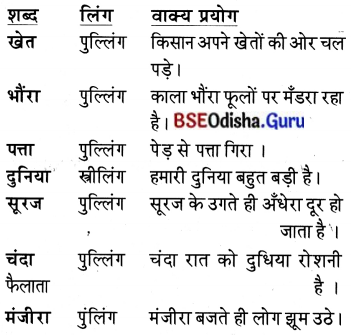
Odisha State Board BSE Odisha 8th Class Sanskrit Solutions Chapter 1 ପରିବେଶଃ Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Sanskrit Solutions Chapter 1 ପରିବେଶଃ
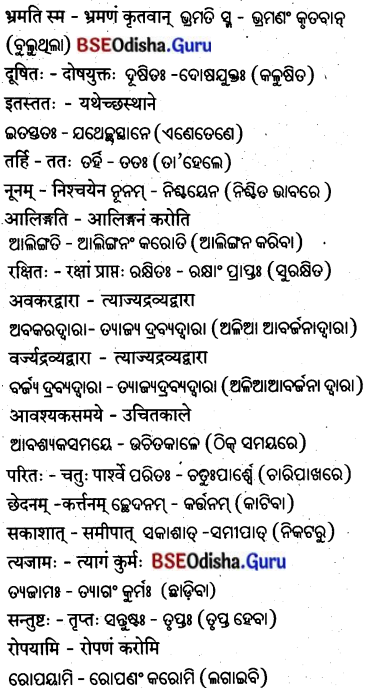
1. एकपदेन उत्तरं कुरुत : (ଏକପଦେନ ଉତ୍ତରାଂ କୁରୁତ ।)
(ଗୋଟିଏ ପଦରେ ଉତ୍ତର ଦିଅ ।)
(क) मनोजः प्रतिदिनं कां प्रणमति ?
ମନୋଜଃ ପ୍ରତିର୍ଦନଂ କାଂ ପ୍ରଣମତି ?
उत्तर: ମାତରଂ
(ख) कया सह मनोज: नदीतटे श्रमति स्म ?
କୟା ସହ ମନୋଜଃ ନଦୀତଟେ ଭ୍ରମତି ସ୍ଵ ?
उत्तर: ମାତ୍ରା
![]()
(ग) अस्मान् परितः कः दृश्यमानः अस्ति ?
ଅସ୍ମାନ୍ ପରିତଃ ଡଃ ଦୃଶ୍ୟମାନଃ ଅସ୍ଥି ?
उत्तर: ପରିବେଶଃ
(घ) रासायनिकसारस्य प्रयोगद्वारा का दूषिता भवति ?
ରାସାୟନିକସାରସ୍ୟ ପ୍ରୟୋଗଦ୍ଵାରା କା ଦୂଷିତା ଭବତି ?
उत्तर: ଭୂମି
(ङ) तैलचालितयानानां धूमद्वारा कः प्रदूषितः भवति ?
ତୈଳଚାଳିତଯାନାନାଂ ଧୂମଦ୍ୱାରା କଃ ପ୍ରଦୂଷିତଃ ଭବତି ?
उत्तर: ବାୟୁ
(च) कथम् अरण्यक्षेत्राणि विनष्टानि भवन्ति ?
କଥମ୍ ଅରଣ୍ୟକ୍ଷେତ୍ରାଣି ବିନଷ୍ଟାନି ଭବନ୍ତି ?
उत्तर: ଶିଳ୍ପୀଗାରସ୍ଥାପନାର୍ଥମ୍
(छ) मातुः सकाशात् कः प्रदूषणविषयं जानाति ?
ମାତୃ ସକାଶାତ୍ ଡଃ ପ୍ରଦୂଷଣବିଷୟଂ ଜାନାତି ?
उत्तर: ପୁନଃ
(ज) कुत्र पुत्रस्य अधिकः विश्वासः अस्ति ?
କୃତ୍ର ପୁତ୍ରସ୍ୟ ଅଧ୍ଵ ବିଶ୍ବାତଃ ଅସ୍ଥି ?
उत्तर: ମାତରି
![]()
(झ) कति वृक्षान् रोपयामि इति पुत्रः शपथं नयति ?
କତି ବୃକ୍ଷାନ୍ ରୋପୟାମି ଇତି ପୁନଃ ଶପଥ୍ୟ ନୟତି ?
उत्तर: ଦଶ
(परिवेशः, मातरि, मातरम्, भूमिः, मात्रा, वायु :, दश, पुत्र:, शिल्पागारस्थापनार्थम्)
2. शून्यस्थानं पूरयत : (ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତ।) (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।)
(क) ………… क: नाम परिवेशः ?
………… କଃ ନାମ ପରିବେଶ ?
उत्तर: ମାତଃ !
(ख) मातः ! केन भावेन स: ………… भवति ?
ମାତଃ ! କେନ ଭାବେନ ସ୍ୱ
उत्तर: ଦୂଷିତଃ
(ग) शिल्पगारस्थापनार्थम् ………… विनष्टानि भवन्ति।
ଶିଳ୍ପଗାରସ୍ଲାପନାର୍ଥମ୍ …………….ବିନଷ୍ଟାନି ଭାବନ୍ତି ?
उत्तर: ଅରଣ୍ୟକ୍ଷେତ୍ରାଣି
(घ) तेन वन्यजीवा: ………… भवन्ति ।
ତେନ ବନ୍ୟଜୀବା ………..ଭବନ୍ତି ।
उत्तर: ବିନଷ୍ଟା
(ङ) प्रतिदिनम् ………… वृद्धिः भवति ।
ପ୍ରତିଦିନମ୍ ………… ବୃଦ୍ଧି ଭବତି ।
उत्तर: ଉତ୍ତାପସ୍ୟ
(च) ………… प्रदूषणविषयं पुत्र: मातुः सकाशात् जानाति ।
………… ପ୍ରଦୂଷଣବିଷୟଂ ପୁନଃ ମାତୁଃ ସକାଶାତ୍ ଜାନାହିଁ ।
उत्तर: ପରିବେଶସ୍ୟ
(छ) ………….. रोपणं कुर्म: ।
………… ରୋପଣଂ କୁର୍ମୀ ।
उत्तर: ବୃକ୍ଷାଣାମ୍
![]()
(ज) तहिं परिवेशः ………….. भवेत् ।
ତହିଁ ପରିବେଶଃ ……… ଭବେତ୍ । ।
उत्तर: ସୁରକ୍ଷିତଃ
(झ) ………. कथनेन पुत्रः तृष्मः भवति ।
……………… କଥନେନ ପୁନଃ ତୃପ୍ତ ଭବତି ।
उत्तर: ମାତୁଃ
(ञ) ………. तस्य अधिकः विश्वासः अस्ति ।
……………… ତସ୍ୟ ଅଧ୍ଵ ବିଶ୍ବାତଃ ଅସ୍ଥି ।
उत्तर: ମାତରି
(मातुः, मातः !, ड़त्तापस्य, मातरि, सुरक्षितः, दूषितः, विनष्टाः, अरण्यक्षेत्राणि, परिवेशस्य, वृक्षाणाम्)
3. मातृभाषया अनुवादं कुरुत :
(ମାତୃଭାଷୟା ଅନୁବାଦଂ କୁରୁତ ।) (ମାତୃଭାଷାରେ ଅନୁବାଦ କର ।)
(क) कृषिक्षेत्रे रासायनिकसारस्य प्रयोगद्वारा भूमि: दूषिता भवति ।
କୃଷିକ୍ଷେତ୍ରେ ରାସାୟନିକ ସାରସ୍ୟ ପ୍ରୟୋଗଦ୍ଵାର। ଭୂମି ଦୂଷିତା ଭବତି ।
ଅନୁବାଦ – କୃଷିକ୍ଷେତ୍ରରେ ରାସାୟନିକ ସାର ପ୍ରୟୋଗଦ୍ଵାରା ଭୂମି ଦୂଷିତ ହେଉଛି ।
(ख) तैलचालितयानानां धूमद्वारा वायु : प्रदूषित: भवति।
ତୈଳଚାଳିତଯାନାନାଂ ଧୂମଦ୍ୱାରା ବାୟୁ ପ୍ରଦୂଷିତଃ ଭବତି ।
ଅନୁବାଦ – ତୈଳଚାଳିତ ଗାଡ଼ିଗୁଡ଼ିକର ଧୂଆଁରେ ବାୟୁ ପ୍ରଦୂଷିତ ହେଉଛି ।
(ग) तेन वन्यजीवाः विनष्टाः भवन्ति ।
ତେନ ବନ୍ୟଜୀବ ବିନଷ୍ଟ ଭବନ୍ତି ।
ଅନୁବାଦ – ତାହାଦ୍ୱାରା ବନ୍ୟପ୍ରାଣୀମାନେ ବିନଷ୍ଟ ହେଉଛନ୍ତି ।
(घ) परिवेशस्य प्रदूषणविषयं पुत्रः मातुः सकाशात् जानाति ।
ପରିବେଶସ୍ୟ ପ୍ରଦୂଷଣବିଷୟଂ ପୁନଃ ମାତୁଃ ସକାଶାତ୍ ଜାନାତି ।
ଅନୁବାଦ – ପରିବେଶ ପ୍ରଦୂଷଣବିଷୟ ପୁଅ ମାଆଠାରୁ ଜାଣଛି ।
![]()
(ङ) अनावश्यकं वस्तु त्यजामः।
ଅନାବଶ୍ୟକଂ ବସ୍ତୁ ତ୍ୟଜାମଃ ।
ଅନୁବାଦ – ଅନାବଶ୍ୟକ ପଦାର୍ଥକୁ ଛାଡ଼ିବା।
(च) मातुः कथनेन पुत्रः सन्तुष्टः भवति ।
ମାତୁଃ କଥନେନ ପୁନଃ ସନ୍ତୁଷ୍ଟି ଭବତି ।
ଅନୁବାଦ – ମାଆର କଥାରେ ପୁଅ ସନ୍ତୁଷ୍ଟ ହୁଏ ।
(छ) मातरि तस्य अधिकः विश्वासः अस्ति |
ମାତରି ତସ୍ୟ ଅଧ୍ୟ ବିଶ୍ୱାସ ଅସ୍ଥି ।
ଅନୁବାଦ – ମାଆଠାରେ ତା’ର ଅଧିକ ବିଶ୍ୱାସ ରହିଛି ।
(ज) अतः नूनम् अहं दश वृक्षान् रोपयामि ।
ଅତଃ ନୂନମ୍ ଅହଂ ଦଶ ବୃକ୍ଷାନ୍ ରୋପୟାମି ।
ଅନୁବାଦ – ଏଣୁ ମୁଁ ନିଶ୍ଚିତ ଦଶଟି ଗଛ ଲଗାଇବି ।
(झ) माता सानन्दं पुत्रं मनोजम् आलिड़ति ।
ମାତା ସାନନ୍ଦ ପୁତ୍ର ମହେଁ”ମ୍ ଆଲିଙ୍ଗତି ।
ଅନୁବାଦ – ମାଆ ଆନନ୍ଦରେ ପୁଅ ମନୋଜକୁ କୋଳକରେ ।
(ज) अतः वक्तुम् उचितम् – “वृक्ष: रक्षति रक्षितः ।”
ଅତଃ ବକ୍ତ୍ରମ୍ ଉଚିତମ୍ -‘‘ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ’’ ।
ଅନୁବାଦ – ଏଣୁ କୁହାଯିବା ଉଚିତ – ବୃକ୍ଷ ତାକୁ ରକ୍ଷା କରେ ଯେ ବୃକ୍ଷକୁ ରକ୍ଷାକରେ ।
![]()
4. शुद्धपदं लिखत । (ଶୁଦ୍ଧ ପଦ ଲେଖ ।)
(ଶୁଦ୍ଧପଦଂ ଲିଖତ ।)
यथा – शः वे रि प =परिवेश:
ଯଥା : ଶଃ ବେ ରି ପ = ପରିବେଶଃ ।
(१) प्र ति ण म = …………
ପ୍ର ତି ଣ ମ = ପ୍ରଣମତି
(२) षि दू तः = ………..
ଷି ଦୂତଃ = ଦୂଷିତଃ
(३) जी वा: व न्य = ………..
ଜୀବାବନ୍ଯ = ବନ୍ଯଜୀବା
(૪) प उ त्ता स्य = ………..
ପ ଭ ଭା ସ୍ୟ = ଉତ୍ତାପସ୍ଯ
(५) सु क्षिर त: = ………..
ସୁ କ୍ଷି ର ତଃ = ସୁରକ୍ଷିତଃ
(६) अ क व रा न् =………..
ଅ କ ବ ରା ନ୍ = ଅବକରାନ୍
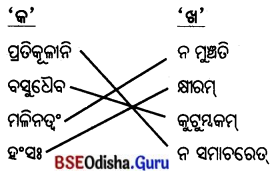
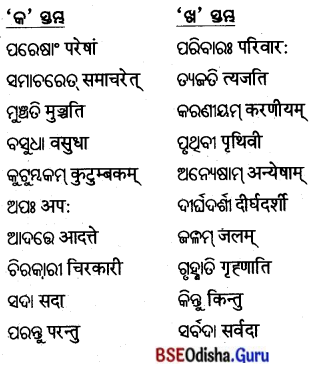
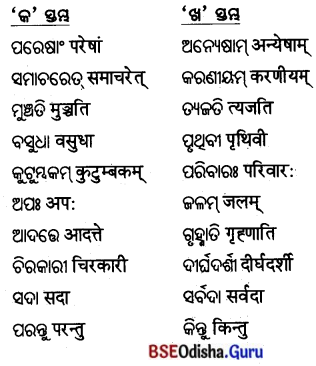
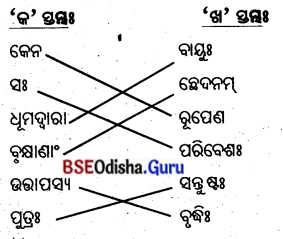
5. स्तम्भमेलनं कुरुतः(ସ୍ତମ୍ଭମେଳନଂ କୁରୁତ ।)
(ସ୍ତମ୍ଭ ମିଳନ କର ।)

उत्तर:
![]()
6. उचितपदेन शून्यस्थानं पूरयत :(ଉଚିତ ପଦେନ ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତ ।)
(ଉଚିତ ପଦରେ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)
(क) एषा मनोजस्य ………… (मात्रा, मातुः, माता)
ଏଷା ମନୋଜସ୍ୟ …………….. (ମାତ୍ରା, ମାତୁଃ,ମାତା )
उत्तर: ମାତା
(ख) स: ………… निवेदयति ।(मात्रे, मातुः, मातृः)
ନି ବେ ଦ ୟତି । (ମାତ୍ରେ, ମାତୁଃ ୫, ମାତୃ)
उत्तर: ମାତ୍ରେ
(ग) ………… केन भावेन स:दूषितः भवति ?(माता, मात, मातुः)
କେନ ଭାବେନ ଡଃ ଦୂଷିତଃ ଭବତି ? (ମାତା, ମାତଃ !, ମାତୁଃ)
उत्तर: ମାତଃ !
(घ) पुत्र: ………… सकाशात् जनिति । (मात्रा, मातुः, मातरम्)
ପୁନଃ ………… ସକାଶାତ୍ ଜାନାତି । (ମାତ୍ରା, ମାତୁଃ, ମାତରମ୍)
उत्तर: ମାତୁଃ
(ङ) ………… तस्य अधिक: विश्वास: अस्ति । (मातारि, मातुः, मात्रे)
……………….. ତସ୍ୟ ଅଧ୍ଵ ବିଶ୍ୱାୟଃ ଅଛି । (ମାତରି, ମାତୁଃ, ମାତ୍ରେ)
उत्तर: ମାତରି
![]()
7. रेखाड्कितपदस्य संशोध्रनं कुरुत। (ରେଖାଙ୍କିତପଦସ୍ୟ ସଂଶୋଧନଂ କୁରୁତ ।)
(ରେଖାଙ୍କିତ ପଦଗୁଡ଼ିକର ସଂଶୋଧନ କର ।)
(क) मनोजः मातरं प्रणमन्ति ।
ମନୋଜଃ ମାତରଂ ପ୍ରଣମନ୍ତି ।
उत्तर:
ମନୋଜଃ ମାତରଂ ପ୍ରଣମତି ।
(ख) पुत्रा: पुनः पृच्छति ।
ପୁନଃ ପୁନଃ ପୃଚ୍ଛତି ।
उत्तर:
ପୁନଃ ପୁନଃ ପୃଚ୍ଛତି ।
(ग) वन्यजीवाः विनाशं गच्छति ।
ବନ୍ୟଜୀବ ବିନାଶଂ ଗଚ୍ଛତି ।
उत्तर:
ବନ୍ୟଜୀବାଃ ବିନାଶଂ ଗଛନ୍ତି ।
(घ) सः शुपथः नयति ।
ସ୍ୱ ଶପଥୀ ନୟତି ।
उत्तर:
ଧଃ ଶପଥ ନୟତି ।
(ङ) वृक्षं रक्षति रक्षितः ।
ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ ।
उत्तर:
ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ ।
![]()
8. वाक्यानि रचयत। (ब।फ्पात्रि खेळ।) (ବାକ୍ୟ ରଚନା କର ।)
(ବାକ୍ୟାନି ରଚୟତ।)
भ्रमति, भवति, नयति, रक्षति, वदति ।
उत्तर:
भ्रमति (ଭ୍ରମତି ) – ବାଳକ ଭ୍ରମତି ।
भवति (ଭବତି) – ଡଃ ଶିକ୍ଷକଃ ଭବତି ।
नयति (ନୟତି) – ମାତା ଜଳଂ ନୟତି ।
रक्षति (ରକ୍ଷତି) – ଈଶ୍ବରଃ ରକ୍ଷତି ।
वदति (ବଦତି) – ରାତଃ ବଦତି।
तव कृते करणीयम् (ତୁମ ପାଇଁ କାମ)
पठत, लिखत च : ପଠତ ଲିଖତ ଚ (ପଢ଼ ଓ ଲେଖ)
प्रथमा विभक्तिः

ପ୍ରଥମା ବିଭବାଃ

द्वितीया विभक्ति:

ଦ୍ବିତୀୟା ବିଭନ୍ତଃ

तृतीया विभक्तिः

ତୃତୀୟା ବିଭବାଃ

![]()
चतुर्थी विभक्ति:

ଚତୁର୍ଥୀ ବିଭନ୍ତଃ

पश्रमी विभक्तिः

ପଞ୍ଚମୀ ବିଭବାଃ

षष्ठी विभक्ति:

ଷଷ୍ଠୀ ବିଭବାଃ

सप्तमी विभक्तिः

ସପ୍ତମୀ ବିଭବାଃ

संवोधने

ସମ୍ବୋଧନେ

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
एकपदेन उत्तरं लिखत। (ଏକପଦେନ ଉତ୍ତରଂ ଲିଖତ।)
1. कः प्रतिदिनं मातरं प्रणमति ?
କଃ ପ୍ରତିଦିନଂ ମାତରଂ ପ୍ରଣମତି ?
उत्तर:
ମନୋଜଃ
![]()
2. नदीतटे मनोज: कया सह श्रमति स्म ?
ନଦୀତଟେ ମନୋଜଃ କୟା ସହ ଭ୍ରମତି ସ୍ମୃ ?
उत्तर:
ମାତ୍ରା
3. मनोज: मात्रा सह कुत्र भ्रमति स्म ?
ମନୋଜଃ ମାତ୍ରା ସହ କୁତ୍ର ଭ୍ରମତି ସ୍ବ ?
उत्तर:
ନଦୀତଟେ
4. मात्रा सह नदीतटे कः भ्रमति स्म ?
ମାତ୍ରା ସହ ନଦୀତଟେ କଃ ଭ୍ରମତି ସ୍ମ ?
उत्तर:
ମନୋଜଃ
5. रासायनिकसारस्य प्रयोगद्वारा भूमिः किं भवति ?
ରାସାୟନିକସାର ପ୍ରୟୋଗଦ୍ଵାରା ଭୂମି କିଂ ଭବତି ?
उत्तर:
ଦୂଷିତା
6. धूमद्वारा क: प्रदूषितः भवति ?
ଧୂମଦ୍ୱାରା କଃ ପ୍ରଦୂଷିତଃ ଭବତି ?
उत्तर:
ବାୟୁ
7. वायु : केन प्रदूषितः भवति ?
ବାୟୁ କେନ୍ ପ୍ରଦୂଷିତଃ ଭବତି ?
उत्तर:
ଧୂମଦ୍ୱାରା
8. शिल्पागारस्थापनार्थं कानि विनष्टानि भवन्ति ?
ଶିଳ୍ପାଗାରସସ୍ଥାପନାର୍ଥୀ କାନି ବିନଷ୍ଟାନି ଭାବନ୍ତି ?
उत्तर:
ଅରଣ୍ୟକ୍ଷେତ୍ରାଣି ।
![]()
9. कुतः पुत्रः प्रदूषणविषयं जानाति ?
କୁତଃ ପୁନଃ ପ୍ରଦୂଷଣବିଷୟଂ ଜାନାତି ?
उत्तर:
ମାତୁଃ
10. दश वृक्षान् रोपयामि इति क: शपथं नयति ?
ଦଶ ବୃକ୍ଷାନ୍ ରୋପୟାମି ଇତି ଡଃ ଶପଥ ନୟତି ?
उत्तर:
ପୁନଃ ମନୋଜଃ
11. का सानन्दं पुत्रम् आलिङ्गति ?
କା ସାନନ୍ଦ ପୁତ୍ରମ୍ ଆଲିଙ୍ଗତି ?
उत्तर:
ମାତା
12. माता सानन्दं कम् आलिद्गति ?
ମାତା ସାନନ୍ଦ କମ୍ ଆଲିଙ୍ଗତି ?
उत्तर:
ପୁତ୍ରମ୍
13. पुत्र पुनः किं करोति ?
ପୁତ୍ର ପୁନଃ କିଂ କରୋତି ?
उत्तर:
ପୃଚ୍ଛତି
14. कः पुनः पृच्छति ?
କଃ ପୁନଃ ପୃଚ୍ଛତି ?
उत्तर:
ପୁନଃ
15. गृहस्य अवकरद्वारा का दूषिता ?
ଗୃହସ୍ୟ ଅବକରଦ୍ୱାରା କା ଦୂଷିତା ?
उत्तर:
ଭୂମି
16. कस्य अवकरद्वारा भूमिः दूषिता भवति ?
କସ୍ୟ ଅବକରଦ୍ୱାରା ଭୂମି ଦୂଷିତା ଭବତି ?
उत्तर:
ଗୃହସ୍ଯ
![]()
17. के विनाशं गच्छन्ति ?
କେ ବିନାଶଂ ଗଛନ୍ତି ?
उत्तर:
ବନ୍ଯଜୀବା
बन्धनीमध्यात् शून्यस्थानं पूरयत।
1. एषा मनोजस्य ………… । (माता, मातरौ, मातरः)
ଏଷା ମନୋଜସ୍ୟ …….। (ମାତା, ମାତରୌ, ମାତର)
उत्तर: ମାତା
2. केन ………… स: दूषित: भवति। (भावम्, भावेन, भावे)
କେନ ………… ସ୍ୱ ଦୂଷିତଃ ଭବତି (ଭାବମ୍, ଭାବେନ, ଭାବେ)
उत्तर: ଭାବେନ
3. स: ………… निवेदयति । (मातुः, मात्रे, मात्रा)
କେନ ………… ସ୍ୱ ଦୂଷିତଃ ଭବତି (ଭାବମ୍, ଭାବେନ, ଭାବେ)
उत्तर: ମାତ୍ରେ
4. पुत्र:- सकाशात् जानाति । (मात्रा, मातुः, मातरम्)
ପୁନଃ ……………ସକାଶାତ୍ ଜାନାତି । (ମାତ୍ରା, ମାତୁଃ, ମାତରମ୍)
उत्तर: ମାତୁଃ
5. ………… तस्य अधिक: विश्वास: अस्ति । (मातरि, मातुः मात्रे)
…………… ତସ୍ୟ ଅଧ୍ବକ ବିଶ୍ୱାୟଃ ଅସ୍ଥି । (ମାତରି,ମାତୁଃ, ମାତ୍ରେ)
उत्तर: ମାତରି
6. ………… रक्षति रक्षितः। (वृक्षाः, वृक्षो, वृक्ष:)
………………… ରକ୍ଷତି ରକ୍ଷିତଃ । (ବୃକ୍ଷା, ବୃକ୍ଷୌ, ବୃକ୍ଷ)
उत्तर: ବୃକ୍ଷ
7. पुत्र: सन्तुष्ट: ………… (भवति, भवतः, भवन्ति)
ପୁନଃ ସନ୍ତୁଷ୍ଟ …………….। (ଭବତି, ଭବତଃ, ଭବନ୍ତ)
उत्तर: ଭବତି
8. मातरि ………… विश्वासः अस्ति । (तम्, तस्य, तेन)
ମାତରି …………ବିଶ୍ୱାସ ଅସ୍ଥି। (ତମ୍, ତସ୍ୟ, ତେନ)
उत्तर: ତସ୍ୟ
9. वन्यजीवा: ………… भवन्ति । (विनष्ट:, विनष्टौ, विनष्टाः)
ବନ୍ଯଜୀବାଃ …………ଭବନ୍ତି । (ବିନଷ୍ଟ, ବିନଷ୍ଟି, ବିନଷ୍ଟା)
उत्तर: ବିନଷ୍ଟା
10. मनोज:नदीतटे ………… स्म।(भ्रमति, भ्रमतः, भ्रमन्ति)
ମନୋଜଃ ନଦୀତଟେ ………… ସ୍ମା (ଭ୍ରମତି, ଭ୍ରମତଃ, ଭ୍ରମନ୍ତି)
उत्तर: ଭ୍ରମତି
![]()
11. माता सानन्दं ………… आलिङ्ग्रति। (पुत्रः,पुत्रम्,पुत्रेण)
ମାତା ସାନନ୍ଦ, …………. ଆଲିଙ୍ଗତି । (ପୁତ୍ର, ପୁତ୍ର, ପୁତ୍ରେଣ)
उत्तर: ପୁତ୍ରମ
12. पुत्र: ………… भवति ।(तृप्तः,तृप्तौ,तृप्ता:)
ପୁନଃ ………………..ଭବତି । (ତୃପ୍ତ, ତୃପ୍ତି, ତୃପ୍ତା)
उत्तर: ତୃପ୍ତି
13. ………… प्रदूषणविषयं पुत्रः मातुः सकाशात् जानाति। (परिवेशस्य,ग्रामस्य,सहरस्य)
………… ପ୍ରଦୂଷଣବିଷୟଂ ପୁନଃ ମାତୁଃ ସକାଶାତ୍ ଜାନାତି । (ପରିବେଶସ୍ୟ, ଗ୍ରାମସ୍ୟ, ସହରସ୍ୟ)
उत्तर: ପରିବେଶସ୍ୟ
14. तर्हि परिवेश:……….. भवेत्।(विनाशः,सुरक्षितः, असुरक्षित)
ତହିଁ ପରିବେଶଃ,……………..ଭବେତ୍ । (ବିନାଶଃ, ସୁରକ୍ଷିତଃ,ଅସୁରକ୍ଷିତଃ)
उत्तर: ସୁରକ୍ଷିତଃ
उत्तरचयनं कुरुत ।(ଉତ୍ତରଚୟନଂ କୁରୁତ।
प्रश्न 1.
मनोजः प्रतिदिनं का प्रणमति?
ମନୋଜଃ ପ୍ରତିଦିନଂ କାଂ ପ୍ରଣମତି ?
(A) ମାତରମ୍
(B) ମାତା
(C) ପିତରମ୍
(D) ଭ୍ରାତରମ୍
उत्तर:
(A) ମାତରମ୍
प्रश्न 2.
कः प्रतिदिनं मातरं प्रणमति?
କଃ ପ୍ରତିଦିନଂ ମାତରଂ ପ୍ରଣମତି ?
(A) ବିଜୟଃ
(B) ମନୋଜଃ
(C) ଅଜୟଃ
(D) ରାଜେଶଃ
उत्तर:
(B) ମନୋଜଃ
![]()
प्रश्न 3.
कया सह मनोजः नदीतटे भ्रमति स्म?
କୟା ସହ ମନୋଜଃ ନଦୀତଟେ ଭ୍ରମତି ସୃ ?
(A) ପିତ୍ରା
(B) ପୁତ୍ରେଣ
(C) ମାତ୍ରା
(D) ସୁମିତ୍ରା
उत्तर:
(C) ମାତ୍ରା
प्रश्न 4.
मात्रा सह नदीतटे क:भूमति स्म?
ମାତ୍ରା ସହ ନତୀତଟେ କଃ ଭ୍ରମତି ସ୍ମ ?
(A) ବିଜୟଃ
(B) ଗୋପାଳ
(C) ସରୋଜଃ
(D) ମନୋଜଃ
उत्तर:
(D) ମନୋଜଃ
प्रश्न 5.
रासायनिकसारस्य प्रयोगद्वारा का दूषिता भवति?
ରାସାୟନିକସାରସ୍ୟ ପ୍ରୟୋଗଦ୍ଵାରା କା ଦୂଷିତା ଭବତି ?
(A) ଭୂମି
(B) ବାୟୁ
(C) ଜଳମ୍
(D) ଗଗନମ୍
उत्तर:
(A) ଭୂମି
प्रश्न 6.
वायु:केन प्रदूषितः भवति?
ବାୟୁ କେନ ପ୍ରଦୂଷିତଃ ଭବଡି ?
(A) ସାର ପ୍ରୟୋଗଦ୍ଵାରା
(B) ଧୂମଦ୍ଵାରା
(C) ଜଳଦ୍ଵାରା
(D) ତୃଣଦ୍ବାରା
उत्तर:
(B) ଧୂମଦ୍ଵାରା
प्रश्न 7.
कथम् अरणयक्षेत्राणि विनश्यन्ति?
କଥମ୍ ଅରଣ୍ୟକ୍ଷେତ୍ରାଣି ବିନଶ୍ୟତି ?
(A) ଗୃହନିର୍ମାଣାର୍ଥମ୍
(B) ନଦୀ ଖୋଦନାର୍ଥମ୍
(C) ଶିଳ୍ପୀଗାରସ୍ଥାପନାର୍ଥମ୍
(D) ମନ୍ଦିରନିର୍ମାଣାର୍ଥମ୍
उत्तर:
(C) ଶିଳ୍ପୀଗାରସ୍ଥାପନାର୍ଥମ୍
प्रश्न 8.
कुतः पुत्रः प्रदूषणविषयं जानाति?
କୃତଃ ପୁନଃ ପ୍ରଦୂଷଣବିଷୟଂ ଜାନାତି ?
(A) ପିତୁଃ
(B) ପୁତ୍ରାତ୍
(C) ଭ୍ରାତଃ
(D) ମାତୁଃ
उत्तर:
(D) ମାତୁଃ
![]()
प्रश्न 9.
कति वृक्षान् रोपयामि झति पुत्रः शपथं नयति?
କତି ବୃତ୍ତାନ୍ ରୋପୟାମି ଇତି ପୁତ୍ର ଶପଥ ନୟତି ?
(A) ପଞ୍ଚ
(B) ଦଶ
(C) ପଞ୍ଚଦଶ
(D) ବିଂଶତି
उत्तर:
(B) ଦଶ
प्रश्न 10.
दश वृक्षान् रोपयामि इति क:शुपथं नयति?
ଦଶ ବୃକ୍ଷାନ୍ ରୋପୟାମି ଇତି ଡଃ ଶପଥ ନୟତି ?
(A) ମାତା
(B) ପୁନଃ
(C) ପିତା
(D) ଭାଇ
उत्तर:
(B) ପୁନଃ
प्रश्न 11.
माता सानन्दे कम् आलिक्रति?
ମାତା ସାନନ୍ଦ କମ୍ ଆଲିଙ୍ଗତି ?
(A) ମାତରମ୍
(B) କନ୍ଯାମ୍
(C) ପୁତ୍ରମ୍
(D) ଭ୍ରାତରମ୍
उत्तर:
(C) ପୁତ୍ରମ୍
प्रश्न 12.
का सानन्दं पुत्रम् आलिद्गति ?
କା ସାନନ୍ଦ ପୁତ୍ରମ୍ ଆଲିଙ୍ଗତି ?
(A) ପିତା
(B) ମନୋଜଃ
(C) କନ୍ଯା
(D) ମାତା
उत्तर:
(D) ମାତା
प्रश्न 13.
कः पुनः पृच्छति ?
(A) ପୁନଃ
(B) ପିତା
(C) ଭ୍ରାତା
(D) ରାମ
उत्तर:
(A) ପୁନଃ
प्रश्न 14.
गृहस्य अवकरद्वारा का दूषिता भवति?
ଗୃହସ୍ୟ ଅବକରଦ୍ଵାରା କା ଦୂଷିତା ଭବତି ?
(A) ବାୟୁ
(B) ଭୂମି
(C) ମ୍ପରିକା
(D) ବସୁଧା
उत्तर:
(B) ଭୂମି
![]()
प्रश्न 15.
धूमद्वारा कः प्रदूषितः भवति?
ଧୂମଦ୍ୱାରା କଃ ପ୍ରଦୂଷିତଃ ଭବତି ?
(A) ଜଳମ୍
(B) ଭୂମି
(C) ବାୟୁ
(D) ଆକାଶଃ
उत्तर:
(C) ବାୟୁ
प्रश्न 16.
के विनाशं गच्छत्ति?
କେ ବିନାଶଂ ଗଛନ୍ତି ?
(A) ବନ୍ଯଜୀବା
(B) ମାନବାଃ
(C) ପଶବ
(D) ବୃକ୍ଷ
उत्तर:
(A) ବନ୍ଯଜୀବା
रेखांकित पदानां संशोधनं कुरुत।
(ରେଖାଙ୍କିତପଦାନାଂ ସଂଶୋଧନଂ କୁରୁତ।)
1. मातरं तस्य अधिक: विश्वास: अस्ति।
ମାତରଂ ତସ୍ୟ ଅଧ୍ବକ ବିଶ୍ୱାସ ଅଛି ।
उत्तर:
ମାତରି ତସ୍ୟ ଅଧ୍ଵକଃ ବିଶ୍ଵାସ ଅସ୍ଥି ।
2. स: शपथं नयन्ति। ଡଃ ଶପୟଂ ନୟତି।
उत्तर:
ଡଃ ଶପୟଂ ନୟତି।
3. पुत्र: पुनः पुच्छन्ति। ପୁନଃ ପୁନଃ ପୁଚ୍ଛନ୍ତି ।
उत्तर: ପୁନଃ ପୁନଃ ପୃଚ୍ଛତି ।
4. स: मातरि निवेदयति।
ସ୍ୱ ମାତରି ନିବେଦୟତି ।
उत्तर:
ଡଃ ମାତ୍ରେ ନିବେଦୟତି।
5. वृक्षेषु च्छेदनं कुर्म :
ବକ୍ଷେଷୁ ଛେଦନଂ କୁର୍ମୀ ।
उत्तर:
ବୃକ୍ଷଣଂ ଛେଦନଂ କୁର୍ମୀ
6. पुत्रा: सन्तुष्ट: भवति ।
ପୁନଃ ସନ୍ତୁଷ୍ଟ ଭବତି ।
उत्तर:
ପୁନଃ ସନ୍ତୁଷ୍ଟ ଭବତି।
7. वृक्षं रक्षति रक्षितः ।
ବ୍ରଣଂ ରକ୍ଷତି ରକ୍ଷିତଃ ।
उत्तर:
ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ ।
8. परिवेशं सुरक्षां करोति ।
ପରିବେଶଂ ସୁରକ୍ଷା କରୋତି ।
उत्तर:
ପରିବେଶସ୍ୟ ସୁରକ୍ଷା କରୋତି।
9. वन्यजीव: विनाशं गच्छन्ति।
ବନ୍ୟଜୀବ ବିନାଶଂ ଗଛନ୍ତି ।
उत्तर:
ବନ୍ୟଜୀବୀ ବିନାଶଂ ଗଛନ୍ତି ।
![]()
10. मातरं सह नदीतटे मनोज: भ्रमति स्म।
ମାତରଂ ସହ ନଦୀତଟେ ମନୋଜଃ ଭ୍ରମତି ସୃ ।
उत्तर:
ମାତ୍ରା
सन्धिविच्छेदं कुरुत।(ସନ୍ଧିବିଚ୍ଛେଦଂ କୁରୁତ।)
1. शिल्पागारस्य (ଶିଳାଗାରସ୍ୟ) = ଶିଳ୍ପ + ଆଗାରସ୍ୟ
2. स्थापनार्थम् (ସ୍ଥାପନାର୍ଥମ୍) = ସ୍ଥାପନା + ଅର୍ଥମ୍
3. इतस्तत: (ଇତସ୍ତତଃ) = ଇତଃ + ତତଃ
सन्धिं कुरुत (ସନ୍ଧି କୁରୁତ।)
1. प्र + नमति = प्रणमति ପ୍ର + ନମତି = ପ୍ରଣମତି
2. इति + आदय: = इत्यादय: ଇତି + ଆଦୟଃ = ଇତ୍ୟାଦୟ
माता, प्रणमति, भ्रमति, वदति, भूमि:, पृच्छति, कुर्मः, पुत्र:, परिवेशः, सुरक्षितः। (କ୍ରିୟାପଦଂ ନିର୍ବାଚୟତ।)
ମାତା, ପ୍ରଣମତି, ଭ୍ରମତି, ବଦତି, ଭୂମି, ପୃଚ୍ଛତି, କୁମଃ, ପୁନଃ, ପରିବେଶଃ, ସୁରକ୍ଷିତଃ ।
उत्तर:
ପ୍ରଣମତି, ଭ୍ରମତି, ବଦତି, ପୃଚ୍ଛତି, କୁର୍ମ
कर्तृपदं चिनुत । (କର୍ତ୍ତୃପଦଂ ଚିନୁତ।)
माता, प्रणमति, भ्रमति, वदति, भूमि:, पृच्छति, कुर्मः, पुत्र:, परिवेश:, सुरक्षित:।
ଆଲିଙ୍ଗତି, ପୁନଃ, ବୃକ୍ଷ, ତ୍ୟଜାମ, ଜାନାତି, ପରିବେଶଃ, ମନୋଜଃ, ବାୟୁ, ବଦତୁ, ବର୍ଷନ୍ତି |
उत्तर:
ପୁନଃ, ବୃକ୍ଷ, ପରିବେଶଃ, ମନୋଜଃ, ବାୟୁ
शब्दानां मातृभाषया अर्थान् लिखत।
(ଶବ୍ଦାନାଂ ମାପୂଜା ମାତୃଭାଷୟା ଅର୍ଥାନ୍ ଲିଖିତ।)
1. मातरम् (ମାତରମ୍) – ମା’ଙ୍କୁ
2. निवेदयंति (ନିବେଦୟତି) – ନିବେଦନ କରୁଛନ୍ତି
3. अवकरद्वारा (ଅବକରଦ୍ୱାରା) – ଆବର୍ଜନା ଦ୍ଵାରା
4. सकाशात् (ସକାଶାତ୍) – ନିକଟରୁ
5. इतस्ततः (ଇତସ୍ତତଃ) – ଏଣେତେଣେ
6. वस्तुः (ବସ୍ତୁ) – ଦ୍ରବ୍ୟ
7. नूनम् (ନୂନମ) – ନିଶ୍ଚୟ
निजभाषया प्रायशः दशभि: वाक्यै : उत्तरं लिखत ।
(ନିଜଭାଷୟ ପ୍ରାୟଶଃ ଦଶତିଃ ବାକ୍ୟୁ ଉତ୍ତରାଂ ଲିଖତ।)
प्रश्न 1.
परिवेशः कथं प्रदूषितः भवति ? केन प्रकारेण तस्य सुरक्षा भवेत् ?
ପରିବେଶଃ କଣଂ ପ୍ରଦୂଷିତଃ ଭବତି ? କେନ ପ୍ରକାରେଣ ତସ୍ୟ ସୁରକ୍ଷା ଭବେତ୍ ?
उत्तर:
ଆମ ଚତୁପାର୍ଶ୍ଵରେ ଯାହା ସବୁ ଦୃଶ୍ୟମାନ ହେଉଛି ତାହା ପରିବେଶ। ଭୂମି, ଜଳ, ଆକାଶ, ବାୟୁ, ବୃକ୍ଷଲତା ଓ ଜୀବମାନେ ବିଶେଷତଃ ପରିବେଶ ନାମରେ ପରିଚିତ । ଏହି ପରିବେଶ ଦିନକୁ ଦିନ ପ୍ରଦୂଷିତ ହେବାକୁ ଲାଗିଛି । ମନୁଷ୍ୟ ସବୁଠୁ ବୁଦ୍ଧିମାନ୍ ଜୀବ ଅଟେ । ତେଣୁ ସେ ନିଜର ସ୍ଵାର୍ଥସାଧନ ପାଇଁ ସ୍ୱବୁଦ୍ଧି ବଳରେ ପରିବେଶକୁ ପ୍ରତିକ୍ଷଣରେ ଦୂଷିତ କରିବାରେ ଲାଗିଛି । ପରିବେଶକୁ ସୁରକ୍ଷିତ ରଖିବା ନିମନ୍ତେ ଆମେ ସମସ୍ତେ ବୃକ୍ଷରୋପଣ କରିବା ଲାଗି ଶପଥ ନେବା ଉଚିତ। କଥାରେ ଅଛି – ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ; ଅର୍ଥାତ୍ ଯଦି ଆମେ ବୃକ୍ଷର ଯତ୍ନନେବା ତେବେ ବୃକ୍ଷ ମଧ୍ୟ ଆମକୁ ରକ୍ଷାକରିବ। ତେଣୁ ବୃକ୍ଷରୋପଣ ଅନିବାର୍ଯ୍ୟ ।
मातृभाषयाअनुवादं कुरुत ।
(ମାତୃଭାଷୟା ଅନୁବାଦଂ କୁରୁତ।)
1. भारती मनोजस्य माता।
ଭାରତୀ ମନୋଜସ୍ୟ ମାତା ।
ଅନୁବାଦ: ଭାରତୀ ମନୋଜର ମାଆ।
2. मनोजः प्रतिदिनं मातरं प्रणमति ।
ମନୋଜଃ ପ୍ରତିଦିନଂ ମାତରଂ ପ୍ରଣମତି ।
ଅନୁବାଦ: ମନୋଜ ପ୍ରତିଦିନ ମାଆଙ୍କୁ ପ୍ରଣାମ କରେ।
3. एकदा मनोज:मात्रा सह नदीतटे श्रमति स्म ।
ଏକଦା ମନୋଜଃ ମାତ୍ରା ସହ ନଦୀତଟେ ଭ୍ରମତି ସୁ ।
ଅନୁବାଦ: ଥରେ ମନୋଜ ମାଆ ସହିତ ନଈକୂଳରେ ବୁଲୁଥିଲା ।
![]()
4. तदा स:मात्रे निवेदयति ।
ତଦା ଡଃ ମାତ୍ରେ ନିବେଦୟତି ।
ଅନୁବାଦ: ସେତେବେଳେ ସେ ମାଆଙ୍କୁ ଜଣାଏ ।
5. मातः!क:नाम परिवेशः;कृपया वदतु ।
ମାତଃ ! ଡଃ ନାମ ପରିବେଶଃ; କୃପୟା ବଦତୁ ।
ଅନୁବାଦ: ମାଆ ! ପରିବେଶ ଅର୍ଥ କ’ଣ ? ଦୟାକରି କୁହନ୍ତୁ ।
6. माता वदति-पुत्र!अस्मान् परितः य:दृश्यमानः अस्ति सः रिवेशः।
ମାତା ବଦତି – ପୁତ୍ର ! ଅସ୍ମାନ୍ ପରିତଃ ଯଃ ଦୃଶ୍ୟମାନଃ ଅସ୍ତି ସ୍ୱ ପରିବେଶଃ ।
ଅନୁବାଦ: ମାଆ କହିଲେ – ପୁତ୍ର ! ଆମ ଚାରିପଟେ ଯାହା ଦେଖାଯାଉଛି ତାହା ପରିବେଶ।
7. भूमि:जलं गगनं जीवा:च विशेषतः परिवेशः इति परिचितः।
ଭୂମି ଜଳଂ ଗଗନଂ ଜୀବ ଚ ବିଶେଷତଃ ପରିବେଶଃ ଇତି ପରିଚିତଃ ।
ଅନୁବାଦ: ଭୂମି, ଜଳ, ଆକାଶ, ବାୟୁ, ବୃକ୍ଷ ଏବଂ ଜୀବ ବିଶେଷକରି ପ୍ରଭୃତି ପରିବେଶ ବୋଲି ପରିଚିତ।
8. पुत्रः पुनः पृच्छति-मातः!केन भावेन स:दूषितः भवति?
ପୁନଃ ପୁନଃ ପୃଚ୍ଛତି – ମାତଃ ! କେନ ଭାବେନ ସ୍ୱ ଦୂଷିତଃ ଭବତି ?
ଅନୁବାଦ; ପୁଅ ପୁଣି ପଚାରିଲା – ମାଆ ! କିପରି ସେ ଦୂଷିତ ହେଉଛି ?
9. नगरस्य शिस्पागारस्य च वर्ज्यद्रव्यद्वारा जल प्रदूषितं भवति।
ନଗରସ୍ୟ ଶିଳ୍ପୀଗାରସ୍ୟ ଚ ବର୍ଜ୍ୟଦ୍ରବ୍ୟଦ୍ଵାରା ଜଳ ପ୍ରଦୂଷିତଂ ଭବତି ।
ଅନୁବାଦ: ନଗର ଓ ଶିଳ୍ପୀଗାରର ବର୍ଜ୍ୟବସ୍ତୁ ଦ୍ବାରା ପାଣି ପ୍ରଦୂଷିତ ହୁଏ ।
10. शिल्पागार-स्थापनार्थम् अरणयक्षेत्राणि विनष्टानि भवन्ति।
ଶିଳ୍ପାଗାର-ସ୍ଥାପନାର୍ଥମ୍ ଅରଣ୍ୟକ୍ଷେତ୍ରାଣି ବିନଷ୍ଟାନି ଭବନ୍ତ
ଅନୁବାଦ: ଶିଳ୍ପୀଗାର ସ୍ଥାପନ ନିମନ୍ତେ ଅରଣ୍ୟ କ୍ଷେତ୍ରଗୁଡ଼ିକ ନଷ୍ଟ ହେଉଛି ।
![]()
11. प्रतिदिनं उत्तापस्य वृद्धि: भवति।
ପ୍ରତିଦିନଂ ଉତ୍ତାପସ୍ୟ ବୃଦ୍ଧି ଭବତି ।
ଅନୁବାଦ: ପ୍ରତିଦିନ ଉତ୍ତାପର ବୃଦ୍ଧି ଘଟୁଛି ।
12. आवश्यकसमये मेघा: न वर्षन्ति।
ଅର୍ଥନା । ଆବଶ୍ୟକସମୟେ ମେଘା ନ ବର୍ଷନ୍ତି |
ଅନୁବାଦ: ଆବଶ୍ୟକ ସମୟରେ ମେଘ ବର୍ଷୁ ନାହିଁ ।
13. सः पुनः मातरं पृच्छति – परिवेशः कथं सुरक्षितः भवेत्?
ନଃ ପୁନଃ ମାତରଂ ପୃଚ୍ଛତି – ପରିବେଶଃ କଥ୍ୟ ସୁରକ୍ଷିତଃ ଭବେତ୍ ?
ଅନୁବାଦ: ସେ ପୁଣିଥରେ ମାଆଙ୍କୁ ପଚାରୁଛି – ପରିବେଶ କିପରି ସୁରକ୍ଷିତ ହେବ ?
संस्कृतभाषया अनुवादं कुरुत।
(ସଂସ୍କୃତଭାଷୟା ଅନୁବାଦ କରୁତ ।)
1. ରମ୍ଭା ଶ୍ରୀଧରସ୍ୟ ମାତା।
उत्तर: रमा श्रीधरस्य माता। ରମା ଶ୍ରୀଧରସ୍ୟ ମାତା ।
2. ମେଘ ହେଉ ନାହିଁ ।
उत्तर: मेघ: न भवति। । ମେଘ ନ ଭବତି।
3. ଜୀବମାନେ ବିନାଶ ଯାଉଛନ୍ତି ।
उत्तर: जीवा: विनाशं गच्छन्ति। ଜୀବା ବିନାଶଂ ଗଛନ୍ତି ।
4. ପିଲାମାନେ ଗଛଗୁଡ଼ିକୁ ଲଗାଉଛନ୍ତି ।
उत्तर: बाला:/ बालका: वृक्षान् रोपयन्ति ବୃକ୍ଷାନ୍ ରୋପୟନ୍ତି ।
5. ପୁଅ ମା’କୁ ନମସ୍କାର କରୁଛି ।
उत्तर: पुत्र: मातरं नमति । ପୁନଃ ମାତରଂ ନମତି ।
6. ମା’ ନଦୀକୂଳରେ ବୁଲୁଛି ।
उत्तर: माता नदीतटे,भ्रमति।ମାତା ନଦୀତଟେ ଭ୍ରମତି।
7. ପୁଅ ଶପଥ ନେଉଛି ।
उत्तर: पुत्र: शपथं नयति। ଦ୍ରୁମ: ୩୩୧ ୩୩। ପୁନଃ ଶପଙ୍ଖ ନୟତି।
प्रथम अनुच्छेदः (ପ୍ରଥମ ଅନୁଚ୍ଛେଦଃ)
भारती मनोजस्य माता । मनोजः प्रतिदिन मातरं प्रणमति । एकदा मनोजः मात्रा सह नदीतटे श्रमति स्म । तदा सः मात्रे निवेदयति – मातः ! कः नाम परिवेशः, कृपया वदतु । माता वदति – पुत्र ! अस्मान् परितः यः दृश्यमानः अस्ति सः परिवेशः ।भूमिः, जलं,गगनं, वायुः, वृक्षाः, जीवाः च विशेषतः परिवेशः इति परिचितः । पुत्रः पुनः पृच्छति – मातः ! केन भावेन सः दूंषितः भवति ? माता वदति, गृहस्य अवकरद्वारा तथा च कृषिक्षेत्रे रासायंनिकसारस्य प्रयोगद्वारा भूमिः दूषिता भवति । नगरस्य शिल्पागारस्य च वर्ज्यव्रव्यद्वारा जलं प्रदूषितं भवति । तैलचालितयानानां धूमद्वारा वायुः प्रदूषितः भवति । शिल्पागारस्थापनार्थम् अरण्यक्षेत्राणि विनष्टानि भवन्ति । वृक्षाणां छेदनं भवति । तेन वन्यजीवाः विनाशं गच्छन्ति । प्रतिदिनम् उत्तापस्य वृद्धिः भवति । आवश्यकसमये मेघाः न वंर्षन्ति ।
![]()
ଭାରତୀ ମନୋଜସ୍ୟ ମାତା । ମନୋଜଃ ପ୍ରତିଦିନଂ ମାତରଂ ପ୍ରଣମତି । ଏକଦା ମନୋଜଃ ମାତ୍ରା ସହ ନଦୀତଟେ ଭ୍ରମତି ସ୍ମ । ତଦା ସ୍ୱ ମାତ୍ରେ ନିବେଦୟତି – ମାତଃ ! କଃ ନାମ ପରିବେଶଃ; କୃପୟା ବଦତୁ । ମାତା ବଦତି – ପୁତ୍ର ! ଅସ୍ମାନ୍ ପରିତଃ ଯଃ ଦୃଶ୍ୟମାନଃ ଅସ୍ତି ଡଃ ପରିବେଶଃ । ଭୂମି ଜଳଂ ଗଗନଂ ବାୟୁ ବୃକ୍ଷା, ଜୀବାଃ ବ ବିଶେଷତଃ ପରିବେଶ ଇତି ପରିଚିତଃ । ପୁନଃ ପୁନଃ ପୃଚ୍ଛତି – ମାତଃ ! କେନ ଭାବେନ ଡଃ ଦୂଷିତଃ ଭବତି ? ମାତା ବଦ୍ଧତି, ଗୃହସ୍ୟ ଅବକରଦ୍ୱାରା। ତଥା ଚ କୃଷିକ୍ଷେତ୍ରେ ରାସାୟନିକ ସାର ସ୍ୟ ପ୍ରୟୋଗଦ୍ଵାରା ଭୂମି ଦୂଷିତା ଭବତି। ନଗରସ୍ୟ ଶିଳ୍ପୀଗାରସ୍ୟ ଚ ବର୍ଜ୍ୟଦ୍ରବ୍ୟଦ୍ଵାରା ଜଳଂ ପ୍ରଦୂଷିତଂ ଭବତି । ତୈଳଚାଳିତଯାନାନାଂ
ଧୂମଦ୍ୱାରା ବାୟୁ ପ୍ରଦୂଷିତଃ ଭବତି । ଶିଳ୍ପାଗାର ସ୍ଥାପନାର୍ଥ ମ୍ ଅରଣ୍ୟକ୍ଷେତ୍ରାଣି ବିନଷ୍ଟାନି ଭବନ୍ତି । ବୃକ୍ଷାମାଂ ଚ୍ଛେଦନଂ ଭବତି । ତେନ ବନ୍ୟଜୀବାଃ ବିନାଶଂ ଗଛନ୍ତି । ପ୍ରତିଦିନମ୍ ଉତ୍ତାପସ୍ୟା ବୃଦ୍ଧି ଭବତି । ଆବଶ୍ୟକସମୟେ ମେଘା ନ ବର୍ଷନ୍ତି ।
ସନ୍ଧି ବିଚ୍ଛେଦ
- ପ୍ରଣମତି = ପ୍ର + ନମତି । ଇତ୍ୟାଦୟଃ = ଇତି + ଆଦୟଃ ।
- ଶିଳ୍ପାଗାରସ୍ୟ = ଶିଳ୍ପ + ଆଗାରସ୍ୟ ।
ଶବ୍ଦାର୍ଥ
ପ୍ରତିଦିନମ୍ – ପ୍ରତିଦିନ । ପ୍ରଣମତି – ପ୍ରଣାମ କରେ । ଏକଦା -ଥରେ । ସହ – ସହିତ । ଭ୍ରମତି ସ୍ମ – ବୁଲୁଥିଲା । ତଦା – ସେ ସମୟରେ । ନିବେଦୟତି – ଜଣାଏ । କଃ ନାମ – ଅର୍ଥ କ’ଣ ? କୃପୟା – ଦୟା କରି । ପରିତଃ -ଚାରିପଟେ । ଦୃଶ୍ୟମାନଃ – ଦେଖାଯାଉଛି । ଗଗନଂ – ଆକାଶ । ଭୃତି – ବୋଲି । ପୁନଃ – ପୁଣି । ଅବକର – ଅପରିଷ୍କାର । ଅଳିଆ ଆର୍ବଜନା । ଭବତି – ହେଉଛି ତୈଳଚାଳିତଯାନାନାଂ – ତେଲଦ୍ୱାରା ଚାଲୁଥିବା ଗାଡ଼ିଗୁଡ଼ିକର ।– ଅରଣ୍ୟକ୍ଷେତ୍ରାଣି – ଜଙ୍ଗଲ ଜମି । ଚ୍ଛେଦନମ୍ – କଟା । ନ ବର୍ଷନ୍ତ – ବର୍ଷନାହାନ୍ତି ।
ଅନୁବାଦ
ଭାରତୀ ମନୋଜର ମାଆ । ମନୋଜ ପ୍ରତିଦିନ ମାଆଙ୍କୁ ପ୍ରଣାମ କରେ । ଥରେ ମନୋଜ ମାଆ ସାଙ୍ଗରେ ନଈକୂଳରେ ବୁଲୁଥିଲା । ସେତେବେଳେ ସେ ମାଆଙ୍କୁ ଜଣାଇଲା – ମାଆ ! ପରିବେଶ ଅର୍ଥ କ’ଣ ? ଦୟାକରି କୁହନ୍ତୁ । ମାଆ କହିଲେ – ହେ ପୁଅ ! ଆମ ଚାରିପଟେ ଯାହା ଦେଖାଯାଉଛି ସେ ହିଁ ପରିବେଶ । ଭୂମି, ଜଳ, ଆକାଶ, ବାୟୁ, ବୃକ୍ଷ, ଜୀବ ବିଶେଷକରି ପରିବେଶ ବୋଲି ପରିଚିତ ଅଟନ୍ତି । ପୁଅ ପୁଣି ପଚାରିଲା – ମାଆ –କିପରି ସେ ଦୂଷିତ ହେଉଛି ।
ମାଆ କହିଲେ ଘର ଅଳିଆ ଆର୍ବଜନା ଦ୍ଵାରା ତଥା କୃଷିକ୍ଷେତ୍ରରେ ରାସାୟନିକ ସାରର ପ୍ରୟୋଗଦ୍ଵାରା ଭୂମି ଦୂଷିତ ହୁଏ । ନଗରର ଓ ଶିଳ୍ପାଗାରର ବର୍ଜ୍ୟବସ୍ତୁ ଦ୍ୱାରା ପାଣି ପ୍ରଦୂଷଣ ହୁଏ । ତେଲପରିଚାଳିତ ଯାନଗୁଡ଼ିକର ଧୂମଦ୍ୱାରା ବାୟୁ ପ୍ରଦୂଷିତ ହୁଏ । ଶିଳ୍ପୀଗାର ସ୍ଥାପନ ନିମନ୍ତେ ଅରଣ୍ୟ କ୍ଷେତ୍ରଗୁଡ଼ିକ ବିନଷ୍ଟ ହେଉଛି । ବୃକ୍ଷଗୁଡ଼ିକ କାଟିଦିଆଯାଉଛି । ତାହାଦ୍ୱାରା ବନ୍ୟପ୍ରାଣୀମାନେ ମୃତ୍ୟୁମୁଖରେ ପଡୁଛନ୍ତି । ପ୍ରତିଦିନ ଉତ୍ତାପର ବୃଦ୍ଧି ଘଟୁଛି । ଆବଶ୍ୟକ ସମୟରେ ମେଘ ବର୍ଷ ନାହିଁ ।
द्वितीय अनुच्छेद: (ଦ୍ବିତୀୟ ଅନୁଚ୍ଛେଦ)
पुत्रः मातुः सकाशात् परिवेशस्य प्रदूषणविषयं जानाति । सः पुनः मातरं पृच्छति – परिवेशः कथं सुरक्षितः भवेत् । माता वदति – यदि वयं गृहस्य शिल्पागारस्य च अवकरान् इतस्ततः न क्षिपामः, निर्दिष्टे स्थाने स्थापयामः, वृक्षाणां रोपणं कुर्मः, अनावश्यकं वस्तु त्यजामः, तर्हि परिवेशः सुरक्षितः भवेत् ।
मातुः कथनेन पुत्रः सन्तुष्टः भवति । मातरि तस्य अधिकः विश्वासः अस्ति । अतः नूनम् अहं दश वृक्षान् रोपयामि, परिवेशस्य सुरक्षां च करोमि इति सः शपथं नयति । माता आनन्देन पुत्रं मनोजम् आलिङ्गति ।
![]()
अतः वक्तुम् उचितम् – “वृक्षः रक्षति रक्षितः।”
ପୁତ୍ର ମାତୁଃ ସକାଶାତ୍ ପରିବେଶସ୍ୟ ପ୍ରଦୂଷଣବିଷୟଂ ଜାନାତି । ଡଃ ପୁନଃ ମାତରଂ ପୃଚ୍ଛତି – ପରିବେଶଃ କଥ୍ୟ ସୁରକ୍ଷିତଃ ଭବେତ୍ । ମାତା ବଦତି – ଯଦି ବୟଂ ଗୃହସ୍ୟ ଶିଳ୍ପାଗାରସ୍ୟ ଚ ଅବକରାନ୍ ଇତସ୍ତତଃ ନ କ୍ଷିପାମଃ, ନିର୍ଦିଷ୍ଟ ସ୍ଥାନେ ସ୍ଥାପୟାମଃ, ବୃକ୍ଷାଣା ରୋପଣଂ କୁର୍ମ, ଅନାବଶ୍ୟକଂ ବସ୍ତୁ ତ୍ୟଜାମ, ତହିଁ ପରିବେଶଃ ସୁରକ୍ଷିତଃ ଭାବେତ୍। ମାତୁଃ କଥନେନ ପୁନଃ ସମ୍ମୁ ଷ୍ଟ ଭବତି । ମାତରି ତସ୍ୟ ଅଧୁନଃ ବିଶ୍ୱାସ ଅସ୍ତି । ଅତଃ ନୂନମ୍ ଅହଂ ଦଶ ବୃକ୍ଷାନ୍ ରୋପୟାମି, ପରିବେଶସ୍ୟ ସୁରକ୍ଷାଂ ଚ କରୋମି – ଇତି ସ୍ୱ ଶପଥ୍ୟ ନୟତି । ମାତା ଆନନ୍ଦେନ ପୁତ୍ର ମନୋଜମ୍ ଆଲିଙ୍ଗତି । ଅତଃ
ବସ୍ତୁମ୍ ଉଚିତମ୍ – ‘ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ’’ । ସନ୍ଧି ବିଚ୍ଛେଦ
ଶିଳ୍ପୀଗାରାନ୍ = ଶିଳ୍ପ + ଆଗାରାନ୍ । ଇତସ୍ତତଃ = ଇତଃ +ତତଃ ।
ଶବ୍ଦାର୍ଥ
ସକାଶାତ୍ – ପାଖରୁ । ଜାନାତି – ଜାଣୁଛି । ପୃଚ୍ଛତି – ପଚାରୁ ଛି । ଭବେତ୍ – ହେବା ଉଚିତ । ଅବକ୍ରାନ୍ ଆବର୍ଜନାଗୁଡ଼ିକୁ । ଇତସ୍ତତଃ – ଏଣେତେଣେ । କ୍ଷିପାମଃ – ଫିଙ୍ଗିବା । ସ୍ଥାପୟାମଃ -ରଖୁ । ତ୍ୟଜାମ – ତ୍ୟାଗ କରିବୁ । ତହିଁ – ତାହା ହେଲେ । ଅସ୍ଥି – ଅଛି । ନୂନମ୍ – ନିଶ୍ଚୟ । ଦଶ ବୃକ୍ଷାନ – ଦଶଟି ଗଛ । ଆଲିଙ୍ଗତି -ଆଲିଙ୍ଗନ କଲା । ଅତଃ – ଏଣୁ । ବସ୍ତୁମ୍ – କହିବା ଉଚିତମ୍ – ଉଚିତ । ବୃକ୍ଷ ରକ୍ଷତି ରକ୍ଷିତଃ – ଯିଏ ବୃକ୍ଷକୁ ରକ୍ଷା କରେ ବୃକ୍ଷ ତାକୁ ରକ୍ଷା କରେ ।
ଅନୁବାଦ
ପୁଅ ମାଆଠାରୁ ପରିବେଶ ପ୍ରଦୂଷଣ ବିଷୟ ଜାଣିଲା । ସେ ବାରମ୍ବାର ମାଆଙ୍କୁ ପଚାରୁଛି – ପରିବେଶ କିପରି ସୁରକ୍ଷିତ ହେବ । ମାଆ କୁହନ୍ତି – ଯଦି ଆମେ ଘର ଓ ଶିଳ୍ପାଗାରର ଆବର୍ଜନା ଏଣେତେଣେ ଫିଙ୍ଗିବା ନାହିଁ ନିର୍ଦ୍ଦିଷ୍ଟ ସ୍ଥାନରେ ରଖୁ, ଗଛଲଗାଇବା, ଅନାବଶ୍ୟକ ପଦାର୍ଥ ତ୍ୟାଗକରିବା; ତେବେ ପରିବେଶ ସୁରକ୍ଷିତ ରହିବ । ମାଆଙ୍କ କଥାରେ ପୁଅ ସନ୍ତୁ ଷ୍ଟ ହେଲା । ମାଆଙ୍କଠାରେ ତା’ର ଅଧିକ ବିଶ୍ଵାସ ରହିଛି । ଏଣୁ ନିଶ୍ଚୟ ମୁଁ ଦଶଟି ଗଛ ଲଗାଇବି । ପରିବେଶର ସୁରକ୍ଷା କରିବି ବୋଲି ସେ ଶପଥ ନେଲା ( ମାଆ ଆନନ୍ଦରେ ପୁଅ ମନୋଜକୁ ଆଲିଙ୍ଗନ କରନ୍ତି । ଏଣୁ କୁହାଯିବା ଉଚିତ ଯେ ବୃକ୍ଷକୁ ରକ୍ଷାକରେ ବୃକ୍ଷ ତାକୁ ରକ୍ଷା କରେ ।
परिवेश:, अवकर:, शिल्पागार:, प्रदूषणाम्,
वृक्षरोपणम्, सुरक्षा, रक्षित
कर्तृपदानि :
मनोज:, माता, मेघा:, वायुः, पुत्रः।
![]()
क्रियापदानि :
प्रणमति, भ्रमति, पृच्छति, गच्छन्ति, वर्षन्ति ।
शब्दार्थ: