Odisha State Board BSE Odisha 9th Class History Important Questions Chapter 5 ଫାସୀବାଦ ଓ ନାଜିବାଦର ବିକାଶ Important Questions and Answers.
BSE Odisha Class 9 History Important Questions Chapter 5 ଫାସୀବାଦ ଓ ନାଜିବାଦର ବିକାଶ
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଇଟାଲୀର ଆର୍ଥିକ ଓ ରାଜନୈତିକ ଅବସ୍ଥା ଶୋଚନୀୟ ହୋଇପଡିଥ୍ଲା କାହିଁକି ?
Answer:
ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧ ପରେ ଇଟାଲୀର ଆର୍ଥିକ ଓ ରାଜନୈତିକ ଅବସ୍ଥା ନିମ୍ନପ୍ରକାର ଥିଲା ।
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ଇଟାଲୀ ଉପନିବେଶ ଲାଭ ଆଶାରେ ମିତ୍ର ଶକ୍ତି ସପକ୍ଷରେ ଯୋଗ ଦେଇଥିଲେ ହେଁ ପ୍ୟାରିସ୍ ଶାନ୍ତ ସମ୍ମିଳନୀରୁ ନିରାଶ ହୋଇ ଫେରିଥିଲା । ବିଜୟୀ ଶକ୍ତି ଭାବରେ ଇଟାଲୀର ଅହମିକା ରହିଲା ନାହିଁ, ବରଂ ସେଥୁରେ ଜାତୀୟ ସମ୍ମାନ ହାନି ହେଲା ।
- ଯୁଦ୍ଧ ପରେ ଦେଶର ଆର୍ଥିକ ଅବସ୍ଥା ଶୋଚନୀୟ ହୋଇପଡ଼ିଥିଲା । ଘୋର ଅଭାବ, ଦାରିଦ୍ର୍ୟ, ବେକାରି, ଶ୍ରମିକ ଅଶାନ୍ତି, ଧର୍ମଘଟ, ହିଂସାକାଣ୍ଡଦ୍ଵାରା ଇଟାଲୀର ଅବସ୍ଥା ବିପଯ୍ୟପ୍ତ ହୋଇପଡ଼ିଥିଲା ।
- ଇଟାଲୀର ତତ୍କାଳୀନ ରାଜା ଭିକ୍ଟର ଇମାନୁଏଲ ତୃତୀୟ ଦେଶରୁ ଅରାଜକତା ଦୂରକରିବା ପାଇଁ ସମର୍ଥ ହେଲେ ନାହିଁ ।
- ଏହି ସମୟରେ ଦେଶରେ ଦେଖା ଦେଇଥିବା କୃଷି ଓ ଶିଳ୍ପ ଶ୍ରମିକଙ୍କ ଆନ୍ଦୋଳନ ଦମନ ପାଇଁ ଶିଳ୍ପପତି, ପୁଞ୍ଜିପତି ଓ ବ୍ୟବସାୟୀମାନେ ସାହାଯ୍ୟ କଲେ । ଫଳରେ ମୁସୋଲିନୀଙ୍କ ଇଟାଲୀରେ ଗଠିତ ଫାସୀବାଦୀ ଦଳକୁ ସାହାଯ୍ୟ କଲେ । ଫଳରେ ମୁସୋଲିନୀଙ୍କ ନେତୃତ୍ଵରେ ପରବର୍ତ୍ତୀ କାଳରେ ଇଟାଲୀରେ ଫାସିଷ୍ଟ ସରକାର ପ୍ରତିଷ୍ଠିତ ହେଲା ।
![]()
୨ । କେଉଁ ପରିସ୍ଥିତିରେ ଜର୍ମାନୀରେ ‘ୱେ ମର୍ ସାଧାରଣତନ୍ତ୍ର’ ପ୍ରତିଷ୍ଠା ହୋଇଥିଲା ? ଏହି ସାଧାରଣତନ୍ତ୍ ଜନସାଧାରଣଙ୍କ ଅବସ୍ଥାରେ ଉନ୍ନତି ଆଣିପାରିଲା ନାହିଁ କାହିଁକି ?
Answer:
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ପରାଜୟ ଓ ଭର୍ସାଇ ସନ୍ଧିର କଠୋର ସର୍ଭାବଳୀ ପାଇଁ ଜର୍ମାନୀ ଜାତି ମର୍ମାହତ ହୋଇଥିଲା ।
- ରାଜନୈତିକ ଅସ୍ଥିରତା ଓ ଆର୍ଥିକ ସଙ୍କଟ ସେମାନଙ୍କୁ ବିଚଳିତ ଓ ବ୍ୟଥ୍ କରି ଦେଇଥ୍ଲା । ଫଳରେ ଦେଶରେ ଦେଖାଦେଇଥିବା ଗଣବିପ୍ଳବର ମୁକାବିଲା କରିନପାରି କାଇଜର ତୃତୀୟ ଉଇଲିୟମ୍ ଦେଶ ଛାଡ଼ି ଚାଲିଯାଇଥିଲେ ।
- ଏହାଦ୍ଵାରା ଜର୍ମାନୀରେ କାଇଜର ଶାସନର ପତନ ଘଟିଲା ଓ ଦେଶରେ ସାଧାରଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠିତ ହେଲା । ତାହାକୁ ‘ୱେମର୍ ସାଧାରଣତନ୍ତ୍ର’ (Weimer Republic) କୁହାଯାଏ ।
- କିନ୍ତୁ ଏହି ରାଜନୈତିକ ପରିବର୍ଷନ ଜନସାଧାରଣଙ୍କର ଅବସ୍ଥାର ଉନ୍ନତି ଆଣିବାରେ ସମ୍ପୂର୍ଣ ବିଫଳ ହୋଇଥିଲା ।
- ଶାସନ ପରି ଚାଳନାରେ ପୁଞ୍ଜିପତି, ବ୍ୟବସାୟୀ ଓ ଶିଳ୍ପପତିମାନଙ୍କର ଆଧୂପତ୍ୟ ଓ ପ୍ରାଧାନ୍ୟ ପୂର୍ବପରି ରହିଲା । ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଦଳମାନଙ୍କ ନେତୃତ୍ୱରେ ଶ୍ରମିକ ଆନ୍ଦୋଳନ ଆରମ୍ଭ ହୋଇ ରାଜନୈତିକ ଅସ୍ଥିରତା ଲାଗି ରହିଲା ।
୩ । କେଉଁ ପରିସ୍ଥିତିର ସୁଯୋଗ ନେଇ ଫାସିବାଦୀ ଚିନ୍ତାଧାରାର ଅଭ୍ୟୁଦୟ ହେଲା ?
Answer:
- ଊନବିଂଶ ଶତାବ୍ଦୀର ଶିଳ୍ପବିପ୍ଳବ ଯୋଗୁଁ କୃଷିକ୍ଷେତ୍ରରେ ବିଜ୍ଞାନର ଉପଯୋଗ ହେବାଦ୍ଵାରା ଉତ୍ପାଦନ ବହୁ ପରିମାଣରେ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହେଲା ।
- କିନ୍ତୁ ଯୁଦ୍ଧ ଯୋଗୁଁ ବାଣିଜ୍ୟ ବ୍ୟବସାୟ ବନ୍ଦହୋଇଯିବାରୁ ଏହି କୃଷିଜାତ ଦ୍ରବ୍ୟ ବିକ୍ରୟ କରିବା ସମ୍ଭବପର ହେଲାନାହିଁ, ଫଳରେ ଉତ୍ପନ୍ନକାରୀ ଦେଶଗୁଡ଼ିକ ବିଶେଷ କ୍ଷତିଗ୍ରସ୍ତ ହେଲେ ଓ କୃଷି ଶ୍ରମିକମାନଙ୍କର ଦୁରବସ୍ଥାର ସୀମା ରହିଲା ନାହିଁ ।
- ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ବିକ୍ରୟ ନହେବା ଫଳରେ ଶିଳ୍ପପତିମାନେ କଳକାରଖାନା ବନ୍ଦ କରିଦେଲେ । ଫଳରେ ଦାରିଦ୍ର୍ୟ ଓ ବେକାରି ବୃଦ୍ଧି ପାଇ ଶାନ୍ତିଶୃଙ୍ଖଳା ବ୍ୟାହତ ହେଲା ।
- ଶ୍ରମିକମାନେ ସେମାନଙ୍କ ଅବସ୍ଥାର ଉନ୍ନତି ଦାବି କରି ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଦଳଗୁଡ଼ିକ ନେତୃତ୍ୱରେ ଆନ୍ଦୋଳନ କଲେ । ଆନ୍ଦୋଳନକୁ ଦମନ କରିବାପାଇଁ ସ୍ୱେଚ୍ଛାଚାରୀ ତଥା ଉଗ୍ରବାଦୀ ଶକ୍ତମାନଙ୍କ ସାହାଯ୍ୟ ନେଲେ ।
- ଫଳରେ କେତେକ ସ୍ଥାନରେ ଜାତୀୟତାବାଦୀ ଓ ଏକଚ୍ଛତ୍ରବାଦୀ ଶକ୍ତି ବା ଫାସୀବାଦୀ ଶକ୍ତିର ଅଭ୍ୟୁଦୟ ହେଲା ।
କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ‘ଫାସିସ୍’ ଶବ୍ଦର ଅର୍ଥ କ’ଣ ? ଫାସୀବାଦୀ ଦଳର ଚିହ୍ନ କ’ଣ ଥିଲା ? ଏହା କେଉଁ ଦେଶରେ ଆରମ୍ଭ ହୋଇଥିଲା ?
Answer:
- ‘ଫାସିସ୍’ ଶବ୍ଦର ଅର୍ଥ ବିଡ଼ାଏ କାଠି ବା କୁରାଢ଼ି ସହିତ ବିଡ଼ାଏ କାଠି ।
- କୁରାଢ଼ି ସହ କାଠିବିଡ଼ା ଫାସୀବାଦୀ ଦଳର ଚିହ୍ନ ଥିଲା । ଏହା ପ୍ରଥମେ ଇଟାଲୀ ଦେଶରେ ଆରମ୍ଭ ହୋଇଥିଲା ।
![]()
୨। ବେନିତୋ ମୁସୋଲିନୀ କେବେ, କେଉଁଠାରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ? ପ୍ରଥମ ଅବସ୍ଥାରେ ସେ କ’ଣ କରୁଥିଲେ ?
Answer:
- ବେନିତୋ ମୁସୋଲିନୀ ୧୮୮୩ ମସିହାରେ ଇଟାଲୀର ରୋମାନାଠାରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ।
- ପ୍ରଥମାବସ୍ଥାରେ ସେ ଶିକ୍ଷକତା କରୁଥିଲେ ।
୩ । ମୁସୋଲିନୀ ଇଟାଲୀର ଶାସନଭାର ଗ୍ରହଣ କଲାପରେ ଦେଶରେ ଦେଖାଦେଇଥୁବ। ପରିବର୍ତ୍ତନ ମଧ୍ୟରୁ ଦୁଇଗୋଟି ଉଲ୍ଲେଖ କର ।
Answer:
- ମୁସୋଲିନୀ ଇଟାଲୀର ଶାସନଭାର ଗ୍ରହଣ କଲାପରେ ୧୯୨୬ ମସିହାରେ ଇଟାଲୀରେ ଫାସୀବାଦୀ ଦଳ ବ୍ୟତୀତ ଅନ୍ୟ ସମସ୍ତ ରାଜନୈତିକ ଦଳକୁ ବେଆଇନ ଘୋଷିତ କରାଗଲା ।
- ପ୍ରଥମାବସ୍ଥାରେ ସେ ଶିକ୍ଷକତା କରୁଥିଲେ । ମୁସୋଲିନୀ ଇଟାଲୀର ଶାସନଭାର ଗ୍ରହଣ କଲାପରେ ଦେଶରେ ଦେଖାଦେଇଥିବା ପରିବର୍ତ୍ତନ ମଧ୍ୟରୁ ଦୁଇଗୋଟି ଉଲ୍ଲେଖ କର ।
୪ । ୧୯୨୯ ରୁ ୧୯୩୩ ମଧ୍ୟରେ ପୃଥିବୀରେ ଦେଖାଦେଇଥିବା ଅର୍ଥନୈତିକ ସଙ୍କଟର ଦୁଇଟି ମୁଖ୍ୟ କାରଣ ଲେଖ ।
Answer:
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ପୃଥିବୀରେ ଏକ ଭୟଙ୍କର ଅର୍ଥନୈତିକ ସଙ୍କଟ ଦେଖାଦେଲା । ମୁଖ୍ୟତଃ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଓ ଇଉରୋପୀୟ ଦେଶମାନଙ୍କରେ ବାଣିଜ୍ୟ ବ୍ୟବସାୟ ବାଧାପ୍ରାପ୍ତ ହେଲା ।
- ଶିଳ୍ପଜାତ ଦ୍ରବ୍ୟଗୁଡ଼ିକର ଉତ୍ପାଦନ ହ୍ରାସ ଓ କ୍ରୟବିକ୍ରୟ ହ୍ରାସ ତଥା ବ୍ୟାଗୁଡ଼ିକରେ ଅଚଳ ଅବସ୍ଥା ଦେଖାଦେଲା ।
୫ । କାହା ନେତୃତ୍ବରେ ଇଟାଲୀରେ ଫାସୀବାଦୀଆନ୍ଦୋଳନ ଆରମ୍ଭ ହେଲା ? କେଉଁମାନଙ୍କୁ ନେଇ ସେ ଇଟାଲୀରେ ଫାସିବାଦୀ ଦଳ ଗଠନ କରିଥିଲେ ?
Answer:
- ବେନିତୋ ମୁସୋଲିନୀଙ୍କ ନେତୃତ୍ବରେ ଇଟାଲୀରେ ଫାସିବାଦୀ ଆନ୍ଦୋଳନ ଆରମ୍ଭ ହେଲା ।
- ଯୁଦ୍ଧଫେରନ୍ତା ବେକାର ସୈନିକ, ଦେଶଭକ୍ତ ନାଗରିକ ଓ ରାଜତନ୍ତ୍ର ବିରୋଧୀ ଲୋକଙ୍କୁ ନେଇସେ ଇଟାଲୀରେ ଫାସୀବାଦୀ ଦଳ ଗଠନ କରିଥିଲେ ।
![]()
୬ | ଫାସୀବାଦର ମୂଳଲକ୍ଷ୍ୟ କ’ଣ ଥିଲା ? ସେମାନେ କେଉଁ ପ୍ରକାର ଶାସନରେ ବିଶ୍ଵାସ କରୁଥିଲେ ?
Answer:
- ହିଂସାତ୍ମକ ପନ୍ଥାଦ୍ବାରା ଜଣେ କିମ୍ବା ମୁଷ୍ଟିମେୟ ବ୍ୟକ୍ତିଙ୍କ ହାତରେ ସମସ୍ତ କ୍ଷମତା କେନ୍ଦ୍ରୀଭୂତ କରି ଦେଶରେ ଏକଚ୍ଛତ୍ର ଶାସନ ପ୍ରତିଷ୍ଠା କରିବା ଫାସୀବାଦର ମୂଳ ଲକ୍ଷ୍ୟ ଥିଲା ।
- ଏହା ବହୁ ଦଳୀୟ ଶାସନକୁ ବିରୋଧ କରୁଥିବାବେଳେ ଏକଦଳୀୟ ଶାସନ ଉପରେ ବିଶ୍ଵାସ କରୁଥିଲା ।
୭ । ହିଟ୍ ଲର୍ ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ କି କାର୍ଯ୍ୟ କରୁଥିଲେ ? ତାଙ୍କୁ କାହିଁକି କାରାଦଣ୍ଡ ଭୋଗ କରିବାକୁ ପଡ଼ିଥିଲ। ? କାରାଗାରରେ ଥିବାବେଳେ ସେ କେଉଁ ପୁସ୍ତକ ଲେଖିଥିଲେ ?
Answer:
- ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧବେଳେ ହିଟଲର୍ ଜଣେ ସୈନିକ ଭାବରେ ଯୁଦ୍ଧରେ ଯୋଗ ଦେଇଥିଲେ ।
- ୧୯୨୩ ମସିହାରେ ବଳପୂର୍ବକ ଜର୍ମାନୀର କରି ହିଟ୍ର୍ କାରାଦଣ୍ଡ ଭୋଗ କରିଥିଲେ। ଜେଲରେ ଥିବାବେଳେ ସେ ‘ମେଁ କାମ୍ଫ’ ବା ‘ମୋର ସଂଘର୍ଷ’ ନାମକ ଏକ ପୁସ୍ତକ ଲେଖୁଥିଲେ ।
୮ । କେଉଁ ଶକ୍ତିମାନଙ୍କୁ ଫାସିବାଦୀ ଶକ୍ତି କୁହାଯାଏ ?
Answer:
- ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଦେଶରେ ଅର୍ଥନୈତି କ ଦୁରବସ୍ଥାର ଉନ୍ନତି ଦାବି କରି ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଦଳଗୁଡ଼ିକ ନେତୃତ୍ଵରେ ହେଉଥିବା ଆନ୍ଦୋଳନ ଦମନ ପାଇଁ ପୁଞ୍ଜିପତି, ଜମିଦାର ଓ ଶିଳ୍ପପତି ମାନେ ଉଗ୍ର ଜାତୀୟତାବାଦୀ ଓ ସ୍ୱେଚ୍ଛାଚାରୀ ଶକ୍ତିମାନଙ୍କ ସାହାଯ୍ୟ ଚାହିଁଲେ ।
- ଏହି ସୁଯୋଗରେ କେତେକ ସ୍ଥାନରେ ଉଗ୍ର ଜାତୀୟତାବାଦୀ ଓ ଏକଚ୍ଛତ୍ରବାଦୀ ଶକ୍ତିମାନଙ୍କର ଉତ୍ଥାନ ହେଲା । ଏମାନଙ୍କୁ ଫାସୀବାଦୀ ଶକ୍ତି କୁହାଯାଏ ।
୯ । ବିଂଶ ଶତାବ୍ଦୀର ପ୍ରଥମାର୍ଦ୍ଧରେ କେଉଁ କେଉଁ ଦେଶରେ ଉଗ୍ର ଜାତୀୟତାବାଦୀ ଚିନ୍ତାଧାରାର ବିକାଶ ଘଟିଲା ଓ ପରବର୍ତ୍ତୀ କାଳରେ ଏହି ଚିନ୍ତାଧାରା କେଉଁ ନାମରେ ପରିଚିତ ହେଲା ?
Answer:
- ବିଂଶ ଶତାବ୍ଦୀର ପ୍ରଥମାର୍ଦ୍ଧରେ ଇଟାଲୀ ଓ ଜର୍ମ।ନୀରେ ଉଗ୍ର ଜାତୀୟତାବାଦୀ ଚିନ୍ତାଧାରାର ବିକାଶ ଘଟିଲା ।
- ପରବର୍ତ୍ତୀ କାଳରେ ଏହି ଚିନ୍ତାଧାରା ‘ଫାସିବାଦ’ ନାମରେ ପରିଚିତ ହେଲା ।
୧୦ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଶିଳ୍ପ ଶ୍ରମିକମାନେ କାହିଁକି ବେକାର ହେଲେ ?
Answer:
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଯୁଦ୍ଧସାମଗ୍ରୀ ଉତ୍ପାଦନ ବନ୍ଦ ହୋଇଯିବାରୁ ଓ ଅନ୍ୟାନ୍ୟ ଶିଳ୍ପଜାତ ଦ୍ରବ୍ୟର ଚାହିଦା କମିଯିବାରୁ ଶିଳ୍ପପତିମାନେ କଳକାରଖାନା ବନ୍ଦ କରିଦେଲେ ।
- ଫଳସ୍ବରୂପ ଲକ୍ଷ ଲକ୍ଷ ଶିଳ୍ପ ଶ୍ରମିକ ବେକାର ହୋଇଗଲେ ।
![]()
୧୧ । ବିଶ୍ଵଯୁଦ୍ଧ ପରେ କେଉଁ କାରଣ ଯୋଗୁଁ କୃଷି ଉତ୍ପାଦନ କରୁଥିବା ଦେଶଗୁଡ଼ିକ ବିଶେଷ କ୍ଷତିଗ୍ରସ୍ତ ହୋଇଥିଲେ ?
Answer:
- ବିଶ୍ଵଯୁଦ୍ଧ ପରେ କୃଷି ଉତ୍ପାଦନ ବୃଦ୍ଧି ପାଇଥିଲେ ମଧ୍ୟ ବାଣିଜ୍ୟ ବ୍ୟବସାୟ ପ୍ରାୟ ବନ୍ଦ ହୋଇଯାଇଥ୍ବାରୁ ସେସବୁ ବିକ୍ରି ହୋଇପାରିଲା ନାହିଁ ।
- କୃଷି ପ୍ରଧାନ ଦେଶଗୁଡ଼ିକରେ କୃଷିଜାତ ଦ୍ରବ୍ୟର ଆବଶ୍ୟକତା ଥିଲେ ମଧ୍ୟ ଲୋକଙ୍କର କ୍ରୟ କ୍ଷମତା ନଥିଲା । ତେଣୁ କୃଷି ଉତ୍ପାଦନ କରୁଥିବା ଦେଶଗୁଡ଼ିକ କ୍ଷତିଗ୍ରସ୍ତ ହେଲେ ।
୧୨ । କାହିଁକି ମୁସୋଲିନୀଙ୍କର ପ୍ରତିପତ୍ତି ଓ କ୍ଷମତ ଯଥେଷ୍ଟ ବୃଦ୍ଧି ପାଇଲା ? କେବେ ଇଟାଲୀରେ ଏକଦଳୀୟ ଶାସନ ପ୍ରତିଷ୍ଠିତ ହେଲା ?
Answer:
- ୧୯୨୪ ମସିହାରେ ଅନୁଷ୍ଠିତ ନିର୍ବାଚନରେ ଫାସୀବାଦୀ ଦଳ ପାର୍ଳ।ମେଣ୍ଝରେ ସଂଖ୍ୟାଗରିଷ୍ଠତା ହାସଲ କରିବାରୁ ମୁସୋଲିନୀଙ୍କର ପ୍ରତିପଭି ଓ କ୍ଷମତା ଯଥେଷ୍ଟ ବୃଦ୍ଧି ପାଇଲା ।
- ୧୯୨୬ ମସିହାରେ ଇଟାଲୀରେ ଏକଦଳୀୟ ଶାସନ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।
୧୩ । ହିଟ୍ଲର୍ ଶାସନ କ୍ଷମତାକୁ ଆସିବା ପରେ ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଦଳଗୁଡ଼ିକୁ କିପରି ଦମନ କଲେ ?
Answer:
- ହିଟଲର୍ ଶାସନ କ୍ଷମତାକୁ ଆସିବାପରେ ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଦଳର ସଙ୍ଗଠନଗୁଡ଼ିକୁ ଭାଙ୍ଗିଦେଲେ ।
- ସେ ସେମାନ ଙ୍କର ସମ୍ପତ୍ତି ବାଜ୍ୟାପ୍ତି କରିଥିଲେ ।
୧୪ । ‘ୱେମର ସାଧାରଣତନ୍ତ୍ର’ କାହାକୁ କୁହାଗଲା ?
Answer:
- ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରବର୍ତ୍ତୀ କାଳରେ ଜର୍ମାନୀରେ ଦେଖାଦେଇଥିବା ଗଣବିପ୍ଳବର ମୁକାବିଲା କରି ନପାରି କାଇଜର ତୃତୀୟ ଉଇଲିୟମ୍ ଦେଶ ଛାଡ଼ି ଚାଲିଗଲେ ।
- ଫଳରେ ଜର୍ମାନୀରେ କାଇଜର ଶାସନର ପତନ ଘଟିଲା ଓ ସାଧାରଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠିତ ହେଲା । ତାହାକୁ ‘ୱେମର୍ ସାଧାରଣତନ୍ତ୍ର’ କୁହାଗଲା ।
୧୫ । ଇଟାଲୀୟମାନେ କାହିଁକି ଫାସୀବାଦର ବିରୋଧ କଲେ ନାହିଁ ?
Answer:
- ଦେଶରୁ ଅରାଜକତା ଦୂର କରିବାପାଇଁ ଫାସୀବାଦୀ ଦଳ ଏକମାତ୍ର ଦଳ ବୋଲି ଭାବି ଇଟାଲୀର ଜନସାଧାରଣ ଫାସୀବାଦର ବିରୋଧ କଲେ ନାହିଁ ।
- ଅପରପକ୍ଷରେ ପୁଞ୍ଜିପତି, ଜମିଦାର ଓ ବ୍ୟବସାୟୀମାନେ ନିଜର ସ୍ଵାର୍ଥ ଓ ସୁବିଧା ଦୃଷ୍ଟିରୁ ଫାସୀବାଦର ବିରୋଧ କରି ନ ଥିଲେ ।
![]()
Objective Type Questions With Answers
A. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
୧। କିଏ ବିପର୍ଯ୍ୟସ୍ତ ଇଟାଲୀର ଶାନ୍ତିଶୃଙ୍ଖଳା ଓ ଆର୍ଥିକ ସ୍ୱଚ୍ଛଳତା ଫେରାଇ ଆଣିବାରେ ସମ୍ପୂର୍ଣ୍ଣ ବିଫଳହୋଇଥିଲେ ?
Answer:
ଇଟାଲୀର ରାଜା ଭିକ୍ଟର ଇମାନୁଏଲ୍ ତୃତୀୟ ବିପର୍ଯ୍ୟସ୍ତ ଇଟାଲୀର ଶାନ୍ତିଶୃଙ୍ଖଳା ଓ ଆର୍ଥିକ ସ୍ୱଚ୍ଛଳତା ଫେରାଇ ଆଣିବାରେ ସମ୍ପୂର୍ଣ୍ଣ ବିଫଳ ହୋଇଥିଲେ ।
୨। ଫାସିବାଦୀ ଆନ୍ଦୋଳନର କର୍ଣ୍ଣଧାର କିଏ ଥିଲେ ?
Answer:
ଫାସିବାଦୀ ଆନ୍ଦୋଳନର କର୍ଣ୍ଣଧାର ବେନିତୋ ମୁସୋଲିନୀ ଥିଲେ ।
୩ । ମୁସୋଲିନୀ କେବେ ଓ କାହିଁକି ଇଟାଲୀର ରାଜଧାନୀ ରୋମ ଅଭିମୁଖେ ଯାତ୍ରା କରିଥିଲେ ?
Answer:
ବଳପୂର୍ବକ କ୍ଷମତା ଅଧିକାର କରି ଏକଚ୍ଛତ୍ର ଶାସନ ପ୍ରତିଷ୍ଠା କରିବା ଉଦ୍ଦେଶ୍ୟରେ ମୁସୋଲିନୀ ୧୯୨୨ ମସିହା ଅକ୍ଟୋବର ୨୮ ତାରିଖ ଦିନ ଇଟାଲୀର ରାଜଧାନୀ ରୋମ୍ ଅଭିମୁଖେ ଯାତ୍ରା କରିଥିଲେ ।
୪ । କିଏ ମୁସୋଲିନୀଙ୍କୁ ଇଟାଲୀରେ ସରକାର ଗଠନ କରିବାକୁ ଆମନ୍ତ୍ରଣ କରିଥିଲେ ?
Answer:
ଇଟାଲୀର ରାଜା ଭିକ୍ଟର ଇମାନୁ ଏଲ ତୃତୀୟ ମୁସୋଲିନୀଙ୍କୁ ସରକାର ଗଠନ କରିବାକୁ ଆମନ୍ତ୍ରଣ କରିଥିଲେ ।
୫। ଦଳଗୁଡ଼ିକ ଶ୍ରମିକ ଆନ୍ଦୋଳନର ନେତୃତ୍ବ ଦଳଗୁଡ଼ିକ ଶ୍ରମିକ ଆନ୍ଦୋଳନର ନେତୃତ୍ୱ ନେଇଥିଲେ ?
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଇଉରୋପର ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଦଳଗୁଡ଼ିକ ଶ୍ରମିକ ଆନ୍ଦୋଳନର ନେତୃତ୍ୱ ନେଇଥିଲେ ।
![]()
୬ | ଫାସିବାଦର ମୂଳ ଲକ୍ଷ୍ୟ କ’ଣ ଥିଲା ?
Answer:
ହିଂସାତ୍ମକ ପନ୍ଥାଦ୍ୱାରା ଜଣେ କିମ୍ବା ମୁଷ୍ଟିମେୟ ବ୍ୟକ୍ତିଙ୍କ ହାତରେ ସମସ୍ତ କ୍ଷମତା କେନ୍ଦ୍ରୀଭୂତ କରି ଏକଚ୍ଛତ୍ର ଶାସନ ପ୍ରତିଷ୍ଠା କରିବା ଫାସୀବାଦର ମୂଳ ଲକ୍ଷ୍ୟ ଥିଲା ।
୭ । ଜର୍ମାନୀରେ କେତେବେଳେ ଓ କାହା ନେତୃତ୍ବର ନାଜି ଆନ୍ଦୋଳନ ଆରମ୍ଭ ହୋଇଥିଲା ?
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଜର୍ମାନୀର ରାଜନୈତିକ ଅସ୍ଥିରତାର ସୁଯୋଗ ନେଇ ହିଟଲର୍ଙ୍କ ନେତୃତ୍ୱରେ ନାଜି ଆନ୍ଦୋଳନ ଆରମ୍ଭ ହୋଇଥିଲା ।
୮ | ‘ମେଁ କାମ୍ପ’ ପୁସ୍ତକ କିଏ ରଚନା କରିଥିଲେ ?
Answer:
‘ମେଁ କାମ୍ପ’ ବା ‘ମୋର ସଂଘର୍ଷ’ ପୁସ୍ତକ ହିଟଲର୍ ରଚନା କରିଥିଲେ ।
୯। କେବେ ହିଟ୍ ଲର୍ ଉଭୟ ରାଷ୍ଟ୍ରପତି ଓ ପ୍ରଧାନମନ୍ତ୍ରୀଙ୍କ କ୍ଷମତା ନିଜ ହାତକୁ ନେଲେ ?
Answer:
ଜର୍ମାନୀର ତତ୍କାଳୀନ ରାଷ୍ଟ୍ରପତି ହିଣ୍ଡେନ୍ବର୍ଗଙ୍କ ମୃତ୍ୟୁପରେ ହିଟ୍ ଲର୍ ଉଭୟ ରାଷ୍ଟ୍ରପତି ଓ ପ୍ରଧାନମନ୍ତ୍ରୀଙ୍କ କ୍ଷମତା ନିଜ ହାତକୁ ନେଲେ ।
୧୦ । କଳାକୁର୍ତ୍ତା ବାହିନୀ କେଉଁମାନଙ୍କୁ କୁହାଯାଉଥିଲା ?
Answer:
ଫାସୀବାଦୀ ଦଳର ତତ୍ତ୍ଵାବଧାନରେ ତାଲିମପ୍ରାପ୍ତ କଳାପୋଷାକ ପିନ୍ଧା ସଶସ୍ତ୍ର ସ୍ଵେଚ୍ଛାସେବକ ବାହିନୀକୁ କଳାକୁର୍ତ୍ତା ବାହିନୀ କୁହାଯାଉଥିଲା ।
୧୧। ହିଟ୍ଲର୍ କିପରି ଭାବରେ ଏକାଧାର ରେ ରାଷ୍ଟ୍ରମୁଖ୍ୟ, ଶାସନମୁଖ୍ୟ ଓ ସାମରିକ ବିଭାଗର ସର୍ବୋଚ୍ଚ କର୍ତ୍ତା ହେଲେ ?
Answer:
ରାଷ୍ଟ୍ରପତି ହିଣ୍ଡେବର୍ଗଙ୍କ ମୃତ୍ୟୁ ପରେ ହିଟ୍ଲର୍ ଏକ ସ୍ୱତନ୍ତ୍ର ଆଇନ ପ୍ରଣୟନ କରି ଉଭୟ ରାଷ୍ଟ୍ରପତି ଓ ଚାନ୍ସେଲରଙ୍କ କ୍ଷମତା ନିଜ ହାତକୁ ନେବା ସହିତ ଏକାଧାରରେ ଜର୍ମାନୀର ରାଷ୍ଟ୍ରମୁଖ୍ୟ, ଶାସନମୁଖ୍ୟ ଓ ସାମରିକ ବିଭାଗର ସର୍ବୋଚ୍ଚ କର୍ତ୍ତା ହେଲେ ।
![]()
୧୨ । ମୁସୋଲିନୀ ଶାସନଭାର ଗ୍ରହଣ କଲାପରେ ଇଟାଲୀରେ ଶିକ୍ଷା ପଦ୍ଧତିରେ କିପରି ବର୍ତ୍ତନ ଘଟିଲା ?
Answer:
ମୁସୋଲିନୀ ଶାସନଭାର ଗ୍ରହଣ କଲାପରେ ଶିକ୍ଷା ପଦ୍ଧତିକୁ ନିୟନ୍ତ୍ରଣ କରାଗଲା ଓ ସାମରିକ ଶିକ୍ଷାକୁ ବାଧ୍ୟତାମୂଳକ କରାଗଲା ।
୧୩। ଜର୍ମାନୀରେ କେଉଁ ଶାସନର ପତନ ପରେ ସାଧାରଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠା ହେଲା ?
Answer:
ଜର୍ମାନୀରେ କାଇଜର୍ ଶାସନର ପତନ ପରେ ସାଧାରଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠା ହେଲା ।
୧୪ । ୧୯୨୯ ରୁ ୧୯୩୩ ମସିହା ମଧ୍ୟରେ ପୃଥିବୀରେ ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଦେଖାଦେଇଥିବା ଉତ୍କଟ ଅର୍ଥନୈତିକ ସଙ୍କଟଦ୍ଵାରା କେଉଁ ଦେଶ ପ୍ରଭାବିତ ହୋଇନଥିଲା ?
Answer:
୧୯୨୯ ରୁ ୧୯୩୩ ମସିହା ମଧ୍ୟରେ ପୃଥିବୀର ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଦେଖାଦେଇଥିବା ଉତ୍କଟ ଅର୍ଥନୈତିକ ସଙ୍କଟଦ୍ବାରା ରୁଷ୍ ଦେଶ ପ୍ରଭାବିତ ହୋଇନଥିଲା ।
B. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।
୧। କୁରାଢ଼ି ସହିତ କାଠିବିଡ଼ାକୁ କେଉଁ ଦଳ ନିଜର ଦଳୀୟ ସଙ୍କେତ ରୂପେ ବ୍ୟବହାର କରୁଥିଲା ?
Answer:
ଫାସୀବାଦୀ ଦଳ
୨ । ଇଟାଲୀ ଦେଶରେ ଫାସୀବାଦୀ ଆନ୍ଦୋଳନର କର୍ଣ୍ଣଧାର କିଏ ଥିଲେ ?
Answer:
ବେନିତୋ ମୁସୋଲିନୀ
୩ । ପ୍ରଥମ ବିଶ୍ଵ ଯୁଦ୍ଧବେଳେ ମୁ ସୋଲିନୀ କି କାର୍ଯ୍ୟ କରିଥିଲେ ?
Answer:
ସୈନିକ
![]()
୪। ଇଟାଲୀରେ ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଆଦର୍ଶରେ ଅନୁପ୍ରାଣିତ ଶ୍ରମିକ ଆନ୍ଦୋଳନକୁ ଦମନ କରିବାପାଇଁ କେଉଁ ଦଳ ଆଗେଇ ଆସିଥିଲା ?
Answer:
ଫାସୀବାଦୀ ଦଳ
୫। ଫାସୀବାଦୀ ଦଳର ତାଲିମପ୍ରାପ୍ତ ସ୍ଵେଚ୍ଛାସେବକଙ୍କ ସଶସ୍ତ୍ର ବାହିନୀକୁ କ’ଣ କୁହାଗଲା ?
Answer:
କଳାକୁର୍ତ୍ତା ବାହିନୀ
୬ । ଇଟାଲୀର କେଉଁ ରାଜା ଭୟଭୀତ ହୋଇ ମୁସୋଲିନୀଙ୍କୁ ସରକାର ଗଠନ କରିବାକୁ ଆମନ୍ତ୍ରଣ କରିଥିଲେ ?
Answer:
ଭିକ୍ଟର୍ ଇମାନୁଏଲ୍ ତୃତୀୟ
୭। ମୁସୋଲିନୀ କେବେ ଫାସୀବାଦୀ ଦଳ ବ୍ୟତୀତ ଅନ୍ୟ ସମସ୍ତ ରାଜନୈତିକ ଦଳକୁ ବେଆଇନ ଘୋଷଣା କରିଦେଲେ ?
Answer:
୧୯୨୬ ମସିହା
୮। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଜର୍ମାନୀରେ ଦେଖାଦେଇଥିବା ଗଣବିପ୍ଳବର ମୁକାବିଲା କରି ନ ପାରି କେଉଁ ସମ୍ରାଟ ଦେଶ ଛାଡ଼ି ନେଦରଲାଣ୍ଡ ଚାଲିଗଲେ ?
Answer:
କାଇଜର ଦ୍ଵିତୀୟ
୯। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ଜର୍ମାନୀରେ ପ୍ରତିଷ୍ଠିତ ସାଧାରଣତନ୍ତ୍ରକୁ କ’ଣ କୁହାଗଲା ?
Answer:
ୱେମର୍ ସାଧାରଣତନ୍ତ୍ର
ଉଇଲିୟମ୍
୧୦ । ହିଟ୍ର୍ କେଉଁ ଦେଶରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ?
Answer:
ଅଷ୍ଟ୍ରିଆ
![]()
୧୧ । କେଉଁ ମସିହାରେ ହିଟ୍ଲର୍ ବଳପୂର୍ବକ ଜର୍ମାନୀର ଶାସନ କ୍ଷମତା ଗ୍ରହଣ କରିବାକୁ ଚେଷ୍ଟା କରି ବିଫଳ ହୋଇଥିଲେ ?
Answer:
୧୯୨୩
୧୨ । ହିଟଲର୍ ତାଙ୍କର କେଉଁ ନୀତି ଯୋଗୁଁ ପୁଞ୍ଜିପତି ଓ ଗଣତନ୍ତ୍ର ବିରୋଧୀ ଶକ୍ତିମାନଙ୍କର ସମର୍ଥନ ଲାଭ କରିଥିଲେ ?
Answer:
ଉଗ୍ର ଜାତୀୟତାବାଦୀ
୧୩ । କ୍ଷମତା ହାସଲ କରିବା ପରେ ହିଟଲର୍ କେଉଁ ସ୍ଥାନରେ ପୁନର୍ବାର ସୈନ୍ୟ ମୁତୟନ କରିଥିଲେ ?
Answer:
ରାଇନ୍ ନଦୀ ଉପତ୍ୟକା
୧୪ । ପୃଥିବୀର ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଅର୍ଥନୈତିକ ସଂକଟ ଦେଖାଯାଇଥିବା ସମୟରେ ରୁଷରେ କିଏ ଶାସନ ମୁଖ୍ୟ ଥିଲେ ?
Answer:
ଷ୍ଟାଲିନ୍
୧୫ । ଇଟାଲୀରେ କଳାକୁର୍ତ୍ତା ବାହିନୀ କିଏ ଗଠନ କରିଥିଲେ ?
Answer:
ବେନିତୋ ମୁସୋଲିନୀ
୧୬ । ହିଟ୍ଲର କେଉଁମାନଙ୍କୁ ଘୃଣା କରୁଥିଲେ ?
Answer:
ଇହୁ ଦୀମାନ ଙ୍କୁ
୧୭ । କେଉଁ ନଦୀ ଉପତ୍ୟକାରେ ହିଟ୍ଲର ପୁନର୍ବାର ସୈନ୍ୟ ମୁତୟନ କରିଥିଲେ ?
Answer:
ରାଇନ୍ ନଦୀ
୧୮ । ହିଟ୍ର ଜର୍ମାନୀର ସର୍ବେସର୍ବା ହେବାପରେ କେଉଁ ସଙ୍ଗଠନଗୁଡ଼ିକୁ ଭାଙ୍ଗି ଦେଇଥିଲେ ?
Answer:
ଶ୍ରମିକ ସଙ୍ଗଠନଗୁଡ଼ିକୁ
![]()
୧୯ । କେ ଉଁ ମାନଙ୍କୁ ହିଟ୍ର ନୃଶଂସଭାବେ ହତ୍ୟା କରିଥିଲେ ?
Answer:
ଇହୁଦୀମାନଙ୍କୁ
୨୦ । ହିଟ୍ର ଶ୍ରମଜୀବୀ ଦଳର ନେତା ହେବାପରେ ଦଳର ନାମ ପରିବର୍ତ୍ତନ କରି କ’ଣ ରଖୁଥିଲେ ?
Answer:
ଜାତୀୟ ସମାଜବାଦୀ ଶ୍ରମିକ ଦଳ / ନାଜି ଦଳ
୨୧ । ଫାସୀବାଦୀ ଶାସନ ପ୍ରତିଷ୍ଠା ପରେ ଇଟାଲୀରେ କେଉଁ ଶିକ୍ଷା ବାଧ୍ୟତାମୂଳକ ହୋଇଥିଲା ?
Answer:
ସାମରିକ ଶିକ୍ଷା
୨୨ । ହିଟ୍ଲର୍ ଜେଲ୍ରେ ଥିବାବେଳେ କେଉଁ ପୁସ୍ତକଟି ରଚନା କରିଥିଲେ ?
Answer:
ମେଁ କାମ୍ପ
୨୩। ଇଟାଲୀର କେଉଁଠାରେ ମୁ ସୋଲି ନୀ ଜନ୍ମ ହୋଇଥିଲେ ?
Answer:
ରୋମାନା
୨୪ । କିଏ ‘ମୋର ସଂଘର୍ଷ’ ପୁସ୍ତକ ରଚନା କରିଥିଲେ ?
Answer:
ହିଟ୍ର
୨୫ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ କେଉଁ ଆଦର୍ଶବାଦ ଇଟାଲୀରେ ପ୍ରସାରଲାଭ କରିଥିଲା ?
Answer:
ଫାସୀବାଦୀ
୨୬ । କେବେ ଜର୍ମାନୀରେ ନାଜିଦଳ ଗଠିତ ହୋଇଥିଲା ?
Answer:
୧୯୨୧ ମସିହା
![]()
୨୭ । କେଉଁ ସମ୍ରାଟଙ୍କ ପଳାୟନ ପରେ ଜର୍ମାନୀରେ ୱେମର୍ ସାଧାରଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍
୨୮ । କେଉଁ ଦଳର ତାଲିମପ୍ରାପ୍ତ ସ୍ଵେଚ୍ଛାସେବକମାନଙ୍କୁ କଳାକୁର୍ତ୍ତା ବାହିନୀ କୁହାଯାଉଥିଲା ?
Answer:
ଫାସୀବାଦୀ ଦଳ
୨୯ । ମୁସୋଲିନୀ କେବେ ଇଟାଲୀର ରାଜଧାନୀ ରୋମ୍ ଅଭିମୁଖେ ଯାତ୍ରା କରିଥିଲେ ?
Answer:
୧୯୨୨ ଅକ୍ଟୋ।ବର ୨୮ ତାରିଖ
୩୦ । ୧୮୮୩ ମସିହାରେ କେଉଁ ବିପ୍ଳବୀ ଜନ୍ମ ଗ୍ରହଣ କରିଥିଲେ ?
Answer:
ମୁସୋଲିନୀ
C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
୧। ମୁ ସୋଲିନୀ __________ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ।
Answer:
୧୮୮୩
୨ । __________ ଦଳର ସ୍ଵେଚ୍ଛାସେବକ ବାହିନୀକୁ କଳାକୁର୍ତ୍ତା ବାହିନୀ କୁହାଯାଏ ।
Answer:
ଫାସିବାଦୀ
![]()
୩ । _________ ମସିହାରେ ନାଜିଦଳ ଗଠିତ ହୋଇଥିଲା ।
Answer:
୧୯୨୧
୪ । ‘ଫାସିସ୍’ ଏକ ______________ ଶବ୍ଦ ।
Answer:
ଲାଟିନ୍
୫ । ଫାସିବାଦୀ ଶାସନ ପ୍ରତିଷ୍ଠା ପରେ ଇଟାଲୀରେ ___________ଶିକ୍ଷା ବାଧ୍ୟତାମୂଳକ ହୋଇଥିଲା ।
Answer:
ସାମରିକ
୬ । ହିର୍ଲର୍ ଜେଲ୍ରେ ଥିଲାବେଳେ __________ ନାମକ ପୁସ୍ତକଟିଏ ରଚନା କରିଥିଲେ ।
Answer:
ମେଁକାମ୍ଫ
୭ । ହିଂସାତ୍ମକ ପନ୍ଥାଦ୍ୱାରା ଜଣେ କିମ୍ବା ମୁଷ୍ଟିମେୟ ବ୍ୟକ୍ତଙ୍କ ହାତରେ ସମସ୍ତ ଶାସନ କ୍ଷମତା କେନ୍ଦ୍ରୀଭୂତ କରି ଦେଶରେ __________ ଶାସନ ପ୍ରତିଷ୍ଠା କରିବା ଫାସୀବାଦର ମୂଳଲକ୍ଷ୍ୟ ଥିଲା ।
Answer:
ଏକଚ୍ଛତ୍ର
୮ | ମୁସୋଲିନୀ ___________ ମସିହାରେ ଇଟାଲୀର ପ୍ରଧାନମନ୍ତ୍ରୀ ହୋଇଥିଲେ ।
Answer:
୧୯୨୨
୯ । _________ ଦଳ ପରେ ଜାତୀୟ ସମାଜବାଦୀ ଶ୍ରମିକ ଦଳ ବା ନାଜିଦଳ ନାମରେ ପରିଚିତ ହେଲା ।
Answer:
ଶ୍ରମଜୀବୀ
![]()
୧୦ । ୧୮୭୧ ମସିହାରୁ ୧୯୧୮ ମସିହା ପର୍ଯ୍ୟନ୍ତ ଜର୍ମାନୀର ସପ୍ର।ଟମାନଙ୍କୁ __________ ବୋଲି କୁହାଯାଉଥିଲା ।
Answer:
କାଇଜର୍
୧୧। ଜର୍ମାନୀରେ _________ ମସିହାରେ ସାଧାରଣ ନିର୍ବ।ଚନ ହୋଇଥିଲା ।
Answer:
୧୯୩୩
୧୨ । ________ ମସିହାରେ ଇଟାଳୀରେ ଫାସୀବାଦୀ ଦଳ ବ୍ୟତୀତ ଅନ୍ୟ ସମସ୍ତ ରାଜନୈତିକ ଦଳକୁ ବେଆଇନ ଘୋଷଣା କରାଯାଇଥିଲା ।
Answer:
୧୯୨୬
୧୩ । ____________ ମସିହାରେ ଯୋଶେଫ୍ ଷ୍ଟାଲିନ୍ଙ୍କଦ୍ୱାରା ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା ପ୍ରବର୍ତ୍ତନ କରାଯାଇଥିଲା ।
Answer:
୧୯୨୮
D. ଠିକ୍ ଉକ୍ତି ପାଇଁ ( ✓) ଓ ଭୁଲ ଉକ୍ତି ପାଇଁ (x) ଲେଖ ।
୧। ଫାସୀବାଦର ମୂଳ ଲକ୍ଷ୍ୟ ହେଲା ହିଂସାତ୍ମକ ଉପାୟରେ ଶାସନ କରିବା ।
୨। ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ପ୍ରଥମେ ଜର୍ମାନୀ ଦେଶରେ ଫାସୀବାଦର ବିକାଶ ଘଟିଥିଲା ।
୩ । କଳାକୁର୍ତ୍ତା ବାହିନୀ ମୁଖ୍ୟତଃ ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀମାନଙ୍କୁ ବିରୋଧ କରୁଥିଲା ।
୪। ଇଟାଲୀରେ ୧୯୨୦ ମସିହାରେ ସାଧାରଣ ନିର୍ବାଚନ ହୋଇଥିଲା ।
୫। ଇଟାଲୀରୁ ସାର୍ବଜନୀନ ଭୋଟ୍ ବ୍ୟବସ୍ଥା ହିଟଲର୍ ଉଠାଇ ଦେଇଥିଲେ ।
୬। ଆଡ଼ଲଫ୍ ହିଟ୍ର୍ ଜର୍ମାନୀ ଦେଶରେ ଜନ୍ମଗ୍ରହଣି କରିଥିଲେ ।
୭। ‘ମୋର ସଂଘର୍ଷ’ ପୁସ୍ତକ ହିଟ୍ଲର୍ ରଚନା କରିଥିଲେ ।
୮। ଇଂରାଜୀ ଭାଷାରୁ ‘ଫାସିସ୍’ ଶବ୍ଦଟି ଆସିଅଛି ।
୯ । ପ୍ୟାରିସ୍ ଶାନ୍ତି ସମ୍ମିଳନୀରେ ଜର୍ମାନୀ ନିରାଶ ହୋଇଥିଲେ ।
୧୦ । ମୁସୋଲିନୀ ଲକ୍ଷ ଲକ୍ଷ ଇହୁଦୀମାନଙ୍କୁ ନୃଶଂସ ଭାବରେ ହତ୍ୟା କରିଥିଲେ ।
![]()
Answer:
୧। (✓)
୨ । (x)
୩ । (✓ )
୪ । (x)
୫ । (x)
୬ । (x)
୭ | (✓)
୮ । (x)
୯ । (x)
୧୦ । (x)
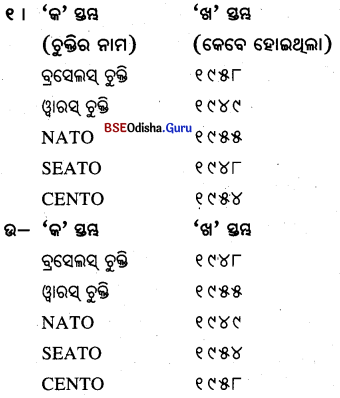
E. ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେ ।


F. ରେଖାଙ୍କିତ ପଦକୁ ପରିବର୍ତ୍ତନ କରି ଭ୍ରମ ସଂଶୋଧନ କର ।
୧। ମୁସୋଲିନ୍ ୧୮୮୨ ମସିହାରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ।
Answer:
୧୮୮୩
୨। ନାଜିଦଳର ସ୍ଵେଚ୍ଛାସେବକମାନଙ୍କୁ ନେଇ କଳାକୁର୍ତ୍ତା ବାହିନୀ ଗଠନ କରାଯାଇଥିଲା ।
Answer:
ଫାସିବାଦୀ
୩ । ମୁସୋଲିନୀ ୧୯୨୦ ମସିହାରେ ଇଟାଲୀର ପ୍ରଧାନମନ୍ତ୍ରୀ ହୋଇଥିଲେ ।
Answer:
୧୯୨୨
![]()
୪ । ଇଟାଲୀର ରୋମ୍ ସହରରେ ମୁସୋଲିନୀ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ।
Answer:
ରୋମାନା
୫। ପଞ୍ଚବାର୍ଷିକ ଯୋଜନାର ପ୍ରବର୍ତ୍ତକ ଥିଲେ ବିନେତୋ ମୁସୋଲିନୀ ।
Answer:
ଯୋଶେଫ୍ ଷ୍ଟାଲିନ୍
୬। କାଇଜର ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍ ଇଟାଲୀ ଦେଶର ଶାସକ ଥିଲେ ।
Answer:
ଜର୍ମାନୀ
୭। ଇହୁଦୀମାନଙ୍କୁ ମୁସୋଲିନୀ ନୃଶଂସଭାବେ ହତ୍ୟା କରିଥିଲେ ।
Answer:
ହିଟଲର
୮। ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧବେଳେ ହିଟଲର ଜଣେ ସେନାପତି ଭାବରେ ଯୁଦ୍ଧରେ ଯୋଗ ଦେଇଥିଲେ ।
Answer:
ସୈନିକ
୯ । କୁରାଢ଼ି ସହ କାଠିବିଡ଼ା ନାଜିଦଳରୁ ସଙ୍କେତ ଥିଲା ।
Answer:
ଫାସୀବାଦୀ ଦଳର
୧୦ । ରୁଷିଆରେ ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା ୧୯୨୦ ମସିହାରେ ନୂତନଭାବେ ପ୍ରବର୍ତ୍ତନ କରାଯାଇଥିଲା ।
Answer:
୧୯୨୮
୧୧ । ନାଜିଦଳର ଚିନ୍ତାଧାରା, ଆଦର୍ଶ ଓ କାର୍ଯ୍ୟକ୍ରମ ମୋର ଅଭିଜ୍ଞତା ପୁସ୍ତକରେ ପ୍ରକାଶ ପାଇଥିଲା ।
Answer:
ମୋର ସଂଘର୍ଷ
![]()
୧୨ । ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧରେ ରୁଷିଆ କେନ୍ଦ୍ରଶକ୍ତି ସପକ୍ଷରେ ଯୋଗ ଦେଇଥିଲା ।
Answer:
ମିତ୍ରଶକ୍ତି
G. ଚାରୋଟି ସମ୍ଭାବ୍ୟ ବିକଳ୍ପ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
Question 1.
ହିଟ୍ର କେଉଁମାନଙ୍କୁ ଘୃଣା କରୁଥିଲେ ?
(A) ମୁସଲମାନ
(B) ଖ୍ରୀଷ୍ଟିଆନ
(C) ପାର୍ସୀ
(D) ଇହୁଦୀ
Answer:
(D) ଇହୁଦୀ
Question 2.
କେଉଁ ନଦୀ ଉପରେ ହିଟ୍ଲର ପୁନର୍ବାର ସୈନ୍ୟ ମୁତୟନ କରିଥିଲେ ?
(A) ନେଭା
(B) ଭଲ୍ଗା
(C) ରେନା
(D) ରାଇନ୍
Answer:
(C) ରେନା
Question 3.
ହିଟ୍ର ଜର୍ମାନୀର ସର୍ବେସର୍ବା ହେବାପରେ କେଉଁ ସଙ୍ଗଠନଗୁଡ଼ିକୁ ଭାଙ୍ଗି ଦେଇଥିଲେ ?
(A) ନାରୀ ସଙ୍ଗଠନ
(B) ଶିକ୍ଷକ ସଙ୍ଗଠନ
(C) ଶ୍ରମିକ ସଙ୍ଗଠନ
(D) ମୂଲିଆ ସଂଘ
Answer:
(C) ଶ୍ରମିକ ସଙ୍ଗଠନ
![]()
Question 4.
କେଉଁମାନଙ୍କୁ ହିଟ୍ର ନୃଶଂସଭାବେ ହତ୍ୟା କରିଥିଲେ ?
(A) ଖ୍ରୀଷ୍ଟିଆନ
(B) ପାର୍ସୀ
(C) ଇହୁଦୀ
(D) ଜୋରାଷ୍ଟର
Answer:
(C) ଇହୁଦୀ
Question 5.
ଇଟାଲୀର ‘କଳାକୁର୍ତ୍ତାବାହିନୀ’ କିଏ ଗଠନ କରିଥିଲେ ?
(A) ଭିକ୍ଟର ଇମାନୁଏଲ
(B) ତୃତୀୟ ଉଇଲିୟମ୍
(C) ମୁସୋଲିନ୍
(D) ହିଟ୍ର
Answer:
(C) ମୁସୋଲିନ୍
Question 6.
ଫାସୀବାଦୀ ଶାସନ ପ୍ରତିଷ୍ଠା ପରେ ଇଟାଲୀରେ କେଉଁ ଶିକ୍ଷା ବାଧ୍ୟତାମୂଳକ ହୋଇଥିଲା ?
(A) ପ୍ରାଥମିକ ଶିକ୍ଷା
(B) ସାମରିକ ଶିକ୍ଷା
(C) ଇଂରାଜୀ ଭାଷା ଶିକ୍ଷା
(D) ଲାଟିନ୍ ଭାଷା ଶିକ୍ଷା
Answer:
(B) ସାମରିକ ଶିକ୍ଷା
Question 7.
ଇଟାଲୀର ନିମ୍ନୋକ୍ତ କେଉଁଠାରେ ମୁସୋଲିନୀ ଜନ୍ମ ହୋଇଥିଲେ ?
(A) ସିସିଲି
(B) ରୋମ୍
(C) ରୋମାନ
(D) ଜୁରିଚ୍
Answer:
(C) ରୋମାନ
Question 8.
କିଏ ‘ମୋର ସଂଘର୍ଷ’ ପୁସ୍ତକ ରଚନା କରିଥିଲେ ?
(A) ରୁଜୁଭେଲଟ୍
(B) କାଂଶିଟନ୍
(C) ଆବ୍ରାହମ୍ ଲିଙ୍କନ୍
(D) ହିଟ୍ର୍
Answer:
(D) ହିଟ୍ର୍
![]()
Question 9.
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ ନିମ୍ନୋକ୍ତ କେଉଁ ଆଦର୍ଶବାଦ ଇଟାଲୀରେ ପ୍ରସାରଲାଭ କରିଥିଲା ?
(A) ନାଜିବାଦ
(B) ଫାସୀବାଦ
(C) ସାମ୍ୟବାଦ
(D) ସମାଜବାଦ
Answer:
(B) ଫାସୀବାଦ
Question 10.
କେବେ ଜର୍ମାନୀରେ ନାଜିଦଳ ଗଠିତ ହୋଇଥିଲା ?
(A) ୧୯୨୦
(B) ୧୯୨୧
(C) ୧୯୨୨
(D) ୧୯୨୪
Answer:
(B) ୧୯୨୧
Question 11.
ନିମ୍ନୋକ୍ତ କେଉଁ ସମ୍ରାଟଙ୍କ ପଳାୟନ ପରେ ଜର୍ମାନୀରେ ୱେମର୍ ସାଧାରଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
(A) ପ୍ରଥମ ଉଇଲିୟମ୍
(B) ତୃତୀୟ ଉଇଲିୟମ୍
(C) ଚତୁର୍ଥ ଉଇଲିୟମ୍
(D) ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍
Answer:
(D) ଦ୍ଵିତୀୟ ଉଇଲିୟମ୍
Question 12.
କେଉଁ ଦଳର ତାଲିମପ୍ରାପ୍ତ ସ୍ଵେଚ୍ଛାସେବକମାନଙ୍କୁ କଳାକୁର୍ତ୍ତା ବାହିନୀ କୁହାଯାଉଥିଲା ?
(A) ନାଜିବାଦୀ
(B) ଫାସୀବାଦୀ
(C) ସାମ୍ୟବାଦୀ
(D) ସମାଜବାଦୀ
Answer:
(B) ଫାସୀବାଦୀ
![]()
Question 13.
୧୮୮୩ ମସିହାରେ କେଉଁ ବିପ୍ଳବୀ ଜନ୍ମ ଗ୍ରହଣ କରିଥିଲେ ?
(A) ଲେନିନ୍
(B) ଜର୍ଜ ବାଂଶିଟନ୍
(C) ହିଟ୍ର୍
(D) ମୁସୋଲିନୀ
Answer:
(D) ମୁସୋଲିନୀ
Question 14.
କାଇଜର ଦ୍ବିତୀୟ ଉଇଲିୟମ୍ କେଉଁ ଦେଶର ଶାସକ ଥିଲେ ?
(A) ଫ୍ରାନ୍ସ
(B) ଇଟାଲୀ
(C) ତୁର୍କୀ
(D) ଜର୍ମାନୀ
Answer:
(D) ଜର୍ମାନୀ
Question 15.
ଉଗ୍ର ଜାତୀୟତାବାଦ କେଉଁ ଚିନ୍ତାଧାରାକୁ ସୂଚାଏ ?
(A) ସାମ୍ୟବାଦ
(B) ଫାସୀବାଦ
(C) ସମାଜବାଦ
(D) ସାମନ୍ତବାଦ
Answer:
(B) ଫାସୀବାଦ
Question 16.
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ପରେ କେଉଁ ଦେଶରେ ପ୍ରଥମେ
(A) ଫ୍ରାନ୍ସ
(B) ଇଂଲଣ୍ଡ
(C) ଇଟାଲୀ
(D) ରୁଷିଆ
Answer:
(C) ଇଟାଲୀ
Question 17.
କେଉଁ ଭାଷାରୁ ଫାସିସ୍ ଶବ୍ଦଟି ଆସିଛି ?
(A) ସଂସ୍କୃତ
(B) ଲାଟିନ୍
(C) ଇଂରାଜୀ
(D) ଜର୍ମାନୀ
Answer:
(B) ଲାଟିନ୍
![]()
Question 18.
କୁରାଢ଼ୀ ସହିତ କାଠିବିଡ଼ାକୁ କେଉଁଦଳ ନିଜର ଦଳୀୟ ସଙ୍କେତ ରୂପେ ବ୍ୟବହାର କରୁଥିଲା ?
(A) ସମାଜବାଦୀ ଦଳ
(B) କମ୍ୟୁନିଷ୍ଟ ଦଳ
(C) ଶ୍ରମିକ ଦଳ
(D) ଫାସୀବାଦୀ ଦଳ
Answer:
(D) ଫାସୀବାଦୀ ଦଳ
Question 19.
ପ୍ରଥମ ବିଶ୍ଵ ୟୁଦ୍ଧ ବେଳେ ମୁସୋଲିନୀ କି କାର୍ଯ୍ୟ କରିଥିଲେ ?
(A) ସୈନିକ
(B) ମେଜର
(C) ସେନାଧ୍ଯକ୍ଷ
(D) ଜାହାଜର କପ୍ତାନ୍
Answer:
(A) ସୈନିକ
Question 20.
ଇଟାଲୀରେ ସମାଜବାଦୀ ଓ ସାମ୍ୟବାଦୀ ଆଦର୍ଶରେ କେଉଁ ଦଳ ଆଗେଇ ଆସିଥିଲା ?
(A) ସାମ୍ୟବାଦୀ ଦଳ
(B) ଫାସୀବାଦୀ ଦଳ
(C) ଏକଚ୍ଛତ୍ରବାଦୀ ଦଳ
(D) ବଲ୍ସେଭିକ୍ ଦଳ
Answer:
(B) ଫାସୀବାଦୀ ଦଳ
Question 21.
ଫାସୀବାଦୀ ଦଳର ତାଲିମପ୍ରାପ୍ତ ସ୍ଵେଚ୍ଛାସେବକଙ୍କ ସଶସ୍ତ୍ର ବାହିନୀକୁ କ’ଣ କୁହାଗଲା ?
(A) ଲାଲକୁର୍ତ୍ତା ବାହିନୀ
(B) କଳାକୁର୍ତ୍ତା ବାହିନୀ
(C) ସବୁଜ ବାହିନୀ
(D) ସିଂହ ବାହିନୀ
Answer:
(B) କଳାକୁର୍ତ୍ତା ବାହିନୀ
![]()
Question 22.
ହିଟ୍ଲର୍ କେଉଁ ଦେଶରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ?
(A) ଅଷ୍ଟ୍ରିଆ
(B) ଜର୍ମାନୀ
(C) ୟୁଗୋସ୍ଲୋଭିଆ
(D) ଫ୍ରାନ୍ସ
Answer:
(A) ଅଷ୍ଟ୍ରିଆ