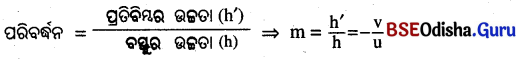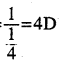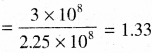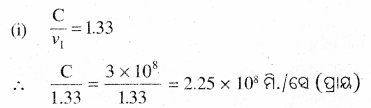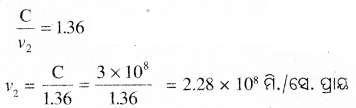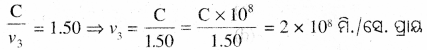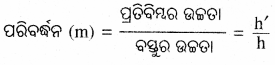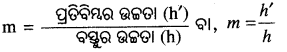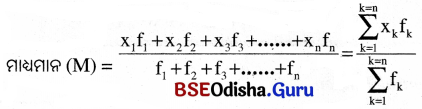Class 10

Odisha State Board BSE Odisha 10th Class Life Science Solutions Chapter 6 ଜନନ  Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Life Science Solutions Chapter 6 ଜନନ

Question 1.
ଉଭିଦରେ ପରିଲକ୍ଷିତ ହେଉଥିବା ଅଲିଙ୍ଗୀଜନ୍ମନ ବର୍ଣ୍ଣନ କର ।
ଭ –
ଉଭିଦରେ ପରିଲକ୍ଷିତ ହେଉଥ‌ିବା ଅଲିଙ୍ଗୀଜନନ ନିମ୍ନୋକ୍ତ ପ୍ରକାରର ହୋଇଥାଏ, ଯଥା – ବିଭାଜନ, କଳିକନ, ରେଣୁଭବନ ଓ ଅଙ୍ଗୀୟ ଜନନ ।

(i) ବିଭାଜନ :

• ବିଭକ୍ତ ହୋଇ ଦୁଇଟି ଅପତ୍ୟ ଜୀବ ସୃଷ୍ଟି ହୋଇଥା’ନ୍ତି । ଏହାକୁ ଦ୍ବିବିଭାଜନ କୁହାଯାଏ ।
• ଭାଗ ଗୋଟିଏ ଗୋଟିଏ ନୂତନ ଜୀବରେ ପରିଣତ ହୋଇଥାଏ । ଏହାକୁ ବହୁବିଭାଜନ କୁହାଯାଏ ।

(ii) କଳିକନ ବା କୋରକୋଦ୍‌ଗମ :

• ଏହି ପ୍ରକ୍ରିୟାରେ କେତେକ ବୀଜାଣୁ ଓ ଏକକୋଷୀ ଶୈବାଳର ନ୍ୟଷ୍ଟି ଓ କୋଷଜୀବକ ଦୁଇଟି ସମାନ ଭାଗରେ ବିଭକ୍ତ ହୋଇ ଦୁଇଟି ଅପତ୍ୟ ଜୀବ ସୃଷ୍ଟି ହୋଇଥା’ନ୍ତି । ଏହାକୁ ଦ୍ଵିବିଭାଜନ କୁହାଯାଏ ।
• କେତେକ ଶୈବାଳଜାତୀୟ ଉଦ୍ଭଦ (ସ୍ପାଇରୋଗାଇରା) କୋଷ ଦୁଇରୁ ଅଧିକ ଭାଗରେ ବିଭାଜିତ ହୋଇ ପ୍ରତ୍ୟେକ ଭାଗ ଗୋଟିଏ ଗୋଟିଏ ନୂତନ ଜୀବରେ ପରିଣତ ହୋଇଥାଏ । ଏହାକୁ ବହୁବିଭାଜନ କୁହାଯାଏ ।

(iii) ରେଣୁଭବନ :

• ଛତୁ ଓ ଫିମ୍ପି ଜାତୀୟ କବିକରେ ଅସଂଖ୍ୟ କଳାରଙ୍ଗର ରେଣୁ (Spore) ଦେଖାଯାଏ । ଏହି ରେଣୁଗୁଡ଼ିକ ନିର୍ଗତ ହୋଇ ଜଳ ବା ବାୟୁରେ ଭାସିବୁଲନ୍ତି ଓ ଅନୁକୂଳ ପରିବେଶ ମିଳିଲେ ଅଙ୍କୁରିତ ହୋଇ ନୂତନ ଉଭିଦ ସୃଷ୍ଟି କରନ୍ତି । ରେଣୁଦ୍ଵାରା ଏ ପ୍ରକାର ଜନନ ପ୍ରକ୍ରିୟାକୁ ରେଣୁଭବନ କୁହାଯାଏ ।
• ୟୁଲୋଥିକସ୍ ପରି ଶୈବାଳରେ 4, 8 ବା ଅଧିକ ଚଳରେଣୁ ସୃଷ୍ଟି ହୋଇଥାନ୍ତି ।
• ପେନିସିଲିୟମ ପରି କବକ ସାଧାରଣତଃ ଅଚଳରେଣୁଦ୍ୱାରା ବଂଶବୃଦ୍ଧି କରନ୍ତି ।
• ପାଇଥମ୍ ପରି କବକ ପରିବେଶ ଅନୁଯାୟୀ ଚଳରେଣୁ ବା ଅଚଳରେଣୁଦ୍ଵାରା ବଂଶବୃଦ୍ଧି କରିଥା’ନ୍ତି ।

Question 2.
ସପୁଷ୍ପକ ଉଦ୍ଭଦରେ ସମାୟନ ପ୍ରକ୍ରିୟାର ବିବରଣୀ ପ୍ରଦାନ କର । ଏହାର ବିଶେଷତ୍ଵ କ’ଣ ?
ଭ –

• ସପୁଷ୍ପକ ଉଦ୍ଭଦରେ ପରାଗରେଣୁ ଗର୍ଭଶୀର୍ଷରେ ପଡ଼ିବା ପରେ ତାହାର ବାହାର ଆବରଣଟି ଫାଟିଯାଏ । ଭିତର ଆବରଣଟି ଗୋଟିଏ ନଳୀ ଆକାରରେ ବାହାରେ ଓ ପରାଗ ଅଙ୍କୁରିତ ହୁଏ ।
• ଏହି ନଳୀ ଗର୍ଭଦଣ୍ଡ ମଧ୍ୟଦେଇ ଭ୍ରୂଣାଶୟ ଆଡ଼କୁ ବଢ଼େ । ଏହାକୁ ପରାଗନଳୀ କୁହାଯାଏ । ପରାଗ ଅଙ୍କୁରିତ ହେବା ସମୟରେ ଏହା ସମବିଭାଜନ ପ୍ରକ୍ରିୟାରେ ବିଭାଜିତ ହୋଇ ପ୍ରଥମେ ଅଙ୍ଗୀୟକୋଷ ଓ ଜନନ କୋଷ ସୃଷ୍ଟି କରେ । ଜନନ କୋଷ ପୁନର୍ବାର ଏହି ପ୍ରକ୍ରିୟାରେ ବିଭାଜିତ ହୋଇ ଦୁଇଟି ପୁଂଯୁଗ୍ମକ ସୃଷ୍ଟିକରେ ।
• ପରାଗନଳୀରେ କିଛି କୋଷରସ ସହିତ ଦୁଇଟି ପୁଂଯୁଗ୍ମକ ଓ ଗୋଟିଏ ନଳୀ ନ୍ୟଷ୍ଟି ଥାଏ । କ୍ରମେ ପରାଗ ନଳୀ ବୀଜରନ୍ଧ୍ର ବାଟଦେଇ ଡିମ୍ବାଶୟରେ ଥିବା ଭ୍ରୂଣାଶୟ ମଧ୍ୟରେ ପ୍ରବେଶ କରେ । ସେଠାରେ ପରାଗନଳୀର ଅଗ୍ରଭାଗଫାଟିଯିବା ଦ୍ଵାରା ପୁଂଯୁଗ୍ମକ ସ୍ତ୍ରୀ ଯୁଗ୍ମକ ବା ଡିମ୍ବକୋଷ ସହିତ ମିଳିତ ହୋଇ ଯୁଗ୍ମକ ଗଠନ କରେ । ଏଥୁରୁ ଭୃଣର ଉତ୍ପତ୍ତି ହୁଏ ।
• ଅନ୍ୟ ପୁଂଯୁଗ୍ମକଟି, ଦ୍ବିତୀୟକ ନ୍ୟଷ୍ଟି ସହିତ ମିଳିତ ହୋଇ ଭୃଣପୋଷ ନ୍ୟଷ୍ଟି ଗଠନ କରେ । ଭ୍ରୂଣପୋଷ ନ୍ୟଷ୍ଟିରୁ ଭ୍ରୂଣପୋଷ ଜାତ ହୁଏ ଏବଂ ଏହା ବର୍ଦ୍ଧିଷ୍ଣୁ ଭୃଣକୁ ପୋଷଣ ଯୋଗାଇଥାଏ । ପରାଗନଳୀରୁ ଦୁଇଟିଯାକ ପୁଂଯୁଗ୍ମକ ଭୂଣାଶୟ ମଧ୍ୟରେ ପ୍ରବେଶ କଲାପରେ ନଳୀ ନ୍ୟଷ୍ଟିଟି ପରାଗନଳୀ ଭିତରେ ନଷ୍ଟ ହୋଇଯାଏ ।

(v) ସପୁଷ୍ପକ ଉଦ୍ଭଦରେ ସମାୟନର ବିଶେଷତ୍ଵ :

• ପୁଂଯୁଗ୍ମକ ଓ ସ୍ତ୍ରୀ ଯୁଗ୍ମକର ମିଳନକୁ ସମାୟନ କୁହାଯାଏ । ପ୍ରକୃତରେ ସପୁଷ୍ପକ ଆବୃତବୀଜୀ ଉଦ୍ଭଦରେ ଦୁଇଟି ସମାୟନ କ୍ରିୟା ଦେଖିବାକୁ ମିଳେ । ପ୍ରଥମଟି ହେଲା, ଗୋଟିଏ ପୁଂଯୁଗ୍ମକ ସହିତ ଡିମ୍ବାଣୁ ବା ଡିମ୍ବକୋଷର ସମାୟନ ଓ ଅନ୍ୟଟି ହେଲା ଦ୍ବିତୀୟକ ନ୍ୟଷ୍ଟି ସହିତ ଦ୍ଵିତୀୟ ପୁଂଯୁଗ୍ଧକର ମିଳନ ।
• ପ୍ରଥମ ପ୍ରକ୍ରିୟାରେ ଯୁଗ୍ଧକ ସୃଷ୍ଟି ହେଉଥ‌ିବାବେଳେ ଦ୍ୱିତୀୟ ପ୍ରକ୍ରିୟାରେ ଭୃଣପୋଷ ନ୍ୟଷ୍ଟି ସୃଷ୍ଟି ହୁଏ । ଯୁଗ୍ମଜର କ୍ରୋମୋଜୋମ୍ ବା ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ଦ୍ବିଗୁଣିତ (2n) ହୋଇଥିବା ବେଳେ ଭୃଣପୋଷର ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ସାଧାରଣତଃ ତ୍ରିଗୁଣିତ (3n) ହୋଇଥାଏ । ସପୁଷ୍ପକ ଉଦ୍ଭଦର ଏହି ପ୍ରକ୍ରିୟାକୁ ଦ୍ବିସମାୟନ କୁହାଯାଏ ।

Question 3.
ଏମିବାର ବହୁ ବିଭାଜନ ବର୍ଣ୍ଣନା କର ।
ଭ –
(i) ଖରାଦିନେ ଏମିବା ରହୁଥ‌ିବା ପୋଖରୀ ବା ଗାଡ଼ିଆର ପାଣି ଶୁଖୁଲେ ବା ଅତ୍ୟଧ୍ଵ ଥଣ୍ଡା ଯୋଗୁଁ ପାଣି ବରଫ ହୋଇଗଲେ, ଏମିବା କୂଟପାଦଗୁଡ଼ିକୁ ପ୍ରତ୍ୟାହାର କରି ନିଜ ଶରୀର ଚାରିପଟେ ତିନିସ୍ତର ବିଶିଷ୍ଟ ଏକ କଠିନ ଆବରଣ ବା କୋଷିକା ତିଆରି କରି ରହେ ।

(ii) ଏହି ସମୟରେ ତା’ର ଚୟାପଚୟ କ୍ରିୟା ହ୍ରାସ ପାଏ । ବାରମ୍ବାର ନ୍ୟଷ୍ଟି ବିଭାଜନଦ୍ୱାରା ଏମିବା ଶରୀରରେ 500-600ଟି ଛୋଟ ନ୍ୟଷ୍ଟି ତିଆରି ହୁଏ ।
(iii) ପ୍ରତ୍ୟେକ ନ୍ୟଷ୍ଟି କିଛି ପରିମାଣର କୋଷଜୀବକଦ୍ବାରା ଆବୃତ ହୋଇ ରହେ । ଏହିପରି ଭାବେ ସୃଷ୍ଟ ଅପତ୍ୟଗୁଡ଼ିକୁ ‘କୁନି ଏମିବା’ (ଏମିବ୍ୟୁଲା) କୁହାଯାଏ ।
(iv) ବର୍ଷାଦିନର ଆଗମନରେ ପରିସ୍ଥିତି ଅନୁକୂଳ ହେଲେ ଏହି କଠିନ ଆବରଣ ଜଳ ସଂସ୍ପର୍ଶରେ ଆସି ଫାଟିଯାଏ । କୋଷିକା ଭିତରେ ଥ‌ିବା ଅପତ୍ୟ କୁନି ଏମିବାମାନେ ବାହାରକୁ ଚାଲିଆସନ୍ତି ।
(v) ପରେ ସେମାନଙ୍କର ଶରୀରରେ କୂଟପାଦ ସୃଷ୍ଟି ହୁଏ ଓ ସେମାନେ ପରିବେଶରୁ ଖାଦ୍ୟ ଗ୍ରହଣ କରି ସାଧାରଣ ଜୀବନ ଯାପନ କରନ୍ତି । ଏମିବାର ଏହି ପ୍ରକାର ବହୁ ବିଭାଜନ ଜନନ କ୍ରିୟାକୁ ସୋରୁଲେସନ ମଧ୍ୟ କୁହାଯାଏ ।

Question 4.
ହାଇଡ୍ରାର ଅଲିଙ୍ଗୀ ଜନନ କିପରି ହୋଇଥାଏ ଲେଖ ।
ଭ –

• ପ୍ରଚୁର ଭାବେ ମିଳେ, ସେତେବେଳେ ସୁସ୍ଥ ଏବଂ ବୟଃପ୍ରାପ୍ତ ହାଇଡ୍ରା କୋରକୋଦ୍‌ଗମ ଉପାୟରେ ବଂଶ ବିସ୍ତାର କରିଥାଏ ।
• ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାର କୋଷ ଏକାଠି ହେବାଦ୍ଵାରା ଏକ ଛୋଟ ଆବୁ ସୃଷ୍ଟିହୁଏ । ଏହି ଅଞ୍ଚଳକୁ କୋରକୋଦ୍‌ଗମ ଅଞ୍ଚଳ କୁହାଯାଏ ।
• ଏହି ଆବୁ ଧୀରେ ଧୀରେ ବଡ଼ ହୁଏ, ଏହା ମଧ୍ୟକୁ ହାଇଡ୍ରା ଶରୀରର ଗୁହାନ୍ତ ପ୍ରବେଶ କରେ । ଆବୁର ଅଗ୍ରଭାଗରେ ତାରା ଆକାରର ଏକ ପାଟି ଓ ପାଟିର ଚାରିପଟେ କର୍ଷିକା ସୃଷ୍ଟିହୁଏ । ଏବେ ଏହା ଏକ ଛୋଟ ହାଇଡ୍ରା ପରି ଦେଖାଯାଏ ।
• ଏହା ମାତୃ ହାଇଡ୍ରା ସହିତ ଲାଗି ରହିଥିଲେ ମଧ୍ୟ ନିଜ କର୍ଷିକା ସାହାଯ୍ୟରେ ଖାଦ୍ୟ ସଂଗ୍ରହ କରେ ।
• ଅପତ୍ୟ ହାଇଡ୍ରାର ସମ୍ପୂର୍ଣ୍ଣ ବୃଦ୍ଧି ପରେ ଏହାର ମୂଳଅଂଶ ସଂକୁଚିତ ହୁଏ । ଏହା ମାତୃ ହାଇଡ୍ରାଠାରୁ ବିଚ୍ଛିନ୍ନ ହୁଏ ଓ ପରିବେଶରୁ ଖାଦ୍ୟ ସଂଗ୍ରହକରି ସାଧାରଣ ଜୀବନଯାପନ କରେ । ଏହି ପ୍ରକ୍ରିୟା ପାଇଁ 48 ରୁ 6 ଘଣ୍ଟା ସମୟ ଲାଗିଥାଏ ।

Question 5.
ମାନବ ପୁରୁଷ ଜନନ ତନ୍ତ୍ରର ଏକ ବିବରଣୀ ଦିଅ ।
ଭ –
ମାନବ ପୁରୁଷ ଜନନ ତନ୍ତ୍ର :
ମାନବ ପୁରୁଷ ଜନନତନ୍ତ୍ରର ମୁଖ୍ୟତଃ ପାଞ୍ଚଟି ଅଂଶ ରହିଛି; ଯଥା –
(i) ଶୁକ୍ରମୁଣି,
(ii) ଶୁକ୍ରାଶୟ (ମୁଷ୍କ),
(iii) ଶୁକ୍ରବାହୀନଳୀ,
(iv) ମୂତ୍ର ମାର୍ଗ,
(v) ଶିଶୁ ଆଦିକୁ ନେଇ ଗଠିତ ।

(i) ଶୁକ୍ରମୁଣି :
ପୁରୁଷ ଶରୀରରେ ଥିବା ଦୁଇଟି ଶୁକ୍ରମୁଣି ମଧ୍ଯରେ ଦୁଇଟି ଶୁକ୍ରାଶୟ ଅଛି । ମାନବ ଶରୀରର ତାପମାତ୍ରା ଅଧ‌ିକ (37°C) ଶୁକ୍ରମୁଣିର ତାପମାତ୍ରା ଏହାଠାରୁ 2°C କମ୍, ଯାହା ଶୁକ୍ରାଣୁ ଉତ୍ପତ୍ତି ପାଇଁ ଅନୁକୂଳ ।

(ii) ଶୁକ୍ରାଶୟ :
(a) ପୁରୁଷ ଶରୀରରେ ଦୁଇଟି ଶୁକ୍ରାଶୟ ରହିଛି । ଏହା ନିଦା ଗୋଲାକାର ପିଣ୍ଡ ଅଟେ ।
(b) ବହୁ ଶୁକ୍ରଜନନ ନଳିକାକୁ ନେଇ ଏହା ଗଠିତ । ଶୁକ୍ଳ ଜନନ ନଳିକାରୁ ଶୁକ୍ରାଣୁ ଉତ୍ପତ୍ତି ହୋଇଥାଏ । ତା’ଛଡ଼ା ଏହି ନଳିକା ବାହାରେ ଓ ବିଭିନ୍ନ ନଳିକାର ଅନ୍ତରାଳରେ ଲେଡିଟ୍ କୋଷ ଦେଖାଯାଏ ।

(iii) ଶୁକ୍ରବାହୀନଳୀ :
ପ୍ରତ୍ୟେକ ଶୁକ୍ରାଶୟରୁ ଗୋଟିଏ ଶୁକ୍ରବାହୀନଳୀ ବାହାରି ଉଦର ଗହ୍ବର ମଧ୍ୟରେ ପ୍ରବେଶ କରେ । ଦୁଇପଟର ନଳୀ ମୂତ୍ରାଶୟର ମୂତ୍ରନଳୀ ସହିତ ମିଶି ମୂତ୍ରମାର୍ଗ ତିଆରି କରନ୍ତି ।

(iv) ମୂତ୍ରମାର୍ଗ :
ଉଭୟ ଶୁକ୍ରରସ ଓ ମୂତ୍ରମାର୍ଗ ଦେଇ ଶିଶୁର ଅଗ୍ରଭାଗରେ ଥ‌ିବା ରନ୍ଧ୍ର ମାଧ୍ୟମରେ ଶରୀର ବାହାରକୁ ବାହାରେ ।

Question 6.
ପରିବାର ନିୟୋଜନର ବିଭିନ୍ନ ପଦ୍ଧତି ବର୍ଣ୍ଣନ କର ।
ଭ –
କୌଣସି ଉପାୟରେ ଶୁକ୍ରାଣୁ ଓ ଡିମ୍ବାଣୁର ମିଳନକୁ ରୋକାଯାଇପାରିଲେ ଗର୍ଭଧାରଣକୁ ଏଡ଼ାଇ ଦିଆଯାଇପାରେ । ପଦ୍ଧତିକୁ ପରିବାର ନିୟୋଜନ କୁହାଯାଏ । ଭାରତ ସରକାର 1952 ମସିହାଠାରୁ ପରିବାର ନିୟୋଜନ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ କରିଛନ୍ତି ।

ବିଭିନ୍ନ ପ୍ରକାର ପରିବାର ନିୟୋଜନ ପଦ୍ଧତି : 
(ii) ପରିବାର ନିୟୋଜନ ପାଇଁ ବ୍ୟବହୃତ ବିଭିନ୍ନ ପ୍ରକାର ଉପାୟ ଦୁଇଭାଗରେ ବିଭକ୍ତ, ଯଥା –
(i) ସ୍ଥାୟୀ ପଦ୍ଧତି,
(ii) ଅସ୍ଥାୟୀ ପଦ୍ଧତି ।

(I) ସ୍ଥାୟୀ ପଦ୍ଧତି :

• ଏହା ଏକ ପ୍ରକାର ଅସ୍ତ୍ରୋପଚାର ପଦ୍ଧତି । ଏହି ପଦ୍ଧତିରେ ମହିଳା ବା ପୁରୁଷଙ୍କୁ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କରାଯାଏ । ଫଳରେ ଭବିଷ୍ୟତରେ ଆଉ ସନ୍ତାନ ଜନ୍ମହେବାର ସମ୍ଭାବନା ନଥାଏ ।
• ଭାରତ ସରକାରଙ୍କର ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମରେ ଚାରି ପ୍ରକାର ଅସ୍ଥାୟୀ ପଦ୍ଧତି ବ୍ୟବହାର କରାଯାଉଛି,

ଭାସେକ୍ଟୋମୀ :
ଭାସେକ୍ଟୋମୀଦ୍ଵାରା ପୁରୁଷର ଦୁଇଟିଯାକ ଶୁକ୍ରବାହୀ ନଳୀକୁ କାଟି ଅଲଗା କରି ବାନ୍ଧି ଦିଆଯାଏ । ଫଳରେ ରେତ ଶୁକ୍ରାଣୁମୁକ୍ତ ଥାଏ । ଏବେ ବିନା ଛୁରୀ ଓ ବିନା ସିଲାଇରେ 10 ରୁ 15 ମିନିଟ୍ ସମୟରେ ଭାସେକ୍ଟୋମୀ

ଟ୍ୟୁବେକ୍ଟୋମୀ : ସ୍ତ୍ରୀ ଶରୀରର ଦୁଇଟିଯାକ ଡିମ୍ବବାହୀନଳୀକୁ କାଟି ବାନ୍ଧି ଦିଆଯାଏ । ଫଳରେ ଡିମ୍ବାଣୁ ଏବଂ ଶୁକ୍ରାଣୁର ମିଳନ ଆଉ ସମ୍ଭବ ହୁଏ ନାହିଁ ।

(II) ଅସ୍ଥାୟୀ ପଦ୍ଧତି :

• ଭାରତ ସରକାରଙ୍କର ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମରେ ଚାରି ପ୍ରକାର ଅସ୍ଥାୟୀ ପଦ୍ଧତି ବ୍ୟବହାର କରାଯାଉଛି, ଯଥା –
  • ପ୍ରତିବନ୍ଧକ ପଦ୍ଧତି (ନିରୋଧ),
  • ହରମୋନ୍ ପଦ୍ଧତି (ଗର୍ଭନିରୋଧକ ବଟିକା),
  • ଅନ୍ତଃ ଗର୍ଭାଶୟ ପଦ୍ଧତି (କପର-ଟି) ଓ
  • ପ୍ରାକୃତିକ ପଦ୍ଧତି ।

Question 7.
ସମବିଭାଜନ (ସୂତ୍ରାୟନ)ର ଏକ ବିବରଣୀ ଦିଅ ।
ଉ-
ସମବିଭାଜନ :
ଜୀବକୋଷର ସମବିଭାଜନ (ସୂତ୍ରାୟନ) ସାଧାରଣତଃ ଦୁଇଟି ପର୍ଯ୍ୟାୟରେ ହୋଇଥାଏ । ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ ନ୍ୟଷ୍ଟିର ବିଭାଜନ ହୁଏ । ଏହାକୁ ନ୍ୟଷ୍ଟି ବିଭାଜନ କୁହାଯାଏ । ପରବର୍ତ୍ତୀ ଅବସ୍ଥାରେ କୋଷଜୀବକର ବିଭାଜନ ହେବାଫଳରେ ବିଭାଜନ ପ୍ରକ୍ରିୟା ସମ୍ପୂର୍ଣ୍ଣ ହୋଇ ଦୁଇଟି ଅପତ୍ୟ କୋଷ ସୃଷ୍ଟି ହୋଇଥାଏ । ଏହା ଏକ ଜଟିଳ ପ୍ରକ୍ରିୟା ଏବଂ ଏହାକୁ ଚାରୋଟି ଅବସ୍ଥାରେ ବିଭକ୍ତ କରାଯାଇଛି, ଯଥା – ଆଦ୍ୟାବସ୍ଥା, ମଧ୍ୟାବସ୍ଥା, ଉତ୍ତରାବସ୍ଥା ଓ ଅନ୍ତିମାବସ୍ଥା ।

(କ) ଆଦ୍ୟାବସ୍ଥା :

• ଆଦ୍ୟାବସ୍ଥାର ଆରମ୍ଭରେ କ୍ରୋମାଟିକ୍ ଜାଲିକା ଦେଖାଯାଏ ।
• ଜାଲିକା କ୍ରମେ ସୁସ୍ପଷ୍ଟ ସ୍ଥୁଳ ରୂପ ଧାରଣ କରି ପରିଶେଷରେ କେତୋଟି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ଗୁଣସୂତ୍ର ଭାବେ ଦୃଶ୍ୟମାନ ହୁଏ ।
• ଆଦ୍ୟାବସ୍ଥାର ଶେଷବେଳକୁ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ଅନୁଲମ୍ବଭାବେ ବିଭାଜିତ ହୋଇଥ‌ିବାର ଦେଖାଯାଏ, କିନ୍ତୁ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରଠାରେ ଲାଗି ରହିଥାଏ ।
• କ୍ରମେ ନିନ୍ୟଷ୍ଟି ଓ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ଅଦୃଶ୍ୟ ହୋଇଯାଏ ଓ କୋଷରେ ଥ‌ିବା ସେଣ୍ଡ୍ରୋଜୋମ୍ ଦୁଇଭାଗରେ ବିଭକ୍ତ ହୋଇ ଦୁଇ ବିପରୀତ ମେରୁ ଆଡ଼କୁ ଗତି କରନ୍ତି ।
• କୋଷର ଦୁଇ ମେରୁ ଅଞ୍ଚଳରେ ତର୍କୁତନ୍ତୁ ଗଠନ ପ୍ରକ୍ରିୟା ଆରମ୍ଭ ହୁଏ ।

(ଖ) ମଧ୍ୟାବସ୍ଥା :

(ii) ମେରୁସ୍ଥିତ ତର୍କୁତନ୍ତୁ କ୍ରମଶଃ ବର୍ଦ୍ଧିତ ହୋଇ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରସହ ସଂଯୁକ୍ତ ହୁଅନ୍ତି ।

(ଗ) ଉତ୍ତରାବସ୍ଥା :

• ଉତ୍ତରାବସ୍ଥାରେ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ର ବିଭାଜିତ ହୁଏ ।
• ତର୍କୁତନ୍ତୁ ସଙ୍କୁଚିତ ହେବାଫଳରେ ଗୁଣସୂତ୍ରର ପ୍ରତ୍ୟେକ ଏକକ ସୂତ୍ର ଦୁଇ ବିପରୀତ୍‌ ମେରୁ ଆଡ଼କୁ ଗତି କରନ୍ତି ।
• ଏହି ସମୟରେ ପ୍ରତ୍ୟେକ ଏକକ ସୂତ୍ର କୋଣାକାର ବା ‘V’ ଆକାର ଧାରଣ କରନ୍ତି ।

(ଘ) ଅନ୍ତଃମାବସ୍ଥା :

• ଅନ୍ତିମାବସ୍ଥାରେ ଅପତ୍ୟ ଗୁଣସୂତ୍ରଗୁଡ଼ିକ କୋଷର ଦୁଇ ମେରୁରେ ଜମା ହୁଅନ୍ତି ।
• କ୍ରମଶଃ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ରପୁଞ୍ଜର ଚତୁର୍ଦ୍ଦିଗରେ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ସୃଷ୍ଟି ହୁଏ ।
• ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ସୂକ୍ଷ୍ମ ଅସ୍ପଷ୍ଟ ହେବା ଆରମ୍ଭ ହେବା ସହ ନିନ୍ୟଷ୍ଟି ମଧ୍ୟ ସୃଷ୍ଟି ହୁଏ ।

କୋଷଜୀବକ ବିଭାଜନ :

• ଉଦ୍ଭିଦ ମାତୃକୋଷର ମଧ୍ୟଭାଗରେ ଏକ କୋଷପଟ୍ଟିକା ଦେଖାଯାଏ । କ୍ରମେ ଏହ ସୁସ୍ପଷ୍ଟ ହୋଇ ମାତୃକୋଷର କୋଷଜୀବକ ଦୁଇଭାଗରେ ବିଭକ୍ତ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ମାତୃକୋଷଟି ଦୁଇଟି ସମରୂପୀ ଅପତ୍ୟ କୋଷରେ ପରିଣତ ହୋଇଥାଏ ।
• ପ୍ରାଣୀ ମାତୃକୋଷରେ କୋଷପଟ୍ଟିକା ତିଆରି ହୁଏନାହିଁ; କେବଳ କୋଷଜୀବକର ସଙ୍କୋଚନ ହୋଇ ଦୁଇଟି ଅପତ୍ୟ କୋଷ ତିଆରି ହୋଇଥାଏ । ।

Question 8.
ଅର୍ଥବିଭାଜନ (ଅର୍ଦ୍ଧାୟନ)ର ପ୍ରଥମ ବିଭାଜନ ବର୍ଣ୍ଣନା କର ।
ଭ –
ଅର୍ଥବିଭାଜନ :
ଅର୍ଥବିଭାଜନଦ୍ୱାରା ଗୋଟିଏ ମାତୃକୋଷରୁ ଚାରୋଟି ଅପତ୍ୟ କୋଷ ସୃଷ୍ଟି ହୁଏ । ପ୍ରତ୍ୟେକ ଅପତ୍ୟକୋଷ ମାତୃକୋଷ ତୁଳନାରେ ଅର୍ଦ୍ଧେକ ସଂଖ୍ୟକ ଗୁଣସୂତ୍ର ବହନ କରେ । ଏହି ପ୍ରକାର ବିଭାଜନକୁ ନୂନକ ବିଭାଜନ କୁହାଯାଏ । ଏହା ଯୁଗ୍ମକ ସୃଷ୍ଟି ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଅଟେ । ଅର୍ଥବିଭାଜନ ଦୁଇଟି ପର୍ଯ୍ୟାୟରେ ସମ୍ପାଦିତ ହୁଏ । ପ୍ରଥମ ବିଭାଜନରେ କୋଷର ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ଅର୍ଦ୍ଧେକ ସଂଖ୍ୟକ ହୋଇଯାଏ ଏବଂ ଦ୍ଵିତୀୟ ବିଭାଜନରେ ନୂତନ ଭାବେ ଗଠିତ କୋଷଗୁଡ଼ିକର ସମବିଭାଜନ ହୁଏ ।

• ଯୁଗ୍ମଜ ଜନନଦ୍ୱାରା ଶୁକ୍ରାଶୟରେ ଶୁକ୍ରାଣୁ ଓ ଡିମ୍ବାଶୟରେ ଡିମ୍ବାଣୁ ସୃଷ୍ଟି ହୋଇଥାଏ । ଶୁକ୍ରାଣୁ ସୃଷ୍ଟି ହେବା ପ୍ରକ୍ରିୟାକୁ ଶୁକ୍ରାଣୁ ଜନନ ଓ ଡିମ୍ବାଣୁ ସୃଷ୍ଟି ହେବା ପ୍ରକ୍ରିୟାକୁ ଡିମ୍ବାଣୁ ଜନନ କୁହାଯାଏ ।
• ଏହି ଜନନର ପ୍ରାବସ୍ଥାଗୁଡ଼ିକ ହେଲା – ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା, ବୃଦ୍ଧି ପ୍ରାବସ୍ଥା ଓ ପରିପକ୍ବନ ପ୍ରାବସ୍ଥା ।
• ଶୁକ୍ରାଣୁ ଜନନର ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥାରେ ‘ମୂଳ ଶୁକ୍ରାଣୁ କୋଷ’’ ଓ ଡିମ୍ବାଣୁ ଜନନରେ ‘ମୂଳ ଡିମ୍ବାଣୁ କୋଷ’’ ଉତ୍ପନ୍ନ ହୁଏ ।
• ବୃଦ୍ଧି ପ୍ରାବସ୍ଥାରେ ମୂଳ ଶୁକ୍ରାଣୁ କୋଷ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷ ଓ ମୂଳ ଡିମ୍ବାଣୁ କୋଷ ବୃଦ୍ଧିପ୍ରାପ୍ତ ହୋଇ ପ୍ରାଥମିକ ଡିମ୍ବାଣୁ କୋଷରେ ପରିଣତ ହୁଏ ।
• ପରିପକ୍ବନ ପ୍ରାବସ୍ଥାରେ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷରୁ ପ୍ରାକ୍ ଶୁକ୍ରାଣୁ କୋଷ ଓ ଶେଷରେ ଶୁକ୍ରାଣୁ ତିଆରି ହୋଇଥାଏ । ସେହିପରି ଗୋଟିଏ ପ୍ରାଥମିକ ଡିମ୍ବାଣୁ କୋଷରୁ ଗୋଟିଏ ଡିମ୍ବାଣୁ ଓ ତିନୋଟି ପୋଲାର ବଡ଼ି ତିଆରି ହୋଇଥାଏ । ପ୍ରଥମ ବିଭାଜନ : ସମବିଭାଜନ ପରି ଏହି ବିଭାଜନକୁ ମଧ୍ଯ ଚାରୋଟି ଅବସ୍ଥାରେ ଅଧ୍ୟୟନ କରାଯାଇପାରେ;

ଯଥା –
(କ) ଆଦ୍ୟାବସ୍ଥା- I
(ଖ) ମାଧ୍ୟାବସ୍ଥା-I
(ଗ) ଉତ୍ତରାବସ୍ଥା -. I ଓ
(ଘ) ଅନ୍ତମାବସ୍ଥା – I

(କ) ଆଦ୍ୟାବସ୍ଥା – I :
ଏହି ଅବସ୍ଥାନଟି ଅପେକ୍ଷାକୃତ ଅଧ୍ବକ ଦୀର୍ଘ ଓ ଜଟିଳ ଅଟେ । ଏହି ଅବସ୍ଥାର ପାଞ୍ଚୋଟି ଉପାବସ୍ଥା ଥାଏ । ସେଗୁଡ଼ିକ ହେଲା – ଲେପ୍ରୋଟିନ୍, ଜାଇଗୋଟିନ୍, ପାକିଟିନ୍, ଡିପ୍ଲୋଟିନ୍ ଏବଂ ଡାଇଆକାଇନେସିସ୍ ।

ଲେପ୍‌ଗୋଟିନ୍ :
1. ହୋଇଥାଏ । ଏହି ଅବସ୍ଥାରେ ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ଯଦିଓ ମାତ୍ର ତାହା ଏକକ ରୂପେ ଦେଖାଯାଆନ୍ତି ।

ଜାଇଗୋଟିନ୍ :
1. ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ପରସ୍ପର ଆଡ଼କୁ ଆକୃଷ୍ଟ ହୁଅନ୍ତି ଓ ଲମ୍ବ ଭାବରେ ଯୋଡ଼ା ଯୋଡ଼ା ହୋଇ ଲାଗି ରହନ୍ତି । ଏହି ଅବସ୍ଥାକୁ ଆପୁଞ୍ଜନ କୁହାଯାଏ ।
2. ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ଯୁଗଳ ବା ଯୋଡ଼ିକୁ ଯୁଗଳ ଗୁଣସୂତ୍ର କୁହାଯାଏ ।

ପାକିଟିନ୍ :
ପାକିଟିନ୍‌ରେ ଗୁଣସୂତ୍ର ସ୍ଥୂଳ ଏବଂ କ୍ଷୁଦ୍ରାକାର ହୁଏ । ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ଲମ୍ବଭାବରେ ଦୁଇଟି ଏକକସୂତ୍ରର ହୋଇଥିବାରୁ ପ୍ରତ୍ୟେକ ଯୁଗଳ ଗୁଣସୂତ୍ର ଗୋଟିଏ ଲେଖାଏଁ ଚତୁଷ୍କ ବା ଚତୁଃଏକକ ସୂତ୍ରରେ ପରିଣତ ହୁଏ ।

ଡିପ୍ରୋଟିନ୍ :
1. ସହିତ ଲାଗିରହି ଅନ୍ୟ ଅଂଶରେ ପୃଥକ୍ ହୋଇଥାନ୍ତି । ହୁଏ । ସେମାନେ କେବଳ କେତେକ ବିନ୍ଦୁରେ ପରସ୍ପର ମଧ୍ୟରେ ଅଂଶ ବିନିମୟ ଦ୍ବାରା ଜିନ୍ ଆଦାନପ୍ରଦାନ ଏହି ମିଳନସ୍ଥଳକୁ କାଏଜ୍‌ମା କୁହାଯାଏ ।
2. ଯୁଗଳ ଗୁଣସୂତ୍ର ଗୁଡ଼ିକର ଏହି ମିଳନସ୍ଥଳ ବା କରନ୍ତି । ଏହି ପ୍ରକ୍ରିୟାକୁ ପାରାନ୍ତରଣ କୁହାଯାଏ ।

ଡାଇଆକାଇନେସିସ୍ :
କିନ୍ତୁ ସ୍କୁଳ ଓ ବର୍ତ୍ତୁଳ ହେବାଦ୍ଵାରା ଅଧିକ ସ୍ପଷ୍ଟ ଦେଖାଯାଆନ୍ତି । ଏହି ଉପାବସ୍ଥାରେ ସେଗୁଡ଼ିକର ଆକୃତି ମୁଦ୍ରିକା ସଦୃଶ । ନିନ୍ୟଷ୍ଟି ଏବଂ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ଏହି ଅବସ୍ଥାରେ ଅଦୃଶ୍ୟ ହୋଇଥାଏ ।

(ଖ) ମଧ୍ୟାବସ୍ଥା – I (Metaphase) :
1.
2. ମେରୁସ୍ଥିତ ତର୍କୁତନ୍ତୁ କ୍ରମଶଃ ବର୍ଦ୍ଧିତ ହୋଇ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରସହ ସଂଯୁକ୍ତ ହୁଅନ୍ତି ।

(ଗ) ଆନାଫେଜ୍ | – I (Anaphase) :
1.
2. ଏକକ ସୂତ୍ର ଦୁଇ ବିପରୀତ ମେରୁ ଆଡ଼କୁ ଗତି କରନ୍ତି ।
3. ଏହି ସମୟରେ ପ୍ରତ୍ୟେକ ଏକକ ସୂତ୍ର କୋଣାକାର ବା ‘V’ ଆକାର ଧାରଣ କରନ୍ତି ।

(ଘ) ଟେଲୋଫେଜ୍ | – I (Telophase):
1.
2. କ୍ରମଶଃ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ରପୁଞ୍ଜର ଚତୁର୍ଦ୍ଦିଗରେ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ସୃଷ୍ଟିହୁଏ ।
3. ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ସୂକ୍ଷ୍ମ ଅସ୍ପଷ୍ଟ ହେବା ଆରମ୍ଭ ହେବା ସହ ନିନ୍ୟଷ୍ଟି ମଧ୍ୟ ସୃଷ୍ଟିହୁଏ ।

Question 9.
ସମବିଭାଜନ ଓ ଅର୍ଥବିଭାଜନ ତୁଳନା କର ।
ଉ-
ସମବିଭାଜନ ଓ ଅର୍ଥବିଭାଜନ ମଧ୍ଯରେ ତୁଳନା :

ସମବିଭାଜନ (ମାଇଟୋସିସ୍)	ଅର୍ଥବିଭାଜନ (ମେଓସିସ୍)
1. ଏହା କାୟିକ କୋଷ, ଆଦି ଜାୟକ କୋଷ ଏବଂ ପରାଗ ମାତୃ କୋଷ ତଥା ମେଗାସ୍କୋର ମାତୃ କୋଷରେ ହୋଇଥାଏ ।	1.ଏହା ଯୁଗ୍ମଜ ସୃଷ୍ଟିପାଇଁ ଉଦ୍ଦିଷ୍ଟ । ତେଣୁ ଏହା କେବଳ ଜନନ କୋଷରେ ଯୁଗ୍ମକ ଜନନ ପ୍ରକ୍ରିୟାରେ ଶେଷ ପର୍ଯ୍ୟାୟରେ ହୋଇଥାଏ ।
2. ଏଥିରେ ମାତୃକୋଷ ଏବଂ ଅପତ୍ୟ କୋଷରେ ଥ‌ିବା ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ସମାନ ରହେ ।	2. ଏହି ବିଭାଜନ ପରେ ଅପତ୍ୟ କୋଷରେ ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ମାତୃ କୋଷରେ ଥିବା ଗୁଣସୂତ୍ର ସଂଖ୍ୟାର ଅର୍ଦ୍ଧେକ ହୋଇଯାଏ ।
3. ଏହି ବିଭାଜନ ବେଳେ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ସ୍ଵାଧୀନ ଭାବରେ ଅର୍ଥାତ୍ ଅନ୍ୟଉପରେ ନିର୍ଭର ନ କରି ବିଭାଜିତ ହୋଇଥାନ୍ତି । ଏଥ‌ିରେ ଆପୁଞ୍ଜନ କିମ୍ବା ଅଂଶ ବିନିମୟ ହୁଏନାହିଁ ।	3. ଏହି ବିଭାଜନର ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ ସଦୃଶ ଗୁଣସୂତ୍ର ଯୋଡ଼ା ଯୋଡ଼ା ହୋଇ ଲାଗି ରହନ୍ତି । ସେମାନଙ୍କ ମଧ୍ୟରେ ଆପୁଞ୍ଜନ ଓ ଅଂଶ ବିନିମୟ ହୁଏ ।
4. ମାଇଟୋସିସ୍‌ର ଉତ୍ତରାବସ୍ଥାରେ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରର ବିଭାଜନ ହେବା ଫଳରେ କ୍ରୋମାଟିଡ୍ ମେରୁଆଡ଼କୁ ଯାଇଥାଏ ।	4. ମେଓସିସ୍ (ପ୍ରଥମ ପର୍ଯ୍ୟାୟ)ର ଉତ୍ତରାବସ୍ଥାରେ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରର ବିଭାଜନ ହୁଏନାହିଁ । ଫଳରେ ସମ୍ପୂର୍ଣ୍ଣ କ୍ରୋମୋଜୋମ୍ ମେରୁଆଡ଼କୁ ଯାଇଥାଏ ।
5. ଏହି ବିଭାଜନରେ ଗୋଟିଏ ମାତୃକୋଷରୁ 2ଟି ଅପତ୍ୟ କୋଷ ଜାତ ହୁଏ ।	5. ଏହି ବିଭାଜନ ଶେଷରେ ଗୋଟିଏ ଆଦି ଜାୟକ କୋଷରୁ 4ଟି ଅପତ୍ୟ କୋଷ ଜାତ ହୁଏ ।

Question 10.
ସଂକ୍ଷେପରେ ଉତ୍ତର ଦିଅ ।
(କ) ଏଚ.ଆଇ.ଭି.ର ଦୂରାନାମ ଓ ବିଶେଷତ୍ଵ ଲେଖ ।
ଭ –

• ଏଚ୍. ଆଇ. ଭି. : ଏହାର ପୂରାନାମ (Human Immunodeficiency Virus -HIV) । ଏଡ଼ସ୍‌ର ଖଳନାୟକ ଏକ ଭୂତାଣୁ ଅଟେ ଯାହାର ନାମ HIV I
• ବିଶେଷତ୍ଵ : ଅନ୍ୟ ଭୂତାଣୁ ପରି ଏହାର ବିଶେଷତ୍ଵ ହେଉଛି ଏହାର ଶରୀର ଗଠନ ଅତି ସରଳ । ମୁଖ୍ୟତଃ ପୁଷ୍ଟିସାରରେ ଗଠିତ ଖୋଳପା ମଧ୍ୟରେ ଭୂତାଣୁର ଆନୁବଂଶିକ ପଦାର୍ଥ ଥାଏ । ଏହା ହେଉଛି RNA I RNA ଥ‌ିବା ଭୂତାଣୁମାନଙ୍କୁ ପଶ୍ଚଭୂତାଣୁ ବା ରେଟ୍ରୋଭାଇରସ୍ କୁହାଯାଏ ।
• ସମାୟନ ବା ନିଷେକ ନ ହୋଇ ଡିମ୍ବାଣୁର ବୃଦ୍ଧିଘଟି ଫଳସୃଷ୍ଟି ହେଲେ ତାହାକୁ ଅସମାୟିତ ଜନନ ବା ଅନିଷେକ ଜନନ କୁହାଯାଏ ।
• କେତେକ ଅପୁଷ୍ପକ ଉଦ୍ଭିଦରେ ଏହା ପରିଲକ୍ଷିତ ହେବା ସହିତ ସପୁଷ୍ପକ ଉଦ୍ଭଦରେ ଏ ପ୍ରକାର ଜନନ ଦେଖାଯାଏ ।
• ଏହି ପଦ୍ଧତିରେ ଜାତ ଫଳ ମଞ୍ଜିଶୂନ୍ୟ ହୋଇଥାଏ । ଏହି ଫଳକୁ ଅସମାୟିତ ଫଳ ବା ମଞ୍ଜିବିହୀନ ଫଳ କୁହାଯାଏ ।

(ଗ) ଯୁଗ୍ମକ ଜନନର ପ୍ରାବସ୍ଥାଗୁଡ଼ିକର ନାମ କ’ଣ ? ଏଥ‌ିରେ କି କି ମୁଖ୍ୟ ଘଟଣା ଘଟିଥାଏ ?
ଉ-
IMG

(i) ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା	(i) ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା
(ii) ବୃଦ୍ଧି ପ୍ରାବସ୍ଥା	(ii) ବୃଦ୍ଧି ପ୍ରାବସ୍ଥା
(iii) ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା	(iii) ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା

• ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା – ଆଦିଜାୟକ କୋଷରୁ ମୂଳ ଶୁକ୍ରାଣୁ କୋଷ ଓ ମୂଳ ଡିମ୍ବାଣୁ କୋଷ ସୃଷ୍ଟିହୁଏ ।
• ବୃଦ୍ଧି ପ୍ରାବସ୍ଥା – ମୂଳ ଶୁକ୍ରାଣୁ କୋଷରୁ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷ ଓ ମୂଳ ଡିମ୍ବାଣୁ କୋଷରୁ ପ୍ରାଥମିକ ଡିମ୍ବାଣୁ କୋଷ ସୃଷ୍ଟି ହୁଏ ।
• ପରିପକ୍ବନ ପ୍ରାବସ୍ଥା – ଏହି ଅବସ୍ଥାରେ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷରୁ 4ଟି ଶୁକ୍ରାଣୁର ସୃଷ୍ଟି ହୁଏ ଓ ପ୍ରାଥମିକ ଡିମ୍ବାଣୁ କୋଷରୁ ଗୋଟିଏ ଡିମ୍ବାଣୁ ଓ ତିନୋଟି ପୋଲାର ବଡ଼ି ତିଆରି ହୁଏ ।

(ଘ) ସ୍ପଞ୍ଜର ଅନ୍ତଃକୋରକୋଦ୍‌ଗମ ବର୍ଣ୍ଣନ କର ।

• ପ୍ରତିକୂଳ ପରିବେଶ ଓ ଖାଦ୍ୟପଦାର୍ଥର ଅଭାବ ଦେଖାଦେଲେ ସଞ୍ଜ ନିଜ ଶରୀର ଭିତରେ ଜମ୍ୟୁଲ୍ ତିଆରି କରେ ।
• ଏହି ପ୍ରକ୍ରିୟାର ପ୍ରାରମ୍ଭରେ ଏକ ସ୍ବତନ୍ତ୍ର ପ୍ରକାରର କେତେକ କୋଷ ଏକତ୍ରିତ ହୁଅନ୍ତି ।
• ଏମାନଙ୍କ ଚାରିପଟେ ଏକ କଠିନ ଆବରଣ ସୃଷ୍ଟି ହୋଇ ଏହା ଜେଡ୍ୟୁଲରେ ପରିଣତ ହୁଏ ।
• ମାଇକ୍ରୋଫାଇଲ୍ ନାମକ ଏକ ରନ୍ଧ୍ରଦ୍ଵାରା ଏହା ବାହାରକୁ ଖୋଲାଥାଏ ।
• ପରିବେଶ ଅନୂକୂଳ ହେଲେ ଜେମ୍ୟୁଲ୍ ଭିତରେ ଥିବା କୋଷଗୁଡ଼ିକ ମାଇକ୍ରୋପାଇଲ ବାଟଦେଇ ବାହାରକୁ ଆସି ନୂଆ ସ୍ପଞ୍ଜ ସୃଷ୍ଟି କରନ୍ତି ।

(ଡ) ଏମିବାର ବହୁବିଭାଜନ କିପରି ହୋଇଥାଏ ଲେଖ ।

• ଖରାଦିନେ ଏମିବା ରହୁଥିବା ପୋଖରୀ, ଗାଡ଼ିଆରୁ ପାଣି ଶୁଖୁଲେ ବା ଅତ୍ୟଧିକ ଥଣ୍ଡା ଯୋଗୁଁ ପାଣି ବରଫ ହୋଇଗଲେ, ଏମିବା କୂଟପାଦଗୁଡ଼ିକୁ ପ୍ରତ୍ୟାହାର କରି ନିଜ ଶରୀର ଚାରିପଟେ ତିନିସ୍ତର ବିଶିଷ୍ଟ ଏକ କଠିନ ଆବରଣ ବା କୋଷିକା ତିଆରି କରି ରହେ ।
• ଏହି ସମୟରେ ତା’ର ଚୟାପଚୟ କ୍ରିୟା ହ୍ରାସପାଏ । ବାରମ୍ବାର ନ୍ୟଷ୍ଟି ବିଭାଜନ ଦ୍ଵାରା ଏମିବା ଶରୀରରେ 500- 600ଟି ଛୋଟ ନ୍ୟଷ୍ଟି ତିଆରି ହୁଏ ।
• ପ୍ରତ୍ୟେକ ନ୍ୟଷ୍ଟି କିଛି ପରିମାଣର କୋଷଜୀବକ ଦ୍ବାରା ଆବୃତ୍ତ ହୋଇ ରହେ । ଏହିପରି ଭାବେ ସୃଷ୍ଟ ଅପତ୍ୟଗୁଡ଼ିକୁ ‘କୁନି ଏମିବା’ ବା ଏମିକ୍ୟୁଲା କୁହାଯାଏ I ବର୍ଷାଦିନର ଆଗମନରେ ପରିସ୍ଥିତି ଅନୁକୂଳ ହେଲେ ଏହି କଠିନ ଆବରଣ ଜଳ ସଂସ୍ପର୍ଶରେ ଆସି ଫାଟିଯାଏ । କୋଷିକା ଭିତରେ ଥ‌ିବା ଅପତ୍ୟ କୁନି ଏମିବାମାନେ ବାହାରକୁ
• ଏମିବାର ଏହି ପ୍ରକାର ବହୁ ବିଭାଜନ ଜନନ କ୍ରିୟାକୁ ସୋରୁଲେସନ ମଧ୍ୟ କୁହାଯାଏ ।

Question 11.
ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ ଲେଖ ।
(କ) ସମାୟନ,
(ଖ) ପରିବାର ନିୟୋଜନର ସ୍ଥାୟୀ ପଦ୍ଧତି,
(ଗ) ଗର୍ଭାଶୟ,
(ଘ) ଅଙ୍ଗବିକାଶ,
(ଙ) ଶୁକ୍ରମୁଣି ।
ଭ –
(କ) ସମାୟନ

• ଯେଉଁ ପ୍ରକ୍ରିୟାରେ ଗୋଟିଏ ପୁଂଯୁଗ୍ମକ, ସ୍ତ୍ରୀ ଯୁଗ୍ମକ ବା ଡିମ୍ବକୋଷ ସହିତ ମିଳିତ ହୋଇ ଯୁଗ୍ମକ ଗଠନ କରେ ତାହାକୁ ସମାୟନ କୁହାଯାଏ । ଏଥୁରୁ ଭୃଣର ଉତ୍ପତ୍ତି ହୋଇଥାଏ ।
• ସପୁଷ୍ପକ ଆବୃତ୍ତବୀଜୀ ଉଦ୍ଭଦରେ ଦୁଇଟି ସମାୟନ ଦେଖାଯାଏ । ଗୋଟିଏ ପୁଂଯୁଗ୍ମକ ସହିତ ଡିମ୍ବାଣୁ ବା ଡିମ୍ବକୋଷର ସମାୟନ ଓ ଅନ୍ୟଟି ଦ୍ଵିତୀୟକ ନ୍ୟଷ୍ଟି ସହିତ ଦ୍ଵିତୀୟ ପୁଂଯୁଗ୍ମକର ମିଳନ । ଦ୍ଵିତୀୟ ପ୍ରକ୍ରିୟାରେ ଭୃଣକୋଷ ନ୍ୟଷ୍ଟି ସୃଷ୍ଟି ହୁଏ । ସପୁଷ୍ପକ ଉଦ୍ଭଦରେ ଏହି ସମାୟନକୁ ଦ୍ଵିସମାୟନ କୁହାଯାଏ ।

(ଖ) ପରିବାର ନିୟୋଜନର ସ୍ଥାୟୀ ପଦ୍ଧତି,

• ଏହା ଏକ ପ୍ରକାର ଅସ୍ତ୍ରୋପଚାର ପଦ୍ଧତି । ଏହି ପଦ୍ଧତିରେ ମହିଳା ବା ପୁରୁଷଙ୍କୁ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କରାଯାଏ । ଫଳରେ ଭବିଷ୍ୟତରେ ଆଉ ସନ୍ତାନ ଜନ୍ମହେବାର ସମ୍ଭାବନା ନଥାଏ ।
• ପୁରୁଷ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାରକୁ ଭାସେକ୍ଟୋମୀ ଓ ମହିଳା ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାରକୁ ଟ୍ୟୁବେକ୍ଟୋମି କୁହାଯାଏ ।

(ଗ) ଗର୍ଭାଶୟ

• ଗର୍ଭାଶୟ ଏକ ଫମ୍ପା ଏବଂ ପେଶୀବହୁଳ ଅଙ୍ଗ । ଏହାର ଲମ୍ବ ପ୍ରାୟ 7.5 ସେ.ମି. ଏବଂ ଚଉଡ଼ା 5.0 ସେ.ମି. ।
• ଏହା ଉଦର ଗହ୍ଵର ନିମ୍ନଭାଗରେ ଠିକ୍ ମୂତ୍ରାଶୟର ପଛକୁ ରହିଛି ।
• ଗର୍ଭାଶୟର ଆଗପଟ ଚଉଡ଼ା ଓ ପଛପଟକୁ ଏହା ନଳିଆ । ଏହି ନଳିଆ ଅଂଶକୁ ଜରାୟୁ ଗ୍ରୀବା (Cervix) କୁହାଯାଏ । ଗର୍ଭାଶୟର ଗ୍ରୀବା ବାହାରକୁ ଉନ୍ମୁକ୍ତ ହୋଇଥାଏ ।

(ଘ) ଅଙ୍ଗବିକାଶ,

• ସମାୟନ ପରେ ପ୍ରାଣୀ ଶରୀରରେ ଯୁଗ୍ଧଜର ବାରମ୍ବାର ବିଭାଜନରୁ ବହୁକୋଷୀ ବ୍ଲାଷ୍ଟଲା ସୃଷ୍ଟି ହୁଏ । ପରେ ଏହା ତିନୋଟି ଜାୟକ ସ୍ତରବିଶିଷ୍ଟ ଗ୍ରାଷ୍ଟ୍ରଲାରେ ପରିଣତ ହୁଏ । ଏହି ତିନୋଟି ଜାୟକ ସ୍ତର ହେଉଛି – ଏକୋଡ଼ର୍ମ, ମେସୋଡ଼ର୍ମ ଓ ଏଣ୍ଡୋଡ଼ର୍ମ ।
• ଅଙ୍ଗ ବିକାଶ ଦ୍ଵାରା ତିନି ପ୍ରକାର ଜାୟକ ସ୍ତରରୁ ବିଭିନ୍ନ ପ୍ରକାର ଟିସୁ, ଅଙ୍ଗ ଓ ଅଙ୍ଗ ତନ୍ତ୍ର ତିଆରି ହୁଏ । ଅଙ୍ଗ ବିକାଶ ପରେ ଗର୍ଭାଶୟରେ ସୃଷ୍ଟି ହୋଇଥବା ପୂର୍ଣ୍ଣ ବିକଶିତ ଶିଶୁ ପ୍ରସବ ଦ୍ୱାରା ମାଆ ଶରୀର ବାହାରକୁ ଆସିଥାଏ ।

(ଙ) ଶୁକ୍ରମୁଣି ।

• ପୁରୁଷ ଶରୀରରେ ଥିବା ଦୁଇଟି ଶୁକ୍ରମୁଣି ମଧ୍ୟରେ ଦୁଇଟି ଶୁକ୍ରାଶୟ ଅଛି ।
• ମାନବ ଶରୀରର ତାପମାତ୍ରା ଅଧିକ (37°C) ଶୁକ୍ରମୁଣିର ତାପମାତ୍ରା ଏହାଠାରୁ 2°C କମ୍, ଯାହା ଶୁକ୍ରାଣୁ ଉତ୍ପତ୍ତି ପାଇଁ ଅନୁକୂଳ ।

Question 12.
ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(କ) କାଲସ୍ କାହାକୁ କୁହାଯାଏ ?
ଉ-
ଟିସୁ ପୋଷଣ ପଦ୍ଧତିରେ ଯେଉଁ ପ୍ରାରମ୍ଭିକ ଟିସୁସମୂହକୁ ସ୍ଵତନ୍ତ୍ର ରୂପେ ସଙ୍ଗଠିକ ପୋଷକ ମାଧମଦ୍ଵାରା ବଢ଼ାଇ ଗୋଟିଏ ଜୀବକୋଷରୁ ଅନେକ ଜୀବକୋଷ ସୃଷ୍ଟି କରାଯାଇଥାଏ, ସେଗୁଡ଼ିକୁ ସାମଗ୍ରିକ ଭାବେ କାଲ୍‌ କୁହାଯାଏ ।

(ଖ) ଡିମ୍ବାଶୟରୁ କେଉଁ ହରମୋନ୍ କ୍ଷରିତ ହୁଏ ?
ଉ-
ଉ- ଡିମ୍ବାଶୟରୁ ଇଷ୍ଟ୍ରୋଜେନ୍ ଓ ପ୍ରୋଜେଷ୍ଟିରନ୍ ନାମକ 2ଟି ହରମୋନ କ୍ଷରିତ ହୁଏ ।

(ଗ) ଅନୁକୂଳ ପରିବେଶରେ ଏମିବା କେଉଁ ପ୍ରକ୍ରିୟା ଦ୍ବାରା ଜନନ କରିଥାଏ ?
ଉ-
ଅନୁକୂଳ ପରିବେଶରେ ଏମିବା ଦ୍ଵିବିଭାଜନ ଓ ବହୁବିଭାଜନ ଦ୍ବାରା ଜନ କରିଥାଏ ।

(ଘ) କେଉଁ ପରିବେଶରେ ହାଇଡ୍ରା କେଉଁ ପ୍ରକ୍ରିୟା ଦ୍ବାରା ଜନନ କରିଥାଏ ?
ଉ-
ଅନୁକୂଳ ପରିବେଶରେ ଓ ପ୍ରଚୁରଖାଦ୍ୟ ପଦାର୍ଥ ମିଳୁଥିବା ବେଳେ ସୁସ୍ଥ ଏବଂ ବୟଃପ୍ରାପ୍ତ ହାଇଡ୍ରା କୋରକୋଦ୍‌ଗମ ଉପାୟରେ ଅଲିଙ୍ଗୀ ଜନନଦ୍ୱାରା ବଂଶବୃଦ୍ଧି କରିଥାଏ ।

(ଙ) ଶୁକ୍ରାଶୟର କେଉଁ କୋଷ ଟେଷ୍ଟୋଷ୍ଟିରନ୍ କ୍ଷରଣ କରେ ?
ଉ-
ଶୁକ୍ରାଶୟ ମଧ୍ୟରେ ଥିବା ଲେଡ଼ିଗ୍ କୋଷରୁ ପୁରୁଷ ହରମୋନ୍ ଟେଷ୍ଟାଷ୍ଟିରନ କ୍ଷରିତ ହୁଏ ।

(ଚ) ଏଡ଼୍ସ୍ ରୋଗ ଚିହ୍ନଟର 2ଟି ଉପାୟ ଲେଖ ।
ଉ –
(i) ଏଲିସା (ELISA Enzyme Linked Immuno Sorbent Assay) ଟେଷ୍ଟ ଦ୍ଵାରା ଏହି ରୋଗ ଚିହ୍ନଟ କରାଯାଇପାରେ । କିନ୍ତୁ ୱେଷ୍ଟର୍ଣ୍ଣ ବ୍ଲୁଟିଙ୍ଗ (Western Blotting) କୌଶଳ ଏଡ଼ସ୍‌ ଚିହ୍ନଟର ସବୁଠାରୁ ବିଶ୍ୱସନୀୟ ଉପାୟ ।

(ଛ) ଭୃଣବନ୍ଧର କାର୍ଯ୍ୟ କ’ଣ ?

• ଭ୍ରୂଣବନ୍ଧ ବା ପ୍ଲାସେଣ୍ଟା ଜରିଆରେ ଗର୍ଭାଶୟ ସହିତ ଭ୍ରୂଣ ଏକ ଜୈବିକ ସମ୍ବନ୍ଧ ସ୍ଥାପନ କରେ । ଭ୍ରୂଣ ଏବଂ
• ଭ୍ରୂଣବନ୍ଧ ଦେଇ ଭ୍ରୂଣ ମାଆ ଶରୀରରୁ ନାଭିରଜ୍ଜୁ ଦ୍ୱାରା ଖାଦ୍ୟ ଓ ଅମ୍ଳଜାନ ଗ୍ରହଣ କରେ । ସେହିପରି ଭ୍ରୂଣ ମଧ୍ୟରୁ ନିର୍ଗତ ବର୍ଜ୍ୟବସ୍ତୁ ପ୍ଲାସେଣ୍ଟା ବାଟଦେଇ ମାଆ ଶରୀରକୁ ଓ ପରେ ବାହାରକୁ ଆସେ ।

Question 13.
ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ ।
(କ) ଲେଡ଼ିଗ୍ କୋଷରୁ କେଉଁ ହର୍ମୋନ୍ କ୍ଷରିତ ହୁଏ ?
ଉ-
ଟେଷ୍ଟେଷ୍ଟେରନ୍

(ଖ) କେଉଁ ମସିହାରୁ ଭାରତରେ ପରିବାର ନିୟୋଜନ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ?
ଉ-
1952

(ଗ) ସାଧାରଣତଃ ସ୍ତ୍ରୀ ଜନନ ତନ୍ତ୍ରର କେଉଁ ସ୍ଥାନରେ ସମାୟନ ଘଟେ ?
ଉ- ହିମ୍ବବାହୀ ନଳୀ ମଧ୍ଯରେ

(ଘ) ଶୁକ୍ରାଣୁ କେଉଁଠାରେ ତିଆରି ହୁଏ ?
ଉ-

(ଙ) ଇଷ୍ଟ୍ରେ କେଉଁ ପ୍ରକାରର ଜନନ ଦେଖାଯାଏ ?
ଉ-

Question 14.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଭୂଣପୋଷର ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ………………… ଅଟେ ।
(ଖ) ସମସ୍ତ ପ୍ରକାର କୋଷ ସୃଷ୍ଟି କରିପାରୁଥିବା କୋଷକୁ ……………………… କୁହାଯାଏ ।
(ଗ) ଶୁକ୍ରମୁଣିର ତାପମାତ୍ରା ମାନବ ଶରୀରର ତାପମାତ୍ରାଠାରୁ ପ୍ରାୟ ………………….. ଡିଗ୍ରୀ କମ୍ ।\
(ଘ) ଇଷ୍ଟ ……………………… ଦ୍ଵାରା ବଂଶବିସ୍ତାର କରିଥାଏ ।
(ଙ) ଏଚ୍.ଆଇ.ଭି.ର ଆନୁବଂଶିକ ପଦାର୍ଥ …………………………. ଅଟେ ।
(ଚ) ଆରଏସ୍ଏ ଥିବା ଭୂତାଣୁଗୁଡ଼ିକୁ ………………………… କୁହାଯାଏ ।
(ଛ) ଏଡ୍‌ସ୍‌ରେ ଆକ୍ରାନ୍ତ ବ୍ୟକ୍ତିଙ୍କ ଶରୀରରେ …………………….. ନାମକ ଶ୍ଵେତରକ୍ତ କଣିକାର ସଂଖ୍ୟା ହ୍ରାସ ପାଏ ।

Answers
(କ) ତ୍ରିଗୁଣିତ (3n)
(ଙ) RNA
(ଘ) ଅଲିଙ୍ଗୀ ଜନନ
(ଛ) ଲିମ୍ଫୋସାଇଟ୍
(ଖ) ପୂର୍ଣ୍ଣବିଭବୀ କୋଷ
(ଗ) 2°°C
(ଚ) ପଶ୍ଚ ଭୂତାଣୁ (ରେଟ୍ରୋଭାଇରସ୍ )

Question 15.
ବାକ୍ୟରେ ଚିହ୍ନିତ ରେଖାଙ୍କିତ ଶବ୍ଦ | ଶବ୍ଦପୁଞ୍ଜକୁ ବଦଳାଇ ଠିକ୍ ବାକ୍ୟ ଲେଖ ।
(କ) ପୁଂଯୁଗ୍ମକ ଓ ସ୍ତ୍ରୀଯୁଗ୍ମକର ମିଳନକୁ ଯୁଗ୍ମକଜନନ କୁହାଯାଏ ।
ଊ-
ପୁଂଯୁଗ୍ମକ ଓ ସ୍ତ୍ରୀଯୁଗ୍ମକର ମିଳନକୁ ସମାୟନ କୁହାଯାଏ ।

(ଖ) ସମାୟନ ନ ହୋଇ ଡିମ୍ବାଣୁର ବୃଦ୍ଧି ଘଟି ଫଳ ସୃଷ୍ଟି ହେଲେ ତାହାକୁ ଅଲିଙ୍ଗୀଜନନ କୁହାଯାଏ ।
ଊ-
ସମାୟନ ନହୋଇ ଡିମ୍ବାଣୁର ବୃଦ୍ଧି ଘଟି ଫଳ ସୃଷ୍ଟି ହେଲେ ତାହାକୁ ଅସମାୟିତ ଜନନ କୁହାଯାଏ ।

(ଗ) ଏଲାଇଜା କୌଶଳ ଏଡ଼ସ୍ ଚିହ୍ନଟ ପାଇଁ ସବୁଠାରୁ ବିଶ୍ୱସନୀୟ ଉପାୟ ।
ଊ-
ୱେଷ୍ଟଟିଙ୍ଗ କୌଶଳ ଏଡ଼ସ୍ ଚିହ୍ନଟ ପାଇଁ ସବୁଠାରୁ ବିଶ୍ୱସନୀୟ ଉପାୟ ।

(ଘ) ଗର୍ଭବତୀ ମହିଳା ଓ ଶିଶୁମାନଙ୍କର ଯତ୍ନ ଓ ସୁରକ୍ଷା ପାଇଁ ଆମ ଦେଶରେ ରାଷ୍ଟ୍ରୀୟ କିଶୋର ସୁରକ୍ଷା
ଊ-
ଗର୍ଭବତୀ ମହିଳା ଓ ଶିଶୁମାନଙ୍କର ଯତ୍ନ ଓ ସୁରକ୍ଷା ପାଇଁ ଆମ ଦେଶରେ ଜନନୀ ସୁରକ୍ଷା ଯୋଜନା କାର୍ଯ୍ୟକାରୀ

(ଙ) ଭୃଣରେ ତିନୋଟି ଜାୟକ ସ୍ତର ତିଆରି ପ୍ରକ୍ରିୟାକୁ ପ୍ରସବ କୁହାଯାଏ ।
ଊ-
ଭ୍ରୂଣରେ ତିନୋଟି ଜାୟକ ସ୍ତର ତିଆରି ପ୍ରକ୍ରିୟାକୁ ଗୀଷ୍ଟ୍ରଲେସନ୍‌ କୁହାଯାଏ ।

Question 16.
ପ୍ରଥମ ଦୁଇଟି ଶବ୍ଦର ସମ୍ପର୍କକୁ ଦେଖ୍ ତୃତୀୟ ସହ ସମ୍ପର୍କିତ ଶବ୍ଦଟି କ’ଣ ହେବ ଲେଖ ।
(i) ଯୁଗ୍ମକ : (n) :: ଯୁଗ୍ମଜ : ……………………..
(ii) ଭାସେକ୍ଟୋମୀ : ଶୁକ୍ରବାହୀ ନଳୀ :: ଟ୍ୟୁବେକ୍ଟୋମୀ : ……………………..
(iii) ଡିମ୍ବାଶୟ : ଇଣ୍ଟ୍ରୋଜେନ୍‌ :: ଶୁକ୍ରାଶୟ : ……………………..
(iv) ନଳୀନ୍ୟଷ୍ଟି : ପୁଂଯୁଗ୍ମକ :: ମେରୁ ନ୍ୟଷ୍ଟି : ……………………..
(v) ଚଳରେଣୁ : ୟୁଲୋଥିକ୍ସ :: ଅଚଳରେଣୁ : ……………………..

Answers
(i) 2n
(ii) ଡିମ୍ବବାହୀ ନାଳୀ
(iii) ଟେଷ୍ଟୋଷ୍ଟିରନ୍
(iv) ଭୃଣପୋଷ
(v) ପେନିସିଲିୟମ୍

Odisha State Board BSE Odisha 10th Class History Notes Chapter 1 ଭାରତୀୟ ଜାତୀୟ ଆନ୍ଦୋଳନରେ ଗାନ୍ଧିଜୀଙ୍କ ଆବିର୍ଭାବ will enable students to study smartly.

BSE Odisha Class 10 History Notes Chapter 1 ଭାରତୀୟ ଜାତୀୟ ଆନ୍ଦୋଳନରେ ଗାନ୍ଧିଜୀଙ୍କ ଆବିର୍ଭାବ

ବିଷୟଭିଭିକ ସୂଚନା ଓ ବିଶ୍ଳେଷଣ

→ ଭାରତୀୟ ଜାତୀୟ ଆନ୍ଦୋଳନରେ ଗାନ୍ଧିଜୀ :

• ପୃଥ‌ିବୀ ଇତିହାସ ପୃଷ୍ଠାରେ ଉଲ୍ଲିଖ୍ ବିଶିଷ୍ଟ ବ୍ୟକ୍ତିମାନଙ୍କ ମଧ୍ୟରେ ଭାରତର ମହାନ୍ ଜନନାୟକ ତଥା ସ୍ଵାଧୀନତା ଆନ୍ଦୋଳନର କର୍ଣ୍ଣଧାର ମହାତ୍ମା ଗାନ୍ଧି ଅନ୍ୟତମ ।
  

ସଂକ୍ଷିପ୍ତ ପରିଚୟ:
ପୂରା ନାମ : ମୋହନଦାସ କରମଚାନ୍ଦ ଚାନ୍ଧି
ଜନ୍ମ ତାରିଖ : ଅକ୍ଟୋବର ୨, ୧୮୬୯
ଜନ୍ମସ୍ଥାନ : ପୋରବନ୍ଦର (ଗୁଜରାଟ)
ବିବାହ : ୧୮୮୨ ଖ୍ରୀଷ୍ଟାବ୍ଦ
ପତ୍ନୀଙ୍କ ନାମ : କସ୍ତୁରବା ଗାନ୍ଧି (ଶ୍ରଦ୍ଧାନାମ – ବା)
ଇଂଲଣ୍ଡ ଯାତ୍ରା : : ୧୮୮୮ ଅକ୍ଟୋବର
ଆଇନ ଶିକ୍ଷା ସମାପ୍ତି : ୧୮୯୧ ଜୁନ୍
ଆଇନ ବ୍ୟବସାୟ ଆରମ୍ଭ : ୧୮୯୫ ଜୁନ୍ (ରାଜକୋଟ ଓ ବମ୍ବେଠାରେ)

→ ଦକ୍ଷିଣ ଆଫ୍ରିକାରେ ଗାନ୍ଧିଜୀଙ୍କ କାର୍ଯ୍ୟାବଳୀ :

• ଦାଦା ଅବଦୁଲ୍ଲା ନାମକ ଜଣେ ଭାରତୀୟ ମୁସଲମାନ ବ୍ୟବସାୟୀଙ୍କ ମୋକଦ୍ଦମା ଲଢ଼ିବାପାଇଁ ଗାନ୍ଧିଜୀ ଦକ୍ଷିଣ ଆଫ୍ରିକାର ନାଟାଲ୍ ନାମକ ସ୍ଥାନକୁ ଯାଇଥିଲେ ।
• ସେଠାରେ କୃଷ୍ଣକାୟ ଆଫ୍ରିକୀୟଙ୍କ ସହ ପ୍ରବାସୀ ଭାରତୀୟମାନେ ଶ୍ୱେତାଙ୍ଗ ଇଂରେଜମାନଙ୍କ ବର୍ଣ୍ଣବୈଷମ୍ୟ ନୀତି ଯୋଗୁଁ ବିଭିନ୍ନ ଅତ୍ୟାଚାରର ସମ୍ମୁଖୀନ ହେଉଥିଲେ ।
• ସେଠାକାର ଭାରତୀୟମାନଙ୍କର ଭୋଟଦାନ ଅଧିକାର ନ ଥିଲା, ସେମାନଙ୍କୁ ନାମ ପଞ୍ଜୀକରଣ କରି ନିର୍ବାଚନ କର ଦେବାକୁ ହେଉଥୁଲା, ଅସ୍ବାସ୍ଥ୍ୟକର ପରିବେଶରେ ବସବାସ କରିବାକୁ ପଡୁଥିଲା ।
• ଭାରତୀୟମାନେ ରେଳଗାଡ଼ିର ପ୍ରଥମ ଶ୍ରେଣୀ ବା ଦ୍ୱିତୀୟ ଶ୍ରେଣୀ କୋଠରିରେ ଯାତ୍ରା କରିପାରୁ ନ ଥିଲେ, ସେମାନଙ୍କୁ ଶ୍ବେତାଙ୍ଗମାନେ ‘କୁଲି’ ବୋଲି ସମ୍ବୋଧନ କରୁଥିଲେ ।
• ଏକଦା ଗାନ୍ଧିଜୀ ରେଳଗାଡ଼ିରେ ପ୍ରଥମ ଶ୍ରେଣୀରେ ଯାତ୍ରା କରୁଥିବାବେଳେ ଶ୍ଵେତାଙ୍କ ସହଯାତ୍ରୀଙ୍କ ଅଭିଯୋଗକ୍ରମେ ରେଳଗାଡ଼ିର ଗାର୍ଡ଼ ଓ ପୋଲିସ୍ ଏକ ଷ୍ଟେସନରେ ତାଙ୍କୁ ତାଙ୍କ ଜିନିଷପତ୍ର ସହ ବାହାରକୁ ଠେଲି ଦେଇଥିଲେ ।
• ଜନସାଧାରଣଙ୍କୁ ସଚେତନ କରିବାପାଇଁ ଗାନ୍ଧିଜୀ ୧୮୯୪ ମସିହାରେ ‘ନାଟାଲ୍ ଭାରତୀୟ କଂଗ୍ରେସ’ ନାମକ ଏକ ରାଜନୈତିକ ଅନୁଷ୍ଠାନ ଗଠନ କରିଥିଲେ ଓ ‘ଇଣ୍ଡିଆନ୍ ଓପିନିଅନ୍’ ନାମକ ଏକ ସମ୍ବାଦପତ୍ରିକା ପ୍ରକାଶ କରିଥିଲେ ।
• ୧୯୦୬ ମସିହାରେ ଦକ୍ଷିଣ ଆଫ୍ରିକା ସରକାର ଆଇନ ପ୍ରଣୟନ କରି ପ୍ରତ୍ୟେକ ଭାରତୀୟଙ୍କୁ ନିଜ ଅଙ୍ଗୁଳି ଛାପିଥ‌ିବା ପ୍ରମାଣପତ୍ର ସବୁ ସମୟରେ ବହନ କରିବା ବାଧ୍ୟତାମୂଳକ କରିଦେଲେ ।
• ଗାନ୍ଧିଜୀ ଏହି ଆଇନ ବିରୋଧରେ ଆନ୍ଦୋଳନ କଲେ ଏବଂ ସତ୍ୟାଗ୍ରହ ଅସ୍ତ୍ର ପ୍ରୟୋଗ କଲେ । ଏଥିପାଇଁ ଗାନ୍ଧିଜୀଙ୍କୁ ଜୋହାନେସବର୍ଗ ଥାଏଟର୍‌ରେ ବନ୍ଦୀ କରି ରଖାଗଲା ।
• ୧୯୦୮ରେ ପ୍ରଣୀତ ଦେଶାନ୍ତର ଗମନ ନିଷେଧ ଆଇନର ବିରୋଧ କରି ଅଧିକାଂଶ ଭାରତୀୟ ନାଟାଲ୍ ସୀମା ପାର ହୋଇ ଟ୍ରାନ୍ସଭାଲ୍ ଗଲେ ଓ ଗିରଫ ହେଲେ । ଗାନ୍ଧିଜୀଙ୍କୁ ମଧ୍ୟ ବନ୍ଦୀ କରାଗଲା ।
• ୧୯୦୮ରେ ପ୍ରଣୀତ ଦେଶାନ୍ତର ଗମନ ନିଷେଧ ଆଇନର ବିରୋଧ କରି ଅଧିକାଂଶ ଭାରତୀୟ ନାଟାଲ୍ ସୀମା ପାର ହୋଇ ଟ୍ରାନ୍ସଭାଲ୍ ଗଲେ ଓ ଗିରଫ ହେଲେ । ଗାନ୍ଧିଜୀଙ୍କୁ ମଧ୍ୟ ବନ୍ଦୀ କରାଗଲା ।
• ୧୯୧୩ ମାର୍ଚ୍ଚ ୧୪ରେ ଦକ୍ଷିଣ ଆଫ୍ରିକା ଉଚ୍ଚତମ ନ୍ୟାୟାଳୟ ନିର୍ଦ୍ଦେଶରେ ଖ୍ରୀଷ୍ଟିଆନ୍ ରୀତିରେ ହୋଇନଥିବା ଓ ଅଣପଞ୍ଜୀକୃତ ଭାରତୀୟମାନଙ୍କ ବିବାହର ସ୍ବୀକୃତି ପ୍ରତ୍ୟାହାର କରାଗଲା ।
• ଗାନ୍ଧିଜୀ ଏହି ଆଇନ ବିରୋଧରେ ଆନ୍ଦୋଳନ କଲେ ଓ ଇଂରେଜ ସରକାର ଆଇନ ପ୍ରତ୍ୟାହାର କରିବାକୁ ବାଧ୍ୟ ହେଲେ ।
• ୧୯୧୫ ଜାନୁୟାରୀ ୧୫ ତାରିଖରେ ଗାନ୍ଧିଜୀ ଭାରତକୁ ଫେରି ଆସିଥିଲେ । ନିଜର ରାଜନୈତିକ ଗୁରୁ ଗୋପାଳକୃଷ୍ଣ ଗୋଙ୍କ ଉପଦେଶ ଅନୁସାରେ ରାଜନୀତିରୁ ଦୂରେଇ ଯାଇ ଭାରତର ବିଭିନ୍ନ ସ୍ଥାନ ଭ୍ରମଣ କରିଥିଲେ ।
• ଦକ୍ଷିଣ ଆଫ୍ରିକାରେ ଗାନ୍ଧିଜୀଙ୍କ ମହାନ୍ ନୀତି ପାଇଁ ବିଶ୍ୱକବି ରବୀନ୍ଦ୍ରନାଥ ଠାକୁର ତାଙ୍କୁ ‘ମହାତ୍ମା’ ଆଖ୍ୟା ଦେଇଥିଲେ ।
• ପ୍ରାରମ୍ଭିକ ସ୍ତରରେ ତାଙ୍କଦ୍ୱାରା ଭାରତରେ ସଙ୍ଗଠିତ କେତେକ ଆନ୍ଦୋଳନ ସଫଳତା ଲାଭ କରିଥିଲା ।

→ ଚମ୍ପାରନ୍ ଆନ୍ଦୋଳନ (୧୯୧୭) :

• ଏହି ଆନ୍ଦୋଳନ ଭାରତରେ ଗାନ୍ଧିଜୀଙ୍କଦ୍ବାରା ସଙ୍ଗଠିତ ପ୍ରଥମ ଆନ୍ଦୋଳନ ଥିଲା
• ବିହାରର ଚମ୍ପାରନ୍ ଜିଲ୍ଲାରେ ଇଂରେଜ ବୃକ୍ଷରୋପଣକାରୀଙ୍କଦ୍ବାରା ଚାଷୀମାନଙ୍କୁ ଜମିର କୋଡ଼ିଏ ଭାଗରୁ ତିନିଭାଗ ଅଞ୍ଚଳରେ ନୀଳ ଉତ୍ପାଦନ କରିବାକୁ ବାଧ୍ୟ କରାଯାଉଥିଲା । ବେଆଇନ ଟିକସ ମଧ୍ୟ ଆଦାୟ କରାଯାଉଥିଲା ।
• ରାଜକୁମାର ଶୁକ୍ଳ ନାମକ ଜଣେ ସ୍ଥାନୀୟ ବାସିନ୍ଦାଙ୍କ ନିମନ୍ତ୍ରଣକ୍ରମେ ଗାନ୍ଧିଜୀ ୧୯୧୭ ମସିହା ଏପ୍ରିଲ୍ ମାସରେ ମୋତିହାରିରେ ପହଞ୍ଚିଲେ । ଏହି ଆନ୍ଦୋଳନର ନେତୃତ୍ଵ ନେଇ ସେ ସଫଳତା ହାସଲ କରିଥିଲେ ।
• ତିନିକାଠିଆ ବ୍ୟବସ୍ଥା ଉଚ୍ଛେଦ ହେଲା ଏବଂ ବେଆଇନ ଭାବେ ଆଦାୟ ଅର୍ଥର ଶତକଡ଼ା ପଚିଶ ଭାଗ ଚାଷୀମାନଙ୍କୁ ଫେରାଇ ଦିଆଗଲା । ଏହା ଥିଲା ଗାନ୍ଧିଜୀଙ୍କ ନେତୃତ୍ଵରେ ପ୍ରଥମ ସଫଳ ଅହିଂସ ଆନ୍ଦୋଳନ ।
• ତିନିକାଠିଆ ବ୍ୟବସ୍ଥା –  ଏହି ବ୍ୟବସ୍ଥାରେ ବିହାରର ଚମ୍ପାରନ୍ ଜିଲ୍ଲାରେ ଚାଷୀମାନଙ୍କୁ ଜମିର କୋଡ଼ିଏ ଭାଗରୁ ତିନି ଭାଗ ଅଞ୍ଚଳରେ ନୀଳ ଉତ୍ପାଦନ କରିବାପାଇଁ ଇଂରେଜ ବୃକ୍ଷ ରୋପଣକାରୀମାନଙ୍କଦ୍ବାରା ବାଧ କରାଯାଇ ସେମାନଙ୍କଦ୍ୱାରା ନିର୍ଦ୍ଧାରିତ ଦରରେ ତାଙ୍କୁ ବିକ୍ରୟ କରିବାକୁ ପଡୁଥିଲା 

→ ଖେଡ଼ା ଆନ୍ଦୋଳନ (୧୯୧୮) :

1. ତତ୍‌କାଳୀନ ରାଜସ୍ୱ ବିଭାଗର ଏକ ନିୟମ ଅନୁଯାୟୀ ଜମିର ସ୍ଵାଭାବିକ ଉତ୍ପାଦନର ଏକ ଚତୁର୍ଥାଂଶରୁ କମ୍ ପରିମାଣରେ ଶସ୍ୟ ଉତ୍ପାଦନ ହେଲେ ଚାଷୀମାନଙ୍କର ରାଜସ୍ୱ ଦେୟ ପରିମାଣ କୋହଳ କରାଯିବାର ବ୍ୟବସ୍ଥା ଥିଲା; କିନ୍ତୁ ୧୯୧୮ ମସିହାରେ ଦୁର୍ଭିକ୍ଷ ସମୟରେ ଖେଡ଼ା ଜିଲ୍ଲାରେ ଶସ୍ୟ ଉତ୍ପାଦନ ବାଧାପ୍ରାପ୍ତ ହୋଇଥିଲେ
   ମଧ୍ୟ ଇଂରେଜ କର୍ମଚାରୀମାନେ ଚାଷୀମାନଙ୍କୁ ସମ୍ପୂର୍ଣ୍ଣ ରାଜସ୍ୱ ଦେବାକୁ ବାଧ୍ୟ କରିଥିଲେ ।
2. ଗାନ୍ଧିଜୀ ଏହା ବିରୋଧରେ ଚାଷୀମାନଙ୍କୁ ସଙ୍ଗଠିତ କରି ସତ୍ୟାଗ୍ରହ କଲେ, ଖଜଣା ଦେୟକୁ ପ୍ରତ୍ୟାଖ୍ୟାନ କଲେ ।
3. ଶେଷରେ ଇଂରେଜ ସରକାର ବାଧ୍ୟତାମୂଳକ ରାଜସ୍ୱ ଆଦାୟରୁ ନିବୃତ୍ତ ହେଲେ; କିନ୍ତୁ ସାମର୍ଥ୍ୟ ଥିବା ଚାଷୀମାନଙ୍କଠାରୁ ଏହା ଆଦାୟ କରିଥିଲେ ।
4. ଏହି ଆନ୍ଦୋଳନରେ ଇନ୍ଦୁଲାଲ ଯାଞ୍ଜିକ୍ ଗାନ୍ଧିଜୀଙ୍କୁ ସହଯୋଗ କରିଥିଲେ ।
5. ଖେଡ଼ା ଜିଲ୍ଲାର ଅଧ୍ୟାବାସୀ ତଥା ଅହମ୍ମଦାବାଦର ବିଶିଷ୍ଟ ଆଇନଜୀବୀ ସର୍ଦ୍ଦାର ବଲ୍ଲଭଭାଇ ପଟେଲ ଏହି ଖେଡ଼ା ଆନ୍ଦୋଳନରେ ସଫଳତାରେ ପ୍ରଭାବିତ ହୋଇ ଗାନ୍ଧିଜୀଙ୍କର ଜଣେ ପ୍ରଧାନ ଅନୁଗାମୀ ହୋଇଗଲେ ।

→ ଅହମ୍ମଦାବାଦ୍ ଲୁଗା କାରଖାନା ଆନ୍ଦୋଳନ :

• ତତ୍‌କାଳୀନ ରାଜସ୍ୱ ବିଭାଗର ଏକ ନିୟମ ଅନୁଯାୟୀ ଜମିର ସ୍ଵାଭାବିକ ଉତ୍ପାଦନର ଏକ ଚତୁର୍ଥାଂଶରୁ କମ୍ ସ୍ଵତନ୍ତ୍ର ଭତ୍ତା ପ୍ରତ୍ୟାହାର କରିନେବାରୁ ଶ୍ରମିକ ଓ ମାଲିକମାନଙ୍କ ମଧ୍ୟରେ କଳହର ସୂତ୍ରପାତ ହୋଇଥିଲା ।
• ଜିଲ୍ଲାପାଳଙ୍କ ଅନୁରୋଧରେ ଗାନ୍ଧିଜୀ ଏକ ଟ୍ରିବ୍ୟୁନାଲ ନିଯୁକ୍ତ କରି ସମସ୍ୟା ସମାଧାନ ପାଇଁ ଉଦ୍ୟମ କଲେ । କିନ୍ତୁ ମାଲିକମାନେ ଏଥୁ ଓହରି ଯିବାରୁ ଗାନ୍ଧିଜୀ ଶ୍ରମିକମାନଙ୍କୁ ଅହିଂସ ଉପାୟରେ ଆନ୍ଦୋଳନ କରିବାକୁ ପ୍ରବର୍ତ୍ତାଇ ନିଜେ ଅନଶନ ଆରମ୍ଭ କଲେ ।
• କଳକାରଖାନାର ମାଲିକମାନେ ଏହି ଆନ୍ଦୋଳନରେ ଭୟଭୀତ ହୋଇ ଶ୍ରମିକମାନଙ୍କ ମଜୁରି ପଞ୍ଚତିରିଶ ଭାଗ ବୃଦ୍ଧି କରିବାପାଇଁ ସମ୍ମତି ପ୍ରଦାନ କରିଥିଲେ ।
• ଏହି ଆନ୍ଦୋଳନଦ୍ଵାରା ଗାନ୍ଧିଜୀ ଜନସାଧାରଣଙ୍କ ମନରେ ‘ସତ୍ୟାଗ୍ରହ’ ପ୍ରତି ଆଗ୍ରହ, ଶ୍ରଦ୍ଧା ଓ ସମ୍ମାନ ଆଣିପାରିଥିଲେ ।
• ‘ପ୍ଲେଗ୍ ବୋନସ୍’’ – ଗୁଜରାଟର ଅହମ୍ମଦାବାଦ୍ୱାରେ ଥ‌ିବା ଲୁଗାକଳଗୁଡ଼ିକର ମାଲିକମାନେ ପ୍ଲେଟ୍ ମହାମାରୀ ପାଇଁ ଶ୍ରମିକମାନଙ୍କୁ ଦେଉଥୁବା ସ୍ବତନ୍ତ୍ର ଭତ୍ତାକୁ ପ୍ଲେଗ୍ ବୋନସ୍ କୁହାଯାଉଥିଲା ।

→ ରାଓଲାତ୍ ଆଇନ ବିରୋଧରେ ଆନ୍ଦୋଳନ (୧୯୧୯) :

• ୧୯୧୯ ମସିହାରେ ଇଂରେଜ ସରକାରଙ୍କଦ୍ଵାରା ପ୍ରଣୀତ ରାଓଲାତ୍ ଆଇନ ବିରୋଧୀ ଆନ୍ଦୋଳନ ଥିଲା ଗାନ୍ଧିଜୀଙ୍କ ପ୍ରଥମ ଜାତୀୟ ସ୍ତରୀୟ ଆନ୍ଦୋଳନ ।
• ପ୍ରଥମ ବିଶ୍ବଯୁଦ୍ଧରେ ଇଂରେଜ ଓ ମିତ୍ରଶକ୍ତିକୁ ବିପୁଳ ସାହାଯ୍ୟ ଓ ସମର୍ଥନ ଦେଇଥ‌ିବା ଭାରତୀୟମାନେ ଯୁଦ୍ଧ ପରେ ରାଜନୀତିକ ଦାବିଗୁଡ଼ିକ ହାସଲ କରିନପାରି ନିରାଶ ହୋଇଥିଲେ । ତେଣୁ ସାମ୍ଭାବ୍ୟ ବିଦ୍ରୋହ ଆଶଙ୍କାରେ ଇଂରେଜ ବିଚାରପତି ରାଓଲାତ୍ରଙ୍କ ଅଧ୍ୟକ୍ଷତାରେ ଏକ କମିଟି ଗଠନ କରାଯାଇ କଠୋର ଆଇନ ପ୍ରଣୟନ କରାଯାଇଥିଲା ।
• ଏହି ଆଇନ ବଳରେ ଇଂରେଜ ସରକାର ଯେ କୌଣସି ଭାରତୀୟଙ୍କୁ ଗିରଫ କରି ବିନା ବିଚାରରେ କାରାଦଣ୍ଡରେ ଦଣ୍ଡିତ କରିପାରିବାର ବ୍ୟବସ୍ଥା ଥିଲା । ୧୯୧୯ ମସିହା ମାର୍ଚ୍ଚ ୧୮ ତାରିଖରେ ଏହି ଆଇନ ଗୃହୀତ ହୋଇଥିଲା । ଗାନ୍ଧିଜୀ ଏହି ଆଇନ ବିରୋଧରେ ଏକ ଗଣ ସତ୍ୟାଗ୍ରହ ପାଇଁ ଆହ୍ୱାନ କରିଥିଲେ ।
• ଗାନ୍ଧିଜୀ ଏହି ଆଇନ ବିରୋଧରେ ଏକ ଗଣ ସତ୍ୟାଗ୍ରହ ପାଇଁ ଆହ୍ବାନ କରିଥିଲେ ।
• ଶ୍ରୀମତୀ ଆନିବେଶାନ୍ତ, ସୁରେନ୍ଦ୍ରନାଥ ବାନାର୍ଜୀ, ଦିନ୍ସ ଏଦୁଲ୍‌ ୱାଚା, ତେଗ୍ ବାହାଦୂର ସାହୁ ଓ ଶ୍ରୀନିବାସ ଶାସ୍ତ୍ରୀଙ୍କ ନେତାଗଣ ଗାନ୍ଧିଜୀଙ୍କ ସତ୍ୟାଗ୍ରହକୁ ବିରୋଧ କରିଥିଲେ ।
• ୧୯୧୯ ମସିହା ଏପ୍ରିଲ୍ ୬ ତାରିଖ ଦିନ ଦେଶବ୍ୟାପୀ ହରତାଳ ପାଳନ କରାଯାଇଥିଲା । ୧୯୧୯ ଏପ୍ରିଲ୍ ୯ ତାରିଖରେ ଗାନ୍ଧିଜୀଙ୍କୁ ଗିରଫ କରାଯାଇ ପରେ ଛାଡ଼ି ଦିଆଯାଇଥିଲା ।
• ୧୯୧୯ ମସିହା ମାର୍ଚ୍ଚ ୨୦ ତାରିଖରେ ଦିଲ୍ଲୀରେ ରାଓଲାତ୍ ଆଇନ ବିରୋଧରେ ହିନ୍ଦୁ ଓ ମୁସଲମାନମାନଙ୍କ ଏକ ଶୋଭାଯାତ୍ରା ଉପରେ ପୋଲିସ୍ ଗୁଳିବର୍ଷଣ କରିଥିଲା ।

→ ଜାଲିଆନାଓ୍ବାଲାବାଗ୍ ହତ୍ୟାକାଣ୍ଡ :

1. ଅମୃତସରର ଜାଲିଆନାଓ୍ବାଲାବାଗ୍‌ଠାରେ ୧୯୧୯ ମସିହା ଏପ୍ରିଲ୍ ୧୩ ତାରିଖରେ ବହୁସଂଖ୍ୟକ ଲୋକ ଦୁଇ ସ୍ଥାନୀୟ ନେତା ଡ. ସତ୍ୟପାଲ ଓ ଡ. ସଇଫୁଦ୍ଦିନ କିଲୁଦଙ୍କ ଗିରଫର ପ୍ରତିବାଦ ଓ ବୈଶାଖୀ ଉତ୍ସବ ପାଳନ ପାଇଁ ଏକ ସଭାରେ ଏକତ୍ରିତ ହୋଇଥିଲେ ।
2. ସହରରେ ସଭାସମିତି କରାଯିବା ଉପରେ ସରକାରଙ୍କଦ୍ଵାରା ପୂର୍ବଦିନ ଘୋଷିତ ନିଷେଧାଜ୍ଞା ବିଷୟରେ ଜନସାଧାରଣ ଅବଗତ ନ ଥିଲେ ।
3. ସଭା ଚାଲିଥିବାବେଳେ ଅମୃତସରର ସାମରିକ ମୁଖ୍ୟ ଜେନେରାଲ ଡାୟାର ହଠାତ୍ ଦଳେ ସୈନ୍ୟଙ୍କ ସହ ପହଞ୍ଚି ବିନା ସତର୍କ ସୂଚନାରେ ନିରସ୍ତ୍ର ଓ ନିରୀହ ଲୋକମାନଙ୍କ ଉପରକୁ ଗୁଳିବର୍ଷଣ କରିଥିଲେ; ଫଳରେ ଅନେକ ଲୋକ ମୃତାହତ ହେଲେ ।
4. ସରକାରୀ ହିସାବ ଅନୁଯାୟୀ ୩୭୯ ଜଣ ମୃତ ଓ ୧୨୦୦ ଜଣ ଆହତ ହୋଇଥିଲେ । ମାତ୍ର ଗାନ୍ଧିଜୀଙ୍କ ନିର୍ଦ୍ଦେଶରେ ହୋଇଥ‌ିବା ତଦନ୍ତ ଅନୁସାରେ ମୃତକଙ୍କ ସଂଖ୍ୟା ୧୨୦୦ ଓ ଆହତଙ୍କ ସଂଖ୍ୟା ୩୬୦୦ ଥିଲା ।
5. ଏହି ବର୍ବରୋଚିତ ହତ୍ୟାକାଣ୍ଡ ସାରା ବିଶ୍ୱକୁ ଚକିତ କରିଦେଇଥିଲା ।
6. ଇଂରେଜ ସରକାରଙ୍କର ଏହି ହତ୍ୟାକାଣ୍ଡର ପ୍ରତିବାଦରେ ବିଶ୍ୱକବି ରବୀନ୍ଦ୍ରନାଥ ଠାକୁର ‘ନାଇଟ୍‌’ ପଦ ଓ ଗାନ୍ଧିଜୀ ‘କାଇଜର-ଇ-ହିନ୍ଦୁ’ ଉପାଧ୍ ପ୍ରତ୍ୟାଖ୍ୟାନ କରିଥିଲେ ।
7. ‘ସାର୍‌’ ଉପାଧ୍ – କୌଣସି ବ୍ୟକ୍ତିର ମହତ୍ ଗୁଣ ବା ରାଜ ସେବା ବା ସାମାଜିକ କ୍ଷେତ୍ରରେ ଅସାଧାରଣ ବୀରତ୍ୱ ପାଇଁ ଇଂରେଜ ସରକାରଙ୍କଦ୍ଵାରା ପ୍ରଦତ୍ତ ନାଇଟ୍‌ ପଦପ୍ରାପ୍ତ ବ୍ୟକ୍ତିଙ୍କୁ ‘ସାର୍’ କୁହାଯାଉଥିଲା ।
8. ‘‘କାଇଜର୍‌-ଇ-ହିନ୍ଦ୍’’ ର ଅର୍ଥ ‘ହିନ୍ଦୁସ୍ଥାନର ସମ୍ରାଟ’’ । ଏହା ଇଂରେଜ ସରକାରଙ୍କଦ୍ବାରା ଗାନ୍ଧିଜୀଙ୍କୁ ତାଙ୍କ ଅସାଧାରଣ ନେତୃତ୍ଵର ସ୍ଵୀକୃତିରୂପେ ପ୍ରଦାନ କରାଯାଇଥିଲା ।

ଐତିହାସିକ ଘଟଣାବଳୀ ଓ ସମୟ:

୧୮୬୯ ଖ୍ରୀ.ଅ. – (ଅକ୍ଟୋବର ୨) ମୋହନଦାସ କରମଚାନ୍ଦ ଗାନ୍ଧିଙ୍କ ଜନ୍ମ ।
୧୮୮୨ ଖ୍ରୀ.ଅ. – ଗାନ୍ଧିଜୀଙ୍କର କସ୍ତୁରବାଙ୍କ ସହ ବିବାହ ।
୧୮୮୮ ଖ୍ରୀ.ଅ. – (ଅକ୍ଟୋବର) ଗାନ୍ଧିଜୀଙ୍କର ବାରିଷ୍ଟରୀ ପଢ଼ିବାପାଇଁ ଇଂଲଣ୍ଡ ଯାତ୍ରା ।
୧୮୯୧ ଖ୍ରୀ.ଅ. – (ଜୁନ୍) ବାରିଷ୍ଟର ଭାବେ ରାଜକୋଟ ଓ ବମ୍ବେଠାରେ ଗାନ୍ଧିଜୀଙ୍କର ଆଇନ ବ୍ୟବସାୟ ଆରମ୍ଭ ।
୧୮୯୪ ଖ୍ରୀ.ଅ. – ଗାନ୍ଧିଜୀଙ୍କଦ୍ବାରା ଦକ୍ଷିଣ ଆଫ୍ରିକାରେ ‘‘ନାଟାଲ୍ ଭାରତୀୟ କଂଗ୍ରେସ’’ ନାମକ ଏକ ରାଜନୈତିକ ଅନୁଷ୍ଠାନ ଗଠନ ।
୧୯୦୬ ଖ୍ରୀ.ଅ. – ଦକ୍ଷିଣ ଆଫ୍ରିକାରେ ଭାରତୀୟମାନେ ନିଜର ଅଙ୍ଗୁଳି ଛାପ ଥିବା ପଞ୍ଜୀକୃତ ପ୍ରମାଣପତ୍ରକୁ ସବୁ ସମୟରେ ନିଜ ସହିତ ବହନ କରିବାପାଇଁ ଆଇନ ପ୍ରଣୟନ ।
୧୯୦୮ ଖ୍ରୀ.ଅ. – (ଅଗଷ୍ଟ) ନାଟାଲ୍ ସୀମା ପାର ହୋଇ ଗାନ୍ଧିଜୀଙ୍କ ଟ୍ରାନ୍ସଭାଲ ଗମନ ଓ ଗିରଫ ।

୧୯୧୩ ଖ୍ରୀ.ଅ. – (ମାର୍ଚ୍ଚ ୧୪) ଦକ୍ଷିଣ ଆଫ୍ରିକାର ଉଚ୍ଚତମ ନ୍ୟାୟାଳୟଦ୍ବାରା ଖ୍ରୀଷ୍ଟିଆନ୍ ରୀତି ଅନୁସାରେ ସମ୍ପାଦିତ ଓ ପଞ୍ଜୀକରଣ ହୋଇ ନଥିବା ଭାରତୀୟମାନଙ୍କର ବିବାହର ସ୍ଵୀକୃତି ପ୍ରତ୍ୟାହାର ।
୧୯୧୫ ଖ୍ରୀ.ଅ. – (ଜାନୁୟାରୀ ୯) ଗାନ୍ଧିଜୀଙ୍କର ଦକ୍ଷିଣ ଆଫ୍ରିକାରୁ ଭାରତକୁ ପ୍ରତ୍ୟାବର୍ତ୍ତନ ।
୧୯୧୬ ଖ୍ରୀ.ଅ. – ଅହମ୍ମଦାବାଦରେ ସାବରମତୀ ନଦୀକୂଳରେ ଗାନ୍ଧିଜୀଙ୍କଦ୍ବାରା ଏକ ଆଶ୍ରମ ପ୍ରତିଷ୍ଠା ।
୧୯୧୭ ଖ୍ରୀ.ଅ. – (ଏପ୍ରିଲ୍) ଚମ୍ପାରନ୍ ଆନ୍ଦୋଳନ ପାଇଁ ଚମ୍ପାରନ୍ ଜିଲ୍ଲାର ସଦର ମହକୁମା ମୋତିହାରିରେ ଗାନ୍ଧିଜୀଙ୍କ ପଦାର୍ପଣ ।
୧୯୧୮ ଖ୍ରୀ.ଅ. – ଗୁଜରାଟର ଖେଡ଼ା ଆନ୍ଦୋଳନ ସଂଘଟିତ ।
୧୯୧୯ ଖ୍ରୀ.ଅ. – ରାଓଲାତ୍ ଆଇନ ବିରୋଧରେ ଗାନ୍ଧିଜୀଙ୍କ ଆନ୍ଦୋଳନ ।
୧୯୧୯ ଖ୍ରୀ.ଅ. – (ମାର୍ଚ୍ଚ ୧୮) ରାଓଲାତ୍ ଆଇନ ଗୃହୀତ ।
୧୯୧୯ ଖ୍ରୀ.ଅ. – (ଏପ୍ରିଲ୍ ୧୩) ଜାଲିଆନାୱାଲାବାଗ୍ ହତ୍ୟାକାଣ୍ଡ ସଂଘଟିତ ।
୧୯୧୯ ଖ୍ରୀ.ଅ. – (ଏପ୍ରିଲ୍ ୧୮) ଗାନ୍ଧିଜୀଙ୍କଦ୍ବାରା ରାଓଲାତ୍ ଆଇନବିରୋଧୀ ଆନ୍ଦୋଳନ ପ୍ରତ୍ୟାହୃତ ।

Odisha State Board BSE Odisha 10th Class Maths Notes Algebra Chapter 2 ଦ୍ବିଘାତ ସମୀକରଣ will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Algebra Chapter 2 ଦ୍ବିଘାତ ସମୀକରଣ

→ ଉପକ୍ରମଣିକା (Introduction) :

• P(x) = ax² + bx + c (a ≠ 0) ଗୋଟିଏ ଦ୍ଵିଘାତ ପଲିନୋମିଆଲ୍ (Quadratic Polynomial), ଯେଉଁଠାରେ a ଓ b ଯଥାକ୍ରମେ x², xର ସହଗ ଏବଂ c ଏକ ଧ୍ରୁବ ସଂଖ୍ୟା ।
• P(x) = 0 ଅର୍ଥାତ୍, ax + bx+c =0, (a ≠0) ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ (Quadratic Equation) ଯେଉଁଠାରେ a, b, c ∈ ଏବଂ a ≠ 0.
• ax² + bx + c = 0, a, b, c e R, a + 0 ଦ୍ଵିଘାତ ସମୀକରଣ ସାଧାରଣ ରୂପ ।
• ‘x’ର ଯେଉଁ ଯେଉଁ ମାନ ପାଇଁ ax² + bx + c = 0 ସମୀକରଣଟି ସିଦ୍ଧ ହୁଏ, ସେହି ମାନଗୁଡିକ ସମୀକରଣର ବୀଜ ବା ମୂଳ (root) କୁହାଯାଏ ।
• ଗୋଟିଏ ଦ୍ଵିଘାତ ସମୀକରଣରେ ଅତିବେଶୀରେ ଦୁଇଟି ବୀଜ ଥାଏ ।

• ଯଦି x = α ପାଇଁ ଦ୍ବିଘାତ ପଲିନୋମିଆଲ୍ ax² + bx + cର ମାନ ଶୂନ ହୁଏ, ତେବେ α କୁ ପଲିନୋମିଆଲ୍‌ର ଏକ ଶୂନ (zero) କୁହାଯାଏ । ଏଠାରେ ମନେରଖୁବାକୁ ହେବ ଯେ, ଦ୍ଵିଘାତ ସମୀକରଣର ‘ଶୂନ’ ଉକ୍ତ ସମୀକରଣର ଏକ ମୂଳ (root) ଅଟେ ।
• ପ୍ରତ୍ୟେକ ଦ୍ଵିଘାତ ପଲିନୋମିଆଲ୍ ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ସହ ସଂପୃକ୍ତ ଅଟେ । ଉଦାହରଣସ୍ୱରୂପ,
  ax² + bx + c ଦ୍ବିଘାତ ପଲିନୋମିଆଲ୍ ax² + bx + c = 0, a ≠ 0 ଦ୍ବିଘାତ ସମୀକରଣ ସହ ସଂପୃକ୍ତ ।

→ ପୂର୍ବବର୍ଗରେ ପରିଣତ କରି ଦ୍ୱିଘାତ ସମୀକରଣର ସମାଧାନ (Solution by completing the squares) :
ମନେକର ଦ୍ବିଘାତ ସମୀକରଣଟି ax² + bx + c = 0, a ≠ 0

→ ବିକଳ୍ପ ପ୍ରଣାଳୀ :
⇒ ax² + bx + c = 0 (a ≠ 0)
⇒ ax² + bx = -c (‘c’ର ପାର୍ଶ୍ଵପରିବର୍ତ୍ତନ କରାଗଲା ।)
⇒ 4a (ax² + bx) = -4ac (ଉଭୟ ପାର୍ଶ୍ଵରେ 4a ଗୁଣନ କଲେ)
⇒ 4a² x² + 4abx= -4ac
⇒ (2ax)² + 2.2ax. b = -4ac
⇒ (2ax)² + 2.2ax.b + b² = b² – 4ac (ଉଭୟ ପାର୍ଶ୍ଵରେ b² ଯୋଗକରାଗଲା ।)
⇒ (2ax + b)² = (±\(\sqrt{(b^2-4ac)}\))² (ଉଭୟ ପାର୍ଶ୍ଵକୁ ପୂର୍ଣବର୍ଗରେ ପରିଣତ କରାଗଲା ।)

(i) ରେ ନିଶ୍ଚିତ ସୂତ୍ରକୁ ଦ୍ବିଘାତ ସୂତ୍ର (Quadratic Formula) କୁହାଯାଏ ।

→ ପ୍ରଭେଦକ (Discriminant) :
b² – 4ac କୁ ax² + bx + c = 0 ଦ୍ଵିଘାତ ସମୀକରଣର ପ୍ରଭେଦକ କୁହାଯାଏ ଓ ଏହାକୁ ‘D’ ଦ୍ଵାରା ସୂଚିତ କରାଯାଏ । ଅର୍ଥାତ୍ D = b² – 4ac ।
ଦ୍ୱିଘାତ ସମୀକରଣ ax² + bx + c = 0 କୁ ବିଚାରକୁ ନେଲାବେଳେ, ସେଥୁରେ a, b ଓ c ରାଶିତ୍ରୟ ପୂର୍ବସଂଖ୍ୟା ଓ a ≠ 0 ।
ମୂଳଦ୍ଵୟକୁ D ମାଧ୍ୟମରେ ପ୍ରକାଶ କଲେ,

→ ମୂଳଦ୍ବୟର ସ୍ବରୂପ (Nature of roots) :
ଦ୍ବିଘାତ ସମୀକରଣର ପ୍ରଭେଦକ (D)କୁ ବିଚାରକୁ ନେଇ ସମୀକରଣଟିର ମୂଳଦ୍ବୟର ସ୍ବରୂପ ନିରୂପଣ କରାଯାଏ ।

• D> 0 ହେଲେ, ମୂଳଦ୍ଵୟ α ଓ ß ବାସ୍ତବ ସଂଖ୍ୟା ଓ ପରସ୍ପରଠାରୁ ପୃଥକ୍ ହେବେ, ଅର୍ଥାତ୍ α ≠ ß ।
• D = 0 ହେଲେ ମୂଳଦ୍ୱୟ ବାସ୍ତବ ସଂଖ୍ୟା ଏବଂ ଏକ ଓ ଅଭିନ୍ନ ହେବେ । ଅର୍ଥାତ୍ α = ß ।
• D < 0 ହେଲେ ମୂଳଦ୍ୱୟ α ଓ ß ବାସ୍ତବ ହେବେ ନାହିଁ ।
• • D > 0 ଏବଂ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା ହେଲେ, ମୂଳଦ୍ଵୟ ପରିମେୟ ଏବଂ ପୃଥକ୍ ହେବେ ।
  • D > 0 ଏବଂ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା ନ ହେଲେ, ମୂଳଦ୍ବୟ ଅପରିମେୟ ଏବଂ ପୃଥକ୍ ହେବେ ।

→ ମୂଳଦ୍ଵୟ ଓ ସହଟ ମଧ୍ୟରେ ସଂପକି (Relation between roots and coefficients) :
ମନେକର ଦ୍ଵିଘାତ ସମୀକରଣଟି ax² + bx + c = 0, (a ≠ 0) ଓ ଏହାର ମୂଳଦ୍ଵୟ α ଓ ß ।

(i) ମୂଳଦ୍ଵୟର ସମଷ୍ଟି :

→ କେତେଗୁଡ଼ିଏ ଜ୍ଞାତବ୍ୟ ଫଳାଫଳ (Some known results) :
ମନେକର ଦ୍ଵିଘାତ ସମୀକରଣଟି ax² + bx + c = 0, (a ≠ 0) ଏବଂ ଏହାର ମୂଳଦ୍ଵୟ α ଓ ß ।
∴ α + ß = \(\frac{-b}{a}\) ଏବଂ αß = \(\frac{c}{a}\)

→ ଦ୍ଵିଘାତ ସମୀକରଣର ଗଠନ (Formation of a quadratic equation) :
ମନେକର ଦ୍ବିଘାତ ସମୀକରଣ ax² + bx + c = 0, (a ≠ 0) ଏବଂ ଏହାର ମୂଳଦ୍ଵୟ α ଓ ß ।
ତେବେ α + ß = \(\frac{-b}{a}\) ଏବଂ αß = \(\frac{c}{a}\)
ବର୍ତ୍ତମାନ ax² + bx + c = 0
⇒ x² + \(\frac{b}{a}\) x + \(\frac{c}{a}\) = 0 (a ଦ୍ବାରା ଉଭୟ ପାର୍ଶ୍ଵକୁ ଭାଗକଲେ ।)
⇒ x² – \(\frac{-b}{a}\) x + \(\frac{c}{a}\) = 0 ⇒ x² – (α + ß) + αß = 0

→ ଦ୍ୱିଘାତ ସମୀକରଣ ରୂପରେ ରୂପାନ୍ତରଣ (Equations reducible to quadratic form) :
ଏପରି ଅନେକ ସମୀକରଣ ଅଛନ୍ତି, ଯେଉଁମାନଙ୍କ ରୂପ ଦ୍ଵିଘାତ ସମୀକରଣର ରୂପ; ଯଥା ax² + bx + c = 0 ନୁହେଁ । ମାତ୍ର ଅଜ୍ଞାତ ରାଶିକୁ ଉପଯୁକ୍ତ ଭାବେ ପରିବର୍ତ୍ତନ କରି ଏମାନଙ୍କୁ ଦ୍ୱିଘାତ ସମୀକରଣ ରୂପକୁ ଆଣି ସମାଧାନ କରିହେବ ।

→ ଦ୍ୱିଘାତ ସମୀକରଣର ପ୍ରୟୋଗ (Application of Quadratic Equaiton) :
କେତେକ ପାଟୀଗାଣିତିକ ପ୍ରଶ୍ନର ସମାଧାନରେ ‘ଦ୍ଵିଘାତ ସମୀକରଣର ସମାଧାନ’ର ଆବଶ୍ୟକତା ପଡ଼ିଥାଏ । ପାଟୀଗାଣିତିକ ପ୍ରଶ୍ନର ତର୍ଜମା ଏବଂ ଅନୁଶୀଳନରେ ଆବଶ୍ୟକ ଥିବା ଉତ୍ତରକୁ ଏକ ଅଜ୍ଞାତରାଶି ରୂପେ ନେଇ ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ଗଠନ କରାଯାଏ । ତତ୍ପରେ ଉକ୍ତ ସମୀକରଣର ସମାଧାନ ପରେ ଇସ୍ପାତ ଉତ୍ତର ମିଳିଥାଏ । ବେଳେବେଳେ ସମୀକରଣର ସମାଧାନରେ ମିଳୁଥିବା ଦୁଇଟି ଉତ୍ତର ମଧ୍ୟରୁ ଗୋଟିଏ, ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଥିବାବେଳେ ଅନ୍ୟଟି ସିଦ୍ଧ କରୁ ନଥାଏ । ଏ କ୍ଷେତ୍ରରେ ସିଦ୍ଧ କରୁଥିବା ମୂଳଟି ପ୍ରଶ୍ନର ଉତ୍ତର ହୋଇଥାଏ ।

Odisha State Board BSE Odisha 10th Class Physical Science Important Questions Chapter 6 ଆଲୋକ- ପ୍ରତିଫଳନ ଓ ପ୍ରତିସରଣ Important Questions and Answers.

BSE Odisha 10th Class Physical Science Important Questions Chapter 6 ଆଲୋକ- ପ୍ରତିଫଳନ ଓ ପ୍ରତିସରଣ

Objective Type Questions with Answers 

A ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

1. ଆପତିତ ରଶ୍ମି ଓ ପ୍ରତିଫଳିତ ରଶ୍ମି ମଧ୍ଯରେ 80° କୋଣ ସୃଷ୍ଟି ହେଲେ ଆପତନ କୋଣର ପରିମାଣ କେତେ ଡିଗ୍ରୀ ?
ଉ –
0°

2. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷ ପୋଲ୍ ଉପରେ ଦର୍ପଣର ପୃଷ୍ଠପ୍ରତି କ’ଣ ହେବ ?
ଉ –
ଅଭିଲମ୍ବ

3. ପୋଲ୍ ଓ ବକ୍ରତା କେନ୍ଦ୍ର ମଧ୍ୟରେ ଥ‌ିବା ଦୂରତାକୁ କ’ଣ କହନ୍ତି ?
ଉ
ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ

4. ଦନ୍ତ ଚିକିତ୍ସକମାନେ କେଉଁ ଦର୍ପଣ ବ୍ୟବହାର କରନ୍ତି ?
ଉ
ଅବତଳ

5. ସାଧାରଣତଃ ଗାଡି ଚାଳକ ପଛପାଖ ଦେଖୁବାପାଇଁ ଗାଡ଼ିରେ କେଉଁ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଇଥାଏ ?
ଉ
ଉତ୍ତଳ

6. ପ୍ରତିସରଣରେ ଆପତନ କୋଣ ଶୂନହେଲେ ପ୍ରତିସରଣ କୋଣ କେତେ ଡିଗ୍ରୀ ହେବ ?
ଉ
45°

7. ବସ୍ତୁ ଅବତଳ ଦର୍ପଣର କେଉଁଠାରେ ରହିଲେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ବାସ୍ତବ, ଓଲଟା ଓ ସମାନ ଆକାରର ପ୍ରତିବିମ୍ବ ଗଠିତ. ହୁଏ ?
ଉ
ବକ୍ରତା କେନ୍ଦ୍ର

8. ସୋଲାର କୁକର୍‌ରେ କେଉଁ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ?
ଉ
ଅବତଳ ଦର୍ପଣ

9. ଅବତଳ ଦର୍ପଣରେ ବସ୍ତୁର କେଉଁ ଅବସ୍ଥାନ ପାଇଁ ପ୍ରତିବିମ୍ବ ପରିବର୍ଦ୍ଧିତ ଆଭାସୀ ଓ ସଳଖ ହେବ ?
ଉ
P ଓ F ମଧ୍ୟରେ

10. ଅବତଳ ଦର୍ପଣରେ ଫୋକସ୍ ଦୂରତା 10 cm ଓ ବସ୍ତୁଟି 20 cm ଦୂରରେ ଅଛି । ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି କ’ଣ ହେବ ?
ଉ
ବାସ୍ତବ ଓ ସମାନ

11. ପୋଠାରୁ ବସ୍ତୁର ଦୂରତାକୁ କେଉଁ ସଙ୍କେତଦ୍ୱାରା ଲେଖାଯାଏ ?
ଉ
u

12. ଗୋଟିଏ ଅବତଳ ଦର୍ପଣରେ ସୃଷ୍ଟ ପ୍ରତିବିମ୍ବ ଆଭାସୀ, ସଳଖ ଓ ବସ୍ତୁଠାରୁ ଆକାରରେ ବଡ଼ । ତାହାହେଲେ ବସ୍ତୁ କେଉଁଠି ଅବସ୍ଥିତ ?
ଉ
ଦର୍ପଣର ପୋଲ୍ ଓ ପ୍ରମୁଖ ଫୋକସ୍ ମଧ୍ୟରେ

13. ବର୍ତ୍ତୁଳ ଦର୍ପଣରେ ତୀର୍ଯ୍ୟକ୍ ଭାବରେ ଆଲୋକ ରଶ୍ମି ପୋଲ୍ ବିନ୍ଦୁଠାରେ ଆପତିତ ହେଲେ ତାହା କିପରି ଭାବରେ ପ୍ରତିଫଳିତ ହୁଏ ?
ଉ
ତୀର୍ଯ୍ୟକ୍ ଭାବରେ

14. ଅବତଳ ଦର୍ପଣ ନିକଟରେ 30 ସେ.ମି. ଦୂରରେ ଥ‌ିବା ବସ୍ତୁର ପ୍ରତିବିମ୍ବ 20 ସେ.ମି. ଦୂରରେ ଉତ୍ପନ୍ନ ହେଲା । ଲେନସ୍‌ର ଫୋକସ୍ ଦୂରତା କେତେ ?
ଉ
60 ସେ.ମି.

15. ବାସ୍ତବ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତାକୁ କେଉଁ ଚିହ୍ନ ରୂପେ ନିଆଯାଏ ?
ଉ
ବିଯୁକ୍ତାତ୍ମକ

16. ଏକ ଦର୍ପଣ ସମ୍ମୁଖରେ 6 m ଦୂରରେ ଗୋଟିଏ ବସ୍ତୁ ଏକ-ଚତୁର୍ଥାଂଶ ପରିବର୍ତ୍ତନ ସୃଷ୍ଟି କଲେ ଦର୍ପଣଟି କ’ଣ ହେବ ?
ଉ
ଉତ୍ତଳ

17. ପ୍ରମୁଖ ଅକ୍ଷର ଉପର ଆଡ଼କୁ +Y ଅକ୍ଷ ଦିଗରେ ଉଚ୍ଚତାର ଚିହ୍ନ କ’ଣ ?
ଉ
ଯୁକ୍ତାତ୍ମକ

18. u, v, f, R ସାଂଖିକ ମାନ ସ୍ଥାପନ କଲାବେଳେ ନୂତନ କେଉଁ ସଙ୍କେତ ପଥ ଅନୁସରଣ କରାଯାଏ ?
ଉ
କାର୍ଟେସିଆନ୍

19. ପରିବର୍ଦ୍ଧନ (m) ର ମୂଲ୍ୟ 1 ଠାରୁ କମ୍ ହେଲେ ପ୍ରତିବିମ୍ବର ଆକୃତିଟି କ’ଣ ହେବ ?
ଉ
ବସ୍ତୁର ଉଚ୍ଚତା ତୁଳନାରେ କ୍ଷୁଦ୍ର

20. ଆପତିତ ରଶ୍ମି ଓ ନିର୍ଗତ ରଶ୍ମି ମଧ୍ୟରେ ଥିବା ବ୍ୟବଧାନ ଦୂରତାକୁ କ’ଣ କହନ୍ତି ?
ଉ
ପାର୍ଶ୍ବବିସ୍ଥାପନ

21. ପରମ ପ୍ରତିସରଣାଙ୍କକୁ କେଉଁ ସଙ୍କେତ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଏ ?
ଉ
n₂₀

22. ଆଲୋକ 1.50 ପ୍ରତିସରଣାଙ୍କ ବିଶିଷ୍ଟ କାଚ ମଧ୍ୟକୁ ପ୍ରବେଶ କଲେ କାଚ ଭିତରେ ଆଲୋକର ବେଗ କେତେ ?
ଉ
2 × 10₈ m/s

23. ଆଲୋକର ବାୟୁରେ ବେଗ ଓ ଅନ୍ୟ ମାଧ୍ୟମରେ ବେଗର ଅନୁପାତକୁ କ’ଣ କୁହାଯାଏ ?
ଉ
ପରମ ପ୍ରତିସରଣାଙ୍କ

24. ପ୍ରତିସରଣାଙ୍କର ଏକକ କ’ଣ ଅଟେ ?
ଉ
ଏକକ ବିହୀନ

25. ବାୟୁ ତୁଳନାରେ ଜଳର ପ୍ରତିସରଣାଙ୍କ ମୁଁ \(\frac { 4 }{ 3 }\)। ଜଳ ତୁଳନାରେ ବାୟୁର ପ୍ରତିସରଣାଙ୍କ କେତେ ?
ଉ
0.75

26. କେଉଁ ମାଧ୍ୟମରେ ପ୍ରତିସରଣାଙ୍କ ସର୍ବନିମ୍ନ ?
ଉ
ଶୂନ୍ୟରେ

27. ଦର୍ପଣରେ ବକ୍ରତା କେନ୍ଦ୍ର ଦେଇ ଅତିକ୍ରମ କରୁଥିବା ଆଲୋକ ରଶ୍ମିର ଆପତନ କୋଣ କେତେ ?
ଉ
0°

28. ବାୟୁରେ ଆଲୋକର ବେଗ 3 x 10⁸ m/s ଓ ମାଧ୍ୟମରେ 1.25 x 10⁸ m/s ହେଲେ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କ କେତେ ?
ଉ
2.4

29. ଆୟତଘନାକାର କାଚ ସ୍ଲାବ୍‌ରେ କେତେ ଥର ପ୍ରତିସରଣ ହୁଏ ?
ଉ
ଦୁଇଥର

30. A, B, C ଓ Dର ପ୍ରତିସରଣାଙ୍କ ଯଥାକ୍ରମେ 1.5, 1.7, 1.3 ଓ 1.4 ହେଲେ କେଉଁଥିରେ ଆଲୋକର ବେଗ ସର୍ବାଧ‌ିକ ?
ଉ
C

31. ଏକ ସମତଳ ଦର୍ପଣରେ ଆପତନ କୋଣ 30° ହେଲେ ପ୍ରତିଫଳନ କୋଣଟି କେତେ ?
ଉ
30°

32. ଉତ୍ତଳ ଲେନ୍ସରେ କାହା ମଧ୍ୟଦେଇ ଗତି କରି ପ୍ରତିସୃତ ରଶ୍ମି ପ୍ରମୁଖ ଅକ୍ଷସହ ସମାନ୍ତର ଭାବେ ଗତିକରେ ?
ଉ
ଫୋକସ୍

33. ଲେନ୍ସର ସମସ୍ତ ଦୂରତା କେଉଁଠାରୁ ମପାଯାଏ ?
ଉ
ଆଲୋକ କେନ୍ଦ୍ର

34. ବସ୍ତୁର କେଉଁଠାରେ ଅବସ୍ଥାନ ପାଇଁ ଉଭଳ ଲେନ୍ସରେ ପ୍ରତିବିମ୍ବ ଅତ୍ୟନ୍ତ ବର୍ଣ୍ଣିତ ହୋଇଥାଏ ?
ଉ
F₁ ଠାରେ

35. ଏକ ଉତ୍ତଳ ଲେନ୍ସରେ ଆଭାସୀ ପ୍ରତିବିମ୍ବ ପାଇଁ ବସ୍ତୁକୁ କେଉଁଠାରେ ରଖୁବା ଆବଶ୍ୟକ ?
ଉ
F₁ ଓ O ମଧ୍ୟରେ

36. 10 ସେ.ମି. ଉଚ୍ଚତାର ଏକ ବସ୍ତୁ ଉତ୍ତଳ ଲେନ୍ସ ଆଗରେ ରଖିଲେ ତା’ର ପ୍ରତିବିମ୍ବ ଲେନ୍ସର ପଛପଟେ 10 ସେ.ମି. ଦୂରରେ ଗଠିତ ହେଲା । ତେବେ ବସ୍ତୁଟି ଲେନ୍ସର କେଉଁଠାରେ ଥିଲା ।
ଉ
2F₁ ଠାରେ

37. ଏକ ଉତ୍ତଳ ଲେନ୍ସର-ଫୋକସ୍ ଦୂରତା 10 ସେ.ମି. ବସ୍ତୁକୁ କେଉଁଠାରେ ରଖୁଲେ ବସ୍ତୁଟି ଓଲଟା ଓ ବସ୍ତୁର ଆକାର ସହ ସମାନ ଆକାରର ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ?
ଉ
20 ସେ.ମି ଦୁରରେ

38. ଉତ୍ତଳ ଲେନ୍ସ ଆଡ଼କୁ ବସ୍ତୁଟି ଗତିକଲେ ପ୍ରତିବିମ୍ବର ଆକାରରେ କ’ଣ ପରିବର୍ତ୍ତନ ହୁଏ ?
ଉ
ସମାନ ରହେ

39. ଅବତଳ ଲେନସ୍‌ରେ ପରିବର୍ତନ ସର୍ବଦା କେତେ ?
ଉ
1 ଠାରୁ ସାନ

40, ଗୋଟିଏ ଉତ୍ତଳ ଲେନସ୍‌ର ସମ୍ମୁଖରେ ବସ୍ତୁ କେଉଁଠି ରହିଲେ ସମାନ ଆକାରର ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ମିଳିପାରିବ ?
ଉ
ଫୋକସ୍ ଦୂରତାର 2 ଗୁଣ ଦୂରତାରେ

41. ଉତ୍ତର ଲେନ୍ସର ପରିବର୍ଜନ – 1 ହେଲେ ବସ୍ତୁଟି ଲେନ୍ସର କେଉଁଠାରେ ରହିବ ?
ଉ
2F₁ ଠାରେ

42. ଉତ୍ତଳ ଲେନ୍ସରେ 4 ଗୁଣ ପରିବର୍ତ୍ତନ ହୋଇ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ଲେନ୍ସଠାରୁ 60 ସେ.ମି. ଦୂରରେ ଗଠିତ ହେଲେ ଉତ୍ତଳ ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତା କେତେ ?
ଉ
12 ସେ.ମି.

43. ଉତ୍ତଳ ଲେନସ୍‌ର ପରିବର୍ଦ୍ଧନ +6 ହେଲେ ବସ୍ତୁଟି କେଉଁଠି ରହିବ ?
ଉ
f ଓ O ମଧ୍ୟରେ

44. କାର୍ଟେସିଆନ୍ ପ୍ରଥା ଅନୁଯାୟୀ ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତାର ସୂତ୍ର କ’ଣ ?
ଉ
f = \(\frac { uv }{ u-v }\)

45. ଉତ୍ତଳ ଲେନ୍ସରେ 0.09 m ଦୂରରେ ଅବସ୍ଥିତ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ 36 cm ଠାରେ ଗଠିତ ହେଲେ ପରିବର୍ତ୍ତନ କେତେ ?
ଉ
40

46. ଲେନ୍ସଗୁଡ଼ିକର ପାୱାର P₁, P₂, ଓ P₃, ହେଲେ ସମୂହ ପାୱାର P = କେତେ ?
ଉ
P₁ + P₂ + P₃

47. 25 cm ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଏକ ଅବତଳ ଲେନ୍ସର ପାୱାର କେତେ ?
ଉ
– 4D

48. ପାୱାର 4D ବିଶିଷ୍ଟ ଉତ୍ତଳ ଲେନ୍ସ କାନ୍ଥଠାରୁ 50 ସେ.ମି. ଦୂରରେ ଅଛି । ଗୋଟିଏ ବସ୍ତୁକୁ କେତେ ଦୂରତାରେ ରଖିଲେ ଏହାର ବାସ୍ତବ ପ୍ରତିବିମ୍ବ କାନ୍ଥରେ ପଡ଼ିବ ?
ଉ
50 ସେ.ମି.

49. A ଓ B ଉଁଭଳ ଲେନ୍‌ସଦ୍ବୟର ଫୋକସ୍ ଦୂରତା ଯଥାକ୍ରମେ 5 ସେ.ମି. ଓ 50 ସେ.ମି. । ଉକ୍ତ ଲେନ୍ସଦ୍ଵୟ ମଧ୍ୟରୁ କାହାର ପାୱାର କେତେ ?
ଉ
20 D ଓ 2 D

50. ଆୟତଘନାକାର କାଚର ମୋଟେଇ କମିଲେ ପାର୍ଶ୍ଵବିସ୍ଥାପନର ପରିମାଣ କ’ଣ ହେବ ?
ଉ
ପ୍ରଥମେ କମେ ଓ ପରେ ବଢ଼େ,

51. ଲେନସ୍‌ର ଫୋକସ୍ ଦୂରତା 20 ସେ.ମି. ହେଲେ ତାହାର ପାୱାର କେତେ ?
ଉ
5D

52. ମାଧ୍ୟମର ପରମ ପ୍ରତିସରଣାଙ୍କ ସେହି ମାଧ୍ୟମରେ ଆଲୋକର ବେଗ ପରସ୍ପରସହ କ’ଣ ?
ଉ
ସମାନ

53. ଉପରୁ ଏକ ଜଳପୂର୍ଣ ଟ୍ୟାଙ୍କକୁ ଚାହିଁଲେ 3m ଗଭୀର ଜଣାପଡ଼େ । ଜଳର ପ୍ରତିସରଣାଙ୍କ 4/3 ହେଲେ ଟାଙ୍କିର ପ୍ରକୃତ ଗଭୀରତା
ଉ
4m

54. ଏକ ଅବତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା 10cm | ଦନ୍ତର ବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ଦେଖୁବାପାଇଁ ଜଣେ ଦାନ୍ତ ଓ ଦର୍ପଣକୁ କେତେ ଦୂରରେ ରଖୁବ ?
ଉ
8cm

55. ପତନ ରଶ୍ମି ଓ ଦର୍ପଣ ମଧ୍ୟରେ କୋଣର ପରିମାଣ 60° ହେଲେ ଆପତିତରଶ୍ମି ଓ ପ୍ରତିଫଳିତ ରଶ୍ମି ମଧ୍ୟରେ କୋଣର
ଉ
120⁰

56. ସିଧାସଳଖ ଲେନସ୍‌ ପାୱାର ମାପିବାପାଇଁ ବ୍ୟବହୃତ ଯନ୍ତ୍ରଟିର ନାମ କ’ଣ ?
ଉ
ଜେନିଭାଲେନ୍ସ ମାପକ

B ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ବିକୀର୍ଶନ ପରିଘଟଣାକୁ ବୁଝାଇବା ପାଇଁ ଆଲୋକକୁ ଏକ ………………. କହନ୍ତି ।
2. ବକ୍ରପୃଷ୍ଠଥବା ଦର୍ପଣକୁ ……………….. କହନ୍ତି ।
3. ଅବତଳ ଦର୍ପଣର ବକ୍ର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଗୋଲକର ………………….. ଆଡ଼କୁ ରହିଥାଏ ।
4. ଉତ୍ତଳ ଦର୍ପଣର ବଜ୍ର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଗୋଲକର ………………….. ର ବିପରୀତ ଦିଗରେ ଥାଏ ।
5. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ମଧ୍ୟବିନ୍ଦୁକୁ ………………… କହନ୍ତି ।
6. ପୋଲ୍ P ଓ ବକ୍ରତାକେନ୍ଦ୍ର C ମଧ୍ୟରେ ଥ‌ିବା ଦୂରତା PC କୁ ……………….. କହନ୍ତି ।
7. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପୋଲ୍ ଓ ଫୋକସ୍ ମଧ୍ୟରେ ଥିବା ଦୂରତାକୁ ……………… କହନ୍ତି ।
8. ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ଵାରକଠାରୁ ………………….. |
9. ……………. ଦର୍ପଣରେ ବସ୍ତୁର ସଳଖ ଓ ପରିବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ଦେଖହୁଏ ।
10. ଦର୍ପଣର ସୂତ୍ରଟି …………………. |
11. ଅବତଳ ଦର୍ପଣର ‘C’ ଠାରେ ବସ୍ତୁର ଅବସ୍ଥିତି ହେଲେ ପ୍ରତିବିମ୍ବର ଅବସ୍ଥିତି ………………….. ଠାରେ ହୋଇଥାଏ ।
12. ଅବତଳ ଦର୍ପଣର F ଠାରେ ବସ୍ତୁର ସ୍ଥିତି ପାଇଁ ପ୍ରତିବିମ୍ବର ସ୍ଥିତି ……………….. ଠାରେ ହୋଇଥାଏ ।
13. ………………… ଦର୍ପଣରେ ସର୍ବଦା ଆଭାସୀ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
14. ମୁଖ୍ୟ ଅକ୍ଷ ପ୍ରତି ସମାନ୍ତର ରଶ୍ମିଗୁଚ୍ଛ ପ୍ରତିଫଳନ ପରେ ଅବତଳ ଦର୍ପଣରେ ………………. ମଧ୍ୟରେଇ ଯାଏ |
15. ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ସମ୍ମୁଖରେ X ସେ.ମି. ଦୂରତାରେ ଅବସ୍ଥିତ ଏକ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ସେହି ସ୍ଥାନରେ ସୃଷ୍ଟି ହେଲେ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ……………………….. ସେ.ମି. ହେବ ।
16. ………………… ପ୍ରତିଫଳନ ପୃଷ୍ଠର ବିସ୍ତୃତି ସୂଚାଏ ।
17. ଦର୍ପଣ ଉପରେ …………………. ଦିଗରୁ ଆଲୋକ ରଶ୍ମି ଆପତିତ ହୁଏ ।
18. …………….. ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ଯୁକ୍ତାତ୍ମକ ।
19. ଶୂନ୍ୟରେ ଆଲୋକର ବେଗ ……………….. ମି. /ସେ. |
20. କ୍ରାଉନ୍ କାଚର ପ୍ରତିସରଣାଙ୍କ …………………. |
21. ………………….. ର ପ୍ରତିସରଣାଙ୍କ ସର୍ବାଧ‌ିକ ।
22. ଲେନସ୍‌ର ……………………… ବିନ୍ଦୁଦେଇ ଯାଇଥ‌ିବା ରଶ୍ମି ବିପଥନ ହୁଏ ନାହିଁ ।
23. ……………… ଲେନ୍‌ସକୁ ଅଭିସାରୀ ଲେନ୍ସ କହନ୍ତି ।
24. ଲେନ୍ସର ପାୱାରକୁ ………………………. ଏକକରେ ମପାଯାଏ ।
25. ଲେନ୍ସର ମଧ୍ୟବିନ୍ଦୁକୁ ………………… କହନ୍ତି ।
26. ସମତଳ ଦର୍ପଣର ପରିବର୍ଦ୍ଧନ …………………….. |
27. ଲେନ୍ସର ସମସ୍ତ ଦୂରତା ଲେନ୍ସର …………….. ଠାରୁ ମପାଯାଏ ।
28. …………………….. ଦର୍ପଣରେ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
29. 4 ମିଟର ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଅବତଳ ଲେନ୍‌ସର ପାୱାର ……………….. ଡାୟପଟର୍ ।
30. ଆଲୋକ ପ୍ରତିସରଣ ନିୟମର ଆବିଷ୍କାରକ ………………………. |
31. ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ଓ ବକ୍ରତା ବ୍ୟାସାର୍ଷର ଅନୁପାତ …………………….. |
32. ଅବତଳ ଦର୍ପଣରେ ଫୋକସ୍ ଦୂରତା 10 cm ଓ ବସ୍ତୁଟି 20 cm ଦୂରରେ ଅଛି । ତେବେ ପ୍ରତିବିମ୍ବଟି ……………………. ହେବ ।
33. …………………… ଲେନ୍ସରେ ସର୍ବଦା ଆଭାସୀ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
34. ବସ୍ତୁର ଅବସ୍ଥିତି 2F₁ ଠାରେ ଥିଲେ ଉତ୍ତଳ ଲେନ୍ସର ପ୍ରତିବିମ୍ବ ଠାରେ ………………………. ଗଠିତ ହେବ ।
35. ଲେନସ୍ ଗୁଡ଼ିକର ପାୱାର P₁, P₂, P₃, ହେଲେ ସମୂହ ମୋଟ ପାୱାର P = …………… ହେବ ।
36. +2.0 D ଓ +0.25 D ପାୱାର ବିଶିଷ୍ଟ ଲେନ୍ସ ମିଶିଲେ ତାହା ଗୋଟିଏ …………………. D ପାୱାର ବିଶିଷ୍ଟ ଲେନ୍ସସର ସମତୁଲ୍ୟ ହୁଏ ।
37. ଲେନ୍ସ ଅଣୁବୀକ୍ଷଣରେ …………………. ଭାବେ ବ୍ୟବହୃତ ହୁଏ ।
38. ଗୋଟିଏ ଚାମଚର ଭିତର ପାଖ …………………….. ଦର୍ପଣ ଆକାରର ।
39. ସମତଳ ଦର୍ପଣରେ ଦର୍ପଣଠାରୁ ବସ୍ତୁର ଦୂରତା ଓ ପ୍ରତିବିମ୍ବର ଦୂରତା ………………….. |
40. ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ଓ ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧର ଅନୁପାତ ……………………… |

Answer:
1. ତରଙ୍ଗ
2. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ
3. କେନ୍ଦ୍ର
4. କେନ୍ଦ୍ର
5. ପୋଲ୍
6. ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ
7. ଫୋକସ୍ ଦୂରତା
8. ବହୁତ ବେଶୀ
9. ଅବତଳ ଦର୍ପଣ
10. \(\frac { 1 }{ u }\) + \(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\)
11. C
12. ଅନନ୍ତ ଦୂରତା
13. ଉତ୍ତଳ ଦର୍ପଣ
14. ଫୋକସ୍
15. \(\frac { X }{ 2 }\)
16. ଦ୍ବାରକ
17. ବାମ
18. ଉତ୍ତଳ
19. 3 × 10⁸ ମି. / ସେ.
20. 1.52
21. ହୀରା
22. ଆଲୋକ କେନ୍ଦ୍ର
23. ଉତ୍ତଳ
24. ଡାୟପ୍‌ର
25. ଆଲୋକ କେନ୍ଦ୍ର
26. (+1)
27. ଆଲୋକ କେନ୍ଦ୍ର
28. ଅବତଳ
29. (-0.25)
30. ସ୍ଲେଲ୍
31. (1:2)
32. ବାସ୍ତବ ଓ ସମାନ
33. ଅବତଳ
34. 2F₂
35. P = P₁ + P₂ + P₃
36. +2.25 D
37. ଅଭିଦୃଶ୍ୟକ
38. ଅବତଳ
39. ସମାନ
40. 1 : 2 କିମ୍ବା 0.5

C ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓) ବା ଭୁଲ ଉକ୍ତି ପାଇଁ (x) ଲେଖ ।

1. ଅନେକ ଆଲୋକୀୟ ଯନ୍ତ୍ରରେ ଏକାଧିକ ଲେନ୍ସ ବ୍ୟବହାର କରାଯାଇଥାଏ ।
2. ଉତ୍ତଳ ଲେନ୍ସର ପାୱାର୍ ବିଯୁକ୍ତାତ୍ମକ ।
3. ଲଘୁ ମାଧ୍ୟମରୁ ଘନ ମାଧ୍ୟମକୁ ଆଲୋକ ଗତି କଲେ ତାହାର ବେଗ ବଢ଼ିଯାଏ ।
4. ବର୍ତ୍ତୁଳାକାର ଲେନ୍ସ ମଝିରେ ଯେଉଁ କ୍ଷୁଦ୍ର ବୃତ୍ତାକାର ପରିସୀମା ଭିତରେ ଲେନ୍ସ ପ୍ରତିସରଣ କରେ ତାହାର ବ୍ୟାସକୁ ଲେନ୍ସର ଦ୍ଵାରକ କୁହାଯାଏ ।
5. ଅବତଳ ଲେନ୍ସରେ ସର୍ବଦା କ୍ଷୁଦ୍ର, ସଳଖ ଓ ଆଭାସୀ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୁଏ ।
6. ଅବତଳ ଦର୍ପଣର x cm ଦୂରରେ ଅବସ୍ଥିତ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ସେହିଠାରେ ସୃଷ୍ଟି ହେଲେ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା 2x ସେ. ମି. |
7. ଗୋଟିଏ ଅବତଳ ଦର୍ପଣରେ ବସ୍ତୁର ଦୂରତା – 10 cm ଓ ଫୋକସ୍ ଦୂରତା + 15 cm ହେଲେ ପ୍ରତିବିମ୍ବର ଦୂରତା + 6 |
8. ଅବତଳ ଦର୍ପଣ କ୍ଷେତ୍ରରେ ବସ୍ତୁର ଅବସ୍ଥାନ ଓ ପ୍ରତିବିମ୍ବ ମଧ୍ଯରେ ସର୍ବନିମ୍ନ ଦୂରତା 0 |
9. ବସ୍ତୁର ଏକ-ପଞ୍ଚମାଂଶ ଆକାରର ପ୍ରତିବିମ୍ବ ଦର୍ପଣଠାରୁ 18 ସେ.ମି. ଦୂରତାରେ ଗଠିତ ହେଲା । ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା 18 ସେ.ମି. ।
10. ଦୁଇଟି ପ୍ରତିଫଳିତ ରଶ୍ମିର ପ୍ରତିଚ୍ଛେଦ ବିନ୍ଦୁରେ ସଳଖ ଆକାରର ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୁଏ ।
11. ବର୍ତ୍ତୁଳ ଦର୍ପଣରେ ତୀର୍ଯ୍ୟକ୍ ଭାବରେ ଆଲୋକ ରଶ୍ମି ପୋଲ୍ ବିନ୍ଦୁଠାରେ ଆପତିତ ହେଲେ ତାହା ତୀର୍ଯ୍ୟକ୍ ଭାବେ ପ୍ରତିଫଳିତ ହୁଏ ।
12. ଅବତଳ ଦର୍ପଣ ନିକଟରେ 30 ସେ.ମି. ଦୂରରେ ଥ‌ିବା ବସ୍ତୁର ପ୍ରତିବିମ୍ବ 20 ସେ.ମି. ଦୂରରେ ଉତ୍ପନ୍ନ ହେଲା । ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା 60 ସେ.ମି. ।
13. ଏକ ବର୍ତ୍ତୁଳ ଦର୍ପଣର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ଓ ଫୋକସ୍ ଦୂରତା ଯଥାକ୍ରମେ R ଓ f ହେଲେ, R = 2f ।
14. ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ଆଗରେ 10 cm ଦୂରରେ ବସ୍ତୁଟି ରଖିଲେ 3 ଗୁଣ ପରିବର୍ଦ୍ଧିତ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ପାଇଁ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ 20 cm ଦୂରରେ ଗଠିତ ହେବ ।
15. ପରିବର୍ଦ୍ଧନ m = + 0.6 ଓ ବସ୍ତୁର ଉଚ୍ଚତା h₁ = 5 cm ହେଲେ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା 3 cm |
16. 20 cm ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଅଭିସାରୀ ଦର୍ପଣ ସମ୍ମୁଖରେ 15 cm ଦୂରରେ ବସ୍ତୁଟି ରହିଲେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ – 30 cm |
17. 2 cm ଉଚ୍ଚତା ବିଶିଷ୍ଟ ବସ୍ତୁର ଅବତଳ ଦର୍ପଣରେ ପରିବର୍ତ୍ତନ 20 cm ହେଲେ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା 40 cm |
18. ପତିତ ରଶ୍ମି ଓ ନିର୍ଗତ ରଶ୍ମି ମଧ୍ୟରେ ଥିବା ବ୍ୟବଧାନ ଦୂରତାକୁ ପାର୍ଶ୍ଵ ବିସ୍ଥାପନ କହନ୍ତି ।
19. ପରମ ପ୍ରତିସରଣାଙ୍କକୁ n₁₂ ସଙ୍କେତ ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଏ ।
20. ଆଲୋକ 1.50 ପ୍ରତିସରଣାଙ୍କ ବିଶିଷ୍ଟ କାଚ ମଧ୍ୟକୁ ପ୍ରବେଶ କଲେ କାଚ ଭିତରେ ଆଲୋକର ବେଗ 2 x 10⁸ m/s |
21. ଏକ ପ୍ରତିସରଣ ପୃଷ୍ଠରେ ଆପତନ କୋଣ 60° ଓ ପ୍ରତିସରଣ କୋଣ 30° ହେଲେ ପ୍ରତିସରଣାଙ୍କ 3 |
22. ସୋଲାର କୁକର୍‌ରେ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।

Answer:
1.✓
2. x
3. F
4. ✓
5. ✓
6. x
7. ✓
8. ✓
9. x
10. x
11.✔
12.✔
13.✔
14. x
15. ✔
16.✔
17.✔
18.✔
19. x
20. ✓
21. ✓
22. x

D ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେଖ ।

E ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

1. ଆଲୋକର ବିକୀର୍ଶନ କାହାକୁ କହନ୍ତି ?
ଉ
ସରଳରେଖାରେ ଗତି କରୁଥିବା ଆଲୋକ ରଶ୍ମି ଗତିପଥରେ ଏକ କ୍ଷୁଦ୍ର ଅସ୍ଵଚ୍ଛ ବସ୍ତୁ ରଖିଲେ ଆଲୋକ ସେହି ଅତିକ୍ଷୁଦ୍ର ବସ୍ତୁ ପାଖରେ ବାଙ୍କିଯାଏ, ଏହାକୁ ଆଲୋକର ବିକୀର୍ଣ୍ଣନ କହନ୍ତି ।

2. ଧୁନିକ କ୍ୱାଣ୍ଟମ୍ ତତ୍ତ୍ବ କ’ଣ ?
ଉ –
ଆଲୋକ କେବଳ ତରଙ୍ଗ ନୁହେଁ କି କେବଳ କଣିକା ନୁହେଁ । ଆଲୋକ ତରଙ୍ଗ ଓ କଣିକା ଉଭୟର ଗୁଣ ପ୍ରଦର୍ଶନ କରେ । ଏହାକୁ ଆଲୋକର ଚୈତ ପ୍ରକୃତି କୁହାଯାଏ ।

3. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ କାହାକୁ କହନ୍ତି ?
ଉ –
ବକ୍ରପୃଷ୍ଠ ବିଶିଷ୍ଟ ପ୍ରତିଫଳନକାରୀ ଦର୍ପଣକୁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ କହନ୍ତି ।

4. ଅବତଳ ଦର୍ପଣ କାହାକୁ କହନ୍ତି ?
ଭ –
ଯେଉଁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଭିତର ଆଡକୁ ବକ୍ର ହୋଇ ରହିଥାଏ ତାହାକୁ ଅବତଳ ଦର୍ପଣ କୁହାଯାଏ । ଉତ୍ତଳ ଦର୍ପଣ କାହାକୁ କହନ୍ତି ?

5. ଡତ୍ତଳ ଦର୍ପଣ କାହାକୁ କହନ୍ତି ?
ଉ –
ଯେଉଁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ବାହାର ଆଡକୁ ବକ୍ର ହୋଇ ରହିଥାଏ ତାହାକୁ ଉତ୍ତଳ ଦର୍ପଣ କୁହାଯାଏ ।

6. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପୋଲ୍ କାହାକୁ କହନ୍ତି ?
ଉ –
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବକ୍ର ପ୍ରତିଫଳନ ପୃଷ୍ଠର ମଧ୍ୟବିନ୍ଦୁକୁ ପୋଲ୍ କହନ୍ତି । ଏହା ସାଧାରଣତଃ (P) ଅକ୍ଷର ଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ ।

7. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବଜ୍ରତା କେନ୍ଦ୍ର କାହାକୁ କହନ୍ତି ?
ଉ –
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ଯେଉଁ ଗୋଲକର ଅଂଶ ହୋଇଥାଏ ସେହି ଗୋଲକର କେନ୍ଦ୍ରକୁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବକ୍ରତା କେନ୍ଦ୍ର କହନ୍ତି ।

8. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ କାହାକୁ କହନ୍ତି ?
ଭ –
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ଯେଉଁ ଗୋଲକର ଅଂଶ ହୋଇଥାଏ, ସେହି ଗୋଲକର ବ୍ୟାସାର୍ଷକୁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର୍ ବଜ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ କହନ୍ତି ।

9. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷ କାହାକୁ କହନ୍ତି ?
ଉ –
ଯେଉଁ ସରଳରେଖା ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପୋଲ୍ ବକ୍ରତା କେନ୍ଦ୍ରକୁ ଯୋଗକରେ ତାହାକୁ ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷ

10. ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ କାହାକୁ କହନ୍ତି ?
ଉ –
ମୁଖ୍ୟ ଅକ୍ଷ ସହ ସମାନ୍ତର ହୋଇ ଆପତିତ ହେଲା ପରେ ପ୍ରତିଫଳିତ ରଶ୍ମିଗୁଡ଼ିକ ଗୋଟିଏ ବିନ୍ଦୁରୁ ଆସିଲା ପରି ଜଣାପଡ଼େ । ଏହି ବିନ୍ଦୁକୁ ଉତ୍କଳ ଦର୍ପଣର ପ୍ରମୁଖ ଫୋକସ୍ କହନ୍ତି ।

11. ଦର୍ପଣର ଦ୍ଵାରକ କାହାକୁ କହନ୍ତି ?
ଉ –
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠର ବ୍ୟାସକୁ ଦର୍ପଣର ଦ୍ଵାରକ କହନ୍ତି ।

12. ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ଓ ଫୋକସ୍ ମଧ୍ୟରେ ଥ‌ିବା ସମ୍ପର୍କଟି ଲେଖ ।
ଉ –
ଏକ କ୍ଷୁଦ୍ର ଦ୍ବାରକ ବିଶିଷ୍ଟ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ବଜ୍ରତା ବ୍ୟାସାର୍କ, ଏହାର ଫୋକସ୍ ଦୂରତାର ଦୁଇଗୁଣ ଅଟେ । R = 2f

13. ଗୋଟିଏ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ 20 ସେ.ମି. ହେଲେ ଫୋକସ୍‌ର ଦୂରତା କେତେ ?
ଉ

14. ଯାନବାହାନର ପଛପାଖ ଦେଖୁବାପାଇଁ କାହିଁକି ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ?
ଉ –
ଉତ୍ତଳ ଦର୍ପଣରେ ବସ୍ତୁର ସର୍ବଦା ସଳଖ ଓ କ୍ଷୁଦ୍ର ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ଏବଂ ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳ ଦୃଶ୍ୟ ହୋଇଥାଏ । ତେଣୁ ଯାନବାହାନରେ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।

15. ଗୋଟିଏ ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ନିଶ୍ଚୟ କର, ଯାହାର ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ 32 ସେ.ମି. ।
ଉ –
R = 32 ସେ.ମି..,
R = 2f ⇒ f = \(\frac { R }{ 2 }\) = \(\frac { 32 }{ 2 }\) = 16 ସେ.ମି.., |
∴ ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା 16 ସେ.ମି..,

16. ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ସମ୍ମୁଖରେ 10 ସେ.ମି. ଦୂରରେ ଗୋଟିଏ ବସ୍ତୁ ରଖିଲେ ସେହି ଦର୍ପଣ 3 ଗୁଣ ପରିବର୍ତ୍ତିତ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ଗଠନ କରେ । ପ୍ରତିବିମ୍ବର ଅବସ୍ଥିତି ନିର୍ଣ୍ଣୟ କର ।
ଉ –
m = -3, u = – 10 cm
m = \(\frac { h’ }{ h }\) = – \(\frac { v }{ u }\) ⇒ – 3 = – \(\frac { v }{ u }\)
∴ v = 3u = 3 x (−10) = − 30 ସେ.ମି.., |
∴ ଦର୍ପଣ ଠାରୁ 30 ସେ.ମି. ଦୂରରେ ବସ୍ତୁଥ‌ିବା ପାର୍ଶ୍ଵରେ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ।

17. ନୂତନ କାର୍ଟେସିଆନ ସଙ୍କେତ ପ୍ରଥା କାହାକୁ କହନ୍ତି ?
ଉ –
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ପ୍ରତିଫଳନ ସମ୍ପର୍କରେ ଆଲୋଚନା କଲାବେଳେ ସାଧାରଣ ଭାବେ ଆଦୃତ ସଙ୍କେତ ପ୍ରଥା ସମୁହକୁ ଅନୁସରଣ କରାଯାଏ । ଏହାକୁ ନୂତନ କାର୍ଟେସିଆନ ସଙ୍କେତ ପ୍ରଥା କହନ୍ତି ।

18. ବସ୍ତୁ ଦୂରତା କାହାକୁ କହନ୍ତି ?
ଉ –
ଗୋଟିଏ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ଏହାର ପୋଠାରୁ ବସ୍ତୁର ଦୂରତାକୁ ବସ୍ତୁ ଦୂରତା (u) କୁହାଯାଏ ।

19. ପ୍ରତିବିମ୍ବର ଦୂରତା କାହାକୁ କୁହାଯାଏ ?
ଉ –
ଦର୍ପଣର ପୋଠାରୁ ପ୍ରତିବିମ୍ବର ଦୂରତାକୁ ପ୍ରତିବିମ୍ବ ଦୂରତା (v) କୁହାଯାଏ ।

20. ଆଲେକର ପ୍ରତିସରଣ କାହାକୁ କହନ୍ତି ?
ଉ–
ଆଲୋକ ରଶ୍ମି ଗୋଟିଏ ମାଧ୍ୟମରୁ ଅନ୍ୟ ଏକ ମାଧ୍ୟମକୁ ଗତିକଲା ବେଳେ ଉଭୟ ମାଧ୍ୟମର ବ୍ୟବଧାନ ପୃଷ୍ଠରେ ଦିଗ ପରିବର୍ତ୍ତନ କରି ଦ୍ୱିତୀୟ ମାଧ୍ୟମରେ ଗତି କରିବାକୁ ଆଲୋକର ପ୍ରତିସରଣ କୁହାଯାଏ ।

21. ପାର୍ଶ୍ଵ ବିସ୍ଥାପନ କାହାକୁ କହନ୍ତି ?
ଉ –
ଆପତିତ ରଶ୍ମି ଓ ନିର୍ଗତ ରଶ୍ମି ମଧ୍ୟରେ ଥିବା ଲମ୍ବ ଦୂରତ୍ବକୁ ପାର୍ଶ୍ଵ ବିସ୍ଥାପନ କହନ୍ତି ।

22. ଆଲୋକ ପ୍ରତିସରଣର ପ୍ରଥମ ନିୟମ ଲେଖ ।
ଉ –
ଆପତିତ ରଶ୍ମି, ପ୍ରତିସୃତ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁରେ ଦୁଇଟି ସ୍ଵଚ୍ଛ ମାଧ୍ୟମର ବ୍ୟବଧାନ ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ ଅଭିଲମ୍ବ ଗୋଟିଏ ସମତଳରେ ରହେ ।

23. ଆଲୋକ ପ୍ରତିସରଣର ଦ୍ବିତୀୟ ନିୟମ ଲେଖ । କିମ୍ବା, ସ୍ମେଲଙ୍କ ପ୍ରତିସରଣ ନିୟମ ଲେଖ ।
ଉ –
ଦୁଇଟି ନିର୍ଦ୍ଦିଷ୍ଟ ମାଧ୍ୟମ ଓ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ବଣ୍ଟର ଆଲୋକ ପାଇଁ ଆପତନ କୋଣର ସାଇନ୍ ଓ ପ୍ରତିସରଣ କୋଣର ସାଇନ୍‌ର ଅନୁପାତ ଏକ ସ୍ଥିରାଙ୍କ ।

24. ପରମ ପ୍ରତିସରଣାଙ୍କ କଣ ?
ଉ –
ଶୂନ୍ୟ ମାଧ୍ୟମ ତୁଳନାରେ ଦ୍ଵିତୀୟ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କକୁ ଦ୍ୱିତୀୟ ମାଧ୍ୟମର ପରମ ପ୍ରତିସରଣାଙ୍କ କହନ୍ତି ।

25. ଉତ୍ତଳ ଲେନ୍ସକୁ ଅଭିସାରୀ ଲେନସ୍ କାହିଁକି କୁହାଯାଏ ?
ଉ –
ଉତ୍ତଳ ଲେନସ୍ ଆଲୋକ ରଶ୍ମିକୁ କେନ୍ଦ୍ରାଭିମୁଖୀ କରେ । ତେଣୁ ଉତ୍ତଳ ଲେନ୍ସକୁ ଅଭିସାରୀ ଲେନ୍ସ କହନ୍ତି ।

26. ଲେନସ୍‌ର ଦ୍ଵାରକ କାହାକୁ କହନ୍ତି ?
ଉ –
ବର୍ତ୍ତୁଳାକାର ଲେନସ୍‌ର ମଝିରେ ଯେଉଁ କ୍ଷୁଦ୍ର ବୃତ୍ତାକାର ପରିସୀମା ଭିତରେ ଲେନସ୍ ପ୍ରତିସରଣ କରେ ତାହାର ବ୍ୟାସକୁ ଲେନସ୍‌ର ଦ୍ଵାରକ କୁହାଯାଏ ।

27. ଲେନସ୍‌ର ପାୱାର୍‌ କ’ଣ ?
ଉ –
ଲେନସ୍‌ଦ୍ୱାରା ହେଉଥ‌ିବା ଅଭିସାରଣ ବା ଅପସାରଣର ମାତ୍ରାକୁ ଲେନସ୍‌ର ପାୱାର କହନ୍ତି । କିମ୍ବା, ଗୋଟିଏ ଲେନସ୍‌ର ଫୋକସ୍ ଦୂରତାର ବିଲୋମୀକୁ ଲେନସ୍‌ର ପାୱାର କହନ୍ତି ।

28. ଲେନସ୍‌ର ପାୱାର ଏକକ କ’ଣ ଓ ଡାୟପ୍‌ଟର କଣ ?
ଉ –
ଲେନସ୍‌ର ପାୱାରର ଏକକ ଡାୟପ୍‌ଟର (D) ।
1 ମିଟର ଫୋକସ୍ ଦୂରତା ଥିବା ଲେନସ୍‌ର ପାଓ୍ବାରକୁ 1 ଡାୟପ୍‌ଟର କହନ୍ତି ।
1D = 1 ମି^-1. ବା 1m^-1.

29. ଅବତଳ ଲେନସ୍‌ର ଫୋକସ୍ ଦୂରତା 2 ମି. ହେଲେ, ତାହାର ପାୱାର କେତେ ?
ଭ –
P = \(\frac { 1 }{ f }\) = – \(\frac { 1 }{ 2 }\) ମି. =- 0.5 ଡାୟପ୍‌ଟର ।

30. ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି କ’ଣ ହେବ ଯେତେବେଳେ ପରିବର୍ତ୍ତନ + 4 ହେବ ।
ଉ –
ପ୍ରତିବିମ୍ବଟି ଆଭାସୀ, ସଳଖ ଓ ବର୍ଣ୍ଣିତ ଏବଂ ଦର୍ପଣର ପଛପଟେ ସୃଷ୍ଟି ହେବ ।

31. କାର୍‌ର ହେଡ୍‌ଲାଇଟ୍‌ରେ ଅବତଳ ଦର୍ପଣ କାହିଁକି ବ୍ୟବହାର କରାଯାଏ ?
ଉ –
କାରର ହେଡ୍‌ଲାଇଟ୍‌ର ପ୍ରତିଫଳକ ରୂପେ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ କାରଣ ଆଲୋକ ରଶ୍ମି ଅଧ୍ଵ ଦୂରକୁ ପଡେ ।

32. ଯାନର ପଛପାର୍ଶ୍ଵ ଦେଖିବା ପାଇଁ କେଉଁ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ଓ କାହିଁକି ?
ଉ –
ଯାନର ପଛ ପାର୍ଶ୍ୱ ଦେଖିବା ପାଇଁ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ । ସଳଖ, ଆଭାସୀ ଓ କ୍ଷୁଦ୍ର ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ । ଯାନର ପଛପଟେ ଥିବା ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳର ଦୃଶ୍ୟ ଦର୍ପଣରେ ପରିଷ୍କାର ଦେଖ୍ହୁଏ ।

33. ଗୋଟିଏ ଲେନ୍ସର ପାୱାର – 2.0 D । ଏହାର ଫୋକସ୍ ଦୂରତା କେତେ ? ଏହା କି ପ୍ରକାର ଲେନସ୍ ?
ଭ –
P = – 2.0 D,
P = \(\frac { 1 }{ f }\) ⇒ f = \(\frac { 1 }{ P }\) = \(\frac { 1 }{ -2.0 }\) ମି.
= – \(\frac { 1 }{ 2 }\) × 100 ସେ. ମି. = – 50 ସେ. ମି. |
ଲେନ୍ସର ପାୱାର ବିଯୁକ୍ତାତ୍ମକ ହେତୁ ଏହା ଏକ ଅବତଳ ଲେନସ୍ ।

34. ଜଣେ ଡାକ୍ତର + 1.5 D. ପାୱାରର ସଂଶୋଧନକାରୀ ଲେନସ୍ ବ୍ୟବହାର କରିବାକୁ ନିର୍ଦ୍ଧାରଣ କରିଛନ୍ତି । ଏହି ଲେନସ୍‌ର ଫୋକସ୍ ଦୂରତା କେତେ ?
ଜ –
– P = \(\frac { 1 }{ f }\) ⇒ 1.5 = \(\frac { 1 }{ f }\) ⇒ f = \(\frac { 1 }{ 1.5 }\) ମି. = \(\frac { 10 }{ 15 }\) ମି. = \(\frac { 2 }{ 3 }\) ମି. = + 0.67

35. ଆଲୋକର ଦ୍ଵୈତ ପ୍ରକୃତି କାହାକୁ କୁହାଯାଏ ?
ଊ–
ଆଧୁନିକ କ୍ୱାଣ୍ଟମ୍ ତତ୍ତ୍ବରୁ ଜଣାଯାଏ ଯେ ଆଲୋକ କେବଳ ତରଙ୍ଗ ନୁହେଁ କି କେବଳ କଣିକା ନୁହେଁ, ଏହା ତରଙ୍ଗ ଓ କଣିକା ଉଭୟର ଗୁଣ ପ୍ରଦର୍ଶନ କରେ ଏବଂ ଏହାକୁ ଆଲୋକର ଦ୍ଵୈତ ପ୍ରକୃତି କହନ୍ତି ।

36. ଉତ୍ତଳ ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବ ଗଠନ ସମ୍ପର୍କରେ ଜାଣିବା ପାଇଁ ବସ୍ତୁର କେଉଁ ଦୁଇଟି ସ୍ଥିତି ବିଚାର କରାଯାଏ ?
ଜ –
(a) ବସ୍ତୁ ଦର୍ପଣଠାରୁ ଅନନ୍ତ ଦୂରତାରେ ରହିଥ‌ିବ ।
(b) ବସ୍ତୁ ଦର୍ପଣ ନିକଟରେ ଏକ ପରିମିତ ଦୂରତାରେ ଥିବ ।

37. ଅବତଳ ଲେନ୍ସରେ କ୍ଷୁଦ୍ରାୟିତ ପ୍ରତିବିମ୍ବର ଆକାର ପାଇଁ ବସ୍ତୁକୁ କେଉଁଠାରେ ରଖାଯାଏ ?
ଉ –
ବସ୍ତୁକୁ ଅନନ୍ତ ଦୂରତା ଓ ଲେନ୍ସର ଆଲୋକ କେନ୍ଦ୍ର ମଧ୍ୟରେ ରଖାଯାଏ ।

38. କେଉଁ ସ୍ଥାନରେ ବସ୍ତୁ ରହିଲେ ଅବତଳ ଦର୍ପଣରେ ଓଲଟା, ବର୍ଣିତ ଓ ବାସ୍ତବ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ?
ଜ –
ଯେତେବେଳେ ବସ୍ତୁଟି (i) ଫୋକସ୍ ଉପରେ ଏବଂ (ii) F ଓ 2F ମଧ୍ୟରେ ରହିବ ସେତେବେଳେ ବାସ୍ତବ, ଓଲଟା ଓ ବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ।

39. ବସ୍ତୁର କେଉଁ ଅବସ୍ଥାନ ପାଇଁ ଅବତଳ ଦର୍ପଣରେ ବର୍ଣ୍ଣିତ ଓ ଆଭାସୀ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ?
ଉ –
ବସ୍ତୁଟି ଫୋକସ୍ ଓ ଦର୍ପଣ ମଧ୍ୟରେ ରହିଲେ ବସ୍ତୁର ଆଭାସୀ ଓ ବର୍ଜିତ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ।

40. ଅବତଳ ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷରେ ଆଲୋକ ରଶ୍ମି ଆପତିତ ହେଲେ ପ୍ରତିଫଳିତ କୋଣର ପରିମାଣ କେତେ ହେବ ?
ଜ –
ଏଠାରେ ଆପତନ କୋଣ (i) = 0°
ତେଣୁ ପ୍ରତିଫଳନ କୋଣ (r) = 0° ହେବ ।

41. ଅବତଳ ଦର୍ପଣରେ ଗୋଟିଏ ପ୍ରତିବିମ୍ବର ବର୍ଦ୍ଧନ + 5 ହେଲେ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି କ’ଣ ହେବ ?
ଉ-
ଏଠାରେ m ଯୁକ୍ତାତ୍ମକ ( ଧନାତ୍ମକ) ତେଣୁ ପ୍ରତିବିମ୍ବଟି ଆଭାସୀ ଓ ସଳଖ ଏବଂ ବସ୍ତୁଠାରୁ 5 ଗୁଣ ହେବ ।

42. ଗୋଟିଏ ଲେନ୍ସର ଦୁଇଟି ପ୍ରମୁଖ ଫୋକସ୍ କିନ୍ତୁ ଦର୍ପଣର ଗୋଟିଏ ପ୍ରମୁଖ ଫୋକସ୍ ଥାଏ କାହିଁକି ?
ଭ –
ଲେନ୍‌ସର ଦୁଇଟି ପ୍ରତିସରଣକାରୀ ପୃଷ୍ଠ ଥିବାବେଳେ ଦର୍ପଣର ଗୋଟିଏ ପ୍ରତିସରଣକାରୀ ପୃଷ୍ଠ ଥାଏ, ତେଣୁ ଲେନ୍ସର ଦୁଇଟି ପ୍ରମୁଖ ଫୋକସ୍ ଓ ଦର୍ପଣର ଗୋଟିଏ ପ୍ରମୁଖ ଫୋକସ୍ ଥାଏ ।

43. ଲେନ୍ସର ପାୱାର କ’ଣ ? ଏହାର ଏକକ ଲେଖ ।
ଭ–
ଲେନ୍‌ସଦ୍ଵାରା ହେଉଥିବା ଅଭିସାରଣ ଓ ଅପସାରଣର ମାତ୍ରାକୁ ଲେନ୍ସର ପାୱାର କୁହାଯାଏ । ଲେନ୍ସର ପାୱାରର ଏକକ ଡାୟପ୍‌ଟର ।

44. ଉତ୍ତଳ ଲେନ୍ସରେ ବସ୍ତୁ ଫୋକସ୍ F ଓ ଆଲୋକ କେନ୍ଦ୍ର ମଧ୍ୟରେ ରହିଲେ ପ୍ରତିବିମ୍ବର ସ୍ଥିତି, ଆକାର ଓ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଲେଖ |
ଜ –
ବସ୍ତୁଟି F₁ ଓ ‘O’ ମଧ୍ୟରେ ରହିଲେ ବସ୍ତୁ ଯେଉଁ ପାର୍ଶ୍ଵରେ ଅଛି ସେହି ପାର୍ଶ୍ବରେ ବର୍ଣ୍ଣିତ, ଆଭାସୀ ଓ ସଳଖ ପ୍ରତିବିମ୍ବ ମିଳିଥାଏ ।

45. ଆଲୋକର ପ୍ରତିଫଳନ କାହାକୁ କହନ୍ତି ?
ଜ –
ଆଲୋକ ରଶ୍ମି ଅସ୍ଵଚ୍ଛ ମସୃଣ ପୃଷ୍ଠ ଉପରେ ପଡ଼ିଲେ ତାହା ବସ୍ତୁକୁ ଭେଦ କରି ନପାରି ଯେଉଁ ମାଧମରୁ ଆସିଥାଏ ସେହି ମାଧ୍ୟମକୁ ଫେରିଯାଏ,ଏହାକୁ ଆଲୋକର ପ୍ରତିଫଳନ କହନ୍ତି ।

46. ସମତଳ ଦର୍ପଣଦ୍ୱାରା ସୃଷ୍ଟି ହେଉଥ‌ିବା ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଲେଖ ।
ଉ-
ସମତଳ ଦର୍ପଣଦ୍ୱାରା ସୃଷ୍ଟି ହେଉଥ‌ିବା ପ୍ରତିବିମ୍ବ ସର୍ବଦା ଆଭାସୀ ଓ ସଳଖ ହୋଇଥାଏ ।

47. ବର୍ତ୍ତୁଳ ଦର୍ପଣର ଦ୍ଵାରକ ଓ ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ମଧ୍ୟରେ ସମ୍ପର୍କ କ’ଣ ?
ଜ –
ବର୍ତ୍ତୁଳ ଦର୍ପଣର ଦ୍ଵାରକ ବକ୍ରତା ବ୍ୟାସାର୍ଷଠାରୁ ବହୁତ କମ୍ ।

48. ଦର୍ପଣର ସୂତ୍ର ଲେଖ ।
ଜ –
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)

49. ଲେନ୍ସର ସୂତ୍ର ଲେଖ ।
ଉ –
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)

50. ଲେନ୍‌ସର ପାୱାର ଓ ଫୋକସ୍ ଦୂରତା ମଧ୍ୟରେ ସମ୍ପର୍କ କ’ଣ ?
ଜ –
P = \(\frac { 1 }{ f }\) ଲେନ୍ସର ଫୋକସ ଦୂରତାର ବିଲୋମୀକୁ ଲେନ୍ସର ପାଓ୍ବାର କୁହାଯାଏ ।

51. କାର୍ଟେସିଆନ୍ ସଙ୍କେତ ପ୍ରଥା କାହାକୁ କହନ୍ତି ?
ଊ–
ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ପ୍ରତିଫଳନ ସଂପର୍କରେ ଆଲୋଚନା କଲାବେଳେ ସାଧାରଣ ଭାବେ ଆଦୃତ ପ୍ରଥା ସମୂହକୁ ଅନୁସରଣ କରାଯାଏ । ଏହାକୁ କାର୍ଟେସିଆନ୍ ସଙ୍କେତ ପ୍ରଥା କହନ୍ତି ।

52. ପ୍ରତିବିମ୍ବର ପରିବର୍ଜନ ନିର୍ଣ୍ଣୟ ପାଇଁ ସୂତ୍ର କ’ଣ ?
ଊ–
ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ଓ ବସ୍ତୁର ଉଚ୍ଚତା, ଅନୁପାତ ଦ୍ୱାରା ପ୍ରତିବିମ୍ବର ପରିବର୍ଦ୍ଧନ ଜଣାପଡ଼ିବ ।

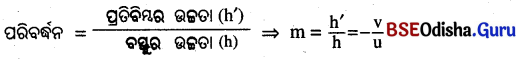
53. n₂₁ କ’ଣ ?
ଊ–

54. ଉତ୍ତଳ ଲେନ୍ସକୁ ଅଭିସାରୀ ଲେନ୍ସ କୁହାଯାଏ କାହିଁକି ?
ଊ–
ଉତ୍ତଳ ଲେନ୍ସ ଆଲୋକ ରଶ୍ମିଗୁଚ୍ଛକୁ କେନ୍ଦ୍ରାଭିମୁଖୀ କରେ । ତେଣୁ ଉଭଳ ଲେନ୍ସକୁ କେନ୍ଦ୍ରାଭିମୁଖୀ ବା ଅଭିସାରୀ ଲେନ୍ସ କୁହାଯାଏ ।

55. ଗୋଟିଏ 25 ସେ.ମି. ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଲେନ୍ସର ପାୱାର କେତେ ?
ଊ–
ଲେନ୍‌ସ୍‌ର ଫୋକସ୍ ତୂରତା (f) = 25 ସେ.ମି. = \(\frac { 1 }{ 4 }\) ମି.
ଲେନ୍ସର ପାୱାର = P = \(\frac { 1 }{ f }\)

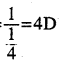
56. ଏକ ଉତ୍ତଳ ଲେନ୍ସର ପାୱାର 10 D ହେଲେ ଫୋକସ୍ ଦୂରତା କେତେ ?
ଊ–
f = \(\frac { 1 }{ p }\) = \(\frac { 1 }{ 10 }\) = \(\frac { 1 }{ 10 }\) × 100 ସେ.ମି. = 10 ସେ.ମି.

F ପ୍ରଥମଯୋଡ଼ିର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟ କରି ଦ୍ବିତୀୟ ଯୋଡ଼ିର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ଅବତଳ ଦର୍ପଣ : ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଭିତର ଆଡ଼କୁ :: ଉତ୍ତଳ ଦର୍ପଣ : ……………………… |
2. ଅବତଳ ଦର୍ପଣ : ଗୋଲକର କେନ୍ଦ୍ର ଆଡକୁ :: ଉତ୍ତଳ ଦର୍ପଣ : …………………. |
3. ବକ୍ରତାକେନ୍ଦ୍ର : C :: ପୋଲ୍ : ……………… |
4. ପୋଲ୍ : ଦର୍ପଣ ଉପରେ :: ବକ୍ରତାକେନ୍ଦ୍ର : …………………. |
5. ଅନନ୍ତ ଦୂରତାରେ ବସ୍ତୁ : ପ୍ରତିବିମ୍ବ F ଠାରେ : F ଠାରେ ବସ୍ତୁ : ……………………. |
6. ବାସ୍ତବ : ଓଲଟା :: ଆଭାସୀ : …………………. |
7. ଆଭାସୀ ପ୍ରତିବିମ୍ବ : ଉତ୍ତଳ ଦର୍ପଣ :: ଆଭାସୀ ଓ ବାସ୍ତବ : ……………………. |
8. ଅବତଳ ଦର୍ପଣ : \(\frac { 1 }{ u }\) + \(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\):: ଉତ୍ତଳ ଦର୍ପଣ : …………………. |
9. ଅବତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା : ବିଯୁକ୍ତ :: ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା : ………………………. |
10. ମୂଳ ବିନ୍ଦୁରୁ ଡାହାଣକୁ : + ve :: ମୂଳବିନ୍ଦୁରୁ ବାମକୁ : …………………. |
11. ପ୍ରମୁଖ ଅକ୍ଷ ଉପରକୁ ଉଚ୍ଚତା : + ve :: ପ୍ରମୁଖ ଅକ୍ଷ ତଳକୁ ଉଚ୍ଚତା : …………………. |
12. ଭାସୀ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା : + ve :: ବାସ୍ତବ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା : …………………………… |
13. ପରିବର୍ଦ୍ଧନର ମୂଲ୍ୟ ଯୁକ୍ତଚିହ୍ନ : ପ୍ରତିବିମ୍ବ ଆଭାସୀ :: ପରିବର୍ତ୍ତନ ମୂଲ୍ୟ ବିଯୁକ୍ତ ଚିହ୍ନ : …………………… |
14.
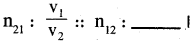
15. ଅବତଳ ଲେନ୍ସ : ଅପସାରୀ :: ଉତ୍ତଳ ଲେନ୍ସ : ……………….. |
16. ଉତ୍ତଳ ଲେନ୍ସ ଫୋକସ୍ ଦୂରତା : + ve :: ଅବତଳ ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତା : …………………. |
17. ପ୍ରତିସରଣାଙ୍କ ସବୁଠାରୁ କମ୍ : ବାୟୁ/ଶୂନ୍ୟ :: ପ୍ରତିସରଣାଙ୍କ ସର୍ବାଧ‌ିକ : ……………………. |
18. ଆଲୋକ କେନ୍ଦ୍ର : ଲେନ୍‌ସ :: ପୋଲ୍ : ……………….. |
19. ଗାଡ଼ିର ହେଡ୍ ଲାଇଟ୍ : ଅବତଳ ଦର୍ପଣ :: ଯାନବାହାନ ପଛପାର୍ଶ୍ବ ଦେଖୁ : …………………. |
20. ଦପଣ: \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) :: ଲେନ୍ସ : …………………. |
21. ଦର୍ପଣ ସମ୍ମୁଖ : ବାସ୍ତବ ପ୍ରତିବିମ୍ବ :: ଦର୍ପଣ ପଛ : ,…………………… |
22. ଜଳର ପ୍ରତିସରଣାଙ୍କ : 1.33 :: କ୍ରାଉନ୍ କାଚ : ……………….. |
23. ଘନ ମାଧ୍ୟମ । ସାନ୍ଦ୍ରତା ଅଧିକ :: ଲଘୁ ମାଧ୍ୟମ : ……………………… |
24. ଫୋକସ୍ ଦୂରତା : ପାୱାର :: ମିଟର : …………………. |
25. ପାୱାର : ଡାୟପ୍‌ଟର :: ଫୋକସ୍ ଦୂରତା : ……………………. |
26. ଫୋକସ୍ ଦୂରତା ବଢିଲେ : ପାୱାର କମେ :: ପାୱାର ବଢ଼ିଲେ : ………………….. |
27. ପ୍ରତିସରଣାଙ୍କ କମ୍ : ଆଲୋକୀୟ ଲଘୁ ମାଧ୍ୟମ :: ପ୍ରତିସରଣାଙ୍କ ଅଧିକ : …………………….. |
28. ଉତ୍ତଳ ଲେନ୍ସ : \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) :: ଅବତଳ ଲେନସ୍ : ……………. |
29. ଉତ୍ତଳ ଲେନ୍ସ : ପାୱାର ଯୁକ୍ତାତ୍ମକ :: ଅବତଳ ଲେନ୍ସ : …………………….. |
30. ଅବତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା : ବିଯୁକ୍ତ (-) :: ଉତ୍ତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା : ………………….. |

Answer:
1. ପ୍ରତିଫଳନ ପୃଷ୍ଠ ବାହାର ଆଡ଼କୁ
2. ଗୋଲକର କେନ୍ଦ୍ରର ବିପରୀତ
3. P
4. ଦର୍ପଣ ବାହାରେ
5. ପ୍ରତିବିମ୍ବ ଅନନ୍ତ ଦୂରତାରେ
6. ସଳଖ
7. ଅବତଳ ଦର୍ପଣ
8. \(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
9. ଯୁକ୍ତ
10. – ve
11. – ve
12. – ve
13. ପ୍ରତିବିମ୍ବ ବାସ୍ତବ
14. (\(\frac{v_2}{v_1}\))
15. ଅଭିସାରୀ
16. (-ve)
17. ହୀରା
18. ଦର୍ପଣ
19. ଉତ୍ତଳ ଦର୍ପଣ
20. \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
21. ଆଭାସୀ
22. 1.52
23. ସାନ୍ଦ୍ରତା କମ୍
24. ଡାୟପଟର
25. ମିଟର
26. ଫୋକସ୍ ଦୂରତା କମ୍
27. ଆଲୋକୀୟ ଘନ ମାଧ୍ୟମ
28. \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
29. ବିଯୁକ୍ତାତ୍ମକ
30. ଯୁକ୍ତ (+)

SUBJECTIVE TYPE QUESTIONS WITH ANSWERS

1. ନୂତନ କାର୍ଟେସିଆନ୍ ସଂକେତ ପ୍ରଥା କାହାକୁ କହନ୍ତି ? ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ବ୍ୟବହୃତ ହେଉଥ‌ିବା ପ୍ରଚଳିତ ସାଙ୍କେତିକ ପ୍ରଥା କ’ଣ ଚିତ୍ର ସହ ବୁଝାଅ । ଦର୍ପଣପାଇଁ ଆବଶ୍ୟକୀୟ ସୂତ୍ର ଲେଖ । ଦର୍ପଣ କ୍ଷେତ୍ରରେ ପରିବର୍ତ୍ତନ କ’ଣ ବୁଝାଅ ।
ଉ –
କାର୍ଟେସିଆନ୍ ସଙ୍କେତ ପ୍ରଥା : ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ପ୍ରତିଫଳନ ସମ୍ପର୍କରେ ଆଲୋଚନା କଲାବେଳେ ସାଧାରଣ ଭାବେ ଯେଉଁ ଆଦୃତ ସଙ୍କେତ ପ୍ରଥାସମୂହକୁ ଅନୁସରଣ କରାଯାଏ ତାହାକୁ ନୂତନ କାର୍ଟେସିଆନ୍ ସଂକେତ ପ୍ରଥା କୁହାଯାଏ । ଏହି ପ୍ରଥାରେ ଦର୍ପଣର ପୋଲ୍ କୁ ମୂଳବିନ୍ଦୁ ନିଆଯାଏ । ଦର୍ପଣର ପ୍ରମୁଖ ଅକ୍ଷକୁ ନିର୍ଦ୍ଦେଶୀ ପଦ୍ଧତିର X- ଅକ୍ଷରୂପେ ନିଆଯାଏ ।

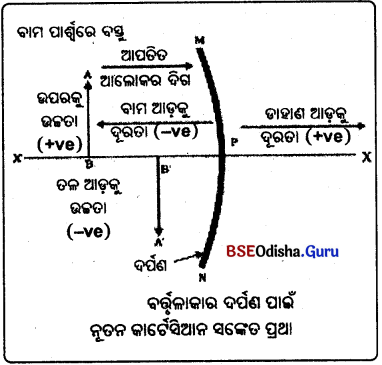
ଆଦୃତ ସଙ୍କେତ ଓ ପ୍ରଥାଗୁଡ଼ିକ ହେଲା :

• ବସ୍ତୁକୁ ସର୍ବଦା ଦର୍ପଣର ବାମପାର୍ଶ୍ଵରେ ରଖାଯାଏ ।
• ପ୍ରମୁଖ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ରହିଥ‌ିବା ଦୂରତାଗୁଡ଼ିକୁ ଦର୍ପଣର ପୋଲ୍ ଠାରୁ ମପାଯାଏ ।
• ଯେଉଁ ଦୂରତାକୁ ମୂଳ ବିନ୍ଦୁର ଡାହାଣ ଆଡ଼କୁ + X ଅକ୍ଷ ଦିଗରେ ମପାଯାଏ ତାହାକୁ ଯୁକ୍ତାତ୍ମକ ଓ ଯାହା ମୂଳବିନ୍ଦୁର ବାମ ଆଡ଼କୁ -X ଅକ୍ଷ ଦିଗରେ ମପାଯାଏ ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।
• ପ୍ରମୁଖ ଅକ୍ଷର ଉପର ଆଡ଼କୁ +Y ଅକ୍ଷ ଦିଗରେ ଲମ୍ବ ଭାବରେ ଯେଉଁ ଦୂରତା ବା ଉଚ୍ଚତା ମପାଯାଏ ତାହାକୁ ଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।
• ପ୍ରମୁଖ ଅକ୍ଷର ଚଳ ଆଡ଼କୁ –Y ଅକ୍ଷ ଦିଗରେ ଲମ୍ବଭାବରେ ଯେଉଁ ଦୂରତା ମପାଯାଏ ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।

ଦର୍ପଣର ସୂତ୍ର :
ଏକ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ପୋଠାରୁ ବସ୍ତୁର ଦୂରତା ‘u’, ପୋଠାରୁ ପ୍ରତିବିମ୍ବର ଦୂରତା ‘v’ ସଙ୍କେତଦ୍ଵାରା, ପୋଲଠାରୁ ଫୋକସ୍ ଦୂରତାକୁ ‘f’ ଦ୍ଵାରା ପ୍ରକାଶ କରାଯାଏ ।
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) ଏହାକୁ ଦର୍ପଣର ସୂତ୍ର କୁହାଯାଏ ।

ପରିବର୍ଦ୍ଧନ :
ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା (h’)ଓ ବସ୍ତୁର ଉଚ୍ଚତା (h) ର ଅନୁପାତକୁ ପରିବର୍ଜନ (m) କୁହାଯାଏ ।
m = \(\frac { h’ }{ h }\) = \(\frac { -v }{ u }\)

2. ଆୟତାକାର କାଚ ସ୍ଲାବ୍‌ ମଧ୍ୟରେ ପ୍ରତିସରଣର ପରୀକ୍ଷା କରି ପରୀକ୍ଷାଲବ୍‌ଧ ତଥ୍ୟ ଲେଖ । ଜଳରେ ଆଲୋକର ବେଗ 2 .25 x 10⁸ m/s ହେଲେ ଜଳର ପ୍ରତିସରଣାଙ୍କ ନିର୍ଣ୍ଣୟ କର । ଶୂନ୍ୟରେ ଆଲୋକର ବେଗ 3 x 10⁸ m/s
ଉ–
ଆବଶ୍ୟକ ଉପକରଣ :
ଧଳା କାଗଜ ଫର୍ଦ୍ଦ, ଡ୍ରଇଂବୋର୍ଡ଼, ଡ୍ରଇଂପିନ୍, ଚାରୋଟି ଆଲପିନ୍, ମୁନିଆ ପେନ୍‌ସିଲ୍, ସ୍କେଲ, ଆୟତଘନାକାର କାଚ ସ୍ଲାବ୍‌ ।

ପର1କ୍ଷଣ :

• ତ୍ରଇଂ ବୋର୍ଡ଼ ଭପରେ ଏକ ଧଳା କାଖଜଫଦକୁ ଡ୍ରଇଂ ପିଦ୍ଵାରା ଲଗାଯାଉ । ଆୟତଘନାକାର କାଚ କ୍ଲବ୍‌କୁ କାଗଜ ମଝିରେ ରଖ୍ ବାହ୍ୟ ସୀମାରେଖାକୁ ପେନ୍‌ସିଲ୍ ସାହାଯ୍ୟରେ ଅଙ୍କନ କରି ABCD ନାମ ଦିଆଯାଉ ।
• କାଗଜ ଉପରେ E ଓ F ନାମକ ଦୁଇଟି ପିନ୍ ଭୂଲମ୍ବ ଭାବରେ ପୋତ ଯେପରିକି E ଓ F ର ମୁନକୁ ଯୋଗ କରୁଥିବା ରେଖା AB ଧାର ପ୍ରତି ତୀର୍ଯ୍ୟକ ହେବ ।
  
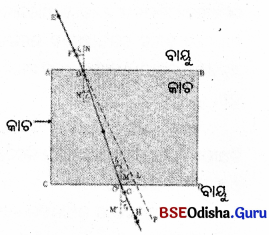
• କ୍ଲବ୍‌ର ଅପର ପାର୍ଶ୍ବରେ G ଓ H ନାମକ ଆଉ ଦୁଇଟି ପିନ୍ କାଗଜ ଉପରେ ଲମ୍ବ ଭାବରେ ଏପରି ପୋତ ଯେପରିକି E ଓ F ପିଦ୍ଵୟର ମୂଳର ପ୍ରତିବିମ୍ବ G ଓ H ପିନର ମୂଳଦ୍ଵୟ ଗୋଟିଏ ସରଳରେଖାରେ ରହିବେ ।
• କାଗଜ ଉପରୁ ସବୁ ପିନ୍ ଓ ସ୍ଲାବ୍‌ କାଢ଼ିଦେଇ E ଓ Fର ସ୍ଥିତି ସୂଚିତ କରୁଥିବା ବିନ୍ଦୁକୁ କାଗଜ ଉପରେ ଯୋଗକରି ସରଳରେଖା ଅଙ୍କନ କଲେ ତାହା AB ଧାରକୁ ଠ ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରିବ । G ଓ H ପିନ୍‌ର ସ୍ଥିତି ସୂଚିତ କରୁଥିବା ବିନ୍ଦୁ ଦୁଇଟିକୁ ଯୋଗକରି ସରଳରେଖା ଅଙ୍କନ କଲେ ତାହା CD ଧାରକୁ ଠା’ ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରିବ ।
• O ଓ ଠି’କୁ କାଗଜ ଉପରେ ଯୋଗ କରାଯାଉ ଏବଂ \(\vec{EF}\) କୁ ବର୍ଦ୍ଧିତ କରାଯାଉ ଏବଂ P ବିନ୍ଦୁ ପର୍ଯ୍ୟନ୍ତ ବିନ୍ଦୁକିତ ରେଖାଦ୍ଵାରା ବଦ୍ଧିତ କରାଯାଉ ।
• ଠ ଓ ଠ’ ଠାରେ ଯଥାକ୍ରମେ ଅଭିଲମ୍ବ NN’ ଓ MM’ ଅଙ୍କନ କରାଯାଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :

• ଠ ଠାରେ ଆଲୋକ ରଶ୍ମି ବାୟୁରୁ କାଚ ମଧ୍ୟକୁ ପ୍ରବେଶ କରି NN’ ଅଭିଲମ୍ବ ଆଡ଼କୁ ବଙ୍କେଇ ଯାଇଛି ।
• ଠ’ ଠାରେ ଆଲୋକ ରଶ୍ମି କାଚରୁ ବାୟୁକୁ ପ୍ରବେଶ କରିଛି ଏବଂ ଅଭିଲମ୍ବଠାରୁ ଦୂରେଇ ଯାଇଛି ।
• ନିର୍ଗତ କୋଣ r₂, ଆପତିତ କୋଣ i ସହ ସମାନ
  ∠r₂ = ∠i |

ସିଦ୍ଧାନ୍ତ
(i) EO ହେଉଛି ଆପତିତ ରଶ୍ମି, ୦୦’ ହେଉଛି ପ୍ରତିସୃତ ରଶ୍ମି, O’H ହେଉଛି ନିର୍ଗତ ରଶ୍ମି ।

(ii) ନିର୍ଗତ ରଶ୍ମି O’H ଆପତିତ ରଶ୍ମି EO ସହ ସମାନ୍ତର । କାରଣ ଆୟତାକାର କାଚ କ୍ଲବ୍‌ର ଦୁଇଟି ସମାନ୍ତର ପୃଷ୍ଠ AB ଓ.CDରେ ଆଲୋକ ରଶ୍ମି ବାଙ୍କିଯିବାର ପରିମାଣ ସମାନ ଓ ବିପରୀତ ।

(iii) ଆଲୋକ ରଶ୍ମି ଗୋଟିଏ ପାର୍ଶ୍ଵକୁ ବିସ୍ଥାପିତ ହୋଇଥାଏ । ବଦ୍ଧିତ ଆପତିତ ରଶ୍ମି ଓ ନିର୍ଗତ ରଶ୍ମି ମଧ୍ୟରେ ଥ‌ିବା ବ୍ୟବଧାନ ଜ୍ୱରଵ୍ଵକୁ ପାର୍ଶ୍ଵ ବିସ୍ଥାପନ କହନ୍ତି |
V = 2.25 × 10₈ m/s
C = 3 x 10₈ m/s, n = 660 ?
n = \(\frac { C }{ v }\)

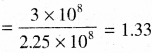
3. ପ୍ରତିସରଣ ନିୟମଗୁଡ଼ିକ ଲେଖ । ନିୟମରୁ ପ୍ରତିସରଣାଙ୍କ କହିଲେ କ’ଣ ବୁଝ ଉଦାହରଣ ସହ ଲେଖ । ଏକ ମାଧ୍ୟମରେ ପ୍ରତିସରଣାଙ୍କ ଓ ଆଲୋକର ବେଗ ମଧ୍ଯରେ ସମ୍ପର୍କ ନିଗମନ କର ।
ଉ-
ଆଲୋକର ପ୍ରତିସରଣ : ଆଲୋକ ଗୋଟିଏ ସ୍ଵଚ୍ଛ ମାଧ୍ୟମରୁ ଆଉ ଏକ ସ୍ଵଚ୍ଛ ମାଧ୍ୟମକୁ ତୀର୍ଯ୍ୟକ ଭାବରେ ପ୍ରବେଶ କଲେ, ତାହାର ସଞ୍ଚାରଣ ଦିଗ ଦ୍ବିତୀୟ ମାଧ୍ୟମରେ ବଦଳିଯାଏ, ଏହାକୁ ଆଲୋକର ପ୍ରତିସରଣ କୁହାଯାଏ ।

ପ୍ରତିସରଣର ପ୍ରଥମ ନିୟମ :
ଆପତିତ ରଶ୍ମି, ପ୍ରତିସୃତ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁରେ ଦୁଇଟି ସ୍ଵଚ୍ଛ ମାଧ୍ୟମର ବ୍ୟବଧାନ ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ ଅଭିଲମ୍ବ ଏକ ସମତଳରେ ଅବସ୍ଥାନ କରିବେ । ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ ଅଭିଲମ୍ବ ଏକ ସମତଳରେ ଅବସ୍ଥାନ କରିବେ ।

ପ୍ରତିସରଣର ଦ୍ବିତୀୟ ନିୟମ : ଦୁଇଟି ନିର୍ଦ୍ଦିଷ୍ଟ ମାଧ୍ୟମ ଓ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷର ଆଲୋକ ପାଇଁ ଆପତନ କୋଣର ସାଇନ୍ (sine) ଓ ପ୍ରତିସରଣ କୋଣର ସାଇନ୍ (sine)ର ଅନୁପାତ ଏକ ସ୍ଥିରାଙ୍କ ।

ପ୍ରତିସରଣାଙ୍କ :
(a) ଆପତନ କୋଣ

• ପ୍ରତିସରଣ କୋଣ ‘r’ ହେଲେ ସ୍କେଲଙ୍କ ନିୟମ ଅନୁଯାୟୀ \(\frac{\sin i}{\sin r}\) ସ୍ଥିରାଙ୍କ |
  ଏହାକୁ ପ୍ରଥମ ମାଧ୍ୟମ ତୁଳନାରେ ଦ୍ଵିତୀୟ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କ କୁହାଯାଏ ।
• ଯଦି ଆଲୋକ ରଶ୍ମି ବାୟୁରୁ କାଚ ମଧ୍ୟରେ ପ୍ରବେଶ କରେ, ତେବେ \(\frac{\sin i}{\sin r}\) କୁ ବାୟୁ ତୁଳନାରେ କାରର ପ୍ରତିସରଣୀଙ୍କ କହନ୍ତି ।
• ଯଦି ଆଲୋକ ରଶ୍ମି ଶୂନ୍ୟରୁ କାଚ ମଧ୍ଯରେ ପ୍ରବେଶ କରେ ତେବେ \(\frac{\sin i}{\sin r}\) କୁ ଶୂନ୍ୟ ତୁଳନାରେ କାରର ପ୍ରତିସରଣୀଙ୍କ କୁହାଯାଏ ।
• ଯଦି ଆଲୋକ ରଶ୍ମି କାଚରୁ ବାୟୁ ମଧ୍ୟରେ ପ୍ରବେଶ କରେ ତେବେ \(\frac{\sin i}{\sin r}\) କୁ କାଢ ତୁଳନାରେ ବାୟୁର ପ୍ରତିସରଣୀଙ୍କ କୁହାଯାଏ ।

(b) ପ୍ରତିସରଣାଙ୍କ ଏକକ ବିହୀନ ।

ଏକ ମାଧ୍ୟମରେ ପ୍ରତିସରଣାଙ୍କ ଓ ଆଲୋକର ବେଗ ମଧ୍ୟରେ ସମ୍ପର୍କ :
ମନେକର ଆଲୋକ ରଶ୍ମି ବାୟୁ ମାଧ୍ୟମରୁ କାଚ ମାଧ୍ୟମକୁ ପ୍ରବେଶ କରୁଛି । ବାୟୁ ଓ କାଚରେ ଆଲୋକର ବେଗ ଯଥା କ୍ରମେ v₁ ଓ v₂ ବେଳେ

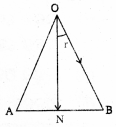
4. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣଦ୍ୱାରା ପ୍ରତିବିମ୍ବ କିପରି ଗଠିତ ହୁଏ ସେଥ‌ିପାଇଁ ଏକ ସରଳ ପରୀକ୍ଷଣ ଦର୍ଶାଅ । ବସ୍ତୁର ବିଭିନ୍ନ ସ୍ଥିତି ଅନୁଯାୟୀ ପ୍ରତିବିମ୍ବର ସ୍ଥିତି, ଆକାର ଓ ପ୍ରକୃତିଗୁଡ଼ିକ ଲେଖ ।
ଉ-
ଆବଶ୍ୟକ ଉପକରଣ : ଅବତଳ ଦର୍ପଣ, ମିଟର ସ୍କେଲ୍, ଚକ୍‌ଖଣ୍ଡ, ଜଳନ୍ତା ମହମବତୀ, କାଗଜ, ପରଦା ।
ସଜ୍ଜ1କରଣ :

• ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ନିଅ । ଏହାର ଫୋକସ୍ ଦୂରତାର ସନ୍ନିକଟ ମାନ ନିର୍ଣ୍ଣୟ କର ।
• ଟେବୁଲ୍ ଉପରେ ଚଦ୍ଵାରା ଏକ ରେଖା ଅଙ୍କନ କରାଯାଉ ।
• ଏକ ଅବତଳ ଦର୍ପଣକୁ ଷ୍ଟାଣ୍ଡରେ ଲଗାଯାଇ ରେଖା ଉପରେ ଏପରି ରଖ ଯେମିତିକି ଦର୍ପଣର ପୋଲ ଠିକ୍ ରେଖା
• ପୂର୍ବରେଖା ସହିତ ସମାନ୍ତର ଭାବେ ଆଉ ଦୁଇଟି ରେଖା ଟାଣ ଯେପରିକି ପାଖାପାଖୁ ଯେକୌଣସି ଦୁଇଟି ରେଖା ମଧ୍ୟରେ ଦୂରତା ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ସହିତ ସମାନ ହେବ ।
• ଉକ୍ତରେଖାର ସ୍ଥିତି ବର୍ତ୍ତମାନ ଦର୍ପଣର ପୋଲ (P) ଫୋକସ୍‌ବିନ୍ଦୁ (F) ଓ ବକ୍ରତାକେନ୍ଦ୍ର (C) ଭେଦ କରିବ, କାରଣ କ୍ଷୁଦ୍ର ଦ୍ବାରକ ବିଶିଷ୍ଟ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣର ଫୋକସ୍ ବିନ୍ଦୁ (F) ଓ ତା’ର ପୋଲ (P) ଓ ବକ୍ରତାକେନ୍ଦ୍ର (C) ର ମଝିରେ ଥାଏ ।
• ଜଳୁଥିବା ମହମବତୀ ନେଇ ୯ ବିନ୍ଦୁର ପଛକୁ ଦୂରରେ ରଖ । ଦର୍ପଣ ସମ୍ମୁଖରେ ଏକ କାଗଜ ପରଦା ରଖ । ପରଦାକୁ ଆଗପଛ କରି ଯେଉଁ ସ୍ଥାନରେ ଉଜ୍ଜ୍ବଳ, ତୀକ୍ଷ୍ଣ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ ସେଠାରେ ପରଦାକୁ ସ୍ଥିର ରଖ୍ ବସ୍ତୁର ତା’ର ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଓ ସ୍ଥିତିକୁ ଲେଖ୍ ରଖ ।
• ମହମବତୀର ଆକାର ସହିତ ପ୍ରତିବିମ୍ବର ଆକାର ତୁଳନା କର । ଜଳନ୍ତା ମହମବତୀକୁ ବିଭିନ୍ନ ସ୍ଥାନରେ ଯଥା :
  • C ଠାରୁ ଅଳ୍ପ ଦୂରରେ
  • ଠିକ୍ C ଉପରେ
  • F ଓ C ମଧ୍ୟରେ
  • ଠିକ୍ F ଉପରେ
  • P ଓ F ମଧ୍ୟରେ ରଖ୍ ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ ଓ ପ୍ରକୃତି ନିର୍ଣ୍ଣୟ କର ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :

• ଅବତଳ ଦର୍ପଣଦ୍ୱାରା ସୃଷ୍ଟି ହେଉଥ‌ିବା କୌଣସି ବସ୍ତୁର ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି, ଅବସ୍ଥାନ ଓ ଆକାର ଦର୍ପଣ ସମ୍ମୁଖରେ ସେହି ବସ୍ତୁର ଅବସ୍ଥାନ ଉପରେ ନିର୍ଭର କରେ ।
• ବସ୍ତୁର ଅବସ୍ଥାନକୁ P, F ଓ C ବିଦୁ୍ୟତ୍ରୟକୁ ଭିତ୍ତିକରି ପ୍ରକାଶ କରାଯାଏ ।
• ବସ୍ତୁର କିଛି ଅବସ୍ଥାନ ପାଇଁ ପ୍ରତିବିମ୍ବ ବାସ୍ତବ ବା ଆଭାସୀ ହୁଏ । ଏହା ସଳଖ ବା ଓଲଟା କିମ୍ବା ବସ୍ତୁ ସହ ସମାନ, ଛୋଟ ବା ବଡ଼ ହୋଇ ପାରେ ।

ସଂକ୍ଷିପ୍ତ ଭତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

1. ଗୋଟିଏ ବର୍ତ୍ତୁଳ ଦର୍ପଣରେ ଗୋଟିଏ ବସ୍ତୁ କେତେ ଦୂରରେ ରଖିଲେ ଏହାର ପ୍ରତିବିମ୍ବ 40 cm ଦୂରରେ ଏକ ପରଦାରେ ସୃଷ୍ଟି ହେବ ଓ ପ୍ରତିବିମ୍ବର ପରିବଦ୍ଧର୍ନ -1 ହେବ ?
ପ୍ରତିବିମ୍ବଟି ପରଦାରେ ସୃଷ୍ଟି ହେଉଥ‌ିବାରୁ ପ୍ରତିବିମ୍ବଟି ବାସ୍ତବ ଏବଂ ଦର୍ପଣଟି ଅବତଳ ଦର୍ପଣ |
V = – 40 cm, m = \(\frac { -v }{ u }\) = -1 ⇒ \(\frac { -(-40) }{ u }\) = – 1 ⇒ u = – 40 cm.
m = – 1 ହେତୁ ବସ୍ତୁ ଓ ପ୍ରତିବିମ୍ବ ଉଚ୍ଚତା ସମାନ ।
ତେଣୁ ବସ୍ତୁଟି ବକ୍ରତା କେନ୍ଦ୍ରଠାରେ ଅଛି ।
R = – 40 cm.
f = \(\frac { -40 }{ 2 }\) = – 20 cm
ଦର୍ପଣର ଫୋକସ୍‌ ଦୂରତା = 20 cm.

2. ଜଳ, ଆଲ୍‌କହଲ୍ ଓ ବେଞ୍ଜିନ୍‌ର ପ୍ରତିସରଣାଙ୍କ ଯଥାକ୍ରମେ 1.33, 1.36 ଓ 1.50 । ସେମାନଙ୍କ ମଧ୍ୟରେ ଆଲୋକର ବେଗ ନିର୍ଣ୍ଣୟ କର । କେଉଁଥରେ ଆଲୋକର ବେଗ ସର୍ବନିମ୍ନ ଓ ସର୍ବାଧ‌ିକ ଲେଖ । (ଶୂନ୍ୟରେ ଆଲୋକର ବେଗ = 3 x 10⁸ ସେ.ମି. )
ଉ-
ଶୂନ୍ୟରେ ଆଲୋକର ବେଗ = 3 x 10⁸ m/s
ଜଳରେ ଆଲୋକର ବେଗ v₁ |

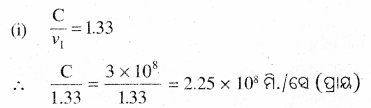
(ii) ଆଲ୍‌କହଲ୍‌ରେ ଆଲୋକର ବେଗ V₂ ହେଲେ,

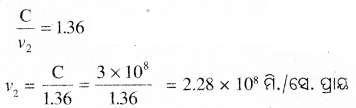
(iii) ବେଞ୍ଜିନ୍‌ରେ ଆଲୋକର ବେଗ V₃

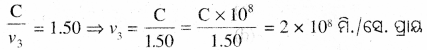
∴ ଜଳରେ ଆଲୋକର ବେଗ ସର୍ବାଧ‌ିକ ଓ ବେଞ୍ଜିନ୍‌ରେ ଆଲୋକର ବେଗ ସର୍ବନିମ୍ନ ।

30 cm ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଗୋଟିଏ ଅବତଳ ଲେନ୍ସ 20 cm ଦୂରରେ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି କରେ । ଲେନ୍ସଠାରୁ କେତେ ଦୂରରେ ବସ୍ତୁଟି ଅଛି ? ରଶ୍ମି ଚିତ୍ର ଅଙ୍କନ କରି ପ୍ରତିବିମ୍ବକୁ ଦେଖାଅ ।
ଉ-
f’ = Φ – 30 cm, y = – 20 cm.
ଲେନ୍ସ ସୂତ୍ର ଅନୁଯାୟୀ,

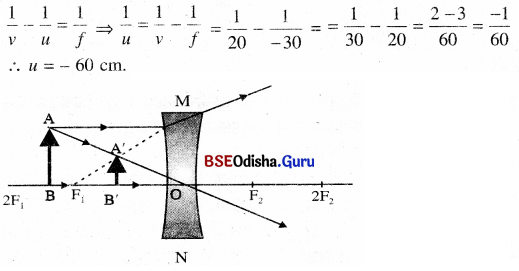
ସୁତରାଂ ବସ୍ତୁଟି ଲେନ୍‌ସଠାରୁ –60 cm ଦୂରରେ ବା 2F ଠାରେ ଅବସ୍ଥିତ ।

4. 30 cm ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଏକ ଉତ୍ତଳ ଲେନ୍ସଠାରୁ 20 cm ଦୂରରେ 10 cm ଉଚ୍ଚତାବିଶିଷ୍ଟ ଏକ ବସ୍ତୁ ଅଛି । ଏହାର ପ୍ରତିବିମ୍ବର ଦୂରତା, ପ୍ରକୃତି ଓ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
ଉ –
h = 10 cm, u = – 20 cm, f = + 30 cm, v = କେତେ ? h’ = କେତେ ?
ଲେନ୍ସର ସୂତ୍ର ଅନୁଯାୟୀ \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
\(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ 30 }\) + \(\frac { 1 }{ -20 }\) = – \(\frac { 1 }{ 60 }\)
v = – 60cm
m = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\) ⇒ m = \(\frac { h’ }{ 10 }\) = \(\frac { -60 }{ -20 }\)
ଆଭାସୀ, ସଳଖ ଓ ପରିବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ ।

5. +2D ଓ – 4D ପାୱାର ବିଶିଷ୍ଟ ଲେନ୍ସ ଦ୍ବୟର ଫୋକସ୍ ଦୂରତା ନିଶ୍ଚୟ କର । – 4D ପାଓ୍ବାର ବିଶିଷ୍ଟ ଲେନ୍‌ସ୍‌ରୁ 100 ମି. ଦୂରରେ ଥ‌ିବା ବସ୍ତୁର ଲେନ୍ସଠାରୁ ପ୍ରତିବିମ୍ବର ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
ଉ –

• ଉତ୍ତଳ ଲେନ୍ସର ଫୋକ୍‌ସ ଦୂରତା : = f = \(\frac { 1 }{ D }\) = \(\frac { 1 }{ 2 }\)m = 50 cm
• ଅବତଳ ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତା = f = \(\frac { 1 }{ D }\) = \(\frac { 1 }{ 4 }\) ମି. = – 25 cm
• P = – 4D, u = 100 cm, v = ?
  ଲେନ୍ସ ସୂତ୍ର ଅନୁଯାୟୀ, \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\), \(\frac { 1 }{ u }\) = \(\frac { 1 }{ -25 }\) + \(\frac { 1 }{ -100 }\) = \(\frac { -5 }{ 100 }\) = – \(\frac { 1 }{ 20 }\)
  v = – 20 cm.

6. ସଙ୍କେତ ପ୍ରଥା କ’ଣ ? ଲେନ୍ସ ପାଇଁ ସଙ୍କେତ ପ୍ରଥାଗୁଡ଼ିକ ଲେଖ ।
ଉ –

• ବସ୍ତୁର ଦୂରତା, ପ୍ରତିବିମ୍ବର ଦୂରତା, ବସ୍ତୁର ଉଚ୍ଚତା, ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ଓ ଲେନ୍‌ସର ଫୋକସ୍‌ର ଦୈର୍ଘ୍ୟକୁ ସଙ୍କେତ ଦେବାପାଇଁ ବ୍ୟବହୃତ ନିୟମର ସମାହାରକୁ ସଙ୍କେତ ପ୍ରଥା କୁହାଯାଏ ।
• ବସ୍ତୁର ଦୂରତା (u), ପ୍ରତିବିମ୍ବର ଦୂରତା (v) ଓ ଫୋକସ୍ ଦୂରତା (f), ଲେନ୍ସର ଆଲୋକ କେନ୍ଦ୍ର ‘O’ ଠାରୁ ମପାଯାଏ ।
• ବସ୍ତୁ ଓ ପ୍ରତିବିମ୍ବର ସମସ୍ତ ଦୂରତା (ଉଚ୍ଚତା )କୁ ମୁଖ୍ୟ ଅକ୍ଷ ଉପରେ ଯୁକ୍ତାତ୍ମକ ଭାବେ ଓ ମୁଖ୍ୟ ଅକ୍ଷତଳେ ବିଯୁକ୍ତାତ୍ମକ ଭାବେ ନିଆଯାଏ ।

7. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ପ୍ରତିଫଳନ ପାଇଁ ପ୍ରଚଳିତ ସଙ୍କେତ ପ୍ରଥା ଉଲ୍ଲେଖ କର ।
ଉ –

• ବସ୍ତୁକୁ ସର୍ବଦା ଦର୍ପଣର ବାମ ପାର୍ଶ୍ଵରେ ରଖାଯାଏ । ପ୍ରମୁଖ ଅକ୍ଷ ସହିତ ସମାନ୍ତର ରହିଥ‌ି ଦୂରତାଗୁଡ଼ିକୁ ଦର୍ପଣର ପୋଠାରୁ ମପାଯାଏ ।
• ଯେଉଁ ଦୂରତାକୁ ମୂଳବିନ୍ଦୁର ଡାହାଣ ଆଡ଼କୁ X- ଅକ୍ଷ ଦିଗରେ ମପାଯାଏ, ତାହାକୁ ଯୁକ୍ତାତ୍ମକ ଓ ଯାହା ମୂଳବିନ୍ଦୁର ବାମ ଆଡ଼କୁ X-ଅକ୍ଷ ଉପରେ ମପାଯାଏ, ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।
• ପ୍ରମୁଖ ଅକ୍ଷର ଉପର ଆଡ଼କୁ Y ଅକ୍ଷ ଦିଗରେ ଲମ୍ବ ଭାବରେ ଯେଉଁ ଦୂରତା ବା ଉଚ୍ଚତା ମପାଯାଏ, ତା’କୁ ଯୁକ୍ତାତ୍ମକ ଓ ପ୍ରମୁଖ ଅକ୍ଷର ତଳଆଡ଼କୁ Y-ଅକ୍ଷ ଦିଗରେ ଲମ୍ବ ଭାବରେ ଯେଉଁ ଦୂରତା ମପାଯାଏ, ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ନିଆଯାଏ ।

8. ଲେନ୍ସର ପାୱାର କହିଲେ କ’ଣ ବୁଝ ? ଗୋଟିଏ ଅବତଳ ଓ ଗୋଟିଏ ଉତ୍ତଳ ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା 50 em ହେଲେ ତାହାର ପାୱାର କେତେ ?
ଉ –
(i)
ଲେନ୍‌ସଦ୍ଵାରା ହେଉଥ‌ିବା ଅଭିସାରଣ ଓ ଅପସାରଣର ମାତ୍ରାକୁ ଲେନ୍ସର ପାୱାର କହନ୍ତି । ଏହା ଫୋକସ୍ ଦୂରତାଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ ହୁଏ । ତେଣୁ ଗୋଟିଏ ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତାର ବିଲୋମୀକୁ ଲେନ୍ସର ପାୱାର କୁହାଯାଏ । P = \(\frac { 1 }{ f }\) |

(ii) ଉତ୍ତଳ ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା f = 50 cm.
P = \(\frac { 1 }{ f }\) = \(\frac { 1 }{ 50 }\) = + 2D

(iii) ଅବତଳ ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା f = – 50 cm
P = \(\frac { 1 }{ f }\) = \(\frac { 1 }{ -50 }\) = -2D

9. ଲୋକର ପ୍ରତିଫଳନ କ’ଣ ? ଏହାର ନିୟମଦ୍ଵୟ ଲେଖ ।
ଉ – ଏକ ଚିକ୍କଣ ଅସ୍ବଚ୍ଛ ପୃଷ୍ଠ ଉପରେ ଆଲୋକ ପଡ଼ିଲେ ତାହାର ଅଧିକାଂଶ ଭାଗ ପ୍ରତିଫଳିତ ହୋଇ ଫେରିଯାଏ । ଆଲୋକର ଗତିପଥରେ ଏକ ପ୍ରକାର ପରିବର୍ତ୍ତନକୁ ପ୍ରତିଫଳନ କୁହାଯାଏ ।

ପ୍ରତିଫଳନର ନିୟମ :

• ଆପତିତ ରଶ୍ମି, ପ୍ରତିଫଳିତ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁରେ ପ୍ରତିଫଳନ ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ
• ଆପତନ କୋଣ ଓ ପ୍ରତିଫଳନ କୋଣ ସମାନ ହୋଇଥାଏ । ପ୍ରତିଫଳନର ଏହି ନିୟମଗୁଡ଼ିକ ପ୍ରତିଫଳକର ବଜ୍ରପୃଷ୍ଠତଳ ସମେତ ଯେକୌଣସି ପୃଷ୍ଠତଳ ପାଇଁ ପ୍ରଯୁଜ୍ୟ ଅଟେ ।
  

10. ଲେନ୍ସ କ’ଣ ? ଏହାର ଅଭିସାରୀ ଓ ଅପସାରୀ ଧର୍ମ କ’ଣ ? ଏହି ଧର୍ମମାନଙ୍କର ପରିମାଣ ଲେନ୍ସର କେଉଁ ଲକ୍ଷଣ ଉପରେ ନିର୍ଭର କରେ ବୁଝାଅ ।
ଉ –

• ଦୁଇଟି ପୃଷ୍ଠଥ‌ିବା ଏକ ସ୍ବଚ୍ଛ ପ୍ରତିସରଣକାରୀ ମାଧ୍ୟମରେ ଗୋଟିଏ ପୃଷ୍ଠ ବା ଉଭୟ ପୃଷ୍ଠ ବକ୍ର ହୋଇଥିଲେ ତାକୁ ଲେନସ୍ କହନ୍ତି ।
• ଉତ୍ତଳ ଲେନ୍ସର ମଝିଅଂଶ ଧାର ଅଂଶଠାରୁ ଅଧ‌ିକ ମୋଟା ହୋଇଥାଏ । ଉତ୍ତଳ ଲେନ୍ସରେ ଆଲୋକ ରଶ୍ମିଗୁଚ୍ଛ ଲେନସ୍‌ ମଝିଆଡ଼କୁ (କେନ୍ଦ୍ରାଭିମୁଖୀ) ଗତିକରେ । ଏହି ଧର୍ମକୁ ଅଭିସାରୀ ଧର୍ମ କହନ୍ତି । ତେଣୁ ଉତ୍ତଳ ଲେନ୍ସକୁ କେନ୍ଦ୍ରାଭିମୁଖୀ ବା ଅଭିସାରୀ ଲେନ୍ସ କହନ୍ତି ।
• ଲେନ୍ସର ଦୁଇଟି ବର୍ତ୍ତୁଳାକାର ପୃଷ୍ଠ ଭିତର ଆଡ଼କୁ ପଶିଯାଇଥାଏ । ତେଣୁ ତାକୁ ଦ୍ବିଅବତଳ ଲେନ୍ସ କହନ୍ତି ।. ଏହାର ଧାର ଅଂଶ ମଝିଠାରୁ ମୋଟା । ଏହି ଲେନ୍ସର ଆଲୋକ ରଶ୍ମି ଧାର ଆଡ଼କୁ ବଙ୍କାଇଥାଏ । ଏହି ଧର୍ମକୁ ଅଭିସାରୀ ଧର୍ମ ଏବଂ ଲେନ୍ସକୁ ଅଭିସାରୀ ଲେନ୍ସ କହନ୍ତି ।
• ଲେନ୍ସର ଅଭିସାରୀ ଓ ଅପସାରୀ ଧର୍ମର ପରିମାଣ ଲେନ୍ସର ପାୱାର ଉପରେ ନିର୍ଭର କରେ ।

11. ଉତ୍ତଳ ଦର୍ପଣଠାରୁ ବସ୍ତୁକୁ ଘୁଞ୍ଚାଇନେଲେ ପ୍ରତିବିମ୍ବର ଅବସ୍ଥିତି ଓ ଆକାର କିପରି ବଦଳିଥାଏ ବୁଝାଅ ।
ଉ –

• ଉତ୍ତଳ ଦର୍ପଣଠାରୁ ବସ୍ତୁକୁ ଘୁଞ୍ଚାଇ ନେଇ ଅନନ୍ତ ଦୂରତାରେ ରଖିଲେ ପ୍ରତିବିମ୍ବ ଫୋକସ୍‌ରେ ଗଠିତ ହେବ । ଅତ୍ୟନ୍ତ କ୍ଷୁଦ୍ର ବିନ୍ଦୁସମ ଆଭାସୀ ଓ ସଳଖ ପ୍ରତିବିମ୍ବ ଗଠିତ ହୁଏ ।
• ଉତ୍ତଳ ଦର୍ପଣଠାରୁ ବସ୍ତୁକୁ ଘୁଞ୍ଚାଇ ଫୋକସ୍ଠାରେ ରଖିଲେ ପ୍ରତିବିମ୍ବ ଦର୍ପଣର ପଛପଟେ P ଓ F ମଧ୍ୟରେ ଗଠିତ ହୁଏ । ପ୍ରତିବିମ୍ବଟି ସଳଖ ଓ କ୍ଷୁଦ୍ର ହୁଏ ।
• ଉତ୍ତଳ ଦର୍ପଣଠାରୁ ବସ୍ତୁକୁ ଘୁଞ୍ଚାଇ ନେଇ ଦର୍ପଣର ପୋଲ୍ ଓ ଫୋକସ୍ ଦୂରତା ମଧ୍ଯରେ ରଖିଲେ ପ୍ରତିବିମ୍ବ ଦର୍ପଣର ପଛପଟେ P ଓ F ମଧ୍ୟରେ ଗଠିତ ହେବ । ପ୍ରତିବିମ୍ବଟି ସଳଖ ଓ କ୍ଷୁଦ୍ର ହେବ ।

12. ଲେନ୍ସର ସୂତ୍ର ଲେଖ । ପରିବର୍ତ୍ତନ କ’ଣ ବୁଝାଅ । ଉତ୍ତଳ ଲେନ୍ସରେ ବସ୍ତୁଟି 12 ସେ.ମି. ଦୂରରେ ରହି ପ୍ରତିବିମ୍ବ 24 ସେ.ମି.ଠାରେ ଗଠିତ ହେଲେ ପରିବର୍ଦ୍ଧନ କେତେ ?
ଉ –
ବସ୍ତୁର ଦୂରତା (u), ପ୍ରତିବିମ୍ବର ଦୂରତା (v) ଓ ଫୋକସ୍ ଦୂରତା (f) ମଧ୍ୟରେ ସମ୍ପର୍କ ହେଲା \(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
ପରିବର୍ଦ୍ଧନ : ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ଓ ବସ୍ତୁର ଉଚ୍ଚତାର ଅନୁପାତକୁ ଲେନ୍ସଦ୍ବାରା ସୃଷ୍ଟ ପରିବର୍ତ୍ତନ କୁହାଯାଏ ।

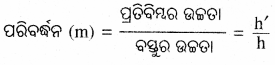
ବସ୍ତୁର ଦୂରତା (u) ଓ ପ୍ରତିବିମ୍ବର ଦୂରତା (v) ହେଲେ, ପରିବର୍ତ୍ତନ (m) = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\)
ଗାଣିତିକ ପ୍ରଣର ସମାଧାନ :
ଏଠାରେ ଏ = 24 69.. 8 u = 12 69.a. I
∴ ପରିବର୍ଦ୍ଧନ (m) = \(\frac { v }{ u }\) = \(\frac { 24 }{ -12 }\) = – 2

13. ବର୍ତ୍ତୁଳ ଲେନ୍ସ ଓ ଦର୍ପଣରେ ଗଠିତ ପ୍ରତିବିମ୍ବକୁ ଆଧାର କରି ସାମଞ୍ଜସ୍ୟ ଥ‌ିବା ଲେନସ୍ ଦର୍ପଣ ଯୋଡ଼ି ଲେଖ ।
ଉ –

• ଉତ୍ତଳ ଲେନ୍ସ ଓ ଅବତଳ ଦର୍ପଣପାଇଁ ବସ୍ତୁ ଫୋକସ୍ ମଧ୍ୟରେ ଅବସ୍ଥାନ କଲେ ପ୍ରତିବିମ୍ବ ଆଭାସୀ, ସଳଖ ଓ ବର୍ଷିତ ହୋଇଥାଏ ।
• ବସ୍ତୁର ଅନ୍ୟ ଯେକୌଣସି ଅବସ୍ଥାନ ପାଇଁ ପ୍ରତିବିମ୍ବ ବାସ୍ତବ, ଓଲଟା ଓ ବିଭିନ୍ନ ଆକୃତିର ହୋଇଥାଏ ।
• ଅବତଳ ଲେନ୍ସ ଓ ଉତ୍ତଳ ଦର୍ପଣପାଇଁ ବସ୍ତୁର ଯେକୌଣସି ଅବସ୍ଥିତିରେ ପ୍ରତିବିମ୍ବ ଆଭାସୀ, ସଳଖ ଓ ବସ୍ତୁ ତୁଳନାରେ ସାନ ହୋଇଥାଏ ।

14. ସମତଳ ଦର୍ପଣରେ ସୃଷ୍ଟ ପ୍ରତିବିମ୍ବର ପ୍ରକୃତି ଓ ଗୁଣ ଦର୍ଶାଅ ।
ଉ –

• ସମତଳ ଦର୍ପଣ ଦ୍ବାରା ସୃଷ୍ଟି ହୋଇଥିବା ପ୍ରତିବିମ୍ବ ସର୍ବଦା ଆଭାସୀ ଓ ସଳଖ ହୋଇଥାଏ ।
• ଏହି ପ୍ରତିବିମ୍ବର ଆକାର ବସ୍ତୁର ଆକାର ସହିତ ସମାନ ହୋଇଥାଏ ।
• ସମତଳ ଦର୍ପଣ ସମ୍ମୁଖରେ ବସ୍ତୁ ଯେତିକି ଦୂରରେ ଥାଏ ତାହାର ପ୍ରତିବିମ୍ବ ଦର୍ପଣର ପଛପଟେ ସେତିକି ଦୂରରେ ରହିଥାଏ ।
• ଏହି ପ୍ରତିବିମ୍ବର ପାର୍ଶ୍ବ ଓଲଟା ହୋଇଥାଏ ।

ଅତିସଂଯିପ୍ର ଉତ୍ତରମ୍ଜଲକ ପ୍ରଣ୍ଟୋତ୍ତର

1. ଉତ୍ତଳ ଦର୍ପଣର ଦୁଇଟି ବ୍ୟବହାର ଲେଖ ।
ଉ –

• କାର, ଟ୍ରକ୍, ବସ୍, ସ୍କୁଟର ଆଦି ଯାନଗୁଡ଼ିକରେ ଉତ୍ତଳ ଦର୍ପଣ ପଛପଟେ ଥିବା ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳକୁ ସଳଖ ଭାବେ
• ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳ ଆଲୋକ ପାଇବା ପାଇଁ ରାସ୍ତା ବତୀଖୁଣ୍ଡରେ ଏହି ଦର୍ପଣକୁ ବ୍ୟବହାର କରାଯାଏ ।

2. ଅବତଳ ଦର୍ପଣ ଓ ଉତ୍ତଳ ଲେନ୍ସକୁ ଜଳ ମଧ୍ୟରେ ରଖିଲେ ସେଗୁଡ଼ିକର ଫୋକସ୍ ଦୈର୍ଘ୍ୟର କିଛି ପରିବର୍ତ୍ତନ ହେବ କି ?
ଉ–

• ଦର୍ପଣର ଫୋକସ୍ ଦୂରତା ମାଧ୍ୟମର ପ୍ରକୃତି ଉପରେ ନିର୍ଭର କରେ ନାହିଁ । ତେଣୁ ପାଣି ଭିତରେ ଅବତଳ ଦର୍ପଣର ଫୋକସ୍ ଦୂରତାର କୌଣସି ପରିବର୍ତ୍ତନ ହେବନାହିଁ ।
• କିନ୍ତୁ ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତା ମାଧ୍ୟମର ପ୍ରକୃତି ଉପରେ ନିର୍ଭର କରେ । ଏଣୁ ପାଣି ଭିତରେ ଉତ୍ତଳ ଲେନ୍ସ, ଫୋକସ୍ ଦୂରତାର ପରିବର୍ତ୍ତନ ହେବ ।

3. ଦର୍ପଣର ପରିବର୍ତ୍ତନ କ’ଣ ଏବଂ ଏହାର ସୂତ୍ରଟି ଲେଖ ।
ଭ–

(i) ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣରେ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୋଇଥିଲାବେଳେ ବସ୍ତୁର ଆକାର ତୁଳନାରେ ପ୍ରତିବିମ୍ବ କେତେ ପରିମାଣରେ ବର୍ଣିତ ହୋଇଛି ତାହାକୁ ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣଦ୍ୱାରା ସୃଷ୍ଟି ହେଉଥ‌ିବା ପରିବର୍ତ୍ତନ କହନ୍ତି । ବସ୍ତୁର ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ଓ ବିସ୍ତୁର ଉଚ୍ଚତାର ଅନୁପାତଦ୍ଵାରା ପ୍ରକାଶ କରାଯାଏ ।

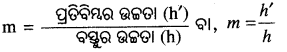
(ii) ବସ୍ତୁର ଦୂରତା (u) ଓ ପ୍ରତିବିମ୍ବର ଦୂରତା (v) ସହିତ ପରିବର୍ତନ (m) ର ସମ୍ପର୍କ ଅଛି । m ର ସର୍ମ୍ପର୍କ ଅଛି | m = \(\frac { h’ }{ h }\) = – \(\frac { v }{ u }\) |

4. ଲେନ୍‌ସକୁ ସ୍ପର୍ଶ ନକରି କହିପାରିବା କି ଏହା ଅବତଳ ବା ଉତ୍ତଳ ?
ଭ–

• ହଁ, ଦର୍ପଣକୁ ବହିପୃଷ୍ଠାର ଅତି ନିକଟରେ ରଖ୍ ବହିର ଲେଖାଗୁଡ଼ିକୁ ଲକ୍ଷ୍ୟ କର ।
• ଯଦି ଲେଖାଗୁଡ଼ିକ ବଡ଼ ବଡ଼ ଦେଖାଯିବ ତେବେ ଲେନ୍ସଟି ଉତ୍ତଳ ଲେନ୍ସ, କିନ୍ତୁ ଯଦି ଲେଖାଗୁଡ଼ିକ ଅତି ସାନ ଦେଖାଯିବ ତେବେ ଲେନ୍ସଟି ଅବତଳ ଲେନ୍ସସ।

5. ଯାନବାହନରେ ଉତ୍ତଳ ଦର୍ପଣ କାହିଁକି ବ୍ୟବହାର କରାଯାଏ ?
ଭ–

• ଉତ୍ତଳ ଦର୍ପଣରେ ପ୍ରତିବିମ୍ବ ସର୍ବଦା ସଳଖ ହୁଏ ଏବଂ ଏକ ବିସ୍ତୀର୍ଣ୍ଣ ଅଞ୍ଚଳର ପ୍ରତିବିମ୍ବକୁ ଛୋଟ କରି ସୃଷ୍ଟି ହୁଏ ।
• ପଛରେ ଆସୁଥିବା ଯାନବାହନକୁ ଦେଖିବାପାଇଁ ଯାନବାହନରେ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।

6. ଦାନ୍ତ ଡାକ୍ତରମାନେ ଦାନ୍ତର ପ୍ରତିବିମ୍ବ ଦେଖୁବାପାଇଁ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରନ୍ତି କାହିଁକି ?
ଭ–

• ଅବତଳ ଦର୍ପଣ ଆଗରେ ଫୋକସ୍‌ଠାରୁ କମ୍ ଦୂରତାରେ ବସ୍ତୁକୁ ରଗ୍‌ ବସ୍ତୁର ଏକ ସଳଖ ଓ ପରିବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହୁଏ ।
• ଦାନ୍ତ ଡାକ୍ତରମାନେ ଦାନ୍ତର ସଳଖ ଓ ପରିବର୍ଦ୍ଧିତ ପ୍ରତିବିମ୍ବ ଦେଖୁବାପାଇଁ ଅବତଳ ଦର୍ପଣ ବ୍ୟବହାର କରନ୍ତି । ବସ୍ତୁର ଘନତା ଓ ଆଲୋକୀୟ ଘନତାଠାରୁ କିପରି ଭିନ୍ନ ?

7. ବସ୍ତୁର ଘନତା ଓ ଆଲୋକୀୟ ଘନତାଠାରୁ କିପରି ଭିନ୍ନ ?
ଭ–

• ଦୁଇଟି ମାଧ୍ୟମକୁ ତୁଳନା କଲେ ଯାହାର ପ୍ରତିସରଣାଙ୍କ ଅଧ୍ଵ ଥୁବ ତାହା ଅନ୍ୟ ମାଧ୍ୟମ ଅପେକ୍ଷା ଅଧିକ ଆଲୋକୀୟ ଘନ ।
• ଯେଉଁ ମାଧ୍ୟମରେ ପ୍ରତିସରଣାଙ୍କ କମ୍ ତାହା ଆଲୋକୀୟ ଲଘୁ ମାଧ୍ୟମ । ଘନ ମାଧ୍ୟମ ଅପେକ୍ଷା ଲଘୁ ମାଧ୍ୟମରେ ଆଲୋକର ବେଗ ଅଧ୍ଯକ ହୁଏ ।
• ଜଳର ବସ୍ତୁତ୍ୱ ସାନ୍ଦ୍ରତା କିରୋସିନ୍‌ଠାରୁ ଅଧିକ ହେଲେ ମଧ୍ୟ କିରୋସିନ୍ ଜଳ ତୁଳନାରେ ଆଲୋକୀୟ ଘନ ମାଧ୍ୟମ ଅଟେ । ବସ୍ତୁର ଘନତା ତା’ର ସାନ୍ଦ୍ରତା ଉପରେ ନିର୍ଭର କରେ ।

8. ଗୋଟିଏ ଅବତଳ ଦର୍ପଣଠାରୁ 30 ସେ.ମି. ଦୂରତାରେ ଥ‌ିବା ଏକ ବସ୍ତୁର ପ୍ରତିବିମ୍ବ ଆଭାସୀ ଓ 2 ଗୁଣ ପରିବର୍ଦ୍ଧିତ ହେଲେ ବସ୍ତୁ ଓ ପ୍ରତିବିମ୍ବ ମଧ୍ୟରେ ବ୍ୟବଧାନ କେତେ ?
ଭ–
(i) ଏଠାରେ ବପ୍ରୁର ଦୂରତା = 30 cm.
ପ୍ରତିବିମ୍ବର ପରିବର୍ଦ୍ଧନ m = +2
\(\frac { -v }{ u }\) = m ⇒ \(\frac { -v }{ -30 }\) = +2 ⇒ – v = – 60
∴ v = 60 ସେ.ମି. |

(ii) ଦର୍ପଣର ପଛପଟେ ପ୍ରତିବିମ୍ବ ଗଠିତ ହେବ ।
ବସ୍ତୁ ଓ ପ୍ରତିବିମ୍ବ ମଧ୍ୟରେ ବ୍ୟବଧାନ = 60 – (–30) = 90 ସେ.ମି ହେବ ।

9. ଏକ ସମତଳ ଦର୍ପଣରେ ପରିବର୍ତ୍ତନ, m = +1 । ଏହାର ଅର୍ଥ କ’ଣ ?
ଭ–

• m = +1 ର ଅର୍ଥ ପ୍ରତିବିମ୍ବର ଉଚ୍ଚତା ସହ ବସ୍ତୁର ଉଚ୍ଚତା ସମାନ ।
• ‘+’ ଚିହ୍ନର ଅର୍ଥ, ପ୍ରତିବିମ୍ବ ସଳଖ ଓ ଆଭାସୀ ।

10. 60 cm ବକ୍ରତା ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଉତ୍ତଳ ଦର୍ପଣର ସମ୍ମୁଖରେ 15 cm ଦୂରରେ ଥ‌ିବା ବସ୍ତୁର ପ୍ରତିବିମ୍ବର ଅବସ୍ଥାନ ଓ ପରିବର୍ଦ୍ଧନ କେତେ ?
ଭ–
(i) u = – 15 cm, R = + 60 cm, f = + 30 cm.
V = କେତେ ? m = କେତେ ?
\(\frac { 1 }{ v }\) + \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\)
\(\frac { 1 }{ v }\) = \(\frac { 1 }{ f }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ 30 }\) – \(\frac { 1 }{ -10 }\) = \(\frac { 4 }{ 30 }\)
v = 7.5 cm
m = \(\frac { -v }{ u }\) = \(\frac { -15 }{ 7.5 }\) = 2
∴ ଆଭାସୀ ଓ 2 ଗୁଣ ପରିବର୍ତ୍ତିତ ପ୍ରତିବିମ୍ବ ସୃଷ୍ଟି ହେବ ।

11. 25 cm ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଏକ ଉତ୍ତଳ ଲେନ୍ସର ପାୱାର କେତେ ହେବ ?
ଭ–
ƒ= 25 cm = \(\frac { 25 }{ 100 }\) ମି. = \(\frac { 1 }{ 4 }\) ମି.
ଲେନ୍ସର ପାୱାର P = \(\frac { 1 }{ f }\) = \(\frac{1}{\frac{1}{4}}\) = 4 ଡାୟୋପ୍‌ଟର +4D.

12. 40 em ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଅବତଳ ଲେନ୍ସର ପାୱାର କେତେ ?
ଉ-
f = – 40 cm = \(\frac { -40 }{ 100 }\) = – \(\frac { 1 }{ 25 }\) ମି.
P = \(\frac { 1 }{ f }\) = \(\frac{1}{\frac{-1}{25}}\) = -2.5 ଡାୟୋପ୍‌ଟର ।

13. ଲେନ୍ସର ପାୱାର କ’ଣ ? 20 cm ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଏକ ଉତ୍ତଳ ଲେନ୍ସର ପାୱାର କେତେ ହେବ ?
ଭ –
(i) ଲେନ୍ସ ପାୱାର – ଗୋଟିଏ ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତାର ବିଲୋମୀକୁ ଲେନ୍ସର ପାୱାର କହନ୍ତି । ଏହାକୁ ‘P’ ଅକ୍ଷରଦ୍ଵାରା ଚିହ୍ନିତ କରାଯାଏ ।
P = \(\frac { 1 }{ f }\), F = ଲେନ୍‌ସର ଫୋକସ୍ ଦୂରତା ।
ଆନ୍ତର୍ଜାତିକ ଏକକ ପଦ୍ଧତିରେ ଲେସର ପାଓ୍ବାରକୁ ଡାୟୋପ୍‌ଟର ଏବଂ ଏହାକୁ ‘D’ ଅକ୍ଷରଦ୍ଵାରା ସୂଚିତ କରାଯାଏ ।

(ii) f = 20 cm = \(\frac { 20 }{ 100 }\) = \(\frac { 1 }{ 5 }\) ମି.
ପାୱାର = P = \(\frac { 1 }{ f }\) = \(\frac{1}{\frac{1}{5}}\) 5 ଡାୟୋପ୍‌ଟର ।

14. ପରମ ପ୍ରତିସରଣାଙ୍କ କ’ଣ ?
ଉ-
(i) ପ୍ରଥମ ମାଧ୍ୟମ ଶୂନ୍ୟ ହେଲେ ଶୂନ୍ୟ ମାଧ୍ୟମ ତୁଳନାରେ ଦ୍ୱିତୀୟ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କ ସେହି ମାଧ୍ୟମର ପରମ ପ୍ରତିସରଣାଙ୍କ କୁହାଯାଏ । ଏହାକୁ n₂₀ ବା n₂ ସଙ୍କେତ ଦ୍ବାରା ଦର୍ଶାଯାଏ ।

(ii) ଆଲୋକର ବେଗ ଶୂନ୍ୟ ମାଧ୍ୟମରେ C ହୁଏ ଅନ୍ୟ ଏକ ମାଧ୍ୟମରେ ଆଲୋକର ବେଗ v ହୁଏ, ତେବେ ଶୂନ୍ୟ ବା ବାୟୁ ମାଧ୍ୟମ ତୁଳନାରେ ସେହି ମାଧ୍ୟମର ପରମ ପ୍ରତିସରଣାଙ୍କ n = \(\frac { C }{ v }\) ହେବ ।

15. ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ କ’ଣ ? ଏହାର ପ୍ରକାରଭେଦ ଦର୍ଶାଅ ।
ଊ –

• ଦର୍ପଣର ପ୍ରତିଫଳନ ପୃଷ୍ଠ ଯଦି ସମତଳ ନ ହୋଇ ବକ୍ର ହୋଇଥାଏ, ତେବେ ଏହାକୁ ବଜ୍ରପୃଷ୍ଠତଳ ବିଶିଷ୍ଟ ଦର୍ପଣ ବା ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ କୁହାଯାଏ ।
• ବର୍ତ୍ତୁଳାକାର ଦର୍ପଣ ଦୁଇଭାଗରେ ବିଭକ୍ତ ।
  ଯଥା : ଅବତଳ ଦର୍ପଣ ଓ ଉତ୍କଳ ଦର୍ପଣ

16. ଆଲୋକର ପ୍ରତିସରଣର ଦୁଇଟି ନିୟମ ଲେଖ ।
ଊ –

• ପତିତ ରଶ୍ମି, ପ୍ରତିସୃତ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁଠାରେ ଦୁଇଟି ସ୍ଵଚ୍ଛ ମାଧ୍ୟମର ବ୍ୟବଧାନ ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ ଅଭିଲମ୍ବ ଗୋଟିଏ ସମତଳରେ ରହେ ।
• ଦୁଇଟି ନିର୍ଦ୍ଦିଷ୍ଟ ମାଧ୍ୟମ ଓ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷର ଆଲୋକ ପାଇଁ ଆପତନ କୋଣର ସାଇନ୍ ଓ ପ୍ରତିସରଣ କୋଣର ସାଇନ୍‌ର ଅନୁପାତ ଏକ ସ୍ଥିରାଙ୍କ ।
  \(\frac{\sin i}{\sin r}\) = ସ୍ଥିରାଙ୍କ । ଏହି ସ୍ଥରାଙ୍କକୁ ପ୍ରଥମ ମାଧ୍ୟମ ତୁଳନାରେ ଦ୍ୱିତୀୟ ମାଧ୍ୟମର ପ୍ରତିସରଣାଙ୍କ କହନ୍ତି ।

17. ଉତ୍ତଳ ଦର୍ପଣର ବ୍ୟବହାର ଲେଖ ।
ଊ –

• ଯାନବାହାନରେ ସାଧାରଣତଃ ପଛପାଖ ଦେଖୁପାଇଁ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ । ଉତ୍ତଳ ଦର୍ପଣରେ ବସ୍ତୁ ଗୁଡ଼ିକର ସର୍ବଦା ସଳଖ, ସାନ ପ୍ରତିବିମ୍ବ ଦେଖାଯାଏ ।
• ରାସ୍ତା କଡ଼ରେ ଜଳୁଥିବା ବିଦ୍ୟୁତ୍ ଖୁଣ୍ଟରେ ଆଲୋକ ପ୍ରତିଫଳକ ରୂପେ ଉତ୍ତଳ ଦର୍ପଣ ବ୍ୟବହାର କରାଯାଏ ।

18. ଆଲୋକର ଦ୍ଵୈତ ପ୍ରକୃତି କ’ଣ ?
ଊ –
(i) ଆଲୋକର ଗତିପଥରେ ଅତି କ୍ଷୁଦ୍ର ଅସ୍ଵଚ୍ଛ କଣିକାଟିଏ ରଖୁ ସେହି କ୍ଷୁଦ୍ର ବସ୍ତୁ ପାଖରେ ବଙ୍କାଇଯାଏ । ଏହାକୁ ଆଲୋକର ପ୍ରକୃତିକୁ ସୂଚାଏ ।ଏହି ତତ୍ତ୍ଵଟି ଆଲୋକ ତରଙ୍ଗ
ଆଲୋକର କଣିକା ତତ୍ତ୍ଵକୁ ପ୍ରମାଣିତ କରୁଛି ।

(ii) ପଦାର୍ଥ ଓ ଆଲୋକ ମଧ୍ଯରେ ହେଉଥିବା ପାରସ୍ପରିକ ପ୍ରକ୍ରିୟା ଅନେକ କ୍ଷେତ୍ରରେ ଆଲୋକ କଣିକା ସଦୃଶ ଗୁଣ ପ୍ରଦର୍ଶନ କରେ । ତେଣୁ କ୍ୱାଣ୍ଟମ୍ ତତ୍ତ୍ବ ଅନୁସାରେ ଆଲୋକ ଉଭୟ ତରଙ୍ଗ ଓ କଣିକାର ଗୁଣ ପ୍ରଦର୍ଶନ କରେ । ଏହାକୁ ଆଲୋକର ଦ୍ଵୈତ ପ୍ରକୃତି କହନ୍ତି ।

19. ସନ୍ନିକଟ ଫୋକସ୍ କ’ଣ ବୁଝାଅ ?
ଊ –

• ଗୋଟିଏ ଅବତଳ ଦର୍ପଣ ସୂର୍ଯ୍ୟ ଆଡ଼କୁ ଦେଖାଇଲେ ଆଲୋକ ରଶ୍ମି କେନ୍ଦ୍ରୀଭୂତ ହୋଇ କାଗଜ ଉପରେ ତୀକ୍ଷ୍ଣ ଉଜ୍ଜଳ ବିନ୍ଦୁ ରୂପରେ ପଡେ । ଏହି ଉଜ୍ଜଳ ବିନ୍ଦୁ ଅବତଳ ଦର୍ପଣର ଫୋକସ୍ ଏବଂ ସୂର୍ଯ୍ୟର ପ୍ରତିବିମ୍ବ ଅଟେ ।
• କାଗଜ ଉପରେ ଫୋକସ୍ ବିନ୍ଦୁରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ପ୍ରତିବିମ୍ବ ଓ ଦର୍ପଣ ମଧ୍ୟରେ ରହିଥ‌ିବା ଦୂରତାକୁ ସନ୍ନିକଟ ଫୋକସ୍ କହନ୍ତି ।

20. ଆଲୋକ ପ୍ରତିଫଳନର ଦୁଇଟି ନିୟମ ଲେଖ ।
ଊ –

• ଆଲୋକ ପ୍ରତିଫଳନ ବେଳେ ଆପତନ କୋଣ ଓ ପ୍ରତିଫଳନ କୋଣ ସମାନ ହୋଇଥାଏ ।
• ପତିତ ରଶ୍ମି, ପ୍ରତିଫଳନ ରଶ୍ମି ଓ ଆପତନ ବିନ୍ଦୁରେ ପ୍ରତିଫଳନ ପୃଷ୍ଠ ପ୍ରତି ଅଙ୍କିତ ଅଭିଲମ୍ବ ଗୋଟିଏ ସମତଳରେ

21. ଗୋଟିଏ 10 ସେ.ମି. ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଅଭିସାରୀ ଲେନ୍ସଠାରୁ 25 ସେ.ମି. ଦୂରରେ ଏକ 5 ସେ.ମି. ଦୈର୍ଘ୍ୟର ବସ୍ତୁ ରହିଛି । ପ୍ରତିବିମ୍ବର ସ୍ଥିତି, ପ୍ରକୃତି ଓ ଆକାର ନିର୍ଣ୍ଣୟ କର ।
ଊ –
ଏଠାରେ h = 5 ସେ.ମି., u = – 25 ସେ.ମି., f = 10 ସେ.ମି.,
ଲେନ୍ସ ସୂତ୍ର ଅନୁଯାୟୀ,
\(\frac { 1 }{ v }\) – \(\frac { 1 }{ u }\) = \(\frac { 1 }{ f }\) ⇒ \(\frac { 1 }{ v }\) – \(\frac { 1 }{ -25 }\) = \(\frac { 1 }{ 10 }\)
⇒ \(\frac { 1 }{ v }\) = \(\frac { 1 }{ 10 }\) – \(\frac { 1 }{ 25 }\) = \(\frac { 5-2 }{ 50 }\) = \(\frac { 3 }{ 50 }\)
⇒ v = \(\frac { 50 }{ 3 }\) ସେ.ମି.,
∴ ପ୍ରତିବିମ୍ବର ଦୂରତା 16.66 ସେ.ମି. ।
ବର୍ଜନ (m) = \(\frac { h’ }{ h }\) = \(\frac { v }{ u }\) ⇒ \(\frac { h’ }{ 5 }\) = \(\frac{\frac{50}{3}}{-25}\)
⇒ \(\frac { h’ }{ 5 }\) = \(\frac { 50 }{ -3×25 }\) ⇒ h’ = \(\frac { 50×5 }{ -3×25 }\) = – 3.33 ସେ.ମି.,
∴ ପ୍ରତିବିମ୍ବ ଲେନ୍ସର ଅପରପାର୍ଶ୍ଵରେ ଗଠିତ ହେବ । ଏହା ବାସ୍ତବ, ଓଲଟା ଏବଂ ବସ୍ତୁଠାରୁ ସାନ ହେବ ।

22. 20 ସେ.ମି. ଓ 50 ସେ.ମି. ଫୋକସ୍ ଦୂରତା ବିଶିଷ୍ଟ ଦୁଇଟି ଲେନ୍ସକୁ ଏକାଠି ଲଗାଇ ରଖାଯାଇଛି । ଏହି ସଂଯୁକ୍ତିର ପାୱାର ଆକଳନ କର ।.
ଊ –
ଗୋଟିଏ ଲେନ୍‌ପର ଫୋକସ୍ ଦୂରତା f₁ = 20 ସେ.ମି., = \(\frac { 1′ }{ 5 }\) ମି.
ଲେନ୍ସର ପାୱାର P₁ = \(\frac { 1 }{ f }\) = 5D
ଅନ୍ୟ ଏକ ଲେନ୍ସର ଫୋକସ୍ ଦୂରତା t₂ = -50 cm = – \(\frac { 1 }{ 2 }\) ମି. P₂ = \(\frac{1}{f_2}\) = -2D
ଲେନ୍ସର ସମାହାର ପାୱାର (P) = P₁ + P₂ = 5D – 2D = 3D

Odisha State Board BSE Odisha 10th Class Life Science Notes Chapter 6 ଜନନ will enable students to study smartly.

BSE Odisha Class 10 Life Science Notes Chapter 6 ଜନନ

→ ଉପକ୍ରମ (Introduction) :
ଜୀବମାନଙ୍କର ଏକ ବିଶେଷତ୍ଵ ହେଉଛି ଜନନ ବା ପ୍ରଜନନ ଜରିଆରେ ବଂଶବିସ୍ତାର କରିବା । ଏହି ପ୍ରକ୍ରିୟା ଦ୍ବାରା ସେମାନେ ଠିକ୍ ନିଜ ପରି ଜୀବ

→ AN ING (Types of Reproduction) :

• ବଂଶବୃଦ୍ଧି ମୁଖ୍ୟତଃ ଦୁଇଟି ଉପାୟରେ ହୋଇଥାଏ, ଯଥା- ଅଲିଙ୍ଗୀ ଜନନ ଏବଂ ଲିଙ୍ଗୀୟ ଜନନ ।
• କେତେକ ଜୀବରେ କେବଳ ଅଲିଙ୍ଗୀ ଜନନଦ୍ୱାରା ଓ ଅନେକ ଜୀବରେ କେବଳ ଲିଙ୍ଗୀୟ ଜନନଦ୍ୱାରା ବଂଶବୃଦ୍ଧି ଘଟିଥାଏ ।
• ଅନ୍ୟ କେତେକ ଜୀବରେ ଉଭୟ ଉପାୟରେ ବଂଶବୃଦ୍ଧି ଘଟିଥାଏ ।
• ଏହା ସମବିଭାଜନ ବା ସୂତ୍ରାୟନ ବା ମାଇଟୋସିସ୍ କିମ୍ବା ଏମାଇଟୋସିସ୍ ପ୍ରକ୍ରିୟାଦ୍ଵାରା ହୋଇଥାଏ ।

→ ଅଲିଙ୍ଗୀ ଜନନ (Asexual Reproduction) :

• ଅଲିଙ୍ଗୀ ଜନନ ପ୍ରକ୍ରିୟା ସାଧାରଣତଃ ଅଣୁଜୀବ ସମେତ କେତେକ ନିମ୍ନ ଶ୍ରେଣୀର ଉଭିଦ ଓ ପ୍ରାଣୀଠାରେ ଦେଖାଯାଏ ।
• ଏହି ପ୍ରକ୍ରିୟାରେ ମାତୃକୋଷ ବା ଜନକ କୋଷ ବିଭାଜିତ ହେବା ଫଳରେ ଅପତ୍ୟ କୋଷ ବା ଅପତ୍ୟ ଜୀବ ସୃଷ୍ଟି ହୁଏ ।
• ଏହା ସମବିଭାଜନ ବା ସୂତ୍ରାୟନ ବା ମାଇଟୋସିସ୍ କିମ୍ବା ଏମାଇଟୋସିସ୍ ପ୍ରକ୍ରିୟାଦ୍ଵାରା ହୋଇଥାଏ ।

→ ଲିଙ୍ଗୀୟ ଜନନ (Sexual Reproduction) :

• ଲିଙ୍ଗୀୟ ଜନନ ପ୍ରକ୍ରିୟାରେ ବଂଶବିସ୍ତାର କରୁଥିବା ଜୀବମାନଙ୍କର ଶରୀରରେ ଦୁଇ ପ୍ରକାର କୋଷ ଥାଏ; ଯଥା – କାୟିକ ବା ସୋମୀୟ କୋଷ ଓ ଜାୟକ କୋଷ ।
• କାୟିକ କୋଷର ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା ଭାବେ ରହିଥାଏ ।
• ଉଦାହରଣସ୍ୱରୂପ ମଣିଷରେ ଏହି ସଂଖ୍ୟା 46 ଓ ମକାରେ 20 । ଏହି ସଂଖ୍ୟାକୁ ଦ୍ବିଗୁଣିତ ବା ଡିପ୍ଲଏଡ୍ ସଂଖ୍ୟା କୁହାଯାଏ ଏବଂ ଏହାକୁ ‘2n’ ଭାବେ ସୂଚିତ କରାଯାଇଥାଏ ।
• ସୋମୀୟ କୋଷ ବିଭାଜନ ଶରୀରର ବୃଦ୍ଧି ଓ ମରାମତି ଆଦି କାର୍ଯ୍ୟ କରିଥାଏ । ଏହି ବିଭାଜନର ବିଶେଷତ୍ଵ ହେଲା ମାତୃକୋଷର କ୍ରୋମୋଜମ୍ ସଂଖ୍ୟା ଓ ଅପତ୍ୟ କୋଷର କ୍ରୋମୋଜୋମ୍ ସଂଖ୍ୟା ସର୍ବଦା ସମାନ ହୋଇଥାଏ ।
• ଜନନ ଅଙ୍ଗ, ଅର୍ଥାତ୍ ପୁରୁଷର ମୁଷ୍କ (ଶୁକ୍ରାଶୟ) ତଥା ସ୍ତ୍ରୀର ଡିମ୍ବାଶୟରେ ଥିବା ଆଦି ଜାୟକ କୋଷ ଏବଂ ସପୁଷ୍ପକ ଉଦ୍ଭଦର ଫୁଲର କେଶରରେ ଥିବା ପରାଗ ମାତୃକୋଷ ତଥା ଫଳିକାରେ ଥ‌ିବା ମେଗାସ୍ପୋର୍ ମାତୃକୋଷରେ ମଧ୍ୟ 2n ସଂଖ୍ୟକ ଗୁଣସୂତ୍ର ରହିଥାଏ ।
• ଏହି କୋଷଗୁଡ଼ିକରୁ ଯୁଗ୍ମକ ଜାତ ହୋଇଥାଏ । ଯୁଗ୍ମକ ଜନନ ପ୍ରକ୍ରିୟାରେ ଯୁଗ୍ମକ ସୃଷ୍ଟ ସମୟରେ ଅର୍ଥବିଭାଜନ ବା ଅନ୍ଧାୟନ ବା ମିଓସିସ୍ ନାମକ ଏକ ବିଶେଷ ପ୍ରକାରର କୋଷ ବିଭାଜନ ହୋଇଥାଏ ।
• ଏଥିଯୋଗୁଁ ଯୁଗ୍ମକରେ ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ଅଧା ହୋଇଯାଏ । ଏହି ସଂଖ୍ୟାକୁ ଏକଗୁଣିତକ ବା ହାଫ୍ଲଏଡ୍ ସଂଖ୍ୟା କୁହାଯାଏ ଏବଂ ଏହାକୁ ‘n’ ଭାବେ ସୂଚିତ କରାଯାଇଥାଏ ।
• ଫୁଯୁଗ୍ମକ ଓ ସ୍ତ୍ରୀ ଯୁଗ୍ଧକର ମିଳନ ବା ସମାୟନ ଫଳରେ ଯୁଗ୍ମଜ ସୃଷ୍ଟି ହୁଏ ।

ଦୁଇ ପ୍ରକାରର ଯୁଗ୍ମକ ଏକାପରି ହୋଇଥିଲେ ସେଗୁଡ଼ିକୁ ସମଯୁଗ୍ମକ ତଥା ସେମାନଙ୍କ ମିଳନକୁ ସମଯୁଗ୍ମନ କୁହାଯାଏ । ଯୁଗ୍ମକ ଦୁଇଟି ଭିନ୍ନ ହୋଇଥିଲେ ସେଗୁଡ଼ିକୁ ଅସମଯୁଗ୍ମକ ତଥା ସେମାନଙ୍କ ମିଳନକୁ ଅସମଯୁଗ୍ମନ କୁହାଯାଏ । ଶୈବାଳ, କବକ ଓ କେତେକ ଆଦିପ୍ରାଣୀ ପରି ଜୀବମାନଙ୍କରେ ଏ ଦୁଇ ପ୍ରକାରର ପ୍ରକ୍ରିୟା ଦେଖା ଯାଇଥାଏ । ଅନ୍ୟ ସବୁ ଉଭିଦ ଓ ପ୍ରାଣୀରେ ଦେଖାଯାଉଥ‌ିବା ବିଶେଷ ପ୍ରକାରର ଅସମଯୁଗ୍ମନକୁ ଡିମ୍ବଯୁଗ୍ମନ କୁହାଯାଏ ।

→ କୋଷ ବିଭାଜନ (Cell division) :

• ଜୀବଜଗତରେ ମୁଖ୍ୟତଃ ଦୁଇ ପ୍ରକାରର କୋଷ ବିଭାଜନ ଦେଖାଯାଏ; ଯଥା- ସମବିଭାଜନ ବା ସୂତ୍ରାୟନ ବା ମାଇଟୋସିସ୍ ଓ ଅର୍ଥବିଭାଜନ ବା ଅଦ୍ଧାୟନ ବା ମିଓସିସ୍ ।
• ମାଇଟୋସିସ୍ କାୟିକ କୋଷରେ ଏବଂ ଆଦି ଜାୟକ କୋଷରେ ସଂଘଟିତ ହେଉଥ‌ିବା ସ୍ଥଳେ ମିଓସିସ୍ ଯୁଗ୍ମକ ସୃଷ୍ଟି ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଅଟେ ।

→ ସମବିଭାଜନ (Mitosis) :

2. ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ ନ୍ୟଷ୍ଟିର ବିଭାଜନ ହୁଏ । ଏହାକୁ ନ୍ୟଷ୍ଟି ବିଭାଜନ କୁହାଯାଏ ।

4. ଏହା ଏକ ଜଟିଳ ପ୍ରକ୍ରିୟା ଏବଂ ଏହାକୁ ଚାରୋଟି ଅବସ୍ଥାରେ ବର୍ଣ୍ଣନା କରାଯାଇପାରେ, ଯଥା ମଧ୍ୟାବସ୍ଥା, ଉତ୍ତରାବସ୍ଥା ଓ ଅନ୍ତିମାବସ୍ଥା ।

→ (କ) ଆଦ୍ୟାବସ୍ଥା (Prophase) :

• ଆଦ୍ୟାବସ୍ଥାର ଆରମ୍ଭରେ କ୍ରୋମାଟିକ୍ ଜାଲିକା ଦେଖାଯାଏ ।
• ଜାଲିକା କ୍ରମେ ସୁସ୍ପଷ୍ଟ ସ୍ଥୂଳ ରୂପ ଧାରଣା କରି ପରିଶେଷରେ କେତୋଟି ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟକ ଗୁଣସୂତ୍ର ଭାବେ ଦେଖାଯାଏ ।
• ଆଦ୍ୟାବସ୍ଥାର ଶେଷବେଳକୁ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ଅନୁଲମ୍ବଭାବେ ବିଭାଜିତ ହୋଇଥିବାର ଦେଖାଯାଏ, କିନ୍ତୁ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରଠାରେ ଲାଗି ରହିଥାଏ ।
• କ୍ରମେ ନିନ୍ୟଷ୍ଟି ଓ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ଅଦୃଶ୍ୟ ହୋଇଯାଏ ଓ କୋଷରେ ଥ‌ିବା ସେଣ୍ଡୋଜୋମ୍ ଦୁଇଭାଗରେ ବିଭକ୍ତ ହୋଇ ଦୁଇ ବିପରୀତ ମେରୁ ଆଡ଼କୁ ଗତି କରନ୍ତି ଓ ସେଠାରେ ତାରକ ଗଠନ କରନ୍ତି ।
• କୋଷର ଦୁଇ ମେରୁ ଅଞ୍ଚଳରେ ତର୍କୁତନ୍ତୁ ଗଠନ ପ୍ରକ୍ରିୟା ଆରମ୍ଭ ହୁଏ ।

→ (ଖ) ମଧ୍ୟାବସ୍ଥା (Metaphase) :

• 
• ମେରୁସ୍ଥିତ ତର୍କୁତନ୍ତୁ କ୍ରମଶଃ ବର୍ଷିତ ହୋଇ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରସହ ସଂଯୁକ୍ତ ହୁଅନ୍ତି ।

→ (ଗ) ଉତ୍ତରାବସ୍ଥା (Anaphase) :

• ଉତ୍ତରାବସ୍ଥାରେ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ର ବିଭାଜିତ ହୁଏ ।
• ତର୍କୁତନ୍ତୁ ସଙ୍କୁଚିତ ହେବାଫଳରେ ଗୁଣସୂତ୍ରର ପ୍ରତ୍ୟେକ ଏକକ ସୂତ୍ର ଦୁଇ ବିପରୀତ ମେରୁ ଆଡ଼କୁ ଗତି କରନ୍ତି ।
• ଏହି ସମୟରେ ପ୍ରତ୍ୟେକ ଏକକ ସୂତ୍ର କୋଣାକାର ବା ‘V’ ଆକାର ଧାରଣ କରନ୍ତି ।

→ (ଘ) ଅନ୍ତମାବସ୍ଥା (Telophase) :

• ଅନ୍ତିମାବସ୍ଥାରେ ଅପତ୍ୟ ଗୁଣସୂତ୍ରଗୁଡ଼ିକ କୋଷର ଦୁଇ ମେରୁରେ ଜମା ହୁଅନ୍ତି ।
• କ୍ରମଶଃ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ରପୁଞ୍ଜର ଚତୁର୍ଦ୍ଦିଗରେ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ସୃଷ୍ଟି ହୁଏ ।
• ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ସୂକ୍ଷ୍ମ ଅସ୍ପଷ୍ଟ ହେବା ଆରମ୍ଭ ହେବା ସହ ନିନ୍ୟଷ୍ଟି ମଧ୍ୟ ସୃଷ୍ଟି ହୁଏ ।

→ କୋଷଜୀବକ ବିଭାଜନ (Cytokinesis) :

• ଉଭିଦ ମାତୃକୋଷର ମଧ୍ୟଭାଗରେ ଏକ କୋଷପଟ୍ଟିକା (Cell plate) ଦେଖାଯାଏ । କ୍ରମେ ଏହା ସୁସ୍ପଷ୍ଟ ହୋଇ କୋଷରେ ପରିଣତ ହୋଇଥାଏ ।
• ପ୍ରାଣୀ ମାତୃକୋଷରେ କୋଷପଟ୍ଟିକା ତିଆରି ହୁଏନାହିଁ; କୋଷଜୀବକର ସଙ୍କୋଚନ ସୂକ୍ଷ୍ମସୂତ୍ର ସାହାଯ୍ୟରେ ହୋଇ ଦୁଇଟି ଅପତ୍ୟ କୋଷ’ ତିଆରି ହୋଇଥାଏ ।

→ ଅର୍ଥବିଭାଜନ (Meiosis) :

•  ଅର୍ଥବିଭାଜନଦ୍ଵାରା ଗୋଟିଏ ମାତୃକୋଷରୁ ଚାରୋଟି ଅପତ୍ୟ କୋଷ ସୃଷ୍ଟି ହୁଏ ।
• ପ୍ରତ୍ୟେକ ଅପତ୍ୟକୋଷ ମାତୃକୋଷ ତୁଳନାରେ ଅର୍ଦ୍ଧେକ ସଂଖ୍ୟକ ଗୁଣସୂତ୍ର ବହନ କରନ୍ତି ।
• ଏହି ପ୍ରକାର ବିଭାଜନକୁ ନୂନକ ବିଭାଜନ ମଧ୍ୟ କୁହାଯାଏ । ଏହା ଯୁଗ୍ମକ ସୃଷ୍ଟି ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ।
• ଅର୍ଥବିଭାଜନ ଦୁଇଟି ପର୍ଯ୍ୟାୟରେ ସମ୍ପାଦିତ ହୁଏ । ପ୍ରଥମ ବିଭାଜନ (Meiosis-I)ରେ କୋଷର ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ଅର୍ଦ୍ଧେକ ସଂଖ୍ୟକ ହୋଇଯାଏ ଏବଂ ଦ୍ଵିତୀୟ ବିଭାଜନ (Meiosis-II) ରେ ନୂତନ ଭାବେ ଗଠିତ କୋଷଗୁଡ଼ିକର ସମବିଭାଜନ ହୁଏ ।

(i) ପ୍ରଥମ ବିଭାଜନ :

• ସମବିଭାଜନ ପରି ଏହି ବିଭାଜନକୁ ମଧ୍ଯ ଚାରୋଟି ଅବସ୍ଥାରେ ଅଧ୍ୟୟନ କରାଯାଇପାରେ; ଯଥା- ଆଦ୍ୟାବସ୍ଥା- 1, ମଧ୍ୟାବସ୍ଥା-I, ଉତ୍ତରାବସ୍ଥା – I ଓ ଅନ୍ତିମାବସ୍ଥା -I।
  • (କ) ଆଦ୍ୟାବସ୍ଥା – 1 : ଆଦ୍ୟାବସ୍ଥା-I ଅପେକ୍ଷାକୃତ ଅଧ୍ବକ ଦୀର୍ଘ ଓ ଜଟିଳ ଅଟେ । ଏହି ଅବସ୍ଥାର ପାଞ୍ଚୋଟି ଉପାବସ୍ଥା ଥାଏ । ସେଗୁଡ଼ିକ ହେଲା – ଲେପ୍‌ଟିନ୍, ଜାଇଗୋଟିନ୍, ପାକିଟିନ୍, ଡିପ୍ଲୋଟିନ୍ ଏବଂ ଡାଇଆକାଇନେସିସ୍ ।
• ଲେପଟୋଟିନ୍ ଉଦ୍ଭାବସ୍ଥାରେ ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ଦୃଶ୍ୟମାନ ହୋଇଥାଏ । ଏହି ଅବସ୍ଥାରେ ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ଯଦିଓ ପୂର୍ବରୁ ଅନୁଦୈର୍ଘ୍ୟକଭାବେ ସମଦ୍ଵିଖଣ୍ଡିତ ହୋଇଥାନ୍ତି ମାତ୍ର ତାହା ଏକକ ରୂପେ ଦେଖାଯାଆନ୍ତି ।
• ଭାବରେ ଯୋଡ଼ା ଯୋଡ଼ା ହୋଇ ଲାଗି ରୁହନ୍ତି । ଏହି ଅବସ୍ଥାକୁ ଆପୁଞ୍ଜନ କୁହାଯାଏ । ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ଯୁଗଳ ବା ଯୋଡ଼ିକୁ ଯୁଗଳ ଗୁଣସୂତ୍ର କୁହାଯାଏ ।
• ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ଯୁଗଳ ବା ଯୋଡ଼ିକୁ ଯୁଗଳ ଗୁଣସୂତ୍ର କୁହାଯାଏ ।
• ପାକିଟିନ୍‌ରେ ଗୁଣସୂତ୍ର ସ୍ଥୂଳ ଏବଂ କ୍ଷୁଦ୍ରାକାର ହୁଏ ।
• ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ଲମ୍ବଭାବରେ ଦୁଇଟି ଏକକସୂତ୍ରର ହୋଇଥିବାରୁ ପ୍ରତ୍ୟେକ ଯୁଗଳ ଗୁଣସୂତ୍ର ଗୋଟିଏ ଲେଖାଏଁ ଚତୁଃଏକକ ସୂତ୍ରରେ ପରିଣତ ହୁଏ ।
• ଡିପ୍ଲୋଟିନ୍‌ରେ ଗୁଣସୂତ୍ରଗୁଡ଼ିକର ପୃଥକୀକରଣ ଆରମ୍ଭ ହୁଏ । ସେମାନେ କେବଳ କେତେକ ବିନ୍ଦୁରେ ପରସ୍ପର ସହିତ ଲାଗିରହି ଅନ୍ୟ ଅଂଶରେ ପୃଥକ୍ ହୋଇଥା’ନ୍ତି । ଏହି ମିଳନସ୍ଥଳକୁ କାଏଜ୍‌ମା କୁହାଯାଏ ।
• ଯୁଗଳ ଗୁଣସୂତ୍ରଗୁଡ଼ିକର ଏହି ମିଳନସ୍ଥଳ ବା କାଏଜ୍‌ମାଟା ନିକଟରେ ସେମାନଙ୍କ ଏକକସୂତ୍ର ମଧ୍ୟରେ ଅଂଶ ବିନିମୟ ଦ୍ବାରା ଜିନ୍ ଆଦାନପ୍ରଦାନ କରନ୍ତି । ଏହି ପ୍ରକ୍ରିୟାକୁ ପାରାନ୍ତରଣ କୁହାଯାଏ ।
• ଡାଇଆକାଇନେସିସ୍‌ରେ ଗୁଣସୂତ୍ରଗୁଡ଼ିକ କ୍ଷୁଦ୍ରାକାର; କିନ୍ତୁ ସ୍ଥୂଳ ଓ ବର୍ଭୁଳ ହେବାଦ୍ୱାରା ଅଧିକ ସ୍ପଷ୍ଟ ଦେଖାଯାଅଛି ଓ ଏହି ଉପାବସ୍ଥାରେ ସେଗୁଡ଼ିକର ଆକୃତି ମୁଦ୍ରିକା ସଦୃଶ ହୋଇଥାଏ । ନିନ୍ୟଷ୍ଟି ଏବଂ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ଏହି ଅବସ୍ଥାରେ ଅଦୃଶ୍ୟ ହୋଇଥାଏ ।
  • (ଖ) ମଧ୍ୟାବସ୍ଥା -I: ଏଥ‌ିରେ ସମବିଭାଜନର ମଧ୍ୟାବସ୍ଥା ପରି ଗୁଣସୂତ୍ରଗୁଡ଼ିକ କୋଷର ମଧ୍ୟସମତଳ ଭାଗକୁ ଚାଲିଆସନ୍ତି । ଏହି ଅବସ୍ଥାରେ ତର୍କୁତନ୍ତୁ ଗୁଣସୂତ୍ରର କେନ୍ଦ୍ରଭାଗ ସହ ସଂଶ୍ଳିଷ୍ଟ ହୁଏ ।
  • (ଗ) ଉତ୍ତରାବସ୍ଥା-I : ଯୁଗଳ ଗୁଣସୂତ୍ରର ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ତାହାର ଦୁଇଟି ଏକକ ସୂତ୍ରସହ କୋଷର ବିପରୀତ ଦିଗକୁ ଦୁଇ ମେରୁ ଆଡ଼କୁ ଗତିକରେ । ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରର ବିଭାଜନ ହୁଏ ନାହିଁ । ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ଏହି ସମୟରେ କୋଣାକାର ବା ‘V’ ଆକାର ଦେଖାଯାଆନ୍ତି ।
  • (ଘ) ଅନ୍ତଃମାବସ୍ଥା-I : ଅର୍ଦ୍ଧେକ ସଂଖ୍ୟକ ଗୁଣସୂତ୍ର କୋଷର ଦୁଇ ବିପରୀତ ମେରୁରେ ଜମାହୋଇ ଦୁଇଟି ନ୍ୟଷ୍ଟି ତିଆରି କରନ୍ତି । ପ୍ରଥମେ ନିନ୍ୟଷ୍ଟି, ପରେ ନ୍ୟଷ୍ଟିଝିଲ୍ଲୀ ସୃଷ୍ଟି ହୁଏ ଏବଂ ଗୁଣସୂତ୍ରଗୁଡ଼ିକ ଆସ୍ତେ ଆସ୍ତେ ଲମ୍ବାଳିଆ ଓ ପରେ ଅସ୍ପଷ୍ଟ ହୋଇଯାଏ ।
• ଏହି ସମୟରେ କୋଷଜୀବକ ଦୁଇଭାଗରେ ବିଭକ୍ତ ହୁଏ ଏବଂ କୋଷକୁ ଦୁଇଟି ଅପତ୍ୟ କୋଷରେ ବିଭକ୍ତ କରେ ।

(ii) ଦ୍ଵିତୀୟ ବିଭାଜନ :

• ଅର୍ଥବିଭାଜନର ପ୍ରଥମ ବିଭାଜନ ପରେ ପରେ ଦ୍ବିତୀୟ ବିଭାଜନ ହୁଏ ଏବଂ ଏହା ଠିକ୍ ସମବିଭାଜନ ପରି ।
• ଏହାର ଚାରୋଟି ଅବସ୍ଥାକୁ ଆଦ୍ୟାବସ୍ଥା -II, ମଧ୍ୟାବସ୍ଥା – II, ଉତ୍ତରାବସ୍ଥା -II ଏବଂ ଅନ୍ତମାବସ୍ଥା – II କୁହାଯାଏ ।

→ ସମବିଭାଜନ ଓ ଅନ୍ଧବିଭାଜନ ମଧ୍ୟରେ ତୁଳନା :
ମାଇଟୋସିସ୍ :

• ଏହା କାୟିକ କୋଷ ଓ ଆଦିଜାୟକ କୋଷରେ ହୋଇଥାଏ ।
• ଏଥିରେ ମାତୃକୋଷ ଏବଂ ଅପତ୍ୟ କୋଷରେ ଥିବା ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ସମାନ ରହେ ।
• ଏହି ବିଭାଜନ ବେଳେ ପ୍ରତ୍ୟେକ ଗୁଣସୂତ୍ର ସ୍ବାଧୀନ ଭାବରେ ଅର୍ଥାତ୍ ଏକ ଅନ୍ୟଉପରେ ନିର୍ଭର ନ କରି ବିଭାଜିତ ହୋଇଥାନ୍ତି । ଏଥ‌ିରେ ଆପୁଞ୍ଜନ କିମ୍ବା ଅଂଶ ବିନିମୟ ହୁଏନାହିଁ ।
• ମାଇଟୋସିସ୍‌ର ଉତ୍ତରାବସ୍ଥାରେ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରର ବିଭାଜନ ହେବା ଫଳରେ କ୍ରୋମାଟିଡ୍ ମେରୁଆଡ଼କୁ ଯାଇଥାଏ । 5. ଏହି ବିଭାଜନରେ ଗୋଟିଏ ମାତୃକୋଷରୁ 2ଟି ଅପତ୍ୟ କୋଷ ଜାତ ହୁଏ ।

→ ମିଓସିସ୍ :

• ଏହା ଯୁଗ୍ମଜ ସୃଷ୍ଟିପାଇଁ ଉଦ୍ଦିଷ୍ଟ । ତେଣୁ ଏହା କେବଳ ଜନନ କୋଷରେ ଯୁଗ୍ମକ ଜନନ ପ୍ରକ୍ରିୟାରେ ଶେଷ ପର୍ଯ୍ୟାୟରେ ହୋଇଥାଏ ।
• ଏହି ବିଭାଜନ ପରେ ଅପତ୍ୟ କୋଷରେ ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ମାତୃକୋଷରେ ଥ‌ିବା ଗୁଣସୂତ୍ର ସଂଖ୍ୟାର ଅର୍ଦ୍ଧେକ ହୋଇଯାଏ ।
• ଏହି ବିଭାଜନର ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ ସଦୃଶ ଗୁଣସୂତ୍ର ଯୋଡ଼ା ଯୋଡ଼ା ହୋଇ ଲାଗି ରହନ୍ତି । ସେମାନଙ୍କ ମଧ୍ୟରେ ଆପୁଞ୍ଜନ ଓ ଅଂଶ ବିନିମୟ ହୁଏ ।
• ମିଓସିସ୍ (ପ୍ରଥମ ପର୍ଯ୍ୟାୟ )ର ଉତ୍ତରାବସ୍ଥାରେ ଗୁଣସୂତ୍ର କେନ୍ଦ୍ରର ବିଭାଜନ ହୁଏନାହିଁ । ଫଳରେ ସମ୍ପୂର୍ଣ୍ଣ କ୍ରୋମଜୋମ୍ ମେରୁଆଡ଼କୁ ଯାଇଥାଏ ।
• ଏହି ବିଭାଜନ ଶେଷରେ ଗୋଟିଏ ଆଦିଜାୟକ କୋଷରୁ 4ଟି ଅପତ୍ୟ କୋଷ ଜାତ ହୁଏ

1. ‘Mitosis’ ମୂଳ ଶବ୍ଦ ‘mitos’ରୁ ଆସିଛି; ‘mitos’ଅର୍ଥ ‘thread’(ସୂତ୍ର ବା ସୂତା)
2. ‘Meiosis’ ମୂଳ ଶବ୍ଦ ‘Meion’ରୁ ଆସିଛି; ଏହାର ଅର୍ଥ ‘to reduce’(କମାଇବା) । କ୍ରୋମୋଜୋମ୍ ସଂଖ୍ୟା ଅଧା ହୋଇଯାଉଥିବାରୁ ଏ ପ୍ରକାର କୋଷ ବିଭାଜନର ନାମ ‘Meiosis’ ରଖାଯାଇଛି ।
3. ‘Mitosis’ର ପ୍ରମୁଖ ଘଟଣା ବା ପରିଣାମ ବା ଗୁରୁତ୍ଵ ହେଉଛି ମାତୃକୋଷରୁ ଜାତ 2ଟି ଅପତ୍ୟ କୋଷ ଭିତରେ ମାତୃକୋଷସ୍ଥିତ ଡିଏନ୍ର ସମବଣ୍ଟନ । ତେଣୁ ଏହାକୁ ‘Equational Division’ କୁହାଯାଏ । ସେହିପରି ‘Meiosis’ର ପ୍ରମୁଖ ଘଟନା ହେଉଛି କ୍ରୋମୋଜୋମ୍ ସଂଖ୍ୟା 2nରୁ nକୁ ହ୍ରାସ ହେବା । ସେ ଦୃଷ୍ଟିରୁ ଏହାକୁ ‘Reductional Division’କୁହାଯାଉଛି।
4. ଓଡ଼ିଆରେ ‘Meiosis’ ପାଇଁ ‘ଅଦ୍ଧାୟନ’ (ଅର୍ଥବିଭାଜନ) ଓ Reductional Division’ ପାଇଁ ‘ନୂନକ ବିଭାଜନ’ – ଏହିପରି 2ଟି ଭିନ୍ନ ଶବ୍ଦ ବ୍ୟବହାର କରାଯାଉଛି, ପ୍ରଥମ ଶବ୍ଦଟି ପ୍ରକ୍ରିୟାର ନାମଭାବେ ଏବଂ ଦ୍ବିତୀୟ ଶବ୍ଦଟି ବିଭାଜନର ପ୍ରମୁଖ ଘଟଣାକୁ ସୂଚାଇବା ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଅଟେ ।
5. Mitosis = ସୂତ୍ରାୟନ ଏବଂ Equational Division = ସମବିଭାଜନ
6. Meiosis = ଅନ୍ଧାୟନ ଏବଂ Reductional Division = ନ୍ୟନକ ରି ଭ।କନ

→ ଉଭିଦରେ ଜନନ (Reproduction) :
ଉଦ୍ଭଦରେ ବଂଶ ବିସ୍ତାର ଉଭୟ ଅଲିଙ୍ଗୀ ଜନନ ଓ ଲିଙ୍ଗୀୟ ଜନନ ପ୍ରକ୍ରିୟାରେ ସମ୍ପନ୍ନ ହୋଇଥାଏ ।

→ ସମଲିଙ୍ଗୀ ପ୍ରଜନନ (Asexual Reproduction) :
ଉଭିଦରେ ଅଲିଙ୍ଗୀ ଜନନ ନିମ୍ନୋକ୍ତ ପ୍ରକାରର ହୋଇଥାଏ, ଯଥା- ବିଭାଜନ, କଳିକନ, ରେଣୁଭବନ ଓ ଅଙ୍ଗୀୟ ଜନନ ।

(i) ବିଭାଜନ (Fission) :

• ଏହି ପ୍ରକ୍ରିୟାରେ କେତେକ ବୀଜାଣୁ ଓ ଏକକୋଷୀ ଶୈବାଳର ନ୍ୟଷ୍ଟି ଓ କୋଷଜୀବକ ଦୁଇଟି ସମାନ ଭାଗରେ ବିଭକ୍ତ ହୋଇ ଦୁଇଟି ଅପତ୍ୟ ଜୀବ ସୃଷ୍ଟି ହୋଇଥା’ନ୍ତି । ଏହାକୁ ଦ୍ବିବିଭାଜନ କୁହାଯାଏ
• କେତେକ ଶୈବାଳଜାତୀୟ ଉଦ୍ଭିଦ (ସ୍ପାଇରୋଗାଇରା) କୋଷ ଦୁଇରୁ ଅଧିକ ଭାଗରେ ବିଭାଜିତ ହୋଇ ପ୍ରତ୍ୟେକ ଭାଗ ଗୋଟିଏ ଗୋଟିଏ ନୂତନ ଜୀବରେ ପରିଣତ ହୋଇଥାଏ । ଏହାକୁ-ବହୁବିଭାଜନ କୁହାଯାଏ ।

(ii) କଳିକନ ବା କୋରକୋଡ଼ଗମ (Budding) :

• ଇଷ୍ଟ ଜାତୀୟ କବକରେ ମୂଳ ମାତୃକୋଷରୁ ଜାତ ଅପତ୍ୟ କୋଷ କଳିକା ବା କୋରକ ଆକାରରେ ସୃଷ୍ଟି ହୋଇଥାଏ ।
• ଏହି କଳିକା କ୍ରମଶଃ ବୃଦ୍ଧିପାଇ ମାତୃକୋଷରୁ ବିଚ୍ଛିନ୍ନ ହୁଏ ଏବଂ ଶେଷରେ ଏକ ପୂର୍ଣାଙ୍ଗ ଇଷ୍ଟକୋଷରେ ପରିଣତ ହୁଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ କଳିକନ ବା କୋରକୋଡ଼ଗମ କୁହାଯାଏ ।

(iii) (Sporulation) :

• ଛତୁ ଓ ଫିମ୍ପି ଜାତୀୟ କବକରେ ଅସଂଖ୍ୟ କଳାରଙ୍ଗର ରେଣୁ (Spore) ଦେଖାଯାଏ । ଏହି ରେଣୁଗୁଡ଼ିକ ନିର୍ଗତ ହୋଇ ଜଳ ବା ବାୟୁରେ ଭାସିବୁଲନ୍ତି ଓ ଅନୁକୂଳ ପରିବେଶ ମିଳିଲେ ଅଙ୍କୁରିତ ହୋଇ ନୂତନ ଉଭିଦ ସୃଷ୍ଟି କରନ୍ତି । ରେଣୁଦ୍ଵାର। ଏ ପ୍ରକାର ଜନନ ପ୍ରକ୍ରିୟାକୁ ରେଣୁଭବନ କୁହାଯାଏ ।
• ୟୁଲୋଥ୍ରିକସ୍ ପରି ଶୈବାଳରେ 4, 8 ବା ଅଧ‌ିକ ଚଳରେଣୁ ସୃଷ୍ଟି ହୋଇଥା’ନ୍ତି ।
• ପେନିସିଲିୟମ ପରି କବକ ସାଧାରଣତଃ ଅଚଳରେଣୁଦ୍ଵାରା ବଂଶବୃଦ୍ଧି କରନ୍ତି ।
• ପାଇଥ୍ୟମ୍ ପରି କବକ ପରିବେଶ ଅନୁଯାୟୀ ଚଳରେଣୁ ବା ଅଚଳରେଣୁଦ୍ବାରା ବଂଶବୃଦ୍ଧି କରିଥାନ୍ତି ।

(iv) ଶାକାହାରୀ ପ୍ରଚାର (Vegetative Propagation):

• ପତ୍ର, ମୂଳ ବା କାଣ୍ଡର କୌଣସି ଅଂଶରୁ ଉଭିଦ ଜାତ ହେଲେ ଏହାକୁ ଅଙ୍ଗୀୟ ଜନନ କୁହାଯାଏ ।
• ଅମରପୋଇର ପତ୍ରଧାରରେ ଥ‌ିବା ଦନ୍ତୁରିତ ଅଂଶ ଓଦାମାଟି ସଂସ୍ପର୍ଶରେ ଆସିଲେ ସେଥୁରୁ ନୂତନ ଗଛ ବାହାରେ ।
• ଶତମୂଳୀ, ଡାଲିଆ ଆଦି ଗଛର ମୂଳରୁ ନୂତନ ଗଛ ବା ଲତା ଜାତ ହେବାର ଦେଖାଯାଏ ।
• କଦଳୀ, ପିଆଜ, ଅଦା, ହଳଦୀ ଆଦି ଭୂନିମ୍ନସ୍ଥ କାଣ୍ଡରୁ ନୂତନ ଗଛ ଜାତ ହୋଇଥାଏ । ଅଙ୍ଗୀୟ ଜନନ ନିମ୍ନୋକ୍ତ ପ୍ରକାରର ହୋଇପାରେ ।

→ (ଳ) ବିଖଣ୍ଡନ | (Fragmentation) :
ସ୍ପାଇରୋଗାଇରା ପରି ଶୈବାଳ ଓ ଅନ୍ୟ କେତେକ ଅପୁଷ୍ପକ ଉଦ୍ଭଦର ଥାଲସ୍ ବିଖଣ୍ଡିତ ହୋଇ ପ୍ରତ୍ୟେକ ଅଂଶ ଗୋଟିଏ ଗୋଟିଏ ସମ୍ପୂର୍ଣ୍ଣ ଉଦ୍ଭଦରେ ପରିଣତ ହେବାର ଦେଖାଯାଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ବିଖଣ୍ଡନ କୁହାଯାଏ ।

→ (ଖ) ଛେଦନ (Cutting) :
ବାକ୍ସଗଛ ଓ ମନିପ୍ଲାଣ୍ଟ ଆଦି ଗଛର କାଣ୍ଡକୁ ଛୋଟ ଛୋଟ କରି କାଟି ମାଟିରେ ପୋତିଲେ କିଛିଦିନ ପରେ ସେଥୁରୁ ନୂତନ ଗଛ ସୃଷ୍ଟିହୁଏ । ଏହାକୁ ଛେଦନ ପ୍ରଣାଳୀ କୁହାଯାଏ । ଉଦାହରଣ – ମନିପ୍ଲାଣ୍ଟ ।

→ (ଗ) କଲମିକରଣ (Grafting) :

• କଲମିକରଣ ପଦ୍ଧତିରେ ଗୋଟିଏ ତରୁଣଗଛର ଅଗ୍ରଭାଗକୁ କାଟି ଦିଆଯାଏ । ଏହି କଟାସ୍ଥାନରେ ଅନ୍ୟ ଗୋଟିଏ ଗଛର କଟାଡାଳ ବା କଲମକୁ କଲମି ମାଟିଦେଇ ବାନ୍ଧି ଦିଆଯାଏ ।
• ଏହି ବନ୍ଧା ସ୍ଥାନକୁ ଅଳ୍ପ ଅଳ୍ପ ପାଣି ଦେଇ ଓଦା ରଖାଯାଏ । କିଛିଦିନ ପରେ ତାହା ଯୋଡ଼ିହୋଇ ସେଠାରେ ନୂତନ ଗଛ ସୃଷ୍ଟି ହୁଏ ।

→ (୧) ଡାଳି କଲମି :

• ଅଳ୍ପ ସମୟ ମଧ୍ୟରେ ନୂଆଗଛ ସୃଷ୍ଟି କରିବାପାଇଁ ଚାଷୀମାନେ ମୁଖ୍ୟତଃ ଡାଳିକଲମି ଉପାୟ ଅବଲମ୍ବନ କରନ୍ତି ।
• ଏହି ପଦ୍ଧତିରେ ଗଛର କୌଣସି ଏକ ଡାଳର କିଛି ଅଂଶରୁ ତ୍ବଚା ବାହାର କରି ମାଟି ପର୍ଯ୍ୟନ୍ତ ବଙ୍କାଇ ଆସି ଓଦା ମାଟିରେ ପୋତି ଦିଆଯାଏ । ଏହି ସ୍ଥାନକୁ କିଛି ଦିନ ଓଦା ରଖିଲେ ପୋତା ହୋଇଥିବା ଅଂଶରୁ କ୍ରମେ ଚେର ବାହାରେ ।
• ଚେର ବାହାରିବା ପରେ ଏହି ଡାଳଟିକୁ ମୂଳଗଛରୁ କାଟି ଅନ୍ୟତ୍ର ଲଗାଇଲେ ତାହା ଏକ ସମ୍ପୂର୍ଣ୍ଣ ନୂତନ ଗଛରେ ପରିଣତ ହୁଏ ।

→ (୨) ଗୁଜି କଲମି (Gootee) :

• ଏଥିପାଇଁ ଗଛର ସୁସ୍ଥ ଓ ପାକଳିଆ ଡାଳକୁ ବାଛି ତା’ର ମୂଳ ଅଂଶର ତ୍ବଚା ବାହାର କରି ଦିଆଯାଏ ।
• କଟା ଅଂଶ ଉପରେ କଲମି ମାଟି [ଗୋବର, କଟା ନଡ଼ା ଓ ପଟୁ ମାଟିର ମିଶ୍ରଣ] ଦେଇ ଅଖା ବା ପଲିଥ୍ଦ୍ୱାରା ତାହାକୁ ବାନ୍ଧି ଦିଆଯାଏ । କଲମି ମାଟି ନଶୁଖୁ ପାଇଁ ସେଥ୍ରେ ପ୍ରତିଦିନ ପାଣି ଦେବାର ବ୍ୟବସ୍ଥା କରାଯାଏ ।
• କିଛିଦିନ ପରେ ଏହି ସ୍ଥାନରୁ ଚେର ବାହାରି କଲମି ମାଟିରେ ବଢ଼େ । ଚେର ଭଲଭାବେ ବଢ଼ିଗଲା ପରେ ଡାଳଟିକୁ କଲମ କୁହାଯାଏ ।
• ଉଦାହରଣ : ପିଜୁଳି, ଗୋଲାପ, ଜାମୁ, କମଳା, କାଗେଜିଲେମ୍ବୁ ଇତ୍ୟାଦି ।

→ ବିଶେଷ ଧରଣର ଜନନ :
(i) ଅସମାୟିତ ଜନନ :

• ସମାୟନ ବା ନିଷେକ ନ ହୋଇ ଡିମ୍ବାଣୁର ବୃଦ୍ଧି ଘଟି ଭ୍ରୂଣ ସୃଷ୍ଟି ହେଲେ ତାହାକୁ ଅସମାୟିତ ଜନନ ବା ଅନିଷେକ ଜନନ କୁହାଯାଏ ।
• କେତେକ ଅପୁଷ୍ପକ ଉଦ୍ଭଦ (ଶୈବାଳ ଓ ଫର୍ଶ)ରେ ଏହା ପରିଲକ୍ଷିତ ହୁଏ । କେତେକ ଉଦ୍ଭଦରେ ସମାୟନ ନହୋଇ ଫଳ ସୃଷ୍ଟି ହୋଇଥାଏ । ଏହାକୁ ଅଯୁଗ୍ନିତ ଫଳନ କୁହାଯାଏ ।
• ସପୁଷ୍ପକ ଉଦ୍ଭଦ (ପିଜୁଳି, ଅଙ୍ଗୁର, କଦଳୀ ଇତ୍ୟାଦି)ରେ ଏ ପ୍ରକାର ଜନନ ଦେଖାଯାଏ । ଏହି ପଦ୍ଧତିରେ ଜାତ ଫଳ ମଞ୍ଜିଶୂନ୍ୟ ହୋଇଥାଏ । ଏହି ଫଳକୁ ଅସାମୟିତ ଫଳ ବା ମଞ୍ଜିବିହୀନ ଫଳ କୁହାଯାଏ ।

(ii) ଟିସୁ ପୋଷଣ (Tissue Culture) :

• ଉଭିଦର ଜୀବନ୍ତକୋଷ, କିମ୍ବା ସେହି କୋଷଗୁଡ଼ିକରୁ ଜାତ ହୋଇଥିବା ଉଭିଦ ପୂର୍ଣବିଭବୀ ବା ସର୍ବକ୍ଷମ । ଅର୍ଥାତ୍ ସେହି ଏକକଗୁଡ଼ିକରେ ଗୋଟିଏ ଉଦ୍ଭଦ ସୃଷ୍ଟି କରିବା କ୍ଷମତା ଥାଏ । ଉଦ୍ଭଦ ଟିସୁର ପୂର୍ଣବିଭବୀ ଗୁଣକୁ ଆଧାର କରି ପାରେନକାଇମା ଭଳି ବିଭେଦିତ ପେଶୀକୁ ଉପଯୁକ୍ତ ପରିମାଣର ପୋଷକ ଅନୁକୂଳ ପରିବେଶ ଯୋଗାଇ ଦେଲେ ତାହା ପୁନଃବିଭାଜନକ୍ଷମ ହୋଇଥାଏ ।
• ଏଣୁ ଏକ ଜୀବନ୍ତ ଜୀବକୋଷ କିମ୍ବା ଜୀବନ୍ତ ଟିସୁକୁ ସ୍ଵତନ୍ତ୍ର ଭାବେ ପ୍ରସ୍ତୁତ ଜୀବାଣୁମୁକ୍ତ ପୋଷକ ମାଧ୍ୟମରେ ବୃଦ୍ଧି କରାଇ ଏକ ପ୍ରତିରୂପୀ ଉଦ୍ଭଦ ସୃଷ୍ଟି ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ କୋଷୀୟ ଗଠନକୁ ଟିସୁ ପୋଷଣ କୁହାଯାଏ ।
• ଏହି ପ୍ରକ୍ରିୟାରେ ପ୍ରଥମେ ଗୋଟିଏ ଉଭିଦର ଉପଯୁକ୍ତ ସୁସ୍ଥ ଓ ତରୁଣଅଂଶ ଚୟନ କରାଯାଏ ପୃଥକ କରାଯାଏ । ତାହାକୁ ବିସ୍ତାପିତ ଅଂଶ ବା ଏକ୍ସପ୍ଲାଣ୍ଟ କୁହାଯାଏ ।
• ଟିସୁ ପୋଷଣଦ୍ୱାରା ଅନିୟମିତ ଭାବେ ସଜ୍ଜିତ ପାରେନକାଇମା ପେଶୀକୋଷଗୁଡ଼ିକର ଏକ ଆକାରବିହୀନ ପିଣ୍ଡକୁ କାଲ୍‌ କୁହାଯାଏ ।
• କାଲ୍ସର ପୁନକର୍ଷଣଦ୍ଵାରା ସେଥୁରୁ ଚାରା ଉଭିଦ ବାହାରେ । ଚାରା ଉଭିଦଗୁଡ଼ିକୁ ନିୟନ୍ତ୍ରିତ ଅବସ୍ଥାରେ ବୃଦ୍ଧି କରାଗଲେ ତାହା ସମ୍ପୂର୍ଣ୍ଣ ଉଭିଦରେ ପରିବର୍ତ୍ତିତ ହୁଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ସୂକ୍ଷ୍ମ ବଂଶବିସ୍ତାର କୁହାଯାଏ ।

→ ସପୁଷ୍ପକ ଉଦ୍ଭଦରେ ଲିଙ୍ଗୀୟ ଜନନ :

• ଆବୃତବୀଜୀ ଉଦ୍ଭଦରେ ଜନତାଂଶଗୁଡ଼ିକ ଫୁଲ ମଧ୍ୟରେ ଥାଏ । ଫୁଲର ବିଭିନ୍ନ ଅଂଶ ହେଲା- ବୃତିମଣ୍ଡଳ, ଦଳମଣ୍ଡଳ, ପୁଂକେଶର ଓ ଫଳିକା ଚକ୍ରର ଫଳିକା ।
• କେବଳ କେଶର ବା କେବଳ ଫଳିକା ଥିବା ଫୁଲକୁ ଏକଲିଙ୍ଗୀ ଫୁଲ କୁହାଯାଏ ଓ ଉଭୟ କେଶର ଓ ଫଳିକା ଥ‌ିବା ଫୁଲକୁ ଦ୍ଵିଲିଙ୍ଗୀ ଫୁଲ କୁହାଯାଏ ।

→ ପରାଗସଙ୍ଗମ ବା ପରାଗଣ (Pollination) :

• ସମାୟନ ପୂର୍ବରୁ ଫୁଲରେ ଥିବା ପରାଗରେଣୁ ବିଭିନ୍ନ ମାଧ୍ୟମରେ ଆସି ଫୁଲର ଗର୍ଭଶୀର୍ଷ (Stigma) ରେ ପଡ଼େ । ଏହାକୁ ପରାଗସଙ୍ଗମ ବା ପରାଗଣ କୁହାଯାଏ ।
• କେତେକ ଉଦ୍ଭଦରେ ଗୋଟିଏ ଫୁଲର ପରାଗରେଣୁ ସେହି ଫୁଲର ଗର୍ଭଶୀର୍ଷରେ ପଡ଼ି ତାହାର ଡିମ୍ବାଣୁକୁ ସମାୟନ କରେ । ଏହାକୁ ସ୍ବ-ପରାଗଣ କୁହାଯାଏ ।
• କିନ୍ତୁ ଅଧିକାଂଶ ଉଦ୍ଭଦରେ ଗୋଟିଏ ଜାତିର ଫୁଲର ପରାଗରେଣୁ ପତଙ୍ଗ, ପକ୍ଷୀ, ଜଳ, ବାୟୁ ଆଦି ମାଧ୍ୟମରେ ଆସି ସେହି ଜାତିର ଅନ୍ୟ ଏକ ଫୁଲର ଗର୍ଭଶୀର୍ଷରେ ପଡ଼େ ଓ ପରେ ଗର୍ଭାଧାନ ହୁଏ । ଏହାକୁ ପରପରାଗଣ କୁହାଯାଏ ।

→ ଫଳିକା ଓ ଗର୍ଭାଶୟ :

• ଫଳିକାର ତିନୋଟି ଅଂଶ ଥାଏ । ଏହାର ସ୍ତ୍ରୀତ ଶେଷଭାଗ ହେଉଛି ଗର୍ଭାଶୟ, ମଧ୍ୟଭାଗଟି ଗର୍ଭଦଣ୍ଡ ଓ ଉପରିଭାଗ ଗର୍ଭଶୀର୍ଷ ନାମରେ ନାମିତ ।
• ସହଡିମ୍ବକଟି ଗୋଟିଏ ବୃନ୍ତଦ୍ୱାରା ଗର୍ଭାଶୟରେ ସଂଯୁକ୍ତ ହୋଇଥାଏ ।
• ଡିମ୍ବକ ମଧ୍ୟରେ ଥ‌ିବା ଡିମ୍ବକାୟାକୁ ଆବୃତ କରି ଗୋଟିଏ ବା ଦୁଇଟି ଆଚ୍ଛଦ ଥାଏ । ଆଚ୍ଛଦ ଅଗ୍ରଭାଗର ମିଳନ ସ୍ଥାନରେ ଗୋଟିଏ ଛିଦ୍ର ରହିଥାଏ ଯାହାକୁ ବୀଜରନ୍ଧ୍ର କୁହାଯାଏ ।
• ଡିମ୍ବକାୟାରେ ଗୋଟିଏ ଭ୍ରୂଣାଶୟ ଥାଏ । ଭ୍ରୂଣାଶୟର ଅଗ୍ରଭାଗରେ ଗୋଟିଏ ଡିମ୍ବକୋଷ ଓ ତାହାର ଦୁଇପାଖରେ ଦୁଇଟି ସହାୟକ କୋଷ ରହିଥାଏ ।
• ବୃନ୍ତଆଡ଼କୁ ତିନିଟି ପ୍ରତିମୁଖ କୋଷିକା ରହିଥାଏ । ଭ୍ରୂଣାଶୟ ମଧ୍ୟଭାଗରେ ଲାଗି ଲାଗି ରହିଥ‌ିବା ଦୁଇଟି ନ୍ୟଷ୍ଟିକୁ ମେରୁନ୍ୟଷ୍ଟି କୁହାଯାଏ ।
• ସମାୟନର ଠିକ୍ ପୂର୍ବରୁ ଏହି ଦୁଇଟି ନ୍ୟଷ୍ଟି ମିଳିତ ହୋଇ ଦ୍ଵିତୀୟକ ନ୍ୟଷ୍ଟିରେ ପରିଣତ ହୁଅନ୍ତି ।

→ ସମାୟନ (Fertilization) :

• ପରାଗରେଣୁ ଗର୍ଭଶୀର୍ଷରେ ପଡ଼ିବା ପରେ ତାହାର ବାହାର ଆବରଣଟି ଫାଟିଯାଏ । ଭିତର ଆବରଣଟି ଗୋଟିଏ ନଳୀ ଆକାରରେ ବାହାରେ ଓ ପରାଗ ଅଙ୍କୁରିତ ହୁଏ ।
• ଏହି ନଳୀ ଗର୍ଭଦଣ୍ଡ ମଧ୍ୟଦେଇ ଭ୍ରୂଣାଶୟ ଆଡ଼କୁ ବଢ଼େ । ଏହାକୁ ପରାଗନଳୀ କୁହାଯାଏ ।
• ପରାଗ ଅଙ୍କୁରିତ ହେବା ସମୟରେ ଏହା ସମବିଭାଜନ ପ୍ରକ୍ରିୟାରେ ବିଭାଜିତ ହୋଇ ପ୍ରଥମେ ଅଙ୍ଗୀୟ କୋଷ ଓ ଜନନ କୋଷ ସୃଷ୍ଟି କରେ
• ଜନନ କୋଷ ପୁନର୍ବାର ଏହି ପ୍ରକ୍ରିୟାରେ ବିଭାଜିତ ହୋଇ ଦୁଇଟି ପୁଂଯୁଗ୍ମକ ସୃଷ୍ଟିକରେ । ପରାଗ ନଳୀରେ କିଛି କୋଷରସ ସହିତ ଦୁଇଟି ପୁଂଯୁଗ୍ମକ ଓ ଗୋଟିଏ ନଳୀ ନ୍ୟଷ୍ଟି ଥାଏ । କ୍ରମେ ପରାଗନଳୀ ବୀଜରନ୍ଧ୍ର ବାଟଦେଇ ପୁଂଯୁଗ୍ମକ ଦୁଇଟି ଭୂଣାଶୟ ମଧକୁ ଚାଲିଆସେ ଓ ଗୋଟିଏ ଫୁଯୁଗ୍ମକ ସ୍ତ୍ରୀ ଯୁଗ୍ମକ ବା ଡିମ୍ବକୋଷ ସହିତ ମିଳିତ ହୋଇ ଯୁଗ୍ମଜ ଗଠନ କରେ । ଏଥୁରୁ ଭ୍ରୂଣର ଉତ୍ପତ୍ତି ହୁଏ ।
• ଅନ୍ୟ ଫୁଯୁଗ୍ମକଟି, ଦ୍ଵିତୀୟକ ନ୍ୟଷ୍ଟି ସହିତ ମିଳିତ ହୋଇ ଭୃଣପୋଷ ନ୍ୟଷ୍ଟି ଗଠନ କରେ । ଭ୍ରୂଣପୋଷ ନ୍ୟଷ୍ଟିରୁ ଭୃଣପୋଷ ଜାତ ହୁଏ ଏବଂ ଏହା ବର୍ଦ୍ଧିଷ୍ଣୁ ଭୃଣକୁ ପୋଷଣ ଯୋଗାଇଥାଏ ।
• ପୁଂଯୁଗ୍ମକ ଓ ସ୍ତ୍ରୀ ଯୁଗ୍ଧକର ମିଳନକୁ ସମାୟନ କୁହାଯାଏ । ସପୁଷ୍ପକ ଆବୃତବୀଜୀ ଉଦ୍ଭଦରେ ଦୁଇଟି ସମାୟନ କ୍ରିୟା ଦେଖବାକୁ ମିଳେ । ପ୍ରଥମଟି ହେଲା, ଗୋଟିଏ ପୁଂଯୁଗ୍ମକ ସହିତ ଡିମ୍ବାଣୁ ବା ଡିମ୍ବକୋଷର ସମାୟନ ଓ ଅନ୍ୟଟି ହେଲା ଦ୍ୱିତୀୟକ ନ୍ୟଷ୍ଟି ସହିତ ଦ୍ୱିତୀୟ ପୁଂଯୁଗ୍ଧକର ମିଳନ । ସପୁଷ୍ପକ ଉଦ୍ଭଦର ଏହି ପ୍ରକ୍ରିୟାକୁ ଦ୍ବିସମାୟନ କୁହାଯାଏ ।
• ସମାୟନ ପରେ ଯୁଗ୍ମଜ ବାରମ୍ବାର ବିଭାଜିତ ହୋଇ ଡିମ୍ବକ ମଧ୍ୟରେ ଏକ ଭ୍ରୂଣ ସୃଷ୍ଟି କରେ । ଭ୍ରୂଣ ଏକ କଠିନ ଆବରଣ ଦ୍ଵାରା ଆବୃତ ହୋଇ ବୀଜ ବା ମଞ୍ଜିରେ ପରିଣତ ହୁଏ । ଏହି ସମୟ ମଧ୍ୟରେ ଡିମ୍ବାଶୟ ବୃଦ୍ଧିପାଇ ଫଳରେ ପରିଣତ ହୁଏ ଏବଂ ବୃତ୍ତି, ଦଳମଣ୍ଡଳ ଆଦି ଶୁଖୁ ଝଡ଼ିଯାଏ ।

→ ପଶୁରେ ପ୍ରଜନନ (Reproduction in Animal) :
କେତେକ ପ୍ରାଣୀରେ ବଂଶବୃଦ୍ଧି କେବଳ ଅଲିଙ୍ଗୀ ଜନନ ବା କେବଳ ଲିଙ୍ଗୀୟ ଜନନଦ୍ୱାରା ହୋଇଥିବାବେଳେ କେତେକଙ୍କଠାରେ ଉଭୟ ପ୍ରକ୍ରିୟା ଦେଖାଯାଇଥାଏ । ପ୍ରାଣୀମାନଙ୍କଠାରେ ଦେଖାଯାଉଥ‌ିବା ଅଲିଙ୍ଗୀ ଜନନର ଦୁଇଟି ସାଧାରଣ ଉପାୟ ହେଉଛି ବିଭାଜନ ଓ କୋରକୋଦ୍‌ଗମ ବା କଳିକନ ।

→  ଅଲିଙ୍ଗୀ ଜନନ :
(i) ବିଭାଜନ (Fission) :

• ବିଭାଜନ ଏକ ଅତି ସରଳ ଜନନ କ୍ରିୟା । ଏହି ପ୍ରକ୍ରିୟା ଦୁଇ ପ୍ରକାରର –
  (କ) ଦ୍ବିବିଭାଜନ ଓ
  (ଖ) ବହୁ ବିଭାଜନ ।

→ (କ) ଦ୍ବିବିଭାଜନ (Binary fission) :

• ଏହି ପ୍ରକାର ଜନନଦ୍ଵାରା ମାତୃ ଜୀବଠାରୁ ଦୁଇଟି ଅପତ୍ୟ ସୃଷ୍ଟି ହୁଅନ୍ତି, ଉଦାହରଣ ଏମିବା । ଏହା ମଧୁର ପାଣିରେ ରହେ । ଅନୁକୂଳ ପରିସ୍ଥିତିରେ ଏମିବା ଶରୀରର ବୃଦ୍ଧି ଘଟେ ।
• ସର୍ବବୃହତ୍ ଆକାରରେ ପହଞ୍ଚିବା ପରେ ନିଜର କୂଟପାଦଗୁଡ଼ିକ ପ୍ରତ୍ୟାହାର କରି ଏହା ପ୍ରାୟ ଗୋଲ ଆକାର ଧାରଣ କରେ । ଏହା ଆଉ ଖାଦ୍ୟ ଗ୍ରହଣ କରେନାହିଁ ଓ କୋଷ ବିଭାଜନ ପାଇଁ ପ୍ରସ୍ତୁତ ହୁଏ ।
• ସମବିଭାଜନଦ୍ୱାରା ଗୋଟିଏ ମାତ୍ର ଏମିବାରୁ ଦୁଇଟି ଅପତ୍ୟ ସୃଷ୍ଟି ହୁଏ ।
• ପାରାମସିଅମ୍ ଓ ଇଉକ୍ଲିନା ମଧ୍ୟ ଦ୍ଵିବିଭାଜନଦ୍ୱାରା ନିଜର ଜନନ କ୍ରିୟା ସମ୍ପାଦନ କରନ୍ତି । କିନ୍ତୁ ପାରାମସିଅମ୍‌କୋ କୋଷ ବିଭାଜନ ଅନୁପ୍ରସ୍ଥ ପୃଷ୍ଠରେ ସମ୍ପାଦିତ ହେଉଥ‌ିବାରୁ ଏହାକୁ ଅନୁପ୍ରସ୍ଥ ଦ୍ବିବିଭାଜନ କୁହାଯାଏ । ଇଉକ୍ଲିନାରେ ବିଭାଜନ ପୃଷ୍ଠ ଅନୁଲମ୍ବ ଭାବେ ହେଉଥ‌ିବାରୁ ଏହାକୁ ଅନୁଲମ୍ବ ଦ୍ବିବିଭାଜନ କୁହାଯାଏ ।

→ (ଖ) ବହୁବିଭାଜନ (Multiple fission) :

• ଖରାଦିନେ ଏମିବା ରହୁଥ‌ିବା ପୋଖରୀ, ଗାଡ଼ିଆରୁ ପାଣି ଶୁଖୁଲେ ବା ଅତ୍ୟଧିକ ଥଣ୍ଡା ଯୋଗୁଁ ପାଣି ବରଫ ହୋଇଗଲେ, ଏମିବା କୂଟପାଦଗୁଡ଼ିକୁ ପ୍ରତ୍ୟାହାର କରି ନିଜ ଶରୀର ଚାରିପଟେ ତିନିସ୍ତର ବିଶିଷ୍ଟ ଏକ କଠିନ ଆବରଣ ବା କୋଷିକା ତିଆରି କରି ରହେ ।
• ଏହି ସମୟରେ ତା’ର ଚୟାପଚୟ କ୍ରିୟା ହ୍ରାସପାଏ । ବାରମ୍ବାର ନ୍ୟଷ୍ଟି ବିଭାଜନଦ୍ୱାରା ଏମିବା ଶରୀରରେ 500- 600ଟି ଛୋଟ ନ୍ୟଷ୍ଟି ତିଆରି ହୁଏ । ପ୍ରତ୍ୟେକ ନ୍ୟଷ୍ଟି କିଛି ପରିମାଣର କୋଷଜୀବକଦ୍ଵାରା ଆବୃତ୍ତ ହୋଇ ରହେ । ଏହିପରି ଭାବେ ସୃଷ୍ଟ ଅପତ୍ୟଗୁଡ଼ିକୁ ‘କୁନି ଏମିବା’ ବା ଏମିକ୍ୟୁଲା କୁହାଯାଏ I ବର୍ଷାଦିନର ଆଗମନରେ ପରିସ୍ଥିତି ଅନୁକୂଳ ହେଲେ ଏହି କଠିନ ଆବରଣ ଜଳ ସଂସ୍ପର୍ଶରେ ଆସି ଫାଟିଯାଏ । କୋଷିକା ଭିତରେ ଥିବା
• ଏମିବାର ଏହି ପ୍ରକାର ବହୁ ବିଭାଜନ ଜନନ କ୍ରିୟାକୁ ସ୍କୋରୁଲେସନ (Sporulation) ମଧ୍ୟ କୁହାଯାଏ ।

ସଂକ୍ରମିତ ମଶା କାମୁଡି଼ବା ସମୟରେ ପ୍ଲାଜମୋଡ଼ିୟମ୍‌ର ସ୍କୋରୋଜୋଏଟ୍ (Sporozoite) ମଣିଷର ରକ୍ତ ପ୍ରବାହ ଦେଇ ଯକୃତ୍ କୋଷ ମଧ୍ୟରେ ପ୍ରବେଶ କରି ବହୁବିଭାଜନଦ୍ୱାରା ବଂଶବୃଦ୍ଧି କରେ । ଏହି ପ୍ରକାର ବହୁ ବିଭାଜନକୁ ସାଇଜୋଗୋନି (Schizogony) କୁହାଯାଏ ।

(ii) କୋରକୋଦ୍‌ଗମ (Budding)

• କେତେକ ଏକକୋଷୀ ପ୍ରାଣୀ, ସ୍ପଞ୍ଜ ଓ ହାଇଡ୍ରାପରି ବହୁକୋଷୀ ପ୍ରାଣୀ କୋରକୋଦ୍‌ଗମ ଉପାୟରେ ଅଲିଙ୍ଗୀ ଜନନଦ୍ୱାରା ନିଜର ବଂଶବିସ୍ତାର କରନ୍ତି ।
• ଏହା ଦୁଇ ପ୍ରକାରର, ଯଥା –
  1. ବାହ୍ୟ କୋରକୋଦ୍‌ଗମ ଓ
  2. ଅନ୍ତଃ କୋରକୋଦ୍‌ଗମ ।

1. ବାହ୍ୟ କୋରକୋଦ୍‌ଗମ (External budding)

• ପରିବେଶ ଯେତେବେଳେ ଅନୁକୂଳ ଓ ଖାଦ୍ୟପଦାର୍ଥ ପ୍ରଚୁର ଭାବେ ମିଳେ, ସେତେବେଳେ ସୁସ୍ଥ ଏବଂ ବୟଃପ୍ରାପ୍ତ ହାଇଡ୍ରା ଏହି ଉପାୟରେ ବଂଶବିସ୍ତାର କରିଥାଏ ।
• ପ୍ରାରମ୍ଭିକ ଅବସ୍ଥାରେ ହାଇଡ୍ରା ଶରୀରର ମଧ୍ୟ ଭାଗରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାର କୋଷ ଏକାଠି ହୋଇ ଏକ ଛୋଟ ଆବୁ ଭଳି କୋରକ ସୃଷ୍ଟି କରେ । ଏହି ଅଞ୍ଚଳକୁ କୋରକୋଦ୍‌ଗମ ଅଞ୍ଚଳ କୁହାଯାଏ ।

2. ଅନ୍ତଃ କୋରକୋଦ୍‌ମ (Internal budding)

• ପ୍ରତିକୂଳ ପରିବେଶ ଓ ଖାଦ୍ୟପଦାର୍ଥର ଅଭାବ ଦେଖାଦେଲେ ସ୍ପଞ୍ଜ ଏହି ପ୍ରଣାଳୀରେ ନିଜ ଶରୀର ଭିତରେ ଜେଡ୍ୟୁଲ୍ ତିଆରି କରି ବଂଶବିସ୍ତାର କରେ ।

→ ପୁନରୁଭବନ (Regeneration) :

• ପୁନରୁଭବନ କୌଣସି ପ୍ରାଣୀର ଏକ ଜନନ କ୍ରିୟା ନୁହେଁ; କିଛି ପ୍ରାଣୀରେ ଏହା ଏକ ସ୍ଵତନ୍ତ୍ର ବ୍ୟବସ୍ଥା ମାତ୍ର ।
• ହାଇଡ୍ରାର ଶରୀରକୁ ଖଣ୍ଡ ଖଣ୍ଡ କରି କାଟିଲେ କିଛିଦିନ ପରେ ପ୍ରତ୍ୟେକ କଟାଖଣ୍ଡରୁ ଗୋଟିଏ ଲେଖାଏଁ ସମ୍ପୂର୍ଣ ପୂର୍ଷବିକଶିତ ହାଇଡ୍ରା ସୃଷ୍ଟି ହୋଇଥାଏ ।

ପ୍ରାଣୀମାନଙ୍କ ଶରୀରରେ ଏକ ପ୍ରକାର ସର୍ବପ୍ରସ୍ତୁ ବା ପୂଷ୍ଠବିଭବୀ କୋଷ (Totipotent cell) ଥାଏ । ଏହା ପ୍ରାଣୀ ଶରୀର ଗଠନ ପାଇଁ ଆବଶ୍ୟକ ଅନ୍ୟ ସମସ୍ତ ପ୍ରକାର କୋଷ ବା ଟିସୁ ତିଆରି କରିପାରେ । ଫଳରେ କଟିଯାଇଥିବା ଅଂଶରୁ ଏକ ନୂଆ ପ୍ରାଣୀ ଜାତ ହୁଏ ।

→ ମାନବର ଲିଙ୍ଗୀୟ ଜନନ (Human Reproduction):

• ମଣିଷ ଗୋଟିଏ ସ୍ତନ୍ୟପାୟୀ ଶ୍ରେଣୀର ପ୍ରାଣୀ ଅଟେ ।
• ପ୍ରଜନନ ଜରିଆରେ ବଂଶବିସ୍ତାର କରିବା ଓ ମାନବଜାତିର ନିରବଚ୍ଛିନ୍ନତା ନିଶ୍ଚିତ କରିବାରେ ଉଭୟ ପୁରୁଷ ଓ ସ୍ତ୍ରୀର ଭୂମିକା ରହିଥାଏ ।

→ ଯୁଗ୍ମକ ଜନନ (Gametogenesis) :

• ଯୁଗ୍ମକ ଜନନଦ୍ୱାରା ଶୁକ୍ରାଶୟରେ ଶୁକ୍ରାଣୁ ଓ ଡିମ୍ବାଶୟରେ ଡିମ୍ବାଣୁ ସୃଷ୍ଟି ହୁଏ ।
• ଶୁକ୍ରାଣୁ ସୃଷ୍ଟି ପ୍ରକ୍ରିୟାକୁ ଶୁକ୍ରାଣୁଜନନ ଓ ଡିମ୍ବାଣୁ ସୃଷ୍ଟି ପ୍ରକ୍ରିୟାକୁ ଡିମ୍ବାଣୁଜନନ କୁହାଯାଏ ।

→ ଶୁକ୍ରାଣୁ ଜନନ (Spermatogenesis) :

• ପୁରୁଷର ଶୁକ୍ରାଶୟ ବହୁସଂଖ୍ୟକ ଶୁକ୍ରୋତ୍ପରି ସୂକ୍ଷ୍ମ ନଳିକା ବା ଶୁକ୍ରଜନ ନଳିକାଦ୍ୱାରା ଗଠିତ । ପ୍ରତ୍ୟେକ ନଳିକାର ଆବରଣରେ ରହିଛି ଆଦି ଜାୟକ କୋଷଦ୍ବାରା ଗଠିତ ଜର୍ମିନାଲ୍ ଏପିଥ୍ଲିୟମ୍ ବା ଜନନ ଅଚ୍ଛଦ ।
• ଏହି ଅଧ୍ଵଚ୍ଛଦରେ ଥ‌ିବା କୋଷରେ ସମବିଭାଜନ ହେବା ଫଳରେ ଉତ୍ପନ୍ନ କୋଷଗୁଡ଼ିକୁ ‘ମୂଳ ଶୁକ୍ରାଣୁ କୋଷ’ କୁହାଯାଏ ।
• ଏହି ପ୍ରକ୍ରିୟା ହେଉଥ‌ିବା ପ୍ରାବସ୍ଥାକୁ ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା କୁହାଯାଏ ।
• ଅନେକ ମୂଳ ଶୁକ୍ରାଣୁ କୋଷ ଗଠିତ ହେଲାପରେ ଏହି କୋଷଗୁଡ଼ିକର ଆକାର ବୃଦ୍ଧି ହୁଏ । କୋଷର ବୃଦ୍ଧି ହୋଇ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଆକାରରେ ପହଞ୍ଚିଲେ ତାହାକୁ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷ କୁହାଯାଏ ।
• ମୂଳ ଶୁକ୍ରାଣୁ କୋଷର ବୃଦ୍ଧିହୋଇ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷ ଏହାପରେ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷରେ ଅଦ୍ଧବିଭାଜନ ପ୍ରକ୍ରିୟା ହେବା ପର୍ଯ୍ୟନ୍ତ ଅବଧିକୁ ବୃଦ୍ଧି ପ୍ରାବସ୍ଥା କୁହାଯାଏ ।
• ଏହାପରେ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷରେ ଅଦ୍ଧବିଭାଜନ ପ୍ରକ୍ରିୟା ହୋଇଥାଏ । ଏହି ବିଭାଜନ ଫଳରେ ଗୋଟିଏ ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷରୁ ଦୁଇଟି ଦ୍ଵିତୀୟକ ଶୁକ୍ରାଣୁ କୋଷ ତିଆରି ହୁଏ।
• ଏହି କୋଷର ଗୁଣସୂତ୍ର ସଂଖ୍ୟା ଅର୍ଦ୍ଧେକ (n) ହୋଇଥାଏ । ଦ୍ୱିତୀୟ ଅର୍ଥ ବିଭାଜନ, ପ୍ରଥମ ଅର୍ଥ ବିଭାଜନ ପରେ ପରେ ହୋଇଥାଏ, ଏହା ସମବିଭାଜନ ପ୍ରକ୍ରିୟାଭଳି ହୋଇଥାଏ । ଏହାଫଳରେ ଦ୍ଵିତୀୟକ ଶୁକ୍ରାଣୁ କୋଷରୁ ଦୁଇଟି ପ୍ରାକ୍ ଶୁକ୍ରାଣୁ କୋଷ ତିଆରି ହୁଏ ।
• ଗତିହୀନ ପ୍ରାକ୍ ଶୁକ୍ରାଣୁ କୋଷରେ ବିଭିନ୍ନ ରକମର ପରିବର୍ତ୍ତନ ଓ ପରିବର୍ଦ୍ଧନ ଅର୍ଥାତ୍ ବିଭେଦନ ହେଲାପରେ ତାହା ଏକ ଗତିଶୀଳ ଶୁକ୍ରାଣୁ ହେବା ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ ପ୍ରକ୍ରିୟାକୁ ସ୍କର୍ମଓଜେନେସିସ୍ କୁହାଯାଏ ।
• ପ୍ରାଥମିକ ଶୁକ୍ରାଣୁ କୋଷରୁ ଶୁକ୍ରାଣୁ ସୃଷ୍ଟି ହେବା ପର୍ଯ୍ୟନ୍ତ ଅବଧୀକୁ ପରିପକ୍ବନ ପ୍ରାବସ୍ଥା କୁହାଯାଏ ।

→ ଶୁକ୍ରାଣୁ (Sperm) :

• ଶୁକ୍ରାଣୁ ଏକ ଲମ୍ବ ଲାଞ୍ଜବିଶିଷ୍ଟ କୋଷ ଅଟେ ।
• ଏହାର ତିନୋଟି ଅଂଶ ରହିଛି; ଯଥା- ଅଗ୍ରଖଣ୍ଡ ବା ହେଡ୍, ମଧ୍ୟଖଣ୍ଡ ଓ ଲାଞ୍ଜ ।
• ଏହାର ଗୋଟିଏ ପାଖରେ ରହିଛି ଅଗ୍ରପିଣ୍ଡକ, ଏହା ପଛକୁ ରହିଛି କୋଷ ନ୍ୟଷ୍ଟି । ମଧ୍ୟଖଣ୍ଡ ଭିତରେ ରହିଛି ମାଇଟୋକଣ୍ଡ୍ରିଆ । ହେଡ୍ ଓ ମିଡ଼ିଲ୍ ପିସ୍ ଭିତରେ ଥ‌ିବା ଗ୍ରୀବା ବା ନେଲ୍‌ରେ ଅଛି ସେଣ୍ଟ୍ରିଓଲ୍, ଠିକ୍ ନ୍ୟଷ୍ଟିକୁ ଲାଗି । ମଧ୍ୟଖଣ୍ଡ ପଛକୁ ଲମ୍ବିଛି ସୂତା ପରି ଲାଞ୍ଜ । ଏହା ଶୁକ୍ରାଣୁର ଚଳନରେ ସାହାଯ୍ୟ କରେ ।

→ ଓଜେନେସିସ୍ (Oogensis) :

• ସ୍ତ୍ରୀଯୁଗ୍ମକ ବା ଡିମ୍ବାଣୁ, ଡିମ୍ବାଣୁ ଜନନ ପ୍ରକ୍ରିୟାରେ ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।
• ଡିମ୍ବାଶୟର ଆବରଣ ସହ ରହିଛି ଆଦି ଜାୟକ କୋଷ । ଏହି କୋଷର ବିଭାଜନ ଫଳରେ ବହୁସଂଖ୍ୟକ ମୂଳ ଡିମ୍ବାଣୁ କୋଷ ଉତ୍ପନ୍ନ ହୁଏ । କୋଷର ବିଭାଜନ, ସମବିଭାଜନ ପ୍ରକ୍ରିୟାରେ ହୋଇଥାଏ ଏବଂ ଏହି ଅବସ୍ଥାକୁ ପ୍ରଗୁଣନ ପ୍ରାବସ୍ଥା କୁହାଯାଏ ।
• ମୂଳ ଡିମ୍ବାଣୁ କୋଷ ତିଆରି ହେଲାପରେ ବୃଦ୍ଧି ପ୍ରାବସ୍ଥାରେ ତାହାର ଆକାରରେ ଉଲ୍ଲେଖନୀୟ ବୃଦ୍ଧି ହୁଏ । ଏହି ସମୟରେ ମୂଳ ଡିମ୍ବାଣୁ କୋଷ ଚାରିପାଖେ କିଛି ଖାଦ୍ୟ ଯୋଗାଉଥ‌ିବା କୋଷ ଘେରି ରହେ ।
• ମୂଳ ଡିମ୍ବାଣୁ କୋଷର ନିର୍ଦ୍ଦିଷ୍ଟ ବୃଦ୍ଧି ଘଟିବା ପରେ ତାହାକୁ ପ୍ରାଥମିକ ଡିମ୍ବାଣୁ କୋଷ କୁହାଯାଏ
• ପରିପକ୍ବନ ପ୍ରାବସ୍ଥାର ପ୍ରଥମ ପର୍ଯ୍ୟାୟରେ ପ୍ରାଥମିକ ଡିମ୍ବାଣୁ କୋଷର ଅର୍ଥବିଭାଜନ ହୁଏ । ଫଳରେ 2ଟି ଅପତ୍ୟ କୋଷ ଜାତ ହୁଏ, ଯେଉଁଥିରେ ଅର୍ଦ୍ଧେକ ସଂଖ୍ୟକ (n)ଗୁଣସୂତ୍ର ରହିଥାଏ ।
• ତେବେ ଅପତ୍ୟ କୋଷ ଦୁଇଟିରେ କୋଷଜୀବକ ପରିମାଣ କମ୍ ବେଶି ହେବାରୁ ଗୋଟିଏ କୋଷର ଆକାର ଅନ୍ୟ କୋଷଠାରୁ ଯଥେଷ୍ଟ ବଡ଼ ହୁଏ । ବଡ଼ କୋଷଟିକୁ ଦ୍ବିତୀୟକ ଡିମ୍ବାଣୁ କୋଷ କୁହାଯାଏ । ଛୋଟ କୋଷଟିକୁ ପ୍ରଥମ ପୋଲାର ବଡ଼ି କୁହାଯାଏ ।
• ଏହି ପ୍ରାବସ୍ଥାର ଦ୍ଵିତୀୟ ପର୍ଯ୍ୟାୟରେ ଦ୍ଵିତୀୟକ ଡିମ୍ବାଣୁ କୋଷ ଏବଂ ପ୍ରଥମ ପୋଲାର ବଡ଼ିର ସମବିଭାଜନ ହୋଇଥାଏ । କିନ୍ତୁ ଯେଉଁ ଦୁଇଟି ଅପତ୍ୟ କୋଷ ହୁଏ ସେମାନଙ୍କ ଆକାର ମଧ୍ୟ ବଡ଼ ଛୋଟ ହୋଇଥାଏ ।
• ବଡ଼ କୋଷଟି ଡିମ୍ବାଣୁ ହୁଏ ଓ ସାନଟି ଦ୍ଵିତୀୟ ପୋଲାର ବଡ଼ ହୁଏ । ସେହିପରି ପ୍ରଥମ ପୋଲାର ବଡ଼ିର ବିଭାଜନ ଫଳରେ ଦୁଇଟି ଅତିରିକ୍ତ ପୋଲାର ବଡ଼ି ତିଆରି ହୁଏ।
• ପରିପକ୍ବନ ପ୍ରାବସ୍ଥାର ଶେଷରେ ଗୋଟିଏ ପ୍ରାଥମିକ ଡିମ୍ବାଣୁ କୋଷରୁ ଗୋଟିଏ ଡିମ୍ବାଣୁ ଓ ତିନୋଟି ପୋଲାର ବଢ଼ି ତିଆରି ହୁଏ ।

→ ପୁରୁଷ ଜନନ ତନ୍ତ୍ର (Male reproduction system) :

• ପୁରୁଷ ଜନନ ତନ୍ତ୍ର ମୁଖ୍ୟତଃ
  (i) ଶୁକ୍ରମୁଣି,
  (ii) ଶୁକ୍ରାଶୟ,
  (iii) ଶୁକ୍ରବାହୀନଳୀ,
  (iv) ମୂତ୍ର ମାର୍ଗ,
  (v) ଶିଶୁ ଆଦିକୁ ନେଇ ଗଠିତ ।

(i) ଶୁକ୍ରମୁଣି (Serotal sac) :

• ପୁରୁଷ ଶରୀରରେ ଥିବା ଦୁଇଟି ଶୁକ୍ରମୁଣି ମଧ୍ୟରେ ଦୁଇଟି ଶୁକ୍ରାଶୟ ଅଛି । ମାନବ ଶରୀରର ତାପମାତ୍ରା ଅଧିକ (37°C) ଶୁକ୍ର ମୁଣିର ତାପମାତ୍ରା ଏହାଠାରୁ 2°C କମ୍, ଯାହା ଶୁକ୍ରାଣୁ ଉତ୍ପତ୍ତି ପାଇଁ ଅନୁକୂଳ । ଏଠାରେ ସୂଚନାଯୋଗ୍ୟ ଯେ ହାତୀ ଓ ତିମି ପରି ସ୍ତନ୍ୟପାୟୀ ପ୍ରାଣୀଙ୍କ ଶୁକ୍ରାଶୟ ଦୁଇଟି ଶରୀର ଭିତରେ ଥାଏ ।

(ii) ଶୁକ୍ରାଶୟ (Testis) :

• ପୁରୁଷ ଶରୀରରେ ଦୁଇଟି ଶୁକ୍ରାଶୟ ବା ମୁଷ୍କ ରହିଛି । ଏହା ନିଦ୍ରା ଗୋଲାକାର ପିଣ୍ଡ ।
  ବହୁ ଶୁକ୍ରଜନନ ନଳିକାକୁ ନେଇ ଏହା ଗଠିତ । ଶୁକ୍ର ଜନନ ନଳିକାରୁ ଶୁକ୍ରାଣୁ ଉତ୍ପତ୍ତି ହୋଇଥାଏ । ତା’ଛଡ଼ା ଏହି ନଳିକା ବାହାରେ ଓ ବିଭିନ୍ନ ନଳିକାର ଅନ୍ତରାଳରେ ଲେଡିଟ୍ କୋଷ ଦେଖାଯାଏ ।

(iii) ଶୁକ୍ରବାହୀନଳୀ (Vas deferens):

• ପ୍ରତ୍ୟେକ ଶୁକ୍ରାଶୟରୁ ଗୋଟିଏ ଶୁକ୍ରବାହୀନଳୀ ବାହାରି ଉଦର ଗହ୍ବର ମଧ୍ୟରେ ପ୍ରବେଶ କରେ । ଦୁଇପଟର ନଳୀ ମୂତ୍ରାଶୟର ମୂତ୍ରନଳୀ ସହିତ ମିଶି ମୂତ୍ରମାର୍ଗ ତିଆରି କରନ୍ତି ।

(iv) ମୂତ୍ରମାର୍ଗ (Urethra) :

• ଉଭୟ ଶୁକ୍ରରସ ଓ ମୂତ୍ର ମୂତ୍ରମାର୍ଗ ଦେଇ ଶିଶୁର ଅଗ୍ରଭାଗରେ ଥ‌ିବା ରନ୍ଧ୍ର ମାଧ୍ୟମରେ ଶରୀର ବାହାରକୁ ବାହାରେ ।

→ ସ୍ତ୍ରୀ ଜନନ ତନ୍ତ୍ର (Female reproductive system) :

• ସ୍ତ୍ରୀ ଜନନ ତନ୍ତ୍ର ମୁଖ୍ୟତଃ ଡିମ୍ବାଶୟ, ଡିମ୍ବବାହୀ ନଳୀ, ଗର୍ଭାଶୟ ଆଦିକୁ ନେଇ ଗଠିତ ।

(i) ଡିମ୍ବାଶୟ (Ovary) :

2. ଏଥୁସହିତ ଡିମ୍ବାଶୟରୁ ଇଡ୍ରୋଜେନ୍ ଓ ପ୍ରୋଜେଷ୍ଟେରନ୍ ନାମକ ଦୁଇଟି ସ୍ତ୍ରୀ-ହରମୋନ୍ କ୍ଷରିତ ହୁଏ ।
3. ଡିମ୍ବାଣୁର ବିକାଶ ଏକ ପ୍ରାଥମିକ ଫଲିକଲ୍ ଭାବେ ଆରମ୍ଭ ହୁଏ । ପରବର୍ତୀ ସମୟରେ ଏହାର ବୃଦ୍ଧି ଘଟି ଏହା ଗ୍ରାଫିଆନ୍‌ ଫଲିକଲ୍‌ର ରୂପ ନିଏ ଏବଂ ଏଥରେ ପରିପକ୍ବ ଡିମ୍ବାଣୁ ଥାଏ ।
4. ଡିମ୍ବାଣୁର ନିଜସ୍ୱ ପ୍ଲାଜମା ଝିଲ୍ଲୀ ଚାରିପଟେ ଜୋନା ପେଲ୍ୟୁସିଡ଼ା ନାମକ ଏକ ଅତିରିକ୍ତ ଝିଲ୍ଲୀ ଥାଏ । ଏହା କିଛି ଫଲିକଲ କୋଷ ଦ୍ଵାରା ଘେରିହୋଇ ରହିଥାଏ । ଏହି ଆବରଣକୁ କରୋନା ରେଡ଼ିଏଟା କୁହାଯାଏ ।
5. ଡିମ୍ବୋତ୍ସର୍ଗ ପରେ ଗ୍ରାଫିଆନ୍ ଫଲିକଲ୍ ଜାଗାରେ କର୍ପସ୍ ଲୁଟିୟମ୍ ସୃଷ୍ଟି ହୁଏ । ଏଥୁରୁ କ୍ଷରିତ ପ୍ରୋଜେଷ୍ଟିରନ୍ ହର୍ମୋନ୍ ଗର୍ଭାବସ୍ଥାକୁ ବଜାୟ ରଖିବାରେ ସହାୟକ ହୋଇଥାଏ ।

(ii) ଡିମ୍ବବାହୀ ନଳୀ (Fallopian tube) :

• ସ୍ତ୍ରୀ ଶରୀରରେ ଏକ ଯୋଡ଼ା ଡିମ୍ବବାହୀ ନଳୀ ରହିଛି । ଏହାର ଲମ୍ବ ପ୍ରାୟ 10 ରୁ 12 ସେ.ମି. ।
• ଡିମ୍ବାଶୟ ପଟକୁ ଥ‌ିବା ଡିମ୍ବବାହୀ ନଳୀର ମୁହଁ କାହାଳୀ ସଦୃଶ । ଅନ୍ୟପଟରେ ଏହା ଜରାୟୁ ବା ଗର୍ଭାଶୟରେ ଖୋଲିଥାଏ ।
• ସାଧାରଣତଃ ଏହି ନଳୀ ମଧ୍ଯରେ ଡିମ୍ବାଣୁ ଓ ଶୁକ୍ରାଣୁର ସମାୟନ ହୋଇ ଯୁଗ୍ମଜ ସୃଷ୍ଟି ହୁଏ । ଯୁଗ୍ମଜଗୁଡ଼ିକ ଗର୍ଭାଶୟରେ ପ୍ରବେଶ କରେ ।

(iii) ଗର୍ଭାଶୟ (Uterus) :

• ଗର୍ଭାଶୟ ଏକ ଫମ୍ପା ଏବଂ ପେଶୀବହୁଳ ଅଙ୍ଗ । ଏହାର ଲମ୍ବ ପ୍ରାୟ 7.5 ସେ.ମି. ଏବଂ ଚଉଡ଼ା 5.0 ସେ.ମି. I ଏହା ଉଦର ଗହ୍ଵର ନିମ୍ନଭାଗରେ ଠିକ୍ ମୂତ୍ରାଶୟର ପଛକୁ ରହିଛି ।
• ଗର୍ଭାଶୟର ଆଗପଟ ଚଉଡ଼ା ଓ ପଛପଟକୁ ଏହା ନଳିଆ । ଏହି ନଳିଆ ଅଂଶକୁ ଜରାୟୁ ଗ୍ରୀବା କୁହାଯାଏ । ଗର୍ଭାଶୟର ଗ୍ରୀବା ବାହାରକୁ ଉନ୍ମୁକ୍ତ ହୋଇଥାଏ ।

→ ସମାୟନ ଓ ସମାୟନ ପରବର୍ତ୍ତୀ ଘଟଣା :

3. ଭୃଣର୍ବନ୍ଧ ବା ପ୍ଲାସେଣ୍ଟା ଜରିଆରେ ଗର୍ଭାଶୟ ସହିତ ଭୃଣ ଏକ ଜୈବିକ ସମ୍ବନ୍ଧ ସ୍ଥାପନ କରେ ।
4. ଭ୍ରୂଣବନ୍ଧ ଦେଇ ଭ୍ରୂଣ ମାଆ ଶରୀରରୁ ନାଭିରଜ୍ଜୁଦ୍ୱାରା ଖାଦ୍ୟ ଓ ଅମ୍ଳଜାନ ଗ୍ରହଣ କରେ । ସେହିପରି ଭୃଣ ମଧ୍ୟରୁ ନିର୍ଗତ ବର୍ଜ୍ୟବସ୍ତୁ ପ୍ଲାସେଣ୍ଟା ବାଟଦେଇ ମାଆ ଶରୀରକୁ ଓ ପରେ ବାହାରକୁ ଆସେ ।
5. ଅନ୍ତଃରୋପଣ ପରେ ମାଷ୍ଟ୍ରଲେସନ୍ ପ୍ରକ୍ରିୟାଦ୍ଵାରା ତିନୋଟି ଜାୟକ ସ୍ତର ବିଶିଷ୍ଟ ଏକ ଗାଝୁଲା ତିଆରି ହୁଏ । ଗାଣ୍ଡୁଲାର ତିନୋଟି ଜାୟକ ସ୍ତର ହେଉଛି ଏକ୍ୱାଡ଼ର୍ମ, ମିସୋଡ଼ର୍ମ ଓ ଏଣ୍ଡୋଡ଼ର୍ମ।
6. ଏବେ ଅଙ୍ଗବିକାଶ ଦ୍ବାରା ଏହି ତିନୋଟି ଜାୟକ ସ୍ତରରୁ ବିଭିନ୍ନ ପ୍ରକାର ଟିସୁ, ଅଙ୍ଗ ଓ ଅଙ୍ଗତନ୍ତ୍ର ତିଆରି ହୁଏ ।
7. ଶେଷ ପର୍ଯ୍ୟାୟରେ ଗର୍ଭାଶୟରେ ସୃଷ୍ଟି ହୋଇଥିବା ପୂଷ୍ଠିବିକଶିତ ଶିଶୁ ପ୍ରସବଦ୍ୱାରା ମାଆ ଶରୀର ବାହାରକୁ ଆସେ ।

ବେଳେବେଳେ ଏକ ଅସାଧାରଣ ଘଟଣା କ୍ରମେ ଅନ୍ତଃରୋପଣ ପ୍ରକ୍ରିୟା ଗର୍ଭାଶୟ ମଧ୍ଯରେ ନ ଡିମ୍ବ ଡିମ୍ବାଣୁବାହୀନଳୀ ମଧ୍ୟରେ ହୁଏ । ଏହାକୁ ଅସ୍ଥାନିକ ଗର୍ଭ (Ectopic pregnancy) କୁହାଯାଏ । ଅସ୍ଥାନିକ ଗର୍ଭଧାରଣ ଯୋଗୁଁ ସାଧାରଣତଃ ସ୍ତ୍ରୀର ମୃତ୍ୟୁ ହୋଇପାରେ । ସମାୟନ ନ ହେଲେ ଡିମ୍ବାଣୁର ଆପେ ଅପେ ମୃତ୍ୟୁହୁଏ ।

→ ପରିବାର ନିୟୋଜନ (Family planning) :

•  ସୁବିଧା ଅନୁଯାୟୀ ପରିବାରର ପିଲା ସଂଖ୍ୟା ସୀମିତ ରଖ୍ ଓ ସନ୍ତାନ ଭିତରେ ଉଚିତ୍ ବ୍ୟବଧାନ ରଖୁବାର ପଦ୍ଧତିକୁ ପରିବାର ନିୟୋଜନ କୁହାଯାଏ ।

→ ବିଭିନ୍ନ ପ୍ରକାରର ପରିବାର ଯୋଜନା ପ୍ରଣାଳୀ (Different types of family planning methods) :

• କୌଣସି ଉପାୟରେ ଶୁକ୍ରାଣୁ ଓ ଡିମ୍ବାଣୁର ମିଳନକୁ ରୋକାଯାଇପାରିଲେ ଗର୍ଭଧାରଣକୁ ଏଡ଼ାଇ ଦିଆଯାଇପାରେ ।
  ପରିବାର ନିୟୋଜନ ପାଇଁ ବ୍ୟବହୃତ ବିଭିନ୍ନ ପ୍ରକାର ଉପାୟ ଦୁଇଭାଗରେ ବିଭକ୍ତ, ଯଥା –
  1. ସ୍ଥାୟୀ ପଦ୍ଧତି
  2. ଅସ୍ଥାୟୀ ପଦ୍ଧତି ।

→ (I) ସ୍ଥାୟୀ ପଦ୍ଧତି (Permanent methods) :

• ଏହା ଏକ ପ୍ରକାର ଅସ୍ତ୍ରୋପଚାର ପଦ୍ଧତି । ଏହି ପଦ୍ଧତିରେ ମହିଳା ବା ପୁରୁଷଙ୍କୁ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କରାଯାଏ । ଫଳରେ ଭବିଷ୍ୟତରେ ଆଉ ସନ୍ତାନ ଜନ୍ମହେବାର ସମ୍ଭାବନା ନଥାଏ।
  ଏହା ଏକ ପ୍ରକାର ଅସ୍ତ୍ରୋପଚାର ପଦ୍ଧତି । ଏହି ପଦ୍ଧତିରେ ମହିଳା ବା ପୁରୁଷଙ୍କୁ ବନ୍ଧ୍ୟାକରଣ ଅସ୍ତ୍ରୋପଚାର କୁହାଯାଏ ।
• ଭାସେକ୍ଟୋମୀ : ଭାସେକ୍ଟୋମୀଦ୍ୱାରା ପୁରୁଷର ଦୁଇଟିଯାକ ଶୁକ୍ରବାହୀ ନଳୀକୁ କାଟି ଅଲଗା କରି ବାନ୍ଧି ଦିଆଯାଏ । ଫଳରେ ରେତ ଶୁକ୍ରାଣୁମୁକ୍ତ ଥାଏ । ଏବେ ବିନା ଛୁରୀ ଓ ବିନା ସିଲାଇରେ 10 ରୁ 15 ମିନିଟ୍ ସମୟରେ ଭାସେକ୍ଟୋମୀ
• ଟ୍ୟୁବେକ୍ଟୋମୀ : ସ୍ତ୍ରୀ ଶରୀରର ଦୁଇଟିଯାକ ଡିମ୍ବବାହୀନଳୀକୁ କାଟି ବାନ୍ଧି ଦିଆଯାଏ । ଫଳରେ ଡିମ୍ବାଣୁ ଏବଂ ଶୁକ୍ରାଣୁର ମିଳନ ଆଉ ସମ୍ଭବ ହୁଏ ନାହିଁ ।

→ (II) ଅସ୍ଥାୟୀ ପଦ୍ଧତି (Temporary methods) :
ଭାରତ ସରକାରଙ୍କର ପରିବାର ନିୟୋଜନ କାର୍ଯ୍ୟକ୍ରମରେ ଚାରି ପ୍ରକାର ଅସ୍ଥାୟୀ ପଦ୍ଧତି ବ୍ୟବହାର କରାଯାଉଛି, ଯଥା

• ପ୍ରତିବନ୍ଧକ ପଦ୍ଧତି (ନିରୋଧ),
• ହରମୋନ୍ ପଦ୍ଧତି (ଗର୍ଭନିରୋଧକ ବଟିକା),
• ଅନ୍ତଃ ଗର୍ଭାଶୟ ପଦ୍ଧତି (କପର-ଟି) ଓ
• ପ୍ରାକୃତିକ ପଦ୍ଧତି ।

→ ମଣିଷ ଜନନ ସମ୍ପର୍କୀୟ ରୋଗ :

• ମଣିଷ ଜନନକ୍ରିୟା ମାଧ୍ୟମରେ ଗନେରିଆ, ସିଫିଲସ୍, ଏଡ୍‌ସ ଭଳି ବିଭିନ୍ନ ପ୍ରକାର ରୋଗ ହୋଇଥାଏ ।

→ ଏଡ୍‌ସ (AIDS : Acquired Immune Deficiency Syndrome) :

• ଏଡସ୍ କୌଣସି ପ୍ରକାର ରୋଗ ନୁହେଁ । ଏହା ମନୁଷ୍ୟ ଶରୀରର ଏକ ଅବସ୍ଥା, ଯେଉଁଥରେ ଶରୀରର ରୋଗ ପ୍ରତିରୋଧ କରିବାକୁ ସମର୍ଥ ହୁଏ ନାହିଁ । ତେଣୁ ଯେ କୌଣସି ରୋଗ ହେଲେ ତାହା ଆଉ ଭଲ ହୁଏ ନାହିଁ।
  AIDS: Acquired Immune Deficiency Syndrome – ଅର୍ଚିତ6ର ଗପ୍ରତି6ରଧାନଶକଆଜି ଅକ।ର ସଂଲକ୍ଷଣ ବା ସମୂହ ।

→ ଏଚ୍. ଆଇ. ଭି. (Human Immunodeficiency Virus – HIV) :

• ଏଡ଼ସ୍‌ର ‘ଖଳନାୟକ’ ଏକ ଭୂତାଣୁ । ଏହି ଭୂତାଣୁର ନାଁ ଏଚ୍.ଆଇ.ଭି. । ଅନ୍ୟ ଭୂତାଣୁ ପରି ଏହାର ଶରୀର ଗଠନ ଅତି ସରଳ । ମୁଖ୍ୟତଃ ପୁଷ୍ଟିସାରରେ ଗଠିତ ଖୋଳପା ମଧ୍ୟରେ ଭୂତାଣୁର ଆନୁବଂଶିକ ପଦାର୍ଥ ଥାଏ । ଏହା ହେଉଛି ଆରଏସ୍ଏ । ଆରିଏନ ଥିବା ଭୂତାଣୁମାନଙ୍କୁ ପଶ୍ଚଭୂତାଣୁ ବା ରେଟ୍ରୋଭାଇରସ୍ (Retrovirus) କୁହାଯାଏ ।

→ ରୋଗ ସମ୍ବନ୍ଧୀୟ (Pathogenecity) :

• ଆମ ରକ୍ତରେ ଥିବା ଶ୍ବେତରକ୍ତ କଣିକାମାନେ ଆମ ଶରୀରକୁ ବାହ୍ୟ ସଂକ୍ରମଣରୁ ରକ୍ଷା କରନ୍ତି । କିନ୍ତୁ ଏଡସ୍‌ରେ ଆକ୍ରାନ୍ତ ବ୍ୟକ୍ତିଙ୍କ ଶରୀରରେ ଟି-ଲିମ୍ଫୋସାଇଟ୍ ନାମକ ଏକ ପ୍ରକାର ଶ୍ୱେତରକ୍ତ କଣିକା ସଂଖ୍ୟା ଦ୍ରୁତଗତିରେ ହ୍ରାସ ପାଏ । ଫଳରେ ସେମାନଙ୍କଠାରେ ମାସାଧ୍ଵ କାଳ ଜ୍ଵର ଲାଗିରହେ ।

→ ଏଡ଼ସ୍ ସଂକ୍ରମଣ :

• ଏଡ଼ସ୍ ସୃଷ୍ଟିକାରୀ ଭୂତାଣୁ ମଣିଷ ଶରୀର ବାହାର ପରିବେଶରେ ଏକ ମିନିଟ୍‌ରୁ ଅଧିକ ସମୟ ବଞ୍ଚିପାରେ ନାହିଁ । ଏହା ଜଣେ ବ୍ୟକ୍ତି ଶରୀରରୁ ସିଧାସଳଖ ଅନ୍ୟଜଣେ ବ୍ୟକ୍ତି ଶରୀରକୁ ସଂକ୍ରମିତ ହୋଇଥାଏ ।
• ଏଡ୍‌ସ୍‌ରେ ଆକ୍ରାନ୍ତ ବ୍ୟକ୍ତିଠାରୁ ରକ୍ତ ଗ୍ରହଣ ଏବଂ ଏଡ଼ସ୍‌ ପୀଡ଼ିତା ମାଆଠାରୁ ତା’ର ଗର୍ଭସ୍ଥ ଶିଶୁକୁ ସଂକ୍ରମଣ ଏହାର କିଛି ଉଦାହରଣ ।

→ ଏଡ୍‌ସ୍ ଚିହ୍ନଟ :

• ରକ୍ତରେ ଆଣ୍ଟିଜେନ୍ ଓ ଆଣ୍ଟିବଡ଼ିର ଉପସ୍ଥିତି ଅନୁସାରେ ପରୀକ୍ଷଣକୁ ଆମେ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରିପାରିବା । ଯଥା : 1. ରାପିଡ୍ ଏଚ୍.ଆଇ.ଭି. ପରୀକ୍ଷଣ (Rapid HIV Test) ଓ 2. ପରମ୍ପରାଗତ ପରୀକ୍ଷାଗାର ପରୀକ୍ଷଣ (Conventional Laboratory Test)
  1. ରାପିଡ଼୍ ଏଚ୍ଆଇଭି ପରୀକ୍ଷଣ : ଏହି ପରୀକ୍ଷଣରେ ବ୍ୟକ୍ତିର ଆଙ୍ଗୁଠି ଟିପରୁ ରକ୍ତ ନେଇ ପରୀକ୍ଷା କରାଯାଇଥାଏ । ଏହି ପରୀକ୍ଷଣ ପାଇଁ 20-30 ମିନିଟ୍ ସମୟ ଲାଗିଥାଏ । ଏଥପାଇଁ ବିଶେଷ ଯନ୍ତ୍ରପାତିର ଆବଶ୍ୟକ ହୋଇନଥାଏ । ଏହି ପରୀକ୍ଷଣ ଭାରତର ସବୁ ରକ୍ତଭଣ୍ଡାରରେ ଉପଲବ୍ଧ ।
  2.  ପରମ୍ପରାଗତ ପରୀକ୍ଷାଗାର ପରୀକ୍ଷଣ : ଏହି ପରୀକ୍ଷଣ ଗୁଡ଼ିକ ହେଉଛି :
     • ଏଲ।ଲକ। (ELISA = Enzyme Linked Immuno Sorbent Assay) 6ଟଷ୍କ୍
     • ଏଲ।ଫା (ELFA = Enzyme Linked Fluorescent Assay) 6ଟଷ୍କ୍
     • ବିଟା (RITA = Recent Infection Testing Algorithm) 6ଟଷ୍କ୍
     • P24 ଟେଷ୍ଟ୍ ଇତ୍ୟାଦି । କିନ୍ତୁ ୱେଷ୍ଟର୍ଣ ବ୍ଲଟିଙ୍ଗ (Western Blotting) କୌଶଳ ଏଡ଼ସ ଚିହ୍ନଟ ପାଇଁ ସବୁଠାରୁ ବିଶ୍ୱସନୀୟ ଉପାୟ ।’
• ଏଡ଼ସ୍ ବିଷୟରେ ଜନସଚେତନତା ସୃଷ୍ଟି କରିବାପାଇଁ ପ୍ରତିବର୍ଷ ଡିସେମ୍ବର ପହିଲା ତାରିଖକୁ ବିଶ୍ବ ଏଡ଼ସ ଦିବସ (World AIDS Day) ଭାବେ ପୃଥ‌ିବୀରେ ସବୁ ଦେଶରେ ପାଳନ କରାଯାଉଛି ।

→ ସନ୍ତାନଧାରଣ ଓ ମା’ଙ୍କ ସ୍ବାସ୍ଥ୍ୟ (Child-bearing & Women’s Health) :

• ଭେଷଜ ବିଦ୍ୟା ସଂଜ୍ଞା ଅନୁଯାୟୀ ମହିଳାଙ୍କର ଗର୍ଭଧାରଣଠାରୁ ସନ୍ତାନ ଜନ୍ମ ହେବା ପର୍ଯ୍ୟନ୍ତ ଘଟୁଥିବା ସମସ୍ତ
• ଏହି ଘଟଣାଦ୍ଵାରା ଗୋଟିଏ ଦେଶର ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ସହିତ ପର ପିଢ଼ିର ସୁସ୍ଥନାଗରିକ ତିଆରି କରିବାପାଇଁ ଯଥେଷ୍ଟ ଅବଦାନ ରହିଛି ।
• କନସଂଖ୍ୟା ବୃଦ୍ଧି ଓ ନିୟନ୍ତ ଣ ଉଇଯ୍ 6େର ମହି କ।ଜ୍ଞର ଅଚଦନ ରହିଛି ।
• ଏକ ଜନକଲ୍ୟାଣକାରୀ ରାଷ୍ଟ୍ରରେ ମହିଳାଙ୍କର ଗର୍ଭଧାରଣଠାରୁ ଶିଶୁ ଜନ୍ମ ତଥା ପ୍ରସବ ପରେ ଉଭୟ ମାଆ ଓ ଶିଶୁର ଯତ୍ନ ନେବା ରାଷ୍ଟ୍ରର ଏକ ମୁଖ୍ୟ ଦାୟିତ୍ଵ ।
• ଏଥୁନିମନ୍ତେ ଗର୍ଭବତୀ ମହିଳା ଓ ଶିଶୁମାନଙ୍କର ଯତ୍ନ ଓ ସୁରକ୍ଷା ପାଇଁ ଆମ ଦେଶର ସମସ୍ତ ସହର ଓ ଗ୍ରାମାଞ୍ଚଳରେ 2005 ମସିହାରୁ ‘ଜାତୀୟ ସ୍ଵସ୍ଥ୍ୟ ମିଶନ’ (National Health Mission) କାର୍ଯ୍ୟକାରୀ ହେଉଛି
• 1. ସବୁ ନାଗରିକଙ୍କ ନିକଟରେ ସ୍ବାସ୍ଥ୍ୟସେବା ପହଞ୍ଚାଇବା,
  2. ପ୍ରାଥମିକ ସ୍ବାସ୍ଥ୍ୟ କେନ୍ଦ୍ରଗୁଡ଼ିକୁ ଶକ୍ତିଶାଳୀ କରିବା,
  3. ସଂକ୍ରମଣ ରୋଗର ପ୍ରତିକାର ଓ ନିୟନ୍ତ୍ରଣ,
  4. ସୁସ୍ଥ ଜୀବନଚର୍ଯ୍ୟା ପାଇଁ ପ୍ରୋତ୍ସାହନ,
  5. ଆଶାକର୍ମୀ ଓ ଅଙ୍ଗନବାଡ଼ି ପରି ସଂସ୍ଥାର ଦୃଢ଼ୀକରଣ ଇତ୍ୟାଦି ।
• କେନ୍ଦ୍ର ସରକାରଙ୍କଦ୍ବାରା
  • (କ) ଜନନୀ ସୁରକ୍ଷା ଯୋଜନା
  • (ଖ) ରାଷ୍ଟ୍ରୀୟ ବାଳ ସ୍ଵାସ୍ଥ୍ୟକଲ୍ୟାଣ ଯୋଜନା
  • (ଗ) ରାଷ୍ଟ୍ରୀୟ କିଶୋର ସୁରକ୍ଷା କାର୍ଯ୍ୟକ୍ରମ ପରି ଅନେକ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହେଉଛି ।

→ ଜନନୀ ସୁରକ୍ଷା ଯୋଜନା :

• ଏହି ଯୋଜନା ମାଧ୍ୟମରେ ଜଣେ ସ୍ତ୍ରୀଲୋକର ପ୍ରସବ ପୂର୍ବକାଳୀନ, ପ୍ରସବକାଳୀନ ଓ ପ୍ରସବ ପରକାଳୀନ ସ୍ବାସ୍ଥ୍ୟର ଯତ୍ନ ପାଇଁ ସମସ୍ତ ବ୍ୟବସ୍ଥା କରାଯାଇଛି । ପ୍ରସବ ପୂର୍ବରୁ ମହିଳାମାନଙ୍କୁ ମାଗଣାରେ ଲୌହ ଓ ଫୋଲିକ୍ ଏସିଡ୍ ବଟିକା ବଣ୍ଟାଯାଉଛି ।
• ତରଫରୁ ମାଗଣା ଆମ୍ବୁଲାନ୍ସର ବ୍ୟବସ୍ଥା କରାଯାଇଛି । ପ୍ରସବ ପରେ ପୌଷ୍ଟିକ ଆହାର ପାଇଁ ଆର୍ଥିକ ପ୍ରୋତ୍ସାହନର କାର୍ଯ୍ୟକ୍ରମ ମଧ୍ୟ ହାତକୁ ନେଇଛନ୍ତି ।
• ବିଶ୍ଵ ସ୍ବାସ୍ଥ୍ୟ ସଂଗଠନ (WHO) ଓ ୟୁନିସେଫ୍ (UNICEF) ପରି ବିଭିନ୍ନ ଆନ୍ତର୍ଜାତୀୟ ସଂସ୍ଥା ମାଆ ଓ ଶିଶୁମାନଙ୍କର ସୁରକ୍ଷା ପାଇଁ ବିଭିନ୍ନ କାର୍ଯ୍ୟକ୍ରମ ମାଧ୍ୟମରେ ବୈଷୟିକ ଓ ଆବଶ୍ୟକ ସ୍ୱାସ୍ଥ୍ୟସେବା ପାଇଁ ଉ ପ କରଣମ।ନ 6ଯ।ଗl କ 6 ଦକଚ୍ଛନ୍ତି
• ସ୍ଵାସ୍ଥ୍ୟସେବାର ଉନ୍ନତି ଯୋଗୁଁ ଭାରତରେ ଗର୍ଭବତୀ ମହିଳାଙ୍କର ମୃତ୍ୟୁହାର ଧୀରେ ଧୀରେ କମିବାରେ ଲାଗିଛ । 1990 ମସିହାରେ ପ୍ରତ୍ୟେକ ଏକ ଲକ୍ଷ ଶିଶୁଜନ୍ମରେ 556 ଜଣ ମାଆଙ୍କର ମୃତ୍ୟୁ ହେଉଥ‌ିବାବେଳେ 2016 ମସିହାବେଳକୁ ମାଆ ମୃତ୍ୟୁହାର ପ୍ରତି ଏକ ଲକ୍ଷ ଶିଶୁ ଜନ୍ମରେ 130ରେ ପହଞ୍ଚିଛି । ସେହିପରି ଶିଶୁ ମୃତ୍ୟୁହାର ମଧ୍ୟ ହ୍ରାସ ପାଇଛି । ଏହାର ଭାରତର ଆନ୍ତର୍ଜାତୀୟ ସ୍ତରରେ ଏକ ବଡ଼ ସଫଳତା ।
  

Odisha State Board BSE Odisha 10th Class Maths Notes Algebra Chapter 1 ସରଳ ସହସମୀକରଣ will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Algebra Chapter 1 ସରଳ ସହସମୀକରଣ

ଉପକ୍ରମଣିକା (Introduction) :

→ ଗୋଟିଏ ଅଜ୍ଞାତ ରାଶି x ରେ ଏକ ସରଳ ସମୀକରଣର ସାଧାରଣ ରୂପ ହେଉଛି ax + b = 0, ଯେଉଁଠାରେ a ≠ 0 ।
ଏଠାରେ à ଓ b ବାସ୍ତବ ସଂଖ୍ୟା ଏବଂ a କୁ xର ସହଗ (Coefficient) ଓ bକୁ ଧ୍ରୁବକ ରାଶି କୁହାଯାଏ ।
ଏଠାରେ ସମୀକରଣଟିର ସମାଧାନ (ମୂଳ) = \(\frac{-b}{2}\) ।

→ ଦୁଇଟି ଅଜ୍ଞାତ ରାଶି x ଓ y ରେ ସରଳରେଖୀୟ ସମୀକରଣର ସାଧାରଣ ରୂପ ax + by + c = 0 ……. (1)
ଯେଉଁଠାରେ a ଓ b ଯଥାକ୍ରମେ x ଓ yର ସହଗ ଓ c ଧ୍ରୁବକ ରାଶି ଏବଂ a, b ଓ ୯ ବାସ୍ତବ ସଂଖ୍ୟା ଅଟନ୍ତି । ଏଠାରେ a ≠ 0 ଓ b ≠ 0 ।

→ xy- ସମତଳରେ y = mx + c ର ଲେଖଚିତ୍ର ଏକ ସରଳରେଖା ହେତୁ ଏହାକୁ ସରଳରେଖୀୟ ସମୀକରଣ (Linear Equation) କୁହଯାଏ ।

→ x = α ଓ y = ß ହେଲେ ଏବଂ ଯଦି ସମୀକରଣଟି aα + bß + c = 0 ହୁଏ, ତେବେ x = α ଓ y = ß ସମୀକରଣର ଏକ ସମାଧାନ ହେବ । ସମାଧାନଟି (α, ß) । xy-ସମତଳରେ (α, ß) ଏକ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (Co-ordinate) ହୋଇଥାଏ ।

ସହ-ସମୀକରଣଦ୍ଵୟର ଜ୍ୟାମିତିକ ପରିପ୍ରକାଶ (Geometrical Representation) :
→ ମନେକର ଦଉ ସହ-ସମୀକରଣଦ୍ଵୟ
a₁x + b₁y + c₁ = 0 … (1)
ଓ a₂x + b₂y + c₂ = 0 … (2)

→ ପ୍ରତ୍ୟେକ ସମୀକରଣ ପାଇଁ ଦୁଇଗୋଟି ସମାଧାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

→ ମନେକର ସମୀକରଣ (1) ଓ (2)ର ଲେଖଚିତ୍ର xy-ସମତଳରେ ଗୋଟିଏ ଗୋଟିଏ ସରଳରେଖା ଯଥାକ୍ରମେ L₁ ଓ L₂ ହେଉ ।
L₁ : a₁x + b₁y + c₁ = 0 ଏବଂ L₂ : a₂x + b₂y + c₂ = 0

→ L₁ ଓ L₂ ସରଳରେଖାଦ୍ବୟର ଛେଦବିନ୍ଦୁ P ନେଇ ଉକ୍ତ ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ ଓ y-ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କରାଯାଉ ।

→ ଚିତ୍ର (i)ରେ L₁ ଓ L₂, ସରଳରେଖାଦ୍ୱୟ ପରସ୍ପର ଛେଦୀ, ସେମାନଙ୍କର କେବଳ ଗୋଟିଏ ଛେଦବିନ୍ଦୁ P ଓ ଏହି ବିଦୁଟି ଉଭୟ L₁ ଓ L₂; ଉପରେ ଅବସ୍ଥିତ । ଏହାର ସ୍ଥାନାଙ୍କ (α, ß) ଅର୍ଥାତ୍‌ x = α ଓ y = ß ଦ୍ବାରା ଉଭୟ ସମୀକରଣ (1) ଓ (2) ସିଦ୍ଧ ହୁଅନ୍ତି ।
ସମୀକରଣ (1) ଓ (2)ର କେବଳ ଗୋଟିଏ (ଅନନ୍ୟ) ସମାଧାନ ରହିବ; ଯଦି ଓ କେବଳ ଯଦି ସମୀକରଣ ଦ୍ବୟ ଦ୍ବାରା ସୂଚିତ ସରଳରେଖାଦ୍ବୟ ପରସ୍ପର ଛେଦୀ ହେବେ ।

→ ଚିତ୍ର (ii)ରେ L₁ ଓ L₂ ସରଳରେଖା ଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ (coincident) ଅର୍ଥାତ୍ ଏକ ଏବଂ ଅଭିନ୍ନ ଅଟନ୍ତି ।
ତେଣୁ ସେମାନଙ୍କର ସାଧାରଣ ବିନ୍ଦୁ ଅସଂଖ୍ୟ । ଅତଏବ ଏ କ୍ଷେତ୍ରରେ ସମୀକରଣ ଦ୍ବୟର ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ ।

→ ଚିତ୍ର (iii)ରେ L₁ ଓ L₂ ସରଳରେଖା ଦ୍ଵୟ ପରସ୍ପର ସହ ସମାନ୍ତର । ଅର୍ଥାତ୍ ସରଳରେଖାଦ୍ଵୟ ପରସ୍ପର ଛେଦୀ ହେବେ ନାହିଁ । ସହ ସମୀକରଣଦ୍ଵୟ ଦ୍ବାରା ସୂଚିତ ସରଳରେଖା ଦୁଇଟି ସମାନ୍ତର ହେଲେ, ସହ-ସମ୍ଭବ। ସମୀକରଣଦ୍ୱୟର ସମାଧାନ ସମ୍ଭବ ନୁହେଁ ।

ଲେଖଚିତ୍ର ଦ୍ବାରା ସହ-ସମୀକରଣଦ୍ଵୟର ସମାଧାନ (Solution of Simultaneous equations by use of Graphs) :
ଏକଘାତୀ ସମୀକରଣର ଲେଖଚିତ୍ର ଏକ ସରଳରେଖା । ଦୁଇଗୋଟି ଏକଘାତୀ ସମୀକରଣ a₁x + b₁y + c₁ = 0 ଏବଂ a₂x + b₂y + c₂ = 0 ର ଲେଖଚିତ୍ର ଅଙ୍କନ କରି ସେମାନଙ୍କ ଛେଦବିନ୍ଦୁ (α, ß) ନିର୍ଣ୍ଣୟ କଲେ, ଦତ୍ତ ସହସମୀକରଣ ଦ୍ଵୟର ସମାଧାନ (α, ß) ହେବ ।

ଲେଖଚିତ୍ର ଅଙ୍କନ ପ୍ରଣାଳୀ :

→ ପ୍ରତ୍ୟେକ ସମୀକରଣ ପାଇଁ ଅତି କମ୍‌ରେ ଦୁଇଟି ସମାଧାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

• ସମୀକରଣଗୁଡ଼ିକୁ y = mx + c ରୂପରେ ଲେଖାଯାଏ ।
• ପ୍ରତି xର ଏପରି ପୂର୍ଣ୍ଣସଂଖ୍ୟାମାନ ନେଇ yର ମଧ୍ୟ ଏକ ଅନୁରୂପ ପୂର୍ଣସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
• ମାନଗୁଡ଼ିକୁ ନେଇ କ୍ରମିତ ଓ ଯୋଡ଼ିମାନ ସ୍ଥିର କରାଯାଏ ।

→ ଲେଖ କାଗଜରେ XOX’ ଓ YOY’ ଅକ୍ଷ – ଅଙ୍କନ କରାଯାଏ ।

→ ପ୍ରତ୍ୟେକ ସମୀକରଣର ସ୍ଥିରୀକୃତ କ୍ରମିତ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଅତି କମ୍‌ରେ ଦୁଇଟି ବିନ୍ଦୁ L₁ ଓ L₂ ସରଳରେଖା ଅଙ୍କନ କରାଯାଏ ।

→ ଯଦି ସେମାନେ (α, ß) ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି, ତେବେ ସମୀକରଣଦ୍ଵୟର ସମାଧାନ (α, ß) ହେବ ।

ସହ-ସମୀକରଣଦ୍ଵୟର ସମାଧାନ ପାଇଁ ସର୍ଭ (Conditions of solvability of two Linear simultaneous equations) :

→ xy-ସମତଳରେ ଦୁଇଟି ସରଳରେଖା ଦତ୍ତ ଥିଲେ ସେମାନେ ଯଦି ପରସ୍ପରକୁ ଛେଦ କରିବେ, ସେମାନଙ୍କର ଗୋଟିଏ ଛେଦବିନ୍ଦୁ ରହିବ । ସରଳରେଖାଦ୍ବୟର ସମୀକରଣ ଦ୍ଵୟ ହେଲେ,
a₁x + b₁y + c₁ = 0 … (1)
a₂x + b₂y + c₂ = 0 … (2)

→ ସରଳରେଖାଦ୍ବୟ ପରସ୍ପରଛେଦୀ ହେଲେ ସେମାନଙ୍କର ଅନନ୍ୟ ସମାଧାନ ରହିବ । ଏ କ୍ଷେତ୍ରରେ ସହ- ସମୀକରଣଦ୍ବୟ ସଙ୍ଗୀତ ଓ ସ୍ବତନ୍ତ୍ର (consistent and independent), ତେବେ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ହେବ ।

→ ଯଦି ସରଳରେଖାଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ ହୁଅନ୍ତି ତେବେ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) ସମୀକରଣଦ୍ଵୟ ସଙ୍ଗୀତ ଓ ପରସ୍ପର ନିର୍ଭରଶୀଳ (consistent and dependent) ହେବେ । ଏ କ୍ଷେତ୍ରରେ ସହ-ସମୀକରଣ ଦ୍ଵୟର ଅସଂଖ୍ୟ ସମାଧାନ ରହିବ ।

→ ଯଦି ସରଳରେଖାଦ୍ବୟ ପରସ୍ପରକୁ ଛେଦ ନ କରିବେ ଏବଂ ସେମାନେ ପରସ୍ପର ସମାନ୍ତର ହେବେ ଓ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) ସର୍ଭ ପୂରଣ ହେବ ଏବଂ ସହ-ସମୀକରଣଦ୍ଵୟ ଅସଙ୍ଗତ (inconsistent) ହେବେ ଅର୍ଥାତ୍ ସହ-ସମୀକରଣଦ୍ୱୟର କୌଣସି ସମାଧାନ ରହିବ ନାହିଁ ।

ମନେରଖ :

ଦ୍ରଷ୍ଟବ୍ୟ : ସମୀକରଣ a₁x + b₁y + = 0 ଓ a₂x + b₂y = 0 ଦ୍ବୟର ଅନନ୍ୟ ସମାଧାନଟି (0, 0);
ଯଦି \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) ଓ ଅସଂଖ୍ୟ ସମାଧାନ ସମ୍ଭବ; ଯଦି \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)। ଏ କ୍ଷେତ୍ରରେ ସମୀକରଣଦ୍ଵୟ ସର୍ବଦା ସଙ୍ଗତ ଅଟନ୍ତି ।

→ (ସହ-ସମୀକରଣ ଦ୍ବୟର ବୀଜଗାଣିତିକ ସମାଧାନ) :
(Algebraic solution of Simultaneous Equations):
a₁x + b₁y + c₁ = 0 ଓ a₂x + b₂y + c₂ = 0 … (2)
ମନେକର ଦତ୍ତ ସହ-ସମୀକରଣ ଦ୍ବୟ ସଙ୍ଗତ ଓ ସ୍ବତନ୍ତ୍ର ।

(a) ପ୍ରତିକଳ୍ପନ ପ୍ରଣାଳୀ (Method of Substitution) :
(b) ଅପସାରଣ ପ୍ରଣାଳୀ (Method of Elimination)
(c) ବକ୍ରଗୁଣନ ପକ୍ଷିଣ (Method of Cross Multiplication)
ଏହି ଦୁଇ ସହସମୀକରଣ 3ଟି ବୀଜଗାଣିତିକ ପ୍ରଣାଳୀ/ପଦ୍ଧତି ସାହାଯ୍ୟରେ ସମାଧାନ କରାଯାଇ ପାରିବ । ଯଥା-

(a) ପ୍ରତିକଳ୍ପନ ପ୍ରଣାଳୀ (Method of Substitution) :
ପ୍ରତିକଳ୍ପନ ପ୍ରଣାଳୀରେ ସହସମୀକରଣଦ୍ଵୟର ସମାଧାନ କରିବାକୁ ହେଲେ, ପ୍ରଥମେ ଏମାନଙ୍କ ମଧ୍ୟରୁ ଯେକୌଣସି ଗୋଟିଏ ସମୀକରଣରୁ y କିମ୍ବା x ର ମାନ ନେଇ ଦ୍ୱିତୀୟ ସମୀକରଣରେ ପ୍ରୟୋଗ କଲେ x କିମ୍ବା y ର ମାନ ନିର୍ଣ୍ଣୟ ହେବ ।
ଉଦାହରଣ : a₁x + b₁y + c₁ = 0 … (1)
ଓ a₂x + b₂y + c₂ = 0 … (2)
ସମାଧାନ :
(i) ମନେକର ସମୀକରଣ (1)କୁ ବିଚାର କରାଯାଇ yକୁ x ମାଧ୍ୟମରେ ପ୍ରକାଶ କରିବା
ଯଦି b₁≠ 0, a₁x + b₁y + c = 0 ⇒ b₁y = -c₂ – a₁x
⇒ y = \(\frac{1}{b_1}(-c_1-a_1 x)\) ……. (3)

(ii) yର ମାନ \(\frac{1}{b_1}(-c_1-a_1 x)\) କୁ ସମୀକରଣ (2) ରେ ବ୍ୟବହାର କଲେ,

→ ଅପସାରଣ ପ୍ରଣାଳୀ (Method of Elimination) :
ଏହି ପ୍ରଣାଳୀରେ ସହସମୀକରଣଦ୍ୱୟର x କିମ୍ବା yର ସହଗମାନଙ୍କୁ ଅପସାରଣ କରାଯାଏ ।
a₁x + b₁y + c₁ = 0 ଓ a₂x + b₂y + c₂ = 0
(i) ମନେକର ଆମେ xକୁ ଅପସାରଣ କରିବା । ସମୀକରଣ (1)ରେ xର ସହଗ a1 କୁ ସମୀକରଣ (2)ର ଉଭୟ ପାର୍ଶ୍ଵରେ ଗୁଣନ କଲେ ଏବଂ ସମୀକରଣ (2)ରେ xର ସହଗ a1କୁ ସମୀକରଣ (1)ର ଉଭୟ ପାର୍ଶ୍ଵରେ ଗୁଣନ କରି ବିୟୋଗ କଲେ,

(ii) y ର ମାନକୁ ସମୀକରଣ (1) [କିମ୍ବା ସମୀକରଣ (2)]ରେ ବ୍ୟବହାର କଲେ,
x = \(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}\) ଲବ୍‌ଧ ହେବ ।
x = \(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}, \quad y=\frac{c_1 a_2-c_2 a_1}{a_1 b_2-a_2 b_1}\) ହେବ ।

(c) ବକ୍ରଗୁଣନ ପକ୍ଷିଣ (Cross Multiplication) :

ଏଠାରେ ସ୍ମରଣ ରହିବା ଉଚିତ ଯେ a₁b₂ – a₂b₁ ≠ 0, ଅର୍ଥାତ୍ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \)
ସମୀକରଣ (4)ରେ ପ୍ରଦତ୍ତ ଉକ୍ତିକୁ ବଜ୍ରଗୁଣନ କୁହାଯାଏ । ଏହାକୁ ସହଜରେ ମନେରଖ୍ ପାଇଁ ନିମ୍ନଲିଖୂ ପଦ୍ଧତି ଅବଲମ୍ବନ କରାଯାଇଥାଏ ।

c₁ = c₂ = 0 ଓ a₁b₂ – a₂b₁ ≠ 0 ହେଲେ, aa₁x + b₁y = 0, a₂x + b₂y = 0 ସମୀକରଣଦ୍ଵୟର ସମାଧାନଟି (0, 0) ଅଟେ । ଏଠାରେ ସମୀକରଣଦ୍ଵୟକୁ ସମ ସହ-ସମୀକରଣ (Homogeneous Simultaneous equation) କୁହାଯାଏ I a₁b₂ – a₂b₁ = 0 ହେଲେ, ସରଳରେଖାଦ୍ଵୟ ଏକ ଓ ଅଭିନ୍ନ ହେବେ ଓ ଦତ୍ତ ସହ-
ଦୁଇଗୋଟି ସହ-ସମୀକରଣ ସମାଧାନ କରିବାକୁ ଦିଆଯାଇଥିଲେ ପ୍ରଥମେ a₁b₂ – a₂b₁ ≠ 0 ସର୍ଭଟି ସତ୍ୟ ବୋଲି ପରୀକ୍ଷା କରିବା ଆବଶ୍ୟକ ।

→ ଅଣ ସରଳରେଖ୍ୟ ସହସମୀକରଣ (Non-Collinear Equation) :
ଅନେକ ସହ-ସମୀକରଣ ଯାହାକି ଏକଘାତୀ ନୁହେଁ, ସେମାନଙ୍କୁ ଆବଶ୍ୟକୀୟ ପରିବର୍ତ୍ତନ କରି ଏକଘାତୀ ରୂପକୁ ଅଣାଯାଇ ପାରିବ ଓ ଉପରେ ଆଲୋଚିତ ବୀଜଗାଣିତିକ ପ୍ରଣାଳୀର ଅବଲମ୍ବନରେ ସମାଧାନ କରିହେବ ।

→ କ୍ରାମରଙ୍କ ନିୟମ (Cramer’s Rule) :
ଦତ୍ତ ଚିତ୍ରଟିକୁ ବିଚାର କର : A = \(\left(\begin{array}{ll}
5 & 7 \\
2 & 1
\end{array}\right)\)

ଏହି ଚିତ୍ରରେ ଲେଖାଯାଇଥ‌ିବା ସଂଖ୍ୟାଗୁଡ଼ିକୁ ଦୁଇଗୋଟି ଧାଡ଼ି (row) ଓ ଦୁଇଗୋଟି ସ୍ତମ୍ଭ (column) ରେ ଲେଖାଯାଇଛି । ସମସ୍ତ ଧାଡ଼ି ଓ ସ୍ତମ୍ଭଗୁଡ଼ିକୁ ଦୁଇଟି ବନ୍ଧନୀ ମଧ୍ଯରେ ରଖାଯାଇଛି । ଏହାକୁ A ରୂପେ ନାମିତ କରାଯାଇଛି । ଏଠାରେ Aକୁ ଏକ 2 × 2 ମାଟ୍ରିକ୍‌ (Matrix) କୁହାଯାଏ । ଆମେ ମଧ୍ୟ 3 × 3, 4 × 4 ମାଟ୍ରିକ୍‌ ଲେଖୁରିବା । ଉଚ୍ଚତର ଗଣିତରେ ମାଟ୍ରିକ୍‌ସର ବ୍ୟବହାର ବହୁଳ ଭାବେ କରାଯାଏ । ଯେହେତୁ ଏଠାରେ ଧାଡ଼ି ସଂଖ୍ୟା ସହ ସ୍ତମ୍ଭ ସଂଖ୍ୟା ସମାନ, ତେଣୁ ଏହି ମାଟ୍ରିକ୍‌ଗୁଡ଼ିକୁ ବର୍ଗ ମାଟ୍ରିକ୍‌ (Square matrix) କୁହାଯାଏ । କେବଳ 2 × 2 ମାଟ୍ରିକ୍‌ସକୁ ଏଠାରେ ବିଚାର କରାଯାଉଛି । ପ୍ରତି ବର୍ଗ ମାଟ୍ରିକ୍‌ସ ସହ ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ସଂଖ୍ୟା ସଂପୃକ୍ତ ଓ ଏହାକୁ ବର୍ଗ ମାଟ୍ରିକ୍‌ସର ଡିଟରମିନାଣ୍ଟ (determinant) କୁହାଯାଏ । ଯଦି ମାଟ୍ରିକ୍‌ A = \(\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right)\) ହୁଏ,

ଉଦାହରଣ \(\frac{1}{x}+\frac{2}{y}\) = 5 (x ≠ 0, y ≠ 0) ଏକ ଅଣସରଳରେଖୀୟ ସମୀକରଣ ।

ଅର୍ଥାତ୍ a + 2b = 5 (ଯେଉଁଠାରେ \(\frac{1}{x}\) = a ଏବଂ \(\frac{1}{y}\) = b)
ତେବେ ଏହାର ଡିଟରମିନାଣ୍ଟ୍ | |A| = \(\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|=a d-b c\) ।

ଉଦାହରଣ :
A = \(\left(\begin{array}{ll}
5 & 7 \\
2 & 1
\end{array}\right)\) ହେଲେ |A| = 5 × 1 – 7 × 2 = 5 – 14 = -9 ଅଟେ ।
ସେହିପରି,

∴ ଡିଟରମିନାଣ୍ଟ ମାଧ୍ୟମରେ ନିର୍ଦେୟ ସମାଧାନ :

x = \(\frac{Δ_x}{Δ}\), y = \(\frac{Δ_y}{Δ}\) ଯେଉଁଠାରେ Δ ≠ 0 କାରଣ ସମୀକରଣଦ୍ଵୟ ସଙ୍ଗତ ହେବା ଆବଶ୍ୟକ ।
ବଜ୍ରଗୁଣନ ପଦ୍ଧତିରେ ଲବ୍‌ଧ ସମାଧାନକୁ ଡିଟରମିନାଣ୍ଟ ମାଧ୍ୟମରେ ଲେଖିଲେ,

ଏହାକୁ ସୁପରିଚିତ Cramer’s ନିୟମ କୁହାଯାଏ । ବଜ୍ରଗୁଣନ ସୂତ୍ର ହିଁ Cramer’s Rule ର ଅନ୍ୟରୂପ ।

→ ପାଟିଗଣିତ ପ୍ରଶ୍ନର ସମାଧାନରେ ପ୍ରୟୋଗ :
ଏକ ଅଜ୍ଞାତ ରାଶି ବିଶିଷ୍ଟ ଏକଘାତୀ ସମୀକରଣ ପ୍ରୟୋଗ କରି ଅନେକ ପାଟିଗଣିତ ପ୍ରଶ୍ନମାନଙ୍କ ସମାଧାନ ସହଜରେ କରାଯାଏ । ସେହିପରି ଦୁଇ ଅଜ୍ଞାତ ରାଶିବିଶିଷ୍ଟ ଏକଘାତୀ ସହ ସମାଧାନରେ ପ୍ରୟୋଗରେ ଜଟିଲ ପାଟିଗଣିତ ପ୍ରଶ୍ନମାନଙ୍କ ସହଜ ସମାଧାନ ହୋଇପାରିବ ।

Odisha State Board BSE Odisha 10th Class History Important Questions Chapter 19 ଶିଳ୍ପର ବିକାଶ Important Questions and Answers.

BSE Odisha Class 10 History Important Questions Chapter 19 ଶିଳ୍ପର ବିକାଶ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୬୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧।. ୧୯୪୭-୪୮ ଆର୍ଥିକ ବର୍ଷରେ ଓଡ଼ିଶାରେ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ପାଇଁ ହରେକୃଷ୍ଣ ମହତାବଙ୍କ କେଉଁ କାର୍ଯ୍ୟ ପ୍ରଶଂସନୀୟ ?
Answer:

• ୧୯୪୭-୪୮ ଆର୍ଥିକ ବର୍ଷରେ ଓଡ଼ିଶାରୁ ମିଳୁଥିବା ଲୁହାପଥର ଓ ମାଙ୍ଗାନିଜକୁ ବ୍ୟବହାର କରି ଏକ ଲୌହ ଓ ଇସ୍ପାତ କାରଖାନା ପ୍ରତିଷ୍ଠା ସମ୍ଭାବନା ପାଇଁ ସର୍ବେକ୍ଷଣ ଆରମ୍ଭ କରାଗଲା ।
• ଓଡ଼ିଶାରେ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ପାଇଁ ଅଣଓଡ଼ିଆ ଭାରତୀୟ ଶିଳ୍ପପତିଙ୍କ ଅନାଗ୍ରହ ଲକ୍ଷ୍ୟକରି ହରେକୃଷ୍ଣ ମହତାବ ବିଦେଶୀ ପୁଞ୍ଜିନିବେଶ ପାଇଁ ଅନୁମତି ଦେବାକୁ ଭାରତ ସରକାରଙ୍କୁ ଅନୁରୋଧ କଲେ ।
• ଓଡ଼ିଶାରେ ଶିଳ୍ପ ବିକାଶର ସମ୍ଭାବନା ଓ ଯୋଜନା ତିଆରି କରିବାପାଇଁ ଆମେରିକାରୁ ଡେଭିଡ୍ ଏଫ୍. ରୋଜେନ୍ ନାମକ ଜଣେ ବୈଷୟିକ ପରାମର୍ଶଦାତାଙ୍କୁ ଓଡ଼ିଶା ଅଣାଯାଇଥିଲା ।
• ସେ ଏକ ପ୍ରତିବେଦନ ମଧ୍ୟ ପ୍ରସ୍ତୁତ କଲେ ।
• ଆହୁରି ମଧ୍ୟ ଓଡ଼ିଶାରେ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ଦିଗରେ ଅନୁକୂଳ ପରିବେଶ ସୃଷ୍ଟି ପାଇଁ ସେ ଅନ୍ୟ କେତେକ ପଦକ୍ଷେପ ନେଇଥିଲେ ।

୨।. ପାରାଦ୍ଵୀପ ବନ୍ଦର ଓଡ଼ିଶାରେ ଆମଦାନୀ ଓ ରପ୍ତାନି ପାଇଁ କ’ଣ ସବୁ ସୁବିଧା ସୁଯୋଗ ସୃଷ୍ଟି କରିପାରିଛି ?
Answer:

• ବିଂଶ ଶତାବ୍ଦୀର ସପ୍ତମ ଦଶକରେ ପାରାଦ୍ବୀପ ବନ୍ଦର ପ୍ରତିଷ୍ଠା ହେଲା ।
• ପ୍ରଥମରୁ ଏଠାରୁ କେବଳ ଲୁହାପଥର ରପ୍ତାନି ହେଉଥିଲା ।
• ପରବର୍ତୀ ସମୟରେ ଏହାର ପଣ୍ୟ ଧାରଣ ଓ ରପ୍ତାନି ଶକ୍ତି ବୃଦ୍ଧି କରାଗଲା ।
• ୧୯୭୫ ମସିହାରେ ପାରାଦ୍ଵୀପକୁ ରେଳଲାଇନ୍‌ଦ୍ବାରା ସଂଯୁକ୍ତ କରାଗଲା ।
• ବର୍ତ୍ତମାନ ଏହି ବନ୍ଦରରୁ ଲୁହାପଥର ସହ ଅନ୍ୟାନ୍ୟ ସାମଗ୍ରୀ ରପ୍ତାନି କରାଯାଉଛି । ଏହା ଓଡ଼ିଶାର ତଥା ଭାରତର ଏକ ପ୍ରମୁଖ ବନ୍ଦରଭାବେ କାର୍ଯ୍ୟ କରୁଛି ।

୩।. ବିଂଶ ଶତାବ୍ଦୀରେ ଓଡ଼ିଶାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିବା ପ୍ରମୁଖ ଶିଳ୍ପଗୁଡ଼ିକର ଏକ ତାଲିକା ପ୍ରସ୍ତୁତ କର ।
Answer:
ବିଂଶ ଶତାବ୍ଦୀରେ ଓଡ଼ିଶାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିବା ପ୍ରମୁଖ ଶିଳ୍ପଗୁଡ଼ିକ ହେଲା

• ଗଞ୍ଜାମ ଜିଲ୍ଲାର ଋଷିକୁଲ୍ୟା ନଦୀକୂଳରେ ଜୟଶ୍ରୀ ରସାୟନ କାରଖାନା ।
• ରାୟଗଡ଼ା ଜିଲ୍ଲାର ଥରଭାଲିଠାରେ ଫେରୋସିଲିକନ୍ କାରଖାନା ।
• କଟକ ଜିଲ୍ଲାର ଚୌଦ୍ଵାରଠାରେ ଫେରେ ଆଏଜ୍ କାରଖାନା ।
• କେନ୍ଦୁଝର ଜିଲ୍ଲାର ଯୋଡ଼ା ଓ ଯାଜପୁର ଜିଲ୍ଲାର ଯାଜପୁର ରୋଡ଼ଠାରେ ଫେରୋ ମାଙ୍ଗାନିଜ୍ କାରଖାନା ।
• ସୁନ୍ଦରଗଡ଼ ଜିଲ୍ଲାର ରାଜଗାଙ୍ଗପୁର ଓ ବରଗଡ଼ ଜିଲ୍ଲାର ବରଗଡ଼ଠାରେ ସିମେଣ୍ଟ କାରଖାନା ଓ ବାଲେଶ୍ଵରଠାରେ

କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୩୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧।. ଶିଳ୍ପ ଭିତ୍ତିଭୂମିର ବିକାଶ ପାଇଁ ମହତାବଙ୍କ ମନ୍ତ୍ରିମଣ୍ଡଳ ନେଇଥ‌ିବା ପଦକ୍ଷେପଗୁଡି଼କ ଉଲ୍ଲେଖ କର ।
Answer:
ଶିଳ୍ପ ଭିତ୍ତିଭୂମିର ବିକାଶ ପାଇଁ ମହତାବଙ୍କ ମନ୍ତ୍ରିମଣ୍ଡଳ ନେଇଥିବା ପଦକ୍ଷେପଗୁଡିକ ହେଲା –

• ବୈଷୟିକ ଶିକ୍ଷାର ପ୍ରସାର, ବିଜ୍ଞାନ ଓ ଶିଳ୍ପର ଗବେଷଣା ପାଇଁ ଏକ ପରିଷଦ ଗଠନ ।
• ଶିଳ୍ପ ବିଭାଗର ପୁନର୍ଗଠନ, ଶିଳ୍ପାୟନ ସମ୍ଭାବନା ବିଷୟରେ ସର୍ବେକ୍ଷଣ ।
• ଶିଳ୍ପଋଣ ନିଗମ ଗଠନ (କ୍ଷୁଦ୍ର ଓ ମଧ୍ୟମ ଶିଳ୍ପ ପାଇଁ), ପ୍ରାଦେଶିକ ଶିଳ୍ପ ଅନୁଦାନ ବ୍ୟବସ୍ଥା ଏବଂ ଶିଳ୍ପ ପରିଷଦ ଗଠନ ।

୨।. ସ୍ଵାଧୀନତା ପରବର୍ତ୍ତୀ କାଳରେ ଓଡ଼ିଶାରେ ପୋତାଶ୍ରୟ, ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଉତ୍ପାଦନ ପାଇଁ କ’ଣ କରାଯାଇଥିଲା ?
Answer:

• ସ୍ଵାଧୀନତା ପରବର୍ତ୍ତୀ କାଳରେ ଓଡ଼ିଶାରେ ଥ‌ିବା ଚାନ୍ଦବାଲି, ଗୋପାଳପୁର ଓ ଧାମରା ପୋତାଶ୍ରୟର ଉନ୍ନତୀକରଣ କରାଗଲା ।
• ଶକ୍ତି ଯୋଗାଣ ପାଇଁ ଚୌଦ୍ଵାର ଓ ବ୍ରହ୍ମପୁରରେ ଦୁଇଟି ଛୋଟ ତାପଜ ବିଦ୍ୟୁତ୍ ଉତ୍ପାଦନ କେନ୍ଦ୍ର, ମାଛକୁଣ୍ଡ ଓ ହୀରାକୁଦରୁ ଜଳବିଦ୍ୟୁତ୍ ଯୋଜନା କାର୍ଯ୍ୟ ଆରମ୍ଭ କରିଥିଲା ।
• ୧୯୫୭ ମସିହାରେ ହୀରାକୁଦ ଜଳବିଦ୍ୟୁତ୍ ପ୍ରକଳ୍ପ କାର୍ଯ୍ୟକାରୀ ହେଲା ।

୩।. ୧୯୫୧-୧୯୮୫ ମଧ୍ୟରେ ଓଡ଼ିଶାରେ ସମୁଦାୟ ଶ୍ରମଶକ୍ତିର ଏକ ଆକଳନ ପ୍ରସ୍ତୁତ କର ।
Answer:

• ୧୯୫୦ ମସିହା ପରଠାରୁ ଅଧ୍ଵରୁ ଅଧ୍ଵ ଓଡ଼ିଆ ଶିଳ୍ପ କାରଖାନାରେ କାର୍ଯ୍ୟ କରିବାକୁ ଆଗେଇ ଆସିଲେ ।
• ୧୯୫୧ ମସିହାରେ ଓଡ଼ିଶାର ସମୁଦାୟ ଶ୍ରମଶକ୍ତିର ଶତକଡ଼ା ୭.୧୪ ଭାଗ ଶ୍ରମିକ କାରଖାନାମାନଙ୍କରେ କାମ କରୁଥିଲେ ।
• ୧୦ ବର୍ଷ ପରେ ୧୯୬୧ ମସିହାରେ ଏହା ପହଞ୍ଚିଲା ୮.୦୫ ପ୍ରତିଶତରେ ଓ ୧୯୮୪-୮୫ ମସିହା ବେଳକୁ ୩, ୯୦,୦୦୦ ଶ୍ରମିକ ଓଡ଼ିଶାର ବିଭିନ୍ନ କଳକାରଖାନାରେ କାମ କରୁଥିଲେ ।

୪।. ଓଡ଼ିଶାରେ ଥ‌ିବା ବିପୁଳ ଲୁହାପଥର ସମ୍ପଦକୁ ଆଧାର କରି କେଉଁସବୁ କମ୍ପାନୀ ସହ ଓଡ଼ିଶା ସରକାର ରାଜିନାମା ପତ୍ର ସ୍ବାକ୍ଷର କରିଛନ୍ତି ?
Answer:
ଓଡ଼ିଶାର ବିପୁଳ ଲୁହାପଥର ସମ୍ପଦକୁ ଆଧାର କରି ଅନେକ କମ୍ପାନୀ ସହ ଓଡ଼ିଶା ସରକାର ରାଜିନାମା ପତ୍ର ସ୍ବାକ୍ଷର କରିଛନ୍ତି; ଯଥା

• ପୋସ୍କୋ ସହିତ ପାରାଦ୍ଵୀପ ନିକଟରେ ନିର୍ମାଣ ହେବାକୁ ଥିବା ବୃହତ୍ ଲୌହଇସ୍ପାତ କାରଖାନା ।
• ଟାଟା ଷ୍ଟିଲ୍‌ ସହିତ ଡୁବୁରିଠାରେ ହେବାକୁ ଥିବା ଏକ ଲୌହ ପ୍ରକଳ୍ପ ।
• ଜିନ୍ଦଲ ଷ୍ଟେନଲେସ୍ ଷ୍ଟିଲ୍‌ ସହିତ ଯାଜପୁର ଜିଲ୍ଲାରେ ପ୍ରସ୍ତାବିତ କାରଖାନା ଇତ୍ୟାଦି ।
• ଜିନ୍ଦଲ ଷ୍ଟିଲ୍‌ ଓ ପାଓ୍ବାର ତରଫରୁ କେନ୍ଦୁଝର ଓ ଅନୁଗୁଳଠାରେ ସ୍ଥାପିତ ହେବାକୁ ଥ‌ିବା ଲୌହ ପ୍ରକଳ୍ପ ।

ସଂଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୨୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧।. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୨୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।
Answer:

• ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତିବେଳକୁ ଓଡ଼ିଶାରେ କଳକାରଖାନା ସଂଖ୍ୟା ଥିଲା ଅତି ନଗଣ୍ୟ ।
• ସେତେବେଳେ ଓଡ଼ିଶାରେ ଗୋଟିଏ କାଗଜକଳ, ଗୋଟିଏ କାଚ କାରଖାନା, ଗୋଟିଏ ସାବୁନ କାରଖାନା ଓ ଦୁଇଟି ମଧ୍ୟମ ଧରଣର ଚିନି କଳ ଥିଲା । ଏହା ବ୍ୟତୀତ କିଛି ଧାନକଳ ଓ ଚିନିକଳ ଥିଲା ।

୨।. ଓଡ଼ିଶାରେ ପ୍ରଥମେ କେଉଁ ଦୁଇଟି ନଦୀବନ୍ଧ ଯୋଜନାର କାର୍ଯ୍ୟ ଆରମ୍ଭ ହେଲା ? ସେଥିମଧ୍ୟରୁ କେଉଁଟି ପ୍ରଥମେ କେବେ କାର୍ଯ୍ୟକାରୀ ହେଲା ?
Answer:

• ଓଡ଼ିଶାରେ ପ୍ରଥମେ ମାଛକୁଣ୍ଡ ଓ ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନା କାର୍ଯ୍ୟ ଆରମ୍ଭ କରିଥିଲା ।
• ସେଥୁମଧ୍ୟରୁ ୧୯୫୭ ମସିହାରେ ହୀରାକୁଦ ଜଳବିଦ୍ୟୁତ୍ ପ୍ରକଳ୍ପ ପ୍ରଥମେ କାର୍ଯ୍ୟକାରୀ ହେଲା ।

୩।. ଡାଲମିଆ କମ୍ପାନୀକୁ ଓଡ଼ିଶା ସରକାର ଓଡ଼ିଶାରେ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ପାଇଁ କ’ଣ ସବୁ ସୁବିଧା ସୁଯୋଗ ପ୍ରଦାନ କରିଥିଲେ ?
Answer:

• ଓଡ଼ିଶା ସରକାର ଡାଲମିଆ କମ୍ପାନୀର ୪୦ ଲକ୍ଷ ଟଙ୍କାର ଅଂଶଧନ କିଣିଥିଲେ ।
• ଭବିଷ୍ୟତରେ ସିମେଣ୍ଟ କିଣିବାପାଇଁ କମ୍ପାନୀକୁ ୫୦ ଲକ୍ଷ ଟଙ୍କା ଅଗ୍ରୀମ ଆକାରରେ ଦେଇଥିଲେ ।

୪।. ରାଉରକେଲା ଲୌହଇସ୍ପାତ ଶିଳ୍ପ କାହା ସହାୟତାରେ କିପରି କାର୍ଯ୍ୟକ୍ଷମ ହୋଇପାରିଛି ?
Answer:

• ଜର୍ମାନୀର ବୈଷୟିକ ସହାୟତାକୁ ଆଧାର କରି ରାଉରକେଲାରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ରାଉରକେଲା ଇସ୍ପାତ କାରଖାନା ।
• ଏହା ଭାରତୀୟ ଇସ୍ପାତ କର୍ତ୍ତୃପକ୍ଷଦ୍ବାରା କାର୍ଯ୍ୟକ୍ଷମ ହୋଇପାରିଛି ।

୫।. ‘ନାଲ୍‌କୋ’ର ପୂରାନାମ କ’ଣ ? ଏହାର ଦୁଇଟି ପ୍ରକଳ୍ପ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer:

• ‘ନାଲ୍‌କୋ’ର ପୂରାନାମ ‘ଜାତୀୟ ଆଲୁମିନିୟମ୍ କମ୍ପାନୀ’ ।
• କୋରାପୁଟ ଜିଲ୍ଲାର ଦାମନଯୋଡ଼ିଠାରେ ଓ ଅନୁଗୁଳ ଜିଲ୍ଲାର ଅନୁଗୁଳଠାରେ ଏହାର ଦୁଇଟି ପ୍ରକଳ୍ପ ଅବସ୍ଥିତ ।

୬।. ମିଗ୍ ବିମାନର ଇଞ୍ଜିନ୍ ତିଆରି କାରଖାନା କାହା ସହାୟତାରେ କେଉଁଠି ନିର୍ମାଣ କରାଯାଇଛି ?
Answer:

• ସୁନାବେଡ଼ାରେ ମିଗ୍ ବିମାନର ଇଞ୍ଜିନ୍ ତିଆରି କାରଖାନା ପ୍ରତିଷ୍ଠିତ ହୋଇଛି ।
• ଏହା ସୋଭିଏତ୍ ରୁଷିଆର ସହଯୋଗରେ ନିର୍ମିତ ହୋଇଛି ।

୭।. ଓଡ଼ିଶାରେ ଫେରୋ ସିଲିକନ୍ ଓ ଫେରୋ ମାଙ୍ଗାନିଜ୍ କାରଖାନା କେଉଁଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:

• ରାୟଗଡ଼ା ଜିଲ୍ଲାର ଥୁରୁଭାଲିଠାରେ ଫେରୋ ସିଲିକନ୍ କାରଖାନା ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
• ଯାଜପୁର ଜିଲ୍ଲାର ଯାଜପୁର ରୋଡ଼ଠାରେ ଫେରୋ ମାଙ୍ଗାନିଜ୍ କାରଖାନା ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।

Objective Type Questions With Answers
A. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।

1. ସ୍ଵାଧୀନତାପ୍ରାପ୍ତି ବେଳକୁ ଓଡ଼ିଶାରେ କେଉଁସବୁ କଳକାରଖାନା ଗଢ଼ିଉଠିଥିଲା ?
Answer:
ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତିବେଳକୁ ଓଡ଼ିଶାରେ ମାତ୍ର ଗୋଟିଏ କାଗଜକଳ, ଗୋଟିଏ କାଚ କାରଖାନା, ଗୋଟିଏ ସାବୁନ କାରଖାନା ଓ ଦୁଇଟି ମଧ୍ୟମ ଧରଣର ଚିନିକଳ ଥିଲା ।

2. କେଉଁ ଦୁଇଟି କାରଣରୁ ଓଡ଼ିଶାରେ ଶିଳ୍ପାୟନ ସମ୍ଭବପର ହୋଇନଥିଲା ?
Answer:
ପ୍ରଥମ କାରଣଟି ହେଲା ଉଦ୍ୟୋଗପତିଙ୍କ ଅଭାବ ଓ ଦ୍ବିତୀୟ କାରଣଟି ଥିଲା ପୁଞ୍ଜିର ଅଭାବ ।

3. କଂଗ୍ରେସର ଦ୍ଵିତୀୟ ମନ୍ତ୍ରୀମଣ୍ଡଳ କେବେ, କାହା ନେତୃତ୍ୱରେ କାର୍ଯ୍ୟ କରିଥିଲା ?
Answer:
ପ୍ରଥମ କାରଣଟି ହେଲା ଉଦ୍ୟୋଗପତିଙ୍କ ଅଭାବ ଓ ଦ୍ବିତୀୟ କାରଣଟି ଥିଲା ପୁଞ୍ଜିର ଅଭାବ ।

4. ଓଡ଼ିଶାରେ ଶିଳ୍ପର ବିକାଶ ପାଇଁ କିଏ କେବେ ପ୍ରଚେଷ୍ଟା କରିଥିଲେ ?
Answer:
୧୯୪୬ ମସିହାରେ ହରେକୃଷ୍ଣ ମହତାବ ଓଡ଼ିଶାରେ ଶିଳ୍ପର ବିକାଶ ପାଇଁ ପ୍ରଚେଷ୍ଟା କରିଥିଲେ ।

5. ଓଡ଼ିଶାରେ ଶିଳ୍ପ ବିକାଶର ମୁଖ୍ୟ ପ୍ରତିବନ୍ଧକ କ’ଣ ଥିଲା ?
Answer:
ଶିଳ୍ପ ବିକାଶ ପାଇଁ ଆବଶ୍ୟକ ଭିତ୍ତିଭୂମିର ଅଭାବ ଓ ଭାରତର ଶିଳ୍ପପତିମାନେ ଓଡ଼ିଶାକୁ ଆସିବାକୁ ଅନାଗ୍ରହ ।

6. ଓଡ଼ିଶାର କେଉଁ ତିନୋଟି ପୋତାଶ୍ରୟର ଉନ୍ନତୀକରଣ କରାଯାଇଥିଲା ?
Answer:
ଏହି ପୋତାଶ୍ରୟଗୁଡ଼ିକ ଥିଲା ଚାନ୍ଦବାଲି, ଗୋପାଳପୁର ଓ ଧାମରା ।

7. ଶକ୍ତିଯୋଗାଣ ପାଇଁ କେଉଁ କେନ୍ଦ୍ରମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
ଶକ୍ତି ଯୋଗାଣ ପାଇଁ ଚୌଦ୍ଵାର ଓ ବ୍ରହ୍ମପୁରରେ ଛୋଟ ତାପଜ ବିଦ୍ୟୁତ୍ ଉତ୍ପାଦନ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।

8. ଓଡ଼ିଶା ଟେକ୍‌ସଟାଇଲ ମିଲ୍ କେଉଁଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
ସ୍ଵାଧୀନତା ପରେ କଟକ ଜିଲ୍ଲାର ଚୌଦ୍ଵାରଠାରେ ଓଡ଼ିଶା ଟେକ୍‌ସଟାଇଲ ମିଲ୍ ନାମରେ ଏକ ଲୁଗାକଳ ପ୍ରତିଷ୍ଠା

9. ମିଗ୍ ବିମାନ ଇଞ୍ଜିନ୍ ତିଆରି କାରଖାନା କେଉଁଠି କାହା ସହାୟତାରେ ନିର୍ମାଣ କରାଯାଇଛି ?
Answer:
ସୋଭିଏତ୍ ଋଷିଆର ସହାୟତାରେ ସୁନାବେଡ଼ାଠାରେ ମିଗ୍ ବିମାନ ଇଞ୍ଜିନ୍ ତିଆରି କାରଖାନା ନିର୍ମାଣ କରାଯାଇଛି ।

10. ଟାଟା କମ୍ପାନୀ ଓ ଜିନ୍ଦଲ କେଉଁଠାରେ ଲୌହ ପ୍ରକଳ୍ପ ସ୍ଥାପନ କରିଛନ୍ତି ?
Answer:
ଟାଟା କମ୍ପାନୀ ଡୁବୁରିଠାରେ ଓ ଜିନ୍ଦଲ ଷ୍ଟେନଲେସ୍ ଷ୍ଟିଲ୍ ଯାଜପୁରଠାରେ ଲୌହ ପ୍ରକଳ୍ପ ସ୍ଥାପନ କରିଛନ୍ତି ।

B. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।

1. ୧୯୪୯-୫୦ ଆର୍ଥିକ ବର୍ଷରେ ଜୟପୁର ଓ ବିଶାଖାପାଟଣା ମଧ୍ୟରେ ଥିବା କେଉଁ ରାସ୍ତାର ଉନ୍ନତୀକରଣ ପାଇଁ ଅର୍ଥ ବ୍ୟବଷ୍ଥ କରାଗଲା ?
Answer:
ସୁନକି ଓ ଜୟପୁର

2. ବୈଷୟିକ ପରାମର୍ଶଦାତା ଡେଭିଡ୍ ଏଫ. ରେଜେନ୍‌ଙ୍କୁ କେଉଁଠାରୁ ଓଡ଼ିଶା ଅଣାଗଲା ?
Answer:
ଆମେରିକା

3. ୧୯୮୪-୮୫ ମସିହାବେଳକୁ କେତେ ସଂଖ୍ୟକ ଓଡ଼ିଆ ଶ୍ରମିକ କଳକାରଖାନାମାନଙ୍କରେ କାମ କରୁଥିଲେ ?
Answer:
୩, ୯୦, ୦୦୦

4. ରାଉରକେଲା ଇସ୍ପାତ କାରଖାନା କେଉଁ ଦେଶର ବୈଷୟିକ ସହାୟତାରେ ନିର୍ମିତ ହୋଇଥିଲା ?
Answer:
ଜର୍ମାନୀ

5. ୧୯୬୧ ମସିହାରେ ଓଡ଼ିଶାର ସମୁଦାୟ ଶ୍ରମଶକ୍ତିର ଶତକଡା କେତେ ଭାଗ ଶ୍ରମିକ କାରଖାନାମାନଙ୍କରେ କାମ କରୁଥିଲେ ?
Answer:
୮.୦୫

6. ଢେଙ୍କାନାଳର କେଉଁଠାରେ ସୂତାକଳ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:
ଗୋବିନ୍ଦପୁର

7. ପଞ୍ଚପତିମାଳି ବକ୍‌ସାଇଟ୍ ଖଣି ଆମ ରାଜ୍ୟର କେଉଁ ଜିଲ୍ଲାରେ ଅବସ୍ଥିତ ?
Answer:
କୋରାପୁଟ

8. ରାୟଗଡ଼ା ଜିଲ୍ଲାର ଥୁରୁଭାଲିଠାରେ କେଉଁ କାରଖାନା ଅଛି ?
Answer:
ଫେରୋସିଲିକନ୍

9. ଆମ ରାଜ୍ୟର ବାଲେଶ୍ଵରଠାରେ କେଉଁ କାରଖାନା ଅଛି ?
Answer:
ଟାୟାର

10. ଆଣବିକ ଶକ୍ତି ଆୟୋଗ ଅଧୀନରେ ଭାରୀଜଳ ପ୍ରକଳ୍ପ ଓଡ଼ିଶାରେ କେଉଁ ସ୍ଥାନରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଛି ?
Answer:
ତାଳଚେର

11. କେଉଁ ଚାଷକୁ ଶିଳ୍ପର ମର୍ଯ୍ୟଦା ଦିଆଯାଇଛି ?
Answer:
ଚିଙ୍ଗୁଡ଼ି ଓ ମାଛଚାଷ

12. ତାଳଚେରଠାରେ ସାର କାରଖାନା କିଏ ପ୍ରତିଷ୍ଠା କରିଥିଲେ ?
Answer:
ଭାରତୀୟ ସାର ନିଗମ

13. ଟିଟାଗଡ଼ ପେପର ମିଲ୍ କେଉଁଠାରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
ଚୌଦ୍ଵାର

14. ଜିନ୍ଦଲ ଷ୍ଟିଲ ଓ ପାୱାର ତରଫରୁ କେଉଁଠାରେ ଲୌହ ପ୍ରକଳ୍ପ ସ୍ଥାପିତ ହେବାକୁ ଅଛି ?
Answer:
କେନ୍ଦୁଝର

15. କେଉଁ ଉଦ୍ଦେଶ୍ୟରେ ଶିଳ୍ପ ବିଦ୍ୟାଳୟମାନଙ୍କରେ ତନ୍ତକାମ, ବଢ଼େଇ କାମ, ସିଲେଇ କାମ ଆଦି ତାଲିମ ଦିଆଗଲା ?
Answer:
କୁଟୀର ଶିଳ୍ପ ଓ କ୍ଷୁଦ୍ରଶିଳ୍ପର ବିକାଶ

16. ଓଡ଼ିଶା ସରକାର ଡାଲମିଆ ସିମେଣ୍ଟ କମ୍ପାନୀର କେତେ ଟଙ୍କା ଅଂଶଧନ କିଣିଥିଲେ ?
Answer:
୪୦ ଲକ୍ଷ ଟଙ୍କା

C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ହରେକୃଷ୍ଣ ମହତାବ ମନ୍ତ୍ରୀମଣ୍ଡଳ ____________________ ମସିହାରେ ଦାୟିତ୍ଵ ଗ୍ରହଣ କରିଥିଲେ ।
Answer:
୧୯୪୬

2. ଓଡ଼ିଶାରେ ପ୍ରଶିକ୍ଷିତ _________________ ସମ୍ବଳର ଅଭାବ ଥିଲା ।
Answer:
ମାନବ

3. ଆମ ରାଜ୍ୟରେ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ଦିଗରେ ________________ ଅନୁକୂଳ ପରିବେଶ ସୃଷ୍ଟି କରିବାପାଇଁ ପଦକ୍ଷେପ ନେଇଥିଲେ ।
Answer:
ହରେକୃଷ୍ଣ ମହତାବ

4. ଶକ୍ତି ଯୋଗାଣପାଇଁ ଚୌଦ୍ୱାର ଓ _________________ ଠାରେ ଦୁଇଟି ଛୋଟ ତାପଜ ବିଦ୍ୟୁତ୍ ଉତ୍ପାଦନ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
Answer:
ବୁହୁପୁର

5. ଡାଲମିଆ କମ୍ପାନୀ ________________ ଠାରେ ଏକ ସିମେଣ୍ଟ କାରଖାନା ସ୍ଥାପନ କରିଥିଲା ।
Answer:
ରାଜଗାଙ୍ଗପୁର

6. ୧୯୪୭-୪୮ ମସିହାରେ ଓଡ଼ିଶାରେ ବୁଣାକର ସମବାୟ ସମିତି ସଂଖ୍ୟା _______________ ଥିଲା ।
Answer:
୧୩୩

7. __________________ ମସିହାରେ ପାରାଦୀପକୁ ରେଳପଥଦ୍ଵାରା ସଂଯୋଗ କରାଯାଇଥିଲା ।
Answer:
୧୯୭୫

8. ଜର୍ମାନୀ ଜ୍ଞାନ କୌଶଳରେ ଆମ ରାଜ୍ୟରେ ________________ ଠାରେ ଏକ ଲୌହଇସ୍ପାତ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
ରାଡରକେଲା

9. ଜାତୀୟ ଆଲୁମିନିୟମ କମ୍ପାନୀ (NALCO)ର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ______________ ଠାରେ ରହିଛି ।
Answer:
ଭୁବନେଶର

10. ୧୯୭୧ ମସିହାରେ ଭାରତୀୟ ସାର ନିଗମ _________________ ଠାରେ ଏକ ସାର କାରଖାନା ପ୍ରତିଷ୍ଠା କରିଥିଲା ।
Answer:
ତାଳଚେର

11. ପାରାଦ୍ଵୀପ ଫସ୍‌ଫେଟ୍ ଲିମିଟେଡ୍ _______________ ମସିହାରେ ଆତ୍ମପ୍ରକାଶ କରିଥିଲା ।
Answer:
୧୯୮୧

12. ସୋଭିଏତ୍ ରୁଷିଆର ସହଯୋଗରେ ସୁନାବେଡ଼ାଠାରେ _______________ ଇଞ୍ଜିନ୍ ତିଆରି କାରଖାନା ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
ମିଗ୍ ବିମାନ୍

13. ‘ଭାରତୀୟ ଆଣବିକ ଶକ୍ତି ଆୟୋଗ’ _________________ ମସିହାରେ ଛତ୍ରପୁରଠାରେ ଏକ ବିରଳ ମୁଭିକା କାରଖାନା ପ୍ରତିଷ୍ଠା କରିଛି ।
Answer:
୧୯୭୮

14. ବଡ଼ମାଳଠାରେ ପ୍ରତିଷ୍ଠା ହୋଇଛି ଏକ ______________ କାରଖାନା ।
Answer:
ଗୋଳାବାରୁଦ

15. ଯାଜପୁର ଜିଲ୍ଲାର ________________ ଠାରେ ଏକ ଝୋଟକଳ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
ଧାନମଣ୍ଡଳ

D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓ ) ଚିହ୍ନ ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (x) ଚିହ୍ନ ଦିଅ ।

1. ସତ୍ୟମ୍ ମହିନ୍ଦ୍ରା ଏକ ମୋଟରଗାଡ଼ି କାରଖାନା ।
Answer:
x

2. ୨୦୦୬ରେ ଓଡ଼ିଶା ତା’ର ନୂତନ ଶିଳ୍ପନୀତି ଘୋଷଣା କରିଥିଲା ।
Answer:
x

3. ଚିଙ୍ଗୁଡ଼ି ଓ ମାଛଚାଷକୁ ବୃହତ୍ ଶିଳ୍ପର ମର୍ଯ୍ୟାଦା ଦିଆଯାଇଛି ।
Answer:
x

4. ବଡ଼ମ୍ବାଠାରେ ଏକ ଚିନିକଳ ସ୍ଥାପିତ ହୋଇଛି ।
Answer:
✓

5. ଧାନମଣ୍ଡଳ ଝୋଟକଳ କଟକ ଜିଲ୍ଲାରେ ଅବସ୍ଥିତ ।
Answer:
x

6. ବିରଳ ମୃତ୍ତିକା କାରଖାନା ତାଳଚେରଠାରେ ଅବସ୍ଥିତ ।
Answer:
x

7. ଭାରୀଜଳ ପ୍ରକଳ୍ପ ବ୍ରହ୍ମପୁରଠାରେ ଅବସ୍ଥିତ ।
Answer:
x

8. କାଚରାମାଳଠାରେ ଗୋଳାବାରୁଦ କାରଖାନା ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
x

9. ୧୯୮୧ ମସିହାଠାରୁ ନାଲ୍‌କୋର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ଭୁବନେଶ୍ୱରଠାରେ କାର୍ଯ୍ୟ କରୁଛି ।
Answer:
✓

10. ରାଉରକେଲା ଷ୍ଟିଲ୍‌ଣ୍ଟ ରୁଷିଆ ସହାୟତାରେ ନିର୍ମାଣ କରାଯାଇଛି ।
Answer:
x

11. କୋରାପୁଟ ଜିଲ୍ଲାର ପଞ୍ଚପତିମାଳିଠାରେ ଆଲୁମିନିୟମ ମିଳିଥାଏ ।
Answer:
x

12. ଓଡ଼ିଶା ସରକାର ଡାଲମିଆ ସିମେଣ୍ଟ କାରଖାନାକୁ ଅନେକ ପ୍ରକାର ସୁବିଧା ପ୍ରଦାନ କରିଥିଲେ ।
Answer:
✓

13. ଓ.ଟି.ଏମ୍. ଢେଙ୍କାନାଳ ଜିଲ୍ଲାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
Answer:
x

14. ଓଡ଼ିଶାରେ ଅବସ୍ଥିତ ଚାରିଗୋଟି ପୋତାଶ୍ରୟର ଉନ୍ନତୀକରଣ କରାଗଲା ।
Answer:
x

15. ପୂର୍ବରୁ ଶକ୍ତି ଯୋଗାଣ ପାଇଁ ଚୌଦ୍ଵାର ଓ ବ୍ରହ୍ମପୁରଠାରେ ଦୁଇଟି ଛୋଟ ତାପଜ ବିଦ୍ୟୁତ୍ ଉତ୍ପାଦନ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
Answer:
✓

16. ଶିଳ୍ପ ଭିତ୍ତିଭୂମିର ବିକାଶ ପାଇଁ କୃଷ୍ଣଚନ୍ଦ୍ର ଗଜପତିଙ୍କ ସରକାର ପଦକ୍ଷେପ ନେଇଥିଲେ ।
Answer:
x

17. ୧୯୪୬ ମସିହାରେ ଓଡ଼ିଶାରେ ମହତାବ ମନ୍ତ୍ରୀମଣ୍ଡଳ ଗଠନ କରିଥିଲେ ।
Answer:
✓

18. ବିଜୁ ପଟ୍ଟନାୟକ ମହାନଦୀ ଓ କାଠଯୋଡ଼ି ଉପରେ ପୋଲ ତିଆରି କାମ ଆରମ୍ଭ କରିଥିଲେ ।
Answer:
x

19. ୧୯୪୭-୪୮ ମସିହାରେ ଓଡ଼ିଶାରେ ସମବାୟ ସମିତି ସଂଖ୍ୟା ଥିଲା ୧୩୩ ।
Answer:
✓

20. ୧୯୫୧ ମସିହାରେ ଶତକଡ଼ା ୭.୧୪ ଭାଗ ଶ୍ରମିକ କଳକାରଖାନାରେ କାମ କରୁଥିଲେ ।
Answer:
✓

E. ‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ମିଳନ କର ।
1.

Answer:

2.

Answer:

3.

Answer:

4.

Answer:

Odisha State Board BSE Odisha 10th Class Maths Notes Algebra Chapter 5 ପରିସଂଖ୍ୟାନ will enable students to study smartly.

BSE Odisha Class 10 Maths Notes Algebra Chapter 5 ପରିସଂଖ୍ୟାନ

→ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା (Central Tendency) :
ଏକାତ୍ମକ ସଂଖ୍ୟା ସମ୍ବନ୍ଧିତ ତଥ୍ୟକୁ ଗୋଟିଏ ସଂଖ୍ୟାରେ ପ୍ରକାଶ କରିବା ଲାଗି ତଥ୍ୟ ଅନ୍ତର୍ଭୁକ୍ତ ସମସ୍ତ ସଂଖ୍ୟାର ସମସ୍ତ ସଂଖ୍ୟାର ପ୍ରତିନିଧ୍ୟ କଲାଭଳି ଗୋଟିଏ ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କରାଯାଏ ଓ ଏହି ପ୍ରତିନିଧୂ ସଂଖ୍ୟାକୁ ତଥ୍ୟାବଳୀର କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତା (Central Tendency) କୁହାଯାଏ।

→ କେନ୍ଦ୍ରୀୟ ପ୍ରବଣତାକୁ ସୂଚାଇବା ପାଇଁ ତିନି ପ୍ରକାର ମାପ ଅଛି –

1. ମାଧ୍ୟମାନ (Mean)
2. ମଧ୍ୟମା (Median) ଏବଂ
3. ଗରିଷ୍ଠକ (Mode) ।

1. ମାଧ୍ୟମାନ – ଗୋଟିଏ ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀ ଅନ୍ତର୍ଗତ ସମସ୍ତ ଲବ୍‌ଧାଙ୍କର ହାରାହାରି ମାପକୁ ତଥ୍ୟାବଳୀର ମାଧ୍ୟମାନ (Mean) କୁହାଯାଏ ।
2. ମଧ୍ୟମା – ବଡ଼ରୁ ସାନ ବା ସାନରୁ ବଡ଼ କ୍ରମରେ ସଜା ଯାଇଥିବା ସମସ୍ତ ଲବ୍‌ଧାଙ୍କର ମଧ୍ୟମ ଲବ୍‌ଧାଙ୍କକୁ ମଧ୍ୟମା (Median) କୁହାଯାଏ ।
3. ଗରିଷ୍ଠକ – କୌଣସି ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀରେ ଥ‌ିବା ସର୍ବାଧ‌ିକ ବାରମ୍ବାରତା ବିଶିଷ୍ଟ ଲବ୍‌ଧାଙ୍କକୁ ଉକ୍ତ ତଥ୍ୟାବଳୀର ଗରିଷ୍ଠକ (Mode) କୁହାଯାଏ ।

→ ମାଧ୍ୟମାନ (Mean) : ଗୋଟିଏ ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀ ଅନ୍ତର୍ଗତ ସମସ୍ତ ଲବ୍‌ଧାଙ୍କର ହାରାହାରି ମାପକୁ ତଥ୍ୟାବଳୀର ମାଧ୍ୟମାନ (Mean) କୁହାଯାଏ ।

(i) ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ନିର୍ଣ୍ଣୟ (Mean of the Individual Series) :

→ ବାରମ୍ବାରତା ବିହୀନ ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ଯମାନ ନିର୍ଣ୍ଣୟ : କୌଣସି ତଥ୍ୟାବଳୀର ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକ x₁, x₂, x₃, …… x_n ହେଲେ ଉକ୍ତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ M ନିମ୍ନ ସୂତ୍ରଦ୍ୱାରା ନିରୂପଣ କରାଯାଏ ।

ଯେଉଁଠାରେ M = ମାଧ୍ୟମାନ, Σ (ସିଗ୍‌ମା) = ସମଷ୍ଟିର ସଂକେତ, x ତଥ୍ୟାବଳୀ ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ
ଲବ୍‌ଧାଙ୍କ, \(\sum_{k=1}^{k=n} x_k\) = x₁ ଠାରୁ x_n ପର୍ଯ୍ୟନ୍ତ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ସମଷ୍ଟି
ଯେଉଁଠାରେ n = ତଥ୍ୟାବଳୀ ଅନ୍ତର୍ଗତ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ସଂଖ୍ୟା ।

ଅର୍ଥାତ୍ M = \(\frac{Σx}{n}\)

→ ବାରମ୍ବାରତା ବିତରଣରେ ପ୍ରକାଶିତ ତଥ୍ୟାବଳୀର ମାଧମାନ ନିର୍ଣ୍ଣୟ (Mean of a frequency distribution) : ଏକ ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀର ଅନ୍ତଗର୍ତ ଲବ୍‌ଧାଙ୍କ (x)ର ମାନ x₁, x₂, x₃, …… x_n ଏବଂ ଏହି ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ବାରମ୍ବାରତା (f) ଯଥାକ୍ରମେ f₁, f₂, f₃, …… f_n ହେଲେ

(ii) ଭାଗ ବିଭକ୍ତ ଏବଂ ବାରମ୍ବାରତା ବିତରଣ ସାରଣୀରେ ପ୍ରକାଶିତ ତଥ୍ୟାବଳୀର ମାଧ୍ଯମାନ ନିର୍ଣ୍ଣୟ(Mean of a Grouped Frequency distribution) :
ପ୍ରତ୍ୟେକ ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ (y) = \(\frac{l_1+l_2}{2}\) (l₁ ଓ l₂ ଯଥାକ୍ରମେ ସଂଭାଗର ନିମ୍ନ ଓ ଊର୍ଦ୍ଧ୍ୱସୀମା) ନିର୍ଣ୍ଣୟ କରାଯାଏ । ତତ୍‌ପରେ fy ଓ Σfy ସ୍ଥିର କରାଯାଏ । ପରବର୍ତୀ ସମୟରେ Σfy କୁ Σf ଦ୍ଵାରା ଭାଗ କରି ମାଧ୍ୟମାନ M ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
∴ ମାଧ୍ୟମାନ (M) = \(\frac{Σfy}{Σf}\)
ଯଦି ଭାଗବିଭକ୍ତ ବାରମ୍ବାରତା ବିତରଣ ସାରଣୀର ମାଧମାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ,
ତେବେ ମାଧ୍ଯମାନ M = A + \(\frac{Σfy’}{Σf}\) ହେବ ।
ଏଠାରେ A = ଆରମ୍ଭ ବିନ୍ଦୁ, Σfy’ = ବିଚ୍ୟୁତିମାନଙ୍କର ସମଷ୍ଟି ଏବଂ Σf = ବାରମ୍ବାରତାର ସମଷ୍ଟି

(iii) ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀ (Short-cut Method) ବା ବିଚ୍ୟୁତି ପ୍ରଣାଳୀ (Deviation Method) : ପୂର୍ବ ପ୍ରଣାଳୀରେ କେତେଗୁଡ଼ିଏ ବଡ଼ ବଡ଼ ସଂଖ୍ୟାର ଗୁଣନ ତଥା ଯୋଗର ଆବଶ୍ୟକ ହୋଇଥାଏ । ଏହି ଅସୁବିଧା ଦୂର କରିବାପାଇଁ ଅନ୍ୟ ଏକ ପ୍ରଣାଳୀ ଅବଲମ୍ବନ କରାଯାଏ ଓ ଏହି ପ୍ରଣାଳୀ ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀ ବା ବିଚ୍ୟୁତି ପ୍ରଣାଳୀ ନାମରେ ଅଭିହିତ ।

ଉଦାହରଣ :
93, 98, 112, 103, 97, 109ର ମାଧ୍ୟମାନ = \(\frac{1}{6}\) (93 + 98 + 112 + 103 + 97 + 109)
= \(\frac{1}{6}\) {(100 – 7) + (100 – 2) + (100 + 12) + (100 + 3) + (100 – 3) + (100 + 9)}
= \(\frac{1}{6}\) [6 × 100+ {(-7) + (-2) + 12 + (3) + (- 3) + 9}]
= \(\frac{1}{6}\) × 6 × 100 + \(\frac{1}{6}\) × 12 = 100 + = \(\frac{1}{6}\) × 12 = 100 + 2 = 102
ଏଠାରେ 100 କୁ ଆରମ୍ଭ ବିନ୍ଦୁ (Working Zero) ବୋଲି କୁହାଯାଏ ।
ଲବ୍‌ଧାଙ୍କରୁ ଆରମ୍ଭ ବିନ୍ଦୁକୁ ବିୟୋଗ କରି ଲବ୍‌ଧାଙ୍କର ବିଚ୍ୟୁତି (Deviation) ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ବିଚ୍ୟୁତି (x’) ଯଥାକ୍ରମେ -7, -2, 12, 3, -3, 9 ।
Σx’ = (-7) + (-2) + 12 + 3 + (-3) + 9 = 12
ମାଧ୍ୟମାନ (M) = A + \(\frac{1}{n}\) Σx’= 100 + \(\frac{1}{6}\) × 12 = 100 + 2 = 102

ଦ୍ରଷ୍ଟବ୍ୟ : 100 ପରିବର୍ତ୍ତେ ଯେକୌଣସି ଆରମ୍ଭ ବିନ୍ଦୁ ନେଇ ମାଧମାନ ନିର୍ଣ୍ଣୟ କଲେ ଉତ୍ତରରେ କୌଣସି ପରିବର୍ତ୍ତନ ହେବନାହିଁ ।
ସଂକ୍ଷିପ୍ତ ପ୍ରଣଳୀ : ଆରମ୍ଭ ବିନ୍ଦୁ ଓ ବିଚ୍ୟୁତି ସାହାଯ୍ୟରେ ମାଧମାନ ନିର୍ଣ୍ଣୟ ପ୍ରଣାଳୀକୁ ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀ କୁହାଯାଏ ।

(iv) ସୋପାନ-ବିଚ୍ୟୁତି ପ୍ରଣାଳୀ (Step-deviation method) :
ଏହି ପ୍ରଣାଳୀ ଏକ ଅତି ସରଳୀକୃତ ଏବଂ ଅତି ସଂକ୍ଷିପ୍ତ ହିସାବ ସଂପୃକ୍ତ ପ୍ରଣାଳୀ । ପୂର୍ବବର୍ଣ୍ଣିତ ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀ * ଭଳି ଏହି ପ୍ରଣାଳୀରେ ମଧ୍ୟ ଆରମ୍ଭ ବିନ୍ଦୁ ଏବଂ ସଂପୃକ୍ତ ବିଚ୍ୟୁତି ମାନଙ୍କର ଆବଶ୍ୟକତା ପଡ଼ିଥାଏ । ସଂପୃକ୍ତ ବିଚ୍ୟୁତିମାନଙ୍କର ଥ‌ିବା ସାଧାରଣ ଗୁଣନୀୟକ ଦ୍ବାରା ବିଚ୍ୟୁତିକୁ ଭାଗକରି ଏହି ସୂତ୍ର ପ୍ରୟୋଗ କରାଯାଏ ।
ମାଧ୍ୟମାନ M = A + \(\frac{Σfy’}{Σf}\) × c

ଆରମ୍ଭ ବିନ୍ଦୁ = A, y’ =
Σfy’ = ବାରମ୍ବାରତା f ଓ y’ର ଗୁଣଫଳର ସମଷ୍ଟି
f = ବାରମ୍ବାରତା,
Σf = ବାରମ୍ବାରତାମାନଙ୍କର ସମଷ୍ଟି ।

→ ମାଧ୍ଯମାନ ସମ୍ବନ୍ଧୀୟ କେତେକ ଉପାଦେୟ ତଥ୍ୟ (Some useful Results on Mean) :
x₁, x₂, x₃, …… x_n ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ଯମନ M ହେଲେ,

• x₁ + a, x₂ + a, x₃ + a ……. x_n + a ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧମାନ M + a ହେବ ।
• x₁ – a, x₂ – a, x₃ – a ……… x_n – a ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ଯମାନ M – a ହେବ ।
• ax₁, ax₂, ax₃ ………… ax_n ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ଯମାନ Ma ହେବ ଯେତେବେଳେ a ≠ 0 ।
• \(\frac{x_1}{a}, \frac{x_2}{a}, \frac{x_3}{a}, ………. \frac{x_n}{a}\) ଲବ୍‌ଧାଙ୍କଗୁଡ଼ିକର ମାଧ୍ଯମାନ \(\frac{M}{a}\) ହେବ ଯେତେବେଳେ a ≠ 0 ।

→ ମଧ୍ୟମା (Median) :

(a) ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିଶ୍ଚୟ :
(i) ଲବ୍‌ଧାଙ୍କ ସଂଖ୍ୟା n ଅଯୁଗ୍ମ ହେଲେ ତଥ୍ୟାବଳୀର ଗୋଟିଏ ମଧ୍ଯମ ସ୍ଥାନ ଥାଏ ଓ ତାହା ହେଉଛି \(\frac{n+1}{2}\) ତମ ସ୍ଥାନ । ଏଣୁ ଏ କ୍ଷେତ୍ରରେ \(\frac{n+1}{2}\) ତମ ସ୍ଥାନୀୟ ଲବ୍‌ଧାଙ୍କ ହିଁ ଦତ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମ ଲବ୍‌ଧାଙ୍କ ।

(ii) ଲବ୍‌ଧାଙ୍କ ସଂଖ୍ୟା n ଯୁଗ୍ମ ହେଲେ ତଥ୍ୟାବଳୀର ଦୁଇଟି ମଧ୍ଯମ ସ୍ଥାନ ଥାଏ ଓ ସେ ଦୁଇଟି ହେଲା \(\frac{n}{2}\) ତମ ଓ (\(\frac{n}{2}\)+1) ତମ ସ୍ଥାନ । ଏ କ୍ଷେତ୍ରରେ ଦୁଇଟି ମଧ୍ୟମ ସ୍ଥାନ ଥ‌ିବାରୁ ସେହି ଦୁଇ ସ୍ଥାନୀୟ ଲବ୍‌ଧାଙ୍କ ଦ୍ବୟର ହାରାହାରି ନେଇ ଦତ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
ଅର୍ଥାତ୍ ଊର୍ଦ୍ଧ୍ବ ବା ଅଧଃ କ୍ରମରେ ସଜ୍ଜିତ ଦତ୍ତ ତଥ୍ୟାବଳୀର ଲବ୍‌ଧାଙ୍କ ସଂଖ୍ୟା n ହେଉ ।

n ଅଯୁଗ୍ମ ହେଲେ, ମଧ୍ୟମା (M_d) = \(\frac{n+1}{2}\) ତମ ଲବ୍‌ଧାଙ୍କ
n ଯୁଗ୍ମ ହେଲେ ମଧ୍ୟମା (M_d) = \(\frac{1}{2}\) {\(\frac{n}{2}\) ତମ ଲବ୍‌ଧାଙ୍କ + (\(\frac{n}{2}\) + 1) ତମ ଲବ୍‌ଧାଙ୍କ }

(b) ବାରମ୍ବାରତା ବିତରଣରେ (ଭାଗ ବିଭକ୍ତ ହୋଇ ନଥବା) ପ୍ରକାଶିତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିଶ୍ଚୟ :
ଯେଉଁ ଲବ୍‌ଧାଙ୍କର ରାଶିକୃତ ବାରମ୍ବାରତା ମଧ୍ଯମ ସ୍ଥାନ (M) ଅପେକ୍ଷା ଠିକ୍ ବୃହତ୍ତମ ସେହି ଲବ୍‌ଧାଙ୍କ ହିଁ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା କୁହାଯାଏ ।

(c) ଭାଗ ବିଭକ୍ତ ଏବଂ ବାରମ୍ବାରତା ବିତରଣ ପ୍ରକାଶିତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିଶ୍ଚୟ :

• ବାରମ୍ବାରତା ବିତରଣ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀ ସର୍ବଦା ଅଧଃ ବା ଊର୍ଦ୍ଧ୍ଵ କ୍ରମରେ ସଜ୍ଜିତ ହୋଇ ରହିଥାଏ । ତେଣୁ ଏ କ୍ଷେତ୍ରରେ ଦତ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମ ଲବ୍‌ଧାଙ୍କ ନିର୍ଣୟ କଲେ ହିଁ ମଧ୍ୟମା ମିଳିଥାଏ ।
• n ଯୁଗ୍ମ ହେଉ ବା ଅଯୁଗ୍ମ ହେଉ \(\frac{n}{2}\) ତମ ସ୍ଥାନକୁ ତଥ୍ୟାବଳୀର ମଧ୍ୟମ ସ୍ଥାନ ନିଆଯାଇପାରେ ( ଅବଶ୍ୟ ଯେଉଁଠି ‘n’ ର ମାନ ଅପେକ୍ଷାକୃତ ବୃହତ୍) ।
• ଭାଗବିଭକ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମ ସ୍ଥାନଟି ଯେଉଁ ସଂଭାଗ ଅନ୍ତର୍ଗତ ହୋଇଥାଏ, ସେହି ସଂଭାଗକୁ ମଧ୍ୟମା ସଂଭାଗ କୁହାଯାଏ ।
• ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ ଲାଗି ପ୍ରଥମେ ଭାଗ ବିଭକ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା-ସଂଭାଗ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
• ପ୍ରତ୍ୟେକ ସଂଭାଗର ରାଶିକୃତ ବାରମ୍ବାରତା (cf) ନିର୍ଣ୍ଣୟ କରି ସାରିବା ପରେ ଯେଉଁ ସଂଭାଗର ରାଶିକୃତ ବାରମ୍ବାରତା ତଥ୍ୟାବଳୀର ମଧ୍ୟମ ସ୍ଥାନ (M) ଅପେକ୍ଷା ଠିକ୍ ବୃହତ୍ତର ହେବ ସେହି ସଂଭାଗ ହିଁ ମଧ୍ୟମା – ସଂଭାଗ ହେବ ।

ମଧ୍ୟମା ନିର୍ଣ୍ଣୟର ସୂତ୍ର : ମଧ୍ୟମା (M) = 1 + \(\frac{m-c}{f}\) × i
M = ମଧ୍ୟମା ସ୍ଥାନ,
l = ମଧ୍ୟମା ସଂଭାଗର ନିମ୍ନସୀମା
f = ମଧ୍ୟମା ସଂଭାଗର ବାରମ୍ବାରତା,
c = ମଧ୍ୟମା ସଂଭାଗର ଠିକ୍ ପୂର୍ବବର୍ତ୍ତା ସଂଭାଗର ରାଶିକୃତ ବାରମ୍ବାରତା
ଏବଂ i = ସଂଭାଗ ବିସ୍ତାର ।

ଅନ୍ତର୍ଭୁକ୍ତ (Inclusive) ସଂଭାଗୀକରଣରେ ପ୍ରକାଶିତ ସଂଭାଗଗୁଡ଼ିକୁ ବହିର୍ଭୁକ୍ତ ( Exclusive) କରିବାକୁ ହେଲେ ପ୍ରଥମ ସଂଭାଗର ଉଚ୍ଚ ସୀମା ଏବଂ ଦ୍ଵିତୀୟ ସଂଭାଗର ନିମ୍ନସୀମା ମଧ୍ୟରେ ଅନ୍ତର ସ୍ଥିର କରି ତା’ର ଅର୍ଦ୍ଧେକକୁ ପ୍ରତ୍ୟେକ ସଂଭାଗ ନିମ୍ନ ସୀମାରୁ ବିୟୋଗ କରାଯାଏ ସଂଭାଗୀକରଣକୁ ବହିର୍ଭୁକ୍ତ ସଂଭାଗୀକରଣ ବିଶିଷ୍ଟ କରାଯାଇଥାଏ ।

(d) ରାଶିକୃତ ବାରମ୍ବାରତା ସୂଚକ ଲେଖ (Ogive) ସାହାଯ୍ୟରେ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ :
ବାରମ୍ବାରତା ବିତରଣ ସାରଣୀ ଅନ୍ତର୍ଭୁକ୍ତ ତଥ୍ୟାବଳୀର ରାଶିକୃତ ବାରମ୍ବାରତା ସୂଚକ ଲେଖ (Ogive) ସାହାଯ୍ୟରେ ମଧ୍ୟ ଉକ୍ତ ସାରଣୀରେ ପ୍ରଦତ୍ତ ତଥ୍ୟାବଳୀର ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ । ନିମ୍ନ ସୋପାନଗୁଡ଼ିକୁ ଅନୁଧ୍ୟାନ କରି ଲେଖଚିତ୍ର ଅଙ୍କନ କର ।

• ରାଶିକୃତ ବାରମ୍ବାରତା ପ୍ରଥମେ ସ୍ଥିର କରାଯିବ ।
• x-ଅକ୍ଷ ଓ y-ଅକ୍ଷରେ ଯଥାକ୍ରମେ ଲବ୍‌ଧାଙ୍କ ଏବଂ ରାଶିକୃତ ବାରମ୍ବାରତା ନିଆଯାଏ ।
• ନେଇ ଗ୍ରାଫ୍ ଅଙ୍କନ କରାଗଲେ ଉଦ୍ଦିଷ୍ଟ ଲେଖ (Ogive) ମିଳିବ ।
• Ogive ଅଙ୍କନ କରି ତଥ୍ୟାବଳୀର ମଧ୍ୟମସ୍ଥାନ ନିର୍ଣ୍ଣୟ କରାଯାଏ । ମଧ୍ଯମ ସ୍ଥାନ ନୈଇ ବୃକ୍ଷ ଉପରେ) ଏକ ବିନ୍ଦୁ (P) ଗ୍ରାଫ୍ ଉପରେ ନିଆଯାଉ, ଯାହାର ରାଶିକୃତ ବାରମ୍ବାରତା ବା ମଧ୍ଯମ ସ୍ଥାନ \(\frac{n}{2}\) ବା \(\frac{n+1}{2}\) ଲବ୍‌ଧାଙ୍କ ସହ ସମାନ ହେବ ।
• P ବିନ୍ଦୁରୁ x-ଅକ୍ଷ ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ତଥ୍ୟାବଳୀର ମଧ୍ୟମାକୁ ସୂଚାଇବ ।

→ ଗରିଷ୍ଠକ (Mode) :

ସଂଜ୍ଞା : କୌଣସି ତଥ୍ୟାବଳୀରେ ସର୍ବାଧ୍ଵକବାର ରହିଥିବା ଲବ୍‌ଧାଙ୍କ (ଲବ୍‌ଧାଙ୍କ ମାନ) ହିଁ ଉକ୍ତ ତଥ୍ୟାବଳୀର ଗରିଷ୍ଠକ । ଭାଗ ବିହୀନ ବାରମ୍ବାରତା ବଣ୍ଟନରେ ସର୍ବାଧ୍ଵକ ବାରମ୍ବାରତା ବିଶିଷ୍ଟ ଲବ୍‌ଧାଙ୍କ ବା ଲବ୍‌ଧାଙ୍କ ମାନ ହିଁ ଉକ୍ତ ବଣ୍ଟନର ଗରିଷ୍ଠକ ।
ଦ୍ରଷ୍ଟବ୍ୟ : ଯଦି କୌଣସି ତଥ୍ୟାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ଲବ୍‌ଧାଙ୍କମାନଙ୍କର ବାରମ୍ବାରତା ସମାନ । ତେବେ ଉକ୍ତ ତଥ୍ୟାବଳୀର ଗରିଷ୍ଠକ ନାହିଁ ବୋଲି କହିବା । ନିମ୍ନ ତଥ୍ୟାବଳୀକୁ ଲକ୍ଷ୍ୟ କର । 3, 5, 7, 3, 8, 5,8, 7 ଏଠାରେ କୌଣସି ଗରିଷ୍ଠକ ନାହିଁ ।

ଗୋଟିଏ ତଥ୍ୟାବଳୀର ମାଧମାନ (M), ମଧ୍ୟମା (M_d) ଏବଂ ଗରିଷ୍ଠକ (M₀) ମଧ୍ୟରେ ଏକ ସାଧାରଣ ସମ୍ବନ୍ଧ ରହିଛି । ଏହା ଏକ ଆନୁଭବିକ ସମ୍ବନ୍ଧ ( Empirical Relation) ଅଟେ ।
ସମ୍ବନ୍ଧଟି ହେଲା : M₀ =3M_d – 2M

Odisha State Board BSE Odisha 10th Class History Important Questions Chapter 20 ଭିଭିଭୂମିର ବିକାଶ Important Questions and Answers.

BSE Odisha Class 10 History Important Questions Chapter 20 ଭିଭିଭୂମିର ବିକାଶ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୬୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧।. କେଉଁସବୁ ଆଧାରକୁ ନେଇ ଭିତ୍ତିଭୂମିର ବିକାଶ ସମ୍ଭବ ହୋଇଥାଏ ? ଏହା ଓଡ଼ିଶାରେ କିପରି ସମ୍ଭବ ହୋଇପାରିବ ?
Answer:

• କେତୋଟି ନିର୍ଦ୍ଦିଷ୍ଟ ଆଧାରକୁ ନେଇ ଭିଭିଭୂମିର ବିକାଶ ସମ୍ଭବ ହୋଇଥାଏ ।
• ସେଗୁଡ଼ିକ ହେଲା– ଜଳସେଚନ, ରାସ୍ତାଘାଟର ଉନ୍ନତୀକରଣ ଓ ଗମନାଗମନର ସୁବିଧା, ପରିବହନ ପାଇଁ ସୁବିଧା ସୁଯୋଗ ଓ ରେଳପଥର ବିକାଶ, ବିମାନଘାଟୀ ଓ ପୋତାଶ୍ରୟର ବ୍ୟବସ୍ଥା, ମାନବ ସମ୍ବଳର ବିକାଶ, ଅର୍ଥଯୋଗାଣ ବ୍ୟବସ୍ଥା ଇତ୍ୟାଦି ।
• ପର୍ଯ୍ୟଟନ ପାଇଁ ଆତିଥ୍ୟ ଯୋଗାଣର ବ୍ୟବସ୍ଥା, ଉଦ୍ୟୋଗପତିମାନଙ୍କୁ ପ୍ରଶିକ୍ଷଣ ଓ ସରକାରୀ ପ୍ରୋତ୍ସାହନ ।
• ଏସବୁକୁ ବିଚାରକୁ ନେଇ ସ୍ଵାଧୀନତା ପରେ ଓଡ଼ିଶାର ବିକଶିତ ଭୂଭିଭୂମି ବିଷୟରେ ବିଚାର କରାଯାଇପାରେ ।
• ଏହିସବୁ ବ୍ୟବସ୍ଥା ବିକଶିତ ହେଲେ ରାଜ୍ୟରେ କୃଷି, ଶିଳ୍ପ, ପର୍ଯ୍ୟଟନ ଓ ସାମାଜିକ ସଂହତି ସମ୍ଭବ ହେବ । ରାଜ୍ୟରେ ଆଞ୍ଚଳିକ ବୈଷମ୍ୟ ରହିବ ନାହିଁ । ସବୁ ଜିଲ୍ଲାର ସମତୁଲ ବିକାଶ ସମ୍ଭବ ହେବ ।

୨।. ଓଡ଼ିଶାରେ ମାନବ ସମ୍ବଳର ବିକାଶ ପାଇଁ କେଉଁସବୁ ପଦକ୍ଷେପ ନିଆଯାଇଛି ଉଲ୍ଲେଖ କର ।
Answer:

• ଏକ ସୁସ୍ଥ ଓ ପ୍ରଶିକ୍ଷିତ ମାନବ ସମ୍ବଳ ସୃଷ୍ଟି ପାଇଁ ଓଡ଼ିଶା ସରକାରଙ୍କ ତରଫରୁ ବିଭିନ୍ନ କାର୍ଯ୍ୟକ୍ରମ ଗ୍ରହଣ କରାଯାଇଛି । ବୈଷୟିକ ଶିକ୍ଷା ପାଇଁ ଶିଳ୍ପ ତାଲିମ କେନ୍ଦ୍ର, ଯାନ୍ତ୍ରିକ ବିଦ୍ୟାଳୟ ଓ ଯାନ୍ତ୍ରିକ ମହାବିଦ୍ୟାଳୟମାନ କାର୍ଯ୍ୟ କରୁଛନ୍ତି । ନୂଆ ନୂଆ ଜ୍ଞାନବିଜ୍ଞାନ; ଯଥା – ସୂଚନା ପ୍ରଯୁକ୍ତିବିଦ୍ୟା, କମ୍ପ୍ୟୁଟର ବିଜ୍ଞାନ, ଜୀବ ବୈଷୟିକ ବିଦ୍ୟା ଶିକ୍ଷାକ୍ଷେତ୍ରରେ ବିଭିନ୍ନ ଅନୁଷ୍ଠାନ ରହିଛି ।
• ଏହାବ୍ୟତୀତ ଓଡ଼ିଶାରେ ଅଛି କଳା, ବିଜ୍ଞାନ ଓ ବାଣିଜ୍ୟ ପାଠ୍ୟକ୍ରମ ସମ୍ପର୍କିତ ଅନେକ କଲେଜ । ଶିକ୍ଷକମାନଙ୍କୁ ପ୍ରଶିକ୍ଷଣ ଦେବାପାଇଁ ଅଧିକାଂଶ ଜିଲ୍ଲାରେ ଶିକ୍ଷକ ପ୍ରଶିକ୍ଷଣ ମହାବିଦ୍ୟାଳୟମାନ ଅଛି ।
• ଶିଳ୍ପ, ମାନବ ସମ୍ବଳ, ଗ୍ରାମ୍ୟ ଉନ୍ନୟନ କାର୍ଯ୍ୟର ପରିଚାଳନା ପାଇଁ ବାଣିଜ୍ୟ ବିଦ୍ୟାଳୟମାନ ଓଡ଼ିଶାର ଯୁବକମାନଙ୍କୁ ପ୍ରଶିକ୍ଷଣ ପ୍ରଦାନ କରୁଛନ୍ତି । ପର୍ଯ୍ୟଟନ ଓ ଶିଳ୍ପରେ ଉପଯୋଗୀ ହେଲାଭଳି ପ୍ରଶିକ୍ଷଣର ବ୍ୟବସ୍ଥା, ପର୍ଯ୍ୟଟନ ଓ ହୋଟେଲ ପରିଚାଳନା ପାଇଁ ଶିକ୍ଷାଦେବା ପାଇଁ ଭୁବନେଶ୍ୱର ସମେତ ଅନ୍ୟ ସହରମାନଙ୍କରେ ଶିକ୍ଷାନୁଷ୍ଠାନମାନ ଖୋଲିଛି ।
• ଓଡ଼ିଶାର ଐତିହ୍ୟ ଓ ସଂସ୍କୃତି ବିଷୟରେ ପ୍ରଶିକ୍ଷଣ ଦିଆଯାଇ ପର୍ଯ୍ୟଟକ ପଥପ୍ରଦର୍ଶକମାନଙ୍କୁ ପ୍ରଶିକ୍ଷଣ ଦିଆଯାଇଛି ।
• ଓଡ଼ିଶାର ଚାରୁକଳା ଓ ହସ୍ତଶିଳ୍ପ ସମ୍ପର୍କରେ ଶିକ୍ଷାଦେବା ପାଇଁ ପ୍ରଶିକ୍ଷଣ କେନ୍ଦ୍ରମାନ କାର୍ଯ୍ୟକରୁଛି ।

୩। ଓଡ଼ିଶାରେ କେଉଁସବୁ ଯୋଜନା ମାଧ୍ୟମରେ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଯୋଗାଇ ଦେବାର ବ୍ୟବସ୍ଥା ସରକାର ଗ୍ରହଣ କରିଛନ୍ତି ସଂକ୍ଷେପରେ ଲେଖ ।
Answer:

• ଓଡ଼ିଶାର ଗ୍ରାମାଞ୍ଚଳକୁ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଯୋଗାଇ ଦେବାରେ ରାଜୀବ ଗାନ୍ଧି ଗ୍ରାମୀଣ ବିଦ୍ୟୁତୀକରଣ ଯୋଜନା ୨୦୦୬ ମସିହାରୁ ଉଲ୍ଲେଖନୀୟ କାର୍ଯ୍ୟ କରୁଅଛି ।
• କୁଟୀର ଜ୍ୟୋତି ଯୋଜନା ମଧ୍ୟ ଓଡ଼ିଶାବାସୀଙ୍କ ପାଇଁ ବେଶ୍ ସହାୟକ ହୋଇପାରିଛି ।
• ୨୦୦୭ ମସିହାରୁ ଓଡ଼ିଶା ସରକାର ଆରମ୍ଭ କରିଛନ୍ତି ବିଜୁ ଗ୍ରାମଜ୍ୟୋତି ଯୋଜନା ।
• ଏହି ଯୋଜନା ଅନୁଯାୟୀ ୧୦୦ରୁ କମ୍ ଲୋକ ବସବାସ କରୁଥିବା ଗ୍ରାମମାନଙ୍କୁ ବିଦ୍ୟୁତଶକ୍ତି ଯୋଗାଇ ଦିଆଯାଉଛି ।
• ଏହାଛଡ଼ା କୃଷି ଓ ଶିଳ୍ପକ୍ଷେତ୍ରକୁ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଯୋଗାଇଦେବାକୁ ଓଡ଼ିଶା ସରକାର ପ୍ରଚେଷ୍ଟା ଜାରି ରଖୁଛନ୍ତି ।

୪। ପର୍ଯ୍ୟଟନ କ୍ଷେତ୍ରରେ ଓଡ଼ିଶା ସରକାର କେଉଁସବୁ ନୂତନ ବ୍ୟବସ୍ଥାମାନ ଗ୍ରହଣ କରିଛନ୍ତି ?
Answer:

• ପର୍ଯ୍ୟଟକମାନଙ୍କ ସୁବିଧା ପାଇଁ ଓଡ଼ିଶା ସରକାର ଭୁବନେଶ୍ବର, ପୁରୀ, କୋଣାର୍କ ସୁବର୍ଣ୍ଣ ତ୍ରିଭୁଜ ଓ ରାଜ୍ୟର ଅନ୍ୟାନ୍ୟ ପର୍ଯ୍ୟଟନ କ୍ଷେତ୍ରମାନଙ୍କରେ ଅନେକ ହୋଟେଲ ଓ ଅତିଥ୍‌ଗୃହ ଖୋଲିଛନ୍ତି ।
• ପର୍ଯ୍ୟଟନସ୍ଥଳୀମାନଙ୍କରେ ଓଡ଼ିଶା ସରକାର ପାନ୍ଥନିବାସ ଓ ପାଛିକାମାନ ନିର୍ମାଣ କରିଛନ୍ତି ।
• ଚିଲିକା, ଭିତରକନିକାରେ ଜଳଯାତ୍ରା ପାଇଁ ସରକାରୀ ବୋଟ୍ ଯୋଗାଇ ଦେଇଛନ୍ତି ।
• ସରକାରୀ ପାନ୍ଥନିବାସ ସାଙ୍ଗକୁ ବଡ଼ ବଡ଼ ପର୍ଯ୍ୟଟନସ୍ଥଳୀରେ ଘରୋଇ ହୋଟେଲମାନ ଖୋଲାଯାଇଛି ।
• ଯାତ୍ରୀମାନଙ୍କୁ ସୁବିଧାରେ ନେବା ଆଣିବାପାଇଁ ଟୁରିଷ୍ଟ୍ ବସ୍ ମଧ୍ୟ ଯୋଗାଇ ଦିଆଯାଇଛି ।

କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୩୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧।. ସ୍ଵାଧୀନତୋତ୍ତର ଓଡ଼ିଶାରେ ଜଳସେଚନର ସୁବିଧା ପାଇଁ କେଉଁସବୁ ସ୍ଥାୟୀ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହେଉଛି ?
Answer:

• ଓଡ଼ିଶାରେ ପ୍ରବାହିତ ନଦୀଗୁଡ଼ିକରେ ବନ୍ଧ ବା ଆନିକଟ ନିର୍ମାଣ କରାଯାଇ କେନାଲ ଯୋଗେ ଜଳସେଚନର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
• ମହାନଦୀ ତ୍ରିକୋଣଭୂମି ଅଞ୍ଚଳରେ ତାଳଦଣ୍ଡା, ମାଛଗାଁ, କେନ୍ଦ୍ରାପଡ଼ା, ପଟ୍ଟାମୁଣ୍ଡାଇ କେନାଲଦ୍ଵାରା ହଜାର ହଜାର ହେକ୍ଟର ଜମି ଜଳସେଚିତ ହୋଇଥାଏ ।
• ଅବିଭକ୍ତ ପୁରୀ ଜିଲ୍ଲା ଆଠଟି କେନାଲଦ୍ଵାରା ଜଳସେଚିତ ହେଉଛି ।

୨।. ପ୍ରଧାନମନ୍ତ୍ରୀ ଗ୍ରାମ ସଡ଼କ ଯୋଜନା କେଉଁଠାରେ ଓ କ’ଣ ପାଇଁ କାର୍ଯ୍ୟକାରୀ ହେଉଛି ?
Answer:

• ପ୍ରଧାନମନ୍ତ୍ରୀ ଗ୍ରାମ ସଡ଼କ ଯୋଜନାରେ ଗାଁଗହଳରେ ଅନେକ ପକ୍‌କା ରାସ୍ତା ନିର୍ମାଣ କରାଯାଇଛି ।
• ପ୍ରତି ଗାଁକୁ ସବୁଦିନିଆ ରାସ୍ତା ନିର୍ମାଣରେ ଯଥେଷ୍ଟ ଅଗ୍ରଗତି ହାସଲ କରାଯାଇ ପାରିଛି ।
• ଓଡ଼ିଶାର ରାଜଧାନୀ ଭୁବନେଶ୍ଵର ଓ ପ୍ରମୁଖ ସହରମାନଙ୍କ ଆଭ୍ୟନ୍ତରୀଣ ରାସ୍ତାଗୁଡ଼ିକୁ ଉନ୍ନତ ମାନର ଓ ପ୍ରଶସ୍ତ କରାଯାଇଛି ।

୩।. ଜାତୀୟ ରାଜପଥ ୫, ୫(A) ଏବଂ ୬ କେଉଁ ସ୍ଥାନରୁ କେଉଁ ସ୍ଥାନକୁ ଲମ୍ବିଛି ଏବଂ ଏହାର ଲମ୍ବ କେତେ କିଲୋମିଟର ?
Answer:

• ଜାତୀୟ ରାଜପଥ ୫ – ମୟୂରଭଞ୍ଜର ଝାଡ଼ପୋଖରିଆଠାରୁ ଗୋଳନ୍ତରା ନିକଟସ୍ଥ ଆନ୍ଧ୍ର-ଓଡ଼ିଶା ସୀମାସହ ସଂଯୋଗ କରୁଛି । ଏହାର ଲମ୍ବ ୪୮୮ କି.ମି. ।
• ଜାତୀୟ ରେଳପଥ ୫(A) – ଧାନମଣ୍ଡଳଠାରୁ ପାରାଦ୍ବୀପକୁ ସଂଯୋଗ କରୁଛି । ଏହାର ଲମ୍ବ ୭୭ କି.ମି. I
• ଜାତୀୟ ରାଜପଥ ୬ – ଓଡ଼ିଶା ଛତିଶଗଡ଼ ସୀମାଠାରୁ ଓଡ଼ିଶା ପଶ୍ଚିମବଙ୍ଗ ସୀମା ପର୍ଯ୍ୟନ୍ତ ଲମ୍ବିଛି । ଏହାର ଲମ୍ବ ୪୬୨ କି.ମି. ।

୪।. ପାରାଦ୍ଵୀପ ବନ୍ଦରକୁ ଭିଭିକରି ଓଡ଼ିଶାରେ କେଉଁସବୁ କଳକାରଖାନା ଗଢ଼ିଉଠିଛି ?
Answer:

• ୧୯୭୫ ମସିହାରେ ପାରାଦ୍ବୀପକୁ ରେଳପଥ ସହିତ ସଂଯୁକ୍ତ କରାଗଲା ।
• ଏହି ବନ୍ଦରକୁ ଭିଭିକରି ପାରାଦ୍ବୀପ ନିକଟବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ପାରାଦ୍ବୀପ ଫସ୍‌ଫେଟ୍‌ସ୍ କାରଖାନା ସ୍ଥାପିତ ହୋଇଛି ।
• ପାରାଦ୍ଵୀପଠାରେ ଏକ ତୈଳ ବିଶୋଧନାଗାର ନିର୍ମାଣ କରାଯାଉଛି ।

୫।. ଶିଳ୍ପ ବିକାଶର ଜୀବନରେଖା କାହାକୁ କୁହାଯାଏ ? ଏଥ‌ିପାଇଁ ଓଡ଼ିଶାରେ କ’ଣସବୁ ବ୍ୟବସ୍ଥା କରାଯାଇଛି ?
Answer:

• ଶିଳ୍ପ ବିକାଶର ଜୀବନରେଖା ହେଉଛି ବିଦ୍ୟୁତ୍ ଶକ୍ତି ।
• ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ସମୟରେ ଓଡ଼ିଶାରେ ଦୁଇଟି ତାପଜ ବିଦ୍ୟୁତ୍ କେନ୍ଦ୍ର ଥିଲା । ଗୋଟିଏ ଚୌଦ୍ଵାର ଓ ଅନ୍ୟଟି ବ୍ରହ୍ମପୁରରେ ଥିଲା ।
• ୧୯୫୭ ମସିହାରେ ହୀରାକୁଦ ଡ୍ୟାମ୍‌ ଜଳ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଉତ୍ପାଦିତ ହେଉଥିଲା । ସମୟକ୍ରମେ ଓଡ଼ିଶାରେ ପରେ ୬ଟି ଜଳବିଦ୍ୟୁତ୍ ପ୍ରକଳ୍ପ କାର୍ଯ୍ୟକ୍ଷମ ହୋଇଛି ।

୬।. ଭିତ୍ତିଭୁମିର ବିକାଶ ହେଲେ କେଉଁସବୁ ସୁଫଳ ମିଳେ ?
Answer:

• ଭିତ୍ତିଭୂମିର ବିକାଶ ହେଲେ ସବୁ ବ୍ୟବସ୍ଥା ବିକଶିତ ହେବ, ଫଳରେ ରାଜ୍ୟରେ କୃଷି, ଶିଳ୍ପ, ପର୍ଯ୍ୟଟନ ଓ ସାମାଜିକ ସଂହତି ସମ୍ଭବ ହେବ ।
• ରାଜ୍ୟରେ ଆଞ୍ଚଳିକ ବୈଷମ୍ୟ ରହିବ ନାହିଁ ।
• ସବୁ ଜିଲ୍ଲାର ସମତୁଲ ବିକାଶ ସମ୍ଭବ ହେବ ।

ସଂଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୨୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧। ଓଡ଼ିଶା ରାଜ୍ୟ ବିଦ୍ୟୁତ୍ ପରିଷଦର କାର୍ଯ୍ୟ କେଉଁ ଦୁଇଗୋଟି ନିଗମକୁ ଦିଆଯାଇଥିଲା ?
Answer:

• ଓଡ଼ିଶା ରାଜ୍ୟ ବିଦ୍ୟୁତ୍ ପରିଷଦର କାର୍ଯ୍ୟ ଦୁଇଗୋଟି ନିଗମକୁ ଦିଆଯାଇଥିଲା ।
• ପ୍ରଥମଟି ହେଲା ଓଡ଼ିଶା ଗ୍ରୀଡ୍ ନିଗମ ଓ ଦ୍ବିତୀୟଟି ହେଲା – ଓଡ଼ିଶା ଜଳବିଦ୍ୟୁତ୍ ଶକ୍ତି ନିଗମ

୨। ବିଦ୍ୟୁତ୍ ବିତରଣ ପାଇଁ ଓଡ଼ିଶା ସରକାର କେଉଁ ସଂସ୍ଥାକୁ ଦାୟିତ୍ବ ଦେଇଛନ୍ତି ?
Answer:

• ବିଦ୍ୟୁତ୍ ବିତରଣ ପାଇଁ ଓଡ଼ିଶା ସରକାର ୱେସ୍କୋ, ନେସ୍କୋ, ସାଉଥ୍ ଓ ସେସ୍କୋ ନାମକ ଚାରିଗୋଟି ଘରୋଇ ସଂସ୍ଥାକୁ ଦାୟିତ୍ଵ ଦେଇଛନ୍ତି ।
• ସେସ୍କୋ ଏବେ ସେସୁରେ ପରିଣତ ହୋଇଛି ।

୩। ‘ବିଜୁ ଗ୍ରାମଜ୍ୟୋତି ଯୋଜନା’ କେବେଠାରୁ ଓ କ’ଣ ପାଇଁ କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ?
Answer:

• ୨୦୦୭ ମସିହାରୁ ଓଡ଼ିଶା ସରକାର ବିଜୁ ଗ୍ରାମଜ୍ୟୋତି ଯୋଜନା ଆରମ୍ଭ କରିଛନ୍ତି ।
• ଏହି ଯୋଜନା ଅନୁଯାୟୀ ୧୦୦ରୁ କମ୍ ଲୋକ ବସବାସ କରୁଥିବା ଗ୍ରାମମାନଙ୍କୁ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଯୋଗାଇ

୪।. ପୂର୍ବତଟ ରେଳପଥ କେବେ ଶୁଭାରମ୍ଭ ହୋଇଥିଲା ଓ ଏହା କେବେ କାର୍ଯ୍ୟକ୍ଷମ ହେଲା ?
Answer:

• ୧୯୯୬ ମସିହା ଅଗଷ୍ଟ ୮ ତାରିଖରେ ପୂର୍ବତଟ ରେଳପଥ ଶୁଭାରମ୍ଭ ହୋଇଥିଲା ।
• ୨୦୦୩ ମସିହା ଏପ୍ରିଲ୍ ମାସରେ ଏହା କାର୍ଯ୍ୟକ୍ଷମ ହୋଇଥିଲା ।

୫।. ଭାରତରେ କେବେ ରେଳପଥ ଆରମ୍ଭ ହୋଇଥିଲା ଓ ଓଡ଼ିଶାରେ କେବେ ପ୍ରଥମେ ରେଳଗାଡ଼ି ଚାଲିଥିଲା ?
Answer:

• ୧୮୫୩ ମସିହାରେ ଭାରତରେ ରେଳପଥ ଆରମ୍ଭ ହୋଇଥିଲା ।
• ୧୮୯୭ ମସିହାରେ ଓଡ଼ିଶାରେ ପ୍ରଥମେ ରେଳଗାଡ଼ି ଚାଲିଥିଲା ।

୬।. ଓଡ଼ିଶାରେ କେତୋଟି ବିମାନ ଅବତରଣ କେନ୍ଦ୍ର ଓ କେତୋଟି ହେଲିପ୍ୟାଡ୍ ଅଛି ?
Answer:

• ଓଡ଼ିଶାରେ ୧୩ ଗୋଟି ବିମାନ ଅବତରଣ କେନ୍ଦ୍ର ଅଛି ।
• ଏହା ବ୍ୟତୀତ ଓଡ଼ିଶାରେ ୧୬ଟି ହେଲିପ୍ୟାଡ଼ ଅଛି ।

୭। ପଞ୍ଚାୟତ ସ୍ତରରେ କୃଷକମାନଙ୍କୁ ବୈଷୟିକ ସହାୟତା ଓ ପରାମର୍ଶ ଏବଂ ଆର୍ଥିକ ସହାୟତା ପ୍ରଦାନ ପାଇଁ କି ବ୍ୟବସ୍ଥା କରାଯାଇଛି ?
Answer:

• ପଞ୍ଚାୟତମାନଙ୍କରେ ନିଯୁକ୍ତ ଗ୍ରାମ୍ୟ କୃଷିକର୍ମୀମାନେ କୃଷକମାନଙ୍କୁ ବୈଷୟିକ ସହାୟତା ଓ ପରାମର୍ଶ ପ୍ରଦାନ କରୁଛନ୍ତି ।
• କୃଷକମାନଙ୍କୁ ଆବଶ୍ୟକବେଳେ ଆର୍ଥିକ ସହାୟତା ପ୍ରଦାନ କରିବାପାଇଁ ସମବାୟ ସଂସ୍ଥା ଓ ବ୍ୟାଙ୍କମାନଙ୍କ ଜରିଆରେ ଋଣ ପ୍ରଦାନର ବ୍ୟାପକ ବ୍ୟବସ୍ଥା ହୋଇଛି ।

Objective Type Questions With Answers
A ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।

1. ଓଡ଼ିଶା କେବେ ଏକ ସ୍ଵତନ୍ତ୍ର ପ୍ରଦେଶ ଭାବରେ ଆତ୍ମପ୍ରକାଶ କରିଥିଲା ?
Answer:
୧୯୩୬ ମସିହାରେ ଓଡ଼ିଶା ଏକ ସ୍ବତନ୍ତ୍ର ପ୍ରଦେଶ ଭାବରେ ଆତ୍ମପ୍ରକାଶ କରିଥିଲା ।

2. କେଉଁ ତିନିଗୋଟି କାରଣପାଇଁ ଓଡ଼ିଶାର ଭିତ୍ତିଭୂମିର ବିକାଶ ହୋଇପାରି ନଥିଲା ?
Answer:
ରାଜନୈତିକ ଅସ୍ଥିରତା, ଦ୍ବିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧ ଓ ଭାରତଛାଡ଼ ଆନ୍ଦୋଳନ ପାଇଁ ଓଡ଼ିଶାର ଭିତ୍ତିଭୂମିର ବିକାଶ ହୋଇପାରି ନଥିଲା ।

3. ଓଡ଼ିଶାରେ ଭିତ୍ତିଭୂମିର ବିକାଶଧାରା କେବେ ତ୍ବରାନ୍ବିତ ହୋଇଥିଲା ?
Answer:
ଦେଶ ସ୍ଵାଧୀନ ହେବା ଓ ବିଶେଷକରି ଓଡ଼ିଶା ସହିତ ଗଡ଼ଜାତ- ଗୁଡ଼ିକରେ ମିଶ୍ରଣ ପରେ ଭିତ୍ତିଭୂମିର ବିକାଶଧାରା ତ୍ବରାନ୍ବିତ ହୋଇଥିଲା ।

4. ମହାନଦୀ ତ୍ରିକୋଣଭୂମି ଅଞ୍ଚଳରେ କେଉଁସବୁ କେନାଲ ସାହାଯ୍ୟରେ ଜଳସେଚନ କରାଯାଇଥାଏ ?
Answer:
ତାଳଦଣ୍ଡା କେନାଲ, ମାଛଗାଁ କେନାଲ, କେନ୍ଦ୍ରାପଡ଼ା କେନାଲ, ପଟ୍ଟାମୁଣ୍ଡାଇ କେନାଲଦ୍ୱାରା ହଜାର ହଜାର ହେକ୍ଟର ଜମିକୁ ଜଳସେଚିତ କରାଯାଇଥାଏ ।

5. ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନାଦ୍ଵାରା କେଉଁ ଦୁଇଟି ଜିଲ୍ଲାରେ ଜଳସେଚନ କରାଯାଇଥାଏ ?
Answer:
ବରଗଡ଼ ଜିଲ୍ଲା ଓ ସମ୍ବଲପୁର ଜିଲ୍ଲାକୁ ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନାରେ ଜଳସେଚନ କରାଯାଇଥାଏ ।

6. ହୀରାକୁଦ ବ୍ୟତୀତ ଓଡ଼ିଶାରେ ଆଉ କେଉଁସବୁ ଜଳ ପ୍ରକଳ୍ପ କାର୍ଯ୍ୟକାରୀ ହୋଇଅଛି ?
Answer:
ହୀରାକୁଦ ବ୍ୟତୀତ ରେଙ୍ଗାଲି ପ୍ରକଳ୍ପ, ହ୍ରଦଗଡ଼ ପ୍ରକଳ୍ପ, ଅପର କୋଲାବ, ବାଲିମେଳା ଓ ଇନ୍ଦ୍ରାବତୀ ପ୍ରକଳ୍ପ କାର୍ଯ୍ୟକାରୀ ହୋଇଅଛି।

7. ଭୁବନେଶ୍ଵର ଓ ଚିପିଲିମାଠାରେ କୃଷି ପାଇଁ କେଉଁ ଅନୁଷ୍ଠାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:
ଭୁବନେଶ୍ୱରଠାରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଛି ‘ଓଡ଼ିଶା କୃଷି ବୈଷୟିକ ବିଶ୍ୱବିଦ୍ୟାଳୟ’ ଓ ଚିପିଲିମାଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ‘କୃଷି ମହାବିଦ୍ୟାଳୟ’ ।

8. ଭାରତରେ ଓ ଓଡ଼ିଶାରେ କେବେ ରେଳ ଚଳାଚଳ ଆରମ୍ଭ ହୋଇଥିଲା ?
Answer:
ଭାରତରେ ରେଳପଥ ଆରମ୍ଭ ହୋଇଥିଲା ୧୮୫୩ ମସିହାରେ ଓ ଓଡ଼ିଶାରେ ପ୍ରଥମ ରେଳଗାଡ଼ି ଚାଲିଥିଲା ୧୮୯୭ ମସିହାରେ ।

9. ଇଷ୍ଟକୋଷ୍ଟ ରେଳବାଇ ଜୋନ୍ କ’ଣ ?
Answer:
ଏହି ରେଳବାଇ ଜୋନ୍‌ରେ ସମ୍ବଲପୁର, ଖୋର୍ଦ୍ଧାରୋଡ଼ ଓ ୱାଲିଟିଅର ଡିଭିଜନ କାର୍ଯ୍ୟ କରିଥାଏ ।

10. ଓଡ଼ିଶାର ମୁଖ୍ୟ ବିମାନ ବନ୍ଦର କେଉଁଟି ?
Answer:
ଭୁବନେଶ୍ଵରଠାରେ ଥ‌ିବା ବିଜୁ ପଟ୍ଟନାୟକ ବିମାନ ବନ୍ଦର ଓଡ଼ିଶାର ମୁଖ୍ୟ ବିମାନ ବନ୍ଦର ଅଟେ ।

11. ଟାଟା କମ୍ପାନୀ ସହାୟତାରେ କେଉଁ ବନ୍ଦର ନିର୍ମାଣ କରାଯାଇଛି ?
Answer:
ଟାଟା କମ୍ପାନୀ ସହାୟତାରେ ଧାମରାଠାରେ ଏକ ବୃହତ୍ ବନ୍ଦର ନିର୍ମାଣ କରାଯାଇଛି ।

12. ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ୬ଟି ବିଦ୍ୟୁତ୍ ପ୍ରକଳ୍ପର ନାମ ଲେଖ ।
Answer:
ହୀରାକୁଦ ଜଳବିଦ୍ୟୁତ୍ ପ୍ରକଳ୍ପ, ବାଲିମେଳା ପ୍ରକଳ୍ପ, ରେଙ୍ଗାଲି, ଅପର କୋଲାବ, ଅପର ଇନ୍ଦ୍ରାବତୀ ଓ ମାଛକୁଣ୍ଡ ଜଳବିଦ୍ୟୁତ୍ ପ୍ରକଳ୍ପ କାର୍ଯ୍ୟକାରୀ ହେଉଛି ।

B. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।

1. ସାମାଜିକ ଐକ୍ୟ ଓ ଆର୍ଥନୈତିକ ସମୃଦ୍ଧିର ପ୍ରଥମ ଆବଶ୍ୟକତା କ’ଣ ?
Answer:
ଭିତ୍ତିଭୂମି

2. ବିଜୁ ଗ୍ରାମଜ୍ୟୋତି ଯୋଜନା କାହାଦ୍ଵାରା ପ୍ରବର୍ତ୍ତିତ ହୋଇଛି ?
Answer:
ଓଡ଼ିଶା ସରକାର

3. କେଉଁ ଜାତୀୟ ରାଜପଥଟି ଓଡ଼ିଶା ଝାଡ଼ଖଣ୍ଡ ସୀମାରୁ ଚମ୍ପୁଆ ଦେଇ ପରଶୋରା ପର୍ଯ୍ୟନ୍ତ ଯାଇଛି ?
Answer:
ଜାତୀୟ ରାଜପଥ – ୭୫

4. ୫ ନମ୍ବର ଜାତୀୟ ରାଜପଥର ଦୈର୍ଘ୍ୟ କେତେ ?
Answer:
୪୮୮ କି.ମି.

5. ପୂର୍ବତଟ ରେଳପଥର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ କେଉଁଠାରେ ଅଛି ?
Answer:
ଭୁବନେଶର

6. ସ୍ଵାଧୀନତାପ୍ରାପ୍ତି ବେଳକୁ ଓଡ଼ିଶାରେ ରେଳପଥର ଦୈର୍ଘ୍ୟ କେତେ କି.ମି. ଥୁଲା ?
Answer:
୯୧୪ କି.ମି.

7. ସମ୍ବଲପୁରର କେଉଁଠାରେ ଏକ କୃଷି ମହାବିଦ୍ୟାଳୟ ରହିଛି ?
Answer:
ଚିପିଲିମା

8. ଓଡ଼ିଶାରେ ଥିବା ଜାତୀୟ ରାଜପଥଗୁଡ଼ିକ ଦୈର୍ଘ୍ୟ କେତେ କି.ମି. ?
Answer:
୩୬୫୫

9. ଜାତୀୟ ରାଜପଥ ନଂ ୪୩ର ଦୈର୍ଘ୍ୟ କେତେ କି.ମି. ?
Answer:
୧୫୨ କି.ମି.

10. ଜାତୀୟ ରାଜପଥ ନଂ ୨୦୩A କେଉଁ ଦୁଇଟି ସ୍ଥାନକୁ ଯୋଗ କରିଛି ?
Answer:
ପୁରୀ ଓ ସାତପଡ଼ା

11. ଜାତୀୟ ରାଜପଥ ନଂ ୨୩ ତାଳଚେରଠାରେ କେଉଁ ଜାତୀୟ ରାଜପଥ ସହିତ ମିଶିଛି ?
Answer:
ଜାତୀୟ ରାଜପଥ ନଂ ୪୨

12. ବିଜୁ ପଟ୍ଟନାୟକ ବିମାନବନ୍ଦରରେ କେବେଠାରୁ ଏକ ଏୟାର କାର୍ଗୋ କମ୍ପ୍ଲେକ୍ସ କାର୍ଯ୍ୟ କରୁଛି ?
Answer:
୧୯୯୫ ଅଗଷ୍ଟ ମାସ

13. ଜଳବିଦ୍ୟୁତ୍ ଓ ତାପଜ ବିଦ୍ୟୁତକୁ ମିଶାଇ ଓଡ଼ିଶାର ନିଜସ୍ଵ ବିଦ୍ୟୁତ୍ ଉତ୍ପାଦନ ସାମର୍ଥ୍ୟ କେତେ ମେଗାଓ୍ବାଟ୍ ଥିଲା ?
Answer:
୨୮୫୬

14. .ବିଦ୍ୟୁତ୍ ସଂସ୍କାର ଆଇନ ୧୯୯୫ କେଉଁ ଉଦ୍ଦେଶ୍ୟରେ କାର୍ଯ୍ୟକାରୀ ହେଲା ?
Answer:
ବିଦ୍ୟୁତ୍ ଶକ୍ତିର ଉତ୍ପାଦନ ଓ ସୁଷମ ବଣ୍ଟନ ପାଇଁ

15. ଟାଟା କମ୍ପାନୀଦ୍ଵାରା କେଉଁଠାରେ ଏକ ବୃହତ୍ ବନ୍ଦର ନିର୍ମିତ ହୋଇଛି ?
Answer:
ଧାମରା

16. ସମ୍ବଲପୁର, ଖୋର୍ଦ୍ଧାରୋଡ଼ ଓ ୱାଲଟିଅର୍ ଡିଭିଜନକୁ ନେଇ କାର୍ଯ୍ୟ କରୁଥିବା ରେଳବାଇ ଜୋନ୍ ?
Answer:
ଇଷ୍ଟକୋଷ୍ଟ ରେଳବାଇ ଜୋନ୍

C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ୧୯୩୬ ମସିହାରୁ ______________ ମସିହା ପର୍ଯ୍ୟନ୍ତ ଓଡ଼ିଶା ଥିଲା ପରାଧୀନ ଭାରତର ଏକ ପ୍ରଦେଶ ।
Answer:
୧୯୪୭

2. ଦ୍ବିତୀୟ ବିଶ୍ଵଯୁଦ୍ଧ ୧୯୩୯ରୁ _____________ ମସିହା ପର୍ଯ୍ୟନ୍ତ ଚାଲିଥିଲା ।
Answer:
୧୯୪୫

3. ୧୯୪୨ ମସିହାରେ ଆମ ଦେଶରେ _______________ ଆନ୍ଦୋଳନ ଚାଲିରହିଥିଲା ।
Answer:
ଭାରତଛାଡ଼

4. ଆମ ରାଜ୍ୟରେ ସମର୍ଥ ଲୋକଙ୍କ ମଧ୍ୟରୁ ଶତକଡ଼ା, ________________ ଭାଗ ଲୋକ କୃଷିକ୍ଷେତ୍ରରେ କାମ କରନ୍ତି ।
Answer:
୬୫

5. ସମ୍ବଲପୁର ନିକଟସ୍ଥ ______________ ଠାରେ ଏକ କୃଷି ମହାବିଦ୍ୟାଳୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
ଚିପିଲିମା

6. ଚଳଚ୍ଚିତ୍ର ଶିଳ୍ପ ପାଇଁ ଓଡ଼ିଶାରେ _______________ ଟି ରେଳବାଇ ଜୋନ୍ କାର୍ଯ୍ୟ କରୁଅଛି ।
Answer:
୧୬

7. ଚଳଚ୍ଚିତ୍ର ଶିଳ୍ପ ପାଇଁ ଓଡ଼ିଶାରେ _______________ ଷ୍ଟୁଡ଼ିଓ କାର୍ଯ୍ୟ କରୁଅଛି ।
Answer:
କଳିଙ୍ଗ

8. ପୂର୍ବତଟ ରେଳପଥର ମୂଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ____________________ ଠାରେ ଅବସ୍ଥିତ ।
Answer:
ଭୁବନେଶ୍ୱର

9. _______________ ରାଜପଥ ଭୁବନେଶ୍ଵରଠାରୁ ପୁରୀ, ବାଲିଘାଇ ଦେଇ କୋଣାର୍କ ପର୍ଯ୍ୟନ୍ତ ଯାଇଛି ।
Answer:
୨୦୩ ଜାତାୟ

10. ପ୍ରଥମେ ପରାଦ୍ବୀପ ବନ୍ଦରରୁ ____________ ବିଦେଶକୁ ରପ୍ତାନି ହେଉଥିଲା ।
Answer:
ଲୁହାପଥର

11. ଭୁବନେଶ୍ୱର ବିମାନ ବନ୍ଦର ବ୍ୟତୀତ ଓଡ଼ିଶାରେ _______________ ଟି ବିମାନ ଅବତରଣ କେନ୍ଦ୍ର ରହିଛି ।
Answer:
୧୩

12. ଗୋପାଳପୁର ବନ୍ଦର _______________ ମସିହାଠାରୁ ଏକ ପ୍ରଥମ ଶ୍ରେଣୀର ବନ୍ଦରଭାବେ କାର୍ଯ୍ୟ କରୁଅଛି ।
Answer:
୧୯୮୭

13. ଭାରତରେ ପ୍ରଥମ ରେଳପଥ ଆରମ୍ଭ ହୋଇଥିଲା _______________ ମସିହାରେ ।
Answer:
୧୮୫୩

14. ବର୍ତ୍ତମାନ ଓଡ଼ିଶାରେ _______________ ଟି ଜଳ ବିଦ୍ୟୁତ୍ ପ୍ରକଳ୍ପ କାର୍ଯ୍ୟକ୍ଷମ ହେଉଛି ।
Answer:
୬

15. ୧୯୯୬ ମସିହାରେ ପୂର୍ବତଟ ରେଳପଥର ଶୁଭ ଦେଇଥିଲେ ପ୍ରଧାନମନ୍ତ୍ରୀ ______________ ।
Answer:
ଦେବଗୌଡ଼ା

D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓) ଚିହ୍ନ ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (x) ଚିହ୍ନ ଦିଅ ।

1. ଦ୍ଵିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧ ୧୯୧୪ ମସିହାରେ ଆରମ୍ଭ ହୋଇଥିଲା ।
Answer:
x

2. ଓଡ଼ିଶାରେ ୮୦ ଭାଗ ଲୋକ କୃଷିକ୍ଷେତ୍ରରେ କାମ କରନ୍ତି ।
Answer:
x

3. ୧୯୩୬ ମସିହାରେ ଓଡ଼ିଶା ସ୍ବତନ୍ତ୍ର ପ୍ରଦେଶରେ ପରିଣତ ହୋଇଥିଲା ।
Answer:
✓

4. କେନ୍ଦ୍ରୀୟ ଧାନ ଗବେଷଣା କେନ୍ଦ୍ର ବରଗଡ଼ଠାରେ ଅବସ୍ଥିତ ।
Answer:
x

5. ମତ୍ସ୍ୟ ଗବେଷଣା କେନ୍ଦ୍ର ଚିଲିକାଠାରେ ଅବସ୍ଥିତ ।
Answer:
x

6. ଚିପିଲିମାଠାରେ ଏକ ଶିଳ୍ପ ମହାବିଦ୍ୟାଳୟ ରହିଛି ।
Answer:
x

7. ବର୍ତ୍ତମାନ ଓଡ଼ିଶାର ରାଜପଥ ସଂଖ୍ୟା ୧୫ରେ ପହଞ୍ଚିଛି ।
Answer:
✓

8. ଗାଁ ଗହଳରେ ପକ୍କା ସଡ଼କ ରାଜୀବ ଯୋଜନାରେ କାର୍ଯ୍ୟକାରୀ ହେଉଛି ।
Answer:
x

9. ୧୮୩୫ରେ ଭାରତରେ ପ୍ରଥମ ରେଳପଥ ଆରମ୍ଭ ହେଲା ।
Answer:
x

10. ଓଡ଼ିଶାରେ ପ୍ରଥମେ ରେଳଗାଡ଼ି ଚାଲିଥିଲା ୧୮୭୯ରେ ।
Answer:
x

11. ପୂର୍ବତଟ ରେଳପଥର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ଭୁବନେଶ୍ଵରରେ ୨୦୦୩ ମସିହାରେ କାର୍ଯ୍ୟକ୍ଷମ ହୋଇଥିଲା ।
Answer:
✓

12. ପାରାଦ୍ଵୀପଠାରେ ଏକ ତୈଳ ବିଶୋଧନାଗାର ନିର୍ମାଣ କରାଯାଇଛି ।
Answer:
✓

13. ଶିଳ୍ପ ବିକାଶର ଜୀବନରେଖା ହେଉଛି ବିଦ୍ୟୁତ୍ଵଶକ୍ତି ।
Answer:
✓

14. ସ୍ଵାଧୀନତା ବେଳକୁ ଓଡ଼ିଶାରେ ତିନୋଟି ତାପଜ ବିଦ୍ୟୁତ୍ କେନ୍ଦ୍ର ଥିଲା ।
Answer:
x

15. ଓଡ଼ିଶାର ତାଳଚେରଠାରେ ଏକ ତାପଜ ବିଦ୍ୟୁତକେନ୍ଦ୍ର ସ୍ଥାପିତ ହୋଇଛି ।
Answer:
✓

16. ଗୋପାଳପୁରଠାରେ ୧୯୮୭ ମସିହାଠାରୁ ଏକ ମଧ୍ୟମ ଶ୍ରେଣୀର ବନ୍ଦର କାର୍ଯ୍ୟ କରୁଅଛି ।
Answer:
✓

17. ରାଜୀବ ଗାନ୍ଧି ଗ୍ରାମୀଣ ବିଦ୍ୟୁତକରଣ ଯୋଜନା ୨୦୦୭ ମସିହାରୁ କାର୍ଯ୍ୟକରୁଛି ।
Answer:
x

18. ବିଜୁ ଗ୍ରାମ୍ୟଜ୍ୟୋତି ଯୋଜନା ଆମ ରାଜ୍ୟରେ ୨୦୦୬ ମସିହାରୁ କାର୍ଯ୍ୟ କରୁଅଛି ।
Answer:
x

19. ପର୍ଯ୍ୟଟକମାନଙ୍କ ସୁବିଧା ପାଇଁ ଭୁବନେଶ୍ୱର, ପୁରୀ, କୋଣାର୍କକୁ ନେଇ ସୁବର୍ଣ୍ଣ ତ୍ରିଭୁଜ ଗଠନ କରାଯାଇଛି ।
Answer:
✓

20. ଚଳଚ୍ଚିତ୍ର ଶିଳ୍ପ ପାଇଁ ଓଡ଼ିଶାରେ କଳିଙ୍ଗ ଷ୍ଟୁଡ଼ିଓ ଭଳି ଅନୁଷ୍ଠାନ କାର୍ଯ୍ୟ କରୁଅଛି ।
Answer:
✓

21. ଓଡ଼ିଶା ବୈଦ୍ୟୁତିକ ସଂସ୍କାର ଆଇ ୧୯୯୬ ମସିହା ଏପ୍ରିଲ ୧ରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ।
Answer:
✓

22. ଓଡ଼ିଶାରେ ୧୬ଟି ହେଲିପ୍ୟାଡ଼ ରହିଛି ।
Answer:
✓

23. ବର୍ତ୍ତମାନ ଭାରତରେ ୯ଟି ରେଳବାଇ ଜୋନ୍ କାମ କରୁଅଛି ।
Answer:
x

E. ‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ମିଳନ କର ।
1.

Answer:

2.

Answer:

3.

Answer:

4.

Answer:

Odisha State Board BSE Odisha 10th Class Odia Solutions Chapter 4 ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Odia Solutions Chapter 4 ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ

ପାଠ୍ୟପୁସ୍ତକସ୍ଥ ପ୍ରଶ୍ନାବଳୀର ଉତ୍ତର

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂ ଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question ୧ ।
ପ୍ରତ୍ୟେକର ତିନୋଟି ଲେଖାଏଁ ପ୍ରତିଶବ୍ଦ ଲେଖ ।
ସିନ୍ଧୁ, ପର୍ବତ, ଆକାଶ

ଶବ୍ଦ	ପ୍ରତିଶବ୍ଦ
ସିନ୍ଧୁ	ସାଗର, ସମୁଦ୍ର, ପାରାବାର, ଜଳଧ୍ଵ
ପର୍ବତ	ଅଚଳ, ପାହାଡ଼, ମହୀଧର, ଗିରି, ଶୈଳ, ଭୂଧର
ଆକାଶ	ଅମ୍ବର, ଗଗନ, ବ୍ୟୋମ, ବିହାୟସ

Question ୨।
ନିମ୍ନଲିଖତ ଶବ୍ଦମାନଙ୍କର ଗଦ୍ୟରୂପ ଲେଖ ।
ପ୍ରାପତି, ଜନମି, ଦଇବ
Answer:
ପ୍ରାପତି – ପ୍ରାପ୍ତି
ଜନମି – ଜନ୍ମି
ପାଇବ – ଦୈବ

Question ୩ ।
ନିମ୍ନଲିଖ୍ ଶବ୍ଦଗୁଡ଼ିକର ବିପରୀତାର୍ଥବୋଧକ ଶବ୍ଦ ଲେଖ ।
ଆଶା, ନିଃଶ୍ଵାସ, ପ୍ରସନ୍ନ, ଜ୍ୟେଷ୍ଠ, ଜନ୍ମ, ପୁଣ୍ୟ, ବିରସ
Answer:
ଆଶା – ନିରାଶ
ପ୍ରସନ୍ନ – ବିଷଣ୍ଣ/ଅପ୍ରସନ୍ନ
ଜନ୍ମ – ମୃତ୍ୟୁ
ବିରସ – ହରଷ/ପ୍ରଫୁଲ୍ଲ
ନିଃଶ୍ବାସ – ପ୍ରଶ୍ଵାସ
ଜ୍ୟେଷ୍ଠ – କନିଷ୍ଠ
ପୁଣ୍ୟ – ପାପ

Question ୪।
ନିମ୍ନଲିଖ ଶବ୍ଦମାନଙ୍କୁ ନେଇ ସାର୍ଥକ ବାକ୍ୟ ରଚନା କର ।
ପିତୃବ୍ୟ, ବ୍ୟୋମ, ପ୍ରସନ୍ନ, ଅନୁଜ, ସତ୍ଵର
Answer:
ପିତୃବ୍ୟ – ପିତୃବ୍ୟଙ୍କୁ ପିତା ସମ ଭକ୍ତି ଓ ସମ୍ମାନ କରିବା ଉଚିତ ।
ବ୍ୟୋମ – ସକ୍ଷାମାନେ ବ୍ୟୋମରେ ବିହାର କରୁଥିବାରୁ ସେମାନଙ୍କୁ ବ୍ୟୋମବାର। କୁହାଯାଏ।
ପ୍ରସନ୍ନ – ସମସ୍ତ ପ୍ରଶ୍ନର ସଠିକ୍ ଉତ୍ତର ଦେଇଥିବାରୁ ଶିକ୍ଷକ ରାମ ଉପରେ ପ୍ରସନ୍ନ ହେଲେ ।
ଅନୁଜ – ଶ୍ରୀରାମ ଅନୁଜ ଲକ୍ଷ୍ମଣ ଓ ପତ୍ନୀ ମାତାଙ୍କ ସହ ବନଗମନ କରିଥିଲେ ।
ପତ୍ଵର – ଗୁରୁଜନଙ୍କ ଆଦେଶ ସତ୍ୱର ପାଳନାୟ।

Question ୫।
ସନ୍ଧିବିଚ୍ଛେଦ କର ।
ବଜ୍ରାଘାତ, ପ୍ରତ୍ୟୁତ୍ତର, ନିଃଶ୍ଵାସ
Answer:
ବଜ୍ରାଘାତ, = ବଜ୍ର + ଆଘାତ
ପ୍ରତ୍ୟୁତ୍ତର = ନିଃ + ଶ୍ଵାସ
ନିଃଶ୍ଵାସ = ପ୍ରତି + ଉତ୍ତର

Question ୬ ।
ବ୍ୟାସବାକ୍ୟ ସହ ସମାସର ନାମ ଲେଖ ।
ବିଭୂତିଭୂଷଣ, ବିଂଶତିକର, ଦେବରିପୁ, ହୀନପରାକ୍ରମ
Answer:
ବିଭୂତିଭୂଷଣ – ବିଭୂତି ଯାହାର ଭୂଷଣ ସେ – ବହୁବ୍ରୀହି ସମାସ,
ବିଭୂତିରେ ଭୂଷିତ ଯେ – ଉପପଦ ତତ୍‌ପୁରୁଷ ସମାସ
ବିଂଶତିକର – ବିଂଶତି କର ଯାହାର ସେ – ବହୁ ବ୍ରାହି ସମାସ
ବିଂଶ କର ଯାହାର – ଉପପଦ ତତ୍‌ପୁରୁଷ ସମାସ
ଦେବରିପୁ – ଦେବତାମାନଙ୍କର ରିପୁ – ଷଷ୍ଠୀ ତପୁରୁଷ ସମାସ
ହାନ ପରାକ୍ରମ – ହାନ ଅଟେ ପରିକ୍ରମ – ମଧ୍ୟପଦ ଲୋପା କମ୍ପଧାରୟ ସମାସ

Question ୭।
କେଁ କେଁ ଭଳି ଆଉ ପାଞ୍ଚଗୋଟି ଧ୍ଵନ୍ୟାତ୍ମକ ଯୁଗ୍ମ ଶବ୍ଦ ଲେଖ ।
Answer:
ପେଁ ପେଁ, ମେଁ ମେଁ, ହେଁ ହେଁ, ମେଁ ମେଁ, ଚେଁ ଚେଁ

କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପୂନୋତ୍ତର

Question ୮।
ସିନ୍ଧୁକୁ ପୋତିବାପାଇଁ ରାମଚନ୍ଦ୍ର କାହିଁକି ସ୍ଥିର କଲେ ?
Answer:
ଲଙ୍କାଗଡ଼ରୁ ସୀତାଙ୍କୁ ଉଦ୍ଧାର କରିବା ନିମନ୍ତେ ସମୁଦ୍ର ଅତିକ୍ରମ କରିବା ଆବଶ୍ୟକ ଥିବାରୁ ରାମଚନ୍ଦ୍ର ସିନ୍ଧୁକୁ ପୋତିବାପାଇଁ ସ୍ଥିର କଲେ ।

Question ୯ ।
କବିତାରେ ରାଘବ ଶବ୍ଦଟି କାହା ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟବହାର କରାଯାଇଛି ?
Answer:
କବିତାରେ ରାଘବ ଶବ୍ଦଟି ରାମଚନ୍ଦ୍ରଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟବହାର କରାଯାଇଛି।

Question ୧୦ ।
ବରୁଣଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ ରାମଚନ୍ଦ୍ର କ’ଣ କଲେ ?
Answer:
ବରୁଣଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ ରାମଚନ୍ଦ୍ର ଅନାହାରରେ ରହିଲେ ଓ କୁଶଶଯ୍ୟାରେ ଶୟନ କଲେ ।

Question ୧୧ ।
ରାବଣ ଶୁକ, ସାରଣଙ୍କ ମାଧ୍ୟମରେ ବିଭୀଷଣଙ୍କ ପାଖକୁ କି ବାର୍ତ୍ତା ପଠାଇଲେ ?
Answer:
ରାବଣ ଶୁକ, ସାରଣ ମନ୍ତ୍ରୀଦ୍ଵୟଙ୍କ ମାଧ୍ୟମରେ ବିଭୀଷଣଙ୍କ ନିକଟକୁ ବାର୍ତ୍ତା ଦେଇ କହିଥିଲେ ଯେ ଯେହେତୁ ଜ୍ୟେଷ୍ଠଭ୍ରାତା ପିତୃତୁଲ୍ୟ ଅଟନ୍ତି; ତେଣୁ ସେ ଯଦିବା କ୍ରୋଧବଶତଃ ତାଙ୍କ ପ୍ରତି କିଛି କଟୁଭାଷା ପ୍ରୟୋଗ କରିଛନ୍ତି ତାହା ଧର୍ତ୍ତବ୍ୟ ନୁହେଁ ବା ସେହି ଉକ୍ତିକୁ ତିକ୍ତତୁଲ୍ୟ ମନେକରିବା ଉଚିତ ନୁହେଁ । ଏତଦ୍‌ଭିନ୍ନ ରାଜ ଐଶ୍ବର୍ଯ୍ୟର ପ୍ରାଚୁର୍ଯ୍ୟକୁ ତ୍ୟାଗକରି

Question ୧୨ ।
ଅଙ୍ଗଦ ନିକଟକୁ ରାବଣ କି ସନ୍ଦେଶ ପ୍ରେରଣ କଲେ ?
Answer:
ଅଙ୍ଗଦ ପ୍ରତି ରାବଣଙ୍କ ବାର୍ତ୍ତା ଥୁଲା ଯେ ପିତାଙ୍କ ଶତ୍ରୁକୁ ଭକ୍ତି କଲେ କଦାପି ପୁଣ୍ୟାର୍ଜନ ହୁଏ ନାହିଁ । ତେଣୁ ପତୃବ୍ୟ ସୁଗ୍ରୀବଙ୍କ ସହ ବିବାଦ ରଚନା କରି ସେ ତୁରନ୍ତ ସୈନ୍ୟ ପ୍ରତ୍ୟାହାରପୂର୍ବକ ସେମାନଙ୍କ ସଙ୍ଗ୍ ତ୍ୟାଗ କରନ୍ତୁ ।

Question ୧୩।
ରାବଣର ବାର୍ତ୍ତା ନେଇ ଅଙ୍ଗଦ ନିକଟକୁ କିଏ ଆସିଥିଲେ ?
Answer:
ରାବଣର ବାର୍ତ୍ତା ନେଇ ଅଙ୍ଗଦ ନିକଟକୁ ରାବଣଙ୍କର ଦୁଇଜଣ ମନ୍ତ୍ରୀ ଶୁକ ଓ ସାରଣ ଆସିଥିଲେ ।

Question ୧୪ ।
ରାବଣର ବାର୍ତ୍ତା ଶୁଣି ଅଙ୍ଗଦ କି ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ କଲେ ?
Answer:
ରାବଣର ବାର୍ତ୍ତା ଶ୍ରବଣ ମାତ୍ରକେ ଅଙ୍ଗଦ ଭୀଷଣ ଉତ୍ତେଜିତ ହୋଇପଡ଼ିଥିଲେ । କ୍ରୋଧରେ ଶୂନ୍ୟକୁ ବଜ୍ର ସମ ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିଥିଲେ ।

Question ୧୫ ।
ମନ୍ତ୍ରୀଦ୍ୱୟ ରାବଣ ନିକଟରେ କି ଉକ୍ତି ପ୍ରକାଶ କଲେ?
Answer:
ମନ୍ତାଦ୍ଵୟ ବିଭାଷଣଙ୍କୁ ପ୍ରଦାନ କରିଥିବା ବାର୍ତ୍ତାର ପ୍ରତ୍ୟୁତ୍ତର ଏବଂ ପାର୍ତ୍ତା ଶ୍ରବଣରେ ଅଙ୍ଗନାଙ୍କ ପ୍ରତକ୍ରୟା ସମ୍ପର୍କିତ ଉକ୍ତି ପ୍ରକାଶ କରିଥିଲେ। ବିଭୀଷଣ ଲଙ୍କପତିଙ୍କ ବାର୍ତ୍ତାର ପ୍ରତ୍ୟୁତ୍ତର ଥିଲା ‘ଯଦି ଜ୍ୟେଷ୍ଠଭ୍ରାତା ଦେବୀ ସୀତାଙ୍କୁ ସସମ୍ମାନେ ରାମଚନ୍ଦ୍ରଙ୍କୁ ନିଃସର୍ଭ ସମର୍ପଣ କରନ୍ତି ତେବେ ସେ ଲଙ୍କାପୁରୀକୁ ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବେ’’ଉକ୍ତି ମନ୍ତ୍ରୀଦ୍ବୟ ରାବଣ ନିକଟରେ ପ୍ରକାଶ କରିଥିଲେ ।

Question ୧୬ ।
ଅଙ୍ଗଦଙ୍କ ଶକ୍ତ ଚାପୁଡ଼ା ପ୍ରହାରରେ ମନ୍ତ୍ରୀଦ୍ଵୟଙ୍କର କି ଅବସ୍ଥା ହୋଇଥାନ୍ତା ?
Answer:
ଅଙ୍ଗଦଙ୍କ ଶୂନ୍ୟରେ ଚାପୁଡ଼ା ପ୍ରହାର ଏପରି ଶକ୍ତିଶାଳୀ ଥିଲା ଯେ ବିଶାଳ ବିନ୍ଧ୍ୟ ପର୍ବତ ସେହି ଆଘାତରେ ଚୂର୍ଣ୍ଣ ବିଚୂର୍ଣ୍ଣ ହୋଇଯାଇଥାଆନ୍ତି । ଅଥବା ପାଞ୍ଜାଳଗାମା ହୋଇଯାଇଥାଆନ୍ତ୍ରା ବାହା ନିଶ୍ଚିତଭାବେ ମନ୍ତ୍ରଦ୍ୱୟଙ୍କର ପ୍ରାଣଘାତକ ହୋଇଥାଆନ୍ତା। କେବଳ ଧର୍ମ ବଳରୁ ସେହି ଆଘାତରୁ ସେମାନେ ପ୍ରାଣ ବଞ୍ଚାଇବାରେ ସମର୍ଥ ହେଲେ ବୋଲି ମନ୍ତ୍ରୀଦ୍ଵୟ କହିଥିଲେ।

Question ୧୭ ।
ଶ୍ରୀରାମଙ୍କ ସୈନ୍ୟ ସଂଖ୍ୟା କେତେ ବୋଲି ମନ୍ତ୍ରୀଦ୍ଵୟ କଳନା କଲେ ?
Answer:
ସମୁଦ୍ରର ଜଳରାଶିରେ ସୃଷ୍ଟ ତଥା ପରିଦୃଷ୍ଟ ଶଙ୍ଖମାନଙ୍କ ସଂଖ୍ୟା ଯେତେ ଶ୍ରୀରାମଙ୍କ ସୈନ୍ୟସଂଖ୍ୟା ସେତେ ଶଙ୍ଖଠାରୁ ଅଧ୍ଵକ ବା ଅଗଣିତ ବୋଲି ମନ୍ତ୍ରୀଦ୍ୱୟ କଳନା କଲେ ।

Question ୧୮ ।
ସମୁଦ୍ର ତରିବା ନିମନ୍ତେ ରାଘବ କ’ଣ ପାଞ୍ଚିଥିଲେ ?
Answer:
ସମୁଦ୍ର ଲଙ୍ଘନ ନିମନ୍ତେ ସେତୁ ସ୍ଥାପନ ପାଇଁ ରାଘବ ବରୁଣ ଦେବତାଙ୍କୁ ସନ୍ତୁଷ୍ଟ କରିବାକୁ ଉଚିତ ମନେ କରି ତାଙ୍କ ପ୍ରୀତ୍ୟର୍ଥେ ଅନାହାର ରହିବା ସହ କୁଶଶଯ୍ୟାରେ ଶୟନ କରିବେ ବୋଲି ପାଞ୍ଚିଥିଲେ ।

ପପ୍ରସଙ୍ଗ ପରଳାର୍ଥ

Question ୧୯ ।
ବିସ୍ମଇ ନିଃଶ୍ବାସ ତେଜି ବରୁଣ ପ୍ରସନ୍ତେ
ବିନାଶନରେ ଶୟନ ସେ ଦର୍ଭଶୟନେ ଯେ ।
Answer:
ବିସ୍ମଇ ନିଶ୍ଵାସ …………………..ଦର୍ଭ ଶୟନେ ଯେ ।’’
ପ୍ରଦତ୍ତ ପଦ୍ୟାଂଶଟି କବି ସମ୍ରାଟ ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ କାଳଜୟୀ କାବ୍ୟ ବୈଦେହାଶ ବିଳାସ କାବ୍ୟର ଚତ୍ବାରିଂଶତମ ଛାନ୍ଦର ପ୍ରଥମାଂଶ ଚାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁଚଳ ଶୀର୍ଷକ କବିତାରୁ ଉଦ୍ଧତା ଏଠାରେ କବି ଶ୍ରୀରାମଙ୍କ ଲଙ୍କାଭିଯାନ ନିମନ୍ତେ ଆୟୋଜିତ ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣର ସଫଳତା ନିମନ୍ତେ ଆଚରିତ ସାତ୍ତ୍ଵିକ ନିଷ୍ଠା ଉପରେ ଆଲୋକପାତ କରିଛନ୍ତି ।ସେତୁ ନିର୍ମାଣ ପାଇଁ ଅମାପ ବଳଶାଳୀ ବାନର ସୈନ୍ୟମାନେ ସମୁଦ୍ରରେ ବିଶାଳ ଗିରିଖଣ୍ଡମାନ ନିକ୍ଷେପ କରିବାକୁ ଲାଗିଲେ । ମାତ୍ର ସେ ସମସ୍ତ ଅତଳ ଜଳଧୂ ଗର୍ଭରେ ବିଲୀନ ହେବାକୁ ଲାଗିଲା । କେବଳ ଫି ଫି କାର ଶବ୍ଦ ବ୍ୟତୀତ ସାମାନ୍ୟ ବୁଦ୍‌ବୁଦ ମଧ୍ୟ ପରିଦୃଷ୍ଟ ହେଲାନାହିଁ । ସାଗର ଜଳର ଏତାଦୃଶ ଆଚରଣ ଶ୍ରୀରାମଙ୍କୁ ବିସ୍ମିତ କଲା । କାର୍ଯ୍ୟାରମ୍ଭରେ କୌଣସି ତ୍ରୁଟି ବିଚ୍ୟୁତି ରହିଥ‌ିବା ସନ୍ଦେହ କରି ରାମଚନ୍ଦ୍ରଙ୍କ ମନ ଆନ୍ଦୋଳିତ ହେବାକୁ ଲାଗିଲା

ତାଙ୍କର ହୃଦ୍‌ବୋଧ ହେଲା ଯେ ବରୁଣ ଦେବଙ୍କ ସହାୟତା ବିନା ସମୁଦ୍ରରେ ସେତୁନିର୍ମାଣ ଅସମ୍ଭବ । ତେଣୁ ଜଳଦେବତାଙ୍କୁ ସନ୍ତୁଷ୍ଟ କରିବାପାଇଁ ସେ ଆହାର ତ୍ୟାଗ କରି ଅନଶନରେ ରହିଲେ ଏବଂ କୋମଳ ଶଯ୍ୟା ପରିବର୍ତ୍ତେ କର୍କଶ କୁଶଶଯ୍ୟାରେ ଶୟନ କରି ବରୁଣ ଦେବଙ୍କ ଅନୁଗ୍ରହ କାମନା କଲେ । କୌଣସି ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ ଶୁଭକର୍ମ ଆରମ୍ଭ କରିବା ପୂର୍ବରୁ ଦୈବୀକୃପା କାମନା କରିବା ଯେ ସର୍ବାଦୌ ଆବଶ୍ୟକ ଏହା ନରଦେହୀ ଭଗବାନ୍ ଶ୍ରୀରାମ ହୃଦୟଙ୍ଗମ କଲେ । ତେଣୁ ବରୁଣ ଦେବଙ୍କ ପ୍ରତ୍ୟର୍ଥେ ସେ ଉପବାସ ତଥା କୁଶଶଯ୍ୟାରେ ଶୟନ ପାଇଁ ନିଷ୍ପତ୍ତି ନେଲେ ।

Question ୨୦ ।
ବିଭୂତିକି ଭୁଞ୍ଜୁଥୁଲୁ ବିଭୂତିଭୂଷଣେ
ବଡ଼କୁଳେ ଜନମି ଶରଣ କି କାରଣେ ଯେ ?
Answer:
ବିଭୂତିକି ଭୁଞ୍ଚୁଥୁଲୁ …………………. କି କାରଣେ ଯେ ।
ପ୍ରୋକ୍ତ ପଦ୍ୟାଟି କରିସମ୍ରାଟ ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ କାଳଜୟୀ ବୈଦେହାଶ ବିଳାସ କାବ୍ୟର ଚତ୍ବାରିଂଶତମ ଛାନ୍ଦ।ନ୍ତ୍ରର୍ଗତ ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୁଳ ଶାର୍ଷିକ କବିତାରୁ ଆନୀତ ଏଠାରେ କବି ଅନୁଜ ବିଭୀଷଣଙ୍କ ପ୍ରତି ଜ୍ୟେଷ୍ଠ ଦଶାନନଙ୍କ ପ୍ରେରିତ ବାର୍ତ୍ତା ଉପରେ ଆଲୋକପାତ କରିଛନ୍ତି । ବିଭୀଷଣ ଜ୍ୟେଷ୍ଠଭ୍ରାତା ଦଶାନନର ଭତ୍ସନା ଓ କଟୁବାଣୀ ସହ୍ୟ କରି ନପାରି ଲଙ୍କା ତ୍ୟାଗପୂର୍ବକ ଶ୍ରୀରାମଙ୍କ ଶରଣାପନ୍ନ ହୋଇଥିଲେ । କାଳେ ସେ ଶତ୍ରୁ ସମ୍ମୁଖରେ ଗୁପ୍ତ ତଥ୍ୟ ପ୍ରକାଶ କରିଦେବେ, ଏହି ଭୟରେ ରାବଣ ତା’ର ପ୍ରମୁଖ ମନ୍ତ୍ରୀ ଶୁକ ଓ ସାରଣଙ୍କୁ ଦୂତରୂପେ ଶ୍ରୀରାମଙ୍କ ଶିବିରକୁ ପଠାଇ ସେମାନଙ୍କ ମାଧ୍ୟମରେ ବିଭୀଷଣଙ୍କ ପ୍ରତି ବାର୍ତ୍ତା ପ୍ରେରଣ କରିଥିଲା । ବିଭୀଷଣଙ୍କ ପ୍ରତି ପ୍ରଦତ୍ତ ବାର୍ତ୍ତାରେ ସେ କହିଥିଲା ଯେ ଜ୍ୟେଷ୍ଠଭ୍ରାତା ପିତୃତୁଲ୍ୟ ସମ୍ମାନାସ୍ପଦ ଅଟନ୍ତି । କ୍ରୋଧବଶତଃ ସେ ଯଦିବା କିଛି କଟୁ ଜଣେ ସାମାନ୍ୟ ତପାଚାରୀଠାରେ ନିଜକୁ ସମର୍ପଣ କରି ତା’ର ଶରଣପ୍ରାର୍ଥୀ ହେବା ଅପମାନଜନକ । ଏଣୁ ଲଙ୍କାନଗରୀକୁ ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବା ତାଙ୍କ ପକ୍ଷେ ଶ୍ରେୟସ୍କର ହେବ ବୋଲି ଦଶାର୍ଜନ କନିଷ୍ଠଭ୍ରାତା ବିଭୀଷଣଙ୍କୁ ବାର୍ତ୍ତା ମାଧ୍ୟମରେ ଶତ୍ରୁ ଶିବିରରୁ ପୃଥକ୍ କରିବାକୁ ଚେଷ୍ଟା କରିଥିଲା ।

Question ୨୧ ।
ବାଜିଥିଲେ ଚୂର୍ଣ ବା ପାତାଳେ ଭଜିଥ‌ିବ
ବିନ୍ଧ୍ୟ ଭାନୁ ତୋଷି ହେଲେ ବଞ୍ଚାଇ ଦଇବ ଯେ ।
Answer:
ବାଜିଥିଲେ ଚୂର୍ଖ ………….. ବଞ୍ଚାଇ ଦଇବ ଯେ ।
ପ୍ରଦତ୍ତ ପଦ୍ୟାଶଟି କବି ସମ୍ରାଟ ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ ରଚିତ ‘ବୈଦେହୀଶ ବିଳାସ’ କାବ୍ୟର ଚତ୍ୱାରିଂଶତମ ଛାନ୍ଦ ଅନ୍ତର୍ଗତ ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ ଶାର୍ଷିକ କବିତାରୁ ଉଘୃତା ଏଠାରେ କବି ଉତ୍‌କ୍ଷିପ୍ତ ଅଙ୍ଗଦଙ୍କ କ୍ରୋଧଯୁକ୍ତ ବଜ୍ରସମ ସଶକ୍ତ ଚପୋଟାଘାତର ଭୟଙ୍କରିତା ସମ୍ପର୍କରେ ଉଲ୍ଲେଖ କରିଛନ୍ତି ।

ଲଙ୍କପତି ଦଣାନନଦ୍ୱ।ରା ପ୍ରେରିତ ଶୁକ ଓ ସାରଣ ମନ୍ତ୍ରୀଦ୍ଵୟ ସାଗର ତଟଦେଶସ୍ଥ ଶ୍ରୀରାମଙ୍କ ଶିବିରରେ ଉପସ୍ଥିତ ହୋଇ ପ୍ରଥମେ ବିଭାଷଶଙ୍କୁ ବୌଷଭ୍ରତା ଲଙ୍କାଧାଶ ରାବ ଶଙ୍କ ବାର୍ତ୍ତା ପ୍ରଦାନ କଲେ। ତତ୍ ପରେ କିସ୍ମିଯ୍ୟା ଯୁବରାଜ ଅଙ୍ଗତାଙ୍କୁ ରାଜାଙ୍କ ନିର୍ଦ୍ଦେଶାନୁସାରେ ବାର୍ତ୍ତା ଦେଇ କହିଥିଲେ ଯେ, ପିତା ଶତ୍ରୁ ନିକଟରେ ଆନୁଗତ୍ୟ ପ୍ରକାଶ କରି ତାଙ୍କ ନିକଟରେ ଶରଣାପନ୍ନ ହୋଇ ରହିବାରେ କଦାପି ପୁଣ୍ୟାର୍ଜନ ହୁଏନାହିଁ । ଏହି ବାର୍ତ୍ତା ଶ୍ରବଣ କଲାମାତ୍ରେ ଅଙ୍ଗଦ କ୍ରୋଧଜର୍ଜରିତ ହୋଇ ଶୂନ୍ୟକୁ ଏପରି ଏକ ସଶକ୍ତ ଚାପୁଡ଼ା ପ୍ରହାର କଲେ ଯାହା ବିଶାଳ ବିନ୍ଧ୍ୟ ପର୍ବତରେ ବାଜିଥିଲେ ତାହାକୁ ଚୂର୍ଣ୍ଣବିଚୂର୍ଣ୍ଣ କରିଦେଇ ଥାଆନ୍ତା; ଅଥବା ଆଘାତର ତ। ବ୍ରତାରେ ତାହା ରସାତଳଗାମା ହୋଇଥା’ନ୍ତା ସୂର୍ଯ୍ୟଙ୍କ ଗତିପଥରେ ଅନ୍ତରାୟ ସୃଷ୍ଟି କରୁଥିବ ସଦ୍ୟ ପର୍ବତ ପାତାଳଗାମୀ ହୋଇଥିଲେ ଭାନୁଦେବ ନିଜ ପଥର ପ୍ରତିବନ୍ଧକ ଦୂର ହେଲା ବୋଲି ହୁଏତ ଆନନ୍ଦିତ ହୋଇଥାଆନ୍ତେ । ମନ୍ତ୍ରୀଦ୍ୱୟ ଏହି ଉକ୍ତିରୁ ଅଙ୍ଗଦଙ୍କ ଶକ୍ତିର ଦୃଢ଼ତା ସହଜରେ ଅନୁମିତ ହୁଏ ।

ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question ୨୨ ।
ଲଙ୍କାଯାତ୍ରା ନିମନ୍ତେ ରାଘବଙ୍କ ପ୍ରୟାସ ବର୍ତ୍ତନ କର ।
କିମ୍ବା,ରାବଣଦ୍ଵାରା ଅପହୃତା ସୀତାଙ୍କୁ ଉଦ୍ଧାର କରିବା ନିମନ୍ତେ ରାମଚନ୍ଦ୍ରଙ୍କ ପ୍ରାକ୍ ପ୍ରସ୍ତୁତି ସମ୍ପର୍କରେ ଆଲୋଚନା କର ।
Answer:
ଉତ୍କଳ ସାହିତ୍ୟର ମଧ୍ୟଯୁଗ ତଥା କାବ୍ୟଯୁଗର ଦିଗ୍ବଳୟ ଯେଉଁ ପ୍ରଜ୍ଞାପୁରୁଷଗଣଙ୍କର ପ୍ରାଜ୍ଞ ଚେତନାରେ ବଣ୍ଡିଳ ତଥା ଉପଭୋଗ୍ୟ ହୋଇଛି, ସେହି ସାରସ୍ଵତ ସାଧକଗଣଙ୍କ ମଧ୍ୟରେ କବିସମ୍ରାଟ ଉପେନ୍ଦ୍ର ଭଞ୍ଜ ଅନ୍ୟତମ । ଶାବ୍ଦିକ ବୈଶିଷ୍ଟ୍ୟ, ଆଳଙ୍କାରିକ ମାଧୁର୍ଯ୍ୟ, ଛନ୍ଦୋବଦ୍ଧ ଶୈଳୀର ନୈପୁଣ୍ୟ ତଥା ବୌଦ୍ଧିକ ଚେତନାର ଗାମ୍ଭୀର୍ଯ୍ୟପୂର୍ଣ୍ଣ ସୃଷ୍ଟିନିଚୟ ସେହି ପ୍ରଚଣ୍ଡ ପ୍ରତିଭାଦୀପ୍ତ ସାଧକଶ୍ରେଷ୍ଠଙ୍କର ଅନନ୍ୟ ବିଦ୍‌ବତ୍ତାର ଅଭିବ୍ୟକ୍ତି ‘କୋଟି ବ୍ରହ୍ମାଣ୍ଡ ସୁନ୍ଦରୀ’, ‘ରସିକ ହାରାବଳୀ’, ‘ପ୍ରେମ ସୁଧାନିଧ୍’, ‘ଲାବଣ୍ୟବତୀ’, ‘ବୈଦେହୀଶ ବିଳାସ’ ଭଳି କାବ୍ୟସମୂହ ଏହି ଯୁଗାନ୍ତକାରୀ ସ୍ରଷ୍ଟାଙ୍କର ଅନୁପମ ପ୍ରତିଭାର ନିଦର୍ଶନ। କବିଙ୍କର ସର୍ବଶ୍ରେଷ୍ଟ ବିଜଗ୍ଧ କାବ୍ୟ ‘ବୈଦେହାଶ ବିଳାସ’ ର ପ୍ରତ୍ୱାରିଂଶତମ ଛାନ୍ଦର ପ୍ରଥମାଂଶ ‘କାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୁଳ’ ଶାର୍ଷିକ କବିତା ଟିରେ କରି ସମ୍ରାଟ ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ ଲଙ୍କା ଅଭିଯାନ ନିମନ୍ତେ ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣର ଶୁଭାରମ୍ଭ ପ୍ରସଙ୍ଗ ଉପସ୍ଥାପନ କରିଛନ୍ତି।

ମାତା ଜାନକୀ ଦଶାନନର ଲଙ୍କାପୁରୀରେ ଅବସ୍ଥାନ କରୁଥିବା ଅବଗତ ହେଲାପରେ ଶ୍ରୀରାମଚନ୍ଦ୍ର ମର୍କଟ ଓ ଭଲ୍ କ ସୈନ୍ୟଙ୍କ ସହ ଲଙ୍କାଭିଯାନ ପାଇଁ ନିଷ୍ପତ୍ତି ନେଇଛନ୍ତି । ଅଭିଯାନର ପ୍ରଥମ ପ୍ରତିବନ୍ଧକ ସମୁଦ୍ର ଲଂଘନ ପାଇଁ ସେ ହନୁମାନ, ସୁଗ୍ରୀବ, ଅଙ୍ଗଦ, ଜାମ୍ବବାନ ଓ ବିଭୀଷଣଙ୍କ ସହ ମନ୍ତ୍ରଣା କରି ସେତୁବନ୍ଧ ନିର୍ମାଣ ଅବଶ୍ୟମ୍ଭାବୀ ବୋଲି ଅନୁଭବ କରିଛନ୍ତି । ସାଗର-ସେତୁ ନିର୍ମାଣ ଯୋଜନାରେ ବାନର ଓ ଭଲ୍ କ ସୈନ୍ୟମାନଙ୍କ ଗଭୀର ଉତ୍ସାହ ଲକ୍ଷ୍ୟକରି ରାଘବ କାର୍ଯ୍ୟାରମ୍ଭ ପାଇଁ ନିର୍ଦ୍ଦେଶ ଦେଇଛନ୍ତି । ଆଦେଶ ପ୍ରାପ୍ତି ମାତ୍ରେ ହନୁମାନଙ୍କ ନେତୃତ୍ୱରେ କପିସୈନ୍ୟମାନେ ବିଶାଳ ପର୍ବତ ଖଣ୍ଡମାନ ସମୁଦ୍ର ମଧ୍ୟକୁ ନିକ୍ଷେପ କରିଛନ୍ତି; କିନ୍ତୁ ପ୍ରକାଣ୍ଡ ଗିରିଖଣ୍ଡମାନ ଗଭୀର ଜଳରେ ପତିତ ହେବାମାତ୍ରେ ଅତଳ ଜଳଧୂଗର୍ଭରେ ବିଲୀନ ହେବାପରି ପ୍ରତୀୟମାନ ହୋଇଛି । ସାଧାରଣତଃ ଜଳରେ କୌଣସି ବସ୍ତୁ ପଡ଼ିବାମାତ୍ରେ ବୁଦ୍‌ବୁଦ ଉତ୍ପନ୍ନ ହୋଇଥାଏ । ମାତ୍ର ପର୍ବତ ପରି ବିଶାଳ ଶିଳାଖଣ୍ଡମାନ ସମୁଦ୍ର ଜଳରେ ବୁଡ଼ିଲା ପରେ ସାମାନ୍ୟ ବୁଦ୍‌ବୁଦ ମଧ୍ୟ ସୃଷ୍ଟି ହୋଇନାହିଁ । କେବଳ ଜଳ ମଧ୍ୟରୁ ‘ଫି ଫି’ କାର ଶବ୍ଦ ମାତ୍ର ନିର୍ଗତ ହୋଇଛି । କବି ସମ୍ରାଟଙ୍କ ଭାଷାରେ-

‘ବୁଡ଼ିଗଲା ପକାଇଲେ କପି ଯେତେ ଗିରି
ବୁଦ୍‌ବୁଦ ନ ଦିଶେ ଜଳ ଫି ଫି କୃତ କରି ଯେ ।’’

ସମୁଦ୍ର ଜଳର ଏପରି ଅବିଶ୍ଵାସ୍ୟ ଆଚରଣ ରାଘବଙ୍କୁ ବିସ୍ମିତ କରିଛି। କାର୍ଯ୍ୟାରମ୍ଭରେ ହୁଏତ କୌଣସି ତ୍ରୁଟିବିଚ୍ୟୁତି ହେତୁ ଏପରି ଅଘଟଣ ସୃଷ୍ଟି ହେଲା ବୋଲି ତାଙ୍କ ମନରେ ସଂଶୟ ଜାତ ହୋଇଛି। ସେତୁ ନିର୍ମାଣ ଭିନ୍ନ ଲଙ୍କାଗଡ଼କୁ ପ୍ରବେଶ କରିବାପାଇଁ ଅନ୍ୟ କୌଣସି ବିକଳ୍ପ ବ୍ୟବସ୍ଥା ଅସମ୍ଭବ, କାରଣ ଲଙ୍କାଗଡ଼ର ଚତୁର୍ଦ୍ଦିଗ ସାଗର ପରିବେଷ୍ଟିତ। ଶତ୍ରୁ ଆକ୍ରମଣରୁ ସୁରକ୍ଷିତ ରଖିବାପାଇଁ ଦଶାନନ ହୁଏତ ଏପରି ଏକ ସ୍ଥାନକୁ ନିଜ ରାଜ୍ୟଭାବେ ନିର୍ବାଚନ କରିଛି। ଏତଦ୍‌ଭିନ୍ନ ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣ ନହେଲେ ମାତା ଜାନକୀଙ୍କୁ ଉଦ୍ଧାର କରିବା କଦାପି ସମ୍ଭବ ନୁହେଁ । ଲଙ୍କାଭିଯାନର ପ୍ରାରମ୍ଭିକ ପର୍ଯ୍ୟାୟରେ ବିଘ୍ନ ସୃଷ୍ଟି ହେବାର କାରଣ ଅନୁଧ୍ୟାନ କରିଛନ୍ତି ଶ୍ରୀରାମ। ରାଘବ ଅନୁଭବ କରିଛନ୍ତି ଯେ ହୁଏତ ବରୁଣଦେବଙ୍କ ଅନୁମତି ବିନା ସେତୁବନ୍ଧ କାର୍ଯ୍ୟାରମ୍ଭ କରିବା ତାଙ୍କ ପକ୍ଷେ ଏକ ତ୍ରୁଟିପୂର୍ଣ୍ଣ ନିଷ୍ପତ୍ତି ଥିଲା । ବରୁଣ ଦେବତାଙ୍କ ସହାୟତା ବିନା ସେହି ନିର୍ମାଣକାର୍ଯ୍ୟ କଦାପି

ସମ୍ଭବ ନୁହେଁ ବୋଲି ତାଙ୍କର ହୃଦ୍‌ବୋଧ ହୋଇଛି । ଜଳ ଦେବତାଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ ସେ ପାନାହାର ପରିତ୍ୟାଗ ପୂର୍ବକ ଅନଶନ କରିଛନ୍ତି ଏବଂ ସୁଖଶଯ୍ୟା ପରିହାର କରି ଶୟନ ନିମିତ୍ତ କୁଶଶଯ୍ୟାକୁ ଆଦରି ନେଇଚନ୍ତି । କବିଙ୍କ ଭାଷାରେ

“ବିସୃଚ୍ଚ ନିଶ୍ୱାସ ତେଜି ବରୁଣ ପ୍ରସନ୍ନେ
ବିନାଶନରେ ଶୟନ ସେ ଗର୍ଭଶୟ ନେ ଯୋ”

ମର୍ଯ୍ୟାଦା ପୁରୁଷୋତ୍ତମ ନରଦେହୀ ନାରାୟଣଙ୍କ ମନରେ ପ୍ରତ୍ୟୟ ସୃଷ୍ଟି ହୋଇଛି ଯେ ସେତୁ ନିର୍ମାଣ ପରି ଏକ ମହାନ୍ କାର୍ଯ୍ୟର ଶୁଭାରମ୍ଭ ପୂର୍ବରୁ ଯାହାକିଛି ପ୍ରାଥମିକ ଭଗବତ୍ କ୍ରିୟା ସଂପାଦନ କରାଯିବା ବିଧେୟ ସେଥ‌ିରେ ସେ ଅବଶ୍ୟ ତ୍ରୁଟି କରିଛନ୍ତି । କେବଳ ସେଇଥପାଇଁ ସମୁଦ୍ର ଜଳ ଅଦ୍ଭୁତ ଆଚରଣ ପ୍ରଦର୍ଶନ କରିଛି । ତ୍ରୁଟି ସଂଶୋଧନ ପୂର୍ବକ ପ୍ରାୟଶ୍ଚିତ୍ତ ସ୍ଵରୂପ ବରୁଣଦେବଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ ତାଙ୍କୁ ଅବଶ୍ଯ ଶାରୀରିକ କ୍ଳେଶ ସହ୍ୟ କରିବା ତଥା ଅନଶନରେ ରହି ଅନୁମତି ପ୍ରାପ୍ତି ନିମିତ୍ତ ପ୍ରାର୍ଥନା କରିବାକୁ ହେବ । ଏହା ଅନୁଭବ କରି ଶୁଦ୍ଧପୂତଭାବେ ଦୈହିକ କଷ୍ଟ ସ୍ୱୀକାର କରି ଜଳ ଦେବତାଙ୍କୁ ପ୍ରସନ୍ନ କରାଇବାପାଇଁ ପ୍ରୟାସ କରିଛନ୍ତି । ଶ୍ରୀରାମଙ୍କର ଏତାଦୃଶ ପଦକ୍ଷେପରୁ ସ୍ପଷ୍ଟ ପ୍ରତୀତ ହୁଏ ଯେ କୌଣସି ଶୁଭକର୍ମର ଶୁଭାରମ୍ଭ ପୂର୍ବରୁ ଭଗବତ୍ ଆଶିର୍ବାଦ ଅବଶ୍ୟ କରଣୀୟ।

Question ୨୩।
ପଠିତ କବିତାରୁ ରାବଣର କୂଟନୀତି ସମ୍ପର୍କରେ ଆଲୋଚନା କର।
କିମ୍ବା,ଲଙ୍କପତି ରାବଣ ଥିଲେ ଜଣେ କୂଟନୀତି ବିଶାରଦ। ଉକ୍ତିଟିର ଯଥାର୍ଥତା ପଠିତ କବିତା ଅବଲମ୍ବନରେ ଆଲୋଚନା କର।
Answer:
ଉତ୍କଳ ସାହିତ୍ୟର ମଧ୍ୟଯୁଗ ତଥା ରାତିଯୁଗ ଯେଉଁ ସାରସ୍ୱିତ ସାଧକତଶଙ୍କ ଚେତନାସ୍ନାତ ଅବ୍ତାନରେ ରଦ୍ଧିମନ୍ତ ରସସିକ୍ତ ଓ ହୃଦୟସ୍ପର୍ଶୀ ହୋଇଉଠିଛି, ସେମାନଙ୍କ ମଧ୍ୟରେ କବିସମ୍ରାଟ ଉପେନ୍ଦ୍ର ଭଞ୍ଜ ଅଗ୍ରଗଣ୍ୟ । ସାରସ୍ଵତ ସାଧନାରେ ଚିରତଲ୍ଲୀନ ଏହି ପ୍ରଜ୍ଞାପୁରୁଷଙ୍କର ଶାବ୍ଦିକ ବୈଭବ, ଆଳଙ୍କାରିକ ନୈପୁଣ୍ୟ, ବୈଦ୍ଧିକ କଳ୍ପନା ତଥା ପ୍ରାଜ୍ଞ ଚେତନାରେ ସମୃଦ୍ଧ ଲେଖନୀ ତାଙ୍କ ସୃଷ୍ଟିନିଚୟକୁ ଯେପରିଭାବେ ଉପଭୋଗ୍ୟ କରିଛି, ତା’ର ପଟାନ୍ତର ନାହିଁ । ‘ବୈଦେହୀଶ ବିଳାସ’, ‘କୋଟି ବ୍ରହ୍ମାଣ୍ଡ ସୁନ୍ଦରୀ’, ‘ଲାବଣ୍ୟବତୀ’, ‘ପ୍ରେମ ସୁଧାନିଧ୍ଵ’, ‘ରସିକ ହାରାବଳୀ’ ଓ ‘ସୁଭଦ୍ରା ପରିଣୟ ’ ଭଳି ସୁଧାସ୍ରାବୀ କାବ୍ୟନିଚୟ କବିଙ୍କ ଅନନ୍ୟ ପ୍ରତିଭାର ବଳିଷ୍ଠ ନିଦର୍ଶନ ।

କବିଙ୍କ ସର୍ବଶ୍ରେଷ୍ଠ ରାମକଥା କାବ୍ୟ ‘ବୈଦେହୀଶ ବିଳାସ’ ଅନ୍ତର୍ଗତ ଚତ୍ବାରିଂଶ ଛାନ୍ଦରୁ ଗୃହୀତ ‘ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁଜଳ ‘ଶୀର୍ଷକ କବିତାରେ କବି ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ ଲଙ୍କାଭିଷାନ ନିମନ୍ତେ ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣର ଶୁଭାରମ୍ଭ ଦର୍ଶନରେ ଦଶାନନର କୁଟନୈତିକ ଦୁରଭିପକ୍ଷି ପଥା ବିଭାଷଣର ରାମଭକ୍ତ ଓ ଅଙ୍ଗକର ଶକ୍ତର ପର।କାଷ୍ଠା ଦଶନରେ ରାବଣର ହତଚୂପା କବିଙ୍କ ସର୍ବଶ୍ରେଷ୍ଠ ରାମକଥା କାବ୍ୟ ‘ବୈଦେହାଶ ବିଳାସ’ ଅନ୍ତର୍ଗତ ଚତ୍ବାରିଂଶ ଛାନ୍ଦରୁ ଗୃହାତ ‘ରାଘରଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ’ ଶୀର୍ଷକ କବିତାରେ କବି ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ ଲଙ୍କାଭିଯାନ ନିମନ୍ତେ ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣର ଶୁଭାରମ୍ଭ ଦର୍ଶନରେ ଦଶାନନର କୁଟନୈତିକ ଦୁରଭିପକ୍ଷି ପଥା ବିଭାଷଣର ରାମଭକ୍ତ ଓ ଅଙ୍ଗକର ଶକ୍ତର ପର।କାଷ୍ଠା ଦଶନରେ ରାବଣର ହତଚୂପା ଶୁକ ଓ ସାରଣ ମନ୍ତ୍ରୀଙ୍କ ଛତ୍ରଭଙ୍ଗାଦି ପ୍ରସଙ୍ଗକୁ ଶାବ୍ଦିକ ଯାଦୁ ବଳରେ ସୁଖପାଠ୍ୟ କରିଛନ୍ତି ।

ସତୀ ଜାନକୀଙ୍କ ଉଦ୍ଧାର ନିମନ୍ତେ ଲଙ୍କାଗଡ଼ ଆକ୍ରମଣ ଓ ଦଶାନନ ସହ ଯୁଦ୍ଧ ଅପରିହାର୍ଯ୍ୟ ବୋଲି ଅନୁଭବ କରି ଲଙ୍କାଭିଯାନ ନିମନ୍ତେ ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣର ଶୁଭାରମ୍ଭ କରିଛନ୍ତି ମର୍ଯ୍ୟାଦା ପୁରୁଷୋତ୍ତମ ଶ୍ରୀରାମ । ସମୁଦ୍ରତଟରେ ସୈନ୍ୟସାମନ୍ତଙ୍କ ସତୀ ଜାନକୀଙ୍କ ଉଦ୍ଧାର ନିମନ୍ତେ ଲଙ୍କାଗଡ଼ ଆକ୍ରମଣ ଓ ଦଶାନନ ସହ ଯୁଦ୍ଧ ଅପରିହାର୍ଯ୍ୟ ବୋଲି ଅନୁଭବ କରି ଲଙ୍କାଭିଯାନ ନିମନ୍ତେ ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣର ଶୁଭାରମ୍ଭ କରିଛନ୍ତି ମର୍ଯ୍ୟାଦା ପୁରୁଷୋତ୍ତମ ଶ୍ରୀରାମ । ସମୁଦ୍ରତଟରେ ସୈନ୍ୟସାମନ୍ତଙ୍କ ସହ ପ୍ରସ୍ତୁତ ହେଉଥିବା ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ ସୈନ୍ୟଙକଳନା ଓ ରଣକୌଶଳ ଅନୁଧାନ କରିବା ଉପଲକ୍ଷ୍ୟରେ ଦଶାନନ ତା’ର ଦୁଇ ପ୍ରମୁଖ ମନ୍ତ୍ରୀ ଶୁକ ଓ ସାରଣଙ୍କୁ ଦୂତ ରୂପେ ପ୍ରେରଣ କରିଛି । ଚର ପ୍ରେରଣ ପଶ୍ଚାତ୍‌ରେ ତା’ର ଉଦ୍ଦେଶ୍ୟ ଥିଲା ଭିନ୍ନ ।

ରାବଣ ଆଶଙ୍କା କରୁଥିଲା ହୁଏତ ଗୃହଭେଦୀ ବିଭୀଷଣ, ଲଙ୍କାଗଡ଼ ସମ୍ପର୍କିତ ଗୁପ୍ତତଥ୍ୟ ତଥା ରାକ୍ଷସୀ ସେନାଙ୍କ ଶକ୍ତି ସାମର୍ଥ୍ୟ ବିଷୟରେ ଶତ୍ରୁକୁ ଅବଗତ କରାଇପାରେ । ତେଣୁ ତା’ର ମନ ପରିବର୍ତ୍ତନ କରାଇ ତାକୁ ଲଙ୍କା ଫେରାଇ ଆଣିବାକୁ ସେ ମନ୍ତ୍ରୀଦ୍ୱୟଙ୍କ ଜରିଆରେ ବାର୍ତ୍ତା ପ୍ରେରଣ କରିଥିଲା । ବାସ୍ତବରେ ସେ ସେହି ବାର୍ତ୍ତା ମାଧ୍ୟମରେ ବିଭୀଷଣକୁ ଶତ୍ରୁଠାରୁ ଦୂରେଇ ଦେବାକୁ ଇଚ୍ଛା କରିଥିଲା । ସେହି ବାର୍ତ୍ତାରେ ସେ କହିଥିଲା ଯେ ଜ୍ୟେଷ୍ଠଭ୍ରାତା ପିତୃତୁଲ୍ୟ ସମ୍ମାନାସ୍ପଦ ଅଟନ୍ତି । କ୍ରୋଧ ପରବଶ ହୋଇ ଯଦିଓ ସେ କନିଷ୍ଠ ପ୍ରତି କଟୁବାକ୍ୟ ପ୍ରୟୋଗ କରିଛନ୍ତି, ତାହା କଦାପି ଧର୍ଭବ୍ୟ ନୁହେଁ । ପ୍ରତିକ୍ରିୟାଶୀଳ ହୋଇ ନିଜ ଜ୍ୟେଷ୍ଠଭ୍ରାତାଙ୍କ ସଙ୍ଗ ତ୍ୟାଗକରି ତାଙ୍କ ବିରୁଦ୍ଧରେ ଯାଇ ଶତ୍ରୁ ଶିବିରରେ ଅବସ୍ଥାନ କରିବା ଆଦୌ ସମୀଚୀନ ନୁହେଁ। ମହାପରାକ୍ରମୀ ଅଗ୍ରଜର

ଶତ୍ରୁଭାବେ ବିବେଚିତ ଜଣେ ବନବାସୀଠାରେ ଶରଣାପନ୍ନ ହେବା ବୁଦ୍ଧିମତ୍ତାର କାର୍ଯ୍ୟ ନୁହେଁ । ଏତଦ୍‌ଭିନ୍ନ ମହାନ୍ ରାଜକୁଳରେ ଜନ୍ମଲାଭ କରି ଜଣେ ଅତି ସାଧାରଣ ବ୍ୟକ୍ତିଠାରେ ଆତ୍ମସମର୍ପଣ କରିବା, ସର୍ବୋପରି ନିଜ ସହୋଦରକୁ ବିରୋଧ କରି ଶତ୍ରୁକୁ ସାହାଯ୍ୟ କରିବା ସର୍ବାଦୌ ଅନୁଚିତ ତଥା ଅବିବେକିତାର କାର୍ଯ୍ୟ । ବିଭୀଷଣଙ୍କୁ ଶତ୍ରୁ ରାମଚନ୍ଦ୍ରଙ୍କଠାରୁ ପୃଥକ୍ କରିବାପାଇଁ ଦଶାନନ ମନ୍ତ୍ରୀଦ୍ଵୟଙ୍କ ମାଧ୍ୟମରେ ଏହିପରି କୂଟନୈତିକ ବାର୍ତ୍ତା ପ୍ରେରଣ କରିଥିଲା । କବିଙ୍କ ଭାଷାରେ-

“ବିଭୂତିକି ଭୁଞ୍ଜୁଅନୁ ବିକୃତି ଭୂଷଣେ
ବଡ଼କୁଳେ ଜନମି ଶରଣ କି କାରଣେ ଯୋ”

କେବଳ ବିଭୀଷଣ ନୁହେଁ ବାଳୀ ପୁତ୍ର ଅଙ୍ଗଦ ପ୍ରତି ଭିନ୍ନ ଏକ କୂଟନୀତିପୂର୍ଣ୍ଣ ବାର୍ତ୍ତା ପ୍ରେରଣ କରିଥିଲା ରାବଣ । ଦଶାନନ ଜାଣିଥିଲା ଯେ ରାମଚନ୍ଦ୍ର କିସ୍କିନ୍ଧ୍ୟାର ବାନର ଓ ଭଲ୍ କ ସୈନ୍ୟମାନଙ୍କ ସହାୟତାରେ ଲଙ୍କା ଆକ୍ରମଣ କରିବାକୁ ସାହସ କରିଛନ୍ତି । ତେଣୁ କିଷ୍କିନ୍ଧ୍ୟା ଯୁବରାଜ ଅଙ୍ଗଦଙ୍କୁ ଶ୍ରୀରାମଙ୍କ ବିରୋଧରେ ଉତ୍ତେଜିତ କରି ପୃଥକ୍ କରାଇପାରିଲେ ଶତ୍ରୁପକ୍ଷ ଅଚିରେ ଦୁର୍ବଳ ହୋଇପଡ଼ିବ ଓ ସେ ଅକ୍ଳେଶରେ ଯୁଦ୍ଧରେ ବିଜୟଲାଭ କରିବେ । ତେଣୁ ମନ୍ତ୍ରୀ ଶୁକ ଓ ସାରଣଙ୍କ ଜରିଆରେ ଅଙ୍ଗଦ ପ୍ରତି ବାର୍ତ୍ତା ଦେଇ ସେ ଜଣାଇଥିଲା ଯେ, ପିତାଙ୍କ ଶତ୍ରୁକୁ ସମର୍ଥନ କରିବା ବା ପିତାଶତୁଠାରେ ଶରଣାପନ୍ନ ହେବାରେ ପୁଣ୍ୟାର୍ଜନ ହୁଏନାହିଁ । ବରଂ ପିତୃହନ୍ତାକୁ ଉପଯୁକ୍ତ ଶାସ୍ତି ଦେବା ବାଞ୍ଛନୀୟ । ତେଣୁ ପିତୃବ୍ୟ ସୁଗ୍ରୀବ ସହ ବିବାଦ କରି ସେ ତୁରନ୍ତ ନିଜ ସୈନ୍ୟବଳ ସହ କିଷ୍କିନ୍ଧ୍ୟା ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବା ହିଁ ଜଣେ ସ୍ବାଭିମାନୀ ପୁତ୍ର ପକ୍ଷେ ସମୀଚୀନ ହେବ । କବିଙ୍କ ଭାଷାରେ-

‘‘ବୋଲ ଅଙ୍ଗଦକୁ ପିତା ଶତ୍ରୁ ଭକ୍ତି ପୁଣ୍ୟ
ବାଦ ରଚାଇ ପିତୃବ୍ୟ ବାହୁଡ଼ାଅ ସୈନ୍ୟ ଯେ।’’

କୂଟନୀତି ବିଶାରଦ ଦଶାନନ ଯେଉଁ ଦୁରଭିସନ୍ଧି ରଖ୍ ବିଭୀଷଣ ଓ ଅଙ୍ଗଦଙ୍କ ପ୍ରତି ଚତୁର ବାର୍ତ୍ତା ପ୍ରେରଣ କରିଥିଲା, ଯେପରିଭାବେ ମାୟାମୃଗ ପ୍ରେରଣ କରିଥିଲା ଓ ଯତି ବେଶରେ ଯାଇ ସତୀ ଜାନକୀଙ୍କୁ ହରଣ କରିଥିଲା, ତହିଁରୁ ତା’ର ବିଚକ୍ଷଣ କୂଟନୀତିର ପରିଚୟ ମିଳେ । ବାସ୍ତବିକ ରାବଣ କେବଳ ଯେ ଜଣେ ମହାପରାକ୍ରମଶାଳୀ ଦୁର୍ଭାନ୍ତ ଶାସକ ଥିଲା ତାହା ନୁହେଁ, ରାଜନୀତିର ପ୍ରମୁଖ ଦିଗ କୂଟନୀତିରେ ତା’ର ଗଭୀର ଦକ୍ଷତା ଥିଲା ।

Question ୨୪ ।
ପଠିତ କବିତା ଭିଭିରେ ସମାଜ ପ୍ରତି ଥ‌ିବା ବାର୍ତ୍ତାଗୁଡ଼ିକ ଲେଖୁ ସାନଭାଇ ନିକଟକୁ ପତ୍ର ଲେଖ ।
Answer:

ନେତାଜୀ ଛାତ୍ରାବାସ, କଟକ
ତା ………………………..

ଶ୍ରଦ୍ଧେୟ ଦୀପୁ,

ମୋର ସ୍ନେହ ନେବୁ। ଗତକାଲି ତୋର ଚିଠି ପାଇଲି । ତୁ ପରୀକ୍ଷାରେ ଭଲ କରୁଛୁ ବୋଲି ଜାଣି ଖୁସି ଲାଗିଲା । ଏହିପରି ମନ ଦେଇ ପଢ଼ାପଢ଼ି କଲେ ତୁ ବାର୍ଷିକ ପରୀକ୍ଷାରେ ଶ୍ରେଣୀରେ ପ୍ରଥମସ୍ଥାନ ଅଧିକାର କରିବୁ । ଆଜି ତୋ ପାଖକୁ କିଛି ଗୁରୁତ୍ଵପୂର୍ଣ କର୍ଭବ୍ୟ ବିଷୟରେ ଦୁଇଧାଡ଼ି ଲେଖୁଛି । ଆମ ସାହିତ୍ୟ ବହିର ‘ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ’ କବିତାରେ କବି ଉପେନ୍ଦ୍ର ଭଞ୍ଜ ପାଠକମାନଙ୍କ ପାଇଁ କିଛି ଉପଦେଶ ଦେଇଛନ୍ତି । ଗତକାଲି ସେ ସମ୍ପର୍କରେ ଶିକ୍ଷକ ଶ୍ରେଣୀରେ ଆଲୋଚନା କରିଥିଲେ । ସମାଜରେ ଚଳିବାକୁ ହେଲେ ସେସବୁ ପ୍ରତି ଆମକୁ ସଚେତନ ରହିବାକୁ ପଡ଼ିବ ।

ଦୀପୁ, ଯେ କୌଣସି କାମ ଆରମ୍ଭ କରିବା ପୂର୍ବରୁ ଠାକୁରଙ୍କୁ ପ୍ରଣାମ କରି ଆଶୀର୍ବାଦ କାମନା କରିବା ସବୁଠାରୁ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ । ଏପରିକି ପାଠପଢ଼ାରେ ବସିବା ପୂର୍ବରୁ ଈଶ୍ବରଙ୍କୁ ଧ୍ୟାନ କରି ପଢ଼ା ଆରମ୍ଭ କରିବୁ । ଠାକୁରଙ୍କ ଶରଣାପନ୍ନ ହେଲେ ତାଙ୍କ ଆଶୀର୍ବାଦରୁ ସ୍ମରଣଶକ୍ତି ବୃଦ୍ଧି ହେବ ଏବଂ କଷ୍ଟକର ବୋଧ ହେଉଥ‌ିବା ପାଠକୁ ଆୟତ୍ତ କରିବାରେ କିଛି ଅସୁବିଧା ହେବ ନାହିଁ । ତୁ ଜାଣିଲେ ଆଶ୍ଚର୍ଯ୍ୟ ହେବୁ ଯେ ରାମଚନ୍ଦ୍ର ସମୁଦ୍ରରେ ସେତୁ ନିର୍ମାଣ ପୂର୍ବରୁ ବରୁଣଦେବଙ୍କୁ ପ୍ରାର୍ଥନା କରିନଥ୍ ବାରୁ ବାନରସେନାଙ୍କଦ୍ୱାରା ସମୁଦ୍ରରେ ପକାଇଥିବା ପର୍ବତମାନ ପୁରିଯିବାକୁ ଲାଗିଲା ତେଣୁ ଚରୁଶଦେବଙ୍କୁ ସନ୍ତୁଷ୍ଟ କରିବାପାଇଁ ଅନଶନରେ ରହି ସେ କୁଶଶଯ୍ୟାରେ ଶୟନ କରିଥ୍ଲୋ

ଦୀପୁ ତୁ ତ ଜାଣିଥୁବୁ, ବିଭୀଷଣ ରାବଣକୁ ତ୍ୟାଗ କରି ଶ୍ରୀରାମଙ୍କ ନିକଟରେ ଶରଣ ପଶିଥିଲା ଏବଂ ଲଙ୍କା ଆକ୍ରମଣବେଳେ ରାବଣର ସମର କୌଶଳ ତଥା ଲଙ୍କାନଗରୀ ସମ୍ପର୍କିତ ଗୁପ୍ତ ତଥ୍ୟ ରାମଚନ୍ଦ୍ରଙ୍କୁ ଜଣାଇଥିଲା । ସେଥ‌ିପାଇଁ ତାକୁ ଗୃହଭେଦୀ ବିଭୀଷଣ ବୋଲି କୁହାଯାଏ । ଏକଥା ଅବଶ୍ୟ ସତ୍ୟ ଯେ ଘର ଓ ପରିବାର ସମ୍ପର୍କିତ ଗୁପ୍ତ କଥା ଅନ୍ୟ ଆଗରେ ପ୍ରକାଶ କରିବା କଦାପି ଉଚିତ ନୁହେଁ । ପରିବାରରେ ରହିଲେ ଗୁରୁ ଗୁରୁଜନମାନେ ଯଦିବା କେବେ କ୍ରୋଧବଶତଃ କିଛି କଟୁକଥା କହିଦିଅନ୍ତି, ସେଥ‌ିରେ ଗୁରୁତ୍ଵ ଦେଇ ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ କରିବା ଆଦୌ ଉଚିତ ନୁହେଁ । ନଚେତ୍ ଖଳଲୋକମାନେ ଗୃହଶାନ୍ତି ନଷ୍ଟ କରିବାକୁ ସୁଯୋଗ ପାଇବେ । ତେଣୁ ବାପା, ଦାଦା ବା ଅନ୍ୟ ଗୁରୁଜନ ଯଦି କେବେ କିଛି ମନକୁ ବାଧୁବା ଭଳି କଥା କୁହନ୍ତି, ତେବେ ସେ କଥାକୁ ଗୁରୁତ୍ଵ ନଦେଇ ସେମାନଙ୍କଠାରେ ଭକ୍ତି ରଖୁ ।

ଶେଷରେ ସବୁଠୁ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ କଥା ପଦେ ଲେଖୁଛି । ଈଶ୍ୱରଙ୍କ ଆଶୀର୍ବାଦ ବିନା ମଣିଷ କଦାପି କୌଣସି କାର୍ଯ୍ୟରେ ସଫଳତା ଲାଭ କରିପାରିବ ନାହିଁ । ଆମ ବାପା, ମାଆ ଆମ ପାଇଁ ଜୀବନ୍ତ ଦେବତା ପରି । ତେଣୁ ତାଙ୍କ କଥା ମାନି ଚଳୁଥିବୁ । ବାପା, ବୋଉଙ୍କୁ ମୋର ଭୂମିଷ୍ଠ ପ୍ରଣାମ ଜଣାଇ ରହୁଛି। ଇତି ।

ତୋର ମଙ୍ଗଳାକାଙ୍ କ୍ଷା ଭାଇ

ଠିକ ଶା

ପ୍ରେରକ	ପ୍ରାପ୍ତେଷୁ
ପାଚକ କାନୁନଗୋ ।	ଶ୍ରା ଦାପକ କାନୁନ୍‌ଗୋ
ନେତାଜା ଛାତ୍ରାବାସ	ମାର୍ଗତ – ଶ୍ରା ସବ୍ୟସାଚୀ କାନୁନ୍‌ଗୋ
ରେଭେନ୍ସା କଲିଜିଏଟ, ଫୁଲ	ଗ୍ରା – ପାର୍ବତୀପୁର
ପୋ – ଚାନ୍ଦିନାଗ୍ରୈକ	ପୋ – ଅସୁରେଶ୍ଵର
ଜ଼ି – କଟକ	ଜି. – କଟକ
ପିନ୍ – ୭୫ ୩୦୦୨	ପିନ୍ – ୨୫୯୨୦୯

ତୁମ ପାଇଁ କାମ

Question ୨୫ ।
ସେତୁବନ୍ଧ ସମ୍ବନ୍ଧୀୟ ଚିତ୍ର ସଂଗ୍ରହ କରି ତୁମ ଶ୍ରେଣୀଗୃହ କାନ୍ଥରେ ସଂଲଗ୍ନ କର ।

Question ୨୬ ।
ବୈଦେହୀଶ ବିଳାସ ପୁସ୍ତକରୁ ତୁମକୁ ଭଲ ଲାଗୁଥ‌ିବା ପଦଗୁଡ଼ିକୁ ଲେଖୁ ରଖୁ ଆବୃତ୍ତି କର ।
[ସୂଚନା : ‘ତୁମ ପାଇଁ କାମ’ର ଉତ୍ତରଗୁଡ଼ିକ ଛାତ୍ରଛାତ୍ରୀମାନେ ଶିକ୍ଷକଙ୍କ ସହାୟତା ନେଇ ପ୍ରସ୍ତୁତ କରନ୍ତୁ ।]

ବଷ୍ଥନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

ବିଗତ ବର୍ଷର ହାଇସ୍କୁଲ ପରୀକ୍ଷା (ବାର୍ଷିକ ଓ ସପ୍ଲିମେଣ୍ଟାରୀ)ର ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ରାବଣକୁ କିଏ ‘ଦେବରିପୁ’ ବୋଲି ସମ୍ବୋଧନ କରିଥିଲେ ?
Answer:
ଶୁକାପାରଣ

Question 2.
କାହାକୁ ସନ୍ତୁଷ୍ଟ କରିବାପାଇଁ ରାଘବ ଅନଶନ କରି କୁଶଶଯ୍ୟାରେ ଶୟନ କରିଥିଲେ ?
Answer:
ବରୁଣ ଦେବତା

Question 3.
କେଉଁ ଦେବତାଙ୍କୁ ପ୍ରସନ୍ନ କରିବାକୁ ଶ୍ରୀରାମଚନ୍ଦ୍ର ଉପବାସ ରହି କୁଶ ଉପରେ ଶୟନ କରିଥିଲେ ?
Answer:
ବରୁଣ

Question 4.
ଶୁକସାରଣ କେଉଁ ରୂପ ଧରି ବିଭୀଷଣ ଓ ଅଙ୍ଗଦଙ୍କ ନିକଟକୁ ଯାଇଥିଲେ ?
Answer:
ବିତକ

Question 5.
ଅଙ୍ଗଦର ପିତୃବ୍ୟ କିଏ ?
Answer:
ରାମଚନ୍ଦ୍ରଙ୍କୁ ପରାକ୍ରମହାନ ଭାବି

Question 6.
ବିରସ ରାବଣ ମନ୍ଦହାସ କରିଥିଲା କାହିଁକି ?
Answer:
ବୈଦେଶ ବିଳାସ

Question 7.
‘ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ’ କବିତାଟି କେଉଁ କାବ୍ୟର ଅଂଶବିଶେଷ ?
Answer:
ବୈଦେହାଶ ବିଲାସ

Question 8.
ରାବଣର ବାର୍ତ୍ତା ନେଇ ଅଙ୍ଗଦ ନିକଟକୁ କିଏ ଆସିଥିଲେ ?
Answer:
ଶୁକସାରଣ .

Question 9.
ବରୁଣଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ ରାମଚନ୍ଦ୍ର କେଉଁ ଶଯ୍ୟାରେ ଶୟନ କରିଥିଲେ ?
Answer:
କୁଶଶଯ୍ୟା

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

A. ଚାରିଗୋଟି ବିକଳ୍ପ ଉତ୍ତର ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ।

Question 1.
‘ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ’ କବିତାଟି କେଉଁ କାବ୍ୟରୁ ଆନୀତ ?
Answer:
‘ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ’ କବିତାଟି କବି ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ ରଚିତ ‘ବୈଦେହୀଶ ବିଳାସ’ କାବ୍ୟରୁ ଆନୀତ ।

Question 2.
‘ବୈଦେହୀଶ ବିଳାସ’ କାବ୍ୟରେ କେଉଁ ମହାନ୍ ପୁରୁଷଙ୍କ କଥା ବର୍ଣ୍ଣନା କରାଯାଇ ଅଛି ।
Answer:
‘ବୈଦେହୀଶ ବିଳାସ’ କାବ୍ୟରେ ମର୍ଯ୍ୟାଦା ପୁରୁଷ ପ୍ରଭୁ ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ କଥା ବର୍ଣ୍ଣନା କରାଯାଇଛି ।

Question 3.
ରାମଚନ୍ଦ୍ର ସମୁଦ୍ରରେ ବନ୍ଧ ବାନ୍ଧିବାପାଇଁ କେଉଁ ଦେବତାଙ୍କୁ ପ୍ରସନ୍ନ କରିବାକୁ ଚାହିଁଥିଲେ?
Answer:
ରାମଚନ୍ଦ୍ର ସମୁଦ୍ରରେ ବନ୍ଧ ବାନ୍ଧିବାପାଇଁ ବରୁଣ ଦେବତାଙ୍କୁ ପ୍ରସନ୍ନ କରିବାକୁ ଚାହିଁଥିଲେ ।

Question 4.
ରାବଣ ଦୂତ ମାଧ୍ୟମରେ ବିଭୀଷଣଙ୍କ ନିକଟକୁ କି ବାର୍ତ୍ତା ପଠାଇଥିଲେ ?
Answer:
ରାବଣ ନିଜର ମନ୍ତ୍ରୀ ଶୁକ ଓ ସାରଣକୁ ଦୂତରୂପେ ପଠାଇଥଳେ ।

Question 5.
ରାବଣ ଦୂତ ମାଧ୍ୟମରେ ବିଭୀଷଣଙ୍କ ନିକଟକୁ କି ବାର୍ତ୍ତା ପଠାଇଥିଲେ ?
Answer:
ରାବଣ ହତ ମାଧ୍ୟମରେ ବିଭାଷଶଙ୍କ ନିକଟକୁ କ୍ରେଧବଶତଃ କହଥ୍ ବା ପିତୃତୁଲ୍ୟ ଅଗ୍ରଜଙ୍କ କଥାରେ ବିମୁଖ ହୋଇ ଲଙ୍କାର ବିପୁଳ ଐଶ୍ବର୍ଯ୍ୟକୁ ତ୍ୟାଗକରି ଓ ଉଚ୍ଚବଂଶଜ ହୋଇ ବନବାସୀର ଶରଣାପନ୍ନ ହେବା ଉଚିତ ନୁହେଁ ବୋଲି ବାର୍ତ୍ତା ପଠାଇଥିଲେ ।

Question 6.
ରାବଣ ଅଙ୍ଗଦଙ୍କ ନିକଟକୁ କି ବାର୍ତ୍ତା ପଠାଇଥିଲେ ?
Answer:
ପିତୃହନ୍ତାର ଶରଣାପନ୍ନ ନ ହୋଇ ପିତୃବ୍ୟଙ୍କ ସହ ବିବାଦ ସୃଷ୍ଟିକରି ସୈନ୍ୟବଳ ସହ ନିଜ ରାଜ୍ୟକୁ ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବାକୁ ରାବଣ ଅଙ୍ଗଦ ନିକଟକୁ ବାର୍ତ୍ତା ପ୍ରେରଣ କରିଥିଲେ ।

Question 7.
ବିଭୀଷଣ ଲଙ୍କା ପ୍ରତ୍ୟାବର୍ତ୍ତନ ପାଇଁ କେଉଁ ସର୍ଭ ରଖୁଥିଲେ ?
Answer:
ଜ୍ୟେଷ୍ଠଭ୍ରାତା ସତୀ ସୀତାଙ୍କୁ ନିଃସର୍ଭ ପ୍ରତ୍ୟର୍ପଣ କଲେ ହିଁ ବିଭୀଷଣ ଲଙ୍କା ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବେ ବୋଲି ସର୍ଭ ରଖୁଥିଲେ ।

Question 8.
ରାମଚନ୍ଦ୍ର କାହିଁକି ବିସ୍ମିତ ହେଲେ ?
Answer:
କପିମାନେ ସମୁଦ୍ରରେ ପକାଉଥବା ଗିରିଖଣ୍ଡମାନ ବୁଡ଼ିଯାଉଥିବାରୁ ରାମଚନ୍ଦ୍ର ବିସ୍ମିତ ହୋଇଥିଲେ ।

Question 9.
ଜ୍ୟେଷ୍ଠଭ୍ରାତା କାହା ସହ ତୁଳନୀୟ ?
Answer:
ଜ୍ୟେଷ୍ଠଭ୍ରାତା ପିତାଙ୍କ ସହ ତୁଳନୀୟ ।

Question 10.
କବିତାରେ ବିଂଶତିକର ବୋଲି କବି କାହାକୁ କହିଛନ୍ତି ?
Answer:
ରାବଣର କୋଡ଼ିଏଟି ହାତ ଥ‌ିବାରୁ କବିତାରେ କବି ତାଙ୍କୁ ବିଂଶତିକର ବୋଲି କହିଛନ୍ତି ।

Question 11.
ସମୁଦ୍ର ତରିବାପାଇଁ ରାମଚନ୍ଦ୍ର କି ପାଞ୍ଚ କରିଥିଲେ ?
Answer:
ସମୁଦ୍ର କରିବାପାଇଁ ରାମଚନ୍ଦ୍ର ଅନଶନତ୍ପର୍ଚ୍କ କୁଶାସନରେ ଶୟନ କରି ଜଳାଧ୍ପତି ବରୁଶଦେବଙ୍କ ପ୍ରାତ୍ୟର୍ଥେ ଉପାସନା କରିଥିଲେ ।

Question 12.
କବିତାରେ ‘ରାଘବ’ଶବ୍ଦଟି କାହା ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟବହାର କରାଯାଇଛି ?
Answer:
କବିତାରେ ‘ରାଘବ’ ଶବ୍ଦଟି ରାମଚନ୍ଦ୍ରଙ୍କ ଉଦ୍ଦଶ୍ୟରେ ବ୍ୟବହାର କରାଯାଇଛିା

Question 13.
‘ବୈଦେହୀଶ ବିଳାସ’ ଭିନ୍ନ ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ ରଚିତ ଅନ୍ୟ ଦୁଇଗୋଟି କାବ୍ୟର ନାମ ଲେଖ ।
Answer:
‘ବୈଦେହୀଶ ବିଳାସ’ ଭିନ୍ନ ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ ରଚିତ ଅନ୍ୟ ଦୁଇଗୋଟି କାବ୍ୟର ନାମ ହେଉଛି ‘ଲାବଣ୍ୟବତୀ’ ଓ କୋଟି ବ୍ରହ୍ମାଣ୍ତସୁନ୍ଦରା

Question 14.
ଅଙ୍ଗଦଙ୍କ ଶକ୍ତ ଚାପୁଡ଼ା ପ୍ରହାର କିପରି ଭୟଙ୍କର ଥିଲା ବୋଲି ମନ୍ତ୍ରୀଦ୍ୱୟ ବର୍ଣ୍ଣନା କଲେ ?
Answer:
ଅଙ୍ଗଦଙ୍କ ଶକ୍ତ ଚାପୁଡ଼ା ବଜ୍ରଠାରୁ ଭୟଙ୍କର ଥିଲା ବୋଲି ମନ୍ତ୍ରୀଦ୍ୱୟ ବର୍ଣ୍ଣନା କରିଥିଲେ ।

Question 15.
ବିରସ ରାବଣ ମନ୍ଦହାସ କରିଥିଲା କାହିଁକି ?
Answer:
ରାମଚନ୍ଦ୍ରଙ୍କୁ ପରାକ୍ରମହୀନ ବୋଲି ଭାବି ବିରସ ରାବଣ ମନ୍ଦହାସ କରିଥିଲା ।

Question 16.
ରାମଚନ୍ଦ୍ର ସମୁଦ୍ରରେ ସେତୁ ବାନ୍ଧିବାପାଇଁ କାହିଁକି ସ୍ଥିର କଲେ ?
Answer:
ରାବଣଦ୍ୱାରା ଅପହୃତା ସୀତାଙ୍କୁ ଉଦ୍ଧାର କରିବାପାଇଁ ରାମଚନ୍ଦ୍ର ସମୁଦ୍ରରେ ସେତୁ ବାନ୍ଧିବାପାଇଁ ସ୍ଥିର କଲେ ।

(B) ଗୋଟିଏ ପଦ ବା ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ ।

Question 1.
‘ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ’ କବିତାଟି କେଉଁ କାବ୍ୟାର ଅଂଶବିଶେଷ ?
Answer:
ବୈଦେହୀଶ ବିଳାସ

Question 2.
‘ରାମକାବ୍ୟ’ କହିଲେ କେଉଁ କାବ୍ୟକୁ ବୁଝାଏ ?
Answer:
ବୈଦେହୀଶ ବିଳାସ

Question 3.
‘ବୈଦେହୀଶ ବିଳାସ’ କାବ୍ୟ କେତେ ଛାନ୍ଦ ବିଶିଷ୍ଟ ?
Answer:
ବାଉନ

Question 4.
ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୁଳ’ କବିତାଟି ‘ବୈଦେହୀଶ ବିଳାସ’ କାବ୍ୟର କେତେତମ ଛାତରୁ ଆନୀତ?
Answer:
ଚାଳିଶ

Question 5.
କିଏ ସୀତାଙ୍କୁ ଅପହରଣ କରିଥିଲେ ?
Answer:
ରାବଣ

Question 6.
ଅଙ୍ଗଦ କେଉଁ ରାଜ୍ୟର ରାଜପୁତ୍ର ଥିଲା ?
Answer:
କିଷ୍କିନ୍ଧ୍ଯା

Question 7.
ଉପେନ୍ଦ୍ର ଭଞ୍ଜ କେଉଁ ରାଜବଂଶରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ?
Answer:
ଘୁମୁସର

Question 8.
କବି ସମ୍ରାଟ୍ କେଉଁ ମନ୍ତ୍ର ଜପି କବିତ୍ଵ ଲାଭ କରିଥିଲେ ?
Answer:
ରାମତାରକ

Question 9.
କେଉଁ କୃତିଟି ଉପେନ୍ଦ୍ରଙ୍କ ପଦ୍ୟାତ୍ମକ ଶବ୍ଦକୋଷ ?
Answer:
ଗାତାର୍ତ୍ତି ଧାନ

Question 10.
କେଉଁ ବାକ୍ୟଟି କବିସମ୍ରାଟଙ୍କ ଗୀତାତ୍ମକ ଆଳଙ୍କାରିକ କୃତି ଅଟେ ?
Answer:
ରସପଞ୍ଚକ

Question 11.
ଗିରିମାନ ବୁଡ଼ିଗଲାବେଳେ କେବଳ କେଉଁ ଶବ୍ଦ ଶୁଣାଯାଉଥିଲା ?
Answer:
ଫି ଫି କାର ଶବ୍ଦ

Question 12.
ରାମଚନ୍ଦ୍ର ଆଶ୍ଚର୍ଯ୍ୟାନ୍ବିତ ହୋଇ କ’ଣ ତ୍ୟାଗ କରିଥିଲେ ?
Answer:
ନିଃଶ୍ବାସ

Question 13.
କବିତାରେ ‘ବୁଧେ’ କେଉଁ ଅର୍ଥରେ ପ୍ରଯୁକ୍ତ ହୋଇଛି ?
Answer:
ପଣ୍ଡିତମାନେ

Question 14.
‘ବିଭୂତିଭୂଷଣ’ ବିଶେଷଣ ପଦଟି କାହା ଉଦ୍ଦେଶ୍ୟରେ କଥିତ ?
Answer:
ରାମଚନ୍ଦ୍ର

Question 15.
ବିତରଣେ ସାଗର କି ପାଞ୍ଚ ପଚାରିଲା – ଏଠାରେ ‘ପାଞ୍ଚ’ ଶବ୍ଦ କେଉଁ ଅର୍ଥରେ ବ୍ୟବହୃତ ?
Answer:
ଉପାୟ

Question 16.
‘ଜଳାଧୂପତି’ କେଉଁ ଦେବତାଙ୍କୁ କୁହାଯାଇଛି ?
Answer:
ବରୁଣ

Question 17.
କବିତାରେ ‘ରାଘବ’ ଶବ୍ଦଟି କାହା ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟବହାର କରାଯାଇଛି ?
Answer:
ରାମଚନ୍ଦ୍ର

Question 18.
ରାବଣର ବାର୍ତ୍ତାନେଇ ଅଙ୍ଗଦ ନିକଟକୁ କିଏ ଆସିଥିଲେ ?
Answer:
ଶୁକ ଓ ସାରଣ

Question 19.
କେଉଁମାନେ ସାଗରଜଳରେ ଗିରିମାନ ପକାଉଥିଲେ ?
Answer:
କପିମାନେ

Question 20.
ରାମଚନ୍ଦ୍ର କାହିଁକି ବିନାଶନରେ କୁଶାସନରେ ଶୟନ କରିଥିଲେ ?
Answer:
ବରୁଣଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ

Question 21.
କିଏ ବିଭୀଷଣଙ୍କର ଜ୍ୟେଷ୍ଠଭ୍ରାତା ଥିଲେ ?
Answer:
ରାବଣ

Question 22.
କବିତାରେ ‘ରାବଣାନୁଜ’ କାହାକୁ ସମ୍ବୋଧନ କରାଯାଇଛି ?
Answer:
ବିଭୀଷଣ

Question 23.
‘ଶଙ୍ଖ’ କହିଲେ କେତେ ସଂଖ୍ୟାକୁ ବୁଝାଏ ?
Answer:
ଲକ୍ଷ କୋଟି ସଂଖ୍ୟକ

Question 24.
ଶଙ୍ଖ କେଉଁ ଶ୍ରେଣୀର ଜୀବ ଅଟେ ?
Answer:
ସାମୁଦ୍ରିକ

Question 25.
ବିହ।ୟସ ଏହି ଶବ୍ଦର ଅର୍ଥ କ’ଣ ?
Answer:
ଆକାଶ

Question 26.
ରାବଣ କାହାକୁ ହୀନପରାକ୍ରମଶାଳୀ ବୋଲି ବିବେଚନା କରିଥିଲେ ?
Answer:
ରାମଚନ୍ଦ୍ରଙ୍କୁ

Question 27.
ରାମଚନ୍ଦ୍ର କେଉଁଥିରେ ସିନ୍ଧୁକୁ ପୋତିବାପାଇଁ ବିଚାର କରିଥିଲେ ?
Answer:
ପର୍ବତରେ

Question 28.
‘ବୈଦେହୀଶ ବିଳାସ’ – କାବ୍ୟର କବି କିଏ ?
Answer:
ଉପେନ୍ଦ୍ର ଭଞ୍ଜ

Question 29.
‘ବୈଦେହୀଶ ବିଳାସ’ କାବ୍ୟଟି କେଉଁ ଆଦ୍ୟବର୍ଣ୍ଣ ନିୟମରେ ରଚିତ ?
Answer:

Question 30.
ଦଶଶିର କିଏ ?
Answer:
ରାବଣ

Question 31.
ରାବଣ କାହାକୁ ଚର କରି ପଠାଇଥିଲା?
Answer:
ଶୁକ ଓ ସାରଣଙ୍କୁ

Question 32.
ଜ୍ୟେଷ୍ଠଭ୍ରାତା କାହା ସହିତ ତୁଳନୀୟ ?
Answer:
ପିତା ସହିତ

Question 33.
ଅଙ୍ଗଦଙ୍କ ପିତାଙ୍କ ନାମ କ’ଣ ?
Answer:
ବାଳୀ

Question 34.
‘ପିତୃବ୍ୟ’ କହିଲେ କାହାକୁ ବୁଝାଏ ?
Answer:
ପିତାଙ୍କ ସାନଭାଇଙ୍କୁ

Question 35.
ଅଙ୍ଗଦଙ୍କ ପିତାଙ୍କ ଶତ୍ରୁ କିଏ ?
Answer:
ରାମଚନ୍ଦ୍ର

Question 36.
ଅଙ୍ଗଦଙ୍କ ପିତୃବ୍ୟଙ୍କ ନାମ କ’ଣ ?
Answer:
ସୁଗ୍ରୀବ

Question 37.
ବିଂଶତିକର – କହିଲେ କାହାକୁ ବୁଝାଏ ?
Answer:
ରାବଣକୁ

Question 38.
ସୀତାଙ୍କୁ ସମର୍ପଣ କଲେ ଲଙ୍କା ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବେ ବୋଲି କିଏ କହିଥିଲେ?
Answer:
ବିଭୀଷଣ

(C) ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

Question 1.
ବିଭାଷଶର ଜ୍ୟଷ୍ଠଭ୍ରାତା ……………….. ଅଟନ୍ତି
Answer:
ରାବଣ,

Question 2.
ଅଙ୍ଗଦ …………………. ଙ୍କ ଚାପୁଡ଼ା ମାରିଲେ।
Answer:
ଆକାଶ

Question 3.
ସୁଶ ଓ ସାରଣା ରାବଣର ………………… ଥିଲ୍ଲୀ
Answer:
ଦୁଇମନ୍ତ୍ରୀ

Question 4.
ବିଭାଷଣ …………………… ଙ୍କ ନିକଟରେ ଶରଣ ପଶିଥିଲେ ।
Answer:
ରାମଚନ୍ଦ୍ରଙ୍କ

Question 5.
‘ଚୈଦେହୀଶ ବିଳାସ୍ଥ – କାବ୍ୟର କବି ହେଉଛନ୍ତି …………… ।
Answer:
ଉପେନ୍ଦ୍ର ଭଞ୍ଜ

Question 6.
ଚାରୁଶଙ୍କୁ ସନ୍ତୁଷ୍ଟ କରିବାପାଇଁ ରାଘବ ଅନଶନ କରି ………………….. ଶଯ୍ୟାରେ ଶୟନ କରିଥିଲେ।
Answer:
କୁଶ,

Question 7.
…………………………… ଦେବତାଙ୍କୁ ପ୍ରସନ୍ନ କରିବାକୁ ଶ୍ରୀରାମଚନ୍ଦ୍ର ଉପବାସ ରହି କୁଶ ଉପରେ ଶୟନ କରିଥିଲେ।
Answer:
ବରୁଣ,

Question 8.
ଶୁକ ଓ ସାରଣ ……………….. ରୂପ ଧରି ବିଭାଷଣ ଓ ଅଙ୍ଗଦଙ୍କ ନିକଟକୁ ଯାଇଥିଲେ।
Answer:
ବତକ,

Question 9.
ଅଙ୍ଗଦର ପିତୃବ୍ୟ ………………… ଥିଲେ।
Answer:
ସୁଗ୍ରୀବ,

Question 10.
ରାବଶର ବାର୍ତ୍ତା ନେଇ ଅଙ୍ଗଦ ନିକଟକୁ …………………… ଆସିଥିଲେ।
Answer:
ଶୁକ ଓ ସାରଣ,

Question 11.
ଗିରିମାନ ଗୁଡ଼ିଗଲ।ବେଳେ କେବଳ …………………. ଶବ୍ଦ ଶୁଣାଯାଉଥ୍ଲା
Answer:
ଫି ଫି କାର,

Question 12.
‘ଚିଭୂତି ଭୂଷଣ ବିଶେଷଣ ପଦଟି ……………….. ଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ କୁହାଯାଇଛି।
Answer:
ରାମଚନ୍ଦ୍ର

Question 13.
ରାବଣ’ ………………… ଙ୍କୁ ହାତପାରାକ୍ରମଶାଳା ବୋଲି ବିବେଚନା କରିଥିଲେ।
Answer:
ରାମଚନ୍ଦ୍ର

Question 14.
ରାବଣ ………………….କୁ ଚର କରି ପଠାଇଥିଲା ।
Answer:
ଶୁକ ଓ ସାରଣ

Question 15.
ଶୁକ ଓ ପାରଣ ବାର୍ତ୍ତା ନେଇ …………………… ଙ୍କ ନିକଟକୁ ଯାଇଥାଲୋ
Answer:
ଅଙ୍ଗଦ ଓ ବିଭୀଷଣ

(D) ଠିକ୍ ଉକ୍ତି ପାଇଁ ‘T” ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ F” ଲେଖ

1. ଅଙ୍ଗଦଙ୍କ ପିତାଙ୍କ ନାମ ସୁଗ୍ରୀବ ।
2. ପିତାଙ୍କ ବନ୍ଧୁଙ୍କୁ ‘ପିତୃବ୍ୟ’ କୁହାଯାଏ ।
3. ‘ବିଂଶତିକର’ କହିଲେ ରାବଣକୁ ବୁଝାଏ ।
4. ରାମଚନ୍ଦ୍ରଙ୍କର ଅନ୍ୟ ନାମ ‘ରାଘବ’ ଅଟେ ।
5. ଶୁକ ଓ ସାରଣ ରାବଣଙ୍କର ମନ୍ତ୍ରୀ ଥିଲେ ।
6. ରାମଚନ୍ଦ୍ର ଇନ୍ଦ୍ରଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ ବିନାଶନରେ କୁଶାସନରେ ଶୟନ କରିଥିଲେ।
7. ‘ଶଙ୍ଖ’ କହିଲେ କୋଟି ସଂଖ୍ୟକ ସଂଖ୍ୟାକୁ ବୁଝାଏ ।
8. ପର୍ବତରେ ସିନ୍ଧୁକୁ ପୋତିବାପାଇଁ ରାମଚନ୍ଦ୍ର ବିଚାର କରିଥିଲେ ।
9. ବିଭୀଷଣ ରାବଣର ଅଗ୍ରଜ ଥିଲେ ।
10. ରାବଣର ବାର୍ତ୍ତା ଶୁଣି ଅଙ୍ଗଦ ଶୂନ୍ୟକୁ ବଜ୍ରସମ ଚାପୁଡ଼ା ପ୍ରହାର କଲେ ।
11. ସାଗର ଅତିକ୍ରମ ନିମନ୍ତେ ରାମଚନ୍ଦ୍ର କୁଶଶଯ୍ୟାରେ ଶୟନ କରିଛନ୍ତି ବୋଲି ଦୂତଦ୍ଵୟ ଲକ୍ଷ୍ମଣଙ୍କୁ କହିଥିଲେ ।
12. ରାମଚନ୍ଦ୍ରଙ୍କ କୁଶଶଯ୍ୟା ଶୟନ କଥା ଶୁଣି ରାବଣ ଅଳ୍ପ ହସି ରାମଚନ୍ଦ୍ରଙ୍କୁ ହୀନପରାକ୍ରମଶାଳୀ ବୋଲି କହିଲେ ।
13. ଅଙ୍ଗଦଙ୍କ ପିତୃବ୍ୟ ହେଉଛନ୍ତି ବାଳୀ ।
14. ହନୁମାନଙ୍କ ପିତା ହେଉଛନ୍ତି ସୁଗ୍ରୀବ ।
15. ବରୁଣ ହେଉଛନ୍ତି ଜଳାଧୂପତି ।
Answer:
1. ଅଙ୍ଗଦଙ୍କ ପିତାଙ୍କ ନାମ ସୁଗ୍ରୀବ । (F)
2. ପିତାଙ୍କ ବନ୍ଧୁଙ୍କୁ ‘ପିତୃବ୍ୟ’ କୁହାଯାଏ । (F)
3. ‘ବିଂଶତିକର’ କହିଲେ ରାବଣକୁ ବୁଝାଏ । (T)
4. ରାମଚନ୍ଦ୍ରଙ୍କର ଅନ୍ୟ ନାମ ‘ରାଘବ’ ଅଟେ । (T)
5. ଶୁକ ଓ ସାରଣ ରାବଣଙ୍କର ମନ୍ତ୍ରୀ ଥିଲେ । (T)
6. ରାମଚନ୍ଦ୍ର ଇନ୍ଦ୍ରଙ୍କୁ ପ୍ରସନ୍ନ କରିବାପାଇଁ ବିନାଶନରେ କୁଶାସନରେ ଶୟନ କରିଥିଲେ। (F)
7. ‘ଶଙ୍ଖ’ କହିଲେ କୋଟି ସଂଖ୍ୟକ ସଂଖ୍ୟାକୁ ବୁଝାଏ । (F)
8. ପର୍ବତରେ ସିନ୍ଧୁକୁ ପୋତିବାପାଇଁ ରାମଚନ୍ଦ୍ର ବିଚାର କରିଥିଲେ । (T)
9. ବିଭୀଷଣ ରାବଣର ଅଗ୍ରଜ ଥିଲେ । (F)
10. ରାବଣର ବାର୍ତ୍ତା ଶୁଣି ଅଙ୍ଗଦ ଶୂନ୍ୟକୁ ବଜ୍ରସମ ଚାପୁଡ଼ା ପ୍ରହାର କଲେ । (T)
11. ସାଗର ଅତିକ୍ରମ ନିମନ୍ତେ ରାମଚନ୍ଦ୍ର କୁଶଶଯ୍ୟାରେ ଶୟନ କରିଛନ୍ତି ବୋଲି ଦୂତଦ୍ଵୟ ଲକ୍ଷ୍ମଣଙ୍କୁ କହିଥିଲେ । (F)
12. ରାମଚନ୍ଦ୍ରଙ୍କ କୁଶଶଯ୍ୟା ଶୟନ କଥା ଶୁଣି ରାବଣ ଅଳ୍ପ ହସି ରାମଚନ୍ଦ୍ରଙ୍କୁ ହୀନପରାକ୍ରମଶାଳୀ ବୋଲି କହିଲେ ।
13. ଅଙ୍ଗଦଙ୍କ ପିତୃବ୍ୟ ହେଉଛନ୍ତି ବାଳୀ । (F)
14. ହନୁମାନଙ୍କ ପିତା ହେଉଛନ୍ତି ସୁଗ୍ରୀବ । (F)
15. ବରୁଣ ହେଉଛନ୍ତି ଜଳାଧୂପତି । (T)

(E) ସ୍ତମ୍ଭ ମିଳନ କର ।

Question 1.
‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସମ୍ପର୍କ ଥିବା ଶବ୍ଦକୁ ଯୋଗ କର ।

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ଘୁମୁସର ରାଜବଂଶ	ବୈଦେହୀଶ ବିଳାସ
ରାମତୀରକ ମନ୍ତ୍ର	କବିତ୍ଵ ଲାଭ
ଗାତାତ୍ମକ ଆଳଙ୍କାରିକ କୃତି	ରସପଞ୍ଚକ
ରାମ କାବ୍ୟ	ସେତୁ କାକ୍ଷିବା
ପାତାଙ୍କୁ ଉଦ୍ଧି।ର	ଉପେନ୍ଦ୍ର ଭଞ୍ଜ

Answer:

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ଘୁମୁସର ରାଜବଂଶ	ଉପେନ୍ଦ୍ର ଭଞ୍ଜ
ରାମତୀରକ ମନ୍ତ୍ର	କବିତ୍ଵ ଲାଭ
ଗାତାତ୍ମକ ଆଳଙ୍କାରିକ କୃତି	ରସପଞ୍ଚକ
ରାମ କାବ୍ୟ	ବୈଦେହୀଶ ବିଳାସ
ପାତାଙ୍କୁ ଉଦ୍ଧି।ର	ସେତୁ କାକ୍ଷିବା

 

Question 2.
‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସମ୍ପର୍କ ଥିବା ଶବ୍ଦକୁ ଯୋଗ କର ।

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ବିନାଶନରେ ଶୟନ	ବର୍ତ୍ତିକ ସ୍ୱରୂପ
ଜ୍ୟେଷ୍ଠ ଭ୍ରାତ।	ତଳ ପ୍ରହାରିଲା
ବାଦ ରଚାଇ ପିତୃବ୍ୟ	ବାହୁଡ଼ାଅ ସୈନ୍ୟ
ବିହାୟସେ ବିହରି	ପିତା ପରି
ବଜ୍ରାଘାତ ସମ	ବରୁଣ  ପ୍ରସନ୍ନେ

Answer:

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ବିନାଶନରେ ଶୟନ	ବରୁଣ  ପ୍ରସନ୍ନେ
ଜ୍ୟେଷ୍ଠ ଭ୍ରାତ।	ପିତା ପରି
ବାଦ ରଚାଇ ପିତୃବ୍ୟ	ବାହୁଡ଼ାଅ ସୈନ୍ୟ
ବିହାୟସେ ବିହରି	ବର୍ତ୍ତିକ ସ୍ୱରୂପ
ବଜ୍ରାଘାତ ସମ	ତଳ ପ୍ରହାରିଲା

Question 3.
‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସମ୍ପର୍କ ଥିବା ଶବ୍ଦକୁ ଯୋଗ କର ।

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ଶୁକ ସାରଣ	ରାଜାଙ୍କ ସାନଭାଇ
ଅଙ୍ଗଦ	ରାବଣର ଭ୍ରାତା
ରିଭାଷଣ	ରାବଶର ମନ୍ତ୍ରୀ
ପିତୃବ୍ୟ	ରାମଚନ୍ଦ୍ର
ରାଘବ	ବାଳା ପୁତ୍ର

Answer:

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ଶୁକ ସାରଣ	ରାବଶର ମନ୍ତ୍ରୀ
ଅଙ୍ଗଦ	ବାଳା ପୁତ୍ର
ରିଭାଷଣ	ରାବଣର ଭ୍ରାତା
ପିତୃବ୍ୟ	ରାଜାଙ୍କ ସାନଭାଇ
ରାଘବ	ରାମଚନ୍ଦ୍ର
ଶଙ୍ଖ	ସଂଖ୍ୟା ବିଶେଷ

କବି ପରିଚୟ

ଉତ୍କଳ ସାହିତ୍ୟର ମଧ୍ୟଯୁଗ ବା. ଛନ୍ଦଯୁଗ ବା ରୀତିଯୁଗର ସମୃଦ୍ଧ ସାରସ୍ଵତ ସୃଷ୍ଟି ଯେଉଁ ବାଣୀସାଧକମାନଙ୍କର ଅତନ୍ଦ୍ର ସାଧନାରେ ସମୁନ୍ନତ, ରସସିକ୍ତ, ଭାବୋଦ୍ଦୀପକ ତଥା ଉପଭୋଗ୍ୟ ସେମାନଙ୍କ ମଧ୍ୟରେ କବିସମ୍ରାଟ ଉପେନ୍ଦ୍ର ଭଞ୍ଜ ଯେ ଅଗ୍ରଗଣ୍ୟ ଏଥ‌ିରେ ସନ୍ଦେହର ଅବକାଶ ନାହିଁ । ଅପୂର୍ବ ଶବ୍ଦ ସଂଯୋଜନାର ବୈଶିଷ୍ଟ୍ୟ, କଳାମଞ୍ଜୁଳ ଭାଷାବୈଭବ, ସାଙ୍ଗୀତିକତାର ମାଧୁର୍ଯ୍ୟ, ଆଳଙ୍କାରିକ ଛନ୍ଦୋବଦ୍ଧ ଶୈଳୀର ନୈପୁଣ୍ୟ, ଭାବୋଦ୍ଦୀପକ ଚେତନାର ଗାମ୍ଭୀର୍ଯ୍ୟ, ସର୍ବୋପରି ଅଲୌକିକ କଇ୍ଚନାପ୍ରସ୍ତତ ତଥା ପ୍ରେରଣିକ ବିଷୟ ଚକ୍ଷୟ ଚୟନ କରିଙ୍କର ବହୁଶାପ୍ତଦଶିତା ତଥା ପ୍ରଜ୍ଞ।ଦାପ୍ତ ପ୍ରତିଭାର ପରିଚାୟକା

କଳିଙ୍ଗ ହୃଦୟନିଧ୍ ଏହି ପ୍ରଜ୍ଞ।ପୁ ରୁଷଙ୍କର ଜନ୍ମ ସପ୍ତଦଶ ଶତାବ୍ଦୀର ଶେଷଭାଗରେ ଘୁମୁସର ରାଜବଂଶରେ ହୋଇଥିଲା ପିତା ନୀଳକଣ୍ଠ ଭଞ୍ଜ ଓ ପିତାମହ ଧନଞ୍ଜୟ ଭଞ୍ଜଙ୍କ କାବ୍ୟ-ଶାସ୍ତ୍ର-ବିନୋଦନ ମଧ୍ଯରେ କାଳାତିବାହିତ କରି କବି ହୋଇଥିଲେ ଶାବ୍ଦିକ ତଥା ଆଳଙ୍କାରିକ ଚେତନାରେ ସୁପଣ୍ଡିତ । ଉତ୍କଳର ପୁରପଲ୍ଲୀରେ ସେ ଯେପରି ବ୍ୟାପକ ଓ ବହୁଳଭାବେ ପରିଚିତ, ଆଦୃତ ଓ ସମ୍ମାନିତ ତାହା ଲକ୍ଷ୍ୟକରି ଉତ୍କଳମଣି ଗୋପବନ୍ଧୁ ଯଥାର୍ଥରେ କହିଥିଲେ-

“ସୃଜିଶ ସ୍ଵସ୍ତେ ଓଡ଼ିଆଙ୍କ ଭାଷା
ଗଢ଼ିଛ ଓଡ଼ିଆ ଜାତି
ତବଜନ୍ମ ସ୍ଥାନ ଓଡ଼ିଶାରୁ ଆନ
ଭ।ରିଲେ ବିଦାରେ ଛାତି।
ସେ ମଧ୍ୟ ପୂର୍ବରୁ କହିଥିଲେ-
ଗାଏ ତୁମ୍ଭ ଗାତ ସଭାରେ ପଣ୍ଡିତ
ପଥେ ପାନ୍ତ୍ର ଦୃଷ୍ଟମନା
ବିଲେ ବୋଲେ ଚକ୍ଷା ଅନ୍ତଃପୁରେ ଯୋଷା
ନୃତ୍ୟରଙ୍ଗେ ବାରାଙ୍ଗ। ।”

ପିତା ଓ ପିତାମହଙ୍କ ଯୋଗ୍ୟ ଉତ୍ତରାଧିକାରୀ ଭାବେ ଲୋକୋତ୍ତର କବିପ୍ରତିଭା ପ୍ରାପ୍ତ ହୋଇଥିଲେ ଉପେନ୍ଦ୍ର ଭଞ୍ଜ। କବିଙ୍କ ଜୀବନରେ । ତେଣୁ ‘ବ’ କରିଥିଲେ ସେ । ଏତଦ୍‌ଭିନ୍ନ ତାଙ୍କ ରାମତାରକ ମନ୍ତ୍ରରେ ସିଦ୍ଧି ଲାଭ ପରେ ସେହି ପ୍ରତିଭାର ଅଲୌକିକ ସ୍ଫୁରଣ ଘଟିଥିଲା ଆଦ୍ୟ ନିୟମରେ ‘ବୈଦେହୀଶ ବିଳାସ’ ମହାକାବ୍ୟକୁ ସୀତାରାମଙ୍କ ପ୍ରୀତ୍ୟର୍ଥେ ରଚନା କାଳଜୟୀ ଲେଖନୀରୁ ଝରି ପଡ଼ିଥିଲା ‘ଲାବଣ୍ୟବତୀ’, ‘କୋଟି ବ୍ରହ୍ମାଣ୍ଡସୁନ୍ଦରୀ’, ‘ପ୍ରେମ ସୁଧାନିଧ୍’, ‘କଳା କଉତୁକ’, ‘ରସିକ ହାରାବଳୀ’, ‘ଅବନା ରସତରଙ୍ଗ’ ଓ ‘ସୁଭଦ୍ରା ପରିଣୟ’ ପରି ମହାର୍ଘ ରସୋତ୍ତୀର୍ଣ କାବ୍ୟସମୂହ । ତତ୍‌ସହିତ. ‘ଛାନ୍ଦ ଭୂଷଣ’, ‘ରସପଞ୍ଚକ’ ଭଳି ଗୀତାତ୍ମକ ଆଳଙ୍କାରିକ କୃତି ଓ ‘ଗୀତାଭିଧାନ’ ନାମକ ପଦ୍ୟାତ୍ମକ ଶବ୍ଦକୋଷ ଉପେନ୍ଦ୍ରଙ୍କ ଅଳଙ୍କାରମନସ୍କ ପାଣ୍ଡିତ୍ୟ ଏବଂ କବିଖ୍ୟାତିର କାଳଜୟୀ କୃତି । ତାଙ୍କ ରଚିତ ଚଉପଦୀ ଓ ଚଉତିଶା ଓଡ଼ିଆ ଗୀତିକବିତା ଧାରାରେ ଅପରୂପ ସୃଷ୍ଟି ରୂପେ ବିବେଚିତ ହୋଇଛି ।

ପୃଜନା ଭିମୁଖ୍ୟ:

ପିତାମହ ଧନଞ୍ଜୟ ଭଞ୍ଜଙ୍କଦ୍ଵାରା ଅନୁପ୍ରେରିତ ହୋଇ ଉପେନ୍ଦ୍ର ଭଞ୍ଜ ସାହିତ୍ୟ ଚର୍ଚ୍ଚାରେ ମନୋନିବେଶ କରିଥିଲେ। ସେ ଥିଲେ କାବ୍ୟ-ସାହିତ୍ୟର ସର୍ବଶ୍ରେଷ୍ଠ ବିନ୍ଧାଣୀ । ବିଷୟ-ବିନ୍ୟାସ, ଶବ୍ଦଗୁମ୍ଫନ, ଅଳଙ୍କାର ପ୍ରୟୋଗ, ପ୍ରକୃତି ଚିତ୍ରଣ ଓ ନାୟକ ନାୟିକାଙ୍କ ରୂପ ବର୍ଣ୍ଣନାରେ ତାଙ୍କର ଅସାଧାରଣ କୃତିତ୍ଵ ଓ କବିତ୍ଵର ପରିଚୟ ସ୍ପଷ୍ଟ ପରିଫଳିତ ।

କବିତାର ପୃଷ୍ଠଭୂମି

ରାମତାରକ ମନ୍ତ୍ରସିଦ୍ଧ, ପ୍ରଥଯଶା କବି ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ ସର୍ବଶ୍ରେଷ୍ଠ କାବ୍ୟ ‘ବୈଦେହୀଶ ବିଳାସ’, ବୈଦେହୀ ଓ ତାଙ୍କର ଈଶ ବା ପ୍ରଭୁ ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ ଲୀଳାବିଳାସ ବର୍ଣ୍ଣିତ ଏକ ଅନନ୍ୟ ବିଦଗ୍ଧ ଗ୍ରନ୍ଥ । ବାଉନ ଛାନ୍ଦ ବିଶିଷ୍ଟ ଏହି ଗ୍ରନ୍ଥରେ ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ ଜନ୍ମରହସ୍ୟଠାରୁ ଆରମ୍ଭ କରି ସମ୍ପୂର୍ଣ୍ଣ ରାମାୟଣର କଥାବସ୍ତୁକୁ ପର୍ଯ୍ୟାୟକ୍ରମେ ଉପସ୍ଥାପନ କରିଛନ୍ତି କବି । ପଠିତ ‘ରାଘବଙ୍କ ଲଙ୍କା ଯାତ୍ରାନୁକୂଳ’ ଶୀର୍ଷକ କବିତାଟି କବିସମ୍ରାଟଙ୍କ ଚିନ୍ମୟ କାବ୍ୟ ‘ବୈଦେହୀଶ ବିଳାସ’ ର ଚତ୍ବାରିଂଶ ଛନ୍ଦରୁ ନିର୍ବାଚିତ ପ୍ରଥମାଂଶ । ‘ବ’ ଆଦ୍ୟବର୍ଣ୍ଣ’ ନିୟମରେ ରଚିତ ପଦ୍ୟଟି ‘ଆଶାବରୀ’ ରାଗରେ ପ୍ରତିବନ୍ଧିତ।

ଲଙ୍କାର ରାଜା ଦଶାନନଙ୍କଦ୍ଵାରା ଅପହୃତା ସୀତାଙ୍କ ଅନ୍ଵେଷଣରେ ଘନ ଅରଣ୍ୟ ମଧ୍ୟରେ ବୁଲୁଥିଲାବେଳେ ଶ୍ରୀରାମ ଓ ଅନୁଜ ଲକ୍ଷ୍ମଣ ଆହତ ଜଟାୟୁକୁ ଭେଟିଲେ । ସତୀ ସୀତାଙ୍କୁ ଲଙ୍କପତି ରାବଣ ଅପହରଣ କରି ପୁଷ୍ପକ ବିମାନରେ ଲଙ୍କାପୁରୀ ନେଇଯାଇଥିବାର ସମ୍ବାଦ ସେମାନେ ତାହାଠାରୁ ଅବଗତ ହେଲେ । ଶ୍ରୀରାମ ସୁଗ୍ରୀବଙ୍କ ସହ ମିତ୍ରତା ସ୍ଥାପନ କରି କିଷ୍କିନ୍ଧ୍ୟାରେ ବାଳୀକୁ ବଧ କଲେ । ଶ୍ରୀରାମଙ୍କ ନିର୍ଦ୍ଦେଶମତେ କପିଶ୍ରେଷ୍ଠ ହନୁମାନ ଦୂତ ରୂପେ ସମୁଦ୍ର ଲଙ୍ଘନ କରି ରାବଣପୁରୀ ଲଙ୍କାଗଡ଼ରେ ମା’ ଜାନକୀଙ୍କୁ ଠାବ କଲେ ଓ ତାଙ୍କଠାରୁ ରତ୍ନହାର ଆଣି ରାମଚନ୍ଦ୍ରଙ୍କୁ ଦେଇ ତାଙ୍କ ମନରେ ଲଙ୍କାପୁରୀରେ ସୀତାଙ୍କ ଅବସ୍ଥାନ ସମ୍ପର୍କିତ ସନ୍ଦେହ ମୋଚନ କରାଇଲେ । ପରେ ପରେ ଲଙ୍କପତି ରାବଣର ଅନୁଜ ବିଭୀଷଣ ଶ୍ରୀରାମଙ୍କୁ ସାକ୍ଷାତ୍ କରି ତାଙ୍କର ଶରଣାପନ୍ନ ହେଲା ଏବଂ ଲଙ୍କାପୁରୀ ସମ୍ପର୍କରେ ବହୁ ତଥ୍ୟ ତାଙ୍କୁ ଅବଗତ କରାଇଲା । ଶ୍ରୀରାମ ଲକ୍ଷ୍ମଣଙ୍କ ସହ କିସ୍କିନ୍ଧ୍ୟାରାଜ ସୁଗ୍ରୀବ, କପିବର ହନୁମାନ, ବାଳୀପୁତ୍ର ଅଙ୍ଗଦ, ନଳ, ନୀଳଙ୍କ ସମେତ ସମସ୍ତ ବାନର ସୈନ୍ୟ ଓ ଜାମ୍ବବାନଙ୍କ ନେତୃତ୍ୱରେ ସୈନ୍ୟମାନେ ଲଙ୍କାଭିଯାନ ପାଇଁ ପ୍ରସ୍ତୁତ ହୋଇ ସମୁଦ୍ର ତଟରେ ଉପସ୍ଥିତ ହେଲେ ।

କବିତାର ମର୍ମବାଣୀ

ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କ ମନରେ ପତ୍ନୀ ଜାନକୀଙ୍କୁ ଫେରିପାଇବାର ଆଶା ଦୃଢ଼ୀଭୂତ ହେଲା। ବାନର ଓ ଭଲ୍ଲୁକ ସୈନ୍ୟଙ୍କ ସହାୟତାରେ ସେ ସମୁଦ୍ରରେ ସେତୁ ବାନ୍ଧି ଲଙ୍କାନଗରୀ ଆକ୍ରମଣ କରିବାପାଇଁ ଯୋଜନା ପ୍ରସ୍ତୁତ କଲେ । ସମୁଦ୍ରରେ ସେତୁ ବାନ୍ଧିବାପାଇଁ ବାନରମାନେ ପର୍ବତପ୍ରମାଣ ବିଶାଳ ପ୍ରସ୍ତରଖଣ୍ଡମାନ ବୋହିନେଇ ସମୁଦ୍ରରେ ନିକ୍ଷେପ କଲେ । ମାତ୍ର ସେ ସମସ୍ତ ଗଭୀର ଜଳରାଶି ମଧ୍ୟରେ ଡୁବିଯାଇ ଅଦୃଶ୍ୟ ହେବାକୁ ଲାଗିଲା । ଏପରିକି ଜଳ ମଧ୍ୟରେ ସାମାନ୍ୟ ବୁଦ୍‌ବୁଦ ମଧ୍ୟ ସୃଷ୍ଟି ହେଲା ନାହିଁ । କେବଳ ଜଳ ମଧ୍ୟରୁ ଯାହା ଫି ଫି ଶବ୍ଦ ଶୁଣାଗଲା । ତଦ୍ବାରା କେବଳ ଜଳର ଗଭୀରତା ହିଁ ଅନୁମିତ ହେଉଥିଲା । ଅଗାଧ ଜଳରାଶି ମଧ୍ୟରେ ବିଶାଳ ପର୍ବତଖଣ୍ଡମାନଙ୍କ ଏତାଦୃଶ ମଜ୍ଜନ ଲକ୍ଷ୍ୟକରି ଶ୍ରୀରାମ ବିସ୍ମିତ ହେଲେ । ବରୁଣ ଦେବତାଙ୍କୁ ହୁଏତ ପ୍ରସନ୍ନ ନ କଲେ ସେ ସେତୁ ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ସଫଳ ହୋଇପାରିବେ ନାହିଁ ବୋଲି ଚିନ୍ତା କଲେ । ଏହା ଭାବି ବରୁଣଦେବଙ୍କ ପ୍ରୀତ୍ୟର୍ଥେ ‘ସେ ଅନାହାରରେ ରହିଲେ ଓ କୋମଳ ଶେଯ ପରିବର୍ତ୍ତେ କୁଶଶଯ୍ୟାରେ ଶୟନ କଲେ । ଶବ୍ଦାଳଙ୍କାର ସମ୍ରାଟ ଭଞ୍ଜଙ୍କ ଭାଷାରେ

‘ବିସ୍ମଇ ନିଃଶ୍ବାସ ତେଜି ବରୁଣ ପ୍ରସନ୍ନେ
ବିନାଶନରେ ଶୟନ ସେ ଦର୍ଭଶୟନେ ଯେ।’’

ତତ୍ପରେ କବିସମ୍ରାଟ ପ୍ରସଙ୍ଗ ପରିବର୍ତ୍ତନର ସୂଚନା ପ୍ରଦାନ କରିଛନ୍ତି । ଶତ୍ରୁପକ୍ଷର ଗତିବିଧୂ ଓ ଯୋଜନା ସମ୍ପର୍କରେ ଅବଗତ ହେବା ନିମିତ୍ତ ଦଶାନନ ଶୁକ ଓ ସାରଣ ନାମକ ଦୁଇ ପ୍ରମୁଖ ମନ୍ତ୍ରୀଙ୍କୁ ଦୂତ ରୂପେ ସମୁଦ୍ର ତଟକୁ ପ୍ରେରଣ କଲା । ବିଶେଷତଃ ସେମାନଙ୍କ ଜରିଆରେ ସେ ତା’ର କନିଷ୍ଠ ଭ୍ରାତା ବିଭୀଷଣ ଓ ବାଳୀପୁତ୍ର ଅଙ୍ଗଦ ଉଦ୍ଦେଶ୍ୟରେ କିଛି ଗୁରୁତ୍ଵପୂର୍ଣ ବାର୍ତ୍ତା ପ୍ରେରଣ କରିଥିଲା । କନିଷ୍ଠ ଭ୍ରାତା ପ୍ରତି ତା’ର ସନ୍ଦେଶର ସାରାଂଶ ଏହି ଯେ ଜ୍ୟେଷ୍ଠଭ୍ରାତା ପିତୃତୁଲ୍ୟ ଗୁରୁଜନ ଅଟନ୍ତି। ଯଦି କ୍ରୋଧବଶତଃ ଆଗପଛ ବିଚାର ନ କରି ସେ କୌଣସି କଟୁକ୍ତି ପ୍ରୟୋଗ କରିଥାଆନ୍ତି, ତାହା ଧର୍ଭବ୍ୟ ନୁହେଁ କିମ୍ବା ସେହି ଉକ୍ତିକୁ ତିକ୍ତ ତୁଲ୍ୟ ମନେକରିବା ଉଚିତ ନୁହେଁ ଏବଂ ତହିଁରେ ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ କରିବା ମଧ୍ୟ ଆଦୌ ସମୀଚୀନ ନୁହେଁ । ସ୍ଵର୍ଣ୍ଣଲଙ୍କା ରାଜପୁରୀରେ ଅବସ୍ଥାନ କରି ରାଜ ଐଶ୍ବର୍ଯ୍ୟର ପ୍ରାଚୁର୍ଯ୍ୟ ମଧ୍ୟରେ ତଥା ନିର୍ଭୟରେ ସେ କାଳାତିପାତ କରୁଥିଲେ । ଉଚ୍ଚକୁଳରେ ଜାତ ହୋଇ ଏକ ସାଧାରଣ ବନବାସୀ ତପସ୍ବୀର ଶରଣାପନ୍ନ ହେବା ଯେ ଅପମାନସୂଚକ ଅନ୍ତତଃ ସେ ଏହା ଅନୁଭବ କରିବା ଆବଶ୍ୟକ । ଏହି କଥା ବିଭୀଷଣକୁ କହିବାପାଇଁ ନିର୍ଦ୍ଦେଶ ଦେଇଥିଲା ଲଙ୍କାଧୂପତି ।

ବାଳୀପୁତ୍ର ଅଙ୍ଗଦ ପ୍ରତି ବାର୍ତ୍ତା ପ୍ରେରଣା କରି ରାବଣ କହିଥିଲା ଯେ ପିତାର ଶତ୍ରୁଠାରେ ଆନୁଗତ୍ୟ ପ୍ରକାଶ କରି ତଥା ଭକ୍ତି ପ୍ରଦର୍ଶନ କରିବାରେ କଦାପି ପୁଣ୍ୟ ଅର୍ଜନ ହୁଏ ନାହିଁ । ନିଜ ପିତୃହନ୍ତା ପ୍ରତି କଠୋର ହେବା ପରିବର୍ତ୍ତେ ତା’ ପାଖରେ ନିଜକୁ ସମର୍ପଣ କରିବା ସ୍ବୀୟ ଆତ୍ମସମ୍ମାନବୋଧର ପରିପନ୍ଥୀ ମାତ୍ର । ତେଣୁ ପିତୃବ୍ୟ ସୁଗ୍ରୀବ ସହ ବିବାଦ ସୃଷ୍ଟି କରି ବାନର ସୈନ୍ୟସାମନ୍ତଙ୍କ ସହ ସେମାନଙ୍କ ସଙ୍ଗିତ୍ୟାଗ କରିବା ସର୍ବାଦୌ ସମୀଚୀନ ହେବ। କବିସମ୍ରାଟଙ୍କ ଭାଷାରେ-

“ବୈଲ ଅଙ୍ଗବକୁ ପିତା ଶତୁ ଭକ୍ତି ପୁଣ୍ୟ
ବାଦ ରଚାଇ ପିତୃବ୍ୟ ବାହୁଡାଆ ସୈନ୍ୟ ଯୋ”

ଲଙ୍କପତି ରାବଣର ଆଦେଶକୁ ଶିରୋଧାର୍ଯ୍ୟ କରି ମନ୍ତ୍ରୀଦ୍ଵୟ ଦାୟିତ୍ଵ ନିର୍ବାହ ନିମନ୍ତେ ଆକାଶ ମାର୍ଗରେ ଯାତ୍ରା କଲେ । ବର୍ଷକ (ଟିଟ୍ଟିଭ ପକ୍ଷୀ | ଟେଣ୍ଟେଇ ପକ୍ଷୀ) ରୂପ ଧାରଣ କରି ସମୁଦ୍ର ଉପରଦେଇ ଉଡ଼ିଗଲାବେଳେ ‘କେଁ କେଁ ଟିହୋ’’ ବୋଲି ଉଚ୍ଚସ୍ଵରରେ ଶବ୍ଦ କରିବାକୁ ଲାଗିଲେ । ‘ତୁମ୍ଭେ କିଏ, କିଏ ତୁମ୍ଭେ’’ ବୋଲି ସେମାନଙ୍କ ଶବ୍ଦରୁ ଅର୍ଥ ପ୍ରତିଧ୍ଵନିତ ହେବାକୁ ଲାଗିଲା । ଦଶାନନର ନିର୍ଦେଶାନୁସାରେ ବିଭୀଷଣ ଓ ଅଙ୍ଗଦକୁ ସମସ୍ତ କଥା କହିବାରୁ ଅଙ୍ଗଦ କ୍ରୋଧାନ୍ବିତ ହୋଇ ସେମାନଙ୍କୁ ପ୍ରହାର କରିବାକୁ ଉଦ୍ୟତ ହେଲା । ତେଣୁ ଭୟରେ ନିଜ ଜୀବନ ରକ୍ଷା କରିବାକୁ ଯାଇ ସେମାନେ ପ୍ରାଣ ବିକଳରେ ସେହି ସ୍ଥାନ ତ୍ୟାଗ କରି ଲଙ୍କା ପ୍ରତ୍ୟାବର୍ତ୍ତନ କଲେ।

ଲଙ୍କାପୁରୀରେ ପହଞ୍ଚି ବିଶ୍ରବାନନ୍ଦନ ରାବଣ ସମ୍ମୁଖରେ ମନ୍ତ୍ରୀଦ୍ୱୟ ବିସ୍ତୃତଭାବେ ସମସ୍ତ ବିବରଣୀ ଅବତାରଣା କଲେ । ଲଙ୍କପତିଙ୍କ ବାର୍ତ୍ତାର ଉତ୍ତର ଦେବାକୁ ଯାଇ ବିଭୀଷଣ କହିଥିଲେ ଯେ ଯଦି ଜ୍ୟେଷ୍ଠଭ୍ରାତା ଅବିଳମ୍ବେ ଦେବୀ ସୀତାଙ୍କୁ ସସମ୍ମାନେ ଶ୍ରୀରାମଚନ୍ଦ୍ରଙ୍କୁ ନିଃସର୍ଭ ସମର୍ପଣ କରନ୍ତି, ତେବେ ସେ ଅବଶ୍ୟ ଲଙ୍କା ପ୍ରତ୍ୟାବର୍ତ୍ତନ କରିବେ । ତତ୍‌ପରେ ଅଙ୍ଗଦଙ୍କର ପ୍ରତିକ୍ରିୟା ବର୍ଣ୍ଣନା କରି କହିଲେ ଯେ ବାର୍ତ୍ତା ଶ୍ରବଣ ମାତ୍ରେ ଅଙ୍ଗଦ ଭୀଷଣ ଭାବେ କ୍ରୋଧାନ୍ବିତ ହୋଇଉଠିଥିଲେ ଏବଂ ଶୂନ୍ୟରେ ବଜ୍ରସମ ଏକ ସଶକ୍ତ ଚାପୋଡ଼ା ପ୍ରହାର କରିଥିଲେ । କେବଳ ଧର୍ମ ବଳରୁ ସେମାନେ ପ୍ରାଣରକ୍ଷା କରିବାରେ ସମର୍ଥ ହେଲେ ବୋଲି ମନ୍ତ୍ରୀଦ୍ୱୟ ପ୍ରକାଶ କଲେ।

ସେହି ଚାପୋଡ଼ା ପ୍ରହାର ଏପରି ଶକ୍ତିଶାଳୀ ଥିଲା ଯେ ସେହି ଆଘାତ ବିନ୍ଧ୍ୟପର୍ବତକୁ ଚୂର୍ଣ୍ଣବିଚୂର୍ଣ୍ଣ କରି ଦେଇଥାଆନ୍ତା ଅଥବା ସେହି ବିଶାଳ ପର୍ବତ ପାତାଳକୁ ଭେଦକରି ଯାଇଥାଆନ୍ତା । ଯେଉଁ ବିକ୍ଷ୍ୟ ପର୍ବତ ସୂର୍ଯ୍ୟଦେବଙ୍କ ଗତିପଥରେ ବ୍ୟାଘାତ ସୃଷ୍ଠି କରିଥାଏ ତାହା ପାରାଲିଗାମା ହୋଇଥିଲେ ପ୍ରତିବନ୍ଧିକ ହର ହେଲା ବୋଲି ଭାନୁଦେବ ହୁଏତ ପ୍ରୀତ ହୋଇଥାଆନ୍ତେ । ତତ୍‌ପରେ ସୈନ୍ୟ କଳନା କରିବାପାଇଁ ‘ସୈନ୍ୟସଂଖ୍ୟା କେତେ’ ବୋଲି ପ୍ରଶ୍ନ କରିବାରୁ ଉତ୍ତରରେ ସେ କହିଥିଲେ ଯେ ସମୁଦ୍ରରେ ସୃଷ୍ଟ ଓ ପରିଦୃଷ୍ଟ ଶଙ୍ଖମାନଙ୍କ ସଂଖ୍ୟାଠାରୁ ସେମାନଙ୍କ ସୈନ୍ୟସଂଖ୍ୟା ବହୁଗୁଣେ ଅଧ‌ିକ ଅର୍ଥାତ୍ ଶଙ୍ଖାତୀତ ବା ଅଗଣିତ । କବିଙ୍କ ଭାଷାରେ-

“ବଳ କେତେ ବୋଗୁଁ ବୋଲେ ଯେତେ ଶଙ୍ଖ ସେହି
ବାରି ରାଶିରେ ଜନିତ ତେତେ ଶଙ୍ଖ ନାହିଁ ଯେ ।’’

ଶ୍ରୀରାମ ଓ ଲକ୍ଷ୍ମଣ ସେସୈନ୍ୟ ସାଗର ଲଙ୍ଘନ କରିବାପାଇଁ କି ବ୍ୟବସ୍ଥା କରୁଛନ୍ତି ବୋଲି ଦଶାନନ ମନ୍ତ୍ରୀଦ୍ୱୟଙ୍କୁ ପଚାରିବାରୁ ଉତ୍ତରରେ ସେମାନେ କହିଥିଲେ ଯେ ସାଗରକୁ ଅତିକ୍ରମ କରିବା ନିମିତ୍ତ ରାମଚନ୍ଦ୍ର ବରୁଣଦେବଙ୍କୁ ସନ୍ତୁଷ୍ଟ କରିବା କାର୍ଯ୍ୟରେ ମଗ୍ନ ଅଛନ୍ତି । ସେଥ‌ିପାଇଁ ସେ କୁଶଶଯ୍ୟାରେ ଶୟନ କରୁଛନ୍ତି । ଶତ୍ରୁପକ୍ଷର ଲଙ୍କାପୁରୀ ଆକ୍ରମଣ ସମ୍ବାଦରେ ପୂର୍ବରୁ ସାମାନ୍ୟ ଚିନ୍ତିତ ଥିବା ରାବଣ ମନ୍ତ୍ରୀଙ୍କଠାରୁ ଏକଥା ଶୁଣିବା ପରେ ସ୍ମିତହାସ୍ୟ ପ୍ରକାଶ କଲା ଓ ତାଚ୍ଛଲ୍ୟ ପ୍ରକାଶ କରି କହିଲା ଯେ ଏପରି ନୂନପରାକ୍ରମ ବିଶିଷ୍ଟ ବନଚାରୀ ତପସ୍ଵୀ ରାମ ଓ ତା’ପରି ମହାପରାକ୍ରମୀ ଲଙ୍କାଧୀଶ ପ୍ରତି ବା କି କ୍ଷତି ପହଞ୍ଚାଇ ପାରିବ।

କଠିନ ଶବ୍ଦାର୍ଥ ଓ ଗିଷ୍ଠଶା

• ରାଘବ – ରାମଚନ୍ଦ୍ର (ରଘୁକୁଳରେ ଜାତ)
• କପି – ବାନର (ରାମଙ୍କ ସେନା)
• ରୁଦ୍ବବୁଦ – ପାଣି ଫୋଟକା (ପାଣିରେ ପଦାର୍ଥ ପଡ଼ିଲେ ଜଳର ରୁଦ୍ବବୁଦ)
• ଗିରି – ପର୍ବତ
• ସିକ୍ଷୁ – ସମୁଦ୍ର
• ଫିଫି କୃତ – ଫିଫି କାର ଶବ୍ଦ
• ବରୁଣ – ଜୁଲାଧିପତି
• ବିସ୍ତର – ବିସ୍ତାରେ/ଆଶୁର୍ଯ୍ୟାନ୍ୱିତ ହୋଇ
• ବିନାଶନରେ – ବିସ୍ଥୟରେ/ଆଶୂର୍ଯ୍ୟାନ୍ୱିତ ହୋଇ
• ବିନାଶନରେ – ବିନା ଅଶନରେ ଅର୍ଥାତ୍ ଅନାହାରରେ
• ଗର୍ଭ – କୁଶ
• ବୁଧେ – ପଠାଇଲା
• ଶୁକ, ପାରଣ – ରାବଣର ଦୁଇ ମନ୍ତ୍ରୀ (ଏମାନେ ପକ୍ଷୀ ରୂପ ଧାରଣ କରି ସାୟା ରଚନାରେ ସମର୍ଥ)
• ବିଭୂତି – ଐଶର୍ଯ୍ୟ
• ଚାର – ହୃତ
• ବିଭୂତିଭୂଷଣ – ଭସ୍ମଭୂଷଣ ଏଠରେ ରାମଚନ୍ଦ୍ରଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ କଥିତ
• ବାଦ ରଚାଇ – କଳହ ଷଷ୍ଠି କରି
• ଅଙ୍ଗଦ – କିମ୍ନିଯ୍ୟାର ରାଜା ବାଳାଙ୍କ ପୁତ୍ର
• ପିତୃବ୍ୟ – ରାଜାଙ୍କର ସାନଭାଇ/ଦାଦା ବା ଖୁଡୁତା
• ବିହାୟ ସେ – ଆକାଶରେ
• ବିହରି – ଭ୍ରମଣ କରି
• ବର୍ତ୍ତିକ – ଟେଣ୍ଟେଇ ବା ଟିଙ୍କିଭ ପକ୍ଷା/ବତକ
• ଧୃତ – ଧାରଣ କରି
• ସତ୍ୱର – ଶୀଘ୍ର
• ବିଂଶତିକର – ବିଂଶବାହୁ/ରାବଣ
• ତଳ – କରତାଳ, ଏଠାରେ ଚାପୁଡ଼ା ଅର୍ଥରେ ବ୍ୟବହୃତ
• ବିଖ୍ୟାତ କରୁ – ପ୍ରକାଶ କରିବାକୁ
• ବୋଧ – ଜାଣି
• ବିର୍ଯ୍ୟ – ପର୍ବତର ନାମ
• ତେବରିପୁ – ଦେବତାମାନଙ୍କ ଶତ୍ରୁ, ଏଠାରେ ରାବଣକୁ ବୁଝାଉଛି
• ଜଳିତ – ଫେରାଇ ଦେଉ
• ଶଙ୍ଖ – ସାମୁଦ୍ରିକ ଜୀବ
• ଚିତରଶେ – ପାରି ହେବାପାଇଁ
• ଅଙ୍ଗ ଦେବାରୁ – ଶରୀର ଦେବାରୁ
• ପାଞ୍ଚ – ଉପାୟ
• ଚଳ – ସୈନ୍ୟ
• ଚିହେ – ବିଧାନ କରେ
• ମନ୍ଦ – ଅଳ୍ପ
• ଚିରସ – ଦୁଃଖ/ବିମର୍ଷ
• ମନ୍ଦ – ଅଳ୍ପ
• ମନ୍ଦହାସ – ସ୍ଥିତହାସ/ଅଳ୍ପହସ
• ବୁଧେ – ପଶ୍ରିତ ମାନେ
• କୁଶ – ଏକପ୍ରକାର କୃଶବିଶେଷ

Odisha State Board BSE Odisha 10th Class History Important Questions Chapter 18 କୃଷିର ବିକାଶ Important Questions and Answers.

BSE Odisha Class 10 History Important Questions Chapter 18 କୃଷିର ବିକାଶ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୬୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧।. ସ୍ଵାଧୀନତା ପରବର୍ତ୍ତୀ କାଳରେ ଚାଷୀମାନଙ୍କ ସୁବିଧା ପାଇଁ ତତ୍‌କାଳୀନ ଓଡ଼ିଶା ସରକାର କ’ଣ କରିଥିଲେ ?
Answer:

• ସ୍ଵାଧୀନତା ପରବର୍ତ୍ତୀ କାଳରେ ଓଡ଼ିଶାର ତତ୍‌କାଳୀନ ମୁଖ୍ୟମନ୍ତ୍ରୀ ହରେକୃଷ୍ଣ ମହତାବ ଜମିଦାରୀ ପ୍ରଥା ଉଚ୍ଛେଦ କରିବାପାଇଁ ଓଡ଼ିଶା ବିଧାନସଭାରେ ଏକ ବିଧେୟକ ଆଗତ କରିଥିଲେ ।
• ପରେ ଷଷ୍ଠ ଦଶକରେ ଜମିଦାରୀ ପ୍ରଥା ଉଚ୍ଛେଦ ଆଇନ କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ।
• ଆଚାର୍ଯ୍ୟ ବିନୋବା ଭାବେଙ୍କ ଭୂଦାନ ଆନ୍ଦୋଳନ ମାଧ୍ୟମରେ ସଂଗୃହୀତ ଜମି ୧୯୫୫ ମସିହାରୁ ଚାଷୀମାନଙ୍କ ମଧ୍ୟରେ ବାଣ୍ଟି ଦିଆଗଲା ।
• ଆଦିବାସୀ କୃଷକମାନଙ୍କର ଜମି ଯେପରି ଅଣଆଦିବାସୀମାନେ ନେଇ ନ ଯାଆନ୍ତି ସେଥ୍ପାଇଁ ବ୍ୟବସ୍ଥା କରଯାଇଥିଲା ।
• ଭାଗଚାଷୀମାନଙ୍କର ସ୍ଵାର୍ଥର ସୁରକ୍ଷା କରାଯାଇଥିଲା ।

୨।. ‘ଟେଣ୍ଟ୍‌ ରିଲିଫ୍’ ସମ୍ପର୍କରେ ଏକ ସଂକ୍ଷିପ୍ତ ସୂଚନା ପ୍ରଦାନ କର ।
Answer:

• ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟ ସମୟରେ ଲୋକମାନଙ୍କୁ କାମଧନ୍ଦା ଯୋଗାଇ ଦେବାପାଇଁ ସରକାର ‘ଟେଷ୍ଟ୍ ରିଲିଫ୍’ କାର୍ଯ୍ୟ ପ୍ରକ୍ରିୟା ଆରମ୍ଭ କରିଥିଲେ ।
• ଏହି କାର୍ଯ୍ୟ ବ୍ୟବସ୍ଥା ସରକାରୀ ଅର୍ଥରେ କାର୍ଯ୍ୟକାରୀ ହୁଏ ।
• ଏହା ବିଶେଷ କରି ଗାଁଗହଳିରେ କରାଯାଇଥାଏ ।
• ଲୋକମାନେ ରାସ୍ତାଘାଟ, ପୋଖରୀ ଖୋଳା ପ୍ରଭୃତି କାମରେ ଶ୍ରମଦାନ କରନ୍ତି ଓ ଶ୍ରମଦାନ ବଦଳରେ ସେମାନଙ୍କୁ ଅର୍ଥ ବା ଖାଦ୍ୟଶସ୍ୟ ମିଳେ ।
• ‘ରିଲିଫ୍’ ଭଳି ଏହା ଏକ ମାଗଣା ପ୍ରାପ୍ତି ବ୍ୟବସ୍ଥା ନୁହେଁ ।

୩।. ଓଡ଼ିଶାର ସର୍ବବୃହତ୍ ବହୁମୁଖୀ ଯୋଜନା କାହାକୁ କୁହାଯାଏ ? ଏହି ଯୋଜନା ସମ୍ବନ୍ଧରେ ଏକ ସଂକ୍ଷିପ୍ତ ସୂଚନା ପ୍ରଦାନ କର ।
Answer:

• ଓଡ଼ିଶାରେ ଜଳସେଚନ ଓ ବନ୍ୟା ନିୟନ୍ତ୍ରଣ ପାଇଁ ସର୍ବବୃହତ୍ ବହୁମୁଖୀ ନଦୀବନ୍ଧ ଯୋଜନା ହେଉଛି ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନା ।
• ମହାନଦୀ ତ୍ରିକୋଣଭୂମି ଅଞ୍ଚଳରେ ବନ୍ୟା ନିୟନ୍ତ୍ରଣ କରିବା, ସମ୍ବଲପୁର, ବଲାଙ୍ଗୀର ଜିଲ୍ଲାରେ ଜଳସେଚନର ବ୍ୟବସ୍ଥା କରିବା ଓ ଜଳବିଦ୍ୟୁତ୍ ଶକ୍ତି ଉତ୍ପାଦନ କରିବା ଏହି ଯୋଜନାର ଉଦ୍ଦେଶ୍ୟ ଥିଲା ।
• ଏହାର କାର୍ଯ୍ୟ ୧୯୪୮ ମସିହାରେ ଆରମ୍ଭ ହୋଇ ୧୯୫୬ ମସିହାରେ ଶେଷ ହୋଇଥିଲା ।
• ଏହି ଜଳଭଣ୍ଡାରରେ ମାଛ ଚାଷ କରିବା ଥିଲା ଅନ୍ୟ ଏକ ଉଦ୍ଦେଶ୍ୟ ।
• ଏହି ଯୋଜନାଟି କେନ୍ଦ୍ରୀୟ ଜଳ ଆୟୋଗଦ୍ଵାରା ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ?

କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୩୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧। କୃଷି ଗବେଷଣା କେନ୍ଦ୍ର ଓ ପ୍ରୟୋଗଶାଳା କାହିଁକି ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
Answer:

• କୃଷି ସମ୍ବନ୍ଧୀୟ ଜ୍ଞାନ କୃଷକମାନଙ୍କ ନିକଟରେ ପହଞ୍ଚାଇବାପାଇଁ ସରକାର ଅନେକ କୃଷି ଗବେଷଣା କେନ୍ଦ୍ର ସ୍ଥାପନ କରିଥିଲେ ।
• ଜମିର ଉର୍ବରତା ବଜାୟ ରଖିବାପାଇଁ ଓଡ଼ିଶା ସରକାର ବିଭିନ୍ନ ପ୍ରୟୋଗଶାଳା ପ୍ରତିଷ୍ଠା କରିଥିଲେ ।
• ଆଧୁନିକ ପ୍ରଣାଳୀରେ କୃଷି ପାଇଁ ପ୍ରଦର୍ଶନୀ କୃଷିକ୍ଷେତ୍ରମାନ ପ୍ରସ୍ତୁତ କରାଗଲା ।

୨।. ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ଭାରତରେ କିଏ, କେବେ ଆରମ୍ଭ କରିଥିଲେ ? ଏହାର ଖସଡ଼ା କିଏ ପ୍ରସ୍ତୁତ କରିଥିଲେ ?
Answer:

• ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ଭାରତରେ ଲର୍ଡ଼ କର୍ଡୱାଲିସ୍ ପ୍ରଚଳନ କରିଥିଲେ ।
• ଏହା ୧୭୯୩ ମସିହାରେ ଆରମ୍ଭ କରାଯାଇଥିଲା ।
• ଏହି ବନ୍ଦୋବସ୍ତର ଖସଡ଼ା ପ୍ରସ୍ତୁତ କରିଥିଲେ ସାର୍ ଜନ୍ ସୋର୍ ।

୩ । ସମବାୟ ବ୍ୟାଙ୍କ କାହିଁକି ପ୍ରତିଷ୍ଠା କରାଗଲା ? ଏହା କେବେ ଓ କିପରି ପ୍ରତିଷ୍ଠା କରାଗଲା.?
Answer:

• କୃଷକମାନଙ୍କୁ ଚାଷକାର୍ଯ୍ୟ ଆରମ୍ଭ ସମୟରେ ସ୍ଵଳ୍ପ ସୁଧହାରରେ ଋଣ ଯୋଗାଇ ଦେବାପାଇଁ ସମବାୟ ବ୍ୟାଙ୍କ ପ୍ରତିଷ୍ଠା କରାଗଲା ।
• ଏହା ୧୯୪୮ ମସିହାରେ ପ୍ରତିଷ୍ଠିତ ହେଲା ।
• ସରକାରୀ ମୂଳଧନରେ ଏହି ବ୍ୟାଙ୍କ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।

୪।. ଓଡ଼ିଶାର କୃଷକମାନେ ଏବେ ମଧ୍ୟ ସମସ୍ୟା ଘେରରେ ରହିଛି କିପରି ? ଏହାର ସମାଧାନର ପନ୍ଥା କ’ଣ ?
Answer:

• ଏବେବି ବନ୍ୟା, ମରୁଡ଼ି ଓ ବାତ୍ୟା ଓଡ଼ିଶାର କୃଷକମାନେ ପାଇଁ ସମସ୍ୟା ସୃଷ୍ଟି କରୁଛି ।
• କୃଷକର ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଠିକ୍ ମୂଲ୍ୟରେ ବିକ୍ରି ହୋଇପାରୁ ନାହିଁ । ଅଭାବୀ ବିକ୍ରିଦ୍ୱାରା ଠିକ୍ ମୂଲ୍ୟ ନ ପାଇବାରୁ ତା’ର ଆର୍ଥିକ ସ୍ଥିତି ଦୋହଲି ଯାଉଛି ।
• ଏସବୁ ସମସ୍ୟା ଘେରରୁ କୃଷକମାନଙ୍କୁ ଉଦ୍ଧାର କରିବାପାଇଁ କୃଷିର ଉନ୍ନତି ତଥା ଗ୍ରାମାଞ୍ଚଳର ବିକାଶ ପାଇଁ ଦୃଷ୍ଟି ଦେବା ନିତାନ୍ତ ଆବଶ୍ୟକ ।

ସଂଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୨୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।

୧। ଭୂଦାନ ଆନ୍ଦୋଳନରେ ମୁଖ୍ୟ ପୁରୋଧା କିଏ ଥିଲେ ଓ ତାଙ୍କର ମୂଳ ନାମ କ’ଣ ଥିଲା ?
Answer:

• ଭୂଦାନ ଆନ୍ଦୋଳନର ମୁଖ୍ୟ ପୁରୋଧା ଥିଲେ ଆଚାର୍ଯ୍ୟ ବିନୋବା ଭାବେ ।
• ତାଙ୍କର ମୂଳ ନାମ ଥିଲା ବିନାୟକ ନରହରି ଭାବେ ।

୨।.‘ଟେଷ୍ଟ୍ ରିଲିଫ୍’ କ’ଣ ? ଏହା ରିଲିଫ୍‌ଠାରୁ କିପରି ଭିନ୍ନ ?
Answer:

• ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟ ସମୟରେ ଲୋକମାନଙ୍କୁ କାମଧନ୍ଦା ଯୋଗାଇ ଦେବାପାଇଁ ସରକାର ‘ଟେଷ୍ଟ ରିଲିଫ୍’ କାର୍ଯ୍ୟ ପ୍ରକ୍ରିୟା ଆରମ୍ଭ କରିଥିଲେ ।
• ରିଲିଫ୍’ ବ୍ୟବସ୍ଥାରେ ମାଗଣାରେ ଲୋକମାନଙ୍କୁ ଦ୍ରବ୍ୟ ଓ ଟଙ୍କା ବିତରଣ କରାଯାଏ; ମାତ୍ର ଟେଷ୍ଟ୍ ରିଲିଫ୍ ଏକ ମାଗଣା ପ୍ରାପ୍ତି ବ୍ୟବସ୍ଥା ନୁହେଁ, ବରଂ ଏଥ‌ିରେ ଶ୍ରମଦାନ ବଦଳରେ ଅର୍ଥ ବା ଖାଦ୍ୟଶସ୍ୟ ପ୍ରଦାନ କରାଯାଏ ।

୩। ହୀରାକୁଦ ବ୍ୟତୀତ ଓଡ଼ିଶାରେ ଆଉ କେଉଁସବୁ ଜଳସେଚନ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହେଉଛି ?
Answer:

• ହୀରାକୁଦ ବ୍ୟତୀତ ଆନ୍ଧ୍ରପ୍ରଦେଶର ସହଯୋଗରେ ମାଛକୁଣ୍ଡ ଯୋଜନା, କୋରାପୁଟର ଅପର କୋଲାବ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହେଉଛି ।
• ଏହା ବ୍ୟତୀତ ଇନ୍ଦ୍ରାବତୀ ଯୋଜନା, ରେଙ୍ଗାଲି-ଭୀମକୁଣ୍ଡ ଯୋଜନା ମଧ୍ୟ କାର୍ଯ୍ୟକାରୀ ହେଉଛି ।

୪।. ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନା କାହାଦ୍ଵାରା ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ଅଞ୍ଚଳର ବନ୍ୟା ନିୟନ୍ତ୍ରଣ କରିବାପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଥିଲା ?
Answer:

• ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନାଟି କେନ୍ଦ୍ରୀୟ ଜଳ ଆୟୋଗଦ୍ଵାରା ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ।
• ଏହି ଯୋଜନାଟି ମହାନଦୀ ତ୍ରିକୋଣଭୂମି ଅଞ୍ଚଳରେ ବନ୍ୟା ନିୟନ୍ତ୍ରଣ କରିବାପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଥିଲା ।

୫।. କୌଶଲ୍ୟାଗଙ୍ଗଠାରେ କେଉଁ ଦୁଇଟି କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:

• କୌଶଲ୍ୟାଗଙ୍ଗଠାରେ ପ୍ରଥମତଃ ଏକ କେନ୍ଦ୍ରୀୟ ମଧୁରଜଳ ମତ୍ସ୍ୟଚାଷ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
• ଦ୍ଵିତୀୟତଃ ସେଠାରେ ରାଜ୍ୟ ସରକାରଙ୍କ କୃଷି ଗବେଷଣା କେନ୍ଦ୍ର ମଧ୍ୟ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।

୬।. ଓଡ଼ିଶାରେ କୃଷି ବିଜ୍ଞାନ କେନ୍ଦ୍ରମାନ କେବେ ଓ କ’ଣ ପାଇଁ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:

• ୧୯୭୬ ମସିହାରୁ ଓଡ଼ିଶାରେ ଅନେକ କୃଷି ବିଜ୍ଞାନ କେନ୍ଦ୍ରମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
• ଆଖପାଖ ଅଞ୍ଚଳର କୃଷକମାନଙ୍କ ଦିଗ୍‌ଦର୍ଶନ ଦେବା ଉଦ୍ଦେଶ୍ୟରେ ଏଗୁଡ଼ିକ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।

Objective Type Questions With Answers
A. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।

1. ଓଡ଼ିଶାର ଅଧିକାଂଶ ଲୋକଙ୍କର ପ୍ରମୁଖ ଜୀବିକା କ’ଣ ଥିଲା ?
Answer:
କୃଷି ଓଡ଼ିଶାର ଅଧିକାଂଶ ଲୋକଙ୍କର ମୁଖ୍ୟ ଜୀବିକା ଥିଲା ।

2. ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ଆମ ଦେଶରେ କେବେ ଆରମ୍ଭ କରାଯାଇଥିଲା ?
Answer:
ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ଲର୍ଡ଼ କର୍ଡୱାଲିସ୍ ୧୭୯୩ ମସିହାରେ ଆମ ଦେଶରେ ଆରମ୍ଭ କରିଥିଲେ ।

3. ଭୂଦାନ ଆନ୍ଦୋଳନରେ କେଉଁ କାର୍ଯ୍ୟ କରାଯାଇଥିଲା ?
Answer:
୧୯୫୫ ମସିହାରେ ଭୂଦାନ ଆନ୍ଦୋଳନରେ ସଂଗୃହୀତ ଜମିଗୁଡ଼ିକୁ ଚାଷୀମାନଙ୍କ ମଧ୍ୟରେ ବାଣ୍ଟି ଦିଆଯାଇଥିଲା ।

4. କେବେଠାରୁ ଗୋତି ଶ୍ରମିକ ପ୍ରଥା ଉଚ୍ଛେଦ କରାଯାଇଥିଲା ?
Answer:
୧୯୪୮ ମସିହାରେ ଗୋତି ଶ୍ରମିକ ପ୍ରଥା ଉଚ୍ଛେଦ କରାଯାଇଥିଲା ।

5. ଆମ ରାଜ୍ୟରେ ସମବାୟ ସଂସ୍ଥାମାନ କ’ଣ ପାଇଁ ଗଠନ କରାଯାଇଥିଲା ?
Answer:
କୃଷକମାନଙ୍କୁ ଚାଷକାର୍ଯ୍ୟ ଆରମ୍ଭ ସମୟରେ ସ୍ୱଳ୍ପ ସୁଧହାରରେ ଋଣ ଯୋଗାଇ ଦେବାପାଇଁ ସମବାୟ ସଂସ୍ଥାମାନ ଗଠନ କରାଯାଇଥିଲା ।

6. ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନା କ’ଣ ପାଇଁ କରାଯାଇଥିଲା ?
Answer:
ଜଳସେଚନ ଓ ବନ୍ୟା ନିୟନ୍ତ୍ରଣ ପାଇଁ ଓଡ଼ିଶାରେ ସର୍ବବୃହତ୍ ହୀରାକୁଦ ବହୁମୁଖୀ ନଦୀବନ୍ଧ ଯୋଜନା କରାଯାଇଥିଲା ।

7. ଓଡ଼ିଶାରେ ହୀରାକୁଦ ବ୍ୟତୀତ ଆଉ କେତୋଟି ନଦୀବନ୍ଧ ଯୋଜନାର ନାମ ଲେଖ ।
Answer:
ଆନ୍ଧ୍ରପ୍ରଦେଶ ସହଯୋଗରେ ମାଛକୁଣ୍ଡ ଯୋଜନା, କୋରାପୁଟର ଅପର କୋଲାବ ଯୋଜନା, ଇନ୍ଦ୍ରାବତୀ ଯୋଜନା, ରେଙ୍ଗାଲି, ଭୀମକୁଣ୍ଡ ଯୋଜନା ଓଡ଼ିଶାରେ କାର୍ଯ୍ୟକାରୀ ହେଉଛି ।

8. ଓଡ଼ିଶା ସରକାର କୃଷି ବ୍ୟତୀତ ଆଉ କେଉଁସବୁ କାର୍ଯ୍ୟକୁ ପ୍ରୋତ୍ସାହନ ଯୋଗାଇ ଆସୁଛନ୍ତି ?
Answer:
କୃଷି ବ୍ୟତୀତ ଓଡ଼ିଶା ସରକାର ଗୋପାଳନ, ମତ୍ସ୍ୟଚାଷ, କୁକୁଡ଼ା ପାଳନ ପ୍ରଭୃତି କାର୍ଯ୍ୟକୁ ପ୍ରୋତ୍ସାହନ ଯୋଗାଇ ଆସୁଛନ୍ତି ।

9. ପଶୁମାନଙ୍କର ସୁରକ୍ଷା ପାଇଁ ସରକାର କେବେ ଆଇନ ପ୍ରଣୟନ କରିଥିଲେ ?
Answer:
ପଶୁମାନଙ୍କୁ ସଂକ୍ରାମକ ରୋଗରୁ ରକ୍ଷା କରିବାପାଇଁ ୧୯୪୯ ମସିହାରେ ସରକାର ଏକ ଆଇନ ପ୍ରଣୟନ କରିଥିଲେ ।

10. ଓଡ଼ିଶାର କୃଷକମାନଙ୍କର ମୁଖ୍ୟ ସମସ୍ୟାଗୁଡ଼ିକ କ’ଣ ?
Answer:
ଓଡ଼ିଶାର କୃଷକମାନେ ଏବେ ବନ୍ୟା, ମରୁଡ଼ି ଓ ବାତ୍ୟା ଭଳି ସମସ୍ୟାର ସମ୍ମୁଖୀନ ହେଉଛନ୍ତି ।

11. କୃଷକମାନଙ୍କୁ ପ୍ରଶିକ୍ଷଣ ଓ ଦିଗ୍‌ଦର୍ଶନ ଦେବାରେ କେଉଁ ଅନୁଷ୍ଠାନ କାର୍ଯ୍ୟ କରିଥାଏ ?
Answer:
‘ଓଡ଼ିଶା କୃଷି ଓ ବୈଷୟିକ ବିଶ୍ୱବିଦ୍ୟାଳୟ’ କୃଷକମାନଙ୍କୁ ପ୍ରଶିକ୍ଷଣ ଓ ଦିଗ୍‌ଦର୍ଶନ ଦେବାରେ ସାହାଯ୍ୟ କରିଥାଏ ।

12. କେବେଠାରୁ ଓଡ଼ିଶାରେ ଅନେକ କୃଷି ବିଜ୍ଞାନ କେନ୍ଦ୍ରମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:
୧୯୭୬ ମସିହାଠାରୁ ଓଡ଼ିଶାରେ ଅନେକ କୃଷିବିଜ୍ଞାନ କେନ୍ଦ୍ରମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।

B. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।

1. ବନ୍ୟାଦାଉରୁ ଫସଲକୁ ରକ୍ଷା କରିବା ପାଇଁ କ’ଣ ତିଆରି କରାଗଲଶ ?
Answer:
ଲୁଣି ଓ ନଦୀ ବନ୍ଧ

2. ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନା କାହାଦ୍ବାରା କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ?
Answer:
କେନ୍ଦ୍ରୀୟ ଜଳ ଆୟୋଗ

3. ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ଖସଡ଼ା କିଏ ପ୍ରସ୍ତୁତ କରିଥିଲେ ?
Answer:
ସାର୍ ଜନ୍ ସୋର୍

4. ବିନୋବା ଭାବେଙ୍କ ମୂଳ ନାମ କ’ଣ ଥିଲା ?
Answer:
ବିନାୟକ ନରହରି ଭାବେ

5. ଜମିଦାରୀ ଉଚ୍ଛେଦ ଆଇନ କେଉଁ ଦଶକରେ କାର୍ଯ୍ୟକାରୀ ହୋଇଥିଲା ?
Answer:
ଷଷ୍ଠ

6. ଭୂଦାନ ଆନ୍ଦୋଳନ ସମୟରେ ବିନୋବା ଭାବେ ଯେଉଁ ଜମି ସଂଗ୍ରହ କରିଥିଲେ ତାକୁ ଚାଷୀମାନଙ୍କୁ କେବେ ବାଣ୍ଟି ଦିଆଯାଇଥିଲା ?
Answer:
୧୯୫୫

7. ଟେଷ୍ଟ ରିଲିଫ୍ ଯୋଜନାରେ ଶ୍ରମଦାନ ବଦଳରେ କ’ଣ ପ୍ରଦାନ କରାଯାଏ ?
Answer:
ଅର୍ଥ ବା ଶସ୍ୟଦାନ

8. ଜମିର ଉର୍ବରତା ବଜାୟ ରଖିବା ପାଇଁ ସରକାର କେଉଁଗୁଡ଼ିକ ପ୍ରତିଷ୍ଠା କରିଥିଲେ ?
Answer:
ପୁୟୋଗଶାଳା

9. ମହାନଦୀ ତ୍ରିକୋଣଭୂମି ଅଞ୍ଚଳରେ ବନ୍ୟା ନିୟନ୍ତ୍ରଣ କେଉଁ ଯୋଜନା ମାଧ୍ୟମରେ କରାଯାଇ ପାରିଛି ?
Answer:
ହୀରାକୁଦ ଡ୍ୟାମ୍

10. ଗାଁ ଗହଳରେ ପଶୁଡାକ୍ତରମାନଙ୍କୁ ନିଯୁକ୍ତି ଦିଆଯିବାର ଉଦ୍ଦେଶ୍ୟ କ’ଣ ଥିଲା ?
Answer:
ଗୋଧନର ସୁରକ୍ଷା

11. ଜଳସେଚନ ସୁବିଧା ନ ଥ‌ିବା ସ୍ଥାନରେ କି ବ୍ୟବସ୍ଥା କରାଗଲା ?
Answer:
ଉଠା ଜଳସେଚନ

12. ଆମ ରାଜ୍ୟରେ କୃଷିର ବିକାଶ ପାଇଁ କେତୋଟି ନିର୍ଦ୍ଦେଶାଳୟ କାର୍ଯ୍ୟ କରୁଅଛି ?
Answer:
୪ଗୋଟି

13. ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ କିଏ ପ୍ରଚଳନ କରିଥିଲେ ?
Answer:
ଲର୍ଡ଼ କଣ୍ଠୱାଲିସ୍

14. ରିଲିଫ୍ ଏକ କେଉଁ ପ୍ରକାର ବ୍ୟବସ୍ଥା ?
Answer:
ମାଗଣା ପ୍ରାପ୍ତି ବ୍ୟବସ୍ଥା

15. ଅଧ୍ବକ ଖାଦ୍ୟଶସ୍ୟ ଉତ୍ପାଦନ କର’ ଯୋଜନାରେ କେଉଁ ଜମିକୁ ଚାଷୋପଯୋଗୀ କରାଗଲା ?
Answer:
ପତିତ ଜମି

C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ଭୂଦାନ ଆନ୍ଦୋଳନରୁ ସଂଗୃହୀତ ଜମିକୁ ______________ ମସିହାରେ ଚାଷୀମାନଙ୍କୁ ବାଣ୍ଟି ଦିଆଯାଇଥିଲା ।
Answer:
୧୯୫୫

2. ଆଚାର୍ଯ୍ୟ ବିନୋବୀ ଭାବେ _________________ ଆନ୍ଦୋଳନର ପୁରୋଧା ଥ୍ ଲେ।
Answer:
ଭୂଦାନ

3. ପ୍ରାକୃତିକ ବିପର୍ଯ୍ୟୟ ଯୋଗୁଁ କ୍ଷତିଗ୍ରସ୍ତ କୃଷକମାନଙ୍କୁ ________________ ଋଣ ଦିଆଯାଇଥାଏ ।
Answer:
ତକାଭି

4. ‘ଅଧ୍ଵ ଖାଦ୍ୟଶସ୍ୟ ଉତ୍ପାଦନ କର’ ଯୋଜନାରେ _________________ ଜମିକୁ ଚାଷୋପଯୋଗୀ କରାଯାଇଥାଏ ।
Answer:
ପତିତ

5. ଜମିର ଉର୍ବରତା ବଜାୟ ରଖୁବାପାଇଁ ଓଡ଼ିଶା ସରକାର ବିଭିନ୍ନ __________________ ପ୍ରତିଷ୍ଠା କରିଥିଲେ ।
Answer:
ପୁୟୋଗଶାଳା

6. ଜଳସେଚନ ଓ ବନ୍ୟା ନିୟନ୍ତ୍ରଣ ପାଇଁ ଓଡ଼ିଶାରେ _______________ ନଦୀବନ୍ଧ ନିର୍ମାଣ କରାଯାଇଛି ।
Answer:
ହାରାକୁଦ

7. __________________ ମସିହାରେ ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନା କାର୍ଯ୍ୟ ସମାପ୍ତ ହୋଇଥିଲା ।
Answer:
୧୯୫୬

8. ମାଛକୁଣ୍ଡ ଯୋଜନା __________________ ରାଜ୍ୟର ସହଯୋଗରେ ନିର୍ମାଣ କରାଯାଇଛି ।
Answer:
ଆନ୍ଧ୍ରପ୍ରଦେଶ

9. ଜଳସେଚନ ସୁବିଧା ନଥ‌ିବା ସ୍ଥାନମାନଙ୍କରେ _____________________ ଜଳସେଚନର ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
Answer:
ଉଠା

10. ଗୋଧନର ସୁରକ୍ଷାପାଇଁ ଗାଁ ଗହଳରେ ________________ ଡାକୁରମାନଙ୍କ ନିପୁକି ମିଳିଛି ।
Answer:
ପଶୁ

11. ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟ ଠିକ୍ ମୂଲ୍ୟରେ ବିକ୍ରି ହୋଇନପାରିବାକୁ ________________ କୁହାଯାଏ ।
Answer:
ଅଭାବୀ ବିକ୍ରି

12. ଓଡ଼ିଶାରେ କୃଷିର ବିକାଶ ପାଇଁ କୃଷି ବିଭାଗ ଅଧୀନରେ ________________ ଟି ନିର୍ଦ୍ଦେଶାଳୟ କାର୍ଯ୍ୟ କରୁଛି ।
Answer:
୪

13. ପଶୁ ସମ୍ପଦର ଉନ୍ନତି ପାଇଁ _______________ ନିର୍ଦ୍ଦେଶାଳୟ କାର୍ଯ୍ୟ କରୁଛି ।
Answer:
ପଶୁଧନ

14. କେନ୍ଦ୍ରୀୟ ମଧୁର ଜଳ ମତ୍ସ୍ୟଚାଷ କେନ୍ଦ୍ର ___________________ ଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
କୌଶଲ୍ୟାଗଙ୍ଗ

15. ________________ ମସିହାଠାରୁ ରାଜ୍ୟରେ ଅନେକ କୃଷି ବିଜ୍ଞାନ କେନ୍ଦ୍ରମାନ ଖୋଲାଯାଇଛି ।
Answer:
୧୯୭୬

D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓) ଚିହ୍ନ ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (×) ଚିହ୍ନ ଦିଅ ।

1. ୧୯୫୪ ମସିହାରେ ଭୂଦାନ ଆନ୍ଦୋଳନର ସଂଗୃହୀତ ଜମି ବଣ୍ଟାଯାଇଥିଲା ।
Answer:
x

2. ଭୂଦାନ ଆନ୍ଦୋଳନର ମୁଖ୍ୟ ପୁରୋଧା ଥିଲେ ଆଚାର୍ଯ୍ୟ କୃପାଳିନୀ ।
Answer:
x

3. ସମବାୟ ସଂସ୍ଥାଦ୍ୱାରା ଚାଷୀମାନଙ୍କୁ ସ୍ୱଳ୍ପ ସୁଧହାରରେ ଋଣ ଯୋଗାଇ ଦିଆଗଲା ।
Answer:
✓

4. ୧୯୪୮ ମସିହାରେ ରାଜ୍ୟ ସମବାୟ ବ୍ୟାଙ୍କ୍ ପ୍ରତିଷ୍ଠା ହୋଇଥିଲା ।
Answer:
✓

5. ତକାଭି ଋଣ ଶିଳ୍ପପତିମାନଙ୍କୁ ପ୍ରଦାନ କରାଯାଇଥାଏ ।
Answer:
x

6. ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ୧୭୯୪ରେ ପ୍ରଚଳନ କରାଯାଇଥିଲା ।
Answer:
x

7. ଟେଷ୍ଟ ରିଲିଫ୍ରେ ବିପର୍ଯ୍ୟୟ ସମୟରେ ଲୋକମାନଙ୍କୁ କାମଧନ୍ଦା ଯୋଗାଇ ଦିଆଯାଏ ।
Answer:
✓

8. ଟେଷ୍ଟ ରିଲିଫ୍ କାର୍ଯ୍ୟ ବ୍ୟବସ୍ଥା ଯାହା ସରକାରୀ ଅର୍ଥରେ କାର୍ଯ୍ୟକାରୀ ହୁଏ ।
Answer:
✓

9.ଟେଷ୍ଟ ରିଲିଫ୍ କାର୍ଯ୍ୟ ବ୍ୟବସ୍ଥା ଯାହା ସରକାରୀ ଅର୍ଥରେ କାର୍ଯ୍ୟକାରୀ ହୁଏ ।
Answer:
x

10. ବିନ୍ୟାଦାଉରୁ ଫସଲକୁ ରକ୍ଷା କରିବାପାଇଁ ଲୁଣି ଓ ନଦୀବନ୍ଧମାନ ତିଆରି କରାଯାଇଛି ।
Answer:
✓

11. ଜଳସେଚନ ଓ ବନ୍ୟା ନିୟନ୍ତ୍ରଣ ପାଇଁ ଓଡ଼ିଶାରେ ହୀରାକୁଦ ନଦୀବନ୍ଧ ନିର୍ମାଣ କରାଯାଇଛି ।
Answer:
✓

12. ୧୯୫୬ ମସିହାରେ ହୀରାକୁଦ ନଦୀବନ୍ଧ ଯୋଜନା କାର୍ଯ୍ୟ ଆରମ୍ଭ ହୋଇଥିଲା ।
Answer:
x

13. ସାକ୍ଷୀଗୋପାଳଠାରେ ମତ୍ସ୍ୟ ଗବେଷଣା କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
x

14. ଜଳସେଚନ ସୁବିଧା ନ ଥିବା ସ୍ଥାନମାନଙ୍କରେ କେନାଲ ଜଳସେଚନ ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
Answer:
x

15. ହୀରାକୁଦ ନଦୀବନ୍ଧଦ୍ବାରା ସମ୍ବଲପୁର ଓ ବଲାଙ୍ଗୀର ଜିଲ୍ଲାରେ ଜଳସେଚନ କରାଯାଇଥାଏ ।
Answer:
✓

16. ପଶୁମାନଙ୍କୁ ସଂକ୍ରାମକ ରୋଗରୁ ରକ୍ଷା କରିବାପାଇଁ ୧୯୪୮ ମସିହାରେ ଏକ ଆଇନ ପ୍ରଣୟନ କରାଯାଇଛି ।
Answer:
x

17. ମହାନଦୀ, ଧାମରା, ସୁବର୍ଣ୍ଣରେଖା ଓ ଚିଲିକାରେ ମତ୍ସ୍ୟଜୀବୀମାନଙ୍କୁ ପ୍ରୋତ୍ସାହନ ଯୋଗାଇ ଦିଆଯାଉଛି ।
Answer:
✓

18. ‘ଅଭାବୀ ବିକ୍ରୀ’ ବ୍ୟବସାୟୀମାନଙ୍କ ପାଇଁ କ୍ଳେଶଦାୟକ ହୋଇଥାଏ ।
Answer:
x

19. କୌଶଲ୍ୟାଗଙ୍ଗଠାରେ ରାଜ୍ୟ ସରକାରଙ୍କର ଏକ କୃଷି ଗବେଷଣା କେନ୍ଦ୍ର ରହିଛି ।
Answer:
✓

20. ୧୯୭୬ ମସିହାରୁ ଅନେକ କୃଷି ବିଜ୍ଞାନ କେନ୍ଦ୍ର ଓଡ଼ିଶାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
Answer:
✓

21. ଓଡ଼ିଶାରେ କୃଷି ବିଭାଗ ଅଧୀନରେ ୩ ଗୋଟି ନିର୍ଦ୍ଦେଶାଳୟ କାର୍ଯ୍ୟ କରୁଅଛି ।
Answer:
x

22. ନ୍ଧ୍ରପ୍ରଦେଶ ସରକାରଙ୍କର ସହାୟତାରେ ମାଛକୁଣ୍ଡ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ।
Answer:
✓

E. ‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ମିଳନ କର ।