Odisha State Board CHSE Odisha Class 12 History Solutions Chapter 3 ଷୋଡ଼ଶ ମହାଜନପଦ Questions and Answers.
CHSE Odisha Class 12 History Chapter 3 Questions and Answers in Odia Medium
ବସ୍ତୁନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ସମ୍ଭାବ୍ୟ ଚାରୋଟି ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
୧ । ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ର ବାରାଣସୀ ନାମରେ ପରିଚିତ ?
(କ) କୋଶଳ
(ଖ) ମଗଧ
(ଗ) କାଶୀ
(ଘ)ଭଜ୍ୱ
Answer:
(ଗ) କାଶୀ
୨। ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ରର ରାଜଧାନୀ ଥିଲା ଶ୍ରାବସ୍ତୀ ?
(କ) କୋଶଳ
(ଖ) ଅଙ୍ଗ
(ଗ) କୁରୁ
(ଘ) ପାଞ୍ଚଳ
Answer:
(କ) କୋଶଳ
୩ । ଉତ୍ତର ପ୍ରଦେଶର ଆଧୁନିକ ଅଯୋଧ୍ୟାକୁ ନେଇ ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ର ଗଠିତ ହୋଇଥିଲା ?
(କ) ଅଙ୍ଗ
(ଖ) ମଗଧ
(ଗ) କୋଶଳ
(ଘ) ଚେଦୀ
Answer:
(ଗ) କୋଶଳ
୪ । ଚମ୍ପା ନିମ୍ନୋକ୍ତ କେଉଁ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ?
(କ) ଅଙ୍ଗ
(ଖ) ଚେଦୀ
(ଗ) ମଗଧ
(ଘ) ବତ୍ସ୍
Answer:
(କ) ଅଙ୍ଗ
![]()
୫। ରାଜଗୃହ କେଉଁ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ?
(କ) ଅଙ୍ଗ
(ଖ) ମଗଧ
(ଗ) କୋଶଳ
(ଘ) ଚେଦୀ
Answer:
(ଖ) ମଗଧ
୬। ଆଧୁନିକ ଦିଲ୍ଲୀ ଓ ମିରଟ ଜିଲ୍ଲାକୁ ନେଇ ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ର ଗଠିତ ହୋଇଥିଲା ?
(କ) କୁରୁ
(ଖ) ପାଞ୍ଚଳ
(ଗ) ମତ୍ସ୍ୟ
(ଘ) ସୁରସେନ
Answer:
(କ) କୁରୁ
୭। ଆଧୁନିକ ରୋହିଲାଖଣ୍ଡ ଅଞ୍ଚଳରେ ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ର ଗଠିତ ହୋଇଥିଲା ?
(କ) ମତ୍ସ୍ୟ
(ଖ) ସୁରସେନ
(ଗ) ପାଞ୍ଚଳ
(ଘ) ଆସାକା
Answer:
(ଗ) ପାଞ୍ଚାଳ
୮ । ବିରାଟ ନଗରୀ ନିମ୍ନୋକ୍ତ କେଉଁ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ?
(କ) ମତ୍ସ୍ୟ
(ଖ) ଆସାକା
(ଗ) ଅବନ୍ତୀ
(ଘ) କୋଶଳ
Answer:
(କ) ମତ୍ସ୍ୟ
![]()
୯ । ମଥୁରା କେଉଁ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ?
(କ) ସୁରସେନ
(ଖ) କୁରୁ
(ଗ) କୋଶଳ
(ଘ) କାଶୀ
Answer:
(କ) ସୁରସେନ
୧୦ । ଅବନ୍ତୀ ରାଷ୍ଟ୍ରର ପଡ଼ୋଶୀ ରାଷ୍ଟ୍ରର ନାମ କ’ଣ ଥିଲା ?
(କ) ଭଜି
(ଖ) ଆସାକା
(ଗ) ମଲ୍ଲ
(ଘ) ମତ୍ସ୍ୟ
Answer:
(ଖ) ଆସାକା
୧୧ । ପୋଟନା ନିମ୍ନୋକ୍ତ କେଉଁ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ?
(କ) ମତ୍ସ୍ୟ
(ଖ) ପାଞ୍ଚଳ
(ଗ) କୁରୁ
(ଘ) ଆସାକା
Answer:
(ଘ) ଆସାକା
୧୨ । ଆଧୁନିକ କାଶ୍ମୀର, ପାକିସ୍ତାନର ପେଶୱାର ଓ ରାଓଲପିଣ୍ଡି ଜିଲ୍ଲାକୁ ନେଇ ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ର ଗଠିତ ହୋଇଥିଲା ?
(କ) କମ୍ବୋଜ
(ଖ) ମଗଧ
(ଗ) ଗାନ୍ଧାର
(ଘ) ତକ୍ଷଶିଳା
Answer:
(ଗ) ଗାନ୍ଧାର
୧୩ । ତକ୍ଷଶିଳା କେଉଁଥିପାଇଁ ପ୍ରସିଦ୍ଧ ?
(କ) ବାଣିଜ୍ୟକେନ୍ଦ୍ର
(ଖ) ଶିକ୍ଷାକେନ୍ଦ୍ର
(ଗ) ତୀର୍ଥସ୍ଥାନ
(ଘ) ବୃଦ୍ଧଙ୍କ ଜନ୍ମସ୍ଥାନ
Answer:
(ଖ) ଶିକ୍ଷାକେନ୍ଦ୍ର
![]()
୧୪ । ପୁଞ୍ଜୁସାତି କେଉଁ ରାଜ୍ୟର ରାଜା ଥିଲେ ?
(କ) ଗାନ୍ଧାର
(ଖ) କମ୍ବୋଜ
(ଗ) ମଗଧ
(ଘ) ବିଦେହ
Answer:
(କ) ଗାନ୍ଧାର
୧୫ । କପିଳବାସ୍ତୁ ଏକ ___________ ରାଷ୍ଟ୍ର ।
(କ) ଗଣତାନ୍ତ୍ରିକ
(ଖ) ରାଜତାନ୍ତ୍ରିକ
(ଗ) ଏକସଂଘୀୟ ରାଷ୍ଟ୍ର
(ଘ) ଦ୍ବି-ସଂଘୀୟ ରାଷ୍ଟ୍ର
Answer:
(କ) ଗଣତାନ୍ତ୍ରିକ
B. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
୧। କାଶୀ ଜନପଦ ଏକ _________ ରାଷ୍ଟ୍ର ଥିଲା ।
Answer:
ରାଜତାନ୍ତ୍ରିକ
୨ । ଅଙ୍ଗ ଜନପଦର ରାଜଧାନୀର ନାମ ଥିଲା ___________ ।
Answer:
ଚମ୍ପା
୩ । କୌଶାସ୍ତ୍ରୀ ____________ ର ରାଜଧାନୀ ଥିଲା ।
Answer:
ବସ ଜନପଦ
୪। ସୁରସେନ ଜନପଦରେ _____________ ବଂଶ ଶାସନ କରୁଥିଲେ ।
Answer:
ଯାଦବ
![]()
୫। ଆଧୁନିକ ____________ କୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ଅବନ୍ତୀ ରାଷ୍ଟ୍ର ।
Answer:
ମାଲୱା
C. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
୧। ମହାବୀରଙ୍କ ମାତା କେଉଁ ରାଜକନ୍ୟା ଥିଲେ ?
Answer:
ମହାବୀରଙ୍କ ମା’ ତ୍ରିଶଳା ଥିଲେ ଲିଚ୍ଛବୀ ରାଜକନ୍ୟା ।
୨ । ପୁରାତନ କାଶୀ ରାଷ୍ଟ୍ର ବର୍ତ୍ତମାନ କେଉଁ ନାମରେ ପରିଚିତ ?
Answer:
ପୁରାତନ କାଶୀ ରାଷ୍ଟ୍ର ବର୍ତ୍ତମାନ ବାରାଣସୀ ନାମରେ ପରିଚିତ ।
୩ । ମହାବୀରଙ୍କ ମାତା କେଉଁ ରାଜକନ୍ୟା ଥିଲେ ?
Answer:
ମହାବୀରଙ୍କ ମା’ ତ୍ରିଶଳା ଥିଲେ ଲିଚ୍ଛବୀ ରାଜକନ୍ୟା ।
୪। ଆସାକା ଜନପଦ କେଉଁ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ଥିଲା ?
Answer:
ଆସାକା ଜନପଦ ଗୋଦାବରୀ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ଥିଲା ।
![]()
D. ଭ୍ରମ ସଂଶୋଧନ କର ।
୧। ମହାବୀରଙ୍କ ମାତାଙ୍କ ନାମ ଥିଲା ମାୟାଦେବୀ ।
Answer:
ମହାବୀରଙ୍କ ମାତାଙ୍କ ନାମ ଥଲା ତ୍ରିଶିଳା ।
୨ । ବୌଦ୍ଧ ଧର୍ମର ପ୍ରତିଷ୍ଠାତା ଥିଲେ ମହାବୀର ।
Answer:
ବୌଦ୍ଧ ଧର୍ମର ପ୍ରତିଷ୍ଠାତା ଥିଲେ ଗୌତମ ବୁଦ୍ଧ ।
୩ । ବିମ୍ବିସାର କୋଶଳର ରାଜା ଥିଲେ ।
Answer:
ବିମ୍ବିସାର ମଗଧର ରାଜା ଥିଲେ ।
୪। କାଶୀର ଦକ୍ଷିଣରେ କୋଶଳ ରାଜ୍ୟ ଥିଲା ।
Answer:
କାଶୀର ଉତ୍ତରରେ କୋଶଳ ରାଜ୍ୟ ଥିଲା ।
୫। ‘ରାଜଗୃହ’ ପୁରାତନ କୋଶଳ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ।
Answer:
ରାଜଗୃହ ପୁରାତନ ମଗଧ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ।
![]()
ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ଦୁଇଟି / ତିନୋଟି ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
୧ । ‘ଅଙ୍ଗ’ ଜନପଦ କେଉଁଠି ଅବସ୍ଥିତ ଥିଲା ? ମଗଧର କେଉଁ ଶାସକ ଅଙ୍ଗ ରାଜ୍ୟକୁ ମଗଧରେ ଅନ୍ତର୍ଭୁକ୍ତ କରିଥିଲେ ?
Answer:
- ‘ଅଙ୍ଗ’ ଜନପଦ ମଗଧର ପଡ଼ୋଶୀ ରାଷ୍ଟ୍ର ରୂପେ ପୂର୍ବ ବିହାରରେ ଅବସ୍ଥିତ ଥିଲା ।
- ମଗଧର ରାଜା ବିମ୍ବିସାରଙ୍କ ସମୟରେ ଏହା ମଗଧରେ ଅନ୍ତର୍ଭୁକ୍ତ ହେଲା ।
୨ । ପୁରାତନ କୋଶଳ ରାଷ୍ଟ୍ର ବର୍ତ୍ତମାନର କେଉଁ ସ୍ଥାନରେ ଗଢ଼ିଉଠିଥିଲା ? ଏହାର ରାଜଧାନୀର ନାମ କ’ଣ ଥିଲା ?
Answer:
- ପୁରାତନ କୋଶଳ ରାଷ୍ଟ୍ର ଉତ୍ତର ପ୍ରଦେଶର ଆଧୁନିକ ଅଯୋଧ୍ୟାକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ।
- ଏହାର ରାଜଧାନୀ ଥିଲା ଶ୍ରାବସ୍ତୀ ।
୩ । ପୁରାତନ ମଗଧ ରାଷ୍ଟ୍ର ଆଧୁନିକ କେଉଁ ସ୍ଥାନକୁ ନେଇ ସୃଷ୍ଟି ହୋଇଥିଲା ? ଏହାର ପୁରାତନ ରାଜଧାନୀର ନାମ କ’ଣ ଥିଲା ?
Answer:
- ପୁରାତନ ମଗଧ ରାଷ୍ଟ୍ର ଆଧୁନିକ ପାଟନା ଓ ଗୟା ଜିଲ୍ଲାକୁ ନେଇ ସୃଷ୍ଟି ହୋଇଥିଲା ।
- ଏହା ପୁରାତନ ରାଜଧାନୀର ନାମ ଥିଲା ରାଜଗୃହ ।
୪ । ବସ୍ତ୍ର ରାଷ୍ଟ୍ର କେଉଁଠି ଅବସ୍ଥିତ ଥିଲା ? ଏହା କେଉଁ ଅଞ୍ଚଳକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ?
Answer:
- ‘ବସ’ ରାଷ୍ଟ୍ର ଅବନ୍ତୀ ରାଷ୍ଟ୍ରର ଉତ୍ତର-ପୂର୍ବ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ଥିଲା ।
- ଏହା ଆଲ୍ଲାହାବାଦ ଓ ତତ୍ସଂଲଗ୍ନ ଅଞ୍ଚଳକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ।
୫ | ଜନପଦ କେଉଁ ଅଞ୍ଚଳକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ? ଏହାର ପ୍ରସିଦ୍ଧ ସହର କ’ଣ ଥିଲା ?
Answer:
- ‘କୁରୁ ଜନପଦ’ ଆଧୁନିକ ଦିଲ୍ଲୀ ଓ ମିରଟ ଅଞ୍ଚଳକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ।
- ହସ୍ତିନାପୁର ଓ ଇନ୍ଦ୍ରପ୍ରସ୍ଥ ଏହାର ଦୁଇଟି ପ୍ରଧାନ ସହର ଥିଲା ।
![]()
୬। ପୁରାତନ ‘ଗାନ୍ଧାର’ ଜନପଦ କେଉଁ ଅଞ୍ଚଳକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ? ଏହାର ରାଜଧାନୀର ନାମ କ’ଣ ଥିଲା ?
Answer:
- ପୁରାତନ ଗାନ୍ଧାର ଜନପଦ ଆଧୁନିକ କାଶ୍ମୀର, ପାକିସ୍ତାନର ପେଶ୍ୱର ଓ ରାୱଲପିଣ୍ଡି ଜିଲ୍ଲାକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ।
- ଏହାର ରାଜଧାନୀର ନାମ ଥିଲା ତକ୍ଷଶିଳା ।
୭ । ପୁରାତନ କାଳରେ ମାନବ ସମାଜରେ କେତୋଟି ଜାତି ଥିଲା ? ସେଗୁଡ଼ିକର ନାମ କ’ଣ ଥିଲା ?
Answer:
- ପୁରାତନ କାଳରେ ମାନବ ସମାଜକୁ ଚାରିଗୋଟି ଜାତିରେ ବିଭକ୍ତ କରାଯାଇଥିଲା ।
- ସେମାନେ ଥିଲେ ବ୍ରାହ୍ମଣ, କ୍ଷତ୍ରିୟ, ବୈଶ୍ୟ ଓ ଶୂଦ୍ର ।
୮ | ଖ୍ରୀ.ପୂ. ଷଷ୍ଠ ଶତାବ୍ଦୀରେ କେତୋଟି ପ୍ରମୁଖ ଧର୍ମର ଆବିର୍ଭାବ ହୋଇଥିଲା ? ସେଗୁଡ଼ିକର ନାମ କ’ଣ ଥିଲା ?
Answer:
- ଖ୍ରୀ.ପୂ. ଷଷ୍ଠ ଶତାବ୍ଦୀରେ ଦୁଇଗୋଟି ପ୍ରମୁଖ ଧର୍ମର ଆବିର୍ଭାବ ହୋଇଥିଲା ।
- ସେଗୁଡ଼ିକର ନାମ ହେଲା ଜୈନଧର୍ମ ଓ ବୌଦ୍ଧଧର୍ମ ।
B. ପାଞ୍ଚଟି ଛଅଟି ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
୧। ଖ୍ରୀ.ପୂ. ଷଷ୍ଠ ଶତାବ୍ଦୀ କେଉଁ ତିନିଗୋଟି କାରଣରୁ ଗୁରୁତ୍ୱପୂର୍ଣ୍ଣ ଥିଲା ?
Answer:
ଖ୍ରୀ.ପୂ. ଷଷ୍ଠ ଶତାବ୍ଦୀ ନିମ୍ନୋକ୍ତ ତିନିଗୋଟି କାରଣରୁ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଥିଲା; ସେଗୁଡ଼ିକ ହେଲା –
- ଏହି ସମୟରେ ଭାରତରେ ୧୬ଟି ମହାଜନପଦ ବା ରାଷ୍ଟ୍ରର ଉତ୍ପତ୍ତି ହୋଇଥିଲା ।
- ଭାରତରେ ବୌଦ୍ଧଧର୍ମ ଓ ଜୈନଧର୍ମର ଆବିର୍ଭାବ ଘଟିଥିଲା ।
- ପୃଥିବୀରେ ବିଭିନ୍ନ ସ୍ଥାନରେ ଧର୍ମକ୍ଷେତ୍ରରେ ପରିବର୍ତ୍ତନ ଆସିଥିଲା । ଚୀରେ କନ୍ଫୁସିୟସ୍ ଓ ଲାଓସେଙ୍କ ଆବିର୍ଭାବ ଘଟିଥିଲା ।
![]()
୨ । ‘ମଗଧ’ ମହାଜନପଦର ନିମ୍ନୋକ୍ତ ତିନିଗୋଟି ମୁଖ୍ୟ କଥା ହେଲା ।
Answer:
- ମଗଧ ଏକ ସାମ୍ରାଜ୍ୟରେ ପରିଣତ ହୋଇଥିଲା ।
- ବିମ୍ବିସାର ଓ ଅଜାତଶତ୍ରୁ ଭଳି ବଳିଷ୍ଠ ରାଜାମାନେ ମଗଧକୁ ଏକ ସାମ୍ରାଜ୍ୟର ରୂପ ଦେଇଥିଲେ ।
- ଆଧୁନିକ ପାଟନା ଓ ଗୟା ଜିଲ୍ଲାକୁ ନେଇ ତତ୍କାଳୀନ ମଗଧ ରାଷ୍ଟ୍ର ଗଠିତ ହୋଇଥିଲା ।
୩ । କୁରୁ ରାଜ୍ୟ ସମ୍ପର୍କରେ ଲେଖ ।
Answer:
- କୁରୁ ରାଜ୍ୟ ସେତେବେଳେ ଆଧୁନିକ ଦିଲ୍ଲୀ ଓ ମିରଟକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା ।
- ହସ୍ତିନାପୁର ଓ ଇନ୍ଦ୍ରପ୍ରସ୍ଥ ଏହାର ପ୍ରଧାନ ସହର ଥିଲା ।
- କୁରୁ ରାଜ୍ୟ ଷଷ୍ଠ ଶତାବ୍ଦୀବେଳକୁ ଏହାର ଗୁରୁତ୍ଵ ହରାଇ ବସିଥିଲା ।
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ଖ୍ରୀଷ୍ଟପୂର୍ବ ଷଷ୍ଠ ଶତାବ୍ଦୀରେ ଭାରତର ରାଜନୈତିକ ଅବସ୍ଥା କିପରି ଥିଲା ତାହାର ସଂକ୍ଷିପ୍ତ ବିବରଣୀ ପ୍ରଦାନ କର ।
Answer:
ଖ୍ରୀ.ପୂ. ଷଷ୍ଠ ଶତାବ୍ଦୀରେ ଭାରତବର୍ଷ ଅନେକ ସ୍ବାଧୀନ ରାଷ୍ଟ୍ରରେ ବିଭକ୍ତ ହୋଇଥିଲା । ଏହି ସ୍ବାଧୀନ ରାଷ୍ଟ୍ରଗୁଡ଼ିକର ଶାସକମାନେ ନିଜ ନିଜର କ୍ଷମତା ତଥା ସାମ୍ରାଜ୍ୟ ବୃଦ୍ଧି ପାଇଁ ସଦାସର୍ବଦା ପରସ୍ପର ବିରୁଦ୍ଧରେ ଯୁଦ୍ଧରେ ଲିପ୍ତ ରହୁଥିଲେ । ଜୈନ ଭଗବତୀ ସୂତ୍ର ଏବଂ ବୌଦ୍ଧ ଅଙ୍ଗୁଭର ନିକାୟ ଗ୍ରନ୍ଥଦ୍ଵୟରୁ ଷୋହଳଟି ରାଷ୍ଟ୍ର ବା ମହାଜନପଦ ସମ୍ବନ୍ଧରେ ସୂଚନା ମିଳିଥାଏ । ଅଙ୍ଗୁରର ନିକାୟ ଓ ଅନ୍ୟାନ୍ୟ ବୌଦ୍ଧଗ୍ରନ୍ଥଗୁଡ଼ିକରୁ ସୂଚନା ମିଳେ ଯେ, ବୁଦ୍ଧଙ୍କ ଆବିର୍ଭାବ ଘଟିବା ପୂର୍ବରୁ ଏହି ସ୍ଵାଧୀନ ରାଷ୍ଟ୍ରଗୁଡ଼ିକର ପତନ ଘଟିଥିଲା । ଏହି ଷୋହଳଟି ମହାଜନପଦର ନାମ ହେଲା— କାଶୀ, କୋଶଳ, ଅଙ୍ଗ, ମଗଧ, ଭଜି ଗଣତନ୍ତ୍ର, ମଲ୍ଲ, ଚେଦୀ, ବତ୍ସ, କୁରୁ, ପାଞ୍ଚାଳ, ମତ୍ସ୍ୟ, ସୁରସେନ, ଆସାକା, ଗାନ୍ଧାର, ଅବନ୍ତୀ, କମ୍ବୋଜ ।
- କାଶୀ – ମହାଜନପଦଗୁଡ଼ିକ ମଧ୍ୟରେ କାଶୀ ଥିଲା ବିଶେଷ ଶକ୍ତିଶାଳୀ । ବାରାଣସୀ ଥୁଲା ଏହାର ରାଜଧାନୀ । କାଶୀର ରାଜା ବ୍ରହ୍ମଦତ୍ତ କୋଶଳ ଅଧିକାର କରିଥିବାର ଜଣାଯାଏ । କାଳକ୍ରମେ କାଶୀ ରାଜ୍ୟର ସମୃଦ୍ଧିରେ ଈର୍ଷାନ୍ବିତ ହୋଇ ଅନ୍ୟାନ୍ୟ ମହାଜନପଦଗୁଡ଼ିକ ତାହାର ବିରୋଧ କରିଥିଲେ ଏବଂ କ୍ରମାଗତ ସଂଘର୍ଷ ତଥା ଯୁଦ୍ଧ ଯୋଗୁ କାଶୀ ରାଜ୍ୟର ପତନ ଘଟିଥିଲା ।
- କୋଶଳ – ଆଧୁନିକ ଅଯୋଧ୍ୟା ଅଞ୍ଚଳକୁ ନେଇ କୋଶଳ ରାଜ୍ୟ ଗଠିତ ହୋଇଥିଲା । ଗୋମତୀ ଓ ସର୍ପିକ ନଦୀଦ୍ୱୟ ଏହି ରାଜ୍ୟର ଯଥାକ୍ରମେ ଦକ୍ଷିଣ ଓ ପୂର୍ବରେ ସୀମା ନିର୍ଦ୍ଧାରଣ କରୁଥିଲେ । ଶ୍ରାବସ୍ତୀ ଥିଲା ଏହାର ରାଜଧାନୀ ଏବଂ ପ୍ରଧାନ ସହର । କ୍ରମେ କୋଶଳ ଓ ମଗଧ ମଧ୍ୟରେ ନିଜ ନିଜର ରାଜନୈତିକ ପ୍ରାଧାନ୍ୟ ପାଇଁ ତୀବ୍ର ପ୍ରତିଦ୍ବନ୍ଦିତାର ସୂତ୍ରପାତ ହୋଇଥିଲା । ପରବର୍ତ୍ତୀ କାଳରେ କୋଶଳ ମଗଧର ଅଂଶବିଶେଷରେ ପରିଣତ ହୋଇଥିଲା ।
![]()
- ଅଙ୍ଗ – ମଗଧ ରାଜ୍ୟର ପୂର୍ବରେ ଅଙ୍ଗ ରାଜ୍ୟ ଅବସ୍ଥିତ ଥିଲା । ଚମ୍ପା ନଦୀ ଥିଲା ଅଙ୍ଗ ଓ ମଗଧରାଜ୍ୟ ଦ୍ଵୟର ସୀମାରେଖା । ଚମ୍ପା ନଗରୀ ଅଙ୍ଗ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା । ଏହା ଏକ ବାଣିଜ୍ୟ ଓ ବ୍ୟବସାୟର କେନ୍ଦ୍ରସ୍ଥଳୀ ଥିଲା । ଅଙ୍ଗ ଓ ମଗଧ ରାଜ୍ୟଦ୍ୱୟ ମଧ୍ୟରେ ତୀବ୍ର ପ୍ରତିଦ୍ବନ୍ଦିତା ଲାଗି ରହିଥିଲା । ପରିଶେଷରେ ମଗଧର ରାଜା ବିମ୍ବିସାର ଅଙ୍ଗ ରାଜ୍ୟକୁ ନିଜ ସାମ୍ରାଜ୍ୟଭୁକ୍ତ କରିଥିଲେ ।
- ମଗଧ – ଆଧୁନିକ ପାଟଣା ଓ ଗୟା ଜିଲ୍ଲାଦ୍ୱୟକୁ ନେଇ ତତ୍କାଳୀନ ମଗଧ ରାଜ୍ୟ ଗଠିତ ହୋଇଥିଲା । ଏହି ରାଜ୍ୟର ଉତ୍ତରରେ ଗଙ୍ଗାନଦୀ ଏବଂ ପଶ୍ଚିମରେ ସୋନନଦୀ ପ୍ରବାହିତ ହେଉଥିଲା । ଗିରିବ୍ରଜ ଏହାର ରାଜଧାନୀ ଥିଲା । ପରବର୍ତ୍ତୀ କାଳରେ ରାଜଗୃହକୁ ରାଜଧାନୀ ସ୍ଥାନାନ୍ତରିତ କରାଯାଇଥିଲା । ପୁନର୍ବାର ରାଜଗୃହ ପରିବର୍ତ୍ତେ ପାଟଳୀପୁତ୍ରଠାରେ ମଗଧର ରାଜଧାନୀ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା । ବେଦ ଓ ଜୈନଗ୍ରନ୍ଥଗୁଡ଼ିକରେ ମଗଧର ପ୍ରଥମ କେତେଜଣ ରାଜାମାନଙ୍କ ସମ୍ବନ୍ଧରେ ସୂଚନା ରାଜଧାନୀ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା । ବେଦ ଓ ଜୈନଗ୍ରନ୍ଥଗୁଡ଼ିକରେ ମଗଧର ପ୍ରଥମ କେତେଜଣ ରାଜାମାନଙ୍କ ସମ୍ବନ୍ଧରେ ସୂଚନା ବିଶେଷ ବୃଦ୍ଧି ପାଇଥଲା ।
- ଭଜି – ଭଜି ଗଣତନ୍ତ୍ର ଗଙ୍ଗାନଦୀର ଉତ୍ତରରେ ଅବସ୍ଥିତ ଥିଲା । ଏହା ଆଠଗୋଟି ଗୋଷ୍ଠୀ ବା ଦଳକୁ ନେଇ ଗଠିତ ହୋଇଥିଲା । ଏଗୁଡ଼ିକ ମଧ୍ୟରେ ଲିଚ୍ଛବି, ଜ୍ଞାତ୍ରିକ, ଭଜି ଓ ବିଦେହ ଗୋଷ୍ଠୀ ବିଶେଷ ଉଲ୍ଲେଖଯୋଗ୍ୟ । ଅନ୍ୟାନ୍ୟ ଗୋଷ୍ଠୀଗୁଡ଼ିକ ସମ୍ବନ୍ଧରେ ସଠିକ୍ ବିବରଣୀ ସଂଗୃହୀତ ହୋଇନାହିଁ । ବୈଶାଳୀ ବା ଆଧୁନିକ ମୁଜାଫରପୁର ଭଜି ଗଣତନ୍ତ୍ରର ରାଜଧାନୀ ଥିଲା ।
- ମଲ୍ଲ ବା ମାଳବ – ମଲ୍ଲ ବା ମାଳବ ରାଜ୍ୟ ଭଜି ଗଣତନ୍ତ୍ରର ଉତ୍ତରରେ ଅବସ୍ଥିତ ଥିଲା । ଏହା କୁଲୁ ନଦୀଦ୍ଵାରା ଦୁଇଟି ଅଂଶରେ ବିଭକ୍ତ ହୋଇଥିଲା । ଗୋଟିଏ ଅଂଶର ରାଜଧାନୀ ଥୁଲା କୁଶୀନରା ଏବଂ ଅନ୍ୟ ଅଂଶର ରାଜଧାନୀ ଥିଲା ପାବା । ପ୍ରଥମେ ଏହି ରାଜ୍ୟରେ ରାଜତନ୍ତ୍ର ଶାସନ ପ୍ରଚଳିତ ଥିଲା । ମାତ୍ର ମଗଧର ରାଜା ବିମ୍ବିସାରଙ୍କ ସମୟବେଳକୁ ଏହି ରାଜ୍ୟରେ ଗଣତନ୍ତ୍ର ଶାସନ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା । ସମ୍ରାଟ ଅଜାତଶତ୍ରୁ ମଲ୍ଲ ରାଜ୍ୟକୁ ମଗଧ ସାମ୍ରାଜ୍ୟଭୁକ୍ତ କରିଥିଲେ ।
- ଚେଦୀ – ଆଧୁନିକ ବୁନ୍ଦେଲଖଣ୍ଡ ଏବଂ ଏହାର ପାର୍ଶ୍ଵବର୍ତ୍ତୀ ଅଞ୍ଚଳ ଏହି ରାଜ୍ୟର ଅନ୍ତର୍ଭୁକ୍ତ ଥିଲା । ଶୁଭ୍ରମତୀ ଏହାର ରାଜଧାନୀ ଥିଲା । ମତ୍ସ୍ୟ ଓ କାଶୀ ଏବଂ ଚେଦୀ ରାଷ୍ଟ୍ର ମଧ୍ୟରେ ସୁସମ୍ପର୍କ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।
- ବତ୍ସ – ଗଙ୍ଗାନଦୀର ଦକ୍ଷିଣରେ ବସ୍ତ୍ର ରାଜ୍ୟ ଅବସ୍ଥିତ ଥିଲା । ଏହା ଏକ ପ୍ରଧାନ ବାଣିଜ୍ୟକେନ୍ଦ୍ର ଥିଲା । କୋଶମ୍ବୀ ଏହାର ରାଜଧାନୀ ଥିଲା । କୋଶମ୍ବୀ ଆହ୍ଲାବାଦ ନିକଟବର୍ତ୍ତୀ ଯମୁନା ନଦୀ କୂଳରେ ଅବସ୍ଥିତ ଥିଲା । ବସ୍ତ୍ରରାଜା ଦଧିବାହନଙ୍କ ପୁତ୍ର ଉଦୟନ, ଅବନ୍ତୀର ରାଜା ପ୍ରଦ୍ୟୋତ ଏବଂ ମଗଧର ରାଜା ବିମ୍ବିସାର ବୁଦ୍ଧଙ୍କ ସମସାମୟିକ ଥିଲେ ।
- କୁରୁ – ପାଲୀ ଗ୍ରନ୍ଥରୁ ଜଣାଯାଏ ଯେ, ଖ୍ରୀ.ପୂ. ଷଷ୍ଠ ଶତକରେ ଯୁଧୁଷ୍ଠିରଙ୍କ ବଂଶଧରମାନେ କୁରୁ ରାଜ୍ୟରେ ଶାସନ କରୁଥିଲେ । ଦିଲ୍ଲୀ ନିକଟବର୍ତ୍ତୀ ଇନ୍ଦ୍ରପ୍ରସ୍ଥ ଥିଲା ଏହି ରାଜ୍ୟର ରାଜଧାନୀ । ମୋଟାମୋଟି ଭାବରେ ଆଧୁନିକ ଦିଲ୍ଲୀ ଏବଂ ମିରଟ ଜିଲ୍ଲାକୁ ନେଇ କୁରୁ ରାଜ୍ୟ ଗଠିତ ହୋଇଥିଲା ।
- ପାଞ୍ଚାଳ – ରୋହିଲାଖଣ୍ଡ ଓ ମଧ୍ୟ-ଭାରତର ଦୋଆବ ଅଞ୍ଚଳକୁ ନେଇ ପାଞ୍ଚାଳ ରାଜ୍ୟ ଗଠିତ ହୋଇଥିଲା । ଗଙ୍ଗାନଦୀ ଏହି ରାଜ୍ୟକୁ ଦୁଇଭାଗରେ ବିଭକ୍ତ କରିଥିଲା; ଯଥା – ଉତ୍ତର ପାଞ୍ଚାଳ ଓ ଦକ୍ଷିଣ ପାଞ୍ଚାଳ । ଅହିଛତ୍ର ଓ କାମ୍ପିଲ୍ୟ ଯଥାକ୍ରମେ ଉତ୍ତର ପାଞ୍ଚାଳ ଓ ଦକ୍ଷିଣ ପାଞ୍ଚାଳର ରାଜଧାନୀ ଥିଲା । ବୌଦ୍ଧ ସାହିତ୍ୟରୁ ଜଣାଯାଏ ଯେ ଉତ୍ତର ପାଞ୍ଚାଳ ଅଧିକାର କରିବାପାଇଁ ପାଞ୍ଚାଳ ଓ କୁରୁ ରାଜ୍ୟଦ୍ୱୟ ମଧ୍ୟରେ ସଂଘର୍ଷ ଲାଗିଥିଲା ।
![]()
- ମତ୍ସ୍ୟ – ଆଧୁନିକ ଜୟପୁର ଅଞ୍ଚଳ ସହିତ ତତ୍କାଳୀନ ମତ୍ସ୍ୟ ରାଜ୍ୟକୁ ଚିହ୍ନଟ କରାଯାଇଅଛି । ବିରାଟ ନଗରୀ ଥିଲା ଏହାର ରାଜଧାନୀ ।
- ସୁରସେନ – ଯମୁନା ନଦୀକୂଳରେ ଅବସ୍ଥିତ ସୁରସେନ ରାଜ୍ୟର ରାଜଧାନୀ ଥିଲା ମଥୁରା । ମହାଭାରତ ଓ ପୁରାଣମାନଙ୍କରୁ ଜଣାଯାଏ ଯେ, ଯଦୁବଂଶର ରାଜାଗଣ ଏହି ରାଜ୍ୟରେ ରାଜତ୍ଵ କରୁଥୁଲେ ।
- ଆସାକା – ଗୋଦାବରୀ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ଥିବା ଆସାକା ରାଜ୍ୟର ରାଜଧାନୀ ଥୁଲା ପୋଟାଳ ବା ପୋଟନା ! ବାୟୁ ପରାଣରେ ଉଲ୍ଲେଖ ଅଛି ଯେ ଆସାକାର ରାଜାମାନେ ଥିଲେ ଈକ୍ଷାକୁ ବଂଶୀୟ ।
- ଅବନ୍ତୀ – ଆଧୁନିକ ଉଜ୍ଜୟିନୀ ଏବଂ ନର୍ମଦା ଉପତ୍ୟକାର କେତେକାଞ୍ଚଳକୁ ନେଇ ଅବନ୍ତୀରାଜ୍ୟ ଗଠିତ ହୋଇଥିଲା । ବିନ୍ଧ୍ୟ ପର୍ବତମାଳା ଏହି ରାଜ୍ୟକୁ ଦୁଇଭାଗରେ ବିଭକ୍ତ କରିଥିଲା । ଉଜ୍ଜୟିନୀ ଏହାର ରାଜଧାନୀ ଥିଲା । ଅବନ୍ତୀର ରାଜା ଚନ୍ଦ୍ରପ୍ରଦ୍ୟୋତ କୋଶାମ୍ବୀର ରାଜା ଉଦୟନଙ୍କର ସମସାମୟିକ ଥିଲେ । ବୌଦ୍ଧଗ୍ରନ୍ଥରୁ ଜଣାଯାଏ ଯେ, ରାଜା ଚନ୍ଦ୍ରପ୍ରଦ୍ୟୋତ ବିଶେଷ ପ୍ରଭାବଶାଳୀ ଥିଲେ । ପୁରାଣରେ ଉଲ୍ଲେଖ ଅଛି, ଅବନ୍ତୀର ଯଦୁବଂଶୀୟ ରାଜାମାନେ ଅବନ୍ତୀ, ବିଦର୍ଭ ଆଦି ନଗରୀ ପ୍ରତିଷ୍ଠା କରିଥିଲେ ।
- ଗାନ୍ଧାର – ଆଧୁନିକ କାଶ୍ମୀର, ପାକିସ୍ତାନର ପେଶୱାର ଓ ରାୱଲପିଣ୍ଡି ଜିଲ୍ଲାକୁ ନେଇ ଗାନ୍ଧାର ରାଷ୍ଟ୍ର ଗଠିତ ହୋଇଥିଲା । ତକ୍ଷଶିଳା ଥିଲା ଏହାର ରାଜଧାନୀ । ଷଷ୍ଠ ଶତାବ୍ଦୀର ଶେଷ ସମୟ ବେଳକୁ ଗାନ୍ଧାର ଜନୈକ ପାରସ୍ୟ ରାଜାଙ୍କଦ୍ବାରା ଅଧିକୃତ ହୋଇଥିଲା । ପୁଞ୍ଜୁସାତି ଥିଲେ ଏହି ରାଜ୍ୟର ରାଜା ।
- କମ୍ବୋଜ – ଭାରତର ଉତ୍ତର-ପଶ୍ଚିମ ସୀମାନ୍ତ ଅଞ୍ଚଳକୁ ନେଇ କମ୍ବୋଜ ରାଷ୍ଟ୍ର ଗଠିତ ହୋଇଥିଲା । ଦ୍ଵାରକା ଥିଲା ଏହାର ରାଜଧାନୀ । ମହାଭାରତରୁ ଜଣାଯାଏ ଯେ, ଏଠାରେ ପ୍ରଥମେ ରାଜତନ୍ତ୍ର ଶାସନ ପ୍ରଚଳିତ ଥିଲା; କିନ୍ତୁ ପରବର୍ତ୍ତୀ କାଳରେ ଏଠାରେ ଗଣତନ୍ତ୍ର ଶାସନ ପ୍ରଚଳନ କରାଯାଇଥିଲା ।


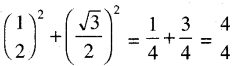
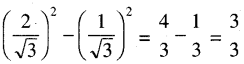
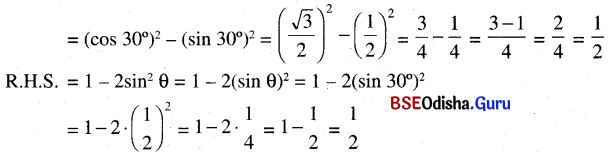
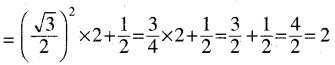

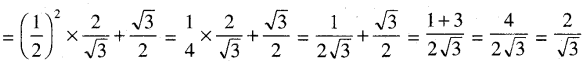
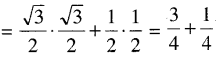
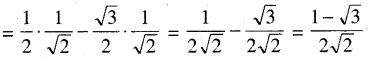
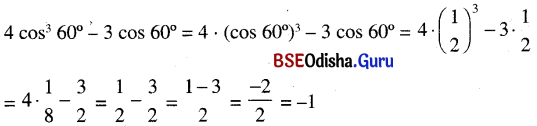
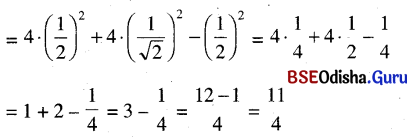
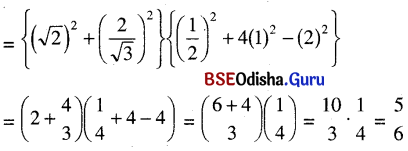
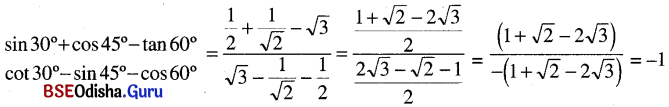




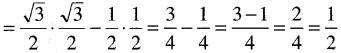
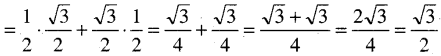
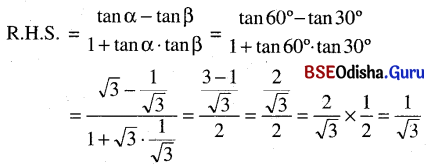
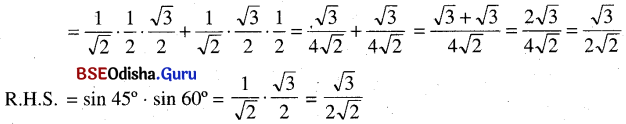
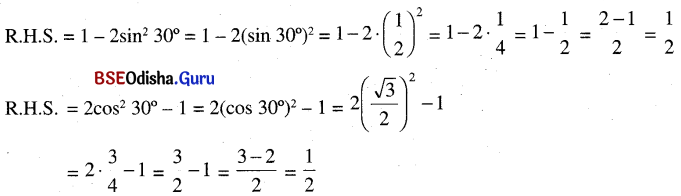





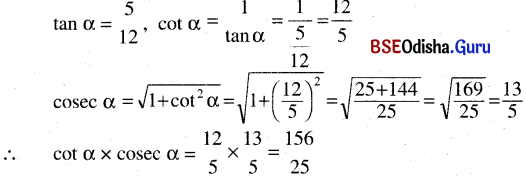
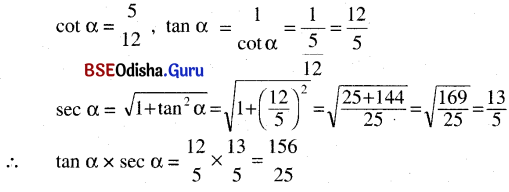



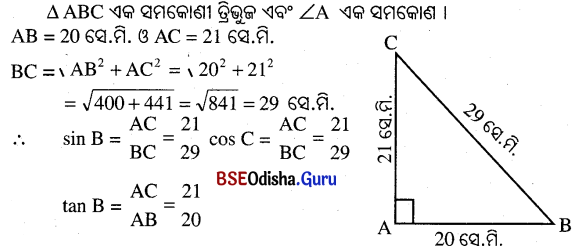
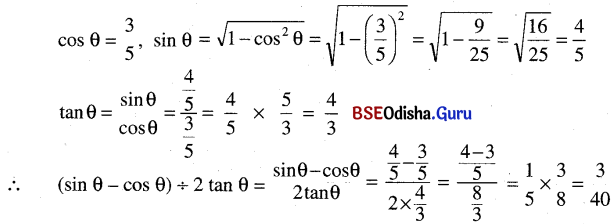




 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ) (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)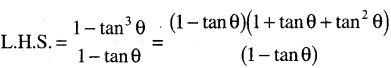
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ) (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)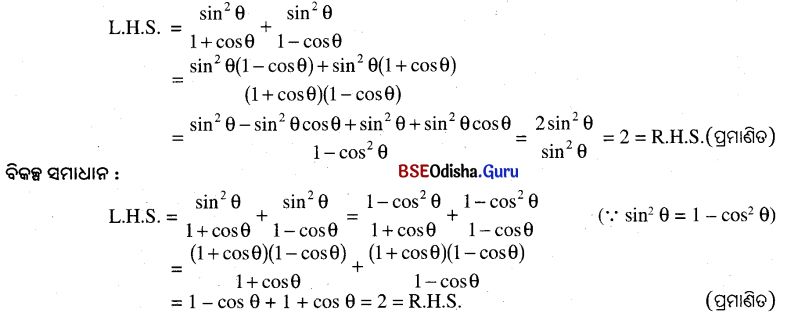
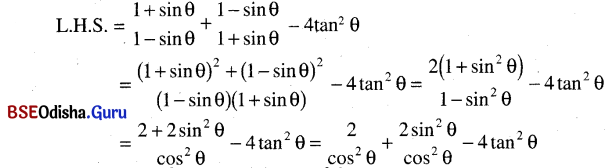
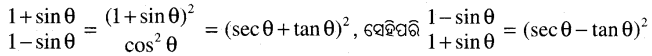
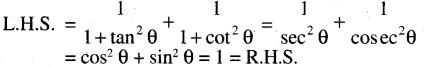 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)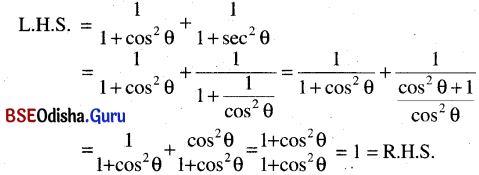 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)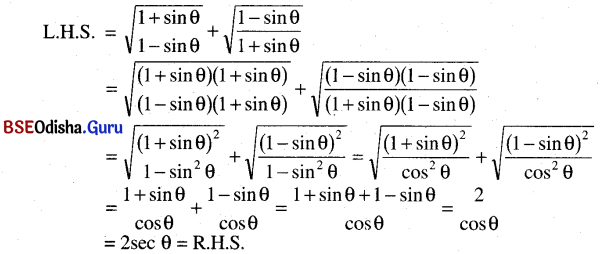 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ) (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)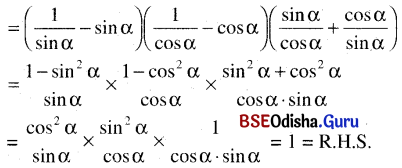 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)