Class 6

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 8 ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା Ex 8.3 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 8 ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା Ex 8.3

Question 1.
ନିମ୍ନ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ –
(କ) (+5) ଏକ ପୂର୍ଣସଂଖ୍ୟା, (-6) ଏକ ପୂର୍ଣସଂଖ୍ୟା ।
(+5) + (-6) = (-1), ଏଠାରେ ପୂର୍ବସଂଖ୍ୟା ଦୁଇଟିର ଯୋଗଫଳ ଏକ ପୂର୍ବସଂଖ୍ୟା ହେଲା।
ଏଥୁରୁ ଯୋଗ ପ୍ରକ୍ରିୟା କେଉଁ ନିୟମ ପାଳନ କରୁଥିବାର ଜଣାପଡିଲା ?
ସମାଧାନ:
ଏଥ୍ରୁ ଯୋଗ ପ୍ରକ୍ରିୟା ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରୁଥିବାର ଜଣାପଡ଼ିଲା ।

(ଖ) ପୂର୍ବସଂଖ୍ୟାରେ ଯୋଗ ପ୍ରକ୍ରିୟା ଅଭେଦ ନିୟମ ପାଳନ କରେ- ଗୋଟିଏ ଉଦାହରଣ ଦେଇ ବୁଝାଅ । 
ସମାଧାନ:
(+3) + (0) = +3, (0) + (+3) = +3 
∴ (+3) + (0) = 0 + (+3) = +3
∴ ପୂର୍ଣ ସଂଖ୍ୟାରେ ଯୋଗ ପ୍ରକ୍ରିୟା ଅଭେଦ ନିୟମ ପାଳନ କରେ । 

(ଗ) ଗୋଟିଏ ଧନାତ୍ମକ ପୂର୍ବସଂଖ୍ୟା ନିଅ। ଏହାର ଯୋଗାତ୍ମକ ବିଲୋମୀ ନିଶ୍ଚୟ କର। ତୁମେ ନେଇଥିବା ଧନାତ୍ମକ ସଂଖ୍ୟା ଓ ତାହାର ଯୋଗାତ୍ମକ ବିଲୋମୀର ସମଷ୍ଟି କେତେ ହେବ ସ୍ଥିର କର।
ସମାଧାନ:
+5 ର ଯୋଗାତ୍ମକ ବିଲୋମୀ -5 ।
(+5) + (-5) = 0
∴ ଧନାତ୍ମକ ସଂଖ୍ୟା ଓ ତାହାର ଯୋଗାତ୍ମକ ବିଲୋମୀର ସମଷ୍ଟି 0 ।

Question 2.
ଏହା (+1) କୁ ସୂଋଏ, ସେହିପରି ଏହା (-)କୁ ସୂଋଏ ତେବେ ନିମ୍ନ ଯୋଗଫଳକୁଡ଼ିକୁ ସ୍ଥିର କର।

ସମାଧାନ:

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.4 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.4

Question 1.
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଭାଗକ୍ରିୟା କରି ଭାଗଫଳ ଓ ଭାଗଶେଷ ନିର୍ଣ୍ଣୟ କର ଏବଂ ଭାଗକ୍ରିୟା ଠିକ୍ ଅଛି କି ନାହିଁ ପରୀକ୍ଷା କର।

(କ) 7772 ÷ 58
ସମାଧାନ:

∴ 7772 ÷ 58 = ଭାଗଫଳ 134 ଓ ଭାଗଶେଷ 0 l 
ପରୀକ୍ଷା : ଭାଜ୍ୟ = ଭାଜକ × ଭାଗଫଳ + ଭାଗଶେଷ
= 58 × 134 + 0 = 7772 + 0 = 7770 = ଭାଜ୍ୟ
∴ ଭାଗକ୍ରିୟାଟି ଠିକ୍ ଅଛି ।

(ଖ) 6324 ÷ 245
ସମାଧାନ:

∴ 6324 ÷ 245 = ଭାଗଫଳ 25 ଓ ଭାଗଶେଷ 199 l 
ପରୀକ୍ଷା : ଭାଜ୍ୟ = ଭାଜକ × ଭାଗଫଳ + ଭାଗଶେଷ
= 245 × 25 + 199 = 6125 + 199 = 6324
∴ ଭାଗକ୍ରିୟାଟି ଠିକ୍ ଅଛି ।

(ଗ) 16025 ÷ 1000
ସମାଧାନ:

∴ 16025 ÷ 1000 = ଭାଗଫଳ 16 ଓ ଭାଗଶେଷ 25 l 
ପରୀକ୍ଷା : ଭାଜ୍ୟ = ଭାଜକ × ଭାଗଫଳ + ଭାଗଶେଷ
= 1000 × 16 + 25 = 16000 + 25 = 16025
∴ ଭାଗକ୍ରିୟାଟି ଠିକ୍ ଅଛି ।

(ଘ) 6906 ÷ 35
ସମାଧାନ:

∴ 6906 ÷ 35 = ଭାଗଫଳ 197 ଓ ଭାଗଶେଷ 11 l 
ପରୀକ୍ଷା : ଭାଜ୍ୟ = ଭାଜକ × ଭାଗଫଳ + ଭାଗଶେଷ
= 35 × 197 + 11 = 6895 + 11 = 6906
∴ ଭାଗକ୍ରିୟାଟି ଠିକ୍ ଅଛି ।

(ଙ) 12345 ÷ 975
ସମାଧାନ:

∴ 12345 ÷ 975 = ଭାଗଫଳ 12 ଓ ଭାଗଶେଷ 645 l 
ପରୀକ୍ଷା : ଭାଜ୍ୟ = 975 × 12 + 645
= 11700 + 645 = 12345

∴ ଭାଗକ୍ରିୟାଟି ଠିକ୍ ଅଛି ।

(ଚ) 5436 ÷ 300
ସମାଧାନ:

∴ 5436 ÷ 300 = ଭାଗଫଳ 18 ଓ ଭାଗଶେଷ 36 l 
ପରୀକ୍ଷା : ଭାଜ୍ୟ = 300 × 18 + 36
= 5400 + 36 = 5436
∴ ଭାଗକ୍ରିୟାଟି ଠିକ୍ ଅଛି ।

Question 2.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର –

(କ) 104 ÷ 104 = ………
ସମାଧାନ
1

(ଖ) 305 ÷ ……… = 305
ସମାଧାନ:
1

Question 3. 
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଦତ୍ତ ସଂଖ୍ୟାକୁ ବନ୍ଧନୀ ମଧ୍ୟରେ ଥିବା ପ୍ରତ୍ୟେକ ସଂଖ୍ୟା ଦ୍ଵାରା ଭାଗ କର ଓ କେଉଁ ସଂଖ୍ୟା ଦ୍ୱାରା ମୂଳ ସଂଖ୍ୟାଟି ବିଭାଜ୍ୟ ତାହା ଲେଖ ।

(କ) 306 [2, 3, 4, 5, 6]
ସମାଧାନ:
306 [2, 3, 4, 5, 6]
306 ÷ 2 = 153
306 ÷ 3 = 102
306 ÷ 4 = 76 ପଡ଼ି ଭାଗଶେଷ 2 ବଳିଲା 
306 ÷ 5 = 61 ପଡ଼ି ଭାଗଶେଷ 1 ବଳିଲା
306 ÷ 6=51
∴ 306 ସଂଖ୍ୟାଟି 2, 3 ଓ 6 ଦ୍ୱାରା ବିଭାଜ୍ୟ ।

(ଖ) 1701 [6, 7, 8, 9] 
ସମାଧାନ:
1701 [6, 7, 8, 9]
1701 ÷ 6 = 283 ପଡ଼ି 3 ବଳିଲା
1701 ÷ 7 = 243
1701 ÷ 8 = 212 ପଡ଼ି 5 ବଳିଲା
1701 ÷ 9 = 189
∴ 1701 ସଂଖ୍ୟାଟି 7 ଓ 9 ଦ୍ୱାରା ବିଭାଜ୍ୟ ।

(ଗ) 3564 [7, 8, 9, 11]
ସମାଧାନ:
3564 [7, 8, 9, 11]
3564 ÷ 7 = 509 ପଡ଼ି 1 ବଳିଲା
3564 ÷ 8 = 445 ପଡ଼ି 4 ବଳିଲା
3564 ÷ 9 = 396
3564 ÷ 11 = 324
∴ 3564 ଟି 9 ଓ 11 ଦ୍ବାରା ବିଭାଜ୍ୟ ।

Question 4.
ଛ’ ଅଙ୍କ ବିଶିଷ୍ଟ କେଉଁ କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟା 74.ଦ୍ୱାରା ବିଭାଜ୍ୟ?
ସମାଧାନ:
ଛଅ ଅଙ୍କ ବିଶିଷ୍ଟ କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟା 100000 ।
100000 ÷ 74 =  ଭାଗଫଳ 1351 ଓ ଭାଗଶେଷ 26
74 – 26 = 48
∴ 100000 + 48 = 100048 ∴ ସଂଖ୍ୟାଟି 100048 

Question 5.
ଚାରିଅଙ୍କ ବିଶିଷ୍ଟ କେଉଁ ବୃହତ୍ତମ ସଂଖ୍ୟା 48 ଦ୍ୱାରା ବିଭାଜ୍ୟ ?
ସମାଧାନ:
ଚାରିଅଙ୍କ ବିଶିଷ୍ଟ ବୃହତ୍ତମ ସଂଖ୍ୟା = 9999
9999 ÷ 48 = ଭାଗଫଳ 208 ଓ ଭାଗଶେଷ 15
∴ 9999 – 15 = 9984 ∴ ସଂଖ୍ୟାଟି 9984 ।

Question 6.
କେଉଁ ସଂଖ୍ୟାକୁ 24 ଦ୍ୱାରା ଭାଗକଲେ 18 ଭାଗଫଳ ପଡ଼ି 9 ଭାଗଶେଷ ରହିବ ।
ସମାଧାନ:
ଏଠାରେ ଭାଜକ = 24, ଭାଗଫଳ = 18 ଭାଗଶେଷ = 9
ଭାଜ୍ୟ = ଭାଜକ × ଭାଗଫଳ + ଭାଗଶେଷ
= 24 × 18 + 9 = 432 + 9 = 441

Question 7.
ଜଣେ କୃଷକଙ୍କ ପାଖରେ 700 ଚାରାଗଛ ଥିଲା । ସେ ପ୍ରତିଧାଡ଼ିରେ 32ଟି ଲେଖାଏଁ ଚାରାଗଛ ଲଗାଇଲେ । ତାଙ୍କ ପାଖରେ କେତୋଟି ଚାରାଗଛ ବଳିଥିବ?
ସମାଧାନ:
32ଟି ଚାରାଗଛ ଲଗାଯାଏ l ଟି ଧାଡ଼ିରେ ।
700 ଟି ଚାରାଗଛ ଲଗାଯିବ 700 + 32 = 21 ଧାଡ଼ି ଲଗାଯାଇ 28ଟି ବଳିବ ।
∴ ତାଙ୍କ ପାଖରେ 28ଟି ଚାରା ଗଛ ବଳିଥ‌ିବ ।

Question 8.
ଏକ ପ୍ରେକ୍ଷାଳୟରେ ପ୍ରତି ଧାଡ଼ିରେ 36 ଟି ଲେଖାଏଁ ଚଉକି ରଖାଯାଇଥିଲା । ତେବେ ଅତିକମ୍‌ରେ କେତୋଟି ଧାଡ଼ିରେ 600 ଦର୍ଶକ ବସି ପାରିବେ ଏବଂ କେତୋଟି ଚଉକି ବଳିବ?
ସମାଧାନ:
ଗୋଟିଏ ଧାଡ଼ିରେ ପଡ଼ିଥିବା ଚଉକି ସଂଖ୍ୟା = 36 ଅର୍ଥାତ୍ ଗୋଟିଏ ଧାଡ଼ିରେ 36 ଜଣ ଲୋକ ବସନ୍ତି ।
600 ଜଣ ଦର୍ଶକ 600 + 36 = 16 ଟି ଧାଡ଼ିରେ ବସି 24 ଜଣ ଦର୍ଶକ ବଳିପଡ଼ିବେ ।
24 ଜଣ ଦର୍ଶକ ବସିବେ ଅନ୍ୟଏକ ଧାଡ଼ିରେ ।
ଧାଡ଼ିସଂଖ୍ୟା = 16 + 1 = 17 ଟି
ଗୋଟିଏ ଧାଡ଼ିରେ ପଡ଼ିଥିବା 36ଟି ଚଉକିରେ 24 ଜଣ ଦର୍ଶକ ବସିଲାପରେ ବଳିଥିବା ଚଉକିସଂଖ୍ୟା 36 – 24 = 12
∴ 600 ଜଣ ଲୋକ 12ଟି ଧାଡ଼ିରେ ଲୋକ ବସିପାରିବେ ଓ 12 ଟି ଚଉକି ବଳିବ ।

Question 9.
(କ) 1325 ରୁ ଅତିକମ୍‌ରେ କେତେ ବିୟୋଗ କଲେ ବିୟୋଗ ଫଳ 36 ଦ୍ବାରା ବିଭାଜ୍ୟ ହେବ?
ସମାଧାନ:

1325 ÷ 36 = ଭାଗଫଳ 36 ଓ ଭାଗଶେଷ 29
∴ 1325 ରୁ ଅତିକମ୍‌ରେ 29 ବିୟୋଗ କଲେ ବିୟୋଗଫଳ 36 ଦ୍ବାରା ବିଭାଜ୍ୟ ହେବ ।

(ଖ) 1325 ସହ ଅତିକମ୍‌ରେ କେତେ ଯୋଗକଲେ ତାହା 42 ଦ୍ଵାରା ବିଭାଜ୍ୟ ହେବ?
ସମାଧାନ:

1325 ÷ 42 = ଭାଗଫଳ 31 ଓ ଭାଗଶେଷ 23 । 42 – 23 = 19
∴ 1325 ରେ ଅତି କମ୍‌ରେ 19 ଯୋଗକଲେ ତାହା 42 ଦ୍ବାରା ବିଭାଜ୍ୟ ହେବ ।

Question 10. 
(କ) 102 କୁ 12 ଦ୍ବାରା ଭାଗ କର ଏବଂ ନିମ୍ନସ୍ଥ ଶୂନ୍ୟସ୍ଥାନରେ ଭାଗଫଳ ଓ ଭାଗଶେଷ ଲେଖ । 102 କୁ 12 ଦ୍ବାରା ଭାଗକଲେ ଭାଗଫଳ = ………. , ଭାଗଶେଷ = …….. ।
ସମାଧାନ:
102 କୁ 12 ଦ୍ବାରା ଭାଗକଲେ, ଭାଗଫଳ = 8 , ଭାଗଶେଷ = 6 ।

(ଖ) 102 କୁ 8 ଦ୍ଵାରା ଭାଗ କର ଏବଂ ନିମ୍ନସ୍ଥ ଶୂନ୍ୟସ୍ଥାନରେ ଭାଗଫଳ ଓ ଭାଗଶେଷ ଲେଖ । 102 କୁ 8 ଦ୍ବାରା ଭାଗକଲେ ଭାଗଫଳ = …… , ଭାଗଶେଷ = ……. ।
ସମାଧାନ:
102 କୁ 8 ଦ୍ଵାରା ଭାଗକଲେ ଭାଗଫଳ = 12, ଭାଗଶେଷ 6 ।

Question 11.
ପ୍ରଶ୍ନ ନଂ 10 ରେ ଦେଖ‌ିଲେ, 102 ଭାଜ୍ୟ ହୋଇଥିବାବେଳେ, ଭାଜକ 12 ହେଲେ ଭାଗଫଳ 8;
ଭାଜକ 8 ହେଲେ ଭାଗଫଳ 12 ଏବଂ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଭାଗଶେଷ 6 l
ବର୍ତ୍ତମାନ 106 କୁ 12 ଦ୍ବାରା ଭାଗକରି ଭାଗଫଳ ଓ ଭାଗଶେଷ ନିର୍ଣ୍ଣୟ କର ।
ଉ – 106 ÷ 12 = ଭାଗଫଳ 8 ଓ ଭାଗଶେଷ 10 ।
106 କୁ ପୂର୍ବ ଭାଗଫଳ ଦ୍ଵାରା ଭାଗକରି ଭାଗଫଳ ଓ ଭାଗଶେଷ କେତେ ହେଉଛି ସ୍ଥିର କର ।
ଉ – 106 ÷ 8 = ଭାଗଫଳ 13 ଓ ଭାଗଶେଷ 2 ।
ପ୍ରଶ୍ନ 10ରେ ଦେଖୁଥିଲେ, ଭାଜକ 12 ବେଳେ ଭାଗଫଳ 8 ଏବଂ ଭାଜକ 8 ହେଲେ ଭାଗଫଳ 12 । 
ମାତ୍ର ଏହି ପ୍ରଶ୍ନର ଭାଗକ୍ରିୟା କ୍ଷେତ୍ରରେ, ଭାଜକ 12 ହେଲେ ଭାଗଫଳ ଯେତେ ପାଇଲ, ସେହି ସଂଖ୍ୟାକୁ ଭାଜକ ନେଇ ଭାଗକ୍ରିୟା କଲାବେଳେ ଭାଗଫଳ 12 ହେଲା କି? କାହିଁକି ହେଲା ନାହିଁ?
ଉ – ପ୍ରଶ୍ନ ନଂ 10ର ଉଭୟ କ୍ଷେତ୍ରରେ ଭାଗଶେଷ < ଭାଜକ ।
କିନ୍ତୁ ଏହି ପ୍ରଶ୍ନର ଦ୍ବିତୀୟ ଭାଗରେ ଯଦି 106 ÷ 8 = 12 ପଡ଼ି 10 ବଳନ୍ତା ତେବେ ଏଠାରେ ଭାଗଶେଷ > ଭାଜକ ହୁଅନ୍ତା ।
ଏହା ହରଣ ପ୍ରକ୍ରିୟାରେ ସମ୍ଭବ ନୁହେଁ ।

Question 12. 
ଯଦି ଗୋଟିଏ ସଂଖ୍ୟାକୁ 15 ଦ୍ବାରା ଭାଗକଲେ କୌଣସି ଭାଗଶେଷ ନ ରହେ, ତେବେ ସେହି ସଂଖ୍ୟାକୁ ଅନ୍ୟ କେଉଁ ସଂଖ୍ୟାଦ୍ଵାରା ଭାଗକଲେ ମଧ୍ୟ କୌଣସି ଭାଗଶେଷ ରହିବ ନାହିଁ ।
ସମାଧାନ:
ଯଦି ଗୋଟିଏ ସଂଖ୍ୟାକୁ 15 ଦ୍ଵାରା ଭାଗକଲେ କୌଣସି ଭାଗଶେଷ ନ ରହେ, ତେବେ ସେହି ସଂଖ୍ୟାକୁ 15ର ଗୁଣନାୟକ 3 ଓ 5 ଦ୍ବାରା ଭାଗକଲେ ମଧ୍ୟ କୌଣସି ଭାଗଶେଷ ରହିବ ନାହିଁ ।

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 8 ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା Ex 8.2 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 8 ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା Ex 8.2

Question 1.
ଗୋଟିଏ ସଂଖ୍ୟାରେଖା ଅଙ୍କନ କରି ସେଥିରେ ପୂର୍ଣ୍ଣସଂଖ୍ୟାମାନ ଚିହ୍ନଟ କର । ସେହି ସଂଖ୍ୟାରେଖା ସାହାଯ୍ୟରେ ନିମ୍ନ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:

(କ) -3 ସୂଚକ ବିନ୍ଦୁଠାରୁ ସେହି ସଂଖ୍ୟାର ଯୋଗାତ୍ମକ ବିଲୋମୀ (ବା ବିପରୀତ ସଂଖ୍ୟା) ସଂଖ୍ୟା ସୂଚକ ବିନ୍ଦୁର ଦୂରତା କେତେ ଏକକ ?
ସମାଧାନ:
-3 ର ଯୋଗାତ୍ମକ ବିଲୋମୀ (ବା ବିପରୀତ ସଂଖ୍ୟା) = 3
-3 ସୂଚକ ବିନ୍ଦୁଠାରୁ 3 ସୂଚକ ବିନ୍ଦୁର ଦୂରତା = 3 – (–3) = 3 + 3 = 6 ଏକକ

(ଖ) -7 ସୂଚକ ବିନ୍ଦୁ ଓ -4 ସୂଚକ ବିନ୍ଦୁ ମଧ୍ୟରେ ଦୂରତା କେତେ ?
ସମାଧାନ:
-7 ସୂଚକ ବିନ୍ଦୁ ଓ -4 ସୂଚକ ବିନ୍ଦୁ ମଧ୍ୟରେ ଦୂରତା = -4 – (-7) = -4 + 7 = 3

(ଗ) +7 ସୂଚକ ବିନ୍ଦୁ ଓ + 4 ସୂଚକ ବିନ୍ଦୁ ମଧ୍ୟରେ ଦୂରତା କେତେ ?
ସମାଧାନ:
+7 ସୂଚକ ବିନ୍ଦୁ ଓ +4 ସୂଚକ ବିନ୍ଦୁ ମଧ୍ୟରେ ଦୂରତା = 7 – 4 = 3

Question 2.
ସଂଖ୍ୟାରେଖାଟିଏ ଅଙ୍କନ କରି ସେଥ‌ିରେ ପୂର୍ବସଂଖ୍ୟା ମାନଙ୍କୁ ଚିହ୍ନଟ କର । ସେହି ସଂଖ୍ୟା ରେଖାକୁ ଦେଖୁ ନିମ୍ନ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:

(କ) -2 ସୂଚକ ବିନ୍ଦୁ ପାଖରୁ 4 ଏକକ ବାମକୁ ଆସିଲେ କେଉଁ ସଂଖ୍ୟା ସୂଚକ ବିନ୍ଦୁ ପାଖରେ ପହଞ୍ଚିବ ? 
ସମାଧାନ:
-2 ବିନ୍ଦୁ ପାଖରେ 4 ଏକକ ବାମକୁ ଆସିଲେ, -2 – 4 = -6 ସୂଚକ ବିନ୍ଦୁ ପାଖରେ ପହଞ୍ଚିବ ।

(ଖ) +4 ସୂଚକ ବିନ୍ଦୁଠାରୁ 7 ଏକକ ବାମକୁ ଆସିଲେ କେଉଁ ସଂଖ୍ୟା ପାଖରେ ପହଞ୍ଚିବ ?
ସମାଧାନ:
+4 ସୂଚକ ବିନ୍ଦୁଠାରୁ 7 ଏକକ ବାମକୁ ଆସିଲେ +4 – 7 = -3 ସୂଚକ ବିନ୍ଦୁ ପାଖରେ ପହଞ୍ଚିବ ।

(ଗ) -5 ସୂଚକ ବିନ୍ଦୁ ପାଖରୁ 4 ଏକକ ଡ଼ାହାଣକୁ ଆସିଲେ କେଉଁ ସଂଖ୍ୟା ପାଖରେ ପହଞ୍ଚିବ ?
ସମାଧାନ:
-5 ସୂଚକ ବିନ୍ଦୁ ପାଖରୁ 4 ଏକକ ଡାହାଣକୁ ଆସିଲେ –5 + 4 = -1 ସୂଚକ ବିନ୍ଦୁ ପାଖରେ ପହଞ୍ଚିବ ।

(ଘ) -2 ସୂଚକ ବନ୍ଧୁଠାରୁ 5 ଏକକ ଡ଼ାହାଣକୁ ଗଲେ, କେଉଁ ସଂଖ୍ୟା ପାଖରେ ପହଞ୍ଚିବ ?
ସମାଧାନ:
-2 ସୂଚକ ବିନ୍ଦୁଠାରୁ 5 ଏକକ ଡାହାଣକୁ ଗଲେ –2 + 5 = 3 ସୂଚକ ବିନ୍ଦୁ ପାଖରେ ପହଞ୍ଚିବ ।

Question 3.
ସଂଖ୍ୟାରେଖା ସାହାଯ୍ୟରେ ଯୋଗକର । ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନ ସମାଧାନ ପାଇଁ ଗୋଟିଏ ସଂଖ୍ୟାରେଖାର ସାହାଯ୍ୟ ନିଅ।
(କ) (+3) + (+2)
ସମାଧାନ:

ଏଣୁ (+3) + (+2) = +5

(ଖ) (-2) + (+5)
ସମାଧାନ:

(-2) + (+5) = +3

(ଗ) (+8) + (-3)
ସମାଧାନ:

(+8) + (-3) = +5

(ଘ) (-7) + (+4)
ସମାଧାନ:

(-7) + (+4) = -3

(ଙ) (-3) + (-4)
ସମାଧାନ:

(-3) + (-4) = -3 – (+4) = -3 – (+4) = -7

(ଚ) (+5) + (0)
ସମାଧାନ:

(+5) + (0) = +5

Question 4.
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନ ଲାଗି ଗୋଟିଏ ସଂଖ୍ୟାରେଖା ଅଙ୍କନ କରି ବିୟୋଗ କର ।
(କ) (+5) – (+3)
ସମାଧାନ:

(+5) – (+3) = +2

(ଖ) (+7) – (-4)
ସମାଧାନ:

(+7) – (-4) = (+7) + (4) = +11

(ଗ) (+5) – (+8)
ସମାଧାନ:

(+5) – (+8) = -3

(ଘ) (+4) – (-7)
ସମାଧାନ:

(+4) – (-7) = (+4) + (+7) = +11

(ଙ) (-4) – (+3)
ସମାଧାନ:

(-4) – (+3) = -7

(ଚ) (-6) – (-5)
ସମାଧାନ:

(-6) – (-5) = -6 + (+5) = -1

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 8 ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା Ex 8.1 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 8 ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା Ex 8.1

Question 1.
ନିମ୍ନ ପରିସ୍ଥିତିମାନଙ୍କର ବିପରୀତ ପରିସ୍ଥିତି ଲେଖ ।
(କ) ଜନସଂଖ୍ୟା ବୃଦ୍ଧି
ସମାଧାନ:
ଜନସଂଖ୍ୟା ହ୍ରାସ

(ଖ) ବ୍ୟାଙ୍କରେ ଟଙ୍କା ଜମା କରିବା
ସମାଧାନ:
ବ୍ୟାଙ୍କରୁ ଟଙ୍କା ଉଠାଇବା

(ଗ) ବ୍ୟୟ କରିବା
ସମାଧାନ:
ଆୟ କରିବା

(ଘ) ଉତ୍ତରକୁ ଯିବା
ସମାଧାନ:
ଦକ୍ଷିଣକୁ ଯିବା

(ଙ) ତାପମାତ୍ରା ହ୍ରାସ
ସମାଧାନ:
 ତାପମାତ୍ରା ବୃଦ୍ଧି

(ଚ) 500 ଖ୍ରୀଷ୍ଟାବ୍ଦ
ସମାଧାନ:
500 ଖ୍ରୀଷ୍ଟପୂର୍ବ

Question 2.
‘+’ ବା ‘–’ ଚିହ୍ନ ବ୍ୟବହାର କରି ଲେଖ ।
(କ) 400 ଟଙ୍କା ଲାଭ
ସମାଧାନ:
+400 ଟଙ୍କା

(ଖ) ଡାହାଣକୁ 4 କି.ମି.
ସମାଧାନ:
+4 କି.ମି.

(ଗ) ବ୍ୟାଙ୍କରୁ 300 ଟଙ୍କା ଉଠାଣ
ସମାଧାନ:
–300 ଟଙ୍କା

(ଘ) 5 ଗୋଲ୍‌ରେ ହାରିବା
ସମାଧାନ:
-5 ଗୋଲ୍‌

(ଙ) ଭୂପୃଷ୍ଠ ଠାରୁ 200 ମି. ଉଚ୍ଚ
ସମାଧାନ:
+200 ମିଟର 

(ଚ) 2,00,000 ଟଙ୍କା ଆୟ
ସମାଧାନ:
+2,00,000 ଟଙ୍କା

Question 3.
ନିମ୍ନ ସଂଖ୍ୟା ଯୋଡ଼ିମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଗୁଡ଼ିକ ବିପରୀତ ସଂଖ୍ୟାଯୋଡ଼ି ଚିହ୍ନଟ କର । 
(2, -3) (-5, 5) (-7, -8) (-1, 0) (-11, +11) (17, -17)
ସମାଧାନ:
ବିପରୀତ ସଂଖ୍ୟା ଯୋଡ଼ି ହେଲା
(-5, 5) (-11, +11) (17, -17)

Question 4.
ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିବସରେ ଭାରତର ଛଅଟି ସ୍ଥାନର ତାପମାତ୍ରାକୁ ନିମ୍ନରେ ଦିଆଯାଇଛି ।

ସ୍ଥାନ	ତାପମାତ୍ରା
ସିଆଚାନ	0°C ରୁ 10°C କମ୍
ଭୁବନେଶ୍ୱର	0°C ରୁ 22°C ଅଧିକ
ସିମଳା	0°C ରୁ 3°C କମ୍
ଦାରି ଙ୍ଗିବାଢ଼ି	0°C ରୁ 1°C କମ୍
କୋରାପୁଟ	0°C ରୁ 8°C ଅଧିକ
ଲଦାଖ	0°C ରୁ 8°C କମ୍

(କ) ପ୍ରତ୍ୟେକ ସ୍ଥାନର ତାପମାତ୍ରାକୁ ପୂର୍ବସଂଖ୍ୟାରେ ପ୍ରକାଶ କର।
ସମାଧାନ:

ସ୍ଥାନ	ତାପମାତ୍ରା
ସିଆଚାନ	-10°C
ଭୁବନେଶ୍ୱର	+22°C
ସିମଳା	-3°C
ଦାରି ଙ୍ଗିବାଢ଼ି	-1°C
କୋରାପୁଟ	+8°C
ଲଦାଖ	-8°C

(ଖ) ଗୋଟିଏ ସଂଖ୍ୟାରେଖା ଅଙ୍କନ କରି ପ୍ରତ୍ୟେକ ସ୍ଥାନର ତାପମାତ୍ରାକୁ ସେଥ‌ିରେ ସୂଚାଅ ।
ସମାଧାନ:

(ଗ) କେଉଁ ସ୍ଥାନର ତାପମାତ୍ରା ସବୁଠାରୁ ଅଧିକ ଓ କେଉଁ ସ୍ଥାନର ତାପମାତ୍ରା ସବୁଠାରୁ କମ୍ ?
ସମାଧାନ:
ଭୁବନେଶ୍ଵରର ତାପମାତ୍ରା ସବୁଠାରୁ ଅଧିକ ଓ ସିଆଚୀନ୍‌ର ତାପମାତ୍ରା ସବୁଠାରୁ କମ୍ ।

Question 5.
ନିମ୍ନରେ ଥିବା କ୍ରମଗୁଡ଼ିକ ମଧ୍ୟରୁ ଠିକ୍ କ୍ରମକୁ ଚିହ୍ନାଅ।
3 < 4
ସମାଧାନ:
3 < 4 (✓)

-7 > -8
ସମାଧାନ:
-7 > -8 (✓)

-9 > +5 
ସମାଧାନ:
-9 > +5 (✗)

-3 < 0
ସମାଧାନ:
-3 < 0 (✓)

-8 < +2
ସମାଧାନ:
-8 < +2 (✓)

+1 > -300
ସମାଧାନ:
+1 > -300 (✓)

-0 < 0
ସମାଧାନ:
-0 < 0 (✗)

Question 6.
ଦତ୍ତ ସଂଖ୍ୟାମାନଙ୍କର ବିପରୀତ ସଂଖ୍ୟା ଲେଖ।
(କ) 7
ସମାଧାନ:
7 ର ବିପରୀତ ସଂଖ୍ୟା = -7

(ଖ) -9
ସମାଧାନ:
-9 ର ବିପରୀତ ସଂଖ୍ୟା = -(-9) = 9

(ଗ) -10
ସମାଧାନ:
-10 ର ବିପରୀତ ସଂଖ୍ୟା = -(-10) = 10

(ଘ) 0
ସମାଧାନ:
0 ର ବିପରୀତ ସଂଖ୍ୟା = 0

(ଙ) 17
ସମାଧାନ:
17 ର ବିପରୀତ ସଂଖ୍ୟା = -17

Question 7.
ନିମ୍ନସ୍ଥ ପୂର୍ବସଂଖ୍ୟା ଦୁଇଟିର ମଧ୍ୟବର୍ତୀ ପୂର୍ବସଂଖ୍ୟାଗୁଡ଼ିକୁ ସାନରୁ ବଡ଼ କ୍ରମରେ ଲେଖ ।
(କ) 2 ଓ 8
ସମାଧାନ:
2 ଓ 8 ର ମଧ୍ୟବର୍ତ୍ତୀ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଗୁଡ଼ିକ ହେଲା : 3 , 4, 5, 6, 7 ।

(ଖ) -3 ଓ -7
ସମାଧାନ:
-3 ଓ -7 ର ମଧ୍ୟବର୍ତ୍ତୀ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଗୁଡ଼ିକ ହେଲା : -6, -5, -4 ।

(ଗ) -5 ଓ +2
ସମାଧାନ:
-5 ଓ +2 ର ମଧ୍ୟବର୍ତ୍ତୀ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଗୁଡ଼ିକ ହେଲା : -4, -3, -2, -1, 0, 1 ।

(ଘ) -1 ଓ +1
ସମାଧାନ:
-1 ଓ +1 ର ମଧ୍ୟବର୍ତ୍ତୀ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଗୁଡ଼ିକ ହେଲା : 0

(ଙ) -7 ଓ 0
ସମାଧାନ:
-7 ଓ 0 ର ମଧ୍ୟବର୍ତ୍ତୀ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଗୁଡ଼ିକ ହେଲା : -6, -5, -4, -3, -2, -1 ।

Question 8.
ଖାଲି ଘରେ >, < ଓ = ଚିହ୍ନମାନଙ୍କ ମଧ୍ୟରୁ ଉପଯୁକ୍ତ ଚିହ୍ନ ବସାଅ, ଯେପରି କ୍ରମ ଠିକ୍ ରହିବ।
(କ) 2 _______ -5
ସମାଧାନ:
>

(ଖ) -7 _______ 3
ସମାଧାନ:
<

(ଗ) 0 _______ -4
ସମାଧାନ:
>

(ଘ) 0 _______ -0
ସମାଧାନ:
=

(ଙ) -0 _______ -3
ସମାଧାନ:
>

(ଚ) -3 _______ -7
ସମାଧାନ:
>

Question 9.
ନିମ୍ନ ଉକ୍ତିଗୁଡ଼ିକ ମଧ୍ୟରୁ ଠିକ୍ ଉକ୍ତିକୁ ବାଛି ତୁମ ଖାତାରେ ଲେଖ ।
(କ) କ୍ଷୁଦ୍ରତମ ପୂର୍ଣ୍ଣସଂଖ୍ୟା ହେଉଛି 0 ।
(ଖ) -225 ଅପେକ୍ଷା -80 ସାନ ।
(ଗ ) -444 ଅପେକ୍ଷା 0 ସାନ ।
(ଘ) -2 < 0 < 7 
(ଙ) -0 = 0
(ଚ) ଶୂନ (0) ଧନାତ୍ମକ ବା ଋଣାତ୍ମକ ନୁହେଁ ।
ସମାଧାନ:
(ଘ), (ଙ), (ଚ) ଠିକ୍

Question 10.
(କ) ସାନରୁ ବଡ଼ କ୍ରମରେ ସଜାଅ।
5, 0, -11, 14, -20, 25, -4
ସମାଧାନ:
ସାନରୁ ବଡ଼ କ୍ରମ : -20 < -11 < -4 < 0 < 5 < 14 < 25

(ଖ) ବଡ଼ରୁ ସାନକ୍ରମରେ ସଜାଅ।
-8, 2, 5, -6, 0, 15, -111
ସମାଧାନ:
ବଡ଼ରୁ ସାନକ୍ରମ : 15 > 5 > 2 > 0 > -6 > -8 > -111

Question 11.
ସଂଖ୍ୟାରେଖାକୁ ଦେଖ୍, ନିମ୍ନ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
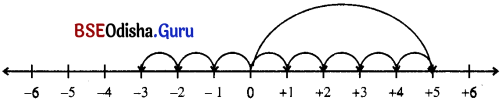
(କ) + 5 ସୂଚକ ବିନ୍ଦୁଠାରୁ ଡାହାଣକୁ 3 ଏକକ ଦୂର ଗଲେ, କେଉଁ ସଂଖ୍ୟା ପାଇବ ?
(ଖ) 5 ସୂଚକ ବିନ୍ଦୁଠାରୁ ବାମକୁ 3 ଏକକ ଦୂର ଗଲେ, କେଉଁ ସଂଖ୍ୟା ପାଇବ ?
(ଗ) + 7 ସୂଚକ ବିନ୍ଦୁଠାରୁ କେତେ ଏକକ ଦୂରରେ – 4 ସୂଚକ ବିନ୍ଦୁ ରହିଛି ?
(ଘ) -7 ସୂଚକ ବିନ୍ଦୁଠାରୁ ଯେତିକି ଦୂରରେ –4 ସୂଚକ ବିନ୍ଦୁ ରହିଛି, -7 ସୂଚକ ବିନ୍ଦୁର ବାମକୁ ପାଖକୁ ସେତିକି ଦୂରରେ କେଉଁ ସଂଖ୍ୟା ରହିଛି ?
ସମାଧାନ:

(କ) +5 ସୂଚକ ବିନ୍ଦୁଠାରୁ ଡାହାଣକୁ 3 ଏକକ ଦୂର ଗଲେ, 5 + 3 = +8 ସଂଖ୍ୟା ମିଳିବ । 
(ଖ) +5 ସୂଚକ ବାମକୁ 3 ଏକକ ଦୂର ଗଲେ 5 – 3 = +2 ସଂଖ୍ୟା ମିଳିବ ।
(ଗ) +7 ସୂଚକ ବିନ୍ଦୁଠାରୁ 7 – (-4) = 7 + 4 = 11 ଏକକ ଦୂରରେ -4 ସୂଚକ ବିନ୍ଦୁ ରହିଛି । 
(ଘ) -7 ସୂଚକ ବିନ୍ଦୁଠାରୁ -4 – (-7) = 4 + 7 = 3 ଏକକ ଦୂରରେ -4 ସୂଚକ ବିନ୍ଦୁ ରହିଛି ।
-7 ସୂଚକ ବିନ୍ଦୁର ବାମ ପାଖକୁ 3 ଏକକ ଦୂରରେ = -7 – 3 = -10 ସୂଚକ ବିନ୍ଦୁ ରହିଛି ।

Question 12.
ସଂଖ୍ୟାରେଖା ଉପରେ ।
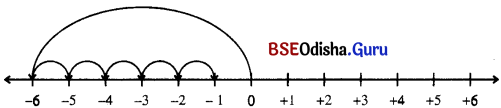
(କ) –3 ଓ –8 ସୂଚକ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ କେତେ ?
ସମାଧାନ:
–3 ଓ –8 ସୂଚକ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ବ୍ୟବଧାନ = -3 – (-8) = -3 + 8 = 5 ଏକକ

(ଖ) –2 ଓ +3 ସୂଚକ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ଦୂରତା କେତେ ?
ସମାଧାନ:
–2 ଓ +3 ସୂଚକ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ଦୂରତା = 3 – (-2) = 3 + 2 = 5 ଏକକ ।

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.3 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.3

Question 1. 
ନିମ୍ନସ୍ଥ ପ୍ରତ୍ୟେକ ଉକ୍ତ ପାଖରେ ସ୍ଵାଭାବିକ ସଂଖ୍ୟାର ବିଭିନ୍ନ ପ୍ରକ୍ରିୟା ସମ୍ବନ୍ଧୀୟ ନିୟମଗୁଡ଼ିକର ନାମ ଲେଖ ।

(କ) 5 × 8 = 8 × 5
ସମାଧାନ:
ଗୁଣନର କ୍ରମବିନିମୟୀ ନିୟମ

(ଖ) ଦୁଇଟି ସ୍ଵାଭାବିକ ସଂଖ୍ୟାର ଗୁଣଫଳ ଏକ ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ।
ସମାଧାନ:
ଗୁଣନର ସଂବୃତ୍ତି ନିୟମ

(ଗ) (8 × 5) × 3 = 8 × (5 × 3) = (8 × 3) × 5
ସମାଧାନ:
ଗୁଣନର ସହଯୋଗୀ ନିୟମ

(ଘ) 5 × 1 = 1 × 5 = 5, 12 × 1 = 1 × 12 = 12, 308 × 1 = 1 × 308 = 308
ସମାଧାନ:
ଗୁଣନର ଅଭେଦ ନିୟମ

(ଙ) (7 + 5) × 3 = 7 × 3 + 5 × 3
ସମାଧାନ:
ଯୋଗ ଉପରେ ଗୁଣନର ବଣ୍ଟନ ନିୟମ

(ଚ) (12 – 4) × 5 = 12 × 5 – 4 × 5
ସମାଧାନ:
ବିୟୋଗ ଉପରେ ଗୁଣନର ବଣ୍ଟନ ନିୟମ

Question 2. 
ନିମ୍ନ ଉଦାହରଣଟି ଦେଖ। ସେହି ଅନୁଯାୟୀ ପରବର୍ତୀ ଗୁଣନ କାର୍ଯ୍ୟ ସମ୍ପାଦନ କର।
ଉଦାହରଣ : 37 × 14 = (30 + 7) × 14
= 30 × 14 + 7 × 14
= 420 + 98
= 518

(କ) 118 × 12
ସମାଧାନ:
118 × 12
= (100 + 18) × 12
= 100 × 12 + 18 × 12
= 1200 + 216
= 1416

(ଖ) 98 × 16
ସମାଧାନ:
98 × 16
= (90 + 8) × 16
= 90 × 16 + 8 × 16
= 1440 + 128
= 1568

(ଗ) 206 × 18
ସମାଧାନ:
206 × 18
= (200 + 6) × 18
= 200 × 18 +6 × 18
= 3600 + 108
= 3708

(ଘ) 512 × 28
ସମାଧାନ:
512 × 28
= (500 + 12) × 28
= 500 × 28 + 12 × 28
= 14000 + 336
= 14336

Question 3. 
(କ) ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ସମୂହ ମଧ୍ୟରେ କେଉଁ ସଂଖ୍ୟାକୁ ଗୁଣନାତ୍ମକ ଅଭେଦ କୁହାଯାଏ?
ସମାଧାନ:
1କୁ ଗୁଣନାତ୍ମକ ଅଭେଦ କୁହାଯାଏ ।

(ଖ) କେଉଁ ନିୟମ ଆମକୁ ତିନିଗୋଟି ସ୍ଵାଭାବିକ ସଂଖ୍ୟାର ଗୁଣଫଳ ନିର୍ଣ୍ଣୟ କରିବାରେ ସାହାଯ୍ୟ କରେ?
ସମାଧାନ:
ସହଯୋଗୀ ନିୟମ ଆମକୁ ତିନିଗୋଟି ସ୍ଵାଭାବିକ ସଂଖ୍ୟାର ଗୁଣଫଳ ନିର୍ଣ୍ଣୟ କରିବାରେ ସାହାଯ୍ୟ କରେ ।

(ଗ) 12 × 7 × 5 ର ଗୁଣଫଳ ନିର୍ଣ୍ଣୟ କରିବା ଲାଗି ସଂଖ୍ୟାଗୁଡ଼ିକୁ ଉପଯୁକ୍ତ କ୍ରମରେ ନେଇ ସହଯୋଗୀ ନିୟମ ପ୍ରୟୋଗ କର।
ସମାଧାନ:
12 × 7 × 5 = 12 × (7 × 5) = 12 × (5 × 7) = (12 × 5) × 7

Question 4.
(କ) (15 + 5) × 6
ସମାଧାନ:
(15 + 5) × 6
= 15 × 6 + 5 × 6
= 90 + 30
= 120

(ଖ) (12 + 7) × 5
ସମାଧାନ:
(12 + 7) × 5
= 12 × 5 + 7 × 5
= 60 + 35
= 95

(ଗ) 4 × (8 + 6)
ସମାଧାନ:
4 ×(8 + 6)
= 4 × 8 + 4 × 6
= 32 + 24
= 56

(ଘ) (15 + 12) × 4
ସମାଧାନ:
(15 + 12) ×4
= 15 × 4 + 12 × 4
= 60 + 48
= 108

(ଙ) 8 × (17 – 9)
ସମାଧାନ:
8 × (17 – 9)
= 8 × 17 – 8 × 9
= 136 – 72
= 64

(ଚ) (324 – 220) × 5
ସମାଧାନ:
(324 – 220) × 5
= 324 × 5 – 220 × 5
= 1620 – 1100
= 520

Question 5. 
ଉପଯୁକ୍ତ ନିୟମ ପ୍ରୟୋଗ କରି ସରଳ କର –

(କ) 398 × 7 + 398 × 3
ସମାଧାନ:
398 × 7 + 398 × 3
= 398 (7 + 3)
= 398 × 10
= 3980

(ଖ) 8265 × 163 + 8265 × 37
ସମାଧାନ:
8265 × 163 + 8265 × 37
= 8265 (163 + 37)
= 8265 × 200
= 1653000

(ଗ) 15625 × 15625 – 15625 × 5625
ସମାଧାନ:
15625 × 15625 – 15625 × 5625
= 15625 × (15625 – 5625)
= 15625 × 10000
= 156250000

(ଘ) 887 × 10 × 461 – 361 × 8870
ସମାଧାନ:
887 × 10 × 461 – 361 × 8870
= 8870 × 461 – 361 × 8870
= 8870 × (461 – 361)
= 8870 × 100
= 887000

Question 6. 
ଜଣେ ଦୋକାନୀ ଗୋଟିଏ ସପ୍ତାହରେ 9785 ଟଙ୍କା ଦାମ୍‌ର 115 ଗୋଟି ଟେଲିଭିଜନ ବିକ୍ରୟ କଲେ । ତେବେ ମୋଟ ବିକ୍ରିଦାମ ବାବଦକୁ ସେ କେତେ ଟଙ୍କା ପାଇଲେ?
ସମାଧାନ:
ଗୋଟିଏ ଟିଭିର ବିକ୍ରିଦାମ୍ 9785 ଟଙ୍କା ।
∴ 115 ଟି ଟିଭିର ବିକ୍ରିଦାମ୍ = 9785 × 115 ଟଙ୍କା
= 9785 (100 + 15) = 9785 × 100 + 9785 × 15
= 978500 + 146775 = 11,25,275 ଟଙ୍କା ।

Question 7.
ଜଣେ ବ୍ୟବସାୟୀ ପ୍ରତି ରିକ୍ସାରେ ତିନି ବସ୍ତା ରଉଳ ଓ 8 ବସ୍ତା ଡାଲି ବୋଝେଇ କରି ହାଟକୁ ପଠାନ୍ତି । ଗୋଟିଏ ହାଟ ପାଳିରେ ସେ 8ଟି ରିକ୍ସା ବୋଝେଇ କରି ଋଉଳ ଓ ଡାଲି ହାଟକୁ ପଠାଇଲେ । ତେବେ ସେହି ହାଟ ପାଳିରେ ସେ ମୋଟ କେତେ ବସ୍ତା ଜିନିଷ ହାଟକୁ ପଠାଇଲେ?
ସମାଧାନ:
ଉ ପ୍ରତି ରିକ୍ସାରେ 3 ବସ୍ତା ଚାଉଳ ଓ 8 ବସ୍ତା ଡାଲି ଯାଏ ।
∴ 8 ଟି ରିକ୍ସାରେ ଯିବ = 8(3 + 8) = 8 × 11 = 88 ବସ୍ତା
∴ 8 ଟି ରିକ୍ସାରେ ସେ 88 ବସ୍ତା ଜିନିଷ ହାଟକୁ ପଠାଇଲେ ।

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.1 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.1

Question 1. 
ଗୋଟିଏ ତ୍ରିଭୁଜ ଅଙ୍କନ କରି ନାମକରଣ କର । ତା’ର ଶୀର୍ଷବିନ୍ଦୁ, କୋଣ ଓ ବାହୁଗୁଡିକର ନାମ ଲେଖ । 
ସମାଧାନ:

କଖଗ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ = କ, ଖ ଓ ଗ କୋଣ = ∠ଖକଗ, ∠କଖଗ ଓ ∠କଗଖ ବାହୁ = \(\overline{\mathrm{କଖ}}\), \(\overline{\mathrm{ଖଗ}}\) ଓ \(\overline{\mathrm{କଗ}}\)

Question 2. 
ବୃତ୍ତରେ ତା’ର ବ୍ୟାସାର୍ଦ୍ଧ ଓ କେନ୍ଦ୍ରକୁ ଦର୍ଶାଅ ।
ସମାଧାନ:

ବୃତ୍ତର କେନ୍ଦ୍ର = ‘କ’
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = \(\overline{\mathrm{କଖ}}\)

Question 3. 
ନିମ୍ନ ମାପବିଶିଷ୍ଟ କୋଣଗୁଡିକୁ ସୂକ୍ଷ୍ମକୋଣ, ସମକୋଣ ଓ ସ୍ଥୂଳକୋଣରେ ବର୍ଗୀକରଣ କର ।
30°, 175°, 90°, 45°, 89°, 115°, 95°, 20°
ସମାଧାନ:
ସୂକ୍ଷ୍ମକୋଣ =30°, 45°, 89°, 20° 
ସମକୋଣ = 90°
ସ୍ଥୂଳକୋଣ = 175°, 115°, 95°
ଯେଉଁ କୋଣର ପରିମାଣ 90° ରୁ କମ୍ ତାହାକୁ ସୂକ୍ଷ୍ମକୋଣ, ଯେଉଁ କୋଣର ପରିମାଣ 90° ତାହାକୁ ସମକୋଣ ଏବଂ ଯେଉଁ କୋଣର ପରିମାଣ 90° ରୁ ବେଶୀ ଓ 180ରୁ କମ୍ ତାହାକୁ ସ୍ଥୂଳକୋଣ କୁହାଯାଏ ।

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 2 ସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ଅଧ୍ବକ ଆଲୋଚନା Ex 2.5 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 2 ସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ଅଧ୍ବକ ଆଲୋଚନା Ex 2.5

Question 1.
ଯଦି ଦୁଇଟି ସଂଖ୍ୟାର ଲ.ସା.ଗୁ. 16 ଓ ସେ ଦ୍ଵୟର ଗୁଣଫଳ 64 ହୁଏ ତେବେ ତା’ର ଗ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କର । 
ସମାଧାନ:
ସଂଖ୍ୟା ଦ୍ବୟର ଲ.ସା.ଗୁ = 16 ଏବଂ ସଂଖ୍ୟା ଦ୍ଵୟର ଗୁଣଫଳ = 64 ।
ଗ.ସା.ଗୁ. = ସଂଖ୍ୟାଦ୍ଵୟର ଗୁଣଫଳ + ଲ.ସା.ଗୁ. = 64 + 16 = 4 

Question 2.
ତିନୋଟି ସଂଖ୍ୟାର ଗୁଣଫଳ ସର୍ବଦା ତା’ର ଗ.ସା.ଗୁ. ଓ ଲ.ସା.ଗୁ.ର ଗୁଣଫଳ ସହିତ ସମାନ ଅଟେ କି? 
ସମାଧାନ:
ତିନୋଟି ସଂଖ୍ୟାର ଗୁଣଫଳ ସର୍ବଦା ତା’ର ଗ.ସା.ଗୁ. ଓ ଲ.ସା.ଗୁର ଗୁଣଫଳ ସହିତ ସମାନ ନୁହେଁ ।
ଉଦାହରଣ – 4,6 ଓ 8 ର ଲ ସା.ଗୁ = 24 ଓ ଗ.ସା.ଗୁ  = 2
ଲ.ସା.ଗୁ. × ଗ.ସା.ଗୁ = 24 × 2 = 48
ସଂଖ୍ୟାତ୍ରୟର ଗୁଣଫଳ = 4 × 6 × 8 = 192

Question 3.
ଦୁଇଟି ସଂଖ୍ୟାର ଗ.ସା.ଗୁ. ଓ ଲ.ସା.ଗୁ. ଯଥାକ୍ରମେ 13 ଓ 1989 ଅଟେ । ଯଦି ସେଥ୍ମଧ୍ୟରୁ ଗୋଟିଏ ସଂଖ୍ୟା 117 ହୁଏ, ତେବେ ଅନ୍ୟ ସଂଖ୍ୟାଟି କେତେ?
ସମାଧାନ:
ଦୁଇଟି ସଂଖ୍ୟାର ଗ.ସା.ଗୁ = 13, ଲ.ସା.ଗୁ. = 1989 ଓ ଗୋଟିଏ ସଂଖ୍ୟା = 117
ଲ.ସା.ଗୁ. × ଗ.ସା.ଗୁ. = 1989 × 13 = 25857
ପ୍ରଥମ ସଂଖ୍ୟା × ଦ୍ବିତୀୟ ସଂଖ୍ୟା = 25857
ପ୍ରଥମ ସଂଖ୍ୟା = 117 ହେଲେ ଦ୍ବିତୀୟ ସଂଖ୍ୟା = 25857 + 117 = 221
∴ ଅନ୍ୟ ସଂଖ୍ୟାଟି 221 

Question 4.
ଦୁଇଟି ସଂଖ୍ୟାର ଗ.ସା.ଗୁ. 14 ଓ ଲ.ସା.ଗୁ. 204 ହୋଇପାରିବ କି ? କାରଣ ସହିତ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
ସଂଖ୍ୟାଦୟର ଗ.ସା.ଗୁ. ସେମାନଙ୍କର ଲ.ସା.ଗୁର ଏକ ଗୁଣନୀୟକ ହେବ । ତେଣୁ ଗ.ସା.ଗୁ. ଦ୍ବାରା ଲ.ସା.ଗୁ ବିଭାଜ୍ୟ ହେବ ।
204 ÷ 14 = 14 ଭାଗଫଳ ଓ ଭାଗଶେଷ 8 ।
204, 14 ଦ୍ବାରା ବିଭାଜ୍ୟ ନୁହେଁ ।
∴ ଯେଉଁ ସଂଖ୍ୟା ଦୁଇଟିର ଗ.ସା.ଗୁ 14, ସେମାନଙ୍କର ଲ.ସା.ଗୁ. 204 ହୋଇପାରିବ ନାହିଁ ।

Question 5. 
ଗୋଟିଏ ବିଦ୍ୟାଳୟର ଷଷ୍ଠ ଶ୍ରେଣୀରେ ଦୁଇଟି ବିଭାଗ ଅଛି । ସେ ଦୁଇଟି ହେଲେ A ଓ B  A ବିଭାଗରେ ଛାତ୍ରଛାତ୍ରୀ ପ୍ରତି 32 ଦିନର ବ୍ୟବଧାନରେ ପ୍ରତିଯୋଗିତା ଆୟୋଜନ କରନ୍ତି । B ବିଭାଗର ଛାତ୍ର-ଛାତ୍ରୀମାନେ ଏହି ପ୍ରତିଯୋଗିତା 36 ଦିନର ବ୍ୟବଧାନରେ ଆୟୋଜନ କରନ୍ତି । ଦୁଇଟି ବିଭାଗ ବର୍ଷ ଆରମ୍ଭର ପ୍ରଥମ ଦିନ ପ୍ରତିଯୋଗିତା ଆୟୋଜନ କରନ୍ତି । ଏଠାରେ କ୍ଷୁଦ୍ରତମ ଦିନ ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର, ଯେତେଦିନ ପରେ ଉଭୟ ବିଭାଗର ପ୍ରତିଯୋଗିତା ଏକା ଦିନରେ ହେବ ।
ସମାଧାନ:
ଷଷ୍ଠ ଶ୍ରେଣୀର A ବିଭାଗର ଛାତ୍ରଛାତ୍ରୀ 32 ଦିନ ବ୍ୟବଧାନରେ ଓ B ବିଭାଗର ଛାତ୍ରଛାତ୍ରୀ 36 ଦିନ ବ୍ୟବଧାନରେ ପ୍ରତିଯୋଗିତା ଆୟୋଜନ କରନ୍ତି ।
ଏଠାରେ 32 ଓ 36 ର ଲ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ ।

∴ ଲ.ସା.ଗୁ. = 2 × 2 × 8 × 9 = 288
288 ଦିନ ପରେ ଉଭୟ ବିଭାଗର ପ୍ରତିଯୋଗିତା ଆରମ୍ଭ ଏକା ଦିନରେ ହେବ ।

Question 6.
10,000 ର ନିକଟତମ ଦୁଇଟି ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର ଯାହା 2, 3, 4, 5, 6 ଓ 7 ପ୍ରତ୍ୟେକ ଦ୍ୱାରା ସମ୍ପୂର୍ଣ୍ଣଭାବେ ବିଭାଜ୍ୟ ହେବ ।

∴ ଲ.ସା.ଗୁ. = 2 × 3 × 2 × 5 × 7 = 420
10,000 ÷ 420 = 23 ଭାଗଫଳ ଓ ଭାଗଶେଷ 340
420 – 340 = 80
∴ ଗୋଟିଏ ସଂଖ୍ୟା = 10000 + 80 = 10080
ଅନ୍ୟ ସଂଖ୍ୟାଟି = 10000 – 340 = 9660

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.1 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.1

Question 1. 
କ୍ଷୁଦ୍ରତମ ସ୍ଵାଭାବିକ ସଂଖ୍ୟା କେତେ?
ସମାଧାନ:
1

Question 2. 
ପ୍ରତ୍ୟେକ ସଂଖ୍ୟାର ବାମରେ ତା’ର ପୂର୍ବବର୍ତୀ ସଂଖ୍ୟା ଓ ଡ଼ାହାଣରେ ତା’ର ପରବର୍ତୀ ସଂଖ୍ୟା ଲେଖ।

(କ) _____, 28, _____
ସମାଧାନ:
27, 28, 29

(ଖ) _____, 248, _____
ସମାଧାନ:
247, 248, 249

(ଗ) _____, 567, _____
ସମାଧାନ:
566, 567, 568

(ଘ) _____, 3856, _____
ସମାଧାନ:
3855, 3856, 3857

(ଙ) _____, 5000, _____
ସମାଧାନ:
4999, 5000, 5001

(ଚ) _____, 99999, _____
ସମାଧାନ:
99998, 99999, 100000

Question 3.
(କ) 57 ଠାରୁ କ୍ଷୁଦ୍ରତର କେତୋଟି ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ଅଛି?
ସମାଧାନ:
56 ଟି

(ଖ) 48 ଓ 216 ମଧ୍ୟରେ କେତୋଟି ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ଅଛି?
ସମାଧାନ:
216 – 48 – 1 = 167

(ଗ) 5729 ର ପରବର୍ତୀ ତିନୋଟି କ୍ରମିକ ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ଲେଖ।
ସମାଧାନ:
5730, 5731, 5732

Question 4. 
(କ) ଏକକ ଅଙ୍କ 5 ହୋଇଥିବା କ୍ଷୁଦ୍ରତମ ଛଅ ଅଙ୍କବିଶିଷ୍ଟ ସଂଖ୍ୟା ଲେଖ। 
ସମାଧାନ:
100005

(ଖ) ଏକକ ଅଙ୍କ 7 ହୋଇଥିବା ବୃହତ୍ତମ ସାତ ଅଙ୍କବିଶିଷ୍ଟ ସଂଖ୍ୟା ଲେଖ ।
ସମାଧାନ:
9999997

(ଗ) ଛଅଅଙ୍କ ବିଶିଷ୍ଟ କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟାଠାରୁ ସାତଅଙ୍କ ବିଶିଷ୍ଟ ବୃହତ୍ତମ ସଂଖ୍ୟା ପର୍ଯ୍ୟନ୍ତ (ଉଭୟ ସଂଖ୍ୟାକୁ ମିଶାଇ) କେତୋଟି ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ଅଛି?
ସମାଧାନ:

∴ ଛଅ ଅଙ୍କ ବିଶିଷ୍ଟ କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟାଠାରୁ ସାତଅଙ୍କ ବିଶିଷ୍ଟ ବୃହତ୍ତମ ସଂଖ୍ୟା ପର୍ଯ୍ୟନ୍ତ 9900000 ଟି ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ଅଛି ।

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.6 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.6

Question 1. 

(କ) ନିମ୍ନଲିଖିତ ମାପବିଶିଷ୍ଟ କୋଣମାନଙ୍କର ଅନୁପୂରକ କୋଣର ମାପ ନିର୍ଣ୍ଣୟ କର ।
6°, 15°, 29°, 30°, 45°, 75°
ସମାଧାନ:
(i) 6° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 6°) = 84°
(ii) 15° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 15°) = 75°
(iii) 29° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 29°) = 61°
(iv) 30° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 30°) = 60°
(v) 45° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 45°) = 45°
(vi) 75° ର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 75°) = 15°

(ଖ) ନିମ୍ନଲିଖତ ମାପବିଶିଷ୍ଟ କୋଣମାନଙ୍କର ପରିପୂରକ କୋଣର ମାପ ନିର୍ଣ୍ଣୟ କର । 
27°, 52°, 70°, 110°, 145°, 150°
ସମାଧାନ:
(i) 27° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 27°) = 153°
(ii) 52° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 52°) = 128°
(iii) 70° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 70°) = 110°
(iv) 110° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 110°) = 70°
(v) 145° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 145°) = 35°
(vi) 150° ର ପରିପୂରକ କୋଣର ମାପ = (180° – 150°) = 30°

Question 2.
(କ) 45° 45′ ମାପ ବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ ଓ ପରିପୂରକ କୋଣର ମାପ ନିର୍ଣ୍ଣୟ କର । (1° = 60′)। 
ସମାଧାନ:
45° 45′ ମାପ ବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ମାପ = (90° – 45° 45′) = 44° 15′
45° 45′ ମାପ ବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ମାପ = (180° – 45° 45′) = 134° 15′

(ଖ) 48° ମାପବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ପରିପୂରକ କୋଣର ପରିମାଣ କେତେ?
ସମାଧାନ:
48° ମାପବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ପରିମାଣ = (90° – 48°) = 42° 
42° ମାପବିଶିଷ୍ଟ କୋଣର ପରିପୂରକ କୋଣର ପରିମାଣ = (180° – 42°) = 138° 
∴ 48° ମାପବିଶିଷ୍ଟ କୋଣର ଅନୁପୂରକ କୋଣର ପରିପୂରକ କୋଣର ପରିମାଣ 138° ।

Question 3. 
ନିମ୍ନ ମାପବିଶିଷ୍ଟ ଯୋଡ଼ିମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ ଯୋଡ଼ି ପରସ୍ପର ଅନୁପୂରକ ଓ କେଉଁ ଯୋଡ଼ି ପରସ୍ପର ପରିପୂରକ ଚିହ୍ନଟ କର ।

(କ) 68°, 22°
ସମାଧାନ:
68°, 22° → 68° + 22° = 90° (ଅନୁପୂରକ)

(ଖ) 163°, 17°
ସମାଧାନ:
163°, 17° → 163° + 17° = 180° (ପରିପୂରକ)

(ଗ) 73°, 17°
ସମାଧାନ:
73°, 17° → 73° + 17° = 90° (ଅନୁପୂରକ)

(ଘ) 80°, 10°
ସମାଧାନ:
80°, 10° → 80° + 10° = 90° (ଅନୁପୂରକ)

(ଙ) 42°, 138°
ସମାଧାନ:
42°, 138° → 42° + 138° = 180° (ପରିପୂରକ)

(ଚ) 90°, 90°
ସମାଧାନ:
90°, 90° → 90° + 90° = 180° (ପରିପୂରକ)

Question 4.
ଚିତ୍ର ଅଙ୍କନକରି ଅନୁପୂରକ କୋଣ ଓ ପରିପୂରକ କୋଣ ଯୋଡ଼ିମାନଙ୍କର ଉଦାହରଣ ଦିଅ ।
ସମାଧାନ:

ଚିତ୍ର-I ରେ ∠ABD ଓ ∠CBD ଯୋଡ଼ି ପରସ୍ପର ଅନୁପୂରକ ।
ଚିତ୍ର – II ଓ ଚିତ୍ର – III ର ∠MNP ଓ ∠XYZ ପରସ୍ପର ଅନୁପୂରକ ।

ଚିତ୍ର-IV ରେ ∠ACD ଓ ∠BCD ଯୋଡ଼ି ପରସ୍ପର ପରିପୂରକ ।
ଚିତ୍ର – V ଓ ଚିତ୍ର – VI ର ∠POR ଓ ∠EFG ଯୋଡ଼ି ପରସ୍ପର ପରିପୂରକ ।

Question 5. 
ତୁମ ଆଖପାଖରେ ଥିବା ବସ୍ତୁମାନଙ୍କ ମଧ୍ୟରୁ ପରସ୍ପର ପ୍ରତି ସମକୋଣରେ ରହୁଥ‌ିବା ବସ୍ତୁମାନଙ୍କର ତିନୋଟି ଉଦାହରଣ ଦିଅ।
ସମାଧାନ:
ଆମ ଆଖପାଖରେ ଥ‌ିବା ବସ୍ତୁମାନଙ୍କ ମଧ୍ୟରୁ ପରସ୍ପର ପ୍ରତି ସମକୋଣରେ ରହୁଥିବା ବସ୍ତୁଗୁଡ଼ିକ ହେଲା – 
(i) ଫଟୋଫ୍ରେମ୍ (ii) ଦୁଆର ବନ୍ଧ (iii) ଟେବୁଲ୍ ଗୋଡ଼

Question 6. 
ଗୋଟିଏ ଟ୍ରାଫିକ୍ ପୋଲିସ୍ ପୂର୍ବକୁ ମୁହଁ କରି ଠିଆ ହୋଇଛି। ଯଦି ସେ ତା’ର ବାମକୁ କ୍ରମାନ୍ୱୟରେ

ସମାଧାନ:

(କ) ଏକ ସମକୋଣ 
ସମାଧାନ:
ପୂର୍ବରୁ ଏକ ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ଉତ୍ତର ଦିଗକୁ ରହିବ । 

(ଖ) ଦୁଇ ସମକୋଣ
ସମାଧାନ:
ପୂର୍ବରୁ ଦୁଇ ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ପଶ୍ଚିମ ଦିଗକୁ ରହିବ ।

(ଗ) ତିନି ସମକୋଣ
ସମାଧାନ:
ପୂର୍ବରୁ ତିନି ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ଦକ୍ଷିଣ ଦିଗକୁ ରହିବ । 

(ଘ) ଚାରି ସମକୋଣ ଘୂରେ, ତେବେ ପ୍ରତି ଥର ଘୂରିବା ପରେ ତା’ର ମୁହଁ କେଉଁ ଦିଗକୁ ରହିବ?
ସମାଧାନ:
ପୂର୍ବରୁ ଚାରି ସମକୋଣ ବାମକୁ ଘୂରିଲେ ମୁହଁ ପୁନଶ୍ଚ ପୂର୍ବ ଦିଗକୁ ରହିବ ।

Question 7. 
କି ପ୍ରକାର କୋଣ ସୃଷ୍ଟି ହେବ?
ସମାଧାନ:

(କ) ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଦକ୍ଷିଣକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ। 
ସମାଧାନ:
ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଦକ୍ଷିଣକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ, ସମକୋଣ (90°) ସୃଷ୍ଟି ହେବ ।

(ଖ) ଗୋଟିଏ ବିନ୍ଦୁରୁ ଉତ୍ତର ଓ ଉତ୍ତର ପୂର୍ବକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ ।
ସମାଧାନ:
ଗୋଟିଏ ବିନ୍ଦୁରୁ ଉତ୍ତର ଓ ଉତ୍ତର ପୂର୍ବକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ ସୂକ୍ଷ୍ମକୋଣ (45°) ସୃଷ୍ଟି ହେବ ।

(ଗ) ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଉତ୍ତରକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ।
ସମାଧାନ:
ଗୋଟିଏ ବିନ୍ଦୁରୁ ପୂର୍ବ ଓ ଉତ୍ତରକୁ ଦୁଇଟି ରଶ୍ମି ଅଙ୍କନ କଲେ ସମକୋଣ (90°) ସୃଷ୍ଟି ହେବ ।

Question 8. 
(କ) ଯେଉଁ କୋଣର ପରିମାଣ ତା’ର ଅନୁପୂରକ କୋଣର ପରିମାଣର ଦୁଇଗୁଣ, ତା’ର ପରିମାଣ କେତେ? 
ସମାଧାନ:
ମନେକର ଅନୁପୂରକ କୋଣର ପରିମାଣ l ଗୁଣ ଓ କୋଣଟିର ପରିମାଣ 2 ଗୁଣ ।
1 ଗୁଣ + 2 ଗୁଣ = 3 ଗୁଣ, 3 ଗୁଣ = 90°
1 ଗୁଣ = \(\frac{90^{\circ}}{3}\) = 30°, 2 ଗୁଣ = 30° × 2 = 60°
∴ କୋଣର ପରିମାଣ 60° ।

(ଖ) ଯେଉଁ କୋଣର ପରିମାଣ ତା’ର ପରିପୂରକ କୋଣର ପରିମାଣର ଦୁଇଗୁଣ, ତା’ର ପରିମାଣ କେତେ?
ସମାଧାନ:
ମନେକର ପରିପୂରକ କୋଣର ପରିମାଣ 1 ଗୁଣ ଓ କୋଣଟିର ପରିମାଣ 3 ଗୁଣ ।
1 ଗୁଣ + 2 ଗୁଣ = 3 ଗୁଣ, 3 ଗୁଣ = 180°, 1 ଗୁଣ = \(\frac{180^{\circ}}{3}\) = 60°
2 ଗୁଣ = 60° × 2 = 120°
∴ କୋଣଟିର ପରିମାଣ 120°

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 7 ବ୍ୟାବସାୟିକ ଗଣିତ Ex 7.5 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 7 ବ୍ୟାବସାୟିକ ଗଣିତ Ex 7.5

Question 1.
35, 48, 31 ଓ 22 ର ହାରାହାରି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

ହାରାହାରି ମୂଲ୍ୟ = \(\frac{35+48+31+22}{4}\) = \(\frac{136}{4}\) = 34

Question 2.
ଖଲିଲ୍ ବାବୁ ତାଙ୍କର ଥିବା ତିନିଗୋଟି ସାଇକେଲ୍ ଲାଗି ତିନୋଟି ସିକଭର କିଣିଲେ। ଗୋଟିକର ଦାମ 28 ଟଙ୍କା, ଆଉ ଗୋଟିକର ଦାମ୍ 24 ଟଙ୍କା ଓ ଅନ୍ୟଟିର ଦାମ୍ 23 ଟଙ୍କା । ତେବେ ସେ କିଣିଥିବା ସିକଭର ଗୁଡ଼ିକର ଗୋଟା ପ୍ରତି ହାରାହାରି ଦାମ୍ କେତେ ?
ସମାଧାନ:
ସିଭର୍ ତିନୋଟିର ଦାମ୍ ଯଥାକ୍ରମେ 28 ଟଙ୍କା, 24 ଟଙ୍କା ଓ 23 ଟଙ୍କା । 
ସିଭର ତିନୋଟିର ମୋଟ ଦାମ୍ = 28 ଟଙ୍କା + 24 ଟଙ୍କା + 23 ଟଙ୍କା = 75 ଟଙ୍କା

= \(\frac{75}{3}\) ଟଙ୍କା = 25 ଟଙ୍କା
∴ ଖଲିଲ୍‌ବାବୁ କିଣିଥିବା ସିଟ୍ କଭରଗୁଡ଼ିକର ଗୋଟା ପ୍ରତି ହାରାହାରି ଦାମ୍ 25 ଟଙ୍କା ।

Question 3.
ଜଣେ କ୍ରିକେଟ୍ ଖେଳାଳି ପାଞ୍ଚଟି ଏକଦିବସୀୟ ଖେଳରେ 45, 30, 102, 113 ଓ 70 ରନ୍ କରିଥିଲେ । ତେବେ ସେ ଖେଳ ପ୍ରତି ହାରାହାରି କେତେ ରନ୍ କରିଥିଲେ ?
ସମାଧାନ:
ମୋଟ ରନ୍ = 45 + 30 + 102 + 113 + 70 = 360

= \(\frac{360}{5}\) = 72
∴ ସେ ଖେଳପ୍ରତି ହାରାହାରି 72 ରନ୍ କରିଥିଲେ ।

Question 4.
ଛଅଟି ପିଲାଥିବା ଗୋଟିଏ ଦଳରେ ପିଲା ପ୍ରତି ହାରାହାରି ବୟସ 10 ବର୍ଷ ହେଲେ, ସେମାନଙ୍କର ମୋଟ ବୟସ କେତେ ?
ସମାଧାନ:
ଦଳରେ ଥିବା ପିଲାସଂଖ୍ୟା = 6 ଓ ପିଲାପ୍ରତି ହାରାହାରି ବୟସ = 10 ବର୍ଷ

ବା, ମୋଟ ବୟସ = ହାରାହାରି ବୟସ × ପିଲାସଂଖ୍ୟା = 10 × 6 = 60
∴ ସେମାନଙ୍କର ମୋଟ ବୟସ 60 ବର୍ଷ ଥିଲା ।

Question 5.
ବାରଟି ଥଳିରେ ଥ‌ିବା ମୋଟ ଚିନିର ଓଜନ 111 କି. 600 ଗ୍ରାମ୍ ହେଲେ, ଥଳି ପ୍ରତି ଚିନିର ହାରାହାରି ଓ ଜନ କେତେ ?
ସମାଧାନ:
ଥଳି ସଂଖ୍ୟା = 12, ମୋଟ ଚିନିର ଓଜନ = 111 କି. 600 ଗ୍ରା. = 111600 ଗ୍ରାମ୍

∴ ଥଳି ପ୍ରତି ଚିନିର ହାରାହାରି ଓଜନ 9 କି. 300 ଗ୍ରାମ୍ ।

Question 6.
ସାତ ଖଣ୍ଡ ବହିର ମୋଟ ଦାମ୍ 310 ଟଙ୍କା ଏବଂ ଅନ୍ୟ ତିନି ଖଣ୍ଡ ବହିର ଖଣ୍ଡ ପ୍ରତି ହାରାହାରି ଦାମ୍ 68 ଟଙ୍କା ହେଲେ, ଉକ୍ତ ଦଶଟିଯାକ ବହିର ଖଣ୍ଡ ପ୍ରତି ହାରାହାରି ଦାମ୍ ସ୍ଥିର କର ।
ସମାଧାନ:
7 ଖଣ୍ଡ ବହିର ମୋଟ୍ ଦାମ୍ = 310 ଟଙ୍କା
3 ଖଣ୍ଡ ବହିର ଖଣ୍ଡ ପ୍ରତି ହାରାହାରି ଦାମ୍ = 68 ଟଙ୍କା
3 ଖଣ୍ଡ ବହିର ମୋଟ୍ ଦାମ୍ = ହାରାହାରି ଦାମ୍ × ବହିସଂଖ୍ୟା = 68 × 3 = 204 ଟଙ୍କା
ମୋଟ ବହି ସଂଖ୍ୟା = 7 + 3 = 10 ଖଣ୍ଡ
10 ଖଣ୍ଡ ବହିର ମୋଟ ଦାମ୍ = 310 ଟଙ୍କା + 204 ଟଙ୍କା = 514 ଟଙ୍କା ।

= \(\frac{514}{10}\) ଟଙ୍କା = ଟ. 51.40 ପଇସା

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.5 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 3 ଜ୍ୟାମିତିରେ ମୌଳିକ ଧାରଣା Ex 3.5

Question 1. 
ଚିତ୍ର ଦେଖି ଖାତାରେ ଉତ୍ତର ଲେଖ ।

(କ) ଚିତ୍ରରେ ଥିବା କୋଣଟିର ନାମ କ’ଣ ଲେଖ। 
ସମାଧାନ:
∠PQR

(ଖ) ଏହାର ଶୀର୍ଷବିନ୍ଦୁ ଓ ବାହୁମାନଙ୍କର ନାମ ଲେଖ। 
ସମାଧାନ:
ଏହାର ଶୀର୍ଷବିନ୍ଦୁ O ଓ \(\overrightarrow{\mathrm{OP}}\) ଓ \(\overrightarrow{\mathrm{OR}}\) ବାହୁ ।

(ଗ) ଏହି କୋଣର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ଓ ବହିଃସୁ ବିନ୍ଦୁର ନାମ ଲେଖ।
ସମାଧାନ:
ଏହି ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ Y ଓ ବହିଃସୁ ବିନ୍ଦୁ X ।

Question 2. 
ନିମ୍ନସ୍ଥ ବାକ୍ୟମାନଙ୍କରେ ଥ‌ିବା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।

(କ) ଗୋଟିଏ କୋଣର _____ ଗୋଟି ଶୀର୍ଷବିନ୍ଦୁ ଓ _____ ଗୋଟି ବାହୁ ଥାଏ।
ସମାଧାନ:
ଏକ, ଦୁକ

(ଖ) _____ ଚିହ୍ନଟି ହେଉଛି ଚିତ୍ରରେ ଥ‌ିବା କୋଣର ସାଙ୍କେତିକ ଚିହ୍ନ।
ସମାଧାନ:
∠

(ଗ) ଦୁଇଟି ସରଳରେଖା ପରସ୍ପରକୁ ଛେଦ କଲେ _____  ଗୋଟି କୋଣ ଉତ୍ପନ୍ନ ହୁଏ ।
ସମାଧାନ:
ଚାରି

Question 3. 
ସ୍କେଲ୍ ଓ ପେନ୍‌ସିଲ ସାହାଯ୍ୟରେ ତୁମ ଖାତାରେ ଦୁଇଟି କୋଣ ଅଙ୍କନ କରି ସେମାନଙ୍କ ନାମ ଦିଅ ।
ସମାଧାନ:

Question 4. 

(କ) ପାର୍ଶ୍ଵସ୍ଥ ଚିତ୍ରରେ କେତୋଟି କୋଣ ଅଛି?
ସମାଧାନ:
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ୫ ଟି କୋଣ ଅଛି

(ଖ) କେବଳ ଶୀର୍ଷବିନ୍ଦୁକୁ ନେଇ କେଉଁ କେଉଁ କୋଣର ନାମକରଣ କରାଯାଇପାରିବ?
ସମାଧାନ:
∠BAD ବା ∠A ଏବଂ ∠BCD ବା ∠C

(ଗ) କେଉଁ କୋଣମାନଙ୍କର ଏକ ସାଧାରଣ ବାହୁ ଅଛି?
ସମାଧାନ:
∠ABD ଓ ∠ABC ର ସାଧାରଣ ବାହୁ \(\overline{\mathrm{AB}}\)
∠ADB ଓ ∠ADC ର ସାଧାରଣ ବାହୁ \(\overline{\mathrm{AD}}\)
∠ABD ଓ ∠CBD ର ସାଧାରଣ ବାହୁ \(\overline{\mathrm{BD}}\)
∠ADB ଓ ∠CBD ର ସାଧାରଣ ବାହୁ \(\overline{\mathrm{BD}}\)
∠CBD ଓ ∠CBA ର ସାଧାରଣ ବାହୁ \(\overline{\mathrm{BC}}\)
∠CDA ଓ ∠CDB ର ସାଧାରଣ ବାହୁ \(\overline{\mathrm{CD}}\)