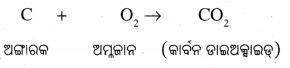Odisha State Board BSE Odisha 7th Class Science Solutions Chapter 1 ପଦାର୍ଥ Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Science Solutions Chapter 1 ପଦାର୍ଥ
Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ପଦାର୍ଥର ତରଲାଦଗାରେ ନିଦପୁ ______ ଥାଏ, କିନ୍ତୁ ନିର୍ଦ୍ଦିଷ୍ଟ ______ ନ ଥାଏ ।
(ଖ) ପଦାର୍ଥର ଗ୍ୟାସ।ୟାବମାରେ କଣିକାଗୁଡିକ ମଧ୍ୟରେ ଥିବା ପାରମରିକ ଆକପଣ ବିକ ______ ଥାଏ ।
(ଗ) ଯେଉଁ ବିଶୁଦ୍ଧ ପଦାର୍ଥର ପରମାଣୁଗୁଡ଼ିକ ସହଧର୍ମୀ ହୋଇଥାଏ, ତାହାକୁ ______ କୁହାଯାଏ ।
(ଘ) ବାୟୁ ଗୋଟିଏ ______ ପଦାର୍ଥ, କିନ୍ତୁ ଅଙ୍ଗାରକାମ୍ଳ ଗୋଟିଏ ______ ପଦାର୍ଥ |
(ଙ) ଗୋଟିଏ ସେକକ ପଦାଥରେ ________ ପ୍ରକାର ଅଣୁ ନ ଥାଏ ।
Solution:
(କ) ଆୟତନ, ଆକୃତି
(ଖ) ସବୁଠାରୁ କମ୍
(ଗ) ମୌଳିକ ପଦାର୍ଥ
(ଘ) ମିଶ୍ର, ଯୌଗିକ
(ଙ) ଭିନ୍ନ ଭିନ୍ନ

Questions 2.
ନିମ୍ନଲିଖୂତ ପଦାର୍ଥଗୁଡ଼ିକରୁ ମୌଳିକ, ଯୌଗିକ ଓ ମିଶ୍ରଣକୁ ଅଲଗା କରି ଲେଖ । କ୍ଲୋରିନ୍, ପାରଦ ବା ମର୍କୁରି, ଲାଇମ୍ ବା ଚୂନ, ଚିନି ସର୍ବତ, ଗନ୍ଧକାମ୍ଳ, ଫିରୀ, ବରଫ, କ୍ଷୀର, ହୀରା, ଲୁଣ
Solution:
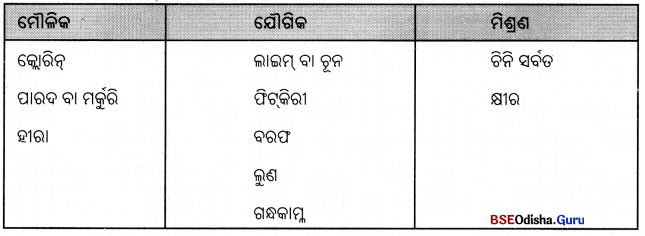
Question 3.
ପ୍ରତୀକ ଓ ସଂକେତ ବ୍ୟବହାର କରି ନିମ୍ନଲିଖ ପଦାର୍ଥ ଗୁଡ଼ିକୁ ଲେଖ ।
(କ) ପାପାନିକାର ପରମାଣ୍ଡ
(ଖ) କ୍ଲୋରିନ୍ ଅଣୁ
(ଗ) ଚୂନପାଣିର ସଂକେତ
(ଘ) ଯବକ୍ଷାରଜାନର ଅଣୁ
Solution:
(କ) ମାଙ୍ଗାନିଜ୍ର ପରମାଣୁ – Mn
(ଖ) କ୍ଲୋରିନ୍ ଅଣୁ – Cl2
(ଗ) ଚୂନପାଣିର ସଂକେତ – Ca(OH)2
(ଘ) ଯବକ୍ଷାରଜାନର ଅଣୁ – N2
Question 4.
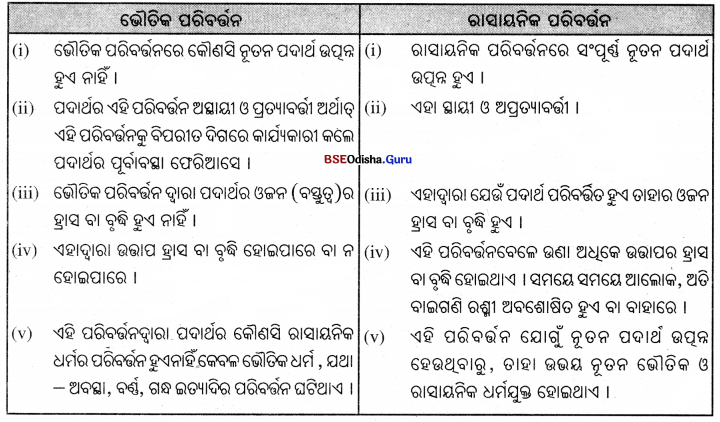
ଯୌଗିକ ଓ ମିଶ୍ରଣ ଭିତରେ ଦୁଇଟି ପାର୍ଥକ୍ୟ ଲେଖ ।
Solution:
| ଯୌଗିକ |
ମିଶ୍ରଣ |
| (i) ଦୁଇ ବା ତତୋଧ୍ଵ ମୌଳିକ ପଦାର୍ଥ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଥନ୍ତ୍ରପାତରେ ରାସାୟନିକ ପୃକ୍ତୟଦ୍ଵାରା ସଯୁକ୍ତ ହୋଇ ଯେଉଁ ନୂତନ ପଦାର୍ଥ ସୃଷ୍ଟି କରନ୍ତି ତାହାକୁ ଯୌଗିକ ପଦାର୍ଥ କିହାଯାଏ |
ରଦାହରଣ ଜଳ (H2O) |
(i) ଯେଉଁ ପଦାର୍ଥରେ ଏକାଧ୍ଵ ମୌଳିକ ବା ଯୌଗିକ ବା ଉଭୟ ମୌଳିକ ଓ ଯୌଗିକ ମିଶିକରି ଥାଏ, ତାହାକୁ ମିଶ୍ରଣ କୁ ହାଯାଏ । ଏମାନେ କୌଣସି |
| (ii) ଯୌଗିକରେ ଉପାଦାନଗୁଡ଼ିକ ନିଜସ୍ୱ ଧର୍ମ ହରାରଥା’ନ୍ତି | |
(ii) ମିଶ୍ରଣରେ ଉପାଦାନଗୁଡ଼ିକର ନିଜସ୍ବ ଗୁଣ ଅପରିବର୍ତିତ ରହିଥାଏ । |
Question 5.
ଯେଉଁ ମୌଳିକର ଅଣୁରେ ଏକରୁ ଅଧିକ ପରମାଣୁ ଥାଏ, ସେହିପରି ମୌଳିକର ତିନିଗୋଟି ଉଦାହରଣ ଦିଅ ।
Solution:
ଉଦାହରଣ – ଉଦ୍ଜାନ (H2) ଅମ୍ଳଜାନ (O2) ଏବଂ ଯବକ୍ଷାରଜାନ (ND2)

Question 6.
ତୁମେ ଜାଣିଛ O2, ଏବଂ O3, ଗୋଟିଏ ଅନ୍ୟଟିର ସମସ୍ଥାନିକ । ତେବେ ଏହି ଦୁଇଟି, ଦୁଇଟି ଭିନ୍ନ ପଦାର୍ଥ, O3 ର ନାମ ଲେଖ ଓ ଏହା ଆଜିକାଲି ସବୁଠାରେ କାହିଁକି ଆଲୋଚନା ହେଉଛି, ସଂକ୍ଷେପରେ ଲେଖ ।
Solution:
02, ଓ O3, ଗୋଟିଏ ଅନ୍ୟଟିର ସମସ୍ଥାନିକ । ତେବେ ଏହି ଦୁଇଟି ଭିନ୍ନ ପଦାର୍ଥ ।
O2 – ଅମ୍ଳଜାନର ସଂକେତ ଏବଂ O3 – ଓଜୋନ୍ର ସଂକେତ ।
- ବାୟୁମଣ୍ଡଳର ‘ଷ୍ଟ୍ରାଟୋସ୍ପିୟର୍’’ ସ୍ତରରେ O3, ବା ଓଜୋନ୍ ସୃଷ୍ଟି ହୋଇଥାଏ ।
- ଏହା ସୂର୍ଯ୍ୟରୁ ଆସୁଥିବା ମାରାତ୍ମକ ଅଲ୍ଟ୍ରାଭାଇଓଲେଟ୍ ବା ଅତିବାଇଗଣୀ ରଶ୍ମିକୁ ଶୋଷି ଦେଇଥାଏ ।
- କ୍ଲୋରୋଫ୍ଲୋରୋ କାର୍ବନ (CFC) ଏହି ଓଜୋନ୍ ଅଣୁକୁ ନଷ୍ଟ କରିଦେଇଥାଏ । ଏହାକୁ ଓଜୋନ୍ ସ୍ତରର ଛିଦ୍ର କୁହାଯାଏ । ଫଳରେ ମାରାତ୍ମକ ଚର୍ମ କର୍କଟ ରୋଗର ପ୍ରାଦୁର୍ଭାବ ପୃଥିବୀ ପୃଷ୍ଠରେ ବୃଦ୍ଧି ପାଇଥାଏ ।
Question 7.
ପ୍ରୋଟିଏମ୍, ଡିଉଟେରିୟମ୍ ଓ ଟ୍ରାଇଟିୟମ୍, ଉଦ୍ଜାନର ତିନିଗୋଟି ସମସ୍ଥାନିକ । ଜଳର ସଂକେତ H2O ଓ ଏଦ୍ବାର ବ୍ୟବହାର ଦହକ | ତିରଟେରିଯାପ ଓ ଥମ୍ନକାନରୁ ପ୍ରସ୍ତୁତ ଯୌଗିକର ନାମ ଓ ଫକେତ ଲେଖା ଏବଂ ସେଦ୍ୱି ମେଟିକର ଦ୍ୟଦହାଇ କାଣ କାଣିଶ୍ଚ ଲେଖ |
Solution:
- ପ୍ରୋଟିଏମ୍, ଡିଉଟେରିୟମ୍ ଓ ଟ୍ରାଇଟିୟମ୍, ଉଦ୍ଜାନର ତିନିଗୋଟି ସମସ୍ଥାନିକ ।
- ଜଳର ସଂକେତ H2O |
- ଡିଉଟେରିୟମ୍ ଓ ଅମ୍ଳଜାନରୁ ପ୍ରସ୍ତୁତ ଯୌଗିକର ନାମ ଭାରୀଜଳ ଓ ଏହାର ସଂକେତ D2O । ଏହାକୁ ଭାରୀଜଳ କୁହାଯାଏ ।
Question 8.
ଗୋଟିଏ ଧାତୁ ଓ ଅଧାତୁର ନାମ ଓ ସଂକେତ ଲେଖ, ଯାହା ସାଧାରଣ ତାପମାତ୍ରାରେ ତରଳ ଅବସ୍ଥାରେ ଥାଏ ।
Solution:
- ପାରଦ ଏକ ତରଳ ଧାତବ ମୌଳିକ । ଏହାର ସଂକେତ – Hg |
- ବ୍ରୋମିନ୍ ଏକ ତରଳ ଅଧାତୁ । ଏହାର ସଂକେତ Br |
ବିପଯୁବସ୍ତୁ ସପୂଜାପ ପୂଚନା ଓ ବିଶେଷଣ :
→ ପ୍ରାକୃତିକ ଓ ମନୁଷ୍ୟକୃତ ପଦାର୍ଥ :
(i) ଆମ ଚତୁପାର୍ଶ୍ଵରେ ଆମେ ଅନେକ ପଦାର୍ଥ ଦେଖୁ । ଏହି ପଦାର୍ଥଗୁଡ଼ିକୁ ମୁଖ୍ୟତଃ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା –
(a) ପ୍ରାକୃତିକ ପଦାର୍ଥ ଓ (b) ମନୁଷ୍ୟକୃତ ପଦାର୍ଥ ।
(ii) ଜଳ, କାଠ, କୋଇଲା, ଖଣିଜ ପଦାର୍ଥ,ବାୟୁ ମୃତ୍ତିକା ଇତ୍ୟାଦି ପ୍ରାକୃତିକ ପଦାର୍ଥ ଅଟେ ।
(iii) ଆମେ ବ୍ୟବହାର କରୁଥିବା ଲୁଗାପଟା, ଆସବାବ ପତ୍ର, ବାସନକୁସନ, ଖାଦ୍ୟ ଓ ପାନୀୟ, ଜୀବନ ରକ୍ଷାକାରୀ ଔଷଧ, କୃଷିକ୍ଷେତ୍ରରେ ବ୍ୟବହାର ହେଉଥିବା ସାର ଓ କୀଟନାଶକ, ପ୍ଲାଷ୍ଟିକ ବସ୍ତୁ, କାଗଜ, କାଳି, ବିଭିନ୍ନ ଯାନବାହନ ଲତ୍ୟାଦି ମନ୍ମଯ୍ୟକର ପଦାର୍ଥ ଅଟେ |
→ ତୁମ ପାଇଁ କାମ :
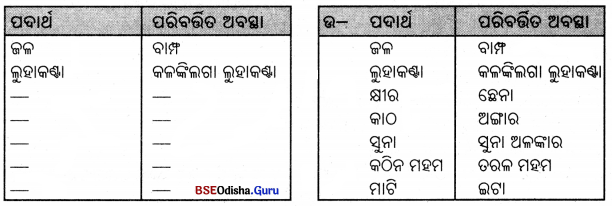
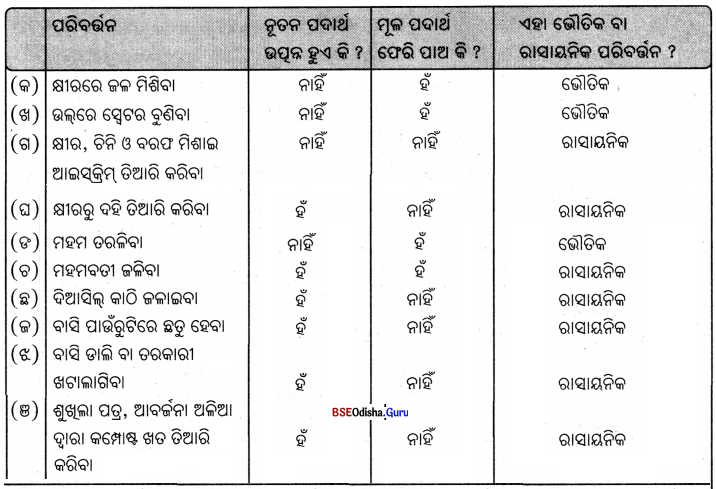
ତୁମେ ବ୍ୟବହାର କରୁଥିବା ଓ ଘରେ ବାହାରେ ଦେଖୁଥିବା ଦଶଗୋଟି ପଦାର୍ଥର ତାଲିକା କର । ସେଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁ ଗୁଡ଼ିକ ପ୍ରାକୃତିକ ପଦାର୍ଥ ଓ କେଉଁଗୁଡ଼ିକ ମନୁଷ୍ୟକୃତ ପଦାର୍ଥ ବାଛ । ନିମ୍ନ ସାରଣୀଟି ତୁମ ଖାତାରେ ତିଆରି କରି ପୂରଣ କର ।
Solution:

→ ପଦାର୍ଥର ଗୁଣ :
- ପ୍ରତ୍ୟେକ କଠିନ ପଦାର୍ଥର ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ଓ ଆୟତନ ଅଛି ।
- ତରଳ ପଦାର୍ଥର କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ନାହିଁ । ଏହାର ଆକୃତି ଧାରକ ପାତ୍ରର ଆକୃତି ଅନୁସାରେ ବଦଳିଥାଏ । କିନ୍ତୁ ଏହାର ନିର୍ଦ୍ଦିଷ୍ଟ ଆୟତନ ଅଛି ।
- ଗ୍ୟାସୀୟ ପଦାର୍ଥର ନିର୍ଦ୍ଦିଷ୍ଟ ଆୟତନ ଓ ଆକୃତି ନଥାଏ ।
→ ତୁମପାଇଁ କାପ :
(କ) ଗୋଟିଏ କାଚ ଗ୍ଲାସ୍ରେ ଜଳନେଇ, ଗ୍ଲାସ୍ର ବାହାର ପଟେ ଗୋଟିଏ ଦାଗ ଦେଇ ଭିତରେ ଥିବା ଜଳର ଉପର ସ୍ତରକୁ ଚିହ୍ନିତ କର । ପଥର ଖଣ୍ଡଟିକୁ ଧୀରେ ଗ୍ଲାସ୍ ଭିତରେ ଥିବା ପାଣିରେ ବୁଡ଼ାଇ ଦିଅ । ଗ୍ଲାସ୍ ଭିତରେ ଥିବା ଜଳ ସ୍ତରର ପରିବର୍ତ୍ତନ ହେଲାକି ? ଜଳସ୍ତରର ଯଦି ପରିବର୍ତ୍ତନ ହେଲା, କାହିଁକି ଏପରି ଦ୍ରେଲା ?
Solution:
ହଁ, ଗ୍ଲାସ ଭିତରେ ଥିବା ଜଳସ୍ତରର ପରିବର୍ତ୍ତନ ହେଲା । କାରଣ ପଥରଟି ଗ୍ଲାସ୍ ଭିତରେ ଯେତିକି ପରିମାଣର ସ୍ଥାନ ଅଧିକାର କଲା, ସେତିକି ଆୟତନର ଜଳ, ଦାଗ ଉପରକୁ ଉଠିଗଲା ।
(ଖ) ବିଭିନ୍ନ ଆକୃତିର ତିନି -ଚାରୋଟି କାଚ ବୋତଲ ସଂଗ୍ରହ କର । ପ୍ରତି ବୋତଲରେ ଏକ ଗ୍ଲାସ୍ ଜଳ ଭର୍ତ୍ତିକର । ବିଭିନ୍ନ ବୋତଲରେ ଜଳର ଆକୃତି ଲକ୍ଷ୍ୟ କର ।
ଏକା ପରିମାଣର ଜଳ ବିଭିନ୍ନ ବୋତଲରେ ଥିବାବେଳେ ସେହି ଜଳର ଆକୃତି ଏକାପରି ଅଟେ କି ?
Solution:
ନାଁ, ବିଭିନ୍ନ ବୋତଲରେ ଏକା ପରିମାଣର ଜଳଥିଲେ ମଧ୍ୟ ସେହି ଜଳର ଆକୃତି ଏକାପରି ନୁହେଁ, କାରଣ ତରଳ ପଦାର୍ଥର କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ନାହିଁ । ଏହାର ଆକୃତି ଧାରକ ପଦାର୍ଥର ଆକୃତି ଅନୁସାରେ ବଦଳୁଥାଏ ।
ପ୍ରଶ୍ନ ୧ । ଧୂପକାଠିରୁ ବାହାରୁଥିବା ଧୂଆଁ, ବାୟୁ, ଜେଟ୍ ପ୍ଲେନ୍ରୁ ବାହାରୁଥିବା ଧୂଆଁର କିଛି ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ଅଛି କି ? ଏଥୁରୁ କେଉଁ ସିଦ୍ଧାନ୍ତରେ ତୁମେ ଉପନୀତ ହେଲ ?
Solution:
ଧୂପକାଠିରୁ ବାହାରୁଥିବା ଧୂଆଁ, ବାୟୁ, ଜେଟ୍, ପ୍ଲେନ୍ରୁ ବାହାରୁଥିବା ଧୂଆଁର କିଛି ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ନାହିଁ । ଏଥୁରୁ ଆମେ ଏହି ସିଦ୍ଧାନ୍ତରେ ଉପନୀତ ହେଲୁ ଯେ ଗ୍ୟାସୀୟ ପଦାର୍ଥର ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ନ ଥାଏ ।
(ଗ) ଉପର (ଖ)ରେ ବ୍ୟବହୃତ ହୋଇଥିବା ଯେକୌଣସି ଗୋଟିଏ ଖାଲି ବୋତଲର ଓଜନ ନିର୍ଣ୍ଣୟ କର । ଏଥିପାଇଁ ତୁମ ସ୍କୁଲରେ ଥିବା ସ୍କିଙ୍ଗ୍ ବାଲାନ୍ସକୁ ବ୍ୟବହାର କରିପାର । ତା’ପରେ ସେହି ବୋତଲରେ ଜଳ ପୁରାଇ ଓଜନ ନିର୍ଣ୍ଣୟ କର । ଏହି ଦୁଇଟି ଓଜନ ମଧ୍ୟରେ ଥିବା ପାର୍ଥକ୍ୟ ତୁମପାଇଁ କାମ ବାହାର କର । ଏହାଦ୍ଵାରା କେଉଁ ସିବିନ୍ତ୍ରରେ ଉପନୀତ ହେଲ |
Solution:
ପ୍ରଥମେ କାଚ ବୋତଲ ଓ ପରେ ବୋତଲ ସହ ଜଳର ଓଜନକୁ ମାପ କରାଯାଉ । ଜଣାଯିବ ଯେ ଉଭୟ ଓଜନର ପାର୍ଥକ୍ୟ ଜଳର ଓଜନ ସହିତ ସମାନ । ଏଥୁ ଆମେ ଜାଣିଲୁ ଯେ ପ୍ରତ୍ୟେକ ପଦାର୍ଥର ବସ୍ତୁତ୍ଵ ଥାଏ ଓ ତାହା କିଛି ସ୍ଥାନ ଅଧ୍ୟାର କରିଥାଏ ।

→ ତୁମପାଇଁ କାପ:
ଗୋଟିଏ ବେଲୁନ୍ରେ ବାୟୁ ଭର୍ତ୍ତିକରି ସୂତାଦ୍ୱାରା ବାନ୍ଧି ଓଜନ କର । କ’ଣ ଲକ୍ଷ୍ୟ କଲ ?
Solution:
ବାୟୁ ଗୋଟିଏ ଗ୍ୟାସୀୟ ପଦାର୍ଥ । ଏହାର ନିର୍ଦ୍ଦିଷ୍ଟ ଆୟତନ ଓ ଆକୃତି ନ ଥାଏ ମାତ୍ର ଓଜନ ଅଛି । ମାତ୍ର ବେଲୁନ୍ ମଧ୍ୟରେ ଥିବା ବାୟୁର ଓଜନ, ଆୟତନ ଓ ଆକାର ଅଛି । ବାୟୁକୁ ଆମେ ଦେଖ୍ ନପାରିଲେ ମଧ୍ୟ ଏହା ଏକ ପଦାର୍ଥ ।
ପ୍ରଶ୍ନ ୨ । ତାପ, ଆଲୋକ, ଅଙ୍ଗାର, ମୋବାଇଲ୍ ଫୋନ୍ ଓ ଶବ୍ଦ ପଦାର୍ଥ କି ? ଏମାନଙ୍କ ମଧ୍ୟରୁ ପଦାର୍ଥଗୁଡ଼ିକ ବାଛ ।
Solution:
ଅଙ୍ଗାର, ମୋବାଇଲ୍ ଫୋନ୍ ପଦାର୍ଥ ଅଟେ, କିନ୍ତୁ ତାପ, ଆଲୋକ ଓ ଶବ୍ଦ ପଦାର୍ଥ ନୁହଁନ୍ତି । ପଦାର୍ଥର ଓଜନ, ଆୟତନ ଓ ଆକାର ଅଛି । ତେଣୁ ଅଙ୍ଗାର ଓ ମୋବାଇଲ୍ ଫୋନ୍ ପଦାର୍ଥ ଶ୍ରେଣୀଭୁକ୍ତ ।
ପ୍ରଶ୍ନ ୩ । ପାଖରେ ଥାଇ ଦିଶଇ ନାହିଁ
ରାଗିଲେ ସେ ସବୁ ଭାଙ୍ଗି ଦିଏ
କହରେ ପିଲେ, କହ ସେ କିଏ ?
Solution:
ବାୟୁ ବା ପବନ ।
ପଦାର୍ଥର ବିଭିନ୍ନ ଅବସ୍ଥା :
(i) ପ୍ରତ୍ୟେକ ପଦାର୍ଥର ତିନୋଟି ଅବସ୍ଥା ଅଛି; ଯଥା – (କ) କଠିନ ଅବସ୍ଥା, (ଖ) ତରଳ ଅବସ୍ଥା ଓ ଦେଖିବାକୁ ପାଉ । ପଦାର୍ଥ ଗୋଟିଏ ଅବସ୍ଥାରୁ ଅନ୍ୟ ଗୋଟିଏ ଅବସ୍ଥାକୁ ରୂପାନ୍ତରିତ ହୋଇଥାଏ । ଏହା ଏକ ଭୌତିକ ପରିବର୍ତ୍ତନ ଅଟେ । ଏହି ସମୟରେ ପଦାର୍ଥର ଭୌତିକ ଗୁଣର ପରିବର୍ତ୍ତନ ହୋଇଥାଏ ।
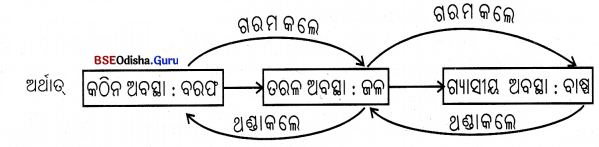
(ii) କଠିନ ବରଫ ତରଳିଲେ ଜଳ ଉତ୍ପନ୍ନ ହୁଏ, ଯାହା ପଦାର୍ଥର ତରଳ ଅବସ୍ଥା । ତରଳ ଜଳକୁ ଗରମ କଲେ ତାହା ବାଷ୍ପରେ ପରିଣତ ହୁଏ ଓ ଏହା ଜଳର ଗ୍ୟାସୀୟ ଅବସ୍ଥା । ସେହିପରି ବାଷ୍ପ ଥଣ୍ଡା ହୋଇ ଜଳରେ ପରିଣତ ହୁଏ ଓ ଜଳମଧ୍ଯ ଅତ୍ୟଧିକ ଥଣ୍ଡାହୋଇ ବରଫରେ ପରିଣତ ହୋଇଥାଏ ।
(କ) ପଦାର୍ଥର କଠିନ ଅବସ୍ଥା ଏହି ଅବସ୍ଥାରେ ପଦାର୍ଥର ନିଜସ୍ବ ଆକାର, ଆୟତନ ଓ ବସ୍ତୁତ୍ଵ ଥାଏ । ଏହାକୁ ଯେଉଁଠାରେ ରଖିଲେ ମଧ୍ୟ ଏହା କିଛି ସ୍ଥାନ ଅଧିକାର କରେ । ଉଦାହରଣ – ପଥର, ବରଫଖଣ୍ଡ, କାଠ, ଇଟା ।
(ଖ) ପଦାର୍ଥର ତରଳ ଅବସ୍ଥା – ଏହି ଅବସ୍ଥାରେ ପଦାର୍ଥର ନିଜସ୍ୱ ଆୟତନ ଓ ବସ୍ତୁତ୍ଵ ଥାଏ, କିନ୍ତୁ ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ନଥାଏ । ତରଳ ଅବସ୍ଥାରେ ପଦାର୍ଥର ଆକୃତି ଧାରକ ପାତ୍ରର ଆକୃତି ଉପରେ ନିର୍ଭର କରେ । ତରଳ ପଦାର୍ଥ ଯେଉଁ ପାତ୍ରରେ ରଖାଯାଇଥାଏ, ସେହି ଆକୃତି ପ୍ରାପ୍ତ ହୋଇଥାଏ । ଉଦାହରଣ – ଜଳ, ତେଲ, କ୍ଷୀର
(ଗ) ପଦାର୍ଥର ଗ୍ୟାସୀୟ ଅବସ୍ଥା – ଏହି ଅବସ୍ଥାରେ ପଦାର୍ଥର କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ଓ ଆୟତନ ନଥାଏ, ମାତ୍ର ବସ୍ତୁତ୍ଵ ଥାଏ । ସାମାନ୍ୟ ତାପ ଓ ଚାପର ତାରତମ୍ୟ ହେଲେ ଏହାର ଆୟତନ ହ୍ରାସ ବୃଦ୍ଧି ଘଟେ । ଗ୍ୟାସୀୟ ପଦାର୍ଥଗୁଡ଼ିକୁ ସର୍ବଦା ଆବଦ୍ଧ ପାତ୍ରରେ ରଖାଯାଏ । ଗ୍ୟାସୀୟ ପଦାର୍ଥକୁ ଯେଉଁ ଆବଦ୍ଧ ପାତ୍ରରେ ରଖାଯାଏ, ତାହା ସେହି ପାତ୍ର ମଧ୍ଯରେ ସଂପୂର୍ଣ୍ଣ ରୂପେ ବ୍ୟାପିଥାଏ । ଉଦାହରଣ – ଅମ୍ଳଜାନ, ଉଦ୍ଜାନ, ଯବକ୍ଷାରଯାନ ।
→ ମନେରଖ :
ରନ୍ଧନଗ୍ୟାସ୍ ଓ ଡାକ୍ତରଖାନାରେ ଇସ୍ପାତ୍ ଟାଙ୍କି ମଧ୍ୟରେ ଥିବା ଅମ୍ଳଜାନ ଗ୍ୟାସ୍ ଯେତେବେଳେ ଉଚ୍ଚ ଚାପଯୁକ୍ତ ହୋଇ ରହିଥାଏ ସେତେବେଳେ ତାହା ତରଳ ଅବସ୍ଥାରେ ଥାଏ । ରେଗୁଲେଟର ସାହାଯ୍ୟରେ ଯେତେବେଳେ ଟାଙ୍କି ମୁହଁ ଖୋଲାଯାଏ ତାହା ବାୟୁମଣ୍ଡଳୀୟ ଚାପ ପାଇ ପୁଣି ବାଷ୍ପୀୟ ଅବସ୍ଥାକୁ ଆସିଯାଏ ।
ବାୟୁ ମଣ୍ଡଳରେ ଥିବା ଅମ୍ଳଜାନ ଗ୍ୟାସୀୟ ଅବସ୍ଥାରେ ହିଁ ରହିଥାଏ । କାରଣ ବାୟୁମଣ୍ଡଳୀୟ ତାପମାତ୍ରା ଓ ଚାପରେ ଏହା ଗୋଟିଏ ଗ୍ୟାସୀୟ ପଦାର୍ଥ ଅଟେ ।
→ ପଦାର୍ଥର ପ୍ରକୃତି :
କଠିନ ପଦାର୍ଥ :
- ସ୍ଥିର ତାପମାତ୍ରାରେ କଠିନ ପଦାର୍ଥର ଆକାର, ଆକୃତି ଓ ଆୟତନର କୌଣସି ପରିବର୍ତ୍ତନ ହୁଏ ନାହିଁ ।
- କାଠିନ ପଦାର୍ଥକ ସେକେଣସି ଷ୍ଠାନରେ ରଖାଯାଲପାରିବ |
→ ଉଇଲ ପଦାର୍ଥ :
- ସ୍ଥିତ ତାପମାତ୍ରାରେ ପରଲ ପଦାର୍ଥର ଆୟତନ ଅପରିବର୍ତ୍ତିତ୍ ରହେ କିଛି ଏହ୍ରାସ ଆକାର ଥାକତି ଧାରକପାତ୍ରର ଆକୃତି ଅନୁସାରେ ବଦଳିଥାଏ ।
- ତରଳ ପଦାର୍ଥ ରଖିବାପାଇଁ ଗୋଟିଏ ପାତ୍ରର ଆବଶ୍ୟକ ହୋଇଥାଏ । ତାହା ଖୋଲା ବା ଆବଦ୍ଧ ହୋଇପାରେ । ନଚେତ୍ ତରଳ ପଦାର୍ଥ ଉର୍ଦ୍ଧ୍ବରୁ ନିମ୍ନକୁ ବହିଯାଇଥାଏ ।
→ ଗ୍ୟାସୀୟ ପଦାର୍ଥ :
- ସ୍ଥିର ତାପମାତ୍ରାରେ ଗ୍ୟାସୀୟ ପଦାର୍ଥର ଆକାର, ଆୟତନ ଓ ଆକୃତି ଆବଦ୍ଧ ଧାରକ ପାତ୍ରର ଆକାର, ଆୟତନ ଓ ଆକୃତି ଅନୁସାରେ ହୋଇଥାଏ ।
- ଗ୍ୟାସୀୟ ପଦାର୍ଥକୁ ସର୍ବଦା ଆବଦ୍ଧ ପାତ୍ରରେ ରଖୁବାକୁ ହୁଏ । ନଚେତ୍ ଗ୍ୟାସୀୟ ପଦାର୍ଥ ପାତ୍ରରୁ ବାହାରିଯାଇ ବାୟୁମଣ୍ଡଳକୁ ଚାଲିଯାଏ ।
ପଦାର୍ଥର ତିନି ସାଧାରଣ ଅବସ୍ଥାର ଅନ୍ତଃ-ରୂପାନ୍ତରଣ (Inter-Conversion) :
ତାପର ପ୍ରୟୋଗରେ କଠିନ ପଦାର୍ଥ ତରଳ ପଦାର୍ଥରେ ରୂପାନ୍ତରିତ ହୁଏ । ତରଳ ପଦାର୍ଥକୁ ଉତ୍ତପ୍ତ କଲେ ଗ୍ୟାସୀୟ ପଦାର୍ଥରେ ପରିବର୍ତ୍ତିତ ହୁଏ । ଗ୍ୟାସୀୟ ପଦାର୍ଥକୁ ଥଣ୍ଡାକଲେ ତାହା ତରଳ ଅବସ୍ଥାକୁ ଆସିଥାଏ । ତରଳ ପଦାର୍ଥକୁ ଥଣ୍ଡା କଲେ ତାହା ପୁନଶ୍ଚ କଠିନାବସ୍ଥାକୁ ଫେରିଆସେ । ପଦାର୍ଥର ଏହି ତିନୋଟି ଅବସ୍ଥାର ଗୋଟିକରୁ ଅନ୍ୟଟିକୁ ହେଉଥିବା ପରିବର୍ତ୍ତନକୁ ଅନ୍ତଃ-ରୂପାନ୍ତରଣ କୁହାଯାଏ ।

ଳେନାଲ – ଯେଉଁ ତାପମାତ୍ରାରେ ବରଫ ତରଳି ଜଳରେ ପରିଣତ ହୁଏ, ତାହାକୁ ଜଳର ଗଳନାଙ୍କ (Melting Point) କୁହାଯାଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ଗଳନ (Melting) କୁହାଯାଏ ।
ହି ମାଙ୍କ – ଯେଉଁ ତାପମାତ୍ରାରେ ଜଳକୁ ଊର୍ଦ୍ଧ୍ବପାତନ ହିମାଙ୍କ (Freezing point) କୁହାଯାଏ ।
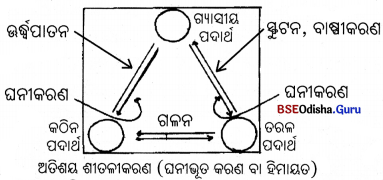
ସ୍ଫୁଟନାଙ୍କ – ଯେଉଁ ତାପମାତ୍ରାରେ ଜଳ ଫୁଟି ବାମ୍ଫ(steam)ରେ ପରିଣତ ହୁଏ ତାହାକୁ ଜଳର ସ୍ଫୁଟନାଙ୍କ (Boiling Point) କୁହାଯାଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ସ୍ଫୁଟନ କୁହାଯାଏ ।
ବାଷ୍ପୀକରଣ – ଜଳର ତାପମାତ୍ରା ସ୍ଫୁଟନ (୧୦୦° ସେ. ) ନହେଲେ ମଧ୍ୟ ସାଧାରଣ ତାପମାତ୍ରାରେ ଏହା ଗ୍ୟାସୀୟ ଅବସ୍ଥା (ଜଳୀୟ ବାଷ୍ପ) ପ୍ରାପ୍ତ ହୋଇଥାଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ବାଷ୍ପୀକରଣ କୁହାଯାଏ ।
ଜଳକୁ ଉତ୍ତପ୍ତ କରି ତାପମାତ୍ରାକୁ ୧୦୦° ସେ. (ସ୍ଫୁଟନାଙ୍କ) କଲେ ସ୍ଫୁଟନ ଘଟି ଜଳ ଗ୍ୟାସୀୟ ଅବସ୍ଥା (ବାମ୍ଫ) ପ୍ରାପ୍ତ ହୁଏ ।
ଊର୍ଦ୍ଧ୍ବପାତନ – କଠିନ ନାଫ୍ଲିନ୍ ଗୁଣ୍ଡକୁ ଉତ୍ତପ୍ତ କଲେ ତାହା ନ ତରଳି ଏକ କଠିନ ପଦାର୍ଥର ଆସ୍ତରଣ ସୃଷ୍ଟିହୁଏ । ଏହି ନାଫ୍ଲିନ୍ ବାଷ୍ପ ଥଣ୍ଡା ହୋଇ କଠିନ ଅବସ୍ଥାର ଏକ ଆସ୍ତରଣ ହୁଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ଊର୍ଷପାତନ କୁହାଯାଏ ।
ପ୍ରଶ୍ନ ୪ । ଗନ୍ଧକର୍ପୁର, ଆୟୋଡିନ୍ ଦାନା, ଆମୋନିୟମ୍ କ୍ଲୋରାଇଡ୍ ଲବଣ ଇତ୍ୟାଦି କଠିନ ପଦାର୍ଥକୁ ନେଇ କିଛି ସମୟ ଉତ୍ତପ୍ତ କଲେ , କ’ଣ ହେବ ?
Solution:
ଗନ୍ଧକର୍ପୁର, ଆୟୋଡି଼ନ୍ ଦାନା, ଆମୋନିୟମ୍ କ୍ଲୋରାଇଡ୍ ଲବଣ ଇତ୍ୟାଦି କଠିନ ପଦାର୍ଥକୁ ଉତ୍ତପ୍ତ କଲେ ତରଳ ନ ହୋଇ ତାହା ବାଷ୍ପ ହୋଇଥାଏ । ଏହି ବାଷ୍ପ ଥଣ୍ଡା ହୋଇ ତରଳ ଅବସ୍ଥାକୁ ନ ଆସି ପୁନଶ୍ଚ କଠିନ ଅବସ୍ଥା ପ୍ରାପ୍ତ ହୋଇଥାଏ । ଏଗୁଡ଼ିକୁ ଉଦ୍ବାୟୀ କଠିନ ପଦାର୍ଥ କୁହାଯାଏ ।
ଉଦ୍ବାୟୀ କଠିନ ପଦାର୍ଥ – କେତେକ କଠିନ ପଦାର୍ଥ ଅଛି ଯାହାକୁ ଉତ୍ତପ୍ତ କଲେ ତାହା ତରଳ ପଦାର୍ଥରେ ପରିଣତ ନ ହୋଇ ସିଧା ଗ୍ୟାସୀୟ ଅବସ୍ଥା ପ୍ରାପ୍ତ ହୋଇଥାନ୍ତି ଏବଂ ଥଣ୍ଡା ହେଲେ ସେମାନଙ୍କର ଗ୍ୟାସୀୟ ଅବସ୍ଥା ତରଳ ଅବସ୍ଥାକୁ ନ ଆସି କଠିନ ଅବସ୍ଥା ପ୍ରାପ୍ତ ହୋଇଥାଏ । ଏହିଭଳି କଠିନ ପଦାର୍ଥଗୁଡ଼ିକ ଏକ ସ୍ବତନ୍ତ୍ର ପ୍ରକାର କଠିନ ପଦାର୍ଥ ଏବଂ ଏଗୁଡ଼ିକୁ ଉଦ୍ବାୟୀ କଠିନ ପଦାର୍ଥ କୁହାଯାଏ ।
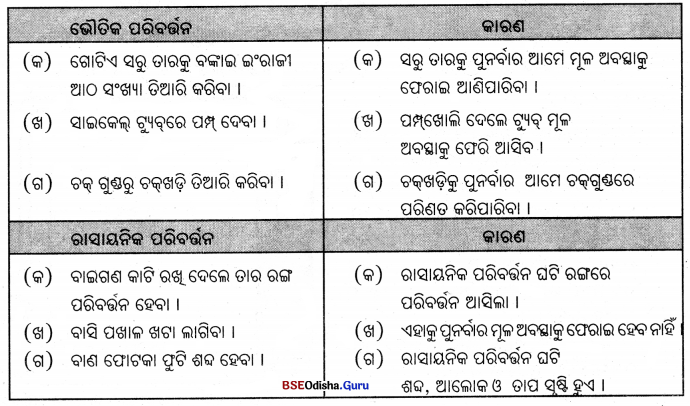
ଗଳନ, ସ୍ଫୁଟନ, ବାଷ୍ଟୀକରଣ, ଘନୀକରଣ ପରି ଉର୍ଦ୍ଧପାତନ ମଧ୍ୟ ଗୋଟିଏ ଭୌତିକ ପରିବର୍ତ୍ତନ ।
→ ପଦାର୍ଥର ଗଠନ :
(i) କେତେଗୁଡିଏ ଜାଣିକାନ୍ତି ନେଲ ପ୍ରତ୍ୟେକ ପଦାର୍ଥ ଗଠିତ | ଏଦ୍ୱି କଣିକାଗୁଗିକ ମଧ୍ୟରେ ଏକ ପ୍ରକାର ର୍ଥାକଗଣ ବଳ ଥାଏ ।
(ii) ପଦାର୍ଥର କଣିକାଗୁଡ଼ିକ ମଧ୍ୟରେ କିଛି ଶୂନ୍ୟସ୍ଥାନ ଥାଏ ଏବଂ କଣିକାଗୁଡ଼ିକ ନିର୍ଦ୍ଦିଷ୍ଟ ରୂପରେ ସଜ୍ଜା ହୋଇ ରହିଥାଆନ୍ତି । ଯେହେତୁ ପଦାର୍ଥର କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ଅବସ୍ଥାରେ ତାହାର କଣିକା ମଧ୍ୟରେ ଥିବା ଆକର୍ଷଣ ବଳ ଭିନ୍ନ ଭିନ୍ନ ଅଟେ, ତେଣୁ ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ଶୂନ୍ୟସ୍ଥାନର ପରିମାଣ ଓ ସେଗୁଡ଼ିକର ସଜ୍ଜା ଭିନ୍ନ ଭିନ୍ନ
ହୋଇଥାଏ ।
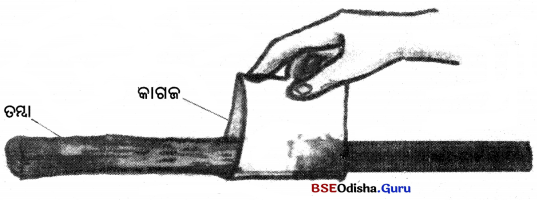
(iii) କଠିନ ଅବସ୍ଥାରେ ପାଖାପାଖ୍ କଣିକା ମଧ୍ୟରେ ଥିବା ଶୂନ୍ୟସ୍ଥାନର ପରିମାଣ ସବୁଠାରୁ କମ୍ । ତେଣୁ ଏହି ଅବସ୍ଥାରେ ଦୁଇଟି କଣିକା ମଧ୍ୟରେ ଥିବା ଆକର୍ଷଣ ବଳ ସବୁଠାରୁ ତୀବ୍ର ଅଟେ । ଏହି ପ୍ରବଳ ଆକର୍ଷଣ ଯୋଗୁ, କଠିନ ଆକୃତି ସ୍ଥିର ଅଟେ । କଠିନ ପଦାର୍ଥର କିଛି ଅଂଶ ଅଲଗା କରିବାପାଇଁ ହାତୁଡ଼ି ବା ସେହିପରି କିଛି ଜିନିଷ ବ୍ୟବହାର କରିବାକୁ ପଡ଼ିଥାଏ ।
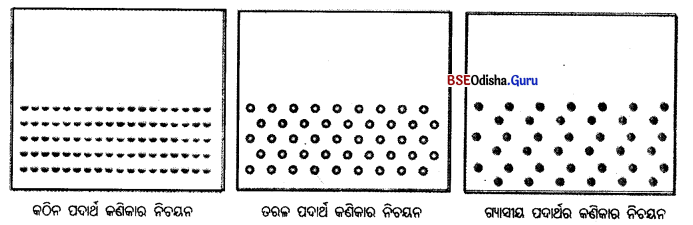
(iv) ତରଳ ଅବସ୍ଥାରେ ପଦାର୍ଥର କଣିକାଗୁଡ଼ିକ ମଧ୍ୟରେ ଥିବା ଦୂରତ୍ୱ ସାମାନ୍ୟ
(v)ତେଣୁ ସେମାନଙ୍କ ମଧ୍ୟରେ ଥିବା ଆକର୍ଷଣ ବଳ କମ୍ । ଏଣୁ ତରଳ ପଦାର୍ଥର ନିର୍ଦ୍ଦିଷ୍ଟ ଆକୃତି ନାହିଁ । ଏହା ଧାରକ ପାତ୍ରର ଆକୃତି ନେଇଥାଏ । ତରଳ ପଦାର୍ଥ ଊର୍ଦ୍ଧ୍ବରୁ ନିମ୍ନକୁ ଗତି କରିଥାଏ ଓ ଏହା କଣିକାଗୁଡ଼ିକ ପ୍ରାୟତଃ ଏକାଠି ଥାଆନ୍ତି । ଗ୍ୟାସୀୟ ପଦାର୍ଥରେ କଣିକାଗୁଡ଼ିକ ମଧ୍ୟରେ ଅତ୍ୟଧିକ ଦୂରତ୍ବ ହେତୁ ପାରସ୍ପରିକ ଆକର୍ଷଣ ବଳ ଅତି କମ୍ ।
ବାହାରକୁ ଚାଲିଯାଏ ।
→ ପଦାର୍ଥର ଣ୍ଡୋଶୀ ବିରାଗ :
- ଭୌତିକ ଥଟସ୍ଥା ହଶିକୋଣରୁ ପଦାର୍ଥକୁ ତିନି ପ୍ତକାରରେ କିଣନ୍ତ କରାଯାଲଥାଏ |
ଯଥା – (କ) କଠିନାବସ୍ଥା, (ଖ) ତରଳାବସ୍ଥା, (ଗ) ଗ୍ୟାସୀୟାବସ୍ଥା ।
- ପଦାର୍ଥଗ୍ମତିକ୍ତ ସେମନଙ୍କର ରାସାୟନିକ ସଂରଚନା (constitution) ଓ ଫକ୍ମତି (composition) ଅନ୍ତମାନ ମୌଳିକ, ଯୌଗିକ ଓ ମିଶ୍ରଣ ରୂପେ ବିଭକ୍ତ କରାଯାଏ ।
- ଯେଉଁ ପଦାର୍ଥ ଗୁଡ଼ିକରେ କେବଳ ଗୋଟିଏ ପ୍ରକାର କଣିକା ଥାଏ, ସେଗୁଡ଼ିକୁ ବିଶୁଦ୍ଧ ପଦାର୍ଥ କୁହାଯାଏ । ମୌଳିକ ଓ ଯୌଗିକ ଏହି ପ୍ରକାରର ବିଶୁଦ୍ଧ ପଦାର୍ଥ ଅଟନ୍ତି । ତମ୍ବାତାର, ସୁନା ଆଦି ବିଶୁଦ୍ଧ ପଦାର୍ଥ ।
- ଆଉ କେତେକ ପଦାର୍ଥ ଅଛି, ଯେଉଁଥିରେ ଏକରୁ ଅଧିକ ପ୍ରକାରର କଣିକା ଥାଏ । ଏହିଭଳି ପଦାର୍ଥକୁ ମିଶ୍ର ପଦାର୍ଥ ବା ମିଶ୍ରଣ କୁହାଯାଏ । କୋଇଲା ଏକ ମିଶ୍ର ପଦାର୍ଥ ।
- ପଦାର୍ଥଗୁଡ଼ିକ ଯେକୌଣସି କ୍ଷେତ୍ରରୁ ସଂଗୃହିତ ହେଲେ ମଧ୍ୟ ସେମାନଙ୍କର ବିଶୁଦ୍ଧ ଅବସ୍ଥାରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପଦାର୍ଥରେ ଥିବା କଣିକାଗୁଡ଼ିକ ଏକାଭଳି ଦେଖାଯାଏ । ଏହିଭଳି ସରଳତମ ବିଶୁଦ୍ଧ ପଦାର୍ଥକୁ ମୌଳିକ କୁହାଯାଏ ।
ସାଧାରଣ ତାପମାତ୍ରାରେ ଅଙ୍ଗାରକ, ଫସଫରସ୍, ଗନ୍ଧକ, ଆୟୋଡ଼ିନ୍, ସୁନା, ରୂପା, ଦସ୍ତା, ଆଲୁମିନିୟମ୍, ସୀସା ଇତ୍ୟାଦି କଠିନ ମୌଳିକ । ପାରଦ ଓ ବ୍ରୋମିନ ତରଳ ମୌଳିକ । ଉଦ୍ଜାନ, ଅମ୍ଳଜାନ, ଯବକ୍ଷାରଜାନ, କ୍ଲୋରିନ୍, ହିଲିୟମ୍ ଇତ୍ୟାଦି ଗ୍ୟାସୀୟ ମୌଳିକ ।
ଆଜି ପର୍ଯ୍ୟନ୍ତ ଜାଣିଥୁବା ୧୧୫ ଟି ମୌଳିକ ମଧ୍ୟରୁ ୮୮ଟି ମୌଳିକ ପ୍ରାକୃତିକ ଓ ୨୭ଟି ମୌଳିକ ମନୁଷ୍ୟକୃତ
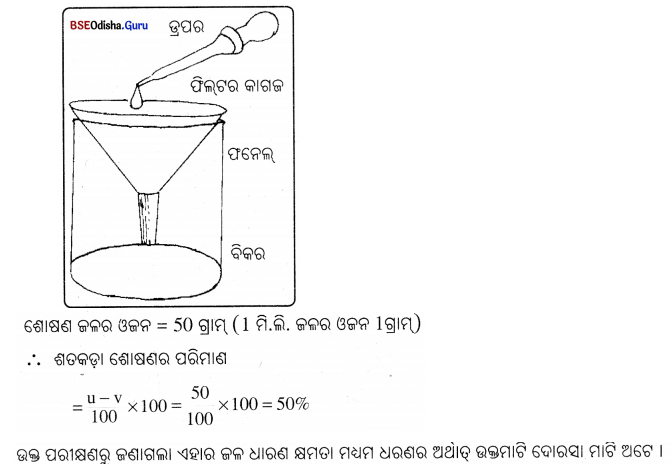
ପ୍ରଶ୍ନ ୬ । ଫିଲଟର୍ ପାଣି ବିଶୁଦ୍ଧ ପଦାର୍ଥ କି ? ତୁମ ଉତ୍ତରର ଯଥାର୍ଥତା ବୁଝାଅ ।
Solution:
ଫିଲଟର୍ ପାଣି ବିଶୁଦ୍ଧ ପଦାର୍ଥ ନୁହେଁ । ଏହା ଏକ ମିଶ୍ରଣ । ଏଥୁରେ ଧାତବଲବଣ ଓ ଅମ୍ଳଜାନ ଦ୍ରବୀଭୂତ ହୋଇଥାଏ ।
→ ମେଲକରି ପୂଜାରେଦ :
(i) ମୌଳିକ ଗୁଡ଼ିକୁ ସେମାନଙ୍କର ଗୁଣ ଅନୁଯାୟୀ ତିନି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – ଧାତୁ (Metal), ଅଧାତୁ (Non-metal) ଉପଧାତୁ (Metalloid) |
(a) ଧାତୁ – ଧାତୁରୁ ତାର ଓ ପାତ୍ର ପସ୍ତୁତ କରାଯାଇପାରେ । ଧାତୁ ମଧ୍ୟ ତାପ ଓ ବିଦ୍ୟୁତ୍ର ସୁପରିବାହୀ । ଲୁହା, ଦସ୍ତା, ତମ୍ବା, ସୀସା, ଆଲୁମିନିୟମ, ସୁନା,ରୁପା, ଜିଙ୍କ୍, ମାଗ୍ନେସିୟମ୍ , କ୍ୟାଲସିୟମ୍ ଇତ୍ୟାଦି କଠିନ ଧାତବ ମୌଳିକର ଉଦାହରଣ ।
(b) ଅଧାତୁ – ଅଙ୍ଗାରକ, ଗନ୍ଧକ, ଫସ୍ଫରସ ଇତ୍ୟାଦି କଠିନ ଅଧାତୁ ମୌଳିକ ଅଟନ୍ତି । ଉଦ୍ଜାନ, ଅମ୍ଳଜାନ, ଯବକ୍ଷାରଜାନ, କ୍ଲୋରିନ୍, ହିଲିୟମ୍, ଇତ୍ୟାଦି ବାଷ୍ପୀୟ ଅଧାତୁ ମୌଳିକ ଅଟନ୍ତି ।
(c) ଉପଧାତୁ – ଯେଉଁ ମୌଳିକ ଉଭୟ ଧାତୁ ଓ ଅଧାତୁ ଉଭୟର ଗୁଣ ପ୍ରଦର୍ଶନ କରନ୍ତି, ସେମାନଙ୍କୁ ଉପଧାତୁ କୁହାଯାଏ । ଆର୍ସେନିକ୍, ବୋରନ୍, ସିଲିକନ୍ ଆଦି ଉପଧାତୁ ।

→ ବ୍ରୋମିନ ଏକମାତ୍ର ତରଳ ଅଧାତୁ ମୌଳିକ ଅଟେ ।
(ii) ପ୍ରାକୃତିକ ମୌଳିକ ପଦାର୍ଥକୁ ନେଇ ଆମ ପୃଥିବୀର ଭୂତ୍ଵକ ଗଠିତ ହୋଇଛି । ଭୂତ୍ଵକର ୯୯ ଭାଗ ପାର୍ଶ୍ଵ ସ୍ଥ ୧୦ଟି ମୌଳିକକୁ ନେଇ ଗଠିତ ।
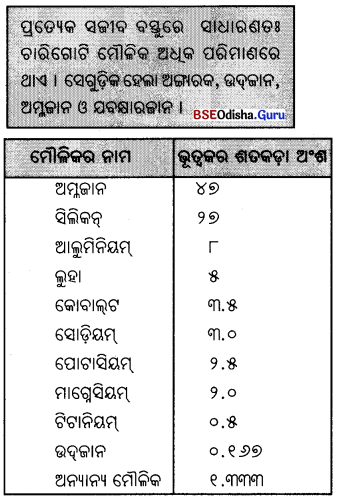
ଆଲୁମିନିୟମ୍ ସେଗୁଡ଼ିକ ହେଲା ଅଙ୍ଗାରକ, ଉଦ୍ଜାନ, ଅମ୍ଳଜାନ ଓ ଯବକ୍ଷାରଜାନ ।
(iii) ଉଦ୍ଜାନ ସବୁଠାରୁ ହାଲୁକା ଓ ଦହନଶୀଳ ମୌଳିକ । କିନ୍ତୁ ଅମ୍ଳଜାନ, ଅନ୍ୟାନ୍ୟ ପଦାର୍ଥର ଦହନରେ ସାହାଯ୍ୟ କରେ । ଉଦ୍ଜାନ ଓ ମାଗ୍ନେସିୟମ୍ ସୃଷ୍ଟି ହୁଏ ।
ଯୌଗିକ :
ଦୁଇ ବା ତତୋଽଧ୍ଵକ ମୌଳିକ ନିଜ ନିଜ ମଧ୍ୟରେ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରି ଯେଉଁ ନୂତନ ପଦାର୍ଥ ଉତ୍ପନ୍ନ କରନ୍ତି, ତାହାକୁ ଯୌଗିକ ପଦାର୍ଥ କୁହାଯାଏ । ଯୌଗିକ ପଦାର୍ଥର ଗୁଣ ଏହାର ମୂଳ ମୌଳିକ ପଦାର୍ଥର ଗୁଣଠାରୁ ଭିନ୍ନ ହୋଇଥାଏ । ଉଦାହରଣ ସ୍ୱରୂପ, ଅଙ୍ଗାରକାମ୍ଳ,ଚିନି, ଲୁଣ, ଜଳ, ଚକ୍ଖଡ଼ି, ଗ୍ଲୁକୋଜ୍, ଖାରସୋଡ଼ା, ଭିନେଗାର୍ ଇତ୍ୟାଦି ଯୌଗିକ ଅଟନ୍ତି । ଉଦାହରଣ – ୫୬ ଗ୍ରାମ୍ ଲୁହାଗୁଣ୍ଡ, ୩୨ ଗ୍ରାମ୍ ଗନ୍ଧକ ସହ ରାସାୟନିକ ସଂଯୋଗ ଘଟାଇ ୮୮ ଗ୍ରାମ୍ ଫେରସ୍ ସଲ୍ଫାଇଡ୍ ନାମକ ଯୌଗିକ ପଦାର୍ଥ ଉତ୍ପନ୍ନ କରେ ।
ମିଶ୍ରଣ :
(i) ଯେଉଁ ପଦାର୍ଥରେ ଏକାଧ୍ଵ ମୌଳିକ ବା ଯୌଗିକ ବା ଉଭୟ ମୌଳିକ ଓ ଯୌଗିକ ମିଶିକରିଥାଏ, ତାହାକୁ ମିଶ୍ରଣ କୁହାଯାଏ | ମିଶ୍ରଣ ଦୁଇ ପ୍ରକାରର ; ଯଥା – ସମଜାତୀୟ ମିଶ୍ରଣ ଓ ବିଷମ ଜାତୀୟ ମିଶ୍ରଣ । ମିଶ୍ରଣ ଗୋଟିଏ ବିଶୁଦ୍ଧ ପଦାର୍ଥ ନୁହେଁ । ଉଦାହରଣ ସ୍ୱରୂପ, ବାୟୁ, ଜଳ, ଚିନିସରବତ, ବାରମଜା ମିକ୍ର ଆଦି ମିଶ୍ରଣ ଅଟନ୍ତି ।
(iii) ମିଶ୍ରଣଗୁଡ଼ିକରେ ଥିବା ଉପାଦାନଗୁଡ଼ିକର ଗୁଣ ଅପରିବର୍ତ୍ତିତ ରହିଥାଏ, ମିଶ୍ରଣଗୁଡ଼ିକ ମିଶି ଉତ୍ପନ୍ନ କରିବାବେଳେ କୌଣସି ରାସାୟନିକ ପରିବର୍ତ୍ତନ ହୋଇ ନ ଥାଏ, ଉପାଦାନଗୁଡ଼ିକ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ଓଜନର ଅନୁପାତରେ
(iii) ପରୀକ୍ଷାଗାରରେ ବିଭିନ୍ନ ମିଶ୍ରଣକୁ ବିଭିନ୍ନ ଉପାୟରେ ପୃଥକ କରାଯାଇଥାଏ । ଏଥିପାଇଁ ଅବକ୍ଷେପଣ (Sedimentation), ଉତଳାଦ୍ରାନ (Decantation), ପରିସ୍ତବଣ (Filtration), ପାଦନ (Distilation), ଊର୍ଦ୍ଧ୍ବପାତନ୍ (Sublimation) ଆଦି ବିଜ୍ଞାନଗାର ପଦ୍ଧତି ଅବଲମ୍ବନ କରାଯାଏ ।
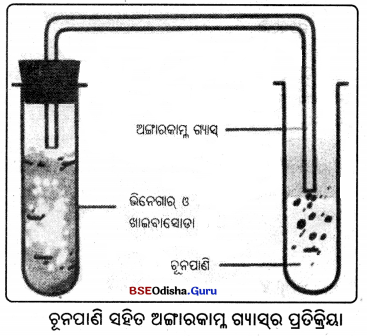
ପ୍ରଶ୍ନ ୭ । (i) ଅଙ୍ଗାରକାମ୍ଳରେ କେଉଁ କେଉଁ ମୌଳିକ ଥାଏ ?
Solution:
ଅଙ୍ଗାରକାମ୍ଳରେ ଅଙ୍ଗାରକ ଓ ଅମ୍ଳଜାନ ମୌଳିକ ଥାଏ ।
(ii) ଭୋଲଟାମିଟର ଯନ୍ତ୍ରରେ ଜଳ ମଧ୍ୟଦେଇ ବିଦ୍ୟୁତ୍ ପ୍ରବାହିତ କରାଇଲେ କେଉଁ କେଉଁ ମୌଳିକ ଉତ୍ପନ୍ନ ହୁଏ ?
Solution:
ଉଦ୍ଜାନ ଓ ଅମ୍ଳଜାନ ଉତ୍ପନ୍ନ ହୁଏ ।
(iii) ଅଙ୍ଗାରକ, ଉଦ୍ଜାନ ଓ ଅମ୍ଳଜାନ ତିନୋଟି ମୌଳିକ, ଗ୍ଲୁକୋଜ ଗୋଟିଏ ଯୌଗିକ । ଏହାର ଯଥାଯଥ କାରଣ ଲେଖ ।
Solution:
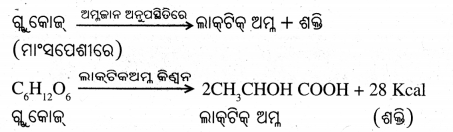
ଅଙ୍ଗାରକ, ଉଦ୍ଜାନ ଓ ଅମ୍ଳଜାନ ପ୍ରତ୍ୟେକ ଏକ ପ୍ରକାରର ପରମାଣୁରେ ଗଠିତ ହୋଇଥିବାରୁ ଏଗୁଡ଼ିକୁ ମୌଳିକ କୁହାଯାଏ । ମାତ୍ର ଗ୍ଲୁକୋଜ (C6H12O6) କାର୍ବନ, ହାଇଡ୍ରୋଜେନ ଓ ଅକ୍ସିଜେନ୍ ତିନି ପ୍ରକାରର ପରମାଣୁରେ ଗଠିତ ହୋଇଅଛି । ତେଣୁ ଗ୍ଲା କୋଜ୍ ଏକ ଯୌଗିକ ଅଟେ ।
(iv) ୮୪ ଗ୍ରାମ୍ ଲୁହାଗୁଣ୍ଡ, ୫୪ ଗ୍ରାମ୍ ଗନ୍ଧକ ସହ ରାସାୟନିକ ସଂଯୋଗ ଘଟାଇଲେ କେତେ ଗ୍ରାମ୍ ଫେରସ୍ ସଲ୍ଫାଇଡ୍ ପ୍ରସ୍ତୁତ ହେବ ?
Solution:
୮୪ ଗ୍ରାମ ଲୁହାଗୁଣ୍ଡ, ୫୪ ଗ୍ରାମ ଗନ୍ଧକ ସହ ରାସାୟନିକ ସଂଯୋଗ ଘଟାଇଲେ (୮୪+୫୪) ଗ୍ରାମ୍ =୧୩୮ ଗ୍ରାମ ଫେରସ୍ ସଲ୍ଫାଇଡ୍ ପ୍ରସ୍ତୁତ ହେବ ।
→ ପରମାଣୁ ଓ ଅଣୁ :
ପରମାଣୁ :
- ପ୍ରତ୍ୟେକ ମୌଳିକ ପଦାର୍ଥ ଅନେକ ଗୁଡ଼ିଏ କ୍ଷୁଦ୍ର କଣିକାର ସମଷ୍ଟି । ମୌଳିକର ଏହି କ୍ଷୁଦ୍ରତମ କଣିକାକୁ ପରମାଣୁ କୁହାଯାଏ ।
- ଗୋଟିଏ ମୌଳିକର ସବୁ ପରମାଣୁ ଗୋଟିଏ ପ୍ରକାରର ହୋଇଥାଏ ।
- କେତେକ ମୌଳିକ ଅଛନ୍ତି ଯେଉଁମାନଙ୍କର ଏକାଧିକ ପ୍ରକାରର ପରମାଣୁ ଥାଏ । ସେହିଭଳି ପରମାଣୁଗୁଡ଼ିକୁ ସମସ୍ଥାନିକ ବା ଆଇସୋଟୋପ୍ (Isotope) କହନ୍ତି । ମୂଳ ମୌଳିକର ଗୁଣ ତାହାର ସମସ୍ଥାନିକ ପରମାଣୁରେ ପରିଲକ୍ଷିତ ହୋଇଥାଏ । ଉଦାହରଣ ସ୍ୱରୂପ, କାର୍ବନ 12 ଓ କାର୍ବନ 14, ପ୍ରୋଟିୟମ୍ (1H), ଡିଉଟେରିୟମ (2H) ଓ ଟ୍ରାଇଟିୟମ୍ (3H)
ଅଣୁ :
- ଯୌଗିକ ପଦାର୍ଥ ଅନେକ ଗୁଡ଼ିଏ କ୍ଷୁଦ୍ର କଣିକାର ସମଷ୍ଟି । ଯୌଗିକର ଏହି କ୍ଷୁଦ୍ରତମ କଣିକାକୁ ଅଣୁ କୁହାଯାଏ ।
- ଯୌଗିକର ଗୁଣ ଏହାର ଅଣୁରେ ମଧ୍ୟ ପରିଲକ୍ଷିତ ହୁଏ । ଯୌଗିକରେ ଯେଉଁ ଯେଉଁ ମୌଳିକ ସଂଯୁକ୍ତ ହୋଇଥାଏ. ସେହି ଯୌଗିକର ଅଣୁରେ ସେହି ମୌଳିକର ପରମାଣୁ ଥାଏ ।
- କଠିନ ମୌଳିକଗୁଡ଼ିକର ଅଣୁ ଗୋଟିଏ ଲେଖାଏଁ ପରମାଣୁରେ ଗଠିତ । ଉଦାହରଣ – ଗନ୍ଧକ (S), ଅଙ୍ଗାରକ (C), ଲୌହ (Fe), ତମ୍ବା (Cu) ଇତ୍ୟାଦି ।
- ଗ୍ୟାସୀୟ ମୌଳିକ ଅଣୁରେ ଦୁଇଟି ଲେଖାଏଁ ପରମାଣୁ ଥାଏ । ଉଦାହରଣ – ଉଦ୍ଜାନ (H2), ଅମ୍ଳଜାନ (O2), ଯବକ୍ଷାରଜାନ (N2) ଇତ୍ୟାଦି ।
ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାରେ ମୌଳିକ ଓ ଯୌଗିକମାନଙ୍କର ଅଣୁ ଓ ପରମାଣୁ ଅଂଶ ଗ୍ରହଣ କରନ୍ତି ।

ମୌଳିକର ପ୍ରତୀକ (Symbol of Elements):
(i) ମୌଳିକର ସଂପୂର୍ଣ୍ଣ ନାମ ପରିବର୍ତ୍ତେ ବ୍ୟବହୃତ ହେଉଥିବା ସାଂକେତିକ କ୍ଷୁଦ୍ରନାମକୁ ମୌଳିକର ପ୍ରତୀକ କୁହାଯାଏ ।
(ii) ପ୍ରତୀକରେ ସେହି ମୌଳିକର ପ୍ରଥମ ଅକ୍ଷରଟି ବା ପ୍ରଥମ ଦୁଇଟି ଅକ୍ଷର ବ୍ୟବହୃତ ହୋଇଥାଏ । ମୌଳିକର ଲାଟିନ୍ ବା ଗ୍ରୀକ୍ନାମକୁ ଇଂରାଜୀ ଅକ୍ଷରଦ୍ବାରା ପ୍ରକାଶ କରାଯାଏ ।
(iii) କେତେକ ମୌଳିକର ଅଣୁ ଏହାର ପରମାଣୁଠାରୁ ଭିନ୍ନ । ଉଦାହରଣ ସ୍ଵରୂପ ଉଦ୍ଜାନ ମୌଳିକର ଅଣୁରେ ଦୁଇଟି ପରମାଣୁ ଥାଏ । ତେଣୁ ଉଦ୍ଜାନ ଅଣୁକୁ ଭିନ୍ନ ଏକ ଉପାୟରେ ଦର୍ଶାଯାଇଥାଏ । ତାହାକୁ ଆଣବିକ ସଂକେତ କୁହାଯାଏ । ଉଦ୍ଜାନର ଆଣବିକ ସଂକେତ H2, ଅମ୍ଳଜାନର ଆଣବିକ ସଂକେତ O2, ଯବକ୍ଷାରଜାନର ଆଣବିକ ସଂକେତ N2, ଇତ୍ୟାଦି ।
→ କେତେଗୋଟି ମୌଳିକର ନାମ ଓ ପ୍ରତୀକ
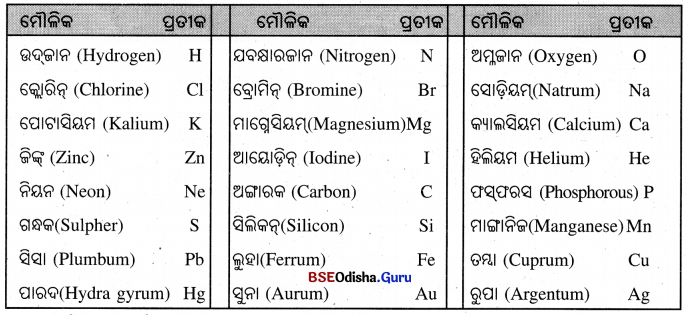
ଯୌଗିକ ପଦାର୍ଥ ଓ ତାହାର ଆଣବିକ ସଂକେତ :
(i) ଦୁଇ ବା ତତୋଽଧ୍ଵକ ମୌଳିକ ପଦାର୍ଥ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଅନୁପାତରେ ରାସାୟନିକ ପ୍ରକ୍ରିୟାଦ୍ଵାରା ସଂଯୁକ୍ତ ହୋଇ ଯେଉଁ ପଦାର୍ଥ ସୃଷ୍ଟି କରନ୍ତି, ତାହାକୁ ଯୌଗିକ ପଦାର୍ଥ କହନ୍ତି ।
(ii) ଯୌଗିକ ପଦାର୍ଥର ଗୁଣ ଏହାର ମୂଳ ମୌଳିକ ପଦାର୍ଥର ଗୁଣଠାରୁ ଭିନ୍ନ । ଯୌଗିକ ପଦାର୍ଥର ଏହି କ୍ଷୁଦ୍ରତମ କଣିକାକୁ ଅଣୁ କୁହାଯାଏ । ଯୌଗିକ ପଦାର୍ଥର ସମସ୍ତ ଗୁଣ ଏହି ଅଣୁରେ ଦେଖିବାକୁ ମିଳେ ।
ଉଦାହରଣ – (କ) ଦୁଇଟି ଉଦଜାନ ପରମାଣୁ ଗୋଟିଏ ଅମ୍ଳଜାନ ପରମାଣୁ ସହ ରାସାୟନିକ ପ୍ରକ୍ରିୟାଦ୍ୱାରା ସଂଯୁକ୍ତ ହୋଇ ଗୋଟିଏ ଜଳ ଅଣୁ (H2O) ସୃଷ୍ଟି କରନ୍ତି । ଏଠାରେ ଜଳଅଣୁର ଆଣବିକ ସଂକେତ H2O ।
(ଖ) ଖାଦ୍ୟରେ ବ୍ୟବହାର କରୁଥିବା ସାଧାରଣ ଲୁଣ ଅଣୁରେ ଗୋଟିଏ ସୋଡ଼ିୟମ୍ ପରମାଣୁ ଓ ଗୋଟିଏ କ୍ଲୋରିନ୍ ପରମାଣୁ ଥାଏ, ତେଣୁ ସାଧାରଣ ଲୁଣର ସଂକେତ ହେଉଛି NaCl ।
→ କେତେକ ପୌଗିକ ଓ ସେମାନଙ୍କର ର୍ଥାଣବିକ ଫକେତ
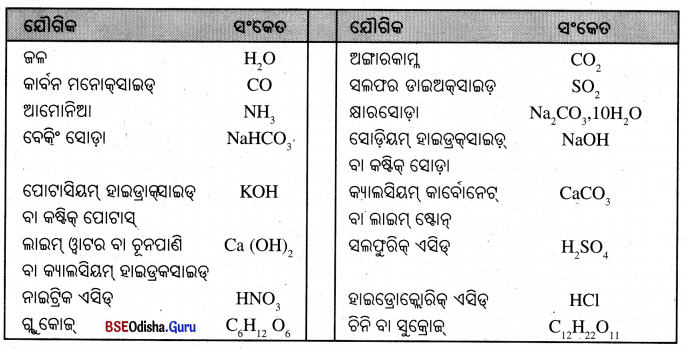
→ ଆପ, କାଣିବା :
- ଜଳ, ବାୟୁ, ଘରଦ୍ଵାର, କାଠ, କୋଇଲା, ଇତ୍ୟାଦିକୁ ପଦାର୍ଥ କୁହାଯାଏ ।
- କେତେକ ପଦାର୍ଥ ପ୍ରାକୃତିକ ଓ ଅନ୍ୟ କେତେକ ମନୁଷ୍ୟକୃତ ।
- ପ୍ରତ୍ୟେକ ପଦାର୍ଥର ବସ୍ତୁତ୍ଵ ଥାଏ ଓ ତାହା କିଛି ସ୍ଥାନ ଅଧିକାର କରିଥାଏ ।
- ପଦାର୍ଥ ତିନିପ୍ରକାର ଅବସ୍ଥାରେ ରହିପାରେ, ଯଥା : କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ।
- ପଦାର୍ଥର ତିନି ଅବସ୍ଥାର ଭୌତିକ ଧର୍ମ ଯଥା : ଆକାର, ଆକୃତି ଭିନ୍ନ ଭିନ୍ନ ହୋଇଥାଏ ।
- ପଦାର୍ଥ ତିନି ପ୍ରକାର ଯଥା : ମୌଳିକ, ଯୌଗିକ ଓ ମିଶ୍ରଣ ।
- ମୌଳିକ ଓ ଯୌଗିକ ପଦାର୍ଥଗୁଡ଼ିକ ବିଶୁଦ୍ଧ ପଦାର୍ଥ ଅଟନ୍ତି ।
- ମିଶ୍ରଣର ଉପାଦାନଗୁଡ଼ିକର ପୃଥକୀକରଣ କରିବା ସହଜ ।
- ମୌଳିକର କ୍ଷୁଦ୍ରତମ କଣିକାକୁ ପରମାଣୁ ଓ ଯୌଗିକର କ୍ଷୁଦ୍ରତମ କଣିକାକୁ ଅଣୁ କୁହାଯାଏ ।
![]()
![]()
![]()
![]()