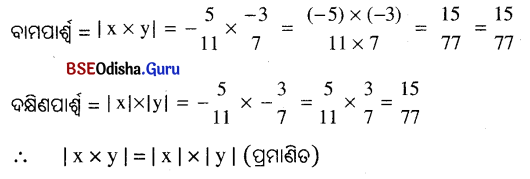Class 7

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.8 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.8

Question 1.
ନିମ୍ନଲିଖତ ପରିମେୟ ସଂଖ୍ୟାମାନଙ୍କର ପରମ ମାନ ନିଶ୍ଚୟ କର ।

(କ) \(\frac{1}{-5}\)
ସମାଧାନ:
\(\frac{1}{5}\)

(ଖ) \(\frac{1}{2}\)
ସମାଧାନ:
\(\frac{1}{2}\)

(ଗ) \(\frac{-3}{-2}\)
ସମାଧାନ:
\(\frac{3}{2}\)

(ଘ) \(\frac{-26}{21}\)
ସମାଧାନ:
\(\frac{26}{21}\)

Question 2.
x ର ନିମ୍ନ ମାନଗୁଡ଼ିକୁ ନେଇ ପ୍ରମାଣ କର ଯେ |x| = |-x|

(କ) 4
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = |x| = |4| = 4, ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = |-x| = |-4| = 4
∴ |x| = |-x|  (ପ୍ରମାଣିତ)

(ଖ) -9
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = |x| = |-9| = 9, ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = |-x| = |-(-9)| = |9| = 9
∴ |x| = |-x|  (ପ୍ରମାଣିତ)

(ଗ) \(\frac{-3}{7}\)
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = |x| = |\(\frac{-3}{7}\)| = \(\frac{3}{7}\), ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = |-x| = |-(\(\frac{-3}{7}\))| = \(\frac{3}{7}\)
∴ |x| = |-x|  (ପ୍ରମାଣିତ)

(ଘ) \(\frac{3}{-8}\)
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = |x| = |\(\frac{3}{-8}\)| = \(\frac{3}{8}\)
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = |-x| = |-(\(\frac{3}{-8}\))| = \(\frac{3}{8}\)
∴ ବାମପାର୍ଶ୍ଵ= ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ  (ପ୍ରମାଣିତ)

Question 3.
x ଓ y ର ନିମ୍ନ ମାନଗୁଡ଼ିକୁ ନେଇ ପ୍ରମାଣ କର ଯେ |x + y| = |x| + |y|

(କ) x = \(\frac{2}{3}\), y = \(\frac{1}{5}\)
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = |x + y| = \(\frac{2}{3}+\frac{1}{5}=\frac{10+3}{15}=\frac{13}{15}\)
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = |x| + |y| = \(\frac{2}{3}+\frac{1}{5}=\frac{10+3}{15}=\frac{13}{15}\)
∴ |x × y| = |x| × |y|  (ପ୍ରମାଣିତ)

(ଖ) x = \(\frac{-3}{4}\), y = \(\frac{-3}{2}\)
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = |x + y| = \(\frac{-3}{4}+\left(-\frac{3}{2}\right)=-\frac{3}{4}-\frac{3}{2}=\frac{-3-6}{4}=-\frac{9}{4}=\frac{9}{4}\)
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = |x| + |y| = \(-\frac{3}{4}+-\frac{3}{2}=\frac{3}{4}+\frac{3}{2}=\frac{3+6}{4}=\frac{9}{4}\)
∴ |x × y| = |x| × |y|  (ପ୍ରମାଣିତ)

Question 4.
x ଓ y ର ନିମ୍ନ ମାନଗୁଡ଼ିକୁ ନେଇ |x + y| < (|x| + |y|) ସତ୍ୟ କି ନାହିଁ ପରୀକ୍ଷା କର ।

(କ) x = -8, y = 5
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = |x + y| = |-8 + 5| = |-3| = 3
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = |x| + |y| = |-8| +|5| = 8 + 5 = 13
∴ |x + y| < (|x| + |y|)  (ସତ୍ୟ)

(ଖ) x = \(\frac{4}{3}\), y = \(\frac{-7}{9}\)
ସମାଧାନ:

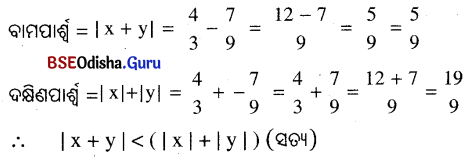
Question 5.
x ଓ y ର ନିମ୍ନ ମାନଗୁଡ଼ିକୁ ନେଇ ପ୍ରମାଣ କର ଯେ |x × y| = |x| × |y|

(କ) x = \(\frac{-4}{5}\), y = \(\frac{2}{3}\)
ସମାଧାନ:

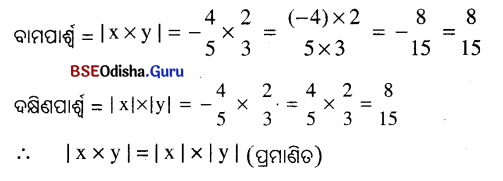
(ଖ) x = \(-\frac{5}{11}\), y = \(\frac{-3}{7}\)
ସମାଧାନ:

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.7 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.7

Question 1.
ଗୋଟିଏ ତ୍ରିଭୁଜର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟର ପରିମାଣ ଯଥାକ୍ରମେ 2 \(\frac{1}{3}\) ସେ.ମି. 3 \(\frac{1}{2}\) ସେ.ମି. ଓ 4 \(\frac{2}{5}\) ସେ.ମି. ହେଲେ, ତ୍ରିଭୁଜଟିର ପରିସୀମା କେତେ ?
ସମାଧାନ:
{ତ୍ରିଭୁଜର ପରିସୀମା = ବାହୁ ତ୍ରୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି}
ତ୍ରିଭୁଜର ପରିସୀମା = 2 \(\frac{1}{3}\) ସେ.ମି., 3 \(\frac{1}{2}\) ସେ.ମି. ଓ 4 \(\frac{2}{5}\) ସେ.ମି. = \(\left(\frac{7}{3}+\frac{7}{2}+\frac{22}{5}\right)\) ସେ.ମି. 
= \(\frac{10 \times 7+15 \times 7+6 \times 22}{30}\) ସେ.ମି. = \(\frac{70+105+132}{30}\) ସେ.ମି.
= \(\frac{307}{30}\) ସେ.ମି. = 10 \(\frac{7}{30}\) ସେ.ମି.
∴ ତ୍ରିଭୁଜର ପରିସୀମା 10 \(\frac{7}{30}\) ସେ.ମି.

Question 2.
କମଳବାବୁ ତାଙ୍କ ଘର ପାଖରୁ \(\frac{2}{5}\) କି.ମି. ଉତ୍ତର ଦିଗ ଆଡ଼କୁ ଯିବା ପରେ 1 \(\frac{3}{4}\) କି.ମି. ଦକ୍ଷିଣ ଦିଗ ଆଡ଼କୁ ଚାଲିଲେ । ତେବେ ସେ ତାଙ୍କ ଘରଠାରୁ କେଉଁ ଦିଗରେ କେତେ ଦୂରରେ ଅଛନ୍ତି?

ସମାଧାନ:
କମଳବାବୁ ଉତ୍ତରକୁ ଗଲେ \(\frac{2}{5}\) କି.ମି. । ସେଠାରୁ ଦକ୍ଷିଣକୁ ଗଲେ = 1 \(\frac{3}{4}\) ବା \(\frac{7}{4}\) କି.ମି.
ଘରଠାରୁ ଦକ୍ଷିଣ ଦିଗକୁ ଯାଇଥିବା ଅଧ‌ିକ ରାସ୍ତାର ଦୈର୍ଘ୍ୟ = \(\left(\frac{7}{4}-\frac{2}{5}\right)\) କି.ମି.
= \(\frac{35-8}{20}\) କି.ମି. = \(\frac{27}{20}\) ବା 1 \(\frac{7}{20}\) କି.ମି.
∴ କମଳବାବୁ ତାଙ୍କ ଘରଠାରୁ ଦକ୍ଷିଣ ଦିଗରେ 1 \(\frac{7}{20}\) କି.ମି. ଦୂରରେ ଅଛନ୍ତି ।

Question 3.
ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟାର ଯୋଗଫଳ -9 । ସେମାନଙ୍କ ମଧ୍ୟରୁ ଗୋଟିଏ \(\frac{15}{8}\) ହେଲେ ଅନ୍ୟଟି କେତେ?
ସମାଧାନ:
ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟାର ଯୋଗଫଳ = -9 । ସେମାନଙ୍କ ମଧ୍ୟରୁ ଗୋଟିଏ ସଂଖ୍ୟା = \(\frac{15}{8}\)
ଅନ୍ୟ ସଂଖ୍ୟାଟି = -9 – \(\frac{15}{8}=-\frac{9}{1}-\frac{15}{8}=\frac{-72-15}{8}=-\frac{87}{8}\)
∴ ଅନ୍ୟ ପରିମେୟ ସଂଖ୍ୟାଟି –\(\frac{87}{8}\) 

Question 4.
ମେରୀ ପ୍ରତିଦିନ 5 \(\frac{2}{3}\) ଘଣ୍ଟା ପଢ଼େ । ସେ ଯଦି 2 \(\frac{4}{5}\) ଘଣ୍ଟା ଗଣିତ ଓ ବିଜ୍ଞାନ ପଢୁଥାଏ, ତେବେ ସେ କେତେ ସମୟ ଅନ୍ୟ ବିଷୟ ଗୁଡ଼ିକୁ ପଢ଼ିଥାଏ?
ସମାଧାନ:
ମେରୀ ପ୍ରତିଦିନ ପଢ଼େ 5 \(\frac{2}{3}\) ବା \(\frac{17}{3}\)ଘଣ୍ଟା । ଗଣିତ ଓ ବିଜ୍ଞାନ ପଢ଼େ = 2 \(\frac{4}{5}\) ବା \(\frac{14}{5}\) ଘଣ୍ଟା
ଅନ୍ୟ ବିଷୟ ପଢ଼େ = \((\frac{17}{3}-\frac{14}{5})\) ଘଣ୍ଟା । = \(\frac{85-42}{15}\) ଘଣ୍ଟା । = \(\frac{43}{15}\) ବା 2 \(\frac{13}{15}\)ଘଣ୍ଟା ।
∴ ମେରୀ 2 \(\frac{13}{15}\) ଘଣ୍ଟା ଅନ୍ୟ ବିଷୟଗୁଡ଼ିକୁ ପଢ଼ିଥାଏ ।

Question 5.
9 \(\frac{4}{3}\) ଓ 5 \(\frac{5}{6}\) ର ଯୋଗଫଳ ଓ 11 \(\frac{2}{5}\) ଓ 7 \(\frac{1}{3}\) ର ଯୋଗଫଳ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ କେତେ?
ସମାଧାନ:

Question 6.
ଗୋଟିଏ ବର୍ଗାକୃତି ପଡ଼ିଆର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 5 \(\frac{3}{4}\) ମି ହେଲେ ସେହି ପଡ଼ିଆର କ୍ଷେତ୍ରଫଳ ଓ ପରିସୀମା ନିର୍ଣ୍ଣୟ କର । ଏହି ପଡ଼ିଆର ଚାରିପାଖରେ ବାଡ଼ ତିଆରି କରିବା ପାଇଁ ମିଟରକୁ 8 ଟଙ୍କା ହିସାବରେ ମୋଟ କେତେ ଖର୍ଚ୍ଚ ହେବ?
ସମାଧାନ:
ବର୍ଗ କ୍ଷେତ୍ରର ପରିସୀମା = 4 × ବାହୁର ଦୈର୍ଘ୍ୟ
ବର୍ଗ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (ବାହୁର ଦୈର୍ଘ୍ୟ)²
ବର୍ଗାକାର ପଡ଼ିଆର ଦୈର୍ଘ୍ୟ = 5 \(\frac{3}{4}\) ବା \(\frac{23}{4}\) ମିଟର ।
ବର୍ଗାକାର କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (ବାହୁର ଦୈର୍ଘ୍ୟ)² = (\(\frac{23}{4}\) ମିଟର)² = \(\frac{529}{16}\) ବର୍ଗମିଟର ।
= 33 \(\frac{1}{16}\) ବର୍ଗମିଟର ।
∴ ପଡ଼ିଆର ପରିସୀମା = 4 × ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = 4 × \(\frac{23}{4}\) ମିଟର = 23 ମିଟର ।
ପଡ଼ିଆର ଚାରିପାଖରେ ବାଡ଼ଦେବାକୁ 1 ମିଟରକୁ ଖର୍ଚ୍ଚ ହୁଏ 8 ଟଙ୍କା । 
∴ 23 ମିଟରକୁ ଖର୍ଚ୍ଚ ହେବ = 23 × 8 ଟଙ୍କା = 184 ଟଙ୍କା ।

Question 7.
କେଉଁ ସଂଖ୍ୟାକୁ \(\frac{-8}{5}\) ଦ୍ଵାରା ଗୁଣିଲେ ଗୁଣଫଳ 36 ହେବ?
ସମାଧାନ:
ସଂଖ୍ୟାଦ୍ବୟର ଗୁଣଫଳ 36 । ଗୋଟିଏ ସଂଖ୍ୟା \(-\frac{8}{5}\)
ଅନ୍ୟ ସଂଖ୍ୟାଟି = 36 ÷ (\(\frac{-8}{5}\)) = 36 × (-\(\frac{5}{8}\)) = \(\frac{-36 \times 5}{8}=-\frac{45}{2}\) ବା -22 \(\frac{1}{2}\)
∴ -22 \(\frac{1}{2}\) କୁ \(\frac{-8}{5}\) ଦ୍ଵାରା ଗୁଣିଲେ ଗୁଣଫଳ 36 ହେବ ।

Question 8.
ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟାର ଗୁଣଫଳ \(\frac{-16}{9}\) । ସେମାନଙ୍କ ମଧ୍ୟରୁ ଗୋଟିଏ \(\frac{-4}{3}\) ହେଲେ ଅନ୍ୟଟି କେତେ?
ସମାଧାନ:
ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟାର ଗୁଣଫଳ = \(\frac{-16}{9}\) । ଗୋଟିଏ ସଂଖ୍ୟା = \(\frac{-4}{3}\)
ଅନ୍ୟ ସଂଖ୍ୟାଟି = \(\left(-\frac{16}{9}\right) \div\left(-\frac{4}{3}\right)=-\frac{16}{9} \times\frac{-3}{4}=\frac{(-16) \times(-3)}{9 \times 4}=\frac{48}{36}=\frac{4}{3}\)
∴ ଅନ୍ୟ ପରିମେୟ ସଂଖ୍ୟାଟି \(\frac{4}{3}\)

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 8 ବ୍ୟାବହାରିକ ଗଣିତ InText Questions Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 8 ବ୍ୟାବହାରିକ ଗଣିତ InText Questions

ନିଜେ କରି ଦେଖ :
1. ତୁମ ଶ୍ରେଣୀରେ ଗୋଟିଏ ଦିନରେ ଅନୁପସ୍ଥିତ ଥ‌ିବା ପିଲାସଂଖ୍ୟା, ସମୁଦାୟ ପିଲାସଂଖ୍ୟାର କେତେ ଶତକଡ଼ା ?
ସମାଧାନ:

2. ତୁମ ଶ୍ରେଣୀରେ ଗଣିତରେ 30 ରୁ କମ୍ ନମ୍ବର ରଖୁଥ‌ିବା ପିଲାସଂଖ୍ୟା ସମୁଦାୟ ପିଲାସଂଖ୍ୟାର କେତେ ଶତକଡ଼ା ?
ସମାଧାନ:

ନିଜେ ସମାଧାନ କର:
ଜଣେ ଦୋକାନୀ 4 ଟି ଲେମ୍ବୁକୁ 3 ଟଙ୍କାରେ କିଣିଲା ଏବଂ 3 ଟିକୁ 4 ଟଙ୍କା ଦରରେ ସବୁଯାକ ବିକିଦେଲା । ତେବେ ତା’ର ଶତକଡ଼ା କେତେ ଲାଭ ବା କ୍ଷତି ହେଲା ?
ସମାଧାନ:
4 ଓ 3 ର ଲ.ସା.ଗୁ. = 12 । ମନେକର ଦୋକାନୀଟି 12 ଟି ଲେମ୍ବୁ କିଣିଥିଲା ।
4 ଟି ଲେମ୍ବୁର କ୍ରୟମୂଲ୍ୟ = 3 ଟଙ୍କା
12 ଟି ଲେମ୍ବୁର କ୍ରୟମୂଲ୍ୟ = 3× 3 ଟ. = 9 ଟଙ୍କା
3 ଟି ଲେମ୍ବୁର ବିକ୍ରୟ ମୂଲ୍ୟ 4 ଟଙ୍କା ।
12 ଟି ଲେମ୍ବୁର ବିକ୍ରୟ ମୂଲ୍ୟ = 4 x 4 ଟଙ୍କା = 16 ଟଙ୍କା
ଲାଭ = ବିକ୍ରୟ ମୂଲ୍ୟ – କ୍ରୟମୂଲ୍ୟ = 16 ଟ. – 9 ଟ. = 7 ଟଙ୍କା

∴ ଦୋକାନୀର 77 \(\frac{7}{9}\)% ଲାଭ ହେଲା ।

ସମାଧାନ କର :
ଗୋଟିଏ ପାଣିଟାଙ୍କିରେ 12 ଟି ପାଇପ୍ ଲଗାଯାଇଛି । 8 ଟି ପାଇପ୍ ଖୋଲାଥ୍ଲେ ଟାଙ୍କିଟି 6 ଘଣ୍ଟାରେ ପୂର୍ଣ୍ଣହୁଏ । ତେବେ ସମସ୍ତ ପାଇପ୍ ଖୋଲାରହିଲେ ଟାଙ୍କିଟି କେତେ ଘଣ୍ଟାରେ ପୂର୍ଣ ହେବ ? 
ସମାଧାନ:
ପାଇପ୍ ସଂଖ୍ୟା ବଢ଼ିଲେ ପାଣିଟାଙ୍କି ପୂଣ୍ଣହେବା ସମୟ କମିବ । ତେଣୁ ଏହା ପ୍ରତିଲୋମୀ ଚଳନ ।
ଏଠାରେ ପାଇପ୍ ସଂଖ୍ୟାକୁ x ଓ ସମୟକୁ y ଘଣ୍ଟା ନେଇ ସାରଣୀଟିଏ ପ୍ରସ୍ତୁତ କଲେ –

x (ପାଇପ୍ ସଂଖ୍ୟା)	x1 = 12	x2 = 8
y (ସମୟ) ଘଣ୍ଟାରେ	y1 = ?	y2 = 6

x ଓ y ମଧ୍ୟରେ ପ୍ରତିଲୋମୀ ଚଳନ ହେତୁ x₁y₂ = x₂y₁
⇒ 12 × y₁ = 8 × 6
⇒ y₁ = \(\frac{8 \times 6}{12}\) = 4
∴ ସମସ୍ତ ପାଇପ୍ ଖୋଲା ରହିଲେ ଟାଙ୍କିଟି 4 ଘଣ୍ଟାରେ ପୂର୍ଣ୍ଣ ହେବ ।

ଉତ୍ତର ନିର୍ଣ୍ଣୟ କର :
ଦୁଇ ଜଣ ସାଙ୍ଗ A ଓ B ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟ ଲାଗି ସ୍କୁଟର ଚଳାଇବାକୁ ଆରମ୍ଭ କଲେ । A ଘଣ୍ଟାପ୍ରତି 54 କି.ମି. ବେଗରେ ସ୍କୁଟର ଚଳାଇ ନିର୍ଦ୍ଧାରିତ ସମୟ ମଧ୍ୟରେ 36 କି.ମି. ଦୂରତା ଅତିକ୍ରମ କଲେ । B ସେହି ସମୟ ମଧ୍ୟରେ 30 କି.ମି. ଦୂରତା ଅତିକ୍ରମ କଲେ, ତେବେ B କେତେ ବେଗରେ ସ୍କୁଟର ଚଳାଉଥିଲେ ?
ସମାଧାନ:
A ର ବେଗ (s) = 54 କି.ମି./ଘଣ୍ଟା ଓ ଦୂରତା (d) = 36 କି.ମି. ।

∴ B ଘଣ୍ଟା ପ୍ରତି 45 କି.ମି. ବେଗରେ ସ୍କୁଟର ଚଳାଉଥିଲା ।

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 4 ଘାତାଙ୍କ ଓ ଘାତରାଶି Ex 4.3 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 4 ଘାତାଙ୍କ ଓ ଘାତରାଶି Ex 4.3

Question 1.
(କ) ଆଲୋକର ବେଗ ସେକେଣ୍ଡ ପ୍ରତି 300,000,000 ମିଟର । ଏହି ବେଗକୁ ପ୍ରାମାଣିକ ରୂପରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:
300,000,000 ର ପ୍ରାମାଣିକ ରୂପ = 3 × 103 ମି. = 3.0 × 10⁸ ମିଟର ।

(ଖ) ପୃଥ‌ିବୀଠାରୁ ଚନ୍ଦ୍ରର ହାରାହାରି ଦୂରତା ପ୍ରାୟ 384000000 ମିଟର । ଉକ୍ତ ଦୂରତାର ପ୍ରାମାଣିକ ରୂପ ଲେଖ
ସମାଧାନ:
384000000 ର ପ୍ରାମାଣିକ ରୂପ = 3.84 × 100000000 ମି. = 3.84 × 10⁸ ମି.

Question 2.
ନିମ୍ନରେ କେତେଗୁଡ଼ିଏ ସଂଖ୍ୟାର ପ୍ରାମାଣିକ ରୂପ ଦିଆଯାଇଛି । ସଂଖ୍ୟାଟିକୁ ଲେଖ ।

(କ) 9.8 × 10⁴
ସମାଧାନ:
9.8 × 10⁴ = \(\frac{98}{10}\) × 10⁴ = 98 × 10^4-1 = 98 × 10³ = 98000

(ଖ) 1.385 × 10⁷
ସମାଧାନ:
1.385 × 10⁷ = \(\frac{1385}{10^3}\) × 10⁷ = 1385 × 10^7-3  = 1385 × 10⁴ = 13850000

(ଗ) 5.15 × 10¹⁰
ସମାଧାନ:
5.15 × 10¹⁰ = \(\frac{515}{10^2}\) × 10¹⁰ = 515 × 10^10-2 = 515 × 10⁸ = 51500000000

(ଘ) 3.9 × 10¹¹
ସମାଧାନ:
3.9 × 10¹¹ = 3.9 × 10 × 10¹⁰ = 39 × 10¹⁰ = 390,000,000,000

Question 3.
ନିମ୍ନରେ ଦିଆଯାଇଥବା ପ୍ରତ୍ୟେକ ଉକ୍ତିରେ ଥିବା ସଂଖ୍ୟାର ପ୍ରାମାଣିକ ରୂପ ଲେଖ ।

(କ) ପୃଥିବୀର ବ୍ୟାସ ପ୍ରାୟ 1,27,56,000 ମିଟର ।
ସମାଧାନ:
1,27,56,000 ମିଟର = 1.2756 × 10⁷ ମିଟର ।

(ଖ) ସୂର୍ଯ୍ୟର ବ୍ୟାସ ପ୍ରାୟ 1,400,000,000 ମିଟର।
ସମାଧାନ:
1,400,000,000 ମିଟର = 1.4 × 10⁹ ମିଟର ।

(ଗ) ଶନି ଗ୍ରହଠାରୁ ସୂର୍ଯ୍ୟର ଦୂରତା ପ୍ରାୟ 1,433,500,000,000 ମିଟର। 
ସମାଧାନ:
1,433,500,000,000 ମିଟର = 1.4355 × 10¹² ମିଟର ।

(ଘ) ପୃଥିବୀରେ ପ୍ରାୟ 1,353,000,000 ଘନ କି.ମି. ସମୁଦ୍ର ଜଳ ଅଛି ।
ସମାଧାନ:
1,353,000,000 ଘନ କି.ମି. = 1.353 × 10⁹ ଘନ କି.ମି. ।

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 4 ଘାତାଙ୍କ ଓ ଘାତରାଶି Ex 4.2 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 4 ଘାତାଙ୍କ ଓ ଘାତରାଶି Ex 4.2

Question 1.
ଘାତାଙ୍କୀୟ ନିୟମ ବ୍ୟବହାର କରି ଏକ ଘାତରାଶିରେ ପରିଣତ କର ।

(କ) 2³ × 2⁴ × 2⁵
ସମାଧାନ:
2³ × 2⁴ × 2⁵ = 2³⁺⁴⁺⁵ = 2¹²

(ଖ) 6¹⁵ ÷ 6¹²
ସମାଧାନ:
6¹⁵ ÷ 6¹² = 6^15-12 = 6³

(ଗ) a³ × a⁷
ସମାଧାନ:
a³ × a⁷ = a³⁺⁷ = a¹⁰

(ଘ) 7 × 7²
ସମାଧାନ:
7 × 7² = 7¹ × 7² = 7¹⁺² = 7³

(ଙ) 5² ÷ 5³
ସମାଧାନ:
5² ÷ 5³ = 5^2-3 = 5^-1

(ଚ) 2⁵ × 3⁵
ସମାଧାନ:
2⁵ × 3⁵ = (2 × 3)⁵ = 6⁵

(ଛ) a⁴ × a⁵
ସମାଧାନ:
a⁴ × a⁵ = a⁴⁺⁵ = a⁹

(ଜ) (3⁴)³ × (2⁶)²
ସମାଧାନ:
(3⁴)³ × (2⁶)² = 3^4×3 × 2^6×2 = 3¹² × 2¹² = (3 × 2)¹² = 6¹²

(ଝ) (2¹⁰ ÷ 2⁸) × 2³
ସମାଧାନ:
(2¹⁰ ÷ 2⁸) × 2³ = 2^10-8 × 2³ = 2² × 2³ = 2²⁺³ = 2⁵

Question 2.
ସରଳ କରି ଏକ ଘାତରାଶିରେ ପରିଣତ କର ।

(କ) \(\frac{2^3 \times 3^4 \times 4}{3 \times 3^3}\)
ସମାଧାନ:
\(\frac{2^3 \times 3^4 \times 4}{3 \times 3^3}\) = \(\frac{2^3 \times 3^4 \times 4}{3^{1+3}}=\frac{2^3 \times 3^4 \times 4}{3^4}\) = 2³ × 4 = 2³ × 2² = 2³⁺² = 2⁵

(ଖ) \(\frac{3 \times 7 \times 11^8}{21 \times 11^3}\)
ସମାଧାନ:
\(\frac{3 \times 7 \times 11^8}{21 \times 11^3}\) = \(\frac{21 \times 11^8}{21 \times 11^3}=\frac{11^8}{11^3}\) = 11^8-3 = 11⁵

(ଗ) [(5²)³ × 5⁴] ÷ 5⁷
ସମାଧାନ:
[(5²)³ × 5⁴] ÷ 5⁷=[5^2×3 × 5⁴] + 5⁷
= [5⁶ × 5⁴] + 5⁷ = 5⁶⁺⁴ ÷ 5⁷ = 5¹⁰ ÷ 5⁷ = 5^10-7 = 5³

(ଘ) 25⁴ ÷ 5³
ସମାଧାନ:
25⁴ ÷ 5³ = (5²)⁴ ÷ 5³ = 5^2×4 + 5³ = 5⁸ ÷ 5³ = 5^8-3 = 5⁵

(ଙ) \(\frac{3^7}{\mathbf{3}^4 \times \mathbf{3}^3}\)
ସମାଧାନ:
\(\frac{3^7}{\mathbf{3}^4 \times \mathbf{3}^3}\) = \(\frac{3^7}{3^{4+3}}=\frac{3^7}{3^7}\) = 3^7-7 = 3⁰

(ଚ) \(\frac{2^4 \times a^53}{4^2 \times a}\)
ସମାଧାନ:
\(\frac{2^4 \times a^53}{4^2 \times a}\) = \(\frac{16 \times a^5}{16 \times a}=\frac{a^5}{a}\) = a^5-1 = a⁴

(ଛ) (2³ × 2)² ÷ 2⁵
ସମାଧାନ:
(2³ × 2)² ÷ 2⁵ = (2³⁺¹)² ÷ 2⁵ =(2⁴)² ÷ 2⁵
= 2^4×2 ÷ 2⁵ = 2⁸ ÷ 2⁵ = 2^8-5 = 2³

(ଜ) \(\frac{a^5}{a^3}\) × a⁸
ସମାଧାନ:
\(\frac{a^5}{a^3}\) × a⁸ = (a^5-3) × a⁸ = a² × a⁸ = a²⁺⁸ = a¹⁰

Question 3.
ନିମ୍ନ ସଂଖ୍ୟାମାନଙ୍କୁ ମୌଳିକ ସଂଖ୍ୟା ଆଧାର ବିଶିଷ୍ଟ ଏକାଧ୍ଵ ଘାତରାଶିର ଗୁଣଫଳ ରୂପେ ପ୍ରକାଶ କର ।

(କ) 270
ସମାଧାନ:
270 = 2 × 3 × 3 × 3 × 5 = 2¹ × 3³ × 5¹

(ଖ) 768
ସମାଧାନ:
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁸ × 3¹

(ଗ) 108 × 192
ସମାଧାନ:
108 × 192 = (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= 2² × 3³ × 2⁶ × 3 = (2² × 2⁶) × (3³ × 3) = 2²⁺⁶ × 3³⁺¹ = 2⁸ × 3⁴

(ଘ) 729 × 64
ସମାଧାନ:
729 × 64 = 3 × 3 × 3 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2 = 3⁶ × 2⁶

Question 4.
ସରଳ କର :

(କ) {(4²)}²
ସମାଧାନ:
{(4)²}² = 4^2×2 = 4⁴ = 4 × 4 × 4 × 4 = 256

(ଖ) (6)³ ÷ (6)
ସମାଧାନ:
(6)³ ÷ (6) = 6^3-1 = 6² = 36

(ଗ) (2)³ × (3)³ ÷ (6)³
ସମାଧାନ:
(2)³ × (3)³ ÷ (6)³ = \(\frac{2^3 \times 3^3}{6^3}=\frac{(2 \times 3)^3}{6^3}=\frac{6^3}{6^3}\) = 1

(ଘ) (5)² × (5)⁴ ÷ (5)²
ସମାଧାନ:
(5)² × (5)⁴ ÷ (5)² = 5² × 5^4-2 = 5² × 5² = 5²⁺² = 5⁴ = 625

(ଙ) \(\frac{\left(2^5\right) \times 7^3}{8^3 \times 7}\)
ସମାଧାନ:
\(\frac{\left(2^5\right) \times 7^3}{8^3 \times 7}\) = \(\frac{2^5 \times 7^3}{\left(2^3\right)^3 \times 7}=\frac{2^5 \times 7^3}{2^9 \times 7}=\frac{2^5 \times 7^2 \times 7}{2^5 \times 2^4 \times 7}=\frac{7^2}{2^4}=\frac{49}{16}\)

(ଚ) \(\frac{3^2 \times 10^5 \times 25}{5^3 \times 6^4}\)
ସମାଧାନ:
\(\frac{3^2 \times 10^5 \times 25}{5^3 \times 6^4}\) = \(\frac{3^2 \times(2 \times 5)^5 \times 5^2}{5^3 \times(2 \times 3)^4}=\frac{3^2 \times 2^5 \times 5^5 \times 5^2}{5^3 \times 2^4 \times 3^4}\)

\(=\frac{2^5}{2^4} \times \frac{3^2}{3^2\cdot 3^2} \times \frac{5^{5+2}}{5^3}\) = \(2^{5-4} \times \frac{1}{3^2} \times 5^{7-3}\) = \(=2 \times\frac{1}{9} \times 5^4=\frac{2}{9} \times 625\) = \(\frac{1250}{9}\)

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 8 ବ୍ୟାବହାରିକ ଗଣିତ Ex 8.8 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 8 ବ୍ୟାବହାରିକ ଗଣିତ Ex 8.8

Question 1.
ଗୋଟିଏ ସ୍ଫୁଟର ଘଣ୍ଟା ପ୍ରତି 40 କି.ମି. ବେଗରେ ଗତି କଲେ 800 ମି. ରାସ୍ତାକୁ କେତେ ସେକେଣ୍ଡରେ ଅତିକ୍ରମ କରିବ ?
ସମାଧାନ: 
ଏଠାରେ ସ୍କୁଟରର ବେଗ (s) = 40 କି.ମି./ଘଣ୍ଟା

= \(\frac{1}{50}\) × 3600 ସେକେଣ୍ଡ = 72 ସେକେଣ୍ଡ ବା 1 ମିନିଟ୍ 12 ସେକେଣ୍ଡ ।
∴ ସ୍କୁଟରଟି 800 ମି. ରାସ୍ତାକୁ 1 ମିନିଟ୍ 12 ସେକେଣ୍ଡରେ ଅତିକ୍ରମ କରିବ ।

Question 2.
ଗୋଟିଏ ଟ୍ରେନ୍‌ର ଦୈର୍ଘ୍ୟ 600 ମି. । ଗୋଟିଏ ଖୁଣ୍ଟକୁ ଏହା 40 ସେକେଣ୍ଡରେ ଅତିକ୍ରମ କଲେ ଏହାର ଘଣ୍ଟା ପ୍ରତି ବେଗ କେତେ ?
ସମାଧାନ: 
ଟ୍ରେନ୍ ଏକ ଖୁଣ୍ଟକୁ ଅତିକ୍ରମ କରିବା ଅର୍ଥ ନିଜ ଦୈର୍ଘ୍ୟକୁ ଅତିକ୍ରମ କରିବାକୁ ହେବ ।
ଦୂରତା (d) = 600 ମିଟର ଓ ସମୟ (t) = 40 ସେକେଣ୍ଡ

= 15 × 3600 ମି. / ଘଣ୍ଟା = 54 କି.ମି. / ଘଣ୍ଟା 
∴ ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ବେଗ 54 କି.ମି. ।

Question 3.
ସୋନାଲି ପାଦରେ ଚାଲିଚାଲି ଗୋଟିଏ 400 ମି. ଲମ୍ବ ପୋଲକୁ 5 ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କଲେ, 2 ଘଣ୍ଟାରେ କେତେ ବାଟ ଯିବ ?
ସମାଧାନ: 
5 ମିନିଟ୍‌ରେ ସୋନାଲି ଯାଏ 400 ମିଟର ।
1 ମିନିଟ୍‌ରେ ସୋନାଲି ଯାଏ = \(\frac{490}{5}\) ମିଟର = 80 ମିଟର
1 ଘଣ୍ଟା ବା 60 ମିନିଟ୍‌ରେ ସୋନାଲି ଯାଏ 60 × 80 ମି. = 4800 ମି.
ସୋନାଲି 2 ଘଣ୍ଟାରେ ଯିବ = 4800 ମି. × 2 = 9600 ମି. = \(\frac{9600}{1000}\) କି.ମି. = 9.6 କି.ମି. ।
∴ ସୋନାଲି 2 ଘଣ୍ଟାରେ 9.6 କି.ମି. ବାଟ ଯିବ ।

Question 4.
କିଶୋର ବାବୁ ଘଣ୍ଟା ପ୍ରତି 30 କି.ମି. ବେଗରେ ଯାଇ ଗୋଟିଏ ସ୍ଥାନରେ 6 ଘଣ୍ଟାରେ ପହଞ୍ଚିଲେ । କେତେ ବେଗରେ ଯାଇଥିଲେ ସେହି ସ୍ଥାନରେ ସେ 3 ଘଣ୍ଟାରେ ପହଞ୍ଚାନ୍ତେ ?
ସମାଧାନ: 
କିଶୋର ବାବୁ 1 ଘଣ୍ଟାରେ ଯାଆନ୍ତି 30 କି.ମି. ।
ସେ 6 ଘଣ୍ଟାରେ ଯିଟେ 6 × 30 କି.ମି. = 180 କି.ମି.
∴ ସ୍ଥାନଟିର ଦୂରତ୍ୱ = 180 କି.ମି.

∴ 60 କି.ମି./ଘଣ୍ଟା ବେଗରେ ଯାଇଥିଲେ ସେହି ସ୍ଥାନରେ କିଶୋର ବାବୁ 3 ଘଣ୍ଟାରେ ପହଞ୍ଚିଥାନ୍ତେ ।

Question 5.
ଘଣ୍ଟା ପ୍ରତି 90 କି.ମି. ବେଗରେ ଗତି କରୁଥ‌ିବା ଗୋଟିଏ ଟ୍ରେନ୍ ପ୍ଲାଟଫର୍ମରେ ଛିଡ଼ା ହୋଇଥବା ଗୋଟିଏ ଲୋକକୁ 20 ସେକେଣ୍ଡରେ ଅତିକ୍ରମ କଲେ, ଟ୍ରେନ୍‌ର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ: 
ଟ୍ରେନ୍‌ଟି 1 ଘଣ୍ଟା ବା 3600 ସେକେଣ୍ଡରେ ଯାଏ 90 କି.ମି. ବା 90000 ମିଟର ।
∴ 1 ସେକେଣ୍ଡରେ ଟ୍ରେନ୍‌ଟି ଯାଏ \(\frac{90000}{3600}\) ମିଟର = 25 ମିଟର
20 ସେକେଣ୍ଡରେ ଯିଟେ = 20 × 25 ମି. = 500 ମିଟର
∴ ଟ୍ରେନ୍‌ଟି ଏକ ଲୋକକୁ ଅତିକ୍ରମ କରିବା ଅର୍ଥ ନିଜ ଦୈର୍ଘ୍ୟକୁ ଅତିକ୍ରମ କରିବା । 
∴ ଟ୍ରେନ୍‌ଟିର ଦୈର୍ଘ୍ୟ 500 ମି. ।

Question 6.
ଦିପ୍ତି ଘଣ୍ଟାପ୍ରତି 60 କି.ମି. ବେଗରେ ଘରଠାରୁ କିଛି ଦୂରତାକୁ 30 ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରି, ସେହି ସ୍ଥାନରୁ ଘଣ୍ଟା ପ୍ରତି 72 କି.ମି. ବେଗରେ ଯାଇ ଅଫିସ୍‌ରେ 30 ମିନିଟ୍‌ରେ ପହଞ୍ଚେ । ତା’ ଘରଠାରୁ ଅଫିସ୍ କେତେ ଦୂର ? 
ସମାଧାନ: 
ଦିପ୍ତି 1 ଘଣ୍ଟାରେ ଯାଏ 60 କି.ମି. ।
ଦିପ୍ତି 30 ମିନିଟ୍ ବା \(\frac{1}{2}\) ଘଣ୍ଟାରେ ଯିବ 60 × \(\frac{1}{2}\) କି.ମି. = 30 କି.ମି. ।
ଅର୍ଥାତ୍ ଦିପ୍ତିର ଘରଠାରୁ ନିର୍ଦ୍ଦିଷ୍ଟ ସ୍ଥାନ ମଧ୍ୟରେ ଦୂରତା = 30 କି.ମି. ।
ପୁନଶ୍ଚ ଦିପ୍ତି 1 ଘଣ୍ଟାରେ ଯାଏ 72 କି.ମି. ।
ଦିପ୍ତି 30 ମିନିଟ୍ ବା \(\frac{1}{2}\) ଘଣ୍ଟାରେ ଯିବ 72 × \(\frac{1}{2}\) କି.ମି. = 36 କି.ମି.
ଅର୍ଥାତ୍ ନିର୍ଦ୍ଦିଷ୍ଟ ସ୍ଥାନଠାରୁ ଦିପ୍ତିର ଅଫିସ୍ ମଧ୍ଯରେ ଦୂରତା = 36 କି.ମି. ।
∴ ଦିପ୍ତି ଘରଠାରୁ ଅଫିସର ଦୂରତା = 30 କି.ମି. + 36 କି.ମି. = 66 କି.ମି.

Question 7.
ଗୋଟିଏ ଟ୍ରେନ୍ 30 ସେକେଣ୍ଟରେ ଗୋଟିଏ ବତୀଖୁଣ୍ଟକୁ ଓ ଗୋଟିଏ 300 ମିଟର ପୋଲକୁ ଏକ ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କଲେ ଟ୍ରେନ୍‌ର ଦୈର୍ଘ୍ୟ ଓ ଘଣ୍ଟା ପ୍ରତି ବେଗ କେତେ ?
ସମାଧାନ: 
ଏକ ଟ୍ରେନ୍ ଗୋଟିଏ ବତୀଖୁଣ୍ଟକୁ 30 ସେକେଣ୍ଡ ବା \(\frac{1}{2}\) ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରେ \(\frac{1}{2}\) ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରେ ଅର୍ଥାତ୍ ନିଜର ଦୈର୍ଘ୍ୟ ।
ଟ୍ରେନ୍‌ଟି 300 ମିଟର ପୋଲକୁ 1 ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରେ ଅର୍ଥାତ୍ ନିଜର ଦୈର୍ଘ୍ୟ ଓ 300 ମିଟର ପୋଲକୁ 1 ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରେ ।
ଟ୍ରେନ୍‌ଟି 300 ମିଟର ଦୈର୍ଘ୍ୟକୁ 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\) ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରେ ।
ଟ୍ରେନ୍‌ଟି \(\frac{1}{2}\) ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରେ 300 ମିଟର ।
ଟ୍ରେନ୍‌ଟି 1 ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରିବ = 300 ÷ \(\frac{1}{2}\) = 300 × 2 = 600 ମିଟର ।
ଟ୍ରେନ୍‌ଟି 60 ମିନିଟ୍‌ରେ ଅତିକ୍ରମ କରିବ = 600 ମି. × 60 = 36000 ମି. = 36 କି.ମି. ।
∴ ଟ୍ରେନ୍‌ର ଦୈର୍ଘ୍ୟ 300 ମିଟର ଓ ଘଣ୍ଟା ପ୍ରତି ବେଗ 36 କି.ମି. ।

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 9 ପ୍ରତିସମତା ଓ ସର୍ବସମତା Ex 9.4 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 9 ପ୍ରତିସମତା ଓ ସର୍ବସମତା Ex 9.4

Question 1.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ, A͞B = C͞B, A͞D = C͞D । ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।

(କ) Δ ABD ଓ Δ CBD ର କେଉଁ କେଉଁ ବାହୁ ସର୍ବସମ ?
ସମାଧାନ:
Δ ABD ଓ Δ CBD ରେ AB ≅ C͞B, B͞D ≅ BD, DA ≅ DC ।

(ଖ) ଚିତ୍ରରେ ଥିବା Δ ABD ଓ Δ CBD ସର୍ବସମ କି ? ଯଦି ତୁମ ଉତ୍ତର ‘ହଁ’ , କାରଣ ଲେଖ । ଯଦି ତୁମ ଉତ୍ତର ‘ନାହିଁ’, କାରଣ ଲେଖ ।
ସମାଧାନ:
Δ ABD ≅ Δ CBD କାରଣ ତ୍ରିଭୁଜଦ୍ଵୟ ବା-ବା-ବା ସର୍ବସମତା ସର୍ଭକୁ ପୂରଣ କରୁଛି ।

(ଗ) Δ ABD ଏବଂ Δ CBD ର କେଉଁ କେଉଁ କୋଣ ସର୍ବସମ ?
ସମାଧାନ:
∠A ≅ ∠C, ∠ABD ≅ ∠CBD ଏବଂ ∠ADB ≅ ∠CDB

(ଘ) B͞D କେଉଁ କେଉଁ କୋଣକୁ ସମଦ୍ବିଖଣ୍ଡ କରେ ?
ସମାଧାନ:
BD, ∠ABC ଓ ∠ADC କୋଣଦ୍ଵୟକୁ ସମନ୍ଦିଖଣ୍ଡ କରେ ।

(ଙ) Δ ABD ≅ Δ BDC ଲେଖିବା ଠିକ୍ ହେବ କି ? ତୁମ ଉତ୍ତରର କାରଣ ଲେଖ ।
ସମାଧାନ:
Δ ABD ≅ Δ BDC ଲେଖିବା ଠିକ୍ ହେବ ନାହିଁ । କାରଣ A ↔ B, B ↔ D ଓ D ↔ C ନୁହେଁ ।

Question 2.
ଦୁଇଟି ସର୍ବସମ ତ୍ରିଭୁଜ ଅଙ୍କନ କରି ପ୍ରମାଣ କର ଯେ “ସର୍ବସମ ତ୍ରିଭୁଜରେ ସର୍ବସମ ବାହୁମାନଙ୍କର ସମ୍ମୁଖୀନ କୋଣମାନେ ଅନୁରୂପ’’।
ସମାଧାନ:
(i) ଗୋଟିଏ ଡ୍ରଇଁ କାଗଜ ଉପରେ ଯେ କୌଣସି ଗୋଟିଏ Δ ଅଙ୍କନ କର (ଚିତ୍ର : କ) ଓ ତା’ର ନାମ ଦିଅ Δ ABC । ସେହି କାଗଜ ଉପରେ BC ର ଦୈର୍ଘ୍ୟ ସଙ୍ଗେ ସମାନ ଦୈର୍ଘ୍ୟର ରେଖାଖଣ୍ଡଟିଏ ଅଙ୍କନ କର (ଚିତ୍ର : ଖ) ଓ ତା’ର ନାମ ଦିଅ OR ।


(ii) ତୁମ କମ୍ପାସରେ AB ର ଦୈର୍ଘ୍ୟ ସଙ୍ଗେ ସମାନ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ Qକୁ କେନ୍ଦ୍ରକରି ଗୋଟିଏ ଚାପ ଅଙ୍କନ କର (ଚିତ୍ର : ଗ) ।

(iii) ପୁନଶ୍ଚ, କମ୍ପାସ୍‌ରେ AC ର ଦୈର୍ଘ୍ୟ ସଙ୍ଗେ ସମାନ ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ R କୁ କେନ୍ଦ୍ର କରି ଗୋଟିଏ ଚାପ ଅଙ୍କନ କର, ଯେପରି ତାହା ପୂର୍ବରୁ ଅଙ୍କିତ ଚାପକୁ ଛେଦ କରିବ (ଚିତ୍ର : ଘ)

(iv) ଏହି ଛେଦବିନ୍ଦୁର ନାମ ‘P’ ଦିଅ ।
(v) ବର୍ତ୍ତମାନ P͞Q ଓ PR ଅଙ୍କନ କର । Δ PQR ମିଳିଲା ।
(vi) ଏବେ ABC ତ୍ରିଭୁଜର ଅବିକଳ ନକଲ ତିଆରି କର ।
(vii) ଏହାକୁ Δ PQR ଉପରେ ରଖ, ଯେପରି Δ ABC ର ଶୀର୍ଷବିନ୍ଦୁ A ଉପରେ Δ PQR ର ଶୀର୍ଷବିନ୍ଦୁ P ରହିବ ।
(viii) Δ ABC ଓ Δ PQR ର କୋଣମାନଙ୍କୁ ମାପିଲେ ∠A ≅∠P, ∠B ≅ ∠Q ଓ ∠C ≅ ∠R ।
ଏଥୁରୁ ପ୍ରମାଣିତ ହେଲା ଯେ, “ସର୍ବସମ ତ୍ରିଭୁଜର ସର୍ବସମ ବାହୁମାନଙ୍କର ସମ୍ମୁଖୀନ କୋଣମାନ ସର୍ବସମ’’ ।
Δ ABC ଓ Δ PQR ମଧ୍ୟରେ AB = PQ ଓ BC = QR

(କ) CA ସହ Δ PQR ର କେଉଁ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ହେଲେ Δ ABC ≅ Δ PQR ହେବ ?
ସମାଧାନ:
CA ସହ Δ PQR ର RP ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ହେଲେ Δ ABC ≅ Δ PQR ହେବ ।

(ଖ) Δ ABC ≅ Δ POR ହେଲେ, ଶୂନ୍ୟସ୍ଥାନରେ କ’ଣ ଲେଖାଯିବ ?
ଶୀର୍ଷବିନ୍ଦୁ A ର ଅନୁରୂପ _________
ଶୀର୍ଷବିନ୍ଦୁ B ର ଅନୁରୂପ _________
ଶୀର୍ଷବିନ୍ଦୁ C ର ଅନୁରୂପ _________
ସମାଧାନ:
ଶୀର୍ଷବିନ୍ଦୁ A ର ଅନୁରୂପ ଶୀର୍ଷବିନ୍ଦୁ P
ଶୀର୍ଷବିନ୍ଦୁ B ର ଅନୁରୂପ ଶୀର୍ଷବିନ୍ଦୁ Q
ଶୀର୍ଷବିନ୍ଦୁ C ର ଅନୁରୂପ ଶୀର୍ଷବିନ୍ଦୁ R

Question 3.
ନିମ୍ନସ୍ଥ ଚିତ୍ରମାନଙ୍କରେ ବାହୁ-ବାହୁ-ବାହୁ ସର୍ବସମତା ସର୍ଭ ଅନୁସାରେ ସର୍ବସମ ହେଉଥ‌ିବା ତ୍ରିଭୁଜ ମାନଙ୍କର ନାମ ଲେଖ ?
(କ)

ସମାଧାନ:
Δ ABC ≅ Δ RPQ

(ଖ)

ସମାଧାନ:
Δ ABD ≅ Δ ACD

(ଗ)

ସମାଧାନ:
Δ LMN ≅ Δ STR

Question 4.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB = AC ଓ D, B͞C ର ମଧ୍ୟ ବିନ୍ଦୁ । ଏହି ଚିତ୍ର ଦେଖି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

Δ ADB ≅ Δ ______
∠ABD ≅ ∠ ______
∠BAD ≅ ∠ ______
∠ADB ≅ ∠ ______
ଦୁଇଟି ତ୍ରିଭୁଜର ସର୍ବସମତାର ଆଉ ଗୋଟିଏ ସର୍ଭ ସଂପର୍କରେ ଆଲୋଚନା କରିବା ।
ସମାଧାନ:
Δ ADB ≅ Δ ADC
∠ABD ≅ ∠ACD
∠BAD ≅ ∠CAD
∠ADB ≅ ∠ADC

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.4 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.4

Question 1.
ନିମ୍ନଲିଖ ପରିମେୟ ସଂଖ୍ୟାମାନଙ୍କର ଗୁଣଫଳ ନିର୍ଣ୍ଣୟ କର ।

(କ) \(\frac{7}{24}\) × -16
ସମାଧାନ:
\(=\frac{7}{24} \times \frac{(-16)}{1}=\frac{-16 \times 7}{24 \times 1}=\frac{-8 \times 2 \times 7}{8 \times 3}=\frac{-2 \times 7} {3}=\frac{-14}{3}\)

(ଖ) \(\frac{-3}{5}\) × 2
ସମାଧାନ:
= \(-\frac{3}{5} \times \frac{2}{1}=\frac{-3 \times 2}{5 \times 1}=\frac{-6}{5}=-1 \frac{1}{5}\)

(ଗ) \(\frac{-7}{6}\) × (-24)
ସମାଧାନ:
= \(\frac{(-7)}{6} \times \frac{(-24)}{1}=\frac{(-7) \times(-24)}{6 \times 1}=\frac{7 \times 24}{6}=\frac{7 \times 4 \times 6}{6}\) = 7 × 4 = 28

(ଘ) \(\frac{5}{7} \times\left(\frac{-2}{3}\right)\)
ସମାଧାନ:
= \(\frac{5 \times(-2)}{7 \times 3}=-\frac{-10}{21}\)

(ଙ) \(\frac{9}{8} \times \frac{32}{7}\)
ସମାଧାନ:
= \(\frac{9 \times 32}{8 \times 7}=\frac{9 \times 8 \times 4}{8 \times 7}=\frac{9 \times 4}{7}=\frac{36}{7}=5 \frac{1}{7}\)

(ଚ) \(\frac{50}{7} \times \frac{14}{7}\)
ସମାଧାନ:
= \(\frac{50}{7} \times \frac{2}{1}=\frac{50 \times 2}{7 \times 1}=\frac{100}{7}=14 \frac{2}{7}\)

(ଛ) \(\frac{4}{7} \times \frac{2}{7}\)
ସମାଧାନ:
= \(\frac{4 \times 2}{7 \times 7}=\frac{8}{49}\)

(ଜ) \(\frac{13}{15} \times \frac{25}{26}\)
ସମାଧାନ:
\(=\frac{13 \times 25}{15 \times 26}=\frac{13 \times 5 \times 5}{3 \times 5 \times 2 \times 13}=\frac{5}{3 \times 2}=\frac{5}{6}\)

Question 2.
ସରଳ କର ।

(କ) \(\left(\frac{-16}{15} \times \frac{20}{8}\right)-\left(\frac{15}{5} \times \frac{35}{5}\right)\)
ସମାଧାନ:

(ଖ) \(\left(\frac{13}{8} \times \frac{12}{13}\right)+\left(\frac{-4}{9} \times \frac{3}{2}\right)\)
ସମାଧାନ:

Question 3.
ପ୍ରମାଣ କର x × y = y × x ଯେତେବେଳେ

(କ) x = \(\frac{1}{2}\), y = \(\frac{3}{5}\)
ସମାଧାନ:

(ଖ) x = \(\frac{2}{7}\), y = \(\frac{-11}{8}\)
ସମାଧାନ:

(ଗ) x = \(\frac{3}{5}\), y = \(\frac{2}{9}\)
ସମାଧାନ:

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.3 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.3

Question 1.
ପ୍ରଥମ ପରିମେୟ ସଂଖ୍ୟାରୁ ଦ୍ଵିତୀୟ ପରିମେୟ ସଂଖ୍ୟାକୁ ବିୟୋଗ କର ।

(କ) \(\frac{11}{2}, \frac{5}{4}\)
ସମାଧାନ:
\(=\frac{11 \times 2-5 \times 1}{4}=\frac{22-5}{4}=\frac{17}{4}=4 \frac{1}{4}\)

(ଖ) \(\frac{-3}{11}, \frac{7}{11}\)
ସମାଧାନ:
= \(\frac{-3}{11}+\frac{-7}{11}=\frac{(-3)+(-7)}{11}=\frac{-10}{11}\)

(ଗ) \(\frac{5}{4}, \frac{-4}{3}\)
ସମାଧାନ:
= \(\frac{5}{4}+\frac{4}{3}=\frac{5 \times 3+4 \times 4}{4 \times 3}=\frac{15+16}{12}=\frac{31}{12}=2 \frac{7}{12}\)

(ଘ) \(\frac{5}{42},\left(\frac{-6}{21}\right)\)
ସମାଧାନ:
= \(\frac{5}{42}+\frac{6}{21}=\frac{5+6 \times 2}{42}=\frac{5+12}{42}=\frac{17}{42}\)

Question 2.
ମାନ ନିର୍ଣ୍ଣୟ କର ।

(କ) \(\frac{6}{7}-\frac{-5}{7}\)
ସମାଧାନ:
= \(\frac{6}{7}+\frac{5}{7}=\frac{6+5}{7}=\frac{11}{7}=1 \frac{4}{7}\)

(ଖ) \(\frac{7}{24}-\frac{5}{36}\)
ସମାଧାନ:
= \(\frac{7}{24}+\left(\frac{-5}{36}\right)=\frac{7 \times 3+(-5) \times 2}{72}=\frac{21+(-10)}{72}=\frac{11}{72}\)

(ଗ) \(\frac{9}{10}-\frac{7}{-15}\)
ସମାଧାନ:
= \(\frac{9}{10}+\frac{7}{15}=\frac{9 \times 3+7 \times 2}{30}=\frac{27+14}{30}=\frac{41}{30}=1 \frac{11}{30}\)

(ଘ) \(\frac{8}{23}-\frac{5}{11}\)
ସମାଧାନ:
\(=\frac{8}{23}+\left(\frac{-5}{11}\right)=\frac{8 \times 11+(-5) \times 23}{23 \times 11}=\frac{88+(-115)}{253}=\frac{-27}{253}\)

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 9 ପ୍ରତିସମତା ଓ ସର୍ବସମତା Ex 9.3 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 9 ପ୍ରତିସମତା ଓ ସର୍ବସମତା Ex 9.3

Question 1.
ଯଦି Δ POR ଓ Δ LMN ସର୍ବସମ ହୋଇଥା’ନ୍ତି, ତେବେ ନିମ୍ନସ୍ଥ ଶୂନ୍ୟସ୍ଥାନରେ କ’ଣ ଲେଖାଯିବ ?
(କ) Δ PQR ≅ Δ ……., Δ QRP ≅ Δ …….
ସମାଧାନ:
Δ PQR ≅ Δ LMN, Δ QRP ≅ Δ MNL

(ଖ) P ↔ ……., Q͞R = …….
ସମାଧାନ:
P ↔ L, Q͞R = MN

(ଗ) P͞Q ≅ ……., Q͞R ≅ …….
ସମାଧାନ:
P͞Q ≅ L͞M, Q͞R ≅ M͞N

(ଘ) P͞Q ର ଅନୁରୂପ ……., ∠R ର ଅନୁରୂପ …….
ସମାଧାନ:
P͞Q ର ଅନୁରୂପ L͞M, ∠R ର ଅନୁରୂପ ∠N

Question 2.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

Δ ABD ≅ …….
B͞C ର ଅନୁରୂପ …….
A͞B ≅ ……..
A͞D ର ଅନୁରୂପ ……..
ସମାଧାନ:
Δ ABD ≅ Δ CBD
B͞C ର ଅନୁରୂପ BA
A͞B ≅ CB
A͞D ର ଅନୁରୂପ CD

Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 8 ବ୍ୟାବହାରିକ ଗଣିତ Ex 8.5 Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Maths Solutions Chapter 8 ବ୍ୟାବହାରିକ ଗଣିତ Ex 8.5

Question 1.
ନିମ୍ନ ସାରଣୀ ଗୁଡ଼ିକରୁ କେଉଁ ଗୁଡ଼ିକରେ ଥିବା ଚଳରାଶି x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ରହିଛି କୁହ ।
(କ)

x	12	8	36
y	72	48	216

ସମାଧାନ:

ଏଠାରେ x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ରହିଛି ।

(ଖ)

x	2	3	4
y	4	9	16

ସମାଧାନ:

∴ ଏଠାରେ x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ନାହିଁ ।

(ଗ)

x	5	10	15
y	10	15	20

ସମାଧାନ:

ଏଠାରେ x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ନାହିଁ ।

(ଘ)

x	48	24	12
y	24	12	6

ସମାଧାନ:

ତେଣୁ ଏଠାରେ x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ଅଛି ।

Question 2.
ସଳଖ ଚଳନରେ ଦିଆଯାଇଥିବା ସାରଣୀଗୁଡ଼ିକରେ ଥିବା ତାରକା ଚିହ୍ନିତ ସ୍ଥାନ ଲାଗି ଉପଯୁକ୍ତ ମାନ ନିଶ୍ଚୟ କର ।

(କ)

x	10	18	☆
y	220	☆	484

ସମାଧାନ:
ମନେକର

x	10	18	n
y	220	m	484

(ଖ)

x	14	2	☆
y	☆	4	76

ସମାଧାନ:
ମନେକର

x	14	2	n
y	m	4	76

Question 3.
ଚଳନ ଧାରାରେ ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ସମାଧାନ କର ।
(କ) ଗୋଟିଏ କାରଖାନାରେ ଗୋଟିଏ ସପ୍ତାହରେ (ରବିବାର ଦିନ କାରଖାନା ବନ୍ଦ ଥାଏ) 840 ଟିଣ ରଂଗ ତିଆରି କରାଗଲେ, 4200 ଟିଣ ରଂଗ ତିଆରି ଲାଗି କେତେ ଦିନ ଲାଗିବ ?
ସମାଧାନ:
ଅଧୂକ ଦିନରେ ଅଧ୍ଵ ଟିଣ ରଙ୍ଗ ପ୍ରସ୍ତୁତ ହୋଇପାରେ । ଏଣୁ ଦିନ ସଂଖ୍ୟା ଓ ରଙ୍ଗର ପରିମାଣ ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ଅଛି ।
ଦିନ ସଂଖ୍ୟାକୁ x ଓ ରଙ୍ଗଟିଣ ସଂଖ୍ୟାକୁ y ନେଇ ସାରଣୀଟି ପ୍ରସ୍ତୁତ କଲେ –

x (ଦିନ ସଂଖ୍ୟା)	x1 = 6	x2 = ?
y (ରଙ୍ଗଟିଣ ସଂଖ୍ୟା)	y1 = 840	y2 = 4200

x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ହେତୁ x₁y₂ = x₂y₁
⇒ 6 × 4200 = x₂ × 840
⇒ x₂ = \(\frac{6×4200}{840}\) = 30
∴ 4200 ଟିଣ ରଙ୍ଗ ତିଆରି ଲାଗି 30 ଦିନ ଲାଗିବ ।

(ଖ) ଗୋଟିଏ 12 ମିଟର ଉଚ୍ଚ ସ୍ତମ୍ଭର ଛାଇ 20 ମିଟର ହେଲେ, ସେହି ସମୟରେ କେତେ ଉଚ୍ଚ ସ୍ତମ୍ଭର ଛାଇ 30 ମିଟର ହେବ? 26 ମିଟର ଉଚ୍ଚ ସ୍ତମ୍ଭର ଛାଇ କେତେ ମିଟର ହେବ ?
ସମାଧାନ:
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସମୟରେ ସ୍ତମ୍ଭର ଉଚ୍ଚତା ବଢ଼ିଲେ ତା’ର ଛାଇର ଦୈର୍ଘ୍ୟ ବଢ଼ିଥାଏ ଏବଂ ସ୍ତମ୍ଭର ଉଚ୍ଚତା କମିଲେ ତା’ର ଛାଇର ଦୈର୍ଘ୍ୟ କମିଥାଏ ।
ସ୍ତମ୍ଭର ଉଚ୍ଚତା ଓ ଛାଇର ଦୈର୍ଘ୍ୟ ମଧ୍ୟରେ ସଳଖ ଚଳନ ଅଛି ।
ସ୍ତମ୍ଭର ଉଚ୍ଚତାକୁ x ଓ ଛାଇର ଦୈର୍ଘ୍ୟକୁ y ନେଇ ସାରଣୀଟି ପ୍ରସ୍ତୁତ କଲେ –

x (ସ୍ତମ୍ଭର ଉଚ୍ଚତା) ମିଟରରେ	x1 = 12	x2 = ?	x3 = 26
y (ଛାଇର ଦୈର୍ଘ୍ୟ) ମିଟରରେ	y1 = 20	y2 = 30	y3 = ?

x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ହେତୁ x₁y₂ = x₂y₁

(ଗ) ଗୋଟିଏ ପରିବାରରେ ସପ୍ତାହକୁ 10 କି.ଗ୍ରା ଋଉଳ ଖର୍ଜ ହେଲେ ତାଙ୍କର ଜାନୁୟାରୀ 1 ତାରିଖରୁ ଫେବୃୟାରୀ 11 ତାରିଖ ପର୍ଯ୍ୟନ୍ତ ମୋଟ୍ କେତେ କି.ଗ୍ରା. ଋଉଳ ଖର୍ଚ୍ଚ ହେବ ?
ସମାଧାନ:
ଅଧିକ ଦିନରେ ଅଧିକ ପରିମାଣର ଚାଉଳ ଖର୍ଚ୍ଚ ହେବ ।
ତେଣୁ ଦିନ ସଂଖ୍ୟା ଓ ଚାଉଳର ପରିମାଣ ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ରହିଛି ।
ଦିନ ସଂଖ୍ୟାକୁ x ଓ ଚାଉଳ ଖର୍ଚ୍ଚ ପରିମାଣ y ନେଇ ସାରଣୀଟି ପ୍ରସ୍ତୁତି କଲେ –

ଦିନ ସଂଖ୍ୟା (x)	x1 = 7	x2 = 31 + 11 = 42
ଚାଉଳ ଖର୍ଚ୍ଚ ପରିମାଣ (କି.ଗ୍ରା.ରେ) (y)	y1 = 10	y2 = ?

ସଳଖ ଚଳନପାଇଁ x₁y₂ = x₂y₁
⇒ 7 × y₂ = 42 × 10
⇒ y₂ = \(\frac{42×10}{7}\) କି.ଗ୍ରା. = 60 କି.ଗ୍ରା. 
∴ ଜାନୁୟାରୀ l ତାରିଖରୁ ଫେବୃୟାରୀ 11 ତାରିଖ ପର୍ଯ୍ୟନ୍ତ ମୋଟ 60 କି.ଗ୍ରା. ଚାଉଳ ଖର୍ଚ୍ଚ ହେବ ।

(ଘ) ଗୋଟିଏ କାମ କରିବା ପାଇଁ 2 ବସ୍ତା ସିମେଣ୍ଟ ସହ 12 ବସ୍ତା ବାଲି ମିଶାଯାଇଥାଏ। ତେବେ ସେହି କାମ ଲାଗି 60 ବସ୍ତା ବାଲି ସହ କେତେ ବସ୍ତା ସିମେଣ୍ଟ ମିଶାଯିବ ? 23 ବସ୍ତା ସିମେଣ୍ଟ ସହ କେତେ ବସ୍ତା ବାଲି ମିଶାଯିବ ? 
ସମାଧାନ:
ଅଧିକ ସିମେଣ୍ଟରେ ଅଧିକ ବାଲି ମିଶାଯାଇଥାଏ ଓ କମ୍ ସିମେଣ୍ଟରେ କମ୍ ବାଲି ମିଶା ଯାଇଥାଏ ।
ସିମେଣ୍ଟ ବସ୍ତାର ସଂଖ୍ୟାକୁ (x) ଓ ବାଲି ବସ୍ତାର ସଂଖ୍ୟାକୁ (y) ନେଇ ସାରଣୀଟି ପ୍ରସ୍ତୁତ କଲେ –

ସିମେଣ୍ଟ ବସ୍ତାସଂଖ୍ୟା (x)	x1 = 2	x2 = ?	x3 = 23
ବାଲିବସ୍ତା ସଂଖ୍ୟା (y)	y1 = 12	y2 = 60	y3 = ?

ସଳଖ ଚଳନପାଇଁ x₁y₂ = x₂y₁
⇒ 2 × 60 = x₂ × 12
⇒ x₂ = \(\frac{2×16}{12}\)
ପୁନଶ୍ଚ x₁y₃ = y₁x₃
⇒ 2 x y₃ = 12 x 23
⇒ y₃ = \(\frac{12×23}{2}\) = 138
∴ 60 ବସ୍ତା ବାଲି ସହ 10 ବସ୍ତା ସିମେଣ୍ଟ ମିଶାଯିବ ଓ 23 ବସ୍ତା ସିମେଣ୍ଟ ସହ 138 ବସ୍ତା ବାଲି ମିଶିବ ।

(ଙ) ଗୋଟିଏ ବିଦ୍ୟାଳୟରେ ଷଷ୍ଠ ଶ୍ରେଣୀରେ ପଢୁଥୁବା 30 ଜଣ ଛାତ୍ରୀଙ୍କ ଲାଗି ପୋଷାକ ତିଆରି ଲାଗି କପଡ଼ା କିଣିବା ଖର୍ଚ୍ଚ 2100 ଟଙ୍କା ହେଲା । ତେବେ 7ମ ଶ୍ରେଣୀରେ ପଢୁଥୁବା 22 ଜଣ ଛାତ୍ରୀଙ୍କ ଲାଗି ପୋଷାକ ତିଆରି ପାଇଁ କେତେ ଟଙ୍କା ଦାମର କପଡ଼ା କିଣିବା ଆବଶ୍ୟକ ହେବ ?
ସମାଧାନ:
ଛାତ୍ରୀଙ୍କ ସଂଖ୍ୟା ଅଧିକ ହେଲେ ତାଙ୍କ ପାଇଁ ଆବଶ୍ୟକ କପଡ଼ା ନିମିତ୍ତ ଖର୍ଚ୍ଚର ପରିମାଣ ଅଧିକ ହେବ ।
ଏଣୁ ଛାତ୍ରୀଙ୍କ ସଂଖ୍ୟା ଏବଂ ସେମାନଙ୍କ ପାଇଁ ଆବଶ୍ୟକ କପଡ଼ା ନିମିତ୍ତ ଖର୍ଚ୍ଚ ମଧ୍ୟରେ ସଳଖ ଚଳନର ସମ୍ବନ୍ଧ ରହିଛି ।
ଛାତ୍ରୀଙ୍କ ସଂଖ୍ୟାକୁ x ଓ ସେମାନଙ୍କ ପାଇଁ ଆବଶ୍ୟକ କପଡ଼ା ନିମିତ୍ତ ଖର୍ଚ୍ଚକୁ y ନେଇ ସାରଣୀଟି ପ୍ରସ୍ତୁତ କଲେ –

ଛାତ୍ରୀଙ୍କ ସଂଖ୍ୟା (x)	x1 = 30	x2 = 22
ଖର୍ଚ୍ଚର ପରିମାଣ (y) (ଟଙ୍କାରେ)	y1 = 2100	y2 = ?

x ଓ y ମଧ୍ୟରେ ସଳଖ ଚଳନ ସମ୍ପର୍କ ହେତୁ x₁y₂ = x₂y₁
⇒ 30 × y₂ = 22 × 2100
⇒ y₂ = \(\frac{22×2100}{20}\) = 1540
∴ 7ମ ଶ୍ରେଣୀରେ ପଢୁଥ‌ିବା 22 ଜଣ ଛାତ୍ରୀଙ୍କ ଲାଗି ପୋଷାକ ତିଆରି ପାଇଁ 1540 ଟଙ୍କା ଦାମ୍‌ର କପଡ଼ା କିଣିବା ଆବଶ୍ୟକ ହେବ ।