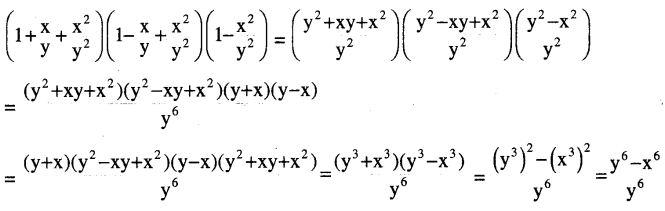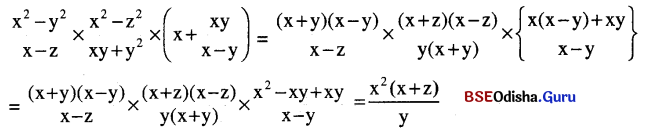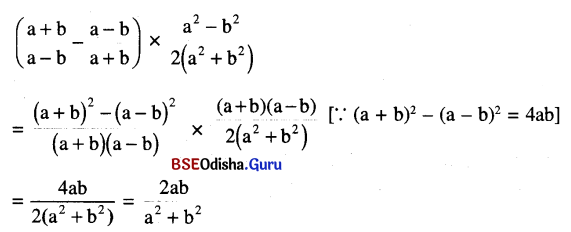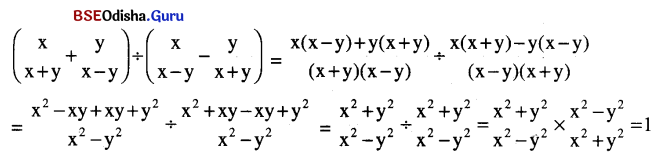Class 9

Odisha State Board BSE Odisha 9th Class History Important Questions Chapter 15 ଓଡ଼ିଶାର ଐତିହ୍ୟ Important Questions and Answers.

BSE Odisha Class 9 History Important Questions Chapter 15 ଓଡ଼ିଶାର ଐତିହ୍ୟ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

୧। କଳିଙ୍ଗ ଶୈଳୀ ଉପରେ ଏକ ଟିପ୍ପଣୀ ପ୍ରଦାନ କର ।
Answer:

• ଓଡ଼ିଶାର ମନ୍ଦିର ସ୍ଥାପତ୍ୟ ଶୈଳୀକୁ ‘କଳିଙ୍ଗ ଶୈଳୀ’ କୁହାଯାଏ । ଭାରତର ଅନ୍ୟ ସ୍ଥାନମାନଙ୍କରେ ନିର୍ମିତ ମନ୍ଦିରଗୁଡ଼ିକର ଶୈଳୀଠାରୁ କଳିଙ୍ଗ ଶୈଳୀ ସମ୍ପୂର୍ଣ୍ଣ ଭିନ୍ନ ଅଟେ ।
• ଷଷ୍ଠ ଶତାବ୍ଦୀର ଶେଷ ଭାଗରେ ବା ସପ୍ତମ ଶତାବ୍ଦୀର ଆରମ୍ଭରେ କଳିଙ୍ଗ ଶୈଳୀରେ ନିର୍ମିତ ଭୁବନେଶ୍ଵରରେ ଭଗ୍ନାବସ୍ଥାରେ ଥ‌ିବା ଲକ୍ଷ୍ମଣେଶ୍ୱର, ଭରତେଶ୍ୱର ଏବଂ ଶତ୍ରୁଗ୍ନେଶ୍ୱର ମନ୍ଦିରଗୁଡ଼ିକ ସର୍ବପୁରାତନ ଅଟେ ।
• ଏହି ଶୈଳୀର ମନ୍ଦିରଗୁଡ଼ିକ ମଧ୍ୟରେ ଭୌମକର ଶାସନ କାଳରେ ନିର୍ମିତ ଭୁବନେଶ୍ୱରର ଶିଶିରେଶ୍ୱର, ବୈତାଳ ଓ ମାର୍କଣ୍ଡେଶ୍ଵର ମନ୍ଦିର, ସୋମବଂଶୀ ରାଜତ୍ଵ କାଳରେ ନିର୍ମିତ ମୁକ୍ତେଶ୍ଵର, ରାଜାରାଣୀ, ବ୍ରହ୍ମେଶ୍ଵର ଓ ଲିଙ୍ଗରାଜ ମନ୍ଦିର ପ୍ରଧାନ ଅଟେ ।
• ପରବର୍ତ୍ତୀ ଗଙ୍ଗବଂଶର ରାଜତ୍ଵ ସମୟରେ ନିର୍ମିତ ହୋଇଥବା ମନ୍ଦିରଗୁଡ଼ିକ ମଧ୍ୟରେ ପୁରୀର ଜଗନ୍ନାଥ ମନ୍ଦିର, କୋଣାର୍କର ସୂର୍ଯ୍ୟ ମନ୍ଦିର, ଭୁବନେଶ୍ଵରର ମେଘେଶ୍ବର, ଅନନ୍ତ ବାସୁଦେବ, ଭାସ୍କରେ ଶ୍ଵର ମନ୍ଦିର ଓ ସାରିଦେଉଳ ଆଦି ଏହି ଶୈଳୀର ଜ୍ଵଳନ୍ତ ନିଦର୍ଶନ ଅଟେ ।

୨। ଓଡ଼ିଶାର ବୌଦ୍ଧକୀର୍ତ୍ତିଗୁଡ଼ିକ ଉପରେ ଏକ ଟିପ୍ପଣୀ ଲେଖ ।
Answer:

• ଓଡ଼ିଶାର ବୌଦ୍ଧଧର୍ମର ଅଭୁତ୍ଥାଥା ସହିତ ତାଳ ଦେଇ ଅନେକ ବୌଦ୍ଧ ବିହାର ଓ ଉପାସନା ଗୃହ ଗଢ଼ି ଉଠିଥିଲା ।
• ରତ୍ନଗିରି, ଉଦୟଗିରି ଓ ଲଳିତଗିରିର ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ଖନନରୁ ଅନୈକ ସଂଖ୍ୟାରେ ବୌଦ୍ଧସ୍ତୂପ, ଚୈତ୍ୟଗୃହ, ମଠ ଓ ବୌଦ୍ଧ ମୂର୍ତ୍ତିକଳା ଆବିଷ୍କୃତ ହୋଇ ପୁରାତନ ଓଡ଼ିଶାର ସ୍ଥାପତ୍ୟ ଓ ଭାସ୍କର୍ଯ୍ୟର ପ୍ରମାଣ ଦେଇଥାଏ ।
• ଗଞ୍ଜାମ ଜିଲ୍ଲାର ବୁଢ଼ାଖୋଲ ପାହାଡ଼ରୁ ଅନେକ ବୌଦ୍ଧକୀର୍ତ୍ତିର ଧ୍ଠସାବଶେଷ ଆବିଷ୍କୃତ ହୋଇଛି ।
• ଏତଦ୍‌ବ୍ୟତୀତ କଟକ ଜିଲ୍ଲାର ବାଣେଶ୍ଵରନାସି ଓ ଚୌଦ୍ଵାର, ଯାଜପୁର ଜିଲ୍ଲାର ଯାଜପୁର, ପୁରୀ ଜିଲ୍ଲାର କୁରୁମ, ଖୋର୍ଦ୍ଧା ଜିଲ୍ଲାର ଅଚ୍ୟୁତ ରାଜପୁର, ’ମୟୂରଭଞ୍ଜ ଜିଲ୍ଲାର ଖୁଚିଙ୍ଗ, ବାଲେଶ୍ଵର ଜିଲ୍ଲାର ଅଯୋଧ୍ୟା, ଭଦ୍ରକ ଜିଲ୍ଲାର ଖଡ଼ିପଦା ଓ ସୋଲାପୁର, ବରଗଡ଼ ଜିଲ୍ଲାର ଗଣିଆପାଲୀ, ବୌଦ୍ଧ ଜିଲ୍ଲାର ବୌଦ୍ଧ ପ୍ରଭୃତି ସ୍ଥାନଗୁଡ଼ିକରୁ ଆବିଷ୍କୃତ ଅନେକ ବୌଦ୍ଧ କୀର୍ତ୍ତିର ଧ୍ବଂସାବଶେଷ ପ୍ରାଚୀନ ଓଡ଼ିଶାର ସ୍ଥାପତ୍ୟ ଓ ଭାସ୍କର୍ଯ୍ୟର ପରିଚୟ ଦିଏ ।

୩ । ଉଦୟଗିରି ଓ ଖଣ୍ଡଗିରିଠାରେ ଥ‌ିବା ଜୈନ ଗୁମ୍ଫାଗୁଡ଼ିକ ସମ୍ପର୍କରେ ସଂକ୍ଷେପରେ ବର୍ଣ୍ଣନା କର ।
Answer:

1. ଭୁବନେଶ୍ୱର ନିକଟସ୍ଥ ଉଦୟଗିରି ଓ ଖଣ୍ଡଗିରିଠାରେ ଥ‌ିବା ଜୈନ ଗୁମ୍ଫାଗୁଡ଼ିକରେ ଚମତ୍କାର ଭାସ୍କର୍ଯ୍ୟ ଦେଖିବାକୁ ମିଳେ ।
2. ଖ୍ରୀ.ପୂ. ପ୍ରଥମ ଶତାବ୍ଦୀରେ ସମ୍ରାଟ ଖାରବେଳଙ୍କ ସମୟରେ ନିର୍ମିତ ଖଣ୍ଡଗିରି, ଉଦୟଗିରିର କେତେକ ଗୁମ୍ଫା ଦ୍ବିତଳ ବିଶିଷ୍ଟ ଏବଂ ଗୁମ୍ଫାଗୁଡ଼ିକର ଖୋଦିତ ମୂର୍ତ୍ତିକଳା ଅତ୍ୟନ୍ତ ମନୋରମ ଅଟେ ।
3. ଉଦୟଗିରିର ରାଣୀଗୁମ୍ଫା ସବୁଠାରୁ ବଡ଼ ଓ ସବୁଠାରୁ ସୁନ୍ଦର ଗୁମ୍ଫା ଅଟେ ।
4. ଉଦୟଗିରି ନିକଟସ୍ଥ ଖଣ୍ଡଗିରି ପାହାଡ଼ରେ ପନ୍ଦରଟି ଜୈନଗୁମ୍ଫା ରହିଛି ।
5. ସେହି ଗୁମ୍ଫାଗୁଡ଼ିକରେ ମଧ୍ୟ ସୁନ୍ଦର ଦେଖାଯାଏ ।

କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

୧ । ଐତିହ୍ୟ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ଗୋଟିଏ ଜାତିର ଗୌରବୋଜ୍ଜଳ ଅତୀତର କୀର୍ତ୍ତିରାଜି ସମ୍ବଳିତ ସଂସ୍କୃତି, ସାହିତ୍ୟ, ଧର୍ମ, କଳା, ସ୍ଥାପତ୍ୟ,ପରମ୍ପରା ଓ ଜୀବନଶୈଳୀର ଆଲେଖ୍ୟ ଉତ୍ତର ପିଢ଼ିଙ୍କ ପାଇଁ ପ୍ରେରଣାର ଉତ୍ସ ହୋଇଥିଲେ, ସେଗୁଡ଼ିକୁ ସେ ଜାତିର ଐତିହ୍ୟ କୁହାଯାଏ ।

୨। ଓଡ଼ିଶାର କେଉଁ ସ୍ଥାନର ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ଖନନରୁ ଅନେକ ସଂଖ୍ୟାରେ ବୌଦ୍ଧସ୍ତୂପ, ଚୈତ୍ୟଗୃହ, ମଠ ଓ ବୌଦ୍ଧ ମୂର୍ତ୍ତିକଳା ଆବିଷ୍କୃତ ହୋଇଛି?
Answer:
ଓଡ଼ିଶାର ରତ୍ନଗିରି, ଉଦୟଗିରି ଓ ଲଳିତଗିରିର ପ୍ରତ୍ନତାତ୍ତ୍ୱିକ ଖନନରୁ ଅନେକ ସଂଖ୍ୟାରେ ବୌଦ୍ଧ ସ୍ତୂପ, ଚୈତ୍ୟ ଗୃହ, ମଠ ଓ ବୌଦ୍ଧ ମୂର୍ତ୍ତିକଳା ଆବିଷ୍କୃତ ହୋଇଛି ।

୩ । ପଞ୍ଚସଖା କେଉଁମାନଙ୍କୁ କୁହାଯାଏ ?
Answer:
ବଳରାମ ଦାସ, ଜଗନ୍ନାଥ ଦାସ, ଅଚ୍ୟୁତାନନ୍ଦ ଦାସ, ଯଶୋବନ୍ତ ଦାସ ଓ ଅନନ୍ତ ଦାସଙ୍କୁ ଓଡ଼ିଶାର ପଞ୍ଚସଖା କୁହାଯାଏ ।

୪। ଓଡ଼ିଶାରେ ହସ୍ତତନ୍ତରୁ ପ୍ରସ୍ତୁତି କେଉଁ ସାମଗ୍ରୀ ବିଶ୍ବର ପ୍ରାୟ ସମସ୍ତ ଦେଶରେ ଓଡ଼ିଶା ପାଇଁ ସୁଖ୍ୟାତି ଆଣିଛି ?
Answer:

• ଓଡ଼ିଶାରେ ହସ୍ତତନ୍ତରୁ ପ୍ରସ୍ତୁତ ସମ୍ବଲପୁର ଓ ବଲାଙ୍ଗୀରର ପଶାପାଲି ଶାଢ଼ି; ସମ୍ବଲପୁର, ବଲାଙ୍ଗୀର, ବରଗଡ଼ ଓ ସୋନପୁରର ବୋମକାଇ ପାଟ, ଗଞ୍ଜାମ ଜିଲ୍ଲାର ବ୍ରହ୍ମପୁରର ମଠା ଶାଢ଼ି ଆଦି ବିଦେଶରେ ଖୁବ୍ ଆଦୃତି ଲାଭ କରିଛି ।
• ଏହାଛଡ଼ା କଟକ ଜିଲ୍ଲାର ନୂଆପାଟଣା ଓ ମାଣିଆବନ୍ଧ ଶାଢ଼ି, ଖୋର୍ଦ୍ଧା ଜିଲ୍ଲାର ଲୁଙ୍ଗି, ଗାମୁଛା ଆଦି ହସ୍ତତନ୍ତରୁ ପ୍ରସ୍ତୁତ ସାମଗ୍ରୀ ବିଶ୍ବର ପ୍ରାୟ ସମସ୍ତ ଦେଶରେ ଓଡ଼ିଶା ପାଇଁ ସୁଖ୍ୟାତି ଆଣିଛି ।

୫। ବୈଶାଖ ମାସର ପ୍ରଥମ ଦିନକୁ କ’ଣ ଭାବରେ ପାଳନ କରାଯାଇଥାଏ ? ଏହି ଦିନ ମଙ୍ଗଳାଙ୍କୁ କ’ଣ ସମର୍ପଣ କରାଯାଏ ?”
Answer:

• ବୈଶାଖ ମାସର ପ୍ରଥମ ଦିନ ଓଡ଼ିଆ ପଞ୍ଜିକାର ନବବର୍ଷର ପ୍ରଥମ ଦିନ ଓ ପ୍ରଥମ ପର୍ବ ‘ବିଷୁବ ସଂକ୍ରାନ୍ତି’ ଭାବରେ ପାଳନ କରାଯାଏ ।
• ଏହିଦିନ ଦେବୀ ମଙ୍ଗଳାଙ୍କ ନିକଟରେ ବେଲରୁ ପ୍ରସ୍ତୁତ ଏକ ସୁସ୍ୱାଦୁ ପାନୀୟ ବା ପଣା ସମର୍ପଣ କରାଯାଇ ସେବନ କରାଯାଏ ।

୬ | କଳିଙ୍ଗର ସାଧବମାନେ ଅତୀତରେ କେଉଁ କେଉଁ ସ୍ଥାନକୁ ବାଣିଜ୍ୟ ବ୍ୟବସାୟ କରିବାକୁ ଯାଉଥିଲେ ?
Answer:
କଳିଙ୍ଗର ସାଧବମାନେ ଅତୀତରେ ଜାଭା, ସୁମାତ୍ରା, ବାଲି, ବୋର୍ଣ୍ଣିଓ ଦ୍ଵୀପପୁଞ୍ଜ ତଥା ଅନ୍ୟାନ୍ୟ ଦକ୍ଷିଣ- ପୂର୍ବ ଏସୀୟ ଦେଶମାନଙ୍କୁ ବାଣିଜ୍ୟ ବ୍ୟବସାୟ କରିବାକୁ ଯାଉଥିଲେ ।

୭ । ଇକତ୍ ଢାଞ୍ଚା କେଉଁଥୁରୁ ସୃଷ୍ଟି ହୋଇଛି ବୋଲି ବିଶ୍ଵାସ କରାଯାଏ ?
Answer:
ବୟନ କଳାର ବୈଶିଷ୍ଟ୍ୟ ଇକତ୍ ଢାଞ୍ଚା ଓଡ଼ିଶାର ପ୍ରାଚୀନ ସାମୁଦ୍ରିକ କାର୍ଯ୍ୟକଳାପର ପ୍ରଭାବରୁ ସୃଷ୍ଟି ହୋଇଛି ବୋଲି ବିଶ୍ଵାସ କରାଯାଏ ।

୮। ଓଡ଼ିଶାର କେଉଁ ଅଞ୍ଚଳ ରୁପାର ତାରକାସୀ କାମ ପାଇଁ ପ୍ରସିଦ୍ଧ ଓ କାହିଁକି ?
Answer:

1. ଓଡ଼ିଶାର କଟକ ସହର ରୁପାର ଆଦିବାସୀ କାମ ପାଇଁ ମ୍ରସିଦ୍ଧ।
2. ରୁପାର ସୂକ୍ଷ୍ମ କାରୁକାର୍ଯ୍ୟ ଖଚିତ ସୁନ୍ଦର କୋଣାର୍କ ଚକ୍ର, ଦେବଦେବୀ ଓ ମନ୍ଦିରମାନଙ୍କର ପ୍ରତିଛବି, ପଶୁପକ୍ଷୀ, ଗଛ, ଡାଳ, ଫୁଲ, ପତ୍ର ଆଦି ପ୍ରସ୍ତୁତ କରି କଟକର କାରିଗରମାନେ ସେମାନଙ୍କର କୌଣକର ପରାକାକ୍ଷ୍ମ। ପ୍ରଦର୍ଣନ କରିବା ସହ ବାଦେଶରେ ଯଶ ଅର୍ଜନ କରିଛନ୍ତି ।

୯ । ଓଡ଼ିଶାର କେତୋଟି ଲୋକନୃତ୍ୟ ଓ ଆଦିବାସୀ ନୃତ୍ୟର ନାମ ଲେଖ ।
Answer:

• ଓଡ଼ିଶାର ଲୋକନୃତ୍ୟଗୁଡ଼ିକର ନାମ ହେଲା ରଣପା ନାଚ, ଚଇତି ଘୋଡ଼ାନାଚ, ଦଣ୍ଡ ନାଚ ଓ ନାଗା ନାଚ, କେଳାକେଲୁଣୀ ନାଚ, ଘୁମୁରା ନାଚ, ଛଉ ନାଚ, ଡାଲଖାଇ ନାଚ, ରସକେଲୀ ନାଚ ଇତ୍ୟାଦି ।
• ଓଡ଼ିଶାର ଆଦିବାସୀ ନୃତ୍ୟଗୁଡ଼ିକ ମଧ୍ୟରେ କରମା, ଗଦବା, କେଦ୍ରୁ, ଝୁମର, କୋୟା, ପରଜା ଇତ୍ୟାଦି ଅନ୍ୟତମ ।

୧୦ । ଓଡ଼ିଶାର କେତୋଟି ଲୋକ ସଙ୍ଗୀତର ନାମ ଲେଖ ।
Answer:
ଓଡ଼ିଶାର କେତୋଟି ଲୋକ ସଙ୍ଗୀତର ନାମ ହେଲା, ଚମ୍ପୁ, ଛାନ୍ଦ, ଚଉତିଶା, କୋଇଲି ଗୀତ, ଜଣାଣ ଓ ଭଜନ ଇତ୍ୟାଦି ।

୧୧ । କେଉଁ ଚିତ୍ରକଳା ଓଡ଼ିଶାର ଚିତ୍ରକଳାର ସ୍ୱତନ୍ତ୍ରତାର ପରିଚୟ ଦିଏ ? ଏହା କେଉଁ ଶତାବ୍ଦୀରୁ ସୃଷ୍ଟି ହୋଇଛି ?
Answer:

• ପଟ୍ଟଚିତ୍ର ଓଡ଼ିଶାର ଚିତ୍ରକଳାର ସ୍ବତନ୍ତ୍ରତାର ପରିଚୟ ଦିଏ ।
• ଏହା ଦ୍ଵାଦଶ ଶତାବ୍ଦୀରୁ ସୃଷ୍ଟି ହୋଇଛି ।

୧୨ । କଟକର କେଉଁ କେଉଁ ଅଞ୍ଚଳରେ ମସ୍‌ଦ୍‌ମାନ ଦେଖିବାକୁ ମିଳେ ?
Answer:
କଟକର ଦରଘା ବଜାରଠାରେ କଦମ୍ବରସୁଲ୍,ଦିଓ୍ବାନ ବଜାରଠାରେ ସର୍ବପୁରାତନ ତାତର ଖାଁ ମସ୍ତିଦ୍ ଓ ବାଲୁବଜାରଠାରେ ଜୁମ୍ମା ମସ୍‌ଜିଦ୍ ଦେଖିବାକୁ ମିଳେ ।

Objective Type Questions With Answers
A. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।

୧। ରତ୍ନଗିରି ପାହାଡ଼ କେଉଁ ପ୍ରଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
ରତ୍ନଗିରି ପାହାଡ଼ ଓଡ଼ିଶା ପ୍ରଦେଶରେ ଅବସ୍ଥିତ ।

୨। କୋଣାର୍କ ମନ୍ଦିର କେଉଁ ଶୈଳୀର ସ୍ବାତନ୍ତ୍ର୍ୟ ପ୍ରତିପାଦନ କରେ ?
Answer:
କୋଣାର୍କ ମନ୍ଦିର କଳିଙ୍ଗ ଶୈଳୀର ସ୍ବାତନ୍ତ୍ର୍ୟ ପ୍ରତିପାଦନ କରେ ।

୩ । ‘କୋଟି ବ୍ରହ୍ମାଣ୍ଡ ସୁନ୍ଦରୀ’ କିଏ ଲେଖୁଥିଲେ ?
Answer:
କବି ସମ୍ରାଟ ଉପେନ୍ଦ୍ର ଭଞ୍ଜ ‘କୋଟି ବ୍ରହ୍ମାଣ୍ଡ ସୁନ୍ଦରୀ’ ଲେଖୁଲେ ।

୪। ଫକୀରମୋହନଙ୍କର ପ୍ରମୁଖ କୄତିମାନଙ୍କର ନାମ କଣ ?
Answer:
‘ଛ’ମାଣ ଆଠଗୁଣ୍ଠ’, ‘ମାମୁ’, ‘ପ୍ରାୟଶ୍ଚିତ୍ତ’ ଓ ‘ଲଛମା’ ଫକୀରମୋହନଙ୍କର କେତେକ ପ୍ରମୁଖ କୃତି ଅଟେ ।

୫ । ମଧୁସୁଦନ ରାଓ କାହା ଅନୁକରଣରେ ସନେଟ୍ ଲେଖୁଥ‌ିଲେ ?
Answer:
ମଧୁସୂଦନ ରାଓ ସେକସପିଅର୍ ଓ ମିଲଟନ୍‌ଙ୍କ ଶୈଳୀର ଅନୁକରଣରେ ସନେଟ୍ ଲେଖୁଥିଲେ ।

୬ । ଭୁବନେଶ୍ୱରର ରାଜାରାଣୀ ମନ୍ଦିର କାହା ରାଜତ୍ଵ କାଳରେ ନିର୍ମିତ ହୋଇଥିଲା ?
Answer:
ସୋମବଂଶୀ ରାଜତ୍ଵ କାଳରେ ଭୁବ ନେ ଶ୍ଵ ର ର ରାଜାରାଣୀ ମନ୍ଦିର ନିର୍ମିତ ହୋଇଥିଲା ।

୭। ପର୍ଶୁରାମେଶ୍ଵର ମନ୍ଦିର କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer:
ଭୁବନେଶ୍ୱରଠାରେ ପର୍ଶୁରାମେଶ୍ଵର ମନ୍ଦିର ଅବସ୍ଥିତ ।

୮ । ଓଡ଼ିଶା ଆଫଗାନମାନଙ୍କଦ୍ୱାରା କେବେ ଅଧୂକୃତ ହୋଇଥିଲା ?
Answer:
୧୫୬୮ ଖ୍ରୀ.ଅ.ରେ ଓଡ଼ିଶା ଆଫଗାନ୍‌ମାନଙ୍କଦ୍ୱାରା ଅଧିକୃତ ହୋଇଥିଲା ।

୯ । ଉଦୟଗିରିର ସବୁଠାରୁ ବଡ଼ ଗୁମ୍ଫାର ନାମ କ’ଣ ?
Answer:
ଉଦୟଗିରିର ସବୁଠାରୁ ବଡ଼ ଗୁମ୍ଫାର ନାମ ହେଉଛି ରାଣୀଗୁମ୍ଫା ।

୧୦। ‘ଓଡ଼ିଆ ଭାଗବତ’ କିଏ ରଚନା କରିଛନ୍ତି ?
Answer:
ଜଗନ୍ନାଥ ଦାସ ‘ଓଡ଼ିଆ ଭାଗବତ’ ରଚନା କରିଛନ୍ତି ।

୧୧। ଓଡ଼ିଆ ସାହିତ୍ୟରେ କାବ୍ୟଯୁଗ କେବେ ଆରମ୍ଭ ହେଲା ?
Answer:
ଓଡ଼ିଶାର ଐତିହ୍ୟରେ ଜଗନ୍ନାଥ ଚେତନାର ମାହାତ୍ମ୍ୟ କାବ୍ୟଯୁଗ ଆରମ୍ଭ ହେଲା ।

୧୨ । ‘ଗୀତ ଗୋବିନ୍ଦ’ର ରଚୟିତା କିଏ ?
Answer:
‘ଗୀତ ଗୋବିନ୍ଦ’ର ରଚୟିତା ହେଉଛନ୍ତି ଓଡ଼ିଶାର ପ୍ରଖ୍ୟାତ ସଂସ୍କୃତ କବି ଜୟଦେବ ।

୧୩ । ଓଡ଼ିଶାର ଐତିହ୍ୟରେ କେଉଁ ଚେତନାର ମାହାତ୍ମ୍ୟ ଅତ୍ୟନ୍ତ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ?
Answer:
ଓଡ଼ିଶାର ଐତିହ୍ୟରେ ଜଗନ୍ନାଥ ଚେତନାର ମାହାତ୍ମ୍ୟ ଚେତନାର ମାହାତ୍ମ୍ୟ ଅତ୍ୟନ୍ତ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ।

୧୪ । ଖଣ୍ଡଗିରି ପାହାଡ଼ରେ କେତୋଟି ଗୁମ୍ଫା ରହିଛି ?
Answer:
ଖଣ୍ଡଗିରି ପାହାଡ଼ରେ ୧୫ଟି ଗୁମ୍ଫା ରହିଛି ।

୧୫ । ବାପ୍‌ଟିଷ୍ଟ ଚର୍ଜ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer:
କଟକର ତିନିକୋଣିଆ ବଗିଚାରେ ବାପ୍‌ଟିଷ୍ଟ ଚର୍ଚ୍ଚ ଅବସ୍ଥିତ । 

୧୬। କେଉଁଥରେ ଭାରତ ମହାସାଗରର ଦ୍ଵୀପପୁଞ୍ଜକୁ କଳିଙ୍ଗୋଡ୍ର ଦେଶ ଭାବେ ବର୍ଣ୍ଣନା କରାଯାଇଛି ?
Answer:
ମଧ୍ୟଯୁଗୀୟ ବୌଦ୍ଧଗ୍ରନ୍ଥ ‘ଆର୍ଯ୍ୟ ମଞ୍ଜୁଶ୍ରୀ ମୂଳକଳ୍ପ’ରେ ଭାରତ ମହାସାଗରର ଦ୍ଵୀପପୁଞ୍ଜକୁ କଳିଙ୍ଗୋଡ୍ର ଦେଶ ଭାବେ ବର୍ଣ୍ଣନା କରାଯାଇଛି ।

୧୭ । ଓଡ଼ିଶାର କେଉଁ ନୃତ୍ୟ ଶାସ୍ତ୍ରୀୟ ନୃତ୍ୟଭାବେ ଭାରତର ଏକ ପ୍ରଧାନ ମାନ୍ୟତା ପାଇଛି ?
Answer:
ଓଡ଼ିଶାର ଓଡ଼ିଶୀ ନୃତ୍ୟ ଭାରତର ଏକ ପ୍ରଧାନ ଶାସ୍ତ୍ରୀୟ ନୃତ୍ୟ ଭାବେ ମାନ୍ୟତା ପାଇଛି ।

୧୮। କେଉଁ ନୃତ୍ୟ ଶୈଳୀକୁ ମାହାରୀ ଶୈଳୀ କୁହାଯାଏ ?
Answer:
ସଙ୍ଗୀତର ତାଳ ଓ ରାଗ ସହିତ ସମନ୍ଵୟ ରକ୍ଷାକରି ନୃତ୍ୟ ପରି ବେ ଷଣ କରୁଥ‌ିବା ନଉଁ କୀମାନଙ୍କ ନୃତ୍ୟଶୈଳୀକୁ ମାହାରୀ ଶୈଳୀ କୁହାଯାଏ ।

B. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।

୧। ମୁକ୍ତେଶ୍ଵର ମନ୍ଦିର କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer:
ଭୁବନେଶ୍ୱର

୨। ଭୁବନେଶ୍ଵରର କପିଳେଶ୍ଵର ମନ୍ଦିର କେଉଁ ଶାସନ ସମୟରେ ନିର୍ମିତ ହୋଇଥିଲା ?
Answer:
ସୂର୍ଯ୍ୟବଂଶୀ ଗଜପତି

୩ । ‘ଗୀତ ଗୋବିନ୍ଦ’ର ରଚୟିତା କିଏ ?
Answer:
ଜୟଦେବ

୪। କେଉଁ ନୃତ୍ୟ ଶୈଳୀରୁ ଓଡ଼ିଶୀ ନୃତ୍ୟର ସୃଷ୍ଟି ହୋଇଛି ?
Answer:
ମାହାରୀ ନାଚ

୫। ଓଡ଼ିଶାର ମନ୍ଦିର ସ୍ଥାପତ୍ୟ ଶୈଳୀକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
କଳିଙ୍ଗ ଶୈଳୀ

୬। କେଉଁ ପୁସ୍ତକରେ କଳିଙ୍ଗର ରାଜାଙ୍କୁ ‘ମହୋଦଧୂପତି’ ଭାବରେ ଚିତ୍ରଣ କରାଯାଇଛି ?
Answer:
କାଳିଦାସଙ୍କ ରଘୁବଂଶମ୍

୭ । ଓଡ଼ିଶାରେ କେଉଁ ପର୍ବରେ ଚାଷୀ ବିଲରେ ବିହନ ବୁଣିବା ଆରମ୍ଭ କରେ ?
Answer:
ଅକ୍ଷୟ ତୃତୀୟା

୮। ନୂଆଖାଇ ପର୍ବ ଅନ୍ୟ କେଉଁ ନାମରେ ମଧ୍ୟ ପ୍ରସିଦ୍ଧ ?
Answer:
ନବାନ୍ନ ଭକ୍ଷଣ

୯ । ଓଡ଼ିଶାର କେଉଁ ସ୍ଥାନ ଧନୁଯାତ୍ରା ପାଇଁ ସମଗ୍ର ଭାରତରେ ପ୍ରସିଦ୍ଧ ଲାଭ କରିଛି ?
Answer:
ବରଗଡ଼

୧୦ । ମୁସଲମାନ୍ ଭକ୍ତ ସାଲବେଗ ଓଡ଼ିଶାର ଘରେ ଘରେ କେଉଁଥିପାଇଁ ପରିଚିତ ?
Answer:
ଜଗନ୍ନାଥ ଜଣାଣ

୧୧ । ସୂର୍ଯ୍ୟଙ୍କର ଉତ୍ତରାୟଣ ଗତି କେଉଁ ମାସରେ ହୁଏ ?
Answer:
ମାଘ ମାସ

୧୨ । କେଉଁ ଅମାବାସ୍ୟା ଦିନ ମହାଳୟା ପର୍ବ ପାଳନ କରାଯାଏ ?
Answer:
ଆଶ୍ୱିନ ଅମାବାସ୍ୟା

୧୩ । ଶ୍ରାବଣ ମାସର ଅମାବାସ୍ୟାଟି କ’ଣ ଭାବରେ ପାଳନ କରାଯାଏ ?
Answer:
ଚିତାଲାଗି ଅମାବାସ୍ୟା

୧୪ । କେଉଁ ସଂକ୍ରାନ୍ତିକୁ ନବବର୍ଷର ପ୍ରଥମ ଦିନ ଭାବରେ ପାଳନ କରାଯାଏ ?
Answer:
ବିଷୁବ ସଂକ୍ରାନ୍ତି

୧୫ । ଓଡ଼ିଶାର ନୌବାଣିଜ୍ୟ କେଉଁ ଶତାବ୍ଦୀରୁ ଆରମ୍ଭ ହୋଇଥିବାର ସୂଚନା ମିଳିଥାଏ ?
Answer:
ତୃତୀୟ ଶତାବ୍ଦୀ

୧୬ । ଓଡ଼ିଶାର କେଉଁ ସହର ‘ତାରକାସି କାମ’ ପାଇଁ ପ୍ରସିଦ୍ଧ ଅଟେ ?
Answer:
କଟକ ସହର

୧୭ । ପଟ୍ଟଚିତ୍ରର ପରମ୍ପରା ଓଡ଼ିଶାରେ କେଉଁ ଶତାବ୍ଦୀରୁ ଚଳି ଆସୁଛି ?
Answer:
ଦ୍ଵାଦଶ ଶତାବ୍ଦୀ

୧୮ । ତାତର ଖାଁ ମସ୍‌ଜିଦ୍‌ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer:
କଟକ

୧୯ । ଓଡ଼ିଶାରେ ସ୍ନେହ, ପ୍ରେମ, ଭ୍ରାତୃଭାବର ପ୍ରତୀକ ରୂପେ କାହାଙ୍କୁ ଗ୍ରହଣ କରାଯାଇଛି ?
Answer:
ଶ୍ରୀଜଗନ୍ନାଥ

୨୦ । ମାଗଧୀ-ପ୍ରାକୃତ ଭାଷାରୁ କେଉଁ ଭାଷାର ଉତ୍ପତ୍ତି ହୋଇଛି ?
Answer:
ଓଡ଼ିଆ

୨୧ । କିଏ ‘ରୁଦ୍ରସୁଧାନିଧ୍’ ରଚନା କରିଥିଲେ ?
Answer:
ଅବଧୂତ ନାରାୟଣ ସ୍ବାମୀ

୨୨ । ‘ରସକଲ୍ଲୋଳ’ କାହାର ସର୍ବଶ୍ରେଷ୍ଠ କୃତି ଥିଲା ?
Answer:
ଦୀନକୃଷ୍ଣ ଦାସ

୨୩ । ଗ୍ରାମ୍ୟ ଜୀବନଭିତ୍ତିକ ପଲ୍ଲୀଚିତ୍ର କେଉଁ କବିଙ୍କ ରଚନାରୁ ସ୍ପଷ୍ଟ ବାରିହୁଏ ?
Answer:
ନନ୍ଦକିଶୋର ବଳ

୨୪ । ଗଞ୍ଜାମ ଜିଲ୍ଲାର କେଉଁ ପାହାଡ଼ରେ ବୌଦ୍ଧକୀର୍ତ୍ତିର ଧ୍ଵଂସାବଶେଷ ଦେଖିବାକୁ ମିଳେ ?
Answer:
ବୁଢ଼ାଖୋଲ ପାହାଡ଼

୨୫ । ଭୁବନେଶ୍ଵରର ‘ପର୍ଶୁରାମେଶ୍ବର’ ମନ୍ଦିର କେଉଁ ଶୈଳୀରେ ନିର୍ମିତ ହୋଇଛି ?
Answer:
କଳିଙ୍ଗ ଶୈଳୀ

C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

୧ । ଓଡ଼ିଶାରେ ସ୍ନେହ, ପ୍ରେମ, ଭ୍ରାତୃଭାବର ପ୍ରତୀକ ରୂପେ ________ ଙ୍କୁ ଗ୍ରହଣ କରାଯାଇଛି ।
Answer:
ଶ୍ରୀଜଗନ୍ନାଥ

୨ । ମାଗଧୀ-ପ୍ରାକୃତ ଭାଷାରୁ ______ ଭାଷାର ଉତ୍ପ ହୋଇଛି ।
Answer:
ଓଡ଼ିଆ

୩ । _______ ‘ରୁଦ୍ରସୁଧାନିଧ୍’ ରଚନା କରିଥିଲେ ।
Answer:
ଅବଧୂତ ନାରାୟଣ ସ୍ବାମୀ

୪ । ‘ରସକଲ୍ଲୋଳ’ — ଙ୍କ ସର୍ବଶ୍ରେଷ୍ଠ କୃତି ଥିଲା ।
Answer:
ଦୀନକୃଷ୍ଣ ଦାସ

୫ । ଗ୍ରାମ୍ୟ ଜୀବନଭିତ୍ତିକ ପଲ୍ଲୀଚିତ୍ର କବି _______ ଙ୍କ ରଚନାରୁ ସ୍ପଷ୍ଟ ବାରିହୁଏ ।
Answer:
ନନ୍ଦକିଶୋର ବଳ

୬ । ଧଉଳି ପାହାଡ଼ ______ ନଦୀ କୂଳରେ ଅବସ୍ଥିତ ।
Answer:
ଦୟା

୭ । ଗଞ୍ଜାମ ଜିଲ୍ଲାର _________ ପାହାଡ଼ରୁ ବୌଦ୍ଧକୀର୍ତ୍ତିର ଧ୍ବଂସାବଶେଷ ଦେଖିବାକୁ ମିଳେ ।
Answer:
ବୁଢ଼ାଖୋଲ

୮ । ଭୁବନେଶ୍ଵରର ପର୍ଶୁ ରାମେଶ୍ଵର ମନ୍ଦିର _________ ଶୈଳୀରେ ନିର୍ମିତ ହୋଇଛି ।
Answer:
କଳିଙ୍ଗ

୯ । ________ ବଂଶର ଶାସନର ପତନ ପରେ ଓଡ଼ିଶାରେ ମନ୍ଦିର ନିର୍ମାଣର ସମାପ୍ତି ଘଟିଥିଲା ।
Answer:
ସୂର୍ଯ୍ୟ

୧୦ । ରୋମାନ୍ କ୍ୟାଥଲିକ୍ ଚର୍ଚ୍ଚ _________ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ।
Answer:
କାଠଯୋଡ଼ି

୧୧ । ପଶାପାଲି ଶାଢ଼ି ପାଇଁ _______ ବିଶ୍ବପ୍ରସିଦ୍ଧ ।
Answer:
ସମ୍ବଲପୁର

୧୨ । କେନ୍ଦୁଝର ଜିଲ୍ଲାର ______ ଶିଳ୍ପ ଓଡ଼ିଶାର ଐତିହ୍ୟ ବହନ କରେ ।
Answer:
ଟେରାକୋଟା

୧୩। ବୈଶାଖ ଶୁକ୍ଳପକ୍ଷ ତୃତୀୟା ଦିନ _______ ପର୍ବ ପାଳିତ ହୁଏ ।
Answer:
ଅକ୍ଷୟ ତୃତୀୟା

D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓) ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (✗) ଲେଖ ।

୧। ସାରଳା ଦାସଙ୍କ ରଚିତ ‘ରାମାୟଣ’ ଓଡ଼ିଶାର ପୌରାଣିକ କାବ୍ୟଜଗତର ଏକ ଅମୂଲ୍ୟ କୃତି ।
୨ । ଜଗନ୍ନାଥ ଦାସଙ୍କ ‘ମହାଭାରତ’ ଓଡ଼ିଶାରେ ସର୍ବାଧ‌ିକ ଆଦୃତ ଓ ସମ୍ମାନିତ ।
୩ । କାବ୍ୟଯୁଗରେ ସର୍ବାଧ‌ିକ ଲୋକପ୍ରିୟତା ଲାଭ କରିଥିବା ‘ରସକଲ୍ଲୋଳ’ ଉପେନ୍ଦ୍ର ଭଞ୍ଜଙ୍କ କୃତି ଥିଲା ।
୪। ଓଡ଼ିଆ ସାହିତ୍ୟର ପ୍ରଥମ କବି ରାଧାନାଥ ରାୟଙ୍କ ସର୍ବଶ୍ରେଷ୍ଠ କୀର୍ତ୍ତି ହେଉଛି ‘ପ୍ରଣୟ ବଲ୍ଲରୀ’ ।
୫। ପିଲାଙ୍କ କବିତା ‘ନାନାବାୟା ଗୀତ’ ନନ୍ଦକିଶୋର ବଳ ରଚନା କରିଥିଲେ ।
୬। ଖୁଚିଙ୍ଗ ଓଡ଼ିଶାର କୋରାପୁଟ ଜିଲ୍ଲାରେ ଅବସ୍ଥିତ ।
୭। ଓଡ଼ିଶାର ମନ୍ଦିର ସ୍ଥାପତ୍ୟ ଶୈଳୀକୁ କଳିଙ୍ଗ ଶୈଳୀ କୁହାଯାଏ ।
୮। ୧୫୬୭ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଓଡ଼ିଶା ଆଫଗାନ୍‌ମାନଙ୍କ ଦ୍ବାରା
୯। ମୁକ୍ତେଶ୍ଵର ମନ୍ଦିରକୁ ‘ଓଡ଼ିଶା ସ୍ଥାପତ୍ୟ କଳାର ମଣି’ ବୋଲି କୁହାଯାଏ ।
୧୦ । ପୁରୀ ଜିଲ୍ଲାର ବୀରମହାରାଜପୁର ଗ୍ରାମରେ ପଟ୍ଟଚିତ୍ର ଅଙ୍କନ ଏକ କୌଳିକ ବୃତ୍ତି ।

Answer:
୧। (×)
୨ । (×)
୩ । (×)
୪। (×)
୫ । (✓)
୬। (×)
୭। (✓)
୮। (×)
୯।  (✓)
୧୦। (×)

E ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେଖ ।

F. ରେଖାଙ୍କିତ ପଦକୁ ପରିବର୍ତ୍ତନ କରି ଭ୍ରମ ସଂଶୋଧନ କର ।

୧। ପ୍ରତିବର୍ଷ ଏପ୍ରିଲ ମାସ ୧୫ ତାରିଖକୁ ବିଶ୍ଵ ଐତିହ୍ୟ ଦିବସ ରୂପେ ପାଳନ କରାଯାଏ ।
Answer:
୧୮

୨ । ହାତୀ ଗୁମ୍ଫା ଶିଳାଲେଖ ମୁକୁନ୍ଦଦେବଙ୍କ ରାଜତ୍ୱ କାଳରେ ତଥ୍ୟ ପ୍ରଦାନ କରିଥାଏ ।
Answer:
ଖାରବେଳ

୩। ସାରଳା ଦାସ ଓଡ଼ିଆ ଭାଗବତ ରଚନା କରିଥିଲେ ।
Answer:
ଓଡ଼ିଆ ମହାଭାରତ

୪। ଗାଥା କବିତା କେଶବ-କୋଇଲିର ଲେଖକ ଥିଲେ ଅର୍ଜନ ଦାସ ।
Answer:
ମାର୍କଣ୍ଡଦାସ

୫। ଜଗନ୍ନାଥ ରଥର ନାମ ଦର୍ପଦଳନ ।
Answer:
ନନ୍ଦିଘୋଷ

୬। ଓଡ଼ିଶାର ବଲାଙ୍ଗୀର ଶୀତଳଷଷ୍ଠୀ ଯାତ୍ରା ପାଇଁ ପ୍ରସିଦ୍ଧି ଲାଭ କରିଛି ।
Answer:
ସମ୍ବଲପୁର

୭। ଅଶୋକାଷ୍ଟମୀ ଦିନ ମହାପ୍ରଭୁ ଜଗନ୍ନାଥଙ୍କ ରଥଯାତ୍ରା ଅନୁଷ୍ଠିତ ହୁଏ ।
Answer:
ଲିଙ୍ଗରାଜ

୮। ଆଶ୍ୱିନ ମାସର ଅମାବାସ୍ୟା ଦିନ ସାବିତ୍ରୀ ବ୍ରତ ପାଳନ କରାଯାଏ ।
Answer:
ମହାଳୟା

୯ । କୋଣାର୍କକୁ ତୁଳସୀ କ୍ଷେତ୍ର କୁହାଯାଇଥାଏ ।
Answer:
ଅର୍କକ୍ଷେତ୍ର

୧୦ । ଓଡ଼ିଶାର ବାଳକାଟି ତମ୍ବାପାତ୍ର ନିର୍ମାଣ କରିବା ପାଇଁ ପ୍ରସିଦ୍ଧ ।
Answer:
କଂସା ପିତ୍ତଳ ବାସନ

୧୧ । ରାଉରକେଲାକୁ ରୌପ୍ୟ ନଗରୀ କୁହାଯାଏ ।
Answer:
ଇସ୍ପାତ ନଗରୀ

୧୨ । ‘ସ୍ତୁତି ଚିନ୍ତାମଣି’ ଅରକ୍ଷିତ ଦାସ ଲେଖୁଥିଲେ ।
Answer:
ଭୀମ ଭୋଇ

୧୩ । ‘ଇନ୍ଦୁମତୀ’ କାବ୍ୟ ରଚୟିତା ଥିଲେ ରାଧାନାଥ ରାୟ ।
Answer:
ଗଙ୍ଗାଧର ମେହେର

୧୪ । ମଠା ଶାଢ଼ି ପାଇଁ ସମ୍ବଲପୁର ପ୍ରସିଦ୍ଧ ।
Answer:
ବ୍ରହ୍ମପୁର

୧୫ । କଦମରସୁଲ ମସ୍‌ଜିଦ୍ ବକ୍ସି ବଜାରରେ ଅବସ୍ଥିତ ।
Answer:
ଦରଘା ବଜାର ।

G. ଚାରୋଟି ସମ୍ଭାବ୍ୟ ବିକଳ୍ପ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

Question 1.
ସୂର୍ଯ୍ୟଙ୍କର ଉତ୍ତରାୟଣ ଗତି ନିମ୍ନୋକ୍ତ କେଉଁ ମାସରେ ??
(A) ଶ୍ରାବଣ
(B) ମାଘ
(C) ଆଶ୍ବିନ
(D) ଫାଲଗୁନ
Answer:
(B) ମାଘ

Question 2.
କେଉଁ ଅମାବାସ୍ୟା ଦିନ ମହାଳୟା ପର୍ବ ପାଳନ କରାଯାଏ ?
(A) ଆଷାଢ଼
(B) ଆଶ୍ବିନ
(C) କାର୍ତିକ
(D) ଚୈତ୍ର
Answer:
(B) ଆଶ୍ବିନ

Question 3.
ଶ୍ରାବଣ ମାସର ଅମାବାସ୍ୟାଟି କ’ଣ ଭାବରେ ପାଳନ କରାଯାଏ ?
(A) ଦୀପାବଳୀ
(B) ମହାଳୟା
(C) ଚିତାଲାଗି ଅମାବାସ୍ୟା
(D) ବୋଇତ ବନ୍ଦାଣ
Answer:
(C) ଚିତାଲାଗି ଅମାବାସ୍ୟା

Question 4.
କେଉଁ ସଂକ୍ରାନ୍ତିକୁ ନବବର୍ଷର ପ୍ରଥମ ଦିନ ଭାବରେ ପାଳନ କରାଯାଏ ?
(A) ମକର ସଂକ୍ରାନ୍ତି
(B) ବିଷୁବ ସଂକ୍ରାନ୍ତି
(C) ରଜ ସଂକ୍ରାନ୍ତି
(D) କୁମ୍ଭ ସଂକ୍ରାନ୍ତି
Answer:
(B) ବିଷୁବ ସଂକ୍ରାନ୍ତି

Question 5.
ଓଡ଼ିଶାର ନୌବାଣିଜ୍ୟ କେଉଁ ଶତାବ୍ଦୀରୁ ଆରମ୍ଭ ହୋଇଥିବାର ସୂଚନା ମିଳିଥାଏ ?
(A) ପ୍ରଥମ ଶତାବ୍ଦୀ
(B) ତୃତୀୟ ଶତାବ୍ଦୀ
(C) ଦ୍ଵିତୀୟ ଶତାବ୍ଦୀ
(D) ପଞ୍ଚମ ଶତାବ୍ଦୀ
Answer:
(B) ତୃତୀୟ ଶତାବ୍ଦୀ

Question 6.
ଓଡ଼ିଶାର କେଉଁ ସହର ‘ତାରକାସି କାମ’ ପାଇଁ ପ୍ରସିଦ୍ଧ ଅଟେ ?
(A) କଟକ
(B) ବ୍ରହ୍ମପୁର
(C) ସମ୍ବଲପୁର
(D) ବାଲେଶ୍ଵର
Answer:
(A) କଟକ

Question 7.
ପଟ୍ଟଚିତ୍ରର ପରମ୍ପରା ଓଡ଼ିଶାରେ କେଉଁ ଶତାବ୍ଦୀରୁ ଚଳି ଆସୁଛି ?
(A) ନବମ
(B) ଏକାଦଶ
(C) ଦଶମ
(D) ଦ୍ଵାଦଶ
Answer:
(D) ଦ୍ଵାଦଶ

Question 8.
ତାତର ଖାଁ ମସ୍‌ଜିଦ୍ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
(A) କଟକ
(B) ସମ୍ବଲପୁର
(C) ପୁରୀ
(D) ବ୍ରହ୍ମପୁର
Answer:
(B) ସମ୍ବଲପୁର

Question 9.
ଓଡ଼ିଶାରେ ସ୍ନେହ, ପ୍ରେମ, ଭ୍ରାତୃଭାବର ପ୍ରତୀକ ରୂପେ କାହାଙ୍କୁ ଗ୍ରହଣ କରାଯାଇଛି ?
(A) ଶ୍ରୀଜଗନ୍ନାଥ
(B) ଲିଙ୍ଗରାଜ
(C) ଶ୍ରୀଲୋକନାଥ
(D) ଅଲାରନାଥ
Answer:
(A) ଶ୍ରୀଜଗନ୍ନାଥ

Question 10.
ମାଗଧୀ-ପ୍ରାକୃତ ଭାଷାରୁ କେଉଁ ଭାଷାର ଉତ୍ପ ହୋଇଛି ?
(A) ସଂସ୍କୃତ
(B) ଓଡ଼ିଆ
(C) ବଙ୍ଗଳା
(D) ମରାଠୀ
Answer:
(B) ଓଡ଼ିଆ

Question 11.
‘ରସକଲ୍ଲୋଳ’ କାହାର ସର୍ବଶ୍ରେଷ୍ଠ କୃତି ଥିଲା ?
(A) ଦୀନକୃଷ୍ଣ ଦାସ
(B) ଉପେନ୍ଦ୍ରଭଞ୍ଜ
(C) ଅବଧୂତ ନାରାୟଣ ସ୍ଵାମୀ
(D) ବଳରାମ ଦାସ
Answer:
(A) ଦୀନକୃଷ୍ଣ ଦାସ

Question 12.
ଗ୍ରାମ୍ୟ ଜୀବନଭିଭିକ ପଲ୍ଲୀଚିତ୍ର ନିମ୍ନୋକ୍ତ କେଉଁ କବିଙ୍କ ରଚନାରୁ ସ୍ପଷ୍ଟ ବାରିହୁଏ ?
(A) ନନ୍ଦକିଶୋର ବଳ
(B) ମଧୁସୂଦନ ରାଓ
(C) ଗଙ୍ଗାଧର ମେହର
(D) କୌଣସିଟି ନୁହେଁ
Answer:
(A) ନନ୍ଦକିଶୋର ବଳ

Question 13.
ଗଞ୍ଜାମ ଜିଲ୍ଲାର କେଉଁ ପାହାଡ଼ରୁ ବୌଦ୍ଧକୀର୍ତ୍ତିର ଧ୍ବଂସାବଶେଷ ଦେଖିବାକୁ ମିଳେ ?
(A) ବଣିଆ
(B) ରମ୍ଭାଖୋଲ
(C) ବୁଢ଼ାଖୋଲ
(D) ଚିତ୍ରଗିରି
Answer:
(C) ବୁଢ଼ାଖୋଲ

Question 14.
ଭୁବନେଶ୍ଵରର ‘ପର୍ଶୁରାମେଶ୍ଵର’ ମନ୍ଦିର କେଉଁ ଶୈଳୀରେ ନିର୍ମିତ ହୋଇଛି ?
(A) ଆର୍ଯ୍ୟ
(B) କଳିଙ୍ଗ
(C) ଦ୍ରାବିଡ଼
(D) କୌଣସିଟି ନୁହେଁ
Answer:
(B) କଳିଙ୍ଗ

Question 15.
କେଉଁ ବଂଶର ଶାସନର ପତନ ପରେ ଓଡ଼ିଶାରେ ମନ୍ଦିର ନିର୍ମାଣର ସମାପ୍ତି ଘଟିଥିଲା ।
(A) ଗଙ୍ଗବଂଶ
(B) ସୋମବଂଶ
(C) ସୂର୍ଯ୍ୟବଂଶ
(D) ଚନ୍ଦ୍ରବଂଶ
Answer:
(C) ସୂର୍ଯ୍ୟବଂଶ

Question 16.
ପଶାପାଲି ଶାଢ଼ି ପାଇଁ ନିମ୍ନୋକ୍ତ କେଉଁ ସ୍ଥାନଟି ବିଶ୍ବପ୍ରସିଦ୍ଧ ?
(A) ସମ୍ବଲପୁର
(B) ମାଣିଆବନ୍ଧ
(C) କଟକ
(D) ବାଲେଶ୍ଵର
Answer:
(A) ସମ୍ବଲପୁର

Question 17.
କେନ୍ଦୁଝର ଜିଲ୍ଲାର କେଉଁ ଶିଳ୍ପ ଓଡ଼ିଶାର ଐତିହ୍ୟ ବହନ କରେ ?
(A) ତାରକସି
(B) କଂସାବାସନ
(C) ଟେରାକୋଟା
(D) ସପମଶିଣା
Answer:
(C) ଟେରାକୋଟା

Question 18.
କେଉଁ ନୃତ୍ୟଶୈଳୀରୁ ଓଡ଼ିଶୀ ନୃତ୍ୟର ସୃଷ୍ଟି ହୋଇଛି ?
(A) ଦଣ୍ଡନାଚ
(B) ଛଉନାଚ
(C) ପାଇକନାଚ
(D) ମାହାରୀନାଚ
Answer:
(D) ମାହାରୀନାଚ

Question 19.
‘ଓଡ଼ିଆ ଭାଗବତ’ କିଏ ରଚନା କରିଛନ୍ତି ?
(A) ବଳରାମ ଦାସ
(B) ଜଗନ୍ନାଥ ଦାସ
(C) କାର୍ମଣ୍ଡ ଦାସ
(D) ଯଶୋବନ୍ତ ଦାସ
Answer:
(B) ଜଗନ୍ନାଥ ଦାସ

Question 20.
ଭୁବନେଶ୍ଵର ନିକଟବର୍ତ୍ତୀ ପାହାଡ଼ରେ କେଉଁ କୀର୍ତ୍ତି ଖଣ୍ଡଗିରି ଓ ଉଦୟଗିରି ଦେଖିବାକୁ ମିଳେ ?
(A) ବୌଦ୍ଧ କୀର୍ତ୍ତି
(B) ଜୈନ କୀର୍ତ୍ତି
(C) ଉତ୍କଳ କୀର୍ତ୍ତି
(D) ଗୁମ୍ଫା କୀର୍ତି
Answer:
(B) ଜୈନ କୀର୍ତ୍ତି

Question 21.
ଚମତ୍କାର ସ୍ଥାପତ୍ୟ ଓ ଭାସ୍କର୍ଯ୍ୟ ଯୋଗୁଁ କେଉଁ ମନ୍ଦିରକୁ ‘ଓଡ଼ିଶା ସ୍ତାପତ୍ୟ କଳାର ମଣି’ ବୋଲି କୁହାଯାଏ ?
(A) ମୁକ୍ତେଶ୍ଵର ମନ୍ଦିର
(B) କୋଣାର୍କ ମନ୍ଦିର
(C) ଲିଙ୍ଗରାଜ ମନ୍ଦିର
(D) ରାଜରାଣୀ ମନ୍ଦିର
Answer:
(A) ମୁକ୍ତେଶ୍ଵର ମନ୍ଦିର

Question 22.
ସ୍ଥାପତ୍ୟ ଓ ଭାସ୍କର୍ଯ୍ୟ ପାଇଁ ଓଡ଼ିଶାର କେଉଁ ମନ୍ଦିରକୁ ବିଶ୍ଵର ଏକ ଐତିହ୍ୟ ସ୍ମାରକୀ ରୂପେ ମାନ୍ୟତା ଦିଆଯାଇଛି ?
(A) ମୁକ୍ତେଶ୍ଵର ମନ୍ଦିର
(B) କୋଣାର୍କ ମନ୍ଦିର
(C) ଲିଙ୍ଗରାଜ ମନ୍ଦିର
(D) ରାଜରାଣୀ ମନ୍ଦିର
Answer:
(B) କୋଣାର୍କ ମନ୍ଦିର

Question 23.
କଟକରେ ସ୍ଥାପିତ କେଉଁ ମୁସଲମାନ କୀର୍ତ୍ତି ହିନ୍ଦୁ ଓ ଭାବରେ ପରିଗଣିତ ?
(A) କଦମ୍ ରସୁଲ
(B) ତାତା ଖାଁ ମସ୍‌ଜିଦ୍
(C) ଜୁମ୍ମା ମସ୍‌ଜିଦ୍
(D) କବର ସ୍ଥାନ
Answer:
(A) କଦମ୍ ରସୁଲ

Question 24.
ରାଣୀଗୁମ୍ଫା କେଉଁ ପାହାଡ଼ରେ ରହିଛି ?
(A) ଖଣ୍ଡଗିରି
(B) ଉଦୟଗିରି
(C) ଦଉଳିଗିରି
(D) ରତ୍ନଗିରି
Answer:
(B) ଉଦୟଗିରି

Question 25.
କୋଣାର୍କ ସୂର୍ଯ୍ୟ ମନ୍ଦିରର ନିର୍ମାତା କେଉଁ ବଂଶର ରାଜା ଥିଲେ ?
(A) ସୋମବଂଶ
(B) ଗଙ୍ଗବଂଶ
(C) ସୂର୍ଯ୍ୟବଂଶ
(D) ଭୋଇବଂଶ
Answer:
(B) ଗଙ୍ଗବଂଶ

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(d) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(d)

Question 1.
ଘାତାଙ୍କୀୟ ସମୀକରଣଗୁଡ଼ିକ ବାଛ ।
(i) 3x = 4
(ii) 3^x = 4
(iii) \(\frac{1}{3^x}\) = 81
(iv) \(\frac{3}{4}\) x = 1
(v) 3^x-2 = 27
(vi) 2^2x – 4 = 0
ସମାଧାନ:
(iii) \(\frac{1}{3^x}\) = 81 ⇒ 3^-x = 3⁴
(v) 3^x-2 = 27 ⇒3^x-2 = 3³
(vi) 2^2x – 4 = 0 ⇒ 2^2x = 4 ⇒ 2^2x = 2⁴
ଏହି ତିନୋଟି ଘାତାଙ୍କୀୟ ସମୀକରଣ ଅଟେ; ଯେଉଁଠାରେ a > 0 ଏବଂ a ≠ 1, x, y ∈ R

Question 2.
ସମାଧାନ କର :

(i) 4^y = 8
ସମାଧାନ:
4^y = 8 (2²)^y = 2³ ⇒ 2^2y = 2³ ⇒ 2y = 3 ⇒ y = \(\frac{3}{2}\)

(ii) \(\frac{1}{2^x}\) = 16
ସମାଧାନ:
\(\frac{1}{2^x}\) = 16 ⇒ 2^-x = 2⁴ ⇒ -x = 4 ⇒ x = -4

(iii) 2^x – 8 = 0
ସମାଧାନ:
2^x – 8 = 0 ⇒ 2^x = 8 ⇒ 2^x = 2³ ⇒ x = 3

(iv) 3^y = 3√3
ସମାଧାନ:
3^y = 3√3 ⇒ 3^y = 3^{\(\frac{1}{3}\)} ⇒ y = \(\frac{1}{3}\)

(v) \(\frac{1}{7^{-y}}\) = 49
ସମାଧାନ:
\(\frac{1}{7^{-y}}\) = 49 ⇒ 7^y = 7² ⇒ y = 2

(vi) 6^x = \(\frac{1}{1296}\)
ସମାଧାନ:
6^x = \(\frac{1}{1296}\) ⇒ 6^x = 6^-4 ⇒ x = -4

Question3.
ସମାଧାନ କର :

(i) 2^2x = 16
2^2x = 16 ⇒ 2^2x = 24 ⇒ 2x = 4 ⇒ x = \(\frac{4}{2}\) = 2
ସମାଧାନ:

(ii) 3^x+2 = 81
ସମାଧାନ:
3^{x+ 2} = 81 ⇒ 3^{x + 2} = 3⁴ ⇒ x + 2 = 4 ⇒ x = 4 – 2 = 2

(iii) 5^y = 5. √5
ସମାଧାନ:
5^y = 5. √5 5^y = 5^{1+ \(\frac{1}{2}\)}  ⇒ 5^y = 5 ^{\(\frac{2+1}{2}\)} ⇒ 5^y = 5 ^{\(\frac{3}{2}\)} ⇒ y = \(\frac{3}{2}\)

(iv) 25^x = 125
ସମାଧାନ:
25^x = 125 ⇒ 5^2x = 5³ ⇒ 2x = 3 ⇒ x = \(\frac{3}{2}\)

(v) 4^{3x + 1} = 64
ସମାଧାନ:
4^3x+1 = 64 ⇒ 4^{3x+ 1} = 4⁴ ⇒ 3x + 1 = 4 ⇒ 3x = 4 – 1 ⇒ 3x = 3 ⇒ x = 1

Question 4.
ସମାଧାନ କର :

(i) (√3)^{x + 5} = (3√3)^2x
ସମାଧାନ:
(√3)^{x + 5} = (3√3)^2x  ⇒ 3^{\(\frac{x+5}{2}\)}  ⇒ 3^{\(\frac{2x}{3}\)}  ⇒ \(\frac{x+5}{2}\) = \(\frac{2x}{3}\)
⇒ 3x + 15 = 4x ⇒ 4x – 3x = 15 ⇒ x = 15

(ii) 3^{y + 2} × 27^{3 – y} = 2187
ସମାଧାନ:
3^{y + 2} × 27^{3 – y} = 2187 ⇒ 3^{y + 2} × (3³)^3-y = 37 ⇒ 3^{y + 2} × 3^9-3y = 37 ⇒ 3^{y + 2 + 9-3y} = 37
⇒ 3^11-2y = 3⁷ ⇒ 11 – 2y = 7 ⇒ -2y = 7- 11 = -4
⇒ 2y = 4 ⇒ y = \(\frac{4}{2}\) = 2

(iii) 4^x+1 + 2^2x = 40
ସମାଧାନ:
4^x+1 + 2^2x = 40
⇒ 4^{x + 1} + 4^x = 40
⇒ 4x × 4 + 4^x = 40
⇒ 4^x (4 + 1) = 40
⇒ 2^2x × 5 = 40
⇒ 2^2x = \(\frac{40}{5}\) = 8 = 2³
⇒ 2x = 3 ⇒ x = \(\frac{3}{2}\)

(iv) 3^x+5 – 3^x+3 = \(\frac{8}{3}\)
ସମାଧାନ:
3^x+5 – 3^x+3 = \(\frac{8}{3}\) ⇒ 3^x+3 3(3² – 1) = \(\frac{8}{3}\)
⇒ 3^x+3 (8) = \(\frac{8}{3}\) ⇒ 3^x+3 = \(\frac{8}{3} \times \frac{1}{8}=\frac{1}{3}\)
⇒ 3^x+3 = 3^-1 = x + 3 = -1
⇒ x = -1 – 3 = -4

(v) 4 × 2^x-1 = 8^x
ସମାଧାନ:
4 × 2^x-1 = 8^x ⇒ 2² × 2^x-1 = 2^3x
⇒ 2^2+x-1 = 2^3x ⇒ x + 1 = 3x
⇒ 3x = x – 1
⇒ 2x = 1 ⇒ x = \(\frac{1}{2}\)

(vi) 3^x+2 + 3^x = 30
ସମାଧାନ:
3^x+2 + 3^x = 30
⇒ 3x (3² + 1) = 30 ⇒ 3^x (10) = 30
⇒ 3^x = \(\frac{30}{10}\) = 3¹ ⇒ x = 1

(vii) 3^x+2 + 3^x+4 = 810
ସମାଧାନ:
3^x+2 + 3^x+4 = 810
⇒ 3^x+2 (1 + 3²) = 810
⇒ 3^x+2 (10) = 810 ⇒ 810
⇒ 3^x+2 = \(\frac{810}{10}\) = 81⇒ 3^{x+ 2} = 3⁴
⇒ x + 2 = 4 ⇒ x = 4 – 2 = 2

(viii) 2^3-x × 4^2x-1 = 16
ସମାଧାନ:
2^3-x × 4^2x-1 = 16
⇒ 2^3-x × 2^2(2x–1) = 16
⇒ 2^{3 – x + 4x- 2} = 2⁴
⇒ 2^{3x + 1} = 2⁴
⇒ 3x + 1 = 4
⇒ 3x = 4 – 1 = 3 ⇒ x = \(\frac{3}{3}\) = 1

(ix) 2^x+2 × 3^x-1 = 288
ସମାଧାନ:
2^x+2 × 3^x-1 = 288
⇒ 2^x × 2² × 3^x × \(\frac{1}{3}\) = 288
⇒ (2^x × 3^x) × (2² × \(\frac{1}{3}\)) = 288
⇒ 6^x × \(\frac{4}{3}\) = 288
⇒ 6^x = 288 × \(\frac{3}{4}\) = 72 × 3 = 216
⇒ 6^x = 6³ ⇒ x = 3

(x) 9^x – 4 × 3^x+1 + 27 = 0
ସମାଧାନ:
9^x – 4 × 3^x+1 + 27 = 0
⇒ (3^x)² – 4 × 3^x – 3 + 27 = 0
⇒ (3^x)² – 12 × 3^x + 27 = 0
ମନେକର 3^x = y
ପ୍ରଦତ୍ତ ସମୀକରଣଟି y² – 12y + 27 = 0
⇒ y² – 9y – 3y + 27 = 0
⇒ y (y – 9) – 3 (y – 9) = 0
⇒ (y – 9) (y – 3) = 0
⇒ y – 9 = 0 ବା y – 3 = 0
⇒ y = 9 ବା y = 3
3^x = 3² ବା3^x = 3¹
(y = 3^x ସଂସ୍ଥାପନ କଲେ)
x = 2 ବା x = 1
∴ ନିର୍ଣ୍ଣୟ ସମାଧାନ 1 ଓ 2 ।

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(a)

Question 1.
2, 3, 5, 8 ଓ – 1 ମାନଗୁଡ଼ିକ ମଧ୍ୟରୁ ଅଜ୍ଞାତ ରାଶିର କେଉଁ ଏକ ବା ଏକାଧ୍ଵ ମାନ ଦ୍ୱାରା ସମୀକରଣଟି ସିଦ୍ଧ ହେବ ନିର୍ଣ୍ଣୟ କର ।

(i) (x + 1)² – 2x = x² + 1
ସମାଧାନ:
(x + 1)² – 2x = x² + 1, ବାମପାର୍ଶ୍ଵ = (x + 1)² – 2x = x² + 1 + 2x – 2x = x² + 1 = ଦକ୍ଷିଣପାର୍ଶ୍ବ
ଏହାର ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ । ତେଣୁ xର ସମସ୍ତ ମାନ ପାଇଁ ଏହି ସମୀକରଟି ସିଦ୍ଧ ହେବ ।

(ii) 6 (2y – 1) – 5 (y + 3) = 3 (y + 5) – 24
ସମାଧାନ:
6 (2y – 1) – 5 (y + 3) = 3 (y + 5) – 24
⇒ 12y – 6 – 5y – 15 = 3y + 15 – 24
⇒ 7y – 21 = 3y – 9 ⇒ 4y = 12 ⇒ y = 3
ଏଠାରେ yର ମାନ 3 ଅଟେ । କାରଣ y ପରିବର୍ତ୍ତେ 3 ନେଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ଵ ସହ ସମାନ ହେବ ।

(iii) (3 – z) + 2 (1 + z) = 13 – 2 (z + 1)
ସମାଧାନ:
(3 – z) + 2 (1 + z) = 13 – 2 (z + 1)
⇒ 3 – z + 2 + 2z = 13 – 2z – 2
⇒ z + 5 = 11 – 2z ⇒ 3z = 6 ⇒ z = 2
ଏଠାରେ z ର ମାନ 2 ଅଟେ । କାରଣ z ପରିବର୍ତ୍ତେ 2 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

(iv) 6x + 10 = 2 (x + 12) + 9 (x – 1)
ସମାଧାନ:
6x + 10 = 2 (x + 12) + 9 (x – 1)
⇒ 6x + 10 = 2x + 24 + 9x – 9
⇒ 11x + 15 = 6x + 10
⇒ 5x = -5 ⇒ x = -1
ଏଠାରେ x ର ମାନ -1 ଅଟେ । କାରଣ x ପରିବର୍ତ୍ତେ -1 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

(v) 3 (x – 4) + 6 = 2 (x + 2) – 2
ସମାଧାନ:
3 (x – 4) + 6 = 2 (x + 2) – 2
⇒ 3x – 12 + 6 = 2x + 4 – 2
⇒ 3x-6 = 2x + 2 ⇒ x = 8
ଏଠାରେ x ର ମାନ 8 ଅଟେ । କାରଣ x ପରିବର୍ତ୍ତେ 8 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

(vi) 3x + 9 – (3x – 5) – (5x + 4) = 0
ସମାଧାନ:
3x + 9- (3x – 5) – (5x + 4) = 0
⇒ 3x + 9 – 3x + 5 – 5x – 4 = 0
⇒ -5x = -10 ⇒ x = 2
ବି.ଦ୍ର.: ଅଜ୍ଞାତ ରାଶି ପରିବର୍ତ୍ତେ 2, 3, 5, 8 ଓ – 1 ନେଇ ପରୀକ୍ଷା କରି ଦର୍ଶାଯାଇ ପାରେ ଯେ,
ଅଜ୍ଞାତ ରାଶିର କେଉଁ ମାନ ବା କେଉଁ ମାନଗୁଡ଼ିକ ପାଇଁ ସମୀକରଣଟି ସିଦ୍ଧ ।
ଏଠାରେ xର ମାନ 2 ଅଟେ । କାରଣ xର ମାନ 2 ବସାଇଲେ ବାମପାର୍ଶ୍ଵ ଦକ୍ଷିଣପାର୍ଶ୍ବ ସହ ସମାନ ହେବ ।

Question 2.
ନିମ୍ନଲିଖ ସମୀକରଣମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ସଙ୍ଗତ, କେଉଁଟି ଅସଙ୍ଗତ, କେଉଁଟି ଅଭେଦ ଓ କେଉଁମାନେ ଅନୁରୂପ ନିର୍ଣ୍ଣୟ କର ।

(i) (5x – 1)³ = 125x³ – 15x (5x – 1) – 1
ସମାଧାନ:
(5x – 1)³ = 125 x³ – 15x (5x – 1) – 1
⇒ (5x – 1)³ = (5x – 1)³
∴ ବାମପାର୍ଶ୍ବ = ଦକ୍ଷିଣପାର୍ଶ୍ଵ, ତେଣୁ ଏହା ଏକ ଅଭେଦ ଅଟେ ।

(ii) (x – 5)² = 2 (x – 3) + (x + 2) (x – 2) – 1
ସମାଧାନ:
(x – 5)² = 2(x – 3) + (x + 2) (x – 2) – 1
⇒ x² – 10x + 25 = 2x – 6 + x² – 4 – 1 ⇒ -10x – 2x = -25 – 11
⇒ -12x = -36 ⇒ x = \(\frac{36}{12}\) = 3
∴ ଏହି ସମୀକରଣଟି ସଙ୍ଗତ ଅଟେ ।

(iii) 4x + 3 – (11x – 18) = 0
ସମାଧାନ:
4x + 3 – (11x – 18) = 0 ⇒ 4x + 3 – l11x + 18 = 0
⇒ – 7x + 21 = 0 ⇒ 7x = 21 ⇒ x = \(\frac{21}{7}\) = 3
∴ ଏହି ସମୀକରଣଟି ସଙ୍ଗତ ଅଟେ ଏବଂ ଏହା (ii)ର ଅନୁରୂପ ଅଟେ ।

(iv) 3 (x + 3) (x – 5) = (x – 3)² + (x – 6) (x + 6) + (x + 3) (x – 3) – 9
ସମାଧାନ:
3 (x + 3) (x- 5) = (x – 3)² + (x – 6) (x + 6) + (x + 3) (x – 3) – 9
⇒ 3 (x² – 5x + 3x – 15) = x² – 6x + 9 + x² – 36 + x² – 9 – 9
⇒ 3x² – 6x – 45 = 3x² – 6x – 45
∴ ଏହି ସମୀକରଣଟିରେ ବାମପାର୍ଶ୍ବ = ଦକ୍ଷିଣପାର୍ଶ୍ବ । ତେଣୁ ଏହା ଏକ ଅଭେଦ ଅଟେ ।

(v) 3 (x + 2a) – 2b = 2 (x + a) + b
ସମାଧାନ:
3 (x + 2a) – 2b = 2 (x + a) + b ⇒ 3x + 6a – 2b = 2x + 2a + b
⇒ 3x – 2x + 6a – 2a = b + 2b ⇒ x + 4a = 3b ⇒ x = 3b – 4a
∴ xର ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମାନ ପାଇଁ ସିଦ୍ଧ ହେଉଥ‌ିବାରୁ ଏହା ଏକ ସଙ୍ଗତ ସମୀକରଣ ଅଟେ ।

(vi) 3 (x + 2) = 4 (2x – 1) – 5 (x + 3)
ସମାଧାନ:
3 (x + 2) = 4 (2x – 1) – 5 (x + 3) ⇒ 3x + 6 = 8x – 4 – 5x – 15
⇒ 3x – 8x + 5x = -19 – 6 ⇒ 8x – 8x = -25 ⇒ 0 = -25
∴ xର ମାନ ନିର୍ଣ୍ଣୟ ଅସମ୍ଭବ ହେତୁ ଏହି ସମୀକରଣଟି ଅସଙ୍ଗତ ଅଟେ ।

Question 3.
ସମାଧାନ କର :

(i) 2 (3x – 1) – 3(x + 2) = 1
ସମାଧାନ:
2 (3x – 1)- 3 (x + 2) = 1
⇒ 6x – 2 – 3x – 6 = 1
⇒ 6x – 3x – 2 – 6 = 1
⇒ 3x – 8 = 1 ⇒ 3x = 1 + 8
⇒ 3x = 9 ⇒ x = \(\frac{9}{3}\) = 3
∴ ନିର୍ଦେୟ ସମାଧାନ 3 ।

(ii) (x + 3) (x – 5) – 15 = x (x – 1)
ସମାଧାନ:
(x + 3) (x – 5) – 15 = x (x – 1)
⇒ x (x – 5) + 3 (x- 5)- 15 = x² – x
⇒ x² – 5x + 3x – 15- 15 = x² – x
⇒ x² – x² – 5x + 3x + x = 15 + 15
⇒ -x = 30 ⇒ x = -30
∴ ନିର୍ଦେୟ ସମାଧାନ -30 ।

(iii) 3 (x + a) – b = 2(x + b) + a
ସମାଧାନ:
3 (x + a) – b = 2 (x + b) + a
⇒ 3x + 3a – b = 2x + 2b + a
⇒ 3x – 2x = 2b + a – 3a + b
⇒ x = 2b + b + a – 3a
⇒ x = 3b – 2a
∴ ନିର୍ଦେୟ ସମାଧାନ 3b – 2a ।

(iv) (x – 5)² + 2(x – 3) – (x + 2)(x – 2) – 1
ସମାଧାନ:
(x – 5)² + 2 (x – 3) = (x + 2) (x – 2) – 1
⇒ x² – 10x + 25 + 2x- 6 = x² – 4 – 1
⇒ x² – x² – 8x = -4 – 1 – 25 + 6
⇒ -8x = -24 ⇒ 8x = 24
⇒ x = \(\frac{24}{8}\) = 3
∴ ନିର୍ଦେୟ ସମାଧାନ 3 ।

(v) (x – 3)² = 2x (x – 1) – x (x + 3) – 2
ସମାଧାନ:
(x – 3)² = 2x (x – 1) – x (x + 3) – 2
⇒ x² – 6x + 9 = 2x² – 2x – x² – 3x – 2
⇒ x² + x² – 2x² – 6x + 2x + 3x = -2 – 9
⇒ -x = -11 ⇒ x = 11
∴ ନିର୍ଦେୟ ସମାଧାନ 11 ।

(vi) (x + 2)² = 3x (x + 1) – 2x (x – 1)
ସମାଧାନ:
(x + 2)² = 3x (x + 1) – 2x (x – 1)
⇒ x² + 4x + 4 = 3x² + 3x – 2x² + 2x
⇒ x² – 3x² + 2x² + 4x – 3x – 2x + 4 = 0
⇒ 3x² – 3x² + 4x – 5x = -4
⇒ – x = -4 ⇒ x = 4
∴ ନିର୍ଦେୟ ସମାଧାନ 4 ।

Question 4.
ସମାଧାନ କର :

(i) x – \(\frac{2 x-1}{3}=\frac{x-2}{4}+\frac{1}{3}\)
ସମାଧାନ:

(ii) \(\frac{2-3 x}{4}+\frac{3-2 x}{5}\) = 2 – x
ସମାଧାନ:

(iii) \(\frac{3 x}{4}-\frac{5 x}{6}+2=\frac{x}{12}\)
ସମାଧାନ:

(iv) (2x – 1) – \(\frac{5(x+3)}{6}=\frac{x+5}{2}\) – 4
ସମାଧାନ:

(v) \(\frac{x-(7-8 x)}{9 x-(3+4 x)}=\frac{2}{3}\)
ସମାଧାନ:

(vi) \(\frac{x}{5}+\frac{x}{2}\) = 7
ସମାଧାନ:

Question 5.
ସମାଧାନ କର :

(i) \(\frac{1}{x+1}+\frac{1}{x+4}=\frac{2}{x+3}\)
ସମାଧାନ:

(ii) \(\frac{2}{x}+\frac{1}{2 x}-\frac{5}{x+2}\) = 0
ସମାଧାନ:

(iii) \(\frac{2}{x+1}-\frac{3}{2 x+2}=\frac{1}{2 x+3}\)
ସମାଧାନ:

(iv) \(\frac{6}{2 x+3}+\frac{4}{x-2}=\frac{7}{x+6}\)
ସମାଧାନ:

(v) \(\frac{2}{x+1}-\frac{6}{2 x-1}+\frac{3}{3 x+2}\) = 0
ସମାଧାନ:

(vi) \(\frac{2}{2 x-3}+\frac{5}{(2 x-3)^2}=\frac{3}{3 x-2}\)
ସମାଧାନ:

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(b)

Question 1.
ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।

(i) x ଓ y ରେ ଏକଘାତୀ ସମୀକରଣର ବ୍ୟାପକ ରୂପଟିକୁ ଲେଖ ।
ସମାଧାନ:
ax + by + c = 0 ( a ≠ 0 ଏବଂ b ≠ 0)

(ii) x ଓ y ରେ ଏକଘାତୀ ସମୀକରଣର ଲେଖଚିତ୍ରଟିର ସ୍ଵରୂପ କ’ଣ ହେବ ?
ସମାଧାନ:
ଏକ ସରଳରେଖା

(iii) x-ଅକ୍ଷର ସମୀକରଣଟି ଲେଖ ।
ସମାଧାନ:
x-ଅକ୍ଷର ସମୀକରଣଟି y = 0 ।

(iv) y-ଅକ୍ଷର ସମୀକରଣଟି ଲେଖ ।
ସମାଧାନ:
y ଅକ୍ଷର ସମୀକରଣଟି x = 0

(v) (3, 0) ବିନ୍ଦୁ ଦେଇ y-ଅକ୍ଷସହ ସମାନ୍ତର ସରଳରେଖାର ସମୀକରଣଟିକୁ ଲେଖ
ସମାଧାନ:
(3, 0) ବିନ୍ଦୁ ଦେଇ y-ଅକ୍ଷସହ ସମାନ୍ତର ସରଳରେଖାର ସମୀକରଣ x = 3

(vi) (0, –2) ବିନ୍ଦୁ ଦେଇ x-ଅକ୍ଷ ସହ ସମାନ୍ତର ସରଳରେଖାର ସମୀକରଣଟିକୁ ଲେଖ ।
ସମାଧାନ:
(0, – 2) ବିନ୍ଦୁ ଦେଇ x-ଅକ୍ଷ ସହ ସମାନ୍ତର ସରଳରେଖାର ସମୀକରଣ y = -2

(vii) ମୂଳ ବିନ୍ଦୁଗାମୀ ସରଳରେଖାର ସମୀକରଣଟିର ବ୍ୟାପକ ରୂପକୁ ଲେଖ ।
ସମାଧାନ:
ମୂଳବିନ୍ଦୁଗାମୀ ସରଳରେଖାର ସମୀକରଣଟିର ବ୍ୟାପକ ରୂପ y = mx ।

(viii) (2, 3) ବିନ୍ଦୁ 2x + 3y + 6 = 0 ସରଳରେଖା ଉପରିସ୍ଥ ହେବ କି ?
ସମାଧାନ:
(2, 3) ବିନ୍ଦୁଟି 2x + 3y + 6 = 0 ସରଳରେଖା ଉପରିସ୍ଥ ହୁହେ‍ଁ
କାରଣ 2 × 2 + 3 × 3 + 6 = 4 + 9 + 6 = 19 ≠ 0

(ix) (1, -1) ବିନ୍ଦୁ 3x + 4y + 1 = 0 ସରଳରେଖା ଉପରିସ୍ଥ ହେବ କି ?
ସମାଧାନ:
(1, -1) ବିନ୍ଦୁ, 3x + 4y + 1 = 0 ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ; କାରଣ
3(1) + 4(-1) + 1 = 3 – 4 + 1 = 4 – 4 = 0

(x) x = 0 ଓ y = 0 ସରଳରେଖା ଦ୍ଵୟର ଛେଦ ବିନ୍ଦୁଟିର ସ୍ଥାନଙ୍କ ଲେଖ ।
ସମାଧାନ:
x = 0 ଓ y = 0 ସରଳରେଖା ଦ୍ଵୟର ଛେଦ ବିନ୍ଦୁ (0, 0)

Question 2.
ନିମ୍ନରେ ଦିଆଯାଇଥବା ସରଳରେଖାମାନଙ୍କୁ y = mx + c ରୂପରେ ଲେଖି m ଓ c ନିରୂପଣ କର ।

(i) 2x + 4y – 7 = 0
ସମାଧାନ:
2x + 4y – 7 = 0 ⇒ 4y = -2x + 7 ⇒ y = \(\frac{-2}{4}\) x + \(\frac{7}{4}\) ⇒ y = (\(\frac{-1}{2}\)) x + \(\frac{7}{4}\)
∴ ଏଠାରେ m = –\(\frac{1}{2}\) ଏବଂ c = \(\frac{7}{4}\)

(ii) x – 2y + 5 = 0
ସମାଧାନ:
x – 2y + 5 = 0 ⇒ x + 5 = 2y ⇒ y = \(\frac{1}{2}\) x + \(\frac{5}{2}\)
∴ ଏଠାରେ m = –\(\frac{1}{2}\) ଏବଂ c = \(\frac{5}{2}\)

(iii) 3x – 4y = 0
ସମାଧାନ:
3x – 4y = 0 ⇒ 3x = 4y ⇒ y = \(\frac{3}{4}\) x + 0
∴ ଏଠାରେ m = \(\frac{3}{4}\) ଏବଂ c = 0

Question 3.
x – 2y + 5 = 0 ସରଳରେଖା ଉପରିସ୍ଥ ବିନ୍ଦୁମାନଙ୍କୁ ଦତ୍ତ ବିନ୍ଦୁମାନଙ୍କରୁ ଚିହ୍ନଟ କର ।

(i) (1, 3)
ସମାଧାନ:
ଦତ୍ତ ସମୀକରଣରେ (1, 3) ଅର୍ଥାତ୍ x = 1 ଓ y = 3 ଲେଖୁଲେ 1 – 2 × 3 + 5 = 6 – 6 = 0
ସୁତରାଂ P(1, 3) ବିନ୍ଦୁଟି ଦତ୍ତ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ।

(ii) (2, 4)
ସମାଧାନ:
ଦତ୍ତ ସମୀକରଣରେ (2, 4) ଅର୍ଥାତ୍ x = 2 ଓ y = 4 ଲେଖୁଲେ 2 – 2 × 4 + 5 = 7 – 8 = -1 ≠ 0
ସୁତରାଂ ॰ P (2, 5) ବିନ୍ଦୁଟି ଦତ୍ତ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ନୁହେଁ ।

(iii) (2, 5)
ସମାଧାନ:
ଦତ୍ତ ସମୀକରଣରେ (2, 5) ଅର୍ଥାତ୍ x = 2 ଓ y = 5 ଲେଖୁଲେ 2 – 2 × 5 + 5 = 7 – 10 = -3 ≠ 0
ସୁତରାଂ P (2, 5) ବିନ୍ଦୁଟି ଦତ୍ତ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ନୁହେଁ ।

(iv) (-1, 2)
ସମାଧାନ:
ଦତ୍ତ ସମୀକରଣରେ (-1, 2) ଅର୍ଥାତ୍ x = -1 ଓ y = 2 ଲେଖୁଲେ -1 – 2(2) + 5 = -5 + 5 = 0
ସୁତରାଂ P (-1, 2) ବିନ୍ଦୁଟି ଦତ୍ତ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ।

(v) (7, -6)
ସମାଧାନ:
ଦତ୍ତ ସମୀକରଣରେ (7, -6) ଅର୍ଥାତ୍ x = 7 ଓ y = 6 ଲେଖୁଲେ 7 – 2(-6) + 5 = 12 + 12 = 24 ≠ 0
ସୁତରାଂ P (7, -6) ବିନ୍ଦୁଟି ଦତ୍ତ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ।

(vi) (-3, 1)
ସମାଧାନ:
ଦତ୍ତ ସମୀକରଣରେ (-3, 1) ଅର୍ଥାତ୍ x = -3 ଓ y = 1 ଲେଖୁଲେ -3 – 2 (1) + 5 = -5 + 5 = 0
ସୁତରାଂ P (-3, 1) ଦତ୍ତ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ।

Question 4.
ନିମ୍ନଲିଖୂତ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ P₁ ଓ P₂ ଦେଇ ଅଙ୍କିତ ସରଳରେଖା \(\overleftrightarrow{\mathbf{P}_1 \mathbf{P}_2}\) ର ସ୍ଲୋପ୍ ନିର୍ଣ୍ଣୟ କର ।

(i) P₁(1, 2) ଓ P₂(2, 3)
ସମାଧାନ:
P₁(1, 2) ଓ P₂(2, 3); ଏଠାରେ x₁ = 1; y₁ = 2 ଏବଂ x₂ = 2 y₂ = 3
∴ \(\overleftrightarrow{\mathbf{P}_1 \mathbf{P}_2}\) ର ସ୍ଲୋପ୍ = \(\frac{y_2-y_1}{x_2-x_1}=\frac{3-2}{2-1}=\frac{1}{1}\) = 1 (∴ ସରଳରେଖାର ସ୍ଲୋପ୍ = \(\frac{y – ସ୍ଥାନାଙ୍କଦ୍ବୟରଅନ୍ତର}{x – ସ୍ଥାନାଙ୍କଦ୍ବୟରଅନ୍ତର}\) )

(ii) P₁(-1, 2) ଓ P₂(5, 7)
ସମାଧାନ:
P₁(-1, 2) ଓ P₂(5, 7); ଏଠାରେ x₁ = -1; y₁ = 2 ଏବଂ x₂ = 5 y₂ = 7
∴ \(\overleftrightarrow{\mathbf{P}_1 \mathbf{P}_2}\) ର ସ୍ଲୋପ୍ = \(\frac{y_2-y_1}{x_2-x_1}=\frac{7-2}{5-(-1)}=\frac{5}{5+1}=\frac{5}{6}\)

(iii) P₁(-2, -3) ଓ P₂(-4, -5)
ସମାଧାନ:
P₁(-2, -3) ଓ P₂(-4, -5); ଏଠାରେ x₁ = -2; y₁ = -3 ଏବଂ x₂ = -4 y₂ = -5
∴ \(\overleftrightarrow{\mathbf{P}_1 \mathbf{P}_2}\) ର ସ୍ଲୋପ୍ = \(\frac{y_2-y_1}{x_2-x_1}=\frac{-5-(-3)}{-4-(-2)}=\frac{-5+3}{-4+2}=\frac{-2}{-2}\) = 1

(iv) P₁(2, -4) ଓ P₂(0, 6)
ସମାଧାନ:
P₁(2, -4) ଓ P₂(0, 6); ଏଠାରେ x₁ = 2; y₁ = -4 ଏବଂ x₂ = 0 y₂ = 6
∴ \(\overleftrightarrow{\mathbf{P}_1 \mathbf{P}_2}\) ର ସ୍ଲୋପ୍ = \(\frac{y_2-y_1}{x_2-x_1}=\frac{6-(-4)}{0-2}=\frac{6+4}{-2}=\frac{10}{-2}\) = -5

(v) P₁(0, 0) ଓ P₂(1, 1)
ସମାଧାନ:
P₁(0, 0) ଓ P₂(1, 1); ଏଠାରେ x₁ = 0; y₁ = 0 ଏବଂ x₂ = 1 y₂ = 1
∴ \(\overleftrightarrow{\mathbf{P}_1 \mathbf{P}_2}\) ର ସ୍ଲୋପ୍ = \(\frac{y_2}{x_2}=\frac{1}{1}\) = 1 (∴ ମୂଳବିନ୍ଦୁଗାମୀ ସରଳରେଖାର m = \(\frac{y}{x}\))

(vi) P₁(0, 0) ଓ P₂(-1, 1)
ସମାଧାନ:
P₁(0, 0) ଓ P₂(-1, 1); ଏଠାରେ x₁ = 0; y₁ = 0 ଏବଂ x₂ = -1 y₂ = 1
∴ \(\overleftrightarrow{\mathbf{P}_1 \mathbf{P}_2}\) ର ସ୍ଲୋପ୍ = \(\frac{y_2}{x_2}=\frac{1}{-1}\) = -1

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 5(a)

Question 1.
ଭୁଲ୍ ଥିଲେ ଠିକ୍ କର ।

(i) ମୂଳ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 0) ।
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

(ii) ପ୍ରଥମ ପାଦ (Q₁) ଉପରିସ୍ଥ (x, y)ରେ x > 0, y < 0 ।
ସମାଧାନ:
ପ୍ରଥମ ପାଦ (Q₁) ଉପରିସ୍ଥ (x, y)ରେ x > 0, y > 0
ଅଥବା ଚତୁର୍ଥ ପାଦ (Q₄) ଉପରିସ୍ଥ (x, y)ରେ x > 0, y < 0

(iii) ଦ୍ଵିତୀୟ ପାଦ (Q₂) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y < 0 
ସମାଧାନ:
ଦ୍ଵିତୀୟ ପାଦ (Q₂) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y > 0
ଅଥବା ତୃତୀୟ ପାଦ (Q₃) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y < 0 

(iv) ତୃତୀୟ ପାଦ (Q₃) ଉପରିସ୍ଥ (x, y) ରେ x < 0, y < 0 
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

(v)  ଚତୁର୍ଥ ପାଦ (Q₄) ଉପରିସ୍ଥ (x, y) ରେ x > 0 , y > 0 ।
ସମାଧାନ:
ପ୍ରଥମ ପାଦ (Q₁) ଉପରିସ୍ଥ (x, y) ରେ x > 0, y > 0
ଅଥବା ଚତୁର୍ଥ ପାଦ (Q₄) ଉପରିସ୍ଥ (x, y) ରେ x > 0 , y < 0 l

(vi) x-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, y) ।
ସମାଧାନ:
x-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, 0) ।
ଅଥବା y- ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, y) ।

(vii) y- ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, 0) ।
ସମାଧାନ:
y-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, y) ।
ଅଥବା x-ଅକ୍ଷ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, 0) ।

(viii) Q₁ ∪ Q₂ ∪ Q₃ ∪ Q₄ = R²
ସମାଧାନ:
Q₁ ∪ Q₂ ∪ Q₃ ∪ Q₄ ∪ {(x, 0) : x ∈ R} ∪ {(0, y) : y ∈ R} = R²

(ix) R² ର ଦକ୍ଷିଣ ଅର୍ଥ ସମତଳ = Q₁ ∪ Q₂
ସମାଧାନ:
R² ର ଊର୍ଦ୍ଧ୍ବ ଅର୍ଥ ସମତଳ = Q₁ ∪ Q₂

(x) R² ର ଦକ୍ଷଶ ଅକ୍ଷ ସମତଳ ।
ସମାଧାନ:
R² ର ଦକ୍ଷିଣ ଅର୍ଥ ସମତଳ = Q₃ ∪ Q₄
ଅଥବା R² ର ଊର୍ଦ୍ଧ୍ବ ଅର୍ଷ ସମତଳ = Q₁ ∪ Q₂

(xi) (-3, -2) ବିନ୍ଦୁଟି ଦ୍ବତୀୟ ପାଦରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

(xii) (1.2, -1) ବିନ୍ଦୁଟି ଦ୍ବିତୀୟ ପାଦରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
(1.2, -1) ବିନ୍ଦୁଟି ଚତୁର୍ଥ ପାଦରେ ଅବସ୍ଥିତ ।

(xiii) (-0.5 , √2) ବିନ୍ଦୁଟି ପ୍ରଥମ ପାଦରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
(-0.5 , √2) ବିନ୍ଦୁଟି ଦ୍ବିତୀୟ ପାଦରେ ଅବସ୍ଥିତ ।

(xiv) (x, y) = (-2, 3) ହେଲେ, x = -2 ଓ y = 3
ସମାଧାନ:
ଠିକ୍ ଅଛି ।

Question 2.
ସମତଳରେ x- ଓ y- ଅକ୍ଷ ଅଙ୍କନ କରି ନିମ୍ନଲିଖତ ବିନ୍ଦୁମାନଙ୍କୁ ଲେଖ କାଗଜ ଉପରେ ଦତ୍ତ କ୍ରମିତ ଯୋଡ଼ି ସାହାଯ୍ୟରେ ଚିହ୍ନଟ କର । (ଲେଖ କାଗଜରେ ପ୍ରତ୍ୟେକ ଅକ୍ଷରେ 1 ସେ.ମି. ଦୈର୍ଘ୍ୟକୁ 1 ଏକକ ନିଅ ।)
(i) P₁(2, 2)
(ii) P₂(-3, 2)
(iii) P₃(2, -3)
(iv) P₄(-4, -4)
(v) P₅(-3, 4)
(vi) P₆(0, 3)
(vii) P₇(3, 0)
(viii) P₈(0, -4)
ଉ – X ଓ Y ଉଭୟ ଅକ୍ଷରେ 1 ସେ.ମି. = 1 ଏକକ ।

Question 3.
ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ

(i) ସଂଖ୍ୟାରେଖା \(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ର ମାତ୍ରା କେତେ ?
ସମାଧାନ:
ସଂଖ୍ୟାରେଖା \(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ଗାେଟିଏ  ର ମାତ୍ରା କେତେ 

(ii) xy- ସମତଳର ମାତ୍ରା କେତେ ?
ସମାଧାନ:
xy- ସମତଳର ଦୁଇଟି ମାତ୍ରା କେତେ 

(iii) ସମତଳ ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି କେଉଁ ଗଣିତଜ୍ଞଙ୍କ ଦ୍ୱାରା ଆବିଷ୍କୃତ ହୋଇଥିଲା ?
ସମାଧାନ:
ସମତଳ ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ଗଣିତଞ Rene Descartes ଙ୍କ ଦ୍ୱାରା ଆବିଷ୍କୃତ ହୋଇଥିଲା

(iv) xy-ସମତଳ କୁ x-ଅକ୍ଷ ଓ y-ଅକ୍ଷ କେତେଗୋଟି ପାଦରେ ବିଭକ୍ତ କରନ୍ତି ?
ସମାଧାନ:
xy-ସମତଳ କୁ x-ଅକ୍ଷ ଓ y-ଅକ୍ଷ ଚାରୋଟି ପାଦରେ ବିଭକ୍ତ କରନ୍ତି 

(v) \(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ଅକ୍ଷର ଧନାତ୍ମକ ଦିଗ କେଉଁଟି ?
ସମାଧାନ:
\(\overleftrightarrow{\mathrm{X}^{\prime} \mathbf{X}}\) ଅକ୍ଷର ଧନାତ୍ମକ ଦିଗ \(\overrightarrow{O X}\)

(vi) \(\overleftrightarrow{\mathrm{Y}^{\prime} \mathbf{Y}}\) ଅକ୍ଷର ଋଣାତ୍ମକ ଦିଗ କେଉଁଟି ?
ସମାଧାନ:
\(\overleftrightarrow{\mathrm{Y}^{\prime} \mathbf{Y}}\) ଅକ୍ଷର ଋଣାତ୍ମକ ଦିଗ \(\overrightarrow{\mathrm{OY}^{\prime}}\)

(vii) ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତିରେ ଜ୍ୟାମିତିକ ଚର୍ଚ୍ଚା ପାଇଁ ଗଣିତର କେଉଁ ଶାଖାଟିର ପ୍ରୟୋଗ କରାଯାଇଥାଏ ?
ସମାଧାନ:
ବୀଜଗଣିତ (Algebra)

(viii) P(5, 4) ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ ଓ y-ସ୍ଥାନାଙ୍କ କେତେ ?
ସମାଧାନ:
P(5, 4) ବିନ୍ଦୁର x-ସ୍ଥାନାଙ୍କ 5 ଓ y-ସ୍ଥାନାଙ୍କ 4

Question 4.
A(0, y) , B(7, 0), C(-2, 5), D (3, -4) ଏବଂ E (−1,1) ବିନ୍ଦୁଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁ ବିନ୍ଦୁ ବା ବିନ୍ଦୁଗୁଡ଼ିକ କେଉଁ ବୃତ୍ତପାଦରେ ଅଥବା କେଉଁ କେଉଁ ଅକ୍ଷରେ ଅବସ୍ଥିତ ଲେଖ ।
ସମାଧାନ:
A (0, y) ବିନ୍ଦୁଟି y- ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ। B (7, 0) ବିନ୍ଦୁଟି x- ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ।
C (–2, 5) ବିନ୍ଦୁଟି ଦ୍ୱିତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ । D (3, – 4) ବିନ୍ଦୁଟି ଚତୁର୍ଥ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
E (−1, 1) ବିନ୍ଦୁଟି ଦ୍ୱିତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।

Question 5.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) x > 0, y > 0 ହେଲେ, p(x, -y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(ii) x < 0, y < 0 ହେଲେ, p(x, -y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iii) x>0, y < 0 ହେଲେ p (−x, y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iv) x ∈ R, y < 0 ହେଲେ, p(x, y) ________ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(v) x < 0, y = R ହେଲେ, p (x, y) ________ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(vi) x > 0, y > 0 ହେଲେ, p (-x, -y) ________ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
ସୂଚନା : (ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ୍ ଉତ୍ତରଗୁଡ଼ିକୁ ତର୍ଜମା କର ।)

(i) x > 0, y > 0 ହେଲେ, p(x, -y) Q₄ ଚତୁର୍ଥ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(ii) x < 0, y < 0 ହେଲେ, p(x, -y) Q₂ ଦ୍ୱିତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iii) x > 0, y < 0 ହେଲେ, P (-x, y) Q₃ ତୃତୀୟ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।
(iv) x ∈ R, y < 0 ହେଲେ, P(x, y) ଅଧଃ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(v) x < 0, y = R ହେଲେ, p (x, y) ବୀମ ଅର୍ଷତଳରେ ଅବସ୍ଥିତ ।
(vi) x > 0, y > 0 ହେଲେ, p (-x, -y) Q₃ ବୃତ୍ତପାଦରେ ଅବସ୍ଥିତ ।

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(e) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(e)

Question 1.
ଠିକ୍ ଉକ୍ତି ପାର୍ଶ୍ୱସ୍ଥ କୋଠରି ମଧ୍ୟରେ ‘✓’ ଚିହ୍ନ ଓ ଭୁଲ ଉକ୍ତି ପାର୍ଶ୍ୱସ୍ଥ କୋଠରି ମଧ୍ୟରେ ‘✗’ ଚିହ୍ନ ଦିଅ ।

(i) \(\frac{x}{2}+\frac{y}{3}=\frac{x+y}{5}\)
ସମାଧାନ:
✗

(ii) \(\frac{x}{y-z}-\frac{x}{z-y}\) = 0
ସମାଧାନ:
✗

(iii) \(\frac{1}{x-y}+\frac{1}{y-x}\) = 0
ସମାଧାନ:
✓

(iv) \(\frac{x-y}{z}+\frac{y-z}{x}+\frac{z-x}{y}\) = 0
ସମାଧାନ:
✗

(v) \(\frac{x-1}{x}+\frac{y-1}{y}=\frac{1}{y}-\frac{1}{x}\)
ସମାଧାନ:
✓

(vi) \(\frac{1}{x-y}+\frac{1}{y-z}+\frac{1}{z-x}\) = 0
ସମାଧାନ:
✗

Question 2.
ସରଳ କର :

(i) \(\frac{1}{x+y}+\frac{1}{x-y}\)
ସମାଧାନ:
= \(\frac{x-y+x+y}{(x+y)(x-y)}=\frac{2 x}{x^2-y^2}\)

(ii) \(\frac{x}{x-y}-\frac{y}{x+y}\)
ସମାଧାନ:

(iii) \(\frac{a-b}{a b}+\frac{b-c}{b c}+\frac{c-a}{c a}\)
ସମାଧାନ:

(iv) \(\frac{x-y}{x+y}-\frac{x+y}{x-y}\)
ସମାଧାନ:

(v) \(\frac{1}{x^2-y^2}-\frac{1}{(x-y)^2}\)
ସମାଧାନ:

(vi) \(\frac{a^2}{a+b}\) – a + b
ସମାଧାନ:

(vii) \(\frac{1}{x+2 y}+\frac{1}{x-2 y}+\frac{2 x}{4 y^2-x^2}\)
ସମାଧାନ:

(viii) \(\frac{a+b}{a-b}+\frac{a-b}{a+b}+\frac{a^2+b^2}{b^2-a^2}\)
ସମାଧାନ:

(ix) \(\frac{1}{x-1}-\frac{1}{x-1}+\frac{1}{x+2}-\frac{1}{x+2}\)
ସମାଧାନ:

(x) \(\frac{3 x+1}{x-3}-\frac{x-3}{3 x+9}-\frac{5 x^2+24 x}{2 x^2-18}\)
ସମାଧାନ:

Question 3.
ସରଳ କର :

(i) \(\frac{x^3 y}{a z^2} \times \frac{y^3 z}{b x^2} \times \frac{z^3 x}{c y^2}\)
ସମାଧାନ:
= \(\frac{x^4 y^4 z^4}{a b c x^2 y^2 z^2}=\frac{x^2 y^2 z^2}{a b c}\)

(ii) \(\frac{x-y}{x+y} \times \frac{x^2+x y}{x^2 y-y^3}\)
ସମାଧାନ:

(iii) \(\frac{x^3+y^3}{x^2-y^2} \times \frac{x^3-y^3}{x^4+x^2y^3+y^4}\)
ସମାଧାନ:

(iv) \(\frac{x^2-7 x+10}{x^2-5 x-14} \times \frac{x^3+8}{x^3-8}\)
ସମାଧାନ:

(v) \(\left(1+\frac{x}{y^2}+\frac{x^2}{y^2}\right)\left(1-\frac{x^2}{y^2}+\frac{x^2}{y^2}\right)\left(1-\frac{x^2}{y^2}\right)\)
ସମାଧାନ:

ବିକଳ୍ପ ସଣାଳା –

(vi) \(\frac{x^2-y^2}{x-z} \times \frac{x^2-z^2}{x y+y^2} \times\left(x+\frac{x y}{x-y}\right)\)
ସମାଧାନ:

(vii) \(\left(\frac{a+b}{a-b}-\frac{a-b}{a+b}\right) \times \frac{a^2-b^2}{2\left(a^2+b^2\right)}\)
ସମାଧାନ:

(viii) \(\left(\frac{\mathbf{x}}{\mathbf{x}+\mathbf{y}}+\frac{\mathbf{y}}{\mathbf{x}-\mathbf{y}}\right) \div\left(\frac{\mathbf{x}}{\mathbf{x}-\mathbf{y}}-\frac{\mathbf{y}}{\mathbf{x}+\mathbf{y}}\right)\)
ସମାଧାନ:

(ix) \(\frac{x^3+y^3}{(x-y)^2+3 x y} \div \frac{(x+y)^2-3 x y}{x^3-y^3} \times \frac{x y}{x^2-y^2}\)
ସମାଧାନ:

(x) \(\frac{(a+b)^2+(a-b)^2}{(a+b)^2-(a-b)^2} \div \frac{a^4-b^4}{2 a b(a-b)} \times \frac{a^2-b^2}{a}\)
ସମାଧାନ:

(xi) \(\frac{a^2+3 a-18}{a^2-4} \div \frac{a^2-36}{a^2-5 a-14}\)
ସମାଧାନ:

(xii) \(\frac{3 a^2+a-4}{2 a^2-a-3} \div \frac{3 a^2-2 a-8}{2 a^2-7 a+6}\)
ସମାଧାନ:

Question 4.
ସରଳ କର :

(i) \(\frac{1}{1+\frac{1}{1+\frac{1}{1-\frac{1}{x}}}}\)
ସମାଧାନ:

(ii) \(\frac{a}{a-\frac{a-1}{1-\frac{1}{a+1}}}\)
ସମାଧାନ:

(iii) \(\frac{y}{y^2-\frac{y^3-1}{y+\frac{1}{y+1}}}\)
ସମାଧାନ:

(iv) \(\frac{\mathbf{x}}{\mathbf{x}-\frac{1}{\mathbf{x}-\frac{\mathbf{x}}{\mathbf{1}+\mathbf{x}}}}\)
ସମାଧାନ:

Odisha State Board BSE Odisha 9th Class Political Science Important Questions Chapter 3 ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ Important Questions and Answers.

BSE Odisha Class 9 Political Science Important Questions Chapter 3 ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ

Subjective Type Questions With Answers
ସଂଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

୧। ସମାଜବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀ କ’ଣ ବୁଝାଅ ।
Answer:

• ସମ୍ବିଧାନର ଧାରା ୩୮, ୩୯, ୪୧, ୪୨, ୪୩ରେ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀର କରାଯାଇଛି ।
• ସମ୍ବିଧାନର ଧାରା ୩୮ରେ ଜନସାଧାରଣଙ୍କ ହିତ ପାଇଁ ରାଷ୍ଟ୍ର ଏକ ସାମାଜିକ ବ୍ୟବସ୍ଥା ସୃଷ୍ଟି କରି ଜାତୀୟ ଜୀବନର ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ସାମାଜିକ, ଅର୍ଥନୈତିକ ଓ ରାଜନୈତିକ ନ୍ୟାୟ ପ୍ରଦାନ କରିବାପାଇଁ ବର୍ଣ୍ଣ ନ କରାଯାଇଛି ।
• ସମ୍ବିଧାନର ଧାରା ୩୯ରେ ସମସ୍ତ ନାରୀ ଓ ଜୀବିକା ଅର୍ଜନ ପନ୍ଥା ଯୋଗାଇବା, ଜାତୀୟ ସମ୍ପତ୍ତିକୁ ନ୍ୟାୟୋଚିତ ଭାବେ ବଣ୍ଟନ କରିବା, ଦେଶର ସମ୍ପତ୍ତି ଅଳ୍ପ ବ୍ୟକ୍ତିଙ୍କ ହାତରେ କେନ୍ଦ୍ରୀଭୂତ ନ ହେବାପାଇଁ ବ୍ୟବସ୍ଥା କରିବା, ନାରୀ ଓ ପୁରୁଷ ସମାନ କାର୍ଯ୍ୟ ପାଇଁ ସମାନ ପାରିଶ୍ରମିକ ପାଇବା ତଥା ଶ୍ରମିକ ଶ୍ରେଣୀର ସ୍ୱାର୍ଥରକ୍ଷା ପାଇଁ ବ୍ୟବସ୍ଥା କରିବାପାଇଁ ରାଷ୍ଟ୍ରକୁ ନିର୍ଦ୍ଦେଶ ଦିଆଯାଇଛି ।
• ଏହାଛଡ଼ା ଶିଶୁ ଓ ଯୁବକ ଏବଂ ଯୁବତୀମାନଙ୍କୁ ଶୋଷଣମୁକ୍ତ କରି ସମସ୍ତଙ୍କୁ ତୁରନ୍ତ ତଥା ସମାନ ନ୍ୟାୟ ପ୍ରଦାନ କରାଯିବାପାଇଁ ଦେବାପାଇଁ ରାଷ୍ଟ୍ରକୁ ନିର୍ଦ୍ଦେଶ ଦିଆଯାଇଛି ।
• ସମ୍ବିଧାନର ଧାରା ୪୧ରୁ ୪୩ ମଧ୍ୟରେ ବେକାର, ବୃଦ୍ଧ, ଅକର୍ମଣ୍ୟ ଓ ରୁଗ୍ଣ ପ୍ରଦାନ କରିବା, କାର୍ଯ୍ୟ କ୍ଷେତ୍ରରେ ପ୍ରଦାନ କରିବା, କାର୍ଯ୍ୟ କ୍ଷେତ୍ରରେ ସମସ୍ତ ଅନୁକୂଳ ବ୍ୟବସ୍ଥା କରିବା ଓ ବ୍ୟବସ୍ଥା କରିବା ନିମନ୍ତେ ରାଷ୍ଟ୍ରକୁ ନିର୍ଦ୍ଦେଶ ଦିଆଯାଇଛି ।

୨। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀରେ ଗାନ୍ଧିଜୀଙ୍କ ପ୍ରଭାବ କିପରି ପଡ଼ିଛି ?
Answer:

• ଭାରତକୁ ଏକ ପ୍ରଗତିଶୀଳ ତଥା ଆଦର୍ଶ ରାଷ୍ଟ୍ରଭାବେ ଗଠନ କରିବା ପାଇଁ ମହାତ୍ମା ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀରେ ଧାରା ୪୦, ୪୫, ୪୬, ୪୭, ୪୮ରେ ଗାନ୍ଧିବାଦୀ ଆଦର୍ଶଗୁଡ଼ିକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଛି । ସେହି ନିର୍ଦ୍ଦେଶ ଦିଆଯାଇଛି ।
• ସ୍ୱାୟତ୍ତ ଶାସନ ପାଇଁ ଦେଶର ପ୍ରତ୍ୟେକ ଅଞ୍ଚଳରେ ଗ୍ରାମ ପଞ୍ଚାୟତମାନ ପ୍ରତିଷ୍ଠା କରିବା ଏବଂ ଗ୍ରାମାଞ୍ଚଳରେ କୁଟୀର ଶିଳ୍ପର ପ୍ରତିଷ୍ଠା ଓ ପ୍ରସାର କରିବାପାଇଁ ରାଷ୍ଟ୍ରକୁ ନିର୍ଦ୍ଦେଶ ଦିଆଯାଇଛି ।
• ଆର୍ଥିକ ଅବସ୍ଥାରେ ଉନ୍ନତି ଆଣିବା ଓ ଔଷଧ ବ୍ୟତୀତ ଅନ୍ୟ କ୍ଷେତ୍ରରେ ନିଶା ଓ ମାଦକ ବ୍ୟତୀତ ଅନ୍ୟ କ୍ଷେତ୍ରରେ ନିଶା ଓ ମାଦକ ଦ୍ରବ୍ୟର ବ୍ୟବହାର ନିଷିଦ୍ଧ କରିବାପାଇଁ ରାଷ୍ଟ୍ରକୁ ନିର୍ଦ୍ଦେଶ ଦିଆଯାଇଛି ।
• ରାଷ୍ଟ୍ରରେ ଗୋ-ହତ୍ୟା ନିବାରଣ ପାଇଁ ରାଷ୍ଟ୍ରକୁ ନିର୍ଦ୍ଦେଶ ଦିଆଯାଇଛି ।
• ବିଶେଷଭାବରେ ଛଅ ବର୍ଷରୁ ଚଉଦ ବର୍ଷ ମଧ୍ୟରେ ଥ‌ିବା ପ୍ରତ୍ୟେକ ବାଳକ ଓ ବାଳିକାଙ୍କୁ ମାଗଣା ଓ ବାଧ୍ୟତାମୂଳକ ଶିକ୍ଷା ପ୍ରଦାନ ଦିଆଯାଇଛି ।

କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

୧। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀରେ କେଉଁ ବିଷୟରେ ଉଲ୍ଲେଖ କରାଯାଇଛି ?
Answer:

• କରିଥିଲେ ଯେ ନାଗରିକମାନଙ୍କ ପାଇଁ ରାଜନୈତିକ ସ୍ଵାଧୀନତା ଯେପରି ଆବଶ୍ୟକ ସେହିପରି ଭାବରେ ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ସ୍ଵାଧୀନତା ମଧ୍ୟ ଆବଶ୍ୟକ ରହିଛି ।
• ଦେଶର ଗରିବ, ପଛୁଆବର୍ଗ, ଶିଶୁ ଓ ମହିଳା ଏବଂ ଅନ୍ୟାନ୍ୟ ଅବହେଳିତ ଲୋକମାନଙ୍କ ବିକାଶ ପାଇଁ ପ୍ରଚେଷ୍ଟା କରାଗଲେ ଦେଶର ପ୍ରଗତି ଘଟିବ । ସେଥ‌ିପାଇଁ ଭାରତର କରାଯାଇଛି ।

୨। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ପାଳନ ସମ୍ପର୍କରେ କିପରି ବର୍ଣ୍ଣନା କରାଯାଇଛି ?
Answer:

• କରିବାପାଇଁ ରାଷ୍ଟ୍ର ବାଧ୍ୟ ନୁହେଁ । ଏଗୁଡ଼ିକର ପାଳନ ପାଇଁ ନ୍ୟାୟାଳୟର ଆଶ୍ରୟ ନିଆଯାଇ ପାରିବ ନାହିଁ ।
• ଅବଶ୍ୟ ଜନମତକୁ ସମ୍ମାନ ପ୍ରଦର୍ଶନ କରି ପ୍ରତ୍ୟେକ ସରକାର ଏହି ନିର୍ଦ୍ଦେଶାବଳୀ ପାଳନ କରିବାକୁ ଉଦ୍ୟମ କରିଥାଆନ୍ତି ।

୩। ମୌଳିକ ଅଧୂର ଓ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ କେଉଁ କେଉଁ ମୂଳଦୁଆ ପ୍ରସ୍ତୁତ କରିଥାଏ ?
Answer:

• ମୌଳିକ ଅଧ୍ୟାର ରାଜନୈତିକ ଗଣତନ୍ତ୍ର ପାଇଁ ମୂଳଦୁଆ ପ୍ରସ୍ତୁତ କରିଥାଏ ।
• ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ଗଣତନ୍ତ୍ରର ମୂଳଦୁଆ ପ୍ରସ୍ତୁତ କରିଥାଏ ।

୪ । କେଉଁ ଅତ୍‌ରଗୁଡ଼ିକୁ ସରକାର ସମ୍ମାନ ପ୍ରଦର୍ଶନ କରିବାକୁ ବାଧ୍ୟ ଅଟନ୍ତି ଓ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀକୁ ସରକାର କିପରି କାର୍ଯ୍ୟକାରୀ କରିଥା’ନ୍ତି ?
Answer:

• ମୌଳିକ ଅସ୍କାରଗୁଡ଼ିକୁ ସମ୍ମାନ ପ୍ରଦର୍ଶନ କରିବାକୁ ସରକାର ବାଧ୍ୟ ଅଟନ୍ତି ।
• ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀକୁ ସରକାର ପାଳନ କରିବାକୁ ଆଇନତଃ ବାଧ୍ୟ । କେବଳ ଏହି ନିର୍ଦ୍ଦେଶାବଳୀ ପଛରେ ଜନମତର ଗୁରୁତ୍ୱକୁ ଉପଲବ୍ଧି କରି ସରକାର ଏହାକୁ କାର୍ଯ୍ୟକାରୀ କରାନ୍ତି ।

୫ । ମୌଳିକ ଅଧ୍ୟାର ବ୍ୟକ୍ତିର ସୁରକ୍ଷାର ଏକ ପ୍ରାଚୀର ରୂପେ କିପରି କାର୍ଯ୍ୟ କରୁଛି ଓ କ’ଣ ଭାରତରେ ‘ଜନମଙ୍ଗଳ ରାଷ୍ଟ୍ର’ ପ୍ରତିଷ୍ଠା କରିବାରେ ସହାୟକ ହେଉଛି ?
Answer:

•  ଦେଶ ଯେପରି ପୋଲିସ୍ ରାଷ୍ଟ୍ରରେ ପରିଣତ ନ ହେବ, ସେଥ‌ିପାଇଁ ମୌଳିକ ଅଧ୍ୟାର ବ୍ୟକ୍ତିର ସୁରକ୍ଷାର ପ୍ରାଚୀର ଭଳି କାର୍ଯ୍ୟ କରୁଛି ।.
• ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ଭାରତରେ ‘ଜନମଙ୍ଗଳ ରାଷ୍ଟ୍ର’ ପ୍ରତିଷ୍ଠା କରିବାରେ ସାହାଯ୍ୟ କରୁଛି ।

୬ | ସମ୍ବିଧାନର ଧାରା ୪୧ରୁ ଧାରା ୪୩ ମଧ୍ୟରେ ନାଗରିକମାନଙ୍କୁ କେଉଁ କେଉଁ ସାମାଜିକ ନିରାପତ୍ତା ପ୍ରଦାନ କରାଯାଇଛି ?
Answer:

• ସମ୍ବିଧାନର ଧାରା ୪୧ରୁ ଧାରା ୪୩ ମଧ୍ୟରେ ବେକାର, ବୃଦ୍ଧ, ଅକର୍ମଣ୍ୟ ଓ ରୁଗ୍ଣ ଲୋକମାନଙ୍କ ପାଇଁ ରାଷ୍ଟ୍ର ସମସ୍ତ ସହାୟତା ଓ ସାହାଯ୍ୟ ପ୍ରଦାନ କରୁଛି ।
• କାର୍ଯ୍ୟ କ୍ଷେତ୍ରରେ ଶ୍ରମିକମାନଙ୍କର ଅବସର ବିନୋଦନ ପାଇଁ ଅନୁକୂଳ ବ୍ୟବସ୍ଥା କରିବା ସହି ତ ଶିଳ୍ପାନୁ ଷ୍ଠାନ ପରିଚାଳନାରେ ଦିଆଯାଉଛି ।

Objective Type Questions With Answers
A ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।

୧। ଭାରତ ସମ୍ବିଧାନର କେଉଁ ଭାଗ ଓ କେ ଉଁ ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ମଧ୍ୟରେ ବିଷୟରେ ଉଲ୍ଲେଖ କରାଯାଇଛି ?
Answer:
ଭାରତର ସମ୍ବିଧାନର ଚତୁର୍ଥ ଭାଗରେ ଧାରା ୩୬ରୁ ଧାରା ୫୧ ମଧ୍ୟରେ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ବିଷୟରେ ଉଲ୍ଲେଖ କରାଯାଇଛି ।

୨। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀକୁ କାର୍ଯ୍ୟକାରୀ କରିବା କେଉଁମାନଙ୍କର ମୌଳିକ କର୍ତ୍ତବ୍ୟ ?
Answer:
ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀକୁ କାର୍ଯ୍ୟକାରୀ କରିବା କେନ୍ଦ୍ର ଓ ରାଜ୍ୟ ସରକାରଙ୍କର ମୌଳିକ କର୍ତ୍ତବ୍ୟ।

୩ । ମୌଳିକ ଅଧିକାର କେଉଁ କ୍ଷେତ୍ରରେ ମୂଳଦୁଆ ପକାଇଥାଏ ।
Answer:
ମୌଳିକ ଅଧିକାର କେଉଁ କ୍ଷେତ୍ରରେ ମୂଳଦୁଆ ପାଇଁ ମୂଳଦୁଆ ପକାଇଥାଏ ।

୪। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ କେଉଁ କ୍ଷେତ୍ରରେ ମୂଳଦୁଆ ପକାଇଥାଏ ?
Answer:
ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ଗଣତନ୍ତ୍ରର ମୂଳଦୁଆ ପକାଇଥାଏ ।

୫। କେଉଁ ଲକ୍ଷ୍ୟ ରଖ୍ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ପ୍ରଣୟନ କରାଯାଇଛି ?
Answer:
ରୂପେ ଗଠନ କରିବାର ଲକ୍ଷ୍ୟ ରଖୁ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ପ୍ରଣୟନ କରାଯାଇଛି ।

୬ | ସମ୍ବିଧାନର ଧାରା ୩୮ରେ କ’ଣ ବର୍ଣ୍ଣ ନା କରାଯାଇଛି ?
Answer:
ସମ୍ବିଧାନର ଧାରା ୩୮ରେ କରାଯାଇଛି ଜନସାଧାରଣଙ୍କର ହିତ ପାଇଁ ରାଷ୍ଟ୍ର ଏକ ମହାନ୍ ଜୀବନର ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ସାମାଜକ, ସାମାଜିକ ବ୍ୟବସ୍ଥା ସୃଷ୍ଟି କରିବ; ଯାହାଦ୍ୱାରା ଜାତୀୟ ଜୀବନର ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ସାମାଜକ, ଅର୍ଥନୈତିକ ଓ ରାଜନୈତିକ ନ୍ୟାୟ ପ୍ରତିଫଳିତ ହେବ ।

୭। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀର ଗୁରୁତ୍ବ ଉପରେ ଡକ୍ଟର ଆମ୍ବେଦକର କିଭଳି ମତ ପ୍ରକାଶ କରିଛନ୍ତି ?
Answer:
ନିର୍ଦ୍ଦେଶାବଳୀର ମୂଲ୍ୟବୋଧ ଅଧ‌ିକ ଏବଂ ଏହା ଡକ୍ଟର ଆମ୍ବେଦକରଙ୍କ ମତରେ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ଅର୍ଥନୈତିକ ଗଣତନ୍ତ୍ର ପ୍ରତିଷ୍ଠାରେ ସହାୟକ ହୋଇଥାଏ ।

୮। ସରକାର ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ପାଳନ କରିବାରେ ଆନ୍ତରିକତା ନ ଦେଖାଇଲେ କ’ଣ ହୁଏ ?
Answer:
ସରକାର ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ପାଳନ କରିବାର ଆନ୍ତରିକତା ନ ଦେଖାଇଲେ, ଲୋକପ୍ରିୟତା ହରାଇଥା’ନ୍ତି ।

୯। ଭାରତ ସମ୍ବିଧାନର ୭୩ତମ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ କେଉଁ ସୁଯୋଗ ସୃଷ୍ଟି କରାଯାଇଛି ?
Answer:
ଭାରତ ସମ୍ବିଧାନର ୭୩ତମ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ ପଞ୍ଚାୟତଗୁଡ଼ିକୁ ଅଧିକ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇ ସେଗୁଡ଼ିକୁ ଲୋକାଭିମୁଖୀ କରାଯାଇଛି ।

୧୦ । ୭୪ତମ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ କାହାକୁ ଅଧ୍ଵ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ?
Answer:
୭୪ତମ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ ପୌର ପାଳିକାଗୁଡ଼ିକୁ ଅଧିକ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ।

B ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।

୧। ଦରିଦ୍ର ଶ୍ରେଣୀର ବ୍ୟକ୍ତିଙ୍କୁ ମାଗଣା ଆଇନ ସହାୟତା ଯୋଗାଇ ଦିଆଯିବା ପାଇଁ ସମ୍ବିଧାନର କେଉଁ ଧାରାରେ କୁହାଯାଇଛି ?
୨। ସମ୍ବିଧାନର କେଉଁ ଭାଗରେ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ଉଲ୍ଲେଖ କରାଯାଇଛି ?
୩। ଜାତୀୟ ଜୀବନର ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ସାମାଜିକ, ହେବାପାଇଁ ସମ୍ବିଧାନର କେଉଁ ଧାରାରେ କୁହାଯାଇଛି ?
୪। ସମ୍ବିଧାନର କେଉଁ ସଂଶୋଧନ ଆଇନ ବଳରେ ପଞ୍ଚାୟତଗୁଡ଼ିକୁ ଅର୍ଧକ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ?
୫। ୭୪ତମ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ କାହାକୁ ଅଧ୍ଵକ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ?
୬ । ସରକାର କେଉଁ ଯୋଜନା ମାଧ୍ୟମରେ ଦେଶରେ ବିଭିନ୍ନ ବିକାଶମୂଳକ କାର୍ଯ୍ୟକ୍ରମ କାର୍ଯ୍ୟକାରୀ କରଛନ୍ତି ?
୭। ସମ୍ବିଧାନର ୨୫ ତମ ସଂଶୋଧନ କାହା ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଥିଲା ?
୮। କୁଟୀର ଶିଳ୍ପର ପ୍ରତିଷ୍ଠା ଓ ପ୍ରସାର କରାଯିବା କେଉଁ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ?

Answers:
୧ । ଧାରା ୩୯
୨ । ୪ର୍ଥ ଭାଗ
୩ । ଧାରା -୩୮
୪ । ୭୩ ତମ
୫ । ପୌରପାଳିକା
୬ । ପଞ୍ଚବାର୍ଷିକ ଯୋଜନା
୭ । ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ
୮ । ଗାନ୍ଧିବାଦୀ

C ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

୧। ସମ୍ବିଧାନର ___________ ଧାରାରେ ଜାତୀୟ ସମ୍ପଭିର ସୁଷମ ବର୍ଣ୍ଣନ ବିଷୟରେ କୁହାଯାଇଛି ।
Answer:
ଚତୁର୍ଥ

୨। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ __________ ଆଇନତଃ ବାଧ୍ୟ ନୁହେଁ ।
Answer:
ରାଷ୍ଟ୍ର,

୩ । ______________କୁ ସମ୍ମାନ ପ୍ରଦର୍ଶନ କରି ପ୍ରତ୍ୟେକ ସରକାର ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ପାଳନ କରିବାକୁ ଉଦ୍ୟମ କରିଥାଆନ୍ତି ।
Answer:
ଜନମତ

୪। ମୌଳିକ ଅଧିକାର ଯୋଗୁଁ ନାଗରିକମାନଙ୍କର _________________ ଭିତ୍ତିଭୂମି ସୁଦୃଢ଼ ହୋଇଥାଏ ।
Answer:
ରାଜନୈତିକ

୫। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀର ସୀମା _________________ ।
Answer:
ବ୍ୟାପକ

୬ | ଭାରତର ସମ୍ବିଧାନ ____________ ଚିନ୍ତାଧାରାଦ୍ୱାରା ପ୍ରଭାବିତ ହୋଇଛି ।
Answer:
ସମାଜବାଦୀ

୭। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀରେ ______________ ଚିନ୍ତାଧାରା ପ୍ରତିଫଳିତ ହୋଇଛି ।
Answer:
ସମାଜବାଦୀ

୮। ସମ୍ବିଧାନର _________________ ଧାରାରେ ଜାତୀୟ ସମ୍ପତ୍ତିକୁ ନ୍ୟାୟୋଚିତ ଭାବେ ବଣ୍ଟନ କରାଯିବ ବୋଲି ବର୍ଣ୍ଣିତ ହୋଇଛି ।
Answer:
୩୯

୯ । କୁଟୀର ଶିଳ୍ପର ପ୍ରତିଷ୍ଠା ଓ ପ୍ରସାର କରାଯିବା _____________ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ।
Answer:
ଗାନ୍ଧିବାଦୀ

୧୦ । ଭାରତରେ ସର୍ବତ୍ର ସମାନ ପ୍ରକାରର ଦେୱାନୀ ଆଇନ ବର୍ଣ୍ଣନା କରାଯାଇଛି ।
Answer:
ଉଦାରବାଦୀ

୧୧ । ଶିଶୁ ଓ ଯୁବକ ଏବଂ ଯୁବତୀମାନଙ୍କୁ ଶୋଷଣମୁକ୍ତ କରାଯିବାପାଇଁ ____________ ନିର୍ଦ୍ଦେଶାବଳୀରେ ବର୍ଣ୍ଣନା କରାଯାଇଛି ।
Answer:
ସମାଜବାଦୀ

୧୨ । ଆଧୁନିକ ବୈଜ୍ଞାନିକ ପ୍ରଣାଳୀରେ କୃଷି ଓ ପଶୁପାଳନ କ୍ଷେତ୍ର ରେ ଉନ୍ନତି କରାଯିବାପାଇଁ ___________ ନିର୍ଦ୍ଦେଶାବଳୀରେ ବର୍ଣ୍ଣନା କରାଯାଇଛି ।
Answer:
ଉଦାରବାଦୀ

୧୩ । __________________ ଙ୍କ ମତରେ ଅର୍ଥନୈତିକ ଗଣତନ୍ତ୍ର ପ୍ରଚଳିତ ହେବା ଗାନ୍ଧିବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀ ସହାୟକ ହୋଇଥାଏ ।
Answer:
ଡକ୍ଟର ଆମ୍ବେଦକର

୧୪। ________________ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀକୁ ‘ମହନୀୟ ଆକାଂକ୍ଷା’ ବୋଲି ଅଭିହିତ କରିଥିଲେ ।
Answer:
ଆଇଭର ଜେନିଙ୍ଗସ୍‌

D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓ ) ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (X) ଚିହ୍ନ ଦିଅ ।

୧। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀକୁ କାର୍ଯ୍ୟକାରୀ କରିବା କେନ୍ଦ୍ର ଓ ରାଜ୍ୟ ସରକାରଙ୍କ ମୌଳିକ କର୍ତ୍ତବ୍ୟ ।
୨ । ମୌଳିକ କର୍ତ୍ତବ୍ୟ ସାମାଜିକ ଓ ଅର୍ଥନୈତିକ ଗଣତନ୍ତ୍ରର ମୂଳଦୁଆ ମଜବୁତ୍ କରିଥାଏ ।
୩। ଭାରତକୁ ଏକ ସମାଜବାଦୀ ଜନମଙ୍ଗଳ ରାଷ୍ଟ୍ର ଭାବେ ଗଠନ କରିବା ମୌଳିକ ଅଧିକାରର ଲକ୍ଷ୍ୟ ।
୪। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ନାସ୍ତିବାଚକ ।
୫। ମାଗଣା ଆଇନ ସହାୟତା ଯୋଗାଇଦେବା ସମାଜବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଗତ ।
୬। ରାଷ୍ଟ୍ର ଗୋ-ହତ୍ୟା ନିବାରଣ କରିବା ଗାନ୍ଧିବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଗତ ।
୭ । ଭାରତରେ ସର୍ବତ୍ର ସମାନ ପ୍ରକାରର ଦେୱାନୀ ଆଇନ ପ୍ରଚଳିତ ହେବା ଗାନ୍ଧିବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀ ଅନ୍ତର୍ଗତ ।
୮ | ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ଏକ ‘ମହନୀୟ ଆକାଂକ୍ଷା’ ବୋଲି ଆଇଭର ଜେନିଙ୍ଗସ୍ କହିଥିଲେ ।
୯। ରାଷ୍ଟ୍ରରେ ସୁଶାସନ ପ୍ରତିଷ୍ଠା ଲାଗି ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀର ବିଶେଷ ମହତ୍ତ୍ଵ ଓ ଗୁରୁତ୍ଵ ରହିଛି ।
୧୦। ୭୪ ତମ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ ପଞ୍ଚାୟତଗୁଡ଼ିକୁ ଅଧ‌ିକ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ।

Answers:
୧। (√)
୨ । (×)
୩। (×)
୪। (×)
୫। (√)
୬। (√)
୭ । (×)
୮ | (√)
୯। (√)
୧୦। (×)

E ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେଖ ।

F. ରେଖାଙ୍କିତ ପଦକୁ ପରିବର୍ତ୍ତନ କରି ଭ୍ରମ ସଂଶୋଧନ କର ।

୧। ଭାରତର ସମ୍ବିଧାନର ତୃତୀୟ ଭାଗରେ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ ବିଷୟରେ ଉଲ୍ଲେଖ କୁହାଯାଇଛି ।
୨। ମୌଳିକ ଅଧିକାର ସାମାଜିକ ଗଣତନ୍ତ୍ରର ମୂଳଦୁଆ ପକାଇଥାଏ ।
୩। ଦରିଦ୍ର ଲୋକମାନଙ୍କୁ ମାଗଣାରେ ଆଇନ ସେବା ପ୍ରଦାନ କରିବାପାଇଁ ସମ୍ବିଧାନର ଧାରା ୩୮ରେ କୁହାଯାଇଛି ।
୪। ସମ୍ବିଧାନର ୪୪ତମ ସଂଶୋଧନ ଆଇନ ବଳରେ ପଞ୍ଚାୟତଗୁଡ଼ିକୁ ଅଧ‌ିକ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ।
୫। କୁଟୀର ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା କରିବା ସମାଜବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ।
୬। ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀର ସୀମା ସୀମିତ ଅଟେ ।
୭। ଭାରତର ସମ୍ବିଧାନ ଉଦାରବାଦୀ ଚିନ୍ତାଧାରାଦ୍ୱାରା ପ୍ରଭାବିତ ହୋଇଛି ।
୮। ସମ୍ବିଧାନର ୩୮ ଧାରାରେ ଜାତୀୟ ସମ୍ପଭିର ସୁଷମ ବର୍ଣ୍ଣନ ବିଷୟରେ କୁହାଯାଇଛି ।
୯। ଡକ୍ଟ ର ଆମ୍ବେଦକର ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ କହିଥିଲେ ।
୧୦ । ନାଗରି କ ମାନଙ୍କର ମୌଳିକ ଅଧ୍ୟାର ଯୋଗୁଁ ସେମାନଙ୍କର ସାମାଜିକ ଭିତ୍ତିଭୂମି ସୁଦୃଢ଼ ହୋଇଥାଏ ।

Answers:
୧ । ଚତୁର୍ଥ
୨ । ରାଜନୈତିକ
୩ । ୩୯
୪ । ୭୩ତମ
୫ । ଗାନ୍ଧିବାଦୀ
୬ । ବ୍ୟାପକ
୭ । ସମାଜବାଦୀ
୮ । ୩୯
୯ । ଆଇଭର ଜେନିଙ୍ଗସ୍‌
୧୦ । ରାଜନୈତିକ

G ଚାରୋଟି ସମ୍ଭାବ୍ୟ ବିକଳ୍ପ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

1. ନିମ୍ନୋକ୍ତ କେଉଁ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ ପଞ୍ଚାୟତଗୁଡ଼ିକୁ ଅଧ୍ଵ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ?
(A) ୭୧ତମ
(B) ୭୨ତମ
(C) ୭୩ତମ
(D) ୭୪ତମ
Answer:
(C) ୭୩ତମ

2. ନିମ୍ନୋକ୍ତ କେଉଁ ସମ୍ବିଧାନ ସଂଶୋଧନ ଆଇନ ବଳରେ ପୌର ପାଳି କାଗୁଡ଼ିକୁ ଅଧିକ କ୍ଷମତା ପ୍ରଦାନ କରାଯାଇଛି ?
(A) ୬୪ତମ
(B) ୬୮ତମ
(C) ୭୨ତମ
(D) ୭୪ତମ
Answer:
(C) ୭୨ତମ

3. ନିମ୍ନୋକ୍ତ ମଧ୍ଯରୁ କିଏ ମତବ୍ୟକ୍ତ କରିଥିଲେ ଯେ ‘ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀର ମୂଲ୍ୟବୋଧ ଅଧ୍ବକ’ ?
(A) ମହାତ୍ମା ଗାନ୍ଧି
(B) ଜବାହରଲାଲ ନେହେରୁ
(C) ରାଜେନ୍ଦ୍ର ପ୍ରସାଦ
(D) ଡକ୍ଟର ଆମ୍ବେଦକର
Answer:
(D) ଡକ୍ଟର ଆମ୍ବେଦକର

4. ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଉଦାରବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ?
(A) ରାଷ୍ଟ୍ର ଗୋ-ହତ୍ୟା ନିବାରଣ କରିବ
(B) ଶିଶୁ ଓ ଯୁବକ ଏବଂ ଯୁବତୀମାନଙ୍କୁ ଶୋଷଣମୁକ୍ତ
(C) ଆନ୍ତର୍ଜାତିକ କ୍ଷେତ୍ରରେ ଶାନ୍ତି ଓ ନିରାପତ୍ତା ପ୍ରତିଷ୍ଠା ନିମନ୍ତେ ରାଷ୍ଟ୍ର ଉଚିତ ପଦକ୍ଷେପ ଗ୍ରହଣ କରିବ
(D) କୁଟୀର ଶିଳ୍ପର ପ୍ରତିଷ୍ଠା ଓ ପ୍ରସାର କରାଯିବ
Answer:
(C) ଆନ୍ତର୍ଜାତିକ କ୍ଷେତ୍ରରେ ଶାନ୍ତି ଓ ନିରାପତ୍ତା ପ୍ରତିଷ୍ଠା ନିମନ୍ତେ ରାଷ୍ଟ୍ର ଉଚିତ ପଦକ୍ଷେପ ଗ୍ରହଣ କରିବ

5. ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଗାନ୍ଧିବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ନୁହେଁ ?
(A) ଶ୍ରମିକ ଶ୍ରେଣୀର ସ୍ଵାର୍ଥରକ୍ଷା କରାଯିବ
(B) କୁଟୀର ଶିଳ୍ପର ପ୍ରତିଷ୍ଠା ଓ ପ୍ରସାର କରାଯିବ
(C) ସ୍ୱାୟତ୍ତ ଶାସନ ପ୍ରତିଷ୍ଠା ପାଇଁ ଦେଶର ପ୍ରତ୍ୟେକ ଅଞ୍ଚଳରେ ଗ୍ରାମପଞ୍ଚାୟତ ପ୍ରତିଷ୍ଠା କରାଯିବ
(D) ରାଷ୍ଟ୍ର ଗୋହତ୍ୟା ନିବାରଣ କରିବ
Answer:
(A) ଶ୍ରମିକ ଶ୍ରେଣୀର ସ୍ଵାର୍ଥରକ୍ଷା କରାଯିବ

6. ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ସମାଜବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ?
(A) ଔଷଧ ବ୍ୟତୀତ ଅନ୍ୟ କ୍ଷେତ୍ରରେ ନିଶା ଓ ମାଦକ
(B) ରାଷ୍ଟ୍ର ନ୍ୟାୟପାଳିକା ବିଭାଗକୁ କାର୍ଯ୍ୟପାଳିକା
(C) ଆନ୍ତର୍ଜାତିକ କ୍ଷେତ୍ରରେ ଶାନ୍ତ ଓ ନିରାପତ୍ତା ପ୍ରତିଷ୍ଠା
(D) ସମସ୍ତ ନାରୀ ଓ ପୁରୁଷ ନାଗରିକମାନଙ୍କୁ ସମାନ
Answer:
(D) ସମସ୍ତ ନାରୀ ଓ ପୁରୁଷ ନାଗରିକମାନଙ୍କୁ ସମାନ

7.ସମ୍ବିଧାନର ଚତୁର୍ଥ ଭାଗରେ ନିମ୍ନୋକ୍ତ କେଉଁ ଧାରା ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଗାନ୍ଧିବାଦୀ ନିର୍ଦ୍ଦେଶାବଳୀର ଅନ୍ତର୍ଭୁକ୍ତ ନୁହେଁ ?
(A) ଧାରା ୩୬ରୁ ୩୮
(B) ଧାରା ୩୮ରୁ ୪୨
(C) ଧାରା ୩୬ରୁ ୫୧
(D) ଧାରା ୪୧ରୁ ୫୧
Answer:
(C) ଧାରା ୩୬ରୁ ୫୧

8. ମୌଳିକ ଅଧ୍ୟାର ଯୋଗୁଁ ନାଗରିକମାନଙ୍କର ନିମ୍ନୋକ୍ତ କେଉଁ ଭିତ୍ତିଭୂମି ସୁଦୃଢ଼ ହୋଇଥାଏ ?
(A) ରାଜନୈତିକ
(B) ଅର୍ଥନୈତିକ
(C) ସାମାଜିକ
(D) ସାଂସ୍କୃତିକ
Answer:
(A) ରାଜନୈତିକ

9. ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ କାର୍ଯ୍ୟକାରୀ କରିବା କେନ୍ଦ୍ର ଓ ରାଜ୍ୟ ସରକାରଙ୍କର :
(A) ମୌଳିକ ଅଧ୍ୟାର
(B) ମୌଳିକ ଦାୟିତ୍ଵ
(C) ମୌଳିକ କର୍ତ୍ତବ୍ୟ
(D) ମୌଳିକ ଲକ୍ଷ୍ୟ
Answer:
(C) ମୌଳିକ କର୍ତ୍ତବ୍ୟ

10. ସମ୍ବିଧାନର ଧାରା ୩୯ରେ କେଉଁ ନିର୍ଦ୍ଦେଶାବଳୀ ସମ୍ପର୍କରେ ବର୍ଣ୍ଣନା କରାଯାଇଛି ?
(A) ଗାନ୍ଧିବାଦୀ
(B) ସମାଜବାଦୀ
(C) ଉଦାରବାଦୀ
(D) ଆନ୍ତର୍ଜାତୀୟବାଦୀ
Answer:
(B) ସମାଜବାଦୀ

11. କେଉଁଟି ସୁଶାସନର ସାମର୍ଥ୍ୟ ମାପିବାପାଇଁ ଏକ ନିର୍ଭରଯୋଗ୍ୟ ମାପକାଠି ?
(A) ମୌଳିକ ଅଧ୍ୟାର
(B) ମୌଳିକ କର୍ଭବ୍ୟ
(C) ମୌଳିକ ଲକ୍ଷ୍ୟ
(D) ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀ
Answer:
(B) ମୌଳିକ କର୍ଭବ୍ୟ

12. ସମ୍ବିଧାନର କେଉଁ ଧାରାରେ ନାଗରିକମାନଙ୍କୁ ସାମାଜିକ ନିରାପତ୍ତା ପ୍ରଦାନ କରାଯାଇଛି ?
(A) ଧାରା ୩୪
(B) ଧାରା ୩୬
(C) ଧାରା ୪୦ ରୁ ୪୧
(D) ଧାରା ୪୧ ରୁ ୪୩
Answer:
(D) ଧାରା ୪୧ ରୁ ୪୩

13. କେଉଁମାନଙ୍କୁ ମାଗଣା ଆଇନ ସହାୟତା ଯୋଗାଇ ଉଲ୍ଲେଖ ଅଛି ?
(A) କୃଷି ଶ୍ରମିକ
(B) ଶିଳ୍ପ ଶ୍ରମିକ
(C) ଦରିଦ୍ରଶ୍ରେଣୀ
(D) ଶିଶୁ
Answer:
(C) ଦରିଦ୍ରଶ୍ରେଣୀ

14. କିଏ ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ ନିର୍ଦ୍ଦେଶାବଳୀକୁ ‘ମହନୀୟ ଆକାଂକ୍ଷା’ ବୋଲି ଅଭିହିତ କରିଥିଲେ ?
(A) ବି.ଆର୍.ଆମ୍ବେଦକର
(B) ଜବାହରଲାଲ ନେହେରୁ
(C) ଆଇଭର୍‌ ଜେନିଙ୍ଗ୍‌ସ୍
(D) ସର୍ଦାର ପଟେଲ
Answer:
(C) ଆଇଭର୍‌ ଜେନିଙ୍ଗ୍‌ସ୍

15. କେଉଁଟି ନାଗରିକମାନଙ୍କୁ ପ୍ରଦାନ କରାଯାଇଥିବା ସାମାଜିକ ନିରାପତ୍ତା ଅଟେ ?
(A) ବେକାର, ବୃଦ୍ଧ, ଅକର୍ମଣ୍ୟ ଓ ରୁଗ୍ ଣ
(B) ନାରୀ ଓ ପୁରୁଷଙ୍କୁ ସମାନ ପ୍ରକାରର କାର୍ଯ୍ୟ ପାଇଁ
(C) ରାଷ୍ଟ୍ରଦ୍ୱାରା ଗୋହତ୍ୟା ନିବାରଣ
(D) ଆଧୁନିକ ବୈଜ୍ଞାନିକ ପ୍ରଣାଳୀରେ କୃଷି ଓ
Answer:
(A) ବେକାର, ବୃଦ୍ଧ, ଅକର୍ମଣ୍ୟ ଓ ରୁଗ୍ ଣ

16. ସମ୍ବିଧାନର କେଉଁ ଧାରାରେ ଜନସାଧାରଣଙ୍କ ହିତ ପାଇଁ ଏକ ସାମାଜିକ ବ୍ୟବସ୍ଥା ସୃଷ୍ଟି କରିବାପାଇଁ ଉଲ୍ଲେଖ ଅଛି ?
(A) ଧାରା ୩୪
(B) ଧାରା ୩୫
(C) ଧାରା ୩୮
(D) ଧାରା ୩୯
Answer:
(C) ଧାରା ୩୮

17. ରାଷ୍ଟ୍ରରେ ସୁଶାସନ ପ୍ରତିଷ୍ଠା ଲାଗି କେଉଁ ନିର୍ଦ୍ଦେଶାବଳୀର ବିଶେଷ ମହତ୍ତ୍ଵ ଓ ଗୁରୁତ୍ଵ ରହିଛି ?
(A) ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ
(B) ଉଦାରବାଦୀ
(C) ଗାନ୍ଧିବାଦୀ
(D) ସମାଜବାଦୀ
Answer:
(A) ରାଷ୍ଟ୍ରନୀତି ନିୟାମକ

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(d) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(d)

Question 1.
ଗ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କର :

(i) xy², x²y
ସମାଧାନ:
xy² = x × y × y
x²y = x × x × y
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ.

(ii) 6a³b², 8a²b³
ସମାଧାନ:
6a³b² = 2 × 3 × a × a × a × b × b
8a²b³ = 2 × 2 × 2 × a × a × b × b × b
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ.. = 2 × a × a × b × b = 2a²b²

(iii) 12a²b⁴c, 15ab²c³
ସମାଧାନ:
12a²b⁴c = 2 × 2 × 3 × a × a × b × b × b × b × c
15ab²c³ =3 × 5 × a × b × b × c × c × c
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = 3 × a × b × b × c = 3ab²c

(iv) x²y², x³y, xy³
ସମାଧାନ:
x²y² = x × x × y × y
x³y = x × x × x × y
xy³ = x × y × y × y
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = xy

(v) 144x³y⁹z⁷, 108x⁶y⁶z⁶
ସମାଧାନ:
144x³y⁹z⁷ = 2² × 2² × 3² × x³ × y³ × y³ × y³ × z × z⁶
108x⁶y⁶z⁶ = 2² × 3² × 3 × x³ × x³ × y³ × y³ × z⁶
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = 2² × 3² × x³ × y³ × y³ × z⁶ = 36x³y⁶z⁶

Question 2.
ଗ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କର :

(i) x² – 1, x² + x
ସମାଧାନ:
x² – 1 = (x + 1) ( x – 1)
x² + x = x(x + 1)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (x + 1)

(ii) a³ – ab², a³ – b³
ସମାଧାନ:
a³ – ab² = a(a² – b²) = a(a + b) (a – b)
a³ – b³ = ( a – b) (a² + ab + b²)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (a – b)

(iii) 4a² – b², b² – 2ab
ସମାଧାନ:
4a² – b² = (2a)² – (b)² = (2a + b) (2a – b)
b² – 2ab = -(2ab – b²) = -b(2a – b)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (2a – b)

(iv) (x – 1)³, (1 – X)²
ସମାଧାନ:
(x – 1)³ = (x – 1) (x – 1) (x – 1)
(1 – x)² = {-(x – 1)}² = (x – 1)(x – 1)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (x – 1)(x – 1) = (x – 1)²

(v) x² – xy + y², x⁴ + x²y² + y⁴
ସମାଧାନ:
(x² – xy + y²) = (x² – xy + y²)
(x⁴ + x²y² + y⁴) = (x² + xy + y²)(x² – xy + y²)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (x² – xy + y²)

(vi) 6(a² – 4b²), 10(a³ – 8b³)
ସମାଧାନ:
6(a² – 4b²) = 2 × 3 {(a)² – (2b)²}
= 2 × 3 (a + 2b) (a- 2b) 10(a³ – 8b³)
= 2 × 5 {(a)³ – (2b)³}
= 2 x 5 (a – 2b) (a² + 2ab + 4b²)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = 2(a – 2b)

(vii) x² + 7x + 12, x² + 9x + 20
ସମାଧାନ:
x² + 7x + 12 = x² + 4x + 3x + 12
= x (x + 4) + 3 (x + 4)
= (x + 4) (x + 3)
x² + 9x + 20 = x² + 5x + 4x + 20
= x (x + 5) + 4(x + 5)
= (x + 5) ( x + 4)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (x + 4)

(viii) 4x³ – 9x, 16x³ + 54, 2x² + 5x + 3
ସମାଧାନ:
4x³ – 9x = x (4x² – 9) = x {(2x)² – (3)²} = x (2x + 3)(2x – 3)
16x³ + 54 = 2(8x³ + 27) = 2{(2x)³ + (3)³}
= 2 (2x + 3) (4x² – 6x + 9)
2x² + 5x + 3 = 2x² + 3x + 2x + 3
= x (2x + 3) + 1(2x + 3) = (2x + 3) (x + 1)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (2x + 3)

(ix) a² – b² – c² – 2bc, a² + b² – c² + 2ab
ସମାଧାନ:
a² – b² – c² + 2bc = a² – (b² + c² – 2bc) = (a)² – (b- c)² = (a + b – c) (a – b + c)
a² + b² – c² + 2ab = (a² + b² + 2ab) – c² = (a + b)² – (c)² = (a + b + c) (a + b – c)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (a + b – c)

(x) a² – b² – c² – 2bc, b² – c² – a² – 2ca, c² – a² – b² – 2ab
ସମାଧାନ:
a² – b² – c² – 2bc = a² – (b² + c² + 2bc) = (a)² – (b + c)² = (a + b + c)(a – b – c)
b² – c² – a² – 2ca = b² – (c² + a² + 2ca) = (b)² – (c + a)² = (b + c + a)(b – c – a)
c² – a² – b² – 2ab = c² – (a² + b² + 2ab) = (c)² – (a + b)² = (c + a + b)(c – a – b)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (a + b + c)

(xi) 8a² – 14 ab + 6b², 15a² + 18ab – 33b², 9a²b – 7ab² – 2b³
ସମାଧାନ:
8a² – 14ab + 6b² = 2(4a² – 7ab + 3b²) = 2 (4a² – 4ab -3ab + 3b²)
= 2 {4a(a – b) -3b(a – b)} = 2(a – b)(4a – 3b)}
15a² + 18ab – 33b² = 15a² + 33ab – 15ab – 33b²
= 3a(5a + 11b) – 3b(5a + 11b) = (5a + 11b)(3a – 3b) = 3(5a + 11b)(a – b)
9a²b – 7ab² – 2b³ = b(9a² – 7ab – 2b²)
= b(9a² – 9ab + 2ab – 2b²) = b{9a (a – b) + 2b(a – b)} = b(a – b) (9a + 2b)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (a – b)

(xii) (a + b) x² – (2a + b) bx + ab², (a- b) x² – (2a – b) bx + ab²
ସମାଧାନ:
(a + b)x² – (2a + b) bx + ab²
= (a + b)x² – {(a + b) + a} bx + ab² = (a + b)x² – (a + b)bx – abx + ab²
= (a + b)x (x – b) – ab(x – b) = (x – b) {(a + b) x – ab}
= (x – b) (ax + bx – ab)
(a- b)x² – (2a – b)bx + ab²
= (a – b)x² – {(a – b) + a} bx + ab² = (a – b)x² – (a – b)bx – abx + ab²
= (a – b) x (x – b) – ab(x – b) = (x – b) (x (a – b) – ab} = (x – b) (ax – bx – ab)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (x – b)

(xiii) c² – 2ab – a² – b², a³ + b³ + c³ – 3abc, b² – 2ca – c² – a²
ସମାଧାନ:
c² – 2ab – a² – b² = c² – (2ab + a² + b²)
= c² – (a² + b² + 2ab) = c² – (a + b)² = {c + (a + b)}{c – (a + b)}
= (c + a + b) (c – a – b) = (a + b + c) (c – a – b)
a³ + b³ + c³ – 3abc = (a + b + c) (a² + b² + c² – ab – bc – ca)
b² – 2ca – c² – a² = b² – (2ca + c² + a²)
= b² – (a² + c² + 2ca) = b² – (a + c)² = {b + (a + c)} {b – (a + c)}
= (b + a + c) (b – a – c) = (a + b + c) (b – a – c)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (a + b + c)

(xiv) a³ – b³ – c³ – 3abc, a² – b² – c² – 2bc
ସମାଧାନ:
a³ – b³ – c³ – 3abc
= a³ + (-b)³ + (-c)³ – 3a (-b) (-c)
= {a + (-b) + (-c)} {a² + (-b)² + (-c)² – a (-b) – (-b) (-c) – (-c) a}
= (a – b – c) (a² + b² + c² + ab – bc + ca)
a² – b² – c² – 2bc = a² – (b² + c² + 2bc) = a² – (b + c)²
= {a + (b + c)} {a – (b + c)} = (a + b + c) (a – b – c)
∴ ନିର୍ଣ୍ଣେୟ ଗ.ସା.ଗୁ. = (a – b – c)

Question 3.
ଲ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କର :

(i) 3a³b, 4a²b
ସମାଧାନ:
3a³b = 3 × a³ × b, 4a²b = 2² × a² × b
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2² × 3 × a³ × b = 12a³b

(ii) 6a²b³, 4a³b⁴
ସମାଧାନ:
6a²b³ = 2 × 3 × a² x b³, 4a³b⁴ = 2² × 3 × a³ × b⁴
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2² × 3 × a³ × b⁴ = 12a³b⁴

(iii) 20a²b³c⁴, 34a³c⁵
ସମାଧାନ:
20a²b³c⁴ = 2² × 5 × a² × b³ × c⁴, 34a³c⁵ = 2 × 17 × a³ × c⁵
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2² × 5 × 17 × a³ × b³ × c⁵ = 340a³b³c⁵

(iv) 3a²b, 4ab², 6ab
ସମାଧାନ:
3a²b= 3 × a² × b, 4ab² = 2² × a × b², 6ab = 2 × 3 × a × b
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2² × 3 × a² × b² = 12a²b²

(v) 25x³y²z², 30x²y³z³, x³y³z²
ସମାଧାନ:
25x³y²z² = 5² × x³ × y² × z², 30x²y³z³ = 2 × 3 × 5 × x² × y³ × z³
x³y³z² = x³ × y³ × z²
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2 × 3 × 5² × x³ × y³ × z³ = 150x³y³z³

Question 4.
ଲ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କର :

(i) a² + ab, ab – b²
ସମାଧାନ:
a² + ab = a(a + b), ab – b² = b (a – b)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = ab(a + b) ( a – b) = ab ( a² – b²)

(ii) 3(x² – y²), 4(x² + xy)
ସମାଧାନ:
3(x² – y²) = 3 ( x + y) (x – y), 4(x² + xy) = 4x ( x + y)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 3 × 4 × x(x + y)(x – y) = 12x (x² – y²)

(iii) x³ + y³, x²y + xy²
ସମାଧାନ:
x³ + y³ = (x + y) (x² – xy + y²), x²y + xy² = xy (x + y)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = xy (x + y)(x² – xy + y²) xy (x³ + y³)

(iv) 6a³b – 12a²b², 8a³ – 64b³
ସମାଧାନ:
6a³b – 12a²b² = 6a²b(a – 2b) = 2 × 3a²b(a – 2b)
8a³ – 64b³ = 8(a³ – 8b³) = 8{(a)³ – (2b)³} = 2³ (a – 2b) (a² + 2ab + 4b²)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2³ × 3 × a² × b(a – 2b) (a² + 2ab + 4b²) = 24a²b (a³ – 8b³)

(v) (x – y)³, x² – y²
ସମାଧାନ:
(x – y)³ = (x – y)³, (x² – y²) = (x + y) ( x – y)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = (x + y) ( x – y)³

(vi) x² – xy, (x – y)², x² – y²
ସମାଧାନ:
x² – xy = x (x – y), (x – y)² = (x – y)², x² – y² = (x + y) (x – y)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = x(x – y)² (x + y)

(vii) 6(a + b)², 8(a² – b²), 12 (a – b)²
ସମାଧାନ:
6(a + b)² = 2x³ (a + b)², 8(a² – b²) = 2³ (a + b)(a – b), 12(a – b)² = 2² × 3 (a – b)²
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2³ × 3 (a + b)² (a – b)² = 24(a² – b²)²

(viii) 2x² + 5x – 3, 4x² – 4x + 1
ସମାଧାନ:
2x² + 5x- 3 = 2x² + 6x – x – 3 = 2x (x + 3) – 1 (x + 3) = (x + 3) (2x – 1)
4x² – 4x + 1 = (2x)² – 2.2x.1 + (1)² = (2x – 1)²
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = (2x – 1)² (x + 3)

(ix) 3a² + 8a + 4, a² + 2a
ସମାଧାନ:
3a² + 8a + 4 = 3a² + 6a + 2a + 4 = 3a (a + 2) + 2 (a + 2) = (a + 2) ( 3a + 2)
a² + 2a = a ( a + 2)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = a(a + 2)(3a + 2)

(x) 6x² – 5x – 6, 4x³ – 12x² + 9x
ସମାଧାନ:
6x² – 5x – 6 = 6x² – 9x + 4x – 6 = 3x (2x – 3) + 2 (2x – 3) = (2x – 3)(3x + 2)
4x³ – 12x² + 9x = x (4x² – 12x + 9) = x {(2x)² – 2.2x.3 + (3)²} = x (2x – 3)²
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = x (2x – 3)² (3x + 2)

(xi) 3x³ + 5x² – 2x, 6x² + 14x + 4, 9^x3 – x
ସମାଧାନ:
3x³ + 5x² – 2x = x (3x² + 5x – 2) = x (3x² + 6x – x – 2)
= x {3x (x + 2) – 1(x + 2)} = x (x + 2) (3x – 1)
6x² + 14x + 4 = 2(3x² + 7x + 2) = 2(3x² + 6x + x + 2)
= 2{3x (x + 2) + 1 (x + 2)} = 2 (x + 2)(3x + 1)
9x³ – x = x (9x² – 1) = x {(3x)² – (1)²} = x(3x + 1) (3x – 1)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 2x (x + 2) (3x + 1) (3x – 1) = 2x (x + 2) (9x² – 1)

(xii) x² + xy + yz + zx, y² + xy + yz + zx, z² + xy + yz + zx
ସମାଧାନ:
x² + xy + yz + zx = x² + xy + zx + yz = x (x + y) + z(x + y) = (x + y) ( x + z)
y² + xy + yz + zx = y² + yz + xy + zx = y (y + z) + x(y + z) = (y + z ) (x + y)
z² + xy + yz + zx = z² + zx + yz + xy = z(z + x) + y(z + x) = (z + x) (y + z)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = (x + y) ( y + z) (z + x)

(xiii) a² – ab – ac + bc, b² – bc – ab + ca, c² – ca – bc + ab
ସମାଧାନ:
a² – ab- ac + bc = a (a – b) – c (a – b) = (a – b) (a – c) = -(a – b)(c – a)
b² – bc – ab + ca = b(b- c)- a(b – c) = (b – c )(b – a) = -(b – c)(a – b)
c² – ca- bc + ab = c(c – a) – b(c – a) = (c – a) (c – b) = -(c – a)(b – c)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = -(a – b) (b – c)(c – a)

(xiv) a² – b² – c² – 2bc, b² – c² – a² – 2ca, c² – a² – b² – 2ab
ସମାଧାନ:
a² – b² – c² – 2bc = a² – (b² + c² + 2bc) = (a)² – (b + c)² = (a + b + c)(a – b – c)
b² – c² – a² – 2ca = b² – (c² + a² + 2ca) = (b)² – (c + a)² = (a + b + c)(b – c – a)
c² – a² – b² – 2ab = c² – (a² + b² + 2ab) = (c)² – (a + b)² = (a + b + c)(c – a – b)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = (a + b + c)(a – b – c)(b – c – a)(c – a – b)

(xv) a⁴ + a²b² + b⁴, a³ + b³, a³ – b³
ସମାଧାନ:
a⁴ + a²b² + b⁴ = (a² + ab + b²) (a² – ab + b²)
a³ + b³ = (a + b) (a² – ab + b²), a³ – b³ = (a – b) (a² + ab +b²)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = (a + b) (a – b) (a² + ab + b²) (a² – ab + b²)
= {(a + b) (a² – ab + b²)} {(a – b) (a² + ab + b²)}
= (a³ + b³) (a³ – b³) = a⁶ – b⁶

(xvi) a⁶ – b⁴, (a + b)³, a² – b²
ସମାଧାନ:
a⁶ – b⁶ = (a³)² – (b³)² = (a³ + b³)(a³ – b³) = (a + b) (a² – ab + b²) (a – b) (a² + ab + b²)
(a + b)³ = (a + b)³, a² – b² = (a + b) (a – b)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = (a + b)³ (a- b) (a² + ab + b²) (a² – ab + b²)

(xvii) a³ + b³ – 1 – 3ab,a³ + (b – 1)³, a² – 2a + 1 – b²
ସମାଧାନ:
a³ + b³ – 1 + 3ab = a³ + b³ + (-1)³ – 3(a) (b) (-1)
= {a + b + (-1)} {a² + b² + (-1)² – ab – b (-1) – (-1) a}
= (a + b – 1) (a² + b² + 1 – ab + b + a)
a³ + (b – 1)³ = {a + (b – 1)} {a² – a (b – 1) + (b – 1)²}
= (a + b – 1) (a² – ab + a + b² – 2b + 1) = (a + b – 1) (a² + b² – ab + a – 2b + 1)
a² – 2a + 1 – b² = (a – 1)² – b² = (a – 1 + b) (a – 1 – b)
= (a + b – 1) (a – b – 1)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = (a + b – 1) (a – b – 1)
(a² + b² + 1 – ab + b + a) (a² + b² – ab + a – 2b + 1)

(xviii) (x – y)³ + (y – z)³ + (z – x)³, (x – y)³ – (z – y)³ – (x – z)³
ସମାଧାନ:
(x – y)³ +(y – z)³ + (z – x)³
ମନେକର x – y = a, y – z = b, z – x = c
a + b + c = x – y + y – z + z – x
⇒ a + b + c = 0 ⇒ a³ + b³ + c³ = 3abc
⇒ (x – y)³ + (y – z)³ + (z – x)³ = 3 (x – y) (y – z) (z – x) (abcର ମାନ ସଂସ୍ଥ।ପନ କଳେ)
(x – y)³ – (z – y)³ – (x – z)³
ମନେକର x – y = a, z – y = b, x – z = c
a – b – c = (x – y) – (z – y) – (x – z) = x – y – z + y – x + z = 0
a – b – c = 0 ହେଲେ a³ – b³ – c³ = 3a (-b) (-c) = 3abc
(x – y)³ – (z – y)³ – (x – z)³ = 3 (x – y) (z – y) (x – z)
= 3(x – y) {-(y – z)} {-(z – x)} = 3 (x – y) (y – z) (z – x)
∴ ନିର୍ଣ୍ଣେୟ ଲ.ସା.ଗୁ. = 3 (x – y) (y – z) (z – x)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(b)

Question 1.
ନିମ୍ନଲିଖତ ସମୀକରଣମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ଦ୍ୱିଘାତ ସମୀକରଣ ନିଶ୍ଚୟ କର ।

(i) 3x² – 4x = -4x + 5
ସମାଧାନ:
ଯେଉଁ ସମୀକରଣର ସର୍ବୋଚ୍ଚ ଘାତ 2 ତାହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ଅଟେ ।
3x² – 4x = -4x + 5 ⇒ 3x² – 5 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(ii) x³ – 2x² + 4 = x³ + 2x
ସମାଧାନ:
x³ – 2x² + 4 = x³ + 2x
⇒ -2x² – 2x + 4 = 0 ⇒ 2x² + 2x – 4 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(iii) x + \(\frac{3}{x}\) = x² (x ≠ 0)
ସମାଧାନ:
x + \(\frac{3}{x}\) = x² + 3 = x³ ⇒ x³ – x² – 3 = 0
(ଏହି ସମୀକରଣଟିର ସର୍ବୋଚ୍ଚ ଘାତ 3 ତେଣୁ ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ ନୁହେଁ ।)

(iv) x + \(\frac{1}{x}\) = 2 (x ≠ 0)
ସମାଧାନ:
x + \(\frac{1}{x}\) = 2 ⇒ \(\frac{x^2+1}{x}\) ⇒ x² + 1 = 2x ⇒ x² – 2x + 1 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(v) (x + 3)² = 0
ସମାଧାନ:
(x + 3)² = 0 ⇒ x² + 6x + 9 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(vi) \(\frac{1}{x}\) x² + \(\frac{3}{2}\) x – \(\frac{5}{4}\) = 0
ସମାଧାନ:
\(\frac{1}{x}\) x² + \(\frac{3}{2}\) x – \(\frac{5}{4}\) = 0
⇒ \(\frac{2 x^2+6 x-5}{4}\) ⇒ 2x² + 6x – 5 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(vii) 3x² = 2x + 7
ସମାଧାନ:
3x² = 2x + 7 ⇒ 3x² – 2x – 7 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(viii) (3x + 2)² – (x + 4)² = (x – 3)
ସମାଧାନ:
(3x + 2)² – (x + 4)² = (x – 3)
⇒ 9x² + 4 + 6x- x² – 16 – 8x = x- 3 ⇒ 8x² – 2x – 12 = x – 3
⇒ 8x² – 3x – 9 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(ix) 7x² + 9 = 0
ସମାଧାନ:
7x² + 9 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

(x) 4x = 3 + 6x²
ସମାଧାନ:
4x = 3 + 6x² ⇒ 6x² – 4x + 3 = 0 (ଏହା ଏକ ଦ୍ଵିଘାତ ସମୀକରଣ)

Question 2.
ପ୍ରତ୍ୟେକ ସମୀକରଣ ପାର୍ଶ୍ଵରେ ଥ‌ିବା ସଂଖ୍ୟାମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ କେଉଁ ସଂଖ୍ୟାଦ୍ଵାରା ସମୀକରଣ ସିଦ୍ଧ ହେବ ନିର୍ଣ୍ଣୟ କର ।
ପ୍ରତ୍ୟେକ ଦ୍ୱିଘାତ ସମୀକରଣ ତାଙ୍କର ମୂଳଦ୍ଵାରା ସିଦ୍ଧ ହୁଅନ୍ତି ।

(i) x² – 3x = 0 (0, 1, 2, 3)
ସମାଧାନ:
x² – 3x = 0 ⇒ x (x – 3) = 0
⇒ x = 0 ବା x = 3 ∴ ଏହି ସମୀକରଣଟିର ମୂଳଦ୍ଵୟ 0 ଓ 3 ‍।
ବିକଳ୍ପ ସମାଧାନ:
ଏଠାରେ ଯେଉଁ ସଂଖ୍ୟାଦ୍ୱୟ ପାଇଁ ସମୀକରଣଟି ‘0’ ହେବ ସେହି ସଂଖ୍ୟାଦ୍ବୟ ଦ୍ୱିଘାତ ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।
x² – 3x = 0 (0 ଓ 3 ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।)

(ii) 3x² – 12 = 0 (1, -1, 2, -2)
ସମାଧାନ:
3x² – 12 = 0 ⇒ 3x² = 12 ⇒ x² = 4
⇒ x = ±√4 = ± 2 ∴ ଏହି ସମୀକରଣଟିର ମୂଳଦ୍ଵୟ 2 ଓ -2 ‍।
ବିକଳ୍ପ ସମାଧାନ:
ଏଠାରେ ଯେଉଁ ସଂଖ୍ୟାଦ୍ୱୟ ପାଇଁ ସମୀକରଣଟି ‘0’ ହେବ ସେହି ସଂଖ୍ୟାଦ୍ବୟ ଦ୍ୱିଘାତ ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।
3x² – 12 = 0 (2 ଓ -2 ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।)

(iii) x² – 3x + 2 = 0 (0, 1, 2, 3)
ସମାଧାନ:
x² – 3x + 2 = 0 ⇒ x² – 2x – x + 2 = 0
⇒ x (x – 2) – 1 (x – 2) = 0
⇒ (x – 2)(x + 1) ⇒ x – 2 = 0 ବା x – 1 = 0 ⇒ x = 2 ବା x = 1
∴ ଏହି ସମୀକରଣଟିର ମୂଳଦ୍ଵୟ 2 ଓ 1 ‍।
ବିକଳ୍ପ ସମାଧାନ:
ଏଠାରେ ଯେଉଁ ସଂଖ୍ୟାଦ୍ୱୟ ପାଇଁ ସମୀକରଣଟି ‘0’ ହେବ ସେହି ସଂଖ୍ୟାଦ୍ବୟ ଦ୍ୱିଘାତ ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।
x² – 3x + 2 = 0 (2 ଓ 1 ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।)

(iv) x² + √2x – 4 = 0 (√2, -√2, 2√2, -2√2)
ସମାଧାନ:
x² + √2x – 4 = 0 ⇒ x2 + 2√2x – √2x – 4 = 0
⇒ x (x + 2√2) – √2 (x + 2√2 ) = 0
(x + 2√2) (x – √2) = 0 ⇒ x + 2√2 =0 ବା x – √2 = 0
x = -2√2, x = √2
∴ ଏହି ସମୀକରଣଟିର ମୂଳଦ୍ଵୟ -2√2 ଓ √2 ‍।
ବିକଳ୍ପ ସମାଧାନ:
ଏଠାରେ ଯେଉଁ ସଂଖ୍ୟାଦ୍ୱୟ ପାଇଁ ସମୀକରଣଟି ‘0’ ହେବ ସେହି ସଂଖ୍ୟାଦ୍ବୟ ଦ୍ୱିଘାତ ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।
x² + √2x – 4 = 0 (-2√2 ଓ √2 ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।)

(v) x² – x – 2 = 0 (1, 0, -1, 2)
ସମାଧାନ:
x² – x – 2 ⇒ x² – 2x + x – 2 = 0 ⇒ x (x – 2) + 1(x – 2) = 0
⇒ (x – 2) (x + 1) = 0 ⇒ x – 2 = 0 ବା x + 1 = 0 ⇒ x = 2 ବା x = -1
∴ ଏହି ସମୀକରଣଟିର ମୂଳଦ୍ଵୟ 2 ଓ -1 ‍।
ବିକଳ୍ପ ସମାଧାନ:
ଏଠାରେ ଯେଉଁ ସଂଖ୍ୟାଦ୍ୱୟ ପାଇଁ ସମୀକରଣଟି ‘0’ ହେବ ସେହି ସଂଖ୍ୟାଦ୍ବୟ ଦ୍ୱିଘାତ ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।
x² – x – 2 = 0 (2 ଓ -1 ସମୀକରଣକୁ ସିଦ୍ଧ କରୁଛି ।)

Question 3.
ସମାଧାନ କର :

(i) 7x² = \(\frac{1}{28}\)
ସମାଧାନ:
7x² = \(\frac{1}{28}\)
⇒ x² = \(\frac{1}{196}\)
⇒ x = ± \(\sqrt{\frac{1}{196}}=\pm \frac{1}{14}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ \(\frac{1}{14}\) ଓ \(\frac{-1}{14}\) ।

(ii) 5x² = 3x
ସମାଧାନ:
5x² = 3x
⇒ 5x² – 3x = 0
⇒ x (5x – 3) = 0
⇒ x = 0 କିମ୍ବ। 5x – 3 = 0
⇒ x = 0 କିମ୍ବ। x = \(\frac{3}{4}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ 0 ଓ \(\frac{3}{4}\) ।

(iii) x² – 3x + 2 = 0
ସମାଧାନ:
x² – 3x + 2 = 0
⇒ x² – 2x – x + 2 = 0
⇒ x (x – 2) – 1 (x – 2) = 0
⇒ (x – 2) (x – 1) = 0
⇒ x -2 = 0 କିମ୍ବ। x – 1 = 0
⇒ x = 2 କିମ୍ବ। x = 1
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ 2 ଓ 1

(iv) (x + 1) (x + 2) = 30
ସମାଧାନ:
(x + 1) (x + 2) = 30
⇒ x²  + x + 2x + 2 – 30 = 0
⇒ x²  + 3x – 28 = 0
⇒ x²  + 7x – 4x – 28 = 0
⇒ x (x + 7) – 4 (x + 7) = 0
⇒ (x + 7) (x – 4) = 0
⇒ x + 7 = 0 କିମ୍ବ। x – 4 = 0
⇒ x = -7 କିମ୍ବ। x = 4
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ -7 ଓ 4

(v) √3x² – x – 2√3 = 0
ସମାଧାନ:
√3x² – x – 2√3 = 0
⇒ √3x² – 3x + 2x – 2√3 = 0
⇒ √3x (x – √3) + 2 (x – √3) = 0
⇒ (x – √3)(√3x + 2) = 0
⇒ x – √3 = 0 √3x +2 = 0
⇒ x = √3 କିମ୍ବ। x = \(\frac{-2}{\sqrt{3}}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ √3 ଓ \(\frac{-2}{\sqrt{3}}\)

(vi) 2x² – 5x – 3 = 0
ସମାଧାନ:
2x² – 5x – 3 = 0
⇒ 2x² – 6x + x – 3 = 0
⇒ 2x (x – 3) + 1 (x – 3) = 0
⇒ (x – 3) (2x + 1) = 0
⇒ x – 3 = 0 କିମ୍ବ। 2x + 1 = 0
⇒ x = 3 କିମ୍ବ। x = \(\frac{-1}{2}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ 3 ଓ \(\frac{-1}{2}\) 

(vii) x² + ax = 2a²
ସମାଧାନ:
x² + ax = 2a²
⇒ x² + ax – 2a² = 0
⇒ x² + 2ax – ax – 2a² = 0
⇒ x (x + 2a) – a (x + 2a) = 0
⇒ (x + 2a) (x – a) = 0
⇒ x + 2a = 0 କିମ୍ବ। x – a = 0
⇒ x = -2a କିମ୍ବ। x = a
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ a ଓ -2a

(viii) x² + 2ax + a² – b² = 0
ସମାଧାନ:
x² + 2ax + a² – b² = 0
⇒ x² + 2ax + a² = b²
⇒ (x + a)² = b²
⇒ x + a = ± √b²
⇒ x + a = ± b
∴ x + a = b କିମ୍ବ। x + a = -b
⇒ x = b – a କିମ୍ବ। x = -(a + b)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ (b – a) ଓ -(a + b)

Question 4.
ସମାଧାନ କର :

(i) \(\frac{3}{x+2}-\frac{1}{x}=\frac{4}{15}\)
ସମାଧାନ:
⇒ \(\frac{3 x-(x+2)}{x(x+2)}=\frac{4}{15}\)
⇒ \(\frac{3 x-x-2}{x^2+2 x}=\frac{4}{15}\)
⇒ 4 (x² + 2x) = 15 (2x – 2)
⇒ 4x² + 8x = 30x – 30
⇒ 4x² + 8x – 30x + 30 = 0
⇒ 4x² – 22x + 30 = 0
⇒ 4x² – 12x – 10x + 30 = 0
⇒ 4x (x – 3) – 10 (x – 3) = 0
⇒ (x – 3) (4x – 10) = 0
⇒ x – 3 = 0 କିମ୍ବ। 4x – 10 = 0
⇒ x = 3 କିମ୍ବ। x = \(\frac{10}{4}=\frac{5}{2}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ 3 ଓ \(\frac{5}{2}\)

(ii) \(\frac{5}{3 x-2}+\frac{3}{x+2}\) = 1
ସମାଧାନ:
⇒ \(\frac{5(x+2)+3(3 x-2)}{(3 x-2)(x+2)}\) = 1
⇒ 5x + 10 + 9x – 6 = (3x – 2) (x + 2)
⇒ 14x + 4 = 3x² + 6x – 2x – 4
⇒ 3x² + 4x – 4 = 14x + 4
⇒ 3x² + 4x – 14x – 4 – 4 = 0
⇒ 3x² – 10x – 8 = 0
⇒ 3x² – 12x + 2x – 8 = 0
⇒ 3x (x – 4) + 2 (x – 4) = 0
⇒ (x – 4) (3x + 2) = 0
⇒ x – 4 = 0 ବା 3x + 2 = 0
⇒ x = 4 ବା x = \(-\frac{2}{3}\)
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ 4 ଓ \(-\frac{2}{3}\)

(iii) \(\frac{x+1}{x+3}-\frac{1-x}{3+2 x}\) = 2
ସମାଧାନ:
⇒ \(\frac{(x+1)(2 x+3)-(x+3)(1-x)}{(x+3)(2 x+3)}\) = 2
⇒ \(\frac{\left(2 x^2+3 x+2 x+3\right)-\left(x-x^2+3-3 x\right)}{2 x^2+6 x+3 x+9}\)
⇒ (2x² + 5x + 3) – (- x² – 2x + 3) = 2 (2x² + 9x + 9)
⇒ 2x² + 5x + 3 + x² + 2x- 3 = 4x² + 18x + 18
⇒ 3x² + 7x – 4x² – 18x – 18 = 0
⇒ -x² – 11x – 18 = 0
⇒ x² + 11x + 18 = 0
⇒ x² + 9x + 2x + 18 = 0
⇒ x (x + 9) + 2 (x + 9) = 0
⇒ (x + 9) (x + 2) = 0
⇒ x + 9 = 0 ବା x + 2 = 0
⇒ x = -9 ବା x = -2
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ -9 ଓ -2

(iv) \(\frac{x}{x+1}+\frac{x+1}{x}=\frac{5}{2}\)
ସମାଧାନ:
⇒ \(\frac{x^2+(x+1)^2}{x(x+1)}=\frac{5}{2}\)
⇒ \(\frac{x^2+x^2+2 x+1}{x^2+x}=\frac{5}{2} \Rightarrow \frac{2 x^2+2 x+1}{x^2+x}=\frac{5}{2}\)
⇒ 5(x² + x) = 2 (2x² + 2x + 1)
⇒ 5x² + 5x = 4x² + 4x + 2
⇒ 5x² – 4x² + 5x – 4x – 2 = 0
⇒ x² + x – 2 = 0
⇒ x² + 2x – x – 2 = 0
⇒ x (x + 2) – 1 (x + 2) = 0
⇒ (x – 1) (x + 2) = 0
⇒ x – 1 = 0 ବା x + 2 = 0
⇒ x = 1 ବା x = -2
∴ ନିର୍ଣ୍ଣେୟ ସମାଧାନ 1 ଓ -2

Question 5.
(i) x² – 7x + a = 0 ସମୀକରଣର ଗୋଟିଏ ବୀଜ 3 ହେଲେ, aର ମାନ ନିର୍ଣ୍ଣୟ କର ଓ ସମୀକରଣର ଅନ୍ୟ ବୀଜଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
x² – 7x + a = 0 ସମୀକରଣର ଗୋଟିଏ ବୀଜ 3।
⇒ (3)² – 7(3) + a = 0 ⇒ 9 – 21 + a = 0
⇒ a – 12 = 0⇒ a = 12
a = 12 ହେଲେ ସମୀକରଣଟି x² – 7x + 12 = 0
⇒ x² – 4x – 3x + 12 = 0
⇒ x (x – 4) – 3(x – 4) = 0 ⇒ (x – 3) (x – 4) = 0
⇒ x – 3 = 0 କିମ୍ବା x – 4 = 0 ⇒ x = 3 କିମ୍ବା x = 4
∴ ସମୀକରଣଟିର ଅନ୍ୟ ବୀଜ 4 । ∵ ପୂର୍ବରୁ ଗୋଟିଏ ବୀଜ 3 ଦତ୍ତ ଅଛି ।
∴ a ର ମାନ 12 ଏବଂ ସମୀକରଣର ଅନ୍ୟ ବୀଜଟି 4 ।

(ii) x² + ax – 15 = 0) ସମୀକରଣର ଗୋଟିଏ ବୀଜ 5 ହେଲେ, ଥର ମାନ ନିର୍ଣ୍ଣୟ କର ଓ ସମୀକରଣର ଅନ୍ୟ ବୀଜଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
x² + ax – 15 = 0 ସମୀକରଣର ଗୋଟିଏ ବୀଜ 5 ।
⇒ (5)² + a(5) – 15 = 0 ⇒ 25 + 5a – 15 = 0
⇒ 10 + 5a = 0 ⇒ 10 = -5a ⇒ a = \(\frac{10}{-5}\) = -2
aର ମାନ – 2 ହେଲେ ସମୀକରଣଟି x² – 2x – 15 = 0 ⇒ x² – 5x + 3x – 15 = 0
⇒ x (x – 5) + 3 (x – 5) = 0 ⇒ (x – 5) (x + 3) = 0
⇒ x – 5 = 0 ବା x + 3 = 0 ⇒ x = 5 ବା x = -3
∴ ସମୀକରଣର ଅନ୍ୟ ବୀଜଟି -3 ∵ ଗୋଟିଏ ବୀଜ 5 ଦତ୍ତ ଅଛି ।
∴ aର ମାନ – 2 ଓ ସମୀକରଣର ଅନ୍ୟ ବୀଜଟି – 3 ।

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 4 ବୀଜଗାଣିତିକ ସମୀକରଣ Ex 4(c)

Question 1.
ଦୁଇଗୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟାର ବର୍ଗର ସମଷ୍ଟି 221 ହେଲେ ସଂଖ୍ୟାଦ୍ୱୟ ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର କ୍ରମିକ ଗଣନ ସଂଖ୍ୟା ଦ୍ୱୟ x ଓ x + 1 ।
ପ୍ରଶାନୁସାରେ x² + (x + 1)² = 221 ⇒ x² + x² + 2x + 1 = 221
⇒ 2x² + 2x + 1 – 221 = 0 ⇒ 2x² + 2x – 220 = 0
⇒ x² + x – 110 = 0 (ଉଭୟ ପାର୍ଶ୍ଵକୁ 2 ଦ୍ବାରା ଭାଗକଲେ ।)
⇒ x² + 11x – 10x – 110 = 0 ⇒ x (x + 11) − 10 (x + 11) = 0
⇒ (x + 11) (x – 10) = 0 ⇒ x + 11 = 0 ବା x – 10 = 0
⇒ x = -11 ବା x = 10 ଏଠାରେ x = -11 (ଋଣାତ୍ମକ) । ତେଣୁ x = 10 ହେବ
ଗୋଟିଏ ଗଣନ ସଂଖ୍ୟା 10 ହେଲେ ଅନ୍ୟଟି = 10 + 1 = 11
∴ କ୍ରମିକ ସଂଖ୍ୟାଦ୍ଵୟ 10 ଏବଂ 11 ।

Question 2.
କୌଣସି ସଂଖ୍ୟା ତାହାର ବର୍ଗ ସହିତ ସମାନ ହେଲେ ସଂଖ୍ୟାଟି ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର ସଂଖ୍ୟାଟି x
ପ୍ରଶ୍ନନୁସାରେ x² = x ⇒ x² – x = 0 ⇒ x(x – 1) = 0
⇒ x = 0 ବା x – 1 = 0 ⇒ x = 0 ବା 1
∴ ସଂଖ୍ୟାଟି 0 ବା 1

Question 3.
51 କୁ ଏପରି ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କର ଯେପରି ଭାଗ ଦ୍ବୟର ଗୁଣଫଳ 378 ହେବ ।
ସମାଧାନ:
ସମାଧାନ ମନେକର ଗୋଟିଏ ସଂଖ୍ୟା = x ଓ ଅନ୍ୟ ସଂଖ୍ୟାଟି = 51 – x
ପ୍ରଶ୍ନନୁସାରେ, x (51 – x) = 378 = 0 ⇒ 51 – x² = 378 ⇒ x² – 51x + 378 = 0
⇒ x² – 42x – 9x + 378 = 0 ⇒ x (x – 42) – 9(x – 42) = 0
⇒ (x – 42)(x – 9) = 0 ⇒ x – 42 = 0 ବା x – 9 = 0
⇒ x = 42 ବା x = 9
ଯଦି x = 42 ହୁଏ ତେବେ ଅନ୍ୟ ସଂଖ୍ୟାଟି 9 । ସେହିପରି ଯଦି x = 9 ହୁଏ, ତେବେ ଅନ୍ୟ ସଂଖ୍ୟାଟି 42 ।
∴ ସଂଖ୍ୟାଦ୍ଵୟ 42 ଓ 9 1

Question 4.
କୌଣସି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ଏହାର କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟର ଦୁଇଗୁଣରୁ 1 ସେ.ମି. କମ୍ ଏବଂ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ 1 ସେ.ମି. ଅଧ୍ଵ ହେଲେ, ତ୍ରିଭୁଜର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସମକୋଣୀ ତ୍ରିଭୁଜର କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟ = x ସେ.ମି.
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x – 1 ସେ.ମି. ଓ ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ = (x + 1) ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, x² + (x + 1)² = (2x – 1)²
⇒ x² + x² + 2x + 1 = 4x² – 4x + 1
⇒ 2x² – 4x² + 2x + 4x + 1 – 1 = 0
⇒ -2x² + 6x = 0
⇒ 2x² – 6x = 0 ⇒ 2x(x – 3) = 0
⇒ x = 0 (ଏହା ଅସମ୍ଭବ) ବା x – 3 = 0 ⇒ x = 3
 କ୍ଷୁଦ୍ରତମ ବାହୁର ଦୈର୍ଘ୍ୟ = 3 ସେ.ମି.
ଅନ୍ୟ ବାହୁର ଦୈର୍ଘ୍ୟ = x + 1 = 3 + 1 = 4 ସେ.ମି.
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x – 1 = 2 × 3 – 1 = 6 – 1 = 5 ସେ.ମି.
∴ ତ୍ରିଭୁଜର ତିନି ବାହୁର ଦୈର୍ଘ୍ୟ 3 ସେ.ମି., 4 ସେ.ମି. ଓ 5 ସେ.ମି. ।

Question 5.
କୌଣସି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଲଗ୍ନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 5x ସେ.ମି. ଓ 3x – 1 ସେ.ମି. ଏବଂ ଏହାର କ୍ଷେତ୍ରଫଳ 60 ବର୍ଗ ସେ.ମି. ହେଲେ, ତ୍ରିଭୁଜର ବାହୁ ତ୍ରୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
କୌଣସି ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟ 5x ସେ.ମି. ଓ 3x – 1 ସେ.ମି. ।
କ୍ଷେତ୍ରଫଳ = 60 ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1}{2}\) (5x) (3x – 1) = 60 ⇒ 15x² – 5x = 120
⇒ 15x² – 5x – 120 = 0 ⇒ 5(3x² – x – 24) = 0
⇒ 3x² – x – 24 = 0 ⇒ 3x² – 9x + 8x – 24 = 0
⇒ 3x (x – 3) + 8 (x – 3) = 0 ⇒ (x – 3)(3x + 8) = 0
⇒ x – 3 = 0 ବା 3x + 8 = 0 ⇒ x = 3 ବା x = \(\frac{-8}{3}\) (ଏହା ଅସମ୍ଭବ)
ସମକୋଣ ସଂଲଗ୍ନ ବାହୁଦ୍ୱୟ 5x = 5 × 3 = 15 ସେ.ମି. ଏବଂ 3x – 1 = 3 × 3 – 1 = 8 ସେ.ମି. ।
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ \(\sqrt{15^2+8^2}=\sqrt{225+64}=\sqrt{289}\) = 17 ସେ.ମି. ।
∴ ସମକୋଣୀ ତ୍ରିଭୁଜର ବାହୁ ତ୍ରୟର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି., 15 ସେ.ମି. ଓ 17 ସେ.ମି. ।

Question 6.
କୌଣସି ଏକ ସଂଖ୍ୟା ଓ ଏହାର ବ୍ୟତ୍‌କ୍ରମ ସଂଖ୍ୟା (Reciprocal)ର ସମଷ୍ଟି \(\frac{17}{4}\) ହେଲେ, ସଂଖ୍ୟାଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସଂଖ୍ୟାଟି x ଓ ଏହାର ବ୍ୟୁତ୍‌କ୍ରମ \(\frac{1}{x}\)
ପ୍ରଶ୍ନନୁସାରେ, x + \(\frac{1}{x}\) = \(\frac{17}{4}\) ⇒ \(\frac{x^2+1}{x}=\frac{17}{4}\)
⇒ 4x² + 4 = 17x ⇒ 4x² – 17x + 4 = 0
⇒ 4x² – 16x – x + 4 = 0 ⇒ 4x (x – 4) – 1 (x + 4) = 0
⇒ (x – 4) (4x – 1) = 0 ⇒ x – 4 = 0 ବା 4x – 1 = 0
⇒ x = 491 x = \(\frac{1}{4}\)
ଯଦି x = 4 ହୁଏ, ତେବେ ଏହାର ବ୍ୟତ୍‌କ୍ରମ \(\frac{1}{4}\) ହେବ ।
ପୁନଶ୍ଚ ଯଦି x = \(\frac{1}{4}\) ହୁଏ, ତେବେ ଏହାର ବ୍ୟତ୍‌କ୍ରମ 4 ହେବ ।
∴ ସଂଖ୍ୟାଟି 4 କିମ୍ବା \(\frac{1}{4}\) ।

Question 7.
କୌଣସି ଏକ ଆୟତାକାର କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ ପ୍ରସ୍ଥ ଅପେକ୍ଷା ୫ ମି. ଅଧ୍ବକ । ଯଦି ଉକ୍ତ ଆୟତାକାର କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ 308 ବର୍ଗ ମି. ହୁଏ, ତେବେ ଏହାର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତାକାର କ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = x ମି. ଓ ଦୈର୍ଘ୍ୟ = (x + 8) ମି.
ଆୟତାକାର କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (x + 8) x ବର୍ଗ ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, (x + 8) x = 308 = x² + 8x – 308 = 0
⇒ x² + 22x – 14x – 308 = 0 ⇒ x (x + 22) – 14 (x + 22) = 0
⇒ (x – 14) (x + 22) = 0 ⇒ x – 14 = 0 କିମ୍ବା x + 22 = 0
⇒ x = 14 କିମ୍ବା x = -22 (ଏହା ଅସମ୍ଭବ)
ଆୟତାକାର କ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = 16 ମି. ଓ ଦୈର୍ଘ୍ୟ = x + 8 = 14 + 8 = 22 ମିଟର ।
∴ ଆୟତାକାର କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ 22 ମିଟର ଓ ପ୍ରସ୍ଥ 14 ମିଟର ।

Question 8.
ଗୋଟିଏ ଶ୍ରେଣୀର ପିଲାମାନେ ଭ୍ରମଣରେ ଯିବା ପାଇଁ 3600 ଟଙ୍କା ଭଡ଼ାରେ ଏକ ବସ୍ ବରାଦ କଲେ । କିନ୍ତୁ ଶେଷବେଳକୁ ସେମାନଙ୍କ ମଧ୍ୟରୁ 3 ଜଣ ପିଲା ଓହରି ଯିବାରୁ ପ୍ରତ୍ୟେକଙ୍କୁ ଆଉ ଚାଳିଶ ଟଙ୍କା ଲେଖାଏଁ ଅଧିକ ଦେବାକୁ ପଡ଼ିଲା । ପ୍ରଥମରୁ କେତେ ପିଲା ଯିବା ପାଇଁ ମନସ୍ଥ କରିଥିଲେ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ପ୍ରଥମରୁ x ଜଣ ପିଲା ଭ୍ରମଣକୁ ଯିବାପାଇଁ ମନସ୍ଥ କରିଥିଲେ ।
x ଜଣ ପିଲା ଟଙ୍କା ପାଇଁ 3600 ବସ୍ ଭଡ଼ା ପଡ଼ିଥିଲେ
ପ୍ରତି ଜଣକୁ ଦେବାକୁ ପଡ଼ିଥା’ନ୍ତା = \(\frac{3600}{x-3}\) ଟଙ୍କା
3 ଜଣ ପିଲା ଓହରିଯିବାରୁ ଭ୍ରମଣପାଇଁ ଗଲେ = (x – 3) ଜଣ
(x – 3) ଜଣ ପିଲା ପାଇଁ 3600 ଟଙ୍କା ବସ୍‌ଭଡ଼ା ପଡ଼ିଲେ ପ୍ରତ୍ୟେକକୁ ଭଡ଼ା ଦେବାକୁ ପଡ଼ିବ = \(\frac{3600}{x-3}\) ଟଙ୍କା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{3600}{x-3}-\frac{3600}{x}\) = 40 ⇒ 3600 (\(\frac{1}{x-3}-\frac{1}{x}\)) = 40
⇒ \(\frac{1}{x-3}-\frac{1}{x}=\frac{40}{3600} \Rightarrow \frac{x-x+3}{x(x-3)}=\frac{1}{90}\)
⇒ x (x – 3) = 3 × 90 ⇒ x² – 3x – 270 = 0
⇒ x² – 18x + 15x – 270 = 0 ⇒ x (x – 18) + 15 (x – 18) = 0
⇒ (x – 18) (x + 15) = 0 ⇒ x – 18 = 0 ବା x + 15 = 0
⇒ x = 18 ବା x = -15 (ଅସମୃବ)
∴ ପ୍ରଥମରୁ 18 ଜଣ ପିଲା ଭ୍ରମଣ ପାଇଁ ମନସ୍ଥ କରିଥିଲେ ।

Question 9.
ତିନିଗୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟାର ବର୍ଗର ସମଷ୍ଟି 110 ହେଲେ ସଂଖ୍ୟା ତିନୋଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ତିନୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟା x, x + 1 ଓ (x + 2 )
ପ୍ରଶ୍ନ।ନୁସାରେ, x² + (x + 1)² + (x + 2)² = 110
⇒ x² + x² + 2x + 1 + x² + 4x + 4 = 110
⇒ 3x² + 6x + 5 = 110 ⇒ 3x² + 6x + 5 – 110 = 0
⇒ 3x² + 6x – 105 = 0 ⇒ 3 (x² + 2x – 35) = 0
⇒ x² + 2x – 35 = 0 (ଉଭୟ ପାର୍ଶ୍ଵକୁ 3 ଦ୍ବାରା ଭାଗକଲେ ।)
⇒ x² + 7x – 5x – 35 = 0 ⇒ x (x + 7) – 5 (x + 7) = 0
⇒ (x + 7) (x – 5) = 0 ⇒ x + 7 = 0 ବା x – 5 = 0
⇒ x = -7 (ଏହା ଅସମ୍ଭବ) ବା x = 5
⇒ x + 1 = 5 + 1 = 6, x + 2 = 5 + 2 = 7
∴ ତିନିଗୋଟି କ୍ରମିକ ଗଣନ ସଂଖ୍ୟା 5, 6 ଓ 7 1

Question 10.
ଦୁଇଗୋଟି କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ବର୍ଗର ସମଷ୍ଟି 290 ହେଲେ ସଂଖ୍ୟା ଦୁଇଟି ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାଦ୍ଵୟ x ଓ x + 2 ।
ପ୍ରଶ୍ନ।ନୁସାରେ, x² + (x + 2)² = 290 ⇒ x² + x² + 4x + 4 – 290 = 0
⇒ 2x² + 4x – 286 = 0 ⇒ 2(x² + 2x – 143) = 0
⇒ x² + 2x – 143 = 0
⇒ x² + 13x – 11x – 143 = 0 ⇒ x (x + 13) – 11 (x + 13) = 0
⇒ (x + 13) (x – 11) = 0 ⇒ x + 13 = 0 ବା x – 11 = 0
⇒ x = -13 ବା x = 11
⇒ x = -13 ହେଲେ x + 2 = -13 + 2 = -11
⇒ x= 11 ହେଲେ x + 2 = 11 + 2 = 13
∴ କ୍ରମିକ ଅଯୁଗ୍ମ ସଂଖ୍ୟାଦ୍ୱୟ – 13 ଓ – 11 ବା 11 ଓ 13 

Question 11.
ଏକ ଆୟତ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଅପେକ୍ଷା 2 ମିଟର ଅଧୂକ । ଯଦି କ୍ଷେତ୍ରଟିର କ୍ଷେତ୍ରଫଳ 48 ବର୍ଗ ମିଟର ହୁଏ, ତେବେ ଆୟତକ୍ଷେତ୍ରର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତକ୍ଷେତ୍ରର ପ୍ରସ୍ଥ = x ମିଟର ଓ ଦୈର୍ଘ୍ୟ = (x + 2) ମିଟର ।
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = (x + 2) x ବର୍ଗ ମିଟର ।
ପ୍ରଶ୍ନ।ନୁସାରେ, x (x + 2) = 48 ⇒ x² + 2x = 48
⇒ x² + 2x – 48 = 0 ⇒ x² + 8x – 6x – 48 = 0
⇒ x (x + 8)- 6 (x + 8) = 0 ⇒ (x – 6) (x + 8) = 0
⇒ x – 6 = 0 ବା x + 8 = 0 ⇒ x = 6 ବା x = -8 (ଏହା ଅସମ୍ଭବ)
ପ୍ରସ୍ଥ = 6 ସେ.ମି., ଦୈର୍ଘ୍ୟ = x + 2 = 6 + 2 = 8 ସେ.ମି. ।
ଆୟତକ୍ଷେତ୍ରର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 8 ସେ.ମି. ଓ 6 ସେ.ମି. ।

Question 12.
ଏକ ମୋଟର ଲଞ୍ଚ ନଦୀ ସ୍ରୋତର ଅନୁକୂଳରେ 36 କି.ମି. ଯାତ୍ରା କରି ଯାତ୍ରା ଆରମ୍ଭ ସ୍ଥାନକୁ ଫେରି ଆସିବାକୁ ସମୁଦାୟ 8 ଘଣ୍ଟା ସମୟ ନେଲା । ଯଦି ସ୍ରୋତର ଘଣ୍ଟା ପ୍ରତି ବେଗ 6 କି.ମି. ହୁଏ, ତେବେ ସ୍ଥିର ଜଳରେ ଲଞ୍ଚଟିର ଘଣ୍ଟାପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ମୋଟର ଲଞ୍ଚର ସ୍ଥିର ଜଳରେ ଘଣ୍ଟା ପ୍ରତି ବେଗ = x କି.ମି. ।
ସ୍ରୋତର ଘଣ୍ଟା ପ୍ରତି ବେଗ = 6 କି.ମି. ।
ସ୍ରୋତର ଅନୁକୂଳରେ ଲଞ୍ଚଟି 1 ଘଣ୍ଟାରେ ଯିବ = (x + 6) କି.ମି. ।
ସ୍ରୋତର ପ୍ରତିକୂଳରେ ଲଞ୍ଚଟି 1 ଘଣ୍ଟାରେ ଯିବ = (x – 6) କି.ମି. ।
ସ୍ରୋତର ଅନୁକୂଳରେ ଲଞ୍ଚଟିକୁ 36 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ = \(\frac{36}{x+6}\) ଘଣ୍ଟା
ସ୍ରୋତର ପ୍ରତିକୂଳରେ ଲଞ୍ଚଟିକୁ 36 କି.ମି. ଯିବାକୁ ସମୟ ଲାଗିବ = \(\frac{36}{x=6}\) ଘଣ୍ଟା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{36}{x+6}+\frac{36}{x-6}\) = 8 ⇒ 36(\(\frac{1}{x+6}+\frac{1}{x-6}\)) = 8
⇒ \(\frac{x-6+x+6}{(x+6)(x-6)}=\frac{8}{36}\) ⇒ \(\frac{2 x}{x^2-36}=\frac{8}{36}\)
⇒ \(\frac{x}{x^2-36}=\frac{4}{36}=\frac{1}{9}\) ⇒ x² – 36 = 96
⇒ x² – 9x – 36 = 0 ⇒ x² – 12x + 3x – 36 = 0
⇒ x (x – 12) + 3 (x – 12) = 0 ⇒ (x – 12) (x + 3) = 0
⇒ x – 12 = 0 ବା x + 3 = 0 ⇒ x = 12 ବା x = -3 (ଅସମୃବ)
∴ ମୋଟର ଲଞ୍ଚର ଘଣ୍ଟାପ୍ରତି ବେଗ 12 କି.ମି. ।

Question 13.
ଦୁଇଗୋଟି ବର୍ଗାକାର କ୍ଷେତ୍ର ମଧ୍ୟରୁ ଗୋଟିକର ବାହୁର ଦୈର୍ଘ୍ୟ ଅପରଟିର ଦୁଇ ଗୁଣରୁ ଏକ ମିଟର କମ୍ । ଯଦି କ୍ଷେତ୍ରଦ୍ଵୟର କ୍ଷେତ୍ରଫଳମାନଙ୍କ ଅନ୍ତର 56 ବର୍ଗ ମିଟର ହୁଏ, ତେବେ ଦୁଇଟି ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = x ମିଟର ।
 ଅନ୍ୟ ଏକ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = (2x – 1) ମିଟର ।
କ୍ଷେତ୍ରଦ୍ୱୟର କ୍ଷେତ୍ରଫଳ ଯଥାକ୍ରମେ x² ବର୍ଗ ମି. ଏବଂ (2x – 1)² ବର୍ଗ ମି.
ପ୍ରଶ୍ନ।ନୁସାରେ, (2x- 1)² – x² = ବର୍ଗ ମି. ⇒ 4x² – 4x + 1 – x² = 56
⇒ 3x² – 4x + 1 – 56 = 0 ⇒ 3x² – 4x – 55 = 0
⇒ 3x² – 15x + 11x – 55 = 0 ⇒ 3x (x – 5) + 11 (x – 5) = 0
⇒ (x – 5)(3x + 11) = 0 ⇒ x – 5 = 0 ବା 3x + 11 =0
⇒ x = 5 ବା 3x= -11 ⇒ x = 5 ବା x = \(\frac{-11}{3}\)
ଏଠାରେ x = \(\frac{-11}{3}\) (ଅସମୃବ)
x = 5 ମି. ହେଲେ 2x – 1 = 2 × 5 – 1 = 10 – 1=9 ମି.
ବର୍ଗକ୍ଷେତ୍ରଦ୍ଵୟର ବାହୁର ଦୈର୍ଘ୍ୟ 5 ମି. ଓ 9 ମି. ।

Question 14.
ଦୁଇଟି ଗଣନ ସଂଖ୍ୟା ମଧ୍ୟରୁ ଗୋଟିଏ ଅପରଟିର ତିନି ଗୁଣରୁ ଦୁଇ କମ୍ । ଯଦି ସଂଖ୍ୟା)ଦ୍ୱୟର ବର୍ଗର ଅନ୍ତର 312 ହୁଏ, ତେବେ ସଂଖ୍ୟାଦ୍ଵୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ ଗଣନ ସଂଖ୍ୟା = x, ପ୍ରଶ୍ନନୁସାରେ ଅନ୍ୟ ଗଣନ ସଂଖ୍ୟା = 3x – 2 
ପ୍ରଶ୍ନ।ନୁସାରେ, (3x- 2)² – x² = 312 ⇒ 9x² – 12x + 4 – x² = 312
⇒ 8x² – 12x + 4 – 312 = 0 ⇒ 8x² – 12x – 308 = 0
⇒ 4 (2x² – 3x – 77) = 0
⇒ 2x² – 3x – 77 = 0 (ଉଭୟ ପାର୍ଶ୍ଵକୁ 4 ଦ୍ବାରା ଭାଗକଲେ ।)
⇒ 2x² – 14x + 11x – 77 = 0 ⇒ 2x(x – 7) + 11(x – 7) = 0
⇒ (x – 7)(2x + 11) = 0 ⇒ x – 7 = 0 ବା 2x + 11 =0
ଯଦି x – 7 = 0 ହୁଏ, ତେବେ x = 7
ଯଦି 2x + 11 = 0 ହୁଏ, ତେବେ 2x = -11 ⇒ x = \(\frac{-11}{3}\) (ଏହା ଅସମ୍ଭବ)
x = 7 ହେଲେ 3x – 2 = 3 × 7 – 2 = 21 – 2 = 19
∴ ଗଣନ ସଂଖ୍ୟାଦ୍ଵୟ 7 ଓ 19 ।

Question 15.
ଦୁଇଟି ଷ୍ଟେସନ୍ Á ଓ B ମଧ୍ୟରେ ଦୂରତା 192 କି.ମି. । ଏକ ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍ A ରୁ Bକୁ ଯିବାକୁ ଯେତିକି ସମୟ ନିଏ ଏକ ପାସେଞ୍ଜର ଟ୍ରେନ୍ ତା’ଠାରୁ ଦୁଇଘଣ୍ଟା ଅଧିକ ସମୟ ନିଏ । ଯଦି ପାସେଞ୍ଜର ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ ଦୃତଗାମୀ ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ ଠାରୁ 16 କି.ମି. କମ୍ ହୁଏ, ତେବେ ଟ୍ରେନ୍‌ଦ୍ଵୟର ହାରାହାରି ଘଣ୍ଟା ପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
 A ଓ B ଦୁଇଟି ଷ୍ଟେସନ ମଧ୍ୟରେ ଦୂରତା = 192 କି.ମି.
ମନେକର ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ = x କି.ମି.
ପାସେଞ୍ଜର ଟ୍ରେନ୍‌ର ଘଣ୍ଟାପ୍ରତି ହାରାହାରି ବେଗ = (x – 16) କି.ମି. ।
192 କି.ମି. ବାଟ ଯିବାକୁ ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍‌କୁ ସମୟ ଲାଗିବ = \(\frac{192}{x}\) ଘଣ୍ଟା (∴ ସମୟ =\(\frac{ଦୂରତା}{ବେଗ}\)
192 କି.ମି. ଯିବାକୁ ପାସେଞ୍ଜର ଟ୍ରେନ୍‌କୁ ସମୟ ଲାଗିବ = \(\frac{192}{x-16}\) ଘଣ୍ଟା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{192}{x-16}-\frac{192}{x}\) = 2 ⇒ 192(\(\frac{1}{x-16}-\frac{1}{x}\)) = 2 ⇒ \(\frac{1}{x-16}-\frac{1}{x}=\frac{2}{192}\)
⇒ \(\frac{x-x+16}{x(x-16)}=\frac{1}{96}\) ⇒ x(x – 16) = 16 × 96
⇒ x² – 16x – 1536 = 0 ⇒ x² – 48x + 32x – 1536 = 0
⇒ x(x – 48) + 32(x – 48) = 0 ⇒ (x – 48) (x + 32) = 0
⇒ x – 48 = 0 କିମୃ। x + 32 = 0 ⇒ x = 48 କିମୃ। x = -32 (ଏହା ଅସମ୍ଭବ)
∴ ଦ୍ରୁତଗାମୀ ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ = 48 କି.ମି. ।
ପାସେଞ୍ଜର ଟ୍ରେନ୍‌ର ଘଣ୍ଟା ପ୍ରତି ହାରାହାରି ବେଗ = x – 16 = 48 – 16 = 32 କି.ମି. ।

Question 16.
ଗୋଟିଏ ନୌକାର ଘଣ୍ଟା ପ୍ରତି ବେଗ ସ୍ଥିର ଜଳରେ 11 କି.ମି. । ଏହା ସ୍ରୋତର ପ୍ରତିକୂଳରେ 12 କି.ମି. ଗତିକରି ପୁନଶ୍ଚ ଅନୁକୂଳରେ ଫେରିଆସିବାକୁ ମୋଟ 2 ଘଣ୍ଟା 45 ମିନିଟ୍ ସମୟ ନେଲା ତେବେ ସ୍ରୋତର ଘଣ୍ଟାପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସ୍ରୋତର ବେଗ = x କି.ମି.|ଘଣ୍ଟା । ଦତ୍ତ ଅଛି ନୌକାର ବେଗ = 11 କି.ମି. /ଘଣ୍ଟା ।
∴ ସ୍ରୋତର ଅନୁକୂଳରେ ନୌକାର ବେଗ (11 + x) କି.ମି. /ଘଣ୍ଟା
ଏବଂ ପ୍ରତିକୂଳରେ ନୌକାର ବେଗ = (11 – x) କି.ମି. /ଘଣ୍ଟା 
ସ୍ରୋତର ଅନୁକୂଳରେ 12 କି.ମି. ଅତିକ୍ରମ କରିବା ପାଇଁ ସମୟ ଲାଗିବ = \(\frac{12}{11+x}\) ଘଣ୍ଟା
ଏବଂ ସ୍ରୋତର ପ୍ରତିକୂଳରେ 12 କି.ମି. ଅତିକ୍ରମ କରିବା ପାଇଁ ସମୟ ଲାଗିବ = \(\frac{12}{11-x}\) ଘଣ୍ଟା
ପ୍ରଶ୍ନ।ନୁସାରେ, \(\frac{12}{11+x}+\frac{12}{11-x}\) = 2 \(\frac{45}{60}\) ବା 2 \(\frac{3}{4}\) ⇒ \(\frac{132-12 x+132+12 x}{(11+x)(11-x)}=\frac{11}{4}\)
⇒ \(\frac{264}{121-x^2}=\frac{11}{4}\) ⇒ 1056 = 1331 – 11x²
⇒ 11x² = 1331 – 1056 = 275 ⇒ x² = \(\frac{275}{11}\) ⇒ x = √25 = 5
∴ ସ୍ରୋତର ଘଣ୍ଟା ପ୍ରତି ବେଗ 5 କି.ମି. ।

Question 17.
ଗୋଟିଏ ଗାଈଗୋଠର ଏକ ଚତୁର୍ଥାଂଶ ଦୃଷ୍ଟିଗୋଚର ହେଉଥିଲେ । ଗୋଠରେ ଥ‌ିବା ଗାଈ ସଂଖ୍ୟାର ବର୍ଗମୂଳର ଦୁଇଗୁଣ ସଂଖ୍ୟକ ଗାଈ ପାହାଡ଼ର ପାଦଦେଶରେ ଚରୁଥିଲେ ଏବଂ ଅବଶିଷ୍ଟ 15 ଟି ଗାଈ ନଦୀକୂଳରେ ଚରୁଥିଲେ । ତେବେ ଗୋଠରେ କେତୋଟି ଗାଈ ଥିଲେ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗାଈ ଗୋଠରେ x²ଟି ଗାଈ ଥିଲେ । ଦୃଷ୍ଟିଗୋଚର ହେଉଥ‌ିବା ଗାଈ ସଂଖ୍ୟା = \(\frac{x^2}{4}\)
ପାହାଡ଼ର ପାଦ ଦେଶରେ ବୁଲୁଥ‌ିବା ଗାଈ ସଂଖ୍ୟା = 2x  ନଦୀକୂଳରେ ଚରୁଥିବା ଗାଈ ସଂଖ୍ୟା = 15
ପ୍ରଶ୍ନ।ନୁସାରେ, x² = \(\frac{x^2}{4}\) + 2x + 15 ⇒ x² = \(\frac{x^2+8 x+60}{4}\)
⇒ 4x² – x² – 8x- 60 = 0 ⇒ 3x² – 8x – 60 = 0
⇒ 3x² – 18x + 10x – 60 = 0 ⇒ 3x (x – 6) + 10 (x-  6) = 0
⇒ (x – 6) (3x + 10) = 0 ⇒ x – 6 = 0 ଘଣ୍ଟା  3x + 10 = 0
⇒ x = 6 ଘଣ୍ଟା x = \(\frac{-10}{3}\) (ଏହା ଅସମ୍ଭବ)
⇒ x² = 6² = 36
∴ ଗୋଠରେ 36ଟି ଗାଈ ଥିଲେ ।
ବିକଳ୍ପ ପ୍ରଣାଳୀ : ମନେକର ଗୋଠରେ ଥିବା ଗାଈ ସଂଖ୍ୟା = x
∴ ଦୃଷ୍ଟିଗୋଚର ହେଉଥୁବା ଗାଈ ସଂଖ୍ୟା = \(\frac{x}{4}\)
ପ୍ରଶ୍ନନୁସାରେ, x= \(\frac{x}{4}\) + 2√x + 15 ⇒ \(\frac{3x}{4}\) – 15=2√x
⇒ 3x – 60 = 8√x ⇒ 9x² + 3600 – 360x = 64x
⇒ 9x² – 424x + 3600 = 0 ⇒ (x – 36) (9x – 100) = 0 ⇒ x = 36
∴ ଗୋଠରେ ଥ‌ିବା ଗାଈ ସଂଖ୍ୟା 36 ।

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(c)

Question 1.
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଠିକ୍ ଉତ୍ତରଟିକୁ ବାଛି ଲେଖ ।

(i) x² – 3x + 2 ର ଉତ୍ପାଦକ ଦ୍ଵୟ
(a) (x – 2) ଓ (x + 1)
(b) (x + 2) ଓ (x – 1)
(c) (x – 2) ଓ (x – 1)
(d) (x + 2) ଓ (x + 1)
ସମାଧାନ:
(x – 2) ଓ (x + 1)
x² – 3 + 2 = x² – (2 + 1) x + 2 . 1 = (x – 2) (x – 1)

(ii) ଏକ ଦ୍ୱିଘାତୀ ପଲିନୋମିଆଲ୍‌ର ଉତ୍ପାଦକ ଦ୍ବୟ (x – 1) ଓ (x – 3) ହେଲେ ପଲିନୋମିଆଲ୍‌ଟି
(a) x² – 4x – 3
(b) x² – 4x + 3
(c) x² + 4x – 3
(d) x² + 4x + 3
ସମାଧାନ:
x² – 4x + 3
(x – 1) (x – 3) = x² – (1 + 3) x + (1) (3) = x² – 4x + 3

(iii) x – y ର ଉତ୍ପାଦକ ମାନ
(a) (x² + y²) (x + y) (x – y)
(b) (x² – y²) (x – y) (x + y)
(c) (x² + y²) (x + y)²
(d) (x² + y²) (x – y)
ସମାଧାନ:
(x² + y²) (x + y) (x – y)
x⁴ – y⁴ = (x²)² – (y²)² = (x² + y²) (x² – y²) = (x² + y²) (x + y) (x – y)

(iv) 8a³ – b³ – 12a²b + 6ab² ର ଉତ୍ପାଦକଗୁଡ଼ିକ
(a) (2a – b), (2a + b), (2a + b)
(b) (2a + b) (2a + b) (2a + b)
(c) (2a – b), (2a – b), (2a + b)
(d) (2a – b), (2a – b), (2a – b)
ସମାଧାନ:
(2a – b) (2a – b) (2a – b)
8a³ – b³ – 12a²b + 6ab² = (2a)³ – b³ – 3.2a.b(2a – b)
= (2a – b)³ = (2a – b) (2a – b) (2a – b)

(v) 625 + 25x⁴ + x⁸ ର ଉତ୍ପାଦକଗୁଡ଼ିକ
(a) (25 + 5x² + x⁴) (25 – 5x² + x⁴)
(b) (25 + 5x² + x⁴) (25 + 5x² – x⁴)
(c) (25 + 5x⁴ + x⁴) (25 – 5x⁴ + x⁴)
(d) (25 – 5x⁴ + x⁴)(25 + 5x⁴ – x⁴)
ସମାଧାନ:
(25 + 5x² + x⁴) (25 – 5x² + x⁴)
625 + 25x⁴ + x⁸ = 5⁴ + 5²(x²)² + (x²)⁴
= {5² + 5x² + (x²)²} {5² – 5x² + (x²)²} = (25 + 5x² + x⁴) (25 – 5x² + x⁴)

(vi) 1 – a³ + b³ + 3ab ର ଗୋଟିଏ ଉତ୍ପାଦକ
(a) (1 – a + b)
(b) (1 – a – b)
(c) (1 + a + b)
(d) (1 + a – b)
ସମାଧାନ:
(1 – a + b)
1 – a³ + b³ + 3ab
= (1 – a + b) {1² + a² + b² – (1) (-a) – (-a) (b) – (b) (1)}
= (1 – a + b) (1 + a² + b² + a + ab – b)

(vii) (2x – 3y)³ + (3y – 4z)³ + (4z – 2x)³ ର ଉତ୍ପାଦକଗୁଡ଼ିକ ହେଲେ
(a) 6(2x – 3y)(3y – 4z) (2z – x)
(b) 3(2x – 3y) (3y – 4z) (2z – x)
(c) 60xyz
(d) ଏଥୁମଧ୍ୟରୁ କୌଣସିଟି ନୁହେଁ
ସମାଧାନ:
6 (2x – 3y) (3y – 4z) (2z – x)
2x – 3y + 3y – 4z + 4z – 2x = 0
(2x – 3y)³ + (3y – 4z)³ + (4z – 2x)³ = 3 (2x – 3y) (3y – 4z) (4z – 2x)
= 6 (2x – 3y) (3y – 4z) (2z – x)(∵ a + b + c = 0 ହେଲେ a³ + b³ + c³ = 3abc)

(viii) (28)³ + (-15)³ + (-13)³ ର ସରଳୀକୃତ ମାନ
(a) 8190
(b) 16380
(c) 24570
(d) 4095
ସମାଧାନ:
16380
28 – 15 -13 = 0
∴ (28)³ + (-15)³ + (-13)³ = 3 (28) (-15) (-13) = 16380
(∵ a + b + c = 0 ହେଲେ a³ + b³ + c³ = 3abc)

(ix) (a – b)³ + (b – c)³ + (c – a)³ ର ମାନ
(a) 3abc
(b) 3a³b³c³
(c) 3(a – b) (b – c)(c – a)
(d) {a – (b + c)}³
ସମାଧାନ:
3(a – b) (b – c) (c – a)
(a – b)³ + (b – c)³ + (c – a)³ = 3(a – b) (b – c) (c – a)
(∵ (a – b) + (b – c) + (c – a) = 0)

(x) 2x² – x – 1 ର ଗୋଟିଏ ଉତ୍ପାଦକ
(a) 2x – 1
(b) x + 1
(c) x – 1
(d) x + 2
ସମାଧାନ:
(x – 1)
2x² – x – 1 = 2x² – 2x + x – 1
= 2x (x – 1) + 1 (x – 1) = (x – 1) (2x + 1)
∴ 2x² – x – 1 ର ଏକ ଉତ୍ପାଦକ (x – 1)

Question 2.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।

(i) 2x² – x – 1
ସମାଧାନ:
2x² – x – 1 = 2x² – 2x + x – 1
= 2x(x – 1) + 1(x – 1) = (x – 1) (2x + 1)

(ii) 2x² – 3x + 1
ସମାଧାନ:
2x² – 3x + 1 = 2x² – 2x – x + 1
= 2x (x – 1) – 1 (x – 1) = (x – 1) (2x – 1)

(iii) 5x² – x – 4
ସମାଧାନ:
5x² – x – 4 = 5x² – 5x + 4x – 4
= 5x (x – 1) + 4 (x – 1) = (x – 1) (5x + 4)

(iv) 4x² – 5x – 6
ସମାଧାନ:
4x² – 5x – 6 = 4x² – 8x + 3x – 6
= 4x(x – 2) + 3 (x – 2) = (4x + 3) (x – 2)

(v) 3x² + 11x + 6
ସମାଧାନ:
3x² + 11x + 6 = 3x² + 9x + 2x + 6
= 3x (x + 3) + 2 (x + 3) = (3x + 2) (x + 3)

(vi) 7x² + x – 6
ସମାଧାନ:
7x² + x – 6 = 7x² + 7x – 6x – 6
= 7x (x + 1) – 6 (x + 1) = (7x – 6) (x + 1)

(vii) 2x² + 5x – 7
ସମାଧାନ:
2x² + 5x – 7 = 2x² + 7x – 2x – 7
= x (2x + 7) – 1 (2x + 7) = (2x + 7) (x – 1)

(viii) 4x² – 5x + 1
ସମାଧାନ:
4x² – 5x + 1 = 4x² – 4x – x + 1
= 4x (x – 1) – 1 (x – 1) = (4x – 1) (x – 1)

(ix) 4x² – 3x – 7
ସମାଧାନ:
4x² – 3x – 7 = 4x² – 7x + 4x – 7
= x (4x – 7) + 1 (4x – 7) = (4x – 7) (x + 1)

Question 3.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
[a³ + b³ = (a + b) (a² – ab + b²), a³ – b³ = (a – b) (a² + ab + b²)]

(i) 25a⁴ – 16b²
ସମାଧାନ:
25a⁴ – 16b² = (5a²)² – (4b)² = (5a² + 4b)(5a² – 4b)

(ii) 9 – 64p²q²
ସମାଧାନ:
9 – 64p²q² = (3)² – (8pq)² = (3 + 8pq)(3 – 8pq)

(iii) 8x³ + 27y³
ସମାଧାନ:
8x³ + 27y³ = (2x)³ + (3y)³ = (2x + 3y){(2x)² – 2x.3y + (3y)²}
= (2x + 3y)(4x² – 6xy + 9y²)

(iv) 8x³ – 27y³
ସମାଧାନ:
8x³ – 27y³ = (2x)³ – (3y)³ = (2x – 3y){(2x)² + 2x.3y + (3y)²}
= (2x – 3y)(4x² + 6xy + 9y²)

(v) (a + b)² – 9
ସମାଧାନ:
(a + b)² – 9 = (a + b)² – 32 = (a + b + 3) (a + b – 3)

(vi) (2a + 5)² – 16
ସମାଧାନ:
(2a + 5)² – 16 = (2a + 5)² – 42 = (2a + 5 + 4) (2a + 5 – 4) = (2a + 9) (2a + 1)

(vii) (x + 2y)² – (x – y)²
ସମାଧାନ:
(x + 2y)² – (x – y)² = {(x + 2y) + (x – y)} {x + 2y) – (x – y)}
= (x + 2y + x – y) (x + 2y – x + y) = (2x + y) (3y) = 3y (2x + y)

(viii) 4(a + 2p)² – 9 (2a – p)²
ସମାଧାନ:
4 (a + 2p)² – 9 (2a – p)² = {2 (a + 2p)}² – {3 (2a – p)}²
= (2a + 4p)² – (6a – 3p)² = (2a + 4p + 6a- 3p) (2a + 4p – 6a + 3p) = (8a + p) (7p – 4a)

(ix) 75 (2a – b + 1)² – 12 (a + b)²
ସମାଧାନ:
75 (2a – b + 1)² – 12 (a + b)² = 3 {25 (2a – b + 1)² – 4 (a + b)²}
= 3 [{5 (2a – b + 1)}² – {2 (a + b)²}] = 3 {(10a – 5b + 5)² – (2a + 2b)²]
= 3 (10a – 5b + 5 + 2a + 2b) (10a – 5b + 5 – 2a – 2b) = 3 (12a – 3b + 5) (8a – 7b + 5)

(x) (a + b)³ – 8c³
ସମାଧାନ:
(a + b)³ – 8c³ = (a + b)³ – (2c)³
= (a + b – 2c) {(a + b)² + (a + b)2c + (2c)²}
= (a + b – 2c) (a² + 2ab + b² + 2ca + 2bc + 4c²)
= (a + b – 2c) (a² + b² + 4c² + 2ab + 2bc + 2ca)

(xi) p⁴ – 27pq⁶
ସମାଧାନ:
p⁴ – 27pq⁶ = p(p³ – 27q⁶)
= p{p³ – (3q²)³} = p(p – 3q²) {p² + 3pq² + (3q²)²} = p(p – 3q²) (p² + 3pq² + 9q⁴)

(xii) 1 – (a + 2)³
ସମାଧାନ:
1 – (a + 2)³ = 1³ – (a + 2)³ = (1 – a – 2) {1² + a + 2 + (a + 2)²}
= (- a – 1) (1 + a + 2 + a² + 4a + 4) = -(a + 1) (a² + 5a + 7)

(xiii) 8 – (2x – 3)³
ସମାଧାନ:
8 – (2x – 3)³ = 2³ – (2x – 3)³ = (2 – 2x + 3) {2² + 2 (2x – 3) + (2x – 3)²}
= (-2x + 5) (4 + 4x – 6 + 4x² – 12x + 9) = (5 – 2x) (4x² – 8x + 7)

(xiv) 320p⁶q – 5p²q⁷
ସମାଧାନ:
320 p⁶q – 5p²q⁷ = 5p²q (64p⁴ – q⁶)
= 5p²q {(8p²)² – (q³)²} = 5p²q (8p² + q³) (8p² – q³)

(xv) 1 + (a + 2)³
ସମାଧାନ:
1 + (a + 2)³ = 1³ + (a + 2)³ = (1 + a + 2) {1² – 1(a + 2) + (a + 2)²}
= (a + 3) (1 – a – 2 + a² + 4a + 4) = (a + 3) (a² + 3a + 3)

(xvi) 8 + (2x – 3)³
ସମାଧାନ:
8 + (2x – 3)³ = 2³ + (2x – 3)³ = (2 + 2x – 3) {2² – 2 (2x – 3) + (2x – 3)²}
= (2x – 1) (4 – 4x + 6 + 4x² – 12x + 9) = (2x – 1) (4x² – 16x + 19)

(xvii) a³ + 6a²b + 12ab² + 8b³
ସମାଧାନ:
a³ + 6a²b + 12ab² + 8b³ = a³ + 3a² (2b) + 3 . a . (2b)² + (2b)³
= (a + 2b)³ = (a + 2b) (a + 2b) (a + 2b)

(xviii) a³ + 9a² + 27a + 27
ସମାଧାନ:
a³ + 9a² + 27a + 27 = a³ + 3a² . 3 + 3 . a . 3² + 3³ = (a + 3)³
= (a + 3) (a + 3) (a + 3)

(xix) 8 – 36p + 54p² – 27p³
ସମାଧାନ:
8 – 36p + 54p² – 27p³ = 2³ – 3. 2² 3p + 3 . 2 (3p)² – (3p)³
= (2 – 3p)³ = (2 – 3p) (2 – 3p) (2 – 3p)

(xx) (b – q)³ – (c – q)³ – 3 (b – c) (b – q) (c – q)
ସମାଧାନ:
(b – q)³ – (c – q)³ – 3 (b – c) (b – q) (c – q)
ମନେକର b – q = x ଓ c – q = y
∴ x – y = (b – q) – (c – q) = b – q – c + q = b – c
ପ୍ରଦତ୍ତ ପଲିନୋମିଆଲ୍‌ଟି x³ – y³ – 3 (x – y) (xy) = x³ – y³ – 3xy (x – y) = (x – y)³
= {(b – q) – (c – q)}³ (x ଓ yର ମାନ ବସାକଳେ)
= (b – c)³ = (b – c) (b – c) (b – c)

Question 4.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
a⁴ + a²b² + b⁴ = (a² + ab + b²)(a² – ab + b²)

(i) a⁴ + a² + 1
ସମାଧାନ:
a⁴ + a² + 1
= a⁴ + 1 + a² = (a²)² + (1)² + a² = (a² + 1)² – 2 . a². 1 + a²
= (a² + 1)² – 2a² + a² = (a² + 1)² – a² = (a² + 1 + a) (a² + 1 – a)
= (a² + a + 1)(a² – a + 1)

(ii) a⁴b⁴ + a²b² + 1
ସମାଧାନ:
a⁴b⁴ + a²b² + 1 = (ab)4 + (ab)² 1² + 1⁴
= (a²b² + ab + 1) (a²b² – ab + 1)

(iii) 16a⁴ + 36a²b² + 81b⁴
ସମାଧାନ:
16a⁴ + 36a²b² + 81b⁴ = (4a²)² + 36a²b² + (9b²)²
= (4a²)² + (9b²)² + 72a²b² – 72a²b² + 36a²b² [72a²b² ଯେ।ଗ ଓ ବିୟେ।ଗ କରି]
= (4a² + 9b²)² – 36a²b² = (4a² + 9b²)² – (6ab)²
= (4a² + 9b² + 6ab) (4a² + 9b² – 6ab) = (4a² + 6ab + 9b²) (4a² – 6ab + 9b²)
ବିକଳ୍ପ ସମାଧାନ –
16a⁴ + 36a²b² + 81b⁴ = (4a²)² + (9b²)² + 36a²b²
= (4a² + 9b²)² – 2 . 4a² . 9b² + 36a²b² = (4a² + 9b²)² – 36a²b²
= (4a2 + 9b²)² – (6ab)² = (4a² + 9b² + 6ab) (4a² + 9b² – 6ab)
= (4a² + 6ab + 9b²) (4a² – 6ab + 9b²)

(iv) a⁸ + a⁴ + 1
ସମାଧାନ:
a⁸ + a⁴ + 1 = (a²)⁴ + (a²)² . 1² + 1⁴
= {(a²)² + a² . 1 + 1²} {(a²)² – a² . 1 + 1²} = (a⁴ + a² + 1) (a⁴ – a² + 1)
= (a⁴ + a² . 1² + 1⁴) (a⁴ – a² + 1) = (a² + a + 1) (a² – a + 1) (a⁴ – a² + 1)

(v) x⁴ + 4
ସମାଧାନ:
x⁴ + 4 = (x²⁾² + (2)² = (x²)² + (2)² + 4x² – 4x²
= (x² + 2)² – (2x)² = (x² + 2 + 2x) (x² + 2 – 2x) = (x² + 2x + 2) (x² – 2x + 2)

(vi) 2a⁴ + 8b⁴
ସମାଧାନ:
2a⁴ + 8b⁴ = 2(a⁴ + 4b⁴) = 2{(a²)² + (2b²)² + 4a²b² – 4a²b²}
= 2{(a² + 2b²)² – (2ab)²} = 2 {a² + 2b² + 2ab) (a² + 2b² – 2ab)}
= 2(a² + 2ab + 2b²) (a² – 2ab + 2b²)

(vii) 36a⁴ + 9b⁴
ସମାଧାନ:
36a⁴ + 9b⁴ = 9 (4a⁴ + b⁴) = 9 {(2a²)² + (b²)²}
= 9 {(2a² + b²)² – 2 (2a²) b²} = 9 {(2a² + b²)² – 4a²b²}
= 9 {(2a² + b²)² – (2ab)²} = 9(2a² + b² + 2ab) (2a² + b² – 2ab)
= 9 (2a² + 2ab + b²) (2a² – 2ab + b²)

(viii) 4a⁴ + 7a² + 16
ସମାଧାନ:
4a⁴ + 7a² + 16 = (2a²)² + (4)² + 16a² – 16a² + 7a²
= (2a² + 4)² – 9a² = (2a² + 4)² – (3a)² = (2a² + 4 + 3a) (2a² + 4 – 3a)
= (2a² + 3a + 4) (2a² – 3a + 4)

(ix) a⁴ + 2a²b² + 9b⁴
ସମାଧାନ:
a⁴ + 2a²b² + 9b⁴ = a⁴ + 9b⁴ + 2a²b²
= (a²)² + (3b²)² + 6a²b² – 6a²b² + 2a²b² =  (a² + 3b²)² – 4a²b²
= (a² + 3b²)² – (2ab)² = (a² + 3b² + 2ab) (a² + 3b² – 2ab)
= (a² + 2ab + 3b²) (a² – 2ab + 3b²)

(x) a⁴ – 3a² + 1
ସମାଧାନ:
a⁴ – 3a² + 1 = (a²)² + (1)² – 3a²
= (a²)² + (1)² – 2a² + 2a² – 3a² (2a² ଯେ।ଗ ଓ ବିୟେ।ଗ କରି)
= (a² – 1)² – (a)² = (a² – 1 + a) (a² – 1 – a) = (a² + a – 1) (a² – a – 1)

(xi) 25a⁴ – 19a²b² + 9b²
ସମାଧାନ:
25a⁴ – 19a²b² + 9b⁴ = (5a²)² + (3b²)² – 19a²b²
= (5a² + 3b²)² + 2 . 5 a² . 3b² – 19 a²b²
= (5a² + 3b²)² – 49 a²b² = (5a² + 3b²) – (7ab)²
= (5a² + 3b² + 7ab) (5a² + 3b² – 7ab) = (5a² + 7ab + 3b²) (5a² – 7ab + 3b²)

(xii) 9x² + y² + 6xy – 4z²
ସମାଧାନ:
9x² + y² + 6xy – 4z² = (3x)² + y² + 2 . 3x . y – (2z)²
= (3x + y)² – (2z)² = (3x + y + 2z) (3x + y – 2z)

(xiii) 16 – x² – 24y + 9y²
ସମାଧାନ:
16 – x² – 24y + 9y² = 16 – 24y + 9y² – x2
= 4² – 2 . 4 . 3y + (3y)² – x² = (4 – 3y)² – x² = (4 – 3y + x) (4 – 3y – x)

(xiv) (a² – b²) (x² – y²) – 4abxy
ସମାଧାନ:
(a² – b²) (x² – y²) – 4abxy = a²x² – a²y² – b²x² + b²y² – 4abxy
= a²x² + b²y² – 2abxy – a²y² – b²x² – 2abxy
= (a²x² + b²y² – 2abxy) – (a²y² + b²x² + 2abxy)
= {(ax)² + (by)² – 2(ax) (by)} – {(ay)² + (bx)² + 2(ay) (bx)}
= (ax – by)² – (ay + bx)² = (ax – by + ay + bx) (ax – by – ay – bx)

(xv) (a² + b²)(x² – y²) – 2ab (x² + y²)
ସମାଧାନ:
(a² + b²)(x² – y²) – 2ab (x² + y²)
= a²x² – ay² + b²x² – b²y² – 2abx² – 2aby²
= a²x² + b²x² – 2abx² – a²y² – b²y² – 2aby²
= (a²x² + b²x² – 2abx²) – (a²y² + b²y² + 2aby²)
= {(ax)² + (bx)² – 2ax . bx} – {(ay)² + (by)² + 2ay . by}
= (ax – bx)² – (ay + by)² = (ax – bx + ay + by) (ax – bx – ay – by)
= {x (a – b) + y (a + b)} {x (a – b) – y(a + b)}

Question 5.
ଉତ୍ପାଦକରେ ବିଶ୍ଳେଷଣ କର ।
(a³ + b³ + c³ – 3abc = (a + b + c) (a² + b² + c² – ab – bc – ca)

(i) a³ + b³ + x³ – 3abx
ସମାଧାନ:
a³ + b³ + x³ – 3abx
= (a + b + x) (a² + b² + x² – ab – bx – ax)

(ii) 8a³ + b³ + c³ – 6abc
ସମାଧାନ:
8a³ + b³ + c³ – 6abc = (2a)³ + b³ + c³ – 3(2a) (b) (c)
= (2a + b + c) { (2a)² + b² + c² – 2a . b. bc – c . 2a}
= (2a + b + c) (4a² + b² + c² – 2ab – bc – 2ca)

(iii) a³ + b³ – 8 + 6ab
ସମାଧାନ:
a³ + b³ – 8 + 6ab = a³ + b³ + (-2)³ – 3a . b(-2)
= (a + b – 2) { a² + b² + (-2)² – ab – b (-2) – (-2) a}
= (a + b – 2) (a² + b² + 4 – ab + 2b + 2a)

(iv) l – 27m³ – n³ – 9 lmn
ସମାଧାନ:
l³ – 27m³ – n³ – 9lmn = l³ + (- 3m)³ + (- n)³ – 3l(-3m) (-n)
= {l + (-3m) + (-n)} {l² + (-3m)² + (- n)² – l(-3m) – (-3m) (-n) – (-n) l}
= (l – 3m – n) (l² + 9m² + n² + 3lm – 3mn + nl)

(v) (a – b)³ + (c – b)³ + (a – c)³ – 3 (a – b) (b – c) (c – a)
ସମାଧାନ:
(a – b)³ + (c – b)³ + (a- c)³ – 3 (a – b) (b – c) (c – a)
ମନେକର a – b = x, b – c = y, c – a = z ⇒ c – b = -y ⇒ a – c = -z
ପ୍ରଦତ୍ତ ପଲିନୋମିଆଲ୍‌ଟି x³ + (-y)³ + (-z)³ – 3(x) (-y) (-z)
= {x + (-y) + (-z)} {x² + (-y)² + (-z)² – x (-y) – (-y) (-z) – (-z) x}
= (x – y – z) (x² + y² + z² + xy – yz + zx)
= {(a – b) – (b – c) – (c – a)} {(a – b)² + (b – c)² + (c – a)² +(a – b) (b – c) – (b – c) (c – a) + (c – a) (a – b) x, y ଓ zର ମାନ ବସାକଳେ,
= (a – b – b + c – c + a) (a² – 2ab + b² + b² – 2bc + c² + c² – 2ca + a² + ab – ca – b² + bc – bc + ab + c² – ca + ca – bc – a² + ab)
= (2a – 2b) (a² + b² + c² + ab – 3bc – 3ca)
= 2 (a – b) (a² + b² + c² + ab – 3bc – 3ca)

(vi) a⁶ + 4a³ – 1
ସମାଧାନ:
a⁶ + 4a³ – 1 = a⁶ + a³ – 1 + 3a³ = (a2)³ + a³ + (-1)³ – 3. a² .a(-1)
= (a² + a – 1) {(a²)² + (a)² + (-1)² – a².a – a(-1) – (-1)a²}
= (a² + a – 1) (a⁴ + a² + 1 – a³ + a + a²) = (a² + a – 1)(a⁴ – a³ + 2a² + a + 1)

(vii) x³ + 72 – 24x
ସମାଧାନ:
x³ + 72 – 24x = x³ + 64 + 8 – 24x
= x³ + 4³ + 2³ – 3. x. 4. 2 = (x + 4 + 2)(x² +  4² + 2² – x. 4 – 4. 2 – 2. X)
= (x + 4 + 2)(x² + 16 + 4 – 4x – 8 – 2x)
= (x + 6)(x² + 16 + 4 – 8 – 6x)
= (x + 6)(x² – 16 + 12)

(viii) m⁶ + 7m³ – 8
ସମାଧାନ:
m⁶ + 7m³ – 8 = m⁶ + m³ – 8 + 6m³
= (m²)³ + m³ + (-2)³ – 3m² .m(-2)
= (m² + m – 2) {(m²)² + m² + (2)² – m² . m – m (-2) – (-2) m²}
= (m² + m – 2)(m⁴ + m² + 4 – m³ + 2m + 2m²)
= (m² + 2m – m – 2)(m⁴ – m³ + 3m² + 2m + 4)
= {m(m + 2) – 1(m + 2)}(m⁴ – m³ +3m² + 2m + 4)
= (m + 2)(m – 1)(m⁴ – m³ + 3m² + 2m + 4)

(ix) a⁶ + \(\frac{1}{a^6}\) + 2 (a ≠ 0)
ସମାଧାନ:

(x)  r⁶ + 45r³ – 8
ସମାଧାନ:
r⁶ + 45r³ – 8 = r⁶  + 27r³ – 8 + 18r³
= (r²)³ + (3r)³ + (-2) – 3 . r² . 3r (-2)
= (r² + 3r – 2) {(r²)² + (3r)² + (2)² – r² 3r – 3r (-2) – (-2) r²)
= (r² + 3r – 2)(r⁴ + 9r² + 4 – 3r³ + 6r + 2r²)
= (r² + 3r – 2)(r⁴ – 3r³ – t – 11r² + 6r + 4)

(xi) 16x³ – 54y⁶ – 2z³ – 36xy²z
ସମାଧାନ:
16x³ – 54y⁶ – 2z³ – 36xy²z = 2 { 8x³ – 27y⁶ –  z³ – 18xy²z)}
= 2 {(2x)³ + (-3y²)³ + (-z)³ – 3 (2x) (-3y²) (-z))
= 2{2x + (-3y²) + (-z)) {(2x)² + (-3y²)² + (-z)² – (2x) (-3y²) – (-3y²) (-z) – (-z) (2x)}
= 2(2x – 3y² – z) (4x² + 9y⁴ + z² + 6xy² – 3y²z + 2zx)

(xii) a³ + b³ – \(\frac{1}{27}\) c³ + abc
ସମାଧାନ:

(xiii) 27a³ – 8b⁶ + 125 c³ + 90ab²c
ସମାଧାନ:
27a³ – 8b⁶ + 125 c³ + 90 ab²c = (3a)³ + (- 2b²)³ + (5c)³ – 3(3a) (- 2b²) (5c)
= {3a + (-2b²) + 5c} {(3a)² + (-2b²)² + (5c)² – (3a) (-2b²) – (-2b²) (5c) – (5c) (3a)}
= (3a – 2b² + 5c) (9a² + 4b⁴ + 25c² + 6ab² + 10b²c – 15 ca)

(xiv) (2x + 3)³ + (3x – 2)³ – (5x + 1)³
ସମାଧାନ:
(2x + 3)³ + (3x – 2)³ – (5x + 1)³
ମନେକର 2x + 3 = a, 3x- 2 = b, 5x + 1 = c
∴ a + b – c = 2x + 3 + 3x – 2 – 5x – 1=0
a + b – c = 0 ହେଲେ a³ + b³ – c³ = -3abc
∴(2x + 3)³ + (3x – 2)³ – (5x + 1)³ = -3 (2x + 3) (3x – 2) (5x + 1)
(a, b ଓ cର ମାନ ବସାକଳେ)

Question 6.
a + b + c = 0 ହେଲେ ଦର୍ଶାଅ ଯେ, a³ + b³ + c³ = 3 abc
ସମାଧାନ:
L.H.S. = a³ + b³ + c³ = a³ + b³ + c³ – 3abc + 3abc
= (a + b + c) (a² + b² + c² –  ab – bc – ca) + 3abc
= (0) (a² + b² + c² – ab – bc – ca) + 3abc
= 0 + 3abc = 3abc = R.H.S. (ପ୍ରମାଣିତ)

Question 7.
(x – y)³ + (y – z)³ + (z – x)³ ର ଉତ୍ପାଦକଗୁଡ଼ିକୁ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର x – y = a, y – z = b, z – x = c
∴ a + b + c = x – y + y – z + z – x ⇒ a + b + c = 0
ପ୍ରଦତ୍ତ ପଲିନୋମିଆଲ୍‌ଟି = a³ + b³+ c³ = 3abc (∵ a + b + c = 0)
∴ (x – y)³ + (y – z)³ + (z – x)³ = 3(x – y) (y – z) (z – x)

Question 8.
ଦର୍ଶାଅ ଯେ, x³ + y³ + z³ – 3xyz = \(\frac{1}{2}\) {(x – y)² + (y – z)² + (z – x)²}
ସମାଧାନ:
x³ + y³ + z³ – 3xyz
= (x + y + z) (x² + y² + z² – xy – yz – zx)
= \(\frac{1}{2}\) (x + y + z) (2x² + 2y² + 2z² – 2xy – 2yz – 2zx)
= \(\frac{1}{2}\) (x + y + z) (x² – 2xy + y² + y² – 2yz + z² + z² – 2zx + x²}
= \(\frac{1}{2}\) (x + y + z) {(x – y)² + (y – z)² + (z – x)²}
∴ x³ + y³ + z³ = \(\frac{1}{2}\) {(x – y)² + (y – z)² + (z – x)²}