Odisha State Board BSE Odisha 9th Class Political Science Important Questions Chapter 9 ଭାରତ ଓ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ Important Questions and Answers.
BSE Odisha Class 9 Political Science Important Questions Chapter 9 ଭାରତ ଓ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ
Subjective Type Questions With Answers
ସଂଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସାଧାରଣ ସଭାର ଗଠନ ଓ କାର୍ଯ୍ୟାବଳୀ ବର୍ଣ୍ଣନା କର ।
Answer:
- ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସମସ୍ତ ସଦସ୍ୟ – ରାଷ୍ଟ୍ରର ପ୍ରତିନିଧ୍ ମାନକ୍ତ ଗଠିତ । ପ୍ରତ୍ୟେକ ସଦସ୍ୟ ରାଷ୍ଟ୍ର ଏହି ଗୋଟିଏ ମାତ୍ର ଭୋଟ ଦେବାର ଅଧିକାର ରହିଛି ।
- ସାଧାରଣ ସଭାର ମୁଖ୍ୟ କାର୍ଯ୍ୟାବଳୀ :
(କ) ସାଧାରଣ ସଭାରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ର ସଂଘ ପରି ସରଭୁକ୍ତ ସମସ୍ତ ବିଷୟ ଉପରେ ବିତର୍କ ବା ଆଲୋଚନା କରାଯାଇଥାଏ ।
(ଖ) ନ୍ୟାସ ପରିଷଦର କାର୍ଯ୍ୟକୁ ସାଧାରଣ ସଭା ତଦାରଖ କରିବା ସହିତ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ର ସଂଘରେ ସର୍ଭାବଳୀ ସମ୍ପର୍କିତ ନିୟମାବଳୀ ସାଧାରଣ ସଭାରେ ଅନୁମୋଦିତ ହୋଇଥାଏ ।
(ଗ) ସାଧାରଣ ସଭାରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ଆମେରିକାର ଅଟକଳ ଅନୁମୋଦିତ ହୋଇଥାଏ ।
(ଘ) ସାଧାରଣ ସଭାରେ ପରିଷଦର ୧୦ ଜଣ ଅସ୍ଥାୟୀ ସଦସ୍ୟ, ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ପରିଷଦର ୧୮ଜଣ ସଦସ୍ୟ ଓ ଆନ୍ତ ର୍ଜାତି କ ନ୍ୟୟାଲୟର ବିବାରପତି ହୋଇଥା’ନ୍ତି ।
(ଙ) ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦର ଆବଶ୍ୟକ ସଂଶୋଧନ ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ପ୍ରସ୍ତାବ ସାଧାରଣ ସଭାର ଦୁଇ- ତୃତୀୟାଂଶ ସଦସ୍ୟଙ୍କ ସମର୍ଥନ ଓ ନିରାପତ୍ତା ପରିଷଦର ସମସ୍ତ ସ୍ଥାୟୀ ଗୃହୀତ ହେବା ପରେ କାର୍ଯ୍ୟକାରୀ ହୁଏ ।

୨। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ନିରାପତ୍ତା ପରିଷଦ କ’ଣ ଓ ଏଥିରେ ଥିବା ସ୍ଥାୟୀ ଓ ଅସ୍ଥାୟୀ ରାଷ୍ଟ୍ରମାନଙ୍କର ଭୂମିକା ସମ୍ପର୍କରେ ଲେଖ ।
Answer:
- ନିରାପତ୍ତା ପରିଷଦ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର କାର୍ଯ୍ୟପାଳିକା ଅଙ୍ଗ । ସନନ୍ଦର ଧାରା ୨୩ ଅନୁସାରେ ୧୯୬୬ ମସିହା ଜାନୁୟାରୀ ୧ ସର୍ବମୋଟ ୧୫ ଗୋଟି ରାଷ୍ଟ୍ର ସଦସ୍ୟ ଅଛନ୍ତି ।
- ୧୫ଗୋଟି ରାଷ୍ଟ୍ର ମଧ୍ୟରୁ ୫ ଗୋଟି ସ୍ଥାୟୀ ସଦସ୍ୟ ରାଷ୍ଟ୍ର ରହିଛନ୍ତି । ସେହି ରାଷ୍ଟ୍ରଗୁଡ଼ିକ ହେଉଛି – ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଇଂଲାଣ୍ଡ, ଫ୍ରାନ୍ସ, ରୁଷିଆ ଓ ଚୀନ୍ । ଏମାନେ ବୃହତ୍ ଶକ୍ତି ନାମରେ ପରିଚିତ ।
- ୧୦ ଗୋଟି ଅସ୍ଥାୟୀ ସଦସ୍ୟ ରାଷ୍ଟ୍ର ପ୍ରତି ଦୁଇ ବର୍ଷ ପାଇଁ ସାଧାରଣ ସଭାଦ୍ଵାରା ନିର୍ବାଚିତ ହୁଅନ୍ତି । ଏଠାରେ ବିଶ୍ଵର ସମସ୍ତ ଅଞ୍ଚଳକୁ ସମାନ ପ୍ରତିନିଧୂ ମିଳିବାପାଇଁ ଏପରି ଦ୍ୱି- ବାର୍ଷିକ ନିର୍ବାଚନ ବ୍ୟବସ୍ଥା କରାଯାଇଛି ।
- ନିରାପତ୍ତା ପରିଷଦରେ ଜଣେ ଅଧ୍ୟକ୍ଷ ଅଛନ୍ତି । ଏହି ପରିଷଦର ସମସ୍ତ ନିଷ୍ପଭି ନିଆଯାଏ । ପ୍ରତ୍ୟେକ ରାଷ୍ଟ୍ରଙ୍କର ଗୋଟିଏ ଲେଖାଏଁ ଭୋଟ ଦେବା ଅଧିକାର ରହିଛି । ଦୁଇଟି ପ୍ରଣାଳୀର ନିଷ୍ପତ୍ତି ଗ୍ରହଣ କରାଯାଏ । ପ୍ରଥମଟି ହେଉଛି – ନିୟମ ବା ପଦ୍ଧତି ସମ୍ପର୍କିତ ସମ୍ପର୍କିତ ।
- ପରିଷଦର ନିଷ୍ପତ୍ତି ପାଇଁ ବିଚାର କରାଯାଏ, ସଦସ୍ୟଙ୍କ ସେତେବେଳେ ପାଞ୍ଚ ଜଣ ସ୍ଥାୟୀ ସଦସ୍ୟଙ୍କ ସହିତ ନଅଜଣ ସଦସ୍ୟଙ୍କ ସମର୍ଥନ ସଦସ୍ୟ ପ୍ରସ୍ତାବ ସପକ୍ଷରେ ଭୋଟ ନ ଦିଅନ୍ତି, ହେଲା ବୋଲି କୁହାଯାଏ ।
୩ । ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ନ୍ଯାସ ପରିଷଦ ଏବଂ ଅର୍ଥନୈତିକ ଏବଂ ସାମାଜିକ ପରିଷଦର ଗଠତ ଓ କାର୍ଯ୍ୟ ବର୍ଣନା କର ।
Answer:
- ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଅଧୀନରେ ଥିବା ଅନୁନ୍ନତ ଅଞ୍ଚଳ ଏବଂ କୌଣସି ରାଷ୍ଟ୍ରର ପରିସୀମା ଆନ୍ତର୍ଜାତିଙ୍କୁ ଅଞ୍ଚଳମାନଙ୍କର ରହିଛି ।
- ଏଥରେ ନିରାପତ୍ତା ପରିଷଦର ୫ଜଣ ସ୍ଥାୟ ସଦସ୍ୟଙ୍କ ବ୍ୟତୀତ ଅନ୍ୟ ସଦସ୍ୟମାନେ ପ୍ରତି ତିନି ବର୍ଷ ପାଇଁ ସାଧାରଣ ସଭାଦ୍ୱାରା ନିର୍ବାଚିତ ହୋଇ ପ୍ରତିବର୍ଷ ଦୁଇଥର ବୈଠକରେ ମିଳିତ ହୁଅନ୍ତି ।
- ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ପରିଷଦ ୫୪ ଜଣ ସଦସ୍ୟଙ୍କୁ ନେଇ ଗଠିତ । ଏହି ସଦସ୍ୟମାନେ ସାଧାରଣ ସଭାଦ୍ଵାରା ପ୍ରତି ତିନି ବର୍ଷ ପାଇଁ ନିର୍ବାଚିତ ହୋଇଥାଆନ୍ତି ।
- ବିଶ୍ଵର ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ସମସ୍ୟାର ରାଷ୍ଟ୍ରସଂଘକୁ ବିଭିନ୍ନ ପ୍ରସ୍ତାବ ଦେଇଥାଏ ।

୪। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଗଠନ ପାଇଁ ହେଇଥବ । ଉଦ୍ୟମଗୁଡ଼ିକୁ ଆଲୋଚନା କର ।
Answer:
- ଦ୍ଵିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧ ଚାଲୁଥିବା ସମୟରେମିତ୍ରଶକ୍ତିର ରାଷ୍ଟ୍ର ମୁଖ୍ୟମାନେ ବିଶ୍ୱ ଶାନ୍ତି ପ୍ରତିଷ୍ଠା ଦିଗରେ ରଣକୌଶଳ ସ୍ଥିର କରିବାପାଇଁ ଏକ ବୈଠକରେ ମିଳିତ ହୋଇଥିଲେ ।
- ଆନ୍ତର୍ଜାତିକ ସ୍ତରରେ ଶାନ୍ତି ଓ ନିରାପତ୍ତା ରକ୍ଷା ପ୍ରତିଷ୍ଠା ପାଇଁ ଉଦ୍ୟମ ଚାଲିଲା ।
- ୧୯୪୧ ମସିହା ଅଗଷ୍ଟ ୧୪ ତାରିଖ ଦିନ ଏକ ଯୁଦ୍ଧ ଜାହାଜରେ ତଦାନୀନ୍ତ ନ ଆମରି କାର ରାଷ୍ଟ୍ରପତି ଫ୍ରାଙ୍କ୍ ଲିନ୍ ରୁ ଜଭେଲ୍ ଟ ଓ ବ୍ରିଟିଶ୍ ପ୍ରଧାନମନ୍ତ୍ରୀ ଉଇନ୍ଷ୍ଟନ୍ ଚର୍ଚ୍ଚିଲ ମିଳିତ ହୋଇ ବିଶ୍ୱଶାନ୍ତି ପ୍ରତିଷ୍ଠା ପାଇଁ ‘ଆଟ୍ଲାଣ୍ଟିକ୍ ସନନ୍ଦ’ ଜାରି କରିଥିଲେ ।
- ଏହି ସନନ୍ଦରେ ବାକ୍ ସ୍ଵାଧୀନତା ଓ ଧର୍ମଗତ ସ୍ଵାଧୀନତା, ଅବାଧ ଜଳଯାତ୍ରା, ନିରାପତ୍ତା ଓ ନିରସ୍ତ୍ରୀକରଣ ଏବଂ ଆନ୍ତର୍ଜାତିକ ଶାନ୍ତି ଓ କରିବାପାଇଁ ଏକ ବିଶ୍ବସ୍ତରୀୟ ସଂଗଠନ ପ୍ରତିଷ୍ଠା ପାଇଁ ଉଦ୍ୟମ ଚାଲିଲା ।
- ୧୯୪୫ ମସିହା ଅପ୍ରେଲ ୨୫ ତାରିଖଠାରୁ ଜୁନ୍ ୨୬ ତାରିଖ ମଧ୍ୟରେ ୫୧ ଗୋଟି ରାଷ୍ଟ୍ରର ସାନ୍ ଫ୍ରାନ୍ ସି ସ୍କୋ ସହରରେ ଏକ ସମ୍ମିଳନୀରେ ମିଳିତ ହେଇ ସଂପୃକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦ ପ୍ରସ୍ତୁତି ଉଦ୍ୟମକୁ ସଫଳ କରିଥିଲେ ଓ ଜାତିସଂଘ ଗଠିତ ହୋଇଥିଲା ।
୫।ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘଦ୍ୱାରା ବିଭିନ୍ନ ଆନ୍ତର୍ଜାତିକ ସମସ୍ୟର ସାଧାନ ବିଷ୍ଟୟରେ ସଂଷ୍ଟପରେ ବର୍ଣ୍ଣନା କର ।
Answer:
- ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ମୁଖ୍ୟ କାର୍ଯ୍ୟ ହେଉଛି ପୃଥିବୀରେ ଶାନ୍ତି ବଜାୟ ରଖୁବା ଏବଂ ସମସ୍ତ କରିବା ।
- ୧୯୮୮ ମସିହାରେ ପୃଥିବୀରେ ଶାନ୍ତିରକ୍ଷା ଦିଗରେ ରାଷ୍ଟ୍ରସଂଘ ନିଜର ସଫଳତା ପାଇଁ ନୋବେଲ ଶାନ୍ତି ପୁରସ୍କାରରେ ସମ୍ମାନିତ ହୋଇଛି ।ମାନବାଧିକାରର ସୁରକ୍ଷା ଦିଗରେ ନାରୀ ଓ ପୁରୁଷ ସମସ୍ତଙ୍କୁ ସମାନ ରାଷ୍ଟ୍ରସଂଘର ଭୂମିକା ପ୍ରଶଂସନୀୟ ।
- ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ବିଭିନ୍ନ ବିବାଦୀୟ ସ୍ଥାନକୁ ଶାନ୍ତି ରକ୍ଷା ଉଦ୍ଦେଶ୍ୟରେ ସେନାବାହିନୀ ପ୍ରେରଣ କରି ସେଠାରେ ଶାନ୍ତି ପ୍ରତିଷ୍ଠା ଦିଗରେ ବହୁ ସଫଳତା ପାଇଛି ।
- ବହୁ ଆନ୍ତର୍ଜାତିକ ସମସ୍ୟା, ଯଥା — ଦକ୍ଷିଣ ସମସ୍ୟା, କୋରିଆ ସମସ୍ୟା, ଇରାକ୍ – ଇରାନ୍ ଯୁଦ୍ଧ, ଆଫଗାନିସ୍ତାନ ସମସ୍ୟା, ଭିଏତ୍ନାମ ଯୁଦ୍ଧ ସମସ୍ୟା, ନାୟି ୟାର ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି, କାଶ୍ମୀର ସମସ୍ୟା ଇତ୍ୟାଦି ବହୁ ବିବାଦୀୟ କ୍ଷେତ୍ର ରେ ସଂଯୁକ୍ତ ପ୍ରଚେଷ୍ଟା ଓ ଭୂମିକା ବିଶେଷ ଭାବରେ
- ବିଶ୍ଵର ନିରସ୍ତ୍ରୀକରଣ ପ୍ରକ୍ରିୟାକୁ ସଫଳ କରାଯାଇଛି । ପରମାଣୁ ଶକ୍ତିର ଶାନ୍ତିପୂର୍ଣ୍ଣ ‘ ନି ର ସ୍ତ୍ରୀକ ର ଣ କରାଯାଇଛି । ଉଦ୍ୟମ ସର୍ବଦା ପ୍ରଶଂସନୀୟ ।
କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ଦ୍ବିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧ ଚାଲୁଥିବା ସମୟରେ ମିତ୍ରଶକ୍ତିର ରାଷ୍ଟ୍ର ମୁଖ୍ୟମାନଙ୍କର ପ୍ରଧାନ ଉଦ୍ଦେଶ୍ୟ କ’ଣ ଥିଲା ?
Answer:
ଦ୍ବିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧ ଚାଲୁଥିବା ସମୟରେ ମିତ୍ରଶକ୍ତିର ରାଷ୍ଟ୍ର ମୁଖ୍ୟମାନ ଙ୍କ ର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ ଥିଲା । ଆନ୍ତର୍ଜାତିକ ସ୍ତରରେ ଶାନ୍ତି ପ୍ରତିଷ୍ଠା କରିବା ଓ ନିରାପତ୍ତା ରକ୍ଷା କରିବାପାଇଁ ଏକ ବିଶ୍ୱସ୍ତରୀୟ ସଂଗଠନ ପ୍ରତିଷ୍ଠା କରିବା ।
୨। କେଉଁ ଦୁଇଜଣ ରାଷ୍ଟ୍ରମୁଖ୍ୟ, କେଉଁଠାରେ ମିଳିତ ହୋଇ ଓ କେବେ ‘ଆଣ୍ଟିକ ସନନ୍ଦ’ ଜାରି କରିଥିଲେ ?
Answer:
ଆମେରିକାର ରାଷ୍ଟ୍ରପତି ଫ୍ରାଙ୍କ୍ଲିନ୍ ରୁଜ୍ଭେଲଟ୍ ଓ ବ୍ରିଟିଶ୍ ପ୍ରଧାନମନ୍ତ୍ରୀ ଉଇନ୍ଷ୍ଟନ୍ ଚର୍ଚ୍ଚିଲ୍ ଉତ୍ତର ଆଣ୍ଟିକ ମହାସାଗରରେ ଥିବା ଏକ ଯୁଦ୍ଧ ଜାହାଜରେ ମିଳିତ ହୋଇ ୧୯୪୧ ମସିହା ଅଗଷ୍ଟ ମାସ ୧୪ ତାରିଖ ଦିନ ଆଟ୍ଲାଣ୍ଟିକ୍ ସନନ୍ଦ ଜାରି କରିଥିଲେ ।

୩। ଦ୍ଵିତୀୟ ବିଶୁଯୁଦ୍ଧ ପରେ କେଉଁ ତିନୋଟି ରାଷ୍ଟ୍ର ଓ କାହିଲି ବିଶ୍ୱଶାନ୍ତି ପ୍ରତିଷ୍ଠାର ଆବଶ୍ୟକତା ଅନୁ ଭବ କରିଥିଲେ ?
Answer:
ଦ୍ବିତୀୟ ବିଶ୍ବଯୁଦ୍ଧ ପରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ବ୍ରିଟେନ୍ ଓ ସୋଭିଏତ୍ ରୁଷ୍ ରାଷ୍ଟ୍ରତ୍ରୟ ବିଶ୍ୱଯୁଦ୍ଧରେ ଘଟିଥିବା ମୃତାହତଙ୍କ ସଂଖ୍ୟା, ବ୍ୟାପକ କ୍ଷୟକ୍ଷତି, ପରମାଣୁ ଶକ୍ତିର ବିଭୀଷିକାକୁ ଉପଲବ୍ଧ କରି ବିଶ୍ୱ ଶାନ୍ତି ପ୍ରତିଷ୍ଠାର ଆବଶ୍ୟକତା ଅନୁ ଭବ କରିଥିଲେ ।
୪। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ଧାରା ଓ ଅଧ୍ୟାୟ ବିଷୟରେ ସଂକ୍ଷେପରେ ଲେଖ ।
Answer:
- ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦ ସବକମେଟ ୧୦,୦୦୦ ଶବ୍ଦ ସମ୍ବଳିତ ।
- ଏହି ସନନ୍ଦ ୧୧୧ ଟି ଧାରା ଓ ଏହା ୧୯ଟି ଅଧ୍ୟାୟରେ ବିଭକ୍ତ ହୋଇଛି ।
୫। କେତୋଟି ରାଷ୍ଟ୍ର ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ମୂଳ ସଦସ୍ୟ ରାଷ୍ଟ୍ର ହେବାର ସୌଭାଗ୍ୟ ଲାଭ କରିଥିଲେ ଓ କିପରି ?
Answer:
- ୫୧ ଗୋଟି ରାଷ୍ଟ୍ର ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ‘ମୂଳ ସଦସ୍ୟ’ ହେବାର ସୌଭାଗ୍ୟ ଲାଭ କରିଥିଲେ ।
- ଏହି ରାଷ୍ଟ୍ର ଗୁଡ଼ିକ ସାନ୍ ଫ୍ରାନ୍ ସିସ୍କୋ । ସମ୍ମିଳନୀରେ ଯୋଗଦାନ କରି ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦରେ ପ୍ରଥମେ ସ୍ଵାକ୍ଷର ପ୍ରଦାନ କରିଥିବାରୁ ସେହି ରାଷ୍ଟ୍ରଗୁଡ଼ିକୁ ‘ମୂଳ ସଦସ୍ୟ ରାଷ୍ଟ୍ର’ କୁହାଯାଉଛି ।
୬। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘରେ କେଉଁ ରାଷ୍ଟ୍ରମାନଙ୍କୁ ଓ କିପରି ନୂତନ ସଦସ୍ୟ ରୂପେ ଗ୍ରହଣ କରାଯାଇପାରିବ ?
Answer:
ନିରାପତ୍ତା ପରିଷଦର ଅନୁମୋଦନ କ୍ରମେ, ସନନ୍ଦର ବ୍ୟବକୁ ମାନି ଚଲିବାକୁ ପ୍ରତିଶୂତିବତ୍ତ ରାଷ୍ଟ୍ରମାନକୁ ‘ସାଧାରଣ ସଭା’ର ଅନୁମତି ମିଳିବା ପରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ର ସଂଘର ନୂତନ ସଦସ୍ୟ ରୂପେ ଗ୍ରହଣ କରାଯାଇପାରିବ ।
୭। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର କୌଣସି ରାଷ୍ଟ୍ରକୁ କେଉଁ ପଦ୍ଧତିରେ ବହିଷ୍କାର କରାଯାଇପାରିବ ?
Answer:
ନିରାପତ୍ତା ପରିଷଦର ଅନୁମୋଦନକ୍ରମେ ସନନ୍ଦର ବ୍ୟବସ୍ଥାକୁ ବାରମ୍ବାର ଭଙ୍ଗ କରୁଥିବା ଯେକୌଣସି ରାଷ୍ଟ୍ରକୁ ‘ସାଧାରଣ ସଭା’ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସଦସ୍ୟ ପଦରୁ ବହିଷ୍କାର କରିପାରନ୍ତି ।
୮। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଅଧୀନରେ କାର୍ଯ୍ୟ କରୁଥିବା ସାଧାରଣ ସଭାକୁ କାହିଲି ‘ପୃଥିବୀର ପଞ୍ଚାୟତ’ ଆଖ୍ୟା ଦିଆଯାଇଛି ?
Answer:
- ସାଧାରଣ ସଭାରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସମସ୍ତ ସଦସ୍ୟ – ରାଷ୍ଟ୍ରର ପ୍ରତି ନିଧ୍ ମାନେ ଆଲୋଚନା ଓ ବିତର୍କ ମାଧ୍ୟମରେ ବିଭିନ୍ନ ଆନ୍ତର୍ଜାତିକ ସମସ୍ୟାର ସମାଧାନ
- ତେଣୁ ଏହାକୁ ‘ପୃଥିବୀର ପଞ୍ଚାୟତ’ ଆଖ୍ୟା ଦିଆଯାଇଛି ।

୧୦। ସାଧାରଣ ସଭାର କେତୋଟି କମିଟି ରହିଛି ଓ ସେଗୁଡ଼ିକ କ’ଣ କ’ଣ ?
Answer:
ସାଧାରଣ ସଭାର ସାତଗୋଟି କମିଟି ରହିଛି । ସେଗୁଡ଼ିକ
(କ) ରାଜନୈତିକ ଏବଂ ନିରାପତ୍ତା କମିଟି
(ଖ) ଅର୍ଥନୈତିକ କମିଟି
(ଗ) ସାମାଜିକ ସଂସ୍ଥା ଓ ସାଂସ୍କୃତିକ କମିଟି
(ଘ) ନ୍ଯାସ କମିଟି
(ଙ) ପ୍ରଶାସନିକ ଓ ବଜେଟ୍ କମିଟି
(ଚ) ଆଇନଗତ କମିଟି
(ଛ) ସ୍ଵତନ୍ତ୍ର – ରାଜନୈତିକ କମିଟି
୧୧ । ସାଧାରଣ ସଭାରେ କିପରି ନିଷ୍ପତ୍ତି ନିଆଯାଏ ?
Answer:
- ସମସ୍ତ ସରଳ ଓ ସହଜ ସମସ୍ୟାର ସମାଧାନ ସାଧାରଣ ସଭାର ବୈଠକରେ ଉପସ୍ଥିତ ସମସ୍ତ ସଦସ୍ୟଙ୍କର ସାଧାରଣ ସଂଶୋଧନ (୫୦% + ୧) ମତ ବା ସମର୍ଥନ ଅନୁସାରେ ନିଷ୍ପଭି ହୋଇଥାଏ ।
- ଅନ୍ୟ ସମସ୍ତ ଜରୁରି ବା ଗୁରୁତର ସମସ୍ୟାର ସମାଧାନ ନିଷ୍ପତ୍ତି ଉପସ୍ଥିତ ସମସ୍ତ ସଦସ୍ୟଙ୍କ ନିଆଯାଏ । ଅର୍ଥାତ୍ ସାଧାରଣ ସଭାରେ ସମସ୍ତ ନିଷ୍ପତ୍ତି କେବଳ ‘ଭୋଟଦାନ’ ବା ‘ମତଦାନ’ ମାଧ୍ୟମରେ ନିଆଯାଏ ।
୧୨ । ସାଧାରଣ ସଭାର ଆଲୋଚନା ବା ବିତର୍କମୂଳକ କାର୍ଯ୍ୟ କ’ଣ ?
Answer:
ମାଧ୍ୟମରେ ସାଧାରଣ ସଭାର ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ପରିସରଭୁକ୍ତ ସମସ୍ତ ବିଷୟ ଉପରେ ବିତର୍କ ବା ଆଲୋଚନା କରାଯାଇଥାଏ । ପାଲେଷ୍ଟାଇନ୍, ଭାରତ- ପାକିସ୍ତାନ ବିବାଦ, ଆଫ୍ରିକାର ବର୍ଣ୍ଣବୈଷମ୍ୟ ଇତ୍ୟାଦି ସମସ୍ୟାତିକ ସାଧାରଣ ସଭାରେ ଆଲୋଚିତ ହୋଇଛି ।
୧୩ । ନିରାପତ୍ତା ପରିଷଦର କେତୋଟି କାର୍ଯ୍ୟ ରହିଛି ଓ ସେଗୁଡ଼ିକ କ’ଣ କ’ଣ ?
Answer:
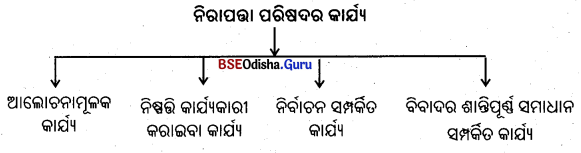
ନିରାପତ୍ତା ପରିଷଦର ଚାରିପ୍ରକାର କାର୍ଯ୍ୟ ରହିଛି । ଯଥା –
(କ) ଆଲୋଚନାମୂଳକ କାର୍ଯ୍ୟ
(ଖ) ନିଷ୍ପତ୍ତି କାର୍ଯ୍ୟକାରୀ କରାଇବା କାର୍ଯ୍ୟ
(ଗ) ନିର୍ବାଚନ ସମ୍ପର୍କିତ କାର୍ଯ୍ୟ
(ଘ) ନିବାଦର ଶାନ୍ତିରକ୍ଷା ସାଧାନ ସମ୍ପର୍କିତ କାର୍ଯ୍ୟ

୧୭। ସଚିବାଳୟର ମହାସଚିବ ହେବାପାଇଁ ଜଣେ ଲୋକର କେଉଁସବୁ ଯୋଗ୍ୟତା ଥିବା ଦରକାର ?
Answer:
- ସାଧାରଣ ସଭା ଓ ନିରାପ୍ଭା ପରିଷଦହରା ଗ୍ରହଣଯୋଗ୍ୟ ଜଣେ ବ୍ୟକ୍ତି ମହାସଚିବ ହେବା ବାଞ୍ଛନୀୟ ।
- ସେ ଜଣେ ବିଚକ୍ଷଣ ରାଷ୍ଟ୍ର ନୀତି ଜ୍ଞ ଓ ସୁପ୍ରଶାସକ ହୋଇଥିବା ଆବଶ୍ୟକ ।
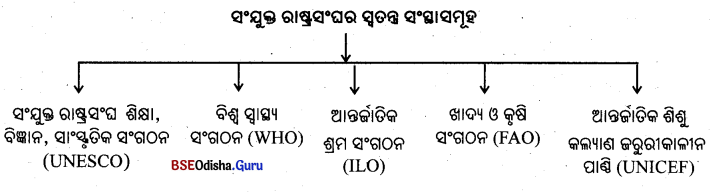
୧୮। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଅଧୀନରେ କାର୍ଯ୍ୟ କରୁଥିବା ଖାଦ୍ୟ ଓ କୃଷି ସଂଗଠନର କାର୍ଯ୍ୟ ଲେଖ ।
Answer:
- ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଅଧୀନରେ କାର୍ଯ୍ୟ କରୁଥିବା ଖାଦ୍ୟ ଓ କୃଷି ସଂଗଠନ ୧୯୪୫ ମସିହାରେ ଗଠିତ ହୋଇଥିଲା । ବିଶ୍ୱରେ କୃଷି ଉତ୍ପାଦନ ବୃଦ୍ଧି ଓ କୃଷି ଉନ୍ନୟନ ମାଧ୍ୟମରେ ଜୀବନଧାରଣର ମାନ ବୃଦ୍ଧି କରିବା ଏହି ସଂଗଠନର ମୁଖ୍ୟ ଉଦ୍ଦେଶ୍ୟ ।
- ଏହି ସଂଗଠନଦ୍ୱାରା ପ୍ରୋତ୍ସାହିତ ହୋଇ
୧୯ । ବିଶ୍ବବ୍ୟାଙ୍କ କେଉଁ ଉଦ୍ଦେଶ୍ୟରେ ଗଠିତ ହୋଇଛି ଓ ଏହାର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ କେଉଁଠାରେ ରହିଛି ?
Answer:
- ପୃଥିବୀର ବିଭିନ୍ନ ଦେଶରେ ପୁନଃନିର୍ମାଣ ଓ ଆର୍ଥିକ ବିକାଶ ପାଇଁ ବିଶ୍ବବ୍ୟାଙ୍କ କାର୍ଯ୍ୟ କରୁଛି ।
- ଏହାର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ଆମେରିକାର ୱାଶିଂଟନ୍ରେ ଅବସ୍ଥିତ ।
Objective Type Questions With Answers
A ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
୧। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ କେବେ ଜନ୍ମ ନେଇଥିଲା ?
Answer:
ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ୧୯୪୫ ମସିହା ଅକ୍ଟୋବର ମାସ ୨୪ ତାରିଖ ଦିନ ଜନ୍ମ ନେଇଥିଲା ।
୨। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ର ସଂଘର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer:
ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ନିୟୁୟର୍କ ସହରରେ ଅବସ୍ଥିତ ।
୩ । ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସାଧାରଣ ସଭା ପ୍ରତିବର୍ଷ କେତେ ଥର ବୈଠକରେ ମିଳିତ ହୁଏ ?
Answer:
ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସାଧାରଣ ସଭା ପ୍ରତିବର୍ଷ ଗୋଟିଏ ଥର ବୈଠକରେ ମିଳିତ ହୁଏ ।

୪। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସାଧାରଣ ସଭାରେ କେତେ ଉପସଭାପତି ଥାଆନ୍ତି ?
Answer:
ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସାଧାରଣ ସଭାରେ ୭ଜଣ ଉପସଭାପତି ଥାଆନ୍ତି।
୫। ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer:
ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ “ଦି ହେର୍” ସହରରେ ଅବସ୍ଥିତ ।
୬। କେଉଁ ସମୟରେ ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ଅଧ୍ୟକ୍ଷ ନିର୍ଣ୍ଣାୟକ ଭୋଟ ଜରିଆରେ ନିଷ୍ପତ୍ତି ଧାର୍ଯ୍ୟ କରନ୍ତି ?
Answer:
ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟରେ ନିଷ୍ପତ୍ତି ନେବା ସମୟରେ ସପକ୍ଷ ଓ ବିପକ୍ଷ ମତ ସମାନ ହେଲେ ଅଧ୍ୟକ୍ଷ ନିଜର ନିର୍ଣ୍ଣାୟକ ଭୋଟ ଜରିଆରେ ନିଷ୍ପତ୍ତି ଧାର୍ଯ୍ୟ କରନ୍ତି ।
୭। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସଚିବାଳୟର କେତେ କର୍ମଚାରୀ ରହିଛନ୍ତି?
Answer:
ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସଚିବାଳୟର ପ୍ରଶାସନି କ କାର୍ଯ୍ୟରେ ପ୍ରାୟ ୪୪ ହଜାର କର୍ମଚାରୀ ରହିଛନ୍ତି ।
୯। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସବୁ ବିଭାଗମାନଙ୍କଦ୍ୱାରା ଗୃହୀତ ହୋଇଥିବା ସମସ୍ତ ପ୍ରସ୍ତାବଗୁଡ଼ିକୁ କାର୍ଯ୍ୟକାରୀ କରାଇବା ଦାୟିତ୍ଵ କାହାର ?
Answer:
ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସବୁ ବିଭାଗମାନଙ୍କଦ୍ୱାରା ଗୃହୀତ ହୋଇଥୁ ସମସ୍ତ ପ୍ରସ୍ତାବଗୁଡ଼ିକୁ କାର୍ଯ୍ୟକାରୀ କରାଇବାର ଦାୟିତ୍ଵ ମହାସଚିବଙ୍କର।
୧୦। ମହାସଚିବ କେତେ ବର୍ଷ ପାଇଁ ନିଯୁକ୍ତ ହୁଅନ୍ତି ?
Answer:
ମହାସଚିବ ୫ବର୍ଷ ପାଇଁ ନିଯୁକ୍ତ ହୁଅନ୍ତି ।
୧୧। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ଖାଦ୍ୟ ଓ କୃଷି ସଂଗଠନ କେବେ ଗଠିତ ହୋଇଥିଲା ?
Answer:
ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ଖାଦ୍ୟ ଓ କୃଷି ସଂଗଠନ ୧୯୪୫ ମସିହାରେ ଗଠିତ ହୋଇଥିଲା ।
୧୨ । କେଉଁ ଦିଗରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘକୁ ସର୍ବଦା ଭାରତ ସାହାଯ୍ୟ ଓ ସହଯୋଗର ହାତ ବଢ଼ାଇଛି ?
Answer:
ବିଭିନ୍ନ ଆନ୍ତର୍ଜାତିକ ସମସ୍ୟାର ସମାଧାନ ଦିଗରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘକୁ ସର୍ବଦା ଭାରତ ସାହାଯ୍ୟ ଓ ସହଯୋଗର ହାତ ବଢ଼ାଇଛି ।
୧୩। ଭାରତର କେଉଁ ନୀତି ଉପରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଦୃଢ଼ ଆସ୍ଥା ସ୍ଥାପନ କରିଛି ?
Answer:
ଭାରତର ନିରପେକ୍ଷ ବୈଦେଶିକ ନୀତି ଉପରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଦୃଢ଼ ଆସ୍ଥା ସ୍ଥାପନ କରିଛି ।
୧୪। ଭାରତର କେଉଁ ଆଭିମୁଖ୍ୟକୁ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ସର୍ବଦା ସମ୍ମାନ ପ୍ରଦର୍ଶନ କରିଛି ?
Answer:
ବର୍ଣ୍ଣବୈଷମ୍ୟ ଦୂରୀକରଣ, ଆନ୍ତର୍ଜାତିକ ମହିଳା ସଶକ୍ତିକରଣ ଇତ୍ୟାଦି କ୍ଷେତ୍ରରେ ଭାରତର ସ୍ପଷ୍ଟ ଆଭିମୁଖ୍ୟକୁ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ସର୍ବଦା ସମ୍ମାନ ପ୍ରଦର୍ଶନ କରିଛି ।
୧୫ । ଭାରତ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘରୁ କେଉଁସବୁ କ୍ଷେତ୍ରରେ ସହାୟତା ପାଇଛି ?
Answer:
ଶିକ୍ଷା, ବିଜ୍ଞାନ ଓ ସାଂସ୍କୃତିକ ସଂଗଠନ ଏବଂ ଶିଶୁ କଲ୍ୟାଣ ଜରୁରିକାଳୀନ ପାଣ୍ଠିରୁ ଭାରତ ବହୁତ ସହାୟତା ପାଇଛି ।
B ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।
୧। ବିଶ୍ଵବ୍ୟାଙ୍କ (World Bank) ର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
୨। ଆନ୍ତର୍ଜାତିକ ଶିଶୁ କଲ୍ୟାଣ ଜରୁରିକାଳୀନ ପାଣ୍ଠି (UNICEF) କେବେ ଗଠିତ ହୋଇଥିଲା ?
୩। ପୃଥିବୀରେ ଶାନ୍ତିରକ୍ଷା ଦିଗରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ନିଜର ସଫଳତା ପାଇଁ କେବେ ନୋବେଲ୍ ଶାନ୍ତି ପୁରସ୍କାର ପାଇଥିଲା ?
୪। ପ୍ରତିବର୍ଷ କେଉଁ ତାରଖଟିକୁ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ପ୍ରତିଷ୍ଠା ଦିବସ ଭାବେ ପାଳନ କରାଯାଇଥାଏ ?
୫। ୧୯୪୫ ମସିହାରେ କୃଷିର ଉନ୍ନତି ପାଇଁ ମିଳିତ ଜାତିସଂଘଦ୍ବାରା କେଉଁ ଅନୁଷ୍ଠାନ ଗଠିତ ହୋଇଥିଲା ?
୬ । ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ଆୟବ୍ୟୟ ଅଟକଳ ବା ବଜେଟ୍ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର । କେଉଁଠାରେ ଅନୁମୋଦିତ ହୋଇଥାଏ ?
୭। ୨୦୧୧ ମସିହା ସୁଦ୍ଧା ପୃଥିବୀର କେତୋଟି ଦେଶ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସଦସ୍ୟ ଅଛନ୍ତି ?
୮। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦରେ ସର୍ବମୋଟ କେତୋଟି ଶବ୍ଦ ରହିଛି ?
୯। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ପ୍ରଥମ ଅଧିବେଶନ କେଉଁଦିନ ବସିଥୁଲା ?
୧୦ । ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ପ୍ରଥମ ଅଧିବେଶନ କେଉଁଠାରେ ବସିଥିଲା ?
୧୧ । ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ତୃତୀୟ ଧାରା ଅନୁସାରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ର ସଂଘର ସମସ୍ତ ସଦସ୍ୟ ରାଷ୍ଟ୍ର କୁ ମୁଖ୍ୟତଃ କେତୋଟି ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଛି ?
୧୨ । ପ୍ରତ୍ୟେକ ସଦସ୍ୟ-ରାଷ୍ଟ୍ର ସାଧାରଣ ସଭାକୁ କେତେଜଣ ଲେଖାଏଁ ପ୍ରତିନିଧ୍ ପଠାଇଥାଆନ୍ତି ?
୧୩ । ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ପରିଷଦର ସଦସ୍ୟ ସଂଖ୍ୟା କେତେ ?
୧୪ । ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର କେତେଜଣ ବିଚାରପତିଙ୍କୁ ନେଇ ‘କୋରମ୍’ ଗଠିତ ହୁଏ ?
୧୫ । ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ଅଧ୍ୟକ୍ଷଙ୍କ କାର୍ଯ୍ୟକାଳ କେତେ ବର୍ଷ ?
୧୬ । ‘ୟୁନିସେଫ୍’ ସଂସ୍ଥା କେବେ ଗଠିତ ହୋଇଥିଲା ?
୧୭ । ‘ଆଟ୍ଲାଣ୍ଟିକ୍ ସନନ୍ଦ’ ପ୍ରସ୍ତୁତ କରିବାରେ କେଉଁ ବ୍ରିଟିଶ୍ ପ୍ରଧାନମନ୍ତ୍ରୀ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ?
୧୮ । ‘ସାନ୍ଫ୍ରାନ୍ସିସ୍କୋ’ ସମ୍ମିଳନୀରେ ମୋଟ କେତୋଟି ରାଷ୍ଟ୍ରର ପ୍ରତିନିଧ୍ଵ ଯୋଗ ଦେଇଥିଲେ ?
Answers
୧ । ୱାଶିଂଟନ୍
୨। ୧୯୪୬ ଡିସେମ୍ବର ୧୧ ତାରିଖ
୩। ୧୯୮୮ ମସିହା
୪। ଅକ୍ଟୋବର ୨୪
୫। ଖାଦ୍ୟ ଓ କୃଷି ସଙ୍ଗଠନ
୬। ସାଧାରଣ ସଭା
୭। ୧୯୩ଟି
୮। ୧୦,୦୦୦ଟି
୯। ୧୯୪୬ ଜୁନ୍ ୧୦
୧୦। ଲଣ୍ଡନ
୧୧। ୨ଟି
୧୨। ୫ ଜଣ
୧୩। ୫୪
୧୪। ୯ ଜଣ
୧୫। ୩ ବର୍ଷ, ।
୧୬।୧୯୪୬
୧୭। ଉଇନ୍ ଷ୍ଟନ୍ ଚର୍ଚ୍ଚିଲ
୧୮। ୫୧ଟି

C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
୧। ____________ ମସିହାରେ ଦ୍ୱିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧର ପରିସମାପ୍ତି ଘଟିଲା ।
Answer:
୧୯୪୫
୨। ଆଟ୍ଲାଣ୍ଟିକ୍ ସନନ୍ଦ_____________ ମସିହାରେ ଜାରି କରାଯାଇଥିଲା ।
Answer:
୧୯୪୧
୩ । ଫ୍ରାଙ୍କ୍ଲିନ୍ ରୁଡ୍ଭେଲ୍ଟଟ _________________ ଦେଶର ରାଷ୍ଟ୍ରପତି ଥିଲେ ।
Answer:
ଆମେରିକା
୪। ଜରୁରି ପରିସ୍ଥିତି ଉପୁଜିଲେ _______________ ଘଣୀ ସମୟ ମଧ୍ୟରେ ସାଧାରଣ ସଭା ଜରୁରି ବୈଠକରେ ମିଳିତ ହୋଇଥାଏ ।
Answer:
୨୪
୫। ସାଧାରଣ ସଭାର ସଦସ୍ୟମାନଙ୍କଦ୍ୱାରା ନିରାପଭା ପରିଷଦର ___________ ଜଣ ଅସ୍ଥାୟୀ ସଦସ୍ୟ ନିର୍ବାଚିତ ହୋଇଥାଆନ୍ତି ।
Answer:
୧୦
୬। ସାଧାରଣ ସଭାର ସଦସ୍ୟମାନଙ୍କଦ୍ୱାରା ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ପରିଷଦର _____________ ଜଣ ସଦସ୍ୟ ନିର୍ବାଚିତ ହୋଇଥା’ନ୍ତି ।
Answer:
୧୮
୭। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘରେ ସର୍ବମୋଟ ____________ ଗୋଟି ରାଷ୍ଟ୍ର ସଦସ୍ୟ ରହିଛନ୍ତି ।
Answer:
୧୯୩

୮। ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ______________ ଜଣ ବିଚାରପତି ଅଛନ୍ତି ।
Answer:
୧୫
୯। ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ବିଚାରପତିମାନଙ୍କର _____________ ବର୍ଷ |
Answer:
୯
୧୦। ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ପ୍ରତି ____________ ବର୍ଷରେ ଏକ ତୃତୀୟାଂଶ ବିଚାରପତି ଅବସର ଗ୍ରହଣ କରନ୍ତି ।
Answer:
୩
୧୧ । ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ଉପାଧ୍ୟକ୍ଷ ________ ବର୍ଷ ପାଇଁ ନିର୍ବାଚିତ ହୋଇଥା’ନ୍ତି ।
Answer:
୩
୧୨। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସଚିବାଳୟର ମୁଖ୍ୟ ହେଉଛନ୍ତି ___________ ।
Answer:
ମହାସଚିବ
D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓ ) ଓ ଭୁଲ୍ ଉକ୍ତି ପାଇଁ (X) ଚିହ୍ନ ଦିଅ ।
୧। ସାମାଜିକ ଏବଂ ଅର୍ଥନୈତିକ ପରିଷଦର ସଦସ୍ୟ ସଂଖ୍ୟା ୫୪।
୨। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘକୁ ୧୯୮୭ ମସିହାରେ ନୋବେଲ ଶାନ୍ତି ପୁରସ୍କାର ପ୍ରଦାନ କରାଯାଇଥିଲା ।
୩। ପ୍ରତିବର୍ଷ ଡିସେମ୍ବର ୧୫ ତାରିଖକୁ ‘ବିଶ୍ୱ ମାନବାଧିକାର ଦିବସ’ ରୂପେ ପାଳନ କରାଯାଇଥାଏ ।
୪। ଦ୍ଵିତୀୟ ବିଶ୍ୱଯୁଦ୍ଧର ପରିସମାପ୍ତି ୧୯୪୬ ମସିହାରେ ହୋଇଥିଲା ।
୫। ୧୯୪୫ ମସିହା ଅକ୍ଟୋବର ୨୪ ତାରିଖରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଜନ୍ମ ନେଇଥିଲା ।
୬। ୨୦୧୧ ମସିହା ସୁଦ୍ଧା ପୃଥିବୀର ୧୯୩ଟି ରାଷ୍ଟ୍ର ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସଦସ୍ୟ ଥିଲେ ।
୭। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦ ୦୬ ଗୋଟି ଭାଷାରେ ଲେଖାଯାଇଛି ।
୮। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ପ୍ରଥମ ଅଧିବେଶନ ୧୯୪୬ ଜୁନ୍ ୧୦ ତାରିଖରେ ଲଣ୍ଡନଠାରେ ବସିଥିଲା ।
୯। ‘ILO’ ଶ୍ରମିକମାନଙ୍କର କଲ୍ୟାଣ ସାଧନ ପାଇଁ କାମ କରିଥାଏ ।
୧୦। UNICEF ଶି ଶୁ ମାନଙ୍କର କଲ୍ୟାଣ ପାଇଁ କାମ କରିଥାଏ ।
୧୧। ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ଦି ହେଗ୍ରାଠାରେ ଅବସ୍ଥିତ ।
୧୨ । ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସଚିବାଳୟରେ ପ୍ରାୟ ୪୫ ହଜାର କର୍ମଚାରୀ ଅଛନ୍ତି ।
୧୩।‘ବିଶ୍ବବ୍ୟାଙ୍କ’ର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ଜେନି ଭାଠାରେ ଅବସ୍ଥିତ ।
Answers
୧। (√)
୨। (×)
୩ ।(×)
୪ । (×)
୫। (√)
୬ | (√)
୭। (×)
୮। (√)
୯। (√)
୧୦। (√)
୧୧। (√)
୧୨। (×)
୧୩ । (×)

E ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେଖ ।




F. ରେଖାଙ୍କିତ ପଦକୁ ପରିବର୍ତ୍ତନ କରି ଭ୍ରମ ସଂଶୋଧନ କର ।
୧। ‘ବିଶ୍ଵ ମାନବାଧ୍ୟାର ଦିବସ’ ପ୍ରତିବର୍ଷ ମାର୍ଚ୍ଚ ୧୦ ତାରିଖରେ ପାଳନ କରାଯାଇଥାଏ ।
୨। ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ବିଚାରପତିଙ୍କର କାର୍ଯ୍ୟକାଳ ୧୦ ବର୍ଷ |
୩। ନ୍ୟାସ ପରିଷଦର ବୈଠକ ପ୍ରତି ବର୍ଷ ପାଞ୍ଚ ଥର ବସିଥାଏ ।
୪। ‘ନୋବେଲ ଶାନ୍ତି ପୁରସ୍କାର’ ୧୯୮୦ ମସିହାରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘକୁ ପ୍ରଦାନ କରାଯାଇଥିଲା ।
୫। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ‘ସନନ୍ଦ’ରେ ୧୧୦ଟି ଧାରା ରହିଛି ।
୬। ୧୯୪୭ ମସିହାରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ଜନ୍ମ ହୋଇଥିଲା ।
୭। ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ଆଂଶିଟନ ସହରରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ ଅବସ୍ଥିତ ।
୮। ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦ ଛଅ ଗୋଟି ଭାଷାରେ ଲେଖାଯାଇଛି ।
୯। ଫ୍ରାଙ୍କ୍ଲିନ୍ ରୁଜ୍ଭେଲଟ୍ର ରୁଷିଆର ରାଷ୍ଟ୍ରପତି ଥିଲେ ।
୧୦। ପୃଥିବୀର ବିଭିନ୍ନ ରାଷ୍ଟ୍ରକୁ ଋଣ ମଞ୍ଜୁର କରିବା ଷ୍ଟେଟ୍ବ୍ୟାଙ୍କର ମୁଖ୍ୟ କାର୍ଯ୍ୟ ।
୧୧। ଜେନେଭା ସହରଟି ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାରେ ଅବସ୍ଥିତ ।
୧୨ । ନ୍ୟାସ ପରିଷଦକୁ ପୃଥିବୀର ପଞ୍ଚାୟତ କୁହାଯାଇଥାଏ ।
୧୩ । ପ୍ରତି ବର୍ଷ ଅକ୍ଟୋବର ମାସ ୨୫ ତାରିଖକୁ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘ ଦିବସ ଭାବେ ପାଳନ କରାଯାଏ ।
୧୪ । ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ପ୍ରଥମ ସନନ୍ଦରେ ପ୍ରଥମେ ୫୦ ଗୋଟି ରାଷ୍ଟ୍ର ସ୍ବାକ୍ଷର ପ୍ରଦାନ କରିଥିଲେ ।
୧୫। ‘ଭିଟୋ’ କ୍ଷମତା କେବଳ ନିରାପତ୍ତା ପରିଷଦର ଅସ୍ଥାୟୀ ସଦସ୍ୟଙ୍କୁ ପ୍ରଦାନ କରାଯାଇଥାଏ ।
Answers
୧। ଡିସେମ୍ବର
୨।୯
୩। ଦୁଇ ଥର
୪। ୧୯୮୮
୫।୧୧୧
୬। ୧୯୪୫
୭। ନିୟୁୟର୍କ
୮। ପାଞ୍ଚ
୯। ଆମେରିକାର
୧୦। ବିଶ୍ୱ ବ୍ୟାଙ୍କ୍,
୧୧ । ସୁଇଜରଲ୍ୟାଣ୍ଡ
୧୨। ସାଧାରଣ ସଭା
୧୩୮୨୪
୧୪।୫୧
୧୫ । ସ୍ଥାୟୀ ।

G. ଚାରୋଟି ସମ୍ଭାବ୍ୟ ବିକଳ୍ପ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
1.୨୦୧୧ ମସିହା ସୁଦ୍ଧା ପୃଥିବୀର ନିମ୍ନୋକ୍ତ କେତୋଟି ଦେଶ ରାଷ୍ଟ୍ରସଂଘର ସଦସ୍ୟ ଅଛନ୍ତି ?
(A) ୧୮୩
(B) ୧୮୫
(C) ୧୯୦
(D) ୧୯୩
Answer:
(D) ୧୯୩
2. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦରେ ସର୍ବମୋଟ କେ ଶବ୍ଦ ରହିଛି ?
(A) ୧୦,୦୦୦
(B) ୧୫,୦୦୦
(C) ୨୦,୦୦୦
(D) ୨୫,୦୦୦
Answer:
(A) ୧୦,୦୦୦
3. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ପ୍ରଥମ ଅଧିବେଶନ ନିମ୍ନୋକ୍ତ କେଉଁ ମସିହାରେ ବସିଥିଲା ?
(A) ୧୯୪୫
(B) ୧୯୪୬
(C) ୧୯୪୭
(D) ୧୯୪୮
Answer:
(B) ୧୯୪୬
4. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ପ୍ରଥମ ଅଧିବେଶନ ନିମ୍ନୋକ୍ତ କେଉଁଠାରେ ବସିଥିଲା ?
(A) ନିୟୁୟର୍କ
(B) ଲଣ୍ଡନ
(C) ପ୍ୟାରିସ୍
(D) ୱାଶିଂଟନ୍
Answer:
(B) ଲଣ୍ଡନ
5. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ତୃତୀୟ ଧାରା ଅନୁସାରେ ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ର ସଂଘର ସମସ୍ତ ସଦସ୍ୟ ରାଷ୍ଟ୍ରକୁ ମୁଖ୍ୟତଃ କେତୋଟି ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଛି ?
(A) ୨ଟି
(C) ୪ଟି
(B) ୩ ଟି
(D) ୫ଟ
Answer:
(A) ୨ଟି
6. କେତେଜଣ ଲେଖାଏଁ ପ୍ରତିନିଧ୍ ପଠାଇଥାଆନ୍ତି ?
(A) ୪ ଜଣ
(B) ୫ ଜଣ
(C) ୬ ଜଣ
(D) ୭ ଜଣ
Answer:
(B) ୫ ଜଣ
7. ଅର୍ଥନୈତିକ ଓ ସାମାଜିକ ପରିଷଦର ସଦସ୍ୟ ସଂଖ୍ୟା କେତେ ?
(A) ୫୦
(C) ୫୪
(B) ୫୨
(D) ୫୭
Answer:
(C) ୫୪
8. ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ନିମ୍ନୋକ୍ତ କେତେଜଣ ବିଚାରପତିଙ୍କୁ ନେଇ ‘କୋରମ୍’ ଗଠିତ ହୁଏ ?
(A) ୭ ଜଣ
(B) ୬ ଜଣ
(C) ୮ ଜଣ
(D) ୯ ଜଣ
Answer:
(D) ୯ ଜଣ

9. ଆନ୍ତର୍ଜାତିକ ନ୍ୟାୟାଳୟର ଅଧ୍ୟକ୍ଷଙ୍କ କାର୍ଯ୍ୟକାଳ କେତେ ବର୍ଷ ?
(A) ୧ ବର୍ଷ
(B) ୨ ବର୍ଷ
(C) ୩ ବର୍ଷ
(D) ୪ ବର୍ଷ
Answer:
(C) ୩ ବର୍ଷ
10. ୟୁନିସେଫ୍ ସଂସ୍ଥା ନିମ୍ନୋକ୍ତ କେବେ ଗଠିତ ହୋଇଥିଲା ?
(A) ୧୯୪୫
(B) ୧୯୪୬
(C) ୧୯୪୭
(D) ୧୯୪୮
Answer:
(B) ୧୯୪୬
11. କେବେ ଦ୍ଵିତୀୟ ବିଶ୍ବଯୁଦ୍ଧର ପରିସମାପ୍ତି ଘଟିଥିଲା ?
(A) ୧୯୪୨ ମସିହା
(B) ୧୯୪୩ ମସିହା
(C) ୧୯୪୫ ମସିହା
(D) ୧୯୪୬ ମସିହା
Answer:
(C) ୧୯୪୫ ମସିହା
12. ଫ୍ରାଙ୍କ୍ଲିନ୍ ରୁଜ୍ଭେଲ୍ଟ କେଉଁ ଦେଶର ରାଷ୍ଟ୍ରପତି ଥିଲେ ?
(A) ଜାପାନ
(B) ଜର୍ମାନୀ
(C) ଆମେରିକା
(D) ଇରାକ୍
Answer:
(C) ଆମେରିକା
13. ଉଇନ୍ଷ୍ଟନ୍ ଚର୍ଚ୍ଚିଲ୍ କେଉଁ ଦେଶର ପ୍ରଧାନମନ୍ତ୍ରୀ ଥିଲେ ?
(A) ଜର୍ମାନୀ
(B) ବ୍ରିଟେନ୍
(C) ରୁଷିଆ
(D) ଇରାନ୍
Answer:
(B) ବ୍ରିଟେନ୍
14. ସାନ୍ଫ୍ରାନ୍ସିସ୍କୋ ସମ୍ମିଳନୀ କେଉଁ ବର୍ଷ ଅନୁଷ୍ଠିତ ହୋଇଥିଲା ?
(A) ୧୯୪୨
(B) ୧୯୪୩
(C) ୧୯୪୫
(D) ୧୯୪୬
Answer:
(C) ୧୯୪୫
15. କେଉଁ ସମ୍ମିଳନୀ ଥିଲା ବିଶ୍ଵ ସଙ୍ଗଠନ ପ୍ରତିଷ୍ଠା ଦିଗରେ ଏକ ଚୂଡ଼ାନ୍ତ ପଦକ୍ଷେପ ?
(A) ଭର୍ସାଇ
(B) ୟାଲ୍ଟା
(C) ସାନ୍ଫ୍ରାନ୍ସିସ୍କୋ
(D) ଡମ୍ଵାରଟନ୍ ଓକ୍
Answer:
(C) ସାନ୍ଫ୍ରାନ୍ସିସ୍କୋ
16. ସାନ୍ଫ୍ରାନ୍ସିସ୍କୋ ସମ୍ମିଳନୀରେ କେତେଗୋଟି ରାଷ୍ଟ୍ରର ପ୍ରତିନିଧୂ ଯୋଗ ଦେଇଥିଲେ ?
(A) ୪୫
(B) ୪୬
(C) ୪୮
(D) ୫୧
Answer:
(D) ୫୧
17. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ମୁଖ୍ୟ କାର୍ଯ୍ୟାଳୟ କେଉଁଠାରେ ଅବସ୍ଥିତ ?
(A) ସାନ୍ଫ୍ରାନ୍ସିସ୍କୋ
(B) ପ୍ୟାରିସ୍
(C) ଲଣ୍ଡନ
(D) ନିଉୟର୍କ
Answer:
(D) ନିଉୟର୍କ
18. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ‘ସନନ୍ଦ’ରେ ସର୍ବମୋଟ କେତୋଟି ଧାରା ରହିଛି ?
(A) ୧୧୧
(B) ୧୧୩
(C) ୧୨୨
(D) ୧୩୨
Answer:
(A) ୧୧୧

19. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘର ସନନ୍ଦ କେତେଗୋଟି ଭାଷାରେ ଲିଖ୍ତର ?
(A) ଦୁଇ
(B) ତିନି
(C) ଚାରି
(D) ପାଞ୍ଚ
Answer:
(D) ପାଞ୍ଚ
20. ସଂଯୁକ୍ତ ରାଷ୍ଟ୍ରସଂଘରେ କେତେଗୋଟି ରାଷ୍ଟ୍ର ମୂଳ ସଦସ୍ୟ ଭାବେ ପରିଚିତ ?
(A) ୪୮
(C) ୫୩
(B) ୫୧
(D) ୫୫
Answer:
(B) ୫୧
![]()
![]()

![]()
![]()
![]()
![]()