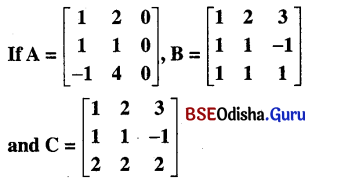
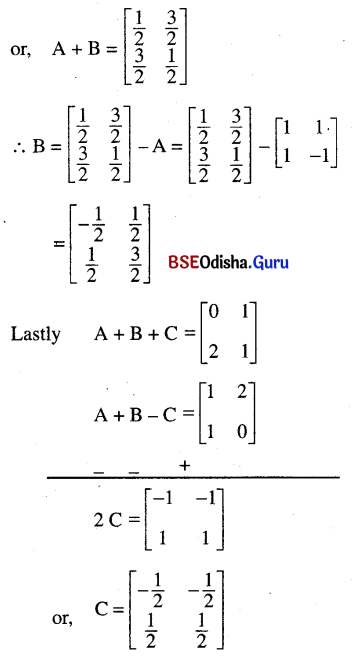
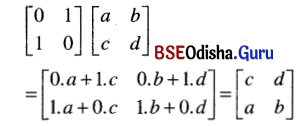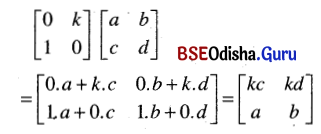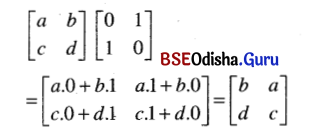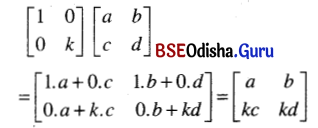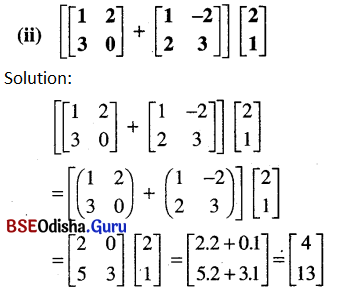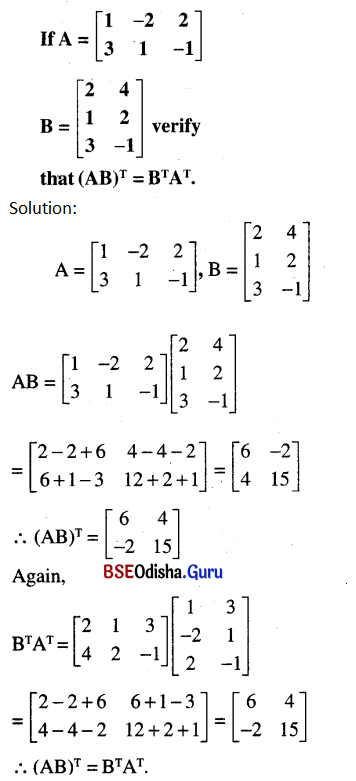Odisha State Board BSE Odisha 7th Class English Solutions Follow-Up Lesson 7 Silver Textbook Exercise Questions and Answers.
BSE Odisha Class 7 English Solutions Follow-Up Lesson 7 Silver
BSE Odisha 7th Class English Follow-Up Lesson 7 Silver Text Book Questions and Answers
Session – 1
I. Pre-Reading
- Socialization:
- You have read the poem Cobweb’. You have seen how a poem is made of a simple sight – the sight of a cobweb on telephone wires. The poem ends with moon — how the moon turns the cobweb into magic white. Now we’ll read. enjoy and see how again a poem is made out of a ver common sight — the moonlit night. Let’s read the poem.
( ତମେ ‘ବଢିଆଣୀ ଜାଲ’ କବିତାଟି ପଢ଼ିଲ । ଜାଣିଲ କିଭଳି ସାଧାରଣ ଦୃଶ୍ୟକୁ କବିତାରେ ସଜାଇ ଦିଆଯାଏ – ଯେପରି ଟେଲିଫୋନ ତାରକୁ ଘେରି ରହିଥିବା ବୁଢ଼ିଆଣୀ ଜାଲ । କବିତାଟି ଚନ୍ଦ୍ର ଶବ୍ଦରେ ପରିସମାପ୍ତ ହୋଇଛି – ଜହ୍ନ ଆଲୁଅ କିଭଳି ବୁଢ଼ିଆଣୀ ଜାଲକୁ ଯାଦୁକରୀ ଶୁଭ୍ର ରଙ୍ଗରେ ରଞ୍ଜିତ କରିଦେଉଛି । ବର୍ତ୍ତମାନ ଚାଲ ପଢ଼ିବା, ଉପଭୋଗ କରିବା ଏବଂ ଦେଖବା କିଭଳି ଏକ ସାଧାରଣ ଦୃଶ୍ୟରୁ ଆଉ ଏକ କବିତା ରଚନା କରାଯାଇଛି – ଚନ୍ଦ୍ରାଲୋକିତ ରଜନୀ । ଚାଲ କବିତାଟିକୁ ପାଠ କରିବା ।)
![]()
II. While Reading
Text
• Read the poem silently and answer the questions that follow.
( କବିତାଟିକୁ ନୀରବରେ ପାଠ କର ଏବଂ ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ । )
Slowly, silently, now the moon
Walks the night in her silver shoon;
This way, and that, she peers, and sees
Silver fruit upon silver trees;
One by one the casements catch
Her beams beneath the silvery thatch;

Couched in his kennel, like a log.
With paws of silver sleeps the dog;
From their shadowy cote the white breasts peep
Of doves in a silver-feathered sleep;
A harvest mouse goes scampering by.
With silver claws, and silver eye;
And moveless fish in the water gleam,
By silver reeds in a silver stream.
Walter de la Mare
ଧୀରେ ଧୀରେ ନୀରବରେ ଚାଲିଥାଏ ଜହ୍ନ
ରାତିସାରା ଚାଲିଥାଏ ଶୁଭ୍ର ଜୋତା ପରିଧାନ କରି;
ରାତ୍ରିସାରା ଚାଲିଥାଏ ଶୁଭ୍ର ଜୋତା ପରିଧାନ କରି;
ଏବଂ ଦେଖେ ଶୁଭ୍ର ଫଳସବୁ ସଫେଦ ବୃକ୍ଷରେ;
ଏକ ପରେ ଏକ ବାତାୟନ | ଝରକା ପଥରେ
ପ୍ରବେଶ ତା’ର କିରଣ ଚାଳକୁ ତ ସଫେଦ ବନାଇ;
ପଡ଼ି ରହିଥାଏ ତ କୁକୁର କାଠଗଣ୍ଡି ତୁଲ୍ୟ ତା’ କୋଠିରେ
ଶୋଇରହେ ଊର୍ଦ୍ଧ୍ୱମୁଖୀ ପଞ୍ଝା ତା’ ସଫେଦ ସଜରେ ବନେଇ;
ଛାୟାଯୁକ୍ତ ପର ଦେହ ଉଙ୍କିମାରେ ଧବଳ ହିଆରେ
କପୋତଟି ଶୋଇ ରହେ ଧବଳ ପର-ପରଦାର ତଳେ;
ଅମଳ ବେଳର ମୂଷା ଧାଇଁଯାଏ ଦ୍ରୁତ ପଦଚାଳି
ରୂପେଲି ପଞ୍ଝା ଏବଂ ରୂପେଲି ଚାହାଣି ସମ୍ଭାଳି;
ନିସ୍ତେଜ ମାଛମାନେ ଜଳ ତଳେ ଚକ୍ରଚକ୍ କାତି ଝଲସାଇ
ଥାଆନ୍ତି ତ ରମେଲି ତଣ ଏବଂ ରୁପେଲି ଝରଣା ହସାଇ ।
![]()
Notes And Glossary
moon (ମୁନ୍) – ଜହ୍ନ
shoon (ସୁନ୍) – ଯୋତା
peer – ଖୋଜିବା ପରି
silver (ସିଲଭର) – ରୂପେଲି
casement (କେସ୍ମେଣୁ) – ଝରକା
beams (ବିମ୍ସ) – ଆଲୋକ | କରଣ
beneath (ବି) – ତଳେ
thatch (ଥ୍ୟାଚ୍) – ମୋଟା କେଶ
couched (କାଉଚ) – ଶୋଇ ରହିଥିଲା
kennel (କେନେଲ୍) – କୁକୁର ରହିବା ଘର
log (ଲଗ) – କାଠଗଣ୍ଡି
paws (ପଢ) – ଖାବଲ୍
breasts (ବ୍ରେଷ୍ଟସ୍) – ଛାତିସବୁ
Peep (ପିପ୍) – ଦେଖୁଛି |
doves (ଡୋଭସ୍) – କପୋତସବୁ
feather (ଫ୍ଲିଦର) – ପର/ଡେଣା
harvest (ହାରଭେଷ୍ଟ) – ଅମଳ/ଉତ୍ପାଦନ
mouse (ମାଉସ୍) – ମୂଷା
scamper (ସ୍କାମ୍ପର) – ତରବର ହୋଇ ଚାଲିଯିବା
claws (କ୍ଲଜ୍) – ଅପେକ୍ଷା କର
moveless (ମୁଭେସ୍) – ସ୍ଥିର
gleam (ଗ୍ଲିମ୍ ) – ଚକ୍କ୍ କରୁଥୁବା
reeds (ରିଡ଼ସ) – ଜଳାଶୟ କୂଳରେ ଥିବା ଘାସ
Follow the steps of the main lesson. ( ମୂଳପାଠ୍ୟର ସୋପାନଗୁଡ଼ିକୁ ଅନୁସରଣ କର ।)
Comprehension Questions
Question 1.
What is the poem about?
( କବିତାଟି କେଉଁ ବିଷୟରେ ?)
Answer:
The poem is about the moon.
Question 2.
How does the moon walk?
(ଜହ୍ନ କିପରି ପଦଚାଳନା କରେ ?)
Answer:
The moon walks very slowly and silently the whole night. She wears silver shoes while walking.
Question 3.
“Shoon” is an old word for “shoe”. Why does the shoe look like silver?
(‘Shoon’ ‘Shoe’ ର ପ୍ରାଚୀନ ଶବ୍ଦ । ଜୋତା କାହିଁକି ରୂପେଲି | ସଫେଦ ପ୍ରତୀୟମାନ ହୁଏ ?)
Answer:
The beams of the moon is silvery. So the moon appears to wear shoes of silver.
Question 4.
How is ‘peer’ slightly different from ‘see’ ? See the dictionary?
(‘Peer’ (ଉଙ୍କି ମାରିବା) ‘see’ (ଦେଖିବା) ଠାରୁ ଅଳ୍ପ ଟିକିଏ ଅଲଗା କିପରି ? ଶବ୍ଦକୋଷ ଦେଖୁ ସ୍ଥିର କର ।)
Answer:
Peer means look searchingly while see means perceive with eyes.
Question 5.
What does the moon see first?
(ଜହ୍ନ ପ୍ରଥମେ କ’ଣ ଦେଖେ ?)
Answer:
First, the moon sees the silver fruit upon silver trees.
![]()
Question 6.
Why do the fruit and tree look silvery?
(କାହିଁକି ଗଛର ଫଳ ଏବଂ ନିଜେ ଗଛ ରୂପେଲି ଦେଖାଯାଏ ?)
Answer:
The moon beam falls on the trees and fruit and turns them into silvery.
Question 7.
Casement’ is an old word for ’window’ and ’ beneath’ is an old word for ’below’. Where are the windows?
(‘Casement’ ‘window’ ର ଏବଂ ‘beneath’ ‘below’ ର ପ୍ରାଚୀନ ଶବ୍ଦ । ଝରକାସବୁ କେଉଁଠି ଥାଏ ? )
Answer:
The windows are below the silvery thatch.
Question 8.
Where does the dog sleep?
(କୁକୁରଟି କେଉଁଠି ଶୁଏ ? )
Answer:
The dog sleeps in its kennel.
Question 9.
The dog sleeps like a log- a piece of wood. What does this tell about the dog’s sleep?
(କୁକୁରଟି ଖଣ୍ଡେ କାଠଗଣ୍ଡି ଭଳି ଶୋଇ ରହିଥାଏ । ଏହା କୁକୁରର ସୁପ୍ତି (ଶୋଇବା) ବାବଦରେ କ’ଣ କହେ ?)
Answer:
“The dog sleeps like a log”. This expression shows that the dog is in deep sleep. It is seen like a log is lying.
Question 10.
Why do its paws look silvery?
(ତାହାର (କୁକୁରର) ପଞ୍ଝା କାହିଁକି ରୂପେଲି ଦିଶେ ?)
Answer:
When the white moonbeam falls on the paws of the dog, they look like silvery.
Question 11.
Can you guess why the dog does not look silvery?
(ଅନୁମାନ କରିପାରିବ କି କାହିଁକି କୁକୁର ରୂପେଲି ଦେଖାଯାଏ ନାହିଁ ?)
Answer:
The dog was inside the kennel but his paws were outside the kennel. So the moonbeams reflect on his paws not on its body. So the dog does not look silvery.
Question 12.
Where does the dove sleep?
(କପୋତ କେଉଁଠି ଶୁଏ ?)
Answer:
The dove sleeps in its shadowy cote.
Question 13.
The breast of the dove peeps out. Silver-feather sleep – the feather looks silvery. What about the head of the dove? Can you think how the dove is sleeping?
(କପୋତର ଛାତି ବାହାରକୁ ଉଙ୍କିମାରେ । ରୂପେଲି ପର ତଳେ ନିଦ୍ରା- ପରସବୁ ରୂପେଲି ଦେଖାଯାଏ । କମୋଦର ମଣ୍ଡ କିଭଳି ଦେଖାଯାଏ ? ଚିନ୍ତା କରିପାରଛ ତ କପୋତ କିଭଳି ଶୋଇଛି ? )
Answer:
The dove in its shadowy cote sleeps keeping its breast out. Its head is hidden inside its feather.
Question 14.
Who goes scampering by (running very fast)?
(କିଏ ତରବର ହୋଇ ଦୃତଗତିରେ ଚାଲିଯାଏ ? )
Answer:
A harvest mouse goes scampering by.
Question 15.
Everyone is asleep. Why is the mouse awake?
(ପ୍ରତ୍ୟେକ ଶୟନରତ । ମୂଷା କାହିଁକି ଜାଗ୍ରତ ଥାଏ ?)
Answer:
Everyone is asleep in the cool moon light, but the mouse is awake. Because it collects its food in silent night.
![]()
Question 16.
Why does the fish gleam (dazzle)?
(ମାଛମାନେ କାହିଁକି ଚକ୍କ୍ ଦିଶନ୍ତି ?)
Answer:
When the moon light falls on moveless fish, it looks white.
Question 17.
Where is the fish?
(ମାଛସବୁ କେଉଁଠି ଥାଆନ୍ତି ?)
Answer:
The fish is in the stream water.
Question 18.
When everyone is asleep, why is the poet awake?
(ଯେତେବେଳେ ସମସ୍ତେ ଶୋଇ ରହିଥାନ୍ତି, କବି ସେତେବେଳେ କାହିଁକି ଜାଗ୍ରତ ଥାଆନ୍ତି ?)
Answer:
When everybody is asleep, the poet is awake because he wants to watch the natural beauty in the moonlit night.
Session – 2
III. Post-Reading
1. Comprehension Activities
(a) MCQs: Fill in the blanks from the alternatives given
Question 1.
The moonlight first falls on _____________?
(A) dog
(B) dove
(C) fish
(D) tree
Answer:
(D) tree
Question 2.
At last the moonlight falls on ____________?
(A) fruits
(B) fish
(C) dog
Answer:
(B) fish
![]()
Question 3.
Round the word which is on odd one out?
(i) window, thatch, tree, dog
(ii) fish, dove, mouse, fruit
Answer:
(i) dog
(ii) fruit
(b) Match the items under A with items under B. (Question with Answer)

Answer:
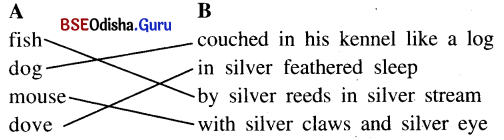
Session – 3
2. Vocabulary
(a) Learn the spelling of the following words using the four steps method- Look > Cover > Write > Verify
beam, peer, harvest, kennel, cote, claws, stream
(b) Solve the following crossword puzzle. Use the clues given. (Question with Answer)
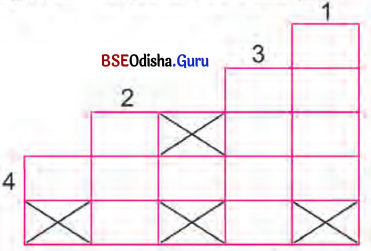
Answer:
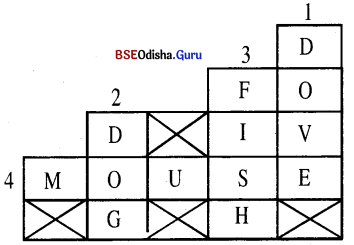
Down: Across :
1. In silver feathered sleep
2. Like a log
3. Moveless
4. Goes scampering by
![]()
Session – 4
3. Writing:
(a) In 2(b), you have already matched items under A with items under B. Now write four sentences joining the items with ‘is’, the first one is done for you.
Fish + silver reeds in silver stream.
1. The fish is by silver reeds in silver stream.
2. The dog is couched in his kennle like a log.
3. The mouse is with silver clause and silver eye.
4. The dove is in silver feathered sleep.
(b) You can summarise the poem using only one type of sentence. Write as many sentences of this type as you can. The first one is done for you using
the word ‘tree’ given in the bracket, (trees, fruits, window, dog ………………..)
1. The moonlight falls on the tree and it looks silvery.
Answer:
2. The moonlight falls on the fruits and they look silvery.
3. The moonlight falls on the window and it looks silvery.
4. The moonlight falls on the paws of the dog and they look silvery.
5. The moonlight falls on the white breast of the dove and it looks silvery.
6. The moonlight falls on the claws of the mouse and they look silvery.
7. The moonlight falls on the stream water and it looks silvery.
(c) Answer the following questions.
Question 1.
What is the poem about?
Answer:
The poem is about the moon.
Question 2.
What does the moon see first?
Answer:
The moon sees the silver fruit upon silver trees first.
Question 3.
Where does the dog sleep?
Answer:
The dog sleeps in its kennel.
Question 4.
Where does the dove sleep?
Answer:
The dove sleeps in its shadowy cote.
Question 5.
Who goes scampering by?
Answer:
A harvest mouse goes scampering by under the moonlight.
Question 6.
Where is the fish?
Answer:
The fish is by the silver stream with reeds on its bank.
![]()
Notes And Glossary
beneath (ବିନିଥ୍) – under (ତଳେ)
casements (କେସ୍ମେଣ୍ଟ୍ସ୍) – windows (ଝରକା)
ceaseless (ସିକ୍ସ୍) – non-stop, without rest (ଅହରହ )
cobwebs (କୋବଓ୍ବେବ) – spider net (ବୁଢ଼ିଆଣୀ ଜାଲ)
couched (କୋଚ୍) – slept (ଶୋଇ ରହିଥିବା )
gleam (ଗ୍ଲିମ୍ ) – shine (ଝଲସୁଥିବା ବା ଚକ୍କ୍ କରୁଥୁବା)
kennel (କେନେଲ୍,) – small shelter for a dog (କୁକୁର ରହିବା ଘର)
peers (ପିଅର୍ସ୍) – to look (ଖୋଜିବା ପରି ଦେଖିବା)
pours (ପୋର୍ସ୍) – gives in plenty (ଢାଳିବା, ବହୁପରିମାଣରେ ଦେବା)
reeds (ରିଡ୍ସ୍) – grass like water plants (ନଦୀ ଝରଣା କୂଳରେ ଥିବା)
scampering (ସ୍କାମ୍ପରଇ) – moving quickly, running (ତରବରିଆ ଭାବେ)
shadowy cote (ସାଡୋ କୋଟ୍) – (here) less bright wings of the dove (ଅସ୍ପଷ୍ଟ)
shoon (ସୁନ୍) – shoe (ଜୋତା)
silver feathered (ସିଲଭର୍ ଫିଦର୍ଡ୍) – feathers look like silver colour (ଦେଖାଯାଉଥିବା ପର)
spider (ସ୍କାଇଡର) – web spinning insect (ବୁଢ଼ିଆଣୀ)
spindles (ସିଣ୍ଡଲ୍ – here, spider’s weaving instrument (ପ୍ରାକୃତିକ ତାକୁଡ଼ି)
stretch (ଷ୍ଟେଟ୍) – long and continuous (ବିସ୍ତାରିତ ହୋଇଥିବା)
thatch – roof of straw (ଚାଳ ଛପର)
weaver (ୱିଭର୍) – one who weaves thread / cloth (ବୁଣାଳି, ଲୁଗା)
BSE Odisha 7th Class English Solutions Follow-Up Lesson 7 Silver Important Questions and Answers
(A) Choose the right answer from the options.
Question 1.
The moon walks in the sky?
(a) silently
(b) slowly
(c) speedily
(d) hopingly
Answer:
(b) slowly
Question 2.
While walking the moon wears?
(a) silver shoes
(b) black shoes
(c) grey shoes
(d) red shoes
Answer:
(a) silver shoes
![]()
Question 3.
The moon is personified as a _____________?
(a) boy
(b) girl
(e) lady
(d) old lady
Answer:
(c) Lady
Question 4.
The dog sleeps in ______________?
(a) its house
(b) its kennel
(c) its stay
(d) its stable
Answer:
(b) its kennel
Question 5.
The breast of the dove looks silvery?
(a) it is naturally white,
(b) somebody paints it white
(c) the moonbeam falls on it.
(d) none of these
Answer:
(c) The moonbeam falls on it.
Question 6.
The poem is by _______________?
(a) W. Wordsworth
(b) Robert Frost
(c) Walter de la Mare
(d) none of these
Answer:
(c) Walter de la Mare
(B) Answer the following questions.
Question 1.
How does the moon walks?
Answer:
The moon walks slowly wearing silver shoes on her feet.
![]()
Question 2.
Why does every object of nature looks white?
Answer:
Every object of nature looks white because the white moon beam falls on them.