Prasanna

Odisha State Board BSE Odisha 6th Class Science Important Questions Chapter 6 ବସ୍ତୁର ଓ ପଦାର୍ଥର ପରିବର୍ତ୍ତନ Important Questions and Answers.

BSE Odisha Class 6 Science Important Questions Chapter 6 ବସ୍ତୁର ଓ ପଦାର୍ଥର ପରିବର୍ତ୍ତନ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ମନୁଷ୍ୟକୃତ ପରିବର୍ତ୍ତନ କ’ଣ ? ଦୁଇଟି ଉଦାହରଣ ଦିଅ ।
ଉ –

• ମନୁଷ୍ୟଦ୍ଵାରା ପଦାର୍ଥର ଯେଉଁ ପରିବର୍ତ୍ତନ ଘଟେ ତା’କୁ ମନୁଷ୍ୟକୃତ ପରିବର୍ତ୍ତନ କୁହାଯାଏ ।
• ତୁଳାରୁ ସୂତା ହେବା, ସୁନା ଓ ରୁପାରୁ ଅଳଙ୍କାର ତିଆରି ହେବା ଆଦି ମନୁଷ୍ୟକୃତ ପରିବର୍ତ୍ତନ ।

Question 2.
ଭୌତିକ ପରିବର୍ତ୍ତନ କ’ଣ ? ଦୁଇଟି ଉଦାହରଣ ଦିଅ ।
ଉ –

• ଯେଉଁ ପରିବର୍ତ୍ତନରେ କୌଣସି ନୂତନ ପଦାର୍ଥ ସୃଷ୍ଟି ହୁଏ ନାହିଁ, ତାହାକୁ ଭୌତିକ ପରିବର୍ତ୍ତନ କୁହାଯାଏ ।
• କାଚ ଗ୍ଲାସ୍ ଭାଙ୍ଗିଯିବା, ଟେବୁଲକୁ ଭାଙ୍ଗି ଖଣ୍ଡ ଖଣ୍ଡ କରିବା ଆଦି ଭୌତିକ ପରିବର୍ତ୍ତନ ।

Question 3.
ଅପ୍ରତ୍ୟାବର୍ତୀ ପ୍ରତିକ୍ରିୟା କ’ଣ ? ଦୁଇଟି ଉଦାହରଣ ଦିଅ ।
ଉ –

• ଯେଉଁ ପ୍ରତିକ୍ରିୟା କେବଳ ଗୋଟିଏ ଦିଗରେ ଘଟିଥାଏ, ତାହାକୁ ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ ପ୍ରତିକ୍ରିୟା କୁହାଯାଏ ।
• କ୍ଷୀର ଦହିରେ ପରିଣତ ହେବା, ମଞ୍ଜିରୁ ଗଜା ହେବା ଆଦି ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ ପ୍ରତିକ୍ରିୟା ।

Question 4.
ଶଗଡ଼ ଚକରେ ନାଲ କିପରି ମଡ଼ାଯାଏ ?
ଉ –

• ପ୍ରଥମେ ଲୁହାରେ ତିଆରି ନାଲକୁ ଉତ୍ତପ୍ତ କରିବାଦ୍ଵାରା ଏହା ପ୍ରସାରିତ ହୁଏ ।
• ଉତ୍ତପ୍ତ ହେବାପରେ ନାଲଟିକୁ ଚକ ଚାରିପାଖରେ ଲଗାଇ ଥଣ୍ଡା କଲେ ଚକରେ ନାଲ ଲାଗିଯାଏ ।

Question 5.
ପ୍ରାକୃତିକ ପରିବର୍ତ୍ତନ କ’ଣ ? ଦୁଇଟିର ଉଦାହରଣ ଦିଅ ।
ଉ –

• ପ୍ରାକୃତିକ ଉପାୟରେ ଘଟୁଥ‌ିବା ପରିବର୍ତ୍ତନଗୁଡ଼ିକୁ ପ୍ରାକୃତିକ ପରିବର୍ତ୍ତନ କହନ୍ତି ।
• ଓଦାଲୁଗା ଶୁଖୁ, ପିଲାଟି ବୁଢ଼ା ହେବା ଆଦି ପରିବର୍ତ୍ତନ ପ୍ରାକୃତିକ ପରିବର୍ତ୍ତନ ।

ଦୀର୍ଘ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ଗୋଟିଏ ରାସାୟନିକ ପରିବର୍ତ୍ତନ ଘଟିଲା ବୋଲି ଜାଣିବା କିପରି, ଏକ ଉଦାହରଣ ସହ ଲେଖ ।
ଉ –

• ତିଆକୁ ଅଧ୍ବକ ଉତ୍ତପ୍ତ କଲେ ଶେଷରେ ଏକ କଳା ରଙ୍ଗର କଠିନ ପଦାର୍ଥ ପରୀକ୍ଷା ନଳୀର ତଳେ ରହିଯିବ ଏହି ପଦାର୍ଥର ରାସାୟନିକ ନାମ କପର ଅକ୍‌ସାଇଡ୍ । ଏଥୁରୁ ଆଉ ତୁତିଆ ପ୍ରସ୍ତୁତ ହୋଇ ପାରିବ ନାହିଁ । ତେଣୁ ଏହି ପରିବର୍ତ୍ତନଟି ସ୍ଥାୟୀ ଓ ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ ।
• ଏହି ପରିବର୍ତ୍ତନଗୁଡ଼ିକର ଶେଷରେ ମିଳୁଥିବା ଉତ୍ପାଦଗୁଡ଼ିକ ଗୋଟିଏ ଗୋଟିଏ ନୂତନ ପଦାର୍ଥ । ତେଣୁ ଏହି ପରିବର୍ତ୍ତନରେ ରାସାୟନିକ ପରିବର୍ତ୍ତନ ଘଟିଲା ବୋଲି ଜାଣିବା ।

Question 2.
ଉଦାହରଣ ଦେଇ ଦ୍ରବ, ଦ୍ରାବକ, ଦ୍ରବଣ ଓ ଦ୍ରବଣୀୟତା କ’ଣ ବୁଝାଅ ।
ଉ –

• ଦ୍ରବ ଓ ଦ୍ରାବକର ମିଶ୍ରଣକୁ ଦ୍ରବଣ କହନ୍ତି; ଯଥା – ଚିନିପାଣି, ଲୁଣପାଣି ।
• ଚିନିପାଣିରେ ଚିନି ଦ୍ରାବ ଓ ଲୁଣ ପାଣିରେ ଲୁଣ ହେଉଛି ସ୍ରାବ ।
• ଚିନିପାଣି ଓ ଲୁଣପାଣିରେ ପାଣି ହେଉଛି ଦ୍ରାବକ ।
• ଜଳରେ ଦ୍ରବୀଭୂତ ହୋଇପାରୁଥିବା ଚିନି ଓ ଲୁଣ ଭଳି ପଦାର୍ଥର ଏହି ଗୁଣକୁ ଦ୍ରବଣୀୟତା କହନ୍ତି ।

Question 3.
ଏକ ପରୀକ୍ଷା ସାହାଯ୍ୟରେ ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ ପରିବର୍ତ୍ତନ କ’ଣ ବୁଝାଅ ।
ଉ –
ପରୀକ୍ଷା :
(i) ଗୋଟିଏ ମହମବତିକୁ ଜଳାଇ ଚିନାମାଟିର ପ୍ଲେଟ୍ ଉପରେ ରଖୁ । ଏହାପରେ ଜଳୁଥିବା ମହମବତିକୁ ଲକ୍ଷ୍ୟକଲୁ ।

(ii) ଦେଖୁ ମହମବତିଟି ଜଳି ଜଳି ଲିଭିଗଲା । ମହମବତୀଟି ମହମରେ ତିଆରି । ମହମ ଏକ ଦହନୀୟ ପଦାର୍ଥ ହୋଇଥ‌ିବାରୁ ସେଥ‌ିରେ ଥ‌ିବା ସଳିତାରେ ନିଆଁ ଲଗାଇଲେ ତାହା ଜଳିବ ।
(iii) ମହମବତି ଜଳିଲାବେଳେ କିଛି ମହମ ତରଳିଯାଏ । ସେଥୁରୁ କିଛି ତଳକୁ ବୋହିଆସେ । ଅବଶିଷ୍ଟ ତରଳ ମହମ ଜଳିଯାଏ ।
(iv) ମହମବତି ଜଳିଲାବେଳେ ଆଲୋକ ଓ ଉତ୍ତାପ ଦିଏ । ମହମବତି ଜଳିସାରିବାବେଳକୁ ଏହାର ଅଧ୍ଵ ଭାଗ ସରିଯାଇଥାଏ । ତାହା ଆଉ ଫେରିବା ସମ୍ଭବ ନୁହେଁ ।
(v) ପ୍ଲେଟ୍‌ରେ ଥ‌ିବା କଠିନ ମହମକୁ ନେଇ ପୁଣି ଜଳିପାରୁଥିବା ମହମବତି ତିଆରି କରାଯାଇପାରିବ ।
ସିଦ୍ଧାନ୍ତ : ଏହି ତଥ୍ୟକୁ ଅନୁଶୀଳନକଲେ ଆମେ ଦେଖୁ ଯେ ମହମବତିର ଜ୍ଵଳନବେଳେ ମହମର ଦୁଇ ପ୍ରକାର ପରିବର୍ତ୍ତନ ହୋଇଥାଏ । ପ୍ରଥମତଃ ଦହନ ଓ ତଦ୍ଵଜନିତ କ୍ଷୟ । ଏହା ଏକ ସ୍ଥାୟୀ ପରିବର୍ତ୍ତନ । ଏହା ମଧ୍ୟ ଏକ ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ ପରିବର୍ତ୍ତନ ।

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶୋଉର

Question 1.
ନିମ୍ନଲିଖତ ପରିବର୍ତ୍ତନଗୁଡ଼ିକ ଭିତରୁ କେଉଁଟି ପ୍ରତ୍ୟାବର୍ତୀ ଓ କେଉଁଟି ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ ପରିବର୍ତ୍ତନ ସାରଣୀ କାଟି ଲେଖ ।
ଉ –
ଚାଉଳରୁ ଭାତହେବା, ଫୁଲରୁ ଫଳ ହେବା, ଜଳ ବାଷ୍ପରେ ପରିଣତ ହେବା, ଲାଜକୁଳୀ ପତ୍ର ନଇଁଯିବା, ଗଜା ବଢ଼ି ଛୋଟ ଗଛ ହେବା, ଦୁଧ ଦହିରେ ପରିଣତ ହେବା ।

Question 2.
ପ୍ରାକୃତିକ ପରିବର୍ତ୍ତନ ଓ ମନୁଷ୍ୟକୃତ ପରିବର୍ତ୍ତନର ଏକ ତାଲିକା ପ୍ରସ୍ତୁତ କର ।
ଉ –

Question 3.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଓଦାଲୁଗା ଶୁଖୁଯିବା ଏକ …………… ପରିବର୍ତ୍ତନ ।
(ଖ) ରୁପାରୁ ଗହଣା କରିବା ଏକ …………… ପରିବର୍ତ୍ତନ ।
(ଗ) କାଠକୁ ଜଳାଇ ଅଙ୍ଗାର ତିଆରି କରିବା …………… ପରିବର୍ତ୍ତନ ।
(ଘ) ବରଫକୁ ତରଳାଇ ଜଳ ପାଇବା ………….. ପରିବର୍ତ୍ତନ ।
(ଙ) ଦ୍ରାବକରେ ଯେତେବେଳପର୍ଯ୍ୟନ୍ତ ସ୍ରାବ ଦ୍ରବୀଭୂତ ହେଉଥାଏ, ସେତେବେଳ ପର୍ଯ୍ୟନ୍ତ ଦ୍ରବଣକୁ ………………କୁହାଯାଏ ।
(ଚ) ଯେଉଁ ଦ୍ରବଣ ଅଧିକ ଦ୍ରାବ ଦ୍ରବୀଭୂତ କରିପାରେ ନାହିଁ, ସେଭଳି ଦ୍ରବଣକୁ ……………… କୁହାଯାଏ ।
ଉ –
(କ) ପ୍ରାକୃତିକ
(ଖ) ମନୁଷ୍ୟକୃତ
(ଗ) ସ୍ଥାୟୀ ବା ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ
(ଘ) ଅସ୍ଥାୟୀ ବା ପ୍ରତ୍ୟାବର୍ତ୍ତୀ
(ଙ) ଅସଂତୃପ୍ତ ଦ୍ରବଣ
(ଚ) ସଂତୃପ୍ତ ଦ୍ରବଣ

Question 4.
ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତର ବାଛି ଲେଖ ।

(କ) କେଉଁଟି ଦହନୀୟ ପଦାର୍ଥ ନୁହେଁ ?
(i) ମହମ
(ii) କାଗଜ
(iii) କିରୋସିନି
(iv) ଲୁହା
ଉ –
(iv) ଲୁହା

(ଖ) ଚିନିକୁ ଗରମକଲେ ଶେଷରେ ଏହା କଳା ପଡ଼ିଯିବ । ଏହା କି ପ୍ରକାର ପରିବର୍ତ୍ତନ ?
(i) ଅସ୍ଥାୟୀ
(ii) ପ୍ରତ୍ୟାବର୍ତ୍ତୀ
(iii) ରାସାୟନିକ
(iv) ଭୌତିକ
ଉ –
(iii) ରାସାୟନିକ

(ଗ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କିଏ ଦ୍ରବୀଭୂତ ହୋଇପାରେ ?
(i) କଠିନ
(ii) ତରଳ
(iii) ଗ୍ୟାସୀୟ
(iv) ସମସ୍ତ
ଉ –
(iv) ସମସ୍ତ

(ଘ) ତୁତିଆକୁ ଗରମ କଲେ ଶେଷରେ ଏହାର ରଙ୍ଗ କିପରି ହୁଏ ?
(i) କଳା
(ii) ଧଳା
(iii) ନୀଳ
(iv) ଲାଲ
ଉ –
(i) କଳା

(ଙ) କେଉଁଟି ପ୍ରାକୃତିକ ପରିବର୍ତ୍ତନ ?
(i) କପାରୁ ସୂତା କରିବା
(ii) କାଠ ଜାଳିବା
(iii) ସୁନାରୁ ଗହଣା କରିବା
(iv) ବରଫ ତରଳିବା
ଉ –
(iv) ବରଫ ତରଳିବା

(ଚ) ମାଗ୍ନେସିୟମ୍ ତାର ଜଳି ଯେଉଁ ପାଉଁଶ ସୃଷ୍ଟିକରେ ତା’ର ରଙ୍ଗ କିପରି ହେବ ?
(i) କଳା
(ii) ଲାଲ
(iii) ଧଳା
(iv) ହଳଦିଆ
ଉ –
(iii) ଧଳା

(ଛ) ଜଳରେ ପୋଡ଼ା ଚୂନଗୁଣ୍ଡ ମିଶାଇଲେ କ’ଣ ହେବ ?
(i) ଜଳ ଥଣ୍ଡା ହେବ
(ii) ଜଳ ଗରମ ହେବ
(iii) ଜଳର ତାପମାତ୍ରା ଅପରିବର୍ତିତ ରହିବ
(iv) କେଉଁଟି ନୁହେଁ
ଉ –
(ii) ଜଳ ଗରମ ହେବ

(ଜ) ସ୍ବଚ୍ଛ ଚୂନପାଣିକୁ କିଛି ସମୟ ରଖିଦେଲେ ପାତ୍ରର ତଳଭାଗରେ ଗୋଟିଏ ଧଳା ପଦାର୍ଥ ଜମିଯିବ; ତାହା ହେଉଛି –
(i) କ୍ୟାଲସିୟମ୍ ଅକ୍‌ସାଇଡ୍
(ii) କ୍ୟାଲସିୟମ୍ ହାଇଡ୍ରିକସାଇଡ୍
(iii) କ୍ୟାଲସିୟମ୍ କ୍ଲୋରାଇଡ୍
(iv) କ୍ୟାଲସିୟମ କାର୍ବୋନେଟ୍
ଉ –
(iv) କ୍ୟାଲସିୟମ କାର୍ବୋନେଟ୍

Question 5.
ବାମ ପାର୍ଶ୍ଵରେ ଥ‌ିବା ଶବ୍ଦଦ୍ୱୟର ସମ୍ପର୍କକୁ ଦେଖ୍ ଦକ୍ଷିଣ ପାର୍ଶ୍ଵର ଶବ୍ଦ ସହିତ ଖାପଖାଉଥ‌ିବା ଶବ୍ଦଟିକୁ ଶୂନ୍ୟସ୍ଥାନରେ ଲେଖ ।
(କ) ମାଟିରୁ ଇଟା କରିବା : ମନୁଷ୍ୟକୃତ :: ଓଦାଲୁଗା ଶୁଖୁ : ……………. ।
(ଖ) କାଠ ଜଳି ଅଙ୍ଗାର ହେବା : ସ୍ଥାୟୀ ପରିବର୍ତ୍ତନ :: ବରଫ ତରଳିବା : ……………. ।
(ଗ) ମିଶ୍ରି ମୁଣ୍ଡା ଭାଙ୍ଗି ଗୁଣ୍ଡ କରିବା : ଭୌତିକ ପରିବର୍ତ୍ତନ :: ଲୁହାରେ କଳଙ୍କି ଲାଗିବା : ……………. ।
(ଘ) ଚିନି : ଦ୍ରାବ :: ଚିନିପାଣି : ……………. ।
(ଙ) କାଠ କୋଇଲା ଜଳିବା : ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ :: ଲୁଣପାଣି ବାଷ୍ପ ହେବା : ……………. ।
ଉ –
(କ) ପ୍ରାକୃତିକ
(ଖ) ଅସ୍ଥାୟୀ
(ଗ) ରାସାୟନିକ
(ଘ) ଦ୍ରବଣ
(ଡ) ପ୍ରତ୍ୟାବର୍ତ୍ତୀ

Question 6.
ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(କ) ଗୋଟିଏ ଦ୍ରାବକରେ ବିଭିନ୍ନ ଦ୍ରାବର ଦ୍ରବଣୀୟତା ସମାନ ହୋଇଥାଏ ।
(ଖ) ତୁତିଆକୁ ଗରମ କଲେ ମ୍ୟାଗ୍ନେସିୟମ୍ ଅକ୍‌ସାଇଡ୍ ନାମକ ରାସାୟନିକ ପଦାର୍ଥ ସୃଷ୍ଟି ହୁଏ ।
(ଗ) ଦ୍ରବଣୀୟତା ଏକ ରାସାୟନିକ ପରିବର୍ତ୍ତନ ।
(ଘ) ସୁଚ୍ଛ ଚୂନପାଣିକୁ ସରବତ ନଳୀ ଦ୍ଵାରା ଫୁଙ୍କିଲେ ଏହାର ରଙ୍ଗ କଳା ହୁଏ ।
(ଙ) କାଠରୁ ଟେବୁଲ ତିଆରି ହେବା ଅପ୍ରତ୍ୟାବର୍ତ୍ତୀ ପରିବର୍ତ୍ତନ ।
ଉ –
(କ) ଗୋଟିଏ ଦ୍ରାବକରେ ବିଭିନ୍ନ ଦ୍ରାବର ଦ୍ରବଣୀୟତା ଭିନ୍ନ ଭିନ୍ନ ହୋଇଥାଏ ।
(ଖ) ତୁତିଆକୁ ଗରମ କଲେ କପର ଅକ୍‌ସାଇଡ୍ ନାମକ ରାସାୟନିକ ପଦାର୍ଥ ସୃଷ୍ଟି ହୁଏ ।
(ଗ) ଦ୍ରବଣୀୟତା ଏକ ଭୌତିକ ପରିବର୍ତ୍ତନ ।
(ଘ) ସ୍ଵଚ୍ଛ ଚୂନପାଣିକୁ ସରବତ ନଳୀ ଦ୍ଵାରା ଫୁଙ୍କିଲେ ଏହାର ରଙ୍ଗ ଧଳା ହୁଏ ।
(ଙ) କାଠରୁ ଟେବୁଲ ତିଆରି ହେବା ପ୍ରତ୍ୟାବର୍ତ୍ତୀ ପରିବର୍ତ୍ତନ ।

Question 7.
‘କ’ ସ୍ତମ୍ଭର ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସଂପର୍କ ବାଛ ।

ଉ –

Odisha State Board BSE Odisha 7th Class Geography Solutions Chapter 5 ବ୍ୟାବହାରିକ ଭୂଗୋଳ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Geography Solutions Chapter 5 ବ୍ୟାବହାରିକ ଭୂଗୋଳ

୧ । ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ସଂକ୍ଷିପ୍ତ ଉତ୍ତର ଲେଖ ।

Question କ.
ବ୍ୟାବହାରିକ ଭୂଗୋଳ କହିଲେ କ’ଣ ବୁଝାଏ ?
Answer:

• ଭୂଗୋଳଲବ୍ଧ ଜ୍ଞାନକୁ ମଣିଷର ଦୈନନ୍ଦିନ କାର୍ଯ୍ୟକଳାପରେ ପ୍ରୟୋଗ କରିବାର ପଦ୍ଧତିକୁ ବ୍ୟାବହାରିକ ଭୂଗୋଳ କୁହାଯାଏ ।
• ଭୂଗୋଳ ଏକ କ୍ଷେତ୍ର ବିଜ୍ଞାନ ହୋଇଥିବାରୁ ଏଥିରେ ବିଭିନ୍ନ ସ୍ଥାନ ବା ଅଞ୍ଚଳ ସମ୍ବନ୍ଧରେ ପ୍ରତ୍ୟକ୍ଷ ନିରୀକ୍ଷଣ ବା ଅଧ୍ୟୟନର ଆବଶ୍ୟକତା ଥାଏ । ଭୌଗୋଳିକ ତଥ୍ୟ ସଂଗ୍ରହ ପାଇଁ ବିଭିନ୍ନ ବୈଜ୍ଞାନିକ ଯନ୍ତ୍ରପାତି ବା ପରିମାପକ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ।
• ଏହି ଯନ୍ତ୍ର ଦ୍ଵାରା ପାଣିପାଗ ଓ ଜଳବାୟୁକୁ ପ୍ରଭାବିତ କରୁଥିବା ଉପାଦାନଗୁଡ଼ିକର ମାତ୍ରା ବା ପରିମାଣ ସମ୍ପର୍କରେ ଜାଣିହୁଏ ।

Question ଖ.
କେଉଁ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ବାୟୁ ତାପମାତ୍ରାର ନିରବଚ୍ଛିନ୍ନ ରେକର୍ଡ଼ ସମ୍ଭବ ?
Answer:
ଥର୍ମୋଗ୍ରାଫ୍ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ବାୟୁ ତାପମାତ୍ରାର ନିରବଚ୍ଛିନ୍ନ ରେକର୍ଡ଼ ସମ୍ଭବ ।

Question ଗ.
କେଉଁ ଚାପମାନ ଯନ୍ତ୍ରର ବହୁଳ ବ୍ୟବହାର କରାଯାଏ ଓ କାହିଁକି ?
Answer:
ଆନି ରଏଡ୍ ଚାପମାନ ଯନ୍ତ୍ରର ବହୁଳ ବ୍ୟବହାର କରାଯାଏ । କାରଣ ଏହା ଆକାରରେ ଛୋଟ ଓ ନେବା ଆଣିବା ପାଇଁ ସହଜ ।

Question ଘ.
ଆପେକ୍ଷିକ ଆର୍ଦ୍ରତା କ’ଣ ?
Answer:

• ବାୟୁ କୌଣସି ନିର୍ଦ୍ଦିଷ୍ଟ ପରିମାଣର ଜଳୀୟବାଷ୍ପ ଧରି ରଖୂପାରେ । ତେବେ ବାୟୁରେ ପ୍ରକୃତପକ୍ଷେ ଜଳୀୟବାଷ୍ପ କମ୍ ବେଶୀ ଥାଇପାରେ ।
• ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରାରେ ବାୟୁରେ ଥିବା ଜଳୀୟବାଷ୍ପର ପରିମାଣ ତଥା ସେହି ତାପମାତ୍ରାରେ ବାୟୁର ଜଳୀୟବାଷ୍ପ ଧାରଣ କ୍ଷମତାର ଅନୁପାତକୁ ଶତାଂଶରେ ପ୍ରକାଶ କରିବାକୁ ବାୟୁର ଆପେକ୍ଷିକ ଆର୍ଦ୍ରତା କୁହାଯାଏ ।

Question ଙ.
ପବନର ବେଗ ମାପିବା ପାଇଁ କେଉଁ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ?
Answer:
ପବନର ବେଗ ମାପିବା ପାଇଁ ପବନ ବେଗମାପକ ଯନ୍ତ୍ର ବା ଆନିମୋମିଟର ବ୍ୟବହାର କରାଯାଏ ।

Question ଚ.
ପାଗର ଭାବୀ ସୂଚନା କାହିଁକି ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ?
Answer:

• ଆମର ନିତିଦିନିଆ ଜୀବନକୁ ପାଣିପାଗ ବିଶେଷଭାବେ ପ୍ରଭାବିତ କରିଥାଏ ।
• କୃଷିକାର୍ଯ୍ୟ, ସମୁଦ୍ରରେ ମାଛଧରା, ଜଳ, ସ୍ଥଳ ତଥା ଆକାଶପଥରେ ଯାତାୟାତ ଅନୁକୂଳ ପାଣିପାଗ ଉପରେ ନିର୍ଭର କରେ ।
• ବନ୍ୟା, ବାତ୍ୟା ଓ ଅନାବୃଷ୍ଟି ଆଦିର ପ୍ରାକ୍-ସୂଚନା ଆମକୁ ଅନେକ ସମ୍ଭାବ୍ୟ ବିପଦରୁ ସାହାଯ୍ୟ କରେ । ତେଣୁ ପାଗର ଭାବୀ ସୂଚନା ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ।

Question ଛ.
ସ୍ଵଳ୍ପକାଳୀନ ଭାବୀ ସୂଚନାର ଆବଶ୍ୟକତା କ’ଣ ?
Answer:

• ସ୍ଵଳ୍ପକାଳୀନ ଭାବୀ ସୂଚନାରୁ ଝଡ଼ବାତ୍ୟା, ଅତ୍ୟଧିକ ବୃଷ୍ଟିପାତ, ହିମପାତ, ଶିଶିରପାତ, ବାଲୁକା ଓ ଧୂଳିଝଡ଼ ଇତ୍ୟାଦି ସମ୍ବନ୍ଧୀୟ ତଥ୍ୟ ମିଳେ ।
• ଏହା ତିନିଦିନ ବା ୭୨ ଘଣ୍ଟା ପାଇଁ ପ୍ରତିଦିନ ଦୁଇଥର ଲେଖାଏଁ ଦିଆଯାଇଥାଏ ।

Question କ.
ଦୀର୍ଘକାଳୀନ ଭାବୀ ସୂଚନା କିପରି ସୂଚିତ ହୋଇଥାଏ ?
Answer:

• ବିଭିନ୍ନ ବୈଜ୍ଞାନିକ ପଦ୍ଧତି ତଥା ଗାଣିତିକ ସୂତ୍ର ବ୍ୟବହାର କରି ଦୀର୍ଘକାଳୀନ ଭାବୀ ସୂଚନା ଦିଆଯାଏ ।
• ଏପରିକି ଆମ ରାଜ୍ୟରେ ପ୍ରଚଳିତ ପଞ୍ଜିକାରେ ଗ୍ରହ- ନକ୍ଷତ୍ର ଆଦିର ଅବସ୍ଥିତି ତଥା ସମ୍ବନ୍ଧକୁ ବିଚାରକୁ ନେଇ ଦୀର୍ଘକାଳୀନ ପାଗର ଭାବୀ ସୂଚନା ଦିଆଯାଇଥାଏ ।

Question ଝ.
ସମୋଳରେଖା କ’ଣ ?
Answer:

• ସମୁଦ୍ର ପତ୍ତନରୁ ସମାନ ଉଚ୍ଚତାରେ ଥିବା ସ୍ଥାନଗୁଡ଼ିକୁ ମାନଚିତ୍ରରେ ଯୋଗ କରୁଥିବା ରେଖାକୁ ସମୋଚ୍ଚରେଖା କୁହାଯାଏ ।
• ଏହି ରେଖାଗୁଡ଼ିକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟବଧାନରେ ଟଣାଯାଇଥାଏ ।

୨ । ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

Question କ.
ହାଇଗ୍ଲୋମିଟର ଓ ଆନିମୋମିଟର
Answer:

Question ଖ.
ଦୈନିକ ଭାବୀ ସୂଚନା ଓ ସ୍ଵଳ୍ପକାଳୀନ ଭାବୀ ସୂଚନା
Answer:

୩ । ସଂକ୍ଷିପ୍ତ ଟିପ୍‌ପଣୀ ଲେଖ ।

Question କ.
ପାରଦ ତାପମାନ ଯନ୍ତ୍ର :
Answer:

• ପାରଦ ତାପମାନ ଯନ୍ତ୍ରରେ ବାୟୁର ତାପମାତ୍ରା ନିଶ୍ଚୟ କରାଯାଏ । ଏହା ଡିଗ୍ରୀ ଏକକରେ ପ୍ରକାଶ କରାଯାଏ ।
• ସାଧାରଣତଃ ତିନି ପ୍ରକାରର ତାପମାନ ଯନ୍ତ୍ର ବ୍ୟବହୃତ ହୋଇଥାଏ; ଯଥା – (୧) ସେଲ୍‌ସିୟସ୍ ତାପମାନ ଯନ୍ତ୍ର, (୨) ଫାରେନ୍‌ହିଟ୍ ତାପମାନ ଯନ୍ତ୍ର ଏବଂ (୩) ରିଉମାର୍ ତାପମାନ ଯନ୍ତ୍ର ।
• ଆମ ଦେଶରେ ସେଲ୍‌ସିୟସ୍ ତାପମାନ ଯନ୍ତ୍ର ବ୍ୟବହୃତ ହୁଏ । ଦିନରାତି ୨୪ ଘଣ୍ଟା ମଧ୍ୟରେ ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ଜାଣିବାପାଇଁ ‘U’ ଆକାର ବିଶିଷ୍ଟ ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ତାପମାନ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ।

Question ଖ.
ବୃଷ୍ଟିମାପକ ଯନ୍ତ୍ର :
Answer:

• ବୃଷ୍ଟିମାପକ ଯନ୍ତ୍ର ବା ରେନ୍ଗଗଳ୍ପରେ ବୃଷ୍ଟିପାତର ପରିମାଣ ନିରୂପଣ କରାଯାଏ ।
• ଏହି ଯନ୍ତ୍ରଟି ୧୨.୫ ସେ.ମି.ରୁ ୨୦ ସେ.ମି. ବ୍ୟାସବିଶିଷ୍ଟ ଏକ ତମ୍ବା ସିଲିଣ୍ଡର ଓ ଏଥରେ ସେହି ସମାନ ବ୍ୟାସବିଶିଷ୍ଟ ଏକ ତମ୍ବା କାହାଳୀର ନିମ୍ନଭାଗ ଏକ କାଚଜାର୍ ବା ତମ୍ବାପାତ୍ର ମଧ୍ୟକୁ ପ୍ରବେଶ କରିଥାଏ ।
• ସମୁଦାୟ ସିଲିଣ୍ଡରକୁ ଅନ୍ୟ ଏକ ଟିଣ ଖୋଳ ଦ୍ଵାରା ଆବୃତ କରି ରଖାଯାଇଥାଏ ।
• ସାଧାର ଣତଃ ଖୋଲାପଡ଼ିଆରେ ଏହି ଯନ୍ତ୍ରକୁ ରଖାଯାଇଥାଏ । ଏହାର ନିଘାଂଶ ମାଟିତଳେ ଓ ଉପର ଅଂଶଟି ମାଟି ଉପରୁ ପ୍ରାୟ ୩୦ ସେ.ମି. ଉଚ୍ଚତାରେ ରହିଥାଏ ।
• ବୃଷ୍ଟିପାତ ପରିମାଣକୁ ଅନ୍ୟ ଏକ ମାପପାତ୍ର ଦ୍ବାରା ମାପ କରାଯାଏ । ଏଥିରେ ଥ‌ିବା ଇଞ୍ଚ ବା ମିଲିମିଟର ମାପ ଦାଗରୁ ବର୍ଷାର ପରିମାଣ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

Question ଗ.
ରଙ୍ଗ ପରସ୍ତ୍ରୀକରଣ :
Answer:

• ଭୂପୃଷ୍ଠର ବିଭିନ୍ନ ଉଚ୍ଚ ନୀଚ ଭୂମିରୂପକୁ ଦର୍ଶାଇବା ପାଇଁ ରଙ୍ଗ ପରସ୍ତୀକରଣ ପ୍ରଣାଳୀ ବହୁଳ ଭାବରେ ଆଦୃତ ହୋଇଛି । ଏହି ପ୍ରଣାଳୀରେ ରଙ୍ଗର ଘନତ୍ବରେ ହ୍ରାସବୃଦ୍ଧିଦ୍ୱାରା ବିଭିନ୍ନ ଭୂମି ରୂପର ପ୍ରଦର୍ଶନ କରାଯାଇଥାଏ ।
• ମାନଚିତ୍ରରେ ଉଚ୍ଚ ଅଞ୍ଚଳକୁ ଗାଢ଼ ରଙ୍ଗ ଓ ନିମ୍ନ ଭୂମିଗୁଡ଼ିକୁ ଅପେକ୍ଷାକୃତ ହାଲୁକା ରଙ୍ଗ ଦିଆଯାଇଥାଏ ।
• ସେହିପରି ସମୁଦ୍ରର ଗଭୀରତା ଦର୍ଶାଇବା ପାଇଁ ଅଳ୍ପ ଗଭୀରତା ବିଶିଷ୍ଟ ସମୁଦ୍ର ଅଞ୍ଚଳକୁ ହାଲୁକା ନୀଳରଙ୍ଗ ଓ ଗଭୀର ସମୁଦ୍ରକୁ ଗାଢ଼ ନୀଳରଙ୍ଗ ବ୍ୟବହାର କରାଯାଏ ।
• ଏହି ପଦ୍ଧତିରେ ସ୍ଥାନର ପ୍ରକୃତ ଉଚ୍ଚତା ତଥା କ୍ରମ ନିମ୍ନତା ସଠିକ୍‌ଭାବେ ଦର୍ଶାଇ ହୁଏ ନାହିଁ ।

୪ । ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(କ) ୨୪ ଘଣ୍ଟା ମଧ୍ୟରେ ବାୟୁର ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ଜାଣିବାପାଇଁ ବ୍ୟବହୃତ ତାପମାନ ଯନ୍ତ୍ର ଇଂରାଜୀ ଅକ୍ଷର ______ ଆକୃତି ବିଶିଷ୍ଟ । (V, U, W, X)
Answer:
U

(ଖ) ସମୁଦ୍ର ପତ୍ତନରେ ବାୟୁଚାପ _______ ସେଣ୍ଟିମିଟର ପାରଦ ସ୍ତମ୍ଭର ଉଚ୍ଚତା ସଙ୍ଗେ ସମତା ରକ୍ଷା କରେ । (୭୦, ୭୬, ୮୦, ୮୬)
Answer:
୭୬

(ଗ) ହାଇଡ୍ରୋମିଟର ଯନ୍ତ୍ର ବାୟୁର ________ ମାପିବାରେ ସାହାଯ୍ୟ କରେ । (ଦିଗ, ବେଗ, ଆର୍ଦ୍ରତା, ଶୁଷ୍କତା)
Answer:
ଆର୍ଦ୍ରତା

BSE Odisha 7th Class Geography Notes Chapter 5 ବ୍ୟାବହାରିକ ଭୂଗୋଳ

ବ୍ୟାବହାରିକ ଭୂଗୋଳ :

• ଭୂଗୋଳ ଲଜ୍ଜାଜ୍ଞାନକୁ ମଣିଷର ଦୈନନ୍ଦିନ କାର୍ଯ୍ୟକଳାପରେ ପ୍ରୟୋଗ କରିବାର ପଦ୍ଧତିକୁ ବ୍ୟାବହାରିକ ଭୂଗୋଳ କୁହାଯାଏ ।
• ପାଣିପାଗ ଓ ଜଳବାୟୁ ସମ୍ବନ୍ଧୀୟ ତଥ୍ୟ ସଂଗ୍ରହ ପାଇଁ ବିଭିନ୍ନ ବୈଜ୍ଞାନିକ ଯନ୍ତ୍ରପାତି ତଥା ପରିମାପକ ଯନ୍ତ୍ରର ଆବଶ୍ୟକତା ପଡ଼େ ।
• ଏହି ଯନ୍ତ୍ରଗୁଡ଼ିକ ଦ୍ୱାରା ଆମେ ବାୟୁର ତାପମାତ୍ରା, ଚାପ, ଆର୍ଦ୍ରତା, ପବନର ବେଗ ଓ ଦିଗ, ବୃଷ୍ଟିପାତର ପରିମାଣ ଆଦି ଜାଣିପାରୁ ।

ତାପମାତ୍ରା ନିରୂପଣ :

• ବାୟୁର ତାପମାତ୍ରା ନିରୂପଣ ନିମିତ୍ତ ତିନିପ୍ରକାର ତାପମାନ ଯନ୍ତ୍ର ବ୍ୟବହୃତ ହୁଏ, ଯଥା – (i) ସେଲ୍ ସିୟସ୍, (ii) ଫାରେନ୍‌ହିଟ୍ ଓ (iii) ରିଜମାରୁ ।
• ଯେଉଁ ଡିଗ୍ରୀ ତାପମାତ୍ରାରେ ଜଳ ବାଷ୍ପ ହୁଏ, ତାହା ସ୍ଫୁଟନାଙ୍କ ଓ ଯେଉଁ ଡିଗ୍ରୀ ତାପମାତ୍ରାରେ ଜଳ ବରଫରେ ପରିଣତ ହୁଏ, ତାକୁ ହିମାଙ୍କ କୁହାଯାଏ ।
• ନିମ୍ନସ୍ଥ ସାରଣୀର ପ୍ରତ୍ୟେକ ତାପମାନ ଯନ୍ତ୍ରର ହିମାଙ୍କ ଓ ସ୍ଫୁଟନାଙ୍କ ଜାଣିବା :

• ଆମ ଦେଶରେ ସେଲ୍ ସିୟସ୍ ସ୍କେଲ ବ୍ୟବହାର କରାଯାଏ ।
• ଆମ ଶରୀରର ତାପମାତ୍ରା ଫାରେନ୍‌ହିଟ୍ ଡିଗ୍ରୀରେ ପ୍ରକାଶ କରାଯାଏ ।
• ଆମ ଶରୀରର ସାଧାରଣ ତାପମାତ୍ରା = ୯୮.୬°F ।
  • ଦିନରାତି ୨୪ ଘଣ୍ଟା ମଧ୍ୟରେ ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ଜାଣିବା ପାଇଁ ‘U’-ଆକାରର ଏକ ସ୍ଵତନ୍ତ୍ର ତାପମାନ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ।
  • ସର୍ବୋଚ୍ଚ ଓ ସର୍ବନିମ୍ନ ତାପମାନ ଯନ୍ତ୍ରର ବାମପାର୍ଶ୍ଵ ବାହୁ ସର୍ବନିମ୍ନ ତାପମାତ୍ରା ଏବଂ ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ ବାହୁ ସର୍ବୋଚ୍ଚ ତାପମାତ୍ରା ଦର୍ଶାଇଥାଏ ।
  • ଥର୍ମୋଗ୍ରାଫ୍ ଯନ୍ତ୍ର ଦ୍ବାରା କ୍ରମାଗତଭାବେ ତାପମାତ୍ରା ରେକର୍ଡ଼ କରାଯାଉଛି ।

ବାୟୁ ଚାପ :

• ବାୟୁ ଚାପ ମାପିବା ନିମିତ୍ତ ପାରଦ ଚାପମାନ ଯନ୍ତ୍ର (Mercury Barometer) ଏବଂ ଆନି ରଏଡ୍ ଚାପମାନ ଯନ୍ତ୍ର (Ancroid Barometer) ବ୍ୟବହାର କରାଯାଏ ।
• ପାରଦ ବାରୋମିଟର (ଚାପମାନ ଯନ୍ତ୍ର)ର ପାରଦ ସ୍ତମ୍ଭ ଉଚ୍ଚତ ସମୁଦ୍ର ପତ୍ତନରେ ୭୬ ସେ.ମି. ହୋଇଥାଏ ।
• ପାରଦ ଚାପମାନ ଯନ୍ତ୍ର ଓ ଆନିରଏଡ୍ ଚାପମାନ ଯନ୍ତ୍ର ମଧ୍ୟରେ ତୁଳନା :

ପବନ ଦିଗବାରେଣୀ ଯନ୍ତ୍ର (ଉଇଣ୍ଡଭେନ୍) :

ପବନ କେଉଁ ଦିଗରୁ ବହୁଛି ଜାଣିବାପାଇଁ ପବନ ଦିଗବାରେଣୀ ଯନ୍ତ୍ର ବା ଉଇଣ୍ଡଭେଡ୍ ଯନ୍ତ୍ର ବ୍ୟବହାର କରାଯାଏ ।

ପବନ ବେଗମାପକ ଯନ୍ତ୍ର (ଆନିମୋମିଟର) :

ଆନିମୋମିଟର ଯନ୍ତ୍ର ଦ୍ବାରା ପବନର ବେଗ ମପାଯାଏ ।

ଆପେକ୍ଷିକ ଆର୍ଦ୍ରତା :

ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରାରେ ବାୟୁରେ ଥିବା ଜଳୀୟବାଷ୍ପର ପଇଁ ମାଣ ତଥା ସେହି ତାପମାତ୍ରାରେ ବାୟୁ ର ଜଳୀୟବାଷ୍ପ ଧାରଣ କ୍ଷମତାର ଅନୁପାତକୁ ଶତାଂଶରେ ପ୍ରକାଶ କରିବାକୁ ବାୟୁର ଆପେକ୍ଷିକ ଆର୍ଦ୍ରତା କୁହାଯାଏ ।

ହାଇଡ୍ରୋମିଟର ଯନ୍ତ୍ର ଦ୍ବାରା ବାୟୁର ଆପେକ୍ଷିକ ଆର୍ଦ୍ରତା ମପାଯାଏ ।

‘ଆର୍ଦ୍ର ଓ ଶୁଷ୍କ ବଲ୍‌ବ ହାଇକ୍ରୋମିଟରରେ ବାୟୁର ଆର୍ଦ୍ରତା ମାପିବାର ପଦ୍ଧତି :

• ଏହି ହାଇଡ୍ରୋମିଟରରେ ଥ‌ିବା ଦୁଇଟି ତାପମାନ ଯନ୍ତ୍ରରୁ ଗୋଟିଏ ସାଧାରଣ ତାପମାତ୍ରା ନିର୍ଣ୍ଣୟ କରେ । ଅନ୍ୟ ତାପମାନ ଯନ୍ତ୍ରଟି ମସ୍‌ଲିନ୍‌ କନାରେ ଗୁଡ଼ାଇ ଜଳପାତ୍ରରେ ବୁଡ଼ାଇ ରଖାଯାଏ ।
• ଫଳରେ ମସ୍‌ଲିନ୍‌ କନାରୁ ଜଳ ବାଷ୍ପୀଭୂତ ହେବା କାରଣରୁ ବଲ୍‌ବଟି ଥଣ୍ଡା ରହେ ଓ କମ୍ ତାପମାତ୍ରା ରେକର୍ଡ଼ କରେ । ଉଭୟ ତାପମାନ ଯନ୍ତ୍ର ତାପମାତ୍ରାରେ ଥିବା ପାର୍ଥକ୍ୟକୁ ହିସାବ କରି ଏକ ନିର୍ଦ୍ଧାରିତ ସାରଣୀ ସାହାଯ୍ୟରେ ଆପେକ୍ଷିକ ଆର୍ଦ୍ରତା ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

ବୃଷ୍ଟି ମାପକ ଯନ୍ତ୍ର :

ବୃଷ୍ଟିମାପକ ଯନ୍ତ୍ରକୁ ରେନ୍ଗଗଜ କୁହାଯାଏ ।

ଗଠନ :

• ଏହି ଯନ୍ତ୍ରଟି ୧୨.୫ ସେ.ମି.ରୁ ୨୦ ସେ.ମି. ବ୍ୟାସବିଶିଷ୍ଟ ଏକ ତମ୍ବା ସିଲିଣ୍ଡର । ଏହା ଭିତରେ ସମାନ ବ୍ୟାସବିଶିଷ୍ଟ ଏକ ତମ୍ବା କାହାଳୀର ନିମ୍ନଭାଗ ଏକ କାଚ ଜାର୍ ବା ତମ୍ବାପାତ୍ର ମଧ୍ୟକୁ ପ୍ରବେଶ କରିଥାଏ ।
• ଟିଣ ଖୋଳ ଦ୍ୱାରା ସମ୍ପୂର୍ଣ୍ଣ ଆବୃତ ଏହି ଯନ୍ତ୍ରର ନିମାଂଶକୁ ମାଟିତଳେ ଓ ଉପର ଅଂଶ ମାଟିଠାରୁ ପ୍ରାୟ ୩୦ ସେ.ମି. ଉଚ୍ଚତାରେ ରଖାଯାଇଥାଏ ।

ବୃଷ୍ଟିପାତର ପରିମାଣ ନିଷ୍କ୍ରିୟ :

ମାପପାତ୍ର ଓ ବୃଷ୍ଟିମାପକ ଯନ୍ତ୍ରରେ ଥିବା କାହାଳୀ ମୁହଁର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ ଦ୍ଵାରା ବୃଷ୍ଟିପାତ ପରିମାଣ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।

ବୃଷ୍ଟିପାତର ପରିମାଣ ସାଧାରଣତଃ ମିଲିମିଟର । ମି.ମି. ଏକକରେ ପ୍ରକାଶ କରାଯାଏ ।

ପାଣିପାଗର ଭାବୀ ସୂଚନା :

ପାଣିପାଗ ଭାବୀ ସୂଚନା ସାଧାରଣତଃ ତିନିଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଛି ।

ଭୂମିରୂପ :

• ପୃଥ‌ିବୀର ବିଭିନ୍ନ ଭୂମିରୂପ ଦେଖିବାକୁ ମିଳେ, ଯଥା- ପାହାଡ଼, ପର୍ବତ, ମାଳଭୂମି, ସମତଳ ଭୂମି, ଉପତ୍ୟକା, ବିସ୍ତୃତ ସମୁଦ୍ରଶଯ୍ୟା ଇତ୍ୟାଦି ।
• ଭୂମିରୂପର ଉଚ୍ଚତା ୩୦୦ ମିଟରରୁ କମ୍ ଥିଲେ ତାହା ପାହାଢ଼ ଏବଂ ୩୦୦ ମିଟରରୁ ଅଧ‌ିକ ଥିଲେ ତାହା ପର୍ବତ ।
• ସମୁଦ୍ର ପତ୍ତନରୁ ବହୁ ଉଚ୍ଚରେ ଥିବା ବିସ୍ତୃତ ସମପ୍ରାୟ ଭୂମିକୁ ମାଳଭୂମି କୁହାଯାଏ । ଏହାର ଚତୁଃପାର୍ଶ୍ବ ସ୍ଥ ଢାଲୁ ।
• ଦୁଇଟି ସଂଲଗ୍ନସ୍ଥ ଉଚ୍ଚଭୂମି ମଧ୍ୟବର୍ତ୍ତୀ ନିମ୍ନଭୂମିକୁ ଉପତ୍ୟକା କୁହାଯାଏ ।

• କୌଣସି ପର୍ବତମାଳାର ଶିଖର ମଧ୍ୟବର୍ତ୍ତୀ ଅପେକ୍ଷାକୃତ ନିମ୍ନଭୂମି ଦେଇ ବ୍ୟବହୃତ ଯାତାୟାତ ପଥକୁ ଗିରିପଥ କୁହାଯାଏ ।

ମାନଚିତ୍ରରେ ଭୂମିରୂପ ଦର୍ଶାଇବାର ଭିନ୍ନ ଭିନ୍ନ ପ୍ରଣାଳୀ :

• କାଗଜପୃଷ୍ଠ ଦୁଇ ପରିସର (ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ), ମାତ୍ର ଭୂସ୍ଥିରୂପଗୁଡ଼ିକ ତିନି ପରିସରବିଶିଷ୍ଟ (ଦୈର୍ଘ୍ୟ, ଉଚ୍ଚତା ଓ ପ୍ରସ୍ଥ) ।
• ମାନଚିତ୍ରରେ ଉଚ୍ଚ ନୀଚ ଭୂମିରୂପକୁ ଦର୍ଶାଇବା ପାଇଁ ମୁଖ୍ୟ ଦୁଇଟି ପ୍ରଣାଳୀ ହେଉଛି : (i) ରଙ୍ଗ ପରସ୍ତୀକରଣ ଓ (ii) ସମୋଚ୍ଚରେଖା ପ୍ରଣାଳୀ ।

ରଙ୍ଗ ପରସ୍ତୀକରଣ :

ରଙ୍ଗର ଘନତ୍ଵରେ ହ୍ରାସବୃଦ୍ଧି ଦ୍ଵାରା ଭୂମିରୂପଗୁଡ଼ିକର ପ୍ରଦର୍ଶନ ପଦ୍ଧତିକୁ ରଙ୍ଗ ପରସ୍ତ୍ରୀକରଣ କୁହାଯାଏ ।

କେଉଁ ଭୂମିରୂପ ପାଇଁ କେଉଁ ରଙ୍ଗ ବ୍ୟବହାର ହୁଏ :

ସମୋଚ୍ଚରେଖା :

ସମୁଦ୍ର ପତ୍ତନରୁ ସମାନ ଉଚ୍ଚତାରେ ପୂ ବ । ସ୍ଥାନଗୁଡ଼ିକୁ ମାନଚିତ୍ରରେ ଯୋଗ କରୁଥିବା ରେଖାକୁ ସେ ମ ଜ ର ଖ । କୁହାଯାଏ ।

• ସମୋଚ୍ଚ ରେ ଖାଗୁ ଡ଼ି କ ୫୦ ଫୁଟ, ୧୦୦ ଫୁଟ, ୧୫ ମିଟର, ୩୦ ମିଟର ଆଦି ବ୍ୟବଧାନ ରେ ଟଣାଯାଇଥାଏ ।
• ସମୋଚ୍ଚରେଖାଗୁଡ଼ିକ ପାଖାପାଖୁ ଥିଲେ ଢାଲୁ ଅଧିକ ହୋଇଥାଏ ଏବଂ ବ୍ୟବଧାନ କମ୍ ଥିଲେ ଢାଲୁ କମ୍ ହୋଇଥାଏ ।

କେତେକ ଭୌଗୋଳିକ ଶବ୍ଦାବଳୀ

• ସ୍ଫୁଟନାଙ୍କ : ଯେଉଁ ଡିଗ୍ରୀ ତାପମାତ୍ରାରେ ଜଳ ବାଷ୍ପରେ ପରିଣତ ହୁଏ, ତାକୁ ସ୍ଫୁଟନାଙ୍କ କୁହାଯାଏ ।
• ହିମାଙ୍କ : ଯେଉଁ ଡିଗ୍ରୀ ତାପମାତ୍ରାରେ ଜଳ ବରଫରେ ପରିଣତ ହୁଏ, ତାକୁ ହିମାଙ୍କ କୁହାଯାଏ ।
• ଡିଗ୍ରୀ : ତାପମାତ୍ରା ମାପିବାର ଏକକ ।
• ଥର୍ମୋଗ୍ରାଫ୍ : ପାଗ ପର୍ଯ୍ୟବେକ୍ଷଣ କେନ୍ଦ୍ର ମାନଙ୍କରେ କ୍ରମାଗତ ଭାବେ ତାପମାତ୍ରା ରେକର୍ଡ଼ କରିବାପାଇଁ ବ୍ୟବହୃତ ହେଉଥିବା ଯନ୍ତ୍ର ।
• ବାରୋମିଟର : ବାୟୁ ଚାପ ମାପିବା ଯନ୍ତ୍ର ।
• ଉଇଣ୍ଡଭେନ୍ : ପବନ ଦିଗ ନିର୍ଣ୍ଣୟ କରିବା ଯନ୍ତ୍ର ।
• ଆନିମୋମିଟର : ପବନର ବେଗ ମାପକ ଯନ୍ତ୍ର ।

• ହାଇଡ୍ରୋମିଟର : ବାୟୁର ଆପେକ୍ଷିକ ଆର୍ଦ୍ରତା ମାପୁଥ‌ିବା-ଯନ୍ତ୍ର ।
• ରଙ୍ଗ ପରସ୍ତୀକରଣ : ରଙ୍ଗର ଘନତ୍ଵରେ ହ୍ରାସବୃଦ୍ଧି ଦ୍ଵାରା ମାନଚିତ୍ରରେ ବିଭିନ୍ନ ଭୂମିରୂପ ପ୍ରଦର୍ଶନ ପଦ୍ଧତିକୁ ରଙ୍ଗ ପରସ୍ତୀକରଣ କୁହାଯାଏ ।
• ସମୋଚ୍ଚରେଖା : ସମୁଦ୍ର ପତ୍ତନରୁ ସମାନ ଉଚ୍ଚତାରେ ଥିବା ସ୍ଥାନଗୁଡ଼ିକୁ ମାନଚିତ୍ରରେ ଯୋଗ କରୁଥିବା ରେଖା ।
• ସ୍ଥାନିକ ଉଚ୍ଚତା : ମାନଚିତ୍ରରେ ଆବଶ୍ୟକ କ୍ଷେତ୍ରରେ କେତେକ ନିର୍ଦ୍ଦିଷ୍ଟ ସ୍ଥାନର ଉଚ୍ଚତା ଦିଆଯାଇଥିଲେ ତାହାକୁ ସ୍ଥାନିକ ଉଚ୍ଚତା କୁହାଯାଏ ।

Odisha State Board BSE Odisha 6th Class Science Important Questions Chapter 5 ବସ୍ତୁର ପ୍ରକାରଭେଦ Important Questions and Answers.

BSE Odisha Class 6 Science Important Questions Chapter 5 ବସ୍ତୁର ପ୍ରକାରଭେଦ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ବସ୍ତୁଗୁଡ଼ିକର ପ୍ରକାରଭେଦ କିପରି କରାଯାଏ ?
ଉ –

• ପ୍ରତ୍ୟେକ ବସ୍ତୁର କେତେଗୁଡ଼ିଏ ଗୁଣ ଥାଏ ।
• ଏହି ଗୁଣକୁ ଆଧାର କରି ବସ୍ତୁଗୁଡ଼ିକର ପ୍ରକାରଭେଦ କରାଯାଇଥାଏ ।

Question 2.
ବସ୍ତୁଗୁଡ଼ିକର ସାଦୃଶ୍ୟ ଓ ପାର୍ଥକ୍ୟକୁ କିପରି ବୁଝିହୁଏ ?
ଉ –
ଯେତେବେଳେ ଅନେକ ବସ୍ତୁକୁ ନେଇ ଅନୁଧ୍ୟାନ କରାଯାଇଥାଏ, ସେତେବେଳେ ସେଗୁଡ଼ିକ ମଧ୍ୟରେ ଥିବା ସାଦୃଶ୍ୟ ଓ ପାର୍ଥକ୍ୟ ବୁଝିହୁଏ ।

Question 3.
ବସ୍ତୁର ଗୁଣଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଗୁଡ଼ିକ ଜଣାପଡ଼େ ?
ଉ –

• ବସ୍ତୁର ଗୁଣଗୁଡ଼ିକ ମଧ୍ୟରୁ ଏହାର ବାହ୍ୟରୂପ, ବର୍ଣ୍ଣ, ରୁକ୍ଷତା, କଠିନତା ଜଣାପଡ଼େ ।
• ଆହୁରି ମଧ୍ୟ ଜଳରେ ଦ୍ରବଣୀୟତା, ଜଳଠାରୁ ଓଜନିଆ କି ହାଲୁକା, ଉଜ୍ଜଳତା ଆଦି ଜାଣିହୁଏ ।

Question 4.
ପ୍ରତ୍ୟେକ ବସ୍ତୁରେ ଥ‌ିବା ଦୁଇଟି ମୌଳିକ ଗୁଣ ଲେଖ ।
ଉ –

• ବସ୍ତୁ କିଛି ସ୍ଥାନ ଅଧିକାର କରି ରହେ ।
• ବସ୍ତୁର ବସ୍ତୁତ୍ଵ ରହିଥାଏ ।

Question 5.
ଉଜ୍ଜଳତା କ’ଣ ? ଦୁଇଟ ଉଜ୍ଜଳ ବସ୍ତୁର ନାମ ଲେଖ ।
ଉ –

• ବସ୍ତୁର ଚକ୍‌କ୍ ଦେଖାଯାଉଥ‌ିବା ଗୁଣକୁ ଉଜ୍ଜ୍ବଳତା କୁହାଯାଏ ।
• ଷ୍ଟିଲ୍‌ ଚାମଚ ଓ ଆଲୁମିନିୟମ୍ ଗିନା ଦୁଇଟି ଉଜ୍ଜଳ ବସ୍ତୁ ।

Question 6.
ଅଳ୍ପ ସ୍ଵଚ୍ଛ ବସ୍ତୁ କାହାକୁ କହନ୍ତି ?
ଉ –
ଯେଉଁ ବସ୍ତୁ ଦେଇ ଆଲୋକ ଆଂଶିକ ଭାବରେ ଗତି କରିପାରେ, ତାହାକୁ ଅଳ୍ପସ୍ଵଚ୍ଛ ବସ୍ତୁ କୁହାଯାଏ । ଉଦାହରଣ – ଟ୍ରେନିଂ ପେପର, ଘଷାକାଚ, ତେଲଲଗା କାଗଜ ।

ଦୀର୍ଘ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ତୁମକୁ ଡଷ୍ଟର, କାଠଖଣ୍ଡ, ଅଙ୍ଗାର, ସଫାବାଲି, ଚକ୍‌ଖଡ଼ି, ଷ୍ଟିଲ୍ ଚାମଚ ଦିଆଗଲା । ତୁମେ ହାତଲଗାଇ ସେଗୁଡ଼ିକର ଉପର ଅଂଶକୁ ଅନୁଭବ କର । କ’ଣ ଜାଣିଲ ଲେଖ ।
ଉ –

• ପ୍ରତ୍ୟେକ ବସ୍ତୁର ରଙ୍ଗ ଏକା ପ୍ରକାର ନୁହେଁ ।
• ସବୁ ବସ୍ତୁ କଠିନ ବା ନରମ ନୁହଁନ୍ତି ।
• ସବୁ ବସ୍ତୁର ବାହ୍ୟରୂପ ଏକାପରି ଚିକ୍‌କଣ ନୁହେଁ ।

Question 2.
ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
(କ) ପ୍ରାକୃତିକ ଓ କୃତ୍ରିମ
ଉ –

(ଖ) ସ୍ବଚ୍ଛ ଓ ଅସ୍ବଚ୍ଛ

Question 3.
ତୁମେ ବସ୍ତୁଗୁଡ଼ିକର ଶ୍ରେଣୀ ବିଭାଗ କରିବାକୁ କି କି ପଦକ୍ଷେପ ନେବ ଉଲ୍ଲେଖ କର ।
ଉ –
ବସ୍ତୁଗୁଡ଼ିକର ଶ୍ରେଣୀ ବିଭାଗ କରିବା ପାଇଁ ନିମ୍ନଲିଖ ପଦକ୍ଷେପ ନେବାକୁ ହେବ ।

• ପ୍ରଥମେ ନିରୀକ୍ଷଣ କରି ତାହା ସ୍ଵଚ୍ଛ ବା ଅସ୍ବଚ୍ଛ, ରଙ୍ଗହୀନ ବା ରଙ୍ଗୀନ ବୋଲି ଜାଣିବା ।
• ତା’ପରେ ସ୍ପର୍ଶ କରି ତାହା ଚିକ୍‌କଣ ବା ଆବଡ଼ାଖାବଡ଼ା ଦେଖୁ ।
• ପୁଣି ବସ୍ତୁଗୁଡ଼ିକୁ ହାତରେ ଟେକି ତାହା ହାଲୁକା ବା ଓଜନିଆ ପରୀକ୍ଷା କରି ଜାଣିବା ।
• ପରିଶେଷରେ ବସ୍ତୁଗୁଡ଼ିକ ମଧ୍ୟରେ ଥିବା ସାଦୃଶ୍ଯ ଓ ପାର୍ଥକ୍ୟର ତାଲିକା କରିବା ।

Question 4.
ଜଳ ଓ କାଚ ମଧ୍ଯରେ ଦୁଇଟି ସାମଞ୍ଜସ୍ୟ ଓ ଦୁଇଟି ପାର୍ଥକ୍ୟ ଲେଖ ।
ଉ –
ସାମଞ୍ଜସ୍ୟ :

• ଜଳ ଓ କାଚ ଉଭୟେ ସ୍ବଚ୍ଛ ।
• ଜଳ ଓ କାଚ ଉଭୟେ ଯୌଗିକ ପଦାର୍ଥ ।

ପାର୍ଥକ୍ୟ :

• ଜଳ ଏକ ଚରଳପଦାର୍ଥ କିନ୍ତୁ କାଚ ଏକ କଠିନ ପଦାର୍ଥ ।
• ଜଳପୃଷ୍ଠ ନରମ କିନ୍ତୁ କାଚପୃଷ୍ଠ ଟାଣ ।

Question 5.
ନିମ୍ନ ସାରଣୀରେ ଥ‌ିବା ବସ୍ତୁର ଗୁଣ ଓ ପ୍ରକାରଭେଦ ପୂରଣ କର ।

ଉ –

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶୋଉର

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ବସ୍ତୁର ……………….. କୁ ଆଧାର କରି ପ୍ରକାରଭେଦ କରାଯାଏ ।
(ଖ) ……………… ଗୋଟିଏ ମୂଳ ପଦାର୍ଥରୁ ତିଆରି ହୋଇଥାଏ ।
(ଖ) ମନୁଷ୍ୟ ତିଆରି ବସ୍ତୁକୁ …………. କୁହାଯାଏ ।
(ଘ) ମାଟି ଏକ ………… ବସ୍ତୁ ଅଟେ ।
(ଙ) ଷ୍ଟିଲ ଚାମଚର ବାହ୍ୟ ରୂପ …………….. ଅଟେ ।
ଉ –
(କ) ଗୁଣ
(ଖ) ବସ୍ତୁ
(ଗ) କୃତ୍ରିମ ବସ୍ତୁ
(ଘ) ପ୍ରାକୃତିକ
(ଙ) ଅନୁଜ୍ବଳ

Question 2.
(କ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ପ୍ରାକୃତିକ ବସ୍ତୁ ?
(i) ଚୌକି
(ii) କାଠ
(iii) ଟେବୁଲ
(iv) ଝରକା
ଉ –
(ii) କାଠ

(ଖ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି କୃତ୍ରିମ ବସ୍ତୁ ନୁହେଁ ?
(i) କାଚ
(ii) ପଥର
(iii) କଣ୍ଢେଇ
(iv) ମାଟି
ଉ –
(iv) ମାଟି

(ଗ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଉଜ୍ଜଳ ବସ୍ତୁ ?
(i) ଚଡ଼ି
(ii) ପ୍ଲାଷ୍ଟିକ୍ ପାନିଆ
(iii) ଅଙ୍ଗାର
(iv) ଷ୍ଟିଲ୍ ଚାମଚ୍
ଉ –
(iv) ଷ୍ଟିଲ୍ ଚାମଚ୍

(ଘ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଅଳ୍ପ ସ୍ବଚ୍ଛ ?
(i) କାଚ ଗ୍ଲାସ୍
(ii) କାର୍ଡବୋର୍ଡ
(iii) କାଠପଟା
(iv) ତେଲଘସା କାଗଜ
ଉ –
(iv) ତେଲଘସା କାଗଜ

(ଙ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଜଳରେ ଦ୍ରବଣୀୟ ?
(i) କିରୋସିନି
(ii) ଚିନି
(iii) ସଫା ବାଲି
(iv) କୁଟା ବା ନଡା ଖଣ୍ଡ
ଉ –
(ii) ଚିନି

Question 3.
ବାମ ପାର୍ଶ୍ଵର ସଂପର୍କକୁ ଦେଖ୍ ଡାହାଣ ପାର୍ଶ୍ଵର ସଂପର୍କ ଲେଖ ।
କ) କାଠ : ଅସ୍ୱଚ୍ଛ : : କାଚ : ………… ।
(ଖ) ଚିନି : ବ୍ରବଶୀୟ :: ………………. ଅଦ୍ରବଣୀୟ ।
(ଗ) ସୁନା : ଧାତୁ : : ଅଙ୍ଗାର : ……………………. ।
(ଘ) ପାଣିରେ ବୁଡ଼ିଯିବା : ଗୋଡ଼ି : : ଭାସିବା : ……………….. ।
(ଙ) ମଣିଷ : ସଜୀବ : : କମ୍ପ୍ୟୁଟର : ……………….. ।
(ଚ) ମହମବତି : ଅନୁଜ୍ଜ୍ବଳ : : ଷ୍ଟିଲପ୍ଲାସ୍ : ……………….. ।
(ଛ) ସୋଲ : ନରମ : : ସାବୁନ : ……………….. ।
ଉ –
(କ) ସ୍ବଚ୍ଛ
(ଖ) ବାଲି
(ଗ) ଅଧାତୁ
(ଘ) ସୋଲ
(ଙ) ନିର୍ଜୀବ
(ଚ) ଉତ୍କଳ
(ଛ) କଠିନ

Question 4.
ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(କ) କାଗଜ ହେଉଛି ପ୍ରାକୃତିକ ବସ୍ତୁ ।
(ଖ) ଲୁହା ତାପ କୁପରିବାହୀ ।
(ଗ) ଯେଉଁ ବସ୍ତୁ ମଧ୍ୟଦେଇ ଆଲୋକ ଗତି କରିପାରେ ନାହିଁ, ତାହା ସ୍ଵଚ୍ଛ ବସ୍ତୁ ।
(ଘ) ଯାହାର ଜୀବନ ଅଛି ତାହା ନିର୍ଜୀବ ବସ୍ତୁ ।
(ଙ) ୟୁରିଆ ସାର ଜଳରେ ଦ୍ରବଣୀୟ ।
ଉ –
(କ) କାଗଜ ହେଉଛି କୃତିମ ବସ୍ତୁ ।
(ଖ) ଲୁହା ତାପ ସୁପରିବାହୀ ।
(ଗ) ଯେଉଁ ବସ୍ତୁ ମଧ୍ୟଦେଇ ଆଲୋକ ଗତି କରିପାରେ ନାହିଁ, ତାହା ଅସ୍ବଚ୍ଛ ବସ୍ତୁ ।
(ଙ) ୟୁରିଆ ସାର ଜଳରେ ଦ୍ରବଣୀୟ ।

Question 5.
‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସଂପର୍କ ବାଛ ।
(କ)

ଉ –

(ଖ)

ଉ –

(ଗ)

ଉ –

Odisha State Board CHSE Odisha Class 12 Sociology Solutions Unit 1 ଭାରତୀୟ ସମାଜର ପରିଚୟ Objective Questions.

CHSE Odisha 12th Class Sociology Unit 1 Objective Questions in Odia Medium

ବସ୍ତୁନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
(କ) ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

୧। କେଉଁ ରାଜାଙ୍କ ନାମ ଅନୁସାରେ ଦେଶର ନାମ ଭାରତ ହୋଇଛି ?
(କ) ଭରତ
(ଖ) ଦୁଷ୍ମନ୍ତ
(ଗ) ସମୁଦ୍ରଗୁପ୍ତ
(ଘ) ସୃଦ୍ରଗୁପ୍ତ
Answer:
(କ) ଭରତ

୨। ନିଗ୍ରିଟୋମାନେ ଭାରତର ସର୍ବପ୍ରଥମ ଅଧ୍ୟାସୀ ବୋଲି କିଏ କହିଥିଲେ ?
(କ) ରିସ୍‌ଲେ
(ଖ) ଜେ.ଏଚ୍.ହଟନ୍
(ଗ) ଏ.ସି.ହଡ଼ନ୍
(ଘ) ବି.ଏସ୍.ଗୁହା
Answer:
(ଖ) ଜେ.ଏଚ୍.ହଟନ୍

୩। ନିମ୍ନଲିଖତ କେଉଁ ନୃବିଜ୍ଞାନୀ ରିସ୍‌ଲେଙ୍କ ପ୍ରଜାତୀୟ ବିଭାଗୀକରଣ ତୃଟିପୂର୍ଣ ବୋଲି ମତ ଦେଇଛନ୍ତି ।
(କ) ଡି.ଏନ୍.ମଜୁମଦାର
(ଖ) ବି.ଏସ୍. ଗୁପ୍ତା
(ଗ) ଏ.ସି.ହଡ଼ନ୍
(ଘ) ଜେ.ଏଚ୍.ହଟନ୍
Answer:
(କ) ଡି.ଏନ୍.ମଜୁମଦାର

୪। କେଉଁ ପ୍ରଜାତି ଅନ୍ତର୍ଭୁକ୍ତ ନ ଥିବାରୁ ନୃବିଜ୍ଞାନୀମାନେ ରିସ୍‌ଲେଙ୍କ ପ୍ରଜାତୀୟ ବିଭାଗୀକରଣକୁ ତ୍ରୁଟିପୂର୍ଣ୍ଣ ବୋଲି ଅଭିହିତ କରିଛନ୍ତି ?
(କ) ନରଡ଼ିକ୍
(ଖ) ଆର୍ଯ୍ୟ
(ଗ) ଦ୍ରାବିଡ଼
(ଘ) ନିଗ୍ରିଟୋ
Answer:
(ଘ) ନିଗ୍ରିଟୋ

୫। କିଏ ଭାରତର ଜନସଂଖ୍ୟାକୁ ୫ଟି ପ୍ରଜାତିରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
(କ) ଏ.ସି.ହଡ଼ନ୍
(ଖ) ରିସ୍‌ଲେ
(ଗ) ଜେ.ଏଚ୍.ହଟନ୍
(ଘ) ବି.ଏସ୍.ଗୁହା
Answer:
(କ) ଏ.ସି.ହଡ଼ନ୍

୬। କିଏ ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ ପ୍ରାକ୍ ଦ୍ରାବିଡ଼ିଆଜ୍‌, ଦ୍ରାବିଡ଼ିଆନ୍, ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟାନ୍, ଇଣ୍ଡୋ-ଆଲ୍‌ପାଇନ୍ ଏବଂ ମଙ୍ଗୋଲିଆନ୍ ଆଦି ଭାବରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
(କ) ରିସ୍‌ଲେ
(ଖ) ଏ.ସି.ହଡ଼ନ୍
(ଗ) ଜେ.ଏଚ୍.ହଟନ୍
(ଘ) ବି.ଏସ୍.ଗୁହା
Answer:
(ଖ) ଏ.ସି.ହଡ଼ନ୍

୭। କିଏ ଭାରତର ଜନସଂଖ୍ୟାକୁ ନିଗ୍ରିଟୋ, ପ୍ରୋଟୋ ଅଷ୍ଟ୍ରାଲଏଡ, ମଙ୍ଗୋଲଏଜ୍, ମେଡ଼ିଟେରାନିଆନ୍, ୱେଷ୍ଟର୍ନ ବ୍ରୋସିସେଫାଲ୍ ଏବଂ ନର୍ଜିକ୍ ଆଦି ପ୍ରଜାତିରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
(କ) ହଟନ୍
(ଖ) ରିସ୍‌ଲେ
(ଗ) ଗୁହା
(ଘ) ହଡ଼ନ୍
Answer:
(ଗ) ଗୁହା

୮। କିଏ ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟନ, ତୁର୍କୋ-ଇରାନିଆନ୍, ସ୍କାଇଥୋଦ୍ରାବିଡ଼ିଆଟ୍, ଦ୍ରାବିଡ଼ିଆନ୍, ମଙ୍ଗୋଲଏଡ, ଆର୍ଯ୍ୟ-ଦ୍ରାବିଡ଼ିଆନ୍‌ ଓ ମଙ୍ଗୋଲଏକ-ଦ୍ରାବିଡ଼ିଆନ୍ ଆଦି ପ୍ରଜାତିରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
(କ) ଗୁହା
(ଖ) ହଟନ୍
(ଗ) ମକୁମଦାର
(ଘ) ରିସ୍‌ଲେ
Answer:
(ଘ) ରିସ୍‌ଲେ

୯। ସ୍ୱତନ୍ତ୍ର ଦୈହିକ ଗୁଣାବଳୀମାନ ଥିବା ଲୋକମାନଙ୍କର ସମଷ୍ଟିକୁ କ’ଣ କହନ୍ତି ?
(କ) ପ୍ରଜାତି
(ଖ) ଜାତି
(ଗ) ଭାଷା
(ଘ) ବର୍ଷ
Answer:
(କ) ପ୍ରଜାତି

୧୦ । ଭାରତ ଭାଷାର ଏକ ସଂଗ୍ରହାଳୟ’’ . କିଏ କହିଥିଲେ ?
(କ) ହରବର୍ଟ ରିସ୍‌
(ଖ) ଏ.ଆର୍.ଦେଶାଇ
(ଗ) ଜେ.ଏଚ୍.ହଟନ୍
(ଘ) ଏ.ସି.ହଡ଼ନ୍
Answer:
(ଖ) ଏ.ଆର୍.ଦେଶାଇ

୧୧ । ୧୯୬୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେତୋଟି ଭାଷା ଅଛି ?
(କ) ୨୦୦୦
(ଖ) ୧୪୫୨
(ଗ) ୧୬୫୨
(ଘ) ୧୫୫୨
Answer:
(ଗ) ୧୬୫୨

୧୨ । ଭାରତର ସମୁଦାୟ ଭାଷାଗୁଡ଼ିକୁ କେତୋଟି ଭାଷାଗତ ପରିବାରରେ ବିଭକ୍ତ କରାଯାଇଛି ?
(କ) ୨
(ଖ) ୫
(ଗ) ୩
(ଘ) ୪
Answer:
(ଘ) ୪

୧୩ ୫ କିଏ ତାଙ୍କ ‘ଭାରତର ଭାଷାଗତ ସର୍ଭେ’ରେ ଉଲ୍ଲେଖ କରିଛନ୍ତି ଯେ ଭାରତରେ ୧୭୯ ଭାଷା ଏବଂ ୫୪୪ ଡାଇଲେକ୍‌ଟିକ୍ ଅଛି?
(କ) ଗ୍ରୀସନ୍ (Grierson)
(ଖ) ରିସ୍ ଲେ(Risley)
(ଗ) ଗୁହା(Guha)
(ଘ) ହଟନ (Hutton)
Answer:
(କ) ଗ୍ରୀସନ୍ (Grierson)

୧୪ । ତାମିଲ ଭାଷା କେଉଁ ଭାଷା ପରିବାର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ?
(କ) ଆର୍ଯ୍ୟ ଭାଷା ପରିବାର
(ଖ) ଦ୍ରାବିଡ଼ିଆନ୍
(ଗ) ଅଷ୍ଟ୍ରିକ୍
(ଘ) ସିନୋ ତିବେତାନ୍
Answer:
(ଖ) ଦ୍ରାବିଡ଼ିଆନ୍

୧୫ । ଓଡ଼ିଆ ଭାଷା କେଉଁ ଭାଷା ପରିବାର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ?
(କ) ଅଷ୍ଟ୍ରିକ୍
(ଖ) ଦ୍ରାବିଡ଼ିଆନ୍
(ଗ) ଲଣେୃ‍।-ଆର୍ଯ୍ୟ
(ଘ) ସିନୋ ତିବେତାନ୍
Answer:
(ଗ) ଲଣେୃ‍।-ଆର୍ଯ୍ୟ

୧୬ । ନିମ୍ନଲିଖତ ଭାଷା ମଧ୍ୟରୁ ଭାରତର ରାଷ୍ଟ୍ରଭାଷା କିଏ ?
(କ) ଇଂରାଜୀ
(ଖ) ଓଡ଼ିଆ
(ଗ) ଊର୍ଦ୍ଧ୍ବ
(ଘ) ହିନ୍ଦୀ
Answer:
(ଘ) ହିନ୍ଦୀ

୧୭ । ଆମ ରାଷ୍ଟ୍ରଭାଷା ହିନ୍ଦୀ କେଉଁ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟେ ?
(କ) ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ
(ଖ) ଦ୍ରାବିଡ଼
(ଗ) ଅଷ୍ଟ୍ରିକ୍
(ଘ) ସିନୋ ତିବେତାନ
Answer:
(କ) ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ

୧୮। ଆମ ସମ୍ବିଧାନ କେତେଗୋଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରିଛି ?
(କ) ୧୫
(ଖ) ୧୮
(ଗ) ୧୯
(ଘ) ୨୧
Answer:
(ଖ) ୧୮

୧୯ । ଭାରତରେ ଅଧିକାଂଶ ଲୋକ କେଉଁ ଭାରତୀୟ ଭାଷାରେ କଥା ହୁଅନ୍ତି ?
(କ) ଇଂରାଜୀ
(ଖ) ତାମିଲ୍
(ଗ) ହିନ୍ଦୀ
(ଘ)
Answer:
(ଗ) ହିନ୍ଦୀ

୨୦ । କେଉଁ ଭାଷା ଆଇନ ହିନ୍ଦୀକୁ ଭାରତର କାର୍ଯ୍ୟକାରୀ ଭାଷା ଭାବେ ଘୋଷଣା କଲା ?
(କ) ୧୯୪୭
(ଖ) ୧୯୫୦
(ଗ) ୧୯୫୧
(ଘ) ୧୯୬୩
Answer:
(ଘ) ୧୯୬୩

୨୧ । ୧୯୩୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେତୋଟି ଧାର୍ମିକ ସମୂହ ଥିଲା ?
(କ) ୧୦
(ଖ) ୧୨
(ଗ) ୮
(ଘ) ୬
Answer:
(କ) ୧୦

୨୨ । ସିହା ଏବଂ ସୁନୀ କେଉଁ ଧର୍ମର ଦୁଇଟି ସଂପ୍ରଦାୟ ଅଟନ୍ତି ?
(କ) ହିଦୁ
(ଖ) ଇସ୍‌ଲାମ୍
(ଗ) ବୌଦ୍ଧ
(ଘ) କୈନ
Answer:
(ଖ) ଇସ୍‌ଲାମ୍

୨୩। ଶୈବ, ଶାକ୍ତ, ବୈଷ୍ଣବ ଇତ୍ୟାଦି କେଉଁ ଧର୍ମର ସଂପ୍ରଦାୟ ଅଟେ ?
(କ) ଶିଖ୍
(ଖ) ପାର୍ସୀ
(ଗ) ହିନ୍ଦୁ
(ଘ) ବୌଦ୍ଧ
Answer:
(ଗ) ହିନ୍ଦୁ

୨୪ । ହୀନଯାନ ଏବଂ ମହାଯାନ କେଉଁ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ଅଟେ ?
(କ) ହିନ୍ଦୁ
(ଖ) ଶିଖ୍
(ଗ) ଜୈନ
(ଘ) ବୌଦ୍ଧ
Answer:
(ଘ) ବୌଦ୍ଧ

୨୫ । ଦିଗମ୍ବର ଓ ଶ୍ୱେତାମ୍ବର କେଉଁ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ଅଟେ ?
(କ) ଜୈନ
(ଖ) ବୌଦ୍ଧ
(ଗ) ହିନ୍ଦୁ
(ଘ) ଶିଖ୍
Answer:
(କ) ଜୈନ

୨୬ । ଭାରତରେ ହିନ୍ଦୁମାନଙ୍କର ସଂଖ୍ୟା ସମୁଦାୟ ଜନସଂଖ୍ୟାର କେତେ ଭାଗ ?
(କ) ୨୦
(ଖ) ୮୨
(ଗ) ୮୫
(ଘ) ୮୦
Answer:
(ଖ) ୮୨

୨୭ । ପ୍ରୋଟେଷ୍ଟାଣ୍ଟ ଏବଂ କ୍ୟାଥୋଲିକ୍ କେଉଁ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ଅଟେ ?
(କ) ଶିଖ୍
(ଖ) ଖ୍ରୀଷ୍ଟ
(ଗ) ହିନ୍ଦୁ
(ଘ) କୈନ
Answer:
(ଖ) ଖ୍ରୀଷ୍ଟ

୨୮ । ନିମ୍ନଲିଖୂତ ଧର୍ମମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ ଧର୍ମ ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଧାର୍ମିକ ସମୂହ ଅଟେ ?
(କ) ଶିଖ୍
(ଖ) ହିନ୍ଦୁ
(ଗ) ଇସ୍‌ଲାମ୍
(ଘ) କୈନ
Answer:
(ଗ) ଇସ୍‌ଲାମ୍

୨୯ । କେଉଁ ମୋଗଲ ସମ୍ରାଟ ହିନ୍ଦୁ ମୁସଲିମ୍ ଏକତା ପ୍ରତିଷ୍ଠା ପାଇଁ ଉଦ୍ୟମ କରିଥିଲେ ?
(କ) ବାବର
(ଖ) ହୁମାୟୁନ୍
(ଗ) ଆକବର
(ଘ) ଶାହାକାହାନ୍
Answer:
(ଗ) ଆକବର

୩୦ । ନିମ୍ନଲିଖ କେଉଁ ଭାଷା ପ୍ରାଚୀନ ଭାରତରେ ଏକତା ଆଣିବାରେ ସହାୟକ ହେଉଥିଲା ?
(କ) ହିଦା
(ଖ) ଇଂରାଜୀ
(ଗ) ଊର୍ଦ୍ଧ୍ବ
(ଘ) ସଂସ୍କୃତ
Answer:
(ଘ) ସଂସ୍କୃତ

୩୧ । ‘‘ଭାରତର ଏକତା ମୁଖ୍ୟତଃ ଧାର୍ମିକ ଅଟେ’– ଏକଥା କିଏ କହିଥିଲେ ?
(କ) ଏସ୍.ଏନ୍.ଶ୍ରୀନିବାସ
(ଖ) ମାକାଇଭର
(ଗ) ଏ.ଆର୍.ଦେଶାଇ
(ଘ) ସି.ଏଚ୍.କୁଲେ
Answer:
(କ) ଏସ୍.ଏନ୍.ଶ୍ରୀନିବାସ

୩୨ । ଭାରତର ଚତୁଃପାର୍ଶ୍ବରେ ପ୍ରାକୃତିକ ପ୍ରାଚୀର ଏହାର କେଉଁ ଏକତାକୁ ଦର୍ଶାଇଥାଏ ?
(କ) ରାଜନୈତିକ
(ଖ) ଭୌଗୋଳିକ
(ଗ) ସାଂସ୍କୃତିକ
(ଘ) ଧାମିକ
Answer:
(ଖ) ଭୌଗୋଳିକ

୩୩ । ଭାରତର ଅତି ପ୍ରାଚୀନ ସୃଷ୍ଟି ଏହାର କେଉଁ ଏକତାକୁ ଦର୍ଶାଇଥାଏ ?
(କ) ଭୌଗୋଳିକ
(ଖ) ରାଜନୈତିକ
(ଗ) ଐତିହାସିକ
(ଘ) ପୁରୁଶା
Answer:
(ଗ) ଐତିହାସିକ

୩୪ । ସର୍ବପ୍ରଥମେ ଭାରତରେ ମନୁଷ୍ୟର ଆର୍ବିଭାବ କେବେ ହୋଇଥିଲା ?
(କ) ୫୦୦୦ ବର୍ଷ ପୂର୍ବେ
(ଖ) ୨୦୦୦ ବର୍ଷ ପୂର୍ବେ
(ଗ) ୧୦,୦୦୦ ବର୍ଷ ପୂର୍ବେ
(ଘ) ୫,୦୦,୦୦୦ ବର୍ଷ ପୂର୍ବେ
Answer:
(ଘ) ୫,୦୦,୦୦୦ ବର୍ଷ ପୂର୍ବେ

୩୫ । ହିନ୍ଦୁ ଉପତ୍ୟକାର ସଭ୍ୟତା କେବେ ସୃଷ୍ଟି ହୋଇଥିଲା ?
(କ) ଖ୍ରୀ.ପୂ. ୨୫୦୦
(ଖ) ଖ୍ରୀ.ପୂ. ୧୫୦୦
(ଗ) ଖ୍ରୀ.ପୂ. ୧୭୦୦
(ଘ) ଖ୍ରୀ.ପୂ. ୫୦୦୦
Answer:
(କ) ଖ୍ରୀ.ପୂ. ୨୫୦୦

୩୬ । ଭାରତର ଭୌଗୋଳିକ ଅଞ୍ଚଳ ଗୁଜରାଟରୁ ଆସାମ ପର୍ଯ୍ୟନ୍ତ କେତେ ମାଇଲ୍ ପରିବ୍ୟାପ୍ତ ଅଟେ ?
(କ) ୨୦୦୦ ମାଇଲ୍
(ଖ) ୧୫୦୦ ମାଇଲ୍
(ଗ) ୩୦୦୦ ମାଇଲ୍
(ଘ) ୨୫୦୦ ମାଇଲ୍
Answer:
(ଖ) ୧୫୦୦ ମାଇଲ୍

୩୭ । ଇଣ୍ଡିଆ ଶବ୍ଦଟି କେଉଁ ଶବ୍ଦରୁ ଆସିଛି ?
(କ) ଭାରତ
(ଖ) ଇଦୁ
(ଗ) ଇଣ୍ଡସ୍
(ଘ) ଗଙ୍କ।
Answer:
(ଗ) ଇଣ୍ଡସ୍

୩୮ । ଭାରତର ପବିତ୍ର ଭୌଗୋଳିକତା ଏହାର କେଉଁ ଏକତାକୁ ଦର୍ଶାଇଥାଏ ?
(କ) ରାଜନୈତିକ
(ଖ) ଭୌଗୋଳିକ
(ଗ) ଧାର୍ମିକ
(ଘ) ସାଂସ୍ମତିକ
Answer:
(ଘ) ସାଂସ୍ମତିକ

୩୯ । ଭାରତର ଅବସ୍ଥିତି କେଉଁ ଗୋଲାର୍ଦ୍ଧରେ ରହିଅଛି ?
(କ) ଦକ୍ଷିଣ
(ଖ) ଉତ୍ତର
(ଗ) ଉତ୍ତୟ
(ଘ) କୌଣସିଟି ନୁହେଁ
Answer:
(ଗ) ଉତ୍ତୟ

୪୦ । ଆମ ଦେଶର ସୀମାକୁ କେତୋଟି ଦେଶ ଲାଗିଛି ?
(କ) ଦୁଇଟି
(ଖ) ସାତଟି
(ଗ) ପାଞ୍ଚ
(ଘ) ଚାରିଟି
Answer:
(ଖ) ସାତଟି

୪୧ । ହିମାଳୟର ଉତ୍ତର ଭାଗକୁ କ’ଣ କୁହାଯାଏ ?
(କ) ହିମାଳ
(ଖ) ହିମାଦ୍ରି
(ଗ) ଣିୱାଲିକ୍
(ଘ) ଗାଙ୍ଗେୟ ସମତଳଭୂମି
Answer:
(ଖ) ହିମାଦ୍ରି

୪୨ । ହିମାଳୟର ଦକ୍ଷିଣଭାଗର ଅଂଶବିଶେଷକୁ କ’ଣ କୁହାଯାଏ ?
(କ) ହିମାଦ୍ରି
(ଖ) ହିମାଚଳ
(ଗ) ପଞ୍ଜାବ
(ଘ) ସିଲିକ୍
Answer:
(ଘ) ସିୱାଲିକ୍

୪୩ । ଭାରତର ମଧ୍ୟଭାଗରେ କେଉଁ ପର୍ବତମାଳା ରହିଅଛି ?
(କ) ପୂର୍ବଘାଟ
(ଖ) ପଶ୍ଚିମଘାଟ
(ଗ) ମଧ୍ୟପ୍ରଦେଶ
(ଘ) ବିନ୍ଧ୍ୟ ଓ ସାତପୁରା
Answer:
(ଘ) ବିନ୍ଧ୍ୟ ଓ ସାତପୁରା

୪୪ । ସୁନ୍ଦରବନ ତ୍ରିକୋଣଭୂମି କେଉଁ ନଦୀର ମୁହାଣରେ ସୃଷ୍ଟି ହୋଇଅଛି ?
(କ) ନର୍ମଦା ଓ ତାୟୀ
(ଖ) କୃଷ୍ଣା ଓ କାବେରୀ
(ଗ) ଗଙ୍ଗା ଓ ଯମୁନା
(ଘ) ଗଙ୍ଗା ଓ ବ୍ରହ୍ମପୁତ୍ର
Answer:
(ଗ) ଗଙ୍ଗା ଓ ବ୍ରହ୍ମପୁତ୍ର

୪୫ । ଭାରତର ଉତ୍ତରସ୍ଥ ସମତଳଭୂମିର ଦକ୍ଷିଣ ଭାଗରେ କ’ଣ ଅବସ୍ଥିତ ?
(କ) ଗାଙ୍ଗେୟ ସମତଳଭୂମି
(ଖ) ଦାକ୍ଷିଣାତ୍ୟ ମାଳଭୂମି
(ଗ) ସାମୁଦ୍ରିକ ଉପକୂଳୀୟ ସମତଳ ଅଞ୍ଚଳ
(ଘ) ପଶ୍ଚିମଘାଟ ପର୍ବତମାଳା
Answer:
(ଖ) ଦାକ୍ଷିଣାତ୍ୟ ମାଳଭୂମି

୪୬ । ୨୦୧୧ ଜନଗଣନା ଅନୁସାରେ ଦେଶର ଜନସଂଖ୍ୟାର ଘନତା ବର୍ଗ କି.ମି. ପ୍ରତି କେତେ ରହିଅଛି ?
(କ) ୧୧୭
(ଖ) ୭୭
(ଗ) ୩୨୧
(ଘ) ୩୮୪
Answer:
(ଘ) ୩୮୪

୪୭ । ଭାରତର କେଉଁ ରାଜ୍ୟ ହେଉଅଛି କମ୍ ଜନସଂଖ୍ୟା ଘନତ୍ବ ରାଜ୍ୟ ?
(କ) କେରଳ
(ଖ) ଆସାମ
(ଗ) ଅରୁଣାଚଳ ପ୍ରଦେଶ
(ଘ) ଓଡ଼ିଶା
Answer:
(ଗ) ଅରୁଣାଚଳ ପ୍ରଦେଶ

୪୮ । ୨୦୧୧ ମସିହାରେ ଭାରତର ଆୟୁ ପ୍ରତ୍ୟାଶା କେତେ ରହିଅଛି ?
(କ) ୫୮ ବର୍ଷ
(ଖ) ୬୫ ବର୍ଷ
(ଗ) ୭୦ ବର୍ଷ
(ଘ) ୫୦ବର୍ଷ
Answer:
(ଗ) ୭୦ ବର୍ଷ

୪୯ । ଭାରତ ସମଗ୍ର ଜନସଂଖ୍ୟାର କେତେ ଭାଗ ମହିଳା ଜନସଂଖ୍ୟା ଅଛି ?
(କ) ୫୧.୫%
(ଖ) ୪୮.୫%
(ଗ) ୫୦%
(ଘ) ୬୧%
Answer:
(ଖ) ୪୮.୫%

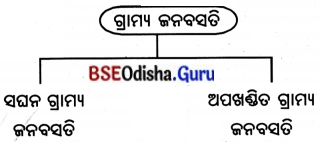
୫୦ । ୨୦୧୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତର କେତେ ପ୍ରତିଶତ ଲୋକ ଗ୍ରାମାଞ୍ଚଳରେ ବସବାସ କରନ୍ତି ?
(କ) ୩୧.୨୦
(ଖ) ୮୦
(ଗ) ୬୮.୮୦
(ଘ) ୮୫
Answer:
(ଗ) ୬୮.୮୦

୫୧ । ଭାରତର ସର୍ବୋଚ୍ଚ ଜନସଂଖ୍ୟା ବିଶିଷ୍ଟ ନଗରଟି କିଏ ?
(କ) ଦିଲ୍ଲୀ
(ଖ) ଜଜଲିତା
(ଗ) ମୁମ୍ବାଇ
(ଘ) ଚେନୃ।ଇ
Answer:
(ଗ) ମୁମ୍ବାଇ

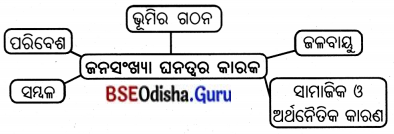
୫୨ । ଭାରତର ସହରୀ ଜନସଂଖ୍ୟାର ଅଭିବୃଦ୍ଧିର କାରଣ କ’ଣ ?
(କ) ଦାରିଦ୍ର୍ୟ
(ଖ) ସହର ଚଳଶି
(ଗ) ଜନସଂଖ୍ୟାର ସ୍ଥାନାନ୍ତରଣ ଓ ଦ୍ରୁତ ସହରୀକରଣ
(ଘ) ବେକାର
Answer:
(ଗ) ଜନସଂଖ୍ୟାର ସ୍ଥାନାନ୍ତରଣ ଓ ଦ୍ରୁତ ସହରୀକରଣ

୫୩ ’ଭୌଗୋଳିକ ଅଞ୍ଚଳ ଦୃଷ୍ଟିକୋଣରୁ ଭାରତ ବିଶ୍ବର ବୃହତ୍ ରାଷ୍ଟ୍ରଗୁଡ଼ିକ ମଧ୍ୟରେ କେଉଁ ସ୍ଥାନରେ ରହିଅଛି ?
(କ) ତୃତୀୟ
(ଖ) ଦ୍ବିତୀୟ
(ଗ) ସପ୍ତମ
(ଘ) ଅଷ୍ଟମ
Answer:
(ଗ) ସପ୍ତମ

୫୪ । ବିଶ୍ଵ ଜନସଂଖ୍ୟାର ଶତକଡ଼ା କେତେ ଭାଗ ଲୋକ ଭାରତରେ ବାସ କରନ୍ତି ?
(କ) ୨.୪%
(ଖ) ୧୭.୫%
(ଗ) ୧୭.୬%
(ଘ) ୯.୯୬ %
Answer:
(କ) ୨.୪%

୫୫ । ଭାରତର ସଂପୂର୍ଣ୍ଣ କ୍ଷେତ୍ରଫଳ କେତେ ?
(କ) ୩୨ ଲକ୍ଷ ୮୭ ହଜାର ୨୬୩ ବର୍ଗ କିଲୋମିଟର
(ଖ) ୨୦ ଲକ୍ଷ ୭୫ ହଜାର ୪୦୦ ବର୍ଗ କିଲୋମିଟର
(ଗ) ୩୦ ଲକ୍ଷ ୮୦ ହଜାର ୫୦୦ ବର୍ଗ କିଲୋମିଟର
(ଘ) ୨୫ ଲକ୍ଷ ୮୭ ହଜାର ୨୬୩ ବର୍ଗ କିଲୋମିଟର
Answer:
(କ) ୩୨ ଲକ୍ଷ ୮୭ ହଜାର ୨୬୩ ବର୍ଗ କିଲୋମିଟର

୫୬ । ଭାରତର ଜନସଂଖ୍ୟା ୨୦୧୧ ଜନଗଣନା ତଥ୍ୟାନୁସାରେ କେତେ ଅଟେ ?
(କ) ୧୧୮କୋଟି ୮୦ ଲକ୍ଷ ୫ ହଜାର ୨୦୦
(ଖ) ୧୦୨ କୋଟି ୮୬ ଲକ୍ଷ ୧୦ ହଜାର ୩୨୮
(ଗ) ୧୨୧ କୋଟି ୧ ଲକ୍ଷ ୯୩ ହଜାର ୪୨୨
(ଘ) ୧୦୫ କୋଟି ୯୦ ଲକ୍ଷ ୨୦ ହଜାର ୫୩୦
Answer:
(ଗ) ୧୨୧ କୋଟି ୧ ଲକ୍ଷ ୯୩ ହଜାର ୪୨୨

୫୭ । ‘‘ଭାରତ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପରିସର ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଥିବା ଏବଂ ବହୁଧା ସ୍ବତନ୍ତ୍ର ବଂଶଗତ ଗୁଣ ଧାରଣା କରିଥିବା ଏକ ବୃହତ୍ ଜୈବିକ ମାନବ ସମୂହ ପ୍ରଜାତି ଅଟେ’’ ଏହା କାହାର ମତ ?
(କ) ପ୍ରଫେସର ଡି. ଏନ୍ ମଜୁମ୍ଦାର
(ଖ) ସାର ହର୍ବଟ୍ ରିଜଲେ
(ଗ) ଏ.ଡବ୍ଲ୍ୟୁ. ଗ୍ରୀନ୍
(ଘ) ପ୍ରଫେସର ସି.ବି. ମେମୋରିଆ
Answer:
(ଗ) ଏ.ଡବ୍ଲ୍ୟୁ. ଗ୍ରୀନ୍

୫୮ । ‘ଟ୍ରାଇବାଲ୍ ଡେମୋଗ୍ରାଫି ଅଫ୍ ଇଣ୍ଡିଆ’ ପୁସ୍ତକର ଲେଖକ କିଏ ?
(କ) ବି. କୁପୁସ୍ୱାମୀ
(ଖ) ରବିନ୍ ଫକସ୍
(ଗ) ଡି.ଏଚ୍. ମଜୁମ୍ଦାର
(ଘ) ସି.ବି.ମେମୋରିଆ
Answer:
(ଘ) ସି.ଜି.ମେମୋରିଆ

(ଖ) ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

୧। _____________ ବିଭିନ୍ନତାରେ ଏକତାର ଏକ ସୁନ୍ଦର ଉଦାହରଣ ।
Answer:
ଭାରତ

୨। ______________ ନଦୀର ନାମ ଅନୁସାରେ ଭାରତର ନାମ ଇଣ୍ଡିଆ ହୋଇଛି ।
Answer:
ଇଣ୍ଡସ୍ ବା ସିନ୍ଧୁ

୩ । ସିନ୍ଧୁ ନଦୀ ବର୍ତ୍ତମାନ_____________ ଦେଶରେ ଅଛି ।
Answer:
ପାକିସ୍ତାନ

୪। _________________ ଆକ୍ରମଣକାରୀମାନେ ଭାରତକୁ ହିନ୍ଦୁସ୍ଥାନ କହିଥିଲେ ।
Answer:
ମୁସଲିମ୍

୫। ସଂପ୍ରତି ଭାରତର ଭୌଗୋଳିକ ଅଞ୍ଚଳ କାଶ୍ମୀରରୁ କେପ୍ କମୋରିନ୍ ପର୍ଯ୍ୟନ୍ତ ______________ ମାଇଲ୍ ଏବଂ ଗୁଜରାଟରୁ ଆସାମ ପର୍ଯ୍ୟନ୍ତ______________ ମାଇଲ୍ ପର୍ଯ୍ୟନ୍ତ ପରିବ୍ୟାପ୍ତ ।
Answer:
୨୦୦୦, ୧୫୦୦

୬। ଧାର୍ମିକ, ଭାଷାଗତ ଓ ଦୈହିକ ଗୁଣ ଉପରେ ପର୍ଯ୍ୟବସିତ ସାମୂହିକ ପାର୍ଥକ୍ୟକୁ _______________ କରନ୍ତି ।
Answer:
ବିଭିନ୍ନତା

୭। କେତେଗୁଡ଼ିଏ ସ୍ୱତନ୍ତ୍ର ଦୈହିକ ଲକ୍ଷଣ ଥିବା ଲୋକଙ୍କର ସମଷ୍ଟିକୁ_____________ କୁହାଯାଏ ।
Answer:
ପ୍ରଜାତି

୮। ହର୍‌ବର୍ଟ ରିସ୍‌ଲେ ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ ______________ ଟି ପ୍ରଜାତୀୟ ପ୍ରକାରରେ ବର୍ଗୀକରଣ କରିଛନ୍ତି ।_______________
Answer:
୭

୯ । ବି.ଏସ୍.ଗୁହା ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ ______________ ଟି ପ୍ରଜାତିରେ ବିଭାଜିତ କରିଛନ୍ତି ।
Answer:
୬

୧୦ | _____________ ରିସ୍‌କ ବର୍ଗୀକରଣକୁ ଏକ ଭାଷାଗତ ବିଭାଜନ ବୋଲି କହି ସମାଲୋଚନା କରିଛନ୍ତି ।
Answer:
ଡି.ଏନ୍.ମଜୁମଦାର

୧୧ । _____________ ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ ୫ଟି ପ୍ରଜାତୀୟ ପ୍ରକାରରେ ବିଭାଜିତ କରିଛନ୍ତି ।
Answer:
ଏ.ସି.ହଡ଼ନ୍

୧୨ । ନିଗ୍ରିଟୋମାନେ ଭାରତର ପ୍ରଥମ ଅଧିବାସୀ ଥିଲେ ବୋଲି ____________ ମତ ଦେଇଥିଲେ ।
Answer:
ଜେ.ଏଚ୍.ହଟନ୍

୧୩ । _____________ ଙ୍କ ମତରେ ଭାରତ ଭାଷାର ଏକ ସଂଗ୍ରହାଳୟ ଅଟେ ।
Answer:
ଏ.ଆର୍.ଦେଶାଇ

୧୪ । ୧୯୬୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ _____________ ଟି ଭାଷା ଓ କଥାତ ଭାଷା ରହିଛି ।
Answer:
୧୬୫୨

୧୫ । ଭାରତର ସମସ୍ତ ଭାଷାକୁ ମୁଖ୍ୟତଃ ______________ ଟି ଭାଷା ପରିବାରଭୁକ୍ତ କରାଯାଇଛି ।
Answer:
୪

୧୬ । ___________ ଆମର ଜାତୀୟ ଭାଷା ଅଟେ ।
Answer:
ହିଦା

୧୭ । ଆମ ସମ୍ବିଧାନ ସମୁଦାୟ ___________ ଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରିଛି ।
Answer:
୧୮

୧୮ । ହିନ୍ଦୀ _____________ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟେ ।
Answer:
ଇଣୋୁ-ଆର୍ପ୍ୟ

୧୯। ____________ ଧର୍ମ ଭାରତର ଏକ ପ୍ରମୁଖ ଧର୍ମ ଅଟେ ।
Answer:
ହିନ୍ଦୁ

୨୦ । ସମୁଦାୟ ଜନସଂଖ୍ୟାର _____________ ଭାଗରୁ ଊର୍ଦ୍ଧ୍ବ ଲୋକ ହିନ୍ଦୁ ଧର୍ମାବଲମ୍ବୀ ଅଟନ୍ତି ।
Answer:
୮୨

୨୧ । ଭାରତରେ ମୁସ୍‌ଲିମ୍‌ଙ୍କ ସଂଖ୍ୟା ସମୁଦାୟ ଜନସଂଖ୍ୟାର ____________ ଭାଗରୁ ଊର୍ଦ୍ଧ୍ବ ଅଟେ ।
Answer:
୧୨

୨୨। ______________ ଧର୍ମ ଏକ ବହୁ ସଂପ୍ରଦାୟ ବିଶିଷ୍ଟ ଧର୍ମ ଅଟେ ।
Answer:
ହିନ୍ଦୁ

୨୩ । ଦିଗମ୍ବର ଓ ଶ୍ୱେତାମ୍ବର ______________ ଧର୍ମର ଦୁଇ ପ୍ରମୁଖ ସଂପ୍ରଦାୟ ଅଟେ ।
Answer:
ଜୈନ

୨୪ । ହୀନଯାନ ଓ ମହାଯାନ ____________ ଧର୍ମର ଦୁଇ ପ୍ରଧାନ ସଂପ୍ରଦାୟ ଅଟେ ।
Answer:
ବୌଦ୍ଧ

୨୫ । _____________ ସଭ୍ୟତା ପୃଥ‌ିବୀର ସବୁଠୁ ପ୍ରାଚୀନ ସଭ୍ୟତା ଅଟେ ।
Answer:
ସିନ୍ଧୁ ଉପତ୍ୟକାର

୨୬ । ___________ ବର୍ଷ ପୂର୍ବେ ପ୍ରଥମ ମନୁଷ୍ୟର ଆର୍ବିଭାବ ଭାରତରେ ଘଟିଥିଲା ବୋଲି ବିଶ୍ବାସ କରାଯାଏ ।
Answer:
୫,୦୦,୦୦୦

୨୭ । ଭାରତର ସମୁଦାୟ ଭୌଗୋଳିକ ଅଞ୍ଚଳ ହେଉଛି ___________ ବର୍ଗ କି.ମି. ।
Answer:
୩୨,୮୦,୪୮୩

୨୮। _____________ ଏକ ଧର୍ମନିରପେକ୍ଷ ଦେଶ ।
Answer:
ଭାରତ

୧୯। _____________ ଙ୍କ ମତରେ ଭାରତର ଏକତା ମୁଖ୍ୟତଃ ଧାର୍ମିକ ଅଟେ ।
Answer:
ଶ୍ରୀନିବାସ

୩୦। ____________ ର ବାସଗୃହ କୁହାଯାଏ ।
Answer:
ବରଫ

୩୧ । ପୌରାଣିକ କିମ୍ବଦନ୍ତୀରୁ ଜଣାପଡ଼େ _______________ ଙ୍କ ନାମାନୁସାରେ ଆମ ଦେଶର ନାମ ଭାରତବର୍ଷ ଅଟେ |
Answer:
ଭରତ

୩୨ । ଭାରତ ________________ ମହାଦେଶର ଏକ ଉପଦ୍ୱୀପ ଅଟେ ।
Answer:
ଏସିଆ

୩ । ଭାରତ ଏକ ____________ ରାଷ୍ଟ୍ର ଅଟେ ।
Answer:
ଧର୍ମନିରପେକ୍ଷ

୩୪ । ଭାରତ _____________ ବୃହତ୍ତମ ରାଷ୍ଟ୍ର ରୂପେ ଖ୍ୟାତିଲାଭ କରିଅଛି ।
Answer:
ସପ୍ତମ

୩୫ । ଭାରତ ବିଶ୍ବର _________ ଜନବହୁଳ ରାଷ୍ଟ୍ର ଅଟେ ।
Answer:
ଦିୃତାୟ

୩୬ । ୨୦୦୧ ଜନଗଣନାନୁଯାୟୀ ଭାରତର ଜନସଂଖ୍ୟା _________ କୋଟି __________ ଲକ୍ଷ _________ ହଜାର ___________ ଅଟେ ।
Answer:
୧୦୨ କୋଟି ୮୬ ଲକ୍ଷ ୧୦ ହଜାର ୩୨୮ ।

୩୭ । ଭାରତର ଇତିହାସ ___________ ଅଟେ ।
Answer:
ଅତି ପ୍ରାଚୀନ

୩୮ । ଭାରତର ଭୌଗୋଳିକ ପରିସୀମା ପୂର୍ବରୁ ପଶ୍ଚିମକୁ ______________ କିଲୋମିଟର ।
Answer:
୨, ୯୩୩

୩୯ । ଭାରତର ଭୌଗୋଳିକ ପରିସୀମା ଉତ୍ତରରୁ ଦକ୍ଷିଣକୁ ____________ କିଲୋମିଟର ।
Answer:
୩, ୨୧୪

୪୦ । ଭାରତର କ୍ଷେତ୍ରଫଳ __________ ବର୍ଗ କିଲୋମିଟର ।
Answer:
୩୨ ଲକ୍ଷ ୮୭ ହଜାର ୨୬୩

୪୧ । ହିମାଳୟ ପାର୍ବତ୍ୟାଞ୍ଚଳ, ଦାକ୍ଷିଣାତ୍ୟ ମାଳଭୂମି, ____________ ଓ ____________ ଅଞ୍ଚଳକୁ ନେଇ ଭାରତ ନିଜର ପରିଚୟ ପ୍ରଦାନ କରେ ।
Answer:
ଉତ୍ତରସ୍ଥ ସମତଳଭୂମି, ଉପକୂଳବର୍ତ୍ତୀ ସମତଳ

୪୨ । ସାଧାରଣ ___________ ଗୁଣଗୁଡ଼ିକ ପ୍ରଜାତିର ସଦସ୍ୟମାନେ ଧାରଣ କରିଥା’ନ୍ତି ।
Answer:
ବଂଶୃଗତ

୪୩ । ଆର୍ଯ୍ୟ, ଦ୍ରାବିଡ଼ୀୟ ପ୍ରଜାତି ଏକ ____________ ପ୍ରଜାତି ଅଟନିୃ ।
Answer:
ମିଶି୍ତ

୪୪ । ମଙ୍ଗୋଲୀୟ ଓ ଦ୍ରାବିଡ଼ମାନଙ୍କ ଆନ୍ତଃବିବାହରୁ _______________ ପ୍ରଜାତିର ସୃଷ୍ଟି ହୋଇଅଛି ।
Answer:
ମଙ୍ଗୋଲୀୟ- ଦ୍ରାବିଡ଼ୟ

୪୫ । ଦ୍ରାବିଡ଼ୀୟମାନେ ସାଧାରଣତଃ ଭାରତର _____________ ଭାଗରେ ବସତି ସ୍ଥାପନ କରିଅଛନ୍ତି ।
Answer:
ଦକ୍ଷିଣ

୪୬। ______________ ସର୍ବ ପୁରାତନ ଜଙ୍ଗଲୀ ଜନଜାତି ବୋଲି ନୃ-ବିଜ୍ଞାନୀ ଏ.ସି. ହାଚ୍ଛନ୍ ମତପୋଷଣ କରିଅଛନ୍ତି ।
Answer:
ପ୍ର।କ୍-ଦ୍ରାବିଡ଼ୟ

୪୭ । ମାଲୟେସିଆର ________________ ପ୍ରଜାତି ସର୍ବପ୍ରଥମେ ଉତ୍ତର ଭାରତରେ ପ୍ରବେଶ କରି ହିମାଳୟର ପାଦଦେଶରେ ବାସ କରିଥିଲେ।
Answer:
ନିଗ୍ରିଟୋ

୪୮ । ________________ ଜାତୀୟ ପ୍ରଜାତି ସିନ୍ଧୁ ସଭ୍ୟତାର ପ୍ରତିଷ୍ଠାତା ବୋଲି ବିଶ୍ଵାସ କରାଯାଏ । _____________
Answer:
ପ୍ରୋଟୋ-ଅଷ୍ଟ୍ରେଲୀୟ

୪୯ । ହିମାଳୟରେ ବାସ କରୁଥିବା ନାଗା ଜନଜାତି ___________________ ଜାତୀୟ ପ୍ରଜାତି ଅଟେ ।
Answer:
ମଙ୍ଗୋଲୀୟ

୫୦ । ପ୍ରାଚ୍ୟ ଦେଶବାସୀୟ ପ୍ରଜାତିକୁ ____________ ପ୍ରଜାତି କୁହାଯାଏ ।
Answer:
ସେମେଟିକ୍

୫୧ । ଭାରତୀୟ ସମ୍ବିଧାନର _______________ ପରିଚ୍ଛେଦରେ ୨୨ ଗୋଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରାଯାଇଅଛି ।
Answer:
ଅଷ୍ଟମ

୫୨ । ୨୦୦୧ ଜନଗଣନାନୁଯାୟୀ ଭାରତର ଜନସଂଖ୍ୟା ______________ ଅଟେ ।
Answer:
୧୦୨ କୋଟିରୁ ଉର୍ଦ୍ଧ୍ବ

୫୩ । ଭାରତୀୟ ସମ୍ବିଧାନର ଅଷ୍ଟମ ପରିଚ୍ଛେଦରେ _______________ ଗୋଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରାଯାଇଅଛି ।
Answer:
୨୨

୫୪ । ସର୍ବବୃହତ୍ ଭାଷା ଓ ମାତୃଭାଷାଗୁଡ଼ିକ _______________ ଭାଷାର ଅନ୍ତର୍ଗତ ଅଟନ୍ତି ।
Answer:
ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟଭାଷା

୫୫ । ଓଡ଼ିଶାର ପାର୍ବତ୍ୟାଞ୍ଚଳରେ ବାସ କରୁଥିବା ଜନଜାତିମାନେ ______________ ଉପଭାଷା ବ୍ୟବହାର କରିଥା’ନ୍ତି ।
Answer:
କୋଇ

୫୬ । ଧର୍ମଗତ ବିବିଧତା ଭାରତର ଜାତୀୟ ସଂହତିର ____________ ଅଟନ୍ତି ।
Answer:
ଭପାଦାନ

୫୭ । କେ.ଏମ୍. ପାନିକରଙ୍କ ମତରେ ହିନ୍ଦୁଧର୍ମର ସାମାଜିକ ସଂରଚନା ___________ ଓ __________ ମୌଳିକ ଅନୁଚ୍ଛେଦ ସହିତ ଜଡ଼ିତ ।
Answer:
ଜାତି ବ୍ୟବସ୍ଥା, ଯୌଥ ପରିବାର

୫୮ । ଖ୍ରୀଷ୍ଟଧର୍ମର ମୂଳମନ୍ତ୍ର ______________ ଅଟେ ।
Answer:
ପ୍ରେମ

୫୯ । ବୁଦ୍ଧଦେବ ଦର୍ଶାଇଥବା ମାର୍ଗକୁ ___________ ମାର୍ଗ କୁହାଯାଏ ।
Answer:
ଆର୍ଯ୍ୟ ଅଷ୍ଟାଙ୍ଗ

୬୦ । ଇତିହାସର ସୁଦୀର୍ଘ କାହାଣୀ ଓ ଘଟଣାଗୁଡ଼ିକୁ ବିବିଧତା ମଧ୍ୟରେ ____________ ର ମୂଳମନ୍ତ୍ରରେ ବାନ୍ଧି ରଖୂରିଅଛି ।
Answer:
ଏକତା

୬୧ । ଭାରତର ଭୌଗୋଳିକ ପରିସୀମା ___________ ଠାରୁ ___________ ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପ୍ତ ଅଟେ ।
Answer:
କାଶ୍ମୀର କୁମାରିକା

(ଗ) ଭ୍ରମ ସଂଶୋଧନ କର ।

୧। ଓଡ଼ିଶା ବିଭିନ୍ନତାରେ ଏକତାର ଏକ ସୁନ୍ଦର ଉଦାହରଣ ଅଟେ ।
Answer:
ଭାରତ ବିଭିନ୍ନତାରେ ଏକତାର ଏକ ସୁନ୍ଦର ଦାହରଣ ଅଟେ ।

୨। ଆମ ଦେଶ ଭାରତ ରାଜା ଦୁଷ୍ମନ୍ତଙ୍କ ନାମ ଅନୁସାରେ ନାମିତ ।
Answer:
ଆମ ଦେଶ ଭାରତ ରାଜା ଭରତଙ୍କ ନାମ ଅନୁସାରେ ନାମିତ ।

୩ । ଗଙ୍ଗା ନଦୀ ନାମ ଅନୁସାରେ ଆମ ଦେଶ ନାମିତ ହୋଇଛି ।
Answer:
ସିନ୍ଧୁ ବା ଇଣ୍ଡସ୍ ନଦୀ ନାମ ଅନୁସାରେ ଆମ ଦେଶ ନାମିତ ।

୪। ସଂପ୍ରତି ସିନ୍ଧୁ ବା ଇଣ୍ଡସ୍ ନଦୀ ଭାରତରେ ପ୍ରବାହିତ ।
Answer:
ସଂପ୍ରତି ସିନ୍ଧୁ ବା ଇଣ୍ଡସ୍ ନଦୀ ପାକିସ୍ତାନରେ ପ୍ରବାହିତ ।

୫। ଗ୍ରୀକ୍‌ମାନେ ଭାରତକୁ ହିନ୍ଦୁସ୍ଥାନ ନାମ ଦେଇଥିଲେ ।
Answer:
ମୁସଲିମ୍ ଆକ୍ରମଣକାରୀମାନେ ଭାରତକୁ ହିନ୍ଦୁସ୍ଥାନ ନାମ ଦେଇଥିଲେ ।

୬୮ ସ୍ୱତନ୍ତ୍ର ଦୈହିକ ଲକ୍ଷଣମାନ ଥିବା ଦଳେ ଲୋକଙ୍କର ସମଷ୍ଟିକୁ ଜାତି କୁହାଯାଏ ।
Answer:
ସ୍ବତନ୍ତ୍ର ଦୈହିକ ଲକ୍ଷଣମାନ ଥିବା ଦଳେ ଲୋକଙ୍କର ସମଷ୍ଟିକୁ ପ୍ରଜାତି କୁହାଯାଏ ।

୭ । ଭାରତର ଜନସଂଖ୍ୟାର ସବୁଠୁ ଗ୍ରହଣୀୟ ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣ ହଟନ୍ ପ୍ରଦାନ କରିଥିଲେ ।
Answer:
ଭାରତର ଜନସଂଖ୍ୟାର ସବୁଠୁ ଗ୍ରହଣୀୟ ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣ ରିସ୍‌ଲେ ଓ ଗୁହା ପ୍ରଦାନ କରିଥିଲେ ।

୮। ସାର ହର୍‌ବର୍ଗ ରିସ୍‌ଲେ ଭାରତୀୟ ଜନସଂଖ୍ୟାର ୫ଟି ପ୍ରଜାତୀୟ ବିଭାଜନ ପ୍ରଦାନ କରିଛନ୍ତି ।
Answer:
ସାର ହରବର୍ଟ ରିସ୍‌ ଭାରତର ଜନସଂଖ୍ୟାର ୭ଟି ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣ ପ୍ରଦାନ କରିଛନ୍ତି ।

୯ ୮ କୁଲେ ଭାରତର ଜନସଂଖ୍ୟାର ୬ଟି ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣ ପ୍ରଦାନ କରିଛନ୍ତି ।
Answer:
ବି.ଏସ୍.ଗୁହା ଭାରତର ଜନସଂଖ୍ୟାର ୬ଟି ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣ ପ୍ରଦାନ କରିଛନ୍ତି ।

୧୦ । ମାକାଇଭର ରିସ୍‌ଙ୍କ ବର୍ଗୀକରଣକୁ ଏକ ଭାଷାଗତ ବିଭାଜନ ବୋଲି ସମାଲୋଚନା କରିଥିଲେ ।
Answer:
ଡି.ଏଚ୍. ମଜୁମଦାର ରିସ୍‌ଙ୍କ ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣକୁ ଏକ ଭାଷାଗତ ବିଭାଜନ ବୋଲି ସମାଲୋଚନା କରିଥିଲେ ।

୧୧ । ହଟନ୍‌ଙ୍କ ଅନୁସାରେ ପ୍ରାକ୍-ଦ୍ରାବିଡ଼ମାନେ ଭାରତର ସର୍ବପ୍ରଥମ ଅଧ୍ୟାବାସୀ ଥିଲେ ।
Answer:
ହଟନ୍‌ଙ୍କ ଅନୁସାରେ ନିଗ୍ରିଟୋମାନେ ଭାରତର ସର୍ବପ୍ରଥମ ଅଧିବାସୀ ଥିଲେ ।

୧୨ । ଶ୍ରୀନିବାସଙ୍କ ମତରେ ଭାରତ ଭାଷାମାନଙ୍କର ଏକ ସଂଗ୍ରହାଳୟ ।
Answer:
ଏ.ଆର୍.ଦେଶାଇଙ୍କ ମତରେ ଭାରତ ଭାଷାମାନଙ୍କର ଏକ ସଂଗ୍ରହାଳୟ ଅଟେ ।

୧୩ । ୧୯୬୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ ୨୦୦୦ ଭାଷା ରହିଛି ।
Answer:
୧୯୬୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ ୧୬୫୨ ଭାଷା ଓ ଡାଇଲେକ୍‌ଟିକ୍ ରହିଛି ।

୧୪ । ଭାରତରେ ଦେଖାଯାଉଥ‌ିବା ସମସ୍ତ ଭାଷାକୁ ୨ଟି ଭାଷା ପରିବାରଭୁକ୍ତ କରାଯାଇଛି ।
Answer:
ଭାରତର ସମସ୍ତ ଭାଷାକୁ ୪ଟି ଭାଷା ପରିବାରଭୁକ୍ତ କରାଯାଇଛି ।

୧୫ । ଆମ ସମ୍ବିଧାନର ଅଷ୍ଟମ ଅନୁଚ୍ଛେଦ ୧୫ଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରିଛି ।
Answer:
ଆମ ସମ୍ବିଧାନର ଅଷ୍ଟମ ଅନୁଚ୍ଛେଦ ୧୮ଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରିଛି ।

୧୬ । ଅଧିକାଂଶ ଭାରତୀୟ ତେଲୁଗୁ ଭାଷାରେ କଥା ହୋଇଥା’ନ୍ତି ।
Answer:
ଅଧିକାଂଶ ଭାରତୀୟ ହିନ୍ଦୀ ଭାଷାରେ କଥା ହୋଇଥା’ନ୍ତି ।

୧୭ । ଆମର ଜାତୀୟ ଭାଷା ହେଉଛି ଓଡ଼ିଆ ।
Answer:
ଆମର ଜାତୀୟ ଭାଷା ହେଉଛି ହିନ୍ଦୀ ।

୧୮ । ହିନ୍ଦୀ ଭାଷା ଅଷ୍ଟ୍ରିକ୍ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟେ ।
Answer:
ହିନ୍ଦୀ ଭାଷା ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟେ ।

୧୯ । ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ ଓ ଦ୍ରାବିଡ଼ ଭାଷା ଦୁଇ ଜନଜାତୀୟ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟନ୍ତି ।
Answer:
ଅଷ୍ଟ୍ରିକ୍ ଏବଂ ସିନୋ ତିବେତାନ୍ ଦୁଇ ଜନଜାତୀୟ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟନ୍ତି ।

୨୦ । ଓଡ଼ିଆ ଓ ଉର୍ଦୁ ଭାଷା ଦ୍ରାବିଡ଼ୀୟ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟନ୍ତି ।
Answer:
ତାମିଲ ଓ ତେଲୁଗୁ ଭାଷା ଦ୍ରାବିଡ଼ୀୟ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟନ୍ତି ।

୨୧ । ଭାରତରେ ସର୍ବାଧ‌ିକ ଖ୍ରୀଷ୍ଟ ଧର୍ମାବଲମ୍ବୀ ଲୋକମାନେ ବସବାସ କରନ୍ତି ।
Answer:
ଭାରତରେ ସର୍ବାଧ୍ଯକ ହିନ୍ଦୁ ଧର୍ମାବଲମ୍ବୀ ଲୋକମାନେ ବସବାସ କରିଥାନ୍ତି ।

୨୨ । ରିସ୍‌ଲେଙ୍କ ମତରେ ଭାରତର ଏକତା ମୁଖ୍ୟତଃ ଏକ ଧାର୍ମିକ ଏକତା ଅଟେ ।
Answer:
ଶ୍ରୀନିବାସଙ୍କ ମତରେ ଭାରତର ଏକତା ମୁଖ୍ୟତଃ ଏକ ଧାର୍ମିକ ଏକତା ଅଟେ ।

୨୩ । ଇସ୍‌ଲାମ ଧର୍ମରେ ଏକାଧ୍ଵ ସଂପ୍ରଦାୟ ଦେଖିବାକୁ ମିଳିଥାଏ ।
Answer:
ହିନ୍ଦୁ ଧର୍ମରେ ଏକାଧ୍ଵ ସଂପ୍ରଦାୟ ଦେଖ‌ିବାକୁ ମିଳିଥାଏ ।

୨୪ । ଦିଗମ୍ବର ଓ ଶ୍ୱେତାମ୍ବର ବୌଦ୍ଧ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ।
Answer:
ଦିଗମ୍ବର ଓ ଶ୍ଵେତାମ୍ବର ଜୈନ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ।

୨୫ । ହୀନସ୍ଥାନ ଓ ମହାଯାନ ହିନ୍ଦୁ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ।
Answer:
ହୀନଯାନ ଓ ମହାଯାନ ବୌଦ୍ଧ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ।

୨୬ । ସିହା ଓ ସୁନୀ ଖ୍ରୀଷ୍ଟ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ଅଟେ ।
Answer:
ସିହା ଓ ସୁନ୍ତୀ ଇସ୍‌ଲାମ୍ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ଅଟେ ।

୨୭ । ଧାର୍ମିକ ପାର୍ଥକ୍ୟ ସାଂସ୍କୃତିକ ବିଭିନ୍ନତା ସୃଷ୍ଟି କରିଥାଏ ।
Answer:
ଧାର୍ମିକ ପାର୍ଥକ୍ୟ ଧାର୍ମିକ ବିଭିନ୍ନତା ସୃଷ୍ଟି କରିଥାଏ ।

୨୮ । ୧୯୩୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେବଳ ୭ଟି ଧାର୍ମିକ ସମୂହ ଥିଲା ।
Answer:
୧୯୩୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେବଳ ୧୦ଟି ଧାର୍ମିକ ସମୂହ ଥିଲା ।

୨୯। ଖ୍ରୀଷ୍ଟ ଧର୍ମ ଭାରତର ଏକ ସର୍ବବୃହତ୍ ଧାର୍ମିକ ସମୂହ ।
Answer:
ହିନ୍ଦୁ ଧର୍ମ ଭାରତର ଏକ ସର୍ବବୃହତ୍ ଧାର୍ମିକ ସମୂହ ।

୩୦ । ଶିଖ୍ ଧର୍ମ ଭାରତର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଧାର୍ମିକ ସମୂହ ଅଟେ ।
Answer:
ଇସ୍‌ଲାମ୍ ଧର୍ମ ଭାରତର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଧାର୍ମିକ ସମୂହ ଅଟେ ।

୩୧ । ଗ୍ରୀକ୍ ସଭ୍ୟତା ପୃଥ‌ିବୀର ସର୍ବପ୍ରଥମ ଓ ସର୍ବପ୍ରାଚୀନ ସଭ୍ୟତା ଅଟେ ।
Answer:
ସିନ୍ଧୁ ଉପତ୍ୟକାର ସଭ୍ୟତା ପୃଥ‌ିବୀର ସର୍ବପ୍ରଥମ ଓ ସର୍ବପ୍ରାଚୀନ ସଭ୍ୟତା ଅଟେ ।

୩୨ । ମୋଗଲ ସମ୍ରାଟ ଶାହାଜାହାନ ହିନ୍ଦୁ ମୁସଲିମ୍ ଏକତା ପାଇଁ ଚେଷ୍ଟା କରିଥିଲେ ।
Answer:
ମୋଗଲ ସମ୍ରାଟ ଆକବର ହିନ୍ଦୁ ମୁସଲିମ୍ ଏକତା ପାଇଁ ଚେଷ୍ଟା କରିଥିଲେ ।

୩୩ । ଭାରତର ଭୌଗୋଳିକ ଅଞ୍ଚଳ ୩୦, ୮୦, ୪୮୩ ବର୍ଗ କି.ମି. ପର୍ଯ୍ୟନ୍ତ ପରିବ୍ୟାପ୍ତ ଅଟେ ।
Answer:
ଭାରତର ଭୌଗୋଳିକ ଅଞ୍ଚଳ ୩୨,୮୦,୪୮୩ ବର୍ଗ କି.ମି. ପର୍ଯ୍ୟନ୍ତ ପରିବ୍ୟାପ୍ତ ଅଟେ ।

୩୪ । ଭାରତର ସାଂସ୍କୃତିକ ଏକତା ଏହାର ଚତୁଃପାର୍ଶ୍ବରେ ଥ‌ିବା ପ୍ରାକୃତିକ ପରିସୀମାଦ୍ୱାରା ସମ୍ଭବ ହୋଇପାରିଛି ।
Answer:
ଭାରତର ଭୌଗୋଳିକ ଏକତା ଏହାର ଚତୁଃପାର୍ଶ୍ବରେ ଥିବା ପ୍ରାକୃତିକ ପରିସୀମାଦ୍ୱାରା ସମ୍ଭବ ହୋଇପାରିଛି ।

୩୫ । ଏକ ପ୍ରମୁଖ ଧର୍ମ ଭାବେ ଇସଲାମ୍ ଭାରତର ଧାର୍ମିକ ଏକତାର ଭିତ୍ତିଭୂମି ଅଟେ ।
Answer:
ଏକ ପ୍ରମୁଖ ଧର୍ମ ଭାବେ ହିନ୍ଦୁ ଧର୍ମ ଭାରତର ଧାର୍ମିକ ଏକତାର ଭିତ୍ତିଭୂମି ଅଟେ ।

୩୬ । ଭାରତ ଏକ ଥ୍ଓକ୍ରେଟିକ୍ ବା ଏକ ଧର୍ମରେ ବିଶ୍ବାସୀ ଦେଶ ।
Answer:
ଭାରତ ଏକ ଧର୍ମନିରପେକ୍ଷ ଦେଶ ଅଟେ ।

୩୭ । ‘ବସୁଧୈବ କୁଟୁମ୍ବକମ୍’ ଭାବ ଭାରତୀୟ ଗଣତାନ୍ତ୍ରିକତାର ବାଧକ ଅଟେ ।
Answer:
‘ବସୁଧୈବ କୁଟୁମ୍ବକମ୍’ ଭାବ ଭାରତୀୟ ଗଣତାନ୍ତ୍ରିକତାର ମୂଳମନ୍ତ୍ର ଅଟେ ।

୩୮ । ଇତିହାସ ଭାରତୀୟଙ୍କୁ ଅତୀତର ଘଟଣାବଳୀ ସହିତ ସମନ୍ବୟ ସ୍ଥାପନ ଓ ବର୍ତ୍ତମାନକୁ ନେଇ ଭବିଷ୍ୟତ ଉଜ୍ଜ୍ବଳମୟ କରିବାରେ ସହାୟକ ହୋଇ ନ ଥାଏ ।
Answer:
ଇତିହାସ ଭାରତୀୟଙ୍କୁ ଅତୀତର ଘଟଣାବଳୀ ସହିତ ସମନ୍ବୟ ସ୍ଥାପନ ଓ ବର୍ତ୍ତମାନକୁ ନେଇ ଭବିଷ୍ୟତ ଉଜ୍ଜ୍ବଳମୟ କରିବାରେ ସହାୟକ ହୋଇଥାଏ ।

୩୯ । ବୌଦ୍ଧଧର୍ମର ରୀତି, ନୀତି ଆଦର୍ଶରେ ହିନ୍ଦୁ ଧର୍ମାବଲମ୍ବୀମାନେ ପ୍ରଭାବିତ ହୋଇନଥା’ନ୍ତି ।
Answer:
ବୌଦ୍ଧଧର୍ମର ରୀତି, ନୀତି ଆଦର୍ଶରେ ହିନ୍ଦୁ ଧର୍ମାବଲମ୍ବୀମାନେ ପ୍ରଭାବିତ ହୋଇଥା’ନ୍ତି ।

୪୦ । ଭାରତୀୟ ସମାଜ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଧର୍ମକୁ ପ୍ରାଧାନ୍ୟ ଦେଇଥାଏ ।
Answer:
ଭାରତୀୟ ସମାଜ ବହୁ ଧର୍ମକୁ ପ୍ରାଧାନ୍ୟ ଦେଇଥାଏ

୪୧ । ଭାରତବର୍ଷ ଇଉରୋପର ଏକ ଉପଦ୍ୱୀପ ଅଟେ ।
Answer:
ଭାରତବର୍ଷ ଦକ୍ଷିଣ ଏସିଆର ଏକ ଉପଦ୍ଵୀପ ଅଟେ ।

୪୨ । ଭାରତ ସର୍ବଦା ଭୌଗୋଳିକବାଦକୁ ଗୁରୁତ୍ଵ ଦେଇଥାଏ ।
Answer:
ଭାରତ ସର୍ବଦା ଐକ୍ୟ ଭାବନାକୁ ଗୁରୁତ୍ଵ ଦେଇଥାଏ ।

୪୩ । ଭାରତ ଏକ ଏକଧର୍ମୀ ରାଷ୍ଟ୍ର ଅଟେ ।
Answer:
ଭାରତ ଏକକ ଧର୍ମନିରପେକ୍ଷ ରାଷ୍ଟ୍ର ଅଟେ ।

୪୪ । ବିଭିନ୍ନତା ମଧ୍ୟରେ ବିଭିନ୍ନତା ଭାରତର ମୂଳମନ୍ତ୍ର ଅଟେ ।
Answer:
ବିଭିନ୍ନତା ମଧ୍ୟରେ ଏକତା ଭାରତର ମୂଳମନ୍ତ୍ର ଅଟେ ।

୪୫ । ଭାରତ ମୁଖ୍ୟତଃ ବିଶ୍ବର ପ୍ରଥମ ଜନବହୁଳ ରାଷ୍ଟ୍ର ଅଟେ ।
Answer:
ଭାରତ ମୁଖ୍ୟତଃ ବିଶ୍ବର ଦ୍ବିତୀୟ ଜନବହୁଳ ରାଷ୍ଟ୍ର ଅଟେ ।

୪୬ । ପ୍ରଜାତି ଏକ ବିଧ୍ଵଦ୍ଧ ମାନସିକ ଧାରଣା ଅଟେ ।
Answer:
ପ୍ରଜାତି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଜୈବିକ ଧାରଣା ଅଟେ ।

୪୭ । ସ୍କୋଥୋ -ଦ୍ରାବିଡ଼ୀୟ ଓଡ଼ିଶାରେ ଆଦୌ ପରିଲକ୍ଷିତ ହୋଇ ନ ଥା’ନ୍ତି ।
Answer:
ଠିକ୍ ଅଛି ।

୪୮ । ମଙ୍ଗୋଲ-ଦ୍ରାବିଡ଼ୀୟ ଓଡ଼ିଶାରେ ଆଦୌ ପରିଲକ୍ଷିତ ହୋଇ ନ ଥା’ନ୍ତି ।
Answer:
ମଙ୍ଗୋଲ-ଦ୍ରାବିଡ଼ୀୟ ଓଡ଼ିଶାରେ ପରିଲକ୍ଷିତ ହୋଇଥା’ନ୍ତି ।

୪୯ । ମଙ୍ଗୋଲୀୟଙ୍କର ଉଚ୍ଚତା ଅଧୁକ ଅଟେ ।
Answer:
ମଙ୍ଗୋଲୀୟମାନଙ୍କର ଉଚ୍ଚତା କମ୍ ଅଟେ ।

୫୦ । ନାୟର ମଙ୍ଗୋଲୀୟ ପ୍ରଜାତୀୟ ଅଟନ୍ତି ।
Answer:
ନାୟର ଦ୍ରବିଡ଼ୀୟ ପ୍ରଜାତୀୟ ଅଟନ୍ତି ।

୫୧ । ନାଗା ଜନଜାତି ତିଦ୍ଧତୀୟ-ମଙ୍ଗୋଲୀୟ ଶ୍ରେଣୀୟ ଅଟନ୍ତି ।
Answer:
ନାଗା ଜନଜାତି ମଙ୍ଗୋଲୀୟ ଶ୍ରେଣୀୟ ଅଟନ୍ତି ।

୫୨ । ନଡ଼ିକୁ ରାଜସ୍ଥାନର ସବୁଠାରୁ ଦୁର୍ବଳ ପ୍ରଜାତି ଅଟନ୍ତି ।
Answer:
ନର୍ଜିକ୍ ରାଜସ୍ଥାନର ସବୁଠାରୁ ଶକ୍ତିଶାଳୀ ପ୍ରଜାତି ଅଟନ୍ତି ।

୫୩ । ଭାରତୀୟ ସମ୍ବିଧାନର ପଞ୍ଚମ ପରିଚ୍ଛେଦରେ ୨୨ ଗୋଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରାଯାଇଅଛି ।
Answer:
ଭାରତୀୟ ସମ୍ବିଧାନର ଅଷ୍ଟମ ପରିଚ୍ଛେଦରେ ୨୨ ଗୋଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରାଯାଇଅଛି ।

୫୪ । ଓଡ଼ିଆ ଦ୍ରାବିଡ଼ୀୟ ଭାଷାର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ।
Answer:
ଓଡ଼ିଆ ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ ଭାଷାର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ।

୫୫ । ମୁଣ୍ଡା ଜନଜାତି ଦ୍ରାବଢ଼ୀୟ ଭାଷ ବ୍ୟବହାର କରିଥା’ନ୍ତି ।
Answer:
ମୁଣ୍ଡା ଜନଜାତି ଅଷ୍ଟ୍ରିକ୍ ଭାଷା ବ୍ୟବହାର କରିଥା’ନ୍ତି ।

୫୬ । ମଣିପୁରୀ ଭାଷା ଥାଇ ଉପଭାଷାର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ।
Answer:
ମଣିପୁରୀ ଭାଷା ନେୱାରୀ ଉପଭାଷାର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ।

୫୭ । ହିନ୍ଦୁଧର୍ମ ସେମିଟିକ୍ ଧର୍ମର ଅନ୍ତର୍ଗତ ଅଟନ୍ତି ।
Answer:
ହିନ୍ଦୁଧର୍ମ ଇଣ୍ଡିଜ୍ ମୂଳଧର୍ମର ଅନ୍ତର୍ଗତ ଅଟନ୍ତି ।

୫୮ । ଇସ୍‌ଲାମ୍ ଧର୍ମ ପଞ୍ଚମ ଶତାବ୍ଦୀରେ ଆରବୀୟମାନଙ୍କଦ୍ୱାରା ଭାରତରେ ପ୍ରସାରିତ ହୋଇଥ୍ ଲା ।
Answer:
ଇସ୍‌ଲାମ୍ ଧର୍ମ ଅଷ୍ଟମ ଶତାବ୍ଦୀରେ ଆରବୀୟମାନଙ୍କଦ୍ୱାରା ଭାରତରେ ପ୍ରସାରିତ ହୋଇଥ୍ ଲା ।

୫୯ । ବାଇବେଲ ଇସ୍‌ଲାମ୍ ଧର୍ମର ଧର୍ମଗ୍ରନ୍ଥ ଅଟେ ।
Answer:
କୋରାନ୍ ଇସ୍‌ଲାମ୍ ଧର୍ମର ଧର୍ମଗ୍ରନ୍ଥ ଅଟେ ।

୬୦ । ‘ଘୃଣା’ ଖ୍ରୀଷ୍ଟଧର୍ମର ମୂଳମନ୍ତ୍ର ଅଟେ ।
Answer:
ପ୍ରେମ ଖ୍ରୀଷ୍ଟଧର୍ମର ମୂଳମନ୍ତ୍ର ଅଟେ ।

୬୧ । ଅନ୍ୟ ରାଜ୍ୟ ତୁଳନାରେ ଓଡ଼ିଶା ରାଜ୍ୟରେ ଅଧ‌ିକ ସଂଖ୍ୟକ ଖ୍ରୀଷ୍ଟଧର୍ମାବଲମ୍ବୀ ବାସ କରନ୍ତି ।
Answer:
ଅନ୍ୟ ରାଜ୍ୟ ତୁଳନାରେ କେରଳ ରାଜ୍ୟରେ ଅଧ‌ିକ ସଂଖ୍ୟକ ଖ୍ରୀଷ୍ଟଧର୍ମାବଲମ୍ବୀ ବାସ କରନ୍ତି ।

୬୨ । ଶିଖ୍ ଧର୍ମାବଲମ୍ବୀମାନେ ଦୁଇଗୋଟି ଜିନିଷକୁ ନିଜର ଆୟୁଧ କରିଥା’ନ୍ତି ।
Answer:
ଶିଖ୍ ଧର୍ମାବଲମ୍ବୀମାନେ ପାଞ୍ଚଗୋଟି ଜିନିଷକୁ ନିଜର ଆୟୁଧ କରିଥା’ନ୍ତି ।

୬୩ । ବୁଦ୍ଧଦେବ ଦର୍ଶାଇଥବା ମାର୍ଗକୁ ଦ୍ରାବିଡ଼-ଅଷ୍ଟାଙ୍ଗ ମାର୍ଗ କୁହାଯାଏ
Answer:
ବୁଦ୍ଧଦେବ ଦର୍ଶାଇଥବା ମାର୍ଗକୁ ଆର୍ଯ୍ୟ-ଅଷ୍ଟାଙ୍ଗ ମାର୍ଗ କୁହାଯାଏ ।

୬୪ । ଜୈନଧର୍ମାବଲମ୍ବୀମାନେ ଆତ୍ମଶୁଦ୍ଧି ନିମନ୍ତେ ଉପବାସ ରୁହନ୍ତି ନାହିଁ ।
Answer:
ଜୈନଧର୍ମାଲମ୍ବୀମାନେ ଆତ୍ମଶୁଦ୍ଧି ନିମନ୍ତେ ଉପବାସ ରୁହନ୍ତି ।

୬୫ । ଜୈନଧର୍ମ ହିନ୍ଦୁଧର୍ମ ପରି ଆତ୍ମା, କର୍ମତତ୍ତ୍ଵ, ଜନ୍ମ ଓ ମୃତ୍ୟୁର ଜୀବନଚକ୍ରରେ ବିଶ୍ଵାସ କରେ ନାହିଁ ।
Answer:
ଜୈନଧର୍ମ ହିନ୍ଦୁଧର୍ମ ପରି ଆତ୍ମା, କର୍ମତତ୍ତ୍ବ, ଜନ୍ମ ଓ ମୃତ୍ୟୁର ଜୀବନଚକ୍ରରେ ବିଶ୍ଵାସ କରେ ।

୬୬ । ଶିଳ୍ପପତି ଟାଟା, ପି. ମେହେଟ୍ଟା ଇତ୍ୟାଦି ଜୁଡ଼ାବାଦୀ ଅଟନ୍ତି ।
Answer:
ଶିଳ୍ପପତି ଟାଟା, ପି. ମେହେଟ୍ଟା ଇତ୍ୟାଦି ପାର୍ଶୀଧର୍ମୀ ଅଟନ୍ତି ।

୬୭ । ଜୀବବାଦୀମାନେ ପ୍ରକୃତି ପୂଜନ ତଥା ଭୂତପ୍ରେତକୁ ବିଶ୍ୱାସ କରନ୍ତି ନାହିଁ ।
Answer:
ଜୀବବାଦୀମାନେ ପ୍ରକୃତି ପୂଜନ ତଥା ଭୂତପ୍ରେତକୁ ବିଶ୍ଵାସ କରନ୍ତି ।

(ଘ) ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ ।

୧। ଆମ ଦେଶ ଭାରତର ନାମ କେଉଁ ପ୍ରସିଦ୍ଧ ରାଜାଙ୍କ ନାମ ଅନୁସାରେ ହୋଇଛି ?
Answer:
ଭାରତ

୨। କେଉଁ ନଦୀର ନାମ ଅନୁସାରେ ଭାରତର ନାମ ଇଣ୍ଡିଆ ହୋଇଛି ?
Answer:
ସିନ୍ଧୁ ବା ଇଣ୍ଡସ୍

୩ । ସଂସ୍କୃତି ସିନ୍ଧୁ ନଦୀ କେଉଁ ଦେଶରେ ପ୍ରବାହିତ ହେଉଛି ?
Answer:
ପାକିସୁ।ନ

୪। କେଉଁମାନେ ଭାରତକୁ ହିନ୍ଦୁସ୍ଥାନ ନାମ ପ୍ରଦାନ କରିଥିଲେ ?
Answer:
ମୁସଲିମ୍ ଆକ୍ରମଣକାରୀମାନେ

୫। ବିଭିନ୍ନତାରେ ଏକତାର ଏକ ସୁନ୍ଦର ଉଦାହରଣ କିଏ ?
Answer:
ଆମ ଦେଶ ଭାରତ

୬। ଦୈହିକ, ଧାର୍ମିକ, ଭାଷାଗତ ଗୁଣାବଳୀ ଉପରେ ପର୍ଯ୍ୟବସିତ ଲୋକମାନଙ୍କ ମଧ୍ୟରେ ଦେଖାଦେଉଥ‌ିବା ସାମୂହିକ ପାର୍ଥକ୍ୟକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ବିଭିନ୍ନତା

୭ | ଲୋକମାନଙ୍କ ମଧ୍ୟରେ ଥ‌ିବା ଭାଷାଗତ ବିଭେଦକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ଭାଷାଗତ ବିଭିନ୍ନତା

୮| ଭାରତର ଲୋକମାନଙ୍କ ମଧ୍ୟରେ ପରିଲକ୍ଷିତ ହେଉଥୁବା ଧାର୍ମିକ ପାର୍ଥକ୍ୟକୁ କ’ଣ କୁହନ୍ତି ?
Answer:
ଧାର୍ମିକ ବିଭିନ୍ନତା

୯| ଭାରତର ଲୋକମାନଙ୍କ ମଧ୍ୟରେ ପରିଲକ୍ଷିତ ହେଉଥ‌ିବା ଦୈହିକ ପାର୍ଥକ୍ୟକୁ କ’ଣ କହନ୍ତି ?
Answer:
ପ୍ରକାତାୟ ବିଭିନ୍ନତା

୧୦ । ଭାରତର ଉତ୍ତର ପଶ୍ଚିମରୁ କେଉଁ ଅଞ୍ଚଳ ଅଲଗା ହୋଇଛି ?
Answer:
ଆଫଗାନିସ୍ଥାନ ଓ ପାକିସ୍ତାନ

୧୧ । ଭାରତର ପୂର୍ବ ଅଞ୍ଚଳରୁ କେଉଁ ଅଞ୍ଚଳ ଅଲଗା ହୋଇ ସ୍ବତନ୍ତ୍ର ଦେଶ ହୋଇଛି ?
Answer:
ବଙ୍କଲାଦେଶ

୧୨ । ସ୍ଵତନ୍ତ୍ର ଦୈହିକ ଗୁଣାବଳୀ ଥିବା ଲୋକମାନଙ୍କର ସମଷ୍ଟିକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ପ୍ରକାତି

୧୩ । କିଏ ଭାରତୀୟ ଜନସଂଖ୍ୟାର ସାଂପ୍ରତିକ ବର୍ଗୀକରଣ ପ୍ରଦାନ କରିଥିଲେ ?
Answer:
ବି.ଏସ୍.ଗୁହା

୧୪ । ରିସ୍‌ଲେ ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ କେତେ ପ୍ରକାର ପ୍ରଜାତିରେ ବିଭାଜନ କରିଥିଲେ ?
Answer:
୭ ପ୍ରକାର

୧୫ । ବି.ଏସ୍.ଗୁହା ଭାରତର ଜନସଂଖ୍ୟାକୁ କେତୋଟି ପ୍ରଜାତିରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
Answer:
୬ ୧ଟି

୧୬ । କେଉଁ ସମାଜବିଜ୍ଞାନୀ ରିସ୍‌ଙ୍କ ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣକୁ ଏକ ଭାଷାଗତ ବିଭାଜନ ବୋଲି ସମାଲୋଚନା କରିଥିଲେ ?
Answer:
ଡି.ଏଚ୍. ମଜୁମଦାର

୧୭ । କେଉଁ ପ୍ରଜାତୀୟ ପ୍ରକାରକୁ ଅନ୍ତର୍ଭୁକ୍ତ କରି ନଥ‌ିବାରୁ ରିସ୍‌ଲେଙ୍କ ବର୍ଗୀକରଣକୁ ତ୍ରୁଟିପୂର୍ଣ୍ଣ ବୋଲି ବିଡାର କରାଯାଇଥାଏ ?
Answer:
ନିଗ୍ରିଟୋ

୧୮ । କେଉଁ ପ୍ରଜାତୀୟବିତ୍‌ଙ୍କର ପ୍ରଜାତୀୟ ବର୍ଗୀକରଣ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଓ ଅଧ‌ିକ ଗ୍ରହଣୀୟ ଅଟେ ?
Answer:
ରିସ୍‌ଲେ ଓ ବି.ଏସ୍.ଗୁହା

୧୯ । ଜେ.ଏଚ୍.ହଟନ୍‌ଙ୍କ ମତରେ ଭାରତର ସର୍ବପ୍ରଥମ ଅଧ୍ୟାବାସୀ କେଉଁ ପ୍ରଜାତୀୟ ଲୋକ ?
Answer:
ନିଗ୍ରିଟୋ

୨୦ । ରିସ୍‌ଙ୍କର ସାତ ପ୍ରକାରର ପ୍ରଜାତୀୟ ବିଭାଜନକୁ ମୁଖ୍ୟତଃ କେତେ ପ୍ରକାରକୁ ହ୍ରାସ କରାଯାଇପାରିବ ?
Answer:
ତିନି ପ୍ରକାର

୨୧ । କେଉଁ ନୃବିଜ୍ଞାନୀ ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ ୨ଟି ପ୍ରଜାତିରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
Answer:
ହର୍‌ବର୍ଟ ରିସ୍‌

୨୨ । କେଉଁ ନୃବିଜ୍ଞାନୀ ଭାରତୀୟ ଜନସଂଖ୍ୟାକୁ ୬ଟି ପ୍ରଜାତିରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
Answer:
ବି.ଏସ୍.ଗୁହା

୨୩ । ଏ.ସି.ହଡ଼ନ୍ ଭାରତର ଜନସଂଖ୍ୟାକୁ କେତୋଟି ପ୍ରଜାତିରେ ବିଭକ୍ତ କରିଛନ୍ତି ?
Answer:
୫ଟି

୨୪ । କିଏ କହିଥିଲେ ଯେ ଭାରତ ଭାଷାର ଏକ ସଂଗ୍ରହାଳୟ ଅଟେ ?
Answer:
ଏ.ଆର୍.ଦେଶାଇ

୨୫ । ଭାରତରେ ପ୍ରାକ୍-ଦ୍ରାବିଡ଼, ଦ୍ରାବିଡ଼ିଆନ୍, ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ, ଇଣ୍ଡୋ-ଆଲପାଇନ୍ ଏବଂ ମଙ୍ଗୋଲିଆନ୍ ଆଦି ପ୍ରଜାତିର ଲୋକ ଦେଖାଯାଆନ୍ତି । ଏହା କିଏ କହିଥିଲେ ?
Answer:
ଏ.ସି.ହଡ଼ନ୍

୨୬ । କେଉଁ ନୃବିଜ୍ଞାନୀ ଭାରତର ଜନସଂଖ୍ୟାକୁ ନିଗ୍ରେଟୋ, ପ୍ରୋଟୋ-ଅଷ୍ଟ୍ରୋଲଏଜ୍, ମଙ୍ଗୋଲଏଜ୍, ମେଡ଼ିଟେରାନିଆନ୍,
Answer:
ବି.ଏସ୍. ଗୁହା

୨୭ । ୧୯୬୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେତୋଟି ଭାଷା ଦେଖିବାକୁ ମିଳେ ?
Answer:
୧୬୫୨ ଗୋଟି

୨୮ । ଭାରତରେ ଦେଖାଯାଇଥିବା ବିଭିନ୍ନ ଭାଷାଗୁଡ଼ିକୁ କେତୋଟି ଭାଷା ପରିବାରରେ ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଛି ?
Answer:
୪ଟି

୨୯। ଓଁ ଆମ ସମ୍ବିଧାନର ଅଷ୍ଟମ ଅନୁଚ୍ଛେଦରେ କେତୋଟି ଭାଷାକୁ ସ୍ବୀକୃତି ଦିଆଯାଇଛି ?
Answer:
୧୮ଟି

୩୦ । ଆମର ଜାତୀୟ ଭାଷା କିଏ ?
Answer:
ହିଦା

୩୧ । କେଉଁ ଆଇନ ହିନ୍ଦୀକୁ ଭାରତର କାର୍ଯ୍ୟକାରୀ ଭାଷାଭାବେ ଘୋଷଣା କଲା ?
Answer:
୧୯୬୩ର ଭାଷା ଆଇନ

୩୨ । ଆମ ଦେଶରେ କେଉଁ ଭାଷାକୁ ସହକାରୀ ଭାଷାର ସ୍ଵୀକୃତି ମିଳିଛି ?
Answer:
ଇଂରାକା

୩୩ । ଆମ ଜାତୀୟ ଭାଷା ହିନ୍ଦୀ କେଉଁ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟେ ?
Answer:
ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ ଭାଷା ପରିବାର

୩୪ । ଓଡ଼ିଆ ଭାଷା କେଉଁ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟେ ?
Answer:
ଇଣ୍ଡୋ-ଆର୍ଯ୍ୟ

୩୫ । କେଉଁ ଭାଷା ପରିବାର ଦ୍ଵୟ ଜନଜାତି ଭାଷା ଅଟେ ?
Answer:
ଅଷ୍ଟ୍ରିକ୍ ଏବଂ ସିନୋ ତିବେତାନ

୩୬ । ଭାରତର ସର୍ବାଧ‌ିକ ଲୋକ କେଉଁ ଭାଷାରେ କଥା ହୋଇଥା’ନ୍ତି ?
Answer:
ହିଦା

୩୭ । ଭାରତର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଭାଷା ଭାବେ କେଉଁ ଭାଷା ପରିଚିତ ଅଟେ ?
Answer:
ତେଲୁଗୁ

୩୮ । ମାଲାୟାଲମ୍, କନ୍ନଡ଼, ତାମିଲ ଓ ତେଲୁଗୁ ଆଦି କେଉଁ ଭାଷା ପରିବାରଭୁକ୍ତ ଅଟନ୍ତି ?
Answer:
ଦ୍ରାବିଡ଼ିଆନ୍ ଭାଷା ପରିବାର

୩୯ । ଭାରତରେ ବୃହତ୍ତମ ଧାର୍ମିକ ସମୂହ କିଏ ?
Answer:
ହିଦୁ

୪୦ । ୧୯୩୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେତୋଟି ଧାର୍ମିକ ସମୂହ ଅଛନ୍ତି ?
Answer:
୧୦ଟି

୪୧ । ୧୯୬୧ ଜନଗଣନା ଅନୁସାରେ ଭାରତରେ କେତୋଟି ଧାର୍ମିକ ସମୂହ ଅଛନ୍ତି ?
Answer:
୭ଟି

୪୨ । ଭାରତର ମୋଟ ଜନସଂଖ୍ୟାର କେତେ ଭାଗ ଲୋକ ହିନ୍ଦୁ ଅଟନ୍ତି ?
Answer:
୮୨ ଭାଗ

୪୩ । ଭାରତର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ଧାର୍ମିକ ସମୂହ କିଏ ?
Answer:
ଇସ୍‌ଲାମ୍

୪୪ । ଶୈବ, ଶାକ୍ତ, ଗାଣପତ୍ୟ, ବୈଷ୍ଣବ ଆଦି କେଉଁ ଧର୍ମର ସଂପ୍ରଦାୟ ଅଟନ୍ତି ?
Answer:
ହିଦୁ

୪୫ । ସିହା ଓ ସୁନୀ କେଉଁ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ଅଟେ ?
Answer:
ଇସ୍‌ଲାମ୍

୪୬ । ହୀନଯାନ ଓ ମହାଯାନ କେଉଁ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ଅଟନ୍ତି ?
Answer:
ବୌଦ୍ଧ

୪୭ । ଦିଗମ୍ବର ଓ ଶ୍ୱେତାମ୍ବର କେଉଁ ଧର୍ମର ଦୁଇ ସଂପ୍ରଦାୟ ?
Answer:
କୈନ

୪୮ । ପ୍ରୋଟେଷ୍ଟାଣ୍ଟ ଏବଂ କ୍ୟାଥୋଲିକ୍ କେଉଁ ଧର୍ମର ସଂପ୍ରଦାୟ ?
Answer:
ଖ୍ର।ଷୃ

୪୯ । ଭାରତର ଜନସଂଖ୍ୟାର କେତେ ଭାଗ ଜନସଂଖ୍ୟା ଇସ୍‌ଲାମ୍ ଧର୍ମାବଲମ୍ବୀ ଅଟନ୍ତି ?
Answer:
୧୨ ଭାଗରୁ ଊର୍ଦ୍ଧ୍ବ

୫୦ । କିଏ ପୃଥ‌ିବୀର ସର୍ବପ୍ରାଚୀନ ସଭ୍ୟତା ଭାବେ ପରିଚିତ ?
Answer:
ସିନ୍ଧୁ ସଭ୍ୟତା

୫୧ । ଭାରତର କେଉଁ ଦିଗରେ ହିମାଳୟ ଅବସ୍ଥିତ ?
Answer:
ଭତ୍ତର

୫୨ । ‘‘ଭାରତର ଏକତା ମୁଖ୍ୟତଃ ଧର୍ମ ଉପରେ ପର୍ଯ୍ୟବସିତ’– କିଏ ଏହା କହିଥିଲେ ?
Answer:
ଏମ୍.ଏନ୍.ଶ୍ରୀନିବାସ

୫୩। ଭାରତର ଭୌଗୋଳିକ ଅଞ୍ଚଳ ଗୁଜରାଟଠାରୁ ଆସାମ ପର୍ଯ୍ୟନ୍ତ କେତେ ମାଇଲ୍ ପରିବ୍ୟାପ୍ତ ଅଟେ ?
Answer:
୧୫୦୦

୫୪ । କାଶ୍ମୀରରୁ କେପ୍ କମୋରିନ୍ ପର୍ଯ୍ୟନ୍ତ ଭାରତର ଭୌଗୋଳିକ ସୀମାରେଖା କେତେ ମାଇଲ୍ ?
Answer:
୨୦୦୦

୫୫ । କିଏ ଭାରତକୁ ତିନି ପଟରୁ ପ୍ରାକୃତିକ ପରିସୀମା ଯୋଗାଇଛି ?
Answer:
ସମୁଦ୍ର

୫୬ । ଭାରତର ଉତ୍ତରରେ କିଏ ପ୍ରାକୃତିକ ପରିସୀମା ଭାବେ ଦଣ୍ଡାୟମାନ ?
Answer:
ହିମାଳୟ

୫୭ । ‘ଭାରତମାତା’ ସଂପ୍ରତ୍ୟୟ ଭାରତର କେଉଁ ଏକତାକୁ ଦର୍ଶାଇଥାଏ ?
Answer:
‘ଭାବଗତ ଏକତା’

୫୮ । କେବେ ଭାରତରେ ସର୍ବପ୍ରଥମ ମନୁଷ୍ୟର ଆବିର୍ଭାବ ଘଟିଥିଲା ବୋଲି ବିଶ୍ଵାସ କରାଯାଏ ?
Answer:
ଖ୍ର।.ପୂ.୫,୦୦,୦୦୦

୫୯ । ‘‘ବନ୍ଦେ ମାତରମ୍’’ ସଙ୍ଗୀତ କିଏ ଲେଖୁଥିଲେ ?
Answer:
ବଙ୍କିମଚଦ୍ର

୬୦ । ଭାରତର ସାମାଜିକ ଜୀବନର ପ୍ରତି କ୍ଷେତ୍ରରେ କେଉଁ ଏକତା ଦେଖିବାକୁ ମିଳିଥାଏ ?
Answer:
ସାଂସୁୃକତ ଏକତା

୬୧ । ଦିଲୀ, ଦଶହରା ଓ ହୋଲି ସାରା ଭାରତରେ ସମାନ ଭାବରେ ପାଳିତ ହେଉଥ‌ିବାରୁ ଏହା ଭାରତର କେଉଁ ଏକତାକୁ ଦର୍ଶାଇଥାଏ ?
Answer:
ସାଂସ୍କୃତିକ ଏକତା

୬୨ । ଅଶ୍ଵମେଧ ଯଜ୍ଞର ଆୟୋଜନ ଓ ରାଜ ଚକ୍ରବର୍ତ୍ତୀ ସଂପ୍ରତ୍ୟୟ ଭାରତର କେଉଁ ଏକତାକୁ ଦର୍ଶାଇଥାଏ ?
Answer:
ରାଜନୈତିକ

୬୩ । ୨୦୦୧ ଜନଗଣନା ଅନୁଯାୟୀ ଭାରତର ଜନସଂଖ୍ୟା କେତେ ?
Answer:
୧୦୨ କୋଟି ୮୬ ଲକ୍ଷ ୧୦ହଜାର ୩୨୮ ଅଟେ ।

୬୪ । ପ୍ରଜାତିର ଅର୍ଥ କ’ଣ ?
Answer:
ପ୍ରଜାତି ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଜୈବିକ ଧାରଣା ଅଟେ ?

୬୫। ପ୍ରଜାତି ଏକ ଉଚିତ ବା ବିଧବଦ୍ଧ ଜୈବିକ ଧାରଣା ଅଟେ । ଏହା ଏକ ସମୂହ ଯାହା ଜଣେ ପ୍ରଜାତି କିମ୍ବା କୌଳିକଗୁଣ ନିୟନ୍ତ୍ରକ ଉପାଦାନ ଏବଂ ଉପସମଜାତୀୟତାରେ ଏକତ୍ରିତ ହୋଇଥା’ନ୍ତି – ଏ ଉକ୍ତି କେଉଁ ନ୍ନ- ବିଜ୍ଞାନୀ ଉଲ୍ଲେଖ କରିଅଛନ୍ତି ?
Answer:
ଏ.ଏଲ୍. କ୍ରୋଜର ।

୬୬ । ଇଣ୍ଡୋ- ଆର୍ଯ୍ୟ ପ୍ରଜାତିର ଲୋକମାନେ ଭାରତର କେଉଁ ରାଜ୍ୟରେ ବିଶେଷ ଭାବରେ ଦେଖାଯାଇଥା’ନ୍ତି ?
Answer:
ପୂର୍ବ ପଞ୍ଜାବ, ରାଜସ୍ଥାନ ଏବଂ କାଶ୍ମୀର

୬୭ । ଆର୍ଯ୍ୟ-ଦ୍ରାବିଡ଼ୀୟ ପ୍ରଜାତି ଭାରତର କେଉଁ ରାଜ୍ୟରେ ପରିଲକ୍ଷିତ ହୁଅନ୍ତି ?
Answer:
ଉତ୍ତର ପ୍ରଦେଶ, ରାଜସ୍ଥାନ ଓ ବିହାର

୬୮ । କେଉଁ ପ୍ରକାର ବିବାହରୁ ମଙ୍ଗୋଲ-ଦ୍ରାବିଡ଼ୀୟ ପ୍ରଜାତିର ସୃଷ୍ଟି ହୋଇଅଛି ?
Answer:
ଆନ୍ତଃବିବାହରୁ

୬୯ । ମଙ୍ଗୋଲୀୟ ପ୍ରଜାତିମାନଙ୍କର ଉଚ୍ଚତା କିପରି ଅଟେ ?
Answer:
ମଙ୍ଗୋଲୀୟ ପ୍ରଜାତିମାନଙ୍କର ଉଚ୍ଚତା କମ୍ ଅଟେ ।

୭୦ । ଦ୍ରାବିଡ଼ୀୟମାନେ ସାଧାରଣତଃ ଭାରତର କେଉଁ ଭାଗରେ ବସତି ସ୍ଥାପନ କରିଥା’ନ୍ତି ?
Answer:
ଦ୍ରାବିଡ଼ୀୟମାନେ ସାଧାରଣତଃ ଭାରତର ମଧ୍ୟପ୍ରଦେଶ, ଛୋଟନାଗପୁର, ଚେନ୍ନାଇ ଓ ହାଇଦ୍ରାବାଦରେ
ଦେଖାଯାକଥା ନ୍ତି

୭୧ । କେଉଁ ପ୍ରଜାତି ଭାରତର ସର୍ବପ୍ରାଚୀନ ପ୍ରଜାତିରୂପେ ପରିଚିତ ?
Answer:
ନିଗ୍ରିଟୋ ପ୍ରଜାତି ଭାରତର ସର୍ବପ୍ରାଚୀନ ପ୍ରଜାତି ରୂପେ ପରିଚିତ ।

୭୨ । କେତେ ପ୍ରକାର ପାଲିଓ- ମଙ୍ଗୋଲୀୟ ପ୍ରଜାତି ଭାରତରେ ପରିଲକ୍ଷିତ ହୁଅନ୍ତି ?
Answer:
ଦୁଇ ପ୍ରକାର ପାଲିଓ- ମଙ୍ଗୋଲୀୟ ପ୍ରଜାତି ଭାରତରେ ପରିଲକ୍ଷିତ ହୁଅନ୍ତି ।

୭୩ । ମେଡ଼ିଟେରାନିଆନ୍ ପ୍ରଜାତିଙ୍କୁ ଅନ୍ୟ ଭାଷାରେ କ’ଣ କୁହାଯାଏ ?
Answer:
ମେଡ଼ିଟେରାନିଆନ୍ ପ୍ରଜାତିଙ୍କୁ ଅନ୍ୟ ଭାଷାରେ ପ୍ରକୃତ ଇଉରୋପୀୟ ବୋଲି ମଧ୍ୟ କୁହାଯାଇଥାଏ ।

୭୪ । ପୁରୁଷପ୍ରଧାନ ସାମାଜିକ ବ୍ୟବସ୍ଥା ଓ ପୁରୁଷ ସ୍ଵତ୍ୱାଧିକାର ବ୍ୟବସ୍ଥା ପ୍ରଥମେ କେଉଁ ପ୍ରଜାତିଙ୍କଦ୍ୱାରା ଭାରତରେ ପ୍ରଚଳିତ ହୋଇଥିଲା ?
Answer:
ପୁରୁଷପ୍ରଧାନ ସାମାଜିକ ବ୍ୟବସ୍ଥା ଓ ପୁରୁଷ ସ୍ଵତ୍ୱାଧିକାର ବ୍ୟବସ୍ଥା ପ୍ରଥମେ ନଢ଼ିକ୍ ପ୍ରଜାତିଙ୍କଦ୍ୱାରା ଭାରତରେ ପ୍ରଚଳିତ ହୋଇଥିଲା ।

୭୫ । ବର୍ତ୍ତମାନ ଭାରତରେ ରାଜ୍ୟ ଓ କେନ୍ଦ୍ରଶାସିତ ଅଞ୍ଚଳର ସଂଖ୍ୟା କେତେ ?
Answer:
ବର୍ତ୍ତମାନ ଭାରତରେ ରାଜ୍ୟ ସଂଖ୍ୟା ୨୯ ଓ କେନ୍ଦ୍ରଶାସିତ ଅଞ୍ଚଳର ସଂଖ୍ୟା ୭ ଅଟେ ।

୭୬ । ଭାରତର ସମ୍ବିଧାନର କେଉଁ ପରିଚ୍ଛେଦରେ ଭାରତୀୟ ଭାଷା ସଂଖ୍ୟା ଦର୍ଶାଯାଇଅଛି ?
Answer:
ଭାରତର ସମ୍ବିଧାନର ଅଷ୍ଟମ ପରିଚ୍ଛେଦରେ ଭାରତୀୟ ଭାଷା ସଂଖ୍ୟ ଦର୍ଶାଯାଇଅଛି ।

୭୭ । ଭାରତୀୟ ସମ୍ବିଧାନ କେତେଗୋଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରିଅଛି ?
Answer:
ଭାରତୀୟ ସମ୍ବିଧାନ୨୨ଟି ଭାଷାକୁ ସ୍ବୀକୃତି ପ୍ରଦାନ କରିଅଛି ।

୭୮ । ଭାରତରେ ସର୍ବାଧ‌ିକ ବ୍ୟକ୍ତି କେଉଁ ଭାଷା ପରିବାରର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟନ୍ତି ?
Answer:
ଭାରତରେ ସର୍ବାଧ‌ିକ ବ୍ୟକ୍ତି ଇଣ୍ଡୋ- ଆର୍ଯ୍ୟଭାଷା ପରିବାରର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟନ୍ତି ।

୭୯ । ‘ଦ୍ରାବିଡ଼ୀୟ’ ଶବ୍ଦଟି ସର୍ବପ୍ରଥମେ କେଉଁ ବ୍ୟକ୍ତି ବ୍ୟବହାର କରିଥିଲେ ?
Answer:
‘ଦ୍ରାବିଡ଼ୀୟ’ ଶବ୍ଦଟି ସର୍ବପ୍ରଥମେ ରବର୍ଟ ଏ. କାଲ୍‌ୱେଲ ବ୍ୟବହାର କରିଥିଲେ ।

୮୦ । ଅଷ୍ଟ୍ରିକ୍ ଭାଷା ପରିବାରକୁ କେତେ ବିଭକ୍ତ କରାଯାଇଅଛି ?
Answer:
ଅଷ୍ଟ୍ରିକ୍ ଭାଷା ପରିବାରକୁ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଅଛି ।

୮୧ । ମୁଣ୍ଡା ଉପଭାଷା କେଉଁ ଭାଷା ପରିବାରର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ ?
Answer:
ମୁଣ୍ଡା ଉପଭାଷା ଅଷ୍ଟ୍ରିକ ଭାଷା ପରିବାରର ଅନ୍ତର୍ଭୁକ୍ତ ଅଟେ

୮୨ । ନିକୋବରୀ ଜନଜାତି କେଉଁ କଥ୍ତ ଭାଷାକୁ ବ୍ୟବହାର କରିଥା’ନ୍ତି ?
Answer:
ନିକୋବରୀ ଜନଜାତି ମଙ୍ଖମର କଥ୍ତ ଭାଷାକୁ ବ୍ୟବହାର କରିଥା’ନ୍ତି ?

୮୩ । କେଉଁ ସମୟରୁ (ମସିହା) ଇଂରେଜୀ ଭାଷାକୁ କେନ୍ଦ୍ର ଓ ଆନ୍ତଃପ୍ରଦେଶିକ ଯୋଗାଯୋଗର ସହବନ୍ଧୀ ଅତିରିକ୍ତ ସରକାରୀ ଭାଷାର ମାନ୍ୟତା ଦିଆଗଲା ?
Answer:
୧୯୬୫ ମସିହାରୁ ଇଂରେଜୀ ଭାଷାକୁ କେନ୍ଦ୍ର ଓ ଆନ୍ତଃପ୍ରଦେଶିକ ଯୋଗାଯୋଗର ସହବନ୍ଧୀ ଅତିରିକ୍ତ ସରକାରୀ ଭାଷାର ମାନ୍ୟତା ଦିଆଗଲା ।

୮୪ । ଭାରତରେ ବ୍ୟବହୃତ ଧର୍ମଗୁଡ଼ିକୁ ସାଧାରଣତଃ କେତେଗୋଟି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଅଛି ?
Answer:
ଭାରତରେ ବ୍ୟବହୃତ ଧର୍ମଗୁଡ଼ିକୁ ସାଧାରଣତଃ ୭ଗୋଟି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଅଛି

୮୫ । ୨୦୦୧ ଜନଗଣନାନୁଯାୟୀ ଭାରତର ଜନସଂଖ୍ୟାର କେତେ ଶତାଂଶ ହିନ୍ଦୁ ଅଟନ୍ତି ?
Answer:
୨୦୦୧ ଜନଗଣନାନୁଯାୟୀ ଭାରତରେ ଜନସଂଖ୍ୟାର ୮୦.୫ ଶତାଂଶ ହିନ୍ଦୁ ଅଟନ୍ତି ?

୮.୬. । ହିନ୍ଦୁଧର୍ମର ଲୋକମାନେ ସାଧାରଣତଃ କେତେଗୋଟି ଭାଗରେ ବିଭକ୍ତ ହୋଇଅଛନ୍ତି ?
Answer:
ହିନ୍ଦୁଧର୍ମର ଲୋକମାନେ ସାଧାରଣତଃ ୪ ଗୋଟି ଭାଗରେ ବିଭକ୍ତ ହୋଇଅଛନ୍ତି ।

୮୭ । ଇସ୍‌ଲାମ୍ ଧର୍ମ କେଉଁମାନଙ୍କଦ୍ୱାରା ଭାରତରେ ପ୍ରସାରିତ ହୋଇଅଛି ?
Answer:
ଇସ୍‌ଲାମ୍ ଧର୍ମ ଆରବୀୟମାନଙ୍କଦ୍ୱାରା ଭାରତରେ ପ୍ରସାରିତ ହୋଇଅଛି ।

୮୮ । ଇସ୍‌ଲାମ୍ ଧର୍ମର ପ୍ରତିଷ୍ଠାତାଙ୍କ ନାମ ଉଲ୍ଲେଖ କର ।
Answer:
ଇସ୍‌ଲାମ୍ ଧର୍ମର ପ୍ରତିଷ୍ଠାତା ହେଲେ ମହାପୁରୁଷ ମହମ୍ମଦ ।

୮୯ । ଇସ୍‌ଲାମର ଅର୍ଥ କ’ଣ ?
Answer:
ଇସ୍‌ଲାମ୍‌ର ଅର୍ଥ ହେଉଛି ଆରବୀୟ ଭାଷାରେ ନାମିତ ଆଲ୍ଲା ଯେ କି ଭଗବାନ୍ ତାଙ୍କର ଇଚ୍ଛା ନିକଟରେ ନିଜକୁ ଆତ୍ମସମର୍ପଣ କରିବା ।

୯୦ । ଇସ୍‌ଲାମ୍ ଧର୍ମର ମୌଳିକ ଧର୍ମବିଧୂ ମଧ୍ୟରୁ ଗୋଟିଏ ଉଲ୍ଲେଖ କର ।`
Answer:
ଏକ ଈଶ୍ବର ବିଶ୍ବାସ ।

୯୧ । ୨୦୦୧ ଜନଗଣନାନୁଯାୟୀ ଶତକଡ଼ା କେତେ ଭାଗ ଖ୍ରୀଷ୍ଟଧର୍ମାବଲମ୍ବୀ ଭାରତରେ ଅବସ୍ଥାପିତ ?
Answer:
୨୦୦୧ ଜନଗଣନାନୁଯାୟୀ ଶତକଡ଼ା ୨.୩ ଶତାଂଶ ଖ୍ରୀଷ୍ଟଧର୍ମାବଲମ୍ବୀ ଭାରତରେ ଅବସ୍ଥାପିତ ?

୯୨ । ଭାରତର କେଉଁ ରଜ୍ୟରେ ଅଧୂକ ସଂଖ୍ୟକ ଖ୍ରୀଷ୍ଟଧର୍ମାବଲମ୍ବୀ ବାସ କରିଥା’ନ୍ତି ?
Answer:
ଭାରତର କେରଳ ରାଜ୍ୟରେ ଅଧ‌ିକ ସଂଖ୍ୟକ ଖ୍ରୀଷ୍ଟଧର୍ମାବଲମ୍ବୀ ବାସ କରିଥା’ନ୍ତି ।

୯୩ । ଶିଖ୍ ଧର୍ମର ପବିତ୍ର ଗ୍ରନ୍ଥର ନାମ କ’ଣ ?
Answer:
ଗୁରୁଗ୍ରନ୍ଥସାହିବ

୯୪ । ବୌଦ୍ଧଧର୍ମର ଗ୍ରନ୍ଥର ନାମ ଉଲ୍ଲେଖ କର ।
Answer:
ତ୍ରିଫିଟକ

୯୫ । ବୁଦ୍ଧଦେବଙ୍କ ଆର୍ଯ୍ୟ ଅଷ୍ଟାଙ୍ଗ ମାର୍ଗରୁ ଗୋଟିଏ ମାର୍ଗ ଉଲ୍ଲେଖ କର ।
Answer:
ସମ୍ୟକ୍ ବାକ୍ୟ

୯୬ । ପଞ୍ଚଯାମର ଅର୍ଥ କ’ଣ ?
Answer:
ସମ୍ୟକ୍ ବିଶ୍ବାସ, ସମ୍ୟକ୍ ଜ୍ଞାନ ଓ ସମ୍ୟକ୍ କର୍ମ ଉପରେ ପର୍ଯ୍ୟବସିତ ।

୯୭ । ହିନ୍ଦୁ ଓ ଜୈନଧର୍ମାବଲମ୍ବୀଙ୍କ ମଧ୍ୟରେ ଥିବା ଗୋଟିଏ ସାମଞ୍ଜସ୍ୟ ଉଲ୍ଲେଖ କର ।
Answer:
ନିଜର ଜୀବନଧାରା ଓ ବ୍ୟାବହାରିକ ପଦ୍ଧତିରେ ଅନ୍ୟ ଧର୍ମଠାରୁ ସମ୍ପୂର୍ଣ୍ଣ ଭିନ୍ନ ଅଟେ ।

୯୮ । କେନ୍ଦାଭେସ୍ତା କ’ଣ ?
Answer:
ଜେନ୍ଦାଭେସ୍ତା ପାର୍ଶୀମାନଙ୍କର ଧର୍ମଗ୍ରନ୍ଥ ଅଟେ ।

୯୯ । ସିନାଯୋଗୁ କେଉଁ ଧର୍ମର ମନ୍ଦିର ଅଟେ ?
Answer:
ସିନାଯୋଗୁ ଜୁଡ଼ାବଦୀ ଧର୍ମର ମନ୍ଦିର ଅଟେ ।

୧୦୦ ।‘‘ଯଦି ଭାରତୀୟ ସଂସ୍କୃତିର ପତନ ଘଟିବ ତେବେ ଏସିଆ ବିଲୁପ୍ତ ହୋଇଯିବ’’- ଏହି ଭକ୍ତିଟିକୁ ଉଲ୍ଲେଖ କରିଥିବା ମହାନ୍ ବ୍ୟକ୍ତିଙ୍କର ନାମ ଉଲ୍ଲେଖ କର ।
Answer:
ମହାମ୍। ଗାକ୍ଷି

୧୦୧ । ଭାରତବର୍ଷକୁ ଅନ୍ୟଭାବରେ କେଉଁ ଭୂମି ରୂପେ ଅଭିହିତ କରାଯାଇଅଛି ?
Answer:
ଦେବଭୂମି

୧୦୨ । ଭାରତରେ କେଉଁ ପ୍ରକାର ପରିବାର ପ୍ରାୟତଃ ପରିଲକ୍ଷିତ ହୋଇଆସୁଅଛି ?
Answer
ଯୌଥ ପରିବାର ।

୧୦୩ । ପୁରାଣ ବର୍ଣ୍ଣିତ ହିନ୍ଦୁ ସାହିତ୍ୟରେ ଭାରତ ଉପମହାଦେଶକୁ କେଉଁ ନାମରେ ପରିଚୟ ପ୍ରଦାନ କରାଯାଇଛି ?
Answer:
ଭାରତଖଣ୍ଡ, ଜମ୍ବୁଦ୍ୱୀପ ଏବଂ ଭାରତବର୍ଷ ନାମରେ ପରିଚିତ କରାଯାଇଛି ।

୧୦୪ । ଭାରତର ଭୌଗୋଳିକ ପରିସୀମା କେଉଁଠାରୁ କେଉଁ ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପ୍ତ ହୋଇଅଛି ?
Answer:
କାଶ୍ମୀରଠାରୁ କୁମାରିକା ପର୍ଯ୍ୟନ୍ତ ବ୍ୟାପ୍ତ ।

୧୦୫ । ଭାରତର ଚାରିଗୋଟି ପ୍ରାକୃତିକ ବିଭାଜନ ମଧ୍ୟରୁ ଗୋଟିଏ ଉଲ୍ଲେଖ କର ।
Answer:
ହିମାଳୟ ପାର୍ବତ୍ୟାଞ୍ଚଳ ।

୧୦୬ । ଭାରତର କେଉଁ ସ୍ଥାନକୁ ବରଫ ଓ ମୁନିଋଷିଙ୍କର ବାସସ୍ଥାନ କୁହାଯାଏ ?
Answer:
ହିମାଳୟ ପର୍ବତମାଳାକୁ ବରଫ ଓ ମୁନିଋଷିଙ୍କର ବାସସ୍ଥାନ କୁହାଯାଏ ।

୧୦୭ । ଭାରତର ସୈନ୍ଧବ-ଗାଙ୍ଗେୟ ସମତଳଭୂମି ମଧ୍ଯରେ କେଉଁ ପବିତ୍ର ନଦୀ ପ୍ରବାହିତ ହେଉଅଛି ?
Answer:
ଭାରତର ସୈନ୍ଧବ-ଗାଙ୍ଗେୟ ସମତଳଭୂମି ମଧ୍ଯରେ ସିନ୍ଧୁ, ଗଙ୍ଗା ଓ ବ୍ରହ୍ମପୁତ୍ର ଆଦି ପବିତ୍ର ନଦୀଗୁଡ଼ିକ ପ୍ରବାହିତ ହେଉଅଛି

୧୦୮ । ଭାରତୀୟ ସଂସ୍କୃତି ସାଧାରଣତଃ କେଉଁ ଜୀବନର ଦିଗକୁ ବିଶେଷ ଭାବରେ ପ୍ରଭାବିତ କରୁଅଛି ?
Answer:
ଭାରତୀୟ ସଂସ୍କୃତି ସାଧାରଣତଃ ସୀମାଜିକ ଜୀବନର ଦିଗକୁ ବିଶେଷଭାବରେ ପ୍ରଭାବିତ କରୁଅଛି ।

Odisha State Board BSE Odisha 6th Class Science Solutions Chapter 5 ବସ୍ତୁର ପ୍ରକାରଭେଦ Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Science Solutions Chapter 5 ବସ୍ତୁର ପ୍ରକାରଭେଦ

Question 1.
ନିମ୍ନଲିଖତ ବସ୍ତୁଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟି ପ୍ରାକୃତିକ ନୁହେଁ ?
(କ) କାଠ
(ଖ) କାଗଜ
(ଗ) ଖଣିଜତୈଳ
(ଘ) ମାଟି
ଉ –
(ଖ) କାଗଜ

Question 2.
ନିମ୍ନଲିଖୂ ବସ୍ତୁଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟି ନିର୍ଜୀବ ?
(i)
(କ) ସାପ
(ଖ) ଭାଙ୍ଗିଯାଇଥିବା ତୁମ ଦାନ୍ତ
(ଗ) ଗେଣ୍ଡା
(ଘ) ଗଜାବୁଟ
ଉ –
(i) ଭାଙ୍ଗିଯାଇଥିବା ତୁମ ଦାନ୍ତ

(ii)
(କ) ଗୋଟା ମୁଗ
(ଖ) ମୁଗ ଡାଲି
(ଗ) ଗଜା ମୁଗ
(ଘ) ମୁଗ ଗଛ
ଉ –
(ii) ମୁଗ ଡାଲି

Question 3.
ପ୍ରଥମ ଶବ୍ଦଦ୍ୱୟର ସଂପର୍କକୁ ଦେଖ୍ ତୃତୀୟ ଶବ୍ଦ ସହ ସଂପର୍କିତ ଶବ୍ଦଟି ଶୂନ୍ୟ ସ୍ଥାନରେ ଲେଖ ।
(କ) କାଠ : ଅସ୍ୱଚ୍ଛ : : କାଚ : ……………….. ।
(ଖ) ଚିନି : ବ୍ରବଶୀୟ :: ………………. ଅଦ୍ରବଣୀୟ ।
(ଗ) ସୁନା : ଧାତୁ : : ଅଙ୍ଗାର : ……………………. ।
(ଘ) ପାଣିରେ ବୁଡ଼ିଯିବା : ଗୋଡ଼ି : : ଭାସିବା : ……………….. ।
ଉ –
(କ) ସ୍ବଚ୍ଛ
(ଖ) ବାଲି
(ଗ) ଅଧାତୁ
(ଘ) ସୋଲ

Question 4.
କଠିନ ଓ ନରମ ପ୍ରକାରଭେଦରେ ନିମ୍ନଲିଖତ ବସ୍ତୁଗୁଡ଼ିକୁ ଶ୍ରେଣୀ ବିଭାଗ କର । (ପ୍ରଶ୍ନସହ ଉତ୍ତର)
(କ) ପିନ୍‌କଣ୍ଟା – କଠିନ
(ଖ) ସାବୁନ – କଠିନ
(ଗ) ତୁଳାବିଣ୍ଡା – ନରମ
(ଘ) ବରଫଖଣ୍ଡ – କଠିନ
(ଙ) ରବର ପେଣ୍ଡୁ – ନରମ
(ଚ) ସୋଲ – ନରମ
(ଛ) ଡପେନ୍ ଭିତରେ ଥ‌ିବା ସ୍ପ୍ରିଙ୍ଗ – ନରମ

Question 5.
କେଉଁ ବାକ୍ୟଟି ଠିକ୍ ?
(କ) ତୁମ ବହି ପୃଷ୍ଠାର ଉଜ୍ଜଳତା ଅଛି ।
(ଖ) ୟୁରିଆ ସାର ଜଳରେ ଦ୍ରବଣୀୟ ଅଟେ ।
(ଗ) ସବୁ କାଠ ପାଣିରେ ଭାସେ ।
(ଘ) କାଚ ଏକ ସ୍ବଚ୍ଛ ବସ୍ତୁ ।
ଉ –
(ଖ) ୟୁରିଆ ସାର ଜଳରେ ଦ୍ରବଣୀୟ ଅଟେ ।
(ଘ) କାଚ ଏକ ସ୍ବଚ୍ଛ ବସ୍ତୁ ।

Question 6.
ତଳେ ଦିଆଯାଇଥ‌ିବା ବସ୍ତୁଦ୍ଵୟ ମଧ୍ୟରେ ଥ‌ିବା ଦୁଇଟି ସାଦୃଶ୍ୟ ଓ ଦୁଇଟି ପାର୍ଥକ୍ୟ ଲେଖ ।

ବସ୍ତୁର ପ୍ରକାରଭେଦ Notes :

→ ପଞ୍ଚମ ଅଧ୍ୟାୟ

• ଆମ ଚତୁର୍ଦ୍ଦିଗରେ ଭରିରହିଥିବା ବସ୍ତୁଗୁଡ଼ିକ ବିଭିନ୍ନ ପ୍ରକାରର ଅଟନ୍ତି । ଚେୟାର, ଟେବୁଲ, ଶଗଡ଼, ସାଇକେଲ, ମଟରଗାଡ଼ି, ବାସନକୁସନ, ଖାତା, ବହି, କଲମ, ଟିଭି, ଖେଳନା ଆଦି ଆବଶ୍ୟକତା ଅନୁସାରେ ଭିନ୍ନ ଭିନ୍ନ କାର୍ଯ୍ୟରେ ବ୍ୟବହାର କରୁ ।
• ଏହାବ୍ୟତୀତ ଆମ ପରିବେଶରେ ଗାଈ, ଛେଳି, କୁକୁର, ବିରାଡ଼ି, ବିଲ, ବାଡ଼ିବଗିଚା, ତୋଟା, ପାହାଡ଼ ଆଦି ଅହିଛି ।
• ଏଗୁଡ଼ିକର ଆକାର, ଆକୃତି, ରଙ୍ଗ ବିଭିନ୍ନ ପ୍ରକାର ।
• ପ୍ରତ୍ୟେକ ବସ୍ତୁର କେତେଗୁଡ଼ିଏ ଗୁଣ ଥାଏ । ଏହି ଗୁଣକୁ ଆଧାର କରି ବସ୍ତୁଗୁଡ଼ିକୁ ପ୍ରକାରଭେଦ କରାଯାଇଥାଏ ।

→ ବିଭିନ୍ନ ବସ୍ତୁ ମଧ୍ୟରେ ଥ‌ିବା ସାଦୃଶ୍ୟ ଓ ପାର୍ଥକ୍ୟ :

• ଆମେ ଦେଖୁଥ‌ିବା ଓ ବ୍ୟବହାରକରୁଥିବା ବିଭିନ୍ନ ବସ୍ତୁଗୁଡ଼ିକ ମଧ୍ୟରେ କେତେକ ସାଦୃଶ୍ୟ ଦେଖାଯାଏ ।
• ସବୁ ବସ୍ତୁ ସବୁ କାମରେ ଲାଗନ୍ତି ନାହିଁ; କାରଣ ସବୁ ବସ୍ତୁର ଗୁଣ ସମାନ ନଥାଏ ।
• ଚାଉଳ, ଗହମ, ମାଣ୍ଡିଆ, ଡାଲି, ପନିପରିବା, କ୍ଷୀର, ମାଛ, ମାଂସ, ଅଣ୍ଡା ଆଦି ବସ୍ତୁକୁ ଆମେ ଖାଦ୍ୟ ରୂପରେ ବ୍ୟବହାର କରୁ ।
• କପା, ରେଶମ, ପଶମ, ନାଇଲନ୍ ଆଦିରୁ ତିଆରି ସୂତାରୁ ଆମେ ବ୍ୟବହାର କରୁଥିବା ବସ୍ତ୍ର ପ୍ରସ୍ତୁତ କରାଯାଏ ।
• ଇଟା, ବାଲି, ଗୋଡ଼ି, ମାଟି, ସିମେଣ୍ଟ, ଟିଣ, ଲୁହା, କାଠ, ବାଉଁଶ, ନଡ଼ା, ଟାଇଲ ଆଦି ବ୍ୟବହାର କରି ଆମ ଘର ତିଆରି ହୋଇଥାଏ ।
• ଘର ତିଆରି ପାଇଁ ବ୍ୟବହୃତ ହେଉଥ‌ିବା ବସ୍ତୁକୁ ଆମେ ଖାଦ୍ୟ ରୂପେ ବ୍ୟବହାର କରିପାରିବା ନାହିଁ ।
• ଏସବୁ ବସ୍ତୁର ଗୁଣ ସମାନ ନୁହେଁ । ସେଗୁଡ଼ିକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ରହିଛି ।
• ଯେତେବେଳେ ଅନେକ ବସ୍ତୁକୁ ଅନୁଧ୍ୟାନ କରାଯାଏ, ସେଗୁଡ଼ିକ ମଧ୍ୟରେ ଥିବା ସାଦୃଶ୍ୟ ଓ ପାର୍ଥକ୍ୟକୁ ବୁଝିହୁଏ ।

Question 1.
ନିମ୍ନ ସାରଣୀଟିକୁ ପୂରଣ କର ।

ଉ –

→ ବସ୍ତୁର ଶ୍ରେଣୀ ବିଭାଗ :
ବସ୍ତୁଗୁଡ଼ିକର ଶ୍ରେଣୀବିଭାଗ କରିବାପାଇଁ ନିମ୍ନଲିଖ ପଦକ୍ଷେପ ନେବା ଉଚିତ ।

• ପ୍ରଥମେ ନିରୀକ୍ଷଣ କରି ତାହା ସ୍ବଚ୍ଛ ବା ଅସ୍ବଚ୍ଛ, ରଙ୍ଗହୀନ ବା ରଙ୍ଗୀନ ଜାଣିବା ।
• ତା’ପରେ ସ୍ପର୍ଶ କରି ତାହା ଚିକ୍କଣ ବା ଆବଡ଼ାଖାବଡ଼ା ଜାଣିବା ।
• ତା’ପରେ ଚାପଦେଇ ପରୀକ୍ଷା କରି ତାହା କଠିନ ବା ନରମ ଜାଣିବା ।
• ବସ୍ତୁଗୁଡ଼ିକ ହାତରେ ଟେକି ତାହା ହାଲୁକା ବା ଓଜନିଆ ପରୀକ୍ଷା କରି ଦେଖୁ ।
• ପରିଶେଷରେ ବସ୍ତୁଗୁଡ଼ିକ ମଧ୍ୟରେ ସାଦୃଶ୍ୟ ଓ ପାର୍ଥକ୍ୟର ତାଲିକା କରିବା ।

ବସ୍ତୁର ଗୁଣ ଅନୁସାରେ ଯେତେବେଳେ ଶ୍ରେଣୀ ବିଭାଗ କରାଯାଏ, ଆମେ ଦେଖୁ କେତେକ ବସ୍ତୁ ପ୍ରାକୃତିକ ଓ ଅନ୍ୟ କେତେକ ମନୁଷ୍ୟକୃତ । କେତେକ ବସ୍ତୁ ସଜୀବ ଓ ଅନ୍ୟ କେତେକ ନିର୍ଜୀବ ।

• ପ୍ରାକୃତିକ ଓ କୃତ୍ରିମ – ଯେଉଁ ବସ୍ତୁଗୁଡ଼ିକ ପ୍ରାକୃତିକ ପ୍ରକ୍ରିୟାରେ ସୃଷ୍ଟି ହୋଇଥାଏ ସେଗୁଡ଼ିକୁ ପ୍ରାକୃତିକ ବସ୍ତୁ କୁହାଯାଏ । ଯେଉଁ ବସ୍ତୁଗୁଡ଼ିକ ମଣିଷଦ୍ବାରା ତିଆରି ହୋଇଥାଏ ତାହାକୁ କୃତ୍ରିମ ବସ୍ତୁ କୁହାଯାଏ ।
• ଜୀବ ଓ ନିର୍ଜୀବ – ଯାହାର ଜୀବନ ଅଛି ତାହାକୁ ଜୀବ ଓ ଯାହାର ଜୀବନ ନାହିଁ ତାହାକୁ ନିର୍ଜୀବ କୁହାଯାଏ ।

Question 1.
ସାରଣୀରେ ଥ‌ିବା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର । (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କରାଯାଇଛି ।)

→ ବସ୍ତୁର ଗୁଣ :
ବସ୍ତୁର ଗୁଣ ଅନୁସାରେ ଯେତେବେଳେ ଶ୍ରେଣୀ ବିଭାଗ କରାଯାଏ, ସେତେବେଳେ କେତେକ ବସ୍ତୁ ପ୍ରାକୃତିକ ଓ ଅନ୍ୟ କେତେକ ମନୁଷ୍ୟକୃତ ଏବଂ କେତେକ ବସ୍ତୁ ସଜୀବ ଓ ଅନ୍ୟ କେତେକ ନିର୍ଜୀବ ଆମେ ଦେଖୁ ।
ପ୍ରତ୍ୟେକ ବସ୍ତୁର ଦୁଇଟି ମୌଳିକ ଗୁଣ ଥାଏ; ଯଥା –

• ବସ୍ତୁ କିଛି ସ୍ଥାନ ଅଧିକାର କରେ ।
• ଏହାର ବସ୍ତୁତ୍ଵ ଥାଏ ।

ବସ୍ତୁର ଅନ୍ୟ ଗୁଣଗୁଡ଼ିକ ହେଲା –

• ରଙ୍ଗ ବା ବର୍ଣ୍ଣ
• ପୃଷ୍ଠଭାଗର ମସୃଣତା ଓ ରୁକ୍ଷତା
• ଉଜ୍ଜ୍ବଳତା
• ସ୍ଵଚ୍ଛତା
• ଦ୍ରବଣୀୟତା

ବସ୍ତୁର ଗୁଣଗୁଡ଼ିକ ମଧ୍ୟରୁ ଏହାର ବାହ୍ୟରୂପ, ବର୍ଣ୍ଣ, ରୁକ୍ଷତା, କଠିନତା, ଜଳରେ ଦ୍ରବଣୀୟତା, ଜଳଠାରୁ ଓଜନିଆ କି ହାଲୁକା, ଉଜ୍ଜଳତା ଜାଣିହୁଏ ।

Question 3.
ବସ୍ତୁର ଗୁଣଗୁଡ଼ିକ ସାରଣୀରେ ଲେଖ । (ସାରଣୀରେ ଗୁଣଗୁଡ଼ିକ ଲେଖାଯାଇଛି ।)

→ ତୁମପାଇଁ କାମ – ୧

• ସବୁ ବସ୍ତୁର ରଳଂ ଏକାପ୍ରକାର ନୁହଁନ୍ତି ।
• ସବୁ ବସ୍ତୁ କଠିନ ବା ନରମ ନୁହଁନ୍ତି ।
• ସବୁ ବସ୍ତୁର ବାହ୍ୟ ରୂପ ଏକା ପରି ଚିକ୍କଣ ନୁହେଁ ।

→ ତୁମପାଇଁ କାମ – ୨

• ଚାମଚରେ ଚିନି, ଅଳ୍ପ କିରୋସିନି, ଗୋଟିଏ କାଚବାଟି, ଅଳ୍ପ ସଫାବାଲି ଓ କିଛି କୁଟା ବା ନଡ଼ାଖଣ୍ଡକୁ ପାଖରେ ରଖ ।
• ଚିନି, କିରୋସିନି, କାଚବାଟି ଓ ନଡ଼ାଖଣ୍ଡକୁ ଅଲଗା ଅଲଗା ପାତ୍ରରେ ଥ‌ିବା ଜଳରେ ପକାଇ ଚାମଚ ସାହାଯ୍ୟରେ ଘାଣ୍ଟି ମିଶାଅ ।
  ବସ୍ତୁର ଗୁଣ ଓ ପ୍ରକାରଭେଦ
  
• ସବୁ ବସ୍ତୁ- ଜଳରେ ଦ୍ରବଣୀୟ ନୁହନ୍ତି । ସବୁ ବସ୍ତୁ ଜଳଠାରୁ ଓଜନିଆ ମଧ୍ଯ ନୁହନ୍ତି ।

→ ତୁମପାଇଁ କାମ – ୩

• ଟର୍ଚ୍ଚ ଲାଇଟ୍ ସାମନାରେ ଗୋଟିଏ କାଚ ଗିଲାସ ରଖିଲେ ଟର୍ଚ୍ଚ ଲାଇଟ୍‌ରୁ ଆସୁଥିବା ଆଲୋକ ଗିଲାସ ଭିତର ଦେଇ ଗିଲାସ ଆଗ ପାଖରେ ପଡ଼ିବ ।
• ଟର୍ଚ୍ଚ ଲାଇଟ୍ ଆଗରେ କାର୍ଡ଼ ବୋର୍ଡ଼ ଖଣ୍ଡିକ ରଖୁ ଆଲୋକ କାର୍ଡ଼ବୋର୍ଡ଼ ଦେଇ ଆଗକୁ ଯାଇପାରୁ ନାହିଁ ।
• ଗୋଟିଏ ଅନ୍ଧାରୁଆ ଜାଗାରୁ କାର୍ଡ଼ବୋର୍ଡ଼କୁ ବାହାର କରିଦେଇ, ସେଠାରେ ହାତ ପାପୁଲି ରଖୁଲେ ହାତ ପାପୁଲିର ରଙ୍ଗ ସାମାନ୍ୟ ଲାଲ୍ ଦେଖାଯିବ ।
• ଖଣ୍ଡିଏ ଧଳା କାଗଜ ମଝିରେ ଦୁଇଟୋପୀ ତେଲ ପକାଇ ଘସି ଦିଅ । ଟର୍ଚ୍ଚ ଆଲୋକ ଆଗରେ କିଛି ନଥ‌ିବା ବେଳେ କେବଳ ବାୟୁରେ ଆଲୋକ ଆଗକୁ ଯାଉଛି । ସେହି ଆଲୋକ କାଚ ଗିଲାସ ଦେଇ ମଧ୍ୟ ଯାଇପାରୁଛି ।
• ବାୟୁ ଓ କାଚଭଳି ବସ୍ତୁ ଯାହା ମଧ୍ୟଦେଇ ଆଲୋକ ଯାଇପାରୁଛି, ସେହି ବସ୍ତୁଗୁଡ଼ିକୁ ସ୍ବଚ୍ଛ ବସ୍ତୁ କୁହାଯାଏ ।
• କାର୍ଡ଼ବୋର୍ଡ଼ ଭଳି ବସ୍ତୁକୁ ଅସ୍ବଚ୍ଛ ବସ୍ତୁ କୁହାଯାଏ । ତେଲ ଘସା ହୋଇଥିବା କାଗଜ, ଯାହା ମଧ୍ୟଦେଇ ଆଲୋକ ଆଂଶିକ ଭାବେ ଯାଇପାରୁଛି, ତାକୁ ଅଳ୍ପସ୍ଵଚ୍ଛ ବସ୍ତୁ କୁହାଯାଏ ।

→ ତୁମପାଇଁ କାମ – ୪

• କାଠ, ଅଙ୍ଗାର, କାର୍ଡ଼ବୋର୍ଡ଼, ଚକ୍ ଖଡ଼ି, ପ୍ଲାଷ୍ଟିକ୍ ପାନିଆ ଆଦି ଚକ୍ ଚକ୍ କରୁ ନାହିଁ ।
• ତମ୍ବାତାର ଓ ଆଲୁମିନିୟମ୍ ଗିନା, ଷ୍ଟିଲ୍ ଚାମଚ ଚକ୍ ଚକ୍ ଦେଖାଯିବ । ବସ୍ତୁର ଚକ୍ରକ୍ ଦେଖାଯାଉଥିବା ଗୁଣକୁ ଉଜ୍ଜ୍ବଳତା କୁହାଯାଏ ।
• କାଠ, ଅଙ୍ଗାର, କାର୍ଡ଼ବୋର୍ଡ଼, ଚକ୍‌ଖଡ଼ି ଓ ପ୍ଲାଷ୍ଟିକ୍ ପାନିଆକୁ ଅନୁଜ୍ବଳ ବସ୍ତୁ କୁହାଯାଏ । ତମ୍ବାତାର, ଆଲୁମିନିୟମ୍ ଗିନା, ଷ୍ଟିଲ୍ ଚାମଚକୁ ଉଜ୍ଜ୍ଵଳ ବସ୍ତୁ କୁହାଯାଏ ।

Question 4.
ନିମ୍ନ ସାରଣୀଟି ପୂରଣ କର । (ସାରଣୀ ପୂରଣ କରାଯାଇଛି)

Question 5.
ବସ୍ତୁର ଉଜ୍ଜଳତା ଗୁଣକୁ ନେଇ ଦଶଟି ବସ୍ତୁର ଶ୍ରେଣୀବିଭାଗ କର ।
ଉ –

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 17 ଆବର୍ଜନାର ପରିଚାଳନା Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 17 ଆବର୍ଜନାର ପରିଚାଳନା

Question 1.
କୃଷିଜାତ ଆବର୍ଜନା କ’ଣ ? ଏହାର କିପରି ସଦୁପଯୋଗ କରାଯାଇପାରିବ ?
Solution:
ଉ-କୃଷିଜାତ ଆବର୍ଜନା – ଧାନ ଓ ଗହମ ଆଦିର ଅଗାଡ଼ି ଓ ଚଷୁ , ନଡ଼ିଆର ସଢ଼େଇ ଓ କତା, ବିଭିନ୍ନ ଫଳର ଚୋପା ଓ ମଞ୍ଜି ଆଦି କୃଷିଜାତ ଆବର୍ଜନା ଅଟେ ।
ସଦୁପଯୋଗ :
(i) ଧାନକୁଣ୍ଡାରୁ ତେଲ ପ୍ରସ୍ତୁତ କରାଯାଏ ଓ ଏହି କୁଣ୍ଡା ସହ ସିମେଣ୍ଟ, କାଦୁଅ ଓ ରାସାୟନିକ ପଦାର୍ଥ ମିଶାଇ ଶୀତତାପ ନିୟନ୍ତ୍ରିତ ଇଟା ମଧ୍ୟ ପ୍ରସ୍ତୁତ କରାଯାଏ, କେତେକ କୁଣ୍ଡାକୁ ଜାଳେଣି ରୂପେ ମଧ୍ୟ ବ୍ୟବହାର କରନ୍ତି ।
(ii) ବିଭିନ୍ନ ଫଳର ଚୋପାରୁ କାଗଜ ପ୍ରସ୍ତୁତ କରାଯାଏ ।
(iii) ଏହି ଆବର୍ଜନାକୁ ବିନିଯୋଗ କରି ସୋଡ଼ିୟମ୍ ସିଲିକେଟ ନାମକ ରାସାୟନିକ ଯୌଗିକ ମଧ୍ୟ ପ୍ରସ୍ତୁତ କରାଯାଏ ।
(iv) କେତେକ ଶସ୍ୟର ବିଶୁଦ୍ଧ ଜଳର ତିନିଗୋଟି ବ୍ୟବହାର ଲେଖ ।

Question 2.
ବିଶୁଦ୍ଧ କଲର ଡିନିଗୋଟି ବ୍ୟବହାର ଲେଖ |
Solution:
ଜଳକୁ ବିଶୁଦ୍ଧ କରିବା ଅର୍ଥ ବ୍ୟବହାର କରିବା ପୂର୍ବରୁ ସେଥୁରେ ମିଶିଥିବା ସମସ୍ତ ଆବର୍ଜନାକୁ ନିଷ୍କାସନ କରିବା ଓ ଜଳକୁ ବୀଜାଣୁ ମୁକ୍ତ କରିବା ।
(i) ଆମେ ସମସ୍ତେ ବିଶୁଦ୍ଧ ଜଳକୁ ହିଁ ପାନୀୟ ରୂପେ ବ୍ୟବହାର କରିଥାଉ ।
(ii) ବିଶୁଦ୍ଧ ଜଳ ବ୍ୟବହାର କଲେ ଓ ସେହି ଜଳରେ ଗାଧୋଇଲେ ଜଳ ବାହିତ ରୋଗ; ଯଥା – କଲେରା, ଆମାଶୟ, ଟାଇଫଏଡ଼, କାମଳ, କାଛୁ କୁଣ୍ଡିଆ ଆଦିରୋଗ ହୋଇ ନଥାଏ ।
(iii) ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରିବା, ଦାନ୍ତ ଘଷିବା ଓ ଶୌଚକରିବା ଆଦିରେ ଆମେ ବିଶୁଦ୍ଧ ଜଳ ବ୍ୟବହାର କରିଥାଉ ।

Question 3.
ପୁନଃ ଚକ୍ରଣ ପଦ୍ଧତି କ’ଣ ? ଆବର୍ଜନା ନିଷ୍କାସନରେ ଏହାର ଭୂମିକା କ’ଣ ଆଲୋଚନ କର ।
Solution:
ପୁନଃଚକ୍ରଣ ପଦ୍ଧତି – କେତେକ ଆବର୍ଜନାରୁ ପୁନର୍ବାର ନୂଆ ନୂଆ ଜିନିଷ ପ୍ରସ୍ତୁତ କରାଯାଇଥାଏ । ଏହି ପଦ୍ଧତିକୁ ପୁନଃଚକ୍ରଣ ପଦ୍ଧତି କହନ୍ତି ।
ଭୂମିକା :
(i) ଅଳିଆ ଗଦାରୁ ମିଳୁଥିବା ଛିଣ୍ଡା କନା, କାଗଜ, କୁଟା, କାଠି, ଶୁଖୁଲା ପତ୍ର ଆଦିକୁ କାଗଜ ଶିଳ୍ପରେ ବ୍ୟବହାର କରାଯାଇପାରିବ । ଏଥୁରୁ ପୁନଃ ଚକ୍ରଣ ପଦ୍ଧତିରେ ଗୋଲ କୋଇଲା ଭଳି ଜାଳେଣି ମଧ୍ୟ ପ୍ରସ୍ତୁତ କରାଯାଇ ପାରିବ ।
(ii) ଲୁହା, ପ୍ଲାଟିନମ, ଟିଣ, ଏଲୁମିନିୟମ୍ ଏପରିକି ପ୍ଲାଷ୍ଟିକ ଓ କାଚ ଆଦି ଆବର୍ଜନାକୁ ପୁନଃଚକ୍ରଣ ପଦ୍ଧତିଦ୍ୱାରା ତରଳାଇ ନୂଆ ନୂଆ ଜିନିଷ ସବୁ ପ୍ରସ୍ତୁତ କରାଯାଇପାରିବ ।

Question 4.
ଅପଚୟିତ ଜଳର ଉପଚାରର କୌଶଳଗୁଡ଼ିକ ଲେଖ । ଏଥୁରୁ କେଉଁ କୌଶଳ ସହରର ଦୂଷିତ ଜଳର ଉପଚାର ପ୍ଲାଣ୍ଟରେ ବ୍ୟବହୃତ ହୁଏ ?
Solution:
(i) ଅପଚୟିତ ଜଳର ଉପଚାରର କୌଶଳଗୁଡ଼ିକ ହେଲା – ଭୌତିକ ଉପଚାର, ରାସାୟନିକ ଉପଚାର, ଜୈବିକ ସହରର ପ୍ଲାଣ୍ଟରେ ଏବଂ ଭସାକରଣ ଲତ୍ୟାଦି |
(ii) ଏଥୁରୁ ସହରରେ ଦୂଷିତ ଜଳର ଉପଚାର ପ୍ଲାଣ୍ଟରେ ଭୌତିକ, ରାସାୟନିକ ଓ ଜୈବିକ ଉପଚାର କରାଯାଇଥାଏ ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଜଳରେ _________ ପଦାର୍ଥ ମିଶିଥିଲେ ତା’କୁ ଅପଚୟିତ ଜଳ କୁହାଯାଏ ।
(ii) ଦୂଷିତ ଜଳକୁ _________ କରିବାପାଇଁ ଚୂନ ଓ ବ୍ଲିଚିଂ ପାଉଡ଼ର ରାସାୟନିକ ପଦାର୍ଥ ବାହିତ କୁହାଯାଏ ।
(iii) ହଇଜା, ଅମାଶୟ ଓ ଟାଇଫଏଡ଼କୁ _________ ବାହିତ ରୋଗ କୁହାଯାଏ ।
(iv) ଦୂଷିତ ଜଳର _________ ଫଳରେ ପଟୁମାଟି ଓ ଜୈବିକ ଗ୍ୟାସ ବାହାରେ ।
(v) ପ୍ରତ୍ୟେକ ଆବର୍ଜନାର _________ କରି ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଇପାରେ ।
(vi) ଘରୁ ବାହାରୁଥିବା ଦୂଷିତ ଜଳକୁ _________ କୁହାଯାଏ ।
(vii) ଦୂଷିତ ଜଳର ଉପଚାର _________ ରେ କରାଯାଏ ।
(viii) ଆମେ _________ କାଳକୁ ପାନୀୟ କଲରୁପେ ବ୍ୟବହାର କରୁ |
(ix) 2005 ମସିହା ମାର୍ଚ୍ଚ 22 ତାରିଖକୁ _______ ଦିବସ ରୂପେ ପାଳନ କରାଯାଏ ।
(x) ଅପଚାୟିତ ଜଳରେ ଥିବା ପୋଷକ ମଧ୍ୟରୁ _______ ଅନପରମ |
(xi) ଜଳକୁ ବୀଜାଣୁମୁକ୍ତ କରିବାକୁ ସେଥ‌ିରେ _______ ବଟିକା ମିଶାଯାଏ ।
(xii) _______ ଗଛ ସବୁଠାରୁ ଅଧ‌ିକ ଅପରିଷ୍କାର ଜଳ ଶୋଷଣ କରିଥାଏ ।
Solution:
(i) ଦୂଷିତ
(ii) ବିଶୁଦ୍ଧ
(iii) ଜଳ
(iv) ଉପଚାର
(v) ପୁନଃଚକ୍ରଣ
(vi) ସୁଏଜ୍ ବା ନାଳ
(vii) ଦୂଷିତ ଜଳ
(viii) ବଟିକା
(ix) ବିଶ୍ଵ ଜଳ
(x) ଯବଶାରକାନ
(xi) କ୍ଲୋରିନ୍
(xii) ଇଉକାଲିପଟାସ୍

II. ବାମପାର୍ଶ୍ଵର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଦକ୍ଷିଣପାର୍ଶ୍ଵର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ମାଟି : ଅଜୈବିକ ପଦାର୍ଥ :: ମନୁଷ୍ୟ ମଳ : _________
(ii) ଆଖୁଛେଦା : ଶିଳ୍ପ ଆବର୍ଜନା :: ନଡ଼ିଆକତା : _________
(iii) ପ୍ଲାଷ୍ଟିକ୍ ପଲିଥୁନ୍ : କଠିନ ଆବର୍ଜନା :: ନର୍ଦ୍ଦମା ପାଣି : _________
Solution:
(i) ଜୈବିକ ପଦାର୍ଥ,
(ii) କୃଷି ଆବର୍ଜନା,
(iii) ତରଳ ଆବର୍ଜନା

III. ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।
(a) କେଉଁଟି ଜୈବ- ନିମ୍ନକରଣ ଅଯୋଗ୍ୟ ଆବର୍ଜନା ?
(i) ରବର
(ii) ଦଳ
(iii) ମଳମୂତ୍ର
(iv) ପଣ୍ଡ
Solution:
(i) ରବର

(b) କେଉଁଟି ପୁନଃଚକ୍ରଣ ଯୋଗ୍ୟ ଆବର୍ଜନା ନୁହେଁ ?
(i) ପଲିଥୁନ୍ ବ୍ୟାଗ୍
(ii) ଚିରା କାଗଜ
(iii) ଟିଣ
(iv) ମଟର ଗାଡ଼ି ଧୂଆଁ
Solution:
(iv) ମଟର ଗାଡ଼ି ଧୂଆଁ

(c) ଚଷୁ କେଉଁ ପ୍ରକାର ଆବର୍ଜନା?
(i) ଶିଳ୍ପ ଜନିତ
(ii) କୃଷି ସମ୍ପର୍କିତ
(iii) ଗୃହକାର୍ଯ୍ୟ ଜନିତ
(iv) ପ୍ରାଣୀଜ
Solution:
(ii) କୃଷି ସମ୍ପର୍କିତ

(d) ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଭୂତାଣୁ ଜନିତ ରୋଗ ?
(i) ହଇଜା
(ii) ଟାଇଫଏଡ
(iii) ଚର୍ମରୋଗ
(iv) କାମଳ
Solution:
(iv) କାମଳ

(e) ବଡ଼ ବଡ଼ ସହରରେ ମେଳା ମହୋତ୍ସବ ହେଉଥ‌ିବା ସ୍ଥାନରେ ପରିବେଶକୁ ପରିଷ୍କାର ରଖୁବାକୁ କେଉଁ ପ୍ରକାର ପାଇଖାନା ବ୍ୟବହାର କରାଯାଏ ?
(i) ସେପ୍‌ଟିକ୍ ଟ୍ୟାକ୍
(ii) ବରପାଲି
(iii) ଭ୍ରାମ୍ୟମାଣ
(iv) ଟ୍ରେଞ୍ଚ୍
Solution:
(iii) ଭ୍ରାମ୍ୟମାଣ

IV. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ମାର୍ଚ୍ଚ ୨୦ ତାରିଖକୁ ଆମେ ‘‘ବିଶ୍ବ ଜଳ ଦିବସ’’ ରୂପେ ପାଳନ କରୁଛେ ।
(ii) ମାଟି, ଗୋଡ଼ି ଓ ପାଉଁଶ ଜୈବିକ ପଦାର୍ଥରେ ଅନ୍ତର୍ଭୁକ୍ତ ।
(iii) ପରିଷ୍କାର ଜଳକୁ ଜୀବାଣୁ ମୁକ୍ତ କରିବାପାଇଁ ସେଥ୍ରେ ନାଇଟ୍ରୋଜେନ୍‌ଦ୍ୱାରା ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଏ ।
(iv) ଆନ୍ତ୍ରିକଜ୍ଵର ଓ କାମଳ ବାୟୁବାହିତ ରୋଗ ଅଟନ୍ତି ।
(v) ପ୍ରତ୍ୟେକ ଆବର୍ଜନାର ପୁନଃଚକ୍ରଣ କରି ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଇପାରିବ ନାହିଁ ।
Solution:
(i) ମାର୍ଚ୍ଚ ୨୨ ତାରିଖକୁ ଆମେ ‘ବିଶ୍ବ ଜଳ ଦିବସ’’ ରୂପେ ପାଳନ କରୁଛେ ।
(ii) ମାଟି, ଗୋଡ଼ି ଓ ପାଉଁଶ ଅଜୈବିକ ପଦାର୍ଥରେ ଅନ୍ତର୍ଭୁକ୍ତ ।
(iii) ପରିଷ୍କାର ଜଳକୁ ଜୀବାଣୁ ମୁକ୍ତ କରିବାପାଇଁ ସେଣ୍ଡ୍‌ରେ କ୍ଲୋରିନ୍ କିମ୍ବା ଓଜୋନ୍‌ଦ୍ୱାରା ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଏ ।
(iv) ଆନ୍ତଃକଜ୍ଵର ଓ କାମଳ ଜଳବାହିତ ରୋଗ ଅଟନ୍ତି ।
(v) ପ୍ରତ୍ୟେକ ଆବର୍ଜନାର ପୁନଃଚକ୍ରଣ କରି ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଇପାରିବ ।

V. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ଆବର୍ଜନା କେତେ ପ୍ରକାର ଓ କ’ଣ କ’ଣ ?
(ii) କେବେଠାରୁ ‘ବିଶ୍ବ ଜଳ ଦିବସ’ ପାଳନ କରାଯାଉଛି ?
(iii) ଆନ୍ତର୍ଜାତିକ ସ୍ତରରେ ବିଶୁଦ୍ଧ ଜଳ ପାଇଁ କି ପ୍ରକାର ପଦକ୍ଷେପ ନିଆଯାଉଛି ?
(iv) ଜଳ କିପରି ଦୂଷିତ ହୁଏ ?
(v) ଆବର୍ଜନା ମିଶା ଜଳକୁ କ’ଣ କହନ୍ତି ?
(vi) ପରିମଳ ବ୍ୟବସ୍ଥାକୁ କାର୍ଯ୍ୟକାରୀ କରୁଥିବା ଏକ ସଂସ୍ଥାର ନାମ ଲେଖ ।
Solution:
(i) ଆବର୍ଜନା ତିନି ପ୍ରକାର; ଯଥା – କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ।
(ii) 2005 ମସିହା ମାର୍ଚ୍ଚ 22 ତାରିଖଠାରୁ ‘ବିଶ୍ବ ଜଳ ଦିବସ’ ପାଳନ କରାଯାଉଛି ।
(iii) ଆନ୍ତର୍ଜାତିକ ସ୍ତରରେ ବିଶୁଦ୍ଧ ଜଳ ପାଇଁ 2005ରୁ 2015 ଦଶନ୍ଧିକୁ ‘ଜୀବନ ପାଇଁ ଜଳ’ ପ୍ରକଳ୍ପକୁ କାର୍ଯ୍ୟକାରୀ କରିବାକୁ ପଦକ୍ଷେପ ନିଆଯାଉଛି ।
(iv) ତରଳ ଆବର୍ଜନାର କାରକମାନେ ଜଳକୁ ପ୍ରଦୂଷିତ କରନ୍ତି । ସେମାନେ ହେଲେ ଶିଳ୍ପଜନିତ, କୃଷିଜନିତ ଓ ଗୃହକାର୍ଯ୍ୟଜନିତ ।
(v) ଆବର୍ଜନା ମିଶା ଜଳକୁ ଅପଚୟିତ ଜଳ କହନ୍ତି ।
(vi) ପରିମଳ ବ୍ୟବସ୍ଥାକୁ କାର୍ଯ୍ୟକାରୀ କରୁଥିବା ଏକ ସଂସ୍ଥା ହେଲା ‘ସୁଲଭ ଇଣ୍ଟରନ୍ୟାସନାଲ’ ।

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 15 ଜଳ – ଅମୂଲ୍ୟ ପ୍ରାକୃତିକ ସମ୍ପଦ Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 15 ଜଳ – ଅମୂଲ୍ୟ ପ୍ରାକୃତିକ ସମ୍ପଦ

Question 1.
କାବପାଇଁ ଲାଲର ଅନ୍ୟଲତା ଲେଖ |
Solution:
ଜଳ, ବାୟୁ, ସୂର୍ଯ୍ୟାଲୋକ ଆଦି ଅସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ । ଆମେ ବ୍ୟବହାର କରୁଥିବା ପଦାର୍ଥଗୁଡ଼ିକ ମଧ୍ୟରୁ ଜଳ ହେଉଛି ଗୋଟିଏ ଅତି ଦରକାରୀ ପଦାର୍ଥ । ଆମ ପୃଥ‌ିବୀ ପୃଷ୍ଠର ଶତକଡ଼ା 71 ଭାଗ ଜଳାବୃତ । ଭୂପୃଷ୍ଠର 7 ଭାଗରୁ 5 ଭାଗ ହେଉଛି କେବଳ ସମୁଦ୍ର ଜଳ । ତେଣୁ ଆମ ପୃଥ‌ିବୀକୁ ଜଳଗ୍ରହ କହନ୍ତି ।
ର୍ଥାତଶ୍ୟକତା :
(i) ଗଛଲତା, ପଶୁପକ୍ଷୀ ଓ ମଣିଷ କେହି ଜଳ ବିନା ବଞ୍ଚିପାରିବେ ନାହିଁ । ଏଣୁ ଜଳର ଅନ୍ୟନାମ ‘ଜୀବନ’ ।
(ii) ଆମେ ବିଶୁଦ୍ଧ ପାନୀୟ ଜଳକୁ ପିଇବା ପାଇଁ ବ୍ୟବହାର କରିଥାଉ । ଧୋଇବା ଓ ରାନ୍ଧିବା ତଥା ସ୍ୱାସ୍ଥ୍ୟରକ୍ଷା ପାଇଁ ମଧ୍ୟ ଜଳ ବ୍ୟବହାର କରିଥାଉ । ମିଳିତ ଜାତିସଙ୍ଘ ର ସୂଚନା ଅନୁଯାୟୀ ଜଣେ ବ୍ୟକ୍ତି ପିଇବା, ଧୋଇବା, ରାନ୍ଧିବା ତଥା ସ୍ୱାସ୍ଥ୍ୟରକ୍ଷା ପାଇଁ ଦୈନିକ ମୋଟ 50 ଲିଟର ଜଳ ବ୍ୟବହାର କରିଥାଏ ।
(iii) ଜଳ ଆମ ଶରୀରରେ ରକ୍ତ ପ୍ରବାହିତ ହେବାରେ, ଅପରିଷ୍କାର ଜିନିଷ ବାହାର କରିବାରେ (ମୂତ୍ର, ଝାଳ ଓ ଲୁହ ଆକାରରେ) ସାହାଯ୍ୟ କରିଥାଏ ।
(iv) ସବୁଜ ଉଦ୍ଭଦ, ମୃଭିକାରୁ ଜଳ ଓ ଖଣିଜ ଲବଣ ନେଇ ବାୟୁମଣ୍ଡଳରୁ ଅଙ୍ଗାରକାମ୍ଳ ଗ୍ରହଣ କରି, ସୂର୍ଯ୍ୟାଲୋକକୁ ସବୁଜକଣା ଦ୍ବାରା ବନ୍ଧନ କରି ପତ୍ରରେ ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରିଥାଏ । ଆମେ ଖାଦ୍ୟ ପାଇଁ ପ୍ରତ୍ୟକ୍ଷ ଓ ପରୋକ୍ଷ ଭାବେ ସବୁଜ ଉଭିଦ ଉପରେ ନିର୍ଭର କରିଥାଉ ।
(v) କଳକାରଖାନାରେ ମଧ୍ୟ ଜଳ ବ୍ୟବହାର କରାଯାଏ । ଜଳବିଦ୍ୟୁତ୍ ଜଳର ସ୍ରୋତ ସାହାଯ୍ୟରେ ହିଁ ଉତ୍ପନ୍ନ କରାଯାଏ ।
(vi) ଜଳଚର ଜୀବମାନେ ଜଳରେ ହିଁ ବାସ କରନ୍ତି ।

ସଂଶିପ୍ତଧାମା ପ୍ରଣୋଉର :

Question 1.
କଲଭ ବିଭିନି ଥବିସ୍ଥାପତିକ ଲେଖ |
Solution:
ଜଳ ସାଧାରଣତଃ ତିନୋଟି ଅବସ୍ଥାରେ ରହିଥାଏ ।
(i) କଠିନ – ବରଫ ଆକାରରେ,
(ii) ତରଳ – ଜଳ ଆକାରରେ ଓ
(iii) ଗ୍ୟାସୀୟ – ଜଳୀୟବାଷ୍ପ ଆକାରରେ
କଠିନ – ମେରୁ ଓ ଉଚ୍ଚ ପର୍ବତ ଶୀର୍ଷାଞ୍ଚଳରେ ଏହା ଅତି ଶୀତଳ ହୋଇ ବରଫ ଆକାରରେ ଥାଏ । ତୁମେ ଖାଉଥ‌ିବା ଆଇସ୍‌କ୍ରିମ୍ ମଧ୍ୟ ଏହାର କଠିନ ଅବସ୍ଥା ।
ତରଳ – ନଦୀ, ଝରଣା, ସମୁଦ୍ର, ପୋଖରୀ, ଗାଡ଼ିଆ, କୂପ, ନଳକୂପ ଆଦିରେ ଜଳ ତରଳ ଅବସ୍ଥାରେ ରହିଥାଏ । ଆମେ ପ୍ରତିଦିନ ଏହି ଜଳକୁ ହିଁ ପାଣିକଳରୁ ବା ନଳକୂପରୁ ଉଠାଇ ବ୍ୟବହାର କରିଥାଉ । ଏପରିକି ଚ୍ଚଶାଲଲ ମଧ୍ୟ ଆମେ ସଂଗ୍ରହ କରି ବ୍ୟବହାର କରୁ |
କିନ୍ତି ଭରକ୍ କଲର ଖ୍ୟାପାଯ୍ୟ ଗ୍ୟାସୀୟ – ସୂଯ୍ୟ ତାପର ପ୍ରତକରେ କଳ ବାଣ୍ଟରେ ପରିଣତ ହୋଇ ଆକାଶରେ ମେଣ ମୂଶ୍ଲି କରେ | ତଦନ କାର୍ଯ୍ୟ କଲାବେଳେ ଜଳ ବାମ୍ଫ ହେବା ଆମେ ଦେଖିଥାଉ । ବାଷ୍ପକୁ ଦେଖୁହୁଏ ନାହିଁ ମାତ୍ର ; ବାମ୍ଫକୁ ଦେଖୁହୁଏ ଅବସ୍ଥା ।

Question 2.
ଜଳଚକ୍ର ସମ୍ବନ୍ଧରେ ସଂକ୍ଷିପ୍ତ ବିବରଣୀ ଦିଅ ।
Solution:
ଜଳଚକ୍ର ଚାଲୁରଖିବା ପାଇଁ ମୁଖ୍ୟତଃ କେତୋଟି ଜଳବାୟୁ ସଂକ୍ରାନ୍ତୀୟ ପ୍ରାକୃତିକ ଘଟଣା ଦାୟୀ । ଏଗୁଡ଼ିକ ହେଉଛି – ବାଷ୍ପୀକରଣ, ଘନୀକରଣ ଇତ୍ୟାଦି । ଜଳଚକ୍ର ମୁଖ୍ୟତଃ ଭୂପୃଷ୍ଠ, ବାୟୁମଣ୍ଡଳ ଏବଂ ସମୁଦ୍ର ଭିତରେ ପ୍ରାୟ ସୀମିତ ରହେ ।
କିପରି ଚାଲୁରହେ –
(i) ଜଳଚକ୍ର ଚାଲୁରଖୁବା ପାଇଁ ବାଷ୍ପୀକରଣ ଓ ଘନୀକରଣ ଆଦି ପ୍ରାକୃତିକ ଘଟଣା ଦାୟୀ । ସୌରଶକ୍ତି ଦ୍ଵାରା ଏହା ଘନୀଭୂତ ହୁଏ ଏବଂ ବର୍ଷାରୂପେ ମାଧ୍ୟାକର୍ଷଣ ଶକ୍ତିର ପ୍ରଭାବରେ ପୃଥ‌ିବୀକୁ ଫେରିଆସେ ।
(ii) ଏହି ବର୍ଷାର କିଛି ଅଂଶ ପୃଥ‌ିବୀରେ ପହଞ୍ଚିବା ପୂର୍ବରୁ ବାଷ୍ପୀକରଣଦ୍ଵାରା ପୂନର୍ବାର ବାୟୁମଣ୍ଡଳକୁ ଫେରିଯାଏ । ବର୍ଷାଜଳର ଏକ ବଡ଼ଭାଗ ସମୁଦ୍ରରେ ପଡ଼େ, କିଛିଭାଗ ପୁଷ୍କରଣୀ ଆଦିରେ ଓ ଆଉ କିଛି ଭୂତଳଜଳ ଭାବରେ ମାଟିତଳେ ସଞ୍ଚିତ ହୋଇ ରହେ ।
(iii) ଉଭିଦର ଉଚ୍ଛେଦନ ଦ୍ୱାରା ଶ୍ଵାସକ୍ରିୟା ଓ ଥପନ ଆଦି ଅନ୍ୟ ପ୍ରକ୍ରିୟା ତୁଳନାରେ ଅଧ‌ିକ ଜଳ ପରିବେଶରେ ପ୍ରବେଶ କରେ । ତଥାପି ଉସେଦନ, ଶ୍ଵାସକ୍ରିୟା ଓ ଅନ୍ୟ ସମସ୍ତ ଜୈବିକ ପ୍ରକ୍ରିୟାରୁ ପରିବେଶକୁ ଆସୁଥିବା ଜଳର ପରିମାଣ ଖୁବ କମ୍ ।

Question 3.
ଜଳ ହିଁ ଜୀବନ – ବୁଝାଅ ।
Solution:
(i) ଜଳ ହେଉଛି ଜୀବ ଶରୀରର ଏକ ପ୍ରଧାନ ଉପାଦାନ । ଆଦି ଜୀବକର ଜଳୀୟଅଂଶର ପରିମାଣ ଶତକଡ଼ା ପ୍ରାୟ 65- 95 ଭାଗ ।
(ii) ଆଦି ଜୀବକକୁ ତଥା କୋଷ ଓ ଅଙ୍ଗ ପ୍ରତ୍ୟଙ୍ଗକୁ ସଠିକ ବା ଉତ୍ତମ ଅବସ୍ଥାରେ ରଖୁବା ଏବଂ ସେଥ‌ିରେ ଚାଲୁ ରହିଥ‌ିବା ସମସ୍ତ ଜୈବିକ ପ୍ରକ୍ରିୟାକୁ ସୁଚାରୁରୂପେ ସଂଘଟିତ କରାଇବାରେ ଜଳର ଅବଦାନ ଉଲ୍ଲେଖନୀୟ ।
(iii) କାରଣ ଜଳ ମାଧ୍ୟମରେ ହିଁ ଶରୀର ମଧ୍ୟରେ ସମସ୍ତ ରାସାୟନିକ ପ୍ରକ୍ରିୟା ଚାଲିଥାଏ । ଏହି କାରଣରୁ ‘ଜଳହିଁ ଜୀବନ’ କହିଲେ ଅତ୍ୟୁକ୍ତି ହେବନାହିଁ । ଏହା ବିନା ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ଜୀବନ ସୃଷ୍ଟି ଓ ସଂରକ୍ଷଣ ଅସମ୍ଭବ ।

Question 4.
ତ୍ତିଶାର କଲ ସମଦ ବିଶପ୍ରେର ଲେଖା |
Solution:
(i) ମହାନଦୀ , ବ୍ରାହ୍ମଣୀ, ବୈତରଣୀ, ଋଷିକୂଲ୍ୟା, ସୁବର୍ଣ୍ଣରେଖା, ବୁଢ଼ାବଳଙ୍ଗ, ବଂଶଧାରା, ନାଗାବଳୀ, ଇନ୍ଦ୍ରାବତୀ ସମ୍ପଦ । ଏମାନଙ୍କ ବ୍ୟତୀତ ପୋଖରୀ, କୂପ ଓ ଭୂତଳ ଜଳ ମଧ୍ୟ ଏହି ଜଳ ସମ୍ପଦର ଅନ୍ତର୍ଭୁକ୍ତ ।
(ii) ଚିଲିକା ଏବଂ ସୁଦୀର୍ଘ ସମୁଦ୍ର ସମ୍ଭାର ମଧ୍ଯ ଓଡ଼ିଶାର ଜଳସମ୍ପଦ ହିସାବରେ ଗଣାଯାଏ । କାରଣ ଏହାକୁ ମାଛଚାଷ ଲୋକେ ବର୍ଷାଜଳକୁ ଅମଳ କରି ସେମାନଙ୍କର ଆବଶ୍ୟକତା ମେଣ୍ଟାଇ ଥାଆନ୍ତି । ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଜଣେ ବ୍ୟକ୍ତି ମିଳିତ ଜାତିସଂଘର ସୂଚନା ଅନୁଯାୟୀ ପ୍ରତିଦିନ ________ ଲିଟର ଜଳ ବ୍ୟବହାର କରେ ।
(ii) ________ କୁ ଜଳଗ୍ରହ କୁହାଯାଏ ।
(iii) ହୀରାକୁଦ ନଦୀବନ୍ଧର ଦୈର୍ଘ୍ୟ ________ କି.ମି. ।
(iv) ଜଳ ________ ବାଷ୍ପୀୟ ଅବସ୍ଥାରେ ଥାଏ ।
(v) ________ ନବା ଉପରେ ହାରାକୁଦ ନଦାବନ୍ଧ ଯୋଜନା କରାଯାଲନ୍ଥି |
(vi) ________ ରେ ମିଳୁଥିବା ଜଳକୁ ଭୂତଳ ଜଳ କହିପାରିବା ।
(vii) ପୃଥ‌ିବୀର ପ୍ରଥମ ଜୀବନର ଅଣୁ ________ ରେ ହିଁ ସୃଷ୍ଟି ହୋଇଥିଲା ।
(viii)‘ବିଶ୍ବ ଜଳ ଦିବସ’ ମାର୍ଚ୍ଚମାସ ________ ତାରିଖରେ ପାଳିତ ହୁଏ ।
(ix) ପୃଥ‌ିବୀ ମହାଶୂନ୍ୟରୁ ________ ଭାବେ ଦୃଶ୍ୟମାନ ହୁଏ ।
(x) ମୋଟ ଜଳର ________ ଭାଗ ମଧୁର ଜଳ ।
(xi) ବାଷ୍ପ ଓ ବାମ୍ଫ ମଧ୍ୟରୁ ________ କୁ ଦେଖ୍ହୁଏ ।
Solution:
(i) 50,
(ii) ପୃଥ‌ିବୀ,
(iii) 25,
(iv) ବାଷ୍ପୀୟ,
(v) ମହାନଦୀ,
(vi) ନଳକୂପ,
(vii) ଜଳ,
(vii) 22,
(viii) ନୀଳଗ୍ରହ,
(ix) 2.5,
(x) ବାମ୍ଫ

II. ବାମପାର୍ଶ୍ବର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଦକ୍ଷିଣପାର୍ଶ୍ଵର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଅନାବୃଷ୍ଟି : ଜଙ୍ଗଲ କ୍ଷୟ :: ସ୍ୱଳ୍ପ ବୃଷ୍ଟି : ________
(ii) ବିଶ୍ଵଜଳ ଦିବସ : ମାର୍ଚ୍ଚ 12 ତାରିଖ :: ବିଶ୍ୱ ଜଳ ନିୟନ୍ତ୍ରଣ ଦିବସ : ________
(iii) ମୋଟ ଜଳର 97.5 ଭାଗ : ସମୁଦ୍ରଜଳ :: ମୋଟ ଜଳର 2.5 ଭାଗ : ________
(iv) ପୃଥ‌ିବୀ : ଜଳଗ୍ରହ :: ମହାଶୂନ୍ୟ : ________
Solution:
(i) ଜଳସ୍ତର ନିମ୍ନକରଣ,
(ii) ଅକ୍ଟୋବର 18 ତାରିଖ,
(iii) ମଧୁର ଜଳ,
(iv) ନୀଳଗ୍ରହ

III. ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(i) ନିମ୍ନୋକ୍ତ ବାକ୍ୟରୁ କେଉଁଟି ଜଳାଭାବ ପାଇଁ ଦାୟୀ ନୁହେଁ ?
(କ) ଶିଳ୍ପର ଦ୍ରୁତବୃଦ୍ଧି
(ଖ) କନଫଖ୍ୟା ଦ୍ୱବି
(ଗ) ଅଧ୍ବକ ବୃଷ୍ଟିପାତ
(ଘ) ଜଲଣପର ପରିଚାଳନା

(ii) ପୃଥ‌ିବୀର ଦୀର୍ଘତମ ନଦୀବନ୍ଧଟି କେଉଁ ନଦୀ ଉପରେ ତିଆରି କରାଯାଇଛି ?
(କ) ବ୍ରାହ୍ମଣୀ
(ଖ) ମହାନଦା
(ଗ) ନାଗାରଲା
(ଘ) ତୈତରଣୀ

(iii) ମେଘ ଜଳର କେଉଁ ଅବସ୍ଥା ?
(କ) କଠିନ
(ଖ) ତଳେ
(ଗ) ଗ୍ୟାପାସ
(ଘ) କେଉଁଟି ନୁହେଁ

(iv) ପୃଥ‌ିବୀକୁ କେଉଁ ଗ୍ରହର ଆଖ୍ୟା ଦିଆଯାଇଛି ?
(କ) ଜଳଗ୍ରହ
(ଖ) ନୀଳଗ୍ରହ
(ଗ) ଲୋକପ୍ରତ ଗ୍ରହ
(ଘ) ଣାତଳଗ୍ରହ

(v) ପୃଥ‌ିବୀର ଦୀର୍ଘତମ ନଦୀବନ୍ଧଟି କିଏ ?
(କ) ବାଲିମେଳା
(ଖ) ହାରାକୁଦ
(ଗ) ଲଦ୍ରାବତୀ
(ଘ) କୋଲାର

(vi) ଅଦରକାରୀ ଜଳ ମୃତ୍ତିକାରେ ଥ‌ିବା ଛିଦ୍ର ଦେଇ ମାଧ୍ୟାକର୍ଷଣ ଯୋଗୁଁ ତଳକୁ ପ୍ରବେଶ କରିବା ପ୍ରକ୍ରିୟାକୁ କ’ଣ କହନ୍ତି ?
(କ) ପାଦନ
(ଖ) ପରିସ୍ରବଣ
(ଗ) ଅନ୍ତଃ ପରିସ୍ରବଣ
(ଘ) ଭବିପାଦନ

(vii) କେଉଁଟି ପୃଥବୀର ସମୁଦାୟ ଜଳପାଇଁ ଉଦ୍ଦିଷ୍ଟ ?
(କ) ନଦୀ ଓ ହ୍ରଦରେ ଜଳର ପରିମାଣ ନିର୍ଦ୍ଦିଷ୍ଟ ମାତ୍ରା ଅଟେ ।
(ଖ) ରୁପଲ କାଳର ପ୍ରିରିମାଣ ନିଦିଶ ଅଟେ |
(ଗ) ସମୁଦ୍ର ଓ ମହାସାଗରରେ ଜଳର ପରିମାଣ ସ୍ଥିର ଅଟେ ।
(ଘ) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ସ୍ଥିର ।
Solution:
(i) ଅଧ୍ବକ ବୃଷ୍ଟିପାତ
(ii) ମହାନଦୀ
(v) ହୀରାକୁଦ
(iii) ଗ୍ୟାସୀୟ
(iv) ଜଳଗ୍ରହ
(vi) ଅନ୍ତଃ ପରିସ୍ରବଣ
(vii) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ସ୍ଥିର ।

IV. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ସମଗ୍ର ପୃଥ‌ିବୀ ପୃଷ୍ଠର ଶତକଡ଼ା ୨୧ ଭାଗ ଜଳାବୃତ୍ତ ।
(ii) ପୃଥ‌ିବୀରେ ହ୍ରଦ ଓ ନଦୀଜଳର ପରିମାଣଠାରୁ ଭୂତଳଜଳର ପରିମାଣ କମ୍ ।
(iii) ଗ୍ରାମାଞ୍ଚଳରେ ରହୁଥିବା ଲୋକମାନେ ଜଳ ଅଭାବ ଭୋଗ କରିଥା’ନ୍ତି ।
(iv) ଜଳସେଚନ ପାଇଁ ନଦୀ ହିଁ ଏକମାତ୍ର ଉତ୍ସ ଅଟେ ।
(v) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ମଧ୍ଯରୁ ଲବଣାକ୍ତ ଜଳ ଅତିକମ୍ ।
Solution:
(i) ସମଗ୍ର ପୃଥ‌ିବୀ ପୃଷ୍ଠର ଶତକଡ଼ା ୭୧ ଭାଗ ଜଳାବୃତ୍ତ ।
(ii) ପୃଥ‌ିବୀରେ ହ୍ରଦ ଓ ନଦୀଜଳର ପରିମାଣଠାରୁ ଭୂତଳଜଳର ପରିମାଣ ଅଧିକ ।
(iii) ସହରାଞ୍ଚଳରେ ରହୁଥିବା ଲୋକମାନେ ଜଳ ଅଭାବ ଭୋଗ କରିଥା’ନ୍ତି ।
(iv) ଜଳସେଚନ ପାଇଁ ବର୍ଷାଜଳ, ନଦୀଜଳ, ପୋଖରୀଜଳ ଇତ୍ୟାଦି ଗୋଟିଏ ଗୋଟିଏ ଉତ୍ସ ଅଟେ ।
(v) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ମଧ୍ୟରୁ ଲବଣାକ୍ତ ଜଳ ବେଶି ।

V. ‘କ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦର ମେଳନ କର ।

VI. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ‘ବିଶ୍ବ ଜଳ ଦିବସ’ କେବେ ପାଳିତ ହୁଏ ?
(ii) ଆମ ପୃଥ‌ିବୀକୁ ଜଳଗ୍ରହ କାହିଁକି କୁହାଯାଏ ?
(iii) ଜଣେ ବ୍ୟକ୍ତିର ଦୈନିକ କେତେ ଲିଟର ଜଳ ଆବଶ୍ୟକ ?
(iv) ମହାଶୂନ୍ୟରୁ ପୃଥ‌ିବୀ ନୀଳ କାହିଁକି ଦେଖାଯାଏ ?
(v) ବିଶ୍ଵ ଜଳବର୍ଷ କେବେ ଓ କାହିଁକି ପାଳନ ହୋଇଥିଲା ?
(vi) ପୃଥ‌ିବୀରେ ମୋଟ ଜଳର ପରିମାଣ କେତେ ?
(vii) ପୃଥ‌ିବୀର ମୋଟ ଲୁଣି ସମୁଦ୍ରଜଳର ପରିମାଣ କେତେ ଶତାଂଶ ?
(viii)ପୃଥ‌ିବୀର ମୋଟ ମଧୁର ଜଳର ପରିମାଣ କେତେ ଶତାଂଶ ?
(ix) ଓଡ଼ିଶାର କେଉଁ ଜଳ ପ୍ରକଳ୍ପଟି ସର୍ବୋତ୍ତମ ଓ ବିଖ୍ୟାତ ?
(x) ପୃଥ‌ିବୀର ବୃହତ୍ତମ ନଦୀବନ୍ଧ କିଏ ଓ ଏହାର ଲମ୍ବ କେତେ ?
Solution:
(i) ‘ବିଶ୍ବ ଜଳ ଦିବସ’ ମାର୍ଚ୍ଚ 22 ତାରିଖରେ ପାଳିତ ହୁଏ ।
(ii) ଆମ ପୃଥ‌ିବୀର ଶତକଡ଼ା 71 ଭାଗ ଜଳ । ତେଣୁ ଆମ ପୃଥ‌ିବୀକୁ ଜଳଗ୍ରହ କୁହାଯାଏ ।
(iii) ଜଣେ ବ୍ୟକ୍ତିର ଦୈନିକ 50 ଲିଟର ଜଳ ଆବଶ୍ୟକ ।
(iv) ପୃଥ‌ିବୀରେ ବହୁ ପରିମାଣର ଜଳର ସମ୍ଭାର ଯୋଗୁଁ ମହାଶୂନ୍ୟରୁ ପୃଥ‌ିବୀ ନୀଳ ଦେଖାଯାଏ ।
(v) ବିଶ୍ୱ ଜଳ ବର୍ଷ 2003 ମସିହାରେ ମଧୁର ଜଳ ସମ୍ବନ୍ଧରେ ସଚେତନତା ସୃଷ୍ଟି ପାଇଁ ପାଳନ ହୋଇଥିଲା ।
(vi) ପୃଥ‌ିବୀରେ ମୋଟ ଜଳର ପରିମାଣ 140 କୋଟି ଘନ କିଲୋମିଟର ।
(vii) ପୃଥ‌ିବୀର ମୋଟ ଲୁଣି ସମୁଦ୍ରଜଳର ପରିମାଣ 97.5 ଶତାଂଶ ଅଟେ ।
(viii)ପୃଥ‌ିବୀର ମୋଟ ମଧୁର ଜଳ ପରିମାଣ 2.5 ଶତାଂଶ ଅଟେ ।
(ix) ଓଡ଼ିଶାର ହୀରାକୁଦ ନଦୀବନ୍ଧ ଜଳ ପ୍ରକଳ୍ପଟି ସର୍ବୋତ୍ତମ ଓ ବିଖ୍ୟାତ ।
(x) ହୀରାକୁଦ ପୃଥ‌ିବୀର ବୃହତ୍ତମ ନଦୀବନ୍ଧ ଓ ଏହାର ଲମ୍ବ 25 କି.ମି. ।

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 16 ଜଙ୍ଗଲ ସମ୍ପଦ Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 16 ଜଙ୍ଗଲ ସମ୍ପଦ

Question 1.
ଜଙ୍ଗଲ ହିଁ ଜୀବଜଗତ ପାଇଁ ଅମ୍ଳଜାନ ଯୋଗାଉଥ‌ିବା ‘ପ୍ରାକୃତିକ କାରଖାନା’ – ବୁଝାଅ ।
Solution:
(i)
ଭାବେ ସବୁଜ ଉଦ୍ଭିଦ ଉପରେ ନିର୍ଭର କରିଥାଉ ।
(ii) ସବୁଜ ଉଭିଦ ବାୟୁମଣ୍ଡଳରୁ ଅଙ୍ଗାରକାମ୍ଳ ଓ ମୃଭିକାରୁ ଜଳ ସଂଗ୍ରହ କରି ସବୁଜକଣାଦ୍ୱାରା ସୂର୍ଯ୍ୟାଲୋକ ଉଭିଦ ଅମ୍ଳଜାନ ଛାଡ଼ିଥାଏ, ଯାହାକି ପ୍ରତ୍ୟେକ ସଜୀବର ଶ୍ଵାସକ୍ରିୟା ପାଇଁ ନିହାତି ଜରୁରୀ ।
(iii) ସବୁଜ ଉଦ୍ଭଦ ହିଁ ବାୟୁମଣ୍ଡଳରେ ଅଙ୍ଗାରକାମ୍ଳ ଗ୍ୟାସ ପରିମାଣକୁ ନିୟନ୍ତ୍ରଣ କରି ଜୀବଜଗତକୁ ଅମ୍ଳଜାନ ଯୋଗାଇଥାଏ ।
(iv) ଜଙ୍ଗଲରେ ଥ‌ିବା ଉଭିଦମାନେ ହିଁ ଏହାର ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥା’ନ୍ତି । ଏହାକୁ ଜୀବଜଗତ ପାଇଁ ଅମ୍ଳଜାନ ଯୋଗାଉଥ‌ିବା ‘‘ପ୍ରାକୃତିକ କାରଖାନା’’ କୁହାଯାଏ ।

Question 2.
ନବୀକରଣ ଯୋଗ୍ୟ ଓ ନବୀକରଣ ଅଯୋଗ୍ୟ ସମ୍ପଦ କାହାକୁ କୁହାଯାଏ, ଉଦାହରଣ ସହ ବୁଝାଅ ।
Solution:
(i) ଯେଉଁ ପ୍ରାକୃତିକ ସମ୍ପଦକୁ ନଷ୍ଟ କରିଦେଲେ ପୁନର୍ବାର ନୂତନ ଭାବେ ସୃଷ୍ଟି ହୋଇପାରୁଥିବ କିମ୍ବା ଅନବରତ ବ୍ୟବହାର କରୁଥିଲେ ମଧ୍ୟ ସରୁ ନଥ‌ିବ ସେହି ସମ୍ପଦକୁ ନବୀକରଣ ଯୋଗ୍ୟ ସମ୍ପଦ କୁହାଯାଏ |
(ii) ଜଙ୍ଗଲ ଜାତ ପଦାର୍ଥ, ପ୍ରାଣୀଜାତ ପଦାର୍ଥ, କୃଷିଜାତ ଦ୍ରବ୍ୟ, ଜଳ, ବାୟୁ, ମୃରିକା ଆଦି ନବୀକରଣଯୋଗ୍ୟ ସମ୍ପଦ ।
ନବାକରଣ ଅଯୋଗ୍ୟ ସମଦ –
(i) ଯେଉଁ ପ୍ରାକୃତିକ ସମ୍ପଦଗୁଡ଼ିକ ଅନବରତ ବ୍ୟବହାରଦ୍ଵାରା ସରିଗଲେ, ସେଗୁଡ଼ିକର ପୁନଃ ଭରଣ ସମ୍ଭବ ହୁଏ ନାହିଁ ବା ଆଉ ମିଳେ ନାହିଁ ସେଗୁଡ଼ିକୁ ନବୀକରଣ ଅଯୋଗ୍ୟ ସମ୍ପଦ କୁହାଯାଏ ।
(ii) କୋଇଲା, ଖଣିଜତୈଳ, ଧାତୁପିଣ୍ଡ ଆଦି ନବୀକରଣ ଅଯୋଗ୍ୟ ସମ୍ପଦ ।

Question 3.
“‘ପ୍ରାକୃତିକ ଭାରସାମ୍ୟ’’ର ଅର୍ଥ କ’ଣ ? ଉଦାହରଣ ସହ ବୁଝାଅ ।
(i) ଜୀବମଣ୍ଡଳର ପ୍ରତ୍ୟେକ ଜୀବ ଅନ୍ୟ ଜୀବଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ । ସେହିପରି ପରିବେଶ ମଧ୍ୟ ଜୀବ ଉପରେ ପ୍ରଭାବ ପକାଇଥାଏ । ତେଣୁ ଜୀବ ଓ ପରିବେଶ ଉଭୟ ଉଭୟଙ୍କର ଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ ।
(ii) ଏହା ଫଳରେ ଜୀବ ଓ ତା’ର ପରିବେଶର ଭୌତିକ, ଜୈବିକ ତଥା ଅଜୈବିକ ପାରିପାର୍ଶ୍ବକ କାରକମାନଙ୍କ ମଧ୍ୟରେ ସର୍ବଦା ଏକ ପାରସ୍ପରିକ କ୍ରିୟା ଚାଲୁଥିବାରୁ ପରିବେଶରେ ଏକ ଭାରସାମ୍ୟ ସମ୍ଭବ ହେଉଛି ।
ଭଦାହରଣ –
(i) ଯଦି ଜଙ୍ଗଲରେ ହରିଣଙ୍କ ସଂଖ୍ୟା ବିଢ଼ିଯିବ ତେବେ ସେମାନେ ସମସ୍ତ ତୃଣ ଖାଇଯିବେ । ଫଳରେ ତୃଣ ସବୁ ସରିଯିବ ଏବଂ ତୃଣଭୋଜୀ ପ୍ରାଣୀସବୁ ଖାଦ୍ୟ ନପାଇ ମୃତ୍ୟୁବରଣ କରିବେ । ଏହାପରେ ମାଂସାଶୀ ପ୍ରାଣୀମାନେ ଖାଦ୍ୟ ନପାଇ ମୃତ୍ୟୁବରଣ କରିବେ ।
(ii) ସୁତରାଂ ପରିସଂସ୍ଥାରୁ ତୃଣ ଲୋପ ପାଇଲେ ସମସ୍ତ ତୃଣଭୋଜୀ ଓ ମାଂସାଶୀ ପ୍ରାଣୀ ନିଶ୍ଚିହ୍ନ ହୋଇଯିବେ । କିନ୍ତୁ ତାହା ହେଉନାହିଁ । ଏହି ପ୍ରାକୃତିକ ପ୍ରକ୍ରିୟା ‘‘ ଖାଦ୍ୟଶୃଙ୍ଖଳ’’ ମାଧ୍ୟମରେ ଚାଲୁ ରହିଛି
(iii) ପ୍ରକୃତିର ଏହି ବିଚିତ୍ର ସ୍ୱ ନିୟନ୍ତ୍ରତ ଓ ସୁନିୟନ୍ତ୍ରିତ ବ୍ୟବସ୍ଥାକୁ ‘ପ୍ରକୃତିର ଭାରସାମ୍ୟ’’ ବା ‘ପରିବେଶ ସନ୍ତୁଳନ’’ କୁହାଯାଏ ।

Question 4.
ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ପ୍ରାକୃତିକ ସନ୍ତୁଳନକୁ ଦିପଯଅସ୍ତ୍ର କରିବାରେ ମ୍ଲଖ ଅଫ ବୀଣା – ବ୍ଲଖାଥ |
Solution:
ସଭ୍ୟତାର ଅଗ୍ରଗତି ଅନୁଯାୟୀ ମଣିଷ ଅନେକ ସମୟରେ ସ୍ୱେଚ୍ଛାଚାରୀଭାବେ ପୋଷକଚକ୍ର ଓ ହେଲା ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ।
ଜନସଂଖ୍ୟା ବୃଦ୍ଧି – ବର୍ତ୍ତମାନ ଏହାକୁ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ବୋଲି ନ କହି ଜନ ବିସ୍ଫୋରଣ କୁହାଯାଉଛି ।
(i) ଶିକ୍ଷାର ଅଭାବ ଓ ଆର୍ଥିକ ଅନଗ୍ରସରତା ଯୋଗୁଁ ଏହି ସମସ୍ୟା ଭୟାବହ ରୂପ ନେଇଛି ।
(ii) ଏହି ଜନସଂଖ୍ୟା ଗୁଣୋତ୍ତର ଅନୁକ୍ରମରେ ବଢ଼ିଚାଲିଛି । କିନ୍ତୁ କୃଷି କ୍ଷେତ୍ରରେ ଉନ୍ନତ କୌଶଳ ପ୍ରୟୋଗ ସତ୍ତ୍ଵେ ଖାଦ୍ୟ ଉତ୍ପାଦନ ଏହି କ୍ରମରେ ବଢ଼ୁନାହିଁ କିମ୍ବା ବଢ଼ିବା ମଧ୍ୟ ସମ୍ଭବ ନୁହେଁ ।
(iii) ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଫଳରେ ଖାଦ୍ୟ ଉତ୍ପାଦନ, ଜଙ୍ଗଲ ସମ୍ପଦ, ଭୂତଳ ଭଣ୍ଡାର, ଜଳ ସମ୍ପଦ, ବାୟୁ ମଣ୍ଡଳ, ସ୍ବାସ୍ଥ୍ୟ, ଶକ୍ତି ଉତ୍ପାଦନ ଆଦି କ୍ଷେତ୍ରରେ ସମସ୍ୟା ସୃଷ୍ଟି ହୋଇଛି । ଏହା ଫଳରେ ପରିବେଶ ବିଭିନ୍ନ ସଂକଟ ଦେଖା ଦେଉଛି ।

Question 5.
ଜଲଚକ୍ରର ନ।ପାରାତ ଚିତ୍ର ଦିଅ |
Solution:

Question 6.
ଅମ୍ଳଜାନ ଓ ଅଙ୍ଗାରକ ଚକ୍ରର ଏକ ନାମାଙ୍କିତ ଚିତ୍ର ଦିଅ ।
Solution:

Question 7.
ଜୀବାଣୁ ଓ କବକ ପରି ଅପଘଟକମାନେ ନ ଥିଲେ ଆମର କି ଅସୁବିଧା ହୁଅନ୍ତା, ଲେଖ ।
Solution:
(i) ବୀଜାଣୁ ଓ କବକ ପରି ମୃତୋପଜୀବୀ ଅଣୁଜୀବମାନେ ମୃତଜୀବ ଶରୀରକୁ ଅପଘଟିତ କରି ମାଟିରେ ମିଶାଇ ଜମାହୋଇ ପରିବେଶକୁ ଅପରିଷ୍କାର କରିବେ ଓ ଏହା ଆମର ବାସପୋଯୋଗୀ ହୋଇପାରିବ ନାହିଁ ।
(ii) ଅପଘଟକମାନେ ଅପଘଟନ ପ୍ରକ୍ରିୟାରେ ଉପାଦେୟ ପୋଷକଗୁଡ଼ିକୁ ପରିବେଶ ମଧ୍ୟକୁ ମୁକ୍ତ କରିଥା’ନ୍ତି । ଏଣୁ ଏହା ବ୍ୟାହତ ହେବ । ଫଳରେ ପରିବେଶର ଭାରସାମ୍ୟ ନଷ୍ଟ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ଏଥ‌ିରେ ଜୀବନଧାରଣ ଅସମ୍ଭବ ହେବ ।

Question 8.
କଲଲ ନଗର କୁପରିଣାମଗ୍ନତିକ ଲେଖା |
Solution:
ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଦୃଷ୍ଟିରୁ ମନୁଷ୍ୟ ତା’ର ବିଭିନ୍ନ ଆବଶ୍ୟକତା ଯଥା – ଖାଦ୍ୟ, ବାସଗୃହ, ରାସ୍ତାଘାଟ, କଳକାରଖାନା, ଜଳସେଚନ ଆଦି ସ୍ଥାପନ ପାଇଁ ଅବିରତ ଭାବେ ଜଙ୍ଗଲ ନଷ୍ଟ କରିଚାଲିଛି । ଏହାଦ୍ଵାରା ଜୀବଜଗତରେ ନାହିଁ ନ ଥ‌ିବା କ୍ଷତି ଘଟୁଛି ।
(i) ଜଙ୍ଗଲ କ୍ଷୟ ହେବାଦ୍ଵାରା ବନ୍ୟଜନ୍ତୁମାନଙ୍କର ପ୍ରାକୃତିକ ବାସସ୍ଥାନ ଧ୍ବସ୍ତବିଧ୍ବସ୍ତ ହେବା ଫଳରେ କେତେକ ପ୍ରାଣୀ ଜୀବମଣ୍ଡଳରୁ ସମ୍ପୂର୍ଣ୍ଣ ବିଲୁପ୍ତ ହୋଇଗଲେଣି ଓ ଆଉ କେତେକ ବିଲୋପ ହେବାକୁ ଲାଗିଲେଣି ।
(ii) କଲଂଲ ଶ୍ରୟଦ୍ଵାରା ମହିଳା ଶାସ୍ ଶଟ୍ମଛି | କଲଂଲ ଶ୍ରଯଦ୍ୱାରା ପୋଇଲ ଟାଧାପ୍ରାପ୍ତ ହେବା ପରେ ପଟିଙ୍ଗ ସ୍ଥାନ ଖାଦ୍ୟଶୃଙ୍ଗଳ ବ୍ୟାହତ ହେଉଛି ।

Question 9.
କଲଂଲକ୍ ବାଣ ନିଶିଦ ହୋଇଗଲେ ଜ’ଣ ହେବ |
Solution:
(i) ଜଙ୍ଗଲରୁ ବାଘ ନିଶ୍ଚିହ୍ନ ହୋଇଗଲେ ହରିଣପରି ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କ ସଂଖ୍ୟା ବଢ଼ିଯିବ, କାରଣ ତାଙ୍କୁ ମାରି ଖାଇବା ପାଇଁ ବାଘ ନଥ‌ିବେ ।
(ii) ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କ ସଂଖ୍ୟା ଅହେତୁକ ଭାବେ ବଢ଼ିଯିବାରୁ ସେମାନଙ୍କୁ ଖାଦ୍ୟ ମିଳିବ ନାହିଁ, ତୃଣ ଓ ଅନ୍ୟାନ୍ୟ ଉଭିଦ ସଂଖ୍ୟା ଦ୍ରୁତ ଗତିରେ ହ୍ରାସ ପାଇ ଜଙ୍ଗଲ ଏକ ଟାଙ୍ଗରା ଭୂଇଁରେ ପରିଣତ ହେବ ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ବାୟୁମଣ୍ଡଳରେ ଅଙ୍ଗାରକାମ୍ଳର ପରିମାଣ ହେଲା _______ |
(ii) ଗୁଜରାଟର ଗିର୍ ଅଭୟାରଣ୍ୟ _______ ପାଇଁ ଭାରତ ପ୍ରସିଦ୍ଧ ।
(iii) _______ ଠାରେ ସାମୁଦ୍ରିକ କଇଁଛମାନଙ୍କ ପାଇଁ ଆଶ୍ରୟସ୍ଥଳୀ ସ୍ଥାପନ କରାଯାଇଛି ।
(iv) ହିମାଳୟର ଜଙ୍ଗଲରେ _______ ଦେଖାଯାଆନ୍ତି ।
(v) ପୁରୀ ସମୁଦ୍ର କୂଳରେ _______ ଗଛର ବଣ ଥିବାର ଦେଖାଯାଏ ।
Solution:
(i) 0.04%,
(ii) ପିଦ୍ର୍-ପ୍ରକଳ୍ପ,
(iii) ଭିତର କନିକା,
(iv) ଚମରୀଗାଈ,
(v) ଝାଉଁ

II. ବାମପାର୍ଶ୍ବର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଦକ୍ଷିଣପାର୍ଶ୍ବର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଖାଇଁ : : ଗୁଜରାଟର ଗିର୍ ଜଙ୍ଗଲ :: ଚମରୀ ଗାଈ : _______
(ii) ଜାତୀୟ ଉଦ୍ୟାନ : 73 :: ଅଭୟାରଣ୍ୟ : _______
(iii) ଶିମିଳିପାଳ : ସଂରକ୍ଷିତ ଜୀବମଣ୍ଡଳ :: ଭିତର କନିକା :: _______
(iv) ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ : ଚିଲିକା :: ଜାତୀୟ ଉଦ୍ୟାନ : _______
(v) ମୃତ୍ତିକା : ପ୍ରାକୃତିକ ସମ୍ପଦ :: ଜଙ୍ଗଲ : _______
Solution:
(i) ହିମାଳୟର ଜଙ୍ଗଲ,
(ii) 416,
(iii) ଜାତୀୟ ଉଦ୍ୟାନ,
(iv) ଭିତର କନିକା,
(v) ପ୍ରାକୃତିକ କାରଖାନା

III. ପ୍ରତି ପ୍ରଶ୍ନର ନିମ୍ନରେ ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ଦିଆଯାଇଛି । ସେଥୁମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(କ) ଚାଉଳ, ଡାଲି ଆଦି
(i) ନବୀକରଣ – ଯୋଗ୍ୟ ସମ୍ପଦ
(ii) ନବୀକରଣ – ଅଯୋଗ୍ୟ ସମ୍ପଦ
(iii) ପୁନଃଚକ୍ରଣ – ଖାଦ୍ୟ ସମ୍ପଦ
(iv) ପୁନଃଚକ୍ରଣ – ଅଯୋଗ୍ୟ ସମ୍ପଦ
Solution:
(i) ନବୀକରଣ – ଯୋଗ୍ୟ ସମ୍ପଦ

(ଖ) ବୀଜାଣୁମାନେ ହେଲେ
(i) ଉତ୍ପାଦକ
(ii) ଭକ୍ଷକ
(iii) ଅପଘଟକ
(iv) ପୋଷକ
Solution:
(iii) ଅପଘଟକ

(ଗ) ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଯେଉଁ କ୍ରମରେ ବଢ଼ିଚାଲିଛି ତାହା ହେଲା
(i) ଗୁଣୋତ୍ତର ଅନୁକ୍ରମ
(ii) ସମାନ୍ତର ଅନୁକ୍ରମ
(iv) ଗାଣିତିକ ଅନୁକ୍ରମ
(iii) ଜ୍ୟାମିତିକ ଅନୁକ୍ରମ
Solution:
(i) ଗୁଣୋତ୍ତର ଅନୁକ୍ରମ

(ଣ) କଳାହାରଖାନାଦ୍ଵାରା ଯେଉ ପ୍ରହଗଣ ତତିଚାଲିଛି ତାହା ହେଲା –
(i) ବାୟୁ
(ii) ଜଳ
(iii) ମୁଭିକା
(iv) ସମଗ୍ର ପରିବେଶ
Solution:
(iv) ସମଗ୍ର ପରିବେଶ

(ଙ) ଜୀବମଣ୍ଡଳରେ ଯେଉଁ ଗ୍ୟାସ୍ ଦିନକୁ ଦିନ ବଢ଼ିଚାଲିଛି ତା’ ହେଲା –
(କ) ନଳାକରଣ – ଯୋଗ୍ୟ ସମବ
(ଖ) ଆପଣକ
(ଗ) ଗୁଣୋତ୍ତର ଅନୁକ୍ରମ
(ପ) ସମଗ୍ର ପରିବେଶ
(ଙ) ଆପଣକ
Solution:
(ଖ) ଆପଣକ

IV. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ଜଙ୍ଗଲ, ବାୟୁ ଓ ଜଳ ସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(ii) ମାଳ ଅଞ୍ଚଳରେ ଥିବା ଜଙ୍ଗଲରେ ଆମ୍ବ, ଖଜୁରୀ ଅଧ‌ିକ ପରିମାଣରେ ଦେଖାଯାଏ ।
(iii) ‘ବନ୍ୟ ଜୀବନ ସୁରକ୍ଷା ଆଇନ’ ୧୯୭୨ ମସିହାରେ ସଂଶୋଧନ କରାଯାଇଛି ।
(iv) ଆମ ରାଜ୍ୟର ଚିଲିକା ହ୍ରଦକୁ ଏକ ସଂରକ୍ଷିତ ଜୀବମଣ୍ଡଳ ରୂପେ ମାନ୍ୟତା ଦିଆଯାଇଛି ।
(v) ଜଙ୍ଗଲ ସୁରକ୍ଷା ପାଇଁ ଦେଶରେ ୧୨ଟି ଜାତୀୟ ଉଦ୍ୟାନ ସଂସ୍ଥା ରହିଛି ।
Solution:
(i) ଜଙ୍ଗଲ, ବାୟୁ ଓ ଜଳ ଅସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(ii) ମାଳ ଅଞ୍ଚଳରେ ଥିବା ଜଙ୍ଗଲରେ ଶାଳ, ପିଆଶାଳ ଓ ମହୁଲ ଗଛ ଅଧ୍ଵ ପରିମାଣରେ ଦେଖାଯାଏ ।
(iii) ‘ବନ୍ୟ ଜୀବନ ସୁରକ୍ଷା ଆଇନ’ ୧୯୯୧ ମସିହାରେ ସଂଶୋଧନ କରାଯାଇଛି ।
(iv) ଆମ ରାଜ୍ୟର ଚିଲିକା ହ୍ରଦକୁ ଏକ ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ ରୂପେ ମାନ୍ୟତା ଦିଆଯାଇଛି ।
(v) ଜୀବମଣ୍ଡଳ ସଂରକ୍ଷିତ ପାଇଁ ଦେଶରେ ୧୨ଟି ଜାତୀୟ ଉଦ୍ୟାନ ସଂସ୍ଥା ରହିଛି ।

V. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ବାୟୁମଣ୍ଡଳର ତାପମାତ୍ରା ସହିତ କାହାର ସମ୍ପର୍କ ଅଛି ?
(ii) ପ୍ରାକୃତିକ ସମ୍ପଦ କ’ଣ ?
(iii) ପ୍ରାକୃତିକ ସମ୍ପଦ କେତେ ପ୍ରକାର ଓ କ’ଣ କ’ଣ ?
(iv) କେତେଗୁଡ଼ିଏ ପ୍ରାକୃତିକ ସମ୍ପଦର ନାମ ଲେଖ ।
(v) ଅପଘଟନ କ’ଣ ?
(vi) ଭାରତ ସ୍ବାଧୀନ ହେବା ସମୟରେ ଭାରତର କେତେ ଅଂଶରେ ଜଙ୍ଗଲ ଥିଲା ?
(vii) ଅପଘଟକ କାହାକୁ କହନ୍ତି ?
(viii)ଓଡ଼ିଶାର କେଉଁଠି ସଂରକ୍ଷିତ ଜୈବମଣ୍ଡଳ ଅଛି ?
(ix) ଓଡ଼ିଶାର କେଉଁଠି ବ୍ୟାଘ୍ର ସଂରକ୍ଷଣ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହୋଇଛି
(x) ଓଡ଼ିଶାର କେଉଁଠି ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ ଅଛି ?
(xi) ଅଙ୍ଗାରକାମ୍ଳର ମାତ୍ରା କାହିଁକି ବଢୁଛି ?
Solution:
(i) ବାୟୁମଣ୍ଡଳର ତାପମାତ୍ରା ସହିତ ଅଙ୍ଗାରକାମ୍ଳର ସମ୍ପର୍କ ଅଛି ।
(ii) ପ୍ରକୃତିରୁ ମିଳୁଥିବା ମାଟି, ପାଣି, ପବନ, ଜଙ୍ଗଲ ପ୍ରଭୃତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(iii) ପ୍ରାକୃତିକ ସମ୍ପଦ ଦୁଇ ପ୍ରକାରର – (a) ସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ (b) ଅସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ
(iv) ମାଟି, ପାଣି, ପବନ, ଜଙ୍ଗଲ, ପଶୁପକ୍ଷୀ, ଖଣିଜ ସମ୍ପଦ ସୂର୍ଯ୍ୟାଲୋକ ପ୍ରଭୃତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(v) ମୃତ ଜୀବଶରୀର କେତେକ ଅଣୁଜୀବମାନଙ୍କ ଦ୍ଵାରା ପଚି ମାଟିରେ ମିଶିବା ପ୍ରକ୍ରିୟାକୁ ଅପଘଟନ କୁହାଯାଏ ।
(vi) ଭାରତ ସ୍ବାଧୀନ ହେବା ସମୟରେ ଭାରତର 45 ଶତାଂଶ ଅଂଶରେ ଜଙ୍ଗଲ ଥିଲା ।
(vii) ଯେଉଁ ମୃତୋପଜୀବୀ ଅଣୁଜୀବମାନଙ୍କଦ୍ଵାରା ମୃତଜୀବ ଶରୀର ପଚି ମାଟିରେ ମିଶିଯାଏ, ସେମାନଙ୍କୁ ଅପଘଟକ କୁହାଯାଏ ।
(vii) ଓଡ଼ିଶାର ଶିମିଳିପାଳଠାରେ ସଂରକ୍ଷିତ ଜୈବମଣ୍ଡଳ ଅଛି ।
(ix) ଓଡ଼ିଶାର ଶିମିଳିପାଳଠାରେ ବ୍ୟାଘ୍ର ସଂରକ୍ଷଣ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ।
(x) ଓଡ଼ିଶାର ଚିଲିକାରେ ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ ଅଛି ।
(xi) ଜନସଂଖ୍ୟା ବୃଦ୍ଧି, ଅଧ୍ଵ ଗାଡ଼ିମଟର ଓ କଳକାରଖାନା ଯୋଗୁଁ ଅଙ୍ଗାରକାମ୍ଳର ମାତ୍ରା ବଢୁଛି ।

Odisha State Board BSE Odisha 6th Class Science Important Questions Chapter 8 ପରିସ୍ଥାନ Important Questions and Answers.

BSE Odisha Class 6 Science Important Questions Chapter 8 ପରିସ୍ଥାନ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
କେଉଁ କେଉଁ ଅଙ୍ଗ ଜଳଜ ପ୍ରାଣୀମାନଙ୍କ ଉପଯୋଜନରେ ସହାୟକ ହୋଇଥାଏ ?
ଉ –
ଜଳଜ ପ୍ରାଣୀମାନଙ୍କର ଶରୀର, ଆକୃତି, ଗାଲି, ଲାଞ୍ଜର ଉପସ୍ଥିତି, କାତି କିମ୍ବା ଲାଳଯୁକ୍ତ ଶରୀର, ପରଦାଯୁକ୍ତ ପକ୍ଷ ଆଦି ଉପଯୋଜନରେ ସହାୟକ ହୋଇଥାଏ ।

Question 2.
ସ୍ଥଳଚର ଓ ଜଳଚର ପ୍ରାଣୀମାନେ କେଉଁ କେଉଁ ପରିସ୍ଥାନରେ ରହିଥା’ନ୍ତି ?
ଉ –

• ସ୍ଥଳଚର ପ୍ରାଣୀମାନେ ଜଙ୍ଗଲ, ମରୁଭୂମି, ତୃଣଭୂମି, ପାର୍ବତ୍ୟାଞ୍ଚଳ ଆଦିରେ ରହିଥା’ନ୍ତି ।
• ଜଳଚର ପ୍ରାଣୀମାନେ ନଦୀ, ହ୍ରଦ, ପୋଖରୀ, ସମୁଦ୍ର ଇତ୍ୟାଦିରେ ରହିଥା’ନ୍ତି ।

Question 3.
ଉପଯୋଜନ କ’ଣ ଏକ ଉଦାହରଣ ଦେଇ ଲେଖ ।
ଉ –

• ପରିବେଶ ଓ ପରିବେଶର ପରିବର୍ତ୍ତନ ସହ ତାଳଦେଇ ପ୍ରତ୍ୟେକ ଜୀବର ଗାଠନିକ ଓ କ୍ରିୟାତ୍ମକ ପରିବର୍ତ୍ତନକୁ ଉପଯୋଜନ କୁହାଯାଏ ।
• ଓଟର ପାଦଗୁଡ଼ିକ ମରୁବାଲିରେ ଚାଲିବାପାଇଁ ଓ ତା’ର ପିଠି ଉପରେ ଥ‌ିବା କୁଜଟି ଖାଦ୍ୟାଭାବ ସମୟରେ ସହାୟତା କରେ । ଓଟର ଏହି ପରିବର୍ତ୍ତନଗୁଡ଼ିକ ଦ୍ଵାରା ସେ ମରୁଭୂମିରେ ବଞ୍ଚରେ ।

Question 4.
ପରିସ୍ଥାନ ପରିବର୍ତ୍ତନ ହେଲେ କ’ଣ ଅସୁବିଧା ହେବ ?
ଉ –

• ପରିସ୍ଥାନ ପରିବର୍ତ୍ତନ ହେଲେ ପରିବେଶରେ ସନ୍ତୁଳନ ବିପର୍ଯ୍ୟସ୍ତ ହୋଇଯିବ ।
• ଏହାର କୁ ପ୍ରଭାବ ସମଗ୍ର ଜୀବଜଗତ ଉପରେ ପଡ଼ିବ । ଫଳରେ କେତେକ ଜାତିର ଜୀବ ନିଶ୍ଚିହ୍ନ ହେବାର

Question 5.
ପରିବେଶରେ ଅପଘଟକର ଭୂମିକା କ’ଣ ?
ଉ –

• କେତେକ ଅଣୁଜୀବ ଉଭିଦ ଓ ପ୍ରାଣୀଙ୍କ ଶରୀରରୁ ଖାଦ୍ୟ ସଂଗ୍ରହ କରିଥାଆନ୍ତି, ସେମାନଙ୍କୁ ଅପଘଟକ କୁହାଯାଏ ।
• ଅନ୍ୟ କେତେକ ଜୀବ ଯଥା ବୀଜାଣୁ, କବକ ଇତ୍ୟାଦି ଉଭିଦ ଓ ପ୍ରାଣୀଙ୍କ ମୃତ ଶରୀରରୁ ଖାଦ୍ୟ ସଂଗ୍ରହ କରି ସେମାନେ କେତେକ ଆବଶ୍ୟକ ଉପାଦାନ ଯଥା – ଯବକ୍ଷାରଜାନ ପରିବେଶକୁ ଛାଡ଼ନ୍ତି ।

Question 6.
ପରିସ୍ଥାନ ଅନୁସାରେ ପ୍ରାଣୀମାନଙ୍କୁ କେତେ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି, ତାହା କ’ଣ କ’ଣ ?
ଉ –

• ପରିସ୍ଥାନ ଅନୁସାରେ ପ୍ରାଣୀମାନଙ୍କୁ ତିନିଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି ।
• ସେଗୁଡ଼ିକ ହେଲା – ସ୍ଥଳଚର, ଜଳଚର ଓ ବାୟବୀୟ ।

ଦୀର୍ଘ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ଉଭିଦମାନଙ୍କର ପରିସ୍ଥାନ ବିଷୟରେ ସଂକ୍ଷେପରେ ଲେଖ ।
ଉ –

• ପରିସ୍ଥାନକୁ ନେଇ ଉଭିଦମାନଙ୍କୁ ତିନି ଭାଗରେ ବିଭକ୍ତ କରାଯାଏ; ଯଥା – ମରୁଜ, ଆର୍ଦ୍ରଭୂମିଜ ଓ ଜଳଜ ।
• ଜଳାଭାବ ଅଞ୍ଚଳରେ ବଢ଼ିପାରୁଥିବା ଉଭିଦଗୁଡ଼ିକ ମରୁଜ; ଯଥା – ସପ୍ତଫେଣୀ, ନାଗଫେଣୀ ।
• ଜଳାଭାବ ଓ ଜଳାଧିକ୍ୟ ନଥ‌ିବା ଅଞ୍ଚଳର ଉଭିଦଗୁଡ଼ିକ ଆର୍ଦ୍ରଭୂମିଜ; ଯଥା – ଧାନ, ଆମ୍ବ ।
• ସମ୍ପୂର୍ଣ୍ଣ ଜଳ ଭିତରେ ବା ଜଳାଧ୍ୟାକ୍ୟ ଅଞ୍ଚଳର ଉଭିଦଗୁଡ଼ିକ ଜଳଜ; ଯଥା – ପଦ୍ମ, ଚିଙ୍ଗୁଡ଼ିଆ ଦଳ ।

Question 2.
ଉଭିଦମାନଙ୍କର ପରିସ୍ଥାନ ବିଷୟରେ ସଂକ୍ଷେପରେ ଲେଖ ।
ଉ –

• ପରିସ୍ଥାନ ଅନୁସାରେ ଉଭିଦମାନଙ୍କୁ ତିନିଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – (i) ମରୁଜ, (ii) ଆର୍ଦ୍ରଭୂମିଜ ଓ (iii) ଜଳଜ ।
• ଜଳାଭାବ ବା ଜଳାଧ୍ୟାକ୍ୟ ନଥ‌ିବା ଅଞ୍ଚଳର ଉଭିଦକୁ ଆଦ୍ରଭୂମିଜ ଉଭିଦ କୁହାଯାଏ ।
• ଜଳାଧ୍ୟାକ୍ୟ ଅଞ୍ଚଳରେ ଥ‌ିବା ଉଭିଦକୁ ଜଳଜ ଉଭିଦ କୁହାଯାଏ ।

Question 3.
ପରିସ୍ଥାନ କ’ଣ ? ଉପାଦାନ ଅନୁସାରେ ପରିସ୍ଥାନର ଜୀବମାନଙ୍କୁ କେତେ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି ଉପଯୋଜନ ଲେଖ ।
ଉ –

• ପରିସ୍ଥାନ – ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କର ବାସସ୍ଥାନ ଓ ତା’ର ଚତୁଃପାର୍ଶ୍ୱକୁ ପରିସ୍ଥାନ କୁହାଯାଏ ।
• ଉପାଦାନ ଅନୁସାରେ ଯେ କୈଣସି ପରିସ୍ଥାନର ଜୀବମାନଙ୍କୁ ତିନିଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – (କ) ଉତ୍ପାଦକ, (ଖ) ଭକ୍ଷକ ଓ (ଗ) ଅପଘଟକ ।
  • (କ) ଉଦ୍ଭିଦ ନିଜପାଇଁ ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରିବାସହ ଅନ୍ୟ ସବୁ ଜୀବପାଇଁ ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରେ । ତେଣୁ ସମସ୍ତ ଉଭିଦକୁ ଉତ୍ପାଦକ କୁହାଯାଏ ।
  • (ଖ) ଉଦ୍ଭଦଦ୍ୱାରା ପ୍ରସ୍ତୁତ ଖାଦ୍ୟ ପ୍ରତ୍ୟକ୍ଷରେ ବା ପରୋକ୍ଷରେ ପ୍ରାଣୀମାନେ ଖାଇଥା’ନ୍ତି । ତେଣୁ ସମସ୍ତ ପ୍ରାଣୀଙ୍କୁ ଭକ୍ଷକ କୁହାଯାଏ ।
  • (ଗ) ବୀଜାଣୁ, କବକ ଆଦି ଜୀବ ଉଦ୍ଭଦ ଓ ପ୍ରାଣୀଙ୍କ ଶରୀରରୁ ଖାଦ୍ୟ ସଂଗ୍ରହ କରିଥା’ନ୍ତି । ତେଣୁ ବୀଜାଣୁ, କବକକୁ ଅପଘଟକ କୁହାଯାଏ ।

Question 4.
ଉପଯୋଜନ କ’ଣ ? ଏହା ଅନୁସାରେ ମରୁଭୂମିରେ ରହୁଥ‌ିବା ଜୀବମାନଙ୍କ ସମ୍ପର୍କରେ ଲେଖ ।
ଉ –

• ପରିବେଶ ପରିବର୍ତ୍ତନ ସହ ତାଳଦେଇ ପ୍ରତ୍ୟେକ ଜୀବର ଗାଠନିକ ଓ କ୍ରିୟାତ୍ମକ ପରିବର୍ତ୍ତନକୁ ଉପଯୋଜନ କୁହାଯାଏ ।
• ମରୁଭୂମିରେ ରହୁଥିବା ସପ୍ତଫେଣୀ ଓ ସିଜୁର ପାଣିର ଆବଶ୍ୟକତା କମ୍ ଥାଏ । ସପ୍ତଫେଣୀ ଓ ସିଜୁରେ ପତ୍ର ରୂପାନ୍ତରିତ ହୋଇ କଣ୍ଟା ଓ ମୋଟା ପତ୍ର ହୁଏ, ଫଳରେ ବାଷ୍ପୀମୋଚନ ବିଶେଷ ଭାବରେ ହୋଇପାରେ ନାହିଁ ।
• ଓଟର ପାଦଗୁଡ଼ିକ ମରୁବାଲିରେ ଚାଲିବାକୁ ସହାୟକ ହୋଇଥାଏ । ଓଟର ପିଠିରେ ଥ‌ିବା କୁଜଟି ଖାଦ୍ୟାଭାବ ସମୟରେ ସହାୟତା କରେ ।
• ମରୁଭୂମିରେ ରହୁଥ‌ିବା ସାପ, ମୂଷା ଆଦି ଜୀବମାନେ ଦିନରେ ବାଲି ଭିତରେ ରହିପାରନ୍ତି ।

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶୋଉର

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଉଦ୍ଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କ ବାସସ୍ଥାନ ଓ ତା’ର ଚତୁଃପାର୍ଶ୍ଵକୁ ………….. କହନ୍ତି ।
(ଖ) ଲତାଜାତୀୟ ଉଦ୍ଭିଦର କାଣ୍ଡ ଆଗରେ …………….. ଥାଏ ।
(ଗ) ଅପଘଟକମାନେ ପରିବେଶକୁ ……………… ଛାଡ଼ନ୍ତି ।
(ଘ) ଉଦ୍ଭଦକୁ ……………… କୁହାଯାଏ ।
(ଙ) ପରିସ୍ଥାନ ହେଉଛି …………. ର ଏକ ଅଂଶବିଶେଷ ।
(ଚ) ବାୟବୀୟ ପ୍ରାଣୀ କହିଲେ ମୁଖ୍ୟତଃ ……………… ଙ୍କୁ ବୁଝାଏ ।
(ଛ) ଓଟର …………….. ତାକୁ ଖାଦ୍ୟାଭାବ ସମୟରେ ସାହାଯ୍ୟ କରେ ।
ଉ –
(କ) ପରିସ୍ଥାନ
(ଖ) ଆକର୍ଷୀ
(ଗ) ଯବକ୍ଷାରଜାନ
(ଘ) ଉତ୍ପାଦକ
(ଙ) ପରିବେଶ
(ଚ) ପକ୍ଷୀମାନ
(ଛ) ଓଟର

Question 2.
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନତଳେ ଦିଆଯାଇଥିବା ଚାରିଗୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

(କ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଏକ ଜୈବିକ କାରକ ?
(i) କବକ
(ii) ଆଲୋକ
(iii) ଜଳ
(iv) ତାପ
ଉ –
(i) କବକ

(ଖ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଏକ ଅଜୈବିକ କାରକ ?
(i) ବୀଜାଣୁ
(ii) କବକ
(iii) ମୁଭିକା
(iv) ଉଭିଦ
ଉ –
(iii) ମୁଭିକା

(ଗ) ସପ୍ତଫେଣୀ ଉଦ୍ଭଦର ପତ୍ରଗୁଡ଼ିକ କେଉଁଥରେ ରୂପାନ୍ତରିତ ହୋଇଥାଏ ?
(i) କାଣ୍ଡ
(ii) ଫୁଲ
(iii) କଣ୍ଟା
(iv) ମୂଳ
ଉ –
(iii) କଣ୍ଟା

(ଘ) ମାଛ କେଉଁଥିରେ ଶ୍ଵାସକ୍ରିୟା କରେ ?
(i) ଡେଣା
(ii) ନାକ
(iii) ପାଟି
(iv) ଗାଲି
ଉ –
(iv) ଗାଲି

(ଙ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଏକ ଅପଘଟକ ?
(i) ବୀଜାଣୁ
(ii) ଉଭିଦ
(iii) ପିମ୍ପୁଡ଼ି
(iv) ମାଙ୍କଡ଼
ଉ –
(i) ବୀଜାଣୁ

Question 3.
ପ୍ରଥମ ଯୋଡ଼ା ଶବ୍ଦଦ୍ଵୟର ସମ୍ପର୍କକୁ ଦେଖୁ ଦ୍ଵିତୀୟ ଯୋଡ଼ାର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ପ୍ରାଣୀ : ଭକ୍ଷକ :: ଉଭିଦ : ………………. ।
(ଖ) ପ୍ରାଣୀ : ଜୈବିକ କାରକ :: ତାପ : ………………. ।
(ଗ) ଅପଘଟକ : କବକ :: ବାୟବୀୟ ପ୍ରାଣୀ : ………………. ।
(ଘ) ଖଜୁରୀ : ମରୁଜ :: ସପ୍ତଫେଣୀ : ………………. ।
(ଙ) ମଣିଷ : ଫୁସ୍‌ଫୁସ୍‌ :: ମାଛ : ………………. ।
ଉ –
(କ) ଉତ୍ପାଦକ
(ଖ) ଅଜୈବିକ କାରକ
(ଗ) ପକ୍ଷୀ
(ଘ) ମରୁଜ
(ଙ) ଗାଲି

Question 4.
ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(କ) କଙ୍କଡ଼ା ପାଟି ସାହାଯ୍ୟରେ ଶ୍ଵାସକ୍ରିୟା କରେ ।
(ଖ) ଖାଦ୍ୟ ସଞ୍ଚୟ ପାଇଁ ସପ୍ତଫେଣୀ ଗଛର କାଣ୍ଡ ମାଂସଳ ହୋଇଥାଏ ।
(ଗ) ଓଟର କଢ ତାପ ସଞ୍ଚୟ କରିଥାଏ ।
(ଙ) ବାୟବୀୟ ପ୍ରାଣୀ ମୁଖ୍ୟତଃ ପଶୁଙ୍କୁ ବୁଝାଏ ।
ଉ –
(କ) କଙ୍କଡ଼ା ଗାଲି ସାହାଯ୍ୟରେ ଶ୍ଵାସକ୍ରିୟା କରେ ।
(ଖ) ଜଳ ସଞ୍ଚୟ ପାଇଁ ସପ୍ତଫେଣୀ ଗଛର କାଣ୍ଡ ମାଂସଳ ହୋଇଥାଏ ।
(ଗ) ଓଟର କୁଜ ଜଳ ଓ ଖାଦ୍ୟ ସଞ୍ଚୟ କରିଥାଏ ।
(ଘ) କଖାରୁ ଗଛ ଆକର୍ଷୀ ସହାୟତାରେ ଉପରକୁ ଉଠେ ।
(ଙ) ବାୟବୀୟ ପ୍ରାଣୀ ମୁଖ୍ୟତଃ ପକ୍ଷୀଙ୍କୁ ବୁଝାଏ ।

Question 5.
‘କ’ ସ୍ତମ୍ଭର ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସଂପର୍କ ବାଛ ।

ଉ –

Odisha State Board BSE Odisha 8th Class Geography Important Questions Chapter 4 ଶିଳ୍ପ Important Questions and Answers.

BE Odisha Class 8 Geography Important Questions Chapter 4 ଶିଳ୍ପ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ପିଟ୍ସବର୍ଗ ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ରର ଭୌଗୋଳିକ ଗୁରୁତ୍ଵ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର ।
Answer:

• ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଇସ୍ପାତନଗରୀ ପିନ୍ସବର୍ଗର ଅବସ୍ଥିତି ଇସ୍ପାତ ଶିଳ୍ପ ପାଇଁ ଅନୁକୂଳ ।
• ଏଠାରେ କୋଇଲା ସମେତ କେତେକ କଞ୍ଚାମାଲ ଆସିଥାଏ ।
• 150 କି.ମି. ଦୂରରେ ଥିବା ମିନେସୋଟାରୁ ଲୁହାପଥର ଟ୍ରେନ୍‌ଯୋଗେ ଶସ୍ତାରେ ପରିବହନ ହୋଇ ଅଣାଯାଏ ।
• ଶସ୍ତା ପରିବହନ ପାଇଁ ବୃହତ୍ ହ୍ରହ ଜଳପଥ ମଧ୍ଯ ସୁବିଧା ଯୋଗାଇଦିଏ ।
• ଓହିଓ, ମନୋଗାହେଲା ଏବଂ ଆଲେଘେନି ନଦୀରୁ ପ୍ରଚୁର ଜଳ ମିଳିଥାଏ । ତେଣୁ ପିଟ୍‌ସବର୍ଗଠାରେ ବଡ଼ ବଡ଼ ଇସ୍ପାତ ଶିଳ୍ପ ଗଢ଼ିଉଠିଛି ।

Question 2.
ଓସାକା କାର୍ପାସ ଶିଳ୍ପର ଗୁରୁତ୍ଵ ବୁଝାଅ ।
Answer:

• ‘ଜାପାନର ମାଞ୍ଚେଷ୍ଟର’ ଓସାକା ଉପସାଗର କୂଳରେ ଅବସ୍ଥିତ ଏକ ବନ୍ଦର ଓ ପରିବହନ କେନ୍ଦ୍ର ।
• ସାକାକୁ ଘେରିରହିଥିବା ସୁବିସ୍ତୃତ ସମତଳଭୂମି ଶିଳ୍ପ ସ୍ଥାପନ ପାଇଁ ସୁବିଧାଜନକ ।
• ଏଠାକାର ଆର୍ଦ୍ର ଜଳବାୟୁ, ପରିବହନ ସୁବିଧା, କଞ୍ଚାମାଲ ପାଇଁ ଆବଶ୍ୟକ ରାସାୟନିକ ଦ୍ରବ୍ୟ ନିକଟବର୍ତ୍ତୀ ଅଞ୍ଚଳରୁ ସହଜରେ ସଂଗ୍ରହ ଏବଂ ଜାପାନ ଭଳି ଜନବହୁଳ ରାଷ୍ଟ୍ରରେ କାର୍ପାସବତ୍ସର ଚାହିଦା ଶିଳ୍ପର ପ୍ରସାରରେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଛି ।
• ଓଡ଼ୋ ନଦୀରୁ ଶିଳ୍ପପାଇଁ ପ୍ରଚୁର ଜଳ ମିଳିବାସହ ବନ୍ଦର ସୁବିଧା ଥୁବାରୁ ତୁଳା ଆମଦାନି କରିବା ଓ ବସ୍ତ୍ର ରପ୍ତାନି କରିବା ସହଜ ହୋଇପାରିଛି ।
• ଏଠାକାର ବସ୍ତ୍ର ଉତ୍ତମ ମାନର ତଥା ଶସ୍ତା ହୋଇଥିବାରୁ ଏହାର ଭଲ ବଜାର ଚାହିଦା ରହିଛି ।

Question 3.
କେଉଁ କେଉଁ ଭୌଗୋଳିକ ଅବସ୍ଥା ଉପରେ ନିର୍ଭର କରି ଅହମ୍ମଦାବାଦରେ କାର୍ପାସ ଶିଳ୍ପ ଗଢ଼ିଉଠିଛି ?
Answer:

• ସାବରମତୀ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ଅହମ୍ମଦାବାଦ ଗୁଜରାଟ ରାଜ୍ୟରେ ଅବସ୍ଥିତ । ଏହି ରାଜ୍ୟ କପାଚାଷ ପାଇଁ ଭାରତରେ ଖ୍ୟାତିଲାଭ କରିଛି । ଏହା କଞ୍ଚାମାଲ ଯୋଗାଣକୁ ନିଶ୍ଚିତ କରିଛି ।
• ଅହମ୍ମଦାବାଦର ଦକ୍ଷିଣରେ ମୁମ୍ବାଇ ଏବଂ ପଶ୍ଚିମରେ କାଣ୍ଡଲା ବନ୍ଦର ଅବସ୍ଥିତ । ତେଣୁ ବନ୍ଦର ମାଧ୍ୟମରେ ଯନ୍ତ୍ରପାତି ଆମଦାନି ଓ ରପ୍ତାନିର ସୁବିଧା ମିଳୁଛି ।
• ନଦୀକୂଳରେ ଅବସ୍ଥିତ ହୋଇଥିବାରୁ କାରଖାନା ଏବଂ ଶିଳ୍ପାଞ୍ଚଳ ପାଇଁ ମଧୁର ଜଳ ମିଳିଥାଏ ।
• ଏଠାରେ କୁଶଳୀ ଓ ଅର୍ଥକୁଶଳୀ ଶ୍ରମିକଙ୍କର ଅଭାବ ନାହିଁ ।
• ଅହମ୍ମଦାବାଦ ସହରଟି ଏକ ବୃହତ୍ ବାଣିଜ୍ୟ ଏବଂ ପରିବହନ କେନ୍ଦ୍ର । ତେଣୁ ବିଭିନ୍ନ ଅଞ୍ଚଳକୁ ବସ୍ତ୍ର, କପଡ଼ା ପଠାଇବା ସମ୍ଭବ ହୋଇପାରୁଛି ।

Question 4.
ଜାମସେଦପୁରଠାରେ ଥିବା ଟାଟା ଲୌହଇସ୍ପାତ ଶିଳ୍ପର ବିକାଶ ଉପରେ ଏକ ବିବରଣୀ ଲେଖ ।
Answer:

• ଭୌଗୋଳିକ ଦୃଷ୍ଟିରୁ ଜାମ୍‌ସେପୁର ହିଁ ଦେଶର ସବୁଠାରୁ ସୁବିଧାଜନକ ସ୍ଥିତିରେ ଥ‌ିବା ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ର ।
• ଅବସ୍ଥିତି : ବେଙ୍ଗଲ୍-ନାଗପୁର ରେଳପଥ ବର୍ତ୍ତମାନର ହାୱଡ଼ା- ମୁମ୍ବାଇ ରେଳପଥର କାଳିମାଟି ଷ୍ଟେସନଠାରୁ 32 କି.ମି. ଦୂରରେ ଅବସ୍ଥିତ ।
• କଞ୍ଚାମାଲ ଉପଲବ୍‌ଧର ସୁବିଧା : ନିକଟସ୍ଥ ଝରିଆରୁ କୋଇଲା, ଓଡ଼ିଶା ଓ ଛତିଶଗଡ଼ରୁ ଲୁହାପଥର, ଚୂନପଥର, ଡୋଲୋମାଇଟ୍ ଓ ମାଙ୍ଗାନିଜ ସୁବିଧାରେ ଉପଲବ୍‌ଧ । ହୋଇଥାଏ ।
• ଜଳ ସୁଲଭତା : ଖରକାଇ ଓ ସୁବର୍ଣ୍ଣରେଖା ନଦୀଦ୍ୱୟରୁ ପ୍ରଚୁର ଜଳ କାରଖାନାକୁ ଯୋଗାଇ ଦିଆଯାଏ ।
• ବଜାର ସୁବିଧା : ଅନତିଦୂରରେ ଅବସ୍ଥିତ କୋଲକାତା ନଗରୀ ବିଶାଳ ବଜାର ପାଇଁ ସୁବିଧା ରହିଛି । ଏତଦ୍‌ବ୍ୟତୀତ ସରକାରୀ ପ୍ରୋତ୍ସାହନ ଯୋଗୁ ପୁଞ୍ଜିର ସୁବ୍ୟବସ୍ଥା ରହିଛି ।

Question 5.
ଶିଳ୍ପ ପ୍ରତିଷ୍ଠାନରେ ଦୁର୍ଘଟଣା ହ୍ରାସ ନିମନ୍ତେ କି କି ପଦକ୍ଷେପ ନିଆଯାଇପାରିବ ଦର୍ଶାଅ ।
Answer:

• ଶିଳ୍ପାଞ୍ଚଳଗୁଡ଼ିକୁ ଘନ ଜନବସତିପୂର୍ଣ୍ଣ ଅଞ୍ଚଳଠାରୁ ଦୂରରେ ସ୍ଥାପନ କରିବା ଉଚିତ ।
• କଳକାରଖାନା ନିକଟରେ ବସବାସ କରୁଥିବା ଲୋକମାନଙ୍କୁ ଶିଳ୍ପରେ ବ୍ୟବହୃତ ବା ଉତ୍ପାଦିତ ବିଷାକ୍ତ ପଦାର୍ଥର ସଂରକ୍ଷଣ ତଥା ଦୁର୍ଘଟଣା ଘଟିଲେ ଏହାର ସମ୍ଭାବ୍ୟ ପ୍ରଭାବ ସମ୍ବନ୍ଧରେ ସଚେତନ କରାଇବା ଆବଶ୍ୟକ ।
• ଅଗ୍ନି ସତର୍କତା ବା ଅଗ୍ନି ନିର୍ବାପନ ବ୍ୟବସ୍ଥାରେ ଉନ୍ନତିକରଣ କରାଯିବା ଆବଶ୍ୟକ ।
• ବିଷାକ୍ତ ପଦାର୍ଥଗୁଡ଼ିକର ଭଣ୍ଡାର ସୀମିତ ହେବା ଉଚିତ ।
• ଶିଳ୍ପାନୁଷ୍ଠାନମାନଙ୍କରେ ହଠାତ୍ ପ୍ରଦୂଷଣ ହେଲେ ସଙ୍ଗେ ସଙ୍ଗେ ତା’ର ଅପସାରଣ ବ୍ୟବସ୍ଥାରେ ଉନ୍ନତିକରଣ ଆବଶ୍ୟକ ।

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ସଂକ୍ଷେପରେ ଉତ୍ତର ଲେଖ ।

Question 1.
କୁଟୀରଶିଳ୍ପ କ’ଣ ? ଉଦାହରଣସହ ଲେଖ ।
Answer:

• ପରିବାର ସଦସ୍ୟଙ୍କ ସହାୟତାରେ ସ୍ଥାନୀୟ କଞ୍ଚାମାଲ ଓ ସରଳ ଉପକରଣ ସାହାଯ୍ୟରେ ବିଭିନ୍ନ ବସ୍ତୁ ଉତ୍ପାଦନକରଣ କରିବା ପ୍ରକ୍ରିୟାକୁ କୁଟୀରଶିଳ୍ପ କୁହାଯାଏ ।
• ଏଥରେ ବଂଶାନୁକ୍ରମିକ କାରିଗରୀ ଜ୍ଞାନର ଉପଯୋଗ ହୋଇଥାଏ। ଉଦାହରଣ ପିପିଲିର ଚାନ୍ଦୁଆ କାମ ଏବଂ କଟକର ତାରକସୀ କାମ ଓ ନୀଳଗିରିର ପଥର ବାସନ କାମ ଇତ୍ୟାଦି ।

Question 2.
ଅହମ୍ମଦାବାଦରେ ପ୍ରଚୁର କପା ଉତ୍ପାଦନର କାରଣ କ’ଣ ?
Answer:

• ଅହମ୍ମଦାବାଦ ଚତୁଃପାର୍ଶ୍ଵ ଅଞ୍ଚଳ କପାଚାଷ ଅଞ୍ଚଳଭାବେ ପ୍ରସିଦ୍ଧ ।
• କାରଣ ଏହାର ଆର୍ଦ୍ର ଜଳବାୟୁ ଓ କୃଷ୍ଣକାର୍ପାସ ମୃତ୍ତିକା ଏହି ଚାଷ ପାଇଁ ଅନୁକୂଳ ପରିବେଶ ଯୋଗାଇଥାଏ ।

Question 3.
ଓସାକା କାର୍ପାସ ଶିଳ୍ପକୁ କଞ୍ଚାମାଲ ଯୋଗାଉଥିବା ଦେଶଗୁଡ଼ିକର ନାମ ପ୍ରକାଶ କର ।
Answer:
ଓସାକା କାର୍ପାସ ଶିଳ୍ପକୁ କଞ୍ଚାମାଲ ଯୋଗାଉଥିବା ଦେଶଗୁଡ଼ିକ ଇଜିପ୍‌ଟ, ଭାରତ, ଚୀନ୍ ଓ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ।

Question 4.
ଇସ୍ପାତର ବିଶେଷତ୍ଵ କ’ଣ ଓ~ଏଥୁରୁ ମିଶ୍ରଧାତୁ କିପରି କରାଯାଏ ?
Answer:

• ଇସ୍ପାତ ବେଶ୍ ଶକ୍ତ । ଏହାକୁ ସହଜରେ ବିଭିନ୍ନ ଆକୃତି ଦିଆଯାଇପାରେ, କଟାଯାଇପାରେ ଏବଂ ତାରରେ ପରିଣତ କରି ହୁଏ
• ଇସ୍ପାତ ସହିତ ଆଲୁମିନିୟମ୍, ନିକେଲ ଓ ତମ୍ବା ଆଦି କମ୍ମାତ୍ରାରେ ମିଶାଇ ମିଶ୍ରଧାତୁ ପ୍ରସ୍ତୁତ କରାଯାଏ ।

Question 5.
ଲୌହଇସ୍ପାତ ଶିଳ୍ପର ନିବେଶ ଉଲ୍ଲେଖ କର ।
Answer:
କଞ୍ଚାମାଲଭାବେ ଲୁହାପଥର, କୋଇଲା ଓ ଚୂନପଥର, ମାନବ, ଶ୍ରମ, ପୁଞ୍ଜି, ଭୂମି ତଥା ଅନ୍ୟାନ୍ୟ ଆଧାରିକ ସଂରଚନା ଖର୍ଚ୍ଚ ନିବେଶ କରାଯାଏ ।

Question 6.
ଚାରିଗୋଟି କୃଷିଭିତ୍ତିକ ଶିଳ୍ପର ଉଦାହରଣ ଦିଅ ।
Answer:
ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, ଖାଇବା ତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ, ଦୁଗ୍ଧଜାତ ପଦାର୍ଥ ପ୍ରସ୍ତୁତ ।

Question 7.
ଦୁଇଟି ଖଣିଜଭିଭିକ ଶିଳ୍ପ ଓ ଦୁଇଟି ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପର ନାମ ଲେଖ ।
Answer:

• ଖଣିଜଭିଭିକ ଶିଳ୍ପ- ଲୌହଇସ୍ପାତ ଓ ଆଲୁମିନିୟମ୍‌ ଶିଳ୍ପ ।
• ସମୁଦ୍ରଭିତିକ ଶିଳ୍ପ – ସାମୁଦ୍ରିକ ଖାଦ୍ୟ ଉଦ୍ୟୋଗ ଓ ମାଛତେଲ ଉଦ୍ୟୋଗ ।

Question 8.
ଉପଭୋକ୍ତା ଦ୍ରବ୍ୟ ଉତ୍ପାଦନକାରୀ ଶିଳ୍ପର ଉଦାହରଣ ଦିଅ ।
Answer:
ଉପଭୋକ୍ତା ଦ୍ରବ୍ୟ ଉତ୍ପାଦନକାରୀ ଶିଳ୍ପଗୁଡ଼ିକ ହେଲେ ଖାଇବାତେଲ, ଚା’, ସାବୁନ, ପାଉଁରୁଟି, ବିସ୍କୁଟ, ରେଡ଼ିଓ, ଟେଲିଭିଜନ୍ ଶିଳ୍ପ ଇତ୍ୟାଦି ।

Question 9.
ତିନୋଟି କ୍ଷୁଦ୍ର ଶିଳ୍ପ ଓ ତିନୋଟି କୁଟୀର ଶିଳ୍ପର ଉଦାହରଣ ଦିଅ ।
Answer:

• କ୍ଷୁଦ୍ରଶିଳ୍ପ – ଘଣ୍ଟା, ରେଡ଼ିଓ, ଟିଭି ଶିଳ୍ପ ।
• କୁଟୀରଶିଳ୍ପ – ଝୁଡ଼ିବୁଣା, ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି ଓ ଶିଙ୍ଗକାମ ଇତ୍ୟାଦି ।

Question 10.
ଏକ କାର୍ପାସ ଶିଳ୍ପର ନିବେଶ ଓ ପ୍ରକ୍ରିୟାକରଣ ଦର୍ଶାଅ ।
Answer:

• ନିବେଶ – ତୁଳା, ମାନବଶ୍ରମ, ଯନ୍ତ୍ରପାତି, ପରିବହନ ଖର୍ଚ୍ଚ,
• ପ୍ରକ୍ରିୟାକରଣ – ତୁଳାଭିଣା, ସୂତାକଟା, ଲୁଗାବୁଣା, ରଙ୍ଗଲଗା, ଛାପାକାର୍ଯ୍ୟ ଓ ସିଲାଇ ।

Question 11.
ଦୁଇଟି ଶିଳ୍ପ ଦୁର୍ଘଟଣାର ନାମ ଲେଖ । ଏହି ଦୁର୍ଘଟଣାଗ୍ରସ୍ତ ପ୍ରପୀଡ଼ିତ ଲୋକଙ୍କ ଦୁର୍ଦ୍ଦଶାଗୁଡ଼ିକ ଲେଖ ।
Answer:

• ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣା ଓ ଚୀନ୍‌ର ଚୋଙ୍ଗିଙ୍ଗ୍ ଅନ୍ତର୍ଗତ ଗାଓକ୍ସିଆଓ ଗ୍ୟାସ୍ କୂପ ବିସ୍ଫୋରଣ ।
• ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣାଗ୍ରସ୍ତ ଲୋକ ଅନ୍ଧତ୍ବ, ପ୍ରତିରୋଧକାରୀ ଶକ୍ତିହୀନତା ଓ ବିଭିନ୍ନ ପେଟରୋଗରେ, ପୀଡ଼ିତ । ଗାଓକ୍ସିଆଓ ଗ୍ୟାସ୍ କୂପ ଦୁର୍ଘଟଣାଗ୍ରସ୍ତ ଲୋକମାନେ ଆଖୁ, ଚର୍ମ ଓ ଫୁସ୍‌ଫୁସ୍ ଜଳାପୋଡ଼ାରେ ପୀଡ଼ିତ ।

Question 12.
ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ କ’ଣ ? ଉଦାହରଣସହ ବୁଝାଅ ।
Answer:

• ନୂତନଭାବେ ଗଢ଼ିଉଠିଥିବା ଶିଳ୍ପକୁ ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ କୁହାଯାଏ ।
• ଉଦାହରଣସ୍ୱରୂପ- ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା, ସ୍ୱାସ୍ଥ୍ୟ ଓ ସ୍ଵାସ୍ଥ୍ୟସେବା, ଆତିଥ୍ୟ ଏବଂ ଶିକ୍ଷା ।

Question 13.
ମାଞ୍ଚେଷ୍ଟର କାହିଁକି ପ୍ରସିଦ୍ଧ ?
Answer:

• ମାଞ୍ଚେଷ୍ଟର ଇଂଲଣ୍ଡର ଏକ କାର୍ପାସ ଓ ବୟନ ଶିଳ୍ପର ପ୍ରଧାନ ସହର ।
• ଏଠାରେ ଶିଳ୍ପବିପ୍ଳବ ପରେ କଳତନ୍ତ ବୟନଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ହେଲା । ଭାରତରୁ କଞ୍ଚାମାଲ ରୂପେ ତୁଳା ଓ ଝୋଟ ଆମଦାନୀ କରାଯାଉଥିଲା ।

Question 14.
ଭାରତର ବେଙ୍ଗାଲୁରୁ ବ୍ୟତୀତ ଆଉ ଚାରିଗୋଟି ସୂଚନା ପ୍ରଯୁକ୍ତିବିଦ୍ୟା କେନ୍ଦ୍ରର ନାମ ଲେଖ ।
Answer:
ଭାରତର ଚାରିଗୋଟି ସୂଚନା ପ୍ରଯୁକ୍ତିବିଦ୍ୟା କେନ୍ଦ୍ରଗୁଡ଼ିକ ହେଲେ ଗୁଡ଼ଗାଓଁ, ପୁଣେ, ଭୁବନେଶ୍ବର ଓ ଥୁରୁ ଅନନ୍ତପୁରମ୍ ।

Question 15.
ଭାରତର ଚାରିଗୋଟି ଶିଳ୍ପାଞ୍ଚଳର ନାମ ଲେଖ ।
Answer:

• ଭାରତର ଚାରୋଟି ଶିଳ୍ପାଞ୍ଚଳର ନାମ ହେଲା-
• ମୁମ୍ବାଇ- ପୁଣେ ଶିଳ୍ପାଞ୍ଚଳ
• ବେଙ୍ଗାଲୁରୁ-ତାମିଲନାଡୁ ଅଞ୍ଚଳ
• ହୁଗୁଳି ଅଞ୍ଚଳ
• ଅହମ୍ମଦାବାଦ–ଭଦୋଦରା ଶିଳ୍ପାଞ୍ଚଳ ।

Question 16.
ଶିଳ୍ପ କହିଲେ କ’ଣ ବୁଝାଯାଏ ?
Answer:

• ଯେଉଁ ଅର୍ଥନୀତିକ କାର୍ଯ୍ୟକଳାପଦ୍ବାରା ନୂତନ ସାମଗ୍ରୀ ପ୍ରସ୍ତୁତକରିବା ସହ ଖଣିଜଦ୍ରବ୍ୟ ଉତ୍ତୋଳନ ତଥା ସେବା ଯୋଗାଇ ଦିଆଯାଏ ତାହାକୁ ଶିଳ୍ପ କୁହାଯାଏ ।
• ଉଦାହରଣସ୍ୱରୂପ ଲୌହଇସ୍ପାତ ଶିଳ୍ପରୁ ବିଭିନ୍ନ ଇସ୍ପାତ ସାମଗ୍ରୀ ପ୍ରସ୍ତୁତ କରାଯାଏ । କୋଇଲା ଖନନ ଶିଳ୍ପରେ କୋଇଲା ଉତ୍ପାଦନ କରାଯାଏ ।
• ପରିବହନ, ଯୋଗାଯୋଗ, ପର୍ଯ୍ୟଟନ ଆଦି ମଧ୍ଯ ସେବାରିରିକ ଶିଳ୍ପ ।

Question 17.
ଭାରତୀୟ ସୂଚନା ପ୍ରଯୁକ୍ତି ଶିଳ୍ପସଂସ୍ଥାର ନାମ ଲେଖ ।
Answer:
ଭାରତରେ ସୂଚନା ପ୍ରଯୁକ୍ତି ଶିଳ୍ପ ସଂସ୍ଥାର ନାମ ହେଲା – ଇନ୍‌ଫୋସିସ୍, ୱିପ୍ରୋ ଓ ସତ୍ୟମ୍ ।

Question 18.
ଗୋଟିଏ ଦେଶ ପାଇଁ ଶିଳ୍ପର ବିକାଶ କାହିଁକି ମହତ୍ତ୍ଵପୂର୍ଣ ? ଦୁଇଟି କାରଣ ଲେଖ ।
Answer:

• ଶିଳ୍ପ ପ୍ରତି ଦ୍ଵାରା ଲୋକ ମାନଙ୍କୁ କର୍ମସଂସ୍ଥାନ ମିଳିଥାଏ ।
• ଏହାଦ୍ୱାରା ବ୍ୟବସାୟ ବାଣିଜ୍ୟ କାରବାର ବୃଦ୍ଧିପାଏ ଏବଂ ଦେଶର ଆୟ ମଧ୍ୟ ବଢ଼େ ।
• ଜଣେ ଶିଳ୍ପ ଶ୍ରମିକ, ଜଣେ କୃଷି ଶ୍ରମିକଠାରୁ ଅଧିକ ମଜୁରି ପାଏ ।
• ଶିଳ୍ପାୟନ ଦେଶକୁ ଅର୍ଥନୀତି କ୍ଷେତ୍ରରେ ସମୃଦ୍ଧ କରେ ।

Question 19.
ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ପାଇଁ କେଉଁ କେଉଁ କାରଣଗୁଡ଼ିକ ମୁଖ୍ୟତଃ ଦାୟୀ ?
Answer:

• କଞ୍ଚାମାଲର ଉପଲବ୍ଧି
• ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ପାଇଁ ଆବଶ୍ୟକ ଜମି
• ଜଳ
• କୁଶଳୀ ଓ ଶସ୍ତା ଶ୍ରମିକ, ଶକ୍ତି, ପୁଞ୍ଜି, ପରିବହନ ଓ ବଜାର ଇତ୍ୟାଦି
• ଏତଦ୍‌ବ୍ୟତୀତ ସରକାରଙ୍କଦ୍ୱାରା ରିହାତି ଦରରେ ଉପରୋକ୍ତ ଆନୁଷଙ୍ଗିକ ବ୍ୟବସ୍ଥା ଯୋଗାଇଦେବା ଆବଶ୍ୟକ ।

Question 20.
କେଉଁ ଶିଳ୍ପକୁ ଆଧୁନିକ ଶିଳ୍ପର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ଏବଂ କାହିଁକି ?
Answer:

• ଲୌହ-ଇସ୍ପାତ ଶିଳ୍ପକୁ ଆଧୁନିକ ଶିଳ୍ପର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ।
• କାରଣ ଏହା ଏକ ମୌଳିକ ଶିଳ୍ପ । ଏହାର ଉତ୍ପାଦକୁ ଅନ୍ୟାନ୍ୟ ଶିଳ୍ପରେ କଞ୍ଚାମାଲ ରୂପେ ବ୍ୟବହାର କରାଯାଏ ।
• ଜଳଜାହାଜ, ରେଳଗାଡ଼ି, ଟ୍ରକ୍, ବସ୍, ଅଟୋ, ସାଇକେଲ ଆଦି ଯାନବାହନଗୁଡ଼ିକ ଲୌହ-ଇସ୍ପାତରେ ତିଆରି ।
• ଛୁଞ୍ଚଠାରୁ ଆରମ୍ଭ କରି ସେଫ୍‌ଟିପିନ୍ ପର୍ଯ୍ୟନ୍ତ ଅନେକ ଘରକରଣା ଜିନିଷ, ତୈଳଖଣି ଖନନ ପାଇଁ ଯନ୍ତ୍ରପାତି, ଚାଷକାର୍ଯ୍ୟ, ସୁଉଚ୍ଚ ଅଟ୍ଟାଳିକାରେ ବ୍ୟବହୃତ ଇସ୍ପାତ ଫ୍ରେମ୍ ଆଦି ଇସ୍ପାତରୁ ତିଆରି ।

ଭୌଗୋଳିକ କାରଣ ଦର୍ଶାଅ ।

Question 1.
ମୁମ୍ବାଇ ଭାରତର ଅନ୍ୟତମ ଆଧୁନିକ କାର୍ପାସ ବୟନଶିଳ୍ପ କେନ୍ଦ୍ର ରୂପେ ପରିଗଣିତ ।
Answer:
ମୁମ୍ବାଇର ଉଷ୍ଣ ଆର୍ଦ୍ର ଜଳବାୟୁ, ଯନ୍ତ୍ରପାତି ଆମଦାନୀ ପାଇଁ ବନ୍ଦର । ସୁବିଧା, କଞ୍ଚାମାଲର ସୁଲଭତା ଏବଂ କୁଶଳୀ ଶ୍ରମିକ ଆଦି ଏହାକୁ ଆଧୁନିକ କାର୍ପାସ ବୟନ ଶିଳ୍ପ କେନ୍ଦ୍ର ରୂପେ ପରିଣତ କରିବାରେ ସହାୟକ ହେଲା ।

Question 2.
ଲୌହଇସ୍ପାତ ଶିଳ୍ପର ବିକାଶ ହିଁ ଭାରତରେ ଶିଳ୍ପ ବିକାଶର ଦ୍ଵାର ଖୋଲିଦେଲା ।
Answer:

• ପ୍ରତ୍ୟେକ ଶିଳ୍ପାନୁଷ୍ଠାନ ସେମାନଙ୍କର ମୌଳିକ ଆଧାରିକ ସଂରଚନା ନିମନ୍ତେ ଲୌହଇସ୍ପାତ ଶିଳ୍ପ ଉପରେ ନିର୍ଭରଶୀଳ ।
• ଲୌହଇସ୍ପାତର ଶେଷ ଉତ୍ପାଦର୍‌ବେ ଲୁହା ବା ଇସ୍ପାତକୁ କଞ୍ଚାମାଲ ଭାବେ ଦ୍ଵିତୀୟକ ଉତ୍ପାଦନକାରୀ ସଂସ୍ଥା, ରୋଲିଂ ମିଲ୍ ଟ୍ରକ୍ ନିର୍ମାଣ, ମଟରଗାଡ଼ି ଯନ୍ତ୍ରାଂଶ, କୃଷି ଯନ୍ତ୍ରପାତି, ରେଳଧାରଣା, କଳକବଜା, ଟିଣଚଦର, କେବୁଲ ଓ ତାର ଉତ୍ପାଦନକାରୀ ଶିଳ୍ପସଂସ୍ଥାରେ ବ୍ୟବହାର କରାଯାଏ ।
• ତେଣୁ ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ରକୁ ଭିରି କରି ଭାରତରେ ଅନେକ ଶିଳ୍ପସଂସ୍ଥା ଗଢ଼ିଉଠିଛି ।

Question 3.
ଖଣିଜରିରିକ ଶିଳ୍ପଗୁଡ଼ିକୁ ମୌଳିକ ଶିଳ୍ପ କୁହାଯାଏ ।
Answer:

• ଖଣିଜରିରିକ ଶିଳ୍ପଗୁଡ଼ିକ ବିଭିନ୍ନ ଖଣିଜପଦାର୍ଥକୁ କଞ୍ଚାମାଲ ରୂପେ ବ୍ୟବହାର କରିଥା’ନ୍ତି । ଏଠାରୁ ପ୍ରସ୍ତୁତ ସାମଗ୍ରୀ ଅନ୍ୟାନ୍ୟ ଶିଳ୍ପରେ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହୃତ ହୁଏ । ଉଦାହରଣସ୍ୱରୂପ– ଲୌହଇସ୍ପାତ ଶିଳ୍ପରେ ଲୁହାପଥର କଞ୍ଚାମାଲ ଓ ଲୁହା ବା ଇସ୍ପାତ ଉତ୍ପାଦ ହୋଇଥାଏ ।
• ଲୁହା କଞ୍ଚାମାଲ ଭାବେ ଭାରୀ ଯନ୍ତ୍ରପାତି, ରେଳଡ଼ବା ନିର୍ମାଣ ତଥା ଜଳଜାହାଜ କାରଖାନା ଆଦିରେ ମୁଖ୍ୟ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହୃତ ହୁଏ ।

Question 4.
କାର୍ପାସ ବୟନ ଶିଳ୍ପ ପୃଥ‌ିବୀର ଏକ ପୁରାତନ ଶିଳ୍ପ
Answer:

• ଅଷ୍ଟାଦଶ ଶତାବ୍ଦୀରେ ସୂତା ଓ ହସ୍ତତନ୍ତଦ୍ୱାରା ବୟନଶିଳ୍ପର ବିକାଶ ଆରମ୍ଭ ହୋଇଥିଲା ।
• ଏହି ଶତାବ୍ଦୀରେ କଳତନ୍ତ୍ରଦ୍ଵାରା ଏହି ଶିଳ୍ପର ପ୍ରସାର ପ୍ରଥମେ ଗ୍ରେଟ୍‌ବ୍ରିଟେନ୍ ଓ ପରେ ଅନ୍ୟ ଅଞ୍ଚଳକୁ କଳତନ୍ତ୍ରର ପ୍ରସାର ଘଟିଲା, ତେଣୁ ଏହା ଏକ ପୁରାତନ ଶିଳ୍ପ ।

Question 5.
ଇସ୍ପାତ ଆଧୁନିକ ଶିଳ୍ପଜଗତର ମେରୁଦଣ୍ଡ ସଦୃଶ।
Answer:

• ଛୁଅ, ସେଫଟିପିଠାରୁ ଆରମ୍ଭ କରି ଜଳଜାହାଜ, ରେଳଗାଡ଼ି, ଟ୍ରକ୍, ବସ୍, ଅଟୋ, ସାଇକେଲ୍‌ ଆଦି ବିଭିନ୍ନ ଜିନିଷରେ ଇସ୍ପାତର ବ୍ୟବହାର ହୋଇଥାଏ।
• ଲୌହ-ଇସ୍ପାତର ବହୁଳ ବ୍ୟବହାର ଯୋଗୁ ଏହାକୁ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ।

ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

1. କୃଷିଭିତ୍ତିକ ଶିଳ୍ପ ଓ ଖଣିଳଭିଭିକ ଶିଳ୍ପ :
Answer:

2. ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପ ଓ ଜଙ୍ଗଲଭିତ୍ତିକ ଶିଳ୍ପ :
Answer:

3. କୁଟୀର ଶିଳ୍ପ ଓ କ୍ଷୁଦ୍ର ଶିଳ୍ପ :
Answer:

4. ପ୍ରାକୃତିକ ତନ୍ତୁ ଓ ମନୁଷ୍ୟକୃତ ତନ୍ତୁ :
Answer:

5. କ୍ଷୁଦ୍ର ଶିଳ୍ପ ଓ ବୃହତ୍ ଶିଳ :
Answer:

6. ବ୍ୟକ୍ତି ମାଲିକାନା ଓ ସରକାରୀ ମାଲିକାନା :
Answer:

7. ଦ୍ଵୈତ ମାଲିକାନା ଓ ସମବାୟ ଶିଳ୍ପ :
Answer:

ପରୀକ୍ଷା ଉପଯୋଗୀ ସମ୍ଭାବିତ ପ୍ରଶ୍ନୋତ୍ତର
ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନୋତ୍ତର

ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।1. ______ ରାଜ୍ୟ ସର୍ବପ୍ରଥମେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଆଇନ୍ ପ୍ରଣୟନ କରିଥିଲେ ।
Answer:
କର୍ଣାଟକ

2. ଆମେରିକାର ସିଲିକନ୍ ଉପତ୍ୟକା ______ ଉପତ୍ୟକାର ଏକ ଅଂଶ ।
Answer:
ଶାନ୍ତାକ୍କାରା

3. ଶାନ୍ତାକାରୀ ଉପତ୍ୟକା ______ ପର୍ବତ ସହ ସଂଲଗ୍ନ ।
Answer:
ରକି

4. ଓସାକାର ______ ଶିଳ୍ପ କଞ୍ଚାମାଲ ପାଇଁ ବାହାର ଦେଶ ଉପରେ ନିର୍ଭରଶୀଳ ।
Answer:
ବୟନ

5. କଳତନ୍ତ ପ୍ରଥମେ ______ ଦେଶରେ ପ୍ରସାରିତ ହୋଇଥିଲା ।
Answer:
ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍

6. ଲିନେନ୍ ______ ତନ୍ତୁ ଅଟେ ।
Answer:
ପ୍ରାକୃତିକ

7. ବୃହତ୍ ହ୍ରଦ ଅଞ୍ଚଳରୁ ______ସାହାଯ୍ୟରେ ଲୁହାପଥର ପିଟ୍ସବର୍ଗକୁ ଆସିଥାଏ।
Answer: ଟ୍ରନ୍‌

8. ପିଟସ୍‌ବର୍ଗଠାରୁ ମିନେସୋଟାର ଦୂରତା ______କି.ମି. ।
Answer:
୧୫୦୦

9. ରୋଲିଂ ମିଲ୍ ______ କାରଖାନା ସହ ସଂପୃକ୍ତ ।
Answer:
ଲୌହ-ଇସ୍ପାତ

10. ଜାମସେଦପୁର ଝାଡ଼ଖଣ୍ଡର ______ ଜିଲ୍ଲାରେ ଅବସ୍ଥିତ ।
Answer:
ସିଂହଭୂମି

ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

Question 1.
ପ୍ରାଥମିକ ଉତ୍ପାଦ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ପ୍ରକୃତିଦର ଜିନିଷଗୁଡ଼ିକ ପ୍ରତ୍ୟକ୍ଷ ଭାବରେ ବ୍ୟବହାର ହୋଇପାରେ ସେଗୁଡ଼ିକୁ ପ୍ରାଥମିକ ଉତ୍ପାଦ କୁହାଯାଏ।

Question 2.
ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ଆର୍ଥନୀତିକ କାର୍ଯ୍ୟକଳାପଦ୍ଵାରା ନୂତନ ସାମଗ୍ରୀ ପ୍ରସ୍ତୁତ କରିବା ସହ ଖଣିଜ ଦ୍ରବ୍ୟ ଉତ୍ତୋଳନ ତଥା ସେବା ଯୋଗାଇ ଦିଆଯାଏ, ତାହାକୁ ଶିଳ୍ପ କୁହାଯାଏ।

Question 3.
ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମୁଦ୍ରଭିଭିକ ଶିଳ୍ପରେ ସାଗର ତଥା ମହାସାଗରରୁ ଉପଲବ୍ଧ ବିଭିନ୍ନ ପଦାର୍ଥକୁ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହାର କରାଯାଏ। ସାମୁଦ୍ରିକ ଖାଦ୍ୟ ଉଦ୍ୟୋଗ ଏବଂ ମାଛତେଲ ଉଦ୍ୟୋଗ ଏହାର ଉଦାହରଣ।

Question 4.
କେଉଁ କାର୍ଯ୍ୟଗୁଡ଼ିକ କୁଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
Answer:
ଝୁଡ଼ିବୁଣା, ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି ଏବଂ ଅନ୍ୟାନ୍ୟ ହସ୍ତଶିଳ୍ପଗୁଡ଼ିକ କୁଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।

Question 5.
କେଉଁ କାର୍ଯ୍ୟଗୁଡ଼ିକ କ୍ଷୁଦ୍ରଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
Answer:
ଘଣ୍ଟା, ରେଡ଼ିଓ ଓ ଟିଭି କ୍ଷୁଦ୍ରଶିଳ୍ପର ଅନ୍ତର୍ଗତ।

Question 6.
ବ୍ୟକ୍ତି ମାଲିକାନା କାହାକୁ କୁହାଯାଏ ?
Answer:
କୌଣସି ବ୍ୟକ୍ତି ବା ଏକାଧ୍ଵକ ବ୍ୟକ୍ତିଙ୍କ ମିଳିତ ମାଲିକାନାରେ ଚାଲୁଥିବା ଶିଳ୍ପ ସଂସ୍ଥାଗୁଡ଼ିକ ବ୍ୟକ୍ତି ମାଲିକାନାଭୁକ୍ତ ଶିଳ୍ପସଂସ୍ଥା ଅଟେ । ଉଦାହରଣ ଟାଟା ଲୌହ-ଇସ୍ପାତ କାରଖାନା।

Question 7.
ସରକାରୀ ଶିଳ୍ପ କ’ଣ ?
Answer:
ସରକାରୀ ଶିଳ୍ପ ସଂସ୍ଥାଗୁଡ଼ିକର ମାଲିକାନା ଓ ପରିଚାଳନା ସରକାରଙ୍କ ଦ୍ଵାରା ହୋଇଥାଏ। ଉଦାହରଣ ହିନ୍ଦୁସ୍ଥାନ ଏରୋନଟିକ୍‌ସ୍ ଲିମିଟେଡ଼।

Question 8.
ସମବାୟ ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମବାୟ ଶିଳ୍ପ ସଂସ୍ଥାଗୁଡ଼ିକ କଞ୍ଚାମାଲ ଉତ୍ପାଦନକାରୀ ବା ଯୋଗାଣକାରୀ ଶ୍ରମିକ କିମ୍ବା ଉଭୟଙ୍କ ମାଲିକାନାରେ ପରିଚାଳିତ ହୋଇଥାଏ। ଯଥା ସମ୍ବଲପୁରୀ ବସ୍ତ୍ରଶିଳ୍ପ ଓ ଅମୁଲ ଦୁଗ୍ଧ ଉତ୍ପାଦନକାରୀ ସଂସ୍ଥା ।

Question 9.
ଶିଳ୍ପ ବ୍ୟବସ୍ଥା କାହାକୁ ନେଇ ଗଢ଼ା ହୋଇଥାଏ ?
Answer:
ଏକ ଶିଳ୍ପ ବ୍ୟବସ୍ଥା ନିବେଶ, ପ୍ରକ୍ରିୟାକରଣ ଓ ଉତ୍ପାଦକୁ ନେଇ ଗଢ଼ା ।

Question 10.
ନିବେଶ କାହାକୁ କୁହାଯାଏ ?
Answer:
ନିବେଶ କହିଲେ କଞ୍ଚାମାଲ, ଶ୍ରମିକ, ଭୂମି, ପରିବହନ, ଶକ୍ତି, ଅନ୍ୟାନ୍ୟ ଆଧାରିକ ସଂରଚନା ଓ ବିକାଶ ନିମନ୍ତେ ବିନିଯୁକ୍ତ ପୁଞ୍ଜିକୁ ବୁଝାଏ ।

Question 11.
ଆଧାରିକ ସଂରଚନା କାହାକୁ କୁହାଯାଏ ?
Answer:
ବିଦ୍ୟୁତ୍‌କରଣ, ଯୋଗାଯୋଗ, ସଡ଼କ ଓ ରେଳପଥ, ଶିକ୍ଷାନୁଷ୍ଠାନ, ଚିକିତ୍ସାଳୟ ଇତ୍ୟାଦି ବ୍ୟବସ୍ଥାକୁ ଆଧାରିକ ସଂରଚନା କୁହାଯାଏ।

Question 12.
ପ୍ରକ୍ରିୟାକରଣ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଶିଳ୍ପ ସଂସ୍ଥାରେ କଞ୍ଚାମାଲରୁ ଉତ୍ପାଦ ସୃଷ୍ଟି ହେବାପାଇଁ ଯେଉଁସବୁ କାର୍ଯ୍ୟପନ୍ଥା ଗ୍ରହଣ କରାଯାଏ, ତାକୁ ପ୍ରକ୍ରିୟାକରଣ କୁହାଯାଏ।

Question 13.
ଉତ୍ପାଦକ’ଶ?
Answer:
ଶିଳ୍ପ ସଂସ୍ଥାରୁ ସର୍ବଶେଷରେ ବାହାରୁଥିବା ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟକୁ ଉତ୍ପାଦ କୁହାଯାଏ ଏବଂ ଏଥୁରୁ ଆୟ ମିଳିଥାଏ।

Question 14.
ଭୋପାଳରେ କେବେ ଶୃଚ୍ଛଜନିତ ଦୁର୍ଘଟଣା ହୋଇଥିଲା ?
Answer:
୧୯୮୪ ମସିହା ଡିସେମ୍ବର ୩ ତାରିଖରେ ଭୋପାଳରେ ମର୍ମନ୍ତୁଦ ଶିଳ୍ପ ଦୁର୍ଘଟଣା ହୋଇଥିଲା ।

Question 15.
ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ନୂତନ ଭାବେ ଗଢ଼ିଉଠିଥିବା ଶିଳ୍ପକୁ ‘ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ’ ଆଖ୍ୟା ଦିଆଯାଇଛି । ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା, ସ୍ୱାସ୍ଥ୍ୟ ସେବା, ଆତିଥ୍ୟ ଏବଂ ଶିକ୍ଷା ଆଦି ଏହାର ଅନ୍ତର୍ଭୁକ୍ତ ।

Question 16.
କାଲିଫର୍ଣିଆ କାହିଁକି ପ୍ରସିଦ୍ଧ ?
Answer:
ସୂଚନା ପ୍ରଯୁକ୍ତିବିଦ୍ୟାର ପ୍ରମୁଖ କ୍ଷେତ୍ରଭାବେ କେନ୍ଦ୍ରୀୟ କାଲିଫର୍ନିଆର ସିଲିକନ୍ ଉପତ୍ୟକା ପ୍ରସିଦ୍ଧ ।

Question 17.
ଭାରତର କେଉଁ ସ୍ନାନ ପ୍ରଯୁକ୍ତିବିଦ୍ୟା କ୍ଷେତ୍ରରେ ଅଗ୍ରଣୀ ?
Answer:
ଭାରତର ବେଙ୍ଗାଲୁରୁ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା କ୍ଷେତ୍ରରେ ଅଗ୍ରଣୀ।

Question 18.
ବ୍ଲାଷ୍ଟ୍ର ଫର୍‌ନେସ୍‌ର କାମ କ’ଣ ?
Answer:
ଲୁହାପଥର ତରଳାଇବାକୁ ବ୍ଲାଷ୍ଟ୍ର ଫର୍‌ନେସ୍‌ର ଆବଶ୍ୟକତା ହୋଇଥାଏ ।

Question 19.
ମିଶ୍ରଧାତୁ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଇସ୍ପାତ୍ ବେଶ୍ ଶକ୍ତି ଏବଂ ଏହାକୁ ସହଜରେ ବିଭିନ୍ନ ଆକୃତି ଦିଆଯାଇପାରେ, କଟାଯାଇପାରେ ଏବଂ ତାରରେ ପରିଣତ କରି ହୁଏ। ଏହା ସହିତ ମାଙ୍ଗାନିଜ, ନିକେଲ ଓ କ୍ରୋମିୟମ୍ ମିଶ୍ରଣ କରାଯାଇ ଏକ ସ୍ଵତନ୍ତ୍ର ଧରଣର ଇସ୍ପାତ୍ ପ୍ରସ୍ତୁତ କରାଯାଏ। ଏହାକୁ ମିଶ୍ରଧାତୁ କୁହାଯାଏ।

Question 20.
କାହାକୁ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ?
Answer:
ଲୁହାକୁ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ।

Question 21.
କେଉଁ ସ୍ଥାନମାନଙ୍କରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ସ୍ଵାପନ କରାଯାଏ ?
Answer:
କଞ୍ଚାମାଲ, ଶସ୍ତା ଶ୍ରମିକ, ପରିବହନ ଓ ବଜାର ସୁବିଧା ଥିବା ସ୍ଥାନମାନଙ୍କରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ସ୍ଥାପନ କରାଯାଏ।

Question 22.
କର୍ଣାଟକର କେଉଁଠାରେ ଲୌହ-ଇସ୍ପାତ କାରଖାନା ରହିଛି ?
Answer:
କର୍ଣ୍ଣାଟକର ଭଦ୍ରାବତୀ ଓ ବିଜୟନଗରଠାରେ ଲୌହ-ଇସ୍ପାତ୍ର କାରଖାନା ରହିଛି ।

Question 23.
ଆନ୍ଧ୍ରପ୍ରଦେଶର କେଉଁଠାରେ ଲୌହଇସ୍ପାତ୍ କାରଖାନା ରହିଛି ?
Answer:
ଆନ୍ଧ୍ରପ୍ରଦେଶର ବିଶାଖାପାଟଣାରେ ଲୌହ-ଇସ୍ପାତ କାରଖାନା ରହିଛି ।

Question 24.
ଓଡ଼ିଶାର କେଉଁଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି ?
Answer:
ଓଡ଼ିଶାର ରାଉରକେଲାଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି।

Question 25.
ଦୁର୍ଗାପୁର ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
Answer:
ପଶ୍ଚିମବଙ୍ଗ ରାଜ୍ୟରେ ଦୁର୍ଗାପୁର ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ଅବସ୍ଥିତ ।

Question 26.
ତାମିଲନାଡୁର କେଉଁଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି ?
Answer:
ତାମିଲନାଡୁର ସାଲେମଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି।

Question 27.
କେଉଁ ନଦୀଦ୍ୱୟର ସଂଗମସ୍ଥଳରେ ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
ସୁବର୍ଣ୍ଣରେଖା ଓ ଖରକାଇ ନଦୀଦ୍ୱୟର ସଂଗମସ୍ଥଳରେ ଟାଟା ଲୌହ- ଇସ୍ପାତ୍ କାରଖାନା ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।

Question 28.
ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
Answer:
ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ଝାଡ଼ଖଣ୍ଡ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ।

Question 29.
ପିଟ୍‌ସ୍‌ବର୍ଗ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁଠି ଅବସ୍ଥିତ ?
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାରେ ପିଟ୍‌ସ୍‌ବର୍ଗ ଲୌହ ଇସ୍ପାତ୍ କାରଖାନା ଅବସ୍ଥିତ ।

Question 30.
ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଲୁହାପଥର କିପରି ଆସିଥାଏ ?
Answer:
ବୃହତ୍ ହ୍ରଦ ଅଞ୍ଚଳରୁ ଟ୍ରେନ୍‌ଯୋଗେ ଲୁହାପଥର ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଆସିଥାଏ।

Question 31.
କେଉଁ ନଦୀ ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଜଳ ଯୋଗାଇଥାଏ ?
Answer:
ଓହିଅ, ମନୋଗାହେଲା ଏବଂ ଆଲେଘେନି ନଦୀରୁ ପ୍ରଚୁର ଜଳ ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଯୋଗାଇଥାଏ।

Question 32.
ପଞ୍ଚହ୍ରଦ ମଧ୍ୟରେ କେଉଁଟି ବୃହତ୍ତମ ?
Answer:
ସୁପିରିଅର

Question 33.
କେଉଁଗୁଡ଼ିକ ପ୍ରାକୃତିକ ତନ୍ତୁ ଅଟେ ?
Answer:
ପଶମ, ରେଶମ, ତୁଳା, ଲିନେନ୍ ଓ ଝୋଟ ପ୍ରାକୃତିକ ତନ୍ତୁ ଅଟନ୍ତି ।

Question 34.
କେଉଁଗୁଡ଼ିକ ମନୁଷ୍ୟକୃତ ତନ୍ତୁ ଅଟେ ?
Answer:
ନାଇଲନ, ପଲିଷ୍ଟର ଓ ରେୟନ୍ ମନୁଷ୍ୟକୃତ ତନ୍ତୁ ଅଟେ।

Question 35.
କେବେଠାରୁ କାର୍ପାସ ବୟନଶିଳ୍ପର ବିକାଶ ହେଲା ?
Answer:
ଅଷ୍ଟାଦଶ ଶତାବ୍ଦୀରେ କାର୍ପାସ ବୟନଶିଳ୍ପର ବିକାଶ ହେଲା।

Question 36.
ପ୍ରଥମେ କେଉଁଠାରେ କଳତନ୍ତର ପ୍ରସାର ଘଟିଲା ?
Answer:
ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍‌ରେ କଳତନ୍ତର ପ୍ରସାର ଘଟିଲା ।

Question 37.
ସୁନାଜରି କାମ କାର୍ପାସ ବସ୍ତ୍ର ପାଇଁ ଭାରତର କେଉଁ ସ୍ଥାନ ପ୍ରସିଦ୍ଧ ?
Answer:
ସୁରତ୍ ଓ ଉଦୋଦରା ସୁନାଜରି କାମ ଓ କାର୍ପାସ୍ ବସ୍ତ୍ର ପାଇଁ ଭାରତ ପ୍ରସିଦ୍ଧ ।

Question 38.
ଢାକାର କେଉଁ କାମ ପୃଥବୀ ପ୍ରସିଦ୍ଧ ?
Answer:
ଢାକାର ମସ୍‌ଲିନ୍ କାର୍ପାସ୍‌ବସ୍ତ୍ର ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ।

Question 39.
କେଉଁ ମସିହାରେ ଭାରତରେ ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ବୟନଶିଳ ମୁମ୍ବାଇରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
୮୫୪ ମସିହାରେ ଭାରତରେ ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ବୟନଶିଳ୍ପ ମୁମ୍ବାଇରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।

Question 40.
ମସଲିପଟ୍ଟନମ୍ବର କେଉଁ କାର୍ପାସ୍ବବସ୍ତ୍ର ପୃଥ‌ିବୀରେ ବେଶ୍ ଆଦୃତ ?
Answer:
ମସଲିପଟ୍ଟନମ୍‌ର ଚିନ୍‌ଜେନ୍ କାର୍ପାସବସ୍ତ୍ର ପୃଥ‌ିବୀରେ ବେଶ୍ ଆଦୃତ ।

Question 41.
କାହାକୁ ‘ଭାରତର ମାଞ୍ଚେଷ୍ଟର’ କୁହାଯାଏ ?
Answer:
ଅହମ୍ମଦାବାଦକୁ ଭାରତର ମାଞ୍ଚେଷ୍ଟର କୁହାଯାଏ ।

Question 42.
ଅହମ୍ମଦାବାଦ କେଉଁ ରାଜ୍ୟରେ ଓ କେଉଁ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ?
Answer:
ଅହମ୍ମଦାବାଦ ଗୁଜରାଟ ରାଜ୍ୟର ନର୍ମଦା ନଦୀକୂଳରେ ଅବସ୍ଥିତ ।

Question 43.
କେବେ ଅହମ୍ମଦାବାଦରେ ପ୍ରଥମ କାର୍ପାସ ବୟନଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
୧୮୫୯ ମସିହାରେ ଅହମ୍ମଦାବାଦରେ ପ୍ରଥମ କାର୍ପାସ ବୟନଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।

Question 44.
ମାଞ୍ଚେଷ୍ଟର କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
ମାଞ୍ଚେଷ୍ଟର ଇଂଲଣ୍ଡରେ ଅବସ୍ଥିତ ।

Question 45.
ଓସାକା କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
ଓସାକା ଜାପାନରେ ଅବସ୍ଥିତ ।

Question 46.
କାହାକୁ ‘ଜାପାନର ମାଞ୍ଚେଷ୍ଟର’ କୁହାଯାଏ ?
Answer:
ଓସାକାକୁ ଜାପାନର ମାଞ୍ଚେଷ୍ଟର କୁହାଯାଏ।

Question 47.
ଓସାକା କାହିଁକି ପ୍ରସିଦ୍ଧ ?.
Answer:
ଓସାକା ଜାପାନର ଏକ ପ୍ରମୁଖ ବୟନଶିଳ୍ପ କେନ୍ଦ୍ର ଅଟେ।

Question 48.
ସୂଚନା ଓ ପ୍ରଯୁକ୍ତିବିଦ୍ୟା ପାଇଁ ଭାରତର କେଉଁ ସ୍ଥାନ ପ୍ରସିଦ୍ଧ ?
Answer:
ସୂଚନା ଓ ପ୍ରଯୁକ୍ତିବିଦ୍ୟା ପାଇଁ ଭାରତର ବେଙ୍ଗାଲୁରୁ ପ୍ରସିଦ୍ଧ।

Question 49.
କାଲିଫର୍ଣିଆ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାକେନ୍ଦ୍ର କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
କାଲିଫର୍ଷିଆ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାକେନ୍ଦ୍ର ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାରେ ଅବସ୍ଥିତ ।

Question 50.
ସିଲିକନ୍ ମାଳଭୂମି କାହାକୁ କୁହାଯାଏ ?
Answer:
ବେଙ୍ଗାଲୁରୁକୁ ସିଲିକନ୍ ମାଳଭୂମି କୁହାଯାଏ।

ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ ।

1. କାହାଦ୍ଵାରା କଞ୍ଚାମାଲକୁ ଲୋକଙ୍କ ପାଇଁ ଉପଯୋଗୀ ଦ୍ରବ୍ୟର ପରିଣତ କରିଥାଏ ?
Answer: ଉଦ୍ୟୋଗ ବା ଶିଳ୍ପ

2. ଶିଳ୍ପ ପ୍ରତିଷ୍ଠାଦ୍ୱାରା ଲୋକଙ୍କୁ କ’ଣ ମିଳିଥାଏ ?
Answer: କର୍ମ ସଂସ୍ଥାନ

3. କେଉଁ ଶିଳ୍ପଗୁଡ଼ିକ ପ୍ରାଣୀ ଓ ଉଭିଦ ଆଧାରିତ ବସ୍ତୁକୁ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହାର କରିଥାନ୍ତି ?
Answer: କୃଷିଭିର୍ଭିକ ଶିଳ୍ପ

4. ରେଳଡ଼ବା ନିର୍ମାଣର ମୁଖ୍ୟ କଞ୍ଚାମାଲ କ’ଣ ଅଟେ ?
Answer: ଲୁହା

5. ମାଛତେଲ ଉଦ୍ୟୋଗ କେଉଁ ଶିଳ୍ପର ଉଦାହରଣ ?
Answer: ସମୁଦ୍ରଭିଭିକ

6. ଅନେକ କ୍ଷେତ୍ରରେ କ’ଣ ସହର ଓ ନଗର ଆଦିର ବିକାଶ ଓ ଅଭିବୃଦ୍ଧିର କାରଣ ହୋଇଥାଏ ?
Answer: ଶିଳ୍ପାୟନ

7. ସିଲିକନ ଉପତ୍ୟକା ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer: କେନ୍ଦ୍ରୀୟ କାଲିଫର୍ଣ୍ଣିଆ

8. ଆଧୁନିକ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ କାହାକୁ କୁହାଯାଏ ?
Answer: ଇସ୍ପାତ

9. ଟାଟା ଲୌହ ଇସ୍ପାତ କାରଖାନା ଯେଉଁ ସ୍ଥାନରେ ଅବସ୍ଥିତ ତାହାର ନାମ କ’ଣ ?
Answer: ସାକ୍‌

10. ଜାପାନର ଓସାକା ବୟନ ଶିଳ୍ପ କେନ୍ଦ୍ର ପାଇଁ କେଉଁ ନଦୀରୁ ଜଳ ମିଳିଥାଏ ?
Answer: ଓଡ଼ୋ

ଭୌଗୋଳିକ ଶବ୍ଦଗୁଡ଼ିକୁ ଗୋଟିଏ ଗୋଟିଏ ବାକ୍ୟରେ ଲେଖ ।

1. ଅହମ୍ମଦାବାଦ :
Answer: ଭାରତର ମାଞ୍ଚେଷ୍ଟର ।

2. ଓସାକ
Answer: ଜାପାନର ମାଞ୍ଚେଷ୍ଟର ।

3. ମସ୍‌ଲି ନ :
Answer: ଢାକାର ନିର୍ମିତ ଏକ ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ ବସ୍ତ୍ର ।

4. ମସଲି ପଟନମ୍ :
Answer: ଚିନ୍‌ନ୍ କାର୍ପାସ ବସ୍ତ୍ରପାଇଁ ପ୍ରସିଦ୍ଧ ଅଞ୍ଚଳ ।

5. ଟିସ୍କୋ।
Answer: ଟାଟା ଲୌହଇସ୍ପାତ କାରଖାନାର ସଂକ୍ଷିପ୍ତ ନାମ ।

6. ସାଲେମ୍ :
Answer: ତାମିଲନାଡୁରେ ଅବସ୍ଥିତ ଏକ ଲୌହଇସ୍ପାତ କାରଖାନା ।

7. ମିଶ୍ରଧାତୁ :
Answer: ଇସ୍ପାତସହ ଆଲୁମିନିୟମ୍, ନିକେଲ ଓ ତମ୍ବା ଆଦି ଧାତୁ ମିଶାଇ ପ୍ରସ୍ତୁତ କରାଯାଉଥୁବା ଧାତୁ ।

8. ମିଥାଇଲ ଆଇସୋସାଇନେଟ୍ :
Answer: ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣାରେ ନିର୍ଗତ ଅତି ବିଷାକ୍ତ ବାଷ୍ପ ।

9. ଅମୁଲ :
Answer: ଆନନ୍ଦ ମିଲ୍‌କ ଇଉନିୟନ ଲିମିଟେଡ଼ର ସଂକ୍ଷିପ୍ତ ନାମ।

10. ଦ୍ୱୈତ ମାଲିକାନା ଲୁକ୍ତ ସଂସ୍ଥା :
Answer: ଉଭୟ ସରକାରୀ ଓ କୌଣସି ବ୍ୟକ୍ତି ବା ଏକାଧୁକ ବ୍ୟକ୍ତିଙ୍କ ମିଳିତ ତତ୍ତ୍ଵାବଧାନ ଓ ମାଲିକାନାରେ ପରିଚାଳିତ ଶିଳ୍ପ।

ଅସଂପର୍କିତ ଶବ୍ଦଟିକୁ ବାଛ ।

1. ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, କାଠମଣ୍ଡ, ଖାଇବାତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ ।
Answer: କାଠମଣ୍ଡ

2. ଲୌହଇସ୍ପାତ ଶିଳ୍ପ, ଭାରୀଯନ୍ତ୍ରପାତି, ରେଳଡ଼ବା ନିର୍ମାଣ, ଚମଡ଼ା ଶିଳ୍ପ ।
Answer: ଚମଡ଼ା ଶିଳ୍ପ

3. ମାଛତେଲ ଉଦ୍ୟୋଗ, କାଗଜଶିକ, ଔଷଧ ପ୍ରସ୍ତୁତକାରୀ ଶିଳ୍ପ, ଗୃହନିର୍ମାଣ ଶିଳ୍ପ ।
Answer: ମାଛ ତେଲ ଉଦ୍ୟୋଗ

4. ଘଣ୍ଟା, ରେଡ଼ିଓ, ଟିଭି, ଝୁଡ଼ିବୁଣା।
Answer: ଝୁଡ଼ିବୁଣା

5. ଝୁଡ଼ି, ଘଣ୍ଟା, ମାଟିହାଣ୍ଡି, ତାରକସି କାମ ।
Answer: ଘଣ୍ଟା

6. ମଟରଗାଡ଼ି ନିର୍ମାଣ, ଜାହାଜ ନିର୍ମାଣ, ଟିଭି, ଭାରୀଯନ୍ତ୍ରପାତି ।
Answer: ଟିଭି

7. ମୁମ୍ବାଇ-ପୁଣେ, ବେଙ୍ଗାଲୁରୁ-ତାମିଲନାଡୁ ଅଞ୍ଚଳ, କୋଲକାତା- ଭୁବନେଶ୍ଵର, ଗୁଡ଼ଗାଓଁ-ଦିଲ୍ଲୀ ।
Answer: କୋଲକାତା-ଭୁବନେଶ୍ଵର

8. ଇସ୍ପାତ, ମାଙ୍ଗାନିଜ, ଚୂନପଥର, ନିକେଲ।
Answer: ଚୂନପଥର

9. ଦିଲ୍ଲୀ, ଭିଲାଇ, ଦୁର୍ଗାପୁର, ବର୍ଣ୍ଣପୁର ।
Answer: ଦିଲ୍ଲୀ

10. HAL, CESCO, SAIL, BHEL
Answer: CESCO

ଠିକ୍ ଉକ୍ତ ପାଖରେ ଠିକ୍ ଚିହ୍ନ ( ✓ ) ଓ ଭୁଲ୍ ଭକ୍ତି ପାଖରେ ଭୁଲ୍ ଚିହ୍ନ ( ✗ ) ଦିଅ ।

1. ଭଦ୍ରାବତୀ ଓ ବିଜୟ ନଗର କର୍ଣାଟକରେ ଅବସ୍ଥିତ। — ଚିହ୍ନ ( ✓ )
2. ଋଷ କାର୍ଯ୍ୟରେ ମୁଖ୍ୟତଃ କାଠ ଯନ୍ତ୍ରପାତି ବ୍ୟବହୃତ ହୁଏ । — ଚିହ୍ନ ( ✗ )
3. ପୃଥ‌ିବୀର ମୁଖ୍ୟ ଶିଳ୍ପାଞ୍ଚଳଗୁଡ଼ିକ ନାତିଶୀତୋଷ୍ଣ ଅଞ୍ଚଳରେ ଅବସ୍ଥିତ । — ଚିହ୍ନ ( ✓ )
4. ଯୋଗାଯୋଗ ବ୍ୟବସ୍ଥାକୁ ଆଧାରିକ ସଂରଚନା କୁହାଯାଏ । — ଚିହ୍ନ ( ✓ )
5. ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ ବୃହତ୍ ଶିଳ୍ପ ଅଟେ । — ଚିହ୍ନ ( ✗ )
6. ଶିଳ୍ପ ଶ୍ରମିକ କୃଷିଶ୍ରମିକ ଠାରୁ କମ୍ ମଜୁରି ପାଇଥାଏ। — ଚିହ୍ନ ( ✗ )
7. ପରିବହନ ଓ ଯୋଗାଯୋଗ ଆଦି ସେବା ଶିଳ୍ପର ଅନ୍ତର୍ଭୁକ୍ତ। — ଚିହ୍ନ ( ✓ )
8. କୋଇଲା ଖନନ ଏକ ଶିଳ୍ପ ଅଟେ । — ଚିହ୍ନ ( ✓ )
9. ଘଣ୍ଟା ଶିଳ୍ପ କୂଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଭୁକ୍ତ । — ଚିହ୍ନ ( ✗ )
10. ଓହିଓ ନଦୀ ରୁଷିଆରେ ଅବସ୍ଥିତ । — ଚିହ୍ନ ( ✗ )
11. ଚିନ୍‌ନ୍ ପାଇଁ କାଲିକଟ୍ ପ୍ରସିଦ୍ଧ ଥିଲା । — ଚିହ୍ନ ( ✗ )
12. ଭାରତର ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ବୟନ ଶିଳ୍ପ ବମ୍ବେଠାରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା । — ଚିହ୍ନ ( ✓ )
13. ପାନିପତ୍ ଆମ ଦେଶର ଏକ ପ୍ରମୁଖ କାର୍ପାସ୍ ବୟନ ଶିଳ୍ପକେନ୍ଦ୍ର । — ଚିହ୍ନ ( ✓ )
14. ବେଙ୍ଗାଲୁରୁରେ ସର୍ବାଧକ ଶିକ୍ଷାନୁଷ୍ଠାନ ଓ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଦାନ କରୁଥିବା ଅବସ୍ଥିତ । — ଚିହ୍ନ ( ✓ )
15. ବେଙ୍ଗଲୁରୁ ଉପକୂଳବର୍ତ୍ତୀ ସମତଳ ଅଞ୍ଚଳରେ ଅବସ୍ଥିତ। — ଚିହ୍ନ ( ✗ )

Objective Type Questions With Answers
ସ୍ତମ୍ଭ ମିଳନ କର ।

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ________ ଦ୍ଵାରା ଆୟ ବୃଦ୍ଧି ପାଇଥାଏ।
(କୃଷି, ଖଣିଜ ଉତ୍ତୋଳନ, ମତ୍ସ୍ୟ ସଂଗ୍ରହ, ବାଣିଜ୍ୟ କାରବାର)
Answer: ବାଣିଜ୍ୟ କାରବାର

2. ଭାରୀ ଯନ୍ତ୍ରପାତି, ରେଳଡବା ନିର୍ମାଣ ________କାରଖାନା ଅନ୍ତର୍ଗତ ।
(କୃଷିଭିଭିକ, ଖଣିଜଭିର୍ଭିକ, ସମୁଦ୍ରଭିଭିକ, ଜଙ୍ଗଲଭିଭିକ
Answer: ଖଣିଜଭିଭିକ

3. ଚମଡ଼ା ଶିଳ୍ପ ______ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।
(କୃଷିଭିତ୍ତିକ, ଜଙ୍ଗଲଭିଭିକ, ଖଣିଜଭିଭିକ, ସମୁଦ୍ରାଭିଭିକ)
Answer: କୃଷିଭ୍ରିକ

4. ଗୃହନିର୍ମାଣ ଶିଳ୍ପ ______ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।
(କୃଷିଭିଭିକ, ଖଣିଜଭିରିକ, ଜଙ୍ଗଲଭିଭିକ, ସମୁଦ୍ରଭିଭିକ)
Answer: ଜଙ୍ଗଲ ଭିଭିକ

5. ______ ପରିବାର ସଦସ୍ୟଙ୍କଦ୍ଵାରା କରାଯାଇଥାଏ।
(କ୍ଷୁଦ୍ରଶିଳ୍ପ, ବୃହତ୍ ଶିଳ୍ପ, କୁଟୀର ଶିଳ୍ପ, ଯାନ୍ତ୍ରିକ ଶିଳ୍ପ)
Answer: କୁଟୀର ଶିଳ୍ପ

6. ମଟର ଗାଡ଼ି ଓ ଭାରୀ ଯନ୍ତ୍ରପାତି ______ ର ଅନ୍ତର୍ଗତ ।
(କୁଟୀରଶିଳ୍ପ, କ୍ଷୁଦ୍ରଶିଳ୍ପ, ଜଙ୍ଗଲଭିଭିକ ଶିଳ୍ପ, ବୃହତ୍‌ଶିଳ୍ପ)
Answer: ବୃହତ୍‌ଶିଳ୍ପ

7. ମାଲିକାନା ଦୃଷ୍ଟିରୁ ଶିଳ୍ପକୁ ______ ଭାଗରେ ଭାଗ କରାଯାଇଛି ।
(ଏକ, ଦୁଇ, ତିନି, ଊରି)
Answer: ଗରି

8. ଟାଟା ଲୌହ ଇସ୍ପାତ କାରଖାନା ______ ଶିଚ୍ଛର ଅନ୍ତର୍ଗତ ।
(ବ୍ୟକ୍ତିମାଲିକାନା, ସରକାରୀ ମାଲିକାନା, ଦ୍ଵୈତ ମାଲିକାନା, ସମବାୟ ସଂସ୍ଥା)
Answer: ବ୍ୟକ୍ତିମାଲିକାନା

9. ଶିଳ୍ପସଂସ୍ଥାରୁ ସର୍ବଶେଷରେ ବାହାରୁଥ‌ିବା ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟକୁ ______ କୁହାଯାଏ ।
(ନିବେଶ, ଉତ୍ପାଦ, କାରକ, ଆଧାରିକ ସଂରଚନା)
Answer: ଉତ୍ପାଦ

10. ୧୯୮୪ ମସିହା ଡିସେମ୍ବର ୩ ତାରିଖ ଦିନ ଭାରତର, _______ସହରରେ ଶିଳ୍ପଜନିତ ଦୁର୍ଘଟଣା ହୋଇଥିଲା।
(ଭୋପାଳ, ଚେନ୍ନାଇ, ରାୟପୁର, ଜୟପୁର)
Answer: ଗୋପାଳ

11. ୨୦୦୫ ମସିହାରେ ପୃଥ‌ିବୀର _______ ଦେଶରେ ଶିଳ୍ପ ଦୁର୍ଘଟଣା ହୋଇ ଅନେକ ଲୋକଙ୍କର ମୃତ୍ୟୁ ଘଟିଥିଲା।
(ଭାରତ, ଜାପାନ, ଚୀନ, ଇଂଲଣ୍ଡ)
Answer: ଚୀନ

12. କାଲିଫର୍ଡିଆ _______ଦେଶରେ ଅବସ୍ଥିତ ।
( ରୁଷିଆ, ଜାପାନ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଚୀନ)
Answer: ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା

13. କାଲିଫର୍ଡିଆର ସିଲିକନ୍ _______ କ୍ଷେତ୍ରରେ ଅଗ୍ରଣୀ।
( ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା, ଶିକ୍ଷା, ଶିଳ୍ପ, ସ୍ଵାସ୍ଥ୍ୟ)
Answer: ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା

14. ଭାରତର _______ ସହର ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାରେ ଅଗ୍ରଣୀ ସହର ।
(ପୁନେ, ଅହମ୍ମଦାବାଦ, ବେଙ୍ଗାଲୁରୁ, ମହୀଶୂର)
Answer: ବେଙ୍ଗାଲୁରୁ

15. ଲୌହ ଇସ୍ପାତ ଶିଳ୍ପ _______ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।
(କୁଟୀର, କ୍ଷୁଦ୍ର, ସମବାୟ, ମୌଳିକ)
Answer: ମୌଳିକ

16. _______ କୁ ଆଧୁନିକ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ କୁହାଯାଏ।
(ସୁନା, ଲୁହା, ଇସ୍ପାତ, ତମ୍ବା)
Answer: ଇସ୍ପାତ

17. ୧୯୪୭ ମସିହା ପୂର୍ବରୁ _______ ଲୌହ ଇସ୍ପାତ କାରଖାନା ଥିଲା ।
(ଗୀଉରକେଲା, ବୋକାରୋ, ବର୍ଣ୍ଣପୁର, ଜାମସେଦ୍‌ପୁର)
Answer: ଜାମସେଦପୁର

18. ଜାମସେଦ୍‌ପୁର ଲୌହ-ଇସ୍ପାତ କାରଖାନା _______ ଅବସ୍ଥିତ।
(ଝାଡ଼ଖଣ୍ଡ, ଉତ୍ତରାଖଣ୍ଡ, ଛତିଶଗଡ଼, ଓଡ଼ିଶା)
Answer: ଝାଡ଼ଖଣ୍ଡ

19. ଟାଟା ଲୌହ-ଇସ୍ପାତ କାରଖାନାର ସଂକ୍ଷିପ୍ତ ନାମ _______|
(ପୋସ୍କୋ, ଟିସ୍କୋ, ସେସ୍କୋ, ନେସ୍କୋ)
Answer: ଟିସ୍କୋ

20. _______ ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ ଶିଳ୍ପକେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା ହୋଇଥିଲା।
(1906, 1907, 1908, 1909)
Answer: 1907

21. ପିଟ୍‌ସ୍‌ବର୍ଗ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା,_______ଦେଶରେ ଅବସ୍ଥିତ ।
(ଭାରତ, ଇଂଲଣ୍ଡ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ରୁଷିଆ)
Answer: ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା

22. ପ୍ରଥମେ _______ଦେଶରେ କଳତନ୍ତର ପ୍ରସାର ଘଟିଥିଲା।
(ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍, ଭାରତ, ଜର୍ମାନୀ)
Answer: ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍

23. ଢାକାର _______ କାର୍ପାସ ବସ୍ତ୍ର ପୃଥୁବୀ ପ୍ରସିଦ୍ଧ ।
(ମସ୍‌ଲିନ, ଚିନ୍‌ନ, କାଲିକୋ, ସୁନା ଜରିକାମ)
Answer: ମସ୍‌ନ

24. ମସଲିପଟନମ୍ବର _______ କାର୍ପାସ ବସ୍ତ୍ର ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ ।
(ମସଲିନ୍, ଚିନ୍‌ନ, କାଲିକୋ, ସୁନା ଜରିକାମ)
Answer: ଚିନ୍‌ନ୍

25. କାଲିକଟର _______ କାର୍ପାସ ବସ୍ତ୍ର ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ ।
( ମସଲିନ୍, ଚିନ୍‌ନ, କାଲିକୋ, ସୁନା ଜରିକାମ)
Answer: କାଲିକୋ

26. _______ ଭାରତର ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ୍ ବୟନଶିଳ୍ପ ମୁମ୍ବାଇରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।
(1851, 1852, 1853, 1854)
Answer: 1854

27. ଅହମଦାବାଦ _______ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ।
(ନର୍ମଦା, ସାବରମତୀ, ତାଣ୍ଡୀ, ମାହୀ)
Answer: ସାବରମ

28. _______ ପ୍ରଥମେ ଅହମ୍ମଦାବାଦରେ କାର୍ପାସ ବୟନ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।
(1856, 1857, 1858, 1859)
Answer: 1859

29. _______ କୁ ଭାରତର୍‌ ମାଞ୍ଚେଷ୍ଟର କୁହାଯାଏ।
(ଅହମ୍ମଦନଗର, ଅହମ୍ମଦାବାଦ, ହାଇଦ୍ରାବାଦ, ଜୟପୁର)
Answer: ଅହମ୍ମଦାବାଦ

30. ମାଞ୍ଚେଷ୍ଟର _______ ରେ ଅବସ୍ଥିତ ।
(ଭାରତ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଇଂଲଣ୍ଡ, ଜାପାନ)
Answer: ଇଂଲଣ୍ଡ

ସମ୍ଭାବ୍ୟ ଉତ୍ତର ବାଛି ଲେଖ ।

Question 1.
କେଉଁଟି ପ୍ରାଥମିକ ଉତ୍ପାଦର ଅନ୍ତର୍ଗତ ?
(A) ଫଳ ଓ ମୂଳ
(B) ଘଣ୍ଟା ଓ ଯନ୍ତ୍ରପାତି
(C) କଲମ ଓ ମୋବାଇଲ
(D) ଲୁଗା ଓ କାଗଜ
Answer:
(A) ଫଳ ଓ ମୂଳ

Question 2.
କେଉଁଟି ପ୍ରକ୍ରିୟାକରଣ ପରେ ଆମେ ବ୍ୟବହାର କରିଥାଉ ?
(A) କାଗଜ
(B) ଫଳ
(C) ମହୁ
(D) ମୂଳ
Answer:
(A) କାଗଜ

Question 3.
କେଉଁ ସେବା କାର୍ଯ୍ୟକୁ ଶିଳ୍ପର ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଛି ?
(A) ଶିକ୍ଷା ଓ ସ୍ୱାସ୍ଥ୍ୟ
(B) ବ୍ୟାଙ୍କ୍ ଓ ପର୍ଯ୍ୟଟନ
(C) ପରିବହନ ଓ ଯୋଗାଯୋଗ
(D) ବ୍ୟାଙ୍କ୍ ଓ ଶିକ୍ଷା
Answer:
(C) ପରିବହନ ଓ ଯୋଗାଯୋଗ

Question 4.
କେଉଁଟି କୃଷିଭିତ୍ତିକ ଶିଳ୍ପର ସ୍ତର ଅଟେ ?
(A) ଭାରୀ ଯନ୍ତ୍ରପାତି, ରେଳଡ଼ବା ନିର୍ମାଣ, ମାଛତେଲ
(B) ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, ଖାଇବାତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ
(C) ମାଛତେଲ, ଚମଡ଼ାଶିଳ୍ପ, ଯନ୍ତ୍ରପାତି ନିର୍ମାଣ
(D) କାଠମଣ୍ଡ, କାଗଜ, ଆସବାବଶିଳ୍ପ
Answer:
(B) ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, ଖାଇବାତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ

Question 5.
କେଉଁଟି ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପ ଅଟେ ?
(A) ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ ଓ କାର୍ପାସ ବୟନ
(B) ଚମଡ଼ାଶିକ ଓ ଭାରି ଯନ୍ତ୍ରପାତି
(C) ସାମୁଦ୍ରିକ ଉଦ୍ୟୋଗ ଓ ମାଛତେଲ
(D) କାଠମତ୍ସ୍ୟ ଓ କାଗଜଶିଳ୍ପ
Answer:
(C) ସାମୁଦ୍ରିକ ଉଦ୍ୟୋଗ ଓ ମାଛତେଲ

Question 6.
କେଉଁଟି ଜଙ୍ଗଲଭିଭିକ ଶିଳ୍ପ ନୁହେଁ ?
(A) କାଠମଣ୍ଡ
(B) କାଗଜ ଶିକ
(C) ଔଷଧ ପ୍ରସ୍ତୁତକାରୀ ଶିଳ୍ପ
(D) ମଛତେଲ
Answer:
(D) ମଛତେଲ

Question 7.
କେଉଁଟି କୁଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ତାରକସି କାମ
(B) ଝାଡ଼ୁବୁଣା
(C) ମାଟିହାଣ୍ଡି ନିର୍ମାଣ
(D) ଘଣ୍ଟା ନିର୍ମାଣ
Answer:
(D) ଘଣ୍ଟା ନିର୍ମାଣ

Question 8.
କେଉଁଟି କ୍ଷୁଦ୍ରଶିଳ୍ପର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ଘଣ୍ଟା
(B) ରେଡିଓ ନିର୍ମାଣ
(C) ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି
(D) ଟିଭି ତିଆରି
Answer:
(C) ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି

Question 9.
HAL ଏବଂ SAIL(ହିନ୍ଦୁସ୍ତାନ ଏରୋନଟିକ୍‌ସ ଲିମିଟେଡ୍ ଓ ଭାରତୀୟ ଇସ୍ପାତନିଗମ) କେଉଁ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
(A) ବ୍ଯକ୍ତିମାଲିକାନା
(B) ସରକାରୀ ମାଲିକାନା
(C) ଦ୍ଵୈତ ମାଲିକାନା
(D) ସମବାୟ ସଂସ୍ଥା
Answer:
(B) ସରକାରୀ ମାଲିକାନା

Question 10.
କେଉଁଟି ଦ୍ଵୈତ ମାଲିକାନା ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
(A) ଟାଟା ଲୌହଇସ୍ପାତ
(B) ଭାରତୀୟ ଇସ୍ପାତ ନିଗମ
(C) ମାରୁତି ଉଦ୍ୟୋଗ
(D) ଅମୁଲ ଶିଳ୍ପ
Answer:
(C) ମାରୁତି ଉଦ୍ୟୋଗ

Question 11.
ସମ୍ବଲପୁରୀ ବସ୍ତଶିଳ୍ପ ଓ ଅମୁଲ ଦୁଗ୍ଧ ଉତ୍ପାଦନକାରୀ ସଂସ୍ଥା କେଉଁ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
(A) ବ୍ୟକ୍ତି ମାଲିକାନା
(B) ସରକାରୀ ମାଲିକାନା
(C) ଦ୍ଵୈତ ମାଲିକାନା
(D) ସମବାୟ ସଂସ୍ଥା
Answer:
(D) ସମବାୟ ସଂସ୍ଥା

Question 12.
କେଉଁଟି ଆଧାରିକ ସଂରଚନାର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ବିଦ୍ୟୁତକରଣ
(B) କଞ୍ଚାମାଲ
(C) ଯୋଗାଯୋଗ
(D) ସଡ଼କ
Answer:
(B) କଞ୍ଚାମାଲ

Question 13.
କେଉଁଟି ଶିଳ୍ପ ବ୍ୟବସ୍ଥାର ନିବେଶର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) କଞ୍ଚାମାଲ
(B) ଶ୍ରମିକ
(C) ଭୂମି
(D) ଅରଣ୍ୟ
Answer:
(D) ଅରଣ୍ୟ

Question 14.
ଶିଳ୍ପସଂସ୍ଥାରେ କଞ୍ଚାମାଲରୁ ଉତ୍ପାଦ ସୃଷ୍ଟି ହେବାପାଇଁ ଯେଉଁସବୁ କାର୍ଯ୍ୟପନ୍ଥା ଗ୍ରହଣ କରାଯାଏ, ତାହାକୁ କ’ଣ କୁହାଯାଏ ?
(A) କାରକ
(B) ନିବେଶ
(C) ପ୍ରକ୍ରିୟାକରଣ
(D) ଉତ୍ପାଦ
Answer:
(C) ପ୍ରକ୍ରିୟାକରଣ

Question 15.
କେଉଁଟି ଭାରତର ଶିଳ୍ପାଞ୍ଚଳ ନୁହେଁ ?
(A) ମୁମ୍ବାଇ – ପୁଣେ
(B) ବେଙ୍ଗାଲୁରୁ – ତାମିଲନାଡୁ
(C) ଗୁଡଗାଓଁ – ଦିଲ୍ଲୀ – ମିରଟ୍
(D) କଟକ – ଓଡ଼ିଶା
Answer:
(D) କଟକ – ଓଡ଼ିଶା

Question 16.
କେଉଁଟି ପୃଥ‌ିବୀର ଶିଳ୍ପାଞ୍ଚଳ ନୁହେଁ ?
(A) ଆମେରିକା ପୂବାଂଶ
(B) ପାକିସ୍ଥାନର ପୂର୍ବାଶ
(C) ପଶ୍ଚିମ ଓ କେନ୍ଦ୍ରୀୟ ୟୁରୋପ
(D) ପୂର୍ବ ଏସିଆ ଓ ପୂର୍ବ ୟୁରୋପ
Answer:
(B) ପାକିସ୍ଥାନର ପୂର୍ବାଶ

Question 17.
କେଉଁଟି ‘ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ’ର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
(B) ସ୍ଵାସ୍ଥ୍ୟ ଓ ସ୍ଵାସ୍ଥ୍ୟ ସେବା
(C) ଆତିଥ୍ୟ ଓ ସେବା
(D) ଲୌହ-ଇସ୍ପାତ ଶିଳ୍ପ
Answer:
(D) ଲୌହ-ଇସ୍ପାତ ଶିଳ୍ପ

Question 18.
କେଉଁଟି ଇସ୍ପାତ ଧାତୁ ପ୍ରସ୍ତୁତିରେ ବ୍ୟବହାର କରାଯାଏ ନାହିଁ ?
(A) ମାଙ୍ଗାନିକ
(B) ଆଲୁମିନିୟମ୍
(C) ନିକେଲ
(D) କ୍ରୋମିୟମ୍
Answer:
(B) ଆଲୁମିନିୟମ୍

Question 19.
କେଉଁ ଲୌହ-ଇସ୍ପାତ କାରଖାନା ଭିନ୍ନ ଅଟେ ?
(A) ଝାଡ଼ଖଣ୍ଡ – ଜାମସେଦ୍‌ପୁର
(B) ଓଡ଼ିଶା – ରାଉରକେଲା
(C) ତାମିଲନାଡୁ – ଭଦ୍ରାବତୀ
(D) ପଶ୍ଚିମବଙ୍ଗ – ଦୁର୍ଗାପୁର
Answer:
(C) ତାମିଲନାଡୁ – ଭଦ୍ରାବତୀ

Question 20.
କେଉଁ ନଦୀଦ୍ୱୟରୁ ଜାମସେଦପୁର ଲୌହଇସ୍ପାତ୍ କାରଖାନାକୁ ପ୍ରଚୁର ଜଳ ଯୋଗାଇ ଦିଆଯାଇଥାଏ ?
(A) ମହାନଦୀ ଓ ବ୍ରାହ୍ମଣୀ
(B) ଗୋଦାବରୀ ଓ କୋଏନା
(C) ଖରକାଇ ଓ ସୁବର୍ଣ୍ଣରେଖା
(D) ସୁବର୍ଣ୍ଣରେଖା ଓ ବୁଢାବଳଙ୍ଗ
Answer:
(C) ଖରକାଇ ଓ ସୁବର୍ଣ୍ଣରେଖା

Question 21.
ଟାଟା ଲୌହ-ଇସ୍ପାତ କାରଖାନାଟି କେଉଁ ରେଳପଥ ନିକଟରେ ଅବସ୍ଥିତ ?
(A) ହାୱଡ଼ା – ଦୁର୍ଗାପୁର
(B) ହାୱଡ଼ା ଚନ୍ଦନନଗର
(C) ହାୱଡ଼ା – ମୁମ୍ବାଇ
(D) ହାୱଡ଼ା – ସାଲିମାର
Answer:
(C) ହାୱଡ଼ା – ମୁମ୍ବାଇ

Question 22.
ଭଦ୍ରାବତୀ ଓ ବିଜୟନଗର ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
(A) ଓଡ଼ିଶା
(B) କର୍ଣାଟକ
(C) ପଶ୍ଚିମବଙ୍ଗ
(D) ତାମିଲନାଡୁ
Answer:
(B) କର୍ଣାଟକ

Question 23.
କେଉଁଟି କାର୍ପାସ ଶିଳ୍ପରେ ଅଗ୍ରଣୀ ଦେଶ ନୁହେଁ ?
(A) ଭାରତ
(B) ଚୀନ
(C) ଜାପାନ
(D) ଶ୍ରୀଲଙ୍କା
Answer:
(D) ଶ୍ରୀଲଙ୍କା

Question 24.
ସୁନା ଜରିକାମ କାର୍ପାସ ବସ୍ତ୍ର କେଉଁ ଅଞ୍ଚଳରେ ପ୍ରସ୍ତୁତ କରାଯାଏ ?
(A) ସୁରତ ଓ ଇଦୋଦରା
(B) ଜୟପୁର ଓ ଆଜମିର
(C) ପୁନେ ଓ ମୁମ୍ବାଇ
(D) ନାଗପୁର ଓ ଥାନେ
Answer:
(A) ସୁରତ ଓ ଇଦୋଦରା

Question 25.
କେଉଁଟି କାର୍ପାସ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) କୋଏମ୍ବାଟୁର
(B) କାନପୁର
(C) ଚେନ୍ନାଇ
(D) ବର୍ଣ୍ଣପୁର
Answer:
(D) ବର୍ଣ୍ଣପୁର

Question 26.
ଅହମ୍ମଦାବାଦରେ କାର୍ପାସ ବୟନ ଶିଳ୍ପ ଗଢ଼ିଉଠିବାର କାରଣ କ’ଣ ?
(A) କଞ୍ଚାମାଲର ସୁଲଭତା
(B) ପୁଞ୍ଜି
(C) ଶ୍ରମ
(D) ପରିବହନ
Answer:
(A) କଞ୍ଚାମାଲର ସୁଲଭତା

Question 27.
କାହାକୁ ‘ଜାପାନର ମାଞ୍ଚେଷ୍ଟର’ କୁହାଯାଏ ?
(A) ଟୋକିଓ
(B) ଓସାକା
(C) ସିକାଗୋ
(D) କ୍ରିଟୋ
Answer:
(B) ଓସାକା

Question 28.
କେଉଁ ନଦୀରୁ ଓସାକା ବୟନଶିଳ୍ପ ପାଇଁ ପ୍ରଚୁର ଜଳ ଯୋଗାଇଥାଏ ?
(A) ଓଜୋ
(B) ସିଜୋ
(C) କ୍ଲିଟୋ
(D) ମିତୃବିସି
Answer:
(A) ଓଜୋ

Question 29.
ଭାରତର କେଉଁଠାରେ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାର ପ୍ରଧାନ କେନ୍ଦ୍ର ଅଟେ ?
(A) ମୁମ୍ବାଇ
(B) ଦିଲ୍ଲୀ
(C) ବେଙ୍ଗାଲୁରୁ
(D) ମହୀଶୂର
Answer:
(C) ବେଙ୍ଗାଲୁରୁ

Question 30.
କାହାକୁ ଭାରତର ସିଲିକନ ମାଳଭୂମି କୁହାଯାଏ ?
(A) ବେଙ୍ଗାଲୁରୁ
(B) ରାୟପୁର
(C) କୋଲକାତା
(D) ଭୁବନେଶ୍ଵର
Answer:
(A) ବେଙ୍ଗାଲୁରୁ

Question 31.
“କାଲିଫର୍ନିଆର ସିଲିକନ୍ ଉପତ୍ୟକା” କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
(A) ଜାପାନ
(B) ଜର୍ମାନୀ
(C) ରୁଷିଆ
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
Answer:
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା

Question 32.
କେବେ କର୍ଣାଟକ ସରକାର ସର୍ବପ୍ରଥମେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଆଇନ ପ୍ରଣୟନ କରିଥିଲେ ?
(A) 1991
(B) 1992
(C) 1993
(D) 1994
Answer:
(B) 1992

Question 33.
କେଉଁଟି ସିଲିକନ ଉପତ୍ୟକାର ବିଶେଷତ୍ଵ ନୁହେଁ ?
(A) ନାତିଶୀତୋଷ ଜଳବାୟୁ
(B) ଆକର୍ଷିତ ସୁନିର୍ମଳ ପରିବେଶ
(C) ପରିବହନ ସୁଯୋଗ
(D) ଅସ୍ୱାସ୍ଥ୍ୟକର ପରିବେଶ
Answer:
(D) ଅସ୍ୱାସ୍ଥ୍ୟକର ପରିବେଶ

Question 34.
ଭାରତର କେଉଁ ସହରରେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାର ନୂତନ କେନ୍ଦ୍ରମାନ ଗଢ଼ିଉଠି ନାହିଁ ?
(A) ମୁମ୍ବାଇ
(B) ରାୟପୁର
(C) ନୂଆଦିଲ୍ଲୀ
(D) ହାଇଦ୍ରାବାଦ
Answer:
(B) ରାୟପୁର

Question 35.
ଇନ୍‌ଫୋସିସ୍ ଓ ୱିପ୍ରୋ କେଉଁ ଶିଳ୍ପ ସଂସ୍ଥାର ଅଟନ୍ତି ?
(A) ଲୌହ-ଇସ୍ପାତ
(B) କାର୍ପାସ
(C) ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
(D) କାଗଜ
Answer:
(C) ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା

Question 36.
ଆମେରିକୀୟ କମ୍ପାନୀଗୁଡ଼ିକ ସେମାନଙ୍କର କୁଶଳୀ କର୍ମୀମାନଙ୍କୁ ନିଯୁକ୍ତି ଦେଇ ଶସ୍ତା ଓ ସମକୁଶଳୀ ଭାବରେ କେଉଁମାନଙ୍କୁ ନିଯୁକ୍ତି ଦେଇଥାନ୍ତି ?
(A) ଭାରତୀୟ
(B) ଚୀନା
(C) ରୁଷିଆ
(D) ଜାପାନୀ
Answer:
(A) ଭାରତୀୟ

Question 37.
କେଉଁଟି ବୃହତ୍ ହ୍ରଦ ଅଞ୍ଚଳର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ସୁପିରିଅର୍
(B) ଭିକ୍ଟୋରିଆ
(C) ହ୍ୟୁରନ୍
(D) ମିଚିଗାନ୍
Answer:
(B) ଭିକ୍ଟୋରିଆ

Question 38.
କେଉଁ ଶିଳ୍ପଟି ପୃଥ‌ିବୀର ଏକ ପୁରାତନ ଶିଳ୍ପ ?
(A) ଲୌହଇସ୍ପାତ
(B) କାର୍ପାସ ବୟନ
(C) ଖଣିଜ ଉତ୍ତୋଳନ
(D) ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
Answer:
(B) କାର୍ପାସ ବୟନ

Question 39.
ଭବୋଦରା କେଉଁଥିପାଇଁ ପ୍ରସିଦ୍ଧ ?
(A) କାଲିକୋ ବସ୍ତ୍ର
(B) ଚିଜେନ୍
(C) ସୁନା ଜରିବସ୍ତ୍ର
(D) ମସ୍‌ଲିନ୍
Answer:
(C) ସୁନା ଜରିବସ୍ତ୍ର

Question 40.
1854 ମସିହାରେ କେଉଁଠାରେ ଭାରତର ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?.
(A) କୋଲକାତା
(B) ସୁରତ୍
(C) ମୁମ୍ବାଇ
(D) ଅହମ୍ମଦାବାଦ
Answer:
(C) ମୁମ୍ବାଇ

Question 41.
କେଉଁ ନଦୀକୂଳରେ ଅହମ୍ମଦାବାଦ ସହର ଅବସ୍ଥିତ ?
(A) ଇରାବତୀ
(B) କାବେରୀ
(C) ନର୍ମଦା
(D) ସାବରମତି
Answer:
(D) ସାବରମତି

Question 42.
ଜାତୀୟ ବୟନଶିଳ୍ପର ଉତ୍ପାଦିତ ସାମଗ୍ରୀର କେତେଭାଗ ବିଦେଶକୁ ରପ୍ତାନି ହୁଏ ?
(A) 1/2
(B) 1/3
(C) 1/5
(D) 2/3
Answer:
(B) 1/3

Question 43.
କେଉଁଟି ସେବାଶିଳ୍ପ ନୁହେଁ ?
(A) ପରିବହନ
(B) ପର୍ଯ୍ୟଟନ
(C) ଯୋଗାଯୋଗ
(D) କୋଇଲା ଖନନ
Answer:
(D) କୋଇଲା ଖନନ

Question 44.
କେବେ ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣା ଘଟିଥିଲା ?
(A) 1984 Dec 3rd
(B) 1989 Jan 13
(C) 1988 Mar 31
(D) 1999 Aug 13
Answer:
(A) 1984 Dec 3rd

Question 45.
ଭଦ୍ରାବତୀ ଲୌହଇସ୍ପାତ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
(A) ଆନ୍ଧ୍ରପ୍ରଦେଶ
(B) ମଧ୍ୟପ୍ରଦେଶ
(C) କର୍ଣ୍ଣାଟକ
(D) ତାମିଲନାଡୁ
Answer:
(C) କର୍ଣ୍ଣାଟକ

Question 46.
କେଉଁ ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ରଟି ପଶ୍ଚିମବଙ୍ଗରେ ଅବସ୍ଥିତ ?
(A) ଟିସ୍କୋ
(B) ଭିଲାଇ
(C) ବୋକାରୋ
(D) ବର୍ଣ୍ଣପୁର
Answer:
(D) ବର୍ଣ୍ଣପୁର

Question 47.
ଓଡ଼ୋ ନଦୀ କେଉଁ ଶିଳ୍ପକୁ ପ୍ରଚୁର ପାଣି ଯୋଗାଏ ?
(A) କାର୍ପାସ ବୟନ
(B) ଲୌହଇସ୍ପାତ
(C) କୋଇଲା ଖନନ
(D) ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
Answer:
(A) କାର୍ପାସ ବୟନ

Question 48.
କେଉଁ ରାଜ୍ୟ ସର୍ବପ୍ରଥମେ 1992 ମସିହାରେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଆଇନ୍ ପ୍ରଣୟନ କରିଥିଲା ?
(A) ମହାରାଷ୍ଟ୍ର
(B) ତାମିଲନାଡୁ
(C) କର୍ଣ୍ଣାଟକ
(D) ଆନ୍ଧ୍ରପ୍ରଦେଶ
Answer:
(C) କର୍ଣ୍ଣାଟକ

Odisha State Board BSE Odisha 7th Class Geography Solutions Chapter 4 ଜୈବମଣ୍ଡଳ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Geography Solutions Chapter 4 ଜୈବମଣ୍ଡଳ

୧ । ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକର ସଂଜ୍ଞା ଲେଖ ।

Question କ.
ପ୍ରାକୃତିକ ପରିବେଶ :
Answer:
ଜଳ, ସ୍ଥଳ, ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କୁ ନେଇ ଗଠିତ ପରିବେଶକୁ ପ୍ରାକୃତିକ ପରିବେଶ କୁହାଯାଏ ।

Question ଖ.
ଜୈବମଣ୍ଡଳ :
Answer:
ଅଶ୍ମମଣ୍ଡଳ, ବାୟୁମଣ୍ଡଳ ଓ ବାରିମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଥୁବା ତଥା ଜୀବନ ଧାରଣ ପାଇଁ ଆବଶ୍ୟକ ଉପାଦାନ ଥ‌ିବା ପତଳା ସ୍ତରକୁ ଜୈବମଣ୍ଡଳ କୁହାଯାଏ ।

Question ଗ.
ପରିସଂସ୍ଥା :
Answer:
ଜୈବିକ ଓ ଅଜୈବିକ (ଭୂମିରୂପ, ଜଳବାୟୁ, ମୃରିକା) ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଯୋଗୁଁ ସୃଷ୍ଟ ପରିବେଶକୁ ପରିସଂସ୍ଥା କୁହାଯାଏ ।

Question ଘ.
ଜୀବାଳୀ :
Answer:
ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଭୌଗୋଳିକ ସୀମାରେଖା ଭିତରେ ଥ‌ିବା ସମସ୍ତ ଛୋଟ ବଡ଼ ପରିସଂସ୍ଥାର ସମାହାରକୁ ଜୀବାଳୀ (Biome) କୁହାଯାଏ ।

Question କ.
ଖାଦ୍ୟ ଶୃଙ୍ଖଳ :
Answer:
କୌଣସି ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କୁହାଯାଏ ।

Question ଚ.
ଖାଦ୍ୟ ଜାଲକ :
Answer:
କୌଣସି ପରିସଂସ୍ଥାରେ ଛନ୍ଦାଛନ୍ଦି ହୋଇ ରହିଥ‌ିବା ଖାଦ୍ୟଶୃଙ୍ଖଳଗୁଡ଼ିକୁ ଖାଦ୍ୟ ଜାଲକ (Food Web) କୁହାଯାଏ ।

Question ଛ.
ମୃତ୍ତିକା :
Answer:
ମୃତ୍ତିକା ହେଉଛି କଠିନ (ଶିଳାରେଣୁ ଓ ଜୈବିକ ପଦାର୍ଥ), ତରଳ (ଜଳ) ଓ ଗ୍ୟାସୀୟ (ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ ଓ ଉଦ୍‌ଜାନ ଭଳି ଗ୍ୟାସ) ପଦାର୍ଥର ସମାହାର ।

୨। ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

Question କ.
କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ଓ ନାତିଶୀତୋଷ୍ଣ ତୃଣଭୂମି
Answer:

Question ଖ.
ଦୋରସା ମାଟି ଓ କାଦୁଆ ମାଟି
Answer:

Question ଗ.
ଅବଶିଷ୍ଟ ମୃତ୍ତିକା ଓ ଅପସୃତ ମୃତ୍ତିକା
Answer:

Question ଘ.
ତୃଣଭୋଜୀ ପ୍ରାଣୀ ଓ ମାଂସାଶୀ ପ୍ରାଣୀ
Answer:

Question ଙ.
ଉତ୍ପାଦକ ଓ ଭକ୍ଷକ
Answer:

୩ । ସ୍ତମ୍ଭ ଦୁଇଟି ମଧ୍ୟରେ ସମ୍ପର୍କ ସ୍ଥାପନ କରି ଲେଖ ।

Answer:

୪ । କାରଣ ଦର୍ଶାଅ ।

Question କ.
ମେରୁ ଅଞ୍ଚଳରେ ପ୍ରାଣୀମାନଙ୍କର ଚମଡ଼ା ଅଧ୍ବକ ଲୋମଯୁକ୍ତ ।
Answer:

• ମେରୁ ଅଞ୍ଚଳରେ ବର୍ଷର ୧୦ ମାସ ଅଧିକ ଥଣ୍ଡା ଅନୁଭୂତ ହୁଏ ।
• ପ୍ରବଳ ଶୀତରୁ ରକ୍ଷା ପାଇବା ନିମନ୍ତେ ମେରୁ ଅଞ୍ଚଳର ପ୍ରାଣୀମାନଙ୍କର ଚମଡ଼ା ଅଧିକ ଲୋମଯୁକ୍ତ । ଲୋମ ତାପର କୁପରିବାହୀ ଥିବାରୁ ଶୀତର ପ୍ରଭାବରୁ ସେମାନେ ରକ୍ଷା ପାଆନ୍ତି ।

Question ଖ.
ସରଳବର୍ଗୀୟ ଅରଣ୍ୟରେ ଶଙ୍କୁ ଆକାରର ବୃକ୍ଷ ଦେଖାଯାଏ ।
Answer:

• ସରଳବର୍ଗୀୟ ଅରଣ୍ୟ ଥିବା ଅଞ୍ଚଳରେ ତୁଦ୍ରାଞ୍ଚଳ ଅପେକ୍ଷା ଅଧିକ ତୁଷାରପାତ ହୋଇଥାଏ ।
• ଶଙ୍କୁ ଆକାର ବୃକ୍ଷରେ ତୁଷାରପାତ ହେଲେ ତାହା ଶୀଘ୍ର ଖସି ଭୂମିରେ ପଡ଼ିବା ସୁବିଧାଜନକ ହୋଇଥାଏ । ତେଣୁ ସରଳବର୍ଗୀୟ ଅରଣ୍ୟରେ ଶଙ୍କୁ ଆକାରର ବୃକ୍ଷ ଦେଖାଯାଏ ।

Question ଗ.
ଓଟକୁ ମରୁଭୂମିର ଜାହାଜ କୁହାଯାଏ ।
Answer:

• ଓଟ ଦୀର୍ଘଦିନ ଧରି ପାଣି ନ ପିଇ ବଞ୍ଚି ରହିପାରେ ଏବଂ ବାଲୁ କାରାଶି ଉପରେ ସହଜରେ ଯିବାଆସିବା କରିପାରେ ।
• ତେଣୁ ଓଟକୁ ‘ମରୁଭୂମିର ଜାହାଜ’ କୁହାଯାଏ ।

୫ । ଖାଦ୍ୟ ଓ ଖାଦକ ସମ୍ପର୍କ ଅନୁସାରେ କ୍ରମରେ ସଜାଅ ।

Question କ.
ବାଳିଆ, ପତ୍ର, ବ୍ୟାକ୍ଟେରିଆ, ଛୋଟ ମାଛ, ଜିଆ
Answer:
ପୁତ୍ର ← ଜିଆ ← ଛୋଟ ମାଛ ← ବାଳିଆ ← ବ୍ୟାକ୍ଟେରିଆ

Question ଖ.
ସର୍ବଭୁକ୍, ପ୍ରାଥମିକ ଭକ୍ଷକ, ଉତ୍ପାଦକ, ଦ୍ବିତୀୟକ ଭକ୍ଷକ ଉତ୍ପାଦକ
Answer:
← ପ୍ରାଥମିକ ଭକ୍ଷକ ← ଦ୍ଵିତୀୟକ ଭକ୍ଷକ← ସର୍ବରୁକ୍

Question ଗ.
ଘାସ, ବାଘ, ହରିଣ, ବ୍ୟାକ୍ଟେରିଆ
Answer:
ଘାସ ← ହରିଣ ← ବାଘ ← ବ୍ୟାକ୍ଟେରିଆ

୬। ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(କ) ଆର୍ଜେଣ୍ଟିନାର ତୃଣଭୂମିକୁ ______ କୁହାଯାଏ । (ଡାଉନ୍ସ, ପମ୍ପାସ, ପ୍ରେରୀ, ଷ୍ଟେପ୍)
Answer:
ପମ୍ପାସ

(ଖ) ପୃଥ‌ିବୀର ପଶୁଶାଳା _______ ତୃଣଭୂମି ଅଟେ । (କାମ୍ବୋସ, ସାଭାନ୍ନା, ଲିଆନୋସ, ଷ୍ଟେପ୍)
Answer:
ସାଭାନ୍ନା

(ଗ) କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ଅଞ୍ଚଳରୁ _____ ଏକ ପ୍ରାଣୀ । (ବାଇସନ୍, ୱାଲରସ, ଗୟଳ, ଜିରାଫ୍)
Answer:
ଜିରାଫ୍

(ଘ) ପୃଥ୍ବୀର ରୁଟି ଝୁଡ଼ି ______ ତୃଣଭୂମି ଅଟେ । (ସାଭାନ୍ନା, ଲିଆନୋସ, ପମ୍ପାସ, କ୍ୟାମ୍ବୋସ)
Answer:
ପମ୍ପାସ

ଙ) ସାଧାରଣ କଥାବାର୍ତ୍ତାର ଶବ୍ଦ _______ ଡେସିବେଲ୍ । (୨୫, ୫୫, ୧୦୦, ୧୦୫)
Answer:
୨୫

୭। ସଂକ୍ଷେପରେ ଉତ୍ତର ଦିଅ ।

Question କ.
ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କ’ଣ ଉଦାହରଣ ସହ ବୁଝାଅ ।
Answer:

• ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କୁହାଯାଏ ।
• ଖାଦ୍ୟ ଶୃଙ୍ଖଳରେ ଥିବା ପ୍ରତ୍ୟେକ ଶ୍ରେଣୀଭୁକ୍ତ ଜୀବ ଏକ କଡ଼ି ପରି କାମ କରିଥାଏ । ଗୋଟିଏ କଡ଼ି ‘ଖାଦ୍ୟ’ ହେଲେ ଅନ୍ୟଟି ‘ଖାଦକ’ । ସେହିପରି ‘ଖାଦକ’ କଢ଼ି ଖାଦ୍ୟ ହେଲାବେଳେ ପରବର୍ତ୍ତୀ କଡ଼ି ଖାଦକ ହୁଏ ।
• ଉଦାହରଣ : ବିଭିନ୍ନ ପୋକଡୋକ ଆଦିକୁ ବେଙ୍ଗ ଖାଇଥାଏ । ବେଙ୍ଗକୁ ଛୋଟ ସାପ, ଛୋଟ ସାପକୁ ବଡ଼ ସାପ, ବଡ଼ ସାପକୁ ନେଉଳ, ନେଉଳକୁ ଛଞ୍ଚାଣ ଖାଇ ବଞ୍ଚିଥାନ୍ତି । ପ୍ରାଣୀମାନେ ମରିଗଲା ପରେ ସେଗୁଡ଼ିକୁ ବ୍ୟାକ୍ଟେରିଆ ଅପଘଟନ କରି ମାଟିରେ ମିଶାଏ ।

ପୋକଜୋକ ← ବେଙ୍ଗ ← ଛୋଟ ସାପ ← ବଡ଼ ସାପ ← ନେଉଳ ← ଛଞ୍ଚାଣ ← ବ୍ୟାକ୍ଟେରିଆ

Question ଖ.
ଜୈବ ଭାରସାମ୍ୟ କହିଲେ କ’ଣ ବୁଝାଯାଏ ?
Answer:

• ଖାଦ୍ୟ-ଖାଦକ ସମ୍ପର୍କ ଦୃଷ୍ଟିରୁ ଶକ୍ତି ପିରାମିଡ଼ର ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ ଜୀବ ସଂଖ୍ୟା ହ୍ରାସ ପାଇବା ଜରୁରୀ ।
• ପ୍ରତ୍ୟେକ ସ୍ତରର ପ୍ରାଣୀମାନଙ୍କ ମଧ୍ୟରେ ସଂଖ୍ୟାଗତ ସୁସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା ହୁଏ । ଏହିପରି ସଂଖ୍ଯାଗତ ସୁସମ୍ପର୍କକୁ ଜୈବ ଭାରସାମ୍ୟ କୁହାଯାଏ ।
• ଅତ୍ୟଧିକ ଜଙ୍ଗଲ ଧ୍ଵଂସ ଫଳରେ ବିଭିନ୍ନ ଶକ୍ତି ସ୍ତର ମଧ୍ଯରେ ସଂଖ୍ୟାଗତ ସୁସମ୍ପର୍କ ନଷ୍ଟ ହେଉଛି । ଫଳରେ ଅନେକ ପ୍ରଜାତିର ବୃକ୍ଷଲତା ଓ ପ୍ରାଣୀ ନିଶ୍ଚିହ୍ନ ହେବାକୁ ବସିଲେଣି । ଫଳରେ ଜୈବ ଭାରସାମ୍ୟ ନଷ୍ଟ ହେବାରେ ଲାଗିଛି ।
• ନିମ୍ନ ସ୍ତରଗୁଡ଼ିକ କ୍ଷତିଗ୍ରସ୍ତ ହେଲେ ଚତୁର୍ଥ ସ୍ତରରେ ଥିବା ମଣିଷ ନିଶ୍ଚିତଭାବେ ବିପଦଗ୍ରସ୍ତ ହେବ । ତେଣୁ ଜୈବ ଭାରସାମ୍ୟ ରକ୍ଷା ଦିଗରେ ଯବାନ ହେବା ଆବଶ୍ୟକ ।

Question ଗ.
କେଉଁ କାରଣଗୁଡ଼ିକ ଦ୍ଵାରା ଜଳ ଦୂଷିତ ହୁଏ ?
Answer:
ନିମ୍ନଲିଖୁତ କାରଣଗୁଡ଼ିକ ଦ୍ୱାରା ଜଳ ଦୂଷିତ ହୁଏ, ଯଥା-

• ବଡ଼ ବଡ଼ ସହରର ନର୍ଦ୍ଦମା ଜଳ, ଆବର୍ଜ ନ ।, କଳକାରଖାନାରୁ ବାହାରୁଥ‌ିବା ମଇଳା ଜଳରେ ମିଶିବା ।
• କୃଷି କ୍ଷେତ୍ରରେ ବ୍ୟବହୃତ ରାସାୟନିକ ସାର ଓ କୀଟନାଶକ ଔଷଧ ଜଳରେ ମିଶିବା ।
• ଭୂକ୍ଷୟ ଦ୍ବାରା ଜୀବଜନ୍ତୁଙ୍କର ପଚାସଢ଼ା ଶବ ଓ ଉଭିଦର ପତ୍ର ପାଣିରେ ପଡ଼ି ପଚିବା ଦ୍ଵାରା ।
• ଘରୋଇ କାର୍ଯ୍ୟ ଦ୍ଵାରା ନିର୍ଗତ ମଇଳା ଓ ଆବର୍ଜନାଯୁକ୍ତ ଜଳ ମିଶିବା ।

Question ଘ.
ଶକ୍ତି ପ୍ରବାହ କ’ଣ ?

• ଉଦ୍ଭଦ ଜଗତ ଉତ୍ପାଦକ ଓ ପ୍ରାଣୀମାନେ ଭକ୍ଷକ ଅଟନ୍ତି ।
• ଉଦ୍ଭିଦ ଦ୍ବାରା ମାଟିରୁ ସଂଗୃହୀତ ଖଣିଜ ଲବଣ ଓ ସୌରଶକ୍ତି ରାସାୟନିକ ଶକ୍ତିରେ ରୂପାନ୍ତରିତ ହୋଇ ରହେ ।
• ତୃଣଭୋଜୀ ପ୍ରାଣୀ ଉଭିଦର ବିଭିନ୍ନ ଅଂଶ ଖାଇବା ଦ୍ବାରା ସେମାନେ ଉଭିଦଠାରୁ କିଛି ପରିମାଣର ରାସାୟନିକ ଶକ୍ତି (ପ୍ରାୟ ଉଭିଦଠାରେ ଥ‌ିବା ଶକ୍ତିର ଏକ-ଦଶମାଂଶ) ଗ୍ରହଣ କରନ୍ତି ।
• ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କଠାରୁ ଏହି ଶକ୍ତି (ପ୍ରାୟ ଏକ- ଦଶମାଂଶ) ମାଂସାଶୀ ପ୍ରାଣୀ ଓ ମନୁଷ୍ୟ ପାଖକୁ ଯାଏ ।
• ପରିସଂସ୍ଥାରେ ଏହିପରି ଶକ୍ତିର ସ୍ଥାନାନ୍ତରଣକୁ ଶକ୍ତି ପ୍ରବାହ କୁହାଯାଏ । ଶକ୍ତି ପ୍ରବାହ ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ହୁଏ ଓ ଶକ୍ତିର ପରିମାଣ ପ୍ରଥମ ସ୍ତରରୁ ଶୀର୍ଷ ସ୍ତର ଆଡ଼କୁ କ୍ରମଶଃ କମିଯାଏ ।

Question ଙ.
ଜଳ, ବାୟୁ ଓ ମୃରିକା ପ୍ରଦୂଷଣ ରୋକିବାପାଇଁ କି କି ପଦକ୍ଷେପମାନ ନିଆଯାଇ ପାରିବ ?
Answer:
ନିମ୍ନଲିଖ୍ଜ ପଦକ୍ଷେପ ନିଆଗଲେ ଜଳ, ବାୟୁ ଓ ମୃତ୍ତିକା ପ୍ରଦୂଷଣକୁ ରୋକି ହେବ, ଯଥା-

• ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ନିୟନ୍ତ୍ରଣ କରିବା ।
• ଜଳ, ଖଣିଜ ଲବଣ ଓ ଅନ୍ୟାନ୍ୟ ଖଣିଜ ଦ୍ରବ୍ୟର ନିୟନ୍ତ୍ରତ ବ୍ୟବହାର କରିବା ।
• ଜଙ୍ଗଲ କ୍ଷୟ ରୋକିବା ସହ ନୂତନ ଜଙ୍ଗଲ ସୃଷ୍ଟି ପାଇଁ ଉଦ୍ୟମ କରିବା ।
• କଳକାରଖାନାରୁ ନିର୍ଗତ ବିଷାକ୍ତ ଧୂଆଁକୁ ବିଭିନ୍ନ ପ୍ରକ୍ରିୟାରେ ବିଶୋଧ କରି ବାୟୁମଣ୍ଡଳକୁ ଛାଡ଼ିବା ଏବଂ ଶିଳ୍ପଜାତ ଆବର୍ଜନାର ପୁନଃଚକ୍ରଣ କରିବା ।
• ରାସାୟନିକ ସାର ଓ କୀଟନାଶକ ଔଷଧର ନିୟନ୍ତ୍ରିତ ବ୍ୟବହାର କରିବା ଏବଂ ଏହା ପରିବର୍ତ୍ତେ ଜୈବସାର ଓ ଜୈବ କୀଟନାଶକର ବ୍ୟବହାର ଉପରେ ଗୁରୁତ୍ବ ଦେବା ।
• ଯାନବାହନରେ କୋଇଲା, ପେଟ୍ରୋଲ, ଡିଜେଲ ଇନ୍ଧନ ପରିବର୍ତ୍ତେ ବିଦ୍ୟୁତ୍ଵଶକ୍ତି, ସି.ଏଚ୍.ଜି. ଗ୍ୟାସ୍ ବ୍ୟବହାର କରିବା ।
• ଜୀବଜନ୍ତୁଙ୍କ ମଳ ଓ ଅନ୍ୟାନ୍ୟ ଜୈବିକ ଆବର୍ଜନାରୁ ବାୟୋଗ୍ୟାସ୍ ଓ ଜୈବିକ ସାର ପ୍ରସ୍ତୁତ କରିବା ।

Question ୫।
ବାକ୍‌ସ ମଧ୍ୟରେ କେତେକ ପ୍ରାଣୀ ଓ ଉଦ୍ଭିଦ ଲୁଚି ରହିଛନ୍ତି ଖୋଜି ବାହାର କର ।

Answer:
ପ୍ରାଣୀ : ବାଇସନ୍, ମିକ୍ସ୍, କୋକିଶିଆଳି, ୱାଲର୍‌ସ, ଆନାକୋଣ୍ଡା, ଧଳା ଭାଲୁ, ଜେବ୍ରା, ସିଲ୍, ଆଣ୍ଟିଲୋପ୍
ଉଭିଦ : ଦେବଦାରୁ, ସିଡାର, ଅଲିଭ୍, ଫାର୍‌, କାକ୍‌ସ, ଓକ୍, ଚେଷ୍ଟନଟ୍, ଜଳପାଇ, ଶାଳ

Question ୯।
ପୃଥ‌ିବୀର ରେଖାଙ୍କିତ ମାନଚିତ୍ର ଅଙ୍କନ କରି ତୃଣଭୂମିଗୁଡ଼ିକ ଦର୍ଶାଅ ।
Answer:

BSE Odisha 7th Class Geography Notes Chapter 4 ଜୈବମଣ୍ଡଳ

ପ୍ରାକୃତିକ ପରିବେଶ :

• ଆମ ଚତୁଃପାର୍ଶ୍ୱସ୍ଥ ଜଳ, ସ୍ଥଳ, ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କୁ ନେଇ ଆମ ପ୍ରାକୃତିକ ପରିବେଶ ଗଠିତ ।
• ପ୍ରାକୃତିକ ପରିବେଶ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ, ଯଥା- ଅଜୈବିକ ପରିବେଶ ଓ ଜୈବିକ ପରିବେଶ ।

• ପୃଥ‌ିବୀର ତିନି ମଣ୍ଡଳ, ଯଥା- ବାୟୁମଣ୍ଡଳ, ଅଂଶୁମଣ୍ଡଳ ଓ ବାରିମଣ୍ଡଳର ମିଳନସ୍ଥଳରେ ଜୈବମଣ୍ଡଳ ଅବସ୍ଥିତ ।
• ଜୈବମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ପ୍ରାଣୀ ଓ ଉଭିଦ ପ୍ରତ୍ୟକ୍ଷ ଓ ପରୋକ୍ଷ ଭାବେ ମୃତ୍ତିକା ଉପରେ ନିର୍ଭରଶୀଳ ।

ମୃତ୍ତିକା :

• ଭୂପୃଷ୍ଠରେ ଏକ ସୂକ୍ଷ୍ମ ପତଳା ସ୍ତର ଭଳି ରହିଥିବା ମୃରିକା କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ପଦାର୍ଥର ସମାହାର ଅଟେ ।
• ମୃତ୍ତିକାର ଉପାଦାନ :
• ଗୋଡ଼ି, ବାଲି, ପଟୁ ଓ କର୍ଦ୍ଦମ ଆକାର ଶିଳାରେଣୁକୁ ନେଇ ମାଟିର ପ୍ରକାରଭେଦ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
• ବିଭିନ୍ନ ପ୍ରକ୍ରିୟାରେ ଶିଳା ଚୂର୍ଣ୍ଣବିଚୁର୍ଣ୍ଣ ହୋଇ ଶିଳାରେଣୁରେ ପରିଣତ ହୁଏ । ଶିଳରେଣୁରେ ଖଣିଜ ଅଂଶ ସହ ଜୈବିକ ଅଂଶ ମିଶି ଏହା ଜଳ ତଥା ଅନ୍ୟାନ୍ୟ ଗ୍ୟାସୀୟ ପଦାର୍ଥ ସଂସ୍ପର୍ଶରେ ଆସି ବିଭିନ୍ନ ଭୌତିକ, ଜୈବିକ ଓ ରାସାୟନିକ ପ୍ରକ୍ରିୟା ଦ୍ଵାରା ମୃତ୍ତିକାରେ ପରିଣତ ହୁଏ ।

• ବାଲି, ପଟୁ ଓ କର୍ଦ୍ଦମର ସୁଷମ ମିଶ୍ରଣରେ ଦୋରସା ମାଟି, ବାଲିର ପରିମାଣ ଅଧିକ ଥିଲେ ବାଲିଆ ମାଟି, କର୍ଦ୍ଦମର ପରିମାଣ ଅଧିକ ଥିଲେ କାଦୁଆ ମାଟି କୁହାଯାଏ ।

ଉତ୍ପତ୍ତିସ୍ଥଳ ଦୃଷ୍ଟିରୁ ଶିଳାର ପ୍ରକାରଭେଦ :

ପରିସଂସ୍ଥା :

• ପ୍ରାକୃତିକ ପରିବେଶର ଜୈବିକ ଓ ଅଜୈବିକ ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧରୁ ପରିସଂସ୍ଥାର ସୃଷ୍ଟି ।
• ପରିସଂସ୍ଥାର ଜୈବିକ ଉପାଦାନ ପ୍ରାଣୀ ଓ ଉଦ୍ଭିଦ ଅଜୈବ ଉପାଦାନ ଜଳ, ବାୟୁ ଓ ମୃଭିକା ଉପରେ ନିର୍ଭରଶୀଳ ।

ଜୀବାଳୀ :

• ବୃହତ୍ ପରିସଂସ୍ଥା ଜୀବାଳୀ ଅଟେ । ସ୍ଥଳଭାଗରେ ଥିବା ସ୍ଵତନ୍ତ୍ର ପ୍ରକାରର ପ୍ରାଣୀ ଓ ଉଭିଦକୁ ନେଇ ଗଠିତ ଜୀବାଳୀ ଅନ୍ୟ ଏକ ଜୀବାଳୀଠାରୁ ଭିନ୍ନ ହୋଇଥାଏ ।
• ଜଳବାୟୁ ଓ ମୃତ୍ତିକା ଦୃଷ୍ଟିରୁ ମହାଦେଶୀୟ ପରିସଂସ୍ଥା ୩ ଭାଗରେ ବିଭକ୍ତ ।

• ପ୍ରତ୍ୟେକ ପରିସଂସ୍ଥା ଜଳବାୟୁ ଓ ମୃରିକା ଦ୍ବାରା ପ୍ରଭାବିତ ହେଉଥ‌ିବାରୁ ସେଠାରେ ଖାପ ଖୁଆଇପାରୁ ନଥ‌ିବା ପ୍ରାକୃତିକ ଉଭିଦ ଓ ବନ୍ୟପ୍ରାଣୀ ଦେଖାଯାନ୍ତି । ଆକାର ପ୍ରକାର ଦୃଷ୍ଟିରୁ ପ୍ରାକୃତିକ ଉଭିଦକୁ ତିନିଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଛି, ଯଥା- ଅରଣ୍ୟ, ତୃଣଭୂମି ଓ କଣ୍ଟାବୁଦା ।

ଅରଣ୍ୟ (ପ୍ରାକୃତିକ ଉଦ୍ଭଦ) :

ଜଳବାୟୁ ଭିତ୍ତିରେ ଅରଣ୍ୟର ପ୍ରକାରଭେଦ, ବିଶେଷତ୍ଵ, ସେଠାରେ ଦେଖାଯାଉଥ‌ିବା ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କ ସମ୍ପର୍କରେ ନିମ୍ନୋକ୍ତ ସାରଣୀର ଜାଣିବା :

ତୃଣଭୂମି :

ଅବସ୍ଥିତି ଦୃଷ୍ଟିରୁ ତୃଣଭୂମି ଦୁଇ ପ୍ରକାରର, ଯଥା – କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି, ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।

କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି :

ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି :

ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିର ନାମ :

ଆଫ୍ରିକାର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ସାଭାନ୍ନା କୁହାଯାଏ । ଏହା ଶିକାରୀର ସ୍ଵର୍ଗ ।
ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ପୃଥ‌ିବୀର ରୁଟି ଝୁଡ଼ି କୁହାଯାଏ ।

କଣ୍ଟାବୁଦା :

• ଅଧ‌ିକ ତାପମାତ୍ରା ଓ ଅତି କମ୍ ବୃଷ୍ଟିପାତ ହେଉଥୁବା ମରୁ ତଥା ଅର୍ଥମରୁ ଅଞ୍ଚଳରେ କଣ୍ଟାବୁଦା ଜାତୀୟ ଉଦ୍ଭଦ ଜନ୍ମିଥାଏ ।
• ଏଠାରେ ଥ‌ିବା ମରୂଦ୍ୟାନମାନଙ୍କରେ ନାଗଫେଣୀ, ଖଜୁରୀ, ସିଜୁ, ବାବୁଲ ଜାତୀୟ ବୃକ୍ଷ ଦେଖାଯାଏ ।

ଚୁନ୍ଦ୍ରା ଭଦ୍ଭଦ :

• ମେରୁ ନିକଟବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ଦୁଇ ମାସ ଗ୍ରୀଷ୍ମଋତୁ ରହେ । ତେଣୁ ଏହି ଋତୁରେ ମସ୍, ଲାଇକେନ୍ ଭଳି ଛୋଟ ଛୋଟ ଗୁଳ୍ମ ଜନ୍ମେ ।
• ମେରୁ ଅଞ୍ଚଳରେ ଦେଖାଯାଉଥିବା ମୁଖ୍ୟ ପ୍ରାଣୀମାନଙ୍କ ମଧ୍ୟରେ ସିଲ୍, ତିମି, ୱାଇରସ୍, ବଲ୍‌ଗା ହରିଣ, ମେରୁଭାଲୁ, ବରଫ କୋକିଶିଆଳୀ, ମେରୁ ପେଚା ଆଦି ପ୍ରଧାନ ।
• ସେହିପରି ଉଚ୍ଚ ପାର୍ବତ୍ୟରେ ଉଚ୍ଚତା ଭେଦରେ ବିଭିନ୍ନ ପ୍ରକାର ଅରଣ୍ୟ ଦୃଷ୍ଟିଗୋଚର ହୁଏ ।

ପ୍ରାକୃତିକ ଭାରସାମ୍ୟ :

ମଣିଷର ଆବଶ୍ୟକତା ବୃଦ୍ଧି ସହ ବିଭିନ୍ନ ପ୍ରଗତିମୂଳକ କାର୍ଯ୍ୟ ନିମିତ୍ତ ବ୍ୟାପକ ଜଙ୍ଗଲ କ୍ଷୟ ହୋଇ ଚାଲୁଛି ।
ଜଙ୍ଗଲ କ୍ଷୟର କାରଣ ଓ ଏହାର କୁଫଳ ନିମ୍ନୋକ୍ତ ରେଖାଚିତ୍ରରୁ ଜାଣିବା :

କୌଣସି ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ଜୈବ (ଉଦ୍ଭିଦ ଓ ପ୍ରାଣୀ) ଓ ଅଜୈବ (ଜଳ, ବାୟୁ ଓ ମୃତ୍ତିକା) ଉପାଦାନ ମଧ୍ଯରେ ଅନବରତ ପଦାର୍ଥ ଓ ଶକ୍ତିର ଆଦାନପ୍ରଦାନ ଚାଲିଥାଏ । ଫଳରେ ପ୍ରାକୃତିକ ଭାରସାମ୍ୟ ବଜାୟ ରହେ ।

ଖାଦ୍ୟଶୃଙ୍ଖଳ :

• ପ୍ରତ୍ୟେକ ପରିସଂସ୍ଥାରେ ଅନେକ ଖାଦ୍ୟଶୃଙ୍ଖଳ ଥାଏ । ପରିସଂସ୍ଥାରେ ଥିବା ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାହିଁ ଖାଦ୍ୟଶୃଙ୍ଖଳ ।
• ଉଦାହରଣ – ବିଭିନ୍ନ ଶସ୍ୟ ଓ ପତ୍ରକୁ ଠେକୁଆ ଖାଇ ବମ୍ବେ, ଠେକୁଆକୁ ହେଟାବାଘ, ହେଟାବାଘକୁ ଅଜଗର ସାପ ଓ ଅଜଗର ସାପ ମଲାପରେ ବ୍ୟାକ୍ଟେରିଆ ତାକୁ ଅପଘଟନ କରି ମାଟିରେ ମିଶାଏ ।

ଖାଦ୍ୟ ଜାଲକ :

• ଖାଦ୍ୟଶୃଙ୍ଖଳଗୁଡ଼ିକ ଛନ୍ଦାଛନ୍ଦି ହୋଇ ରହିଲେ ତାହାକୁ ଖାଦ୍ୟ ଜାଲକ କୁହାଯାଏ ।
• ଶକ୍ତିପ୍ରବାହ : ଉଭିଦର ଖାଦ୍ୟ ପ୍ରସ୍ତୁତିବେଳେ ସୌରଶକ୍ତି ରାସାୟନିକ ଶକ୍ତିଭାବେ ତା’ଠାରେ ସଞ୍ଚିତ ହୋଇ ରହେ । ଉଭିଦକୁ ଖାଉଥ‌ିବା ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କଠାରେ ଏହି ଶକ୍ତିର ସ୍ଥାନାନ୍ତରିତ ହୁଏ । ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କଠାରୁ ଏହା ମାଂସାଶୀ ଓ ମଣିଷ ପାଖକୁ ଶକ୍ତିର ସ୍ଥାନାନ୍ତରଣ ହୁଏ । ଏହାକୁ ଶକ୍ତି ପ୍ରବାହ କୁହାଯାଏ ।

• ଶକ୍ତି ପ୍ରବାହର ପ୍ରଥମ ସ୍ତରରେ ଉଭିଦ, ଦ୍ବିତୀୟ ସ୍ତରରେ ତୃଣଭୋଜୀ, ତୃତୀୟ ସ୍ତରରେ ମାଂସାଶୀ ପ୍ରାଣୀ ଓ ଚତୁର୍ଥ ସ୍ତରରେ ଦ୍ଵିତୀୟ ସ୍ତର ମାଂସାଶୀ ପ୍ରାଣୀ ରହିଥାଏ । ଶକ୍ତି ପ୍ରବାହର ପରିମାଣ ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ କ୍ରମଶଃ ହ୍ରାସ ପାଏ । ଚିତ୍ର ଆକାରରେ ଏହା ପିରାମିଡ୍ ଭଳି ଦେଖାଯାଉଥିବାରୁ ଏହାକୁ ଶକ୍ତି ପିରାମିଡ୍ କୁହାଯାଏ ।
• ଖାଦ୍ୟ-ଖାଦକ ସମ୍ପର୍କ ଦୃଷ୍ଟିରୁ ଶକ୍ତି ପିରାମିଡ଼ର ପ୍ରଥମ ସ୍ତରରୁ ଶେଷ ସ୍ତର ପର୍ଯ୍ୟନ୍ତ ଜୀବସଂଖ୍ୟା କ୍ରମଶଃ ହ୍ରାସ ପାଇବା ଜରୁରୀ ।
• ପ୍ରତ୍ୟେକ ଶକ୍ତି ସ୍ତର ମଧ୍ଯରେ ସଂଖ୍ୟାଗତ ସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା ହେଲେ ଜୈବ ଭାରସାମ୍ୟ ବଜାୟ ରହେ ।
• ବିଭିନ୍ନ କାରଣରୁ ଜୈବ ଭାରସାମ୍ୟ କ୍ଷୟ ହେବାରେ ଲାଗିଛି ।

ପ୍ରଦୂଷଣ ଓ ପରିବେଶ ଅବକ୍ଷୟ :

ମାନବକୃତ କାର୍ଯ୍ୟକଳାପରୁ ସୃଷ୍ଟ ବର୍ଜ୍ୟବସ୍ତୁ ଜଳ, ବାୟୁ, ମୃରିକାରେ ମିଶି ପ୍ରାକୃତିକ ପରିବେଶକୁ ପ୍ରଦୂଷଣ କରନ୍ତି । ପ୍ରାକୃତିକ ପ୍ରଦୂଷଣ କେହିଲେ ବାୟୁ ପ୍ରଦୂଷଣ, ଜଳ ପ୍ରଦୂଷଣ ଓ ମୃତ୍ତିକା ପ୍ରଦୂଷଣକୁ ବୁଝାଏ ।

ବାୟୁ ପ୍ରଦୂଷଣ :

ପ୍ରାକୃତିକ ଓ ମାନବକୃତ କାର୍ଯ୍ୟକଳାପରୁ ବାୟୁ ପ୍ରଦୂଷିତ ହୋଇଥାଏ ।

ବାୟୁ ପ୍ରଦୂଷଣ ନିରାକରଣ ପାଇଁ କେତେକ ପଦକ୍ଷେପ :

• ପେଟ୍ରୋଲ ଓ ଡିଜେଲ୍ ଜାଳେଣି ପରିବର୍ତ୍ତେ ସି.ଏଚ୍.ଜି.ର ବ୍ୟବହାର ।
• କାଠ, କୋଇଲା, ଗୋବର ଘସି ପରିବର୍ତ୍ତେ ଗ୍ୟାସ୍ ବ୍ୟବହାର ।
• ବୃକ୍ଷରୋପଣ ତଥା ସାମାଜିକ ବନୀକରଣ ପାଇଁ ଉଦ୍ୟମ ।

ଜଳ ପ୍ରଦୂଷଣ :

ମୃରିକା ପ୍ରଦୂଷଣ :

ଶବ୍ଦ ପ୍ରଦୂଷଣ :

• ମଣିଷ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତୀବ୍ରତା ବିଶିଷ୍ଟ ଶବ୍ଦକୁ ଗ୍ରହଣ କରିପାରେ, ଯଥା- ସର୍ବାଧ‌ିକ ୭୫ ଡେସିବେଲ୍ ଶବ୍ଦ ମଣିଷର କିଛି କ୍ଷତି କରେ ନାହିଁ ।
• ଏହାଠାରୁ ଅଧ‌ିକ ଡେସିବେଲ୍‌ ଶବ୍ଦ ଶବ୍ଦ ପ୍ରଦୂଷଣ ସୃଷ୍ଟି କରେ ।
• ଶବ୍ଦ ପ୍ରଦୂଷଣ ଦ୍ବାରା ଶ୍ରବଣଶକ୍ତି ହ୍ରାସ, ମୁଣ୍ଡବ୍ୟଥା ଓ ମସ୍ତିଷ୍କ ବିକୃତି ରୋଗ ହେବା ଆଶଙ୍କା ଥାଏ ।

ପରିବେଶକୁ ପ୍ରଦୂଷଣମୁକ୍ତ କରିବାର ଉପାୟ :

କେତେକ ପଦକ୍ଷେପ ଦ୍ଵାରା ଆମେ ଆମ ପ୍ରାକୃତିକ ପରିବେଶକୁ ପ୍ରଦୂଷଣମୁକ୍ତ ରଖୂପାରିବା :

କେତେକ ଭୌଗୋଳିକ ଶବ୍ଦାବଳୀ

• ପ୍ରାକୃତିକ ପରିବେଶ : ଜଳ, ସ୍ଥଳ, ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କୁ ନେଇ ଗଠିତ ପରିବେଶ ।
• ଅଜୈବ ପରିବେଶ : ପ୍ରାକୃତିକ ପରିବେଶ ଅନ୍ତର୍ଗତ ଅଶୁମଣ୍ଡଳ, ବାରିମଣ୍ଡଳ ଓ ବାୟୁମଣ୍ଡଳକୁ ନେଇ ସୃଷ୍ଟ ପରିବେଶ ।
• ଜୈବିକ ପରିବେଶ : ଜୈବମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ପ୍ରାଣୀ ଓ ଉଦ୍ଭଦକୁ ନେଇ ଜୈବିକ ପରିବେଶ ଗଠିତ ।
• ଅବଶିଷ୍ଟ ମୃତ୍ତିକା : ଶିଳା ଚୂର୍ଣ୍ଣ ବିଚୂର୍ଣ ହୋଇ ସେହି ସ୍ଥାନରେ ମୃର୍ତ୍ତିକାରେ ପରିଣତ ହେଲେ ତାହାକୁ ଅବଶିଷ୍ଟ ମୃରିକା କୁହାଯାଏ ।
• ଅପସୃତ ମୃର୍ତ୍ତିକା : ନଦୀ, ହିମବାହ, ବାୟୁପ୍ରବାହ ଦ୍ଵାରା ଅପସୃତ ଶିଳାରେଣୁ ନିମ୍ନଭୂମିରେ ଜମାହୋଇ ସୃଷ୍ଟି ହେଉଥୁବା ମୃରିକା ।
• ପରିସଂସ୍ଥା : ଜୈବିକ ଓ ଅଜୈବିକ ଉପାଦାନ ମଧ୍ଯରେ ଥ‌ିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଯୋଗୁଁ ସୃଷ୍ଟ ପରିବେଶ ।
• ଜୀବାଳୀ : କୌଣସି ବିସ୍ତୀର୍ଣ୍ଣ ସ୍ଥଳଭାଗ ଓ ଜଳଭାଗ ଅନ୍ତର୍ଗତ ବୃହତ୍ ପରିସଂସ୍ଥା ।
• ଟାଇଗା : ସରଳବର୍ଗୀୟ ଅରଣ୍ୟକୁ ରୁଷୀୟ ଭାଷାରେ ଟାଇଗା କୁହାଯାଏ, ଯାହାର ଅର୍ଥ ବିଶୁଦ୍ଧ, ଅସ୍ପୃଶ୍ୟ ।
• ସାଭାନ୍ନା : ଆଫ୍ରିକାର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• କ୍ୟାମ୍ପୋସ୍ : ବ୍ରାଜିଲ୍‌ରେ ଥିବା କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଲିଆନୋସ୍ : ଭେନେଜୁଏଲାରେ ଥିବା କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ପ୍ରେରୀ : ଉତ୍ତର ଆମେରି କାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଷ୍ଟେପ୍ : ମଧ୍ୟ-ଏସିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଡାଉନ୍ସ : ଅଷ୍ଟ୍ରେଲିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ପମ୍ପାସ : ଆର୍ଜେଣ୍ଟିନାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।

• ଭେଲ୍ସ : ଦକ୍ଷିଣ ଆଫ୍ରିକାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଖାଦ୍ୟ ଶୃଙ୍ଖଳ : ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରି ଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୂ ଙ୍ଖ ଳ କୁହାଯାଏ ।
• ଖାଦ୍ୟ ଜାଲକ : ଛନ୍ଦାଛନ୍ଦି ହୋଇ ରହିଥ‌ିବା ଖାଦ୍ୟ ଶୃଙ୍ଖଳକୁ ଖାଦ୍ୟ ଜାଲକ କୁହାଯାଏ ।
• ଶକ୍ତି ପ୍ରବାହ : ପରିସଂସ୍ଥାରେ ପ୍ରଥମ ସ୍ତରରୁ ଦ୍ବିତୀୟ ସ୍ତର, ଦ୍ଵିତୀୟ ସ୍ତରରୁ ତୃତୀୟ ସ୍ତର ଓ ତୃତୀୟ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତରକୁ ଶକ୍ତିର ସ୍ଥାନାନ୍ତରଣ ହେବା ପ୍ରକ୍ରିୟା ।
• ଶକ୍ତି ପିରାମିଡ୍ : ଖାଦ୍ୟ ଶୃଙ୍ଖଳର ପ୍ରତ୍ୟେକ ସ୍ତରରେ ଏକକ ସମୟ ଓ ଅଞ୍ଚଳ ରେ ଆହ ର ଣ କରାଯାଉଥିବା ଶକ୍ତି ପରିମାଣ ଦର୍ଶାଉଥ‌ିବା ପିରାମିଡ୍ ସଦୃଶ ଗ୍ରାଫିକ୍ ଚିତ୍ର ।
• ଜୈବ ଭାରସାମ୍ୟ : ଶକ୍ତି ପିରାମିଡ୍‌ର ପ୍ରତ୍ୟେକ ସ୍ତର ମଧ୍ଯରେ ସଂଖ୍ୟାଗଡ ସୁସମ୍ପର୍କକୁ ଜୈବ ଭାରସାମ୍ୟ କୁହାଯାଏ ।
• ପ୍ରଦୂଷଣ : ପ୍ରାକୃତିକ ପରିବେଶର ଦୂଷିତ ଓ ସଂକ୍ରମିତ ଅବସ୍ଥା ।
• ପ୍ରଦୂଷକ : ପ୍ରଦୂଷଣ କରୁଥିବା ବର୍ଜ୍ୟବସ୍ତୁ ।
• ଡେସିବେଲ୍ : ଶବ୍ଦର ତୀବ୍ରତା ମାପିବାର ଏକକ ।