Prasanna

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 17 ଆବର୍ଜନାର ପରିଚାଳନା Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 17 ଆବର୍ଜନାର ପରିଚାଳନା

Question 1.
କୃଷିଜାତ ଆବର୍ଜନା କ’ଣ ? ଏହାର କିପରି ସଦୁପଯୋଗ କରାଯାଇପାରିବ ?
Solution:
ଉ-କୃଷିଜାତ ଆବର୍ଜନା – ଧାନ ଓ ଗହମ ଆଦିର ଅଗାଡ଼ି ଓ ଚଷୁ , ନଡ଼ିଆର ସଢ଼େଇ ଓ କତା, ବିଭିନ୍ନ ଫଳର ଚୋପା ଓ ମଞ୍ଜି ଆଦି କୃଷିଜାତ ଆବର୍ଜନା ଅଟେ ।
ସଦୁପଯୋଗ :
(i) ଧାନକୁଣ୍ଡାରୁ ତେଲ ପ୍ରସ୍ତୁତ କରାଯାଏ ଓ ଏହି କୁଣ୍ଡା ସହ ସିମେଣ୍ଟ, କାଦୁଅ ଓ ରାସାୟନିକ ପଦାର୍ଥ ମିଶାଇ ଶୀତତାପ ନିୟନ୍ତ୍ରିତ ଇଟା ମଧ୍ୟ ପ୍ରସ୍ତୁତ କରାଯାଏ, କେତେକ କୁଣ୍ଡାକୁ ଜାଳେଣି ରୂପେ ମଧ୍ୟ ବ୍ୟବହାର କରନ୍ତି ।
(ii) ବିଭିନ୍ନ ଫଳର ଚୋପାରୁ କାଗଜ ପ୍ରସ୍ତୁତ କରାଯାଏ ।
(iii) ଏହି ଆବର୍ଜନାକୁ ବିନିଯୋଗ କରି ସୋଡ଼ିୟମ୍ ସିଲିକେଟ ନାମକ ରାସାୟନିକ ଯୌଗିକ ମଧ୍ୟ ପ୍ରସ୍ତୁତ କରାଯାଏ ।
(iv) କେତେକ ଶସ୍ୟର ବିଶୁଦ୍ଧ ଜଳର ତିନିଗୋଟି ବ୍ୟବହାର ଲେଖ ।

Question 2.
ବିଶୁଦ୍ଧ କଲର ଡିନିଗୋଟି ବ୍ୟବହାର ଲେଖ |
Solution:
ଜଳକୁ ବିଶୁଦ୍ଧ କରିବା ଅର୍ଥ ବ୍ୟବହାର କରିବା ପୂର୍ବରୁ ସେଥୁରେ ମିଶିଥିବା ସମସ୍ତ ଆବର୍ଜନାକୁ ନିଷ୍କାସନ କରିବା ଓ ଜଳକୁ ବୀଜାଣୁ ମୁକ୍ତ କରିବା ।
(i) ଆମେ ସମସ୍ତେ ବିଶୁଦ୍ଧ ଜଳକୁ ହିଁ ପାନୀୟ ରୂପେ ବ୍ୟବହାର କରିଥାଉ ।
(ii) ବିଶୁଦ୍ଧ ଜଳ ବ୍ୟବହାର କଲେ ଓ ସେହି ଜଳରେ ଗାଧୋଇଲେ ଜଳ ବାହିତ ରୋଗ; ଯଥା – କଲେରା, ଆମାଶୟ, ଟାଇଫଏଡ଼, କାମଳ, କାଛୁ କୁଣ୍ଡିଆ ଆଦିରୋଗ ହୋଇ ନଥାଏ ।
(iii) ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରିବା, ଦାନ୍ତ ଘଷିବା ଓ ଶୌଚକରିବା ଆଦିରେ ଆମେ ବିଶୁଦ୍ଧ ଜଳ ବ୍ୟବହାର କରିଥାଉ ।

Question 3.
ପୁନଃ ଚକ୍ରଣ ପଦ୍ଧତି କ’ଣ ? ଆବର୍ଜନା ନିଷ୍କାସନରେ ଏହାର ଭୂମିକା କ’ଣ ଆଲୋଚନ କର ।
Solution:
ପୁନଃଚକ୍ରଣ ପଦ୍ଧତି – କେତେକ ଆବର୍ଜନାରୁ ପୁନର୍ବାର ନୂଆ ନୂଆ ଜିନିଷ ପ୍ରସ୍ତୁତ କରାଯାଇଥାଏ । ଏହି ପଦ୍ଧତିକୁ ପୁନଃଚକ୍ରଣ ପଦ୍ଧତି କହନ୍ତି ।
ଭୂମିକା :
(i) ଅଳିଆ ଗଦାରୁ ମିଳୁଥିବା ଛିଣ୍ଡା କନା, କାଗଜ, କୁଟା, କାଠି, ଶୁଖୁଲା ପତ୍ର ଆଦିକୁ କାଗଜ ଶିଳ୍ପରେ ବ୍ୟବହାର କରାଯାଇପାରିବ । ଏଥୁରୁ ପୁନଃ ଚକ୍ରଣ ପଦ୍ଧତିରେ ଗୋଲ କୋଇଲା ଭଳି ଜାଳେଣି ମଧ୍ୟ ପ୍ରସ୍ତୁତ କରାଯାଇ ପାରିବ ।
(ii) ଲୁହା, ପ୍ଲାଟିନମ, ଟିଣ, ଏଲୁମିନିୟମ୍ ଏପରିକି ପ୍ଲାଷ୍ଟିକ ଓ କାଚ ଆଦି ଆବର୍ଜନାକୁ ପୁନଃଚକ୍ରଣ ପଦ୍ଧତିଦ୍ୱାରା ତରଳାଇ ନୂଆ ନୂଆ ଜିନିଷ ସବୁ ପ୍ରସ୍ତୁତ କରାଯାଇପାରିବ ।

Question 4.
ଅପଚୟିତ ଜଳର ଉପଚାରର କୌଶଳଗୁଡ଼ିକ ଲେଖ । ଏଥୁରୁ କେଉଁ କୌଶଳ ସହରର ଦୂଷିତ ଜଳର ଉପଚାର ପ୍ଲାଣ୍ଟରେ ବ୍ୟବହୃତ ହୁଏ ?
Solution:
(i) ଅପଚୟିତ ଜଳର ଉପଚାରର କୌଶଳଗୁଡ଼ିକ ହେଲା – ଭୌତିକ ଉପଚାର, ରାସାୟନିକ ଉପଚାର, ଜୈବିକ ସହରର ପ୍ଲାଣ୍ଟରେ ଏବଂ ଭସାକରଣ ଲତ୍ୟାଦି |
(ii) ଏଥୁରୁ ସହରରେ ଦୂଷିତ ଜଳର ଉପଚାର ପ୍ଲାଣ୍ଟରେ ଭୌତିକ, ରାସାୟନିକ ଓ ଜୈବିକ ଉପଚାର କରାଯାଇଥାଏ ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଜଳରେ _________ ପଦାର୍ଥ ମିଶିଥିଲେ ତା’କୁ ଅପଚୟିତ ଜଳ କୁହାଯାଏ ।
(ii) ଦୂଷିତ ଜଳକୁ _________ କରିବାପାଇଁ ଚୂନ ଓ ବ୍ଲିଚିଂ ପାଉଡ଼ର ରାସାୟନିକ ପଦାର୍ଥ ବାହିତ କୁହାଯାଏ ।
(iii) ହଇଜା, ଅମାଶୟ ଓ ଟାଇଫଏଡ଼କୁ _________ ବାହିତ ରୋଗ କୁହାଯାଏ ।
(iv) ଦୂଷିତ ଜଳର _________ ଫଳରେ ପଟୁମାଟି ଓ ଜୈବିକ ଗ୍ୟାସ ବାହାରେ ।
(v) ପ୍ରତ୍ୟେକ ଆବର୍ଜନାର _________ କରି ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଇପାରେ ।
(vi) ଘରୁ ବାହାରୁଥିବା ଦୂଷିତ ଜଳକୁ _________ କୁହାଯାଏ ।
(vii) ଦୂଷିତ ଜଳର ଉପଚାର _________ ରେ କରାଯାଏ ।
(viii) ଆମେ _________ କାଳକୁ ପାନୀୟ କଲରୁପେ ବ୍ୟବହାର କରୁ |
(ix) 2005 ମସିହା ମାର୍ଚ୍ଚ 22 ତାରିଖକୁ _______ ଦିବସ ରୂପେ ପାଳନ କରାଯାଏ ।
(x) ଅପଚାୟିତ ଜଳରେ ଥିବା ପୋଷକ ମଧ୍ୟରୁ _______ ଅନପରମ |
(xi) ଜଳକୁ ବୀଜାଣୁମୁକ୍ତ କରିବାକୁ ସେଥ‌ିରେ _______ ବଟିକା ମିଶାଯାଏ ।
(xii) _______ ଗଛ ସବୁଠାରୁ ଅଧ‌ିକ ଅପରିଷ୍କାର ଜଳ ଶୋଷଣ କରିଥାଏ ।
Solution:
(i) ଦୂଷିତ
(ii) ବିଶୁଦ୍ଧ
(iii) ଜଳ
(iv) ଉପଚାର
(v) ପୁନଃଚକ୍ରଣ
(vi) ସୁଏଜ୍ ବା ନାଳ
(vii) ଦୂଷିତ ଜଳ
(viii) ବଟିକା
(ix) ବିଶ୍ଵ ଜଳ
(x) ଯବଶାରକାନ
(xi) କ୍ଲୋରିନ୍
(xii) ଇଉକାଲିପଟାସ୍

II. ବାମପାର୍ଶ୍ଵର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଦକ୍ଷିଣପାର୍ଶ୍ଵର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ମାଟି : ଅଜୈବିକ ପଦାର୍ଥ :: ମନୁଷ୍ୟ ମଳ : _________
(ii) ଆଖୁଛେଦା : ଶିଳ୍ପ ଆବର୍ଜନା :: ନଡ଼ିଆକତା : _________
(iii) ପ୍ଲାଷ୍ଟିକ୍ ପଲିଥୁନ୍ : କଠିନ ଆବର୍ଜନା :: ନର୍ଦ୍ଦମା ପାଣି : _________
Solution:
(i) ଜୈବିକ ପଦାର୍ଥ,
(ii) କୃଷି ଆବର୍ଜନା,
(iii) ତରଳ ଆବର୍ଜନା

III. ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।
(a) କେଉଁଟି ଜୈବ- ନିମ୍ନକରଣ ଅଯୋଗ୍ୟ ଆବର୍ଜନା ?
(i) ରବର
(ii) ଦଳ
(iii) ମଳମୂତ୍ର
(iv) ପଣ୍ଡ
Solution:
(i) ରବର

(b) କେଉଁଟି ପୁନଃଚକ୍ରଣ ଯୋଗ୍ୟ ଆବର୍ଜନା ନୁହେଁ ?
(i) ପଲିଥୁନ୍ ବ୍ୟାଗ୍
(ii) ଚିରା କାଗଜ
(iii) ଟିଣ
(iv) ମଟର ଗାଡ଼ି ଧୂଆଁ
Solution:
(iv) ମଟର ଗାଡ଼ି ଧୂଆଁ

(c) ଚଷୁ କେଉଁ ପ୍ରକାର ଆବର୍ଜନା?
(i) ଶିଳ୍ପ ଜନିତ
(ii) କୃଷି ସମ୍ପର୍କିତ
(iii) ଗୃହକାର୍ଯ୍ୟ ଜନିତ
(iv) ପ୍ରାଣୀଜ
Solution:
(ii) କୃଷି ସମ୍ପର୍କିତ

(d) ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଭୂତାଣୁ ଜନିତ ରୋଗ ?
(i) ହଇଜା
(ii) ଟାଇଫଏଡ
(iii) ଚର୍ମରୋଗ
(iv) କାମଳ
Solution:
(iv) କାମଳ

(e) ବଡ଼ ବଡ଼ ସହରରେ ମେଳା ମହୋତ୍ସବ ହେଉଥ‌ିବା ସ୍ଥାନରେ ପରିବେଶକୁ ପରିଷ୍କାର ରଖୁବାକୁ କେଉଁ ପ୍ରକାର ପାଇଖାନା ବ୍ୟବହାର କରାଯାଏ ?
(i) ସେପ୍‌ଟିକ୍ ଟ୍ୟାକ୍
(ii) ବରପାଲି
(iii) ଭ୍ରାମ୍ୟମାଣ
(iv) ଟ୍ରେଞ୍ଚ୍
Solution:
(iii) ଭ୍ରାମ୍ୟମାଣ

IV. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ମାର୍ଚ୍ଚ ୨୦ ତାରିଖକୁ ଆମେ ‘‘ବିଶ୍ବ ଜଳ ଦିବସ’’ ରୂପେ ପାଳନ କରୁଛେ ।
(ii) ମାଟି, ଗୋଡ଼ି ଓ ପାଉଁଶ ଜୈବିକ ପଦାର୍ଥରେ ଅନ୍ତର୍ଭୁକ୍ତ ।
(iii) ପରିଷ୍କାର ଜଳକୁ ଜୀବାଣୁ ମୁକ୍ତ କରିବାପାଇଁ ସେଥ୍ରେ ନାଇଟ୍ରୋଜେନ୍‌ଦ୍ୱାରା ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଏ ।
(iv) ଆନ୍ତ୍ରିକଜ୍ଵର ଓ କାମଳ ବାୟୁବାହିତ ରୋଗ ଅଟନ୍ତି ।
(v) ପ୍ରତ୍ୟେକ ଆବର୍ଜନାର ପୁନଃଚକ୍ରଣ କରି ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଇପାରିବ ନାହିଁ ।
Solution:
(i) ମାର୍ଚ୍ଚ ୨୨ ତାରିଖକୁ ଆମେ ‘ବିଶ୍ବ ଜଳ ଦିବସ’’ ରୂପେ ପାଳନ କରୁଛେ ।
(ii) ମାଟି, ଗୋଡ଼ି ଓ ପାଉଁଶ ଅଜୈବିକ ପଦାର୍ଥରେ ଅନ୍ତର୍ଭୁକ୍ତ ।
(iii) ପରିଷ୍କାର ଜଳକୁ ଜୀବାଣୁ ମୁକ୍ତ କରିବାପାଇଁ ସେଣ୍ଡ୍‌ରେ କ୍ଲୋରିନ୍ କିମ୍ବା ଓଜୋନ୍‌ଦ୍ୱାରା ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଏ ।
(iv) ଆନ୍ତଃକଜ୍ଵର ଓ କାମଳ ଜଳବାହିତ ରୋଗ ଅଟନ୍ତି ।
(v) ପ୍ରତ୍ୟେକ ଆବର୍ଜନାର ପୁନଃଚକ୍ରଣ କରି ବ୍ୟବହାର ଯୋଗ୍ୟ କରାଯାଇପାରିବ ।

V. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ଆବର୍ଜନା କେତେ ପ୍ରକାର ଓ କ’ଣ କ’ଣ ?
(ii) କେବେଠାରୁ ‘ବିଶ୍ବ ଜଳ ଦିବସ’ ପାଳନ କରାଯାଉଛି ?
(iii) ଆନ୍ତର୍ଜାତିକ ସ୍ତରରେ ବିଶୁଦ୍ଧ ଜଳ ପାଇଁ କି ପ୍ରକାର ପଦକ୍ଷେପ ନିଆଯାଉଛି ?
(iv) ଜଳ କିପରି ଦୂଷିତ ହୁଏ ?
(v) ଆବର୍ଜନା ମିଶା ଜଳକୁ କ’ଣ କହନ୍ତି ?
(vi) ପରିମଳ ବ୍ୟବସ୍ଥାକୁ କାର୍ଯ୍ୟକାରୀ କରୁଥିବା ଏକ ସଂସ୍ଥାର ନାମ ଲେଖ ।
Solution:
(i) ଆବର୍ଜନା ତିନି ପ୍ରକାର; ଯଥା – କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ।
(ii) 2005 ମସିହା ମାର୍ଚ୍ଚ 22 ତାରିଖଠାରୁ ‘ବିଶ୍ବ ଜଳ ଦିବସ’ ପାଳନ କରାଯାଉଛି ।
(iii) ଆନ୍ତର୍ଜାତିକ ସ୍ତରରେ ବିଶୁଦ୍ଧ ଜଳ ପାଇଁ 2005ରୁ 2015 ଦଶନ୍ଧିକୁ ‘ଜୀବନ ପାଇଁ ଜଳ’ ପ୍ରକଳ୍ପକୁ କାର୍ଯ୍ୟକାରୀ କରିବାକୁ ପଦକ୍ଷେପ ନିଆଯାଉଛି ।
(iv) ତରଳ ଆବର୍ଜନାର କାରକମାନେ ଜଳକୁ ପ୍ରଦୂଷିତ କରନ୍ତି । ସେମାନେ ହେଲେ ଶିଳ୍ପଜନିତ, କୃଷିଜନିତ ଓ ଗୃହକାର୍ଯ୍ୟଜନିତ ।
(v) ଆବର୍ଜନା ମିଶା ଜଳକୁ ଅପଚୟିତ ଜଳ କହନ୍ତି ।
(vi) ପରିମଳ ବ୍ୟବସ୍ଥାକୁ କାର୍ଯ୍ୟକାରୀ କରୁଥିବା ଏକ ସଂସ୍ଥା ହେଲା ‘ସୁଲଭ ଇଣ୍ଟରନ୍ୟାସନାଲ’ ।

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 15 ଜଳ – ଅମୂଲ୍ୟ ପ୍ରାକୃତିକ ସମ୍ପଦ Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 15 ଜଳ – ଅମୂଲ୍ୟ ପ୍ରାକୃତିକ ସମ୍ପଦ

Question 1.
କାବପାଇଁ ଲାଲର ଅନ୍ୟଲତା ଲେଖ |
Solution:
ଜଳ, ବାୟୁ, ସୂର୍ଯ୍ୟାଲୋକ ଆଦି ଅସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ । ଆମେ ବ୍ୟବହାର କରୁଥିବା ପଦାର୍ଥଗୁଡ଼ିକ ମଧ୍ୟରୁ ଜଳ ହେଉଛି ଗୋଟିଏ ଅତି ଦରକାରୀ ପଦାର୍ଥ । ଆମ ପୃଥ‌ିବୀ ପୃଷ୍ଠର ଶତକଡ଼ା 71 ଭାଗ ଜଳାବୃତ । ଭୂପୃଷ୍ଠର 7 ଭାଗରୁ 5 ଭାଗ ହେଉଛି କେବଳ ସମୁଦ୍ର ଜଳ । ତେଣୁ ଆମ ପୃଥ‌ିବୀକୁ ଜଳଗ୍ରହ କହନ୍ତି ।
ର୍ଥାତଶ୍ୟକତା :
(i) ଗଛଲତା, ପଶୁପକ୍ଷୀ ଓ ମଣିଷ କେହି ଜଳ ବିନା ବଞ୍ଚିପାରିବେ ନାହିଁ । ଏଣୁ ଜଳର ଅନ୍ୟନାମ ‘ଜୀବନ’ ।
(ii) ଆମେ ବିଶୁଦ୍ଧ ପାନୀୟ ଜଳକୁ ପିଇବା ପାଇଁ ବ୍ୟବହାର କରିଥାଉ । ଧୋଇବା ଓ ରାନ୍ଧିବା ତଥା ସ୍ୱାସ୍ଥ୍ୟରକ୍ଷା ପାଇଁ ମଧ୍ୟ ଜଳ ବ୍ୟବହାର କରିଥାଉ । ମିଳିତ ଜାତିସଙ୍ଘ ର ସୂଚନା ଅନୁଯାୟୀ ଜଣେ ବ୍ୟକ୍ତି ପିଇବା, ଧୋଇବା, ରାନ୍ଧିବା ତଥା ସ୍ୱାସ୍ଥ୍ୟରକ୍ଷା ପାଇଁ ଦୈନିକ ମୋଟ 50 ଲିଟର ଜଳ ବ୍ୟବହାର କରିଥାଏ ।
(iii) ଜଳ ଆମ ଶରୀରରେ ରକ୍ତ ପ୍ରବାହିତ ହେବାରେ, ଅପରିଷ୍କାର ଜିନିଷ ବାହାର କରିବାରେ (ମୂତ୍ର, ଝାଳ ଓ ଲୁହ ଆକାରରେ) ସାହାଯ୍ୟ କରିଥାଏ ।
(iv) ସବୁଜ ଉଦ୍ଭଦ, ମୃଭିକାରୁ ଜଳ ଓ ଖଣିଜ ଲବଣ ନେଇ ବାୟୁମଣ୍ଡଳରୁ ଅଙ୍ଗାରକାମ୍ଳ ଗ୍ରହଣ କରି, ସୂର୍ଯ୍ୟାଲୋକକୁ ସବୁଜକଣା ଦ୍ବାରା ବନ୍ଧନ କରି ପତ୍ରରେ ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରିଥାଏ । ଆମେ ଖାଦ୍ୟ ପାଇଁ ପ୍ରତ୍ୟକ୍ଷ ଓ ପରୋକ୍ଷ ଭାବେ ସବୁଜ ଉଭିଦ ଉପରେ ନିର୍ଭର କରିଥାଉ ।
(v) କଳକାରଖାନାରେ ମଧ୍ୟ ଜଳ ବ୍ୟବହାର କରାଯାଏ । ଜଳବିଦ୍ୟୁତ୍ ଜଳର ସ୍ରୋତ ସାହାଯ୍ୟରେ ହିଁ ଉତ୍ପନ୍ନ କରାଯାଏ ।
(vi) ଜଳଚର ଜୀବମାନେ ଜଳରେ ହିଁ ବାସ କରନ୍ତି ।

ସଂଶିପ୍ତଧାମା ପ୍ରଣୋଉର :

Question 1.
କଲଭ ବିଭିନି ଥବିସ୍ଥାପତିକ ଲେଖ |
Solution:
ଜଳ ସାଧାରଣତଃ ତିନୋଟି ଅବସ୍ଥାରେ ରହିଥାଏ ।
(i) କଠିନ – ବରଫ ଆକାରରେ,
(ii) ତରଳ – ଜଳ ଆକାରରେ ଓ
(iii) ଗ୍ୟାସୀୟ – ଜଳୀୟବାଷ୍ପ ଆକାରରେ
କଠିନ – ମେରୁ ଓ ଉଚ୍ଚ ପର୍ବତ ଶୀର୍ଷାଞ୍ଚଳରେ ଏହା ଅତି ଶୀତଳ ହୋଇ ବରଫ ଆକାରରେ ଥାଏ । ତୁମେ ଖାଉଥ‌ିବା ଆଇସ୍‌କ୍ରିମ୍ ମଧ୍ୟ ଏହାର କଠିନ ଅବସ୍ଥା ।
ତରଳ – ନଦୀ, ଝରଣା, ସମୁଦ୍ର, ପୋଖରୀ, ଗାଡ଼ିଆ, କୂପ, ନଳକୂପ ଆଦିରେ ଜଳ ତରଳ ଅବସ୍ଥାରେ ରହିଥାଏ । ଆମେ ପ୍ରତିଦିନ ଏହି ଜଳକୁ ହିଁ ପାଣିକଳରୁ ବା ନଳକୂପରୁ ଉଠାଇ ବ୍ୟବହାର କରିଥାଉ । ଏପରିକି ଚ୍ଚଶାଲଲ ମଧ୍ୟ ଆମେ ସଂଗ୍ରହ କରି ବ୍ୟବହାର କରୁ |
କିନ୍ତି ଭରକ୍ କଲର ଖ୍ୟାପାଯ୍ୟ ଗ୍ୟାସୀୟ – ସୂଯ୍ୟ ତାପର ପ୍ରତକରେ କଳ ବାଣ୍ଟରେ ପରିଣତ ହୋଇ ଆକାଶରେ ମେଣ ମୂଶ୍ଲି କରେ | ତଦନ କାର୍ଯ୍ୟ କଲାବେଳେ ଜଳ ବାମ୍ଫ ହେବା ଆମେ ଦେଖିଥାଉ । ବାଷ୍ପକୁ ଦେଖୁହୁଏ ନାହିଁ ମାତ୍ର ; ବାମ୍ଫକୁ ଦେଖୁହୁଏ ଅବସ୍ଥା ।

Question 2.
ଜଳଚକ୍ର ସମ୍ବନ୍ଧରେ ସଂକ୍ଷିପ୍ତ ବିବରଣୀ ଦିଅ ।
Solution:
ଜଳଚକ୍ର ଚାଲୁରଖିବା ପାଇଁ ମୁଖ୍ୟତଃ କେତୋଟି ଜଳବାୟୁ ସଂକ୍ରାନ୍ତୀୟ ପ୍ରାକୃତିକ ଘଟଣା ଦାୟୀ । ଏଗୁଡ଼ିକ ହେଉଛି – ବାଷ୍ପୀକରଣ, ଘନୀକରଣ ଇତ୍ୟାଦି । ଜଳଚକ୍ର ମୁଖ୍ୟତଃ ଭୂପୃଷ୍ଠ, ବାୟୁମଣ୍ଡଳ ଏବଂ ସମୁଦ୍ର ଭିତରେ ପ୍ରାୟ ସୀମିତ ରହେ ।
କିପରି ଚାଲୁରହେ –
(i) ଜଳଚକ୍ର ଚାଲୁରଖୁବା ପାଇଁ ବାଷ୍ପୀକରଣ ଓ ଘନୀକରଣ ଆଦି ପ୍ରାକୃତିକ ଘଟଣା ଦାୟୀ । ସୌରଶକ୍ତି ଦ୍ଵାରା ଏହା ଘନୀଭୂତ ହୁଏ ଏବଂ ବର୍ଷାରୂପେ ମାଧ୍ୟାକର୍ଷଣ ଶକ୍ତିର ପ୍ରଭାବରେ ପୃଥ‌ିବୀକୁ ଫେରିଆସେ ।
(ii) ଏହି ବର୍ଷାର କିଛି ଅଂଶ ପୃଥ‌ିବୀରେ ପହଞ୍ଚିବା ପୂର୍ବରୁ ବାଷ୍ପୀକରଣଦ୍ଵାରା ପୂନର୍ବାର ବାୟୁମଣ୍ଡଳକୁ ଫେରିଯାଏ । ବର୍ଷାଜଳର ଏକ ବଡ଼ଭାଗ ସମୁଦ୍ରରେ ପଡ଼େ, କିଛିଭାଗ ପୁଷ୍କରଣୀ ଆଦିରେ ଓ ଆଉ କିଛି ଭୂତଳଜଳ ଭାବରେ ମାଟିତଳେ ସଞ୍ଚିତ ହୋଇ ରହେ ।
(iii) ଉଭିଦର ଉଚ୍ଛେଦନ ଦ୍ୱାରା ଶ୍ଵାସକ୍ରିୟା ଓ ଥପନ ଆଦି ଅନ୍ୟ ପ୍ରକ୍ରିୟା ତୁଳନାରେ ଅଧ‌ିକ ଜଳ ପରିବେଶରେ ପ୍ରବେଶ କରେ । ତଥାପି ଉସେଦନ, ଶ୍ଵାସକ୍ରିୟା ଓ ଅନ୍ୟ ସମସ୍ତ ଜୈବିକ ପ୍ରକ୍ରିୟାରୁ ପରିବେଶକୁ ଆସୁଥିବା ଜଳର ପରିମାଣ ଖୁବ କମ୍ ।

Question 3.
ଜଳ ହିଁ ଜୀବନ – ବୁଝାଅ ।
Solution:
(i) ଜଳ ହେଉଛି ଜୀବ ଶରୀରର ଏକ ପ୍ରଧାନ ଉପାଦାନ । ଆଦି ଜୀବକର ଜଳୀୟଅଂଶର ପରିମାଣ ଶତକଡ଼ା ପ୍ରାୟ 65- 95 ଭାଗ ।
(ii) ଆଦି ଜୀବକକୁ ତଥା କୋଷ ଓ ଅଙ୍ଗ ପ୍ରତ୍ୟଙ୍ଗକୁ ସଠିକ ବା ଉତ୍ତମ ଅବସ୍ଥାରେ ରଖୁବା ଏବଂ ସେଥ‌ିରେ ଚାଲୁ ରହିଥ‌ିବା ସମସ୍ତ ଜୈବିକ ପ୍ରକ୍ରିୟାକୁ ସୁଚାରୁରୂପେ ସଂଘଟିତ କରାଇବାରେ ଜଳର ଅବଦାନ ଉଲ୍ଲେଖନୀୟ ।
(iii) କାରଣ ଜଳ ମାଧ୍ୟମରେ ହିଁ ଶରୀର ମଧ୍ୟରେ ସମସ୍ତ ରାସାୟନିକ ପ୍ରକ୍ରିୟା ଚାଲିଥାଏ । ଏହି କାରଣରୁ ‘ଜଳହିଁ ଜୀବନ’ କହିଲେ ଅତ୍ୟୁକ୍ତି ହେବନାହିଁ । ଏହା ବିନା ପୃଥ‌ିବୀ ପୃଷ୍ଠରେ ଜୀବନ ସୃଷ୍ଟି ଓ ସଂରକ୍ଷଣ ଅସମ୍ଭବ ।

Question 4.
ତ୍ତିଶାର କଲ ସମଦ ବିଶପ୍ରେର ଲେଖା |
Solution:
(i) ମହାନଦୀ , ବ୍ରାହ୍ମଣୀ, ବୈତରଣୀ, ଋଷିକୂଲ୍ୟା, ସୁବର୍ଣ୍ଣରେଖା, ବୁଢ଼ାବଳଙ୍ଗ, ବଂଶଧାରା, ନାଗାବଳୀ, ଇନ୍ଦ୍ରାବତୀ ସମ୍ପଦ । ଏମାନଙ୍କ ବ୍ୟତୀତ ପୋଖରୀ, କୂପ ଓ ଭୂତଳ ଜଳ ମଧ୍ୟ ଏହି ଜଳ ସମ୍ପଦର ଅନ୍ତର୍ଭୁକ୍ତ ।
(ii) ଚିଲିକା ଏବଂ ସୁଦୀର୍ଘ ସମୁଦ୍ର ସମ୍ଭାର ମଧ୍ଯ ଓଡ଼ିଶାର ଜଳସମ୍ପଦ ହିସାବରେ ଗଣାଯାଏ । କାରଣ ଏହାକୁ ମାଛଚାଷ ଲୋକେ ବର୍ଷାଜଳକୁ ଅମଳ କରି ସେମାନଙ୍କର ଆବଶ୍ୟକତା ମେଣ୍ଟାଇ ଥାଆନ୍ତି । ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଜଣେ ବ୍ୟକ୍ତି ମିଳିତ ଜାତିସଂଘର ସୂଚନା ଅନୁଯାୟୀ ପ୍ରତିଦିନ ________ ଲିଟର ଜଳ ବ୍ୟବହାର କରେ ।
(ii) ________ କୁ ଜଳଗ୍ରହ କୁହାଯାଏ ।
(iii) ହୀରାକୁଦ ନଦୀବନ୍ଧର ଦୈର୍ଘ୍ୟ ________ କି.ମି. ।
(iv) ଜଳ ________ ବାଷ୍ପୀୟ ଅବସ୍ଥାରେ ଥାଏ ।
(v) ________ ନବା ଉପରେ ହାରାକୁଦ ନଦାବନ୍ଧ ଯୋଜନା କରାଯାଲନ୍ଥି |
(vi) ________ ରେ ମିଳୁଥିବା ଜଳକୁ ଭୂତଳ ଜଳ କହିପାରିବା ।
(vii) ପୃଥ‌ିବୀର ପ୍ରଥମ ଜୀବନର ଅଣୁ ________ ରେ ହିଁ ସୃଷ୍ଟି ହୋଇଥିଲା ।
(viii)‘ବିଶ୍ବ ଜଳ ଦିବସ’ ମାର୍ଚ୍ଚମାସ ________ ତାରିଖରେ ପାଳିତ ହୁଏ ।
(ix) ପୃଥ‌ିବୀ ମହାଶୂନ୍ୟରୁ ________ ଭାବେ ଦୃଶ୍ୟମାନ ହୁଏ ।
(x) ମୋଟ ଜଳର ________ ଭାଗ ମଧୁର ଜଳ ।
(xi) ବାଷ୍ପ ଓ ବାମ୍ଫ ମଧ୍ୟରୁ ________ କୁ ଦେଖ୍ହୁଏ ।
Solution:
(i) 50,
(ii) ପୃଥ‌ିବୀ,
(iii) 25,
(iv) ବାଷ୍ପୀୟ,
(v) ମହାନଦୀ,
(vi) ନଳକୂପ,
(vii) ଜଳ,
(vii) 22,
(viii) ନୀଳଗ୍ରହ,
(ix) 2.5,
(x) ବାମ୍ଫ

II. ବାମପାର୍ଶ୍ବର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଦକ୍ଷିଣପାର୍ଶ୍ଵର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଅନାବୃଷ୍ଟି : ଜଙ୍ଗଲ କ୍ଷୟ :: ସ୍ୱଳ୍ପ ବୃଷ୍ଟି : ________
(ii) ବିଶ୍ଵଜଳ ଦିବସ : ମାର୍ଚ୍ଚ 12 ତାରିଖ :: ବିଶ୍ୱ ଜଳ ନିୟନ୍ତ୍ରଣ ଦିବସ : ________
(iii) ମୋଟ ଜଳର 97.5 ଭାଗ : ସମୁଦ୍ରଜଳ :: ମୋଟ ଜଳର 2.5 ଭାଗ : ________
(iv) ପୃଥ‌ିବୀ : ଜଳଗ୍ରହ :: ମହାଶୂନ୍ୟ : ________
Solution:
(i) ଜଳସ୍ତର ନିମ୍ନକରଣ,
(ii) ଅକ୍ଟୋବର 18 ତାରିଖ,
(iii) ମଧୁର ଜଳ,
(iv) ନୀଳଗ୍ରହ

III. ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(i) ନିମ୍ନୋକ୍ତ ବାକ୍ୟରୁ କେଉଁଟି ଜଳାଭାବ ପାଇଁ ଦାୟୀ ନୁହେଁ ?
(କ) ଶିଳ୍ପର ଦ୍ରୁତବୃଦ୍ଧି
(ଖ) କନଫଖ୍ୟା ଦ୍ୱବି
(ଗ) ଅଧ୍ବକ ବୃଷ୍ଟିପାତ
(ଘ) ଜଲଣପର ପରିଚାଳନା

(ii) ପୃଥ‌ିବୀର ଦୀର୍ଘତମ ନଦୀବନ୍ଧଟି କେଉଁ ନଦୀ ଉପରେ ତିଆରି କରାଯାଇଛି ?
(କ) ବ୍ରାହ୍ମଣୀ
(ଖ) ମହାନଦା
(ଗ) ନାଗାରଲା
(ଘ) ତୈତରଣୀ

(iii) ମେଘ ଜଳର କେଉଁ ଅବସ୍ଥା ?
(କ) କଠିନ
(ଖ) ତଳେ
(ଗ) ଗ୍ୟାପାସ
(ଘ) କେଉଁଟି ନୁହେଁ

(iv) ପୃଥ‌ିବୀକୁ କେଉଁ ଗ୍ରହର ଆଖ୍ୟା ଦିଆଯାଇଛି ?
(କ) ଜଳଗ୍ରହ
(ଖ) ନୀଳଗ୍ରହ
(ଗ) ଲୋକପ୍ରତ ଗ୍ରହ
(ଘ) ଣାତଳଗ୍ରହ

(v) ପୃଥ‌ିବୀର ଦୀର୍ଘତମ ନଦୀବନ୍ଧଟି କିଏ ?
(କ) ବାଲିମେଳା
(ଖ) ହାରାକୁଦ
(ଗ) ଲଦ୍ରାବତୀ
(ଘ) କୋଲାର

(vi) ଅଦରକାରୀ ଜଳ ମୃତ୍ତିକାରେ ଥ‌ିବା ଛିଦ୍ର ଦେଇ ମାଧ୍ୟାକର୍ଷଣ ଯୋଗୁଁ ତଳକୁ ପ୍ରବେଶ କରିବା ପ୍ରକ୍ରିୟାକୁ କ’ଣ କହନ୍ତି ?
(କ) ପାଦନ
(ଖ) ପରିସ୍ରବଣ
(ଗ) ଅନ୍ତଃ ପରିସ୍ରବଣ
(ଘ) ଭବିପାଦନ

(vii) କେଉଁଟି ପୃଥବୀର ସମୁଦାୟ ଜଳପାଇଁ ଉଦ୍ଦିଷ୍ଟ ?
(କ) ନଦୀ ଓ ହ୍ରଦରେ ଜଳର ପରିମାଣ ନିର୍ଦ୍ଦିଷ୍ଟ ମାତ୍ରା ଅଟେ ।
(ଖ) ରୁପଲ କାଳର ପ୍ରିରିମାଣ ନିଦିଶ ଅଟେ |
(ଗ) ସମୁଦ୍ର ଓ ମହାସାଗରରେ ଜଳର ପରିମାଣ ସ୍ଥିର ଅଟେ ।
(ଘ) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ସ୍ଥିର ।
Solution:
(i) ଅଧ୍ବକ ବୃଷ୍ଟିପାତ
(ii) ମହାନଦୀ
(v) ହୀରାକୁଦ
(iii) ଗ୍ୟାସୀୟ
(iv) ଜଳଗ୍ରହ
(vi) ଅନ୍ତଃ ପରିସ୍ରବଣ
(vii) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ସ୍ଥିର ।

IV. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ସମଗ୍ର ପୃଥ‌ିବୀ ପୃଷ୍ଠର ଶତକଡ଼ା ୨୧ ଭାଗ ଜଳାବୃତ୍ତ ।
(ii) ପୃଥ‌ିବୀରେ ହ୍ରଦ ଓ ନଦୀଜଳର ପରିମାଣଠାରୁ ଭୂତଳଜଳର ପରିମାଣ କମ୍ ।
(iii) ଗ୍ରାମାଞ୍ଚଳରେ ରହୁଥିବା ଲୋକମାନେ ଜଳ ଅଭାବ ଭୋଗ କରିଥା’ନ୍ତି ।
(iv) ଜଳସେଚନ ପାଇଁ ନଦୀ ହିଁ ଏକମାତ୍ର ଉତ୍ସ ଅଟେ ।
(v) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ମଧ୍ଯରୁ ଲବଣାକ୍ତ ଜଳ ଅତିକମ୍ ।
Solution:
(i) ସମଗ୍ର ପୃଥ‌ିବୀ ପୃଷ୍ଠର ଶତକଡ଼ା ୭୧ ଭାଗ ଜଳାବୃତ୍ତ ।
(ii) ପୃଥ‌ିବୀରେ ହ୍ରଦ ଓ ନଦୀଜଳର ପରିମାଣଠାରୁ ଭୂତଳଜଳର ପରିମାଣ ଅଧିକ ।
(iii) ସହରାଞ୍ଚଳରେ ରହୁଥିବା ଲୋକମାନେ ଜଳ ଅଭାବ ଭୋଗ କରିଥା’ନ୍ତି ।
(iv) ଜଳସେଚନ ପାଇଁ ବର୍ଷାଜଳ, ନଦୀଜଳ, ପୋଖରୀଜଳ ଇତ୍ୟାଦି ଗୋଟିଏ ଗୋଟିଏ ଉତ୍ସ ଅଟେ ।
(v) ପୃଥ‌ିବୀର ଜଳର ପରିମାଣ ମଧ୍ୟରୁ ଲବଣାକ୍ତ ଜଳ ବେଶି ।

V. ‘କ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦର ମେଳନ କର ।

VI. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ‘ବିଶ୍ବ ଜଳ ଦିବସ’ କେବେ ପାଳିତ ହୁଏ ?
(ii) ଆମ ପୃଥ‌ିବୀକୁ ଜଳଗ୍ରହ କାହିଁକି କୁହାଯାଏ ?
(iii) ଜଣେ ବ୍ୟକ୍ତିର ଦୈନିକ କେତେ ଲିଟର ଜଳ ଆବଶ୍ୟକ ?
(iv) ମହାଶୂନ୍ୟରୁ ପୃଥ‌ିବୀ ନୀଳ କାହିଁକି ଦେଖାଯାଏ ?
(v) ବିଶ୍ଵ ଜଳବର୍ଷ କେବେ ଓ କାହିଁକି ପାଳନ ହୋଇଥିଲା ?
(vi) ପୃଥ‌ିବୀରେ ମୋଟ ଜଳର ପରିମାଣ କେତେ ?
(vii) ପୃଥ‌ିବୀର ମୋଟ ଲୁଣି ସମୁଦ୍ରଜଳର ପରିମାଣ କେତେ ଶତାଂଶ ?
(viii)ପୃଥ‌ିବୀର ମୋଟ ମଧୁର ଜଳର ପରିମାଣ କେତେ ଶତାଂଶ ?
(ix) ଓଡ଼ିଶାର କେଉଁ ଜଳ ପ୍ରକଳ୍ପଟି ସର୍ବୋତ୍ତମ ଓ ବିଖ୍ୟାତ ?
(x) ପୃଥ‌ିବୀର ବୃହତ୍ତମ ନଦୀବନ୍ଧ କିଏ ଓ ଏହାର ଲମ୍ବ କେତେ ?
Solution:
(i) ‘ବିଶ୍ବ ଜଳ ଦିବସ’ ମାର୍ଚ୍ଚ 22 ତାରିଖରେ ପାଳିତ ହୁଏ ।
(ii) ଆମ ପୃଥ‌ିବୀର ଶତକଡ଼ା 71 ଭାଗ ଜଳ । ତେଣୁ ଆମ ପୃଥ‌ିବୀକୁ ଜଳଗ୍ରହ କୁହାଯାଏ ।
(iii) ଜଣେ ବ୍ୟକ୍ତିର ଦୈନିକ 50 ଲିଟର ଜଳ ଆବଶ୍ୟକ ।
(iv) ପୃଥ‌ିବୀରେ ବହୁ ପରିମାଣର ଜଳର ସମ୍ଭାର ଯୋଗୁଁ ମହାଶୂନ୍ୟରୁ ପୃଥ‌ିବୀ ନୀଳ ଦେଖାଯାଏ ।
(v) ବିଶ୍ୱ ଜଳ ବର୍ଷ 2003 ମସିହାରେ ମଧୁର ଜଳ ସମ୍ବନ୍ଧରେ ସଚେତନତା ସୃଷ୍ଟି ପାଇଁ ପାଳନ ହୋଇଥିଲା ।
(vi) ପୃଥ‌ିବୀରେ ମୋଟ ଜଳର ପରିମାଣ 140 କୋଟି ଘନ କିଲୋମିଟର ।
(vii) ପୃଥ‌ିବୀର ମୋଟ ଲୁଣି ସମୁଦ୍ରଜଳର ପରିମାଣ 97.5 ଶତାଂଶ ଅଟେ ।
(viii)ପୃଥ‌ିବୀର ମୋଟ ମଧୁର ଜଳ ପରିମାଣ 2.5 ଶତାଂଶ ଅଟେ ।
(ix) ଓଡ଼ିଶାର ହୀରାକୁଦ ନଦୀବନ୍ଧ ଜଳ ପ୍ରକଳ୍ପଟି ସର୍ବୋତ୍ତମ ଓ ବିଖ୍ୟାତ ।
(x) ହୀରାକୁଦ ପୃଥ‌ିବୀର ବୃହତ୍ତମ ନଦୀବନ୍ଧ ଓ ଏହାର ଲମ୍ବ 25 କି.ମି. ।

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 16 ଜଙ୍ଗଲ ସମ୍ପଦ Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 16 ଜଙ୍ଗଲ ସମ୍ପଦ

Question 1.
ଜଙ୍ଗଲ ହିଁ ଜୀବଜଗତ ପାଇଁ ଅମ୍ଳଜାନ ଯୋଗାଉଥ‌ିବା ‘ପ୍ରାକୃତିକ କାରଖାନା’ – ବୁଝାଅ ।
Solution:
(i)
ଭାବେ ସବୁଜ ଉଦ୍ଭିଦ ଉପରେ ନିର୍ଭର କରିଥାଉ ।
(ii) ସବୁଜ ଉଭିଦ ବାୟୁମଣ୍ଡଳରୁ ଅଙ୍ଗାରକାମ୍ଳ ଓ ମୃଭିକାରୁ ଜଳ ସଂଗ୍ରହ କରି ସବୁଜକଣାଦ୍ୱାରା ସୂର୍ଯ୍ୟାଲୋକ ଉଭିଦ ଅମ୍ଳଜାନ ଛାଡ଼ିଥାଏ, ଯାହାକି ପ୍ରତ୍ୟେକ ସଜୀବର ଶ୍ଵାସକ୍ରିୟା ପାଇଁ ନିହାତି ଜରୁରୀ ।
(iii) ସବୁଜ ଉଦ୍ଭଦ ହିଁ ବାୟୁମଣ୍ଡଳରେ ଅଙ୍ଗାରକାମ୍ଳ ଗ୍ୟାସ ପରିମାଣକୁ ନିୟନ୍ତ୍ରଣ କରି ଜୀବଜଗତକୁ ଅମ୍ଳଜାନ ଯୋଗାଇଥାଏ ।
(iv) ଜଙ୍ଗଲରେ ଥ‌ିବା ଉଭିଦମାନେ ହିଁ ଏହାର ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥା’ନ୍ତି । ଏହାକୁ ଜୀବଜଗତ ପାଇଁ ଅମ୍ଳଜାନ ଯୋଗାଉଥ‌ିବା ‘‘ପ୍ରାକୃତିକ କାରଖାନା’’ କୁହାଯାଏ ।

Question 2.
ନବୀକରଣ ଯୋଗ୍ୟ ଓ ନବୀକରଣ ଅଯୋଗ୍ୟ ସମ୍ପଦ କାହାକୁ କୁହାଯାଏ, ଉଦାହରଣ ସହ ବୁଝାଅ ।
Solution:
(i) ଯେଉଁ ପ୍ରାକୃତିକ ସମ୍ପଦକୁ ନଷ୍ଟ କରିଦେଲେ ପୁନର୍ବାର ନୂତନ ଭାବେ ସୃଷ୍ଟି ହୋଇପାରୁଥିବ କିମ୍ବା ଅନବରତ ବ୍ୟବହାର କରୁଥିଲେ ମଧ୍ୟ ସରୁ ନଥ‌ିବ ସେହି ସମ୍ପଦକୁ ନବୀକରଣ ଯୋଗ୍ୟ ସମ୍ପଦ କୁହାଯାଏ |
(ii) ଜଙ୍ଗଲ ଜାତ ପଦାର୍ଥ, ପ୍ରାଣୀଜାତ ପଦାର୍ଥ, କୃଷିଜାତ ଦ୍ରବ୍ୟ, ଜଳ, ବାୟୁ, ମୃରିକା ଆଦି ନବୀକରଣଯୋଗ୍ୟ ସମ୍ପଦ ।
ନବାକରଣ ଅଯୋଗ୍ୟ ସମଦ –
(i) ଯେଉଁ ପ୍ରାକୃତିକ ସମ୍ପଦଗୁଡ଼ିକ ଅନବରତ ବ୍ୟବହାରଦ୍ଵାରା ସରିଗଲେ, ସେଗୁଡ଼ିକର ପୁନଃ ଭରଣ ସମ୍ଭବ ହୁଏ ନାହିଁ ବା ଆଉ ମିଳେ ନାହିଁ ସେଗୁଡ଼ିକୁ ନବୀକରଣ ଅଯୋଗ୍ୟ ସମ୍ପଦ କୁହାଯାଏ ।
(ii) କୋଇଲା, ଖଣିଜତୈଳ, ଧାତୁପିଣ୍ଡ ଆଦି ନବୀକରଣ ଅଯୋଗ୍ୟ ସମ୍ପଦ ।

Question 3.
“‘ପ୍ରାକୃତିକ ଭାରସାମ୍ୟ’’ର ଅର୍ଥ କ’ଣ ? ଉଦାହରଣ ସହ ବୁଝାଅ ।
(i) ଜୀବମଣ୍ଡଳର ପ୍ରତ୍ୟେକ ଜୀବ ଅନ୍ୟ ଜୀବଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ । ସେହିପରି ପରିବେଶ ମଧ୍ୟ ଜୀବ ଉପରେ ପ୍ରଭାବ ପକାଇଥାଏ । ତେଣୁ ଜୀବ ଓ ପରିବେଶ ଉଭୟ ଉଭୟଙ୍କର ଦ୍ଵାରା ପ୍ରଭାବିତ ହୋଇଥାଏ ।
(ii) ଏହା ଫଳରେ ଜୀବ ଓ ତା’ର ପରିବେଶର ଭୌତିକ, ଜୈବିକ ତଥା ଅଜୈବିକ ପାରିପାର୍ଶ୍ବକ କାରକମାନଙ୍କ ମଧ୍ୟରେ ସର୍ବଦା ଏକ ପାରସ୍ପରିକ କ୍ରିୟା ଚାଲୁଥିବାରୁ ପରିବେଶରେ ଏକ ଭାରସାମ୍ୟ ସମ୍ଭବ ହେଉଛି ।
ଭଦାହରଣ –
(i) ଯଦି ଜଙ୍ଗଲରେ ହରିଣଙ୍କ ସଂଖ୍ୟା ବିଢ଼ିଯିବ ତେବେ ସେମାନେ ସମସ୍ତ ତୃଣ ଖାଇଯିବେ । ଫଳରେ ତୃଣ ସବୁ ସରିଯିବ ଏବଂ ତୃଣଭୋଜୀ ପ୍ରାଣୀସବୁ ଖାଦ୍ୟ ନପାଇ ମୃତ୍ୟୁବରଣ କରିବେ । ଏହାପରେ ମାଂସାଶୀ ପ୍ରାଣୀମାନେ ଖାଦ୍ୟ ନପାଇ ମୃତ୍ୟୁବରଣ କରିବେ ।
(ii) ସୁତରାଂ ପରିସଂସ୍ଥାରୁ ତୃଣ ଲୋପ ପାଇଲେ ସମସ୍ତ ତୃଣଭୋଜୀ ଓ ମାଂସାଶୀ ପ୍ରାଣୀ ନିଶ୍ଚିହ୍ନ ହୋଇଯିବେ । କିନ୍ତୁ ତାହା ହେଉନାହିଁ । ଏହି ପ୍ରାକୃତିକ ପ୍ରକ୍ରିୟା ‘‘ ଖାଦ୍ୟଶୃଙ୍ଖଳ’’ ମାଧ୍ୟମରେ ଚାଲୁ ରହିଛି
(iii) ପ୍ରକୃତିର ଏହି ବିଚିତ୍ର ସ୍ୱ ନିୟନ୍ତ୍ରତ ଓ ସୁନିୟନ୍ତ୍ରିତ ବ୍ୟବସ୍ଥାକୁ ‘ପ୍ରକୃତିର ଭାରସାମ୍ୟ’’ ବା ‘ପରିବେଶ ସନ୍ତୁଳନ’’ କୁହାଯାଏ ।

Question 4.
ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ପ୍ରାକୃତିକ ସନ୍ତୁଳନକୁ ଦିପଯଅସ୍ତ୍ର କରିବାରେ ମ୍ଲଖ ଅଫ ବୀଣା – ବ୍ଲଖାଥ |
Solution:
ସଭ୍ୟତାର ଅଗ୍ରଗତି ଅନୁଯାୟୀ ମଣିଷ ଅନେକ ସମୟରେ ସ୍ୱେଚ୍ଛାଚାରୀଭାବେ ପୋଷକଚକ୍ର ଓ ହେଲା ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ।
ଜନସଂଖ୍ୟା ବୃଦ୍ଧି – ବର୍ତ୍ତମାନ ଏହାକୁ ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ବୋଲି ନ କହି ଜନ ବିସ୍ଫୋରଣ କୁହାଯାଉଛି ।
(i) ଶିକ୍ଷାର ଅଭାବ ଓ ଆର୍ଥିକ ଅନଗ୍ରସରତା ଯୋଗୁଁ ଏହି ସମସ୍ୟା ଭୟାବହ ରୂପ ନେଇଛି ।
(ii) ଏହି ଜନସଂଖ୍ୟା ଗୁଣୋତ୍ତର ଅନୁକ୍ରମରେ ବଢ଼ିଚାଲିଛି । କିନ୍ତୁ କୃଷି କ୍ଷେତ୍ରରେ ଉନ୍ନତ କୌଶଳ ପ୍ରୟୋଗ ସତ୍ତ୍ଵେ ଖାଦ୍ୟ ଉତ୍ପାଦନ ଏହି କ୍ରମରେ ବଢ଼ୁନାହିଁ କିମ୍ବା ବଢ଼ିବା ମଧ୍ୟ ସମ୍ଭବ ନୁହେଁ ।
(iii) ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଫଳରେ ଖାଦ୍ୟ ଉତ୍ପାଦନ, ଜଙ୍ଗଲ ସମ୍ପଦ, ଭୂତଳ ଭଣ୍ଡାର, ଜଳ ସମ୍ପଦ, ବାୟୁ ମଣ୍ଡଳ, ସ୍ବାସ୍ଥ୍ୟ, ଶକ୍ତି ଉତ୍ପାଦନ ଆଦି କ୍ଷେତ୍ରରେ ସମସ୍ୟା ସୃଷ୍ଟି ହୋଇଛି । ଏହା ଫଳରେ ପରିବେଶ ବିଭିନ୍ନ ସଂକଟ ଦେଖା ଦେଉଛି ।

Question 5.
ଜଲଚକ୍ରର ନ।ପାରାତ ଚିତ୍ର ଦିଅ |
Solution:

Question 6.
ଅମ୍ଳଜାନ ଓ ଅଙ୍ଗାରକ ଚକ୍ରର ଏକ ନାମାଙ୍କିତ ଚିତ୍ର ଦିଅ ।
Solution:

Question 7.
ଜୀବାଣୁ ଓ କବକ ପରି ଅପଘଟକମାନେ ନ ଥିଲେ ଆମର କି ଅସୁବିଧା ହୁଅନ୍ତା, ଲେଖ ।
Solution:
(i) ବୀଜାଣୁ ଓ କବକ ପରି ମୃତୋପଜୀବୀ ଅଣୁଜୀବମାନେ ମୃତଜୀବ ଶରୀରକୁ ଅପଘଟିତ କରି ମାଟିରେ ମିଶାଇ ଜମାହୋଇ ପରିବେଶକୁ ଅପରିଷ୍କାର କରିବେ ଓ ଏହା ଆମର ବାସପୋଯୋଗୀ ହୋଇପାରିବ ନାହିଁ ।
(ii) ଅପଘଟକମାନେ ଅପଘଟନ ପ୍ରକ୍ରିୟାରେ ଉପାଦେୟ ପୋଷକଗୁଡ଼ିକୁ ପରିବେଶ ମଧ୍ୟକୁ ମୁକ୍ତ କରିଥା’ନ୍ତି । ଏଣୁ ଏହା ବ୍ୟାହତ ହେବ । ଫଳରେ ପରିବେଶର ଭାରସାମ୍ୟ ନଷ୍ଟ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ଏଥ‌ିରେ ଜୀବନଧାରଣ ଅସମ୍ଭବ ହେବ ।

Question 8.
କଲଲ ନଗର କୁପରିଣାମଗ୍ନତିକ ଲେଖା |
Solution:
ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଦୃଷ୍ଟିରୁ ମନୁଷ୍ୟ ତା’ର ବିଭିନ୍ନ ଆବଶ୍ୟକତା ଯଥା – ଖାଦ୍ୟ, ବାସଗୃହ, ରାସ୍ତାଘାଟ, କଳକାରଖାନା, ଜଳସେଚନ ଆଦି ସ୍ଥାପନ ପାଇଁ ଅବିରତ ଭାବେ ଜଙ୍ଗଲ ନଷ୍ଟ କରିଚାଲିଛି । ଏହାଦ୍ଵାରା ଜୀବଜଗତରେ ନାହିଁ ନ ଥ‌ିବା କ୍ଷତି ଘଟୁଛି ।
(i) ଜଙ୍ଗଲ କ୍ଷୟ ହେବାଦ୍ଵାରା ବନ୍ୟଜନ୍ତୁମାନଙ୍କର ପ୍ରାକୃତିକ ବାସସ୍ଥାନ ଧ୍ବସ୍ତବିଧ୍ବସ୍ତ ହେବା ଫଳରେ କେତେକ ପ୍ରାଣୀ ଜୀବମଣ୍ଡଳରୁ ସମ୍ପୂର୍ଣ୍ଣ ବିଲୁପ୍ତ ହୋଇଗଲେଣି ଓ ଆଉ କେତେକ ବିଲୋପ ହେବାକୁ ଲାଗିଲେଣି ।
(ii) କଲଂଲ ଶ୍ରୟଦ୍ଵାରା ମହିଳା ଶାସ୍ ଶଟ୍ମଛି | କଲଂଲ ଶ୍ରଯଦ୍ୱାରା ପୋଇଲ ଟାଧାପ୍ରାପ୍ତ ହେବା ପରେ ପଟିଙ୍ଗ ସ୍ଥାନ ଖାଦ୍ୟଶୃଙ୍ଗଳ ବ୍ୟାହତ ହେଉଛି ।

Question 9.
କଲଂଲକ୍ ବାଣ ନିଶିଦ ହୋଇଗଲେ ଜ’ଣ ହେବ |
Solution:
(i) ଜଙ୍ଗଲରୁ ବାଘ ନିଶ୍ଚିହ୍ନ ହୋଇଗଲେ ହରିଣପରି ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କ ସଂଖ୍ୟା ବଢ଼ିଯିବ, କାରଣ ତାଙ୍କୁ ମାରି ଖାଇବା ପାଇଁ ବାଘ ନଥ‌ିବେ ।
(ii) ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କ ସଂଖ୍ୟା ଅହେତୁକ ଭାବେ ବଢ଼ିଯିବାରୁ ସେମାନଙ୍କୁ ଖାଦ୍ୟ ମିଳିବ ନାହିଁ, ତୃଣ ଓ ଅନ୍ୟାନ୍ୟ ଉଭିଦ ସଂଖ୍ୟା ଦ୍ରୁତ ଗତିରେ ହ୍ରାସ ପାଇ ଜଙ୍ଗଲ ଏକ ଟାଙ୍ଗରା ଭୂଇଁରେ ପରିଣତ ହେବ ।

ବସ୍ତୁନିଷ୍ ପ୍ରଣୋଉର :

I. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ବାୟୁମଣ୍ଡଳରେ ଅଙ୍ଗାରକାମ୍ଳର ପରିମାଣ ହେଲା _______ |
(ii) ଗୁଜରାଟର ଗିର୍ ଅଭୟାରଣ୍ୟ _______ ପାଇଁ ଭାରତ ପ୍ରସିଦ୍ଧ ।
(iii) _______ ଠାରେ ସାମୁଦ୍ରିକ କଇଁଛମାନଙ୍କ ପାଇଁ ଆଶ୍ରୟସ୍ଥଳୀ ସ୍ଥାପନ କରାଯାଇଛି ।
(iv) ହିମାଳୟର ଜଙ୍ଗଲରେ _______ ଦେଖାଯାଆନ୍ତି ।
(v) ପୁରୀ ସମୁଦ୍ର କୂଳରେ _______ ଗଛର ବଣ ଥିବାର ଦେଖାଯାଏ ।
Solution:
(i) 0.04%,
(ii) ପିଦ୍ର୍-ପ୍ରକଳ୍ପ,
(iii) ଭିତର କନିକା,
(iv) ଚମରୀଗାଈ,
(v) ଝାଉଁ

II. ବାମପାର୍ଶ୍ବର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଦକ୍ଷିଣପାର୍ଶ୍ବର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଖାଇଁ : : ଗୁଜରାଟର ଗିର୍ ଜଙ୍ଗଲ :: ଚମରୀ ଗାଈ : _______
(ii) ଜାତୀୟ ଉଦ୍ୟାନ : 73 :: ଅଭୟାରଣ୍ୟ : _______
(iii) ଶିମିଳିପାଳ : ସଂରକ୍ଷିତ ଜୀବମଣ୍ଡଳ :: ଭିତର କନିକା :: _______
(iv) ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ : ଚିଲିକା :: ଜାତୀୟ ଉଦ୍ୟାନ : _______
(v) ମୃତ୍ତିକା : ପ୍ରାକୃତିକ ସମ୍ପଦ :: ଜଙ୍ଗଲ : _______
Solution:
(i) ହିମାଳୟର ଜଙ୍ଗଲ,
(ii) 416,
(iii) ଜାତୀୟ ଉଦ୍ୟାନ,
(iv) ଭିତର କନିକା,
(v) ପ୍ରାକୃତିକ କାରଖାନା

III. ପ୍ରତି ପ୍ରଶ୍ନର ନିମ୍ନରେ ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ଦିଆଯାଇଛି । ସେଥୁମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
(କ) ଚାଉଳ, ଡାଲି ଆଦି
(i) ନବୀକରଣ – ଯୋଗ୍ୟ ସମ୍ପଦ
(ii) ନବୀକରଣ – ଅଯୋଗ୍ୟ ସମ୍ପଦ
(iii) ପୁନଃଚକ୍ରଣ – ଖାଦ୍ୟ ସମ୍ପଦ
(iv) ପୁନଃଚକ୍ରଣ – ଅଯୋଗ୍ୟ ସମ୍ପଦ
Solution:
(i) ନବୀକରଣ – ଯୋଗ୍ୟ ସମ୍ପଦ

(ଖ) ବୀଜାଣୁମାନେ ହେଲେ
(i) ଉତ୍ପାଦକ
(ii) ଭକ୍ଷକ
(iii) ଅପଘଟକ
(iv) ପୋଷକ
Solution:
(iii) ଅପଘଟକ

(ଗ) ଜନସଂଖ୍ୟା ବୃଦ୍ଧି ଯେଉଁ କ୍ରମରେ ବଢ଼ିଚାଲିଛି ତାହା ହେଲା
(i) ଗୁଣୋତ୍ତର ଅନୁକ୍ରମ
(ii) ସମାନ୍ତର ଅନୁକ୍ରମ
(iv) ଗାଣିତିକ ଅନୁକ୍ରମ
(iii) ଜ୍ୟାମିତିକ ଅନୁକ୍ରମ
Solution:
(i) ଗୁଣୋତ୍ତର ଅନୁକ୍ରମ

(ଣ) କଳାହାରଖାନାଦ୍ଵାରା ଯେଉ ପ୍ରହଗଣ ତତିଚାଲିଛି ତାହା ହେଲା –
(i) ବାୟୁ
(ii) ଜଳ
(iii) ମୁଭିକା
(iv) ସମଗ୍ର ପରିବେଶ
Solution:
(iv) ସମଗ୍ର ପରିବେଶ

(ଙ) ଜୀବମଣ୍ଡଳରେ ଯେଉଁ ଗ୍ୟାସ୍ ଦିନକୁ ଦିନ ବଢ଼ିଚାଲିଛି ତା’ ହେଲା –
(କ) ନଳାକରଣ – ଯୋଗ୍ୟ ସମବ
(ଖ) ଆପଣକ
(ଗ) ଗୁଣୋତ୍ତର ଅନୁକ୍ରମ
(ପ) ସମଗ୍ର ପରିବେଶ
(ଙ) ଆପଣକ
Solution:
(ଖ) ଆପଣକ

IV. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ଜଙ୍ଗଲ, ବାୟୁ ଓ ଜଳ ସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(ii) ମାଳ ଅଞ୍ଚଳରେ ଥିବା ଜଙ୍ଗଲରେ ଆମ୍ବ, ଖଜୁରୀ ଅଧ‌ିକ ପରିମାଣରେ ଦେଖାଯାଏ ।
(iii) ‘ବନ୍ୟ ଜୀବନ ସୁରକ୍ଷା ଆଇନ’ ୧୯୭୨ ମସିହାରେ ସଂଶୋଧନ କରାଯାଇଛି ।
(iv) ଆମ ରାଜ୍ୟର ଚିଲିକା ହ୍ରଦକୁ ଏକ ସଂରକ୍ଷିତ ଜୀବମଣ୍ଡଳ ରୂପେ ମାନ୍ୟତା ଦିଆଯାଇଛି ।
(v) ଜଙ୍ଗଲ ସୁରକ୍ଷା ପାଇଁ ଦେଶରେ ୧୨ଟି ଜାତୀୟ ଉଦ୍ୟାନ ସଂସ୍ଥା ରହିଛି ।
Solution:
(i) ଜଙ୍ଗଲ, ବାୟୁ ଓ ଜଳ ଅସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(ii) ମାଳ ଅଞ୍ଚଳରେ ଥିବା ଜଙ୍ଗଲରେ ଶାଳ, ପିଆଶାଳ ଓ ମହୁଲ ଗଛ ଅଧ୍ଵ ପରିମାଣରେ ଦେଖାଯାଏ ।
(iii) ‘ବନ୍ୟ ଜୀବନ ସୁରକ୍ଷା ଆଇନ’ ୧୯୯୧ ମସିହାରେ ସଂଶୋଧନ କରାଯାଇଛି ।
(iv) ଆମ ରାଜ୍ୟର ଚିଲିକା ହ୍ରଦକୁ ଏକ ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ ରୂପେ ମାନ୍ୟତା ଦିଆଯାଇଛି ।
(v) ଜୀବମଣ୍ଡଳ ସଂରକ୍ଷିତ ପାଇଁ ଦେଶରେ ୧୨ଟି ଜାତୀୟ ଉଦ୍ୟାନ ସଂସ୍ଥା ରହିଛି ।

V. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ବାୟୁମଣ୍ଡଳର ତାପମାତ୍ରା ସହିତ କାହାର ସମ୍ପର୍କ ଅଛି ?
(ii) ପ୍ରାକୃତିକ ସମ୍ପଦ କ’ଣ ?
(iii) ପ୍ରାକୃତିକ ସମ୍ପଦ କେତେ ପ୍ରକାର ଓ କ’ଣ କ’ଣ ?
(iv) କେତେଗୁଡ଼ିଏ ପ୍ରାକୃତିକ ସମ୍ପଦର ନାମ ଲେଖ ।
(v) ଅପଘଟନ କ’ଣ ?
(vi) ଭାରତ ସ୍ବାଧୀନ ହେବା ସମୟରେ ଭାରତର କେତେ ଅଂଶରେ ଜଙ୍ଗଲ ଥିଲା ?
(vii) ଅପଘଟକ କାହାକୁ କହନ୍ତି ?
(viii)ଓଡ଼ିଶାର କେଉଁଠି ସଂରକ୍ଷିତ ଜୈବମଣ୍ଡଳ ଅଛି ?
(ix) ଓଡ଼ିଶାର କେଉଁଠି ବ୍ୟାଘ୍ର ସଂରକ୍ଷଣ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହୋଇଛି
(x) ଓଡ଼ିଶାର କେଉଁଠି ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ ଅଛି ?
(xi) ଅଙ୍ଗାରକାମ୍ଳର ମାତ୍ରା କାହିଁକି ବଢୁଛି ?
Solution:
(i) ବାୟୁମଣ୍ଡଳର ତାପମାତ୍ରା ସହିତ ଅଙ୍ଗାରକାମ୍ଳର ସମ୍ପର୍କ ଅଛି ।
(ii) ପ୍ରକୃତିରୁ ମିଳୁଥିବା ମାଟି, ପାଣି, ପବନ, ଜଙ୍ଗଲ ପ୍ରଭୃତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(iii) ପ୍ରାକୃତିକ ସମ୍ପଦ ଦୁଇ ପ୍ରକାରର – (a) ସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ (b) ଅସରନ୍ତି ପ୍ରାକୃତିକ ସମ୍ପଦ
(iv) ମାଟି, ପାଣି, ପବନ, ଜଙ୍ଗଲ, ପଶୁପକ୍ଷୀ, ଖଣିଜ ସମ୍ପଦ ସୂର୍ଯ୍ୟାଲୋକ ପ୍ରଭୃତି ପ୍ରାକୃତିକ ସମ୍ପଦ ଅଟନ୍ତି ।
(v) ମୃତ ଜୀବଶରୀର କେତେକ ଅଣୁଜୀବମାନଙ୍କ ଦ୍ଵାରା ପଚି ମାଟିରେ ମିଶିବା ପ୍ରକ୍ରିୟାକୁ ଅପଘଟନ କୁହାଯାଏ ।
(vi) ଭାରତ ସ୍ବାଧୀନ ହେବା ସମୟରେ ଭାରତର 45 ଶତାଂଶ ଅଂଶରେ ଜଙ୍ଗଲ ଥିଲା ।
(vii) ଯେଉଁ ମୃତୋପଜୀବୀ ଅଣୁଜୀବମାନଙ୍କଦ୍ଵାରା ମୃତଜୀବ ଶରୀର ପଚି ମାଟିରେ ମିଶିଯାଏ, ସେମାନଙ୍କୁ ଅପଘଟକ କୁହାଯାଏ ।
(vii) ଓଡ଼ିଶାର ଶିମିଳିପାଳଠାରେ ସଂରକ୍ଷିତ ଜୈବମଣ୍ଡଳ ଅଛି ।
(ix) ଓଡ଼ିଶାର ଶିମିଳିପାଳଠାରେ ବ୍ୟାଘ୍ର ସଂରକ୍ଷଣ ଯୋଜନା କାର୍ଯ୍ୟକାରୀ ହୋଇଛି ।
(x) ଓଡ଼ିଶାର ଚିଲିକାରେ ପକ୍ଷୀ ଅଭୟାରଣ୍ୟ ଅଛି ।
(xi) ଜନସଂଖ୍ୟା ବୃଦ୍ଧି, ଅଧ୍ଵ ଗାଡ଼ିମଟର ଓ କଳକାରଖାନା ଯୋଗୁଁ ଅଙ୍ଗାରକାମ୍ଳର ମାତ୍ରା ବଢୁଛି ।

Odisha State Board BSE Odisha 6th Class Science Important Questions Chapter 8 ପରିସ୍ଥାନ Important Questions and Answers.

BSE Odisha Class 6 Science Important Questions Chapter 8 ପରିସ୍ଥାନ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
କେଉଁ କେଉଁ ଅଙ୍ଗ ଜଳଜ ପ୍ରାଣୀମାନଙ୍କ ଉପଯୋଜନରେ ସହାୟକ ହୋଇଥାଏ ?
ଉ –
ଜଳଜ ପ୍ରାଣୀମାନଙ୍କର ଶରୀର, ଆକୃତି, ଗାଲି, ଲାଞ୍ଜର ଉପସ୍ଥିତି, କାତି କିମ୍ବା ଲାଳଯୁକ୍ତ ଶରୀର, ପରଦାଯୁକ୍ତ ପକ୍ଷ ଆଦି ଉପଯୋଜନରେ ସହାୟକ ହୋଇଥାଏ ।

Question 2.
ସ୍ଥଳଚର ଓ ଜଳଚର ପ୍ରାଣୀମାନେ କେଉଁ କେଉଁ ପରିସ୍ଥାନରେ ରହିଥା’ନ୍ତି ?
ଉ –

• ସ୍ଥଳଚର ପ୍ରାଣୀମାନେ ଜଙ୍ଗଲ, ମରୁଭୂମି, ତୃଣଭୂମି, ପାର୍ବତ୍ୟାଞ୍ଚଳ ଆଦିରେ ରହିଥା’ନ୍ତି ।
• ଜଳଚର ପ୍ରାଣୀମାନେ ନଦୀ, ହ୍ରଦ, ପୋଖରୀ, ସମୁଦ୍ର ଇତ୍ୟାଦିରେ ରହିଥା’ନ୍ତି ।

Question 3.
ଉପଯୋଜନ କ’ଣ ଏକ ଉଦାହରଣ ଦେଇ ଲେଖ ।
ଉ –

• ପରିବେଶ ଓ ପରିବେଶର ପରିବର୍ତ୍ତନ ସହ ତାଳଦେଇ ପ୍ରତ୍ୟେକ ଜୀବର ଗାଠନିକ ଓ କ୍ରିୟାତ୍ମକ ପରିବର୍ତ୍ତନକୁ ଉପଯୋଜନ କୁହାଯାଏ ।
• ଓଟର ପାଦଗୁଡ଼ିକ ମରୁବାଲିରେ ଚାଲିବାପାଇଁ ଓ ତା’ର ପିଠି ଉପରେ ଥ‌ିବା କୁଜଟି ଖାଦ୍ୟାଭାବ ସମୟରେ ସହାୟତା କରେ । ଓଟର ଏହି ପରିବର୍ତ୍ତନଗୁଡ଼ିକ ଦ୍ଵାରା ସେ ମରୁଭୂମିରେ ବଞ୍ଚରେ ।

Question 4.
ପରିସ୍ଥାନ ପରିବର୍ତ୍ତନ ହେଲେ କ’ଣ ଅସୁବିଧା ହେବ ?
ଉ –

• ପରିସ୍ଥାନ ପରିବର୍ତ୍ତନ ହେଲେ ପରିବେଶରେ ସନ୍ତୁଳନ ବିପର୍ଯ୍ୟସ୍ତ ହୋଇଯିବ ।
• ଏହାର କୁ ପ୍ରଭାବ ସମଗ୍ର ଜୀବଜଗତ ଉପରେ ପଡ଼ିବ । ଫଳରେ କେତେକ ଜାତିର ଜୀବ ନିଶ୍ଚିହ୍ନ ହେବାର

Question 5.
ପରିବେଶରେ ଅପଘଟକର ଭୂମିକା କ’ଣ ?
ଉ –

• କେତେକ ଅଣୁଜୀବ ଉଭିଦ ଓ ପ୍ରାଣୀଙ୍କ ଶରୀରରୁ ଖାଦ୍ୟ ସଂଗ୍ରହ କରିଥାଆନ୍ତି, ସେମାନଙ୍କୁ ଅପଘଟକ କୁହାଯାଏ ।
• ଅନ୍ୟ କେତେକ ଜୀବ ଯଥା ବୀଜାଣୁ, କବକ ଇତ୍ୟାଦି ଉଭିଦ ଓ ପ୍ରାଣୀଙ୍କ ମୃତ ଶରୀରରୁ ଖାଦ୍ୟ ସଂଗ୍ରହ କରି ସେମାନେ କେତେକ ଆବଶ୍ୟକ ଉପାଦାନ ଯଥା – ଯବକ୍ଷାରଜାନ ପରିବେଶକୁ ଛାଡ଼ନ୍ତି ।

Question 6.
ପରିସ୍ଥାନ ଅନୁସାରେ ପ୍ରାଣୀମାନଙ୍କୁ କେତେ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି, ତାହା କ’ଣ କ’ଣ ?
ଉ –

• ପରିସ୍ଥାନ ଅନୁସାରେ ପ୍ରାଣୀମାନଙ୍କୁ ତିନିଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି ।
• ସେଗୁଡ଼ିକ ହେଲା – ସ୍ଥଳଚର, ଜଳଚର ଓ ବାୟବୀୟ ।

ଦୀର୍ଘ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ଉଭିଦମାନଙ୍କର ପରିସ୍ଥାନ ବିଷୟରେ ସଂକ୍ଷେପରେ ଲେଖ ।
ଉ –

• ପରିସ୍ଥାନକୁ ନେଇ ଉଭିଦମାନଙ୍କୁ ତିନି ଭାଗରେ ବିଭକ୍ତ କରାଯାଏ; ଯଥା – ମରୁଜ, ଆର୍ଦ୍ରଭୂମିଜ ଓ ଜଳଜ ।
• ଜଳାଭାବ ଅଞ୍ଚଳରେ ବଢ଼ିପାରୁଥିବା ଉଭିଦଗୁଡ଼ିକ ମରୁଜ; ଯଥା – ସପ୍ତଫେଣୀ, ନାଗଫେଣୀ ।
• ଜଳାଭାବ ଓ ଜଳାଧିକ୍ୟ ନଥ‌ିବା ଅଞ୍ଚଳର ଉଭିଦଗୁଡ଼ିକ ଆର୍ଦ୍ରଭୂମିଜ; ଯଥା – ଧାନ, ଆମ୍ବ ।
• ସମ୍ପୂର୍ଣ୍ଣ ଜଳ ଭିତରେ ବା ଜଳାଧ୍ୟାକ୍ୟ ଅଞ୍ଚଳର ଉଭିଦଗୁଡ଼ିକ ଜଳଜ; ଯଥା – ପଦ୍ମ, ଚିଙ୍ଗୁଡ଼ିଆ ଦଳ ।

Question 2.
ଉଭିଦମାନଙ୍କର ପରିସ୍ଥାନ ବିଷୟରେ ସଂକ୍ଷେପରେ ଲେଖ ।
ଉ –

• ପରିସ୍ଥାନ ଅନୁସାରେ ଉଭିଦମାନଙ୍କୁ ତିନିଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – (i) ମରୁଜ, (ii) ଆର୍ଦ୍ରଭୂମିଜ ଓ (iii) ଜଳଜ ।
• ଜଳାଭାବ ବା ଜଳାଧ୍ୟାକ୍ୟ ନଥ‌ିବା ଅଞ୍ଚଳର ଉଭିଦକୁ ଆଦ୍ରଭୂମିଜ ଉଭିଦ କୁହାଯାଏ ।
• ଜଳାଧ୍ୟାକ୍ୟ ଅଞ୍ଚଳରେ ଥ‌ିବା ଉଭିଦକୁ ଜଳଜ ଉଭିଦ କୁହାଯାଏ ।

Question 3.
ପରିସ୍ଥାନ କ’ଣ ? ଉପାଦାନ ଅନୁସାରେ ପରିସ୍ଥାନର ଜୀବମାନଙ୍କୁ କେତେ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି ଉପଯୋଜନ ଲେଖ ।
ଉ –

• ପରିସ୍ଥାନ – ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କର ବାସସ୍ଥାନ ଓ ତା’ର ଚତୁଃପାର୍ଶ୍ୱକୁ ପରିସ୍ଥାନ କୁହାଯାଏ ।
• ଉପାଦାନ ଅନୁସାରେ ଯେ କୈଣସି ପରିସ୍ଥାନର ଜୀବମାନଙ୍କୁ ତିନିଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – (କ) ଉତ୍ପାଦକ, (ଖ) ଭକ୍ଷକ ଓ (ଗ) ଅପଘଟକ ।
  • (କ) ଉଦ୍ଭିଦ ନିଜପାଇଁ ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରିବାସହ ଅନ୍ୟ ସବୁ ଜୀବପାଇଁ ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରେ । ତେଣୁ ସମସ୍ତ ଉଭିଦକୁ ଉତ୍ପାଦକ କୁହାଯାଏ ।
  • (ଖ) ଉଦ୍ଭଦଦ୍ୱାରା ପ୍ରସ୍ତୁତ ଖାଦ୍ୟ ପ୍ରତ୍ୟକ୍ଷରେ ବା ପରୋକ୍ଷରେ ପ୍ରାଣୀମାନେ ଖାଇଥା’ନ୍ତି । ତେଣୁ ସମସ୍ତ ପ୍ରାଣୀଙ୍କୁ ଭକ୍ଷକ କୁହାଯାଏ ।
  • (ଗ) ବୀଜାଣୁ, କବକ ଆଦି ଜୀବ ଉଦ୍ଭଦ ଓ ପ୍ରାଣୀଙ୍କ ଶରୀରରୁ ଖାଦ୍ୟ ସଂଗ୍ରହ କରିଥା’ନ୍ତି । ତେଣୁ ବୀଜାଣୁ, କବକକୁ ଅପଘଟକ କୁହାଯାଏ ।

Question 4.
ଉପଯୋଜନ କ’ଣ ? ଏହା ଅନୁସାରେ ମରୁଭୂମିରେ ରହୁଥ‌ିବା ଜୀବମାନଙ୍କ ସମ୍ପର୍କରେ ଲେଖ ।
ଉ –

• ପରିବେଶ ପରିବର୍ତ୍ତନ ସହ ତାଳଦେଇ ପ୍ରତ୍ୟେକ ଜୀବର ଗାଠନିକ ଓ କ୍ରିୟାତ୍ମକ ପରିବର୍ତ୍ତନକୁ ଉପଯୋଜନ କୁହାଯାଏ ।
• ମରୁଭୂମିରେ ରହୁଥିବା ସପ୍ତଫେଣୀ ଓ ସିଜୁର ପାଣିର ଆବଶ୍ୟକତା କମ୍ ଥାଏ । ସପ୍ତଫେଣୀ ଓ ସିଜୁରେ ପତ୍ର ରୂପାନ୍ତରିତ ହୋଇ କଣ୍ଟା ଓ ମୋଟା ପତ୍ର ହୁଏ, ଫଳରେ ବାଷ୍ପୀମୋଚନ ବିଶେଷ ଭାବରେ ହୋଇପାରେ ନାହିଁ ।
• ଓଟର ପାଦଗୁଡ଼ିକ ମରୁବାଲିରେ ଚାଲିବାକୁ ସହାୟକ ହୋଇଥାଏ । ଓଟର ପିଠିରେ ଥ‌ିବା କୁଜଟି ଖାଦ୍ୟାଭାବ ସମୟରେ ସହାୟତା କରେ ।
• ମରୁଭୂମିରେ ରହୁଥ‌ିବା ସାପ, ମୂଷା ଆଦି ଜୀବମାନେ ଦିନରେ ବାଲି ଭିତରେ ରହିପାରନ୍ତି ।

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶୋଉର

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଉଦ୍ଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କ ବାସସ୍ଥାନ ଓ ତା’ର ଚତୁଃପାର୍ଶ୍ଵକୁ ………….. କହନ୍ତି ।
(ଖ) ଲତାଜାତୀୟ ଉଦ୍ଭିଦର କାଣ୍ଡ ଆଗରେ …………….. ଥାଏ ।
(ଗ) ଅପଘଟକମାନେ ପରିବେଶକୁ ……………… ଛାଡ଼ନ୍ତି ।
(ଘ) ଉଦ୍ଭଦକୁ ……………… କୁହାଯାଏ ।
(ଙ) ପରିସ୍ଥାନ ହେଉଛି …………. ର ଏକ ଅଂଶବିଶେଷ ।
(ଚ) ବାୟବୀୟ ପ୍ରାଣୀ କହିଲେ ମୁଖ୍ୟତଃ ……………… ଙ୍କୁ ବୁଝାଏ ।
(ଛ) ଓଟର …………….. ତାକୁ ଖାଦ୍ୟାଭାବ ସମୟରେ ସାହାଯ୍ୟ କରେ ।
ଉ –
(କ) ପରିସ୍ଥାନ
(ଖ) ଆକର୍ଷୀ
(ଗ) ଯବକ୍ଷାରଜାନ
(ଘ) ଉତ୍ପାଦକ
(ଙ) ପରିବେଶ
(ଚ) ପକ୍ଷୀମାନ
(ଛ) ଓଟର

Question 2.
ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନତଳେ ଦିଆଯାଇଥିବା ଚାରିଗୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

(କ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଏକ ଜୈବିକ କାରକ ?
(i) କବକ
(ii) ଆଲୋକ
(iii) ଜଳ
(iv) ତାପ
ଉ –
(i) କବକ

(ଖ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଏକ ଅଜୈବିକ କାରକ ?
(i) ବୀଜାଣୁ
(ii) କବକ
(iii) ମୁଭିକା
(iv) ଉଭିଦ
ଉ –
(iii) ମୁଭିକା

(ଗ) ସପ୍ତଫେଣୀ ଉଦ୍ଭଦର ପତ୍ରଗୁଡ଼ିକ କେଉଁଥରେ ରୂପାନ୍ତରିତ ହୋଇଥାଏ ?
(i) କାଣ୍ଡ
(ii) ଫୁଲ
(iii) କଣ୍ଟା
(iv) ମୂଳ
ଉ –
(iii) କଣ୍ଟା

(ଘ) ମାଛ କେଉଁଥିରେ ଶ୍ଵାସକ୍ରିୟା କରେ ?
(i) ଡେଣା
(ii) ନାକ
(iii) ପାଟି
(iv) ଗାଲି
ଉ –
(iv) ଗାଲି

(ଙ) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଏକ ଅପଘଟକ ?
(i) ବୀଜାଣୁ
(ii) ଉଭିଦ
(iii) ପିମ୍ପୁଡ଼ି
(iv) ମାଙ୍କଡ଼
ଉ –
(i) ବୀଜାଣୁ

Question 3.
ପ୍ରଥମ ଯୋଡ଼ା ଶବ୍ଦଦ୍ଵୟର ସମ୍ପର୍କକୁ ଦେଖୁ ଦ୍ଵିତୀୟ ଯୋଡ଼ାର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ପ୍ରାଣୀ : ଭକ୍ଷକ :: ଉଭିଦ : ………………. ।
(ଖ) ପ୍ରାଣୀ : ଜୈବିକ କାରକ :: ତାପ : ………………. ।
(ଗ) ଅପଘଟକ : କବକ :: ବାୟବୀୟ ପ୍ରାଣୀ : ………………. ।
(ଘ) ଖଜୁରୀ : ମରୁଜ :: ସପ୍ତଫେଣୀ : ………………. ।
(ଙ) ମଣିଷ : ଫୁସ୍‌ଫୁସ୍‌ :: ମାଛ : ………………. ।
ଉ –
(କ) ଉତ୍ପାଦକ
(ଖ) ଅଜୈବିକ କାରକ
(ଗ) ପକ୍ଷୀ
(ଘ) ମରୁଜ
(ଙ) ଗାଲି

Question 4.
ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(କ) କଙ୍କଡ଼ା ପାଟି ସାହାଯ୍ୟରେ ଶ୍ଵାସକ୍ରିୟା କରେ ।
(ଖ) ଖାଦ୍ୟ ସଞ୍ଚୟ ପାଇଁ ସପ୍ତଫେଣୀ ଗଛର କାଣ୍ଡ ମାଂସଳ ହୋଇଥାଏ ।
(ଗ) ଓଟର କଢ ତାପ ସଞ୍ଚୟ କରିଥାଏ ।
(ଙ) ବାୟବୀୟ ପ୍ରାଣୀ ମୁଖ୍ୟତଃ ପଶୁଙ୍କୁ ବୁଝାଏ ।
ଉ –
(କ) କଙ୍କଡ଼ା ଗାଲି ସାହାଯ୍ୟରେ ଶ୍ଵାସକ୍ରିୟା କରେ ।
(ଖ) ଜଳ ସଞ୍ଚୟ ପାଇଁ ସପ୍ତଫେଣୀ ଗଛର କାଣ୍ଡ ମାଂସଳ ହୋଇଥାଏ ।
(ଗ) ଓଟର କୁଜ ଜଳ ଓ ଖାଦ୍ୟ ସଞ୍ଚୟ କରିଥାଏ ।
(ଘ) କଖାରୁ ଗଛ ଆକର୍ଷୀ ସହାୟତାରେ ଉପରକୁ ଉଠେ ।
(ଙ) ବାୟବୀୟ ପ୍ରାଣୀ ମୁଖ୍ୟତଃ ପକ୍ଷୀଙ୍କୁ ବୁଝାଏ ।

Question 5.
‘କ’ ସ୍ତମ୍ଭର ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସଂପର୍କ ବାଛ ।

ଉ –

Odisha State Board BSE Odisha 8th Class Geography Important Questions Chapter 4 ଶିଳ୍ପ Important Questions and Answers.

BE Odisha Class 8 Geography Important Questions Chapter 4 ଶିଳ୍ପ

Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ପିଟ୍ସବର୍ଗ ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ରର ଭୌଗୋଳିକ ଗୁରୁତ୍ଵ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର ।
Answer:

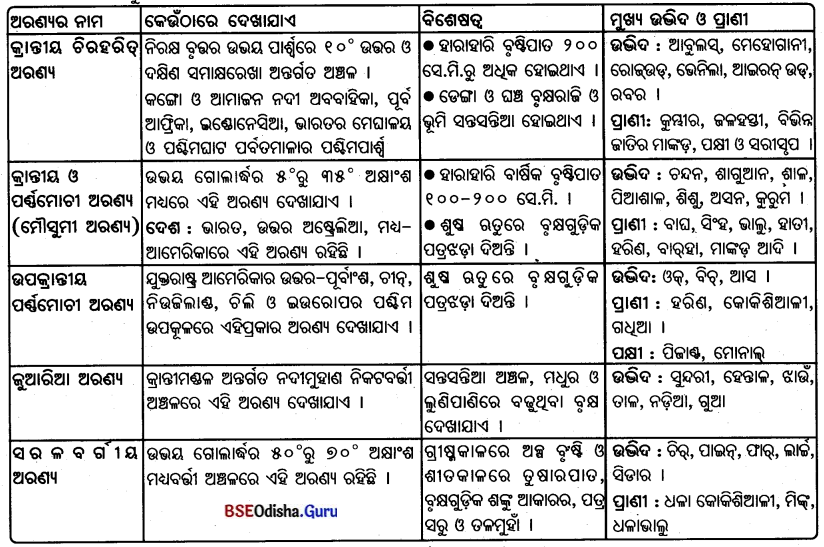
• ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଇସ୍ପାତନଗରୀ ପିନ୍ସବର୍ଗର ଅବସ୍ଥିତି ଇସ୍ପାତ ଶିଳ୍ପ ପାଇଁ ଅନୁକୂଳ ।
• ଏଠାରେ କୋଇଲା ସମେତ କେତେକ କଞ୍ଚାମାଲ ଆସିଥାଏ ।
• 150 କି.ମି. ଦୂରରେ ଥିବା ମିନେସୋଟାରୁ ଲୁହାପଥର ଟ୍ରେନ୍‌ଯୋଗେ ଶସ୍ତାରେ ପରିବହନ ହୋଇ ଅଣାଯାଏ ।
• ଶସ୍ତା ପରିବହନ ପାଇଁ ବୃହତ୍ ହ୍ରହ ଜଳପଥ ମଧ୍ଯ ସୁବିଧା ଯୋଗାଇଦିଏ ।
• ଓହିଓ, ମନୋଗାହେଲା ଏବଂ ଆଲେଘେନି ନଦୀରୁ ପ୍ରଚୁର ଜଳ ମିଳିଥାଏ । ତେଣୁ ପିଟ୍‌ସବର୍ଗଠାରେ ବଡ଼ ବଡ଼ ଇସ୍ପାତ ଶିଳ୍ପ ଗଢ଼ିଉଠିଛି ।

Question 2.
ଓସାକା କାର୍ପାସ ଶିଳ୍ପର ଗୁରୁତ୍ଵ ବୁଝାଅ ।
Answer:

• ‘ଜାପାନର ମାଞ୍ଚେଷ୍ଟର’ ଓସାକା ଉପସାଗର କୂଳରେ ଅବସ୍ଥିତ ଏକ ବନ୍ଦର ଓ ପରିବହନ କେନ୍ଦ୍ର ।
• ସାକାକୁ ଘେରିରହିଥିବା ସୁବିସ୍ତୃତ ସମତଳଭୂମି ଶିଳ୍ପ ସ୍ଥାପନ ପାଇଁ ସୁବିଧାଜନକ ।
• ଏଠାକାର ଆର୍ଦ୍ର ଜଳବାୟୁ, ପରିବହନ ସୁବିଧା, କଞ୍ଚାମାଲ ପାଇଁ ଆବଶ୍ୟକ ରାସାୟନିକ ଦ୍ରବ୍ୟ ନିକଟବର୍ତ୍ତୀ ଅଞ୍ଚଳରୁ ସହଜରେ ସଂଗ୍ରହ ଏବଂ ଜାପାନ ଭଳି ଜନବହୁଳ ରାଷ୍ଟ୍ରରେ କାର୍ପାସବତ୍ସର ଚାହିଦା ଶିଳ୍ପର ପ୍ରସାରରେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଛି ।
• ଓଡ଼ୋ ନଦୀରୁ ଶିଳ୍ପପାଇଁ ପ୍ରଚୁର ଜଳ ମିଳିବାସହ ବନ୍ଦର ସୁବିଧା ଥୁବାରୁ ତୁଳା ଆମଦାନି କରିବା ଓ ବସ୍ତ୍ର ରପ୍ତାନି କରିବା ସହଜ ହୋଇପାରିଛି ।
• ଏଠାକାର ବସ୍ତ୍ର ଉତ୍ତମ ମାନର ତଥା ଶସ୍ତା ହୋଇଥିବାରୁ ଏହାର ଭଲ ବଜାର ଚାହିଦା ରହିଛି ।

Question 3.
କେଉଁ କେଉଁ ଭୌଗୋଳିକ ଅବସ୍ଥା ଉପରେ ନିର୍ଭର କରି ଅହମ୍ମଦାବାଦରେ କାର୍ପାସ ଶିଳ୍ପ ଗଢ଼ିଉଠିଛି ?
Answer:

• ସାବରମତୀ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ଅହମ୍ମଦାବାଦ ଗୁଜରାଟ ରାଜ୍ୟରେ ଅବସ୍ଥିତ । ଏହି ରାଜ୍ୟ କପାଚାଷ ପାଇଁ ଭାରତରେ ଖ୍ୟାତିଲାଭ କରିଛି । ଏହା କଞ୍ଚାମାଲ ଯୋଗାଣକୁ ନିଶ୍ଚିତ କରିଛି ।
• ଅହମ୍ମଦାବାଦର ଦକ୍ଷିଣରେ ମୁମ୍ବାଇ ଏବଂ ପଶ୍ଚିମରେ କାଣ୍ଡଲା ବନ୍ଦର ଅବସ୍ଥିତ । ତେଣୁ ବନ୍ଦର ମାଧ୍ୟମରେ ଯନ୍ତ୍ରପାତି ଆମଦାନି ଓ ରପ୍ତାନିର ସୁବିଧା ମିଳୁଛି ।
• ନଦୀକୂଳରେ ଅବସ୍ଥିତ ହୋଇଥିବାରୁ କାରଖାନା ଏବଂ ଶିଳ୍ପାଞ୍ଚଳ ପାଇଁ ମଧୁର ଜଳ ମିଳିଥାଏ ।
• ଏଠାରେ କୁଶଳୀ ଓ ଅର୍ଥକୁଶଳୀ ଶ୍ରମିକଙ୍କର ଅଭାବ ନାହିଁ ।
• ଅହମ୍ମଦାବାଦ ସହରଟି ଏକ ବୃହତ୍ ବାଣିଜ୍ୟ ଏବଂ ପରିବହନ କେନ୍ଦ୍ର । ତେଣୁ ବିଭିନ୍ନ ଅଞ୍ଚଳକୁ ବସ୍ତ୍ର, କପଡ଼ା ପଠାଇବା ସମ୍ଭବ ହୋଇପାରୁଛି ।

Question 4.
ଜାମସେଦପୁରଠାରେ ଥିବା ଟାଟା ଲୌହଇସ୍ପାତ ଶିଳ୍ପର ବିକାଶ ଉପରେ ଏକ ବିବରଣୀ ଲେଖ ।
Answer:

• ଭୌଗୋଳିକ ଦୃଷ୍ଟିରୁ ଜାମ୍‌ସେପୁର ହିଁ ଦେଶର ସବୁଠାରୁ ସୁବିଧାଜନକ ସ୍ଥିତିରେ ଥ‌ିବା ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ର ।
• ଅବସ୍ଥିତି : ବେଙ୍ଗଲ୍-ନାଗପୁର ରେଳପଥ ବର୍ତ୍ତମାନର ହାୱଡ଼ା- ମୁମ୍ବାଇ ରେଳପଥର କାଳିମାଟି ଷ୍ଟେସନଠାରୁ 32 କି.ମି. ଦୂରରେ ଅବସ୍ଥିତ ।
• କଞ୍ଚାମାଲ ଉପଲବ୍‌ଧର ସୁବିଧା : ନିକଟସ୍ଥ ଝରିଆରୁ କୋଇଲା, ଓଡ଼ିଶା ଓ ଛତିଶଗଡ଼ରୁ ଲୁହାପଥର, ଚୂନପଥର, ଡୋଲୋମାଇଟ୍ ଓ ମାଙ୍ଗାନିଜ ସୁବିଧାରେ ଉପଲବ୍‌ଧ । ହୋଇଥାଏ ।
• ଜଳ ସୁଲଭତା : ଖରକାଇ ଓ ସୁବର୍ଣ୍ଣରେଖା ନଦୀଦ୍ୱୟରୁ ପ୍ରଚୁର ଜଳ କାରଖାନାକୁ ଯୋଗାଇ ଦିଆଯାଏ ।
• ବଜାର ସୁବିଧା : ଅନତିଦୂରରେ ଅବସ୍ଥିତ କୋଲକାତା ନଗରୀ ବିଶାଳ ବଜାର ପାଇଁ ସୁବିଧା ରହିଛି । ଏତଦ୍‌ବ୍ୟତୀତ ସରକାରୀ ପ୍ରୋତ୍ସାହନ ଯୋଗୁ ପୁଞ୍ଜିର ସୁବ୍ୟବସ୍ଥା ରହିଛି ।

Question 5.
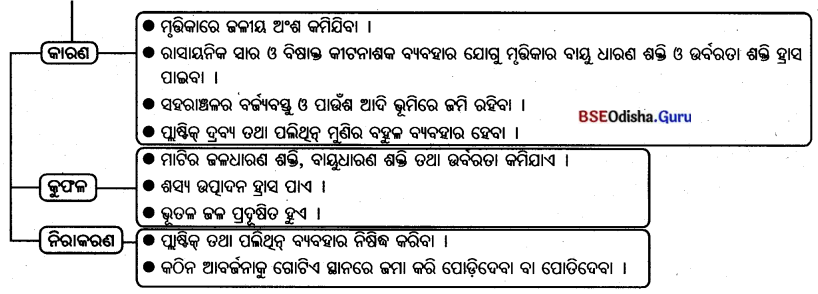
ଶିଳ୍ପ ପ୍ରତିଷ୍ଠାନରେ ଦୁର୍ଘଟଣା ହ୍ରାସ ନିମନ୍ତେ କି କି ପଦକ୍ଷେପ ନିଆଯାଇପାରିବ ଦର୍ଶାଅ ।
Answer:

• ଶିଳ୍ପାଞ୍ଚଳଗୁଡ଼ିକୁ ଘନ ଜନବସତିପୂର୍ଣ୍ଣ ଅଞ୍ଚଳଠାରୁ ଦୂରରେ ସ୍ଥାପନ କରିବା ଉଚିତ ।
• କଳକାରଖାନା ନିକଟରେ ବସବାସ କରୁଥିବା ଲୋକମାନଙ୍କୁ ଶିଳ୍ପରେ ବ୍ୟବହୃତ ବା ଉତ୍ପାଦିତ ବିଷାକ୍ତ ପଦାର୍ଥର ସଂରକ୍ଷଣ ତଥା ଦୁର୍ଘଟଣା ଘଟିଲେ ଏହାର ସମ୍ଭାବ୍ୟ ପ୍ରଭାବ ସମ୍ବନ୍ଧରେ ସଚେତନ କରାଇବା ଆବଶ୍ୟକ ।
• ଅଗ୍ନି ସତର୍କତା ବା ଅଗ୍ନି ନିର୍ବାପନ ବ୍ୟବସ୍ଥାରେ ଉନ୍ନତିକରଣ କରାଯିବା ଆବଶ୍ୟକ ।
• ବିଷାକ୍ତ ପଦାର୍ଥଗୁଡ଼ିକର ଭଣ୍ଡାର ସୀମିତ ହେବା ଉଚିତ ।
• ଶିଳ୍ପାନୁଷ୍ଠାନମାନଙ୍କରେ ହଠାତ୍ ପ୍ରଦୂଷଣ ହେଲେ ସଙ୍ଗେ ସଙ୍ଗେ ତା’ର ଅପସାରଣ ବ୍ୟବସ୍ଥାରେ ଉନ୍ନତିକରଣ ଆବଶ୍ୟକ ।

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ସଂକ୍ଷେପରେ ଉତ୍ତର ଲେଖ ।

Question 1.
କୁଟୀରଶିଳ୍ପ କ’ଣ ? ଉଦାହରଣସହ ଲେଖ ।
Answer:

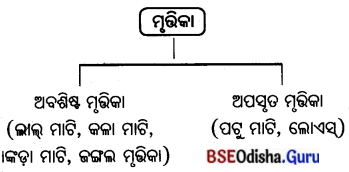
• ପରିବାର ସଦସ୍ୟଙ୍କ ସହାୟତାରେ ସ୍ଥାନୀୟ କଞ୍ଚାମାଲ ଓ ସରଳ ଉପକରଣ ସାହାଯ୍ୟରେ ବିଭିନ୍ନ ବସ୍ତୁ ଉତ୍ପାଦନକରଣ କରିବା ପ୍ରକ୍ରିୟାକୁ କୁଟୀରଶିଳ୍ପ କୁହାଯାଏ ।
• ଏଥରେ ବଂଶାନୁକ୍ରମିକ କାରିଗରୀ ଜ୍ଞାନର ଉପଯୋଗ ହୋଇଥାଏ। ଉଦାହରଣ ପିପିଲିର ଚାନ୍ଦୁଆ କାମ ଏବଂ କଟକର ତାରକସୀ କାମ ଓ ନୀଳଗିରିର ପଥର ବାସନ କାମ ଇତ୍ୟାଦି ।

Question 2.
ଅହମ୍ମଦାବାଦରେ ପ୍ରଚୁର କପା ଉତ୍ପାଦନର କାରଣ କ’ଣ ?
Answer:

• ଅହମ୍ମଦାବାଦ ଚତୁଃପାର୍ଶ୍ଵ ଅଞ୍ଚଳ କପାଚାଷ ଅଞ୍ଚଳଭାବେ ପ୍ରସିଦ୍ଧ ।
• କାରଣ ଏହାର ଆର୍ଦ୍ର ଜଳବାୟୁ ଓ କୃଷ୍ଣକାର୍ପାସ ମୃତ୍ତିକା ଏହି ଚାଷ ପାଇଁ ଅନୁକୂଳ ପରିବେଶ ଯୋଗାଇଥାଏ ।

Question 3.
ଓସାକା କାର୍ପାସ ଶିଳ୍ପକୁ କଞ୍ଚାମାଲ ଯୋଗାଉଥିବା ଦେଶଗୁଡ଼ିକର ନାମ ପ୍ରକାଶ କର ।
Answer:
ଓସାକା କାର୍ପାସ ଶିଳ୍ପକୁ କଞ୍ଚାମାଲ ଯୋଗାଉଥିବା ଦେଶଗୁଡ଼ିକ ଇଜିପ୍‌ଟ, ଭାରତ, ଚୀନ୍ ଓ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ।

Question 4.
ଇସ୍ପାତର ବିଶେଷତ୍ଵ କ’ଣ ଓ~ଏଥୁରୁ ମିଶ୍ରଧାତୁ କିପରି କରାଯାଏ ?
Answer:

• ଇସ୍ପାତ ବେଶ୍ ଶକ୍ତ । ଏହାକୁ ସହଜରେ ବିଭିନ୍ନ ଆକୃତି ଦିଆଯାଇପାରେ, କଟାଯାଇପାରେ ଏବଂ ତାରରେ ପରିଣତ କରି ହୁଏ
• ଇସ୍ପାତ ସହିତ ଆଲୁମିନିୟମ୍, ନିକେଲ ଓ ତମ୍ବା ଆଦି କମ୍ମାତ୍ରାରେ ମିଶାଇ ମିଶ୍ରଧାତୁ ପ୍ରସ୍ତୁତ କରାଯାଏ ।

Question 5.
ଲୌହଇସ୍ପାତ ଶିଳ୍ପର ନିବେଶ ଉଲ୍ଲେଖ କର ।
Answer:
କଞ୍ଚାମାଲଭାବେ ଲୁହାପଥର, କୋଇଲା ଓ ଚୂନପଥର, ମାନବ, ଶ୍ରମ, ପୁଞ୍ଜି, ଭୂମି ତଥା ଅନ୍ୟାନ୍ୟ ଆଧାରିକ ସଂରଚନା ଖର୍ଚ୍ଚ ନିବେଶ କରାଯାଏ ।

Question 6.
ଚାରିଗୋଟି କୃଷିଭିତ୍ତିକ ଶିଳ୍ପର ଉଦାହରଣ ଦିଅ ।
Answer:
ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, ଖାଇବା ତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ, ଦୁଗ୍ଧଜାତ ପଦାର୍ଥ ପ୍ରସ୍ତୁତ ।

Question 7.
ଦୁଇଟି ଖଣିଜଭିଭିକ ଶିଳ୍ପ ଓ ଦୁଇଟି ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପର ନାମ ଲେଖ ।
Answer:

• ଖଣିଜଭିଭିକ ଶିଳ୍ପ- ଲୌହଇସ୍ପାତ ଓ ଆଲୁମିନିୟମ୍‌ ଶିଳ୍ପ ।
• ସମୁଦ୍ରଭିତିକ ଶିଳ୍ପ – ସାମୁଦ୍ରିକ ଖାଦ୍ୟ ଉଦ୍ୟୋଗ ଓ ମାଛତେଲ ଉଦ୍ୟୋଗ ।

Question 8.
ଉପଭୋକ୍ତା ଦ୍ରବ୍ୟ ଉତ୍ପାଦନକାରୀ ଶିଳ୍ପର ଉଦାହରଣ ଦିଅ ।
Answer:
ଉପଭୋକ୍ତା ଦ୍ରବ୍ୟ ଉତ୍ପାଦନକାରୀ ଶିଳ୍ପଗୁଡ଼ିକ ହେଲେ ଖାଇବାତେଲ, ଚା’, ସାବୁନ, ପାଉଁରୁଟି, ବିସ୍କୁଟ, ରେଡ଼ିଓ, ଟେଲିଭିଜନ୍ ଶିଳ୍ପ ଇତ୍ୟାଦି ।

Question 9.
ତିନୋଟି କ୍ଷୁଦ୍ର ଶିଳ୍ପ ଓ ତିନୋଟି କୁଟୀର ଶିଳ୍ପର ଉଦାହରଣ ଦିଅ ।
Answer:

• କ୍ଷୁଦ୍ରଶିଳ୍ପ – ଘଣ୍ଟା, ରେଡ଼ିଓ, ଟିଭି ଶିଳ୍ପ ।
• କୁଟୀରଶିଳ୍ପ – ଝୁଡ଼ିବୁଣା, ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି ଓ ଶିଙ୍ଗକାମ ଇତ୍ୟାଦି ।

Question 10.
ଏକ କାର୍ପାସ ଶିଳ୍ପର ନିବେଶ ଓ ପ୍ରକ୍ରିୟାକରଣ ଦର୍ଶାଅ ।
Answer:

• ନିବେଶ – ତୁଳା, ମାନବଶ୍ରମ, ଯନ୍ତ୍ରପାତି, ପରିବହନ ଖର୍ଚ୍ଚ,
• ପ୍ରକ୍ରିୟାକରଣ – ତୁଳାଭିଣା, ସୂତାକଟା, ଲୁଗାବୁଣା, ରଙ୍ଗଲଗା, ଛାପାକାର୍ଯ୍ୟ ଓ ସିଲାଇ ।

Question 11.
ଦୁଇଟି ଶିଳ୍ପ ଦୁର୍ଘଟଣାର ନାମ ଲେଖ । ଏହି ଦୁର୍ଘଟଣାଗ୍ରସ୍ତ ପ୍ରପୀଡ଼ିତ ଲୋକଙ୍କ ଦୁର୍ଦ୍ଦଶାଗୁଡ଼ିକ ଲେଖ ।
Answer:

• ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣା ଓ ଚୀନ୍‌ର ଚୋଙ୍ଗିଙ୍ଗ୍ ଅନ୍ତର୍ଗତ ଗାଓକ୍ସିଆଓ ଗ୍ୟାସ୍ କୂପ ବିସ୍ଫୋରଣ ।
• ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣାଗ୍ରସ୍ତ ଲୋକ ଅନ୍ଧତ୍ବ, ପ୍ରତିରୋଧକାରୀ ଶକ୍ତିହୀନତା ଓ ବିଭିନ୍ନ ପେଟରୋଗରେ, ପୀଡ଼ିତ । ଗାଓକ୍ସିଆଓ ଗ୍ୟାସ୍ କୂପ ଦୁର୍ଘଟଣାଗ୍ରସ୍ତ ଲୋକମାନେ ଆଖୁ, ଚର୍ମ ଓ ଫୁସ୍‌ଫୁସ୍ ଜଳାପୋଡ଼ାରେ ପୀଡ଼ିତ ।

Question 12.
ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ କ’ଣ ? ଉଦାହରଣସହ ବୁଝାଅ ।
Answer:

• ନୂତନଭାବେ ଗଢ଼ିଉଠିଥିବା ଶିଳ୍ପକୁ ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ କୁହାଯାଏ ।
• ଉଦାହରଣସ୍ୱରୂପ- ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା, ସ୍ୱାସ୍ଥ୍ୟ ଓ ସ୍ଵାସ୍ଥ୍ୟସେବା, ଆତିଥ୍ୟ ଏବଂ ଶିକ୍ଷା ।

Question 13.
ମାଞ୍ଚେଷ୍ଟର କାହିଁକି ପ୍ରସିଦ୍ଧ ?
Answer:

• ମାଞ୍ଚେଷ୍ଟର ଇଂଲଣ୍ଡର ଏକ କାର୍ପାସ ଓ ବୟନ ଶିଳ୍ପର ପ୍ରଧାନ ସହର ।
• ଏଠାରେ ଶିଳ୍ପବିପ୍ଳବ ପରେ କଳତନ୍ତ ବୟନଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ହେଲା । ଭାରତରୁ କଞ୍ଚାମାଲ ରୂପେ ତୁଳା ଓ ଝୋଟ ଆମଦାନୀ କରାଯାଉଥିଲା ।

Question 14.
ଭାରତର ବେଙ୍ଗାଲୁରୁ ବ୍ୟତୀତ ଆଉ ଚାରିଗୋଟି ସୂଚନା ପ୍ରଯୁକ୍ତିବିଦ୍ୟା କେନ୍ଦ୍ରର ନାମ ଲେଖ ।
Answer:
ଭାରତର ଚାରିଗୋଟି ସୂଚନା ପ୍ରଯୁକ୍ତିବିଦ୍ୟା କେନ୍ଦ୍ରଗୁଡ଼ିକ ହେଲେ ଗୁଡ଼ଗାଓଁ, ପୁଣେ, ଭୁବନେଶ୍ବର ଓ ଥୁରୁ ଅନନ୍ତପୁରମ୍ ।

Question 15.
ଭାରତର ଚାରିଗୋଟି ଶିଳ୍ପାଞ୍ଚଳର ନାମ ଲେଖ ।
Answer:

• ଭାରତର ଚାରୋଟି ଶିଳ୍ପାଞ୍ଚଳର ନାମ ହେଲା-
• ମୁମ୍ବାଇ- ପୁଣେ ଶିଳ୍ପାଞ୍ଚଳ
• ବେଙ୍ଗାଲୁରୁ-ତାମିଲନାଡୁ ଅଞ୍ଚଳ
• ହୁଗୁଳି ଅଞ୍ଚଳ
• ଅହମ୍ମଦାବାଦ–ଭଦୋଦରା ଶିଳ୍ପାଞ୍ଚଳ ।

Question 16.
ଶିଳ୍ପ କହିଲେ କ’ଣ ବୁଝାଯାଏ ?
Answer:

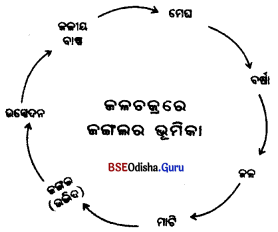
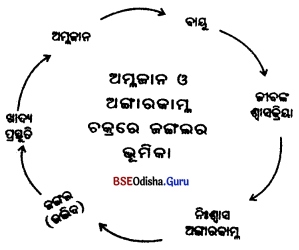
• ଯେଉଁ ଅର୍ଥନୀତିକ କାର୍ଯ୍ୟକଳାପଦ୍ବାରା ନୂତନ ସାମଗ୍ରୀ ପ୍ରସ୍ତୁତକରିବା ସହ ଖଣିଜଦ୍ରବ୍ୟ ଉତ୍ତୋଳନ ତଥା ସେବା ଯୋଗାଇ ଦିଆଯାଏ ତାହାକୁ ଶିଳ୍ପ କୁହାଯାଏ ।
• ଉଦାହରଣସ୍ୱରୂପ ଲୌହଇସ୍ପାତ ଶିଳ୍ପରୁ ବିଭିନ୍ନ ଇସ୍ପାତ ସାମଗ୍ରୀ ପ୍ରସ୍ତୁତ କରାଯାଏ । କୋଇଲା ଖନନ ଶିଳ୍ପରେ କୋଇଲା ଉତ୍ପାଦନ କରାଯାଏ ।
• ପରିବହନ, ଯୋଗାଯୋଗ, ପର୍ଯ୍ୟଟନ ଆଦି ମଧ୍ଯ ସେବାରିରିକ ଶିଳ୍ପ ।

Question 17.
ଭାରତୀୟ ସୂଚନା ପ୍ରଯୁକ୍ତି ଶିଳ୍ପସଂସ୍ଥାର ନାମ ଲେଖ ।
Answer:
ଭାରତରେ ସୂଚନା ପ୍ରଯୁକ୍ତି ଶିଳ୍ପ ସଂସ୍ଥାର ନାମ ହେଲା – ଇନ୍‌ଫୋସିସ୍, ୱିପ୍ରୋ ଓ ସତ୍ୟମ୍ ।

Question 18.
ଗୋଟିଏ ଦେଶ ପାଇଁ ଶିଳ୍ପର ବିକାଶ କାହିଁକି ମହତ୍ତ୍ଵପୂର୍ଣ ? ଦୁଇଟି କାରଣ ଲେଖ ।
Answer:

• ଶିଳ୍ପ ପ୍ରତି ଦ୍ଵାରା ଲୋକ ମାନଙ୍କୁ କର୍ମସଂସ୍ଥାନ ମିଳିଥାଏ ।
• ଏହାଦ୍ୱାରା ବ୍ୟବସାୟ ବାଣିଜ୍ୟ କାରବାର ବୃଦ୍ଧିପାଏ ଏବଂ ଦେଶର ଆୟ ମଧ୍ୟ ବଢ଼େ ।
• ଜଣେ ଶିଳ୍ପ ଶ୍ରମିକ, ଜଣେ କୃଷି ଶ୍ରମିକଠାରୁ ଅଧିକ ମଜୁରି ପାଏ ।
• ଶିଳ୍ପାୟନ ଦେଶକୁ ଅର୍ଥନୀତି କ୍ଷେତ୍ରରେ ସମୃଦ୍ଧ କରେ ।

Question 19.
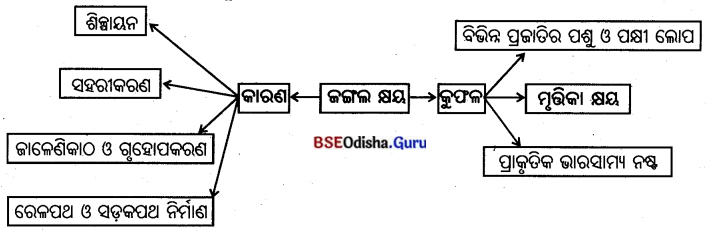
ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ପାଇଁ କେଉଁ କେଉଁ କାରଣଗୁଡ଼ିକ ମୁଖ୍ୟତଃ ଦାୟୀ ?
Answer:

• କଞ୍ଚାମାଲର ଉପଲବ୍ଧି
• ଶିଳ୍ପ ପ୍ରତିଷ୍ଠା ପାଇଁ ଆବଶ୍ୟକ ଜମି
• ଜଳ
• କୁଶଳୀ ଓ ଶସ୍ତା ଶ୍ରମିକ, ଶକ୍ତି, ପୁଞ୍ଜି, ପରିବହନ ଓ ବଜାର ଇତ୍ୟାଦି
• ଏତଦ୍‌ବ୍ୟତୀତ ସରକାରଙ୍କଦ୍ୱାରା ରିହାତି ଦରରେ ଉପରୋକ୍ତ ଆନୁଷଙ୍ଗିକ ବ୍ୟବସ୍ଥା ଯୋଗାଇଦେବା ଆବଶ୍ୟକ ।

Question 20.
କେଉଁ ଶିଳ୍ପକୁ ଆଧୁନିକ ଶିଳ୍ପର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ଏବଂ କାହିଁକି ?
Answer:

• ଲୌହ-ଇସ୍ପାତ ଶିଳ୍ପକୁ ଆଧୁନିକ ଶିଳ୍ପର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ।
• କାରଣ ଏହା ଏକ ମୌଳିକ ଶିଳ୍ପ । ଏହାର ଉତ୍ପାଦକୁ ଅନ୍ୟାନ୍ୟ ଶିଳ୍ପରେ କଞ୍ଚାମାଲ ରୂପେ ବ୍ୟବହାର କରାଯାଏ ।
• ଜଳଜାହାଜ, ରେଳଗାଡ଼ି, ଟ୍ରକ୍, ବସ୍, ଅଟୋ, ସାଇକେଲ ଆଦି ଯାନବାହନଗୁଡ଼ିକ ଲୌହ-ଇସ୍ପାତରେ ତିଆରି ।
• ଛୁଞ୍ଚଠାରୁ ଆରମ୍ଭ କରି ସେଫ୍‌ଟିପିନ୍ ପର୍ଯ୍ୟନ୍ତ ଅନେକ ଘରକରଣା ଜିନିଷ, ତୈଳଖଣି ଖନନ ପାଇଁ ଯନ୍ତ୍ରପାତି, ଚାଷକାର୍ଯ୍ୟ, ସୁଉଚ୍ଚ ଅଟ୍ଟାଳିକାରେ ବ୍ୟବହୃତ ଇସ୍ପାତ ଫ୍ରେମ୍ ଆଦି ଇସ୍ପାତରୁ ତିଆରି ।

ଭୌଗୋଳିକ କାରଣ ଦର୍ଶାଅ ।

Question 1.
ମୁମ୍ବାଇ ଭାରତର ଅନ୍ୟତମ ଆଧୁନିକ କାର୍ପାସ ବୟନଶିଳ୍ପ କେନ୍ଦ୍ର ରୂପେ ପରିଗଣିତ ।
Answer:
ମୁମ୍ବାଇର ଉଷ୍ଣ ଆର୍ଦ୍ର ଜଳବାୟୁ, ଯନ୍ତ୍ରପାତି ଆମଦାନୀ ପାଇଁ ବନ୍ଦର । ସୁବିଧା, କଞ୍ଚାମାଲର ସୁଲଭତା ଏବଂ କୁଶଳୀ ଶ୍ରମିକ ଆଦି ଏହାକୁ ଆଧୁନିକ କାର୍ପାସ ବୟନ ଶିଳ୍ପ କେନ୍ଦ୍ର ରୂପେ ପରିଣତ କରିବାରେ ସହାୟକ ହେଲା ।

Question 2.
ଲୌହଇସ୍ପାତ ଶିଳ୍ପର ବିକାଶ ହିଁ ଭାରତରେ ଶିଳ୍ପ ବିକାଶର ଦ୍ଵାର ଖୋଲିଦେଲା ।
Answer:

• ପ୍ରତ୍ୟେକ ଶିଳ୍ପାନୁଷ୍ଠାନ ସେମାନଙ୍କର ମୌଳିକ ଆଧାରିକ ସଂରଚନା ନିମନ୍ତେ ଲୌହଇସ୍ପାତ ଶିଳ୍ପ ଉପରେ ନିର୍ଭରଶୀଳ ।
• ଲୌହଇସ୍ପାତର ଶେଷ ଉତ୍ପାଦର୍‌ବେ ଲୁହା ବା ଇସ୍ପାତକୁ କଞ୍ଚାମାଲ ଭାବେ ଦ୍ଵିତୀୟକ ଉତ୍ପାଦନକାରୀ ସଂସ୍ଥା, ରୋଲିଂ ମିଲ୍ ଟ୍ରକ୍ ନିର୍ମାଣ, ମଟରଗାଡ଼ି ଯନ୍ତ୍ରାଂଶ, କୃଷି ଯନ୍ତ୍ରପାତି, ରେଳଧାରଣା, କଳକବଜା, ଟିଣଚଦର, କେବୁଲ ଓ ତାର ଉତ୍ପାଦନକାରୀ ଶିଳ୍ପସଂସ୍ଥାରେ ବ୍ୟବହାର କରାଯାଏ ।
• ତେଣୁ ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ରକୁ ଭିରି କରି ଭାରତରେ ଅନେକ ଶିଳ୍ପସଂସ୍ଥା ଗଢ଼ିଉଠିଛି ।

Question 3.
ଖଣିଜରିରିକ ଶିଳ୍ପଗୁଡ଼ିକୁ ମୌଳିକ ଶିଳ୍ପ କୁହାଯାଏ ।
Answer:

• ଖଣିଜରିରିକ ଶିଳ୍ପଗୁଡ଼ିକ ବିଭିନ୍ନ ଖଣିଜପଦାର୍ଥକୁ କଞ୍ଚାମାଲ ରୂପେ ବ୍ୟବହାର କରିଥା’ନ୍ତି । ଏଠାରୁ ପ୍ରସ୍ତୁତ ସାମଗ୍ରୀ ଅନ୍ୟାନ୍ୟ ଶିଳ୍ପରେ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହୃତ ହୁଏ । ଉଦାହରଣସ୍ୱରୂପ– ଲୌହଇସ୍ପାତ ଶିଳ୍ପରେ ଲୁହାପଥର କଞ୍ଚାମାଲ ଓ ଲୁହା ବା ଇସ୍ପାତ ଉତ୍ପାଦ ହୋଇଥାଏ ।
• ଲୁହା କଞ୍ଚାମାଲ ଭାବେ ଭାରୀ ଯନ୍ତ୍ରପାତି, ରେଳଡ଼ବା ନିର୍ମାଣ ତଥା ଜଳଜାହାଜ କାରଖାନା ଆଦିରେ ମୁଖ୍ୟ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହୃତ ହୁଏ ।

Question 4.
କାର୍ପାସ ବୟନ ଶିଳ୍ପ ପୃଥ‌ିବୀର ଏକ ପୁରାତନ ଶିଳ୍ପ
Answer:

• ଅଷ୍ଟାଦଶ ଶତାବ୍ଦୀରେ ସୂତା ଓ ହସ୍ତତନ୍ତଦ୍ୱାରା ବୟନଶିଳ୍ପର ବିକାଶ ଆରମ୍ଭ ହୋଇଥିଲା ।
• ଏହି ଶତାବ୍ଦୀରେ କଳତନ୍ତ୍ରଦ୍ଵାରା ଏହି ଶିଳ୍ପର ପ୍ରସାର ପ୍ରଥମେ ଗ୍ରେଟ୍‌ବ୍ରିଟେନ୍ ଓ ପରେ ଅନ୍ୟ ଅଞ୍ଚଳକୁ କଳତନ୍ତ୍ରର ପ୍ରସାର ଘଟିଲା, ତେଣୁ ଏହା ଏକ ପୁରାତନ ଶିଳ୍ପ ।

Question 5.
ଇସ୍ପାତ ଆଧୁନିକ ଶିଳ୍ପଜଗତର ମେରୁଦଣ୍ଡ ସଦୃଶ।
Answer:

• ଛୁଅ, ସେଫଟିପିଠାରୁ ଆରମ୍ଭ କରି ଜଳଜାହାଜ, ରେଳଗାଡ଼ି, ଟ୍ରକ୍, ବସ୍, ଅଟୋ, ସାଇକେଲ୍‌ ଆଦି ବିଭିନ୍ନ ଜିନିଷରେ ଇସ୍ପାତର ବ୍ୟବହାର ହୋଇଥାଏ।
• ଲୌହ-ଇସ୍ପାତର ବହୁଳ ବ୍ୟବହାର ଯୋଗୁ ଏହାକୁ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ।

ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

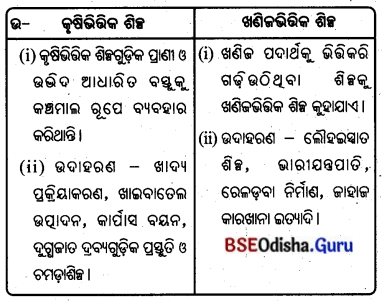
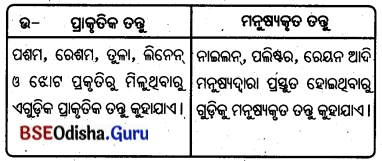
1. କୃଷିଭିତ୍ତିକ ଶିଳ୍ପ ଓ ଖଣିଳଭିଭିକ ଶିଳ୍ପ :
Answer:

2. ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପ ଓ ଜଙ୍ଗଲଭିତ୍ତିକ ଶିଳ୍ପ :
Answer:

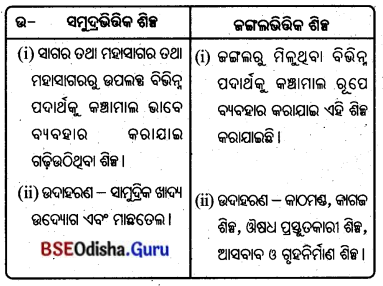
3. କୁଟୀର ଶିଳ୍ପ ଓ କ୍ଷୁଦ୍ର ଶିଳ୍ପ :
Answer:

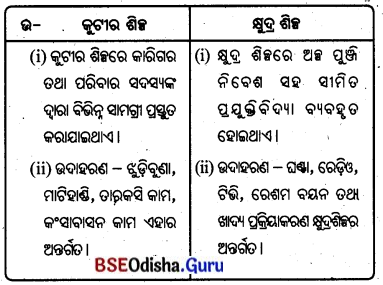
4. ପ୍ରାକୃତିକ ତନ୍ତୁ ଓ ମନୁଷ୍ୟକୃତ ତନ୍ତୁ :
Answer:

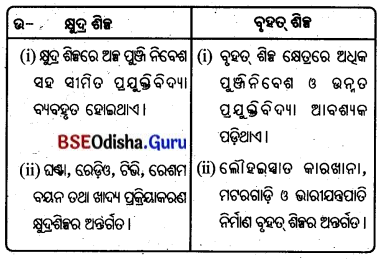
5. କ୍ଷୁଦ୍ର ଶିଳ୍ପ ଓ ବୃହତ୍ ଶିଳ :
Answer:

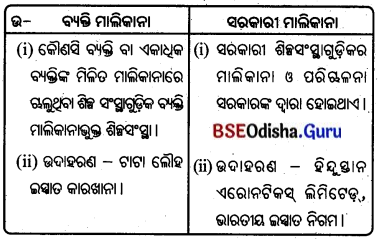
6. ବ୍ୟକ୍ତି ମାଲିକାନା ଓ ସରକାରୀ ମାଲିକାନା :
Answer:

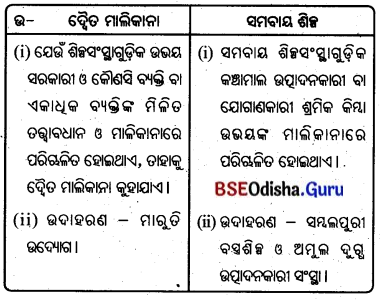
7. ଦ୍ଵୈତ ମାଲିକାନା ଓ ସମବାୟ ଶିଳ୍ପ :
Answer:

ପରୀକ୍ଷା ଉପଯୋଗୀ ସମ୍ଭାବିତ ପ୍ରଶ୍ନୋତ୍ତର
ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନୋତ୍ତର

ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।1. ______ ରାଜ୍ୟ ସର୍ବପ୍ରଥମେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଆଇନ୍ ପ୍ରଣୟନ କରିଥିଲେ ।
Answer:
କର୍ଣାଟକ

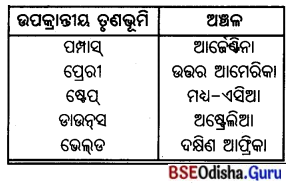
2. ଆମେରିକାର ସିଲିକନ୍ ଉପତ୍ୟକା ______ ଉପତ୍ୟକାର ଏକ ଅଂଶ ।
Answer:
ଶାନ୍ତାକ୍କାରା

3. ଶାନ୍ତାକାରୀ ଉପତ୍ୟକା ______ ପର୍ବତ ସହ ସଂଲଗ୍ନ ।
Answer:
ରକି

4. ଓସାକାର ______ ଶିଳ୍ପ କଞ୍ଚାମାଲ ପାଇଁ ବାହାର ଦେଶ ଉପରେ ନିର୍ଭରଶୀଳ ।
Answer:
ବୟନ

5. କଳତନ୍ତ ପ୍ରଥମେ ______ ଦେଶରେ ପ୍ରସାରିତ ହୋଇଥିଲା ।
Answer:
ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍

6. ଲିନେନ୍ ______ ତନ୍ତୁ ଅଟେ ।
Answer:
ପ୍ରାକୃତିକ

7. ବୃହତ୍ ହ୍ରଦ ଅଞ୍ଚଳରୁ ______ସାହାଯ୍ୟରେ ଲୁହାପଥର ପିଟ୍ସବର୍ଗକୁ ଆସିଥାଏ।
Answer: ଟ୍ରନ୍‌

8. ପିଟସ୍‌ବର୍ଗଠାରୁ ମିନେସୋଟାର ଦୂରତା ______କି.ମି. ।
Answer:
୧୫୦୦

9. ରୋଲିଂ ମିଲ୍ ______ କାରଖାନା ସହ ସଂପୃକ୍ତ ।
Answer:
ଲୌହ-ଇସ୍ପାତ

10. ଜାମସେଦପୁର ଝାଡ଼ଖଣ୍ଡର ______ ଜିଲ୍ଲାରେ ଅବସ୍ଥିତ ।
Answer:
ସିଂହଭୂମି

ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

Question 1.
ପ୍ରାଥମିକ ଉତ୍ପାଦ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ପ୍ରକୃତିଦର ଜିନିଷଗୁଡ଼ିକ ପ୍ରତ୍ୟକ୍ଷ ଭାବରେ ବ୍ୟବହାର ହୋଇପାରେ ସେଗୁଡ଼ିକୁ ପ୍ରାଥମିକ ଉତ୍ପାଦ କୁହାଯାଏ।

Question 2.
ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଯେଉଁ ଆର୍ଥନୀତିକ କାର୍ଯ୍ୟକଳାପଦ୍ଵାରା ନୂତନ ସାମଗ୍ରୀ ପ୍ରସ୍ତୁତ କରିବା ସହ ଖଣିଜ ଦ୍ରବ୍ୟ ଉତ୍ତୋଳନ ତଥା ସେବା ଯୋଗାଇ ଦିଆଯାଏ, ତାହାକୁ ଶିଳ୍ପ କୁହାଯାଏ।

Question 3.
ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମୁଦ୍ରଭିଭିକ ଶିଳ୍ପରେ ସାଗର ତଥା ମହାସାଗରରୁ ଉପଲବ୍ଧ ବିଭିନ୍ନ ପଦାର୍ଥକୁ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହାର କରାଯାଏ। ସାମୁଦ୍ରିକ ଖାଦ୍ୟ ଉଦ୍ୟୋଗ ଏବଂ ମାଛତେଲ ଉଦ୍ୟୋଗ ଏହାର ଉଦାହରଣ।

Question 4.
କେଉଁ କାର୍ଯ୍ୟଗୁଡ଼ିକ କୁଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
Answer:
ଝୁଡ଼ିବୁଣା, ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି ଏବଂ ଅନ୍ୟାନ୍ୟ ହସ୍ତଶିଳ୍ପଗୁଡ଼ିକ କୁଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।

Question 5.
କେଉଁ କାର୍ଯ୍ୟଗୁଡ଼ିକ କ୍ଷୁଦ୍ରଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
Answer:
ଘଣ୍ଟା, ରେଡ଼ିଓ ଓ ଟିଭି କ୍ଷୁଦ୍ରଶିଳ୍ପର ଅନ୍ତର୍ଗତ।

Question 6.
ବ୍ୟକ୍ତି ମାଲିକାନା କାହାକୁ କୁହାଯାଏ ?
Answer:
କୌଣସି ବ୍ୟକ୍ତି ବା ଏକାଧ୍ଵକ ବ୍ୟକ୍ତିଙ୍କ ମିଳିତ ମାଲିକାନାରେ ଚାଲୁଥିବା ଶିଳ୍ପ ସଂସ୍ଥାଗୁଡ଼ିକ ବ୍ୟକ୍ତି ମାଲିକାନାଭୁକ୍ତ ଶିଳ୍ପସଂସ୍ଥା ଅଟେ । ଉଦାହରଣ ଟାଟା ଲୌହ-ଇସ୍ପାତ କାରଖାନା।

Question 7.
ସରକାରୀ ଶିଳ୍ପ କ’ଣ ?
Answer:
ସରକାରୀ ଶିଳ୍ପ ସଂସ୍ଥାଗୁଡ଼ିକର ମାଲିକାନା ଓ ପରିଚାଳନା ସରକାରଙ୍କ ଦ୍ଵାରା ହୋଇଥାଏ। ଉଦାହରଣ ହିନ୍ଦୁସ୍ଥାନ ଏରୋନଟିକ୍‌ସ୍ ଲିମିଟେଡ଼।

Question 8.
ସମବାୟ ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମବାୟ ଶିଳ୍ପ ସଂସ୍ଥାଗୁଡ଼ିକ କଞ୍ଚାମାଲ ଉତ୍ପାଦନକାରୀ ବା ଯୋଗାଣକାରୀ ଶ୍ରମିକ କିମ୍ବା ଉଭୟଙ୍କ ମାଲିକାନାରେ ପରିଚାଳିତ ହୋଇଥାଏ। ଯଥା ସମ୍ବଲପୁରୀ ବସ୍ତ୍ରଶିଳ୍ପ ଓ ଅମୁଲ ଦୁଗ୍ଧ ଉତ୍ପାଦନକାରୀ ସଂସ୍ଥା ।

Question 9.
ଶିଳ୍ପ ବ୍ୟବସ୍ଥା କାହାକୁ ନେଇ ଗଢ଼ା ହୋଇଥାଏ ?
Answer:
ଏକ ଶିଳ୍ପ ବ୍ୟବସ୍ଥା ନିବେଶ, ପ୍ରକ୍ରିୟାକରଣ ଓ ଉତ୍ପାଦକୁ ନେଇ ଗଢ଼ା ।

Question 10.
ନିବେଶ କାହାକୁ କୁହାଯାଏ ?
Answer:
ନିବେଶ କହିଲେ କଞ୍ଚାମାଲ, ଶ୍ରମିକ, ଭୂମି, ପରିବହନ, ଶକ୍ତି, ଅନ୍ୟାନ୍ୟ ଆଧାରିକ ସଂରଚନା ଓ ବିକାଶ ନିମନ୍ତେ ବିନିଯୁକ୍ତ ପୁଞ୍ଜିକୁ ବୁଝାଏ ।

Question 11.
ଆଧାରିକ ସଂରଚନା କାହାକୁ କୁହାଯାଏ ?
Answer:
ବିଦ୍ୟୁତ୍‌କରଣ, ଯୋଗାଯୋଗ, ସଡ଼କ ଓ ରେଳପଥ, ଶିକ୍ଷାନୁଷ୍ଠାନ, ଚିକିତ୍ସାଳୟ ଇତ୍ୟାଦି ବ୍ୟବସ୍ଥାକୁ ଆଧାରିକ ସଂରଚନା କୁହାଯାଏ।

Question 12.
ପ୍ରକ୍ରିୟାକରଣ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଶିଳ୍ପ ସଂସ୍ଥାରେ କଞ୍ଚାମାଲରୁ ଉତ୍ପାଦ ସୃଷ୍ଟି ହେବାପାଇଁ ଯେଉଁସବୁ କାର୍ଯ୍ୟପନ୍ଥା ଗ୍ରହଣ କରାଯାଏ, ତାକୁ ପ୍ରକ୍ରିୟାକରଣ କୁହାଯାଏ।

Question 13.
ଉତ୍ପାଦକ’ଶ?
Answer:
ଶିଳ୍ପ ସଂସ୍ଥାରୁ ସର୍ବଶେଷରେ ବାହାରୁଥିବା ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟକୁ ଉତ୍ପାଦ କୁହାଯାଏ ଏବଂ ଏଥୁରୁ ଆୟ ମିଳିଥାଏ।

Question 14.
ଭୋପାଳରେ କେବେ ଶୃଚ୍ଛଜନିତ ଦୁର୍ଘଟଣା ହୋଇଥିଲା ?
Answer:
୧୯୮୪ ମସିହା ଡିସେମ୍ବର ୩ ତାରିଖରେ ଭୋପାଳରେ ମର୍ମନ୍ତୁଦ ଶିଳ୍ପ ଦୁର୍ଘଟଣା ହୋଇଥିଲା ।

Question 15.
ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ କାହାକୁ କୁହାଯାଏ ?
Answer:
ନୂତନ ଭାବେ ଗଢ଼ିଉଠିଥିବା ଶିଳ୍ପକୁ ‘ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ’ ଆଖ୍ୟା ଦିଆଯାଇଛି । ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା, ସ୍ୱାସ୍ଥ୍ୟ ସେବା, ଆତିଥ୍ୟ ଏବଂ ଶିକ୍ଷା ଆଦି ଏହାର ଅନ୍ତର୍ଭୁକ୍ତ ।

Question 16.
କାଲିଫର୍ଣିଆ କାହିଁକି ପ୍ରସିଦ୍ଧ ?
Answer:
ସୂଚନା ପ୍ରଯୁକ୍ତିବିଦ୍ୟାର ପ୍ରମୁଖ କ୍ଷେତ୍ରଭାବେ କେନ୍ଦ୍ରୀୟ କାଲିଫର୍ନିଆର ସିଲିକନ୍ ଉପତ୍ୟକା ପ୍ରସିଦ୍ଧ ।

Question 17.
ଭାରତର କେଉଁ ସ୍ନାନ ପ୍ରଯୁକ୍ତିବିଦ୍ୟା କ୍ଷେତ୍ରରେ ଅଗ୍ରଣୀ ?
Answer:
ଭାରତର ବେଙ୍ଗାଲୁରୁ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା କ୍ଷେତ୍ରରେ ଅଗ୍ରଣୀ।

Question 18.
ବ୍ଲାଷ୍ଟ୍ର ଫର୍‌ନେସ୍‌ର କାମ କ’ଣ ?
Answer:
ଲୁହାପଥର ତରଳାଇବାକୁ ବ୍ଲାଷ୍ଟ୍ର ଫର୍‌ନେସ୍‌ର ଆବଶ୍ୟକତା ହୋଇଥାଏ ।

Question 19.
ମିଶ୍ରଧାତୁ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଇସ୍ପାତ୍ ବେଶ୍ ଶକ୍ତି ଏବଂ ଏହାକୁ ସହଜରେ ବିଭିନ୍ନ ଆକୃତି ଦିଆଯାଇପାରେ, କଟାଯାଇପାରେ ଏବଂ ତାରରେ ପରିଣତ କରି ହୁଏ। ଏହା ସହିତ ମାଙ୍ଗାନିଜ, ନିକେଲ ଓ କ୍ରୋମିୟମ୍ ମିଶ୍ରଣ କରାଯାଇ ଏକ ସ୍ଵତନ୍ତ୍ର ଧରଣର ଇସ୍ପାତ୍ ପ୍ରସ୍ତୁତ କରାଯାଏ। ଏହାକୁ ମିଶ୍ରଧାତୁ କୁହାଯାଏ।

Question 20.
କାହାକୁ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ ?
Answer:
ଲୁହାକୁ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ ବୋଲି କୁହାଯାଏ।

Question 21.
କେଉଁ ସ୍ଥାନମାନଙ୍କରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ସ୍ଵାପନ କରାଯାଏ ?
Answer:
କଞ୍ଚାମାଲ, ଶସ୍ତା ଶ୍ରମିକ, ପରିବହନ ଓ ବଜାର ସୁବିଧା ଥିବା ସ୍ଥାନମାନଙ୍କରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ସ୍ଥାପନ କରାଯାଏ।

Question 22.
କର୍ଣାଟକର କେଉଁଠାରେ ଲୌହ-ଇସ୍ପାତ କାରଖାନା ରହିଛି ?
Answer:
କର୍ଣ୍ଣାଟକର ଭଦ୍ରାବତୀ ଓ ବିଜୟନଗରଠାରେ ଲୌହ-ଇସ୍ପାତ୍ର କାରଖାନା ରହିଛି ।

Question 23.
ଆନ୍ଧ୍ରପ୍ରଦେଶର କେଉଁଠାରେ ଲୌହଇସ୍ପାତ୍ କାରଖାନା ରହିଛି ?
Answer:
ଆନ୍ଧ୍ରପ୍ରଦେଶର ବିଶାଖାପାଟଣାରେ ଲୌହ-ଇସ୍ପାତ କାରଖାନା ରହିଛି ।

Question 24.
ଓଡ଼ିଶାର କେଉଁଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି ?
Answer:
ଓଡ଼ିଶାର ରାଉରକେଲାଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି।

Question 25.
ଦୁର୍ଗାପୁର ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
Answer:
ପଶ୍ଚିମବଙ୍ଗ ରାଜ୍ୟରେ ଦୁର୍ଗାପୁର ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ଅବସ୍ଥିତ ।

Question 26.
ତାମିଲନାଡୁର କେଉଁଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି ?
Answer:
ତାମିଲନାଡୁର ସାଲେମଠାରେ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ରହିଛି।

Question 27.
କେଉଁ ନଦୀଦ୍ୱୟର ସଂଗମସ୍ଥଳରେ ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
ସୁବର୍ଣ୍ଣରେଖା ଓ ଖରକାଇ ନଦୀଦ୍ୱୟର ସଂଗମସ୍ଥଳରେ ଟାଟା ଲୌହ- ଇସ୍ପାତ୍ କାରଖାନା ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।

Question 28.
ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
Answer:
ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା ଝାଡ଼ଖଣ୍ଡ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ।

Question 29.
ପିଟ୍‌ସ୍‌ବର୍ଗ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁଠି ଅବସ୍ଥିତ ?
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାରେ ପିଟ୍‌ସ୍‌ବର୍ଗ ଲୌହ ଇସ୍ପାତ୍ କାରଖାନା ଅବସ୍ଥିତ ।

Question 30.
ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଲୁହାପଥର କିପରି ଆସିଥାଏ ?
Answer:
ବୃହତ୍ ହ୍ରଦ ଅଞ୍ଚଳରୁ ଟ୍ରେନ୍‌ଯୋଗେ ଲୁହାପଥର ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଆସିଥାଏ।

Question 31.
କେଉଁ ନଦୀ ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଜଳ ଯୋଗାଇଥାଏ ?
Answer:
ଓହିଅ, ମନୋଗାହେଲା ଏବଂ ଆଲେଘେନି ନଦୀରୁ ପ୍ରଚୁର ଜଳ ପିଟ୍‌ସ୍‌ବର୍ଗ ଅଞ୍ଚଳକୁ ଯୋଗାଇଥାଏ।

Question 32.
ପଞ୍ଚହ୍ରଦ ମଧ୍ୟରେ କେଉଁଟି ବୃହତ୍ତମ ?
Answer:
ସୁପିରିଅର

Question 33.
କେଉଁଗୁଡ଼ିକ ପ୍ରାକୃତିକ ତନ୍ତୁ ଅଟେ ?
Answer:
ପଶମ, ରେଶମ, ତୁଳା, ଲିନେନ୍ ଓ ଝୋଟ ପ୍ରାକୃତିକ ତନ୍ତୁ ଅଟନ୍ତି ।

Question 34.
କେଉଁଗୁଡ଼ିକ ମନୁଷ୍ୟକୃତ ତନ୍ତୁ ଅଟେ ?
Answer:
ନାଇଲନ, ପଲିଷ୍ଟର ଓ ରେୟନ୍ ମନୁଷ୍ୟକୃତ ତନ୍ତୁ ଅଟେ।

Question 35.
କେବେଠାରୁ କାର୍ପାସ ବୟନଶିଳ୍ପର ବିକାଶ ହେଲା ?
Answer:
ଅଷ୍ଟାଦଶ ଶତାବ୍ଦୀରେ କାର୍ପାସ ବୟନଶିଳ୍ପର ବିକାଶ ହେଲା।

Question 36.
ପ୍ରଥମେ କେଉଁଠାରେ କଳତନ୍ତର ପ୍ରସାର ଘଟିଲା ?
Answer:
ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍‌ରେ କଳତନ୍ତର ପ୍ରସାର ଘଟିଲା ।

Question 37.
ସୁନାଜରି କାମ କାର୍ପାସ ବସ୍ତ୍ର ପାଇଁ ଭାରତର କେଉଁ ସ୍ଥାନ ପ୍ରସିଦ୍ଧ ?
Answer:
ସୁରତ୍ ଓ ଉଦୋଦରା ସୁନାଜରି କାମ ଓ କାର୍ପାସ୍ ବସ୍ତ୍ର ପାଇଁ ଭାରତ ପ୍ରସିଦ୍ଧ ।

Question 38.
ଢାକାର କେଉଁ କାମ ପୃଥବୀ ପ୍ରସିଦ୍ଧ ?
Answer:
ଢାକାର ମସ୍‌ଲିନ୍ କାର୍ପାସ୍‌ବସ୍ତ୍ର ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ।

Question 39.
କେଉଁ ମସିହାରେ ଭାରତରେ ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ବୟନଶିଳ ମୁମ୍ବାଇରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
୮୫୪ ମସିହାରେ ଭାରତରେ ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ବୟନଶିଳ୍ପ ମୁମ୍ବାଇରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।

Question 40.
ମସଲିପଟ୍ଟନମ୍ବର କେଉଁ କାର୍ପାସ୍ବବସ୍ତ୍ର ପୃଥ‌ିବୀରେ ବେଶ୍ ଆଦୃତ ?
Answer:
ମସଲିପଟ୍ଟନମ୍‌ର ଚିନ୍‌ଜେନ୍ କାର୍ପାସବସ୍ତ୍ର ପୃଥ‌ିବୀରେ ବେଶ୍ ଆଦୃତ ।

Question 41.
କାହାକୁ ‘ଭାରତର ମାଞ୍ଚେଷ୍ଟର’ କୁହାଯାଏ ?
Answer:
ଅହମ୍ମଦାବାଦକୁ ଭାରତର ମାଞ୍ଚେଷ୍ଟର କୁହାଯାଏ ।

Question 42.
ଅହମ୍ମଦାବାଦ କେଉଁ ରାଜ୍ୟରେ ଓ କେଉଁ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ?
Answer:
ଅହମ୍ମଦାବାଦ ଗୁଜରାଟ ରାଜ୍ୟର ନର୍ମଦା ନଦୀକୂଳରେ ଅବସ୍ଥିତ ।

Question 43.
କେବେ ଅହମ୍ମଦାବାଦରେ ପ୍ରଥମ କାର୍ପାସ ବୟନଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?
Answer:
୧୮୫୯ ମସିହାରେ ଅହମ୍ମଦାବାଦରେ ପ୍ରଥମ କାର୍ପାସ ବୟନଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।

Question 44.
ମାଞ୍ଚେଷ୍ଟର କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
ମାଞ୍ଚେଷ୍ଟର ଇଂଲଣ୍ଡରେ ଅବସ୍ଥିତ ।

Question 45.
ଓସାକା କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
ଓସାକା ଜାପାନରେ ଅବସ୍ଥିତ ।

Question 46.
କାହାକୁ ‘ଜାପାନର ମାଞ୍ଚେଷ୍ଟର’ କୁହାଯାଏ ?
Answer:
ଓସାକାକୁ ଜାପାନର ମାଞ୍ଚେଷ୍ଟର କୁହାଯାଏ।

Question 47.
ଓସାକା କାହିଁକି ପ୍ରସିଦ୍ଧ ?.
Answer:
ଓସାକା ଜାପାନର ଏକ ପ୍ରମୁଖ ବୟନଶିଳ୍ପ କେନ୍ଦ୍ର ଅଟେ।

Question 48.
ସୂଚନା ଓ ପ୍ରଯୁକ୍ତିବିଦ୍ୟା ପାଇଁ ଭାରତର କେଉଁ ସ୍ଥାନ ପ୍ରସିଦ୍ଧ ?
Answer:
ସୂଚନା ଓ ପ୍ରଯୁକ୍ତିବିଦ୍ୟା ପାଇଁ ଭାରତର ବେଙ୍ଗାଲୁରୁ ପ୍ରସିଦ୍ଧ।

Question 49.
କାଲିଫର୍ଣିଆ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାକେନ୍ଦ୍ର କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
Answer:
କାଲିଫର୍ଷିଆ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାକେନ୍ଦ୍ର ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାରେ ଅବସ୍ଥିତ ।

Question 50.
ସିଲିକନ୍ ମାଳଭୂମି କାହାକୁ କୁହାଯାଏ ?
Answer:
ବେଙ୍ଗାଲୁରୁକୁ ସିଲିକନ୍ ମାଳଭୂମି କୁହାଯାଏ।

ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ ।

1. କାହାଦ୍ଵାରା କଞ୍ଚାମାଲକୁ ଲୋକଙ୍କ ପାଇଁ ଉପଯୋଗୀ ଦ୍ରବ୍ୟର ପରିଣତ କରିଥାଏ ?
Answer: ଉଦ୍ୟୋଗ ବା ଶିଳ୍ପ

2. ଶିଳ୍ପ ପ୍ରତିଷ୍ଠାଦ୍ୱାରା ଲୋକଙ୍କୁ କ’ଣ ମିଳିଥାଏ ?
Answer: କର୍ମ ସଂସ୍ଥାନ

3. କେଉଁ ଶିଳ୍ପଗୁଡ଼ିକ ପ୍ରାଣୀ ଓ ଉଭିଦ ଆଧାରିତ ବସ୍ତୁକୁ କଞ୍ଚାମାଲ ଭାବେ ବ୍ୟବହାର କରିଥାନ୍ତି ?
Answer: କୃଷିଭିର୍ଭିକ ଶିଳ୍ପ

4. ରେଳଡ଼ବା ନିର୍ମାଣର ମୁଖ୍ୟ କଞ୍ଚାମାଲ କ’ଣ ଅଟେ ?
Answer: ଲୁହା

5. ମାଛତେଲ ଉଦ୍ୟୋଗ କେଉଁ ଶିଳ୍ପର ଉଦାହରଣ ?
Answer: ସମୁଦ୍ରଭିଭିକ

6. ଅନେକ କ୍ଷେତ୍ରରେ କ’ଣ ସହର ଓ ନଗର ଆଦିର ବିକାଶ ଓ ଅଭିବୃଦ୍ଧିର କାରଣ ହୋଇଥାଏ ?
Answer: ଶିଳ୍ପାୟନ

7. ସିଲିକନ ଉପତ୍ୟକା ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର କେଉଁଠାରେ ଅବସ୍ଥିତ ?
Answer: କେନ୍ଦ୍ରୀୟ କାଲିଫର୍ଣ୍ଣିଆ

8. ଆଧୁନିକ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ କାହାକୁ କୁହାଯାଏ ?
Answer: ଇସ୍ପାତ

9. ଟାଟା ଲୌହ ଇସ୍ପାତ କାରଖାନା ଯେଉଁ ସ୍ଥାନରେ ଅବସ୍ଥିତ ତାହାର ନାମ କ’ଣ ?
Answer: ସାକ୍‌

10. ଜାପାନର ଓସାକା ବୟନ ଶିଳ୍ପ କେନ୍ଦ୍ର ପାଇଁ କେଉଁ ନଦୀରୁ ଜଳ ମିଳିଥାଏ ?
Answer: ଓଡ଼ୋ

ଭୌଗୋଳିକ ଶବ୍ଦଗୁଡ଼ିକୁ ଗୋଟିଏ ଗୋଟିଏ ବାକ୍ୟରେ ଲେଖ ।

1. ଅହମ୍ମଦାବାଦ :
Answer: ଭାରତର ମାଞ୍ଚେଷ୍ଟର ।

2. ଓସାକ
Answer: ଜାପାନର ମାଞ୍ଚେଷ୍ଟର ।

3. ମସ୍‌ଲି ନ :
Answer: ଢାକାର ନିର୍ମିତ ଏକ ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ ବସ୍ତ୍ର ।

4. ମସଲି ପଟନମ୍ :
Answer: ଚିନ୍‌ନ୍ କାର୍ପାସ ବସ୍ତ୍ରପାଇଁ ପ୍ରସିଦ୍ଧ ଅଞ୍ଚଳ ।

5. ଟିସ୍କୋ।
Answer: ଟାଟା ଲୌହଇସ୍ପାତ କାରଖାନାର ସଂକ୍ଷିପ୍ତ ନାମ ।

6. ସାଲେମ୍ :
Answer: ତାମିଲନାଡୁରେ ଅବସ୍ଥିତ ଏକ ଲୌହଇସ୍ପାତ କାରଖାନା ।

7. ମିଶ୍ରଧାତୁ :
Answer: ଇସ୍ପାତସହ ଆଲୁମିନିୟମ୍, ନିକେଲ ଓ ତମ୍ବା ଆଦି ଧାତୁ ମିଶାଇ ପ୍ରସ୍ତୁତ କରାଯାଉଥୁବା ଧାତୁ ।

8. ମିଥାଇଲ ଆଇସୋସାଇନେଟ୍ :
Answer: ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣାରେ ନିର୍ଗତ ଅତି ବିଷାକ୍ତ ବାଷ୍ପ ।

9. ଅମୁଲ :
Answer: ଆନନ୍ଦ ମିଲ୍‌କ ଇଉନିୟନ ଲିମିଟେଡ଼ର ସଂକ୍ଷିପ୍ତ ନାମ।

10. ଦ୍ୱୈତ ମାଲିକାନା ଲୁକ୍ତ ସଂସ୍ଥା :
Answer: ଉଭୟ ସରକାରୀ ଓ କୌଣସି ବ୍ୟକ୍ତି ବା ଏକାଧୁକ ବ୍ୟକ୍ତିଙ୍କ ମିଳିତ ତତ୍ତ୍ଵାବଧାନ ଓ ମାଲିକାନାରେ ପରିଚାଳିତ ଶିଳ୍ପ।

ଅସଂପର୍କିତ ଶବ୍ଦଟିକୁ ବାଛ ।

1. ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, କାଠମଣ୍ଡ, ଖାଇବାତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ ।
Answer: କାଠମଣ୍ଡ

2. ଲୌହଇସ୍ପାତ ଶିଳ୍ପ, ଭାରୀଯନ୍ତ୍ରପାତି, ରେଳଡ଼ବା ନିର୍ମାଣ, ଚମଡ଼ା ଶିଳ୍ପ ।
Answer: ଚମଡ଼ା ଶିଳ୍ପ

3. ମାଛତେଲ ଉଦ୍ୟୋଗ, କାଗଜଶିକ, ଔଷଧ ପ୍ରସ୍ତୁତକାରୀ ଶିଳ୍ପ, ଗୃହନିର୍ମାଣ ଶିଳ୍ପ ।
Answer: ମାଛ ତେଲ ଉଦ୍ୟୋଗ

4. ଘଣ୍ଟା, ରେଡ଼ିଓ, ଟିଭି, ଝୁଡ଼ିବୁଣା।
Answer: ଝୁଡ଼ିବୁଣା

5. ଝୁଡ଼ି, ଘଣ୍ଟା, ମାଟିହାଣ୍ଡି, ତାରକସି କାମ ।
Answer: ଘଣ୍ଟା

6. ମଟରଗାଡ଼ି ନିର୍ମାଣ, ଜାହାଜ ନିର୍ମାଣ, ଟିଭି, ଭାରୀଯନ୍ତ୍ରପାତି ।
Answer: ଟିଭି

7. ମୁମ୍ବାଇ-ପୁଣେ, ବେଙ୍ଗାଲୁରୁ-ତାମିଲନାଡୁ ଅଞ୍ଚଳ, କୋଲକାତା- ଭୁବନେଶ୍ଵର, ଗୁଡ଼ଗାଓଁ-ଦିଲ୍ଲୀ ।
Answer: କୋଲକାତା-ଭୁବନେଶ୍ଵର

8. ଇସ୍ପାତ, ମାଙ୍ଗାନିଜ, ଚୂନପଥର, ନିକେଲ।
Answer: ଚୂନପଥର

9. ଦିଲ୍ଲୀ, ଭିଲାଇ, ଦୁର୍ଗାପୁର, ବର୍ଣ୍ଣପୁର ।
Answer: ଦିଲ୍ଲୀ

10. HAL, CESCO, SAIL, BHEL
Answer: CESCO

ଠିକ୍ ଉକ୍ତ ପାଖରେ ଠିକ୍ ଚିହ୍ନ ( ✓ ) ଓ ଭୁଲ୍ ଭକ୍ତି ପାଖରେ ଭୁଲ୍ ଚିହ୍ନ ( ✗ ) ଦିଅ ।

1. ଭଦ୍ରାବତୀ ଓ ବିଜୟ ନଗର କର୍ଣାଟକରେ ଅବସ୍ଥିତ। — ଚିହ୍ନ ( ✓ )
2. ଋଷ କାର୍ଯ୍ୟରେ ମୁଖ୍ୟତଃ କାଠ ଯନ୍ତ୍ରପାତି ବ୍ୟବହୃତ ହୁଏ । — ଚିହ୍ନ ( ✗ )
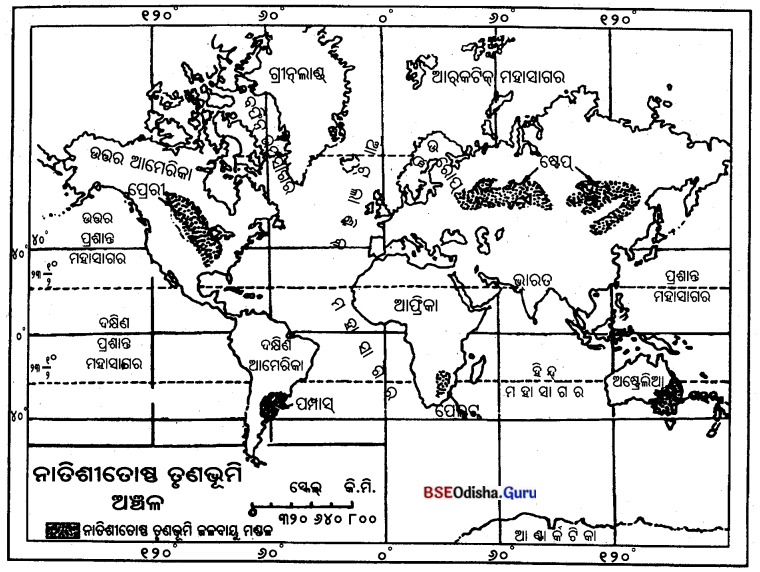
3. ପୃଥ‌ିବୀର ମୁଖ୍ୟ ଶିଳ୍ପାଞ୍ଚଳଗୁଡ଼ିକ ନାତିଶୀତୋଷ୍ଣ ଅଞ୍ଚଳରେ ଅବସ୍ଥିତ । — ଚିହ୍ନ ( ✓ )
4. ଯୋଗାଯୋଗ ବ୍ୟବସ୍ଥାକୁ ଆଧାରିକ ସଂରଚନା କୁହାଯାଏ । — ଚିହ୍ନ ( ✓ )
5. ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ ବୃହତ୍ ଶିଳ୍ପ ଅଟେ । — ଚିହ୍ନ ( ✗ )
6. ଶିଳ୍ପ ଶ୍ରମିକ କୃଷିଶ୍ରମିକ ଠାରୁ କମ୍ ମଜୁରି ପାଇଥାଏ। — ଚିହ୍ନ ( ✗ )
7. ପରିବହନ ଓ ଯୋଗାଯୋଗ ଆଦି ସେବା ଶିଳ୍ପର ଅନ୍ତର୍ଭୁକ୍ତ। — ଚିହ୍ନ ( ✓ )
8. କୋଇଲା ଖନନ ଏକ ଶିଳ୍ପ ଅଟେ । — ଚିହ୍ନ ( ✓ )
9. ଘଣ୍ଟା ଶିଳ୍ପ କୂଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଭୁକ୍ତ । — ଚିହ୍ନ ( ✗ )
10. ଓହିଓ ନଦୀ ରୁଷିଆରେ ଅବସ୍ଥିତ । — ଚିହ୍ନ ( ✗ )
11. ଚିନ୍‌ନ୍ ପାଇଁ କାଲିକଟ୍ ପ୍ରସିଦ୍ଧ ଥିଲା । — ଚିହ୍ନ ( ✗ )
12. ଭାରତର ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ବୟନ ଶିଳ୍ପ ବମ୍ବେଠାରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା । — ଚିହ୍ନ ( ✓ )
13. ପାନିପତ୍ ଆମ ଦେଶର ଏକ ପ୍ରମୁଖ କାର୍ପାସ୍ ବୟନ ଶିଳ୍ପକେନ୍ଦ୍ର । — ଚିହ୍ନ ( ✓ )
14. ବେଙ୍ଗାଲୁରୁରେ ସର୍ବାଧକ ଶିକ୍ଷାନୁଷ୍ଠାନ ଓ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଦାନ କରୁଥିବା ଅବସ୍ଥିତ । — ଚିହ୍ନ ( ✓ )
15. ବେଙ୍ଗଲୁରୁ ଉପକୂଳବର୍ତ୍ତୀ ସମତଳ ଅଞ୍ଚଳରେ ଅବସ୍ଥିତ। — ଚିହ୍ନ ( ✗ )

Objective Type Questions With Answers
ସ୍ତମ୍ଭ ମିଳନ କର ।

Question 1.

Answer:

Question 2.

Answer:

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.

Answer:

ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ________ ଦ୍ଵାରା ଆୟ ବୃଦ୍ଧି ପାଇଥାଏ।
(କୃଷି, ଖଣିଜ ଉତ୍ତୋଳନ, ମତ୍ସ୍ୟ ସଂଗ୍ରହ, ବାଣିଜ୍ୟ କାରବାର)
Answer: ବାଣିଜ୍ୟ କାରବାର

2. ଭାରୀ ଯନ୍ତ୍ରପାତି, ରେଳଡବା ନିର୍ମାଣ ________କାରଖାନା ଅନ୍ତର୍ଗତ ।
(କୃଷିଭିଭିକ, ଖଣିଜଭିର୍ଭିକ, ସମୁଦ୍ରଭିଭିକ, ଜଙ୍ଗଲଭିଭିକ
Answer: ଖଣିଜଭିଭିକ

3. ଚମଡ଼ା ଶିଳ୍ପ ______ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।
(କୃଷିଭିତ୍ତିକ, ଜଙ୍ଗଲଭିଭିକ, ଖଣିଜଭିଭିକ, ସମୁଦ୍ରାଭିଭିକ)
Answer: କୃଷିଭ୍ରିକ

4. ଗୃହନିର୍ମାଣ ଶିଳ୍ପ ______ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।
(କୃଷିଭିଭିକ, ଖଣିଜଭିରିକ, ଜଙ୍ଗଲଭିଭିକ, ସମୁଦ୍ରଭିଭିକ)
Answer: ଜଙ୍ଗଲ ଭିଭିକ

5. ______ ପରିବାର ସଦସ୍ୟଙ୍କଦ୍ଵାରା କରାଯାଇଥାଏ।
(କ୍ଷୁଦ୍ରଶିଳ୍ପ, ବୃହତ୍ ଶିଳ୍ପ, କୁଟୀର ଶିଳ୍ପ, ଯାନ୍ତ୍ରିକ ଶିଳ୍ପ)
Answer: କୁଟୀର ଶିଳ୍ପ

6. ମଟର ଗାଡ଼ି ଓ ଭାରୀ ଯନ୍ତ୍ରପାତି ______ ର ଅନ୍ତର୍ଗତ ।
(କୁଟୀରଶିଳ୍ପ, କ୍ଷୁଦ୍ରଶିଳ୍ପ, ଜଙ୍ଗଲଭିଭିକ ଶିଳ୍ପ, ବୃହତ୍‌ଶିଳ୍ପ)
Answer: ବୃହତ୍‌ଶିଳ୍ପ

7. ମାଲିକାନା ଦୃଷ୍ଟିରୁ ଶିଳ୍ପକୁ ______ ଭାଗରେ ଭାଗ କରାଯାଇଛି ।
(ଏକ, ଦୁଇ, ତିନି, ଊରି)
Answer: ଗରି

8. ଟାଟା ଲୌହ ଇସ୍ପାତ କାରଖାନା ______ ଶିଚ୍ଛର ଅନ୍ତର୍ଗତ ।
(ବ୍ୟକ୍ତିମାଲିକାନା, ସରକାରୀ ମାଲିକାନା, ଦ୍ଵୈତ ମାଲିକାନା, ସମବାୟ ସଂସ୍ଥା)
Answer: ବ୍ୟକ୍ତିମାଲିକାନା

9. ଶିଳ୍ପସଂସ୍ଥାରୁ ସର୍ବଶେଷରେ ବାହାରୁଥ‌ିବା ଉତ୍ପାଦିତ ଦ୍ରବ୍ୟକୁ ______ କୁହାଯାଏ ।
(ନିବେଶ, ଉତ୍ପାଦ, କାରକ, ଆଧାରିକ ସଂରଚନା)
Answer: ଉତ୍ପାଦ

10. ୧୯୮୪ ମସିହା ଡିସେମ୍ବର ୩ ତାରିଖ ଦିନ ଭାରତର, _______ସହରରେ ଶିଳ୍ପଜନିତ ଦୁର୍ଘଟଣା ହୋଇଥିଲା।
(ଭୋପାଳ, ଚେନ୍ନାଇ, ରାୟପୁର, ଜୟପୁର)
Answer: ଗୋପାଳ

11. ୨୦୦୫ ମସିହାରେ ପୃଥ‌ିବୀର _______ ଦେଶରେ ଶିଳ୍ପ ଦୁର୍ଘଟଣା ହୋଇ ଅନେକ ଲୋକଙ୍କର ମୃତ୍ୟୁ ଘଟିଥିଲା।
(ଭାରତ, ଜାପାନ, ଚୀନ, ଇଂଲଣ୍ଡ)
Answer: ଚୀନ

12. କାଲିଫର୍ଡିଆ _______ଦେଶରେ ଅବସ୍ଥିତ ।
( ରୁଷିଆ, ଜାପାନ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଚୀନ)
Answer: ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା

13. କାଲିଫର୍ଡିଆର ସିଲିକନ୍ _______ କ୍ଷେତ୍ରରେ ଅଗ୍ରଣୀ।
( ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା, ଶିକ୍ଷା, ଶିଳ୍ପ, ସ୍ଵାସ୍ଥ୍ୟ)
Answer: ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା

14. ଭାରତର _______ ସହର ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାରେ ଅଗ୍ରଣୀ ସହର ।
(ପୁନେ, ଅହମ୍ମଦାବାଦ, ବେଙ୍ଗାଲୁରୁ, ମହୀଶୂର)
Answer: ବେଙ୍ଗାଲୁରୁ

15. ଲୌହ ଇସ୍ପାତ ଶିଳ୍ପ _______ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ।
(କୁଟୀର, କ୍ଷୁଦ୍ର, ସମବାୟ, ମୌଳିକ)
Answer: ମୌଳିକ

16. _______ କୁ ଆଧୁନିକ ଶିଳ୍ପ ଜଗତର ମେରୁଦଣ୍ଡ କୁହାଯାଏ।
(ସୁନା, ଲୁହା, ଇସ୍ପାତ, ତମ୍ବା)
Answer: ଇସ୍ପାତ

17. ୧୯୪୭ ମସିହା ପୂର୍ବରୁ _______ ଲୌହ ଇସ୍ପାତ କାରଖାନା ଥିଲା ।
(ଗୀଉରକେଲା, ବୋକାରୋ, ବର୍ଣ୍ଣପୁର, ଜାମସେଦ୍‌ପୁର)
Answer: ଜାମସେଦପୁର

18. ଜାମସେଦ୍‌ପୁର ଲୌହ-ଇସ୍ପାତ କାରଖାନା _______ ଅବସ୍ଥିତ।
(ଝାଡ଼ଖଣ୍ଡ, ଉତ୍ତରାଖଣ୍ଡ, ଛତିଶଗଡ଼, ଓଡ଼ିଶା)
Answer: ଝାଡ଼ଖଣ୍ଡ

19. ଟାଟା ଲୌହ-ଇସ୍ପାତ କାରଖାନାର ସଂକ୍ଷିପ୍ତ ନାମ _______|
(ପୋସ୍କୋ, ଟିସ୍କୋ, ସେସ୍କୋ, ନେସ୍କୋ)
Answer: ଟିସ୍କୋ

20. _______ ଟାଟା ଲୌହ-ଇସ୍ପାତ୍ ଶିଳ୍ପକେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା ହୋଇଥିଲା।
(1906, 1907, 1908, 1909)
Answer: 1907

21. ପିଟ୍‌ସ୍‌ବର୍ଗ ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା,_______ଦେଶରେ ଅବସ୍ଥିତ ।
(ଭାରତ, ଇଂଲଣ୍ଡ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ରୁଷିଆ)
Answer: ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା

22. ପ୍ରଥମେ _______ଦେଶରେ କଳତନ୍ତର ପ୍ରସାର ଘଟିଥିଲା।
(ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍, ଭାରତ, ଜର୍ମାନୀ)
Answer: ଗ୍ରେଟ୍ ବ୍ରିଟେନ୍

23. ଢାକାର _______ କାର୍ପାସ ବସ୍ତ୍ର ପୃଥୁବୀ ପ୍ରସିଦ୍ଧ ।
(ମସ୍‌ଲିନ, ଚିନ୍‌ନ, କାଲିକୋ, ସୁନା ଜରିକାମ)
Answer: ମସ୍‌ନ

24. ମସଲିପଟନମ୍ବର _______ କାର୍ପାସ ବସ୍ତ୍ର ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ ।
(ମସଲିନ୍, ଚିନ୍‌ନ, କାଲିକୋ, ସୁନା ଜରିକାମ)
Answer: ଚିନ୍‌ନ୍

25. କାଲିକଟର _______ କାର୍ପାସ ବସ୍ତ୍ର ପୃଥ‌ିବୀ ପ୍ରସିଦ୍ଧ ।
( ମସଲିନ୍, ଚିନ୍‌ନ, କାଲିକୋ, ସୁନା ଜରିକାମ)
Answer: କାଲିକୋ

26. _______ ଭାରତର ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ୍ ବୟନଶିଳ୍ପ ମୁମ୍ବାଇରେ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।
(1851, 1852, 1853, 1854)
Answer: 1854

27. ଅହମଦାବାଦ _______ ନଦୀକୂଳରେ ଅବସ୍ଥିତ ।
(ନର୍ମଦା, ସାବରମତୀ, ତାଣ୍ଡୀ, ମାହୀ)
Answer: ସାବରମ

28. _______ ପ୍ରଥମେ ଅହମ୍ମଦାବାଦରେ କାର୍ପାସ ବୟନ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ।
(1856, 1857, 1858, 1859)
Answer: 1859

29. _______ କୁ ଭାରତର୍‌ ମାଞ୍ଚେଷ୍ଟର କୁହାଯାଏ।
(ଅହମ୍ମଦନଗର, ଅହମ୍ମଦାବାଦ, ହାଇଦ୍ରାବାଦ, ଜୟପୁର)
Answer: ଅହମ୍ମଦାବାଦ

30. ମାଞ୍ଚେଷ୍ଟର _______ ରେ ଅବସ୍ଥିତ ।
(ଭାରତ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ଇଂଲଣ୍ଡ, ଜାପାନ)
Answer: ଇଂଲଣ୍ଡ

ସମ୍ଭାବ୍ୟ ଉତ୍ତର ବାଛି ଲେଖ ।

Question 1.
କେଉଁଟି ପ୍ରାଥମିକ ଉତ୍ପାଦର ଅନ୍ତର୍ଗତ ?
(A) ଫଳ ଓ ମୂଳ
(B) ଘଣ୍ଟା ଓ ଯନ୍ତ୍ରପାତି
(C) କଲମ ଓ ମୋବାଇଲ
(D) ଲୁଗା ଓ କାଗଜ
Answer:
(A) ଫଳ ଓ ମୂଳ

Question 2.
କେଉଁଟି ପ୍ରକ୍ରିୟାକରଣ ପରେ ଆମେ ବ୍ୟବହାର କରିଥାଉ ?
(A) କାଗଜ
(B) ଫଳ
(C) ମହୁ
(D) ମୂଳ
Answer:
(A) କାଗଜ

Question 3.
କେଉଁ ସେବା କାର୍ଯ୍ୟକୁ ଶିଳ୍ପର ଅନ୍ତର୍ଭୁକ୍ତ କରାଯାଇଛି ?
(A) ଶିକ୍ଷା ଓ ସ୍ୱାସ୍ଥ୍ୟ
(B) ବ୍ୟାଙ୍କ୍ ଓ ପର୍ଯ୍ୟଟନ
(C) ପରିବହନ ଓ ଯୋଗାଯୋଗ
(D) ବ୍ୟାଙ୍କ୍ ଓ ଶିକ୍ଷା
Answer:
(C) ପରିବହନ ଓ ଯୋଗାଯୋଗ

Question 4.
କେଉଁଟି କୃଷିଭିତ୍ତିକ ଶିଳ୍ପର ସ୍ତର ଅଟେ ?
(A) ଭାରୀ ଯନ୍ତ୍ରପାତି, ରେଳଡ଼ବା ନିର୍ମାଣ, ମାଛତେଲ
(B) ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, ଖାଇବାତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ
(C) ମାଛତେଲ, ଚମଡ଼ାଶିଳ୍ପ, ଯନ୍ତ୍ରପାତି ନିର୍ମାଣ
(D) କାଠମଣ୍ଡ, କାଗଜ, ଆସବାବଶିଳ୍ପ
Answer:
(B) ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ, ଖାଇବାତେଲ ଉତ୍ପାଦନ, କାର୍ପାସ ବୟନ

Question 5.
କେଉଁଟି ସମୁଦ୍ରଭିତ୍ତିକ ଶିଳ୍ପ ଅଟେ ?
(A) ଖାଦ୍ୟ ପ୍ରକ୍ରିୟାକରଣ ଓ କାର୍ପାସ ବୟନ
(B) ଚମଡ଼ାଶିକ ଓ ଭାରି ଯନ୍ତ୍ରପାତି
(C) ସାମୁଦ୍ରିକ ଉଦ୍ୟୋଗ ଓ ମାଛତେଲ
(D) କାଠମତ୍ସ୍ୟ ଓ କାଗଜଶିଳ୍ପ
Answer:
(C) ସାମୁଦ୍ରିକ ଉଦ୍ୟୋଗ ଓ ମାଛତେଲ

Question 6.
କେଉଁଟି ଜଙ୍ଗଲଭିଭିକ ଶିଳ୍ପ ନୁହେଁ ?
(A) କାଠମଣ୍ଡ
(B) କାଗଜ ଶିକ
(C) ଔଷଧ ପ୍ରସ୍ତୁତକାରୀ ଶିଳ୍ପ
(D) ମଛତେଲ
Answer:
(D) ମଛତେଲ

Question 7.
କେଉଁଟି କୁଟୀର ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ତାରକସି କାମ
(B) ଝାଡ଼ୁବୁଣା
(C) ମାଟିହାଣ୍ଡି ନିର୍ମାଣ
(D) ଘଣ୍ଟା ନିର୍ମାଣ
Answer:
(D) ଘଣ୍ଟା ନିର୍ମାଣ

Question 8.
କେଉଁଟି କ୍ଷୁଦ୍ରଶିଳ୍ପର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ଘଣ୍ଟା
(B) ରେଡିଓ ନିର୍ମାଣ
(C) ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି
(D) ଟିଭି ତିଆରି
Answer:
(C) ମାଟିହାଣ୍ଡି ପ୍ରସ୍ତୁତି

Question 9.
HAL ଏବଂ SAIL(ହିନ୍ଦୁସ୍ତାନ ଏରୋନଟିକ୍‌ସ ଲିମିଟେଡ୍ ଓ ଭାରତୀୟ ଇସ୍ପାତନିଗମ) କେଉଁ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
(A) ବ୍ଯକ୍ତିମାଲିକାନା
(B) ସରକାରୀ ମାଲିକାନା
(C) ଦ୍ଵୈତ ମାଲିକାନା
(D) ସମବାୟ ସଂସ୍ଥା
Answer:
(B) ସରକାରୀ ମାଲିକାନା

Question 10.
କେଉଁଟି ଦ୍ଵୈତ ମାଲିକାନା ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
(A) ଟାଟା ଲୌହଇସ୍ପାତ
(B) ଭାରତୀୟ ଇସ୍ପାତ ନିଗମ
(C) ମାରୁତି ଉଦ୍ୟୋଗ
(D) ଅମୁଲ ଶିଳ୍ପ
Answer:
(C) ମାରୁତି ଉଦ୍ୟୋଗ

Question 11.
ସମ୍ବଲପୁରୀ ବସ୍ତଶିଳ୍ପ ଓ ଅମୁଲ ଦୁଗ୍ଧ ଉତ୍ପାଦନକାରୀ ସଂସ୍ଥା କେଉଁ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ?
(A) ବ୍ୟକ୍ତି ମାଲିକାନା
(B) ସରକାରୀ ମାଲିକାନା
(C) ଦ୍ଵୈତ ମାଲିକାନା
(D) ସମବାୟ ସଂସ୍ଥା
Answer:
(D) ସମବାୟ ସଂସ୍ଥା

Question 12.
କେଉଁଟି ଆଧାରିକ ସଂରଚନାର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ବିଦ୍ୟୁତକରଣ
(B) କଞ୍ଚାମାଲ
(C) ଯୋଗାଯୋଗ
(D) ସଡ଼କ
Answer:
(B) କଞ୍ଚାମାଲ

Question 13.
କେଉଁଟି ଶିଳ୍ପ ବ୍ୟବସ୍ଥାର ନିବେଶର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) କଞ୍ଚାମାଲ
(B) ଶ୍ରମିକ
(C) ଭୂମି
(D) ଅରଣ୍ୟ
Answer:
(D) ଅରଣ୍ୟ

Question 14.
ଶିଳ୍ପସଂସ୍ଥାରେ କଞ୍ଚାମାଲରୁ ଉତ୍ପାଦ ସୃଷ୍ଟି ହେବାପାଇଁ ଯେଉଁସବୁ କାର୍ଯ୍ୟପନ୍ଥା ଗ୍ରହଣ କରାଯାଏ, ତାହାକୁ କ’ଣ କୁହାଯାଏ ?
(A) କାରକ
(B) ନିବେଶ
(C) ପ୍ରକ୍ରିୟାକରଣ
(D) ଉତ୍ପାଦ
Answer:
(C) ପ୍ରକ୍ରିୟାକରଣ

Question 15.
କେଉଁଟି ଭାରତର ଶିଳ୍ପାଞ୍ଚଳ ନୁହେଁ ?
(A) ମୁମ୍ବାଇ – ପୁଣେ
(B) ବେଙ୍ଗାଲୁରୁ – ତାମିଲନାଡୁ
(C) ଗୁଡଗାଓଁ – ଦିଲ୍ଲୀ – ମିରଟ୍
(D) କଟକ – ଓଡ଼ିଶା
Answer:
(D) କଟକ – ଓଡ଼ିଶା

Question 16.
କେଉଁଟି ପୃଥ‌ିବୀର ଶିଳ୍ପାଞ୍ଚଳ ନୁହେଁ ?
(A) ଆମେରିକା ପୂବାଂଶ
(B) ପାକିସ୍ଥାନର ପୂର୍ବାଶ
(C) ପଶ୍ଚିମ ଓ କେନ୍ଦ୍ରୀୟ ୟୁରୋପ
(D) ପୂର୍ବ ଏସିଆ ଓ ପୂର୍ବ ୟୁରୋପ
Answer:
(B) ପାକିସ୍ଥାନର ପୂର୍ବାଶ

Question 17.
କେଉଁଟି ‘ସୂର୍ଯ୍ୟୋଦୟ ଶିଳ୍ପ’ର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
(B) ସ୍ଵାସ୍ଥ୍ୟ ଓ ସ୍ଵାସ୍ଥ୍ୟ ସେବା
(C) ଆତିଥ୍ୟ ଓ ସେବା
(D) ଲୌହ-ଇସ୍ପାତ ଶିଳ୍ପ
Answer:
(D) ଲୌହ-ଇସ୍ପାତ ଶିଳ୍ପ

Question 18.
କେଉଁଟି ଇସ୍ପାତ ଧାତୁ ପ୍ରସ୍ତୁତିରେ ବ୍ୟବହାର କରାଯାଏ ନାହିଁ ?
(A) ମାଙ୍ଗାନିକ
(B) ଆଲୁମିନିୟମ୍
(C) ନିକେଲ
(D) କ୍ରୋମିୟମ୍
Answer:
(B) ଆଲୁମିନିୟମ୍

Question 19.
କେଉଁ ଲୌହ-ଇସ୍ପାତ କାରଖାନା ଭିନ୍ନ ଅଟେ ?
(A) ଝାଡ଼ଖଣ୍ଡ – ଜାମସେଦ୍‌ପୁର
(B) ଓଡ଼ିଶା – ରାଉରକେଲା
(C) ତାମିଲନାଡୁ – ଭଦ୍ରାବତୀ
(D) ପଶ୍ଚିମବଙ୍ଗ – ଦୁର୍ଗାପୁର
Answer:
(C) ତାମିଲନାଡୁ – ଭଦ୍ରାବତୀ

Question 20.
କେଉଁ ନଦୀଦ୍ୱୟରୁ ଜାମସେଦପୁର ଲୌହଇସ୍ପାତ୍ କାରଖାନାକୁ ପ୍ରଚୁର ଜଳ ଯୋଗାଇ ଦିଆଯାଇଥାଏ ?
(A) ମହାନଦୀ ଓ ବ୍ରାହ୍ମଣୀ
(B) ଗୋଦାବରୀ ଓ କୋଏନା
(C) ଖରକାଇ ଓ ସୁବର୍ଣ୍ଣରେଖା
(D) ସୁବର୍ଣ୍ଣରେଖା ଓ ବୁଢାବଳଙ୍ଗ
Answer:
(C) ଖରକାଇ ଓ ସୁବର୍ଣ୍ଣରେଖା

Question 21.
ଟାଟା ଲୌହ-ଇସ୍ପାତ କାରଖାନାଟି କେଉଁ ରେଳପଥ ନିକଟରେ ଅବସ୍ଥିତ ?
(A) ହାୱଡ଼ା – ଦୁର୍ଗାପୁର
(B) ହାୱଡ଼ା ଚନ୍ଦନନଗର
(C) ହାୱଡ଼ା – ମୁମ୍ବାଇ
(D) ହାୱଡ଼ା – ସାଲିମାର
Answer:
(C) ହାୱଡ଼ା – ମୁମ୍ବାଇ

Question 22.
ଭଦ୍ରାବତୀ ଓ ବିଜୟନଗର ଲୌହ-ଇସ୍ପାତ୍ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
(A) ଓଡ଼ିଶା
(B) କର୍ଣାଟକ
(C) ପଶ୍ଚିମବଙ୍ଗ
(D) ତାମିଲନାଡୁ
Answer:
(B) କର୍ଣାଟକ

Question 23.
କେଉଁଟି କାର୍ପାସ ଶିଳ୍ପରେ ଅଗ୍ରଣୀ ଦେଶ ନୁହେଁ ?
(A) ଭାରତ
(B) ଚୀନ
(C) ଜାପାନ
(D) ଶ୍ରୀଲଙ୍କା
Answer:
(D) ଶ୍ରୀଲଙ୍କା

Question 24.
ସୁନା ଜରିକାମ କାର୍ପାସ ବସ୍ତ୍ର କେଉଁ ଅଞ୍ଚଳରେ ପ୍ରସ୍ତୁତ କରାଯାଏ ?
(A) ସୁରତ ଓ ଇଦୋଦରା
(B) ଜୟପୁର ଓ ଆଜମିର
(C) ପୁନେ ଓ ମୁମ୍ବାଇ
(D) ନାଗପୁର ଓ ଥାନେ
Answer:
(A) ସୁରତ ଓ ଇଦୋଦରା

Question 25.
କେଉଁଟି କାର୍ପାସ ଶିଳ୍ପର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) କୋଏମ୍ବାଟୁର
(B) କାନପୁର
(C) ଚେନ୍ନାଇ
(D) ବର୍ଣ୍ଣପୁର
Answer:
(D) ବର୍ଣ୍ଣପୁର

Question 26.
ଅହମ୍ମଦାବାଦରେ କାର୍ପାସ ବୟନ ଶିଳ୍ପ ଗଢ଼ିଉଠିବାର କାରଣ କ’ଣ ?
(A) କଞ୍ଚାମାଲର ସୁଲଭତା
(B) ପୁଞ୍ଜି
(C) ଶ୍ରମ
(D) ପରିବହନ
Answer:
(A) କଞ୍ଚାମାଲର ସୁଲଭତା

Question 27.
କାହାକୁ ‘ଜାପାନର ମାଞ୍ଚେଷ୍ଟର’ କୁହାଯାଏ ?
(A) ଟୋକିଓ
(B) ଓସାକା
(C) ସିକାଗୋ
(D) କ୍ରିଟୋ
Answer:
(B) ଓସାକା

Question 28.
କେଉଁ ନଦୀରୁ ଓସାକା ବୟନଶିଳ୍ପ ପାଇଁ ପ୍ରଚୁର ଜଳ ଯୋଗାଇଥାଏ ?
(A) ଓଜୋ
(B) ସିଜୋ
(C) କ୍ଲିଟୋ
(D) ମିତୃବିସି
Answer:
(A) ଓଜୋ

Question 29.
ଭାରତର କେଉଁଠାରେ ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାର ପ୍ରଧାନ କେନ୍ଦ୍ର ଅଟେ ?
(A) ମୁମ୍ବାଇ
(B) ଦିଲ୍ଲୀ
(C) ବେଙ୍ଗାଲୁରୁ
(D) ମହୀଶୂର
Answer:
(C) ବେଙ୍ଗାଲୁରୁ

Question 30.
କାହାକୁ ଭାରତର ସିଲିକନ ମାଳଭୂମି କୁହାଯାଏ ?
(A) ବେଙ୍ଗାଲୁରୁ
(B) ରାୟପୁର
(C) କୋଲକାତା
(D) ଭୁବନେଶ୍ଵର
Answer:
(A) ବେଙ୍ଗାଲୁରୁ

Question 31.
“କାଲିଫର୍ନିଆର ସିଲିକନ୍ ଉପତ୍ୟକା” କେଉଁ ଦେଶରେ ଅବସ୍ଥିତ ?
(A) ଜାପାନ
(B) ଜର୍ମାନୀ
(C) ରୁଷିଆ
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
Answer:
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା

Question 32.
କେବେ କର୍ଣାଟକ ସରକାର ସର୍ବପ୍ରଥମେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଆଇନ ପ୍ରଣୟନ କରିଥିଲେ ?
(A) 1991
(B) 1992
(C) 1993
(D) 1994
Answer:
(B) 1992

Question 33.
କେଉଁଟି ସିଲିକନ ଉପତ୍ୟକାର ବିଶେଷତ୍ଵ ନୁହେଁ ?
(A) ନାତିଶୀତୋଷ ଜଳବାୟୁ
(B) ଆକର୍ଷିତ ସୁନିର୍ମଳ ପରିବେଶ
(C) ପରିବହନ ସୁଯୋଗ
(D) ଅସ୍ୱାସ୍ଥ୍ୟକର ପରିବେଶ
Answer:
(D) ଅସ୍ୱାସ୍ଥ୍ୟକର ପରିବେଶ

Question 34.
ଭାରତର କେଉଁ ସହରରେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାର ନୂତନ କେନ୍ଦ୍ରମାନ ଗଢ଼ିଉଠି ନାହିଁ ?
(A) ମୁମ୍ବାଇ
(B) ରାୟପୁର
(C) ନୂଆଦିଲ୍ଲୀ
(D) ହାଇଦ୍ରାବାଦ
Answer:
(B) ରାୟପୁର

Question 35.
ଇନ୍‌ଫୋସିସ୍ ଓ ୱିପ୍ରୋ କେଉଁ ଶିଳ୍ପ ସଂସ୍ଥାର ଅଟନ୍ତି ?
(A) ଲୌହ-ଇସ୍ପାତ
(B) କାର୍ପାସ
(C) ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
(D) କାଗଜ
Answer:
(C) ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା

Question 36.
ଆମେରିକୀୟ କମ୍ପାନୀଗୁଡ଼ିକ ସେମାନଙ୍କର କୁଶଳୀ କର୍ମୀମାନଙ୍କୁ ନିଯୁକ୍ତି ଦେଇ ଶସ୍ତା ଓ ସମକୁଶଳୀ ଭାବରେ କେଉଁମାନଙ୍କୁ ନିଯୁକ୍ତି ଦେଇଥାନ୍ତି ?
(A) ଭାରତୀୟ
(B) ଚୀନା
(C) ରୁଷିଆ
(D) ଜାପାନୀ
Answer:
(A) ଭାରତୀୟ

Question 37.
କେଉଁଟି ବୃହତ୍ ହ୍ରଦ ଅଞ୍ଚଳର ଅନ୍ତର୍ଗତ ନୁହେଁ ?
(A) ସୁପିରିଅର୍
(B) ଭିକ୍ଟୋରିଆ
(C) ହ୍ୟୁରନ୍
(D) ମିଚିଗାନ୍
Answer:
(B) ଭିକ୍ଟୋରିଆ

Question 38.
କେଉଁ ଶିଳ୍ପଟି ପୃଥ‌ିବୀର ଏକ ପୁରାତନ ଶିଳ୍ପ ?
(A) ଲୌହଇସ୍ପାତ
(B) କାର୍ପାସ ବୟନ
(C) ଖଣିଜ ଉତ୍ତୋଳନ
(D) ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
Answer:
(B) କାର୍ପାସ ବୟନ

Question 39.
ଭବୋଦରା କେଉଁଥିପାଇଁ ପ୍ରସିଦ୍ଧ ?
(A) କାଲିକୋ ବସ୍ତ୍ର
(B) ଚିଜେନ୍
(C) ସୁନା ଜରିବସ୍ତ୍ର
(D) ମସ୍‌ଲିନ୍
Answer:
(C) ସୁନା ଜରିବସ୍ତ୍ର

Question 40.
1854 ମସିହାରେ କେଉଁଠାରେ ଭାରତର ପ୍ରଥମ ଆଧୁନିକ କାର୍ପାସ ଶିଳ୍ପ ପ୍ରତିଷ୍ଠିତ ହୋଇଥିଲା ?.
(A) କୋଲକାତା
(B) ସୁରତ୍
(C) ମୁମ୍ବାଇ
(D) ଅହମ୍ମଦାବାଦ
Answer:
(C) ମୁମ୍ବାଇ

Question 41.
କେଉଁ ନଦୀକୂଳରେ ଅହମ୍ମଦାବାଦ ସହର ଅବସ୍ଥିତ ?
(A) ଇରାବତୀ
(B) କାବେରୀ
(C) ନର୍ମଦା
(D) ସାବରମତି
Answer:
(D) ସାବରମତି

Question 42.
ଜାତୀୟ ବୟନଶିଳ୍ପର ଉତ୍ପାଦିତ ସାମଗ୍ରୀର କେତେଭାଗ ବିଦେଶକୁ ରପ୍ତାନି ହୁଏ ?
(A) 1/2
(B) 1/3
(C) 1/5
(D) 2/3
Answer:
(B) 1/3

Question 43.
କେଉଁଟି ସେବାଶିଳ୍ପ ନୁହେଁ ?
(A) ପରିବହନ
(B) ପର୍ଯ୍ୟଟନ
(C) ଯୋଗାଯୋଗ
(D) କୋଇଲା ଖନନ
Answer:
(D) କୋଇଲା ଖନନ

Question 44.
କେବେ ଭୋପାଳ ଗ୍ୟାସ୍ ଦୁର୍ଘଟଣା ଘଟିଥିଲା ?
(A) 1984 Dec 3rd
(B) 1989 Jan 13
(C) 1988 Mar 31
(D) 1999 Aug 13
Answer:
(A) 1984 Dec 3rd

Question 45.
ଭଦ୍ରାବତୀ ଲୌହଇସ୍ପାତ କାରଖାନା କେଉଁ ରାଜ୍ୟରେ ଅବସ୍ଥିତ ?
(A) ଆନ୍ଧ୍ରପ୍ରଦେଶ
(B) ମଧ୍ୟପ୍ରଦେଶ
(C) କର୍ଣ୍ଣାଟକ
(D) ତାମିଲନାଡୁ
Answer:
(C) କର୍ଣ୍ଣାଟକ

Question 46.
କେଉଁ ଲୌହଇସ୍ପାତ କେନ୍ଦ୍ରଟି ପଶ୍ଚିମବଙ୍ଗରେ ଅବସ୍ଥିତ ?
(A) ଟିସ୍କୋ
(B) ଭିଲାଇ
(C) ବୋକାରୋ
(D) ବର୍ଣ୍ଣପୁର
Answer:
(D) ବର୍ଣ୍ଣପୁର

Question 47.
ଓଡ଼ୋ ନଦୀ କେଉଁ ଶିଳ୍ପକୁ ପ୍ରଚୁର ପାଣି ଯୋଗାଏ ?
(A) କାର୍ପାସ ବୟନ
(B) ଲୌହଇସ୍ପାତ
(C) କୋଇଲା ଖନନ
(D) ସୂଚନା ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା
Answer:
(A) କାର୍ପାସ ବୟନ

Question 48.
କେଉଁ ରାଜ୍ୟ ସର୍ବପ୍ରଥମେ 1992 ମସିହାରେ ସୂଚନା ଓ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟା ଆଇନ୍ ପ୍ରଣୟନ କରିଥିଲା ?
(A) ମହାରାଷ୍ଟ୍ର
(B) ତାମିଲନାଡୁ
(C) କର୍ଣ୍ଣାଟକ
(D) ଆନ୍ଧ୍ରପ୍ରଦେଶ
Answer:
(C) କର୍ଣ୍ଣାଟକ

Odisha State Board BSE Odisha 7th Class Geography Solutions Chapter 4 ଜୈବମଣ୍ଡଳ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Geography Solutions Chapter 4 ଜୈବମଣ୍ଡଳ

୧ । ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକର ସଂଜ୍ଞା ଲେଖ ।

Question କ.
ପ୍ରାକୃତିକ ପରିବେଶ :
Answer:
ଜଳ, ସ୍ଥଳ, ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କୁ ନେଇ ଗଠିତ ପରିବେଶକୁ ପ୍ରାକୃତିକ ପରିବେଶ କୁହାଯାଏ ।

Question ଖ.
ଜୈବମଣ୍ଡଳ :
Answer:
ଅଶ୍ମମଣ୍ଡଳ, ବାୟୁମଣ୍ଡଳ ଓ ବାରିମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଥୁବା ତଥା ଜୀବନ ଧାରଣ ପାଇଁ ଆବଶ୍ୟକ ଉପାଦାନ ଥ‌ିବା ପତଳା ସ୍ତରକୁ ଜୈବମଣ୍ଡଳ କୁହାଯାଏ ।

Question ଗ.
ପରିସଂସ୍ଥା :
Answer:
ଜୈବିକ ଓ ଅଜୈବିକ (ଭୂମିରୂପ, ଜଳବାୟୁ, ମୃରିକା) ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଯୋଗୁଁ ସୃଷ୍ଟ ପରିବେଶକୁ ପରିସଂସ୍ଥା କୁହାଯାଏ ।

Question ଘ.
ଜୀବାଳୀ :
Answer:
ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଭୌଗୋଳିକ ସୀମାରେଖା ଭିତରେ ଥ‌ିବା ସମସ୍ତ ଛୋଟ ବଡ଼ ପରିସଂସ୍ଥାର ସମାହାରକୁ ଜୀବାଳୀ (Biome) କୁହାଯାଏ ।

Question କ.
ଖାଦ୍ୟ ଶୃଙ୍ଖଳ :
Answer:
କୌଣସି ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କୁହାଯାଏ ।

Question ଚ.
ଖାଦ୍ୟ ଜାଲକ :
Answer:
କୌଣସି ପରିସଂସ୍ଥାରେ ଛନ୍ଦାଛନ୍ଦି ହୋଇ ରହିଥ‌ିବା ଖାଦ୍ୟଶୃଙ୍ଖଳଗୁଡ଼ିକୁ ଖାଦ୍ୟ ଜାଲକ (Food Web) କୁହାଯାଏ ।

Question ଛ.
ମୃତ୍ତିକା :
Answer:
ମୃତ୍ତିକା ହେଉଛି କଠିନ (ଶିଳାରେଣୁ ଓ ଜୈବିକ ପଦାର୍ଥ), ତରଳ (ଜଳ) ଓ ଗ୍ୟାସୀୟ (ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ ଓ ଉଦ୍‌ଜାନ ଭଳି ଗ୍ୟାସ) ପଦାର୍ଥର ସମାହାର ।

୨। ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

Question କ.
କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ଓ ନାତିଶୀତୋଷ୍ଣ ତୃଣଭୂମି
Answer:

Question ଖ.
ଦୋରସା ମାଟି ଓ କାଦୁଆ ମାଟି
Answer:

Question ଗ.
ଅବଶିଷ୍ଟ ମୃତ୍ତିକା ଓ ଅପସୃତ ମୃତ୍ତିକା
Answer:

Question ଘ.
ତୃଣଭୋଜୀ ପ୍ରାଣୀ ଓ ମାଂସାଶୀ ପ୍ରାଣୀ
Answer:

Question ଙ.
ଉତ୍ପାଦକ ଓ ଭକ୍ଷକ
Answer:

୩ । ସ୍ତମ୍ଭ ଦୁଇଟି ମଧ୍ୟରେ ସମ୍ପର୍କ ସ୍ଥାପନ କରି ଲେଖ ।

Answer:

୪ । କାରଣ ଦର୍ଶାଅ ।

Question କ.
ମେରୁ ଅଞ୍ଚଳରେ ପ୍ରାଣୀମାନଙ୍କର ଚମଡ଼ା ଅଧ୍ବକ ଲୋମଯୁକ୍ତ ।
Answer:

• ମେରୁ ଅଞ୍ଚଳରେ ବର୍ଷର ୧୦ ମାସ ଅଧିକ ଥଣ୍ଡା ଅନୁଭୂତ ହୁଏ ।
• ପ୍ରବଳ ଶୀତରୁ ରକ୍ଷା ପାଇବା ନିମନ୍ତେ ମେରୁ ଅଞ୍ଚଳର ପ୍ରାଣୀମାନଙ୍କର ଚମଡ଼ା ଅଧିକ ଲୋମଯୁକ୍ତ । ଲୋମ ତାପର କୁପରିବାହୀ ଥିବାରୁ ଶୀତର ପ୍ରଭାବରୁ ସେମାନେ ରକ୍ଷା ପାଆନ୍ତି ।

Question ଖ.
ସରଳବର୍ଗୀୟ ଅରଣ୍ୟରେ ଶଙ୍କୁ ଆକାରର ବୃକ୍ଷ ଦେଖାଯାଏ ।
Answer:

• ସରଳବର୍ଗୀୟ ଅରଣ୍ୟ ଥିବା ଅଞ୍ଚଳରେ ତୁଦ୍ରାଞ୍ଚଳ ଅପେକ୍ଷା ଅଧିକ ତୁଷାରପାତ ହୋଇଥାଏ ।
• ଶଙ୍କୁ ଆକାର ବୃକ୍ଷରେ ତୁଷାରପାତ ହେଲେ ତାହା ଶୀଘ୍ର ଖସି ଭୂମିରେ ପଡ଼ିବା ସୁବିଧାଜନକ ହୋଇଥାଏ । ତେଣୁ ସରଳବର୍ଗୀୟ ଅରଣ୍ୟରେ ଶଙ୍କୁ ଆକାରର ବୃକ୍ଷ ଦେଖାଯାଏ ।

Question ଗ.
ଓଟକୁ ମରୁଭୂମିର ଜାହାଜ କୁହାଯାଏ ।
Answer:

• ଓଟ ଦୀର୍ଘଦିନ ଧରି ପାଣି ନ ପିଇ ବଞ୍ଚି ରହିପାରେ ଏବଂ ବାଲୁ କାରାଶି ଉପରେ ସହଜରେ ଯିବାଆସିବା କରିପାରେ ।
• ତେଣୁ ଓଟକୁ ‘ମରୁଭୂମିର ଜାହାଜ’ କୁହାଯାଏ ।

୫ । ଖାଦ୍ୟ ଓ ଖାଦକ ସମ୍ପର୍କ ଅନୁସାରେ କ୍ରମରେ ସଜାଅ ।

Question କ.
ବାଳିଆ, ପତ୍ର, ବ୍ୟାକ୍ଟେରିଆ, ଛୋଟ ମାଛ, ଜିଆ
Answer:
ପୁତ୍ର ← ଜିଆ ← ଛୋଟ ମାଛ ← ବାଳିଆ ← ବ୍ୟାକ୍ଟେରିଆ

Question ଖ.
ସର୍ବଭୁକ୍, ପ୍ରାଥମିକ ଭକ୍ଷକ, ଉତ୍ପାଦକ, ଦ୍ବିତୀୟକ ଭକ୍ଷକ ଉତ୍ପାଦକ
Answer:
← ପ୍ରାଥମିକ ଭକ୍ଷକ ← ଦ୍ଵିତୀୟକ ଭକ୍ଷକ← ସର୍ବରୁକ୍

Question ଗ.
ଘାସ, ବାଘ, ହରିଣ, ବ୍ୟାକ୍ଟେରିଆ
Answer:
ଘାସ ← ହରିଣ ← ବାଘ ← ବ୍ୟାକ୍ଟେରିଆ

୬। ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(କ) ଆର୍ଜେଣ୍ଟିନାର ତୃଣଭୂମିକୁ ______ କୁହାଯାଏ । (ଡାଉନ୍ସ, ପମ୍ପାସ, ପ୍ରେରୀ, ଷ୍ଟେପ୍)
Answer:
ପମ୍ପାସ

(ଖ) ପୃଥ‌ିବୀର ପଶୁଶାଳା _______ ତୃଣଭୂମି ଅଟେ । (କାମ୍ବୋସ, ସାଭାନ୍ନା, ଲିଆନୋସ, ଷ୍ଟେପ୍)
Answer:
ସାଭାନ୍ନା

(ଗ) କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ଅଞ୍ଚଳରୁ _____ ଏକ ପ୍ରାଣୀ । (ବାଇସନ୍, ୱାଲରସ, ଗୟଳ, ଜିରାଫ୍)
Answer:
ଜିରାଫ୍

(ଘ) ପୃଥ୍ବୀର ରୁଟି ଝୁଡ଼ି ______ ତୃଣଭୂମି ଅଟେ । (ସାଭାନ୍ନା, ଲିଆନୋସ, ପମ୍ପାସ, କ୍ୟାମ୍ବୋସ)
Answer:
ପମ୍ପାସ

ଙ) ସାଧାରଣ କଥାବାର୍ତ୍ତାର ଶବ୍ଦ _______ ଡେସିବେଲ୍ । (୨୫, ୫୫, ୧୦୦, ୧୦୫)
Answer:
୨୫

୭। ସଂକ୍ଷେପରେ ଉତ୍ତର ଦିଅ ।

Question କ.
ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କ’ଣ ଉଦାହରଣ ସହ ବୁଝାଅ ।
Answer:

• ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କୁହାଯାଏ ।
• ଖାଦ୍ୟ ଶୃଙ୍ଖଳରେ ଥିବା ପ୍ରତ୍ୟେକ ଶ୍ରେଣୀଭୁକ୍ତ ଜୀବ ଏକ କଡ଼ି ପରି କାମ କରିଥାଏ । ଗୋଟିଏ କଡ଼ି ‘ଖାଦ୍ୟ’ ହେଲେ ଅନ୍ୟଟି ‘ଖାଦକ’ । ସେହିପରି ‘ଖାଦକ’ କଢ଼ି ଖାଦ୍ୟ ହେଲାବେଳେ ପରବର୍ତ୍ତୀ କଡ଼ି ଖାଦକ ହୁଏ ।
• ଉଦାହରଣ : ବିଭିନ୍ନ ପୋକଡୋକ ଆଦିକୁ ବେଙ୍ଗ ଖାଇଥାଏ । ବେଙ୍ଗକୁ ଛୋଟ ସାପ, ଛୋଟ ସାପକୁ ବଡ଼ ସାପ, ବଡ଼ ସାପକୁ ନେଉଳ, ନେଉଳକୁ ଛଞ୍ଚାଣ ଖାଇ ବଞ୍ଚିଥାନ୍ତି । ପ୍ରାଣୀମାନେ ମରିଗଲା ପରେ ସେଗୁଡ଼ିକୁ ବ୍ୟାକ୍ଟେରିଆ ଅପଘଟନ କରି ମାଟିରେ ମିଶାଏ ।

ପୋକଜୋକ ← ବେଙ୍ଗ ← ଛୋଟ ସାପ ← ବଡ଼ ସାପ ← ନେଉଳ ← ଛଞ୍ଚାଣ ← ବ୍ୟାକ୍ଟେରିଆ

Question ଖ.
ଜୈବ ଭାରସାମ୍ୟ କହିଲେ କ’ଣ ବୁଝାଯାଏ ?
Answer:

• ଖାଦ୍ୟ-ଖାଦକ ସମ୍ପର୍କ ଦୃଷ୍ଟିରୁ ଶକ୍ତି ପିରାମିଡ଼ର ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ ଜୀବ ସଂଖ୍ୟା ହ୍ରାସ ପାଇବା ଜରୁରୀ ।
• ପ୍ରତ୍ୟେକ ସ୍ତରର ପ୍ରାଣୀମାନଙ୍କ ମଧ୍ୟରେ ସଂଖ୍ୟାଗତ ସୁସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା ହୁଏ । ଏହିପରି ସଂଖ୍ଯାଗତ ସୁସମ୍ପର୍କକୁ ଜୈବ ଭାରସାମ୍ୟ କୁହାଯାଏ ।
• ଅତ୍ୟଧିକ ଜଙ୍ଗଲ ଧ୍ଵଂସ ଫଳରେ ବିଭିନ୍ନ ଶକ୍ତି ସ୍ତର ମଧ୍ଯରେ ସଂଖ୍ୟାଗତ ସୁସମ୍ପର୍କ ନଷ୍ଟ ହେଉଛି । ଫଳରେ ଅନେକ ପ୍ରଜାତିର ବୃକ୍ଷଲତା ଓ ପ୍ରାଣୀ ନିଶ୍ଚିହ୍ନ ହେବାକୁ ବସିଲେଣି । ଫଳରେ ଜୈବ ଭାରସାମ୍ୟ ନଷ୍ଟ ହେବାରେ ଲାଗିଛି ।
• ନିମ୍ନ ସ୍ତରଗୁଡ଼ିକ କ୍ଷତିଗ୍ରସ୍ତ ହେଲେ ଚତୁର୍ଥ ସ୍ତରରେ ଥିବା ମଣିଷ ନିଶ୍ଚିତଭାବେ ବିପଦଗ୍ରସ୍ତ ହେବ । ତେଣୁ ଜୈବ ଭାରସାମ୍ୟ ରକ୍ଷା ଦିଗରେ ଯବାନ ହେବା ଆବଶ୍ୟକ ।

Question ଗ.
କେଉଁ କାରଣଗୁଡ଼ିକ ଦ୍ଵାରା ଜଳ ଦୂଷିତ ହୁଏ ?
Answer:
ନିମ୍ନଲିଖୁତ କାରଣଗୁଡ଼ିକ ଦ୍ୱାରା ଜଳ ଦୂଷିତ ହୁଏ, ଯଥା-

• ବଡ଼ ବଡ଼ ସହରର ନର୍ଦ୍ଦମା ଜଳ, ଆବର୍ଜ ନ ।, କଳକାରଖାନାରୁ ବାହାରୁଥ‌ିବା ମଇଳା ଜଳରେ ମିଶିବା ।
• କୃଷି କ୍ଷେତ୍ରରେ ବ୍ୟବହୃତ ରାସାୟନିକ ସାର ଓ କୀଟନାଶକ ଔଷଧ ଜଳରେ ମିଶିବା ।
• ଭୂକ୍ଷୟ ଦ୍ବାରା ଜୀବଜନ୍ତୁଙ୍କର ପଚାସଢ଼ା ଶବ ଓ ଉଭିଦର ପତ୍ର ପାଣିରେ ପଡ଼ି ପଚିବା ଦ୍ଵାରା ।
• ଘରୋଇ କାର୍ଯ୍ୟ ଦ୍ଵାରା ନିର୍ଗତ ମଇଳା ଓ ଆବର୍ଜନାଯୁକ୍ତ ଜଳ ମିଶିବା ।

Question ଘ.
ଶକ୍ତି ପ୍ରବାହ କ’ଣ ?

• ଉଦ୍ଭଦ ଜଗତ ଉତ୍ପାଦକ ଓ ପ୍ରାଣୀମାନେ ଭକ୍ଷକ ଅଟନ୍ତି ।
• ଉଦ୍ଭିଦ ଦ୍ବାରା ମାଟିରୁ ସଂଗୃହୀତ ଖଣିଜ ଲବଣ ଓ ସୌରଶକ୍ତି ରାସାୟନିକ ଶକ୍ତିରେ ରୂପାନ୍ତରିତ ହୋଇ ରହେ ।
• ତୃଣଭୋଜୀ ପ୍ରାଣୀ ଉଭିଦର ବିଭିନ୍ନ ଅଂଶ ଖାଇବା ଦ୍ବାରା ସେମାନେ ଉଭିଦଠାରୁ କିଛି ପରିମାଣର ରାସାୟନିକ ଶକ୍ତି (ପ୍ରାୟ ଉଭିଦଠାରେ ଥ‌ିବା ଶକ୍ତିର ଏକ-ଦଶମାଂଶ) ଗ୍ରହଣ କରନ୍ତି ।
• ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କଠାରୁ ଏହି ଶକ୍ତି (ପ୍ରାୟ ଏକ- ଦଶମାଂଶ) ମାଂସାଶୀ ପ୍ରାଣୀ ଓ ମନୁଷ୍ୟ ପାଖକୁ ଯାଏ ।
• ପରିସଂସ୍ଥାରେ ଏହିପରି ଶକ୍ତିର ସ୍ଥାନାନ୍ତରଣକୁ ଶକ୍ତି ପ୍ରବାହ କୁହାଯାଏ । ଶକ୍ତି ପ୍ରବାହ ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ହୁଏ ଓ ଶକ୍ତିର ପରିମାଣ ପ୍ରଥମ ସ୍ତରରୁ ଶୀର୍ଷ ସ୍ତର ଆଡ଼କୁ କ୍ରମଶଃ କମିଯାଏ ।

Question ଙ.
ଜଳ, ବାୟୁ ଓ ମୃରିକା ପ୍ରଦୂଷଣ ରୋକିବାପାଇଁ କି କି ପଦକ୍ଷେପମାନ ନିଆଯାଇ ପାରିବ ?
Answer:
ନିମ୍ନଲିଖ୍ଜ ପଦକ୍ଷେପ ନିଆଗଲେ ଜଳ, ବାୟୁ ଓ ମୃତ୍ତିକା ପ୍ରଦୂଷଣକୁ ରୋକି ହେବ, ଯଥା-

• ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ନିୟନ୍ତ୍ରଣ କରିବା ।
• ଜଳ, ଖଣିଜ ଲବଣ ଓ ଅନ୍ୟାନ୍ୟ ଖଣିଜ ଦ୍ରବ୍ୟର ନିୟନ୍ତ୍ରତ ବ୍ୟବହାର କରିବା ।
• ଜଙ୍ଗଲ କ୍ଷୟ ରୋକିବା ସହ ନୂତନ ଜଙ୍ଗଲ ସୃଷ୍ଟି ପାଇଁ ଉଦ୍ୟମ କରିବା ।
• କଳକାରଖାନାରୁ ନିର୍ଗତ ବିଷାକ୍ତ ଧୂଆଁକୁ ବିଭିନ୍ନ ପ୍ରକ୍ରିୟାରେ ବିଶୋଧ କରି ବାୟୁମଣ୍ଡଳକୁ ଛାଡ଼ିବା ଏବଂ ଶିଳ୍ପଜାତ ଆବର୍ଜନାର ପୁନଃଚକ୍ରଣ କରିବା ।
• ରାସାୟନିକ ସାର ଓ କୀଟନାଶକ ଔଷଧର ନିୟନ୍ତ୍ରିତ ବ୍ୟବହାର କରିବା ଏବଂ ଏହା ପରିବର୍ତ୍ତେ ଜୈବସାର ଓ ଜୈବ କୀଟନାଶକର ବ୍ୟବହାର ଉପରେ ଗୁରୁତ୍ବ ଦେବା ।
• ଯାନବାହନରେ କୋଇଲା, ପେଟ୍ରୋଲ, ଡିଜେଲ ଇନ୍ଧନ ପରିବର୍ତ୍ତେ ବିଦ୍ୟୁତ୍ଵଶକ୍ତି, ସି.ଏଚ୍.ଜି. ଗ୍ୟାସ୍ ବ୍ୟବହାର କରିବା ।
• ଜୀବଜନ୍ତୁଙ୍କ ମଳ ଓ ଅନ୍ୟାନ୍ୟ ଜୈବିକ ଆବର୍ଜନାରୁ ବାୟୋଗ୍ୟାସ୍ ଓ ଜୈବିକ ସାର ପ୍ରସ୍ତୁତ କରିବା ।

Question ୫।
ବାକ୍‌ସ ମଧ୍ୟରେ କେତେକ ପ୍ରାଣୀ ଓ ଉଦ୍ଭିଦ ଲୁଚି ରହିଛନ୍ତି ଖୋଜି ବାହାର କର ।

Answer:
ପ୍ରାଣୀ : ବାଇସନ୍, ମିକ୍ସ୍, କୋକିଶିଆଳି, ୱାଲର୍‌ସ, ଆନାକୋଣ୍ଡା, ଧଳା ଭାଲୁ, ଜେବ୍ରା, ସିଲ୍, ଆଣ୍ଟିଲୋପ୍
ଉଭିଦ : ଦେବଦାରୁ, ସିଡାର, ଅଲିଭ୍, ଫାର୍‌, କାକ୍‌ସ, ଓକ୍, ଚେଷ୍ଟନଟ୍, ଜଳପାଇ, ଶାଳ

Question ୯।
ପୃଥ‌ିବୀର ରେଖାଙ୍କିତ ମାନଚିତ୍ର ଅଙ୍କନ କରି ତୃଣଭୂମିଗୁଡ଼ିକ ଦର୍ଶାଅ ।
Answer:

BSE Odisha 7th Class Geography Notes Chapter 4 ଜୈବମଣ୍ଡଳ

ପ୍ରାକୃତିକ ପରିବେଶ :

• ଆମ ଚତୁଃପାର୍ଶ୍ୱସ୍ଥ ଜଳ, ସ୍ଥଳ, ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କୁ ନେଇ ଆମ ପ୍ରାକୃତିକ ପରିବେଶ ଗଠିତ ।
• ପ୍ରାକୃତିକ ପରିବେଶ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ, ଯଥା- ଅଜୈବିକ ପରିବେଶ ଓ ଜୈବିକ ପରିବେଶ ।

• ପୃଥ‌ିବୀର ତିନି ମଣ୍ଡଳ, ଯଥା- ବାୟୁମଣ୍ଡଳ, ଅଂଶୁମଣ୍ଡଳ ଓ ବାରିମଣ୍ଡଳର ମିଳନସ୍ଥଳରେ ଜୈବମଣ୍ଡଳ ଅବସ୍ଥିତ ।
• ଜୈବମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ପ୍ରାଣୀ ଓ ଉଭିଦ ପ୍ରତ୍ୟକ୍ଷ ଓ ପରୋକ୍ଷ ଭାବେ ମୃତ୍ତିକା ଉପରେ ନିର୍ଭରଶୀଳ ।

ମୃତ୍ତିକା :

• ଭୂପୃଷ୍ଠରେ ଏକ ସୂକ୍ଷ୍ମ ପତଳା ସ୍ତର ଭଳି ରହିଥିବା ମୃରିକା କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ପଦାର୍ଥର ସମାହାର ଅଟେ ।
• ମୃତ୍ତିକାର ଉପାଦାନ :
• ଗୋଡ଼ି, ବାଲି, ପଟୁ ଓ କର୍ଦ୍ଦମ ଆକାର ଶିଳାରେଣୁକୁ ନେଇ ମାଟିର ପ୍ରକାରଭେଦ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
• ବିଭିନ୍ନ ପ୍ରକ୍ରିୟାରେ ଶିଳା ଚୂର୍ଣ୍ଣବିଚୁର୍ଣ୍ଣ ହୋଇ ଶିଳାରେଣୁରେ ପରିଣତ ହୁଏ । ଶିଳରେଣୁରେ ଖଣିଜ ଅଂଶ ସହ ଜୈବିକ ଅଂଶ ମିଶି ଏହା ଜଳ ତଥା ଅନ୍ୟାନ୍ୟ ଗ୍ୟାସୀୟ ପଦାର୍ଥ ସଂସ୍ପର୍ଶରେ ଆସି ବିଭିନ୍ନ ଭୌତିକ, ଜୈବିକ ଓ ରାସାୟନିକ ପ୍ରକ୍ରିୟା ଦ୍ଵାରା ମୃତ୍ତିକାରେ ପରିଣତ ହୁଏ ।

• ବାଲି, ପଟୁ ଓ କର୍ଦ୍ଦମର ସୁଷମ ମିଶ୍ରଣରେ ଦୋରସା ମାଟି, ବାଲିର ପରିମାଣ ଅଧିକ ଥିଲେ ବାଲିଆ ମାଟି, କର୍ଦ୍ଦମର ପରିମାଣ ଅଧିକ ଥିଲେ କାଦୁଆ ମାଟି କୁହାଯାଏ ।

ଉତ୍ପତ୍ତିସ୍ଥଳ ଦୃଷ୍ଟିରୁ ଶିଳାର ପ୍ରକାରଭେଦ :

ପରିସଂସ୍ଥା :

• ପ୍ରାକୃତିକ ପରିବେଶର ଜୈବିକ ଓ ଅଜୈବିକ ଉପାଦାନ ମଧ୍ୟରେ ଥ‌ିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧରୁ ପରିସଂସ୍ଥାର ସୃଷ୍ଟି ।
• ପରିସଂସ୍ଥାର ଜୈବିକ ଉପାଦାନ ପ୍ରାଣୀ ଓ ଉଦ୍ଭିଦ ଅଜୈବ ଉପାଦାନ ଜଳ, ବାୟୁ ଓ ମୃଭିକା ଉପରେ ନିର୍ଭରଶୀଳ ।

ଜୀବାଳୀ :

• ବୃହତ୍ ପରିସଂସ୍ଥା ଜୀବାଳୀ ଅଟେ । ସ୍ଥଳଭାଗରେ ଥିବା ସ୍ଵତନ୍ତ୍ର ପ୍ରକାରର ପ୍ରାଣୀ ଓ ଉଭିଦକୁ ନେଇ ଗଠିତ ଜୀବାଳୀ ଅନ୍ୟ ଏକ ଜୀବାଳୀଠାରୁ ଭିନ୍ନ ହୋଇଥାଏ ।
• ଜଳବାୟୁ ଓ ମୃତ୍ତିକା ଦୃଷ୍ଟିରୁ ମହାଦେଶୀୟ ପରିସଂସ୍ଥା ୩ ଭାଗରେ ବିଭକ୍ତ ।

• ପ୍ରତ୍ୟେକ ପରିସଂସ୍ଥା ଜଳବାୟୁ ଓ ମୃରିକା ଦ୍ବାରା ପ୍ରଭାବିତ ହେଉଥ‌ିବାରୁ ସେଠାରେ ଖାପ ଖୁଆଇପାରୁ ନଥ‌ିବା ପ୍ରାକୃତିକ ଉଭିଦ ଓ ବନ୍ୟପ୍ରାଣୀ ଦେଖାଯାନ୍ତି । ଆକାର ପ୍ରକାର ଦୃଷ୍ଟିରୁ ପ୍ରାକୃତିକ ଉଭିଦକୁ ତିନିଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଛି, ଯଥା- ଅରଣ୍ୟ, ତୃଣଭୂମି ଓ କଣ୍ଟାବୁଦା ।

ଅରଣ୍ୟ (ପ୍ରାକୃତିକ ଉଦ୍ଭଦ) :

ଜଳବାୟୁ ଭିତ୍ତିରେ ଅରଣ୍ୟର ପ୍ରକାରଭେଦ, ବିଶେଷତ୍ଵ, ସେଠାରେ ଦେଖାଯାଉଥ‌ିବା ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କ ସମ୍ପର୍କରେ ନିମ୍ନୋକ୍ତ ସାରଣୀର ଜାଣିବା :

ତୃଣଭୂମି :

ଅବସ୍ଥିତି ଦୃଷ୍ଟିରୁ ତୃଣଭୂମି ଦୁଇ ପ୍ରକାରର, ଯଥା – କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି, ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।

କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି :

ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି :

ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିର ନାମ :

ଆଫ୍ରିକାର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ସାଭାନ୍ନା କୁହାଯାଏ । ଏହା ଶିକାରୀର ସ୍ଵର୍ଗ ।
ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ପୃଥ‌ିବୀର ରୁଟି ଝୁଡ଼ି କୁହାଯାଏ ।

କଣ୍ଟାବୁଦା :

• ଅଧ‌ିକ ତାପମାତ୍ରା ଓ ଅତି କମ୍ ବୃଷ୍ଟିପାତ ହେଉଥୁବା ମରୁ ତଥା ଅର୍ଥମରୁ ଅଞ୍ଚଳରେ କଣ୍ଟାବୁଦା ଜାତୀୟ ଉଦ୍ଭଦ ଜନ୍ମିଥାଏ ।
• ଏଠାରେ ଥ‌ିବା ମରୂଦ୍ୟାନମାନଙ୍କରେ ନାଗଫେଣୀ, ଖଜୁରୀ, ସିଜୁ, ବାବୁଲ ଜାତୀୟ ବୃକ୍ଷ ଦେଖାଯାଏ ।

ଚୁନ୍ଦ୍ରା ଭଦ୍ଭଦ :

• ମେରୁ ନିକଟବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ଦୁଇ ମାସ ଗ୍ରୀଷ୍ମଋତୁ ରହେ । ତେଣୁ ଏହି ଋତୁରେ ମସ୍, ଲାଇକେନ୍ ଭଳି ଛୋଟ ଛୋଟ ଗୁଳ୍ମ ଜନ୍ମେ ।
• ମେରୁ ଅଞ୍ଚଳରେ ଦେଖାଯାଉଥିବା ମୁଖ୍ୟ ପ୍ରାଣୀମାନଙ୍କ ମଧ୍ୟରେ ସିଲ୍, ତିମି, ୱାଇରସ୍, ବଲ୍‌ଗା ହରିଣ, ମେରୁଭାଲୁ, ବରଫ କୋକିଶିଆଳୀ, ମେରୁ ପେଚା ଆଦି ପ୍ରଧାନ ।
• ସେହିପରି ଉଚ୍ଚ ପାର୍ବତ୍ୟରେ ଉଚ୍ଚତା ଭେଦରେ ବିଭିନ୍ନ ପ୍ରକାର ଅରଣ୍ୟ ଦୃଷ୍ଟିଗୋଚର ହୁଏ ।

ପ୍ରାକୃତିକ ଭାରସାମ୍ୟ :

ମଣିଷର ଆବଶ୍ୟକତା ବୃଦ୍ଧି ସହ ବିଭିନ୍ନ ପ୍ରଗତିମୂଳକ କାର୍ଯ୍ୟ ନିମିତ୍ତ ବ୍ୟାପକ ଜଙ୍ଗଲ କ୍ଷୟ ହୋଇ ଚାଲୁଛି ।
ଜଙ୍ଗଲ କ୍ଷୟର କାରଣ ଓ ଏହାର କୁଫଳ ନିମ୍ନୋକ୍ତ ରେଖାଚିତ୍ରରୁ ଜାଣିବା :

କୌଣସି ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ଜୈବ (ଉଦ୍ଭିଦ ଓ ପ୍ରାଣୀ) ଓ ଅଜୈବ (ଜଳ, ବାୟୁ ଓ ମୃତ୍ତିକା) ଉପାଦାନ ମଧ୍ଯରେ ଅନବରତ ପଦାର୍ଥ ଓ ଶକ୍ତିର ଆଦାନପ୍ରଦାନ ଚାଲିଥାଏ । ଫଳରେ ପ୍ରାକୃତିକ ଭାରସାମ୍ୟ ବଜାୟ ରହେ ।

ଖାଦ୍ୟଶୃଙ୍ଖଳ :

• ପ୍ରତ୍ୟେକ ପରିସଂସ୍ଥାରେ ଅନେକ ଖାଦ୍ୟଶୃଙ୍ଖଳ ଥାଏ । ପରିସଂସ୍ଥାରେ ଥିବା ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାହିଁ ଖାଦ୍ୟଶୃଙ୍ଖଳ ।
• ଉଦାହରଣ – ବିଭିନ୍ନ ଶସ୍ୟ ଓ ପତ୍ରକୁ ଠେକୁଆ ଖାଇ ବମ୍ବେ, ଠେକୁଆକୁ ହେଟାବାଘ, ହେଟାବାଘକୁ ଅଜଗର ସାପ ଓ ଅଜଗର ସାପ ମଲାପରେ ବ୍ୟାକ୍ଟେରିଆ ତାକୁ ଅପଘଟନ କରି ମାଟିରେ ମିଶାଏ ।

ଖାଦ୍ୟ ଜାଲକ :

• ଖାଦ୍ୟଶୃଙ୍ଖଳଗୁଡ଼ିକ ଛନ୍ଦାଛନ୍ଦି ହୋଇ ରହିଲେ ତାହାକୁ ଖାଦ୍ୟ ଜାଲକ କୁହାଯାଏ ।
• ଶକ୍ତିପ୍ରବାହ : ଉଭିଦର ଖାଦ୍ୟ ପ୍ରସ୍ତୁତିବେଳେ ସୌରଶକ୍ତି ରାସାୟନିକ ଶକ୍ତିଭାବେ ତା’ଠାରେ ସଞ୍ଚିତ ହୋଇ ରହେ । ଉଭିଦକୁ ଖାଉଥ‌ିବା ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କଠାରେ ଏହି ଶକ୍ତିର ସ୍ଥାନାନ୍ତରିତ ହୁଏ । ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କଠାରୁ ଏହା ମାଂସାଶୀ ଓ ମଣିଷ ପାଖକୁ ଶକ୍ତିର ସ୍ଥାନାନ୍ତରଣ ହୁଏ । ଏହାକୁ ଶକ୍ତି ପ୍ରବାହ କୁହାଯାଏ ।

• ଶକ୍ତି ପ୍ରବାହର ପ୍ରଥମ ସ୍ତରରେ ଉଭିଦ, ଦ୍ବିତୀୟ ସ୍ତରରେ ତୃଣଭୋଜୀ, ତୃତୀୟ ସ୍ତରରେ ମାଂସାଶୀ ପ୍ରାଣୀ ଓ ଚତୁର୍ଥ ସ୍ତରରେ ଦ୍ଵିତୀୟ ସ୍ତର ମାଂସାଶୀ ପ୍ରାଣୀ ରହିଥାଏ । ଶକ୍ତି ପ୍ରବାହର ପରିମାଣ ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ କ୍ରମଶଃ ହ୍ରାସ ପାଏ । ଚିତ୍ର ଆକାରରେ ଏହା ପିରାମିଡ୍ ଭଳି ଦେଖାଯାଉଥିବାରୁ ଏହାକୁ ଶକ୍ତି ପିରାମିଡ୍ କୁହାଯାଏ ।
• ଖାଦ୍ୟ-ଖାଦକ ସମ୍ପର୍କ ଦୃଷ୍ଟିରୁ ଶକ୍ତି ପିରାମିଡ଼ର ପ୍ରଥମ ସ୍ତରରୁ ଶେଷ ସ୍ତର ପର୍ଯ୍ୟନ୍ତ ଜୀବସଂଖ୍ୟା କ୍ରମଶଃ ହ୍ରାସ ପାଇବା ଜରୁରୀ ।
• ପ୍ରତ୍ୟେକ ଶକ୍ତି ସ୍ତର ମଧ୍ଯରେ ସଂଖ୍ୟାଗତ ସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା ହେଲେ ଜୈବ ଭାରସାମ୍ୟ ବଜାୟ ରହେ ।
• ବିଭିନ୍ନ କାରଣରୁ ଜୈବ ଭାରସାମ୍ୟ କ୍ଷୟ ହେବାରେ ଲାଗିଛି ।

ପ୍ରଦୂଷଣ ଓ ପରିବେଶ ଅବକ୍ଷୟ :

ମାନବକୃତ କାର୍ଯ୍ୟକଳାପରୁ ସୃଷ୍ଟ ବର୍ଜ୍ୟବସ୍ତୁ ଜଳ, ବାୟୁ, ମୃରିକାରେ ମିଶି ପ୍ରାକୃତିକ ପରିବେଶକୁ ପ୍ରଦୂଷଣ କରନ୍ତି । ପ୍ରାକୃତିକ ପ୍ରଦୂଷଣ କେହିଲେ ବାୟୁ ପ୍ରଦୂଷଣ, ଜଳ ପ୍ରଦୂଷଣ ଓ ମୃତ୍ତିକା ପ୍ରଦୂଷଣକୁ ବୁଝାଏ ।

ବାୟୁ ପ୍ରଦୂଷଣ :

ପ୍ରାକୃତିକ ଓ ମାନବକୃତ କାର୍ଯ୍ୟକଳାପରୁ ବାୟୁ ପ୍ରଦୂଷିତ ହୋଇଥାଏ ।

ବାୟୁ ପ୍ରଦୂଷଣ ନିରାକରଣ ପାଇଁ କେତେକ ପଦକ୍ଷେପ :

• ପେଟ୍ରୋଲ ଓ ଡିଜେଲ୍ ଜାଳେଣି ପରିବର୍ତ୍ତେ ସି.ଏଚ୍.ଜି.ର ବ୍ୟବହାର ।
• କାଠ, କୋଇଲା, ଗୋବର ଘସି ପରିବର୍ତ୍ତେ ଗ୍ୟାସ୍ ବ୍ୟବହାର ।
• ବୃକ୍ଷରୋପଣ ତଥା ସାମାଜିକ ବନୀକରଣ ପାଇଁ ଉଦ୍ୟମ ।

ଜଳ ପ୍ରଦୂଷଣ :

ମୃରିକା ପ୍ରଦୂଷଣ :

ଶବ୍ଦ ପ୍ରଦୂଷଣ :

• ମଣିଷ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତୀବ୍ରତା ବିଶିଷ୍ଟ ଶବ୍ଦକୁ ଗ୍ରହଣ କରିପାରେ, ଯଥା- ସର୍ବାଧ‌ିକ ୭୫ ଡେସିବେଲ୍ ଶବ୍ଦ ମଣିଷର କିଛି କ୍ଷତି କରେ ନାହିଁ ।
• ଏହାଠାରୁ ଅଧ‌ିକ ଡେସିବେଲ୍‌ ଶବ୍ଦ ଶବ୍ଦ ପ୍ରଦୂଷଣ ସୃଷ୍ଟି କରେ ।
• ଶବ୍ଦ ପ୍ରଦୂଷଣ ଦ୍ବାରା ଶ୍ରବଣଶକ୍ତି ହ୍ରାସ, ମୁଣ୍ଡବ୍ୟଥା ଓ ମସ୍ତିଷ୍କ ବିକୃତି ରୋଗ ହେବା ଆଶଙ୍କା ଥାଏ ।

ପରିବେଶକୁ ପ୍ରଦୂଷଣମୁକ୍ତ କରିବାର ଉପାୟ :

କେତେକ ପଦକ୍ଷେପ ଦ୍ଵାରା ଆମେ ଆମ ପ୍ରାକୃତିକ ପରିବେଶକୁ ପ୍ରଦୂଷଣମୁକ୍ତ ରଖୂପାରିବା :

କେତେକ ଭୌଗୋଳିକ ଶବ୍ଦାବଳୀ

• ପ୍ରାକୃତିକ ପରିବେଶ : ଜଳ, ସ୍ଥଳ, ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କୁ ନେଇ ଗଠିତ ପରିବେଶ ।
• ଅଜୈବ ପରିବେଶ : ପ୍ରାକୃତିକ ପରିବେଶ ଅନ୍ତର୍ଗତ ଅଶୁମଣ୍ଡଳ, ବାରିମଣ୍ଡଳ ଓ ବାୟୁମଣ୍ଡଳକୁ ନେଇ ସୃଷ୍ଟ ପରିବେଶ ।
• ଜୈବିକ ପରିବେଶ : ଜୈବମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ପ୍ରାଣୀ ଓ ଉଦ୍ଭଦକୁ ନେଇ ଜୈବିକ ପରିବେଶ ଗଠିତ ।
• ଅବଶିଷ୍ଟ ମୃତ୍ତିକା : ଶିଳା ଚୂର୍ଣ୍ଣ ବିଚୂର୍ଣ ହୋଇ ସେହି ସ୍ଥାନରେ ମୃର୍ତ୍ତିକାରେ ପରିଣତ ହେଲେ ତାହାକୁ ଅବଶିଷ୍ଟ ମୃରିକା କୁହାଯାଏ ।
• ଅପସୃତ ମୃର୍ତ୍ତିକା : ନଦୀ, ହିମବାହ, ବାୟୁପ୍ରବାହ ଦ୍ଵାରା ଅପସୃତ ଶିଳାରେଣୁ ନିମ୍ନଭୂମିରେ ଜମାହୋଇ ସୃଷ୍ଟି ହେଉଥୁବା ମୃରିକା ।
• ପରିସଂସ୍ଥା : ଜୈବିକ ଓ ଅଜୈବିକ ଉପାଦାନ ମଧ୍ଯରେ ଥ‌ିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଯୋଗୁଁ ସୃଷ୍ଟ ପରିବେଶ ।
• ଜୀବାଳୀ : କୌଣସି ବିସ୍ତୀର୍ଣ୍ଣ ସ୍ଥଳଭାଗ ଓ ଜଳଭାଗ ଅନ୍ତର୍ଗତ ବୃହତ୍ ପରିସଂସ୍ଥା ।
• ଟାଇଗା : ସରଳବର୍ଗୀୟ ଅରଣ୍ୟକୁ ରୁଷୀୟ ଭାଷାରେ ଟାଇଗା କୁହାଯାଏ, ଯାହାର ଅର୍ଥ ବିଶୁଦ୍ଧ, ଅସ୍ପୃଶ୍ୟ ।
• ସାଭାନ୍ନା : ଆଫ୍ରିକାର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• କ୍ୟାମ୍ପୋସ୍ : ବ୍ରାଜିଲ୍‌ରେ ଥିବା କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଲିଆନୋସ୍ : ଭେନେଜୁଏଲାରେ ଥିବା କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ପ୍ରେରୀ : ଉତ୍ତର ଆମେରି କାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଷ୍ଟେପ୍ : ମଧ୍ୟ-ଏସିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଡାଉନ୍ସ : ଅଷ୍ଟ୍ରେଲିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ପମ୍ପାସ : ଆର୍ଜେଣ୍ଟିନାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।

• ଭେଲ୍ସ : ଦକ୍ଷିଣ ଆଫ୍ରିକାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
• ଖାଦ୍ୟ ଶୃଙ୍ଖଳ : ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରି ଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୂ ଙ୍ଖ ଳ କୁହାଯାଏ ।
• ଖାଦ୍ୟ ଜାଲକ : ଛନ୍ଦାଛନ୍ଦି ହୋଇ ରହିଥ‌ିବା ଖାଦ୍ୟ ଶୃଙ୍ଖଳକୁ ଖାଦ୍ୟ ଜାଲକ କୁହାଯାଏ ।
• ଶକ୍ତି ପ୍ରବାହ : ପରିସଂସ୍ଥାରେ ପ୍ରଥମ ସ୍ତରରୁ ଦ୍ବିତୀୟ ସ୍ତର, ଦ୍ଵିତୀୟ ସ୍ତରରୁ ତୃତୀୟ ସ୍ତର ଓ ତୃତୀୟ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତରକୁ ଶକ୍ତିର ସ୍ଥାନାନ୍ତରଣ ହେବା ପ୍ରକ୍ରିୟା ।
• ଶକ୍ତି ପିରାମିଡ୍ : ଖାଦ୍ୟ ଶୃଙ୍ଖଳର ପ୍ରତ୍ୟେକ ସ୍ତରରେ ଏକକ ସମୟ ଓ ଅଞ୍ଚଳ ରେ ଆହ ର ଣ କରାଯାଉଥିବା ଶକ୍ତି ପରିମାଣ ଦର୍ଶାଉଥ‌ିବା ପିରାମିଡ୍ ସଦୃଶ ଗ୍ରାଫିକ୍ ଚିତ୍ର ।
• ଜୈବ ଭାରସାମ୍ୟ : ଶକ୍ତି ପିରାମିଡ୍‌ର ପ୍ରତ୍ୟେକ ସ୍ତର ମଧ୍ଯରେ ସଂଖ୍ୟାଗଡ ସୁସମ୍ପର୍କକୁ ଜୈବ ଭାରସାମ୍ୟ କୁହାଯାଏ ।
• ପ୍ରଦୂଷଣ : ପ୍ରାକୃତିକ ପରିବେଶର ଦୂଷିତ ଓ ସଂକ୍ରମିତ ଅବସ୍ଥା ।
• ପ୍ରଦୂଷକ : ପ୍ରଦୂଷଣ କରୁଥିବା ବର୍ଜ୍ୟବସ୍ତୁ ।
• ଡେସିବେଲ୍ : ଶବ୍ଦର ତୀବ୍ରତା ମାପିବାର ଏକକ ।

Odisha State Board BSE Odisha 6th Class Science Important Questions Chapter 2 ଖାଦ୍ୟର ଶ୍ରେଣୀ ବିଭାଗ Important Questions and Answers.

BSE Odisha Class 6 Science Important Questions Chapter 2 ଖାଦ୍ୟର ଶ୍ରେଣୀ ବିଭାଗ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟର ଉଦାହରଣ ଦିଅ ଏବଂ ଏହାର କାର୍ଯ୍ୟ ଉଲ୍ଲେଖ କର ।
ଉ –

• ଚାଉଳ, ଚିନି, ଗୁଡ଼, ଆଳୁ, ମାଣ୍ଡିଆ, ମକା, ସାରୁ, ବାଜରା, ଅଟା, କନ୍ଦମୂଳ ଇତ୍ୟାଦି ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟ ।
• ଶ୍ଵେତସାର କାର୍ଯ୍ୟ କରିବାପାଇଁ ଶକ୍ତି ଯୋଗାଏ । ବଳକା ଶ୍ଵେତସାର ଶରୀରରେ ଚର୍ବି ଆକାରରେ ଜମାହୋଇ ରହେ, ଯେଉଁଥୁରୁ ଆବଶ୍ୟକ ସମୟରେ ଶକ୍ତି ମିଳେ । ଏହି ଖାଦ୍ୟ ଅଭାବରେ ମାରାସ୍‌ମସ୍ ରୋଗ ହୁଏ ।

Question 2.
ମାରାସମସ୍ ଓ କ୍ଲାସିଓର୍କର୍ ରୋଗ ଦୁଇଟିର ଲକ୍ଷଣମାନ ଲେଖ ।
ଉ –

• ମାରାସମସ୍ ରୋଗର ଲକ୍ଷଣଗୁଡ଼ିକ ମଧ୍ୟରେ ପତଳା ଝାଡ଼ା ହେବ, ବୃଦ୍ଧିରେ ବାଧା, ଶରୀର କ୍ଷୀଣ ହେବା, କେଶ କହରା ହେବା ଇତ୍ୟାଦି ପ୍ରଧାନ ।
• କ୍ଲାସିଓର୍କର୍ ରୋଗର ଲକ୍ଷଣଗୁଡ଼ିକ ମଧ୍ୟରେ ଗୋଡ଼, ହାତ, ମୁହଁ ଫୁଲିଯିବା ଓ ମୁଣ୍ଡରୁ କେଶ ଉପୁଡ଼ିଯିବା ଇତ୍ୟାଦି ପ୍ରଧାନ ।

Question 3.
ଭିଟାମିନ୍ ‘C’ କେଉଁଥୁରୁ ମିଳେ ଓ ଏହାର ଅଭାବରେ କେଉଁ କେଉଁ ରୋଗ ହୁଏ ?
ଉ –

• କମଳା, ଲେମ୍ବୁ, ପିଜୁଳି, ଟମାଟୋ, ଅଁଳା, କଞ୍ଚାଲଙ୍କା, ତଟକା ପନିପରିବା ଆଦିରୁ ଭିଟାମିନ୍ ‘C’ ମିଳେ ।
• ଭିଟାମିନ୍ C ଅଭାବରେ ସ୍କର୍ଭି ରୋଗ ହୁଏ, ଦାନ୍ତ ମାଢ଼ିରୁ ରକ୍ତ ପଡ଼େ ଓ ଘା’ ଶୁଖେ ନାହିଁ ।

Question 4.
ଗର୍ଭବତୀ ମାଆମାନେ ଅଧ୍ବକ ପୁଷ୍ଟିସାର ଓ ଲୌହଯୁକ୍ତ ଖାଦ୍ୟ ଖାଇବା ଉଚିତ କାହିଁକି ?
ଉ –

• ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟ ପିଲାମାନଙ୍କ ଶରୀର ବୃଦ୍ଧି ଓ ନୂତନ କୋଷ ସୃଷ୍ଟି କରିବାରେ ସାହାଯ୍ୟ କରେ ।
• ଲୌହଯୁକ୍ତ ଖାଦ୍ୟ ରକ୍ତ ତିଆରିରେ ସାହାଯ୍ୟ କରେ । ତେଣୁ ଗର୍ଭବତୀ ମାଆମାନେ ଅଧିକ ପୁଷ୍ଟିସାର ଓ ଲୌହଯୁକ୍ତ ଖାଦ୍ୟ ଖାଇବା ଉଚିତ ।

Question 5.
ଶ୍ରମିକମାନେ ଅଧ୍ଵ ଶ୍ଵେତସାରଯୁକ୍ତ ଖାଦ୍ୟ ଖାଇବା ଉଚିତ କାହିଁକି ?
ଉ –

• ଶ୍ରମିକମାନେ କଠିନ ଶାରୀରିକ ପରିଶ୍ରମ କରନ୍ତି । ସେଥ୍ପାଇଁ ଅଧିକ ଶକ୍ତି ଆବଶ୍ୟକ ।
• ଶ୍ଵେତସାରଯୁକ୍ତ ଖାଦ୍ୟରୁ ମିଳୁଥିବା ଶକ୍ତି ଶାରୀରିକ ପରିଶ୍ରମ ଲାଗି ବଳ ଦେଇଥାଏ । ତେଣୁ ସେମାନେ ଅଧୂକ ଶ୍ଵେତସାରଯୁକ୍ତ ଖାଦ୍ୟ ଖାଇବା ଉଚିତ।

Question 6.
ଶ୍ଵେତସାର ଓ ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟ ମଧ୍ୟରେ ଦୁଇଟି ସାମଞ୍ଜସ୍ୟ ଲେଖ ।
ଉ-
ସାମଞ୍ଜସ୍ୟ :

• ଉଭୟ ଶ୍ଵେତସାର ଓ ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟ ଉଭୟ ଆମର ପୋଷକଯୁକ୍ତ ଖାଦ୍ୟ ।
• ଶ୍ଵେତସାର ଓ ପୁଷ୍ଟିସାର ଉଭୟ ଖାଦ୍ୟ ଶରୀରକୁ ଶକ୍ତି ଯୋଗାଏ ।

Question 7.
ଅପପୁଷ୍ଟି ଜନିତ ରୋଗ କ’ଣ ? ୨ଟିର ନାମ ଲେଖ ।
ଉ-

• ଉପଯୁକ୍ତ ପୋଷକର ଅଭାବରେ ଯେଉଁ ରୋଗ ହୁଏ, ତାକୁ ଅପପୁଷ୍ଟି ଜନିତ ରୋଗ କହନ୍ତି ।
• ମାରାସ୍‌ମସ୍ ଓ କ୍ଵାସିଓକର ୨ଟି ଅପପୁଷ୍ଟି ଜନିତ ରୋଗ ଅଟେ ।

Question 8.
ଭିଟାମିନ୍ B₁₂ର ଦୁଇଟି କାର୍ଯ୍ୟ
ଉ-
(i) ରକ୍ତରେ ଲେଖ ।
(ii) ସ୍ନାୟୁମାନଙ୍କର କାର୍ଯ୍ୟକୁ ତ୍ୱରାନ୍ଵିତ କରେ ।

Question 9
ସ୍ନେହସାର ଖାଦ୍ୟର ୨ଟି କାର୍ଯ୍ୟ ଲେଖ ।
ଉ-

• ସ୍ନେହସାର ଖାଦ୍ୟ ଶରୀରକୁ କାର୍ଯ୍ୟକରିବା ପାଇଁ ଶକ୍ତି ଯୋଗାଏ ।
• ଏହା ଆମର ଚର୍ମକୁ ଚିକ୍‌କଣ ରଖେ ।

Question 10.
ପୋଷକ କ’ଣ ? ବିଭିନ୍ନ ପ୍ରକାର ପୋଷକର ନାମ ଲେଖ ।
ଉ-

• ଖାଦ୍ୟ ପଦାର୍ଥରେ କେତେକ ରାସାୟନିକ ପଦାର୍ଥ ଥାଏ ସେହି ପଦାର୍ଥକୁ ପୋଷକ କହନ୍ତି ।
• ପୋଷକଗୁଡ଼ିକ ହେଲା- ଶ୍ଵେତସାର, ସ୍ନେହସାର, ପୁଷ୍ଟିସାର, ଧାତୁସାର, ଜୀବସାର ଓ ଜଳ ।

Question 11.
ସ୍ନେହସାର ଶରୀର ପାଇଁ କି ଉପକାର କରେ ?
ଉ-

• ସ୍ନେହସାର ଖାଦ୍ୟ ଶରୀରକୁ କାର୍ଯ୍ୟ କରିବା ପାଇଁ ଶକ୍ତି ଯୋଗାଏ ।
• ଏହା ଆମର ଚର୍ମକୁ ଚିକ୍‌କଣ ରଖେ ।

ଦୀର୍ଘ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ମାରାସ୍‌ମସ୍ ଓ କ୍ଵାସିଓର୍କର ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
ଉ –

ମାରାସ୍‌ମସ୍	କ୍ଵାସିଓର୍କର
(i) ଶ୍ଵେତସାର ଅଭାବଜନିତ ରୋଗକୁ ମାରସ୍‌ମସ୍ କହନ୍ତି ।	(i) ପୁଷ୍ଟିସାର ଅଭାବଜନିତ ରୋଗକୁ କ୍ଳାସିଓର୍କର କହନ୍ତି ।
(ii) ମାରାସ୍‌ମସ୍ ଭୋଗୁଥ‌ିବା ରୋଗୀର ପତଳା ଝାଡ଼ା, ବୃଦ୍ଧିରେ ବାଧା, ଶରୀର କ୍ଷୀଣ ଓ କେଶ କହରା ହୁଏ ।	(ii) କ୍ଲାସିଓର୍କର ଭୋଗୁଥିବା ରୋଗୀର ଗୋଡ଼, ହାତ, ମୁହଁ ଫୁଲିଯାଏ ଓ ମୁଣ୍ଡରୁ କେଶ ଉପୁଡ଼ିଯାଏ ।

Question 2.
ଆୟୋଡ଼ିନଯୁକ୍ତ ଲବଣ କେଉଁଥରୁ ମିଳେ ? ଏହାର କାର୍ଯ୍ୟ ଅଭାବଜନିତ ରୋଗର ନାମ ଲେଖ ।
(i) ସଜନା ଛୁଇଁ, ସମୁଦ୍ର ମାଛ, ସମୁଦ୍ର କୂଳବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ହେଉଥ‌ିବା ପରିବା ଓ ଫଳରୁ ଆୟୋଡ଼ିଯୁକ୍ତ ଲବଣ ମିଳିଥାଏ ।
(ii) ଆୟୋଡ଼ିଯୁକ୍ତ ଲବଣ ଥାଇରଏଡ଼ ଗ୍ରନ୍ଥିକୁ କାର୍ଯ୍ୟକ୍ଷମ କରାଏ ।
(iii) ଏହାର ଅଭାବରେ ଗଳଗଣ୍ଡ ରୋଗ ଓ ପିଲାର ମାନସିକ ବିକାଶରେ ବାଧା ସୃଷ୍ଟି କରାଇଥାଏ ।

Question 3.
ସୁଷମ ଖାଦ୍ୟ କ’ଣ ? ୧୨ ବର୍ଷ ବୟସର ପିଲାପାଇଁ ନିରାମିଷାଶୀ ସୁଷମ ଖାଦ୍ୟଦ୍ରବ୍ୟର ପରିମାଣର ଏକ ତାଲିକା ଲେଖ ।
ଉ –
ସୁଷମ ଖାଦ୍ୟ – ଜଣେ ବ୍ୟକ୍ତିର ଆବଶ୍ୟକତା ଅନୁସାରେ ପ୍ରତ୍ୟେକ ଉପାଦାନ ରହିଥ‌ିବା ଖାଦ୍ୟକୁ ସୁଷମ ଖାଦ୍ୟ କୁହାଯାଏ ।
୧୦-୧୨ ବର୍ଷ ପିଲାଙ୍କର ସୁଷମ ଖାଦ୍ୟ ତାଲିକା –

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶୋଉର

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଖାଦ୍ୟ ପଦାର୍ଥରେ ଥ‌ିବା ରାସାୟନିକ ପଦାର୍ଥକୁ ………… କୁହାଯାଏ ।
(ଖ) ଅଟାକୁ …………. ଦ୍ରବଣରେ ମିଶାଇଲେ ଗୀତନାଳ ବର୍ଣ୍ଣ ହୋଇଥାଏ l
(ଗ) ତୁତିଆର ରାସାୟନିକ ନାମ ………… ।
(ଘ) ……….. ରୋଗ ଭୋଗୁଥିବା ରୋଗୀର ଗୋଡ଼, ହାତ, ମୁହଁ ଫୁଲିଯାଏ ।
(ଙ) ସ୍ନାୟୁମାନଙ୍କ କାମ ପାଇଁ …………. ଭିଟାମିନ୍ ଦରକାର ।
(ଚ) ଲହୁଣି …………. ଜାତୀୟ ଖାଦ୍ୟ ।
(ଛ) ଭିଟାମିନ୍ ‘C’ ଅଭାବରେ ………….. ରୋଗ ହୁଏ ।
(ଜ) ଆମେ ଦୈନିକ ………….. ଗ୍ଲାସ୍ ପାଣି ପିଇବା ଦରକାର ।
ଉତ୍ତର –
(କ) ପୋଷକ
(ଖ) ଆୟୋଡ଼ିନ୍
(ଗ) କପର ସଲଫେଟ୍
(ଘ) କ୍ବାସିଓକର
(ଙ) B₁₂
(ଚ) ସ୍ନେହସାର
(ଛ) ସ୍କର୍ଭି
(ଜ) 8 – 10

Question 2.
ପ୍ରତି ପ୍ରଶ୍ନତଳେ ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ଦିଆଯାଇଛି । ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

(କ) କେଉଁ ପ୍ରକାର ଖାଦ୍ୟ ଶରୀର ଗଠନ ଓ କ୍ଷୟ ପୂରଣ କରେ ?
(i) ସ୍ନେହସାର
(ii) ପୁଷ୍ଟିସାର
(iii) ଶ୍ଵେତସାର
(iv) ଖଣିଜ ଲବଣ
ଉ –
(କ) ପୁଷ୍ଟିସାର
(ଖ) ଗାଈ କ୍ଷୀରରେ କେଉଁ ଭିଟାମିନ୍ ନଥାଏ ?
(i) A
(ii) B
(iii) C
(iv) D
ଉ –
(ଖ) C

(ଗ) ସୂର୍ଯ୍ୟକିରଣ ଚର୍ମରେ ପଡ଼ିଲେ କେଉଁ ଭିଟାମିନ୍ ତିଆରି ହୁଏ ?
(i) A
(ii) B
(iii) E
(iv) D
ଉ –
(ଗ) D

(ଘ) ଶ୍ଵେତସାର ଅଭାବରେ କେଉଁ ରୋଗ ହୁଏ ?
(i) କ୍ଵାସିଓକର୍
(ii) ମାରାସ୍ମସ୍
(iii) କାମଳ
(iv) ଏଡ୍‌ସ
ଉ –
(ଘ) ମାରାସ୍‌ମସ୍

(ଙ) ତୈଳବୀଜରେ କେଉଁ ଜାତୀୟ ଖାଦ୍ୟ ଥାଏ ?
(i) ଶ୍ଵେତସାର
(ii) ପୁଷ୍ଟିସାର
(iii) ସ୍ନେହସାର
(iv) ଜୀବସାର
ଉ –
(ଡ) ସ୍ନେହସାର

(ଚ) ନିମ୍ନଲିଖ କେଉଁଥରେ ଭିଟାମିନ୍ E ଥାଏ ?
(i) ସୋରିଷ ତେଲ
(ii) ନଡ଼ିଆତେଲ
(iii) ରାଶିତେଲ
(iv) ବାଦାମ ତେଲ
ଉ –
(ଚ) ରାଶିତେଲ

(ଛ) କେଉଁ ଭିଟାମିନ୍ ଅଭାବରେ ଅଷ୍ଟିଓମାଲେସିଆ ରୋଗ ହୁଏ ?
(i) A
(ii) B
(iii) E
(iv) D
ଉ –
(ଛ) D

(ଜ) ଲୋହିତ କୋଷିକା ତିଆରି ପାଇଁ କେଉଁ ଭିଟାମିନ୍ ଦରକାର ?
(i) B₁₂
(ii) B₁
(iii) K
(iv) D
(iv) C
ଉ –
(ଜ) B₁₂

Question 3.
ନିମ୍ନରେ ଦିଆଯାଇଥିବା ପ୍ରଶ୍ନର ବାମପାର୍ଶ୍ଵର ଦୁଇ ଶବ୍ଦର ସମ୍ପର୍କକୁ ଦେଖ୍ ଡାହାଣ ପାର୍ଶ୍ଵର ଶବ୍ଦ ପାଖରେ ଥ‌ିବା ଶୂନ୍ୟ ସ୍ଥାନରେ ଉପଯୁକ୍ତ ଶବ୍ଦ ଲେଖ ।
(କ) ପୁଷ୍ଟିସାର : ଶରୀର ଗଠନ :: ଶ୍ଵେତସାର : ……….. ।
(ଖ) ରକ୍ତ ଜମାଟ ବାନ୍ଧିବା : ଭିଟାମିନ୍ K :: ବନ୍ଧ୍ୟାରୋଗ ଦୂରହେବା : ……….. ।
(ଗ) ଶ୍ଵେତସାର : ମାରାସ୍‌ମସ୍ :: ପୁଷ୍ଟିସାର : ……….. ।
(ଘ) ଲୌହଯୁକ୍ତ ଲବଣ : ରକ୍ତହୀନତା :: ଆୟୋଡ଼ିଯୁକ୍ତ ଲବଣ : ……….. ।
(ଙ) ତୁତିଆ : କପର ସଲ୍‌ଫେଟ୍ :: ଲୁଣ : ……….. ।
(ଚ) ସଜନା ଛୁଇଁ : ଆୟୋଡ଼ିଯୁକ୍ତ ଲବଣ :: ସଜନା ଶାଗ : ……….. ।
(ଛ) କାଞ୍ଜି : ଭିଟାମିନ୍ B :: ବନ୍ଧାକୋବି : ……….. ।
(ଜ) ଭିଟାମିନ୍ B : ଜଳରେ ଦ୍ରବଣୀୟ :: ଭିଟାମିନ୍ A : ……….. ।
ଉ –
(କ) କାର୍ଯ୍ୟ କରିବାପାଇଁ ଶକ୍ତି
(ଖ) ଭିଟାମିନ୍ E
(ଗ) କ୍ଵାସିଓକ୍‌ର
(ଙ) ସୋଡ଼ିୟମ୍‌ କ୍ଲୋରାଇଡ୍
(ଚ) ଲୌହଯୁକ୍ତ ଲବଣ
(ଛ) ଭିଟାମିନ୍ K

Question 4.
ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(କ) ପ୍ରତ୍ୟେକ ଖାଦ୍ୟ ପଦାର୍ଥରେ ଥିବା କେତେକ ରାସାୟନିକ ପଦାର୍ଥକୁ ଶ୍ଵେତସାର କୁହାଯାଏ ।
(ଖ) ଅନ୍ଧାରକଣା ରୋଗ ଭିଟାମିନ୍ – B ଅଭାବରେ ହୋଇଥାଏ ।
(ଗ) ରକ୍ତରେ ଥିବା ଲୋହିତ କୋଷିକା ତିଆରିରେ ଭିଟାମିନ୍ -E ସାହାଯ୍ୟ କରେ ।
(ଘ) ଭିଟାମିନ୍ – E ଅଭାବରେ ସ୍କର୍ଭିରୋଗ ହୁଏ ।
(ଙ) ସୋଡ଼ିୟମ୍‌ କ୍ଲୋରାଇଡ୍ ଲବଣ ଦାନ୍ତ ଓ ଅସ୍ଥି ଗଠନରେ ସାହାଯ୍ୟ କରେ ।
ଉ –
(କ) ପ୍ରତ୍ୟେକ ଖାଦ୍ୟ ପଦାର୍ଥରେ ଥ‌ିବା କେତେକ ରାସାୟନିକ ପଦାର୍ଥକୁ ପୋଷକ କୁହାଯାଏ ।
(ଖ) ଅନ୍ଧାରକଣା ରୋଗ ଭିଟାମିନ୍ – A ଅଭାବରେ ହୋଇଥାଏ ।
(ଗ) ରକ୍ତରେ ଥ‌ିବା ଲୋହିତ କୋଷିକା ତିଆରିରେ ଭିଟାମିନ୍ -B₁₂ ସାହାଯ୍ୟ କରେ ।
(ଘ) ଭିଟାମିନ୍ – C ଅଭାବରେ ସ୍କର୍ଭିରୋଗ ହୁଏ ।
(ଙ) କାସିୟମ୍ ଲବଣ ଦାନ୍ତ ଓ ଅସ୍ଥି ଗଠନରେ ସାହାଯ୍ୟ କରେ ।

Question 5.
ଠିକ୍ ଉତ୍ତର ପାଖରେ (✓) ଚିହ୍ନ ଓ ଭୁଲ୍ ଉତ୍ତର ପାଖରେ (*) ଚିହ୍ନ ଦିଅ ।
(କ) ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟ ଚର୍ମକୁ ଚିକ୍କଣ କରାଏ । (✗)
(ଖ) ଭିଟାମିନ୍ ‘C’ ଅଭାବରେ ବେରିବେରି ରୋଗ ହୁଏ । (✗)
(ଗ) ବିଭିନ୍ନ ପ୍ରକାର ଶାଗରେ ଭିଟାମିନ୍ – K ଥାଏ । (✓)
(ଘ) ଖାଦ୍ୟ ଖାଇବା ସହିତ ଦୈନିକ ୫-୬ ଗିଲାସ ପାଣି ପିଇବା ଦରକାର । (✗)
(ଙ) ସୁଷମ ଖାଦ୍ୟ ଆମକୁ ସମସ୍ତ ପୋଷାକ ଯୋଗାଇଥାଏ । (✓)

Question 6.
‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସଂପର୍କ ବାଛ ।
(କ)

ଉ –

(ଖ)

ଉ –

Odisha State Board BSE Odisha 6th Class Science Important Questions Chapter 4 ଦୈନନ୍ଦିନ ଜୀବନରେ ବ୍ୟବହୃତ ବସ୍ତୁ Important Questions and Answers.

BSE Odisha Class 6 Science Important Questions Chapter 4 ଦୈନନ୍ଦିନ ଜୀବନରେ ବ୍ୟବହୃତ ବସ୍ତୁ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ରେଶମ ବସ୍ତ୍ର କିପରି ତିଆରି କରାଯାଏ ?
ଉ –

• ରେଶମ ପୋକ ଏକ କୋଷା ତିଆରି କରେ ।
• ସେହି କୋଷାରୁ ରେଶମ ତନ୍ତୁ ବାହାରେ ଓ ଏହାକୁ ରେଶମ ବସ୍ତ୍ର ତିଆରିରେ ବ୍ୟବହାର କରାଯାଏ ।

Question 2.
ନଳିତାରୁ ଝୋଟ କିପରି ପ୍ରସ୍ତୁତ କରାଯାଏ ଲେଖ ।
ଉ –

• ନଳିତା ଗଛକୁ କାଟି ବିଡ଼ା ବନ୍ଧାଯାଏ । ସେହି ନଳିତା ଗଛ ବିଡ଼ାକୁ ଗଡ଼ିଆ ପାଣିରେ ପ୍ରାୟ ୧୫ ଦିନ ପର୍ଯ୍ୟନ୍ତ ବୁଡ଼ାଇ ରଖାଯାଏ ।
• ଗଛର ବକଳ ପଚିଗଲାପରେ ତାକୁ ବାଡ଼େଇ ଝୋଟ ତନ୍ତୁ ବାହାର କରାଯାଏ ଓ ଖରାରେ ଶୁଖାଇ ରଖାଯାଏ ।

Question 3.
ତନ୍ତୁ ସାହାଯ୍ୟରେ କ’ଣ ବୁଣାଯାଏ ଓ ଓଡ଼ିଶାର କେଉଁଠାରେ ତନ୍ତଲୁଗା ବୁଣାଯାଏ ?
ଉ –

• ତନ୍ତ ସାହାଯ୍ୟରେ ଶାଢ଼ୀ, ଗାମୁଛା ଆଦି ବୁଣାଯାଏ ।
• ଆମ ଓଡ଼ିଶାର ସମ୍ବଲପୁର, ସୋନପୁର, ଆଠଗଡ଼, ବ୍ରହ୍ମପୁର ଆଦି ଅଞ୍ଚଳରେ ତନ୍ତ ଲୁଗା ବୁଣାଯାଏ ।

Question 4.
ଦୁଇଟି ପ୍ରାଣୀଜ ତନ୍ତୁ ଓ ଦୁଇଟି ଉଭିଦଜାତ ତନ୍ତୁର ନାମ ଲେଖ ।
ଉ –

• ରେଶମ ଓ ପଶମ – ପ୍ରାଣୀଜ ତନ୍ତୁ
• କପା ଓ ଝୋଟ – ଉଭିଦଜ ତନ୍ତୁ

Question 5.
ନଡ଼ିଆ ଗଛର ତନ୍ତୁ କ’ଣ ? ଏଥୁରୁ କ’ଣ ତିଆରି ହୁଏ ?
ଉ –

• ନଡ଼ିଆ ଛଡ଼ାଇଦେଲେ ଏହାର ଚୋପା ବାହାରେ । ଏହାକୁ ନଡ଼ିଆକତା କହନ୍ତି । ନଡ଼ିଆକତାକୁ ନଡ଼ିଆ ଗଛର ତନ୍ତୁ କହନ୍ତି ।
• ଏହି ତନ୍ତୁରେ ଦଉଡ଼ି, ରସି, ପାପୋଛ, ଗଦି ଆଦି ତିଆରି ହୁଏ ।

Question 6.
ପ୍ରାକୃତିକ ତନ୍ତୁ ଓ କୃତ୍ରିମ ତନ୍ତୁ ମଧ୍ଯରେ ପାର୍ଥକ୍ୟ ଲେଖ ।
ଉ –

• ପ୍ରାକୃତିକ ତନ୍ତୁ ପ୍ରାଣୀ ଓ ଉଦ୍ଭଦରୁ ପ୍ରସ୍ତୁତ କରାଯାଏ ।
• କିନ୍ତୁ କୃତ୍ରିମ ତନ୍ତୁ ରାସାୟନିକ ପଦାର୍ଥରୁ ପ୍ରସ୍ତୁତ କରାଯାଏ । ତେଣୁ ଶରୀର ଉପରେ ଏହାର କୁପ୍ରଭାବ ରହିଛି ।

Question 7.
ଚର୍ମରୋଗୀମାନଙ୍କୁ ନାଇଲନ୍, ପଲିଷ୍ଟର ଆଦିରେ ତିଆରି ପୋଷାକ ପିନ୍ଧିବାକୁ ବାରଣ କରାଯାଏ ।
ଉ –

• ନାଇଲନ୍, ପଲିଷ୍ଟର ଆଦି ତନ୍ତୁ କୃତ୍ରିମ ତନ୍ତୁ । ଏଗୁଡ଼ିକ ରାସାୟନିକ ପଦାର୍ଥରୁ ପ୍ରସ୍ତୁତ କରାଯାଇଥାଏ ।
• ଏପରି ବସ୍ତ୍ରର ଶରୀର ଉପରେ କୁପ୍ରଭାବ ଥାଏ । ତେଣୁ ଡାକ୍ତରମାନେ ଚର୍ମରୋଗୀମାନଙ୍କୁ ଏପରି ବସ୍ତ୍ର ପିନ୍ଧିବାକୁ ବାରଣ କରିଥାନ୍ତି ।

Question 8.
ପ୍ରାକୃତିକ ତନ୍ତୁ ଓ କୃତ୍ରିମ ତନ୍ତୁ ମଧ୍ୟରେ ଥ‌ିବା ଗୋଟିଏ ସାମଞ୍ଜସ୍ୟ ଓ ଗୋଟିଏ ପାର୍ଥକ୍ୟ ଲେଖ ।
ଉ –

• ପ୍ରାକୃତିକ ତନ୍ତୁ ଓ କୃତ୍ରିମ ତନ୍ତୁ ଉଭୟରୁ ପୋଷାକ ତିଆରି ହୁଏ ।
• ପ୍ରାକୃତିକ ତନ୍ତୁ ନିର୍ମିତ ପୋଷାକ ଶରୀର ପାଇଁ ସ୍ବାସ୍ଥ୍ୟପ୍ରଦ ହୋଇଥିବା ବେଳେ କୃତ୍ରିମ ତନ୍ତୁ ନିର୍ମିତ ବସ୍ତ୍ର ଶରୀର ପାଇଁ ହାନିକାରକ ।

ଦୀର୍ଘ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
କପା ଚାଷ ବିଷୟରେ ସଂକ୍ଷିପ୍ତ ଟିପ୍‌ପଣୀ ଲେଖ ।
ଉ –

• କପା ଚାଷ ପାଇଁ କୃଷ୍ଣ କାର୍ପାସ ମୃତ୍ତିକା ଓ ଉଷ୍ମ ଜଳବାୟୁ ଉପଯୁକ୍ତ ଅଟେ ।
• ଏହି ମୁଭିକାର ଜଳଧାରଣ ଶକ୍ତି ଅଧ୍ଵ ।
• ମାଟି ଶୁଖୁଲେ ଫାଟିଯାଏ; ଫଳରେ ବାୟୁ ପ୍ରବେଶ କରିବା ସହଜ ହୁଏ ଓ ଅଣୁଜୀବମାନେ ଭଲ ବଢ଼ିପାରନ୍ତି ।
• ଆମ ଦେଶର ମହାରାଷ୍ଟ୍ର ଓ ଗୁଜରାଟରେ ଅଧିକ କପାଚାଷ କରାଯାଏ । ସେଥ‌ିପାଇଁ ମୁମ୍ବାଇ, ସୁରଟ,

Question 2.
କୃତ୍ରିମ ତନ୍ତୁ କ’ଣ ଓ କୃତ୍ରିମ ତନ୍ତୁରୁ ତିଆରି କପଡ଼ା ପିନ୍ଧିବାକୁ ଡାକ୍ତରମାନେ କାହିଁକି ମନାକରିଥା’ନ୍ତି ?
ଉ –

• କୃତ୍ରିମ ଉପାୟରେ ତିଆରି ହୋଇଥିବା ତନ୍ତୁକୁ କୃତ୍ରିମ ତନ୍ତୁ କହନ୍ତି ।
• ନାଇଲନ୍, ପଲିଷ୍ଟର, ଟେରିଲିନ୍ କପଡ଼ା କୃତ୍ରିମ ତନ୍ତୁରୁ ତିଆରି ହୋଇଥାଏ ।
• କୃତ୍ରିମ ତନ୍ତୁରୁ ତିଆରି କପଡ଼ା ବହୁତ ଟାଣ ଓ ବହୁଦିନ ପର୍ଯ୍ୟନ୍ତ ଛିଣ୍ଡେ ନାହିଁ ।
• ଏହି କପଡ଼ା ରାସାୟନିକ ପଦାର୍ଥରୁ ତିଆରି ହେଉଥ‌ିବାରୁ ଶରୀର ଉପରେ ଏହାର କୁପ୍ରଭାବ ରହିଛି । ଚର୍ମରୋଗ ହୋଇଥିଲେ ଡାକ୍ତର ଏପ୍ରକାର ପୋଷାକ ପିନ୍ଧିବାକୁ ମନାକରିଥା’ନ୍ତି ।

Question 3.
ଆମ ଓଡ଼ିଶାର କେନ୍ଦ୍ରାପଡ଼ା ଜିଲ୍ଲାରେ ନଳିତା ଚାଷ କରାଯାଏ କାହିଁକି ?
ଉ –

• ନଳିତା ଚାଷ ପାଇଁ ପଟୁମାଟି ଆବଶ୍ୟକ ।
• ପଟୁମାଟି ଥାଏ ଫଳରେ ବେଶି ନଳିତା ଚାଷ କରାଯାଏ ।
• କେନ୍ଦ୍ରାପଡ଼ା ନିକଟରେ ଚିତ୍ରୋତ୍ପଳା, ମହାନଦୀ ଆଦି ନଦୀ ପ୍ରବାହିତ ହୋଇଛି । ଏହାର ଉପକୂଳ ଅଞ୍ଚଳରେ ପଟୁମାଟି ଥାଏ ଫଳରେ ବେଶି ନଳିତା ଚାଷ କରାଯାଏ ।
• ତେଣୁ କେନ୍ଦ୍ରାପଡ଼ା ଜିଲ୍ଲାରେ ନଳିତା ଚାଷ କରାଯାଏ ।

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶୋଉର

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଗରମ ଦିନେ ……………. ବସ୍ତ୍ର ପିନ୍ଧିବାକୁ ଭଲ ଲାଗେ ।
(ଖ) ସୂତା …………. ରୁ ତିଆରି ହେଉଛି ।
(ଗ) ପଶମ ମୁଖ୍ୟତଃ …………….. ଲୋମରୁ ମିଳିଥାଏ ।
(ଘ) କପା ଚାଷ ପାଇଁ …………. ମୁଭିକା ଉପଯୁକ୍ତ ଅଟେ ।
(ଙ) ଓଡ଼ିଶାର ……………… ଜିଲ୍ଲାରେ ନଳିତା ଚାଷ ହୁଏ ।
(ଚ) ଓଡ଼ିଶାର ତନ୍ତବୁଣା ……………… ଶାଢ଼ୀର ଆଦର ଭାରତ ବାହାରେ ଅଛି ।
(ଛ) ଗାନ୍ଧିଜୀ …………. ଓ …………. ରେ ସୂତା କାଟୁଥିଲେ ।
(ଜ) …………… ତନ୍ତୁର ସୂତାରେ ସ୍ଵେଟର, ମଫଲର, ଚଦର ଇତ୍ୟାଦି ତିଆରି କରାଯାଏ ।
ଉ –
(କ) ସୂତା
(ଖ) ତନ୍ତୁ
(ଗ) ମେଣ୍ଢା
(ଘ) କୃଷ୍ଣକାର୍ପାସ
(ଙ) କେନ୍ଦ୍ରାପଡ଼ା
(ଚ) ପାଟ
(ଛ) ତକଲି, ଅରଟ
(ଜ) ପଶମ

Question 2.
ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତର ବାଛି ଲେଖ ।

(କ) କେଉଁ ତନ୍ତୁଟି ଉଭିଦ ଓ ପ୍ରାଣୀଠାରୁ ମିଳେ ନାହିଁ ?
(i) ରେଶମ
(ii) ପଶମ
(iii) ପଲିଷ୍ଟର
(iv) ତୁଳା
ଉ –
(iii) ପଲିଷ୍ଟର

(ଖ) ନାଇଲନ୍ ଓ ଟେରିଲିନ୍ ବସ୍ତ୍ର ପିନ୍ଧିଲେ କେଉଁ ରୋଗ ହୁଏ ?
(i) ହୃଦ୍‌ରୋଗ
(ii) ମଧୁମେହ
(ii) ଚର୍ମରୋଗ
(iv) କର୍କଟ
ଉ –
(ii) ଚର୍ମରୋଗ
(ଗ) କେଉଁଟି ପ୍ରାକୃତିକ ତନ୍ତୁ ?
(i) ପଲିଷ୍ଟର
(ii) ପଶମ
(iii) ଟେରିଲିନ୍
(iv) ନାଇଲନ୍
ଉ –
(ii) ପଶମ
(ଘ) ରେଶମ ପୋକ କ’ଣ ତିଆରି କରେ ?
(i) ଫେଣା
(ii) ଗାତ
(iii) ବସା
(iv) କୋଷା
ଉ –
(iv) କୋଷା

(ଙ) ଭାରତର କେଉଁ ରାଜ୍ୟରେ ଅଧ‌ିକ କପାଚାଷ କରାଯାଏ ?
(i) ମହାରାଷ୍ଟ୍ର
(ii) ପଞ୍ଜାବ
(iii) କେରଳ
(iv) ପଶ୍ଚିମବଙ୍ଗ
ଉ –
(i) ମହାରାଷ୍ଟ୍ର

(ଚ) କେଉଁଟି ପ୍ରାକୃତିକ ତନ୍ତୁ ନୁହେଁ ?
(i) ଚମଡ଼ା
(ii) ପଶମ
(iii) ରେଶମ
(iv) ଡେକ୍ରନ
ଉ –
(iv) ଡେକ୍ରନ

(ଛ) ଶୀତଦିନେ କେଉଁ ବସ୍ତ୍ର ପିନ୍ଧାଯାଏ
(i) ରେଶମ
(ii) କାର୍ପାସ
(iii) ପଶମ
(iv) ପଲିଷ୍ଟର
ଉ –
(iii) ପଶମ

(ଜ) କପାଚାଷ ପାଇଁ କେଉଁ ଜଳବାୟୁ ଆବଶ୍ୟକ ?
(i) ଶୀତଳ
(ii) ଉଷ୍ଣ
(iii) ନୀତିଶୀତାଷ୍ଣ
(iv) ଆର୍ଦ୍ର
ଉ –
(ଜ) ଉଷ୍ଣ

Question 3.
ପ୍ରଥମ ଯୋଡ଼ା ଶବ୍ଦଦ୍ଵୟର ସମ୍ପର୍କକୁ ଦେଖୁ ଦ୍ବିତୀୟ ଯୋଡ଼ାର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ରେଶମ : ପ୍ରାକୃତିକ ତନ୍ତୁ : : ପଲିଷ୍ଟର : ………………… ।
(ଖ) କପା ଚାଷ : କୃଷ୍ଣ କାର୍ପାସ ମୃତ୍ତିକା : : ଝୋଟ ଚାଷ : ………………… ।
(ଗ) ରେଶମ ପୋକ : ରେଶମ : : ଚମରୀ ଗାଈ : ………………… ।
(ଘ) ମଫଲର : ପଶମ ତନ୍ତୁ : : ପାପୋଛ : ………………… ।
(ଙ) ତୁଳା : କପା : : ଝୋଟ : ………………… ।
ଉ –
(କ) କୃତ୍ରିମ ତନ୍ତୁ
(ଖ) ପଟୁମାଟି
(ଗ) ପଶମ
(ଘ) ତନ୍ତୁ
(ଙ) ନଳିତା

Question 4.
୪। ରେଖାଙ୍କିତ ପଦ ନବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(କ) ରେଶମ ପୋକର ଅଣ୍ଡାରୁ ରେଶମ ମିଳେ ।
(ଖ) ନାଇଲନ ଗୋଟିଏ ପ୍ରାକୃତିକ ତନ୍ତୁ ।
(ଗ) ହସ୍ତ ପ୍ରସ୍ତୁତ କପଡ଼ାକୁ ଖଦଡ଼ କୁହାଯାଏ ।
(ଘ) ଗାଈ ଲୋମରୁ ପଶମ ମିଳିଥାଏ ।
(ଙ) କପାଚାଷ ପାଇଁ ଆର୍ଦ୍ର ଜଳବାୟୁ ଆବଶ୍ୟକ ।
ଉ –
(କ) ରେଶମ ପୋକର କୋଷାରୁ ରେଶମ ମିଳେ ।
(ଖ) ନାଇଲନ୍ ଗୋଟିଏ କୃତ୍ରିମ ତନ୍ତୁ ।
(ଗ) ହସ୍ତ ପ୍ରସ୍ତୁତ କପଡ଼ାକୁ ଖଦଡ଼ କୁହାଯାଏ ।
(ଘ) ଚମରୀଗାଈ ଲୋମରୁ ପଶମ ମିଳିଥାଏ ।
(ଙ) କପାଚାଷ ପାଇଁ ଉଷ୍ଣ ଜଳବାୟୁ ଆବଶ୍ୟକ ।

Question 5.
‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସଂପର୍କ ବାଛ ।
(କ)

ଉ –

(ଖ)

ଉ –

(ଗ)

ଉ –

Odisha State Board BSE Odisha 6th Class Science Important Questions Chapter 3 ଖାଦ୍ୟ ପଦାର୍ଥର ପରିଷ୍କରଣ Important Questions and Answers.

BSE Odisha Class 6 Science Important Questions Chapter 3 ଖାଦ୍ୟ ପଦାର୍ଥର ପରିଷ୍କରଣ

ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ହାତରେ ବାଛିବା ପ୍ରଣାଳୀ କ’ଣ ? ଗୋଟିଏ ଉଦାହରଣଦେଇ ଲେଖ ।
ଉ –

• ଯେଉଁ ପ୍ରଣାଳୀରେ ଆଙ୍ଗୁଠି ଦ୍ଵାରା ଧରିହେଉଥବା ପଦାର୍ଥକୁ ପୃଥକ୍ କରାଯାଇଥାଏ, ତାହାକୁ ହାତରେ ବାଛିବା ପ୍ରଣାଳୀ କୁହାଯାଏ ।
• ଚାଉଳରେ ମିଶିଥିବା ଗୋଡ଼ି, କାଠି ଓ ମଲା ଚାଉଳକୁ ଏହି ପ୍ରଣାଳୀରେ ପୃଥକ୍ କରାଯାଏ ।

Question 2.
ଧାନ କିପରି ଅମଳ କରାଯାଏ ।
ଉ –

• ଧାନପେଣ୍ଡା କଟାହୋଇ ଆସିଲେ ବେଙ୍ଗଳା ସାହାଯ୍ୟରେ ଧାନ ଅମଳ କରାଯାଏ ।
• ଧାନ ନଡ଼ାରେ ରହିଥିଲେ ତାକୁ ଭାଡ଼ି ବା ଘୋଡ଼ିଆ ସାହାଯ୍ୟରେ ପିଟାଯାଇ ଅମଳ କରାଯାଏ ।

Question 3.
କୁଲା ଓ ଚାଲୁଣିଦ୍ଵାରା କି କାର୍ଯ୍ୟ କରାଯାଏ ?
ଉ –

• କୁଲାଦ୍ଵାରା ପାଛୁଡ଼ିବା ଓ ଉଡ଼େଇବା କାର୍ଯ୍ୟ କରାଯାଏ ।
• ଚାଲୁଣିଦ୍ଵାରା ଚଲେଇବା କାର୍ଯ୍ୟ କରାଯାଏ ।

Question 4.
ପାଛୁଡ଼ିବା କହିଲେ କ’ଣ ?

• ଯେଉଁ ପ୍ରଣାଳୀରେ ହାଲୁକା ପଦାର୍ଥ ଓଜନିଆ ପଦାର୍ଥଠାରୁ ଅଲଗା କରାଯାଇଥାଏ, ସେହି ପ୍ରଣାଳୀକୁ ପାଛୁଡିବା କୁହାଯାଏ ।
• ଉଦାହରଣସ୍ୱରୂପ ଚାଉଳକୁ କୁଲା ସାହାଯ୍ୟରେ ପାଛୁଡ଼ି ଦେଲେ ସେଥୁରେ ରହିଥିବା କୁଣ୍ଡା ଓ ହାଲୁକା କାଠି

Question 5.
ହରଡ଼ ଡାଲିରେ ସୁଜି ମିଶିଯାଇଥିଲେ କିପରି ପୃଥକ୍ କରିବ ?
ଉ –

• ସୁଜିର ଆକାର ହରଡ଼ ଡାଲିର ଆକାରଠାରୁ କ୍ଷୁଦ୍ର ହୋଇଥିବାରୁ ଚଲେଇବା ପ୍ରଣାଳୀରେ ସୁଜିକୁ ହରଡ଼ ଡାଲିରୁ ପୃଥକ୍ କରିହେବ ।
• ମିଶ୍ରିତ ସୁଜି ଓ ଡାଲିକୁ ଏକ ଚାଲୁଣିରେ ରଖ୍ ଚଲେଇଲେ ଚାଲୁଣିର ରନ୍ଧ୍ରଦେଇ ସୁଜି ବାହାରିଯିବ ଓ ଡାଲି ଚାଲୁଣିରେ ରହିଯିବ ।

ଦୀର୍ଘ ପ୍ରଶ୍ନୋତ୍ତର

Question 1.
ଏକ ଉଦାହରଣ ସହ ଆସ୍ରବଣ ଓ ଅବକ୍ଷେପଣ କ’ଣ ବୁଝାଅ ।
ଉ –

• ଗୋଟିଏ ପାତ୍ରରେ କିଛି ଚାଉଳ ନେଇ ସେଥୁରେ ଜଳ ମିଶାଅ । ଭଲ ଭାବରେ ଏହାକୁ ଗୋଳାଇଦିଅ ।
• କିଛି ସମୟ ସ୍ଥିର ଭାବରେ ରହିବାପରେ ଜଳରେ ହାଲୁକା କୁଣ୍ଡା, କାଠି, ଧୂଳି ଭାସିବ । ପାତ୍ରର ତଳେ ଗୋଡ଼ି, ବାଲି ଓ ଚାଉଳ ବସିଯିବ ।
• ଏହାପରେ ଧୀରେ ଧୀରେ ଉପର ଜଳକୁ ଅନ୍ୟ ଏକ ପାତ୍ରକୁ ଢାଳିଲେ, ସେଥୁ ଧୂଳି, କୁଣ୍ଡା ଓ କାଠି ଚାଲିଯିବ ।
• ଜଳ ସହିତ ହାଲୁକା କଠିନ ପଦାର୍ଥକୁ ଅନ୍ୟ ଏକ ପାତ୍ରକୁ ଢାଳିବା ପ୍ରଣାଳୀକୁ ଆଶ୍ରବଣ କହନ୍ତି । ତଳେ କଠିନ ଓଜନିଆ ପଦାର୍ଥ ବସିଯିବା ପ୍ରଣାଳୀକୁ ଅବକ୍ଷେପଣ କୁହାଯାଏ ।

Question 2.
କୁଲାରେ ପାଛୁଡ଼ି ଅଲଗା କରାଯାଉଥିବା ୪ଟି ମିଶ୍ରଣର ନାମ ଲେଖ ।
ଉ –

• କୁଲାରେ ପାଛୁଡ଼ିବା ଦ୍ଵାରା ହାଲୁକା ପଦାର୍ଥ ଓଜନିଆ ପଦାର୍ଥଠାରୁ ଅଲଗା ହୋଇଯାଏ । ଏହାକୁ ପାଛୁଡ଼ିବା ପ୍ରଣାଳୀ କୁହନ୍ତି । ଏହାଦ୍ଵାରା ନିମ୍ନୋକ୍ତ ମିଶ୍ରଣଗୁଡ଼ିକ ଅଲଗା କରାଯାଇପାରିବ –
• ଧାନରୁ ଅଗାଡ଼ି, କାଠି, ପତ୍ର।
• ଗ୍ରହମରୁ କଣିଆ ଗହମ, କାଠି, ପତ୍ର।
• ଚାଉଳରେ ମିଶିଥ‌ିବା କୁଣ୍ଡା ।
• ପେଶି, ରାଶି, ସୋରିଷ ଇତ୍ୟାଦି ତୈଳବୀଜରେ ମିଶିଥିବା ପତ୍ର, କାଠି ।

Question 3.
ଚାଲୁଣି ସାହାଯ୍ୟରେ ଚଲେଇ କେଉଁ ଖାଦ୍ୟପଦାର୍ଥକୁ ପରିଷ୍କାର କରାଯାଏ, ତାହାର ୪ଟି ଉଦାହରଣ ଦିଅ ।
ଉ –
ଚାଲୁଣି ସାହାଯ୍ୟରେ ନିମ୍ନଲିଖ୍ ଖାଦ୍ୟ ପଦାର୍ଥକୁ ଚଲେଇ ପରିଷ୍କାର କରାଯାଏ

• ମୁଢ଼ିରୁ ବାଲି ଅଲଗା କରିବା
• ଚୁନାରୁ ଚାଉଳ ଅଲଗା କରିବା
• ଧାନରୁ ଅଗାଡ଼ି ଓ କୁଟା ଆଦି ଅଲଗା କରିବା
• ଚୁଡ଼ାରୁ କୁଣ୍ଡା ଅଲଗା କରିବା

Question 4.
ପରିସ୍ରବଣ ପ୍ରଣାଳୀ କ’ଣ ସଂକ୍ଷେପରେ ବୁଝାଅ ।
ଉ –

• ଯେଉଁ ପ୍ରଣାଳୀ ଦ୍ଵାରା ତରଳ ପଦାର୍ଥରେ ରହିଥିବା ଅଦ୍ରବଣୀୟ କଠିନ ପଦାର୍ଥରୁ ତରଳ ପଦାର୍ଥରୁ ପୃଥକ୍ କରାଯାଏ, ତାହାକୁ ପରିସ୍ରବଣ କୁହାଯାଏ ।
• ଘରେ ଚା’ ଛାଣିବାପାଇଁ କନାର ବା ତାରର ଅଥବା, ପ୍ଲାଷ୍ଟିକ୍ ର ଜାଲି ବ୍ୟବହାର ଫିଲ୍‌ଟର୍ ପେପର୍ ବା ଚୁଟିଙ୍ଗ୍ ପେପର୍ ବ୍ୟବହାର କରାଯାଇଥାଏ ।
  ବିଜ୍ଞାନାଗାର ରେ ପରି ସ୍ରବଣ ପାଇଁ କାଚଫୁଲଣା, ଫୁଲଣା ଧାରକ ଷ୍ଟାଣ୍ଡ, ଦୁଇଟି ବିକର୍‌, ଖଣ୍ଡିଏ ସରୁ କାଚଦଣ୍ଡ, ଫିଲ୍ମର ପେପର୍ ଆବଶ୍ୟକ ହୋଇଥାଏ ।
• ବୃତ୍ତାକାର ଫିଲଟର୍ ପେପର୍‌କୁ ଚାରିଭାଙ୍ଗ କରି ଚାରି ପରସ୍ତରୁ ଗୋଟିଏ ପରସ୍ତକୁ ଟାଣି ଫୁଲଣା ବା ଫନେଲ୍ ଆକାର କରି ଫୁଲଣାରେ ରଖ୍ (ଚିତ୍ରରେ ଦେଖାଗଲାପରି) ଓ ଫୁଲଣାକୁ ଷ୍ଟାଣ୍ଡ ଧାରକରେ ରଖ୍ କାଚଦଣ୍ଡକୁ ତେରଛା ଧରି ଧୀରେ ଧୀରେ ଅଦ୍ରାବ୍ୟ ଭାସମାନ କଠିନ ପଦାର୍ଥ ମିଶିଥିବା ତରଳ ପଦାର୍ଥକୁ ଢଳାଯାଏ ।
• ଫଳରେ ଫୁଲଣା ତଳେଥିବା ବିକକୁ ପରିଷ୍କାର ତରଳ ପଦାର୍ଥ (ପରିଷ୍କୃତ) ଚାଲିଯାଏ ଓ ଫିଲ୍‌ଟର୍ କାଗଜ ଉପରେ ଅଦ୍ରାବ୍ୟ (ଅବଶେଷ) ରହିଯାଏ ।

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶୋଉର

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ପାଛୁଡ଼ିବା ଓ ଉଡ଼ାଇବା ପ୍ରଣାଳୀ ପାଇଁ ………………… ବ୍ୟବହାର କରାଯାଏ ।
(ଖ) ଆଜିକାଲି ………………… ସାହାଯ୍ୟରେ ଉଡ଼ାଯାଉଛି ।
(ଗ) …………….. ପ୍ରଣାଳୀରେ ତଳେ ପଦାର୍ଥରେ ରହିଥିବା ଅଦ୍ରବଣୀୟ କଠିନ ତରଳ ପଦାର୍ଥରୁ ପୃଥକ କରାଯାଇପାରେ ।
(ଘ) ପରିସ୍ରବଣ ପ୍ରଣାଳୀରେ ଫିଲ୍ଗର୍ ପେପର୍ ବଦଳରେ ………. ପେପର୍ ବ୍ୟବହାର କରାଯାଏ ।
(ଙ) ଜଳ ସହିତ ମିଶି ରହିଥ‌ିବା ଅଦ୍ରବଣୀୟ ହାଲୁକା ପଦାର୍ଥକୁ ………… ପ୍ରଣାଳୀରେ ପୃଥକ୍ କରାଯାଏ ।
ଉ –
(କ) କୁଲା
(ଖ) ବିଦ୍ୟୁତ୍ ପଙ୍ଖା
(ଗ) ପରିସ୍ରବଣ
(ଘ) ବ୍ଳଟିଇଂ ପେପର
(ଙ) ଆସ୍ରବଣ

Question 2.
ନିମ୍ନରେ ଦିଆଯାଇଥିବା ପ୍ରଶ୍ନର ବାମ ପାର୍ଶ୍ବର ଦୁଇଟି ଶବ୍ଦର ସଂପର୍କକୁ ଦେଖ୍ ଡାହାଣ ପାର୍ଶ୍ଵର ଶବ୍ଦ ପାଖରେ ‘?” ସ୍ଥାନରେ ଉପଯୁକ୍ତ ଶବ୍ଦ ଲେଖ ।
(କ) ଚାଉଳରୁ ମଲା ଚାଉଳ ଅଲଗା କରିବା : ହାତରେ ବାଛିବା :: ଲେମ୍ବୁ ସରବତରୁ ଲେମ୍ବୁ ମଞ୍ଜି ଅଲଗା କରିବା : (?) ।
(ଖ) ଛାଣିବା : ପରିସ୍ରବଣ :: ଧୀରେ ଧୀରେ ଢାଳିବା : (?) ।
(ଗ) କୁଲା : ପାଛୁଡ଼ିବା :: ଫିଲ୍‌ଟର୍‌ ପେପର୍ : (?) ।
(ଘ) ବିରି ଅମଳକରିବା : ବେଙ୍ଗଳା :: ମେଥ୍ ପରିଷ୍କାର କରିବା : (?) ।
(ଙ) ଗୋଳିଆ ପାଣି : ଅବକ୍ଷେପଣ ଓ ଆସ୍ରବଣ :: ଚା’ ପାଣି : (?) ।
(ଚ) ମୁଢ଼ିରୁ ବାଲି : ଚାଲୁଣି :: ଧାନରୁ ଅଗାଡ଼ି : (?) ।
ଉ –
(କ) ପରିସ୍ରବଣ
(ଖ) ଆସ୍ରବଣ
(ଗ) ପରିସ୍ରବଣ
(ଘ) ଆସ୍ରବଣ ଓ ଅବକ୍ଷେପଣ
(ଙ) ପରିସ୍ରବଣ
(ଚ) ପବନରେ ଉଡ଼େଇବା

Question 3.
ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତର ବାଛି ଲେଖ ।

(କ) ଅଟାରୁ ଚୋକଡ଼ ବାହାର କରିବାକୁ କ’ଣ ଆବଶ୍ୟକ ?
(i) କୁଲା
(ii) ଚାଲୁଣି
(iii) ବିଦ୍ୟୁତ ପଙ୍ଖା
(iv) ବ୍ଲଟିଂପେପର୍
ଉ –
(ii) ଚାଲୁଣି

(ଖ) ନଡ଼ାରେ ଶସ୍ୟ ରହିଥିଲେ କ’ଣ କରାଯାଏ ?
(i) ବେଙ୍ଗଳା ପକାଯାଏ
(ii) ଛଣାଯାଏ
(iii) ପିଟାଯାଏ
(iv) ବଛାଯାଏ
ଉ –
(iii) ପିଟାଯାଏ

(ଗ) ଗହମରେ ମିଶି ରହିଥ‌ିବା କାଠିକୁ କେଉଁ ପ୍ରଣାଳୀରେ ପୃଥକ୍ କରାଯାଏ ?
(i) ଚଲେଇବା
(ii) ହାତବଛା
(iii) ଆସ୍ରବଣ
(iv) ପରିସ୍ରବଣ
ଉ –
(ii) ହାତବଛା

(ଘ) କେଉଁଟି ଅଲଗା କରିହେବ ନାହିଁ ?
(i) ଅଟାରେ ବେସନ ମିଶିଥିଲେ
(ii) ଡାଲିରେ ସୁଜି ମିଶିଥିଲେ
(iii) ଚାଉଳରେ କୁଣ୍ଡା ମିଶିଥିଲେ
(iv) ଚୁଡ଼ାରେ ଧାନଚୋପା ମିଶିଥିଲେ
ଉ –
(i) ଅଟାରେ ବେସନ ମିଶିଥିଲେ

(ଙ) ଜଳରେ ଭାସୁଥିବା କୁଣ୍ଡାକୁ କେଉଁ ପ୍ରଣାଳୀରେ ପୃଥକ କରାଯାଏ ?
(i) ଚଲେଇବା
(ii) ପରିସ୍ରବଣ
(iii) ଅମଳ
(iv) ଆସ୍ରବଣ
ଉ –
(ଡ) ଆସ୍ରବଣ

(ଚ) ଛଣାକାଗଜ କେଉଁଥରେ ବ୍ୟବହୃତ ହୁଏ ?
(i) ପରିସ୍ରବଣ
(ii) ଅବକ୍ଷେପଣ
(iii) ଚାଲୁଣି
(iv) ଆସ୍ରବଣ
ଉ –
(i) ପରିସ୍ରବଣ

(ଛ) ଧାନ ଉଡ଼େଇବା ପାଇଁ କେଉଁଟି ଆବଶ୍ୟକ ?
(i) ବିଞ୍ଚଣା
(ii) କୁଲା
(iii) ଚାଲୁଣି
(iv) ଚାଲୁଣି
ଉ –
(ii) କୁଲା

Question 4
ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(କ) ଚାଉଳରେ କୁଣ୍ଡା ଥିଲେ ତାକୁ ବାଡ଼େଇ ବାଡ଼େଇ ଅଲଗା କରାଯାଏ ।
(ଖ) ଚାଉଳରୁ ଗୋଡ଼ିକୁ ଅଲଗା କରିବା ପାଇଁ ଉଡ଼ାଇବା ପ୍ରଣାଳୀ ଅବଲମ୍ବନ କରାଯାଏ ।
(ଗ) ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ବାଲିକୁ ହାତବଛା ପ୍ରଣାଳୀରେ ପରିଷ୍କାର କରାଯାଏ ।
(ଘ) ଜଳରେ ବାଲି ମିଶିଥିଲେ ପୃଥକୀକରଣ ଆସ୍ରବଣ ପ୍ରଣାଳୀରେ କରାଯାଏ ।
(ଙ) ଗହମରେ ମିଶି ରହିଥିବା କାଠିକୁ ଆସ୍ରବଣ ପ୍ରଣାଳୀରେ ପୃଥକ୍ କରାଯାଏ ।
ଉ –
(କ) ଚାଉଳରେ କୁଣ୍ଡା ଥିଲେ ତାକୁ ପାଛୁଡ଼ି (କୁଲାରେ) ଅଲଗା କରାଯାଏ ।
(ଖ) ଚାଉଳରୁ ଗୋଡ଼ିକୁ ଅଲଗା କରିବା ପାଇଁ ହାତବଛା ପ୍ରଣାଳୀ ଅବଲମ୍ବନ କରାଯାଏ ।
(ଗ) ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ବାଲିକୁ ଚାଲୁଣି ସାହାଯ୍ୟରେ ପରିଷ୍କାର କରାଯାଏ ।
(ଘ) ଜଳରେ ବାଲି ମିଶିଥିଲେ ପୃଥକୀକରଣ ପରିସ୍ରବଣ ପ୍ରଣାଳୀରେ କରାଯାଏ ।
(ଙ) ଗହମରେ ମିଶି ରହିଥିବା କାଠିକୁ ଆସ୍ରବଣ ପ୍ରଣାଳୀରେ ପୃଥକ୍ କରାଯାଏ ।

Question 5.
‘କ’ ସ୍ତମ୍ଭ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ସଂପର୍କ ବାଛ ।
(କ)

ଉ –

Odisha State Board BSE Odisha 6th Class Science Solutions Chapter 2 ଖାଦ୍ୟର ଶ୍ରେଣୀ ବିଭାଗ Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Science Solutions Chapter 2 ଖାଦ୍ୟର ଶ୍ରେଣୀ ବିଭାଗ

Question 1.
ଦିଆଯାଇଥ‌ିବା ଖାଦ୍ୟ ତାଲିକାରୁ କେଉଁଟି କେଉଁ ଶ୍ରେଣୀର ଖାଦ୍ୟ ଚିହ୍ନଟ କରି ସଂପୃକ୍ତ କୋଠରିରେ ଲେଖ ।

ଉ –

Question 2.
କେଉଁଗୁଡ଼ିକ ଠିକ୍, (✓) ଚିହ୍ନ ଦେଇ ଦର୍ଶାଅ ।
(କ) ସୂର୍ଯ୍ୟ କିରଣରେ ଭିଟାମିନ୍ ‘D’ ଥାଏ ।
(ଖ) ଅଁଳାରେ ଭିଟାମିନ୍ ‘C’ ଥାଏ ।
(ଗ) ଶୁଖୁଆରେ ଅଧିକ ସ୍ନେହସାର ରହିଛି ।
(ଘ) ସୁଷମ ଖାଦ୍ୟ ଶରୀରର ଆବଶ୍ୟକତା ପୂରଣ କରେ ।
(ଙ) ରକ୍ତହୀନତା ହୋଇଥିଲେ ସମୁଦ୍ର ମାଛ ଖାଇବା ଉଚିତ ।
(ଚ) ଭିଟାମିନ୍ ‘K’ ସଜନା ଛୁଇଁରେ ମିଳେ ନାହିଁ ।
(ଛ) ଅନ୍ଧାରକଣା ଭୋଗୁଥିବା ବ୍ୟକ୍ତି ଗାଜର ଖାଇବା ଅନୁଚିତ ।
(ଜ) କ୍ଷୀରରେ ସମସ୍ତ ପ୍ରକାର ଭିଟାମିନ୍ ଥାଏ ।
ଉ –
(କ) ସୂର୍ଯ୍ୟ କିରଣରେ ଭିଟାମିନ୍ ‘D’ ଥାଏ । (✓)
(ଖ) ଅଁଳାରେ ଭିଟାମିନ୍ ‘C’ ଥାଏ । (✓)
(ଗ) ଶୁଖୁଆରେ ଅଧିକ ସ୍ନେହସାର ରହିଛି । (✗)
(ଘ) ସୁଷମ ଖାଦ୍ୟ ଶରୀରର ଆବଶ୍ୟକତା ପୂରଣ କରେ । (✓)
(ଙ) ରକ୍ତହୀନତା ହୋଇଥିଲେ ସମୁଦ୍ର ମାଛ ଖାଇବା ଉଚିତ । (✓)
(ଚ) ଭିଟାମିନ୍ ‘K’ ସଜନା ଛୁଇଁରେ ମିଳେ ନାହିଁ । (✓)
(ଛ) ଅନ୍ଧାରକଣା ଭୋଗୁଥିବା ବ୍ୟକ୍ତି ଗାଜର ଖାଇବା ଅନୁଚିତ । (✓)
(ଜ) କ୍ଷୀରରେ ସମସ୍ତ ପ୍ରକାର ଭିଟାମିନ୍ ଥାଏ । (✓)

Question 3.
ଦୁଇଟି ବା ତିନୋଟି ବାକ୍ୟରେ କାରଣ ଲେଖ ।
(କ) ଖାଦ୍ୟରେ ତନ୍ତୁଯୁକ୍ତ ଖାଦ୍ୟ ରହିବା ଆବଶ୍ୟକ ।
ଉ –

• ଖାଦ୍ୟରେ ତନ୍ତୁଯୁକ୍ତ ଖାଦ୍ୟ ନ ରହିଲେ ଝାଡ଼ା ପରିଷ୍କାର ହୁଏ ନାହିଁ । ଖାଦ୍ୟନଳୀରୁ ମଳ ବାହାର କରିବାରେ
• ପେଟରୁ ମଳ ଭଲ ଭାବରେ ବାହାରି ନଗଲେ ଶରୀରରେ ବିଭିନ୍ନ ରୋଗ ସୃଷ୍ଟି ହୋଇଥାଏ । ତେଣୁ ଖାଦ୍ୟରେ ତନ୍ତୁଯୁକ୍ତ ଖାଦ୍ୟ ରହିବା ଆବଶ୍ୟକ ।

(ଖ) ଆମିଷ ଖାଉ ନଥିବା ପିଲା ଅଧ୍ଵ ପରିମାଣର କ୍ଷୀର, ଡାଲି, ବାଦାମ ଖାଇବା ଆବଶ୍ୟକ ।
ଉ –

• ମାଛ, ମାଂସ ଓ ଅଣ୍ଡାରେ ପୁଷ୍ଟିସାର ଅଧିକ ପରିମାଣରେ ଥାଏ ।
• ଆମିଷ ଖାଉ ନଥିବା ପିଲା ମାଛ, ମାଂସ ଓ ଅଣ୍ଡାରେ ଥିବା ପୁଷ୍ଟିସାର କ୍ଷୀର, ଡାଲି, ବାଦାମରୁ ପାଇଥାଏ । ପିଲାମାନଙ୍କ ଶରୀର ବୃଦ୍ଧି ନିମିତ୍ତ ଆମିଷ ଖାଉ ନଥୁବା ପିଲା ଅଧ୍ଵ ପରିମାଣରେ କ୍ଷୀର, ଡାଲି, ବାଦାମ. ଖାଇବା ଆବଶ୍ୟକ ।

(ଗ) ଚକ୍ରଧରକୁ ଅନ୍ଧାରରେ ଦେଖାଯାଉ ନାହିଁ ।
ଉ –

• ଚକ୍ରଧରକୁ ଭିଟାମିନ୍ – ‘A’ ଅଭାବରୁ ଅନ୍ଧାରକଣା ରୋଗ ହୋଇଛି ।
• ତେଣୁ ଚକ୍ରଧରକୁ ଅନ୍ଧାରରେ ଦେଖାଯାଉ ନାହିଁ ।

(ଘ) ପିଲାମାନଙ୍କର ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟର ଆବଶ୍ୟକତା ବେଶୀ ।
ଉ –

• ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟ ପିଲାମାନଙ୍କର ଶରୀର ବୃଦ୍ଧିରେ ସାହାଯ୍ୟ କରେ ।
• ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟଗୁଡ଼ିକ ହେଉଛି ମାଛ, ମାଂସ, ଅଣ୍ଡା, ଡାଲି, ଛତୁ, ସୋୟାବିନ୍ ଇତ୍ୟାଦି ।

(ଙ) ପାହାଡ଼ିଆ ଅଞ୍ଚଳର ଲୋକମାନଙ୍କର ଗଳଗଣ୍ଡ ରୋଗ ହେବାର ସମ୍ଭାବନା ଅଧିକ ।
ଉ –

• ପାହାଡ଼ିଆ ଅଞ୍ଚଳରେ ହେଉଥ‌ିବା ଖାଦ୍ୟ ପଦାର୍ଥରେ ଆୟୋଡ଼ିନ୍‌ର ଅଭାବ ଥାଏ ।
• ରକ୍ତରେ ଆୟୋଡ଼ିନ ଅଭାବଯୋଗୁଁ ଗଳଗଣ୍ଡ ରୋଗ ହୁଏ । ତେଣୁ ପାହାଡ଼ିଆ ଅଞ୍ଚଳର ଲୋକମାନଙ୍କର ଗଳଗଣ୍ଡ ରୋଗ ହେବାର ସମ୍ଭାବନା ଥାଏ ।

Question 4.
ତଳେ ଦିଆଯାଇଥ‌ିବା ପ୍ରତ୍ୟେକ ପୋଷକ ପାଇଁ ଦୁଇଟି ଖାଦ୍ୟ ପଦାର୍ଥର ନାମ ଲେଖ ।
(କ) ପୁଷ୍ଟିସାର – ……………….. – …………………..
(ଖ) ଭିଟାମିନ୍ C. – ……………….. – ………………
(ଗ) ଖଣିଜ ଲବଣ – ……………….. – …………………..
ଉ –
(କ) ଡାଲି, ମାଛ
(ଖ) କମଳା, ପିଜୁଳି
(ଗ) ଚୂନାମାଛ, ସଜନା ଛୁଇଁ

Question 5.
ଶାଗରେ କେଉଁଟି ନଥାଏ ?
(କ) ଖଣିଜ ଲବଣ (ଖ) ତନ୍ତୁ (ଗ) ଭିଟାମିନ୍ (ଘ) ସ୍ନେହସାର
ଉ –
(ଘ) ସ୍ନେହସାର

Question 6.
ଯଦି ସବୁ ଗାଈ ଓ ମଇଁଷି ଲୋପପାଇଯାଆନ୍ତି; ତାହାହେଲେ କ୍ଷୀର, ଦହି, ଘିଅ, ଛେନା ବ୍ୟତୀତ ଆଉ ଯେଉଁସବୁ ଖାଦ୍ୟ ପଦାର୍ଥ ମିଳିବ ନାହିଁ, ସେହି ମଧ୍ୟରୁ ଦୁଇଟିର ନାମ ଲେଖ ।
ଉ –
ଲହୁଣି, ରାବିଡ଼ି

Question 7.
ଗୋଟିଏ ବଦ୍ଧିଷ୍ଣୁ ଶିଶୁର ଓ ଜଣେ ବୃଦ୍ଧର ଖାଦ୍ୟର ଆବଶ୍ୟକତା ମଧ୍ୟରେ ଥ‌ିବା ପାର୍ଥକ୍ୟ ଯୁକ୍ତି ସହ ସଂକ୍ଷେପରେ ଲେଖ ।
ଉ –

ଖାଦ୍ୟର ଶ୍ରେଣୀ ବିଭାଗ Notes :

→ ଉପକ୍ରମ :
(i) ଆମେ ଖାଉଥ‌ିବା ବିଭିନ୍ନ ପ୍ରକାର ଖାଦ୍ୟରେ ଚାଉଳ, ଡାଲି, ପନିପରିବା, ଚିନି, ଅଣ୍ଡା, ମାଂସ, ମାଛ, ଛେନା, କ୍ଷୀର, ଚୁଡ଼ା, ମୁଢ଼ି, ପିଜୁଳି, କମଳା, କାକୁଡ଼ି, ଲଙ୍କା, ଲେମ୍ବୁ, ଅଟା, ବାଜ୍‌, ମାଣ୍ଡିଆ, ଗୁଡ଼, ଘିଅ, ତେଲ ଇତ୍ୟାଦି ପଦାର୍ଥ ବ୍ୟବହାର କରିଥାଉ ।
(ii) ଆମେ ଖାଦ୍ୟାଭାବରେ ଯାହାସବୁ ଖାଉଛେ ସେ ସବୁର ଆବଶ୍ୟକତା ଆମ ଶରୀର ପାଇଁ ରହିଛି ।
(iii) ଖାଦ୍ୟ ଆମ ଶରୀର ବୃଦ୍ଧିରେ ସାହାଯ୍ୟ କରେ ଓ କାମ କରିବାପାଇଁ ଶକ୍ତି ଯୋଗାଇଥାଏ ।
(iv) ଶରୀରରେ ରୋଗ ପ୍ରତିରୋଧକ ଶକ୍ତି ସୃଷ୍ଟି କରେ । ଖାଦ୍ୟ ପଦାର୍ଥରେ ଥ‌ିବା ରାସାୟନିକ ପଦାର୍ଥକୁ ପୋଷକ କୁହାଯାଏ ।
(v) ଭିନ୍ନ ଭିନ୍ନ ଖାଦ୍ୟପଦାର୍ଥରେ ଏହି ପୋଷକ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଥାଏ । ତେଣୁ ସୁସ୍ଥ ରହିବାପାଇଁ ଆମେ ବିଭିନ୍ନ ପ୍ରକାର ଖାଦ୍ୟ ଖାଇବ! ଆବଶ୍ୟକ । ଖାଦ୍ୟରେ ଥ‌ିବା ମୁଖ୍ୟ ପୋଷକକୁ ଆଧାର କରି ଖାଦ୍ୟକୁ ପାଞ୍ଚ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା – ଶ୍ଵେତସାର, ପୁଷ୍ଟିସାର, ସ୍ନେହସାର, ଭିଟାମିନ୍ ବା ଜୀବସାର, ଖଣିଜ ଲବଣ ।

(vi) ଶରୀରର ଆବଶ୍ୟକତା ପୂରଣ କରିବାପାଇଁ ଜଳ ଓ ତନ୍ତୁ ଜାତୀୟ ଖାଦ୍ୟର ଆବଶ୍ୟକତା ରହିଛି ।

• ପ୍ରତ୍ୟେକ ଖାଦ୍ୟରେ ପ୍ରାୟ ସମସ୍ତ ପ୍ରକାର ପୋଷକ ଅଳ୍ପ ବା ବେଶି ପରିମାଣରେ ଥାଏ । ଯେଉଁ ଖାଦ୍ୟରେ ଯେଉଁ ପୋଷକ ଅଧିକ ପରିମାଣରେ ଥାଏ ତାକୁ ଆମେ ସେହି ଜାତୀୟ ଖାଦ୍ୟ କରିଥାଉ ।
• ଖାଦ୍ୟରେ ଥ‌ିବା ମୁଖ୍ୟ ପୋଷକକୁ ଆଧର କରି ଖାଦ୍ୟକୁ ବିଭିନ୍ନ ବିଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି ।
  

• ଖଣିଜ ଲବଣ ବା ଧାତୁସାର

→ ଖାଦ୍ୟର ଶ୍ରେଣୀବିଭାଗ :
ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟର ଚିହ୍ନଟ ପ୍ରଣାଳୀ :
ତୁମପାଇଁ କାମ : 1
ଗୋଟିଏ ଏକ ଚାମଚ ଅଟା ନେଇ ସେଥ‌ରେ ୩/୪ ଚାମଚ ପାଣି ମିଶାଇ ଭଲ ଭାବରେ ଗୋଳାଇଦିଅ । ସେହି ପାଣିଆ ଅଟାରେ ୨-୩ ବୁନ୍ଦା ସାଙ୍ଗେ ସାଙ୍ଗେ ପ୍ରସ୍ତୁତ ହୋଇଥିବା ଆୟୋଡି଼ନ୍‌ ଦ୍ରବଣ ମିଶାଅ । ଏହାକୁ ଚାମଚ ସାହାଯ୍ୟରେ ଭଲ ଭାବରେ ଘାଣ୍ଟିଦିଅ । ଆୟୋଡ଼ିନ୍ ଦ୍ରବଣ ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟକୁ ଗାଢ଼ ନୀଳ ରଙ୍ଗ କରିଦିଏ ।

ଆୟୋଡ଼ିନ୍ ଦ୍ରବଣ ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟକୁ ଗାଢ଼ ନୀଳରଙ୍ଗ କରିଦିଏ ।
ସିଝା ଆଳୁ, ଚୁଡ଼ା, ଚାଉଳ, ଅଟା, ମୁଢ଼ି, କନ୍ଦମୂଳ, ଚିନି, ସାରୁ, ଓଲୁଅ, ବାଜରା, ମାଣ୍ଡିଆ ଆଦି ଶ୍ଵେତସାର ଜାତୀୟ ଖାଦ୍ୟ ।

ତୁମପାଇଁ କାମ : 2
ସିଝା ଆଳୁ, ଚୁଡ଼ାଗୁଣ୍ଡ, ସୋରିଷ ତେଲ, ଡାଲିଗୁଣ୍ଡ, କ୍ଷୀରକୁ ଅଲଗା ଅଲଗା ଗିଲାସରେ ନେଇ ସେଥ‌ିରେ ଆୟୋଡିନ୍ ଦ୍ରବଣ ମିଶାଅ । କେଉଁ କେଉଁ କ୍ଷେତ୍ରରେ ଗାଢ଼ ରଙ୍ଗ ହେଲା ଦେଖ । ନିମ୍ନ ସାରଣୀଟିକୁ ପୂରଣ କର ।
ଡ –

ଗାଢ଼ ନୀଳ ରଙ୍ଗ ହେଲ	ଗାଢ଼ନୀଳ ରଙ୍ଗ ହେଲା ନାହିଁ
ସିଝା ଆଳୁ	ଡାଲିଗୁଣ୍ଡ, କ୍ଷୀର
ଚୁଡ଼ା ଗୁଣ୍ଡ	ଗାଢ଼ନୀଳ

→ ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟର ଚିହ୍ନଟ ପ୍ରଣାଳୀ :
ତୁମପାଇଁ କାମ : ୨
ଗୋଟିଏ ସ୍ବଚ୍ଛ ପ୍ଲାଷ୍ଟିକ ବୋତଲ ନେଇ ସେଥ‌ିରେ ଅଳ୍ପ ଗୁଣ୍ଡଡାଲି ପୂରାଅ । ଡ୍ରପର ସାହାଯ୍ୟରେ ସେଥ‌ିରେ ୮-୧୦ ବୁନ୍ଦା ପାଣି ମିଶାଅ । ଏହାପରେ ସେଥ‌ିରେ ଦୁଇବୁନ୍ଦା ତୁତିଆ ଦ୍ରବଣ (କପର ସଲଫେଟ୍) ଓ ୮-୧୦ ବୁନ୍ଦା କ୍ଷାରସୋଡ଼ାର ଦ୍ରବଣ ମିଶାଅ । ଠିପି ଲଗାଅ ଓ ଏହାକୁ ଭଲ ଭାବରେ ହଲାଅ, ଯେପରି ଦ୍ରବଣଗୁଡ଼ିକ ମିଶିଯିବ । କିଛି ସମୟ ଗୋଟିଏ ସ୍ଥାନରେ ସ୍ଥିର ଭାବରେ ରଖୁଦିଅ ।

• ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟ ତୁଡିଆ ( କପର ସଲଫେଟ୍) ଦ୍ରବଣ ସହ ମିଶିଲେ ଦ୍ରବଣଟି ବାଇଗଣି ରଙ୍ଗ ହୁଏ ।

୨ । କ୍ଷୀର, ବାଇଗଣ ଚକଟା, ଅଣ୍ଡାଲାଳ, ଭାତ ନେଇ ପରୀକ୍ଷାଟି କର । କେଉଁ କ୍ଷେତ୍ରରେ ବାଇଗଣି ରଙ୍ଗ ହେଉଛି ତଳ ସାରଣୀରେ ଲେଖ ।

ଗାଢ଼ ନୀଳ ରଙ୍ଗ ହେଲ	ଗାଢ଼ନୀଳ ରଙ୍ଗ ହେଲା ନାହିଁ
ଡାଲି ଗୁଣ୍ଡ	ଭାତ
କ୍ଷୀର	ବାଇଗଣ ଚକଟା
ଅଣ୍ଡାଲାଳ

ଡାଲି, ଅଣ୍ଡାଲାଳ, କ୍ଷୀର, ମାଛ, ମାଂସ, ସୋୟାବିନ୍, ଛତୁ ଆଦି ପୁଷ୍ଟିସାର ଜାତୀୟ ଖାଦ୍ୟ ।

→ ସ୍ନେହସାର ଜାତୀୟ ଖାଦ୍ୟର ଚିହ୍ନଟ ପ୍ରଣାଳୀ :
ତୁମପାଇଁ କାମ : ୩
କେତେଖଣ୍ଡ ଧଳା କାଗଜ ନିଅ । ଅଟା, ସିଝାଆଳୁ, ଚିନାବାଦାମ ଗୁଣ୍ଡ, କୋରାଯାଇଥିବା ପାକଳ ନଡ଼ିଆ, ସୋରିଷ ଗୁଣ୍ଡ ଅଲଗା ଅଲଗା କାଗଜରେ ଘସି ଗୁଣ୍ଡ ପଦାର୍ଥଗୁଡ଼ିକୁ କାଗଜ ଉପରୁ ଝାଡ଼ିଦେଇ କାଗଜକୁ ଖରାରେ କିଛି ସମୟ ଶୁଖାଇ ଦିଅ । ଦେଖୁ ଯେଉଁ କାଗଜଟି ତେଲିଆ ଦେଖାଯାଉଛି, ସେଥୁରେ ଘସାଯାଇଥିବା ପଦାର୍ଥରେ ତେଲ ଅଛି । ଯେଉଁ କାଗଜ ତେଲିଆ ଦେଖା ଯାଉନାହିଁ, ସେଥୁରେ ଘସାଯାଇଥ‌ିବା ଖାଦ୍ୟ ପଦାର୍ଥରେ ତେଲ ନାହିଁ ବା କମ୍ ପରିମାଣରେ ରହିଛି ।
(i) ସ୍ନେହସାର ଜାତୀୟ ଖାଦ୍ୟରେ ଅଧୂକ ପରିମାଣରେ ତେଲ ଥାଏ ।
(ii) ଚିନାବାଦାମ, ସୋରିଷ, ନଡ଼ିଆ, ସୂର୍ଯ୍ୟମୁଖୀ ମଞ୍ଜି, ରାଶି, ଅତସୀ, କୁସୁମ, ଜଡ଼ା, ମାଛ ଓ ମାଂସର ଚର୍ବି, ଅଣ୍ଡାର କେଶର, ଗାଈ ଓ ମଇଁଷି ଘିଅ, ଲହୁଣି ଆଦି ସ୍ନେହସାର ଜାତୀୟ ଖାଦ୍ୟ ।

• ଯେଉଁ ସ୍ନେହସାର ଉଦ୍ଭଦରୁ ମିଳେ ତାହା ଉଦ୍ଭଜ ସ୍ନେହସାର ଏବଂ ଯାହା ପ୍ରାଣୀଙ୍କଠାରୁ ମିଳେ ତାହାକୁ ପ୍ରାଣୀଜ ସ୍ନେହସାର କୁହାଯାଏ ।
• ଖାଦ୍ୟରେ ଶ୍ଵେତସାର, ପୁଷ୍ଟିସାର, ସ୍ନେହସାର, ଭିଟାମିନ୍ ଓ ଖଣିଜ ଲବଣ ଥାଏ । ଏହା ମଧ୍ୟ ଆମ ଶରୀର ପାଇଁ ଏକାନ୍ତ ଆବଶ୍ୟକ ।

→ ପୋଷକ ଆମ ଶରୀର ପାଇଁ ଆବଶ୍ୟକ :
(i) ଖାଦ୍ୟରେ ଥ‌ିବା ଭିନ୍ନ ଭିନ୍ନ ପୋଷକ ଭିନ୍ନ ଭିନ୍ନ କାର୍ଯ୍ୟ କରନ୍ତି ଓ ଭିନ୍ନ ଭିନ୍ନ ଉତ୍ସରୁ ମିଳିଥାଆନ୍ତି ।

(ii) ଶ୍ଵେତସାର, ସ୍ନେହସାର ଓ ପୁଷ୍ଟିସାର ଅଭାବରେ ଅପପୁଷ୍ଟିଜନିତ ରୋଗ ହୋଇଥାଏ ।
(iii) ଶ୍ଵେତସାର ଅଭାବରେ ମାରାସମସ୍ ରୋଗ ହୁଏ । ଏହି ରୋଗର ଲକ୍ଷଣଗୁଡ଼ିକ ହେଲା- ପତଳାଝାଡ଼ା ହେବା, ବୃଦ୍ଧିରେ ବାଧା, ଶରୀର କ୍ଷୀଣ ହେବା, କେଶ କହରା ହେବା ଇତ୍ୟାଦି ।
(iv) ପୁଷ୍ଟିସାର ଅଭାବରେ କ୍ଲାସିଓକର୍ ରୋଗ ହୁଏ । ଏହି ରୋଗର ଲକ୍ଷଣଗୁଡ଼ିକ ହେଲା ଗୋଡ଼, ହାତ, ମୁହଁ
(v) ଜୀବସାର ବା ଭିଟାମିନ୍ ଆମ ଆଖୁ, ଦାନ୍ତ, ଅସ୍ଥିକୁ ସୁସ୍ଥ ରଖିବା ସଙ୍ଗେ ସଙ୍ଗେ ଶରୀରର ରୋଗ ପ୍ରତିରୋଧକ କ୍ଷମତା ବଢ଼ାଇଥାଏ । ଏହି ଭିଟାମିନ୍‌ର ଅଭାବରେ ବିଭିନ୍ନ ପ୍ରକାର ରୋଗ ହୁଏ ।

(vi) ଏତଦ୍‌ବ୍ୟତୀତ ଭିଟାମିନ୍ B,, B, Bj ଓ B, ରହିଛି । ସାଧାରଣତଃ ମାଛ, ମାଂସ, ଅଣ୍ଡା, କ୍ଷୀର, କଲିଜା ଆଦିରେ ଭିଟାମିନ୍ B,, ଥାଏ । ଭିଟାମିନ୍ B, ରକ୍ତରେ ଥିବା ଲୋହିତ କୋଷିକା ତିଆରିରେ ସାହାଯ୍ୟ କରିଥାଏ ଏବଂ ସ୍ନାୟୁମାନଙ୍କ କାମପାଇଁ ମଧ୍ୟ ଏହା ଦରକାର ହୁଏ ।

• ଭିଟାମିନ୍ B ଓ ଭିଟାମିନ୍ C ଜଳରେ ଦ୍ରବଣୀୟ; କିନ୍ତୁ ଭିଟାମିନ୍ A, D, E ଓ K ସ୍ନେହସାରରେ ଦ୍ରବଣୀୟ ।

(vii) ଗାଈ ଓ ମଇଁଷି କ୍ଷୀରରେ ଭିଟାମିନ୍ C ବ୍ୟତୀତ ଅନ୍ୟ ସମସ୍ତ ପୋଷକ ଥାଏ ।
(viii) ଖାଦ୍ୟପଦାର୍ଥରେ ଥ‌ିବା ଖଣିଜ ଲବଣ ଆମ ଶରୀରର ଅନେକ କାର୍ଯ୍ୟରେ ଲାଗିଥାଏ । ଏହାର ଅଭାବରେ

• ଲୁଣର ରାସାୟନିକ ନାମ ସୋଡ଼ିୟମ୍‌ କ୍ଲୋରାଇଡ୍ ।

→ ତନ୍ତୁଜାତୀୟ ଖାଦ୍ୟ :

• କେତେକ ଖାଦ୍ୟରେ ଅଧୂକ ପରିମାଣରେ ତନ୍ତୁ ଥାଏ ।
• ତନ୍ତୁ ଶରୀର ପାଇଁ ଏକ ପୋଷକ ନହେଲେ ମଧ୍ୟ ଏହା ଖାଦ୍ୟ ନଳୀରୁ ମଳ ବାହାର କରିବାରେ ସାହାଯ୍ୟ କରେ । ଝାଡ଼ା ପରିଷ୍କାର ନହେଲେ ତନ୍ତୁଯୁକ୍ତ ଖାଦ୍ୟ ଖାଇବା ଉଚିତ ।
• ଚୋପାଲଗା କଞ୍ଚାଫଳ ଓ ମଞ୍ଜି, ଚୋପାଲଗା କଞ୍ଚା ପରିବା; ଯଥା – ଟମାଟୋ, ମୂଳା, ଗାଜର, ବିଟ୍, କାକୁଡ଼ି, ଚକିପେଶା ଅଟା, ଚୋପାଲଗା ଡାଲି ଓ ସମସ୍ତ ପ୍ରକାର ଶାଗରେ ତନ୍ତୁ ଥାଏ । ପନିପରିବାରେ ତନ୍ତୁ ଅଂଶ ଅଧ୍ୟା ଥାଏ । ସବୁଦିନ ସାଲାଡ୍ ଖାଇବା ଉଚିତ ।

→ ସୁଷମ ଖାଦ୍ୟ :

• ଆମେ ଗୋଟିଏ ପ୍ରକାର ଖାଦ୍ୟ ନ ଖାଇ ବିଭିନ୍ନ ପ୍ରକାର ଖାଦ୍ୟକୁ ମିଶାଇ ଖାଇଲେ ଆମ ଶରୀର ଆବଶ୍ୟକ ପୋଷକ ପାଇପାରିବ ।
• ଜଣେ ଲୋକ ପାଇଁ ବିଭିନ୍ନ ପୋଷକ ଥିବା ଆବଶ୍ୟକୀୟ ଖାଦ୍ୟର ପରିମାଣ ଲୋକଟିର ବୟସ, ଲିଙ୍ଗ, ତଥା ସେ କରୁଥିବା କାର୍ଯ୍ୟ ଉପରେ ନିର୍ଭର କରେ ।
• ଛୋଟ ଶିଶୁଟିଏ ପାଇଁ ଯେଉଁ ଖାଦ୍ୟ ଆବଶ୍ୟକ, ତାହା ତୁମପାଇଁ ଉପଯୁକ୍ତ ହୋଇ ନପାରେ ।
• ଯୁବକର ଉତ୍ତମ ସ୍ୱାସ୍ଥ୍ୟ ପାଇଁ ଆବଶ୍ୟକ ହେଉଥ‌ିବା ଖାଦ୍ୟ ବୃଦ୍ଧର ଖାଦ୍ୟଠାରୁ ଭିନ୍ନ ।
• ଆବଶ୍ୟକତା ପାଠ ପଢୁଥିବା, ଅଫିସରେ କାମ କରୁଥିବା ଲୋକଙ୍କ ଖାଦ୍ୟଠାରୁ ଭିନ୍ନ ଅଟେ ।
  • ବ୍ୟକ୍ତିର ଆବଶ୍ୟକତା ଅନୁସାରେ ଖାଦ୍ୟ ଉପାଦାନମାନ ଯୋଗାଇ ଦେଉଥ‌ିବା ଖାଦ୍ୟକୁ ସୁଷମ ଖାଦ୍ୟ କୁହାଯାଏ
  • ସୁଷମ ଖାଦ୍ୟର ତାଲିକା ପ୍ରସ୍ତୁତ କଲାବେଳେ ଲୋକଟିର ବୟସ, ଲିଙ୍ଗ, ତଥା ସେ କରୁଥିବା କାର୍ଯ୍ୟ ବିଚାରକୁ ନିଆଯାଏ ।
  • ଶରୀରର ଆବଶ୍ୟକତାକୁ ପୂରଣ କରୁଥିବା ଉପଯୁକ୍ତ ପରିମାଣର ଖାଦ୍ୟପଦାର୍ଥଗୁଡ଼ିକୁ ନେଇ ସୁଷମ ଖାଦ୍ୟର ତାଲିକା କରାଯାଏ ।
    ୧୦-୧୨ ବର୍ଷ ପିଲାଙ୍କର ଖାଦ୍ୟ ତାଲିକା :
    
  • ନିରାମିଷ ଭୋଜନ କରୁଥିବା ବ୍ୟକ୍ତି ଦୈନିକ ଚିନାବାଦାମ ଖାଇବା ଉଚିତ ।
  • ଖାଦ୍ୟ ଖାଇବା ସହିତ ଦୈନିକ ୮-୧୦ ଗିଲାସ ପାଣି ପିଇବା ଦରକାର ।

Odisha State Board BSE Odisha 7th Class Science Important Questions Chapter 8 ମାଟି (ମୃତ୍ତିକା) Important Questions and Answers.

BSE Odisha Class 7 Science Important Questions Chapter 8 ମାଟି (ମୃତ୍ତିକା)

Question 1.
ବୈଜ୍ଞାନିକ କାରଣ ଦର୍ଶାଅ :

(କ) ମୃତ୍ତିକା କ୍ଷୟ ଜମିର ଅନୁର୍ବରତା ପାଇଁ ଦାୟୀ ।
Solution:
(i) ମୃତ୍ତିକା କ୍ଷୟ ପାଇଁ ଜଳ ଓ ବାୟୁ ମୁଖ୍ୟତଃ ଦାୟୀ ।
(ii) ଅଧିକ ବେଗରେ ବୃଷ୍ଟିପାତ ହେଲେ ଜଳବିନ୍ଦୁ ମାଟିରେ ବାଡ଼େଇ ହୋଇ ମାଟିକଣାଗୁଡ଼ିକୁ ଅଲଗା କରିଦିଏ । ଫଳରେ ପୃଷ୍ଠ ମୃତ୍ତିକାରେ ଥ‌ିବା ଜୈବପଦାର୍ଥ ଓ ଖଣିଜ ଲବଣ ଧୋଇ ହୋଇ ସ୍ଥାନାନ୍ତରିତ ହୁଏ ।
(iii) ଅଧୁକ ବେଗରେ ଖରାଦିନେ ପବନ ବୋହିଲେ ମାଟିର ଉପର ସ୍ତରରୁ ଧୂଳି ଉଡ଼ି ସ୍ଥାନାନ୍ତରିତ ହୁଏ । ଏହି ମାଟିରେ ଥ‌ିବା ଜୈବପଦାର୍ଥ ଓ ଖଣିଜ ଲବଣ ଆଦି ମଧ୍ୟ ସ୍ଥାନାନ୍ତରିତ ହୋଇ ମାଟିକୁ ଅନୁର୍ବର କରିଦିଏ । ଏଣୁ ମୃଭିକା କ୍ଷୟ ଜମିର ଅନୁର୍ବରତା ପାଇଁ ଦାୟୀ ହୋଇଥାଏ ।

(ଖ) ମୃତ୍ତିକା ସଂରକ୍ଷଣ କରିବା ପାଇଁ ବୃକ୍ଷରୋପଣ କରିବା ନିହାତି ଆବଶ୍ୟକ ।
Solution:
(i) କଲେ ଉଭିଦର ଚେର ମାଟିକୁ ଜାବୁଡ଼ିଧରି ଏହାକୁ ସ୍ଥାନାନ୍ତରିତ ହେବାକୁ ସୁଯୋଗ ଦିଏ ନାହିଁ । ଏଣୁ ପଡ଼ିଆରେ ଘାସ ଥିଲେ, ଗୋରୁ ଚାରଣ ବାରଣ କରିବା ଉଚିତ୍ ।
(ii) ଏହାଛଡ଼ା ଉଭିଦ ମାନଙ୍କର ଡାଳପତ୍ର ମାଟିକୁ ଘୋଡ଼ାଇରଖ୍ ପାଣି, ପବନ ଓ ସୂର୍ଯ୍ୟତାପ ପ୍ରକୋପରୁ ଏହାକୁ
(iii) ଗଛଲତାର ଶୁଖୁଲା ଡାଳପତ୍ର ମାଟି ଉପରେ ପଡ଼ିରହି ଉପରୁ ତଳକୁ ଦିଏ ଏବଂ ମୃତ୍ତିକା କ୍ଷୟ ରୋକିବାରେ ସାହାଯ୍ୟ କରେ । ଏଣୁ ମୃର୍ତ୍ତିକା ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।

Question 2.
(କ) ପୃଷ୍ଠମୃତ୍ତିକା ଓ ଉପମୃତ୍ତିକା

(ଖ) ବାଲିଆ ମାଟି ଓ ଦୋରସା ମାଟି

(ଗ) ଲାଲ୍ ମାଟି ଓ କଳା ମାଟି

(ଘ) ପଟୁ ମାଟି ଓ ପାହାଡ଼ିଆ ମାଟି

Question 3.
ହ୍ୟୁମସ୍ କ’ଣ ? ଏହାର ଆବଶ୍ୟକତା ଲେଖ ।
Solution:
(i) ତାହାର ବିଘଟନରେ ଯେଉଁ ଅଂଶ ଗଠିତ ହୁଏ, ତାହାକୁ ହ୍ୟୁମସ୍ କହନ୍ତି ।
(ii) ଏହା ଦେଖିବାକୁ ଚିକ୍କଣ ଓ ଅଠାଳିଆ । ଏହା ମାଟିକୁ ଉର୍ବର କରେ ଫଳରେ ଏପରି ମାଟିରେ ଫସଲ କଲେ ଥ‌ିବାରୁ ଏହା ଉର୍ବର ।

Question 4.
ମାଙ୍କଡ଼ା ମାଟି ବା ମୋରମ୍ କାହାକୁ କହନ୍ତି ? ଆମ ରାଜ୍ୟରେ ଏହା କେଉଁଠି ଦେଖାଯାଏ ?
Solution:
(i) ଲାଲମାଟି ସହ କାଦୁଅ ଓ ଗୋଡ଼ି ମିଶିଲେ ମାଙ୍କଡ଼ା ମାଟି ବା ମୋରମ ସୃଷ୍ଟି ହୁଏ । ଏହା ଅନୁର୍ବର ମାଟି ।
(ii) ଆମ ରାଜ୍ୟର ଖୋର୍ଦ୍ଧା ଓ ଭୁବନେଶ୍ୱର ଅଞ୍ଚଳରେ ଏହି ମାଟି ଦେଖାଯାଏ ।

Question 5.
ମୃତ୍ତିକାର ଉପାଦାନଗୁଡ଼ିକ କ’ଣ ?
Solution:
(i) ବାଲି, କାଦୁଅ, ଜୈବପଦାର୍ଥ ଓ ଶିଳାରେ ଥ‌ିବା ଲବଣ ମିଶି ମାଟି ସୃଷ୍ଟି ହୁଏ । ଏଥରେ ପ୍ରଧାନତଃ ଦୁଇଟି ଉପାଦାନ ଦେହାବଶେଷ ଓ ମଳମୂତ୍ର ଏବଂ ଉଭିଦର ବିଘଟନରୁ ହ୍ୟୁମସ୍ ସୃଷ୍ଟି ହୋଇଥାଏ । ଏହା ହେଉଛି ମାଟିର ଜୈବିକ ଭପାଦାନ |
(ii) ଦେଖାଯାଏ; ଯଥା – ସରୁବାଲି, ମୋଟାବାଲି, ସରୁଗରଡ଼ା ଓ ବାଲିଗରଡ଼ା ।

ସଂଶିପ୍ତଧାମା ପ୍ରଣୋଉର :

I. ଉପଯୁକ୍ତ ଶବ୍ଦଦ୍ୱାରା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ମୃଭିକା ଏକ _________ ଉର୍ବର ।
(ii) ମୃଭିକା କ୍ଷୟ ମାଟିର _________ କମାଇଥାଏ ।
(iii) ମୃତ୍ତିକାରେ ସବୁଠାରୁ ଅଧିକ _________ ଉପାଦାନ ଥାଏ ।
(iv) _________ ମାଟି ସବ୍ଲଠାରୁ ଭରର |
(v) ମାଟିରେ _________ ରହିଲେ ତାହାର ରଙ୍ଗ ଧୂସର ହୁଏ ।
(vi) 70 ରୁ 80 ଭାଗ ବାଲିଥିବା ମୃତ୍ତିକାକୁ _________ କୁହାଯାଏ ।
(vii) ଧାନଚାଷପାଇଁ _________ ମାଟି ଉତ୍ତମ ।
(viii) _________ ମାଟିରେ ପନିପରିବା ଚାଷ କରାଯାଏ ।
(ix) _________ ଦ୍ଵାରା ମୃତ୍ତିକା କ୍ଷୟ ରୋକାଯାଇ ପାରିବ ।
(x) ବାଲିଆ ଓ କାଦୁଆ ଉପାଦାନ ସମପରିମାଣରେ ମିଶି _________ ଗଠିତ ହୋଇଥାଏ ।
(xi) ମୃତ୍ତିକାର ଦ୍ଵିତୀୟ ସ୍ତରରେ _________ ର ପରିମାଣ ଅଧ୍ଵ ଥାଏ ।
(xii) କୃଷ୍ଣ ମୃତ୍ତିକା (କଳାମାଟି) _________ ଚାଷ ପାଇଁ ଅଧ‌ିକ ଉପଯୋଗୀ ।
(xiii) ଲୋହିତ ମୃତ୍ତିକା ମାଙ୍ଗାନିଜ ଲବଣ ଓ _________ ମାଟିରେ ପନିପରିବା ଚାଷ କରାଯାଏ ।
(xiv) _________ ମାଟିରେ ଶତକଡ଼ା 50 – 60 ଭାଗ ଛିଦ୍ରସ୍ଥାନ ଥାଏ ।
(xv) ବାଲିଆ ମାଟିର ଜଳଧାରଣ କ୍ଷମତା _________ |
(xvi) ଉଦ୍ଭଦ ନିଜର ପୁଷ୍ଟି ପାଇଁ ମାଟିତଳୁ _________ ଓ _________ ଶୋଷଣ କରେ ।
(xvii) ଲାଲ୍ ମାଟିରେ, _________ ଓ _________ ର ଲବଣ ପରିମାଣ ଅଧ୍ଵ ଥାଏ ।
(xviii) ଧାଲା ମାଟିରେ _________ ଓ _________ ଅଧ୍ୟକ ପରିମାଣରେ ଥାଏ ।
(xix) କଳା ମାଟିରେ _________ ଓ _________ ର ଲବଣ ଅଧିକ ଥାଏ ।
(xx) ଓଡ଼ିଶାର _________ ଓ _________ ଅଥଲରେ ମାଇତା ମାଟି ଦେଖାଯାଏ |
(xxi) ମଟାଳ ମାଟିରେ _________ ରୁ _________ ଭାଗ ଛିଦ୍ରସ୍ଥାନ ଥାଏ ।
(xxii) _________ ମାଟିରେ କଲଧାରଣ ଯମତା ସଢାଧିକ ଓ _________ ମାଟିରେ ସର୍ବନିମ୍ନ ।
(xxiii) _________ ଓ _________ ମୃତ୍ତିକା ଅବକ୍ଷୟର ମୁଖ୍ୟ ପ୍ରାକୃତିକ କାରକ ଅଟନ୍ତି |
Solution:
(i) ପ୍ରାକୃତିକ
(ii) ଉର୍ବରତା
(iii) ଅଜୈବିକ
(iv) ପଟୁ
(v) ହ୍ୟୁମସ
(vi) ବାଲିଆ
(vii) ମମାନ
(viii) ଦୋରସା
(ix) ବୃକ୍ଷରୋପଣ
(x) ଦୋରସା ମାଟି
(xi) ଖଣିଜ ପଦାର୍ଥ
(xii) କପା
(xiii) ଲତ୍ରର
(xiv)ମଟାଳ
(xv) ସନ୍ଦନିମ୍ନ
(xvi) ଜଳ, ପୋଷକ
(xix) ଲୌହ, ମ୍ୟାଗ୍ନେସିୟମ୍
(xx) ଖୋର୍ଦ୍ଧା, ଭୁବନେଶ୍ଵର
(xxi)50,60
(xxii) ମଟାଳ, ବାଲିଆ
(xxiii) ଜଳ, ବାୟୁ
(xvii) ଲୌହ, ମାଙ୍ଗାନିଜ
(xviii) ଚୂନ, ଆଲୁମିନିୟମ୍‌ ଅକ୍‌ସାଇଡ୍

II. ବାମପାର୍ଶ୍ବରେ ଥ‌ିବା ଶବ୍ଦଦ୍ୱୟର ସମ୍ପର୍କକୁ ଦେଖୁ ଦକ୍ଷିଣପାର୍ଶ୍ବର ଶବ୍ଦର ସମ୍ପର୍କିତ ଶବ୍ଦଟି ଲେଖ ।
(i) ଧାନ : ମଟାଳ :: ପନିପରିବା : _________
(ii) ଚିନାବାଦାମ : ବାଲିଆ :: ନଳିତା : _________
(iii) ପ୍ରଥମ ସ୍ତର ମୃତ୍ତିକା : ଉର୍ବର :: ଦ୍ଵିତୀୟ ସ୍ତର ମୃତ୍ତିକା : _________
(iv) ବୃକ୍ଷରୋପଣ : ମୃତ୍ତିକା ସଂରକ୍ଷଣ :: ଜଙ୍ଗଲ ଉଚ୍ଛେଦ _________
(v) ମରୁମାଟି : ରାଜସ୍ଥାନ :: ମାଙ୍କଡ଼ା ମାଟି : _________
(vi) ସର୍ବାଧ‌ିକ ଜଳଧାରଣ କ୍ଷମତା : ମଟାଳ ମାଟି :: _________
(vii) କଳାମାଟି : ଲୌହ ଓ ମାଗ୍ନେସିୟମ :: ଲାଲମାଟି : _________
(viii) ହ୍ୟୁମସ୍ : ଧୂସର :: ବକ୍‌ସାଇଟ : _________
(ix) ଟାଙ୍ଗରା ଜମିରେ କାଜୁବାଦାମ ଚାଷ : ମୃତ୍ତିକା ସଂରକ୍ଷଣ :: ବକ୍‌ସାଇଟ : _________
(x) ଦୋରସା ପଟୁ ମାଟି : ମକା :: କୃଷ୍ଣମୃତ୍ତିକା : _________
Solution:
(i) ବୋରପା
(ii) ମଟାଳ
(iii) ଅନୁର୍ବର
(iv) ମୃତ୍ତିକାକ୍ଷୟ
(v) ଖୋର୍ଦ୍ଧା
(vi) ବାଲିଆ ମାଟି
(vii) ମାଙ୍ଗାନିଜ ଓ ଲୌସ
(viii) ଧାଳା
(ix) ମୃତ୍ତିକା କ୍ଷୟ
(x) କାପା

III. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ପ୍ରଶ୍ନତଳେ ଦିଆଯାଇଛି । ସେଥୁମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

(i) ମାଟିରେ ଥବା ମୋଟା ବାଲିର ବ୍ୟାସ ପ୍ରାୟ –
(କ) 2.0 ରୁ 5.0 ମି.ମି.
(ଖ) 0.02 ରୁ 0.2 ମି.ମି.
(ଗ) 0.7 ରୁ 2.0 ମି.ମି.
(ଘ) 0.002 ରୁ 0.02 ମି.ମି.
Solution:
(ଘ) 0.002 ରୁ 0.02 ମି.ମି.

(ii) ଯେଉଁ ମାଟିରେ ବକ୍‌ସାଇଟ୍ ଅବ୍ଲକ ପରିମାଣରେ ଥାଏ ତାହାକୁ କେଉଁ ପ୍ରକାର ମାଟି କହନ୍ତି ?
(କ) ଲାଲମାଟି
(ଖ) ମଶାଳ ମାଟି
(ଗ) ଧୁସରମାନି
(ଘ) ଧଲାମାଟି
Solution:
(ଘ) ଧଲାମାଟି

(iii) ଝାଉଁ ଗଛ ପାଇଁ କେଉଁ ମାଟି ଉପଯୋଗୀ ?
(କ) ବାଲିଆ ମାଟି
(ଖ) ମଶାଳ ମାଟି
(ଗ) ଦୋରସା ମାଟି
(ଘ) ପଟୁ ମାଟି
Solution:
(କ) ବାଲିଆ ମାଟି

(iv) ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟିର ମୃତ୍ତିକା ଗଠନରେ ଭୂମିକା ନାହିଁ ?
(କ) ଉକା
(ଖ) ସୁଯକରିଣ
(ଗ) ସୂର୍ଯ୍ୟକିରଣ
(ଘ) ବିକ୍ଳି
Solution:
(ଘ) ବିକ୍ଳି

(v) ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ଅତି ଉର୍ବର ମୃତ୍ତିକା ?
(କ) ପୃଷ୍ଠ ମୃତ୍ତିକା
(ଖ) ମୃତ ମୂରିକା
(ଗ) ଭପସ୍ଣିକା
(ଘ) ବାଲିଥା ମୂଶିକା
Solution:
(କ) ପୃଷ୍ଠ ମୃତ୍ତିକା

(vi) ଯେଉଁ ମାଟିର ଜଳଧାରଣ କ୍ଷମତା ସର୍ବାଧ୍ଵକ ସେହି ମାଟି ପାଇଁ ନିମ୍ନୋକ୍ତ କେଉଁ ଫସଲ ଉପଯୁକ୍ତ ?
(କ) ଆଳୁ
(ଖ) ଚିନାବାଦାମ୍
(ଗ) କତା
(ଘ) ସୂର୍ଯ୍ୟମୁଖୀ
Solution:
(ଗ) କତା

(vii) ମାଟିରେ କେଉଁଟି ଅଧୂକ ରହିଲେ ମାଟି ଉର୍ବର ହୋଇଥାଏ ?
(କ) ହ୍ୟୁମସ୍
(ଖ) ଲୌହ ଅକ୍‌ସାଇଡ
(ଗ) ବାୟୁ
(ଘ) ତକ୍ସାଲଟ
Solution:
(କ) ହ୍ୟୁମସ୍

(viii) ନଈକୂଳ ଅତଡ଼ା ଖାଉଥିଲେ ମୃତ୍ତିକାକ୍ଷୟ କିପରି ରୋକିବାକୁ ହେବ ?
(କ) ପଥର ବନ୍ଧ ତିଆରି କରି
(ଖ) ବୃକ୍ଷରୋପଣ କରି
(ଗ) ସୋପାନପ୍ରଣାଳୀ ବ୍ୟବହାର କରି
(ଘ) ବୃଷ୍ଟିପାତ
Solution:
(ଘ) ବୃଷ୍ଟିପାତ

IV. ‘କ’ ସ୍ତମ୍ଭରେ ଥ‌ିବା ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ସଂଯୋଗ କର ।

V. ରେଖାଙ୍କିତ ପଦ ନ ବଦଳାଇ ଭ୍ରମ ଥିଲେ ସଂଶୋଧନ କର ।
(i) ମଟାଳ ମାଟିରେ ଶତକଡ଼ା 50-60 ଭାଗ ଛିଦ୍ରସ୍ଥାନ ଥାଏ ।
(ii) ସର୍ବାଧ‌ିକ ଜଳଧାରଣ କ୍ଷମତା ଦୋରସା ମାଟିର ଥାଏ ।
(iii) ଯେଉଁ ପ୍ରକ୍ରିୟାରେ ଉପର ପାଣି ମାଟି ଦେଇ ତଳକୁ ଗଲା, ତାହାକୁ ଶୋଷଣ କହନ୍ତି ।
(iv) ଛୋଟ ବାଲିଗରଡ଼ାର ହାରାହାରି ବ୍ୟାସ 0.02 ରୁ 0.2 ଅଟେ ।
(v) ମାଟି ସୃଷ୍ଟି ହେବା ଏକ ଅତ୍ୟନ୍ତ ଦୃଢ଼ ପ୍ରକ୍ରିୟା ।
Solution:
(i) ମଟାଳ ମାଟିର ଶତକଡ଼ା 30 40 ଭାଗ ଛିଦ୍ରସ୍ଥାନ ଥାଏ ।
(ii) ସର୍ବାଧ‌ିକ ଜଳଧାରଣ କ୍ଷମତା ମଟାଳ ମାଟିର ଥାଏ ।
(iii) ଯେଉଁ ପ୍ରକ୍ରିୟାରେ ଉପର ପାଣି ମାଟି ଦେଇ ତଳକୁ ଗଲା । ତାହାକୁ ଅବଶୋଷଣ କହନ୍ତି ।
(iv) ମୋଟା ବାଲିର ହାରାହାରି ବ୍ୟାସ 0.02 ରୁ 0.2 ଅଟେ ।
(v) ମାଟି ସୃଷ୍ଟି ହେବା ଏକ ଅତ୍ୟନ୍ତ ମନ୍ଥର ପ୍ରକ୍ରିୟା ।

VI. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
(i) ରଙ୍ଗର ବିଭିନ୍ନତାକୁ ନେଇ ମାଟିର ପ୍ରକାର ଲେଖ ।
(ii) କଳାମାଟିରେ କେଉଁ ଲବଣ ଥାଏ ?
(iii) ଉପାଦାନ ଅନୁସାରେ ମାଟି କେତେ ପ୍ରକାର ଓ କ’ଣ କ’ଣ ?
(iv) । ସେ.ମି. ମାଟି ସୃଷ୍ଟି ହେବାକୁ କେତେ ସମୟ ଲାଗେ ?
(v) ମାଟିର ଉପର ସ୍ତରକୁ କ’ଣ କହନ୍ତି ?
(vi) ଭୂ-ଶିଳାସ୍ତର କାହାକୁ କୁହାଯାଏ ?
(vii) ଅବଶୋଷଣ କାହାକୁ କହନ୍ତି ?
(viii) ଶୋଷଣ କ’ଣ ?
(ix) ଉଦ୍ଭଦ ମାଟିରୁ କ’ଣ ପାଏ ?
(x) ମାଟିର ଉପାଦାନଗୁଡ଼ିକ କ’ଣ ?
Solution:
(i) ରଙ୍ଗର ବିଭିନ୍ନତାକୁ ନେଇ ମାଟି ଚାରି ପ୍ରକାର; ଯଥା – ଲାଲ, କଳା, ଧଳା ଓ ଧୂସର ।
(ii) କଳାମାଟିରେ ଲୁହା ଓ ମାଗ୍ନେସିୟମ ଲବଣ ଥାଏ ।
(iii) ଉପାଦାନ ଆଧାରରେ ମାଟି ଚାରି ପ୍ରକାର; ଯଥା- ବାଲିଆ, ଦୋରସା, ମଟାଳ ଓ କାଦୁଆ ।
(iv) ସେ.ମି. ମାଟି ସୃଷ୍ଟି ହେବାକୁ ପ୍ରାୟ 500ରୁ 1000 ବର୍ଷ ସମୟ ଲାଗେ ।
(v) ମାଟିର ଉପର ସ୍ତରକୁ ହ୍ୟୁମସ୍ କହନ୍ତି ।
(vi) ମାଟିର ଭିତରର ତୃତୀୟସ୍ତରକୁ ଭୂ-ଶିଳାସ୍ତର କହନ୍ତି ।
(vii) ଭୂପୃଷ୍ଠରୁ ଜଳ ମାଟିଭେଦ କରି ମାଟିର ଭିତର ସ୍ତରକୁ ଯିବା ପ୍ରକ୍ରିୟାକୁ ଅବଶୋଷଣ କୁହାଯାଏ ।
(viii)ମାଟିର ଅଭ୍ୟନ୍ତରରୁ ଜଳ ମାଟିର ଉପରକୁ ସଞ୍ଚରିତ ହୋଇ ଆସିବା ପ୍ରକ୍ରିୟାକୁ ଶୋଷଣ କୁହାଯାଏ ।
(ix) ଉଦ୍ଭଦ ମାଟିରୁ ଜଳ ଓ ଖଣିଜ ଲବଣ ପାଏ ।
(x) ବାଲି, ପଟୁ, କାଦୁଅ ଓ ଖଣିଜଲବଣ ମାଟିର ଉପାଦାନ ଅଟନ୍ତି ।