Odisha State Board BSE Odisha 8th Class History Important Questions Chapter 3 ଇଂରେଜ ଶାସନକୁ ପ୍ରତିରୋଧ Important Questions and Answers.
BSE Odisha Class 8 History Important Questions Chapter 3 ଇଂରେଜ ଶାସନକୁ ପ୍ରତିରୋଧ
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧ । ଖୋର୍ଦ୍ଧାରାଜାଙ୍କ ମନ୍ତ୍ରୀଭାବେ ଜୟୀରାଜଗୁରୁଙ୍କ କାର୍ଯ୍ୟାବଳୀ ଉଲ୍ଲେଖ କର ।
Answer:
ଅଭିଭାବକ ଭାବେ କାର୍ଯ୍ୟ :
- ରାଜା ଦିବ୍ୟସିଂହଦେବଙ୍କ ମୃତ୍ୟୁ ପରେ ତାଙ୍କର ନାବାଳକ ପୁତ୍ର ଦ୍ଵିତୀୟ ମୁକୁନ୍ଦଦେବ ରାଜା ହେଲାପରେ ଜୟୀ ରାଜଗୁରୁ ତାଙ୍କର ଅଭିଭାବକଭାବେ କାର୍ଯ୍ୟ କଲେ ।
- ୧୭୮୯ ଖ୍ରୀ.ଅ.ରେ ସେ ସମସ୍ତ ପ୍ରକାର ଶାସନ ନିୟନ୍ତ୍ରଣ କ୍ଷମତା ହାତକୁ ନେଲେ ।
ଦୁର୍ଭିକ୍ଷ :
ସେହି ସମୟରେ ଛୋଟ ଛୋଟ ରାଜ୍ୟଗୁଡ଼ିକ ମଧ୍ୟରେ ଅନ୍ତଯୁଦ୍ଧ ଚାଲିଥିଲା ଏବଂ ଦୁର୍ଭିକ୍ଷ ପଡ଼ିବାରୁ ଘୋର ସଂକଟ ଦେଖାଦେଲା । ଏହି ସମୟରେ ଜୟୀ ରାଜଗୁରୁଙ୍କ ଭୂମିକା ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଥିଲା ।
ଆଖଡ଼ାଶାଳ :
ପାଇକମାନଙ୍କୁ ଯୁଦ୍ଧବିଦ୍ୟାରେ ତାଲିମ ଦେବାପାଇଁ ସେ ଆଖଡ଼ାଶାଳ ପ୍ରତିଷ୍ଠା କରି ସେମାନଙ୍କୁ ଦେଶପ୍ରେମରେ ଉଦ୍ବୁଦ୍ଧ କରାଇଥିଲେ ।
ଦେଶଭକ୍ତି :
ଇଂରେଜମାନେ ବିଶ୍ୱାସଘାତକତା କରିବାରୁ ଜୟୀ ରାଜଗୁରୁ ରାଜାଙ୍କୁ ସେମାନଙ୍କ ବିରୋଧରେ ଯୁଦ୍ଧ କରିବାକୁ ପରାମର୍ଶ ଦେଇଥିଲେ । ଯଦିଓ ଖୋର୍ଦ୍ଧା ଶେଷରେ ଇଂରେଜ ଶାସନାଧୀନ ହେଲା, ତଥାପି ଜୟୀ ରାଜଗୁରୁଙ୍କ ଦେଶଭକ୍ତି ଓ ତ୍ୟାଗ ଚିରସ୍ମରଣୀୟ ।

୨ । ପାଇକ ବିଦ୍ରୋହର ଅବସାନ କିପରି ଘଟିଥିଲା ?
Answer:
ବିଦ୍ରୋହୀମାନଙ୍କ ଆତ୍ମସମର୍ପଣ :
ପାଇକ ବିଦ୍ରୋହକୁ ଦମନ କରିବା ପାଇଁ ଇଂରେଜମାନେ ଆପ୍ରାଣ ଉଦ୍ୟମ କଲେ । ଫଳରେ ଅନେକ ବିଦ୍ରୋହୀ ଆତ୍ମସମର୍ପଣ କଲେ ।
ସମ୍ପତ୍ତି ବ୍ୟାଜାପ୍ତି :
ବକ୍ସି ଜଗବନ୍ଧୁ ଆତ୍ମସମର୍ପଣ ନ କରିବାରୁ ୧୮୨୩ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଇଂରେଜ ସରକାର ତାଙ୍କର ସମସ୍ତ ସମ୍ପତ୍ତି ବାଜ୍ୟାପ୍ତ କରିଦେଲେ ।
ଘୋଷଣା :
ସେ ଆତ୍ମସମର୍ପଣ କଲେ ତାଙ୍କୁ ସସମ୍ମାନେ ବୃତ୍ତି ଦିଆଯିବ ବୋଲି ଇଂରେଜ ସରକାର ଘୋଷଣା କଲେ ।
ଆତ୍ମସମର୍ପଣ :
ତେଣୁ ଦୀର୍ଘଦିନର ଆତ୍ମଗୋପନ ପରେ ୧୮୨୫ ଖ୍ରୀ.ଅ. ମେ ମାସରେ କଟକ ସହରରେ ଇଂରେଜ ସରକାରଙ୍କ ନିକଟରେ ସେ ଆତ୍ମସମର୍ପଣ କଲେ ।
ନଜରବନ୍ଦୀ :
ତାଙ୍କୁ କଟକ ସହରରେ ନଜରବନ୍ଦୀ କରି ରଖାଗଲା ଓ ପାଇକ ବିଦ୍ରୋହର ଅବସାନ ଘଟିଲା ।
୩ । ସିପାହୀ ବିଦ୍ରୋହର ରାଜନୈତିକ କାରଣ ଲେଖ ।
Answer:
ନିମ୍ନଲିଖୂତ ରାଜନୈତିକ କାରଣଗୁଡ଼ିକ ସିପାହୀ ବିଦ୍ରୋହ ପାଇଁ ଦାୟୀ ଥିଲା ।
ରାଜ୍ୟବିସ୍ତାର ନୀତି :
- ଇଂରେଜମାନେ ଭାରତକୁ ବାଣିଜ୍ୟ କରିବାକୁ ଆସି ଶାସନ ଡୋରି ଧରିବାର ଲକ୍ଷ୍ୟ ପୋଷଣ କଲେ ।
- ୱେଲସ୍ଲିଙ୍କ ସାମନ୍ତ ସନ୍ଧି ପ୍ରଥା ଏବଂ ଡେଲ୍ହାଉସୀଙ୍କ ରାଜ୍ୟସ୍ୱତ୍ୱ ଲୋପନୀତିଦ୍ଵାରା ଅନେକ ଦେଶୀୟ ରାଜ୍ୟ ଇଂରେଜ ସାମ୍ରାଜ୍ୟଭୁକ୍ତ ହୋଇଥିଲା ।
ସମ୍ରାଟଙ୍କ ସ୍ଥାନାନ୍ତରଣ :
- ମୋଗଲ ସମ୍ରାଟ ବାହାଦୁର ଶାହାଙ୍କୁ ଦିଲ୍ଲୀର ଲାଲକିଲ୍ଲାରୁ କୁତବ ଅଞ୍ଚଳକୁ ପଠାଇ ଦିଆଗଲା ।
- ଅଯୋଧ୍ୟାକୁ ଇଂରେଜ ସାମ୍ରାଜ୍ୟରେ ମିଶାଇ ଦିଆଗଲା ।
- ପେଶବା ଦ୍ଵିତୀୟ ବାଜିରାଓଙ୍କ ମୃତ୍ୟୁପରେ ତାଙ୍କ ପୋଷ୍ୟପୁତ୍ର ନାନାସାହେବଙ୍କ ଭତ୍ତା ବନ୍ଦ କରି ଦିଆଗଲା ।

୪ । ମହାରାଣୀ ଭିକ୍ଟୋରିଆଙ୍କ ଘୋଷଣାପତ୍ରରେ କି କି ବ୍ୟବସ୍ଥାମାନ ଉଲ୍ଲେଖ କରାଯାଇଥିଲା ?
Answer:
ମହାରାଣୀଙ୍କ ଘୋଷଣାପତ୍ରରେ କେତେକ ବ୍ୟବସ୍ଥା ଉଲ୍ଲେଖ ଥିଲା; ଯଥା—
- କମ୍ପାନୀ ଶାସନ କାଳରେ ଦେଶୀୟ ରାଜାମାନଙ୍କ ସହ ହୋଇଥିବା ଚୁକ୍ତି ଅପରିବର୍ତ୍ତିତ ରହିବ ।
- ଦେଶୀୟ ରାଜାମାନଙ୍କ କ୍ଷମତା, ସମ୍ମାନ ଓ ପଦମର୍ଯ୍ୟାଦା ଅକ୍ଷୁଣ୍ଣ ରହିବ ।
- ଭାରତୀୟମାନଙ୍କ ଧର୍ମବିଶ୍ଵାସ ଉପରେ ହସ୍ତକ୍ଷେପ କରାଯିବ ନାହିଁ ।
- ଭାରତୀୟମାନଙ୍କ ମୌଳିକ ପରମ୍ପରା, ସାମାଜିକ ରୀତିନୀତି ଉପରେ ହସ୍ତକ୍ଷେପ କରାଯିବ ନାହିଁ ।
- ଜାତି-ଧର୍ମ-ବର୍ଣ୍ଣ ନିର୍ବିଶେଷରେ ଭାରତୀୟମାନଙ୍କୁ ଯୋଗ୍ୟତାଭିଭିକ ନିଯୁକ୍ତି ଦିଆଯିବ ।
୫ | ୧୮୫୭ ବିଦ୍ରୋହରେ ଓଡ଼ିଶାର ଭୂମିକା ବର୍ଣ୍ଣନା କର ।
Answer:
ନେତୃତ୍ବ :
- ୧୮୫୭ ଜାତୀୟ ବିଦ୍ରୋହ କାଳରେ ଭାରତର ଅନ୍ୟାନ୍ୟ ଅଞ୍ଚଳ ପରି ଓଡ଼ିଶାରେ ଉଲ୍ଲେଖନୀୟ ଘଟଣା ଘଟିଥିଲା ।
- ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ସମ୍ବଲପୁରଠାରେ ୧୮୫୭ ବିଦ୍ରୋହର ନେତୃତ୍ୱ ନେଇଥିଲେ । ସେ ତାନ୍ତିଆ ତୋପେ, ଲକ୍ଷ୍ମୀବାଈ ଓ ନାନାସାହେବଙ୍କ ସମକକ୍ଷ ଥିଲେ ।
ସୁରେନ୍ଦ୍ର ସାଏଙ୍କ ଭୂମିକା :
- ୧୮୫୭ ଜୁଲାଇ ୩୧ ତାରିଖ ଦିନ ବିଦ୍ରୋହୀମାନେ ହଜାରୀବାଗ ଜେଲ୍ ଭାଙ୍ଗି ବନ୍ଦୀମାନଙ୍କୁ ମୁକ୍ତ କରିଦେଲେ । ବନ୍ଦୀମାନଙ୍କ ମଧ୍ୟରେ ସୁରେନ୍ଦ୍ର ସାଏ ଓ ତାଙ୍କ ସାନ ଭାଇ ଉଦନ୍ତ ସାଏ ଥିଲେ । ସେମାନେ ସମ୍ବଲପୁର ଆସି ଇଂରେଜମାନଙ୍କ ବିରୁଦ୍ଧରେ ଆଦିବାସୀମାନଙ୍କୁ ସଙ୍ଗଠିତ କରିଥିଲେ ।
- ଜମିଦାର, ଗୌନ୍ତିଆ ଓ ମାନ୍ୟଗଣ୍ୟ ବ୍ୟକ୍ତିମାନେ ତାଙ୍କୁ ସ୍ଵାଗତ କରିଥିଲେ । ଇଂରେଜ ସେନାପତି ଲି ତାଙ୍କ ସଶସ୍ତ୍ର ଆବିର୍ଭାବରେ ଭୟଭୀତ ହୋଇ ତାଙ୍କ ନିବେଦନପତ୍ର ଉଚ୍ଚ କର୍ତ୍ତୃପକ୍ଷଙ୍କ ବିଚାର ପାଇଁ ପଠାଇଦେବାକୁ ପ୍ରତିଶ୍ରୁତି ଦେଲେ ।
- କିଛି ଦିନ ଅପେକ୍ଷା ପରେ ତାଙ୍କୁ ବିଚାର ନମିଳିବାରୁ ସୁରେନ୍ଦ୍ର ସାଏ ଆଦିବାସୀ, ସାଧାରଣ ଜନତା,ଜମିଦାର ଗୌନ୍ତିଆଙ୍କ ସହାୟତାରେ ବିଦ୍ରୋହ କରିଥିଲେ ।
- ଇଂରେଜମାନଙ୍କ ସହ ଲଢ଼େଇ ମଧ୍ୟରେ ସୁରେନ୍ଦ୍ର ସାଏ ନିଜ ଭାଇ ଛବିଳ ସାଏଙ୍କୁ ହରାଇଥିଲେ । ବିଦ୍ରୋହୀମାନେ କ୍ୟାପ୍ଟେନ୍ ଉଙ୍କୁ ମଧ୍ୟ ହତ୍ୟା କରିଥିଲେ । ଦୀର୍ଘଦିନ ଯୁଦ୍ଧକରି ସୁରେନ୍ଦ୍ର ସାଏ ୧୮୬୪ ମସିହା ଜାନୁୟାରୀ ମାସ ୨୩ ତାରିଖରେ ଇଂରେଜମାନଙ୍କଦ୍ୱାରା ବନ୍ଦୀ ହେଲେ ଏବଂ ଅସିରଗଡ଼ ଦୁର୍ଗରେ ଆଜୀବନ ବନ୍ଦୀ ଜୀବନ କାଟିଥିଲେ ।

ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ଖୋର୍ଦ୍ଧାରେ ବିଦ୍ରୋହ କାହିଁକି ହୋଇଥିଲା ? ଏହି ବିଦ୍ରୋହର ନେତୃତ୍ବ କିଏ ନେଇଥିଲେ ?
Answer:
- ଇଂରେଜମାନଙ୍କ ଓଡ଼ିଶା ଅଧିକାର ପ୍ରତିବାଦରେ ଖୋର୍ଦ୍ଧାରେ ବିଦ୍ରୋହ ହୋଇଥିଲା ।
- ଜୟୀ ରାଜଗୁରୁ ଏହି ବିଦ୍ରୋହର ନେତୃତ୍ଵ ନେଇଥିଲେ ।
୨। ଓଡ଼ିଶାର ଶାସନ ଇଂରେଜମାନଙ୍କ ହାତକୁ କିପରି ଗଲା ? କିଏ ଇଂରେଜମାନଙ୍କୁ ବିରୋଧ କରି ଶହୀଦ ହୋଇଥିଲେ ?
Answer:
- ଇଂରେଜମାନେ ୧୮୦୩ରେ ଓଡ଼ିଶା ଉପକୂଳବର୍ତ୍ତୀ ଅଞ୍ଚଳ ଅଧିକାର କରି ଶାସନ ପ୍ରତିଷ୍ଠା କରିବା ଫଳରେ ଓଡ଼ିଶା ଶାସନ ମରହଟ୍ଟାମାନଙ୍କ ହାତରୁ ଆସି ଇଂରେଜମାନଙ୍କ ହାତକୁ ଗଲା ।
- ଜୟୀ ରାଜଗୁରୁ ଇଂରେଜମାନଙ୍କୁ ବିରୋଧ କରି ଶହୀଦ ହୋଇଥିଲେ ।
୩ । କେବେ, କେଉଁଠାରେ ଏବଂ କାହା ନେତୃତ୍ଵରେ ପାଇକମାନେ ଇଂରେଜ ଶାସନ ବିରୋଧରେ ବିଦ୍ରୋହ ଆରମ୍ଭ କରିଥିଲେ ?
Answer:
୧୮୧୭ ମସିହାରେ, ଖୋର୍ଦ୍ଧାରେ ଏବଂ ଖୋର୍ଦ୍ଧା ରାଜାଙ୍କର ସେନାପତି ବକ୍ସି ଜଗବନ୍ଧୁଙ୍କ ନେତୃତ୍ୱରେ ପାଇକମାନେ ଇଂରେଜ, ଶାସନ ବିରୋଧରେ ବିଦ୍ରୋହ ଆରମ୍ଭ କରିଥିଲେ ।
୪ । ବକ୍ସି ଜଗବନ୍ଧୁ କେଉଁ କାରଣରୁ ଇଂରେଜ ଶାସନର ବିରୋଧୀ ହେଲେ ?
Answer:
- ବକ୍ସି ଜଗବନ୍ଧୁ ଇଂରେଜ ସରକାରଙ୍କ ଚକ୍ରାନ୍ତରେ ରାଜାଙ୍କଠାରୁ ପାଇଥିବା ଚୋଡ଼ଙ୍ଗମଣ୍ଡଳ ଜମିଦାରୀ ହରାଇଲେ ।
- ସେଥିପାଇଁ ସେ କ୍ଷୁବ୍ଧ ହୋଇ ଇଂରେଜ ଶାସନର ବିରୋଧୀ ହେଲେ ।

୫ । ଘୁମୁସର ରାଜ୍ୟର କେଉଁ ରାଜାଙ୍କୁ ଇଂରେଜମାନେ କାହିଁକି ଗାଦିଚ୍ୟୁତ କଲେ ?
Answer:
- ଘୁମୁସର ରାଜ୍ୟର ରାଜା ଧନଞ୍ଜୟ ଭଞ୍ଜଙ୍କୁ ଇଂରେଜମାନେ ଗାଦିଚ୍ୟୁତ କରିଥିଲେ ।
- କାରଣ ସେ ନିର୍ଦ୍ଧାରିତ ସମୟରେ କର ଦେଇପାରି ନଥିଲେ ।
୬ । ବିଦ୍ରୋହୀ ସିପାହୀମାନେ କାହାକୁ କେଉଁଠାରେ ଭାରତର ସମ୍ରାଟଭାବେ ଘୋଷଣା କଲେ ?
Answer:
ବିଦ୍ରୋହୀ ସିପାହୀମାନେ ବୃଦ୍ଧ ମୋଗଲ ସମ୍ରାଟ୍ ଦ୍ୱିତୀୟ ବାହାଦୂର ଶାହା ଜାଫରଙ୍କୁ ଦିଲ୍ଲୀଠାରେ ଭାରତର ସମ୍ରାଟ୍ ଭାବେ ଘୋଷଣା କଲେ ।
୭ । ମଙ୍ଗଳ ପାଣ୍ଡେ କାହିଁକି ଇଂରେଜ ଅଫିସରଙ୍କୁ ହତ୍ୟାକଲେ ?
Answer:
- ମଙ୍ଗଳ ପାଣ୍ଡେ ଏନ୍ଫିଲଡ୍ ବନ୍ଧୁକ ବ୍ୟବହାର କରିବାକୁ ସ୍ପଷ୍ଟ ମନା କରିଦେଲେ ।
- ଇଂରେଜ ଅଫିସର ତାଙ୍କୁ ବାଧ୍ୟ କରିବାରୁ ସେ ରାଗିଯାଇ ସେହି ବନ୍ଧୁକରେ ଇଂରେଜ ଅଫିସରଙ୍କୁ ହତ୍ୟା କରିଥିଲେ ।
୮ । ଇଂରେଜ ସରକାର ସିପାହୀମାନଙ୍କ ବ୍ୟକ୍ତିଗତ ଧର୍ମବିଶ୍ଵାସରେ କିପରି ହସ୍ତକ୍ଷେପ କରିଥିଲେ ?
Answer:
- ଇଂରେଜ ସରକାର ସିପାହୀମାନଙ୍କ ସ୍ଥାନୀୟ ଟୋପି ଓ ପଗଡ଼ି ପିନ୍ଧିବା ଉପରେ କଟକଣା ଜାରି କଲେ ।
- ସମୁଦ୍ର ପାର ହୋଇ ଦେଶ ବାହାରେ ଯୁଦ୍ଧ କରିବାପାଇଁ ଆଇନ କଲେ ।

୯ । ନାନାସାହେବ କିଏ ? ତାଙ୍କର ମନ୍ତ୍ରୀ କିଏ ଥିଲେ ?
Answer:
- ନାନାସାହେବ ପେଶବା ଦ୍ଵିତୀୟ ବାଜିରାଓଙ୍କ ପୋଷ୍ୟପୁତ୍ର ଥିଲେ ।
- ତାନ୍ତିଆ ତୋପେ ତାଙ୍କର ମନ୍ତ୍ରୀ ଥିଲେ ।
୧୦ । କେଉଁମାନଙ୍କୁ ସର୍ବରାକର କୁହାଯାଏ ? ବକ୍ସି ସେମାନଙ୍କଦ୍ୱାରା କିପରି କ୍ଷତିଗ୍ରସ୍ତ ହେଲେ ?
Answer:
- ଖଜଣା ଅସୁଲ କରି ଜମିଦାର ବା ସରକାରଙ୍କଠାରେ ଦାଖଲ କରୁଥିବା କର୍ମଚାରୀଙ୍କୁ ସର୍ବରାକର କୁହାଯାଏ ।
- ସର୍ବରାକରଙ୍କ କୂଟ ଚକ୍ରାନ୍ତ ଫଳରେ ବକ୍ସି ନିଜ ଜମିଦାରୀ ହରାଇଥିଲେ ।
୧୧ । ଜାଗିରୀ କ’ଣ ? ବକ୍ସି କେଉଁ ଜାଗିରୀ ହରାଇଥିଲେ ?
Answer:
- ସୈନିକ ବା ଅନ୍ୟାନ୍ୟ କୌଣସି କାର୍ଯ୍ୟ କରିବା ପାଇଁ ପ୍ରାପ୍ତ ପୁରସ୍କାରସ୍ଵରୂପ ଜମିକୁ ଜାଗିରୀ କୁହାଯାଏ ।
- ବକ୍ସି ଚୋଡ଼ଙ୍ଗମଣ୍ଡଳର ଜାଗିରୀ ହରାଇଥିଲେ ?
୧୨ । ଇଂରେଜ ସରକାରଙ୍କ କେଉଁ ଦୁଇଟି ନୀତିଦ୍ଵାରା ଅଧ୍ବକାଂଶ ଦେଶୀୟ ରାଜ୍ୟ ଇଂରେଜ ସାମ୍ରାଜ୍ୟଭୁକ୍ତ ହେଲା ?
Answer:
ଲର୍ଡ ୱେଲେସ୍ଲିଙ୍କ ସାମନ୍ତ ସନ୍ଧି ଏବଂ ଲର୍ଡ ଡେଲ୍ହାଉସୀଙ୍କ ରାଜ୍ୟସ୍ଵତ୍ଵ ଲୋପନୀତିଦ୍ୱାରା ଅନେକ ଦେଶୀୟ ରାଜ୍ୟ ଇଂରେଜ ସାମ୍ରାଜ୍ୟଭୁକ୍ତ ହେଲା ।

୧୩ । କେବେ କେଉଁଠାରେ ବକ୍ସି ଜଗବନ୍ଧୁ ଇଂରେଜମାନଙ୍କ ନିକଟରେ ଆତ୍ମସମର୍ପଣ କରିଥିଲେ ?
Answer:
୧୮୨୫ ଖ୍ରୀ.ଅ. ମେ’ମାସରେ କଟକଠାରେ ବକ୍ସି ଜଗବନ୍ଧୁ ଇଂରେଜମାନଙ୍କ ନିକଟରେ ଆତ୍ମସମର୍ପଣ କରିଥିଲେ ।
୧୪ । ଦିଲ୍ଲୀରେ ବିଦ୍ରୋହ ଦମନ ପରେ କେଉଁ ମୋଗଲ ସମ୍ରାଟଙ୍କୁ ବନ୍ଦୀ କରାଯାଇଥିଲା ? ତାଙ୍କୁ କେଉଁଠାରେ ରଖାଗଲା ?
Answer:
- ଦିଲ୍ଲୀରେ ବିଦ୍ରୋହ ଦମନ ପରେ ମୋଗଲ ସମ୍ରାଟ ଦ୍ବିତୀୟ ବାହାଦୁର ଶାହା ଜାଫରଙ୍କୁ ବନ୍ଦୀ କରାଗଲା ।
- ତାଙ୍କୁ ମିଆଁମାରର ରେଙ୍ଗୁନସ୍ଥିତ ମାଣ୍ଡାଲେ ଜେଲରେ ବନ୍ଦୀକରି ରଖାଗଲା ।
୧୫ । ଘୁମୁସରର ବିଦ୍ରୋହୀ ନେତା ଦୋରା ବିଶୋଇଙ୍କୁ ଧରିବାପାଇଁ ଇଂରେଜମାନେ କେତେ ଟଙ୍କା ପୁରସ୍କାର ଘୋଷଣା କରିଥିଲେ ? ଦୋରା ବିଶୋଇଙ୍କ ମୃତ୍ୟୁ କେଉଁଠି ହୋଇଥିଲା ?
Answer:
- ଘୁମୁସରର ବିଦ୍ରୋହୀ ନେତା ଦ୍ଵାରା ବିଶୋଇଙ୍କୁ ଧରିବାପାଇଁ ଇଂରେଜ ସରକାର ପାଞ୍ଚ ହଜାର ଟଙ୍କା ପୁରସ୍କାର ଘୋଷଣା କରିଥିଲେ ।
- ମାନ୍ଦ୍ରାଜଠାରେ ତାଙ୍କର ମୃତ୍ୟୁ ହୋଇଥିଲା ।
୧୬ । ବୀର ସୁରେନ୍ଦ୍ର ସାଏ କେଉଁଠାରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ? ତାଙ୍କର ପିତାଙ୍କ ନାମ କ’ଣ ଥିଲା ?
Answer:
- ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ସମ୍ବଲପୁରର ଖୁଣ୍ଡା ଗ୍ରାମରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ।
- ତାଙ୍କ ପିତାଙ୍କ ନାମ ଥିଲା ଧରମ ସିଂହ ।
୧୭ । ସିପାହୀ ବିଦ୍ରୋହବେଳେ ଭାରତର ଗଭର୍ଣ୍ଣର ଜେନେରାଲ୍ କିଏ ଥିଲେ ? ବିଦ୍ରୋହ ଦମନ କରିବାପାଇଁ କେଉଁ ଶାସକମାନେ ତାଙ୍କୁ ସାହାଯ୍ୟ କରିଥିଲେ ?
Answer:
- ସିପାହୀ ବିଦ୍ରୋହବେଳେ ଭାରତର ଗଭର୍ଣ୍ଣର ଜେନେରାଲ୍ ଲର୍ଡ କ୍ୟାଟିଂ ଥିଲେ ।
- ବିଦ୍ରୋହ ଦମନ କରିବାପାଇଁ ତାଙ୍କୁ ପଞ୍ଜାବ, ନେପାଳ ଓ ହାଇଦ୍ରାବାଦର ଶାସକ ସାହାଯ୍ୟ କରିଥିଲେ ।

୧୮ । ଇଷ୍ଟଇଣ୍ଡିଆ କମ୍ପାନୀ କେଉଁ ଦୁଇଟି ବିଷୟ ଉପରେ ବେଶି ଗୁରୁତ୍ଵ ଦେଉଥିଲେ ?
Answer:
ଇଷ୍ଟଇଣ୍ଡିଆ କମ୍ପାନୀ –
- ବାଣିଜ୍ୟ କ୍ଷେତ୍ରରେ ଏକଚାଟିଆ କାରବାର କରିବା ଏବଂ,
- ଭାରତୀୟ ବଣିକମାନଙ୍କ ସହ ପ୍ରତିଯୋଗିତା ନକରିବା ଉପରେ ବେଶି ଗୁରୁତ୍ଵ ଦେଉଥିଲା ।
ଅତି ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର (ଗୋଟିଏ ବାକ୍ୟରେ)
୧। ଜୟୀ ରାଜଗୁରୁଙ୍କ ପିତାଙ୍କ ନାମ କ’ଣ ଥିଲା ?
Answer:
ଜୟୀ ରାଜଗୁରୁଙ୍କ ପିତାଙ୍କ ନାମ ଥିଲା ଚାନ୍ଦ ରାଜଗୁରୁ ।
୨ । ଜୟୀ ରାଜଗୁରୁଙ୍କ ଜ୍ଞାନ ଗରିମାରେ ମୁଗ୍ଧ ହୋଇ କିଏ ତାଙ୍କୁ ରାଜସଭାକୁ ନେବାକୁ ଚାହିଁଥିଲେ ?
Answer:
ଜୟୀ ରାଜଗୁରୁଙ୍କ ଜ୍ଞାନ ଗରିମାରେ ମୁଗ୍ଧ ହୋଇ ଆଠଗଡ଼ ରାଜା ତାଙ୍କୁ ନିଜ ଦରବାରକୁ ନେବାକୁ ଚାହିଁଥିଲେ ।
୩ । ଧର୍ମାନ୍ତରିତ ଭାରତୀୟମାନଙ୍କୁ ଇଂରେଜ ସରକାର କି ପ୍ରକାର ସୁବିଧା ଦେଇଥୁଲେ ?
Answer:
ଧର୍ମାନ୍ତରିତ ଭାରତୀୟଙ୍କ ପୈତୃକ ସମ୍ପତ୍ତି ଉପରେ ଅଧ୍ଵର ରହିବ ବୋଲି ଇଂରେଜ ସରକାର ଆଇନ ପ୍ରଣୟନ କରିଥିଲେ ।
୪। ସିପାହୀ ବିଦ୍ରୋହରେ ଅଂଶଗ୍ରହଣ କରିଥିବା ଓଡ଼ିଶାର କେଉଁ ବ୍ୟକ୍ତି ସ୍ମରଣୀୟ ?
Answer:
ସିପାହୀ ବିଦ୍ରୋହରେ ଅଂଶଗ୍ରହଣ କରିଥିବା ଓଡ଼ିଶାର ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ସ୍ମରଣୀୟ ।

୫ | ସିପାହୀ ବିଦ୍ରୋହ ଶେଷରେ ନାନାସାହେବଙ୍କ ଅବସ୍ଥା କ’ଣ ହେଲା ?
Answer:
ସିପାହୀ ବିଦ୍ରୋହ ଶେଷରେ କାନପୁରଠାରେ ନାନାସାହେବ ପରାସ୍ତ ହୋଇ ନେପାଳର ଜଙ୍ଗଲ ଅଞ୍ଚଳକୁ ପଳାୟନ କରିଥିଲେ ।
୬ | ମୁକୁନ୍ଦଦେବ କେବେ ପିପିଲିଠାରେ ଇଂରେଜମାନଙ୍କୁ ଆକ୍ରମଣ କରିଥିଲେ ?
Answer:
ମୁକୁନ୍ଦଦେବ ୧୮୦୪ ମସିହା ଅକ୍ଟୋବର ମାସରେ ପିପିଲିଠାରେ ଇଂରେଜମାନଙ୍କୁ ଆକ୍ରମଣ କରିଥିଲେ ।
୭ । କେବେ ଇଂରେଜମାନେ ମରହଟ୍ଟାମାନଙ୍କଠାରୁ ଓଡ଼ିଶାର ଶାସନ କ୍ଷମତା ନିଜ ହାତକୁ ନେଲେ ?
Answer:
୧୮୦୩ ମସିହାରେ ଇଂରେଜମାନେ ମରହଟ୍ଟାମାନଙ୍କଠାରୁ ଓଡ଼ିଶାର ଶାସନ କ୍ଷମତା ନିଜ ହାତକୁ ନେଲେ ।
୮ | ୧୮୫୭ ସିପାହୀ ବିଦ୍ରୋହବେଳେ ଭାରତର ଗଭର୍ଣ୍ଣର ଜେନେରାଲ କିଏ ଥିଲେ ?
Answer:
୧୮୫୭ ସିପାହୀ ବିଦ୍ରୋହବେଳେ ଭାରତର ଗଭର୍ଣ୍ଣର ଜେନେରାଲ୍ ଥିଲେ ଲର୍ଡ କ୍ୟାନିଂ ।
୯ । ୧୮୧୭ ମସିହାରେ କାହା ନେତୃତ୍ଵରେ ପାଇକ ବିଦ୍ରୋହ ହୋଇଥିଲା ?
Answer:
୧୮୧୭ ମସିହାରେ ବକ୍ସି ଜଗବନ୍ଧୁଙ୍କ ନେତୃତ୍ୱରେ ପାଇକ ବିଦ୍ରୋହ ହୋଇଥିଲା ।
୧୦ । ମଙ୍ଗଳ ପାଣ୍ଡେ କେଉଁଠାରେ ଜଣେ ଇଂରେଜ ଅଫିସରଙ୍କୁ ଗୁଳି କରିଥିଲେ ?
Answer:
ମଙ୍ଗଳ ପାଣ୍ଡେ ବଙ୍ଗର ବାରାକପୁରଠାରେ ଜଣେ ଇଂରେଜ ଅଫିସରଙ୍କୁ ଗୁଳି କରିଥିଲେ ।

୧୧ । ଇଂରେଜ ସରକାର ଘୁମୁସରର କେଉଁ ରାଜାଙ୍କୁ କର ନ ଦେବାରୁ ଗାଦିଚ୍ୟୁତ କରିଥିଲେ ?
Answer:
ଇଂରେଜ ସରକାର ଘୁମୁସରର ରାଜା ଧନଞ୍ଜୟ ଭଞ୍ଜଙ୍କୁ କର ନ ଦେବାରୁ ଗାଦିଚ୍ୟୁତ କରିଥିଲେ ।
୧୨ । ଚକରା ବିଶୋଇ କିଏ ?
Answer:
ଚକରା ବିଶୋଇ ଘୁମୁସରର କନ୍ଧ ବିଦ୍ରୋହର ଅନ୍ୟତମ ମହାନ୍ ନେତା ଥିଲେ ।
୧୩ । କେନ୍ଦୁଝରର କେଉଁ ରାଜାଙ୍କୁ ଓଡ଼ିଶାର ତତ୍କାଳୀନ କମିଶନର ରେଭେନ୍ସା ଅନ୍ୟାୟ ଭାବରେ ଶାସନ ଗାଦିରୁ ବଞ୍ଚିତ କରିଥିଲେ ?
Answer:
କେନ୍ଦୁଝରର ରାଜା ଗଦାଧର ଭଞ୍ଜଙ୍କ ପୋଷ୍ୟପୁତ୍ର ବୃନ୍ଦାବନ ଭଞ୍ଜଙ୍କୁ ଓଡ଼ିଶାର ତତ୍କାଳୀନ କମିଶନର ରେଭେନ୍ସା ଅନ୍ୟାୟ ଭାବରେ ଶାସନ ଗାଦିରୁ ବଞ୍ଚିତ କରିଥିଲେ ।
୧୪ । ରତ୍ନା ନାୟକ କିଏ ଥିଲେ ?
Answer:
ରତ୍ନା ନାୟକ କେନ୍ଦୁଝର ଭୂୟାଁ ବିଦ୍ରୋହର ଅନ୍ୟତମ ନେତା ଥିଲେ ।
୧୫ । ୧୮୨୦ ମସିହାରେ ମୟୂରଭଞ୍ଜର କୋହ୍ଲମାନେ କେଉଁ ରାଜାଙ୍କ ବିରୁଦ୍ଧରେ ବିଦ୍ରୋହ କଲେ ?
Answer:
୧୮୨୦ ମସିହାରେ ମୟୂରଭଞ୍ଜର କୋହ୍ଲମାନେ ସିଂହଭୂମର ରାଜା ଘନଶ୍ୟାମ ସିଂହଙ୍କ ବିରୁଦ୍ଧରେ ବିଦ୍ରୋହ କଲେ ।

Objective Type Questions With Answers
A. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
୧ । କାନପୁରଠାରେ _________ ଙ୍କ ନେତୃତ୍ୱରେ ବିଦ୍ରୋହ ପରିଚାଳିତ ହେଉଥିଲା ।
Answer:
ନାନା ସାହେବ
୨ । ଇଂରେ ଜମାନେ ___________ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଓଡ଼ିଶାର ଶାସନ କ୍ଷମତା ନିଜ ହାତକୁ ନେଇଥିଲେ ।
Answer:
୧୮୦୩
୩ । ବକ୍ସି ଜଗବନ୍ଧୁ _________ ଙ୍କୁ ଖୋର୍ଦ୍ଧାର ରାଜା ରୂପେ ଘୋଷଣା କରିଥିଲେ ।
Answer:
ଦ୍ଵିତୀୟ ମୁକୁନ୍ଦଦେବ
୪ । ଦୋରା ବିଶୋଇଙ୍କ ପୁତୁରା __________ କନ୍ଧ ସମ୍ପ୍ରଦାୟର ମହାନ୍ ନେତା ଥିଲେ ।
Answer:
ଚକରା ବିଶୋଇ
୫। ବିଦ୍ରୋହ କାଳରେ ସିପାହୀମାନେ _________ ଙ୍କୁ ଭାରତର ଶାସକ ଭାବରେ ଘୋଷଣା କଲେ ।
Answer:
ମୋଗଲ ସମ୍ରାଟ ଦ୍ବିତୀୟ ବାହାଦୁର – ଶାହ ଜାଫର

୬ | ୧୮୧୭ ମସିହାରେ ବିଦ୍ରୋହୀ ପାଇକମାନେ ପ୍ରଥମେ __________ ଥାନା ଆକ୍ରମଣ ହୋଇଥିଲେ ।
Answer:
ବାଣପୁର
୭ । ଇଂରେଜମାନଙ୍କୁ ନିର୍ଦ୍ଧାରିତ କର ଦେଇନପାରି ଘୁମୁସର ରାଜା __________ ଗାଦିଚ୍ୟୁତ କରିଥିଲେ ।
Answer:
ଧନଞ୍ଜୟ ଭଞ୍ଜ
୮ | ଧରଣୀଧର ଭୂୟାଁ ____________ ମସିହାରେ ଇଂରେଜମାନଙ୍କ ବିରୋଧୀ ମେଳିର ନେତୃତ୍ୱ ନେଇଥିଲେ ।
Answer:
୧୮୯ ୮
୯ । କେନ୍ଦୁଝରର ଭୂୟାଁମାନେ କେନ୍ଦୁଝରର ରାଜା _________ ଙ୍କୁ ସମର୍ଥନ କରୁନଥୁଲେ ।
Answer:
ଧନୁର୍ଜୟ ଭଞ୍ଜ
୧୦ । ଇଂରେଜମାନେ __________ ଙ୍କୁ ଅନ୍ୟାୟଭାବରେ କେନ୍ଦୁଝର ରାଜଗାଦିରୁ ବଞ୍ଚ କରିଥିଲେ ।
Answer:
ବୃନ୍ଦାବନ ଭଞ୍ଜ
୧୧। __________ ଖୋର୍ଦ୍ଧା ରାଜାଙ୍କର ସେନାପତି ଥିଲେ ।
Answer:
ବକ୍ସି ଜଗବନ୍ଧୁ
୧୨ । ଇଂରେଜମାନେ _________ ମସିହାରେ ବକ୍ସି ଜଗବନ୍ଧୁଙ୍କ ସମ୍ପତ୍ତି ବାଜ୍ୟାପ୍ତ କରିଥିଲେ ।
Answer:
୧୮୨୩

୧୩ । ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧବେଳେ ଇଂରେଜ ସରକାର __________ ରେ କାର୍ଯ୍ୟ କରିବାପାଇଁ ଆଦିବାସୀମାନଙ୍କୁ ପଠାଇବାକୁ ଚେଷ୍ଟା କରିଥିଲେ ।
Answer:
ଫ୍ରାନ୍ସ
୧୪ । ୧୮୧୦ ମସିହାରେ ଇଂରେଜ ଶାସକ __________ ଙ୍କୁ ମୟୂରଭଞ୍ଜର ରାଜା ରୂପେ ସ୍ଵୀକାର କଲେ ।
Answer:
ତ୍ରିବିକ୍ରମ ଭଞ୍ଜ
୧୫ । ବୀର ସୁରେନ୍ଦ୍ର ସାଏଙ୍କୁ ୧୮୪୦ ମସିହାରେ ___________ ଜେଲକୁ ପଠାଯାଇଥିଲା ।
Answer:
ହଜାରିବାଗ
୧୬ । ସୁରେନ୍ଦ୍ର ସାଏ ___________ ଦୁର୍ଗରେ ଆଜୀବନ ବନ୍ଦୀ ଭାବରେ ରହିଥିଲେ ।
Answer:
ଅସିରଗଡ଼
B. ନିମ୍ନୋକ୍ତ ବାକ୍ୟଗୁଡ଼ିକ ମଧ୍ୟରୁ ଠିକ୍ ବାକ୍ୟଗୁଡ଼ିକ ପାଖରେ (✓) ଚିହ୍ନ ଓ ଭୁଲ୍ ବାକ୍ୟଗୁଡ଼ିକ ପାଖରେ (✗) ଚିହ୍ନ ଦିଅ ।
୧। ୧୮୫୭ ମସିହା ଭାରତ ଇତିହାସରେ ଏକ ସ୍ମରଣୀୟ ବର୍ଷ ।
୨ । ତାନ୍ତିଆ ତୋପେ ନାନା ସାହେବଙ୍କ ସେନାପତି ଥିଲେ ।
୩ । ୧୮୦୩ ମସିହାରେ ଓଡ଼ିଶାର ଶାସନ ମରହଟ୍ଟାମାନଙ୍କ ହାତରୁ ଇଂରେଜମାନଙ୍କ ହାତକୁ ଗଲା ।
୪ । ୧୮୯୮ ମସିହାରେ କେନ୍ଦୁଝରରେ ସଙ୍ଗଠିତ ଭୂୟାଁ ବିଦ୍ରୋହକୁ ରତ୍ନାମେଳି କୁହାଯାଏ ।
୫ । ସରକାରଙ୍କ ନୀତିକୁ ନାପସନ୍ଦକରି ଷ୍ଟକ୍ୱେଲ ୧୮୩୧ ମସିହାରେ ନିଜ ପଦବୀରୁ ଇସ୍ତଫା ଦେଲେ ।
୬ | ଇଂଲଣ୍ଡ ରାଣୀଙ୍କ ପ୍ରତିନିଧ୍ୟାବରେ ଭାରତରେ ଶାସନ କରୁଥିବା ବ୍ୟକ୍ତି ଭାଇସ୍ଏ ରୂପେ ପରିଚିତ ହେଲେ ।
୭ । ଲର୍ଡ କ୍ୟାମିଂ ଦିଲ୍ଲୀଠାରେ ରାଣୀ ଭିକ୍ଟୋରିଆଙ୍କ ଘୋଷଣାପତ୍ର ପାଠ କରିଥିଲେ ।
୮। ବକ୍ସି ଜଗବନ୍ଧୁ ଖୋର୍ଦ୍ଧା ରାଜାଙ୍କର ସେନାପତି ଥିଲେ ।
୯। ଇଂରେଜମାନେ ପ୍ରଜାଙ୍କଠାରୁ କଉଡ଼ି ଆକାରରେ ଖଜଣା ଆଦାୟ କଲେ ।
୧୦ । ଇଂରେଜ ସରକାରଙ୍କ ଚକ୍ରାନ୍ତରେ ବକ୍ସି ଜଗବନ୍ଧୁଙ୍କୁ ଚୋଡ଼ଙ୍ଗମଣ୍ଡଳର ଜାଗିରୀ ହରାଇଲେ ।
୧୧ । ଦୋରା ବିଶୋଇ ଘୁମୁସର ରାଜା ଧନଞ୍ଜୟ ଭଞ୍ଜଙ୍କ ବିରୋଧୀ ଥିଲେ ।
୧୨ । ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ତାଙ୍କ ସମର୍ଥକମାନଙ୍କୁ ୫ ଭାଗରେ ବିଭକ୍ତ କରିଥିଲେ ।
୧୩ । ୧୮୫୭ ମସିହା ମାର୍ଚ୍ଚ ମାସ ୨୯ ତାରିଖ ଦିନ ସିପାହୀ ମଙ୍ଗଳପାଣ୍ଡେ ବଙ୍ଗର ବାରାକ୍ପୁରଠାରେ ଏନ୍ଫିଲଡ୍ ବନ୍ଧୁକ ବ୍ୟବହାର କରିବାକୁ ସ୍ପଷ୍ଟ ମନା କରିଥିଲେ ।
୧୪ । କାନପୁରଠାରେ ନାନା ସାହେବ ପରାସ୍ତ ହୋଇ ବ୍ରହ୍ମଦେଶର ଜଙ୍ଗଲ ଅଞ୍ଚଳକୁ ପଳାୟନ କରିଥିଲେ ।
୧୫ । ସପାହୀ ବିଦ୍ରୋହ ପରେ ଭାରତର ଶାସନ କ୍ଷମତା ଇଂଲଣ୍ଡର ରାଣୀ ଭିକ୍ଟୋରିଆଙ୍କ ହାତକୁ ଯାଇଥିଲା ।

Answer:
୧। (✓ )
୨ । (✗ )
୩ । (✓ )
୪ । (✗ )
୫ । (✗ )
୬ | (✓ )
୭ । (✗ )
୮। (✓ )
୯। (✗ )
୧୦ । (✓ )
୧୧ । ( ✗)
୧୨ । (✗ )
୧୩ । ( ✓)
୧୪ । (✗ )
୧୫ । (✓ )
C. ରେଖାଙ୍କିତ ଶବ୍ଦଗୁଡ଼ିକୁ ପରିବର୍ତ୍ତନ ନକରି ଭ୍ରମ ସଂଶୋଧନ କର ।
୧। ୧୮୦୪ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଖୋର୍ଦ୍ଧାରେ ହୋଇଥିବା ବିଦ୍ରୋହର ନେତୃତ୍ବ ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ନେଇଥିଲେ ।
Answer:
୧୮୦୪ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଖୋର୍ଦ୍ଧାରେ ହୋଇଥିବା ବିଦ୍ରୋହର ନେତୃତ୍ବ ଜୟୀ ରାଜଗୁରୁ ନେଇଥିଲେ ।
୨ । ଇଂରେଜ ପ୍ରଶାସକ କଣ୍ଠୱାଲିସ୍ ଖୋର୍ଦ୍ଧାରାଜାଙ୍କୁ କବଳିତ କରିବାକୁ ଯାଇ କୂଟନୀତି ଅବଲମ୍ବନ କରିଥିଲେ ।
Answer:
ଇଂରେଜ ପ୍ରଶାସକ କର୍ଣ୍ଣେଲ ହର୍କୋର୍ଟ ଖୋର୍ଦ୍ଧାରାଜାଙ୍କୁ କବଳିତ କରିବାକୁ ଯାଇ କୂଟନୀତି ଅବଲମ୍ବନ କରିଥିଲେ ।
୩ । ୧୮୧୦ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଖୋର୍ଦ୍ଧା ଇଂରେଜମାନଙ୍କର ଅଧ୍ୟାତ ହେଲା ।
Answer:
୧୮୦୪ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଖୋର୍ଦ୍ଧା ଇଂରେଜମାନଙ୍କର ଅଧିକୃତ ହେଲା ।

୪ । ୧୮୩୫ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଇଂରେଜ ସରକାର ଉତ୍ତର ଓଡ଼ିଶାର ଘୁମୁସର ଅଧ୍ୟାର କରି କନ୍ଧମାନଙ୍କ ଉପରେ ପ୍ରଭୁତ୍ଵ ବିସ୍ତାର କରିଥିଲେ ।
Answer:
୧୮୩୫ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଇଂରେଜ ସରକାର ଦକ୍ଷିଣ ଓଡ଼ିଶାର ଘୁମୁସର ଅଧିକାର କରି କନ୍ଧମାନଙ୍କ ଉପରେ ପ୍ରଭୁତ୍ଵ ବିସ୍ତାର କରିଥିଲେ ।
୫। ରାଜା ଧନଞ୍ଜୟ ଭଞ୍ଜ ଖୋର୍ଦ୍ଧାର ରାଜା ଥିଲେ ।
Answer:
ରାଜା ଧନଞ୍ଜୟ ଭଞ୍ଜ ଘୁମୁସରର ରାଜା ଥିଲେ ।
୬ । ୧୮୧୦ ମସିହାରେ ଇଂରେଜମାନେ ତ୍ରିବିକ୍ରମ ଭଞ୍ଜଙ୍କୁ ସମ୍ବଲପୁରର ରାଜା ରୂପେ ସ୍ଵୀକାର କରିଥିଲେ ।
Answer:
୧୮୧୦ ମସିହାରେ ଇଂରେଜମାନେ ତ୍ରିବିକ୍ରମ ଭଞ୍ଜଙ୍କୁ ମୟୂରଭଞ୍ଜର ରାଜାରୂପେ ସ୍ଵୀକାର କରିଥିଲେ ।
୭ | ୧୮୩୦ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ କୋହ୍ଲମାନେ ସିଂହଭୂମ ରାଜା ଘନଶ୍ୟାମ ସିଂହଙ୍କ ବିରୁଦ୍ଧରେ ବିଦ୍ରୋହ କରିଥିଲେ ।
Answer:
୧୮୨୦ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ କୋହ୍ଲମାନେ ସିଂହଭୂମ ରାଜା ଘନଶ୍ୟାମ ସିଂହଙ୍କ ବିରୁଦ୍ଧରେ ବିଦ୍ରୋହ କରିଥିଲେ ।
୮ | ପ୍ରଥମ ବିଶ୍ୱଯୁଦ୍ଧ ସମୟରେ ଇଂରେଜ ସରକାର ଜାପାନରେ କାର୍ଯ୍ୟ କରିବାପାଇଁ ଆଦିବାସୀମାନଙ୍କୁ ପଠାଇବାକୁ ଚେଷ୍ଟାକଲେ ।
Answer:
ପ୍ରଥମ ବିଶ୍ଵଯୁଦ୍ଧ ସମୟରେ ଇଂରେଜ ସରକାର ଫ୍ରାନ୍ସରେ କାର୍ଯ୍ୟ କରିବାପାଇଁ ଆଦିବାସୀମାନଙ୍କୁ ପଠାଇବାକୁ ଚେଷ୍ଟା କଲେ ।
୯ । ନାନା ସାହେବ ପେଶବା ଦ୍ୱିତୀୟ ବାଜିରାଓଙ୍କ ଭାଇ ଥିଲେ ।
Answer:
ନାନା ସାହେବ ପେଶବା ଦ୍ଵିତୀୟ ବାଜିରାଓଙ୍କ ପୋଷ୍ୟପୁତ୍ର ଥିଲେ ।

୧୦ । ଲର୍ଡ ଡେଲ୍ହାଉସୀ ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ପ୍ରଚଳନ କରିଥିଲେ ।
Answer:
ଲର୍ଡ କଣ୍ଠୱାଲିସ୍ ଚିରସ୍ଥାୟୀ ବନ୍ଦୋବସ୍ତ ପ୍ରଚଳନ କରିଥିଲେ ।
୧୧ । କନ୍ଧ ଓ କୋହ୍ଲ ଆଦିବାସୀମାନେ ସୁରେନ୍ଦ୍ର ସାଏଙ୍କ ବିଦ୍ରୋହକୁ ସମର୍ଥନ ଜଣାଇଥିଲେ ।
Answer:
ଗଣ୍ଡ ଓ ବିଂଝାଲ ଆଦିବାସୀମାନେ ସୁରେନ୍ଦ୍ର ସାଏଙ୍କ ବିଦ୍ରୋହକୁ ସମର୍ଥନ ଜଣାଇଥିଲେ ।
୧୨ । ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ତାଙ୍କ ସମର୍ଥକ ବିଦ୍ରୋହୀମାନଙ୍କୁ ୫ ଭାଗରେ ବିଭକ୍ତ କରିଥିଲେ ।
Answer:
ବୀର ସୁରେନ୍ଦ୍ର ସାଏ ତାଙ୍କ ସମର୍ଥକ ବିଦ୍ରୋହୀମାନଙ୍କୁ ୪ ଭାଗରେ ବିଭକ୍ତ କରିଥିଲେ ।
D. ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
୧। ନିମ୍ନୋକ୍ତ କିଏ କାନପୁରଠାରେ ସିପାହୀ ବିଦ୍ରୋହର ନେତୃତ୍ବ ନେଇଥିଲେ ?
(କ) ଝାନ୍ସୀ ରାଣୀ ଲକ୍ଷ୍ମୀବାଈ
(ଖ) ସୁରେନ୍ଦ୍ର ସାଏ
(ଗ) ନାନା ସାହେବ
(ଘ) କନୱାର ସିଂ
Answer:
(ଗ) ନାନା ସାହେବ

୨। ଓଡ଼ିଶା ଶାସନ ଦାୟିତ୍ଵ ଇଂରେଜମାନେ ନିମ୍ନୋକ୍ତ କେତେ ମସିହାରେ ନିଜ ହାତକୁ ନେଇଥିଲେ ?
(କ) ୧୮୦୩
(ଖ) ୧୮୧୮
(ଗ) ୧୮୧୭
(ଘ) ୧୮୨୫
Answer:
(କ) ୧୮୦୩
୩ । ଦୋରା ବିଶୋଇ ନିମ୍ନୋକ୍ତ କେଉଁ ସମ୍ପ୍ରଦାୟର ନେତା ଥିଲେ ?
(କ) ମୁଣ୍ଡା
(ଖ) କୋହ୍ଲ
(ଗ) କନ୍ଧ
(ଘ) ଜୁଆଙ୍ଗ
Answer:
(ଗ) କନ୍ଧ
୪। ନିମ୍ନୋକ୍ତ କିଏ ନାନା ସାହେବଙ୍କ ମନ୍ତ୍ରୀ ଥିଲେ ?
(କ) ରାଓ ସାହେବ
(ଖ) ତାନ୍ତିଆ ତୋପେ
(ଗ) କନ୍ର ସିଂ
(ଘ) ମହମ୍ମଦ ଉଲ୍ଲା
Answer:
(ଖ) ତାନ୍ତିଆ ତୋପେ
୫ । ଲର୍ଡ କ୍ୟାଚିଂ ନିମ୍ନୋକ୍ତ କେତେ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଭାରତରେ ପ୍ରଥମ ଭାଇସ୍ରାଏ ହେଲେ ?
(କ) ୧୮୪୬
(ଖ) ୧୮୫୭
(ଗ) ୧୮୫୮
(ଘ) ୧୮୯୧
Answer:
(ଗ) ୧୮୫୮
୬ । ୧୮୨୫ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ବକ୍ସି ଜଗବନ୍ଧୁ ବିଦ୍ୟାଧର ନିମ୍ନୋକ୍ତ କେଉଁ ସ୍ଥାନରେ ଆତ୍ମସମର୍ପଣ କରିଥିଲେ ?
(କ) ପୁରୀ
(ଖ) ଖୋର୍ଦ୍ଧା
(ଗ) ଜୟପୁର
(ଘ) କଟକ
Answer:
(ଘ) କଟକ

୭ । ନିମ୍ନୋକ୍ତ ମଧ୍ଯରୁ କିଏ ପେଶବା ଦ୍ଵିତୀୟ ବାଜିରାଓଙ୍କ ପୋଷ୍ୟପୁତ୍ର ଥିଲେ ?
(କ) ନାନା ସାହେବ
(ଖ) ରାଓସାହେବ
(ଗ) କନୱାର ସିଂ
(ଘ) ଚକରା ବିଶୋଇ
Answer:
(କ) ନାନା ସାହେବ
୮। ସମ୍ବଲପୁରରେ କିଏ ସିପାହୀ ବିଦ୍ରୋହର ନେତୃତ୍ବ ନେଇଥିଲେ ?
(କ) ନାନା ସାହେବ
(ଖ) ତାନ୍ତିଆ ତୋପେ
(କ) ନାନା ସାହେବ
(ଘ) ବୀର ସୁରେନ୍ଦ୍ର ସାଏ
Answer:
(ଘ) ବୀର ସୁରେନ୍ଦ୍ର ସାଏ
୯ । ୧୮୬୮ ମସିହାରେ ହୋଇଥିବା ‘ରତ୍ନାମେଳି’ ବିଦ୍ରୋହର ନେତୃତ୍ୱ ନିମ୍ନୋକ୍ତ କିଏ ନେଇଥିଲେ ?
(କ) ଧନଞ୍ଜୟ ଭଞ୍ଜ
(ଖ) ଧନୁର୍ଜୟ ଭଞ୍ଜ
(ଗ) ଧରଣୀଧର ଭୂୟାଁ
(ଘ) ରତ୍ନା ନାୟକ
Answer:
(ଘ) ରତ୍ନା ନାୟକ
୧୦ । ନିମ୍ନୋକ୍ତ କେତେ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଏଡ୍ଫିଲଡ୍ ନାମକ ଏକ ବନ୍ଧୁକ ବ୍ୟବହାର କରିବାପାଇଁ ସିପାହୀମାନଙ୍କୁ ବାଧ୍ୟ କରାଗଲା ?
(କ) ୧୮୦୩
(ଖ) ୧୮୨୫
(ଗ) ୧୮୮୫
(ଘ) ୧୮୫୭
Answer:
(ଘ) ୧୮୫୭
୧୧ । ନିମ୍ନୋକ୍ତ କେତେ ଖ୍ରୀଷ୍ଟାବ୍ଦରେ ଇଂରେଜ ସରକାର ବକ୍ସିଙ୍କ ସମ୍ପତ୍ତିକୁ ବାଜ୍ୟାପ୍ତ କରିଥିଲେ ?
(କ) ୧୧୧୮
(ଖ) ୧୮୨୫
(ଗ) ୧୮୨୩
(ଘ) ୧୮୧୭
Answer:
(ଗ) ୧୮୨୩

୧୨ । ନାନା ସାହେବ କେଉଁଠାରେ ପରାସ୍ତ ହୋଇ ନେପାଳର ଜଙ୍ଗଲ ଅଞ୍ଚଳକୁ ପଳାୟନ କରିଥିଲେ ?
(କ) ଦିଲ୍ଲୀ
(ଖ) କାନପୁର
(ଗ) ବମ୍ବେ
(ଘ) ଝାନ୍ସୀ
Answer:
(ଖ) କାନପୁର
E. ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହିତ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ମିଳନ କର ।
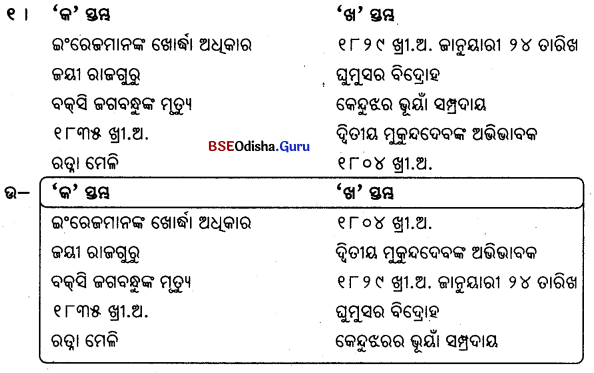
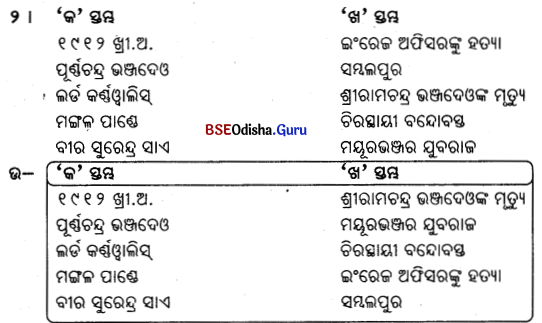
F. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଦିଅ ।
୧। ଇଂରେଜମାନେ କେବେ ଓଡ଼ିଶା ଅଧୂକାର କରିଥିଲେ ?
Answer:
୧୮୦୩ ମସିହା
୨। ଜୟୀ ରାଜଗୁରୁ କାହାର ଉପଦେଷ୍ଟା ଓ ଆଧ୍ୟାତ୍ମିକ ଗୁରୁ ଥିଲେ ?
Answer:
ଖୋର୍ଦ୍ଧା ରାଜା

୩ । ବକ୍ସି ଜଗବନ୍ଧୁ କେଉଁଠାରେ ଆତ୍ମ ସମର୍ପଣ କରିଥିଲେ ?
Answer:
କଟକ
୪ । ବେଠି କ’ଣ ?
Answer:
ବିନା ବେତନ ବା ପାରିଶ୍ରମିକରେ ବାଧ୍ୟତାମୂଳକ ସେବା
୫। ପାଇକ ବିଦ୍ରୋହ କେବେ ହୋଇଥିଲା ?
Answer:
୧୮୧୭ ମସିହା
୬ | ସିପାହୀ ବିଦ୍ରୋହ କେବେ ହୋଇଥିଲା ?
Answer:
୧୮୫୭ ମସିହା
୭ । ଭାରତର ପ୍ରଥମ ଶହୀଦ କିଏ ?
Answer:
ମଙ୍ଗଳ ପାଣ୍ଡେ
୮ | ଓଡ଼ିଶାର ପ୍ରଥମ ଶହୀଦ କିଏ ?
Answer:
ଜୟୀ ରାଜଗୁରୁ
୯ । ସିପାହୀମାନେ କେଉଁ ବନ୍ଧୁକ ବ୍ୟବହାର କରିବାକୁ ବିରୋଧ କରି ବିଦ୍ରୋହ କରିଥିଲେ ?
Answer:
ରୟାଲ୍ ଏନ୍ଫିଲ୍
୧୦ । ସୁରେନ୍ଦ୍ର ସାଏ ସମ୍ବଲପୁରର କେଉଁ ଗ୍ରାମରେ ଜନ୍ମଗ୍ରହଣ କରିଥିଲେ ?
Answer:
ଖୁଣ୍ଡା.
୧୧। ଚିରସ୍ତାୟୀ ବନ୍ଦୋବସ୍ତ କିଏ ପ୍ରଚଳନ କରିଥିଲେ ?
Answer:
ଲର୍ଡ଼ କଣ୍ଠୱାଲିସ୍

୧୨। ସୁରେନ୍ଦ୍ର ସାଏଙ୍କୁ କେଉଁଠାରେ ଆଜୀବନ ବନ୍ଦୀ କରି ରଖାଯାଇଥିଲା ?
Answer:
ଅସିରଗଡ଼ ଦୁର୍ଗ
୧୩। ଭାରତର ପ୍ରଥମ ଭାଇସ୍ରାଏ କିଏ ଥିଲେ ?
Answer:
ଲର୍ଡ଼ କ୍ୟାଟିଂ
![]()


![]()