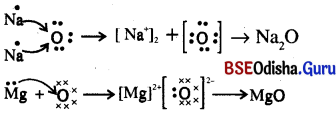Odisha State Board BSE Odisha 10th Class Physical Science Solutions Chapter 3 ଧାତୁ ଓ ଅଧାତୁ Textbook Exercise Questions and Answers.
BSE Odisha Class 10 Physical Science Solutions Chapter 3 ଧାତୁ ଓ ଅଧାତୁ
Question 1.
ନିମ୍ନଲିଖତ କେଉଁ ଯୋଡ଼ା ବିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା କରେ ।
(a) ସୋଡ଼ିୟମ୍ କ୍ଲୋରାଇଡ୍ ଦ୍ରବଣ ଏବଂ ତମ୍ବାଧାତୁ ।
(b) ମ୍ୟାଗ୍ନେସିୟମ୍ କ୍ଲୋରାଇଡ୍ ଦ୍ରବଣ ଏବଂ ଏଲୁମିନିୟମ୍ ଧାତୁ ।
(c) ଫେରସ୍ ସଲ୍ଫେଟ୍ ଦ୍ରବଣ ଏବଂ ସିଲ୍ଭର୍ ଧାତୁ । ତମ୍ବା ଧାତୁ ।
(d) ସିଲ୍ଭର୍ ନାଇଟ୍ରେଟ୍ ଦ୍ରବଣ ଏବଂ ଧାତୁ
Answer:
(d) ସିଲ୍ଭର ନାଇଟ୍ରେଟ୍ ଦ୍ରବଣ ଓ ତମ୍ବା
Question 2.
ନିମ୍ନଲିଖ କେଉଁ ପ୍ରଣାଳୀ ଲୁହା ତାୱାକୁ କଳଙ୍କି ନିରୋଧପାଇଁ ବିନିଯୋଗ କରିହେବ ?
(a) ଗ୍ରୀକ୍ ପ୍ରୟୋଗ ଦ୍ଵାରା
(b) ରଙ୍ଗ ପ୍ରଲେପ ଦ୍ଵାରା
(c) ଜିଙ୍କର ଆବରଣ ପ୍ରୟୋଗ ଦ୍ଵାରା
(d) ତପତୋକ୍ର ସମସ୍ତ ପ୍ରଣାଳ1 ଦ୍ବ|ରା
Answer:
(c) ଜିଙ୍କର ଆବରଣ ପ୍ରୟୋଗ ଦ୍ଵାରା ।
Question 3.
ଗୋଟିଏ ମୌଳିକ ଅମ୍ଳଜାନ ସହ ପ୍ରତିକ୍ରିୟା କରି ଗୋଟିଏ ଉଚ୍ଚ ଗଳନାଙ୍କ ବିଶିଷ୍ଟ ଯୌଗିକ ସୃଷ୍ଟି କରେ । ଏହା ଜଳରେ ଦ୍ରବଣୀୟ । ନିମ୍ନ ଉତ୍ତରରୁ ଉକ୍ତ ମୌଳିକଟି ବାଛ ।
(a) କ୍ୟାଲ୍ସିୟମ୍
(b) କାରନ୍
(c) ପିଲିକନ୍
(d) ଆଇନ୍
Answer:
(a) କ୍ୟାଲ୍ସିୟମ୍
Question 4.
ଖାଦ୍ୟ ଡବାଗୁଡ଼ିକରେ ଜିଙ୍କଦ୍ୱାରା ପ୍ରଲେପ ନ ହୋଇ ଟିଣରେ ହୋଇଥାଏ କାରଣ–
(a) ଜିଙ୍କ୍ ଟିଣଠାରୁ ଅଧିକ ମୂଲ୍ୟବାନ ଅଟେ ।
(b) ଜିଙ୍କ୍ ଟିଣଠାରୁ ଉଚ୍ଚ ଗଳନାଙ୍କ ବିଶିଷ୍ଟ ।
(c) ଜିଜ୍ ଟିଣଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ।
(d) ଜିଙ୍କ୍ ଟିଣଠାରୁ କମ୍ ପ୍ରତିକ୍ରିୟାଶୀଳ ।
Answer:
(c) ଜିଙ୍କ୍ ଟିଣଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ।
Question 5.
ତୁମକୁ ଗୋଟିଏ ହାତୁଡ଼ି, ଗୋଟିଏ ବ୍ୟାଟେରୀ, ଗୋଟିଏ ବଲ୍ , ତାର ଏବଂ ଗୋଟିଏ ସ୍ଵିଚ୍ ଦିଆଯାଇଛି ।
(a) ଧାତୁ ଏବଂ ଅଧାତୁର ନମୁନାକୁ ଚିହ୍ନଟ କରିବାପାଇଁ ଏଗୁଡ଼ିକୁ କିପରି ବ୍ୟବହାର କରିବ ?
(b) ଏହି ପରୀକ୍ଷାର ଉପଯୋଗିତାକୁ ନିର୍ଣ୍ଣୟ (Assess) କରି ଧାତବ ଏବଂ ଅଧାତବ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ |
Answer:
(a)
(i) ପ୍ରଦତ୍ତ ନମୁନାକୁ ହାତୁଡ଼ି ସାହାଯ୍ୟରେ ପିଟିଲେ ଯଦି ତାହା ପ୍ରସାରିତ ହୋଇ ପତଳା ତେବେ ତାହା ଧାତୁ । ଯଦି ନମୁନାଟି ଭାଙ୍ଗି ଗୁଣ୍ଡ ହୋଇଯାଏ ତେବେ ତାହା ଅଧାତୁ ।
(ii) ଧାତୁକୁ ହାତୁଡ଼ିରେ ଆଘାତ କଲେ ସେଥୁରୁ ଧ୍ଵନି ବାହାରେ, କିନ୍ତୁ ଅଧାତୁରୁ କୌଣସି ଧ୍ବନି ବାହାରେ ନାହିଁ ।
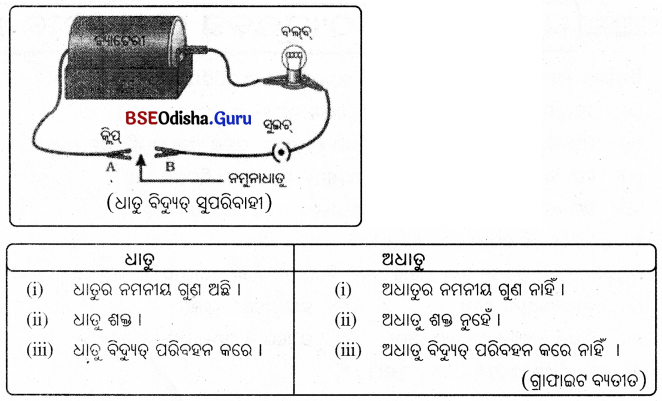
(b) ବ୍ୟାଟେରୀ, ବଲ୍ବ, ତାର ଓ ସ୍ଵିକୁ ନେଇ ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ହେବାଭଳି ପରିପଥ ପ୍ରସ୍ତୁତ କରାଯାଉ, ପରିପଥର A ଓ B ପ୍ରାନ୍ତରେ ନମୁନାକୁ ଲଗାଇ ସୁଇଚ୍ ON କଲେ ଯଦି ବଲ୍ବ ଜଳିବ ତେବେ ନମୁନାଟି ଧାତୁ, ନଚେତ୍ ଅଧାତୁ ।
Question 6.
ଏମ୍ପୋଟେରିକ୍ ଅକ୍ସାଇଡ୍ କହିଲେ କ’ଣ ବୁଝ ? ଏହି ଅକ୍ସାଇଡ୍ର ଦୁଇଟି ଉଦାହରଣ ଦିଅ ।
Answer:
ଯେଉଁ ଧାତବ ଅକ୍ସାଇଡ୍ ଉଭୟ ଅମ୍ଳ ଓ କ୍ଷାରକ ସହ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରି ଲବଣ ଓ ଜଳ ସୃଷ୍ଟିକରେ ତାହାକୁ ଉଭୟ ଧର୍ମୀ ଅକ୍ସାଇଡ୍ ବା ଏମ୍ପୋଟେରିକ୍ ଅକ୍ସାଇଡ କହନ୍ତି ।
ଉଦାହରଣ :
ଜିଙ୍ଗ୍ ଅକ୍ସାଇଡ୍ (ZnO) ଓ ଆଲୁମିନିୟମ୍ ଅକ୍ସାଇଡ୍ (Al203) ଦୁଇଟି ଏମୋଟେରିକ୍ ଅକ୍ସାଇଡ୍ ।
ZnO + 2HC → ZnCl2 + H2O
ZnO + 2NaOH → Na2 ZnO2 + H2O
Al2O3 + 6HCI → 2AlCl3 + 3H2O
Al2O3 + 2NaOH → 2NaAlO2 + H2O

Question 7.
ଦୁଇଟି ଧାତୁର ନାମ ଦର୍ଶାଅ ଯାହାକି ହାଇଡ୍ରୋଜେନ୍କୁ ଲଘୁ ଅମ୍ଳରୁ ବିସ୍ଥାପନ କରେ ଏବଂ ଦୁଇଟି ଧାତୁର ନାମ ଦର୍ଶାଅ ଯାହା ଏପରି କରେ ନାହିଁ ।
Answer:
(i) ସକ୍ରିୟତା ଅନୁ କ୍ରମରେ ହାଇଡ୍ରୋଜେନ୍ ଉପରେ ଥିବା ଯେକୌଣସି ଦୁଇଟି ମୌଳିକ ନେଲେ ତାହା ହାଇଡ୍ରୋଜେନକୁ ବିସ୍ଥାପନ କରିବ । ଲଘୁ ଅମ୍ଳରୁ ହାଇଡ୍ରୋଜେନ୍, ମ୍ୟାଗ୍ନେସିୟମ୍ ଓ ଆଲୁମିନିୟମ୍କୁ ବିସ୍ଥାପନ କରିବ ।
(ii) କପର ଓ ସିଲ୍ଭର ଲଘୁ ଅମ୍ଳରୁ ହାଇଡ୍ରୋଜେନ୍କୁ ବିସ୍ଥାପନ କରେ ନାହିଁ ।
Question 8.
ବୈଦ୍ୟୁତିକ ଶୋଧନ ଗୋଟିଏ ଧାତୁ M ପାଇଁ, ଏନୋଡ୍, କ୍ୟାଥୋଡ୍ ଏବଂ ବୈଦ୍ୟୁତିକ ବିଶ୍ଳେଷ୍ୟ ରୂପେ କାହାକୁ ନିଆଯିବ ?
Answer:
ଅଶୋଧ ଧାତୁ Mକୁ ଏନୋଡ୍ ରୂପେ,ବିଶୁଦ୍ଧ ଧାତୁ Mକୁ କ୍ୟାଥୋଡ୍ ରୂପେ ଏବଂ ଧାତୁ Mର ଲବଣକୁ ବୈଦ୍ୟୁତିକ ବିଶ୍ଳେଷ୍ୟରୂପେ ନିଆଯିବ ।
Question 9.
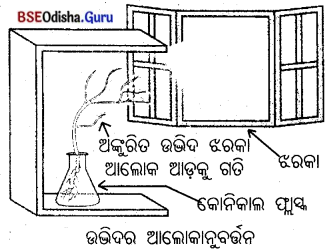
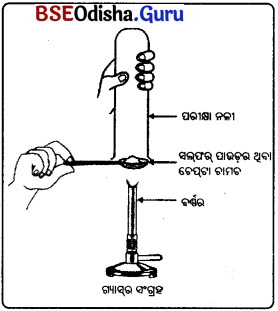
ଜଣେ ଚେପ୍ଟା ଚାମଚରେ ସଲ୍ଫର ପାଉଡ଼ର ନେଇ ଉତ୍ତପ୍ତ କଲା ଏବଂ ଗୋଟିଏ ପରୀକ୍ଷାନଳୀକୁ ଓଲଟାଇ ବାହାରୁଥିବା ଗ୍ୟାସ୍କୁ ସଂଗ୍ରହ କଲା । (ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ହେଲାପରି)
(a) ଗ୍ୟାସ୍ର କ୍ରିୟାଶୀଳତା
(i) ଶୁଷ୍କ ଲିଟମସ୍ କାଗଜ ଉପରେ କ’ଣ ହେବ ?
ଉ : ଶୁଷ୍କ ଲିଟମସ୍ କାଗଜ ଉପରେ କୌଣସି ପ୍ରତିକ୍ରିୟା ହେବ ନାହିଁ । ଅର୍ଥାତ୍ ଗ୍ୟାସ୍ର କ୍ରିୟାଶୀଳତା ଅପରିବତ୍ତତ ରହିବ ।
(ii) ଆର୍ଦ୍ର ଲିଟମସ୍ କାଗଜ ଉପରେ କ’ଣ ହେବେ ?
ଉ : ଆର୍ଦ୍ର ନୀଳ ଲିଟମସ୍ କାଗଜ ଲାଲ୍ ହେବ ।
(b) ସୃଷ୍ଟି ହୋଇଥ୍ ପ୍ରତିକ୍ରିୟାର ଏକ ସମତୁଲ
ଉ :

Question 10.
ଲୁହାର କଳଙ୍କି ନିରୋଧ ପାଇଁ ଦୁଇଟି ଉପାୟ ଲେଖ ।
Answer:
(a) ଗାନାଇଜିଙ୍ଗ୍ (ଜିଙ୍କ୍ ଲେପନ) : ଏହି ପ୍ରଣାଳୀରେ ଜିଙ୍କର ଏକ ପତଳା ସ୍ତରର ଆଚ୍ଛାଦନ ଦ୍ଵାରା ଲୁହାକୁ କଳଙ୍କି ନିରୋଧ କରାଯାଇ ପାରିବ ।
(b) ରଙ୍ଗ ଲେପନ: ଲୌହ ପଦାର୍ଥ ଉପରେ ରଙ୍ଗର ଲେପ ଦେଇ କଳଙ୍କିରୋଧ କରାଯାଇପାରିବ ।
Question 11.
ଅଧାତୁ ସହ ଅକ୍ସିଜେନ୍ର ସଂଯୋଗ ହେଲେ କେଉଁ ପ୍ରକାରର ଅକ୍ସାଇଡ୍ ଉତ୍ପନ୍ନ ହୁଏ ?
Answer:
ଅଧାତୁ ସହ ଅକ୍ସିଜେନ୍ ସଂଯୋଗ ହେଲେ ଅମ୍ଳୀୟ ବା ନିରପେକ୍ଷ ଅକ୍ସାଇଡ୍ ଉତ୍ପନ୍ନ ହୁଏ ।
ଉଦାହରଣ:
ଅମ୍ଳୀୟ ଅକ୍ସାଇଡ୍ – CO2, SO2
ନିରପେକ୍ଷ ଅକ୍ସାଇଡ୍ – H2O, CO, N2O
Question 12.
କାରଣ ଦର୍ଶାଅ ।
Answer:
(a) ପ୍ଲାଟିନମ, ସୁନା ଏବଂ ରୁପା ଗହଣା ତିଆରିରେ ବ୍ୟବହୃତ ହୁଏ ।
ଉ :
(i) ପ୍ଲାଟିନମ୍, ସୁନା ଓ ରୁପା ସବୁଠାରୁ କମ୍ ପ୍ରତିକ୍ରିୟାଶୀଳ ଧାତୁ । ଏଗୁଡ଼ିକ ସହଜରେ ବାୟୁଦ୍ବାରା କ୍ଷୟପ୍ରାପ୍ତ ହୁଅନ୍ତି ନାହିଁ ।
(ii) ଏଗୁଡ଼ିକ ଅତି ନମନୀୟ, ତନ୍ୟ ଓ ଉଜ୍ଜଳ । ତେଣୁ ଏଗୁଡ଼ିକ ଗହଣା ତିଆରିରେ ବ୍ୟବହୃତ ହୁଏ
(b) ତେଲ ଭିତରେ ସୋଡ଼ିୟମ୍, ପୋଟାସିୟମ୍କୁ ଓ ଲିଥ୍ୟମ୍କୁ ରଖାଯାଏ ।
ଉ :
(i) ପୋଟାସିୟମ୍, ସୋଡ଼ିୟମ୍ ଓ ଲିଥ୍ମ୍ ସାଧାରଣ ତାପମାତ୍ରାରେ ଏତେ ଜୋରରେ ପ୍ରତିକ୍ରିୟା କରେ ଯେ ସେଗୁଡ଼ିକରେ ନିଆଁ ଲାଗିଯାଏ ।
(ii) ତେଣୁ ଦୁର୍ଘଟଣାଜନିତ ନିଆଁରୁ ରକ୍ଷା ପାଇବା ପାଇଁ ସେଗୁଡ଼ିକୁ ସର୍ବଦା କିରୋସିନ୍ରେ ବୁଡ଼ାଇ ରଖାଯାଏ ।
(c) ଯଦିଓ ଏଲୁମିନିୟମ୍ ଏକ ଉଚ୍ଚ କ୍ରିୟାଶୀଳ ମୌଳିକ, ତଥାପି ଏହାକୁ ରନ୍ଧନ ବାସନକୁସନ ତିଆରିରେ ବ୍ୟବହାର କରାଯାଏ ।
(i) ଏଲୁମିନିୟମ୍ କ୍ଷୟରୋଧୀ ଓ ତାପର ସୁପରିବାହୀ । ଏହାର ପୃଷ୍ଠଦେଶ ଅକ୍ସାଇଡ୍ର ଏକ ପ୍ରତିକ୍ରିୟାହୀନ ସ୍ତର ସୃଷ୍ଟିକରେ ।
(ii) ଏହି ଅକ୍ସାଇଡ୍ର ଆସ୍ତରଣ ଧାତୁକୁ ସଂକ୍ଷାରଣରୁ ରକ୍ଷାକରେ । ତେଣୁ ଏହାକୁ ରନ୍ଧନ ବାସନକୁସନ ତିଆରିରେ କରାଯାଏ ।
(d) ଧାତୁ ନିଷ୍କାସନ ପ୍ରଣାଳୀରେ କାର୍ବୋନେଟ୍ ଓ ସଲଫାଇଡ୍ ଧାତୁପିଣ୍ଡକୁ ଅକ୍ସାଇଡ୍ରେ ପରିଣତ କରାଯାଏ ।
ଉ : ଧାତବ ଅକ୍ସାଇଡ୍କୁ ସହଜରେ ବିଜାରଣ କରି ସେଥୁରୁ ଧାତୁ ନିଷ୍କାସନ କରାଯାଇ ପାରିବ । କିନ୍ତୁ ସଲଫାଇଡ୍ ଓ କାର୍ବୋନେଟ୍ ଧାତୁପିଣ୍ଡରୁ ଧାତୁ ନିଷ୍କାସନ ସହଜରେ କରାଯାଇ ପାରିବ ନାହିଁ ।

Question 13.
ତୁମ୍ଭେମାନେ ଦେଖୁଥିବା ମଳିନ ପଡ଼ିଥିବା ତମ୍ବା ପାତ୍ରଗୁଡ଼ିକ ଲେମ୍ବୁ ଏବଂ ତେନ୍ତୁଳି ରସଦ୍ଵାରା ସଫା କରାଯାଏ । କାହିଁକି ଏହି ଖଟାଜାତୀୟ ପଦାର୍ଥ ଦ୍ଵାରା ପାତ୍ରଗୁଡ଼ିକ ସଫା କରିବା ସମ୍ଭବ ହୁଏ ? ବୁଝାଅ । ମଳିନ ପଡ଼ିଥିବା ତମ୍ବା ପାତ୍ରଗୁଡ଼ିକ ଉପରେ କପର କାର୍ବୋନେଟ୍ର ଏକ ସ୍ତର ଥାଏ ।
Answer:
(i) ମଳିନ ପଡ଼ିଥିବା ତମ୍ବା ପାତ୍ରଗୁଡ଼ିକ ଉପରେ କପର କାର୍ବୋନେଟ୍ର ଏକ ସ୍ତର ଥାଏ ।
(ii) କ୍ଷାରୀୟ କପର କାର୍ବୋନେଟ୍ ଜଳରେ ଅଦ୍ରବଣୀୟ । କିନ୍ତୁ ଲେମ୍ବୁରସ ଏବଂ ତେନ୍ତୁଳି ରସ ଭଳି ଅମ୍ଳରେ ଦ୍ରୁତ ଦ୍ରବଣୀୟ । ତେଣୁ ସହଜରେ ତମ୍ବା ପାତ୍ରଗୁଡ଼ିକ ସଫା ହୋଇଯାଏ ।
Question 14.
ଧାତୁ ଏବଂ ଅଧାତୁ ମଧ୍ୟରେ ଥିବା ରାସାୟନିକ ଧର୍ମଗୁଡ଼ିକର ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
Answer:
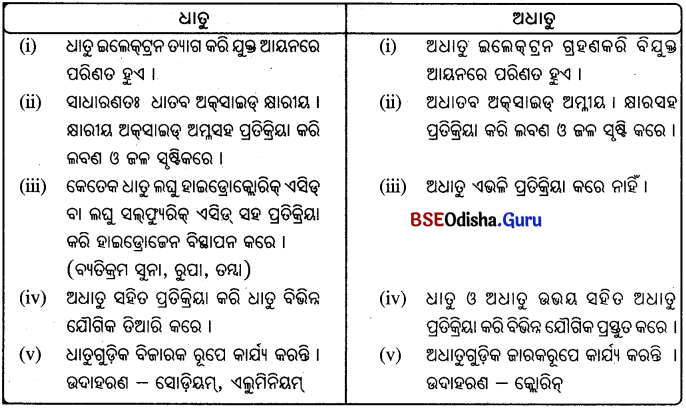
Question 15.
ଗୋଟିଏ ଲୋକ ଦୁଆର ଦୁଆର ବୁଲି ନିଜକୁ ବଣିଆ ବୋଲି କହିଲା । ସେ ପୁରୁଣା ଏବଂ ମାନ୍ଦା ସୁନା ଅଳଙ୍କାରକୁ ନୂତନ କରିଦେବ ବୋଲି ପ୍ରତିଶ୍ରୁତି ଦେଲା । ନିଃସନ୍ଦେହରେ ଜଣେ ଭଦ୍ର ମହିଳା ଏକ ଯୋଡ଼ା ଚୁଡ଼ି ତାକୁ ଦେବାରୁ ସେ ତାକୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦ୍ରବଣରେ ବୁଡ଼ାଇଦେଲା । ଏହାପରେ ସେହି ଚୁଡ଼ିଗୁଡ଼ିକ ନୂଆପରି ଚକ୍ ଚକ୍ ହୋଇଗଲା । ମାତ୍ର ତା’ର ଓଜନ ବହୁତ କମିଗଲା । ସେହି ସ୍ତ୍ରୀଲୋକଟି ଅଶାନ୍ତ ହୋଇ କିଛି ସମୟ ଯୁକ୍ତିତର୍କ କଲାପରେ
Answer:
(i) ଲୋକଟି ବ୍ୟବହାର କରିଥିବା ଉକ୍ତ ଦ୍ରବଣର ନାମ ଆକ୍କାରେଜିଆ ବା ଅମ୍ଳରାଜ। ସଦ୍ୟ ପ୍ରସ୍ତୁତ ଗାଢ଼ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍ ଏବଂ ଗାଢ଼ ନାଇଟ୍ରିକ୍ ଏସିଡ୍ର 3 : 1 ମିଶ୍ରଣ । ଏ ଦୁଇ ଅମ୍ଳ ମଧ୍ୟରୁ କୌଣସିଟି ସୁନାକୁ ଦ୍ରବୀଭୂତ କରିପାରେ ନାହିଁ । କିନ୍ତୁ ଏହାର ମିଶ୍ରଣ ସୁନାକୁ ଦ୍ରବୀଭୂତ କରିପାରେ ।
(ii) ଅମ୍ଳରାଜରେ ଏକ ଯୋଡ଼ା ଚୁଡ଼ିକୁ ପକାଇବା ଦ୍ଵାରା କିଛି ସୁନା ଦ୍ରବୀଭୂତ ହୋଇଗଲା, ଫଳରେ ଓଜନରେ
Question 16.
ଗରମ ପାଣି ଟାଙ୍କି ପାଇଁ ଷ୍ଟିଲ୍ ପରିବର୍ତ୍ତେ ତମ୍ବା କାହିଁକି ବ୍ୟବହାର କରାଯାଏ ?
Answer:
(i) ଷ୍ଟିଲ୍ ଲୁହାରେ ତିଆରି ଯାହାକି ଗରମପାଣିର ବାମ୍ଫ ସହ ପ୍ରତିକ୍ରିୟା କରେ; କିନ୍ତୁ କପର ପ୍ରତିକ୍ରିୟା କରେ ନାହିଁ ।
3Fe(s) + 4H2O → Fe3O4(s) + 4H2(g)
( ଗରମ)
(ii) ଷ୍ଟିଲ୍ ତୁଳନାରେ ତମ୍ବାର ଗଳନାଙ୍କ ଅତି ଉଚ୍ଚ ଏବଂ ତମ୍ବା ମଧ୍ୟ ଅଧିକ ତାପ ସୁପରିବାହୀ । ତେଣୁ ଗରମ ପାଣି ଟାଙ୍କି ପାଇଁ ଷ୍ଟିଲ୍ ପରିବର୍ତ୍ତେ ତମ୍ବା ବ୍ୟବହାର କରାଯାଏ ।
ପ୍ରଶ୍ନବଳୀ ଓ ଉତ୍ତର:
Question 1.
ଗୋଟିଏ ଧାତୁର ଉଦାହରଣ ଦିଅ ଯାହାକି
(i) ସାଧାରଣ ତାପମାତ୍ରାରେ ତରଳ ଅଟେ
(ii) ସହଜରେ ଛୁରୀରେ କଟାଯାଇ ପାରିବ
(iii) ତାପର ସୁପରିବାହୀ
(iv) ତାପର କୁପରିବାହୀ
Answer:
(i) ପାରଦ, (ii) ସୋଡ଼ିୟମ୍, (iii) ରୁପା, ଲୁହା, (iv) ଲେଡ଼
Question 2.
ନମନୀୟ ଓ ତନ୍ୟର ଅର୍ଥ ବୁଝାଅ ।
Answer:
ନମନୀୟ – ଧାତୁକୁ ଆଘାତ କରି ଚଦରରେ ପରିଣତ କରିବା ଗୁଣକୁ ନମନୀୟ ଗୁଣ କହନ୍ତି ।
ତନ୍ୟ – ଧାତୁଗୁଡ଼ିକ ତାରରେ ରୂପାନ୍ତରଣ ହେବା ଗୁଣକୁ ତନ୍ୟ ଗୁଣ କହନ୍ତି ।
Question 3.
ସୋଡ଼ିୟମ୍କୁ କାହିଁକି କିରୋସିନ୍ ତେଲରେ ବୁଡ଼ାଇ ରଖାଯାଏ ?
Answer:
ସୋଡ଼ିୟମ ଅତ୍ୟନ୍ତ ପ୍ରତିକ୍ରିୟାଶୀଳ ଧାତୁ ହୋଇଥିବାରୁ ଏହା ବାୟୁ ସଂସ୍ପର୍ଶରେ ଆସିଲେ ଜଳିଯାଏ । ସୋଡ଼ିୟମ୍ ସାଧାରଣ ତାପମାତ୍ରାରେ ଅମ୍ଳଜାନ ଓ ଜଳୀୟବାଷ୍ପ (ଆର୍ଦ୍ର ବାୟୁ) ସହ ପ୍ରତିକ୍ରିୟା କରେ । କିନ୍ତୁ କିରୋସିନ୍ରେ ବୁଡ଼ାଇ ରଖିଲେ ସୋଡ଼ିୟମ୍ ପ୍ରତିକ୍ରିୟା କରେ ନାହିଁ ।

Question 4.
ନିମ୍ନଲିଖୁତ ପ୍ରତିକ୍ରିୟା ପାଇଁ ରାସାୟନିକ ସମୀକରଣ ଲେଖ ।
(i) ଆଇରନ୍ ସହିତ ବାମ୍ଫ
(ii) କ୍ୟାଲ୍ସିୟମ୍ ଏବଂ ପୋଟାସିୟମ୍ ସହିତ ଜଳ ।
Answer:

Question 5.
ଚାରୋଟି ଧାତୁର ନମୁନା A, B, C ଏବଂ D ନିଆଯାଇଛି ଏବଂ ଗୋଟିଏ ଧାତୁକୁ ପକାଯାଇଛି । ଫଳାଫଳକୁ ନିମ୍ନସାରଣୀରେ ଲେଖା ଧାତୁ |
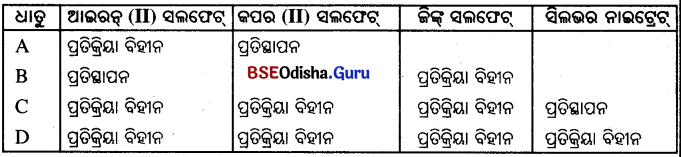
ଉପରୋକ୍ତ ସାରଣୀ ବ୍ୟବହାର କରି A, B, C ଏବଂ D ଧାତୁ ବିଷୟରେ ନିମ୍ନଲିଖ୍ତ ପ୍ରଶ୍ନର ଉତ୍ତର ଦିଅ |
(i) କେଉଁ ଧାତୁଟି ସବୁଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ଅଟେ ?
ଉ : B ଧାତୁଟି ସବୁଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ଅଟେ
(ii) B ଧାତୁକୁ କପର (II) ସଲଫେଟ୍ ଦ୍ରବଣ ସହ ମିଶାଇଲେ କ’ଣ ଦେଖୁବ ?
ଉ : B ଧାତୁ ଆଇରନ୍ଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ଏକ ଆଇରନ୍ କପରଠାରୁ ଅଧ୍ଵ ପ୍ରତିକ୍ରିୟାଶୀଳ । ତେଣୁ B ଧାତୁ କର୍ପରଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ । ତେଣୁ କପର ସଲଫେଟ୍ ଦ୍ରବଣରୁ କପ୍କୁ ବିସ୍ଥାପିତ କରିବ । :
B + CuSO4 → Cu + BSO4
(iii) ପ୍ରତିକ୍ରିୟାଶୀଳତାର ଅଧଃକ୍ରମରେ A, B, C ଏବଂ D ଧାତୁକୁ ସଜାଇ ଲେଖ ।
ଉ : ଧାତୁ B > ଧାତୁ A > ଧାତୁ C > ଧାତୁ D
Question 6.
ଗୋଟିଏ ପ୍ରତିକ୍ରିୟାଶୀଳ ଧାତୁ ସହ ଲଘୁ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍ ମିଶାଇଲେ କେଉଁ ଗ୍ୟାସ୍ ପାଇବ ? ଲୁହା ସହିତ ଲଘୁ H2SO4 ର ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାକୁ ସମୀକରଣ ସହ ଲେଖ ।
Answer:
ଗୋଟିଏ ପ୍ରତିକ୍ରିୟାଶୀଳ ଧାତୁ ସହ ଲଘୁ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍ ମିଶାଇଲେ ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ସୃଷ୍ଟି ହେବ
Fe(s) + H2SO4 (aq) → FeSO4(aq) + H2(g)
Question 7.
ଜିକ୍ ସହିତ ଆଇରନ୍ (II) ସଲ୍ଫେଟ୍କୁ ମିଶାଇଲେ କ’ଣ ପର୍ଯ୍ୟବେକ୍ଷଣ କରିବ ? ଏହି ରାସାୟନିକ ପ୍ରତିକ୍ରିୟାଟିକୁ ସମୀକରଣ ସହ ଲେଖ ।
Answer:
ଜିଙ୍କ୍ ଆଇରନ୍ଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ । ତେଣୁ ଜିଙ୍କ୍କୁ ଆଇରନ୍ ସଲଫେଟ୍ ସହ ମିଶାଇଲେ ଜିଙ୍କ୍ ଆଇରନକୁ
Zn(s) + FeSO4(aq) → ZnSO4(aq) + Fe
Question 8.
(i) ସୋଡ଼ିୟମ୍, ଅକ୍ସିଜେନ୍ ଏବଂ ମ୍ୟାଗ୍ନେସିୟମ୍ର ଇଲେକ୍ଟ୍ରନ୍ ସଂରଚନା ଲେଖ । (ଏହାକୁ ବିନ୍ଦୁଦ୍ଵାରା ଚିହ୍ନିତ କର)
ଉ :

(ii) ଇଲେକ୍ଟ୍ରନ ସ୍ଥାନାନ୍ତରଦ୍ୱାରା (Na2O) ଏବଂ (MgO)ର ଗଠନ ଦର୍ଶାଅ ।
ଉ :
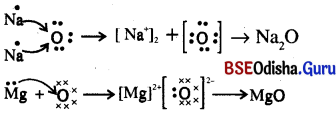
(iii) ଏହି ଯୌଗିକଗୁଡ଼ିକରେ କେଉଁ ଆୟନସବୁ ରହିଅଛି ?
ଉ : Na2O ରେ Na+ ଓ O2- ଏବଂ MgO ରେ Mg2+ ଓ O2- ଏନାୟନ୍ ସବୁ ରହିଅଛି ।
Question 9.
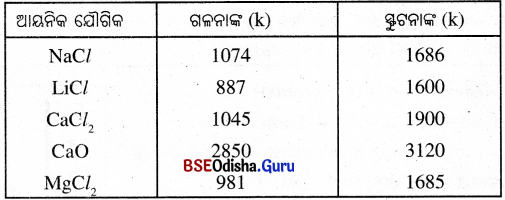
ଆୟନିକ ଯୌଗିକର କାହିଁକି ଉଚ୍ଚ ଗଳନାଙ୍କ ହୁଏ ?
Answer:
ଆୟନିକ ଯୌଗିକର ପରମାଣୁଗୁଡ଼ିକ ପରସ୍ପର ସହିତ ଦ୍ରୁତ ରାସାୟନିକ ବନ୍ଧଦ୍ୱାରା ବାନ୍ଧିହୋଇ ରହିଥାନ୍ତି । ଆୟନିକ ଯୌଗିକର ଶକ୍ତ ଅନ୍ତଃ ଆୟନୀୟ ଆକର୍ଷଣ ଭାଙ୍ଗିବା ପାଇଁ ପ୍ରଚୁର ଶକ୍ତି ଆବଶ୍ୟକ । ତେଣୁ ଆୟନିକ ଯୌଗିକର ଗଳନାଙ୍କ ଉଚ୍ଚ ହୋଇଥାଏ ।
Question 10.
ନିମ୍ନଲିଖୂତ ପଦଗୁଡ଼ିକୁ ବୁଝାଇ ଲେଖ ।
(i) ଖଣିଜ
(ii) ଧାତୁପିଣ୍ଡ
(iii) ଗାର୍ଲ୍
Answer:
(i) ଖଣିଜ – ପ୍ରକୃତିରେ ଭୂତ୍ବକ୍ରୁ ମିଳୁଥିବା ମୌଳିକ ବା ଯୌଗିକକୁ ଖଣିଜ କୁହାଯାଏ ।
(ii) ଧାତୁପିଣ୍ଡ – ଯେଉଁ ଖଣିଜରୁ ଧାତୁକୁ ନିଷ୍କାସନ କରିବା ଲାଭଜନକ ହୋଇଥାଏ, ସେହି ଖଣିଜକୁ ଓର୍ ବା ଧାତୁପିଣ୍ଡ କୁହାଯାଏ ।
(iii) ଗାଙ୍ଗ୍ – ଧାତୁପିଣ୍ଡରେ ମିଶିରହିଥିବା ମାଟି, ବାଲି ଆଦି ଅପଦ୍ରବକୁ ଗାଙ୍ଗୁ କୁହାଯାଏ ।

Question 11.
ମୁକ୍ତ ଭାବରେ ପ୍ରକୃତିରୁ ମିଳୁଥିବା ଦୁଇଟି ଧାତୁର ନାମ ଲେଖ ।
Answer:
ସୁନା, ପ୍ଲାଟିନମ୍
Question 12.
କେଉଁ ରାସାୟନିକ ପ୍ରଣାଳୀ ବ୍ୟବହାର କରି ଧାତବ ଅକ୍ସାଇଡ୍ରୁ ଧାତୁ ନିଷ୍କାସନ କରାଯାଏ ?
Answer:
ବିଜାରଣ ପଦ୍ଧତି ବ୍ୟବହାର କରି ଧାତବ ଅକ୍ସାଇଡ୍ରୁ ଧାତୁ ନିଷ୍କାସନ କରାଯାଏ ।
Question 13.
ଜିଙ୍କ୍, ମ୍ୟାଗ୍ନେସିୟମ୍ ଏବଂ ତମ୍ବାର ଧାତବ ଅକ୍ସାଇଡ୍ଗୁଡ଼ିକୁ ନିମ୍ନଧାତୁ ସହ ଉତ୍ତପ୍ତ କରାଗଲା । ମ୍ୟାଗ୍ନେସିୟମ୍

କେଉଁ କ୍ଷେତ୍ରରେ ଅପସାରଣ ପ୍ରତିକ୍ରିୟା ହେବାର ଦେଖିପାରିବ ?
Answer:
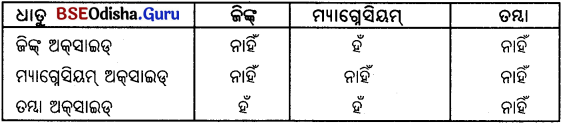
Question 14.
କେଉଁ ଧାତୁ ସହଜରେ ସଂକ୍ଷାରଣ ହୋଇପାରେ ନାହିଁ ?
Answer:
ସୁନା, ରୁପା ଓ ପ୍ଲାଟିନମ୍
Question 15.
ମିଶ୍ରଧାତୁ କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ଧାତୁ ଓ ଅଧାତୁ କିମ୍ବା ଧାତୁ ଓ ଧାତୁ କିମ୍ବା ଧାତୁ ଓ ଉପଧାତୁର ମିଶ୍ରଣକୁ ମିଶ୍ରଧାତୁ କୁହାଯାଏ ।
କାର୍ଯ୍ୟାବଳୀ (Activity):
କାର୍ଯ୍ୟାବଳୀ -1 (Activity-1)
(a) ଧାତବ ଦୀପ୍ତି ବା ଧାତବ ଉଜ୍ଜଳତା :
ବିଶୁଦ୍ଧ ଅବସ୍ଥାରେ ଧାତୁଗୁଡ଼ିକ ଚକ୍ ଚକ୍ କରୁଥବାରୁ, ଏହି ଗୁଣକୁ ଧାତବ ଦୀପ୍ତି କୁହାଯାଏ
ପରୀକ୍ଷା ପଦ୍ଧତି:
ବାଲିକାଗଜ ଦ୍ବାରା ପ୍ରତ୍ୟେକ ନମୁନା ଧାତୁକୁ ଭଲଭାବରେ ଘଷ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
ଘଷାଯାଇଥିବା ପାର୍ଶ୍ଵ ଓ ଘଷା ଯାଇନଥିବା ଅଂଶକୁ ଦେଖୁଲେ ଜଣାଯାଏ ଯେ ଘଷାଯାଇଥିବା ପାର୍ଶ୍ୱ
ସିଦ୍ଧାନ୍ତ:
ବିଶୁଦ୍ଧ ଅବସ୍ଥାରେ ଧାତୁର ପୃଷ୍ଠ ଚକ୍ ଚକ୍ କରେ । ଧାତୁର ଏହି ଧର୍ମକୁ ଧାତବ ଦୀପ୍ତି ବା ଧାତବ ଉଜ୍ଜ୍ବଳତା କୁହାଯାଏ ।
କାର୍ଯ୍ୟାବଳୀ -2 (Activity-2)
(b) ଧାତୁଗୁଡ଼ିକ ଦୃଢ଼ ବା ଶକ୍ତ:
ଆବଶ୍ୟକ ଉପକରଣ:
ଲୁହା, ତମ୍ବା, ଏଲୁମିନିୟମ୍ ଏବଂ ମ୍ୟାଗ୍ନେସିୟମର ଛୋଟ ଖଣ୍ଡ ନିଅ । ସୋଡ଼ିୟମ ଖଣ୍ଡ ଚାପି ଶୁଖାଅ ଓ ୱାସ ଉପରେ ରଖ ।
ପରୀକ୍ଷା ପଦ୍ଧତି:
ପ୍ରତ୍ୟେକ ଖଣ୍ଡକୁ ଧାରୁଆ ଛୁରିରେ କାଟିବାକୁ ଚେଷ୍ଟାକର ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
ଲୁହା, ତମ୍ବା, ଏଲୁମିନିୟମ୍ ସହଜରେ ଛୁରୀଦ୍ଵାରା କାଟି ହେଉନାହିଁ; କିନ୍ତୁ ସୋଡ଼ିୟମ ଧାତୁ ସହଜରେ
ସିଦ୍ଧାନ୍ତ:
ସାଧାରଣତଃ ଧାତୁ ଗୁଡ଼ିକ ଦୃଢ଼ ବା ଶକ୍ତ । କିନ୍ତୁ ସୋଡ଼ିୟମ ପରି ଧାତୁର ଦୃଢ଼ତା ଅନ୍ୟଧାତୁଠାରୁ କମ୍ ( ନରମ ) ।

କାର୍ଯ୍ୟାବଳୀ -3 (Activity-3)
(c) ଧାତୁଗୁଡ଼ିକ ଦୃଢ଼ ବା ଶକ୍ତ:
ଆବଶ୍ୟକୀୟ ଉପକରଣ:
ଲୁହା, ଜିଙ୍କ୍, ଲେଡ୍ ଏବଂ ତମ୍ବାର ଧାତୁ ଖଣ୍ଡ ମାନ ନିଅ ।
ପରୀକ୍ଷା ପଦ୍ଧତି:
ଏକ ଲୁହା ଖଣ୍ଡ ଉପରେ ଯେ କୌଣସି ଧାତୁକୁ ରଖ୍ ହାତୁଡ଼ିରେ ଚାରିପାଞ୍ଚ ଥର ଆଘାତ କର । ଏହି ପରି ଅନ୍ୟ ଧାତୁ ଖଣ୍ଡକୁ ରଖ୍ ଆଘାତ କରି ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
ଧାତୁଖଣ୍ଡକୁ ବାରମ୍ବାର ଆଘାତକଲେ ତାହା ପତଳା ଚଦର ପରି ହୋଇଯାଉଛି ।
ସିଦ୍ଧାନ୍ତ:
ଧାତୁ ପ୍ରସାରଣଶୀଳ ବା ନମନୀୟ । ଧାତୁର ଏହି ଗୁଣକୁ ନମନୀୟତା କୁହାଯାଏ । ସୁନା ଓ ରୁପାର ନମନୀୟଗୁଣ ସର୍ବାଧିକ ।

କାର୍ଯ୍ୟାବଳୀ -4 (Activity-4)
(d) କାର୍ଯ୍ୟ|ଚ୍ଳ| (Ductility):
ଆବଶ୍ୟକ ଉପକରଣ:
ଲୁହା, ତମ୍ବା, ଏଲୁମିନିୟମ, ଲେଡ୍ ଇତ୍ୟାଦି ଧାତୁ ନିଆଯାଉ । ପରୀକ୍ଷା ପଦ୍ଧତି: ଧାତୁଗୁଡ଼ିକୁ ଗରମ କରି ଚିମୁଟାରେ ଟଣାଯାଉ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
ଧାତୁଗୁଡ଼ିକୁ ଚିମୁଟାରେ ଟାଣିଲେ ଧାତୁରୁ ତାର ମିଳୁଛି ।
ସିଦ୍ଧାନ୍ତ:
ଧାତୁ ତାରରେ ପରିଣତ ହେବା ଗୁଣକୁ ତନ୍ୟତା କୁହାଯାଏ ।
କାର୍ଯ୍ୟାବଳୀ -5 (Activity-5)
(e) ଧାତୁ ଗୁଡ଼ିକ ତାପ ସୁପରି ବାହୀ ଓ ଭଚ୍ଚଗଳନାକ ଚିଣିଷ୍ଟ:
ଆବଶ୍ୟକ ଉପକରଣ:
ଟଣ୍ଡେ ତମ୍ବା ଜିମ୍ବା ଏଲୁମିନିୟମ୍ ତାର, କ୍ଲାମ୍ପ ଷ୍ଟାଣ୍ଡ, ସ୍ପିରିଟ୍ ଲ୍ୟାମ୍ପ କିମ୍ବା ମହମବତୀ, ମହମ, ପିନ୍ କଣ୍ଟା ।
ପରୀକ୍ଷା ପଦ୍ଧତି:
ତମ୍ବା ତାରଖଣ୍ଡ ନେଇ ଗୋଟିଏ କ୍ଲାମ୍ପ ସାହାଯ୍ୟରେ ଷ୍ଟାଣ୍ଡରେ ଧରି ରଖାଯାଉ । ମହମ ସାହାଯ୍ୟରେ ଗୋଟିଏ ପିନ୍ କଣ୍ଟାକୁ ତାରର ମୁକ୍ତ ପ୍ରାନ୍ତରେ ଯୋଡ୍ ରଖାଯାଉ । ସ୍ପିରିଟ୍ ଲ୍ୟାମ୍ପ/ ମହମବତୀ ସାହାଯ୍ୟରେ ତାରର ମଝି ସ୍ଥାନରେ ଗରମ କରାଯାଉ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
କିଛି ସମୟପରେ ମହମ ତରଳିବାକୁ ଆରମ୍ଭକରିବ ଏବଂ ପିକଣ୍ଟାଟି ତଳକୁ ଖସି ପଡ଼ିବ । କିନ୍ତୁ ଧାତବ ତାର, ତରଳୁ ନାହିଁ ।
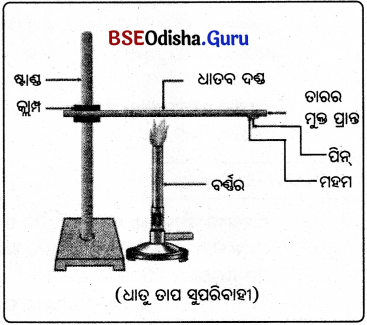
ସିଦ୍ଧାନ୍ତ:
ଧାତୁ ଗୁଡ଼ିକ ତାପ ସୁପରିବାହୀ ଏବଂ ଉଚ୍ଚ ଗଳନାଙ୍କ ବିଶିଷ୍ଟ ।
ରୁପା ଓ ତମ୍ବା ହେଉଛି ସବୁଠାରୁ ଉତ୍ତମ ତାପ ପରିବାହୀ । ଲେଡ୍ ଓ ପାରଦ ଅପେକ୍ଷାକୃତ କମ୍ ତାପ ପରିବାହୀ
କାର୍ଯ୍ୟାବଳୀ -6 (Activity-6)
(f) ଧାତୁ ବିଦ୍ୟୁତ୍ ପରିବହନ କରେ:
ଆବଶ୍ୟକ ଉପକରଣ: ବ୍ୟାଟେରୀ, ସୁଇଚ୍, ନମୁନା ଧାତୁ, କ୍ଳିପ୍ , ରବର କିମ୍ବା PVC ଭଳି ପଦାର୍ଥ ଦ୍ଵାରା ଆବୃତ ପରିବାହୀ ତାର, ବିଦ୍ୟୁତ୍ ହୋଲଡର ସହ ବଲ୍ବ ।
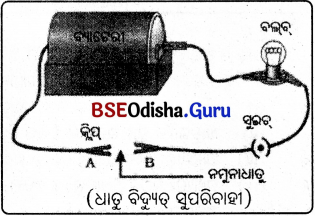
ପରୀକ୍ଷା ପଦ୍ଧତି :
ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥିବା ଭଳି ଉପକରଣଗୁଡ଼ିକୁ ବିଦ୍ୟୁତ୍ ପରିପଥରେ ସଂଯୋଗ କରାଯାଉ । A ଓ B ଅଗ୍ରମଧ୍ଯରେ ପରୀକ୍ଷା ପାଇଁ ଥିବା ନମୁନା ଧାତୁଟିକୁ ସଂଯୋଗ କରାଯାଉ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ :
ବିଦ୍ୟୁତ୍ ବଲବଟି ଜଳୁଛି ।
ସିଦ୍ଧାନ୍ତ :
ଧାତୁ ବିଦ୍ୟୁତ୍ ପରିବହନ କରେ ।
(g) ଧାତୁ ଧ୍ୱନି ସୃଷ୍ଟିକରେ:
ଆବଶ୍ୟକ ଉପକରଣ: ନମୁନା ଧାତୁ କିମ୍ବା ବିଦ୍ୟାଳୟ ଧାତବ ପିଟା ଘଣ୍ଟା କିମ୍ବା କଠିନ ପଦାର୍ଥ । ମନ୍ଦିରଗୁଡ଼ିକର ଘଣ୍ଟ,
ପରୀକ୍ଷା:
ନମୁନା ଧାତୁଖଣ୍ଡ ନେଇ ଯେ କୌଣସି କଠିନ ପଦାର୍ଥ ଦ୍ଵାରା ଆଘାତ କରାଯାଉ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
ଧାତୁକୁ କଠିନ ବସ୍ତୁରେ ଆଘାତ କଲେ ଧ୍ଵନି ସୃଷ୍ଟି ହୁଏ ।
ଅଧାତୁ (Non-metals):
ଅଧାତୁ ଗୁଡ଼ିକ ତିନୋଟି (କଠିନ ତରଳ ଓ ଗ୍ୟାସୀୟ) ଅବସ୍ଥାରେ ଦେଖାଯାନ୍ତି । କଠିନ ଅବସ୍ଥାରେ ମିଳୁଥିବା ଅଧାତୁ – କାର୍ବନ, ସଲଫର୍, ଆୟୋଡ଼ିନ୍ ଇତ୍ୟାଦି । ତରଳ ଅବସ୍ଥାରେ ମିଳୁଥିବା ଅଧାତୁ – ବ୍ରୋମିନ୍ ଗ୍ୟାସୀୟ ଅବସ୍ଥାରେ ମିଳୁଥିବା ଅଧାତୁ – ହାଇଡ୍ରୋଜେନ୍, ଅକ୍ସିଜେନ୍, କ୍ଲୋରିନ୍, ନାଇଟ୍ରୋଜେନ୍, ଫ୍ଲୋରିନ୍, ହିଲିୟମ, ନିୟନ ଓ ଆର୍ଗନ ।

କାର୍ଯ୍ୟାବଳୀ -7 (Activity-7)
ଆବଶ୍ୟକ ଉପକରଣ:
କାର୍ବନ, ସଲ୍ଫର ଓ ଆୟୋଡ଼ିନ୍ର କିଛି ନମୁନା ସଂଗ୍ରହ କରାଯାଉ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
ଏହି ଅଧାତୁଗୁଡ଼ିକୁ ନେଇ କାର୍ଯ୍ୟାବଳୀ-1ରୁ କାର୍ଯ୍ୟାବଳୀ-7 ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ ପରୀକ୍ଷା କରି ନିମ୍ନ ସାରଣୀରେ ଲିପିବଦ୍ଧ କରାଯାଉ ।
ଅଧାତୁ ସମ୍ବନ୍ଧୀୟ ପର୍ଯ୍ୟବେକ୍ଷଣ ସାରଣୀ
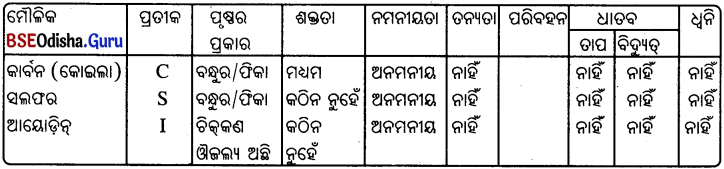
ସିଦ୍ଧାନ୍ତ :
ଧାତୁ ଓ ଅଧାତୁକୁ କେବଳ ଭୌତିକ ଧର୍ମ ଅନୁଯାୟୀ ବର୍ଗୀକରଣ କରାଯାଇ ପାରିବ ନାହିଁ କାରଣ ଏଥରେ ଅନେକ
- ସାଧାରଣ ତାପମାତ୍ରାରେ ସମସ୍ତ ଧାତୁ କଠିନ; କିନ୍ତୁ ପାରଦ ତରଳ ।
- ଧାତୁଗୁଡ଼ିକ ଉଚ୍ଚ ଗଳନାଙ୍କ ବିଶିଷ୍ଟ କିନ୍ତୁ ଗାଲିୟମ୍ ଏବଂ ସୀସିୟମ୍ ଅତି ନିମ୍ନ ଗଳନାଙ୍କ ବିଶିଷ୍ଟ ।
- ଆୟୋଡ଼ିନ୍ ଏକ ଅଧାତୁ ହେଲେ ମଧ୍ୟ ଏହାର ଧାତବ ଔଜଲ୍ୟ ଅଛି ।
- ମୁଖ୍ୟତଃ କଠିନ ଅଧାତୁଗୁଡ଼ିକ ନରମ; କିନ୍ତୁ କାର୍ବନର ଏକ ରୂପ ହୀରା ଯାହାକି ଗୋଟିଏ କଠିନତମ ପ୍ରାକୃତିକ ଅପରରୂପ (allotrope) ।
- ଧାତୁଗୁଡ଼ିକ କଠିନ; କିନ୍ତୁ କ୍ଷାରୀୟ ଧାତୁ (Alkali metals) ( ସୋଡ଼ିୟମ୍, ଲିଥ୍ୟମ, ପୋଟାସିୟମ୍ ଇତ୍ୟାଦି) ନରମ ଯାହାକୁ ଛୁରୀରେ କଟାଯାଇପାରିବ।
- ଅଧାତୁ ବିଦ୍ୟୁତ୍ କୁପରିବାହୀ; କିନ୍ତୁ କାର୍ବନର ଏକ ଅପର ରୂପ ଗ୍ରାଫାଇଟ୍ ବିଦ୍ୟୁତ୍ ପରିବହନ କରେ ।
କାର୍ଯ୍ୟାବଳୀ -8 (Activity-8)
ଆବଶ୍ୟକ ଉପକରଣ:
ସଲଫର ପାଉଡ଼ର, ଜଳ, ଲିଟ୍ସ୍ କାଗଜ, ପରୀକ୍ଷାନଳୀ
ପରୀକ୍ଷଣ:
ସଲଫର ପାଉଡ଼ରକୁ ଜାଳି ଉତ୍ପନ୍ନ ହେଉଥିବା ଧୂଆଁକୁ ଏକ ପରୀକ୍ଷାନଳୀରେ ସଂଗ୍ରହ କରାଯାଉ । ଏହି ପରୀକ୍ଷାନଳୀରେ କିଛି ଜଳ ମିଶାଇ ଜୋରରେ ହଲାଇଦିଅ । ଏହି ଦ୍ରବଣରେ ନୀଳ ଓ ନାଲି ଲିଟମସ୍ କାଗଜ ବୁଡ଼ାଇ ପରୀକ୍ଷା କରାଯାଉ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
ଦ୍ରବଣ ନୀଳ ଲିଟମସ୍ କାଗଜକୁ ନାଲି କରିବ । କିନ୍ତୁ ନାଲି ଲିଟ୍ସ୍ କାଗଜର ରଙ୍ଗରେ କୌଣସି ପରିବର୍ତ୍ତନ ହେବ ନାହିଁ ।
ସିଦ୍ଧାନ୍ତ:
ଅମ୍ଳ ନୀଳ ଲିଟମସ୍ କାଗଜକୁ ଲାଲ୍ କରିଥାଏ । ଏଠାରେ SO2 ର ଜଳୀୟ ଦ୍ରବଣ ଅମ୍ଳୀୟ ଅଟେ । ଅଧାତବ ଅକ୍ସାଇଡ୍ର ଜଳୀୟ ଦ୍ରବଣ ଅମ୍ଳୀୟ ।
ସମୀକରଣ S + 02 → SO2
SO2 + H2O → H2SO3 (AM&NA UF)
କାର୍ଯ୍ୟାବଳୀ -9 (Activity-9)
ଆବଶ୍ୟକ ଉପକରଣ:
ଏଲୁମିନିୟମ୍, ତମ୍ବା, ଲୁହା, ଲେଡ୍, ମ୍ୟାଗ୍ନେସିୟମ, ଜିଙ୍କ୍, ସୋଡ଼ିୟମ୍, ସୁନା ଓ ରୁପା ଧାତୁର ନମୁନା ସଂଗ୍ରହ କର ।
ପରୀକ୍ଷଣ:
ଉପର ଲିଖ୍ ଧାତୁର ନମୁନା ଗୁଡ଼ିକୁ ଚିମୁଟାରେ ଧରି ନିଆଁରେ ଜଳାଯାଉ । ସୃଷ୍ଟି ହୋଇଥିବା ଉତ୍ପାଦଗୁଡ଼ିକୁ ସଂଗ୍ରହ କରାଯାଉ । ଧାତୁର ପୃଷ୍ଠ ଏବଂ ଉତ୍ପାଦକ ଥଣ୍ଡା ହେବାକୁ ଦିଅ । ଉତ୍ପାଦଗୁଡ଼ିକୁ ଜଳରେ ଦ୍ରବୀଭୂତ କରିବାକୁ ରେଷ୍ଠ| ଇର|ତ୍ପ|ଉ |
ପର୍ଯ୍ୟବେକ୍ଷଣ:
- ମ୍ୟାଗ୍ନେସିୟମ ଧାତୁ ସହଜରେ ଜଳିଲା ଏବଂ ଉଜ୍ଜ୍ଵଳ ଆଲୋକ ଶିଖା ଦେଖାଗଲା ।
- ଧାତୁର ପୃଷ୍ଠଟି ରୂପେଲୀ ଧଳା ରଙ୍ଗର ଦେଖାଗଲା ।
- ସୋଡ଼ିୟମ୍ ସହଜରେ ଜଳିଲା ଏବଂ ସୁନେଲୀ ହଳଦିଆ ରଙ୍ଗର ଶିଖା ଦେଖାଗଲା ।
ସିଦ୍ଧାନ୍ତ:
- ଅକ୍ସିଜେନ ସହ ପ୍ରତିକ୍ରିୟାଶୀଳତାର ହ୍ରାସ ଅନୁସାରେ
Na > Mg > Al > Zn > Fe > Pb > Cu
- ସୋଡ଼ିୟମ ଅକ୍ସାଇଡ ଜଳରେ ଦ୍ରବଣୀୟ ।
- ଆଲୁମିନିୟମ, କପର, ଲୌହ, ଲେଡ୍, ମ୍ୟାଗ୍ନେସିୟମ୍, ଜିଙ୍କ୍ ଆଦି ଧାତୁର ଅକ୍ସାଇଡ୍ ଜଳରେ ଅଦ୍ରବଣୀୟ ।
- ଅଧିକାଂଶ ଧାତୁ ଅକ୍ସିଜେନ୍ ସହିତ ପ୍ରତିକ୍ରୟାକରି ଧାତବ ଅକ୍ସାଇଡ ସୃଷ୍ଟିକରେ ।
ଧାତୁ + ଅକ୍ସିଜେନ → ଧାତବ ଅକ୍ସାଇଡ୍
ଉଦାହରଣ:
(i) କପର ବାୟୁର ଉପସ୍ଥିତିରେ ଉତ୍ତପ୍ତ ହେଲେ ଅକ୍ସିଜେନ ସହ ମିଶି କଳାରଙ୍ଗର କପର

(ii) ଏଲୁମିନିୟମ୍ ଅକ୍ସିଜେନ ସହ ମିଶି ଏଲୁମିନିୟମ୍ ଅକ୍ସାଇଡ ସୃଷ୍ଟି କରେ ।
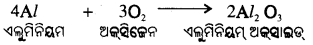
ଉଭୟଧର୍ମୀ ଅକ୍ସାଇଡ୍ ବା ଏମ୍ପୋଟେରିକ୍ ଅକ୍ସାଇଡ୍ :
ଯେଉଁ ଧାତବ ଅକ୍ସାଇଡ୍ ଉଭୟ ଅମ୍ଳସହ ଓ କ୍ଷାରସହ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରି ଲବଣ ଓ ଜଳ ସୃଷ୍ଟିକରେ ତାହାକୁ ଉଭୟଧର୍ମୀ ଅକସାଇଡ୍ ବା ଏମ୍ପୋଟେରିକ୍ ଅକ୍ସାଇଡ୍ (amphoteric oxide) କହନ୍ତି ।
Al2O3 + 6HCI → 2ACl3 + 3H2O
Al2O3 + 2NaOH → 2NaAlO3 + H2O
(ସୋଡ଼ିୟମ୍ ଏଲୁମିନେଟ୍)
ଅଧିକାଂଶ ଧାତବ ଅକ୍ସାଇଡ୍ ଜଳରେ ଅଦ୍ରବଣୀୟ ; କିନ୍ତୁ କିଛି ଧାତବ ଅକ୍ସାଇଡ ଜଳରେ ଦ୍ରବୀଭୂତ ହୋଇ କ୍ଷାର (Alkali) ସୃଷ୍ଟି କରନ୍ତି । ସୋଡ଼ିୟମ ଅକ୍ସାଇଡ୍ ଏବଂ ପୋଟାସିୟମ୍ ଅକ୍ସାଇଡ୍ ଜଳରେ ଦ୍ରବୀଭୂତ ହୋଇ କ୍ଷାର ସୃଷ୍ଟି କରନ୍ତି ।
Na2O(s) + H2O(l) → 2NaOH(aq)
K2O(s) + H2O(l) → 2KOH(aq)
(iii) ପୋଟାସିୟମ୍ ଓ ସୋଡ଼ିୟମ୍ ପରି ଧାତୁକୁ ବାହାରେ ରଖୁଦେଲେ ଜୋର୍ରେ ପ୍ରତିକ୍ରିୟା ହୁଏ ଏବଂ ସେଗୁଡ଼ିକରେ ନିଆଁ ଲାଗିଯାଏ ।
(iv) ଲୁହାକୁ ଉତ୍ତପ୍ତକଲେ ଜଳେ ନାହିଁ କିନ୍ତୁ ଲୁହାର ଗୁଣ୍ଡକୁ ଅଗ୍ନିଶିଖାରେ ଛିଞ୍ଚିଦେଲେ ଖୁବ୍ଶୀଘ୍ର ଜଳିଯାଏ ।
ରୁପା ଓ ସୁନା ଅକ୍ସିଜେନ ସହ ଏପରିକି ଉଚ୍ଚ ତାପମାତ୍ରାରେ ମଧ୍ୟ ପ୍ରତିକ୍ରିୟା କରନ୍ତି ନାହିଁ ।
ସିଦ୍ଧାନ୍ତ:
- ଧାତୁଗୁଡ଼ିକ ଅକ୍ସିଜେନ ସହ ସମାନ ବେଗରେ ପ୍ରତିକ୍ରିୟା କରନ୍ତି ନାହିଁ ।
- ବିଭିନ୍ନ ଧାତୁ ଅକ୍ସିଜେନ୍ ସହ ଭିନ୍ନ ଭିନ୍ନ ପ୍ରତିକ୍ରିୟାଶୀଳତା ପ୍ରଦର୍ଶନ କରନ୍ତି ।
- ପୋଟାସିୟମ୍ ଓ ସୋଡ଼ିୟମ୍ ସବୁଠାରୁ ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ଧାତୁ ।
- ମ୍ୟାଗ୍ନେସିୟମ୍ର ପ୍ରତିକ୍ରିୟା କମ୍ ।
- ଜିଙ୍କ, ଲୁହା, ତମ୍ବା ଏବଂ ଲେଡ୍କୁ ଅକ୍ସିଜେନ ଉପସ୍ଥିତିରେ ଜଳାଇଲେ ଏଗୁଡ଼ିକର ପ୍ରତିକ୍ରିୟାଶୀଳତା କ୍ରମ ବିଷୟରେ କୌଣସି ସୂଚନା ମିଳେ ନାହିଁ ।
- ସାଧାରଣ ତାପମାତ୍ରାରେ ମ୍ୟାଗ୍ନେସିୟମ୍, ଏଲୁମିନିୟମ୍, ଜିଙ୍କ୍, ଲେଡ୍ ଇତ୍ୟାଦି ଧାତୁଗୁଡ଼ିକର ପୃଷ୍ଠତଳରେ ଏକ ପତଳା ଅକ୍ସାଇଡ୍ ଆବରଣ ରହିଥାଏ । ସଂରକ୍ଷୀ ଅକ୍ସାଇଡ୍ର ସ୍ତର ଧାତୁକୁ ଅଧିକ ଜାରଣରୁ ରକ୍ଷାକରେ ।
- ତମ୍ବା ନିଆଁରେ ଜଳେ ନାହିଁ । ମାତ୍ର ଉତ୍ତପ୍ତ ଧାତୁ କପର (II) ଅକ୍ସାଇଡ୍ର ଏକ କଳା ଆବରଣ ଦ୍ଵାରା ଆଚ୍ଛାଦିତ ହୋଇଥାଏ ।
ମନେତଟ:
ଏନୋଡ଼ାଇଜିଂ ଏଲୁମିନିୟମ୍ରେ ଏକ ମୋଟା ଅକ୍ସାଇଡ୍ ପ୍ରଲେପ ଦେବାର ଏକ ପ୍ରଣାଳୀ । ଏଲୁମିନିୟମ୍ ବାୟୁରେ ରହିଲେ ଏକ ପତଳା ଅକ୍ସାଇଡ଼ର ଆବରଣ ସୃଷ୍ଟି କରେ । ଏହି ଏଲୁମିନିୟମ୍ ଅକ୍ସାଇଡ୍ର ପ୍ରଲେପ ଅଧିକ ସଂକ୍ଷାରଣ ହେବାକୁ ପ୍ରତିରୋଧ କରେ ।
ଏନୋଡ଼ାଇଜିଂ ପଦ୍ଧତିରେ ପରିଷ୍କାର ଏଲୁମିନିୟମ୍କୁ ଏନୋଡ଼ରେ ସଂଯୁକ୍ତ କରି ଲଘୁ ସଫ୍ୟୁରିକ୍ ଅମ୍ଳରେ ବୈଦ୍ୟୁତିକ ବିଶ୍ଳେଷଣ କରାଯାଏ । ଏନୋଡ଼ରେ ସୃଷ୍ଟି ହୋଇ ଅକ୍ସିଜେନ୍ ଏଲୁମିନିୟମ୍ ସହ ପ୍ରତିକ୍ରିୟା କରି ଏହା ଉପରେ ଏକ ମୋଟା ପ୍ରତିରୋଧ ଜାରଣ ଅକ୍ସାଇଡ୍ ଆବରଣ ସୃଷ୍ଟି କରେ ।
(b) ଧାତୁର ଜଳ ସହିତ ପ୍ରତିକ୍ରିୟା | (Reaction of Metals with Water):

କାର୍ଯ୍ୟାବଳୀ -10 (Activity-10)
ଆବଶ୍ୟକ ଉପକରଣ:
ଏଲୁମିନିୟମ୍, ତମ୍ବା, ଲୁହା, ଲେଡ୍ ମ୍ୟାଗ୍ନେସିୟମ୍, ଜିଙ୍କ୍, ସୋଡ଼ିୟମ, ସୁନା, ରୁପା ଧାତୁର ନମୁନା, ବିକର ଓ ଥଣ୍ଡା ଜଳ ।
ପରୀକ୍ଷଣ:
ସଂଗୃହୀତ ନମୁନାର ଛୋଟ ଖଣ୍ଡକୁ ଅଲଗା ଅଲଗା ବିକର୍ରେ ଅଧା ପର୍ଯ୍ୟନ୍ତ ଥଣ୍ଡାଜଳ ପୂରାଇ ରଖ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
- ସୋଡ଼ିୟମ, ପୋଟାସିୟମ ଏବଂ କ୍ୟାଲସିୟମ ଜଳ ସହିତ ପ୍ରତିକ୍ରିୟା କଲେ ବର୍ଦ୍ଧିତ ପ୍ରତିକ୍ରିୟାଶୀଳତା ଅନୁଯାୟୀ
କ୍ୟାଲସିୟମ୍ < ପୋଟାସିୟମ୍ < ସୋଡ଼ିୟମ୍
- ହଁ ସୋଡ଼ିୟମ୍ ଓ ପୋଟାସିୟମ ଧାତୁ ଜଳ ସହ ପ୍ରତିକ୍ରିୟା କରି ନିଆଁ ସୃଷ୍ଟି କଲା ।
- କିଛି ସମୟ ପରେ କ୍ୟାଲସିୟମ୍ ଭାସିବାକୁ ଆରମ୍ଭ କଲା ।
ପରୀକ୍ଷଣ:
ଯେଉଁ ଧାତୁଗୁଡ଼ିକ ଥଣ୍ଡା ଯେଉଁ ଧାତୁଗୁଡ଼ିକ ଥଣ୍ଡା କିମ୍ବା ଜଳରେ ପ୍ରତିକ୍ରିୟା କଲାନାହିଁ, ସେଗୁଡ଼ିକୁ ଅଧା ବିକର ଗରମ ପାଣିରେ ପକାଅ । ଗରମ ପାଣିରେ ପ୍ରତିକ୍ରିୟା କଲାନାହିଁ, ସେଗୁଡ଼ିକ ବାମ୍ଫ ସହ ପ୍ରତିକ୍ରିୟା କରେ । ମ୍ୟାଗ୍ନେସିୟମ୍ ଓ କ୍ୟାଲସିୟମ୍ ଥଣ୍ଡାଜଳରେ କମ୍ ମାତ୍ରାରେ ପ୍ରତିକ୍ରିୟା କରନ୍ତି କିନ୍ତୁ ଫୁଟନ୍ତା ପାଣିରେ ତୀବ୍ର ବେଗରେ ପ୍ରତିକ୍ରିୟା କରନ୍ତି ।
Mg + H2O → MgO + H2
Zn + H2O → ZnO + H2
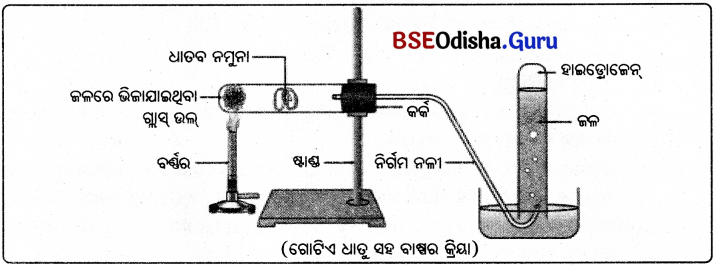
ଏଲୁମିନିୟମ୍ ଲୌହ, ଜିଙ୍କ୍ ବାମ୍ଫସହ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରେ ।
ଲେଡ୍, କପର, ସୁନା ଓ ରୁପା ଆଦି ଧାତୁ ଜଳସହ ରାସାୟନିକ ପ୍ରତିକ୍ରିୟା କରନ୍ତି ନାହିଁ ।
ସୋଡ଼ିୟମ୍ > ପୋଟାସିୟମ୍ > କ୍ୟାଲସିୟମ୍ > ମ୍ୟାଗ୍ନେସିୟମ୍ > ଏଲୁମିନିୟମ୍ > ଲୌହ > ସୀସା > ତମ୍ବା > ରୁପା > ପାରଦ > ସୁନା ।
ସିଦ୍ଧାନ୍ତ :
(i) ଧାତୁ + ଜଳ → ଧାତବ ଅକ୍ସାଇଡ୍ + ହାଇଡ୍ରୋଜେନ
(ii) ଧାତବ ଅକ୍ସାଇଡ୍ + ଜଳ → ଧାତବ ହାଇଡ୍ରକ୍ସାଇଡ୍
(iii) ସୋଡ଼ିୟମ୍ ପୋଟାସିୟମ୍ ଭଳି ଧାତୁ ଥଣ୍ଡାଜଳ ସହ ତୀବ୍ର ପ୍ରତିକ୍ରିୟା କରେ ।
2K(s) + 2H2O(l) → 2KOH(aq) + H2(g) + ତାପଶକ୍ତି
(iv) 2Na(s) + 2H2O(l) → 2NaOH(aq) + H2(g) + ତାପଶକ୍ତି
କ୍ୟାଲସିୟମ୍ ଜଳସହ କମ୍ ତୀବ୍ରତାରେ ପ୍ରତିକ୍ରିୟା କରେ ।
Ca(s) + 2H2O(l) → Ca(OH)2(aq) + H2(g)
(v) କ୍ୟାଲ୍ସିୟମ୍ ଜଳରେ ଭାସେ କାରଣ ଉତ୍ପନ୍ନ ହେଉଥିବା ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ର ଫୋଟକାଗୁଡ଼ିକ ଧାତୁର ଉପର ଭାଗରେ ଲାଖ୍ ରହିଯାଏ ।
(vi) ମ୍ୟାଗ୍ନେସିୟମ୍ ଗରମ ପାଣି ସହିତ ପ୍ରତିକ୍ରିୟା କରି ମ୍ୟାଗ୍ନେସିୟମ୍ ହାଇଡ୍ରକ୍ସାଇଡ୍ ଓ ହାଇଡ୍ରୋଜେନ ଗ୍ୟାସ୍ ଉତ୍ପନ୍ନ କରେ । ଏହାର ପୃଷ୍ଠଭାଗରେ ଲାଗିଥିବା ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ର ଫୋଟକା ଯୋଗୁଁ ଏହା ଭାସିବାକୁ ଆରମ୍ଭ କରେ ।
(vii) ଏଲୁମିନିୟମ୍, ଲୌହ, ଜିଙ୍କ୍ ପରି ଧାତୁ ବାମ୍ଫସହ ପ୍ରତିକ୍ରିୟା କରି ଧାତବ ଅକ୍ସାଇଡ୍ ଏବଂ ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ସୃଷ୍ଟିକରେ ।
2Al(s) + 3H2O(g) → Al2O3(s) + 3H2(g)
3Fe(s) + 4H2O(g) → Fe3O4(s) + 4H2(g)
ଲେଡ୍, ତମ୍ବା, ରୁପା, ସୁନା ଆଦୌ ଜଳସହ ପ୍ରତିକ୍ରିୟା କରନ୍ତି ନାହିଁ ।

କାର୍ଯ୍ୟାବଳୀ -11 (Activity-11)
ଆବଶ୍ୟକ ଉପକରଣ:
ସୋଡ଼ିୟମ୍ ଓ ପୋଟାସିୟମ ବ୍ୟତୀତ ଅନ୍ୟ ଧାତୁର ନମୁନା ସଂଗ୍ରହକର । ନମୁନା ମଳିନ ପଡ଼ିଥିଲେ ବାଲି କାଗଜରେ ଘଷି ସଫାକର ।
ପରୀକ୍ଷା:
- ଲଘୁ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍ ଥିବା ପରୀକ୍ଷାନଳୀରେ ନମୁନାଗୁଡ଼ିକୁ ଅଲଗା ଅଲଗା ଭର୍ତ୍ତି କର ।
- ଥର୍ମୋମିଟରକୁ ପରୀକ୍ଷାନଳୀ ମଧ୍ଯରେ ରଖି । ଏହାର ବଲ୍ବ ଏସିଡ୍ ଭିତରେ ବୁଡ଼ିରହୁ ।
ପର୍ଯ୍ୟବେକ୍ଷଣ:
କେତେକ ପରୀକ୍ଷାନଳୀରୁ ଫୋଟକା ବିଭିନ୍ନ ବେଗରେ ବାହାରୁଛି ଲକ୍ଷ୍ୟକର ।
ସିଦ୍ଧାନ୍ତ :
(i) ମ୍ୟାଗ୍ନେସିୟମ୍ ତୀବ୍ରଭାବରେ ପ୍ରତିକ୍ରିୟା କରୁଛି ଏବଂ ସବୁଠାରୁ ଦ୍ରୁତବେଗରେ ଫୋଟକା ସୃଷ୍ଟି ହେଉଛି ।
(ii) ମ୍ୟାଗ୍ନେସିୟମ୍ ଥିବା ପରୀକ୍ଷାନଳୀର ତାପମାତ୍ରା ଅଧିକ ।
(iii) Mg > Al > Zn > Fe (କ୍ରମରେ ପ୍ରତିକ୍ରିୟାଶୀଳତା କମିଥାଏ)
(iv) ତମ୍ବା, ରୁପା, ସୁନା, ଲଘୁ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଅମ୍ଳ ସହ ପ୍ରତିକ୍ରିୟା କରନ୍ତି ନାହିଁ ।
(v)
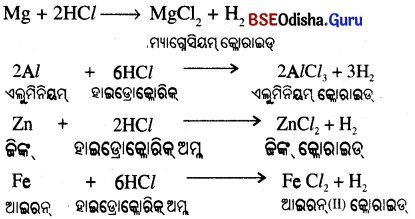
କୌଣସି ଧାତୁ HNO3 ସହ ପ୍ରତିକ୍ରିୟା କଲେ ହାଇଡ୍ରୋଜେନ୍ ଗ୍ୟାସ୍ ନିର୍ଗତ ହୁଏ ନାହିଁ କାରଣ HNO3 ସବଳ ଜାରକ ।
ଉତ୍ପନ୍ନ ହେଉଥିବା ହାଇଡ୍ରୋଜେନକୁ ଜାରଣ କରି ଜଳ ସୃଷ୍ଟିକରେ ଏବଂ ନିଜେ ବିଜାରିତ ହୋଇ ଯେକୌଣସି ନାଇଟ୍ରୋଜେନ୍ ଅକ୍ସାଇଡ୍ (N2O, NO, NO2,) ହୁଏ ।
କିନ୍ତୁ ମ୍ୟାଗ୍ନେସିୟମ୍ (Mg) ଓ ମାଙ୍ଗାନିଜ (Mn) ଲଘୁ ନାଇଟ୍ରିକ ଏସିଡ଼୍ ସହ ପ୍ରତିକ୍ରିୟା କରି H2 ଗ୍ୟାସ୍ ନିର୍ଗତ
ଅମ୍ଳରାଜ :
ଅମ୍ଳରାଜ(Aquaregia) ହେଉଛି ସଦ୍ୟ ପ୍ରସ୍ତୁତ ଗାଢ଼ ହାଇଡ୍ରୋକ୍ଲୋରିକ୍ ଏସିଡ୍ ଏବଂ ଗାଢ଼ ନାଇଟ୍ରିକ ଏସିଡ୍ 3 : 1 ଅନୁପାତର ଏକ ମିଶ୍ରଣ । ଏହି ଦୁଇ ଅମ୍ଳମଧ୍ୟରୁ କୌଣସିଟି ସୁନାକୁ ଦ୍ରବୀଭୂତ କରିପାରେ ନାହିଁ । କିନ୍ତୁ ଏହାର ମିଶ୍ରଣ ସୁନାକୁ ଦ୍ରବୀଭୂତ କରିପାରେ । ଆକ୍ସାରେଜିଆ (ଅମ୍ଳରାଜ) ଏକ ଭଲ ସଂକ୍ଷାରଣ, ଦ୍ରବୀଭୂତ କରିବାର କ୍ଷମତା ରହିଛି ।

କାର୍ଯ୍ୟାବଳୀ -12 (Activity-12)
ଆବଶ୍ୟକ ଉପକରଣ:
ଖଣ୍ଡିଏ ସଫା ତମ୍ବାତାର, ଲୁହା କଣ୍ଟା, ଆଇରନ୍ ସଲଫେଟ୍ ଦ୍ରବଣ, କପର ସଲ୍ଫେଟ ଦ୍ରବଣ । ଆଇରନ୍ ସଲଫେଟ୍ ଦ୍ରବଣ ନେଇ ସେଥୁରେ ତମ୍ବାତାରଟିକୁ
ପରୀକ୍ଷଣ:
ଗୋଟିଏ ପରୀକ୍ଷାନଳୀରେ ଆଇରନ୍ ସଲଫେଟ୍ ଦ୍ରବଣ ନେଇ ସେଥିରେ ତମ୍ବାତାରଟିକୁ ଏବଂ ଅନ୍ୟ ଏକ ପରୀକ୍ଷାନଳୀରେ କପଟ ସଲଫେଟ୍ ଦ୍ରବଣ ନେଇ ସେଥିରେ ଲୁହାକଣ୍ଟା ଭର୍ତ୍ତି କର ।
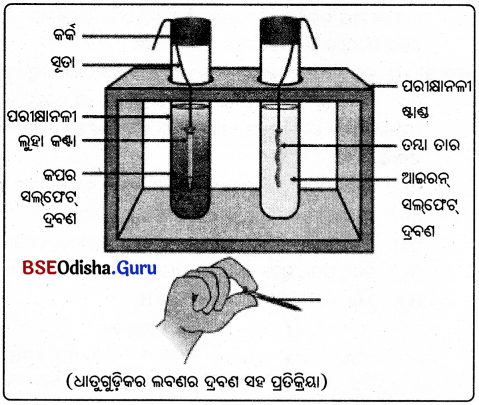
ପର୍ଯ୍ୟବେକ୍ଷଣ:
20 ମିନିଟ୍ ପର୍ଯ୍ୟନ୍ତ ପରୀକ୍ଷଣଟିକୁ ଲକ୍ଷ୍ୟକର ।
ସିଦ୍ଧାନ୍ତ:
(i) ଯେଉଁ ପରୀକ୍ଷାନଳୀରେ କପର ସଲଫେଟ୍ ଦ୍ରବଣରେ ଲୁହାକଣ୍ଟାଟିକୁ ଭର୍ତି କରାଯାଇଥିଲା, ସେହି ପରୀକ୍ଷାନଳୀରେ ନିମ୍ନ ପ୍ରତିକ୍ରିୟା ଲକ୍ଷ୍ୟ କରାଗଲା

(ii) ନୀଳରଙ୍ଗର CuSO4 ଦ୍ରବଣ କ୍ରମଶଃ ସବୁଜ ଦ୍ରବଣରେ ପରିଣତ ହୋଇ ମାଟିଆଲାଲ୍ କପର ବାହାରିବ । ଏ ପ୍ରକାର ପ୍ରତିକ୍ରିୟାର ନାମ ହେଉଛି ପ୍ରତିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା ।
(iii) ଏ ପ୍ରକାର ପ୍ରତିକ୍ରିୟାର ନାମ ହେଉଛି ପ୍ରତିସ୍ଥାପନ ପ୍ରତିକ୍ରିୟା ଅଧ୍ଵ ପ୍ରତିକ୍ରିୟାଶୀଳ ଧାତୁ କମ୍ ପ୍ରତିକ୍ରିୟାଶୀଳ ଧାତୁକୁ ସେମାନଙ୍କର ଦ୍ରବଣୀୟ ଯୌଗିକରୁ କିମ୍ବା ତରଳ ଅବସ୍ଥାରୁ ବିସ୍ଥାପନ କରେ । ସାଧାରଣ ଭାବେ କୁହାଯାଇପାରିବ ଯେ ଯଦି ଧାତୁ A, ଧାତୁ Bକୁ ଏହାର ଦ୍ରବଣରୁ ବିସ୍ଥାପନ କରେ ତେବେ Bଠାରୁ A ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ହେବ ।
ଧାତୁ A + Bର ଲବଣ ଦ୍ରବଣ → Aର ଲବଣ ଦ୍ରବଣ + ଧାତୁ B B ଠାରୁ A ଅଧିକ ପ୍ରତିକ୍ରିୟାଶୀଳ ।
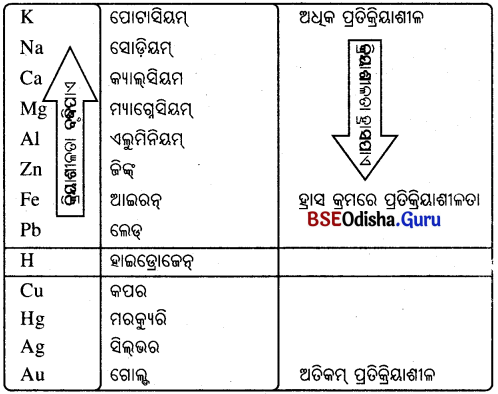
ପ୍ରତିକ୍ରିୟାଶୀଳତାର ଅନୁକ୍ରମ (The Reactivity Series):
ପ୍ରତିକ୍ରିୟାଶୀଳତାର ଅନୁକ୍ରମ ହେଉଛି କେତେକ ଧାତୁର ସକ୍ରିୟତାର ଅଧଃକ୍ରମ ସଜ୍ଜାର ସାରଣୀ ।
ସକ୍ରିୟତାର ଅନୁକ୍ରମ : ଧାତୁର ଆପେକ୍ଷିକ ଓ ପ୍ରତିକ୍ରିୟାଶୀଳତା
କାର୍ଯ୍ୟାବଳୀ -13 (Activity-13)
ଆବଶ୍ୟକ ଉପକରଣ :
ବିଜ୍ଞାନାଗାରରେ ଯେକୌଣସି ଲବଣର ନମୁନା ; ଯଥା – ସୋଡ଼ିୟମ କ୍ଲୋରାଇଡ୍, ପୋଟାସିୟମ ଆୟୋଡାଇଡ୍, ବ୍ରେରିୟମ୍ କ୍ଲୋରାଇଡ୍ ସଂଗ୍ରହ କର ।
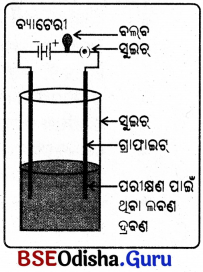
ପରୀକ୍ଷଣ:
- ଏହିସବୁ ଲବଣର ଭୌତିକ ସ୍ଥିତି ଲକ୍ଷ୍ୟକର ।
- ଧାତବ ଚେପ୍ଟା ଚାମଚରେ ଗୋଟିଏ ଧାତୁର କିଛି ନମୁନା ନେଇ ସିଧାସଳଖ ଗରମ କର । ସେହିପରି ଅନ୍ୟ ନମୁନାଗୁଡ଼ିକୁ ମଧ୍ୟ ନେଇ ଅନୁରୂପ ଭାବେ ଗରମ କର ।
- ନମୁନାଗୁଡ଼ିକୁ ଜଳ, ପେଟ୍ରୋଲ ଏବଂ କିରୋସିନ୍ରେ ଦ୍ରବୀଭୂତ କରିବା ପାଇଁ ଚେଷ୍ଟାକର ।
- ଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ହେଲାପରି ବିଦ୍ୟୁତ୍ ପରିପଥ ତିଆରି କରି ଲବଣର ଦ୍ରବଣରେ ଇଲେକ୍ଟ୍ରୋଡ୍ ଦଣ୍ଡକୁ ବୁଡ଼ାଅ ।
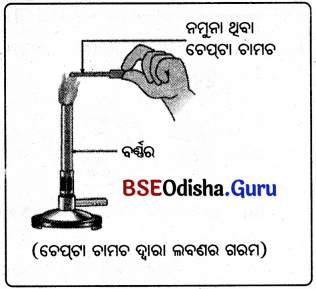
ପର୍ଯ୍ୟବେକ୍ଷଣ:
- ନମୁନାଗୁଡ଼ିକରେ ଭୌତିକ ସ୍ଥିତି ହେଉଛି କଠିନ । ଏହି ନମୁନାଗୁଡ଼ିକ ଶିଖାର ବର୍ଣ୍ଣ ବଦଳାଇଲା । ଯୌଗିକଗୁଡ଼ିକ ତରଳିଲା ନାହିଁ ।
- ଏଗୁଡ଼ିକ ଜଳରେ ଦ୍ରବଣୀୟ କିନ୍ତୁ ପେଟ୍ରୋଲ ଏବଂ କିରାସିନ୍ରେ ଦ୍ରବଣୀୟ ନୁହଁନ୍ତି ।
- ଆୟନିକ, ଯୌଗିକ କଠିନ ଅବସ୍ଥାରେ ବିଦ୍ୟୁତ୍ ପରିବହନ କରନ୍ତି ନାହିଁ; କିନ୍ତୁ ଲବଣ ଦ୍ରବଣରେ ବିଦ୍ୟୁତ୍ ପରିବହନ କରେ ।
ସିଦ୍ଧାନ୍ତ:
ଆୟନିକ୍ ଯୌଗିକର ଧର୍ମ;
- ୟନିକ୍ ଯୌଗିକଗୁଡ଼ିକ କଠିନ : ଆୟନିକ ଯୌଗିକଗୁଡ଼ିକ ଯୁକ୍ତାତ୍ମକ ଏବଂ ବିଯୁକ୍ତାତ୍ମକ ଆୟନ ମଧ୍ୟରେ ଦୃଢ଼ ଆକର୍ଷଣ ବଳ ଯୋଗୁଁ ଏଗୁଡ଼ିକ କଠିନ ଏବଂ କିଛି ପରିମାଣରେ ଶକ୍ତ । ଏହି ଯୌଗିକଗୁଡ଼ିକ ସାଧାରଣତଃ ଭଙ୍ଗୁର ଏବଂ ଚାପ ପ୍ରୟୋଗ ଫଳରେ ଖଣ୍ଡ ଖଣ୍ଡ ହୋଇ ଭାଙ୍ଗିଯାଏ ।
- ଗଳନାଙ୍କ ଓ ସ୍ଫୁଟନାଙ୍କ : ଆୟନିକ ଯୌଗିକଗୁଡ଼ିକର ଉଚ୍ଚ ଗଳନାଙ୍କ ଏବଂ ଉଚ୍ଚ ସ୍ଫୁଟନାଙ୍କ ଥାଏ । ଆୟନଗୁଡ଼ିକ ମଧ୍ୟରେ ଥିବା ଶକ୍ତ ଆନ୍ତଃ ଆୟନୀୟ ଆକର୍ଷଣ ଭାଙ୍ଗିବା ପାଇଁ ବିପୁଳ ପରିମାଣର ଶକ୍ତି ଆବଶ୍ୟକ ହୋଇଥାଏ ।
- ଦ୍ରବଣୀୟତା : ଏହି ଯୌଗିକଗୁଡ଼ିକ ସାଧାରଣତଃ ଜଳରେ ଦ୍ରବଣୀୟ କିନ୍ତୁ କିରୋସିନ୍, ପେଟ୍ରୋଲ ଆଦି ଦ୍ରାବକରେ ଅଦ୍ରବଣୀୟ ।
- ବିଦ୍ୟୁତ୍ ପରିବହନ କରନ୍ତି : କଠିନ ଅବସ୍ଥାରେ ଆୟନିକ ଯୌଗିକଗୁଡ଼ିକ ବିଦ୍ୟୁତ୍ ପରିବହନ କରେ ନାହିଁ । କିନ୍ତୁ ତରଳ ଅବସ୍ଥାରେ ଆୟନ ମୁକ୍ତ ହେବାରୁ ଏଗୁଡ଼ିକ ବିଦ୍ୟୁତ୍ ପରିବହନ କରିପାରେ ।

କାର୍ଯ୍ୟାବଳୀ -14 (Activity-14)
ଆବଶ୍ୟକ ଉପକରଣ : ତିନୋଟି ପରୀକ୍ଷାନଳୀ, ପ୍ରତ୍ୟେକଟିରେ ପରିଷ୍କୃତ ଲୁହା କଣ୍ଟା, କର୍କ, ପାତିତ ଜଳ, ନିର୍ଜଳୀୟ କ୍ୟାଲସିୟମ୍ କ୍ଲୋରାଇଡ୍ , ତେଲ
ପରୀକ୍ଷଣ:
- ପରୀକ୍ଷାନଳୀ ତିନୋଟିର ନାମକରଣ A, B ଓ C ଦିଅ । ପ୍ରତ୍ୟେକ ପରୀକ୍ଷାନଳୀରେ ଲୁହା କଣ୍ଟା ରଖ । À ନଳୀରେ କିଛି ଜଳ ଢାଳି କର୍କଦ୍ଵାରା ବନ୍ଦ କର।
- B ନଳୀରେ ଫୁଟାହୋଇଥିବା ପାତିତ ଜଳ ଢାଳ । ପ୍ରାୟ 1 ମିଲିଲି ତେଲ ମିଶାଇ କର୍କ ଦ୍ଵାରା ବନ୍ଦ କର । ତେଲ ଜଳରେ ଭାସିବ ଏବଂ ବାୟୁ ଜଳରେ ଦ୍ରବୀଭୂତ କରାଇ ଦେବ ନାହିଁ ।
- C ପରୀକ୍ଷାନଳୀରେ କିଛି ନିର୍ଜଳୀୟ କ୍ୟାଲସିୟମ୍ କ୍ଲୋରାଇଡ ନେଇ ନଳୀରେ | ରଖ ଓ କର୍କଦ୍ଵାରା ବନ୍ଦକର । ପରୀକ୍ଷା ନଳୀକୁ କିଛିଦିନ ରଖିଦିଅ । ।
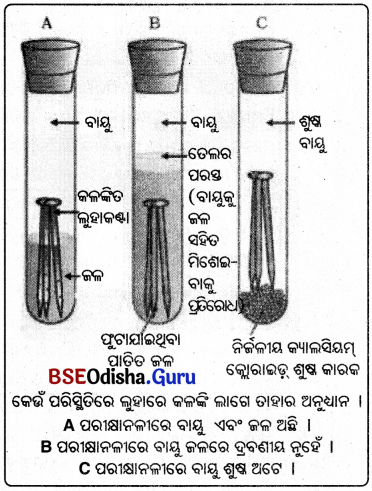
ପର୍ଯ୍ୟବେକ୍ଷଣ:
- A ପରୀକ୍ଷାନଳୀରେ ଥିବା ଲୁହାକଣ୍ଟାରେ କଳଙ୍କି ଲାଗିଛି ।
- B ଓ C ପରୀକ୍ଷାନଳୀରେ ଥିବା ଲୁହାକଣ୍ଟାଗୁଡ଼ିକରେ କଳଙ୍କି ଲାଗିନାହିଁ ।
- À ପରୀକ୍ଷାନଳୀରେ କଣ୍ଟାଗୁଡ଼ିକ ଉଭୟ ଜଳ ଓ ବାୟୁ ସଂସ୍ପର୍ଶ ଆସିବା ଫଳରେ କଳଙ୍କି ଲାଗିଲା ।
- B ପରୀକ୍ଷାନଳୀରେ କଣ୍ଟାଗୁଡ଼ିକ କେବଳ ଜଳ ସଂସ୍ପର୍ଶରେ ଆସିଲା । C ପରୀକ୍ଷାନଳୀର କଣ୍ଟାଗୁଡ଼ିକ କେବଳ ଶୁଷ୍କବାୟୁ ସଂସ୍ପର୍ଶରେ ଆସିଲା ।
ସିଦ୍ଧାନ୍ତ:
ଉଭୟ ବାୟୁ ଓ ଜଳ ସଂସ୍ପର୍ଶରେ ଆସିଲେ ଲୌହ ବସ୍ତୁରେ କଳଙ୍କି ଲାଗେ ।
ସଂକ୍ଷାରଣର ପ୍ରତିରୋଧ (Prevention of Corrosion):
ସଂକ୍ଷାରଣର ପ୍ରତିରୋଧ ପାଇଁ ନିମ୍ନଲିଖତ ଉପାୟଗୁଡ଼ିକ ଅବଲମ୍ବନ କରାଯାଇଥାଏ ।
- ତୈଳଦ୍ଵାରା: ଧାତୁ ନିର୍ମିତ ପଦାର୍ଥ ଉପରେ ତୈଳ ଜାତୀୟ ପଦାର୍ଥ ଲେପନ କଲେ ଧାତୁ ଆର୍ଦ୍ର ବାୟୁର ସଂସ୍ପର୍ଶରେ ଆସେନାହିଁ । ଫଳରେ ସଂକ୍ଷାରଣ ହୁଏ ନାହିଁ।
- ଗ୍ରୀଜଦ୍ଵାରା: ଶ୍ରୀଜଲେପ ଦେଲେ କଳଙ୍କି ଲାଗେ ନାହିଁ ।
- ରଙ୍ଗ ଲେପନଦ୍ଵାରା କ୍ଷୟରୋଧ କରାଯାଏ ।
- ଜିଙ୍କ୍ ଲେପନ (ଗାନାଇଜିଙ୍ଗ୍) – ଜିଙ୍କର ଏକ ପତଳା ସ୍ତରର ଆଚ୍ଛାଦନ ଦ୍ବାରା ଷ୍ଟିଲ ଓ ଲୁହାକୁ କଳଙ୍କି ଲାଗିବାରେ ପ୍ରତିରୋଧ କରାଯାଇ ପାରିବ । ଜିଙ୍କ ଆବରଣ ନଷ୍ଟ ହେଲେ ମଧ୍ୟ ଜିଙ୍କ ଲେପିତ ଜିନିଷ ଗୁଡ଼ିକ କଳଙ୍କି ଲାଗିବାରୁ ସୁରକ୍ଷିତ ରହିଥାଏ ।
- ଇଲେକ୍ଟ୍ରୋସ୍ଟେଟିଂ ଦ୍ଵାରା : ଲୁହାରେ ନିର୍ମିତ ଦ୍ରବ୍ୟାଦିଗୁଡ଼ିକ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ସାହାଯ୍ୟରେ ଅନ୍ୟଧାତୁର ପ୍ରଲେପଦ୍ବାରା କ୍ଷୟରୋଧ କରାଯାଏ ।
- ଟିନିଂ ଦ୍ଵାରା: ବଜାରରେ ମିଳୁଥିବା ଟିଣ ଡବା ଲୁହାରେ ତିଆରି । ଏହି ଲୁହାଡ଼ବା ଉପରେ ଟିଣର ଲେପ ଦିଆଯାଇଛି । ତେଣୁ ସେହିଡବାରେ କଳଙ୍କି ଲାଗିପାରେ ନାହିଁ ।
- କେତକ ମିଶ୍ରଧାତୁରେ ଆଦୌ କଳଙ୍କି ଲାଗେନାହିଁ । ବିଶୁଦ୍ଧ ଲୁହା ନରମ ଅଟେ । ମାତ୍ର ଅଳ୍ପ ପରିମାଣର କାର୍ବନ (0.05%) ସହ ମିଶାଇଲେ ତାହା ଶକ୍ତ ଓ କଠିନ ହୋଇଯାଏ ।
ଲୁହାରେ ନିକେଲ୍ ଓ କ୍ରୋମିୟମ୍ ମିଶିଲେ ଷ୍ଟେନ୍ଲେସ୍ ଷ୍ଟିଲ୍ ମିଳେ ଯାହାକି ଶକ୍ତ ହୁଏ ଓ କଳଙ୍କି ଲାଗେନାହିଁ ।
ମିଶ୍ରଧାତୁ (Alloy) – ଦୁଇ ବା ଅଧ୍ଵ ଧାତୁର କିମ୍ବା ଧାତୁ ଓ ଉପଧାତୁ କିମ୍ବା ଧାତୁ ଓ ଅଧାତୁର ମିଶ୍ରଣକୁ ମିଶ୍ରଧାତୁ କହନ୍ତି । ଏହା ସମଜାତୀୟ ଅଟେ ।
ପାରଦର ମିଶ୍ରଧାତୁକୁ ଅମାଲ୍ଗାମ୍ କୁହାଯାଏ । ପିତ୍ତଳ ହେଉଛି ତମ୍ବା ଏବଂ ଜିଙ୍କ୍ (Cu ଓ Zn) ର ଏକ ମିଶ୍ର ଧାତୁ ।
ବ୍ରୋଞ୍ଜ୍ ହେଉଛି ତମ୍ବା ଏବଂ ଟିଣ (Cu ଓ Sn) ର ଏକ ମିଶ୍ରଧାତୁ ।
ସୋଲ୍ଡର ହେଉଛି ସୀସା ଓ ଟିଣ (Pb ଓ Sn) ର ଏକ ମିଶ୍ରଧାତୁ ।
ବିଶୁଦ୍ଧ ସୁନା 24 କ୍ୟାରେଟ୍ ନାମରେ ଜଣାଶୁଣା । ତାହା ଅତ୍ୟନ୍ତ ନରମ ହୋଇଥିବାରୁ ସେଥିରେ ଅଳଙ୍କାର ତିଆରି ହୋଇପାରେ ନାହିଁ । ଏହାକୁ ଶକ୍ତ କରିବା ପାଇଁ ଏଥିରେ ରୁପା କିମ୍ବା ତମ୍ବା ମିଶାଯାଏ । ସାଧାରଣତଃ 22 କ୍ୟାରେଟ୍ ସୁନା ଅଳଙ୍କାର ତିଆରି ପାଇଁ ବ୍ୟବହୃତ ହୁଏ । ଅର୍ଥାତ୍ 22 ଭାଗ ବିଶୁଦ୍ଧ ସୁନା ସହ 2 ଭାଗ ତମ୍ବା କିମ୍ବା ରୁପା ମିଶାଯାଇ ମିଶ୍ରଧାତୁ ପ୍ରସ୍ତୁତ କରାଯାଏ । 1600 ବର୍ଷ ପୂର୍ବେ ଦିଲ୍ଲୀର କୁତୁବ୍ମିନାର ଠାରେ ନିର୍ମିତ ହୋଇଥିବା ଲୌହସ୍ତମ୍ଭର ଉଚ୍ଚତା 8 ମିଟର ଏବଂ ଓଜନ 6 ଟନ୍ । ଏହି ଲୌହସ୍ତମ୍ଭ ଏପରି ପ୍ରଣାଳୀରେ ନିର୍ମିତ ହୋଇଥିଲା ଯେ ଏହା ଏବେବି କଳଙ୍କହୀନ ଅବସ୍ଥାରେ ରହିଛି ।
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()