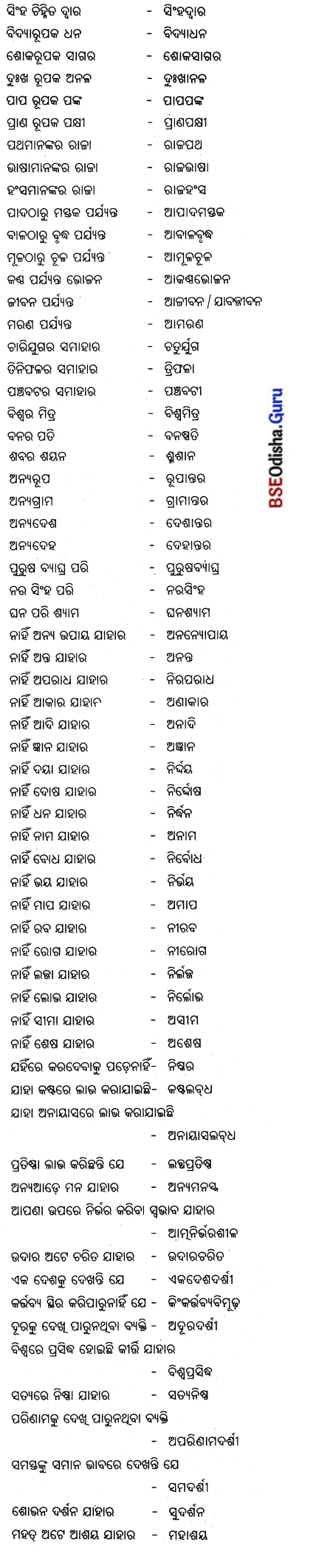
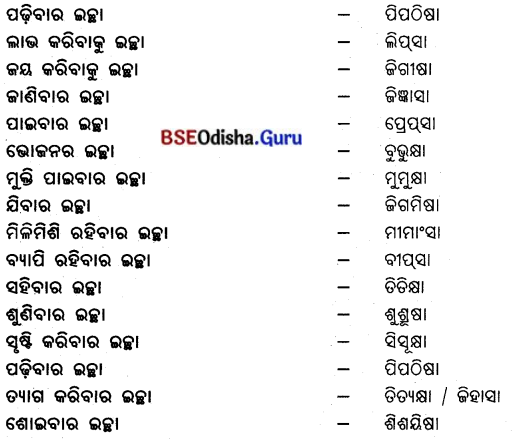
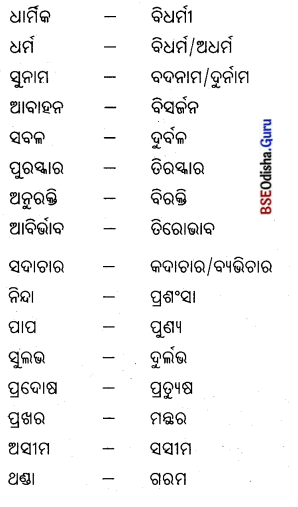
Odisha State Board CHSE Odisha Class 12 Sanskrit Solutions Poem 2 गीतासौरभम् Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Sanskrit Poem 2 गीतासौरभम् Question Answer
१. एकेन वाक्येन उत्तरं लिखत –
(ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।)
(क) कुत्र ते अधिकारः अस्ति ?
Solution:
କର୍ମଣି ଏବଂ ତେ ଅଧୂକାରଃ ଅସ୍ଥି ।
(ख) कुत्र तव सङ्गः मा अस्तु ?
Solution:
ଅକର୍ମଣି ତେ ସଙ୍ଗୀ ମା ଅସ୍ତୁ ।
(ग) कः स्थितधी : ?
Solution:
ଦୁ:ଖେଯୁ ଅନ୍ମହ୍ବିଗ୍ନମନା: ସ୍ନଖେଣ୍ଟ ବିଗତସ୍ନଦୃ ବାତରାଗଲ ଦେଖା ସ୍ନନି: ଉପବେ ।
(घ) भगवान् कदा आत्मानं सृजति ?
Solution:
ଯଦା ଯଦା ହି ଧର୍ମସ୍ୟ ଗ୍ଳାନିଂ ଭବତି ଅଧର୍ମସ୍ୟ ଅଭ୍ୟୁତ୍ଥାନଂ ଭବତି ତଦା ଭଗବାନ୍ ଆତ୍ମାନଂ ସୃଜତି।
(ङ) पण्डिताः केषु समदर्शनं कुर्वन्ति ?
Solution:
ବିଦ୍ୟାବିନୟସଂପନ୍ନ ବ୍ରାହ୍ମଣେ, ଗବି, ହସ୍ତିନି, ଶୁନି, ଶୁପାକେ ଚ ଇତି ଏତେଷୁ ପଣ୍ଡିତଃ ସମଦର୍ଶନଂ କୁର୍ବନ୍ତି ।
(च) कः वेदवित् ?
Solution:
ଅଶ୍ୱତ୍ଥମ୍ ଊର୍ଧମୂଳମ୍ ଅଧଃଶାଖମ୍ ଅବ୍ୟୟଂ ପ୍ରାଦୁଃ ଛନ୍ଦସି ଯସ୍ୟ ପଶ୍ଚିନି, ଯଃ ତଂ ବେଦ ସ ବେଦବିତ୍ ।
(छ) सात्त्विकप्रियाः आहाराः के ?
Solution:
ଆୟୁ ସତ୍ତ୍ବବଳାରୋଗ୍ୟସୁଖପ୍ରୀତିବିବର୍ଣନା ରସ୍ୟ ସ୍ନିଗ୍ଧା ସ୍ଥିରଃ ହୃଦ୍ୟା ଚ ସାତ୍ତ୍ଵିକପ୍ରିୟା ଆହାରାଃ ଭବନ୍ତି ।
(ज) परमात्मा की दृशं जनं मेक्षायिष्यति ?
Solution:
ସର୍ବଧର୍ମାନ୍ ପରିତ୍ୟଜ୍ୟ ଭଗବନ୍ତ ଯେ ଶରଣଂ ଗଚ୍ଛନ୍ତି ତେଭିଂ ଜନେଭ୍ୟ ସର୍ବପାପେଭ୍ୟ ପରମାତ୍ମା ମୋକ୍ଷୟିଷ୍ଯତି ।

२. एकेन पदेन उत्तरं लिखत
(ଏକ ପଦରେ ଉତ୍ତର ଲେଖ)
(क) कस्य मृत्युः ध्रुवः ?
Solution:
ଜାତସ୍ୟ ।
(ख) कामात् कः अभिजायते ?
Solution:
କ୍ରୋଧଃ ।
(ग) परधर्मः कीदृश: ?
Solution:
ଭୟାବହଃ ।
(घ) कः आत्मनः बन्धुः ?
Solution:
ଆତ୍ମା ।
(ङ) ईश्वरः वेदानां मध्ये कः ?
Solution:
ସାମବେଦଃ ।
(च) कः वेदवित् ?
Solution:
ପୁରୁଷୋତ୍ତମଃ ।
(छ) कर्मफलत्यागात् किं लभ्यते ?
Solution:
ଶାନ୍ତଃ ।
(ज) नरकस्य द्वारं कतिविधम् ?
Solution:
ନିଃ ।
३. बन्धनीमध्यात् उपयुक्तं पदं निरूप्य शून्यस्थानं पूरयत
(ବନ୍ଧନୀମଧ୍ଯରୁ ଉପଯୁକ୍ତ ପଦ ନିରୂପଣ କରି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)
(क) मा _____ कदाचन । (कर्मसु, फलेषु, भोगेषु)
Solution:
ଫଳେଷୁ
(ख) _____ ध्रुवं मृतस्य च । (जन्म, , मृत्युः, स्वर्गः )
Solution:
ଜନ୍ମ
(ग) क्रोधात् भवति _____ । (कामः, संम्मोहः, बुद्धिनाशः )
Solution:
ସଂଶୋହଃ
(घ) स्वधर्मे निधनं _____ । (ज्ञानं, प्रेयः, श्रेयः)
Solution:
ଶ୍ରେୟଃ
(ङ) परमात्मा इन्द्रियेषु _____ । (चक्षुः,,हस्तः, मनः )
Solution:
ମନଃ
(च) ज्ञानात् विशिष्यते _____ । (ध्यानं, प्रेम, स्तुतिः)
Solution:
ଧ୍ୟାନମ୍
(छ) सत्त्वस्थाः गच्छन्ति _____ । (ऊर्ध्वम्, अधः, मध्यम्)
Solution:
ଊର୍ଧମ୍
(ज) नरकस्य त्रिविधं द्वारं _____ । (गच्छेत् त्यजेत् पश्येत्)
Solution:
ତ୍ୟଜେତ୍

४ . उत्कलभाषया आङ्गलभाषया वा अनुवादं कुरुत
(ଓଡ଼ିଆ ଅଥବା ଇଂରାଜୀରେ ଅନୁବାଦ କର |)
(क) जातस्य …………………………………………………. अर्हसि ।।२।।
Solution:
ଯେ ଜନ୍ମ ହୋଇଛି ତା’ର ମୃତ୍ୟୁ ସୁନିଶ୍ଚିତ ଏବଂ ଯେ ମୃତ୍ୟୁଲାଭ କରିଛି ତାହାର ଜନ୍ମ ନିଶ୍ଚିତ । ତେଣୁ ଏହା ଯେତେବେଳେ ଅପରିହାର୍ଯ୍ୟ କର୍ତ୍ତବ୍ୟ ସଂପାଦନରେ ପଛେଇବା ଉଚିତ ନୁହେଁ କି ଦୁଃଖ ପ୍ରକାଶ କରିବା ଉଚିତ ନୁହେଁ ।
(ख) ध्यायतो ……………………………………………. क्रोधोऽभिजायते ||४||
Solution:
ବ୍ୟକ୍ତି ଇନ୍ଦ୍ରିୟଭୋଗ୍ୟ ବିଷୟବସ୍ତୁକୁ ଚିନ୍ତା କରୁଥିଲାବେଳେ ସେଗୁଡ଼ିକ ପ୍ରତି ତା’ର ଆସକ୍ତି ଜାତ ହୁଏ ଏବଂ ଏ ପ୍ରକାର ଆସକ୍ତିରୁ କାମନା ଜାତ ହୁଏ ଏବଂ କାମନାରୁ କ୍ରୋଧ ଜାତ ହୁଏ ।
(ग) विद्याविनय ………………………………………. समदर्शिनः ||९||
Solution:
ପଣ୍ଡିତମାନେ ବିଦ୍ୟା ଏବଂ ବିନୟସଂପନ୍ନ ବ୍ରାହ୍ମଣଠାରେ ଓ ଚାଣ୍ଡାଳଠାରେ, ତଥା ଗାଭୀଠାରେ, ହାତୀଠାରେ ଓ ସମଭାବାପନ୍ନ ହୋଇଥା’ନ୍ତି ।
(घ) पत्रं पुष्पं ……………………………………………… प्रयतात्मनः ।।१३।।
Solution:
ଯେଉଁ ବ୍ୟକ୍ତି ଭକ୍ତି ସହକାରେ ପତ୍ର, ଫୁଲ, ଫଳ ଓ ଜଳ ମୋତେ ଅର୍ପଣ କରେ, ସେହି ଶୁଦ୍ଧଚେତ୍ତାର ଭକ୍ତିରେ ଅର୍ପିତ ସେସବୁକୁ ମୁଁ ଗ୍ରହଣ କରେ।
(ङ) ऊध्वंगच्छन्ति ………………………………………… तामसाः ।।१८।।
Solution:
ଯେଉଁମାନେ ସତ୍ତ୍ଵଗୁଣରେ ସ୍ଥିତ, ସେମାନେ କ୍ରମେ ଊର୍ଦ୍ଧ୍ବକୁ ଗତି କରି ଉଚ୍ଚତର ଲୋକକୁ ଯା’ନ୍ତି, ଯେଉଁମାନେ ରଜୋଗୁଣରେ ସ୍ଥିତ ସେମାନେ ଏ ଧରାଧାମରେ ରହନ୍ତି ଏବଂ ଯେଉଁମାନେ ଘୃଣିତ କର୍ମ ଆଚରଣ କରି ତମୋଗୁଣରେ ସ୍ଥିତ ସେମାନେ ନିମ୍ନକୁ ନର୍କାନୁଗାମୀ ହୁଅନ୍ତି।
(च) त्रिविधं ……………………………………………… त्यजेत् ।।२०।।
Solution:
ନର୍କକୁ ଯିବାର ତିନିଗୋଟି ଦ୍ଵାର ହେଉଛି – କାମ, କ୍ରୋଧ ତଥା ଲୋଭ | ପ୍ରତ୍ୟେକ ସୁସ୍ଥମନା ମନୁଷ୍ୟ ଏ ତିନିଟିକୁ ତ୍ୟାଗ କରିବା ଉଚିତ । କାରଣ ଏମାନେ ଆତ୍ମାର ଅଧୋଗତି ବିଧାନ କରନ୍ତି।
(छ) सर्वधर्मान् …………………………………………. मा शुचः ।।२२।।
Solution:
ସମସ୍ତ ପ୍ରକାର ଧର୍ମ ତ୍ୟାଗ କରି କେବଳ ମୋର ଶରଣାପନ୍ନ ହୁଅ। ମୁଁ ତୁମକୁ ସମସ୍ତ ପ୍ରକାର ପାପକର୍ମର ପ୍ରକ୍ରିୟାରୁ ମୁକ୍ତି ଦେଇପାରିବି। ଏଥରେ ଭାବନା ବା ଦୁଃଖ କରନାହିଁ ।
५. सन्धिं कुरुत
(ସନ୍ଧି କର ।)
कर्मणि + एव, ध्रुवः + मृत्युः, मुनिः + उच्यते, क्रोधः + अभिजायते, सु + अनुष्ठितात्, उद्धरेत् + आत्मना, माम् + एव नास्ति + अत्र ।
Solution:
କର୍ମଣି + ଏବ = କପଶ୍ୟେବ
ଧ୍ରୁନଃ + ମୃତ୍ୟୁ = ଧ୍ରୁବ
ମୁନିଃ + ଉଚ୍ୟତେ = ମୁନିରୁଚ୍ୟତେ
କ୍ରୋଧଃ + ଅଭିଜାୟତେ = କ୍ତୋଧୋଽରିକାୟରେ
ସୁ + ଅନୁଷ୍ଠିତାତ୍ = ସ୍ଵନୁଷ୍ଠିତାତ୍
ଉଦ୍ଧରେତ୍ + ଆତ୍ମନା = ଉଦ୍ଧରେଦାମ୍ନା
ମାମ୍ + ଏବ = ମାନେବ ।
ନାସ୍ତି + ଅତ୍ର = ନାସ୍ତ୍ୟତ୍ର ।
६. सन्धिविच्छेदं कुरुत
(ସନ୍ଧିବିଚ୍ଛେଦ କର ।)
सङ्गस्तेषु, सम्मोहः, तदात्मानम्, चैव, आत्मैव, मामेव, मद्भावम्, भक्त्युपहृतम्, मनश्चास्मि, त्यागच्छान्तिः, एतत्त्रयम् ।
Solution:
ସଙ୍ଗସ୍ତେଷୁ = ସରଃ + ତେଣୁ
ସଶୋହଃ = ସମ୍ + ମୋହ
ତଦାତ୍ମାନମ୍ = ତତ୍ + ଆତ୍ମାନମ୍
ଚୈବ = ଚ + ଏବ
ଆଜୈବ = ଆତ୍ମା + ଏବ
ମାମେବ = ମାମ୍ + ଏବ
ମଦ୍ବମ୍ = ମତ୍ + ଭାବମ୍
ଭଲ୍ୟୁପହୃତମ୍ = ଭକ୍ତ + ଉପହୃତମ୍
ମନଶ୍ଚାସ୍ତି = ମନଃ + ଚ + ଅସ୍ତି
ତ୍ୟାଗାଚ୍ଛାନ୍ତି = ତ୍ୟାଗାତ୍ + ଶାନ୍ତି
ଏତତ୍ତ୍ଵୟମ୍ = ଏତତ୍ + ତ୍ରୟମ୍

७. रेखाङ्कितपदानां सकारणं विभक्तिं निरूपयत
(ରେଖାଙ୍କିତ ପଦଗୁଡ଼ିକର ସକାରଣ ବିଭକ୍ତି ନିରୂପଣ କର ।)
(क) मा ते सङ्गोऽस्त्वकर्मणि ।
Solution:
ତେ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ ।
(ख) जातस्य हि ध्रुवो मृत्युः ।
Solution:
ଜାତସ୍ୟ = ନିର୍ଦ୍ଧାରଣେ ୬ଷ୍ଠୀ ।
(ग) सुखेषु विगतस्पृहः ।
Solution:
ସୁଖେଷୁ = ଅଧିକରଣେ ୭ମୀ ।
(घ) सङ्गात् कामः संजायते ।
Solution:
ସଙ୍ଗୀତ୍ = ‘ଜନିକର୍ତ୍ତୃପ୍ରକୃତି’ ଯୋଗେ ୫ମୀ ।
(ङ) परधर्मात् विगुणः स्वधर्मः श्रेयान् ।
Solution:
ପରଧର୍ମାତ୍ = ଅପାଦାନେ ୫ମୀ ।
(च) अहं भक्त्या जातुं शक्यः ।
Solution:
ଭକ୍ତ = ହେତୌ ୩ୟା ।
(छ) तस्मात् एतत्त्रयं त्यजेत् ।
Solution:
ତସ୍ମାତ୍ = ହେତୌ ୫ମୀ ।
(ज) भूतानामस्मि चेतना ।
Solution:
ଭୂତାନାମ୍ = ନିର୍ଦ୍ଧାରଣେ ୬ଷ୍ଠୀ ।
(झ) त्वां सर्वपापेभ्यो मोक्षयिष्यामि ।
Solution:
ପରଧର୍ମାତ୍ = ଅପାଦାନେ ୫ମୀ ।
८. सविग्रहं समासनाम लिखत
(ବ୍ୟାସବାକ୍ୟ ସହ ସମାସ ନାମ ଲେଖ ।)
अकर्मणि, विगतस्पृहः, स्थितधीः, बुद्धिनाशः, परधर्मः, भक्त्युपहृतम्, कर्मफलत्यागः, सात्त्विकप्रियाः, सर्वपापेभ्यः ।
Solution:
ଅକର୍ମଣି = ନ କର୍ମଣି (ନଞ୍ଚ୍ ତତ୍)
ବିଗତତଃ = ବିଗତଃ ସ୍ପୃହାଃ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ)
ସ୍ଥିତଧୀ = ସ୍ଥିତାଃ ଧୀ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ)
ପରଧର୍ମ = ବୁଦ୍ଧେ ନାଶଃ ( ୬୩ ତତ୍)
ଭଲ୍ୟୁପହୃତମ୍ = ପରସ୍ୟ ଧର୍ମ (୬ଷ୍ଠୀ ତତ୍)
ଭଲ୍ୟୁପହୃତମ = ଭକ୍ତ ଉପହୃତମ୍ (୩ୟା)
କର୍ମଫଳତ୍ୟାଗ = କର୍ମଶଃ ଫଳମ୍, ତସ୍ୟ ତ୍ୟାଗ (୬ଷ୍ଠୀ ତତ୍)
ସାତ୍ତ୍ଵିକପ୍ରିୟା = ସାତ୍ତ୍ଵିକା ପ୍ରିୟା ଯେସାଂ ତେ (ବହୁବ୍ରୀହିଃ)
ସର୍ବପାପେଭ୍ୟ = ସର୍ବ ପାପଃ, ତେଭିଂ (କର୍ମଧାରୟ)
९. शून्यस्थाने प्रकृतिं / प्रत्ययं वा लिखत
(ଶୂନ୍ୟସ୍ଥାନରେ ପ୍ରକୃତି / ପ୍ରତ୍ୟୟ ଲେଖ ।)
व्यवस्थितः – वि + अव् + …… + क्त: ।
Solution:
ସ୍ଥା |
प्रवृत्तः प्र + वृत् + …… ।
Solution:
କ୍ତ |
शोचितुं – ………….. + तुमुन् ।
Solution:
ଶୋଚ୍
ध्यायतः – ध्यै + ………… ।
Solution:
କ୍ତ
निधनं – नि + ………… + ल्युट् ।
Solution:
ହନ୍
प्रवेष्टुं प्र + विश् + ……….. ।
Solution:
ତୁମୁନ୍
त्यागः – त्यज् + ………. ।
Solution:
ଘଞ୍ଚ୍
परित्यज्य – परि + …….. + ल्यप् ।
Solution:
ତ୍ୟକ୍

१० दत्तपदानि व्यवहृत्य वाक्यानि रचयत
(ପ୍ରଦତ୍ତ ପଦଗୁଡ଼ିକୁ ବ୍ୟବହାର କରି ବାକ୍ୟଗଠନ କର ।)
ध्रुवम्, कामः, श्रेयान् पण्डितः, मुक्त्वा, ज्ञानम्, द्वारम्, आहारः, शरणम् ।
Solution:
ଧ୍ରୁବମ୍ (ନିଶ୍ଚିତ) = ତସ୍ୟ ମରଣଂ ଧ୍ରୁବମ୍ ।
କାମଃ ( କାମ) = ସଙ୍ଗୀତ୍ କାମଃ ସଂଜାୟତେ ।
ପଣ୍ଡିତଃ ( ବିଦ୍ଵାନ) = ଶତଶ୍ଳୋକେନ ପଣ୍ଡିତଃ ।
ମୁକ୍ତା ( ମୁକ୍ତି କରି) = ବ୍ୟାଧଃ ପକ୍ଷିନ୍ ମୁକ୍ତା ଅବଦତ୍ ।
ଜ୍ଞାନମ୍ (ଜ୍ଞାନ) = ସଂସ୍କୃତସ୍ୟ ଜ୍ଞାନମ୍ ଅସ୍ଵାଭିଂ କରଣୀୟା ।
ଦ୍ଵାରମ୍ (ଦ୍ଵାର) = ଦ୍ଵାରଂ କପାଟେନ ଆବଦ୍ଧ ।
ଆହାରଃ (ଖାଦ୍ୟ) = ସର୍ବଦା ସାତ୍ତ୍ଵିକା ଆହାରାଃ ଖାଦେୟଃ ।
ଶରଣମ୍ (ଶରଣ) = ତ୍ଵମେବ ଶରଣଂ ମମ ।
११. अधोलिखितानां रेखाङ्कितपदानां मूलधातु – पुरुष – काल निरूपणं कुरुत
(ନିମ୍ନଲିଖିତ ଲେଖାକରି ପଦଗ୍ମତିକାର ମୂଳଧାତୁ – ପୁରୁଷ – କାଲ ନିର୍ମାଣ କାର |)
(क) न त्वं शोचितुमर्हसि ।
Solution:
ଅର୍ହସି = ଅର୍ହ ଧାତୁ ମଧ୍ୟମ ପୁରୁଷ ଲଟ୍ ଲକାର (ବର୍ତ୍ତମାନ କାଳ) ।
(ख) स्थितधीः मुनिः उच्यते ।
Solution:
ଉଚ୍ୟତେ = ବଚ୍ ଧାତୁ ,ପ୍ରଥମ ପୁରୁଷ ଲଟ୍ ଲକାର (ବର୍ତ୍ତମାନ କାଳ) ।
(ग) बुद्धिनाशात् प्रणश्यति ।
Solution:
ପ୍ରଣଶ୍ୟତି = ପ୍ର ଉପସର୍ଗ ପୂର୍ବକ ନଶ୍ ଧାତୁ ପ୍ରଥମ ପୁରୁଷ ବର୍ତ୍ତମାନ କାଳ ।
(घ) मध्ये तिष्ठन्ति राजसाः ।
Solution:
ତିପନ୍ = ସ୍ପା ଧାତୁ ପ୍ରଥମ ପୁରୁଷ ଲଟ୍ ଲକାର (ବର୍ତ୍ତମାନ କାଳ) ।
(ङ) मामेकं शरणं व्रज ।
Solution:
ବ୍ରଜ = ବ୍ରଜ୍ ଧାତୁ ମଧ୍ୟମ ପୁରୁଷ ଏକବଚନ ଲଟ୍ ଲକାର (ବର୍ତ୍ତମାନ କାଳ) ।
१२. अधोलिखितानां पदानां मूलशब्द- लिङ्ग – विभक्ति वचन निरुपणं कुरुत ।
(ନିମ୍ନଲିଖତ ପଦଗୁଡ଼ିକର ମୂଳଶବ୍ଦ – ଲିଙ୍ଗ – ବିଭକ୍ତି – ବଚନ ନିରୂପଣ କର ।)
(क) मा फलेषु कदाचन ।
Solution:
ଫଳେଷୁ = ଫଳ ଶବ୍ଦ କ୍ଲବଲିଙ୍ଗ ସପ୍ତମୀ ବିଭକ୍ତି ବହୁବଚନ ।
(ख) ध्रुवं जन्म मृतस्य च ।
Solution:
ମୃତସ୍ୟ = ମୃତ ଶବ୍ଦ ପୁଂଲିଙ୍ଗ ଷଷ୍ଠୀ ବିଭକ୍ତି ଏକବଚନ ।
(ग) पुंसः तेषु सङ्गः उपजायते ।
Solution:
ପୁଂଧଃ = ପୁମସ୍ ଶବ୍ଦ ପୁଂଲିଙ୍ଗ ଷଷ୍ଠୀ ବିଭକ୍ତି ଏକବଚନ ।
(घ) सम्मोहात् स्मृतिविभ्रमः ।
Solution:
ମରେହାତ = ସଂମୋହ ଶବ୍ଦ ପୁଂଲିଙ୍ଗ ପଞ୍ଚମୀ ବିଭକ୍ତି ଏକବଚନ ।
(ङ) परित्राणाय साधुनां विनाशाय च दुष्कृताम् ।
Solution:
ପରିତ୍ରାଣାୟ = ପରିତ୍ରାଣ ଶବ୍ଦ ପୁଂଲିଙ୍ଗ ଚତୁର୍ଥୀ ବିଭକ୍ତି ଏକବଚନ ।
(च) न आत्मानम् अवसादयेत् ।
Solution:
ଆମ୍ବାନମ୍ = ଆତ୍ମନ୍ ଶବ୍ଦ ପୁଂଲିଙ୍ଗ ଦ୍ଵିତୀୟା ବିଭକ୍ତି ଏକବଚନ ।
(छ) दैवी ह्येषा गुणमयी मम माया ।
Solution:
ଦୈବୀ = ଦୈବୀ ଶବ୍ଦ ସ୍ତ୍ରୀଲିଙ୍ଗ ପ୍ରଥମା ବିଭକ୍ତି ଏକବଚନ ।
(ज) रस्याः स्निग्धाः स्थिरा हृद्या आहाराः सात्तिकप्रियाः ।
Solution:
ରସ୍ୟା = ରସ୍ୟ ଶବ୍ଦ ପୁଂଲିଙ୍ଗ ପ୍ରଥମା ବିଭକ୍ତି ବହୁବଚନ ।

१३. प्रतिशब्दद्वयं लिखत ।
(ଦୁଇଟି ପ୍ରତିଶବ୍ଦ ଲେଖ |)
ब्राह्मणः, कलेवर:, पत्रम्, वासवः, पापम् ।
Solution:
ବ୍ରାହ୍ମଣୀ = ଦ୍ବିଜଃ, ବିପଃ ।
କଳେବରଃ = ଶରୀରମ୍, ଗାତ୍ରମ୍ ।
ପତ୍ରମ୍ = ପଶ୍ଚିମ୍, ପଲାଶମ୍ ।
ବାସବ: = ଇନ୍ଦ୍ର, ଦେବରାଜଃ ।
ପାପମ୍ = ଅଘମ୍, ଏନସ୍ ।
१४. स्त्रीप्रत्यये रूपं लिखत ।
(ସ୍ତ୍ରୀ ପ୍ରତ୍ୟୟ ରୂପ ଲେଖ। )
मुनि, विगुण, ब्राह्मण, हस्तिन्, बन्धु, सात्त्विक ।
ମୁନି = ମୁନୀ
ବ୍ରାହ୍ମଣ = ବ୍ରାହ୍ମଣୀ
ବନ୍ଧୁ = ବନ୍ଦୀ / ବନ୍ଧୁ
ବିଗୁଣ = ବିଗୁଣା
ହସ୍ତିନ୍ = ହସ୍ପିନୀ
ସାତ୍ତ୍ଵିକ = ସାତ୍ତ୍ଵିକୀ
ପଚାଷା ଭପଯୋଗା ଅତିରିକୃ ପୃହୋଇର
1. कोष्ठकमध्यात् उपयुक्तं पदं निरूप्य शून्यस्थानं पूरयत ।
(ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ପଦ ନିରୂପଣ କରି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)
1. कर्मण्येवाधिकारस्ते मा _____ कदाचन ।
Solution:
କର୍ମଣ୍ୟବାଧିକାରସ୍ତେ ମା ଫଳେଷୁ କଦାଚନ ।
2. मा कर्म _____ हेतुर्भूः । (मूल, फल, शाखा)
Solution:
ମା କର୍ମ ଫଳ ହେତୁଭଃ ।
3. जातस्य हि _____ मृत्युः । (सदा, कृतो, ध्रुवो)
Solution:
ଜାତସ୍ୟ ହି ଧ୍ରୁବୋ ମୃତ୍ୟୁ ।
4. जातस्य ध्रुव _____ । ( व्याधिः, मृत्युः, गेहः )
Solution:
ଜାତସ୍ୟ ହି ଧ୍ରୁବୋ ମୃତ୍ୟୁ ।
5. _____ जन्म मृतस्य च । (ध्रुवं, नित्यं, वृथा )
Solution:
ଧ୍ରୁବଂ ଜନ୍ମ ମୃତସ୍ୟ ଚ ।
6. तस्मादपरिहार्येऽर्थे न त्वं _____ अर्हसि । (बाधितुम्, शोचितुम्, काङ्खितुम्)
Solution:
ତସ୍ମାଦପରିହାର୍ଯ୍ୟଽର୍ଥେ ନ ତଂ ଶୋଚିତୁମ୍ ଅର୍ହସି ।
7. दुःखेष्वनुद्विग्नमनाः _____ विगतस्पृहः । ( गतेषु, गृहेषु, सुखेषु)
Solution:
ଦୁଃଖେଷ୍ଠନୁଦ୍ବିଗ୍ନମନାଃ ସୁଖେଷୁ ବିଗତସ୍ପୃହ ।
8. वीतरागभयक्रोधः स्थितधीः _____ उच्यते । ( मुनिः, गुरुः, कवि: )
Solution:
ବୀତରାଗଭୟକ୍ରୋଧଃ ସ୍ଥିତଧୀ ମୁନିଃ ଉଚ୍ୟତେ ।
9. ध्यायतो विषपान् पुंसः _____ स्तेषूपजायते । ( सङ्ग, रङ्ग, भङ्ग)
Solution:
ଧାୟତୋ ବିଷୟାନ୍ ପୁଂସ ସଙ୍ଗ ସ୍ତେତୂପଜାୟତେ ।
10. सङ्गात् संजायते _____ । (भाव:, रागः, कामः )
Solution:
ସଙ୍ଗୀତ୍ ସଂଜାୟତେ କାମଃ ।
11. _____ क्रोधोऽभिजायते । (रागात्, भावात्, कामात्)
Solution:
କାମାତ୍ କ୍ରୋଧୋଽଭିଜାୟତେ ।
12. कामात् _____ अभिजायते । (भाव:, सङ्गः, क्रोधः )
Solution:
କାମାତ୍ କ୍ରୋଧଃ ଅଭିଜାୟତେ ।
13. क्रोधात् भवि _____ । (सम्मोह:, संयोग:, संशय:)
Solution:
କ୍ରୋଧାତ୍ ଭବତି ସମ୍ମୋହ ।
14. सम्मोहात् _______ विभ्रमः । (शृति, स्मृति, वुद्धि)
Solution:
ସମ୍ମୋହାତ୍ ସ୍ମୃତି ବିଭ୍ରମଃ ।
15. _____ नाशात् प्रणश्यति । (स्मृति, वृद्धि, शृति)
Solution:
ବୁଦ୍ଧି ନାଶାତ୍ ପ୍ରଣଶ୍ୟତି ।
16. _______ निधनं श्रेयः । (अधर्मे, स्वधर्मे, विधर्मे )
Solution:
ସ୍ୱଧର୍ମେ ନିଧନଂ ଶ୍ରେୟଃ ।
17. स्वधर्मे _______ श्रेयः । (पतनं, निधनं, गमनं)
Solution:
ସ୍ୱଧର୍ମେ ନିଧନଂ ଶ୍ରେୟଃ ।
18. परधर्मो _______ । (भयावहः, दयावहः, विवर्जितः )
Solution:
ପରଧର୍ମେ ଭୟାବହଃ ।

19. यदा यदा हि _______ ग्लानिर्भवति भारत । (कामस्य, रागस्य, धर्मस्य )
Solution:
ଯଦା ଯଦା ହି ଧର୍ମସ୍ୟ ଗ୍ଳାନିର୍ଭବତି ଭାରତ ।
20. परित्राणाय _______ विनाशाय च दुष्कृताम् । ( भक्तानां, रक्तानां साधूनां )
Solution:
ପରିତ୍ରାଣାୟ ସାଧୁନାଂ ବିନାଶୟ ଚ ଦୁଷ୍କୃତାମ୍ ।
21. आत्मैव ध्यात्मनो बन्धुरात्मैव _______ आत्मनः । (रिपुः, मित्रम्, गुरु: )
Solution:
ଆତ୍ମବ ହ୍ୟାତ୍ମନୋ ବନ୍ଧୁରାସୈବ ରିପୁ ଆତ୍ମନଃ ।
22. आत्मैव ह्यात्मनो _______ आत्मैव रिपुरात्मनः । (शत्रुः, वन्धुः, दुःखः)
Solution:
ଆସୈବ ହ୍ୟାତ୍ମନୋ ବନ୍ଧୁ ଆମ୍ଭେବ ରିପୁରାତ୍ମନଃ ।
23. दैवी ह्येषा _______ मम माया दुरत्यया । (विधिमयी, भवमयी, गुणमयी)
Solution:
ଦୈବୀ ଜ୍ୟେଷା ଗୁଣମୟୀ ମମ ମାୟା ଦୁରତ୍ୟୟା ।
24. दैवी ह्येषा गुणमयी मम _______ दूरत्यया । (कोप:, इच्छा, माया)
Solution:
ଦୈବୀ ଜ୍ୟେଷା ଗୁଣମୟୀ ମମ ମାୟା ଦୁରତ୍ୟୟା ।
25. मामेव ये प्रपद्यन्ते _______ एतां तरन्ति ते । ( विद्याम्, वाञ्छाम्, मायाम्)
Solution:
ମାମେବ ଯେ ପ୍ରପଦ୍ୟନ୍ତେ ମାୟାମ୍ ଏତାଂ ତରନ୍ତି ତେ ।
26. अन्तकाले च मामेव स्मरन् . कलेवरम् । (मुक्त्वा, नीत्वा, त्यक्त्वा)
Solution:
ଅନ୍ତକାଳେ ଚ ମାମେବ ସ୍ମରନ୍ ମୁକ୍ତା କଳେବରମ୍ ।
27. अन्तकाले च मामेव . मुक्त्वा कलेवरम् । ( स्पृशन्, विलपन्, स्मरन् )
Solution:
ଅନ୍ତକାଳେ ଚ ମାମେବ ସ୍ମରନ୍ ମୁକ୍ତା କଳେବରମ୍ ।
28. पत्रं पुष्पं फलं _______ यो मे भक्त्या प्रयच्छति । ( तोयं, मूलं, क्षीरं)
Solution:
ପତ୍ର ପୁଷ୍ପ ଫଳ ତୋୟାଂ ଯେ ମେ ଭକ୍ତ ପ୍ରୟଚ୍ଛତି ।
29. पत्रं पुष्पं फलं तोयं यो मे _______ प्रयच्छति । (भक्त्या, मान्या, मत्या)
Solution:
ପତ୍ର ପୁଷ୍ପ ଫଳ ତୋୟାଂ ଯୋ ମେ ଭକ୍ତ ପ୍ରୟଚ୍ଛତି ।
30. वेदानां _______ अस्मि । (सामवेदः, ऋग्वेद, यजुर्वेद : )
Solution:
ବେଦାନାଂ ସାମବେଦଃ ଅଗ୍ନି ।
31. देवानामस्मि _______ । (राघव:, माधवः, वासव:)
Solution:
ଦେବାନାମସ୍ତି ବାସତଃ ।
32. भूतानामस्मि _______ । ( कामना, भावना, चेतना )
Solution:
ଭୂତାନାମସ୍ତି ଚେତନା ।
33. श्रेयो हि ज्ञानम् _______ । (अज्ञानात्, अभावात्, अभ्यासात्)
Solution:
ଶ୍ରେୟୋ ହି ଜ୍ଞାନମ୍ ଅଭ୍ୟାସାତ୍ ।
34. ज्ञानात् _______ विशिष्यते । (मौनं, ध्यानं, त्यागम्)
Solution:
ଲାନାତ୍ ଧ୍ୟାନ ବିଣିଯ୍ୟରେ ।
35. त्यागात् _______ रनन्तरम् । (कान्ति, भ्रान्ति, शान्ति)
Solution:
ତ୍ୟାଗାତ୍ ଶାନ୍ତି ରନନ୍ତରମ୍ ।
36. ऊर्ध्वं गच्छन्ति _______ । (सत्त्वस्था:, राजसाः, तामसाः)
Solution:
ରଧିଂ ଗଛନ୍ତି ସତ୍ତମା ।
37. मध्ये तिष्ठन्ति _______ । (सत्त्वस्थाः, राजसाः, तामसाः)
Solution:
ମଧ୍ୟେ ଡିପନ୍ତି ରାକସା ।
38. जघन्यगुणवृत्तिस्था अधो गच्छन्ति _______ । (सात्त्विकाः, राजसाः, तामसाः )
Solution:
ଘନ୍ୟଗୁଣବୃତ୍ତିସ୍ଥା ଅଧୋ ଗଛନ୍ତି ତାମସା ।
39. छन्दांसि यस्य _______ यस्तं वेद स वेदवित् । (पर्णानि, शाखा:, फलानि )
Solution:
ଛନ୍ଦସି ଯସ୍ୟ ପର୍ଶୁନି ଯସ୍ତଂ ବେଦ ସ ବେଦବିତ୍ ।
40. त्रिविधं नरकस्येदं _______ नाशनमात्मनः । (द्वां, विलं, गृहं)
Solution:
ତ୍ରିବିଧ୍ୱଂ ନରକସ୍ୟଦଂ ଦ୍ବାରଂ ନାଶନମାତ୍ମନଃ ।
41. _______ क्रोधस्तथा लोभस्तस्मादेतत्रयं त्यजेत् । (काम:, रागः, भावः)
Solution:
କାମଃ କ୍ରୋଧସ୍ତଥା ଲୋଭସ୍ତସ୍ମାଦେତତ୍ତ୍ୱୟଂ ତ୍ୟଜେତ୍ !
42. रस्याः स्निग्धाः स्थिरां हृद्या _______ सात्त्विकप्रियाः । (पानीया:, ग्राह्याश्च, आहारा 🙂
Solution:
ରସ୍ୟା ସ୍ନିଗ୍ଧା ସ୍ଥିରାଂ ହୃଦ୍ୟା ଆହାରାଃ ସାତ୍ତ୍ଵିକପ୍ରିୟା ।
43. सर्वधर्मान् परित्यज्य _______ एकं शरणं व्रज । (माम्, तम्, यम्)
Solution:
ସର୍ବଧର୍ମାନ୍ ପରିତ୍ୟଜ୍ୟ ମାମ୍ ଏବଂ ଶରଣଂ ବ୍ରଜ ।
अतिसंक्षेपेण उत्तरं लिखत :
1. कर्मण्येव ते किं वर्तते ?
Solution:
ର୍ଥଧ୍କାର:
2. कुत्र ते अधिकारः अस्ति ?
Solution:
କମାଣ
3. कस्य मृत्युः ध्रुवः ?
Solution:
କାରମ୍ୟ
4. मृतस्य किं ध्रुवम् ?
Solution:
କଳ୍କ
5. अपरिहार्य्येऽर्थे त्वं किं कर्तुं न अर्हसि ?
Solution:
ଶୋଚିତୁମ୍
6. ध्यायतो विषयान् पुंसः किमुपजायते ?
Solution:
ସଙ୍ଗ
7. सङ्गात् किं संजायते ?
Solution:
କାମଃ
8. कस्मात् कामः संजायते ?
Solution:
ସଙ୍ଗୀତ୍
9. कस्मात् क्रोधोऽभिजायते ?
Solution:
କାମାତ୍
10. कस्मात् सम्मोहः भवति ?
Solution:
କ୍ରୋଧାତ୍
11. कस्मात् स्मृतिविभ्रमः भवति ?
Solution:
ସମ୍ମୋହାତ୍
12. कस्मात् बुद्धिनाश: भवति ?
Solution:
ସ୍ମତିଭ୍ରଂଶାତ୍
13. स्वधर्मे किं श्रेयः ?
Solution:
ନିଧନମ୍
14. परधर्मः किम्भूत: ?
Solution:
ଉଯାବହ
15. केषां परित्राणाय भगवान् युगे युगे सम्भवति ?
Solution:
ଦୁଷ୍କୃତାମ୍
16. केषां विनाशाय भगवान् युगे युगे सम्भवति ?
Solution:
ଦୁଯତାମ

17. किमर्थं युगे युगे भगवान् सम्भवति ?
Solution:
ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ
18. आत्मना किमुद्धरेत् ?
Solution:
ଆତ୍ମାନମ୍
19. कः आत्मनः बन्धु ?
Solution:
ଆତ୍ମା
20. कः आत्मनः रिपुः ?
Solution:
ଆତ୍ମା
21. वेदानां भगवान् कः ?
Solution:
ସାମବେଦ
22. देवानां भगवान् कः ?
Solution:
ବାସଦ:
23. इन्द्रियाणां भगवान् कः ?
Solution:
ମନଃ
24. भूतानां भगवान् कः ?
Solution:
ଚେତନା
25. अभ्यासात् किं श्रेयः ?
Solution:
ଜ୍ଞାନମ୍
26. ज्ञानं कस्मात् श्रेयः ?
Solution:
ଅଭ୍ଯାସାତ୍
27. कस्मात् ध्यानं विशिष्यते ?
Solution:
ଜ୍ଞାନମ୍
28. ज्ञानात् किं विशिष्यते ?
Solution:
ଧ୍ୟାନମ୍
29. कर्मफलत्यागः कस्मात् भवति ?
Solution:
ଧ୍ୟାନାତ୍
30. कस्मात् शान्तिः भवति ?
Solution:
ତ୍ୟାଗାତ୍
31. सत्त्वस्थाः क्व गच्छन्ति ?
Solution:
ଉର୍ଧମ
32. ऊर्ध्वं के गच्छन्ति ?
Solution:
ସତ୍ତ୍ବସ୍ଥା
33. राजसाः कुत्र तिष्ठन्ति ?
Solution:
ମଧ୍ୟ
34. मध्ये के तिष्ठन्ति ?
Solution:
ରାଜସା
35. तामसाः कुत्र गच्छन्ति ?
Solution:
ଅଧଃ
36. के अधो गच्छन्ति ?
Solution:
ତାମସା
37. त्रिविधं नरकस्य किं भवति ?
Solution:
ଦ୍ବାରମ୍
38. कस्य त्रिविधं द्वारं भवति ?
Solution:
ନରକସ୍ୟ
39. किं परित्यज्य भगवन्तं शरणं व्रज़ ?
Solution:
ସର୍ବଧର୍ମାନ୍
40. भगवान् केभ्यः मोक्षयिष्यति ?
Solution:
ସର୍ବପାପେଭ୍ୟ
संक्षेपेण उत्तरं लिखत :
1. कर्मविषये भगवान् अर्जुनं किमुक्तवान् ?
Solution:
ଭଗବାନ୍ ଅର୍ଜୁନଂ କଣ୍ଠତବାନ୍ ଯତ୍ – ହେ ଅର୍ଜୁନ ! କର୍ମଣି ଏବ ତେ ଅଧିକାରଃ ଅସ୍ଥି । କର୍ମଫଳେଷୁ ତେ ଅଧିକାରଃ ନାସ୍ତି । ଅତଃ ଫଳେଚ୍ଛା ତ୍ୟକ୍ସା ସ୍ଵକର୍ତ୍ତବ୍ୟ କୁରୁ । ନଂ କଦାପି କର୍ମବିମୁଖ ନ ଭବ । ପୁନଶ୍ଚ ନଂ କର୍ମଫଳସ୍ୟ କାରଣଂ ନ ଇବ । କର୍ମଣି ତବ ମମତ୍ୱ ନ ଧ୍ୟାତ୍ !
2. जन्ममृत्युविषये भगवान् किमुक्तम् ?
Solution:
ଅସ୍ଥିନ୍ ସଂସାରେ ଯଃ ଜାୟତେ ତସ୍ୟ ମରଣଂ ସୁନିଶ୍ଚିତମ୍ । ପୁନଶ୍ଚ ଯସ୍ୟ ମୃତ୍ୟୁ ଭବତି ଡଃ ଜୀବ ଜନ୍ମମୃତ୍ଯୁଚକ୍ର ବିହାତଂ ନ ଶକ୍ନୋତି । ଏତତ୍ ତୁ ଅପରିହାର୍ଯ୍ୟ ବିଷୟ ଭବତି । ଅସ୍କ୍ରିନ୍ ବିଷୟ ହେ ଅର୍ଜୁନ ! ତବ ଶୋକଃ ନ କରଣୀୟଂ । କେବଳଂ କ୍ଷତ୍ରିୟୋଚିତଂ କର୍ମ କୁରୁ ।
3. मुने: लक्षणं किम् ?
Solution:
ଯଃ ଜନଃ ସର୍ବାନ୍ କାମାନ୍ ପରିତ୍ୟଜତି ପୁନଶ୍ଚ ଦୁଃଖେଷୁ ଅନୁଦ୍ବିଗ୍ନମନା ଭବତି, ସୁଖେଷୁ ବିଗତସ୍ପୃହଃ ଭବତି ସ୍ୱ ମୁନଃ । ଅପି ଚ ଯସ୍ୟ ରାଗ-ଭୟ-କ୍ରୋଧଃ ଚ ଅତୀତଃ ଭବତି ଡଃ ମୁନଃ ଭବତି ।
4. पुरुषः कथं प्रणश्यति ?
Solution:
ଯଃ ଜନଃ ସାଂସାରିକଃ ବିଷୟାନ୍ ସଦା ଚିନ୍ତୟତି, ତସ୍ମିନ୍ ବିଷୟ ଆସକ୍ତ ଭବତି । ତସ୍ୟ ମନସି ବିଷୟଭୋଗବିଳାସଂ ଜାୟତେ । ଯଦି କାମନା ପରିପୂର୍ଣ୍ଣ ନ ଭବତି ତହିଁ ମନସି କ୍ରୋଧଭାବମ୍ ଆୟାତି । କ୍ରୋଧାତ୍ ସମ୍ମୋହ ଜନସ୍ୟ ସ୍ମତିଃ ବିଭ୍ରମତି । ସ୍ମୃତିଭ୍ରଂଶାତ୍ ବୁଦ୍ଧି ନଶ୍ୟତି । ଅନ୍ତତଃ ଗଢ଼ା ବୁଦ୍ଧିନାଶାତ୍ ଏବଂ ମନୁଷ୍ୟ ମୃତ୍ୟୁ ଭବତି ।
5. स्वधर्मपरधर्मयोर्मध्ये को भेदः ?
Solution:
ଅସ୍ଥିନ୍ ସଂସାରେ କର୍ମାନୁସାରୀ ମାନବାନାଂ ଜନ୍ମ ଭବତି । ଜନ୍ମନଃ ମାନବାନାଂ କୃତେ ସ୍ଵଧର୍ମପାଳନମ୍ ଏକାନ୍ତମ୍ ଆବଶ୍ୟକୀୟମ୍ । ଯଦ୍ୟପି ସ୍ୱଧର୍ମ ଭବତି ତଥାପି ସ୍ଵଧର୍ମ ଶ୍ରେୟସ୍କରଃ ଅନୁଷ୍ଟେୟଶ୍ଚ ଭବତି । ସ୍ୱଧର୍ମେ ନିଧନଂ ବରଂ ପରନ୍ତୁ ପରଧର୍ମୀ ଭୟାବହିଃ । ସ୍ବଧର୍ମ ପରଧର୍ମୟୋ ଅୟଂ ଭେଦଃ ଅସ୍ଥି ।
6. कदा धर्मस्य ग्लानिः भवति ?
Solution:
ଯଦା ଅସ୍ମିନ୍ ସଂସାରେ ସଦାଚାରିତାଂ ନିରପରାଧାନାଂ ଦୁର୍ବଳାନାମ୍ ଉପରି ଦୁରାଚାରିଣୀ ପାପାନାମ୍ ଅତ୍ୟାଚାରଃ ବର୍ଧତେ ତସ୍ମିନେବ କାଳେ ଅଧର୍ମସ୍ୟ ଅଭ୍ୟୁତ୍ଥାନଂ ଭବତି, ଧର୍ମସ୍ୟ ଗ୍ଳାନିଂ ଭବତି ଚ । ସଂସାରେ ଅଧର୍ମ ଅତ୍ୟାଚାରଃ, ପାପଃ ବର୍ଧନଂ ଭବତି ।
7. भगवान् कदा आत्मानं सृजति ?
Solution:
ହେ ଭାରତ ! ଅହଂ ପ୍ରାଣିନାମ୍ ଈଶ୍ଵରଃ । ପ୍ରାଣିଜାତଂ ମୟା ରଚିତମ୍ । ଅହଂ ସଂସାରାତୀତଃ ତ୍ରିଗୁଣାତୀତ । ତଥାପି ଯୋଗମାୟାମ୍ ଉପାଶ୍ରିତ୍ୟ ଯୁଗେ ଯୁଗେ ଭୂଲୋକେ ଆତ୍ମାନଂ ସୃଜାମି । ଯଦା ଯଦା ଅସ୍ଥିନ୍ ସଂସାରେ ଧର୍ମସ୍ୟ କ୍ଷୟଂ ଅଧର୍ମସ୍ୟ ଅଭ୍ୟୁତ୍ଥାନଂ ଚ ଭବତି, ତଦା ହି ଅହମ୍ ଆତ୍ମାନଂ ସୃଜାମି ।

8. भगवान् किमर्थं सम्भवति ?
Solution:
ଯଦା ଅସ୍ମିନ୍ ସଂସାରେ ଧର୍ମସ୍ୟ ଗ୍ଳାନିଃ ଭବତି, ଅଧର୍ମସ୍ୟ ଅଭ୍ୟୁତ୍ଥାନଂ ଭବତି ତଦା ଭଗବାନ୍ ଆତ୍ମାନଂ ସୃଜତି । ପୁନଶ୍ଚ ସାଧୁନାଂ ପରିତ୍ରାଣାୟ, ଦୁଷ୍କୃତାଂ ବିନାଶାୟ, ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ ଚ ଭଗବାନ୍ ଯୁଗେ ଯୁଗେ ସମ୍ଭବତି ।
9. भगवतः माया कीदृशी ?
Solution:
ସଂସାରୋଽୟଂ ତ୍ରିଗୁଣାତ୍ମକଃ । ଗୁଣା ସତ୍ତ୍ଵ-ରଜ-ତମ ଭେଦେନ ତ୍ରିବିଧା । ଭଗବତଃ ମାୟା ତୁ ତ୍ରିଗୁଣମୟୀ । ଇୟଂ ମାୟା ଦୁରତ୍ୟୟା ଭବତି । କୋଽପି ପ୍ରାଣୀ ଭଗବତଃ ମାୟାଂ ତରିତଂ ନ ଶକ୍ନୋତି । ପରନ୍ତୁ ଯେ ଭଗବତଃ ଶରଣାପନଂ ଭବନ୍ତି ତେ ଏବ ଦୈବୀ ତ୍ରିଗୁଣମୟୀ ଦୁରତ୍ୟୟା ଚ ମାୟାମ୍ ଅବଶ୍ୟ ତରିଷ୍ୟନ୍ତି ।
10. के भगवद् भावं याति ?
Solution:
ଅଶ୍ବିନ୍ ସଂସାରେ ସର୍ବେ ଭଗବତଃ ଆଶ୍ରୟଂ ଲଭନ୍ତେ । ମୃତ୍ୟୁକାଳେ ଯେ ଜିତ୍ୟତାୟୀ ଭଗବନ୍ତମେବ ସ୍ମରନ୍ତି ତେ ଅବଶ୍ୟ ମୋକ୍ଷ ପ୍ରାପ୍ଲା ବନ୍ତି । ବିଷ୍ଣୁଲୋକଂ ଗଛନ୍ତି । ଅସ୍ଥିନ୍ ବିଷୟେ କିମପି ସଂଦେହ ନାସ୍ତି । ଅତଃ ମୃତ୍ୟୁକାଳେ ଭଗବତଃ ସ୍ମରଣଂ କରଣୀୟମ୍ ।
11. भगवान् किं किम् अश्नाति ?
Solution:
ଭଗବତେ ଭକ୍ତ, ପତ୍ର, ପୁଷ୍ପ, ଫଳଂ, ତୋୟଂ ଚ ପ୍ରଦଦାତି ତହିଁ ଡଃ ନୂନମେବ ଗ୍ରହଣ କରିଷ୍ଯତି । ଭକ୍ତ ଯତ୍କିମପି ଭଗବତ ପ୍ରଦୀୟତେ ତତ୍ ଏବ ଡଃ ଭକ୍ଷୟତି । ଭକ୍ତସ୍ୟ ଚିରଂ ସଦା ଶୁଦ୍ଧ ନିଷ୍କାମଂ ଚ ସ୍ୟାତ୍ ।
12. भगवतः महिमा कीदृशी ?
Solution:
ଶ୍ରୀମଦ୍ଭଗବଦ୍ଗୀତାୟାଂ ଦଶମାଧ୍ୟାୟେ ବିଭୂତିଯୋଗନାମ ଅଧ୍ୟାୟେ ଭଗବତଃ ମହିମା ବର୍ଣ୍ଣିତଂ ଭବତି । ସଂସାରୋଽୟଂ ଭଗବତଃ ବିଶେଷା ମହିମା ଭବତି । ଭବବାନ୍ ଋଗାଦିବେଦାନାଂ ମଧ୍ୟ ସାମବେଦଃ, ଦେବାନାଂ ମଧ୍ୟ ବାସବାଃ, ଇନ୍ଦ୍ରିୟାନାଂ ମନଃ ଭୂତାନଂ ଚେତନା ଚ ଇତି ଭଗବତଃ ମହିମା ଅସ୍ଥି ।
13. मनुष्यानां गतिः कीदृशी भवति ?
Solution:
ସତ୍ତ୍ଵାଦିଗୁଣ ପ୍ରଧାନାନାଂ ସାଧକାନାଂ ଗତଃ ବିବିଧା ଭବତି । ସତ୍ତ୍ବଗୁଣାତ୍ ଜ୍ଞାନଂ, ରଜୋଗୁଣାତ୍ ଲୋଭଃ, ତମୋଗୁଣାତ୍ ମୋହଃ ଅଜ୍ଞାନଞ୍ଚ ଜାୟତେ । ସାର୍କାଜନା ସ୍ଵର୍ଗଲୋକଂ, ରାଜସିକାଂ ନର୍କଲୋକଂ ଗଛନ୍ତି । ଜନାନାମ୍ ଇଦୃଶୀ ଗତିର୍ଭବତି ।
14. के अधः गच्छन्ति ?
Solution:
ଅସ୍ଥିନ୍ ସଂସାରେ ତ୍ରିପ୍ରକାରକଂ ଜନଃ ସନ୍ତି । ସତ୍ତ୍ଵଗୁଣଯୁକ୍ତା ତାମସା ଚ । ଗୁଣାନୁସାରଂ ମନୁଷ୍ୟାନାଂ ଗତିଃ ଭିନ୍ନ ଭବତି । ସସ୍ଥା ଊର୍ଧ ନାମ ସ୍ଵର୍ଗ ଗଚ୍ଛନ୍ତି, ରାଜସା ମର୍ତ୍ତ୍ୟ ତିଷ୍ଠନ୍ତି, ପରନ୍ତୁ ଜଘନ୍ୟଗୁଣବୃତ୍ତିସ୍ଥା ତାମସା ଅଧଃ ଗଛନ୍ତି
15. कः वेदवित् ?
Solution:
ସଂସାରୋଽୟଂ ବିଚିତଂ ଭବତି । ଅୟମ୍ ଅଶ୍ୱତ୍ଥବୃକ୍ଷ ସଦୃଶଂ ଊର୍ଦ୍ଧ୍ୱ ଚ ବିଦ୍ୟତେ । ପରନ୍ତୁ ସଂସାରରୂପ ଅଶ୍ୱତ୍ଥବୃକ୍ଷସ୍ୟ ମୂଳମ୍ ଉର୍ରେ ଶାଖା ଛନ୍ଦସି ପର୍ଶୁନି ଭବନ୍ତି । ଇଙ୍ଖ ବୃକ୍ଷ ଯଃ ବେଦଃ ମଃ ବେଦବିତ୍ ଭବତି ।
16. सात्त्विकप्रियाः आहारा: के ?
Solution:
ଆହାରୋଽପି ତ୍ରିଗୁଣାତ୍ମକମ୍ । ସପ୍ତାହାରଃ, ରାଜସିକାହାରଃ, ତାମସିକାହାରୟେତି । ସାତ୍ତ୍ଵିକପ୍ରିୟା ଆହାରାଃ ଆୟୁବର୍ଷକା, ବୁଦ୍ଧିବର୍ଷକା, ବଳବର୍ଷକା, ଆରୋଗ୍ୟଦାୟକା, ସୁଖବର୍ଷକା, ପ୍ରୀତିବର୍ଷକା, ରସ୍ୟା, ସ୍ନିଗ୍ଧା, ସ୍ଥିରଃ, ହୃଦ୍ୟା ଚ ଭବନ୍ତି । ସାତ୍ତ୍ଵିକପ୍ରିୟଜନା ଏତାଦୃଶମ୍ ଆହାରଂ ସ୍ଵୀକୁର୍ବନ୍ତି ।
17. परमात्मा कीदृशं जनं मोक्षयिष्यति ?
Solution:
ଭଗବାନ୍ ଶ୍ରୀକୃଷ୍ଣ ଗୀତାୟାମ୍ ଅର୍ଜୁନଂ ମୋକ୍ଷସ୍ୟ ମାର୍ଗ କଥୁତବାନ୍ । ଯଦା ଅର୍ଜୁନସ୍ୟ ମୋହଜାତଃ ତଦା ଭଗବାନ୍ ତମ୍ ଉପଦେଶ ଦତ୍ତବାନ୍ – ହେ ଅର୍ଜୁନ ! ସର୍ବଧର୍ମାନ୍ ପରିତ୍ୟଜ୍ୟ ଭଗବନ୍ତ ଯେ ଶରଣଂ ଗଛନ୍ତି ତେଭ୍ୟ ଜନେଭ୍ୟ ସର୍ବପାପେଭ୍ୟ ପରମାତ୍ମା ମୋକ୍ଷୟିଷ୍ୟତି । ଅସ୍ଥିନ୍ ବିଷୟ ସଂଦେହ ନାସ୍ତି ।
दीर्घप्रश्नोत्तरम्
1. भगवान् श्रीकृष्णः गीतायां किम् उपदेशं प्रदत्तम् ।
Solution:
ଉପଦେଶଂ ଦଦାତି ତତ୍ ସର୍ବେଷା ମାନବାନାଂ କୃତେ ଭବତି । ଅସ୍ଥିନ୍ ସଂସାରେ କର୍ମଣି ଏବଂ ଅଧିକାରଃ ଅସ୍ଥି ଫଳେଷୁ କଦାଚନ ଅଧିକାରଃ ନାସ୍ତି । ଯଃ ଜନଃ ସଂସାରେ ଜାତଃ ତସ୍ୟ ମରଣଂ ତୁ ଧ୍ରୁବଂ ପୁନଶ୍ଚ ଯଃ ମୃତଃ ତସ୍ୟ ଜନ୍ମ ଏବଂ ନିଶ୍ଚିତଃ । ଦୁଃଖେଷୁ ଅନୁଦ୍ବିଗ୍ନମନାଃ ସୁଖେଷୁ ବିଗତସ୍ପୃହ ବୀତରାଗ-ଭୟ-କ୍ରୋଧଃ ଚ ଜନଃ ସ୍ଥିତପ୍ରଜ୍ଞ ଭବତି । ବିଷୟାସତଃ ମନୁଷ୍ୟାମାଂ ବିନାଶଃ ଭବତି । ସ୍ୱଧର୍ମେ ନିଧନଂ ଶ୍ରେୟଃ ପରନ୍ତୁ ପରଧର୍ମୀ ଭୟାବହିଃ । ପଣ୍ଡିତଃ ସମଦର୍ଶନଃ ଭବନ୍ତି । ଭଗବନ୍ତଃ ଯେ ଶରଣାପନ୍ନ ଯାନ୍ତି ତେ ମାୟାମୟଂ ସଂସାରଂ ତରନ୍ତି । କାମ, କ୍ରୋଧଃ, ଲୋଭଃ ଚ ଆତ୍ମନାଶକଃ ନରକସ୍ୟ ତ୍ରିବିଧ୍ୱଂ ଦ୍ବାରଂ ଭବତି । ସଂସାରସ୍ବରୂପ ଅଶ୍ବତ୍ ଯଃ ଜାନାତି ଧଃ ବେଦବିତ୍ । ଏତାଦୃଶୀ ବିବିଧା ଶିକ୍ଷା ଅତ୍ର ପ୍ରଦୀୟତେ ।
2. कर्माचरणविषये भगवान् अर्जुनं किमवदत् ?
Solution:
କର୍ମାଚରଣବିଷୟ ଭଗବାନ୍ ଅର୍ଜୁନଂ କଥୟତି ଯତ୍ – ହେ ଅର୍ଜୁନ୍ । ନିଷ୍କାମକର୍ମଣ ଏବଂ ତବ ଅଧିକାରଃ ଅସ୍ଥି । କ୍ଷତ୍ରିୟକୁଳେଜାତଃ ତବ କ୍ଷାତ୍ରକର୍ମଣି ଏବଂ ଅଧିକାରଃ ବର୍ଗତେ । କର୍ମଶଃ ଫଳେଷୁ ତବ ଅଧିକାରଃ ନାସ୍ତି । କର୍ମ ମନୁଷ୍ଯାଧୀନଂ ଭବତି ପରନ୍ତୁ ଫଳଂ ପ୍ରାରବ୍ଧଧୀନଂ ଭଗବଦଧୀନଂ ବା ଭବତି । ଅତଃ ଫଳେଚ୍ଛାତ୍ୟକ୍ତା ସ୍ଵକର୍ତ୍ତବ୍ୟ ସମାଚାର । କ୍ଷତ୍ରିୟୋଚିତଂ କର୍ମ ଭବତି ଯୁଦ୍ଧମ୍ ଇତି । ସାଧାରଣତଃ ଅସ୍ଥିନ୍ ସଂସାରେ ମନୁଷ୍ୟ ଫଳକାମନୟା କର୍ମ କରୋତି । ଅତଃ ଫଳସ୍ୟ କାରଣଂ ଭବତି । ପରନ୍ତୁ ହେ ଅର୍ଜୁନ୍ । ବଂ ତାଦୃଶଂ ମା ଭବ । ଯଦି ସ୍ୱଧର୍ମ ପାଳନଂ ତଂ ନ କରିଷ୍ଯସି ତହିଁ ଅବଶ୍ୟମ୍ ଅଧୋଗତଂ ପ୍ରାପ୍ସ୍ୟତି । ଅତଃ ତ୍ଵ କ୍ଷତ୍ରିୟୋଚିତଂ କର୍ମ ନାମ ଯୁଦ୍ଧ କୁରୁ । ଯତଃ ସ୍ଵଧର୍ମପାଳନଂ ଶ୍ରେଷ୍ଠକର୍ମ ରୂପେଣ ଅଭିହିତମ୍ ।
गीतासोरशम् (ଗୀତାସୌରଭମ୍ )
ଶ୍ଳୋକ – ୧
कर्मण्येवाधिकारस्ते मा फलेषु कदाचन ।
मा कर्मफलहेतुर्भूर्माते सङ्गोऽस्त्वकर्मणि ।। १ ।।
କର୍ମଣ୍ୟବାଧ୍ୟକାରସ୍ତେ ମା ଫଳେଷୁ କଦାଚନ ।
ମା କର୍ମଫଳହେତୁର୍ଭୂମାତେସଙ୍ଗୋଽକର୍ମଣି ॥୧॥|
ଅନ୍ବୟ – କର୍ମଣି ଏବ ଅଧିକାରଃ ତେ (ଅସ୍ଥି), ଫଳେଷୁ ମା (ଅସ୍ଥି); କଦାଚନ କର୍ମଫଳ ହେତୁଃ ମା ଭୂ, ଅକର୍ମଣି – ତେ ସଙ୍ଗ ମା ଅସ୍ତୁ ।
ଶବ୍ଦାର୍ଥ – କର୍ମଣି = ନିର୍ଦ୍ଦିଷ୍ଟ କର୍ତ୍ତବ୍ୟ । ଏବ = ହିଁ । ନିଶ୍ଚିତଭାବେ । ଅଧିକାରଃ = ଅଧିକାର । ତେ = ତୁମର । ଫଳେଷୁ = ଫଳରେ । ମା = ନୁହେଁ । କଦାଚନ = କେବେହେଲେ । କର୍ମଫଳ = କର୍ମଫଳରେ । ହେତୁଃ =କାରଣ । ଭୂ = ହୁଅ । ଅକର୍ମଣି = ଅକାର୍ଯ୍ୟରେ । ସଙ୍ଗ = ଆସକ୍ତ । ଅସ୍ତୁ = ହେଉ ।
ଅନୁବାଦ – କର୍ତ୍ତବ୍ୟ କର୍ମ ସମ୍ପାଦନ କରିବାର ଅଧିକାର ତୁମର ଅଛି । କିନ୍ତୁ କର୍ମଫଳରେ ତୁମର ଅଧିକାର କେବେହେଲେ ଆସକ୍ତ ହୁଅନାହିଁ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ୟ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟଭାଗସ୍ଥ ଭଗବାବ୍ୟାସ ବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭୀଷ୍ମପର୍ବାନ୍ତର୍ଗତଃ ଶ୍ରୀମଦ୍ଭଗବଦ୍ଗୀତାୟା ଦ୍ଵିତୀୟାଧ୍ୟୟ ସାଂଖ୍ୟଯୋଗାତ୍ ଆନୀତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ଭଗବାନ୍ ଶ୍ରୀକୃଷ୍ଣ ଅର୍ଜୁନଂ କର୍ମାଧ୍ୟାକାରପ୍ରସଙ୍ଗ ବର୍ଣ୍ଣିତମ୍ |
ସାଧାରଣତଃ କର୍ତ୍ତବ୍ୟ ତ୍ରିବିଧମ୍ ନିର୍ଦ୍ଦିଷ୍ଟ କର୍ଭବ୍ୟ, ଯଥେଚ୍ଛୁକର୍ମ କର୍ମଶୂନ୍ୟତା ଚ ଅର୍ଜୁନଂ ପ୍ରତି ଭଗବତଃ ଉପଦେଶଂ
ଯତ୍ – ହେ ଅର୍ଜୁନ ! କର୍ମଣି ଏବଂ ତେ ଅଧିକାରଃ ଅସ୍ଥି । କଦାଚନ ଫଳେଷୁ ଅଧିକାରଃ ନାସ୍ତି । ଅତଃ ତଂ କଦାଚନ କର୍ମଫଳ ହେତୁ ମା ଭୂ । ଅପିଚ ଅକର୍ମଣି ତେ ସଙ୍ଗ ମା ଅସ୍ତୁ । ଅତଃ ତଂ ନିଷ୍କାମକର୍ମ କୁରୁ ଇତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – କର୍ମଣ୍ୟବାଧ୍ୱକାରସ୍ତେ = କର୍ମଣି + ଏବଂ + ଅଧୂକାରଃ + ତେ | କର୍ମଫଳହେତୁର୍ଭୂମାଁତେସଙ୍ଗେଽସ୍ଵକର୍ମଣ = କର୍ମଫଳହେତୁଃ + ଭୂ + ମା + ତେ + ସଙ୍ଗ + + ଅସ୍ତୁ + ଅକର୍ମଣି ।
ସମାସ – କର୍ମଫଳହେତୁଃ = କର୍ମଶଃ ଫଳମ୍ (୬ଷ୍ଠ ତତ୍), ତସ୍ୟ ହେତୁଃ (୬ଷ୍ଠ ତତ୍) । ଅକର୍ମଣି = ନ କର୍ମଣି (ନଞ୍ଚ୍ ତତ୍) ।
ପୃକତିପ୍ରତ୍ୟୟ – ଅଧୂକାରଃ = ଅଧୂ + କୃ + ଘଞ୍ଚ୍ ।
ଶ୍ଳୋକ – ୨
जातस्य हि ध्रुवो मृत्युर्ध्रुवं जन्म मृतस्य च ।
तस्मादपरिहार्येऽर्थे न त्वं शोचितुमर्हसि ||२||
ଜାତସ୍ୟ ହି ଧ୍ରୁବୋ ମୃତ୍ଯୁଧ୍ରୁବଂ ଜନ୍ମ ମୃତସ୍ୟ ଚ ।
ତସ୍ମାଦପରିହାର୍ଯ୍ୟଽର୍ଥେ ନ ତ୍ରିଂ ଶୋଚିତୁମର୍ହସି ||୨||
ଅନ୍ବୟ – ଜାତସ୍ୟ ହି ମୃତ୍ୟୁ ଧ୍ରୁମଃ ମୃତସ୍ୟ ଜନ୍ମ ଧ୍ରୁବଂ ଚ । ତସ୍ମାତ୍ ଅପରିହାର୍ଯ୍ୟ ଅର୍ଥେ ତଂ ଶୋଚିତୁଃ ନ ଅର୍ହସି ।
ଶବ୍ଦାର୍ଥ – ଜାତସ୍ୟ = ଯେ ଜନ୍ମ ହୋଇଛି । ହି = ଯେହେତୁ । ମୃତ୍ୟୁ : ସେହିହେତୁରୁ । ତେଣୁ । ଅପରିହାର୍ଯ୍ୟ ଯୋଗ୍ୟ / ଉଚିତ ।
ଅନୁବାଦ – ଯେ ଜନ୍ମ ହୋଇଛି ତା’ର ମୃତ୍ୟୁ ସୁନିଶ୍ଚିତ ଏବଂ ଯେ ମୃତ୍ୟୁଲାଭ କରିଛି ତାହାର ଜନ୍ମ ନିଶ୍ଚିତ ତେଣୁ ଏହା ଯେତେବେଳେ ଅପରିହାର୍ଯ୍ୟ କର୍ତ୍ତବ୍ୟ ସଂପାଦନରେ ପଛେଇବା ଉଚିତ ନୁହେଁ କି ଦୁଃଖ ପ୍ରକାଶ କରିବା ଉଚିତ ନୁହେଁ ଆନୀତଃ | ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ଜୀବନସ୍ୟ ଚରମିଂ ତଥା ମରମଂ ରହସ୍ୟ ବର୍ଣ୍ଣିତମ୍ |
ନିୟତଃ ନିୟମେନ ସୃଷ୍ଟି ଇୟଂ ପରିଚାଳିତା । ‘ଚକ୍ରବତ୍ ପରିବର୍ତ୍ତନ୍ତେ ଦୁଃଖାନି ଚ ସୁଖାନି ଚ।’ ଅସ୍ଥିନ୍ ସଂସାରେ ମନୁଷ୍ୟାମାଂ ଜନ୍ମ ମୃତ୍ୟୁ ଚ ଚକ୍ରାକାରେଣ ଘୂର୍ଣାୟମାନଂ ଭବତି । ସଂସାରେଽସ୍ମିନ୍ ଯସ୍ୟ ଜନ୍ମ ଭବତି ତତ୍ସ୍ୟ ମୃତ୍ୟୁ ସୁନିଶ୍ଚିତମ୍ । ପରମେଶ୍ଵରସ୍ୟ ଇଚ୍ଛାମାତ୍ରେଣ ସର୍ବ ପରିଚାଳିତଂ ଭବତି । କୁରୁକ୍ଷେତ୍ରସ୍ୟ ସମରାଙ୍ଗଣେ କ୍ଷତ୍ରିୟରୂପେଣ ଅର୍ଜୁନସ୍ୟ ଯୁଦ୍ଧ ତୁ ପରମକର୍ତ୍ତବ୍ୟ ଭବତି । ସ୍ଵକର୍ତ୍ତବ୍ୟସ୍ୟ ପୁରତଃ କସ୍ୟ ମୃତ୍ୟୁ ନାପେକ୍ଷ୍ୟତେ । କର୍ତ୍ତବ୍ୟ ସମାହିତେ ସତି ଯଦି କୋଽପି ସ୍ଵଜନସ୍ୟ ମୃତ୍ୟୁ ଭବତି ତହିଁ ଅନୁଶୋଚନା ନ କରଣୀୟମ୍ । ସ୍ବକର୍ଭବ୍ୟାତ୍ ଚ୍ୟୁତଃ ମନୁଷ୍ୟ ପାପେ ଲିପ୍ତ ଭବତି । ଅତଃ ମୃତ୍ୟୁ ଅବଶ୍ୟମ୍ଭାବୀ । ଜୀବନସ୍ୟ ଏତାଦୃଶ ସତ୍ୟତା ଉପଲବିଂ କୃତ୍ୱା ଅନୁଶୋଚନଂ ନ କୁର୍ଯ୍ୟାତ୍ । ସଦୈବ ସ୍ଵକୀୟକର୍ତ୍ତବ୍ୟ ସମ୍ପାଦନେ ବ୍ରତୀ ଭବେତ୍ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ମୃତ୍ୟୁର୍ଧବମ୍ = ମୃତ୍ୟୁ + ଧ୍ରୁବମ୍ । ତସ୍ମାଦପରିହାର୍ଯ୍ୟର୍ଥେ = ତସ୍ମାତ୍ + ଅପରିହାର୍ଯ୍ୟ + ଅର୍ଥେ । ଶୋଚିତୁମର୍ହସି = ଶୋଚିତୁମ୍ + ଅର୍ହସି |
ସମାସ – ଅପରିଦ୍ଵାମ୍ୟୌ = ନ ପରିହାର୍ଯ୍ୟ, ତସ୍ମିନ୍ (ନଞ୍ଚ୍ ତତ୍) ।
ମୂତସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ଧ୍ରୁମଃ, ମୃତ୍ୟୁ ରଂ, ଜନ୍ମ = କର୍ଭରି ୧ ମା । ତସ୍ମାଦ୍ = ହେତୌ ୫ମୀ । ଅପରିହାର୍ଯ୍ୟ, ଅର୍ଥେ = ଅଧୂକରଣେ ୭ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଜାତଃ = ଜନ୍ + କ୍ତ । ଶୋଚିତୁମ୍ = ଶୋଚ୍ + ଣିଚ୍ + ତୁମୁନ୍ ।

ଶ୍ଳୋକ – ୩
दुःखेष्वनुद्विग्नमनाः सुखेषु विगतस्पृहः |
वीतरागभयक्रोधः स्थितधीर्मुनिरुच्यते ||३||
ଦୁଃଖେଷ୍ଠନୁବିଗ୍ନମନାଃ ସୁଖେଷୁ ବିଗତତଃ |
ବାତରାଗଭୟକ୍ତେଧ ସିଉଧାମ୍ବନିର୍ଦ୍ୟତେ ||୩||
ଅନ୍ବୟ – ଦୁଃଖେଷୁ ଅନୁଦ୍ବିଗ୍ନମନାଃ ସୁଖେଷୁ ବିଗତସ୍ପୃହ ବୀତରାଗଭୟକ୍ରୋଧଃ ସ୍ଥିତଧୀ ମୁନଃ ଉଚ୍ୟତେ। ଦୁଃଖେଷୁ = ବିଭିନ୍ନ ପ୍ରକାର ଦୁଃଖରେ । ଅନୁଦ୍ବିଗ୍ନମନା = ଉଦ୍ବିଗ୍ନ ନହୋଇ । ସୁଖେଷୁ = ସୁଖରେ । ବିଗତସ୍ପୃହ = ଅତ୍ୟଧିକ ଆଗ୍ରହ ପ୍ରକାଶ ନ କରି । ବୀତ = ମୁକ୍ତ । ରାଗ = ଆସକ୍ତି । ଭୟ = ଭୟ । କ୍ରୋଧଃ = ରାଗ । ସ୍ଥିତଧୀ = ସ୍ଥିରମତି ବା ବୁଦ୍ଧି । ମୁନଃ = ଋଷି / ମନନଶୀଳ ।
ଅନୁବାଦ – ବିବିଧ ଦୁଃଖ ତଥା ତ୍ରିତାପରେ ଯେ ବିଚଳିତ ହୁଏନାହିଁ, ସୁଖରେ ଯେ ଆନନ୍ଦବିଭୋର ହୁଏନାହିଁ ଏବଂ ଯେ ଆସକ୍ତି (ରାଗ), ଭୟ ଏବଂ କ୍ରୋଧରୁ ମୁକ୍ତ ତାଙ୍କୁ ସ୍ଥିତପ୍ରଜ୍ଞ ମୁନି ବୋଲି କୁହାଯାଏ ।
ତ୍ୟାଖ୍ୟା – ଶଂସିତ ଶ୍ଳୋକଃ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟଭାଗାତ୍ ଆନୀତଃ । ଅୟଂ ସଂଗୃହିତଃ । ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ସ୍ଥିତପ୍ରଜ୍ଞସ୍ୟ ଲକ୍ଷଣଂ ବର୍ଣ୍ଣିତମ୍ ।
ଦୁଃଖ ତ୍ରିବିଧମ୍ – ଆଧ୍ୟାତ୍ମକମ୍, ଆଦୈବିକମ୍, ଆଭୌତିକଂ ଚେତି । ଏଷ୍ଣୁ ତ୍ରିବଧଦୁଃଖେଷୁ ଯଃ ଉଦ୍ବିଗ୍ନାଂ ନ ଭବତି, ସ୍ୱୟମେବ ସ୍ଥିରଃ ଭବତି ପୁନଶ୍ଚ ସୁଖପ୍ରାପ୍ତିକାଳେଽପି ଆନନ୍ଦବିଭୋରଂ ନ ଭବତି, ଅର୍ଥାତ୍ ସୁଖ ଦୁଃଖ ଚ ସମାନରୂପେଣ ପଶ୍ୟତି ଧଃ ସ୍ଥିତପ୍ରଜ୍ଞ ଭବତି । ଇନ୍ଦ୍ରିୟାଶାଂ ସୁଖଭୋଗଂ ଭବତି ଆସକ୍ତି, ଏତତ୍ ରହିତଂ ତୁ ଅନାସିକ୍ତ ଇତି କଥ୍ୟତେ । ଲୋଭଶୂନ୍ୟ ଭୟଶୂନ୍ୟ ଅନାସଭ୍ରଂ ଚ ଯଃ ଭବତି ସ ସ୍ଥିତଧୀ ମନସି ରାଗ-ଭୟ-କ୍ରୋଧଃ ଚ ନ ଭବତି ଏତାଦୃଶ ଶାନ୍ତଚେତ୍ତା ମୁନଃ ଭବିତୁମ୍ ଅର୍ହସି । ଅତଃ ଉଚ୍ୟତେ-ଦୁଃଖେଷୁ ଅନୁଦ୍ବିଗ୍ନମନାଃ ସୁଖେଷୁ ବିଗତସ୍ପୃହ ବୀତରାଗଭୟକ୍ରୋଧଃ ମୁନଃ ସ୍ଥିତଧୀ ଉଚ୍ୟତେ । ‘ନାସୌ ମୁନଃ ଯସ୍ୟ ମତଂ ନ ଭିନ୍ନମ୍ ।’ ଇତି ଉକ୍ତଧାରେଣ ସ୍ଥିତପ୍ରଜ୍ଞସ୍ୟ ଲକ୍ଷଣଂ ନିର୍ଣ୍ଣୀତମ୍ । ଏତଦ୍ ବିଷୟମ୍ ଅତୀବ ମନୋଜ୍ଞ ଗ୍ରହଣୀୟଂ ସ୍ପୃହଣୀୟଂ ଚ ଭବତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଦୁଃଖେଷ୍ଠନୁଦ୍ବିଗ୍ନମନାଃ = ଦୁଃଖେଷୁ + ଅନୁଦ୍ବିଗ୍ନମନାଃ । ସ୍ଥିତଧୀର୍ମୁନିରୁଚ୍ୟତେ =ସ୍ଥିତଧୀ + ମୁନିଃ + ଉଚ୍ୟତେ ।
ଅନୁଦ୍ବିଗ୍ନମନାଃ = ଉଦ୍ବିଗ୍ନ ମନଃ ଯସ୍ୟ ଡଃ ତେ (ବହୁବ୍ରୀହିଃ), ନ ଉଦ୍ବିଗ୍ନମନାଃ (ନଞ୍ଚ୍ ତତ୍) । ବିଗତସ୍ପୃହଃ = ବିଗତଃ ସ୍ପୃହା ଯସ୍ୟ ଡଃ ( ବହୁବ୍ରୀହିଃ) । ସ୍ଥିତଧୀ = ସ୍ଥିତାଃ ଧୀ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) ।
ସକାରଣବିଭକ୍ତି – ଦୁଃଖେଷୁ, ସୁଖେଷୁ = ଅଧିକରଣେ ୭ମୀ । ଅନୁଦ୍ବିଗ୍ନମନଃ, ବିଗତସ୍ପୃହ, ବୀତରାଗଭୟକ୍ରୋଧଃ, ସ୍ଥିତଧୀ, ମୁନଃ = ଉକ୍ତ କର୍ମଣି ୧ ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ରାଗ = ରଞ୍ଜ୍ + ଘଞ୍ଜ୍ । କ୍ରୋଧଃ = କୃଧୂ + ଘଞ୍ଚ୍ । ସ୍ଥିତଃ = ସ୍ଲା + କ୍ତ ।
ଶ୍ଳୋକ – ୪
ध्यायतो विषयान् पुंसः सङ्गस्तेषूपजायते ।
सङ्गात् संजायते कामः कामात् क्रोधोऽभिजायते ।।४।।
ଧ୍ୟାଯ୍ତୋ ବିଷୟନ ଫୁସ: ସଲଂସ୍ତେତ୍ପପ୍ରଦାୟରେ |
ସଙ୍ଗୀତ୍ ସଂଜାୟତେ କାମଃ କାମାତ୍ କ୍ରୋଧାଽଭିଜାୟତେ || ୪ ||
ଅନ୍ବୟ – ବିଷୟାନ୍ ଧ୍ୟାୟତଃ ପୁଂଧଃ ତେଷୁ (ବିଷୟେଷୁ) ସଙ୍ଗୀ ଉପଜାୟତେ । ସଙ୍ଗୀତ୍ କାମ ସଂଜାୟତେ, କାମାତ୍ କ୍ରୋଧଃ ଅଭିଜାୟତେ |
ଣଦାର୍ଥ – ବିଷୟାନ୍ = ଇନ୍ଦ୍ରିୟଭୋଗ୍ୟ ବିଷୟମାନଙ୍କୁ । ଧ୍ୟାୟତଃ = ଚିନ୍ତା କଲାବେଳେ । ପୁଂନଃ = ପୁରୁଷର | ତେଣୁ = ଇନ୍ଦ୍ରିୟଭୋଗ୍ୟ ବିଷୟବସ୍ତୁରେ । ସଙ୍ଗ = ଆସକ୍ତି । ଉପଜାୟତେ = ବୃଦ୍ଧିଲାଭ କରେ । ସଙ୍ଗୀତ୍ = ସଂଜାୟତେ = ବୃଦ୍ଧିଲାଭ କରେ । କାମଃ = କାମନା । କାମାତ୍ = କାମନାରୁ । କ୍ରୋଧଃ = କ୍ରୋଧ ବା ରାଗ । ଅଭିଜାୟତେ = ଜାତ ହୁଏ ।
ଅନୁବାଦ – ବ୍ୟକ୍ତି ଇନ୍ଦ୍ରିୟଭୋଗ୍ୟ ବିଷୟବସ୍ତୁକୁ ଚିନ୍ତା କରୁଥିଲାବେଳେ ସେଗୁଡ଼ିକ ପ୍ରତି ତା’ର ଆସକ୍ତି ଜାତ ହୁଏ ଏବଂ ଏ ପ୍ରକାର ଆସକ୍ତିରୁ କାମନା ଜାତ ହୁଏ ଏବଂ କାମନାରୁ କ୍ରୋଧ ଜାତ ହୁଏ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ‘ ଗୀତାସୌରଭମ୍ ପଦ୍ୟାତ୍ ଆନୀତଃ । ଭଗବାନ୍ ବ୍ୟାସବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭୂତ୍ରା କୀଦୃଶଂ ଭାବଂ ସମାଗଚ୍ଛତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ସାଂସାରିକ ଜୀବନଂ ନିର୍ବାହୟିତୁ ମନୁଷ୍ୟ ବିଭିନ୍ନେଷୁ ବିଷୟେଷୁ ସଂଲଗ୍ନ ଭବତି । ବିଷୟ ଅପି ମନୁଷ୍ୟାନ୍ ଆକର୍ଷୟନ୍ତି । ବିଷୟାନାଂ ଧ୍ୟାନଂ କୁର୍ବନ୍ତଃ ଜନଃ ତେଷୁ ବିଷୟେଷୁ ସଙ୍ଗ ଭବନ୍ତି । ବିଷୟସଙ୍ଗୀତ୍ ମନସି କାମଃ ଭାବାଃ ଚ ଜାୟତେ । ପୁନଶ୍ଚ ଯଦା କାମନାୟା ପରିପୂରଣଂ ନ ଭବତି ତଦା କ୍ରୋଧଭାବ ଜାୟତେ । ଅତଃ ମନୁଷ୍ୟ ସଦୈବ ବିଷୟାତ୍ ଧାନଂ ନ କୁର୍ଯ୍ୟାତ୍ । ଅନାସକ୍ତ ପୁରୁଷ ପରମାର୍ଥୀ ପ୍ରାପ୍ଳୁତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ସଙ୍ଗସ୍ତେଷ୍ଠପଜାୟତେ = ସଙ୍ଗୀ + ତେଷୁ + ଉପଜାୟତେ | କ୍ରୋଧୋଽଭିଜାୟତେ = କ୍ରୋଧଃ + ଅଭିଜାୟତେ |
ସକାରଣବିଭକ୍ତି – ଧ୍ୟାୟତଃ, ପୁଂନଃ = ସଙ୍ଗୀ + ତେଷୁ + ଉପଜାୟତେ । କ୍ରୋଧୋଽଭିଜାୟତେ = କ୍ରୋଧଃ + ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ବିଷୟାନ୍ = କର୍ମଣି ୨ୟା । ସଙ୍ଗୀ, କାମ, କ୍ରୋଧଃ = କଉଁରି ୧ ମା । ତେଷୁ = ଅଧିକରଣେ ୭ମୀ । ସଙ୍ଗାତ, କାମାତ୍ = ‘ଜନିକର୍ତ୍ତୃପ୍ରକୃତି’ ଯୋଗେ ୫ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – କାମଃ = କମ୍ + ଘଞ୍ଜ୍ । କ୍ରୋଧଃ = କୃଧୂ + ଘଞ୍ଚ୍ । ଧାୟତଃ =
ଶ୍ଳୋକ – ୫
क्रेाधाद् भवति सम्मोहः सम्मोहात् स्मृतिविभ्रमः ।
स्मृतिभ्रंशाद् बुद्धिनाशेो वुद्धिनाशात् प्रणश्यति || ५ ||
କ୍ରୋଧାଦ୍ ଭବତି ସହ ସମ୍ମୋହାତ୍ ସ୍ମୃତିବିଭ୍ରମଃ ।
ସ୍ମୃତିଭ୍ରଂଶାଦ୍ ବୁଦ୍ଧିନାଶୋ ବୁଦ୍ଧିନାଶାତ୍ ପ୍ରଣଶ୍ୟତି ॥ ୫ ||
ଅନ୍ବୟ – କ୍ରୋଧାଦ୍ ସମ୍ମୋହଃ ଭବତି, ସମ୍ମୋହାତ୍ ସ୍ମୃତିବିଭ୍ରମଃ (ଭବତି), ସ୍ମୃତିଭ୍ରଂଶାଦ୍ ବୁଦ୍ଧିନାଶଃ ( ଭବତି), ବୁଦ୍ଧିନାଶାତ୍ ପ୍ରଣଶ୍ୟତି |
ଣଦାର୍ଥ – କ୍ରୋଧାତ୍ = କ୍ରୋଧରୁ । ସଂମୋହଃ = ପୂର୍ଣମୋହ ବା ଅଜ୍ଞାନ । ଭବତି = ଜାତ ହୁଏ । ସଂମୋହାତ୍ = ମୋହରୁ । ସ୍ମୃତି = ସ୍ମୃତିର | ବିଭ୍ରମ = ବିଭ୍ରମ | ସ୍ମୃତିଭ୍ରଂଶାତ୍ = ସ୍ମୃତିନାଶରୁ । ବୁଦ୍ଧିନାଶଃ = ବୁଦ୍ଧି ନଷ୍ଟ । ବୁଦ୍ଧିନାଶାତ୍ =ବୁଦ୍ଧିବିନଷ୍ଟତାରୁ । ପ୍ରଣଶ୍ୟତି = ମୃତ୍ୟୁ ବା ଅଧୋପତନ ହୁଏ ।
ଅନ୍ମବାଦ – କ୍ରୋଧରୁ ମୋହ ଜାତ ହୁଏ ଏବଂ ମୋହରୁ ସ୍ମୃତିବିଭ୍ରମ ହୁଏ । ସ୍ମୃତିବିଭ୍ରମ ହେଲେ ବୁଦ୍ଧି ନାଶ ହୁଏ ଏବଂ ଯେତେବେଳେ ବୁଦ୍ଧି ନଷ୍ଟ ହୋଇଯାଏ, ସେତେବେଳେ ବ୍ୟକ୍ତିର ମୃତ୍ୟୁ ବା ଅଧୋପତନ ହୁଏ |
ବ୍ୟାଖ୍ୟା – ଶପିଙ ଶୋଇ ବ୍ୟାସବିରଚିତ ମହରାରଗଣ୍ଡସ୍ୟ ଭାପବାନ୍ତ୍ରଗତ ଣ୍ଡାମହ୍ଭଗହଣାତାମା ସାଂଖ୍ୟଯୋଗନାମ ଦ୍ବିତୀୟାଧ୍ୟାୟାତ୍ ଆନୀତଃ । ଅୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ୟ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ମନୁଷ୍ୟସ୍ୟ ଅଧୋପତନଂ କର୍ଡିଂ ଭବତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ସାଂସାରିକ ଭୋଗବାସନାୟାଂ ଲିପ୍ତ ମନୁଷ୍ୟସ୍ୟ ମନସି ପ୍ରଥମତଃ ଆସ କାମନା ଅଚରିତାର୍ଥ ସନ୍ କ୍ରୋଧଃ ଜାୟତେ । ଅତ୍ୟଧିକ କ୍ରୋଧଃ ମନୁଷ୍ୟ ହିତାହିତଂ ଜ୍ଞାନଂ ନ ଭବତି । ମୋହବଶାତ୍ ଅଜ୍ଞାନାତ୍ ବା ସ୍ମୃତିବିଭ୍ରମଃ ତସ୍ୟ ବୁଦ୍ଧି ନାଶଂ ଯାତି । ମନୁଷ୍ୟତାଂ ସର୍ବସ୍ୱ ଭବତି ବୁଦ୍ଧି ବିବେକଃ ତିଷ୍ଠତି । ସ୍ୱ ଅଧୋପତିତଃ ଭବତି । ସାଂସାରାର୍ଣ୍ଣବେ ଭାସମାନଃ ପ୍ରାୟଃ ବିଷୟାନ୍ ପ୍ରତି ଅନାସକ୍ତିମାଧ୍ୟମେନ ଭଗବତଃ କୃପା ଲଭ୍ୟତେ । ଅତଃ ଚିନ୍ତନଂ ଚ କରଣୀୟମ୍ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ସହଃ = ସମ୍ + ମୋହ ।
ଜାୟତେ । ଅସ୍ମାତ୍ କାମନାୟା ଜନ୍ମ ଭବତି । ଜ୍ଞାନଶୂନ୍ୟ ସମ୍ମୋହିତଂ ଚ କରୋତି | ତଥ୍ୟ ଭବତି । କିମପି ସୂତୌ ନ ତିଷ୍ଠତି । ଅନେନ ବିଭ୍ରମେନ ଚ । ଯଦି ନଶ୍ୟତି ବୁଦ୍ଧି ତହିଁ ମନୁଷ୍ୟସ୍ୟ ସତ୍ତାପି ନ ଭବତି । ଅତଃ ସଦୈବ ପରମେଶ୍ଵରସ୍ୟ ଧ୍ୟାନଂ ତଥା ମନମଃ ସ୍ଥିରତା, ବିଷୟବାସନା ରାହିତ୍ୟମ୍, ଈଶ୍ବର
ସମାସ – ସ୍ମୃତିବିଭ୍ରମଃ = ସ୍ଵତଃ ବିଭ୍ରମଃ (୬୩ ତତ୍) । ବୁଦ୍ଧିନାଶଃ = ବୁଦ୍ଧି ନାଶଃ ( ୬ଷ୍ଠ ତତ୍) । ସ୍ମୃତିଭ୍ରଂଶାତ୍ ସ୍ଵତଃ ଭ୍ରଂଶ ତସ୍ମାତ୍ (୬ଷ୍ଠୀ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – କ୍ରୋଧାତ୍, ସଂମୋହାତ୍, ସ୍ମୃତିଭ୍ରଂଶାତ୍, ବୁଦ୍ଧିନାଶାତ୍ = ଜନିକର୍ତ୍ତୃପ୍ରକୃତି ଯୋଗେ ୫ମୀ | ସଂମ୍ମୋହଃ, ସ୍ମୃତିବିଭ୍ରମ, ବୁଦ୍ଧିନାଶଃ = କଉଁରି ୫ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସଂହିଃ = ସମ୍ + ମୁହ + ଘଞ୍ଚ୍ । ସ୍ମୃତି = ସ୍କୃ + ସ୍କ୍ରିନ୍ । ବିଭ୍ରମ = ବି + ଭ୍ରମ୍ + ଅଚ୍ ।
ଶ୍ଳୋକ – ୬
श्रेयान् स्वधर्मे विगुणः परधर्मात् स्वनुष्ठितात् ।
स्वधर्मे निधनं श्रेयः परधर्मो भयावह || ६ ||
ଶ୍ରେୟାନ୍ ସ୍ଵଧର୍ମେ ବିଗୁନଃ ପରଧର୍ମାତ୍ ସ୍ୱନୁଷ୍ଠିତାତ୍ ।
ସ୍ଵଧର୍ମେ ନିଧନଂ ଶ୍ରେୟଃ ପରଧର୍ମୋ ଭୟାବହିଃ ॥ ୬ ||
ଅନ୍ବୟ – ସ୍ଵନୁଷ୍ଠିତାତ୍ ପରଧର୍ମାତ୍ ବିଗୁନଃ (ଅପି) ସ୍ଵଧର୍ମୀ ଶ୍ରେୟାନ, ସ୍ଵଧର୍ମେ ନିଧନଂ ଶ୍ରେୟଃ ପରଧର୍ମୀ ଭୟାବହିଃ ।
ଶବ୍ଦାର୍ଥ – ଶ୍ରେୟାନ୍ = ବରଂ ଉତ୍ତମ । ସ୍ଵଧର୍ମୀ = ବ୍ୟକ୍ତିର ନିଜ ଧର୍ମ ବା ନିର୍ଦ୍ଦିଷ୍ଟ ଧର୍ମ । ବିଗୁନଃ = ଦୋଷଯୁକ୍ତ ହେଲେ ସୁଦ୍ଧା । ପରଧର୍ମାତ୍ = ଅନ୍ୟ ନିମିତ୍ତ ଉଦ୍ଦିଷ୍ଟ ଧର୍ମ ଅପେକ୍ଷା । ସ୍ୱନୁଷ୍ଠିତାତ୍ = ଭଲଭାବରେ କରିବା ଅପେକ୍ଷା । ସ୍ଵଧର୍ମେ ନିଜ ଧର୍ମରେ । ନିଧନଂ = ମୃତ୍ୟୁ । ଶ୍ରେୟଃ = ଉତ୍ତମ । ପରଧର୍ମ = ଅନ୍ୟର ଧର୍ମ । ଭୟାବହିଃ = ବିପଦପୂର୍ଣ୍ଣ ।
ଅନ୍ମବାଦ – ଅନ୍ୟର ଧର୍ମ ବା କର୍ମ ଆଚରଣ କରିବା ଅପେକ୍ଷା ନିଜର ଧର୍ମ ବା କର୍ମ ଯେତେ ଦୋଷଯୁକ୍ତ ହେଲେ ମଧ୍ୟ ତାହାକୁ ହିଁ ଆଚରଣ କରିବା ଉଚିତ । ଅନ୍ୟର ଧର୍ମାଚରଣ କରିବା ଅପେକ୍ଷା ନିଜର ଧର୍ମ ବା କର୍ମରେ ସ୍ଥିର ରହି ମୃତ୍ୟୁବରଣ କରିବା ବରଂ ଭଲ । କାରଣ ଅନ୍ୟର ଧର୍ମ ବା କର୍ମ ଅନୁସରଣ କରିବା ବିପଦପୂର୍ଣ୍ଣ ।
ସକାରଣବିଭକ୍ତି – କର୍ମଯୋଗନାମ ତୃତୀୟାଧ୍ୟାୟାତ୍ ଆନୀତଃ । ଅୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ୟ ଅସ୍ମିନ୍ ଶ୍ଳୋକେ କର୍ମଯୋଗସ୍ୟ ମାହାତ୍ମ୍ୟ ତଥା ସ୍ଵଧର୍ମପାଳନପ୍ରସଙ୍ଗ ବର୍ଣ୍ଣିତମ୍ । ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ କର୍ମଯୋଗସ୍ୟ ମାହାତ୍ମ୍ୟ ତଥା ସ୍ଵଧର୍ମପାଳନପ୍ରସଙ୍ଗ ବର୍ଣ୍ଣିତମ୍ |
ସାଂସାରିକଜନଃ ସ୍ୱକୀୟଂ କର୍ତ୍ତବ୍ୟମ୍ ଅବଶ୍ୟ କରଣୀୟମ୍ । ମାନବାନାଂ କୃତେ ମାନବଧର୍ମୀ ଶ୍ରେଷ୍ଠ ଭବତି । ସ୍ଵଧର୍ମ ଶ୍ରେୟାନ୍ । ପୁନଶ୍ଚ ସ୍ୱଧର୍ମେ ନିଧନଂ ଶ୍ରେୟଃ ପରନ୍ତୁ ପରଧର୍ମୀ ଭୟାବହିଃ ଭବତି । ଅତଃ ସଦୈବ ସ୍ୱଧର୍ମାଚରଣଂ କୁମ୍ୟୁ । ହେ ଅର୍ଜୁନଃ ! ସ୍ଵଂ କ୍ଷତ୍ରିୟୋଚିତଃ ଧର୍ମ ନାମ ଯୁଦ୍ଧ କୁରୁ । ଯଥା ସ୍ଵଧର୍ମସ୍ୟ ମହତ୍ତ୍ୱ ବର୍ଣ୍ଣିତଂ ତଦେବ ସ୍ପୃହଣୀୟଂ ଗ୍ରହଣୀୟଂ ଚ ଇତଡି |
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଭୟାବହିଃ = ଭୟ + ଆବହିଃ । ସ୍ଵନୁଷ୍ଠିତାତ୍ = ସୁ + ଅନୁଷ୍ଠିତାତ୍ ।
ସମାସ – ସ୍ଵଧର୍ମୀ = ସ୍ଵସ୍ୟ ଧର୍ମୀ (୬ଷ୍ଠୀ ତ୍ତ୍) । ପରଧର୍ମାତ୍ = ପରସ୍ୟ ଧର୍ମୀ, ତସ୍ମାତ୍ (୬ଷ୍ଠ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ସ୍ଵନୁଷ୍ଠିତାତ୍, ପରଧର୍ମାତ୍ = ଅପାଦାନେ ୫ମୀ । ସ୍ଵଧର୍ମୀ = ଅଧିକରଣେ ୭ମୀ । ଶ୍ରେୟଃ, ପରଧର୍ମୀ = କଉଁରି ୧ ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଧର୍ମୀ = ଧୃ + ମନ୍ ।

ଶ୍ଳୋକ – ୭
यदा यदा हि धर्मस्य ग्लानिर्भवति भारत !
अभ्युत्थानमधर्मस्य तदात्मानं सृजाम्यहम् ||७||
ଯଦା ଯଦା ହି ଧର୍ମସ୍ୟ ଗ୍ଳାନିର୍ଭବତି ଭାରତ ।
ଅଭ୍ୟୁତ୍ଥାମ୍ ଧର୍ମସ୍ୟ ତଦାତ୍ମାନଂ ସୃଜାମ୍ୟହମ୍ ॥ ୭||
ଅନ୍ବୟ – ଭାରତ ! ଯଦା ଯଦା ହି ଧର୍ମସ୍ୟ ଗ୍ଳାନିଃ ଭବତି ଅଧର୍ମସ୍ୟ ଅଭ୍ୟୁତ୍ଥାନଂ ( ଭବତି) ତଦା ଅହମ୍ ଆତ୍ମାନଂ ତ୍ସକାମି |
ଶବ୍ଦାର୍ଥ – ଭାରତ ! = ହେ ଭରତବଂଶଜ । ଯଦା = ଯେତେବେଳେ । ଯଦା = ଯେଉଁଠାରେ । ହି = ନିଶ୍ଚିତଭାବେ । ଧର୍ମସ୍ୟ = ଧର୍ମର । ଗ୍ଳାନିଃ = ଅପଚୟ । ଭବତି = ହୁଏ, ଦେଖାଯାଏ । ଅଧର୍ମସ୍ୟ = ଅଧର୍ମର । ଅଭ୍ୟୁତ୍ଥାନଂ = ଉନ୍ନତି । ତଦା = ସେତେବେଳେ । ଅହମ୍ = ମୁଁ । ଆତ୍ମାନଂ = ନିଜକୁ । ସୃଜାମି = ପ୍ରକାଶିତ କରେ ।
ଅନୁବାଦ – ହେ ଭରତବଂଶଜ ! ଯେଉଁଠାରେ ଏବଂ ଯେତେବେଳେ ଧର୍ମର ଗ୍ଲାନି (ଅପଚୟ) ଦେଖାଦିଏ ଏବଂ ଅଧର୍ମର ଅଭ୍ୟୁତ୍ଥାନ (ଉନ୍ନତି) ହୁଏ, ସେତେବେଳେ ମୁଁ ଅବତରଣ କରେ ବା ଆବିର୍ଭୂତ ହୁଏ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ‘ ଗୀତାସୌରଭମ୍ ପଦ୍ୟାତ୍ ଆନୀତଃ । ଭଗବାନ୍ ବ୍ୟାସ ବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ସୃଷ୍ଟି ଆବିର୍ଭାବାଃ ବା କଦା ଭବତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ସଂସାରୋଽୟଂ ଭଗବତଃ ସୃଷ୍ଟି । ମନୁଷ୍ୟତାଂ ଧର୍ମୀ ହି ମୂଳମ୍ । ଜୀବନନିର୍ବାହାର୍ଥମ୍ ଅସ୍ଥିନ୍ ସଂସାରେ ଧର୍ମ ଆଚରଣୀୟ ଭବତି । ପରନ୍ତୁ ସ୍ବାର୍ଥୀ ମନୁଷ୍ୟ ସ୍ବଉଦ୍ଦେଶ୍ୟ ପରିପୂରଣାର୍ଥମ୍ ଅଧର୍ମମ୍ ଆଚରତି । ଧର୍ମ ପୁଣ୍ୟ ଚ ବିହାୟ ଜନଃ ଅଧର୍ମ ପାପଂ ଚ ଆଚରନ୍ତି । ସଂସାରାତ୍ ଧର୍ମସ୍ୟ ଗ୍ଳାନିଃ ଭବତି ପୁନଶ୍ଚ ଅଧର୍ମସ୍ୟ ଅଭ୍ୟୁତ୍ଥାନଂ ଭବତି । ଅସ୍ଥିନ୍ ଏବ କାଳେ ଭଗବାନ୍ ଆତ୍ମାନଂ ସୃଜତି ସଂସାରେ ଆବିର୍ଭୂତଃ ଚ ଭବତି । ସାଧୁନାଂ ପରିତ୍ରାଣାୟ ଦୁଷ୍କୃତାନ୍ ବିନାଶାୟ ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ ଚ ଭଗବାନ୍ ଆତ୍ମାନଂ ସୃଜତି । ହେ ଭାରତ ! ଅହଂ ଧର୍ମସଂସ୍ଥାପନାୟ ଯୁଗେ ଯୁଗେ ସଂଭବାମି । ଭବବତଃ ଉକ୍ତ ଯାଥାର୍ଥ୍ୟମ୍ ଅସ୍ଥି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଗ୍ଳାନିର୍ଭବତି = ଗ୍ଳାନିଃ + ଭବତି । ଅଭ୍ୟୁତ୍ଥାନମଧର୍ମସ୍ୟ = ଅଭି +ଉତ୍ + ସ୍ଥାନମ୍ + ଅଧର୍ମସ୍ୟ । ତଦାତାନଂ = ତଦା + ଆତ୍ମାନମ୍ । ସୃଜାମ୍ୟହମ୍ = ସୃଜାମି + ଅହମ୍ ।
ସମାସ – ଅଧର୍ମସ୍ୟ = ନ ଧର୍ମୀ, ତସ୍ୟ (ନଞ୍ଚ୍ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ଭାରତ ! = ସମ୍ବୋଧନେ ୧ମା । ଧର୍ମସ୍ୟା, ଅଧର୍ମସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ଅହମ୍ = କର୍ଭରି ୧ମ । ଆତ୍ମାନଂ = କର୍ମଣି ୨ୟା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଗ୍ଳାନି = ଗ୍ଲୋ + ସ୍କ୍ରିନ୍ । ଅଭ୍ୟୁତ୍ଥାନମ୍ = ଅଭି + ଉତ୍ + ସ୍ପା + ଲ୍ୟୁଟ୍ ।
ଶ୍ଳୋକ – ୮
परित्राणाय साधूनां विनाशाय च दुष्कृताम् ।।
धर्मसंस्थापनार्थाय सम्भवामि युगे युगे ||८||
ପରିତ୍ରାଣାୟ ସାଧୁନାଂ ବିନାଶାୟ ଚ ଦୁଷୃତାମ୍ ।
ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ ସମ୍ଭବାମି ଯୁଗେ ଯୁଗେ ॥ ୮॥
ଅନ୍ବୟ – ସାଧୂନ୍ୟ ପରିତ୍ରାଣାୟ, ଦୁଷ୍ମତାଂ ବିନାଶାୟ, ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ ଚ (ଅହଂ) ଯୁଗେ ଯୁଗେ ସମ୍ଭବାମି |
ଶବ୍ଦାର୍ଥ – ସାଧୁନାଂ = ସଜ୍ଜନମାନଙ୍କର । ପରିତ୍ରାଣାୟ ଉଦ୍ଧାର ନିମନ୍ତେ | ଦୁଷ୍କୃତାମ୍ = ଦୁର୍ବୃର୍ତ୍ତିମାନଙ୍କର । ବିନାଶାୟ = ବିନାଶ ନିମିତ୍ତ | ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ = ଧର୍ମର ପ୍ରତିଷ୍ଠା ନିମନ୍ତେ । ଯୁଗେ ଯୁଗେ = ଯୁଗ ଯୁଗରେ । ସମ୍ଭବାମି = ଆବିର୍ଭୂତ ହୁଏ ।
ସାଧୁ ବା ସଜନମାନଙ୍କର ଉଦ୍ଧାର ବା ରକ୍ଷା ନିମନ୍ତେ ଓ ଦୁର୍ବୃତ୍ତମାନଙ୍କର ବିନାଶ ନିମନ୍ତେ ତଥା ଧର୍ମର ପ୍ରତିଷ୍ଠା ନିମନ୍ତେ ମୁଁ ଯୁଗେ ଯୁଗେ ଅବତୀର୍ଣ୍ଣ ହୁଏ । ଶ୍ଳୋକେ ଭଗବାନ୍ କିମର୍ଥ୍ୟ ଯୁଗେ ଯୁଗେ ସମ୍ଭବତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ । ପାପେ ନିମଗ୍ନାଂ ଭବନ୍ତି । ସଜନାଃ ଅକୁଳା ଭବନ୍ତି । ଦୃଷ୍କୃତଃ ବାତାବରଣମ୍ ଆଚ୍ଛନ୍ତଃ ଭବତି । ଅସ୍ଥିନ୍ ଏବ କାଳେ ଭଗବାନ୍ ଆଚରତି । ସଂସାରୋଽୟଂ ପାପପୂର୍ଣ୍ଣ ଭବତି । ଜନଃ ସ୍ଵାର୍ଥପରା ପ୍ରଭାବଂ ବିସ୍ତାରୟତ୍ତି । ସଜନାନ୍ ପୀଡ଼ୟନ୍ତି ଚ । ସର୍ବତ୍ରୈବ ହିଂସାୟା ଆବିର୍ଭୂତଃ ଭବତି । ସ୍ଵୟଂ ଭଗବତା ଶ୍ରୀକୃଷ୍ଣନ ଅର୍ଜୁନଃ କଥ୍ୟତେ ଯତ୍ ସାଧୁନାଂ ପରିତ୍ରାଣାୟ ଦୁଷ୍କର୍ମକାରିତାଂ ବିନାଶାୟ ଧମସମ୍ଵାପନାଆପ୍ ଚ କ୍ଷ୍ବଗେ କ୍ଷ୍ବଗେ ଅହିଂ ସପୂବାମି | ବସ୍ତୁତ ଭଗବତ ଧରାବତରଣ ତିଶ୍ୱକଲମପ ଉନତି |
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଦୁଷୃତାମ୍ = ଦୁଃ + କୃତାମ୍ । ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ = ଧର୍ମସଂସ୍ଥାପନ + ଅର୍ଥାୟ ।
ସମାସ – ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ = ଧର୍ମସ୍ୟ ସଂସ୍ଥାପନମ୍ (୬ଷ୍ଠ ତତ୍), ତଥ୍ୟ ଅର୍ଥମ୍, ତସ୍ମି (୬୩ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ପରିତ୍ରାଣାୟ, ବିନାଶାୟ, ଧର୍ମସଂସ୍ଥାପନାର୍ଥାୟ = ନିମିତ୍ତାର୍ଥେ ୪ ର୍ଥୀ । ସାଧୁନାଂ, ଦୁଷ୍କୃତାମ୍ ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ଯୁଗେ ଅଧୂକରଣେ ୭ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସଂଭବ: = ସମ୍ + ଭୂ + ଅଚ୍ ।
ଶ୍ଳୋକ – ୯
विद्याविनयसंपन्ने ब्राह्मणे गवि हस्तिनि ।
शुनि चैव श्वपाके च पण्डिताः समदर्शिनः || ९ ||
ବିଦ୍ୟାବିନୟସଂପନ୍ନେ ବ୍ରାହ୍ମଣେ ଗବି ହସ୍ତିନି |
ଶୁନି ଚୈବ ଶ୍ୱପାକେ ଚ ପଣ୍ଡିତଃ ସମଦର୍ଶନଃ ॥ ୯ ॥
ଅନ୍ବୟ – ପଣ୍ଡିତଃ ବିଦ୍ୟାବିନୟସଂପନ୍ନେ ବ୍ରାହ୍ମଣେ ଶୁପକେ ଚ ଗବି ହସ୍ତିନି ଶୁନି ଚ ଏବଂ ସମଦର୍ଶନଃ (ଭାବନ୍ତି) ।
ଶବ୍ଦାର୍ଥ – ପଣ୍ଡିତଃ = ପଣ୍ଡିତମାନେ । ବିଦ୍ୟା = ଶିକ୍ଷା । ବିନୟ = ବିନୟଭାବ । ସମ୍ପନ୍ନ = ପୂର୍ଣଭାବେ ଅଧିକୃତ । ହସ୍ତିନି = ହାତୀଠାରେ । ଶୁନି = କୁକୁରଠାରେ । ଚ = ଓ | ଏବ = ହିଁ | ସମଦର୍ଶନଃ = ସମାନ ଦୃଷ୍ଟିରେ ଦେଖନ୍ତି ।
ଅନୁବାଦ – ପଣ୍ଡିତମାନେ ବିଦ୍ୟା ଏବଂ ବିନୟସଂପନ୍ନ ବ୍ରାହ୍ମଣଠାରେ ଓ ଚାଣ୍ଡାଳଠାରେ, ତଥା ଗାଭୀଠାରେ, ହାତୀଠାରେ ଓ କ୍ମକ୍ସରଠାରେ ଦସମହାପନ ହେଲଥା’ନ୍ତି |
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟାତ୍ ଆନୀତଃ । ଅୟଂ ଭଗବାନ୍ ବ୍ୟାସବିରଚିତଂ ଶ୍ଳୋକେ ପଣ୍ଡିତଃ କୁତ୍ର ସମଦର୍ଶନଃ ଭବନ୍ତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ଅଜ୍ଞଜନା ସଂସାରୋଽୟଂ ଭିନ୍ନଭିନ୍ନ ରୂପେଣ ପଶ୍ୟନ୍ତି । ସ୍ଵଳ୍ପବୁଦ୍ଧିବଳେନ ଅୟଂ ନରଃ ଅୟଂ ବାନରଃ ଇତି ଚିନ୍ତୟନ୍ତି । ମନୁଷ୍ୟ ତଥା ମନୁଷ୍ୟତରଂ ପ୍ରାଣିନଃ ଭିନ୍ନଭିନ୍ନ ରୂପେଣ ଇତି ଅବଗଣୟନ୍ତି । ପରନ୍ତୁ ପଣ୍ଡିତାନାଂ ସ୍ବଭାବଂ ତୁ ଭିନଂ ଭବତି । ତେଷା ଦର୍ଶନଂ ତୁ ଭିନ୍ନ ସମଭାବାପନଂ ଚ ଭବତି । ଅତଃ ତେ ସମସ୍ତଂ ସଂସାରମ୍ ଏକରୂପେଣ ଅବଲୋକୟନ୍ତ । ପଣ୍ଡିତାଃ ବିଦ୍ୟାବିନୟସମ୍ପନ୍ନ ବ୍ରାହ୍ମଣେ, ଗବି, ହସ୍ତିନି, ଶୁନି, ଶୁପାକେ ଚାଣ୍ଡାଳେ ବା ଚ ଏବଂ ସମଦର୍ଶନଃ ଭବନ୍ତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଚୈବ = ଚ + ଏବ ।
ସମାସ – ବିଦ୍ୟାବିନୟସଂପନ୍ନ = ବିଦ୍ୟା ଚ ବିନୟ ଚ (ଦ୍ବନ୍ଦ୍ବ) ତ ସମ୍ପନ୍ନମ୍, ତସ୍ମିନ୍ (୬ଷ୍ଠ ତତ୍) । ଶ୍ଵପାକେ ଶ୍ଵାନଂ ପାଚୟତି ଯଃ ସ୍ୱ, ତସ୍ମିନ୍ (ବହୁବ୍ରୀହୀ) । ପଣ୍ଡିତଃ ପଣ୍ଡା ବେଦୋଜ୍ୱଳା ବୁଦ୍ଧି ଯସ୍ୟ ସ୍ୱ, ତେ (ବହୁବ୍ରୀହିଃ) । ସମଦର୍ଶନଃ = = ସମଃ ଦର୍ଶୀ ତେ (କର୍ମଧାରୟ) ।
ସକାରଣବିଭକ୍ତି – ପଣ୍ଡିତାଃ = କଉଁରି ୧ ମା । ବିଦ୍ୟାବିନୟସଂପନ୍ନ, ବ୍ରାହ୍ମଣେ, ଗବି, ହସ୍ତିନି, ଶୁନି, ଶୁପାକେ = ଅଧିକରଣେ ୭ମୀ ।
ଶ୍ଳୋକ – ୧୦
उद्धरेदात्मनात्मानं नात्मानमवसादयेत् ।
आत्मैव ह्यात्मनो बन्धुरात्मैव रिपुरात्मनः ||१०||
ଉତ୍ତରେଦାତ୍ମନାତ୍ମାନାଂ ନାତ୍ମାନମବସାଦୟେତ୍ ।
ଆଜୈବ ହ୍ୟାତ୍ମନୋ ବନ୍ଧୁରାଜୈବ ରିପୁରାତ୍ମନଃ ॥ ୧୦ ||
ଅନ୍ବୟ – ଆତ୍ମନା ଆତ୍ମାନମ୍ ଉଦ୍ଧରେତ୍ ଆତ୍ମାନଂ ନ ଅବସାଦୟେତ୍ । ହି ଆତ୍ମା ଏବଂ ଆତ୍ମନଃ ବନ୍ଧୁ ଆତ୍ମା ଏବ ଆତ୍ମନଃ ରିପୁ ।
ଶବ୍ଦାର୍ଥ – ଆତ୍ମନା = ମନ ସାହାଯ୍ୟରେ । ଆତ୍ମାନମ୍ = ବଦ୍ଧଜୀବାତ୍ମାକୁ । ଉଦ୍ଧରେତ୍ = ଉଦ୍ଧାର କରିବା ଉଚିତ । ଅବସାଦତ୍ = ଅଧୋଗତି କରାଇବା । ହି ଯେହେତୁ । ଆତ୍ମା = ମନ | ଏବ = ହିଁ | ଆତ୍ମନଃ ବଦ୍ଧଜୀବାତ୍ମାର ବନ୍ଧୁ = ମିତ୍ର । ରିପଃ = ଶତ୍ରୁ ।
ଅନୁବାଦ – ବ୍ୟକ୍ତି ମନ ସାହାଯ୍ୟରେ ନିଜକୁ ଉପରକୁ ଉଠାଇବା ଉଚିତ, ତଳକୁ ନେବା ଉଚିତ ନୁହେଁ । ମନ ବଦ୍ଧଜୀବାତ୍ମାର ବନ୍ଧୁ ତଥା ଶତ୍ରୁ ମଧ୍ୟ ଅଟେ ।
‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟଭାଗେ ସନ୍ନିବେଶିତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ଆଲୋଦ୍ଧାରପ୍ରସଙ୍ଗ ବର୍ଣ୍ଣିତମ୍ । ଆତ୍ମନଃ ବର୍ଷିତମ୍ ।
ସଂସାରୋଽୟଂ ପରମାତ୍ମନଃ ସୃଷ୍ଟି । ଅତ୍ର ସାଂସାରିକଃ ଜୀନଃ ସଦୈବ ପରମାକର୍ଷିତଃ ଭବତି । ଜୀବ ସ୍ଵସ୍ୟରକ୍ଷଣାର୍ଥମ୍ ଚ ଭବତି । ଆତ୍ମରକ୍ଷଣମ୍ ଆତ୍ମଦର୍ଶନଂ ପ୍ରତ୍ୟେକଜୀବସ୍ୟ ମୂଳଉଦ୍ଦେଶ୍ୟ ଭବେତ୍ । ଆମ୍ଭୋଦ୍ଧାରଂ କଣଂ ବା ଭବେତ୍ ? ଅନେନ ପ୍ରସଙ୍ଗେନ ଭଗବତଃ ଉକ୍ତ ଯତ୍– ଆତ୍ମନା ଜୀବାତ୍ମା ବା ଆତ୍ମାନମ୍ ଉଦ୍ଧରେତ୍, ଆତ୍ମାନଂ ନ ଅବସାଦୟେତ୍ ଚ । ହି ଆତ୍ମା ଏବ ଆତ୍ମନଃ ବନ୍ଧୁ, ଆତ୍ମା ଏବ ଆତ୍ମନଃ ରିପୁ ଚ ଭବତି । ଜୀବ ସ୍ଵସ୍ୟ ରକ୍ଷଣାର୍ଥୀ ସ୍ୱୟମେବ ପ୍ରଯତ୍ନଶୀଳ ଭବେତ୍ ।
ନାତ୍ମାନମବସାଦୟେତ୍ = ନ + ଆତ୍ମାନମ୍ + ଅବସାଦୟେତ୍ । ଆଜୈବ = ଆତ୍ମା + ଏବ । ହ୍ୟାତ୍ମନଃ = ହି + ଆତ୍ମନଃ । ବନ୍ଧୁରାଜୈବ = ବନ୍ଧୁ + ଆତ୍ମା + ଏବ । ରିପୁରାତ୍ମନଃ = ରିପଃ + ଆତ୍ମନଃ ।
କର୍ମଣି ୨ୟା । ଆତ୍ମା = ଏବଂ ଯୋଗେ ୧ ମା । ରିପୁ = କଉଁରୀ ୧ ମା । ଆତ୍ମାନଃ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ |
ଶ୍ଳୋକ – ୧୧
दैवी ह्येषा गुणमयी मम माया दुरत्यया ।
मामेव ये प्रपद्यन्ते मायामेतां तरन्ति ते ।।११।।
ଦୈବୀ ଜ୍ୟେଷା ଗୁଣମୟୀ ମମ ମାୟା ଦୁରତ୍ୟୟା ।
ମାମେବ ଯେ ପ୍ରପଦ୍ୟନ୍ତେ ମାୟାମେତାଂ ତରନ୍ତି ତେ ॥୧୧||
ଅନ୍ବୟ – ଗୁଣମୟୀ ମମ ଏଷା ଦୈବୀ ମାୟା ଦୁରତ୍ୟୟା ହି ଯେ ମାଂ ପ୍ରପଦ୍ୟନ୍ତେ ତେ ଏବ ଏତାଂ ମାୟାଂ ତରନ୍ତି ।
ଶବ୍ଦାର୍ଥ – ତ୍ରିଗୁଣମୟୀ ପ୍ରକୃତି । ମମ = ମୋର । ଏଷା = ଏହି । ଦୈବୀ = ଦେବୀ । ମାୟା = ଶକ୍ତି | ଯେହେତୁ । ଯେ = ଯେଉଁମାନେ । ମାଂ = ମୋତେ । ପ୍ରପଦ୍ୟନ୍ତେ = ଅତିକ୍ରମ କରିବା ବଡ଼ କଠିନ । ହି = ଶରଣରେ ଆସନ୍ତି । ତେ = ସେମାନେ । ଏବ = ହିଁ । ଏତାଂ ମାୟାମ୍ = ଏହି ମାୟାଶକ୍ତିକୁ |
ଅନ୍ମବାଦ – ଭୂତ ପ୍ରକୃତିର ତ୍ରିଗୁଣଯୁକ୍ତ ମୋର ଏହି ଦୈବୀ ମାୟାଶକ୍ତିକୁ ଅତିକ୍ରମ କରିବା ବଡ଼ କଠିନ । କିନ୍ତୁ ଯେଉଁମାନେ ମୋର ଶରଣରେ ଆସିଥା’ନ୍ତି ସୋମାନେ ଅତି ମନ୍ତ୍ରଣରେ ଏହ୍ରାକୁ ଅତିକ୍ରମ କରିଯା’ନ୍ତି |
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟାତ୍ ଆନୀତଃ । ଅୟଂ ଭଗବାନ୍ ବ୍ୟାସବିରଚିତଃ ଶ୍ଳୋକେ ଦୈବୀମାୟା କର୍ଡିଂ ତରଣୀୟଂ ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ମାୟାପ୍ରପଞ୍ଚୋଽୟଂ ସଂସାରଃ । ଭଗବାନ୍ ତୁ ସ୍ଵୟଂ ମାୟାଧରଃ । ତସ୍ୟ ମାୟୟା ଜଗତ୍ଵବ୍ୟାପ୍ତ ବା ଭବତି । ସାଂସାରିକ ମନୁଷ୍ୟ ନ ଜାନାତି ଦୈବୀମାୟାଂ ପରନ୍ତୁ ସଂସାର ସର୍ବସ୍ଵସୁଖଭୋଗଂ ପ୍ରାୟୁମ୍ ଅଧିକାଧି ମାୟାୟାମ୍ ଆପୁ ତଃ ଭବତି । ମାୟା ତ୍ରିଗୁଣାମ୍ବିକା ଭବତି । ସତ୍ତ୍ଵ-ରଜ-ତମ ତ୍ରିଗୁଣାମ୍ବିକା ଭବତି ମାୟା । ଅତଃ ଭଗବାନ୍ କଥୟତି ଯତ୍-ମମ ଏଷା ଦୈବୀ ଗୁଣମୟୀ ମାୟା ହିଁ ଦୁରତ୍ୟୟା । ପରନ୍ତୁ ଯେ ମାମ୍ ଏବ ପ୍ରପଦ୍ୟନ୍ତେ, ତେ ଏତାଂ ମାୟାଂ ତରନ୍ତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଜ୍ୟେଷା ହି + ଏଷା । ମାମେବ = ମାମ୍ + ଏବ । ମାୟାମେତାଂ = ମାୟାମ୍ + ଏତାମ୍ ।
ସକାରଣବିଭକ୍ତି – ମମ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ମାମ୍, ମାୟାମ୍, ଏତାମ୍ = କର୍ମଣି ୨ୟା । ଯେ, ଏଷା, ଗୁଣମୟୀ, ତେ, ଦୈବୀ, ମାୟା କଉଁରି ୧ ମା ।

ଶ୍ଳୋକ – ୧୨
अन्तकाले च मामेव स्मरन् मुक्त्वा कलेवरम् ।
यः प्रयाति स मद्भावं याति नास्त्यत्र संशयः ।।१२।।
ଅନ୍ତକାଳେ ଚ ମାମେବ ସ୍ମରନ୍ ମୁକ୍ତା କଳେବରମ୍ ।
ଯଃ ପ୍ରୟାତି ସ ମଦ୍ବଂ ଯାତି ନାସ୍ଥ୍ୟତ୍ର ସଂଶୟଃ || ୧୨ ||
ଅନ୍ବୟ – ଯଃ ଅନ୍ତକାଳେ ମାମ୍ ଏବ ସ୍ମରନ୍ କଳେବରଂ ମୁକ୍ତା ପ୍ରୟାତି ସ ମଦ୍ବଂ ଯାତି ଚ ଅତ୍ର ସଂଶୟଃ ନାସ୍ତି ।
ଶବ୍ଦାର୍ଥ – ଯଃ = ଯେ । ଅନ୍ତକାଳେ = ଜୀବନର ଶେଷ ସମୟରେ । ମାମ୍ = ମୋତେ । ଏବ = ହିଁ | ସ୍ଵରନ୍ ସ୍ମରଣ କରି । କଳେବରମ୍ = ଶରୀର। ମୁକ୍ତା = ତ୍ୟାଗକରି। ପ୍ରୟାତି = ଯାଏ । ଡଃ = ସେ । ମଦ୍ବମ୍ = ମୋ ପ୍ରକୃତି ବା ସ୍ଵଭାବକୁ। ଯାତି = ପ୍ରାପ୍ତ ହୁଏ । ଅତ୍ର = ଏଥିରେ । ସଂଶୟଃ = ସନ୍ଦେହ ।
ଅନ୍ନବାଦ – ଯେ ମୃତ୍ୟୁ ସମୟରେ କେବଳ ମୋତେ ସ୍ମରଣ କରି ଶରୀର ତ୍ୟାଗକରେ ସେ ସଙ୍ଗେ ସଙ୍ଗେ ମୋ ପ୍ରକୃତିକୁ ପ୍ରାପ୍ତ ହୁଏ । ଏଥିରେ କୌଣସି ସନ୍ଦେହ ନାହିଁ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟାତ୍ ଆନୀତଃ । ଅୟଂ କବିବ୍ୟାସକୃତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭଗବଦ୍ଭାବଂ ପ୍ରସ୍ତୋତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ବିଷୟଭୋଗବାସନାୟାଂ ନିଷ୍ପେଷିତଂ ଭବତି । ଈପ୍ସିତଂ ପ୍ରାପୁଂ ପ୍ରୟାସଂ କରୋତି । ଚିନ୍ତା ତଥା ମୋହମଧ୍ୟ କଦା ଜୀବନସ୍ୟ ଅନ୍ତଃ ଭବତି ଡଃ ନ ଜାନାତି । ଅନ୍ତକାଳେଽପି ତଦେବ କାମନା ସାଂସାରିକ ଭାବନା ଚ ମନସି ତିଷ୍ଠତି । ଜନ୍ମଜନ୍ମାନ୍ତରେ ପୀଡ଼ା ପ୍ରାପ୍ତ ଭବତି, ମୁଭିଂ ନ ଲଭତେ । ଅତଃ ଭଗବାନ୍ ଅର୍ଜୁନଂ ଆଦିଶତି ଯତ୍-ଅନ୍ତକାଳେ ଚ ଯଃ ମାମ୍ ଏବ ସ୍ମରନ୍ କଳେବରଂ ମୁକ୍ତା ପ୍ରୟାତି, ଡଃ ମଦ୍ବଂ ଯାତି ଇତି ଅତ୍ର ସଂଶୟଃ ନାସ୍ତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ମାମେବ = ମମ୍ + ଏବ | ମଦ୍ଭାବଂ = ମତ୍ + ଭାବମ୍ | ନାସ୍ତ୍ୟତ୍ର = ନାସ୍ତି + ଅତ୍ର |
ସମାସ – ଅନ୍ତକାଳେ = ଅନ୍ତସ୍ୟ କାଳୀ, ତସ୍ମିନ୍ (୬ଷ୍ଠ ତତ୍) | ମଦ୍ଭାବଂ = ମମ ଭାବମ୍ (୬ଷ୍ଠୀ ତତ୍) |
ଯଃ, କଃ = କଉଁରି ୧ ମା । ମାମ୍, କଳେବରମ୍, ମନ୍ଦମ୍ = କର୍ମଣି ୨ୟା । ଅନ୍ତକାଳେ = ଅଧିକରଣେ ୭ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସ୍ମରନ୍ = ସ୍କୃ + ଶତ୍ରୁ । ମୁକ୍ତା = ମୁଚ୍ + ଭ୍ରାତ୍। ସଂଶୟ =
ଶ୍ଳୋକ – ୧୩
पत्रं पुष्पं फलं तोयं यो मे भक्त्या प्रयच्छति ।
तदहं भक्त्युपहृतमश्नामि प्रयतात्मनः ।।१३।।
ପତ୍ର ପୁଷ୍ପ ଫଳ ତୋୟାଂ ଯୋ ମେ ଭକ୍ତ ପ୍ରୟଚ୍ଛତି ।
ତଦହ୍ ଭର୍ପଦ୍ରତମଶ୍ନାମି ପ୍ରତଶ୍ଳନ: ।।१३।।
ଅନ୍ବୟ – ଯଃ ଭକ୍ତ ପତ୍ର ପୁଷ୍ପ ଫଳଂ ତୋୟାଂ (ଚ) ମେ ପ୍ରୟଚ୍ଛତି, ପ୍ରୟତାନଃ ଭକ୍ତି ଉପହୃତଂ ତତ୍ (ସର୍ବମ୍) ଅହମ୍ ଅଣ୍ଡାମି |
ଶବ୍ଦାର୍ଥ – ଯଃ = ଯେ। ଭକ୍ତା = ଭକ୍ତିରେ । ପତ୍ର = ପତ୍ର । ପୁଷ୍ପ = ଫୁଲ। ଫଳ = ଫଳ। ତୋୟଂ = ଜଳଂ । ମେ = ମୋତେ । ପ୍ରଯଚ୍ଛତି = ଅର୍ପଣ କରେ । ପ୍ରୟତାତ୍ମନଃ = ସେହି ଶୁଦ୍ଧଚେତ୍ତା । ଭକ୍ତ ଉପହୃତମ୍ = ଭକ୍ତିରେ ଅର୍ପିତ । ତତ୍ ସେସବୁକୁ । ତାହା। ଅହମ୍ = ମୁଁ । ଅଣ୍ଡାମି = ଗ୍ରହଣ କରେ।
ଅନୁବାଦ – ଯେଉଁ ବ୍ୟକ୍ତି ଭକ୍ତି ସହକାରେ ପତ୍ର, ଫୁଲ, ଫଳ ଓ ଜଳ ମୋତେ ଅର୍ପଣ କରେ, ସେହି ଶୁଦ୍ଧଚେଭାର ଭକ୍ତିରେ ଅର୍ପିତ ସେସବୁକୁ ମୁଁ ଗ୍ରହଣ କରେ ।
ବ୍ୟାଖ୍ୟା – ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ଭଗବାନ୍ ଭକ୍ତଭ୍ୟ କିଂ କିଂ ଗୃହ୍ମାତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ । ଭକ୍ତାନାଂ ଭଗବାନ୍ । ଉଲ୍ଲେଭ୍ୟ ଭଣ୍ଡିଂ ସଦୈବ ଇଚ୍ଛତି । ଭକ୍ତ ସଦୈବ କିମପି କିମପି ପ୍ରାପ୍ୟର୍ଥୀ ଭଗବରଂ ପୂଜୟତି । ପୂଜାମାଧମେନ କିମପି ପ୍ରଦାତୁମ୍ ଇଚ୍ଛତି । ତସ୍ୟାଦ୍ଦେଶ୍ୟ ଭବତି ପ୍ରଭୂତ ଧନସୁଖାଦିକଂ ପ୍ରାପ୍ତି । ଅଳ୍ପମାତ୍ର ଦତ୍ତ୍ୱ ପ୍ରଚୁରଂ ପ୍ରାସ୍ତୁମ୍ ଇଚ୍ଛତି ଭକ୍ତ ! ଅନେନ ରାଜସୟା ଡଃ ଭଣ୍ଡିଂ ତ୍ୟଜତି । କେବଳମ୍ ଔପଚାରିକତୟା ପୂଜାପାଠ୍ୟ ମନ୍ତ୍ରଗାନଂ ଫଳପୁଷ୍ପାର୍ଘ୍ୟ ଚ ପ୍ରୟଚ୍ଛତି । ପରନ୍ତୁ ଭଗବାନ୍ ସ୍ଵୟମେବ ଅର୍ଜୁନମାଧମେନ ସର୍ବାନ୍ ଭକ୍ତାନ୍ କଥୟତି ଯତ୍-ଯଃ ଜନଃ ମେ ଭକ୍ତା ପତ୍ର ପୁଷ୍ପ ଫଳଂ ତୋୟଂ ଚ ପ୍ରୟଚ୍ଛତି, ଅହଂ ପ୍ରୟତାତ୍ମନଃ ଶୁଦ୍ଧଚିତ୍ତସ୍ୟ ତସ୍ୟ ଭଲ୍ୟୁପହୃତଂ ତତ୍ ସର୍ବମ୍ ଅକ୍ଲାମି । ଅତଃ ସର୍ବେ ଭଗବନ୍ତମ୍ ଅବଶ୍ୟ ଭଣ୍ଡିଂ କୁର୍ଯ୍ୟ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ତଦହଂ = ତତ୍ + ଅହମ୍ । ଭଲ୍ୟୁପହୃତମଣ୍ଡାମି = ଭକ୍ତ + ଉପହୃତମ୍ + ଅଶ୍ମାମି । ପ୍ରୟତାତ୍ମନଃ = ପ୍ରୟତ + ଆତ୍ମନଃ ।
ସମାସ – ଭକ୍ତିଭପହ୍ନତମ୍ବ = ଭକ୍ତ ଉପହୃତମ୍ (୩ୟା ତତ୍) । ପ୍ରିୟତଆତ୍ମନଃ = ପ୍ରୟତଃ ଆତ୍ମା ଯସ୍ୟ ଡଃ ତଥ୍ୟ (ବହୁବ୍ରୀହିଂ)।
ସକାରଣବିଭକ୍ତ – ଯଃ, ଅହମ୍ କଉଁରି ୧ ମା । ଭକ୍ତ = ସହାର୍ଥେ ୩ୟା । ଯେ = = ସଂପ୍ରଦାନେ ୪ର୍ଥୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଭକ୍ତି = ଭଜ୍ + ସ୍କ୍ରିନ୍ । ଉପହୃତମ୍ = ଉପ + ହୃ + କ୍ତ |
ଶ୍ଳୋକ – ୧୪
वेदानां सामवेदोऽस्मि देवानामस्मि वासवः ।
इन्द्रियाणां मनश्चास्मि भूतानामस्मि चेतना || १४ ||
ବେଦାନ ସାମବେଦୋଽସି ଦେବାନଂମସି ବାମଦ: |
ଇନ୍ଦ୍ରିୟାଣା ମନଶ୍ଚାସ୍ତି ଭୂତାନାମସ୍ତି ଚେତନା ॥ ୧୪ ||
ଅନ୍ବୟ – ବେଦାନାଂ ସାମବେଦଃ (ଅହଂ) ଅସ୍ଥି, ଦେବାନାଂ ବାସବଂ (ଅହଂ) ଅସ୍ଥି, ଇନ୍ଦ୍ରିୟାନାଂ ମନଃ (ଅହଂ) ଅସ୍ଥି, ଭୂତାନାଂ ଚେତନା ( ଅହଂ) ଅସ୍ଥି ଚ ।
ସମାସ – ବେଦାନ = ବେଦମାନଙ୍କର ମଧ୍ୟରେ । ସାମବେଦଃ = ସାମବେଦ । ଅସ୍ଥି = ଅଟେ । ଦେବାନାଂ = ଦେବତାମାନଙ୍କ ମଧ୍ୟରେ । ବାସବ = ଦେବରାଜ ବା ଇନ୍ଦ୍ର । ଇନ୍ଦ୍ରିୟାନାଂ = ଇନ୍ଦ୍ରିୟମାନଙ୍କ ମଧ୍ୟରେ । ମନଃ = = ଜୀବମାନଙ୍କ ମଧ୍ୟରେ । ଚେତନା = ଚୈତନ୍ୟ ବା ଜୀବନଶକ୍ତି । ଅସ୍ଥି = ଅଟେ !
ଅନୁବାଦ – ବେଦମାନଙ୍କ ମଧ୍ୟରେ (ମୁଁ) ସାମବେଦ, ଦେବତାମାନଙ୍କ ମଧ୍ୟରେ (ମୁଁ) ଇନ୍ଦ୍ର, ଇନ୍ଦ୍ରିୟମାନଙ୍କ ମଧ୍ୟରେ (ମୁଁ) ମନ ଏବଂ ଜୀବମାନଙ୍କ ମଧ୍ୟରେ (ମୁଁ) ଚେତନା ବା ଜୀବନଶକ୍ତି ଅଟେ ।
ବ୍ୟାଖ୍ୟା – ବିଭୂତିଯୋଗନାମ ଦଶମାଧ୍ୟାୟାତ୍ ଆନୀତଃ । ଅୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅଶ୍ବିନ୍ ଶ୍ଳୋକେ ଭଗବାନ୍ ଅର୍ଜୁନସ୍ୟ ପୁରତଃ ସ୍ଵକୀୟ ବିଭୂତିଃ ମହିମା ବା ବର୍ଣ୍ଣୟତି । ଭଗବତଃ ମହିମା ମନୁଷ୍ୟାନାଂ କୃତେ ଅଗୋଚରଃ ଭବତି । ଏତଦେବ ସମ୍ଭବଂ ଭବତି କେବଳଂ ଭଗବତଃ ଇଚ୍ଛାମାତ୍ରେଣ । ଯଦି ଭଗବାନ୍ ଇଚ୍ଛତି ତହିଁ ଜୀବୀ ତଥ୍ୟ ମହିମାଂ ଜ୍ଞାତୁଃ ସମର୍ଥ ଭବତି ଅନ୍ୟଥା ନ । ସ୍ଵକୀୟଂ ଶ୍ରେଷ୍ଠତା ବର୍ଣ୍ଣୟିତ୍ଵ ଭଗବାନ୍ କଥୟତି ଯତ୍-ହେ ଅର୍ଜୁନ ! ବେଦାନାଂ ମଧ୍ୟ ଅହଂ ସାମବେଦଃ ଅସ୍ଥି । ଅତଃ ବେଦେଷୁ ସାମବେଦଃ ଶ୍ରେଷ୍ଠ ଭବତି । ଦେବାନାଂ ମଧ୍ୟ ଅହଂ ବାସବ ଅସ୍ଥି । ଦେବରାଜ ଇନ୍ଦ୍ର ଅତଃ ଶ୍ରେଷ୍ଠ । ଇନ୍ଦ୍ରିୟାଣା ମନଃ ଅହଂ ଅସ୍ଥି । ଅତଃ ଏକାଦଶଇନ୍ଦ୍ରିୟ ମଧ୍ୟ ମନଃ ଶ୍ରେଷ୍ଠ ଭବତି । ଭୂତାନାମ୍ ଅହଂ ଚେତନା ଅସ୍ଥି । ସଂସାରେ ଯେ ପ୍ରାଣିନଃ ସନ୍ତୋ ତନ୍ମଧେ ଭଗବାନ୍ ଚେତନାରୂପେଣ ବିଦ୍ୟମାନଃ ଚ ଭବତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ସାମବେଦୋଽସ୍ମି = ସାମବେଦଃ + ଅସ୍ଥି । ଦେବାନାମସ୍କି = ଦେବାନାମ୍ + ଅସ୍ଥି । ମନଶାସ୍ତି = ମନଃ + ଚ + ଅସ୍ଥି। ଭୂତନାମସ୍ତି = ଭୂତାନାମ୍ + ଅସ୍ଥି ।
ସମାସ – ସାମବେଦଃ = ସାମ ନାମ ବେଦଃ (ମଧ୍ୟପଦଲୋପୀ କର୍ମଧାରାୟ) ।
ସକାରଣବିଭକ୍ତ – ବେଦନାଂ, ଦେବାନାଂ, ଇନ୍ଦ୍ରିୟାଣଂ, ଭୂତାନାମ୍ ନିର୍ଦ୍ଧାରଣେ ୬ଷ୍ଠୀ । ସାମବେଦଃ, ବାସନଃ, ମନଃ, ଚେତନା = କଉଁରି ୧ ମା। |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ବେଦଃ =ବିଦ୍ + ଘଞ୍ଚ୍ ଦେବାଃ = ଦିବ୍ + ଅଚ୍।
ଶ୍ଳୋକ – ୧୫
भक्त्या त्वनन्यया शक्य अहमेवंविधाऽर्जुन !
ज्ञातुं द्रष्टुं च तत्त्वेन प्रवेष्टुं च परंतप ! ।।१५।।
ଭକ୍ତା ଦ୍ଵନନ୍ୟୟା ଶକ୍ୟ ଅହମେବଂବିଧୋଽର୍ଜୁନ ।
ଜ୍ଞାନଂ ଦ୍ରୁଟିଂ ଚ ତତ୍ତ୍ଵେନ ପ୍ରବେଜିଂ ଚ ପରଂତପ | ୧୫ ||
ଅନ୍ବୟ – ପରଂତପ ! ଅନନ୍ୟୟା ଭକ୍ତ ତୁ ଏବଂବିଧଃ ଅହଂ ଜ୍ଞାନଂ ଶକ୍ୟ, (ଏବଂବିଧଃ ଅହଂ) ଦ୍ରସ୍ତୁ (ଶକ୍ୟ), ଅର୍ଜୁନ ! ତତ୍ତ୍ଵେନ ପ୍ରବେଜିଂ (ଶକ୍ୟ) ଚ |
ଶବ୍ଦାର୍ଥ – ପରଂତପ ! = ହେ ଶ୍ରେଷ୍ଠ ତପସ୍ବି ! ଅନନ୍ୟୟା = ସକାମ କର୍ମରେ ବା କାଳ୍ପନିକ ଜ୍ଞାନରେ ମିଶ୍ରିତ ନ ହୋଇ । ଭକ୍ତା = ଭକ୍ତିଦ୍ଵାରା । ତୁ = କିନ୍ତୁ । ଏବଂବିଧଃ ଏହିପରି। ଅହଂ = ମୁଁ । ଜ୍ଞାତୁ ଜାଣିବାକୁ । ଶକ୍ୟ = ସକ୍ଷମ । ଦ୍ରଷ୍ଟୁ = ଦେଖିବାକୁ । ଅର୍ଜୁନ = ହେ ଅର୍ଜୁନ । ତତ୍ତ୍ଵେନ = ବାସ୍ତବରେ । ପ୍ରବେଜିଂ = ପ୍ରବେଶ କରିବାକୁ । ଚ = ଏବଂ |
ଅନୁବାଦ – ହେ ପରମ ତପସ୍ବି ! କେବଳ ଅନନ୍ୟ ଭକ୍ତି ବଳରେ (ଭକ୍ତ) ମୋର ପ୍ରକୃତ ସ୍ଵରୂପକୁ ଜାଣିବାକୁ ସକ୍ଷମ ହେବ; ମୁଁ ଯେପରି ପ୍ରକୃତ ସ୍ଵରୂପରେ ବର୍ତ୍ତମାନ ତୁମ ଆଗରେ ଦଣ୍ଡାୟମାନ ହୋଇଛି, ଠିକ୍ ଏହି ସ୍ଵରୂପକୁ ଭକ୍ତ ଜାଣିପାରିବ। ଏହି ପ୍ରକାର ମୁଁ ପ୍ରତ୍ୟକ୍ଷ ଭାବରେ ଦୃଷ୍ଟିଗୋଚର ହୋଇପାରିବି । କେବଳ ଏହି ପ୍ରକାରେ ତୁମେ ମୋର ରହସ୍ୟକୁ ଭେଦ କରିପାରିବ |
ଅନନ୍ୟୟା ଭକ୍ତ ଭଗବତଃ ଜ୍ଞାନଂ କର୍ଡିଂ କରଣୀୟ ଅଗ୍ନିନ୍ ସଂସାରେ ବଦ୍ଧଜୀବସ୍ୟ ପରମାଂ ପ୍ରଯନୁଶୀଳୀ ଭବେତ୍ । ଭଗବତଃ ଜ୍ଞାନଂ ତସ୍ୟ ସ୍ଵୟଂ ଭଗବତା ଶ୍ରୀକୃଷ୍ଣନ ଗୀତାୟାମ୍ ଅର୍ଜୁନଂ ତଦେବ ବର୍ଣ୍ଣିତମ୍ । ଚରମଂ ଲକ୍ଷ୍ୟ ଭବତି ଭଗବତ୍ ତତ୍ତ୍ଵସ୍ୟ ଜ୍ଞାନମ୍ । ଏତଦ ସ ସଦୈବ ସ୍ୱରୂପଂ, ତସ୍ମିନ୍ମଧ୍ଯ ପ୍ରବେଶଂ ଚ ସର୍ବମେବ ଅନନ୍ୟୟା ଭକ୍ତ ସଂଭବଂ ଭବତି । ପ୍ରତି କଥୟତି – ହେ ପରଂତପ ଅର୍ଜୁନ ! ଅନନ୍ୟୟ ଭକ୍ତ ତୁ ଜନଃ ଏବଂବିଧଃ ଚତୁର୍ଭୁଜଃ ସ୍ଵରୂପମ୍ ଅହଂ ତତ୍ତ୍ଵେନ ଜ୍ଞାତଂ ଦ୍ରଷ୍ଣୁ ପ୍ରବେଜିଂ ଚ ଶକ୍ୟ । ଭକ୍ତିମାଧମେନ ଜନା ଭଗବରଂ ଜ୍ଞାନଂ, ଦୁଷ୍ଟ, ପ୍ରବେଷ୍ଟୁ ଚ ସମର୍ଥା ଭବିଷ୍ଯତ୍ତି । ଅତଃ ଭକ୍ତି ଏବ ଶକ୍ତି ଇତି କଥ୍ୟତେ ।
ସନ୍ଧିବିଛେଦ – ତନନଜଣା = ତୁ + ଅନନ୍ୟୟା । ଅହମେବଂବିଧୋଽର୍ଜୁନ = ଅହମ୍ + ଏବଂବିଧଃ + ଅର୍ଜୁନ ।
ସମାସ – ଅନନ୍ୟୟା = ନ ଅନ୍ୟ, ତୟା (ନଞ୍ଚ୍ ତତ୍) । ଅର୍ଜୁନଃ = ଅରୀନ୍ ଶତ୍ରୁନ୍ ଜୟତି ଯଃ (ଉପପଦ ତତ୍)।
ସକାରଣବିଭକ୍ତି – ପରଂତପ !, ଅର୍ଜୁନ ! = ସମ୍ବୋଧନେ ୧ମା । ଅନନ୍ୟୟା, ଭକ୍ତା = କରଣେ ୩ୟା । ଭରେନ = କରଣେ ୩ଯ୍ବା |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଶକ୍ୟ = ଶକ୍ + ପଣ୍ । ଜ୍ଞାତୁ ଜ୍ଞା + ତୁମୁନ୍ । ଦ୍ରଷ୍ଟ = ଦୃଶ୍ + ତୁମୁନ୍ । ପ୍ରବେଜିଂ = ପ୍ର + ବିଶ୍ + ତୁମୁନ୍ ।

ଶ୍ଳୋକ – ୧୬
श्रेया हि ज्ञानमभ्यासात् ज्ञानाद्ध्यानं विशिष्यते ।
ध्यानात् कर्मफलत्यागः त्यागाच्छान्तिरनन्तरम् ।।१६।।
ଶ୍ରେୟୋ ହି ଜ୍ଞାନମଭ୍ୟାସାତ୍ ଜ୍ଞାନାଦ୍ଵାନଂ ବିଶିଷ୍ୟତେ ।
ଧ୍ୟାନାତ୍ କର୍ମଫଳତ୍ୟାଗ ତ୍ୟାଗାଚ୍ଛାନ୍ତରନନ୍ତରମ୍ ॥ ୧୬ ||
ଅନ୍ବୟ – ଅଭ୍ୟାସାତ୍ ଜ୍ଞାନଂ ହି ଶ୍ରେୟ, ଜ୍ଞାନାତ୍ ଧ୍ୟାନଂ, ଧ୍ୟାନାତ୍ କର୍ମଫଳତ୍ୟାଗ ବିଶିଷ୍ୟତେ, ତ୍ୟାଗାତ୍ ଅନନ୍ତରଂ
ଶବ୍ଦାର୍ଥ – ଜ୍ଞାନାତ୍ = ଜ୍ଞାନଠାରୁ । ଧ୍ୟାନଂ ଧ୍ୟାନ । ଧ୍ୟାନୀତ୍ = ଧ୍ୟାନଠାରୁ । କର୍ମଫଳତ୍ୟାଗ = ସକ୍ଷମ କର୍ମର ଫଳତ୍ୟାଗ। ବିଶିଷ୍ୟତେ = ଶ୍ରେଷ୍ଠ ଅଟେ । ତ୍ୟାଗାତ୍ = ତ୍ୟାଗଠାରୁ । ଅନନ୍ତରମ୍ = ପରେ । ଶାନ୍ତଃ = ଶାନ୍ତି ।
ଅଭ୍ୟାସ ଯୋଗ ଅପେକ୍ଷା ଜ୍ଞାନ ଶ୍ରେଷ୍ଠ, ଜ୍ଞାନଠାରୁ ଧ୍ୟାନ ଉତ୍ତମ ଏବଂ ଧ୍ୟାନଠାରୁ କର୍ମଫଳ ତ୍ୟାଗ ଉତ୍ତମ । କାରଣ କର୍ମଫଳ ତ୍ୟାଗ ପରେ ହିଁ ଶାନ୍ତି ଲାଭ ହୁଏ ।
ବ୍ୟାଖ୍ୟା – ଶମିିତ: ଶ୍ଳୋକ: ମଦୃପ: ବ୍ୟାସବିରଚିତଂ ମଦ୍ରାଭାରତଣ୍ଡଳଦ ଭାଷପବାନ୍ତ୍ରଗତ: ଣ୍ଡାମହଉଗଦଗାତାୟା ଭକ୍ତିଯୋଗନାମ ଦ୍ବାଦଶାଧ୍ୟାୟାତ୍ ଆନୀତଃ । ଅକ୍ଷାଂ ପଠିତ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ଭଗବତଃ ପ୍ରାପ୍ତି ଉପାୟଂ ବର୍ଣ୍ଣିତମ୍ ।
ଭଗବତଃ ପ୍ରାପ୍ତେ ବିଭିନେଷୁ ଉପାୟେଷୁ କର୍ମଫଳତ୍ୟାଗ ସର୍ବଶ୍ରେଷ୍ଠ ଭବତି । ଅନେନ ମନୁଷ୍ୟ ସର୍ବୋତ୍ତମଂ ସୁଙ୍ଖ ପରମାନନ୍ଦ ଚ ପ୍ରଶ୍ନୋତି । ସଂସାରସ୍ୟ ସର୍ବଶ୍ରେଷ୍ଠ ପ୍ରାଣୀ ଭବତି ମନୁଷ୍ୟ ତଥାପି ତଥ୍ୟ ମନସି ଦୁଃଖମ୍, ଅଶାନ୍ତଃ, ନିରାନନ୍ଦଯୁକ୍ତ ଚ ଭାବନା ଆୟାତି । ତସ୍ୟ ଦୁଃଖସ୍ୟାନ୍ତ ନ ଭବତି । କାମନାୟା ଉତ୍ତୁଙ୍ଗଶିଖରଂ ସ ନିର୍ମାତି । ଏକ ଏବଂ କାମନାୟା ବିନାଶେନ ଅପରସ୍ୟା ଜାତା ଭବତି । କାମନାୟା ବିନାଶେନ ଦୁଃଖସ୍ୟ ବିନାଶମ୍ ଇତ୍ୟେବ ବାଣୀ ତଂ ନ ଆକର୍ଷୟତି । ଅତଃ ଅଭ୍ୟାସାତ୍ ଜ୍ଞାନଂ ଶ୍ରେୟମ୍, ଜ୍ଞାନାତ୍ ଧ୍ୟାନଂ ଶ୍ରେୟମ୍, ଧ୍ୟାନାତ୍ କର୍ମଫଳତ୍ୟାଗ ଶ୍ରେୟଃ ବିଶିଷ୍ୟତେ ବା, ତ୍ୟାଗାତ୍ ଅନନ୍ତରଂ ଶାନ୍ତଃ ଲଭତେ । ଯାବତ୍ ମନୁଷ୍ୟ ସ୍ଵକର୍ମଫଳ ଧାରୟତି ତାବତ୍ ଅସୁଖୀ ଅଶାନ୍ତ ଚ ଭବତି । ଯଦା ତୁ ତ୍ୟଜତି ସୁଖଶାନ୍ତି ପ୍ରାଷ୍ଟୋତି । ଅତ ଗୀତାକାରେଣ ଉକ୍ତ ଯତ୍-‘ଅଶାନ୍ତସ୍ୟ କୁତଃ ସୁଖମ୍ ।’
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଜ୍ଞାନମଭ୍ୟସାତ୍ = ଜ୍ଞାନମ୍ + ଅଭ୍ୟାସାତ୍ । ଜ୍ଞାନାଦ୍ଵାନଂ = ଜ୍ଞାନାତ୍ + ଧ୍ୟାନମ୍ । ତ୍ୟାଗାଚ୍ଛାନ୍ତରନନ୍ତରମ୍ = ତ୍ୟାଗାତ୍ + ଶାନ୍ତଃ + ଅନନ୍ତରମ୍ ।
ସମାସ – କର୍ମଫଳତ୍ୟାଗ = କର୍ମଶଃ ଫଳମ୍, ତସ୍ୟ ତ୍ୟାଗ (୬ଷ୍ଠ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ଅଭ୍ୟାସାତ୍, ଧ୍ୟାନାତ୍ = ଅପାଦାନେ ୫ମୀ । ଜ୍ଞାନମ୍, ଧ୍ୟାନମ୍ = କର୍ଭରି ୧ ମା। ତ୍ୟାଗାତ୍ = ଅନନ୍ତରମ୍ ଯୋଗେ ୫ମୀ |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଶ୍ରେୟଃ = ଶ୍ରି + ଅଚ୍। ଶାନ୍ତଃ = ଶମ୍ + ସ୍କ୍ରିନ୍ । ତ୍ୟାଗ = ତାଜ୍ + ଘଞ୍ଚ୍ । ଜ୍ଞାନମ୍ = ଜ୍ଞା + ଲୁଟ୍ ।
ଶ୍ଳୋକ – ୧୭
अध्यात्मज्ञाननित्यत्वं तत्त्वज्ञानार्थदर्शनम् ।
एतज् ज्ञानमिति प्रोक्तमज्ञानं यदतोऽन्यथा ।।१७।।
ର୍ଥଧ୍ୟାତ୍ନକାନନିତ୍ୟତ୍ବ ତତ୍ଵକାନାର୍ଥଦଣ |
ଏତକ୍ ଦ୍ବାନମିତି ପ୍ରୋକ୍ତମଳାନ ଯଦଣୋଽଦାଥା ||१७।।
ଅନ୍ବୟ – ଅଧ୍ୟାତ୍ମଜ୍ଞାନନିତ୍ୟତଂ ତତ୍ତ୍ୱଜ୍ଞାନାର୍ଥଦର୍ଶନମ୍ ଇତି ଏତତ୍ ଜ୍ଞାନଂ ପ୍ରୋକ୍ତମ୍, ଅତଃ ଅନ୍ୟଥା ଯତ୍ (ତତ୍)
ଶବ୍ଦାର୍ଥ – ଅଧ୍ୟାତ୍ମଜ୍ଞାନନିତ୍ୟଙ୍ଖ = ଆତ୍ମା ସମ୍ବନ୍ଧୀୟ ଜ୍ଞାନର ନିତ୍ୟଭାବ । ତତ୍ତ୍ୱଜ୍ଞାନାର୍ଥଦର୍ଶନମ୍ = ତତ୍ତ୍ୱଜ୍ଞାନବିଷୟବସ୍ତୁ ଦର୍ଶନ। ଇତି = ବୋଲି (ଏହିପରି) । ଏତତ୍ = ଏସବୁ । ଜ୍ଞାନଂ କୁହାଯାଇଛି । ଅତଃ= ଏହାଠାରୁ । ଅନ୍ୟଥା = ଭିନ୍ନ । ଯତ୍ = ଯାହା । ଅଜ୍ଞାନମ୍ = ଅଜ୍ଞାନ। = ଜ୍ଞାନ ।
ଅନୁବାଦ – ଆତ୍ମଜ୍ଞାନ ଉପରେ ଗୁରୁତ୍ଵ ଆରୋପ ଓ ତତ୍ତ୍ୱଜ୍ଞାନ ଲାଭ କରିବା ନିମନ୍ତେ ଜିଜ୍ଞାସୁ ହେବା ଇତ୍ୟାଦି ଜ୍ଞାନ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ କିଂ ଜ୍ଞାନମ୍ ଇତି ଭଗବାନ୍ ବ୍ୟାଖ୍ୟାନଂ କୃତମ୍ ।
ଆତ୍ମାନୁଭୂତୌ ଭକ୍ତିଯୋଗୀ ବାସ୍ତବ ମାର୍ଗ ଭବତି । ଆତ୍ମା ପରମାତ୍ମା ମଧେ ଶ୍ଵାଶ୍ୱତଃ ସମ୍ବନ୍ଧ ଭବତି । ଭକ୍ତି ଏବ ନିତ୍ୟ ଶାସ୍ଵତଃ ଚ । ଅତଃ ଗୀତାୟାମ୍ ଉକ୍ତମ୍ – ‘ବଦନ୍ତି ତତ୍ ତତ୍ତ୍ବବିଦଃ ତତ୍ତ୍ୱ ଯଜ୍ଞାନାମ୍ ଅନ୍ବୟମ୍’ । ପରମତତ୍ତ୍ୱାନୁଭୂତୌ ଭଗବଦ୍ ଅନୁଭୂତିଃ ସର୍ବଶ୍ରେଷ୍ଠ ତଥା ସର୍ବାନ୍ତଃ ଭବତି । ଭଗବତଃ ଜ୍ଞାନଂ ତତ୍ତ୍ଵାର୍ଥଦର୍ଶନଂ ଚ ଅବଶ୍ୟ କରଣୀୟମ୍ । ଇଦମେବ ଜ୍ଞାନସ୍ୟ ପୂର୍ଣତ୍ୱମ୍ । ଅତଃ ଆତ୍ମଜ୍ଞାନଂ ତତ୍ତ୍ୱଜ୍ଞାନଂ ଚ ପ୍ରକୃଷ୍ଟଜ୍ଞାନମ୍ । ଏତଦ୍ ଅତିରିକ୍ତ ଅନ୍ୟ ସର୍ବମ୍ ଅଜ୍ଞାନମ୍ । ଅତଃ ସର୍ବେ ଅଜ୍ଞାନଂ ବିହାୟ ଜ୍ଞାନଂ କରଣୀୟମ୍ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଅଧ୍ + ଆତ୍ମଜ୍ଞାନନିତ୍ୟତ୍ଵମ୍ । ତତ୍ତ୍ୱଜ୍ଞାନାର୍ଥଦର୍ଶନମ୍ = ତତ୍ତ୍ଵଜ୍ଞାନ + ଜ୍ଞାନମ୍ + ଇତି । ପ୍ରୋକ୍ତମଜ୍ଞାନଂ = ପ୍ରୋକ୍ତମ୍ + ଅଜ୍ଞାନମ୍। ଯଦତୋଽନ୍ୟଥା = ଯତ୍ + ଅତଃ + ଅନ୍ୟଥା |
ସମାସ – ଅଧ୍ୟାତ୍ମ = ଆତ୍ମନି ଇତି (ଅବ୍ୟୟୀଭାବ) । ତତ୍ତ୍ୱଜ୍ଞାନମ୍ = ତତ୍ତ୍ଵାନାଂ ଜ୍ଞାନମ୍ (୬ଷ୍ଠୀ ତତ୍) । ଅଜ୍ଞାନମ୍ = ନ ଜ୍ଞାନମ୍ (ନଞ୍ଚ୍ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ଜ୍ଞାନମ୍, ଅଜ୍ଞାନମ୍ = କଉଁରି ୧ ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଦର୍ଶନମ୍ = ଦୃଶ୍ + ଲ୍ୟୁଟ୍ । ଜ୍ଞାନମ୍ = ଜ୍ଞା + ଲ୍ୟୁଟ୍ । ପ୍ରୋକ୍ତମ୍ = ପ୍ର + ବଚ୍ + କ୍ତ ।
ଶ୍ଳୋକ – ୧୮
ऊर्ध्वं गच्छन्ति सत्त्वस्था मध्ये तिष्ठन्ति राजसाः ।
जघन्यगुणवृत्तिस्था अधा गच्छन्ति तामसाः ।। १८ ।।
ଊର୍ଦ୍ଧ୍ଵ ଗଛନ୍ତି ସତ୍ତ୍ଵସ୍ଥା ମଧ୍ୟ ତିଷ୍ଠନ୍ତି’ ରାଜସା ।
ଜଘନ୍ୟଗୁଣବୃଭିସ୍ମା ଅଧୋ ଗଛନ୍ତି ତାମସା ||୧୮||
ଅନ୍ବୟ – ସତ୍ତ୍ଵସ୍ଥା ଊର୍ଧ ଗଛନ୍ତି, ରାଜସା ମଧ୍ୟ ତିଷ୍ଠନ୍ତି, ଜଘନ୍ୟଗୁଣବୃତ୍ତିସ୍ଥା ତାମସା ଅଧଃ ଗଛନ୍ତି ।
ଶବ୍ଦାର୍ଥ – ସତ୍ତ୍ଵସ୍ଥା = ଯେ ସତ୍ତ୍ଵଗୁଣରେ ସ୍ଥିତ । ଊର୍ଦ୍ଧ୍ଵ = ଉପରକୁ ବା ସ୍ଵର୍ଗକୁ । ଗଛନ୍ତି = ଯାଆନ୍ତି । ରାଜସ୍ୱ = ଯେଉଁମାନେ ରଜୋଗୁଣରେ ସ୍ଥିତ । ମଧ୍ୟ = ମଝିରେ ବା ମର୍ତ୍ତ୍ୟରେ । ତିଷ୍ଠନ୍ତି = ରୁହନ୍ତି । ଜଘନ୍ୟଗୁଣବୃଭିସ୍ତା = ଘୃଣିତ ଗୁଣ ବୃତ୍ତିରେ ସ୍ଥିତ । ତାମସା = ଯେଉଁମାନେ ତମୋଗୁଣରେ ସ୍ଥିତ । ଅଧଃ = ତଳକୁ ବା ନର୍କକୁ । ଗଛନ୍ତି = ଯାଆନ୍ତି ।
ଅନୁବାଦ – ଯେଉଁମାନେ ସତ୍ତ୍ଵଗୁଣରେ ସ୍ଥିତ, ସେମାନେ କ୍ରମେ ଊର୍ଦ୍ଧ୍ବକୁ ଗତି କରି ଉଚ୍ଚତର ଲୋକକୁ ବା ସ୍ଵର୍ଗକୁ ଯା’ନ୍ତି, ଯେଉଁମାନେ ରଜୋଗୁଣରେ ସ୍ଥିତ ସେମାନେ ଏ ଧରାଧାମରେ ରହନ୍ତି ଏବଂ ଯେଉଁମାନେ ପୃଣିତ କର୍ମ ଆଚରଣ କରି ତମୋଗୁଣରେ ସ୍ଥିତ ସେମାନେ ନିମ୍ନକୁ ନର୍କାନୁଗାମୀ ହୁଅନ୍ତି।
ବ୍ୟାଖ୍ୟା – ଉଦ୍ଧୃତଃ ଶ୍ଳୋକଃ ମହାମହିମମହର୍ଷି ବ୍ୟାସବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭୀଷ୍ମ ପର୍ବାନ୍ତର୍ଗତଃ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ତ୍ରିଗୁଣସମ୍ପନ୍ତଃ ଗତିଃ କୁତ୍ର ଭବତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ଗୁଣ ତ୍ରିବିଧଃ-ସତ୍ତ୍ଵ-ରଜ-ତମଶ୍ଚ । ସତ୍ତ୍ବଗୁଣସମ୍ପତଃ ବ୍ୟକ୍ତି ସାତ୍ତ୍ଵିକଃ, ରଜୋଗୁଣସମ୍ପରଃ ବ୍ୟକ୍ତି ରାଜସିକଃ, ତମୋଗୁଣସମ୍ପନ୍ତଃ ବ୍ୟକ୍ତି ତାମସିକଣ୍ଠ ଭବତି । ତଦ୍ବତ୍ ସକଳବିଶ୍ୱବ୍ରହ୍ମାଣ୍ଡସ୍ୟ ସ୍ଥିତିଃ ଅପି ତ୍ରିଗୁଣାତ୍ମକମ୍ । ସ୍ବର୍ଗ ଦ୍ୟୁଲୋକଂ ଚ ସତ୍ତ୍ବଗୁଣସମ୍ପନ୍ନମ୍ । ମର୍ତ୍ତ୍ୟଲୋକଂ ରଜୋଗୁଣସମ୍ପନ୍ନମ୍, ନର୍କ ତମୋଗୁଣପୂର୍ଣ୍ଣ ଚ ଭବତି । ମନୁଷ୍ୟାଽପି ତ୍ରିଗୁଣସମ୍ପନ୍ନ ଭବତି । ସସ୍ଥା ଉତଂ ନାମ ସ୍ଵର୍ଗ ଗଛନ୍ତି । ରାଜସ୍ୱ ମଧ୍ୟ ମର୍ତ୍ତ୍ୟ ଚ ତିଷ୍ଠନ୍ତି, ଜଘନ୍ୟଗୁଣବୃତ୍ତିସ୍ଥା ତାମସା ଅଧଃ ନାମ ନର୍କ ଗଛନ୍ତି । ଏତାଦୃଶରୂପେଣ ମନୁଷ୍ୟତାଂ ଗତିଃ ଭବତି ।
ବ୍ୟାକରଣ:
ସମାସ – ସତ୍ତ୍ଵସ୍ଥା = ସତ୍ତ୍ଵେ ତିଷ୍ଠନ୍ତି ଯେ (ଉପପଦ ତତ୍) । ରାଜସା = ରଜସି. ତିଷ୍ଠନ୍ତି ଯେ (ଉପପଦ୍ ତତ୍)। = ଜଘନ୍ୟ ଗୁନଃ (କର୍ମଧାରୟ) ତସ୍ୟ ବୃତିଃ ( ୬ଷ୍ଠ ତତ୍), ତସ୍ମିନ୍ ତିଷ୍ଠନ୍ତି ଯେ (ଉପପଦ ତତ୍) । ତାମସା = ତମସି ତିଷ୍ଠନ୍ତି ଯେ (ଉପପଦ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ସତ୍ତ୍ଵସ୍ଥ୍ୟ, ରାଜସା, ଜଘନ୍ୟଗୁଣବୃତ୍ତିସ୍ଥା, ତାମସା = କଉଁରି ୧ମା। ଊନଂ = କର୍ମ ୨ୟା । ମଧ୍ୟ = ଅଧୂକରଣେ ୭ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ବୃଷ୍ଟି = ବୃତ୍ + ସ୍କ୍ରିନ୍ ।
ଶ୍ଳୋକ – ୧୯
ऊर्ध्वमूलमधः शाखमश्वत्थं प्राहुरव्ययम् ।
छन्दांसि यस्य पर्णानि यस्तं वेद स वेदवित् ||१९||
ଊର୍ଧମୂଳମଧଃଶାଖମଶ୍ଵତ୍ଥ ପ୍ରାହୁରବ୍ୟୟମ୍ ।
ଛନ୍ଦସି ଯସ୍ୟ ପର୍ଶୁନି ଯସ୍ତଂ ବେଦ ସ ବେଦବିତ୍ ॥ ୧୯ ||
ଅନ୍ଵୟ – (ବେଦୀ) (ରଂ) ଅଶ୍ଵତ୍ଥମ୍ ଊର୍ଧମୂଳମ୍, ଅଧଃଶାଖମ୍ ଅବ୍ୟୟଂ ପ୍ରାଦୁଃ ଛନ୍ଦସି ଯସ୍ୟ ପଶ୍ଚିନି, ଯଃ ତଂ ବେଦ, ସ ବେଦବିତ୍।
ଶବ୍ଦାର୍ଥ – ଊର୍ଧମୂଳମ୍ = ମୂଳ ଊର୍ଦ୍ଧ୍ବକୁ । ଅଧଃ = ତଳକୁ । ଶାଖାମ୍ = ଶାଖାସବୁ। ଅଶ୍ବତ୍ = ଅଶ୍ଵତ୍ଥ ବୃକ୍ଷ । ପ୍ରାଦୁଃ = କୁହାଯାଏ । ଅବ୍ୟୟମ୍ = ଶାଶ୍ବତ । ଛନ୍ଦାସି ବେଦମନ୍ତ୍ରମାନ । ଯସ୍ୟ = ଯାହାର । ପର୍ଶୁନି = ପତ୍ରସବୁ । ଯଃ = ଯେ । ତଂ = ତାହା । ବେଦ = ଜାଣେ। କଃ = ସେ । ବେଦବିତ୍ = ବେଦଜ୍ଞ ଅଟେ। |
ବ୍ୟାକରଣ:
ଅନୁବାଦ – ଏକ ଅଶ୍ଵତ୍ଥ ବୃକ୍ଷ ଅଛି ଯାହାର ମୂଳସବୁ ଊର୍ଦ୍ଧ୍ବକୁ ଓ ଶାଖାସବୁ ତଳକୁ ଏବଂ ଯାହାର ପତ୍ରସବୁ ବେଦମନ୍ତ୍ର ଅଟେ । ଏହା କ୍ଷଣସ୍ଥାୟୀ ଓ ଅବିନାଶୀ । ଯେ ଏହି ବୃକ୍ଷକୁ ଜାଣେ ସେ ବେଦଜ୍ଞ ଅଟେ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାମହିମ ମହର୍ଷି ବ୍ୟାସବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭୀଷ୍ମ ପର୍ବାନ୍ତର୍ଗତଃ ଶ୍ରୀମଦ୍ଭଗବଦ୍ଗୀତାୟା ପୁରୁଷୋତ୍ତମଯୋଗୀ ନାମ ପଞ୍ଚଦଶାଧ୍ୟାୟତ୍ ଆନୀତଃ । ଅୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ସଂସାରମ୍ ଅଶ୍ୱତ୍ଥବୃକ୍ଷରୂପେଣ ବର୍ଣ୍ଣିତମ୍ ।
ଭଗବାନ୍ ସଂସାର ସ୍ୟ ସ୍ୱରୂପମ୍ ଅବବୋଧୟିତୁଃ କଥୟତି ଯତ୍-ହେ ଅର୍ଜୁନ ! ସଂସାରୋଽୟଂ ମାୟାପୂର୍ଣ୍ଣ ମ୍ ଅଶ୍ୱତ୍ଥବୃକ୍ଷସଦୃଶମ୍ । ଯସ୍ୟ ମୂଳମ୍ ଊର୍ଦ୍ଧ୍ୱ ଶାଖା ଚ ନିମ୍ନଦେଶ ବିଦ୍ୟତେ । ଅସ୍ୟ ତାତ୍ପର୍ଯ୍ୟ ଭବତି ଯତ୍ନ-ବ୍ରହ୍ମ ସଂସାରଷ୍ଟେ ମୂଳମ୍ । ସଂସାରରୂପବୃକ୍ଷସ୍ୟ ମୂଳମ୍ ଊର୍ଷେ ପରମେଶ୍ଵରସ୍ୟ ସମୀପେ ବର୍ଷତେ । ଅସ୍ୟ ଶାଖା ତୁ ମର୍ତ୍ତ୍ୟ ମନୁଷ୍ୟଲୋକେ ବିଦ୍ୟମାନା ଭବତି । ଛନ୍ଦସ ବେଦସମୂହଃ ପଣ୍ଡାନି ଭବନ୍ତି । ଯମ୍ ଏବ ଅବ୍ୟୟଂ ପ୍ରାହୁ । ସଂସାରସ୍ୟ ବିନାଶଂ ନାସ୍ତି ଇତି । ତଂ ସଂସାରରୂପମ୍ ଅଶ୍ୱତ୍ ଯଃ ବେଦଃ ସ ବେଦବିତ୍ ଭବତି । ସଂସାରସ୍ୟ ପ୍ରକୃତସ୍ବରୂପଂ ବେଦଜ୍ଞମେବ ଜାନାତି ।
ସନ୍ଧିବିଚ୍ଛେଦ – ଊର୍ଧମୂଳମଧଃଶାଖମଶ୍ଵତ = ଊର୍ଧମୂଳମ୍ + ଅଧଃଶାଖମ୍ + ଅଶ୍ୱତ୍ଥମ୍ । ପ୍ରାହୁରବ୍ୟୟମ୍ = ପ୍ରାଦୁଃ + ଅବ୍ୟୟମ୍ । ଯସ୍ତଂ = ଯଃ + ତମ୍ ।
ସମାସ – ଊର୍ଧମୂଳମ୍ = ଊର୍ଧମୂଳ ଯସ୍ୟ ସ, ତମ୍ (ବହୁବ୍ରୀହିଃ) । ଅଧଃଶାଖମ୍ = ଅଧଃ ଶାଖା ଯସ୍ୟ ଡଃ, ତମ୍ (ବହୁବ୍ରୀହିଂ)। ଅବ୍ୟୟମ୍ = ନ ବ୍ୟୟମ୍ (ନଞ୍ଚ୍ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ଅଶ୍ଵତ୍, ଊର୍ଧମୂଳ, ଅଧଃଶଙ୍ଖ, ଅବ୍ୟୟଂ, ତମ୍ = କର୍ମଣି ୨ୟା । ଯଃ, କଃ = ୧ମା । ଯସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ବେଦଃ = ବିଦ୍ + ଘଞ୍ଚ୍ |
ଶ୍ଳୋକ – ୨୦
त्रिविधं नरकस्येदं द्वारं नाशनमात्मनः ।
कामः क्रेाधस्तथा लाभस्तस्मादेतत्त्रयं त्यजेत् ||२०||
ତ୍ରିବିଧ୍ୱଂ ନରକସ୍ୟଦଂ ଦ୍ବାରଂ ନାଶନମାତ୍ମନଃ ।
କାମଃ କ୍ରୋଧସ୍ତଥା ଲୋଭସ୍ତସ୍ମାଦେତତ୍ତ୍ଵୟଂ ତ୍ୟଜେତ୍ ॥ ୨୦ ||
ଅନ୍ନକ୍ଷ – କାପ: କ୍ତେଧ: ତଥା ଲେଉ: କଦ ଦ୍ୱିବିଧମ୍ ଆଣ୍ଡନ: ନଣନ ନରକମଥତାରପ୍, ତମାଦ ଏଉତ୍ ପ୍ରମ ତ୍ୟକେତ |
ଶଦାର୍ଥ – କାମ: = କାମ | କ୍ରେଧ: = କ୍ରେଧ | ତଥା = ତଥା | ଲୋତ = ଲୋକ | ଲଦଂ = ଏଦ୍ | ତିସାର = ସେଦ୍ରିଦ୍ରେତୁ / ଗେଣ୍ଡ | ତିନିଟିକୁ ତ୍ୟାଗ କରିବା ଉଚିତ | କାରଣ ଏମାନେ ଆତ୍ମାର ଅଧୋଗତି ବିଧାନ କରନ୍ତି |
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାମହିମ ମହର୍ଷି ବ୍ୟାସବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭୀଷ୍ମ ପର୍ବାନ୍ତର୍ଗତଃ ଶ୍ରୀମଦ୍ଭଗବଦ୍ଗୀତାୟା ପୁରୁଷୋତ୍ତମଯୋଗୀ ନାମ ପଞ୍ଚଦଶାଧ୍ୟାୟତ୍ ଆନୀତଃ । ଅୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ସଂସାରମ୍ ଅଶ୍ୱତ୍ଥବୃକ୍ଷରୂପେଣ ବର୍ଣ୍ଣିତମ୍ ।
କାମଃ ନାମ ବାସନା ଲାଳସା ଚ ସଦୈବ ମନୁଷ୍ୟାନ୍ ଆକର୍ଷତି । ସ୍ବକୀୟ କାମଭାବନାଂ ଚରିତାର୍ଥୀ କର୍ଡିଂ ସ୍ୱ ଯତ୍ନବାନ୍ ଭବତି । ସ୍ବପ୍ରଯନ ଯଦ୍ୟପି କାମନା ପରିପୂରିତଂ ନ ଭବତି ତହିଁ ମନସି କ୍ରୋଧଃ ଭାବ ସମୁଦେତି । ଲୋଭଃ ଅପି ମନୁଷ୍ୟାନ୍ ଆକର୍ଷୟତି । କାମାସକ୍ତ ପୁରୁଷ ସଦା ଲୋଭବଶବର୍ତ୍ତୀ ଭବତି । ଅନେନ ମନୁଷ୍ୟ ସ୍ବବିନାଶଂ ସାଧୟତି । ଏତଦ ଏତେ ନର୍କସ୍ୟ ତ୍ରିବିଧ୍ୱଂ ଦ୍ବାରରୂପେଣ ବର୍ଥ୍ୟତେ । ଅତଃ ଭଗବତଃ ନିର୍ଦ୍ଦେଶଂ ଯତ୍ ଏତଦ୍ ତ୍ରିବିଧ୍ୱଂ ନର୍କସ୍ୟ ଦ୍ଵାରଂ ତ୍ରୟଂ ତ୍ୟଜେତ୍ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ନରକସ୍ଯଦମ୍ = ନରକସ୍ୟ + ଇଦମ୍ । ନାଶନମାତ୍ମନଃ = ନାଶନମ୍ + ଆତ୍ମନଃ। କ୍ରୋଧସ୍ତଥା = ଲୋଭଃ + ତସ୍ମାତ୍ + ଏତତ୍ + ତ୍ରୟମ୍ ।
ସକାରଣବିଭକ୍ତି – କାମଃ, କ୍ରୋଧଃ, ଲୋଭଃ, ଇଦମ୍ = କଉଁରି ୧ ମା । ଆତ୍ମନଃ = ସମ୍ବନ୍ଧେ ୬ଷ୍ଠୀ । ନରକସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ତସ୍ମାତ୍ = ହେତୌ ୫ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – କମ୍ + ଘଞ୍ଜ୍ । କ୍ରୋଧଃ = କୃଧୂ + ଘଞ୍ଜ୍ । ଲୋଭ = ଲୁଭ + ଘଞ୍ଜ୍ ।

ଶ୍ଳୋକ – ୨୧
आयुः सत्वबलारोग्यसुखप्रीतिविवर्द्धना ।
रस्याः स्निग्धाः स्थिरा हृद्या आहाराः सात्त्विकप्रियाः ।।२१।।
ଆୟୁ ସତ୍ଵବଳାରୋଗ୍ୟସୁଖପ୍ରୀତିର୍ବିବର୍ଦ୍ଧନା ।
ରସ୍ୟ ସ୍ନିଗ୍ଧା ସ୍ଥିରା ହୃଦ୍ୟା ଆହାରାଃ ସାତ୍ତ୍ଵିକପ୍ରିୟ || ୨୧ ||
ଅନ୍ବୟ – ସାତ୍ତ୍ଵିକା ଆହାରାଃ ଆୟୁ ସତ୍ତ୍ଵବଳାରୋଗ୍ୟ ସୁଖ ପ୍ରୀତିବିବର୍ଣନାଃ ରସ୍ୟ ସ୍ନିଗ୍ଧା ସ୍ଥିରଃ ହୃଦ୍ୟା ପ୍ରିୟା (ଚ ଭବନ୍ତି) |
ଶବ୍ଦାର୍ଥ – ସାତ୍ତ୍ଵିକା = ସାତ୍ତ୍ଵିକ । ଆହାରାଃ = ଖାଦ୍ୟ । ଆୟୁ = ଆୟୁଷ । ସତ୍ଵ = ଅସ୍ଥିତ୍ଵ । ବଳ = ସୁଖ ବା ଆନନ୍ଦ। ପ୍ରୀତି = ସନ୍ତୋଷ । ବିବର୍ଷନଃ = ବୃଦ୍ଧିକାରକ। ରସ୍ୟା = ଆରୋଗ୍ୟ = ସ୍ଵାସ୍ଥ୍ୟ । ସ୍ନିଗ୍ଧା = ଚର୍ବିଯୁକ୍ତ। ସ୍ଥିରଃ = ରସଯୁକ୍ତ । ଦୀର୍ଘକାଳସ୍ଥାୟୀ । ହୃଦ୍ୟା = ହୃଦୟର ଆନନ୍ଦଦାୟକ । ପ୍ରିୟା = ସ୍ଵାଦୁକର ।
ଅନୁବାଦ – ସାତ୍ତ୍ଵିକ ଖାଦ୍ୟ ଆୟୁଷ ବୃଦ୍ଧିକରେ, ବ୍ୟକ୍ତିର ସ୍ଥିତିକୁ ବିଶୁଦ୍ଧ କରେ ଏବଂ ବଳ, ସ୍ୱାସ୍ଥ୍ୟ, ସୁଖ ଓ ସନ୍ତୋଷ ଦିଏ। ଏ ପ୍ରକାର ପୁଷ୍ଟିକର ଖାଦ୍ୟ ସୁମିଷ୍ଟ, ରସଯୁକ୍ତ, ସ୍ନିଗ୍ଧ ଏବଂ ସ୍ଵାଦୁକର ଅଟେ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାମହିମ ମହର୍ଷି ବ୍ୟାସବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭୀଷ୍ମ ପର୍ବାନ୍ତର୍ଗତଃ ଶ୍ରୀମଦ୍ଭଗବଦ୍ଗୀତାୟା ପୁରୁଷୋତ୍ତମଯୋଗୀ ନାମ ପଞ୍ଚଦଶାଧ୍ୟାୟତ୍ ଆନୀତଃ । ଅୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ସଂସାରମ୍ ଅଶ୍ୱତ୍ଥବୃକ୍ଷରୂପେଣ ବର୍ଣ୍ଣିତମ୍ ।
ଆହାରୋଽପି ତ୍ରିଗୁଣାତ୍ମକମ୍ । ସପ୍ତାହାରଃ, ରାଜସିକାହାରଃ ତାମସିକାହାରୟେତି । ଅତ୍ର ସାତ୍ତ୍ଵିକାହାରଃ ବିଷୟ ବର୍ଣ୍ଣିତଂ ଭବତି । ସାତ୍ତ୍ଵିକପ୍ରିୟା ଆହାରାଃ ଆୟୁବର୍ଣକଃ, ବୁଦ୍ଧିବର୍ଷକା, ବଳବର୍ଷକା, ଆରୋଗ୍ୟଦାୟକା, ସୁଖବର୍ଷକା, ପ୍ରୀତିବର୍ଷକା, ରସ୍ୟା, ସ୍ନିଗ୍ଧା, ସ୍ଥିରଃ, ହୃଦ୍ୟା ଚ ଭବନ୍ତି । ସାତ୍ତ୍ଵିକଜନା ଏତାଦୃଶମ୍ ଆହାରଂ ସ୍ବୀକୁର୍ବନ୍ତି । ଏତାଦୃଶଃ ଆହାରଃ ଅସ୍ମାକଂ କାମ୍ଯ ଭବେତ୍ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ସତ୍ତ୍ଵେବଳାରୋଗ୍ୟସୁଖପ୍ରୀତିବିବର୍ଣ୍ଣନା = ସର୍ବଳ + ଆରୋଗ୍ୟସୁଖପ୍ରୀତିର୍ବିବର୍ଦ୍ଧନା।
ସମାସ – ସତ୍ତ୍ଵେବଳାରୋଗ୍ୟସୁଖପ୍ରୀତିବିବର୍ଦ୍ଧନା = ସତ୍ତ୍ୱେ ଚ ବରଂ ଚ ଆରୋଗ୍ୟ ଚ ସୁଙ୍ଖ ଚ ପ୍ରୀତିଃ ଚ ବିବର୍ଷନଃ ଚ ସାତ୍ତ୍ଵିକା ପ୍ରିୟା ଯେସାଂ, ତେ (ବହୁବ୍ରୀହିଂ)।
ସକାରଣବିଭକ୍ତି – ଆୟୁ, ରସ୍ୟା, ସ୍ନିଗ୍ଧା, ସୁରାଃ, ହୃଦ୍ୟା, ପ୍ରିୟଃ, ସାତ୍ତ୍ଵିକା, ଆହାରାଃ = କଉଁରି ୧ ମା। |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ପ୍ରୀତିଃ = ପ୍ରୀଣ୍ + ସ୍କ୍ରିନ୍ ।
ଶ୍ଳୋକ – ୨୨
सर्वधर्मान् परित्यज्य मामेकं शरणं व्रज ।
अहं त्वां सर्वपापेभ्येा मोक्षयिष्यामि मा शुचः ।। २२ ।।
ସର୍ବଧର୍ମାନ୍ ପରିତ୍ୟଜ୍ୟ ମାମେକଂ ଶରଣଂ ବ୍ରଜ ।
ଅହଂ ତାଂ ସର୍ବପାପେଭ୍ୟ ମୋକ୍ଷୟିଷ୍ୟାମି ମା ଶୁନଃ || ୨୨ ||
ଅନ୍ବୟ – ସର୍ବଧର୍ମାନ୍ ପରିତ୍ୟଜ୍ୟ ଏବଂ ମାଂ ଶରଣଂ ବ୍ରଜ। ଅହଂ ତାଂ ସର୍ବପାପେଭ୍ୟା ମୋକ୍ଷୟିଷ୍ୟାମି, ମା ଶୁନଃ ।
ସମାସ –ସର୍ବଧର୍ମାନ୍ = ସମସ୍ତ ପ୍ରକାର ଧର୍ମ । ପରିତ୍ୟଜ୍ୟ = ପରିତ୍ୟାଗ କରି । ଏକମ୍ =କେବଳ । ମାମ୍ = ମୋତେ । ଶରଣମ୍ = ଶରଣ । ବ୍ରଜ = ଯାଅ | ଅହଂ = ମୁଁ । ତାଂ = ତୁମକୁ । ମୋକ୍ଷୟିଷ୍ୟାମି = ମୁକ୍ତ କରିବି । ମା ଶୁନଃ = ଦୁଃଖ କରନାହିଁ ।
ଅନୁବାଦ – ସମସ୍ତ ପ୍ରକାର ଧର୍ମତ୍ୟାଗ କରି କେବଳ ମୋର ଶରଣାପନ୍ନ ହୁଅ। ମୁଁ ତୁମକୁ ସମସ୍ତ ପ୍ରକାର ପାପକର୍ମର ପ୍ରକ୍ରିୟାରୁ ମୁକ୍ତି ଦେଇପାରିବି। ଏଥରେ ଭାବନା ବା ଦୁଃଖ କର ନାହିଁ |
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାମହିମ ମହର୍ଷି ବ୍ୟାସବିରଚିତଂ ମହାଭାରତଗ୍ରନ୍ଥସ୍ୟ ଭୀଷ୍ମ ପର୍ବାନ୍ତର୍ଗତଃ ଶ୍ରୀମଦ୍ଭଗବଦ୍ଗୀତାୟା ପୁରୁଷୋତ୍ତମଯୋଗୀ ନାମ ପଞ୍ଚଦଶାଧ୍ୟାୟତ୍ ଆନୀତଃ । ଅୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ‘ଗୀତାସୌରଭମ୍’ ପଦ୍ୟ ସନ୍ନିବେଶିତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ସଂସାରମ୍ ଅଶ୍ୱତ୍ଥବୃକ୍ଷରୂପେଣ ବର୍ଣ୍ଣିତମ୍ ।
ଶରଣଂ ଜୀବସ୍ୟା ପରମକର୍ତ୍ତବ୍ୟମ୍ ଇତି ବର୍ଣ୍ଣିତମ୍ । ଈଶସୃଷ୍ଟି ଅୟଂ ସଂସାରଃ । ଅସ୍ଥିନ୍ ଚ । ସାଂସାରିକ ଧର୍ମାନ୍ ନିର୍ବାହୟିତଂ ଜୀବା ଶ୍ରୀକୃଷ୍ଣନ ଅର୍ଜୁନମାଧମେନ ସର୍ବଜୀବାନାଂ ଅର୍ଜୁନ ! ସର୍ବଧର୍ମାନ୍ ପରିତ୍ୟଜ୍ୟ ଏବଂ ମାଂ ସଂସାରେ ବଦ୍ଧଜୀବା ସୃଜୀବନନିର୍ବାହାର୍ଥୀ କିମପି କିମପି ଧର୍ମମ୍ ଆଚରନ୍ତି ଗୃହ୍ନାନ୍ତି ପାପେ ନିମଗ୍ନା ଭବନ୍ତି । ବଦ୍ଧଜୀବସ୍ୟ ସାଂସାରିକ ମୋହ ତ୍ୟାଗାମିଂ ସ୍ଵୟଂ ଭଗବତା କୃତେ ମାନବଜାତଃ ଉଦ୍ଧରଣାର୍ଥୀ ପ୍ରଯତମାନଂ ଭବତି । ଅତଃ କଥୟତି – ହେ ଶରଣଂ ବ୍ରଜ । ଅହଂ ତାଂ ସର୍ବପାପେଭ୍ୟ ମୋକ୍ଷୟିଷ୍ୟାମି, ବଂ ଶୋଚନା ମା କୁରୁ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ମାସକର = ମାମ୍ + ଏକମ୍ ।
ସମାସ – ସର୍ବଧର୍ମାନ୍ = ସର୍ବ ଧର୍ମ ତାନ୍ (କର୍ମଧାରୟ) । ସର୍ବପାପେଭ୍ୟ = ସର୍ବ ପାପଃ, ତେଭିଂ (କର୍ମଧାରୟ ) ।
ସକାରଣବିଭକ୍ତି – ସର୍ବଧର୍ମାନ୍ = କର୍ମଣି ୨ୟା । ମାମ୍, ଏକମ୍, ଶରଣଂ ୧ ମା । ତାଂ = କର୍ମଣି ୨ୟା । ସର୍ବପାପେଭ୍ୟ = ଅପାଦାନେ ୫ମା |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ପତିପ୍ୟାକ୍ = ପରି + ବ୍ୟକ୍ + ଲ୍ୟପ୍ |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()