Odisha State Board BSE Odisha 7th Class Odia Solutions Chapter 15 ଏ ମଣିଷକୁ ପଥର କଲା କିଏ Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Odia Solutions Chapter 15 ଏ ମଣିଷକୁ ପଥର କଲା କିଏ
ପାଠ୍ୟପୁସ୍ତକସ୍ଥ ଅଭ୍ୟାସ କାର୍ଯ୍ୟର ଉତ୍ତର
Question ୧।
ଉତ୍ତର କୁହ ।
(କ) ପାହାଡ଼ ତଳ ବଣଭୂଇଁକି ସଫା କରାଗଲା କାହିଁକି ?
Answer:
ରାଜାଙ୍କ ଆଦେଶରେ ମଧୁପୁରଗଡ଼ର ଗଡ଼ପାହାଡ଼ ତଳିରେ ରାଜପ୍ରାସାଦ ନିର୍ମାଣ କରାଯିବା ସ୍ଥିର କରାଗଲା । ସେଥିପାଇଁ ପାହାଡ଼ ତଳ ବଣଭୂଇଁକୁ ସଫା କରାଗଲା ଓ ପାହାଡ଼ କାଟି ଭୂମିକୁ ସମତଳ କରାଗଲା ।
(ଖ) ସେ ପାହାଡ଼ର ନାଆଁ କ’ଣ ଥିଲା ?
Answer:
ଦିଗଦିଗନ୍ତ ବ୍ୟାପୀ ଜଙ୍ଗଲ ମଧ୍ୟରେ ରହିଥିବା ମଧୁପୁରଗଡ଼ ପାହାଡ଼କୁ ଲୋକେ ଗଡ଼ ଓ ରାଜପ୍ରାସାଦ ନିର୍ମାଣ ପରେ ନାମକରଣ କରିଥିଲେ । ପାହାଡ଼ର ନାଆଁ ଥିଲା ‘ଗଡ଼ପର୍ବତ’ ।
(ଗ) ରାଜା ପାହାଡ଼ କୋଳରୁ କେଉଁ ଶବ୍ଦ ଶୁଣିବାକୁ ପାଇଲେ ?
Answer:
ପାହାଡ଼ କୋଳରୁ ରାଜା ପଥରକଟାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ଶୁଣିବାକୁ ପାଇଲେ । ତାହା ଥିଲା ପଥର କୋରଡ଼ବାସୀ ଭୀମ ଦାସର ପଥରକଟାର ଶବ୍ଦ ଯାହାକି ରାଜାଙ୍କ ନିଦ୍ରାରେ ବ୍ୟାଘାତ ସୃଷ୍ଟି କରିଥିଲା ।
(ଘ) ସେହି ଶବ୍ଦ କିଏ ଓ କିପରି ସୃଷ୍ଟି କରୁଥିଲା ?
Answer:
ପଥରକଟାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ପାହାଡ଼ର କୋରଡ଼ ମଧ୍ୟରୁ ଭାସି ଆସୁଥିଲା । ତାହା ଥିଲା ପର୍ବତର କୋରଡ଼ରେ ବାସ କରୁଥିବା ଭୀମ ଦାସର ପଥରକଟାର ଶବ୍ଦ । ଗଡ଼ ନିର୍ମାଣ ହେଲାପରେ ମଧ୍ୟ ଭୀମ ଦାସର ପଥରକଟା ଶବ୍ଦ ବନ୍ଦ ହୋଇନଥିଲା । ସେ ପୂର୍ବବତ୍ ପଥରକଟା କାର୍ଯ୍ୟରେ ଲିପ୍ତ ରହୁଥିଲା ।
(ଙ) ସେହି ଶବ୍ଦ ବନ୍ଦ କରିବା ପାଇଁ ରାଜା କାହିଁକି ଆଦେଶ ଦେଲେ ?
Answer:
ରାଜଉଆସ ନିର୍ମାଣ ହେଲାପରେ ତା’ ମଧ୍ୟରେ ବିଳାସବ୍ୟସନର ସମସ୍ତ ବ୍ୟବସ୍ଥା ସଂପୂର୍ଣ୍ଣ ହେଲା । କିନ୍ତୁ ଭୀମ ଦାସର ପଥରକଟାର ଶବ୍ଦ ରାଜାଙ୍କ ନିଦ୍ରାରେ ବ୍ୟାଘାତ ସୃଷ୍ଟିକଲା । ସେହି ଶବ୍ଦ କେଉଁଠାରୁ ଆସୁଥିଲା ତାହା ରାଜା ଜାଣିନଥୁଲେ । ମାତ୍ର ରାଜାଙ୍କ ସୁନିଦ୍ରାପାଇଁ ସେହି ଶବ୍ଦ ବନ୍ଦ କରିବା ଜରୁରୀ ଥିଲା । ତେଣୁ ତାହା ତୁରନ୍ତ ବନ୍ଦ କରିବାପାଇଁ ରାଜା ଆଦେଶ ଦେଇଥିଲେ ।
(ଚ) ଭୀମ ଦାସକୁ ନିଜ ଉଆସକୁ ନେଇ ରାଜା ତା’ପାଇଁ କ’ଣ କଲେ ?
Answer:
ରାଜଉଆସ ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ଭୀମ ଦାସର ଅବଦାନ ସମ୍ପର୍କରେ ଜାଣିଲା ପରେ ତା’ପାଇଁ ରାଜା ଉଆସ ମଧ୍ୟରେ ଏକ ସ୍ଵତନ୍ତ୍ର ଘରର ବ୍ୟବସ୍ଥା କଲେ । ତା’ ପାଇଁ ନୂଆ ଲୁଗା ଆଣିଲେ ଓ ନୂଆ ଖଟ ତିଆରି କରାଇଲେ । ସେଠାରେ ତା’ର ଯେପରି କିଛି ଅସୁବିଧା ନହୁଏ ସେଥିପାଇଁ ଚାକରବାକର ମଧ୍ୟ ଖଞ୍ଜି ଦେଲେ । ସେଠାରେ ଭୀମ ଦାସ ରାଜସମ୍ମାନ ସହ ରହିବାପାଇଁ ରାଜା ସମସ୍ତ ବ୍ୟବସ୍ଥା କରିଥିଲେ ।
![]()
Question ୨।
ଦୁଇ ବା ତିନୋଟି ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
(କ) ପାହାଡ଼ ସବୁ ଦେଖିଲା, ସବୁ ସହିଲା, ମାତ୍ର କିଛି କରିପାରିଲା ନାହିଁ କାହିଁକି ?
ଯେଉଁଦିନ ଟମକ ବଜାଇ ରଜାଘର ଲୋକେ ପାହାଡ଼ ତଳଟାକୁ ମାପିଦେଇ, ସେଦିନଠାରୁ ଜଙ୍ଗଲ ସଫା ହୋଇ ପାହାଡ଼ ତଡ଼ାହେବା ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ କାର୍ଯ୍ୟଧାରାକୁ ପାହାଡ଼ ଖାଲି ନୀରବରେ ଦେଖୁଲା । କାଠୁରିଆର କୁଠାରାଘାତରେ ଗୋଟିକ ପରେ ଗୋଟିଏ ଗଛ ଟଳି ପଡୁଥିବା ଓ ଜଙ୍ଗଲର ବନ୍ୟଜନ୍ତୁମାନଙ୍କୁ ଗୁଳି, ଶର ଓ ଖଣ୍ଡାରେ ହତ୍ୟା କରାଯାଉଥିବା ପରି ମାନବର ସବୁ ଅତ୍ୟାଚାରକୁ ମୁଣ୍ଡ ପାତି ସହିନେବା ଛଡ଼ା ପାହାଡ଼ର କିଛି ଉପାୟ ନଥିଲା । ପାହାଡ଼ରୁ ବଡ଼ ବଡ଼ ପଥର ଖଣ୍ଡମାନ କଟାଯାଉଥିଲେ ମଧ୍ୟ ମୂକ ପାହାଡ଼ କିଂକର୍ତ୍ତବ୍ୟବିମୂଢ଼ ହୋଇ କୌଣସି ପ୍ରତିବାଦ
(ଖ) ଗଡ଼ ନିର୍ମାଣ କାର୍ଯ୍ୟ କିପରି ସମାପ୍ତ ହେଲା ?
ଲାଗିପଡ଼ିଲେ । ନଅର ମଧ୍ଯରେ ସୁନ୍ଦର ଉଆସ, ରଙ୍ଗୀନ ଆଲୋକ ପାଇଁ ଦୀପମାଳା ଇତ୍ୟାଦି ଖଞ୍ଜି ପ୍ରାସାଦଟିକୁ ଅପୂର୍ବ ସାଜସଜ୍ଜାରେ ମଣ୍ଡିତ କଲେ । ଗଡ଼ ନିର୍ମାଣ ପରେ ପରେ ତା’ମଧ୍ୟରେ ଆହୁରି କେତେ ଘର, ପାଚେରୀ, ଦେବୀମନ୍ଦିର ଆଦି ଯଥାସ୍ଥାନରେ ନିର୍ମିତ ହେଲା । ସମସ୍ତ ରାଜକଳ୍ପନାକୁ କର୍ମଚାରୀମାନେ ଯଥାବିଧ୍ କାର୍ଯ୍ୟକାରୀ କରାଇଲେ ଓ ନିର୍ମାଣକାର୍ଯ୍ୟ ଯଥା ସମୟରେ ସମାପ୍ତ ହେଲା ।
(ଗ) ସେ ରାତିରେ ନିଦରେ ଶୋଉଛି, ମାତ୍ର ଯୌବନର ସ୍ୱପ୍ନ ଦେଖୁନାହିଁ ଏକଥା କେଉଁ ପ୍ରସଙ୍ଗରେ କୁହାଯାଇଛି ?
Answer:
ଏକଥା ଭୀମ ଦାସ ପ୍ରସଙ୍ଗରେ କୁହାଯାଇଛି । ଭୀମ ଦାସ ଅନ୍ୟମାନଙ୍କ ପରି ରକ୍ତମାଂସ ଦେହଧାରୀ ମଣିଷ ଥିଲା । ସୁଖ ସ୍ୱାଚ୍ଛନ୍ଦ୍ୟରେ ରହି ଜୀବନକୁ ଉପଭୋଗ କରିବାର କାମନା ମଧ୍ଯ ତା’ ମନରେ ସୃଷ୍ଟିହେବା ସ୍ଵାଭାବିକ । ମାତ୍ର ସଭ୍ୟ ସମାଜର ସବୁ ଅତ୍ୟାଚାରକୁ ମଥାପାତି ସହିନେଇଥିଲା ସେ । ବିଳାସପୂର୍ଣ୍ଣ ପ୍ରାସାଦ ତଥା ସୁରମ୍ୟ ଗଡ଼ ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ନିୟୋଜିତ ହୋଇଥିଲେ ମଧ୍ୟ ରାଜକୀୟ ଶୋଷଣର ଶିକାର ହୋଇ ଜୀବନର ସମସ୍ତ ସୁଖରୁ ସେ ବଞ୍ଚତ ଥିଲା । ୧୫ ବର୍ଷ ବୟସରୁ ସେ ଦୀର୍ଘ ଷାଠିଏ ବର୍ଷକାଳ ପଥର କାଟି ଚାଲିଥିଲା । ଏହା ମଧ୍ୟରେ ତା’ର ଯୌବନ ଅତିକ୍ରାନ୍ତ ହୋଇ ବାର୍ଦ୍ଧକ୍ୟ ଆସିଯାଇଛି । ଯନ୍ତ୍ରବତ୍ କାର୍ଯ୍ୟ କରିଚାଲିବା ଭିତରେ ସେ ଯୌବନର ଉପସ୍ଥିତିକୁ ମଧ୍ୟ ଜାଣି ପାରିନଥିଲା ।
(ଘ) ଭୀମ ଦାସକୁ ରାଜା ନିଜ ଉଆସକୁ ଆଣିବା ମୂଳରେ କି ଉଦ୍ଦେଶ୍ୟ ଥିଲା ?
Answer:
ରାଜାଙ୍କ ନିଦ୍ରାରେ ବ୍ୟାଘାତ ସୃଷ୍ଟି କରୁଥିବା ପଥରକଟାର ଠିକ୍ ଠକ୍ ଶବ୍ଦ ବନ୍ଦ କରିବାପାଇଁ ପାଇକମାନେ ଚାବୁକ୍ ଦେଇ ଭୀମ ଦାସକୁ ବାରଣ କଲେ ମଧ୍ୟ ପଟରକଟା ବନ୍ଦ ହୋଇନଥିଲା । ଦିନେ ପାରିକୁ ଯାଇ ସ୍ବୟଂ ରାଜା ଭୀମ ଦାସକୁ ପଥରକଟା କାର୍ଯ୍ୟରେ ନିମଗ୍ନ ଥିବା ଲକ୍ଷ୍ୟକରି ତା’ ସମ୍ପର୍କରେ ସମସ୍ତ ତଥ୍ୟ ବୁଝିଲେ ଏବଂ ନଅର ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ସାରା ଜୀବନ ଉତ୍ସର୍ଗ କରିଥିବା ଲୋକଟିକୁ ସୁଖଶାନ୍ତିରେ ଶେଷଜୀବନ କଟାଇବାପାଇଁ ଉଆସ ମଧ୍ୟରେ ରଖାଇବାର ସମସ୍ତ ବ୍ୟବସ୍ଥା କରାଇଲେ । ଜଙ୍ଗଲ କାଟି ପାହାଡ଼ ତାଡ଼ି ଗୋଟିଏ ଅଗମ୍ୟ ଅପନ୍ତରା ଅଞ୍ଚଳକୁ ରାଜଉଆସରେ ପରିଣତ କରିଥିବା କାର୍ଯ୍ୟର ମୁଖ୍ୟ ବିନ୍ଧାଣିର ଦୁରବସ୍ଥା ଲକ୍ଷ୍ୟକରି ରାଜା ଦୁଃଖ ପ୍ରକାଶ କରିଥିଲେ ଓ ତା’ ଅବଦାନ ପାଇଁ ଉପଯୁକ୍ତ ମର୍ଯ୍ୟାଦା ଦେବାକୁ ରାଜଉଆସକୁ ଅଣାଇବାର ବନ୍ଦୋବସ୍ତ କରାଇଥିଲେ ।
Question ୩।
ଭୀମ ଦାସ ରାଜଉଆସରେ ରହିଲା ନାହିଁ କାହିଁକି ?
Answer:
ପନ୍ଦର ବର୍ଷ ବୟସରୁ ମଧୁପୁରଗଡ଼ ଜଙ୍ଗଲ ପାହାଡ଼ ଭିତରେ ଯନ୍ତ୍ରବତ୍ ଦିନରାତି ଜଙ୍ଗଲ ସଫେଇ ଓ ପଥରକଟା କାର୍ଯ୍ୟରେ ନିଯୁକ୍ତ ରହିଥିଲେ ମଧ୍ୟ ବଣର ଫଳମୂଳ ଆହାରରେ ଜୀବନ କଟାଇ ଓ ପଥର ଚଟାଣରେ କ୍ଲାନ୍ତି ମେଣ୍ଟାଇ ସେ ଆନନ୍ଦରେ ଥିଲା । ପ୍ରକୃତି କୋଳରେ ଜୀବନ କାଟି ଆଜୀବନ କର୍ମମୁଖର ଜୀବନ ଧରି ସେ ପାଉଥିଲା ପରମ ଶାନ୍ତି । ତେଣୁ ଚାକରବାକର ଗହଣରେ, ବିଳାସପୂର୍ଣ୍ଣ ଗୃହର ଆଧୁନିକ ପରିପାଟୀରେ ସେ ଅଣନିଃଶ୍ୱାସୀ ହୋଇପଡ଼ିଲା । ତେଣୁ ସେ ସେଠାରେ ମଧ୍ୟ ପଥର ଖୋଜିଲା । ମାଟି, ଗୋଡ଼ି, ପଥର ସହ ସାରାଜୀବନ କାଟିଥ୍ୟା ଭୀମ ଦାସ ରାଜ ଉଆସରେ
ଶାନ୍ତି ନପାଇ ପୁନରାୟ ଗଡ଼ପର୍ବତ ତଳିକୁ ଚାଲିଯାଇଥିଲା ।
![]()
Question ୪।
ପ୍ରସଙ୍ଗ ସହ ସରଳାର୍ଥ ଲେଖ ।
(କ) ମର୍ତ୍ତ୍ୟର ମରୁଭୂମିରେ ସ୍ଵର୍ଗର ଅମରାବତୀର ଛାୟା ପଡ଼ିଲା ।
Answer:
ମର୍ତ୍ତ୍ୟରେ ……………………………. ଛାୟା ପଡ଼ିଲା ।
ଉଦ୍ଧୃତାଂଶଟି ଗୋଦାବରୀଶ ମହାପାତ୍ରଙ୍କ ଲିଷ୍କୃତ ‘ଏ ମଣିଷକୁ ପଥର କଲା କିଏ’ ଗଳ୍ପରୁ ଉଦ୍ଧୃତ। ମଧୁପୁରଗଡ଼ର ବିସ୍ତୀର୍ଣ୍ଣ ଜଙ୍ଗଲରେ ରାଜନଅର ତିଆରି ହେବ। ପରିବେଶକୁ କିପରି ସୌନ୍ଦର୍ଯ୍ୟପୂର୍ଣ୍ଣ କରିଦେଲା ତାହା ଏଠା। ବର୍ଣ୍ଣିତ । ବହୁଦୂର ବ୍ୟାପି ମଧୁପୁରଗଡ଼ ପାହାଡ଼ତଳି ଅଞ୍ଚଳ ଘନଜଙ୍ଗଲ ଓ ଶ୍ଵାପଦସଙ୍କୁଳ ଥିଲା । ରାଜାଙ୍କର ଲୋକେ ଗଛ କାଟି, ଜଙ୍ଗଲ ସଫାକରି ନଅର ତୋଳା କାମ ଆରମ୍ଭ କଲେ। ପଥର କାରିଗର ଭୀମ ଦାସ ପାହାଡ଼ରୁ ପଥର କାଟି କାଟି ରାସ୍ତାଘାଟ, ନଅର, ପାଚେରି ଇତ୍ୟାଦି ତୋଳିବାରେ ସାହାଯ୍ୟ କଲା। ସୁନ୍ଦର ଉଆସ, ତା’ଭିତରେ ଦୀପମାଳା ଓ ଆଲୋକସଜ୍ଜା, ରାସ୍ତାଘାଟ, ଦେବଦେବୀ ମନ୍ଦିର କେତେ ଯେ କ’ଣ ନିର୍ମାଣ କରାଗଲା ତା’ର ହିସାବ ନାହିଁ। ଯେଉଁ ଜଙ୍ଗଲରେ କେବଳ ହିଂସ୍ରଜନ୍ତୁ ଓ ଜଙ୍ଗଲୀ ମଣିଷ ରହୁଥିଲେ, ଯାହାକି ନୀରବ, ନିସ୍ତବ୍ଧ ଥିଲା, ସେଠାରେ ସୌନ୍ଦର୍ଯ୍ୟ ପରିପୂର୍ଣ୍ଣ ଜନପଦ ସୃଷ୍ଟି ହୋଇଥିଲା। ତେଣୁ ଏଠାରେ ମଧୁପୁରଗଡ଼କୁ ମର୍ତ୍ତ୍ୟର ଅମରାବତୀ ବୋଲି କୁହାଯାଇଛି।
(ଖ ) ସେ ଦିନରେ ବାଟ ଚାଲୁଛି ମାତ୍ର କାହାକୁ ପଥ ପଚାରୁ ନାହିଁ ।
Answer:
ସେ ଦିନରେ …………………………. ପଚାରୁ ନାହିଁ ।
ଉକ୍ତ ଗଦ୍ୟାଶଟି ଗୋଦାବରୀଶ ମହାପାତ୍ରଙ୍କ ଲିଖିତ “ଏ ମଣିଷକୁ ପଥର କଲା କିଏ” ଗଳ୍ପରୁ ଆସିଅଛି । ପଥର କାମ କରି କରି ଭୀମଦାସ କିପରି ପ୍ରତିକ୍ରିୟାହୀନ ମଣିଷ ପାଲଟି ଯାଇଥିଲା, ତାହା ଏଠାରେ ଆଲୋଚ୍ୟ। ଶିଳ୍ପୀ ଭୀମଦାସ ମଧୁପୁରଗଡ଼ ନିର୍ମାଣ ପାଇଁ ପାହାଡ଼ରୁ ପ୍ରଥମେ ପଥର କାଟିଥିଲା। ଦିନଦିନ, ମାସମାସ, ବର୍ଷବର୍ଷ ଧରି ଷାଠିଏ ବର୍ଷ କାଳ ଭୀମଦାସ ଖରା, ବର୍ଷ, ଶୀତ, କାକର ଖାଇ ପଥର କାଟି ରାଜଉଆସ, ବିହାର ଉଦ୍ୟାନ, ମନ୍ଦିର, ରାସ୍ତାଘାଟ ସବୁକିଛି କରିଥିଲା। ତା’ର କୈଶୋରର ଚପଳତା, ଯୌବନର ଜ୍ୟୋତି, କୋମଳ କଥା, ଚିକ୍କଣ-ଶରୀର ଏବେ ବାର୍ଦ୍ଧକ୍ୟରେ ପହଞ୍ଚୁଛି । ପଥର କାଟି କାଟି ସତେଯେପରି ସେ ନିଜେ ପଥର ପାଲଟି ଯାଇଛି । ସେ ବାଟ ଚାଲୁଛି କିନ୍ତୁ ରାସ୍ତା ପଚାରୁ ନାହିଁ, ଚାହୁଁଛି, କିନ୍ତୁ କିଛି ଦେଖୁନାହିଁ। କାମ କରୁଛି, କିନ୍ତୁ କିଛି ଜାଣି ପାରୁନାହିଁ । ସେ ନିର୍ବାକୁ ନିଶ୍ଚଳ ଓ ପ୍ରତିକ୍ରିୟାହୀନ ହୋଇ କେବଳ କାମ କରିଛାଲିଛି।
(ଗ) ରାଜା ମନକୁ ମନ ଅତର୍କିତ ପ୍ରଶ୍ନ କଲେ, ‘‘ଏ ମଣିଷକୁ ପଥର କଲା କିଏ ???
Answer:
ରାଜା ମନକୁ ……………………………… କଲା କିଏ ?
ଉକ୍ତ ଗଦ୍ୟାଶଟି ଗୋଦାବରୀଶ ମହାପାତ୍ରଙ୍କ ଲିଖିତ “ ଏ ମଣିଷକୁ ପଥର କଲା କିଏ” ଗଳ୍ପରୁ ଉଦ୍ଧୃତ। ପଥର ପରି ମଣିଷଟିଏ ଭୀମ ଦାସଙ୍କୁ ଦେଖ୍ ରାଜା ବିସ୍ମିତ ହୋଇଥିବା କଥା ଏଠାରେ ଗାଳ୍ପିକ ପ୍ରକାଶ କରିଛନ୍ତି |
ପଥର କଟାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ବାରି ରାଜା ଭୀମ ଦାସ ପାଖରେ ପହଞ୍ଚିଲେ। କିନ୍ତୁ ଭୀମ ଦାସ କିଛି କହିଲାନି କିମ୍ବା ରାଜାଙ୍କୁ ଚାହିଁଲାନି। ରାଜା ତାକୁ ରାଜଉଆସକୁ ଡକାଇ ନେଇ ସମ୍ମାନ ସହକାରେ ବିଶ୍ରାମ ନେବାପାଇଁ କହିଲେ। କିନ୍ତୁ ଉଆସ ଭିତରେ ସେ ପଥର ଖୋଜିଲା। ତା’ପରଦିନ ସେ ଉଆସରେ ନଥିଲା। ରାଜା ତାକୁ ଖୋଜି ଖୋଜି ପଥର କାଟୁଥିବାର ଦେଖିଲେ।
ରାଜାଙ୍କୁ ଦେଖୁ ମଧ୍ୟ ତା’ର ମନରେ କିଛି ଭାବାନ୍ତର ଆସି ନଥିଲା। ତେଣୁ ଏ ମଣିଷକୁ କିଏ ପଥର କରିଦେଲା ବୋଲି ରଜା ଦୁଃଖରେ ନିଜକୁ ନିଜେ ପ୍ରଶ୍ନ ପଚାରିଲେ ଏବଂ ନିଜେ ମଧ୍ୟ ଉତ୍ତର ଦେଇଥିଲେ। ଯେ ରାଜା ହିଁ ତାକୁ ପଥର କରି ଦେଇଛନ୍ତି। ଅତୀତରେ ରାଜାଙ୍କର ନିଷ୍ଠୁର ସ୍ଵଭାବ ଓ ଅବହେଳା ଯୋଗୁଁ ଏ ମଣିଷର ଆଶା ଓ ଭାବନା ସବୁ ମରିଯାଇଛି। ସେଥିପାଇଁ ‘ରାଜା’ ଶବ୍ଦଟା ଶୁଣିବା ମାତ୍ରକେ ଭୀମ ଦାସ ରାଜାଙ୍କୁ କୁଣ୍ଡାଇ ଧରି ଚିତ୍କାର କରିଉଠିଥିଲା ।
Question ୪।
(କ) ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ‘ଖ’ ସ୍ତମ୍ଭରେ ଥିବା ଶବ୍ଦର ସମ୍ପର୍କ ଯୋଡ଼ି ବାକ୍ୟ ଗଠନ କର ।
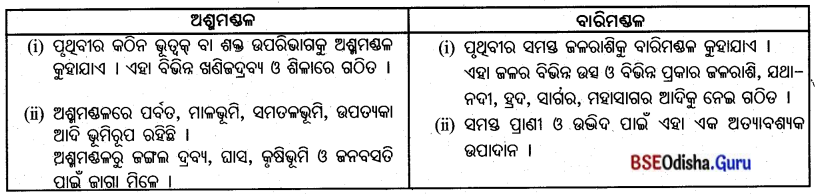
| ‘କ’ ସ୍ତ୍ରମ୍ଭ | ‘ଖ’ ସ୍ତ୍ରମ୍ଭ |
| ଅବ୍ୟକ୍ତ | ଜନତା |
| ଗୋପନୀୟ | ଛାତ୍ର |
| ଭାତତ୍ରସ୍ତ | ଦେବତା |
| ଜ୍ଞାନଲିପ୍ସ୍ | ଦୃଶ୍ୟ |
| ରମଶାୟ | ଜାବନ |
| ନିରଳସ | ବିଷୟ |
Answer:
| ‘କ’ ସ୍ତ୍ରମ୍ଭ | ‘ଖ’ ସ୍ତ୍ରମ୍ଭ |
| ଅବ୍ୟକ୍ତ | ଦେବତା |
| ଗୋପନୀୟ | ବିଷୟ |
| ଭାତତ୍ରସ୍ତ | ଜନତା |
| ଜ୍ଞାନଲିପ୍ସ୍ | ଛାତ୍ର |
| ରମଶାୟ | ଦୃଶ୍ୟ |
| ନିରଳସ | ଜାବନ |
- ଦେବତାଙ୍କ ଅବ୍ୟକ୍ତ ଅବଦାନ ବିଶ୍ଵସୃଷ୍ଟିରେ ମାନବକୁ ବଞ୍ଝାରେ ସହାୟକ ହୋଇଛି ।
- ଭୀତତ୍ରସ୍ତ ଜନତାଙ୍କ ମନରେ ସାନ୍ତନା ଦେବା ପାଇଁ ସରକାର ଗଣମାଧ୍ୟମରେ ସାହାଯ୍ୟ ନେଲେ । ଜ୍ଞାନଲିପ୍ସୁ ଛାତ୍ର ଜୀବନରେ ବହୁ ଉନ୍ନତି କରେ ।
- ପ୍ରକୃତିର ରମଣୀୟ ଦୃଶ୍ୟ ମନରେ ଶାନ୍ତି ଆଣିଦିଏ ।
- ନିରଳସ ଜୀବନ ଓ ଈଶ୍ୱରୀୟ ଭାବନା ମଣିଷକୁ ମହତ କରେ ।
Question ୫।
ନିମ୍ନରେ ଦିଆଯାଇଥବା ଶବ୍ଦଗୁଡ଼ିକର ଦୁଇଟି ଲେଖାଏଁ ପ୍ରତିଶବ୍ଦ ଲେଖ ।
ପାହାଡ଼, ଫୁଲ, ପକ୍ଷୀ, ଦିନ, ଗଛ, ମଣିଷ
Answer:
ପାହାଡ଼ – ଶୈଳ, ଗିରି
ପକ୍ଷୀ – ବିହଗ, ବିହଙ୍ଗମ
ଗଛ – ବୃଷ, ପାଦପ
ଫୁଲ – ପୁଷ୍ପ, ସୁମନ
ଦିନ – ଦିବସ, ଅହ୍ନ
ମଣିଷ – ନର, ମନୁଷ୍ୟ
![]()
Question ୬।
ନିମ୍ନଲିଖତ ଶବ୍ଦଗୁଡ଼ିକୁ ବ୍ୟବହାର କରି ବାକ୍ୟଗଠନ କର ।
ପ୍ରଚଣ୍ଡ, ଭୀତତ୍ରସ୍ତ, ଦୁର୍ଭେଦ୍ୟ, ବିସ୍ତୀର୍ଣ୍ଣ, ଅତ୍ୟାଚାର, ସୀମା, ପହୁଡ଼,
Answer:
ପ୍ରଚଣ୍ଡ – ପ୍ରଚଣ୍ଡ ଗ୍ରୀଷ୍ମରେ ନଦୀ, ନାଳ ଶୁଷ୍କ ହୋଇଯାଏ ।
ଭୀତତ୍ରସ୍ତ – ସୁନାମିର ଭୟାବହତା ଲୋକଙ୍କୁ ଭୀତତ୍ରସ୍ତ କଲା ।
ଦୁର୍ଭେଦ୍ୟ – ଦୁର୍ଭେଦ୍ୟ ଅରଣ୍ୟ ହିଁ ହିଂସ୍ରଜନ୍ତୁଙ୍କ ଆବାସସ୍ଥଳୀ ।
ଅତ୍ୟାଚାର – ଇଂରେଜ ଶାସକଙ୍କ ଅତ୍ୟାଚାର ରେ ଅତିଷ୍ଠ ହୋଇ ଭାରତୀୟମାନେ ବିଦ୍ରୋହ ଆରମ୍ଭ କରିଥିଲେ ।
ସୀମା – ଜମିର ସୀମା ଚିହ୍ନଟ କରିବାକୁ ଅମିନ ଆସିଥିଲେ ।
ପହୁଡ଼ – ଶ୍ରୀଜଗନ୍ନାଥଙ୍କ ପହୁଡ଼ ହେବା ପୂର୍ବରୁ ଆମେ ଦର୍ଶନ କରିବା ସୁଯୋଗ ପାଇଲୁ ।
ନିରଳସ – ଗୋପବନ୍ଧୁ ନିରଳସ ଜୀବନ ଶୈଳୀରେ ବିଶ୍ଵାସ କରୁଥିଲେ ।
Question ୭।
ପ୍ରାୟ ୧୫୦ଟି ଶବ୍ଦ ମଧ୍ଯରେ ଉତ୍ତର ଲେଖ ।
(କ) ମଧୁପୁରଗଡ଼ ପାହାଡ଼ ସହିତ ଭୀମ ଦାସର କି ସମ୍ପର୍କ ଥିଲା ?
Answer:
ଭୀମ ଦାସକୁ ବାଦ୍ ଦେଇ ମଧୁପୁରଗଡ଼ର ଇତିହାସ ରଚନା କରାଯାଇ ପାରିବ ନାହିଁ । ଗଡ଼ ନିର୍ମାଣର ପ୍ରତିଟି ଧୂଳିକଣା ଭୀମର ହାତସ୍ପର୍ଶ ପାଇଛି । ଏକଦା ମଧୁପୁରଗଡ଼ ପାହାଡ଼ତଳି ଅଞ୍ଚଳ ଥିଲା ଦୁର୍ଭେଦ୍ୟ ଅରଣ୍ୟ, ହିଂସ୍ରଜନ୍ତୁଙ୍କ ଆବାସସ୍ଥଳୀ । ସେହି ଅଞ୍ଚଳକୁ ପରିଷ୍କାର କରି ରାଜନଅର ନିର୍ମାଣ କରିବାକୁ ରାଜା ସିଦ୍ଧାନ୍ତ ନେଲାପରେ ଭୟସଙ୍କୁଳ ଅଗମ୍ୟ ଜଙ୍ଗଲ ଅଞ୍ଚଳରେ କାର୍ଯ୍ୟାରମ୍ଭ କରିବାକୁ ଆସିଥିଲେ ରାଜକର୍ମଚାରୀ । ମାତ୍ର ସେହି ଅଞ୍ଚଳ ବିଷୟରେ ଅଜ୍ଞ ଥିବାରୁ ସେମାନଙ୍କୁ ଭୀମ ଦାସର ସହାୟତା ନେବାକୁ ପଡ଼ିଥିଲା । ଟମକ କାଠିଠାରୁ ଆରମ୍ଭ କରି ଜଙ୍ଗଲର ଗଛକଟା ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ କାର୍ଯ୍ୟରେ ଭୀମ ଦାସ ହିଁ ସେମାନଙ୍କ ମାର୍ଗଦର୍ଶକ ସାଜିଥିଲା । ଜଙ୍ଗଲ ସଫାହେଲା ପରେ ପାହାଡ଼ ତଡ଼ା କାର୍ଯ୍ୟ ଓ ପଥରକଟା କାର୍ଯ୍ୟର ମୁଖ୍ୟ ସେ ହିଁ ଥିଲା । ପର୍ବତରୁ ପଥର ଫଟାଇ ସୁନ୍ଦର ରାଜନଥର ନିର୍ମାଣ ହେଲା । ଜଙ୍ଗଲ କାଟି, ପାହାଡ଼ ଭାଙ୍ଗି କେବଳ ଗଡ଼ ନିର୍ମାଣ ପରେ କାର୍ଯ୍ୟର ସମାପ୍ତି ଘଟିନଥିଲା । ପରେ ପରେ ଗଢ଼ିଉଠିଥିଲା କେତେ ଘର, ପାଚେରୀ, ଦେବୀ ମନ୍ଦିର ଇତ୍ୟାଦି ।
ଏଇ ଭଙ୍ଗାଗଢ଼ା ଭିତରେ କେତେ କାରିଗର, ଶିଳ୍ପୀ କାଳଗର୍ଭରେ ମରିହଜି ଗଲେ । ମାତ୍ର ଭୀମ ଦାସର ପଥରକଟା କାର୍ଯ୍ୟର ସମାପ୍ତି ନଥୁଲା । ମଧୁପୁରଗଡ଼ ପର୍ବତର ଅନ୍ଧାରିଆ ଗହ୍ଵର ମଧ୍ୟରେ ମାନବର ପ୍ରଥମ ସ୍ବର ଭୀମ ଦାସହିଁ ଶୁଣାଇଥିଲା । ବଣ, ପାହାଡ଼, ତରୁଲତା ସହ ନିବିଡ଼ ଭାବେ ପରିଚିତ ଭୀମ ଦାସ ନିଜ ହତିଆର ଧରି ପଥର କାଟି ଚାଲିଥିଲା ଦିନ ଦିନ, ମାସ ମାସ ଓ ବର୍ଷ ବର୍ଷ ଧରି । ଦୀର୍ଘ ଷାଠିଏ ବର୍ଷ କାଳ ଖରା, ବର୍ଷା, ଶୀତ, କାକର ସହି ସେ ଗଡ଼ପର୍ବତ ତଳି ଅଞ୍ଚଳକୁ ରମଣୀୟ ଉଆସରେ ପରିଣତ କରିଥିଲା । ଅକର୍ମ ଶିଳାକୁ ଅଭିନବ ବେଶରେ ସଜାଇ ସୁଦୃଶ୍ୟ ରାଜନଅର ନିର୍ମାଣରେ ସେ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲା । ପନ୍ଦର ବର୍ଷ ବୟସରୁ ପଥରକଟା କାର୍ଯ୍ୟରେ ନିଯୁକ୍ତ ହୋଇ ଜୀବନର ସବୁ ସୁଖ ସ୍ବାଚ୍ଛନ୍ଦ୍ୟକୁ ସେ ଜଳାଞ୍ଜଳି ଦେଇଥିଲା । ମଧୁପୁରଗଡ଼ର ରାଜପୁରୀ, ଦେବୀ ମନ୍ଦିର, ନଅର, ଉଆସ, ବିହାର, ଉଦ୍ୟାନ କୌଣସିଠାରେ ଏପରି ଖଣ୍ଡିଏ ହେଲେ ପଥର ନାହିଁ, ଯେଉଁଥରେ କି ଭୀମଦାସର ହାତ ବାଜିନାର୍ହି।
(ଖ) ଗଡ଼ ତିଆରି ପରେ ଭୀମ ଦାସ କ’ଣ କଲା ?
Answer:
ମଧୁପୁରଗଡ଼ ନିର୍ମାଣ କାର୍ଯ୍ୟରେ ଭୀମ ଦାସ ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲା । ଜଙ୍ଗଲ ସଫା ହେବାଠାରୁ ଆରମ୍ଭ କରି ପାହାଡ଼ ତଡ଼ା ହେବା, ପଥର କାଟି ପ୍ରାସାଦ ନିର୍ମାଣ କରିବା ଆଦି ପ୍ରତ୍ୟେକଟି କାର୍ଯ୍ୟ ପଛରେ ଥିଲା ଭୀମ ଦାସର ହାତ ! ଗଡ଼ ନିର୍ମାଣ କାର୍ଯ୍ୟ ଶେଷହେବା ପରେ ମଧ୍ୟ ଭୀମ ଦାସର ପଥରକଟା କାର୍ଯ୍ୟ ସମାପ୍ତ ହୋଇ ନଥିଲା । ରାଜ ଉଆସ ପରେ ଗଡ଼ ଭିତରେ ବହୁ ସୁଦୃଶ୍ୟ ଘର, ପାଚେରୀ, ଦେବୀ ମନ୍ଦିର, ଏହିପରି ଗୋଟାକ ପରେ ଗୋଟାଏ ନିର୍ମାଣ କାର୍ଯ୍ୟ ଚାଲୁ ରହିଥିଲା। ଭୀମ ଦାସ ପଥର କାଟି ଯୋଗାଇ ଚାଲିଥିଲା । ସେହିସବୁ ନିର୍ମାଣ କାର୍ଯ୍ୟ ନିମନ୍ତେ ଦିନ ଦିନ, ମାସ ମାସ, ବର୍ଷ ବର୍ଷ ଧରି ଭୀମ ଦାସ ଖରାବର୍ଷା, ଶୀତ କାକରକୁ ଖାତିର ନକରି ଗଡ଼ପର୍ବତ ତଳେ ପଥର କାଟି ଚାଲିଥିଲା ।
ଅକର୍ମ ଶିଳାକୁ ଚିକ୍କଣ କରି ଉଆସକୁ ରମଣୀୟ କରିବା ଦାୟିତ୍ଵ ସତେଯେପରି ତା’ ଉପରେ ନ୍ୟସ୍ତ ଥିଲା । ଭୀମ ଦାସର ବୃତ୍ତି ଥିଲା ପଥରକଟା, ଜଙ୍ଗଲ ତା’ର ଘର ଓ ତା’ର ଖାଦ୍ୟ ବଣର ଫଳମୂଳ । ଗଡ଼ପର୍ବତର ଅନ୍ଧାରିଆ ଗୁହା ଭିତରେ ରହି ରାଜପୁରୀ, ଦେବୀମନ୍ଦିର, ନଅର, ଉଆସ, ବିହାର ଓ ଉଦ୍ୟାନ ପାଇଁ ସେ ପଥର ଯୋଗାଇ ଚାଲିଥିଲା । ଆଉ ପଥରର ଆବଶ୍ୟକତା ନାହିଁ ବୋଲି କହିଲା ପରେ ମଧ୍ୟ ତା’ର କାର୍ଯ୍ୟ ବନ୍ଦ ହୋଇନଥିଲା । ଏକ ମେସିନ୍ ପରି ସେ ତା’ର ପଥରକଟା କାମ କରି ଚାଲିଥିଲା । ସେ ପଥର କାଟି କାଟି ନିଜେ ଯେପରି ପଥର ପାଲଟି ଯାଇଥିଲା ।
(ଗ) ପାହାଡ଼ ତଳେ କିପରି ଗଡ଼ ନିର୍ମାଣ କରାଗଲା ?
Answer:
କାହିଁ କେତେ କାଳରୁ ବଣ ଜଙ୍ଗଲଘେରା ମଧୁପୁରଗଡ଼ ପର୍ବତ ତଳେ ରାଜନଅର ନିର୍ମାଣ କରିବା ସ୍ଥିର ହେଲାପରେ ରାଜାଙ୍କ ନିର୍ଦ୍ଦେଶରେ କର୍ମଚାରୀମାନେ ଅଗମ୍ୟ ବନପଥରେ ଟମକ ବଜାର ମାପଚୁପ ଆରମ୍ଭ କଲେ । ହିଂସ୍ର ବନ୍ୟଜନ୍ତୁ ଭରା ଜଙ୍ଗଲରୁ ଗଛକଟା କାର୍ଯ୍ୟ ଭୀମ ଦାସ ହାତରେ ଆରମ୍ଭ ହେଲା । ଅଳ୍ପ କେଇଦିନ ମଧ୍ୟରେ ପାହାଡ଼ତଳି ଜଙ୍ଗଲ ସଫା ହୋଇଗଲା । ବନ୍ୟ ପଶୁପକ୍ଷୀମାନେ ଶିକାରୀର ତୀର, ଗୁଳି ଓ ଖଣ୍ଡା, ବର୍ଚ୍ଛାରେ ପ୍ରାଣ ଦେଲେ । ପରେ ପରେ ପାହାଡ଼ ତାଡ଼ିବା କାର୍ଯ୍ୟ ଆରମ୍ଭ ହେଲା । ଭୀମ ଦାସ ହିଁ ପାହାଡ଼ ତାଡ଼ିବା କାର୍ଯ୍ୟର ମୁଖ୍ୟ ଦାୟିତ୍ଵରେ ରହିଲା । ପାହାଡ଼ ଭଙ୍ଗାଯାଇ ଗୋଟା ଗୋଟା ପଥର, ଶଗଡ଼ ଶଗଡ଼ ରଙ୍ଗମାଟି, କେତେ ଗୋଡ଼ି, ଧୂଳି ପାହାଡ଼ତଳି ଅଞ୍ଚଳକୁ ବୁହାହୋଇ ଆସିଲା ।
ଗଡ଼ପର୍ବତ ତଳେ ରାଜପ୍ରସାଦ ନିର୍ମାଣ କାର୍ଯ୍ୟ ଆରମ୍ଭ ହେଲା । ସୁନ୍ଦର ଉଆସ ଭିତରେ ରଙ୍ଗୀନ ଦୀପମାଳା ଓ ଅପୂର୍ବ ସାଜସଜ୍ଜା ଖଞ୍ଜି ଦିଆଗଲା । ବିଳାସ ବ୍ୟସନର ସମସ୍ତ ବ୍ୟବସ୍ଥା ଉଆସ ମଧ୍ଯରେ ରଖାଯାଇ ବାଇଦ ବାଜଣା ଓ ଆନନ୍ଦ ଉତ୍ସବର ଆୟୋଜନ କରାଗଲା । ରାଜା ଓ ରାଣୀ ଉଆସରେ ରହି ନଅରକୁ କିପରି ଆହୁରି ସୁନ୍ଦର କରାଯାଇ ପାରିବ ତା’ର ଯୋଜନା କଲେ । ପ୍ରଜାମାନଙ୍କ ପାଇଁ ଗଡ଼ ମଧ୍ଯରେ ବାସଗୃହ ନିର୍ମାଣ ହେଲା । ପରେ ପରେ ନିର୍ମାଣ ହେଲା ଦେବୀମନ୍ଦିର, ବିହାର, ଉଦ୍ୟାନ ଓ ରାଜପଥ । ଏ ସମସ୍ତ ନିର୍ମାଣ ପାଇଁ ଆବଶ୍ୟକ ପଥର କାଟି ଯୋଗାଇବାର ଦାୟିତ୍ଵ ସତେ ଯେପରି ଭୀମ ଦାସ ଉପରେ ନ୍ୟସ୍ତ ଥିଲା । ସେଥିପାଇଁ ତା’ କର୍ମରେ ବିରାମ ନଥିଲା । ନଅର ଓ ଗଡ଼ ନିର୍ମାଣ ପାଇଁ ପଥର ଯୋଗାଇ ଯୋଗାଇ ସେ ସତେ ଯେପରି ପଥର ପାଲଟି ଯାଇଥିଲା । ନିର୍ମାଣ କାର୍ଯ୍ୟ ସମାପ୍ତ ହୋଇଛି ବୋଲି କହିଲା ପରେ ମଧ୍ୟ ଭୀମ ଦାସ ପଥର କାଟି ଚାଲିଥିଲା ।
(ଘ) ‘ଏ ମଣିଷକୁ ପଥର କଲା କିଏ’ – ଏପରି ନାମକରଣର ବିଶେଷତ୍ବ କ’ଣ ?
Answer:
ଗଳ୍ପର ବିଷୟବସ୍ତୁକୁ ଆଧାର କରି ଗଳ୍ପର ନାମକରଣ କରାଯାଇଥାଏ । ପଥର ଏକ ନିର୍ଜୀବ ବସ୍ତୁ । ତା’ର ଅନୁଭବ କରିବାର ଶକ୍ତି ନଥାଏ, ହୃଦୟ ନଥାଏ କି ମନ ବୋଲି କିଛି ନଥାଏ । ତାକୁ ଯେଉଁ କାର୍ଯ୍ୟ ପାଇଁ ରଖାଯାଏ, ସେହିଠାରେ ହିଁ ସେ ପଡ଼ିରହେ । ସେ କାହାରି କଥା ଶୁଣି ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ କରିପାରେ ନାହିଁ । ଦୁଃଖ-ସୁଖ, ଭଲ-ମନ୍ଦ,
ଭୀମ ଦାସ ଚରିତ୍ରକୁ ଲେଖକ ସେହିପରି ପଥର ସହ ତୁଳନା କରିଛନ୍ତି । ସେ ଆମରି ପରି ରକ୍ତମାଂସ ଦେହଧାରୀ ମଣିଷ ହେଲେ ମଧ୍ୟ ପଥରକଟା କାର୍ଯ୍ୟରେ ନିଯୁକ୍ତ ହେଲାପରେ ସେ ଯେପରି ପଥର ପାଲଟି ଯାଇଥିଲା । ମଧୁପୁର ଗଡ଼ପର୍ବତ କନ୍ଦର ଥିଲା ତା’ର ଘର । ବଣର ଫଳମୂଳ ଥିଲା ତା’ର ଆହାର । ପ୍ରକୃତି କୋଳରେ ହସି, ଖେଳି, ନାଚି, ଗାଇ ବୁଲୁଥିବା ଭୀମ ଦାସ ଉପରେ ଯେଉଁଦିନଠାରୁ ଜଙ୍ଗଲ ସଫେଇ ଓ ପଥରକଟା ଦାୟିତ୍ଵ ନ୍ୟସ୍ତ କରାଗଲା, ସେ କୌଣସି ପ୍ରତିବାଦ କରିନଥିଲା । ରାଜାଙ୍କ ଆଦେଶ ତା’ପାଇଁ ଥିଲା ସବୁଠୁ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ । ତେଣୁ ରାଜପ୍ରାସାଦ, ଗଡ଼, ମନ୍ଦିର, ବିହାର ସବୁ କିଛି ନିର୍ମାଣ ପାଇଁ ସେ ପଥର କାଟି ଯୋଗାଇ ଚାଲିଥିଲା । ଏପରିକି ରାଜାଙ୍କ ନିଦ୍ରାରେ ବ୍ୟାଘାତ ସୃଷ୍ଟି କରୁଥିବା ପଥର କଟାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ବନ୍ଦ କରିବାକୁ ସିପାହି ତାକୁ ଚାବୁକ୍ ଦେଇ ବାରଣ କଲେ ମଧ୍ୟ ସେ ତା’ର କାର୍ଯ୍ୟରୁ ବିରତ ହୋଇନଥିଲା ।
ତା’ପାଇଁ ଉଆସରେ ସମସ୍ତ ରାଜକୀୟ ବ୍ୟବସ୍ଥା କରି, ଶେଷ ଜୀବନକୁ ଶାନ୍ତିରେ କାଟିବାକୁ କୁହାଗଲେ ମଧ୍ୟ ସେ ପୁଣି ଫେରିଯାଇଥିଲା ସେହି ଗଡ଼ପର୍ବତ ଖୋଲକୁ ଓ ଚିରାଚରିତ ଢଙ୍ଗରେ ପଥର କାଟିବା କାର୍ଯ୍ୟରେ ବ୍ୟସ୍ତ ରହିଲା । ତା’ପାଇଁ ଉଆସର ବିଳାସପୂର୍ଣ୍ଣ ବ୍ୟବସ୍ଥା ଆକର୍ଷଣୀୟ ନଥୁଲା, କି ରାଜକୀୟ ଖାଦ୍ୟ ପ୍ରତି ମଧ୍ୟ ତା’ର ରୁଚି ନଥିଲା । ପ୍ରକୃତିର କୋଳ ଥିଲା ତା’ପାଇଁ ଆନନ୍ଦପ୍ରଦ, କର୍ମରେ ଥିଲା ତା’ର ଆନନ୍ଦ । ପଥରକଟା ବନ୍ଦ କରିବାପାଇଁ ପାଇକମାନଙ୍କ ଚାବୁକ ମାଡ଼ ମଧ୍ୟ ତା’ ମନରେ କୌଣସି ପ୍ରତିକ୍ରିୟା କରିନଥିଲା ସତେରେଯପରି ପଥର କାଟି କାଟି ସେ ପଥର ହୋଇଯାଇଥିଲ। ଗଳ୍ପଟିର ବିଷୟବସ୍ତୁକୁ ଲକ୍ଷ୍ୟ କଲେ ନାମକରଣ ସାର୍ଥକତା ଉପଲବ୍ କରିହୁଏ ।
ତୁମପାଇଁ କାମ :
ଭୀମ ଦାସ ପରି ଚରିତ୍ର ଥିବା ଅନ୍ୟ କୌଣସି ଗଳ୍ପ ଖୋଜି ପଢ଼ ।
ପରିବେଶ ନଷ୍ଟ କରି ବଡ଼ ପ୍ରାସାଦ ତିଆରି କରିବା ଘଟଣାକୁ ନେଇ ଗଳ୍ପଟିଏ ଲେଖ ।
Answer:
ପିଲାମାନେ ଶିକ୍ଷକ ବା ଅଭିଭାବକଙ୍କ ପରାମର୍ଶ ନେଇ ନିଜେ ସଂଗ୍ରହ କରିବେ ।
ଅଭ୍ୟାସ ପାଇଁ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
Question ୧।
ମଧୁପୁରଗଡ଼ ଜଙ୍ଗଲରେ ହାହାକାର ପଡ଼ିଗଲା କାହିଁକି ?
Answer:
ଉକ୍ତ ଗଳ୍ପରେ ଗାଳ୍ପିକ ଗୋଦାବରୀଶ ମହାପାତ୍ର ପ୍ରକୃତି ଉପରେ ମଣିଷର ଅତ୍ୟାଚାର କଥା ଅତି ସୁନ୍ଦର ଓ ସାବଲୀଳ ଭାଷାରେ ପ୍ରକାଶ କରିଛନ୍ତି । କେଉଁ ଆଦିମ କାଳରୁ ମଧୁପୁରଗଡ଼ ପାହାଡ଼ ତା’ର କୋଳରେ ଶ୍ୟାମଳ ବନରାଜି, ପଶୁପକ୍ଷୀଙ୍କୁ ଧରି ଆତି ଆନନ୍ଦରେ ଥିଲା। ହଠାତ୍ ଦିନେ ସହରୀ ସଭ୍ୟତାର ନାଗରା ବଜାଇ ଲୋକମାନେ ପାହାଡ଼ ତଳି ଅଞ୍ଚଳ ମାପଚୁପ କଲେ। ତା’ପରେ ଚାଲିଲା ଜଙ୍ଗଲ ସଫା କାର୍ଯ୍ୟ। ଅସୁମାରୀ ଗଛ ହଣା ହେଲା, ବଣବୁଦା ସଫା କରାଗଲା, ପଶୁପକ୍ଷୀଙ୍କୁ ଗୁଳି, ଶର, ଖଣ୍ଡାରେ ହତ୍ୟା କରାଗଲା। ଦୁର୍ଭେଦ୍ୟ ଜଙ୍ଗଲ ବିସ୍ତୀର୍ଣ୍ଣ ପ୍ରାନ୍ତରରେ ପରିଣତ ହେଲା। ଜଙ୍ଗଲର ଜୀବଜନ୍ତୁ, ତରୁଲତା ସମସ୍ତଙ୍କ ଭିତରେ ଭୟ ଓ ଆଶଙ୍କା ଦେଖାଦେଲା। ବନରାଜ୍ୟରେ ହାହାକାର ପଡ଼ିଗଲା।
![]()
Question ୨।
“ଏ ମଣିଷକୁ ପଥର କଲା କିଏ ?” – ଗଳ୍ପର ଏପରି ନାମକରଣ କରାଯିବାର କାରଣ କ’ଣ ?
କିମ୍ବା, “ଏ ମଣିଷକୁ ପଥର କଲା କିଏ ? ” – ରାଜା କାହାକୁ ଲକ୍ଷ୍ୟକରି ଏକଥା କହିଛନ୍ତି ?
Answer:
‘ଏ ମଣିଷକୁ ପଥର କଲା କିଏ ?’ ଗଳ୍ପରେ ପଥର କାଟି କାଟି ରାଜଉଆସ ବନାଇ, ଆଧୁନିକ ସଭ୍ୟତାର ରୂପ ଦେଇ ଶିଳ୍ପୀ ଭୀମ ଦାସ କିପରି ନିଜେ ପଥର ପାଲଟି ଯାଇଥିଲା, ତାହା ଗାଳ୍ପିକ୍ ବର୍ଣନା କରିଛନ୍ତି । ମଧୁପୁର ପାହାଡ଼ର ପଥର କାଟିବା ଦାୟିତ୍ଵ ରାଜା ପନ୍ଦର ବର୍ଷୀୟ କିଶୋର ଭୀମ ଦାସକୁ ଦେଇଥିଲେ। ରାଜପୁରୀ, ଦେବମନ୍ଦିର, ନଅର, ଉଆସ, ବିହାର, ଉଦ୍ୟାନ ଯେଉଁ ପଥରରେ ତିଆରି ହେଲା ସବୁଥରେ ଭୀମ ଦାସର ହାତ ବାଜିଛି। କେତେ ଦିନ, ମାସ, ବର୍ଷ ବିତିଯାଇଛି ତା’ର ହିସାବ ନାହିଁ । ସେ ପଥରକଟା କାମରେ ଖାଇବା, ପିଇବା ଏବଂ ନିଜର ଭୋବିଳାସ ସବୁ ଭୁଲିଯାଇଛି । ଖରା, ବର୍ଷା, ଶୀତ, କାକର ସହି କୌଣସି ପ୍ରତିକ୍ରିୟା ପ୍ରକାଶ ନ କରି କେବଳ ପଥର କାଟି ଚାଲିଛି ଭୀମ ଦାସ । ଶେଷରେ ସେ ଅଶୀବର୍ଷୀୟ ବୃଦ୍ଧ ହୋଇଯାଇଛନ୍ତି। କିନ୍ତୁ ସମସ୍ତ ସୁଖ ସୁବିଧା, ବିଳାସ ଯାହା ପାଇଁ ମିଳିଲା, ରାଜା ଦିନେହେଲେ ସେହି ଶିଳ୍ପୀ କଥା ବୁଝିବାକୁ ଚେଷ୍ଟା କରିନାହାନ୍ତି । ପଥର କାଟି କାଟି ସତେ ଯେପରି ସେ ପଥର ପାଲଟି ଯାଇଛି । ତେଣୁ ଯୁବରାଜ ଭୀମ ଦାସଠାରେ ନିର୍ଲିପ୍ତ, ନିର୍ବାକ୍, ନିଷ୍ପନ୍ଦ ଭାବ ଲକ୍ଷ୍ୟକରି ଏପରି କହିଛନ୍ତି।
Question ୩।
ଯୁବରାଜ କିପରି ଭୀମ ଦାସର ସନ୍ଧାନ ପାଇଲେ ?
Answer:
କିପରି ବିକାଶ ଘଟିଛି, ତାହା ଏଠାରେ ଗାଳ୍ପିକ ଗୋଦାବରୀଶ ମହାପାତ୍ର ବର୍ଣ୍ଣନା କରିଛନ୍ତି। ରାଜାଙ୍କ ପରେ ଯୁବରାଜ ଗାଦିରେ ବସିଲେ । ୟା ଭିତରେ ପଚାଶ ବର୍ଷ ଅତିକ୍ରମ କରିଗଲା। କିନ୍ତୁ ଭୀମ ଦାସର ପଥର କାଟିବାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ବନ୍ଦ ହୋଇ ନ ଥିଲା। ଯୁବରାଜ ସେହି ଠକ୍ ଠକ୍ ଶବ୍ଦ ବାରି ଗୀତ, ଗୁହା, କୁଞ୍ଜ ପାର ହୋଇ ଭୀମ ଦାସ ନିକଟରେ ପହଞ୍ଚିଲେ । ଯେଉଁ ଶବ୍ଦ ତାଙ୍କର ଶୟନରେ ବାଧା ସୃଷ୍ଟି କରୁଥିଲା, ସେହି ଶବ୍ଦ ସୃଷ୍ଟି କରୁଥିବା ଶିଳ୍ପୀ ପାଖରେ ପହଞ୍ଚି ଜଣେ ଯାଇଛ୍ଛା ତେଶୁ ଯୁବରାଜ ଭାମ ଦାସଠାରେ ନିଲିପ୍ତ, ନିର୍ବାକ, ନିଷନ୍ଦ ଭାବ ଲକ୍ଷ୍ୟକରି ଏପରି କହିଛନ୍ତି।
Question ୪।
ରାଜା ଭୀମ ଦାସକୁ ଉଆସକୁ କାହିଁକି ଆଣିଥିଲେ ?
Answer:
ମଧୁପୁରଗଡ଼ ଉଆସରୁ କେତେ ରାଜା ଗଲେ । ଶେଷରେ ଯୁବରାଜ ଗାଦିରେ ବସିଲେ । ରାଜାଙ୍କ ଶାନ୍ତନିଦ୍ରାରେ ବ୍ୟାଘାତ ସୃଷ୍ଟି କରୁଥିବା ଭୀମ ଦାସର ପଥରକଟା ଶବ୍ଦ ବନ୍ଦ କରିବାପାଇଁ ପାଇକମାନେ ତାକୁ ଚାବୁକ୍ରେ ପିଟିଲେ। ଶେଷରେ ରାଜା ନିଜେ ଜଙ୍ଗଲ ଭିତରେ ଶବ୍ଦ ବାରି ସେହି ଶିଳ୍ପୀ ନିକଟରେ ପହଞ୍ଚିଲେ। ରାଜା ଭୀମ ଦାସର କର୍ତ୍ତବ୍ୟ ପରାୟଣତା, ନିଃସ୍ୱାର୍ଥଭାବ, ନିର୍ଲିପ୍ତ ଭାବନା ଲକ୍ଷ୍ୟ କରି ଦୁଃଖିତ ହେଲେ। ଯେଉଁ ଶିଳ୍ପୀ ଜଙ୍ଗଲ କାଟି, ପାହାଡ଼ ତାଡି ନିଜର ସୁଖସ୍ୱାଚ୍ଛନ୍ଦ୍ୟକୁ ବଳିଦେଇ ରାଜଉଆସକୁ ସ୍ଵର୍ଗର ନନ୍ଦନକାନନ କରାଇ ପାରିଛି, ତା’ ପାଇଁ ତାଙ୍କ ମନରେ ସମବେଦନା ଭାବ ସୃଷ୍ଟି ହେଲା । ପରିଶ୍ରମର ଉପଯୁକ୍ତ ମର୍ଯ୍ୟାଦା ଓ ସୁଖଶାନ୍ତି ଦେବାପାଇଁ ରାଜା ଭୀମ ଦାସକୁ ଉଆସକୁ ନେଇଆସିଲେ।
ଅତିସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର
Question ୧।
ଜଙ୍ଗଲ ଜୀବଜନ୍ତୁ ଚମକି ଉଠିଥିଲେ କାହିଁକି ?
Answer:
ଟମକ ବଜାଇ ପାହାଡ଼ ତଳ ଅଞ୍ଚଳ ଜଙ୍ଗଲକୁ ମାପ କରାଇବାକୁ ଆସିଥିବା ଲୋକମାନଙ୍କ କାର୍ଯ୍ୟକୁ ଦେଖୁ ଜଙ୍ଗଲର ଜୀବଜନ୍ତୁ ଚମକି ଉଠିଥିଲେ ।
Question ୨।
ବନରାଜ୍ୟରେ ହାହାକାର ପଡ଼ିଗଲା କାହିଁକି ?
Answer:
କାଠୁରିଆଙ୍କ କୁଠାରଘାତରେ ପାହାଡ଼ ତଳର ଭୀଷଣ ଦୁର୍ଭେଦ୍ୟ ଜଙ୍ଗଲ ଏକ ବିସ୍ତୀର୍ଣ୍ଣ ପ୍ରାନ୍ତରରେ ପରିଣତ ହେଲା ।
![]()
Question ୩।
ଜଙ୍ଗଲବାସୀ ଜୀବଗଣକୁ କିପରି ଲୋପ କରିବାକୁ ଚେଷ୍ଟା କରାଗଲା ?
Answer:
ଜଙ୍ଗଲବାସୀ ଜୀବଗଣକୁ ଗୁଳି, ଶର, ଖଣ୍ଡା ବଳରେ ଲୋପ କରିବାକୁ ଚେଷ୍ଟା କରାଗଲା।
Question ୪।
ରାଜ ନଅରରେ କେଉଁସବୁ ବ୍ୟବସ୍ଥା କରାଗଲା ?
Answer:
ରାଜ ନଅରରେ ସୁନ୍ଦର ଉଆସ, ତା’ ଭିତରେ ଦୀପମାଳା, ଅପୂର୍ବ ସାଜସଜ୍ଜାର ବ୍ୟବସ୍ଥା ହୋଇଥିଲା। ପାଚେରୀ, ଦେବୀମନ୍ଦିର ଆଦି ନିର୍ମାଣ କରାଗଲା।
Question ୫।
ମଧୁପୁରଗଡ଼ରେ କାହାର ବିରାମ ହେଲା ନାହିଁ ?
Answer:
ମଧୁପୁରଗଡ଼ରେ ଘରତୋଳାର ବିରାମ ହେଲା ନାହିଁ।
Question ୬।
କାହାର ପ୍ରଥମ ଚୋଟ ଗଛ ଦେହରେ ବାଜିଥିଲା ଓ ପ୍ରଥମ ପଥର ଖଣ୍ଡ ସେ ତାଡ଼ିଥିଲା ?
Answer:
ଭୀମ ଦାସର ପ୍ରଥମ ଚୋଟ ଗଛ ଦେହରେ ବାଜିଥିଲା ଓ ପ୍ରଥମ ପଥର ଖଣ୍ଡ ସେ ତାଡ଼ିଥିଲା।
Question ୭।
ପାଇକ ଭୀମ ଦାସକୁ କ’ଣ କରିବାକୁ କହିଲେ ?
Answer:
ରାଜାଙ୍କ ନିର୍ଦ୍ଦେଶରେ ପାଇକ ଭୀମ ଦାସ ପିଠିରେ ଚାବୁକ ଦେଇ ପଥରକଟା ବନ୍ଦ କରିବାକୁ କହିଲେ।
Question ୮।
ରାଜା କାହାପାଇଁ ଉଆସ ଭିତରେ ଏକ ସ୍ଵତନ୍ତ୍ର ଘର ଠିକ୍ କଲେ ?
Answer:
ରାଜା ଭୀମ ଦାସ ପାଇଁ ଉଆସ ଭିତରେ ଏକ ସ୍ଵତନ୍ତ୍ର ଘର ଠିକ୍ କଲେ।
![]()
Question ୯।
ରାଜା ଅବାକ୍ ହୋଇ ପୁଣି ସେହି ପର୍ବତଗୁହା ଆଡ଼କୁ କାହିଁକି ଗଲେ ?
Answer:
ରାଜା ସକାଳୁ ଭୀମ ଦାସକୁ ଘରେ ନ ଥିବାର ଦେଖିଲେ; ତେଣୁ ସେ ଅବାକ୍ ହୋଇ ପୁଣି ସେଇ ପର୍ବତ ଗୁହା ଆଡ଼କୁ ଗଲେ ।
Question ୧୦।
ଭୀମ ଦାସ ରାଜାଙ୍କୁ ନିବିଡ଼ ଭାବରେ ଜାକି ଧରି କାହିଁକି ଚିତ୍କାର କଲା ?
Answer:
ଭୀମ ଦାସ ପଥର କାଟିବା ଆଦେଶ ପାଇବା ପରେ କାର୍ଯ୍ୟକରି ଚାଲିଥିଲା। ନିଜ ଜୀବନକୁ ପଥର କରିବା ଭିତରେ ସେ ରାଜାଙ୍କୁ କେବେହେଲେ ଦେଖୁ ନ ଥିଲା ପରି ନିବିଡ଼ ଭାବରେ ଜାକି ଧରି ରାଜା ରାଜା ବୋଲି ଚିତ୍କାର କଲା।
ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନେ।ତ୍ତର
Question ୧।
କାହାର ଶବ୍ଦ ପାହାଡ଼କୋଳରୁ ଭାସିଆସୁଥିଲା ?
(କ) ହିଂସ୍ରଜନ୍ତୁଙ୍କର ଶବ୍ଦ
(ଖ) ପଥରକଟାର ଶବ୍ଦ
(ଗ) ଜଳର କଳକଳ ଶବ୍ଦ
(ଘ) ପବନର ସୁ ସୁ ଶବ୍ଦ
Answer:
(ଖ) ପଥରକଟାର ଶବ୍ଦ
Question ୨।
ଜା ଭୀମ ଦାସର ପଥରକଟାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ବନ୍ଦ କରିବାକୁ କାହିଁକି ଆଦେଶଦେଲେ ?
(କ) ରାଣୀ ରାଜାଙ୍କ ପାଖରେ ଅଭିଯୋଗ କରିବାରୁ
(ଖ) ଯୁବରାଜ ରାଜାଙ୍କ ନିକଟରେ ଅଭିଯୋଗ କରିବାରୁ
(ଗ) ଅମରାବତୀର ସ୍ପର୍ଶ ରାଜଉଆସରେ ନହେବାରୁ
(ଘ) ରାଜାଙ୍କ ପହଡ଼ରେ ବ୍ୟାଘାତ ଲାଗିବାରୁc
Answer:
(ଘ) ରାଜାଙ୍କ ପହଡ଼ରେ ବ୍ୟାଘାତ ଲାଗିବାରୁc
![]()
Question ୩।
ରାଜା କାହାକୁ ଉଆସକୁ ନେଇଆସିଲେ ?
(କ) ଯୁବରାଜଙ୍କୁ
(ଖ) ଗଡ଼ବାସାଙ୍କୁ
(ଗ) ଭାଗ ଦାସଙ୍କୁ
(ଘ) ଅମରାବତାକୁ
Answer:
(ଗ) ଭାଗ ଦାସଙ୍କୁ
Question ୪।
ଠିକ୍ ପଚାଶ ବର୍ଷ ପରେ ରାଜା କେଉଁଠାକୁ ଗଲେ ?
(କ) ପ୍ରାନ୍ତ୍ରରକୁ
(ଖ) ପାରିଧିକୁ
(ଗ) ମଧୁପୁର ଗଡ଼ଙ୍କୁ
(ଘ) ଶିକାରକୁ
Answer:
(ଖ) ପାରିଧିକୁ
Question ୫।
କେଉଁ ଲେଖାଟି ଗୋଦାବରୀଶ ମହାପାତ୍ରଙ୍କ ଲେଖନୀ
(କ) ଗରିବର ଭଗବାନ
(ଖ) ଜୀବନ ରହସ୍ୟ
(ଗ) ଗନ୍ଦାର ମାୟା
(ଘ) ନାଳମାଷ୍ଟ୍ରାଣା
Answer:
(ଖ) ଜୀବନ ରହସ୍ୟ
Question ୬।
ହାଡ଼ି ହାତକୁ ଟମକ କାଠି କାଟି କିଏ ଦେଇଥିଲା ?
(କ) ମନ୍ତ୍ରୀ
(ଖ) ରାଜା
(ଗ) ଭାମ ଦାସ
(ଘ) କ୍ଷୁବରାଜ
Answer:
(ଗ) ଭାମ ଦାସ
![]()
Question ୭।
କେଉଁମାନେ ଅବ୍ୟକ୍ତ ଭାଷାରେ କୁହାକୁହି ହେଲେ – ‘ଏ ରାଜ୍ୟରେ ପୁଣି ଏ କ’ଣ ?
(କ) ରାଜ୍ୟବାସୀ
(ଖ) ଗଛପତ୍ର
(ଗ) ବନବାସା
(ଘ) ଜାଗଜନ୍ତୁ
Answer:
(ଖ) ଗଛପତ୍ର
Question ୮।
ଏଠାରେ କାହା ସମ୍ବନ୍ଧରେ କୁହାଯାଇଛି – ‘ତା’ର ଇତିହାସ କେହି ଜାଣନ୍ତି ନାହିଁ’’ ?
(କ) ପାହାଡ଼ର
(ଖ) ଗଛପତ୍ର
(ଗ) ଉଆସର
(ଘ) ରାଜାଙ୍କର
Answer:
(କ) ପାହାଡ଼ର
Question ୯।
‘ପହୁଡ଼ ବେଳ, ପହୁଡ଼ ବେଳ – କାମ ବନ୍ଦ କର-ବନ୍ଦ କର- ବନ୍ଦ କର ।’’ – ଏହା କାହାର ଉକ୍ତି ?
(କ) ରାଜାଙ୍କର
(ଖ) ରାଣୀଙ୍କର
(ଗ) ଯୁବରାଜଙ୍କର
(ଘ) ପାଇକର
Answer:
(ଘ) ପାଇକର
![]()
Question ୧୦।
‘ସେ ସେହିଠାରେ ପ୍ରଥମେ ହସିଥିଲା, ସେହିଠାରେ ପ୍ରଥମେ ଗୀତ ବୋଲିଥିଲା ।’-ଏଠାରେ ‘ସେ’ କାହାକୁ ସୂଚାଉଛି ?
(କ) ଭାମ ଦାସ
(ଖ) ରାଜା
(ଗ) ପାଇକ
(ଘ) ପଥର
Answer:
(କ) ଭାମ ଦାସ
ଗାଞ୍ଜିକ ପରିଚୟ :
ସତ୍ୟବାଦା ସାହିତ୍ୟ ଗୋଷ୍ଠାର ସାଧକମାନଙ୍କ ପ୍ରେରଣା ପାଇ ଗୋଦାବରୀଶ ମହାପାତ୍ର ସାହିତ୍ୟ ସାଧନାରେ ବ୍ରତୀ ହୋଇଥିଲେ । ସେ ଥିଲେ ଏକାଧାରରେ ଜଣେ କବି, ଗାଳ୍ପିକ, ରମ୍ୟରଚନାର ସ୍ରଷ୍ଟା, ଭଗ୍ର ଦେଶପ୍ରେମୀ ତଥା ପ୍ରକୃତିପ୍ରେମୀ । କବିତା, ଗଳ୍ପ, ଉପନ୍ୟାସ ତଥା ଅନ୍ୟାନ୍ୟ ସାହିତ୍ୟିକ ରଚନା ସୃଷ୍ଟି କରିବାରେ ସେ ଥିଲେ ସ୍ଵତନ୍ତ୍ର ମର୍ଯ୍ୟାଦାର ଅଧ୍ କାରା ସମାଜର ବା ସାଧାରଣ ଘଟଣାକୁ ଅସାଧାରଣ ଭଙ୍ଗୀରେ ଉପସ୍ଥାପନ କରିବା ତାଙ୍କ ରଚନାର ବୈଶିଷ୍ଟ୍ୟ । ତାଙ୍କର ସମସ୍ତ ରଚନାରେ ମାନବିକ ସମ୍ବେଦନଶୀଳତା, ମୂଲ୍ୟବୋଧ, ସମାଜ ସଚେତନତା ଏବଂ ସଂସ୍କାର ପ୍ରୟାସ ପରିଲକ୍ଷିତହୁଏ । ସେ ‘ନିଆଁଖୁଣ୍ଟା’ ପତ୍ରିକାର ପ୍ରତିଷ୍ଠା ଓ ସମ୍ପାଦନା କରି ସାମାଜିକ ଦୁର୍ନୀତି ବିରୋଧରେ ‘ଟୁଆଁଟୁଇଁ’ ନାମକ ଅନ୍ୟ ଏକ ପତ୍ରିକା ମଧ୍ୟ ତାଙ୍କଦ୍ୱାରା ପ୍ରକାଶିତ ହେତ୍ତଥ୍ଲା । ତାଙ୍କ ସାରସ୍ଵତ ସୃଷ୍ଟିଗୁଡ଼ିକ ମଧ୍ୟରେ ‘କଣ୍ଟା ଓ ଫୁଲ’, ‘ଉଠ କଙ୍କାଳ’, ‘ନୀଳ ମାଷ୍ଟରାଣୀ’, ଓ ‘ମୁଁ ଦିନେ ମନ୍ତ୍ରୀ ଥୁଲି’ ଗ୍ରନ୍ଥ ଅତ୍ୟନ୍ତ ଲୋକପ୍ରିୟ ।
ଗଞ୍ଜିର ପୃଷ୍ଠଭୂମି :
ଆଲୋଚ୍ୟ ଗଳ୍ପ ‘ଏ ମଣିଷକୁ ପଥର କଲା କିଏ’ ପ୍ରାବନ୍ଧିକଙ୍କ ଏକ ସଂସ୍କାରଧର୍ମୀ ରଚନା । ଆଧୁନିକ ସହରୀ ସଭ୍ୟତା ପ୍ରଭାବରେ ଆମ ଚତୁଃପାର୍ଶ୍ୱସ୍ଥ ରମ୍ୟ ପ୍ରାକୃତିକ ପରିବେଶ କିପରି ଧ୍ୱଂସାଭିମୁଖୀ ହେଉଛି ଏବଂ ସରଳ ମଣିଷ ଜୀବନର ସୁଖଶାନ୍ତି କିପରି ବ୍ୟାହତ ହେଉଛି ଲେଖକ ଏଥିରେ ତାହା ବର୍ଣ୍ଣନା କରିଛନ୍ତି ।
ଗଳ୍ପର ସାରକଥା :
ମଧୁପୁରଗଡ଼ ପାହାଡ଼ ଓ ଏହାର ତଳି ବିସ୍ତୀର୍ଣ୍ଣ ଜଙ୍ଗଲ ଅଞ୍ଚଳରେ ରାଜପ୍ରାସାଦ ଓ ଜନପଦ ନିର୍ମାଣ କରିବାପାଇଁ ରାଜାଦେଶ ଆସିଲା। ନାଗରା ଦିଆଯାଇ ପାହାଡ଼ ତଳ ମପାଗଲା । ପରେ ପରେ ଜଙ୍ଗଲ ସଫା କାର୍ଯ୍ୟ ଆରମ୍ଭ କରି ଦିଆଗଲା । ଏକ ମନୋରମ ସବୁଜ ବନାନୀ ଦିନ କେଇଟାରେ ବିସ୍ତୀର୍ଣ୍ଣ ପ୍ରାନ୍ତରରେ ପରିଣତ ହୋଇଗଲା। ଜଙ୍ଗଲ ପରେ ପରେ ପାହାଡ଼ ଉପରେ ଆରମ୍ଭ ହେଲା ଅତ୍ୟାଚାର । ପାହାଡ଼ ଫଟାଇ ପଥର, ଗୋଡ଼ି, ମାଟିଧୂଳିକୁ ସମତୁଲ କରି ରାଜନଅର ନିର୍ମାଣ ଆରମ୍ଭ ହେଲା । ବିଳାସପୂର୍ଣ୍ଣ ରାଜପ୍ରାସାଦ ନିର୍ମାଣ ପରେ ମଧ୍ୟ କାମ ସରିଲା ନାହିଁ । ଏହାର ଚତୁଃପାର୍ଶ୍ବରେ ଆଉ କେତେ ଘର, ପାଚେରୀ, ମନ୍ଦିର ଗୋଟିକ ପରେ ଗୋଟିଏ ଗଢ଼ିଉଠିଲା । ରାଜାଙ୍କ କଳ୍ପନାକୁ ରୂପ ଦେବାପାଇଁ ବହୁ ପ୍ରସ୍ତାବ ଆଗତ ହୋଇ କାର୍ଯ୍ୟକାରା ହେବାକୁ ଲାଗିଲା ମଧୁପୁରଗଡ଼ର ଗଡ଼ପର୍ବତରୁ ପଥରକଟା ଓ ଘରତୋଳା କାର୍ଯ୍ୟ ତ୍ବରାନ୍ବିତ ହୋଇ ପାହାଡ଼ ତଳି ଅଞ୍ଚଳ ଏକ ବିରାଟ ଜନପଦରେ ପରିଣତ
ହେଲା । ବୁଢ଼ାରାଜାଙ୍କ ଅମଳରେ ଆରମ୍ଭ ହୋଇଥିବା ନିର୍ମାଣକାର୍ଯ୍ୟ ଯୁବରାଜଙ୍କ ଅମଳରେ ମଧ୍ୟ ପୂର୍ବବତ୍ ଚାଲୁରହିଲା ।
ପ୍ରଥମରୁ ଡେଙ୍ଗୁରାପିଟା କାଠି ତିଆରି କରିବା, ଜଙ୍ଗଲର ଗଛକଟା କାର୍ଯ୍ୟ ଆରମ୍ଭ କରିବା, ଏପରିକି ଗଡ଼ପର୍ବତରୁ ପ୍ରଥମ କରି ପଥର ତାଡ଼ିବା କାର୍ଯ୍ୟ ଆରମ୍ଭ କରିଥିବା ଭୀମ ଦାସର କାର୍ଯ୍ୟରେ ବିରାମ ନଥିଲା । ସକାଳୁ ସନ୍ଧ୍ୟାଯାଏ ପାହାଡ଼ ଭିତରୁ ପଥର କାଟିବାର ଠକ୍ ଠକ୍ ଶବ୍ଦ କେବେ ବି ବନ୍ଦ ନଥିଲା । ପଥରକଟାକୁ ନିଜ ବୃତ୍ତି ଭାବେ ଧରିନେଇଥବା ସେଇ ମଣିଷଟା ଜଙ୍ଗଲରେ ରହି ବଣ ଫଳମୂଳ ଖାଇ ବଞ୍ଚୁଥିଲା । ଚାକଚକ୍ୟପୂର୍ଣ୍ଣ ବିଳାସମୟ ରାଜଉଆସମାନଙ୍କରେ ସୁଖ ସମ୍ପଦର ପ୍ରାଚୁର୍ଯ୍ୟ ମଧ୍ୟରେ ରହି କେହି ଦିନେ ମଧ୍ଯ ଭୀମ ଦାସ ବିଷୟରେ ପଚାରି ନଥିଲେ । ଦିନ, ମାସ, ବର୍ଷ ଧରି ଷାଠିଏ ବର୍ଷକାଳ ଖରା, ବର୍ଷା, ଶୀତ, କାକରରେ ଗଡ଼ପର୍ବତ ତଳିକୁ ରମଣୀୟ ଉଆସରେ ପରିଣତ କରିଥିବା ଲୋକଟି ସଭିଙ୍କ ଦୃଷ୍ଟି ଆଢୁଆଳରେ ରହି ପୂର୍ବପରି ତା’ ନିତ୍ୟନୈମିତ୍ତିକ ପଥରକଟା କାର୍ଯ୍ୟରେ ବୁଡ଼ି ରହିଥିଲା । ପନ୍ଦର ବର୍ଷର କିଶୋର ଭୀମ ଦାସ ତା’ର ଯୌବନ କାଳର ସମସ୍ତ ଶକ୍ତିକୁ ପଥରକଟା କାର୍ଯ୍ୟରେ ନିଃଶେଷ କରି ଆଜି ଅଶୀବର୍ଷ ବୟସର ବାର୍ଦ୍ଧକ୍ୟରେ ଉପନୀତ ହୋଇଥିଲେ ମଧ୍ୟ ପର୍ବତ ଭିତରେ ତା’ର ପଥରକଟାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ପ୍ରତି କେହି ଦିନେ ହେଲେ କର୍ଣ୍ଣପାତ କରିନଥିଲେ ।
ଦିନେ ପଥରକଟାର ଠକ୍ ଠକ୍ ଶବ୍ଦ ରାଜାଙ୍କ ନିଦ୍ରାରେ ବ୍ୟାଘାତ ସୃଷ୍ଟି କରିବାରୁ ରାଜାଦେଶରେ ପାଇକସୈନ୍ୟ ଭୀମ ଦାସ ପିଠିରେ ଚାବୁକ୍ ଦେଇ ପହୁଡ଼ ବେଳେ ପଥରକଟା ବନ୍ଦ କରିବାକୁ ଆଦେଶ ଦେଇଗଲେ । ମାତ୍ର ମୂକ ଭୀମ ଦାସର ପଥରକଟା ବନ୍ଦ ହୋଇନଥିଲା । ଦିନେ ରାଜା ପାରିସ୍ ଉଦ୍ଦେଶ୍ୟରେ ଜଙ୍ଗଲ ମଧ୍ୟକୁ ପ୍ରବେଶ କରି ପଥର କଟାଳି ଭୀମ ଦାସକୁ ତା’ର ଚିରାଚରିତ କାମରେ ବୁଡ଼ିରହିଥିବା ଲକ୍ଷ୍ୟକଲେ । ତା’ ବିଷୟରେ ସବୁ ଜାଣିବା ପରେ ଦୟାପରବଶ ହୋଇ ଲୋକଙ୍କଦ୍ବାରା ତାକୁ ରାଜଧାନୀକୁ ନେଇଆସି ଏକ ସୁରମ୍ୟ ଗୃହରେ ରଖାଇବାର ବ୍ୟବସ୍ଥା କରାଇଥିଲେ । ଚାକରବାକର ଗହଣରେ ସମ୍ମାନର ସହ ତା’ ରହିବାର ସୁବନ୍ଦୋବସ୍ତ କରାଗଲା । ମାତ୍ର ଭୀମ ଦାସ ଖୋଜୁଥିଲା ସେହି ପାହାଡ଼କୁ ଓ ପଥରକୁ । ରାଜା ଯେତେବେଳେ କହିଥିଲେ ଯେ ତା’ ହାତକଟା ପଥର ଘରେ ସେ ରହୁଛି ବୋଲି ସେତେବେଳେ ଭୀମ ଚଟାଣକୁ କୁଣ୍ଢାଇ ପକାଇ ‘ମୋ ପଥର’, ‘ମୋ ପଥର’ କହି କାନ୍ଦି ଉଠିଥିଲା ।
ସେଦିନ ରାତିରେ ଭୀମ ଦାସ ସେ ଘର ଛାଡ଼ି ଚାଲିଯାଇଥିଲା ସେହି ପାହାଡ଼ ନିକଟକୁ । ତା’କୁ ଖୋଜି ଖୋଜି ରାଜା ତା’ ନିକଟରେ ପହଞ୍ଚିଲାବେଳକୁ ସେ ତା’ର ପଥରକଟା ହତିଆର ସବୁ ସଜାଡ଼ୁଥିଲା । ତା’ର ଆଚରଣ, ଗତିବିଧ୍ ରାଜାଙ୍କୁ ବିସ୍ମିତ କରିଥିଲା । ତାଙ୍କ କଣ୍ଠରୁ ଅଜାଣତରେ ବାହାରି ଆସିଲା, ‘ଏ ମଣିଷକୁ ପଥର କଲା କିଏ ? ’’ ସେହି କେତୋଟି ଶବ୍ଦ ପର୍ବତରେ ଧକ୍କା ଖାଇ ପ୍ରତିଧ୍ଵନିତ ହୋଇଉଠୁଥିଲା । ରାଜାଙ୍କ ପରିଚୟ ପାଇଲା ପରେ ଭୀମ ଦାସ ତାଙ୍କୁ କୁଣ୍ଢାଇ ପକାଇ କହିଲା ‘ରାଜା ! ମୋ ରାଜା ! ଯେ ମୋତେ ପଥର କାଟିବାକୁ ଆଦେଶ ଦେଇଥିଲେ ସେହି ମୋର ରାଜା ।’’ ସେ ପଥର କାଟିବା ଭିତରେ କେବେହେଲେ ରାଜାଙ୍କୁ ଦେଖୁଥିଲା । ସେ ରାଜାଙ୍କୁ ଜୋରରେ କୁଣ୍ଢାଇ ଧରି ‘ରାଜା’, ‘ରାଜା’ ବୋଲି ଚିତ୍କାର। ପର୍ବତରେ ପ୍ରତିଧ୍ଵନିର ଶେଷ ଶବ୍ଦ ଶୁଭିଲା, ‘ହା-ହା-ହା-ଆ’। ପର୍ବତର ଏହି ଉପହାସ ମଧ୍ଯରେ ରାଜା ନିଜର ଉତ୍ତର ପାଇସାରିଥିଲେ ।
କଠିନ ଶବ୍ଦ।ର୍ଥ :
- ଆଦ୍ୟ – ଆରମ୍ଭ ।
- ଅବ୍ୟକ୍ତ – ଯାହା କହିହେବ ନାହିଁ ।
- ଦର୍ଭେଦ୍ୟ – ଯାହା ଭେଦ କରିବା କଷ୍ଟକର ।
- ପ୍ରାନ୍ତର – ପଡ଼ିଆ ।
- ଶ୍ରୀହୀନ – ଶୋଭା ହୀନ ରୂ ପିଲା ବି ଣ୍ୟ ହଜିଯାଇଥିବା
- ରାଷ୍ଟ୍ର ହେଲା – ସମ୍ବାଦ ଚାରିଆଡ଼େ ପ୍ରସାରିତ ହେଲା । ପ୍ରଚାରିତ ହେଲା ।
- ପିଶାଚ – ଅସୁର / ଭୟଙ୍କର ରୂପଧାରୀ ରାକ୍ଷସ ।
- ଯୁବରାଜ – ରାଜାଙ୍କର ପୁଅ ।
- ପାରିଧ – ଶିକାର ।
- ବୃକୋଦର – ଭୀମ ।
- ଅମରାବତ – ସ୍ୱର୍ଗପୁର ।
- ଟମକ – ନାଗରା ।
- ଆରକ୍ତ – ଲାଲ ।
- ଜରା – ବାର୍ଦ୍ଧକ୍ୟ ।
- ଭୀମକର୍ମା – ଭୟଙ୍କର କାର୍ଯ୍ୟରେ ରତ ବ୍ୟକ୍ତି ।
- ଲିପ୍ – ଲାଭ କରିବାକୁ ଇଚ୍ଛା କରୁଥିବା ଲୋକ ।
- ଗହ୍ବର – ଗାତ।
- ରମଣୀୟ – ଅତି ସୁନ୍ଦର ।