Odisha State Board BSE Odisha 9th Class History Important Questions Chapter 9 ସାମରିକ ଗୋଷ୍ଠୀ ଗଠନ : ସଶସ୍ତ୍ରୀକରଣ ପାଇଁ ପ୍ରତିଦ୍ବନ୍ଦିତା Important Questions and Answers.
BSE Odisha Class 9 History Important Questions Chapter 9 ସାମରିକ ଗୋଷ୍ଠୀ ଗଠନ : ସଶସ୍ତ୍ରୀକରଣ ପାଇଁ ପ୍ରତିଦ୍ବନ୍ଦିତା
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ଉତ୍ତର ଆଟଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଂଗଠନ (NATO) କେବେ, କାହା ନେତୃତ୍ଵରେ ଓ କ’ଣ ପାଇଁ ଗଠିତ ହୋଇଥିଲା ?
Answer:
- ପଶ୍ଚିମ ଓ ମଧ୍ୟ ଇଉରୋପରେ ନିଜ ପ୍ରାଧାନ୍ୟ ବିସ୍ତାର ଓ ସୋଭିଏତ୍ ରୁଷର ପ୍ରତିପତ୍ତିକୁ ପ୍ରତିହତ କରିବାପାଇଁ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ୧୯୪୯ ମସିହା ଏପ୍ରିଲ୍ ୪ ତାରିଖରେ ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ ଗଠନ କରିଥିଲା ।
- ଏଥିରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ସହିତ କାନାଡ଼ା, ବେଲଜିୟମ୍ , ହଲାଣ୍ଡ, ଲକ୍ସେମ୍ବର୍ଗ, ଡେନ୍ମାର୍କ, ନରୱେ, ଆଇସ୍ଲାଣ୍ଡ, ବ୍ରିଟେନ୍, ଫ୍ରାନ୍ସ ଓ ପର୍ତ୍ତୁଗାଲ୍ ଯୋଗ ଦେଇଥିଲେ ।
- ଏହି ଚୁକ୍ତିରେ ଚୁକ୍ତିଭୁକ୍ତ ଗୋଟିଏ ଦେଶ ଉପରେ ଆକ୍ରମଣ ହେଲେ ସମସ୍ତ ସଭ୍ୟ ଦେଶ ଉପରେ ଆକ୍ରମଣ ହେଲା ବୋଲି ଧରିନେବାପାଇଁ ଏଥରେ ଉଲ୍ଲେଖ ଥିଲା ।
- ଫେବୃୟାରୀ ୧୯୫୨ରେ ଗ୍ରୀସ୍ ଓ ତୁର୍କୀ ଏବଂ ମେ ୧୯୫୫ରେ ଜର୍ମାନୀ ସଂଯୁକ୍ତ ସାଧାରଣତନ୍ତ୍ର ବା ପଶ୍ଚିମ ଜର୍ମାନୀ ଏହି ସାମରିକ ଚୁକ୍ତିରେ ଯୋଗ ଦେଇଥିଲେ ।
- ଏହା ଫଳରେ ୧୯୪୯ ମସିହା ପରେ ସାମ୍ୟବାଦୀମାନେ ପଶ୍ଚିମ ଇଉରୋପ ଓ ଆଟ୍ଲାଣ୍ଟିକ୍ ଅଞ୍ଚଳରେ କ୍ଷମତା ବିସ୍ତାର କରିପାରିଲେ ନାହିଁ ।
![]()
୨। ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଓ ସୋଭିଏତ୍ ରୁଷ୍ ନେତୃତ୍ୱରେ କେବେ ଓ କେଉଁ ସାମରିକ ଚୁକ୍ତିଗୁଡ଼ିକ ସଂଗଠିତ ହୋଇଥିଲା ?
Answer:
- ୧୯୪୯ ମସିହା ଏପ୍ରିଲ ୪ ତାରିଖରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ରୁଷ୍ଠ ପ୍ରତିପରିକୁ ପ୍ରତିରୋଧ କରିବାକୁ ଯାଇ ୧୧ଟି ଦେଶର ସହଯୋଗରେ ‘ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ରୁକ୍ତି ସଂଗଠନ’ ଗଢ଼ିଥିଲା । ୧୯୫୨ ମସିହାରେ ଗ୍ରୀସ୍ ଓ ତୁର୍କୀ ଏବଂ ୧୯୫୫ ମସିହାରେ ଜର୍ମାନୀ ଏହି ଚୁକ୍ତିରେ ଯୋଗ ଦେଇଥିଲେ ।
- ୧୯୫୪ ମସିହାରେ ଅଷ୍ଟ୍ରେଲିଆ, ନିଉଜିଲାଣ୍ଡ ଏବଂ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ମଧ୍ୟରେ ‘ଆନ୍ସ୍ ରାଜିନାମା’ (ANZUS PACT) ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
- ୧୯୫୪ ମସିହା ସେପ୍ଟେମ୍ବର ୮ ତାରିଖ ଦିନ ରୁଷ୍ ଓ ସାମ୍ୟବାଦୀ ଚୀନ୍ର ପ୍ରଭାବକୁ ହ୍ରାସ କରିବାପାଇଁ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ନେତୃତ୍ୱରେ ‘ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଂଗଠନ’ ଗଠିତ ହୋଇଥିଲା । ସେହିଭଳି ୧୯୫୫ ମସିହାରେ ‘ବାଗଦାଦ୍ ଚୁକ୍ତି’ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ଯାହା ପରେ କେନ୍ଦ୍ରୀୟ ଚୁକ୍ତି ସଙ୍ଗଠନ ନାମରେ ନାମିତ ହେଲା ଓ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଏଥୁରେ ଯୋଗଦେଲା ।
- ଏହିସବୁ ମେଣ୍ଟ ଗଠନ ବିରୋଧରେ ସାମ୍ୟବାଦୀ ରାଷ୍ଟ୍ରମାନେ ରୁଷ୍ ନେତୃତ୍ବରେ ପୋଲାଣ୍ଡର ରାଜଧାନୀ ୱାରସ୍ଠାରେ ୧୯୫୫ ମସିହାରେ ରାଜଧାନୀ ୱାରସ୍ଠାରେ ୧୯୫୫ ମସିହାରେ ‘ୱାରସ୍ ଚୁକ୍ତି’ ନାମକ ଏକ ସାମରିକ ଚୁକ୍ତିରେ ଆବଦ୍ଧ ହୋଇଥିଲେ ।
୩ । ୱାରସ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ ଉପରେ ଏକ ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ ଲେଖ ।
Answer:
- ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ସାମରିକ ମେଣ୍ଟ ଗଠନ ବିରୋଧରେ ସୋଭିଏତ୍ ରୁଷ୍ ନେତୃତ୍ୱରେ ତା’ର ଅନୁ ଗାମୀ ଇଉରୋପୀୟ ସାମ୍ୟବାଦୀ ରାଷ୍ଟ୍ରମାନେ ୧୯୫୫ ମସିହା ମେ ୧ ତାରିଖରେ ୱାରସ୍ ଚୁକ୍ତି ସ୍ୱାକ୍ଷର କଲେ ।
- ପୋଲାଣ୍ଡର ରାଜଧାନୀ ୱାର୍ସଠାରେ ସୋଭିଏତ୍ ରୁଷ୍, ପୋଲାଣ୍ଡ, ହଙ୍ଗେରୀ, ରୁ ମାନିଆ, ବୁଲ୍ ଗେରି ଆ, ଆଲ୍ ବାନି ଆ, ଚେକୋସ୍ଲୋଭାକିଆ ଓ ଜର୍ମାନ୍ ଗଣତାନ୍ତ୍ରିକ ସାଧାରଣତନ୍ତ୍ର ବା ପୂର୍ବ ଜର୍ମାନୀ ମଧ୍ୟରେ ଗଠିତ ଏହି ସାମରିକ ମେଣ୍ଟ ଶୀତଳ ଯୁଦ୍ଧକୁ ତୀବ୍ରତର କରିବାରେ ସହାୟକ ହୋଇଥିଲା ।
- ଚୁକ୍ତି ସ୍ୱାକ୍ଷରକାରୀ ରାଷ୍ଟ୍ରମାନେ ପୁଞ୍ଜିବାଦୀ ରାଷ୍ଟ୍ରଙ୍କର ଆକ୍ରମଣକୁ ମିଳିତଭାବେ ପ୍ରତିରୋଧ କରିବେ ବୋଲି ଘୋଷଣା କରିଥିଲେ ।
- ରସ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ, ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ ଭଳି ଶୀତଳ ଯୁଦ୍ଧ ସମୟରେ ପ୍ରମୁଖ ସାମରିକ ମେଣ୍ଟ ଭାବେ କାର୍ଯ୍ୟ କଲା ।
![]()
୪। ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ (SEATO) ଉପରେ ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ ପ୍ରଦାନ କର ।
Answer:
- ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆରେ ରୁଷ୍ ଓ ସାମ୍ୟବାଦୀ ଚୀନ୍ର ପ୍ରଭାବକୁ ହ୍ରାସ କରିବା ନିମନ୍ତେ ୧୯୫୪ ମସିହା ସେପ୍ଟେମ୍ବର ୮ ତାରିଖ ଦିନ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ନେତୃତ୍ଵରେ ‘ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ‘ଚୁକ୍ତି ସଙ୍ଗଠନ’ (SEATO) ଗଠିତ ହୋଇଥିଲା ।
- ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ବ୍ରିଟେନ୍, ଫ୍ରାନ୍ସ, ଅଷ୍ଟ୍ରେଲିଆ, ନିଉଜିଲାଣ୍ଡ, ଥାଇଲାଣ୍ଡ, ପାକିସ୍ତାନ ଓ ଫିଲିପାଇନ୍ସ ଏହାର ସଭ୍ୟ ହୋଇଥିଲେ । ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ ଢାଞ୍ଚାରେ ଏହାର ନୀତିମାନ ନିର୍ଦ୍ଧାରିତ ହୋଇଥିଲା ।
- ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆରେ ଯେକୌଣସି ଭାବରେ ପ୍ରତିରୋଧ କରି ସେହି ଅଞ୍ଚଳରେ ନିରାପତ୍ତା ରକ୍ଷା କରିବେ ବୋଲି ସ୍ଥିର ହେଲା ।
- କିନ୍ତୁ ଭିଏତ୍ନାମ୍ ଯୁଦ୍ଧ ସମୟରେ ଏହି ଚୁକ୍ତିର କାର୍ଯ୍ୟକାରିତା ପରୀକ୍ଷିତ ହୋଇଥିଲା । ଦୀର୍ଘକାଳ ଯୁଦ୍ଧ ପରେ ସୋଭିଏତ୍ ସମର୍ଥ ଉତ୍ତର ଭିଏତ୍ନାମ୍, ୧୯୭୫ ମସିହାରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ସମର୍ଥା ଦକ୍ଷିଣ ଭିଏତ୍ନାମ୍ ଉପରେ ବିଜୟ ହାସଲ କରିଥିଲା ।
- ଫଳସ୍ୱରୂପ, ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ମର୍ଯ୍ୟାଦା କ୍ଷୁଣ୍ଣ ହୋଇଥିଲା ଏବଂ ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନର ପରିସମାପ୍ତି ଘଟିଥିଲା ।
୫। ବାଗ୍ବାଦ୍ ଚୁକ୍ତି ଉପରେ ଏକ ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ ଲେଖ ।
Answer:
- ୧୯୫୫ ମସିହାରେ ଇରାକ୍ଟର ରାଜଧାନୀ ବାଦଠାରେ ବ୍ରିଟେନ୍, ତୁର୍କୀ, ଇରାକ୍, ଇରାନ୍ ଓ ପାକିସ୍ତାନ ମଧ୍ୟରେ ଏକ ସାମରିକ ଚୁକ୍ତି ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
- ଏହା ‘ବାଗ୍ଦାଦ୍ ଚୁକ୍ତି’ ନାମରେ ପରିଚିତ ।
- ୧୯୫୮ ମସିହାରେ ରାଜତନ୍ତ୍ରର ପତନ ଫଳରେ ଇରାକ୍ ଏହି ମେଣ୍ଟରୁ ଓହରିଗଲା ଏବଂ ଏହାପରେ ଏହି ଚୁକ୍ତିର ନାମ ‘କେନ୍ଦ୍ରୀୟ ଚୁକ୍ତି ସଙ୍ଗଠନ’ ରଖାଗଲା ।
- ଏଥୁରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ନୂତନ ସଭ୍ୟରୂପେ ଯୋଗ ଦେଇଥିଲା ।
କ୍ଷୁଦ୍ର ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧ । ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ କେବେ ଓ କାହିଁକି ଗଠିତ ହୋଇଥିଲା ? କେଉଁମାନେ ଏହାର ସଭ୍ୟ ରାଷ୍ଟ୍ର ଥିଲେ ?
Answer:
- ୧୯୫୪ ମସିହା ସେପ୍ଟେମ୍ବର ୮ ତାରିଖରେ ଦକ୍ଷିଣ ପୂର୍ବ ଏସିଆରେ ରୁଷ୍ ଓ ସାମ୍ୟବାଦୀ ଚୀନ୍ର ପ୍ରଭାବକୁ ହ୍ରାସ କରିବାପାଇଁ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ନେତୃତ୍ୱରେ ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ ଗଠିତ ହୋଇଥିଲା ।
- ଏଥିରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, ବ୍ରିଟେନ୍, ଫ୍ରାନ୍ସ, ଅଷ୍ଟ୍ରେଲିଆ, ନିଉଜିଲାଣ୍ଡ, ଥାଇଲାଣ୍ଡ, ଫିଲିପାଇନ୍ସ ଓ ପାକିସ୍ତାନ ସଭ୍ୟ ରାଷ୍ଟ୍ର ଥିଲେ ।
![]()
୨। ୱାରସ୍ ବୁକ୍ତି କେବେ, କେଉଁଠାରେ କେଉଁ ଉଦ୍ଦେଶ୍ୟରେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ? କେଉଁ କେଉଁ ଦେଶ ମଧ୍ୟରେ ଏହି ଚୁକ୍ତି ହୋଇଥିଲା ?
Answer:
- ୧୯୫୫ ମସିହାରେ ପୋଲାଣ୍ଡର ରାଜଧାନୀ ୱାରସ୍ଠାରେ ୱାରସ୍ ଚୁକ୍ତି ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା । ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ସାମରିକ ମେଣ୍ଟ ଗଠନ ବିରୋଧରେ ଏହି ମେଣ୍ଟ ଗଠନ କରାଯାଇଥିଲା ।
- ସୋଭିଏତ୍ ରୁଷ୍, ପୋଲାଣ୍ଡ, ହଙ୍ଗେରୀ, ରୁ ମାନି ଆ, ବୁଲ୍ ଗେରିଆ, ଆଲ୍ ବାନିଆ, ଚେକୋସ୍ଲୋଭାକିଆ ଓ ଜର୍ମାନ୍ ଗଣତାନ୍ତ୍ରିକ ସାଧାରଣତନ୍ତ୍ର ବା ପୂର୍ବ ଜର୍ମାନୀ ମଧ୍ୟରେ ଏହି ଚୁକ୍ତି ହୋଇଥିଲା ।
୩ । ଆନ୍ ସ୍ ରାଜିନାମା କେବେ ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ? ଏହା କେଉଁଥିପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଥିଲା ?
Answer:
- ୧୯୫୧ ମସିହାରେ ଅଷ୍ଟ୍ରେଲିଆ, ନିଉଜିଲାଣ୍ଡ ଓ ଯୁକ୍ତ ରାଷ୍ଟ୍ର ଆମେରିକା ମଧ୍ୟରେ ଆନ୍ଜସ୍ ରାଜିନାମା ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
- ପ୍ରଶାନ୍ତ ମହାସାଗରୀୟ ଅଞ୍ଚଳରେ ଶାନ୍ତି ପ୍ରତିଷ୍ଠା ତଥା ମିଳିତ ପ୍ରତିରକ୍ଷା ବ୍ୟବସ୍ଥା ପରିଚାଳନା ନିମନ୍ତେ ଏହି ଚକ୍ତି ଉଦ୍ଦିଷ୍ଟ ଥିଲା ।
୪ । କିଏ କାହିଁକି ‘ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ’ ଗଢ଼ିଥିଲା ?
Answer:
- ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ‘ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ’ ଗଢ଼ିଥିଲା ।
- ପଶ୍ଚିମ ଓ ମଧ୍ୟ ଇଉରୋପରେ ନିଜର ପ୍ରାଧାନ୍ୟ ବିସ୍ତାର ଓ ସୋଭିଏତ୍ ରୁଷ୍ ପ୍ରତିପତ୍ତିକୁ ପରାହତ କରିବା ଏହାର ଉଦ୍ଦେଶ୍ୟ ଥିଲା ।
୫ । କେବେ ଓ କାହିଁକି ‘ବାଗଦାଦ୍ ଚୁକ୍ତି’ର ନାମ ପରିବର୍ତ୍ତନ ହୋଇ କେନ୍ଦ୍ରୀୟ ଚୁକ୍ତି ସଙ୍ଗଠ ନ ରଖାଗଲା ?
Answer:
- ୧୯୫୮ ମସିହାରେ ରାଜତନ୍ତ୍ରର ପତନ ଫଳରେ ଇରାକ୍ ବାଗଦାଦ୍ ଚୁକ୍ତିରୁ ଓହରିଗଲା ।
- ଏହାପରେ ଏହି ଚୁକ୍ତିର ନାମ ପରିବର୍ତ୍ତିତ ହୋଇ ‘କେନ୍ଦ୍ରୀୟ ଚୁକ୍ତି ସଙ୍ଗଠନ’ ରଖାଗଲା ।
୬ । କେବେ ‘ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ’ ଗଠିତ ହୋଇଥିଲା ? ଏଥୁରେ କେଉଁ କେଉଁ ଦେଶ ଯୋଗ ଦେଇଥିଲେ ?
Answer:
- ୧୯୪୯ ମସିହା ଏପ୍ରିଲ୍ ୪ ତାରିଖରେ ‘ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ’ ଗଠିତ ହୋଇଥିଲା ।
- ଏଥିରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା, କାନାଡ଼ା, ବେଲ୍ ଜିୟମ୍, ହଲାଣ୍ଡ, ଲକ୍ସେମ୍ବର୍ଗ, ଡେନ୍ମାର୍କ, ନରୱେ, ଆଇସ୍ଲାଣ୍ଡ, ବ୍ରିଟେନ୍, ଫ୍ରାନ୍ ସ, ଇଟାଲୀ ଓ ପର୍ଶୁ ଗାଲ୍ ଯୋଗ ଦେଇଥିଲେ ।
![]()
Objective Type Questions With Answers
A. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଲେଖ ।
୧। ଶୀତଳ ଯୁଦ୍ଧ ଯୋଗୁଁ ଦୁଇ ମହାଶକ୍ତିଙ୍କ ନେତୃତ୍ୱରେ ପୃଥିବୀ କେତେ ଭାଗରେ ବିଭକ୍ତ ହୋଇଥିଲା ଓ କ’ଣ କ’ଣ?
Answer:
ଶୀତଳ ଯୁଦ୍ଧ ଯୋଗୁଁ ଦୁଇ ମହାଶକ୍ତିଙ୍କ ନେତୃତ୍ୱରେ ପୃଥିବୀ ଦୁଇଭାଗରେ ବିଭକ୍ତ ହୋଇଥିଲା; ଯଥା – ସାମ୍ୟବାଦୀ ଗୋଷ୍ଠୀ ଓ ପୁଞ୍ଜିବାଦୀ ଗୋଷ୍ଠୀ ।
୨। ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ କେବେ ଗଢ଼ାଯାଇଥିଲା ?
Answer:
ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ ଏପ୍ରିଲ ୪, ୧୯୪୯ ମସିହାରେ ଗଢ଼ାଯାଇଥିଲା ।
୩ । ଗ୍ରୀସ୍ ଓ ତୁର୍କୀ ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନରେ କେବେ ଯୋଗ ଦେଇଥିଲେ ?
Answer:
ଗ୍ରୀସ୍ ଓ ତୁର୍କୀ ୧୯୫୨ ମସିହାରେ ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନରେ ଯୋଗ ଦେଇଥିଲେ ।
୪। ବ୍ରସେଲସ୍ ଚୁକ୍ତି କେବେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ?
Answer:
୧୯୪୮ ମସିହାରେ ବ୍ରସେଲସ୍ ଚୁକ୍ତି ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ।
୫। ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ ବା SEATO କେବେ ଗଠିତ ହୋଇଥିଲା ?
Answer:
୧୯୫୪ ମସିହା ସେପ୍ଟେମ୍ବର ୮ ତାରିଖ ଦିନ ଦକ୍ଷିଣ- ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ ବା SEATO ଗଠିତ ହୋଇଥିଲା ।
![]()
୬। କେଉଁ ଘଟଣାରୁ ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନର ପରିସମାପ୍ତି ଘଟିଥିଲା ?
Answer:
ଦୀର୍ଘଦିନ ଯୁଦ୍ଧ ହେବା ପରେ ୧୯୭୫ ମସିହାରେ ସୋଭିଏତ୍ ସମର୍ଥ ଉତ୍ତର ଭିଏତ୍ନାମଠାରୁ ଯୁଦ୍ଧରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ସମର୍ଥାତ ଦକ୍ଷିଣ ଭିଏତ୍ନାମ୍ ହାରିଯିବା ପରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକାର ମର୍ଯ୍ୟାଦା କ୍ଷୁଣ୍ଡ ହୋଇଥ୍ଲା ଏବଂ ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ବୁ୍କ୍ତି ସଙ୍ଗଠନର ପରିସମାପ୍ତି ଘଟିଥିଲା ।
୭ । କେବେ ଓ କାହିଁକି ବାଦ୍ ଚୁକ୍ତିରୁ ଇରାକ୍ ଓହରି ଯାଇଥିଲା ?
Answer:
୧୯୫୮ ମସିହାରେ ରାଜତନ୍ତ୍ରର ପତନ ଯୋଗୁଁ ଇରାକ୍ ବାଦ୍ ଚୁକ୍ତିରୁ ଓହରି ଯାଇଥିଲା ।
୮ । ୱାରସ୍ ଚୁକ୍ତି କେବେ ଓ କାହା ମଧ୍ୟରେ ହୋଇଥିଲା ?
Answer:
ୱାରସ୍ ଚୁକ୍ତି ୧୯୫୫ ମସିହା ମେ ୧ ତାରିଖରେ ସୋଭିଏତ୍ ରୁଷ୍ ଓ ତା’ର ଅନୁଗାମୀ ଇଉରୋପୀୟ ସାମ୍ୟବାଦୀ ରାଷ୍ଟ୍ରମାନଙ୍କ ମଧ୍ୟରେ ହୋଇଥିଲା ।
୯ । ୱାରସ୍ କେଉଁ ଦେଶର ରାଜଧାନୀ ଥିଲା ?
Answer:
ୱାରସ୍ ପୋଲାଣ୍ଡର ରାଜଧାନୀ ଥିଲା ।
୧୦ । କେବେ ସୋଭିଏତ୍ ସଂଘର ବିଲୟ ଘଟିଥିଲା
Answer:
୧୯୯୧ ମସିହାରେ ସୋଭିଏତ୍ ସଂଘର ବିଲୟ ଘଟିଥିଲା ।
୧୧ । ୧୯୮୫ ମସିହାରେ ସୋଭିଏତ୍ ପଲିଟିବ୍ୟୁରୋ ସାଧାରଣ ସମ୍ପାଦକ କିଏ ହୋଇଥିଲେ ?
Answer:
୧୯୮୫ ମସିହାରେ ମିଖାଇଲ୍ ଗୋର୍ବାଚେଭ୍ ସୋଭିଏତ୍ ପଲିଟିବ୍ୟୁରୋ ସାଧାରଣ ସମ୍ପାଦକ ହୋଇଥିଲେ ।
![]()
B. ଗୋଟିଏ ଶବ୍ଦରେ ଉତ୍ତର ଲେଖ ।
୧। ଦକ୍ଷିଣ ପୂର୍ବ ଏସିଆରେ ରୁଷ୍ ଓ ସାମ୍ୟବାଦୀ ଚୀନ୍ର ପ୍ରଭାବକୁ ହ୍ରାସ କରିବା ନିମନ୍ତେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା କେଉଁ ସାମରିକ ମେଣ୍ଟ ଗଠନ କରିଥିଲା ?
Answer:
SEATO
୨। କେଉଁ ଯୁଦ୍ଧ ସମୟରେ ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ (SEATO)ର କାର୍ଯ୍ୟକାରିତା ପରୀକ୍ଷିତ ହୋଇଥିଲା ?
Answer:
ଭିଏତ୍ନାମ ଯୁଦ୍ଧ
୩ । କେଉଁ ଘଟଣା ପରେ ଦକ୍ଷିଣ ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନର ପରିସମାପ୍ତି ଘଟିଥିଲା ?
Answer:
ଭିଏତ୍ନାମ୍ ଯୁଦ୍ଧରେ ଆମେରିକାର ମର୍ଯ୍ୟାଦା କ୍ଷୁଣ୍ଣ
୪। ‘ବାଗ୍ଦାଦ୍ ଚୁକ୍ତି’ର ପରିବର୍ତ୍ତିତ ନାମ କ’ଣ ?
Answer:
କେନ୍ଦ୍ରୀୟ ଚୁକ୍ତି ସଂଗଠନ ବା CENTO
୫। ‘ୱାର୍ସ ଚୁକ୍ତି’ କେବେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ?
Answer:
୧୯୫୫ ମେ ୧
୬। ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଓ ସୋଭିଏତ୍ ରୁଷ୍ ମଧ୍ୟରେ ଉତ୍ତେଜନା ହ୍ରାସ ଓ ଶୀତଳ ଯୁଦ୍ଧର ଏକ ନୂତନ ରୂପର ନାମ କ’ଣ ?
Answer:
ଦେତା
![]()
୭। କେଉଁ ସମୟ ମଧ୍ୟରେ ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ଓ ସୋଭିଏତ୍ ରୁଷ୍ ମଧ୍ୟରେ କ୍ରମାଗତ ଉତ୍ତେଜନା ଏକ ଆଣବିକ ଯୁଦ୍ଧରେ ରୂପାନ୍ତରିତ ହୋଇ ସମଗ୍ର ପୃଥିବୀକୁ ଧ୍ୱଂସାଭିମୁଖୀ କରିଦେବ ବୋଲି ସେମାନଙ୍କର ଧାରଣା ହେଲା ?
Answer:
୧୯୬୯ ରୁ ୧୯୭୮
୮ । ସୋଭିଏତ୍ ରୁଷର କେଉଁ ନେତାଙ୍କ ସଂସ୍କାରମୂଳକ ନୀତି ଶୀତଳ ଯୁଦ୍ଧର ଅବସାନ ନିମନ୍ତେ ମାର୍ଗ ପ୍ରସ୍ତୁତ କରିଥିଲା ?
Answer:
ମିଖାଇଲ୍ ଗୋର୍ବାଚୋଭ୍
୯୮ ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ କେବେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ?
Answer:
୧୯୪୯ ଏପ୍ରିଲ ୪
୧୦ । ବ୍ରସେଲସ୍ ଚୁକ୍ତି କେବେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ?
Answer:
୧୯୪୮ ମସିହା
୧୧ । ସୋଭିଏତ୍ ସାମ୍ୟବାଦୀ ଦଳର ସମସ୍ତ ନୀତି କାହାଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ ହେଉଥିଲା ?
Answer:
ସୋଭିଏତ୍ ପଲିଟିବ୍ୟୁରୋ
୧୨ । ‘ସାନ୍ ସାସାଲଭେଡ଼ର’ କାହାର ରାଜଧାନୀ ଥିଲା ?
Answer:
ଏଲ୍ ସାଲ୍ ଭେଡ଼ର
୧୩ । ପୃଥିବୀରେ ସାମରିକ ଗୋଷ୍ଠୀ ଗଠନ କରିବାରେ କେଉଁ ଦେଶ ଆଗୁଆ ଥିଲା ?
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
୧୪ । ଜର୍ଜ ବୁଶ୍ ଓ ବୋରିସ୍ ୟେଲସିନ୍ କେବେ ଶୀତଳ ଯୁଦ୍ଧର ଅବସାନ ଘୋଷଣା କରିଥିଲେ ?
Answer:
୧୯୯୨ ମସିହା
୧୫ । ସୋଭିଏତ୍ ସଂଘର ବିଲୟ କେବେ ଘଟିଥିଲା ?
Answer:
୧୯୯୧ ଡିସେମ୍ବର
![]()
୧୬ । ୧୯୫୮ ମସିହାରେ କେଉଁ ଦେଶରେ ରାଜତନ୍ତ୍ରର ପତନ ଘଟିଥିଲା ?
Answer:
ଇରାକ୍
୧୭ । ରୁଷ୍ କେଉଁ ରାଷ୍ଟ୍ରପତିଙ୍କ ସମୟରେ ଆମେରିକା ଓ ରୁଷ୍ ମଧ୍ୟରେ ସମ୍ପର୍କରେ ଉନ୍ନତି ହେଲା ?
Answer:
ଗୋର୍ବାଚେଭ୍
୧୮ । ଶୀତଳ ଯୁଦ୍ଧର ଅବସାନ ପାଇଁ ଆମେରିକାର କେଉଁ ରାଷ୍ଟ୍ରପତି ମୁଖ୍ୟ ଭୂମିକା ଗ୍ରହଣ କରିଥିଲେ ?
Answer:
ଜର୍ଜ ବୁଶ୍
୧୯ । ଶୀତଳ ଯୁଦ୍ଧ ସମୟରେ କେଉଁ ରାଷ୍ଟ୍ର ସାମ୍ୟବାଦୀ ଗୋଷ୍ଠୀର ନେତୃତ୍ଵ ନେଇଥୁଲା ?
Answer:
ସୋଭିଏତ୍ ରୁଷ୍
୨୦ । ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ କେଉଁ ମସିହାରେ ଗଠିତ ହୋଇଥିଲା ?
Answer:
୧୯୫୪ ମସିହା
C. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
୧ । __________ ମସିହାରେ ସୋଭିଏତ୍ ସଂଘର ବିଲୟ ଘଟିଥିଲା ।
Answer:
୧୯୯୧
୨ । ଇରାନ୍ ବିଦ୍ରୋହ _________ ମସିହାରେ ହୋଇଥିଲା ।
Answer:
୧୯୭୯
![]()
୩ । ________ ମସିହାରେ ବାଦ୍ ଚୁକ୍ତି ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ।
Answer:
୧୯୫୫
୪ । __________ ଚୁକ୍ତି ଆଧାରରେ ପଶ୍ଚିମ ଇଉରୋପୀୟ ଐକ୍ୟ ପ୍ରତିଷ୍ଠା ନିମନ୍ତେ ଏକ ଯୋଜନା ପ୍ରସ୍ତୁତ କରାଯାଇଥିଲା ।
Answer:
ବ୍ରସେଲସ୍
୫ । ୧୯୫୨ ମସିହାରେ _________ ର ପ୍ରତିଷ୍ଠା ନିମନ୍ତେ ପ୍ୟାରିସ୍ତାରେ ଏକ ଚୁକ୍ତି ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ।
Answer:
ଇଉରୋପୀୟ ପ୍ରତିରକ୍ଷା ଗୋଷ୍ଠୀ
୬। ପଶ୍ଚିମ ଇଉରୋପୀୟ ରାଷ୍ଟ୍ରଙ୍କ ମଧ୍ୟରେ ବୁଝାମଣା ନିମନ୍ତେ ୧୯୫୪ ମସିହାରେ ___________ ଠ।ରେ ଏକ ସମ୍ମିଳନୀ ଆୟୋଜନ କରାଯାଇଥିଲା ।
Answer:
ଲଣ୍ଡନ
୭ । __________ ମସିହାରେ ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଙ୍ଗଠନ ଗଢ଼ି ଉଠିଥିଲା ।
Answer:
୧୯୪୯
୮ । ଦକ୍ଷିଣ ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଂଗଠନ (SEATO) ର ଅବସାନ __________ ମସିହାରେ ହୋଇଥିଲା ।
Answer:
୧୯୭୫
![]()
୯ । ୧୯୫୮ ମସିହାରେ _________ ଦେଶ କେନ୍ଦ୍ରୀୟ ଚୁକ୍ତି ସଂଗଠନରେ ଯୋଗ ଦେଇଥିଲା ।
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
୧୦ । ଆନଜସ୍ ରାଜି ନାମା’ ___________ ମସିହାରେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
Answer:
୧୯୫୧
୧୧ । ଉତ୍ତର ଆଟଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଂଗଠନ (NATO) __________ ଦେଶର ନେତୃତ୍ୱରେ ଗଠିତ ହୋଇଥିଲା ।
Answer:
ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
୧୨ । ପ୍ରଶାନ୍ତ ମହାସାଗରୀୟ ଅଞ୍ଚଳରେ ଶାନ୍ତି ପ୍ରତିଷ୍ଠା ପାଇଁ _________ ରାଜିନାମା ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
Answer:
ଆନଜସ୍
୧୩ । ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆରେ ରୁଷ୍ ଓ ଚୀନ୍ର ସାମ୍ୟବାଦୀ ପ୍ରଭାବକୁ ହ୍ରାସ କରିବା ପାଇଁ _________ ଗଠିତ ହୋଇଥିଲା ।
Answer:
ଦକ୍ଷିଣ ପୂର୍ବ ଏସିଆ ସଙ୍ଗଠନ ବା SEATO
D. ଠିକ୍ ଉକ୍ତି ପାଇଁ (✓) ବା ଭୁଲ ଉକ୍ତି ପାଇଁ (✗) ଲେଖ ।
୧। ଉତ୍ତର ଆଟ୍ଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଂଗଠନ (NATO)ରେ ଦଶଗୋଟି ରାଷ୍ଟ୍ର ଭାଗ ନେଇଥିଲେ ।
୨। ଜର୍ମାନୀ ୧୯୫୪ ମସିହାରେ NATO ରେ ଯୋଗ ଦେଇଥିଲା ।
୩ । ପ୍ରଶାନ୍ତ ମହାସାଗରୀୟ ଅଞ୍ଚଳରେ ଶାନ୍ତିପ୍ରତିଷ୍ଠା ପାଇଁ ଆନ୍ସ୍ ରାଜିନାମା ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
୪। ବ୍ରସେଲସ୍ ଚୁକ୍ତି ୧୯୪୭ରେ ସ୍ବାକ୍ଷରିତ ହୋଇଥିଲା ।
୫। ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆରେ ରୁଷ୍ ଓ ଚୀନ୍ର ସାମ୍ୟବାଦୀ ପ୍ରଭାବକୁ ହ୍ରାସ କରିବାପାଇଁ SEATO ଗଠିତ ହୋଇଥିଲା ।
୬ । SEATO ର ନେତୃତ୍ୱ ସୋଭିଏତ୍ ରୁଷ ନେଇଥିଲା ।
୭। ୧୯୫୫ ମସିହା ସେପ୍ଟେମ୍ବର ୮ ତାରିଖରେ SEATO ଗଠିତ ହୋଇଥିଲା ।
୮। ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା ୧୯୭୪ରେ ଦକ୍ଷିଣ ଭିଏତ୍ନାମ୍ ଉପରେ ବିଜୟ ହାସଲ କରିଥିଲା ।
୯ । ‘ବାଦ୍ ଚୁକ୍ତି’ ୧୯୫୪ ମସିହାରେ ସ୍ଵାକ୍ଷରିତ ହୋଇଥିଲା ।
୧୦ । ପାକିସ୍ତାନ ‘ବାଦ୍ ଚୁକ୍ତି’ରେ ସଦସ୍ୟ ନଥିଲା ।
![]()
Answer:
୧। (✗)
୨। (✗)
୩ । (✓)
୪ । (✗)
୫ । (✓)
୬ । (✗)
୭ । (✗)
୮ । (✗)
୯ । (✗)
୧୦ । (✗)
E. ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେଖ ।
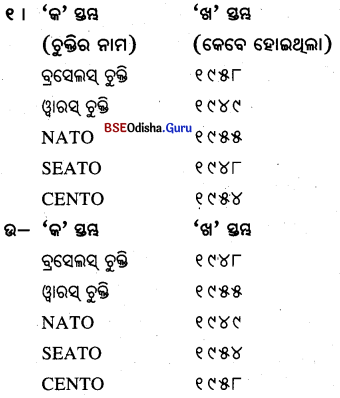

F. ରେଖାଙ୍କିତ ପଦକୁ ପରିବର୍ତ୍ତନ କରି ଭ୍ରମ ସଂଶୋଧନ କର ।
୧। ଦକ୍ଷିଣ ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଂଗଠନରେ ୭ଗୋଟି ରାଷ୍ଟ୍ର ସଭ୍ୟ ଥିଲେ ।
Answer:
୮ ଗୋଟି
୨। ୧୯୫୫ ମସିହା ମେ’ ମାସ ୧ ତାରିଖରେ ଆନଜସ୍ ଚୁକ୍ତି ସ୍ୱାକ୍ଷରିତ ହୋଇଥିଲା ।
Answer:
ୱାରସ୍ ଚୁକ୍ତି
୩ । ପାକିସ୍ତାନ ୱାରସ ଚୁକ୍ତିରେ ସାମିଲ ହୋଇଥିଲା ।
Answer:
ବାଗଦାଦ୍
୪ । ୧୯୭୮ ମସିହା ଦେତାର ଅବସାନ ଘଟିଥିଲା ।
Answer:
୧୯୭୯
୫। ସୋଭିଏତ ସଂଘର ବିଲୟ ୧୯୯୦ ମସିହାରେ ଘଟିଥିଲା ।
Answer:
୧୯୯୧
![]()
୬ । ଉତ୍ତର ଆଟଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଂଗଠନ (NATO) ୧୯୫୦ ଏପ୍ରିଲ୍ ୪ ତାରିଖରେ ଗଠିତ ହୋଇଥିଲା ।
Answer:
୧୯୪୯
୭। ୧୯୫୮ ମସିହାରେ ଇରାନ୍ ବାଦ୍ ଚୁକ୍ତିରୁ ଓହରି ଯାଇଥିଲା ।
Answer:
ଇରାକ୍
୮। ଆନଜସ୍ ରାଜିନାମାରେ ୪ଗୋଟି ଦେଶ ସ୍ବାକ୍ଷର କରିଥିଲେ ।
Answer:
୩ ଗୋଟି
୯ । ବୋରିସ୍ ୟେଲସିନ୍ଙ୍କ ସଂସ୍କାରମୂଳକ ନୀତି ଶୀତଳ ଯୁଦ୍ଧର ଅବସାନ ନିମନ୍ତେ ମାର୍ଗ ପ୍ରସ୍ତୁତ କରିଥିଲା ।
Answer:
ମିଖାଇଲ୍ ଗୋର୍ବାଚୋ
୧୦ । କେନ୍ଦ୍ର ରୁଷ୍ ମଣ୍ଡଳର ରାଷ୍ଟ୍ରପତି ଥିଲେ ମିଖାଇଲ ଗୋର୍ବାଚେଲୁ ।
Answer:
ବୋରିସ୍ ୟେଲସିନ୍ ।
G. ଚାରୋଟି ସମ୍ଭାବ୍ୟ ବିକଳ୍ପ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।
Question 1.
ଶୀତଳ ଯୁଦ୍ଧ ସମୟରେ ନିମ୍ନୋକ୍ତ କେଉଁ ରାଷ୍ଟ୍ର ସାମ୍ୟବାଦୀ ଗୋଷ୍ଠୀର ନେତୃତ୍ୱ ନେଇଥିଲା ?
(A) ଆମେରିକା
(B) ଚୀନ୍
(C) ସୋଭିଏତ୍ ରୁଷ୍
(D) ଜାପାନ
Answer:
(C) ସୋଭିଏତ୍ ରୁଷ୍
Question 2.
ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଙ୍ଗଠନ ନିମ୍ନୋକ୍ତ କେଉଁ ମସିହାରେ ଗଠିତ ହୋଇଥିଲା ?
(A) ୧୯୫୧
(C) ୧୯୫୩
(B) ୧୯୫୨
(D) ୧୯୫୪
Answer:
(D) ୧୯୫୪
![]()
Question 3.
କେବେ ଇରାକ୍ ବାଗଦାଦ୍ ଚୁକ୍ତିରୁ ଓହରିଗଲା ?
(A) ୧୯୫୬
(B) ୧୯୫୭
(C) ୧୯୫୮
(D)୧୯୫୯
Answer:
(C) ୧୯୫୮
Question 4.
କେଉଁ ସାମ୍ୟବାଦୀ ରାଷ୍ଟ୍ର ‘ୱାରସ୍ ଚୁକ୍ତି’ର ସଦସ୍ୟ ନ ଥିଲା ?
(A) ପୋଲାଣ୍ଡ
(B) ହଙ୍ଗେରୀ
(C) ବୁଲଗେରିଆ
(D) ଚୀନ୍
Answer:
(D) ଚୀନ୍
Question 5.
ନିମ୍ନୋକ୍ତ କେଉଁ ମସିହାରେ ସୋଭିଏତ୍ ସଂଘର ବିଲୟ ଘଟିଥିଲା ?
(A) ୧୯୯୦
(B) ୧୯୯୧
(C) ୧୯୯୨
(D) ୧୯୯୫
Answer:
(B) ୧୯୯୧
Question 6.
କେବେ ନୂତନ ଶୀତଳ ଯୁଦ୍ଧର ସୂତ୍ରପାତ ହୋଇଥିଲା?
(A) ୧୯୭୭
(B) ୧୯୭୮
(C) ୧୯୭୯
(D) ୧୯୮୦
Answer:
(C) ୧୯୭୯
Question 7.
ନିମ୍ନୋକ୍ତ କେଉଁ ‘ମସିହାରେ ଆନ୍ସ୍ ରାଜିନାମା ସ୍ଵାକ୍ଷରିତ ହୋଇଥିଲା ?
(A) ୧୯୪୮
(B) ୧୯୪୯
(C) ୧୯୫୦
(D) ୧୯୫୧
Answer:
(B) ୧୯୪୯
Question 8.
କେବେ ବାଗ୍ଦାଦ୍ ଚୁକ୍ତି କେନ୍ଦ୍ରୀୟ ଚୁକ୍ତି ସଂଗଠନ ନାମରେ ନାମିତ ହେଲା ?
(A) ୧୯୪୯ ମସିହା
(B) ୧୯୫୨ ମସିହା
(C) ୧୯୫୫ ମସିହା
(D) ୧୯୫୮ ମସିହା
Answer:
(D) ୧୯୫୮ ମସିହା
![]()
Question 9.
କେବେ ଦେର୍ତାର ଅବସାନ ଘଟିଲା ?
(A) ୧୯୭୮ ମସିହା
(B) ୧୯୭୯ ମସିହା
(C) ୧୯୮୫ ମସିହା
(D) ୧୯୯୦ ମସିହା
Answer:
(D) ୧୯୯୦ ମସିହା
Question 10.
କେବେ ଇରାକ୍ ‘ବାଗଦାଦ୍ ଚୁକ୍ତି’ ରୁ ଓହରିଗଲା ?
(A) ୧୯୬୦
(B) ୧୯୫୮
(C) ୧୯୫୬
(D) ୧୯୬୧
Answer:
(B) ୧୯୫୮
Question 11.
କେଉଁ ଚୁକ୍ତି ଆଧାରରେ ପଶ୍ଚିମ ଇଉରୋପୀୟ ସଂଘ ପ୍ରତିଷ୍ଠିତ ହେଲା ?
(A) ବ୍ରସେଲସ୍
(B) ମ୍ୟୁନିକ୍
(C) ଆଟଲାଣ୍ଟା
(D) ତାସ୍କେଣ୍ଟ୍
Answer:
(A) ବ୍ରସେଲସ୍
Question 12.
କେବେ ଶୀତଳ ଯୁଦ୍ଧର ପରିସମାପ୍ତି ଘଟିଲାବୋଲି ଘୋଷଣା କରାଗଲା ?
(A) ୧୯୯୧
(B) ୧୯୯୨
(C) ୧୯୯୩
(D) ୧୯୯୪
Answer:
(B) ୧୯୯୨
Question 13.
କେଉଁ ମସିହା ପରେ ସାମ୍ୟବାଦୀମାନେ ପଶ୍ଚିମ ଇଉରୋପ ଓ ଆଟଲାଣ୍ଟିକ୍ ଅଞ୍ଚଳରେ କ୍ଷମତା ବିସ୍ତାର କରିପାରି ନଥିଲେ ?
(A) ୧୯୪୨
(B) ୧୯୪୬
(C) ୧୯୪୯
(D) ୧୯୫୨
Answer:
(C) ୧୯୪୯
Question 14.
୧୯୫୨ ମସିହା ମେ ମାସ ୨୭ ତାରିଖରେ ଇଉରୋପୀୟ ପ୍ରତିରକ୍ଷା ଗୋଷ୍ଠୀର ପ୍ରତିଷ୍ଠା ନିମନ୍ତେ କେଉଁଠାରେ ଏକ ଚୁକ୍ତି ସାକ୍ଷରିତ ହୋଇଥିଲା ?
(A) ପ୍ୟାରିସ୍
(B) ପୋଲାଣ୍ଡ
(C) ହଲାଣ୍ଡ
(D) ନରୱେ
Answer:
(A) ପ୍ୟାରିସ୍
![]()
Question 15.
୧୯୫୪ ମସିହା ୨୮ ସେପ୍ଟେମ୍ବରରୁ ୩ ଅକ୍ଟୋବର ପର୍ଯ୍ୟନ୍ତ କେଉଁଠାରେ ପଶ୍ଚିମ ଇଉରୋପୀୟ ରାଷ୍ଟ୍ରଙ୍କ ମଧ୍ୟରେ ବୁଝାମଣା ନିମନ୍ତେ ଏକ ସମ୍ମିଳନୀର ଆୟୋଜନ କରାଯାଇଥିଲା ?
(A) ସ୍ପେନ
(B) ଜାପାନ
(C) ଲଣ୍ଡନ
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
Answer:
(C) ଲଣ୍ଡନ
Question 16.
ଇଉରୋପୀୟ ପ୍ରତିରକ୍ଷା ଗୋଷ୍ଠୀ ଗଠନକୁ କେଉଁ ଦେଶ ସମର୍ଥନ କରିନଥିଲେ ?
(A) ଇଂଲାଣ୍ଡ
(B) ପଶ୍ଚିମ ଜର୍ମାନୀ
(C) ଫ୍ରାନ୍ସ
(D) ନେଦରଲାଣ୍ଡ
Answer:
(C) ଫ୍ରାନ୍ସ
Question 17.
କେବେ ପଶ୍ଚିମ ଇଉରୋପୀୟ ସଂଘ ଜନ୍ମ ନେଇଥିଲା ?
(A) ୧୯୪୨
(B) ୧୯୪୫
(C) ୧୯୪୮
(D) ୧୯୪୯
Answer:
(C) ୧୯୪୮
Question 18.
ଦକ୍ଷିଣ -ପୂର୍ବ ଏସିଆରେ ରୁଷ୍ ଓ ସାମ୍ୟବାଦୀ ଚୀନ୍ର ପ୍ରଭାବକୁ ହ୍ରାସ କରିବା ନିମନ୍ତେ ୧୯୫୪ ମସିହା ସେପ୍ଟେମ୍ବର ୮ ତାରିଖ ଦିନ କାହା ନେତୃତ୍ବରେ ଦକ୍ଷିଣ- ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଂଗଠନ ଗଠିତ ହୋଇଥିଲା ?
(A) ସୋଭିଏତ୍ ରୁଷ୍
(B) ସ୍ପେନ
(C) ଇଟାଲୀ
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
Answer:
(D) ଯୁକ୍ତରାଷ୍ଟ୍ର ଆମେରିକା
Question 19.
ପାକିସ୍ତାନ କେଉଁ ସଂଗଠନର ସଦସ୍ୟ ଥିଲା ?
(A) ସିଆଟୋ
(B) ୱାର୍ସ ଚୁକ୍ତି
(C) ନାଟୋ
(D) ବାଗ୍ଦାଦ୍ ଚୁକ୍ତି
Answer:
(A) ସିଆଟୋ
![]()
Question 20.
କେବେ ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଂଗଠନର ପରିସମାପ୍ତି ଘଟିଥିଲା ?
(A) ୧୯୭୦
(B) ୧୯୭୨
(C) ୧୯୭୫
(D) ୧୯୭୬
Answer:
(C) ୧୯୭୫
Question 21.
୧୯୫୫ ମସିହାରେ ଇରାକ୍ ର ରାଜଧାନୀ ବାଗ୍ଦାରେ କେଉଁ ଚୁକ୍ତି ସାକ୍ଷରିତ ହୋଇଥିଲା ?
(A) ୱାର୍ସ ଚୁକ୍ତି
(B) ବାଦ୍ ଚୁକ୍ତି
(C) ଲଣ୍ଡନ ଚୁକ୍ତି
(D) ନାଟୋ
Answer:
(B) ବାଦ୍ ଚୁକ୍ତି
Question 22.
କେଉଁ ଦେଶ ଉତ୍ତର ଆଟଲାଣ୍ଟିକ୍ ଚୁକ୍ତି ସଂଗଠନର ସଭ୍ୟ ନୁହେଁ ?
(A) ଆଇସ୍ଲାଣ୍ଡ
(B) ନରୱେ
(C) ପର୍ତ୍ତୁଗାଲ
(D) ନେଦରଲାଣ୍ଡ
Answer:
(D) ନେଦରଲାଣ୍ଡ
Question 23.
କେଉଁ ଦେଶ ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଂଗଠନର ସଭ୍ୟ ନୁହେଁ ?
(A) ସୋଭିଏତ୍ ରୁଷ୍
(B) ଫ୍ରାନ୍ସ
(C) ବ୍ରିଟେନ୍
(D) ଅଷ୍ଟ୍ରେଲିଆ
Answer:
(A) ସୋଭିଏତ୍ ରୁଷ୍
Question 24.
ଦକ୍ଷିଣ-ପୂର୍ବ ଏସିଆ ଚୁକ୍ତି ସଂଗଠନରେ କେତେଜଣ ସଭ୍ୟ ଥିଲେ ?
(A) ୬ ଜଣ
(B) ୮ ଜଣ
(C) ୧୦ ଜଣ
(D) ୧୨ ଜଣ
Answer:
(B) ୮ ଜଣ
![]()
Question 25.
ୱାର୍ସ ଚୁକ୍ତିରେ କେତୋଟି ରାଷ୍ଟ୍ର ଯୋଗ ଦେଇଥିଲେ ?
(A) ୮ଟି
(B) ୧୫ଟି
(C) ୧୬ଟି
(D) ୧୮ଟି
Answer:
(A) ୮ଟି