Bhagya

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 13 Three Dimensional Geometry Ex 13(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Exercise 13(c)

Question 1.
State which of the following statements are true (T) or false (F):
(a) The line \(\frac{x-1}{2}=\frac{y-1}{2}=\frac{z-1}{2}\) pass through the origin.
Solution:
True

(b) The lines \(\frac{x+2}{-k}=\frac{y-3}{k}=\frac{z+4}{k}\) and \(\frac{x-4}{-4}=\frac{y-3}{k}=\frac{z+1}{2}\) are perpendicular every value of k.
Solution:
True

(c) The line \(\frac{x+5}{-2}=\frac{y-3}{1}=\frac{z-2}{3}\) lies on the plane x – y + z + 1 = 0
Solution:
False

(d) The line \(\frac{x-2}{3}=\frac{1-y}{4}=\frac{5-z}{1}\) is parallel to the plane 2x – y – 2z = 0
Solution:
False

(e) The line \(\frac{x+3}{-1}=\frac{y-2}{3}=\frac{z-1}{4}\) is perpendicular to the plane 3x – 3y + 3z – 1 = 0
Solution:
False

Question 2.
Fill in the blanks by choosing the correct alternative from the given ones:
(a)

[parallel, perpendicular, coincident]
Solution:
perpendicular.

(b) The line passing through (-1, 0, 1) and perpendicular to the plane x + 2y + 1 = 0 is _____.

Solution:
\(\frac{x+1}{1}=\frac{y}{2}=\frac{z-1}{0}\)

(c) The line \(\frac{x+1}{2}=\frac{y-6}{1}=\frac{z-4}{0}\) is _____. [parallel to x-axis, perpendicular to y-axis, perpendicular to z-axis]
Solution:
perpendicular to. z-axis

(d) If the line \(\frac{x-3}{2}=\frac{y+k}{-1}=\frac{z+1}{-5}\) lies on the plane 2x – y + z – 7 = 0; then k = -(2, -1, -2)
Solution:
2

(e) If l, m, n be d.cs. of a line, then the line is perpendicular to the plane x – 3y + 2z + 1 = 0 if _____. [(i) l = 1, m = -3, n = 2, (ii) \(\frac{l}{1}=\frac{m}{-3}=\frac{n}{2}\) , (iii) l – 3m + 2n = 0]
Solution:
\(\frac{l}{1}=\frac{m}{-3}=\frac{n}{2}\)

Question 3.
Find the equation of lines joining the points.
(i) (4, -6, 1) and (0, 3, -1)
Solution:
Equation of the line joining the points (4, -6, 1) and (0, 3, -1) is

(ii) (a, a, a) and (a, 0, a)
Solution:
Equation of the line joining the points (a, a, a) and (a, 0, a) is

(iii) (2, 1, 3) and (4, -2, 5).
Solution:
Equation of the line joining the points (2, 1, 3) and (4, -2, 5) is

Question 4.
Write the symmetric form of equation of the following lines:
(i) x-axis
Solution:
D.cs. of x-axis are < 1, 0, 0 >.
x-axis passes through the origin.
So the equation of x-axis in symmetrical form is
\(\frac{x-0}{1}=\frac{y-0}{0}=\frac{z-0}{0}\)

(ii) y = b, z = c
Solution:
Given line in unsymmetrical from is y = b, z = c
⇒ y – b = 0 and z – c = 0.
The straight line is parallel to x-axis.
D.rs. of the straight line are < 0, 0, k >.
So the equation of the line is
\(\frac{y-b}{0}=\frac{z-c}{0}=\frac{x}{k}\)

(iii) ax + by + d = 0, 5z = 0
Solution:
Given lines ax + by + d = 0, 5z = 0

(iv) x – 2y = 3, 2x + y – 5z = 0;
Solution:
Given straight line is x – 2y – 3 = 0 … (1)
and 2x + y – 5z = 0 … (2)
Putting z = 0 in (1) and (2) we get x – 2y – 3 = 0 and 2x + y = 0.
Solving we get y = -2x and x + 4x – 3 = 0

(v) 4x + 4y – 5z – 12 = 0, 8x + 12y – 13z = 32;
Solution:
Given straight line in unsymmetrical form is
4x + 4y – 5z – 12 = 0 … (1)
8x + 12y – 13z – 32 = 0 … (2)
Putting z = 0 in (1) and (2) we get
4x + 4y – 12 = 0 ⇒ x + y – 3 =0
8x + 12y – 32 = 0 ⇒ 2x + 3y – 8 = 0
Solving we get

(vi) 3x – 2y + z = 1, 5x + 4y – 6z = 2
Solution:
Given straight line is
3x – 2y + z – 1 = 0 … (1)
and 5x – 4y + 6z – 2 = 0 … (2)
Putting x = 0 in (1) and (2) we get

Question 5.
(a) Obtain the equation of the line through the point (1, 2, 3) and parallel to the line x – y + 2z – 5 = 0, 3x + y + z = -6
Solution:
Equation of the straight line through

(b) Find the equation of the line through the point (3, -1, 2) and parallel to the planes x + y + 2z – 4 = 0 and 2x – 3y + z + 3 = 0
Solution:
Equation of the straight line through the point (3, -1, 2) is

Question 7.
(a) Show that the line passing through the points (a₁, b₁, c₁) and (a₂, b₂, c₂) passes through the origin, if a₁a₂ + b₁b₂ + c₁c₂ = p₁p₂, where p₁ and p₂ are distances of the points from origin.
Solution:
The equation of the line passing through the points (a₁, b₁, c₁) and (a₂, b₂, c₂) is

(b) Prove that the lines x = az + b, y = cz + d and x = a₁z + b₁, y = c₁z + d₁ are perpendicular if aa₁ + cc₁ + 1 = 0.
Solution:
Given lines are
x – az – b = 0 = y – cz – d … (1)
and x – a₁z – b₁ = 0 and < l₂, m₂, n₂ > … (2)
Let < l₁, m₁, n₁ > and < l₂, m₂, n₂ > be the d.cs. of the lines (1) and(2)

D.rs. of the two lines are < a, c, 1 > and < a₁, c₁, 1 >.
If the lines are perpendicular then the sum of product of d.rs. is zero.
So aa₁ + cc₁ + 1 = 0 (Proved)

Question 8.
Find the points of intersection of the line \(\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{-1}\) and the plane 2x + y + a = 9.
Solution:
Given line is \(\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{-1}\) = r (say)
∴ Any point on (1) is (r + 1, 3r – 2, -r + 1)
If it lies on the plane 2x + y + z – 9 = 0 then
2 (r + 1) + 3r – 2 + (-r + 1) – 9 = 0
or, 2r + 3r – r + 2 – 2 + 1 – 9 = 0
or, 4r = 8, or, r = 2
∴ The point of intersection is (3, 4, -1).

Question 9.
Find the coordinates of the point where the line joining (3, 4, -5) and (2, -3, 1), meets the plane 2x + y + z – 7 = 0.
Solution:
The straight line joining the points (3, 4, -5) and (2, -3, 1) is
\(\frac{x-3}{2-3}=\frac{y-4}{-3-4}=\frac{z+5}{1+5}\)
or, \(\frac{x-3}{-1}=\frac{y-4}{-7}=\frac{z+5}{6}\) = r (say)
Any point on the line is
(-r + 3, -7r + 4, 6r – 5)
If this point is the point of intersection of the line with the plane 2x + y + z – 7 = 0 then
2 (-r + 3) + (-7r + 4) + 6r – 5 – 7 = 0
or, -2r + 6 – 7r + 4 + 6r – 12 = 0
or, -3r = 2 or, r = \(\frac{-2}{3}\)
∴ The point of intersection is
\(\left(\frac{11}{3}, \frac{26}{3}, \frac{-27}{3}\right) \text { i.e., }\left(\frac{11}{3}, \frac{26}{3},-9\right)\).

Question 10.
(a) Find the distance of the point (-1, -5, -10) from the point of intersection of the line \(\frac{x-2}{2}=\frac{y+1}{4}=\frac{z-2}{12}\) and the plane x – y + z = 5.
Solution:
Given line is
\(\frac{x-2}{2}=\frac{y+1}{4}=\frac{z-2}{12}\) = z
Any point on (1) is (2r + 2, 4r – 1, 12r + 2).
If this point is the point of intersection of the line with the plane
x – y + z = 5
then 2r + 2 – 4r + 1 + 12r + 2 = 5
or, 10r = 0, or, r = 0
The point of intersection is (2, -1, 2).
Distance between the points (-1, -5, -10) and the point of intersection of the given line and plane.
= \(\sqrt{9+16+144}=\sqrt{169}\) = 13

(b) Find the image of the point (2, -1, 3) in the plane 3x – 2y + z – 9 = 0
Solution:

Let A = (2, -1, 3)
Let B be the image point of A with respect to the plane
3x – 2y + z – 9 = 0 … (1)
Then AB is normal to the plane.
Again let C be the point of intersection of the line with the plane (1).
Again as B is the image point of A then C must be the mid-point of AB.
Now d.rs. of AB are < 3, -2, 1 > because AB is perpendicular to the plane.
Eqn. of the line AB is

Question 11.
Prove that the lines, \(\frac{x+3}{2}=\frac{y+5}{3}=\frac{z-7}{-3}\) and \(\frac{x+1}{4}=\frac{y+1}{5}=\frac{z+1}{-1}\) are coplanar.
Find the equation of the plane containing them.
Solution:
Given lines are

Two lines are co-planar if either they are parallel or intersecting. Now the line (1) and (2) are not parallel because their d.rs. are not proportional. So we shall show that they are intersecting.
Any point on (1) is (2r₁ – 3, 3r₁ – 5, -3r₁ + 7)
Any point on (2) is (4r₂ – 1, 5r₂ – 1, -r₂ – 1)
If the lines are intersecting then for some values of r₁ and r₂.
2r₁ – 3 = 4r₂ – 1 … (3)
3r₁ – 5 = 5r₂ – 1 … (4)
-3r₁ + 7 = -r₂ – 1 … (5)
From (3) we get r₁ = \(\) = 2r₂ + 1
Putting it in (4) we get 6r₂ + 3 – 5 = 5r₂ – 1
or, r₂ = 1. Again r₁ = 3
With these values r₁ = 3, r₂ = 1
We see that eqn. (5) is satisfied. So the straight lines are intersecting. Hence they are coplanar.
The equation of the plane containing the line (1) is:
a (x + 3) + b (y + 5) + c (z – 7) = 0 … (6)
where 2a + 3b – 3c = 0 … (6)
If the plane (6) contains the line (2) then
4a + 5b – c = 0 … (8)
Solving (7) and (8) we get

Equation of the plane is
6 (x + 3) – 5 (y + 5) – 1 (z – 7) = 0
or, 6x – 5y – z = 0

Question 12.
Prove that the lines \(\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}\) and 3x – 2y + z + 5 = 0 = 2x + 3y + 4z – 4 are co-planar.
Solution:
Given lines are
\(\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}\) = r (say) … (1)
and 3x – 2y + z + 5 = 0
= 2x + 3y + 4z – 4 … (2)
Any point on (1) and (2) are coplanar if they are either parallel or intersecting. If the line are intersecting then
3 (3r – 4) – 2 (5r – 6) + (-2r + 1) + 5 = 0 … (3)
and 2 (3r – 4) + 3 (5r – 6) + 4 (-2r + 1) – 4 = 0 … (4) are consistent.
Solving (3) we get
9r – 12 – 10r + 12 – 2r + 1 + 5 = 0
or, -3r + 6 = 0 or, r = 2
For r = 2, eqn (4) is satisfied. Thus the lines are intersecting and hence they are co-planar. (Proved)

Question 13.
Show that the lines 7x – 4y + 7z + 16 = 0 = 4x + 3y – 2z + 3 and x – 3y + 4z + 6 = z – y + z + 1 intersect. Find the coordinates of their point of intersection and equation of the plane containing them.
Solution:
Let < l₁, m₁, n₁ > and < l₂, m₂, n₂ > be the d.cs. of the lines.
7x – 4y + 7z + 16 = 0 = 4x + 3y – 2z + 3 … (1)
and x – 3y + 4z + 6 = 0 = x – y + z + 1 … (2)
Then 7l₁ – 4m₁ + 7n₁ = 0
4l₁ + 3m₁ – 2n₁ = 0

Question 14.
Show that the line joining the points (0, 2, -4) and (-1 , 1, -2) and the lines joining the points (-2, 3, 3) and (-3, -2, 1) are co-planar. Find their point of intersection.
Solution:
The eqn. of the line joining the points (0, 2, -4) and (-1, 1, -2) is

The lines (1) and (2) are coplanar if either they are parallel or intersecting. These lines are not parallel. So we have to prove that they are intersecting.
Any point on (1) is (-r₁, -r₁ + 2, 2r₁ – 4)
Any point on (2) is (-r₂ – 2, -5r₂ + 3, -2r₂ + 3)
If two lines are intersecting then for some r₁ and r₂
-r₁ = -r₂ – 2 … (1)
-r₁ + 2 = -5r₂ + 3 … (2)
2r₁ – 4 = -2r₁ + 3 … (3)
From (3), r₁ = r₂ + 2

Question 15.
Show that the lines x – mz – a = 0 = y – nz – b and x – m’z’ – a’ = 0 = y – n’z’ – b’ intersect, if (a – a’) (n – n’) = (b – b’) (m – m’).
Solution:
Given lines are
x – mz – a = 0 = y – nz – b … (1)
and x – m’z’ – a’ = 0 = y – n’z’ – b … (2)
Putting z = 0 in (1) we get x = a and y = b.
So (a, b, 0) is a point on (1).
Again putting z = 0 in (2) we get x = a’, y = b’.
So (a’, b’, 0) is a point on (2).
Let < L₁, M₁, N₁ > and < L₂, M₂, N₂ > be the d.cs. of the lines (1) and (2).
Then L₁ – mN₁ = 0, M₁ – nN₁ = 0

or, n (a’ – a) + b (m – m’)
= n’ (a’ – a) + b (m – m’)
⇒ (a – a’) (n – n’) = (b – b’) (m – m’) (Proved)

Question 16.
Proved that the line \(\frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-3}{1}\) lies on the plane 7x + 5y + z = 0
Solution:
Given line is
\(\frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-3}{1}\) = r (say) … (1)
Any point on (1) is (2r + 1, -3r – 2, r + 3)
The straight line lies on the plane 7x + 5y + z = 0 … (2)
if every point of the line lies on (2).
Now 7 × (2r + 1) + 5 (-3r -2) + (r + 3)
= 14r + 7 – 15r – 10 + r + 3 = 0
Thus the point (2r + 1, -3r – 2, r + 3) lies on (2).
Hence the straight line lies on the plane. (Proved)

Question 17.
(a) Find the angle between the plane x + y + 4 = 0 and the line \(\frac{x+3}{2}=\frac{y-1}{1}=\frac{z+4}{-2}\).
Solution:

(b) Find the angle between the plane 4x + 3y + 5z – 1 = 0 and the line \(\frac{x+3}{2}=\frac{y-1}{3}=\frac{z+4}{6}\).
Solution:
Given plane and the line have equations
4x + 3y + 5z – 1 = 0 … (1)

Question 18.
(a) Find the equation of the line passing through the point (1, 0, -1) and intersecting the lines x = 2y = 2z; 3x + 4y – 1 = 0 = 4x + 5z – 2.
Solution:
Given lines are x = 2y = 2z … (1)
and 3x + 4y – 1 = 0 = 4x + 5z – 2 … (2)
Any plane containing the line (1)
i.e., x – 2y = 0 and y – z = 0 is
x – 2y + k₁ (y – z)= 0 = 0
or, x + (k₁ – 2) y – k₁z = 0
If it passes through the point (1, 0, -1) then 1 + k₁ = 0 or, k₁ = -1
The plane containing the line (1) and passing through the point (1, 0, -1) is x – 3y + z = 0
Again any plane containing the line (2) is
3x + 4y – 1 + k₂ (4x + 5z – 2) = 0
or, (3 + 4k₂) x + 4y + 5k₂z – (2k₂ + 1) = 0
If it passes through the point (1, 0, -1) then
3 + 4k₂ – 5k₂ – 2k₂ – 1 = 0
or, 3k₂ = 2 or, k₂ = \(\frac{2}{3}\)
The equation of the plane through the line (2) and passing through (1, 0, -1) is

(b) A line with direction ratios < 2, 1, 2 > meets each of the lines x = y + a = z and x + a = 2y = 2z. Find the coordinates of the points of intersection.
Solution:
Given lines are
x = y + a = z and x + a = 2y = 2z
These can be written in symmetrical form as
\(\frac{x}{1}=\frac{y+a}{1}=\frac{z}{1}\) = r₁ (say)
and \(\frac{x+a}{2}=\frac{y}{1}=\frac{z}{1}\) = r₂ (say)
Any point on (1) is (r₁, r₁ – a, r₁)
Any point on (2) is (2r₂ – a, r₂, r₂)
Suppose that the line meets the lines (1) and (2) at P and Q respectively.
Let P = (r₁, r₁ – a, r₁), Q = (2r₂ – a, r₂, r₂)
D.rs. of PQ are
< r₁ – 2r₂ + a, r₁ – r₂ – a, r₁ – r₂ >
But given that d.rs. are < 2, 1, 2 >.
So \(\frac{r_1-2 r_2+a}{2}=\frac{r_1-r_2-a}{1}=\frac{r_1-r_2}{2}\)
From the 1st two ratios we get
r₁ – 2r₂ + a = 2r₁ – 2r₂ – 2a ⇒ r₁ = 3a
From the last two ratios we get
2r₁ – 2r₂ – 2a = r₁ – r₂
⇒ r₁ = r₂ + 2a ⇒ 3a = r₂ + 2a ⇒ r₂ = a
∴ P (3a, 2a, 3a), Q = (a, a, a)
∴ The co-prdinates of the points of intersection and (3a, 2a, 3a) and (a, a, a).

Question 19.
Obtain the co-ordinates of the foot of the perpendicular drawn from the point (3, -1, 11) to the line \(\frac{x}{2}=\frac{y-2}{3}=\frac{z-3}{4}\). Obtain the equation of the perpendicular also.
Solution:

Let P be the given point (3, -1, 11).
Draw PM perpendicular from P onto the straight line.
Any point on (1) is (2λ, 3λ + 2, 4λ + 3)
Let M = (2λ, 3λ + 2, 4λ + 3)
D.rs. of PM are 2λ – 2, 3λ + 3, 4λ – 8
As PM is perpendicular to the line then
(2λ – 3) . 2 +3 (3λ + 3) + (4λ – 8) . 4 = 0
or, 4λ – 6 + 9λ + 9 + 16λ – 32 = 0
or, 29λ – 29 = 0 or, λ = 1
∴ The foot of the perpendicular is (2, 5, 7)
Equation of the perpendicular line is
\(\frac{x-3}{2-3}=\frac{y+1}{5+1}=\frac{z-11}{7-11}\)
or, \(\frac{x-3}{1}=\frac{y+1}{-6}=\frac{z-11}{4}\)

Question 20.
Find the perpendicular distance of the point (-1, 3, 9) from the line \(\frac{x-13}{5}=\frac{y+8}{-8}=\frac{z-31}{1}\).
Solution:
Let P be the point (-1, 3, 9).
Suppose that M is the foot of the perpendicular drawn from P onto the straight line.
\(\frac{x-13}{5}=\frac{y+8}{-8}=\frac{z-31}{1}\) = λ (say)
Let M = (5λ + 13, -8λ – 8, λ + 31)
D.rs. of PM are
< 5λ + 14, -8λ – 11, λ + 22 >
As PM is perpendicular to the line (1) then
5 (5λ + 14) – 8 (-8λ – 11) + λ + 22 = 0
or, 25λ + 64λ + λ + 70 + 88 + 22 = 0
or, 90λ = -180 or, λ = -2
Thus M = (3, 8, 29)
Distance PM = \(\sqrt{(3+1)^2+(8-3)^2+(29-9)^2}\)
= \(\sqrt{16+25+400}\) = \(\sqrt{441}\) = 21

Question 21.
Find the distance of the point (1, -2, 3) from the plane x – y + z = 5, measured parallel to the line \(\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}\).
Solution:
Let P be the point (1, 2, 3). Draw the straight line PM parallel to the line

Question 22.
Find the distance of the point (1, -1, -10) from the line \(\frac{x-4}{1}=\frac{y+3}{-4}=\frac{z+1}{7}\) measured parallel to the line \(\frac{x+2}{2}=\frac{y-3}{-3}=\frac{z-4}{8}\).
Ans.
Let P be the point (1, -1, -10). Equation of the line through P parallel to the line

∴ Distance of the point (1, -1, -10) from the given line is √308.

Question 23.
Find the equation of plane through the point (2, 0, -3) and containing the line 3x + y + z – 5 = 0 = x – 2y + 4z + 4
Solution:
Any plane containing the line
3x + y + z – 5 = 0 = x – 2y + 4z + 4
3x + y + z – 5 + k (x – 2y + 4z + 4) = 0
or, (3 + k) x + (1 – 2k) y + (1 + 4k) z + (4k – 5) = 0 … (1)
If this plane contains the point (2, 0, -3) then
2 (3 + k)² + (1 – 2k) . 0 + (1 + 4k) . (-3) + 4k – 5 = 0
⇒ 6 + 2k – 3 – 12k + 4k – 5 = 0
⇒ -6k – 2 = 0 ⇒ k = –\(\frac{1}{3}\)
Required plane is
\(\left(3-\frac{1}{3}\right) x+\left(1+\frac{2}{3}\right) y+\left(1-\frac{4}{3}\right) z+\left(-\frac{4}{3}-5\right)\) = 0
⇒ 8x + 5y – z – 19 = 0

Question 24.
Find the equation of the plane containing the line x + 2 = 2y – 1 = 3z and parallel to the line x = 1 – 5y = 2z – 7. Also find the shortest distance between the two lines.
Solution:
Given line is x + 2 = 2y – 1 = 3z
[x – 2y + 3 = 0
2y – 3z – 1 = 0] … (1)
Any plane containing the line (1) is
(x – 2y + 3) + k (2y – 3z – 1) = 0
or, x + (2k – 2) y – 3kz + (3 – k) = 0… (2)
Again given that the plane (2) is parallel to the line
x = 1 – 5y = 2z – 7
⇒ \(\frac{x}{10}=\frac{y-\frac{1}{5}}{-2}=\frac{z-\frac{7}{2}}{5}\) … (3)
D.rs. of the line (3) are < 10, -2, 5 >
If the plane (2) is parallel to the line (3) then the normal plane (2) is perpendicular to the line (3). D.rs. of the normal of the plane(2) are
< 1, 2k – 2, -3k >.
Thus 10 – 2 (2k – 2) – 15 k = 0
⇒ 10 – 4k + 4 – 15k = 0

We have to find the shortest distance between the lines (3) and (4). The shortest distance is the line segment perpendicular to both the lines. Let < l, m, n > be the d.cs. of the shortest distance.
Then 6l + 3m + 2n = 0
10l – 2m+ 5n = 0
Solving we get

Question 25.
Find the equation of the two planes through the origin and parallel to the line \(\frac{x-1}{2}=\frac{y+3}{-1}=\frac{z+1}{-2}\) and at a distance \(\frac{5}{3}\) from it.
Solution:
Equation of the plane through the origin is ax + by + cz = 0 … (1)
If the plane (1) is parallel to the line

⇒ 9b² = 4a² + 4b² + 4c²
⇒ 4a² – 5b² + 4c² = 0 … (4)
From (3) we get b = 2a – 3c.
Putting it in (4) we get
4a² – 5 × 4 (a – c)² + 4c² = 0
⇒ a² – 5a² – 5c² + 10ac + c² = 0
⇒ -4a² – 4c² + 10ac = 0
⇒ 2a² + 2c² – 5ac = 0
⇒ 2a² + 2c² – 4ac – ac = 0
⇒ 2a (a – 2c) – c (a – 2c) = 0
⇒ (a – 2c) (2a – c) = 0

∴ The plane is x – 2y + 2z = 0
Hence the planes are
2x + 2y + z = 0 and x – 2y + 2z = 0.

Question 26.
Find the equation of the straight line perpendicular to the line \(\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-6}{7}\) and lying in the plane x – 2y + 4z – 51 = 0.
Solution:
Let < l, m, n > be the d.cs. of the straight line perpendicular to the line.

D.rs. of the line is < -6, 1, 2 >.
Again let A be the point of intersection of the line with the line (1).
Let A = (3r + 2, 4r – 1, 7r + 6)
Then this point a lies also on the plane (2).
So 3r + 2 – 8r + 2 + 28r + 24 – 51 =0
or, 23r – 23 = 0 or, r = 1
∴ A = (5, 3, 13)
Hence the equation of the required line is
\(\frac{x-5}{-6}=\frac{y-3}{1}=\frac{z-13}{2}\)

Question 27.
Find the shortest distance between the lines \(\frac{x-3}{3}=\frac{y-8}{-1}=\frac{z-3}{1}\) and \(\frac{x+3}{-3}=\frac{y+7}{2}=\frac{z-6}{4}\). Find also the equation of the line of shortest distance.
Solution:
Given lines are

Any point on the line (1) and (2) are P (3 + 3α, 8 – α, 3 + α) and Q (-3 – 3β, -7 + 2β, 6 + 4β) respectively.
D.r.s. of PQ are < 6 + 3α + 3β, 15 – α – 4β >
D.r.s. of the lines are < 3, -1, 1 > and < -3, 2, 4 > respectively.
PQ is perpendicular to the given lines.
∴ 3 (6 + 3α + 3β) – (15 – α – 2β) + 1 (-3 + α – 4β) = 0
and -3 (6 + 3α + 3β) + 2 (15 – α – 2β) + 1 (-3 + α – 4β)
⇒ 18 + 9α + 9β – 15 + α + 2β – 3 + α – 4β = 0
and -18 – 9α – 9β + 30 – 2α – 4β – 12 + 4α – 16β = 0
⇒ 11a + 7b = 0
and -7a – 29b = 0
⇒ a = b = 0
co-ordinates P and Q are (3, 8, 3) and (-3, -7, 6) respectively.
The shortest distance

Question 28.
Show that the shortest distance between the lines x + a = 2y = -12z and x = y + 2a = 6z – 6a is 2a.
Solution:
Given lines are
x + a = 2y = -12z
and x = y + 2a – 6z – 6a

Question 29.
Find the length and equation of the line of shortest distance between the lines 3x – 9y + 5z = 0 = x + y – z and 6x + 8y + 3z – 13 = 0 = x + 2y + z – 3
Solution:
Given lines are
3x – 9y + 5z = 0
x + y – z = 0 … (1)
and 6x + 8y + 3z – 13 = 0
x + 2y + z – 3 = 0 … (2)
Let us consider the line (1)
Now z = x + y
∴ 3x – 9y + 5 ( x + y) = 0
⇒ 8x – 4y = 0 ⇒ 2x = y
Again y = z – x
∴ 3x – 9 (z – x) + 5z = 0
⇒ 12x – 4z = 0
⇒ 3x = z
∴ 6x = 3y = 2z

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 13 Three Dimensional Geometry Ex 13(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Exercise 13(a)

Question 1.
Fill in the blanks in each of the following questions by choosing the appropriate answer from the given ones.
(a) The number of lines making equal angles with coordinate axes is _______. [1, 2, 4, 8]
Solution:
8

(b) The length of the projection of the line segment joining (1, 3, -1) and (3, 2, 4) on z-axis is _______. [1, 3, 4, 5]
Solution:
5

(c) If a line is perpendicular to z-axis and makes an angle measuring 60° with x-axis, then the angle it makes with y-axis measures _______. [30°, 60°, 90°, 120°]
Solution:
30°

(d) If the distance between the points (-1, -1, z) and (1, -1, 1) is 2 then z = _______. [1, √2, 2, 0]
Solution:
1

Question 2.
Which of the following statements are true (T) or false (F):
(a) The line through (1, -1, 2) and (-2, -1, 2) is always perpendicular to z-axis.
Solution:
True

(b) The line passing through (0, 0, 0) and (1, 2, 3) has direction cosines (-1, -2, -3)
Solution:
False

(c) if l, m, n be three real numbers proportional to the direction cosines of a line L, then l² + m² + n² = 1.
Solution:
False

(d) If α, β, γ be any three arbitrary angles then cos α, cos β, cos γ can always be considered as the direction cosines of a line.
Solution:
False

(e) If two lines are perpendicular to a third line, then the direction ratios of the two lines are proportional.
Solution:
False

Question 3.
(a) Show that the points (3, -2, 4), (1, 1, 1) and (-1, 4, -1) are collinear.
Solution:
Let A = (3, -2, 4), B = (1, 1, 1) and C = (-1, 4, -2)
D. rs of AB are < -2, 3, -3 >
D. rs of BC are < -2, 3, -3 >
As D.rs of AB are same as d.rs of BC it follows that A, B, C lie on the same straight line.
So the points are collinear. (Proved)

(b) Show that points (0, 1, 2), (2, 5, 8), (5, 6, 6) and (3, 2, 0) form a parallelogram.
Solution:
Let A = (0, 1, 2), B = (2, 5, 8), C = (5, 6, 6), D = (3, 2, 0)

∴ BC = AD
Thus the opposite sides of the quadrilateral ABCD are equal, hence it is a parallelogram.

Question 4.
(a) Find the co-ordinates of the foot of the perpendicular from the point (1, 1, 1) on the line joining (1, 4, 6) and (5, 4, 4).
Solution:

Let P = (1, 1, 1), A = (1, 4, 6) and B = (5, 4, 4)
Let Q be the foot of the perpendicular drawn from P on AB. Suppose that Q divides AB into the ratio m:n.

⇒ 4 (4m) – 2 (3m + 5n) = 0
16m – 6m – 10n = 0
⇒ 10m 10n = 0
⇒ m = n
∴ Q = (3, 4, 5)

(b) Find the co-ordinates of the point where the perpendicular from the origin meets the line joining the points (-9, 4, 5) and (11, 0, -1).
Solution:
Let A = (-9, 4, 5) and B = (11, 0, -1)

Let OM be the perpendicular drawn onto the line segment AB. Suppose that M divides AB into the ratio m:n.
Then co-ordinates of

D.rs. of AB are < 20, -4, -6 >
As OM is perpendicular on to AB, then
20 (11m – 9n) – 4 (4n) – 6 (-m + 5n) = 0
⇒ 220m – 180n – 16n + 6m – 30n = 0
⇒ 226m – 226n = 0
⇒ m = n
∴ The ratio is \(\frac{m}{n}=\frac{1}{1}\)
∴ Co-ordinates of M are (1, 2, 2).

(c) Prove that the points P(3, 2, -4), Q (5, 4, -6) and R (9, 8, -10) are collinear.
Solution:
Given that P = (3, 2, -4), Q = (5, 4, -6), R = (9, 8, -10)
D. rs. of PQ are < 2, 2, -2 >
D. rs. of QR are < 4, 4, -4 >
i.e., < 2, 2, -2 >
Thus D.rs. of PQ and QR are same. So P, Q, R lie on the same straight line.
Hence P, Q, R are collinear. (Proved)

(d) If P (1, y, z) lies on the line through (3, 2, -1) and (-4, 6, 3) find y & z.
Solution:
Let A = (3, 2, -1), B = (-4, 6, 3)
Suppose that P (1, y, z) divides AB into the ratio m:n.

Question 5.
(a) If A, B, C, D are the points (6, 3, 2), (3, 5, 7), (2, 3, -1) and (3, 5, -3) respectively, then find the projection of \(\overline{A B} \text { on } \overleftrightarrow{CD}\).
Solution:
Given that
A = (6, 3, 2), B = (3, 5, 7), C = (2, 3, -1), D = (3, 5, -3)

(b) The projections of a line segment \(\overline{OP}\), through origin O, on the coordinate axes are 6, 2, 3. Find the length of the line segment \(\overline{OP}\) and its direction cosines.
Solution:

(c) The projections of a line segment of x, y and z-axis respectively are 12, 4, 3. Find the length and the direction cosines of the line segment.
Solution:
Let the length of the line segment be ‘r’ and suppose that it makes angles α, β, γ with the axes.
Then r cos α = 12, r cos β = 4 and r cos γ = 3

Question 6.
(a) If A, B, C are the points (1, 4, 2), (-2, 1, 2) and (2, -3, 4) respectively then find the angles of the triangle ABC.
Solution:

Given that A = (1, 4, 2), B = (-2, 1, 2) and C = (2, -3, 4)
D.r.s. of AB are < -3, -3, 0 >
D.r.s. of BC are < 4, -4, 2 >
D.r.s. of AC are < 1, -7, 2 >

(b) Find the acute angle between the lines passing through (-3, -1, 0), (2, -3, 1) and (1, 2, 3), (-1, 4, -2) respectively.
Solution:
Let A = (-3, -1, 0), B = (2, -3, 1), C = (1, 2, 3), D = (-1, 4, -2)
D.rs. of AB are < 5, -2, 1 >
D.rs. of CD are < -2, 2, -5 >

(c) Prove that measure of the angle between two main diagonals of a cube is cos^-1\(\frac{1}{3}\).
Solution:

Let OABCDEFG be a cube of side ‘a’. Choose the vertex ‘O’ as origin, the line OA as x-axis, OE as y-axis and OC as z-axis.
Then
A = (a, 0, 0), B = (a, 0, a), C = (0, 0, a), D = (0, a, a), E = (0, a, 0), F = (a, a, 0) and G = (a, a, a)
The main diagonals are OG and BE
D.rs. of OG are < a, a, a >.

(d) Prove that measure of the angle between the diagonal of a face and the diagonal of a cube, drawn from a vertex is cos^-1\(\sqrt{\frac{2}{3}}\).
Solution:
See the figure of (c)
Consider the face OABC.
Let us find the angle between AC and AD.
D.rs. of AC are < -a, 0, a >

(e) Find the angle which a diagonal of a cube makes with one of its edges.
Solution:
See the figure of (c).
Let us find the angle between the edge AB and diagonal AD.

(f) Find the angle between the lines whose dcs. l, m, n are connected by the relation, 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0
Solution:
Given that 3l + m + 5n = 0 … (1)
6mn – 2nl + 5lm = 0 … (2)
From (1) we get
n = –\(\frac{3 l+m}{5}\)
Putting it in (2) we get
(6m – 2l) . (-\(\frac{3 l+m}{5}\)) + 5lm = 0
⇒ -18lm + 6l² – 6m² + 2lm + 25lm = 0
⇒ 6l² – 6m² + 9lm = 0
⇒ 2l² – 2m² + 3lm = 0
⇒ 2l² + 4lm – lm – 2m² = 0
⇒ 2l (l + 2m) – m (1 + 2m)
⇒ (l + 2m) (2l – m) = 0
⇒ l + 2m = 0 or, 2l – m = 0

Case (i) Let l + 2m = 0

Case (ii) Let 2l – m = 0

Question 7.
Show that measures of the angles between the four diagonals, of a rectangular paralle-lopiped whose edges are a, b, c are cos^-1\(\left(\frac{a^2 \pm b^2 \pm c^2}{a^2+b^2+c^2}\right)\).
Solution:

Let OABCDEFG be a rectangular parallelopiped whose edges are a, b, c.
Choose O as origin, OA as x-axis, OE as y-axis and OC as z-axis.
Then A = (a, 0, 0), B = (a, 0, c), C = (0, 0, c), D = (0, b, c), E = (0, b, 0), F = (a, b, 0), G = (a, b, c)
The four diagonals are OG, EB, AD and CF.
D. rs. of OG are < a, b, c >
D. rs. of EB are < a, -b, c >
D. rs. of AD are < -a, b, c >
D. rs. of CF are < a, b, -c >
Angle between OG and EB.

Similarly find the angles between the other diagonals. Thus the angles between the four diagonals are cos^-1\(\left(\frac{a^2 \pm b^2 \pm c^2}{a^2+b^2+c^2}\right)\).

Question 8.
If l₁, m₁, n₁ and l₂, m₂, n₂ are the direction cosines of two mutually perpendicular lines show that the d.cs. of the line perpendicular to both of them are m₁n₂ – n₁m₂, n₁l₂ – l₁n₂, l₁m₂ – m₁l₂
Solution:
Let < l₁, m₁, n₁ > and < l₂, m₂, n₂ > be the d.cs. of two mutually perpendicular straight lines.
Then l₁l₂ + m₁m₂ + n₁n₂ = 0 … (1)
Let < l, m, n > be the d.cs. of the straight line perpendicular to the above lines.
Then ll₁ + mm₁ + nn₁ = 0 … (2)
ll₂ + mm₂ + nn₂ = 0 … (3)
Solving (2) and (3) for l, m, n we get

Odisha State Board BSE Odisha 10th Class Physical Science Solutions Chapter 8 ବିଦ୍ୟୁତ୍ Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Physical Science Solutions Chapter 8 ବିଦ୍ୟୁତ୍

ପ୍ରଶ୍ନ 1 ରୁ 4 ମଧ୍ୟରେ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନ ପାଇଁ ଦିଆଯାଇଥ‌ିବା ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।

Question 1.
ଖଣ୍ଡିଏ ତାରର ପ୍ରତିରୋଧ ହେଉଛି R । ଏହି ତାରକୁ ପାଞ୍ଚଟି ସମାନ ଭାଗରେ ବିଭକ୍ତ କରାଗଲା ଏବଂ ଏଗୁଡ଼ିକୁ ସମାନ୍ତରାଳ ସଂଯୋଗ କରାଗଲା । ଏହି ସଂଯୋଗର ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ R’ ହେଲେ, R/R’ ହେଲେ
(a) 1/25
(b) 1/5
(c) 5
(d) 25
Answer:
(d) 25

Question 2.
ନିମ୍ନୋକ୍ତ ପଦମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ବିଦ୍ୟୁତ୍ ପାଓ୍ବାର ସୂଚାଉ ନାହିଁ ?
(a) I²R
(b) IR²
(c) VT
(d) V²/R

Question 3.
220 V ଓ 100 W ଲେଖାଥ‌ିବା ଗୋଟିଏ ବଲ୍‌ବକୁ 110 V ଲାଇନ୍‌ରେ ଲଗାଇଲେ ପାୱାର ହେବ
(a) 100W
(b) 75 W
(c) 50 W
(d) 25 W
Answer:
(d) 25 W

Question 4.
ଏକା ବସ୍ତୁରୁ ତିଆରି ସମାନ ଦୈର୍ଘ୍ୟ ଓ ସମାନ ବ୍ୟାସ ବିଶିଷ୍ଟ ଦୁଇଟି ପରିବାହୀ ତାରକୁ ଯଥାକ୍ରମେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ଓ ସମାନ୍ତରାଳ ସଂଯୋଗ କରାଗଲା । ଉଭୟ କ୍ଷେତ୍ରରେ ବିଭବାନ୍ତର ସମାନ ହେଲେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ଓ ସମାନ୍ତରାଳ ସଂଯୋଗରେ ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ତାପର ଅନୁପାତ
(a) 1:2
(b) 2:1
(c) 1 : 4
(d) 4:1
Answer:
(c) 1 : 4

Question 5.
ପରିପଥର ଦୁଇଟି ବିନ୍ଦୁ ମଧ୍ୟରେ ବିଭବାନ୍ତର ମାପିବା ପାଇଁ ଭୋଲ୍‌ଟମିଟର କେମିତି ସଂଯୋଗ କରାଯାଏ ?
Answer:
ପରିପଥ ସହ ସମାନ୍ତରଭାବେ ଦୁଇଟି ବିନ୍ଦୁ ମଧ୍ୟରୁ + ପାର୍ଶ୍ଵ ବିନ୍ଦୁକୁ ଭୋଲଟମିଟର + ଅଗ୍ରସହ ଏବଂ ପରିପଥର ଅନ୍ୟ ଏକ ବିଯୁକ୍ତ (–) ଅଗ୍ରଥ‌ିବା ବିନ୍ଦୁକୁ ଭୋଲ୍‌ମିରର ବିଯୁକ୍ତ ଅଗ୍ରସହ ସମାନ୍ତରଭାବେ ସଂଯୁକ୍ତ କରାଯାଏ ।

Question 6.
ଖଣ୍ଡିଏ ତମ୍ବା ତାରର ବ୍ୟାସ 0.5 mm ଓ ପ୍ରତିରୋଧ 1.6 × 10^-8Ω m । 10 Ω ପ୍ରତିରୋଧ ବିଶିଷ୍ଟ ଏଭଳି ତାରର ଦୈର୍ଘ୍ୟ କେତେ ? ବ୍ୟାସ ଦୁଇଗୁଣ ହେଲେ ପ୍ରତିରୋଧ କେତେ ହେବ ?
Answer:
ଏଠାରେ R = 10 Ω,
d = 0.5 mm,
ପ୍ରତିରୋଧତା (ρ) = 1.6 x 10^-8Ω m
r = \(\frac { d }{ 2 }\) = \(\frac { 0.5 }{ 2 }\) = 0.25 mm = 0.25 x 10^-3 ମିଟର
A = πr² = 3.14 x (0.25 x 10^-3)²ମି². = 1962.50 x 10^-10 m² = 1962 x 10^-8 m²
ଆମେ ଜାଣୁ L = \(\frac { R.A }{ ρ }\) = \(\frac{10 \times 19.625 \times 10^{-8}}{1.6 \times 10^{-8}}\) m = 122.65
R = ρ \(\frac { L }{ A }\) = ρ \(\frac{\mathrm{L}}{\pi r^2}\)Ω, ବ୍ୟାସ = 2 x 2r = 4r ⇒ ବ୍ୟାସାର୍ଦ୍ଧ = \(\frac { 4r }{ 2 }\) = 2r
R = ρ \(\frac{\mathrm{L}}{\pi π(2r)^2}\) = ρ \(\frac{\mathrm{L}}{\pi π4r^2}\) = \(\frac { 1 }{ 4 }\) (ρ \(\frac{\mathrm{L}}{\pi πr^2}\))
ଅର୍ଥାତ୍ ବ୍ୟାସ 2 ଗୁଣ ହେଲେ ପ୍ରତିରୋଧ \(\frac { 1 }{ 4 }\) ଗୁଣ ହେବ।
∴ ପ୍ରତିରୋଧ = \(\frac { 10 }{ 4 }\) = 2 – 5 Ω

Question 7.
ଗୋଟିଏ ପ୍ରତିରୋଧୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ହିଁ ଓ ତହିଁରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ Iର ପରିମାଣ ନିମ୍ନରେ ଦିଆଯାଇଛି ।

V ଓ I ମଧ୍ଯରେ ଗ୍ରାଫ୍‌ଟିଏ ଅଙ୍କନ କରି ପ୍ରତିରୋଧୀର ପ୍ରତିରୋଧ ନିର୍ଣ୍ଣୟ କର ।
Answer:
CF = 6.7 – 3.4 = 3.3 ଅର୍ଥାତ୍ ବିଭବାନ୍ତର ପରିବର୍ତ୍ତନ = 3.3 V
BF = 2 – 1 = 1 ଅର୍ଥାତ୍ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିବର୍ତ୍ତନ = 1A

Question 8.
ଗୋଟିଏ ପ୍ରତିରୋଧୀର ଦୁଇ ପ୍ରାନ୍ତ ସହ ଏକ 12V ବ୍ୟାଟେରୀ ସଂଯୁକ୍ତ ହୋଇଛି । ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ପରିମାଣ 2.5 m ହେଲେ ପ୍ରତିରୋଧୀର ପ୍ରତିରୋଧ ନିର୍ଣ୍ଣୟ କର ।
Answer:
ଏଠାରେ V = 12 V, I= 2.5 mA = 2.5 x 10^-3 A (∵ 1mA = 10^-3 A)
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ R = \(\frac { V }{ I }\) = \(\frac{12 \mathrm{~V}}{2.5 \times 10^{-3} \mathrm{~A}}\) = 4800 Ω
∴ ପ୍ରତିରୋଧୀର ପ୍ରତିରୋଧ = 4800 Ω |

Question 9.
ଏକ 9V ବ୍ୟାଟେରୀ ଗୋଟିଏ 12 Ω ପ୍ରତିରୋଧୀ ସହ ସଂଯୁକ୍ତ । ପ୍ରତିରୋଧୀରେ କେଉଁ ପରିମାଣର ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଉଛି ?
Answer:
ଏଠାରେ R = 12 Ω, V = 9 V, ଓମ୍ବକ ନିପ୍ନମ ଅନୁପାରେ V = IR
⇒ I = \(\frac { V }{ R }\) = \(\frac { 9V }{ 12Ω }\) = 0.75 A

Question 10.
କେତୋଟି 176 Ω ପ୍ରତିରୋଧୀର ସମାନ୍ତରାଳ ସଂଯୋଗ 220V ଲାଇନ୍‌ରୁ 5A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ନେବ ?
Answer:
ଏଠାରେ I = 5A, V = 220 V, R = 176 Ω
ମନେକର xଟି 176 Ω ପ୍ରତିରୋଧୀର ସମାନ୍ତରାଳ ସଂଯୋଗ 220 V ଲାଇନ୍‌ରୁ 5A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବ ।
∴ \(\frac { 1 }{ R }\) = \(\frac { 1 }{ 176 }\) + \(\frac { 1 }{ 176 }\) + …………..x ଟି = \(\frac { x }{ 176 }\) ⇒ R = \(\frac { 176 }{ x }\) Ω
I = \(\frac { V }{ R }\) ⇒ 5 = \(\frac{220}{\frac{176}{x}}\)
⇒ \(\frac { x }{ 176 }\) = \(\frac { 220 }{ 5 }\) ⇒ x = \(\frac { 176×5 }{ 220 }\) = 4
∴ 4 ଟି 176 Ω ପ୍ରତିରୋଧୀ ଅ|ରଣ୍ୟକ |

Question 11.
ତିନୋଟି ପ୍ରତିରୋଧୀ ମଧ୍ୟରୁ ପ୍ରତ୍ୟେକର ପ୍ରତିରୋଧ 6Ω । ଏଗୁଡ଼ିକୁ କିଭଳି ଭାବେ ସଂଯୋଗ କଲେ ସମତ୍ରଳ୍ୟ ପ୍ରତିରୋଧ ତ୍ରେ (i) 9Ω (ii) 4Ω ?
(i) R₁ = R₂ = R₃ = 6Ω
ଏଠାରେ ଦୁଇଟିକୁ ସମାନ୍ତର ସଂଯୋଗକରି ସେମାନଙ୍କର ମିଳିତ ପ୍ରତିରୋଧ ସହିତ ଗୋଟିଏ ପକ୍ତିରେ ସଂଯୋଗ କରାଯିବ ।
ସମାନ୍ତର ସଂଯୋଗ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\)
= \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\) = \(\frac { 2 }{ 6 }\) = \(\frac { 1 }{ 3 }\)Ω
⇒ R = 3Ω
ପଭକ୍ତି ସଂଯୋଗ = 3Ω + 6Ω = 9Ω

(ii) ଦୁଇଟିକୁ ପଙ୍‌କ୍ତିରେ ସଂଯୋଗକରି ପଙ୍‌କ୍ତି ସଂଯୋଗର ମିଳିତ ପ୍ରତିରୋଧ ସହିତ ଅନ୍ୟ ଏକ ସମାନ୍ତର ସଂଯୋଗ କରାଯାଡ |
R₁ = 6 + 6 = 12 Ω, R₂ = 6Ω
ସମାନ୍ତରାଳ ସଂଯୋଗ
(\(\frac { 1 }{ R }\)) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\) = \(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 6 }\) = \(\frac { 1+2 }{ 12 }\) = \(\frac { 1 }{ 4 }\)
⇒ R = 3Ω

Question 12.
220 V ଲାଇନ୍‌ରେ ଲାଗିପାରୁଥିବା କେତେଗୁଡ଼ିଏ ବଲ୍‌ବର ପାଓ୍ବାର ହେଉଛି 10 W । ଯଦି ସର୍ବୋଚ୍ଚ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ 5 A ହୁଏ ତେବେ କେତୋଟି ବଲ୍‌ବକୁ ସେହି ଲାଇନ୍‌ରେ ସମାନ୍ତରାଳ ଭାବେ ସଂଯୋଗ କରାଯାଇପାରିବ ?
Answer:
ଏଠାରେ V = 220 V, P = 10 W, I = 5A
ପ୍ରତ୍ୟେକ ବଲ୍‌ବର ପ୍ରତିରୋଧ (R) = \(\frac{\mathrm{V}^2}{\mathrm{P}}\) = \(\frac{\mathrm{(220)}^2}{\mathrm{10}}\) = 4840 Ω
ମନେକର xଟି ବଲ୍‌ବ ସମାନ୍ତର ସଂଯୋଗରେ ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ R_eq ।
\(\frac{1}{\mathrm{R}_eq}\) = \(\frac { 1 }{ 4840 }\) + \(\frac { 1 }{ 4840 }\) + ………. ଟି ସଂଖ୍ୟକ = \(\frac { x }{ 4840 }\) ⇒ \(\frac{1}{\mathrm{R}_eq}\) = \(\frac { 4840 }{ x }\) Ω
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁଯାୟୀ, \(\frac{1}{\mathrm{R}_eq}\) = \(\frac { V }{ I }\)
⇒\(\frac { 4840 }{ x }\) = \(\frac { 220 }{ 5 }\) ⇒ x = \(\frac { 4840×5 }{ 220 }\) = 110
∴ 110 ଟି 10 W ବଲ୍‌ବ 220 V ଲାଇନ୍‌ରେ ଲାଗିଲେ 5A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହୁଏ ।

Question 13.
220 V ଲାଇନ୍‌ରେ ଲଗାଯାଇଥିବା ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଚୁଲାରେ ଦୁଇଟି 24 Ω ପ୍ରତିରୋଧ ବିଶିଷ୍ଟ ତାର କୁଣ୍ଡଳୀ ଅଛି । କୁଣ୍ଡଳୀ ଦୁଇଟିକୁ ଅଲଗା ଅଲଗା, ପଙ୍‌କ୍ତିରେ ଓ ସମାନ୍ତର ଭାବେ ବ୍ୟବହାର କଲେ ପ୍ରତି କ୍ଷେତ୍ରରେ କେତେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବ ?
Answer:
(i) ଦୁଇଟି କୁଣ୍ଡଳୀକୁ ଅଲଗା ଅଲଗା ଲଗାଇଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ I = \(\frac { V }{ R }\) = \(\frac { 220V }{ 24Ω }\) = 9.2 Ω

(ii) ଦୁଇଟି କୁଣ୍ଡଳୀକୁ ପଙକ୍ତିରେ ସଂଯୋଗ କଲେ
ମୋଟ ପ୍ରତିରୋଧ (R) = 24 + 24 = 48 Ω, ବିଦ୍ୟୁତ୍ ସ୍ରୋତ (I) = \(\frac { V }{ R }\) = \(\frac { 220 }{ 48 }\) = 4.58 A

(iii) ଦୁଇଟି କୁଣ୍ଡଳୀକୁ ସମାନ୍ତରାଳ ସଂଯୋଗ କଲେ \(\frac { 1 }{ R }\) = \(\frac { 1 }{ 24 }\) + \(\frac { 1 }{ 24 }\) = \(\frac { 1+1 }{ 24 }\) = \(\frac { 2 }{ 24 }\) = \(\frac { 1 }{ 12 }\) ⇒ R = 12
ବିଦ୍ୟୁତ୍ ସ୍ରୋତ (I) = \(\frac { V }{ R }\) = \(\frac { 220 }{ 12 }\) = 18.33 A

Question 14.
ନିମ୍ନୋକ୍ତ ପରିପଥଗୁଡ଼ିକରେ 2 Q ପ୍ରତିରୋଧୀରେ ବ୍ୟବହାର ହେଉଥ‌ିବା ପାୱାରର ତୁଳନା କର ।
(i) 1Ω ଓ 2Ω ପ୍ରତିରୋଧୀ ସହ ଗୋଟିଏ 6V ବ୍ୟାଟେରୀର ପଙ୍‌କ୍ତି ସଂଯୋଗ ଏବଂ
(ii) 12 Ω ଓ 2 Ω ପ୍ରତିରୋଧୀ ସହ ଗୋଟିଏ 4 V ବ୍ୟାଟେରୀର ସମାନ୍ତରାଳ ସଂଯୋଗ ।
Answer:
(i) ପଙ୍‌କ୍ତି ସଂଯୋଗ ହୋଇଥିବାରୁ ମୋଟ ପ୍ରତିରୋଧ R = 1 + 2 = 3Ω
V = 6V, I = \(\frac { V }{ R }\) = \(\frac { 6 }{ 3 }\) = 2A
2 Ω ପ୍ରତିରୋଧୀଦ୍ଵାରା ବ୍ୟବହୃତ ପାଓ୍ବାର (P) = I²R = 2² x 2 = 8 ୱାଟ୍

(ii) 12 Ω2 ଓ 2 Ω ପ୍ରତିରୋଧୀଗୁଡ଼ିକ ସମାନ୍ତରାଳ ସଂଯୋଗ ହୋଇଥିବାରୁ 2Ω ପ୍ରତିରୋଧୀ ପାଇଁ ବିଭବାନ୍ତର 4V |
2 Ω ପ୍ରତିରୋଧୀଦ୍ଵାରା ବ୍ୟବହୃତ ପାୱାର = \(\frac{\mathrm{V}^2}{\mathrm{R}}\) = \(\frac{\mathrm{4}^2}{\mathrm{2}}\) = 8 ୱାଟ୍

Question 15.
ଗୋଟିଏ 100 W – 220 V ଓ ଗୋଟିଏ 60 W – 220 V ବିଦ୍ୟୁତ୍ଵବତୀ ଏକ 220 V ଲାଇନ୍‌ରେ ସମାନ୍ତର ଭାବେ ସଂଯୁକ୍ତ ହୋଇଛି । ଏହା ଲାଇନ୍‌ରୁ କେତେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ନେଉଛି ?
Answer:
ଦ୍ତଇଟି ଚଢା ବ୍ୟତତ୍ବାବ କରୁଥିବା ପାୱାର = 100 W + 60 W = 160 W V = 220 V
ଭୋଲ୍ଟେଜ୍ V = 220 V
P = VI ⇒ 1 = \(\frac { P }{ V }\) = \(\frac { 160 }{ 220 }\) = 0.727 A
∴ ଲାଇନରୁ 0.727 ଏମ୍ପିୟର ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଉଛି ।

Question 16.
କେଉଁଟି ବେଶି ଶକ୍ତି ବ୍ୟବହାର କରେ ? 1 ଘଣ୍ଟା ଚାଲୁଥ‌ିବା ଗୋଟିଏ 250 W ଟିଭି ସେଟ୍ ନା 10 ମିନିଟ୍ ଚାଲୁଥ‌ିବା ଗୋଟିଏ 1200 W ଟୋଷ୍ଟର ?
Answer:
1 ଘଣ୍ଟା ଚାଲୁଥିବା ଗୋଟିଏ 250 W ଟିଭିସେଟ୍ ଖର୍ଚ୍ଚକରୁଥିବା ଶକ୍ତି (W) = Pt
= 250 W x 1h = 250 Wh
10 ମିନିଟ୍ ଚାଲୁଥ‌ିବା ଗୋଟିଏ 1200 W ଟୋଷ୍ଟର = 1200 W x 10 ମିନିଟ୍
= 1200 W x \(\frac { 10 }{ 60 }\)h = 1200 W
∴ ଟିଭି ସେଟ୍‌ଟି ଅଧ୍ଯକ ଶକ୍ତି ବିନିଯୋଗ କରୁଛି ।

Question 17.
ଗୋଟିଏ 8 Ω ହିଟର 2 ଘଣ୍ଟା ଧରି ଲାଇରୁ 15 A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ନିଏ । ହିଟର୍‌ରେ ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ତାପର ହାର ନିର୍ଣ୍ଣୟ କର ।
Answer:
R = 8Ω, t = 2h, I = 15 A
ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ତାପର ହାର = ପାୱାର (ଶକ୍ତି)
H = \(\frac{\mathrm{I}^2 \mathrm{Rt}}{\mathrm{t}}\) = I²R
H = I²R= 15² × 8 = 225 x 8 = 1800 ୱାଗ୍ 31 = 1800 J/sec.
∴ ହିଟର୍‌ରେ ଉତ୍ପନ୍ନ ହେଉଥିବା ତାପର ହାର 1800 J/s |

Question 18.
ବୁଝାଅ :
(a) ବିଦ୍ୟୁତ୍ ବତୀର ଫିଲାମେଣ୍ଟ ପାଇଁ ଟଙ୍ଗଷ୍ଟନ୍ ଧାତୁ କାହିଁକି ବ୍ୟବହାର କରାଯାଏ ?
ଉ :
ଟଙ୍ଗ୍‌ଷ୍ଟନର ତାରର ପ୍ରତିରୋଧ’ବହୁତ ଅର୍ଧ ଏବଂ ଗଳନାଙ୍କ ଉଚ୍ଚ (3410°C) ହେତୁ, ‘ ଏହାକୁ ବିଦ୍ୟୁତ୍ ବତୀର ଫିଲାମେଣ୍ଟ୍‌ ପାଇଁ ବ୍ୟବହାର କରାଯାଏ ।

(b) ପାଉଁରୁଟି ଟୋଷ୍ଟର ଓ ଇସ୍ତ୍ରୀ ଭଳି ବିଦ୍ୟୁତ୍ ତାପନ ସାମଗ୍ରୀରେ କାହିଁକି ଶୁଦ୍ଧ ଧାତୁ ପରିବର୍ତ୍ତେ ମିଶ୍ରଧାତୁ ବ୍ୟବହାର କରାଯାଏ ?
ଉ :
ମିଶ୍ରଧାତୁର ପ୍ରତିରୋଧ ମୂଳ ଧାତୁଗୁଡ଼ିକର ପ୍ରତିରୋଧଠାରୁ ଅଧ‌ିକ ଏବଂ ମିଶ୍ରଧାତୁଗୁଡ଼ିକ ଉଚ୍ଚ ତାପମାତ୍ରାରେ ସହଜରେ ଜାରିତ ହୁଏ ନାହିଁ । ତେଣୁ ପାଉଁରୁଟି ଟୋଷ୍ଟର ଓ ଇସ୍ତ୍ରୀଭଳି ବିଦ୍ୟୁତ୍ ତାପନ ସାମଗ୍ରୀରେ ମିଶ୍ରଧାତୁ ବ୍ୟବହାର କରାଯାଏ ।

(c) ଗୃହ ବିଦ୍ୟୁତ୍ ପରିପଥରେ କାହିଁକି ପଙ୍‌ ସଂଯୋଗ ବ୍ୟବହାର କରାଯାଏ ନାହିଁ ?
ଉ :
ନିମ୍ନଲିଖତ କାରଣଗୁଡ଼ିକ ଯୋଗୁ ଗୃହ ବିଦ୍ୟୁତ୍ ପରିପଥରେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ବ୍ୟବହାର କରାଯାଏ ନାହିଁ ।

• ପଙ୍‌କ୍ତି ସଂଯୋଗ କଲେ ଗୋଟିଏ ଉପକରଣ ଅଚଳ ହୋଇଗଲେ ସମୁଦାୟ ପରିପଥଟି ବିଚ୍ଛିନ୍ନ ହୋଇଯାଏ । ଅନ୍ୟ ଉପକରଣ ଗୁଡ଼ିକ କାର୍ଯ୍ୟ କରେ ନାହିଁ।
• ସମୂହ ପ୍ରତିରୋଧ ଅଧ୍ଯକ ହୋଇଯାଏ ଫଳରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବହୁ ପରିମାଣରେ ହ୍ରାସପାଏ ।
• ପଙ୍‌କ୍ତିରେ ସଂଯୋଗ ଉପକରଣଗୁଡ଼ିକୁ ଏକ ସମୟରେ ବ୍ୟବହାର କରିବାକୁ ପଡ଼ିବ ।
• ଆବଶ୍ୟକ ଅନୁଯାୟୀ ସ୍ଵିଚ୍ ଗୁଡ଼ିକ ମୁଦିତ କିମ୍ବା ମୁକ୍ତ କରିପାରିବା ନାହିଁ ।

(d) ତାରର ପ୍ରତିରୋଧ କିଭଳି ଭାବେ ତା’ର ପ୍ରସ୍ଥଚ୍ଛେଦ କ୍ଷେତ୍ରଫଳ ଉପରେ ନିର୍ଭର କରେ ?
ଉ :
ଆମେ ଜାଣୁ R ∝ \(\frac { 1 }{ A }\)
⇒ R ∝ \(\frac{1}{\pi r^2}\) ⇒R ∝ \(\frac{1}{\mathrm{r}^2}\)
ତାରର ପ୍ରସ୍ଥଚ୍ଛେଦ କ୍ଷେତ୍ରଫଳ କମିଲେ ପ୍ରତିରୋଧ ବଢ଼େ, ପ୍ରସ୍ଥଚ୍ଛେଦ କ୍ଷେତ୍ରଫଳ ବଢ଼ିଲେ ପ୍ରତିରୋଧ ହ୍ରାସପାଏ ।

(e) ବିଦ୍ୟୁତ୍ ପରିବହନ ପାଇଁ ସାଧାରଣତଃ ତମ୍ବା ଓ ଏଲୁମିନିୟମ୍ ତାର କାହିଁକି ବ୍ୟବହାର କରାଯାଏ ?
ଉ :
ତମ୍ବା ଓ ଏଲୁମିନିୟମ୍ ଧାତୁର ପ୍ରତିରୋଧ କମ୍ ହେତୁ ସେଗୁଡ଼ିକୁ ବିଦ୍ୟୁତ୍ ପରିବହନ ପାଇଁ ବ୍ୟବହାର କରାଯାଏ ।

ପ୍ରଶ୍ନବଳୀ ଓ ଉତ୍ତର:

Question 1.
ବିଦ୍ୟୁତ୍ ପରିପଥ କହିଲେ କ’ଣ ତ୍ରଝ୍ ?
Answer:
ଏକ ଅବିଚ୍ଛିନ୍ନ ଓ ମୁଦିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ପଥକୁ ବିଦ୍ୟୁତ୍ ପରିପଥ କୁହାଯାଏ ।

Question 2.
ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଏକକର ସଂଜ୍ଞା ଦିଅ ।
Answer:
ବିଦ୍ୟୁତ୍ ସ୍ରୋତର SI ଏକକ ହେଉଛି ଏମିୟର (A) । ଗୋଟିଏ ପରିବାହୀରେ ପ୍ରତି ସେକେଣ୍ଡରେ l କୁଲମ୍ ଚାର୍ଜ ପ୍ରବାହିତ ହେଉଥିଲେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ ହେବ । ଏମ୍ପିୟର ହେବ ।

Question 3.
କେତୋଟି ଇଲେକ୍‌ଟ୍ରନର ଚାର୍ଜ ସମଷ୍ଟି ଏକ କୁଲମ୍ ହିସାବ କରି ଦେଖାଅ ।
Answer:
ଗୋଟିଏ ଇଲେକ୍‌ଟ୍ରନର ଚାର୍ଜର ପରିମାଣ = 1.6 x 10^-19 C
ମନେକର n ଟି ଇଲେକ୍‌ଟ୍ରନର ଚାର୍ଜ = 1 କୁଲମ୍
⇒ n x 1.6 x 10^-19 C = 1 C
⇒ n = \(\frac{1}{1.6 \times 10^{-19}}\) = \(\frac{10^{19}}{1 \cdot 6}\) = \(\frac{10 \times 10^{18}}{1.6}\) = 6.25 x 10¹⁸ ଇଲେକଟ୍ରନ (6 x 10¹⁸ ପ୍ରାୟ )
∴ 6 x 10⁸ ସଂଖ୍ୟକ ଇଲେକଟ୍ରନ ଚାର୍ଜର ସମଷ୍ଟି 1 କୁଲମ ।

Question 4.
କେଉଁ ଉପାୟରେ ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ସ୍ଥିର ରଖାଯାଇପାରେ ?
Answer:
ବିଦ୍ୟୁତ୍ ସେଲ୍ ବା ବ୍ୟାଟେରୀ ସଂଯୋଗ କଲେ ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ସ୍ଥିର ରଖାଯାଇପାରେ ।

Question 5.
ଦୁଇଟି ବିନ୍ଦୁ ମଧ୍ୟରେ ବିଭବାନ୍ତର 1V କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ପରିବାହୀର ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ 1 କୁଲମ୍ ଚାର୍ଜ ସ୍ଥାନାନ୍ତରଣ ହୋଇ ସମ୍ପାଦିତ କାର୍ଯ୍ୟ 1 ଜୁଲ ହେଲେ ପ୍ରାନ୍ତଦ୍ଵୟ ମଧ୍ଯରେ ବିଭବାନ୍ତର 1 ଭୋଲ୍ଡ ହେବ ।

Question 6.
ଗୋଟିଏ 12V ବ୍ୟାଟେରୀ ମଧ୍ୟଦେଇ 1C ଚାର୍ଜ ପ୍ରବାହିତ ହେବାରେ କେତେ ଶକ୍ତି ଆବଶ୍ୟକ ହୁଏ ?
Answer:
ଏଠାରେ V = 12 V, Q = 1 C
ଶକ୍ତି (W) = V.Q = 12V × 1C = 12 J = 12 ଜୁଲ୍ |

Question 7.
ଗୋଟିଏ ପରିବାହୀର ପ୍ରତିରୋଧ କେଉଁ କେଉଁ କାରକ ଉପରେ ନିର୍ଭର କରେ ?
Answer:
ଗୋଟିଏ ପରିବାହୀର ପ୍ରତିରୋଧ ନିମ୍ନଲିଖୁ କାରକ ଉପରେ ନିର୍ଭର କରେ –

• ପରିବାହୀର ଦୈର୍ଘ୍ୟ (l)
• ପରିବାହୀର ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ (A)
• ପରିବାହୀ ନିର୍ମିତ ପଦାର୍ଥର ପ୍ରତିରୋଧ (p)

Question 8.
ଗୋଟିଏ ବସ୍ତୁରୁ ତିଆରି ଖଣ୍ଡିଏ ମୋଟା ତାର ଓ ଖଣ୍ଡିଏ ସରୁ ତାର ଅଲଗା ଅଲଗା ଭାବେ ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଲାଇନ୍‌ରେ ସଂଯୁକ୍ତ ହେଲେ କେଉଁଥ‌ିରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବେଶି ସହଜ ହେବ ? କାହିଁକି ?
Answer:
(i) ଗୋଟିଏ ବସ୍ତୁରୁ ତିଆରି ଖଣ୍ଡିଏ ମୋଟା ତାର ଓ ଖଣ୍ଡିଏ ସରୁ ତାର ଅଲଗା ଭାବେ ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଲାଇନ୍‌ରେ ସଂଯୁକ୍ତ ହେଲେ ମୋଟା ତାରରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବେଶି ସହଜ ହେବ ।

(ii) କାରଣ ମୋଟା ତାରର ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ ଅଧ‌ିକ ହୋଇଥିବାରୁ ପ୍ରତିରୋଧ କମ୍ । ତେଣୁ ଇଲେକ୍‌ଟ୍ରନ୍‌ ଅଧ୍ଵ ସହଜରେ ଗତି କରିପାରିବ । କିନ୍ତୁ ସରୁ ତାରର ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ କମ୍ ଓ ପ୍ରତିରୋଧ ଅଧ୍ଵ । ତେଣୁ ଇଲେକ୍‌ଟ୍ରନ୍ ତା’ର ପରମାଣୁ ସହ ଧକ୍‌କା ଖାଇ କମ୍ ବେଗରେ ଗତି କରିବ ।

Question 9.
ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଉପାଂଶର ପ୍ରତିରୋଧକୁ ସ୍ଥିର ରଖ୍ ତା’ର ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥ‌ିବା ବିଭବାନ୍ତରକୁ ଅଧା କରି ଦିଆଗଲା । ତା’ ଭିତରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ କିଭଳି ପରିବର୍ତ୍ତିତ ହେବ ?
Answer:
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁଯାୟୀ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରା ଓ ପ୍ରତିରୋଧରେ V ∝ I
ତେଣୁ ବିଭବାନ୍ତର ଅଧା ହେଲେ ତା’ ଭିତରେ ପ୍ରବାହିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ମଧ୍ଯ ଅଧା ହେବ ।

Question 10.
ବିଦ୍ୟୁତ୍ ଟୋଷ୍ଟର ଓ ବିଦ୍ୟୁତ୍ ଇସ୍ତ୍ରୀର କୁଣ୍ଡଳୀଗୁଡ଼ିକୁ କାହିଁକି ବିଶୁଦ୍ଧ ଧାତୁ ବଦଳରେ ମିଶ୍ରଧାତୁରୁ ତିଆରି କରାଯାକଥାଏ ?
Answer:

• ମିଶ୍ରଧାତୁର ପ୍ରତିରୋଧ ମୂଳ ଧାତୁଗୁଡ଼ିକଠାରୁ ଅଧିକ ।
• ମିଶ୍ରଧାତୁ ଉଚ୍ଚ ତାପମାତ୍ରାରେ ସହଜରେ ଜାରିତ ହୁଏ ନାହିଁ ।
• ମିଶ୍ରଧାତୁର ଗଳନାଙ୍କ ଉଚ୍ଚ ହୋଇଥାଏ । ତେଣୁ ବିଦ୍ୟୁତ୍ ଟୋଷ୍ଟର ଓ ବିଦ୍ୟୁତ୍ ଇସ୍ତ୍ରୀରେ କୁଣ୍ଡଳୀଗୁଡ଼ିକ ବିଶୁଦ୍ଧ ଧାତୁ ବଦଳରେ ମିଶ୍ରଧାତୁରେ ତିଆରି କରାଯାଏ ।

Question 11.
ସାରଣୀ ମଧ୍ଯରେ ଦିଆଯାଇଥ‌ିବା ତଥ୍ୟ ବ୍ୟବହାର କରି ଉତ୍ତର ଦିଅ ।
Answer:
(a) ଲୌହ ଓ ପାରଦ ମଧ୍ୟରୁ କେଉଁଟି ଉତ୍ତମ ପରିବାହୀ ?
ଉ :
ଲୌହତ ପ୍ରତିରୋଧୁତା = 10.0 × 10^-8 Ω m
ପାରଦର ପ୍ରତିରୋଧୁତା = 94.0 × 10^-8 Ω m
ଲୌହର ପ୍ରତିରୋଧ ପାରଦର ପ୍ରତିରୋଧ ଠାରୁ କମ୍ । ତେଣୁ ଲୌହ ପାରଦ ଅପେକ୍ଷା ଉତ୍ତମ ପରିବାହୀ ।

(b) କେଉଁ ପଦାର୍ଥଟି ସର୍ବୋତ୍କୃଷ୍ଟ ପରିବାହୀ ?
ଉ :
ରୁପାର ପ୍ରତିରୋଧ ସର୍ବନିମ୍ନ (1-60 x 10^-8 Ωm) । ତେଣୁ ରୁପା ସର୍ବୋତ୍କୃଷ୍ଟ ପରିବାହୀ ।

Question 12.
ଏକ ପରିପଥରେ ଗୋଟିଏ ବ୍ୟାଟେରୀ, 5Ω ପ୍ରତିରୋଧ, 8Ω ପ୍ରତିରୋଧ, 12Ω ପ୍ରତିରୋଧ ଓ ଗୋଟିଏ ପ୍ଲଗ୍ କି ର ପଙ୍‌କ୍ତି ସଂଯୋଗ ହୋଇଛି । ବ୍ୟାଟେରୀରେ ତିନୋଟି 2V ସେଲ୍ ଅଛି । ପରିପଥର ଚିତ୍ର କର ।
Answer:
ଦତ୍ତ ଅନ୍ମପାୟ1 ବିଦ୍ୟୁତପରିପଥ

Question 13.
ପୂର୍ବ ପ୍ରଶ୍ନରେ ଦିଆଯାଇଥିବା ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ମାପିବା ପାଇଁ ଗୋଟିଏ ଏମିଟର୍ ଏବଂ 12Ω ପ୍ରତିରୋଧର ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ମାପିବା ପାଇଁ ଗୋଟିଏ ଭୋମିଟର ଲଗାଯାଇଛି । ଚିତ୍ରଟି କର । ଏମିଟର୍ ଓ ଭୋଲ୍ଟ ମିଟର୍‌ର ପାଠ୍ୟଙ୍କ କେତେ ହେବ ?
Answer:
R₁ = 5Ω, R₂ = 8Ω, R₃ = 12Ω
ମୋଟ ଭୋଲ୍ଟେଜ (V) = 3 x 2 = 6 V
ସମସ୍ର ପଥ ପଡକ୍ରି ସଂଯୋଗ ହୋଚ୍ଚଥିବାରୁ
ମୋଟ୍ ପ୍ରତିରୋଧ (R)
= R₁ + R₂ + R₃
= (5 + 8 + 12) Ω = 25 Ω
ଏମିଟରର ପାଠ୍ୟଙ୍କ (I) = \(\frac { V }{ R }\) = \(\frac { 6 }{ 25 }\) = 0 . 24 A
ଭୋଲ୍ଲମିଟର ପାଠ୍ୟଙ୍କ (V) = IR = 0·24 × 12 = 2.88 V

Question 14.
ନିମ୍ନୋକ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକର ସମାନ୍ତରାଳ ସଂଯୋଗ ହୋଇଛି । ପ୍ରତି କ୍ଷେତ୍ରରେ ସମୂହ ପ୍ରତିରୋଧ କେତେ ହେବ ବିଚାର କର ।
(a) 1Ω ଓ 10⁶Ω

(b) 1Ω, 10³ Ω & 10⁶Ω
R₁ = 1Ω, R₂ = 10⁶ Ω ସମୂହ ପ୍ରତିରୋଧ R |
ସୂତ୍ର ଅନୁଯାୟୀ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\)
\(\frac { 1 }{ R }\) = \(\frac { 1 }{ 1 }\) + \(\frac{1}{\mathrm{R}_6}\) = \(\frac{10^6+1}{10^6}\) = \(\frac { 1000000+1 }{ 1000000 }\) = \(\frac { 100000 }{ 1000000 }\)
⇒ R = \(\frac { 100000 }{ 1000001 }\) = 0.9 Ω
ସମୂହ ପ୍ରତିରୋଧ < 10

(b) R₁ = 1Ω, R₂ = 10³Ω, R₃ = 10⁶Ω
ସମାନ୍ତରାଳ ସଂଯୋଗରେ ସମୂହ ପ୍ରତିରୋଧ = R
ସୂତ୍ର ଅନୁଯାୟୀ ତୁ ତୂ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\) + \(\frac{1}{\mathrm{R}_3}\) = \(\frac { 1 }{ 1 }\) + \(\frac{1}{10^3}\) + \(\frac{1}{10^6}\) Ω

Question 15.
ଗୋଟିଏ 220V ବିଦ୍ୟୁତ୍ ଲାଇନ୍ ସହ ଗୋଟିଏ 100 Ω ବଲ୍‌ବ, ଗୋଟିଏ 50 Ω ଟୋଷ୍ଟର ଓ 500 Ω ଘର ପାଣି ଫିଲ୍ଟର’ ସମାନ୍ତରାଳ ଭାବେ ସଂଯୁକ୍ତ ହୋଇଛି । ସେହି ବିଦ୍ୟୁତ୍ ଲାଇନ୍ ସହ ଗୋଟିଏ ଇସ୍ତ୍ରୀ ମଧ୍ୟ ଲଗାଯାଇଛି । ଇସ୍ତ୍ରୀ ଆବଶ୍ୟକ କରୁଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବଲ୍‌ବ, ଟୋଷ୍ଟର ଓ ଫିଲ୍‌ଟରରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ସମଷ୍ଟିସହ ସମାନ । ଏହି ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ କେତେ ଏବଂ ଇସ୍ତ୍ରୀର ପ୍ରତିରୋଧ କେତେ ?
Answer:
ଗୋଟିଏ ବଲ୍‌ବର ପ୍ରତିରୋଧ R₁ 100 Ω
ଗୋଟିଏ ଟୋଷ୍ଟରର ପ୍ରତିରୋଧ R₂ = 50 Ω
ଗୋଟିଏ ପାଣି ଫିଲ୍ଟଟରର ପ୍ରତିରୋଧR₃ = 500 N
ସମୂହ ପ୍ରତିରୋଧ = R
ସୂତ୍ର ଅନୁଯାୟୀ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\) + \(\frac{1}{\mathrm{R}_3}\)
⇒ \(\frac { 1 }{ R }\) = \(\frac { 1 }{ 100 }\) + \(\frac { 1 }{ 50 }\) + \(\frac { 1 }{ 500 }\) = \(\frac { 5+10+1 }{ 500 }\) = \(\frac { 16 }{ 500 }\)
⇒ R = \(\frac { 500 }{ 16 }\) = 31 – 25Ω
ଇସ୍ତ୍ର1ର ପ୍ରତିରୋଧ = 31 – 25Ω , V = 220 V
ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ I = \(\frac { V }{ R }\) = \(\frac { 220V }{ 31 – 25Ω }\) = 7.04A

Question 16.
ବିଦ୍ୟୁତ୍ ଉପକରଣଗୁଡ଼ିକୁ ବ୍ୟାଟେରୀ ସହ ସମାନ୍ତର ଭାବେ ସଂଯୋଗ କଲେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ତୁଳନାରେ କ’ଣ ସୁବିଧା ହୁଏ ?
Answer:
ଉପକରଣଗୁଡ଼ିକୁ ସମାନ୍ତରାଳ ଭାବେ ସଂଯୁକ୍ତ କଲେ ପରିପଥର ସମୁଦାୟ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବିଭିନ୍ନ ଉପକରଣ ଆବଶ୍ୟକତା ଅନୁସାରେ ପାଇଥାଏ । କିନ୍ତୁ ପଙ୍‌କ୍ତି ସଂଯୋଗରେ ପ୍ରତିରୋଧ ଗୁଡ଼ିକ ସମାନ ପରିମାଣର ବିତ୍ର୍ୟତ ପ୍ରୋତ ପାଇଥାନ୍ତି |

ଠିକ୍ ଠିକ୍ କାର୍ଯ୍ୟ କରିପାରିବ । କିନ୍ତୁ ପଙ୍‌କ୍ତି ସଂଯୋଗରେ ଗୋଟିଏ ଉପକରଣ ଅଚଳ ହୋଇଗଲେ ସମୁଦାୟ

Question 17.
ତିନୋଟି ପ୍ରତିରୋଧର ପରିମାଣ 2Ω, 3Ω ଓ 6Ω । ଏଗୁଡ଼ିକର କେମିତି ସଂଯୋଗ କରିବ ଯାହାଫଳରେ ସମୂହ ପ୍ରତିରୋଧ ହେବ (a) 4Ω (b) 1Ω ?
Answer:
ସମୂହ ପ୍ରତିରୋଧ 4Ω ପାଇବା ପାଇଁ 3Ω ଓ 6Ω ଥ‌ିବା ପ୍ରତିରୋଧକୁ ସମାନ୍ତର ସଂଯୋଗ ଏବଂ 2Ωକୁ ପଲ୍ଲିରେ ସଂଯୋଗ କରାଯିବ ।

R₁ = 2Ω, R₂ = 3Ω, R₃ = 6Ω
3Ω ଓ 6Ω ପ୍ରତିରୋଧ ଦ୍ଵୟର ସମୂହ ପ୍ରତିରୋଧ R₄
\(\frac{1}{\mathrm{R}_4}\) = \(\frac{1}{\mathrm{R}_2}\) + \(\frac{1}{\mathrm{R}_3}\) = \(\frac { 1 }{ 3 }\) + \(\frac { 1 }{ 6 }\) = \(\frac { 2+1 }{ 6 }\) = \(\frac { 1 }{ 2 }[/latex ] ⇒ R₄ = 2Ω
ତିନୋଟି ପ୍ରତିରୋଧର ସମ୍ବହ ପ୍ରତିରୋଧ (R) = R₁ + R₄ = 2Ω + 2Ω = 4Ω

(b) ପ୍ରତିରୋଧ ତିନୋଟିକୁ ସମାନ୍ତରାଳ ସଂଯୋଗ କଲେ ସମୂହ ପ୍ରତିରୋଧ = R

Question 18.
ଗୋଟିଏ ଲେଖାଏଁ 4Ω, 8Ω, 12Ω ଓ 24Ω ପ୍ରତିରୋଧ ଦିଆଯାଇଛି । ଏଗୁଡ଼ିକର ସଂଯୋଗରୁ ମିଳୁଥିବା
(a) ସର୍ବୋଚ୍ଚ ପ୍ରତିରୋଧ କେତେ ?
(b) ସର୍ବନିମ୍ନ ପ୍ରତିରୋଧ କେତେ ?
Answer:
R₁ = 4Ω,
R₂ = 8Ω,
R₃ = 12Ω,
R₄ = 24Ω

(a) ସମସ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକୁ ପଂକ୍ତିରେ ସଂଯୋଗ କଲେ
ସର୍ବୋଚ୍ଚ ପ୍ରତିରୋଧ R = R₁ + R₂ + R₃ + R₄
= 4 + 8 + 12 + 24 = 48Ω

(b) ସମସ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକୁ ପଂକ୍ତିରେ ସଂଯୋଗ କଲେ
[latex]\frac { 1 }{ R }\) = \(\frac { 1 }{ 4 }\) + \(\frac { 1 }{ 8 }\) + \(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 24 }\) = \(\frac { 6+3+2+1 }{ 24 }\) = \(\frac { 12 }{ 24 }\) = \(\frac { 1 }{ 2 }\)
∴ ସର୍ବନିମ୍ନ ପ୍ରତିରୋଧ, R = 2Ω

Question 19.
ବୈଦ୍ୟୁତିକ ହିଟର୍‌ର ତାର କୁଣ୍ଡଳୀ ଉତ୍ତପ୍ତ ହେଉଥିଲାବେଳେ ସଂଯୋଗୀ ତାର କାହିଁକି ଉତ୍ତପ୍ତ ହୁଏ ନାହିଁ ?
Answer:
ଆମେ ଜାଣୁ H = I²Rt
ଅର୍ଥାତ୍ H ∝ R
ବୈଦ୍ୟୁତିକ ହିଟର୍ ତାର କୁଣ୍ଡଳୀର ପ୍ରତିରୋଧ ଅଧ୍ବକ । ତେଣୁ ଅଧିକ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ତାପଶକ୍ତିରେ ରୂପାନ୍ତରିତ ହୋଇ ଅଧ‌ିକ ତାପ ଓ ଆଲୋକ ଦିଏ । କିନ୍ତୁ ସଂଯୋଗୀ ତାରର ପ୍ରତିରୋଧ ତାର କୁଣ୍ଡଳୀର ପ୍ରତିରୋଧ ତୁଳନାରେ ବହୁତ କମ୍ । ତେଣୁ ତାହା ଉତ୍ତପ୍ତ ହୁଏନାହି ।

Question 20.
ଗୋଟିଏ 20 Ω ପ୍ରତିରୋଧ ବିଶିଷ୍ଟ ବୈଦ୍ୟୁତିକ ଇସ୍ତ୍ରୀରେ 5A ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହେଉଛି । 30 s ରେ କେତେ ତାପ ଉତ୍ପନ୍ନ ହେବ ?
Answer:
ଏଠାରେ R = 20Ω, I = 5A, t = 30 s
H = I²Rt = 5² × 20 × 30 = 15000 ଜ୍ତଲ୍ = 15 କିଲୋଜ୍ତଲ୍

Question 21.
ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଦ୍ଵାରା ପ୍ରଦତ୍ତ ଶକ୍ତିର ହାର କେଉଁ କାରକ ଉପରେ ନିର୍ଭର କରେ ?
Answer:
ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଦ୍ଵାରା ପ୍ରଦତ୍ତ ଶକ୍ତିର ହାର ବିଦ୍ୟୁତ୍ ପାଓ୍ବାର ଉପରେ ନିର୍ଭର କରେ ।

Question 22.
ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ମୋଟର୍ 220 V ବିଦ୍ୟୁତ୍ ଲାଇନ୍‌ରୁ 5A ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ନିଏ । ମୋଟର୍‌ର ପାୱାର୍‌ କେତେ ? 2 ଘଣ୍ଟାରେ ଏହା କେତେ ଶକ୍ତି ବ୍ୟୟ କରିବ ?
Answer:
ଏଠାରେ I = 5A, V = 220V, t = 2 ଘଣ୍ଟା = 7200 ସେକେଣ୍ଡ
P = VI = 220 x 5 = 1100 W
ବ୍ୟୟିତ ଶକ୍ତି = ପାୱାର × ସମୟ = P x t
= 1100 W × 2 × 7200 ସେ = 7920000 ଜ୍ତଲ୍ = 7.92 × 10⁶ J

କାର୍ଯ୍ୟାବଳୀ (Activity)

କାର୍ଯ୍ୟାବଳୀ- 1 (Activity-1)

ଆବଶ୍ୟକୀୟ ଉପକରଣ :
ଗୋଟିଏ 0.5 m ଦୈର୍ଘ୍ୟର ନିକ୍ରୋମ ତାର XY, ଏକ ଏମିଟର (A), ପ୍ଲଗ୍‌ବି, ପରିବାହୀ ତାର, 1.5 V ବିଶିଷ୍ଟ 4ଟି ସେଲ୍, ଗୋଟିଏ ଭୋଲଟ୍‌ଟର । ନିକ୍ରୋମ – (ନିକେଲ + କ୍ରୋମିୟମ୍ + ମାଙ୍ଗାନିଜ + ଲୌହ) ଏଲୟ ।

ପରୀକ୍ଷଣ :
ଚିତ୍ରରେ ଦର୍ଶାଇଲା ଭଳି ପରିପଥଟିଏ ତିଆରି କର, ଯେଉଁଥ୍ରେ 0.5 ମି ଦୈର୍ଘ୍ୟର ନିକ୍ରୋମ ତାର XY ଏମିଟରକୁ ପଙ୍‌କ୍ତିରେ ଏବଂ ଭୋଲ୍‌ଟମିଟରକୁ ସମାନ୍ତର ସଂଯୋଗ କରାଯାଏ ।

ପ୍ରଥମେ ଗୋଟିଏ ସେଲ୍ ନେଇ ଏମିଟରକୁ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ମୂଲ୍ୟାଙ୍କ ଏବଂ ଭୋଲ୍ସମିଟରରୁ ନିକ୍ରୋମ ତାରର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥିବା ବିଭବାନ୍ତର Vର ମୂଲ୍ୟ ପଢ଼ି ସାରଣୀରେ ଲେଖ ।

ସେହିଭଳି ଦୁଇଟି ସେଲ୍, ତିନୋଟି ସେଲ୍, ଚାରୋଟି ସେଲ୍‌ ସଂଯୋଗକରି ପ୍ରତ୍ୟେକ ଥର ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ଓ ବିଭବାନ୍ତର \(\frac { V }{ I }\) ର ମୂଲ୍ୟାଙ୍କ ଲେଖୁରଖ ଏବଂ ମୁଁ ବାହାର କର ।

ପଯ୍ୟରେକ୍ଷଣ :

ବିଦ୍ୟୁତ୍ ସ୍ରୋତକୁ X ଅକ୍ଷରେ ଓ ବିଭବାନ୍ତରକୁ Y ଅକ୍ଷରେ ସୂଚାଇ ଲେଖଚିତ୍ର ଅଙ୍କନ କଲେ ଗ୍ରାଫ୍‌ଟି ଏକ ସରଳରେଖା ହୁଏ ।
V ଓ I ଗ୍ରାଫ୍‌ଟି ଏକ ସରଳରେଖା ହେବ ଓ ଏହା ଆଦ୍ୟବିନ୍ଦୁ ଠକୁ ଭେଦ କରିବ ।

ସିଦ୍ଧାନ୍ତ :
(i) V ଓ I ର ଗ୍ରାଫ୍ ସରଳରେଖାରୁ ଜଣାଯାଏ ଯେ, ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥ‌ିବା ବିଦ୍ୟୁତ୍‌ବିଭବ ପାର୍ଥକ୍ୟ ବଢ଼ିଲେ ବିଦ୍ଯୁସ୍ରୋତ ସେହି ଅନୁସାରେ ବଢ଼େ । V ଓ I ସମାନୁପାତୀ ।

(ii) V ଓ I ର ଅନୁପାତ ସ୍ଥିରାଙ୍କ ଅର୍ଥାତ୍ \(\frac { V }{ I }\) = R

ପ୍ରତିରୋଧ :
ତାରର ବିଦ୍ୟୁତ୍ ବିଭବ ପାର୍ଥକ୍ୟ ଓ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ର ଭାଗଫଳକୁ ନିର୍ଦ୍ଦିଷ୍ଟ ତାରଟିର ପ୍ରତିରୋଧ R କୁହାଯାଏ ।

ଓମ୍‌ଙ୍କ ନିୟମ :
‘‘ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରାରେ ଥିବା କୌଣସି ଏକ ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥିବା ବିଭବାନ୍ତର ପରିବାହୀରେ ପ୍ରବାହିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସହ ସମାନୁପାତୀ’’ ।

• ସାଙ୍କେତିକ ଭାଷାରେ ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ V ∝ I କିମ୍ବା \(\frac { V }{ I }\) = R = ସ୍ଥିରାଙ୍କ
  V = IR, R = \(\frac { V }{ I }\) ବା I = \(\frac { V }{ R }\)
• ଖଣ୍ଡିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଧାତବ ତାର ଓ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରା ପାଇଁ R ଏକ ସ୍ଥିରାଙ୍କ । ଏହାକୁ ତାରର ପ୍ରତିରୋଧ (resistance) କୁହାଯାଏ |
• ପ୍ରତିରୋଧ ପରିବାହୀର ଏକ ଗୁଣ । ଏହା ଯୋଗୁଁ ଚାର୍ଜର ପ୍ରବାହ କମିଯାଏ ।
• ପ୍ରତିରୋଧର SI ଏକକ ହେଉଛି ଓମ୍ (Ω) ।
• ଯଦି କୌଣସି ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥ‌ିବା ବିଦ୍ୟୁତ୍ ବିଭବାନ୍ତର IV ହୁଏ ଏବଂ ସେଥ‌ିରେ IA ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହେଉଥାଏ, ତେବେ ପ୍ରତିରୋଧ (R) ହେବ 1Ω ।

I = \(\frac { V }{ R }\) ରୁ ଜଣାଯାଏ ଯେ, ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିଭବାନ୍ତର V ପାଇଁ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ I ପରିବାହୀର ପ୍ରତିରୋଧ R ସହ ପ୍ରତିଲୋମାନ୍ତପାତ1 (inversely proportional) |
(vi) ବିଭବାନ୍ତରକୁ ସ୍ଥିରରଖ୍ ପ୍ରତିରୋଧକୁ ଦୁଇଗୁଣ କଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଅଧା ହେବ ।
(vii) ବିଦ୍ୟୁତ୍ ପ୍ରବାହକୁ କମ୍ ବେଶୀ କରିବା ପାଇଁ ପରିବର୍ତ୍ତୀ ପ୍ରତିରୋଧ ବା ରିଓଷ୍ଟାଟ୍ ନାମକ ଉପକରଣ ବ୍ୟବହାର କରାଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 2 (Activity – 2)
ଆବଶ୍ୟକ ଉପକରଣ: ଖଣ୍ଡିଏ ନିକ୍ରୋମ ତାର, ଗୋଟିଏ ଟର୍ଚ୍ଚ ବଲ୍‌ବ, ଗୋଟିଏ 10W ବଲ୍‌ବ, 0-5A ବିସ୍ତାର ଥ‌ିବା ଗୋଟିଏ ଏମିଟର, ଗୋଟିଏ ପ୍ଲଗ୍ କି, କିଛି ସଂଯୋଜୀତାର ଓ 4ଟି 1.5 volt ଶୁଷ୍କ ସେଲ୍ ।

ପରୀକ୍ଷଣ :

• ଉପରୋକ୍ତ ଉପକରଣଗୁଡ଼ିକୁ ନେଇ ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥ‌ିବା ଭଳି ପରିପଥଟିଏ ତିଆରି କର । XY ହେଉଛି ପରିପଥର ଏକ ଶୂନ୍ୟସ୍ଥାନ |
• ପ୍ରଥମେ ନିକ୍ରୋମ ତାରକୁ XY ମଧ୍ୟରେ ଥ‌ିବା ଶୂନ୍ୟସ୍ଥାନ ମଧ୍ୟରେ ରଖ୍ ପ୍ଲଗ୍ ଚାବିକୁ ବନ୍ଦକରି ପରିପଥ ମୁଦିତ କର ।
• ଏହି ସମୟରେ ଏମିଟର ପାଠ୍ୟଙ୍କ ଟିପିରଖ
• ସେହିପରି 10W ବଲ୍‌ବ ଏବଂ ଏକ ଟର୍ଚ୍ଚ ବଲ୍‌ବ ଲଗାଇ ପୂର୍ବପରି ପରିପଥକୁ ମୁଦିତ କରି ଏମିଟରର ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।

ପଯ୍ୟରେକ୍ଷଣ :

• ତିନୋଟି ଉପାଂଶ କ୍ଷେତ୍ରରେ ଏମିଟର ପାଠ୍ୟଙ୍କ ପରସ୍ପରଠାରୁ ଭିନ୍ନ ।
• ବିଭିନ୍ନ ଉପାଂଶ ବିଦ୍ୟୁତ୍ ପ୍ରବାହକୁ ଭିନ୍ନ ଭିନ୍ନ ମାତ୍ରାରେ ପ୍ରତିରୋଧ କରେ ।
• ପରିବାହୀରେ ଇଲେକ୍‌ଟ୍ରନ ଗତିରୁ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ । ମାତ୍ର ପରିବାହୀରେ ରହିଥ‌ିବା ବହୁ ସଂଖ୍ୟକ ପରମାଣୁ ଯୋଗୁଁ ଇଲେକ୍‌ଟ୍ରନ ଗୁଡ଼ିକ ଅବାଧ ଭାବେ ଗତି କରିପାରନ୍ତି ନାହିଁ । ଇଲେକ୍‌ଟ୍ରନ୍‌ର ଗତି ପରମାଣୁଦ୍ୱାରା ପ୍ରତିରୋଧର ସମ୍ମୁଖୀନ ହୁଏ ।

ସିଦ୍ଧାନ୍ତ :

• ଯେଉଁ ପଦାର୍ଥ ଖୁବ୍ କମ୍ ପରିମାଣର ପ୍ରତିରୋଧ ଦିଏ ତାକୁ ସୁପରିବାହୀ (Good conductor) କୁହାଯାଏ ।
• ଯେଉଁ ପଦାର୍ଥ କିଛି ପରିମାଣର ପ୍ରତିରୋଧ ଦେଖାଏ ତାକୁ ପ୍ରତିରୋଧୀ ବା ରେଜିଷ୍ଟର (Resistor) କହନ୍ତି ।
• ଅଧ‌ିକ ପ୍ରତିରୋଧ ଦେଖାଉଥ‌ିବା ପଦାର୍ଥକୁ କୁପରିବାହୀ (Poor conductor) କହନ୍ତି ।
• ପ୍ରତିରୋଧ ବହୁତ ବେଶୀହେଲେ ପଦାର୍ଥକୁ ବିଦ୍ୟୁତ୍‌ରୋଧୀ (Insulator) କୁହାଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 3 (Activity – 3)
ଆବଶ୍ୟକ ଉପକରଣ : ଗୋଟିଏ ସ୍କେଲ, ଗୋଟିଏ ଏମିଟର, ଖଣ୍ଡିଏ ନିକ୍ରୋମ ତାର ଓ ଗୋଟିଏ ପ୍ଲଗ୍ କି ।
ଦ୍ତରଖଣ୍ଡ ନିକ୍ରୋମ ଭାଇ ନିଥ ଯାହାର ଦୈର୍ଘ୍ୟ (l) ସମାନ; କିନ୍ତୁ ମୋଟେଇ ଭିନ୍ନ ଭିନ୍ନ । ଅନ୍ୟ ଏକ ନିକ୍ରୋମ ତାର ନିଅ ଯାହାର ଦୈର୍ଘ୍ୟ ପ୍ରଥମର 2ଗୁଣ (2I) ଏବଂ ଟଣ୍ଡେ ତମ୍ବାତାର ନିଅ

ପରୀକ୍ଷଣ :
ଚିତ୍ର ଅନୁସାରେ ପରିପଥଟିଏ ପ୍ରସ୍ତୁତ କର ।

• I ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ (1) ଚିହ୍ନିତ ନିକ୍ରୋମ ତାର ନେଇ ପରିପଥ ମୁଦିତ କରି ଏମିଟର ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।
• ପ୍ରଥମ ନିକ୍ରୋମ ତାରର ମୋଟେଇ ସହ ସମାନ କିନ୍ତୁ ଦୈର୍ଘ୍ୟ ଦୁଇଗୁଣ (21) ନିକ୍ରୋମ ତାର ନେଇ ଏମିଟର ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।
• ପ୍ରଥମ ନିକ୍ରୋମ ତାରର ଦୈର୍ଘ୍ୟ ସହ ସମାନ (l) ମାତ୍ର ମୋଟେଇ ଅଧିକ (ପ୍ରସ୍ଥଚ୍ଛେଦ ଅଧ୍ବକ) ନେଇ ଏମିଟର୍‌ର
• ନିକ୍ରୋମ ତାରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥଚ୍ଛେଦ ସହ ସମାନ ଏକ ତମ୍ବାତାର ଚିତ୍ରରେ ଚିହ୍ନିତ (4) ନେଇ ଏମିଟର୍ ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।
• ବିଭିନ୍ନ ତାପମାତ୍ରାରେ ପରୀକ୍ଷାଟି କରାଯାଉ ।

ପଯ୍ୟରେକ୍ଷଣ :

• ଏକା ପ୍ରକାରର ତାରର ଦୈର୍ଘ୍ୟ ଦୁଇଗୁଣ ହେଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଅଧା ହୁଏ ।
• ତାରର ପ୍ରକାର ଓ ଦୈର୍ଘ୍ୟ ସମାନ ଥାଇ ପ୍ରସ୍ଥଚ୍ଛେଦ ବଢ଼ିଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବଢ଼େ ।
• ତାରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥଛେଦ ସମାନଥାଇ ( ତମ୍ବା ଓ ନିକ୍ରୋମ) ବସ୍ତୁ ବଦଳିଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବଦଳେ ।

ସିଦ୍ଧାନ୍ତ :
ଗୋଟିଏ ସେଲ୍ ନିଆଯାଇଥ‌ିବା ଯୋଗୁଁ ବିଭବାନ୍ତର ସମାନ ରହିଛି । ପରିବାହୀର ପ୍ରତିରୋଧ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସହ ପ୍ରତିଲୋମାନୁପାତୀ । ପ୍ରତିରୋଧ ନିମ୍ନ କାରଣଗୁଡ଼ିକ ଉପରେ ନିର୍ଭର କରେ ।

• ପରିବାହୀର ଦୈର୍ଘ୍ୟ
• ପରିବାହୀର ପ୍ରସ୍ଥଛେତ
• ପରିବାହୀ ଯେଉଁ ପଦାର୍ଥରୁ ତିଆରି ତା’ର ପ୍ରକୃତି
• ପରିବାହୀର ତାପମାତ୍ରା

ପ୍ରତିରୋଧ ସଂଜ୍ଞା ଓ ପ୍ରତିରୋଧତାର ଗାଣିତିକ ବ୍ୟାଖ୍ୟା :
ଅଧିକ ଉନ୍ନତ ପରୀକ୍ଷା ଓ ପର୍ଯ୍ୟବେକ୍ଷଣରୁ ଜଣାପଡ଼ିଛି ଯେ,
(i) ପରିବାହୀ ତାରର ପ୍ରତିରୋଧ ତାରର ଦୈର୍ଘ୍ୟ ସହ ସମାନୁପାତୀ ଓ

(ii) ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ ସହ ପ୍ରତିଲୋମାନୁପାତୀ ଅଟେ
ପ୍ରତିରୋଧର ସଙ୍କେତ R, ତାରର ଦୈର୍ଘ୍ୟର ସଙ୍କେତ | ଓ ପ୍ରସ୍ଥଛେଦର କ୍ଷେତ୍ରଫଳର ସଙ୍କେତ A ହୁଏ ତେବେ
R ∝l (A ସ୍ଥିର ଥିଲେ ) ……………….(i)

ଏବଂ R ∝ \(\frac { 1 }{ A }\) (/ ସ୍ଥିର ଥିଲେ) …(ii)
(i) ଓ (ii) ରୁ ଲେଖୁପାରିବା R ∝ l x \(\frac { 1 }{ A }\) (l ଓ A ବଦଳିଲେ)
⇒ R ∝ \(\frac { 1 }{ A }\) କିମ୍ବା R = p \(\frac { 1 }{ A }\)
ଏଠାରେ p (ଗ୍ରୀକ୍ ଅକ୍ଷର ରୋ (rho)) ହେଉଛି ସମାନୁପାତ ସ୍ଥିରାଙ୍କ ।
(iv) ଏହାକୁ ପରିବାହୀ ବସ୍ତୁର ବିଶିଷ୍ଟ ପ୍ରତିରୋଧ (Specific resistance) ବା ପ୍ରତିରୋଧତା (Resistivity) କୁହାଯାଏ ।

(v) ପ୍ରତିରୋଧତାର SI ଏକକ ହେଉଛି ଓମ୍-ମି. (Ωm) ।

(vi) ଏହା ବସ୍ତୁର ଗୁଣ ଉପରେ ନିର୍ଭର କରେ । ଧାତୁ ଓ ମିଶ୍ରଧାତୁମାନଙ୍କର ପ୍ରତିରୋଧ ଅପେକ୍ଷାକୃତ କମ୍ (10^-8 Ωm ରୁ 10^-6 Ωm )

(vii) ବସ୍ତୁର ପ୍ରତିରୋଧ ଓ ପ୍ରତିରୋଧ ଉଭୟ ତାପମାତ୍ରା ଉପରେ ନିର୍ଭର କରେ ।

20°C ତାପମାତ୍ରାରେ ବସ୍ତୁର ପ୍ରତିରୋଧ

କାର୍ଯ୍ୟାବଳୀ – 4 (Activity – 4)
ଆବଶ୍ୟକ ଉପକରଣ :
ତିନୋଟି ଭିନ୍ନ ଭିନ୍ନ ପ୍ରତିରୋଧ 1Ω, 2Ω, 3Ω,ଗୋଟିଏ 6V ବ୍ୟାଟେରୀ, ଗୋଟିଏ ଏମିଟର, ଗୋଟିଏ ପ୍ଲଗ୍ କି ।

ପରୀକ୍ଷଣ :

• 1Ω, 2Ω ଓ 3Ω ପ୍ରତିରୋଧଗୁଡ଼ିକୁ ପଙକ୍ତିରେ ସଂଯୋଗ କର । ପ୍ଲଗ୍ କିକୁ ବନ୍ଦ କରି ପରିପଥକୁ ମୁଦିତ କର ।
• ଏମିଟର ପାଠ୍ୟଙ୍କ ଲେଖ । ଏମିଟର ସ୍ଥାନ ପରିବର୍ତ୍ତନ କରି ପରିପଥର ପାଠ୍ୟଙ୍କ ଲେଖ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ଯେକୌଣସି ସ୍ଥାନରେ ଏମିଟର ରଖିଲେ ମଧ୍ୟ ଏମିଟର ମଧ୍ୟରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସମାନ ରହୁଛି ।

ସିଦ୍ଧାନ୍ତ :
ପ୍ରତିରୋଧ ମାନଙ୍କ ପକ୍ତି ସଂଯୋଗରେ ପ୍ରତି ପ୍ରତିରୋଧ ଭିତରେ ସମାନ ପରିମାଣର ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହୁଏ ।

କାର୍ଯ୍ୟାବଳୀ -5 (Activity-5)
ଆବଶ୍ୟକ ଉପକରଣ : 3ଟି ପ୍ରତିରୋଧ (R₁, R₂, R₃) ଏକ ଏମିଟର, ଏକ ଭୋଲ୍‌ଟର ପ୍ଲଗ୍ କି ବ୍ୟାଟେରୀ, ପ୍ଲଟଚାବି , ସପୋଖ1 ପରିବାବା

ପରୀକ୍ଷଣ :

• ଚିତ୍ରରେ ଦର୍ଶାଇଲା ଭଳି ଉପକରଣଗୁଡ଼ିକୁ ସଜାଅ ।
• ପ୍ଲଗ୍ କିକୁ ବନ୍ଦକରି ପରିପଥ ମୁଦିତ କର ଏବଂ ଭୋଲଟ୍ମିଟରର ପାଠ୍ୟାକ ଟିପିବଟ |
• ମନେକର V ହେଉଛି ପ୍ରତିରୋଧର ପଙ୍‌କ୍ତି ସଂଯୋଗର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟସ୍ଥ ବିଭବାନ୍ତର ।
• ଭୋଲ୍ସମିଟରକୁ ଖୋଲି ବ୍ୟାଟେରୀର ଦୁଇମୁଣ୍ଡ ସହ ସଂଯୋଗ କରି ବିଭବାନ୍ତର ମାପ ଓ ବିଭବାନ୍ତର ତୁଳନା କର ।
• ଭୋଲ୍ସମିଟରକୁ ପ୍ରତିରୋଧ R₁ ର ଦୁଇପ୍ରାନ୍ତ X ଓ P ସହ ସଂଯୋଗ କରି R₁ ର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ମାପ । ମନେକର ଏହା ହେଉଛି V₁
• ସେହିପରି ପ୍ରତିରୋଧ R₂, ଓ R₃ ର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ରହିଥ‌ିବା ବିଭବାନ୍ତର ମାପ । ସେଗୁଡ଼ିକ ଯଥାକ୍ରମେ V₂ ଓ V₃ ହେଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ପ୍ରତିରୋଧମାନଙ୍କର ଶେଷାଗ୍ରରେ ଉତ୍ପନ୍ନ ବିଭବାନ୍ତରର ସମଷ୍ଟି V ହେବ ।

ସିଦ୍ଧାନ୍ତ :
(i)
V = V₁ + V₂ + V₃
ଅର୍ଥାତ୍ ପ୍ରତିରୋଧଗୁଡ଼ିକର ପଙ୍‌କ୍ତି ସଂଯୋଗ ଜନିତ ବିଭବାନ୍ତର ସେଗୁଡ଼ିକ ପୃଥକ୍ ପୃଥକ୍ ପ୍ରତିରୋଧ ଜନିତ ବିଭବାନ୍ତରର ସମଷ୍ଟି ସହ ସମାନ ।
ଏକାଧ୍ଵ ପ୍ରତିରୋଧର ପଙ୍‌କ୍ତି ସଂଯୋଗ ପରିବର୍ତ୍ତେ ଆମେ କେବଳ ଗୋଟିଏ ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ R ନେଇପାରିବା ଯାହା ମଧ୍ୟଦେଇ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ପ୍ରବାହିତ ହେଉଥ‌ିବ ।
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ V = IR
ଟି ଯାକ ପ୍ରତିରୋଧ ପାଇଁ V₁ = IR₁, V₂ = IR₂, V₃ = IR₃
∴ V = V₁ + V₂ + V₃
⇒ IR = IR₁ + IR₂ + IR₃
ଅର୍ଥାତ୍‌ R = R₁ + R₂ + R₃

ପ୍ରତିରୋଧଗୁଡ଼ିକର ପଙ୍‌କ୍ତି ସଂଯୋଗର ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ ବା ସମୂହ ପ୍ରତିରୋଧ ସମ୍ପୃକ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକର ସମଷ୍ଟି ସହ ସମାନ ।
ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ ସମ୍ପୃକ୍ତ ଯେକୌଣସି ପ୍ରତିରୋଧଠାରୁ ଅଧ୍ଵ ।
ଏହାହିଁ ପକ୍ତି ସଂଯୋଗର ନିୟମ ।
ପଙ୍‌କ୍ତି ସଂଯୋଗର ଅସୁବିଧା :
ପରିପଥରେ କୌଣସି ଏକ ଉପକରଣ କିମ୍ବା ପ୍ରତିରୋଧଶୀଳ ହେଲେ ସମୁଦାୟ ପରିପଥରେ ବିଦ୍ୟୁତ ପ୍ରବାହ ବନ୍ଦ ହୋଇଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 6 (Activity – 6)

ଆବଶ୍ୟକ ଉପକରଣ : ତିନୋଟି ପ୍ରତିରୋଧ
(R₁, R₂ ଓ R₃ ), ଏକ ଏମିଟର, ଭୋଲ୍ସମିଟର, ପ୍ଲଗ୍ କି, ପରିବାହୀ ତାର ।
ପରୀକ୍ଷଣ :

• ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥିବା ଭଳି X ଓ Y ବିନ୍ଦୁ ତି ନୋଟି ପ୍ରତି ରୋଧର ସମାନ୍ତରାଳ ସଂଯୋଗ କର !
• X ଓ Y ମଧ୍ୟରେ ଗୋଟିଏ ଭୋଲ୍ସମିଟର ସଂଯୁକ୍ତ କର । ଏହି ସଂଯୋଗ ସହ ଗୋଟିଏ ବ୍ୟାଟେରୀ, ଗୋଟିଏ ପ୍ଲଗ୍ କି ଓ ଗୋଟିଏ ଏମିଟର ଲଗାଅ ।
• ପ୍ଲଗ୍ କି କୁ ବନ୍ଦ କରି ପରିପଥକୁ ମୁଦିତ କର । ଏମିଟର୍‌ର ପାଠ୍ୟଙ୍କ ଲେଖଖ । ପାଠ୍ୟଙ୍କ I ହେଉ ।
• ଭୋଲ୍ସମିଟରର ପାଠ୍ୟଙ୍କ V ହେଉ ।
• ପ୍ରତିରୋଧ R₁ ସହିତ ଏମିଟର ଲଗାଅ ମନେକର ପାଠ୍ୟଙ୍କ I₁ । ସେହିଭଳି R₂ ଓ R₃ ରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I₂ ଓ I₃ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ : I = I₁ + I₂ + I₃

ସିଦ୍ଧାନ୍ତ :
ପରିପଥର ସମୁଦାୟ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ତିନୋଟି ପ୍ରତିରୋଧରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ପୃଥକ୍ ପୃଥକ୍ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ସମଷ୍ଟି ସହ ସମାନ ।
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ I = \(\frac { V }{ R }\)
ତିନୋଟିଯାକ ପ୍ରତିରୋଧ ପାଇଁ I₁ = \(\frac{\mathrm{V}}{\mathrm{R}_1}\), I₂ = \(\frac{\mathrm{V}}{\mathrm{R}_2}\) , I₃ = \(\frac{\mathrm{V}}{\mathrm{R}_3}\)
\(\frac { V }{ R }\) = \(\frac{\mathrm{V}}{\mathrm{R}_1}\) + \(\frac{\mathrm{V}}{\mathrm{R}_2}\) + \(\frac{\mathrm{V}}{\mathrm{R}_3}\) କିମ୍ବା
\(\frac { 1 }{ R }\) = \(\frac{\mathrm{1}}{\mathrm{R}_1}\) + \(\frac{\mathrm{1}}{\mathrm{R}_2}\) + \(\frac{\mathrm{1}}{\mathrm{R}_3}\)
ପ୍ରତିରୋଧର ସମାନ୍ତରାଳ ସଂଯୋଗର ସମୂହ ପ୍ରତିରୋଧ ବା ସମତୁଲ୍ୟ ପ୍ରତିରୋଧର ବିଲୋମୀ (reciprocal)
ସମ୍ପୃକ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକର ବିଲୋମୀର ସମଷ୍ଟି ସହ ସମାନ ।
ସମାନ୍ତରାଳ ସଂଯୋଗରେ ସମୂହ ପ୍ରତିରୋଧର ମୂଲ୍ୟ ସମ୍ପୃକ୍ତ ଯେକୌଣସି ପ୍ରତିରୋଧର ମୂଲ୍ୟଠାରୁ କମ୍ ।

Odisha State Board CHSE Odisha Class 12 Approaches to English Book 2 Solutions Grammar Word Order Textbook Exercise Questions and Answers.

CHSE Odisha 12th Class Alternative English Grammar Word Order

1. Fill in the blanks with the suitable verb forms relating to the subjects.
(a) One number of the books ____________ been lost (here / has).
(b) Neither boy ____________ Ramesh (is/are)
(c) Whether Sita or Gita wins ____________ does not matter.
(d) Neither Sushma nor Shasmita ____________ well, (do / plays)
(e) Your knowledge in many languages ____________ poor, (is/are)
(f) Dr. Das with his sons and daughters ____________ gone to Puri, (has/have)
(g) A gang of thieves ____________ arrested, (was/were)
(h) My family ____________ early sisters, (is/are)
(i) Rains ____________ welcome (is/are)
(j) The cattle ____________ grazing in the field (is/are)
(k) The public ____________ not accept your view, (do/does)
(l) The committee ____________ divided in their opinion, (was/were)
(m) Your spectacles ____________ nice on me. (look / looks)
(n) The rich ____________ always unhappy, (is/are)
(o) The boy as well as the girls ____________ guilty, (is/are)
(p) Ten minutes ____________ not enough for me. (is/are)
(q) Show and steady ____________ the race (win/wins)
(r) Bread and butter ____________ my favorite subject, (is/are)
(s) The United nations ____________ not functioning well, (is/are)
(t) Mathematics ____________ my favorite subject, (is/are)
(u) Measles ____________ a dreadful disease, (is/are)
(v) Rice and dal ________________ eaten in Odisha. (is/are)
(w) I ____________ your brother, should be respected, (is / am / are)
(x) The father of these children ____________ an innocent fellow, (is/are)
(y) A pair of spectacles ____________ lying on the table, (is/are)
(z) Ten kilometers ____________ not a long way to walk, (is/are)

Answer:
(a) One number of the books has been lost (here / has).
(b) Neither boy is Ramesh (is/are)
(c) Whether Sita or Gita wins does not matter.
(d) Neither Sushma nor Shasmita plays well, (do / plays)
(e) Your knowledge in many languages is poor, (is/are)
(f) Dr. Das with his sons and daughters has gone to Puri, (has/have)
(g) A gang of thieves was arrested, (was/were)
(h) My family are early sisters, (is/are)
(f) Rains are welcome (is/are)
(j) The cattle are grazing in the field (is/are)
(k) The public do not accept your view, (do/does)
(l) The committee were divided in their opinion.
(m) Your spectacles looks nice on me.
(n) The rich are always unhappy.
(o) The boy as well as the girls is guilty.
(p) Ten minutes is not enough for me.
(q) Show and steady wins the race
(r) Bread and butter is my favourite subject.
(s) The United nations is not functioning well.
(t) Mathematics is my favourite subject.
(u) Measles is a dreadful disease.
(v) Rice and dal is eaten in Odisha.
(w) I am your brother, and should be respected.
(x) The father of these children is an innocent fellow.
(y) A pair of spectacles is lying on the table.
(z) Ten kilometers is not a long way to walk.

2. Supply the correct forms of the verbs given in the brackets in relation to their respective subjects.
(a) Economics ____________ difficult subject, (is/are)
(b) “Lines written in March” ____________ a good poem, (is/are)
(c) The audience ____________ enjoying the speech, (was/were)
(d) Three deers ____________ grazing in the park (is/are)
(e) Neither John nor Mary ____________ responsible for the breakage, (is/are)
(f) None of you ____________ correct in your answer, (is/are)
(g) Everyone in the class has ____________ identify cards. (his / their)
(h) Either Mary or her sister ____________ in the house, (was/were)
(i) The number of students ____________ large, (have/has)
(j) A large number of students ____________ applied for admission. (have/has)
(k) The poet and teacher ____________ deed, (is/are)
(l) Two fives ____________ ten. (is/are)
(m) Twice twelve ____________ twenty-four, (is/are)
(n) Two and two ____________ four, (make / makes)
(o) More then one person ____________ signed, (have/has)
(p) No person of the name ____________ here, (lives / five)
(q) In the past, goods ____________ cheap. (was/were)
(r) The man together with his wife ____________ been killed, (have/has)
(s) Rs 50,000 ____________ a big sum (is/are)
(t) The unemployed ____________ living in a precious situation, (is/are)
(u) You who ____________ my brother should not say so. (is/are)
(v) The military ____________ called out to tackle the situation, (was/were)
(w) There ____________ many trees on both sides of the road, (is /are)
(x) Each of the boys ____________ a pen. (have/has)
(y) A committee ____________ appointed to enquire into the matter, (was/were)
(z) He, you, and they ____________ ready, (is/are)

Answers:
(a) Economics is a difficult subject.
(b) “Lines written in March” is a good poem.
(c) The audience were enjoying the speech.
(d) Three deer are growing in the park.
(e) Neither John nor Mary is responsible for the breakage.
(f) None of you are correct in your answer.
(g) Everyone in the class has his identification cards.
(h) Either Mary or her sister was in the house.
(1) The number of students is large.
(j) A large number of students have applied for admission.
(k) The poet and teacher is the deed.
(l) Two fives are ten.
(m) Twice twelve is twenty-four.
(n) Two land two makes four.
(o) More than one person has signed.
(p) No person of the name lives here.
(q) In the past, goods were cheap.
(r) The man together with his wife has been killed.
(s) Rs 50,000 is a big sum.
(t) The unemployed are living in a precious situation.
(u) You who is my brother should not say so.
(v) The military were called out to tackle the situation.
(w) There are many trees on both sides of the road.
(x) Each of the bo vs has a pen.
(y) A committee was appointed to enquire into the matter.
(z) He, you, and they is ready.

3. Concord of nouns, pronouns, possessive, adjectives:
(a) They had a dog. Once ____________ was ill. (he/she / it)
(b) Give the baby ____________ toy. (his / her / its)
(c) The cow lives ____________ calf, (it’s / her)
(d) The car is ____________ (your / yours). The car is (my, mine)
(e) This book is new, ____________ books are old. (these / those)
(f) Everyone of the boys is keen on ____________ success, (his / their)
(g) The cabinet has taken ____________ decision, (it’s / their)
(h) The flock of sheep has done ____________ part well, (her / their)
(i) Neither of the girls have done ____________ part well, (her / their)
(j) I am not one of the ____________ who betray friends, (these / those)
(k) I ____________ your friend, should not be misbehaved, (am / are)
(l) Neither is capable of making ____________ mind, (his / their)

Answers:
(a) They had a dog. Once it was ill.
(b) Give the baby its toy.
(c) The cow lives with her calf.
(d) The car is yours. The car is mine.
(e) This book is new, those books are old.
(f) Every one of the boys is keen on his success.
(g) The cabinet has taken its decision.
(h) The flock of sheep has done its part well.
(i) Neither of the girls has done her part well.
(j) I am not one of those who betray friends.
(k) I am your friend, should not be misbehaved.
(l) Neither is capable of making his mind.

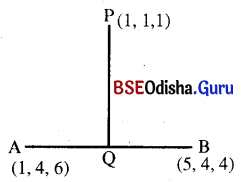
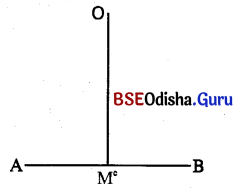
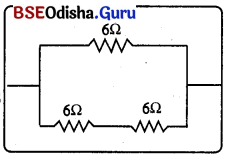
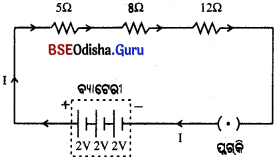
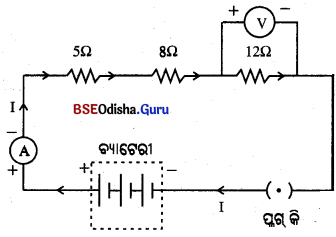
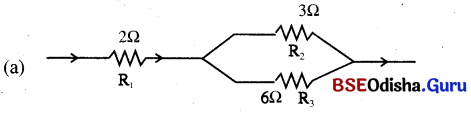
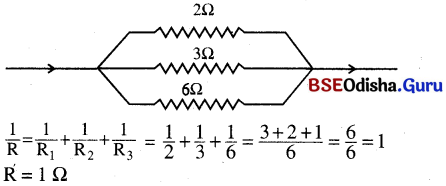
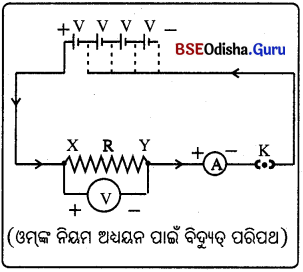
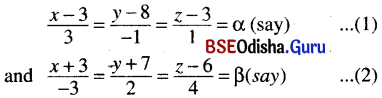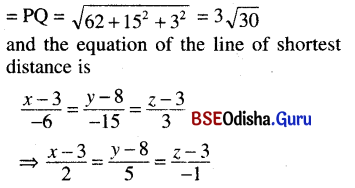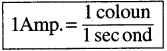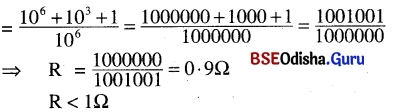Odisha State Board BSE Odisha 10th Class Hindi Solutions व्याकरण विभाग Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Hindi व्याकरण विभाग

लिंग

प्रश्न 1.
दूर का पहाड़ सुन्दर लगता है। रेखांकित शब्द का लिंग बताइए।
उत्तर:
पुंलिंग

प्रश्न 2.
मेरी परीक्षा पन्द्रह दिन सरक गयी है रेखांकित शब्द का लिंग बताइए।
उत्तर:
स्त्रीलिंग

प्रश्न 3.
पंड़ित लड़कों को मुफ्त में पढ़ाते थे रेखांकित शब्द का लिंग बताइए।
उत्तर:
पुंलिंग

प्रश्न 4.
आदमी का इतिहास पुराना है। रेखांकित शब्द का लिंग बताइए।
उत्तर:
पुंलिंग

प्रश्न 5.
‘मांस’ – दिए गए शब्द लिंग निर्णय कीजिए।
उत्तर:
पुंलिंग

प्रश्न 6.
‘मूँछ’ – लिंग निर्णय करो।
उत्तर:
स्त्रीलिंग

प्रश्न 7.
‘दूध’ – लिंग निर्णय करो।
उत्तर:
पुंलिंग

प्रश्न 8.
‘पूँछ’ – लिंग निर्णय करो।
उत्तर:
स्त्रीलिंग

प्रश्न 9.
‘मर्यादा’ – लिंग निर्णय करो।
उत्तर:
स्त्रीलिंग

प्रश्न 10.
‘जान’ – लिंग निर्णय करो।
उत्तर:
स्त्रीलिंग

प्रश्न 11.
‘तलाश’- लिंग निर्णय करो।
उत्तर:
स्त्रीलिंग

प्रश्न 12.
‘नौकर’- सही लिंग परिवर्तन किजिए।
उत्तर:
नौकरानी

प्रश्न 13.
‘बंदर’ शब्द का स्त्रीलिंग रूप है
उत्तर:
बंदरिया

प्रश्न 14
‘आदमी’ का स्त्रीलिंग रूप लिखिए।
उत्तर:
औरत

प्रश्न 15.
‘कवि’ लिंग बदलिए।
उत्तर:
कवयित्री

प्रश्न 16.
‘माली’ – लिंग बदलिए।
उत्तर:
मालिन

प्रश्न 17.
‘पिता’ लिंग बदलिए।
उत्तर:
माता

प्रश्न 18.
‘सेठ’ – लिंग बदलिए।
उत्तर:
सेठानी

वचन

प्रश्न 1.
वचन का आकर्षण बहुवचन में लिखिए।
उत्तर:
वचनों का आकर्षण

प्रश्न 2.
“कलाकृतियाँ” का एकवचन रूप है।
उत्तर:
कलाकृति

प्रश्न 3.
काँटा कम से कम मत बोओ। – रेखांकित शब्द का बहुवचन लिखिए।
उत्तर:
काँटे

प्रश्न 4.
‘घोसले’ का एकवचन रूप है।
उत्तर:
घोसला

प्रश्न 5.
‘दोहा’ का वहुवचन रूप है।
उत्तर:
दोहे

प्रश्न 6.
‘मौसम’ का वहुवचन रूप है।
उत्तर:
मौसम

प्रश्न 7.
‘ऋतु’ का वहुवचन है।
उत्तर:
ऋतुएँ

प्रश्न 8.
‘सूचना’ का बहुवचन है।
उत्तर:
सूचनाएँ

प्रश्न 9.
‘गुफा’ का वहुवचन है।
उत्तर:
गुफाएँ

प्रश्न 10.
‘प्राण’ का बहुवचन है।
उत्तर:
प्राण

प्रश्न 11.
‘सुविधा’ का बहुवचन रूप है।
उत्तर:
सुविधाएँ

प्रश्न 12.
‘गिलहरी’ का वहुवचन रूप है
उत्तर:
गिलहरियाँ

प्रश्न 13.
‘खेत’ का वहुवचन रूप क्या है?
उत्तर:
खेत

प्रश्न 14.
‘सदियाँ’ का एकवचन रूप है।
उत्तर:
सदी

प्रश्न 15.
‘स्मृती’ का बहुवचन रूप है।
उत्तर:
स्मृतियाँ

प्रश्न 16.
‘धारा’ – वचन बदलिए।
उत्तर:
धाराएँ

प्रश्न 17.
‘जहाज’- वचन बदलिए।
उत्तर:
जहाज

प्रश्न 18.
‘कुत्ता’ – वचन बदलिए।
उत्तर:
कुत्

प्रश्न 19.
‘नौकरी’ – वचन बदलिए।
उत्तर:
नौकरियाँ

प्रश्न 20.
‘लकड़ियाँ’ – वचन बदलिए।
उत्तर:
लकड़ी

सर्वनाम ( पुरुषवाचक)

प्रश्न 1.
आपको यह काम करना है। इस वाक्य में प्रयुक्त सर्वनाम है…………….. ।
उत्तर:
यह

प्रश्न 2.
उसको जाने दो। इस वाक्य में प्रयुक्त सर्वनाम है।
उत्तर:
उसको

प्रश्न 3.
उन्होंने काम पूरा कर दिया। इस वाक्य में सर्वनाम है…………….. ।
उत्तर:
उन्होंने

प्रश्न 4.
पुरुषवाचक सर्वनाम नहीं है ……………….।
( ये, मैं, कौन, वह)
उत्तर:
कौन

प्रश्न 5.
प्रश्नवाचक सर्वनाम है………………।
(वे, कौन, यह, उसे)
उत्तर:
कौन

प्रश्न 6.
संबंधवाचक सर्वनाम है ………………. ।
(जो-सो, मैं, कौन, वे)
उत्तर:
जो सो

प्रश्न 7.
सर्वनाम छाँटिए।
( नाम, मोटा, कोई, मकान )
उत्तर:
कोई

प्रश्न 8.
मेरी माताजी खाना पका रही हैं \। इस वाक्य में प्रयुक्त सर्वनाम है………………..।
उत्तर:
मेरी

प्रश्न 9.
……………. नाम क्या है?
उत्तर:
तेरा

प्रश्न 10.
निम्नलिखित में से संबंधवाचक सर्वनाम है ……………….।
(मैं, कौन, जो, कहाँ)
उत्तर:
जो

प्रश्न 11.
मेरी माताजी खाना पका रही हैं। इस वाक्य में प्रयुक्त सर्वनाम है।
उत्तर:
मेरी

प्रश्न 12.
कोई (बहुवचन) + ने = ……………….. ( सही रूप लिखिए)
उत्तर:
किन्होंने

प्रश्न 13.
वह + ने = …………….. ( सही रूप लिखिए)
उत्तर:
उसने

प्रश्न 14.
ये + ने = ………………… ( सही रूप लिखिए)
उत्तर:
इन्होंने

प्रश्न 15.
वाक्य में संज्ञा शब्दों के स्थान पर प्रयुक्त होनेवाले शब्दों को ………………. कहते हैं।
उत्तर:
सर्वनाम

प्रश्न 16.
जिस सर्वनाम से कर्त्ता के विषय में कुछ बताया जाता ……………….. सर्वनाम कहते हैं।
उत्तर:
निजवाचक

प्रश्न 17.
किन्हीं चार प्रश्नों के उत्तर दिजिए। रेखांकित शब्द किस प्रकार का सर्वनाम है?
उत्तर:
अनिश्चयवाचक

कारक

प्रश्न 1.
दूध से दही बनता है। रेखांकित पद किस कारक में है?
उत्तर:
अपादान

प्रश्न 2.
महेश बुखार से पीड़ित है। रेखांकित पद किस कारक में है?
उत्तर:
करण

प्रश्न 3.
बन्दूक से गोली चली। रेखांकित अंश किस कारक में है?
उत्तर:
अपादान

प्रश्न 4.
छात्र ने शिक्षक से दो प्रश्न पूछे। रेखांकित पद किस कारक में है?
उत्तर:
कर्म

प्रश्न 5.
बच्चा साँप से डरता है। रेखांकित पद किस कारक में है?
उत्तर:
कर्म

प्रश्न 6.
मुझ पर भरोसा रखो। रेखांकित पद किस कारक में है?
उत्तर:
अधिकरण

प्रश्न 7.
कटक में बालियात्रा का मेला लगता है। रेखांकित पद किस कारक में है?
उत्तर:
अधिकरण

प्रश्न 8.
पेड़ पर बन्दर बैठा है। रेखांकित पद किस कारक में है?
उत्तर:
अधिकरण

प्रश्न 9.
विनोद माधव से लम्बा है। रेखांकित अंश किस कारक में है?
उत्तर:
अपादान

प्रश्न 10.
माता ने बच्चे को सुलाया। रेखांकित अंश किस कारक में है?
उत्तर:
कर्म

प्रश्न 11.
यह है शब्द संयोजन की बात। रेखांकित अंश किस कारक में है?
उत्तर:
संबंध कारक

प्रश्न 12.
कृपाशंकर घर से स्टेशन आया। रेखांकित अंश किस कारक में है?
उत्तर:
अपादान

परसर्ग / विभक्ति

प्रश्न 1.
वह तकिए……………… बैठा।
उत्तर:
पर

प्रश्न 2.
साँप नेवले ……………. डरता है।
उत्तर:
से

प्रश्न 3.
हृदय द्वार खोलने ……………. कुंजी है।
उत्तर:
की

प्रश्न 4.
पेड़…………………फल गिरा।
उत्तर:
से

प्रश्न 5.
जीवों …………..दया करो।
उत्तर:
पर

प्रश्न 6.
रोगी हैजे ……………… मर गया।
उत्तर:
स

प्रश्न 7.
लोगों की जान ………… जान आई।
उत्तर:
में

प्रश्न 8.
ठाकुर साहब गाड़ी ………… जान आई।
उत्तर:
से

प्रश्न 9.
कृपाशंकर …………. उतरने लगे।
उत्तर:
ने

प्रश्न 10.
उत्कृष्ट कलाओं …………… कई कुली बुलाये।
उत्तर:
का

प्रश्न 11.
क्या तुम्हारे बैठने …………… देश उत्कल।
उत्तर:
का

प्रश्न 12.
गर्व
उत्तर:
से.

प्रश्न 13.
वाणभट्ट …………….. ठेका लिया है?
उत्तर:
ने

प्रश्न 14.
गिल्लू ने मुक्ति ……………. कहो कि मैं भारतीय हूँ।
उत्तर:
की

प्रश्न 15.
मुँह. ……………….. .उफ न निकलने दो अपने लड़के से कहा।
उत्तर:
से

प्रश्न 16.
गाय ………….. घास दो।
उत्तर:
को

प्रश्न 17.
नरेन ……………….भाई पढ़ता है।
उत्तर:
का

प्रश्न 18.
मन …………….. अहंकार को स्थान मत दो।
उत्तर:
में

प्रश्न 19.
मेज ……………… किताबें रखी है।
उत्तर:
पर

प्रश्न 20.
खुले मैदान में, रेत …………… साँस ली।
उत्तर:
पर

क्रिया (सकर्मक और अकर्मक)

प्रश्न 1.
“घोड़ा दौड़ता है” – इस वाक्य में “ दौड़ता ” किस क्रिया का रूप है?
उत्तर:
अकर्मक

प्रश्न 2.
“राम फल खाता है”- इस वाक्य में ‘खाता’ किस क्रिया का रूप है?
उत्तर:
सकर्मक

प्रश्न 3.
सही अकर्मक क्रिया रूप छाँटिए:
(गाना, रोना, खाना, , देना)
उत्तर:
रोना

प्रश्न 4.
अकर्मक क्रिया रूप पहचानिए:
(पढ़ना, मिलना, बहना, कहना)
उत्तर:
बहना

प्रश्न 5.
सही सकर्मक क्रिया रूप छाँटिए:
( रहना, रोना, गाना, सरकाना )
उत्तर:
गाना

प्रश्न 6.
अकर्मक क्रिया रूप चुनिए:
(वनाना, भागना, समझना, पढ़ना)
उत्तर:
भागना

प्रश्न 7.
सही सकर्मक क्रिया रूप पहचानिए:
( उड़ना, कूदना, छोड़ना, याचना )
उत्तर:
छोड़ना

प्रश्न 8.
कौन सा क्रिया रूप अकर्मक है छाँटिए:
(खाना, देखना, मिलना, दौड़ना)
उत्तर:
खाना

प्रश्न 9.
सकर्मक क्रिया रूप छाँटिए:
(सोना, रोना, होना,
उत्तर:
पीना

प्रश्न 10.
सही सकर्मक क्रिया रूप पहचानिए:
(निकलना, सजाना, जीना, वदलना)
उत्तर:
सजाना

प्रेरणार्थक क्रिया रूप

प्रश्न 1.
‘पढ़ना’ – द्वितीय प्रेरणार्थक क्रिया का रूप है…………..।
उत्तर:
पढ़वाना

प्रश्न 2.
‘करना’- प्रथम प्रेरणार्थक क्रिया का रूप है …………….।
उत्तर:
कराना

प्रश्न 3.
‘कहना’ – द्वितीय प्रेरणार्थक क्रिया का रूप है ……………।
उत्तर:
कहलवाना

प्रश्न 4.
‘देखना ‘ – द्वितीय प्रेरणार्थक क्रिया का रूप है ……………..।
उत्तर:
दिखवाना

प्रश्न 5.
‘भीगना’ – द्वितीय प्रेरणार्थक क्रिया का रूप है…………….।
उत्तर:
भीगवाना

प्रश्न 6.
‘रोना’ – द्वितीय प्रेरणार्थक क्रिया का रूप है……………।
उत्तर:
रुलवाना

प्रश्न 7.
‘खाना’ – द्वितीय प्रेरणार्थक क्रिया का रूप है…………..।
उत्तर:
खिलवाना

प्रश्न 8.
‘बनना’ क्रिया का पहला प्रेरणार्थक क्रिया रूप है…………..।
उत्तर:
बनाना

प्रश्न 9.
‘खाना’ क्रिया का सही प्रेरणार्थक क्रिया रूप है……………….।
उत्तर:
खिलाना

प्रश्न 10.
‘सोना’ क्रिया का प्रथम प्रेरणार्थक रूप है
उत्तर:
सुलाना

प्रश्न 11.
‘भेजना’ क्रिया का दूसरा प्रेरणार्थक रूप है
उत्तर:
भेजवाना

प्रश्न 12.
‘लिखना’ क्रिया का द्वितीय प्रेरणार्थक रूप है
उत्तर:
लिखवाना

प्रश्न 13.
‘हँसना’ क्रिया का सही प्रेरणार्थक रूप है
उत्तर:
हँसाना

प्रश्न 14.
‘करना’ क्रिया का द्वितीय प्रेरणार्थक रूप है
उत्तर:
करवाना

प्रश्न 15.
‘पिना’ क्रिया का द्वितीय प्रेरणार्थक रूप हैं-
उत्तर:
पिलवाना

प्रश्न 16.
‘उठना’ क्रिया का प्रथम प्रेरणार्थक रूप है –
उत्तर:
उठाना

प्रश्न 17.
‘समझना’ क्रिया का पहला प्रेरणार्थक रूप है
उत्तर:
समझाना

सही क्रिया पद भरिए

प्रश्न 1.
अनेक सुधी नेता काम में जुट……………..।
उत्तर:
गए

प्रश्न 2.
राम ने एक पुस्तक…………….।
उत्तर:
खरीदी

प्रश्न 3.
आँख भी लाल होकर दुःखने ………………।
उत्तर:
लगी

प्रश्न 4.
उसने चाय पी ………………।
उत्तर:
ली

प्रश्न 5.
सीता ने गीता को ……………..।
उत्तर:
पढ़ाया

प्रश्न 6.
वे चिट्ठियाँ लिख ………….।
उत्तर:
रहे थे

प्रश्न 7.
कृपाशंकर ने कई कुली…………….।
उत्तर:
बुलाये

प्रश्न 8.
उन्हें आज इस पद को महानता ज्ञात……………।
उत्तर:
हुई

प्रश्न 9.
मुसाफिर ने क्रोध पूर्ण नेत्रो से …………..।
उत्तर:
देखा

प्रश्न 10.
अशोक ने वीरत्व की कहानी ……………।
उत्तर:
सुनी

प्रश्न 11.
आपको कुछ सेवा करने का अवसर ………………।
उत्तर:
मिला

प्रश्न 12.
यह नित्य का क्रम हो ……………..।
उत्तर:
गया

प्रश्न 13.
कलिंगवासियों ने जाने दीं पर जमीन नहीं …………….।
उत्तर: दी

प्रश्न 14.
शिक्षक चन्द्रधर शर्मा को नींद नहीं …………………।
उत्तर:
आयी

प्रश्न 15.
पारादीप बन्दरगाह ने नौवाणिज्य को बढ़ावा …………….।
उत्तर:
दिया

विपरीतार्थक शब्द (विलोम )

प्रश्न 1.
‘मृत्यु’ शब्द का सही विलोमरूप …………….।
उत्तर:
जन्म

प्रश्न 2.
‘राजा’ शब्द का सही विपरीत रूप …………….।
उत्तर:
रंक

प्रश्न 3.
‘अपनापन’ शब्द का सही विलोमरूप ……………..।
उत्तर: परायापन

प्रश्न 4.
‘चर’ शब्द का सही विलोम रूप ……………..।
उत्तर:
अचर

प्रश्न 5.
‘हाजिर’ शब्द का सही विपरीत रूप ……………।
उत्तर:
गैरहाजिर

प्रश्न 6.
‘नफा’ शब्द का सही विलोमरूप ……………..।
उत्तर:
नुकसान

प्रश्न 7.
‘कम’ शब्द का सही विलोम रूप ……………।
उत्तर:
ज्यादा

प्रश्न 8.
‘काँटा’ शब्द का सही विलोम रूप ……………..।
उत्तर:
फूल

प्रश्न 9.
‘मोटा’ शब्द का सही विपरीत रूप ………………।
उत्तर:
पतला

प्रश्न 10.
‘पण्डित’ शब्द का सही विपरीत रूप ……………..।
उत्तर:
मूर्ख

प्रश्न 11.
‘उत्तम’ शब्द का सही विलोमरूप …………….।
उत्तर:
मध्यम

प्रश्न 12.
‘सच्चा’ शब्द का सही बिलोमरूप ……………..।
उत्तर:
झूठा

प्रश्न 13.
‘महल’ शब्द का सही विलोम रूप ……………….।
उत्तर:
झोंपड़ी

प्रश्न 14.
‘वसंत’ शब्द का सही विलोम रूप ………………..।
उत्तर:
पत्तझड़

प्रश्न 15.
‘गन्दा’ शब्द का सही विलोम रूप
उत्तर:
साफ

पर्यायवाची शब्द

प्रश्न 1.
‘तलवार’ शब्द का सही समानार्थक रूप……………..।
उत्तर:
कृपाण

प्रश्न 2.
‘कमल’ शब्द का सही समानार्थक रूप……………..
उत्तर:
सरोज

प्रश्न 3.
‘धर’ शब्द का पर्यायवाची रूप ……………..।
उत्तर:
निवास

प्रश्न 4.
‘शरीर’ शब्द का समानार्थक रूप ……………….।
उत्तर:
काया

प्रश्न 5.
‘चवाई’ शब्द का सही पर्यायवाची रुप…………….।
उत्तर:
निन्दक

प्रश्न 6.
‘सौदामिनी’ शब्द का सही पर्यायवाची रूप ……………।
उत्तर:
बिजली

प्रश्न 7.
‘हाथी’ शब्द का सही पर्यायवाची रूप ………………।
उत्तर:
गज

प्रश्न 8.
‘अम्बा’ शब्द का पर्यायवाची रूप ……………..।
उत्तर:
माता

प्रश्न 9.
‘महादेव’ का दूसरा रूप है………………….।
उत्तर:
शिवं

प्रश्न 10.
‘सुधाकर’ शब्द का पर्यायवाची रूप …………………।
उत्तर:
चन्द्र

प्रत्यय

प्रश्न 1.
जो शब्दांश धातु, क्रिया या शब्दों के अंत में लगकर नये शब्दों का निर्माण करते है, उन्हें……………. कहते है।
उत्तर:
प्रत्यय

प्रश्न 2.
‘शक्तिमान’ शब्द से …………. प्रत्ययहै।
उत्तर:
मान

प्रश्न 3.
‘चिकनाई’ में प्रत्यय है……………।
उत्तर:
आई

प्रश्न 4.
‘शैव’ में प्रत्यय है ……………।
उत्तर:
अ

प्रश्न 5.
‘पाठक’ शब्द में प्रत्यय है ……………।
उत्तर:
अक

प्रश्न 6.
‘दर्दनाक’ में प्रत्यय है …………….।
उत्तर:
नाक

प्रश्न 7.
‘शरमालू’ में प्रत्यय है …………….।
उत्तर:
आलू

प्रश्न 8.
‘राष्ट्रीय’ शब्द में प्रत्यय है………….
उत्तर:
ईय

 

प्रश्न 9.
संज्ञा, सर्वनाम मेल से बने शब्द को……………….. जाता है ।
उत्तर:
तद्धितान्त पद

प्रश्न 10.
‘प्रसन्न’ के साथ ‘ता’ प्रत्यय लगाइए ………………. ।
उत्तर:
प्रसन्नता

प्रश्न 11.
‘निर्मलता’ में प्रत्यय ………………..।
उत्तर:
ता

प्रश्न 12.
‘उपजाऊ’ में प्रत्यय है …………..।
उत्तर:
आऊ

प्रश्न 13.
‘ईला’ प्रत्यय प्रयुक्त शब्द है…………..।
उत्तर:
चमकीला

प्रश्न 14.
‘इक’ प्रत्यय प्रयुक्त शब्द है…………….।
उत्तर:
सामाजिक

प्रश्न 15.
‘आस’ प्रत्यय प्रयुक्त शब्द है ……………….।
उत्तर:
मिठास

उपसर्ग

प्रश्न 1.
भाषा में नए शब्दों का निर्माण करने के लिए शब्द के पहले जो शब्दांश जोड़े जाते है, उन्हे ……………….. कहते हैं।
उत्तर:
उपसर्ग

प्रश्न 2.
‘अभिमान’ शब्द से कौन सा उपसर्ग जुड़ा गया है?
उत्तर:
अभि

प्रश्न 3.
‘हर’ उपसर्ग से बना शब्द है……………….।
उत्तर:
हरघड़ी

प्रश्न 4.
‘अनुशासन’ शब्द में उपसर्ग है……………।
उत्तर:
अनु

प्रश्न 5.
‘अन’ उपसर्गवाले शब्द है। …………….।
उत्तर:
अनपढ़

प्रश्न 6.
‘अभि’ उपसर्ग से बना शब्द है……………..
उत्तर:
अभिमान

प्रश्न 7.
‘प्र’ उपसर्ग जोड़ा हुआ शब्द ……………..।
उत्तर:
प्रगति

प्रश्न 8.
‘परा’ उपसर्ग प्रयुक्त शब्द……………….।
उत्तर:
पराजय

प्रश्न 9.
‘सम्’ उपसर्ग प्रयुक्त शब्द ………………।
उत्तर:
संतोष

प्रश्न 10.
‘उत्’ उपसर्ग प्रयुक्त शब्द ……………….।
उत्तर:
उत्कर्ष

प्रश्न 11.
‘परि’ उपसर्ग प्रयुक्त शब्द …………….।
उत्तर:
परिवार

प्रश्न 12.
‘प्रति’ उपसर्ग प्रयुक्त शब्द ……………।
उत्तर:
प्रतिकार

प्रश्न 13.
‘अति’ उपसर्ग प्रयुक्त शब्द ………………।
उत्तर:
अत्याचार

प्रश्न 14.
‘अनु’ उपसर्ग प्रयुक्त शब्द ……………..।
उत्तर:
अनुकूल

प्रश्न 15.
‘अधि’ उपसर्ग प्रयुक्त शब्द …………….।
उत्तर:
अधिकार

प्रश्न 16.
‘ला’ उपसर्ग प्रयुक्त शब्द ……………..।
उत्तर:
लाचार

प्रश्न 17.
‘अनुकूल’ शब्द में कौन-सा उपसर्ग है?
उत्तर:
अनु

प्रश्न 18.
‘सरपंच’ शब्द में कौन-सा उपसर्ग है?
उत्तर:
सर

विशेषण / संज्ञा

प्रश्न 1.
‘कांटा’ शब्द का विशेषण रूप………………….।
उत्तर:
कंटीला

प्रश्न 2.
‘समाज’ शब्द का सही विशेषण रूप ………………।
उत्तर:
सामाजिक

प्रश्न 3.
‘राष्ट्र’ शब्द का सठिक विशेषण रूप …………….।
उत्तर:
राष्ट्रीय

प्रश्न 4.
‘शरीर’ शब्द का सही विशेषण रूप …………….।
उत्तर:
शारीरिक

प्रश्न 5.
‘इच्छा’ शब्द का सही विशेषण रूप बताइए।
उत्तर:
ऐच्छिक

प्रश्न 6.
‘शैक्षिक’ शब्द का मूल रूप वताइए।
उत्तर:
शिक्षा

प्रश्न 7.
‘सोना’ शब्द का सही विशेषण रूप …………..।
उत्तर:
सुनहरा

प्रश्न 8.
‘साल’ शब्द का सही विशेषण रूप ……………।
उत्तर:
सालाना

प्रश्न 9.
‘रंग’ शब्द का सही बिशेषण रूप ……………।
उत्तर:
रंगिला

प्रश्न 10.
‘चाल’ शब्द का सही विशेषण रूप …………..।
उत्तर:
चालु

प्रश्न 11.
‘लौकिक’ शब्द के मूल रूप …………….।
उत्तर:
लोक

प्रश्न 12.
‘शोभा’ शब्द का विशेषण रूप …………..।
उत्तर:
शोभित

प्रश्न 13.
‘अग्नि’ शब्द का सही विशेषण रूप ……………।
उत्तर:
आग्नेय

प्रश्न 14.
‘खिलाड़ी’ का मूल शब्द ………………..।
उत्तर:
खेल

अव्यय

प्रश्न 1.
अचानक वर्षा आ गई रेखांकित शब्द कौन-सा अव्यय है?
उत्तर:
क्रिया विशेषण

प्रश्न 2.
नौकर के हाथ चिट्ठी भेज दो- रेखांकित अंश कौन- सा अव्यय है?
उत्तर:
संबंधसूचक

प्रश्न 3.
कक्षा में लगभग चालीस विद्यार्थी थे – रेखांकित शब्द कौन-सा अव्यय है ?
उत्तर:
क्रिया विशेषण

प्रश्न 4.
तुम पुरी जाओ, नहीं तो मैं जाऊँगा – रेखांकित शब्द कौन-सा अव्यय?
उत्तर:
समुच्चयबोधक

प्रश्न 5.
कुछ शब्द ऐसे होते हैं जिनमें कभी किसी भी स्थिति में परिवर्तन नहीं होता, ऐसे शब्दों को ………… कहते है।
उत्तर:
अव्यय

प्रश्न 6.
जो शब्द दो सजातीय पदों या दो स्वतंत्र उपवाक्यों को जोड़ते या अलग करते हैं, उसे …………… अव्यय कहा जाता है।
उत्तर:
समुच्चयबोधक

प्रश्न 7.
पेड़ लगाएँ जीवन बचाएँ वाक्य में सही अव्यय लगाइए।
उत्तर:
और

प्रश्न 8.
शेर शिकार पर झपटता है- वाक्य में सही अव्यय लगाइए।
उत्तर:
अचानक

प्रश्न 9.
वह अच्छा पढ़ता है, देर से उठता है- वाक्य में सही अव्यय लगाइए ।
उत्तर:
लेकिन

प्रश्न 10.
उनको दिल का दौरा पड़ा, अस्पताल गए हैं – वाक्य में सही अव्यय जोड़िए।
उत्तर:
इसलिए

विविध

प्रश्न 1.
‘बुबै’ शब्द का खड़ीबोली रूप ………….।
उत्तर:
बोए

प्रश्न 2.
‘हिरदै’ शब्द का खड़ीबोली रूप……………।
उत्तर:
हृदय

प्रश्न 3.
‘बाको’ शब्द का खड़ीबोली रूप ……………।
उत्तर:
उसको

प्रश्न 4.
‘तलवार’ शब्द का खड़ीवोली रूप …………… है।
उत्तर:
तलवार

प्रश्न 5
‘खोदना’ शब्द का सही भाववाचक संज्ञारूप …………….. है।
उत्तर:
खुदाई

प्रश्न 6.
‘चतुर’ शब्द का सही भाववाचक संज्ञारूप ………….. है।
उत्तर:
चतुराई

प्रश्न 7.
‘दौड़ना’ शब्द का सही भाववाचक संज्ञारूप ………….. हैं।
उत्तर:
दौड़

प्रश्न 8.
‘दाँत खट्टे करता’ का अर्थ …………. है।
उत्तर:
परास्त करना

प्रश्न 9.
‘जान की वाजी लगाना’ का अर्थ ………….. है।
उत्तर:
जी तोड़ कोशिश करना

प्रश्न 10.
‘बीड़ा उठाना’ का अर्थ …………… है।
उत्तर:
दायित्व संभालना

प्रश्न 11.
‘खुफिया’ शब्द का अर्थ …………….. है।
उत्तर:
गुप्त

प्रश्न 12.
‘मुदर्रिसी’ शब्द का अर्थ …………….।
उत्तर:
शिक्षकता

प्रश्न 13.
‘सलोने’ शब्द का अर्थ ……………..।
उत्तर:
सुन्दर

प्रश्न 14. ‘
अचरज’ का तत्सम रूप है:
उत्तर:
आश्चर्य

प्रश्न 15.
‘कुआँ’ शब्द का सही तत्सम रूप ………………।
उत्तर:
कूप

प्रश्न 16.
‘कचूमर निकालना’ शब्द का सही अर्थ क्या है?
उत्तर:
पीटना

प्रश्न 17.
नीली गाय कौन-सा समास है?
उत्तर:
कर्मधारय

Odisha State Board BSE Odisha 10th Class Physical Science Solutions Chapter 9 ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଚୁମ୍ବକୀୟ ପ୍ରଭାବ Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Physical Science Solutions Chapter 9 ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଚୁମ୍ବକୀୟ ପ୍ରଭାବ

ପ୍ରଶ୍ନ 1 ରୁ 5 ମଧ୍ୟରେ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନ ପାଇଁ ଦିଆଯାଇଥ‌ିବା ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।

Question 1.
ଖଣ୍ଡିଏ ଲମ୍ବା ସଳଖ ତାର ଚାରିପଟେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର କିଭଳି ହୋଇଥାଏ ?
(a) ତାର ପ୍ରତି ଲମ୍ବ ସରଳରେଖା ଦ୍ୱାରା ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୂଚିତ ହୁଏ ।
(b) ତାର ପ୍ରତି ସମାନ୍ତର ସରଳରେଖା ଦ୍ୱାରା ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୂଚିତ ହୁଏ ।
(c) ତାରରୁ ବାହାରୁଥ‌ିବା ଅରୀୟ (Radial) ରେଖା ଦ୍ୱାରା ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୂଚିତ ହୁଏ ।
(d) ତାରକୁ କେନ୍ଦ୍ର କରୁଥିବା ସମକୈନ୍ଦ୍ରିକ ବୃତ୍ତଦ୍ୱାରା ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୂଚିତ ହୁଏ ।
Answer:
(d) ତାରିକୁ କେନ୍ଦ୍ର କରୁଥିବା ସମକୈନ୍ଦ୍ରିକ ବୃତ୍ତଦ୍ୱାରା ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୂଚିତ ହୁଏ ।

Question 2.
ବିଦ୍ୟୁତ୍ ଚୁମ୍ବକୀୟ ପ୍ରେରଣ ହେଉଛି
(a) ବସ୍ତୁକୁ ଚାର୍ଜିତ କରିବା ପଦ୍ଧତି
(b) ଏକ ପଦ୍ଧତି ଯେଉଁଥିରେ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଯୋଗୁଁ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୃଷ୍ଟି ହୁଏ ।
(c) ଏକ ପଦ୍ଧତି ଯେଉଁଥିରେ କୁଣ୍ଡଳୀ ଓ ଚୁମ୍ବକ ମଧ୍ୟରେ ଆପେକ୍ଷିକ ଗତି ଯୋଗୁଁ କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ ।
(d) ବୈଦ୍ୟୁତିକ ମୋଟର୍‌ର କୁଣ୍ଡଳୀକୁ ଘୂରାଇବା ପଦ୍ଧତି ।
Answer:
(୯) ଏକ ପଦ୍ଧତି ଯେଉଁଥିରେ କୁଣ୍ଡଳୀ ଓ ଚୁମ୍ବକ ମଧ୍ୟରେ ଆପେକ୍ଷିକ ଗତି ଯୋଗୁଁ କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ ।

Question 3.
ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଉତ୍ପନ୍ନ କରିବା ପାଇଁ ବ୍ୟବହୃତ ହେଉଥ‌ିବା ସାଧନର ନାମ ହେଉଛି –
(a) ଜେନେରେଟର୍
(b) ଗାଲ୍‌ ଭାନୋମିଟର୍
(c) ଏମିଟର୍
(d) ମୋଟର୍
Answer:
(a) ଜେନେରେଟର୍

Question 4.
ଏ.ସି. ଜେନେରେଟର ଓ ଡି.ସି. ଜେନେରେଟର ମଧ୍ୟରେ ମୁଖ୍ୟ ପ୍ରଭେଦ ହେଉଛି –
(c) ଏ.ସି. ଜେନେରେଟର୍‌ରେ ବିଦ୍ୟୁତ୍ ଚୁମ୍ବକ ଥିବାବେଳେ ଡି.ସି. ଜେନେରେଟର୍‌ରେ ସ୍ଥାୟୀ ଚୁମ୍ବକ ଥାଏ ।
(b) ଡି.ସି. ଜେନେରେଟର୍ ଅଧ‌ିକ ଭୋଲ୍ଟେଜ୍ ଉତ୍ପନ୍ନ କରେ ।
(c) ଏ.ସି. ଜେନେରେଟର୍ ଅଧ‌ିକ ଭୋଲ୍‌ଟେଜ୍ ଉତ୍ପନ୍ନ କରେ ।
(d) ଏ.ସି. ଜେନେରେଟର୍‌ରେ ସ୍କ୍ରିପ୍ ବଳୟ ଥିବାବେଳେ ଡି.ସି. ଜେନେରେଟର୍‌ରେ କମ୍ୟୁଟେଟ୍‌ର ଥାଏ ।
Answer:
(d) ଏ.ସି. ଜେନେରେଟର୍‌ରେ ସ୍କ୍ରିପ୍ ବଳୟ ଥିବାବେଳେ ଡି.ସି. ଜେନେରେଟର୍‌ରେ କମ୍ୟୁଟେଟ୍‌ ଥାଏ ।

Question 5.
ଲଘୁପଥନ ହୋଇଥିବା ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ
(a) ବହୁ ପରିମାଣରେ କମିଯାଏ
(b) ଅପରିର୍ତ୍ତର ରହେ
(c) ବହୁପରିମାଣରେ ବଢ଼ିଯାଏ
(d) ଅରିରତ ଉ|ବେ ବଦଳୁଥାଏ
Answer:
(c) ବହୁ ପରିମାଣରେ ବଢ଼ିଯାଏ

Question 6.
ନିମ୍ନଲିଖୂ ବାକ୍ୟଗୁଡ଼ିକ ଠିକ୍ ବା ଭୁଲ୍ ଦର୍ଶାଅ ।
(a) ବୈଦ୍ୟୁତିକ ମୋଟର୍ ଯାନ୍ତ୍ରିକ ଶକ୍ତିକୁ ବିଦ୍ୟୁତ୍ ଶକ୍ତିରେ ପରିଣତ କରେ ।
(b) ବିଦ୍ୟୁତ୍ ଜେନେରେଟର୍ ବିଦ୍ୟୁତ୍ ଚୁମ୍ବକୀୟ ପ୍ରେରଣ ନିୟମ ଅନୁସାରେ କାର୍ଯ୍ୟ କରେ ।
(c) ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଥ‌ିବା ଏକ ଦୀର୍ଘ ବୃତ୍ତାକାର କୁଣ୍ଡଳୀର କେନ୍ଦ୍ରରେ କ୍ଷେତ୍ର ସମାନ୍ତର ସରଳରେଖା ଦ୍ବାରା ସୂଚିତ ହୁଏ ।
(d) ବିଦ୍ୟୁତ୍ ଯୋଗାଣ କ୍ଷେତ୍ରରେ ଲାଇଭ୍ ତାର ସାଧାରଣତଃ ସବୁଜ ବିଦ୍ୟୁତ୍‌ରୋଧୀ ଦ୍ଵାରା ଚିହ୍ନିତ ହୋଇଥାଏ ।
Answer:
(a) ଭୁଲ୍ (b) ଠିକ୍ (c) ଠିକ୍ (d) ଭୁଲ୍ ।

Question 7.
ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୃଷ୍ଟି କରିବା ପାଇଁ ଦୁଇଟି ଉପାୟର ତାଲିକା କର ।
Answer:
(a) କୃତ୍ରିମ ଓ ପ୍ରାକୃତିକ ଚୁମ୍ବକ
(b) ବିଦ୍ୟୁତ୍ ଚୁମ୍ବକ
(c) ଏକ ପରିବାହୀ, ତାର କୁଣ୍ଡଳୀ ଓ ସଲେନଏଡ୍ ଯେ କି ବିଦ୍ୟୁତ୍ ପରିବହନ କରେ ।

Question 8.
ସଲେନଏଡ୍ କେମିତି ଚୁମ୍ବକ ଭଳି କାର୍ଯ୍ୟ କରେ ? ଗୋଟିଏ ଦଣ୍ଡ ଚୁମ୍ବକ ସାହାଯ୍ୟରେ ବିଦ୍ୟୁତ୍ ପରିବହନ କରୁଥିବା ସଲେନଏଡ୍‌ର ଉତ୍ତର ଓ ଦକ୍ଷିଣ ମେରୁ ନିର୍ଣ୍ଣୟ କରିପାରିବ କି ? ବୁଝାଅ ।
Answer:
(a)

• ସଲେନଏଡ୍ ଏକ ଦଣ୍ଡଚୁମ୍ବକ ପରି କାର୍ଯ୍ୟ କରେ ।
• ସଲେନଏଡ୍ ଯୋଗୁଁ ସୃଷ୍ଟ କ୍ଷେତ୍ର ରେଖା ବଳରେଖାମାନ ଦଣ୍ଡ ଚୁମ୍ବକର୍ ବଳରେଖା ସଦୃଶ ।
• ସଲେନଏଡ୍ ଭିତର ପଟରେ କ୍ଷେତ୍ରରେଖାଗୁଡ଼ିକ ସରଳରୈ ଓ ପରସ୍ପର ସହ ସମାନ୍ତର । ବାହାର ପଟରେ ଗୋଟିଏ ପ୍ରାନ୍ତରୁ ଅନ୍ୟ ପ୍ରାନ୍ତକୁ ଯାଇଛି ।
• ତେଣୁ ଦଣ୍ଡ ଚୁମ୍ବକ ପରି ସଲେନଏଡ୍‌ର ଗୋଟିଏ ପ୍ରାନ୍ତ ଚୁମ୍ବକୀୟ ଉତ୍ତର ମେରୁ ଓ ଅନ୍ୟ ପ୍ରାନ୍ତଟି ଦକ୍ଷିଣ ମେରୁ ଭଳି ଆଚରଣ କରେ ।

(b)
(i) ସଲେନଏଡ୍ ପ୍ରାନ୍ତକୁ ଚାହିଁଲେ ଯଦି ପ୍ରବାହ ଘଣ୍ଟାକଣ୍ଟା ଘୂରିବା ଦିଗରେ ଅର୍ଥାତ୍ ଦକ୍ଷିଣାବର୍ତୀ ପ୍ରବାହ ହେଉଥାଏ, ତେବେ ସେହି ପ୍ରାନ୍ତ ଦକ୍ଷିଣ ମେରୁ ଏବଂ ଯେଉଁ ପ୍ରାନ୍ତରେ ବାମାବର୍ତୀ ପ୍ରବାହ ହେଉଥ‌ିବ ତାହା ଉତ୍ତର ମେରୁ ।

(ii) ଦ୍ଵିତୀୟରେ ଗୋଟିଏ ଦଣ୍ଡଚୁମ୍ବକର ଉତ୍ତର ମେରୁ ସଲେନଏଡ଼ର ଏକ ପ୍ରାନ୍ତ ନିକଟକୁ ନେଲେ ଯଦି ସଲେନଏଡ୍ ଉତ୍ତର ମେରୁ ଆଡ଼କୁ ଆକୃଷ୍ଟ ହୋଇଆସେ ତେବେ ସଲେନଏଡ୍ର ସେହି ପ୍ରାନ୍ତ ଦକ୍ଷିଣ ମେରୁ । ଯଦି ସଲେନଏଡ୍‌ର ସେହି ପ୍ରାନ୍ତ ଦଣ୍ଡ ଚୁମ୍ବକର ଉତ୍ତର ମେରୁଠାରୁ ଦୂରେଇଯାଏ ତେବେ ତାହା ଉତ୍ତର ମେରୁ ହେବ ।

Question 9.
ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ରହିଥ‌ିବା ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବିଶିଷ୍ଟ ପରିବାହୀ ଉପରେ ବଳ କେତେବେଳେ ସର୍ବାଧିକ ହୁଏ ?
Answer:
ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ରହିଥ‌ିବା ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବିଶିଷ୍ଟ ପରିବାହୀ ଉପରେ ବଳ ସର୍ବାଧ‌ିକ ହେବ ଯେତେବେଳେ ପରିବାହୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ହେବ ।

Question 10.
ମନେକର ଗୋଟିଏ କୋଠରୀ ଭିତରେ ତୁମେ ଗୋଟିଏ କାନ୍ଥକୁ ଆଉଜି ବସିଛ । ପଛକାନ୍ଥରୁ ସାମ୍ନା କାନ୍ଥ ଆଡ଼କୁ ଭୂସମାନ୍ତର ଭାବେ ଗତି କରୁଥିବା ଏକ ଇଲେକ୍‌ଟ୍ରନ ଗୁଚ୍ଛ ଗୋଟିଏ ତୀବ୍ର ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ଯୋଗୁଁ ତୁମ ଡାହାଣ ଆଡ଼କୁ ବିକ୍ଷେପିତ ହେଉଛି । ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ କ’ଣ ?
Answer:
ବିଦ୍ୟୁତ୍ ସ୍ରୋତ (I)ର ଦିଗ ଇଲେକ୍‌ଟ୍ରନ ଗୁଚ୍ଛର ବିପରୀତ ଦିଗ ଅଟେ । ଯେହେତୁ ଇଲେକ୍‌ ଟ୍ରନ ରଶ୍ମିଗୁଚ୍ଛ ଗୋଟିଏ ତୀବ୍ର ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ଯୋଗୁ ଡାହାଣ ଆଡ଼କୁ ବିକ୍ଷେପିତ ହେଉଛି, ଫ୍ଲେମିଂଙ୍କ ବାମହସ୍ତ ନିୟମ ପ୍ରୟୋଗ କଲେ ଜଣାଯାଏ ଯେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ଲମ୍ବଭାବରେ ନିମ୍ନମୁଖୀ କାର୍ଯ୍ୟକାରୀ ହେତଛ |

Question 11.
ଗୋଟିଏ ବୈଦ୍ୟୁତିକ ମୋଟର୍‌ର ନାମାଙ୍କିତ ଚିତ୍ର ଅଙ୍କନ କର । ଏହାର ନିୟମ ଓ କାର୍ଯ୍ୟପ୍ରଣାଳୀ ବୁଝାଅ । ମୋଟର୍‌ରେ ବିଖଣ୍ଡିତ ବଳୟର କାର୍ଯ୍ୟ କ’ଣ ?
Answer:
ନିୟମ : ବୈଦ୍ୟୁତିକ ମୋଟର୍ ଏକ ଘୂର୍ଣାୟମାନ ଯନ୍ତ୍ର । ଏହା ବିଦ୍ୟୁତ୍ ଶକ୍ତିକୁ ଯାନ୍ତ୍ରିକ ଶକ୍ତିରେ ରୂପାନ୍ତରିତ କରେ । ଯେକୌଣସି ପରିବାହୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହ କଲେ ତା’ ଚତୁର୍ଦ୍ଦିଗରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୃଷ୍ଟି ହୁଏ । ଯଦି ଏକ ସ୍ଥାୟୀ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହୀ ପରିବାହୀକୁ ରଖାଯାଏ, ତେବେ ଦୁଇଟି ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ପରସ୍ପରକୁ ପ୍ରଭାବିତ କରନ୍ତି । ଫଳରେ ପରିବାହୀଟି ଉପରେ ଏକ ବଳ କାର୍ଯ୍ୟକାରୀ ହୁଏ । ଏହି ବଳ ପ୍ରଭାବରେ ପରିବାହୀଟି ଗତିଶୀଳ ହୁଏ ।

କାର୍ଯ୍ୟପ୍ରଣାଳୀ :

• ବ୍ୟାଟେରୀରୁ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବ୍ରଶ X ଜରିଆରେ କୁଣ୍ଡଳୀ ABCD ରେ ପ୍ରବେଶ କରେ ଓ Y ଜରିଆରେ ପ୍ରସ୍ଥାନ କରେ |
• ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବାହୁ AB ରେ A ରୁ B ଆଡ଼କୁ ଓ CD ରେ C ରୁ D ଆଡ଼କୁ ପ୍ରବାହିତ ହେଉଛି ।
• ଫ୍ଲେମିଂଙ୍କ ବାମହସ୍ତ ନିୟମ ଅନୁସାରେ AB ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳ ତାକୁ ତଳକୁ ଠେଲୁଥିବା ବେଳେ CD ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳ ତାକୁ ଉପରକୁ ଠେଲିବ ।
• କୁଣ୍ଡଳୀ ଓ ଅଖ ଗୋଟିଏ ଅକ୍ଷ ଚାରିପଟେ ଘଣ୍ଟାକଣ୍ଟାର ବିପରୀତ ଦିଗରେ ଘୂରିବ । ପ୍ରବାହିତ ହେବ ।
• ଅର୍ଶଘୂର୍ଶନ ପରେ Q ବ୍ରଶ Xସହ ଓ P ବ୍ରଶ Y ସହ ଲାଗିବ ।
• କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ବିପରୀତ ହୋଇ DCBA ରେ
• ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗର ପରିବର୍ତ୍ତନ AB ଓ CD ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳର ଦିଗ ପରିବର୍ତ୍ତନ କରେ । ପୂର୍ବରୁ ତଳକୁ ଯାଉଥୁବା AB ବର୍ତ୍ତମାନ ଉପରକୁ ଉଠିବ ଏବଂ ପୂର୍ବରୁ ଉପରକୁ ଉଠୁଥ‌ିବା CD ବର୍ତ୍ତମାନ ତଳକୁ ଖସିବ ।
• କୁଣ୍ଡଳୀ ଓ ଅଖ ଏକାଦିଗରେ ଆଉ ଏକ ଅର୍ଦ୍ଧ ଘୂର୍ଣ୍ଣନ କରିବ ।
• ପ୍ରତି ଅର୍ଥ ଘୂର୍ଣ୍ଣନ ପରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଦିଗ ବଦଳି ଚାଲିବ ଏବଂ କୁଣ୍ଡଳୀ ଓ ଅଖ ଘଣ୍ଟାକଣ୍ଟାର ବିପରୀତ ଦିଗରେ ଅନବରତ ଘୂରିଚାଲିବ ।
• ଯେଉଁ ଯନ୍ତ୍ରକୁ ଘୂରାଇବା ଆବଶ୍ୟକ ତାକୁ ଅଖ ସହିତ ସଂଯୁକ୍ତ କରି ଦିଆଯିବ ।

ବିଖଣ୍ଡିତ ବଳୟର କାର୍ଯ୍ୟ :
ବିଖଣ୍ଡିତ ବଳୟ (କମ୍ୟୁଟେଟ୍‌ର) ପରିପଥରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ପ୍ରତି ଅର୍ଷଘୂର୍ଣ୍ଣନରେ ପରିବର୍ତ୍ତନ କରେ । ଫଳରେ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ପରିବର୍ତ୍ତନ ହୁଏ । କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳର ଦିଗ ସେହି ଅନୁସାରେ ପରିବର୍ତ୍ତନ ହୁଏ ଏବଂ କୁଣ୍ଡଳୀକୁ ଅନବରତ ଘୂରିବାରେ ସାହାଯ୍ୟ କରେ ।

Question 12.
ବୈଦ୍ୟୁତିକ ମୋଟର୍ ବ୍ୟବହାର କରୁଥ‌ିବା କିଛି ସାଧନର ନାମ ଲେଖ ।
Answer:
ବିଦ୍ୟୁତ୍ ଚାଳିତ ପଙ୍ଖା, ରେଫ୍ରିଜରେଟର୍, ମିକ୍ସର, ଲୁଗାଧୁଆ ଯନ୍ତ୍ର, କମ୍ପ୍ୟୁଟର, MP-3 ପ୍ଲେୟାର, ପାଣିପମ୍ପ୍, କୁଲର୍‌, ଶୀତତାପ ନିୟନ୍ତ୍ରିତ ଯନ୍ତ୍ର, ଧାନକୁଟା କଳ ।

Question 13.
ବିଦ୍ୟୁତ୍‌ରୋଧୀ ଦ୍ୱାରା ଆଚ୍ଛାଦିତ ତମ୍ବାତାରର ଏକ କୁଣ୍ଡଳୀ ଗୋଟିଏ ଗାଲ୍‌ଭାନୋମିଟର ସହ ସଂଯୁକ୍ତ । ଗୋଟିଏ ଦଣ୍ଡ ଚୁମ୍ବକକୁ ଯଦି
(i) କୁଣ୍ଡଳୀ ମଧ୍ୟକୁ ଠେଲି ଦିଆଯାଏ,
(ii) କୁଣ୍ଡଳୀ ମଧ୍ୟରୁ ବାହାରକୁ କାଢ଼ି ଅଣାଯାଏ,
(iii) କୁଣ୍ଡଳୀ ମଧ୍ୟରେ ସ୍ଥିର ଭାବେ ରଖାଯାଏ, ତା’ ହେଲେ କ’ଣ ହେବ ?
Answer:
ବିଦ୍ୟୁତ୍‌ରୋଧୀ ଦ୍ଵାରା ଆଚ୍ଛାଦିତ ତମ୍ବାତାରର ଏକ କୁଣ୍ଡଳୀ ଗୋଟିଏ ଗାଲ୍‌ଭାନୋମିଟର ସହ ସଂଯୁକ୍ତ । ଗାଲଭାନୋମିଟର କ୍ଷୀଣ ବିଦ୍ୟୁତ୍ ମାପକ ଯନ୍ତ୍ର ।

(i) ଗୋଟିଏ ଦଣ୍ଡ ଚୁମ୍ବକକୁ ଯଦି କୁଣ୍ଡଳୀ ମଧ୍ୟକୁ ଠେଲି ଦିଆଯାଏ ତେବେ ଗାଲଭାନୋମିଟରର ସୂଚୀ ଡାହାଣପଟକୁ ବିକ୍ଷେପିତ ହେବ । ଗାଲଭାନୋମିଟର୍‌ ବିକ୍ଷେପଣର ଅର୍ଥ କୁଣ୍ଡଳୀ ମଧ୍ଯରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହିତ ହୋଇଛି । ବୁମ୍ବକକୁ କୁଣ୍ଡଳୀ ନିକଟକୁ ହଠାତ୍ ନେଲେ କୁଣ୍ଡଳୀରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ପରିବର୍ତ୍ତନ ହୁଏ ଏବଂ କୁଣ୍ଡଳୀରେ ଚୁମ୍ବକୀୟ ବଳରେଖାର ପରିବର୍ତ୍ତନ ହୁଏ । କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ପ୍ରବାହ ଯୋଗୁଁ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସୃଷ୍ଟିହେଲା ଏବଂ ଗାଲ୍‌ଭାନୋମିଟର୍‌ ଡାହାଣକୁ ବିକ୍ଷେପିତ ହେଲା ।

(ii) କୁଣ୍ଡଳୀ ମଧ୍ୟରୁ ବାହାରକୁ କାଢ଼ି ଆଣିଲେ ହଠାତ୍‌ କୁଣ୍ଡଳୀରେ ଚୁମ୍ବକକ୍ଷେତ୍ର ପରିବର୍ତ୍ତନ ହେବ । ଫଳରେ କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ପ୍ରବାହ (ବିପରୀତ) ହେବ, ତେବେ ଗାଲଭାନୋମିଟର ବିକ୍ଷେପ ବାମପଟକୁ ହେବ । କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସୃଷ୍ଟି ହୋଇ ବିପରୀତ ଦିଗରେ ପ୍ରବାହିତ ହେବ ।

(iii) କୁଣ୍ଡଳୀ ମଧ୍ଯରେ ଚୁମ୍ବକକୁ ସ୍ଥିର ରଖୁଲେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା ପରିବର୍ତ୍ତନ ହୁଏନାହିଁ । ଫଳରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଉତ୍ପନ୍ନ ହୁଏ ନାହିଁ । ତେଣୁ ଗାଲଭାନୋମିଟର ବିକ୍ଷେପ ଶୂନ ହେବ ।

Question 14.
ଦୁଇଟି ବୃତ୍ତାକାର କୁଣ୍ଡଳୀ À ଓ B ପାଖାପାଖ୍ ରହିଛି । ଯଦି କୁଣ୍ଡଳୀ A ରେ ବିଦ୍ୟୁତ୍‌ ପ୍ରବାହ ବଦଳେ, କୁଣ୍ଡଳୀ Bରେ କିଛି ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବ କି ? କାରଣ ଦିଅ ।
Answer:
ହଁ, ଯଦି କୁଣ୍ଡଳୀ A ରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବଦଳେ ତେବେ କୁଣ୍ଡଳୀ B ରେ କିଛି ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବ । କାରଣ ଆମେ ଜାଣୁ ଯେ ଯଦି ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ପରିବର୍ତ୍ତନ ହେବ, ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ତୀବ୍ରତା ପରିବର୍ତ୍ତନ ହେବ । ତେଣୁ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ରେଖା ପରିବର୍ତ୍ତନ ହେଲେ B ର ମଧ୍ୟ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ରେଖା ପରିବର୍ତ୍ତନ ହେବ । A ରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବଦଳିବ ଫଳରେ B ରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବ ।

Question 15.
ନିୟମ ଦର୍ଶାଅ ।
Answer:
(i) ସଳଖ ପରିବାହୀରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଜନିତ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେ ଦିଗ ନିର୍ଣ୍ଣୟ କରିବା ପାଇଁ ।
ଡ :
ଦକ୍ଷିଣହସ୍ତ ବୃଦ୍ଧାଙ୍ଗୁଳି ନିୟମ :
ମନେକର ଯେଉଁ ତାରରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଉଛି ତାକୁ ତୁମେ ଡାହାଣ ହାତରେ ଏମିତି ମୁଠାଇ ଧରିଛି ଯେ ବୁଢ଼ା ଆଙ୍ଗୁଳିଟି ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଦିଗରେ ତାର ସହ ସମାନ୍ତର ହୋଇ ଲମ୍ବିରହିଛି ଓ ଅନ୍ୟ ଆଙ୍ଗୁଳିଗୁଡ଼ିକ ତାର ଚାରିପଟେ ବଙ୍କାଇ ହୋଇ ଘେରି ରହିଛି । ଏହି ଆଙ୍ଗୁଳି ଗୁଡ଼ିକର ଟିପ ଯେଉଁ ବୃତ୍ତାକାର ଦିଗର ସୂଚନା ଦେଉଛି ତାହା ହେଉଛି ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବହନ କରୁଥିବା ପରିବାହୀ ଜନିତ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ।

(ii) ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ପ୍ରତି ଲମ୍ବ ଭାବେ ଥ‌ିବା ସଳଖ ପରିବାହୀରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଜନିତ ବଳର ଦିଗ ନିର୍ଣ୍ଣୟ କରିବା ପାଇଁ ।
ଡ :
ଫ୍ଲେମିଂଙ୍କ ବାମହସ୍ତ ନିୟମ :
ବାମହସ୍ତ ବୃଦ୍ଧାଙ୍ଗୁଳି, ତର୍ଜନୀ ଓ ମଧ୍ଯମାକୁ ଏପରି ଖୋଲି ରଖ ଯେପରିକି ସେଗୁଡ଼ିକ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ହୋଇ ରହିବେ । ଯଦି ତର୍ଜନୀ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଓ ମଧ୍ୟମା ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ସୂଚାଏ ତେବେ ପରିବାହୀ ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳର ଦିଗ ବା ପରିବାହୀର ଗତିର ଦିଗ ବୃଦ୍ଧାଙ୍ଗୁଳି ଦ୍ଵାରା ନିର୍ଦ୍ଦେଶିତ ହେବ ।

(iii) କୁଣ୍ଡଳୀଟିଏ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେ ଘୂରୁଥିଲେ ସେଥ‌ିରେ ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ଦିଗ ନିର୍ଣ୍ଣୟ କରିବା ପାଇଁ ।
ଡ :
ଫ୍ଲେମିଂଙ୍କ ଦକ୍ଷିଣହସ୍ତ ନିୟମ :
ଦକ୍ଷିଣ ହସ୍ତର ବୃଦ୍ଧାଙ୍ଗୁଳୀ, ତର୍ଜନୀ ଓ ମଧ୍ଯମାକୁ ଏପରି ଖୋଲି ରଖ ଯେ ସେଗୁଡ଼ିକ ପରସ୍ପର ପ୍ରତି ସମକୋଣରେ ରହିବେ । ତର୍ଜନୀ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଓ ବୃଦ୍ଧାଙ୍ଗୁଳି ପରିବାହୀର ଗତିର ଦିଗ ନିର୍ଦ୍ଦେଶ କଲେ ମଧ୍ୟମା ନିର୍ଦ୍ଦେଶ କରୁଥ‌ିବା ଦିଗରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହେବ ।

Question 16.
ଏକ ନାମାଙ୍କିତ ଚିତ୍ର ସାହାଯ୍ୟରେ ବିଦ୍ୟୁତ୍ ଜେନେରେଟର୍‌ର ନିୟମ ଓ କାର୍ଯ୍ୟପ୍ରଣାଳୀ ବୁଝାଅ । ବ୍ରଶ୍ନର କାର୍ଯ୍ୟ କ’ଣ ?
Answer:
ନିସ୍ତ୍ରମ :
ବିଦ୍ୟୁତ୍ ଜେନେରେଟର୍ ବିଦ୍ୟୁତ୍ ଚୁମ୍ବକୀୟ ପ୍ରେରଣ ପଦ୍ଧତି ଉପରେ ପର୍ଯ୍ୟବସିତ । ବିଦ୍ୟୁତ୍ ଜେନେରେଟର ଏକ ଯନ୍ତ୍ର ଯେଉଁଥରେ ଯାନ୍ତ୍ରିକ ଶକ୍ତି ବିଦ୍ୟୁତ୍ ଶକ୍ତିରେ ପରିଣତ ହୁଏ । ଏଥିରେ ଯାନ୍ତ୍ରିକ ଶକ୍ତି ସାହାଯ୍ୟରେ ଏକ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ଗୋଟିଏ ପରି ବାହୀକୁ ଘୁରାଇ ବିଦ୍ୟୁତ ଉତ୍ପାଦନ କରାଯାଏ ।

ଚୁମ୍ବକ କ୍ଷେତ୍ରରେ ପରିବାହୀର ଗତି ବା ପରିବାହୀ ନିକଟରେ ଚୁମ୍ବକର ଗତି ବା ଯେକୌଣସି ପଦ୍ଧତିରେ ପରିବାହୀ ମଧ୍ୟରେ ଚୁମ୍ବକୀୟ ବଳରେଖାମାନ ପରିବର୍ତ୍ତନ ଫଳରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ବାହକ ବଳ ସୃଷ୍ଟି ହୁଏ । ଏହି ପ୍ରକ୍ରିୟାକୁ ଉପଯୋଗ କରି ବିଦ୍ୟୁତ୍ ଜେନେରେଟର୍ ଗଠିତ ହୋଇଛି ।

ଖଠନ :

• ABCD ଏକ ଘୂର୍ଣାୟମାନ ଆୟତାକାର କୁଣ୍ଡଳୀ । ଏହାକୁ ଏକ ସ୍ଥାୟୀ ଚୁମ୍ବକରେ ଦୁଇମେରୁ ମଧ୍ୟରେ ରଖାଯାଇଛି ।
• ସ୍କ୍ରିପ୍ ବଳୟ R₁ ଓ R₂ ସହିତ ଯଥାକ୍ରମେ B₁ ଓ B₂ ବ୍ରଶ ସଂଯୁକ୍ତ ହୋଇଛି । ବଳୟ ଭିତର ବିଦ୍ୟୁତରୋଧୀ ଏବଂ ବାହାର ପାଖ ବିଦ୍ୟୁତ୍ ସୁପରିବାହୀ ଅଟେ।
• ଅଖ ସହ କୁଣ୍ଡଳୀ ଓ ସ୍କ୍ରିପ୍ ବଳୟ ଘୂରେ । କୁଣ୍ଡଳୀଟି ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ଘୂରେ । ବାହ୍ୟ ପରିପଥ ସହ ବ୍ତଣ୍ ତ୍ରରଟି ସଂପ୍ତକ୍ର |
• ବାହ୍ୟ ପରିପଥରେ ଲାଗିଥିବା ଗାଲ୍‌ଭାନୋମିଟର୍ ଓ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ସୂଚନା ଦିଏ ।

କାର୍ଯ୍ୟ :

• ମନେକର କୁଣ୍ଡଳୀକୁ ଘଣ୍ଟାକଣ୍ଟା ଦିଗରେ ଘୂରାଯାଉଛି ।
• ଯେଉଁ ସମୟରେ କୁଣ୍ଡଳୀର ବାହୁ AB ଉପରକୁ ଉଠେ ସେହି ସମୟରେ CD ବାହୁ ତଳକୁ ଖସେ ।
• ଫ୍ଲେମିଂଙ୍କ ଦକ୍ଷିଣ ହସ୍ତ ନିୟମ ଅନୁସାରେ ବାହୁ AB ରେ A ରୁ B ଆଡ଼କୁ ଏବଂ ବାହୁ CD ରେ C ରୁ D ଆଡ଼କୁ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହୁଏ ।
• ବାହ୍ୟ ପରିପଥରେ ଏହା B₂ ରୁ B₁ ଆଡ଼କୁ ପ୍ରବାହିତ ହୁଏ ।
• କୁଣ୍ଡଳୀରେ ଯେତେ ସଂଖ୍ୟକ ଘେର ରହିବ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସେହି ଅନୁସାରେ ଅଧିକ ହେବ ।
• ଗୋଟିଏ ଅର୍ଶଘୂର୍ଣ୍ଣନ ପରେ AB ଓ CD ସ୍ଥାନ ବଦଳାଇବ । ବର୍ତ୍ତମାନ CD ଉପରକୁ ଉଠିବ ଏବଂ AB ତଳକୁ ଖସିବ । ଫ୍ଲେମିଂଙ୍କ ଦକ୍ଷିଣ ହସ୍ତ ନିୟମ ଅନୁଯାୟୀ କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ DCBA ବିଖରେ ହେଡ୍‌ଚ୍ଚି |
• ବାହ୍ୟ ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ B₁ ରୁ B₂ କୁ ହେବ । ପ୍ରତି ଅର୍ଥ ଘୂର୍ଣ୍ଣନ ପରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ଦିଗର ପରିବର୍ତ୍ତନ ଘଟେ । ଏ ପ୍ରକାର ସ୍ରୋତକୁ ପ୍ରତ୍ୟାବର୍ତ୍ତୀ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ କହନ୍ତି ।
• ଡି.ସି. ବା ସଳଖ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ପାଇଁ ବଳୟ ପରିବର୍ତ୍ତେ ବିଖଣ୍ଡିତ ବଳୟ ବା କମ୍ୟୁଟେଟ୍‌ର ବ୍ୟବହାର କରାଯାଏ ।

ବ୍ରଶ୍ନର କାର୍ଯ୍ୟ
B₁ ଓ B₂ ଦୁଇଟି ସ୍ଥିର ଓ ପରିବାହୀ ବ୍ରଶ୍ନ । ବ୍ରଶ୍ ଏକ ପ୍ରାନ୍ତ ବାହ୍ୟ ପରିପଥ ସହିତ ସଂଯୁକ୍ତ ହୋଇଥାଏ ଓ ଅନ୍ୟ ପ୍ରାନ୍ତ ସ୍କ୍ରିପ୍ ବଳୟ R₁ ଓ R₂ ସହିତ ସଂଯୁକ୍ତ ହୋଇଥାଏ । କୁଣ୍ଡଳୀରେ ଉତ୍ପନ୍ନ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଯୋଗୁଁ ବାହ୍ୟ ପରିପଥରେ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ ।

Question 17.
ବୈଦ୍ୟୁତିକ ଲଘୁପଥନ କେତେବେଳେ ହୁଏ ?
Answer:
ବିଦ୍ୟୁତ୍ ରୋଧୀ ଆବରଣ ନଷ୍ଟ ହୋଇଯିବା ଯୋଗୁ ବା ଉପକରଣରେ ତ୍ରୁଟି ଥିଲେ ଲାଇଭ୍ ତାର ଓ ନିଉଟ୍ରାଲ୍ ତାର ସିଧାସଳଖ ପରସ୍ପରକୁ ସ୍ପର୍ଶ କଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ପରିମାଣ ହଠାତ୍ ବଢ଼ିଯାଏ ଏହାକୁ ଲଘୁ ପଥନ (Short-circuiting) କହନ୍ତି ।

Question 18.
ଭୂ-ତାରର କାର୍ଯ୍ୟ କ’ଣ ? ଧାତବ ଉପକରଣକୁ ଭୂମି ସହ କାହିଁକି ସଂଲଗ୍ନ କରାଯାଏ ?
Answer:
(i) ଘରେ ଫେଜ୍ ତାର ଓ ନିଉଟ୍ରାଲ୍ ସହିତ ଏକ ସବୁଜ ବର୍ଣ୍ଣର ବିଦ୍ୟୁତରୋଧୀ ଦ୍ଵାରା ଆଚ୍ଛାଦିତ ତାରକୁ ଭୂତାର କହନ୍ତି । ଏହାର ଗୋଟିଏ ପ୍ରାନ୍ତ ଧାତବ ଫଳକ ସହ ଓ ଅନ୍ୟ ପ୍ରାନ୍ତ ଘର ବାହାରେ ମାଟିର ଗହୀରରେ ପୋତି ଦିଆଯାଏ । ଏହା ଏକ ନିରାପତ୍ତା ସାଧନ, ଯେଉଁଥରେ ଉଚ୍ଚ ପାଓ୍ବାର ବିଶିଷ୍ଟ ଉପକରଣ ବାହାରେ ମାଟି ସହିତ ସଂଯୁକ୍ତ କରାଯାଇଛି । ଏହା ବ୍ୟବହାରକାରୀ ଓ ଉପକରଣ ଉଭୟକୁ ବିଦ୍ୟୁତ୍ ଆଘାତରୁ ରକ୍ଷାକରେ ।

(ii) ଉଚ୍ଚ ପାଓ୍ବାର ବିଶିଷ୍ଟ ବିଦ୍ୟୁତ୍ ଉପକରଣର ଧାତବ ଖୋଳ ସହିତ ଭୂତାରର ଏକ ପ୍ରାନ୍ତ ଯୋଡ଼ାଯାଇଥାଏ । ଯଦି କେତେବେଳେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଲିକ୍ କରି ଧାତବ ଖୋଳକୁ ଚାଲିଆସେ ତାହା ଭୂତାର ଯୋଗେ ମାଟିକୁ ଚାଲିଯାଏ ଏବଂ ଧାତବ ଉପକରଣକୁ ଛୁଇଁଲେ ଗୁରୁତର ବିଦ୍ୟୁତ୍ ଆଘାତ ଲାଗେନାହିଁ ଓ ଉପକରଣ ନଷ୍ଟ ହୁଏ ନାହିଁ । ଏହି କାରଣରୁ ଉପକରଣକୁ ଭୂମିସହ ସଂଲଗ୍ନ କରାଯାଏ ।

ପ୍ରଶ୍ନବଳୀ ଓ ଉତ୍ତର:

Question 1.
ଦଣ୍ଡ ଚୁମ୍ବକ ନିକଟକୁ ଆଣିଲେ କମ୍ପାସ ସୂଚୀ କାହିଁକି ବିକ୍ଷେପିତ ହୁଏ ?
Answer:
ଉଭୟ ଦଣ୍ଡଚୁମ୍ବକ ଓ କମ୍ପାସ ସୂଚୀର ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ରହିଛି । ଦଣ୍ଡ ଚୁମ୍ବକର ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଏକ ପ୍ରକାର ଚୁମ୍ବକୀୟ ବଳ କମ୍ପାସ ସୂଚୀର ଉଭୟ ମେରୁରେ କାର୍ଯ୍ୟ କରୁଛି । ତେଣୁ ଦଣ୍ଡ ଚୁମ୍ବକ ନିକଟକୁ ଆଣିଲେ କମ୍ପାସ ସୂଚୀ ବିକ୍ଷେପିତ ହୁଏ ।

Question 2.
ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖାର ଧର୍ମଗୁଡ଼ିକ କ’ଣ ?
Answer:

• ଚୁମ୍ବକର ଉତ୍ତର ମେରୁରୁ କ୍ଷେତ୍ରରେଖା ବାହାରି ଦକ୍ଷିଣ ମେରୁରେ ମିଶେ, କିନ୍ତୁ ଚୁମ୍ବକ ଭିତରେ ଦକ୍ଷିଣ ମେରୁରୁ ଉତ୍ତର ମେରୁ ପର୍ଯ୍ୟନ୍ତ ଯାଇଥାଏ । ତେଣୁ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା ଏକ ଅବିଚ୍ଛିନ୍ନ ଓ ମୁଦିତ ରେଖା ।
• ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଆପେକ୍ଷିକ ସାମର୍ଥ୍ୟ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକର ଘନତ୍ଵ ଉପରେ ନିର୍ଭର କରେ ।
• ଯେଉଁଠାରେ କ୍ଷେତ୍ରର ରେଖାଗୁଡ଼ିକ ବେଶି ଲଗାଲଗି ହୋଇଥାଏ, ସେଠାରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ସାମର୍ଥ୍ୟ ଅଧିକ । ସେଠାରେ ଅନ୍ୟ ଏକ ଚୁମ୍ବକର ମେରୁ ଉପରେ ଅଧ‌ିକ ବଳ କାର୍ଯ୍ୟକାରୀ ହୁଏ ।
• ଚୁମ୍ବକୀୟ ରେଖା ପରସ୍ପର ସହ ସମାନ୍ତର ।

Question 3.
ଦୁଇଟି ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା କାହିଁକି ପରସ୍ପରକୁ ଛେଦ କରନ୍ତି ନାହିଁ ?
Answer:
ଦୁଇଟି ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା ପରସ୍ପରକୁ ଛେଦ କରନ୍ତି ନାହିଁ କାରଣ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଗୋଟିଏ ବିନ୍ଦୁରେ ଦୁଇଟି ଦିଗ ନାହିଁ । ଯଦି ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦ କରୁଥାନ୍ତା ତେବେ କମ୍ପାସ ସୂଚୀ ଏକ ସମୟରେ ଦୁଇଟି ଦିଗ ଦର୍ଶାନ୍ତା ।

Question 4.
ଗୋଟିଏ ବୃତ୍ତାକାର ତାର କୁଣ୍ଡଳୀ ଟେବୁଲ ଉପରେ ଭୂସମାନ୍ତର ଭାବେ ରଖାଯାଇଛି । ସେଥ‌ିରେ ଘଣ୍ଟାକଣ୍ଟା ଦିଗରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହତ ହେଉଛି । ଦକ୍ଷିଣ ହସ୍ତ ବୃଦ୍ଧାଙ୍ଗୁଳି ନିୟମ ବ୍ୟବହାର କରି କୁଣ୍ଡଳୀ ଭିତରେ ଓ ବାହାରେ ଚମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ନିରପଣ କର ।
Answer:
ଦକ୍ଷିଣ ହସ୍ତ ବୃଦ୍ଧାଙ୍ଗୁଳି ନିୟମ ବ୍ୟବହାର କଲେ ଜଣାଯାଏ ଯେ କୁଣ୍ଡଳୀ ଭିତରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ନିମ୍ନଗାମୀ (ତଳକୁ) । ଅନ୍ୟପକ୍ଷରେ କୁଣ୍ଡଳୀ ବାହାରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେ ଦିଗ ଉପରକୁ ଅଟେ ।

Question 5.
ଗୋଟିଏ ଅଞ୍ଚଳରେ ଏକ ସମ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ରହିଛି । ଏହାକୁ ଚିତ୍ରରେ ଦେଖାଅ ।
Answer:
ସମଦୂରତାରେ ଓ ସମାନ୍ତର ଚୁମ୍ବକୀୟ ରେଖାଗୁଡ଼ିକ ସମ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ରେଖା ଦର୍ଶାଉଛି ।

Question 6.
ସଠିକ୍ ଉତ୍ତର ବାଛ । ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ସ୍ରୋତଧାରୀ ଦୀର୍ଘ ଓ ସଳଖ ସଲେନଏଡ୍‌ର ଭିତର ଅଂଶରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର
(a) ଶୂନ୍ ଅଟେ
(b) ପ୍ରାନ୍ତଆଡ଼କୁ କମିଯାଏ ।
(c) ପ୍ରାନ୍ତ ଆଡ଼କୁ ବଢ଼େ
(d) ସବୁଠାରେ ସମାନ
Answer:
(d) ସବୁଠାରେ ସମାନ

Question 7.
ଗୋଟିଏ ପ୍ରୋଟନ ଏକ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେ ମୁକ୍ତ ଭାବେ ଗତି କରୁଛି । ତା’ର ନିମ୍ନଲିଖୂତ ଧର୍ମଗୁଡ଼ିକ ମଧ୍ୟରୁ କେଉଁଟିର ପରିବର୍ତ୍ତନ ହୋଇପାରେ ? (ଏକାଧ୍ଵ ଉତ୍ତର ହୋଇପାରେ)
(a) ବସ୍ତୁତ୍ଵ
(b) ବେଗ
(c) ପରିବେଗ
(d) ସଂବେଗ
Answer:
(c) ପରିବେଗ
(d) ସଂବେଗ
କୌଣସି ଚାର୍ଜିତ କଣିକା (ପ୍ରୋଟନ୍) ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ଗତିକଲେ ଏହାର ପରିବେଗ ଓ ସଂବେଗ ପରିବର୍ତ୍ତିତ ହୁଏ ଏବଂ ଏହାର ବେଗ ଓ ବସ୍ତୁତ୍ଵ ଅପରିବର୍ତ୍ତନୀୟ ରହେ ।

Question 8.
ତୁମ ପାଇଁ କାମ 9.7 ରେ ଯଦି

• ରଡ୍ ABରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ ବଢ଼େ;
• ଅଧିକ ଶକ୍ତିଶାଳୀ ଅଶ୍ଵକ୍ଷୁରାକୃତି ଚୁମ୍ବକ ବ୍ୟବହାର କରାଯାଏ; ଏବଂ
• ରଡ୍ AB ର ଦୈର୍ଘ୍ୟ ବଢ଼ିଯାଏ, ତାହେଲେ ରଡ୍ ABର ଗତି କେମିତି ବଦଳିବ ବୋଲି ଭାବୁଛ ?

Answer:
AB ରଡ୍ (ପରିବାହୀର)ର ଦୈର୍ଘ୍ୟ 1, ପ୍ରବାହିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ଏବଂ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର B ମଧ୍ୟରେ ଥିଲେ କାର୍ଯ୍ୟକାରୀ ବଳ (F)ର ପରିମାଣ = F = lIB

• ବିଦ୍ୟୁସ୍ରୋତ I ବଢ଼ିଲେ AB ରଡ୍‌ର ଗତି ବଢ଼ିବ ।
• ଶକ୍ତିଶାଳୀ ଅଶ୍ୱକ୍ଷୁରାକୃତି ଚୁମ୍ବକ ବ୍ୟବହାର କଲେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ପରିମାଣ ତୀବ୍ରତା ବୃଦ୍ଧିପାଏ । ଫଳରେ ABର ଗତି ବଢ଼େ ।
• AB ରଡ଼ର ଦୈର୍ଘ୍ୟ ବଢ଼ିଲେ AB ରଡ୍ ଉପରେ କାର୍ଯ୍ୟକାରୀ ବଳର ପରିମାଣ ବଢ଼େ । ଫଳରେ AB ରଡ୍‌ର ଗତି ବୃଦ୍ଧିପାଏ ।

Question 10.
ଗୋଟିଏ ଯୁକ୍ତ ଚାର୍ଜ ବିଶିଷ୍ଟ କଣିକା (ଆଲ୍‌ଫା କଣିକା) ପଶ୍ଚିମକୁ ଗତି କରୁଥିବା ବେଳେ ଏକ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ଦ୍ବାରା ଉତ୍ତରକୁ ବିକ୍ଷେପିତ ହୁଏ । ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ହେବ
(a) ଦକ୍ଷିଣକୁ
(b) ପୂର୍ବକୁ
(c) ତଳକୁ
(d) ଉପରକୁ
Answer:
(d) ଉପରକୁ (ଫ୍ଲେମିଂଙ୍କ ବାମହସ୍ତ ନିୟମ ଅନୁଯାୟୀ)

Question 11.
ଫ୍ଲେମିଂଙ୍କ ବାମହସ୍ତ ନିୟମ କ’ଣ ?
Answer:
ବାମହସ୍ତର ବୃଦ୍ଧାଙ୍ଗୁଳି, ତର୍ଜନୀ ଓ ମଧମାକୁ ଏପରି ଖୋଲି ରଖ ଯେପରିକି ସେଗୁଡ଼ିକ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ହୋଇ ରହିବେ । ଯଦି ତର୍ଜନୀ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଓ ମଧ୍ୟମା ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ସୂଚାଏ ତେବେ ପରିବାହୀ ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳର ଦିଗ ବା ପରିବାହୀର ଗତିର ଦିଗ ବୃଦ୍ଧାଙ୍ଗୁଳି ଦ୍ଵାରା ନିର୍ଦ୍ଦେଶିତ ହେବ ।

Question 12.
ବୈଦ୍ୟୁତିକ ମୋଟର୍‌ର କାର୍ଯ୍ୟପଦ୍ଧତି ବର୍ଣ୍ଣନା କର ।
Answer:
ଯେକୌଣସି ପରିବାହୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହ କଲେ ତା’ ଚତୁର୍ଦ୍ଦିଗରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୃଷ୍ଟି ହୁଏ । ଯଦି ଏକ ସ୍ଥାୟୀ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହୀ ପରିବାହୀକୁ ରଖାଯାଏ, ତେବେ ଦୁଇଟି ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ପରସ୍ପରକୁ ପ୍ରଭାବିତ କରନ୍ତି । ଫଳରେ ପରିବାହୀ ଉପରେ ଏକ ବଳ କାର୍ଯ୍ୟକରେ । ଏହି ବଳ ପ୍ରଭାବରେ ପରିବାହୀଟି ଗତିଶୀଳ ହୁଏ । ଏହି ନିୟମ ବ୍ୟବହାର କରି ବୈଦ୍ୟୁତିକ ମୋଟର୍ ନିର୍ମାଣ କରାଯାଇଛି । ବୈଦ୍ୟୁତିକ ମୋଟର୍ ବିଦ୍ୟୁତ୍ ଶକ୍ତିକୁ ଯାନ୍ତ୍ରିକ ଶକ୍ତିରେ ପରିଣତ କରେ ।

Question 13.
ମୋଟର୍‌ରେ ବିଖଣ୍ଡିତ ବଳୟର ଆବଶ୍ୟକତା କ’ଣ ?
Answer:
ମୋଟର୍‌ରେ ବିଖଣ୍ଡିତ ବଳୟ ବା କମ୍ୟୁଟେଟ୍‌ ପରିପଥରେ (ଆର୍ମେଚର୍‌ରେ ) ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ପରିବର୍ତ୍ତନ କରେ । ଫଳରେ ଆର୍ମେଚରଟି ନିରବଚ୍ଛିନ୍ନ ଭାବରେ ଏକ ଦିଗରେ ଘୂରୁଥାଏ ।

Question 14.
ଗୋଟିଏ ତାର କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରଦାହ କେଉଁ କେଉଁ ଉପାୟରେ ସୃଷ୍ଟି କରାଯାଇପାରିବ ବର୍ଣ୍ଣନା କର ।
Answer:

• ପରିବାହୀ ନିକଟରେ ଚୁମ୍ବକର ଗତି ଯୋଗୁଁ କିମ୍ବା ଚୁମ୍ବକ ନିକଟରେ ପରିବାହୀର ଗତି ଯୋଗୁଁ ତାର କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ ।
• ପାଖାପାଖୁ ବିଦ୍ୟୁତ୍ ପ୍ରବାହିତ ହେଉଥ‌ିବା କୁଣ୍ଡଳୀ ଓ ବିଦ୍ୟୁତ୍ ପ୍ରବାହିତ ହେଉ ନଥ‌ିବା ତାର କୁଣ୍ଡଳୀଦ୍ଵୟ ମଧ୍ୟରୁ ଯେକୌଣସି ଗୋଟିକରେ ଗତି କିମ୍ବା ନିକଟରେ ଥ‌ିବା ତାର କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ପରିମାଣରେ ପରିବର୍ତ୍ତନ ହେଲେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟିହେବ ।

Question 15.
ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଜେନେରେଟର୍‌ର କାର୍ଯ୍ୟ ପଦ୍ଧତି ବର୍ଣ୍ଣନା କର ।
Answer:

• ବିଦ୍ୟୁତ୍ ଜେନେରେଟର୍ ବିଦ୍ୟୁତ୍ ଚୁମ୍ବକୀୟ ପ୍ରେରଣ ତତ୍ତ୍ବ ଉପରେ ପର୍ଯ୍ୟବସିତ ।
• ଯାନ୍ତ୍ରିକ ଶକ୍ତି ସାହାଯ୍ୟରେ ଏକ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ମଧ୍ୟରେ ଗୋଟିଏ ପରିବାହୀକୁ ଘୂରାଇ ବିଦ୍ୟୁତ୍ ଉତ୍ପାଦନ କରାଯାଏ !
• ମୁଦିତ କୁଣ୍ଡଳୀକୁ ଚୁମ୍ବକୀୟ ମଧ୍ୟରେ ଘୂରାଇଲେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ରେଖା ଓ ମୁଦିତ କୁଣ୍ଡଳୀ ମଧ୍ଯରେ ପରିବର୍ତ୍ତନ ହୁଏ, ଫଳରେ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ବିଭବାନ୍ତର ସୃଷ୍ଟି ହୁଏ । ଏହି ବିଭବାନ୍ତର ଯୋଗୁଁ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସୃଷ୍ଟି ହୁଏ ।

Question 16.
ସଳଖ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର କେତୋଟି ଉତ୍ସର ନାମ ଲେଖ ।
Answer:
ଶୁଷ୍କ ସେଲ୍, ବ୍ୟାଟେରୀ, ଡି.ସି. ଜେନେରେଟର୍‌, ବଟନ୍ ସେଲ୍ (ଘଣ୍ଟା ଓ ଖେଳନାରେ ବ୍ୟବହୃତ ଛୋଟ), ସୌରସେଲ୍ ।

Question 17.
କେଉଁ କେଉଁ ଉତ୍ସରୁ ଏ.ସି. ଉତ୍ପାଦିତ ହୁଏ ?
Answer:
ନ୍ୟୁକ୍ଲିୟର ପାୱାର ପ୍ଲାଣ୍ଟ, ଜଳ ବିଦ୍ୟୁତ୍ କେନ୍ଦ୍ର, ତାପଜ ବିଦ୍ୟୁତ୍ କେନ୍ଦ୍ର ଇତ୍ୟାଦି ଥ‌ିବା A.C. ଜେନେରେଟର୍‌ରୁ ଏସି ଉତ୍ପାଦିତ ହୁଏ ।

Question 18.
ଠିକ୍ ଉତ୍ତର ବାଛ । ଗୋଟିଏ ତମ୍ବାତାର କୁଣ୍ଡଳୀ ଗୋଟିଏ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେ ଘୂରୁଛି । ଉତ୍ପାଦିତ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ଦିଗରେ ପରିବର୍ତ୍ତନ ହୁଏ ।
(a) ଦୁଇଟି ଘୂର୍ଶନ ପରେ
(c) ଅର୍ଶଘୂର୍ଣ୍ଣନ ପରେ
(b) ଗୋଟିଏ ଘୂର୍ଶନ ପରେ
(d) ଏକ – ରତ୍ର୍ଥାଣ ଘୂର୍ଣ୍ଣନ ପରେ
Answer:
(b) ଗୋଟିଏ ଘୂର୍ଶନ ପରେ

Question 19.
ବିଦ୍ୟୁତ୍ ପରିପଥ ଓ ଉପକରଣର ସୁରକ୍ଷା ପାଇଁ ବ୍ୟବହୃତ ଦୁଇଟି ସାଧାରଣ ବ୍ୟବସ୍ଥାର ନାମ ଲେଖ ।
Answer:
ଫ୍ର୍ୟଜ୍ (Fuse) ଓ ଭୂତାର (Earthwire) |

Question 20.
220 V ଓ 5A ରେଟିଂ ବିଶିଷ୍ଟ ଗୋଟିଏ ଗୃହ ପରିପଥରେ ଗୋଟିଏ 2kW ପାୱାର ରେଟିଂର ବିଦ୍ୟୁତ୍ ଚୁଲ୍ଲା ଲଗାଯାଇଛି । ଚୁଲାକୁ ଚାଲୁ କଲେ କ’ଣ ଘଟିପାରେ ବୋଲି ଭାବୁଛ ବୁଝାଅ ।
Answer:
I = \(\frac { P }{ V }\)
= \(\frac { 2k }{ 220V }\)
= \(\frac { 2000w }{ 220V }\) = 9.09A
ବିଦ୍ୟୁତ୍ ସ୍ରୋତ୍ 5A କିନ୍ତୁ ବିଦ୍ୟୁତ୍ ଚୁଲା ତା’ଠାରୁ (୨.୦୨A) ଯଥେଷ୍ଟ ଅଧ‌ିକ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବ୍ୟବହାର କରୁଛି । ତେଣୁ ମ୍ୟୁଜ୍ ତରଳିଯିବ ଓ ପରିପଥ ବିଚ୍ଛିନ୍ନ ହେବ ଏବଂ ବିଦ୍ୟୁତ୍ ଚୁଲ୍ଲା ସୁରକ୍ଷିତ ରହିବ ।

Question 21.
ଗୃହ ବିଦ୍ୟୁତ୍ ପରିପଥରେ ଅଧ‌ିକ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବିପଦ ଦୂର କରିବାପାଇଁ କ’ଣ କରାଯିବା ଉଚିତ ?
Answer:

• ଗୋଟିଏ ପ୍ଲଗ୍ ସକେଟ୍‌ରେ ଏକାଧିକ ଉପକରଣ ସଂଯୋଗ କରିବ ନାହିଁ ।
• ପରିବାହୀ ତାରଗୁଡ଼ିକର ଉନ୍ନତ କୁପରିବାହୀ ଆବରଣ ରହିବା ଦରକାର ।
• ଗୃହ ପରିପଥକୁ ବିଭିନ୍ନ ଭାଗରେ ବିଭକ୍ତ କରି ପ୍ରତ୍ୟେକ ଭାଗରେ ଫ୍ୟୁଜ୍‌ର ବ୍ୟବହାର କରିବା ଆବଶ୍ୟକ ।
• ଅତ୍ୟଧୂକ ପାୱାର ବିନିଯୋଗ କରୁଥିବା ଉପକରଣ; ଯଥା – ରେଫ୍ରିଜରେଟର, ଜଳ ତାପକ (water heater) ଇତ୍ୟାଦି ଏକ ସମୟରେ ବ୍ୟବହାର କରିବା ଉଚିତ ନୁହେଁ ।

କାର୍ଯ୍ୟାବଳୀ (Activity)

କାର୍ଯ୍ୟାବଳୀ – 1(Activity – 1)
ଉଦ୍ଦେଶ୍ୟ :
ପରିବାହୀ ତାରରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଲେ ତାହା ଚୁମ୍ବକ ଭଳି କାର୍ଯ୍ୟକରେ ।

ଆବଶ୍ୟକ ଉପକରଣ :
ଧଳାକାଗଜ ଏକପୃଷ୍ଠା, ଡ୍ରଇଂବୋର୍ଡ଼, ଡ୍ରଇଂ ପିନ୍, ସଳଖ ମୋଟା ତମ୍ବାତାର, କମ୍ପାସ ସୂଚୀ, ପ୍ଲଗ୍ କି, ପ୍ରତିରୋଧ, ବ୍ୟାଟେରୀ, ପରିବାହୀ ତାର ।

ପରୀକ୍ଷଣ :
ଖଣ୍ଡିଏ ସଳଖ ମୋଟା ତମ୍ବା ତାର ନେଇ ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ପରିପଥର ଦୁଇବିନ୍ଦୁ X ଓ Y ମଧ୍ୟରେ ରଖ । ଏହା କାଗଜର ପୃଷ୍ଠତଳ ସହ ଲମ୍ବଭାବରେ ରହୁ ।

କାଗଜ ଉପରେ ଗୋଟିଏ ଛୋଟ କମ୍ପାସ ତାର ପାଖାପାଖୁ ରଖ ଏବଂ କମ୍ପାସ ସୂଚୀର ଅବସ୍ଥିତି ଲକ୍ଷ୍ୟ କର । ପରିପଥକୁ ମୁଦିତ କରି ବିଦ୍ୟୁତ୍ ପ୍ରବାହ କରାଇ କମ୍ପାସ ସୂଚୀକୁ ଲକ୍ଷ୍ୟକର ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବା ପୂର୍ବରୁ ତମ୍ବାତାର ପାଖାପାଖୁ ଥ‌ିବା ସୂଚୀଚୁମ୍ବକ ଉତ୍ତର ଦକ୍ଷିଣ ହୋଇ ରହୁଥିଲା

ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଯୋଗୁଁ କମ୍ପାସ ସୂଚୀର ବିକ୍ଷେପ (Deflection) ହେଲା । କାରଣ ତମ୍ବାତାର XY ରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବା ଫଳରେ ତମ୍ବାତାର ଚାରିପାଖରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୃଷ୍ଟିହେଲା । ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ପ୍ରଭାବରେ କମ୍ପାସ ସୂଚୀ ବିକ୍ଷେପିତ ହେଲା ।

ସିଦ୍ଧାନ୍ତ :
ତମ୍ବାତାରରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଯୋଗୁଁ ତାହାର ଚତୁଃପାର୍ଶ୍ଵରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ସୃଷ୍ଟିହେଲା ଏବଂ ତମ୍ବାତାର ଚୁମ୍ବକ ଭଳି କାର୍ଯ୍ୟ କରେ ।

କାର୍ଯ୍ୟାବଳୀ – 2(Activity – 2)
ଆବଶ୍ୟକ ଉପକରଣ :
ଗୋଟିଏ ଡ୍ରଇଂବୋର୍ଡ଼, ଧଳା କାଗଜ, ପିନ୍, ଦଣ୍ଡ ଚୁମ୍ବକ ଓ ଲୁହାଗୁଣ୍ଡ ।

ପରୀକ୍ଷଣ :

• ଡ୍ରଇଂବୋର୍ଡ଼ ଉପରେ ଧଳାକାଗଜ ପିନ୍ ସାହାଯ୍ୟରେ ଲଗାଇ ଦିଅ ।
• କାଗଜର କେନ୍ଦ୍ରରେ ଗୋଟିଏ ଦଣ୍ଡ ଚୁମ୍ବକ ରଖ ।
• ଦଣ୍ଡ ଚୁମ୍ବକର ଚାରିପାଖରେ କିଛି ଲୁହାଗୁଣ୍ଡ ସମାନ ଭାବରେ ବିଞ୍ଚିଦିଅ ।
• ଡ୍ରଇଂବୋର୍ଡ଼କୁ ଆଙ୍ଗୁଳି ଟିପରେ ଆସ୍ତେ ଆସ୍ତେ ଆଘାତ ଦିଅ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :

• ଲୁହାଗୁଣ୍ଡଗୁଡ଼ିକ ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥିବା ଭଳି ସଜାଇ ହୋଇ ରହିବେ ।
• ଦଣ୍ଡ ଚୁମ୍ବକର ଆଖପାଖରେ ଚୁମ୍ବକର ପ୍ରଭାବ ଯୋଗୁଁ ଲୁହାଗୁଣ୍ଡ ଉପରେ ଏକ ପ୍ରକାର ବଳ କାର୍ଯ୍ୟକାରୀ
• ଏହି ବଳ ଯୋଗୁଁ ଲୁହାଗୁଣ୍ଡ ନିର୍ଦ୍ଦିଷ୍ଟ ଢଙ୍ଗରେ ଚୁମ୍ବକ ଚାରିପାଖେ ସଜାଇ ହୋଇ ରହିଛି ।

ସିଦ୍ଧାନ୍ତ :

• ଚୁମ୍ବକର ପ୍ରଭାବ ଅନୁଭୂତ ହେଉଥ‌ିବା ଅଞ୍ଚଳକୁ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର (Magnetic field) କହନ୍ତି ।
• ଲୁହାଗୁଣ୍ଡ ଯେଉଁ କାଳ୍ପନିକ ରେଖାରେ ସଜାଇ ହେଲା ପରି ଦିଶେ ତାକୁ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା (Magnetic field lines) ବୋଲି ମନେକରାଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 3(Activity – 3)
ଆବଶ୍ୟକ ଉପକରଣ :
ଦଣ୍ଡଚୁମ୍ବକ, ଛୋଟ କମ୍ପାସ, ଡ୍ରଇଂବୋର୍ଡ଼, ଧଳାକାଗଜ, ପିନ୍

ପରୀକ୍ଷଣ :
(i) ଗୋଟିଏ ଦଣ୍ଡଚୁମ୍ବକ ଓ ଗୋଟିଏ ଛୋଟ କମ୍ପାସ ନିଅ ।
(ii) ଗୋଟିଏ ଡ୍ରଇଂବୋର୍ଡ଼ରେ ଖଣ୍ଡିଏ ଧଳା କାଗଜକୁ ପିନ୍ ପୋତି ଲଗାଅ । କାଗଜ ମଝିରେ ଦଣ୍ଡ ଚୁମ୍ବକକୁ ରଖ ।
(iii) ଦଣ୍ଡ ଚୁମ୍ବକର ପରିସୀମାକୁ ପେନ୍‌ସିଲ୍‌ରେ ଗାର ଟାଣି ଚିହ୍ନାଅ ।
(iv) ଦଣ୍ଡ ଚୁମ୍ବକର ଉତ୍ତର ମେରୁ ପାଖରେ କମ୍ପାସଟି ରଖ । ଦେଖୁବ ଯେ କମ୍ପାସର ଦକ୍ଷିଣ ମେରୁ ଦଣ୍ଡ ଚୁମ୍ବକର ଉତ୍ତର ମେରୁ ଆଡ଼କୁ ଆକର୍ଷିତ ହେଉଛି ଏବଂ କମ୍ପାସର ଠାରୁ ବିକର୍ଷଣ ଯୋଗୁଁ ଦୂରେଇ ଯାଉଛି ।

(v) କମ୍ପାସ୍ ସୂଚୀର ଦୁଇପ୍ରାନ୍ତକୁ ପେନ୍‌ସିଲ ଦ୍ୱାରା ଚିହ୍ନିତ କର ।
(vi) ବର୍ତ୍ତମାନ କମ୍ପାସକୁ ଘୁଞ୍ଚାଇ ଅନ୍ୟ ଏକ ସ୍ଥାନରେ ରଖ ଯେମିତିକି ସୂଚୀର ଦକ୍ଷିଣ ମେରୁ ପୂର୍ବରୁ ଉତ୍ତର ମେରୁ ଯେଉଁଠାରେ ଥିଲା ସେହିଠାରେ ରହିବ । ଏବେ ସୂଚୀର ଉତ୍ତର ମେରୁର ସ୍ଥାନ ଚିହ୍ନିତ କର ।
(vii) ଏହି ଭଳି କମ୍ପାସର ସ୍ଥାନ କ୍ରମାଗତ ବଦଳାଇ ଦଣ୍ଡ ଚୁମ୍ବକର ଦକ୍ଷିଣ ମେରୁ ପର୍ଯ୍ୟନ୍ତ ନିଅ ।
(viii) କାଗଜ ଉପରେ ଚିହ୍ନିତ ବିନ୍ଦୁଗୁଡ଼ିକୁ ଯୋଡ଼ି ହାତରେ ଗୋଟିଏ ଚିକ୍କଣ ବା ସୁଗମ ବକ୍ରରେଖା ଅଙ୍କନ କର । ଏହି ରେଖାଟି ଏକ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :

• ମେରୁଆଡ଼କୁ ଆସିଲା ବେଳକୁ କମ୍ପାସ ସୂଚୀର ବିକ୍ଷେପଣ ମାତ୍ରା ବଢୁଛି ।
• ମେରୁ ନିକଟରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ତୀବ୍ରତା ଅଧିକ ।
• ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ରେଖା ଉତ୍ତର ମେରୁରୁ ଦକ୍ଷିଣ ମେରୁ ଆଡ଼କୁ (ଚୁମ୍ବକର ବାହାରେ) ହୋଇଥାଏ ।
• ଚୁମ୍ବକ ମଧ୍ୟରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା ଦକ୍ଷିଣ ମେରୁରୁ ଉତ୍ତର ମେରୁ ପର୍ଯ୍ୟନ୍ତ ଯାଇଥାଏ ।

ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖାର ଧର୍ମ :
(i) ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ରେଖାଗୁଡ଼ିକ ମୁଦିତ ବକ୍ରରେଖା ଅଟନ୍ତି ।

(ii) ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଆପେକ୍ଷିକ ସାମର୍ଥ୍ୟ (Relative strength) କ୍ଷେତ୍ରରେଖାଗୁଡ଼ିକ ଘନତ୍ବ ଉପରେ ନିର୍ଭର କରେ । ଯେଉଁଠାରେ କ୍ଷେତ୍ରରେଖାଗୁଡ଼ିକ ବେଶି ଲଗାଲଗି ହୋଇଥାଏ ସେଠାରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ସାମର୍ଥ୍ୟ ଅଧିକ ଏବଂ ସେଠାରେ ଅନ୍ୟ ଏକ ଚୁମ୍ବକର ମେରୁ ଉପରେ ଅଧ୍ଵ ବଳ କାର୍ଯ୍ୟ କରେ ।

(iii) ଦୁଇଟି ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ରେଖା ପରସ୍ପରକୁ ଛେଦ କରେ ନାହିଁ ।

କାର୍ଯ୍ୟାବଳୀ -4(Activity – 4)

ଆବଶ୍ୟକ ଉପକରଣ :
ଲମ୍ବା ଓ ସଳଖ ତମ୍ବାତାର, 2ଟି ବା 3ଟି 15V ସେଲ୍ ଏବଂ ଗୋଟିଏ ପ୍ଲଗ୍ କି ।

ପରୀକ୍ଷଣ :
(i) ଖଣ୍ଡିଏ ଲମ୍ବା ଓ ସଳଖ ତମ୍ବା ତାର, ଦୁଇଟି ବା ତିନୋଟି 1.5V ସେଲ୍‌ ଏବଂ ଗୋଟିଏ ପ୍ଲଗ୍ କି ନେଇ ପଙକ୍ତିରେ ସଂଯୋଗ କର ।
(ii) ସଳଖ ତାର ସହ ସମାନ୍ତର କରି ଛୋଟ କମ୍ପାସଟିଏ ରଖ ।
(iii) ପ୍ଲଗ୍ କି କୁ ବନ୍ଦକରି ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ କରାଅ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :

• ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଉତ୍ତରରୁ ଦକ୍ଷିଣ ଆଡ଼କୁ ପ୍ରବାହିତ ହେଲେ କମ୍ପାସ ସୂଚୀର ଉତ୍ତର ମେରୁ ପୂର୍ବ ଆଡ଼କୁ ବିକ୍ଷେପିତ ହେବ ।
• ସେଲ୍‌ଗୁଡ଼ିକର ଅଗ୍ର ସଂଯୋଗ ବଦଳାଇଲେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ବଦଳିଯିବ । କମ୍ପାସ ସୂଚୀର ବିକ୍ଷେପ ପୂର୍ବ ପରିବର୍ତ୍ତେ ପଶ୍ଚିମ ଆଡ଼କୁ ହେବ ।

ସିଦ୍ଧାନ୍ତ :
ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ପରିବାହୀରେ ପ୍ରବାହିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ଉପରେ ନିର୍ଭର କରେ ।

କାର୍ଯ୍ୟାବଳୀ – 5 (Activity – 5)
ଆବଶ୍ୟକ ଉପକରଣ :
ଗୋଟିଏ 12V ବ୍ୟାଟେରୀ, ଗୋଟିଏ ରିଓଷ୍ଟାର୍ଟ୍, ଏମିଟର (0.5A), ଗୋଟିଏ ପ୍ଲଗ୍ କି ଓ ଖଣ୍ଡିଏ ଲମ୍ବା ସଳଖ ମୋଟା ତମ୍ବାତାର, ଆୟତାକାର କାର୍ଡ଼ବୋର୍ଡ଼ ।

ପରୀକ୍ଷଣ :
(i) ଖଣ୍ଡିଏ ଆୟତାକାର କାର୍ଡ଼ବୋର୍ଡ଼ ନେଇ ତା ମଧ୍ୟ ବିନ୍ଦୁରେ ତମ୍ବାତାରଟିକୁ ପ୍ରବେଶ କରାଅ । ତାରଟି କାର୍ଡ଼ବୋର୍ଡ଼ର ସମତଳ ପ୍ରତି ଲମ୍ବ ଭାବେ ରହୁ ।
(ii) ଲମ୍ବ ଭାବେ ଥ‌ିବା ସଳଖ ତାରର ପ୍ରାନ୍ତ ସହ ଓ ପ୍ଲଗ୍ କି ସଂଯୋଗ କର ।
(iii) କିଛି ଲୁହାଗୁଣ୍ଡ ନେଇ କାର୍ଡ଼ବୋର୍ଡ଼ ଉପରେ ସମାନ ଭାବେ ବିଞ୍ଚିଦିଅ ।
(iv) ପ୍ଲଗ୍ କି କୁ ବନ୍ଦ କରି ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ କରାଅ ।
(v) ରିଓଷ୍ଟାଟ୍‌ରେ ପରିବର୍ତ୍ତନଶୀଳ ପ୍ରତିରୋଧକୁ ସ୍ଥିର ରଖ୍ ଏମିଟରରେ କେତେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଉଛି ଲକ୍ଷ୍ୟ କର ।
(vi) କାର୍ଡ଼ବୋର୍ଡ଼କୁ ଆଙ୍ଗୁଳି ଟିପରେ ଅଳ୍ପ ଆଘାତ କରି ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) କାର୍ଡ଼ବୋର୍ଡ଼କୁ ଆଙ୍ଗୁଳି ଟିପରେ ଅଳ୍ପ ଆଘାତ କଲେ ଲୁହାଗୁଣ୍ଡ ତାର ଚାରିପାଖେ ସମକୈନ୍ଦ୍ରିକ ବୃତ୍ତ ଆକାରରେ ସଜାଇ ହୋଇ ରହିବେ । କେନ୍ଦ୍ର ପରିବାହୀ ଉପରେ ରହିବ ।

(ii) ଲୁହାଗୁଣ୍ଡର ସମକେନ୍ଦ୍ରିକ ବୃତ୍ତ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଦର୍ଶାଉ ନାହିଁ । ଗୋଟିଏ ଛୋଟ କମ୍ପାସଟିଏ ନେଇ ଗୋଟିଏ ବୃତ୍ତ ଉପରେ ଗୋଟିଏ ସ୍ଥାନରେ ରଖିଲେ ଉତ୍ତର ମେରୁ ଯେଉଁ ଦିଗ ଦେଖାଇବ ତାହା ସେଠାରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ହେବ ।

ସିଦ୍ଧାନ୍ତ :

• ତାରରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ଦିଗକୁ ବିପରୀତ କରିଦେଲେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ବିପରୀତ ହେବ ।
• ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ ବଦଳିଲେ କମ୍ପାସ ସୂଚୀର ବିକ୍ଷେପ ବଦଳିବ ।

କାର୍ଯ୍ୟାବଳୀ – 6 (Activity – 6)
ଆବଶ୍ୟକ ଉପକରଣ :
ଦୁଇଟି ଛିଦ୍ରଯୁକ୍ତ ଆୟତାକାର କାର୍ଡ଼ବୋର୍ଡ଼, ବହୁ ଘେର ବିଶିଷ୍ଟ କୁଣ୍ଡଳୀ, ବ୍ୟାଟେରୀ, ଫ୍ଲଗ୍ କି ଓ ଲୁହାଗୁଣ୍ଡ ।

ପରୀକ୍ଷଣ :
(i) ଦୁଇଟି ଛିଦ୍ର ବିଶିଷ୍ଟ ଆୟତାକାର କାର୍ଡ଼ବୋର୍ଡ଼ଟିଏ ନିଅ । ଛିଦ୍ର ଦୁଇଟି ଭିତରେ ଗୋଟିଏ ବହୁ ଘେର ବିଶିଷ୍ଟ କୁଣ୍ଡଳୀ କାର୍ଡ଼ବୋର୍ଡ଼ର ପୃଷ୍ଠପ୍ରତି ଲମ୍ବ ଭାବେ ଭର୍ତ୍ତି କର ।
(ii) କୁଣ୍ଡଳୀର ଦୁଇ ପ୍ରାନ୍ତକୁ ଗୋଟିଏ ବ୍ୟାଟେରୀ ଓ ପ୍ଲଗ୍ କି ସହ ପଙ୍‌କ୍ତି ସଂଯୋଗ କର ।
(iii) କାର୍ଡ଼ବୋର୍ଡ଼ ଉପରେ କିଛି ଲୁହାଗୁଣ୍ଡ ସମାନ ଭାବେ ବିଞ୍ଚିଦିଅ ।
(iv) ପ୍ଲଗ୍ କି କୁ ବନ୍ଦକରି କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ କରାଅ ।

(v) କାର୍ଡ଼ବୋର୍ଡ଼କୁ ଆଙ୍ଗୁଳିରେ ଆସ୍ତେ ଆସ୍ତେ ଆଘାତ କରି ଦେଖ ଲୁହାଗୁଣ୍ଡଗୁଡ଼ିକ କେମିତି ସଜାଇ ହୋଇ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖାର ଧାରଣା ଦେଉଛି ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ତାରର ଦୁଇବିନ୍ଦୁକୁ କେନ୍ଦ୍ରକରି କେତେଗୁଡ଼ିଏ ସମକୈନ୍ଦ୍ରିକ ବୃତ୍ତରେ ଲୁହାଗୁଣ୍ଡଗୁଡ଼ିକ ସଜାଇ ହୋଇ ରହିବ । ଏହା ବୃତ୍ତାକାର ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଜନିତ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖା ଦର୍ଶାଉଛି ।

ସିଦ୍ଧାନ୍ତ :

• ତାରକୁଣ୍ଡଳୀ ନିକଟରେ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ର ରେଖାଗୁଡ଼ିକ ବୃତ୍ତାକାର ।
• କୁଣ୍ଡଳୀର କେନ୍ଦ୍ର ଆଡ଼କୁ ବୃତ୍ତଗୁଡ଼ିକ ସରଳରେଖା ଭଳି ଦେଖାଯାଆନ୍ତି ।
• ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ତୀବ୍ରତା କୁଣ୍ଡଳୀର କେନ୍ଦ୍ରଠାରେ ଅଧିକ ।

କାର୍ଯ୍ୟାବଳୀ – 7 (Activity – 7)
ଆବଶ୍ୟକ ଉପକରଣ : 5 ସେ.ମି. ଲମ୍ବର ଏଲୁମିନିୟମ ରଡ୍, ପରିବାହୀ ତାର ଅଶ୍ୱକ୍ଷୁରାକୃତି ଚୁମ୍ବକ, ପ୍ଲଗ କି, ବ୍ୟାଟେରୀ ଓ ଷ୍ଟାଣ୍ଡ ।

ପରୀକ୍ଷଣ :

• 5 ସେ.ମି. ଲମ୍ବର ଖଣ୍ଡିଏ ଏଲୁମିନିୟମ ରଡ୍‌କୁ ଦୁଇଟି ସଂଯୋଗକାରୀ ତାରଦ୍ୱାରା ଗୋଟିଏ ଆଧାରରୁ ଭୂସମାନ୍ତର ଭାବେ ଝୁଲାଇଦିଅ ।
• ଗୋଟିଏ ଶକ୍ତିଶାଳୀ ଅଶ୍ଵକ୍ଷୁରାକୃତି ଚୁମ୍ବକ ନେଇ ତା’ର ଉତ୍ତର ମେରୁକୁ ଏଲୁମିନିୟମ୍ ରଡ୍‌ର ତଳପଟେ ଓ ଦକ୍ଷିଣ ମେରୁକୁ ରଡ୍‌ର ଉପର ପଟେ ରଖ ଯେପରିକି ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଉପର ଆଡ଼କୁ ହେବ ।
• ଏଲୁମିନିୟମ୍ ରଡ୍‌କୁ ବ୍ୟାଟେରୀ ଓ ପ୍ଲଗ୍ କି ସହ ପଙ୍‌କ୍ତି ସଂଯୋଗ କର ।
• ପରିପଥକୁ ମୁଦିତ କରି ରଡ୍‌ର B ପ୍ରାନ୍ତରୁ A ପ୍ରାନ୍ତ ଆଡ଼କୁ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ କରାଅ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :

• ଏଲୁମିନିୟମ୍ ରଡ୍ ବାମ ଆଡ଼କୁ ଘୁଞ୍ଚିଯିବ ।
• ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ଓଲଟାଇଲେ ରଡ଼ ଡାହାଣ ଆଡ଼କୁ ଘୁଞ୍ଚିବ ।
• ଯଦି ଚୁମ୍ବକଟିକୁ ଓଲଟାଇ ଦେଇ ଉତ୍ତର ମେରୁକୁ ରଡ୍‌ର ଉପରକୁ ଓ ଦକ୍ଷିଣ ମେରୁକୁ ରଡ୍‌ର ତଳକୁ ରଖାଯାଏ, ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ବିପରୀତ ହେବ । ତେବେ ପରିବାହୀ ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳର ଦିଗ ବିପରୀତ ହେବ ।

ସିଦ୍ଧାନ୍ତ :
ପରିବାହୀ ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳର ଦିଗ

• ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ଓ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଉପରେ ନିର୍ଭର କରେ ।
• ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ପ୍ରତି ଲମ୍ବ ହୁଏ । ସେତେବେଳେ ପରିବାହୀ ସର୍ବାଧ‌ିକ ଘୁଞ୍ଚେ । ଅର୍ଥାତ୍ ବଳର ପରିମାଣ ସର୍ବାଧ‌ିକ ହୁଏ ।

ଫ୍ଲେମିଂକ ବାମହସ୍ତ୍ର ନିଯମ (Fleming’s Left hand Rule):
ବାମହସ୍ତର ବୃଦ୍ଧାଙ୍ଗୁଳି (Thumb), ତର୍ଜନୀ (Fore finger) ଓ ମଧ୍ୟମା (Middle finger) କୁ ଏପରି ଖୋଲି ରଖ ଯେପରି ସେଗୁଡ଼ିକ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ହୋଇ ରହିବ । ଯଦି ତର୍ଜନୀ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଓ ମଧ୍ୟମା ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ଦିଗ ସୂଚାଏ ତେବେ ପରିବାହୀ ଉପରେ କାର୍ଯ୍ୟକାରୀ ହେଉଥ‌ିବା ବଳର ଦିଗ ବା
ପରିବାହୀର ଗତିର ଦିଗ ବୃଦ୍ଧାଙ୍ଗୁଳି ଦ୍ଵାରା ନିର୍ଦ୍ଧାରିତ ହେବ ।

କାର୍ଯ୍ୟାବଳୀ – 8 (Activity-8)
ଆବଶ୍ୟକ ଉପକରଣ :
ତାରକୁଣ୍ଡଳୀ, ଗାଲଭାନୋମିଟର, ଶକ୍ତିଶାଳୀ ଦଣ୍ଡଚୁମ୍ବକ

ପରୀକ୍ଷଣ :

• ବେଶୀ ସଂଖ୍ୟକ ଘେର ବିଶିଷ୍ଟ ତାର କୁଣ୍ଡଳୀଟିଏ (AB) ନିଅ ।
• କୁଣ୍ଡଳୀର ଦୁଇପ୍ରାନ୍ତ କୁ ଗୋଟିଏ ଗାଲ୍‌ଭାନୋମିଟର (G) ସହ ସଂଯୋଗ କର ।
• ଗୋଟିଏ ଶକ୍ତିଶାଳୀ ଦଣ୍ଡଚୁମ୍ବକ ନେଇ ତା’ର ଉତ୍ତର ମେରୁକୁ କୁଣ୍ଡଳୀର ପ୍ରାନ୍ତ B ଆଡ଼କୁ ନିଅ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
(i) ସାମୟିକ ଭାବେ ଗାଲଭାନୋମିଟରର ସୂଚୀ ଡାହାଣ ପଟକୁ ବିକ୍ଷେପିତ ହେବ । ଏଥୁରୁ ଜଣାପଡ଼ୁଛି ଯେ ଚୁମ୍ବକର ଗତି ଯୋଗୁଁ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହେଲା । ଚୁମ୍ବକର ଗତି ବନ୍ଦ ହେବା ମାତ୍ରେ ସୂଚୀର ବିକ୍ଷେପ ଶୂନ୍ ହୋଇଯିବ ।

(ii) ବର୍ତ୍ତମାନ ଚୁମ୍ବକକୁ ଡାହାଣ ଆଡ଼କୁ ଗତିଶୀଳ କରାଇ ଉତ୍ତର ମେରୁକୁ କୁଣ୍ଡଳୀଠାରୁ ଦୂରକୁ ନିଅ । ଏବେ ଦେଖୁବ ଗାଲଭାନୋମିଟରରେ ବିକ୍ଷେପ ବାମପଟକୁ ହେବ । କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସୃଷ୍ଟି ହେଉଛି ଓ ଏହା
ବିପର1ତ ତିଖରେ ପ୍ରବାହିତ ହେଉଛି

(iii) ଚୁମ୍ବକକୁ କୁଣ୍ଡଳୀ ପାଖାପାଖ୍ ସ୍ଥିର ଅବସ୍ଥାରେ ରଖ । ତାର ଉତ୍ତର ମେରୁ କୁଣ୍ଡଳୀର ପ୍ରାନ୍ତ B ଆଡ଼କୁ ରହୁ । ବର୍ତ୍ତମାନ କୁଣ୍ଡଳୀକୁ ଚୁମ୍ବକ ଆଡ଼କୁ ନେଲେ ଗାଲଭାନୋମିଟର ସୂଚୀର ବିକ୍ଷେପ ଡାହାଣ ଆଡ଼କୁ ହେବ । ସେହିଭଳି କୁଣ୍ଡଳୀକୁ ଚୁମ୍ବକଠାରୁ ଦୂରକୁ ନେଲେ ସୂଚୀର ବିକ୍ଷେପ ବାମଆଡ଼କୁ ହେବ ।

(iv) କୁଣ୍ଡଳୀ ଓ ଚୁମ୍ବକ ଉଭୟ ସ୍ଥିର ରହିଲେ ଗାଲଭାନୋମିଟରରେ ବିକ୍ଷେପ ଶୂନ୍ ହୁଏ ।

(v) କୁଣ୍ଡଳୀକୁ ସ୍ଥିର ରଖ୍ ଚୁମ୍ବକର ଉତ୍ତର ମେରୁ ପରିବର୍ତ୍ତେ ଦକ୍ଷିଣ ମେରୁକୁ କୁଣ୍ଡଳୀର ପ୍ରାନ୍ତ B ଆଡ଼କୁ ଗତି କରାଇ ଦେଖ ଯେ ଗାଲଭାନୋମିଟର ସୂଚୀର ବିକ୍ଷେପ ବିପରୀତ ହେବ ।

ସିଦ୍ଧାନ୍ତ :
ଉପର ପରୀକ୍ଷଣରେ ଆମେ ଦେଖୁ ଯେ

• ତାର କୁଣ୍ଡଳୀ ସ୍ଥିର ଥାଇ ଚୁମ୍ବକ ଗତିକଲେ ବା ଚୁମ୍ବକ ସ୍ଥିର ଥାଇ କୁଣ୍ଡଳୀ ଗତି କଲେ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ ।
• ଉଭୟ ଚୁମ୍ବକ ଓ କୁଣ୍ଡଳୀ ସ୍ଥିର ଥିଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହୁଏ ନାହିଁ ।
• ତାର କୁଣ୍ଡଳୀ ଓ ଚୁମ୍ବକ ମଧ୍ୟରେ ଆପେକ୍ଷିକ ଗତି (Relative motion) ହଁ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର କାରଣ ।
• ତାର କୁଣ୍ଡଳୀ ଓ ଚୁମ୍ବକ ମଧ୍ୟରେ ଆପେକ୍ଷିକ ଗତି ଯୋଗୁଁ କୁଣ୍ଡଳୀରେ ଏକ ବିଦ୍ୟୁତ୍ ବିଭବାନ୍ତର ସୃଷ୍ଟି ହୁଏ ।
• ଏହି ବିଭବାନ୍ତର ଯୋଗୁଁ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହୁଏ । ଏହି ବିଭବାନ୍ତରକୁ ପ୍ରେରିତ (Induced potential difference) ଓ ବିଦ୍ୟୁତ୍ ସ୍ରୋତକୁ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ (Induced current) କୁହାଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 9 (Activity – 9)
ପରୀକ୍ଷଣ :
50 ଘେର ଓ 100 ଘେର ବିଶିଷ୍ଟ ଦୁଇଟି ତମ୍ବାତାର କୁଣ୍ଡଳୀ ନେଇ ଏକ ବିଦ୍ୟୁତ୍‌ରୋଧୀ ସିଲିଣ୍ଡର ଉପରେ ଗୁଡ଼ାଅ ।

ସିଦ୍ଧାନ୍ତ :
100 ଘେର ବିଶିଷ୍ଟ କୁଣ୍ଡଳୀ -1 କୁ ଗୋଟିଏ ବ୍ୟାଟେରୀ ଓ ପ୍ଲଗ୍ କି ସହ ପଙ୍‌କ୍ତିରେ ସଂଯୁକ୍ତ କର । 50 ଘେର ବିଶିଷ୍ଟ କୁଣ୍ଡଳୀ – 2 କୁ ଗୋଟିଏ ଗାଲ୍‌ଭାନୋମିଟର ସହ ସଂଯୁକ୍ତ କର ।
ପ୍ଲଗ କିକୁ ବନ୍ଦ କରି କୁଣ୍ଡଳୀ -1 ରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଲେ ଦେଖାଯିବ ଯେ ସୂଚୀଟି ହଠାତ୍ ଗୋଟିଏ ପଟକୁ ବିକ୍ଷେପିତ ହୋଇ ଶୂନ୍‌କୁ ଫେରି ଆସିଲା । ଅର୍ଥାତ୍ କୁଣ୍ଡଳୀ-2 ରେ ସାମୟିକ ଭାବେ ବିଦ୍ୟୁତ୍ ପ୍ରୋତ ପ୍ରବାହିତ ହେଳ |
ପ୍ଲଗ୍ କି କୁ ମୁକ୍ତକରି କୁଣ୍ଡଳୀ-1ରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହକୁ ଶୂନ୍ କରିଦେଲେ ଦେଖୁ ଯେ ଗାଲଭାନୋମିଟର ସୂଚୀଟି ବିପରୀତ ଦିଗକୁ ସାମୟିକ ଭାବେ ବିକ୍ଷେପିତ ହୋଇ ପୁଣି ଶୂନ୍‌କୁ ଫେରି ଆସିବ । ଅର୍ଥାତ୍ ବର୍ତ୍ତମାନ କୁଣ୍ଡଳୀ-2 ରେ ବିପରୀତ ଦିଗରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହେଲା ।
ଏଥରୁ ଜଣାଯାଉଛି ଯେ କୁଣ୍ଡଳୀ -1ରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବଢ଼ି ଏକ ସ୍ଥିର ମୂଲ୍ୟରେ ପହଞ୍ଚିଲା ପରେ ବା କମି ଶୂନ୍‌ରେ ପହଞ୍ଚିଲା ପରେ କୁଣ୍ଡଳୀ-2ରେ ଗାଲଭାନୋମିଟର ସୂଚୀର ବିକ୍ଷେପ ହେଉନାହିଁ ।

ସିଦ୍ଧାନ୍ତ :
କୁଣ୍ଡଳୀ-1 ରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ପରିବର୍ତ୍ତନ ହେଲେ କୁଣ୍ଡଳୀ-2 ରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ବିଭବାନ୍ତର ସୃଷ୍ଟ ହେଉଛି ।
କୁଣ୍ଡଳୀ-1 କୁ ପ୍ରାଥମିକ (Primary) କୁଣ୍ଡଳୀ ଓ କୁଣ୍ଡଳୀ-2 କୁ ଦ୍ୱିତୀୟକ (Secondary) କୁଣ୍ଡଳୀ କୁହାଯାଏ ।

ବ୍ୟାଖ୍ୟା :
ପ୍ରାଥମିକ କୁଣ୍ଡଳୀରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ପରିବର୍ତ୍ତନ ହେଲେ ତା’ ସହ ସଂପୃକ୍ତ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେ ପରିବର୍ତ୍ତନ
ଦ୍ବିତୀୟକ କୁଣ୍ଡଳୀ ସଂପୃକ୍ତ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରରେଖାର ପରିବର୍ତ୍ତନ ଯୋଗୁଁ ହିଁ ଦ୍ବିତୀୟକ କୁଣ୍ଡଳୀରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟିହୁଏ । ଏହାକୁ ବିଦ୍ୟୁତ୍ ଚୁମ୍ବକୀୟ ପ୍ରେରଣ (electromagnetic induction) କୁହାଯାଏ । କୁଣ୍ଡଳୀର ଗତିର ଦିଗ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ପ୍ରତି ଲମ୍ବ ହେଲେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ ସବୁଠୁ ଅଧ୍ୟକ ହୁଏ ।

ଫ୍ଲେମିଂଙ୍କ ଦକ୍ଷିଣ ହସ୍ତ ନିୟମ (Fleming’s Right-Hand Rule):
ଦକ୍ଷିଣ ହସ୍ତର ବୃଦ୍ଧାଙ୍ଗୁଳି, ତର୍ଜନୀ ଓ ମଧ୍ଯମାକୁ ଏପରି ଖୋଲି ରଖ ଯେ ସେଗୁଡ଼ିକ ପରସ୍ପର ପ୍ରତି ସମକୋଣରେ ରହିବ । ତର୍ଜନୀ ଚୁମ୍ବକୀୟ କ୍ଷେତ୍ରର ଦିଗ ଓ ବୃଦ୍ଧାଙ୍ଗୁଳି ପରିବାହୀର ଗତିର ଦିଗ ନିର୍ଦ୍ଦେଶ କଲେ ମଧ୍ୟମା ନିର୍ଦ୍ଦେଶ କରୁଥିବା ଦିଗରେ ପ୍ରେରିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହେବ ।
ଫ୍ଲେମିଂଙ୍କ ଦକ୍ଷିଣ ହସ୍ତ ନିୟମ ସାହାଯ୍ୟରେ ବିଦ୍ୟୁତ୍ ଜେନେରେଟର୍‌ର କାର୍ଯ୍ୟ ପ୍ରଣାଳୀ ବୁଝିହେବ ।

Odisha State Board BSE Odisha 10th Class Life Science Notes Chapter 4 ରେଚନ will enable students to study smartly.

BSE Odisha Class 10 Life Science Notes Chapter 4 ରେଚନ

→ଉପକ୍ରମ (Introduction) :

• ଶରୀରର ବିଭିନ୍ନ କୋଷରେ ଉପଯୁକ୍ତ ଖାଦ୍ୟ ଓ କେତେକ ବିପାଚକଦ୍ୱାରା ଜୈବ ରାସାୟନିକ ପ୍ରକ୍ରିୟା କ୍ରମାଗତ ଭାବେ ସଂଘଟିତ ହୋଇଥାଏ । ଏହି ରାସାୟନିକ ପ୍ରକ୍ରିୟାଦ୍ବାରା କୋଷ ତା’ର ଆବଶ୍ୟକ ଶକ୍ତି ପାଇଥାଏ ।
• ଶରୀରରେ ହେଉଥ‌ିବା ବିଭିନ୍ନ ଚୟାପଚୟ ପ୍ରକ୍ରିୟାରୁ ଜାତ ହେଉଥ‌ିବା ବର୍ଜ୍ୟବସ୍ତୁ ଶରୀର ପାଇଁ ଅଦରକାରୀ ଓ ହାନିକାରକ ଅଟେ । ଶରୀରରେ ଥ‌ିବା ବିଶେଷ ବ୍ୟବସ୍ଥାଦ୍ଵାରା ଏହି ବର୍ଜ୍ୟବସ୍ତୁଗୁଡ଼ିକ ନିଷ୍କାସିତ ହୁଏ ଓ ଶରୀର ଭିତରର ପରିବେଶ ପ୍ରଦୂଷଣମୁକ୍ତ ହୋଇଥାଏ ।
• ବର୍ଜ୍ୟବସ୍ତୁର ନିଷ୍କାସନ ଦ୍ଵାରା କୋଷରେ ହେଉଥ‌ିବା ବିଭିନ୍ନ ଜୈବରାସାୟନିକ କାର୍ଯ୍ୟକଳାପର ସନ୍ତୁଳନ ବଜାୟ ରହେ ଓ ଶରୀର ସୁସ୍ଥ ରହେ । ଏହି ପ୍ରକ୍ରିୟାକୁ ରେଚନ କୁହାଯାଏ ।
• ରେଚନ ତନ୍ତ୍ର ମାଧ୍ୟମରେ ଶରୀରରୁ ଏମୋନିଆ, ୟୁରିଆ, ୟୁରିକ୍ ଏସିଡ୍ ଜାତୀୟ ବର୍ଜ୍ୟବସ୍ତୁର ନିଷ୍କାସନ ହୁଏ ଏବଂ ଶରୀରରେ ଜଳ ଓ ଧାତବ ଲବଣ ଆଦି ପଦାର୍ଥର ସନ୍ତୁଳନ ବଜାୟ ରହେ ।
• ଶରୀରରେ ପୁଷ୍ଟିସାର ଚୟାପଚୟ ଫଳରେ ଏମୋନିଆ ନିର୍ଗତ ହୋଇଥାଏ । ଏମୋନିଆ ଏକ ଗ୍ୟାସୀୟ ପଦାର୍ଥ ଓ ଏହା ଜଳରେ ଅତିମାତ୍ରାରେ ଦ୍ରବଣୀୟ । ଦ୍ରବୀଭୂତ ଏମୋନିଆ ଶରୀର ପାଇଁ କ୍ଷତିକାରକ ଅଟେ ।
• ଜଳଚର ପ୍ରାଣୀ ଶରୀରରୁ ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ଏମୋନିଆକୁ ବିସରଣ ପ୍ରକ୍ରିୟାଦ୍ଵାରା ସିଧାସଳଖ ଜଳୀୟ ପରିବେଶକୁ ନିଷ୍କାସିତ କରିଥାନ୍ତି ।
• ସ୍ଥଳଚର ପ୍ରାଣୀଙ୍କଠାରେ ସେ ସୁବିଧା ନଥ‌ିବାରୁ ସେମାନେ ଶରୀରରେ ଜାତ ହେଉଥ‌ିବା ଏମୋନିଆକୁ ୟୁରିଆ ବା ୟୁରିକ୍ ଏସିଡ୍‌ରେ ପରିଣତ କରି ଶରୀରରୁ ନିଷ୍କାସିତ କରିଥାନ୍ତି ।

ରେଚନ ମାଧ୍ୟମରେ ମଣିଷ ତଥା ଅନ୍ୟ ସମସ୍ତ ସ୍ତନ୍ୟପାୟୀ ପ୍ରାଣୀ, ବେଙ୍ଗ ଜାତୀୟ ଉଭୟଚର, ସାକ୍‌ଜାତୀୟ ମାଛ ଶରୀରରୁ ୟୁରିଆ ତ୍ୟାଗ କରୁଥିବାବେଳେ ପକ୍ଷୀ, ସରୀସୃପ ଓ ପତଙ୍ଗ ଶରୀରରୁ ୟୁରିକ୍ ଏସିଡ୍ ନିଷ୍କାସନ କରିଥା’ଛି ।

→ରେଚନର ଉପଯୋଗିତା :

• ଶରୀରର ଆଭ୍ୟନ୍ତରୀଣ ପରିବେଶ ପ୍ରଦୂଷଣମୁକ୍ତ ରହେ ।
• କୋଷରେ ସମ୍ପାଦିତ ବିଭିନ୍ନ ଜୈବ ରାସାୟନିକ କାର୍ଯ୍ୟକଳାପର ସନ୍ତୁଳନ ବଜାୟ ରହେ ଓ ଶରୀର ସୁସ୍ଥ ରହେ ।

→ବିଭିନ୍ନ ଜୀବଜନ୍ତୁଙ୍କ ବହିଷ୍କାର (Excretion in various Animals) :

• ମଣିଷ ତଥା ସମସ୍ତ ସ୍ତନ୍ୟପାୟୀ ପ୍ରାଣୀ, ବେଙ୍ଗ ଓ ସାଲାମାଣ୍ଡର ଭଳି ଉଭୟଚର ଓ ସାର୍କଜାତୀୟ ମାଛ ଶରୀରରୁ ବୃକ୍‌କଦ୍ଵାରା ୟୁରିଆ ନିଷ୍କାସନ କରିଥା’ନ୍ତି । ୟୁରିଆ ଜଳରେ ଦ୍ରବଣୀୟ ହେତୁ ରକ୍ତରେ ମିଶି ବୃକ୍‌କରେ ପହଞ୍ଚିଥାଏ । ବୃକ୍‌କରେ ରକ୍ତରୁ ୟୁରିଆ ପୃଥକ୍ ହୁଏ ଏବଂ ଜଳରେ ଦ୍ରବୀଭୂତ ହୋଇ ମୂତ୍ର ଆକାରରେ ଶରୀରରୁ ନିଷ୍କାସିତ ହୁଏ ।
• ପକ୍ଷୀ, ସରୀସୃପ ଓ ପତଙ୍ଗ ଏମୋନିଆକୁ ‘ୟୁରିକ୍ ଅମ୍ଳ’ରେ ପରିଣତ କରି ମଳ ସହ ଶରୀରରୁ ନିଷ୍କାସନ କରିଥା’ନ୍ତି । ୟୁରିକ୍ ଅମ୍ଳ ଜଳରେ ପ୍ରାୟ ଅଦ୍ରବଣୀୟ ହୋଇଥିବାରୁ ମୂତ୍ର ତିଆରି ପରେ ଏହା ସହଜରେ ଦ୍ରବଣରୁ ପୃଥକ୍ ହୋଇଯାଏ । ଦ୍ରବଣରେ ଥିବା ଜଳ ପୁନର୍ବାର ଶୋଷିତ ହୋଇ ରକ୍ତକୁ ଚାଲିଯାଏ । ଏଣୁ ଉପରୋକ୍ତ ପ୍ରାଣୀମାନେ ରେଚନ ପ୍ରକ୍ରିୟାରେ ଅଧ୍ୟକ ଜଳକ୍ଷୟ କରନ୍ତି ନାହିଁ ।
• ଏକକୋଷୀ ଏମିବା ‘ପ୍ଲାଜ୍‌ମା ଝିଲ୍ଲୀ’ ଓ ‘ସଙ୍କୋଚିକିଧାନୀ’ (Contractile Vacuole) ଦ୍ୱାରା ବିସରଣ ପ୍ରକ୍ରିୟାରେ ରେଚନ କରିଥାଏ । ଏହା ଏମୋନିଆ ତ୍ୟାଗ କରିଥାଏ ।
• ସଞ୍ଜ୍ ଓ ହାଇଡ୍ରା ପରି ନିମ୍ନବର୍ଗର ପ୍ରାଣୀଙ୍କର ନିର୍ଦ୍ଦିଷ୍ଟ ରେଚନ ଅଙ୍ଗ ନଥାଏ ଏବଂ ଏମାନେ ବିସରଣ ପ୍ରକ୍ରିୟାରେ ଏମୋନିଆ
• ଚେପ୍‌ଟା କୃମି, ଫିତାକୃମି ଓ ଯକୃତ କୃମି ଶିଖା କୋଷ (Flame Cells)ଦ୍ୱାରା ଏମୋନିଆ ତ୍ୟାଗ କରିଥା’ନ୍ତି ।
• ଜିଆ, ଜୋକ ଓ ନେରିସ୍ ନେଫ୍ରିଡ଼ିଆ (Nephridia)ଦ୍ୱାରା ଏମୋନିଆ କିମ୍ବା ୟୁରିଆ ତ୍ୟାଗ କରନ୍ତି ।
• ଝିଣ୍ଟିକା, ଅସରପା ଭଳି ପତଙ୍ଗ ଏବଂ କଙ୍କଡ଼ାବିଛା, ବୁଢ଼ିଆଣୀ ଭଳି କୀଟ ମାପିଝିଆନ୍ ନଳିକା (Malpighian tubules)ଦ୍ୱାରା ୟୁରିକ୍ ଅମ୍ଳ ତ୍ୟାଗ କରନ୍ତି ।

→ପ୍ରାଣୀମାନଙ୍କ ରେଚନ ଅଙ୍ଗର ଗଠନ, ପ୍ରକାରଭେଦ ଓ କାର୍ଯ୍ୟକାରିତାରେ ନିମ୍ନଲିଖ୍ ବିଭିନ୍ନତା ଦେଖିବାକୁ ମିଳିଥାଏ ।

• ଏମିବାର ରେଚନ ଅଙ୍ଗ – ସଂକୋଚିକିଧାନୀ
• ଗଞ୍ଜ, ହାଇଡ୍ରାର ରେଚନ ଅଙ୍ଗ – ନାହିଁ ।
• ଚେପଟାକୃମିର ରେଚନ ଅଙ୍ଗ – ଶିଖାକୋଷ
• ଜିଆ, ଜୋକର ରେଚନ ଅଙ୍ଗ – ନେଫ୍ରିଡ଼ିଆ
• ଝିଣ୍ଟିକାର ରେଚନ ଅଙ୍ଗ – ମାଲପିଝିଆନ୍ ନଳିକା
• ମେରୁଦଣ୍ଡୀ ପ୍ରାଣୀଙ୍କର ରେଚନ ଅଙ୍ଗ – ବୃକ୍‌କ, ଚର୍ମ

→ମଣିଷର ରେଚନ ତନ୍ତ୍ର :
1. ମଣିଷର ରେଚନ ତନ୍ତ୍ର ବୃକ୍‌କ, ମୂତ୍ରସାରଣୀ, ମୂତ୍ରାଶୟ ଓ ମୂତ୍ରମାର୍ଗ ଆଦିକୁ ନେଇ ଗଠିତ ହୋଇଥାଏ ।

→(i) ବୃକ୍‌କର ବାହ୍ୟ ଗଠନ (External structure of Kidney) :
ଅବସ୍ଥିତି :

• ମଣିଷର ମଧ୍ୟଚ୍ଛଦାର ଠିକ୍ ତଳକୁ ଉଦରଗହ୍ଵର ଭିତରେ ଓ ମେରୁଦଣ୍ଡର ଉଭୟ ପାର୍ଶ୍ଵରେ ଦୁଇଟି ବୃକ୍‌କ ରହିଥାଏ ।
• ବୃକ୍‌କର ଆକୃତି ପ୍ରାୟ ଶିମ୍ବ ମଞ୍ଜିପରି । ସୁସ୍ଥ ବୟଃପ୍ରାପ୍ତ ବ୍ୟକ୍ତିର ବୃକ୍‌କର ଲମ୍ବ ପ୍ରାୟ 10 ରୁ 12 ସେ.ମି., ପ୍ରସ୍ଥ ପ୍ରାୟ 5 ରୁ 7 ସେ.ମି. ଓ ମୋଟେଇ ପ୍ରାୟ 3 ସେ.ମି. ଅଟେ ।
• ବୃକ୍‌କର ଭିତର ପାଖରେ ଥିବା ଖାଲୁଆ ସ୍ଥାନଟିକୁ ହାଇଲମ୍ କୁହାଯାଏ ।
• ହାଇଲମ୍ ମଧ୍ୟଦେଇ ବୃକ୍‌କୀୟ ଶିରା, ଧମନୀ ଓ ମୂତ୍ରସାରଣୀ ବୃକ୍‌କ ସହିତ ସଂଯୁକ୍ତ ହୋଇଥାଏ ।
• ମୂତ୍ରସାରଣୀ ଦେଇ ବୃକ୍‌କରୁ ମୂତ୍ର ମୂତ୍ରାଶୟକୁ ଆସିଥାଏ ।

→(ii) ବୃକ୍‌କର ଅନ୍ତଃ ଗଠନ (Internal structure of Kidney) :

• ପ୍ରତ୍ୟେକ ବୃକ୍‌କ ଭିତରେ 10 ଲକ୍ଷରୁ ଅଧିକ ସୂକ୍ଷ୍ମ ବୃକ୍‌କୀୟ ନଳିକା ବା ମୂତ୍ରଜନ ନଳିକା ବା ନେଫ୍ରନ୍ ରହିଥାଏ ।
• ପ୍ରତି ବୃକ୍‌କୀୟ ନଳିକାର ଗୋଟିଏ ପାର୍ଶ୍ଵ ‘କପ୍’ ବା ଗିନା ଆକୃତିର ହୋଇଥାଏ । କପ୍ ଆକୃତିର ପାର୍ଶ୍ଵଟି ବୃକ୍‌କର ବାହାର ପଟକୁ ମୁହେଁଇଥାଏ । ଏହି କପ୍‌କୁ ବାଓମ୍ୟାନ୍ସ କ୍ୟାପ୍‌ସୁଲ କୁହାଯାଏ ।
• ପ୍ରତି ନେଫ୍ରନ୍ ସହ ବୃକ୍‌କୀୟ ଧମନୀର ଗୋଟିଏ ଲେଖାଏଁ ସୂକ୍ଷ୍ମ ଶାଖା (ଏଫରେଣ୍ଟ ଅନ୍ତର୍ବାହୀ ଉପଧମନୀ) ସଂଯୁକ୍ତ ହୋଇଥାଏ ।
• ଏହା ନେଫ୍ରନ୍ ଭିତରେ ପ୍ରବେଶ କରି ଅନେକ ଅତି ସୂକ୍ଷ୍ମ ଶାଖାପ୍ରଶାଖା ବା କୈଶିକନଳୀରେ ପରିଣତ ହୋଇଥାଏ । ଏହିସବୁ କୈଶିକନଳୀ ପରସ୍ପର ସହ ପୁଣି.ମିଶିଯିବାଦ୍ଵାରା ବହିର୍ବାହୀ ଉପଧମନୀ ସୃଷ୍ଟି ହୋଇଥାଏ ।
• କୈଶିକନଳୀଗୁଡ଼ିକର ପ୍ରାଚୀର ଖୁବ୍ ପତଳା ଅଟେ । ଏ ଦୁଇଟି ଉପଧମନୀ ସହ ସଂଶ୍ଳିଷ୍ଟ କୈଶିକନଳୀର ଏହି ଗୁଚ୍ଛକୁ କୈଶିକଗୁଚ୍ଛ ବା ଗ୍ଲୋମେରୁଲସ୍ କୁହାଯାଏ ।
• ବାଓମ୍ୟାନ୍ସ କ୍ୟାପସୁଲର ‘କପ୍’ରେ ଏହା ଯୋଗୁଁହୋଇ ରହିଥାଏ । ରକ୍ତ, ଅନ୍ତର୍ବାହୀ ଉପଧମନୀ ଦେଇ କୈଶିକଗୁଚ୍ଛରେ ପ୍ରବେଶ କରେ ଏବଂ ବହିର୍ବାହୀ ଉପଧମନୀ ଦେଇ ଗୁଚ୍ଛ ବାହାରକୁ ଯାଇଥାଏ ।
• ‘ରକ୍ତଛଣା’ କାର୍ଯ୍ୟ ପାଇଁ ଏହି ବ୍ୟବସ୍ଥା ବେଶ୍ ଉପଯୋଗୀ । ଗ୍ଲୋମେରୁଲସ୍ ଓ ବାଓମ୍ୟାନ୍ସ କ୍ୟାପସୁଲ୍ ମିଶି ମାଲ୍‌ପିଝିଆନ୍ ପିଣ୍ଡ ଗଠନ କରିଥାନ୍ତି ।
• ବୃକ୍‌କୀୟ ନଳିକାର କେତେକ ଅଂଶ ବୃକ୍‌କ ଭିତରେ ଗୁଡ଼େଇ ରହି ଶେଷ ମୁଣ୍ଡଟି ମୂତ୍ର ସଂଗ୍ରହନଳିକା ମଧ୍ଯରେ ପଶିଥାଏ ।
• ମୂତ୍ର ସଂଗ୍ରହ ନଳିକାଗୁଡ଼ିକ ଏକାଠି ହୋଇ ବୃକ୍‌କ ଭିତରେ ଥ‌ିବା ଏକ ଗହ୍ଵର ଭିତରକୁ ଖୋଲିଥା’ନ୍ତି । ଏହି ଗହ୍ଵରଟିକୁ ଗବିଣୀ ବସ୍ତି କୁହାଯାଏ ।
• ପ୍ରତ୍ୟେକ ବୃକ୍‌କରୁ ଗୋଟିଏ ଲେଖାଏଁ ମୂତ୍ରସାରଣୀ ବାହାରି ତଳିପେଟରେ ଥିବା ମୂତ୍ରାଶୟ ଭିତରେ ପଶିଥାଏ ।
• ମୂତ୍ରାଶୟରେ ମୂତ୍ର ସ ହୋଇ ରହେ ଓ ପରିସ୍ରା କଲାବେଳେ ତାହା ମୂତ୍ରମାର୍ଗ ଦେଇ ନିଷ୍କାସିତ ହୋଇଥାଏ ।

→(iii) ଗ୍ଲୋମେରୁଲସ୍‌ର କାର୍ଯ୍ୟ (Function of Glomerulus) :

• ଗ୍ଲୋମେରୁଲସ୍‌ରେ ରକ୍ତଛଣା କାର୍ଯ୍ୟ ସମ୍ପାଦିତ ହୋଇଥାଏ ।
• ଗ୍ଲୋମେରୁଲସ୍ ଭିତରେ ଥ‌ିବା ଅତି ସୂକ୍ଷ୍ମ ରନ୍ଧ୍ରଦେଇ ରକ୍ତରେ ଥିବା ରକ୍ତ କଣିକା ଓ କିଛି ବଡ଼ ଅଣୁବିଶିଷ୍ଟ ପ୍ରୋଟିନ୍ ପରିସ୍ତ୍ରୁତ ହୋଇପାରେ ନାହିଁ । ତେଣୁ ଏହା ବ୍ୟତୀତ ପ୍ରାୟ ଅନ୍ୟ ସମସ୍ତ ଉପାଦାନ ଛାଣି ହୋଇ ବୃକ୍‌କୀୟ ନଳୀକା ଭିତରକୁ ଯାଇଥାଏ ।
• ବୃକ୍‌କୀୟ ନଳିକା ଭିତରେ ପ୍ରବେଶ କରୁଥିବା ଉପାଦାନଗୁଡ଼ିକ ଭିତରେ ଜଳ, ଗ୍ଲୁକୋଜ, ଆମିନୋ ଏସିଡ୍, ୟୁରିଆ, ୟୁରିକ୍ ଏସିଡ୍, କ୍ରିଏଟିନିନ୍, ସୋଡ଼ିୟମ, ପୋଟାସିୟମ୍, କ୍ଲୋରାଇଡ୍ ଆଦି ପ୍ରଧାନ ।
• ଗ୍ଲୁକୋଜ୍ ଓ ଏମିନୋ ଏସିଡ୍ ଭଳି ଉପାଦାନ ଆମ ଶରୀର ପାଇଁ ଅଧିକ ଉପଯୋଗୀ ହୋଇଥିବାରୁ ସେଗୁଡ଼ିକ ନିଷ୍କାସିତ ନ ହୋଇ ବୃକକୀୟ ନଳିକାକୁ ଘେରି ରହିଥିବା କୈଶିକ ରକ୍ତନଳୀ ଭିତରକୁ ପୁନଃଶୋଷିତ ହୋଇଥାଏ ।
• ଏହି କୈଶିକ ରକ୍ତନଳୀମାନ ମିଶି ବୃକ୍‌କୀୟ ଶିରାରେ ପରିଣତ ହୁଏ ।

ମୂତ୍ରରେ ନିଷ୍କାସିତ ହେଉଥ‌ିବା ପଦାର୍ଥମାନଙ୍କ ଭିତରେ ମୁଖ୍ୟତଃ ଜଳ ଓ ୟୁରିଆ ଏବଂ ଅଳ୍ପ ପରିମାଣର ୟୁରିକ୍ ଏସିଡ଼, କ୍ରିଏଟିନିନ୍, ବିଭିନ୍ନ ଲବଣ ଯଥା ସୋଡ଼ିୟମ କ୍ଲୋରାଇଡ୍, ପୋଟାସିୟମ କ୍ଲୋରାଇଡ୍ ଆଦି ପ୍ରଧାନ । ମୂତ୍ରରେ ୟୁରୋକ୍ରୋମ (Urochrome) ନାମକ ବର୍ଷକଣା ଥିବା ହେତୁ ଜଣେ ସୁସ୍ଥ ବ୍ୟକ୍ତିର ପରିସ୍ରା ରଙ୍ଗ ଈଷତ୍ ହଳଦିଆ ହୋଇଥାଏ । ସୁସ୍ଥ ଲୋକର ମୂତ୍ରରେ ଗ୍ଲୁକୋଜ୍, ପ୍ରୋଟିନ୍ ବା କୌଣସି ରକ୍ତକଣିକା ନଥାଏ । ମୂତ୍ରରେ ଏଭଳି କୌଣସି ଉପାଦାନ ଥିଲେ ଅଥବା, ମୂତ୍ରର ବର୍ଷରେ ପରିବର୍ତ୍ତନ ଦେଖାଗଲେ ତାହା ରୋଗର ସୂଚନା ଦିଏ ।

→(iv) କିଡନୀ ର ଅତିରିକ୍ତ କାର୍ଯ୍ୟ (Extra function of kidney) :

• ଶରୀରର ଜଳ ଓ ଧାତବଲବଣ ପରିମାଣର ନିୟନ୍ତ୍ରଣ, ରକ୍ତର ଅମ୍ଳ ଓ କ୍ଷାରୀୟ ମାତ୍ରା ନିୟନ୍ତ୍ରଣ କରୁଥିବା ପଦାର୍ଥମାନଙ୍କ ସନ୍ତୁଳନ ରକ୍ଷା କରିବା, ଶରୀରର ରକ୍ତଚାପ ନିୟନ୍ତ୍ରଣ ଓ ଏରିଥ୍ରୋପୋଇଏଟିନ୍ ନାମକ ହରମୋନ୍ କ୍ଷରଣ କରି ଲୋହିତ ରକ୍ତକଣିକା ତିଆରି କରିବାରେ ସାହାଯ୍ୟ କରିବା ଇତ୍ୟାଦି ବୃକ୍‌କର ଅନ୍ୟ କାର୍ଯ୍ୟ ।
• ପରିସ୍ରବଣ, ପୁନଃଶୋଷଣ, କ୍ଷରଣ ଏବଂ ନିଷ୍କାସନ – ଏହି ଚାରୋଟି ପ୍ରକ୍ରିୟା ମାଧ୍ୟମରେ ବୃକ୍‌କ ଶରୀରର ଅନ୍ତଃପରିବେଶରେ ସନ୍ତୁଳନ ବଜାୟ ରଖେ ।

→ଶରୀରର ଅନ୍ୟ ରେଚନ ଅଙ୍ଗ (Other excretory organs) :
ଚର୍ମ :

• ଶରୀରରୁ ବର୍ଜ୍ୟବସ୍ତୁ କିଛି ପରିମାଣରେ ଝାଳ ଆକାରରେ ଚର୍ମଦେଇ ନିଷ୍କାସିତ ହୋଇଥାଏ । ଝାଳ ତିଆରି ଚର୍ମର ଅନ୍ୟତମ କାର୍ଯ୍ୟ ଓ ଏଥପାଇଁ ଚର୍ମରେ ସ୍ବେଦଗ୍ରନ୍ଥି ରହିଥାଏ ।
• ରକ୍ତରୁ ଧାତବଲବଣ, ସାମାନ୍ୟ ୟୁରିଆ ଶୋଷିତ ହୋଇ ପରେ ଝାଳ ଆକାରରେ ଶରୀରରୁ ନିଷ୍କାସିତ ହୋଇଥାଏ ।
• ଝାଳ ବାଷ୍ପୀଭୂତ ହେବା ଫଳରେ ଶରୀର ଶୀତଳ ହୋଇଥାଏ ।

→ଯକୃତ :

• ପାଚକତନ୍ତ୍ର ସହ ଜଡ଼ିତ ଯକୃତ୍ କିଛି ବର୍ଜ୍ୟବସ୍ତୁ ନିଷ୍କାସନ କରିବାରେ ସହାୟକ ହୋଇଥାଏ ।
• ଚୟାପଚୟରୁ ଉତ୍ପାଦିତ ବର୍ଜ୍ୟ ଯଥା ଖାଉଥ‌ିବା ଔଷଧର ଅବଶିଷ୍ଟାଶ, ମାତ୍ରାଧ‌ିକ ଭିଟାମିନ୍, ଲୋହିତ ରକ୍ତକଣିକାର ବିଖଣ୍ଡନ ପ୍ରକ୍ରିୟାରେ ଜାତ ହେଉଥ‌ିବା ବର୍ଣ୍ଣକଣା ଇତ୍ୟାଦି ପିତ୍ତରସ ସହ ମିଶି ଖାଦ୍ୟନଳୀ ଭିତରକୁ ଯାଇଥାଏ, ପରେ ସେଠାରୁ ମଳ ସହ ନିଷ୍କାସିତ ହୋଇଥାଏ ।

→ଫୁସ୍‌ଫୁସ୍ :
1. ନିଃଶ୍ବାସ ଛାଡ଼ିଲା ବେଳେ ଫୁସ୍‌ଫୁସ୍‌ରୁ ଶରୀରରେ ଉତ୍ପନ୍ନ ଅଙ୍ଗାରକାମ୍ଳ ଓ ଜଳୀୟବାଷ୍ପ ନିଷ୍କାସିତ ହୋଇଥାଏ ।

→ଉଭିଦରେ ରେଚନ (Excretion in plant) :

• ଉଭିଦରେ ରେଚନ ପାଇଁ ପ୍ରାଣୀପରି ସ୍ବତନ୍ତ୍ର ରେଚନ ଅଙ୍ଗ ନଥାଏ । ଚୟାପଚୟ ପ୍ରକ୍ରିୟାରେ ସୃଷ୍ଟିହେଉଥ‌ିବା ବିଭିନ୍ନ ଉପଜାତ ପଦାର୍ଥ ଉଭିଦର କେତେକ ବିଶେଷ ଅଂଶରେ ଗଚ୍ଛିତ ହୋଇ ରହେ ।
• ଖଇର, ଝୁଣା, ଅଠା, କ୍ଷୀର ଏହାର କେତୋଟି ଉଦାହରଣ ଅଟେ ।
• ତେନ୍ତୁଳିରେ ଥ‌ିବା ଟାର୍ଟାରିକ୍ ଅମ୍ଳ, ଲେମ୍ବୁରେ ଥ‌ିବା ସାଇଟ୍ରିକ୍ ଅମ୍ଳ, ସିନା ଗଛରେ ଥ‌ିବା କୁଇନାଇନ୍ ଓ ତମାଖୁ ପତ୍ରରେ ଥ‌ିବା ନିକୋଟିନ ପରି ଉପକ୍ଷାର ଇତ୍ୟାଦି ଏହିପରି କିଛି ଉତ୍ପାଦ ଅଟନ୍ତି ।
• ଏଗୁଡ଼ିକ ଆମର ଉପକାରରେ ଆସନ୍ତି । ଏହି ଅଦରକାରୀ ପଦାର୍ଥଗୁଡ଼ିକ ଯୋଗୁଁ ଉଭିଦର କ୍ଷତି ହୋଇ ନଥାଏ ।
• ଉଭିଦରେ ଷ୍ଟୋମାଟା ଶ୍ଵାସକ୍ରିୟା ସମ୍ପାଦନ କରିବା ସହିତ ଏକ ରେଚନ ଅଙ୍ଗଭଳି କାର୍ଯ୍ୟ କରିଥାଏ ।
• ଉଭିଦମାନେ ବର୍ଜ୍ୟବସ୍ତୁରୁ ମୁକ୍ତ ରହିବାପାଇଁ ବିଭିନ୍ନ ଉପାୟ ଅବଲମ୍ବନ କରିଥା’ନ୍ତି । ଉଭିଦ ଶରୀରରେ ଥ‌ିବା ବଳକା ପାଣି ଉଚ୍ଛେଦନ ପ୍ରକ୍ରିୟାରେ ବାହାରିଯାଇଥାଏ ।

ଅନେକ ଉଦ୍ଭଦରେ ବର୍ଜ୍ୟବସ୍ତୁଗୁଡ଼ିକ କୋଷମଧ୍ଯସ୍ଥ ରସଧାନୀରେ ସଂଗୃହୀତ ହୋଇଥାଏ । ସ୍ଥଳବିଶେଷରେ ସେଗୁଡ଼ିକ ମଧ୍ଯ ପତ୍ରରେ ସଂଗୃହୀତ ହୁଏ ଓ ପରେ ବର୍ଜ୍ୟବସ୍ତୁଭରା ପତ୍ର ଶୁଖ୍ ଝଡ଼ିପଡ଼େ । ରେଜିନ୍ ଓ ଟାନିନ୍ ପରି ବର୍ଜ୍ୟବସ୍ତୁଗୁଡ଼ିକ ପରିପକ୍ବ ଜାଇଲେଟ୍‌ରେ ମଧ୍ଯ ସଂଗୃହୀତ ହୋଇଥାଏ ।

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Additional Exercise Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Additional Exercise

Question 1.
Prove that the sum of the vectors directed from the vertices to the midpoints of opposite sides of a triangle is zero.
Solution:
Let D, E, F are midpoints of side BC, CA and AB of ΔABC

Question 2.
Prove by vector method that the diagonals of a quadrilateral bisect each other iff it is a parallelogram.
Solution:

Question 3.
If G is the centroid of a triangle ABC, prove that \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Solution:

Question 4.
If M is the midpoint of the side B͞C of a triangle ABC, prove that \(\overrightarrow{AB}+\overrightarrow{AC}=2 \overrightarrow{AM}\).
Solution:

Question 5.
If \(\vec{a} \text { and } \vec{b}\) are the vectors represented by the adjacent sides of a regular hexagon, taken in order, what are the vectors represented by the other sides taken in order?
Solution:

Question 6.
If the points with position vectors 10î +3ĵ, 12î – 5ĵ and aî +11ĵ are collinear, find the value of a.
Solution:
Let the points are A, B and C.
As A, B and C are co-llinear.
We have \(\overrightarrow{AB}=\overrightarrow{AC}\)
\(\overrightarrow{AB}=\lambda \overrightarrow{AC}\)
⇒ (12i – 5j) – (10i + 3j)
⇒ λ [(ai + 11j) – (10i + 3j)
⇒ 2i – 8j = (a – 10)λ i + 8λ j
Comparing the components we have
8λ = -8
⇒ λ = -1
(a – 10) (-1) = 2
⇒ -a + 10 = 2
⇒ a = 8

Question 7.
Prove that the four points with position vectors \(2 \vec{a}+3 \vec{b}-\vec{c}, \vec{a}-2 \vec{b}+3 \vec{c}, 3 \vec{a}+4 \vec{b}-2 \vec{c}\) and \(\vec{a}-6 \vec{b}+6 \vec{c}\) are coplanar.
Solution:
Let the points are A, B, C

Question 8.
For any vector \(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) prove that \(\vec{r}=(\vec{r} \cdot \hat{i}) \hat{i}+(\vec{r} \cdot \hat{j}) \hat{j}+(\vec{r} \cdot \hat{k}) \hat{k}\).
Solution:

Question 9.
If two vectors \(\vec{a} \text { and } \vec{b}\) are such \(|\vec{a}|={3},|\vec{b}|=2 \text { and } \vec{a} \cdot \vec{b}={6}\text { find }|\vec{a}+\vec{b}| \text { and }|\vec{a}-\vec{b}|\).
Solution:

Question 10.
If \(\vec{a}\) makes equal angles with î, ĵ and k̂ and has magnitude 3, prove that the angle between \(\vec{a}\) and each of î ,ĵ and k̂ is \(\cos ^{-1}\left(\frac{1}{\sqrt{3}}\right)\).
Solution:

Question 11.
If \(\vec{a}, \vec{b}, \vec{c}\) are such that \(\vec{a} \cdot \vec{b}=\vec{a} \cdot \vec{c}\) then show that \(\vec{a}=\overrightarrow{0} \text { or } \vec{b}=\vec{c} \text { or } \vec{a}\) is perpendicular to \(\vec{b}-\vec{c}\)
Solution:

Question 12.
If \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0},|\vec{a}|={3},|\vec{b}|={5}\text { and }|\vec{c}|=7\), find the angle between \(\vec{a} \text { and } \vec{b}\).
Solution:

Question 13.
If \(\vec{a}, \vec{b}, \vec{c}\) are unit vectors such that \(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\), find the value of \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\).
Solution:

Question 14.
Find the angles which the vector \(\vec{a}=\hat{i}-\hat{j}+\sqrt{2} \hat{k}\) makes with the coordinate axes.
Solution:

Question 15.
Find the angle between \(\vec{a} \text { and } \vec{b}\) if \(|\vec{a} \times \vec{b}|=\vec{a} \cdot \vec{b}\).
Solution:

Odisha State Board BSE Odisha 9th Class Hindi Solutions  Poem 6 साथी ! दुःख से घबराता है ? Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Hindi Solutions Poem 6 साथी ! दुःख से घबराता है ?

प्रश्न और अभ्यास (ପ୍ରଶ୍ନ ଔର୍ ଅଭ୍ୟାସ)

1. इन प्रश्नों के उत्तर दो-तीन वाक्यों में दीजिए:
(ଇନ୍ ପ୍ରଶ୍ନୋ କେ ଉତ୍ତର୍ ଦୋ-ଡ଼ୀନ୍ ବାକ୍ୟା ମେଁ ଦୀଜିଏ) ।
(ଏହି ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦୁଇ-ତିନୋଟି ବାକ୍ୟରେ ଦିଅ ।)

(क) कवि दुःख से न घबराने को क्यों कहते हैं ?
(କବି ଦୁଃଖ୍ ସେ ନ ଘବ୍‌ରାନେ କୋ କେଁ କହ ହେଁ (କବି ଦୁଃଖରେ ନ ଡରିବାକୁ (ବ୍ୟତିବ୍ୟସ୍ତ ନ ହେବାକୁ) କାହିଁକି କହିଛନ୍ତି ।)
उत्तर:
कवि के मत से दुःख से डरने से, रोने- चीखने से दुःख दूर नहीं होता मगर दुःख के बाद सुख आएगा और दुःख सर्वदा नहीं रह सकता। जीवन में दुःख होने के कारण हम सव कर्मतत्पर बने रहते है। दुःख पर विजय प्राप्त करने की कोशिश करना जरुरी है।

(ख) इस कविता का संदेश क्या है- समझाइए।
(ଏହି କବିତାର ବାର୍ତ୍ତା କ’ଣ ଅଟେ – ବୁଝାଅ)
(ଇସ୍ କବିତା କା ସଂଦେଶ କ୍ୟା ହୈ – ସମଝାଇଏ ।
उत्तर:
इस कविता का संदेश यह है कि मानव जीवन में दुःख ज्यादा और सुख बहुत कम होता है। दुःख से डरने से दुःख दूर नहीं होता बरं दुःख से लड़ना सही रास्ता है। इसलिए दुःख को बुरी चीज न मानकर मुक्ति का मार्ग मानना चाहिए।
निम्नलिखित प्रश्नों के उत्तर एक या दो शब्द वाक्यों में दीजिए।

2. निम्नलिखित प्रश्नों के उत्तर एक या दो शब्द वाक्यों में दीजिए।
(ନିମ୍ନଲିଖୂ ପ୍ରଶ୍ନ କେ ଉତ୍ତର୍ ଏକ୍ ୟା ଦୋ ବାର୍କେ ମେଁ ଦୀଜିଏ) ।
(ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଗୋଟିଏ ବା )

(क) कवि ने मुक्ति का बंधन किसे माना है?
(କବି ନେ ମୁକ୍ତି କା ବଂଧନ୍ କିସ୍ ମାନା ହୈ ?)
(କବି ମୁକ୍ତିର ବଂଧନ କାହାକୁ ମାନିଛନ୍ତି ?)
उत्तर:
कवि ने मुक्ति का बंधन दुःख को माना है।

(ख) जीवन के लम्बे पथ पर कौन साथ-साथ चलते हैं?
(ଜୀବନ୍ କେ ଲୟେ ପଥ୍ ପର୍ କୌନ୍ ସାଥ୍‌-ସାଥ୍ ଚଲତେ ହୈ ?)
(ଜୀବନର ଲମ୍ବା ରାସ୍ତାରେ କିଏ ସାଥ୍‌ରେ ଚାଲିଛନ୍ତି ?)
उत्तर:
जीवन के लम्बे पथ पर सुख और दुःख साथ-साथ चलते हैं।

(ग) जीवन की मंजिल तक कौन जाता है?
(ଜୀବନ୍ କୀ ମଂଜିଲ୍ ତକ୍ କୌନ୍ ଜାତା ହୈ ?)
(ଜୀବନର ଲକ୍ଷ୍ୟ ପର୍ଯ୍ୟନ୍ତ କିଏ ଯାଇଛି ?)
उत्तर:
जीवन की मंजिल तक दुःख जाता है।

(घ) जीवन में हलचल कौन लाता है?
(ଜୀବନ୍ ମେଁ ହଲ୍‌ଚଲ୍ କୌନ୍ ଲାତା ହୈ ?)
(ଜୀବନରେ ଏପଟସେପଟ (ଅସ୍ଥିରତା) କିଏ ଆଣିଛି ?)
उत्तर:
दुःख मन की दुर्बलता जीवन में हलचल लाता है।

(ङ) जलती ज्वाला में जलकर क्या लाल बन निकलाता है?
(ଜଲ୍‌ ଜ୍ଵାଲା ମେଁ ଜଲ୍‌କର୍ କ୍ୟା ଲାଲ୍ ବନ୍ ନିକଲ୍‌ତା ହୈ ?)
(ଜଳନ୍ତା ଅଗ୍ନିଶିଖାରେ କିଏ ଜଳି ଲାଲ୍ ହୋଇ ବାହାରୁଛି ?)
उत्तर:
जलती ज्वाला में जलकर लोहा लाल बन निकलता है। लेकिन यहाँ पर मानव-जीवन में दुःख रूपी संघर्ष के कारण व्यक्तित्व का उत्कर्ष प्रतिपादित होता है।

(च) कवि ने किसे धन्यवाद देने को कहा है?
(କବି କାହାକୁ ଧନ୍ୟବାଦ ଦେବାକୁ କହିଛନ୍ତି ?)
उत्तर:
कवि ने दुःख देने वाले व्यक्ति को धन्यवाद देने को कहा इसलिए कि दुःख से ही सुख का मार्ग उन्मुक्त होता है।

(छ) दुःख कब सुख बन जाता है।
(ଦୁଃଖ୍ କବ୍ ସୁଖ ବନ୍ ଜାତା ହୈ ?)
(ଦୁଃଖ କେବେ ସୁଖରେ ପରିଣତ ହୋଇଯାଏ ?)
उत्तर:
दुःख से न डरने से सुख बन जाता है।

3. पंक्तियाँ पूरा कीजिए:
(क) जीवन के………………. सुख दुःख चलते साथ-साथ तब
उत्तर:
लम्बे पथ पर जब

(ख) दुःख जीवन में करता…………………. वह मन की …………… केवल।
उत्तर:
हलचल, दुर्बलता

(ग) जलती ……………….. में जलकर ही ……………………. लाल निकल आता है।
उत्तर:
ज्वाला, लोहा

(घ) एक समय है जब ……………… ही क्या! ……………….. भी साथ न दे पाता है।
उत्तर:
सुख, दुःख

4. सही अर्थ चुनिए: (ଠିକ୍ ଅର୍ଥ ବାଛ)
(क) प्रबल परीक्षा का क्षण क्या है?
(i) सुख
(ii) दुःख
(iii) आनन्द
उत्तर:
(ii) दुःख

(ख) किसमें जलकर ही लोहा लाल निकल आता है?
उत्तर:
(i) दुःख में
(ii) सुख में
(iii) जलती ज्वाला में
उत्तर:
(iii) जलती ज्वाला में

भाषा-ज्ञान (ଭାଷା-ଜ୍ଞାନ)

1. विपरीत अर्थवाले शब्द लिखिए:
(ବିପରାତ ଅର୍ଥ ବୁଝାଉଥବା ଶବ୍ଦ ଲେଖା::)
उत्तर:
कठिन:, बंधन:, दुर्बलताः, दुःख :, मुक्ति:, हार:
कठिन : सरल
दुर्बलता : सबलता
मुक्ति : बन्दी
बंधन : मुक्त
दुःख : सुख
हार : जीत

2. इन शब्दों का वाक्यों में प्रयोग कीजिए:
(ଏହିଶବ୍ଦଗୁଡ଼ିକୁ ବାକ୍ୟରେ ଚ୍ୟବହାର କର)
परीक्षा, समय, मंजिल, बंधन
उत्तर:
परीक्षा- कल हमारी परीक्षा होगी।
समय – हमारे लिए कीमती चीज समय है।
मंजिल – जीवन की मंजिल तक दुःख जाता है।
बंधन – यह संसार मायामोह बंधन में जुड़े हुए है।

3. लिंग वताइए: ( ଲିଙ୍ଗ କୁହ )
लोहा, आग, हार, ज्वाला, पथ, दुःख
उत्तर:
लोहा – पुंलिंग
ज्वाला – स्त्रीलिंग
आग – स्त्रीलिंग
हार – पुंलिंग
पथ – पुंलिंग
दुःख – पुंलिंग

4. बहुवचन रूप लिखिए:
(ବହୁ ବଚନ ରୂପ ଲେଖ;:)
एक, परीक्षा, सपना, मंजिल
उत्तर:
एक: अनेक
परीक्षा : परीक्षाएँ
सपना : सपने
मंजिल : मंजिलें

5. ‘जीवन के लम्बे पथ पर जब’ ……………. में ‘पथ’ संज्ञा है और ‘लम्बे’ विशेषण है जिससे पथ की लम्बाई सूचित हुई है। निम्न वाक्यों में विशेषणों को रेखांकित कीजिए :
(क) कोयल की आवाज …………………… होती है।
उत्तर:
कोयल की आवाज सुरीली होती है।

(ग) हमें …………….. जनता की सेवा करनी चाहिए
उत्तर:
मुझे पाँच रूपये चाहिए।

(ख) मुझे …………….. रूपये चाहिए।
उत्तर:
हमें गरीब जनता की सेवा करनी चाहिए।

(घ) रमेश …………….. छात्र है।
उत्तर:
रमेश एक मेधावी छात्र है।

गृहकार्य:

1. अपने जीवन में आये दुःख के क्षण का वर्णन कीजिए।
2. इस कविता को कंठस्थ कीजिए।
उत्तर :
मुझे आज भी याद है जब छोटा था तब मेरी माँ बहुत बीमार थी। वह उन दिनों अंतिम साँसे गिन रही थी। और एक दिन अचानक वह वावा के लिए इस दुनिया को छोड़कर चली जाती है। अंतिम समय में जब माँ को श्मशान ले जाया जा रहा था उस समय मुझे लगा कि अब माँ घर में आज के नहीं देगी उस समय में बहुत दुःखी हुआ था।

अति संक्षिप्त उत्तरमूलक प्रश्नोत्तर

A. निम्नलिखित प्रश्नों के उत्तर एक वाक्य में दीजिए

प्रश्न 1.
‘साथी ! दुःख से घबराता है?’ कविता किसने लिखा है?
उत्तर:
‘साथी ! दुःख से घबराता है?’ कविता को गोपालदास ‘नीरज’ ने लिखा है।

प्रश्न 2.
कवि ‘नीरज’ का जन्म कब और कहाँ हुआ?
उत्तर:
कवि नीरज का जन्म सन् १९२६ ई. से पुरावली, जिला इटावा (उत्तर प्रदेश) में हुआ।

प्रश्न 3.
‘नीरज’ ने इस कविता में किस बात की सलाह दी है?
उत्तर:
‘नीरज’ ने इस कविता में दुःख से न डरने की सलाह दी है।

प्रश्न 4.
दुःख कब सुख बन जाता है?
उत्तर:
न डरने से दुःख सुख बन जाता है।

प्रश्न 5.
दुःख किसके जीवन में ज्यादा होता है?
उत्तर:
दुःख मानव-जीवन में ज्यादा होता है।

प्रश्न 6.
सही रास्ता क्या है?
उत्तर:
दुःख से लड़ना सही रास्ता है।

प्रश्न 7.
हम सब कर्म तत्पर क्यों बने रहते हैं?
उत्तर:
जीवन में दुःख होने के कारण हम सब कर्म तत्पर बने रहते हैं।

प्रश्न 8.
कवि नीरज के अनुसार दुःख को क्या मानना चाहिए?
उत्तर:
कवि नीरज के अनुसार दुःख को मुक्ति का मार्ग मानना चाहिए।

प्रश्न 9.
जलती ज्वाला में जलकर क्या लाल बन जाता है?
उत्तर:
जलती ज्वाला जलकर लोहा लाल बन जाता है।

प्रश्न 10.
प्रबल परीक्षा का क्षण क्या है?
उत्तर:
प्रबल परीक्षा का क्षण दुःख है।

B. निम्नलिखित प्रश्नों के उत्तर एक शब्द में दीजिए।

प्रश्न 1.
जीवन के लम्बे पथ पर कौन साथ-साथ चलते हैं?
उत्तर:
सुख और दुःख

प्रश्न 2.
किसमें जलकर ही लोहा लाल निकल आता है?
उत्तर:
जलती ज्वाला

प्रश्न 3.
जीवन को मंजिल तक कौन ले जाता है?
उत्तर:
दुःख

प्रश्न 4.
कवि ने किसे धन्यवाद देने को कहा है?
उत्तर:
जिसने हमें दुःख के सपने दिए

प्रश्न 5.
जलती ज्वाला में जलकर लोहा क्या बन निकल आता है?
उत्तर:
लाल

प्रश्न 6.
मनुष्य की दुर्बलता जीवन में क्या लाती है?
उत्तर:
हलचल

प्रश्न 7.
जीवन में हलचल कौन लाता है?
उत्तर:
दुःख

C. रिक्तस्थानों को भरिए।

प्रश्न 1.
दु:ख
उत्तर:
मानब जीवन

प्रश्न 2.
कवि ने मुक्ति का बंधन से माना है।
उत्तर:
दु:ख

प्रश्न 3.
हम सब कर्मतत्पर बने रहते हैं।
उत्तर:
जीवन में दु:ख होने के

प्रश्न 4.
“साथी ! दु:ख से घबराता है ?”‘ यह कविता ने लिखी है
उत्तर:
गोपालदास

प्रश्न 5.
प्रबल परीक्षा का क्षण है।
उत्तर:
दु:ख

प्रश्न 6.
हलचल जीवन में लाता है।
उत्तर:
दु:ख

प्रश्न 7.
जलती ज्वाला में जलकर लाल बन निकलता है।
उत्तर:
लोहा

प्रश्न 8.
को धन्यवाद देना चाहिए।
उत्तर:
दु:ख देने वाले का

प्रश्न 9.
कवि के अनुसार दु:ख का बंधन है।
उत्तर:
मुक्ति

प्रश्न 10.
सुख और दु:ख जीवन के पथ पर साथ-साथ चलते हैं।
उत्तर:
लबै

प्रश्न 11.
दु:ख के समय मनुष्य की होती है।
उत्तर:
परीक्षा

D. सही उत्तर चुनिए।

1. साथी ! दु:ख से घवराता है? कविता के कवि कौन है?
(A) कबीरदास
(B) सूर दास
(C) गोपाल दास
(D) तुलसी दास
उत्तर:
(C) गोपाल दास

2. प्रबल परीक्षा का क्षण क्या है?
(A) सुख
(B) दु:ख
(C) आनंद
(D) चेष्टा
उत्तर:
(B) दु:ख

3. दुर्बलता का अर्थ क्या है?
(A) कमजोरी
(B) काँटा
(C) भारी
(D) कष्ट
उत्तर:
(A) कमजोरी

4. दु:ख पर क्या प्राप्त करने की चेष्टा करते हैं?
(A) विजय
(B) पराजय
(C) डर
(D) हलचल
उत्तर:
(A) विजय

5. जीवन में क्या होने के कारण हम कर्मतत्पर बनते हैं?
(A) हलचल
(B) दु:ख
(C) घृणा
(D) कर्म
उत्तर:
(B) दु:ख

6. कवि का जन्म किस प्रदेश में हुआ था?
(A) उत्तरप्रदेश
(B) हिमाचल प्रदेश
(C) महम प्रदेश
(D) केरल
उत्तर:
(A) उत्तरप्रदेश

7. ‘साथी ! दु:ख से घवराता है’ कविता में कवि अपने साथी को किस से न डरने की सलाह देता है?
(A) दु:ख
(B) सुख
(C) कष्ट
(D) आनंद
उत्तर:
(A) दु:ख

8. ‘जलती ज्वाला में जलकर क्या लाल बन निकलता है?
(A) सीसा
(B) लोहा
(C) पथर
(D) पायल
उत्तर:
(B) लोहा

9. कवि का जन्म कब हुआ था?
(A) सन् 1925 ई. में
(B) सन् 2006 ई. में
(C) सन् 1927 ई. में
(D) सन् 1926 ई. में
उत्तर:
(D) सन् 1926 ई. में

10. दु:ख के बाद क्या आएगा?
(A) प्रेम
(B) मरण
(C) सुख
(D) डर
उत्तर:
(C) सुख

दोहे (ତେ।ହେ)

साथी ! दुःख से घबराता है?
दुःख ही कठिन मुक्ति का बन्धन,
दुःख ही प्रबल परीक्षा का क्षण,
दुःख से हार गया जो मानब,
वह क्या मानब कहलाता है ?
ସାଥୀ ! ଦୁଃଖ୍ ସେ ଘବ୍‌ରାତା ହୈ ?
ଦୁଃଖ୍ ହୀ କଠିନ୍ ମୁକ୍ତି କା ବନ୍ଧନ୍,
ଦୁଃଖ୍ ହୀ ପ୍ରବଲ୍‌ ପରୀକ୍ଷା କା କ୍ଷଣ୍ଢ,
ଦୁଃଖ ସେ ହାର୍ ଗୟା ଜୋ ମାନବ,
ୱହ୍ କ୍ୟା ମାନବ୍ କହିଲାତା ହୈ ?
ଅନୁବାଦ ;
ହେ ବନ୍ଧୁ ଦୁଃଖକୁ ଡର ନାହିଁ । ଦୁଃଖ ହିଁ କଠିନ ମୁକ୍ତିର ବନ୍ଧନ ଏବଂ ପ୍ରଚଣ୍ଡ ପରୀକ୍ଷାର ମୁହୂର୍ତ୍ତ ଅଟେ।

साथी ! दुःख से घबराता है ?
जीवन के लम्बे पथ पर जब
सुख – दुःख चलते साथ-साथ तब
सुख पिछे रह जाया करता दुःख ही मञ्जिल
तक जाता है ।
ସାଥୀ ! ଦୁଃଖ୍ ସେ ଘବ୍ରାତା ହୈ ?
ଜୀୱନ୍ କେ ଲମ୍ବେ ପଥ୍ ପର୍ ଜବ୍
ସୁଖ୍-ଦୁଃଖ୍ ଚଲ୍‌ ସାଥ୍‌-ସାଥ୍ ତବ୍
ସୁଖ୍ ପିଛେ ରହ୍ ଜାୟା କର୍‌ତା ଦୁଃଖ୍ ହୀ ମଞ୍ଜିଲ୍
ତକ୍ ଜାତା ହୈ ।
ଅନୁବାଦ:
ହେ ବନ୍ଧୁ ଦୁଃଖକୁ ଭୟ କର ନାହିଁ । ଏହି ଲମ୍ବା ଜୀବନ ପଥରେ ସୁଖ, ଦୁଃଖ ସମତାଳରେ ଚାଲିଥା’ନ୍ତି; ମାତ୍ର ସୁଖକୁ ପଛରେ ପକାଇ ଦୁଃଖ ଲକ୍ଷ୍ୟସ୍ଥଳ ପର୍ଯ୍ୟନ୍ତ ଅର୍ଥାତ୍ ଅନ୍ତିମ ଅବସ୍ଥା ପର୍ଯ୍ୟନ୍ତ ସାଥ୍‌ରେ ରହିଥାଏ ।

साथी! दु:ख से घबराता है?
दुःख जीवन में करता हलचल,
वह मनकी दुर्बलता केवल,
दुःख को यदि मान न तू तो दुःख ही फिर
सुख बन जाता है।
ସାଥୀ ! ଦୁଃଖ୍ ସେ ଘବ୍ରାତା ହୈ ?
ଦୁଃଖ ଜୀୱନ୍ ମେଁ କର୍‌ତା ହଲ୍‌ଚଲ୍,
ୱହ ମନ୍‌କୀ ଦୁର୍ବଲ୍‌ କେଲ୍,
ଦୁଃଖ୍ କୋ ୟଦି ମାନ୍ ନ ତୂ ତୋ ଦୁଃଖ ହୀ ଫିର୍
ସୁଖ୍ ବନ୍ ଜାତା ହୈ ।
ଅନୁବାଦ:
ହେ ବନ୍ଧୁ ଦୁଃଖକୁ ଭୟ କର ନାହିଁ । ଏହି ଲମ୍ବା ଜୀବନ ପଥରେ ସୁଖ, ଦୁଃଖ ସମତାଳରେ ଚାଲିଥା’ନ୍ତି; ମାତ୍ର ସୁଖକୁ ପଛରେ ପକାଇ ଦୁଃଖ ଲକ୍ଷ୍ୟସ୍ଥଳ ପର୍ଯ୍ୟନ୍ତ ଅର୍ଥାତ୍ ଅନ୍ତିମ ଅବସ୍ଥା ପର୍ଯ୍ୟନ୍ତ ସାଥ୍‌ରେ ରହିଥାଏ ।

साथी ! दु:ख से घबराता है ?
पथ में शूल बिछे तो क्या चल
पथ में आग जी तो क्या जल
जलती ज्वाला में जलकर ही लोहा लाल
निकल आता है ।
ସାଥୀ ! ଦୁଃଖ୍ ସେ ଘବ୍‌ରାତା ହୈ ?
ପଥ୍ ମେଁ ଶୁଲ୍ ବିଛେ ତୋ କ୍ୟା ଚଲ୍
ପଥ୍ ମେଁ ଆର୍ ଜୀ ତୋ କ୍ୟା ଜଲ୍
ଜଲ୍‌ ଜ୍ବାଲା ମେଁ ଜଲ୍‌କର୍ ହୀ ଲୋହା ଲାଲ୍
ନିକଲ୍ ଆତା ହୈ ।
ଅନୁବାଦ :
ହେ ବନ୍ଧୁ ଦୁଃଖକୁ କାହିଁକି ଡରୁଛ, ଜୀବନ ପଥରେ ଅନେକ କଣ୍ଟା ସଦୃଶ ବିପଦ ଆସିଥାଏ । ତାକୁ ଅତିକ୍ରମ କରିବାକୁ ପଡ଼ିବ । ଯେପରିକି କଳାରଙ୍ଗର ଲୁହା ଜଡ଼ିତ ଏ ଜୀବନ ସୁଖମୟ ହୋଇଥାଏ ।

साथी ! दु: से घबराता है ?
धन्यबाद दो उसको जिसने
दिए तुझे दु:ख के तो सपने
एक समय है जब सुख ही क्या! दु:ख भी
साथ न दे पाता है।
साथी ! दुःख से घबंराता है।
ସାଥୀ ! ଦୁଃଖ୍ ସେ ଘବ୍ରାତା ହୈ ?
ଧନ୍ୟବାଦ୍ ଦୋ ଉସ୍କୋ ଜିସ୍‌
ଦିଏ ତୁଝେ ଦୁଃଖ୍ କେ ତୋ ସପନେ,
ଏକ୍ ସମୟ ହୈ ଜବ୍ ସୁଖ ହୀ କ୍ୟା ! ଦୁଃଖ୍ ଭୀ
ସାଥ୍ ନ ଦେ ପାତା ହୈ ।
ସାଥୀ ! ଦୁଃଖ୍ ସେ ଘବରାତା ହୈ ।
ଅନୁବାଦ :
ହେ ବନ୍ଧୁ ଦୁଃଖକୁ ଡର ନାହିଁ, କାରଣ ମଣିଷ ଜୀବନ ଦୁଃଖ ରୂପକ ସଂଘର୍ଷରେ ବ୍ୟକ୍ତିତ୍ଵର ପରାକାଷ୍ଠା ପ୍ରତିପାଦନ କରିଥାଏ । ତେଣୁ ଦୁଃଖ ଦେଉଥିବା ଲୋକଙ୍କୁ ଧନ୍ୟବାଦ । ଏହି ଦୁଃଖରୁ ହିଁ ମୁକ୍ତିର ମାର୍ଗ ସୁଗମ ହୋଇଥାଏ । ଏପରି ସମୟ ଆସେ ଯେତେବେଳେ ସୁଖ ବା ଦୁଃଖ କେହି ସାଥ୍‌ ଦିଅନ୍ତି ନାହିଁ ।

शबनार: (ଶରାର୍ଥି)

मुक्ति – आजादी, स्वतंत्रता (ସ୍ଵାଧୀନ, ସ୍ଵାଧୀନତା ) ।

प्रबल – बड़ा, भारी, प्रचंड ( ଭାରୀ, ପ୍ରଚଣ୍ଡ ) ।

क्षण – घड़ी, पल, वक् (ସମୟ, ସମୟର ଏକ ମୁହୂର୍ତ୍ତକୁ ୩୯ କୁହାଯାଏ, ପର୍ଶୀ ଶବ୍ଦର ପ୍ରୟୋଗ ପୂର୍ବରୁ ଚାଲୁଥିଲା, ଏକ ଏକ ଘଡ଼ି ୩ ଘଣ୍ଟା ସହିତ ସମାନ) ।

मंजिल – लक्ष्य (ଲକ୍ଷ୍ୟ) ।

हलचल – हिलने-डोलने की क्रिया या भाव (ଦୋଳାୟମାନ ହେବା, ଆଲୋଡ଼ିତ ହେବା) ।

दुर्बलता – कमजोरी (କଣ୍ଟା, ପ୍ରତିବନ୍ଧକ) ।

शूल – काँटा (କମ୍‌ର, ଦୁର୍ବଳ) ।

ज्वाला – अग्निशिखा, लौ, लपट (ଅଗ୍ନିଶିଖା) ।

कवि परिचय (କବି ପରିଚୟ)।

गोपालदास ‘नीरज’ का जन्म पुरावली, जिला इटावा (उत्तर प्रदेश) में सन् 1926 ई. में हुआ। बचपन में ही उनके पिता चल बसे। इसलिए ‘नीरज’ ने अपनी चेष्टा से पढ़ा। एम.ए. किया। फिर नौकरी की। अपने को बनाया। ‘संघर्ष’, ‘विभावरी’, ‘नीरज की पाती’, ‘प्राणगीत’, ‘दो गीत’, ‘मुक्तावली’, ‘दर्द दिया है’, ‘बादर बरस गयो’ आदि ‘नीरज’ के लोकप्रिय काव्य संग्रह हैं। ‘नीरज’ के गीतों में जीवन के सहज अनुभव अभिव्यक्त हुए हैं। इसलिए वे सब के मन को छू पाते हैं। गीत गाए जाते हैं तो और भी सरस होते हैं।

Odisha State Board CHSE Odisha Class 12 Alternative English Solutions Grammar Linking Devices Exercise Questions and Answers.

CHSE Odisha Class 12 Alternative English Grammar Linking Devices

What is linking devices?
The devices or tricks or principles that are used to link the sentences in a paragraph by suitable connectives is called linking devices.
Here, linking means connecting and devices means tricks of principles or methods.
There are different types of connectives, such as
(i) By the use of numbering system.
(ii) By the use of personal pronouns.
(iii) By the use of demonstrative.
(iv) By the use of adverbs or conjunctions.

(i) By the use of numbering system.
We can link sentences by the use of words taken from numbering system. Such as – first, second, third etc. or numbering words like firstly, secondly, thirdly etc.
Example:
Trees help us many ways, firstly they provide us food, secondly they provide us shelter, thirdly we use tree branches as fire wood. We can link sentences by the use of personal pronouns like he, she, it, they etc.

(ii) By the use of personal pronouns.
Example:
Vivekananda began a whirlwind tour of India, he urged the necessity ofending the poverty of the masses.

(iii) By the use of demonstrative.
We can also link sentences by the use of demonstrative like this, that, these, those etc.
Example:
Have you visited Netaji’s birth place at Odia Bazar? This place attracts thousands of patriots each year.

(iv) By the use of adverbs or conjunctions.
We can also link sentences by the use of adverbs or conjunctions like at present, at the sometime, above, below in front of, however, therefore etc.
Example:
Our friend Pratap has secured 90% of marks in the +2 Arts, therefore, he should be welcomed in our college Annual Function.

Some Common Connectives:
Some common connectives are given below:
as a result – on the other hand
for this – beside
in addition – either … or
of course – neither nor
in contrast – not only, but also

1. Addition:
also : 1 went to the lèstival with Mr. Patra, Mr. Patra’s son was also with us.
and : She was cooking and her baby was crying.
besides : Besides his salary, he got an allowance of Rs 5,OOO/ from his grand – ther.
further : He is not such a man who will help you. Further he is not present now.
moreover : I am not in a mood to take with them, moreover I am not well.
in addition (to): Mr. Ratha donated Rs 1,00,000/- lÓr the repairing of our game field. In addition to that he had promised to bear the cost of a gallery.

2. Contrast:
yet : I drove first yet, I could not reach the station in time.
Iit : I can’t do you work, but I can engage my friend. Who can help you to complete it.
still : It is true that he is not good still as a near one you must come forward to help ham
though : Though, he is poor, he is honest.
while : He is cruel while his brother is kind.
in spite of : In spite of his illness, he attended the examination in time.

3. Time:
till : He is determined to appear the examination till he passes it.
urtil : You should wait until his arrival.
aller : Police came after the thief has escaped.
when. : 1 saw him when he was playing cricket.
before : I was already there much before the guest arrived.
at last : He worked hard for many years. At least success and fame came to him.
by the time : By the time the doctor arrived, the patient was dead.
finally : At last, we admitted him in the village dispensaiy, finally we took him to district hospital.

4. Choice:
either…. or : Either he or my friend could attend the meeting.
neither …not : Neither Hari nor his sister is present in the school today.

5. Examples:
for example : Odisha is always neglected by the centre. For example, we can take the negligance of Ministry of Railways.
particularly : I like the plays of Shakespeare, particularly, the Macbeth, for instance : Some bacteria help us in many ways. For instance, milk is changed to curd by such a bacteria.
such as : Poets such as Gangadhar Meher, Gopabandhu, Madhusudan as famous in Odisha.

6. Clarification
in other words : Our Principal is a strict disciplinarian. In other words, he wants his students to behave properly.

7. Cause:
because : He did not pass the examination, because he had not read mindfully,
as : Akash could not attend the meeting as he was ill.
since : Since he was sick, he could not attend the Governing Body Meeting,
for : The manager called him on last Sunday for he had an important discussion with him.

8. Intention:
in order that : The baby cried loudly in order that her mother would hurry to her.
so that : The baby who fell into the well shouted loudly so that others could hear him.

9. Effect/Consequence:
thus : Mukesh was selected in the district level in cricket.
so : Last night is rained heavily, so the road is muddy.
consequently : My bike was out of order in the way, Consequently I could not attend the meeting in time.
as a result : He has laboured hard, as a result he will fetch attractive marks.
therefore : You are doing exercise everyday, therefore, we expect a good health from you.

10. Purpose:
so that : We eat so that we can live.

11. Similarity:
likewise : Pratap studied hard, likewise, his brother also studied hard.
similarly : Mr. Mahapatra, purchased a Hero Honda Splendor, similarly, Mr. Panda purchased a similar one.

Task – 1
Read the following carefully. Underline the linking devices present in the text.

Text:
Smoking which may be a pleasure for some people is a source of serious discomfort for their fellows. Further medical authorities express their concern about the effect of smoking on the health not only of those who smoke but also those who must involuntarily inhale the contribution of smokers to the atmosphere. As you are dull, lessly aware a considerable number of our students have joined together in an effort to persuade the university to ban smoking in the classrooms. I believe they are entirety right in their aim. However, I would hope that it is possible to achieve this by an appeal to reason and to concern for other rather than by regulation. Smoking is prohibited by city bye – laws in theatres and in halls used for showing .films as’ well as laboratories where there may be a fire hazard. Elsewhere it is upto our own good sense. I am therefore, asking you to maintain “No Smoking” in the auditorium, classroom and seminar rooms where you teach. This proof of your interest for their health and well – being is very important to a large number of students.

Answer:
Smoking which may be a pleasure for some people is a source of serious discomfort for; their fellows. Further medical authorities express their concern about the effect of smoking on the health not only of those who smoke but also those who must involuntarily inhale the contribution of smokers to the atmosphere. As you are dull, less aware a considerable number of our students have joined together in an effort to persuade the university to ban smoking in the classrooms. I believe they are entirely right in their aim.

However. I would hope that it is possible to achieve this by an appeal to reason and to concern for other rather than by regulation. moking is prohibited by city bye – laws in theatres and in halls used for showing films as well as laboratories where there may be a fire hazard. Elsewhere it is upto our own good sense. I am, therefore, asking you to maintain “No Smoking” in the auditorium, classroom and seminar rooms where you teach. This proof of your interest for their health and well – being is very important to a large number of students.

Task-2
Fill in the blanks by choosing the most appropriate connective from the alternatives given in brackets.
1. She is intelligent ____________ she is beautiful, (so, and, as a result).
2. He was indifferent to his friend’s needs ____________ there was a lot of bad feeling, (but, consequently, in other words)
3. She did not work hard ____________ she came out first in the final examination, (yet, consequently, in other words).
4. I rarely watch T. V. must programmes are terrible, (because, therefore, further)
5. Ramesh first called on his friend. He ____________ went to this station to receive his uncle, (then, till by that time)
6. Trees help us in many ways ____________ it provides us oxygen, (in other words, for example, further).
7. The party didn’t go all that well ____________ it was a disaster (likewise, moreover, in other words)

Answer:
1; She is intelligent and she is beautiful.
2. He was indifferent to his friend’s needs consequently there was a lot of bad feeling.
3. She did not work hard yet she came out first in the final examination.
4. I rarely watch T. V. because most programs are terrible,
5. Ramesh first called on his friend. He then went to this station to receive his uncle.
6. Trees help us in many ways. For example, it provides us with oxygen.
7. The party didn’t go all that well In other words it was a disaster

Task – 3
Use suitable linking devices (connectives) from the box to complete the text below.
also but meanwhile and
but also not only and however
since because in this way
Sita’s sister is an air hostess for a famous International Airline ____________. Sita wants to become one too ____________ She is still too young, the minimum age for an air hostess is twenty ____________. Sita is just over sixteen
____________ she has taken up a job in an office ____________ she ____________ attends evening classes ____________ she wants to improve her French and Japanese. ____________ foreign languages are an essential qualification for an air hostess.
She is gaining experience through her present job ____________ the office where she works is a travel agency. She is learning ____________ how to deal with people ____________ quite a lot about the places she one day hopes to visit.
Answer:
Sita’s sister is an air hostess for a famous International Airline and. Sita wants to become one too but she is still too young, the minimum age for an air hostess is twenty and. Sita is just over sixteen However she has taken up a job in an office meanwhile she also attends evening classes In this way she wants to improve her French and Japanese. Because foreign languages are an essential qualification for an air hostess.
She is gaining experience through her present job since the office where she works is a travel agency. She is learning not only how to deal with people but also quite a lot about the places she one day hopes to visit.

Exercises

1. Linking words and phrases:
In the following letter, the linking words and phrases are missing. Choose the most appropriate phrase from the ones given below and use them appropriately.
Dear Akash,
Remember that I told you I was trying to get a job at ICTL? (1) ____________I finally managed to get one! Of course, I haven’t been working there long, (2) ____________ I can already tell that it’s a wonderful place to work. All the staff, (3) ____________ the directors are very friendly with everybody and (4) ____________ they have marvelous facilities for the employees, (5) ____________ there’s a bar and gum and lots of other things. I’m called the Safety Equipment Officer. It (6) ____________ sounds like an impressive title, but it’s not a very accurate description of what I do. My main job is to provide protective clothing, (7) ____________ overalls, helmets, and so on. I estimate what the different departments will need and (8) ____________ I order it from the suppliers, (9) ____________ I make sure that the various departments have everything they want. (10) ____________ stationery is also my responsibility. (11) ____________ I have the job very interesting. (12) ____________ I get the chance to go all over the factory and to meet everybody. ____________ (13) the play is a lot better than in my old job. (14) ____________ that’s my news. What about you? Drop me a line when you have time. Regards to your family, and best wishes to you.

1.	(a) then	(b) well	(c) and
2.	(a) but	(b) because	(c) so
3.	(a) until	(b) and	(c) even
4.	(a) so	(b) what’smore	(c) on the other hand
5.	(a) for instance	(b) however	(c) even
6.	(a) can	(b) could	(c) may
7.	(a) such as	(b) namely	(c) as
8.	(a) then	(b) after	(c) so
9.	(a) by the way	(b) anyway	(c) in this way
10.	(a) however	(b) although	(c) but
11.	(a) secondly	(b) in other words	(c) also
12.	(a) why	(b) because	(c) then
13.	(a) besides	(b) besides	(c) on the other hand
14.	(a) at the end	(b) any way	(c) after all

Answer:
DearAkash,
Remember that I told you I was trying to get a job at ICTL? (1) Well I finally managed to get one! Of course, I haven’t been working there long, (2) but I can already tell that it’s a wonderful place to work. All the staff, (3) even the directors are very friendly with everybody and (4) what’s more they have excellent facilities for the employees, (5) for instance there’s a bar and gum and lots of other things. I’m called the Safety Equipment Officer. It (6) may sound like an impressive title, but it’s not a very accurate description of what I do. My main job is to provide protective clothing, (7) such as overalls, helmets, and so on. I estimate what the different departments will need and (8) then I order it from the suppliers, (9) In this way I make sure that the various departments have everything they want. (10) however stationary is also my responsibility. (11) In other words I have the job very interesting. (12) Because I get the chance to go all over the factory and to meet everybody (13) Besides the play is a lot better than in my old job. (14) At the end that’s my news. What about your? Drop me a line when you have time. Regards to your family, and best wishes to you.

2. Each of the following sentences has a blank where there should be a linking word or phrase. Put in one of the above words and phrases so that the relation between the two statements is made clear.
1. The pay and conditions are very good ____________ it’s only five minutes walk from where I live.
2. I didn’t apply for the job ____________ I didn’t think I had much chance of getting it.
3. A lot of professional groups, ____________ doctors and lawyers have strong associates that protest
members rights.
4. The hours are short, the pay’ is excellent and the people I work with the very nice ____________ it’s a great job.
5. You ____________ think it’s bring, but in fact, it’s very interesting.
6. All my relatives were at the wedding ____________ my cousins from Australia.
7. At first I didn’t feel happy with so much responsibility ____________ now I feel quite confident that I can manage.
8. There are several things that make it a nice place to live ____________ there’s a park right across the road.

Answer:
1. The pay and conditions are very good. Besides, it’s only five minutes walk from where I live.
2. I didn’t apply for the job, anyway I didn’t think I had much chance of getting it.
3. A lot of professional groups, such as doctors and lawyers have strong associates that protest members’ rights.
4. The hours are short, the pay is excellent, and the people I work with the very nice in other words it’s a great job.
5. You may think it’s boring, but in fact, it’s very interesting.
6. All my relatives were at the wedding. Even my cousins from Australia.
7. At first I didn’t feel happy with so much responsibility but now I feel quite confident that I can manage.
8. There are several things that make it a nice place to live what’s more there’s a park right across the road.

3. Here are words or phrases to indicate logical relationship of thought. Use them in sentences of your own and explain what each signals to the reader.

so	besides	on the contrary
yet	because	in sum
though	anyhow	but
furthermore	on the other hand	for example

Answer:
So: Last night it rained heavily and the river flooded. So, I have to say back. Here, ‘so’ signals effect.
Yet: She prepared hard, yet she failed. Here ‘yet’ signals contrast.
though : Though he is poor he is always first to contribute for any social work. Here ‘though’ signals addition.
furthermore : He was honest, educated, furthermore he is rich. Here ‘furthermore’ signals addition.
besides : The company offers me an alluring salary. Besides it is very close to my dwelling place. Here ‘besides’ signals addition.
because : He could not come to our party, because his fàther was sick. Here ‘because’ signals cause.
any how : I know the work is difficult, but any how we have to accomplish it. Here ‘anyhow’ signals cause.
on the other hand : This talcum power is costly, on the other hand, its quality is poor. ‘Here’ on the other hand signals contrast.
on the contrary : Akash approached Mr. Patra for help, but on the contrary, Mr. Pratap scolded him. Here ‘on the contrary’ signals opposition.
in sum : Mr. Mahapatra has a scooter, a moped and a motor – cycle, in sum, he has three bikes with him. Here ‘in sum’ signals conclusion.
But : He is an honest man, but he is not punctual. Here ‘but’ signals contrast.
for example : Trees are our best friends, our survival completely depend on them, for example, they provide us with oxygen to breath, fruits, leaves and roots and food and cause rain. Here ‘for example’ signals clarification.

Odisha State Board BSE Odisha 8th Class Science Solutions Chapter 11 ବଳ ଓ ଚାପ Textbook Exercise Questions and Answers.

BSE Odisha Class 8 Science Solutions Chapter 11 ବଳ ଓ ଚାପ

Question 1.
ନିମ୍ନ ଉକ୍ତିଗୁଡ଼ିକରେ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ………………… ବଳଦ୍ଵାରା ପାଣି କଢ଼ାଯାଏ ।
(b) ଏକ ଚାର୍ଜିତ ବସ୍ତୁ ଓ ଅଚାର୍ଜିତ ବସ୍ତୁ ମଧ୍ୟରେ …………………… ବଳ ରହିଥାଏ ।
(c) ବସ୍ତା ଭର୍ତ୍ତି ଧାନ ଲଦା ହୋଇ ଯାଉଥିବା ଶଗଡ଼କୁ ………………. କରି ଗତିଶୀଳ କରାଯାଏ ।
(d) ଏକ ଚୁମ୍ବକର ଉତ୍ତର ମେରୁ ଅନ୍ୟ ଏକ ଚୁମ୍ବକର ଉତ୍ତର ମେରୁ ଦ୍ଵାରା …………………… ହୋଇଥାଏ ।
(e) ଏକକ କ୍ଷେତ୍ରଫଳ ପ୍ରତି ଲମ୍ବଭାବରେ ପ୍ରଯୁକ୍ତ ବଳକୁ ……………….. କହନ୍ତି ।

Answers:
(a) ଟଣା
(b) ଆକର୍ଷଣ
(c) ମାଂସପେ ଶୀୟ/ଟଣା
(d) ବିକର୍ଷିତ
(e) ଚାପ

Question 2.
ନିମ୍ନରେ ଦିଆଯାଇଥ‌ିବା ପରିସ୍ଥିତି ଗୁଡ଼ିକରେ ବଳର କାରକ ଓ ଯେଉଁ ବସ୍ତୁ ପ୍ରତି ବଳ ପ୍ରୟୋଗ କରାଯାଏ ସେଗୁଡ଼ିକ ଚିହ୍ନାଅ । ପ୍ରତି ପରିସ୍ଥିତିରେ ବଳ ପ୍ରୟୋଗ ଦ୍ଵାରା କ’ଣ ହୁଏ ଲେଖ ।
(a) ଲେମ୍ବୁରୁ ରସ ବାହାର କରିବା ପାଇଁ ଫାଳେ ଲେମ୍ବୁକୁ ଆଙ୍ଗୁଠିରେ ଧରି ଚିପିବା ବେଳେ ।
(b) ଟୁଥ୍ ପେଷ୍ଟ୍ ଟ୍ୟୁବ୍‌ରୁ ପେଷ୍ଟ୍ ବାହାର କରିବା ବେଳେ ।
(c) କାନ୍ଥରେ ଥିବା କଣ୍ଟାରୁ ଝୁଲୁଥ୍ ସ୍ପ୍ରିଙ୍ଗ୍‌ରୁ ଓଜନିଆ ବସ୍ତୁଟିଏ ଝୁଲାଇଲେ ।
(d) ଉଚ୍ଚଡିଆରେ କିଛି ଉଚ୍ଚତାରେ ରଖାଯାଇଥ‌ିବା ସିଧା ଦଣ୍ଡଟିକୁ ଡିଆଁଳି ଅତିକ୍ରମ କରୁଥିବାବେଳେ ।
ଉ-

Question 3.
କମାର ଲାଲ ଉତ୍ତପ୍ତ ଲୁହାକୁ ପିଟି ପିଟି କଟୁରୀଟିଏ ତିଆରି କରେ । ଏଠାରେ ହାତୁଡ଼ି ଦ୍ଵାରା ପ୍ରଯୁକ୍ତ ବଳ ସାହାଯ୍ୟରେ ଲୁହାଟିରେ କି ପରିବର୍ତ୍ତନ ସୃଷ୍ଟି ହୁଏ ଲେଖ ।
ଉ-
ଏଠାରେ ହାତୁଡ଼ିଦ୍ୱାରା ପ୍ରଯୁକ୍ତ ବଳ ସାହାଯ୍ୟରେ ଲୁହାଟିର ଆକୃତିରେ ପରିବର୍ତ୍ତନ ହୁଏ ।

Question 4.
ଜଣେ ବ୍ୟକ୍ତି ହାତରେ ପାଣି ବାଲ୍‌ଟିଏ ଭୂମିଠାରୁ କିଛି ଉଚ୍ଚତାରେ ଟେକି ଧରିଛନ୍ତି । ବାଲ୍ଟିଟି ଉପରେ କି, କି ବଳ କ୍ରିୟାଶୀଳ ହୁଏ ଲେଖ । ଏହି ବଳମାନଙ୍କ ଦ୍ବାରା ବାଲ୍ଟିର ଗତି ଅବସ୍ଥାରେ ପରିବର୍ତ୍ତନ ହୁଏ କି ? ଆଲୋଚନା କର ।
ଉ-
(i) ବାଲ୍ଟିଟି ଉପରେ ନିମ୍ନଲିଖ ବଳ କାର୍ଯ୍ୟକାରୀ ହୁଏ ।
(a) ବାଲ୍ଟି ଓ ବାଲ୍ଟି ମଧ୍ୟରେ ଥ‌ିବା ପାଣିର ନିମ୍ନମୁଖୀ ଓଜନ ବଳ ।
(b) ବ୍ୟକ୍ତିଟିର ମାଂସପେଶୀୟ ବଳ
(ii) ବାଲ୍ଟିଟି ଭୂମିଠାରୁ କିଛି ଉଚ୍ଚତାରେ ଥାଏ ଓ ପରିଣାମୀ ବଳ ଶୂନ ହେତୁ ବାଲ୍ଟିର ଗତି ଅବସ୍ଥାରେ କିଛି ପରିବର୍ତ୍ତନ ହୁଏ ନାହିଁ ।

Question 5.
ଏକ ଡ୍ରପର୍‌ରେ ଥିବା କାଚନଳୀର ଗୋଜିଆ ମୁଣ୍ଡଟି ଜଳରେ ବୁଡ଼ାଇ, ଏହାର ରବରଟି ଚାପିଲେ କ’ଣ ହୁଏ ଲକ୍ଷ୍ୟକର ଓ ଲେଖ । ତା’ପରେ ରବରଟିରୁ ଚାପ ପ୍ରତ୍ୟାହାର କରିନେଲେ କ’ଣ ହୁଏ ଓ କାହିଁକି ସେପରି ହୁଏ,

• ହୋଇ ବାୟୁ ବାହାରେ । ରବରଟିରୁ ଚାପ ପ୍ରତ୍ୟାହାର କରିନେଲେ ଡ୍ରପର ମଧ୍ୟଦେଇ ଜଳ ଉପରକୁ ଉଠିଆସେ ।
• ପ୍ରଥମ ଅବସ୍ଥାରେ ଡ୍ରପର ମଧ୍ୟରେ ଥ‌ିବା ବାୟୁ ଜଳ ମଧ୍ୟଦେଇ ବାହାରକୁ ବାହାରିଯାଏ । ରବରଟିରୁ ଚାପ ପ୍ରତ୍ୟାହାର କରିନେଲେ ଡ୍ରପର ମଧ୍ୟସ୍ଥ ବାୟୁ ଚାପ କମିଯାଏ । ତେଣୁ ବାହାର ବାୟୁ ଜଳ ଉପରେ ଚାପ ପକାଏ । ତେଣୁ ଜଳ କାଚନଳୀ ମଧ୍ୟଦେଇ ଡ୍ରପର ମଧ୍ୟକୁ ଉଠିଆସେ ।

Question 6.
ଦୈନନ୍ଦିନ ଜୀବନରେ ଠେଲା ବଳ ଓ ଟଣା ବଳ ପ୍ରୟୋଗ ଦ୍ୱାରା ବସ୍ତୁର ଗତି ଅବସ୍ଥାରେ ପରିବର୍ତ୍ତନ ହେଉଥୁବାର, ଦୁଇଟି ଲେଖାଏଁ ଉଦାହରଣ ଲେଖ ।
ଠେଲାବଳ :

• ଘରେ ପଶି କବାଟ ଖୋଲିବା ସମୟରେ ଠେଲାବଳ କାର୍ଯ୍ୟ କରିଥାଏ ।
• ଘର ଚଟାଣରେ ଥ‌ିବା ଧୂଳିକୁ ଝାଡୁରେ ଠେଲାବଳ ପ୍ରୟୋଗ କରି ବାହାର କରାଯାଏ ।

ଟଣାବଳ :

• ଘରର ବାହାରପଟୁ ଥିବା ଝରକା ଟଣାବଳ ପ୍ରୟୋଗ କରି ବନ୍ଦ କରାଯାଏ ।
• କୂଅରୁ ପାଣି କାଢ଼ିବା ବେଳେ ଟଣାବଳ ଆବଶ୍ୟକ ହୋଇଥାଏ ।

Question 7.
“‘ବଳ ବସ୍ତୁର ଆକୃତି ପରିବର୍ତ୍ତନ କରିପାରେ’’ । ଏହାର ଦୁଇଟି ଉଦାହରଣ ଉଲ୍ଲେଖ କର ।
ଉ-

• ଅଟା ଚକଟି ଏହାର ପିଣ୍ଡୁଳାକୁ ବେଲଣାକାଠି ଦ୍ଵାରା ଚାପ ପ୍ରୟୋଗ କରି ରୁଟି, ପୁରିରେ ପରିଣତ କରିବା ।
• କମାରଶାଳରେ ଉତ୍ତପ୍ତ ଲୁହାକୁ ବାଡ଼େଇ ସେଥୁରୁ ଦାଆ, ପନିକି, କଟୁରୀ ଇତ୍ୟାଦି ଦିଆରି କରିବା ।

Question 8.
ନିମ୍ନଲିଖ ପ୍ରତ୍ୟେକ ଉଦାହରଣରେ ପ୍ରଯୁକ୍ତ ବଳ ସଂସ୍ପର୍ଶ ବଳ କି ଅସଂସ୍ପର୍ଶ ବଳ, ଲେଖ ।
(a) ବୁଢ଼ୀମା’ ଛୋଟ ପିଲାଟିକୁ ତେଲ ଘଷୁଛନ୍ତି ।
(b) ଏକ ପାତ୍ରରେ ଥ‌ିବା ଶସ୍ୟଦାନାରେ କିଛି ଲୁହାଗୁଣ୍ଡ ମିଶି ଯାଇଛି ଓ ରାମ ବାବୁ ଖଣ୍ଡିଏ ଚୁମ୍ବକ ଧରି ସେହି ଲୁହାଗୁଣ୍ଡ ଗୁଡ଼ିକୁ ଅଲଗା କରୁଛନ୍ତି ।
(c) ପ୍ଲାଷ୍ଟିକ୍ ପାନିଆରେ ଶୁଖୁଲା କେଶ କୁଣ୍ଡାଇବା ପରେ ପାନିଆଟି ଦ୍ଵାରା ପିଲାଟିଏ ଟୁକୁରା କାଗଜଗୁଡ଼ିକୁ ଉଠାଇ ଆଣୁଛି ।
(d) ତୁମେ ବହିଥାକରୁ ତୁମର ଗଣିତ ବହିଟି ବାହାର
(e) ଜଣେ ବ୍ୟକ୍ତି ରାସ୍ତାରେ ଚାଲିଚାଲି ଯାଉଛନ୍ତି
(f) ପାଚିଲା ଆମ୍ବଟିଏ ଗଛରୁ ଝଡୁଛି ।

Answers:
(a) ସଂସ୍ପର୍ଶ ବଳ (ଟଣାବଳ)
(b) ସଂସ୍ପର୍ଶ ବଳ (ଚୁମ୍ବକୀୟ ବଳ)
(c) ଅସଂସ୍ପର୍ଶ ବଳ (ସ୍ଥିର ବିଦ୍ୟୁତ୍ ବଳ)
(d) ସଂସ୍ପର୍ଶ ବଳ (ଟଣା ବଳ)
(e) ସଂସ୍ପର୍ଶ ବଳ (ଘର୍ଷଣ ବଳ)
(f) ଅସଂସ୍ପର୍ଶ ବଳ (ମାଧ୍ୟାକର୍ଷଣ ବଳ)

(ଛାତ୍ରଛାତ୍ରୀମାନେ ଜାଣିବାପାଇଁ ବିଭିନ୍ନ ବଳର ନାମ ଦିଆଯାଇଛି ।)

Question 9.
ଚାପ ଓ ବଳ ମଧ୍ୟରେ ସଂପର୍କଟି ଲେଖ ।
ଉ-

A = 1 ବର୍ଗ ଏକକ ହେଲେ P = F । ତେଣୁ, ଚାପ ହେଉଛି ଏକକ କ୍ଷେତ୍ରଫଳ ଉପରେ ପ୍ରଯୁକ୍ତ ବଳ ।

Question 10.
ସମକ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଦୁଇଟି ପ୍ଲାଷ୍ଟିକ ନଳ A ଓ B ରେ ଜଳ ଭର୍ତ୍ତି କରିବାରୁ ମୁଁ ନଳରେ ଜଳର ଉଚ୍ଚତା 20 ସେ.ମି. ଓ B ନଳରେ ସେହି ଉଚ୍ଚତା 15 ସେ.ମି. ହେଲା କେଉଁ ନଳର ଭୂମି ଉପରେ ଜଳର ଚାପ ଅଧ୍ଵ ଓ କାହିଁକି, ବୁଝାଅ ।
ଉ-

• A ନଳରେ ଜଳର ଉଚ୍ଚତା = 20 ସେ.ମି. ଓ B ନଳରେ ଜଳର ଉଚ୍ଚତା = 15 60. ।
• A ନଳର ଭୂମି ଉପରେ ଜଳର ଚାପ ଅଧିକ କାରଣ ଏଠାରେ ଜଳପୃଷ୍ଠର ଉଚ୍ଚତା ଅଧିକ ।

Question 11.
ମୁନ ନଥିବା ପିନ୍‌କଣ୍ଟା ଦ୍ଵାରା କିଛି କାଗଜ ଏକାଠି ଗୁଛିବା କଷ୍ଟ ହୁଏ କାହିଁକି, ବୁଝାଅ ।
ଉ-
ମୁନ ନ ଥିଲେ ପିନ୍‌କଣ୍ଟାର ପୃଷ୍ଠକ୍ଷେତ୍ରଫଳ ଅଧିକ ହୋଇଥାଏ, ଫଳରେ ଚାପ କମ୍ ହୁଏ । ଚାପ ଏକ ପରିମେୟ ସଂଖ୍ୟା ଯାହାର ହର କ୍ଷେତ୍ରଫଳ । ଏଠାରେ ପୃଷ୍ଠକ୍ଷେତ୍ରଫଳ ଅଧ‌ିକ ହେତୁ ଚାପ କମ୍ ହୁଏ, ତେଣୁ କିଛି କାଗଜ ଗୁଛିବା କଷ୍ଟ ହୁଏ ।

Question 12.
ଏକ ପ୍ଲାଷ୍ଟିକ୍ ବୋତଲରେ ଗରମ ପାଣି ରଖ୍ ଏହାର ଠିପିଟି ବନ୍ଦ କରାଗଲା । ପ୍ରାୟ 1 ଘଣ୍ଟାପରେ ଦେଖାଗଲା ଯେ ବୋତଲଟି ଚେପା ହୋଇଯାଇଛି । ଏହାର କାରଣ ବୁଝାଅ ।
ଉ-

• ପ୍ଲାଷ୍ଟିକ୍ ବୋତଲରେ ଗରମ ପାଣି ରଖୁ ଏହାର ଠିପିଟି ବନ୍ଦ କରାଗଲା ।
• କିଛି ସମୟପରେ ଗରମପାଣି ଶୀତଳ ହୋଇ ଥଣ୍ଡା ପାଣିରେ ପରିଣତ ହେବ, ଫଳରେ ସେ ପାଣିର ଆୟତନ କମିଯିବ ।
• ତେଣୁ ବୋତଲ ମଧ୍ୟରେ ବାୟୁଚାପ କମିଯିବ । ଫଳରେ ବାହାର ବାୟୁର ସର୍ବଦିଗ ଚାପ ଯୋଗୁଁ ବୋତଲଟି ଚେପା ହୋଇଯିବ ।

Question 13.
ଜଣେ ଧନୁର୍ଦ୍ଧାରୀ ଲକ୍ଷ୍ୟସ୍ଥଳକୁ ଶର ମାରିବା ପାଇଁ ଧନୁରେ ଶରଟି ରଖ୍ ଗୁଣ ଚଢ଼ାଇଲେ । ଲକ୍ଷ୍ୟ ସ୍ଥିର ରଖ୍ ସେ ଶରଟି ଛାଡ଼ିଲେ । ଶରଟି ଲକ୍ଷ୍ୟସ୍ଥଳ ଆଡ଼କୁ ଗତିଶୀଳ ହେଲା । ଏହି ସୂଚନାକୁ ଆଧାରକରି ବନ୍ଧନୀ ମଧ୍ଯରେ ପ୍ରଦତ୍ତ ଶବ୍ଦମାନଙ୍କ ମଧ୍ୟରୁ ଉପଯୁକ୍ତ ଶବ୍ଦଗୁଡ଼ିକ ବ୍ୟବହାର କରି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର । (ମାଂସପେଶୀୟ, ସଂସ୍ପର୍ଶ, ଅସଂସ୍ପର୍ଶ, ମାଧ୍ୟାକର୍ଷଣ, ଘର୍ଷଣ, ଆକୃତି, ଆକର୍ଷଣ)
(a) ଧନୁଟିରେ ଗୁଣ ଦେବାପାଇଁ ଧନୁର୍ଦ୍ଧାରୀ ଯେଉଁ ବଳ ପ୍ରୟୋଗ କରନ୍ତି ତାହା ଧନୁଟିର …………………. ପରିବର୍ତ୍ତନ କରେ ।
(b) ଧନୁରେ ଗୁଣ ଦେବାବେଳେ ଏଥ‌ିରେ ପ୍ରଯୁକ୍ତ ହେଉଥ‌ିବା ବଳ ……………….. ବଳର ଏକ ଉଦାହରଣ ।
(c) ଶବ୍ଦଟିର ଗତି ଅବସ୍ଥାରେ ପରିବର୍ତ୍ତନ ପାଇଁ ଏଥ‌ିରେ ପ୍ରଯୁକ୍ତ ବଳ …………………. ବଳର ଏକ ଉଦାହରଣ ।
(d) ଶରଟି ଲକ୍ଷ୍ୟସ୍ଥଳ ଆଡ଼କୁ ଅଗ୍ରସର ହେଉଥ‌ିବାବେଳେ ଏହା ଉପରେ କ୍ରିୟାଶୀଳ ବଳଗୁଡ଼ିକ ମଧ୍ୟରୁ ଗୋଟିଏ …………………. ଯୋଗୁଁ ଓ ଅନ୍ୟଟି ବାୟୁର ………………….. ଯୋଗୁଁ ସୃଷ୍ଟି ହୋଇଥାଏ ।

Answers:
(a) କୃତି
(b) ମାଂସପେଶୀୟ
(c) ମାଧ୍ୟାକର୍ଷଣ
(d) ମାଧ୍ୟାକର୍ଷଣ, ଘର୍ଷଣ ବଳ

Question 14.
ଏକ କୃତ୍ରିମ ଉପଗ୍ରହକୁ ଏହାର କକ୍ଷରେ ଅବସ୍ଥାପନ କରିବାପାଇଁ ଏକ ରକେଟ୍ ସାହାଯ୍ୟରେ ଏହାକୁ ଉପରକୁ ପଠାଗଲା । ରକେଟ୍ ପ୍ରେରଣ କେନ୍ଦ୍ରରୁ ଠିକ୍ ଛାଡ଼ିବାପରେ ରକେଟ୍ ଉପରେ ଯେଉଁ ଦୁଇଟି ବଳ କ୍ରିୟାଶୀଳ ହୁଅନ୍ତି, ସେମାନଙ୍କର ନାମ ଲେଖ ।
ଉ-
ରକେଟ୍ ପ୍ରେରଣ କେନ୍ଦ୍ରରୁ ଠିକ୍ ଛାଡ଼ିବା ପରେ ରକେଟ୍ ଉପରେ ନିମ୍ନଲିଖ ବଳ କ୍ରିୟାଶୀଳ ହୁଏ – କୃତ୍ରିମ ଉପଗ୍ରହ ଓ ରକେଟ୍‌ର ନିମ୍ନମୁଖୀ ଓଜନ ବଳ (ପୃଥୁବୀର ମହାକର୍ଷଣ ବଳ) ଏବଂ ବାୟୁର ଘର୍ଷଣ ବଳ ।

Question 15.
ଯଦି ଏକ ବସ୍ତୁ ଉପରେ ଦୁଇଟି ବଳ F₁ ଓ F₂ ପରସ୍ପରର ବିପରୀତ ଦିଗରେ କ୍ରିୟାଶୀଳ ହୁଅନ୍ତି, ତେବେ ବସ୍ତୁଟି ଉପରେ କେଉଁ ପରିଣାମୀ ବଳ କ୍ରିୟାଶୀଳ ହୋଇଥାଏ ?
ଉ-
ଯଦି ଏକ ବସ୍ତୁ ଉପରେ ଦୁଇଟି ବଳ F₁ ଓ F2 ପରସ୍ପରର ବିପରୀତ ଦିଗରେ କ୍ରିୟାଶୀଳ ହୁଅନ୍ତି, ତେଣୁ ବସ୍ତୁଟି ଉପରେ F₁ – F₂ ଯଦି F₁ > F₂ ବା F₂ – F₁ ଯଦି F₂ > F₁ ବଳ କ୍ରିୟାଶୀଳ ହୁଏ ।
ଅର୍ଥାତ୍ :

• ଯଦି F₁ = F₂, ତେବେ ପରିମାଣୀ ବଳ = F₁ – F₂ = 0
• ଯଦି F₁ > F₂, ତେବେ ପରିଣାମୀ ବଳ = F₁ – F₂
• ଯଦି F₁ < F₂, ତେବେ ପରିଣାମୀ ବଳ = F₂ – F₁

Question 16.
ଭୂସମାନ୍ତର ଭାବେ ଥ‌ିବା ଏକ ବୃତ୍ତାକାର ପଥରେ ଗୋଟିଏ ବସ୍ତୁ ସମବେଗରେ ଘୂରୁଅଛି । ସେହି ବସ୍ତୁ ଉପରେ କିଛି ବଳ କ୍ରିୟାଶୀଳ ହେଉଛି କି ? କାହିଁକି ?
ଉ-
ଭୂସମାନ୍ତର ଭାବେ ଥ‌ିବା ଏକ ବୃତ୍ତାକାର ପଥରେ ଗୋଟିଏ ବସ୍ତୁ ସମବେଗରେ ଘୁରୁଅଛି । ସେହି ବସ୍ତୁ ଉପରେ ମହାକର୍ଷଣ ବଳ ଓ ମାଧ୍ୟାକର୍ଷଣ ବଳ କ୍ରିୟାଶୀଳ ହେଉଛି ।

• ଏଠାରେ ପୃଥ‌ିବୀ ଓ ଘୂରୁଥୁବା ବସ୍ତୁର ବସ୍ତୁତ୍ଵ ପରସ୍ପରକୁ ଆକର୍ଷଣ କରନ୍ତି । ଏହି ବସ୍ତୁତ୍ଵଜନିତ ବଳ ମହାକର୍ଷଣ ବଳ ।
• ପୃଥ‌ିବୀ ମାଧ୍ୟାକର୍ଷଣ ବଳଦ୍ୱାରା ଘୂରୁଥିବା ବସ୍ତୁକୁ ଆକର୍ଷଣ କରିଥାଏ ।

ଆଉ କ ଣ କରିହେବ -ତୁମ ପାଇଁ କିଛି ଅଧିକ କାର୍ଯ୍ୟ ଓ ପ୍ରକଳ୍ପ :

1. 50 ସେ.ମି. ଲମ୍ବ ଓ 50 ସେ.ମି. ପ୍ରସ୍ଥ ବିଶିଷ୍ଟ ଏକ ବାଲୁକାଶଯ୍ୟା ପ୍ରସ୍ତୁତ କର, ଯେପରିକି ଏହାର ଉଚ୍ଚତା ପ୍ରାୟ 10 ସେ.ମି. ହେବ । କାଠ କିମ୍ବା ପ୍ଲାଷ୍ଟିକ୍‌ର ଏକ ସ୍କୁଲ ନିଅ । ଖଣ୍ଡିଏ ଗ୍ରାଫ୍ କାଗଜରୁ 1 ସେ.ମି. ପ୍ରସ୍ଥର ଦୁଇଟି ଲମ୍ବା ପଟି କାଟ । ଗୋଟିଏ ପଟି ସ୍କୁଲ୍‌ର ଏକ ଗୋଡ଼ ଉପରେ ଏହାର ତଳଠାରୁ ଉପର ଆଡ଼କୁ ଅଠାଦ୍ଵାରା ଲଗାଅ । ଅନ୍ୟଟି କରି ସ୍କୁଲ୍‌ ଧୀରେ ତା ଉପରେ ରଖ, ଯେପରିକି ତୁମର କୌଣସି ଚାପ ଷ୍ଟୁଲ୍‌ ଉପରେ ନ ପଡ଼େ ।

ବର୍ତ୍ତମାନ ବହି ଭଉଁଥିବା ତୁମର ସ୍କୁଲବ୍ୟାଗ, (କିମ୍ବା ଖଣ୍ଡେ ଇଟା ବା ପଥର ପରି ଓଜନିଆ ଜିନିଷ) ଷ୍ଟୁଲ୍‌ ଉପରେ ଧୀରେ ରଖ । ସ୍କୁଲ୍‌ର ଗୋଡ଼ଟି ବାଲି ଭିତରକୁ କିଛି ଦୂର ପଶିଥିବାର ତୁମେ ଲକ୍ଷ୍ୟ କରୁଛ କି ? ତୁମ ପେନ୍‌ସିଲ ଦ୍ବାରା ଗ୍ରାଫ୍ କାଗଜରେ ସେଠାରେ ଏକ ଦାଗ (mark) ଦିଅ । ଏହାପରେ ସ୍କୁଲ୍ ଓ ବ୍ୟାଗ୍ କାଢ଼ିନିଅ ଏବଂ ବାଲିର ଶଯ୍ୟାକୁ ଭଲ ଭାବେ ସମତଳ କରିଦିଅ । ବର୍ତ୍ତମାନ ସ୍କୁଲ୍‌ଟି ଏହି ଶଯ୍ୟା ଉପରେ ଧୀରେ ଓଲଟାଇ ରଖ ଏବଂ ବ୍ୟାଗ୍‌ ତା’ ଉପରେ ରଖିଦିଅ ।

ଏଥର କାଗଜରେ ଦେଇଥ‌ିବା ଦାଗରୁ ତୁମେ ଜାଣିପାରିବ, କେଉଁ କ୍ଷେତ୍ରରେ ସ୍କୁଲ୍‌ କେତେ ବାଲି ଭିତରକୁ ପଶିଛି । ଏଥୁରୁ ସ୍କୁଲ୍ ଓ ବ୍ୟାଗର ଓଜନ ଦ୍ବାରା ବାଲିର ଶଯ୍ୟା ଉପରେ ପଡୁଥିବା ଚାପ କେଉଁ କ୍ଷେତ୍ରରେ ଅଧ୍ଵ ହେଉଛି ଜାଣିପାରିବ, ଏହାର କାରଣ ନିର୍ଣ୍ଣୟ କର । ଉଭୟ କ୍ଷେତ୍ରରେ ଚାପଦ୍ଵୟର ଅନୁପାତ ବି ନିର୍ଣ୍ଣୟ କର । (ଏକ ସରୁ ମୁହଁଥ‌ିବା କାଚ କିମ୍ବା ପ୍ଲାଷ୍ଟିକ୍ ଡିବା ବ୍ୟବହାର କରି ଏହି ପ୍ରକଳ୍ପଟି ମଧ୍ୟ କରାଯାଇପାରିବ) ।
ଉ-
(i) ପ୍ରଥମ କ୍ଷେତ୍ରରେ ଷ୍ଟୁଲ୍‌ର ଚାରିଟି ଗୋଡ଼ର ମୋଟ ଭୂମିର କ୍ଷେତ୍ରଫଳ ଖୁବ୍ କମ୍, ତେଣୁ ଚାପ ଅଧିକ ହେବ ଓ ସ୍କୁଲ୍‌ର ଗୋଡ଼ ବାଲି ମଧ୍ୟକୁ ପ୍ରବେଶ କରିବ ।
(ii) ଦ୍ଵିତୀୟ କ୍ଷେତ୍ରରେ ସ୍କୁଲ୍‌ର ସ୍ପର୍ଶ କ୍ଷେତ୍ରଫଳ ସ୍କୁଲ୍‌ର ଉପର ପଟାର କ୍ଷେତ୍ରଫଳଠାରୁ ବହୁତ ବେଶି । ତେଣୁ ଏ କ୍ଷେତ୍ରରେ ଚାପ ଅଧିକ ହେତୁ ଚାପ ଖୁବ୍ କମ୍ ହେବ । ତେଣୁ ଦ୍ବିତୀୟ କ୍ଷେତ୍ରରେ ସ୍କୁଲ୍‌ ବାଲି ମଧ୍ୟରେ ଖୁବ୍ କମ୍ ପ୍ରବେଶ କରିବ ।

2. ଜଳ ଭଭି ଏକ କାଚଗିଲାସ ନିଅ । ପୋଷ୍ଟକାଡ଼ ପରି ଖଣ୍ଡିଏ ମୋଟା କାଗଜ ଦ୍ଵାରା ଏହାର ମୁହଁଟି ଘୋଡ଼ାଇଦିଅ [ଚିତ୍ର (a) । ବର୍ତ୍ତମାନ ଗୋଟିଏ ହାତରେ ଗିଲାସଟି ଧରି, ଅନ୍ୟ ହାତରେ କାଗଜଟିକୁ ଗିଲାସର ମୁହଁ ଉପରେ [ଚିତ୍ର (b)] ଯେପରିକି ଏହା ପୂରାପୁରି ସିଧା ରହିବ । ଧୀରେ କାଗଜଟି ଉପରୁ ହାତଟି କାଢ଼ିନିଅ [ଚିତ୍ର (c)] । କ’ଣ ଲକ୍ଷ୍ୟ କରୁଛ ? କାଗଜଟି ତଳକୁ ପଡ଼ିଗଲା ଓ ଜଳ ଢାଳି ହୋଇଗଲା କି ?

ଯଦି ସେପରି ହେଲା, କିଛି ଅଧ୍ଵ ସାବଧାନତାର ସହ ପରୀକ୍ଷାଟି ଆଉଥରେ କର । ତୁମେ ଦେଖୁ ଯେ ହାତର ବିନା ସାହାଯ୍ୟରେ କାଗଜଟି ଖସି ନଯାଇ ଗିଲାସରେ ଜଳକୁ ଧରି ରଖୁଛି । ଏପରି କାହିଁକି ହେଉଛି, କାରଣଟି ନିର୍ଣ୍ଣୟ କର । କାଗଜଟି କାଢ଼ିନେଇ ଗିଲାସର ମୁହଁଟି ଏକ କନାଦ୍ଵାରା ଘୋଡ଼ାଇ ପରୀକ୍ଷାଟି ଆଉଥରେ କର [ଚିତ୍ର (d), (e)] । କ’ଣ ଦେଖୁଛ ଓ କାହିଁକି ? ତୁମେ ପାଉଥବା ସିଦ୍ଧାନ୍ତଟି ଲେଖ ।

ଉ-

• ବାୟୁର ଊର୍ଦ୍ଧ୍ବଚାପ ଅଛି । ବାୟୁ ନିମ୍ନମୁଖୀ ଗ୍ଲାସ୍‌ ପୋଷ୍ଟକାର୍ଡ଼ ଉପରେ ଊର୍ଦ୍ଧ୍ବଚାପ ପକାଇବାରୁ ପୋଷ୍ଟକାର୍ଡ଼ଟି ତଳକୁ ଖସିବ ନାହିଁ କି ପାଣି ଢାଳି ହୋଇଯିବ ନାହିଁ ।
• କନାଦ୍ଵାରା ଘୋଡ଼ାଇ ଓଲଟାଇଲେ କନାମଧ୍ୟ ଦେଇ ଜଳ ମଧ୍ୟ ବାୟୁର ଊର୍ଦ୍ଧ୍ବଚାପ ଯୋଗୁ ତଳକୁ ପଡ଼ିବ ନାହିଁ ।

3. ଭିନ୍ନ ଭିନ୍ନ ଆକୃତିର ଯେ କୌଣସି ଚାରୋଟି ପ୍ଲାଷ୍ଟିକ୍ ଦୁଇଟି ବୋତଲରେ ଗୋଟିଏ ଲେଖାଏଁ ଓ ଅନ୍ୟ ଦୁଇଟି ବୋତଲରେ ଦୁଇଟି ଲେଖାଏଁ ରନ୍ଧ୍ର କର । ବର୍ତ୍ତମାନ ତିନୋଟି ସରୁ ପ୍ଲାଷ୍ଟିକ୍ ପାଇପ୍ ବା ନଳୀ ଦ୍ଵାରା ବୋତଲଗୁଡ଼ିକୁ ସଂଯୁକ୍ତ କର (ଚିତ୍ର ) । ସମତଳ ପୃଷ୍ଠ ଉପରେ ରଖ ।

ମହମଦ୍ଵାରା (ଚିତ୍ର ) ଯୋଡ଼ା ଯାଇଥିବା ସ୍ଥାନ ବନ୍ଦ କର, ଯେପରିକି କୌଣସି ବୋତଲରୁ ଜଳ ଝରିଯିବ ନାହିଁ । ଏବେ ଗୋଟିଏ ବୋତଲରେ ଜଳ ଢାଳ । ସେହି ବୋତଲଟି ଆଗ ପୁରିଯାଉଛି ନା ପ୍ରତିଟି ବୋତଲରେ ଜଳ କ୍ରମଶଃ ଭର୍ତ୍ତି ହେଉଛି ? ପ୍ରତି ବୋତଲରେ ଜଳର ପତ୍ତନ ଲକ୍ଷ୍ୟ କର । ଜଳର ପତ୍ତନ ପ୍ରତି ବୋତଲରେ ସମାନ ଦେଖାଯାଉଛି କି ? ଏପରି କାହିଁକି ହେଲା ? ବୁଝିବା ପାଇଁ ଚେଷ୍ଟା କର ।

ଉ-
ଗୋଟିଏ ବୋତଲରେ ଜଳ ଢାଳିଲେ ସବୁ ବୋତଲରେ ଜଳ ସମାନ ଉଚ୍ଚତା ରହିବ । ଏହାକୁ ଜଳର ସମୋଚ୍ଚଶୀଳତା

ପରୀକ୍ଷା ଉପଯୋଗୀ ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତର

ବସ୍ତୁନିଷ୍ଠ ପ୍ରଶ୍ନେ। ଭର

1. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) ବିଶ୍ଵରେ ଥ‌ିବା ଯେକୌଣସି ଦୁଇଟି ବସ୍ତୁ ପରସ୍ପରକୁ ସ୍ପର୍ଶ ନକରି ଆକର୍ଷଣ କଲେ ତାହାକୁ ………………….. ବଳ କୁହାଯାଏ ।
(ii) ବିଶ୍ଵର ସର୍ବତ୍ର ……………………. ବଳ ହୋଇଥାଏ ।
(iii) ପୃଥ‌ିବୀ ଚାରିପଟେ ବାୟୁମଣ୍ଡଳ …………………. କି.ମି. ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ ।
(iv) 0°C ତାପମାତ୍ରାରେ l ବର୍ଗ ସେ.ମି. କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ସ୍ଥାନ ଉପରେ ପଡ଼ୁଥ‌ିବା ବାୟୁର ବଳ ………………….. ଓଜନ ସହ ସମାନ ।
(v) ଚାପ ହେଉଛି …………………. କ୍ଷେତ୍ରଫଳ ପ୍ରତି ପ୍ରଯୁକ୍ତ ବଳ ।
(vi) ଯେକୌଣସି ସଂସ୍ପର୍ଶବଳ ଯାହାଦ୍ଵାରା ପ୍ରୟୋଗ କରାଯାଏ ତାହାକୁ ଉକ୍ତ ବଳର ………………… କୁହାଯାଏ ।
(vii) ଲଗାଲଗି ଦୁଇଟି ପୃଷ୍ଠ ମଧ୍ଯରେ …………………. ଘର୍ଷଣର କାରଣ ଅଟେ ।
(viii) ଦୁଇଟି ଚୁମ୍ବକ ମଧ୍ୟରେ ………………….. ବଳ ଯୋଗୁ ଚୁମ୍ବକୀୟ ବଳ ସମ୍ଭବ ହୋଇଥାଏ ।
(ix) ଦୁଇଟି ଚୁମ୍ବକର ସମମେରୁ ପରସ୍ପରକୁ …………………….. କରନ୍ତି ।
(x) …………………. ବଳଦ୍ଵାରା ଶରୀରକୁ ବଙ୍କାଇ ହୁଏ ।
(xi) ବସ୍ତୁଟିର ବେଗ ‘0’ ହେଲେ, ସେହି ଅବସ୍ଥାକୁ ବସ୍ତୁଟିର …………………… କୁହାଯାଏ ।
(xii) ଠେଲାବଳ ଓ ଟଣାବଳକୁ ମିଳିତଭାବେ …………………. ବଳ କୁହାଯାଏ ।
(xiii) ଯାହାଦ୍ଵାରା ଠେଲାବଳ ବା ଟଣାବଳ ବସ୍ତୁ ଉପରେ ପ୍ରୟୋଗ କରାଯାଏ ତାକୁ ……………….. କରନ୍ତି ।
(xiv) ବଳ ପ୍ରୟୋଗବେଳେ କାରକ ବସ୍ତୁକୁ ସ୍ପର୍ଶ କଲେ ସେ ଧରଣର ବଳକୁ …………………… ବଳ କୁହାଯାଏ ।
(xv) ବଗିଚାରୁ ଘାସ ଉପାଡ଼ିବା ବେଳେ ଘାସ ଉପରେ ………………….. ବଳ ପ୍ରୟୋଗ କରାଯାଏ ।
(xvi) କୌଣସି ବସ୍ତୁ ଉପରେ ଦୁଇ ବିପରୀତ ଦିଗରୁ କ୍ରିୟାଶୀଳ ସମପରିମାଣ ବଳଗୁଡ଼ିକର ପରିଣାମୀ ବଳ …………………….. ହୁଏ ।
(xvii) F₁ ଓ F₂ ବଳ ଏକ ଦିଗରୁ ଏକ ବସ୍ତୁ ଉପରେ କ୍ରିୟାଶୀଳ ହେଲେ ପରିଣାମୀ ବଳ …………………… ହେବ ।
(xviii) ………………. ହେଉଛି ଏକକ କ୍ଷେତ୍ରଫଳ ପ୍ରତି ପ୍ରଯୁକ୍ତ ବଳ ।
(xix) ପୃଥ‌ିବୀପୃଷ୍ଠରେ ବା ପୃଷ୍ଠରୁ କିଛି ଉଚ୍ଚତାରେ ପୃଥ‌ିବୀର କେନ୍ଦ୍ର ଆଡ଼କୁ କାର୍ଯ୍ୟକାରୀ ଆକର୍ଷଣ ବଳକୁ …………………… କହନ୍ତି ।
(xx) ଏକ ଚୁମ୍ବକର ଦକ୍ଷିଣ ମେରୁ ଅନ୍ୟ ଏକ ଚୁମ୍ବକର ଉତ୍ତର ମେରୁ ଦ୍ବାରା ………………….. ହୋଇଥାଆନ୍ତି ।

Answer:
(i) ମହାକର୍ଷଣ
(ii) ମହାକର୍ଷଣ
(iii) 1000
(iv) 1 Kg.
(v) ଏକକ
(vi) କାରକ
(vii) ଆପେକ୍ଷିକ ଗତି
(viii) ଆନ୍ତଃକ୍ରିୟା
(ix) ବିକର୍ଷଣ
(x) ମାଂସପେଶୀୟ
(xi) ସ୍ଥିରାବସ୍ଥା
(xii) ସଂସ୍ପର୍ଶ
(xiii) କାରକ
(xiv) ସଂସ୍ପର୍ଶ
(xv) ଟଣା
(xvi) ଶୂନ
(xvii) F₁ ଓ F₂
(xviii) ଚାପ
(xix) ମାଧ୍ୟାକର୍ଷଣ ବଳ
(xx) ଆକର୍ଷିତ

2. ବାମପାର୍ଶ୍ଵର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟକରି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) ସମମେରୁ : ବିକର୍ଷଣ :: ବିଷମମେରୁ : ………………………।
(ii) ଫୁଲତୋଳା : ଟଣାବଳ :: ବଲମାରିବା : ………………………।
(iii) ସାଧାରଣ ତରାଜୁ : କମାନୀ ତରାଜୁ :: ବସ୍ତୁତ୍ଵ : ………………………।
(iv) ଚୁମ୍ବକର ସମମେରୁ : ବିକର୍ଷଣ :: ବିଷମମେରୁ : ………………………।
(v) ଗାଡ଼ି ଟାଣିବା : ଟଣାବଳ :: କୂଅରୁ ପାଣିକାଢ଼ିବା : ………………………।
(vi) କାଠପେଲିବା : ଠେଲାବଳ :: ଖୁସୁଣିରେ ଗଛରୁ ଆମ୍ବପାରିବା : ………………………।
(vii) ଠେଲାବଳ : ସଂସ୍ପର୍ଶ ବଳ :: ମହାକର୍ଷଣ ବଳ : ………………………।
(viii) ସାଧାରଣ ତରାଜୁ : ବସ୍ତୁତ୍ଵ :: କମାନୀ ତରାଜୁ : ………………………।
(ix) ବିଶ୍ଵରେ ଦୁଇଟି ବସ୍ତୁ : ମହାକର୍ଷଣ ବଳ :: ପୃଥ‌ିବୀ ଓ ଚନ୍ଦ୍ର : ………………………।

Answer:
(i) ଆକର୍ଷଣ
(ii) ଠେଲାବଳ
(iii) ଓଜନ
(iv) ଆକର୍ଷଣ
( v ) ଟଣାବଳ
(vi) ଟଣା ବଳ
(vii) ଅସଂସ୍ପର୍ଶ ବଳ
(viii) ବଳ ( ଓଜନ)
(ix) ମହାକର୍ଷଣ ବଳ

3. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) କୌଣସି ବସ୍ତୁ ଉପରେ ଦୁଇ ବିପରୀତ ଦିଗରୁ କ୍ରିୟାଶୀଳ ହେଉଥ‌ିବା ସମପରିମାଣ ବଳଗୁଡ଼ିକର ବଳ ………………….. ହେବ । (୦, ୨ ଗୁଣ, ଅଧା, ୩ ଗୁଣ)
(ii) 0 ତାପମାତ୍ରାରେ I ବର୍ଗ ସେ.ମି. କ୍ଷେତ୍ରଫଳ ଉପରେ ପଡୁଥ‌ିବା ବାୟୁର ବଳ …………………… କି.ଗ୍ରା. । (0, 1, 2, 3)
(iii) ଧନୁରେ ଗୁଣ ଦେବାବେଳେ ଏଥ‌ିରେ ପ୍ରଯୁକ୍ତ ହେଉଥିବା ବଳ ……………………. ବଳର ଏକ ଉଦାହରଣ । (ମାଧ୍ୟାକର୍ଷଣ, ସଂସ୍ପର୍ଶ, ମାଂସପେଶୀୟ, ଅସଂସ୍ପର୍ଶ)
(iv) ଶରଟିର ଗତି ଅବସ୍ଥାରେ ପରିବର୍ତ୍ତନ ପାଇଁ ଏଥ‌ିରେ ପ୍ରଯୁକ୍ତ ବଳ ……………………… ବଳର ଏକ ଉଦାହରଣ ଅଟେ । (ଘର୍ଷଣ, ସଂସ୍ପର୍ଶ, ମାଂସପେଶୀୟ, ମାଧ୍ୟାକର୍ଷଣ)
(v) ଚୁମ୍ବକୀୟବଳ, ସ୍ଥିର ବିଦ୍ୟୁତ୍ ବଳ ଓ ମହାକର୍ଷଣ ବଳକୁ ମିଳିତଭାବେ ………………….. ବଳ କୁହାଯାଏ । (ସଂସ୍ପର୍ଶ, ଅସଂସ୍ପର୍ଶ, ମାଧ୍ୟାକର୍ଷଣ, ଆକର୍ଷଣ)
(vi) ମାଧ୍ୟାକର୍ଷଣ ବଳ …………………….. ବଳର ଅନ୍ତର୍ଗତ ଅଟେ । (ସଂସ୍ପର୍ଶ, ଅସଂସ୍ପର୍ଶ, ଘର୍ଷଣ, ମହାକର୍ଷଣ)
(vii) ସ୍ଥିର ବିଦ୍ୟୁତ୍ଵଳ ……………………… ବଳର ଅନ୍ତର୍ଗତ ଅଟେ । (ସଂସ୍ପର୍ଶ, ଅସଂସ୍ପର୍ଶ, ଘର୍ଷଣ, ମହାକର୍ଷଣ)
(viii) ଚାପର ଏକକ ……………………….। (N, Nm, Nm², Nm^-2)
(ix) ………………………. ଯନ୍ତ୍ରଦ୍ୱାରା ବାୟୁମଣ୍ଡଳୀୟ ଚାପ ମପାଯାଏ । ( ଲାକ୍ଟୋମିଟର, ବାରୋମିଟର, ଆନିମୋମିଟର, ହାଇଡ୍ରୋମିଟର)
(x) ………………………. ବଳଦ୍ୱାରା କୂଅରୁ ପାଣି କଢ଼ାଇବା ସମ୍ଭବ ଅଟେ । (ଟଣାବଳ, ଠେଲାବଳ, ଚୁମ୍ବକୀୟ ବଳ, ଆକର୍ଷଣ ବଳ)

Answer:
(i) 0
(ii) 1
(iii) ମାଂସପେଶୀୟ
(iv) ମାଧ୍ୟାକର୍ଷଣ
(v) ଅସଂସ୍ପର୍ଶ
(vi) ମହାକର୍ଷଣ
(vii) ଅସଂସ୍ପର୍ଶ
(viii) Nm^-2
(ix) ବାରୋମିଟର
(x) ଟଣାବଳ

4. ‘କ’ ସ୍ତମ୍ଭରେ ଶବ୍ଦସହ ‘ଖ’ ସ୍ତମ୍ଭର ସମ୍ପର୍କିତ ଶବ୍ଦକୁ ମିଳାଅ ।

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) ଚାଲିବା	(i) ମହାକର୍ଷଣ ବଳ
(ii) ସମମେରୁ	(ii) ଅସଂସ୍କର୍ଶଚ୍କ
(iii) 2 ଟି ଚୁମ୍ବକ ମଧ୍ୟରେ ଆନ୍ତଃକ୍ରିୟା ଅସମମେରୁ	(iii) ବିକର୍ଷଣ
(iv) ଆସମମେରୁ	(iv) ବାରୋମିଟର
(v) 2ଟି ପୃଷ୍ଠ ମଧ୍ୟରେ ଆପେକ୍ଷିକଗତି	(v) ମାଧ୍ୟାକର୍ଷଣ ବଳ
(vi) କମାନୀ ତରାଜୁ	(vi) ଚ୍ସ୍ତୁତ୍ଵ
(vii) ଗ୍ରହମାନଙ୍କର ଘୂର୍ଣ୍ଣନ	(vii) ମାଂସପେଶୀୟ ବଳ
(viii) ସାଧାରଣ ତରାଜୁ	(viii) ଓଚ୍ଚନ
(ix) ବସ୍ତୁଉପରେ କ୍ରିୟାଶୀଳ ବଳ	(ix) ଘର୍ଷଣର କାରଣ
(x) ବାୟୁମଣ୍ଡଳୀୟ ଚାପ	(x) ଆକର୍ଷଣ

Answer:

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
(i) ଚାଲିବା	(vii) ମାଂସପେଶୀୟ ବଳ
(ii) ସମମେରୁ	(iii) ବିକର୍ଷଣ
(iii) 2 ଟି ଚୁମ୍ବକ ମଧ୍ୟରେ ଆନ୍ତଃକ୍ରିୟା ଅସମମେରୁ	(ii) ଅସଂସ୍କର୍ଶଚ୍କ
(iv) ଆସମମେରୁ	(x) ଆକର୍ଷଣ
(v) 2ଟି ପୃଷ୍ଠ ମଧ୍ୟରେ ଆପେକ୍ଷିକଗତି	(ix) ଘର୍ଷଣର କାରଣ
(vi) କମାନୀ ତରାଜୁ	(viii) ଓଚ୍ଚନ
(vii) ଗ୍ରହମାନଙ୍କର ଘୂର୍ଣ୍ଣନ	(i) ମହାକର୍ଷଣ ବଳ
(viii) ସାଧାରଣ ତରାଜୁ	(vi) ଚ୍ସ୍ତୁତ୍ଵ
(ix) ବସ୍ତୁଉପରେ କ୍ରିୟାଶୀଳ ବଳ	(v) ମାଧ୍ୟାକର୍ଷଣ ବଳ
(x) ବାୟୁମଣ୍ଡଳୀୟ ଚାପ	(iv) ବାରୋମିଟର