Odisha State Board CHSE Odisha Class 12 Sanskrit Solutions Poem 3 रघुवंशम् Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Sanskrit Poem 3 रघुवंशम् Question Answer
१. एकेन पदेन उत्तरं प्रदीयताम् | (ଏକ ପଦରେ ଉତ୍ତର ଦିଅ ।)
(क) कविः मोहात् केन दुस्तरं सागरं तितीर्षुः वर्त्तते ?
Solution:
ଉଡୁପେନ ।
(ख) रघुवंशे क्षीरनिधौ इन्दुरिव कः राजेन्दुः आसीत् ?
Solution:
ଦିଲ୍ଲୀପ ।
(ग) रविः सहस्रगुणम् उत्स्त्रष्टुं किम् आदत्ते ?
Solution:
ରସମ୍ ।
(घ) धर्मरतेः कस्य जरसा विना वृद्धत्वम् आसीत् ?
Solution:
ରାଜ୍ଞ ( ଦିଲୀପସ୍ୟ) ।
(ङ) दिलीप: यज्ञाय कां दुदोह ?
Solution:
ଗାମ୍ ।

२. एकेन वाक्येन उत्तरं लिख्यताम् (ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।)
(क) हेम्नः विशुद्धिः कथं परीक्ष्यते ?
Solution:
ହେମ୍ୱ ବିଶୁଦ୍ଧି ଶ୍ୟାମିକା ଅପି ବା ଅଗ୍ନି ପରୀକ୍ଷତେ ।
(ख) दिलीपः यादोरत्नैः अर्णव इव इति कथमुक्तम् ?
Solution:
ଭୀମକାନ୍ତଃ ନୃପଗୁଣେ ଦିଲୀପଃ ଉପଜୀବିନାମ୍ ଅଧୃଷ୍ୟଶ୍ଚ ଅଭିଗମ୍ୟଶ୍ଚ ବଭୂବ । ଅତଃ ଉକ୍ତ ଯାଦୋର ଅର୍ଣବ ଇବ ଇତି ॥
(ग) राजा दिलीपः प्रजाभ्यः कथं वलिमग्रहीत् ?
Solution:
ରାଜା ଦିଲୀପଃ ପ୍ରଜାନାଂ ଭୂତ୍ୟର୍ଥମ୍ ଏବ ପ୍ରଜାଭ୍ୟ ବଳିମ୍ ଅଗ୍ରହୀତ୍ ।
(घ) राज्ञो दिलीपस्य फलानुमेया प्रारम्भाः कीदृशाः आसन् ?
Solution:
ରାଜ୍ଞ ଦିଲୀପସ୍ୟ ପ୍ରାରମ୍ଭା ପ୍ରାକ୍ତନାଃ ସଂସ୍କାର ଇବ ଫଳାନୁମେୟା ଆସନ୍ ।
(ङ) कथं दिलीपः प्रजानां पिता आसीत् ?
Solution:
ପ୍ରଜାନାଂ ବିନୟଧାନାତ୍ ରକ୍ଷଣାତ୍ ଭରଣାତ୍ ଅପି ଦିଲୀପଃ ତେରାଂ ପିତା ଆସୀତ୍ ।
३. बन्धनीमध्यात् उपयुक्तं पदं चित्वा शून्यस्थानं पूरयत ( ବନ୍ଧିନା ମଧ୍ୟରୁ ଉପଯୁକ୍ତ ପଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।)
(क) जगत: वन्दे पार्वतीपरमेश्वरौ । ( जनकौ, मातरौ पितरौ )
Solution:
ପିତରେ ।
(ख) प्रांशुलभ्ये फले वामनः उद्वाहु: भवति । ( लोभात्, क्षोभात्, आग्रहात् )
Solution:
ଲୋଭାତ୍ ।
(ग) दिलीपः अगृध्नुः आददे । (धर्मम्, अर्थम्, फलम्)
Solution:
ଅର୍ଥମ୍ ।
(घ) उरगक्षता अड्डलीव प्रियोऽपि त्याज्यः । ( शिष्टः, इष्टः, दुष्टः)
Solution:
ଦୁଷ୍ଟ ।
(ङ) अनन्यशासनां एकपुरीमिव शशास ( देशम्, उर्वीम्, राज्यम्)
Solution:
ଉର୍ବୀମ୍ ।
४. उत्कलभाषया आङ्गलभाषया वा अनुद्यताम् (ଓଡ଼ିଆ ବା ଇଂରାଜୀ ଭାଷାରେ ଅନୁବାଦ କରି ।)
(क) क्व सूर्यप्रभवो बंशः …………………………. उडुपेनास्मि सागरम् ||२||
Solution:
ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଜାତ ହୋଇଥିବା (ପ୍ରସିଦ୍ଧ) ବଂଶ କେଉଁଠି ? ଏବଂ ଅଳ୍ପ ବିଷୟକୁ ମାତ୍ର ଜାଣିଥୁବା ମୋର ବୁଦ୍ଧି କେଉଁଠି ? ମୁଁ ମୋହବଶତଃ ସାମାନ୍ୟ ଡଙ୍ଗାଦ୍ଵାରା ଦୁସ୍ତର ସମୁଦ୍ରକୁ ପାରହେବାକୁ ଇଚ୍ଛା କରୁଛି ।
(ख) तं सन्तः श्रोतुमर्हन्ति …………………………… श्यामिकाऽपि वा ।।१०।।
Solution:
ଭଲ ଓ ମନ୍ଦ ବିଚାର କରିପାରୁଥିବା ସଜ୍ଜନ ସହୃଦୟମାନେ ହିଁ କେବଳ ଏହି ରଘୁବଂଶ ନାମକ ମହାକାବ୍ୟକୁ ଶୁଣିବାପାଇଁ ସମର୍ଥ ହୋଇଥା’ନ୍ତି । ଯେହେତୁ ସୁବର୍ଣ୍ଣର ଶୁଦ୍ଧତା ବା କିଛି ଦୋଷ କେବଳ ଅଗ୍ନିରେ ହିଁ ପରୀକ୍ଷିତ ହୋଇଥାଏ ।
(ग) ज्ञाने मौनं ……………………………………. सप्रसवा इव ।।२२।।
Solution:
(ସେହି ରାଜା ଦିଲୀପ) ଜ୍ଞାନ ଥିଲେ ବି ମୌନ ଆଚରଣ କରୁଥିଲେ, ପ୍ରବଳ ପରାକ୍ରମ ଥିବା ସତ୍ତ୍ବେ ବି କ୍ଷମା ଆଚରଣ କରୁଥିଲେ, ଯାଚକମାନଙ୍କୁ ଦାନ ଦେଇଥିଲେ ବି ନିଜର ପ୍ରଶଂସା କରୁ ନଥିଲେ । ଏହିପରି ତାଙ୍କ ନିକଟରେ ଥିବା ଗୁଣଗୁଡ଼ିକ ପରସ୍ପର ବିରୋଧୀ ହୋଇଥିଲେ ସୁଦ୍ଧା ସେମାନେ ସହୋଦର ଭାଇ ଭଳି ଅବସ୍ଥାନ କରୁଥିବାର ଜଣାପଡୁଥିଲା ।
(घ) सर्वातिरिक्तसारेण ………………………………………. मेरुरिवात्मना ।।१४।।
Solution:
ମହାରାଜ ଦିଲୀପ ନିଜର ସବୁଠାରୁ ଅଧିକ ବଳବାନ୍, ସବୁଠାରୁ ଅଧିକ ତେଜସ୍ବୀ ତଥା ସବୁଠାରୁ ଅଧିକ ଉନ୍ନତ ଶତାରଦ୍ୱାରା ସମସ୍ତ ତ୍ପଥ୍ରାବାକୁ ଅକ୍ତାନ୍ତ କରି ରଦ୍ରିଥିଲେ | ଯେଉଳି ସ୍ପେକ୍ ପର୍ବତ ସବୁଠାରୁ ଅଧ୍କ ପିରତାଯ୍ୟ, ସବୁଠାରୁ ଅଧିକ କାନ୍ତିଯୁକ୍ତ ଏବଂ ସବୁଠାରୁ ଅଧିକ ଉଚ୍ଚତାଯୁକ୍ତ ନିଜର ଶରୀରରେ ସମଗ୍ର ପୃଥିବୀକୁ ଆକ୍ରାନ୍ତ କରି ରହିଛି ।
५. सन्धिं कुरुत (ସନ୍ଧି କାର |)
सूत्रस्य + इव, सः + अहम्, रघूणाम् + अन्वयः, सत् + असत्, मनुः + नाम, क्षीरनिधौ + इव ।
Solution:
ସୂତ୍ରସ୍ୟ + ଇବ = ସୂତ୍ରଧ୍ଯେବ ।
ନଃ + ଅହମ୍ = ସୋଽହମ୍ ।
ରଘୁଣାମ୍ + ଅନ୍ବୟଃ = ରପୂଣାମନ୍ଵୟଃ ।
ସତ୍ + ଅସତ୍ = ସଦସତ୍ ।
ମନୁଃ + ନାମ = ମନୁର୍ନାମ
କ୍ଷୀରନିଧୌ + ଇବ = କ୍ଷୀରନିଧାବିବ ।
६. रेखारूढ़ानां पदानां सकारणं विभक्तिः निरूप्यताम् (ରେଖାଙ୍କିତ ପଦଗୁଡ଼ିକର ସକାରଣ ବିଭକ୍ତି ନିରୂପଣ କର ।)
(क) आगमैः सदृशारम्भः आरम्भसदृशोदयः ।
Solution:
ଆଗମୈ = ତୁଲ୍ୟାର୍ଥେ ୩ୟା ।
(ख) जगतः पितरौ वन्दे पार्वतीपरमेश्वरौ ।
Solution:
ପିତରୌ = କର୍ମଣି ୨ୟା ।
(ग) वैवस्वतो मनुर्नाम माननीयो मनीषिणाम् ।
Solution:
ମନୀଷିଣାମ୍ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ ।
(घ) शास्त्रेष्वकुण्ठिता बुद्धिमौर्वी धनुषि चालता ।
Solution:
ଶାସ୍ତେଷୁ = ଅଧିକରଣେ ୭ମୀ ।
(ङ) ज्ञाने मौनं क्षमा शक्तौ ।
Solution:
ଜ୍ଞାନେ = ଅଧୂକରଣେ ୭ମୀ ।
७. सविग्रहं समासनामानि लिख्यन्ताम् (ବ୍ୟାସବାକ୍ୟ ସହ ସମାସ ନାମ ଲେଖ ।)
वागर्थौ, महाभुजः, वृषस्कन्धः, फलानुमेयाः, अनन्यशासनाम् ।
Solution:
ବାଗର୍ଥୀ = ବାକ୍ ଚ ଅର୍ଥଶ୍ଚ ଇତି (ଦ୍ବନ୍ଦ୍ବ)
ମହାଭୁଜଃ = ମହାନ୍ ଭୁଜଃ (କର୍ମଧାରୟଃ)
ବୃଷସ୍କନ୍ଧ = ବୃଷସ୍ୟ ସ୍କନ୍ଧ ଇବ ସ୍କନ୍ଧ ଯସ୍ୟ ଡଃ (ଉପମାନାର୍ଥକ ବହୁବ୍ରୀହିଃ)
ଫଳାନୁମେୟା = ଫନିଃ ଅନୁମେୟା (୩ୟା ତତ୍)
ଅନନ୍ୟଶାସନାମ୍ = ଅନ୍ୟଶାସନଂ ଯସ୍ୟା ତାମ୍ ( ବହୁବ୍ରୀହିଃ)
८. प्रकृतिं प्रत्ययं च लिखत (ପ୍ରକୃତି ଓ ପ୍ରତ୍ୟୟ ଲେଖ ।)
प्रारम्भाः, त्यागः, दुस्तरम्, तितीर्षुः, लोभात्, प्रसूतः, स्थितः ।
Solution:
ପ୍ରାରମ୍ଭା = ପ୍ର + ଆ + ରଭ୍ + ଘଞ୍ଚ୍ (ବହୁବଚନ)
ଦୁସ୍ତରମ୍ = ଦୁସ୍ + ତୃ + ଖଳ୍
ତିତୀର୍ଷୁ = ତୃ + ସନ୍ + ଉ
ଲୋଭାତ୍ = ଲୁଭ୍ + ଘଞ୍ଚ (୫ମୀ ଏକବଚନ)
ପ୍ରସୂତଃ = ପ୍ର+ ସୂ + କ୍ତ
ସ୍ଥିତଃ = ସୁ + କ୍ତ
९. सन्धिविच्छेदः क्रियताम् (ସନ୍ଧି ବିଚ୍ଛେଦ କର | )
वागर्थाविव, लोभादुद्बाहुः, वंशेऽस्मिन् श्रोतुमर्हन्ति, ह्यग्नौ ।
Solution:
ବାଗର୍ଥାବିବ = ବାକ୍ + ଅର୍ଥେ + ଇବ
ଲୋଭାଦୁଡା଼ହୁ = ଲୋଭାତ୍ + ଉତ୍ + ବାହୁ
ବଂଶେଽମିନ୍ନ = ବଂଶେ + ଅସ୍କ୍ରିନ୍
ଗୋତ୍ନମଦୃନ୍ତି = ଶ୍ରୋତୁମ୍ + ଅହଁନ୍ତି
ଦ୍ବ୍ୟଗୌ = ହି + ଅଗ୍ନି

१०. अधोलिखितपदानि व्यवहृत्य वाक्यरचना कार्या (ନିମ୍ନଲିଖିତ ପଦଗୁଡିକୁ ବ୍ୟବହାର କରି ବାକ୍ୟ ଗଠନ କର ।)
क्व, सागरः, लोभात्, अथवा, योगेन, माननीयः, संस्कारः ।
Solution:
କ୍ (କେଉଁଠି) = ଧଃ ବଞ୍ଚକଃ କ୍ଵସ୍ତେ ?
ସାଗରଃ (ସମୁଦ୍ର) = ତେନ ସାଗରଃ ଦୃଷ୍ଟି ।
ଲୋଭାତ୍ (ଲୋଭରୁ) = ଲୋଭାତ୍ ମରଣ ସୁନିଶିମମ୍ ।
ଅଥବା (ବା) = ରାମଃ ଅଥବା ଶ୍ୟାମଃ ତତ୍ର ଗଚ୍ଛତୁ ।
ଯୋଗେନ (ଯୋଗଦ୍ଵାରା) = ମୁନୟଃ ଯୋଗେନ ଚିତ୍ତବୃରିଂ କୁର୍ବନ୍ତି ।
ସଂସ୍କାରଃ ( ସଂସ୍କାର) = ଅଧୁନା ସମାଜେ କୁସଂସ୍କାରଃ ପ୍ରଚଳିତଃ ।
११. अधोदत्तानां मूलधातुं पुरुषं कालं च निर्णयत (ନିମ୍ନ ପ୍ରଦତ୍ତଗୁଡ଼ିକର ମୂଳଧାତୁ, ପୁରୁଷ ଓ କାଳ ନିରୂପଣ କର ।)
गमिष्यामि, आसीत्, बभूव, शशास ।
Solution:

१२. अधोदत्तानां पदानां मूलशब्द- लिङ्गं – विभक्ति – निरूपणं क्रियताम् (ନିମ୍ନପ୍ରଦତ୍ତ ପଦଗୁଡ଼ି କର ମୂଳଶବ୍ଦ, ଲିଙ୍ଗ, ବିଭକ୍ତି ନିରୂପଣ କର ।)
उडुपेन, सूरिभिः, मितभाषिणाम्, क्षीरनिधौ, आत्मानम्, शक्तौ, जरसा, उर्वीम् ।
Solution:
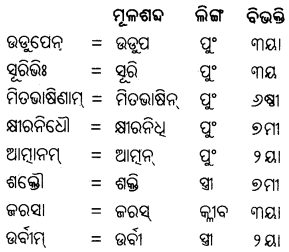
१३. प्रतिशब्दद्वयं लिख्यताम्
सूर्य:, सागरः, वंशः, अग्नि, इन्द्रः, नृपः, पिता, उरगः, पुरी ।
Solution:
ସାଗରଃ = ଭାନୁ, ତପନଃ ।
ମାଗର: = ଅର୍ଥଦଃ, ରତ୍ନାକରଃ ।
ବଂଶ: = ଅନ୍ବୟଂ, ସନ୍ତାନଃ ।
ଅଗ୍ନିଂ = ବହିଃ, ଅନମଃ ।
ଲନ୍ଦ୍ର = ମଘବା, ପାକଶାସନଃ ।
ନ୍ନପ: = ରାଜା, ପାର୍ଥିବ ।
ଯିବା = ଜନକଃ, ତାତଃ ।
ଭରଣ: = ସର୍ପ, ଅହିଂ ।
ପୁରୀ = ନଗରୀ, ପତ୍ତନମ୍ ।
१. कोष्ठकमध्यात् उपयुक्तं पदं चित्वा शून्यस्थानं पूरयत
(ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ପଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)
1. जगत: _______ वन्दे । ( पितरौ, नायकौ, कारकौ)
Solution:
ଜଗତଃ ପିତରୌ ବନ୍ଦେ ।
2. ____ पितरौ वन्दे । (स्वर्गस्य, जगत:, लोकस्य )
Solution:
ଜଗତଃ ପିତରୌ ବନ୍ଦେ ।
3. जगतः पितरौ वन्दे _______ । (राधामाधवौ, लक्ष्मीनारायणौ, पार्वतीपरमेश्वरौ)
Solution:
ଜଗତଃ ପିତରୌ ବନ୍ଦେ ପାର୍ବତୀପରମେଶ୍ଵରୌ ।
4. क्व _______ वंश: । (सूर्यप्रभवः, चन्द्रप्रभवः, शुक्रप्रभवः )
Solution:
5. क्व चाल्पविषया ______ । (गति:, रति:, मतिः)
Solution:
6. तितीर्षुः ______ मोहादुडुपेनास्मि सागरम् । (दुर्भरं, दुर्गमं, दुस्तरं)
Solution:
ତିତୀର୍ଷୁ ଦୁସ୍ତରଂ ମୋହାଦୁଡୁପେନାସ୍ତି ସାଗରମ୍ ।
7. तितीर्षुर्दुस्तरं ______ उड़पेनास्मि सागरम् । ( लोभात्, मोहात्, क्रोधात् )
Solution:
ତିତୀର୍ଷୁର୍ଣ୍ ମୋହାତ୍ ଉଡୁପେନାସ୍ତି ସାଗରମ୍ ।
8. प्रांशुलभ्ये ______ लोभात् उद्वाहुरिव वामनः । (फले. कले. बले)
Solution:
ଭ୍ରାଂଶୁଲଭ୍ୟ ଫଳେ ଲୋଭାତ୍ ଉଦ୍ବାହୁରିବ ବାମନଃ ।
9. प्रांशुलभ्ये फले ______ उद्बाहुरिव वामनः । (लोभात्, `माहात्, क्रोधात्)
Solution:
ଆଂଶୁଲଭ୍ୟ ଫଳେ ଲୋଭାତ୍ ଉଦ୍ବାହୁରିବ ବାମନଃ ।
10. प्रांशुलभ्ये फले लोभात् उद्बाहुरिव ______ । (माधव:, वामन:, केशव:)
Solution:
ଆଂଶୁଲଭ୍ୟ ଫଳେ ଲୋଭାତ୍ ଉଦ୍ବାହୁରିବ ବାମନଃ ।
11. मणौ वज्रसमुत्कीर्णे सूत्रस्येवास्ति मे ______ । ( रति:, मतिः, गति:)
Solution:
ମଣି ବଜ୍ରସମୁଖୀହେଁ ସୂତ୍ରସ୍ୟବାସ୍ତି ମେ ଗତିଃ ।
12. तं सन्तः ______ अर्हन्ति सदसद्व्यक्तिहेतवः । ( ज्ञातुम्, श्रोतुम्, क्रेतुम् )
Solution:
ତଂ ସନ୍ତଃ ଶ୍ରୋତୁମ୍ ଅହଁନ୍ତି ସଦସଦ୍ବ୍ୟକ୍ତିହେତପଃ ।
13. तं ______ श्रोतुमर्हन्ति सदसद्व्यक्तिहेतवः । (सन्त:, विज्ञा:, देवा:)
Solution:
ତଂ ସନ୍ତଃ ଶ୍ରୋତୁମହଁନ୍ତି ସଦସଦ୍ବ୍ୟକ୍ତି ହେତବ ।
14. ______ संलक्ष्यते ह्यग्नौ विशुद्धिः श्यामिकापि वा । (धातोः, शुक्तेः, हेम्नः)
Solution:
ହେମ୍ୱ ସଂଲକ୍ଷ୍ୟତେ ହ୍ୟକ୍ଷ୍ନୌ ବିଶୁଦ୍ଧି ଶ୍ୟାମିକାପି ବା ।
15. वैवस्वतो मनुनीम ______ मनीषिणाम् । ( पूजनीयो, माननीयो, वन्दनीयो)
Solution:
ବୈବସ୍ଵତୋ ମନୁର୍ନାମ ମାନନୀୟୋ ମନୀଷିଣାମ୍ ।
16. वैवस्वतो ______ नीम माननीय मनीषिगणाम् । ( मुनि, मनु, विभु)
Solution:
ବୈବସତୋ ମନୁନାପ ମାନନାମୋ ମନାଶିଶାମ୍ବ ।
17. ______ इति राजेन्द्ररिन्द्रः क्षीरनिधाविव । (महीश, दिलीप, सुरेश)
Solution:
ଦିଲୀପ ଇତି ରାଜେନ୍ଦୁରିଦୁଃ କ୍ଷୀରନିଧାବିବ ।
18. ______ सदृशारम्भ आरम्भसदृशोदयः । (ज्योतिषै:, आगमैः, नैगमैः )
Solution:
ଆଗମୈ ସଦୃଶାରାମ୍ଭ ଆରମ୍ଭସଦୃଶୋଦୟଃ ।
19. न व्यतीयुः ______ तस्य नियन्तुर्नेमियुत्तयः । (पुत्राः, जनाः, प्रजा:)
Solution:
ନ ବ୍ୟତୀୟୁ ପ୍ରଜାଃ ତସ୍ୟ ନିୟନ୍ତୁନୈମିବୃତ୍ତୟଃ ।
20. ______ एव भूत्यर्थं स ताभ्यो वलिमग्रहीत् । ( मुनीनाम्, प्रजानाम्, नराणाम् )
Solution:
ପ୍ରଜାନାମ୍ ଏବ ଭୂତ୍ୟର୍ଥ ସ ତାଭ୍ୟ ବଳିମଗ୍ରହୀତ୍ ।
21. प्रजानामेव भूत्यर्थं स ताभ्यो ______ अग्रहीत् । (वलिम्, करम्, धनम् )
Solution:
ପ୍ରଜାନାମେବ ଭୂତ୍ୟର୍ଥ ସ ତାଭ୍ୟ ବଲିମ୍ ଥିଣ୍ଡଦ୍ରାତ୍ ।
22. सहस्रगुणमुत्स्रष्टुमादत्ते हि ______ रविः । (रसं, जलं, बलं )
Solution:
ସହସ୍ରଶ୍ନମ୍ସ୍କୁପୁମାଦରେ ହି ରସ ରବି: ।
23. सहस्रगुणमुत्स्रष्टुमादत्ते हरसं ______ । (बुध, गुरुः, रविः)
Solution:
ସହସ୍ରଶ୍ନମ୍ସ୍କୁପୁମାଦରେ ହି ରସ ରବି: ।

24. फलानुमेयाः ______ संस्कार: प्राक्तना इव । (प्रारम्भाः, प्रारब्धाः, सञ्चयाः)
Solution:
ଫଲାନ୍ମପେପ୍ରା: ପ୍ରାରମା: ସଂସାରା: ପ୍ତାକୃମା ଲବ ।
25. युगोपात्मानमत्रस्ता भेजे ______ अनातुरः । (कार्यम्, धर्मम्, शास्त्रम्)
Solution:
ଜୁଗୋପାମାନମତ୍ରସ୍ତା ଭେଜେ ଧର୍ମମ୍ ଅନାତୁରଃ ।
26. अगृध्नुराददे सोऽर्थम्. ______ सुखमन्वभूत् । ( अरक्तः, अशक्तः, असक्तः )
Solution:
ଅଗୃଧୁରାଦଦେ ସୋଽର୍ଥମ୍ ଅସନ୍ତଃ ସୁଖମନ୍ତ୍ରଭୂତ୍ ।
27. अगृध्नुराददे सोऽर्थमसक्तः ______ अन्वभूत् । (सुखम्, जयम्, भयम्)
Solution:
ଅଗ୍ଧ୍ଧୁ ରାବଡେ ସୋଽଥମସକ୍ତ: ସ୍କଖମ୍ନ ଅନ୍ନରୁତ୍ ।
28. ______ मौनं क्षमा शाक्तौ त्यागे श्लाघाविपर्ययः । (वेदे, शास्त्रे, ज्ञाने)
Solution:
ଜ୍ଞାନେ ମୌନଂ କ୍ଷମା ଶଭୌ ତ୍ୟାଗେ ଶ୍ଵାଘାବିପର୍ଯ୍ୟୟ ।
29. ज्ञाने मौनं ______ शक्तौ त्यागे श्लाघाविपर्ययः । (क्षमा, दया, स्पृहा)
Solution:
ଜ୍ଞାନେ ମୌନଂ କ୍ଷମା ଶର୍ଥେ ତ୍ୟାଗେ ଶ୍ଵାଘାବିପର୍ଯ୍ୟୟ ।
30. ज्ञाने मौनं क्षमा शक्तौ ______ श्लाघाविपर्ययः । ( कार्ये, शौर्ये, त्यागे)
Solution:
ଅନେ ମୌନଂ କମା ଶକ୍ତବ ପ୍ୟାରେ ଶ୍ରାଣାବିପଣାସମା: ।
31. तस्य ______ आसीद् वृद्धत्वं जरसा विना । (धर्मरते, पुण्यरते:, कर्मरते:)
Solution:
ତସ୍ୟ ଧର୍ମରତେ ଆସୀଦ୍ ବୃଦ୍ଧବଂ ଜରସା ବିନା ।
32. तस्य धर्मरतेरासीद् ______ रजसा विना । (बृद्धत्वं, प्रौढत्वं, बुद्धत्वं)
Solution:
ରଖ୍ୟ ଧମତତେରାମାହ୍ ବଦ୍ଧତ୍ୱ କରମା ବିନା ।
33. ______ विनयाधानाद्रक्षणाद् भरणादपि । (प्रजानां नराणां जनानां )
Solution:
ପୃକାନ ବି ନାମଧାନାଦୃକଣାହ ଉରଣାଦପି ।
34. स ______ पितरस्तासां केवलं जन्महेतवः । ( गुरुः, गुणी, पिता )
Solution:
ସ ପିତା ପିତରସ୍ତାସାଂ କେବଳଂ ଜନ୍ମହେତବ ।
35. स पिता पितरस्तासां केवलं ______ । ( जन्महेतव:, कर्महेतवः, धर्महेतवः)
Solution:
ସ ପିତା ପିତରସ୍ତାସାଂ କେବଳଂ ଜନ୍ମହେତପଃ ।
36. अप्यर्थकामौ तस्यास्तां धर्मं एव ______ । (शरीरिणः, मनीषिणः, तपस्विनः )
Solution:
ଅପ୍ୟର୍ଥକାମୌ ତସ୍ୟାସ୍ତା ଧର୍ମ ଏବଂ ମନୀଷିଣୀ ।
37. अप्यर्थकामौ तस्यास्तां ______ एव मनीषिणः । (धर्म, पुण्य, पाप)
Solution:
ଅପ୍ୟର୍ଥକାମୌ ତସ୍ୟାସ୍ତା ଧର୍ମ ଏବ ମନୀଷିତଃ ।
38. दुदोह गां स ______ सस्याय मघवा दिवम् । ( धर्मीय, पुण्याय, यज्ञाय )
Solution:
ଦୁଦୋହ ମାଂ ସ ଯଜ୍ଞାୟ ସସ୍ୟାୟ ମଘବା ଦିବମ୍ ।
39. दृदोह गां स यज्ञाय सस्याय ______ दिवम् । ( मधवा, वरुणो, सविता )
Solution:
ଦୁଦୋହ ମାଂ ସ ଯଜ୍ଞାୟ ସସ୍ୟାୟ ମଘବା ଦିବମ୍ ।
40. दुदोह गां स यज्ञाय सस्याय मघवा ______ । (जलम्, भुवम्, दिवम्)
Solution:
ଦୁଦୋହ ସାଂ ସ ଯଜ୍ଞାୟ ସସ୍ୟାୟ ମଘବା ଦିବମ୍ ।
41. तथा हि सर्वे तस्यासन् परार्थैकफला ______ । ( जनाः, बुधाः, गुणाः )
Solution:
ତଥା ହି ସର୍ବେ ତସ୍ୟାସନ୍ ପରାର୍ଥେକଫଳା ଗୁଣା ।
42. अनन्यशासनाम् ______ शशासैकपुरीमिव । (भूमिं, पृथ्वीं, उवीं)
Solution:
ଅନନ୍ୟଶାସନାମ୍ ଉର୍ବୀ ଶଶାସୈକପୁରୀମିବ ।
अतिसंक्षेपेण उत्तरं लिखत:
1. ‘रघुवंशम् ‘ महाकाव्यस्य रचयिता क: ?
Solution:
ମଦ୍ରାକରି କାଲିବାସ:
2. कौ जगतः पितरौ ?
Solution:
ପାବତାପରସେଶ୍ୱରୌ
3. पार्वतीपरमेश्वरी, काविव सम्पृक्तौ ?
Solution:
ବାଗଥୋ
4. किमर्थं कविः जगतः पित्रोः वन्दनं करोति ?
Solution:
ବାଗର୍ଥପୃତିପରମେ
5. केन कविः मोहात् सागरं तितीर्षुरस्ति ?
Solution:
ଉରୁସେନ
6. कविः कस्मात् उडुपेन दुस्तरं सागरं तितीर्षुः वर्त्तते ?
Solution:
ମୋହାତ୍
7. कविः किम्भूतं सागरं तितीर्षुरस्ति ?
Solution:
ଦୁସ୍ତରମ୍
8. रघुवंशे वज्रसमुत्कीर्णमणौ कस्य इव कालिदासस्य गतिः अस्ति ?
Solution:
ସୂତ୍ରସ୍ୟ
9. रघुवंशीया राजानः कथं मितभाषिणः ?
Solution:
ସତ୍ୟାୟ
10. रघुवंशीया राजानः सत्याय किं भवन्ति ?
Solution:
ମିତଭାଷିତଃ
11. रघुवंशीया राजानः कथं विजिगीषवः ?
Solution:
ଯଶସେ
12. रघुवंशीया राजान: यशसे किं भवन्ति ?
Solution:
ବିଜିଗୀଷତଃ
13. रघुवशीया राजानः कस्मिन् काले विषयैषिणो भवन्ति ?
Solution:
ଯୌବନେ
14. रघुवंशीया राजानः यौवने किं भवन्ति ?
Solution:
ବିଷୟେଷିଣ
15. रघुवशीया राजानः वार्द्धक्ये किं कुर्वन्ति ?
Solution:
ମ୍ନନିବଢିମ୍ନ
16. के रघुणामन्वयं श्रोतुमर्हन्ति ?
Solution:
ସନ୍ତ୍ର:
17. कीदृश: सन्त: रघुवंशं श्रोतुमर्हन्ति ?
Solution:
ସଦସହବ୍ୟକ୍ତତ୍ତ୍ବେଡବ:
18. हेम्नः विशुद्धिः कुत्र संलक्ष्यते ?
Solution:
ର୍ଥଗେ
19. अग्नौ कस्य विशुद्धि: संलक्ष्यते ?
Solution:
ବ୍ରେସ୍ନ:
20. रघुवंशीय राजानाम् आद्यः राजा कः आसीत् ?
Solution:
ବୈବସ୍ଵତ: ମନୁ:
21. राजा दिलीपः कीदृशः इव उर्वी क्रान्त्वा स्थितः ?
Solution:
ମେରୁ:
22. राजा दिलीपः कीदृशः प्राज्ञः आसीत् ?
Solution:
ଆକାରସଦ୍ୱଶ:
23. राजा दिलीपस्य उदयः किंभूतः आसीत् ?
Solution:
ଆକାରସଦ୍ୱଶ:
24. दिलीपः किमर्थं प्रजानां बलिमग्रहीत् ?
Solution:
ଭୂତ୍ୟର୍ଥମ୍
25. प्रजानां भूत्यर्थं दिलीपः किमग्रहीत् ?
Solution:
ବଲିମ୍
26. कः सहस्रगुणम् उत्स्रष्टुं रसम् आदत्ते ?
Solution:
ରବି:

27. सहस्त्रगुणमुत्स्त्रष्टुं रविः किमादत्ते ?
Solution:
ରସମ୍
28. राजा दिलीपस्य सेना कं बभूव ?
Solution:
ପରିଛଦ:
29. राजा दिलीपस्य मन्त्रणा कीदृशम् आसीत् ?
Solution:
ସଂବୃତମ୍
30. दिलीपस्य बुद्धिः शास्त्रे कीदृशी आसीत् ?
Solution:
ର୍ଥକ୍ରଣିତା
31. दिलीपः कथम् आत्मानं जुगोपः ?
Solution:
ଅତ୍ରପ୍ର: ମନ୍
32. दिलीप: असक्तः किमन्वभूत् ?
Solution:
ସୁଖମ୍
33. अनातुर: दिलीप: किं भेजे ?
Solution:
ଧସମ୍ବ
34. अगृघ्नुः दिलीपः किमाददे ?
Solution:
ଅଅମ୍ଳ
35. दिलीप: ज्ञाने किमासीत् ?
Solution:
ମୌଳମ୍
36. के सप्रसवा इव अभूवन् ?
Solution:
ଣ୍ଡଶା:
37. केषां पितरः तु केवलं जन्महेतवः
Solution:
ପ୍ରଜାନାମ୍
38. के तु प्रजानां केवलं जन्महेतवः अभूवन् ?
Solution:
ପିତରଃ
39. कौ अपि दिलीपस्य धर्मः एव आस्ताम् ?
Solution:
ଅର୍ଥକାମୌ
40. कथं दिलीप गां दुदोह ?
Solution:
ଯଜ୍ଞାୟ
41. यज्ञाय दिलीप: कां दुदोह ?
Solution:
ଗାମ୍
42. कः सस्याय दिवं दुदोह ?
Solution:
ମଶବା
43. के रक्षितुः दिलीपस्य यशः न अनुययुः ?
Solution:
ରାକାନ:
44. का श्रुतौ स्थिता ?
Solution:
ତସ୍କରତା
45. कस्य औषधं सम्मतः आसीत् ?
Solution:
ଆଉମ୍ୟ
46. “क: द्वेष्यः अपि सम्मतः आसीत् ?
Solution:
ଶିଷ୍ଟ
47. कः प्रियः अपि त्याज्यः आसीत् ?
Solution:
ଦୁପ:
48. कः दिलीपं महाभूतसमाधिना विदधे ?
Solution:
ତେଧା:
49. वेधाः दिलीपं केन विदधे ?
Solution:
ମଦ୍ରାରୁତମଧୁନା
50. राजा दिलीप: उवीं कथमिव शशास ?
Solution:
ଏକପୁରାମ୍
51. दिलीप: काम् एकपुरीम् इव शशस ?
Solution:
ରତାମା
संक्षेपेण उत्तरं लिखत :
1. कालिदासः कौ कथं च वन्दते ?
Solution:
ମହାକବି କାଳିଦାଡଃ ଜଗତପିତରୌ ପାର୍ବତୀପରମେଶ୍ଵରୌ ବନ୍ଦତେ । ତୌ କୀଦୃଶୌ ? ବାଗର୍ଥେ ଇବ ସଂପୃକ୍ତେ ବାଗର୍ଥପ୍ରତିପତ୍ତୟେ ବନ୍ଦତେ । କବି ପାର୍ବତୀପରମେଶ୍ଵରୌ ଶବ୍ଦାର୍ଥେନ ସାକଂ ତୁଳିତମ୍ ।
2. कालिदासः कथं दुस्तरं सागर तारिष्यति ?
Solution:
ସୂର୍ଯ୍ୟବଂଶଃ ଅତୀବ ବିଶାଳସାଗରସଦୃଶ । ଅସ୍ଥିନ୍ ବଂଶ ବହବଂ ରାଜାନଃ ଜାତଃ । ଅସ୍ତ୍ୟ ବଂଶସ୍ୟ ବର୍ଣ୍ଣନମ୍ ଅତୀବ ଦୁଷ୍କରମ୍ । କାଳିଦାନଃ ସ୍ଵଳ୍ପବିଷୟା ମତଃ ଆସୀତ୍ । ଅତଃ ମୋହବଶତଃ ନୁନମ୍ ଉପହାସ୍ୟତାଂ ଗମିଷ୍ୟତି ।
3. कालिदासः कथं उपहास्यतां गमिष्यति ?
Solution:
କାଳିଦାନଃ ସ୍ୱୟମେବ କଥୟତି ଯତ୍ ମନ୍ଦକବି । ତଥାପି ଡଃ ଯଶଃ ଇଚ୍ଛତି । ବାମନଃ ଯଥା ଲୋଭାତ୍ ଆଂଶୁଲଭ୍ୟ ଫଳେ ଉଦ୍ବାହୁ ସନ୍ ଉପହାସ୍ୟତାଂ ଯାତି ତଥା କାଳିଦାସ ସ୍ଵଚ୍ଛବୁଦ୍ଧି ସନ୍ ବିଶାଳ ରଘୁବଂଶଂ ରଚୟିତୁମ୍ ଇୟେଷ । ଡଃ ନୁନମ୍ ଉପହାସ୍ୟତାଂ ଗମିଷ୍ୟତି ।
4. रघुवंशे कालिदासस्य कीदृशी गतिः अस्ति ?
Solution:
ମହାକବି କାଳିଦାନଃ ପ୍ରସିଦ୍ଧ ରଘୁବଂଶସ୍ୟ ବର୍ଣ୍ଣନଂ କର୍ତୁମିଚ୍ଛତି । କାବ୍ୟରଚନେ ତସ୍ୟ ଜ୍ଞାନଂ ସ୍ଵଳ୍ପମାସୀତ୍ । ମୋହାତ୍ ସିଂ ରଘୁବଂଶଂ ବର୍ଣ୍ଣୟିତଂ ପ୍ରଯନଂ କୃତବାନ୍ । ବ୍ୟାସବାଲ୍ମୀକ୍ୟାଦୟଃ ପୂର୍ବସୂରିଭିଂ କୃତବାଗ୍ରେ ଅସ୍ମିନ୍ ରଘୁବଂଶେ ବଜ୍ରସମୁତ୍ର୍ରେ ମଣୋ ସୁତ୍ରସ୍ୟ ଇବ କାଳିଦାସସ୍ୟ ଗତିଃ ଅସ୍ତ ।
5. रघुवंशीय राजानः शैशवे किं कृतम् ?
Solution:
ମନୁଷ୍ୟଜୀବନେ ବିବିଧା ଅବସ୍ଥା ଭବନ୍ତି । ତନ୍ମଧେ ଶୈଶବାବସ୍ଥା ଅନ୍ୟତମା । ଇୟଂ ବାଲ୍ୟାବସ୍ଥାରୂପେଣ ପରିଚିତା । ଅସ୍ୟାମ୍ ଅବସ୍ଥାୟାଂ ସର୍ବେ ମାନବା ବିଦ୍ୟାଭ୍ୟାସଂ କୁର୍ବନ୍ତି । ଅତଃ ରଘୁବଂଶୀୟ ରାଜାନୋଽପି ଶୈଶବକାଳେ ବିଦ୍ୟାଭ୍ୟାସଂ କୃତବନ୍ତଃ ।
6. रघुवंशीय राजानः यौवने किं कृतम् ?
Solution:
ରଘୁବଂଶୀୟ ରାଜାନଃ ଜୀବନସ୍ୟ ବିବିଧାବସ୍ଥାନ ଅନୁଭୂୟନ୍ତେ । ବାଲ୍ୟ-ଯୌବନ-ବାର୍ଦ୍ଧକ୍ୟ-ଅନ୍ତଃ ଚ ଚତ୍ବାରଭାଗାନ୍ ତେ ଅବଗତବନ୍ତଃ । ଅତଃ ଶୈଶବେ ବିଦ୍ୟାଭ୍ୟାସଂ, ଯୌବନେ ବିଷୟବାସନୋପଭୋଗ୍ୟ, ବାର୍ଦ୍ଧକ୍ୟ ମୁନିବୃରିଂ, ଅନ୍ତେ ଯୋଗେନ ତନୁ ତ୍ୟକ୍ତବନ୍ତଃ ଚ । ତେ ଯୌବନକାଳେ ବିଷୟାଦି ଭୋଗ କୃତବନ୍ତଃ ।
7. कालिदासः कथं रघुवशं वर्णयितुं प्रेरित: ?
Solution:
ମହାକବି କାଳିଦାସ ସୂର୍ଯ୍ୟବଂଶଂ ରଚୟିତୁମ୍ ଇୟେଷ । ତସ୍ୟ ବୁଦ୍ଧି ସ୍ଵଳ୍ପମାସୀତ୍ । ରଘୁବଂଶଂ ବିଶାଳମାସୀତ୍ । ତନୁବାଗ୍ବିଭବ ଅପି ରଘୁବଂଶୀୟ ରାଜାନାଂ ଗୁଣି କର୍ଣ୍ଣମ୍ ଆଗତ୍ୟ ଚାପଳାୟ ପ୍ରଚୋଦିତଃ ସନ୍ କାଳିଦାନଃ ରଘୁଣାମ୍ ଅନ୍ବୟଂ ବକ୍ଷ୍ୟ ।
8. रघुवंशमहाकाव्यं श्रोतुं के प्रभवन्ति ?
Solution:
ବିଶାଳସୂର୍ଯ୍ୟବଂଶଂ ରଘୁବଂଶଂ ବା ଶ୍ରୋତାଂ ସର୍ବେ ନ ସମର୍ଥା ଭବନ୍ତି । କେବଳଂ ସଦସଦ୍ବ୍ୟକ୍ତିହେତପଃ ସନ୍ତଃ ରଘୁବଂଶମହାକାବ୍ୟ ଶ୍ରୋତୁମ୍ ଅହଁନ୍ତି । ଯଥା ହେମ୍ୱ ବିଶୁଦ୍ଧି ଶ୍ୟାମିକା ଅପି ବା ଅଗ୍ନୀ ସଂଲକ୍ଷ୍ୟତେ ତଥା ରଘୁବଂଶଂ ସଜ୍ଜନେଭ୍ୟ ପଠ୍ୟରେ ।
9. हेम्नः विशुद्धिः कथं परीक्ष्यते ?
Solution:
ପଣ୍ଡିତ କେବଳଂ ରଘୁବଂଶମହାକାବ୍ୟ ଶ୍ରୋତୁଃ ସମର୍ଥା ଭବନ୍ତି । ଅତଃ ଅସ୍ଥିନ୍ ସଂସାରେ ସୁଧୀଜନା କାବ୍ୟସ୍ୟ ଦୋଷାଦୋଷାନ୍ ନିର୍ଣ୍ଣୟନ୍ତି । ଯତଃ ସୁବର୍ଣ୍ଣସ୍ୟ ଶୁଦ୍ଧତା ଶ୍ୟାମିକା ବା ଅଗ୍ନୀ ଏବ ପରୀକ୍ଷ୍ଯତେ । ଅତ୍ର ଅଗ୍ନିନା ସାକଂ ରଘୁବଂଶକାବ୍ୟଂ ତୁଳିତଂ ଭବତି ।
10. कस्मिन् वंशे दिलीपः प्रसूतः ?
Solution:
ଶୁଦ୍ଧିମତି ବୈବସ୍ଵତମନୁବଂଶେ ଶୁଦ୍ଧିମତ୍ତରଃ ରାଜଶ୍ରେଷ୍ଠ ଦିଲୀପଃ କ୍ଷୀରସାଗରେ ଇନ୍ଦୁ ଇବ ଜାତଃ । ମନୁବଂଶଃ ସୂର୍ଯ୍ୟବଂଶଃ ବା ରଘୁବଂଶଃ ରୂପେଣ ଖ୍ୟାତଃ । ଦିଲୀପଃ ଅସ୍ଥିନ୍ ବଂଶେ ଶ୍ରେଷ୍ଠରାଜାରୂପେଣ ଅଜାୟତଃ ।
11. दिलीपस्य शरीरं कीदृशमासीत् ?
Solution:
ବୈବସ୍ୱତମନୋ ବଂଶ ଦିଲୀପଃ ନାମା ରାଜା ଜାତଃ । ସ ସୁନ୍ଦରଃ ଆସୀତ୍ । ତସ୍ୟ ବକ୍ଷସ୍ଥଳଂ ବିଶାଳମ୍, ସ୍କନ୍ଧଦେଶଃ ବୃଷଭସ୍ୟ ଇବ ଆସୀତ୍ । ସ୍ତ୍ରୀ ଶାଳବୃକ୍ଷ ସଦୃଶଃ ଉନ୍ନତଃ ଦୀର୍ଘବାହୁ ଚ ଆସୀତ୍ । ରାଜା ଦିଲୀପଃ କ୍ଷାତ୍ରଧର୍ମସ୍ୟ ମୂର୍ତ୍ତିମାନ୍ ସାକ୍ଷାତ୍ ବିଗ୍ରହଃ ଆସୀତ୍ । ଡଃ ସର୍ବେଭ୍ୟ ଅଧ୍ଵଂ ବଳଶାଳୀ ଆସୀତ୍ ।
12. राजा दिलीपस्य सफलता कीदृशी आसीत् ?
Solution:
ରାଜା ଦିଲୀପଃ ବୁଦ୍ଧିମାନ୍, ସୁନ୍ଦରଃ, ଶାସ୍ତ୍ରଜ୍ଞା, କର୍ମପରାୟଣଶ୍ଚାସୀତ୍ । ତସ୍ୟ ବିଶାଳଶରୀରାନୁରୂପଂ ସୌନ୍ଦର୍ଯ୍ୟମାସୀତ୍ । ତସ୍ୟ ଦର୍ଶନୀୟସ୍ୱରୂପାନୁସାରଂ ଶାସ୍ତେଷୁ ଜ୍ଞାନମଣ୍ଡି । ପୁନଶ୍ଚ ତସ୍ୟ ଶାସ୍ତ୍ରଜ୍ଞାନୁନୁରୂପଂ କର୍ମାନୁଷ୍ଠାନମପି ଆସୀତ୍ । କର୍ମଶଃ ଅନୁରୂପଂ ସଫଳତାଂ ପ୍ରାପ୍ଳୁତି । ଦିଲୀପସ୍ୟ ସର୍ବବିଧ କର୍ମ ସଫଳଂ ଭବତି ।
13. राजा दिलीपः प्रजाभ्यः कथं वलिम् अग्रहीत् ?
Solution:
ପ୍ରଜାପାଳନଂ କରଗ୍ରହଣଂ ଚ ରାଜ୍ଞ ପରମକର୍ତ୍ତବ୍ୟମ୍ । ଇତ୍ୟବ ବଚନମନୁସୃତ୍ୟ ରାଜା ଦିଲୀପଃ ପ୍ରଜାନାଂ ଉନ୍ନତ୍ୟର୍ଥମ୍ ଏବ ତାଭ୍ୟ ଷକ୍ଷାଂଶରୂପଂ କରମ୍ ଅଗ୍ରହୀତ୍ । ତଦର୍ଥଜାତଂ ସ ନାନାବିଧେଷୁ କଲ୍ୟାଣକରେଷୁ କାର୍ଯ୍ୟଶ୍ରୁ ବିନିଯୋଗ୍ଯ ପ୍ରଜାନାମ୍ ଅଶେଷ ହିତଂ ଚକାର । ଯଥା ସୂର୍ଯ୍ୟ ସହସ୍ରଗୁଣଂ ବୃଷ୍ଟି କର୍ଡିଂ ଜଳଂ ହି ଗୃହ୍ଣାତି ।
14. दिलीपस्य शरीरं कीदृशमासीत् ?
Solution:
ଦିଲୀପଃ ଶାସ୍ତ୍ରାନୁସାରଂ ସ୍ଵତ୍ୟନୁସାରଂ ଚ ପ୍ରଜାପାଳନମ୍ ଅକରୋତ୍ । ଡଃ ମନୁପ୍ରୋକ୍ତା ନୀତ୍ୟନୁସାରଂ ପ୍ରଜା ପାଳୟାମାନଃ । ପ୍ରଜା ଅପି ମନୋ ଆରଣ୍ୟ ଆଚରଣ ଅଭ୍ୟସ୍ତା ଆସନ୍ । ଆଚାରମାର୍ଗତ୍ ସାମାନ୍ୟପି ବିଚ୍ୟୁତଃ ନ ଭବନ୍ତି । ଯଥା କୁଶଳସାରଥରିତା ରଥନେମୟ ଇବ ଦିଲୀପସ୍ୟ ପ୍ରଜା ଆଚାରମାନଂ ନ ତ୍ୟକ୍ତବନ୍ତଃ ।
15. दिलीपस्य प्रजापालनं कीदृक् आसीत् ?
Solution:
ମନୁଷ୍ୟଜୀବନେ ଚତୁଃ ପୁରୁଷାର୍ଥୀ ଯଥା – ଧର୍ମ, ଅର୍ଥ, କାମ ମୋକ୍ଷଶ୍ଚ । ରାଜା ଦିଲୀପସ୍ୟ ଅର୍ଥକାମୌ ଧର୍ମୀ ଏବଂ ଆସ୍ତାମ୍ । ରାଜା ସ୍ଥିତୌ ଦଣ୍ଡାନ୍ ଦଣ୍ଡୟତଃ । ରାଜା ପ୍ରସୂତୟେ ପରିଣେତୁ ନାମ କାମଭୋଗଂ କୃତମ୍ । ଅନେନ ରାଜା ଦିଲୀପସ୍ୟ ଅର୍ଥକାମୌ ଅପି ଧର୍ମ ଏବ ଆସ୍ତାମ୍ ।
16. दीलिपस्य अर्थकामौ कीदृशौ आस्ताम् ?
Solution:
ମର୍ତ୍ତ୍ୟ ରାଜା ଦିଲୀପଃ ଯଜ୍ଞାୟ ଶାଂ ଦୁଦୋହ । ଇନ୍ଦ୍ର ଶସ୍ୟାୟ ଦିବଂ ଦୁଦୋହ । ଅନନେ ସଂପଦ୍ ବିନିମୟେନ ଦ୍ରୌ ଉଭୌ ଭୁବନଦ୍ବୟଂ ଦଧତୁଃ । ରାଜା ଦିଲୀପଃ ପୃଥିବ୍ୟା ସ୍ଥିତଃ ସନ୍ ସ୍ଵର୍ଗେପି ସ୍ଵସମ୍ପଦଂ ଲବ୍ଧବାନ୍ ।
17. दिलीपस्य प्रारम्भाः प्राक्तनाः संस्काराः इव कथमासीत् ?
Solution:
ରାଜା ଦିଲୀପସ୍ୟ ଗୁପ୍ତଚରଭାବମ୍ ଅତୀବ ଉନ୍ନତଃ ଆସୀତ୍ । ରାଜ୍ୟ ଶାସନେ ତସ୍ୟ ଗୁପ୍ତବିଚାରଂ ନ କୋଽପି ଜ୍ଞାତୁଃ ପ୍ରଭବତି | ଡଃ ସାମ-ଦାନ-ଦଣ୍ଡାଦି ନୀତିଃ ପ୍ରୟୋଗେଣ ବିଚକ୍ଷତଃ ଆସୀତ୍ | ଯଥା ପୂର୍ବଜନ୍ମାର୍ଜିତଃ ସଂସ୍କାରା ପ୍ରାଣିଶୁ ଚାସୀତ୍ । ତସ୍ୟ ପ୍ରାରମ୍ଭା ଫଳାନୁମେୟା ଭବତି ।
18. राजा दिलीप: कथं सुखमन्वभूत् ?
Solution:
ରାଜା ଦିଲୀପଃ ସଦା ଭୟଶୂନ୍ୟମାସୀତ୍ । ଡଃ ଅନାୟାସେନ ସ୍ଵଶରୀରରକ୍ଷା ଅସୌ ପୁଣ୍ୟାର୍ଜନମ୍ ଅକରୋତ୍ । ଅଲୁବ୍ଧଃ ସନ୍ ଧନସଂଗ୍ରହଂ କୃତବାନ୍ । ପୁନଶ୍ଚ ଅନାସକ୍ତା ମନ୍ନ ସ୍କଖମ୍ ଅନ୍ନରୁତ୍ |
19. राजादिलीपस्य समीपे विरुद्धाः गुणाः कथम् आसन् ?
Solution:
ରାଜା ଦିଲୀପସ୍ୟ ସମୀପେ ପରସ୍ପରବିରୁଦ୍ଧା ଗୁଣା ସମନ୍ବିତା କରୋତି ସ୍ମ । ରୋଗଶୂନ୍ୟ ସନ୍ ସନ୍ ସୁଖମ୍ ଅନୁଭୂତ୍ । ଅଭୂତ୍ । ଜ୍ଞାନେ ମୌନତା, କ୍ଷମା ଶକ୍ତିଶାଳୀତାୟାମ୍, ତ୍ୟାଗେ ଶ୍ଵାଘାବିପର୍ଯ୍ୟୟ ଅନେନ ପ୍ରକାରେଣ ପରସ୍ପର ବିରୁଦ୍ଧଗୁଣା ଗୁଣ- ଅନୁବନ୍ଧିତ୍ଵାତ୍ ସହୋଦର ଇବ ସ୍ଥିତାଃ ।
20. राजा दिलीपः प्रजानां पिता कथमासीत् ?
Solution:
ରାଜାରୂପେଣ ଦିଲୀପଃ ସର୍ବାଷା ପ୍ରଜାନାଂ ପିତୃପଦବାଚ୍ୟ ଆସୀତ୍ । ପିତା ସ୍ଵସ୍ୟ ପୁତ୍ରସ୍ୟ କୃତମ୍ ଯଦେବ କରୋତି ତଦେବ ଦିଲୀପେନ ସ୍ବପ୍ରଜାର୍ଥୀ କୃତଃ । ପ୍ରଜାନାଂ ବିନୟଶିକ୍ଷାଦାନାତ୍, ରକ୍ଷଣାତ୍, ଭରଣାତ୍, ପାଳନପୋଷଣାତ୍ ଧଃ ତାସାଂ ପିତା ଆସୀତ୍ । ପ୍ରକୃତତଃ ପ୍ରଜାନାଂ ଯେ ପିତରଃ ତେ କେବଳଂ ଜନ୍ମହେତବ ଆସନ୍ତି ।
21. कथं तस्करता श्रुतौ एव स्थिता ?
Solution:
ରାଜା ଦିଲୀପଃ ସୁଶାସନଃ ଆସୀତ୍ । ତସ୍ୟ ରାଜତ୍ଵକାଳେ ତସ୍ମିନ୍ ରାଜ୍ୟ ନ କୋଽପି ଚୌରଃ ଆସୀତ୍ । ତସ୍କରତା ନାମ ଚୌର୍ଯ୍ୟବୃତ୍ତି ତଥ୍ୟ ରାଜ୍ୟ ନାସୀତ୍ । ତସ୍ୟ ରାଜ୍ୟେ ଶାନ୍ତି ଶୃଙ୍ଖଳା ଚ ସଦୈବ ଆସ୍ତାମ୍ । ତସ୍ମିନ୍ ରାଜ୍ୟ ନ କୋଽପି କସ୍ୟ ଧନସ୍ୟ ଅପହରଣଂ କରୋତି । ତସ୍କରତା ନ ପ୍ରଜାସୁ ଶବ୍ଦଷୁ ଆସୀତ୍ ଶୁତୌନାମ ବେଦେ ତସ୍କରତା ଶବ୍ଦରୂପେଣ ଆସୀତ୍ ।
22. दिलीपस्य शिष्टदुष्टयोः व्यवहारः कीदृक् आसीत् ?
Solution:
ରାଜାଦିଲୀପଃ ଶିଷ୍ଟାନାଂ କୃତ ଭିନ୍ନ ବ୍ୟବହାରଃ ପୁନଶ୍ଚ ଦୁଷ୍ଟାନାଂ କୃତେ ଭିନ୍ନ ବ୍ୟବହାରଃ ଦ୍ଦେଶ୍ୟ ଅପି ସମ୍ମତଃ । ସଜନଃ ଶତ୍ରୁରାଜ୍ୟ ପ୍ରଦର୍ଶିତେ ସତି ଗ୍ରହଣୀୟଂ ଭବତି । ଦୁର୍ଜନଃ ପ୍ରିୟ ସନ୍ ତ୍ୟାଜ୍ୟ ବର୍ଜନୀୟଂ ଭବତି । ସଜ୍ଜନଃ ଔଷଧମିବ ଗ୍ରାହ୍ୟ, ଦୁର୍ଜନଃ ଉରଗକ୍ଷତାଙ୍ଗୁଳା ଇବ ତ୍ୟାଜ୍ୟ ଇବତି ଚ |
23. राजा दिलीपस्य सर्वेगुणाः किमर्थम् आसन् ?
Solution:
ପଞ୍ଚଭୂତେନ ରାଜା ଦିଲୀପସ୍ୟ ଶରୀରଂ ବିଧ୍ୱଂ ସସ । ଅତଃ ପଞ୍ଚଭୂତେଷୁ ଯଦେବ ଗୁଣା ତଦେବ ଅସ୍ୟ ରାଜ୍ଞ ଦିଲୀପସ୍ୟ ସମୀପେ ବିରାଜତେ । ଅତଃ ରାଜା ଦିଲୀପସ୍ୟ ସର୍ବଗୁଣା ।
24. दिलीपः कीदृशी उर्वी शशास ?
Solution:
ରାଜା ଦିଲୀପଃ ଚକ୍ରବର୍ତ୍ତୀ ସମ୍ରାଟ୍ ଆସୀତ୍ । ଡଃ ଉପଯୁକ୍ତ ପ୍ରଜାନୁରଞ୍ଜତଃ ରାଜା ଆସୀତ୍ । ଡଃ ବେଳାବପ୍ରବଳୟାଂ ପରିଖୀକୃତସଗରାମ୍ ଅନନ୍ୟଶାସନାମ୍ ଉର୍ବୀମ୍ ଏକପୁରୀମ୍ ଇବ ଶଶାସ୍ତ୍ର ।
दीर्घप्रश्नोत्तरम् :
1. रघुवंशस्य संक्षिप्तपरिचयं प्रदत्तः ।
Solution:
ନାମାନୁସାରଂ ଭବତି । ସୂର୍ଯ୍ୟବଂଶଃ ରୂପେଣ ଖ୍ୟାତଃ ଅସ୍ୟ ବଂଶସ୍ୟ ମହତ୍ତ୍ୱ ମହାକବି କାଳିଦାସେନ ସ୍ଵଳ୍ପବୁଦ୍ଧିତୟା ବର୍ଣ୍ଣିତମ୍ । କବି ଅଳ୍ପଶବ୍ଦବିଭବ ସନ୍ତପି ଆଜନ୍ମନଃ ତେଷା ରଘୁଣା ଶ୍ରୁତିମାର୍ଗମାଗତଃ ଗୁଣି ପ୍ରେରିତଃ ଭୂତ୍ଵା ବିନା ବିଚାରଂ ରଘୁବଂଶ ବର୍ଣ୍ଣନରୂପଂ ଚାପଳଂ କର୍ଭୁମିଚ୍ଛତି । ରଘୁବଂଶଂ ତୁ ମନୁବଂଶରୂପେଣ ପ୍ରଖ୍ୟାତଃ । ମନୂନା ସଂଖ୍ୟା ଚତୁର୍ଦ୍ଦଶ । ସମ୍ପ୍ରତି ସପ୍ତମଂ ମନ୍ବନ୍ତରଂ ପ୍ରଚଳତି । ଏତଃ ମନୁଃ ସୂର୍ଯ୍ୟସ୍ୟ ପୁତ୍ରତ୍ୱାତ୍ ବୈବସ୍ବତଃ ମନୁରିତି ଖ୍ୟାତଃ । ଭୂଲୋକେ ସ୍ୱ ସର୍ବେକ୍ଷାଂ ନୃପାଣାମ୍ ଅଗ୍ରଣୀ ଆସୀତ୍ । ବୈବସ୍ଵତଃ ମନୁଃ ଭୂପାଳାନାମ୍ ଆଦିଭୂତଃ ଆସୀତ୍ ସର୍ବପୂଜ୍ୟ ଚ ଆସୀତ୍ । ସୋଽୟଂ ସୂର୍ଯ୍ୟବଂଶସ୍ୟ ରଘୁବଂଶସ୍ୟ ବା ପ୍ରତିଷ୍ଠାତା ବଭୂବ । ଅତଃ କବି କାଳିଦାସ ଭୁବନପ୍ରସିଦ୍ଧାନାଂ ରଘୁବଂଶୀୟାନାଂ ରାଜାନାଂ ଚରିତଂ ବର୍ଷୟତି ।
ଏତେ ରଘୁବଂଶୀୟ ରାଜାନଃ ଜନ୍ମନଃ ଆରଭ୍ୟ ନିଷେକାଦି ସଂସ୍କାରଃ ପବିତ୍ରା ଆସନ୍, ଫଳପ୍ରାପ୍ତି ଯାବତ୍ କର୍ମତତ୍ପ ବଭୂମଃ, ଆସମୁଦ୍ର ଧରାୟା ସାର୍ବଭୌମା ଅଧୀଶ୍ଵରଃ ଜାତା ତଥା ସ୍ବର୍ଗ ଯାବତ୍ ତେଷା ରଥମାର୍ଗ ବ୍ୟାପ୍ତା ଅଭବନ୍ ଚ । ଏତେ ରାଜାନଃ ବିଧୂମ ଅନତିକ୍ରମ୍ୟ ଅଗ୍ନିମ୍ ଆହୂତ୍ୟାଦିଭିଂ ପୂଜିତବନ୍ତୀ, ଅତିଥୀନ୍ ଅର୍ଜିତବନ୍ତୀ, ଅପରାଧାନୁସାରମ୍ ଅପରାଧୂନଃ ଦଣ୍ଡିତବନ୍ତୀ । ସମୁଚିତେ କାଳେ ଜାଗରୂକା ଅଭିବନ୍ ଚ । ସତ୍ପାତ୍ରାୟ ଦାତୁଃ ଧନଂ ସଞ୍ଚବନ୍ତଃ, ସତ୍ୟାୟ ସ୍ଵଚ୍ଛ ଭାଷିତବନ୍ତଃ, ଅନ୍ୟ ପରାଜେତୁ ନ, ଅପିତୁ କୀର୍ତିନିମିତ୍ତ ବିଜୟମ୍ ଇଷ୍ଟବନ୍ତଃ, ସନ୍ତାନାୟ ଭାର୍ଯ୍ୟାଗୃହୀତବନ୍ତୀ ନ ତୁ ଇନ୍ଦ୍ରିୟସୁଖାର୍ଥମ୍ । ଶୈଶବେ ବିଦ୍ୟାଭ୍ୟାସଂ, ଯୌବନେ ବିଷୟଭୋଗ୍ୟ, ବାର୍ଦ୍ଧକ୍ୟ ମୁନିବୃରିଂ, ଅନ୍ତକାଳେ ଯୋଗେନ ତନୁ ତ୍ୟକ୍ତବନ୍ତଃ ଚ । ଏତାଦୃଶସ୍ୟ ରାଜ୍ଞ ଚରିତେନ ରଘୁବଂଶସ୍ୟ
2. राज्ञः दिलीपस्य स्वरूपं वर्णयत ।
Solution:
ଶରୀରଶୋଭା ଅତୀବ ଚମତ୍କାରୀ ଆସୀତ୍ । ତସ୍ୟା ଉରୁସ୍ଥଳଂ ବିପୁଳମ୍ ଆସୀତ୍ । ବୃଷଭସ୍ୟ ସ୍କନ୍ଧ ଇବ ତଥ୍ୟ ସ୍କନ୍ଧସ୍ବୟଂ ବଭୂବ ଶାଳବୃକ୍ଷସମଃ ସ ଉନ୍ନତଃ ଅସୀତ୍ । ତସ୍ୟ ଭୁଜଯୁଗଳଂ ସୁଦୀର୍ଘ ଶରଂ ଚ ଆସୀତ୍ । ଅସୌ ରାଜା ଦିଲୀପଃ ସ୍ବବ୍ୟାପାରାନୁରୂପଂ ଶରୀରଂ ପ୍ରାପ୍ତବାନ୍ । ଡଃ କ୍ଷାତ୍ରଧର୍ମୀ ଇବ ତନ୍ମାମ ମୂର୍ତ୍ତିମାନ୍ ପରାକ୍ରମ ଇବ ସ୍ଥିତଃ । ଡଃ ସର୍ବେଭ୍ୟ ଭୂତେଭ୍ୟ ଅଧିକ ବଳବାନ୍ ଭୂତ୍ବା ତାନି ସର୍ବାଣି ତେଜସା ଅଭିଭୂୟ ଉନ୍ନତଶରୀରେଣ ମେରୁପର୍ବତଃ ଇବ ମହୀ ପୃଥିବୀ ବା ଆକ୍ରମ୍ୟ ସ୍ଥିତଃ । ରାଜା ଦିଲୀପସ୍ୟ ଯଥା ରୂପିଂ ତଥା ପରାକ୍ରମଂ ଶକ୍ତି ଚ ଆସୀତ୍ ।
3. दिलीपस्य राज्यशासनपद्धतिं विशदयत ।
Solution:
ଦିଲ୍ଲୀପେନ ଶାସିତଃ ପ୍ରଜା ସାରଥେ ରଥନେମିବୃଭିବତ୍ ମନୁପ୍ରୋକ୍ତାତ୍ ମାର୍ଗାତ୍ ରେଖାପ୍ରମାଣମପି ନ ବ୍ୟତୀୟୁ । ଯଥା ରବି ସହସ୍ରଗୁନଃ ବର୍ଷତୁଃ ଜଳଂ ଗୃହ୍ଣାତି ତଥାସୌ ଦିଲୀପଃ ପ୍ରଜାନାଂ କଲ୍ୟାଣାୟ ତାଭ୍ୟ ଷକ୍ଷାଂଶରୂପଂ କରମ୍ ଅଗ୍ରହୀତ୍ । ଚତୁରଙ୍ଗବଳଂ ତସ୍ୟ ଉପକରଣଂ, ଶାସ୍ତ୍ରଷୁ ତୀକ୍ଷ୍ଣବୁଦ୍ଧି ଧନୁଷି ଆରୋପିତା ଜ୍ୟା ଚ ତଥ୍ୟ ଅର୍ଥସାଧନଦ୍ବୟଂ ବଭୂବ । ତଥ୍ୟ ଗୂଢ଼ ବିହିତାନି କର୍ମାଣି ପ୍ରାକ୍ତନ ସଂସ୍କାରା ଇବ ଫଳାନୁମେୟାନି ଜାତାନି । ଅର୍ଥେ ନିର୍ଭୟ ସନ୍ ଆତ୍ମାନଂ ରରକ୍ଷ, ଅରୁଗ ସନ୍ ଧର୍ମ ଚଚାର, ନିର୍ଲୋଭଃ ସନ୍ ଅର୍ଥମ୍ ଆଦରେ, ନିରାସକ୍ତ ସନ୍ ସୁଖମ୍ ଅନ୍ଧଭବତ୍ ଚ । ସ ପ୍ରଜାନାଂ ସନ୍ମାର୍ଗପ୍ରଦର୍ଶନାତ୍, ଭାର୍ଯ୍ୟାଗ୍ରହଣଂ କୁର୍ବତଃ ଦିଲୀପସ୍ୟ ଅର୍ଥକାମାଁ ଧର୍ମ ଏବ ଆସ୍ତାମ୍ । ଅସୌ ଦିଲୀପଃ ପ୍ରଜାଭ୍ୟ କରଂ ଗୃହୀତ୍ମା ଯଜ୍ଞକରଣେନ, ଇନ୍ଦ୍ର ସ୍ବର୍ଗ ରିଭିଂ ବିଧାୟ ପ୍ରଚୁର ବୃଷ୍ଟିପାତେନ କ୍ରମଶଃ ମର୍ତ୍ତ୍ୟ ସ୍ବର୍ଗ ଚ ଭୁବନଦ୍ଵୟଂ ପୁପୁଷତଃ ।

ଶ୍ଳୋକ – ୧
वागर्थाविव संपृक्तौ वागर्थप्रतिपत्तये |
जगतः पितरौ वन्दे पार्वतीपरमेश्वरौ ।। १ ।।
ବାଗର୍ଥାବିବ ସଂପୂ ବାଗର୍ଥପ୍ରତିପତ୍ତୟେ ।
ଜଗତଃ ପିତରୌ ବନ୍ଦେ ପାର୍ବତୀ ପରମେଶ୍ଵରୌ || ୧ ||
ଅନ୍ବୟ – (ଅହଂ) ବାଗ ବିବସଂପୃକ୍ତା ଜଗତଃ ପିତରୌ ପାର୍ବତୀପରମେଶ୍ଵରୌ ବାଗର୍ଥ ପ୍ରତିପତ୍ତୟେ ବନ୍ଦେ ।
ଶବ୍ଦାର୍ଥ – ବାଗର୍ଥାବିବ = ଶବ୍ଦ ଏବଂ ଅର୍ଥ ଭଳି । ସଂପୃଭୌ = ସଂପୃକ୍ତ ହୋଇଥିବା । ଜଗତଃ= ଜଗତର । ପିତରୌ = ପିତା ଓ ମାତାଙ୍କୁ | ପାର୍ବତୀପରମେଶ୍ଵରୌ = ପାର୍ବତୀ ଓ ପରମେଶ୍ଵରଙ୍କୁ । ବାଗର୍ଥପ୍ରତିପଭୟେ = ଶବ୍ଦ ଏବଂ ଅର୍ଥ ଉଭୟର ସମ୍ୟକ୍ ଜ୍ଞାନ ନିମନ୍ତେ । ବନ୍ଦେ = ବନ୍ଦନା କରୁଛି ।
ର୍ଥନ୍ମବାଦ – ଶବ୍ଦ ଏବଂ ଅର୍ଥ ଭଳି ନିତ୍ୟଭାବରେ ସଂପୃକ୍ତ ଥିବା ସଂସାରର ପିତା ଓ ମାତା ଭଗବାନ୍ ଶିବ ଓ ପାର୍ବତୀଙ୍କୁ ଶବ୍ଦ ଏବଂ ଅର୍ଥ ବିଷୟରେ ଭଲଭାବେ ଜ୍ଞାନଅର୍ଜନ କରିବାପାଇଁ (ମୁଁ) ବନ୍ଦନା କରୁଅଛି
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋୟାଂ ପଠିତଃ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ‘ରଘୁବଂଶମ୍’ ମହାକାବସ୍ୟ ପ୍ରଥମସର୍ଗୀତ୍ ଆନୀତଃ । ର୍ଥମିନ୍ ଶୋକେ ସ୍ତ୍ରନ୍ଥନିବିମ୍ପରିସରରେ କାବ୍ୟାୟମେ ମଲଂଳାଚରଣ ରୂପେଶ ପାତପରମେଶ୍ଵରରେ ବନ୍ଦନଂ ମଦ୍ରାକବିନା କୃତମ୍ ।
କାବ୍ୟଲକ୍ଷଣ ପରମ୍ପରାନୁସାରେଣ ରଚିତଃ ମହାକବି କାଳିଦାସସ୍ୟ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟମ୍ । ଅସ୍ଥିନ୍ ମହାକାବ୍ୟ ବିନା କୋଽପି କବି କାବ୍ୟରଚୟିତାଂ ନ ସମର୍ଥୀ ଭବତି । ଶବ୍ଦନ ସାକଂ ପାର୍ବତୀ ଅର୍ଥଣ ସହ ମହେଶ୍ଵରଂ ଚ ତୁଳିତମ୍ । କବି ଉପମାଳଂକାରସ୍ୟ ସଫଳପ୍ରୟୋଗମ୍ ଅତ୍ର କୃତମ୍ । ଅତଃ ଉକ୍ତ ଯତ୍ – ବାଗର୍ଥେ ଇବ ସଂପୃଭୌ ଜଗତଃ ପିତରୌ ପାର୍ବତୀପରମେଶ୍ଵରୌ ଶବ୍ଦାର୍ଥ ସମ୍ୟଜ୍ଞାନାର୍ଥୀ ଅହଂ କାଳିଦାସ ଅଭିବାଦୟେ । ସର୍ବେ ଜଗତଃ ପିତରୌ ପାର୍ବତୀପରମେଶ୍ଵରୌ ଅବଶ୍ୟ ବନ୍ଦନଂ କୁର୍ଯ୍ୟ । ଅନେନ କାଳିଦାସସ୍ୟ ଶିବଭକ୍ତି ସୂଚିତଂ ଭବତି ।
ବ୍ୟାକାରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ବାଗର୍ଥବିଦ = ବାକ୍ + ଅର୍ଥେ + ଇବ । ବାଗର୍ଥପ୍ରତିପତ୍ତୟେ = ବାକ୍ + ଅର୍ଥପ୍ରତିପତ୍ତୟେ ।
ସମାସ – ବାଗର୍ଥାବିବ – ବାକ୍ ଚ ଅର୍ଥଶ୍ଚ ଇତି ବାଗାଆଁ (ଦ୍ବନ୍ଦ୍ବ), ତୌ = ବାକ୍ ଚ ଅର୍ଥଶ୍ଚ (ଦ୍ବନ୍ଦ୍ବ), ତ ପ୍ରତିପତିଃ, ତଥ୍ୟ (୬୩ ତତ୍) । ପିତରେ ପରମେଶ୍ଵରୌ = ପାର୍ବତୀ ଚ ପରମେଶ୍ଵରଶ୍ଚ (ଦ୍ବନ୍ଦ୍ବ) । = ମାତା ଚ ପିତା ଚ (ଦ୍ବନ୍ଦ୍ବ), ପାର୍ବତୀ ପରମେଶଭୌ = ପାବାଦା ଚ ପରମେଶ୍ବରଣ (ଦଦ୍ଵ) |
ସକାରଣବିଭକ୍ତି – ବାଗର୍ଥପ୍ରତିପତ୍ତୟେ = ତାଦଥ୍ୟ ବା ନିମିତ୍ତାର୍ଥେ ୪ ର୍ଥୀ । ଜଗତଃ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ପିତରେ, ସଂପୃଲ୍ଲୋ, ପାର୍ବତୀ ପରମେଶ୍ଵରୌ = କର୍ମଣି ୨ୟା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସଂପୃଭୌ = ସମ୍ + ପୃଚ୍ + କ୍ତ (୨ୟା ଦ୍ଵିବଚନ) । ପ୍ରତିପତିଃ = ପ୍ରତି + ପଦ୍ + ସ୍କ୍ରିନ୍ ।
ଶ୍ଳୋକ – ୨
क्व सूर्यप्रभवो वंशः क्व चाल्पविषया मतिः ।
तितीर्षुर्दुस्तरं मोहादुडुपेनास्मि सागरम् ।। २ ।।
କୃ ସୂର୍ଯ୍ୟପ୍ରଭବୋ ବଂଶଃ କ୍ଵ ଚାଳ୍ପବିଷୟା ମତିଃ ।
ତିତୀର୍ଷସ୍ତରଂ ମୋହାଦୁଡୁପେନାସ୍ତି ସାଗରମ୍ ||୨||
ଅନ୍ବୟ – ସୂର୍ଯ୍ୟପ୍ରଭତଃ ବଂଶଃ କ୍ଵ ? ଅଳ୍ପବିଷୟା ମମ ମତିଶ୍ଚ କ୍ବ ? ଅହଂ ମୋହାତ୍ ଉଡୁପେନ୍ ଦୁସ୍ତରଂ ସାଗରଂ ତିତୀର୍ଷୁ ଅସ୍ଥି ।
ଶବ୍ଦାର୍ଥ – ସୂର୍ଯ୍ୟପ୍ରଭବ = ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଜାତ ହୋଇଥିବା । ବଂଶଃ = କୁଳ । କୁ = କେଉଁଠି । ଅଳ୍ପବିଷୟା ମମ ମତିଶ୍ଚ = ଅଳ୍ପବିଷୟକୁ ଜାଣିଥୁବା ମୋର ବୁଦ୍ଧି । ଅହଂ = ମୁଁ । ମୋହାତ୍ = ମୋହ ହେତୁରୁ । ଉଡୁପେନ = ଡଙ୍ଗାଦ୍ଵାରା । ଦୁସ୍ତରଂ ସାଗରଂ = ଦୁସ୍ତର ସମୁଦ୍ରକୁ । ତିତୀର୍ଷୁ ଅଗ୍ନି = ତିତୀର୍ଷୁ ଅଗ୍ନି ପାରହେବାକୁ ଇଚ୍ଛା କରୁଛି |
ଅନୁବାଦ – ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଜାତ ହୋଇଥିବା (ପ୍ରସିଦ୍ଧ) ବଂଶ କେଉଁଠି ? ଏବଂ ଅଳ୍ପ ବିଷୟକୁ ମାତ୍ର ଜାଣିଥୁବା ମୋର ବୁଦ୍ଧି କେଉଁଠି ? ମୁଁ ମୋହବଶତଃ ସାମାନ୍ୟ ଡଙ୍ଗାଦ୍ଵାରା ଦୁସ୍ତର ସମୁଦ୍ରକୁ ପାରହେବାକୁ ଇଚ୍ଛା କରୁଛି ।
ବ୍ୟାଖ୍ୟା – ଉଦ୍ଧୃତଃ ଶ୍ଳୋକ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ୟ ପଦ୍ୟଭାଗସ୍ଥ ମହାକବି କାଳିଦାସ କୃତଃ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ମହାକବି କାଳିଦାସ ସ୍ଵାହଂକାରଂ ବିହାୟ ସ୍ଵଭାବସୁଲଭିଂ ବିନମ୍ରତା ଗୁଣସ୍ୟ ପ୍ରଦର୍ଶନଂ କୃତମ୍ ।
ଗ୍ରନ୍ଥାରମ୍ଭେ ମଙ୍ଗଳାଚରଣାତ୍ ଅନନ୍ତରଂ କବି କାବ୍ୟାର୍ଥୀ ପ୍ରଯନୁବାନ୍ ଆସୀତ୍ । ‘ବିଦ୍ୟା ଦଦାତି ବିନୟମ୍’ । ସ୍ୱୀୟଜ୍ଞାନଂ ଦେବୀସରସ୍ୱତ୍ୟା କୃପାବଳେନ ସୁପ୍ରସିଦ୍ଧ ରଘୁବଂଶଂ ସୂର୍ଯ୍ୟବଂଶଂ ବା ବର୍ଣ୍ଣତୁ ପ୍ରଯତତେ । ଏତଦର୍ଥୀ କବି ସ୍ଵକୀୟ ଅକ୍ଷମଣୀୟତାଂ ଭବତି ତଥା ସ୍ଵଳ୍ପଜ୍ଞାନେନ ସୂର୍ଯ୍ୟବଂଶସ୍ୟ ବର୍ଣ୍ଣନଂ କଠିନଂ ଭବତି । ତଥାପି ମୋହବଶାତ୍ କାଳିଦାନଃ ଅସ୍ୟ ବଂଶସ୍ୟ ବର୍ଣ୍ଣନଂ କର୍ଭୁମିୟେଷ । ଅସ୍ମାତ୍ ଶ୍ଳୋକାତ୍ ସୂର୍ଯ୍ୟବଂଶସ୍ୟ ପ୍ରସିଦ୍ଧି ତଥା ମହାକବୋ ମହାନତା ପ୍ରତିଫଳିତଂ ଭବତି । ଅନ୍ୟଷା କବିନାଂ କୃତେ ଏତଦ୍ ଆଦର୍ଶଶିକ୍ଷଣଂ ଭବତି ।
ବ୍ୟାକାରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଚାକବିପ୍ରମପତି: – ଚ + ଅଳ୍ପବିଷୟାମତିଃ । ତିତୀର୍ଷୁର୍ଦ୍ଧ୍ଵସ୍ତରଂ = ତିତୀର୍ଷୁ + ଦୁସ୍ତରମ୍ । ମୋହାଦୁଡୁପେନାସ୍ତି = ମୋହାତ୍ + ଉଡୁପେନ + ଅସ୍ଥି ।
ସମାସ – ବାଗର୍ଥାବିବ: = ସୂର୍ଯ୍ୟ ପ୍ରଭବ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) । ଅଳ୍ପବିଷୟା = ଅନ୍ତଃ ବିଷୟ ଯସ୍ୟା ସା ( ବହୁବ୍ରୀହିଃ) । ଦୁସ୍ତରମ୍ = ଦୁଃଖେନ ତୀର୍ଯ୍ୟତେ ଇତି, ତମ୍ (ଉପପଦ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ବଂଶଃ, ଅଳ୍ପବିଷୟ, ମତିଃ, ଅହମ୍ = କଉଁରି ୧ ମା। ଦୁସ୍ତରଂ, ସାଗରଂ = କର୍ମଣି ୨ୟା । ମୋହାତ୍ = ହେତୌ ୫ମୀ । ଉଡୁପେନ = କରଣେ ୩ୟା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସୂର୍ଯ୍ୟ = ସ୍କୃ + କ୍ୟପ୍ । ପ୍ରଭବ = ପ୍ର + ଭୁ + ଅପ୍ । ମତିଃ = ମନ୍ + ସ୍କ୍ରିନ୍ । ତିତୀର୍ଷୁ = ତୃ + ସନ୍ + ଉ । ଦୁସ୍ତରମ୍ = ଦୁସ୍ + ତୃ + ଖଳ୍ । ମୋହଃ = ମୁହ୍ + ଘଞ୍ଚ୍ । ଉଡୁପଃ = ଉଡୁ + ପା + କ ।
ଶ୍ଳୋକ – ୩
मन्दः कवियशः प्रार्थी गमिष्याम्युपहास्यताम् ।
प्रांशुलभ्ये फले लोभादुद्वाहुरिव वामनः ||३||
ମନ୍ଦ କବିଯଶଃପ୍ରାର୍ଥୀ ଗମିଷ୍ୟାମ୍ୟପହାସ୍ୟତାମ୍ ।
ପାଂଶୁଲଭ୍ୟ ଫଳେ ଲୋଭାଦୁଡା଼ହୁରିବ ବାମନଃ ॥ ୩ ॥
ଅନ୍ବୟ – ମନ୍ଦ (ତଥାପି) କବିଯଶଃପ୍ରାର୍ଥୀ ଅହଂ ପାଂଶୁଲଭ୍ୟଫଳେ ଲୋଭାତ୍ ଉଦ୍ବାରଃ ବାମନଃ ଇବ ଉପହାସ୍ୟତାଂ ଗମିଷ୍ୟାମି ।
ଶବ୍ଦାର୍ଥ – ମଦଃ = ମୂର୍ଖ । କବିଯଶଃପ୍ରାର୍ଥୀ = କବିର ଯଶ ଅଭିଳାଷୀ । ଅହଂ = ମୁଁ । ପାଂଶୁଲଭିଂ = ଉନ୍ନତ ପୁରୁଷ ପାଇବାଯୋଗ୍ୟ । ଫଳେ = ଫଳ ପ୍ରସଙ୍ଗରେ । ଲୋଭାତ୍ = ଅତ୍ୟନ୍ତ ଲୋଭହେତୁରୁ । ଉଦ୍ବାହୁ ବାମନଃ ଇବ = ବାମନ ଭଳି । ଉପହାସ୍ୟତାଂ ଗମିଷ୍ୟାମି = ଉପହସନୀୟ ହେବି ।
ଅନୁବାଦ – ମୂର୍ଖ ହୋଇ କବିକୀର୍ତି ପାଇବାକୁ ଆଶାକରି ମୁଁ ଯେଭଳି ଏକ ଉନ୍ନତ (ଡେଙ୍ଗା) ପୁରୁଷ ପାଇବାଯୋଗ୍ୟ
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ୟ ‘ ରଘୁବଂଶମ୍’ ପଦ୍ୟଭାଗାତ୍ ଆନୀତଃ । ଅସ୍ୟ ରଚୟିତା ମହାକବି କାଳିଦାସ । ପଞ୍ଚମହାକାବ୍ୟ ମଧେ ଅନ୍ୟତମ ‘ରଘୁବଂଶମ୍’ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମସର୍ଥାତ୍ ଶ୍ଳୋକୋଽୟଂ ସଂଗୃହିତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ କହିଃ ସ୍ୱୟମେବ ମୂର୍ଖମ୍‘ଇତି ମଜ୍ଜା ମହାକାବ୍ୟସ୍ୟ ରଚନେ ଅସାମର୍ଥ୍ୟ ପରିପ୍ରକାଶୟତି । ସୂର୍ଯ୍ୟବଂଶଃ ଇବ ବିଶ୍ୱବିଶୁତଃ ବଂଶଂ ବର୍ଷତୁଃ କବେ ଅସାମର୍ଥ୍ୟମ ଅତ୍ର ବର୍ଣ୍ଣିତଃ । ମୋହାତ୍ କବିଯଶପ୍ରାର୍ଥୀ ସନ୍ କାଳିଦାନଃ ସୂର୍ଯ୍ୟବଂଶଃ ଇବ ସୁବିଶାଳଂ ବଂଶଂ ବର୍ଷତୁଃ ପ୍ରଯବାନ୍ ଭବତି । ଏତତ୍ ତୁ ଉପହସନୀୟଂ ଭବତି । ପ୍ରାଶୁଲଭ୍ୟ ଫଳେ ଲୋଭାତ୍ ବାମନଃ ଉଦ୍ବାହୁ ଇବ କାଳିଦାନଃ ମୋହାତ୍ ପ୍ରଯନଂ କର୍ଭୁମ୍ ଉତିଷ୍ଠତେ । କାଳିଦାସସ୍ୟ ଏତାଦୃଶଂ ଦୁଃସାହସଂ ତୁ ପ୍ରଭୃତୟଃ ସୁମହାନୌ କବୀ କେବଳଂ ବର୍ଣ୍ଣୟିତୁ ଶକ୍ୟତେ ପରନ୍ତୁ ମହାକବି କାଳିଦାସ ନ । ଏତତ୍ ତୁ ମହାକବେ ପ୍ରାଚୀନକବିନ କୃତେ ସମ୍ମାନବୋଧଃ ସ୍ଵସ୍ୟ ନିରହଂକାରଶ୍ଚ ସୂଚୟତି ।
ସନ୍ଦିବିଛେଦ – ଗମିଷ୍ୟାମ୍ୟୁପହାସ୍ୟତାମ୍ = ଗମିଷ୍ୟାମି + ଉପହାସ୍ୟତାମ୍ । ଉଦ୍ବାହୁରିବ = ଉତ୍ + ବାହୁ + ଇବ ।
ସମାସ – କବିଯଶଃ = କବୀନାଂ ଯଶଃ (୬ଷ୍ଠ ତତ୍) । ପାଂଶୁଲଭ୍ୟ = ପାଂଶୁନା ଲଭ୍ୟମ୍, ତସ୍ମିନ୍ (୩ୟା ତତ୍) । ଉତ୍ତୋଳିତଃ ବାହୁର୍ମେନ ଡଃ (ବହୁବ୍ରୀହିଃ) ।
ସକାରଣବିଭକ୍ତି – ମଦଃ = କଉଁରି ୧ ମା । କବିଯଶଃପ୍ରାର୍ଥୀ = କର୍ଭରି ୧ ମା । ଉପହାସ୍ୟତାମ୍ = କର୍ମଣି ୨ୟା ।
ଅଧିକରଣେ ୭ମୀ । ଫଳେ = ବିଷୟାଧ୍ୟାକରଣେ ୭ମୀ । ଲୋଭାତ୍ = ହେତେ ୫ମୀ । ବାମନଃ = ଇବ ଅବ୍ୟୟ ଯୋଗେ ୧ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ପ୍ରାର୍ଥୀ = ପ୍ର + ଅର୍ଥ + ଣିନି । ଉପହାସ୍ୟତାମ୍ = ଉପହାସ + ଣ୍ୟତ୍ + ତଳ୍ + ଟାପ୍ । ଲଭ୍ୟମ୍ = ଲଭ୍ + ଯତ୍ । ଲୋଭୀ = ଲଭ୍ + ଘଞ୍ଚ୍ ।
ଶ୍ଳୋକ – ୪
अथ वा कृतवाग्द्वारे वंशेऽस्मिन्पूर्वसूरिभिः ।
मणौ वज्रसमुत्कीर्णे सूत्रस्येवास्ति मे गतिः || ४ ||
ଅଥ ବା କୃତବାଗ୍ରେ ବଂଶେଽସ୍ମିନ୍ପୂର୍ବସୂରିଭି ।
ମଣି ବଜ୍ରସମୁତ୍ର୍ରେ ସୂତ୍ରସ୍ୟବାସ୍ତି ମେ ଗତିଃ ॥ ୪ ॥
ଅନ୍ବୟ – ଅଥ ବା ପୂର୍ବସୂରିଭିଂ କୃତବାଗ୍ରେ ଅଶ୍ବିନ୍ ବଂଶେ ବଜ୍ରସମୁଣ୍ଡେ ମଣି ସୂତ୍ରସ୍ୟ ଇବ ମେ ଗତିଃ ଅସ୍ତି |
ଶବ୍ଦାର୍ଥ – ଅଥ ବା = ଅନ୍ୟପକ୍ଷରେ । ପୂର୍ବସୂରିଭିଂ = ପ୍ରାଚୀନ କବିମାନଙ୍କଦ୍ଵାରା । କୃତବାଗଦ୍ଵାରେ ହୋଇଥିବା କାବ୍ୟଦ୍ଵାରରେ । ଅସ୍କ୍ରିନ୍ ବଂଶ = ଏହି ସୂର୍ଯ୍ୟବଂଶରେ । ବଜ୍ରସମୁକୀର୍ଷେ = ବଜ୍ରଦ୍ୱାରା ଉତ୍କୀର୍ଣ ହୋଇଥୁବା । ମହୌ = ମଣିରେ । ସୂତ୍ରସ୍ୟ ଇବ = ଗୋଟିଏ ସୂତାର ଗତି ଭଳି। ମମ ଗତିଃ ଅସ୍ତି = ମୋର ପ୍ରବେଶ ହେବ ।
ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ମହାକବି କାଳିଦାସବିରଚିତଂ ‘ ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗାତ୍ ଆନୀତଃ । ଅତ୍ର ଯଦ୍ୟପି ମୂର୍ଖ ତଥାପି ପୂର୍ବକବିଭିଂ ବର୍ଣ୍ଣିତଂ ରାମାୟଣାଦିପ୍ରବନ୍ଧରୂପ ଦ୍ବାରେଣ ମହକବେ ପ୍ରବେଷ୍ଟୁ କାମନା ବିଷୟେ ବର୍ଣ୍ଣିତମ୍ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ପ୍ରାଚୀନ କବିନ୍ ପ୍ରତି କାଳିଦାସସ୍ୟ ଭକ୍ତିପୁତଃ ଶ୍ରଦ୍ଧାଞ୍ଜଳି । ସ୍ଵାହଂକାରଂ ପରିତ୍ୟଜ୍ୟ ବିନୟଂ ପ୍ରଦଶ୍ୟ କବି ‘ରଘୁବଂଶମ୍’ ଇବ ବିଶାଳବଂଶସ୍ୟ ଐତିହ୍ୟଗାଥା ବର୍ଷତୁଃ ପ୍ରଯତତେ । ମହର୍ଷିବାଲ୍ମୀକି, ଭଗବାନ୍ ବ୍ୟାସ ଚ ମହାକବେ ଆଦର୍ଶଭୂତଃ । ଉପମାଳଙ୍କାରଛଳେନ କଥ୍ ଯତ୍ – ବଜ୍ରସମୁଦ୍ଵୀଣ୍ଡେ ମଣୋ ଯଥା ସୂତ୍ରସ୍ୟ ଗତିଃ ଅନାୟାସେନ ଭବତି ତଥା କୃତିଃ ନୂନଂ ପ୍ରଶଂସାହଂ ଭବିଷ୍ୟତି ଅତ୍ର ସନ୍ଦେହଂ ନାସ୍ତି ।
ସନ୍ଧିବିଚ୍ଛେଦ – ବଂଶେଽସ୍ମିନ୍ = ବଂଶେ + ଅସ୍ଥିନ୍ । ସୂତ୍ରସ୍ୟବାସ୍ତି = ସୂତ୍ରସ୍ୟ + ଇବ + ଅସ୍ତି ।
ସମାସ – କୃତବାଗ୍ରେ = ବାଗ୍ ଏବ ଦ୍ଵାରଂ (କର୍ମଧାରୟ), କୃତଂ ବାଦ୍ଵାରଂ ଯସ୍ୟ ତତ୍ ତସ୍ମିନ୍ (ବହୁବ୍ରୀହିଃ) । ପୂର୍ବସୂରିଭି = ପୂର୍ବେ ସୂରୟଃ, ତିଃ (କର୍ମଧାରୟ) । ବଜ୍ରସମୁତ୍ର୍ରେ = ବଜ୍ରଣ ସମୃତ୍, ତସ୍ମିନ୍ (୩ୟା ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ପୂର୍ବସୁରଭି = ଅନୁସ୍ତେ କଉଁରି ୩ୟା । କୃତବାଗଦ୍ଵାରେ, ଅସ୍ମିନ୍, ବଂଶ ୭ମୀ । ବଜ୍ରସମୁକୀର୍ଣ୍ଣ, ମଣି ଅଧିକରଣେ ୭ମୀ । ସୂତ୍ରସ୍ୟ = ସମ୍ବନ୍ଧେ ୬ଷ୍ଠୀ । ମେ = ସମ୍ବନ୍ଧେ ୬ଷ୍ଠୀ |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସମୁତ୍ = ସମ୍ + ଉତ୍ + କୃ + କ୍ତ । ଗତିଃ = ଗମ୍ + ସ୍କ୍ରିନ୍ ।
ଶ୍ଳୋକ – ୫
सोऽहमाजन्मशुद्धानामाफलोदयकर्मणाम् ।
आसमुद्रक्षितीशानामानाकरथवर्त्मनाम् ||५||
ଡଃ ଅହମ୍ ଆଜନ୍ମଶୁଦ୍ଧାନାମ୍ ଆଫଳୋଦୟକର୍ମଣାମ୍,
ଆସମୁଦ୍ରକ୍ଷିତୀଶାନାମ୍ ଆନାକରଥବର୍ତ୍ତନାମ୍ ||୫||
ଶବ୍ଦାର୍ଥ – ସ ଅହମ୍ = ସେହି ମୁଁ ମୂର୍ଖ କବି କାଳିଦାସ । ଆଜନ୍ମଶୁଦ୍ଧାନାମ୍ = ଜନ୍ମ ଆରମ୍ଭରୁ ବିଭିନ୍ନ ସଂସ୍କାରଦ୍ଵାରା ପବିତ୍ରିତ ହୋଇଥିବା । ଆଫଳୋଦୟକର୍ମଣାମ୍ = ଫଳପ୍ରାପ୍ତି ପର୍ଯ୍ୟନ୍ତ କାର୍ଯ୍ୟରତ ଥିବା । ଆସମୁଦ୍ରକ୍ଷିତୀଶାନାମ୍ ଆରମ୍ଭ କରି ପୃଥବୀ ପର୍ଯ୍ୟନ୍ତ ସମସ୍ତ ସସାଗରାଧରାର ଅଧୂପତି । ଆନାକରଥବର୍ତ୍ତନାମ୍ = ସ୍ଵର୍ଗପର୍ଯ୍ୟନ୍ତ ନିଜର ରଥକୁ ଚଳାଉଥିବା ।
ଅନୁବାଦ – ସେହି ମୁଁ (ମୂର୍ଖ କବି କାଳିଦାସ) ଜନ୍ମରୁ ବିଭିନ୍ନ ସଂସ୍କାରଦ୍ଵାରା ଶୁଦ୍ଧ ହୋଇଥବା, ଫଳପ୍ରାପ୍ତି ପର୍ଯ୍ୟନ୍ତ କାର୍ଯ୍ୟ କରୁଥିବା, ସସାଗରାଧରାର ଅଧୂପତି ଭାବରେ ପ୍ରତିଷ୍ଠା ଲାଭ କରିଥିବା, ସ୍ଵର୍ଗ ପର୍ଯ୍ୟନ୍ତ ନିଜର ରଥକୁ ସ୍ଵଦେହରେ
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ମହାକବି କାଳିଦାଡଃ ବିରଚିତଂ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ରଘୁବଂଶୀୟରାଜାନାଂ ଗୁନଃ ତଥା ବୀରତ୍ଵସ୍ୟ ଗାଥା ବର୍ଣ୍ଣିତଂ ଭବତି । ମହାକବି ମୂଳତଃ ରଘୁବଂଶୀୟରାଜାନାଂ ଗୁଣଗାନଂ କରୋତି, ଯତ୍ ତେ ଆଜନ୍ମଶୁଦ୍ଧମ୍ ଆସନ୍ । ବିବିଧସମୟେ ସ୍ମୃତିଶାସ୍ତ୍ରଣ ଭିନ୍ନସଂସ୍କାରମାଧମେନ ତେ ପବିତ୍ରମ୍ ଅଭବନ୍ । ତେ କାର୍ଯ୍ୟାର୍ଥମ୍ ଅତୀବ ଉତ୍ସାହୀ ବଦ୍ଧପରିକରା ଚ ଆସନ୍ । ସିଦ୍ଧିପର୍ଯ୍ୟନ୍ତ ତେ କାର୍ଯ୍ୟ କୁର୍ବନ୍ତି ସ୍ମ । ତେ ଅତୀବ ପରାକ୍ରମଶାଳୀ ଆସନ୍ । ଆସମୁଦ୍ରପର୍ଯ୍ୟନ୍ତ ତେଷା ସାମ୍ରାଜ୍ୟ ବ୍ୟାପ୍ତ ଆସୀତ୍ । ସୂର୍ଯ୍ୟବଂଶୀୟରାଜାନଃ ସ୍ଵକୀୟରଥ ସ୍ଵର୍ଗପର୍ଯ୍ୟନ୍ତ ସଞ୍ଚରଣଂ କୃତ୍ୱା ଇନ୍ଦ୍ରଣ ସାକଂ ବନ୍ଧୁତାମ୍ ଅକୁର୍ବନ୍ । ଦେବାସୁରସଂଗ୍ରାମେ ଆସନ୍ । ପରବର୍ତ୍ତୀକାଳେ ଏତେ ରାଜାନଃ ଆଦର୍ଶଭୂତା ଆସନ୍ ।
ବ୍ୟାକାରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ବଂଶେଽସ୍ମିନ୍ = ପଃ + ଅହମ୍ + ଆଜନ୍ମଶୁଦ୍ଧାନାମ୍ + ଆଫଳ + ଉଦୟକର୍ମଣାମ୍ । ଆସମୁଦ୍ରକ୍ଷିତୀଶାନାମାନାକରଥବର୍ତ୍ତନାମ = ଆସମୁଦ୍ରକ୍ଷିତି + ଈଶାନାମ୍ + ଆନାକରିଥବର୍ତ୍ତନାମ୍ ।
ସମାସ – ଆଜନ୍ମଶୁଦ୍ଧାନାମ୍ = ଜନ୍ମନଃ ଆରଭ୍ୟ, ଆଜନ୍ମ (ଅବ୍ୟୟୀଭାବ), ଆଜନ୍ମନାଶୁଦ୍ଧାନଃ, ଆଜନ୍ମଶୁଦ୍ଧା ତେଷା (ସୁପ୍ସୁପା) । ଆଫଳୋଦୟକର୍ମଣାମ୍ = ଫଳସ୍ୟ ଉଦୟ (୬ଷ୍ଠୀ ତତ୍), ଫଳୋଦୟମଭିବ୍ୟାପ୍ୟ ଇତି (ଅବ୍ୟୟୀଭାବ), ଆଫଳୋଦୟଂ କର୍ମ ଯେସାଂ ତେ, ତେତାଂ (ବହୁବ୍ରୀହିଃ) । ଆସମୁଦ୍ରକ୍ଷିତୀଶାନାମ୍ = କ୍ଷିତଃ ଈଶା (୬ଷ୍ଠ ତତ୍), ସମୁଦ୍ରମ୍ ଅଭିବ୍ୟାପ୍ୟ (ଅବ୍ୟୟୀଭାବ), ଆସମୁଦ୍ର କ୍ଷିତୀଶା, ତେଷା (କର୍ମଧାରୟ) । ଆନାକରଥବର୍ତ୍ତନଃ = ନ ଅକଂ ବିଦ୍ୟତେ ଯତ୍ର (ନିଷେଧାର୍ଥକ ବହୁବ୍ରୀହିଃ), ନାକମ୍ ଅଭିବ୍ୟାପ୍ୟ (ଅବ୍ୟୟୀଭାବ), ରଥସ୍ୟ ବଦ୍ଧ (୬ଷ୍ଠୀ ତତ୍), ଆନାକଂ ରଥବର୍ତ୍ତ ଯେସାଂ ତେ, ତେଷାମ୍ (ବହୁବ୍ରୀହିଃ) ।
ସକାରଣବିଭକ୍ତି – ଧଃ, ଅହମ୍ = କଉଁରି ୧ ମା । ଆଜନ୍ମଶୁଦ୍ଧାନାମ୍, ଆଫଳୋଦୟକର୍ମଣାମ୍, ଆସମୁଦ୍ରକ୍ଷିତୀଶାନାମ୍, ଆନାକାରଥବର୍ତ୍ତନାମ୍ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ |
ଶ୍ଳୋକ – ୬
यथाविधिहुताग्नीनां यथाकामार्चितार्थिनाम् ।
यथापराधदण्डानां यथाकालप्रवोधिनाम् ||६||
ଯଥାବିଧିହ୍ନତାଗ୍ନାନାଂ ଯଥାକାମ।ଣିତାଥିନାପ୍ର |
ପ୍ରଥାପରାଧଦଣ୍ଡାନାଂ ଯଥାକାଳପ୍ରବୋଧ୍ନାମ୍ ||୬||
ଅନ୍ନୟ – ପ୍ରଥାବିଧ୍ହୁଡାଗ୍ନାନାଂ ପ୍ରଥାକାମାଟିଡାଥନଂ, ଯଥାପରାଧଦଣ୍ଡାନାଂ, ଯଥାକାଳସ୍ଥବୋଧ୍ନାଂ (ରଶ୍ନଶାମ୍ନ ଅନ୍ମ୍ନ ବଯ୍ୟେ) |
ଶବ୍ଦାର୍ଥ – ଯଥାବିଧ୍ଵହୁତାଗ୍ନୀନା = ଠିକ୍ ନିୟମ ଅନୁସାରେ ଅଗ୍ନିରେ ଆହୁତି ଦେଉଥିବା । ଯଥାକାମାର୍ଚିତାର୍ଥନାମ୍ ଦଣ୍ଡ ଦେଉଥିବା । ଯଥାକାଳପ୍ରବୋଧୁନାମ୍ = ଠିକ୍ ସମୟରେ ପ୍ରଜାମାନଙ୍କ ରକ୍ଷଣ ପାଇଁ ଜାଗ୍ରତ ଥିବା ।
ଅନୁବାଦ – ରଘୁବଂଶୀୟ ରାଜାମାନେ ଶାସ୍ତ୍ରୀୟ ରୀତି ଅନୁସାରେ ଅଗ୍ନିରେ ଆହୁତି ଦେଉଥିଲେ । ଇଚ୍ଛାନୁସାରେ ଯାଚକମାନଙ୍କର ମନସ୍କାମନା ପୂରଣ କରୁଥିଲେ । ଅପରାଧୀମାନଙ୍କୁ ଯଥାବିଧ୍ଵ ଦଣ୍ଡ ଦେଉଥିଲେ ଏବଂ ପ୍ରଜାମାନଙ୍କୁ ପାଳନ ପୋଷଣ କରିବାପାଇଁ ନିରନ୍ତର ଜାଗ୍ରତ ରହୁଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶପିତ: ଶ୍ଳୋକ: ସଂସଡମାହିତ୍ୟପ୍ୟ ପୁସ୍ତତିପ: ବିରଚିତମ୍ନ ଥମରକତି: ‘ରଶ୍ମବଂଶମ୍ନ’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରଘୁବଂଶୀୟ ରାଜାନାଂ ଗୌରବଂ ତଥା ଗୁଣସ୍ୟ ବର୍ଣ୍ଣନଂ ଭବତି । କୃତ୍ୱା ଯଜ୍ଞ ପ୍ରଜ୍ଜଳିତ ଅଗ୍ନେ ଆହୁରିଂ ପ୍ରଦତ୍ତବାନ୍ । ଯଜ୍ଞେନ ବୃଷ୍ଟି ପ୍ରଜାନାଂ ରାଜ୍ୟସ୍ୟ ବା ମଙ୍ଗଳବିଧାନମ୍ ଅଭବତ୍ । ଆର୍ଥୀନାଂ କୃତେ ପ୍ରଚୁର ପରିମାଣଂ ଦାନଂ ପ୍ରଦତ୍ତବାନ୍ । ଅପରାଧୀନଃ କୃତେ ଉପଯୁକ୍ତ ଦଣ୍ଡ ବ୍ୟବସ୍ଥା ତେନ କୃତଃ । ରାଜ୍ୟସ୍ୟ ସୁବ୍ୟବସ୍ଥାର୍ଥୀ ଶୃଙ୍ଖଳାର୍ଥୀ ଚ ଦଣ୍ଡ ଅବଶ୍ୟ କରଣୀୟମ୍ । ସର୍ବାଗ୍ରେ ପ୍ରଜାପାଳନାଞ୍ଚ ରକ୍ଷଣାର୍ଥ ଚ ତେ ଜାଗ୍ରତଃ ଆସନ୍ । ଏତସ୍ମାତ୍ ରାଜାନାଂ ଧର୍ମ-ଦାନଶୀଳତା -ନ୍ୟାୟଶୀଳତା-ନୀତିଜ୍ଞତା ଚ ସହଜେନ ଅନୁମୀୟତେ | ତସ୍ମିନ୍ କାଳେ ସୁଶାସନ ବ୍ୟବସ୍ଥା ଆସୀତ୍ |
ବ୍ୟାକରଣ:
ସନ୍ଦିବିଛେଦ – ଯଥାବିଧତାଗ୍ନୀନାମ୍ = ଯଥାବିଧୂତ + ଅଗ୍ନୀନାମ୍ । ଯଥାକାମାର୍ଚିତାର୍ଥନାମ୍ = ଯଥାକାମ + ଅର୍ଚିତ + ଅର୍ଥନାମ୍ । ଯଥାପରାଧଦଣ୍ଡାନାମ୍ = ଯଥା + ଅପରାଧଦଣ୍ଡାନାମ୍ ।
ସମାସ – ଯଥାବିଧ୍ଵ = ବିଧୂମନତିକ୍ରମ୍ୟ (ଅବ୍ୟୟୀଭାବ) । ଯଥାବିଧ୍ଵହୁତାଗ୍ନୀନାମ୍ = ଯଥାବିଧ୍ଵ ହୁତଃ ଅଗ୍ନୟଃ ଯଃ, ତେଷାମ୍ ( ବହୁବ୍ରୀହିଃ) । ଯଥାକାମମ୍ = କାମମ୍ ଅନତିକ୍ରମ୍ୟ (ଅବ୍ୟୟୀଭାବ) । ଯଥାକାମାର୍ଚିତାର୍ଥନାମ୍ = ଯଥାକାମମ୍ ଅର୍ଚିତାଃ ଅର୍ଥନଃ ଯେସ୍ତେ, ତେଷାମ୍ (ବହୁବ୍ରୀହିଃ) । ଯଥାପରାଧମ୍ = ଅପରାଧମ୍ ଅନତିକ୍ରମ୍ୟ (ଅବ୍ୟୟୀଭାବ) । ଯଥାପରାଧଦଣ୍ଡାନାମ୍ = ଯଥାପରାଧ୍ୟ ଦଣ୍ଡେ ଯେଷା ତେଷାମ୍ (ବହୁବ୍ରୀହିଃ) । ଯଥାକାଳମ୍ = କାଳମ୍ ଅନତିକ୍ରମ୍ୟ (ଅବ୍ୟୟୀଭାବ) । ଯଥାକାଳପ୍ରବୋଧନାମ୍ = ଯଥାକାଳଂ ପ୍ରବୋଧନଃ, ତେଷାମ୍ (ସୁପ୍ସୁପା) ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ବିଧ୍ଵ = ବି + ଧା + କି । ହୁତଃ = ହୁ + କ୍ତ । କାମଃ ଅର୍ଥୀ = ଅର୍ଥ + ଈନି । ଅପରାଧଃ = କମ୍ + ଘଞ୍ଚ୍ । ଅର୍ଚିତଃ = ଅର୍ଚ + କ୍ତ । ଅପ + ରାଣ୍ଡ୍ + ଘଞ୍ଚ୍ । ପ୍ରବୋଧନୀ = ପ୍ର + ବୁଥ୍ + ଘଞ୍ଚ୍ + ଇନି |
ଶ୍ଳୋକ – ୭
त्यागाय संभृतार्थानां सत्याय मितभाषिणाम् ।
यशसे विजिगीषूणां प्रजायै गृहमेधिनाम् ||७||
ତ୍ୟାଗାସ୍ନ ସଂର୍ତାର୍ଥୀନାଂ ସଭ୍ୟାସ ମିପରାଘିଶାମ୍ବ |
ଯଶସେ ବିଜିଗ୍ରୀଷ୍ମଣା ପ୍ରଜାୟେ ଗୃହମେଧ୍ଵନାମ୍ ॥୭ ||
ଅନ୍ନମ – ତ୍ୟାଗୀୟ ସଂଭୃତାର୍ଥନାଂ, ସତ୍ୟାୟମିତଭାଷିଣାମ୍, ଯଶସେ ବିଜିଗ୍ରୀଷୂଣା, ପ୍ରଜାୟେ ଗୃହମେଧ୍ୱନାମ୍ ।
ଶଦାର୍ଥ – ତ୍ୟାଗାୟ = ତ୍ୟାଗ ନିମନ୍ତେ । ସଂଭୃତାର୍ଥନାମ୍ = ଅର୍ଥ ବା ଧନ ସଞ୍ଚୟ କରୁଥିଲେ । ସତ୍ୟାୟ = ପାଇଁ । ମିତଭାଷିଣାମ୍ = ଖୁବ୍ କମ୍ କଥା କହୁଥିଲେ । ଯଶସେ = ଯଶ ପାଇଁ । ବିଜିଗୀଶୁଣାମ୍ = ଦିଗ୍ବିଜୟ କରୁଥିଲେ । ପ୍ରଜାୟୈ = ସନ୍ତାନ ପାଇଁ । ଗୃହମେଧ୍ଵନାମ୍ = ଗୃହସୁ ଆଶ୍ରମରେ ପ୍ରବେଶ କରୁଥିଲେ ।
ଅନୁବାଦ – (ରଘୁବଂଶୀୟ ରାଜାମାନେ) ସପାତ୍ରରେ ଦାନ ଦେବାପାଇଁ ଧନ ସଂଗ୍ରହ କରୁଥିଲେ, ସତ୍ୟର ପ୍ରସାର ପାଇଁ ଖୁବ୍ କମ୍ କଥା କହୁଥିଲେ, ଯଶଲାଭ ପାଇଁ ରାଜାମାନଙ୍କୁ ଜୟ କରୁଥିଲେ, ଏବଂ ସନ୍ତାନ ଉତ୍ପନ୍ନ ପାଇଁ ହିଁ ଆଶ୍ରମରେ ପ୍ରବେଶ କରୁଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଉଦ୍ଧୃତଃ ଶ୍ଲୋକ ସରସ୍ଵତୀବରପୁନଃ ମହାକବି କାଳିଦାସପ୍ରଣୀତଃ ‘ ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ ଅତ୍ର ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରଘୁବଂଶୀୟ ରାଜାନା ପରୋପକାରଂ ସତ୍ୟ -କର୍ତ୍ତବ୍ୟବୋଧାଦି ଗୁଣାନାଂ ବର୍ଣ୍ଣନଂ ଭବତି |
ରଘୁବଂଶୀୟରାଜାନଃ ବିବିଧାନାଂ ଗୁଣାନାମ୍ ଅଧୁକାରିତଃ ଆସନ୍ । ତେ ପରୋପକାରାୟ ଦାନାୟ ଚ ଧନସଂଗ୍ରହମ୍ ଅକୁର୍ବନ୍ । ତେ ଜ୍ଞାତଂ ଯତ୍ ‘ ପରୋପକାରାୟ ସ୍ଵର୍ଗୀୟ।’ ପୁନଶ୍ଚ ତେ ମିତଭାଷିଣ ଆସନ୍ । ଇଲଂ ତୁ ସତ୍ୟମାସୀତ୍ । ଫଳତଃ କସ୍ମି ନ ଦୁଃଖ୍ୟ ଦୀୟତେ । ‘ମିତଂ ଚ ସାରଂ ଚ ବଡେ ହି ବାଗ୍ମୀତା – ଇତ୍ୟେବ ବତଃ ଅକ୍ଷରୟୋ ତେ ପାଳିତବନ୍ତଃ । ଅନ୍ୟାୟାର୍ଥୀ ନ ଅପିତୃ ସ୍ଵାସ୍ଥ୍ୟ ଯଶବଦ୍ଧନାର୍ଥୀ ତେ ରାଜ୍ୟଜୟମ୍ ଅକୁର୍ବନ୍ । ସାଧାରଣତଃ ମନୁଷ୍ୟ ସ୍ୱସ୍ୟ କାମାଭିଳାଷ ଚରିତାର୍ଥ କରୁଁ ବିବାହଂ କୃତ୍ୱା ଗୃହସ୍ଥାଶ୍ରମେଣ ପ୍ରବିଶତି, ପରନ୍ତୁ ରଘୁବଂଶୀୟା ସ୍ବବଂଶରକ୍ଷାର୍ଥୀ ସନ୍ତାନୋତ୍ପରିଂ ଚ ଗୃହସ୍ଥାଶ୍ରମେ ପ୍ରବେଶଂ କୃତବନ୍ତଃ । ତେ ଅତୀବ ସଂଯମିନଃ ଆସନ୍ । ମହାକବିଂ ଯଥା ଅତ୍ର ରଘୁବଂଶୀୟରାଜାନାଂ ପରୋପକାରଂ, ମିତଭାଷଣଂ, ସତ୍ୟକଥନଂ, ଯଶୋବର୍ଦ୍ଧନଂ, ସଂଯମତାଦି ଗୁଣାନାଂ ବର୍ଣ୍ଣନଂ କୃତଃ ତଦେବ ଅତୀବ ଶିକ୍ଷଣୀୟଃ ଗ୍ରହଣୀୟଶ୍ଚେ ଭବତି ।
ବ୍ୟାକରଣ:
ସମାସ – ସଂଭୃତାର୍ଥାନାମ୍ = ସଂଭୂତଃ ଅର୍ଥ ପୈ, ତେଷାମ୍ (ବହୁବ୍ରୀହିଃ) । ମିତଭାଷିଣାମ୍ = ମିତଂ ଭାଷନ୍ତେ ଇତି, ତେଷା (ଉପପଦ ତତ୍) । ଗୃହମେଧ୍ଵନାମ୍ = ଗୃହୈ ମେଧନ୍ତେ ଇତି, ତେଷା (୪ର୍ଥୀ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ତ୍ୟାଗାୟ, ସତ୍ୟାୟ, ଯଶସେ, ପ୍ରଜାୟୈ = ନିମିତ୍ତାର୍ଥେ ବା ତାଦ୍ୟର୍ଥେ ୪ ର୍ଥୀ । ସଂଭୃତାର୍ଥନାମ, ମିତଭାଷିଣାମ୍, ବିଜିଗୀଷୂଣାମ, ଗ୍ରହମେଧ୍ଵନାମ୍ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ |
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ତ୍ୟାଗ = ତ୍ୟଜ୍ + ଘଞ୍ଚ୍ ସଂଭୂତଃ = ସମ୍ + ଭୃ + କ୍ତ | ଭାଷୀ = ଭାଷ୍ + ଇନି । ବିଜିଗୀତୁଃ ବି + ଜି + ସନ୍ + ଉ ।
ଶ୍ଳୋକ – ୮
शैशवेऽभ्यस्तविद्यानां यौवने विषयैषिणाम् ।
वार्धके मुनिवृत्तीनां योगेनान्ते तनुत्यजाम् ।।८।।
ଶୈଶବେଽଭ୍ୟସ୍ତବିଦ୍ୟାନାଂ ଯୌବନେ ବିଷୟିଷିଣାମ୍ ।
ବାର୍ଧକେ ମୁନିବୃଭାନ ଯୋଗେନାନ୍ତେ ତନ୍ମଣ୍ୟକାମ୍ ||୮||
ର୍ଥନ୍ନୟ – ଶୈଶବେ ଅଭ୍ୟସ୍ତବିଦ୍ୟାନାଂ, ଯୌବନେ ବିଷୟୈଷିଣାମ୍, ବାର୍ଧକେ ମୁନିବୃତ୍ତୀନାମ୍ ଅନ୍ତେ ଯୋଗେନ ତନୁତ୍ୟଜାମ୍ ( ରଘୁଣାମ୍ ଅନ୍ବୟଂ ବକ୍ଷ୍ୟ) ।
ଶଦାର୍ଥ – ଗୌଣରେ = ବାଲ୍ୟାବସ୍ଥାରେ । ଅଭ୍ୟସ୍ତବିଦ୍ୟାନାମ୍ = ସମସ୍ତ ବିଦ୍ୟା ଅଧ୍ୟୟନ କରିଥିଲେ । ଯୌବନେ = = ରୂପ, ରସ, ଗନ୍ଧ ଆଦି ବିଷୟ ଆସ୍ବାଦନ କରିଥିଲେ । ବାଧିକେ = ବୃଦ୍ଧାବସ୍ଥାରେ । ଆଚରଣ କରୁଥିଲେ । ଅନ୍ତେ = ଦେହତ୍ୟାଗ ସମୟରେ । ଯୋଗେନ = ନିରୋଧପୂର୍ବକ । ତନୁତ୍ୟଜାମ୍ = ଦେହତ୍ୟାଗ କରୁଥିଲେ ।
ଅନୁବାଦ – (ରଘୁବଂଶୀୟ ରାଜାମାନେ) ବାଲ୍ୟାବସ୍ଥାରେ ସମସ୍ତ ବିଦ୍ୟା ଅଧ୍ୟୟନ କରୁଥିଲେ, ଯୁବକାବସ୍ଥାରେ ପର୍ଯ୍ୟାୟରେ ଚିତ୍ତବୃତ୍ତି ନିରୋଧ କରି ପ୍ରାଣତ୍ୟାଗ କରୁଥିଲେ । କଥମନୁମୀୟତେ ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ଭାରତୀୟସଂସ୍କୃତୌ ମନୁଷ୍ୟାମାଂ ଜୀବନଂ ଚତୁରାଶ୍ରମେ ଆବଦ୍ଧମ୍ । ଶତାୟୁମନୁଷ୍ୟ ବ୍ରହ୍ମଚର୍ଯ୍ୟ, ଗାର୍ହସ୍ଥ୍ୟ, ବାନପ୍ରସ୍ଥ୍ୟ, ସନ୍ୟାସଂ ଚ ଆଶ୍ରମେ ଜୀବନଂ ନିର୍ବାହୟତି । ପ୍ରତ୍ୟେକସ୍ୟ ଆଶ୍ରମସ୍ୟ କାଳ ପଞ୍ଚବିଂଶତିଃ ସଂବତ୍ସରଃ । ଧର୍ମଶାସ୍ତ୍ର ତଥା ମନୁସ୍ଥ ତୋ ଆଶ୍ରମସ୍ଥ ନିୟମଂ କର୍ତ୍ତବ୍ୟଂ ଚ ଉଲ୍ଲିଖମ୍ । ତଦନୁସାରଂ ରଘୁବଂଶୀୟ ରାଜାନଃ ଶୈଶବେ ବିଦ୍ୟାଭ୍ୟାସମ୍, ଯୌବନେ ବିଷୟୈଷିଣମ୍, ବାର୍ଧକେ ମୁନିବୃଷ୍ଟିମ୍, ଅନ୍ତେ ଯୋଗେନ ତନୁତ୍ୟାଗଂ ଚ କୃତବନ୍ତଃ । ଅତଃ ବସ୍ତୁତଃ ମନୁଷ୍ୟଜୀବନସ୍ୟ ପୁରୁଷାର୍ଥମ୍
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଛେଦ – ଶୈଶବେଽଭ୍ୟସ୍ତ = ଶୈଶବେ + ଅଭ୍ୟସ୍ତ । ବିଷୟୈଷିଣାମ୍ = ବିଷୟ + ଈଷିଣାମ୍ । ଯୋଗେନାନ୍ତେ = ଯୋଗେନ + ଅନ୍ତେ ।
ସମାସ – ଅଭ୍ୟସ୍ତବିଦ୍ୟାନାମ୍ = ଅଭ୍ୟସ୍ତ ବିଦ୍ୟା ଯୌ ତେ, ତେଷାମ୍ (ବହୁବ୍ରୀହିଃ) । ବିଷୟିଷିଣାମ୍ = ବିଷୟାନ୍ ଈଷିତୁଃ ଶୀଳଂ ଯେଷା ତେ, ତେଷାମ୍ (ବହୁବ୍ରୀହିଃ) । ମୁନିବୃତ୍ତୀନାମ୍ = ମୁନୀନାଂ ବୃଦ୍ଧିରିବ ବୃତିଃ ଯେଷାମ୍ (ବହୁବ୍ରୀହିଃ) । ତନୁତ୍ୟଜାମ୍ = ତନୁ ତ୍ୟଜନ୍ତି ଯେ ତେ, ତେଷାମ୍ (ବହୁବ୍ରୀହିଃ) ।
ସକାରଣବିଭକ୍ତି – ଶୈଶବେ, ଯୌବନେ, ବାର୍ଥକେ, ଅନ୍ତେ = ଅଧିକରଣେ ୭ମୀ। ଅଭ୍ୟସ୍ତ ବିଦ୍ୟାନାମ୍, = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ | ଯୋଗେନ = କରଣେ ୩ୟା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଅଭ୍ୟସ୍ତ = ଅଭି + ଅସ୍ + କ୍ତ । ଯୌବନମ୍ = ଯୁବନ୍ + ଅଣ୍ । ବୃତ୍ତି = ବୃତ୍ + ସ୍କ୍ରିନ୍ ଯୋଗ = ଯୁଜ୍ + ଘଞ୍ଚ୍ । ତ୍ୟଜନ୍ତି = ତ୍ୟଜ୍ + କ୍ରିପ୍। ବକ୍ଷ୍ୟ ।

ଶ୍ଳୋକ – ୯
रघूणामन्वयं वक्ष्ये तनुवाग्विभवोऽपि सन् ।
तदगुणौः कर्णमागत्य चापलाय प्रचोदितः ।। ९ ।।
ରତ୍ପଣମନ୍ନକ୍ଷ ବଯ୍ୟେ ତନୁବାଗ୍ନବିରବୋଽପି ସନ୍ନ |
ତଦ୍ଗୁଣି କର୍ସମାଗତ୍ୟ ଚାପଳାୟ ପ୍ରଚୋଦିତଃ ॥ ୯॥
ଅନ୍ବୟ – ଡଃ ଅହଂ ତନୁବାଗ୍ବିଭବ ଅପି ତଦ୍ଗୁଣି କଣ୍ଠମ୍ ଆଗତ୍ୟ ଚାପଳାୟ ପ୍ରଚୋଦିତଃ ସନ୍ ରଘୁଣାମ୍ ଅନ୍ବୟଂ ବାର୍ଯ୍ୟେ |
ଣଦାର୍ଥ – ସ: ର୍ଥଦୃ ସେହି ମୁଁ । ତନୁବାଗ୍ବିଭନଃ ଅପି = ମୋର ଶବ୍ଦବୈଭବ ଖୁବ୍ କମ୍ ଥିଲେ ମଧ୍ୟ । ସେହି ରଘୁବଂଶୀୟ ରାଜାମାନଙ୍କର ଗୁଣରେ । କଣ୍ଠମ୍ ଆଗତ୍ୟ = ଶୁଣି । ଚାପଳାୟ ପ୍ରଚୋଦିତଃ ସନ୍ = ବିନା ରଘୁବଂଶୀୟ ରାଜାମାନଙ୍କର । ଅନ୍ବୟଂ ବକ୍ଷ୍ୟ = ବର୍ଣ୍ଣନା କରୁଛି ।
ଅନୁବାଦ – ରଘୁବଂଶ ବିଷୟରେ ମୁଁ ଅନଭିଜ୍ଞ, ଶବ୍ଦବୈଭବ ମଧ୍ଯ ମୋର ଖୁବ୍ କମ୍ । ତଥାପି ସେ ବଂଶର ମହାନ୍ ଶ୍ନଣ ମୋର କଣ୍ଡଗୋଚର ହୋଲଥ୍ବାରୁ କୌଣସି କଥା ବିଚାର ନ କରି ଅତ୍ୟନ୍ତ ଭମାଦ୍ରିତ ଦ୍ବୋଲ ସେଦ୍ଵି ପ୍ରସିଦ୍ଧି ରାଜାମାନବର ବଂଶକୁ ବର୍ଣ୍ଣନା କରିବି ।
ବ୍ୟାଖ୍ୟା – ଶପିତ: ଶ୍ଳୋକ: ସଂସଡମାହିତ୍ୟପ୍ୟ ପୁସ୍ତତିପ: ବିରଚିତମ୍ନ ଥମରକତି: ‘ରଶ୍ମବଂଶମ୍ନ’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗାତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ କହିଃ ବିଶ୍ଵବିଶ୍ରୁତରଘୁବଂଶଂ ତଥା ତେଷା ରାଜାନାଂ ଗୁଣାବଳୀ ବଣ୍ଡିତମ୍ । ମହାକବେ ସ୍ଵକୀୟ ସାମର୍ଥ୍ୟସ୍ୟ ଅଭିବ୍ୟକ୍ତି ଭବତି ଅସ୍ୟ ଶ୍ଳୋକସ୍ୟ ପ୍ରସଙ୍ଗ । ଅତ୍ର କବିନା ଉକ୍ତ ଯତ୍-ଅସ୍ଥିନ୍ ବଂଶବିଷୟ ମମ ଯଥାର୍ଥଜ୍ଞାନଂ ନାସ୍ତି ଶବ୍ଦବୈଭବମପି ନାସ୍ତି । ତଥାପି ଅସ୍ୟ ବଂଶସ୍ୟ ସୁମହତା ଗୁଣାବଳୀ ତମ୍ ଆକର୍ଷୟତି ଏତାଦୃଶଂ ବଂଶଂ ବର୍ଣ୍ଣନାର୍ଥମ୍ । ଡଃ ଯବାନ୍ ଭବତି ସର୍ବଶ୍ରେଷ୍ଠବଂଶସ୍ୟ ବର୍ଣ୍ଣନାର୍ଥମ୍ । ରାଜାନଃ ଆଦର୍ଶଗୁଣାବଳୀ ଏବଂ ମହାକବେ ସିଦ୍ଧିଲାଭ କରିଷ୍ଯତି ଅତ୍ର ଶଙ୍କା ନାହିଁ । ଯଥାର୍ଡେନ ଉକ୍ତ ଯତ୍ –
” ବିମୌସୁନପଉପି ପ୍ରତଦ୍ର୍ୟମାନ।
ପ୍ତାରଥିମ୍ନଉପଗୁଣା: ନ ପରିତ୍ୟକନ୍ତି |”
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ରଘୁଣାମନ୍ଵୟଂ = ରଘୁଣାମ୍ + ଅନ୍ବୟମ୍ । ତନୁବାଗ୍ବିଭବୋଽପି = ତନୁବାକ୍ + ବିଭବ + ଅପି । କଣ୍ଠମାଗତ୍ୟ = କଶ୍ଚିମ୍ + ଆଗତ୍ୟ !
ସମାସ – ତନୁବାଗ୍ବିଭବ = ତନୁଶ୍ଚାସୌ ବାକ୍ ଚେତି (କର୍ମଧାରୟ), ସୈବ ବିଭବୋ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) | ବାଚଂ ବିଭବ (୬ଷ୍ଠୀ ତତ୍), ତନୁ ବାଗ୍ବିଭବାଃ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) । ତଦ୍ଗୁଣି = ତେଷ ଗୁଣା ତିଃ (୬୩ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ଧଃ, ଅହଂ = କଉଁରି ୧ ମା । ତନୁବାଗ୍ବିଭବାଃ = କଉଁରି ୧ ମା । ତଦ୍ଗୁଣୋ କଉଁରି ୩ୟା । କଶ୍ଚିମ୍ = କର୍ମଣି ୨ୟା । ଚାପଳାୟ = ‘କ୍ରିୟାର୍ଥୋପପଦସ୍ୟ କର୍ମଣି ଚ ସ୍ଥାନିନଃ’ ଯୋଗେ ଚତୁର୍ଥୀ । ରଘୁଣାମ୍ = ଶେଷ ୬ଷ୍ଠୀ । ଅନ୍ବୟଂ = କର୍ମଣି ୨ୟ ।
ପ୍ରକୃତି ପ୍ରତ୍ୟୟ – ଅନ୍ବୟ = ଅନୁ + ଇ + ଅଚ୍ । ଆଗତ୍ୟ = ଆ +ଗମ୍ + ଲ୍ୟପ୍ । ବାପକଃ = ଚପଳ + ଅଣ୍ । ପ୍ରଚୋଦିତଃ = ପ୍ର + ବୃଦ୍ + ଣିଚ୍ + କ୍ତ ।
ଶ୍ଳୋକ – ୧୦
तं सन्तः श्रोतुमर्हन्ति सदसद्व्यक्तिहेतवः ।
हेम्नः संलक्ष्यते ह्यग्नौ विशुद्धिः श्यामिकापि वा ।।१०।।
ଙ ସନ୍ତ: ଣ୍ଡୋତୁମଦୃନ୍ତି ସଦସହ୍ବ୍ୟକ୍ତିଦେବବ: |
ହେମଃ ସଂଲକ୍ଷ୍ୟତେ ହ୍ୟକ୍ଷ୍ନୌ ବିଶୁଦ୍ଧି ଶ୍ୟାମିକାପି ବା ॥ ୧୦ ||
ର୍ଥନ୍ନମ – ସଦସଦ୍ବ୍ୟକ୍ତିହେତପଃ ସନ୍ତଃ ତଂ ଶ୍ରୋତ୍ରୁମ୍ ଅର୍ହନ୍ତି, ହି ହେମ୍ୱ ବିଶୁଦ୍ଧି ଶ୍ୟାମିକା ଅପି ବା ଅଗ୍ନି ସଂଲଯ୍ୟଦେ |
= ଗୁଣ ଏବଂ ଦୋଷ ବିଚାର କରିପାରୁଥିବା । ସନ୍ତଃ = ସେହି ରଘୁବଂଶ ନାମକ ମହାକାବ୍ୟକୁ । ଶ୍ରୋତୁମ୍ = ଶୁଣିବା ପାଇଁ । ଅହଁନ୍ତି = ଯୋଗ୍ୟ ହୋଇଥା’ନ୍ତି । ହି = ଯେହେତୁ । ହେମ୍ୱ = ସୁବର୍ଣ୍ଣର । ବିଶୁଦ୍ଧି ବିଶୁଦ୍ଧତା । ଶ୍ୟାମିକା = କିଛି ମିଶାମିଶି ଦୋଷ । ଅଗ୍ନି ସଂଲକ୍ଷ୍ୟତେ = ଅଗ୍ନିରେ ହିଁ ପ୍ରମାଣିତ ହୋଇଯାଇଥାଏ ।
ଅନୁବାଦ – ଭଲ ଓ ମନ୍ଦ ବିଚାର କରିପାରୁଥିବା ସଜ୍ଜନ ସହୃଦୟମାନେ ହିଁ କେବଳ ଏହି ରଘୁବଂଶ ନାମକ ମହାକାବ୍ୟକୁ ଶୁଣିବାପାଇଁ ସମର୍ଥ ହୋଇଥା’ନ୍ତି । ଯେହେତୁ ସୁବର୍ଣ୍ଣର ଶୁଦ୍ଧତା ବା କିଛି ଦୋଷ କେବଳ ଅଗ୍ନିରେ ହିଁ ପରୀକ୍ଷିତ ଦୃଷ୍ଟିମ୍ ଆକର୍ଷୟତି ।
‘ଅପାରେ କାବ୍ୟ ସଂସାରେ କବିରେବ ପ୍ରଜାପତି – କାବ୍ୟସମ୍ଭାରସ୍ୟ ସ୍ରଷ୍ଟା ଭବତି କବି । କବି କର୍ମ ଭବତି କାବ୍ୟମ୍ । କବିଂ ବିନା କାବ୍ୟସ୍ୟ ସ୍ଥିତି ଅସମ୍ଭବମ୍ । ‘ନ କବିତା ବନିତା କବିନାଂ ବିନା ।’, ଅତଃ କବି ସତତଂ କାବ୍ୟକୃତ୍ୟର୍ଥମ୍ । କାବ୍ୟସ୍ୟ ଶୁଦ୍ଧାଶୁଦ୍ଧ ପରୀକ୍ଷଣାର୍ଥୀ ସହୃଦୟାନ୍ ଆହୃତି । ପାଠକା ସହୃଦୟା ଗୁଣଦୋଷ ପରୀକ୍ଷ୍ୟନ୍ତେ ନିର୍ୟ୍ୟୟନ୍ତେ ଚ । ରଘୁବଂଶମିବ ମହାକାବ୍ୟସ୍ୟ ମାହାତ୍ମ୍ୟ କେବଳଂ ସଜନାଃ କୁର୍ବନ୍ତି ଜାନନ୍ତି ବା । ଯଥା ସୁବର୍ଣ୍ଣସ୍ୟ ଶୁଦ୍ଧତା ଅଗ୍ନି ପରୀକ୍ଷତେ । ଅସ୍ୟ ମହାକାବ୍ୟସ୍ୟ ସଫଳତଂ କେବଳଂ ସହୃଦୟା ଏବ ଜ୍ଞାସ୍ୟନ୍ତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଛେଦ – ଣ୍ଡୋତ୍ନମଦୃନ୍ତି = ଣ୍ଢୋତୁମ + ଥଦ୍ୱିନ୍ତି | ସଦସଦ୍ବ୍ୟକ୍ତିହେତବାଃ = ସତ୍ + ଅସଦ୍ବ୍ୟକ୍ତିହେତପଃ । ହ୍ୟକ୍ଷ୍ନୌ = ହି + ଅଗ୍ନି । ଶ୍ୟାମିକାପିବା = ଶ୍ୟାମିକା + ଅପିବା ।
ସମାସ – ସଦସଦ୍ବ୍ୟକ୍ତିହେତବାଃ = ସଚ୍ଚ ଅସଚ୍ଚ (ଦ୍ବନ୍ଦ୍ବ), ତୟୋ ବ୍ୟକ୍ତି (୬ଷ୍ଠୀ ତତ୍), ତସ୍ୟା ହେତପଃ (୬ଷ୍ଠୀ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ସଦସଦ୍ବ୍ୟକ୍ତିହେତବ, ସନ୍ତଃ = କଉଁରି ୧ ମା । ତଂ = କର୍ମଣି ୨ୟା । ହେମଃ = ସମ୍ବନ୍ଧେ ୬ଷ୍ଠୀ । ଅଗ୍ନି = ଅଧିକରଣେ ୭ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଶ୍ରୋତୁମ୍ = ଶୁ + ତୁମୁନ୍ । ବ୍ୟକ୍ତି = ବି + ଅନଜ୍ + ସ୍କ୍ରିନ୍ । ବିଶୁଦ୍ଧି = ବି + ଶୁଧ୍ + ସ୍କ୍ରିନ୍
ଶ୍ଳୋକ – ୧୧
वैवस्वतो मनुर्नाम माननीय मनीषिणाम् ।
आसीन्महीक्षितामाद्यः प्रणवश्छन्दसामिव ।। ११ ।।
ବୈବସ୍ଵତୋ ମନୁର୍ନାମ ମାନନୀୟୋ ମନୀଷିଣାମ୍ ।
ଆସାନ୍ନଦ୍ରାଘିତାମାଦ୍ୟ: ପ୍ତଶବଶନ୍ଦମାନିବ ||୧୧||
ଅନ୍ନପ – ମନୀଷିଣା ମାନନୀୟ ଛନ୍ଦସାଂ ପ୍ରଣତଃ ଇବ ମହୀକ୍ଷିତାମ୍ ଆଦ୍ୟ ବୈବସ୍ଵତଃ ନାମ ମନୁ ଆସୀତ୍ ।
ଶବ୍ଦାର୍ଥ – ମନୀଷିଣାମ୍ = ପଣ୍ଡିତମାନଙ୍କର । ମାନନୀୟ = ସମସ୍ତ ବେଦର । ପ୍ରଣତଃ ଇବ୍ = ଓଁକାର ସଦୃଶ । ମହୀକ୍ଷିତାମ୍ = ରାଜାମାନଙ୍କର । ଆଦ୍ୟ = ପ୍ରଥମ । ବୈବସ୍ଵତଃ ନାମ = ବୈବସ୍ଵତ ନାମରେ । ମନୁଃ = ମନୁ । ଆସୀତ୍ = ଥିଲେ |
ଅନୁବାଦ – ପଣ୍ଡିତମାନଙ୍କର ପୂଜ୍ୟ ତଥା ସମସ୍ତ ବେଦର ଶ୍ରେଷ୍ଠ ତତ୍ତ୍ଵ ଓଁକାର ଭଳି ରାଜାମାନଙ୍କ ମଧ୍ୟରେ ସର୍ବପ୍ରଥମ ବୈବସ୍ଵତ ନାମରେ ଜଣେ ‘ମନୁ’ ଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ମହାମହିମଃ ପଣ୍ଡିତଃ ମହାକବି କାଳିଦାସକୃତଂ ‘ରଘୁବଂଶମ୍ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗାତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ସୂର୍ଯ୍ୟବଂଶସ୍ୟ ପ୍ରଥମରାଜା ବୈବସ୍ଵତଃ ମନୁଃ ଆସୀତ୍ ଇତି ବର୍ଣ୍ଣିତମ୍ ।
ଅନ୍ତତଃ ମହାକବି କାଳିଦାସ୍ଯ ସୂର୍ଯ୍ୟବଂଶସ୍ୟ ବର୍ଣ୍ଣନଂ କୃତମ୍ । ଅସ୍ୟ ବଂଶସ୍ୟ ପ୍ରଥମ ତଥା ଆଦିମରାଜା ଭବତି ‘ବୈବସ୍ୱତ ମନୁଃ’ ଯଃ ସର୍ବେକ୍ଷାଂ ରାଜାନଂ ମାନ୍ୟା ପୂଜ୍ଯା ଅଗ୍ରଗଣ୍ୟ ଚ ଆସୀତ୍ । ମନୁଃ ଅନେକାଂ ଆସନ୍ । ଅତ୍ର ଉପମା ପ୍ରସଙ୍ଗେନ କାଳିଦାସେନ ଉକ୍ତ ଯତ୍-ଚତୁର୍ବେଦାନାଂ ମୂଳ ତତ୍ତ୍ୱ ଭବତି ପ୍ରଣବ ନାମ ଓଁକାରଃ । ସର୍ବେଷା ମନ୍ତ୍ରାଣାମ୍ ଆଦୌ ଏବ ଓଁକାରଃ ମହାମନ୍ତ୍ରରୂପେଣ ଉଚ୍ଚାର୍ଯ୍ୟତେ । ବୈବସ୍ବତ ମନୁଃ ଓଁକାରେଣ ସହ ତୁଳିତଃ । ‘ବିବସ୍ୱାନ୍’ ଇତି ସୂର୍ଯ୍ୟ ତସ୍ମାତ୍ ଜାତଃ ବୈବସ୍ଵତଃ ତଦେବ ବଂଶଂ ସୂର୍ଯ୍ୟବଂଶମ୍ ଇତି ପ୍ରସିଦ୍ଧମ୍ । ସୂର୍ଯ୍ୟବଂଶମ୍ ଈକ୍ଷାକୁବଂଶଂ, ରଘୁବଂଶମ୍ ଇତି ଉଚ୍ୟତେ । ବଂଶସ୍ୟ ମାହାତ୍ମ୍ୟମ୍ ଅବର୍ଣ୍ଣନୀୟମ୍ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ମନୁର୍ନାମ = ମନୁଃ + ନାମ । ଆସୀନ୍ସହୀକ୍ଷିତାମାଦ୍ୟ ପ୍ରଣବଶ୍ଚନ୍ଦସାମିବ = ପ୍ରଣତଃ +ଛନ୍ଦସାମ୍ + ଇବ ।
ସମାସ – ମହୀକ୍ଷିତାମ୍ = ମହୀ କ୍ଷୟନ୍ତ ଇତି ତେଷା (ଉପପଦ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ବୈବସ୍ଵତଃ = କଉଁରି ୧ ମା। ମନୁ = ୬ଷ୍ଠୀ । ପ୍ରଣତଃ = ‘ଇବ’ ଅବ୍ୟୟ ଯୋଗେ ୧ମା। ମହୀକ୍ଷିତାମ୍ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ଛନ୍ଦସାମ୍ = ନିର୍ଦ୍ଧାରଣେ ୬ଷ୍ଠୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ମାନନୀୟ = ମନ୍ + ଣିଚ୍ + ଅନୀୟର୍ । ମହୀକ୍ଷିତାମ୍ = ମହୀ + କ୍ଷି + କ୍ରିପ୍ + ତୁକ୍ । ପ୍ରଣତଃ = ପ୍ର + ନୁ + ଅପ୍ ।
ଶ୍ଳୋକ – ୧୨
तदन्वये शुद्धिमति प्रसूतः शुद्धिमत्तरः ।
दिलीप इति राजेन्दुरिन्दुः क्षीरनिधाविव ।।१२।।
ତଦନ୍ସୟେ ଶୁଦ୍ଧିମତି ପ୍ରସୂତଃ ଶୁଦ୍ଧିମତ୍ତରଃ ।
ଦିଲୀପ ଇତି ରାଜେନ୍ଦୁରିନ୍ଦୁ କ୍ଷୀରନିଧାବିବ ॥ ୧୨ ||
ଅନ୍ବୟ – ଶୁଦ୍ଧିମତି ତଦନ୍ବୟେ ଶୁଦ୍ଧିମତ୍ତରଃ ଦିଲୀପଃ ଇତି ରାଜେନ୍ଦୁ କ୍ଷୀରନିଧୌ ଇନ୍ଦୁ ଇବ ପ୍ରସୂତଃ ।
ଶବ୍ଦାର୍ଥ – ଶୁଦ୍ଧିମତି = ଅତ୍ୟନ୍ତ ପବିତ୍ରିତା । ତଦନ୍ଵୟେ = ସେହି ବୈବସ୍ଵତ ମନୁଙ୍କର ବଂଶରେ । ଶୁଦ୍ଧିମତ୍ତରଃ = ଅତ୍ୟନ୍ତ ପବିତ୍ରତମ । ଦିଲୀପଃ ଇତି = ଦିଲୀପ ବୋଲି । ରାଜେନ୍ଦୁ = ନୃପଶ୍ରେଷ୍ଠ । କ୍ଷୀରନିଧୌ = କ୍ଷୀରସାଗରରେ । ଇଦୁଃ = ଚନ୍ଦ୍ର । ଇବ ପରି । ପ୍ରସୂତଃ = ଜାତ ହେଲେ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାକବି କାଳିଦାସ୍ଯ ବିରଚିତମ୍ ଅମରକୃତିଃ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଥାତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରଘୁବଂଶସ୍ୟ ପ୍ରମୁଖରାଜା ବୈବସ୍ବତ ମନୋ ଜାତଃ ରଘୋ ପିତା ପରମପ୍ରଭାବଶାଳୀ ଦିଲୀପସ୍ୟ ଜନ୍ମବୃତ୍ତାନ୍ତ ବର୍ଣ୍ଣିତମ୍ ।
ମହାକବି ରଘୁବଂଶସ୍ୟ ବର୍ଣ୍ଣନାରମ୍ଭେ ଆଦି ରାଜା ବୈବସ୍ଵତମନୋ ଉଲ୍ଲେଖ୍ୟ କୃତମ୍ । ରାଜା ରଘୋ ନାମ୍ନା ପ୍ରସିଦ୍ଧ ବଂଶଂ ରଘୁବଂଶମ୍ ଇତି । ରଘୋ ପିତା ସମ୍ରାଟ୍ ଦିଲୀପ । ରାଜା ଦିଲୀପଃ ପବିତ୍ର ରଘୁବଂଶସ୍ୟ ପବିତ୍ରତମଃ ନୃପଃ ଆସୀତ୍ । ଧଃ ରାଜ୍ଞାସୁ ଶ୍ରେଷ୍ଠ ଆସୀତ୍ । କବି ଉପମା ପ୍ରସଙ୍ଗେ ଉକ୍ତ ଯତ୍ – ଯଥା କ୍ଷୀରସାଗରାତ୍ ଚନ୍ଦ୍ରମା ଜାତା ତଥା ସର୍ବେ ଗୁ ସର୍ବାନ୍ ଆକର୍ଷୟତି । ଅତ୍ର ରାଜା ଦିଲୀପଂ ଚନ୍ଦ୍ରମାୟା ସାକଂ ତୁଳନାଂ କ୍ରିୟତେ । ବିଷୟମିଦମ୍ ଅତୀବ ବର୍ଣ୍ଣନୀୟଂ ଭବତି ।
ସନ୍ଧିବିଛେଦ – ତଦନ୍ସ୍ଟେ = ତତ୍ + ଅନୁୟେ । ରାଜେନ୍ଦୁରିନ୍ଦୁ ରାଜା + ଇନ୍ଦୁ + ଇନ୍ଦୁ । କ୍ଷୀରନିଧାବିବ = କ୍ଷୀରନିଧୌ + ଇବ ।
ସମାସ – ତଦୟେ = ସ ଚାସୌ ଅନ୍ବୟଷ୍କୃତି (କର୍ମଧାରୟ), ତସ୍ୟ ଅନ୍ବୟ, ତସ୍ମିନ୍ (୬ଷ୍ଠୀ ତତ୍) । ରାଜେନ୍ଦୁ = ରାଜା ଇନ୍ଦୁ ଇବ (ଉପମିତ କର୍ମଧାରୟ) । କ୍ଷୀରନିଧୌ = କ୍ଷୀରସ୍ୟ ନିଧଃ, ତସ୍ମିନ୍ (୬ଷ୍ଠୀ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ତଦୟେ = ଅଧିକରଣେ ସପ୍ତମୀ । ଶୁଦ୍ଧିମତି = ଅଧୂକରଣେ ସପ୍ତମୀ । ଶୁଦ୍ଧିମତ୍ତରଃ = କଉଁରି ୧ ମା । ଦିଲୀପଃ = ଇତି ଅବ୍ୟୟ ଯୋଗେ ୧ ମା । ଇନ୍ଦୁ = ‘ଇବ’ ଯୋଗେ ୧ମା । କ୍ଷୀରନିଧୌ = ଅଧିକରଣେ ୭ମୀ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଶୁଦ୍ଧି = ଶୁଧ୍ + ସ୍କ୍ରିନ୍ । ପ୍ରସୂତଃ = ପ୍ର + ସୂ + କ୍ତ । ଶୁଦ୍ଧିମତ୍ତରଃ = ଶୁଦ୍ଧି + ମତୁପ୍ + ତରପ୍ । ନିଧ୍ଵ = ନି + ଧା + କି ।
ଶ୍ଳୋକ – ୧୩
व्यूढोरस्को वृषस्कन्धः शालप्रांशुर्महाभुजः ।
आत्मकर्मक्षमं देहं क्षात्रो धर्म इवाश्रितः ।।१३।।
ବ୍ୟଜୋରସ୍ପୋ ବୃଷସ୍କନ୍ଧ ଶାଳୟାଂଶୁର୍ମହାଭୁକଃ ।
ଆତ୍ମକର୍ମକ୍ଷମଂ ଦେହଂ କ୍ଷାତ୍ରା ଧର୍ମ ଇବାଶ୍ରିତଃ । ୧୩ ॥
ଅନ୍ବୟ – ବ୍ଯୂଡ଼ୋରସ୍ଵ, ବୃକ୍ଷସ୍କନ୍ଧ ଶାଳତାଂଶୁ ମହାଭୁଜଃ ଆତ୍ମକର୍ମକ୍ଷମଂ ଦେହମ୍ ଆଶ୍ରିତଃ କ୍ଷାତଃ ଧର୍ମ ଇବ (ସ୍ଥିତଃ) ।
ଶବ୍ଦାର୍ଥ – ବ୍ୟଢ଼େର = ବିପୁଳବକ୍ଷସ୍ଥଳଯୁକ୍ତ । ବୃକ୍ଷସ୍କନ୍ଧି = ବୃଷଭର ସ୍କନ୍ଧ ଭଳି ଉନ୍ନତ ସ୍କନ୍ଧଯୁକ୍ତ । ଶାଳଗ୍ନାଂଶୁ ମହାବାହୁ ବା ଆଜାନୁଲମ୍ବିତ ବାହୁ । ଆତ୍ମକର୍ମକ୍ଷମଂ ଦେହମ୍ ନିଜର କାର୍ଯ୍ୟ = ଶାଳ ବୃକ୍ଷ ଭଳି ଉନ୍ନତ । ମହାଭୁଜଃ କରିବାପାଇଁ ସମର୍ଥ ଦେହ । ଆଶ୍ରିତଃ = ଧାରଣ କରିଥିବା | କ୍ଷାତ୍ର ଧର୍ମ ଇବ = ସାକ୍ଷାତ୍ ମୂର୍ତ୍ତିମାନ୍ କ୍ଷତ୍ରିୟ ଧର୍ମ ସଦୃଶ ।
ଅନ୍ମବାଦ – ରାଜା ଦିଲୀପଙ୍କର ବକ୍ଷସ୍ଥଳ ବିପୁଳ, ବୃଷଭର ସ୍କନ୍ଧ ଭଳି ମହାନ୍ ସ୍କନ୍ଧ, ଶାଳବୃକ୍ଷ ଭଳି ଉନ୍ନତ ବା ଡେଙ୍ଗା, ଆଜାନୁଲମ୍ବିତ ବାହୁ ଥିଲା । ସେ ନିଜର କାର୍ଯ୍ୟ କରିବାପାଇଁ ସାମର୍ଥ୍ୟ ଥବା ଶରୀର ଧାରଣ କରିଥିଲେ । ଜଣାପଡୁଥିଲା ସତେ ଯେପରି ସେ କ୍ଷତ୍ରିୟ ଧର୍ମର ମୂର୍ତ୍ତିମାନ୍ ଅବତାର ଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ସୁପ୍ରସିଦ୍ଧ ‘ରଘୁବଂଶମ୍ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଥାତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲ୍ଲୀପସ୍ୟ ଶାରୀରିକ ଶୋଭାଂ ତଥା ବିବିଧା ଗୁଣା ବଣ୍ଠିତମ୍ ।
ରାଜାଦିଲୀପସ୍ୟ ଶାରୀରିକଶୋଭା ଚମତ୍କାରୀ ଆସୀତ୍ । ତସ୍ୟ ବକ୍ଷସ୍ଥଳମ୍ ଅତି ବିସ୍ତୃତମାସୀତ୍ । ସ୍କନ୍ଧ ବୃଷଭସ୍ୟ ସ୍କନ୍ଧ ଇବ ମହାନ୍ ଆସୀତ୍ । ତଥ୍ୟ ଆଜାନୁଲମ୍ବୀ ସୁଦୀର୍ଘବାହୁ ଆସୀତ୍ । ଶାଳବୃକ୍ଷ ଇବ ଅତୀବ ଉନ୍ନତଃ ଆସୀତ୍ । ଅର୍ଥାତ୍ ତସ୍ୟ ଶରୀରସ୍ୟ ବଳିଷ୍ଠତା, ଦୃଢ଼ତା, ଉନ୍ନତତା ତେଜେମୟତା ଚ ପରଲକ୍ଷିତଂ ଭବତି । ଏତାଦୃଶ ଶରୀରେଣ ଡଃ ଉପଯୁକ୍ତକ୍ଷତ୍ରିୟ ଇବ ପ୍ରତିଭାତି । କ୍ଷତ୍ରିୟସ୍ୟ ମୂର୍ତ୍ତିମନ୍ତଃ ଅବତାରସଦୃଶଃ ଧଃ ଆସୀତ୍ । ବସ୍ତୁତଃ ଶୌର୍ଯ୍ୟ, ତେଜଃ, ଧୈର୍ଯ୍ୟ, ଦକ୍ଷତା, ଯୁଦ୍ଧ, ଦାନମ୍, ଈଶ୍ବରଭାବଂ ଚ ଏତେ ଗୁଣା କ୍ଷତ୍ରିୟାନାଂ ମୌଳିକ ଧର୍ମ ଆସନ୍ । ଏତାଦୃଶଃ ଚାରିତ୍ରିକ ଗୁଣସ୍ୟ ମହନୀୟତା ଅସ୍ଥାକଂ ଧେୟଂ ଜ୍ଞେୟଂ ଭବେତ୍ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଶାଳତାଂଶୁର୍ମହାଭୁଜଃ = ଶାଳତାଂଶୁ + ମହାଭୁଜଃ । ଇବାଶ୍ରିତଃ = ଇବ + ଆଶ୍ରିତଃ ।
ସମାସ – ବ୍ଯୂଢ଼େର = ବ୍ଯୂଢ଼ ଉରଃ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) । ବୃଷସ୍କନ୍ଧ = ବୃଷସ୍ୟ ସ୍କନ୍ଧ ଇବ ସ୍କନ୍ଧ ଯସ୍ୟ ଡଃ (ଉପମାନଗର୍ଭକ ବହୁବ୍ରୀହିଃ) । ଶାଳତାଂଶୁ = ଶାଳ ଇବ ତାଂଶୁ (ଉପମାନ କର୍ମଧାରୟ) । ମହାଭୁକଃ = ତତ୍), ତସ୍ମି କ୍ଷମମ୍ (୪ର୍ଥୀ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ମହାଭୁଜଃ= କଉଁରି ୧ ମା । ଆତ୍ମକର୍ମକ୍ଷମଂ, ଦେହମ୍ = କର୍ମଣି ୨ୟା । ଧର୍ମ = ‘ଇବ’ ଯୋଗେ ୧ମା ।
ପ୍ରକୃତି ପ୍ରତ୍ୟୟ – ବ୍ୟଢ଼ମ୍ = ବି + ବନ୍ଦ୍ + କ୍ତ । ଦେହମ୍ = ଦିହ + ଘଞ୍ଜ୍ । କ୍ଷତ୍ରିୟ = କ୍ଷତ୍ର + ଅଣ୍ । ଧର୍ମୀ = ଧୃ + ମନ୍ । ଆଶ୍ରିତଃ = ର୍ଥା + ଣ୍ଡି + କ୍ |
ଶ୍ଳୋକ – ୧୪
सर्वातिरिक्तसारेण सर्वतेजोभिभाविना ।
स्थितः सर्वोन्नतेनोव क्रान्त्वा मेरुरिवात्मना ।।१४।।
ସବାତିରିକ୍ତସାରେଣ ସବ ସେକେଽଶିରାବିନା |
ସ୍ଥିତଃ ସର୍ବୋନ୍ନତେନୋର୍ବୀ କ୍ରାନ୍ସା ମେରୁରିବାତ୍ମନା ॥ ୧୪ ॥
ଅନୁମ – ସର୍ବାତିରିକ୍ତସାରେଣ ସର୍ବତେଜୋଭିଭାବିନା ସର୍ବୋନ୍ନତେନ ଆହ୍ଵାନା ମେରୁ ଇବ ଉର୍ବୀ କ୍ରାନ୍ସା (ସ୍ଥିତଃ) ।
ଶବ୍ଦାର୍ଥ – ସର୍ବାତିରିକ୍ତସାରେଣ = ସମସ୍ତଙ୍କଠାରୁ ଅଧିକ ବଳଦ୍ଵାରା । ସର୍ବତେଜୋଭିଭାବିନା = ସମସ୍ତଙ୍କଠାରୁ ଅଧିକ ତେକଦ୍ୱାରା | ସବୋନରୋନ= ସବୁଠାରୁ ଉନ୍ନତଦ୍ବାରା । ଆତ୍ମନା = ନିଜର ଶରୀରଦ୍ଵାରା । ମେରୁ ଇବ = ସ୍ମସେବ ପବତ ଭଳି । ଉର୍ବୀ କ୍ରାନ୍ସା = ପୃଥିବୀକୁ ଆକ୍ରାନ୍ତ କରି ରହିଥିଲେ ।
ଅନୁବାଦ – ମହାରାଜ ଦିଲୀପ ନିଜର ସବୁଠାରୁ ଅଧିକ ବଳବାନ୍, ସବୁଠାରୁ ଅଧିକ ତେଜସ୍ବୀ ତଥା ସବୁଠାରୁ ଅଧିକ ଉନ୍ନତ ଶରୀରଦ୍ଵାରା ସମଗ୍ର ପୃଥିବୀକୁ ଆକ୍ରାନ୍ତ କରି ରହିଥିଲେ । ଯେଭଳି ସୁମେରୁ ପର୍ବତ ସବୁଠାରୁ ଅଧୂକ ସ୍ଥିରତାଯୁକ୍ତ, ସବୁଠାରୁ ଅଧିକ କାନ୍ତିଯୁକ୍ତ ଏବଂ ସବୁଠାରୁ ଅଧିକ ଉଚ୍ଚତାଯୁକ୍ତ ନିଜର ଶରୀରରେ ସମଗ୍ର ପୃଥିବୀକୁ ଆକ୍ରାନ୍ତ କରି ରହିଛି ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକ ସୁରଭାରତୀ ସେବକ କବିଲଲାମଭୂତଃ କାଳା ଦାସ କାଳିଦାସ ବିରଚିତମ୍ ଅମରକୃତିଃ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗାତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପଃ ସୁମେରୁପର୍ବତଃ ଇବ ସମସ୍ତଂ ପୃଥିବୀ କ୍ରାନ୍ସାସ୍ଥିତଃ ଇତି ବର୍ଣ୍ଣିତମ୍ ।
‘ଉପମା କାଳିଦାସସ୍ୟ’ – ସଂସ୍କୃତସାହିତ୍ୟ ମହାକବି କାଳିଦାସ ଉପମାଳଂକାର ପ୍ରୟୋଗେ ସିଦ୍ଧହସ୍ତ । ଅସ୍ୟ ନିଦର୍ଶନଂ ତୁ ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ପ୍ରଦତ୍ତମ୍ । କବି ରାଜାଦିଲୀପଂ ସୁମେରୁ ପର୍ବତେନ ସାକଂ ତୁଳିତମ୍ । ଯଥା ସୁମେରୁପର୍ବତଃ ସ୍ଵସ୍ୟ ସର୍ବାଧିକ ସ୍ଥିରତା ସର୍ବାଧିକା କାହିଃ ସର୍ବୋତ୍ତମ ଉଚ୍ଚତା ଚ ବଳେନ ପୃଥ୍ବୀ କ୍ରାନ୍ସା ତିଷ୍ଠତି ତଥା ମହାରାଜା ଦିଲୀପଃ ଅପି ଧରଣୀମାକ୍ରାନ୍ତ୍ ସ୍ଥିତଃ । ତସ୍ୟ ବଳଂ ତୁ ସର୍ବେଶ୍ରାମପେକ୍ଷୟା ଅଧ୍ଵତରଂ ଭବତି । ତସ୍ୟ ତେଜୋଽପି ସର୍ବାଧ୍ଵ । ରାଜ୍ଞ ବଳିଷ୍ଠତା, ସ୍ଥିରତା,
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ସର୍ବତେଜଃ + ଅଭିଭାବିନା । ସର୍ବୋନ୍ନତେନ୍ଫୋର୍ବୀମ୍ = ସର୍ବ + ଉନ୍ନତେନ + ଉର୍ବୀମ୍ । କ୍ରାନ୍ସାମେରୁରିବାଙ୍ଗନା = କ୍ରାନ୍ହାମେରୁ + ଇବ + ଆଜ୍ନନା |
ସମାସ – ସର୍ବାତିରିକ୍ତସାରେଣ = ସର୍ବେଭ୍ୟ ଅତିରିକ୍ତ (୫ମୀ ତତ୍), ସର୍ବାତିରିକ୍ତ ସାରଃ ଯସ୍ୟ ଡଃ ତେନ ସର୍ବଞ୍ଚ ତତ୍ ତେଜଃ ( କର୍ମଧାରୟ), ସର୍ବତେଜଃ ଅଭିଭବିତୁଃ ଶୀଳମସ୍ୟତି, ତେନ ( ବହୁବ୍ରୀହିଃ) ।
ସକାରଣବିଭକ୍ତି – ସର୍ବାତିରିକ୍ତସାରେଣ, ସର୍ବତୋଜୋଭିଭାବିନା, ସର୍ବୋନ୍ନତେନ, ଆତ୍ମନା = କରଣେ ୩ୟା । ମେରୁ = ‘ଇବ’ ଯୋଗେ ୧ମା । ଉର୍ବୀ = କର୍ମଣି ୨ୟା ।
ପୃକଡିପ୍ରତ୍ୟୟ – ଅତିରିକ୍ତ = ଅତି + ରିଚ୍ + କ୍ତ । ସ୍ଥିତଃ = ସୁ + କ୍ତ । କ୍ରାନ୍ସା = କ୍ରମ୍ + କ୍ରାଚ୍ ।
ଶ୍ଳୋକ – ୧୫
आकारसदृशप्रज्ञः प्रज्ञयासदृशागमः ।
आगमैः सदृशारम्भ आरम्भ सदृशोदयः ||१५||
ଆକାରସଦୃଶପ୍ରଜ୍ଞା ପ୍ରଜ୍ଞୟା ସଦୃଶାଗମଃ ।
ଆଗମୈ ସଦୃଶାରମ୍ଭ ଆରମ୍ଭ ସଦୃଶୋଦୟଃ ॥ ୧୫ ॥
ଅନ୍ବୟ – (ସ ଦିଲୀପଃ) ଆକାରସଦୃଶ ପ୍ରଜ୍ଞା, ପ୍ରଜ୍ଞୟା ସଦୃଶାଗମଃ, ଆଗମେ ସଦୃଶାରମ୍ଭ ଆରମ୍ଭ ସଦୃଶୋଦୟ (ଆସୀତ୍) ।
ଶବ୍ଦାର୍ଥ – ଆକାରସଦୃଶ ପ୍ରଜ୍ଞ = ନିଜର ଆକୃତି ସଦୃଶ ବୁଦ୍ଧିମାନ୍ । ପ୍ରଜ୍ଞୟାସଦୃଶାଗମ = ନିଜର ବୁଦ୍ଧି ଅନୁସାରେ ଶାସ୍ତ୍ରର ନୀତିରେ ଧୁରନ୍ଧର ଥିଲେ ! ଆଗମଃ ସଦୃଶାରତଃ ଶାସ୍ତ୍ରୀୟ ନୀତି ଅନୁସାରେ କାର୍ଯ୍ୟ ଆରମ୍ଭ କରୁଥିଲେ । ଆରମ୍ଭ ଯେକୌଣସି କାର୍ଯ୍ୟ ଆରମ୍ଭ କରୁଥିଲେ ତଦନୁରୂପ ଫଳଲାଭ କରୁଥିଲେ ।
ର୍ଥନ୍ମବାନ – (ରାଜା ଦିଲୀପଙ୍କର) ଆକୃତି ଯେଭଳି ଥିଲା ସେହିଭଳି ମଧ୍ଯ ବୁଦ୍ଧି ଥଲା । ବୁଦ୍ଧି ଅନୁରୂପ ତାଙ୍କର ଶାସ୍ତ୍ରୀୟ ପାଣ୍ଡିତ୍ୟ ଥିଲା । ଶାସ୍ତ୍ରୀୟ ପାଣ୍ଡିତ୍ୟ ଅନୁସାରେ ସେ ସମସ୍ତ କାର୍ଯ୍ୟ ଆରମ୍ଭ କରୁଥିଲେ ଏବଂ ଆରମ୍ଭ କରୁଥିବା କାର୍ଯ୍ୟର ସେ ଅନୁରୂପ ଫଳ ଲାଭ କରୁଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଉଦ୍ଧୃତଃ ଶ୍ଳୋକଃ ମହାକବି କାଳିଦାସବିରଚିତଂ ‘ ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରାଜ୍ଞ ଦିଲୀପସ୍ୟ ବିବିଧା ଗୁଣା ଯଥା ସୁନ୍ଦରତା, ବୁଦ୍ଧିମତା, ଶାସ୍ତ୍ରୀୟତା, ନୀତିଜ୍ଞତା, ଭାଗ୍ୟଶାଳୀତା ଚ ବର୍ଣ୍ଣିତଂ ଭବତି ।
ରୂପମାସୀତ୍ ତଥା ସୁବୁଦ୍ଧି ଆସୀତ୍ । ବୁଦ୍ଧାନୁସାରଂ ଚ ବିଦିତମ୍ । ସ୍ଵକୀୟ କାର୍ଯ୍ୟଧାରାଂ ଶାସ୍ତ୍ରୋକ୍ତରୀତ୍ୟା ତଥା ସୁନିଶ୍ଚିତଂ ଫଳମପି ଲଛମ୍ । ଦିଲୀପଃ ଅତ୍ୟନ୍ତ |
ଯଥା ବଂଶଃ ତଥା ଗୁନଃ ରୂପଶ୍ଚ । ସମ୍ରାଟ୍ ଦିଲୀପସ୍ୟ ଯଥା ସୌନ୍ଦର୍ଯ୍ୟ ଶାସ୍ତ୍ରୀୟଜ୍ଞାନମପି ଆସୀତ୍ । ସ୍ବକୀୟ ପାଣ୍ଡିତ୍ୟେନ ସର୍ବଂ ଶାସ୍ତ୍ର ନୀତିନିୟମଂ ସମାହିତମ୍ । ବିଧୂପୂର୍ବକଂ କର୍ତ୍ତବ୍ୟ ସମ୍ପାଦିତମ୍ । ଯଦେବ କାର୍ଯ୍ୟାରତଂ କୃତଂ ଭାଗ୍ୟବାନ୍ ଆସୀତ୍ । କବି ଯଥା ଦିଲୀପସ୍ୟ ଗୁଣାବଳୀ ବର୍ଣିତଂ ତଦେବ ପ୍ରଶଂସାହଃ ଭବତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଛେଦ – ପ୍ରତମ୍ବା ସହଶାଗମ: = ପ୍ରକମ୍ନାସଦୃଶ + ଆଗମ: | ସଦ୍ୱଶାରମ୍ବ = ସଦ୍ଵଶ + ଆରମ୍ | ଆରମ୍ଭସଦୃଶ + ଉଦୟଃ ।
ସମାସ – ଆକାର ସଦୃଶୀ ପ୍ରଜ୍ଞା ଯସ୍ୟ ଡଃ (ବାହୁବ୍ରୀହିଃ) । ସଦୃଶାଗମ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) । ସଦୃଶାରତଃ = ସଦୃଶଃ ଆରମ୍ଭ ଯସ୍ୟ ଡଃ ( ବହୁବ୍ରୀହିଃ) । ଆରମ୍ଭସଦୃଶୋଦୟଃ ସଦୃଶଃ (୩ୟା ତତ୍), ଆରମ୍ଭସଦୃଶଃ ଉଦୟଃ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) ।
ସକାରଣବିଭକ୍ତି – ପ୍ରଜ୍ଞୟା, ଆଗମୈ = ତୁଲ୍ୟାର୍ଥେ ୩ୟା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଆକାରଃ = ଆରମ୍ଭେଣ ଆ +କ୍+ ଘଞ୍ଚ୍ । ଆଗମ = ଆ + ଗମ୍ + ଅପ୍ । ଆରମ୍ଭ = ଆ + ରଭ + ଘଞ୍ଚ୍ ।
ଶ୍ଳୋକ – ୧୬
भीमकान्तैर्नुपगुणैः स बभूवोपजीविनाम् ।
अधृष्यश्चाभिगम्यश्च यादोरन्तैरिवार्णवः || १६ ||
ଭୀମକାନୈପଗୁ ସ ବଭୂବୋପଜୀବିନାମ୍ ।
ଅଧୃଷ୍ୟଣ୍ଟାଭିଗମ୍ୟଷ୍ଟ ଯାହୋରତ୍ରୈରିବାର୍ଣକଃ ॥ ୧୬ ||
ଅନ୍ବୟ – ଭୀମକାନ୍ତଃ ନୃପଗୁଣି ଡଃ ଉପଜୀବିନାଂ ଯାଦୋରତ୍ଯେ ଅର୍ୟତଃ ଇବ ଅଧୃଷ୍ୟଶ୍ଚ ଅଭିଗମ୍ୟଶ୍ଚ ବଭୂବ ।
ଶବ୍ଦାର୍ଥ – ଭୀମକାନ୍ତଃ = ଭୟାନକ ଏବଂ ମନୋରମ । ନୃପଗୁଣି = ରାଜକୀୟ ଗୁଣଦ୍ଵାରା । ଡଃ = = ଜଳଜନ୍ତୁ ମଣିପ୍ରଭୃତିଦ୍ଵାରା । ଅର୍ଶନଃ ଇବ = ସମୁଦ୍ର ଭଳି ଅତ୍ୟନ୍ତ ଭୟଙ୍କର ଫଳରେ ଅନାକ୍ରମ୍ୟ । ଅଭିଗମ୍ୟଶ୍ଚ = `ଯେହେତୁ ଶାନ୍ତ, ଫଳରେ ସେବନୀୟ । ବଭୂବ = ଦିଲୀପ । ଉପଜୀବିନାଂ = ଆଶ୍ରିତମାନଙ୍କର । ଯାଦେର = ଥିଲେ ।
କେହି ଆକ୍ରମଣ କରିପାରନ୍ତି ନାହିଁ, ତଥା ନିଜ ମଧ୍ୟରେ ରତ୍ନ ଥିବାଦ୍ଵାରା ତାହା ସମସ୍ତଙ୍କର ମନୋରମ ଏବଂ ସେବାର ଯୋଗ୍ୟ ହୋଇଥାଏ, ସେହିଭଳି ରାଜା ଦିଲୀପ ନିଜର ଭୟାନକ ତଥା କାନ୍ତ କମନୀୟ ତେଜ, ପ୍ରତାପ, ଦୟା, ଦାକ୍ଷିଣ୍ୟାଦି ରାଜକୀୟ ଗୁଣଦ୍ଵାରା ଅନ୍ୟର ଅନାକ୍ରମ୍ୟ ତଥା ସେବାର ଯୋଗ୍ୟ ମଧ୍ୟ ହୋଇଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ମହାକବି କାଳିଦାସବିରଚିତଃ ‘ରଘୁବଂଶମ୍ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମସର୍ଗତ୍ ଆନୀତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟା ଶାରୀରିକ ଶୋଭା କଥମ୍ ଅର୍ନ୍ତତଃ ଇବ ଆସୀତ୍ ତଦେବ ବର୍ଣ୍ଣିତମ୍ । ତୁଳିତମ୍ । ଯଥା ଅର୍ଶନଃ ତଥା ଅସୌ ରାଜା ଦିଲୀପଃ । ରାଜା ଦିଲୀପଃ ଯଥା ଭୀମ ନାମ ଭୟଂକରଃ ତଥା କାନ୍ତଃ ନାମ ସୌମ୍ୟ ସମଳଂକୃତସନ୍ ଅନାକ୍ରମଣୀୟ ଅନଭିବବଦନୀୟ ଆକର୍ଷଣୀୟଂ ଚ ଆସୀତ୍ । ତଥା ସମୁଦ୍ର ଅପି ଧୀରଃ ଗମ୍ଭୀରଶ୍ଚ ଭବତି ପୁନଃ ମନୋହରଃ ଚ ଭବତି । ସମୁଦ୍ରାଭ୍ୟନ୍ତରେ ବହତଃ ହିଂସ୍ରଜଳଜନ୍ତତଃ ଆସନ୍ ଅପି ତୁ ବିବିଧି ରହିଃ ପରିପୂରିତଃ ଚାସୀତ୍ । ଉପଜୀବିନାଂ କୃତେ ରାଜା ଯଥା ଅପରାଜେୟ ଆଶ୍ରୟଣୀୟ ଚ ବିଶୂଦଭୂବ ତଥା ସମୁଦ୍ରାପି ଉପଜୀବିନାଂ କୃତେ ତଥୈବ ଭବତି । ସମୁଦ୍ରସ୍ୟ ଗୁନଃ ରାଜା ଦିଲୀପସ୍ୟ ସମୀପେ ଦୃଶ୍ୟମାନଂ ଭବତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଭୀମକାନ୍ତେର୍ନ୍ତପଗୁଣି = ଭୀମକାନ୍ତଃ + ନୃପଗୁଣି । ବଭୂବୋପଜୀବିନାମ୍ = ବଭୂବ + ଉପଜୀବିନାମ୍ । ଅଧୃଷ୍ୟଣ୍ଟାଭିଗମ୍ୟଶ୍ଚ = ଅଧୃଷ୍ୟ + ଚ + ଅଭିଗମ୍ୟ + ଚ । ଯାଦୋରତ୍ରୈରିବାର୍ଷିକଃ = ଯାଦୋରର୍ତ୍ତେ + ଇବ + ଅର୍ଥଦଃ ।
ଶବ୍ଦାର୍ଥ – ଭୀମକାନ୍ତଃ = ଭୀମାଶ୍ଚ ତେ କାନ୍ତାଶ୍ଚ, ଡଃ (କର୍ମଧାରୟ) । ନୃପଗୁଣେ (ନଞ୍ଚ୍ ତତ୍) । ଅଭିଗମ୍ୟ = ଅଭିଗନ୍ତୁ ଯୋଗ୍ୟ ଇତି (ଅବ୍ୟୟୀଭାବ) । ଯଦୋର = ଯମାଂସି ଚ ରତ୍ନାନି ଚ, ତିଃ (ଦ୍ବନ୍ଦ୍ବ) ।
ସକାରଣବିଭକ୍ତି – ଭୀମକାନ୍ତେ, ନୃପଗୁଣେ, ଯାଦୋରର୍ତ୍ତି = କରଣେ ୩ୟା । ସ = କଉଁରି ୧ ମା । ଉପଜୀବିନାଂ କୃତ୍ ଯୋଗେ ୬ଷ୍ଠୀ । ଅର୍ଣବ = ଇବ ଯୋଗେ ୧ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଭୀମ = ଭୀ + ମକ୍ । କାନ୍ତଃ = କମ୍ + କ୍ତ । ନୃପ = ନୃ + ପା + କ୍ତ । ଉପଜୀବିନାମ୍ = ଉପ + ଜୀବ୍ + ଣିନି (୬ଷ୍ଠୀ) । ଧୃଷ୍ୟ ଧୃଷ୍ + ଯତ୍ । ଅଭିଗମ୍ୟ = ଅଭି + ଗମ୍ + ଯତ୍ ।

ଶ୍ଳୋକ – ୧୭
रेखामात्रमपि क्षुण्णादामनोर्वर्त्मनः परम् ।
न व्यतीयुः प्रजास्तस्य नियन्तुर्नेमिवृत्तयः ।।१७।।
ରେଖାମାତ୍ରମପି କ୍ଷୁଷ୍ଠାଦା ମନୋର୍ବର୍ତ୍ତନଃ ପରମ୍ ।
ନ ବ୍ୟତୀୟୁ ପ୍ରଜାସ୍ତସ୍ୟ ନିୟନ୍ତୁନୈମିବୃତ୍ତୟଃ ॥ ୧୭ ||
ଅନ୍ବୟ – ନିୟନ୍ତୁ ତଥ୍ୟ ନେମିବୃତ୍ତୟଃ ପ୍ରଜାଃ ଆ ମନୋ କ୍ଷୁଷ୍ଠାତ୍ ବର୍ତ୍ତନଃ ପରଂ ରେଖାମାତ୍ରମ୍ ଅପି ନ ବ୍ୟତୀୟୁ ।
ଶବ୍ଦାର୍ଥ – ନିୟନ୍ତୁ = ସାରଥସଦୃଶ । ତଥ୍ୟ = ସେହି ରାଜା ଦିଲୀପଙ୍କର । ନେମିବୃତ୍ତୟଃ ପ୍ରଜାଃ ଗତି କରୁଥିବା ପ୍ରଜାମାନେ | ଆମନୋ = ମନୁଙ୍କଠାରୁ ଆରମ୍ଭ କରି । କ୍ଷୁଶ୍ଚାତ୍ = ନିର୍ଦ୍ଧାରିତ । ବର୍ତ୍ତନଃ ପରଂ ରେଖାମାତ୍ରମ୍ ଅପି = ତିଳେମାତ୍ର ବା ଇଞ୍ଚେମାତ୍ରେ ବି । ନ ବ୍ୟତୀୟୁ = ବିଚଳିତ ହେଉ ନଥିଲେ ।
ଅନୁବାଦ – ସାରଥ୍ ସଦୃଶ ସେହି ରାଜା ଦିଲୀପଙ୍କର ରଥଚକ୍ର ଭଳି ଗତି କରୁଥିବା ପ୍ରଜାମାନେ ମନୁଙ୍କଠାରୁ ନିର୍ଦ୍ଧାରିତ ହୋଇଥବା ନୀତିପୂର୍ଣ୍ଣ ମାର୍ଗରୁ ତିଳେହେଲେ ମଧ୍ୟ ବିଚ୍ୟୁତ ହେଉ ନଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ‘ରଘୁବଂଶମ୍ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ ସୁଶାସନବଳେନ କରଂ ତସ୍ୟ ପ୍ରଜାଃ ସଦୈବ ମନୋ ମାର୍ଗ ପରିଚାଳିତଂ ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ସୁପ୍ରସିଦ୍ଧ ବଂଶସ୍ୟ ସମ୍ରାଟ ଦିଲୀପସ୍ୟ ସୁଶାସନସ୍ୟ ପ୍ରଭାବେନ ପ୍ରଜା ସୁଶୃଙ୍ଖଳିତଃ ସୁସଂଯତଃ ଚ ଆସନ୍ । ଯଥା ନିୟନ୍ତୁ ଭବନ୍ତି । ରଥଚକ୍ରସ୍ୟ ଧାରଂ ଯଥା ଚଳତି ତାବତ୍ ପ୍ରଜା ମନୋ ନିର୍ଦେଶିତଂ ମାର୍ଗ ପରିଚାଳିତଂ ଭବନ୍ତି । ରେଖାମାତ୍ରମପି ବିଚ୍ୟୁତଃ ଭବନ୍ତି । ଅର୍ଥାତ୍ ଦିଲୀପସ୍ୟ ପ୍ରଶାସନିକ ଦକ୍ଷତା ତଥା ପ୍ରଜାନାଂ ବ୍ୟକ୍ତିତ୍ୱ ଚ ପରିଲକ୍ଷିତଂ ଭବତି ।
= ରେଖାମାତ୍ରମ୍ + ଅପି । କ୍ଷୁଣ୍ଣଦାମନୋନଃ = କ୍ଷୁଷ୍ଠାତ୍ + ଆମନୋ + ବର୍ତ୍ତନଃ । ପ୍ରଜାସ୍ତସ୍ୟ = ପ୍ରଜାଃ + ତସ୍ୟ । ନିୟନ୍ତୁନୈମିବୃତ୍ତୟ = ନିୟତଃ + ନେମିବୃତ୍ତୟଃ ।
ସମାସ – ନେମିବୃତ୍ତୟଃ = ନେମୀନାଂ ବୃତିଃ (୬ଷ୍ଠ ତତ୍), ନେମିବୃତିଃ ଇବ ବୃତିଃ ଯାଆଂ ଡାଃ (ବହୁବ୍ରୀହି) ।
ସକାରଣବିଭକ୍ତି – ଆମନୋ = ‘ଆମର୍ଯ୍ୟାଦାଭିବିଧୌ’ ଯୋଗେ ୫ମୀ । ନିୟୁନ୍ତୁ, ତଥ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ନେମିବୃତ୍ତୟଃ, ପ୍ରଜାଃ = କଉଁରି ୧ ମା । କ୍ଷୁଷ୍ଠାତ୍ = ଅପାଦାନେ ୫ମୀ । ବର୍ତ୍ତନଃ = ପରଂ ଯୋଗେ ୫ମୀ । ରେଖାମାତ୍ରମ୍ = ‘ଅପି’ ଅବ୍ୟୟ ଯୋଗେ ୧ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – କ୍ଷୁଣ୍ଣ = କ୍ଷୁଦ୍ + କ୍ତ । ପ୍ରଜା = ପୂ + ଜନ୍ + ତ । ନିୟୁତଃ = ନି + ଯମ୍ + ତୁଚ୍ (୬ଷ୍ଠୀ ଏକବଚନ) । ବୃତିଃ = ବୃତ୍ + ସ୍କ୍ରିନ୍ ।
ଶ୍ଳୋକ – ୧୮
प्रजानामेव भूत्यर्थं स ताभ्यो वलिमग्रहीत् ।
सहस्रगुणमुत्स्रष्टुमादत्ते हि रसं रविः ।।१८।।
ପ୍ରଜାନାମେବ ଭୃତ୍ୟର୍ଥ୍ୟ ସ ତାଭ୍ୟା ବଳିମଗ୍ରହୀତ୍ ।
ସହସ୍ରଗୁଣମୁସ୍ରଷ୍ଣୁ ମାଦରେ ହିଁ ରସଂ ରବି ॥ ୧୮ ||
ଅନ୍ବୟ – ଡଃ ପ୍ରଜାନାଂ ଭୂତ୍ୟର୍ଥମ୍ ଏବଂ ତାଭ୍ୟ ବଳିମ୍ ଅଗ୍ରହୀତ୍ । ହି ରବି ସହସ୍ରଗୁଣମ୍ ଭସ୍ରଷ୍ଣୁ ରସମ୍ ଆଦତ୍ତେ ।
ଶବ୍ଦାର୍ଥ – କଃ = ସେହି ରାଜା ଦିଲୀପ । ପ୍ରଜାନାମ୍ = ପ୍ରଜାମାନଙ୍କର । ଭୂତ୍ୟର୍ଥମ୍ = ମଙ୍ଗଳ ପାଇଁ । ତାଭ୍ୟ = ସେହି ପ୍ରଜାମାନଙ୍କଠାରୁ । ବଳିମ୍ = କରସ୍ଵରୂପ ଷଷ୍ଠୀଶ । ଅଗ୍ରହୀତ୍ = ଗ୍ରହଣ କରୁଥିଲେ । ହି = ଯେହେତୁ । ରବି ସୂର୍ଯ୍ୟ । ସହସ୍ରଗୁଣମ୍ = ସହସ୍ର ଗୁଣ ଅଧିକ ହିଁ ବର୍ଷା କରିବାପାଇଁ । ରସମ୍ = ଜଳ । ଆଦିରେ = ଗ୍ରହଣ କରନ୍ତି ।
ଅନ୍ତବାଦ – ସେହି ରାଜା ଦିଲୀପ ପ୍ରଜାମାନଙ୍କର ମଙ୍ଗଳ ପାଇଁ ହିଁ ସେମାନଙ୍କଠାରୁ କର ଗ୍ରହଣ କରୁଥିଲେ । ଯେହେତୁ ସହସ୍ର ଗୁଣ ଅଧିକ ବର୍ଷା କରିବାପାଇଁ ସୂର୍ଯ୍ୟ ଜଳଗ୍ରହଣ କରିଥା’ନ୍ତି ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋସଙ୍ଗ ପଠିତ ମହାକଟି କାଲିବାପବିଉଟିଭ: ସ୍ପ୍ରପିବଂ ‘ରଶ୍ମବଂଶମ୍ଭ’ ମଦ୍ରାକାବ୍ୟପ୍ୟ ସ୍ତରମଗାଡ ଆନୀତଃ । ଅସ୍କ୍ରିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ କରଗ୍ରହଣପ୍ରସଙ୍ଗ ବର୍ଣ୍ଣିତମ୍ ।
ରାଜା ଦିଲୀପସ୍ୟ ଶାସନବ୍ୟବସ୍ଥା ସୁଶୃଙ୍ଖଳିତଃ ଆସୀତ୍ । ରାଜା ଦିଲୀପଃ ପ୍ରଜାନାଂ କଲ୍ୟାଶ୍ରାର୍ଥୀ ତାଭ୍ୟ ଏକଷକ୍ଷାଂଶ ବଳିମ୍ ଅଗ୍ରହୀତ୍ । ଅସ୍ୟ ପ୍ରସଙ୍ଗସ୍ୟ ବର୍ଣ୍ଣନଂ କବିକାଳିଦାସେନ ଉପମାଧାରେଣ ପ୍ରଯୁକ୍ତ । ଯଥା ରବି ସହସ୍ରଗୁଣଂ ଜଳଂ ପ୍ରଦାମିଂ ସ୍ଵଜଳଂ ଗୃହ୍ଣାତି ତଥୈବ ଅସୌ ରାଜା ଦିଲୀପଃ ପ୍ରଜାଭ୍ୟ ବଳଂ ଗୃହ୍ଣାତି । ଅତ୍ର ରାଜା ଦିଲୀପଂ ରବିନା ସାକଂ, ବଳଂ ତୁ ଜଳେନ ସହ ତୁଳିତମ୍ । ମହର୍ଷି ମନୁଃ ସ୍ବରଚିତଗ୍ରନ୍ଥି ରାଜ୍ଞ କର୍ତ୍ତବ୍ୟ ପ୍ରସଙ୍ଗେ ଉକ୍ତ ଯତ୍ – ପ୍ରଜାପାଳନଂ କରଗ୍ରହଣଂ ଚ ରାଜ୍ଞ ପରମକର୍ତ୍ତବ୍ୟ ଭବତି । ପ୍ରସଽୟଂ ଯଥା ମହାକବିନା ବର୍ଣିତଃ ତଦେବ ବର୍ଣ୍ଣନୀୟଂ ଭବତି ।
ସନ୍ଧିବିଚ୍ଛେଦ – ପ୍ରଜାନାମେବ = ପ୍ରଜାନାମ୍ + ଏବ । ବଳିମଗ୍ରହୀତ୍ = ବଳିମ୍ + ଅଗ୍ରହୀତ୍ । ସହସ୍ରଗୁଣସ୍ରଷ୍ଣୁମାଦରେ ସହସ୍ରଗୁଣମ୍ + ଉତ୍ + ସ୍ରଷ୍ଟୁମ୍ + ଆଦତ୍ତେ ।
ସମାସ – ସହସ୍ରଗୁଣମ୍ = ସହସ୍ର ଗୁଣୀ ଯସ୍ମିନ୍ କର୍ମଣି ତଦ୍ (ବହୁବ୍ରୀହିଃ) । ଭୂତ୍ୟର୍ଥମ୍ = ଭୂତଃ ଇଦମ୍ (ନିତ୍ୟ) ।
ସକାରଣବିଭକ୍ତି – ପ୍ରଜାନାମ୍ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ତାଭ୍ୟ = କର୍ମଣି ୨ୟା । ରସମ୍ = କର୍ମଣି ୨ୟା । ରବି = କର୍ଭରି ୧ ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଉସ୍ରଷ୍ଟୁମ୍ = ଉତ୍ + ସୃଜ୍ + ତୁମୁନ୍ ।
ଶ୍ଳୋକ – ୧୯
सेना परिच्छदस्तस्य द्वयमेवार्थसाधनम् ।
शास्त्रेष्वकुण्ठिता बुद्धिमौर्वी धनुषि चातता ।।१९।।
ସେନା ପରିଚ୍ଛଦସ୍ତସ୍ୟ ଦ୍ୱୟମେବାର୍ଥସାଧନମ୍ ।
ଶାସ୍ତେଶ୍ବକୁଣ୍ଠିତା ବୁଦ୍ଧିମୌର୍ବୀ ଧନୁଷି ଚାତତା ॥ ୧୯ ||
ର୍ଥନ୍ମସ୍ – ତସ୍ୟ ସେନା ପରିଚ୍ଛଦଃ (ବଭୂବ) ଅର୍ଥସାଧନମ୍ ଦ୍ଵୟମେବ – ଶାସ୍ତେଷୁ ଅକୁଣ୍ଠିତା ବୁଦ୍ଧି, ଧନୁଷି ଆତତା ମୌବା ଚ |
ଶବ୍ଦାର୍ଥ – ତଥ୍ୟ = ସେହି ରାଜା ଦିଲୀପଙ୍କର । ସେନା = ସେନାବାହିନୀ । ପରିଚ୍ଛଦଃ = ଅର୍ଥସାଧନମ୍ = ପ୍ରୟୋଜନସିଦ୍ଧି । ଦ୍ଵୟମେବ = ହିଁ ଦୁଇଟି | ଶାସ୍ତେଷୁ = ଶାସ୍ତ୍ରମାନଙ୍କରେ । ଅକୁଣ୍ଠିତା ବୁଦ୍ଧି = ପ୍ରଖର ବୁଦ୍ଧି | ଧନୁରେ ଆରୋପିତ ହୋଇଥିବା | ମୌର୍ବୀ = ଗୁଣ ।
ଅନୁବାଦ – ପ୍ରୟୋଜନ ସିଦ୍ଧି ପାଇଁ ଦୁଇଟି ମାତ୍ର ଉପାୟ ଥିଲା । ପ୍ରଥମଟି ତାଙ୍କର ଶାସ୍ତ୍ରରେ ଥିବା ପ୍ରଖର ବୁଦ୍ଧି ବା ପାଣ୍ଡିତ୍ୟ ଏବଂ ଅପରଟି ତାଙ୍କର ଧନୁରେ ଆରୋପିତ ହୋଇଥିବା ଗୁଣ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋସଙ୍ଗ ପଠିତ ମହାକଟି କାଲିବାପବିଉଟିଭ: ସ୍ପ୍ରପିବଂ ‘ରଶ୍ମବଂଶମ୍ଭ’ ମଦ୍ରାକାବ୍ୟପ୍ୟ ପ୍ରଥମସର୍ଗତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ନୀତିଶାସ୍ତ୍ରବିଶାରଦଃ ତଥା ଶୌର୍ଯ୍ୟବାନ୍ ରାଜା ଦିଲୀପ ସ୍ୱସ୍ୟ ଅର୍ଥସିଦ୍ଧାର୍ଥୀ ସେନା ଉପରି ନିର୍ଭରଂ ନ କୃତବାନ୍ ଇତି ବିଷୟେ ବର୍ଣ୍ଣିତମ୍ ।
ରଘୁବଂଶୀୟ ରାଜାନଃ ପରାକ୍ରମୀ ଆସନ୍ । ‘ସ୍ବବୀର୍ଯ୍ୟଗୁପ୍ତାହି ମନୋ ପ୍ରସୂତି ।’ ସ୍ଵସ୍ୟ ରକ୍ଷାର୍ଥୀ ତ୍ରେ ପରେଷା ଅନ୍ୱେଷା ବା ଉପରି ନିର୍ଭରଶୀଳା ନାସନ୍ । ରାଜାଦିଲୀପସ୍ୟ ଚତୁରଙ୍ଗସେନା କେବଳମ୍ ଅଳଂକରଣ ରୂପେଣ ସ୍ଥିତା । ଅନ୍ୟାୟେନ ରାଜା କମପି ଆକ୍ରମଣଂ ନ କୃତବାନ୍ । ତସ୍ୟ କୋଽପି ଶତଃ ନାସୀତ୍ । ସ୍ଵସ୍ୟ କାର୍ଯ୍ୟ ସିଦ୍ଧାର୍ଥୀ ରାଜା ଦିଲୀପେନ ଉପାୟଦ୍ୱୟସ୍ୟ ଅବଲମ୍ବନଂ କୃତମ୍ । ଯାସ୍ତେଷୁ ଅକୁଣ୍ଠିତା ବୁଦ୍ଧି, ଧନୁଷି ଆତତା ମୌର୍ବୀ ଚ ତଥ୍ୟ ଦିଲୀପସ୍ୟ ଅର୍ଥସାଧନଦ୍ଵୟମାସୀତ୍ । ରାଜା ଦିଲୀପସ୍ୟ ବୁଦ୍ଧିମତା ତଥା ବୀରତ୍ଵ ପ୍ରଶଂସନୀୟଂ ଭବତି ।
ସନ୍ଧିବିଚ୍ଛେଦ – ପରିଚ୍ଛଦସ୍ତସ୍ୟ = ପରିଚ୍ଛଦଃ + ତସ୍ୟ । ଦ୍ୱୟମେବାର୍ଥସାଧନମ୍ = ଦ୍ଵୟମ୍ + ଏବ + ଅର୍ଥସାଧନମ୍ । ଶାସ୍ତେଷୁ + ଅକୁଣ୍ଠିତା । ବୁଦ୍ଧିମୌର୍ବୀ = ବୁଦ୍ଧି + ମୌର୍ବୀ । ଚାତ = ଚ+ ଆତତା ।
ସମାସ – ଅର୍ଥସାଧନମ୍ = ଅର୍ଥକ୍ୟ ସାଧନମ୍ (୬ଷ୍ଠ ତତ୍) । ଅକୁଣ୍ଠିତା = ନ କୁଣ୍ଠିତା (ନଞ୍ଚ୍ ତତ) ।
ସକାରଣବିଭକ୍ତି – ଶାସ୍ତ୍ରଷୁ, ଧନୁଷି = ଅଧୂକରଣେ ୭ମୀ । ତସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ସେନା, ପରିଚ୍ଛଦଃ = କଉଁରି ୧ ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସାଧନମ୍ = ସାଧ୍ + ଲ୍ୟୁଟ୍ । ମୌର୍ବୀ = ମୁର୍ବା + ଅଣ୍ + ଡୀପ୍ । ଆତତା = ଆ + ତନ୍ + କ୍ତ + ଆପ୍ ।
ଶ୍ଳୋକ – ୨୦
तस्य संवृतमन्त्रस्य गूढाकारेङ्गितस्य च ।
फलानुमेयाः प्रारम्भाः संस्काराः प्राक्तना इव ।। २० ।।
ତସ୍ୟ ସଂବୃତମନ୍ତ୍ରସ୍ୟ ଗୂଢ଼ାକାରେଙ୍ଗିତସ୍ୟ ଚ ।
ଫଳାନୁମେୟା ପ୍ରାରମ୍ଭ ସଂସ୍କାରଃ ପ୍ରାକ୍ତନା ଇବ । ୨୦ ||
ଅନ୍ବୟ – ସଂବୃତମନ୍ତ୍ରସ୍ୟ ଚ ଗୂଢ଼ାକାରେଙ୍ଗିତସ୍ୟ ତସ୍ୟ ପ୍ରାରମ୍ଭ ପ୍ରାକ୍ତନଃ ସଂସ୍କାରଃ ଇବ ଫଳାନୁମେୟା ଆ ସନ୍ ।
ଶବ୍ଦାର୍ଥ – ସଂବୃତମନ୍ତ୍ରସ୍ୟ = ଯାହାର ବିଚାର ବା ମନ୍ତ୍ରଣା ଅତ୍ୟନ୍ତ ଗୋପନୀୟ ଥିଲା = ତାଙ୍କର ହୃଦୟର ଭାବ ମଧ୍ୟ ଆଦୌ ପ୍ରକଟିତ ହୋଇପାରୁ ନଥିଲା । ତସ୍ୟ = ସେହି ରାଜା ଦିଲୀପଙ୍କର । ପ୍ରାରମ୍ଭ = ସମସ୍ତ କାର୍ଯ୍ୟକ୍ରମଗୁଡ଼ିକ । ପ୍ରାକ୍ତନା = ପୁରାତନ । ସଂସ୍କାରଃ ଇବ = ସଂସ୍କାର ଭଳି । ଫଳାନୁମେୟା = ଫଳରୁ ହିଁ ଅନୁମିତ ହେଉଥିଲା ।
ର୍ଥନ୍ମବାଦ – ସେହି ରାଜା ଦିଲୀପଙ୍କର ମନ୍ତ୍ରଣା ଅତ୍ୟନ୍ତ ଗୋପନୀୟ ଥିଲା ଏବଂ ତାଙ୍କର ହୃଦୟର ଭାବ ଆଦୌ ପ୍ରଥମସର୍ଗତ୍ ଆନୀତାଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ ମନ୍ତ୍ରଣା କଲଂ ଗୋପନୀୟମ୍ ଆସୀତ୍ ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ବ୍ୟାଖ୍ୟା – ରାଜକୀୟକାର୍ଯ୍ୟାର୍ଥୀ ଗୁପ୍ତଚରାଣା ନିଯୁକ୍ତା କର୍ତ୍ତବ୍ୟ । ଅନେନ ଗୁପ୍ତଚରେଣ ରାଜା ସ୍ଵକାର୍ଯ୍ୟସ୍ୟ ଗୋପନୀୟତଂ ସିରିଂ ଚ ପ୍ରତିପାଦୟତି । ରାଜ୍ଞ ଦିଲୀପସ୍ୟ ମନ୍ତ୍ରଣା ଅତୀବ ଭୂମତାସୀତ୍ । ‘ ମନସା ଚିରିତଂ କାର୍ଯ୍ୟ ବଚସା ନ ପ୍ରକାଶୟେତ୍।’ ରାଜ୍ୟରକ୍ଷାର୍ଥୀ ଗୋପନୀୟତା ଏକାନ୍ତ ପାଳନୀୟମ୍ । କାର୍ଯ୍ୟସ୍ୟ ଆରମ୍ଭାତ୍ ପ୍ରାକ୍ ଗୋପନୀୟତା ଯଦି ଅବଲକ୍ଷ୍ୟତେ ତହିଁ କାର୍ଯ୍ୟସିଦ୍ଧି ସୁନ୍ଦରଂ ରାଜା ଦିଲୀପସ୍ୟ କାର୍ଯ୍ୟକ୍ରମ ତସ୍ୟାରତଂ ଚ ସିଦ୍ଧିମାତ୍ରେଣ ଫଳପ୍ରାପ୍ତା ଚ ସୂଚିତଂ ଭବତି । ଅର୍ଥାତ୍ ରାଜା ଦିଲୀପସ୍ୟ କାର୍ଯ୍ୟଦକ୍ଷତା ଅନୁମୀୟତେ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଛେଦ – ଗୂଢ଼ାକାରେଙ୍ଗିତଥ୍ୟ = ଗୂଢ଼ାକାର + ଇଙ୍ଗିତସ୍ୟ । ଫଳାନୁମେୟା = ଫଳ + ଅନୁମେୟ ।
ସମାସ – ସହସ୍ରଗୁଣମ୍ = ସଂବୃତଃ (ଗୁପ୍ତ) ମନ୍ତ୍ରୀ ଯସ୍ୟ ଡଃ (ବହୁବ୍ରୀହିଃ) । ଗୂଢ଼ାକାରେଙ୍ଗିତସ୍ୟ = ଆକାରଶ୍ଚ ଇଙ୍ଗିତଞ୍ଚ (ଦ୍ବନ୍ଦ୍ବ), ଗୂଢ଼େ ଆକାରେଙ୍ଗିତ ଯସ୍ୟ ଡଃ, ତସ୍ୟ (ବହୁବ୍ରୀହିଃ) । ଫଳାନୁମେୟୀ = ଫଳି ଅନୁମେୟା (୩ୟା ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ସଂହିତମନ୍ତ୍ରସ୍ୟ, ଗୂଢ଼ାକାରେଙ୍ଗିତସ୍ୟ, ତଥ୍ୟ = ସମ୍ବନ୍ଧେ ୬ଷ୍ଠୀ । ପ୍ରାରମ୍ଭ, ପ୍ରାକ୍ତନଃ = ୧ମା । ସଂସ୍କାରା = ‘ଇବ’ଯୋଗେ ୧ମା । ଫଳାନୁମେୟୀ = କଉଁରି ୧ ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସଂବୃତ = ସମ୍ + ବୃ + କ୍ତ । ଆକାରଃ = ପ୍ର + ଆ + ରଭ + ଘଞ୍ଜ୍ । ସଂସ୍କାରଃ = ସମ୍ + କୃ + ଘଞ୍ଚ୍ ।
ଶ୍ଳୋକ – ୨୧
जुगोपात्मानमत्रस्तो भेजे धर्ममनातुरः ।
अगृध्नुराददे सोऽर्थमसक्तः सुखमन्वभूत् ।।२१।।
ଜୁଗୋପାତ୍ମାନମତ୍ରସ୍ତୋ ଭେଜେ ଧର୍ମମନାତୁରଃ |
ଅଗ୍ନିଧୁରାଦଦେ ସୋଽର୍ଥମସନ୍ତଃ ସୁଖମନ୍ବଭୂତ୍ ॥ ୨୧ ||
ଅନୁୟ – ଧଃ ଅତ୍ରସ୍ତ (ସନ୍) ଆତ୍ମାନଂ କୁଗୋପ, ଅନାତୁରଃ (ସନ୍) ଧର୍ମ ଭେଜେ, ଅଗ୍ନୀଧ୍ରୁ (ସନ୍) ଅର୍ଥମ୍ ଆଦଦେ, ଅସନ୍ତଃ ( ସନ୍) ସୁଖମ୍ ଅନ୍ଧଭୂତ୍ ।
ଶବ୍ଦାର୍ଥ – ଡଃ = ସେହି ରାଜା ଦିଲୀପ | ଅତ୍ରସ୍ତ = ଭୟାତୁର ନ ହୋଇ | ଆତ୍ମାନଂ ଜୁଗୋପ = ନିଜକୁ ରକ୍ଷା କରୁଥିଲେ | ଅନାତୁରଃ = ନୀରୋଗ ହୋଇ | ଧର୍ମ ଆଚରଣ କରୁଥିଲେ । ଅଗ୍ନଧୂ = ଲୋଭାସକ୍ତ ନ ହୋଇ । ଅର୍ଥମ୍ ଆଦିଦେ ଭୟାତୁର ନ ହୋଇ । ଆତ୍ମାନଂ ଜୁଗୋପ = ନିଜକୁ ରକ୍ଷା । ଧର୍ମ ଭେଜେ ଅର୍ଥ ଗ୍ରହଣ କରୁଥିଲେ । ଅସନ୍ତଃ = ଅନାସକ୍ତ ହୋଇ । ସୁଖମ୍ ଅନୁଭୂତ୍ = ସୁଖ ଅନୁଭବ ବା ଉପଭୋଗ କରୁଥିନ୍ଦେ |
ଅନୁବାଦ – ସେହି ରାଜା ଦିଲୀପ ଭୟାତୁର ନ ହୋଇ ନିଜକୁ ରକ୍ଷା କରୁଥିଲେ । ଅରୁଗ୍ଣ ଅବସ୍ଥାରେ ହିଁ ଧର୍ମ ଆଚରଣ କରୁଥିଲେ । ଲୋଭାସକ୍ତ ନ ହୋଇ ଅର୍ଥ ଗ୍ରହଣ କରୁଥିଲେ ଏବଂ ଅନାସକ୍ତ ହୋଇ ସୁଖ ଉପଭୋଗ କରୁଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାମହିମଃ ପଣ୍ଡିତପ୍ରବରଃ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗାତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରାଜାଦିଲୀପସ୍ୟ ସ୍ୱରକ୍ଷଣଂ, ଧର୍ମାଚରଣଂ, ଅର୍ଥୋପାର୍ଜନଂ ସୁଖାନୁଭବଂ ଏତେଷାମ୍ ଉପାୟା ବର୍ଣ୍ଣିତାଃ ।
ରାଜାନଃ ରାଜକୀୟ କାର୍ଯ୍ୟ ପରିଚାଳନାର୍ଥୀ ବିବିଧା ଉପାୟ ଅବଲମ୍ବନଂ କୁର୍ବନ୍ତି । ଯଦା ଭୟମ୍ ଆୟାତି ତଦା ସ୍ୱରକ୍ଷଣଂ ଚିନ୍ତୟନ୍ତି । ରୋଗାକ୍ରାନ୍ତ ସମ୍ ଧର୍ମମ୍ ଆଚରନ୍ତି । ଲୋଭାସନ୍ତୀ ସନ୍ ଧନାର୍ଜନଂ କୁର୍ବନ୍ତି । କାମାସକ୍ତା ସନ୍ ସୁଖୋପଭୋଗଂ କୁର୍ବନ୍ତି । ପରନ୍ତୁ ଅସୌ ରାଜା ଦିଲୀପଃ ଭିନ୍ତଃ ଆସୀତ୍ । ଡଃ ନିର୍ଭିକଃ ସନ୍ ଆତ୍ମାନଂ ଜୁଗୋପ । ନୀରୋଗ ସନ୍ ଧର୍ମମାଚରଣଂ କୃତବାନ୍ । ଅଗୁଧ୍ ସନ୍ ଧନାର୍ଜନଂ କୃତବାନ୍ । ଅନାସକ୍ତ ସନ୍ ସୁଖୋପଭୋଗ୍ୟ କୃତବାନ୍ । ଅନେନ ରାଜ୍ଞ ବ୍ୟକ୍ତିତ୍ୱ ଚାରିତ୍ରିକମହତ୍ତ୍ଵ ଚ ଅନୁମୀୟତେ ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଛେଦ = ଜୁଗୋପ + ଆତ୍ମାନମ୍ + ଅଗ୍ରସ୍ତ । ଧର୍ମମନାତୁରଃ = ଧର୍ମମ୍ + ଅନାତୁରଃ । ଅଗ୍ନିଧୁରାଦଦେ = ଅଗୃଧଃ + ଆଦିଦେ । ସୋଽର୍ଥମନ୍ତଃ = ଡଃ + ଅର୍ଥମ୍ + ଅସନ୍ତଃ । । ସୁଖମନ୍ବଭୂତ = ସୁଖମ୍ + ଅନୁଭୂତ୍ ।
ସମାସ – ଅତ୍ରସ୍ଥ = ନ ତ୍ରସ୍ଥୁ (ନଞ୍ଚ୍ ତତ୍) । ଅନାତୁରଃ = ନ ଆତୁରଃ (ନଞ୍ଜ୍ ତତ୍) । ଅଗ୍ନିଧ୍ଵ = ନ ଗୃଧୁ, (ନଞ୍ଜ୍ ତତ୍) । ଅସନ୍ତଃ = ନ ସକ୍ତା (ନଞ୍ଚ୍ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ନଃ, ଅତ୍ରସ୍ତ, ଅନାତୁରଃ, ଅଗୁଧଃ, ଅସନ୍ତଃ = କଉଁରି ୧ ମା | ଧର୍ମମ୍, ଅର୍ଥମ, ସୁଖମ୍ = କର୍ମଣି ୨ୟା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଧର୍ମ = ଧୃ + ମନ୍ । ଆତୁରଃ = ଆ + ତୁର୍ +କ । ଅସନ୍ତଃ = ନ – ମଞ + କ୍ତ: |
ଶ୍ଳୋକ – ୨୨
ज्ञाने मौनं क्षमा शक्तौ त्यागे श्लाघाविपर्ययः ।
गुणा गुणानुबन्धित्वात्तस्य सप्रसवा इव ।। २२।।
ଜ୍ଞାନେ ମୌନଂ କ୍ଷମା ଶର୍ଭେ ତ୍ୟାଗେ ଶ୍ଳୋଘାବିପର୍ଯ୍ୟୟ ।
ଗୁଣା ଗୁଣାନୁବନ୍ଧିତ୍ଵାତ୍ତସ୍ୟ ସପ୍ରସବା ଇବ ॥ ୨୨ ||
ଅନ୍ବୟ – ଜ୍ଞାନେ ମୌନଂ, ଶସ୍ତେ କ୍ଷମା, ତ୍ୟାଗେ ଶ୍ମାଘାବିପର୍ଯ୍ୟୟ (ଇ) ତଥ୍ୟ ଗୁଣା ଗୁଣାନୁବନ୍ଧିତ୍ଵାତ୍ ସପ୍ରସବା ଇବ ଅଭୂବନ୍ ଇତି ।
ଶବ୍ଦାର୍ଥ – ଜ୍ଞାନେ = ଜ୍ଞାନ ଥିଲେ ବି । ମୌନ ଆଚରଣ କରୁଥିଲେ । ଶସ୍ତେ = ପ୍ରବଳ ପରାକ୍ରମ ଥିଲେ ଅନ୍ୟକୁ ପ୍ରବଳ ଦାନ ଦେଇଥିଲେ ବି । ଶ୍ଵାଘାବିପର୍ଯ୍ୟୟ ତାଙ୍କର ଗୁଣଗୁଡ଼ିକ । ଗୁଣାନୁବନ୍ଧିତ୍ଵାତ୍ = ବିରୋଧୀ ଗୁଣମାନଙ୍କ ପରି ଅବସ୍ଥାନ କରୁଥିଲା ।
ଅନୁବାଦ – (ସେହି ରାଜା ଦିଲୀପ) ଜ୍ଞାନ ଥିଲେ ବି ମୌନ ଆଚରଣ କରୁଥିଲେ । ପ୍ରବଳ ପରାକ୍ରମ ଥିବା ସତ୍ତ୍ବେ ବି କ୍ଷମା ଆଚରଣ କରୁଥିଲେ, ଯାଚକମାନଙ୍କୁ ଦାନ ଦେଇଥିଲେ ବି ନିଜର ପ୍ରଶଂସା କରୁ ନଥିଲେ । ଏହିପରି ତାଙ୍କ ନିକଟରେ ଥବା ଗୁଣଗୁଡ଼ିକ ପରସ୍ପର ବିରୋଧୀ ହୋଇଥିଲେ ସୁଦ୍ଧା ସେମାନେ ସହୋଦର ଭାଇ ଭଳି ଅବସ୍ଥାନ କରୁଥିବାର ଜଣାପଡୁଥିଲା |
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ସଂସ୍କୃତସାହିତ୍ୟସ୍ୟ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ ସମୀପେ ପାରସ୍ପରିକ-ବିରୁଦ୍ଧଗୁଣା କଳଂ ସହୋଦରଃ ଇବ ଅବସ୍ଥାଫୋତେ ତଦେବ ବର୍ଣ୍ଣିତମ୍ ।
ରାଜା ଦିଲୀପସ୍ୟ ସମୀପେ ଅକଳନୀୟଂ ଜ୍ଞାନଂ ଭୂତେ ସତି ସ ମୌନତାଂ ସଂଯମତାଂ ଚ ଆଚରିତବାନ୍ । ସାଧାରଣତଃ ମନୁଷ୍ୟ ଜ୍ଞାନେ ଅହଂକାରୀ ଭବତି । ‘ ଅନୁଜ୍ଞାନଂ ଭୟଙ୍କରମ୍ । ତଥା ମନୁଷ୍ୟ ଯଦି ଶକ୍ତିଶାଳୀ ଭବତି ତହିଁ କମପି ଡଃ କ୍ଷମାଂ ନ କରୋତି । ସଦୈବ ସ୍ଵଶକ୍ତିପ୍ରୟୋଗେନ ଦଣ୍ଡ ପ୍ରଦଦାତି । କ୍ଷମାଂ ଡଃ ବିସ୍ମରତି । ପରନ୍ତୁ ରାଜା ଦିଲୀପଃ ପରାକ୍ରମୀ ଶକ୍ତିଶାଳୀ ଭୂତେ ସତି କ୍ଷମାଶୀଳ ଆସୀତ୍ । ଯଦି କୋଽପି କିଞ୍ଚ୍ କସ୍ମି ଦଦାତି ତହିଁ ଆତ୍ମପ୍ରଶଂସା କରୋତି । ରାଜା ଦିଲୀପଃ ଦାନଶୀଳ ଭୂତେ ସତି ଆତ୍ମପ୍ରଶଂସା ରହିତଃ ଆସୀତ୍ । ସ୍ଵକୀୟପ୍ରଶଂସାଂ କଦାପି ନ କୃତମ୍ । ଅନେନ ପ୍ରକାରେଣ ପରସ୍ପର ବିରୁଦ୍ଧ ସ୍ବଭାବାଃ ଗୁଣା ତସ୍ୟ ଦିଲୀପସ୍ୟ ସମୀପେ ସହୋଦର ଇବ ସହାବସ୍ଥାନଂ କୃତମ୍ । ଏକ ଏବଂ ଗୁନଃ ଅପରସ୍ୟ ଗୁଣସ୍ୟ ସର୍ଜନଃ ଭବତି ।
ବ୍ୟାକରଣ:
ସନ୍ଧିବିଚ୍ଛେଦ – ଗୁଣାନୁବନ୍ଧିତ୍ଵଭସ୍ୟ = ଗୁଣ + ଅନୁବନ୍ଧିତ୍ଵାତ୍ + ତଥ୍ୟ |
ସମାସ – ଶାଘାବିପର୍ଯ୍ୟୟ = ଶୁଘାୟୀ ବିପର୍ଯୟଃ (୬ଷ୍ଠ ତତ୍) । ଗୁଣାନୁବନ୍ଧିତ୍ଵାତ୍ = ଗୁଣାନ୍ ଅନୁବନ୍ଧୁ ଶୀଳଂ = ସମାନଃ ପ୍ରସବାଃ ଯେତାଂ ତେ (ବହୁବ୍ରୀହିଃ) ଯେଷା ତେ, ତସ୍ମାତ୍ (ବହୁବ୍ରୀହିଃ) । ସପ୍ରସବାଃ = ସପାନ: ପ୍ରସବ: ଯେଫା ତେ (ବହୁବାହି:)
ସକାରଣବିଭକ୍ତି – ଜ୍ଞାନେ, ତ୍ୟାଗେ ଗୁଣାନୁବନ୍ଧିତ୍ଵାତ୍ = ହେତୌ ୫ମୀ । ଅଧିକରଣେ ୭ମୀ । ତଥ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ଗୁଣା = କଉଁରି ୧ ମା । ସପ୍ରସବାଃ = ‘ଇବ’ ଯୋଗେ ୧ମା ।
ପୃତ୍କତିପ୍ରତ୍ୟୟ – ଜ୍ଞାନମ୍ = ଜ୍ଞା + ଲ୍ୟୁଟ୍ । ମୌନ = ମୁନି + ଅଣ୍ । ଶକ୍ତି = ଶକ୍ + ସ୍କ୍ରିନ୍ । ତ୍ୟାଗ = ତ୍ୟଜ୍ + ଘଞ୍ଜ୍ । ବିପର୍ଯ୍ୟୟ = ବି + ପରି + ଇ + ଅଚ୍ । ଅନୁବନ୍ଧିନୀ = ଅନୁ + ବନ୍ଦ୍ + ଣିନି ।
ଶ୍ଳୋକ – ୨୩
अनाकृष्टस्य विषयैर्विद्यानां पारदृश्वनः ।
तस्य धर्मरतेरासीद्वृद्धत्वं जरसा विना || २३ ।।
ଅନାକୃଷ୍ଟସ୍ୟ ବିଷୟିର୍ବିଦ୍ୟାନାଂ ପାରଦୃଶ୍ଵନଂ ।
ତସ୍ୟ ଧର୍ମରତେରାସୀଦ୍ବୃଦ୍ଧ ଜରସା ବିନା ॥ ୨୩ ||
ଅନ୍ବୟ – ବିଷଶବ୍ଦାର୍ଥ ଅନାକୃଷ୍ଟସ୍ୟ ବିଦ୍ୟାନାଂ ପାରଦୃଶ୍ଵନଃ ଧର୍ମରତଃ ତଥ୍ୟ ଜରସା ବିନା ବୃଦ୍ଧତ୍ଵ ଆସୀତ୍ ।
ଣଦାର୍ଥ – ବିଯିପୌ: = ରୂପ, ରସ, ଗନ୍ଧ, ଶବ୍ଦ, ସ୍ପର୍ଶାଦି ପଞ୍ଚ ବିଷୟଦ୍ଵାରା | ଅନାକୃଷ୍ଟସ୍ୟ = ଥାତ୍କପ ହୋଇ ନଥିବା | ବିଦ୍ୟାନ ପାରନ୍ତଶ୍ଵନ: = ସମସ୍ତ ବିଦ୍ୟାରେ ପାରଦର୍ଶିତା ହାସଲ କରିଥିବା | ଧର୍ମରତଃ ତଥ୍ୟ = ସେହି ରାଜା ଦିଲୀପଙ୍କର | ଜରସା ବିନା = ବାର୍ଦ୍ଧକ୍ୟ ବିନା ମଧ୍ଯ |
ଅନ୍ମବାଦ – ବିଡିନ୍ନ ବିପକ୍ଷ୍ଜ୍ଜିରା ଆକ୍ବଗୃ ଦ୍ବୋଲ ନଥିବା, ସମସ୍ତ ବ୍ୟାରେ ପାରବଣତା ଦ୍ଵାମଲ କରିଥିବା ସେଦ୍ଵି ଧାର୍ମିକ ରାଜା ଦିଲୀପଙ୍କର ବୃଦ୍ଧାବସୁ ବିନା ମଧ୍ୟ ବୃଦ୍ଧତ୍ଵ ପ୍ରାପ୍ତି ହୋଇଯାଇଥିଲା |
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋସଙ୍ଗ ପଠିତ ମହାକଟି କାଲିବାପବିଉଟିଭ: ସ୍ପ୍ରପିବଂ ‘ରଶ୍ମବଂଶମ୍ଭ’ ମଦ୍ରାକାବ୍ୟପ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ ନ ବୟବୃଦ୍ଧବଂ ଅପିତୁ ଜ୍ଞାନବୃଦ୍ଧବଂ ବିଷୟ ବର୍ଣ୍ଣିତମ୍ ।
ମନୁଷ୍ୟାମାଂ ଜୀବନକ୍ରମଂ ଜନ୍ମନଃ ମୃତ୍ୟୁ ପର୍ଯ୍ୟନ୍ତ ଚତୁରବସ୍ଥା ମାଧ୍ୟମେନ ଗଚ୍ଛତି । ତଦ୍ ଯଥା – ଶୈଶବାଃ, କିଶୋରଃ, ଯୌବନଂ ବାର୍ଷକଂ ଚ । ଜୀବନସ୍ୟ ଅକ୍ତିମାବସ୍ଥା ଭବତି ବାର୍ଦ୍ଧକ୍ୟମ୍ । ଅସ୍ଥିନ୍ ଅବସ୍ଥାୟାଂ ଚର୍ମ ଶିଳଂ ଭବତି, ଅଙ୍ଗାନି ର ଶିଳ ଭବନ୍ତି, କେଶଃ ଶୁକ୍ଳା ଭବନ୍ତି । ପରନ୍ତୁ ସ୍ମୃତିକାରମତେନ ବୃଦ୍ଧବଂ ଯଥା –
‘‘ନ ତେନ ବୃଦ୍ଧା ଭବତି ଯେନାସ୍ୟ ପଳିତଂ ଶିରଃ ।
ଯୋ ବୌକ୍ଷ୍ନଽପଅଧାମ୍ବାନପ୍ର ଦେବା: ମୃବିରଂ ବିଦୃ: ||”
ଏତଃ ବୟୋବୃଦ୍ଧ ଅପରଃ ଜ୍ଞନବୃଦ୍ଧିଷ୍ଟ । ରାଜାଦିଲୀପଃ ନ ବୟଃବୃଦ୍ଧା ଅପିତୁ ଜ୍ଞାନବୃଦ୍ଧି ଆସୀତ୍ । ବିଷୟେ ଅନାକୃଷ୍ଟସ୍ୟ, ବିଦ୍ୟାନାଂ ପାରଦୃଶ୍ଵନଃ ଧର୍ମରତେ ତସ୍ୟ ଦିଲୀପସ୍ୟ ଜରସା ବିନା ବୃଦ୍ଧତ୍ଵମ୍ ଆସୀତ୍ ।
ବ୍ୟାକରଣ :
ସନ୍ଧବିଛେଦ – ବିଶମୌବଦ୍ୟାନାଂ = ବିଷୟଃ + ବିଦ୍ୟାନାମ୍ । ଧର୍ମରତେରାସୀଦ୍ବୃଦ୍ଧ = ଧର୍ମରତଃ + ଆସୀତ୍ + ବୃଦ୍ଧତ୍ଵମ୍ ।
ସପାସ – ଥନାକୁତ୍ସ୍ୟ = ନ ଆକୃଷ୍ଟ, ତଥ୍ୟ (ନଞ୍ଚ୍ ତତ୍ତ୍ଵ) । ଧର୍ମରତଃ = ଧର୍ମେ ରତିଃ ଯସ୍ୟ ଡଃ ତଥ୍ୟ (ବହୁବ୍ରୀହିଃ) ।
ସକାରଣବିଭକ୍ତି – ବିଷୟି = କରଣେ ୩ୟା । ଅନାକୃଷ୍ଟସ୍ୟ, ପାରଦୃଶ୍ଵନଃ, ଧର୍ମରତଃ, ତସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ | ବିଦ୍ୟାନାଂ = ଶେଷେ ୬ଷ୍ଠୀ । ଜରସା = ‘ବିନା’ ଯୋଗେ ୩ୟା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଆକୃଷ୍ଟ = ଆ + କୃଷ୍ + କ୍ତ । ପାରଦୃଶୁନଃ = ପାର + ଦୃଶ୍ + କ୍ରନିପ୍ ।

ଶ୍ଳୋକ – ୨୪
प्रजानां विनयाधानाद्रक्षणाद्भरणादपि ।
स पिता पितरस्तासां केवलं जन्महेतवः || २४ ।।
ପ୍ରଜାନାଂ ବିନୟଧାନାଦ୍ରକ୍ଷଣାଦ୍ରଣାଦପି ।
ସ ପିତା ପିତରସ୍ତାସାଂ କେବଳଂ ଜନ୍ମହେତନଃ ।।୨୪।।
ଅନ୍ବୟ – ପ୍ରଜାନାଂ ବିନୟାଧାନାତ୍, ରକ୍ଷଣାତ୍ ଭରଣାତ୍ ଅପି ଡଃ ପିତା (ଅଭୂତ) । ତାସାଂ ପିତରଃ ତୁ କେବଳଂ ଜନ୍ମହେତବାଃ (ଅଭୂବନ୍) ।
ଣଦାର୍ଥ – ବିଯିପୌ: = ପ୍ରଜାମାନଙ୍କର । ବିନୟଧାନାତ୍ = ନମ୍ରତାଦି ଗୁଣ ଶିକ୍ଷାଦେବା ଫଳରେ । ରକ୍ଷଣାତ୍ = ରକ୍ଷା କରିବା ହେତୁରୁ । ଭରଣାତ୍ = ପାଳନ କରିବା = ସେମାନଙ୍କର ପିତାମାନେ । ତୁ = କିନ୍ତୁ । କେବଳଂ ଜନ୍ମହେତପଃ = କେବଳ ଜନ୍ମହେତୁରୁ ପିତା|
ଅନ୍ମବାଦ: ସେହି ଭାକା ଦିନାପ ଣ୍ତକାଣକକୁ ନମ୍ରତା ଥାଦି ଗୁଣ ଶିକାଦେବୀ ହେତୁରୁ ସେମାନକର ରମଶାଢେକଣ ଏବଂ ପାଳନ କରିବା ହେତୁରୁ ସେମାନଙ୍କର ପ୍ରକୃତ ପିତା ଥିଲେ । କିନ୍ତୁ ସେମାନଙ୍କର ଜନକମାନେ କେବଳ ଜନ୍ମ କରିଥିବା ହେତୁରୁ ପିତୃ ପଦବାଚ୍ୟ ହେଉଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ମହାକବି କାଳିଦାସବିରଚିତଂ ‘ରଘୁବଂଶମ୍ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପଃ କଣଂ ପ୍ରଜାନାଂ ପ୍ରକୃତଃ ପିତା ଆସୀତ୍ ତଦେବ ବର୍ଣ୍ଣିତମ୍ । ପ୍ରଜାନ୍ ବିନୟାଦି ଶିକ୍ଷାମ୍ ଅଦଦାତ୍ । ପ୍ରଜାନାଂ ରକ୍ଷଣଂ ଭରଣଂ ଚ କୃତମ୍ । ଅତଃ ଡଃ ଦିଲୀପଃ ତେଷା ପିତା ଆସୀତ୍ । ଅପରନ୍ତୁ ପ୍ରଜାନାଂ ଯେ ପ୍ରକୃତଃ ପିତରଃ ତେ ତୁ କେବଳଂ ଜନ୍ମହେତପଃ ଅଭୂବନ୍ । ଅସ୍ମାତ୍ ରାଜ୍ଞ ପିତୃତ୍ୱ ସୂଚିତଂ ଭବତି ।
ବ୍ୟାକରଣ :
ସନ୍ଧିବିଚ୍ଛେଦ – ବିନୟଧାନାତ୍ = ବିନୟ + ଆଧାନାତ୍ । ଭରଣାଦପି ଭରଣାତ୍ + ଅପି । ପିତରସ୍ତାସାମ୍ = ପିତରଃ + ତାସାମ୍ ।
ସପାସ – ବିନୟଧାନାତ୍ = ବିନୟସ୍ୟ ଆଧାନମ୍, ତସ୍ମାତ୍ (୬୩ ତତ୍) । ଜନ୍ମହେତବ = ଜନ୍ମନଃ ହେତବାଃ (୬୩ ତତ୍) ।
ସକାଶେବିଇଛି – ପୃକାଙ୍କ = ଶେଷେ ୬ଷ୍ଠୀ । ବିନୟଧାନାତ୍, ଭରଣାତ୍, ରକ୍ଷଣାତ୍ = ହେତୌ ୫ମୀ । ସ୍ୱ, ପିତା, ପିତରଃ = କଉଁରି ୧ ମା ।
ପ୍ରକୃତି ପ୍ରତ୍ୟୟ – ପ୍ରଜା = ପ୍ର + ଜନ୍ + ଡ । ବିନୟ = ବି + ନୀ + ଅଚ୍ । ଭରଣମ୍ = ଭୃ + ଲ୍ୟୁଟ୍ । ରକ୍ଷଣମ୍ = ରକ୍ଷ୍ + ଲ୍ୟୁଟ୍ । ପିତା = ପା + ତୃଚ୍ !
ଶ୍ଳୋକ – ୨୫
स्थित्यै दण्डयतो दण्ड्यान्परिणेतुः प्रसूतये ।
अप्यर्थकामौ तस्यास्तां धर्म एवं मनीषिणः ||२५||
ସ୍ଥିତ୍ୟେ ଦଣ୍ଡୟତୋ ଦଣ୍ଡାରିଣେତୁଃ ପ୍ରସୂତୟେ ।
ଅତ୍ୟର୍ଥକାମୌ ତସ୍ୟାସ୍ତା ଧର୍ମ ଏବଂ ମନୀଷିତଃ ||୨୫||
ଅନ୍ବୟ – ଦଣ୍ଡାନ୍ (ଏବ) ସ୍ଥିତ୍ୟେ ଦଣ୍ଡୟତଃ ପ୍ରସୂତୟେ ପରିଣେତୁଃ ମନୀଷିଣ ତଥ୍ୟ ଅର୍ଥକାମୌ ଅପି ଧର୍ମ ଏବ ଆସ୍ତାମ୍ ।
ଶବ୍ଦାର୍ଥ – ଦଶ୍ୟାନ୍ = ଅପରାଧୀମାନଙ୍କୁ । ସ୍ଥିତ୍ୟେ = ପ୍ରଜାମାନଙ୍କର ମଙ୍ଗଳ ବା ପାଳନ ପାଇଁ । ଦଣ୍ଡୟତଃ ଦେଇଥିବା । ପ୍ରସୂତୟେ = ସନ୍ତାନ ଉତ୍ପନ୍ନ କରିବା ନିମନ୍ତେ । ପରିଣେତୁଃ = ବିବାହ କରିଥିବା । ମନୀଷିଣ ମନିଷୀ । ତସ୍ୟ = ରାଜା ଦିଲୀପଙ୍କର । ଅର୍ଥକାମୌ ଅପି = ଅର୍ଥ ଏବଂ କାମ ମଧ୍ୟ ହୋଇଥିଲା |
ନିମନ୍ତେ ବିବାହ କରିଥିବା ସେହି ବୁଦ୍ଧିମାନ୍ ରାଜା ଦିଲୀପଙ୍କର ଅର୍ଥ ଏବଂ କାମ ଉଭୟ ଧର୍ମରେ ହିଁ ପରିଣତ ହୋଇଯାଇଥିଲା |
କୃତିଃ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମସର୍ଗୀତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ ଅର୍ଥା କାମଶ୍ଚ କଥ୍ୟ ଚତୁର୍ବର୍ଗ ଫଳପ୍ରାପ୍ୟର୍ଥୀ ସର୍ବେ କାମୟନ୍ତ ଯତୋହି ଜୀବନଂ ପୁରୁଷାର୍ଥମ୍ ଉଦ୍ଦିଷ୍ଟ ଭବତି । ଜନାଃ ଅର୍ଥନିମନ୍ତେ ଅପରଜନଂ ପୀଡ଼ୟନ୍ତି । ତଦ୍ବତ୍ ରାଜା ଅପି ପ୍ରଜାନ୍ ଦଣ୍ଡୟତି ଅର୍ଥସ୍ୟ କୃତେ । କାମପ୍ରାପ୍ୟର୍ଥୀ ବିବାହଂ କୁର୍ବନ୍ତି । ପରନ୍ତୁ ରାଜା ଦିଲୀପଃ ପ୍ରଜାରକ୍ଷଣାର୍ଥୀ ପାଳନାର୍ଥୀ ଚ ଦଣ୍ଡ ପ୍ରଦଦାତି । ଦଣ୍ଡପ୍ରଦାନଂ ତୁ ରାଜ୍ଞ ଦିଲୀପସ୍ୟ ଧର୍ମ ଏବ ପ୍ରତିଭାତି । ସ୍ବବଂଶରକ୍ଷାର୍ଥୀ ଦାରପରିଗ୍ରହଣଂ ତେନ କୃତମ୍ । କାମାଭିଳାଷମପି ରାଜ୍ଞ ଧର୍ମସ୍ପେନ ଅଭିବାନକ୍ତି । ଅର୍ଥ କାମଶ୍ଚ ରାଜ୍ଞ ପରମଧର୍ମରୂପେଣ ପରିବର୍ତ୍ତିତଃ ଭବନ୍ତି । ସଦା ଧର୍ମରତଃ ଦିଲୀପଃ ସର୍ବେଷା ପୂଜନୀୟଃ ବନ୍ଦନୀୟଶ୍ଚାସୀତ୍ ।
ବ୍ୟାକରଣ :
ସନ୍ଧିବିଚ୍ଛେଦ – ଅପ୍ୟର୍ଥକାମୌ = ଅପି + ଅର୍ଥକାମାଁ। ତସ୍ୟାସ୍ତା = ତଥ୍ୟ + ଆସ୍ତାମ୍ ।
ସମାସ – ଅର୍ଥକାମୌ = ଅର୍ଥଶ୍ଚ କାମଶ୍ଚ (ଦ୍ବନ୍ଦ୍ବ) ।
ସକାରଣବିଭକ୍ତି – ସ୍ଥିତ୍ୟେ = ତାଦ୍ୟର୍ଥେ ୪ର୍ଥୀ । ଦଣ୍ଡୟତଃ, ପରିଣେତୁଃ, ମନୀଷିଣୀ, ତସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ପ୍ରସୂତ = ନିମିତ୍ତାର୍ଥେ ୪ର୍ଥୀ । ଧର୍ମ = ଏବଂ ଅବ୍ୟୟ ଯୋଗେ ୧ମା ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ସ୍ଥିତିଃ = ସ୍ପା + ସ୍କ୍ରିନ୍ । ଦଣ୍ଡୟନ୍ = ଦଣ୍ଡ୍ + ଶତ୍ରୁ । ଦଣ୍ଡ = ଦଣ୍ଡ୍ + ଯତ୍ । ପ୍ରସୂତି = ପୂ + ସୂ + ସ୍କ୍ରିନ୍ । ଧର୍ମ = ଧୂ + ମନ୍ ।
ଶ୍ଳୋକ – ୨୬
दुदोह गां स यज्ञाय सस्याय मघवा दिवम् ।
संपद्विनिमयेनो भौ दधतुर्भुवद्वयम् ।।२६।।
ଦୁଦୋହ ସାଂ ସ ଯଜ୍ଞାୟ ସସ୍ୟାୟ ମଘବା ଦିବମ୍ ।
ସଂପଦ୍ୱିନିମାସରକୌ ଦଧତୁରୁବନଦ୍ୱୟମ ||२६।।
ଶବ୍ଦାର୍ଥ — ଡଃ ସେହି ରାଜା ଦିଲୀପ । ଯଜ୍ଞାୟ = ଯଜ୍ଞ ପାଇଁ । ମାଂ = ପୃଥିବୀକୁ । ଦୁଦୋହ = ଦୋହନ କଲେ । ଇନ୍ଦ୍ର । ସସ୍ୟାୟ = ଶସ୍ୟ ଉତ୍ପାଦନ ପାଇଁ । ଦିବଂ = ସ୍ଵର୍ଗକୁ । ଏବଂ = ଏହିପରି । ଉଭୌ = ଉଭୟ ରାଜା ଏବଂ = ଉଭୟ ଭୁବନକୁ |
ଅନୁବାଦ – ସେହି ରାଜା ଦିଲୀପ ଯଜ୍ଞ ପାଇଁ ପୃଥିବୀକୁ ଦୋହନ କରୁଥିଲେ (ପ୍ରଜାମାନଙ୍କ– ଠାରୁ ଏକଷକ୍ଷାଂଶ କର ଗ୍ରହଣ କରୁଥିଲେ) । ଇନ୍ଦ୍ର ପୃଥିବୀକୁ ଶସ୍ୟଶାଳୀ କରିବାପାଇଁ ସ୍ଵର୍ଗକୁ ଦୋହନ କରୁଥିଲେ (ସ୍ଵର୍ଗରୁ ମର୍ତ୍ତ୍ୟଲୋକକୁ ବୃଷ୍ଟି କରାଉଥିଲେ)। ଏହିପରି ଉଭୟ ରାଜା ଦିଲୀପ ଏବଂ ଦେବରାଜ ଇନ୍ଦ୍ର ଉଭୟ ସମ୍ପତ୍ତିର ବିନିମୟରେ ଉଭୟଲୋକକୁ ଧାରଣ କରିଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶ୍ଳୋକୋଽୟଂ ପଠିତଃ ମହାକବି କାଳିଦାସ ବିରଚିତ ‘ରଘୁବଂଶମ୍’ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମସର୍ଗତ୍ ଆନୀତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ମହାରାଜା ଦିଲୀପସ୍ୟ ଦେବରାଜ ଇନ୍ଦ୍ରଣ ସାକଂ ମିତ୍ରତା ପ୍ରସଙ୍ଗ ବର୍ଣ୍ଣିତମ୍ ।
ଯଥା ମର୍ତ୍ତ୍ୟ ରାଜା ଦିଲୀପଃ ତଥା ସ୍ଵର୍ଗେ ଦେବରାଜଇନ୍ଦ୍ର ଆସୀତ୍ । ଏକଃ ଭୂଲୋକସ୍ୟ ପାଳକ ଅପରଂ ଦ୍ୟୁଲୋକସ୍ୟ ପାଳକଂ ଚ ଭବତି । ରାଜା ଦିଲୀପଃ ଯଜ୍ଞ କର୍ତ୍ତ୍ୟ ଭୁବଂ ଦୁଦୋହ କରଗ୍ରହଣେନ ହିତାଂ ଚକାର । ଦେବେନ୍ଦ୍ର ସସ୍ୟ ବର୍ଧନଂ ସ୍ବର୍ଗ ଦୁଦୋହ ଦ୍ୟୁଲୋକାତ୍ ବୃଷ୍ଟିମୁପାଦୟାମାସ । ଉଭୌ ରାଜାଦିଲୀପଦେବେନ୍ଦ୍ରୋ ସଂପଦ୍ବିନିମୟେନ ଭୁବନଦ୍ଵୟଂ ଦଧାତୁଃ । ଉଭୌ ରୁବନଦ୍ୱସଂ ଧାରମାମାସ ପୋପମ୍ସ ଚ |
ବିନିମୟେନୋଭୌ = ବିନିମୟନ + ଉଭୌ । ଦଧତୁର୍ଭୁବନଦ୍ଵୟମ୍= ଦଧୁତଃ + ଭୁବନଦ୍ଵୟମ୍ ।
ସମାସ – ସଂପଦ୍ବିନିମୟେନ = ସଂପଦଃ ବିନିମୟ, ତେନ (୬ଷ୍ଠୀ ତତ୍) ।
ସକାରଣବିଭକ୍ତି – ଗାମ୍ = କର୍ମଣି ୨ୟା । ଯଜ୍ଞାୟ, ସସ୍ୟାୟ = ‘କ୍ରିୟାଥୋପପଦସ୍ୟ’ ଯୋଗେ ୪ ର୍ଥୀ । ଦିବମ୍ =
ପ୍ତକ୍ଵତିପୃତସମ୍ – ମସ୍ୟା = ସସ୍ + ଯତ୍ । ସମ୍ପତ୍ = ସମ୍ + ପଦ୍ + କ୍ରିପ୍ ।
ଶ୍ଳୋକ – ୨୭
न किलानुययुस्तस्य राजानो रक्षितुर्यशः !
व्यावृत्ता यत्परस्वेभ्यः श्रुतौ तस्करता स्थिता ।। २७ ।।
ବ୍ୟାବୃତ୍ତା ଯତ୍ରସ୍ଵଭ୍ୟ ଶ୍ରୁତୌ ତସ୍କରତା ସ୍ଥିତା ।୨୭।
ରାଜାନଃ ରକ୍ଷିତଃ ତଥ୍ୟ ଯଶଃ ନ ଅନୁଯତଃ କିଳ, ଯତ୍ ତସ୍କରତା ପରସ୍ଵଭ୍ୟ ବ୍ୟାବୃତ୍ତା (ସତୀ) ଶ୍ରୁତୌ
ଶବ୍ଦାର୍ଥ – ରାଜାନଃ = ରାଜାମାନେ । ରକ୍ଷିତଃ ତଥ୍ୟ = ସେହି ପାଳନକର୍ତ୍ତା ରାଜା ଦିଲୀପଙ୍କର । ଯଶଃ = କୀର୍ତ୍ତିକୁ । ନ = ପରଧନ ଅପହରଣରୁ ବ୍ୟାବୃତ ହୋଇ । ଶ୍ରୁତୌ ସ୍ଥିତା = କର୍ଣ୍ଣଗୋଚର ମାତ୍ର ହେଉଥିଲା ।
ଅନୁବାଦ – ଅନ୍ୟରାଜାମାନେ ପାଳନକର୍ତ୍ତା ସେହି ଯେହେତୁ । ତସ୍କରତା = ଚୌର୍ଯ୍ୟବୃତ୍ତି । ପରସ୍ଵଭ୍ୟ ବ୍ୟାବୃତ୍ତା ରାଜା ଦିଲୀପଙ୍କର ଯଶକୁ ଅନୁକରଣ କରିପାରିଲେ ନାହିଁ ଯେହେତୁ, ପରଧନ ଅପହରଣରୁ ବ୍ୟାବୃତ୍ତ ହୋଇ ଚୌର୍ଯ୍ୟବୃତ୍ତି କେବଳ ଶ୍ରୁତିମାତ୍ରାରେ ଗୋଚର ହେଉଥୁଲା ବା ଖାଲି ଶୁଣାଯାଉଥିଲା ।
ବ୍ୟାଖ୍ୟା – ପ୍ରଥମ ସର୍ଗାତ୍ ଆନୀତଃ । ଅତ୍ର ଅସ୍ଥିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ ଯଶସ୍ବୀତଃ ତଥ୍ୟ ରାଜ୍ୟ ସ୍ଵଚ୍ଛତା ଚ କଥମାସନ୍ ତଦେବ ବର୍ଣ୍ଣିତମ୍ । ଅପି ସୁଖସମୃଦ୍ଧି ପ୍ରଦଦାତି ସ୍ମ । ରାଜା ଦିଲୀପସ୍ୟ ନାସୀତ୍ । ଅତଃ ଅବନ୍ୟା ରାଜାନଃ ଦିଲୀପସ୍ୟ ଅତିଷ୍ଠତ୍ । ଜନାନାଂ ପ୍ରବୃରୌ ତୁ ଚୌର୍ଯ୍ୟବୃତିଃ ନିୟମାବଦ୍ଧ ଚାସୀତ୍ । ତସ୍ୟ ଉଦାରତା ସେବାପରାୟଣତା ଚ ପ୍ରଜାଭ୍ୟ ରାଜ୍ୟ ତସ୍କରତା ଚୌର୍ଯ୍ୟବୃତିଃ ବା ନାସୀତ୍ । କୋଽପି ଚୌର୍ଯ୍ୟକର୍ମଣା ବ୍ୟାପୃତଃ ଯଶଂ କୀର୍ତ୍ତି ଚ ଅନୁକରଣଂ ନ କୃତବନ୍ତଃ । ତସ୍କରତା ଶ୍ରୁତିମାତ୍ରେଣ କେବଳଂ ନାସନ୍ । ଅର୍ଥାତ୍ ତଦାନୀନ୍ତନଃ ସାମାଜିକବ୍ୟବସ୍ଥା ରାଜ୍ଞ ସୁଶାସନଂ ଚ ସୂଚିତଂ ଭବତି ।
ସନ୍ଧିବିଚ୍ଛେଦ – କିଳାନୁପଯୁସ୍ତସ୍ୟ = କିଳ + ଅନୁପଯୁଃ + ତଥ୍ୟ । ରକ୍ଷିତୁର୍ଯ୍ୟଶଃ = ରକ୍ଷିତୁଃ + ଯଶଃ । ଯପ୍ରସ୍ଵଭ୍ୟ = ଯତ୍ + ପରସ୍ଵଭ୍ୟ ।
ସକାରଣବିଭକ୍ତି – ଅନୁଯୟୁ, ରାଜାନୀ, ତସ୍କରତା = ପରେଷା ସ୍ଵାନି, ତେଭ୍ୟ (୬ଷ୍ଠୀ ତତ୍) । କଉଁରି ୧ ମା । ରକ୍ଷିତୁଃ= ଶେଷେ ୬ଷ୍ଠୀ । ଯଶଃ = ତତ୍ + କୃ +
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ବ୍ୟାବୃତ୍ତା = ବି + ଆ + ବୃତ୍ + କ୍ତ + ଟାପ୍ । ଶ୍ରୁତିଃ = ଶୁ + ସ୍କ୍ରିନ୍ ତସ୍କର = ଅତ୍ । ସ୍ଥିତା = ସ୍ଲା + ନ୍ତ + ଟାପ୍ ।
ଶ୍ଳୋକ – ୨୮
द्वेष्योऽपि संमतः शिष्टस्तस्यार्तस्य यथौषधम् ।
त्याज्यो दुष्टः प्रियोऽप्यासीदङ्गुली वोरगक्षता ।। २८।।
ସ୍ଵେଷ୍ୟାପି ସଂମତଃ ଶିଷ୍ଟସ୍ତସ୍ୟାର୍ତସ୍ୟ ଯପୌଷଧମ୍ ।
ତ୍ୟାଜ୍ୟେ ଦୁଷ୍ଟ ପ୍ରିୟୋଽପ୍ୟାସୀଦଙ୍ଗୁଳୀବୋରଗକ୍ଷତା ||୨୮||
ଅନ୍ପପ – ଶିଷ୍ଟ ଦୃଶ୍ୟ ଆପି ଆଇଁସ୍ୟ ଔଷଧ୍ୟ ଯଥା ତଥ୍ୟ ସମ୍ମତଃ ଆସୀତ । ଦୁଷ୍ପ ପ୍ରିୟ ଅପି ଉରଗକ୍ଷତା ଅଙ୍ଗୁଳୀଇବ ତସ୍ୟ ତ୍ୟାଜ୍ୟ ଆସୀତ୍ ।
ଶବ୍ଦାର୍ଥ – ଶିଷ୍ଟ = ସଜ୍ଜନ । ଦ୍ଧେଶ୍ୟ = ଅପି = ଶତ୍ରୁ ହେଲେ ମଧ୍ୟ । ଆର୍ଡସ୍ୟ = ରୋଗୀର । ଔଷଧ୍ୟ ସେହି ରାଜାଙ୍କର ସେ ଗ୍ରହଣୀୟ ଥିଲେ । ଦୁଷ୍ଟ = ଦୁର୍ଜନ । ପ୍ରିୟ ସର୍ପ ଦଂଶନ କରିଥିବା ଅଙ୍ଗୁଳି ଭଳି । ତସ୍ୟ ତ୍ୟାଜ୍ୟ ଆସୀତ୍ = ତାଙ୍କର ଯେପରି ଗ୍ରହଣୀୟ । ତସ୍ୟ ସମ୍ମତଃ ଆସୀତ୍ ଆପଣାର ହେଲେ ମଧ୍ୟ । ଉରଗକ୍ଷତାଅଙ୍ଗୁଳୀ ଇବ = ତ୍ୟାଜ୍ୟ ବା ବର୍ଜନୀୟ ଥିଲା ।
ଅନୁବାଦ – ଯେଭଳି ଔଷଧ କଟୁ ହେଲେ ମଧ୍ୟ ତାହା ରୋଗୀର ଗ୍ରହଣୀୟ ହୋଇଥାଏ । ସେହିପରି ସଜ୍ଜନ ଯେତେ ଶତ୍ରୁ ହେଲେ ମଧ୍ୟ ସେ ରାଜାଙ୍କର ପ୍ରିୟ ବା ଗ୍ରହଣୀୟ ଥିଲେ । ଯେପରି ଏକ ଅଙ୍ଗୁଳିକୁ ସାପ କାମୁଡ଼ି ଦେଲେ ତାହା ଯେତେ ଭଲ ହେଲେ ବି ତାକୁ ବର୍ଜନ କରାଯାଏ, ସେହିପରି କୌଣସି ଦୁଷ୍ଟ ଯେତେ ଆପଣାର ହେଲେ ବି ସେ ରାଜାଙ୍କର ବର୍ଜନୀୟ ଥଲା ।
ଉଦ୍ଧୃତଃ ଶ୍ଳୋକଃ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ସୁପ୍ରସିଦ୍ଧ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମ ସର୍ଗାତ୍ ଆନୀତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରାଜାଦିଲୀପସ୍ୟ ଶିଷ୍ଟଶିଷ୍ଟ ବ୍ୟବହାରପ୍ରସଙ୍ଗ ବର୍ଣ୍ଣିତମ୍ । ଶିଷ୍ଟଶିଷ୍ଟାନ୍ ପ୍ରତି ରାଜ୍ଞ ବ୍ୟବହାରବିରଂ ତୁ ଭିନ୍ନମ୍ ଆସୀତ୍ । ଉପମାଛଳେନ ପ୍ରସଙ୍ଗୋଽୟମ୍ ଉପସ୍ଥାପିତମ୍ । ଯଥା ଔଷଧାଂ ସମ୍ମନଃ ଅପ୍ରିୟୋଽପି ରାଜ୍ଞ ଗ୍ରହଣୀୟଂ ଭବତି ଯତୋହି ତଥ୍ୟ ପ୍ରକୃତିଃ ସ୍ଵଭାବାଃ ଦଂଶତି ସଂପୂର୍ଣ୍ଣଶରୀରେ ବିଷସ୍ୟ ସଞ୍ଚରଣଂ ଭବତି, ଅସ୍ମିନ୍ନବସରେ ଉରଗକ୍ଷତଃ ପ୍ରିୟୋଽପି ତ୍ୟାଜ୍ଯ ଭବତି । ଦୁଷ୍ଟ ବିଷତୁଲ୍ୟ ଭବତି । ଅନେକ ପ୍ରକାରେଣ କଟୁ ଭୂତେ ସତି ରୁଗ୍ଣସ୍ୟ ଗ୍ରାହ୍ୟ ଭବତି ତଥା ବା ସୁଶ୍ରୁ ଭବତି । ଯଦି ଅଙ୍ଗୁଳୀମେକଂ ସର୍ପ ଅଙ୍ଗୁଳୀ ଅବଶ୍ୟ କର୍ତ୍ତନୀୟମ୍ । ତଥୈବ ଦୁଷ୍ଟ ଶିଷ୍ଟଶିଷ୍ଟ ବ୍ୟବହାରଂ ତେନ କୃତମ୍ ।
ବ୍ୟାକରଣ :
ସନ୍ଧିବିଚ୍ଛେଦ – ଦ୍ବେଦ୍ୟୋଽପି = ଦ୍ଧେଶ୍ୟ + ଅପି । ଶିଷ୍ଟସ୍ତସ୍ୟାର୍ଡସ୍ୟ = ଶିଷ୍ଟ + ତଥ୍ୟ + ଆର୍ଡସ୍ୟ । ଯପୌଷଧମ୍ = ଯଥା + ଔଷଧମ୍ । ପ୍ରିୟୋଽପ୍ୟାସୀତ୍ = ପ୍ରିୟଃ + ଅପି + ଆସୀତ୍ । ଅଙ୍ଗୁଳୀବୋରଗକ୍ଷତା = ଅଙ୍ଗୁଳୀ +ଇବ + ଇରଗଣତା |
ସମାସ – ଉରଗକ୍ଷତା = ଉରଗେଣ କ୍ଷତା (୩ୟା ତତ୍) |
ସକାରଣବିଭକ୍ତି – ଶିଷ୍ଟ, ଦୁଷ୍ଟ = କଉଁରି ୧ ମା । ଦେଷ୍ୟ, ପ୍ରିୟ = ଅପି ଯୋଗେ ୧ମା । ଅଙ୍ଗୁଳୀ = ଇବ ଯୋଗେ ୧ ମା । ଆର୍ଡସ୍ୟ, ତଥ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ । ଔଷଧମ୍ = କର୍ମଣି ୨ୟ ।
ପ୍ରକୃତିପ୍ରତ୍ୟୟ – ଦ୍ଧେଶ୍ୟ = ଦ୍ବିଷ୍ + ଣ୍ୟତ୍ ! ସମ୍ମତଃ= ସମ୍ + ମନ୍ + କ୍ତ | ତ୍ୟାଜ୍ୟ = ତ୍ୟଜ୍ + ଣ୍ୟତ୍ । ଦୁଷ୍ଟ ଦୁଷ୍ + .କ୍ତ | ପ୍ରିୟ = ପ୍ରୀଣ୍ + କ୍ତ । କ୍ଷତା = ଶିଷ୍ + କ୍ତ । ଆର୍ଡ = ଆ + କ୍ଷଣ + କ୍ତ + ଟାପ୍ ।
ଶ୍ଳୋକ – ୨୯
तं वेधा विदधे नूनं महाभूतसमाधिना ।
तथा हि सर्वे तस्यासन्परार्थेकफला गुणाः ।। २९ । ।
ତଂ ବେଧା ବିଦଧେ ନୂନଂ ମହାଭୂତସମାଧ୍ଵନା ।
ତଥା ହିଁ ସର୍ବେ ତସ୍ୟାସରାର୍ଥେକଫଳା ଗୁଣା ।।୨୯||
ଅନୂୟ – ବେଧା ତଂ ମହାଭୂତସମାଧ୍ଵନା ବିଦଧ ନୂନଂ, ତଥାହି ତଥ୍ୟ ସର୍ବଗୁଣା ପରାର୍ଥେକଫଳା ଆସନ୍ ।
ଶବ୍ଦାର୍ଥ – ବୈଧଃ = ବ୍ରହ୍ମା । ତଂ = ସେହି ରାଜା ଦିଲୀପଙ୍କୁ । ମହାଭୂତସମାଧ୍ଵନା = ହିଁ ।
ନୂନମ୍ = ସତେ ଯେପରି ନିର୍ମାଣ କରିଥିଲେ। ତଥାହି= ସେହେତୁ । ତସ୍ୟ ସର୍ବେଗୁଣା = ତାଙ୍କର ସମସ୍ତ ଗୁଣଗୁଡ଼ିକ । ପରାଥୈକଫଳା ଆସନ୍ = ପରର ଉପକାର ପାଇଁ ଉଦ୍ଦିଷ୍ଟ ଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ‘ରଘୁବଂଶମ୍’ ମହାକାବ୍ୟସ୍ୟ ପ୍ରଥମସର୍ଗତ୍ ଆନୀତଃ । ଅସ୍ମିନ୍ ଶ୍ଳୋକେ ରାଜା ଦିଲୀପସ୍ୟ ସର୍ବେ ଗୁଣା କଥ୍ୟ ପରୋପକାରାୟ ଭବତି ତଦେବ ବର୍ଣ୍ଣିତମ୍ । ଅସ୍ମାନ୍ ସଂସାରେ ସ୍ୱୟଂସ୍ରଷ୍ଟା ଏବ ସର୍ବାନ୍ ମନୁଷ୍ୟାନ୍ ସୃଜତି । କ୍ଷିତି-ଅପ୍-ତେଜ-ମରୁତ୍-ବ୍ୟୋମ-ଇତ୍ୟେବ ପଞ୍ଚଭୂତେନ ମାନବଶରୀରଂ ନିର୍ମିତମ୍ । ବେଧାଽପି ରାଜାଦିଲୀପସ୍ୟ ଶରୀରଂ ପଞ୍ଚଭୂତେନ ନିର୍ମିତବାନ୍ । ପଞ୍ଚଭୂତୋଽୟଂ ସଂସାରସ୍ୟ ପ୍ରାଣୀନାଂ କୃତେ ମଙ୍ଗଳମୟ ବସ୍ତୁରୂପେଣ ବିବେଚିତଂ ଭବତି । ଅସ୍ୟ ସ୍ୱରୂପଂ ତୁ ରାଜାଦିଲୀପସ୍ୟ ଶରୀରେ ଅନୁଭୂତମ୍ । ପୃଥିବ୍ୟା ସହିଷ୍ଣୁତା କ୍ଷମା ଚ, ଜଳସ୍ୟ ଔଦାର୍ଯ୍ୟତା ଗାମ୍ଭୀର୍ଯ୍ୟତା ଚ, ତେଜସ୍ୱୀ ଜାଜ୍ଜଲ୍ୟତା ଶକ୍ତିମତା ଚ, ମରୁତଃ ଗତିଶୀଳତା ଶୀଘ୍ରତା ଚ, ବ୍ୟାପକତାଦି ବିବିଧା ଗୁଣା,ରାଜ୍ଞ ଦିଲୀପସ୍ୟ ସମୀପେ ଆସନ୍ । ଇମଂ ଗୁଣଂ ଧାରୟିତ୍ୱ ଡଃ ସଦା ପରୋପକାରେଣ ନିରତଃ ଅଭୂତ୍ । ଅସ୍ମାତ୍ ରାଜା- ଦିଲୀପସ୍ୟା ଚାରିତ୍ରିକ ମହତ୍ତ୍ୱ ପ୍ରତୀୟତେ ।
ସନ୍ଧିବିଚ୍ଛେଦ – ତଖ୍ୟାମନ୍ = ତସ୍ୟ + ଆସନ୍ । ପରାମୈକଫଳା = ପର + ଅର୍ଥ + ଏକଫଳା ।
ସମାସ – ମହାଭୂତସମାଧନା = ମହାଭୂତାନାଂ ସମାଧଃ, ତେନ (୬ଷ୍ଠ ତତ୍ତ୍ଵ) । ପରାର୍ଥୀ = ପରାସ୍ୟ ଅର୍ଥ (୬ଷ୍ଠ ତତ୍) ।
ମହାରାଣାରରକ୍ତି – ବେଧଃ, ସର୍ବଗୁଣୀ = କର୍ଭରି ୧ ମା। ତଂ = କରଣେ ୩ୟା । ତସ୍ୟ = ସମ୍ବନ୍ଧ ୬ଷ୍ଠୀ |
ପୃକ୍ଵଜିସ୍ତ୍ୟୟ – ସମାଧା: = ସମ୍ + ଆ + ଧା + କି
ଶ୍ଳୋକ – ୩୦
स वेलावप्रवलयां परिखीकृत सागराम् ।
अनन्यशासनामुर्वी शशासैकपुरीमिव ।। ३० ।।
ସ ବେଳାବପ୍ରବଳୟା ପରିଖୀକୃତସାଗରାମ୍ ।
ଅନନ୍ୟଶାସନାମୁର୍ଥୀ ଶସାସୈକପୁରୀମିବ ॥୩୦॥
ଅନୂୟ – ସ୍ୱୀ ବେଳାବପ୍ରବଳୟାଂ ପରିଖୀକୃତସାଗରାମ୍ ଅନନ୍ୟ ଶାସନାମ୍ ଉର୍ବୀମ୍ ଏକପୁରୀମ୍ ଇବ ଶଶାସ ।
ଶବ୍ଦାର୍ଥ – କଃ = ସେହି ରାଜା ଦିଲୀପ । ବେଳାବପ୍ରବଳୟାମ୍ = ସମୁଦ୍ରକୁ ରୂପକ ପ୍ରାକାର ବେଷ୍ଟିତ । ପଖୀକୃତସାଗରାମ୍ = ଯାହାର ସମୁଦ୍ର ହିଁ ପରିଖା ଭାବରେ ରହିଥିଲା । ଅନନ୍ୟ ଶାସନାମ୍ = ଯାହାକୁ କି ଆଗରୁ କେହି ଶାସନ କରି ନଥିଲେ । ଉର୍ବୀମ୍ = ପୃଥିବୀକୁ । ଏକପୁରମ୍ ଇବ = ଗୋଟିଏ ନଗରୀ ସଦୃଶ । ଶଶାସ୍ତ୍ର = ଶାସନ କରୁଥିଲେ ।
ଅନୁବାଦ – ସେହି ରାଜା ଦିଲୀପ ସାଗରକୂଳରୂପକ ପ୍ରାକାର ମଣ୍ଡିତ ସାଗର ସ୍ଵରୂପ ପରିଖାଯୁକ୍ତ ତଥା ତାଙ୍କ ବିନା ଅନ୍ୟ କେହି ହେଲେ ଶାସନ କରି ନଥିବା ପୃଥିବୀକୁ ଗୋଟିଏ ନଗରୀ ଭଳି ଶାସନ କରୁଥିଲେ ।
ବ୍ୟାଖ୍ୟା – ଶଂସିତଃ ଶ୍ଳୋକଃ ପଠିତଃ ସଂସ୍କୃତପ୍ରଭା ପୁସ୍ତକସ୍ଥ ପଦ୍ୟଭାଗଂ ମହାକବି କାଳିଦାସ ବିରଚିତଂ ‘ ରଘୁବଂଶମ୍ ଇତି ବର୍ଣ୍ଣିତମ୍ ।
ରଘୁବଂଶମ୍ ଏବଂ ପ୍ରାଚୀନଂ ବଂଶମ୍ । ବୈବସ୍ୱତମନୁଃ ଅସ୍ୟ ବଂଶସ୍ୟ ପ୍ରଥମରାଜା ଆସୀତ୍ । ଅସ୍ଥିନ୍ ବଂଶେ ରାଜା ଦିଲୀପଃ ଉପଯୁକ୍ତ ଉତ୍ତରଦାୟାଦଃ ଆସୀତ୍ । ଡଃ ସସାଗରାଧରାୟା ଶାସକଃ । ତସ୍ୟ ରାଜା ଦିଲୀପସ୍ୟ ସାମ୍ରାଜ୍ୟମ୍ ଆସମୁଦ୍ରପର୍ଯ୍ୟନ୍ତ ସୁବିସ୍ତୃତମାସୀତ୍ । ସବଳା ଯସ୍ୟ ପ୍ରାଚୀର, ସାଗର ଯସ୍ୟ ପରୀଖା ଆସୀତ୍ । ତସ୍ୟ ବହିଃ ଶତ୍ରୁ ନାସୀତ୍ । ଦିଲୀପୋହି ଅନନ୍ୟଶାସକ ଆସୀତ୍ । ଏତାଦୃଶ ପୃଥିବୀ ରାଜା ଦିଲୀପଃ ଏକପୁରୀମିବ ଶଶାସ୍ତ୍ର ।
ସନ୍ଧିବିଚ୍ଛେଦ – ଅନନ୍ୟଶାସନାମୁର୍ବୀମ୍ = ଅନନ୍ୟଶାସନାମ୍ + ଉର୍ବୀମ୍ । ଶଶାସୈକପୁରୀମିବ = ଶଶାସ + ଏକପୁରୀମ୍ = ବପ୍ରାଚ୍ୟବ ବଳୟଃ (ରୂପକ କର୍ମଧାରୟଃ), ବେଳା ଏବ ବଜ୍ର ବଳୟା ଯସ୍ୟା ତାମ୍ (ବହୁବ୍ରୀହିଃ) । ପରି ଖୀକୃ ତସାଗରାମ୍ = ପରି ଖୀକୃ ତା ସାଗରାଂ ଯସ୍ୟା = ଅନ୍ୟସ୍ୟ ଶାସନାମ୍ (୬ଷ୍ଠ ତତ୍), ଅବିଦ୍ୟ- ମାନମ୍ ଅନ୍ୟ ଶାସନଂ ଯସ୍ୟା – ଏକପୁରୀମ୍ = ଏକା ଚାସୌ ପୁରୀ ଚେତି (କର୍ମଧାରୟ) । ତାମ୍ ( ବହୁବ୍ରୀହିଃ) । ତାମ୍ (ବହୁବ୍ରୀହିଂ) ।
ସକାରଣବିଭକ୍ତି – ବେଳାବପ୍ରବଳୟାମ୍, ପରିଖୀକୃତସାଗରାମ୍, ଅନନ୍ୟଶାସନାମ, ଉର୍ବୀମ୍ = କର୍ମଣି ୨ୟା । ସ୍ୱ = କଉଁରି ୧ ମା। ଏକପୁରୀମ୍ = ଇବ ଅବ୍ୟୟ ଯୋଗେ ୧ମା ।
ପ୍ରକୃତିପ୍ରତୟ – ଶାସନମ୍ = ଶାସ୍ + ଲ୍ୟୁଟ୍ ।
![]()

![]()
![]()

![]()




