Odisha State Board BSE Odisha 6th Class Geography Important Questions Chapter 5 ପୃଥିବୀର ମଣ୍ଡଳସମୂହ Important Questions and Answers.
BSE Odisha Class 6 Geography Important Questions Chapter 5 ପୃଥିବୀର ମଣ୍ଡଳସମୂହ
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ବାୟୁମଣ୍ଡଳର ବିଭିନ୍ନ ସ୍ତରଗୁଡ଼ିକୁ ଚିତ୍ର ସାହାଯ୍ୟରେ ଦର୍ଶାଅ ଓ ବାୟୁର ବିଭିନ୍ନ ଉପାଦାନଗୁଡ଼ିକର ନାମ ଲେଖ।
Answer:
- ବାୟୁମଣ୍ଡଳକୁ ୫ ଗୋଟି ସ୍ତରରେ ବିଭକ୍ତ କରାଯାଇଛି; ଯଥା—
(୧) ଟ୍ରପୋସ୍ପିଅର
(୨) ଷ୍ଟ୍ରାଟୋସ୍ପିଅର
(୩) ମେସୋସ୍ପିଅର
(୪) ଥର୍ମୋସ୍ପିଅର
(୫) ଏକ୍ସୋସ୍ପିଅର।


- ବାୟୁ କେତେକ ବାଷ୍ପ ଓ ଧୂଳିକଣା ଆଦି ପଦାର୍ଥର ଏକ ଭୌତିକ ମିଶ୍ରଣ। ସେହିସବୁ ଉପାଦାନଗୁଡ଼ିକ ହେଲା— ଯବକ୍ଷାରଜାନ, ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ, ଉଦ୍ଜାନ, ଆର୍ଗନ୍, ଜେନନ୍, ନିଅନ ଓ ଜଳୀୟବାଷ୍ପ।
- ବାୟୁର ମୁଖ୍ୟ ଉପାଦାନ ଯବକ୍ଷାରଜାନର ପରିମାଣ ୭୮% ଓ ଅମ୍ଳଜାନର ପରିମାଣ ୨୧% । ଅନ୍ୟାନ୍ୟ ସମସ୍ତ ବାଷ୍ପର ପରିମାଣ ୧% ।
୨। ଅଶ୍ମମଣ୍ଡଳ ବିଷୟରେ ଯାହାଜାଣ ଲେଖ।
Answer:
- ଅଶ୍ମମଣ୍ଡଳଟି ଭୂତ୍ବକ୍ର ବିଭିନ୍ନ ଶିଳା ଓ ମୃତ୍ତିକାସ୍ତରକୁ ନେଇ ଗଠିତ।
- ଭୂପୃଷ୍ଠରେ ଥିବା ବିଭିନ୍ନ ଉଦ୍ଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କ ଜୀବନଧାରଣ ପାଇଁ ଆବଶ୍ୟକ ଅଧିକାଂଶ ଉପାଦାନ ଏହି ଶିଳା ଓ ମୃତ୍ତିକାରୁ ହିଁ ମିଳିଥାଏ।
- ଅଶ୍ମମଣ୍ଡଳ ପୃଥିବୀର ସାତୋଟି ମହାଦେଶ ଓ ସମୁଦ୍ରତଳକୁ ନେଇ ଗଠିତ ହୋଇଛି। ଏହି ମହାଦେଶଗୁଡ଼ିକ ହେଲା– ଏସିଆ, ଆଫ୍ରିକା, ଉତ୍ତର ଆମେରିକା, ଦକ୍ଷିଣ ଆମେରିକା, ଆଣ୍ଟାର୍କଟିକା, ଇଉରୋପ ଓ ଅଷ୍ଟ୍ରେଲିଆ।
- ଭୂପୃଷ୍ଠରେ ଏହି ମହାଦେଶଗୁଡ଼ିକ ବିସ୍ତୀର୍ଣ୍ଣ ଜଳଭାଗଦ୍ଵାରା ପରସ୍ପରଠାରୁ ଅଲଗା ରହିଛନ୍ତି।
- ପୃଥିବୀର ସ୍ଥଳଭାଗ ସାତଟି ମହାଦେଶ ସହ ବିସ୍ତୀର୍ଣ୍ଣ ଜଳଭାଗ ୪ଟି ମହାସାଗରକୁ ନେଇ ଗଠିତ।
୩। ପୃଥିବୀର ବାରିମଣ୍ଡଳ ବିଷୟରେ ସଂକ୍ଷେପରେ ବର୍ଣ୍ଣନା କର।
Answer:
- ବାରିମଣ୍ଡଳ ପୃଥିବୀପୃଷ୍ଠର ପ୍ରାୟ ଶତକଡ଼ା ୭୧ ଭାଗ ସ୍ଥାନ ଅଧିକାର କରିଛି।
- ଏହି ଜଳ ସାଗର, ମହାସାଗର, ହ୍ରଦ ବ୍ୟତୀତ ପାର୍ବତ୍ୟ ଅଞ୍ଚଳରେ ତୁଷାରରାଶି ଓ ହିମବାହ, ନଦୀ ଓ କେନାଲରେ ପ୍ରବହମାନ ଧାରା, ଭୂଗର୍ଭରେ ସଞ୍ଚ ଜଳ ଓ ବାୟୁମଣ୍ଡଳରେ ଜଳୀୟବାଷ୍ପ ରୂପେ ଥାଏ।
- ଏହି ସମସ୍ତ ଜଳରାଶିକୁ ନେଇ ବାରିମଣ୍ଡଳ ଗଠିତ।
- ସମୁଦାୟ ଜଳରାଶିର ଶତକଡ଼ା ୯୭.୨ ଭାଗ ଜଳ ମହାସାଗର ଓ ସାଗରରେ ରହିଛି। ଏହା ଲବଣାକ୍ତ ହୋଇଥିବାରୁ ପାନୀୟ ଅନୁପଯୋଗୀ।
- ଶତକଡ଼ା ୨.୮ ଭାଗ ଜଳ ପାନୀୟ ଉପଯୋଗୀ । ତାହା ମଧ୍ୟରୁ ଶତକଡ଼ା ପ୍ରାୟ ୨.୭୭ ଭାଗ ଜଳ ବରଫ ଆକାରରେ ଓ ଭୂଗର୍ଭସ୍ଥ ଜଳ ଆକାରରେ ଅଛି। ମାତ୍ର ଶତକଡ଼ା ୦.୦୩ ଭାଗ ଜଳ ପୃଥିବୀପୃଷ୍ଠରେ ଉପଲବ୍ଧ ।
- ପୃଥିବୀପୃଷ୍ଠରେ ଜଳର ପରିମାଣ ଅଧିକ ଥିବାରୁ ଏହା ଜଳୀୟ ଗ୍ରହ ବା ନୀଳଗ୍ରହ ରୂପେ ପରିଚିତ।

(କ) ସଂକ୍ଷେପରେ ଉତ୍ତର ଦିଅ।
୧। ପୃଥିବୀର କେଉଁ କେଉଁ ମହାଦେଶ ସଂପୂର୍ଣ୍ଣ ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଅବସ୍ଥିତ ?
Answer:
- ପୃଥିବୀର ୩ଟି ମହାଦେଶ ସଂପୂର୍ଣ୍ଣ ଭାବରେ ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧରେ ଅବସ୍ଥିତ।
- ସେଗୁଡ଼ିକ ହେଲା– ଉତ୍ତର ଆମେରିକା, ଏସିଆ ଓ ଇଉରୋପ।
୨। ପରିସଂସ୍ଥା କାହାକୁ କୁହାଯାଏ ?
Answer:
- ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାରର ଜଳବାୟୁ, ମୃତ୍ତିକା ଓ ସେହି ଅଞ୍ଚଳରେ ରହୁଥିବା ଜୀବଗୋଷ୍ଠୀକୁ ଦେହ ଏକ ପରିବେଶ ସୃଷ୍ଟି ହୋଇଥାଏ।
- ଏହାକୁ ପରିସଂସ୍ଥା କୁହାଯାଏ।
୩ । ଭୂଗୋଲକୀୟ ଉଷ୍ମତା ବୃଦ୍ଧି ପାଇବାର କାରଣ କ’ଣ ?
Answer:
- ଭୂପୃଷ୍ଠରେ ଥିବା କଳକାରଖାନା, ତାପଜ ଶକ୍ତିକେନ୍ଦ୍ର ଓ ଗମନାଗମନ ପାଇଁ ବ୍ୟବହୃତ ଯାନବାହନରୁ ନିର୍ଗତ ପାଉଁଶ ଓ ଧୂଆଁ ବାୟୁମଣ୍ଡଳକୁ ଦୂଷିତ କରିଥାଏ।
- ଫଳରେ ବାୟୁମଣ୍ଡଳରେ ଅଙ୍ଗାରକାମ୍ଳ ବାଷ୍ପର ପରିମାଣ ବୃଦ୍ଧିପାଇଁ ଭୂଗୋଲକୀୟ ଉଷ୍ଣତା ବୃଦ୍ଧି ହୋଇଥାଏ।
୪। ଆଟ୍ଲାଣ୍ଟିକ୍ ମହାସାଗରର ପୂର୍ବ ଓ ପଶ୍ଚିମରେ କେଉଁ କେଉଁ ମହାଦେଶ ଅବସ୍ଥିତ ?
Answer:
- ଆଟ୍ଲାଣ୍ଟିକ୍ ମହାସାଗରର ପୂର୍ବରେ ଇଉରୋପ ଓ ଆଫ୍ରିକା ଅବସ୍ଥିତ।
- ଏହାର ପଶ୍ଚିମରେ ଉତ୍ତର ଆମେରିକା ଓ ଦକ୍ଷିଣ ଆମେରିକା ଅବସ୍ଥିତ।

୫। ପ୍ରଶାନ୍ତ ମହାସାଗରର କେଉଁ କେଉଁ ଦିଗରେ କେଉଁ ମହାଦେଶ ଅବସ୍ଥିତ ?
Answer:
- ପ୍ରଶାନ୍ତ ମହାସାଗରର ପୂର୍ବରେ ଉତ୍ତର ଆମେରିକା ଓ ଦକ୍ଷିଣ ଆମେରିକା ମହାଦେଶ ଅବସ୍ଥିତ।
- ଏହାର ପଶ୍ଚିମରେ ଏସିଆ ଓ ଦକ୍ଷିଣରେ ଆଣ୍ଟର୍କଟିକା ମହାଦେଶ ଅବସ୍ଥିତ।
(ଖ) ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ।
୧। ଅଶ୍ମମଣ୍ଡଳ ଓ ଜୈବ ମଣ୍ଡଳ :
Answer:
| ଅଶ୍ମମଣ୍ଡଳ |
ଜୈବ ମଣ୍ଡଳ |
- ଅଶ୍ମମଣ୍ଡଳ ଭୂତ୍ବକ୍ର ବିଭିନ୍ନ ଶିଳା ଓ ମୃତ୍ତିକାକୁ ନେଇ ଗଠିତ । ଭୂପୃଷ୍ଠରେ ଥିବା ବିଭିନ୍ନ ଉଦ୍ଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କ ଜୀବନ ଧାରଣ ପାଇଁ ଆବଶ୍ୟକ ଅଧିକାଂଶ ଉପାଦାନ ଏହି ଶିଳା ଓ ମୃତ୍ତିକାରୁ ହିଁ ମିଳିଥାଏ।
- ଏହା ପୃଥିବୀର ସାତୋଟି ମହାଦେଶ ଓ ସମୁଦ୍ରତଳକୁ ନେଇ ଗଠିତ।
|
- ଭୂପୃଷ୍ଠରେ ଏବଂ ଏହାର ଅଳ୍ପକିଛି ଉପର ଓ ଅଳ୍ପକିଛି ତଳକୁ ତିଷ୍ଠି ରହିଥିବା ଜୀବ ଓ ଉଦ୍ଭିଦ ଜଗତକୁ ନେଇ ଜୈବ ମଣ୍ଡଳ ଗଠିତ । ଏହି ମଣ୍ଡଳଟି ସମଗ୍ର ଜୀବଜଗତର ଧାରଣ ଓ ପୋଷଣ କର୍ତ୍ତା।
- ଭୂପୃଷ୍ଠର ମୃତ୍ତିକା, ଜଳ ଓ ବାୟୁଦ୍ୱାରା ଏହି ମଣ୍ଡଳଟି ପରିପୃଷ୍ଠ।
|
୨। ପ୍ରଶାନ୍ତ ମହାସାଗର ଓ ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର :
Answer:
| ପ୍ରଶାନ୍ତ ମହାସାଗର |
ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର |
- ପ୍ରଶାନ୍ତ ମହାସାଗର ପୃଥିବୀର ବୃହତ୍ତ ମ ମହାସାଗର । ଏହା ପୃଥିବୀ ପୃଷ୍ଠର ପ୍ରାୟ ଏକ ତୃତୀୟାଂଶ ସ୍ଥାନ ଅଧୀକାର କରିଛି ।
- ଏସିଆ, ଅଷ୍ଟ୍ରେଲିଆ, ଉତ୍ତର ଆମେରିକା ଓ ଦକ୍ଷିଣ ଆମେରିକା ଏହାର ଉପକୂଳରେ ଅବସ୍ଥିତ।
|
- ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର ପୃଥିବୀର ଦ୍ବିତୀୟ ବୃହତ୍ତମ ମହାସାଗର। ଏହା ପ୍ରାୟ ଇଂରାଜୀ ଅକ୍ଷର ‘S’ ଆକୃତି ସଦୃଶ।
- ଏହି ମହାସାଗରର ଗୋଟିଏ ପାର୍ଶ୍ଵରେ ଉତ୍ତର ଓ ଦକ୍ଷିଣ ଆମେରିକା ମହାଦେଶ ଏବଂ ଅନ୍ୟ ଏକ ପାର୍ଶ୍ଵ ରେ ଇଉରୋପ ଓ ଆଫ୍ରିକା ମହାଦେଶ ଅବସ୍ଥିତ।
|
(ଗ) ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ :
୧। ନୀଳଗ୍ରହ :
Answer:
- ପୃଥିବୀରେ ଜଳଭାଗର ପରିମାଣ ପ୍ରାୟ ଶତକଡ଼ା ୭୧ ଭାଗ ଓ ସ୍ଥଳଭାଗର ପରିମାଣ ପ୍ରାୟ ଶତକଡ଼ା ୨୯ ଭାଗ।
- ପୃଥିବୀରେ ଜଳର ପରିମାଣ ଅଧିକ ହୋଇଥିବାରୁ ଏହାକୁ ଜଳୀୟ ଗ୍ରହ ବା ନୀଳଗ୍ରହ କହନ୍ତି।
୨। ପରିସଂସ୍ଥା :
Answer:
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ପ୍ରକାରର ଜଳବାୟୁ, ମୃତ୍ତିକା ଏବଂ ସେହି ଅଞ୍ଚଳରେ ରହୁଥିବା ପ୍ରାଣୀ ଓ ଉଦ୍ଭିଦମାନଙ୍କୁ ନେଇ ଯେଉଁ ପରିବେଶ ସୃଷ୍ଟି ହୁଏ। ତାହାକୁ ପରିସଂସ୍ଥା କୁହାଯାଏ।

୩। ବାୟୁମଣ୍ଡଳ :
Answer:
- ପୃଥିବୀର ଚତୁଃପାର୍ଶ୍ଵରେ ବାୟୁର ଏକ ସ୍ତର ଢାଙ୍କି ହୋଇ ରହିଛି। ଭୂପୃଷ୍ଠ ପ୍ରାୟ ୧୬୦୦ କିଲୋମିଟର ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବାୟୁମଣ୍ଡଳ ବିସ୍ତୃତ। ଜୀବଜଗତର ଶ୍ଵାସକ୍ରିୟା ପାଇଁ ବାୟୁମଣ୍ଡଳ ଅତ୍ୟନ୍ତ ଆବଶ୍ୟକ।
- ବାୟୁମଣ୍ଡଳର ତାପମାତ୍ରା, ଚାପ, ଘନତ୍ୱ ଆଦି ସବୁଠାରେ ସମାନ ନଥାଏ। ବାୟୁମଣ୍ଡଳରେ ୭୮ ଶତକଡ଼ା ଯବକ୍ଷାରଜାନ ଓ ୨୧ ଭାଗ ଅମ୍ଳଜାନ ରହିଛି।
(ଘ) ଭୌଗୋଳିକ କାରଣ ଦର୍ଶାଅ :
୧। ବାୟୁମଣ୍ଡଳରେ ଅଙ୍ଗାରକାମ୍ଳ ବାଷ୍ପର ପରିମାଣ ଅପେକ୍ଷାକୃତ କମ୍ ଥିଲେ ମଧ୍ୟ ଏହା ଗୁରୁତ୍ବପୂର୍ଣ।
Answer:
- ବାୟୁମଣ୍ଡଳରେ ଅପେକ୍ଷାକୃତ କମ୍ ପରିମାଣରେ ଥିବା ଅଙ୍ଗାରକାମ୍ଳ ବାଷ୍ପ ପୃଥିବୀ ବିକିରଣ କରୁଥିବା ତାପକୁ ଗ୍ରହଣ କରି ପୃଥିବୀର ଉଷ୍ଣତା ରକ୍ଷା କରିବାରେ ସାହାଯ୍ୟକରେ।
- ତାଛଡ଼ା ଉଭିଦ ଜଗତର ଖାଦ୍ୟ ପ୍ରସ୍ତୁତି ପ୍ରକ୍ରିୟାରେ ଏହା ବିଶେଷ ଆବଶ୍ୟକ ହୋଇଥାଏ। ତେଣୁ ଏହା ଖୁବ୍ ଗୁରୁତ୍ବପୂର୍ଣ୍ଣ।
୨। ପର୍ବତ ଆରୋହଣକାରୀମାନେ ସେମାନଙ୍କ ସହିତ ଅମ୍ଳଜାନ ପୂର୍ଣ୍ଣ ଥଳୀ ଦେଇଥାନ୍ତି।
Answer:
- ବାୟୁମଣ୍ଡଳରେ ବାୟୁର ଘନତା ସର୍ବତ୍ର ସମାନ ନଥାଏ। ଭୂପୃଷ୍ଠରୁ ଉଚ୍ଚତାର ବୃଦ୍ଧି ସଙ୍ଗେ ସଙ୍ଗେ ବାୟୁର ଘନତା କ୍ରମଶଃ କମି କମି ଯାଏ।
- ସମୁଦ୍ର ପତ୍ତନରେ ଏହା ସବୁଠାରୁ ଅଧିକ ଏବଂ ପର୍ବତ ଶିଖରରେ ଏହା ବହୁତ କମ୍ ଥାଏ। ତେଣୁ ପର୍ବତ ଶିଖରରେ ଏହା ବହୁତ କମ୍ ଥାଏ। ତେଣୁ ପର୍ବତ ଆରୋହୀମାନେ ଅମ୍ଳଜାନପୂର୍ଣ୍ଣ ଥଳୀ ସାଙ୍ଗରେ ନେ ଇଥାନ୍ତି।

(କ) ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।
(୧) ପୃଥିବୀର ସର୍ବୋଚ୍ଚ ପାର୍ବତ୍ୟ ଶୃଙ୍ଗର ଉଚ୍ଚତା _______ ।
Answer:
୮୮୪୮ ମିଟର
(୨) ଭୂପୃଷ୍ଠର ପ୍ରାୟ _________ ଜଳଭାଗଦ୍ବାରା ବେଷ୍ଟିତ।
Answer:
ତିନି-ଚତୁର୍ଥାଂଶ
(୩) ପୃଥିବୀର ସାତଟି ମହାଦେଶ ଓ ସମୁଦ୍ରତଳକୁ ନେଇ ___________ ଗଠିତ।
Answer:
ଅଶ୍ମମଣ୍ଡଳ
(୪) ପୃଥିବୀକୁ ତା’ର ଚତୁଃପାର୍ଶ୍ବରେ ଏକ _________ ଘେରି ରହିଛି।
Answer:
ବାୟୁମଣ୍ଡଳ
(୫) ପୃଥିବୀର ଗଭୀରତମ ସାମୁଦ୍ରିକ ଖାତ ମାରିଆନା ___________ ମହାସାଗରରେ ଅବସ୍ଥିତ।
Answer:
ପ୍ରଶାନ୍ତ

(୬) ଏଭେରେଷ୍ଟର ଉଚ୍ଚତା ___________ ମିଟର।
Answer:
୮୮୪୮ ମିଟର
(୭) ମାରିଆନାର ଗଭୀରତା ___________ ମିଟର।
Answer:
୧୧୦୨୨ ମିଟର
(୮) ପୃଥିବୀର ବୃହତ୍ତମ ମହାସାଗର _____________।
Answer:
ପ୍ରଶାନ୍ତ ମହାସାଗର
(୯) ପୃଥିବୀପୃଷ୍ଠରେ ଉପଲବ୍ଧ ଜଳର ପରିମାଣ ____________।
Answer:
୦.୦୩ ଭାଗ
(୧୦) ବାୟୁମଣ୍ଡଳରେ ________ ବାଷ୍ପର ପରିମାଣ ଅଧ୍ଵ ହେଲେ ଭୂଗୋଲକୀୟ ତାପମାତ୍ରାରେ କ୍ରମଶଃ ବୃଦ୍ଧି ଘଟିଥାଏ।
Answer:
ଅଙ୍ଗାରକାମ୍ଳ

(ଖ) ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ସଂକ୍ଷେପରେ ଦିଅ।
୧। ସମୁଦାୟ ଜଳରାଶିର ଶତକଡ଼ା କେତେ ଅଂଶ ସାଗର ଓ ମହାସାଗରରେ ଅଛି ?
Answer:
ସମୁଦାୟ ଜଳରାଶିର ଶତକଡ଼ା ୯୭.୨ ଭାଗ ଜଳ ସାଗର ଓ ମହାସାଗରରେ ଅଛି।
୨। ଭୂପୃଷ୍ଠରୁ ପ୍ରାୟ କେତେ କିଲୋମିଟର ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବାୟୁମଣ୍ଡଳ ବିସ୍ତୃତ ?
Answer:
ଭୂପୃଷ୍ଠରୁ ପ୍ରାୟ ୧୬୦୦ କିଲୋମିଟର ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବାୟୁମଣ୍ଡଳ ବିସ୍ତୃତ।
୩। ସବୁଠାରୁ ଉଚ୍ଚରେ ଥିବା ସ୍ତରର ନାମ କ’ଣ ?
Answer:
ସବୁଠାରୁ ଉଚ୍ଚରେ ଥିବା ସ୍ତରର ନାମ ଏକ୍ସୋସ୍ପିଅର।
୪। ବାୟୁର ଦୁଇଟି ମୁଖ୍ୟ ଉପାଦାନର ନାମ ଲେଖ।
Answer:
ବାୟୁର ଦୁଇଟି ମୁଖ୍ୟ ଉପାଦାନର ନାମ ଯବକ୍ଷାରଜାନ ଓ ଅମ୍ଳଜାନ।

୫। ପବନ କାହାକୁ କୁହାଯାଏ ?
Answer:
ପ୍ରବାହିତ ବାୟୁକୁ ପବନ କୁହାଯାଏ।
୬। ପୃଥିବୀର ଗଭୀରତମ ସାମୁଦ୍ରିକ ଖାତର ନାମ କ’ଣ ?
Answer:
ପୃଥିବୀର ଗଭୀରତମ ସାମୁଦ୍ରିକ ଖାତର ନାମ ମାରିଆନା।
୭। ପୃଥିବୀପୃଷ୍ଠରୁ କେତେ ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବାୟୁମଣ୍ଡଳ ବ୍ୟାପି ରହିଛି ?
Answer:
ପୃଥିବୀପୃଷ୍ଠରୁ ପ୍ରାୟ ୧୬୦୦ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବାୟୁମଣ୍ଡଳ ବ୍ୟାପି ରହିଛି।
୮। ପୃଥିବୀର ଦ୍ଵିତୀୟ ବୃହତ୍ତମ ମହାସାଗରର ନାମ କ’ଣ ?
Answer:
ପୃଥିବୀର ଦ୍ବିତୀୟ ବୃହତ୍ତମ ମହାସାଗରର ନାମ ଆଟ୍ଲାଣ୍ଟିକ୍ ମହାସାଗର।
୯। ଏସିଆ ମହାଦେଶର ଦକ୍ଷିଣରେ କେଉଁ ମହାସାଗର ଅଛି ?
Answer:
ଏସିଆ ମହାଦେଶର ଦକ୍ଷିଣରେ ଭାରତ ମହାସାଗର ଅଛି।
୧୦। ଆଟ୍ଲାଣ୍ଟିକ୍ ମହାସାଗରର ଆକୃତି କିପରି ?
ଆଟ୍ଲାଣ୍ଟିକ୍ ମହାସାଗରର ଆକୃତି ଇଂରାଜୀ ଅକ୍ଷର ‘S’ ପରି।

(ଗ) ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ।
୧। ନିମ୍ନଲିଖ ମଧ୍ୟରୁ ପୃଥିବୀରେ ସ୍ଥଳଭାଗର ଆୟତନ ଶତକଡ଼ା କେତେ ?
(A) ୩୯ ଭାଗ
(B) ୨୯ ଭାଗ
(C) ୭୮ ଭାଗ
(D) ୭୧ ଭାଗ
Answer:
(B) ୨୯ ଭାଗ
୨। ଗଡ଼ୱିନ୍ ଅଷ୍ଟିନ୍ କେଉଁ ପର୍ବତରେ ଅବସ୍ଥିତ ?
(A) ହିମାଳୟ
(B) ହିନ୍ଦୁକୁଶ
(C) କ୍ୟୁନଲୁନ୍
(D) କାରାକୋରମ୍
Answer:
(D) କାରାକୋରମ୍
୩। ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁ ପ୍ରଣାଳୀଟି ସୁମେରୁ ମହାସାଗର ସହିତ ପ୍ରଶାନ୍ତ ମହାସାଗରକୁ ସଂଯୁକ୍ତ କରୁଛି ?
(A) ପକ୍ ପ୍ରଣାଳୀ
(B) ବେରିଂ ପ୍ରଣାଳୀ
(C) ଜିଦ୍ରାଲିଟର ପ୍ରଣାଳୀ
(D) ଇଂଲିଶ୍ ପ୍ରଣାଳୀ
Answer:
(B) ବେରିଂ ପ୍ରଣାଳୀ

୪। ନିମ୍ନଲିଖ ମଧ୍ୟରୁ ପୃଥିବୀର ଉଚ୍ଚତମ ଶୃଙ୍ଗ କିଏ ?
(A) ଏଭେରେଷ୍ଟ
(B) ହିନ୍ଦୁକୁଶ
(C) ଭୂଗୋଲକୀୟ
(D) ଗଭୀରତମ
Answer:
(A) ଏଭେରେଷ୍ଟ
୫। ନିମ୍ନଲିଖ ମଧ୍ୟରୁ ପୃଥିବୀର ବୃହତ୍ତମ ମହାସାଗର କିଏ ?
(A) ଭାରତ ମହାସାଗର
(B) ଅମ୍ଳଜାନ
(C) ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର
(D) ପ୍ରଶାନ୍ତ ମହାସାଗର
Answer:
(D) ପ୍ରଶାନ୍ତ ମହାସାଗର
୬। ଭୂପୃଷ୍ଠରେ ଥିବା ସ୍ଥଳଭାଗର ପରିମାଣ କେତେ ?
(A) ୧/୪
(B) ୧/୩
(C) ୨/୩
(D) ୧/୨
Answer:
(A) ୧/୪
୭। ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗରର ଆକୃତି କେଉଁ ଇଂରାଜୀ ଅକ୍ଷର ପରି ?
(A) T
(B) 0
(C) P
(D) S
Answer:
(D) S
୮। ପୃଥିବୀର ବାୟୁମଣ୍ଡଳଟି ଭୂପୃଷ୍ଠରୁ କେତେ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ ?
(A) ୧୬୦୦
(B) ୧୨୦୦
(C) ୪୦୦୦
(D) ୮୦୦୦
Answer:
(A) ୧୬୦୦

୯। ବାୟୁମଣ୍ଡଳରେ କେଉଁ ଗ୍ୟାସ୍ର ପରିମାଣ ସବୁଠାରୁ ଅଧିକ ?
(A) ଅମ୍ଳଜାନ
(B) ଅଙ୍ଗାରକାମ୍ଳ
(C)ଆଟଲାଣ୍ଟିକ୍ ମହାସାଗର
(D) ଯବକ୍ଷାରଜାନ
Answer:
(D) ଯବକ୍ଷାରଜାନ
୧୦। ପୃଥିବୀର ଗଭୀରତମ ସାମୁଦ୍ରିକ ଖାତ ମାରିଆନା କେଉଁ ମହାସାଗରରେ ଅବସ୍ଥିତ ?
(A) ପ୍ର ଶା ନ୍ତ
(B) ଆଟ୍ଲାଣ୍ଟିକ୍
(C) ଶୂନ୍ୟସ୍ଥାନ
(D)ପୃଥିବୀପୃଷ୍ଠରେ
Answer:
(A) ପ୍ର ଶା ନ୍ତ

(ଘ) ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।
1. ପୃଥିବୀର ଗଭୀରତମ ସାମୁଦ୍ରିକ ଖାତ ମାରିଆନା ____________ ମହାସାଗରରେ ଅବସ୍ଥିତ।
(ପ୍ରଶାନ୍ତ, ଆଟ୍ଲାଣ୍ଟିକ୍, ଭାରତ, ସୁମେରୁ)
Answer:
ପ୍ରଶାନ୍ତ
2. ପୃଥିବୀପୃଷ୍ଠରେ ଥିବା ମଧୁର ଜଳର ପରିମାଣ ପ୍ରାୟ ଶତକଡ଼ା __________ ଭାଗ।
(୧.୮, ୧୮ ୩୮, ୪.୮)
Answer:
୧.୮
3. ସୁମେରୁ ମହାସାଗର ସହିତ ପ୍ରଶାନ୍ତ ମହାସାଗରକୁ __________ ପ୍ରଣାଳୀ ସଂଯୁକ୍ତ କରୁଛି ।
(ଜିବ୍ରାଲିଟର, ପକ୍ , ବେରିଂ, ଇଂଲିଶ )
Answer:
ବେରିଂ
4. ବାୟୁମଣ୍ଡଳରେ _____________ ଗ୍ୟାସ୍ ପରିମାଣ ସବୁଠାରୁ ଅଧିକ।
( ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ, ଆରଗନ, ଯବକ୍ଷାରଜାନ)
Answer:
ଯବକ୍ଷାରଜାନ

5. ପୃଥିବୀର ସର୍ବୋଚ୍ଚ ପାର୍ବତ୍ୟ ଶୃଙ୍ଗର ଉଚ୍ଚତା __________ ମିଟର।
(୮୮୪୮, ୮୮୮୪, ୮୪୮୮, ୮୮୮୮ )
Answer:
୮୮୪୮
6. ପୃଥିବୀପୃଷ୍ଠରେ ଉପଲବ୍ଧ ଜଳର ପରିମାଣ ଶତକଡ଼ା __________ ।
(୦.୩ ଭାଗ, ୦.୦୩ ଭାଗ, ୦.୦୦୩ ଭାଗ, ୩ ଭାଗ)
Answer:
୦.୦୩ ଭାଗ
7. ଭୂପୃଷ୍ଠରେ ଥିବା ସ୍ଥଳଭାଗର ପରିମାଣ ________________ ।
[୧/୪’ ୧/୩’ ୨/୩’୧/୨]
Answer:
୧/୪’
8. ବାୟୁମଣ୍ଡଳରେ __________ ବାଷ୍ପର ପରିମାଣ ଅଧ୍ଵ ହେଲେ ଭୂଗୋଲକୀୟ ତାପମାତ୍ରାର କ୍ରମଶଃ ବୃଦ୍ଧି ଘଟିଥାଏ।
( ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ, ଆରଗନ୍, ଯବକ୍ଷାରଜାନ )
Answer:
ଅଙ୍ଗାରକାମ୍ଳ
10. ପୃଥିବୀର ବାୟୁମଣ୍ଡଳଟି ଭୂପୃଷ୍ଠରୁ ________ କି.ମି. ଉଚ୍ଚତା ପର୍ଯ୍ୟନ୍ତ ବିସ୍ତୃତ।
(୧୬୦୦, ୧୨୦୦, ୪୦୦, ୮୦୦)
Answer:
୧୬୦୦

ତୁମ ପାଇଁ କାମ :
- ମନୁଷ୍ୟ ଯେଉଁ ଯେଉଁ କାର୍ଯ୍ୟ ପାଇଁ ଅଶ୍ଵମଣ୍ଡଳ, ବାରିମଣ୍ଡଳ ଓ ବାୟୁମଣ୍ଡଳ ଉପରେ ନିର୍ଭରଶୀଳ ତାହାର ତାଲିକା କର।
Answer:
( ନିଜେ କର।)
- ପୃଥିବୀର ଚିତ୍ର ଅଙ୍କନ କରି ତହିଁରେ ମହାଦେଶ ଓ ମହାସାଗରଗୁଡ଼ିକୁ ରେଖାଙ୍କିତ ଚିତ୍ରରେ ଦର୍ଶାଅ।
Answer:
( ନିଜେ କର।)
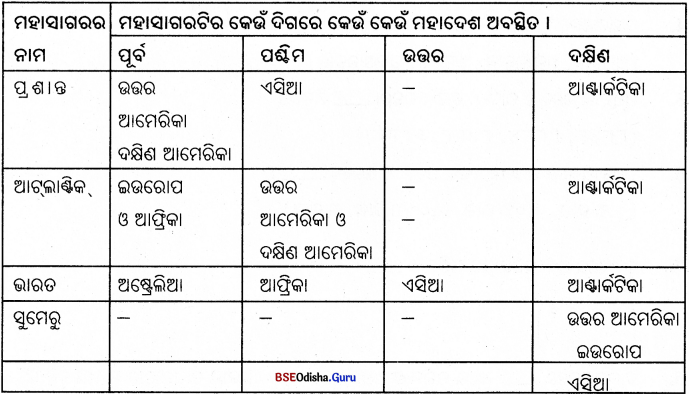
- ମାନଚିତ୍ର ଅଧ୍ୟୟନକରି ପ୍ରଦତ୍ତ ସାରଣୀଟିରେ ବିଭିନ୍ନ ମହାସାଗର ତଟସ୍ଥ ଦେଶଗୁଡ଼ିକର ନାମ ଲେଖ।
( ଦେଶଗୁଡ଼ିକର ନାମ ସାରଣୀରେ ଲେଖୁ ଦିଆଯାଇଛି ।)

![]()