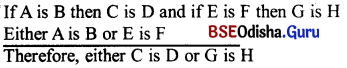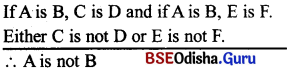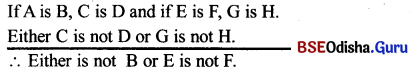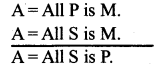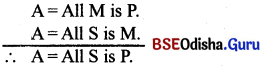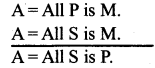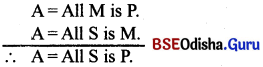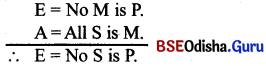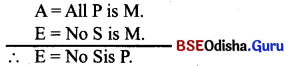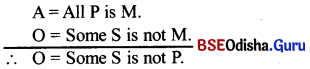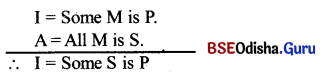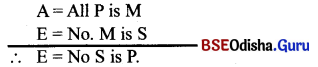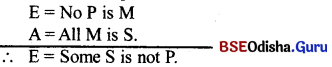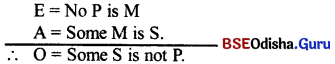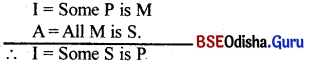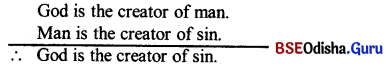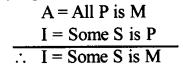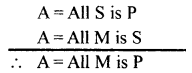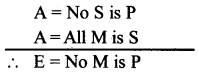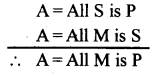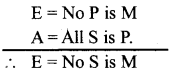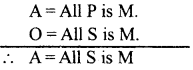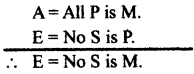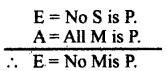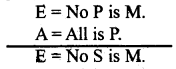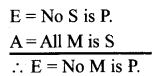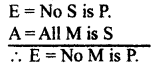Class 12

Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 6 Cost and Revenue Questions and Answers.

CHSE Odisha 12th Class Economics Chapter 6 Question Answer Cost and Revenue

Group – A

Short type Questions with Answers
I. Answer within Two/Three sentence.

Question 1.
What is the shape of Marginal cost curve ?
Answer:
Marginal cost first falls because of the increasing returns from the factors in which MP of the factor increases. Secondly, marginal cost increases because of the diminishing returns from the factors & hence marginal lost becomes U-shaped.

Question 2.
What is shape of Short-run average cost (SAC) curve ?
Answer:
On account of the emergence of stage of increasing & diminishing returns, the AP of the factor increases & diminishes. This has the impact on the short-run Average cost for which it first falls & then rises & becomes U-shaped.

Question 3.
What, is nature of Average fixed Cost (AFC) with the increase in the level of output ?
Answer:
The total fixed cost is fixed in the short-run irrespective of the level of output. So with the increase in the level of output, the fixed cost per unit of output (AFC) goes on decreasing.

Question 4.
What is the relationship between Marginal cost and Average cost ?
Answer:
As long as MC < AC, AC must be falling & when MC > AC, AC must be rising. So, MC=AC at the minimum point of AC.

Question 5.
What is the nature of Variable Cost ?
Answer:
In the Short-run total fixed cost remains fixed & only the variable cost changes with the change in the level of output. So variable cost is the prime cost.

Question 6.
What is the relationship between average revenue and marginal revenue in perfect Competition ?
Answer:
In perfect competition, the goods are hemogeneous & sold at a uniform price by the large number of buyers & sellers So additional revenue from the extra unit sold (MR) & revenue per unit of output (AR) becomes same.

Question 7.
What is the slope of average revenue curve in Monopoly ?
Answer:
Under monopoly, single seller sells the product having no close substitute & if he wants to sell more, it is to reduce the price & vice-versa. So AR curve slopes downward.

Question 8.
Which revenue reflects price of the goods ?
Answer:
Average Revenue (AR) is the total revenue perunit of output \(\left(\frac{\mathrm{TR}}{\mathrm{q}}\right)\). So it reflects price

Question 9.
Which cost is called alternative cost ?
Answer:
The opportunity cost of any goods is the best alternative goods that is sacrificed. So it is called alternative Cost.

Question 10.
Which cost is independent of level of output ?
Answer:
Fixed cost is incurred for the use of fixed factors which remain unchanged in the short- run irrespective of the level of output. So fixed cost is independent of level of output.

Question 11.
What is Total cost ?
Answer:
Both fixed factors & variable factors are employed in the production for which fixed costs as well as variable costs are incurred. So total fixed cost & the total variable cost mixed together indicates total cost.

Question 12.
What is the shape of AR curve in under perfect competition ?
Answer:
Under perfect competition, price of goods remains uniform. So AR curve as well as MR curve is equal & horizontal straight line.

Question 13.
What is slope of AR curve under monopoly ?
Answer:
Under monopoly, if sella- wants to sell more, it is to reduce the price & vice-versa. So the AR curve slopes downward from left to right.

II. Answer within Five/Six sentence :

Question 1.
What is Total Revenue (TR) ?
Answer:
Total Revenue refers to the aggregate of income earned by the seller from the sale of his output. It is the sum of all sales, receipts or income of a price per unit multiplied quantity sold. Thus,
TR = P × Q Where P → Price per unit
Q → Output.

Question 2.
What do you mean by Average Revenue (AR) ?
Answer:
Average Revenue refers to the revenue received per unit. It is the per unit revenue received from the sale of one unit of a commodity. AR is calculated by dividing the Total Revenue by total output. Hence, symbolically,
AR = \(\frac{TR}{Q}\) Where Q – Output
AR is equal to price of the commodity.
AR = \(\frac{PQ}{Q}\) = P where P → Price.

Question 3.
Explain the concept Marginal Revenue (MR).
Answer:
Marginal Revenue refers to the net revenue obtained by selling an additional unit of the commodity. In other words, Marginal Revenue is the change in the total revenue which results from the sale of one more or one less unit of output. Thus, Marginal Revenue is the addition made to the total revenue by selling one more unit of the good.
MR = \(\frac{\Delta \mathrm{TR}}{\Delta \mathrm{Q}}\)
MR_n = TR_n – TR_n-1

Question 4.
Explain the relationship between TR, AR and MR.
Answer:
TR goes on rising as long as MR remains positive. TR becomes maximum when MR is zero. TR starts falling when MR becomes negative and when AR falls MR follows AR, but MR falls at a faster rate than AR. When the AR curve goes on falling the MR curve lies below the AR. When AR rises the MR lies above the AR. The position of the MR is determined by the slope of the AR. When the AR curve is convex to the origin the MR curve is farther from the AR curve. When the AR curve is concave the MR curve lies closer to the AR curve.

(A) WRITE SHORT NOTES ON :

Question 5.
Money Cost.
Answer:
Money cost refers to the monetary expenses incurred by the producer to produce a given quantity of a goods. In other words, the cost of production incurred & expressed in terms of money is called money cost. Money cost is otherwise known as “Nominal cost”. It is expressed as sum of payments made to different factors of production in terms of money. Money cost includes wages for labourers, payment for raw materials, interest, taxes etc.

Question 6.
Accounting Cost.
Answer:
Accounting cost refers to the cost which can be expressed & whose accounts can be maintaned by the accountant. Accounting costs are expressible & hence called explicit cost. These costs are actually paid by the producer for hiring different factors of production. These accounting costs are nothing but the cash payments made to different factor owners such as wage, rent, interest paid in the productive process.

Question 7.
Economic Cost.
Answer:
Economic cost is a broader concept which includes both explicit cost & implicit cost. It takes the direct cost incurred & paid in terms of money to different into account along with the cost arising from land Owned & used by the producer, entrepreneurs self invested capital, self managment etc. Economic cost includes the total cost which covers both the explicit & implicit cost. The net profit is calculated by deducting this economic cost from the total revenue.

Question 8.
Real Cost.
Answer:
Real cost refers to all those efforts, sacrifices, troubles, toils undergone by the factors owners or the members of the society to produce a goods. It is a subjective concept. It also denotes the exertion of all different kinds of labour that are directly or indirectly involved in the production of goods. It is also called social costs’. It can not be meausred quantitatively & hence no monetary reward is paid.

Question 9.
Opportunity Cost.
Answer:
The opportunity cost of anything is the next best alternative that could be produced instead by the same factors or by an equivalent group of factors costing the same amount of money. In other words, the opportunity cost of any good is the next best alternative good that is foregone. For example, a farmer producing wheat in his land can not produce sugar cane simultaneously. So the production of sugar cane is sacrificed. The opportunity cost of producing wheat is the value of sugarcane sacrificed. This opportunity cost is otherwise called transfer cost or alternative cost.

Question 10.
Fixed Cost
Answer:
Fixed costs denote those costs which are incurred for the fixed factors employed in the productive process. Fixed costs remain unchanged irrespective of the level of output. Even at zero level of output, fixed cost is to be borne. The costs incurred towards land or building, plants & machiney insurance charges etc. are included in the category of fixed cost. Fixed costs are otherwise called “Supplementary cost” or indirect cost. It is also called “ overhead cost”.

Question 11.
Variable Cost.
Answer:
Variable costs are those costs which change with the change in the level of output. It increases with the increase in the level of output & decreases with the decrease in the level of output. Variables costs are called “direct cost” & also treated as “prime cost” during the short-run. The wages, the payment for raw materials are the examples of variable costs.

(B) DISTINGUISH BETWEEN

Question 12.
Explicit cost & Implicit Cost.
Answer:

• Explict cost is that cost which is expressible in any form, but implicit cost is inexpressible.
• Explicit cost is actually paid by the producer to hire different factors of production whereas implicit cost includes entrepreneurs self owned & self employed resources for which no payment is actually made.
• Explicit cost can be properly maintained by an accountant but the accounts of implicit cost can not be maintained.
• Gross profit is calculated by deducting only explicit cost from total revenue but net profit is calculated by deducting both implicit & explicit cost.

Question 13.
Money Cost & Real Cost.
Answer:

• Money cost refers to the cost which is paid in terms of money whereas real cost refers to efforts & sacrifices undergone by the factor owners or the members of the society for producing a commodity.
• Money cost is directly borne by the producer but real cost is the “spill over cost” borne by the society as a whole.
• Money cost is incurred through cash payment to factor owners but no real payment is made in respect of real cost.
• Money cost is a quantitative or objective concept but real cost is qualitative or subjective concept.

Question 14.
Fixed cost & Variable Cost.
Answer:

• Fixed costs are those costs incurred for hiring fixed factors like land & building, plant & machinery whereas variable costs are those costs incurred for hiring variable factors like labour, raw materials, fuel etc.
• Fixed costs remain unchanged irrespective of the level of output. It is indepedent of level of output. Variable costs change with the change in the level of output. It depends on the level of output.
• Fixed costs are the supplementaiy or overhead costs that happen only in the short-run but variable costs are the prime cost which happen both in the short-run & in the long-run.
• Fixed cost exist even at zero level of output but variable cost does not appear at zero level of out-put.

Question 15.
Average Cost & Marginal Cost
Answer:

• Average cost is the total cost per unit of output. But marginal cost is the addition made to the total cost for producing one extra unit of good.
• Both average cost & marginal cost are calculated from total cost.
• When average cost is falling, MC < AC
• When average cost is rising, MC > AC
• Marginal cost becomes equal to average cost when average cost is minimum.

Group – B

Long Type Questions With Answers

Question 1.
What are the components of total cost ? How can total cost be derived in the short-run ?
Answer:
Cost of production refers to the total expenditure incurred for producing a given level of output. It is incurred for hiring different factors of production to be employed in the productive process. The concept of cost can be classified on the basis of the time period i.e. short-run & long- run. In traditional theory of cost, cost can be distinguished as short-run costs & long-run costs.

Total cost refers to the aggregate of expenditure incurred towards the various factors of production to produce a given quantity of output. It is the function of output to be produced. It increases or decreases with the increase or decrease in the level of output. In short-run, there are two components of total cost i.e. total fixed cost-(TFC) & total variable cost (TVC). The sum of total fixed cost & total variable cost gives rise to the total cost during short-period. (Mathematically, stated, TG=TFC +TVC.) For the derivation of total cost, these two components must be looked into.

Total Fixed Cost (TFC)
Total fixed cost is the cost incurred for employing fixed factors which are observed to be constant during short-run. Hence, total fixed costs denote to those costs which remain unchanged or constant in the productive process irrespective of the level of output. Thus, total fixed cost is quite independent of level of output. Any change in the level of output does not have any impact on this total fixed cost. Even at zero level of output, total fixed cost is to be borne. These cost are otherwise called overhead or supplementary cost. The cost of building, machinery, land, salaries of the executives etc. are the examples of fixed costs. The total fixed cost curve is a horizontal straight line.

In the figure units of outputs are measured on OX-axis & cost on the OY-axis. TFC is the total fixed cost which is constant (OM) irrespective of the level cost output.
Total Variable Cost-(TVC)
Tota variable costs are those cost which go on changing with the change in the level of output. Any increase in or decrease in level of output causes an increase or decrease in the total variable cost. It is otherwise called prime cost as it is a vital cost concept in the short-run. Expenses towards raw materials, labour power, fuel etc. are the examples of toal variable cost.

In the above figurem units of outputs are measured on OX-axis & cost on OY-axis. For producing OQ amount of output, the variable cost amounts to QR & for higher level of output (OS), it increases to ST. Thus, it is obvious that total variable cost increases with the increase in the level of output & decreases with the decrease in the level of output.

Derivation of TC.
As known total cost is the sum of total fixed cost & total variable cost. This total cost can be numerically derived by summing both these two costs & graphically total cost can be derived through vertical summation of total fixed cost curve & total variable cost curve.

Units of Output	Total Fixed Cost (Rs.)	Total Variable Cost (in Rs.)	Total Cost (in Rs.)
0	10	0	10
1	10	8	18
2	10	13	23
3	10	16	26
4	10	20	30
5	10	26	36
6	10	35	45
7	10	45	55

The numercial analysis as above presents a break-up of total cost (TC) into total fixed cost (TFC) and total variable cost (TVC). It reveals that TFC remains unchanged (Rs. 10) irrespective of the level of output. But TVC increases with the increase in the level of output. Accordingly total cost being the sum of TFC & TVC increases with the increase-in the level of output. The same notion can be explained with the help of graphical analysis.

The above diagram measures units of output on OX- axis & cost on OY-axis The diagram describes that total fixed cost (TFC) remains constant & hence TFC curve is a horizontal straight line indicating OC amount of total fixed cost. But the total variable cost (TVC) increases with the increase in the level of output & thus TVC curve is inverse – S- shaped. As such TC being the vertical summation of TFC & TVC is represented through TC curve.

The figure also exposes that at OQ₁ level of output, the TFC is OC & TVC is Q₁V₁ At this level, TC is found to be Q₁T₁, which is obtained by adding TVC (Q₁V₁) & TFC (OC).

∴ Total cost (TC) at OQ₁ level of output = O₁V₁ + Q₁C = Q₁T₁ Similarly, at higher level of output OQ₂, the TFC remains unchanged at OC level as before & TVC increases to Q₂V₂. AT this level, TC is the sum of TFC (OC) & TVC (O₂V₂) i.e Q₂T₂.
∴ TC at OQ₂ level of output = Q₂V₂ + Q₂C = Q₂T₂
In this manner TC is derived in the short-run TC is found to be the aggregate of TFC & TVC.

Question 2.
Explain Average Cost in the Short-run. How can it be derived ?
Answer:
Average cost is the total cost incurred per unit of output. In the short-run, the analysis of average cost can be made by the way of its compnents exist in the short-run. Short-run is a period during which there are two types of costs like Total fixed cost (TFC) & Total variable cost (TVC). So in order to analyse the short-run average cost, there is need of analysing Average fixed cost (AFC) & Average variable cost (AVC).

Average fixed cost (AFC) :
As one of the components of C in the Short-run, Average fixed cost (AFC) can be defined as fixed cost per unit of output (Q). It can be calculated by dividing units output produced (Q) with the i.e. AFC = \(\frac{TFC}{Q}\)

Nature : As total fixed cost is a constant entity in the short-run cost structure, the AFC continuously falls with the increase in the level of output. Thus AFC gradually declines with the increase in the level of output. Hence, AFC curve slopes downward from left to right & takes the shape of rectangular hyperbola. This curve approachs both the axes but does never touch any axis.

In the figure, it is revealed that when the level of output (measure on OX-axis) increases, the cost (measured on OY-axis) falls. At OQ level of output, AFC is found to QA& when output level increases to OR & OS, the A’FC falls to RB & SC respectively. Thus AFC curve approaches both the axes but does not touch any axis.

Average Variable Cost.
Total variable cost incurred per unit of output is called average vriable cost. It can be calculated by dividing quantity of output (Q) produced with the total variable cost (TVC). Symbolically expressed.
AVC = \(\frac{TVC}{Q}\)
Nature :Average variable cost (AVC) at the intial stage diminishes with the increase in the level of output. After a point AVC increases with the increase in the level of output AVC curve takes the shape of‘U’. The nature & shape of AVC is due to the operation of “Law ofVariable Proportions”.

The figure describes that when the output (measured on OX-axis) increases, the average variable cost (AVQ declines. When output level increases from OAto OB, it falls fromAK to BM. At OB level of output, the AVC is minimum at OC level of output, the AVC is found to CL.
Here, output level OA BM < CL

Derivation of AC
Theoretically, short run AC can be derived from the TC which is composed of TFC & TVC TC = TFC + TVC
⇒ \(\frac{TC}{Q}\) = \(\frac{TFC}{Q}\) + \(\frac{TVC}{Q}\)
⇒ AC = AFC + AVC
The derivation of short-run average cost can be numerically & graphically represented.

Unit of output	TFC (in Rs.)	TVC (in Rs.)	TC (in Rs.)	AFC (in Rs.)	AVC (in Rs)	AC (in Rs.)
1	10	8	18	10	8	18
2	10	13	23	5	6.5	11.5
3	10	16	26	3.3	5.3	8.6
4	10	20	30	2.5	5	7.5
5	10	26	36	2	5.2	7.2
6	10	35	45	1.66	5.83	7.49
7	10	45	55	1.42	6.42	7.84
8	10	60	70	1.25	7.5	8.75

The above analysis indicates that AC is the sum of AFC & AVC. Secondly, it shows that the AFC goes on falling with the increase in the level of output. Thridly. the AVC is found to be falling upto the production of 5th unit of output & afterwards it goes on increasing with the increase in the level of output. On this basis, AC also falls upto the production of 5th unit then increases with the level of output.

GRAPHICAL ANALYSIS
The same principle can be reflected with the help the graph.

The figure reflects the shapes of AFC, AVC & AC curves. Primarily, the AFC curve gradually diminishes with the increase in the level of output. AFC curve takes the shape of a rectangular hyperbola. The AVC curve is U-shaped. At first, it goes on diminishing upto a point & then increases. The minimum point of AVC curve is shown as point ‘G’ in the figure. The AVC curve is thus U- shaped. It goes on diminishing upto the production on the level of output & the increases with the increases in the level of output.

As the AC is the sum of AFC & AVC the graphical structure of the AC curve can be shown through the vertical addition of AFC curve & AVC curve.
At OM level of output, AFC = MA; AVC = MB
Hence AC at OM level = MA + MB = MC
Thus, point C on AC curve is derived.
At OV level of output, AFC = VH; AVC = VG
Hence AC at OV level = VH + VG =-VK
Thus, point K on AC curve is derived.
At ON level of output, AFC = NQ; AVC = NR
Hence AC at ON level = NQ + NR = NT
Thus, point on AC curve is derived. .
At OS level of output, AFC = SD; AVC = SE
Hence AC at OS level = SD + SE = SF
Thus, point F on AC curve is derived.
At length, by joining C, K, T, & F points, the shape of SAC curve can be derived & this shape is just like‘U’.

Question 3.
Discuss the relationship between Marginal cost & Average cost.
Answer:
In the short-run, the cost is classified into fixed cost & variable cost. As such, the total cost incurred for producing a given level of output is assessed as the combination of these total fixed cost & total variable cost. Considering the nature of total fixed cost (TFC), it is observed that there is no change in the TFC irrespective of the level of output & hence stands as a constant entity in the productive process during short-run. Regarding total variable cost (TVC), this cost changes with the change in the level of output & hence treated as “Prime cost” in the cost-structure during short- run.

Marginal Cost & its Nature.
Marginal cost which is enunciated by Austrian school of Economics refers to rate of change of total cost by producing one additional unit of output. The total cost, being the sum of TFC & TVC it increase with the increases in the level of output. Hence Marginal Cost (MC) is defined as an addition made to the total cost coused by an increase in one extra unit produced. Mathematically stated.
MCn = TCn – TCn-1
or, MC = \(\frac{\Delta \mathrm{TC}}{\Delta \mathrm{C}}\)
Where, n → no of units produced
Q → output
Marginal cost is viewed as an extra cost for producing one extra unit more or less. As during short-run, total fixed cost does not change under any circumstances, marginal cost being expressed as change in total cost is no way related to this total fixed cost. It is only associated with Total Variable Cost (TVC) which changes with the change in the level of output. Marginal cost at first stage decreases with the increase in the level of output & afterwards increases. So marginal cost curve is U-shaped.

Average Cost & its Nature :
In the short-run, Average Cost (AC) is also composed of AFC & AVC. It is the cost incurred per unit of output produced. Hence AC = \(\frac{TC}{Q}\)

Average cost breaks into AFC & AVC. AFC regularly decreases with increase in the level of output & AVC, at first stage decreases with the increase in the level of output & then increases with the increases in the level output. Like MC curve, AC curve is also U-shaped.
The nature & behaviour of the AC & MC can be explained with numerical example & graphical illustrations.

Numerical Analysis

Units of Output (units)	Total Cost (in Rs.)	Average Cost (in Rs.)	Marginal Cost (in Rs.)
1	40	40	–
2	60	30	20
3	70	23.3	10
4	76	19	6
5	84	16.8	8
6	96	16	12
7	112	16	16
8	136	17	24
9	162	18	26

The above numercial analysis indicates that the AC & MC both decreases with the increase in the level of output at the first phase of production But MC attains its minimum point much earlier than the AC (producing 4th unit). AC attains its minimum point while 7th unit is produced. At this level, MC = AC. Above this point MC < AC but afterwards AC < MC

The inference drawn with this analysis can also be explained with the help of graphical analysis. In the figure, OX-axis measures output & OY-axis measures cost. SAC & SMC represent short-run Average Cost & short-run Marginal Cost respectively. From the figure, it is obvious that upto the point E, AC > MC & AC is falling. At point E, (minimum point of AC curve) both AC & MC are equal after the point E, MC>AC & AC is increasing.

General Conslusion.
(a) Both Average cost & marginal cost can be calculated from Total cost i.e.
AC = \(\frac{TC}{Q}\) &MC = \(\frac{\Delta \mathrm{TC}}{\Delta \mathrm{Q}}\)
(b) When Average cost is falling, MC < AC (c) At the minimum point of AC, MC = AC (d) When AC is rising MC > AC
The above analysis has discussed the general inter-relationship between AC & MC.

Question 4.
Discuss the relationship among the Total Revenue, Average Revenue & Marginal Revenue.
Answer:
Revenue refers to the money income received from the sale of the product. It is the money receipts earned by the producer by selling its product in the market. Revenue can be expressed in three forms like Total Revenue, Average Revenue & Marginal Revenue.
(a) Total Revenue (TR) : Total Revenue refers to the sum total of income earned the sale of output. It is the total money receipts earned by the producer from the sale of its product. In other words, it is the sum of all sale, receipts or income of a firm.
Total Revenue can be calculated by multiplying price with the quantity sold.
TR = P × Q
P → Unit price
Q → Quantity sold

(b) Average Revenue (AR) : Average Revenue refers to the revenue earned per unit of output. It is the revenue earned by the seller/producer/firm by selling the per unit product. Average Revenue can be obtained by dividing the total revenue with number of units (Q) sold.
Thus, Average Revenue = AR = \(\frac{TR}{Q}\)

(c) Marginal Revenue (MR) : Marginal Revenue is the additional revenue earned from the sale of one extra unit of a good. In other words, it is the addition made to the TR by selling one extra unit of good. Thus, MR is the net revenue obtained from the sale of one additional unit. It is the change in the TR resulting from the sale of one more unit of good. Marginal Revenue can be obtained in the following way.
MRn = TR_n – TR_n-1
n → number of units sold
or, MR = \(\frac{\Delta \mathrm{TR}}{\Delta \mathrm{Q}}\)

Relationship among TR, AR & MR : There exists certain basic relationship among TR, AR & MR. This relationship can be explained under two heads which are classified into perfect competitive market & imperfect market.

(a) Relationship under Perfect competition.
Perfect competition is said to exist when all the goods are homogenous & sold at a uniform price. The relation among there TR, AR & MR can be explained with the following numerical & graphical analysis.
NUMERICAL ANALYSIS

Units of Output	AR (in Rs.)	TR (in Rs.)	MR (in Rs.)
1	10	10	10
2	10	20	10
3	10	30	10
4	10	40	10
5	10	50	10

The above analysis reveals that under perfect competition AR or Price is uniform & hence MR becomes equal to AR. Total Revenue increases at a constant rate with the increase in the units of the product sold.

Graphical Analysis:

In the figure (a), it is observed that TR curve slopes upwards which established TR increase when more & more output are sold. The fig (b) indicates a horizontal straight line because of equality between AR & MR. AR curve coincides with MR due to this relationship.

(b) Relationship among TR, AR & MC under Imperfect Competition :
Under imperfect competition, AR gradually diminishes with the increase in the sale of output. It implies that if the sella” wants to sell more he is to reduce the price & vice – versa. Unlike the perfect competition price is not uniform. The relationship among TR, AR and MR is explained with the following example.

Numerical Analysis

Units (in Rs.)	AR (in Rs.)	TR (in Rs.)	MR
1	10	10	1o
2	9	18	8
3	8	24	6
4	7	28	4
5	6	30	2

The analysis shows that AR gradually decreases with the increase in the sale of output, l R increases at a diminishing rate & MR gradually diminishes.

Graphical Analysis

The figure (a) indicates that TR increase at an increasing rate upto point & then increase at a diminishing rate. It implies that at the stage of diminishing returns TR increases at a diminishing rate & by selling OQ unit of output, it becomes maximum.
The figure (b) indicates that both AR & MR are falling with the increase in the number of units sold & AR is always greater than MR.
Thus, the relationship among TR & MR is found to be in different forms under different market structure.

Question 5.
Describe the nature of various revenue concepts under perfect competition & imperfect competition.
Answer:
Average Revenue (AR) refers to the revenue earned per unit of output. On the other hand marginal revenue refers to the addition made to the total revenue due to the additional sale of one unit, the nature of these differs from each other under different market conditions. In general, there exists certain relationship between these two concepts. But this relationship differs from market to market which is illustrates as follows :
(i) Perfect competition: Under perfect competition, individual firms are price-takers. They bring numerous exercise, no control and influence over the price. The price is determined by the industry as a whole which consists of a number of firms producing identical products. The price is determined by the interaction of market demand and supply for us. When all units of a product are sold at one price, the price equals to the average revenue and the average revenue equals to the marginal revenue. Therefore, under perfect competition the AR, MR and price become equal as shown in the following table.

Price in Rs.	Quantity sold	TR in Rs.	AR in Rs.	MR
5/-	5	25	5	–
5/-	6	30	5	5
5/-	7	35	5	5
5/-	8	40	5	5
5/-	9	45	5	5

The table makes evident that when price is Rs.5/ per unit the total revenue is obtained by multiplying the price with the quantity sold. As more and more quantity is sold the total revenue increases but the AR and MR remain unchanged. The price paid by the consumer is the revenue of the seller. Since price equals to AR and MR the demand curve, AR curve and MR curve coincide as shown in the following diagram.

(ii) Monopoly : A pure monopoly market presents a situation which is exactly opposite of pure competition. A monopolist being the only one seller in respect of a particular commodity controls the supply of the product. There is no substitute to the monopolist’s product. He is the price-maker of his product as he has no rival. Therefore, by restricting his output he can change any price so as to take away the entire consumers expenditure on the commodity. He may boost up his sales by lowering the price of his product or he may raise the price by restricting the supply. Therefore, the average revenue slopes downwards from left to right. But his total revenue remains unchanged and the marginal revenue is zero. The marginal revenue coincides with the ‘X’ axis as shown in the following table and diagram.

Price in Rs.	Unity sold in Rs.	TR in Rs.	AR in Rs.	MR in Rs.
5	8	40	5	0
4	10	40	4	0
2	20	40	2	0
1	40	40	1	0

From the table it may be seen that the monopolist sells more units of his product by lowering the price but his total revenue remains unaffected. Hence, the marginal revenue curve coincides with OX axis as shown in the diagram:

In the diagram the AR curve represents unitary elasticity of demand suggesting that the total revenue of the firm is constant at OP and OP₁ price, though sale increases from OQ to OQ₁ as a result of fall in price from OP to OP₁.

(iii) Imperfect competition: Under imperfect competition market consists of many categories ranging from two sellers to a large number of buyers and selling. In these markets the AR curve is less than perfectly elastic. The elasticity differs from market to market. The demand curve or AR curve has a downward slope. The downward slope of the AR curve indicates that the seller can sell more and more by lowering the price level and vice versa. The corresponding marginal revenue will be less than the falling average revenue. The MR curve will, therefore, lie below the AR curve as shown in the following table and diagram.

Price	Quantity sold	TR	AR	MR
Rs. 5/-	1	5	5	5
Rs. 4/-	2	8	4	3
Rs. 3/-	3	9	3	1
Rs. 2/-	4	8	2	-1
Rs. 1/-	5	5	1	-3

The table shows that as more and more quantity is sold at lower and lower prices the total revenue increases at a diminishing rate. The average revenue also goes on falling but the MR falls at a greater rate than the fall of AR.

The diagram shows that the AR curve falls as more quantity is sold at lower prices and MR curve lies below the AR curve as the former falls at a greater rate than the latter. In this connection it may be noted that when the seller restricts the supply to sell at higher prices the AR curve takes a positive slope which is represented by a rising AR curve. When the AR curve slopes upwards, as shown in the diagram, the MR curve also slopes upwards and lies above the AR.

In a market characterised as monopolistic competition there are many small sellers and buyers. The products are differentiated, although not exact substitutes. A seller under this market structure faces competition from rival sellers. He is a monopolist in the sense that some buyers have preference for his product. Taking advantage of this a seller can charge a little more than his rivals
and sellers or charge a little less and sell more. The AR curve facing a firm in this situation is quite elastic though not perfectly elastic as in pure competition. The AR, therefore, has a gentle slope. The MR curve which slopes downwards lies close to the AR an shown in the diagram:

The diagram shows that the AR curve under the.monopolistic competition being more than unitary elastic the MR curve lies to the right of the mid-point of the perpendicular drawn from the price axis to the AR curve

(iv) Oligopoly : In oligopoly market there is a small number of sellers. The price changed by one invites retaliation from others and the latter may not react to the change in price. If a seller rises the price and other do not follow then the former will face a fall in demand for his product and suffer loss. In such a case the AR curve appears less elastic in some portion and more elastic in another portion. The corresponding MR curve becomes discontinuous as shown in the diagram:

To sum up the AR under perfect competition takes horizontal shape and the MR curve coincides withAR curve. In pure monopoly the AR curve sloped down wards with unitary elasticity throughout its length and the MR curve coincides with the OX horizontal axis.
The AR curve under imperfect competition has a negative slope and the MR curve lies below the AR curve.
Under monopolistic competition AR slopes downwards with more than unitary elasticity and the MR slopes downwards and lies close to the AR.
Under oligopoly the AR curve is indeterminate. It usually takes kinked shape and the MR, which lies below AR becomes discontinuous and slopes downwards at the point of kink.

Group – C

Objective type Questions with Answers
I. Multiple Choice Questions with Answers :

Question 1.
The price paid for the use of factor input is called
(i) factor price
(ii) value of factor
(iii) cost of production
(iv) price of input
Answer:
(iii) cost of production

Question 2.
The functional relationship between cost of production & output is called
(i) production function
(ii) consumption function
(iii) cost function
(iv) All of the above
Answer:
(iii) cost function

Question 3.
Cost is always expressed for a
(i) particular price of a factor
(ii) particular time period
(iii) particular quantity of a factor
(iv) None of the above
Answer:
(ii) particular time period

Question 4.
Change in cost of production occurs due to
(i) change in the level of output
(ii) Change in factor proportion
(iii) change in factory size
(iv)
Answer:
(i) change in the level of output

Question 5.
Cost in economics indicates
(i) only money case
(ii) only real cost
(iii) only economic cost
(iv) only real cost
Answer:
(iii) only economic cost

Question 6.
Money cost is otherwise known as
(i) normal cast
(ii) Prime cost
(iii) overhead cost
(iv) Supplementary cost
Answer:
(i) normal cast

Question 7.
Efforts, pain, sacrifices, troubles etc undertaken by the society due to production is termed as
(i) supplementary cost
(ii) opportunity cost
(iii) real cost
(iv) prime cost
Answer:
(iii) real cost

Question 8.
Producers do not generally bear
(i) Real cost
(ii) supplementary cost
(iii) Alternative cost
(iv) None of the above
Answer:
(i) Real cost

Question 9.
Economic cost comprises of both
(i) Money cost & Real cost
(ii) Explict cost & implicit cost
(iii) Prime cost & overhead cost
(iv) All of the above
Answer:
(ii) Explict cost & implicit cost

Question 10.
Money cost is basically
(i) Accounting cost
(ii) Explicit cost
(iii) implicit cost
(iv) Both (i) and (ii)
Answer:
(iv) Both (i) and (ii)

Question 11.
Real cost is generally borne by the
(i) Enterprereurs
(ii) workers
(iii) Members of the society
(iv) Government
Answer:
(iii) Members of the society

Question 12.
Rent for the self owned building for business is covered under
(i) money cost
(ii) real cost
(iii) opportunity cost
(iv) Both (i) and (ii)
Answer:
(iv) Both (i) and (ii)

Question 13.
The amount from the next best alternative use of a factor which is foregone is called
(i) alternative cost
(ii) supplementary cost
(iii) opportunity cost
(iv) Both (i) and (ii)
Answer:
(i) alternative cost

Question 14.
Suppose a piece of land be best be used for cultivating rice, potato, wheat & sugarcane. Frame rice, it earns 10,000, from potato it earns 15,000 from wheat it earns 9,000. & from sugar cane it earn, 12,000. If it is now used for producing potato, what will be its opportunity cost ?
(i) 15,000
(ii) 10,000
(iii) 12,000
(iv) 9,000
Answer:
(iii) 12,000

Question 15.
Salary of the manager is
(i) variable cost
(ii) fixed cost
(iii) real cost
(iv) None of the above
Answer:
(ii) fixed cost

Question 16.
If the level of output of a factory becomes zero its fixed cost becomes
(i) zero
(ii) decreases
(iii) increases
(iv) remains unaffected
Answer:
(iv) remains unaffected

Question 17.
If the level of output of a unit continuously goes on diminishing, its fixed cost shall
(i) diminish
(ii) remain unchanged
(iii) first diminish & then increase
(iv) become zero
Answer:
(ii) remain unchanged

Question 18.
Which cost remains unaffected irrespective of the level of output
(i) Supplementary cost
(ii) fixed cost
(iii) variable cost
(iv) Both (i) and (ii)
Answer:
(i) Supplementary cost

Question 19.
If the level of output of a factory goes on increasing, the fixed cost curve of it will
(i) slope upward from left toright
(ii) slope downward from left to right
(iii) become a vertical straight line
(iv) become a horizontal straight line
Answer:
(iv) become a horizontal straight line

Question 20.
The elasticity of the fixed cost curve is
(i) perfectly elastic
(ii) perfectly inelastic
(iii) unitary elastic
(iv) relatively more inelastic
Answer:
(i) perfectly elastic

Question 21.
Fixed cost is otherwise known as
(i) prime cost
(ii) supplementary cost
(iii) alternative cost
(iv) none of the above
Answer:
(iii) alternative cost

Question 22.
The emergence of fixed cost & variable cost occurs during
(i) long period
(ii) short-period
(iii) market period
(iv) All of the above
Answer:
(ii) short-period

Question 23.
Variable cost its otherwise known as
(i) prime cost
(ii) alternative cost
(iii) supplementary cost
(iv) overhead cost
Answer:
(i) prime cost

Question 24.
At the initial stage of production if the level of production increases, the average variable cost
(i) increases
(ii) decreases
(iii) remains unaffected
(iv) none of the above
Answer:
(ii) decreases

Question 25.
The shape of the average variable cost is generally
(i) ‘L’ shaped
(ii) ‘V’ shaped
(iii) ‘U’ shaped
(iv) none of the above
Answer:
(iii) ‘U’ shaped

Question 26.
If the level of output increases, the average fixed cost
(i) remains fixed
(ii) decreases
(iii) increases
(iv) both (i) and (ii)
Answer:
(iii) increases

Question 27.
AFC curve takes the shape of a
(i) ‘U’
(ii) L
(iii) Rectangular hyperbola
(iv) Straight line
Answer:
(iii) Rectangular hyperbola

Question 28.
At different levels of output, the total fixed cost
(i) remains constant
(ii) goes on increasing
(iii) goes on diminishing
(iv) first increases & then decreases
Answer:
(i) remains constant

Question 29.
When AC is falling marginal coat curve remains
(i) above the AC curve
(ii) below the AC curve
(iii) constant
(iv) none of the above
Answer:
(ii) below the AC curve

Question 30.
Firm has to bear the loss of
(i) variable cost
(ii) fixed cost
(iii) real cost
(iv) money cost
Answer:
(i) variable cost

Question 31.
Interest on capital borrowed is an example of
(i) alternative cost
(ii) fixed cost
(iii) real cost
(iv) variable cost
Answer:
(ii) fixed cost

Question 32.
Payment forth raw material is an example of
(i) fixed cost
(ii) variable coal
(iii) alternative cost
(iv) real cost
Answer:
(ii) variable cost

Question 33.
Insurance premium of a company is an example of
(j) fixed cost
(ii) variable cost
(iii) real cost
(iv) none of the above
Answer:
(i) fixed cost

Question 34.
Cost per unit of output is called
(i) total cost
(ii) average cost
(iii) marginal coat
(iv) none of the above
Answer:
(ii) average coat

Question 35.
Addition made to the total cost is called
(i) average cost
(ii) supplementary cost
(iii) marginal cost
(iv) All of the above
Answer:
(iii) marginal cost

Question 36.
AC becomes equal to MC when
(i) AC curve cuts MC from below
(ii) AC curve cuts MC at its minimum point.
(w) MC curve cuts AC at its minimum point
(iv) AC curve cuts MC curve from above
Answer:
(iii) MC curve cuts AC at its minimum point

Question 37.
Under perfect competition. AR becomes
(i) greater than MR
(ii) leas than AR
(iii) equal toAR
(iv) can not say
Answer:
(iii) equal to AR

Question 38.
Under pefect competition AR curve takes the shape of a
(i) rectanugal hyperbola
(ii) horizontal straight line
(iii) vertical straight line
(iv) U – shaped
Answer:
(ii) horizontal straight line

Question 39.
Under monopoly, AR curve lies
(i) above the MR curve
(ii) below the MR curve
(iii) equal to MR curve
(iv) none of the above
Answer:
(i) above the MR curve

Question 40.
MC is not related with
(i) fixed cost
(ii) variable cost
(iii) alternative cost
(iv) real cost
Answer:
(ii) variable cost

Question 41.
If AR = MR, AR curve and MR curve become :
(i) Parallel to OY axis
(ii) Parallel to OX axis
(iii) All of the above
(iv) None of the above
Answer:
(ii) Parallel to OX axis

Question 42.
Under perfect competition AR is :
(i) AR = MR
(ii) AR is less than MR
(iii) AR is greater than MR
(iv)
Answer:
(i) AR = MR

Question 43.
Average revenue generally indicates :
(i) MR
(ii) TR
(iii) Price
(iv) Both(i) and (ii)
Answer:
(iii) Price

Question 44.
Average Revenue is equal to :
(i) TR-Te
(ii) TR_n – TR_n-1
(iii) TR/Q
(iv) None of the above
Answer:
(iii) TR/Q

Question 45.
TR is maximum when :
(i) MR is maximum
(ii) MR is zero
(iii) All of the above
(iv) None of the above
Answer:
(ii) MR is zero

Question 46.
Total Revenue at any output is equal to :
(i) Cost per unit multiplied by quantity sold.
(ii) Price per unit multiplied by quantity sold.
(iii) Both (i) and (ii)
(iv) None of the above.
Answer:
(ii) Price per unit multiplied by quantity sold.

Question 47.
If MR is negative, TR remains :
(i) Constant
(ii) Rises
(iii) Falls
(iv) None of the above.
Answer:
(iii) Falls

Question 48.
MRn is :
(i) MRn – TR_n – TR_n-1
(ii) MRn = TR_n-1 – TR_n
(iii) MRn – AR_n – AR_n-1
(iv) None of the above.
Answer:
(i) MRn – TR_n – TR_n-1

Question 49.
Under Monopoly, MR is always.
(i) Greater than AR
(ii) Less than AR
(iii) Both (i) and (ii)
(iv) None of the above
Answer:
(ii) Less than AR

Question 50.
The incremental cost is associated with
(i) total cost
(ii) average cost
(iii) marginal cost
(iv) all of the above
Answer:
(iii) marginal cost

II. Fill in the blanks :

Question 1.
____ function describes the functional relationship between output and cost.
Answer:
Cost

Question 2.
____ costs are nominal costs.
Answer:
Money

Question 3.
Insurance charges are the example of ____ costs.
Answer:
money

Question 4.
Advertising Cost is the example of ____ cost.
Answer:
explicit

Question 5.
Payments for raw materials are ____ costs.
Answer:
explicit

Question 6.
____ Cost includes only explicit cost.
Answer:
Accounting

Question 7.
____ Cost is deducted from total revenue to calculate Gross Profit.
Answer:
Accounting

Question 8.
Net Profit is the difference between total revenue and ____ costs.
Answer:
Economic

Question 9.
Real cost is ____ cost.
Answer:
implicit

Question 10.
Total Variable Cost is ____ when the output is zero.
Answer:
zero

Question 11.
The wage paid to security personnel is ____ cost.
Answer:
Fixed Cost.

Question 12.
Total Variable Cost is inverted ____
Answer:
‘S’ shaped.

Question 13.
____ are‘Overhead Costs’.
Answer:
Fixed Costs

Question 14.
____ cost is prime cost.
Answer:
Variable

Question 15.
Fixed Costs are realised during ____ period
Answer:
Short

Question 16.
AFC ____ throughout with the increase in output.
Answer:
falls

Question 17.
AVC first ____ and then rises.
Answer:
diminishes

Question 18.
AC is ____ shape.
Answer:
U-shaped

Question 19.
Rate of change of Variable Cost for producing one more unit of output is called ____
Answer:
MC

Question 20.
MC cuts AC curve at its ____ point.
Answer:
minimum

Question 21.
____ Revenue at any point is equal to price per unit multiplied by quantity sold.
Answer:
Total

Question 22.
____ Revenue is the revenue per unit of output.
Answer:
Average

Question 23.
Marginal Revenue is the change in ____ Revenue resulting from the sale of one more unit of output.
Answer:
Total

Question 24.
If MR is negative, TR ____
Answer:
falls.

Question 25.
TR is maximum when MR is ____
Answer:
zero.

Question 26.
Under Imperfect Competition, TR ____ at an diminishing rate.
Answer:
increases

Question 27.
Under Perfect Compeition AR = ____
Answer:
MR.

Question 28.
Under monopoly, AR is always ____ than MR.
Answer:
greater

Question 29.
____ revenue generally indicates price.
Answer:
Average

Question 30.
____ = \(\frac{TR}{Q}\)
Answer:
AR

III. Correct the Sentences :

Question 1.
The quantity of output produced increases with the increase in cost of production.
Answer:
Incorrect:
Correct: Cost of production increases with the increase in quantity of output produced

Question 2.
Cost of production relates to demand for goods.
Answer:
Incorrect:
Correct: Cost of production relates to supply of goods.

Question 3.
Real cost is known as nominal cost.
Answer:
Incorrect
Correct: Money cost is known as nominal cost.

Question 4.
Accounting costs include both explicit & implicit cost.
Answer:
Incorrect.
Correct: Accounting costs include only explicit cost.

Question 5.
Transportation cost is a money cost.
Answer:
Correct:

Question 6.
Economic cost covers only explicit cost.
Answer:
Incorrect:
Correct: Economic cost covers both explicit & implicit cost.

Question 7.
Accounting cost is a broad concept but economic cost is a narrow concept.
Answer:
Incorrect:
Correct: Economic cost is a broad concept but accounting cost is a narrow concent.

Question 8.
Money cost is a subjective concept.
Answer:
Incorrect:
Correct: Real cost is a subjective concept.

Question 9.
Money cost is same as real cost.
Answer:
Incorrect:
Correct: Money cost is different from Real cost.

Question 10.
Money cost is a qualitative concept whereas real cost is a quantitative concept.
Answer:
Incorrect:
Correct: Real cost is a qualitative concept whereas money cost is a quantitative concept.

Question 11.
Money cost is otherwise called social cost.
Answer:
Incorrect:
Correct: Real cost is otherwise called social cost.

Question 12.
Real cost is not borne by the producer.
Answer:
Correct.

Question 13.
Money cost is expressed in terms of efforts & sacrifices.
Answer:
Incorrect:
Correct: Real cost is expressed in terms of efforts & sacrifices.

Question 14.
Opportunity cost is transfer cost.
Answer:
Correct.

Question 15.
Real cost is explicit cost.
Answer:
Incorrect :
Correct: Real cost is implicit cost.

Question 16.
Gross profit is calculated by deducting accounting cost from Total Revenue.
Answer:
Correct

Question 17.
Net Profit is calculated by deducting explicit cost from total revenue.
Answer:
Incorrect:
Correct: Net Profit is calculated by deducting economic cost from total revenue.

Question 18.
Fixed cost increases with the increase in the level of output.
Answer:
Incorrect:
Correct: Variable cost increases (or fixed cost remains samel with the increase in the level of output.

Question 19.
Fixed cost is independent of level of output.
Answer:
Correct:

Question 20.
Variable costs are supplementary cost.
Answer:
Incorrect:
Correct: Fixed cost are supplementary cost.

Question 21.
Fixed costs are direct costs.
Answer:
Incorrect:
Correct: Variable costs are direct costs.

Question 22.
Fixed costs are otherwise known as overhead costs.
Answer:
Correct:

Question 23.
Fixed costs become zero when the level of output is zero.
Answer:
Incorrect:
Correct: Fixed cost is positive when the level of output is zero.

Question 24.
Fixed costs are prime costs.
Answer:
Incorrect:
Correct: Variable costs are prime costs.

Question 25.
Insurance charges are real costs.
Answer:
Incorrect:
Correct: Insurance charges are money costs.

Question 26.
Salary of executives is a variable cost.
Answer:
Incorrect:
Correct: Salary of excutives is a fixed cost.

Question 27.
The shape of AC curve is U-shaped.
Answer:
Correct:

Question 28.
Average cost is equal to marginal cost at the maximum point of average cost.
Answer:
Incorrect:
Correct: Average cost is equal to marginal cost at the minimum point of average cost.

Question 29.
Average cost first increases & then decreases with the increase in the level of output.
Answer:
Incorrect:
Correct: Average cost first decreases & the increases with the increase in the level of output.

Question 30.
Marginal cost is associated with fixed cost in the short-run
Answer:
Incorrect:
Correct: Marginal cost is associated with variable cost in the short-run.

Question 31.
Average cost cuts marginal cost curve at its minimum point.
Answer:
Incorrect:
Correct: Marginal cost cuts average cost at its minimum point.

Question 32.
When AC is equal to MC, AC is minimum
Answer:
Incorrect:
Correct: When AC is equal to MC, AC is maximum.

Question 33.
When AC is less than MC, the AC must be falling.
Answer:
Correct

Question 34.
When AC is more than MC. AC must be falling.
Answer:
Correct

Question 35.
Average fixed cost is independent of level of output.
Answer:
Incorrect:
Correct: Total fixed cost is independent of level of output.

Question 36.
AFC is fixed with the increase in level of output.
Answer:
Incorrect
Correct: AFC decreases with the increase in the level of output.

Question 37.
Average cost changes faster than marginal cost.
Answer:
Incorrect
Correct: Marginal cost changes faster than average cost.

Question 38.
Fixed cost arises only in the long-run.
Answer:
Incorrect
Correct: Fixed cost arises only in the short-run.

Question 39.
All the costs are variable in the long run
Answer:
Correct

Question 40.
Total revenue represents price of the goods.
Answer:
Incorrect
Correct: Average revenue represents price of goods.

Question 41.
Average revenue curve is the demand curve.
Answer:
Correct:

Question 42.
In perfect competition, AR>MR.
Answer:
Incorrect:
Correct: In perfect competition AR = MR.

Question 43.
AR increases with the increase in the units of output sold in a perfectly competitive market.
Answer:
Incorrect:
Correct: AR regains same with the increase in the units of output sold in a perefectly competitive market.

Question 44.
Under monopoly, AR < MR.
Answer:
Incorrect:
Correct: Under monopoly, AR > MR

Question 45.
In imperfect market AR increases with the increase in the sale of output.
Answer:
Incorrect:
Correct: In Imperfect market AR decreases with the increase in the sale of output.

Question 46.
Total Revenue at any output is equal to cost per unit multiplied by quantity sold.
Answer:
Incorrect.
Correct: Total Revenue at any point is equal to price per unit multiplied by quantity sold.

Question 47.
Average Revenue is the revenue per unit of output.
Answer:
Correct.

Question 48.
Marginal Revenue is the change in average revenue resulting from the sale of one more unit of output.
Answer:
Incorrect.
Correct : Marginal Revenue is the change in Total Revenue resulting from the sale of one more unit of output.

Question 49.
If MR is negative, TR remains constant.
Answer:
Incorrect.
Correct: If MR is negative, TR falls.

Question 50.
TR is maximum when MR is maximum.
Answer:
Incorrect.
Correct: TR is maximum when MR is zero.

Question 51.
Under Imperfect Competition, TR increases at an increasing rate.
Answer:
Incorrect.
Correct: Under Imperfect Competition, TR increases at an diminishing rate.

Question 52.
If AR = MR, AR curve and MR curve become parallel to OX-axis.
Answer:
Correct.

Question 53.
Under Perfect Competition, AR is greater than MR.
Answer:
Incorrect.
Correct: Under Perfect CompeitionAR = MR.

Question 54.
Under Monopoly, MR is always greater than AR.
Answer:
Incorrect.
Correct: Under monopoly, AR is always greater than MR.

Question 55.
Marginal Revenue generally indicates price.
Answer:
Incorrect.
Correct: Average revenue generally indicates price.

Question 56.
AR = TR-TC
Answer:
Incorrect.
Correct: AR = \(\frac{TR}{Q}\)

IV. Answer the following questions in one word :

Question 1.
What does cost function show ?
Answer:
Cost function shows the functional relationship between cost of production & quantity of output produced.

Question 2.
What is cost of production ?
Answer:
Cost of production refers to the expenses incurred for producing a given level of output.

Question 3.
Which cost is called “Nominal Cost” ?
Answer:
Money cost is called “Nominal cost”.

Question 4.
What is money cost ?
Answer:
The cost of production expressessed in terms of money is called money cost.

Question 5.
What do you mean by accounting cost ?
Answer:
Accounting cost is explicit cost whose accounts can be maintained.

Question 6.
What is a difference between explicit cost & implicit cost ?
Answer:
Explicit cost can be expressed in any form but implicit cost is a hidden cost not expressible.

Question 7.
What is economic cost ?
Answer:
Economic cost is the sum of explicit cost & implicit cost.

Question 8.
Give an example of implicit cost.
Answer:
Payment for entrepreneur’s self invested capital.

Question 9.
How is the net profit calculated ?
Answer:
Net profit is calculated by deducting economic cost from total revenue.

Question 10.
What is real cost ?
Answer:
Real costs are the efforts & sacrifices, troubles, pain etc. undergone for producing a commodity.

Question 11.
Which cost is called social cost ?
Answer:
Real cost is called social cost.

Question 12.
For which cost no real payment is made ?
Answer:
For real cost no real payment is made.

Question 13.
Which cost is direct cost ?
Answer:
Money cost is direct cost.

Question 14.
What is opportunity cost ?
Answer:
Opportunity cost is the cost for the next best alternative good which is foregone.

Question 15.
Which cost is called transfer cost ?
Answer:
Opportunity cost is called transfer cost.

Question 16.
What is fixed cost ?
Answer:
Fixed cost is that cost incurred for hiring fixed factors.

Question 17.
What happens to fixed cost when the level of output increases ?
Answer:
Fixed cost remains unchanged when the level of output increases.

Question 18.
What happens to fixed cost if the level of output is zero ?
Answer:
Fixed cost remains unchanged even at zero level of output.

Question 19.
What is variable cost ?
Answer:
Variable cost refers to that cost incurred for hiring variable factor.

Question 20.
Which cost is called supplementary cost ?
Answer:
Fixed cost is called supplementary cost.

Question 21.
Which cost is called overhead cost ?
Answer:
Fixed cost is called overhead cost.

Question 22.
What is other name of variable cost ?
Answer:
Prime cost is the other name of variable cost.

Question 23.
What happens to variable cost at zero level of output ?
Answer:
Variable cost becomes zero at zero level of output.

Question 24.
What is marginal cost ?
Answer:
Marginal cost is the additional cost incurred for producing one extra unit of good.

Question 25.
What happens to marginal cost if average cost is falling ?
Answer:
Marginal cost is less than average cost if average cost is falling.

Question 26.
What happens to average cost if MC > AC ?
Answer:
Average cost must be rising if MC > AC.

Question 27.
At what point of AC curve, MC curve intersects ?
Answer:
MC curve cuts at the minimum point of the AC curve.

Question 28.
What is revenue ?
Answer:
Revenue refers to the income earned by the producer from the sale of output.

Question 29.
Which concept of revenue represents price ?
Answer:
Average revenue represents price.

Question 30.
Which revenue curve is treated as demand curve ?
Answer:
AR curve is treated as demand curve.

Question 31.
What is the nature of AR under perfect competition ?
Answer:
AR remains same under perfect competition.

Question 32.
What is the reltion between AR & MR under perfect competition ?
Answer:
AR = MR under perfect competition.

Question 33.
What is shape of AR curve under perfect competition ?
Answer:
AR curve is a horizontal straight line under perfect competition.

Question 34.
What is the shape of AR curve in imperfect market ?
Answer:
In imperfect market, AR curve slopes downward from left to right.

Question 35.
What is the relation between AR & MR under imperfect competition ?
Answer:
Under imperfect competition, AR > MR.

Question 36.
What do you mean by ‘revenue’ ?
Answer:
Revenue refers to the income earned by the firm from the sale of its output.

Question 37.
What is TR?
Answer:
TR referse to sum of all types of income earned by the firm from the sale of output.

Question 38.
What is Marginal Revenue (MR) ?
Answer:
Marginal Revenue is the change in total revenue resulting from the sale of one more unit of output.

Question 39.
Under what circumstances AR curve and MR curve become a horizontal straight line and coincide with each other ?
Answer:
AR and MR curves coincide with each other and become a horizontal straight line under perfect competition.

Question 40.
What is the relationship between AR and MR under imperfect competition (monopoly) ?
Answer:
Under imperfect competition (monopoly) AR is greater than MR.

Question 41.
What is the significance of the revenue curves ?
Answer:
The significance of the revenue curve is observed in case of estimation of profits and losses, equilibrium of firm and price-changes.

Question 42.
Which concept of revenue is called Price ?
Answer:
Average Revenue is the same thing as price.

Question 43.
When AR is constant, what is the state of MR ?
Answer:
When AR is constant, MR is also constant and equal to AR.

Question 44.
What is the shape of MR and AR curve under Perfect Competition ?
Answer:
Under Perfect Competition both MR and AR curves are represented by one curve which is parallel to OX-axis.

Question 45.
How are the MR and AR curves under monopoly ?
Answer:
Under monopoly, MR and AR curves are separate from each other and both are downward sloping.

Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 5 Production Questions and Answers.

CHSE Odisha 12th Class Economics Chapter 5 Question Answer Production

Group – A

Short type Questions with Answers
I. Answer within Two/Three sentence.

Question 1.
What is Production ?
Answer:
Production refer to the creation of new goods having value-in-exchange. Hence it creates utility.

Question 2.
What are the stages of Law of variable propertions ?
Answer:
Law of variable proportions operates when some factors are fixed (indivisible) & some factors are variable. In the production process, there observed three stages like stage of increasing returns, stage of diminishing returns & stage of negative returns.

Question 3.
Which is the suitable stage of production ?
AnsWER:
In stage of diminishing returns (second stage) the total product becomes maximum & marginal product of the factor is zero. So it is considered as suitable stage of production.

Question 4.
What happens to the factors in the Long-run ?
Answer:
There are somefactors like building, machineries etc which are indivisible & lumpy in size & hence there supply can not be changed in short-period. As long-run is a pretty long-time, all these factors can be varied & so all the factors are said to be variable in the long-run.

Question 5.
Why does the Law of variable proportions operate ?
Answer:
Because of indivisibility of fixed factors, the return from these factors increases at an increasing rate then diminishing rate with the increase in the quantum of variable factors. It happens due to the gradual effective utilisatiion of these fixed factors & hence law of variable proportions operates with three distinct stages.

Question 6.
Which is the prime factor in the short run ?
Answer:
In short-run, the fixed factor remains unchanged & any change in level of output happens due to change in variable factor. So the variable factors are prime factors in the short run.

Question 7.
Which factor remains unchanged in the short-run ?
Answer:
Fixed factor like building, machinery etc. are indivisible & lumpy. So in the short-run, fixed factors remain unchanged.

Question 8.
In which stage the Production is carried on ?
Answer:
During the stage of diminishing returns, the total product becomes maximum. So it is rational to carry on production during this stage.

Question 9.
Why is the Law of Diminishing Returns more applicable to agriculture ?
Answer:
The law is applicable to agriculture because of ineffective supervision, natural influences, no division of labour, limited land, fall in the fertility of land etc.

Question 10.
Why is the Law of Increasing Returns called law of Decreasing Cost ?
Answer:
It is because as more and more doses of labour and capital are employed initially, the average cost falls as the total product increases at an increasing rate.

Question 11.
What is Average Product (AP)
Answer:
Average product is calculated by dividing the total product by the units of variable factors of production. This is also called per unit production cost of a factor.

Question 12.
What is Marginal Product (MP)
Answer:
The rate at which the total product increases is called marginal product. Marginal product is the addition made to the total product by an increase in one more unit of variable factor of production.

Question 13.
What is total product ?
Answer:
Total product refers to the total amount of goods and services produced with the help of factors of production in a given period. Total product increases at different rates if more and more factors are employed. At the outset, it is more likely to increase at an increasing rate and then it increases at a diminishing rate. At the worst case, it may fall.

Question 14.
Define ‘Law of Variable Proportions’.
Answer:
According to G J. Stigler, “As equal increments of one input are added, the inputs of other productive services being held constant, beyond a certain point, the resulting increments of product will decrease, i.e. marginal product will diminish.”

Question 15.
What do you mean by fixed factors ?
Answer:
Fixed factors are those factors which remain unchanged during the short-run irrespective of the level of output. In other words, fixed factors in the short run undergo no change in order to change the volume of output. It is almost fixed during short-run.

Question 16.
What do you mean by Variable factors ?
Answer:
Variable factors are those factors which undergo a change with the change in the level of output. This is called variable factors in the sense that these factors are to be changed in order to change the level of output during short-run.

II. Answer within Five/Six sentence :

(A) WRITE SHORT NOTES ON :

Question 1.
Production Function:
Answer:
Production function refers to the technological relationship between physical inputs & physical output. It tells a functional relationship between the in puts & output. Thus, it is the relationship between the two variables i.e. inputs & output. It shows that the quantity of output produced depends on the quantity of inputs. Mathmatically stated.
Q = f (a, b, c, d) where Q refers to the output & a, b, c, d are the inputs. T stands for the functional relationship that exists between the two. Simply speaking, the production function describes maximum quantity of output that can be produced with given inputs.

Question 2.
Fixed Factor:
Answer:
During the short-run, the factors of production can be classified into fixed factor & variable factor. Fixed factors are those factor which remain fixed in the short-run. The quantum of these factors remain constant irrespective of the level of output. The example of fixed factors is building, machinary, land etc. which can not be changed in the short-run. Thus, the production in the short-run is carried on with fixed quantity of such factors & variable factor.

Question 3.
Variable Factor:
Answer:
Variable factors are those factors which change with the change in the level of output in the short-run. In the short-run, any increase or decrease in the level of output happens due to the change in variable factors alone. Raw materials, labour etc. are the examples of variable factor. In short-run production function, there observed direct relationship between these variable factors & the level of output.

Question 4.
Relationship between Average Product & marginal product.
Answer:
Average product refers to the output produced per unit of variable product. It can be assessed by dividing amount of variable factor with the total product. On the other hand, marginal product is the addition made to the total product due to the increase in one additional unit of factor. At the intial stage both the marginal & average product increase with the increase amount of variable factor but the change in marginal product is more quicker than the change in average product. As long as marginal product exceeds average product, the average product continues to rise. When marginal product falls short of the average product the average product starts falling. Marginal product becomes equal to average product at the maximum point of the average product.

Question 5.
Marginal Product’:
Answer:
Marginal product is the addition made to the total product caused by an increase in one additional unit of a factor employed. It is the rate of change of total product per unit change in factor. Marginal product at the initial stage of production continues to rise & after a point it starts declining. Marginal product may be positive, zero or negative. In the stage of increasing returns, it becomes positive, in the stage of diminishing return, it is zero & in the stage of negative return it becomes negative.

Question 6.
Why is the law of diminishing returns called the law of increasing costs ?
Answer:
The law of diminishing returns operates when the total output increases less than proportionately as more and more of variable factors are combined with fixed factors. In other words after the optimum level of production the marginal returns go on falling progressively. The average cost of production, therefore, increases when output does not increase in equal proportion to increase in inputs. Hence, the law of diminishing returns amounts to increasing cost and the law is otherwise known as the law of increasing costs.

Question 7.
Describe the concepts of total product, marginal product & average product.
Answer:
Total production refers to the total amount of goods and services produced with the help of factors of production during a given time period. Marginal production refers to change in total production as a result of the employment of one more unit of variable factors. It can be calculated as MP_n = TP_n – TP_n-1, where n refers to the unit. Lastly average production indicates the total production per unit of the variable factor and it is calculated as AP = TP/q where units of variable factor.

Question 8.
Why does the law of variable proportions operate ?
Answer:
This law operates with several assumptions like homogeneous factors, constant technology, variability of factor proportion and short – run time period. This law operates on account of two reasons as Joan Robinson suggests. Firstly, there is a limit to the extent to which one factor can be substituted for other and secondly, two factors are not perfect substitutes.

(B) DISTINGUISH BETWEEN

Question 9.
Short period & Long period.
Answer:
Short period refers to a situation where the time involved is nor too short as in market period nor too long as. in long period. During short period supply cannot fully adjust to change in demand, because the fixed factors like plant and machinery cannot be changed at short notice. Hence, plant size remains unaltered. Production can be increased or decreased to some extent by changing the variable factors only. Demand forces play an important role in determining price in the short period. Firms may reap supernormal profits in the short period.

During long period, supply can fully adjust to demand conditions as all factors are variable during this period. Sufficient time is available to change the plant size by changing the factor inputs. New firms may enter the industry or old firms may quit depending upon the demand conditions. Thus, adjustment between supply and demand becomes possible. Firms earn only normal profits in the long period.

Question 10.
Average product & marginal product.
Answer:
Average product refers to the output produced per unit of variable product. It can be assessed by dividing amount of variable factor with the total product. On the other hand, marginal product is the addition made to the total product due to the increase in one additional unit of factor. At the initial stage both the marginal & average product increase with the increase amount of variable factor but the change in marginal product is more quicker than the change in average product. As long as marginal product exceeds average product, the average product continues to rise. When Marginal Product falls short of the average product the average product starts falling. Marginal product becomes equal to average product at the maximum point of the average product.

Question 11.
Distinguish between TP and MP.
Anwser:

• Total Product is the total amount of output produced during a given time period whereas marginal product (MP) refers to the addition made to the TP caused by an increase in one more unit of variable factor.
• When MP increases, TP increases at an increasing rate.
• When MP diminishes, TP increases at a diminishing rate.
• When MP is zero, TP becomes maximum.
• When MP is -negative, TP starts falling.

Group – B

Long Type Questions With Answers

Question 1.
What is production function ? Make a brief analysis of it.
Answer:
Production is an economic activity that creates new goods having exchange – value. Thus, it is the creation of utility. Production takes place with the combination of four factors of production, ie., land, labour, capital & organisation which can be broadly classified into fixed factor & variable factors. The combination of these factor produces output. In production, there occurs physical transformation of inputs into output. Hence, there exists a relationship between physical inputs & output which is called “ Production function”.

The production function refers to the technological relationship between physical inputs & physical output. It expresses the functional relationship between the two. The relationship between those inputs & outputs is presented in mathematical form which is the production function.” Symbolically .
Q = f (a, b, c, d)
Where Q → quantity of output
a, b, c, d → various inputs
f → function of
The above noted mathematical expression tells about production function. The word function refers to the relationship that exists between one dependent variable (output) & many independent variables (inputs). The production function shows the relationship between the maximum quantity of output produced in the productive process & the quantites of inputs used in that process.

Oh the physical aspects of production inside a firm & state of technology or method of organisation, the production function is quite external to economies. There may be many process of production & for each.of them there is a relationship between various combinations of inputs & the output. So a particular process is adopted & accepted which is well-suited to the enterpreneur. The combination perferred is determined on the basis of market prices of inputs used.

Production function bears an important implication. It expresses the relationship between quantity of output & the requirements & inputs for production. In otherwords, production function relates the various quantities of inputs with the maximum possible output which can be obtained out of the inputs, even the producer is interested in minimising the output from a given combination of inputs. Hence, the production function is considered to be a statement of technical facts which the producer uses to obtairie the least-cost combination of inputs required to produce a given quantity of output.

The form of production function can be determined by the state of technology. It represents the technical choice operate to each producer within a given span of time. A short-period production function differs from long period production function. When technical progRESS takes place, new production function comes into existence.

Production function for all firms may not be uniform. It differs from firm to firm & industry ‘ to industry. There are two types of inputs output relations in production function. First, the relations where quantities of some inputs are fixed while quantities of other inputs vary, secondly, where all the inputs are variable. The first type of production function is termed as short-run production function which is subject to “Law of Variable Proportion” & second one is subject to “Law of Returns to scale” which happens a long-run.
Production function is an essential device in the theory of production, technique of production & objectives & intention of the producer.

Question 2.
Explain the law of variable proportions.
Answer:
Production refers to the creation of goods & services having value in exchange. It takes place with the help of four factors of production like land, labour, capital & organisation which are broadly classified into two types of factors like fixed factor and variable factor. These factors are otherwise known as inputs. Thus, production is viewed as physical transformation of physical inputs into output. The quantum of output depends on the quantity of inputs used. So there observed certain relation between these inputs & output. The technological relationship between physical inputs & output is termed as production function. It expresses the functional relationship between these inputs & output.

This production function describes the maximum quantity of output that can be produced with given inputs. This production function may be short-run production function & long-jun production function. In the short-run, there are some factors kept fixed & at least one factor variable. But in the long run all the factors are variable & output can be increased by changing all the factors. The short-run production function explains that production process in which at least one factor should be variabale & other factors should be fixed. So when one variable factor is added or changed to combine with fixed factor, there occured a change in factor proportions. As the output is increased by changing the factor proportions, the law is so named as “Law of Variable Proportions.” This short-run production function is’ subject to the law of variable proportions.

Law of variable proportions occupies an important place in economics beacuse of its universal implications. This law is also known as “Law of Proportionality”. According to this law, if at least one factor in the combination of factors is varied, keeping other factors constant, beyond a certain point, the marginal product emerging out of this will diminish. This law has’ been variously difined by different economists.

According to GJ. Stigler, “As an equal increments of one input are added, the inputs of other productive services being held constant, beyond a certain point, the resulting increments of the product will diminish i.e. marginal product will diminish.” According to Prof. Benham, “As the proportion of the factor in a combination of factors is increased after a point, first the marginal & then the average product of that factor will diminish.”

From these definitions, it is clear that the increase in variable factor in the combinatin of factors leads to increase in output in different phases. It reveals that the marginal product as well as average product at the initial stage of production starts increasing & after a while both diminish. This law passes through three distinct phases.

Assumptions :,The law of variable proportion is based on following assumptions.

1. (1) State of technology should memain unchanged. It means there should not be any change in technique of production.
2. There should be two types of factors like fixed factors & variable factors in the shout-run.
3. There should be the possibility of change in factor proportions. It means the factors can be combined in varied proportions.
4. The factors employed in the productive process assumed to be homogeneous.

Explanation : The law of variable proportions possessed three distinct stages in which different
nature and behaviour of total product, average product & marginal product is observed. Total product is the aggregate of output produced at a given level of employment of variable factor. Average product denotes the output produced perunit of variable factor. Marginal product is the addition made to the total product caused by an employment of one additional unit of factor. All these products are studied in three stages of law of variable proportions.

Numerical Analysis:

The numerical example illustrates that the marginal product (MP) increases upto the employment of four units of variable factor. The average product also increases till this point. Total product at this point.increases at an increasing rate upto 3rd unit of variable factor & then increases at a diminishing rate. This is the first stage. From the employment of 5th unit of variable factor, the marginal product diminishes & it continues till 8th unit of variable factor. Total product at this stage increases at a diminishing rate. Average product also diminishes. After 8th unit of variable factor employed, marginal product becomes negative. Total product diminishes & average product also diminish. This is the third stage.
Graphical illustration : This notion can also be graphically illustrated as follows.

In the above figure, OX-axis measures quantity, of Variable factor & OY-axis measures the total product, (TP), marginal product (MP) & average product (AP). The figure shows three distinct stages.

Stage -1 : At the initial stage of production when the quantity of variable factor is gradually increased by keeping fixed factors constant, the TP increases at an increasing rate upto the point F, the point of inflexion & then increase at a diminishing rate up to point R. In this stage ON amount of variable factors are employed. Besides, marginal product first increases & then diminishes. The average product increases through out the stage. This first stage is commonly known as “stage of increasing returns which ends when marginal product cuts average product curve at its maximum point or when average product is maximum.

Stage – II: Stage II starts after the point of intersections of marginal product curve with average product curve. In this stage, total product increases at a diminishing rate and attains its maximum points. Mariginal product diminishes & becomes zero at point M . Average product also diminishes. In figure, with the employment of OM units of variable factor, total product becomes maximum & marginal product becomes zero. This stage is known as stage of diminishing returns & it comes to an end when total product is maximum or marginal product is zero.

Stage – III: After marginal product is being zero, further employment of variable factor leads to the emergence of third stage. In this stage, total product starts declining & Marginal product becomes negative. Hence, the variable factors becomes abundant in relation to fixed factor resulting negative marginal product of the variable factor.

Stage of Operation : Now, it is to adjudge which stage is suitable to carry on production. It is quite obvious that both the first & third stage are symmetrical. In the first stage, fixed factor is abundant in relation to variable factor for which fixed factors are not fully utilised. So the total product falls shoft of its maximum point. On the contrary in the third stage total product diminishes & marginal product is negative. So it is quite natural & irrational to opt for producing output in these two stages. As such, second stage i.e. stage of diminishing returns is the suitable stage for production. In this stage, both the factors are properly & effectively utilised & total product becomes maximum. So the rational producer prefers to produce in this stage.

Law of variable proportions gains wide appreciation because of its tremendous implications in the theory of production.

Question 3.
Illustrate the Law of Diminishing Returns. Is this law applicable to only agriculture ?
Answer:
Law of diminishing Returns is a unique law in the theory of production which has wide range of implications & applications. This law is prominently pronounced in the law of variable of proportions which is the generalised version of it. Though, this law becomes a part of the law of the variable proportions, yet it is admittedly conceived as the crucial part of it as it is the a suitable stage of production. Alfred Marshall, the chief architect of this law considers three law of returns corresponding to input-output relationship & thus concludes that diminishing returns quite visible in and applicable to agriculture.

According to Marshall, “An increase in the capital & labour applied in the cultivation of land causes in general a less than proportionate increase in the amount of product raised unless it happens to coincide with an improvement in the art of the agriculture.” In other words, it is observed that in the cultivation of land, if the quantity of land is fixed & the quantity of variable factors like labour & capital is gradually increased, the total production changes less than proportionately. In other way, it can also be read that if the quantity of variable factor is increased & combined with the fixed factor after a point, the resulting total product will diminish.

Assumptions : The law of diminishing returns operates on the basis of following assumptions.

• The art of agriculture should remain unchanged. In generalised form, T is presented “Lai the technique of production should remain constant.
• The variable factor must be homogenous.
• There should be the possibility of change in factor proportions.

Explanation : This law can be explained by the way of numerical & graphical analysis. Marshall presumed land as a fixed factor which is combined with labour & capital, the variable factors. If the number of doses of labour & capital is increased & combined with fixed factor, land the marginal products go on diminishing i.e. total product increases at a diminishing rate.
Numerical Analysis

Unit of land (Fixed Factor)	Units of labour & Capital (variable Factor)	Total Product (TP)	Average Product (MP)	Marginal Product (AP)
1 acre	1	10	10	10
1 acre	2	18	8	9
1 acre	3	24	6	8
1 acre	4	28	4	7
1 acre	5	30	2	6

In the above analysis, it is revealed that with the gradual increase in the doses of labours & capital (1 unit to 5th unit) which is combined with fixed quantity of fixed factor, land (one acre), the marginal product diminishes & total product increases at a diminishing rate. Though this phenomenon does not happen immediately i.e. at the initial phase of production, yet it is the ultimate stage of operation in the productive process. In the analysis, the doses of labour & capital are increased from 1 to 5 units which results a decline in the marginal product from 10 units to 2 units. Total product increases from 10 units to 30 units.

Graphical Analysis : The same explanation can be graphically presented which is as follows :

In the above figure, doses of labours capital (in units) measured on OX-axis & marginal product on OY-axis. It is seen that with the increase in the doses of labour & capital, the marginal products of these factors goes on declinirig. Thus, the same conclusion as in numerical analysis is drawn in this graphical analysis.

Limitations : This law suffers from, certain limitations which are described below.

• The law will not operate if the technique or art of production changes.
• If the cultivation is undertaken for the first time, there may be increasing returns
• The law is not applicable if the factors are perfectly divisible.
• The law will not apply, if the labour & capital are inadequate.

Application of law : Primarily it is believed that the law is applicable to agriculture alone. Trough it is true that the application of this law is more prominently applied to agriculture, yet this law has wide application. This law is universally applied to agriculture, mining, fisheries, manufacturing industries, building etc.

Group – C

Objective type Questions with Answers
I. Multiple Choice Questions with Answers :

Question 1.
Production refers to
(i) creation of material wealth
(ii) creation of utility
(iii) creation of value
(iv) All of the above
Answer:
(ii) creation of utility

Question 2.
Goods which are used in productive process are termed as
(i) inputs
(ii) output
(iii) raw material
(iv) product
Answer:
(i) inputs

Question 3.
The input-out relationship shown in a functional manner is called
(i) input function
(ii) cost function
(iii) production function
(iv) All of the above
Answer:
(iii) production function

Question 4.
The factors which remain unchanged with the change in the level of output are called
(i) variable factors
(ii) fixed factors
(iii) None of the above
Answer:
(ii) fixed factors

Question 5.
Law of variable proportions operates during
(i) short-period
(ii) long period
(iii) market period
(iv) secular period
Answer:
(i) short-period

Question 6.
In law of variable proportions, the first stage is called
(i) stage of diminishing cost
(ii) stage of dminishing returns
(iii) stage in increasing cost
(iv) stage of negative returns
Answer:
(i) stage of diminishing cost

Question 7.
In which stage of law of variable proportions, the fixed factors are found to be abundant in relation to variable factors
(i) stage of increasing returns
(ii) stage of diminishing returns
(iii) stage of negative returns
(iv) all of the above
Answer:
(i) stage of increasing returns

Question 8.
The law of variable proportions is so named because
(i) Fixed factors changes in varied proportions
(ii) The ratio of fixed factor to variable factors change
(iii) The proportion of variable factors change
(iv) All of the above
Answer:
(ii) The ratio of fixed factor to variable factors change

Question 9.
In stage of increasing returns
(i) AP increases through out the stage.
(ii) TP increases at an increasing rate throughout the stage
(iii) MP increases through out the stage
(iv) All of the above
Answer:
(i) AP increases through out the stage.

Question 10.
The stage of increasing returns comes to an end
(i) when TP becomes maximum
(ii) when MP becomes maximum
(iii) when AP becomes maximum
(iv) None of the above
Answer:
(i) when TP becomes maximum

Question 11.
In stage of increasing returns
(i) MP curve cuts AP curve from below
(ii) AP curve cuts MP curve from above
(iii) MP curve cuts AP curve from above
(iv) MP curve cuts AP curve at its minimum point
Answer:
(iii) MP curve cuts AP curve from above

Question 12.
In the stage of increasing returns, the TP increases
(i) at an increasing rate
(ii) at a diminishing rate
(iii) at a cOnstant rate
(iv) initially at increasing rate & then at a diminishing rate
Answer:
(iv) initially at increasing rate & then at a diminishing rate

Question 13.
When MP goes on increasing
(i) TP increases at a diminishing raie
(ii) IP increases al an increasing rate.
(iii) TP increases at a constant rate
(iv) TP remains constant
Answer:
(ii) TP increases at an increasing raie.

Question 14.
As long as MP > AP, AP is
(i) increasing
(ii) diminishing
(iii) constant
(iv) Both increasing & diminishing
Answer:
(i) increasing

Question 15.
As long as MP > AP, AP is
(i) increasing
(ii) diminishing
(iii) Both increasing & diminishing
(iv) constant
Answer:
(ii) diminishing

Question 16.
TP becomes maximum during the stage of
(i) increasing returns
(ii) stage of diminishing returns
(iii) stage of negative return
(iv) None of the above
Answer:
(ii) stage of diminishing returns

Question 17.
When TP is maximum marginal product (MP) is
(i) positive
(ii) zero
(iii) negative
(iv) cannot say
Answer:
(ii) tCtO

Question 18.
TP starts falling when
(i) MP is -ve
(ii) AP is -ve
(iii) Mp is zero
(iv) APiszcro
Answer:
(i) MP is -ve

Question 19.
Which stage is the rational stage for production?
(i) stage of increasing returns
(ii) stage of diminishing returns
(iii) stage of negative returns
(iv) Both stage of increasing & diminishing returns
Answer:
(ii) stage of diminishing returns

Question 20.
Rate of change of total product is called
(i) Average product
(ii) marginal product
(iii) Both marginal & average product
(iv) None of the above
Answer:
(ii) marginal product

Question 21.
Which is the assumption for the law of variable proportions?
(i) All the factors arc homogeneous
(ii) There must be fixed & variable factors
(iii) Fixed factors should be perfectly divisible
(iv) All of the above
Answer:
(iv) All of the above

Question 22.
For which reason, the law of variable proportions operate ?
(i) indivisibility of fixed factor
(ii). indivisibility of variable factor
(iii) factors are perfect substitute for each other
(iv) All of the above
Answer:
(i) indivisibility of fixed factor

Question 23.
Law of variable proportions does not occur if
(i) factors are perfect divisible
(ii) factors are imperfect substitute
(iii) factors are homogeneous
(iv) All of the above
Answer:
(i) factors are perfect divisible

Question 24.
Which is the factor of production?
(i) Land
(ii) Labour
(iii) Capital
(iv) All of the above
Answer:
(iv) All of the above

Question 25.
A black market is not a producer because
(i) it does not earn income
(ii) it is an unethical practice
(iii) money is not involved
(iv) it does not create any value
Answer:
(iv) it does not create any value

Question 26.
Mines & fisheries are subject to the law of
(i) diminishing retursn
(ii) increasing returns
(iii) negative returns
(iv) constant returns
Answer:
(i) diminishing retursn

Question 27.
If on a piece of land, more & more labour & capital is employed after certain point, the output increases
(i) more than proportionately
(ii) less than proportionately
(iii) at constant rate
(iv) None of the above
Answer:
(ii) less than proportionately

Question 28.
If MP decreases & total product increases in this situation shows the stage of
(i) increasing returns
(ii) diminishing returns
(iii) negative returns
(iv) constant returns
Answer:
(ii) diminishing returns

Question 29.
In law of diminishing returns, returns to a variable factor
(i) increases
(ii) diminishes
(iii) remains constant
(iv) None of the above
Answer:
(ii) diminishes

Question 30.
If an acre of land is cultivated more intensively, the output
(i) increases more that proportionately
(ii) increases less than proportionately
(iii) decreases less than proportionately
(iv) increases proportionately.
Answer:
(ii) increases less than proportionately

Question 31.
The rate at which the total product changes is called
(i) average product
(ii) marginal product
(iii) Both (i) and (ii)
(iv) None of the above
Answer:
(ii) marginal product

II. Fill in the blanks :

Question 1.
_____ is the creation of utility.
Answer:
Production

Question 2.
_____ can be resumed with land, labour, capital and organisation.
Answer:
Production

Question 3.
Law of variable proportion is a law for _____
Answer:
short-run production.

Question 4.
According to Law of Variable Proportion, all the factors are _____
Answer:
Variable

Question 5.
Fixed factors, in the _____, remain unchanged/fixed irrespective of the level of output.
Answer:
short-run

Question 6.
Total product _____ at a diminishing rate in the stage of diminishing returns.
Answer:
increases

Question 7.
Stage of _____ is the suitable stage of production.
Answer:
diminishing returns

Question 8.
The marginal product becomes _____ in the second stage.
Answer:
zero

Question 9.
Total Product is maximum when Marginal Product is _____
Answer:
zero

Question 10.
Total Product _____ during the stage of negative returns.
Answer:
falls

Question 11.
_____ product can be zero or negative but not average product.
Answer:
Marginal

Question 12.
The law of _____ returns is more applicable to agriculture.
Answer:
diminishing

Question 13.
The law of variable proportion is a _____ period phenomenon.
Answer:
short-run

Question 14.
The law of diminishing returns is otherwise known as law of _____ cost.
Answer:
increasing

Question 15.
Mines and fisheries are subject to the law of _____ returns.
Answer:
diminishing

Question 16.
The stage of increasing returns operate due to the _____ of factors.
Answer:
indivisibility

Question 17.
Rate of change of total product is called _____
Answer:
Marginal Product

Question 18.
Total product becomes maximum in the stage of _____
Answer:
Diminishing return

Question 19.
The electricity is a _____ factor.
Answer:
variable

Question 20.
The manager employed in an enterprise is a _____ factor.
Answer:
Fixed

III. Correct the Sentences:

Question 1.
Production is the destruction of utility.
Answer:
Incorrect
Correct – Production is the creation of utility.

Question 2.
All the factors are variable in the short-run.
Answer:
Incorrect
Correct: All the factors are variable in the long-run.

Question 3.
Production function is the technical relationship between inputs & output.
Answer:
Correct

Question 4.
Law of variable proportions is applicable in long-run.
Answer:
Incorrect
Correct – Law of variable proportions is applicable in short-run.

Question 5.
Long-run production function is subject to law of variable proportions.
Answer:
Incorrect.
Correct – Short-run production function is subject to law of variable proportions.

Question 6.
In the long-run all the factors are variable.
Answer:
Correct

Question 7.
Machines are the examples of variable factor.
Answer:
Incorrect
Correct – Machines are the examples of fixed factor.

Question 8.
In the short-run, level of output can be increased due to change in fixed factor.
Answer:
Incorrect.
Correct – In the short-run, level of output can be increase due to change in variable factor

Question 9.
Total product becomes maximum in the stage of increasing returns.
Answer:
Incorrect.
Correct – Total product becomes maximum in the stage of diminishing returns.

Question 10.
In the second stage of law of variable proportions, the marginal product is zero.
Answer:
Correct.

Question 11.
In the first stage, the quantity of fixed factors is abundant in relation to variable factor.
Answer:
Correct.

Question 12.
Manager is a variable factor.
Answer:
Incorrect.
Correct – Manager is a fixed factor.

Question 13.
In the short-run, all the inputs can be varied.
Answer:
Incorrect.
Correct – In the long-run, all the inputs can be varied.

Question 14.
Stage of increasing returns & stage of diminishing returns are symmetrical.
Answer:
Incorrect.
Correct – Stage of increasing returns & stage of – ve retuns are symmetrical.

Question 15.
Producers produce in the stage of increasing returns.
Answer:
Incorrect.
Correct – Producer produce in the stage of diminishing returns.

Question 16.
When marginal product is zero, total product is maximum.
Answer:
Incorrect
Correct: When marginal product is zero, total product is maximum.

Question 17.
Marginal Product is maximum in the second stage of law of variable proportions.
Answer:
Incorrect
Correct: Marginal product is maximum in the first stage of law of variable proportions.

Question 18.
When marginal product is – ve. total product is negative.
Answer:
Incorrect
Correct: When marginal product is – ve. total product declines.

Question 19.
Marginal product is the sum of total product.
Answer:
Incorrect
Correct: Total product is the sum of marginal products

Question 20.
Law of diminishing returns is applied to agriculture alone.
Answer:
Incorrect
Correct: Law of diminishing returns is applied to all fields.

Question 21.
Marginal product can never be negative.
Answer:
Incorrect
Correct – Total product can never be negative.

IV. Answer the following questions in one word :

A. ANSWER IN ONE SENTENCE

Question 1.
What is Production ?
Answer:
Production is the creation of goods & services having exchange value, or, Production is the creation of utility.

Question 2.
What do you mean by inputs ?
Answer:
Inputs are those goods & services which are used for further poroduction.

Question 3.
What is fixed factor ?
Answer:
Fixed factor is that factor which remains unchanged irrespective of the level of output.

Question 4.
What is variable factor ?
Answer:
Variable factor is that factor which changes with the change in the level of output.

Question 5.
Give an example of variable factor.
Answer:
Raw material.

Question 6.
What is production function ?
Answer:
Production function refers to the technological relationship between physical inputs & output.

Question 7.
What is short-run ?
Answer:
Short-run or short-period is a short – span of time during which there observed some fixed factor & some variable factors.

Question 8.
What is short-run production function ?
Answer:
Short-run production function is that type of production function in which output is produced with the combination of fixed factors & variable factors.

Question 9.
What is total product ?
Answer:
Total product is aggregate of output produced with a given quantity of inputs.

Question 10.
What is average product ?
Answer:
Average product is the output produced per unit of variable factor.

Question 11.
What is marginal product ?
Answer:
Marginal product refers to the addition made to the total product caused by an increase in one additional unit of factor employed.

Question 12.
How is total product derived from marginal product ?
Answer:
Total product is sum of marginal products.

Question 13.
What happens to total product if marginal product falls ?
Answer:
Total product increases at a diminishing rate when marginal product falls.

Question 14.
What will be the total product if marginal product becomes zero ?
Answer:
Total product is maximum when marginal product is zero.

Question 15.
What happens to total product if marginal product is negative ?
Answer:
Total product diminishes when marginal product is negative.

Question 16.
What is shape of marginal product curve ?
Answer:
Marginal product curve is inverse U- shaped.

Question 17.
During which stage, total product becomes maximum.
Answer:
During the stage of diminishing returns, total product becomes maximum.

Question 18.
At which stage, the producer produces goods ?
Answer:
In the stage of diminishing returns (stage II) the producer produces goods.

Question 19.
What happens to marginal product in the stage of negative returns ?
Answer:
Marginal product becomes negative in the stage of negative returns.

Question 20.
At what point marginal product is to equal average product ?
Answer:
Marginal product is equal to average product at the maximum point of average product curve.

Question 21.
In which stage, total product declines ?
Answer:
In the stage of negative returns, the total product declines.

Odisha State Board CHSE Odisha Class 12 Logic Solutions Chapter 3 Mixed Syllogism Questions and Answers.

CHSE Odisha 12th Class Logic Chapter 3 Question Answer Mixed Syllogism

Group – A

Short type Questions with Answers
I. Answer with in Two/Three sentence.

Question 1.
What is pure syllogism?
Answer:
(i) Pure syllogism is that syllogism where all the constituent propositions are of same type :

(ii) Example:
All men are mortal
Ram is a man.
∴ Ram is mortal.

Question 2.
What is called pure categorical syllogism?
Answer:
(i) If both the premises and the conclusion are categorical, the syllogism is called pure categorical.

(ii) Example:
All men are mortal
All students are men
∴ All students are mortal.

Question 3.
What is called pure hypothetical syllogism?
Answer:
(i) If both the premises and the conclusion are hypothetical, the syllogism is called pure hypothetical.

(ii) Example; If there is light, things are visible
If there is sun, there is light
If there is sun, things are visible.

Question 4.
Pure alternative syllogism.
Answer:
(i) If both the premises and the conclusion are alternative, the syllogism is called pure alternative.

(ii) Example : Madhu is either honest or intelligent
Madhu is either not-honest or industrious.
∴ Madhu is either intelligent or industrious.

Question 5.
Pure disjunctive syllogism.
Answer:
(i) If both the premises and the conclusion are disjunctive, the syllogism is called pure disjunctive.

(ii) Example; All Ministers are not both Muslims and Hindus
∴ All ministers are not both not-Muslims and atheists.

Question 6.
What is mixed syllogism?
Answer:
(i) Mixed syllogism is that syllogism where all the constituent propositions are different types.
(ii) Example; If there is sun then there is light.
There is sun .
∴ There is light.

Question 7.
What is called hypothetical – categorical syllogism?
Answer:
(i) Hypothetical – categorical syllogism is that syllogism where the major premise is hypothetical, minor premise is categorical and the conclusion is categorical.

(ii) Example; If it rains he will not come It rains
∴ He will not come.

Question 8.
What is called disjunctive – categorical syllogism?
Answer:
(i) Disjunctive – categorical syllogism is that syllogism where the major premise is disjuctive, the minor premise is categorical, and the conclusion is categorical.

(ii) Example : Ramesh cannot be bom in both January and June Ramesh bom in January Ramesh is not bom in June.

Question 9.
Alternative – categorical syllogism.
Answer:
(i) Where the major premise alternative, the minor premise is categorical and the conclusion is categorical that is called alternative – categorical syllogism.

(ii) Krishna is either a teacher or a politician Krishna is not a teacher.
∴ Krishna is a politician.

Question 10.
Give an example of simple constructive dilemma.
Answer:
If A is B, C is D and If E is F, C is D
Either A is B or E is F
∴ C is D

Question 11.
State the rules of hypothetical – categorical syllogism.
Answer:
(i) There are two rules in case of hypothetical categorical syllogism.

(ii) These are affirming the antecedent and denying the consequent.

Question 12.
What is called affirming the antecedent rule?
Answer:
Affirming the antecedent rule states that when we affirm the antecedent part of the major premise into the minor premise then in this respect we should affirm the consequent part of the major premise in the conclusion.

Question 13.
Fallacy of denying the antecedent.
Answer:
(i) When we deny the antecedent part of the major premise into the minor premise and consequent part of the major premise in the conclusion then we commit the fallacy of denying the antecedent.

(ii) Example, If there is sun then there is light.
There is no sun
∴ There is no light.

Question 14.
What is called simple constructive dilemma?
Answer:
(i) Simple constructive, dilemma is that dilemma where the conclusion is categorical and affirming the antecedent rule is applied.

(ii) If P then q and if r then q
Either p or r
∴ q

Question 15.
What is called complex destructive dilemma?
Answer:
(i) In a dilemma, if the conclusion is an alternative proposition and denying the consequent rule is applied that is called complex destructive dilemma.

(ii) If p then q and if r then s.
Neither q nor s
Neither p nor r.

II. Answer with in Five/Six sentence :

Question 1.
What is dilemma ?
Answer:
Dilemma is a mixed syllogism in which one premise is compound hypothetical the other premise is alternative and the conclusion is either categorical or alternative. As Dilemma is a combination of two hypothetical categorical syllogism, so the rules of this syllogism are observed dilemma. Example :
If A is B, then C is D and if E is f then G is H.
Either A is B or E is f
Either C is D or G is H.

Question 2.
Explain rebuttal of Dilemma.
Answer:
Rebuttal of Dilemma is done by giving a counter dilemma and showing that the opposite conclusion is also possible under the same circumstance.

Dilemma : If you are kind to your wife, your mother is displeased and if you are cruel to your wife, your mother-in-law is displeased.
Either your mother or your mother in-law is displeased.

Counter dilemma: If T and kind to my wife, my mother-in-law is pleased and if I am cruel to my wife, my mother is pleased.
Either I am kind to my wife or I am cruel to my wife.
∴ Either my mother or mother-in-law pleased.

Question 3.
What is called the fallacy of affirming the consequent?
Answer:
When we affirm the consequent part of the major premise in the minor and the antecedent part of the major premise in the conclusion, then the fallacy arises, which is called the fallacy of affirming the consequent.

Example :
If somebody wins a lottery prize he is
happy These school children are happy.
∴ They have own lottery prizes.

Question 4.
Explain the fallacy of Denying the antecedent
Answer:
When we deny the antecedent part of the major premise in the minor and consequent part of the major premise in the conclusion then we commit a fallacy. Which is called the fallacy of denying the antecedent.

Example :
If there is war, the prices are high.
There is no war
∴ The prices are not high.

Question 5.
Give a symbolic example of constructive form of hypothetical categorical syllogism.
Answer:
It A is B then C is D
A is B
∴ C is D

Question 6.
Give a concrete example of simple constructive dilemma.
Answer:
If you are destined to pass, the reading is unnecessary and if you are destined to fail then reading is unnecessary. Either you are destined to pass or you are destined to fail… Reading is unnecessary.

Question 7.
What is alternative categorical syllogism.
Answer:
Alternative categorical syllogism is a kind of mixed syllogism in which the major premise is an alternative proposition, where as the minor premise and the conclusion are categorical propositions.
For example:
Either P or q
∴ \(\frac{\text { Not } P}{q}\)

Question 8.
Name the fallacy in the following argument. If there is rain, the ground is wet
∴ There is no rain
The ground is not wet
Answer:
The above argument is called the fallacy of denying the antecedent.

Question 9.
State the rules of hypothetical categorical syllogism.
Answer:
There are two rules in hypothetical categorical syllogism.
(i) By affirming the antecedent, we affirm the consequent but not conversely.
(ii) By denying the consequent, we deny the antecedent but not conversely.

Question 10.
Write the different forms of dilemma.
Answer:
There are four types of Dilemma such as :
(a) Simple constructive
(b) Simple destructive
(c) Complex constructive
(d) Complex destructive

Question 11.
Give a symbolic example of complex destructive dilemma.
Answer:
It A is B, C is D and if E is F, G is H.
Either C is not D or G is not H
∴ Either C is not B or E is not F,

Question 12.
Briefly explain the fallacy of Dilemma.
Answer:
The format fallacies of dilemma are affirming the consequents or Denying the antecedents in the minor premise. Further they may be rebutted by taking the horns or escaping between the horns or by the process of rebutal Most dilemmas are formally valid but mate rally false and their falsity may be exposed by one or the other of the above methods of rebutation.

Question 13.
What is Modus pones?
Answer:
There are two kinds of Hypothetical categorical syllogism; such as constructive and Destructive. The constructive form of this kind of Syllogism is technically known as modus ponens. In this form of argument we firm the antecedent of the major premise in the minor premise to affirm the consequent in the conclusion.

Question 14.
What is Modus Tolens?
Answer:
The destructive form of Hypothetical categorical syllogism is known as moduls tollens. In this form of argument we deny the consequent of the major premise in the minor premise to deny the antecedent in the conclusion.
For example:
If there is sun then there is light and there is no light therefore, there is no sun.

Question 15.
Which rule governs Alternative categorical Syllogism?
Answer:
The alternative proposition aims at affirming one alternate by denying the denying the other. So the rule of Alternative categorical syllogism is to deny one alternate in the minor premise and to affirm the other alternate in the conclusion.

Question 16.
Write the different forms of Dilemma.
Answer:
There are four types of Dilemma such as :

1. Simple constructive
2. Simple destructive
3. Complex constructive
4. Complex destructive.

Question 17.
Give concrete example of simple constructive dilemma.
Answer:
If you are destined to pass, the reading unnecessary and if you are destined to fail then reading is unnecessary. Either you are destined to pass or fail. Reading is unnecessary.

Question 18.
Give the concrete example of simple destructive dilemma.
Answer:
If you read Bhagabad Gita, you should obey norms and if you read Bhagabad Gita, you should practise its ethos.
Either you do not obey its norms or you do practise its ethos.
∴ You do not read Bhagabad Gita.

Question 19.
Give the concrete example of complex destructive dilemma.
Answer:
If students are obedient, they must love their teachers and if the students are sincere, they must labour hard.
Either the students do riot love their teachers of the students do not labour hard.
∴ Either the students are not obedient or the students are not sincere.

Question 20.
Define Dilemma.
Answer:
Dilemma is a mixed syllogism, in which the major premise in a compound hypothetical proposition and the minor premise is Alternative and the conclusion is either categorical or Alternative propositions.
Example :
If A is B, C is D and if E is F.
C is D
Either A is B or E is F
C is D

Question 21.
State the ways of refutation of Dilemma.
Answer:
A Dilemma may be refuted in the following three ways.
(a) Taking by One horn
(b) Taking by Two horns
(c) Escaping between the horns.

Question 22.
Write a concrete example of Rebuttal Dilemma.
Answer:
If you speak the truth, people will hate you and if you tell a lie, God will hate you. Either you speak the truth or tell lies.
∴ Either people will hate you or God will hate you.

Rebuttal: If I speak the truth, God will not hate me and of I tell lies, people will not hate. Either I speak the truth or tell lies.
∴ Either God will not hate me or people will not hate

Question 23.
Name the special syllogistic rules of Figure one.
Answer:
There are two special syllogistic rules in the figure one these are,
(1) Major premise must be universal
(2) Minor premise must be affirmative.

Question 24.
What is Reduction?
Answer:
Reduction is the process of proving the validity of the moods of the imperfect figures with the help of the moods of the perfect first figure. Direct reduction is the process of directly transforming a mood of inperfect figure to a mood of perfect figure. Indirect reduction is the process of showing that some moods of 2nd, 3rd and 4th figures are such that the conclusion cannot be false if the premises are true.

Question 25.
What in the direct Reduction of ‘DIMARIS’.
Answer:
DIMARIS – DARII

Group – B

Long Type Questions With Answers

Question 1.
What is Dilemma ? What are its different form?
Answer:
Dilemma is kind of mixed syllogism in which the major premise is a compound hypothetical proposition, the minor premise is alternative and the conclusion is either categorical or alternative.

There are different kinds of dilemma. Based on the nature of the minor premise, dilemma can be either constructive or destructive. If the minor premise affirms the antecedents of the major premise in the minor premise, the dilemma is called constructive. If the minor premise denies the consequents of the major premise, the dilemma is called destructive.

Again, a dilemma can be simple or complex, depending on the nature of the conclusion. If the conclusion of the dilemma is a categorical proposition, it is called simple dilemma. But if the conclusion is an alternative proposition, the dilemma is complex. So, by combining the above, we get four of dilemma. They are-
(a) Simple constructive
(b) Complex constructive
(c) Simple Destructive and
(d) Complex Destructive
Now, let us discuss the above different kind dilemma in details,

(a) Simple constructive Dilemma :
It is a kind of mixed syllogism in which the major premise is a compound-hypothetical proposition, (i.e. a conjunction of two hypothetical propositions), and the minor premise is a disjunctive proposition in which the antecedents of the major premise are affirmed disjunctively, and the conclusion is a categorical proposition. Symbolically it is of the following form:

The above one is the symbolic example complex constructive Dilemma. The dilemma is complex because its conclusion because the antecedents of major premise are affirmed in the minor premise.

(b) Complex constructive Dilemma :
Complex constructive dilemma is an argument, where the major premise is a compound hypothetical, in the minor premise the antecedents of the major premise are disjunctively affirmed and the conclusion is a disjunctive proposition. It is of the following form :

Concrete example :
If Rakesh is in Cuttack, he is in Odisha and if he is in Kolkata, then he is in Bengal
Rakesh is either in Cuttack or in Kolkata
Therefore, he is either in Odisha or in Bengal.

(c) Simple Destructive Dilemma :
In a simple destructive dilemmatic argument the consequents of the compound hypothetical major are alternatively denied in the minor premise and the conclusion is a categorical proposition. In other words, it is a kind of mixed syllogism in which the major premise is a compound hypothetical proposition and the minor premise is a disjunctive proposition in which the consequents of the major premise are alternatively denied. Finally, the conclusion is a denial of a categorical proposition. Symbolically it is of following form:

The above argument is a symbolic example simple Destructive Dilemma. Here the consequence the major premise are denined in the minor premise is destructive. Again, it is simple because the conclusion is categorical proposition.

(d) Complex Destructive Dilemma :
In this kind of dilemma, the major premise is a compound-hypothetical proposition, the minor premise and the conclusion are disjunctive propositions. Moreover, in the minor premise, the con-sequents of the major premise are disjunctively denied.

This is a symbolic form of complex Destructive Dilemma. The Dilemma is complex because conclusion is an alternative proposition. It is destructive because the consequents of the major premise*denied in the minor premise.

These are the four forms of dilemma. We see that looking at how the minor premise is constructive we can know whether the dilemma is constructive destructive. Again, looking at the conclusion, we know whether the dilemma is simple or complex.

Question 2.
How dilemma is refuted? Discuss.
Answer:
A dilemma is either formally valid materially true again a dilemma may be formally involved and materially false. A dilemma may be refuted both formally war or materially way. It is formally refuted when it violates the rules of dilemma and it is materially refuted when it is shown that the premises are materially false. However dilemma may be refuted in the following three ways such as,
(1) Taking by one horn.
(2) Taking by two horn.
(3) Escaping between the horn.

(1) Taking by one horn : Taking by one horn means when one consequent part of the major premise seems to be week. It means when one consequent part does not follow from its one antecedent part, at that time a dilemma is refuted which is called taking by one horn.

Example: If he is intelligent, then he can understand everything else and if he is honest, then he can admit his faults. Either he is intelligent or he is honest
∴ Either he can understand everything else or we can admit his fault.

(2) Taking by two horns : Taking by two horns means when both the consequent parts of the major premise seen to be weak. It means if both consequent part does not follow from its antecedent part does not follow from its antecedent parts then the dilemma is refuted which is called taking by two horns.

Example: If you are fated to be cure then consulting the physician is unnecessary and is you are not fated to be cured then consulting the physician is necessary.
Either you are fated to be cured.
or you are not fated to be cured.
∴ Consulting the physician is necessary.

(3) Escaping between the horns : Escaping between the horns means two puzzlement situation arise then at that time you should help another argument in under to escape from the situation.

Example:
If the day is hot, then you can if go out and if the day is cold then you can not go out.
Either the day is hot or the day is cold .’. You can’t go out.

Question 3.
What is hypothetical – categorical syllogism? Discuss its forms and fallacies.
Answer:
Hypothetical – categorical syllogism is a valid of mixed syllogism in which the major premise is a categorical proposition and the conclusion is a categorical proposition. There are certain rules to be followed for a valid Hypothetical – categorical syllogism which are discussed below.

Rules of Reasoning :
1. By affirming the antecedent of the major premise in the minor premise, we affirm the consequent in the conclusion. Violating this if we affirm the consequent of the major premise in the minor premise, the argument becomes fallacious. It is called the fallacy of affirming the consequent.

When the antecedent is affirmed in the minor premise, so that the consequent is affirmed in the conclusion, it is the constructive form of the argument. It is also called modus ponens.

2. By denying the consequent of the major premise in the minor premise, we deny the antecedent in the conclusion. If we violate this rule and deny the antecedent in the minor premise, the argument becomes fallacious. The fallacy is called the fallacy of denying the antecedent. When the consequent is denied in the minor premise to deny the antecedent in the conclusion, it is the destructive form of the argument or modus Tollens.

Constructive form or modus ponens : For the elaboration of the constructive form of Hypothetical – categorical syllogism let us take the help of examples.

Symbolic example :
Let P and Q stand for any two propositions.
If P then Q
∴ Q

Concrete example :
If there is sun, then there is light.
There is sun
∴ There is light.

The argument given above is a valid form of modus ponens or constructive form of Hypothetical – categorical syllogism. Here the antecedent ‘P’ or There is sun’ is affirmed in the minor premise. In the conclusion the consequent ‘Q’ or ‘There is light’ is affirmed. If we violate this rule and affirm the consequent in the minor premise, we commit the fallacy of affirming the consequent.

Symbolic example of the fallacy :
If P the Q
Not P
∴ Not Q

Concrete example of the fallacy :
If there is sun, there is light.
There is sun.
∴ There is light

The argument is obviously fallacious because presence of light does not necessary imply the presence of sun. There are other sources of light too. The argument is fallacious. The absence of the sun does not mean there will certainly the absence of light. These are the different forms and fallacies of Hypothetical – categorical syllogism.

Question 4.
Explain the disjunctive – categorical syllogism.
Answer:
Disjunctive categorical syllogism is a kind of mixed syllogism in which the major premise is disjunctive, the minor premise is categorical and the conclusion is categorical. It is otherwise called as mixed disjunctive syllogism.

For example; Raja cannot stay both in Odisha and Bihar state at the sometime.
Raja stays in Odisha.
∴ Raja does not stay in the Bihar.

Rule : If we affirm one of the disjuncts in the minor we may deny the other in the conclusion, but not conversely.

Symbolic example :
A cannot both B and C
A is B.
∴ A is rot C.

Concrete example :
A cannot be both honest and cruel.
Joseph is honesty.
∴ Joseph is not cruel.

This form in accordance with the rule. So it is a valid form argument and it is called modus Ponendo Tollens. Let’s take an example in regard to the converse of the rule.

Symbolic example :
A cannot be both B and C
A is not B
∴ A is C

Concrete example :
Suprava cannot be both student of I.A. class and B.A. class.
She is not a student of I. A. class.
She is a student of B.A. class.

In this case we violate the rule and deny one of the disjuncts in the minor premise whereas affirm the other in the conclusion. This is called modus Tollendo Ponens. So this is an invalid form of argument.

Question 5.
State and explain the rules and fallacies of Alternative categoric*! syllogism.
Answer:
Alternative categorical syllogism is a kind of mixed syllogism is a kind of mixed syllogism in which the major premise is an alternative proposition, the minor premise is a categorical proposition and the conclusion is either categorical proposition or alternative proposition.

Rule :
By denying one or more alternants of an alternative proposition, we can affirm the remaining alternants.

(1) Symbolic example
Either A is B or C is D.
A is not B
∴ C is D

Concrete example :
Either the sun is shining or it is raining.
The sun is not shining.
∴ It is raining.

(2) Symbolic example :
A is B or C or D
A is not B
∴ A is either C or D.

Concrete example :
Hari is intelligent or clever or foolish.
Hari is not intelligent
∴ Hari is either clever or foolish.

(3) Symbolic example.
A is B or C or D
A is neither B nor C
∴ A is D.

Concrete example :
Mira is intelligent or clever or foolish.
Mira is neither intelligent nor clever.
∴ Mira is foolish.

Violation of the rule : The rule governing mixed alternative syllogism is violated if by affirming one or more alternants, we deny the remaining alternants.
Symbolic Example;
Either A is B or C.
A is B
∴ A is not C

Concrete example;
Either Elina is clever or foolish Elina is clever.
∴ Elina is not foolish.
This is against the rule governing mixed alternative sylogism. Hence, the argument is invalid.

Group – C

Objective type Questions with Answers
I. Multiple Choice Questions with Answers :

Question 1.
In a simple dilemma, the conclusion is :
(i) Categorical
(ii) Alternative
(iii) Hypothetical
(iv) Either alternative
Answer:
(i) Categorical

Question 2.
The conclusion of a mixed syllogism is always :
(i) Hypothetical
(ii) Disjunctive
(iii) Alternative
(iv) Categorical
Answer:
(iv) Categorical

Question 3.
“When men are pure, Laws are useless. When men are corrupt, Laws are broken. Therefore laws are unnecessary”. This argument in :
(i) Materially true
(ii) Materially false
(iii) Formally true & materially false.
(iv) Formally invalid and materially false.
Answer:
(iii) Formally true & materially false.

Question 4.
Pure syllogism in mainly divided into :
(i) Two types
(ii) Three types
(iii) Four types
(iv) Five types
Answer:
(iii) Four types

Question 5.
Where all the constituent propositions are of categorical that is called what?
(i) Pure categorical syllogism
(ii) Pure hypothetical syllogism
(iii) Pure disjunctive syllogism
(iv) Dilemma
Answer:
(i) Pure categorical syllogism

Question 6.
Where all the constituent propositions are of disjunctive in character that is called which syllogism?
(i) Pure categorical
(ii) Pure hypothetical
(iii) Pure alternative
(iv) Pure disjunctive
Answer:
(iv) Pure disjunctive

Question 7.
If A is B then C is D.
If E is F then A is B.
∴ If E is F then C is D
This is a symbolic example of:

(i) Pure categorical syllogism
(ii) Pure hypothetical syllogism
(iii) Pure alternative syllogism
(iv) Pure disjunctive syllogism
Answer:
(ii) Pure hypothetical syllogism

Question 8.
How many kinds of mixed syllogism are there ?
(i) Two
(ii) Three
(iii) Four
(iv) Five
Answer:
(iii) Four

Question 9.
What is the major premise of mixed hypothetical syllogism?
(i) Hypothetical
(ii) Categorical
(iii) Alternative
(iv) Disjunctive
Answer:
(i) Hypothetical

Question 10.
What is the major premise of mixed alternative syllogism ?
(i) Hypothetical
(ii) Categorical
(iii) Alternative
(iv) Disjunctive
Answer:
(iii) Alternative

Question 11.
What is the major premise of mixed disjunctive syllogism ?
(i) Hypothetical
(ii) Categorical
(iii) Alternative
(iv) Disjunctive
Answer:
(iv) Disjunctive

Question 12.
How many kinds of dilemma are there ?
(i) Two
(ii) Three
(iii) Four
(iv) Five
Answer:
(iii) Four

Question 13.
How many rules are observed in hypothetical categorical syllogism?
(i) Two
(ii) Three
(iii) Four
(iv) Five
Answer:
(i) Two

Question 14.
When we affirm the consequent part of the major premise in the minor premise then we commit which fallacy?
(i) Denying the antecedent
(ii) Affirming the consequent
(iii) Fallacy accent
(iv) Fallacy of accident
Answer:
(ii) Affirming the consequent

Question 15.
When the antecedent of the major premise is denied in the minor, then which fallacy arises?
(i) Denying the antecedent
(ii) Denying consequent
(iii) Affirming the antecedent
(iv) Affirming the consequent
Answer:
(i) Denying the antecedent

Question 16.
In a mixed syllogism, one of the premises is necessarily;
(i) Categorical
(ii) Alternative
(iii) Hypothetical
(iv) Disjunctive
Answer:
(i) Categorical

Question 17.
If there is smoke, then there is fire,
There is fire.
∴ There is smoke.
The fallacy committed here is:
(i) Fallacy of affirming the consequent.
(ii) Fallacy of affirming the antecedent.
(iii) Both of these.
(iv) None of these.
Answer:
(i) Fallacy of affiring the consequent.

Question 18.
Which of the following is are true of a Dilemma?
(i) One of the premises is a compound hypothetical proposition
(ii) The second premise is an alternative proposition.
(iii) The cpnclusibn is either alternative to categorical
(iv) All of these
Answer:
(iv) All of these

Question 19.
The consequents of the hypothetics propositions in the compound hypothetics proposition are same in:
(i) Simple constructive dilemma.
(ii) Simple destructive dilemma,
(iii) Complex constructive dilemma.
(iv) Complex destructive dilemma.
Answer:
(i) Simple constructive dilemma.

Question 20.
A dilemmawhpse conclusion is alternative must be a ;
(i) Simple dilemma
(ii) Complied dilemma
(iii) Constructive dilemma
(iv) Destructive dilemma
Answer:
(ii) Complied dilemma

Question 21.
A dilemma is refuted by:
(i) Showing that if violates a rule.
(ii) Showing that a premise or both of its premises are materially false.
(iii) Rebuttal
(iv) All of the above
Answer:
(iv) All of the above

Question 22.
Which of the following kinds of Dilemma can only be rebutted?
(i) Simple constructive dilemma
(ii) Simple destructive dilemma
(iii) Complex constructive dilemma
(iv) Complex destructive dileittma
Answer:
(iii) Complex constructive dilemma

Question 23.
Which of the following proposition is the conclusion of simple constructive dilemma?
(i) Categorical
(ii) Alternative
(iii) Hypothetical
(iv) Disjunctive
Answer:
(i) Categorical

Question 24.
Which of the following proposition is the conclusion of complex constructive dilemma?
(i) Categorical
(ii) Alternative
(iii) Hypothetical
(iv) Disjunctive
Answer:
(ii) Alternative

Question 25.
Which of the following proposition is the conclusion of complex destructive dilemma?
(i) Categorical
(ii) Alternative
(iii) Hypothetical
(iv) Disjunctive
Answer:
(ii) Alternative

II. Fill in the blanks :

Question 1.
In a hypothetical categorical syllogism the major premise is ______ proposition.
Answer:
Hypothetical proposition

Question 2.
In an alternative categorical syllogism the major premise in ______ proposition.
Answer:
Alternative proposition

Question 3.
In a Disjunctive categorical syllogism to affirm the one is to ______.
Answer:
Deny the other

Question 4.
In a dilemma if both the alternatives are not exhaustive if is called ______.
Answer:
Escaping between the horns.

Question 5.
In the dilemma the conclusion in ______.
Answer:
Either categorical or Alternative.

Question 6.
Traditionally, syllogisms are divided into ______ types.
Answer:
two

Question 7.
Syllogism is mainly classified into ______ and ______.
Answer:
pure, mixed

Question 8.
In a pure syllogism the constituent propositions are of ______.
Answer:
same type

Question 9.
In a mixed syllogism the constituent propositions are of ______.
Answer:
Different types

Question 10.
Pure syllogism is divided into three type; such as ______ and ______.
Answer:
pure categorical, pure alternative and pure disjunctive.

Question 11.
In a syllogism if all the constituents propositions are categorical that is ______ syllogism.
Answer:
pure categorical

Question 12.
In a syllogism if all the propositions are disjunctive that is called ______ syllogiosm.
Answer:
pure disjunctive

Question 13.
In a syllogism if all the propositions are of alternative that is called ______.
Answer:
pure alternative

Question 14.
There are ______ kinds of mixed syllogism.
Answer:
four

Question 15.
In a mixed hypotheical syllogism the major premise is ______.
Answer:
hypothetical proposition

Question 16.
In a mixed disjunctive syllogism the major premise is ______.
Answer:
disjunctive proposition

Question 17.
In a mixed alternative syllogism the minor premise is ______ .
Answer:
categorical proposition

Question 18.
In a mixed hypothetical syllogism the minor premise is ______.
Answer:
categorical proposition

Question 19.
In a dilemma the major premise is ______.
Answer:
a compound hypothetical proposition

Question 20.
In a dilemma the minor premise is ______.
Answer:
Alternative

Question 21.
In a dilemma the conclusion is ______.
Answer:
Higher alternative or categorical

Question 22.
In a mixed hypothetical syllogism to affirm the antecedent is to ______.
Answer:
affirm the consequent

Question 23.
In a mixed hypothetical syllogism to deny the consequent is to ______.
Answer:
Deny the antecedent

Question 24.
In a mixed alternative syllogism to deny any one is to ______.
Answer:
affirm the other

Question 25.
In a mixed disjunctive syllogism to affirm the one is to ______.
Answer:
deny the other

Question 26.
There are ______ forms of dilemma.
Answer:
four

Question 27.
The dilemma is constructive if ______.
Answer:
The antecedants are affirmed in the minor premise.

Question 28.
The dilemma is destructive if ______.
Answer:
The consequents are denied in the minor premise.

Question 29.
The dilemma is simple if ______.
Answer:
The conclusion is and alternative proposition

Question 30.
The dilemma is complex if ______.
Answer:
The conclusion is an alternative proposition.

Question 31.
A hypothetical syllogism is constructive of ______.
Answer:
The antecedent k difirmed in the minor premise.

Question 32.
A hypothetical syllogism is destructive if ______.
Answer:
The antecedent is affirmed in the’minor premise.

Question 33.
The dilemma is formally valid if ______.
Answer:
The rules are correctly observed.

Question 34.
In a dilemma if one consequent does not follow from the antecedent it is called ______.
Answer:
Taking by one horn

Question 35.
In a dilemma if both the consequents do not follow from the antecedent it is called ______.
Answer:
taking by both the honors

Question 36.
In a dilemma if both the alternatives are not exhaustive it is called ______.
Answer:
Escaping between the horns

Question 37.
There are two rules in mixed hypothetical syllogism, such as ______ and ______.
Answer:
Affirming the antecedent, Denying the consequent.

Question 38.
In a dilemma, if the antecedents are affirmed in the premise, it is called from ______.
Answer:
Constructive

Question 39.
In a dilemma, if the consequents are affirmed then ______ fallacy arises.
Answer:
Aflfirmin the consequent

Question 40.
In a dilemma, if the consequents are denied in the premise, it is called ______.
Answer:
Destructive

Question 41.
In a dilemma, if the antecedents are denied in the premise then ______ fallacy arises.
Answer:
Denying the antecedent

Question 42.
If the conclusion of a dilemma is categorical proposition that is called ______ dilemma.
Answer:
Simple

Question 43.
If the conclusion of a dilemma is alternative proposition that is called ______ dilemma.
Answer:
Complex

Question 44.
A dilemma is said to be ______ when is incorrectness is exposed.
Answer:
Rebutted

Question 45.
According to logicians, only ______ form of dilemma can be rebutted.
Answer:
Complex constructive

Question 46.
A dilemma is materially refuted if it is shown that a premise or both the premise are ______.
Answer:
Materially false

Question 47.
The ______ of a dilemma are like the two homess of a dangerous animal.
Answer:
Alternants

III. Correct the Sentences:

Question 1.
In pure syllogism all the constituent propositions are of different types.
Answer:
In mixed syllogism all the constituent propositions are of different types.

Question 2.
In mixed syllogism all the constituent propositions are of same types.
Answer:
In Pure Syllogism all the constituent propositions are of same types.

Question 3.
Mixed Syllogisms are of three types.
Answer:
Mixed syllogisms are of four types.

Question 4.
In a hypothetic 1.1 categorical syl logism, the maj or premise a alternative and the minor premise is categorical.
Answer:
In a hypothetical categorical syllogism, the major premise is hypothetical and the minor premise is categorical proposition.

Question 5.
In a mixed disjunctive syllogism, the major premise is alternative and the minor premise is compound proposition.
Answer:
In a mixed disjunctive syllogism, the major premise is disjunctive proposition and the minor premise is categorical proposition.

Question 6.
The constructive form of the mixed hypothetical syllogism is also called Modus tollens.
Answer:
The constructive form of the mixed hypothetical syllogism is also called Modus Ponens.

Question 7.
The Destructive form of the mixed hypothetical syllogism is also called Pollendo Tollens.
Answer:
The Destructive form of the Mixed hypothetical syllogism is also called Modus Tollens.

Question 8.
There are two forms of dilemma.
Answer:
There are four forms of dilemma.

Question 9.
In case of simple dilemma the conclusion is an alternative proposition.
Answer:
In case of simple dilemma the conclusion is categorical proposition.

Question 10.
In case of complex dilemma the conclusion is categorical proposition.
Answer:
In case of complex dilemma the conclusion is an alternative proposition.

Question 11.
In hypothetical categorical syllogism Ponendo Ponens become valid.
Answer:
In hypothetical categorical syllogism Ponendo Ponens becomes invalid.

Question 12.
In disjunctive – categorical syllogism Tollendo Ponens is valid.
Answer:
In disjunctive – categorical syllogism, Tollendo Ponens is invalid.

Question 13.
In alternative – categorical syllogism, Ponendo Tollens is valid.
Answer:
In alternative categorical syllogism, Ponendo Tollens is invalid.

Question 14.
Simple constructive dilemma can only be refuted.
Answer:
Complex constructive dilemma can only be refuted.

Question 15.
In a mixed disjunctive syllogism, one disjunct is denied to deny the other.
Answer:
In a mixed disjunctive syllogism, one disjunct is affirmed to deny the other.

IV. Answer the following questions in one word:

Question 1.
Syllogisms are mainly classified into how many types?
Answer:
Two

Question 2.
Where all the propositions are of same type that is called what syllogism?
Answer:
Pure

Question 3.
Where all the propositions are of different types that is called what syllogism?
Answer:
Mixed

Question 4.
Mixed syllogism is divided into how many types?
Answer:
Four

Question 5.
How many kinds of dilemma do use have?
Answer:
Four

Question 6.
How many hypothetical propositions are there in the compound hypothetical proposition of a dilemma?
Answer:
Two

Question 7.
What in the method of refutation of a dilemma by constructing its counter dilemma called?
Answer:
Rebuttal

Question 8.
Whether the conclusion of a complex dilemma is alternative or categorical?
Answer:
Alternative

Question 9.
Whether the consequents of the hypothetical propositions in a simple constructive dilemma are same or different?
Answer:
Same

Question 10.
How many alternative propositions are there in a simple dilemma?
Answer:
One

Question 11.
How many alternative propositions are there in a complex dilemma?
Answer:
Two

Question 12.
How many types of rules are there in Hypothtical categorical syllogism?
Answer:
Two

Question 13.
If in a syllogism, one premise is hypothetical and other premise is categorical, what is the name of this mixed syllogism?
Answer:
Hypothetical Categorical

Question 14.
If in a syllogism one premise is disjunctive and other premise is categorical, What is the name of this mixed syllogism.
Answer:
Mixed-Disjunctive

Question 15.
In a mixed hypothetical syllogism, the conclusion is what type of proposition.
Answer:
Categorical

Question 16.
Modus ponens form of mixed hypothetical syllogism is also called what?
Answer:
Constructive

Question 17.
Modus Tollens form of the mixed Hypothetical syllogism is also called what?
Answer:
Destructive

Question 18.
In’ mixed Disjunctive syllogism, the conclusion is what type of proposition.
Answer:
Categorical

Question 19.
If the antecedent part is affirmed, it is called what?
Answer:
Affirming the antecedent

Question 20.
If the consequent part is denied, it is called what?
Answer:
Denying the consequent

Question 21.
If the conclusion of dilemma is categorical, it is called what?
Answer:
Simple

Question 22.
If the conclusion of dilemma is alternative, it is called what?
Answer:
Complex

Question 23.
Which form of dilemma is only rebutted?
Answer:
Complex constructive

Question 24.
How many ways are there by which, a dilemma is refuted?
Answer:
Three

Odisha State Board CHSE Odisha Class 12 Logic Solutions Chapter 2 Syllogism Questions and Answers.

CHSE Odisha 12th Class Logic Chapter 2 Question Answer Syllogism

Group – A

Short type Questions with Answers
I. Answer with in Two/Three sentence!

Question 1.
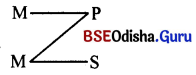
Write the 3rd figure of syllogism.
Answer:

(i) In this figure middle term (m) is present subject place in both the premises.
(ii) The major term (p) is present in the predicate place of the major premise and the minor term is (s) present in the predicate place of the minor premise.

Question 2.
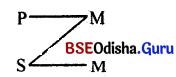
What is the position of the middle term in the fourth figure?

Answer:
(i) Middle term (m) is present in the predicate place of the major premise.
(ii) Middle term is present subject place of the minor premise.

Question 3.
Write any three general rules of syllogism.
Answer:
(i) Rule ‘3 ’ states that middle term must be distributed at least once in any of the premises.
(ii) From two negative premises no conclusion follows (Rule-5)
(iii) From two particular premises no conclusion follows (Rule-8)

Question 4.
Write the valid moods of the 3rd figure.
Answer:
(i) There are six valid moods in the third figure.
(ii) These are : DARAPTI, DATISI, DISAMIS, FELAPTION, FERISON, BOCARDO.

Question 5.
Name the valid moods of 4th figure.
Answer:
(i) There are 5 valid moods in the 4th figure.
(ii) These are BRAMANTIP, CAMENES, FESAPO, FRESISON, DIMARIS.

Question 6.
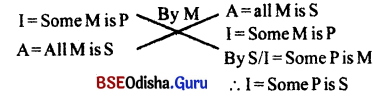
Give the symbolic example of BAROCO.
Answer:
(i) ‘BAROCO’ is the valid mood of 2nd figure.
(ii) Symbolic example;
A = All P is M
O = Some S is not M
∴ O = Some S is not P

Question 7.
Write the names of the perfect moods.
Answer:
(i) There are 4 perfect moods in syllogism.
(ii) These are BARBARA, DARII, CELARENT, FERIO

Question 8.
Write the names of the imperfect moods.
Answer:
(i) There are 15 imperfect moods in syllogis

(ii) These are, CAMESTRES, CESARE, FESTINO, BAROCO, DARAPTI, DATISI, DISAMIS, FELAPTON, FERISON, BOCARDO, BRAMANTIP, CAMENES, FESAPO, FRESISON, DIMARIS.

Question 9.
Write the special syllogistic rules of the first figure.
Answer:
(i) There are two special syllogistic rules in the 1st figure. These are
(ii) Major premise must be universal.
(iii) Minor premise most be affirmative.

Question 10.
State the special syllogistic rules of the 2nd figure.
Answer:

1. There are three special syllogistics rules in the 2nd figure. These are-
2. Major premise must be universal.
3. Conclusion must be negative –
4. Out of two premises, one premise must be negative.

Question 11.
State the special syllogistic rules of the 3rd figure.
Answer:

1. The minor premise must be affirmative.
2. The conclusion must be particular.
3. One of the premises must be universal.

Question 12.
Write the special syllogistic rules of the 4th figure.
Answer:

1. If the major premise is affirmative, the minor premise must be universal.
2. If the minor premises is affirmative the conclusion must be particular.
3. If either premise is negative, the major premise must be universal.

II. Answer within Five/Six sentence :

Question 1.
Why is syllogism called a mediate deductive inference?
Answer:
An inference is said to be mediate if the conclusion is drawn from. More than one premises and it is said to be deductive if the conclusion is never more general that the premises. In a syllogism the conclusion follows form two premises taken jointly and the conclusion cannot be more general than the premises. So a syllogism is called a mediate deductive inference.

Question 2.
How the figure of the syllogism is determined?
Answer: Figure of the syllogism is mainly determined by the position of the middle term. It may be the subject in both the premises, or predicate in both the premises or subject in minor and predicate in major subject in major and predicate in minor. There are four figures which are-

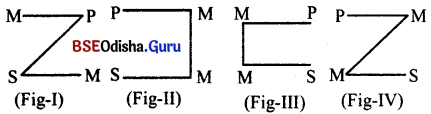
Question 3.
What is the fallacy of illicit minor?
Answer:
In a syllogism, if the minor term (s) is distributed in the conclusion but not distributed minor premise at that time we commit the fallacy of illicit minor.
Example :

In this example the minor term(s) is distributed in the conclusion but it is not distributed in the minor premise, so it leads to the fallacy of illicit minor.

Question 4.
Explain the fallacy of illicit major.
Answer:
In a syllogism, if the major term (p) is distributed in the conclusion but not distributed in the major premise that is called the fallacy of illicit major.
Example :

Here the major term (mortal) is distributed in the conclusion but not distributed in the major premise. So it leads to the fallacy of illicit major.

Question 5.
What is mood of syllogism?
Answer:
Mood of a syllogism is mainly determined by the quality and quantity of the premises. According to quality or quantity the propositions are A. E. I. O. on the basis of quality and quantity (A, E, I, O) the possible combinations are AA, AE, AI, AO, EA, EO, OA, IA, IE, II, 10, OE, 01, OO. According to first group of logicians there are only 16 x 4 = 46 possible moods. According to second group of logicians there are only 64 x 4 = 256 possible moods. According to Aristotle, there are 19 valid moods.

Question 6.
What is the fallacy of illicit Minor?
Answer: When the minor term is distributed in the conclusion without being distributed in the minor premise, we commit the fallacy of illicit minor.
Example :
E = No M is P.
A = All M is S.
E = No S is P
Here the minor term (p) is distributed in the conclusion but not distributed in the minor premise. So we commit the fallacy of illicit minor.

Question 7.
Explain the fallacy of undistributed middle.
Answer:
According to the third general syllogistic rule, middle term must be distributed at least once in any of the premise of a syllogism. But if the middle term is not distributed in any of the premises then we commit the fallacy of undistributed middle.
Example :

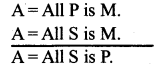
The above example is a fallacy of undistributed middle, because here the middle term (M) is not distributed in any of the premises.

Question 8.
Give a concrete example of valid argument in figure III.
Answer:
E = No men are birds.
A = All men are biped.
∴ O = Some biped beings are not birds.
This is the concrete example of the valid mood of third figure which is called FELAPTON.

Question 9.
Give an example of ‘A’ proposition and find out its converse.
Answer:
A = All men are mortal.
Converse I = some mortal beings are men.
A = All Sis P.
Converse I = Some P is S.

Question 10.
Give concrete example of the mood ‘CESARE’.
Answer:
E = No men are birds.
A = All crows are birds.
E = No crows are men

Question 11.
Give a symbolic example of the mood ‘BRAMANTlP’.
Answer:
A = All P is M
A = All M is S
∴ I = Some S is P.

Question 12.
Give an example of a valid syllogistic argument in which the middle term is distributed in both the premises.
Answer:
E = No M is P
A = All M is S
∴ O = Some S is not P.
This FELAPTON, a valid mood 3rd figure, where the middle term is distributed in both the premises.

Question 13.
Give an example of a valid syllogistic argument in which the major term is distributed in the premise but not in the conclusion.
Answer: A = All P is M
A = A11 M is S.
∴ I = Som S is P
This is BRAMANTlP, a valid mood in 4th figure, I where the major term is distributed in the premises but not distributed in the conclusion.

Question 14.
Write the special syllogistic rules of the figure one.
Answer:
(i) Major premise must be universal
(ii) Minor premise must be affirmative.

Question 15.
Name the moods of the 1st figure to which the following moods can be directly reduced BAROCO, BOCARDO, BRAMANTlP.
Answer:
BAROCO = FERIO. BOCARDO = DARIT. BRAMANTlP = BARBARA.

Question 16.
State the structure of a syllogism.
Answer:
A syllogism is consisted of three propositions, out of which the first two are called premises and the last one is called conclusion. The first proposition of syllogism is called major premise and the second proposition is called Minor premise. It is also consisted of three terms, such as; Major term (P) minor term (S) and middle term (m). The predicate part of the conclusion of a syllogism is called major term (P), the subject part of the conclusion of syllogism is called Minor term (s) and the common term between the premises is cabled middle term (M).

Question 17.
What is syllogism?
Answer:
Syllogism is a kind of mediate form of deductive inference where the conclusion is drawn out of two premises taken jointly but not separately. It is consisted of three terms like-major (p), minor (S) and middle term. It is consted of 3 propositions.
Example :

Question 18.
What is the fallacy of two particular premises.
Answer:
The general syllogistic rule says that if both their premises are particular then no conclusion follows. But if we draw any conclusion, out of two particular premises then we commit the fallacy of two particular premises.
Example:
I = Some mangoes are sweet.
O = Some fruits are not mangoes.
∴ O = Some fruits are not sweet.

Question 19.
Explain the fallacy of “Train of syllogism”?
Answer:
According to the general syllogistic rule, A syllogism must be consisted of three propositions, neither more or nor less. But if a syllogism is consisted of more than three propositions than we commit a fallacy, which is called the fallacy of train of syllogism.
Example :
All animals are mortal.
All men are mortal. Ram is a man
∴ Ram is mortal.
This argument is fallacious because it is consisted of 4 propositions.

Question 20.
What is the fallacy of ‘Four Terms’ ?
Answer:
A syllogism must be consisted of three terms, neither more not less. But if syllogism is consisted of more than three terms, than the fallacy arises, which as called the fallacy of ‘FOUR TERMS’.
Example :
God is the creator of man Man is the creator of sin,
God is the creator of sin.

Question 21.
What is meant by fundamental mood?
Answer:
A fundamental mood is a valid syllogism where the premises are just sufficient fttr the conclusion. Here the middle term is distributed only once and whatever other term is distributed in the premises are also distributed in the conclusion. The following 15 moods are fundamental.
Figure-I = BARBARA, DARII, CELARENT, FERIO.
Figure-II = CAMESTRES, CASARE, FESTINO, BAROCO .
Figure-III = DATISI, DISAM1S, FERISON, BOCARDO
Figure-IV = CAMENES, DIMARIS, FERESION,

Question 22.
Name the valid moods of flgure-III.
Answer:
DARAPTI, DATISI, DISAMIS, FELAPTON, FERISON, BOCARDO.

Question 23.
Name the valid moods of the first figure.
Answer:

1. BARBARA,
2. DARII,
3. CELARENT,
4. FERIO

Question 24.
Write short notes on the strengthed moods.
Answer:
A mood is said to be strengthened, if one of its premises is unnecessarily stronger than what is required to prove the conclusion. In the case of a strengthened mood even if a universal premise be substituted by its corresponding particular proposition, still the same conclusion follows. The following eight moods are strengthened.
Fig I = Barbari, Celaront.
Fig II = Cesaro, Camestrop
Fig III – Darapti, Felapton
Fig IV = Bramantip, Fesapo.

Question 25.
What is called weakened mood?
Answer:
A mood is said to be weakened, if its conclusion is weaker than what i$ justified by its premises. Though the premises can validate a universal conclusion, in a weakened a universal conclusion, the corresponding particular proposition, is drawn as the conclusion. The following five moods are weakened.
Fig I = Barbari, cetaront
Fig II = Cesaro, camestrop
Fig III = Camerop

Question 26.
Write any two general syllogistic rules are :
Answer:
(i) If one of the premise be negative, the conclusion is negative.
(ii) If one of the premise be particular the conclusion must be particular.

Question 27.
Distinguish-between immediate and mediate inference.
Answer:
Immediate inference is a kind of deductive inference in which the conclusion is drawn out of the only one premise.
Example :
All men are mortal.
Some mortal beings are men.

It is divided into 4 types, such as conversion, obversion, inversion and contraposition. Mediate inference is a kind of deductive inference in which the conclusion is drawn out of two premises taken jointly but not separately. It is otherwise called as syllogism.
Example :
A = All men are mortal.
A = All. students are men.
A = All students are mental.

Question 28.
What are the different kinds of inference?
Answer:
Inference is of two kinds, called deductive inference and inductive inference. Deductive inference is again of two kinds called immediate and mediate inference. Mediate inference which is also called syllogism can be pure or mixed.

Question 29.
Name the valid moods of 2nd figure.
Answer:
There are only four valid moods in the second figure. These are; CAMESTRES, CESARE. FESTINO, BAROCO.

Question 30.
Name the valid moods of 4th figure.
Answer:
There are only five valid moods in the fourth figure. These are; BRAMANTIP = AAI, CAMENES = AEE; FESAPO = EAO, FRESISON = E10, DIMARIS = LAI.

Question 31.
Give a symbolic example of BARBARA.
Answer:
Symbolic example of BARBARA.

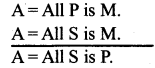
Question 32.
Give the symbolic expression of DARII.
Answer:
Symbolic expression of DARII.

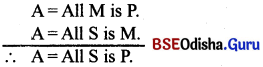
Question 33.
Give the Symbolic expression of CELARENT.
Answer:
Symbolic expression of CELARENT.

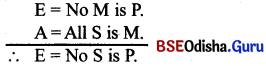
Question 34.
Write the symbolic example of FERIO.
Answer:
Symbolic example of FERIO.

Question 35.
Write the symbolic expression of GAMESTERS.
Answer:
Symbolic expression of GAMESTERS.

Question 36.
Write the symbolic expression of CESARE.
Answer:
Symbolic expression of CESARE.

Question 37.
Write the symbolic expression of FESTINO.
Answer:
Symbolic expression of FESTINO.

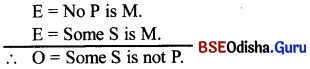
Question 38.
State the symbolic expression of BAROCO.
Answer:
BAROCO is the valid mood of 2nd figure. The symbolic expression of BAROCO

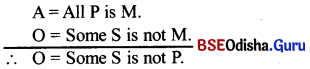
Question 39.
State the symbolic expression of DARAPTI.
Answer:
‘DARAPTI’ is the valid mood of third figure.
The symbolic expression of DARAPTI is →

Question 40.
State the symbolic expression of DISAMIS.
Answer:
‘DISAMIS’ is the valid mood of 3rd figure. The symbolic expression of ‘DISAMIS’ is →

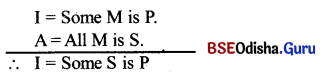
Question 41.
Give the symbolic expression of FELAPTON.
Answer:
‘FELAPTON’ is the valid mood of third figure. The symbolic expression of FELAPTON is →

Question 42.
State the symbolic example of ‘BOCARDO’.
Answer:
‘BOCARDO’ is the valid Mood of third figure. It is symbolic expression is:

Question 43.
State the symbolic example of CAMENES.
Answer:
‘CAMENES’ is the valid mood of 4th figure. It is symbolic expression is;

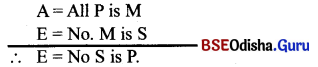
Question 44.
State the symbolic expression of “FESAPO”.
Answer:
‘FESAPO’ is the valid mood of 4th figure.
The symbolic expression of ‘FESAPO’ is →

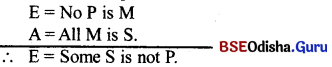
Question 45.
Write the symbolic expression of FRESISON.
Answer:
FRESISON is the valid mood of 4th figure. It is symbolic expression is;

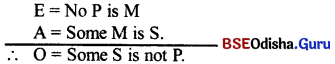
Question 46.
Write the symbolic expression of DIMARIS.
Answer:
DIMARIS is the valid mood of 4th figure.
Its symbolic expression is;

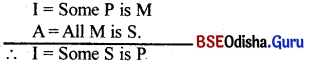
Question 47.
Write the special syllogistic rules of the figure 3.
Answer:
The following are the special rules of the third figure.

1. The minor premise must be affirmative.
2. One of the premises must be universal.
3. The conclusion must be particular.

Question 48.
What is called the fallacy of ‘Four Terms’?
Answer:
According to the general syllogistic rule, syllogism must be consisted of only three terms, neither more or less. But if a syllogism is consisted of more than 3 terms we the commit the fallacy of Four Terms.
Example :

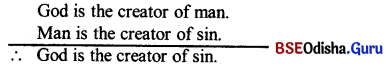
This argument is fallacious because it is consisted of 4 terms.

Question 49.
Why the 1st figure is called perfect figure?
Answer:
According to Aristotle, first figure is called the perfect figure, because it follows a principle what calls is “Dictem deomini etnullo”, which literally means “statement concerning all and none”. According to him the moods of 2nd, 3rd and 4th figure will be tested by transforming to the moods of the 1st figure.

Question 50.
State Aristotles Dictum.
Answer:
For testing the validity of moods Aristotle had framed one rule, which is called “Aristotle’s dictum de omniet nullo”. Which means statements concerning all one none we state the rule thus.

1. It something is true of all of a class, it can be affirmed of some of that class.
2. If something is true of none of a class, it can be denied of some of that class.
   • Example :
     All M is P.
     All S is M.
     All S is P.

Question 51.
State the necessary of reduction in a syllogism.
Answer:
Reduction, in wide sense means transformation of moods of any figure to any other figure but in narrow sense it means changing the moods of 2nd, 3rd & 4th figure to 1st figure. Hence according to Aristotle 1st figure is the perfect figure because the dictem is applicable to the first figure. Hence reduction may be defined as the transformation of the moods to the imperfect figures to die moods of the 1 st figure there by proving the correctness of the moods of the so called imperfectTigures. That is why reduction is necessary.

Question 52.
State the special rules of 4th figures.
Answer:
The special rules of 4th figures are.

1. If the major premise is affirmative, the minor premise must be universal.
2. If any premise is negative, the major premise must be universal. .
3. Both the premises cannot be negative.
4. If the minor premise is affirmative, the conclusion is particular.

Question 53.
State the special syllogistic rules of figure-11.
Answer:
The special rules of figure II are :

1. The major premise must be universal.
2. One of the premises must be negative.
3. The conclusion must be negative.

Question 54.
Name the special syllogistic rules of Figure one.
Answer:
There are two special syllogistic rules in the figure on these are,
(i) Major premise musrte universal.
(ii) Minor premise must be affirmative.

Question 55.
What is Reduction?
Answer:
Reduction is the process of proving the validity of the moods of the imperfect figures with the help of the moods of the perfect first figure. Direct reduction is the process of directly transforming a mOod of imperfect figure to a mood of perfect figure. Indirect reduction is the process of showing that some moods of 2nd, 3rd and 4th figures are such that the conclusion cannot be false if the premises are true.

Question 56.
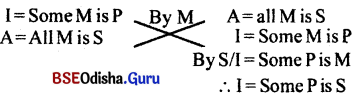
What in the direct Reduction of ‘DIMARIS’.
Answer:
DIMARIS – DARII

Question 57.
Prove : If one premise be negative the conclusion must be negative.
Answer:
One of the rules of syllogism says that both the premises cannot be negative. So there must be one premise affirmative enabling to draw the conclusion and the other one is negative. In negative premises there is no connection between middle term and one of the extremes. But in affirmative premises there is same connection between the middle term and the other extreme. From this it is clear that there lies no connection between both the extremes, hence the conclusion would be a negative proposition.

Question 58.
Prove : Minor premise must be affirmative in the third figure.
Answer:
One of the special syllogistic rule of the figure 3 says that minor premise must be affirmative in the third figure. But if the minor premise be not affirmative then it must be negative. In this case the major premise will be affirmative. If it be so then conclusion must be negative. But if the conclusion be negative then it will always distribute its predicate term, which will never distribute in case of the major premise. As a result of which we will commit the fallacy of illicit major. So it is proved that minor premise must be affirmative in third figure.

Group – B

Long Type Questions With Answers

Question 1.
Prove the following : From two Negative premises, no conclusion follows.
Answer:
The general syllogistic rule 5 says that if both the premises are negative then no conclusion follows. It means if both the premises are negative then the possible combinations may be :
\(\frac{E / O}{E / O}\) = EE,EO,OE,OO
Let’s test the above possible combinations and find whether any conclusion follows or not ?
E = No M is P.
E = No S is M.

In the above combination, the major premise says that M and P both are separated from each other. It means there is not relationship between M and P. And the minor premise says that S and M both are two Negative terms and there is no relationship between them. We have known that conclusion comes when the relation exists between the two premises. But here as there is no relation between so how can we draw a conclusion. So it is proved that if both the premises are negative then there is no conclusion.

Question 2.
Prove the following :
(a) In a valid syllogism, middle term must be distributed at least once
(b) From particular major and negative minor, no conclusion follows.
Answer:
(a) The third general syllogistic rule says that the middfe tend must be distributed at least once in any of the premises. Generally the term distribution means its entire denotation. The middle term is related to the major term in the major premise. It is related again to the minor term in the minor premise, from the nature of these two relations of the major and the minor term with the same middle term, we determine the relation of them in the conclusion.

Is the middle term is used partially in both the premises, then these two P arts may be different form each other. In that case the major term and the minor term are not being related to the same individuals and their mutual relation can not be ascertained. Here we are used to commit the fallacy of undistributed middle. Some M is P some M is S.

But if both the above propositions be plurative, more than half of ‘M’ is taken in both the cases, then naturally P and S are related to the same common individuals. So the conclusion ‘Some S is P’ can be drawn.

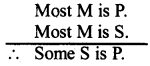
This is an exception to the rule. Logically both the premises we 1 propositions, which distribute no term and the middle term is not at all distributed here.

(b) The General Syllogistic rule (10) says that if the major premise is particular and the minor premise is negative then no conclusion follows. If the major premise is particular and the minor premise is negative then the possible combinations.
May be \(\frac{\mathrm{I} / \mathrm{O}}{\mathrm{E} / \mathrm{O}}\) = IE,IO,OE,OO.

Out of the above four possible combinations we can reject the last two (OE, 00) as per the rule No. 5 (from two negative premises no conclusion follows). And also we can reject (IO) possible combination because both are particular. Let’s test the only possible combination ‘EF’.
I = Some M is P.
E = No S is M.

In the above combination as the middle term (M) is distributed that is why we can draw a conclusion. But if the conclusion be any than it will be negative proposition, which will be distributed its predicate term or major term. But that major term (P) will never distribute in the major premise. So we commit the fallacy of illicit major. Therefore it is proved that from particular major and negative minor, no conclusion follows.

Question 3.
Prove : If both the premises are affirmative the conclusion must be affirmative.
Answer:
If both the premises are affirmative in a syllogism, then the possible combination may be \(\frac{\mathrm{ALI}}{\mathrm{ALI}}\) = AA, AI, LA, II. out of the four possible combinations we can reject the last (II); because from two particular premises no conclusion follows. As per this rule the conclusion will be affirmative from the other three possible combination. But if the conclusion be not affirmative then it must be negative.

Let’s see if the conclusion be negative then what will happen?
Example :
A = All M is P.
A = All S is M.
If the conclusion be negative then it will be either (E or O). But if it be so then major term will be distributed in the conclusion but will never distributed in the conclusion but will never distribute in case of the major premise. As a result of which we will always commit the fallacy of illicit major. So it is proved that if both the premise are affirmative the conclusion must be affirmative.

Question 4.
Explain. From two particular premises, no conclusion follows.
Answer:
If both the premises are particular in a Syllogism then the possible combinations may be \(\frac{\mathrm{IIO}}{\mathrm{IIO}}\) IO, OI, OO out of the above four possible combination we can reject the last possible combination (O O) as both the premises are negative,

Let us test the other possible combination
II = I = Some M is P,
I = Some S is M.
In this possible combination no conclusion follows because the middle term is not distributed in any of the premises. So here we commit the fallacy of undistributed middle.
IO = I = Some M is P.
O = Some S is not M.
In this combinations as the middle term is distributed in the minor premise then we can draw a conclusion. But if the conclusion be any then it will be ‘O’ in which the major term (P) will be distribute but that will never distribute in case of the major premise. As a result of which we commit a fallacy of illicit major.
OI = O = Some M is not P.
I = Some S is M.
In this combination as the middle term is not distributed in any of the premises, we commit the fallacy of undistributed middle, from this above it is prove, that if both the premises are particular in a syllogisms then no conclusion follows.

Question 5.
Prove the following :
(a) In a Syllogism, If one premise is particular the conclusion is particular.
(b) From particular major and Negative minor no conclusion follows.
Answer:
(a) If one of the premise is particular then other premise must be universal and the possible combination may be \(\frac{1 / O}{A / E}\) IA,IE,OA,OE.

Out of the above we can reject the last combination (OE); as per the rule No 5 and ‘IE’ as per the rule No. 10. Let’s test other possible combination like- LA, OA, ‘IA’.

In this combination (IA) only one term is distributed that is the subject of ‘A’. In order to avoid the fallacy of undistributed middle. Suppose we have taken that distributed term as middle term. Then no distributed term is there in the premise. So if we will take the conclusion as T proposition, then no fallacy will be occur. So ‘LA’ combination T comes always.

‘OA’: In this possible combination only two terms are distributed. One the subject of ‘A’ and other is the predicate of ‘O’ proposition out of two distributed terms we should take one as the middle term and other as the major term. Then, here we should remember that the major term in distributed in the .major premise. If we will take particular negative. (O) proposition in case of conclusion then the fallacy of illicit major will never occur. From this above, it is proved that if one of the premise is negative, then conclusion must be negative.

(b) The General Syllogistic rule (10) says that if the major premise is particular and the minor premise is negative then on conclusion follows. If the major premise is particular and the minor premise is negative then the possible combinations may be \(\frac{\mathrm{I} / \mathrm{O}}{\mathrm{E} / \mathrm{I}}\) = IE,IO,OE,OO.

Out of the above four possible combinations we can reject the last two (OE, OO) as per the rule No 5 (From two negative premises no conclusion follows). And also we can reject (IO) possible combination because both are particular. Let’s test the only possible combination ‘IE’.
I = Some M is P.
E = NO’S is M.

In the above combination as the middle term (M) is distributed that is why we can draw a conclusion. But if the conclusion be any then it will be negative proposition, which will be distributed its predicate term or major term. But that major term (P) will never distribute in the major premise. So we commit the fallacy of illicit major.

Question 6.
Prove : From two negative premises, no conclusion follows.
Answer:
The General Syllogistic rule No.5 says that if both the premises are negative then no conclusion follows. If means it both the premises are negative then the possible combinations may
be \(\frac{E / O}{E / O}\) = EE, EO & OO. Let’s test the above possible combinations and find whether any conclusion follows or not ?
E = No M is P.
E = No S is M.

In the above combination, the major premise says that M and P both are separated from each other. It means there is no relationship between M and P. And the minor premise says S and M both are separated. We have known that conclusion comes the relation exists between the two premises. But here as there is not relation between the two premise S So how can we draw a conclusion.
So it is proved that if both the premises are negative, then there is no conclusion.

Question 7.
Prove : Middle term must be distributed at last once in the premises,
Answer:
To be distributed means to be taken in its entire denotation of the term. The middle term is the bond of connection between the two extremes. If it remains undistributed in both the premises, it means it takes only a part of denotation of the major term and also of the minor ten. In that case, it is possible that the extremes are related to different parts of the middle term.

Two such premises can not draw a conclusion because the middle term is unable to link the two extremes. If the middle term is distributed in both the premises, it is still better. If we violate this rule and keep the middle term undistributed in both the premises, it is called the fallacy of undistributed middle. For Example:
A – All Indians are Asians
A – All Pakistanis are Asians
∴ A – All Pakistanis are Indians.

As we see in the above example a false conclusion from two true premises. It is because the middle term remained undistributed in both the premises and failed to related the two extremes in the conclusioii. This can be explained by the help of a diagram

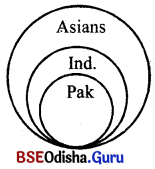
We can see in the above diagram the class extremes, neither by Indians nor by PakistAnswer: So the conclusion gets wrong.

Question 8.
Prove : Major premise must be universal in the first figure.
Answer:
One of the special syllogistic rule of the figure (one) says that major premise must be universal. But if the major premise be not universal in the 1 st figure then it must be particular. If the major premise is particular then in that case the middle term (m), which is the subject cannot be distributed. So the fallacy of “undistributed middle” will arise. But in order to avoid the fallacy of undistributed middle, it must be distributed in the minor premise, where the middle term is predicate. So if we will take minor premise as a negative proposition then it will distribute its predicate and the fallacy of undistributed middle will never occurs.

Again it we take minor premise as Negative proposition (E/o) then in that case major premise will be affirmative and the conclusion will be Negative. If the conclusion will be negative, it will be distribute its major term (P) which will never be distribute in case of the major premise. Because major premise as affirmative cannot be distributed is predicate. So we commit the fallacy of illicit major.

Again we can avoid the fallacy if illicit major if the major term (P) will be distributed in the major premise. If means if the major premise will be negative proposition, it will distribute its predicate (P). But we cannot take any negative proposition in case of the major premise. Because we have already taken the negative proposition in case of minor premise. All the above fallacies arise as we have taken the major premise as particular. So it proved that the major premise must be universal in the first figure.

Question 9.
Prove the following :
(a) Minor Premise must be affirmative in the 1st figure.
(b) ‘O’ proposition cannot be a premise in the 1st figure.
Answer:
(a) The minor Premise must be affirmative in the 1st figure : If the minor premise be not affirmative in the 1st figure then it must be negative. If the minor premise be negative then in that case the major is affirmative. So if the major affirmation and minor is negative, then conclusion must be negative and if the conclusion is a negative proposition it will always distribute its major term (P) which will never distribute in case of major premise as we have taken the major premise is affirmative. So the fallacy will arise, which is called illicit major.

Again this fallacy of illicit major can be avoided if we take the major premise as negative proposition. But we can not take the major into a negative. Because we have taken the minor premise as negative. So form this above discussion it is proved that the minor premise of the first figure must be affirmative but it cannot be negative.

(b) If one premise be O, the other premise must be A, and the conclusion must be O. So the mood is either O A o or AGO. In first figure, both these moods are universal.

O = Some M is not P.
A = All S is M.
∴ O = Some S is not P.
Here, the middle term is not at all distributed. So, it commits the fallacy of undistributed Middle.

A = All M is P.
O = Some S is not M.
∴ O = Some S is not P.
Here, the major term is distributed in the conclusion, but not distributed in the major premise. So it commits the fallacy of Illicit major. Therefore, O cannot be a premise in First figure.

Question 10.
Prove : Major premise must be universal in the first figure.
Answer:
One of the special syllogistic rule of the figure (one) says that major premise must be universal. But if the major premise be not universal in the 1 st figure then it must be particular. If the major premise is particular then in that case the middle term (m), which is the subject cannot be distributed. So the fallacy of “undistributed middle” will arise. But in order to avoid the fallacy of undistributed middle, it must be distributed in the minor premise, where the middle term is predicate. So if we will take minor premise as a negative proposition then it will distribute its predicate and the fallacy of undistributed middle will never occurs.

Again if we take minor premise as Negative proposition (E/o) then in that case major premise will be affirmative and the conclusion will be Negative. If the conclusion will be negative, it will be distribute its major term (P) which will never be distribute in case of the major premise. Because major premise as affirmative cannot be distributed is predicate. So we commit the fallacy of illicit major.

Again we can avoid the fallacy if illicit major if the major term (P) will be distributed in the major premise. If means if the major premise will be negative proposition, it will distribute its predicate (P). But we cannot take any negative proposition in case of the major premise. Because we have already taken the negative proposition in case of minor premise. All the above fallacies arise as we have taken the major premise as particular. So it is proved that the major premise must be universal in the first figure.

11. Explain :
(a) If the conclusion is universal the middle term can be distributed only once.
(b) If the major term in predicate in the major premise, the minor premise must be affirmative.
Answer:
(a) If the conclusion is universal, it is either A or E. In case of A, both the premises are A and only two terms are distributed in the premises. One of them must be the minor term, otherwise there arises the fallacy of illicit minor. So only one term is left distributed for the middle term.

In case of ‘E’, the premises are either EA or AE and three terms are distributed in the premises. Two of these must be the minor and the major terms to avoid the fallacies of the illicit process. So only one term is left distributed for the middle term.
Therefore, when the conclusion is universal the middle term can be distributed only once.

(b) The major term in the major premises if either distributed or undistributed. If it is distributed, then the major premise must be negative. So, in this case, the minor premise must be affirmative. If it is undistributed, then it cannot be distributed in the conclusion and the conclusion must be affirmative. If the conclusion be affirmative, then both the premises must be affirmative.
Therefore, if the major term is predicate in the major premise, the minor premise must be affirmative.

Question 12.
Prove : In the second figure major premise must if ‘I’ a universal and one premise must be negative.
Answer:
The proposition of the middle term in 2nd figure is :

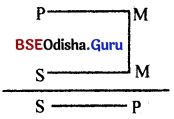
Thus in the second figure the middle term is the predicate in both the premise. Now affirmative proposition do not distribute their predicates but the middle term must be distributed at least once. So there must be a negative premise.

Question 13.
Explain. ‘O’ proposition can not be a major premise in the 4th figure.
Answer:

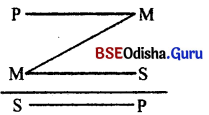
If we take ‘O’ proposition as a premise in figure IV, the other premise must be affirmative. In this case the conclusion will be particular negative (O). Which will always distribute its predicate term or major term (P). But the major term (P) will never distribute in case of the major premise. Because we have taken it as particular proposition, which will never distribute. Major term (P); as a result of which we commit the fallacy of illicit major. So it is proved that O proposition cannot be taken as a premise in figure IV.

Question 14.
Prove the following :
(a) Minor premise is affirmative in the 3rd figure.
(b) Conclusion is particular in the 3rd figure.
(c) At least one premise must be universal in the 3rd figure.
Answer:
(a) One of the special Syllogistic rule of the fig 3 says that minor premise must be affirmative in the 3rd figure. But the major premise be not affirmative then it must be negative. This case the major premise will be affirmative. If it be so then conclusion must be negative, but if the conclusion is negative then it will always distribute its predicate term, which will never distribute in case of the major premise. As a result which we will commit the fallacy of illicit major. So it is proved that minor premise must be affirmative in the 3rd figure.

(b) This rule says that conclusion must be particular in the 3rd figure. But if the conclusion be not particular then it must be universal (A/E). But if the conclusion be universal then the premise will also be universal. But if the conclusion be universal then it will be E proposition, which will distribute its subject term and predicate term. But however may be the predicate term will never be distribute in case of the major premise. As a result of which we will commit the fallacy of illicit major. So it is proved that the conclusion must be particular but should not be universal.

(c) If one of the premises be not universal in the 3rd figure then either both the predicate may be universal or may be particular. If both the premises are particular then no conclusion will follows as per the rule no 8. From two particular premises no conclusion follows. But if both the premises are universal the conclusion will be universal which will commonly distribute its subject term (minor) but it will never distribute in case of the minor premise. So we will commit the fallacy of illicit minor. From this above discussion it is proved that at least one premise must be universal.

Question 15.
Prove the following :
(a) If the conclusion is universal, the middle term can be distributed only once.
(b) If the major term is predicate in the major premise, the minor premise must be affirmative.
Answer:
(a) If the conclusion is universal, it is either A or E.
In the case of A, both the premises are A and only two terms are distributed in the premises. One of them must be the minor term, otherwise there arises the fallacy of illicit Minor. So only one term is left distributed for the middle term.

In the case of E, the premises are either EA or AE and three terms are distributed in the premises. Two of these must be the minor and the major terms to avoid the fallacies of the Illicit Process. So only one term is left distributed for the middle term. Therefore, if the conclusion is universal, the middle term can be distributed only once.

(b) The major term in the major premise is either distributed or undistributed. If it is distributed, then the major premise must be negative. So, in this case, the minor premise must be affirmative. If it is undistributed, then it cannot be distributed in the conclusion and the conclusion must be affirmative. If the conclusion be affirmative, then both the premise must be affirmative. Therefore, if the major term is predicate in the major premise, the minor premise must be affirmative.

Question 16.
Prove the following :
(a) No term will be distributed in the conclusion, if it is not distributed in the premises.
(b) In the fourth figure, if the major premise is O affirmative, the minor premise must be universal.
Answer:
(a) In deductive reasoning the conclusion. Can not be more general than the premises. A term is not distributed in the premises means only a part of the denotation is covered. But if it is distributed in the conclusion, that means we have drawn a conclusion on entire denotation based on part of denotation is a passage from “all” to “some”. Violation of this rule leads to two fallacies.
If the major term is distributed in the conclusion without being distributed in the major premise, it commits the fallacy of Illicit major For example
A-All tigers are animals
E-No. birds are tigers
E-No birds are animals

In the above example the major term “animal” is distributed in the conclusion but not in the premise. Secondly, if the minor term is distributed in the minor premise, it commits the fallacy of Illicit minor, for Example:
A-All snakes are poisonous
A-All snakes are reptiles
∴ A-All reptiles are poisonous
Here the minor term ‘reptiles’ is the predicate of ‘A proposition and so undistributed. But “reptile” is the subject of ‘A’ proposition in the conclusion and distributed. The argument is invalid.

(b) In the fourth figure, the middle term is the predicate in the major premise and subject in the minor premise. As affirmative propositions do not distribute their predicates, the middle term remains undistributed in the major premise. To avoid the fallacy of undistributed middle, it must be distributed in the minor premise, where it is the subject. Only universal propositions distribute their subjects. So, if the major premise is affirmative, the minor premise must be universal in the fourth figure.

Question 17.
Reduce ‘CAMENES’ both directly and indirectly.

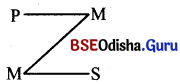
Answer:
Direct Reduction of ‘CAMENES’

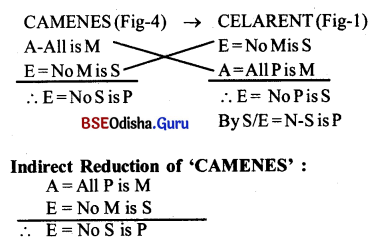
Let’s take the original conclusion of ‘CAMENES’ as false and its contradiction (I = Some S is P) as true. As per the rules of indirect reduction, here let’s take the major premise as true and minor premise as false. Here we should take the contradiction of the original conclusion as a true premise in the minor premise of ‘CAMENES’ which we have taken as false. After taking the value of major premise and minor premise as (true and false) let’s construct the new form of syllogism.

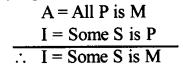
From this above it is said that ‘CAMENES’ is directly reduced to ‘CELARENT’ and indirectly reduced to DAR II.

Question 18.
Reduce ‘BOCARDO’ both directly and indirectly.
Answer:

Direct reduction of ‘BOCARDO’ BOCARDO (Fig-III) → DAR 99 (Fig-I) (Renamed as DOKSAMOSK)

Let’s take the original conclusion as false (F) and its contradiction as true (T) (A = All S is P). Taking this new proposition as the major premise and the original as the major premise and the original minor as minor premise, let’s form a new syllogism.
A = All S is P.
A = All M is S
∴ A = All M is P

Now we can see that the new conclusion is the contradictory of the original major premise. Both cannot be true. One must be false. The original major premise cannot be false because in deductive reasoning the premises are always taken to be true. So the new conclusion is false. The falsity can arise out of two ways.

If we have violated the rules syllogism or there is mistake in the premises. But we have not violated the rules of syllogism for which it is the valid mood ‘BARBARA’ of the perfect 1st figure. So the mistake is in the premises. The minor premise cannot be false as it is the original minor premise. So the mistakeis in the major premise which is the contradictory of the original conclusion. So the original conclusion is proved to be true.

Question 19.
Reduce ‘CAMESTRES’ both directly and indirectly.

Answer:
Direct Reduction of CAMESTRES
CAMESTRES (Fig-2) → CELARENT (Fig = I)
A = All p is M By M
E = No S is p
∴ E = No S is p

E = No S is M
By s/E E = No M is S
A = All P is M
∴ E = No P is S
By s/E = No is P

Indirect reduction of CAMESTRES :
A = All P is M
E = No S is M
∴ E = No S is P

‘Let’s take the original conclusion of ‘CAMESTRES’ as false and its contradiction as true I = Some S is P). Taking this new proposition as the minor premise and the original major as the major, Let’s form a new syllogism.
A = All P is M
I = Some S is P
∴ I = Some S is M

Now we see that the new conclusion is the contradictory of the original minor premise. Both cannot be false: The original major premise cannot be false, because in the deductive reasoning premises are always taken to be true. So the new conclusion is false. The falsity can arise out of two ways. If we have mistake in the premises or if we have violated the rules of syllogism. We have not violated the rules of syllogism for which it is the valid mood ‘DAR99’ Of first figure. SO there is mistake in the premises. The major premise cannot be false because it is the original major premise. So the mistake is in the minor premise which is the contradictory of the original conclusion. So the original conclusion in true. From the above it is said that ‘CAMESTRES’ is directly reduce to ‘CELARENT’ and indirectly reduced to DAR99.

Question 20.
Reduce ‘FELAPTON’ both directly and Indirectly.
Answer:
Direct Reduction of FELAPTON. FELAPTON (Fig-3) → FER90 (Fig-1)

Let’s take the original conclusion of FELAPTON as false and its contradiction as true (All S is P), Taking this new’ proposition as the major premise and the original minor as the minor, Let’s form a new syllogism.

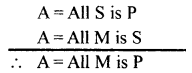
Now we see that the new conclusion is the contrary of the original major premise. Both cannot be true. One must be false. The original major premise cannot be wrong because in deductive reasoning premises are always taken to be true. So the new conclusion is false. The falsity can arise out of two ways. It there is any mistake in the premises or if we have violated the rules of syllogism. We have not violated the rules of syllogism for which it is the valid mood ‘BARBARA’, of first figure. So these is mistake in the premises. The minor premise cannot be false as if in the original minor. So the major premise is wrong. If it is wrong then its contradictory .the original conclusion in true.

Question 21.
Reduce ‘BRAMANTIP’ both directly and indirectly.
Answer:
Direct reduction of BRAMANTIP BRAMANTIP (Fig-4) → BARBARA (Fig = I)

Let’s take the original as false and its contradiction as true. (E = No’S is P). Taking this new proposition as the major premise and the original minor as the minor, let’s form a new syllogism.

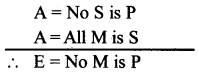
Now we see that the new conclusion is the contrary of the original major premise. Out of two premises, one must be false. The original major premise cannot be false because in deductive reasoning premises are always taken to be true. So the new conclusion is false. The falsity can arise out of two ways. It we have mistake in the premises or if we have violated the rules of syllogism.

We have not violated the rules of syllogism for which it is the valid mood ‘CELARENT’ of the perfect first figure. So there is mistake in the premises. The minor premise cannot be false as it is the original minor premise. So the mistake is in the major premise which is the contrary of the original conclusion. So the original conclusion is proved to be true. From this above it is said that BRAMANTIP is directly reduced to BARBARA and indirectly reduced to CELARENT.

Question 22.
Reduce ‘FESAPO’ both directly and indirectly.
Answer:
Direct Reduction of ‘FESAPO’

Suppose this conclusion is false. If it is false, its contradictory ‘A’ = All is S is P in true. Taking this new proposition as the major premise and the original minor as the minor, let’s form a new syllogism;

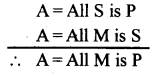
Now we see that the converse of the new conclusion is the contradictory of the original major premise. Both cannot be true. One must be false. The original premise cannot be false as in the deductive reasoning the premises are always taken to be true. So the new conclusion is false. The falsity can arise out of two ways. If there is mistake in the premises or if we have violated the rules of syllogism. We have not violated the rules of syllogism for which it is the valid mood BARBARA’ of 1st figure. So the mistake is in the premises. The minor premise cannot be wrong beca use it is the original minor premise. So the major premise is false which is the contradictory of the original conclusion. So the original conclusion is proved to be true.

Question 23.
Reduce ‘FESTINO’ both directly and indirectly.
Answer:
Direct Reduction of FESTINO

Let’s take the original,conclusion as false and its contradiction (A = All S is P) as true. Taking this new proposition as# the minor premise and the original major as the major, let’s form a new syllogism.

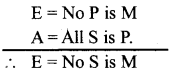
Here we see that the new conclusion in the contradictory of the original minor premise. Both cannot be true. One must be false. The original minor premise cannot be false as in deductive reasoning the original premises are always taken to be true. So the new conclusion is false. This falsity can arise out of two ways. If there is any mistake in the premises or if we have violated the rules of syllogism. We have not violated the rules of syllogism for which it is the valid mood CELARENT of 1st figure. So there is mistake in the premises. The major premise cannot be wrong as it is the original major. So the mistake is in the minor premise. If the minor premise is false, then its contradictory the original conclusion is true.

Question 24.
Explain Aristotle’s Dictum and determine its role in reduction.
Answer:
Aristotle, the father of deductive Logic, has formulated a rule in order to test the validity of syllogistic arguments, that is the fundamental principle of syllogism known as “Dictum de omni et nullo”, which means “Statement concerning all and none”.

Now we can see that the new conclusion is the contradictory of the original minor premise. Both can not be true. One must be false. In deductive syllogism premises are always taken to be true. So the new conclusion is false. The falling can arise out of two ways, if there is mistake in the premises or if we have violated the rules of syllogism. We have not violated the rules of syllogism for which it is the valid mood FERIO of 1st figure. So the mistake is in the premises. The major premise can not be wrong because it is the original major premise. So the falsity lies in the minor promise. If the minor premise is wrong, its contradictory, the original conclusion is true.

Question 25.
Reduce ‘BAROCO’ both directly and indirectly.
Answer:
DIRECT REDUCTION OF “BAROCO” BAROCO (FAKSOKO) → FERIO

Suppose the conclusion is false, It’s false, its contradictory “A = All is P” is true. Taking this new proposition as the minor premise and the original major as the major, lets form a new Syllogism.

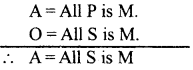
Now we can see that the new conclusion is the contradictory of the original minor premise. Both cannot be true. One must be false. In deductive reasoning the premises are always taken to be true. So the new conclusion is false. The falsity can arise out of two ways. If there is any mistake in the premises or if we have violated the rules of syllogism.

We have not violated the rules of syllogism for which it is the valid mood ‘BARBARA’ of 1 st figure which is the perfect figure. So the mistake is in the premises. The major premise cannot be wrong as it is the original major premise. So the mistake is the minor premise which is the contradictory of the original conclusion. So the original conclusion is proved to be true. From the above it is said that ‘BAROCO’ is directly reduced to FERIO and indirectly reduced to BARBARA.

Question 26.
Reduce ‘DATISI’ both directly and indirectly.
Answer:
DIRECT REDUCTION OF ‘DATISI’

In the above valid mood let’s take the original conclusion “I = Some S is P” is false (F) and its contradiction ‘E’ = No S is P” is true. As per the rules of indirect reduction. Let’s take the original major true (T) and minor premise “I = Some M is S” as false (F). Here we should take the contradiction form of the original conclusion, in case of the minor premise, which we have taken as False.
Let’s construct the new form of Syllogism.

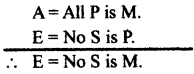
From the above it is proved that ‘DASTI’ is directly reduced to ‘DARIF and indirectly reduced to CAMESTRES.

Question 27.
Reduce ‘DISAMIS’ both directly and indirectly.
Answer:
DIRECT REDUCTION OF ‘DISAMIS’.

Suppose the conclusion is false. If it is false, its contradictory ‘E = No S is P’ is true. Taking this new proposition as the major premise and the original minor as minor, Let us a new syllogism

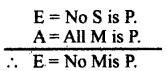
Now we can see that the new conclusion is the contradictory of the original major premise. Both cannot be true. One must be false. The original major premise cannot be wrong because in deductive reasoning premises are always taken to be true. So the new-conclusion is false. The falsity can arise out of two ways. It there is mistake in the premises or if we have violated the rules of syllogism.

We have not violated the rules of syllogism for which it is the valid mood ‘CELARENT’ of the perfect first figure. So the mistake is in the premises. The minor premise cannot be false because it is the original minor premise. So the mistake is in the major premise which is the contradictory of the original conclusion. So the original conclusion is proved to be true. From this above it is said that ‘DISAMIS’ is directly reduced to ‘DARII’ and indirectly reduced to “CLEARENT”.

Question 28.
Reduce “FRESISON” both directly and, indirectly.
Answer:
DIRECT REDUCTION OF “FRESISON”

Suppose the original conclusion is false. It is false. If it is false, its contradictory “A = All S is P” must be true. Taking this new proposition as the minor premise and the original major premise as the major, Let us form a new syllogism:

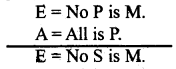
This is ‘CELARENT’ of first figure and ‘p’ as the middle term. Now we see that the converse of the new conclusion is the contradictory of the original minor premise. So both cannot be true together. One must be false. The original minor premise cannot be false as inductive reasoning the original premises are always taken to be true. So the new conclusion and its converse is false. Falsity can arise out of two ways. If there is any mistake in the premises or if we have violated the rules of Syllogism.

We have not violated the rules for which it is the valid mood “CELARENT” of first figure and its converse. So there is mistake in the premises. The major premise cannot be wrong as it is the original major. So the mistake is in the minor premise. If the minor premise is false, then its contradictory, the original Conclusion ‘O’ = some S is not P must be true. Thus ‘FRESISON” is a valid mood of Fourth figure.
From this above it is said that ‘FRESISON’ is directly reduced to ‘FERIO’ and indirectly reduced to CELARENT.

Question 29.
Show that obversion and simple conversion give equivalent conclusions, but partial conversion gives a non-equivalent conclusion.
Answer:
A conclusion is equivalent, if by repeating the same Logical process we obtain the original proposition. It is non-equivalent, if we cannot come back to the original proposition by the repetition of the inferential process. Obversion :

Question 30.
Prove : Major premise must be universal in the A, first figure
Answer:
One of the special Syllogistic rule of the figure (one) says that major premise must be universal. But if the major premise be not universal in the first figure then it must be particular. If the major premise is particular then in that case the middle term (M) which is the subject cannot be distributed. So the fallacy of “undistributed middle” will arise. But in order to avoid the fallacy of undistributed middle, it must be distributed in the minor premise, where the middle term is predicate. So if we will take minor premise as a negative proposition then it will distribute its predicate and the fallacy of undistributed middle will never occur.

Again if we take minor premise as Negative proposition (E/O) then in that case major premise will be affirmative and the conclusion will be negative, it will be distribute its major term (P) which will never be distribute in case of the major premise. Because major premise as affirmative cannot be distributed its predicate. So we commit the fallacy of illicit major. Again we can avoid the fallacy of illicit major if the major term (P) will be distributed in the major premise.

It means if the major premise will be negative proposition, it will distribute. Its predicate (P). But we cannot take-only negative proposition in case of the major premise, Because we have already taken the negative proposition in case of minor premise. All the above fallacies arise as we have taken the major premise as particular. So it is proved that the major premise must be universal in the first figure.

Question 31.
Prove : Major premise must be universal in the 2nd figure.
Answer:
One of the special Syllogistic rule in the 2nd figure (2) says that major premise must be universal But if the major premise be not universal then it must be particular (10). Suppose if we will take major premise as 1 then in the case the middle term will never distribute. So we will take minor premise as ‘E’ proposition. Then the conclusion will be ‘O’ which will always distribute its predicate but will never distribute in case of the major premise, as a result of which we will commit the fallacy of illicit major.

Again it will take major premise as ‘0’ and minor premise as ‘A’ then the conclusion will be ‘O’. If it be so then in the case the major term will be distribute. Which will never distribute in case of major premise and automatically we will commit the fallacy of illicit major. From this above discussion this proved that major premise must be universal in 2nd figure.

Question 32.
Prove the Special Syllogistics rules of 4th figure.
Answer:
(a) If the major premise is affirmative, the minor premise must be universal:
If the major premise is affirmative, it does not distribute it predicate, i.e., the middle term. To avoid the fallacy of undistributed middle, the middle term must be distributed in the minor premise, where it is the subject. So in this case, the minor premise must be universal.

(b) If any premise is negative, the major premise must be universal:
If any premise is negative, the conclusion must be negative and the major term is distributed in the conclusion. To avoid the fallacy of illicit major, the major term must be distributed in the major premise where it is the subject. So in this case, the major must be universal.

(c) Both the premise cannot be negative : If both the-premises are negative no conclusion follows. This is one of the general Syllogist rules. It is started as a special Syllogistic rule of figure IV. In order to make the special Syllogistic rules self-sufficient to determine, the valid mood of this figure.

(d) If the major premise is affirmative, the conclusion is particular. If the minor premise is affirmative, the minor term is not distribute in the minor premise, consequently it can not be distributed in the conclusion, where it is the subject. So, in this case, the conclusion must be particular.

Question 33.
Prove the following :
(a) The middle term cannot be distributed twice in figure I & figure II.
(b) ‘O’ proposition can not be a premise in figure ‘IV’.
Answer:
(a) The position of the terms in fig 1 is :
M P
S M
∴ S P

If the middle term is distributed twice, then the major premise is universal and. the minor premise is negative. The minor premise being negative, the conclusion must be negative and the major premise must be affirmative. In that case, the major term is distributed in the conclusion, but not distributed in the major premise leading to the fallacy of illicit major. So, the middle term cannot be distributed twibe ill Fig. 1.

The Position of the terms in Fig. II is :
P M
S M
∴ S P

If the middle term is distributed twice, then both the premises are negative and no conclusion follows. So, the middle term cannot be distributed twice on Fig. II.

(b) It one premise be 0, the other premise must be A, and the conclusion must be 0. So, the mood is either OAO or AOO in fig I both these moods are invalid.

O – Some M is not P.
A – All S is M.
O – Some S is not P.
Here, the middle term is not at all distributed. So it commits the fallacy of Undistributed Middle.
A – All M is P.
O – Some S is not M.
∴ O – Some S is not P.
Here the major term is distributed in the contusion, but not distributed in the major premise. So, it commits the fallacy of Illicit Major, Therefore O cannot be a premise in Fig.l.

Question 34.
Prove the following :
(a) If in a Syllogism only two terms are distributed twice, the conclusion must be ‘O’.
(b) If in the minor term in predicate in the minor premise the conclusion cannot be ‘A’.
Answer:
(a) Here, of the two distributed terms, one must be the middle term to avoid the fallacy of Undistributed Millde. If the millde term is distributed twice, the conclusion must be particular; i.e., I or O. If is 1, neither the minor nor the major term can be distributed. So the condition ‘two terms distributed twice’ cannot be fulfilled. Thus the only possibility left is that the conclusion is O. The premises, here, are EA and the mood is EAO.

(b) The minor term in the minor premise is either distributed or undistributed. If it is distributed, the minor premise is negative. So, the conclusion cannot be affirmative, i.e. the conclusion cannot be A. If it is undistributed, it cannot be distributed in the conclusion. So the conclusion cannot be universal, i.e. the conclusion cannot be A. Thus, if the minor term is predicate in the minor premise, the conclusion cannot be A.

Question 35.
Why ‘El’ is valid in every figure, but ‘IE’ is valid in None.
Answer:
The major premise ‘E’ distributes the major term and the middle term whatever be their positions. The minor premise does not distribute the middle term, whatever be its position, in whatever figure the argument may be, the distributed and undistributed terms remain the same. The distributed and undistributed terms are adequate to justify the conclusion = 0. where the minor term is undistributed and the major terms is distributed. The rules regarding the quality and quantity are also not violated, if the conclusion in 0. So ‘EIO’ is valid mood in all figures. It is called FERIO in figure one, FESTINO in figure TWO, FERISON in figure three and FRESISON in figure four.

The major premise T does not distribute the major term, whatever be its position. The negative minor premise leads to a Negative conclusion, which distributed its major term. So, we commit the fallacy of illicit major, whatever be the figure of syllogism. So, TEO’ is not valid in any figure.

Question 36.
Reduce ‘CESARE’ both directly and indirectly.
Answer:
Direct Reduction of ‘CESARE’

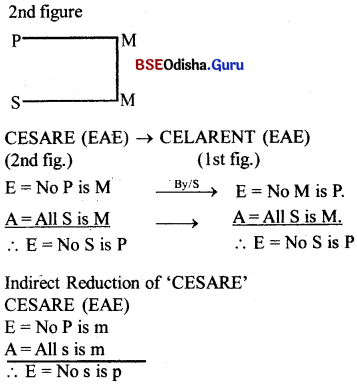
In the above imprefect mood (CESARE) let’s first take the original conclusion (E = N o S is p) as false and its contradiction (I = some S is P) as true. As per the rales of indirect reduction let’s take major premise of CESARE as true and minor premise of CESARE as false. Let’s take the contradiction of the conclusion (I = some S is P) as a new premise in case of the minor premise of ‘CESARE’ which we have taken as false. By taking the major premise of ‘CESARE’ E = No P is M and minor premise I = some S is P, let’s construct the new form of syllogism.

From the above it is said that ‘CESARE’ is directly reduced to CELARENT and indirectly reduced to FERIO.

Question 37.
Reduce ‘DARASPTP both directly and indirectly.
Answer:
Direct Reduction of ‘DARAPTI’

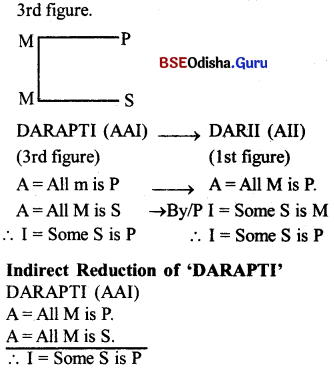
In the above imperfect mood (DARAPTI), Let’s first take its original conclusion (I = Some S is P) as false and its contradiction (E = NO S is P) as true.

As per the rales of indirect reduction let’s take the major premise of DARAPTI as false and minor premise as true. Let’s take the contradiction (E = NO S is P) of the original conclusion as a new premise in case of the major premise of DARAPTI, which we have taken as false. By taking the major premise of DARAPTI as I = Some S is P and minor premise of DARAPTI as A = All M is S, Let’s construct the new form of syllogism.

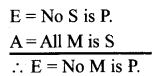
From the above it is said that ‘DARAPTE is directly reduced to ‘DARIE and indirectly reduced to CELARENT.

Question 38.
Reduce ‘FERISON’ both directly and indirectly.
Answer:
Direct Reduction of ‘FERISON’

In the above imperfect mood (FERISON), Let’s first take the original conclusion (O = Some S is not P) as false and its contradiction.
(A = All S is P) as true.

As per the rules of indirect reduction let’s take the major premise of FERISOn (E = No M is P) as false and the minor premise of FERISON (I = Some M is S) as true. Let’s take the contradiction form (A = All S is P) of original conclusion as a new premise in case of the major premise of FERISON, which we have taken as false.

By taking the major premise of ‘FERISON’ as (A = All S is P), minor premise of FERISON ad (I = Some M is S) true, Let’s construct the new form of syllogism.

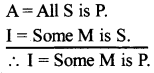
From the above it is said that FERISON is directly reduced to ‘FERIO’ and indirectly reduced to ‘DARII’.

Question 39.
Reduce ‘DIMARIS’ both directly and indirectly.
Answer:
Direct Reduction of ‘DIMARIS’

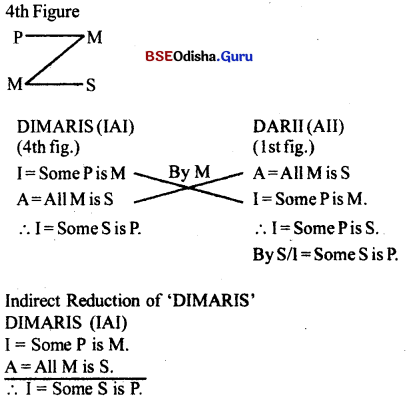
In the above imperfect mood DIMARIS, let’s take first the friginal conclusion (I = Some S is P) as false and its contradiction form (E = No S is P) as true.

As per the rules of indirect reduction, let’s take the major premise of DIMARIS as false and minor premise of DIMARIS as true. Let’s take the contradiction form of the conclusion as a new premise in case of the major premise of ‘DIMARIS’ which we have taken as false.
By taking major premise as (E = No S is P) and minor premise as (A = All M is S), let’s construct the new form of syllogism.

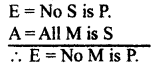
From the above it is said that ‘DIMARIS’ is directly reduced to ‘DARII’ and indirectly reduced to ‘CELARENT’.

Group – C

I. Multiple Choice Questions with Answers :

Question 1.
Syllogism is:
(i) An immediate inference
(ii) A mediate inference
(iii) Both immediate and mediate inference
(iv) None of these
Answer:
(ii) A mediate inference

Question 2.
Pick the odd man out:
(i) Major term
(ii) Minor term
(iii) Middle term
(iv) Equivocal term
Answer:
(iv) Equivocal term

Question 3.
The middle term must be distributed in the premises :
(i) Once
(ii) Twice
(iii) Ateast once
(iv) None of these
Answer:
(iii) Ateast once

Question 4.
In which figure the middle term take the position of the subject in both the premises?
(i) Figure-I
(ii) Figure-II
(iii) Figure-III
(iv) Figure-IV
Answer:
(iii) Figure-III

Question 5.
How many moods are possible in each figure by considering the quality and quantity of only premises?
(i) 16
(ii) 19
(iii) 64
(iv) 256
Answer:
(i) 16

Question 6.
A term which is ret distributed in the premise of a syllogism :
(i) May be distributed in the conclusion
(ii) May or may not be distributed in the conclusion
(iii) Must be distributed in the conclusion
(iv) Must not be distributed in the conclusion
Answer:
(iv) Must not be distributed in the conclusion

Question 7.
From two negative premises, we derive :
(i) A valid conclusion
(ii) An invalid conclusion
(iii) Either a valid or an invalid conclusion
(iv) None the these
Answer:
(ii) An invalid conclusion

Question 8.
Which figure has not weakened moods?
(i) Figure-I
(ii) Figure-II
Answer:
(iii) Figure-Ill

Question 9.
Which of the following is not a weakened mood ?
(i) Barbari
(ii) Camestros
(iii) Darapti
(iv) Camenos
Answer:
(iii) Darapti

Question 10.
In which of the following figures in the AA combination of premises not valid?
(i) Figure-I
(ii) Figure-II
(iii) Figure-III
(iv) Figure-IV
Answer:
(ii) Figure-II

Question 11.
A syllogism is invalid if:
(i) Both the premises are universal
(ii) Both the premises are affirmative
(iii) Both the premises are negative
(iv) One of the premises is negative
Answer:
(iii) Both the premises are negative The mood ‘AAF’ is invalid in :
(i) Figure-I
(ii) Figure-II
(iii) Figure-Ill
(iv) Figure-IV
Answer:
(ii) Figure-II

Question 12.
The mood ‘AAF’ is invalid in:
(i) Figure-I
(ii) Figure-II
(iii) Figure-III
(iv) Figure-IV
Answer:
(ii) Figure-II

Question 13.
Which combination of premises is valid in all figures ?
(i) AA
(ii) AE
(iii) EA
(iv) El
Answer:
(iii) EA

Question 14.
How many propositions are there in syllogism?
(i) Three
(ii) Four
(iii) Five
(iv) Two
Answer:
(i) Three

Question 15.
How many premises are there in syllogism ?
(i) Three
(ii) Four
(iii) Two
(iv) Five
Answer:
(iii) Two

Question 16.
How many terms are there in syllogism?
(i) Two terms
(ii) Three terms
(iii) Four terms
(iv) Five terms
Answer:
(ii) Three terms

Question 17.
The first proposition of a syllogism is called :
(i) Minor premise
(ii) Major Premise
(iii) Conclusion
(iv) None of these
Answer:
(ii) Major premise

Question 18.
The second proposition of a syllogism is called :
(i) Major premise
(ii) Conclusion
(iii) Minor premise
(iv) Conclusion
Answer:
(iii) Minor premise

Question 19.
The third proposition of a syllogism is called.
(i) Major premise
(ii) Minor premise
(iii) Conclusion
(iv) Middle term
Answer:
(iii) Conclusion

Question 20.
The first premise of syllogism is called:
(i) Major premise
(ii) Minor premise
(iii) Conclusion
(iv) None of these
Answer:
(I) Major premise

Question 21.
The second premise of syllogism is called:
(i) Major premise
(ii) Minor premise
(iii) Conclusion
(iv) None of these
Answer:
(i) Minor premise

Question 22.
Hoe many general syllogistic rules are there?
(i) Ten
(ii) Nine
(iii) Eight
(iv) Seven
Answer:
(i) Ten

Question 23.
How many figures are there in syllogism?
(i) Five
(ii) Six
(iii) Four
(iv) Eight
Answer:
(iii) Four

Question 26.
What is the position of middle term in the second figure?
(i) Subject in both the premises
(ii) Predicate in both the premises
(iii) Subject in major and predicate in minor premise
(iv) Predicate in major and subject in minor premise
Answer:
(ii) Predicate in both the premises

Question 27.
What is the position of middle term in the third figure?
(i) Subject in both the premises
(ii) Predicate in both the premises
(iii) Subject in major and predicate in premise
(iv) Predicate in major and subject in premise
Answer:
(i) Subject in both the premises

Question 28.
What is the position of middle term in the fourth figure?
(i) Subject in both the premises
(ii) Predicate in both the premises.
(iii) Subject in major and predicate in minor premise
(iv) Predicate in major and subject in minor premise.
Answer:
(iv) Predicate in major and subject in minor premise.

Question 29.
Subject term of the conclusion of a syllogism is called which term?
(i) Major term
(ii) Minor term
(iii) Middler term
(iv) None of these
Answer:
(ii) Minor term

Question 30.
The predicate term of the conclusion of syllogism is called which term?
(i) Major term
(ii) Minor term
(iii) Middle term
(iv) Cannot say
Answer:
(i) Major term

Question 31.
The term which absent in the conclusion is called which term?
(i) Major term
(ii) Minor term
(iii) Middle term
(iv) None of these
Answer:
(iii) Middle term

Question 32.
There are two terms in major premise, one is major term other is:
(i) Minor term
(ii) Middle term
(iii) Major term
(iv) No other term is present
Answer:
(ii) Middle term

Question 33.
Which term must be distributed at atleast once in any of the premises?
(i) Major term
(ii) Minor term
(iii) Middle term
(iv) None of these
Answer:
(iii) Middle term

Question 34.
If the middle term is not distributed in any of the premises then we commit which fallacy?
(i) Illicit major
(ii) Undistributed Middle
(iii) Illicit minor
(iv) Four terms
Answer:
(ii) Undistributed Middle

Question 35.
If a syllogism is consisted of more than three terms then which fallacy arises?
(i) Illicit major
(ii) Four terms
(iii) Undistributed middle
(iv) Illicit minor
Answer:
(ii) Four terms

Question 36.
When the minor term is distributed in the conclusion without being distributed in the minor premise, we commit which fallacy?
(i) Undistributed middle
(ii) Four terms
(iii) Illicit minor
(iv) Illicit major
Answer:
(iv) Illicit major

Question 37.
When the minor term is distributed in the conclusion without being distributed in the minor premise, we commit which fallacy?
(i) Illicit major
(ii) Illicit minor
(iii) Fallacy of four terms
(iv) Undistributed middle
Answer:
(ii) Illicit minor

Question 38.
Is it correct to say that if both the premises are negative, the conclusion is negative?
(i) Yes
(ii) No
(iii) Partially correct
(iv) Cannot say
Answer:
(ii) No.

Question 39.
When we draw the conclusion out of two negative premises then we commit which fallacy?
(i) Fallacy of two negative premises
(ii) Fallacy of two particular premises
(iii) Fallacy of undistributed middle
(iv) No fallacy arises.
Answer:
(i) Fallacy of two negative premises

Question 40.
If both the premises are affirmative then the conclusion will be what?
(i) Affirmative
(ii) Negative
(iii) Particular
(iv) No conclusion
comes
Answer:
(i) Affirmative

Question 41.
If both the premises are particular then the conclusion will be what?
(i) Affirmative
(ii) Particular
(iii) Negative
(iv) No conclusion comes
Answer:
(ii) Particular

Question 42.
When the major premise be particular and minor premise be negative then the conclusion will be what?
(i) Affirmative
(ii) Negative
(iii) Universal
(iv) No conclusion will be follow
Answer:
(iv) No conclusion will be follow

Question 43.
If one of the premise be particular, the conclusion will be what?
(i) affirmative
(ii) universal
(iii) particular
(iv) none of these
Answer:
(iii) particular

Question 44.
Mood of the syllogism in mainly determined by :
(i) Quality of the premises
(ii) Quantity of the premises
(iii) Both quality and quantity of the premises
(iv) Position of the middle term.
Answer:
(iii) Both quality and quantity of the premises

Question 45.
According to first group of logicians, the number of possible moods of four different figures are:
(i) 16
(ii) 64
(iii) 256
(iv) 4
Answer:
(ii) 64

Question 46.
How many valid mood are in four different figures?
(i) 16
(ii) 64
(iii) 19
(iv) 225
Answer:
(iii) 19

Question 47.
How many valid moods are there in the first figure?
(i) Four
(ii) Three
(iii) Six
(iv) Eight
Answer:
(i) Four

Question 48.
How many valid moods are there in the second figure?
(i) Three
(ii) Four
(iii) Five
(iv) Six
Answer:
(ii) Four

Question 49.
How many valid moods are there in the third figure?
(i) Four
(ii) Five
(iii) Six
(iv) Eight
Answer:
(iii) Six

Question 50.
How many valid moods are in the 4th figure?
(i) Four
(ii) Five
(iii) Six
(iv) Eight
Answer:
(ii) Five

Question 51.
How many fundamental moods are there in syllogism?
(i) 15
(ii) 16
(iii) 18
(iv) 8
Answer:
(i) 15

Question 52.
How many strengthened moods are there in syllogism?
(i) 15
(ii) 16
(iii) 5
(iv) 8
Answer:
(iv) 8

Question 53.
How many weakened moods are there in syllogism ?
(i) five moods
(ii) six moods
(iii) eight moods
(iv) nine moods
Answer:
(i) five moods

II. Fill in the blanks :

Question 1.
Syllogism is a ______ kind of inference.
Answer:
mediate

Question 2.
A syllogism is consisted of _____ proposition .
Answer:
Three

Question 3.
A syllogism is consisted of _____ premises.
Answer:
Two

Question 4.
The two propositions from which the conclusion is drawn in a syllogism are called as _____
Answer:
Premises

Question 5.
The conclusion of a syllogism cannot be more _____ than the premises.
Answer:
general

Question 6.
The three terms in a syllogism occur _____ each in it.
Answer:
Twice

Question 7.
The term which occurs twice in the premises is called as the _____ term.
Answer:
middle

Question 8.
The first proposition of a syllogism is called _____ premise.
Answer:
Major

Question 9.
The second proposition of a syllogism is called _____ premise.
Answer:
Minor

Question 10.
The third proposition of a syllogism is called _____ .
Answer:
Conclusion

Question 11.
The three terms of a syllogism are called _____ and _____ .
Answer:
major, minor, middle term

Question 12.
The predicate of the conclusion is called _____ term.
Answer:
Major term

Question 13.
The subject of the conclusion is called _____term.
Answer:
Minor term

Question 14.
The premise in which the major term occurs is the _____ premise.
Answer:
Major

Question 15.
The premise in which the minor term occur is the _____ premise.
Answer:
Minor

Question 16.
The denotation of the major term is _____ than the denotation of the minor term.
Answer:
more

Question 17.
The symbol of the major term is _____
Answer:
‘P’

Question 18.
The symbol of the minor term is _____
Answer:
‘S’

Question 19.
The symbol of the middle term is _____
Answer:
M’

Question 20.
Syllogisms are of two kinds, namely, _____ and _____ Syllogisms.
Answer:
Pure, mixed

Question 21.
Figure of the syllogism is mainly determined by the position of _____ term.
Answer:
Middle

Question 22.
There are _____ figures in syllogism.
Answer:
Four

Question 23.
The figure _____ is called _____ figure
Answer:
First

Question 24.
In the 1st figure the middle term is _____
Answer:
Subject of the major premise and predicate in the minor premise.

Question 25.
In the second figure the middle term is _____.
Answer:
Predicate of both the premises.

Question 26.
In the third figure middle term is _____.
Answer:
subject of both the premises

Question 27.
In the fourth figure middle term is _____.
Answer:
Predicate of the major premise and subject of the minor premise.

Question 28.
There are _____ general syllogistic rules.
Answer: Ten

Question 29.
If a syllogism is consisted of more than three propositions, we commit _____ fallacy.
Answer:
Train of syllogism

Question 30.
If a syllogism is consisted of more than three terms, we commit the fallacy of _____.
Answer:
Four terms

Question 31.
Middle term must be _____ at least once in an of the premises.
Answer:
Distributed

Question 32.
When the middle term is not distributed in any of the premises we commit _____ fallacy.
Answer:
undistributed middle

Question 33.
When the major term (p) is distributed in the conclusion without being distributed in the major premise at that time _____ fallacy arises.
Answer:
Illicit major

Question 34.
When the minor term(s) is distributed in the conclusion without being distributed in the minor premise at that time we commit _____ fallacy.
Answer:
Illicit minor

Question 35.
If one of the premise be negative then other premise must be _____ .
Answer:
Affirmative .

Question 36.
If one of the premise be negative then the conclusion must be _____ .
Answer:
Negative

Question 37.
If both premises are negative then the conclusion will be _____ .
Answer:
inpossible

Question 38.
From two negative premises if the conclusion will be drawn then _____.
Answer:
The fallacy of two negative premises arises.

Question 39.
If both the premises are affirmative the conclusion will be _____.
Answer:
affirmative :

Question 40.
If both the premises are particular, the conclusion must be _____.
Answer:
particular

Question 41.
Out of two premises, if one premise be particular the conclusion will be _____.
Answer:
particular

Question 42.
From particular major and negative minor _____ conclusion comes.
Answer:
no

Question 43.
Mood of the syllogism is determined by the _____ and _____ if the premises.
Answer:
quality, quantity

Question 44.
According to the 1 st group of logicians, there are _____ moods in syllogism!
Answer:
64

Question 45.
According to second group of logicians there are _____ moods in syllogism.
Answer:
256

Question 46.
According to Aristotle, there are _____ types of valid moods in syllogism.
Answer:
19

Question 47.
The weakened or the sub-altern moods in figure one are _____ and _____.
Answer:
Barbari, celaront

Question 48.
The weakened or the sub-altern moods in figure one are _____ and _____.
Answer:
camestros, cesaro.

Question 49.
There is no sub-altern‘mood in _____.
Answer:
third

Question 50.
The sub-altern mood in figure four is _____.
Answer:
Camenos

Question 51.
Elina Loves Lipina.
Lipika loves Rani.
∴ Rani loves Elina.
Answer:
Four terms

Question 52.
‘BOCARDO’is the valid mood of _____ figure.
Answer:
third

Question 53.
‘DARAPTF’ is the valid mood of _____ figure.
Answer:
third

Question 54.
‘BRAMANTIP’ is the valid mood of _____ figure.
Answer:
Fourth

Question 55.
‘CAMENES’ is the valid mood of _____ figure.
Answer:
fourth

Question 56.
The other name of ‘BAROCO’ is _____ .
Answer:
FAKSOKO

Question 57.
‘DIMARIS’ is the valid mood of _____ figure.
Answer:
fourth

Question 58.
‘FESTINO’ is the valid mood of _____ figure.
Answer:
second

Question 59.
The other name of ‘BOCARDO’ is _____.
Answer:
DOKSAMOSK

Question 60.
Reduction is divided into _____ and _____.
Answer:
direct, indirect

Question 61.
In Reduction the letter ‘M’ means _____.
Answer:
Mutual transposition of the premises

Question 62.
In reduction the letter ‘S’ means _____.
Answer:
Simple conversion

Question 63.
In reduction the letter ‘P’ means _____.
Answer:
partial conversion

Question 64.
In reduction the letter ‘K’ means _____.
Answer:
obversion

Question 65.
‘CAMESTRES’ is directly reduced to _____.
Answer:
CELARENT

Question 66.
‘CESARE’ is directly reduced to _____.
Answer:
CELARENT

Question 67.
‘FESTINO’ is directly reduced to _____ .
Answer:
FERIO

Question 68.
“BAROCO” is directly reduced to _____ .
Answer:
FERIO

Question 69.
‘DARAPTF is directly reduced to _____.
Answer:
DARII

Question 70.
‘DATISI’ is directly reduced to _____ .
Answer:
DARII

Question 71.
‘DISAMIS’ is directly reduced to _____.
Answer:
DARII

Question 72.
FELAPTON is directly reduced to _____.
Answer:
FERIO

Question 73.
‘FERISON’ is directly reduced to _____.
Answer:
FERIO

Question 74.
‘BOCARDO’ is directly reduced to _____.
Answer:
DARII

Question 75.
‘BRAMANTIP’ is directly reduced to _____.
Answer:
BARBARA

Question 76.
‘CAMENES’ is directly reduced to _____.
Answer:
CELARENT

Question 77.
‘FESAPO’ is directly reduced to _____.
Answer:
FERIO

Question 78.
‘FRESISON’ is directly reduced to _____.
Answer:
FERIO

Question 79.
‘DIMARIS’ directly reduced to _____.
Answer:
DARIF

Question 80.
The process of proving the validity of the mood of the imperfect figures with the help of the perfect moods is called _____.
Answer:
Reduction

Question 81.
If the conclusion be ‘A’, the argument must be in _____.
Answer:
figure one

Question 82.
______ proposition cannot be a premise either in figure one or in figure four.
Answer:
‘O’ proposition

Question 83.
The middle term cannot be distributed twice in _____and _____.
Answer:
Figure one and figure two

Question 84.
Figure are _____ fundamental moods in syllogism.
Answer:
15

Question 85.
There are _____ strengthened moody in syllogism.
Answer:
8

Question 86.
There are _____ weakened moods in syllogism.
Answer:
five

Question 87.
If the conclusion is universal, the middle term can be distributed _____.
Answer:
only once

Question 88.
If the major term is predicate in the major premise, the minor premise must be _____.
Answer:
affirmative

Question 89.
If the middle term is distributed twice, the conclusion must be _____.
Answer: particular

Question 90.
In a syllogism if two terms are distributed twice, the conclusion must be _____.
Answer:
‘O’ proposition

Question 91.
If the minor term is predicate in the minor premise, the conclusion cannot be _____.
Answer:
‘A’ proposition

Question 92.
‘BAROCO’ is indirectly reduced to _____.
Answer:
BARBARA

Question 93.
BOCARDO’ is indirectly reduced to _____.
Answer:
CELARENT .

Question 94
‘DARAPTI’ is indirectly reduced to _____.
Answer:
CELARENT ,

Question 95.
‘DARAPTF’ is indirectly reduced to _____
Answer:
CELARENT

Question 96.
‘DISAMIS’ is indirectlyreduced to _____.
Answer:
CELARENT

Question 97.
‘CAMENES’ is indirctly reduced to _____.
Answer:
DARII

Question 98.
‘FEST1NO’ is indirectly reduced to _____.
Answer:
CELARENT

Question 99.
There _____ are special syllogistic rules in the first figure.
Answer:
Two

Question 100.
There are _____ special syllogistic rules in the figure two.
Answer:
Three

Question 101.
There are _____ special syllogistic rules in the figure three.
Answer:
Three

Question 102.
There are _____ special syllogistic rules in the figure four.
Answer:
Four

Question 103.
Major premise must be _____ in the first figure.
Answer:
Universal

Question 104.
Minor premise must be _____ in the first figure.
Answer:
affirmative

Question 105.
In the second figure the major premise is _____ .
Answer:
Universal

Question 106.
In the second figure the conclusion is _____.
Answer:
Negative

Question 107.
In the second figure one premise must be _____.
Answer:
Negative

Question 108.
The minor premise must be _____ in the third figure.
Answer:
Affirmative

Question 109.
At least one premise must be _____ in the third figure.
Answer:
Universal

Question 110.
The conclusion must be _____.
Answer:
Particular

Question 111.
In the fourth figure, if the major premise is affirmative, the minor premise must be _____
Answer:
Universal

Question 112.
Both the premises cannot be _____ in the 4th figure.
Answer:
Negative

Question 113.
If the minor premise is affirmative, the conclusion _____ is in 4th figure.
Answer:
Particular

Question 114.
‘Aristotle’s Dictum de omniet nullo’ means _____.
Answer:
Statements concerning all and none

Question 115.
_____ figure is called perfect figure.
Answer:
First

Question 116.
There are _____ imperfect figures in syllogism perfect moods in syllogism.
Answer:
Three

Question 117.
There are _____ perfect moods in syllogism.
Answer:
Four

Question 118.
There are _____ imperfect mods in syllogism.
Answer:
15

III. Correct the Sentences :

Question 1.
Syllogism is an immediate deductive inference.
Answer:
Syllogism is mediate deductive inference.

Question 2.
Syllogism is consisted of two propositions.
Answer:
Syllogism is consisted of three propositions.

Question 3.
Syllogism is consisted of three premises.
Answer:
Syllogism is consisted of three propositions.

Question 4.
There are four terms in Syllogism.
Answer:
There are three terms in syllogism.

Question 5.
There are five figures in Syllogism.
Answer:
There are four figures in syllogism.

Question 6.
The subject of the conclusion of syllogism is called major term.
Answer:
The subject of the conclusion of syllogism is called minor term.

Question 7.
The predicate of the conclusion of syllogism is called minor term.
Answer:
The predicate of the conclusion of a syllogism is called major term.

Question 8.
The term which is commonly present in both the premises is called minor term.
Answer:
The term which is commonly present in both the premises is called middle term.

Question 9.
The premise, in which the major term is present is called minor premise.
Answer:
The premise, in which the major term in present is called major premise.

Question 10.
The premise, in which the minor term is present is called major premise.
Answer:
The premise, in which the minor term is present is called minor premise.

Question 11.
The symbol of major term is‘S’.
Answer:
the symbol of minor term is ‘S’.

Question 12.
The symbol of minor term is ‘M’
Answer:
The symbol of middle term is ‘M’

Question 13.
The symbol of middle term is ‘P’.
Answer:
The symbol of major term is ‘P’.

Question 14.
There are five figures in Syllogism.
Answer:
There are four figures in Syllogism.

Question 15.
There are 12 general rules in syllogism.
Answer:
There are 10 general rules in syllogism.

Question 16.
Figure of the Syllogism is determined by the position of the major term.
Answer:
Figure of the Syllogism is determined by the position of the middle term.

Question 17.
If the middle term is distributed twice, the conclusion must be universal.
Answer:
If the middle term is distributed twice, the conclusion must be particular.

Question 18.
In the third figure, middle term is present in the predicate place of both the premises.
Answer:
In the second figure, middle term is present in the predicate place of both the premises.

Question 19.
In the second figure, middle term is present in the subject place of both the premises.
Answer:
In the third figure, middle term is present in the subject place of both the premises.

Question 20.
In the first figure middle term is present in the predicate of the major premise and subject in the minor premise.
Answer:
In the fourth figure middle term is present in the predicate of the major premise and subject in the minor premise. .

Question 21.
In the fourth figure, middle term is present in the subject place of the major premise and predicate place of the minor premise.
Answer:
In the first figure, middle term is present in the subject of the major premise and predicate place of minor premise.

Question 22.
In a syllogism, if both the premises are negative, the conclusion must be negative.
Answer:
In a syllogism, if both the premises are negative, no conclusion will be follow.

Question 23.
In a Syllogism, if one of the premise be negative then no conclusion follows.
Answer:
In a syllogism, if one of the premise be negative then the conclusion must be negative.

Question 24.
In a syllogism, if both the premises are affirmative, the conclusion must be Universal.
Answer:
In a syllogism, if both the premises are affirmative, the conclusion must be affirmative.

Question 25.
If both the premises are particular, the conclusion must be particular.
Answer:
If both the premises are particular the conclusion dose not follow.

Question 26.
If one of the premises be particular the conclusion must be negative.
Answer:
If one of the premises be particular, the conclusion must be particular.

Question 27.
From particular major and Negative minor, the conclusion will.be negative.
Answer:
From particular major and Negative minor, No conclusion will be follow.

Question 28.
There are six valid moods in the second figure.
Answer:
There are four valid moods in the second figure.

Question 29.
There are six valid moods in the second figure.
Answer:
There are five valid moods in the 4th figure.

Question 30.
There are eight valid moods in the third figure.
Answer:
There are six valid moods in the third figure.

Question 31.
There are three valid moods in the fourth figure.
Answer:
There are five valid moods in the fourth figure.

Question 32.
‘DARIF is the valid mood of 2nd figure.
Answer:
‘DARIF is the valid mood of first figure.

Question 33.
‘FERIO’is the valid piood of 3rd figure.
Answer:
‘FERIO’ is the valid mood of first figure.

Question 34.
‘FESTINO’ is the valid mood of first figure.
Answer:
‘FESTINO’ is the valid mood of second figure.

Question 35.
‘BAROCO’ is the valid mood of 3rd figure.
Answer:
‘BAROCO’ is the valid mood of second figure.

Question 36.
‘BOCARDO’ is the valid mood of fourth figure.
Answer:
‘BOCARDO’ is the valid mood of third figure.

Question 37.
‘BRAMANTIP’ is the valid mood of third figure.
Answer:
‘BRAMANTIP’ is the valid mood of fourth figure.

Question 38.
‘BAROCO’is the valid mood of fourth figure.
Answer:
‘BAROCO’ is directly reduced to FERIO.

Question 39.
Major premise must be particular in the first figure.
Answer:
Major premise must be universal in the first figure.

Question 40.
Minor premise must be negative in the first figure.
Answer:
Minor premise must be affirmative in the first figure.

Question 41.
In the second figure, major premise must be particular.
Answer:
In the second figure, major premise must be universal.

Question 42.
In the second figure, the conclusion must be affirmative.
Answer:
In the second figure, the conclusion must be negative.

Question 43.
The minor premise must be negative in the third figure.
Answer:
The minor remise must be affirmative in the third figure.

Question 44.
Indirect reduction is also called as Dictum de omni etnullo.
Answer:
Indirect reduction is also called as Reductio ad absurdum.

Question 45.
Camestres can be directly reduce to ceasare.
Answer:
Camestres can be directly reduce to celarent.

Question 46.
If the conclusion is universal, the middle term can be distributed twice.
Answer:
If the conclusion is universal, the middle term can be distributed only once.

Question 47.
If the major term is predicate in the major premise, the minor premise must be negative. Answer: If the major term is predicate in the major premise, the minor premise must be affirmative.

IV. Answer the following questions in one word :

Question 1.
Is syllogism an immediate or mediate inference ?
Answer:
Mediate

Question 2.
How many kinds of syllogism do we have?
Answer:
Two

Question 3.
How many propositions are there in syllogism?
Answer:
Three

Question 4.
How many premises are there in syllogism?
Answer:
Two

Question 5.
How many terms are there in syllogism?
Answer:
Three

Question 6.
The subject of the conclusion of syllogism is called which term?
Answer:
Minor

Question 7.
The predicate of the conclusion of syllogism is called which term?
Answer:
Major

Question 8.
Which term occurs both in the premises but not in the conclusion?
Answer:
Middle

Question 9.
The first proposition of a syllogism is called which premise?
Answer:
Major

Question 10.
The second proposition of a syllogism is called which premise?
Answer:
Minor

Question 11.
The third proposition of a syllogism is called what?
Answer:
Conclusion

Question 12.
Figure of the syllogism is determined by the position of which term in the premises?
Answer:
Middle

Question 13.
How many types of figures are there in syllogism?
Answer:
Four

Question 14.
In which figure middle term in subject in both the premises?
Answer:
Third

Question 15.
In which figure middle term is predicate in both the premises?
Answer:
Second

Question 16.
In which figure middle term in subject is major premise and predicate in minor premise?
Answer:
First

Question 17.
In which figure middle term is predicate in major premise and subject in minor premise?
Answer:
Fourth

Question 18.
Which letter is used for the symbol of major term?
Answer:
‘P’

Question 19.
Which letter is used for the symbol of minor term?
Answer:
‘S’

Question 20.
Which letter is used for the symbol of middle term?
Answer:
‘M’

Question 21.
How many types of general rules are there in syllogism?
Answer:
Ten

Question 22.
Which term must be distributed at least once in any of the premises?
Answer:
Middle

Question 23.
In a syllogism, if one premise is negative, the conclusion must be what?
Answer:
Negative

Question 24.
If one of the premises be particular the conclusion will be what?
Answer:
Particular

Question 25.
If both the premises are affirmative, the conclusion will be what?
Answer:
Affirmative

Question 26.
Is it possible to draw a conclusion out of two negative premises?
Answer:
No

Question 27.
Is it correct to say that from two particular premises, the conclusion will be particular?
Answer:
No

Question 28.
Is it possible to draw a conclusion, from particular major and Negative minor?
Answer:
No

Question 29.
When the major term is distributed in conclusion without being distributed in the premises, we commit which fallacy?
Answer:
Illicit Major

Question 30.
What type of fallacy arises, when the minor term is distributed in the conclusion but not distributed in the premises?
Answer:
Illicit Minor

Question 31.
Which fallacy comes, when the middle term is not distributed in any of the premises?
Answer:
Undistributed Middle

Question 32.
Which fallacy arises, when the conclusion is drawn out of two particular premises?
Answer:
Fallacy of two particular premises.

Question 33.
Which fallacy arises, when the conclusion is drawn from two Negative premises?
Answer:
Fallacy of two Negative premises.

Question 34.
How many valid moods are there in syllogism?
Answer:
19

Question 35.
On the basis of what the mood of the syllogism is determined?
Answer:
Quality & quantity

Question 36.
How many types of valid moods are there in figure one?
Answer:
Four

Question 37.
How many valid moods are there in figure two?
Answer:
Four

Question 38.
How many valid moods are there in figure three ?
Answer:
Six

Question 39.
How many valid moods are there in figure four?
Answer:
Five

Question 40.
‘DARIF’ is the valid mood of which figure?
Answer:
First

Question 41.
‘FERIO’ is the valid mood of which figure?
Answer:
First

Question 42.
‘FESTINO’ is the valid mood of which figure?
Answer:
Second

Question 43.
‘BAROCO’ is the valid mood of which figure?
Answer:
Second

Question 44.
‘DARAPTT is the valid mood of which figure?
Answer:
Third

Question 45.
DISAMIS is the valid mood of which figure?
Answer:
Third

Question 46.
FRESISON is the valid mood of which figure?
Answer:
Fourth

Question 47.
‘CAMENES’ is the valid mood of which figure?
Answer:
Fourth

Question 48.
‘TESAPO’ is the valid mood of which figure?
Answer:
Fourth

Question 49.
How many types of fundamental moods are there in syllogism?
Answer:
15

Question 50.
How many types of strengthened moods one there in syllogism?
Answer:
8

Question 51.
How many types of weakened moods are there in syllogism?
Answer:
5

Question 52.
What is the process of transformation of imperfect mood to perfect moods called?
Answer:
Reduction

Question 53.
Who postulated “Dictum de omniet nullo”?
Answer:
Aristotle

Question 54.
Which figure in perfect?
Answer:
First

Question 55.
How many imperfect figures are there in syllogism?
Answer:
Three

Question 56.
How many perfect figures are there in syllogism?
Answer:
One

Question 57.
How many perfect! moods are there in syllogism?
Answer:
Four

Question 58.
How many imperfect moods are there in syllogism?
Answer:
15

Question 59.
How many types of Reduction are there?
Answer:
Two

Question 60.
‘CAMESTRES’ is directly reduced to what?
Answer:
CELARENT

Question 61.
‘CESARE’ is directly reduced to what?
Answer:
CELARENT

Question 62.
TESTING is directly reduced to what?
Answer:
FERIO

Question 63.
‘BAROCO’ is directly reduced to what?
Answer:
FERIO

Question 64.
‘DARAPTF’ is directly reduced to what?
Answer:
DARII

Question 65.
‘DATISF’ is directly reduced to what?
Answer:
DARII

Question 66.
‘DISAMIS’ is directly reduced to what?
Answer:
DARII

Question 67.
‘FELAPTON’ is directly reduced to what?
Answer:
FERIO

Question 68.
‘FERISON’ is directly reduced to what?
Answer:
FERIO

Question 69.
‘BOCARDO’ is directly reduced to what?
Answer:
DARII

Question 70.
‘BRAMANTIP’ is directly reduced to what?
Answer:
BARBARA

Question 71.
CAMENES’ is directly reduced to what?
Answer:
CELARENT

Question 72.
‘FESAPO’ is directly reduced to what?
Answer:
FERIO

Question 73.
‘FRESISON’ is directly reduced to what?
Answer:
FERIO

Question 74.
‘DIMARIS’ is directly reduced to what?
Answer:
DARII

Question 75.
In Reduction the letter ‘P’ stands for what?
Answer: Partial Conversion
76.
In reduction the letter ‘K’ stands for what ?
Answer:
Obversion

Question 77.
In reduction the letter ‘S’ stands for what ?
Answer:
Simple Conversion

Question 78.
In direct reduction, the letter ‘M’ stands for what?
Answer:
Mutual transposition of the premises.

Question 79.
TESTING is indirectly reduced to what?
Answer:
CELARENT

Question 80.
ELAPTON is indirectly reduced to what?
Answer:
BARBARA

Question 81.
‘DISAMIS’ in indirectly reduced to what?
Answer:
CELARENT

Question 82.
‘BRAMANTIP’ is indirectly reduced to what?
Answer:
CELARENT

Question 83.
‘TESAPO’ is indirectly reduced to what?
Answer:
CELARENT

Question 84.
What is the major premise of first figure?
Answer:
Universal

Question 85.
What is the minor premise of first figure?
Answer:
Affirmative

Question 86.
What is the major premise of second figure?
Answer:
Universal

Question 87.
What is the conclusion of second figure?
Answer:
Negative

Question 88.
One of the two premises of second figure must be what?
Answer:
Negative

Question 89.
The minor premise of third figure must be what?
Answer:
Affirmative

Question 90.
In the third figure, at least one premise must be what?
Answer:
Universal

Question 91.
What is the conclusion of third figure?
Answer:
Particular

Question 92.
In the fourth figure, if the major premise is affirmative then the minor premise must be what?
Answer:
Universal

Question 93.
In the fourth figure, if any premise is negative, the major premie must be what?
Answer:
Universal

Question 94.
In the fourth figure, if the minor premise is affirmative, the conclusion is what?
Answer:
Particular

Question 95.
‘A’ proposition can be the conclusion of which figure?
Answer:
First

Question 96.
Which proposition cannot be the premise of first figure and fourth figure?
Answer:
‘O’ proposition

Question 97.
If the middle term is distributed twice, the conclusion must be what proposition?
Answer:
Affirmative

Question 98.
If in a syllogism only two terms are distributed twice, the conclusion must be what?
Answer:
‘O’ proposition

Question 99.
If the major term is predicate in the major premise, the minor premise must be what?
Answer:
Affirmative

Question 100.
If the minor term is predicate in the minor premise, the conclusion cannot be what?
Answer:
‘A’ proposition

Question 101.
If the minor premise be negative, the major must be what?
Answer:
Universal

Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 4 Demand and Price Elasticity of Demand Questions and Answers.

CHSE Odisha 12th Class Economics Chapter 4 Question Answer Demand and Price Elasticity of Demand

Group – A

Short type Questions with Answers
I. Answer within Two/Three sentence.

Question 1.
What is demand ?
Answer:
Demand refers to willingness to buy a good backed by ability to pay the price at a particular time period. It indicates various quantities of a good purchased at different price level during a particular time period.

Question 2.
What is difference between demand & desire ?
Answer:
Demand is the willingness to buy & ability to pay the price. But desire is only the willingness to buy.

Question 3.
What is demand function ?
Answer:
Demand is a multi-valued function which it establishes functional relationship between price of a goods, other non-pricing factor & quantity demanded.

Question 4.
What is direct demand ?
Answer:
The demand for those goods & services which yields direct satisfaction is called direct demand. The demand for rice breads fruits etc. are the cost of direct demand.

Question 5.
What type of demand is the demand for raw material ?
Answer:
Demand for raw material is a derived demand. It yields indirect satisfaction.

Question 6.
What is “Law of demand” ?
Answer:
Law of demand states that “Other things remaining constant, amount demanded increases with the fall in price & vice-versa”. It shows the inverse relationship between price quantity demand.

Question 7.
What is composite demand ?
Answer:
Demand not for one purpose but for so may purposes is called composite demand. It combines a number of goods.

Question 8.
What is demand schedule ?
Answer:
Demand schedule is a tabular expression showing various quantities of a goods purchased or demanded at different price-level. It is a numerical analysis at law of demand.

Question 9.
What is a demand curve ?
Answer:
Demand curve is a graphical illustation of demand schedule which slopes downward from left to right showing inverse relationship between price & quantity demanded of a good.

Question 10.
What is slope of demand curve ?
Answer:
Demand curve is -negative slope. It slopes downward from left to right.

Question 11.
What is a Giffen goods ?
Answer:
Giffen goods are those inferior goods. The law of demand does not operate in this case.

Question 12.
What do you mean by change in demand ?
Answer:
Change in demand refers to increase or decrease in demand because of change in factors like price of related goods, income of the consumer, population taste & preference etc of the consumer. It is a case shifting of demand curve.

Question 13.
What do mean by conspicuous consumption ?
Answer:
Conspicious consmption refers to the consumption of prestigious goods. Law of demand does not operate in this case.

Question 14.
What is the normal shape of demand curve ?
Answer:
Normally, a demand curve sloped downward from left to right. It has a negative slope.

Question 15.
What happens to demand for tea it price of cofee rises ?
Answer:
The demand for tea increases if price of cofee rises. Because, these are substitute goods.

Question 16.
What happens to demand for a good if future price-hike is anticipated ?
Answer:
The demand for the goods increases if the future price hike is anticipated. It is an exception to law of demand.

Question 17.
What is elasticity of demand ?
Answer:
Elasticity of demand refers to degree of responsiveness of demand as a result of given change in price. It indicates degree of changing in demand as a result of change in price.

Question 18.
What does elasticity of demand measure ?
Answer:
Elasticity to demand measures the effect of change in price of a goods on the quantity demanded of it. It indicates the degree of sensitiveness of change demand due to change in price.

Question 19.
Who propounded the concept of elasticity of demand ?
Answer:
Alfred Marshall proposed to the concept elasticity of demand.

II. Answer within Five/Six sentence :

(A) WRITE SHORT NOTES ON :

Question 1.
Demand.
Answer:
Demand refers to willingness of the consumer to buy a goods backed by his ability to pay the price for it. In other words, demand refers to the quantity of the goods what a consumer is willing to purchase at a given price dining particular time period. Demand is always quoted with the price of goods & is expressed for a particular time-period. Hence demand for a goods comprises of 3 elements like effective desire to purchase a given quantity of goods, price of the goods & time – period.

Question 2.
Demand Function.
Answer:
Demand is a multi-variate concept showing the functional relationship between the demand for a goods & other factors like price of the goods, income of the consumer, price of the related goods etc. Other things remaining constant, there exists inverse relationship between the quantity demanded & price. Symbolically stated Dx = f (Px) in unchanged situation. There is inverse relationship between price of a goods & quantity demanded. In this function price of the goods is an independent factor on whom the demand depends on.

Question 3.
Demand – Schedule.
Answer:
Demand-schedule is a tabular expression showing various quantities of a goods demanded at different price-level. It contains different quantities of a goods demanded at different price-level. It is an information regarding the prices & quantity demanded. Thus it is viewd as a numerical explanation of Taw of demand’. This demand schedule is of two types like individual demand schedule & market demand schedule.

Question 4.
Demand Curve.
Answer:
Demand curve is the graphical or geometrical representation of demand-schedule. Both the demand curve & demand schedule provide the same information on price & quantity demanded of a goods. It graphically illustrates the law of demand. Normally, the demand curve slopes downward from left to right showing a negative inclination. It is because of the inverse relationship between price & quantity demanded. The slope of the demand curve is always negative.

Question 5.
Change in Demand :
Answer:
Demand is a multi-variate function. Demand for any goods depends on the price of goods, price of related goods, income of the consumer, taste & preference etc. If there occurs increase or decrease in demand due to change in factors other than price, it is called change in demand. In case of change in demand, the demand curye shifts either upward or downward. Increase in demand & decrease in demand are two conceptual situations that heppen in change in demand. In increase in demand, more is demanded at same price & same is demanded at higher price. So demand curve shifts upward. In case of decrease in demand, the demand curve shift downward & same is demanded at lower price & less is demaned at same price.

Question 6.
Elasticity of Demand.
Answer:
Elasticity of demand refers to the degree of responsiveness or sensitiveness of quantity demanded to changes in price. It tells how much or to what extent the quantity demanded changes due to a given change in price. It is a quantitative expression of change in quantity demanded. Elasticity of demand can be assessed as a ratio of proportionate change in quantity demanded to proportionate change in price. Elasticity of demand is always -ve & it ranges from 0 to oo & hence with this range it describes five cases of elasticity of demand.

Question 7.
Perfectly Elastic Demand .
Answer:
The demand is said to be perfectly elastic, if a small change in price leads to an infinite change in quantity demanded. In this case, the demand is highly sensitive & responsive which causes an infinite change in quantity demanded due to a small & insignificant change in price. In such case, the value of elasticity of demand is ∞ & the demand curve becomes a horizontal straight line. This concept is quite conceptual & imaginary & is not observed in real world.

Question 8.
Perfectly Inelastic Demand.
Answer:
If any change in price does not create any change in quantity demanded of a goods, the demand for that goods is said to be perfectly inelastic. Here change in price does not have any impact on quantity demanded. The quantity demanded remains Unchanged irrspective of the change in price. In this case, the demand curve takes the shape of a Vertical straight line & the value of elasticity of demand is zero (o). This case of elasticity of demand is not found in real world.

Question 9.
Unitary Elastic Demand.
Answer:
In case of unit elastic demand, a given change in price leads to proportionate change in quantity demanded. For example, if change in prices 10%, the quantity demanded also changes to the extent of 10%. The vaule of elasticity of demand is found to be one (1) & the demand curve in this case takes the shape of a rectangular hyperbola.”

Question 10.
Giffen Goods
Answer:
Giffen goods are special type of inferior goods for which law of demand does not operate. These goods are named after Sir Robert Giffen who is the chief innovator of this good. The income effect of price change for such goods is found to be negative. So when the price of a good falls causing a rise in income, the consumer concerned treates these goods inferior & reduces its consumption. These are the special type of goods whose quantity demanded decreases with the fall in its price & vice-versa.

(B) DISTINGUISH BETWEEN

Question 1.
Demand & Desire
Answer:
Both the concept of demand & desire sound to be synonymous. Both indicates the willingness to have a good. Demand refers to willingness to buy a good backed by ability to pay the price of it.* But the term “desire” is restricted to only willingness to have a good. Demand is quoted with price but desire is not associated with price. Demand is expressed per unit of time, but there is no mentioned of time period in case of desires. Thus in economics, the term ‘demand’ & ‘desires’ are two different terms.

Question 2.
Direct Demand & Derived Demand.
Answer:
The goods which are demand for the direct satisfaction of human wants, the demand is called direct demand. On the contrary, the goods which provides indirect satisfaction & these goods are so demanded, it is called derived demand. The demand for all types of consumers goods such as book, pen, shirt etc are the example of direct demand as all these provide direct satisfaction. On the other hand, the demand for raw materials, machineries etc. are the example of derived demand. Thus, the direct demand is directly associated with direct satisfaction of wants and derived demand is related to indirect satisfaction of wants. i

Question 3.
Individual Demand schedule & Market Demand Schedule.
Answer:
Individual demand schedule is a tabulor expression reflecting different quantities of goods purchased by an individual at different price-level. But the market demand schedule is numerical statement in tabular form showing different quantities of goods demand in the market at different price-level. Both the schedules are framed on the same price but one is exclusively for an individual & other is for the whole market. Individual demand schedule is a numerical expression of individual demand whereas market demand schedule is the numerical expression of market demand. Market demand schedule is a composition of individual demand schedules.

Question 4.
Change in demand & Change in quantity demanded.
Answer:
Change in demand is a multivalued function depending on factors other than price of goods whereas change in quantity demanded is a single valued function depending only on price. Increase & decrease in demand are the. two consequences of change in demand but extension and contraction of demand are the consequence of change in quantity demanded. In case of change in demand, price remains same & non-price factors change; but in change in quantity demanded price changes but non-price factors remain unchanged. In case of change in demand, there is shift of demand curve either upward or downward but there is no change nor shift of demand curve in change in quantity demanded.

Question 5.
Increase in demand & Extension of demand
Answer:
Increase in demand takes place when non-pricing factors change but price remains same whereas extension of demand happens when other non-price factor remain constant but price changes. Increase in demand is a consequence of change in demand but extension of demand is a consequence of change in quantity demanded. In case of increase in demand, more is demanded at same price & same is demanded at higher price; but in extension of demand more is demanded at lower price & vice-versa. In increase in demand, the demand curve shifts upward to the right; but in extension of demand there is no shift of demand curve.

Question 6.
Perfectly elastic demand & Perfectly inelastic demand.
Answer:
Perfectly Elastic Demand : The demand is said to be perfectly elastic if a small change in price leads to an infinite change in quantity demanded. Here, the value of elasticity of demand is infinite (∞) & the demand curve in this case becomes a horizontal straight line.
Perfectly inelastic demand: In perfectly inelastic demand, the quantity demanded remains same irrespective of any change in price. Any fall or rise in price has no impact on quantity demanded & hence the value of elasticity is zero. The demand curve is a vertical straight line.

Group – B

Long Type Questions With Answers

Question 1.
What do you mean by demand ? What are its determinants ?
Answer:
In economics, demand refers to willingness to buy a given quantity of goods backed by ability & willingness to pay the price for it. Thus, the complete meaning of demand comprises of several components like willingness to buy a commodity, ability to pay the price, willingness to spend, price of the commodity & time-period. Thus, demand refers to the quantity of goods what a consumer is willing to purchase at a given price during a particular time period. As such, the demand is always quoted with price & expressed for a particular time period.

According to Benham, “The demand for. anything at a given price is the amount of it which will be bought per unit of time. Hansen defined demand, “By demand, we mean the quantity of a commodity that will be purchased at a particular price and not merely the desire of a thing.”

There are different types of demand like price demand, income demand, cross demand, direct or derived demand, joint or composite demand, competitive or alternative demand.
Factors influencing demand : The demand is a multi-variate function. It is influenced by a number of factors. These factors may be classified into economic, social & political factors or which may directly or indirectly influence demand. The important determinants of demand are described below:

(i) Price of the Commodity : The demand is always quoted with price. It is the basic component or factor of demand which exert its influence. Without price-quotation, the concept of demand remains incomplete. Price & demand for a goods are inversely related. When price of a goods falls or rises, the quantity demanded of it increases or decreases respectively. Thus, there observed direct influence of price on the demand for a goods.

(ii) Price of Related goods : The price of related goods is also an important determinant of
demand. The related goods may be substitute or complementary goods. Any rise in price of a substitute goods has direct influence on the demand for goods. If the price of a substitute goods rises, the quantity demanded of the goods increases & vice-versa. Similarly, the demand for complementary goods changes directly when there is change in price of the goods in question. For example, if the price of tea rises, the quantity demanded of its substitute i.e. coffee increases. On the other hand, if the price of ink rises the quantity demanded of pen decreases. So it is inferred that price of related goods influences the demand.

(iii) Income of the Consumer : Income of the consumer is worth mentioning determinant of the demand. It directly influences the demand for goods. Demand for goods & income of the consumer are directly related. It implies that if the income of the consumer increases, the consumer will be capable of consuming more & thus demand for goods is influenced. Thus, it can be affirmed that other things remaining constant, the demand for a goods increases with the increase in the income of the consumer & vice-versa.

(iv) Taste & preference : Tastes & preferences of the consumer exert influence on the demand. These factors which influenced by habit, customs, fashion etc. influence the demand in either way. With the change in these factors, the demand will certainly change.

(v) Population: Population stands as prominent factor influencing demand. The size & composition of the population influence the demand for goods especially the basic necessary of life i.e., food, clothing, shelter etc. Similarly, the composition of the population builds the demand structure. If majority of people are rich, more luxuries & comfortable items shall be demanded or in case of majority of poor, basis necessaries for life will be demanded. In this way it determines the basis of demand.

(vi) Distribution of income & wealth: Distribution refers to the sharing of national income among the people of a country. This distribution maybe of individual which is personal & functional, regional or sectoral. But, the equality in the distribution of income is highly stressed. If the income distribution maintains equality & uniformity, .it will generate more demand & in case of inequality the demand may be contracted and restricted to a particular class, sector or region.

(vii) Government Policy : Government policy is found to be a crucial factor in moulding the quantum of demand. It considerably influences the demand structure of the community. If scarcity of essential goods is felt, the government may adopt certain restrictive measures like rationing to ensure fair distribution. This measure is essential to avoid acUte scarcity. Similarly taxation policy of the government deters the size & structure of the demand if higher tax rate is imposed.

All these factors significantly influence the demand. The contraction or expansion, increase or decrease in demand can happen due to the variations in these factors. Thus, demand is quitely proved to be multi- dimensional concept because of the presence of these multiple variables.

Question 2.
What do you mean by demand ? Distinguish between individual and marked demand schedules.
Answer:
The demand for any commodity, at a given price, is the quantity which will be bought per unit of time at that price. From this definition of demand two things are quite clear. Firstly, demand always refers to demand at a price. If demand is not related to price, it conveys no sense. To say that the demand for mangoes is 100 kg. fails to convey any sense. It should be always related to price. Secondly, demand always means demand per unit of time. The time may be a day, a week or a month, etc. Therefore, “the demand for any commodity or service is the amount that will be bought at any given price per unit of time.” (Benham).

There is a difference between ‘desire’, ‘need’ and ‘demand’. A desire will become demand only if a consumer has the means to buy a thing and also he is prepared to spend the money. Thus, by demand we mean the various quantities of a given commodity or service which consumers would buy in the market in a given period of time at various prices. According to Pension,
“Demand implies three things –
(a) desire to possess a thing,
(b) means of purchasing it, and
(c) willingness to use those means for purchasing it.”

Again in the words of Shearman-, “To speak of the demand for a commodity in the serise of the mere amount that will be purchased without reference to any price, will be meaningless.” Although there are various kinds of demand, such as cross, income, price demand, unless specified otherwise demand for a good or service refers to price demand, i.e., quantity demanded in relation to price.

Demand schedule depicts the various-Quantities of a commodity which will be demanded at different prices. Quantity demanded will be different at different prices because with an increase in price, demand falls and with a fall in price, demand extends. Demand schedule is of two types, viz. : (i) Individual demand schedule and (ii) Market demand schedule.
(i) Individual demand schedule – Individual demand schedule shows the various quantities demanded by one person at different prices. Individual demand schedule can be shown as follows :

Price (in Rupees)	Demand of Mangoes (in Kgs.)
5	1
4	2
3	3
2	4
1	5

As is clear from the above schedule, the demand for mangoes of a consumer is 1 kg. when the price is rupees 5 per kg. When price falls to Rs.4, demand for mangoes extends to 2 kg. Again demand for mangoes extends to 5 kg. when price is 1 rupee per kg.
Individual demand curve – The individual demand schedule can be explained with the help of the following diagram:

In the diagram OX-axis measures the quantity demanded while OY-axis represents the price of mangoes per kg. When price is Rs. 5 per kg. demand is 1 kg. Likewise when the price is 4 rupees per kg., demand is 2 kg., etc. By combining the A₁, A₂, A₃, A₄, A₅, we get the demand curve DD. This is called the individual demand curve.

(ii) Market demand schedule – If we add up the demand at various prices of all the consumers in the market, we will get the market demand schedule. Let us suppose, there are three consumers A, B and C in the market. If now we add the quantity demanded by A, B and C at different prices, we will get the market demand schedule. It can be shown as follows :

Price (rupees) Per Kg.	Demand of ‘A’ K.g.	Demand of ‘B’ K.g.	‘Demand of ‘C’ Kg.	Total demand in the market(Kgs)
5	1	3	2	6
4	2	4	3	9
3	3	5	4	12
2	4	6	5	15
1	5	7	6	18

When price is rupees 5 per kg. total demand of all consumers is 6 kg., when price is rupees 4, total demand of all the consumers is 9 kgs. etc. Hence a demand schedule may mean a tabular representation of price-quantity relationship.

Market demand curve – Market demand curve can be shown as follows :
On OX-axis, we take the total quantity demanded of mangoes in the market. On OY-axis, we measure the prices. When price is Rs. 5 per kg:, total quantity demanded is 6 kgs. Again when price is Rs. 4 per kg., total quantity demanded goes up to 9 kgs. By joining the points A, B, C, D, E, we get DD – the demand curve – for the market as a whole. Market demand curve can also be known by adding up the individual demand curves. We assume that there are two consumers A and B. If we know the demand curve of A and B, we can find out the market demand curve as follows :

In the following figures (i), (ii) and (iii) we show the demand of consumer A, consumer B and total demand curve respectively. On OX-axis we measure demand and on OY-axis we measure the price. d_a shows the demand of consumer ‘A’ and d_b shows the demand curve of consumer ‘B’. At price OP, the quantity demanded by consumer ‘ A’ is OA while the quantity demanded by consumer ‘B’ at this price is OB. The total demand of consumer ‘A’ and ‘B’ shall

be OA+ OB. In diagram (ii) total demand is OT at price OP. Here OT = OA + OB. When price falls to OP₁ the quantity demanded increases to OA₁ and OB₁ in the case of consumers A and B respectively. Now the market demand at price OP₁ shall be equal to OA₁ + OB₁. In figure (iii) the total demand is OT₁ at price OP₁. Here, OT₁ = OA₁ + OB₁. By joining the points M and N, we get d_m which is the market demand curve.

Question 3.
What is “Law of Demand” ? Explain it with its limitations.
Answer:
“Law of demand” is a unique law in consumption that moulds consumers behaviour while purchasing goods. This law explains the relationship between the price of a goods & its quantity demanded. Thus, the law of demand is a guiding principle in consumption which establishes inverse relationship between price of a goods & its quantity demanded. According to the law of demand, “Other things remaining constant, the amount demanded increases with the fall in its price & decreases with the rise in its price.” In other words, inverse relationship between price & quantity demanded is explained in law of demand.
The explanation of law of demand is associated with the demand function. The demand function expresses the functional relationship between demand & determinants of demand. Mathematically expressed, ‘
Dx = F (Px, Py, Py, Y, T …………….)
Dx → Demand for gods X
Px → Price of goods X
Py,Pz → Price of related goods
Y → Income of the consumers
T → Taste & preference.
Thus, the demand function describes multiple determinants of demand in which price of a goods is important one. If other factors in demand function remain constant, the relationship between price of a goods & quantity demanded becomes the topic of discussion in law of demand. Symbolically expressed,
Dx = f(Px) “other things remaining constant”
Exp
lanation : The law of demand simply illustrates the inverse relationship between price of a goods and quantity demanded in an unchanged situation. If the price of a goods rises, the quantity demanded of it will increase & vice-versa. This notion involved in law of demand which can be explained with the help of numerical analysis & graphical analysis.

Numerical Analysis : The numerical analysis of law of demand can be made with the help of demand schedule. The demand schedule describes various quantities of a goods purchased or demanded at different price level.

DEMAND SCHEDULE

Price of goods ‘A’ (in Rs.)	Quantity of goods ‘A’ (in units)
1	50
2	40
3	30
4	20
5	10

The numerical example as shown in demand schedule reflects that at the lower price i.e. Rs. 1/- the quantity demanded of good ‘A’ is found to be more i.e. 50 units. When price of goods ‘A’ gradually rises the quantity demanded of it declines. For example, when the price rises to Rs. 2,3,4,5, the quantity demanded becomes 40,30,20 & 10 units. It just establishes the inverse relationship between price of a good ‘A’ & its quantity demanded which is the principle in “Law of Demand.”

Graphical Analysis
The same notion can be explained graphically. The graphical illustration of law of demand can be made with the help of demand curve. Demand curve is nothing but the geometrical representation of demand schedule. So the graphical version of demand schedule determines the demand curve.

In the above figure , OX – axis measures the quantity demanded of good§ x & OY-axis measures the price of good A.

The same expression as in demand schedule is found in this diagram. When the price is Rs. 1/- the quantity demanded is 50units. When the price of goods A rises to Rs.2,3,4,5, the quantity denUtnded of it declines to 40,30,20, & 10 units respectively. By joining all these points, the demand curve ‘DD’ is derived.

The traditional shape of demand curve is downward sloping as shown in graph. It is because of the inverse relationship between price of good & its quanity demanded. As such, the demand curve (DD) is found to be negatively sloped.

ASSUMPTIONS:
The law of demand can not be independently explained.” For the operation of law of demand certain assumptions are to be made. Assumptions are the conditions on which the law is based on & explained. The assumptions of law of demand are mentioned below :

• Income of the consumer should be constant
• Price or related goods (substitute & complementary) should be unchanged.
• Taste, preference of the consumer should not change.
• Goods should be the “Normal Goods ”.
• Population should not change.

Limitations : In spite of significant practical value, the law of demand suffers from certain serious & dubious limitations which are as follows :

(i) Income of the consumer : As assumed, the income of the consumer should remain unchanged. But the income is. a flow concept which varies from time to time. As such, the law of demand becomes an invalid statement because of changeability of an income of the consumer.

(ii) Taste & Preference : Taste & preference which are influenced by custom, habit, fashion etc undergo frequent change. So the law of demand loses its stand under the condition of change of taste & preference.

(iii) Price of Related Goods : The price of related goods which assumed to be constant in the explanation of law of demand sounds to be impractical. Because, the price of such goods change frequently due to competitive structure of the market.

(iv) Giffen Goods : Giffen goods are special type of inferior goods for which law of demand does not operate. These goods named after Sir Robert Giffen, an economist of Ireland, are inferior goods for which the income effect is negative. The price of these goods, if falls, shall be treated as inferior goods, for which its quantity demanded falls. As such the law of demand does not operate.

(v) Conspicuous Consumption : The consumption of prestigeous goods or articles of distinction is called conspicuous consumption. For these goods, the law of demand does not hold good. It is because, these goods are consumed for displaying their social status & aristocracy. For these people, these goods are the symbol of status. So, when the price of these goods rises, the people of this special category feels proud to consume more.

(vi) Future – Expectation of Price Change : If any rise in price of the goods is apprehended, the consumer like to purchase more of it at prevailing price. On the other hand, if fall in price is expected in future, people will prefer to consume less at current price. So the law of demand does not stand if there is future expectation of price – change occurs.

(vii) Necessaries for life : The law of demand can not be properly applied to goods which are essential for the survival of human existence. In case of life saving drugs, the people are constrained to consume the required quantity of goods irrespective of the level of prices.

In spite of these limitation, “the law of demand’ is universally accepted as an important law in consumption. It looks into the basic principles involved in the consumers motive in the field of purchasing goods. Thus, the law possesses certain practical significance.

Question 4.
Why does demand curve slope downward ?
Answer:
The downward sloping nature of demand curve is because of its inverse relationship between the price of a goods & its amount purchased. The shape & slope of the demand curve in general is derived from the basic principles involved in ‘Law of demand’. In law of demand, it is learnt that the demand for goods increases with the fall in its price & vice-versa & hence the inverse relationship is established. As such, the demand curve slopes downward from left to right with a negative inclination. Prof. Marshall associated the downward sloping of the demand curve to the law of diminishing marginal utility. But J.R. Hicks & R.GD. Allen ascribed income effect & substitution effect to this tendency. The important & worth mentioning reasons for such downward sloping is discussed below :

(i) Effect of law of Diminishing Marginal Utility : The law of demand is derived from the law of diminishing marginal utility. According to this law, the marginal utility derived from the additional units of a particular goods goes on diminishing. It simply shows that the consumer derives less & less marginal utility from the additional units of the goods. So, the rational consumer compares the marginal utility derived from the goods with its price. He continues consumption till the marginal utility is equal to its price & at this level he feels satisfied. If the price of the goods falls, this reduced price should be equated with marginal utility. So, there is need of reducing marginal utility which happens only by purchasing more. So, it reveals that with lower price, more is purchased. It is because of the effect of law of diminishing marginal utility.

(ii) Price Effect: If a fall in price of a good is experienced while price of other goods or other factors remaining unchanged, its effect on quantity demanded is called “price effect.” This fall in price attracts new consumers to buy more at reduced price. Those who were not purchasing this good because of higher price shall be financially able to purchase it at lower price. Secondly, those who are purchasing less quantity of it because of higher price shall be interested to purchase more of it because of lower price. Overall effect of such fall in price is the increase in quanity demanded. In other words, the quantity demanded of the goods increases with fall in price & hence the demand curve showing the price & quantity demanded relationship slopes downward from left to right.

(iii) Income Effect: The effect of change in income on the quanity demanded is termed as “Income effect”. When there is fall in price of goods, the consumer gains real income because of increase in its purchasing power arising out of fall in price. Thus, at the same income, the consumer is able to purchase more because of such gain in real income. When the price of a goods falls, the consumer gains real income. Now the consumer either purchases the same quantity by spending less or purchases more by spending the same. So, there arises increase in demand because of income effect. As a result, the quantity demanded increases because of initial fall in price of it. So the demand curve slopes downward.

(iv) Substitution Effect: When the price of a goods falls the price of other related goods remains constant, the consumer prefers to substitute low-priced goods for high price goods. This is called substitution effect. So, it clearly indicates that the demand for commodity increases because of favourable substitution effect. The demand curve for this slopes downward from left to right.

(v) Multiple uses of a Goods : A particular goods can be put into several uses i.e. for the satisfaction of urgent needs & less urgent needs. So, when the price of a goods falls, the people will proceed to use it for less urgent wants & ultimately its quantity demanded increases. For example, if the price of coal falls, the people will use it as ordinary fuel which may not happen when its price is high- So, it reflects that the quanity demanded increases with fall in price & vice-versa. As such, the demand curve shows a negative inclination.

Question 5.
Distinguish between extension and increase in demand and contraction and decrease in demand.
Answer:
Generally we don’t differentiate between increase in demand and extension of demand and decrease in demand and contraction of demand. But as a matter of fact they are different concepts. When demand for a commodity changes because of a change in price, it is a case of extension or contraction of demand. But if demand changes because of factors other than price, it is a case of increase or decrease in demand.

Extension of demand – When demand goes up because of a fall in price, it is called extension of demand. For example, if the price of milk falls from 1 rupee 50 paise per litre the demand shall go up from 3 litres to 5 litres. This is a case of extension of demand. This can be shown with the help of the alongside diagram :

When the price is OP, the demand is OQ. Demand rises to OQ₁ when price falls to OP₁, OQ₁ is the extension of demand. In extension of demand, the consumer remains on the same demand curve but moves downwards from left to right.
Increase in demand – Increase in demand may come about in two ways :

• More demand at the same price.
• Same demand at a higher price.

Increase in demand can be shown with the help of the following diagram:

Demand is OR, when price is OP. At this very price OP, demand goes up to OR. Again when price rises to OP, demand remains the same i.e., OR. DD₁ depicts an increase in demand.

Contraction of demand – When demand of a commodity falls because of a rise in its price, it is a case of contraction of demand. For example, the demand for milk is 3 litres when its price is rupee one per litre. Now when price rises to Rs. 2 per litre, demand comes down to 2 litres. Contraction of demand can be shown diagrammatically as follows :

When price is OP, demand is OQ. When price rises to OP₁, demand falls to OQ₁. OQ₁ is the contraction of demand. In this case, the consumer goes upwards from right to left on the same demand curve.

Decrease in demand – Decrease in demand implies two things :
(i) Less demand at the same price.
(ii) Same demand at the lower price.
Decrease in demand can be shown with the help of the following diagram :

Demand in the start is OR when price is OP. At the same price OP, demand falls to OR₁. Again at a lower price OP₁, demand remains the same OR. R₁R is the decrease in demand. D₁D₁ curve depicts decrease in demand. In case of decrease in demand, the demand curve shifts downwards. ,

Question 6.
What do you mean by Elasticity of demand ? Discuss various cases of elasticity of demand.
Answer:
Elasticity of demand is the measure of the degree of change in the amount demanded of the commodity in response to given change in the price of the commodity. When the price of a good changes, quantity demanded of a commodity also changes, but the response is not same for all the commodities. The concept of elasticity of demand captures the magnitude of change or degree of responsiveness of demand to change in price. In other words, elasticity of demand refers to the degree of extension or contraction of demand as a result of given change in price.

Elasticity of demand is a quantitative concept that measures the degree of responsiveness of quanity demanded of a goods to a change in its price. According to Alfred Marshall, “The elasticity (or responsiveness) of demand in a market is great or small according as the amount demanded increases much or little for a given fall in price and diminishes much or little for a given rise in price.” According to Lipsey, “Elasticity of demand may be defined as the ratio of the percentage change in demand to the percentage change in price.” Mathematically stated,

Ed is always negative because it confirms, the inverse relationship between price & quantity demanded. So Ed always has a (-) minus sign.

FIVE CASES OF ELASTICITY OF DEMAND:
There observed five cases of elasticity of demand. The detailed study of these cases are describes below:
Quantity
(i) Perfectly Elastic Demand : The demand is said to be perfectly elastic if a small change in price leads to an infinite change in quantity demanded. Here the value of elasticity of demand is infinite (∞) & the demand curve in this case becomes horizontal straight line.

In this figure, at price OP, the demand is infinite A slight change in price will lead to infinite change in quantity demanded.

(ii) Perfectly inelastic demand: In perfectly inelastic demand the quantity demanded remains same irrespective of any change in price. Any fall or rise in price has no impact on quantity demanded & hence the value of elasticity is zero. The demand curve is a vertical straight line.

In the figure, the demand (OQ) remains the same irrespective of any change in price (OP or OP₁) So the Ed = 0.

(iii) Unitary Elatic Demand : Elasticity of demand is unity if a given change in price exactly creates a proportionate change in quanity demanded. The numerical value of such demand is 1 (one) i.e. Ed = 1

In the figure, DD curve represents unitary elastic demand curve when price falls from OP to OP₁, the quantity demanded increase OQ to OQ₁, which is quite proportionate in nature.

(iv) Relatively more Elastic Demand : The demand is relatively more elastic if any given change in price leads to more than proportionate change in quantity demanded. In this case Ed >1.

The figure shows that when price falls from OP to OP₁, the quantity demanded increases from OQ to OQ₁, which is quite more than proportionate change. ,

(v) Relatively less Elastic Demand : In relatively less elastic demand, any change in price leads to less than proportionate change in quantity demanded. Hence Ed <1.

In figure, DD demand curve shows this relatively less elastic demand. When price falls from OP to OP₁, the quantity demanded increases from OP to OPt the quantity demanded increases from OQ to OQ₁ which is less proportionate change.

Question 7.
What do you mean by Elasticity of demand ? Discuss various factors influencing of elasticity of demand.
Answer:
Elasticity of demand is the measure of the degree of change in the amount demanded of the commodity in response to given change in the price of the commodity. When the price of a goods changes, quantity demanded of a commodity also changes, hut the response is not same for all the commodities. The concept of elasticity of demand captures the magnitude of change or degree of responsiveness of demand to change in price. In other words, elasticity of demand refers to the degree of extension or contraction of demand as a result of given change in price.

Elasticity of demand is a quantitative concept that measures the degree of responsiveness of quanity demanded of a goods to a change in its price. According to Alfred Marshal, “The elasticity (or responsiveness) of demand in a market is great or small according as the amount demanded increase much or little for a given fall in price & diminishes much or little for a given rise in price.” According to Lipsey, “Elasticity of demand may be defined as the ratio of the percentage change in demand to the percentage change in price. Mathematically stated.

Ed is always negative because it confirms the inverse relationship between price & quantity demanded. So Ed always has a (-) minus sign.

FACTORS INFLUENCING ELASTICITY OF DEMAND

Elasticity of demand is not uniform or same for all the commodities or for all the consumers. It may vary from consumer to consumer or commodity to commodity. For some it may be more elastic or for other it may be more inelastic. Besides, some commodities have more elastic demand & some are less elastic in demand. It simply shows that the contraction or expansion of demand does not remain some for any change in price. There are certain factors which influence the elasticity of demand.The important factors determining elasticity of demand are described below :

(a) Nature of Commodity : Goods are classified into three categories like necessary, comforts & luxuries. These classification, through relative in nature, it determines the elasticity of demand. For necessaries which are urgently statisfied or human life are considered to have relatively less elastic demand because the demand for these goods are not significantly affected by the change in price. On the other hand, the comforts & luxuries comprise of less urgent want for which demand is relatively more elastic. Because, the demand for these goods is greatly influenced by the change in price.

(b) Availability of Substitutes : The demand for those goods is found to be more elastic if it has more substitutes. If the price of any goods having a large number of substitutes rises, the quantity demanded of it will fall to a greater extent because the consumers will divert their consumption to its substitutes. On the contrary, if the price of such goods falls its quantity demanded will increase significantly. But if the goods does not have any substitute any change in price will have no influence on its demand as the people are compelled to purchase that only good due to the absence of its substitutes. Hence, the demand for such goods is inelastic or less elastic.

(c) Alternative Uses : The demand for the goods having multiple uses is more elastic & the goods having no alternative uses or single use is found to be less elastic or inelastic. In case of goods having alternative uses, if its price falls the consumer will use it for the satisfaction of less urgent wants. So its quantity demanded increases. On the other hand, if its price rises, the people use it in satisfying more urgent wants. So its quantity demanded will decrease. In the similar manner, the goods which can not be put into several uses, the demand seems to be less elastic as it has only single use & change in price has less impact on it.

(d) Proportion of Income Spent: It the amount spent on goods constitute a very small fraction of the income or total expenditure, then the elasticity of demand is likely to be less. For example, the demand for match box is not greately influenced by the change in its price as the amount of expenditure spent towards this is very less. So the demand for such goods is less elastic or inelastic. On the other hand, if the proportion of income spent on a good is more, the demand becomes more elastic.

(e) Price-level: The price-level of a commodity influences the demand for it. The commodities with high price is more elastic & the commodity having low price is less elastic.

(f) Income-level: The level of income of the consumer will also determine the elasticity demand for goods. The demand is inelastic for higher lower income groups & elastic for middle income groups. The rich persons do not care for the price while purchasing the goods.

(g) Time period : Time period is also an influential factor having effect on elasticity of demand. In short-period, the elasticity of demand remains low as quantity demanded slowly changes with the changes in the price-level. On the contrary, the demand becomes relatively more elastic during long period & it is relatively more inelastic during market period which is very very shot period.

(h) Fashion & habit: The goods & commodities which are in the flow fashion responds slowly to the change in price. If the price of such good changes, the quantity demanded of these goods changes slowly & hence the demand for these is felt to be inelastic. Similarly, the goods which are habitually consumed is also non-responsive to the change in price. If the price of goods which are in habit of the consumer changes, the quantity demanded of these goods changes slowly or sometimes does not change at all. So the demand becomes less elastic or inelastic.

(i) Possibility of Postponement of the Consumption: If the consumption of any goods can be postponed at present moment, the demand for such goods becomes more elastic. If the price of goods rises, the consumer will think it pertinent to postpone the consumption of these goods for future & hence the demand of these goods falls at the present increased price & thus becomes elastic. On the other hand, if the consumption of any goods like lfe-saving drugs can not be postponed it can be consumed irrespective of any price & hence the demand for such goods becomes inelastic.
All these factors mentioned above are found to be prominent features that influence the elasticity of demand to a greater extent. The elasticity of demand whether high or low, depends upon these factors.

Group – C

Objective type Questions with Answers
I. Multiple Choice Questions with Answers :

Question 1.
Which is a component of demand ?
(i) Effective desire
(ii) Price
(iii) Time period
(iv) All of the above
Answer:
(iv) All of the above

Question 2.
Demand is generally and greatly influenced by
(i) Price
(ii) Price of substitute goods
(iii) Supply of goods
(iv) Time period
Answer:
(i) Price

Question 3.
Which of the following is a variable of demand ?
(i) Price
(ii) Income of the consumer
(iii) Price of substitute goods
(iv) All of these
Answer:
(iv) All of these

Question 4.
Which of the followings does not influence demand ?
(i) Income of the consumer
(ii) Price of goods
(iii) Cost of goods
(iv) Price of related goods
Answer:
(iii) Cost of goods

Question 5.
Demand curve has a negative slope due to
(i) Price effect
(ii) Income effect
(iii) Substitution effect
(iv) All of these
Answer:
(iv) All of these

Question 6.
Which is not cause of shift of demand curve?
(i) Change in price
(ii) Change in income
(iii) Change in related price
(iv) Change in Taste
Answer:
(i) Change in price

Question 7.
If a demand curve shifts upward, it is
(i) Expanison of demand
(ii) Increase in demand
(iii) Contraction of demand
(iv) Decrease in demand
Answer:
(ii) Increase in demand

Question 8.
Demand for fertiliser for a farmer is
(i) More elastic
(ii) Less elastic
(iii) Zero elastic
(iv) None Of these
Answer:
(ii) Less elastic

Question 9.
The elasticity of demanf of wine for a drun kard is
(i) Elastic
(ii) Inelastic
(iii) Relatively more elastic
(iv) Relatively less elastic
Answer:
(ii) Inelastic

Question 10.
If the price of cofee falls, the demand for tea shall
(i) Decrease
(ii) Increase
(iii) Remains same
(iv) Can not say
AnsWER:
(i) Decrease

Question 11.
If the price of petrol rises, the demand for motor bike.
(i) Increases
(ii) Decrease
(iii) Remains unaffected
(iv) Can not say
Answer:
(ii) Decrease

Question 12.
Which of the following concepts induces the consumer to consume a good ?
(i) Usefulness of goods
(ii) Utility of a goods
(iii) Pleasure from the goods
(iv) None of the above
Answer:
(ii) Utility of a goods

Question 13.
Which of the followings is the basic objective of the consumer ?
(i) Maximisation of utility
(ii) Best use of goods
(iii) To get satisfaction
(iv) All of the above
Answer:
(i) Maximisation of utility

Question 14.
Which of the followings is a true statement ?
(i) Consumer tries to maximise marginal utility
(ii) Consumer gets maximum satisfaction when marginal utility is maximum
(iii) Marginal Utility can be zero
(iv) Marginal utility can never be negative
Answer:
(iii) Marginal Utility can be zero

Question 15.
Which is not a true statement ?
(i) Marginal utility decreases at an increasing rate
(ii) Marginal utility decreases at decreasing rate
(iii) Margila utility can be zero
(iv) Marginal utility can be negative
Answer:
(i) Marginal utility decreases at an increasing rate

Question 16.
Which statement is correct ?
(i) Marginal utility is the sum of total utilities.
(ii) Marginal utility is derived from the last unit.
(iii) Rate of change of Marginal Utility is the total utility.
(iv) Marginal Utility is the utility derived from additional unit.
Answer:
(iv)Marginal Utility is the utility derived from additional unit.

Question 17.
Marginal utility refers to
(i) Utility from the last unit
(ii) Utility from the additional unit
(iii) Utility from the first unit
(iv) None of the above
Answer:
(iii) Utility from the first unit

Question 18.
If marginal utility is zero, total utility is
(i) Maximum
(ii) Zero
(iii) Minimum
(iv) None of the above
Answer:
(i) Maximum

Question 19.
If TU derived from 5th unit is 50 and from 4th unit it is 35, then MU from 5th unit is
(i) 95
(ii) 15
(iii) 70
(iv) 100
Answer:
(ii) 15

Question 20.
When MU is negative, total utility becomes
(i) negative
(ii) Positive
(iii) decreases
(iv) increases
Answer:
(iii) decreases

Question 21.
Which of following is correct ?
(i) MU_n = TU_n – TU_n-1
(ii) MU_n = TU_n+1 – TU_n-1
(iii) MU_n – TU_n-1 – TU_n
(iv) MU_n – TU_n-1 – TU_n+1
Answer:
(i) MU_n = TU_n – TU_n-1

Question 22.
Which is not true is case of Total Utility ?
(i) Total Utility can never be zero.
(ii) Total utility increases with an increasing rate.
(iii) Total utility increases with a decreasing rate;
(iv) All of the above
Answer:
(i) Total Utility can never be zero.

Question 23.
Which statement is true ?
(i) Marginal utility determines price
(ii) Marginal utility may always be positive ?
(iii) Marginal utility can never be zero
(iv) Marginal utility is always equal to total utility
Answer:
(i) Marginal utility determines price

Question 24.
Demand for a goods refers to willingness to buy a good backed by
(i) ability to pay the price
(ii) ability to earn more income
(iii) adequate desire
(iv) All of the above
Answer:
(i) ability to pay the price

Question 25.
Demand for a good should always be quoted with
(i) income
(ii) Price
(iii) price of related goods
(iv) All of the above
Answer:
(ii) Price

Question 26.
Demand is different from desire in the sense that
(i) Desire is not backed by ability to pay the price
(ii) Desire does not show willingness to buy
(iii) Desire does not indicate consumers preference
(iv) All of the above
Answer:
(iv) All of the above

Question 27.
Which is a factor that influences demand ?
(i) price of a goods
(ii) income of the consumer
(iii) price of related goods
(iv) All of the above
Answer:
(iv) All of the above

Question 28.
The phrase ‘ceteris paribus’ implies.
(i) Other things should be simultaneously changed
(ii) The required factors should change
(iii) All other factors excluding desired factors should remain constant
(iv) All of the above
Answer:
(iii) All other factors excluding desired factors should remain constant

Question 29.
Other things remaining constant if income of the consumer increases, the quantity demand
(i) increases
(ii) decreases
(iii) not attacted
(iv) only price affects
Answer:
(i) increases

Question 30.
In case of an inferior goods, if the price-level falls its quantity demanded
(i) increases
(ii) decreases
(iii) remains unchanged
(iv) None of the above
Answer:
(ii) decreases

Question 31.
Price remaining constant, if we anticipate future rise in prices, the quantity demanded of that good
(i) remains constant
(ii) increases
(iii) decreases
(iv) can not say
Answer:
(ii) increases

Question 32.
If the priceof petrol rises, the demand for car
(i) increases
(ii) decreases
(iii) remains constant
(iv) Both (i) and (ii)
Answer:
(ii) decreases

Question 33.
If price of coffee increases, the quantity demanded of tea
(i) increases
(ii) decreases
(iii) remains constant
(iv) Both (i) and (ii)
Answer:
(i) increases

Question 34.
According to law of demand, usual relationship between price & quantity demanded of a good shows
(i) inverse relationship
(ii) proportional relationship
(iii) direct relationship
(iv) Both(i) & (ii)
Answer:
(i) inverse relationship

Question 35.
Demand curve & demand schedule give the same information on law of demand; but they differ in one respect that is
(i) Demand schdule is in tabular form
(ii) Demand schdule is a numerical analysis
(iii) Demand schedule is of two types
(iv) All of the above
Answer:
(ii) Demand schdule is a numerical analysis

Question 36.
The usual shape of demand curve is
(i) upward sloping
(ii) vertical straight line
(iii) downward sloping
(iv) Horizontal straight line
Answer:
(iii) downward sloping

Question 37.
Demand curve has a negative slope because of
(i) Direct of relationship between price & quantity demanded
(ii) Inverse relationship between price & quantity demanded
(iii) proportional relationship between price & quantity demanded
(iv) All of the above
Answer:
(ii) Inverse relationship between price & quantity demanded

Question 38.
The demand curve describes the inverse relationship between
(i) price & quantity demanded
(ii) income & quantity demanded
(iii) price of related goods & quantity demanded
(iv) All of the above
Answer:
(i) price & quantity demanded

Question 39.
The effect of change in income on quantity demanded of a good is called
(i) price effect
(ii) income effect
(iii) substitution effect
(iv) All of the above
Answer:
(ii) income effect

Question 40.
Change in demand takes place due to
(i) change in price
(ii) change in income
(iii) change in other things
(iv) All of the above
Answer:
(iii) change in other things

Question 41.
In change in demand, the demand curve
(i) remains unchanged
(ii) Shifts upward
(iii) shifts down ward
(iv) either shifts upward or downward
Answer:
(iv) either shifts upward or downward

Question 42.
In case of increase in demand, more is demanded at
(i) higher price
(ii) same price
(iii) At lower price
(iv) All of the above
Answer:
(ii) same price

Question 43.
The law of demand does not operate in ease of
(i) Giffen goods
(ii) inferior goods
(iii) prestigious goods
(iv) All of the above
Answer:
(iv) All of the above

Question 44.
The degree of sensitiveness of demand due to change in price of a good is called
(i) change in demand
(ii) change in quantity demanded
(iii) elasticity of demand
(iv) All of the above
Answer:
(iii) elasticity of demand

Question 45.
Elasticity of demand of a good measures
(i) change in demand
(ii) proportionate change in demand as a result of proportionate change in price
(iii) percentage change in demand as a result of precentage change in price
(iv) Both (ii) and (iii)
Answer:
(iv) Both (ii) and (iii)

Question 46.
The elasticity of demand is always
(i) positive
(ii) negative
(iii) zero
(iv) All of the above
Answer:
(ii) negative

Question 47.
The Ed is always negative because of –
(i) inverse relationship between price & quantity demanded
(ii) proportional relationship between price & quantity demanded
(iii) direct relationship between price & quantity demanded
(iv) All of the above
Answer:
(i) inverse relationship between price & quantity demanded

Question 48.
In case of perfectly elastic demand, the demand curve becomes
(i) vertical straight line
(ii) horizontal straight line
(iii) downward sloping
(iv) Upward sloping
Answer:
(ii) horizontal straight line

Question 49.
The value of perfectly elastic demand is
(i) 0
(ii) +1
(iii) ∞
(iv) -1
Answer:
(iii) ∞

Question 50.
In case of perfectly inelastic demand, the demand curve takes the shape of a
(i) Horizontal straight line
(ii) Downward sloping
(iii) Vertical straight line
(iv) Upward sloping
Answer:
(iii) Vertical straight line

Question 51.
The value of perfectly inelastic demand is
(i) 0
(ii) -1
(iii) +1
(iv) ∞
Answer:
(i) 0

Question 52.
If any given change in price leads to proportionate change in quantity demanded, the demand is said to be
(i) relatively more elastic
(ii) relatively len elastic
(iii) unit elastic
(iv) perfectly elastic
Answer:
(iii) unit elastic

Question 53.
If the price of a goods falls by 25% & quantity demanded of a goods increases by 50%, its demand is said to be
(i) more elastic
(ii) less elastic
(iii) unit elastic
(iv) perfectly elastic
Answer:
(i) more elastic

Question 54.
If the price of a goods falls by 20% but its quantity demanded increases by 10% its demand is said to be
(i) elastic
(ii) inelastic
(iii) unit elastic
(iv) Both (i) and (ii)
Answer:
(ii) inelastic

Question 55.
If the price of a goods falls by 25% & the proportion of income spent on that goods is 35%, the demand for the goods is
(i) elastic
(ii) inelastic
(iii) zero elastic
(iv) cannot say
Answer:
(i) elastic

Question 56.
If the price of a good falls by 10% & the expenditure spent on the goods is 5% the demand is
(i) elastic
(ii) inelastic
(iii) more elastic
(iv) All of the above
Answer:
(ii) inelastic

Question 57.
If a good has a number of substitutes, its demand becomes
(i) elastic
(ii) inelastic
(iii) perfectly elastic
(iv) perfectly inelastic
Answer:
(i) elastic

Question 58.
The demand for petrol is elastic because
(i) it has multiple use
(ii) it has no substitute
(iii) it is used for vehicle
(iv) All of the above
Answer:
(i) it has multiple use

Question 59.
The elasticity of demand for electricity is
(i) more inelastic
(ii) more elastic
(iii) perfectly elastic
(iv) none of the above
Answer:
(ii) more elastic

Question 60.
Which is not a determinant of elasticity of demand ?
(i) Supply of a good
(ii) Cost of production
(iii) Alternative uses of goods
(iv) All of the above
Answer:
(i) Supply of a good

II. Fill in the blanks :

Question 1.
Law of demand reflects the ____ relationship between price of a goods and its quantity demanded.
Answer:
inverse

Question 2.
Demand for any goods refers to the willingness and ability of the consumer for having that goods at a given ____ during a particular time period.
Answer:
price

Question 3.
Demand for any goods is always expressed with the ____of that goods.
Answer:
price

Question .
Demand is a ____ function.
Answer:
multi-valued

Question 5.
Demand for tea ____ with a fall in price of coffee.
Answer:
decreases

Question 6.
Demand for motor-bike ____ with a fall in price of petrol.
Answer:
increases

Question 7.
Price remains unchanged, the demand for goods ____ if the income of the consumer increases.
Answer:
increases

Question 8.
The demand for the commodity goes ____, if the consumers have no taste of the commodity.
Answer:
down

Question 9.
The demand for the old fashioned items ____ with a fall in price of them.
Answer:
diminishes

Question 10.
The demand of cold drinks ____ during winter in spite of a fall in price of it.
Answer:
decreases

Question 11.
According to Law of Demand ____ is purchased at lower price and vice-versa.
Answer:
more

Question 12.
Demand schedule and demand curve provide ____ information.
Answer:
same

Question 13.
Demand curve has a ____ slope.
Answer:
negative

Question 14.
Demand for Giffen’s goods ____ with a fall in its price.
Answer:
decreases

Question 15.
Demand curve for Giffen’s goods is ____ sloping.
Answer:
upward

Question 16.
A change in quantity demanded as a result of change in price of goods is known as ____ of demand.
Answer:
Extension or contraction

Question 17.
The demand curve for a normal goods is a ____ hyperbola.
Answer:
rectangular

Question 18.
Elasticity of demands shows the magnitude of change in demand as a result of change in ____
Answer:
price

Question 19.
In case of perfectly elastic demand the demand curve becomes a ____ straight line.
Answer:
horizontal

Question 20.
In case of perfectly inelastic demand, a fall in price of the goods leads to ____ change in quantity demanded.
Answer:
no

Question 21.
The numerical value of ____ elastic demand is equal to 1.
Answer:
unit

Question 22.
The demand for diamond to a rich person is ____
Answer:
inelastic

Question 23.
The demand for tea is found to be more ____
Answer:
elastic

Question 24.
Demand is ____ for goods having multiple uses.
Answer:
elastic

Question 25.
The demand for medicines is ____ elastic (inelastic)
Answer:
less

Question 26.
The demand is inelastic for ____ income groups.
Answer:
higher

Question 27.
The demand for low priced items is ____
Answer:
inelastic.

Question 28.
The demand for newspaper is ____
Answer:
inelastic.

Question 29.
If a change in demand is followed by proportional change in price, elasticity of demand is ____
Answer:
unitary.

III. Correct the Sentences:

Question 1.
Demand is a single valued function.
Answer:
Incorrect.
Correct : Demand is a multi-valued function.

Question 2.
Demand refers to only the quantity of a good purchased.
Answer:
Incorrect.
Correct: Demand refers to the quantity of goods purchased at a given price during a particular time period.

Question 3.
Demand for any goods is high because price is high.
Answer:
Incorrect.
Correct: Demand for any goods is high because price is low.

Question 4.
Demand for any goods determines its price.
Answer:
Incorrect.
Correct: Price of any goods determines its demand.

Question 5.
Demand for a goods & its price are directly related.
Answer:
Incorrect.
Correct: Demand for a goods & its price are inversely related.

Question 6.
Law of demand describes the inverse relationship between price & quantity demanded.
Answer:
Correct.

Question 7.
In law of demand, changes in quantity demanded is the cause & change in price is the effect.
Answer:
Incorrect.
Correct: In law of demand, change in price is the cause & change in quantity demanded is the effect.

Question 8.
Demand schedule contains the list of goods only.
Answer:
Incorrect.
Correct: Demand schedule contains the list of price & quantities of goods.

Question 9.
Market demand schedule is the sum of indiviaul demand schedules.
Answer:
Correct.

Question 10.
The demand curve is positively sloped.
Answer:
Incorrect
Correct: The demand curve is negatively sloped.

Question 11.
The demand schedule & demand curve provide same information.
Answer:
Correct.

Question 12.
Demand curve is a graphical representation of demand schedule.
Answer:
Correct

Question 13.
When demand for a goods decreases its price falls.
Answer:
Incorrect.
Correct: When price of a goods decreases its demand increases.

Question 14.
In law of demand, the price depends on quantity demanded.
Answer:
Incorrect.
Correct: In law of demand quantity demanded depends on the price.

Question 15.
If price of the substitute goods falls, the quantity demanded of the goods increases.
Answer:
Incorrect.
Correct: If the price of the substitute good falls the quantity demanded of the goods decreases.

Question 16.
It price of petrol rises, the use of car decreases.
Answer:
Correct.

Question 17.
In change in quantity demanded, the demand curve shifts either upward or downward.
Answer:
Incorrect.
Correct: In change in demand, the demand curve shifts either upward or downward.

Question 18.
It price of tea falls, the demand for coffee falls.
Answer:
Correct

Question 19.
In extension of demand, more is demanded at same price.
Answer:
Incorrect
Correct: In increase in demand, more is demanded at same price.

Question 20.
If the income of the consumer increases, the demand for the goods increases.
Answer:
Correct

Question 21.
Demand for Giffen goods increases if its price falls.
Answer:
Incorrect.
Correct: Demand for Giffen goods decrease if its price falls.

Question 22.
Elasticity of demand is a quatitative concept
Answer:
Incorrect
Correct: Elasticity of demand is a quantitative concept.

Question 23.
Elasticity of demand is always negative.
Answer:
Correct.

Question 24.
Elasticity of demand varies from +1 to -1.
Answer:
Incorrect.
Correct: Elasticity of demand varies from 0 to ∞.

Question 25.
In perfectly elastic demand, the demand curve is a vertical straight line.
Answer:
Incorrect
Correct: In perfectly elastic demand, the demand curve is horizontal straight line.

Question 26.
The co-efficient of elasticity is zero when demand is less elastic.
Answer:
Incorrect.
Correct: The co-efficient of elasticity is zero when demand is perfectly inelastic.

Question 27.
If given change in price leads to proportionate change in quantity demanded, the demand is more elastic.
Answer:
Incorrect
Correct: If given change in price leads to proportionate change in quantity demanded, the demand is unit elastic.

Question 28.
Demand for necessaries is inelastic.
Answer:
Correct

Question 29.
The demand for match box is elastic.
Answer:
Incorrect
Correct: The demand for match box is inelastic.

Question 30.
Demand for luxuries is elastic.
Answer:
Correct.

Question 31.
Deman for tea is inelastic.
Answer:
Incorrect
Correct: Demand for tea is elastic.

Question 32.
Demand for goods having more substitutes is elastic.
Answer:
Correct

Question 33.
Coal has high elastic demand.
Answer:
Correct.

Question 34.
Goods having multiple uses has inelastic demand
Answer:
Incorrect
Correct: Goods having multiple uses has elastic demand.

Question 35.
The demand for high priced goods is elastic.
Answer:
Correct

Question 36.
The demand for wine in case of a drunkard is inelastic.
Answer:
Correct

Question 37.
The demand for medicine is elastic.
Answer:
Incorrect
Correct: The demand for medicine is inelastic.

Question 38.
Demand for salt is elastic.
Answer:
Incorrect
Correct: Demand for salt is inelastic.

Question 39.
The demand for goods whose consumption can be postponed is more elastic.
Answer:
Correct

Question 40.
‘Elasticity demand is always negative.
Answer:
Correct

Question 41.
If total expenditure spent on a goods remains same after fall in its price, the demand is unit elastic
Answer:
Correct.

IV. Answer the following questions in one word / One sentence:

Question 1.
What is demand?
Answer:
Demand refers to willingness to buy a goods backed by ability to pay the price at a particular time period.

Question 2.
What is difference between demand & desire ?
Answer:
Demand is the willingness to buy & ability to pay the price but desire is the willingness to buy.

Question 3.
What is demand function ?
Answer:
Demand is a multi-valued function which establishes functional & inverse relationship between price of a goods, other non-pricing factor & quantity demanded.

Question 4.
Which is an independent variable in demand function ?
Answer:
Price of the goods is the independent variable in demand function.

Question 5.
What is direct demand ?
Answer:
The demand for those goods & services which yields diret satisfaction is called direct demand.

Question 6.
What type of demand is the demand for raw material ?
Answer:
Demand for raw material is a derived demand.

Question 7.
What is “Law of demand” ?
Answer:
Law of demand states that “other thing remaining constant amount demanded increases with the fall in price & vice-versa.”

Question 8.
What do you mean by “Ceteris-Paribus” ?
Answer:
Ceteris-Paribus means an unchanged situation or “other thing remaining unchanged”.

Question 9.
What is composite demand ?
Answer:
Demand not for one purpose but for so many purposes is called composite demand ?

Question 10.
What is competitive demand ?
Answer:
Demand for substitutes is competitive demand.

Question 11.
What are the variables in law of demand ?
Answer:
There are two variable like price of goods & quantity demanded in law of demand.

Question 12.
What is demand schedule ?
Answer:
Demand schedule is a tabular expression showing various quantities of a goods purchased or demanded at different price-level.

Question 13.
What is a demand curve ?
Answer:
Demand curve is a graphical illustration of demand schedule which slopes downward from left to right showing an inverse relationship between price & quantity demanded of a goods.

Question 14.
What is the slope of demand curve ?
Answer:
Demand curve is slopes downward from left to right.

Question 15.
What is a substitute goods ?
Answer:
A good can be a substitute of other if both the goods can satsify common wants.

Question 16.
Write two determinants of demand ?
Answer:
Price of related goods & income of the consumer.

Question 17.
What happens to demand for good if the income of the consumer increases ?
Answer:
The demand for goods increases if the income of the consumer increases.

Question 18.
What happens to demand for a good if the price of its substitutes falls ?
Answer:
The demand for good decreases if the price of its substitute falls.

Question 19.
Under what circumstances, the demand curve shifts ?
Answer:
The Demand curve shifts either upward or downward if there is change in the factors other than the price.

Question 20.
What is a Giffen goods ?
Answer:
Giffen goods are those inferior goods for which law of demand does not operate.

Question 21.
What happens to demand for good if its price is expected to rise in future ?
Answer:
The demand for goods increases if its price is expected to rise in future.

Question 22.
What do you mean by change in demand ?
Answer:
Change in demand refers to increase or decrease in demand because of change in factors like price of related goods, income of the consumer, population, taste & preference etc.

Question 23.
What do you mean by conspicuous consumption’ ?
Answer:
Conspicuous consumption refers to the consumption of prestigious goods.

Question 24.
What is the normal shape of demand curve ?
Answer:
Normally a demand curve slopes downward from left to right.

Question 25.
Write two exceptions of law of demand ?
Answer:
Law of demand does not operate in case of Giffen goods & prestigious goods.

Question 26.
Which economic device measures the quantitative change in demand due to change in price ?
Answer:
Elasticity of demand.

Question 27.
What is elasticity of demand ?
Answer:
Elasticity of demand refers to degree of responsiveness of quantity demanded as a result of given change in price.

Question 28.
What does elasticity of demand measure ?
Answer:
Elasticity of demand quantifies the effect of change in price of a goods on the quantity demanded.

Question 29.
How can be the elasticity of demand measured ?
Answer:
Elasticity of demand can be measured by the ratio of proportionate change in quantity demanded to proportionate change in price.

Question 30.
Why is elasticity demand always negative ?
Answer:
Elasticity of demand is always negative because of inverse relationship between price & quantity demanded of a good.

Question 31.
What is limit of the value of elasticity of demand ?
Answer:
The value of elasticity of demand varies from 0 to ∞.

Question 32.
What is the shape of demand curve in case of perfectly elastic demand.
Answer:
In perfectly elastic demand, the demand curve becomes a horizontal straight line.

Question 33.
In which case, the elasticity of demand is zero ?
Answer:
In case of perfectly inelastic demand, the elasticity of demand is zero

Question 34.
What is the elasticity demand for a goods whose demand does not change due to change in price ?
Answer:
The demand for the goods is perefectly inelastic if its demand does not change due to change in price.

Question 35.
If a small changes in price leads to a fall in quantity demanded, state if demand is elastic or inelastic ?
Answer:
If a small changes in price leads to fall in quantity demanded, the demand is elastic.

Question 36.
If any given change in price leads to proportionate change in quantity demanded, state what type of elasticity of demand it is ?
Answer:
If any given change in price leads to proportionate change in quantity demanded it is a case of unit elastic demand.

Question 37.
What is elasticity of demand if the demand does not change due to change in price.
Answer:
The demand for the goods is perefectly inelastic if its demand does not change due to change in price.

Question 38.
What is elasticity of demand for a Newspaper ?
Answer:
The elasticity of demand for the newspapers is inelastic.

Question 39.
What is elasticity of demand for necessary & luxuries ?
Answer:
The demand for necessary is inelastic where for the lusuries it is elastic.

Question 40.
Give an example of a good whose demand is inelastic
Answer:
Salt.

Question 41.
What is the elasticity of demand for a good having substitutes ?
Answer:
The demand for the goods having substitutes is more elastic.

Question 42.
What is the elasticity demand for a goods having alternative uses.
Answer:
The demand for the goods having alternative uses is elastic.

Question 43.
If total expenditure spent on a goods remains same after fall in its price, state what type of elasticity of demand it is ?
Answer:
If total expenditure spent on a goods remains same after fall in its price, the demand for that goods is unit elastic.

Question 44.
If total expenditure spent on a goods increases after fall in its price, state what type of elasticity of demand it is ?
Answer:
The demand is relatively more elastic.

Odisha State Board CHSE Odisha Class 12 Economics Solutions Chapter 3 Laws of Consumption Questions and Answers.

CHSE Odisha 12th Class Economics Chapter 3 Question Answer Laws of Consumption

Group – A

Short type Questions with Answers
I. Answer within Two/Three sentence.

Question 1.
What is Consumption ?
Answer:
Consumption refers to the use of goods & services for the satisfaction of human wants. So when a good is consumed its wants satisfying power (utility) is destroyed.

Question 2.
What happens to Total Utility when marginal Utility is zero ?
Answer:
Marginal utility is the additional utility derived from an extra unit consumed. So when the additional units are continuously consumed, the marginal utility goes on diminishing but the total utility goes on increasing at an diminfshing rate. Hence, when marginal utility becomes zero, total utility is maximum.

Question 3.
What happens to Total Utility when marginal utility is negative ?
Answer:
Marginal utility is the addition made to the total utility caused an one extra unit of a good consumed. When marginal utility is negative, it does not add to the total utility rather subtracts it from total utility. So total utility diminishes.

Question 4.
What is Total utility ?
Answer:
Marginal utility is the additional utility derived from the successive units of a good. With continuous consumption, the additional utility (Marginal utility) derived goes on diminishing which is added to the total utility. Thus total utility is the sum of marginal utilities.

Question 5.
What is the nature of Marginal utility ?
Answer:
On account of increase in level of consumption, the intensity of wants for that goods diminises. So the marginal utility diminishes.

Question 6.
What is the slope of Marginal utility curve ?
Answer:
Marginal utility goes on diminishing withincrease in consumption of additional units of a goods. So marginal utility curve slopes downward.

Question 7.
What happens to total utility becomes when marginal utility is zero ?
Ans. The marginal utility derived from a goods becomes zero when he consumes the required units of that good to maximise his satisfaction. So total utility becomes maximum when MU is zero.

Question 8.
Explain the Marginal utility of money.
Answer:
Money is not a commodity rather it represents a bundle of goods & also having generalised purchasing power. So MU of money can never be zero.

Question 9.
Describe the relationship between price of a commodity and Marginal Utility.
Answer:
A consumer prefers to pay the price on the basis of wants satisfying power of a commodity. So price of a commodity is equal to MU.

Question 10.
What is Marginal Utility ?
Answer:
Marginal utility refers to the addition made to the total utility caused by an increase in one additional unit of a good consumed. It is the utility derived from the extra unit of a good consumed. Marginal utility is otherwise expressed as the rate of change of total utility caused by an extra unit consumed. So MUn = TU_n – TU_n-1

Question 11.
Marginal Utility of Money.
Answer:
Money represents a bundle of commodities Hence, the basic nature of marginal utility does not apply to money. It implies that marginal utility derived from the possession of additional unit of money does not diminish as it possesses a generalised, purchasing power.

II. Answer within Five/Six sentence:

Question 1.
What is Marginal utility?
Answer:
Marginal Utility refers to the addition made to the total utility caused by an increase of one additional unit of a commodity consumed. Thus, marginal utility indicates the rate of change of total utility on account of the consumption of one additional unit of a commodity.
i. e. MU_n = TU_n – TU_n-1
Where, MU_n → Marginal utility derived from n’th units of a goods.
TU_n → Total utility derived from n’th unit of a goods,
n → No. of Units of goods consumed.
Marginal utility derived from various units of a goods goes on diminishing with every increase in the additional units consumed. Thus marginal utility curve bears a negative slope.

Question 2.
What is Total Utility ?
Answer:
Total Utility refers to the sum of utilities derived from all the units of a goods consumed. In other words, it is nothing but the sum of marginal utilities derived from different units of a particular goods.
i. e. TU_n = Σ₁MU_n
The very nature of total utility reflects that it increases with the increase in the number of units consumed but at a diminishing rate. Total utility becomes maximum when marginal utility is found to be zero and it starts diminishing when marginal utility is negative.

Question 3.
What is the relationship between Marginal Utility and Total Utility ?
Answer:
Marginal Utility derived from a goods goes on diminishing when the consumer increases the level of consumption of that goods. But in this case, the total utility increases at a diminishing rate. Secondly, total utility derived from a goods is maximum when marginal utility derived from that goods becomes zero. Thirdly, total utility derived from a goods starts diminishing if the marginal utility from such goods becomes negative. Lastly, the marginal utility derived from a goods may be positive or negative but the total utility may not be negative.

Question 4.
State the relationship between Marginal Utility and Price.
Answer:
The Law of Diminishing Marginal Utility reveals that the consumer will derive less and less satisfaction (utility) from the consumption of successive units of a commodity. In other words, the marginal utility of a commodity diminishes with the increase in the stock of a commodity. On the other hand, the price to be paid for a commodity measures the utility. As such, the consumer shall be reluctant to pay the same price for all the units purchased or consumed due to the declining nature of the marginal utility. So the consumer prepares to purchase the various units of a particular commodity by comparing the utility derived and the price paid for it. So long as the price in the market is less than the utility derived, the consumer has a gain over it and at best, he will go on purchasing the various units of that commodity till the marginal utility derived is equal to its price. At this point the consumer prefers to stop purchasing.

Question 5.
Law of Diminishing Marginal Utility is not applicable to money. Explain.
Answer:
Money represents generalised purchasing power. It does not represent a particular commodity; rather it has a command over a bundle of commodities. This is the reason why the law of diminishing marginal utility is of slow application in case of money. In other words, the marginal utility diminishes comparatively slowly in case of money. But in practical field, one can realise the application of law of diminishing marginal utility in case of money, A man having more stock of money (rich man) is not cautious of spending the money as in case of poor man. But in case of a poor man, a unit of money has greater importance. Thus, for poor man having less stock of money, marginal utility seems to be greater in comparison to that of the rich man with more stock of money.

Question 6.
Explain the relationship between Marginal Utility and Total Utility.
Answer:
Marginal Utility refers to the addition made to the total utility caused by an increase in one more unit consumed. Total utility, on the other hand, is the sum of marginal utilities derived form the consumption of all the units. As the person consumes more and more units of a particular commodity, the marginal utility declines while the total utility increases at a diminishing rate. When marginal utility is found to be zero, total utility becomes maximum. When marginal utility is negative, total utility diminishes.

Question 7.
Total Utility increases at a diminishing rate if consumption of a good increases.
Answer:
The law of diminishing marginal utility is based on the characteristic of human wants, that is, a particular want is satiable. When a person goes on consuming more and more units of a particular commodity, the satisfaction derived from the successive units goes on diminishing. The successive units yield less and less satisfaction. Total utility is the aggregate of marginal utilities derived from the consumption of all the units. Therefore, total utilities increases at a diminishing rate.

Question 8.
‘Law of Equi-marginal Utility’ is otherwise called ‘Law of Substitution’. Why ?
Answer:
As per the law of equi-marginal utility, the consumer attains equilibrium when the marginal utility derived from the last rupee spent on each commodity is equal. If the marginal utility derived from goods Aand B is MUA and MUB respectively and the price of A and B is PA and PB, then law of equi-marginal utility is reflected as
\(\frac{\mathrm{MU}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{A}}}\) = \(\frac{\mathrm{MU}_{\mathrm{B}}}{\mathrm{P}_{\mathrm{B}}}\)
If the fraction deviates from each other i.e., \(\frac{\mathrm{MU}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{A}}}\) = \(\frac{\mathrm{MU}_{\mathrm{B}}}{\mathrm{P}_{\mathrm{B}}}\) the consumer will then substitute goods A for B in order to restore the above equality. That’s why, the law is otherwise called as law of substitution

Question 9.
Consumers, Equilibrium.
Answer:
Equilibrium is general sense refers to the “state of balance” & hence it is free from fluctuation. In this sense, a consumer attains equilibrium when he does not have any tendency either to increase or to decrease the level of consumption. Thus, a consumer shall be in equilibrium when he derives maximum satisfaction from the existing level of consumption. According to law of Equi-marginal utility, a consumer is in equilibrium or derives maximum satisfaction when marginal utility derived from various goods stall be equal or marginal utility derived from various goods shall be proportional to its price.

Question 10.
Consumption.
Answer:
Consumption is the initial process for the satisfaction of human wants. Consumption refers to the use of goods & services for the satisfaction of human wants. A consumer consumes a good because of its utility which is destroyed in the process of consumption. Thus, the destruction of utility is the result of consumption. Hence, consumption is viewed as the destruction of utility.

Question 11.
Marginal Utility & Total Utility.
Answer:

• Marginal utility is the addition made to the total utility caused by an increase in one extra unit possessed. Total utility is the sum of utilities derived from all the successive units.
• Marginal utility is the rate of change of total utility due to the consumption of one additional unit. Total utility is the sum of marginal utilities.
• At the intial stage, both the marginal & total utility are found to be equal.
• When marginal utility is zero, total utility is maximum.
• When marginal utility is negative, total utility declines.
• Marginal utility declines with the increase in the level of consumption but total utility increases at a diminishing rate.

Group – B

Long Type Questions With Answers

Question 1.
What is consumption in Economics ? Point out its importance.
Answer:
Meaning of consumption- Consumption is the pivot of all economic activities. In economic sense satisfaction of want through use of goods and services is called consumption. In order to have goods and services man has to make efforts. The urge to work comes from wants. In this sense the want for food is satisfied by having food-stuff for production of which effort is necessary. Consumption is of two types-consumption of goods and consumption of services. When consumption takes place the utilities contained in the commodities are used up and wants are satisfied. Some people observing this loss of utility in a commodity as a result of consumption define consumption as destruction of utility. But this conception of consumption is not correct always. Consumption may cause using up utilities at the point of consumption or it may take place gradually.

Consultation is of great relevance in the study of Economics. Consumption leads to production. The producers produce such things which consumers like. In this sense the consumer is treated as the king in the market. The producer decides the volume of production basing upon the consumer’s preference. The volume of consumption in our economy is an indicator of the degree of human welfare and the state of development of a country. In developed countries the standard of living is high which implies a high level of consumption and production. In under-developed countries the standard of living is low because of low level of consumption.

Consumption may be direct and indirect. Goods and services which are used directly to satisfy wants are called direct consumption. Indirect consumption refers to use of goods for further production. The former type of goods are called consumer goods and the latter type is known as investment goods. Consumption may be productive and unproductive. Productive consumption leads to increase in productivity. Unproductive consumption refers to consumption of luxuries which is wasteful.

Question 2.
State & explain the law of diminishing marginal utility with its exception ? Or, Make an analysis of law of diminishing marginal utility.
Answer:
The law of diminishing marginal utility is one of the fundamental & important laws of consumption. This law which is intially propounded by Gossen, a French engineer has been developed by Alfred Marshall later on. So this is called Gossen’s first law. This law serves as a basis for the analysis of demand.

The law of diminishing marginal utility explains an important tendency in the consumption of every commodity. When a consumer consumes the additional units of a particular goods, the marginal utility derived from those successive units goes on progressively diminishing. That’s why this law is commonly called as “Law of Diminishing marginal utility.” According to Marshall, “the additional benefit which a person derives from the given increase of his stock of a thing diminishes with every in the stock that he already has.”

This law is based on of a fundamental feature of human wants i.e. a particular want is satiable. It simply shows that when a consumer goes on consuming various units of a particular goods, the intensity of his wants for that goods gradually declines. It tells that the marginal utility derived from the additional units of a particular goods gradually falls & ultimately it becomes zero. Second fact speaks that the goods which are consumed are not perfect substitutes for each other. If so happens, one goods can satisfy a number of wants & hence the law will not operate. As the goods are not perfect substitutes for the satisfaction of various wants the law of diminishing marginal utility operates.
Illustration : The law can better be illustrated with the help of a numerical analysis.

Suppose, a consumer starts consuming different units of apples. When he consumes the first unit of the apple, he is supposed to get 30 units of utilities when he proceeds to consume second units of it, he will get 20 units of utility. Similarly, when he consumes 3rd, 4th, 5th & 6th units of the apple, he will get 15 units, 10 units, 5 units and 2 units of utility respectively. Ultimately, after consuming 7th units the marginal utility becomes zero. It simply shows that the gradual and progressive consumption of additional units of apple, the intensity of wants of the consumer towards apples is progressively declining. Furthermore, if the consumer is biased to consume the eighth units of apple, he will confront with the negative satisfaction and the marginal utility become negative (-2). This numerical notion is reflected in the following table :

Units of apple	Marginal Utility (in units)	Total Utility (in units)
1	30	30
2	20	50
3	15	65
4	10	75
5	5	80
6	2	82
7	0	82
8	-2	80

The table just reflects the theoretical illustration as mentioned above. This table reflects that the marginal utility derived from the successive units of apple goes on diminishing progressively but the total utility goes on increasing at a diminishing rate with the increase in the level of consumption. Secondly, the total utility is found to be the sum of the marginal utilities derived from the different units of the apples consumed.

Graphical Illustration : The law of diminishing marginal utility can also be graphically presented in the following manner :

The above figure measures units of the goods on OX-axis & marginal utility derived from OY-axis.
It is observed that the consumer derives 30 units of utilities by consuming 1st unit of the apple. Similarly by consuming 2nd, 3rd, 4th, 5th, and 6th.units of apple, the consumer gets 20,15, 10, 5,2 units of utilities respectively. Furthermore, the consumer gets zero utility by consuming 7th unit of apple and utility becomes -ve (-2) after the consumer consumes the 8units.

The marginal utility curve shows a diminishing trend throughout the period of consumption & it touches the OX-axis at point ‘7’ which shows that the marginal utility derived from the seventh unit is zero & by consuming the 8th unit the consumer gets -ve utility (-2) for which the curve crosses the OX-axis. Above all, the marginal utility curve slopes downward from left to right reflecting the diminishing nature of marginal utility.

Assumptions:
The law of diminishing marginal utility is based on several assumptions. For the operation of this law, the following conditions are to be taken into consideration.
(i) Homogeneous Units : The unitsjof the goods consumed should be identical in all respect. These units must be similar in quality, quantity, size etc for the operation of the law. If the units of the goods are not homogenous, the law of diminishing marginal utility may not operate. .

(ii) Continuous Consumption : The law of diminishing marginal utility stands valid in case of continuous consumption. There should not be any time gap between the consumption of successive units. The consumption should be continuous and regular so that the law will effectively operate.

(iii) Suitable quantity or size to be consumed : The units of the goods which are consumed should be of suitable size or quantity should be suitable. The units should not be so small or quantity should not so little.

(iv) No change in taste habit, fashion etc: The taste, habit, fashion etc should remain unchanged during the period of consumption. The operation of law depends on the constancy of such factors.

(v) Mental condition of the consumers : The consumer is assumed to be rational. His mental condition should be sound & this condition should remain unchanged during the period of consumption.

(vi) No change in the price of goods : The price of the goods should remain constant. If the price of the goods falls, the consumer may consume more of it by reducing the consumption as its substitutes and as such, the law becomes invalid.

(vii) No change in the income of the consumer : The income of the consumer is assumed to be constant. If the income of the consumer changes during the period of consumption, it may influence the consumer’s-behaviour and the law may not operate

Exceptions /Limitations:
The law of diminishing marginal utility suffers from a number of exceptions or limitations. Some of the limitations are. mentioned below :

• Measurability, of Utility : The law presumes that the utility is measurable in cardinal terms. Being a subjective concept, it is impracticable to measure utility in numerical terms.
• Rare and Curious things : The law does not operate in case of the collection of rare and curious things like old coins, old stamps, rare ancient goods, painting etc. In such case, the marginal utility is never felt to be diminishing.
• Conspicuous Consumption : The consumption of those luxurious goods which displays the social status, aristocracy and social prestige of the consumer is termed as conspicuous consumption. In case of such consumption, the law does not operate.
• Indivisible goods : The operation of the law is not felt in case of the consumption of indivisible goods.
• Abnormal Persons : The law is exclusively for the rational consumers. It is not applicable to the misers, mad persons & other abnormal persons.
• Change in taste, fashion and habits : In case of the change in taste, fashion and habit, the law does not operate.
• Initial Consumption : The law does not operate in case of initial consumption. In other words, the operation of law is not realised the stage of initial consumption.

In spite of these limitations, the law of diminishing marginal utility carries tremendous significance. It acts as a basis for the analysis of demand, theory of value, consumers surplus, taxation & other fields of consumption.

Question 2.
What is law of equi-marginal utility ? Explain it with diagram.
Or, How does the consumer attain equilibrium ? Explain the Principle of equilibrium.
Or, Explain the law of substitution ? Why is the law so named ?
Answer:
The law of equimarginal utility occupies an important place in the theory of consumptioti. This law is otherwise called “Gossen’s Second Law” which states the principle for attaining equilibrium in the field of consumption. This fundamental law of consumption describes the rules and principles for getting maximum satisfaction from the consumption of various goods with limited resources.

Admittedly, a consumer confronts with unlimited wants. But he possesses limited resources by which he can satisfy these wants. So he pursues to satisfy these wants with the limited resources in such a manner that he can get maximum satisfaction. In other words, the consumer tries to be in equilibrium while satisfying his unlimited wants with limited resources. Equilibrium is a situation in which the consumer has no tendency either to increase or to decrease the level of consumption. It is only possible if he derives maximum satisfaction. So the consumer is said to be in equilibrium when he gets maximum satisfaction in the field of consumption.

In the context of consumers equilibrium, the law of equi-marginal utility states that a consumer will be in equilibrium or a consumer derives maximum satisfaction when the marginal utilities derived from the different commodities are equal. Suppose a consumer consumes two goods X & Y„ he will be in equilibrium when marginal utility derived from X becomes equal to marginal utility derived from Y i.e.,
i.e. MUx = MUy
It is quite obvious from the law of diminishing marginal utility that a consumer shall go on consuming various units of a particular goods till marginal utility derived from it will be equal to price paid for it. Incase of good X, the consumer stops his consumption when marginal utility derived from it is equal to its price i.e.
i-e MUx = Px
As such, he will start the consumption of Y after this point is achieved & will continue till marginal utility derived from good Y is.equal to its price. i-e MUy = Py
As the marginal utilities are derived from the different goods are .equal, the prices of those goods must be equal. The equality of price of various goods in real market is quite imaginary. So, if the prices are found to be unequal, the law of equi-margnial utility states that a consumer will be in equilibrium when marginal utility derived from a good is proportional to its price. So this law is otherwise called “law of proportionality”. In this case, the consumer derives maximum satisfaction when the utility derived from the last rupee spent on each commodity will be equal. In our example, it is expressed as
\(\frac{\mathrm{MU}_{\mathrm{X}}}{\mathrm{P}_{\mathrm{X}}}\) = \(\frac{\mathrm{MU}_{\mathrm{Y}}}{\mathrm{P}_{\mathrm{Y}}}\)

The equality between the marginal utilities or the equality between \(\frac{MU}{P}\) for two goods may heppen at different level of consumption. But the most feasible combination is that which can be purchased with the given money income. Hence, the equality of \(\frac{MU}{P}\) for various goods must be equal to marginal utility of money which is asumed to be constant. In our example,
\(\frac{\mathrm{MU}_{\mathrm{X}}}{\mathrm{P}_{\mathrm{X}}}\) = \(\frac{\mathrm{MU}_{\mathrm{X}}}{\mathrm{P}_{\mathrm{X}}}\) = MUm
Where MUm represents marginal utility of money, or MUx = MUy = MUm.

If the \(\frac{\mathrm{MU}_{\mathrm{X}}}{\mathrm{P}_{\mathrm{X}}}\) becomes greater than \(\frac{\mathrm{MU}_{\mathrm{Y}}}{\mathrm{P}_{\mathrm{Y}}}\) the consumer shall prefer to substitute good X for Y so that the equality between the two will be restored & the consumer will get maximum satisfaction. For this, the law is called “law of substitution”.
Numercial Analysis.
This notion can be explained with the help of a numerical analysis which is as follows :

Units of. commodities in terms of Money	Marginal Utility X	Marginal Utility Y
1	20	18
2	18	16
3	15	14
4	12	12
5	9	10

In the numerical analysis, it is observed that the marginal utility of goods is equal to marginal utility of good Y when he consumes 4th unit of X and 4th unit of Y. Let the consumer has Rs.20 to spend on these two goods. Suppose, the price of X & price of Y is Rs 2 & Rs 3 respectively. With this a consumer shall be in equilibrium when he purchases 4 units of X & 4 units of Y. No other combinations can give him more satisfaction than this.
Graphical Analysis : The graphical analysis of the law can make this presumption more clear.

This figure measures unit of money on GX-axis which also represents the units of commodities in terms of money & OY-axis measures marginal utility.
The figure shows marginal utility curve for good X & Y which slope downward. It is obvious from the figure that MUx is equal to MUy when 4units of X & 4 units of Y are consumed. Any deviation of it will make the consumer a looser. To establish this let the consumer reduces his consumption of X & now consumer 3 units of X. To compensate this loss, the consumer may perfer to consume one more unit of Y i.e. 5 unit. In this circumstances, it is clear from the figure that the loss due to the reduction of the consumption of X is more than the gain due to increase in one additional unit of X. So, the consumer’s equilibrium is not assured. Thus, the previous combintaion is construed as real combintaion that ensures maximum satisfaction. ,

Limitations:

• Measurability of Utility : The law presumes measurability of utility. But the utility is a subjective concept which can not be measured in cardinal or numerical terms.
• In applicable to free goods : The law does not operate in case of free good as no payment is involved.
• Not applicable to indivisible goods : The law is ineffective for indivisible goods like Car, T.V. Because the marginal utility of car not be compared with that of pen.
• Taste, fashion, Custom, Habit: If the consumer is biased by the taste, fashion, habit, custom, the law will lose its significance.
• Not applicable to irrational man: The law may operate if the consumer is rational. In case of irrational or ignorant consumer, the law does not operate. Through the law suffers from these demerits, it has got practical significance in case of production, distribution publlic finance, planning etc.

Group – C

Objective type Questions with Answers
I. Multiple Choice Questions with Answers :

Question 1.
What hapens to utility of a goods, if it is consumed ?
(i) increases
(ii) decreases
(iii) remains same
(iv) destroyed
Answer:
(iv) destroyed

Question 2.
Which of the following determines the price of a goods ?
(i) utility
(ii) marginal utility
(iii) Demand
(iv) supply
Answer:
(ii) marginal utility

Question 3.
Diamond is more costly because its
(i) Marginal utility is more
(ii) Total utility is more
(iii) Demand is more
(iv) All of the above
Answer:
(i) Marginal utlity is more

Question 4.
For which MU can never be zero ?
(i) Water
(ii) Apple
(iii) Money
(iv) All of these
Answer:
(iii) Money

Question 5.
Which law guides the consumer to gain maximum satisfaction ?
(i) Law of demand
(ii) Law of dimenshing MU
(iii) Law of supply
(iv) Law of Equi-marginal utility
Answer:
(iv) Law of Equi-marginal utility

Question 6.
Which is not an assumption of Law of Diminishing MU ?
(i) Homegeneous units
(ii) Short time interval
(iii) Unchanged Taste and Preference
(iv) Marginal utility of money should by zero
Answer:
(iv) Marginal utility of money should by zero

Question 7.
Which is derived from Law of Dimenshing Marginal Utility ?
(i) Mu of money is zero
(ii) MU = Price
(iii) MU > Price
(iv) MU < Price
Answer:
(ii) MU = Price

Question 8.
For which the law of diminishing MU is not applicable ?
(i) Consumers goods
(ii) Material goods
(iii) Indivigible goods
(iv) Private goods
Answer:
(ii) Material goods

Question 9.
For which the practical importance of Law of equi-marginal utility is felt ?
(i) Production
(ii) Consumption
(iii) Distribution
(iv) All of the above
Answer:
(ii) Consumption

Question 10.
Which is the meaning of consumption ?
(i) creation of utility
(ii) destruction of utility
(iii) creation of satisfaction
(iv) All of the above
Answer:
(ii) destruction of utility

Question 11.
If a consumer goes on consuming the additional units of a goods, the wants satisfying power of the good
(i) increases
(ii) diminishes
(iii) first increases & then decreases
(iv) remain unchanged
Answer:
(ii) diminishes

Question 12.
If a consumer consumes a good, the total utility
(i) decreases
(ii) increases
(iii) remains some
(iv) can not say
Answer:
(ii) increases

Question 13.
The satisfaction derived from the consumption of additional units of a good goes on
(i) increasing
(ii) diminishing
(iii) remains unchanged
(iv) None of the above
Answer:
(ii) diminishing

Question 14.
As per the law of diminishing marginal utility, the increase in level of consumption cause a
(i) increase in MU
(ii) increase in TU
(iii) decrease in MU
(iv) decrease in TU
Answer:
(iii) decrease in MU

Question 15.
Marginal utility curve generally takes the shape of
(i) vertical straight line
(ii) horizontal straight line
(iii) upward sloping
(iv) downward sloping
Answer:
(iv) downward sloping

Question 16.
When marginal utility is zero, the TU becomes
(i) zero
(ii) minimum
(iii) maximum
(iv) negative
Answer:
(iii) maximum

Question 17.
With increase in level of consumption, total utility derived from the goods goes on
(i) increasing at an increasing rate
(ii) diminishing
(iii) increasing at a diminishing rate
(iv) increasing
Answer:
(iii) increasing at a diminishing rate

Question 18.
When marginal utility is negative, the total utility
(i) remains unaffected
(ii) diminishes
(iii) increases
(iv) first increases & then decreases
Answer:
(ii) diminishes

Question 19.
Which is the assumption of law of diminishing marginal utility ?
(i) Income of the consumer should remain constant
(ii) consumption must be continuous
(iii) Goods must be homogeneous
(iv) All of the above
Answer:
(iv) All of the above

Question 20.
For the operation of the law of diminishing marginal utility, the units of the good must be
(i) big in size
(ii) identical
(iii) very small
(iv) no specific size is required
Answer:
(ii) identical

Question 21.
Law of diminishing marginal utility does not operate in case of
(i) drunkard
(ii) rational man
(iii) consumer
(iv) producer
Answer:
(i) drunkard

Question 22.
Which law provides a base for consumers equilibrium ?
(i) Law of diminishing marginal utility
(ii) Law of Equi-marginal utility
(iii) Law of demand
(iv) All of the above
Answer:
(ii) Law of Equi-marginal utility

Question 23.
Which is not the other name of the law of equi-marginal utility ?
(i) Law of maximum happiness
(ii) Law of substitution
(iii) Law of maximum satisfaction
(iv) Law of maximum utility
Answer:
(iii) Law of maximum satisfaction

Question 24.
In order to get maximum satisfaction, the marginal utilities derived from various goods should be
(i) maximum (ii) equal
(iii) unequal
(iv) Both (i) and (ii)
Answer:
(ii) equal

Question 25.
According to law of equi-marginal utility, the marginal utility derived from a good must be
(i) proportional to its price
(ii) equal to its price
(iii) equal to MU of money
(iv) All of the above
Answer:
(i) proportional to its price

Question 26.
While purchasing goods with fixed income a rational consumer is guided by;
(i) Law of demand
(ii) Law of supply
(iii) Law of Equi-marginal utility
(iv) Law of diminishing marginal utility
Answer:
(iii) Law of Equi-marginal utility

Question 27.
Law of equi-marginal utility does not operate in ease of
(i) Divisible of goods
(ii) rational consumer
(iii) unlimited resources
(iv) All of the above
Answer:
(iii) unlimited resources

Question 28.
Law of eqi-marginal utility is based on
(i) Wants are competitive
(ii) A particular want is satiable
(iii) Wants are complementary
(iv) All of the above
Answer:
(i) Wants are competitive

Question 29.
The Most important assumptions of ‘Law of Diminishing Marginal Utility’ is :
(i) Commodity must be homogenous
(ii) Consumption must be continuous
(iii) Sufficient quantity is to be consumed
(iv) All of the above
Answer:
(iv) All of the above

Question 30.
The most important limitations of Law of Diminishing Marginal Utility is
(i) Abnormal Person
(ii) Indivisible goods
(iii) Gififen goods
(iv) Both (i) and (ii)
Answer:
(iv) Both (i) and (ii)

Question 31.
A consumer will attain equlibrium when :
(i) \(\frac{\text { M.U.x }}{\text { Px }}\) = \(\frac{\text { M.U.y }}{\text { Py }}\)
(ii) MUx = MUy
(iii) \(\frac{\text { M.U.x }}{\text { Py }}\) = \(\frac{\text { M.U.y }}{\text { Px }}\)
(iv) None of the above
Answer:
(iii) \(\frac{\text { M.U.x }}{\text { Py }}\) = \(\frac{\text { M.U.y }}{\text { Px }}\)

Question 32.
The most important assumptions of Law of Equi-marginalutility are:
(i) Utility of a commodity is cardinally measurable.
(ii) Marginal utility of money remains constant.
(iii) Income of the consumer is constant.
(iv) Both (i) and (ii)
Answer:
(iv) Both (i) and (ii)

Question 33.
In which of the following cases the law of Diminishing Marginal Utility is not applicable ?
(i) Love
(ii) Money
(iii) Stamp collection
(iv) All of the above
Answer:
(iv) All of the above

Question 34.
The relationship between marginal utility and total utility is :
(i) Total utility increases at an increasing rate after a point.
(ii) When marginal utility becomes zero, total utility becomes maximum.
(iii) Total utility starts falling when marginal utility becomes negative.
(iv) Both (ii) and (iii)
Answer:
(iv) Both (ii) and (iii)

Question 35.
Marginal Utility is
(i) Want satisfying power of a commodity.
(ii) The sum of utilities of all successive units of a commodity.
(iii) The addition to the total utility caused by an increase of one commodity possessed.
(iv) None of the above.
Answer:
(iii) The addition to the total utility caused by an increase of one commodity possessed.

Question 36.
When marginal utility is zero, the total utility is:
(i) Zero
(ii) Negative
(ii) Maximum
(iv) None of the above.
Answer:
(iii) Maximum

Question 37.
Marginal Utility of money can be:
(i) Zero
(ii) Negative
(iii) Neither zero nor negative
(iv) None of the above.
Answer:
(iii) Neither zero nor negative.

Question 38.
The law of equi-rnarginal utility is also known as:
(i) Law of substitution.
(ii) Law of maximum satisfaction.
(iii) Law of proportionality
(iv) All of the above.
Answer:
(iv) All of the above.

II. Fill in the blanks :

Question 1.
Consumption refers to the ____ of utility.
Answer:
Destruction

Question 2.
As the quantity of commodity consumed increases, total utility also increases at a ____
Answer:
Diminishing rate.

Question 3.
____ is the rate of change of total utility.
Answer:
Marginal utility

Question 4.
Price of a commodity is always equal to ____ utility.
Answer:
marginal

Question 5.
Total utility becomes ____ when marginal utility is zero.
Answer:
maximum

Question 6.
____ utility can never be negative.
Answer:
Total

Question 7.
Total utility may ____ when marginal utility is negative.
Answer:
diminish

Question 8.
Marginal utility curve has a ____
Answer:
Diminish

Question 9.
While consuming, a consumer stops his consumption when marginal utility derived from a commodity is equal to ____
Answer:
Price

Question 10.
Utility is a ____ concept.
Answer:
Subjective

Question 11.
According to Marshall marginal utility of money remains ____
Answer:
Constant

Question 12.
Price of a commodity reflects ____ utility.
Answer:
Marginal

Question 13.
Marginal utility of liquor in case of a drunkard ____ instead of felling.
Answer:
Rises

Question 14.
The consumer is in equlibrium when marginal utility derived from different commodities is ____
Answer:
equal.

Question 15.
Law of ____ guides the consumer for deriving maximum satisfaction.
Answer:
equi-marginal utility

III. Correct the Sentences:
Correct them, if necessary, without changing the words underlined.

Question 1.
Consumption is the creation of utility.
Answer:
Incorrect
Correct: Consumption is the destruction of utility.

Question 2.
Utility is an objective concept.
Answer:
Incorrect
Correct: Utility is a subjective concept

Question 3.
Utility is assumed to be a cardinal concept.
Answer:
Correct

Question 4.
Marginal utility is the sum of utilities.
Answer:
Incorrect
Correct; Total utility is the sum of utilities.

Question 5.
Rate of change of total utility is the marginal utility.
Answer:
Correct.

Question 6.
When a consumer consumes the additional units of a goods, marginal utility increases but total utility decreases at a diminishing rate.
Answer:
Incorrect
Correct: When a consumer consumes the additional unite of a goods, margina utility decreases. but total utility increases at a diminishing rate.

Question 7.
Total utility is the additional utility derived from the consumption of an extra units of a goods.
Answer:
Incorrect
Correct: Marginal utility is the additional utility derived from the consumption of an extra units of a goods.

Question 8.
When marginal utility is zero, total utility is zero.
Answer:
Incorrect
Correct: When marginal utility is zero, total utility is maximum.

Question 9.
Marginal utility can never be negative.
Answer:
Incorrect
Correct: Total utility can never be neeative.

Question 10.
Total utility goes on increasing even if marginal utility is negative.
Answer:
Incorrect
Correct: Total utility declines when marginal utility is negative.

Question 11.
Marginal utility is a static concept.
Answer:
Incorrect
Correct: Marginal utility is a moving concept.

Question 12.
Marginal utility tends to be equal to price.
Answer:
Correct

Question 13.
Utility derived from the last unit is the marginal utility.
Answer:
Incorrect
Correct: Utility derived from the additional unit is the marginal utility.

Question 14.
Marginal utility curve has a positive slope.
Answer:
Incorrect
Correct: Marginal utility curve has a negative slope.

Question 15.
Total utility of a goods determines the price.
Answer:
Incorrect
Correct: Marginal utility of a goods determines the price.

Question 16.
Consumer is in equilibrium when total utility derived from different goods are equal.
Answer:
Incorrect
Correct: Consumer is in equilibrium, when marginal utility derived from different goods are equal.

Question 17.
Marginal utility is inversely related to price.
Answer:
Incorrect
Correct: Marginal utility is directly related to price.

Question 18.
Law of equi-marginal utility is called “Law of substitution”.
Answer:
Correct

Question 19.
In law of equi-marginal utility, marginal utility is equal to its price.
Answer:
Incorrect
Correct: In law of equi-marginal utility, marginal utility is proportional to its price.

Question 20.
Law of equi-marginal utility is called law of proportionality
Answer:
Correct

IV. Answer the following questions in one word/one sentence :

Question 1.
What is meaning of consumption ?
Answer:
Consumption refers to the use of goods & services for the satisfaction of human wants.

Question 2.
Who is called as a rational consumer ?
Answer:
A rational consumer is one who tries to maximise his utility.

Question 3.
Who is the consuming unit ?
Answer:
Consumer is the consuming unit.

Question 4.
What is utility ?
Answer:
Utility is the wants satisfying power of a commodity.

Question 5.
What is Total Utility ?
Answer:
Total utility is the sum of utilities derived from all the successive units consumed.

Question 6.
What is marginal utility ?
Answer:
Marginal utility is the addition made to the total utility caused by an increase in one additional unit of a good consumed.

Question 7.
What happens to total utility when the units of goods consumed increases ?
Answer:
When the units of goods consumed increase, the total utility increases at a diminishing rate.

Question 8.
What is the nature of marginal utility ?
Answer:
Marginal utility derived from a goods diminishes with every increase in the units of that goods consumed.

Question 9.
What happens to total utility’ when marginal utility is zero ?
Answer:
When marginal utility is zero, the total utility is maximum.

Question 10.
What happens to total utility when marginal utility is negative ?
Answer:
Total utility decreases when marginal utility is -ve.

Question 11.
When marginal utility becomes equal to total utility ?
Answer:
At the initial stage of consumption, marginal utility is equal to total utility.

Question 12.
Who propounded the law of diminishing marginal utility ?
Answer:
Alfred Marshall.

Question 13.
What is law of diminishing marginal utility ?
Answer:
According to Marshall, “the additional benefit what a person derives from the given increase of his stock of a thing diminishes with every increase in the stock that he already has.”

Question 14.
What does the law of diminishing marginal utility show ?
Answer:
The law of diminishing marginal utility shows the relationship between marginal utility derived from various units of a goods & the quantity of it consumed.

Question 15.
To what extent a consumer goes on consuming various units of a goods ?
Answer:
A consumer goes on consuming various units of a goods till marginal utility derived is equal to its price.

Question 16.
What should be the nature of commodity for the operation of law of diminishing marginal utility ?
Answer:
The units of the commodity must be homogeneous.

Question 17.
Does marginal utility of money become zero ?
Answer:
No, marginal utility of money can never be zero.

Question 18.
Why does marginal utility of money not become zero ?
Answer:
Marginal utility of money does not become zero because money is not a commodity rather it represents a bundle of commodities.

Question 19.
What is the relationship between marginal utility & price ?
Answer:
Marginal utility derived from a goods should be equal to its price.

Question 20.
Which law is called “Gossen’s first law.”
Answer:
Law of diminishing marginal utility is called to “Gossen’s first law”.

Question 21.
State two exceptions of law of diminishing marginal utility.
Answer:
The law does not operate in case of indivisible goods & rare collections.

Question 22.
What is equilibrium ?
Answer:
Equilibrium is a state of balance.

Question 23.
When does consumer attain equilibrium ?
Answer:
Consumer is said to be in equilibrium when he has no tendency either to increase or to decrease the level of consumption.

Question 24.
What happens to utility when consumer attains equilibrium ?
Answer:
Utility is maximised when consumer attains equilibrium.

Question 25.
Which law explains the consumers equilibrium ?
Answer:
Law of equi-marginal utility explains the consumers’ equilibrium.

Question 26.
Which law is called “Gossen’s second law” ?
Answer:
Law of equimarginal utility is called Gossen’s second law.

Question 27.
What does the law of equi-marginal utility state ?
Answer:
Law of equi-marginal utility states that a consumer will be in equilibrium when the marginal utility derived from different goods are equal.

Question 28.
What relationship between marginal utility & price exists in case of consumer’s equilibrium ?
Answer:
The marginal Utility is proportional to its price in case of consumer’s equilibrium.

Question 29.
How can be the marginal utility of money measured ?
Answer:
Marginal utility of money can be measured by dividing marginal utility of a commodity by its price.

Question 30.
Which law is called the “Law of substitution”.
Answer:
Law of equi-marginal utility.