Odisha State Board BSE Odisha 6th Class English Solutions Test-2(A) Textbook Exercise Questions and Answers.
BSE Odisha Class 6 English Solutions Test-2(A)
BSE Odisha 6th Class English Test-2(A) Text Book Questions and Answers
□ The figures in the right-hand margin indicate the marks for each question.
1. Write the following names of persons in English.
(Teacher will provide names of six persons in Odia.)
ଡାକ୍ତର ରାଜେନ୍ଦ୍ର ପ୍ରସାଦ
ରଣଜିତ ସିଂହ
ଅରବିନ୍ଦ ଘୋଷ
ବାଘା ଜତିନ
ସମ୍ରାଟ ଅଶୋକ |
ରାଜା ଦଶରଥ
Answer:
Doctor Rajendra Prasad
Ranjit Singh
Aurobindo Ghose
Bagha Jatin
Emperor Ashok
King Dasaratha
2. Write the following names of places in English.
(Teacher will provide names of six places in Odia.)
ପୁଡୁଚେରୀ |
ଶ୍ରୀ ଲଙ୍କା
ବିଜୟ ନାଗର
ମଥୁରା |
ମୁମ୍ବାଇ |
କପିଳାସ
Answer:
Puducherry
Srilanka
Vijaya Nagar
Mathura
Mumbai
Kapilas
![]()
3. Your teacher will give a dictation of twelve words. Listen to him/her and write.
Answer:
village
classmate
friend
decided
deaf
Good Morning
fever
Germany
soldier
quarters
country
understand
4. Given below are some words. Your teacher will read aloud seven of them. Tick those s/he reads aloud.
language, young, neither, retire, gunny bag, religious, sight, greedy, weather, straightened, beautiful, special, elephant, bicycle
[Listen to your teacher carefully and tick those words as he reads aloud.]
5. Your teacher will read aloud a paragraph. Listen to him/her and fill in the gaps. (Question with Answer)
Once there lived a poor man in a village. He had a rich classmate. He lived in a town. They did not meet for a long time. In the meantime, the rich friend had problems with his ear and became deaf. His friend in the village could not know this.
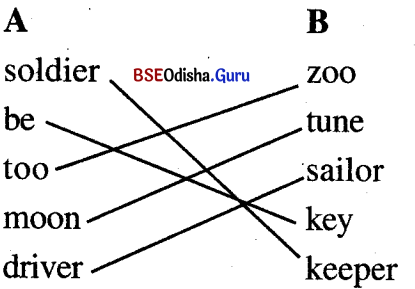
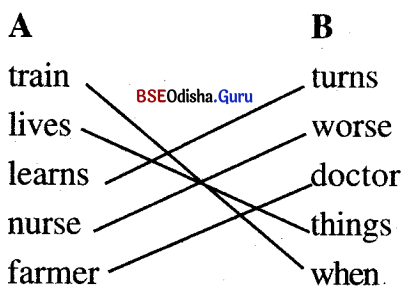
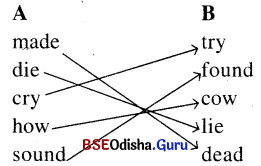
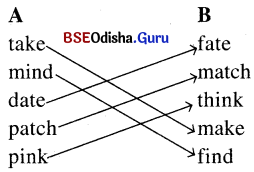
6. Match the words which sound alike at the end. (Question with Answer)
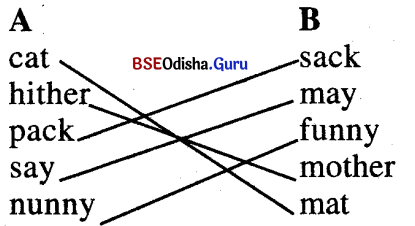
Answer:
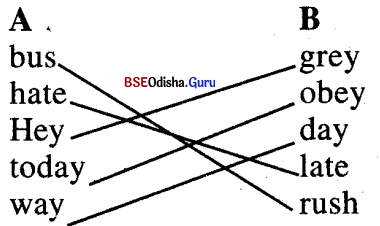
![]()
7. Read The poem and answer the questions incomplete sentences.
There was a dog and there was a cat.
One very thin and the other is fat.
Neither of them was a pet.
But the cat always sat on a mat.
and claimed she was a loving pet.
Question (i)
Who were there in the poem?
Answer:
In the poem, there were a dog and a cat.
Question (ii)
How were they?
Answer:
One was very thin and the other was fat.
Question (iii)
Were they pets?
Answer:
No, neither of them was a pet.
Question (iv)
Who sat on a mat?
Answer:
The cat always sat on a mat.
Question (v)
What did the cat claim?
Answer:
The cat claimed that she was a loving pet.
(vi)
Who was very thin?
Answer:
The dog was very thin.
![]()
8. Read the following paragraph and answer the questions in complete sentences.
“There is a special school in Karagudi. It is special because it is not for children. Can you guess for whom it is ? It is for baby elephants. Who teaches them? The elephant trainers teach them. Like our schools, they have a timetable. They learn, play and eat according to this timetable.
Question (i)
What is there in Karagudi?
Answer:
There is a special school in Karagudi.
Question (ii)
Why is this school special?
Answer:
This school is special because it is not for children.
Question (iii)
Who are the students?
Answer:
Baby elephants are the students.
Question (iv)
Who are the teachers?
Answer:
The elephant trainers are the teachers.
Question (v)
What do they have like our schools?
Answer:
Like our schools, they have a timetable.
Question (vi)
How do they follow it?
Answer:
According to this timetable, they learn, play, and eat in the special school.
![]()
9. Read the following poem and answer the questions in complete sentences.
It was a very cool night And there
was no crab in sight.
The fox looked for one
But there was none.
“Where did they go ?”
Not even one in sight!
They must be in their holes If
I’m right.”
Question (i)
How was the night?
Answer:
It was a very cool night.
Question (ii)
What was not in sight?
Answer:
There was no crab in sight.
Question (iii)
Who looked for the crab?
Answer:
The fox looked for the crab.
Question (iv)
Did he find one?
Answer:
No, he did not find any crab, because there was none.
Question (v)
Where did they go?
Answer:
They must have been in their holes.
Question (vi)
Who were there in the poem?
Answer:
There were the fox and the crab in the poem.
![]()
10. Read the following paragraph and answer the questions in complete sentences.
Mahagiri was a big elephant. He was trained at a special school. He was bought by a merchant. The merchant made a lot of money by putting Mahagiri to work. The elephant was often sent to the forest to carry heavy logs of wood. Sometimes, he carried people from one place to another. Once, he even carried a bridegroom to the bride’s house! At times he was sent to a famous temple in a village nearby to lead the festival procession.
Question (i)
What is this paragraph about?
Answer:
This paragraph is about an elephant.
Question (ii)
Who was Mahagiri?
Answer:
Mahagiri was a big elephant.
Question (iii)
Where was Mahagiri trained?
Answer:
Mahagiri was trained at a special school.
Question (iv)
Who bought it?
Answer:
A merchant bought it.
Question (v)
How did the merchant make a lot of money?
Answer:
The merchant made a lot of money by putting Mahagiri to work.
Question (vi)
Why was the elephant often sent to the forest?
Answer:
The elephant was often sent to the forest to carry heavy logs of wood.
Question (vii)
What did he sometimes carry?
Answer:
Sometimes, he carried people from one place to another.
Question (viii)
What did he once even carry?
Answer:
Once, he even carried a bridegroom to the bride’s house.
Question (ix)
Where was he sent to at times?
Answer:
At times he was sent to a famous temple in a village nearby.
![]()
Question (x)
Why was he sent to a famous temple?
Answer:
He was sent to a famous temple to lead the festival procession.




 I like bats
I like bats







 not built a nest. One day the crow was not in her nest. The cuckoo threw away the eggs and laid her own eggs there. The crow did not know this. She sat over the eggs for some days. Young ones came out. She took care of them. But when the young ones grew? up, they sang like cuckoos. So she drove them away. From that day the crow always drives away the cuckoo.
not built a nest. One day the crow was not in her nest. The cuckoo threw away the eggs and laid her own eggs there. The crow did not know this. She sat over the eggs for some days. Young ones came out. She took care of them. But when the young ones grew? up, they sang like cuckoos. So she drove them away. From that day the crow always drives away the cuckoo.