Class 6

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି Ex 9.5 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି Ex 9.5

Question 1.
ତଳେ ଦିଆଯାଇଥିବା ସାରଣୀକୁ ପୂରଣ କର, ଯେପରି ସାମାନ୍ତରିକ ଚିତ୍ର ସମ୍ବନ୍ଧରେ ‘ହଁ’ ବା ‘ନାହିଁ’ ପୂରଣ କରାଯାଇଛି । (ପ୍ରଶ୍ନ ସହ ଉତ୍ତର)

ସମାଧାନ:

Question 2.
ପ୍ରତ୍ୟେକ ଉକ୍ତିର ତଳେ ଥିବା ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ତଥ୍ୟ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(କ) ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର _________ ସମାନ ହେଲେ ଚିତ୍ରଟି ରମ୍ବସ୍ ହୁଏ ।
(କୋଣର ପରିମାଣ, ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ, କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ)
ସମାଧାନ:
ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ

(ଖ) ଏକ _________ ର କୋଣମାନ ସମକୋଣ ହେଲେ ଚିତ୍ରଟି ଆୟତଚିତ୍ର ହେବ ।
(ବର୍ଗଚିତ୍ର, ସାମାନ୍ତରିକ ଚିତ୍ର, ରମ୍ବସ)
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ର

(ଗ) ଏକ ଆୟତଚିତ୍ରର _________ ସମାନ ହେଲେ ଚିତ୍ରଟି ବର୍ଗଚିତ୍ର ହେବ ।
(ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ, ସମସ୍ତ କୋଣର ପରିମାଣ )
ସମାଧାନ:
ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ

(ଘ) କୌଣସି ଚତୁର୍ଭୁଜର ଏକ ଯୋଡ଼ା ବିପରୀତ ବାହୁ ସମାନ୍ତର ହେଲେ ଚିତ୍ରଟି _________ ହେବ ।
(ରମ୍ବସ, ବର୍ଗଚିତ୍ର, ଟ୍ରାପିଜିୟମ୍ )
ସମାଧାନ:
ଟ୍ରାପିଜିୟମ୍

(ଙ) କୌଣସି ଚତୁର୍ଭୁଜର ଦୁଇଯୋଡ଼ା ବିପରୀତ ବାହୁ ସମାନ୍ତର ହେଲେ ଚିତ୍ରଟି _________ ହେବ ।
(ବର୍ଗଚିତ୍ର, ଆୟତଚିତ୍ର, ସାମାନ୍ତରିକ ଚିତ୍ର)
ସମାଧାନ:
ସାମାନ୍ତରିକ ଚିତ୍ର

(ଚ) ABCD ଚତୁର୍ଭୁଜର A͞B ସମାନ୍ତର C͞D, A͞D ସମାନ୍ତର BC ଏବଂ ∠ABC ର ପରିମାଣ 90° ହେଲେ ଚତୁର୍ଭୁଜଟି ଏକ _________ ହେବ ।
(ରମ୍ବସ, ଆୟତଚିତ୍ର, ବର୍ଗଚିତ୍ର)
ସମାଧାନ:
ଆୟତଚିତ୍ର

Question 3.
ନିମ୍ନସ୍ଥ ଉକ୍ତିମାନଙ୍କ ମଧ୍ୟରୁ ଠିକ୍ ଉକ୍ତି ଶେଷରେ ଠିକ୍ ଚିହ୍ନ (✓) ଓ ଭୁଲ୍ ଉକ୍ତି ଶେଷରେ ଛକି ଚିହ୍ନ (✗) ବସାଅ ।
(କ) ଆୟତଚିତ୍ରର ପ୍ରତ୍ୟେକ କୋଣ ଏକ ସମକୋଣ । 
ସମାଧାନ:
✓

(ଖ) ଆୟତଚିତ୍ରର ବିପରୀତ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ।
ସମାଧାନ:
✓

(ଗ) ଏକ ବର୍ଗଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ।
ସମାଧାନ:
✓

(ଘ) ଏକ ରମ୍ବସର ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ । 
ସମାଧାନ:
✓

(ଙ) ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ।
ସମାଧାନ:
✗

(ଚ) ଟ୍ରାପିଜିୟମ୍‌ର ବିପରୀତ ବାହୁ ସମାନ୍ତର ।
ସମାଧାନ:
✗

Question 4.
ଏକ ଚତୁର୍ଭୁଜର ସମସ୍ତ ବାହୁ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଓ ସମସ୍ତ କୋଣ ସମପରିମାଣ ବିଶିଷ୍ଟ ହେଲେ ଆମେ ତାକୁ ସୁଷମ ଚତୁର୍ଭୁଜ କହୁ । ତେବେ ସୁଷମ ଚତୁର୍ଭୁଜଟି କିଏ ଲେଖ ।

ସମାଧାନ:
ସୁଷମ ଚତୁର୍ଭୁଜଟି ବର୍ଗଚିତ୍ର ।

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି Ex 9.4 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି Ex 9.4

Question 1.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର ଚିତ୍ର ଅଙ୍କନ କରି ତାହାର ନାମ PQRS ଦିଅ । ଏହାର ସମସ୍ତ ବାହୁ, କୋଣ ଓ ଶୀର୍ଷବିନ୍ଦୁ ଓ କଣ୍ଠର ନାମ ଲେଖ ।
ସମାଧାନ:

ବାହୁ : P͞Q, Q͞R, R͞S, P͞S
କୋଣ : ∠QPS, ∠PQR, ∠QRS, ∠RSP
ଶୀର୍ଷବିନ୍ଦୁ : P, Q, R ଓ S
କର୍ଣ୍ଣ : P͞R ଓ Q͞S

Question 2.

(କ) ∠B ର ବିପରୀତ କୋଣ _________ ଓ ∠A ର ବିପରୀତ କୋଣ _________ ।
ସମାଧାନ:
∠D, ∠C

(ଖ) D͞A ବାହୁର ସଂଲଗ୍ନ କୋଣ ଦୁଇଟି ହେଲେ _________ ଓ _________ ।
ସମାଧାନ:
∠BAD, ∠ADC

(ଗ) ଚତୁର୍ଭୁଜଟିରେ ଗୋଟିଏ ବାହୁର _________ ଗୋଟି ସଂଲଗ୍ନ କୋଣ ଥାଏ ।
ସମାଧାନ:
ଦୁଇ

(ଘ) B ଶୀର୍ଷବିନ୍ଦୁର ବିପରୀତ ଶୀର୍ଷବିନ୍ଦୁ ହେଉଛି _________ ।
ସମାଧାନ:
D

(ଙ) _________ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ _________ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟଠାରୁ ଅଧିକ ।
ସମାଧାନ:
A͞C, B͞D

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 5 ଭଗ୍ନ ସଂଖ୍ୟା Ex 5.4 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 5 ଭଗ୍ନ ସଂଖ୍ୟା Ex 5.4

Question 1. 
ନିମ୍ନରେ ଥ‌ିବା ପ୍ରତ୍ୟେକ ଚିତ୍ର ପ୍ରକୃତ ଭଗ୍ନ ସଂଖ୍ୟା ବା ମିଶ୍ର ସଂଖ୍ୟା ସୁରଉଛି ଲେଖ।

ସମାଧାନ:
\(\frac{1}{4}\), 2 \(\frac{1}{3}\), 1 \(\frac{3}{6}\) ବା 1 \(\frac{1}{2}\)

Question 2. 
ନିମ୍ନ ମିଶ୍ରସଂଖ୍ୟାଗୁଡ଼ିକୁ ଅପ୍ରକୃତ ଭଗ୍ନସଂଖ୍ୟାରେ ପରିଣତ କର।

(କ) 3 \(\frac{2}{3}\)
ସମାଧାନ:
= \(\frac{3 \times 3+2}{3}=\frac{11}{3}\)

(ଖ) 2 \(\frac{2}{3}\)
ସମାଧାନ:
= \(\frac{2 \times 3+2}{3}=\frac{8}{3}\)

(ଗ) 1 \(\frac{5}{8}\)
ସମାଧାନ:
= \(\frac{1 \times 8+5}{8}=\frac{13}{8}\)

Question 3. 
ନିମ୍ନ ଅପ୍ରକୃତ ଭଗ୍ନସଂଖ୍ୟାଗୁଡ଼ିକୁ ମିଶ୍ରସଂଖ୍ୟାରେ ପ୍ରକାଶ କର।

(କ) \(\frac{18}{7}\)
ସମାଧାନ:

(ଖ) \(\frac{20}{9}\)
ସମାଧାନ:

(ଗ) \(\frac{23}{8}\)
ସମାଧାନ:

Question 4. 
ନିମ୍ନ ଭାଗକ୍ରିୟାଗୁଡ଼ିକର ଭାଗଫଳକୁ ମିଶ୍ରସଂଖ୍ୟାରେ ପ୍ରକାଶ କର।

(କ) 19 ÷ 5
ସମାଧାନ:

(ଖ) 24 ÷ 7
ସମାଧାନ:

(ଗ) 34 ÷ 13
ସମାଧାନ:

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 6 ଦଶମିକ ସଂଖ୍ୟା Ex 6.3 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 6 ଦଶମିକ ସଂଖ୍ୟା Ex 6.3

Question 1.
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଦୁଇଟିଯାକ ଦଶମିକ ସଂଖ୍ୟାକୁ ଚିତ୍ରରେ ଦେଖାଅ ଓ ବଡ଼ ସଂଖ୍ୟାଟିକୁ ଚିହ୍ନାଅ ।

(କ) 0.47 ଓ 0.3
ସମାଧାନ:

(ଖ) 0.5 ଓ 0.05
ସମାଧାନ:

(ଗ) 1.5 ଓ 0.68
ସମାଧାନ:

Question 2. 
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଥ‌ିବା ଦଶମିକ ସଂଖ୍ୟାମଧ୍ୟରୁ କେଉଁଟି ବଡ଼?

(କ) 0.93 ଏବଂ 0.093
ସମାଧାନ:

(ଖ) 1.1 ଏବଂ 1.01
ସମାଧାନ:

(ଗ) 0.83 ଏବଂ 0.038
ସମାଧାନ:

(ଘ) 1.5 ଏବଂ 1.50
ସମାଧାନ:

(ଙ) 0.099 ଏବଂ 0.19
ସମାଧାନ:

Question 3. 
ତୁମ ମନରୁ ଯେ କୌଣସି ଦୁଇଟି ଦଶମିକ ସଂଖ୍ୟା ନିଅ ଓ ସେ ଦୁଇଟି ମଧ୍ଯରେ ବଡ଼ ସଂଖ୍ୟାଟିକୁ ବାଛ | ତୁମେ ବଡ଼ ସଂଖ୍ୟାଟିକୁ କିପରି ଚିହ୍ନଟ କଲେ ଲେଖ।
ସମାଧାନ:

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି InText Questions Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି InText Questions

1. ନିମ୍ନ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
(କ) ∠A ର ସମ୍ମୁଖୀନ ବାହୁ କିଏ ?
ସମାଧାନ:
B͞C

(ଖ) କେଉଁ ବାହୁର ଦୈର୍ଘ୍ୟକୁ ‘a’ ରୂପେ ନାମିତ କରାଯାଏ ?
ସମାଧାନ:
B͞C

(ଗ) B͞C ର ଦୈର୍ଘକୁ କିପରି ନାମିତ କରାଯିବ ?
ସମାଧାନ:
a

(ଘ) A͞B ଓ A͞C ର ଛେଦରେ ଗଠିତ ଶୀର୍ଷବିନ୍ଦୁର ନାମ କ’ଣ ?
ସମାଧାନ:
A ବିନ୍ଦୁ

2. B͞A ଓ C͞A ବାହୁଦ୍ୱୟର ଅନ୍ତର୍ଗତ କୋଣ ହେଉଛି ∠BAC ।
ସେହିପରି, A͞B ଓ B͞C ର ଅନ୍ତର୍ଗତ କୋଣ ∠ABC ।
B͞C ଓ A͞C ର ଅନ୍ତର୍ଗତ କୋଣର ନାମ କହ ।
ସମାଧାନ:
∠ACB

3. ପାର୍ଶ୍ୱସ୍ଥ ABC ତ୍ରିଭୁଜକୁ ଦେଖ ଓ ତଳେ ଦିଆଯାଇଥବା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

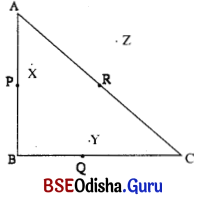
(i) Δ ABC ______, ______ ଓ ______ ରେଖାଖଣ୍ଡ ତ୍ରୟର ସମାହାର।
ସମାଧାନ:
A͞B, B͞C, C͞A

(ii) P ବିନ୍ଦୁଟି ______ ବାହୁ ଉପରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
A͞B

(iii) Q ବିନ୍ଦୁଟି ______ ବାହୁ ଉପରେ ଅବସ୍ଥିତ।
ସମାଧାନ:
B͞C

(iv) R ବିନ୍ଦୁଟି ______ ବାହୁ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ।
ସମାଧାନ:
C͞A

(v) A,B,C ବିନ୍ଦୁ ବ୍ୟତୀତ ଚିତ୍ରରେ ______, ______ ଓ ______ ବିନ୍ଦୁ ତିନୋଟି ଅବସ୍ଥିତ ।
ସମାଧାନ:
P, Q, R

(vi) X, Y ଓ Z ବିଦୁ୍ୟତ୍ରୟ ତ୍ରିଭୁଜ ଉପରେ (ଅର୍ଥାତ୍‌ ତ୍ରିଭୁଜର କୌଣସି ବାହୁ ଉପରେ) ଅବସ୍ଥିତ ନୁହନ୍ତି । ତେବେ ସେଗୁଡ଼ିକ କେଉଁଠି ଅବସ୍ଥିତ ?
ସମାଧାନ:
X ଓ Y ବିନ୍ଦୁ ଧର ଅନ୍ତର୍ଦେଶରେ ଅବସ୍ଥିତ ଏବଂ Z ବିନ୍ଦୁ ତ୍ରିଭୁଜର ବହିର୍ଦେଶରେ ଅବସ୍ଥିତ ।

ପ୍ରଶ୍ନ : ଚିତ୍ର ଦେଖ୍ ପ୍ରଶ୍ନର ଉତ୍ତର ଲେଖ ।

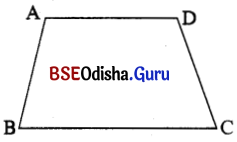
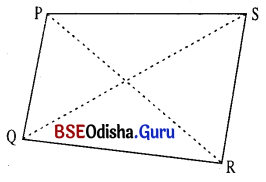
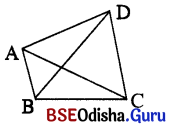
1. ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ଥିବା ଚତୁର୍ଭୁଜର ନାମ କ’ଣ ?
ସମାଧାନ:
ABCD ଚତୁର୍ଭୁଜ ।

2. ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ଥିବା ଚାରିଯୋଡ଼ା ସନ୍ନିହିତ ବାହୁର ନାମ ଲେଖ ।
ସମାଧାନ:
A͞B ଓ B͞C, B͞C ଓ C͞D, C͞D ଓ D͞A, A͞D ଓ A͞B

3. ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ଥିବା ଚତୁର୍ଭୁଜର ଦୁଇଯୋଡ଼ା ବିପରୀତ ବାହୁର ନାମ ଲେଖ ।
ସମାଧାନ:
A͞B ଓ C͞D, A͞D ଓ B͞C

4. ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ A ଓ B ଶୀର୍ଷବିନ୍ଦୁ ଛଡ଼ା ଅନ୍ୟ କେଉଁ ଯୋଡ଼ା ଶୀର୍ଷବିନ୍ଦୁ ସନ୍ନିହିତ ଓ କେଉଁ ଯୋଡ଼ା ଶୀର୍ଷବିନ୍ଦୁ ବିପରୀତ ଚିତ୍ରରୁ ବାଛି ଲେଖ ।
ସମାଧାନ:
B ଓ C, C ଓ D, D ଓ A ଶୀର୍ଷବିନ୍ଦୁ ସନ୍ନିହିତ ।
A ଓ C ଏକ ଯୋଡ଼ା ବିପରୀତ ଶୀର୍ଷବିନ୍ଦୁ ଛଡ଼ା B ଓ D ବିପରୀତ ଶୀର୍ଷବିନ୍ଦୁ ।

5. ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ଥ‌ିବା ଚତୁର୍ଭୁଜର କ୍ରମିକ କୋଣ ଓ ବିପରୀତ କୋଣର ନାମ ଲେଖ ।
ସମାଧାନ:
∠ABC, ∠BCD, ∠CDA, ∠BAD – କ୍ରମିକ କୋଣ ।
∠ABC ର ବିପରୀତ ∠CDA, ∠BAD ର ବିପରୀତ ∠BCD
ଏବଂ ∠ABC ର ବିପରୀତ ∠ADC ।

ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରକୁ ଦେଖ୍ ଉତ୍ତର ଦିଅ ।

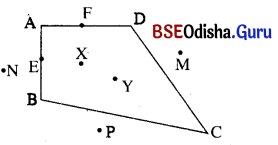
(କ) କେଉଁ ବିନ୍ଦୁଗୁଡ଼ିକ ଚତୁର୍ଭୁଜ ଉପରିସ୍ଥ ବିନ୍ଦୁ ? 
ସମାଧାନ:
E ଓ F

(ଖ) କେଉଁ ବିନ୍ଦୁଗୁଡ଼ିକ ଚତୁର୍ଭୁଜର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ? 
ସମାଧାନ:
X ଓ Y

(ଗ) କେଉଁ ବିନ୍ଦୁଗୁଡ଼ିକ ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ ବିନ୍ଦୁ ?
ସମାଧାନ:
M, N ଓ P

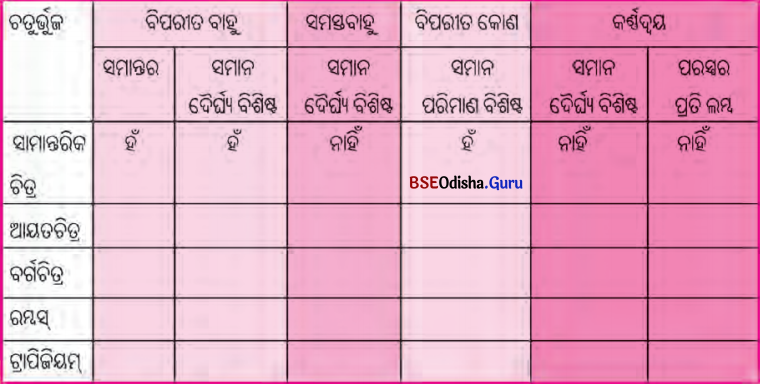
ବିଭିନ୍ନ ପ୍ରକାର ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣ ମଧ୍ୟରେ ସମ୍ପର୍କ:
ପ୍ରତ୍ୟେକ ପ୍ରକାର ଚତୁର୍ଭୁଜର ଯେଉଁ ଚିତ୍ରଗୁଡ଼ିକ ଆଗରୁ ଦିଆଯାଇଛି, ସେହି ଚିତ୍ରରୁ କୋଣମାନଙ୍କର ପରିମାଣ ତୁମ ପ୍ରୋଟ୍ରାକ୍ଟର ସାହାଯ୍ୟରେ ମାପ । ସାରଣୀରେ ଖାଲିଥିବା ଘରେ ‘ଠିକ୍’ ବା ‘ଭୁଲ’ ଲେଖ ।

ଚତୁର୍ଭୁଜର ନାମ	ବିପରୀତ କୋଣ ମାନଙ୍କର ପରିମାଣ ସମାନ	ଗ୍ୱରେଟି ଯାକ କୋଣର ପରିମାଣ ସମାନ
ଆୟତଚିତ୍ର
ବର୍ଗଚିତ୍ର
ସାମାନ୍ତରିକ ଚିତ୍ର
ରମ୍ବସ୍
ଟ୍ରାପିଜିୟମ୍

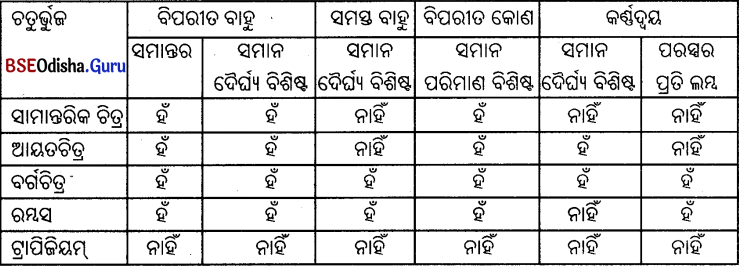
ସମାଧାନ:

ଚତୁର୍ଭୁଜର ନାମ	ବିପରୀତ କୋଣ ମାନଙ୍କର ପରିମାଣ ସମାନ	ଗ୍ୱରେଟି ଯାକ କୋଣର ପରିମାଣ ସମାନ
ଆୟତଚିତ୍ର	ଠିକ୍	ଠିକ୍
ବର୍ଗଚିତ୍ର	ଠିକ୍	ଠିକ୍
ସାମାନ୍ତରିକ ଚିତ୍ର	ଠିକ୍	ଭୁଲ
ରମ୍ବସ୍	ଠିକ୍	ଭୁଲ
ଟ୍ରାପିଜିୟମ୍	ଭୁଲ	ଭୁଲ

କହିଲ ଦେଖ୍:
ବୃତ୍ତର ବ୍ୟାସ ଜଣାଥିଲେ ଏହାର ବ୍ୟାସାର୍ଷ କିପରି ବାହାରିବ ।
ସମାଧାନ:
ବୃତ୍ତର ବ୍ୟାସର ଅଧା କରିଦେଲେ ବା 2 ଦ୍ବାରା ଭାଗକଲେ ବ୍ୟାସାର୍ଦ୍ଧ ବାହାରିବ ।

ଚିତ୍ର ଦେଖ୍ ଉତ୍ତର ଦିଅ ।

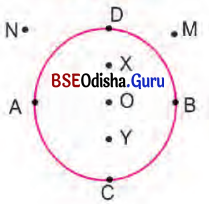
(କ) C,D,A ଓ ______ ବିନ୍ଦୁ ଗୁଡ଼ିକ ବୃତ୍ତ ଉପରେ ଅବସ୍ଥିତ।
ସମାଧାନ:
B

(ଖ) M ଓ ______ ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁ ଅଟନ୍ତି ।
ସମାଧାନ:
N

(ଗ) X,O ଓ ______  ବୃତ୍ତର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ଅଟନ୍ତି ।
ସମାଧାନ:
Y

ଉତ୍ତର ଲେଖ: (ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କରାଯାଇଛି ।)
(କ) \(\widehat{\mathrm{DAC}}\), \(\widehat{\mathrm{DBC}}\), _________ ଓ _________ ଦତ୍ତ ବୃତ୍ତର ଗୋଟିଏ ଗୋଟିଏ ଚାପ ।
ସମାଧାନ:
\(\widehat{\mathrm{ACB}}\) ଓ \(\widehat{\mathrm{ADB}}\)

(ଖ) \(\widehat{\mathrm{DBC}}\) ଚାପର _________ ଓ _________ ଦୁଇଟି ପ୍ରାନ୍ତ ବିନ୍ଦୁ ।
ସମାଧାନ:
D, C

(ଗ) \(\widehat{\mathrm{ADB}}\) ଚାପ ଓ _________ ଚାପର ସଂଯୋଗରେ ସମୁଦାୟ ବୃତ୍ତଟି ଗଠିତ ହୁଏ ।
ସମାଧାନ:
\(\widehat{\mathrm{ACB}}\)

(ଘ) \(\widehat{\mathrm{ACB}}\) ଚାପର A ବିନ୍ଦୁ ଓ _________ ବିନ୍ଦୁ ବ୍ୟତୀତ ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁ ଚାପର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
ସମାଧାନ:
B

ନିଜେ କରି ଦେଖ:
ତଳେ ଦିଆଯାଇଥବା ଚିତ୍ର ପରି କାଗଜରେ ସ୍କେଲ୍ ଓ କମ୍ପାସ୍ ଦ୍ୱାରା ବିଭିନ୍ନ ଚିତ୍ର ପ୍ରସ୍ତୁତ କରି ବୃତ୍ତଖଣ୍ଡ, ବୃତ୍ତକଳା ଓ ଅର୍ଥବୃତ୍ତ ଚିହ୍ନଟ କର ।

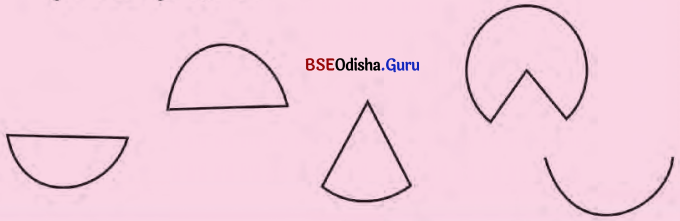
ସମାଧାନ:

ତୁମ ପରିବେଶରେ କେଉଁ କେଉଁଠାରେ କୋନ୍ ଆକୃତିର ଘନବସ୍ତୁ ଦେଖୁଛ ଲେଖ ।
ସମାଧାନ:
ନଟୁ, ଟୋପି, କାହାଳୀ, ଶୁଖୁଲା ବାଲିଗଦା, ଧାନ, ମୁଗ ଆଦି ଶସ୍ୟ ଗଦାକରି ରଖିଲେ ତାହା କୋନ୍ ଆକୃତି ପରି ଦେଖାଯାଏ ।

ଚିତ୍ରଦେଖ୍ ଉତ୍ତର ଦିଅ ।

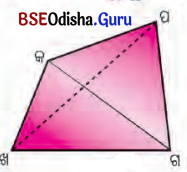
(କ) ତ୍ରିଭୁଜାକାର ବିଶିଷ୍ଟ ପିରାମିଡ୍‌ର ପୃଷ୍ଠସଂଖ୍ୟା କେତେ ?
ସମାଧାନ:
4ଟି

(ଖ) ତ୍ରିଭୁଜାକାର ବିଶିଷ୍ଟ ପିରାମିଡ୍ରର ଧାର ସଂଖ୍ୟା କେତେ ?
ସମାଧାନ:
6ଟି

(ଗ) ଏହା ଶୀର୍ଷ ସଂଖ୍ୟା କେତେ ?
ସମାଧାନ:
4ଟି

ତଳେ ଦିଆଯାଇଥ‌ିବା ଭଳି ଏକ ସାରଣୀ ତିଆରି କରି ଖାଲିଘରେ ଉତ୍ତର ଲେଖ । (ପ୍ରଶ୍ନ ସହ ଉତ୍ତର)

ଆକୄତିର ନାମ	ପୃଷ୍ଠ ସଂଖ୍ୟା	ଧାର ସଂଖ୍ୟା	ଣୀର୍ଷ ସଂଖ୍ୟା
ଆୟତଘନ
ସମଘନ
ସିଲିଣ୍ଡର୍
ଗୋଲକ
କୋନ୍
ପ୍ରିଜିମ୍

ସମାଧାନ:

ଆକୄତିର ନାମ	ପୃଷ୍ଠ ସଂଖ୍ୟା	ଧାର ସଂଖ୍ୟା	ଣୀର୍ଷ ସଂଖ୍ୟା
ଆୟତଘନ	6	12	8
ସମଘନ	6	12	8
ସିଲିଣ୍ଡର୍	3	2	ନାହିଁ
ଗୋଲକ	1	ନାହିଁ	ନାହିଁ
କୋନ୍	1	1	1
ପ୍ରିଜିମ୍	5	9	6

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 6 ଦଶମିକ ସଂଖ୍ୟା Ex 6.2 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 6 ଦଶମିକ ସଂଖ୍ୟା Ex 6.2

Question 1. 
ନିମ୍ନ ଭଗ୍ନସଂଖ୍ୟାଗୁଡ଼ିକୁ ଦଶମିକ ସଂଖ୍ୟାରେ ପ୍ରକାଶ କର ।

(କ) \(\frac{7}{10}\)
ସମାଧାନ:
0.7

(ଖ) \(\frac{7}{100}\)
ସମାଧାନ:
0.07

(ଗ) \(\frac{11}{100}\)
ସମାଧାନ:
0.11

(ଘ) \(\frac{135}{100}\)
ସମାଧାନ:
= \(1 \frac{35}{100}=1+\frac{35}{100}\) = 1.35

(ଙ) \(\frac{27}{5}\)
ସମାଧାନ:
= \(\frac{27 \times 2}{5 \times 2}=\frac{54}{10}=5 \frac{4}{10}=5+\frac{4}{10}\) = 5.4

(ଚ) \(\frac{16}{5}\)
ସମାଧାନ:
= \(\frac{16 \times 2}{5 \times 2}=\frac{32}{10}=3 \frac{2}{10}=3+\frac{2}{10}\) = 3.2

(ଛ) \(\frac{35}{2}\)
ସମାଧାନ:
= \(\frac{35 \times 5}{2 \times 5}=\frac{175}{10}=17+\frac{5}{10}=10+7+\frac{5}{10}\) = 17.5

Question 2. 
ନିମ୍ନ ଦଶମିକ ସଂଖ୍ୟା ଗୁଡ଼ିକୁ ସାଧାରଣ ଭଗ୍ନସଂଖ୍ୟାରେ ପ୍ରକାଶ କର।

(କ) 12.3
ସମାଧାନ:
= 10 + 2 + \(\frac{3}{10}=12+\frac{3}{10}=12 \frac{3}{10}=\frac{123}{10}\)

(ଖ) 17.53
ସମାଧାନ:
= 10 + 7 + \(\frac{5}{10}+\frac{3}{100}=17+\frac{53}{100}=\frac{1753}{100}\)

(ଗ) 8.23
ସମାଧାନ:
= 8 + \(\frac{2}{10}+\frac{3}{100}=8+\frac{23}{100}=8 \frac{23}{100}=\frac{823}{100}\)

(ଘ) 31.7
ସମାଧାନ:
= 30 + 1 + \(\frac{7}{10}=31+\frac{7}{10}=31 \frac{7}{10}=\frac{317}{10}\)

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 6 ଦଶମିକ ସଂଖ୍ୟା Ex 6.1 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 6 ଦଶମିକ ସଂଖ୍ୟା Ex 6.1

Question 1.
ନିମ୍ନଲିଖତ ଗୁଡ଼ିକୁ ଦଶମିକରେ ଲେଖ ।

ଣତକ 100	ଦଶକ 10	ଏକକ 1	ଦଣାଂଣ \(\frac{1}{10}\)
2	3	4	5
	1	5	7
1	0	0	3
		3	7

ସମାଧାନ:

ଣତକ 100	ଦଶକ 10	ଏକକ 1	ଦଣାଂଣ \(\frac{1}{10}\)
2	3	4	5	234.5
	1	5	7	15.7
1	0	0	3	100.3
		3	7	3.7

Question 2. 
ଖାଲିୱାନ ପୂରଣକର ।
(କ) 23 ସେ. ମି. 5 ସେ. ମି. = _____ ସେ. ମି.
ସମାଧାନ:
23.5

(ଖ) 55 ସେ. ମି. = _____ ସେ. ମି.
ସମାଧାନ:
5.5

Question 3.
ନିମ୍ନ ସାରଣୀର ଖାଲିସ୍ଥାନ ପୂରଣ କର ।

ମନେରଖ : ଏକ ଦଶମିକ ଭଗ୍ନସଂଖ୍ୟାକୁ ଦଶମିକ ସଂଖ୍ୟା ମଧ୍ୟ କୁହାଯାଏ ।
ସମାଧାନ:

କହିଲ ଦେଖ୍ : ଦୁଇ ଦଶ ଛଅ ଦଶାଂଶକୁ ଦଶମିକରେ ଲେଖୁଲେ କେଉଁ ସଂଖ୍ୟା ହେବ?
ସମାଧାନ: ଦୁଇ ଦଶ ଛଅ ଦଶାଂଶ = 20 + \(\frac{6}{10}\) = 20.6

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 5 ଭଗ୍ନ ସଂଖ୍ୟା Ex 5.8 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 5 ଭଗ୍ନ ସଂଖ୍ୟା Ex 5.8

ଯୋଗଫଳ ନିଶ୍ଚୟ କର ।

1. \(\frac{2}{3}\) ଓ \(\frac{1}{3}\)
ସମାଧାନ:
= \(\frac{2+1}{3}=\frac{3}{3}\) = 1

2. \(\frac{3}{8}+\frac{1}{8}\)
ସମାଧାନ:
= \(\frac{3+1}{8}=\frac{4}{8}=\frac{1}{2}\)

3. \(\frac{1}{9}+\frac{2}{9}+\frac{5}{9}\)
ସମାଧାନ:
= \(\frac{1+2+5}{9}=\frac{8}{9}\)

4. \(1 \frac{2}{5}+2 \frac{1}{5}\)
ସମାଧାନ:
= \(\frac{7}{5}+\frac{11}{5}=\frac{7+11}{5}=\frac{18}{5}=3 \frac{3}{5}\)

5. \(2 \frac{1}{7}+3 \frac{2}{7}\)
ସମାଧାନ:
= \(\frac{15}{7}+\frac{23}{7}=\frac{15+23}{7}=\frac{38}{7}=5 \frac{3}{7}\)

6. \(\frac{1}{5}+\frac{3}{10}\)
ସମାଧାନ:

7. \(\frac{3}{8}+\frac{5}{16}\)
ସମାଧାନ:

8. \(\frac{5}{8}+\frac{5}{12}\)
ସମାଧାନ:

9. \(\frac{4}{9}+\frac{5}{12}\)
ସମାଧାନ:

10. \(1 \frac{3}{8}+2 \frac{5}{12}\)
ସମାଧାନ:

11. \(1 \frac{2}{5}+2 \frac{3}{10}+3 \frac{1}{2}\)
ସମାଧାନ:

12. \(1 \frac{1}{10}+2 \frac{1}{15}+3 \frac{1}{6}\)
ସମାଧାନ:

ବିୟୋଗଫଳ ନିର୍ଣ୍ଣୟ କର ।

13. \(\frac{3}{8}-\frac{1}{8}\)
ସମାଧାନ:
= \(\frac{3-1}{8}=\frac{2}{8}=\frac{1}{4}\)

14. \(\frac{7}{12}-\frac{5}{12}\)
ସମାଧାନ:
= \(\frac{7-5}{12}=\frac{2}{12}=\frac{1}{6}\)

15. \(\frac{2}{3}-\frac{5}{12}\)
ସମାଧାନ:

16. \(\frac{7}{18}-\frac{2}{9}\)
ସମାଧାନ:

17. \(\frac{5}{12}-\frac{1}{6}\)
ସମାଧାନ:

18. \(1 \frac{2}{3}-\frac{5}{6}\)
ସମାଧାନ:

19. \(2 \frac{3}{8}-1 \frac{1}{4}\)
ସମାଧାନ:

20. \(3 \frac{5}{12}-2 \frac{3}{8}\)
ସମାଧାନ:

21. \(3 \frac{7}{10}-2 \frac{8}{15}\)
ସମାଧାନ:

22. 2 – 1 \(\frac{3}{5}\)
ସମାଧାନ:
= \(\frac{2}{1}-\frac{8}{5}=\frac{2 \times 5-8 \times 1}{5}=\frac{10-8}{5}=\frac{2}{5}\)

23. 3 – 2 \(\frac{7}{8}\)
ସମାଧାନ:
= \(\frac{3}{1}-\frac{23}{8}=\frac{3 \times 8-23 \times 1}{8}=\frac{24-23}{8}=\frac{1}{8}\)

24. 2 – 1 \(\frac{5}{12}\)
ସମାଧାନ:

Question 25. 
ଦୋକାନରୁ ସରିତା \(\frac{2}{5}\) ମିଟର ଲମ୍ବର ଓ ଲଳିତା \(\frac{3}{4}\) ମିଟର ଲମ୍ବର ରିବନ କିଣିଲେ । ଉଭୟ ମୋଟ କେତେ ଦୈର୍ଘ୍ୟର ରିବନ୍ କିଣିଲେ?
ସମାଧାନ:
ସରିତା ରିବନ୍ କିଣିଲେ \(\frac{2}{5}\) ମିଟର ଓ ଲଳିତା ରିବନ୍ କିଣିଲେ \(\frac{3}{4}\) ମିଟର
ମିଟର ଓ ଲଳିତା ମିଣି ରିବନ୍ କିଣିଲେ = \(\frac{2}{5}\) ମି. + \(\frac{3}{4}\) ମି. = \(\frac{2 \times 4+3 \times 5}{20}\) ମି.
= \(\frac{8+15}{20}\) ମି. = \(\frac{23}{20}\) ମି. = 1 \(\frac{3}{20}\) ମି.
ଉଭୟ ମୋଟ 1 \(\frac{3}{20}\) ମିଟର ରିବନ କିଣିଲେ ।

Question 26. 
ବିଦ୍ୟାଳୟ ହତା ଚାରିପାଖରେ ଥରେ ଗଲି ଆସିବାକୁ ନିଲୁ 2 \(\frac{1}{5}\) ମିନିଟ୍ ସମୟ ନିଏ। ସେତିକି ବାଟ ସ୍ଫୁଲିବା ପାଇଁ ଜିତୁ \(\frac{7}{4}\) ମିନିଟ୍ ସମୟ ନିଏ। ଦୁଇଜଣଙ୍କ ମଧ୍ୟରୁ କିଏ କମ୍ ସମୟ ନିଏ ଓ କେତେ କମ୍ ସମୟ ନିଏ?

ସମାଧାନ:
ହତା ଚାରିପାଖରେ ଗଲି ଆସିବାକୁ ନିଲୁଲୁ ସମୟ ଲାଗେ 2 \(\frac{1}{5}\) ମିନିଟ୍ ଓ କିତୁକୁ ସମୟ ଲାଗେ \(\frac{7}{4}\) ମିନିଟ୍
\(2 \frac{1}{5}-\frac{7}{4}=\frac{11}{5}-\frac{7}{4}=\frac{11 \times 4-7 \times 5}{20}=\frac{44-35}{20}=\frac{9}{20}\) ମିନିଟ୍
ଦୁଇଜଣଙ୍କ ମଧ୍ୟରୁ କିତୁ \(\frac{9}{20}\) ମିନିଟ୍ କମ୍ ସମୟ ନିଏ

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି Ex 9.7 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 9 ସମତଳ ଉପରିସ୍ଥ ଜ୍ୟାମିତିକ ଆକୃତି Ex 9.7

Question 1.
ପ୍ରତ୍ୟେକରୁ ଦୁଇଟି ଲେଖାଏଁ ଉଦାହରଣ ଦିଅ ।
ଆୟତଘନ, ସମଘନ, ଗୋଲକ, ପ୍ରିଜିମ୍, ସିଲିଣ୍ଡର୍, କୋନ୍
ସମାଧାନ:
ଆୟତଘନ – ଇଟା, ଦିଆସିଲି ବାକ୍ସ
ସମଘନ – ଲୁଡୁଗୋଟି, ଚାରିକୋଣିଆ ବାକ୍ସ
ଗୋଲକ – ଫୁଟବଲ୍, କାଚଗୋଲି
ପ୍ରିଜିମ୍ – ପ୍ରିଜିମ୍‌କୃତ କାଚ
ସିଲିଣ୍ଡର – ରୁଲବାଡ଼ି, ପେନ୍‌ସିଲ
କୋନ୍ – କାହାଳୀ, ନଟୁ

Question 2.
କେଉଁ ପ୍ରକାର ଆକୃତି ଲେଖ।
(କ) ତୁମର ଜ୍ୟାମିତି ବାକ୍ସ
ସମାଧାନ:
ଆୟତଘନ

(ଖ) ଗୋଟିଏ ଇଟା
ସମାଧାନ:
ଆୟତଘନ

(ଗ) ଦିଆସିଲି ବାକ୍ସ
ସମାଧାନ:
ଆୟତଘନ

(ଘ) ଗୋଟିଏ ରୁଲ୍ ବାଡ଼ି
ସମାଧାନ:
ସିଲିଣ୍ଡର

(ଙ) ଗୋଟିଏ ଲୁଡୁଗୋଟି
ସମାଧାନ:
ସମଘନ

(ଚ) କ୍ରିକେଟ୍ ବଲ୍
ସମାଧାନ:
ଗୋଲକ

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.2 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 4 ସ୍ଵାଭାବିକ ସଂଖ୍ୟା Ex 4.2

Question 1. 
ସହଯୋଗୀ ନିୟମ ଅନୁଯାୟୀ ଦୁଇଟି ଉପାୟରେ ଯୋଗଫଳ ନିଶ୍ଚୟ କର।

(କ) 12 + 9 + 8 = (12 + 9) + 8 = ……… + ……. = …….
ସମାଧାନ:
= 21 + 8 = 29

(ଖ) 12 + 9 + 8 = 12 + (9 + 8) = ….. + ……. = …….
ସମାଧାନ:
= 12 + 17 = 29

Question 2. 
(କ) ସ୍ଵାଭାବିକ ସଂଖ୍ୟା ସମୂହ ଅନ୍ତର୍ଭୁକ୍ତ ପ୍ରତ୍ୟେକ ସଂଖ୍ୟା, ତା’ର ପୂର୍ବବର୍ତୀ ସଂଖ୍ୟାଠାରୁ କେତେ ଅଧିକ? 
ସମାଧାନ:
1 ଅଧିକ

(ଖ) ସବୁଠୁ ଛୋଟ ସ୍ଵାଭାବିକ ସଂଖ୍ୟା କେଉଁଟି?
ସମାଧାନ:
1

(ଗ) ସବୁଠୁ ବଡ଼ ସ୍ଵାଭାବିକ ସଂଖ୍ୟା କିଏ କହିପାରିବ କି?
ସମାଧାନ:
କହିହେବ ନାହି‍ଁ

(ଘ) ଖୁବ୍ ବଡ଼ ସଂଖ୍ୟାଟିଏ ଭାବ । ତା’ର ଠିକ୍ ପରବର୍ତୀ ସଂଖ୍ୟାଟି ତୁମେ ଭାବିଥୁବା ସଂଖ୍ୟାଠାରୁ କେତେ ବଡ଼? 
ସମାଧାନ:
1 ବଡ଼

Question 3. 
536 + 718  + 464 ର ଯୋଗଫଳ ନିର୍ଣ୍ଣୟ କରିବାକୁ ଦିଆଯାଇଛି । କ୍ରମ ବିନିମୟୀ ଓ ସହଯୋଗୀ ନିୟମ ପ୍ରୟୋଗ କର ଯେପରି ଯୋଗ କ୍ରିୟାଟି ସହଜ ହେବ ।
ସମାଧାନ:
536 + 718 + 464 = 536 + (718 + 464) = 536 + (464 + 718) (ବିନିମୟୀ ନିୟମ)
= (536 + 464) + 718 (ସହଯୋଗୀ ନିୟମ)
= 1000 + 718 = 1718

Question 4. 
ନିମ୍ନ ଯୋଗକାର୍ଯ୍ୟ ଗୁଡ଼ିକୁ ସହଜ ହେବା ଭଳି ସଂଖ୍ୟାଗୁଡ଼ିକୁ ସଜାଇ ଯୋଗକର ।

(କ) 417 + 384 + 583
ସମାଧାନ:
417 + 384 + 583
=(417 + 583) + 384
= 1000 + 384
= 1384

(ଖ) 2536 + 1205 + 7464
ସମାଧାନ:
2536 + 1205 + 7464
= (2536 + 7464) + 1205
= 10000 + 1205
= 11205

(ଗ) 654 + 333 + 346
ସମାଧାନ:
654 + 333 + 346
=(654 + 346) + 333
= 1000 + 333
= 1333

(ଘ) 2062 + 353 + 1438 + 547
ସମାଧାନ:
2062 + 353 + 1438 + 547
= (2062 + 1438) + (353 + 547)
= 3500 + 900 = 4400

Question 5. 
ନିମ୍ନ ବିୟୋଗ କଥାଗୁଡ଼ିକୁ ଯୋଗ କଥାରେ ଲେଖ । 

(କ) 9 – 5 = 4
ସମାଧାନ:
9 –  5 = 4 (ବିୟୋଗ କଥା)
4 + 5 = 9 (ଯୋଗ କଥା)

(ଖ) 12 – 7 = 5
ସମାଧାନ:
12 – 7 = 5 (ବିୟୋଗ କଥା)
5 + 7 = 12 (ଯୋଗ କଥା)

(ଗ) 316 – 285 = 31
ସମାଧାନ:
316 – 285 = 31 (ବିୟୋଗ କଥା)
31 + 285 = 316 (ଯୋଗ କଥା)

Question 6. 
ଗୋଟିଏ ଗ୍ରାମର ଲୋକ ସଂଖ୍ୟା 1500 | ଯଦି ସେହି ଗ୍ରାମର ପୁରୁଷ ସଂଖ୍ୟା 489 ଓ ମହିଳା ସଂଖ୍ୟା 512 ହୁଏ, ତେବେ ପିଲାଙ୍କ ସଂଖ୍ୟା କେତେ?
ସମାଧାନ:
ଗ୍ରାମର ପୁରୁଷ ସଂଖ୍ୟା 489 ଜଣ ଓ ମହିଳା ସଂଖ୍ୟା 512 ଜଣ । 
∴ ଗ୍ରାମର ପୁରୁଷ ଓ ମହିଳା ସଂଖ୍ୟା ମିଶି = 489 + 512 = 1001 ଜଣ 
ଗ୍ରାମର ମୋଟ ଲୋକସଂଖ୍ୟା 1500 ଜଣ ।
∴ ପିଲାଙ୍କ ସଂଖ୍ୟା = 1500 – 1001 = 499 ଜଣ ।

Question 7. 
ଶୋଭନ୍ ପାଖରେ 52,718 ଟଙ୍କା ଥିଲା | ସେ କରଜ ଶୁଝିଲା 5000 ଟଙ୍କା ଓ 2500 ଟଙ୍କା ଦାମ୍‌ର ଗୋଟିଏ ସାଇକେଲ୍ କିଣିଲା । ତା’ପାଖରେ ବଳକା କେତେ ଟଙ୍କା ରହିଲା?
ସମାଧାନ:

Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 5 ଭଗ୍ନ ସଂଖ୍ୟା Ex 5.3 Textbook Exercise Questions and Answers.

BSE Odisha Class 6 Maths Solutions Chapter 5 ଭଗ୍ନ ସଂଖ୍ୟା Ex 5.3

Question 1.

ଉପରିସ୍ଥ ସଂଖ୍ୟାରେଖାରେ 0 ଓ 1 କୁ ସୂୠଉଥ‌ିବା ବିଦୁ୍ୟଦ୍ଵୟ ମଧ୍ୟବର୍ତୀ ସଂଖ୍ୟାରେଖାର ଅଂଶକୁ ସମାନ ଦଶ ଭାଗରେ ଏବଂ 1 ଓ 2 କୁ ସୂରଉଥବା ବିନ୍ଦୁ ଦୁଇଟି ମଧ୍ୟବର୍ତୀ ସଂଖ୍ୟାରେଖାର ଅଂଶକୁ ଋରିଗୋଟି ସମାନ ଭାଗରେ ପରିଣତ କରାଯାଇଛି । ବିଭାଜକ ବିନ୍ଦୁଗୁଡ଼ିକୁ A, B, C ଆଦି ନାମ ଦିଆଯାଇଛି । କେଉଁ ବିନ୍ଦୁଦ୍ଵାରା କେଉଁ ସଂଖ୍ୟା ସୂଚିତ ତାହା ନିମ୍ନରେ ଲେଖ ।

(କ) A ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{1}{10}\)

(ଖ) C ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{3}{10}\)

(ଗ) E ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{5}{10}\) ବା \(\frac{1}{2}\)

(ଘ) G ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{7}{10}\)

(ଙ) । ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{9}{10}\)

(ଚ) K ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
1 \(\frac{2}{4}\)  1 \(\frac{1}{2}\)

(ଛ) B ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{2}{10}\) ବା \(\frac{1}{5}\)

(ଜ) D ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{4}{10}\) ବା \(\frac{2}{5}\)

(ଝ) F ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{6}{10}\) ବା \(\frac{3}{5}\)

(ଞ) H ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
\(\frac{8}{10}\) ବା \(\frac{4}{5}\)

(ଟ) J ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
1 \(\frac{1}{4}\)

(ଠ) L ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା _____ ।
ସମାଧାନ:
1 \(\frac{3}{4}\)

Question 2. 
ନିମ୍ନ ସଂଖ୍ୟାଗୁଡ଼ିକୁ ସଂଖ୍ୟାରେଖାରେ ସ୍ଥାପନ କର ।
ସମାଧାନ:

(କ) \(\frac{3}{4}\)
ସମାଧାନ:
C ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା = \(\frac{3}{4}\)

(ଖ) 1 \(\frac{1}{3}\)
ସମାଧାନ:
M ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା = 1 \(\frac{1}{3}\)

(ଗ) 2 \(\frac{1}{4}\)
ସମାଧାନ:
P ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା = 2 \(\frac{1}{4}\)

(ଘ) 3 \(\frac{1}{3}\)
ସମାଧାନ:
S ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା = 3 \(\frac{1}{3}\)

(ଙ) 4 \(\frac{1}{2}\)
ସମାଧାନ:
X ଦ୍ଵାରା ସୂଚିତ ସଂଖ୍ୟା = 4 \(\frac{1}{2}\)

Question 3.
(କ) ସଂଖ୍ୟାରେଖା ଉପରିସ୍ଥ କେଉଁ ଦୁଇଟି ପାଖାପାଖୁ ପୂର୍ଣ୍ଣସଂଖ୍ୟା ମଧ୍ୟରେ ସମସ୍ତ ପ୍ରକୃତ ଭଗ୍ନସଂଖ୍ୟା ଅବସ୍ଥିତ? 
ସମାଧାନ:
ସଂଖ୍ୟାରେଖା ଉପରିସ୍ଥ 0 ଓ 1 ପୂର୍ଣ୍ଣସଂଖ୍ୟା ମଧ୍ୟରେ ସମସ୍ତ ପ୍ରକୃତ ଭଗ୍ନସଂଖ୍ୟା ଅବସ୍ଥିତ ।

(ଖ) ସଂଖ୍ୟାରେଖା ଉପରିସ୍ଥ କେଉଁ ଦୁଇଟି ପାଖାପାଖୁ ପୂର୍ବସଂଖ୍ୟା ମଧ୍ୟରେ 2 \(\frac{1}{5}\) ଅବସ୍ଥିତ?
ସମାଧାନ:
2 \(\frac{1}{5}\) = 2 + \(\frac{1}{5}\) ∴ 2 < 2 \(\frac{1}{5}\) < 3
ସଂଖ୍ୟାରେଖା ଉପରିସ୍ଥ 2 ଓ 3 ପୂର୍ଣ୍ଣସଂଖ୍ୟା ମଧ୍ୟରେ 2 \(\frac{1}{5}\) ଅବସ୍ଥିତ

Question 4.
(କ) \(\frac{15}{4}\) କୁ ସଂଖ୍ୟାରେଖାରେ ଦର୍ଶାଇବା ଲାଗି ପ୍ରଥମେ କ’ଣ କରିବାକୁ ହେବ?
ସମାଧାନ:
\(\frac{15}{4}\) କୁ ସଂଖ୍ୟାରେଖାରେ ଦର୍ଶାଇବା ଲାଗି ତାହାକୁ ମିଶ୍ର ସଂଖ୍ୟାରେ ପ୍ରକାଶ କରିବାକୁ ହେବ ।

(ଖ) କେଉଁ ଦୁଇଟି ପାଖାପାଖ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ମଧ୍ୟରେ \(\frac{15}{4}\) ଅବସ୍ଥିତ?
ସମାଧାନ:
\(\frac{15}{4}=3 \frac{3}{4}=3+\frac{3}{4}\), 3 ଓ 4 ପୂର୍ବସଂଖ୍ୟା ମଧ୍ୟରେ \(\frac{15}{4}\) ଅବସ୍ଥିତ

(ଗ) ଉକ୍ତ ପୂର୍ବସଂଖ୍ୟା ସୂଚକ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ସଂଖ୍ୟାରେଖାର ଅଂଶକୁ କେତେ ସମାନ ଭାଗ କରିବାକୁ ହେବ?
ସମାଧାନ:
ଉକ୍ତ ପୂର୍ବସଂଖ୍ୟା ସୂଚକ ବିଦୁ୍ୟଦ୍ୱୟ ମଧ୍ୟବର୍ତ୍ତୀ ସଂଖ୍ୟାରେଖାର ଅଂଶକୁ 4 ସମାନ ଭାଗ କରିବାକୁ ହେବ ।

(ଘ) \(\frac{15}{4}\) କୁ ମିଶ୍ର ସଂଖ୍ୟାରେ ପରିଣତ କରି ଏହାକୁ ସଂଖ୍ୟାରେଖାରେ ଦର୍ଶାଅ।
ସମାଧାନ: