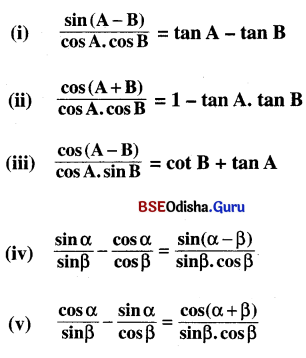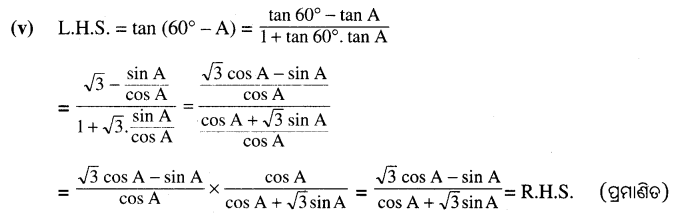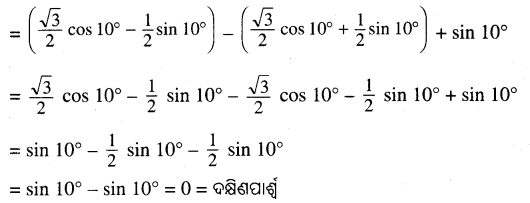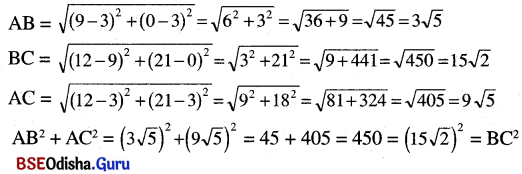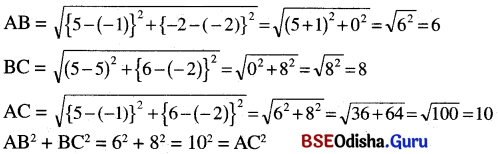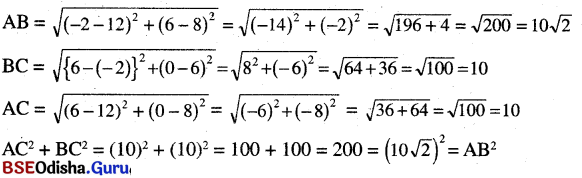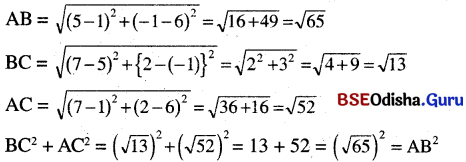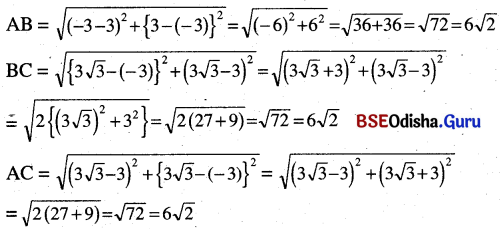Odisha State Board BSE Odisha 10th Class History Solutions Chapter 15 ଭାରତରେ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ଜ୍ଞାନର ବିକାଶ Textbook Exercise Questions and Answers.
BSE Odisha Class 10 History Solutions Chapter 15 ଭାରତରେ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ଜ୍ଞାନର ବିକାଶ
୧. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୬୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।
(କ) ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ବିଦ୍ୟାର ଉପଯୋଗିତା ସମ୍ପର୍କରେ ଜବାହରଲାଲ ନେହେରୁଙ୍କର ମତ କ’ଣ ଥିଲା ?
Answer:
- ଜବାହରଲାଲ ନେହେରୁ ତାଙ୍କ ପ୍ରଧାନମନ୍ତ୍ରୀତ୍ଵ କାଳ (୧୯୪୬ – ୧୯୬୪)ରେ ଭାରତରେ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ଜ୍ଞାନର ବିକାଶ ପାଇଁ ଅକ୍ଲାନ୍ତ ଚେଷ୍ଟା କରିଥିଲେ ।
- ନେହେରୁଙ୍କର ଦୃଢ଼ ବିଶ୍ଵାସ ଥିଲା ଯେ କେବଳ ବିଜ୍ଞାନ ହିଁ କ୍ଷୁଧା, ଦାରିଦ୍ର୍ୟ, ଅପରିଚ୍ଛନ୍ନତା, ନିରକ୍ଷରତା, ଅନ୍ଧବିଶ୍ଵାସ, ପ୍ରାକୃତିକ ସମ୍ବଳର ଅସଦ୍ ବିନିଯୋଗ ପ୍ରଭୃତି ଭାରତର ଗୁରୁତର ସମସ୍ୟାଗୁଡ଼ିକର ସମାଧାନ କରିପାରିବ ।
- ଦେଶର ଅର୍ଥନୈତିକ, ସାମାଜିକ ଓ ସାଂସ୍କୃତିକ ପ୍ରଗତି ପାଇଁ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ବିଦ୍ୟା ଯେ ଅପରିହାର୍ଯ୍ୟ ତାହା ନେହେରୁ ଉପଲବ୍ଧ କରିଥିଲେ ।
- ବୈଜ୍ଞାନିକ ଗବେଷଣା ଓ ବୈଷୟିକ ଜ୍ଞାନ ଯେ ଭାରତର ପ୍ରତିରକ୍ଷା ବ୍ୟବସ୍ଥାକୁ ଶକ୍ତିଶାଳୀ କରିବ ସେ ବିଷୟ ଜବାହରଲାଲ ନେହେରୁ ସ୍ପଷ୍ଟ କରିଦେଇଥିଲେ ।
- ସୁତରାଂ ଭାରତର ସର୍ବାଙ୍ଗୀନ ଉନ୍ନତି ପାଇଁ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ବିଦ୍ୟା ସହାୟକ ବୋଲି ନେହେରୁ ମତ ଦେଇଥିଲେ ।
(ଖ) ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପରେ ଭାରତରେ କୃଷି ଓ ଶିଳ୍ପର ବିକାଶ ନିମନ୍ତେ କ’ଣ କରାଯାଇଛି ?
Answer:
- ସ୍ଵାଧୀନତା ପ୍ରାପ୍ତି ପରେ କୃଷିକ୍ଷେତ୍ରରେ ବିଜ୍ଞାନ ଶିକ୍ଷାର ବ୍ୟାପକ ପ୍ରୟୋଗ କରିବାପାଇଁ ବ୍ୟବସ୍ଥା ହେଲା ।
- ବିଂଶ ଶତାବ୍ଦୀର ସପ୍ତମ ଦଶକରେ ରାସାୟନିକ ସାର ଓ ଅଧିକ ଉତ୍ପାଦନକ୍ଷମ ବିହନର ବହୁଳ ବ୍ୟବହାର, ସୁବ୍ୟବସ୍ଥିତ ଜଳସେଚନ ବ୍ୟବସ୍ଥା ଫଳରେ ଉତ୍ପାଦନ ବୃଦ୍ଧି ପାଇଲା ଓ ସବୁଜ କ୍ରାନ୍ତି ସମ୍ଭବ ହେଲା ।
- ୧୯୭୧ ମସିହାରେ କେନ୍ଦ୍ରରେ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ମନ୍ତ୍ରଣାଳୟ ନାମରେ ଏକ ସ୍ବତନ୍ତ୍ର ବିଭାଗ ସୃଷ୍ଟି କରାଗଲା । ଜୈବ ପ୍ରଯୁକ୍ତି ବିଦ୍ୟାର ବିକାଶ ଓ କୃଷି କ୍ଷେତ୍ରରେ ଏହାର ବିନିଯୋଗ ଲାଭଦାୟକ ହେଲା ।
- ଶିଳ୍ପ କ୍ଷେତ୍ରରେ ବିଶେଷକରି ଲୌହ ଓ ଇସ୍ପାତ ଶିଳ୍ପ କ୍ଷେତ୍ରରେ ମଧ୍ୟ ପ୍ରଗତି ପାଇଁ ଚେଷ୍ଟା କରାଗଲା ।
- ୧୯୭୩ ମସିହାରେ ‘ଭାରତୀୟ ଇସ୍ପାତ ପ୍ରାଧ୍ଵରଣ ଲିମିଟେଡ୍’ ନାମକ ସରକାରୀ ସଂସ୍ଥା ସ୍ଥାପନ କରାଯାଇ ଭାରତରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିବା ପାଞ୍ଚଟି ଏକୀକୃତ ଇସ୍ପାତ ପ୍ରକଳ୍ପର ପରିଚାଳନା ଭାର ହାତକୁ ନିଆଗଲା ।
![]()
(ଗ) ପରମାଣୁ ଶକ୍ତିର ବିକାଶ ପାଇଁ ଭାରତ ସରକାର କି କି ପଦକ୍ଷେପ ନେଇଛନ୍ତି ?
Answer:
- ପରମାଣୁ ଶକ୍ତିର ବିକାଶ ପାଇଁ ୧୯୪୮ ମସିହା ଅଗଷ୍ଟ ମାସରେ ବିଶିଷ୍ଟ ବୈଜ୍ଞାନିକ ହୋମି ଜାହାଙ୍ଗୀର ଭାବାଙ୍କ ଅଧ୍ୟକ୍ଷତାରେ ‘ପରମାଣୁ ଶକ୍ତି ଆୟୋଗ’ ଗଠନ କରାଗଲା ।
- ୧୯୫୪ ମସିହାରେ ଏକ ସ୍ଵତନ୍ତ୍ର ‘ପରମାଣୁ ଶକ୍ତି ବିଭାଗ’ ଖୋଲାଗଲା ।
- ୧୯୫୬ ମସିହାରେ ଟ୍ରମ୍ବେଠାରେ ପ୍ରଥମ ଆଣବିକ ରିଆକ୍ଟର ଓ ଭାବା ଆଣବିକ ଗବେଷଣା କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଛି । ଏହାର ଅଧୀନରେ ଅପ୍ସରା, ସର୍କସ, ଜେରଲିନା, ଧ୍ରୁବ ପ୍ରଥମ ଓ ଦ୍ୱିତୀୟ, ପୂର୍ଣ୍ଣିମା, କାମିନୀ ପ୍ରଭୃତି ରିଆକ୍ଟର କାର୍ଯ୍ୟକ୍ଷମ ହେଲା ।
- ଭାବା ଆଣବିକ ଗବେଷଣା କେନ୍ଦ୍ର ତତ୍ତ୍ୱାବଧାନରେ ଅନେକ ଗବେଷଣା କେନ୍ଦ୍ର ପଶ୍ଚିମବଙ୍ଗ, କାଶ୍ମୀର ଓ କର୍ଣ୍ଣାଟକଠାରେ ଗଢ଼ିଉଠିଲା । ୧୯୮୪ ମସିହାରେ ଇନ୍ଦୋରଠାରେ ଉନ୍ନତ ବୈଷୟିକ ଜ୍ଞାନକେନ୍ଦ୍ର ନାମକ ଏକ ଗବେଷଣା ସଂସ୍ଥା ପ୍ରତିଷ୍ଠା କରାଗଲା ।
- ଭାରତ ପ୍ରଥମଥର ପାଇଁ ୧୯୭୪ ମସିହା ମେ ୧୮ରେ ଓ ଦ୍ବିତୀୟଥର ପାଇଁ ୧୯୯୮ ମସିହା ମେ ୧୧ ଓ ୧୩ରେ ରାଜସ୍ଥାନର ପୋଖରାନ୍ଠାରେ ପରମାଣୁ ବୋମା ପରୀକ୍ଷଣ କରିଥିଲା ।
(ଘ) ପ୍ରତିରକ୍ଷା କ୍ଷେତ୍ରରେ ଭାରତର ଅଗ୍ରଗତି ସମ୍ପର୍କରେ ସୂଚନା ଦିଅ ।
Answer:
- ପ୍ରତିରକ୍ଷା କ୍ଷେତ୍ରରେ ଭାରତର ଅଗ୍ରଗତି ଉଦ୍ଦେଶ୍ୟରେ ୧୯୫୮ ମସିହାରେ ପ୍ରତିରକ୍ଷା ଗବେଷଣା ଓ ଉନ୍ନୟନ ସଙ୍ଗଠନ ଗଠିତ ହେଲା ।
- ୧୯୮୩ ମସିହାରେ ଏକୀଭୂତ ନିୟନ୍ତ୍ରିତ କ୍ଷେପଣାସ୍ତ୍ର କାର୍ଯ୍ୟକ୍ରମ ହାତକୁ ନିଆଯାଇ ବିଭିନ୍ନ ଧରଣର କ୍ଷେପଣାସ୍ତ୍ରର ଯଥା – ଅଗ୍ନି, ପୃଥ୍ବୀ, ଧନୁଶ, ଆକାଶ, ତ୍ରିଶୂଳ ଓ ନାଗ ଆଦିର ବିକାଶ କରାଗଲା । ,
- ଏହି କ୍ଷେପଣାସ୍ତ୍ରଗୁଡ଼ିକର ପରୀକ୍ଷା ପାଇଁ ଓଡ଼ିଶାର ଚାନ୍ଦିପୁରଠାରେ ଏକ କ୍ଷେପଣାସ୍ତ୍ର ପରୀକ୍ଷଣ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଗଲା ।
- ପ୍ରତିରକ୍ଷା ଗବେଷଣା ଓ ଉନ୍ନୟନ ସଙ୍ଗଠନ ତିନି ବାହିନୀ (ସ୍ଥଳ, ଜଳ ଓ ଆକାଶ) ପାଇଁ ପ୍ରତିରକ୍ଷା ସାମଗ୍ରୀ ଉତ୍ପାଦନ ଓ ତା’ର ଗୁଣବତ୍ତା ପରୀକ୍ଷା କରିବାରେ ପ୍ରଶଂସନୀୟ କାର୍ଯ୍ୟ କରୁଛି ।
- ପ୍ରତିରକ୍ଷା ପାଇଁ ବ୍ୟବହୃତ ଯାନବାହନ, ଗୋଳାବାରୁଦ, ବୈଦ୍ୟୁତିକ ଯନ୍ତ୍ରପାତି, ଜଳଜାହାଜ ଓ ବୁଡ଼ାଜାହାଜ ମଧ୍ୟ ଭାରତରେ ଉତ୍ପାଦିତ ହେଉଛି ।
(ଙ) ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ବିଦ୍ୟାର ବିକାଶ ଫଳରେ ଭାରତ କିପରି ଲାଭବାନ୍ ହୋଇଛି ?
Answer:
- ଦେଶରେ ଉପଲବ୍ଧ ବିଜ୍ଞାନ ଓ ବୈଷୟକ ବିଦ୍ୟାର ବିକାଶ ଫଳରେ ସମସ୍ତ କ୍ଷେତ୍ରରେ ବୈପ୍ଳବିକ ପରିବର୍ତ୍ତନ
- ଖାଦ୍ୟଶସ୍ୟ ଓ ଅନ୍ୟାନ୍ୟ ଖାଦ୍ୟସାମଗ୍ରୀ ଉତ୍ପାଦନ କ୍ଷେତ୍ରରେ ଭାରତ ସ୍ବାବଲମ୍ବୀ ହୋଇପାରିଛି ।
- ଶିଳ୍ପ କ୍ଷେତ୍ରରେ ଭାରତ ପାରଦର୍ଶିତା ହାସଲ କରିପାରିଛି ଓ ଶକ୍ତି କ୍ଷେତ୍ରରେ ସ୍ଵାବଲମ୍ବୀ ହୋଇପାରିଛି ।
- ପ୍ରତିରକ୍ଷା କ୍ଷେତ୍ରରେ ସ୍ବଦେଶୀ ଜ୍ଞାନକୌଶଳ ପ୍ରୟୋଗ କରି ଦେଶ ଶକ୍ତିଶାଳୀ ହୋଇପାରିଛି ।
- ମହାକାଶ ଗବେଷଣା, ସାମୁଦ୍ରିକ ବିଜ୍ଞାନ ଗବେଷଣା ଓ ପରିବେଶ ବିଜ୍ଞାନ ସମ୍ପର୍କରେ ଜ୍ଞାନ ଆହରଣ ଓ ବିନିଯୋଗ ସମ୍ଭବପର ହେବା ସହିତ ମାନବ ସମ୍ବଳକୁ ପ୍ରଶିକ୍ଷିତ ଓ ଦକ୍ଷ କରାଯାଇପାରିଛି ।
![]()
୨. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ପ୍ରାୟ ୨୦ ଗୋଟି ଶବ୍ଦରେ ଲେଖ ।
(କ) କେଉଁ ଉଦ୍ଦେଶ୍ୟରେ ଭାରତର ବୈଷୟିକ ଅନୁଷ୍ଠାନମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ?
Answer:
- ଦେଶର ଅର୍ଥନୈତିକ, ସାମାଜିକ ଓ ସାଂସ୍କୃତିକ ପ୍ରଗତି ପାଇଁ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ବିଦ୍ୟା ଯେ ଅପରିହାର୍ଯ୍ୟ ତାହା ନେହେରୁ ଓ ତତ୍କାଳୀନ ଭାରତର ନେତୃବୃନ୍ଦ ଉପଲବ୍ଧ କରିଥିଲେ ।
- ତେଣୁ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ କ୍ଷେତ୍ରରେ ଉଚ୍ଚତର ଓ ମୂଲ୍ୟବୋଧଭିଭିକ ଶିକ୍ଷା ପାଇଁ ଭାରତର ବିଭିନ୍ନ ସ୍ଥାନରେ ବୈଷୟିକ ଅନୁଷ୍ଠାନମାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଛି ।
(ଖ) ଭାରତୀୟ ଇସ୍ପାତ ପ୍ରାଧ୍ଵରଣ ଲିମିଟେଡ୍ କେବେ ଗଠିତ ହେଲା ଓ କେବେ କାର୍ଯ୍ୟ ଆରମ୍ଭ କଲା ?
Answer:
- ‘ଭାରତୀୟ ଇସ୍ପାତ ପ୍ରାଧକରଣ ଲିମିଟେଡ୍’ ୧୯୭୩ ମସିହାରେ ଗଠିତ ହେଲା ।
- ଏହି ସଂସ୍ଥା ସେହି ବର୍ଷ କାର୍ଯ୍ୟ ଆରମ୍ଭ କଲା ।
(ଗ) ଜବାହରଲାଲ ନେହେରୁ ଆଣବିକ ଶକ୍ତି କ୍ଷେତ୍ରକୁ କାହିଁକି ଗୁରୁତ୍ଵ ଦେଉଥିଲେ ?
Answer:
- ନେହେରୁଙ୍କ ମତ ଥିଲା ପରମାଣୁ ଶକ୍ତି ସାମାଜିକ, ଅର୍ଥନୈତିକ ଓ ରାଜନୈତିକ କ୍ଷେତ୍ରରେ ବୈପ୍ଳବିକ ପରିବର୍ତ୍ତନ ଆଣିବ ଓ ଭାରତର ପ୍ରତିରକ୍ଷା ବ୍ୟବସ୍ଥାକୁ ସୁଦୃଢ଼ କରିବ ।
- ତେଣୁ ଜବାହରଲାଲ ନେହେରୁ ଆଣବିକ ଶକ୍ତି କ୍ଷେତ୍ରକୁ ଅଧିକ ଗୁରୁତ୍ଵ ଦେଉଥିଲେ ।
(ଘ) ଭାବା ଆଣବିକ ଗବେଷଣା କେନ୍ଦ୍ର କେବେ ଏବଂ କେଉଁଠାରେ ପ୍ରତିଷ୍ଠା କରାଗଲା ?
Answer:
- ଭାବା ଆଣବିକ ଗବେଷଣା କେନ୍ଦ୍ର ୧୯୫୬ ମସିହାରେ ପ୍ରତିଷ୍ଠା କରାଗଲା ।
- ଏହା ଟ୍ରମ୍ବେଠାରେ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
(ଙ) ଭାରତ କେବେ ଏବଂ କେଉଁଠାରେ ତା’ର ପ୍ରଥମ ପରମାଣୁ ବୋମା ବିସ୍ଫୋରଣ କରିଥିଲା ?
Answer:
- ଭାରତ ତା’ର ପ୍ରଥମ ପରମାଣୁ ବୋମା ବିସ୍ଫୋରଣ ୧୯୭୪ ମସିହା ମେ ମାସ ୧୮ ତାରିଖରେ କରିଥିଲା ।
- ଏହା ରାଜସ୍ଥାନର ପୋଖରାନ୍ଠାରେ ହୋଇଥିଲା ।
(ଚ) କେଉଁ କାରଣରୁ ଭାରତ ତା’ର ପ୍ରତିରକ୍ଷା ବ୍ୟବସ୍ଥାକୁ ଦୃଢ଼ କରିବାର ଆବଶ୍ୟକତା ଉପଲବ୍ଧ କଲା ?
Answer:
- ୧୯୬୨ ମସିହାରେ ଚୀନ୍-ଭାରତ ଯୁଦ୍ଧରେ ଭାରତୀୟ ସୈନ୍ୟବାହିନୀର ଦୁର୍ବଳତା ଭାରତୀୟମାନଙ୍କୁ ସତର୍କ
- ତେଣୁ ଭାରତ ତା’ର ପ୍ରତିରକ୍ଷା ବ୍ୟବସ୍ଥାକୁ ଦୃଢ଼ କରିବାର ଆବଶ୍ୟକତା ଉପଲବ୍ କଲା ।
![]()
(ଛ) ୧୯୬୩ ମସିହାରେ କେଉଁଠାରେ ଏକ ରକେଟ୍ ଉକ୍ଷେପଣ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ଏବଂ ଏହାର ନାମ କ’ଣ ରଖାଯାଇଥିଲା ?
Answer:
- ୧୯୬୩ ମସିହାରେ କେରଳର ଥୁରୁବନନ୍ତପୁରମ୍ଠାରେ ଏକ ରକେଟ୍ ଉକ୍ଷେପଣ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ।
- ଏହାର ନାମ ଥୁମ୍ବା ବିଷୁବୀୟ ରକେଟ୍ ଉକ୍ଷେପଣ କେନ୍ଦ୍ର ରଖାଯାଇଥିଲା ।
(ଜ) ଭାରତ ତିଆରି ପ୍ରଥମ କୃତ୍ରିମ ଉପଗ୍ରହର ନାମ କ’ଣ ଏବଂ ଏହା କେଉଁଦିନ ମହାକାଶକୁ ପ୍ରେରଣ।
Answer:
- ଭାରତ ତିଆରି ପ୍ରଥମ କୃତ୍ରିମ ଉପଗ୍ରହର ନାମ ଥିଲା ‘ଆର୍ଯ୍ୟଭଟ୍ଟ’ ।
- ଏହା ୧୯୭୫ ମସିହା ଏପ୍ରିଲ୍ ୧୯ ତାରିଖରେ ମହାକାଶକୁ ପ୍ରେରଣ କରାଯାଇଥିଲା ।
(ଝ) ଭାରତର ପ୍ରଥମ ଯୋଗାଯୋଗ ଉପଗ୍ରହ କେବେ ମହାକାଶକୁ ପ୍ରେରିତ ହେଲା ଏବଂ ତାହାର ନାମ କ’ଣ ?
Answer:
- ଭାରତର ପ୍ରଥମ ଯୋଗାଯୋଗ ଉପଗ୍ରହ ୧୯୮୧ ମସିହା ଜୁନ୍ ୧୯ ତାରିଖରେ ମହାକାଶକୁ ପ୍ରେରିତ ହେଲା ।
- ଏହାର ନାମ ଥିଲା ‘ଆପଲ୍’ ।
(ଞ) ଭାରତ ମହାକାଶରେ ଛାଡ଼ିଥିବା କୃତ୍ରିମ ଉପଗ୍ରହଗୁଡ଼ିକ ମୁଖ୍ୟତଃ କେଉଁ କ୍ଷେତ୍ରରେ ଉପଯୋଗୀ ହୋଇପାରିଛି ?
Answer:
ଭାରତ ମହାକାଶରେ ଛାଡ଼ିଥିବା କୃତ୍ରିମ ଉପଗ୍ରହଗୁଡ଼ିକ ମୁଖ୍ୟତଃ ଦୁଇଟି କ୍ଷେତ୍ରରେ ଉପଯୋଗୀ ହୋଇପାରିଛି । ସେଗୁଡ଼ିକ ହେଲା– (କ) ଯୋଗଯୋଗ, (ଖ) ପାଣିପାଗର ପୂର୍ବାନୁମାନ ।
୩. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନର ଉତ୍ତର ଗୋଟିଏ ବାକ୍ୟରେ ଲେଖ ।
(କ) କେବେ ଭାରତର ପ୍ରଥମ ଜାତୀୟ ପରୀକ୍ଷାଗାରର ଭିତ୍ତିପ୍ରସ୍ତର ସ୍ଥାପନ କରାଯାଇଥିଲା ?
Answer:
ଭାରତର ପ୍ରଥମ ଜାତୀୟ ପରୀକ୍ଷାଗାରର ଭିତ୍ତିପ୍ରସ୍ତର ୧୯୪୭ ମସିହା ଜାନୁଆରୀ ୪ ତାରିଖରେ ସ୍ଥାପନ କରାଯାଇଥିଲା ।
(ଖ) ବୈଜ୍ଞାନିକ ଓ ଶିଳ୍ପ ଗବେଷଣା କେନ୍ଦ୍ରର ପ୍ରଥମ ଅଧ୍ୟକ୍ଷ କିଏ ଥିଲେ ?
Answer:
ବୈଜ୍ଞାନିକ ଓ ଶିଳ୍ପ ଗବେଷଣା କେନ୍ଦ୍ରର ପ୍ରଥମ ଅଧ୍ୟକ୍ଷ ଥିଲେ ଭାରତର ପ୍ରଥମ ପ୍ରଧାନମନ୍ତ୍ରୀ ଜବାହରଲାଲ ନେହେରୁ ।
![]()
(ଗ) କେଉଁ ଅନୁଷ୍ଠାନ ଢାଞ୍ଚାରେ ଭାରତରେ ବୈଷୟିକ ଶିକ୍ଷାନୁଷ୍ଠାନ ଗଠନ କରାଗଲା ?
Answer:
ଆମେରିକାର ମାଶାଚୁସେଟ୍ସ ବୈଷୟିକ ଶିକ୍ଷାନୁଷ୍ଠାନ ଢାଞ୍ଚାରେ ଭାରତରେ ବୈଷୟିକ ଶିକ୍ଷାନୁଷ୍ଠାନ ଗଠନ କରାଗଲା ।
(ଘ) ଭାରତର କେନ୍ଦ୍ରୀୟ ଶାସନରେ କେବେ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ମନ୍ତ୍ରଣାଳୟ ସୃଷ୍ଟି କରାଗଲା ?
Answer:
ଭାରତର କେନ୍ଦ୍ରୀୟ ଶାସନରେ ୧୯୭୧ ମସିହାରେ ବିଜ୍ଞାନ ଓ ବୈଷୟିକ ମନ୍ତ୍ରଣାଳୟ ସୃଷ୍ଟି କରାଗଲା ।
(ଡି) କେବେ ଭାରତର କେନ୍ଦ୍ରୀୟ ଶାସନରେ ଏକ ସ୍ଵତନ୍ତ୍ର ପରମାଣୁ ଶକ୍ତି ବିଭାଗ ଖୋଲାଯାଇଥିଲା ?
Answer:
ଭାରତର କେନ୍ଦ୍ରୀୟ ଶାସନରେ ୧୯୫୪ ମସିହାରେ ଏକ ସ୍ବତନ୍ତ୍ର ପରମାଣୁ ଶକ୍ତି ବିଭାଗ ଖୋଲାଯାଇଥିଲା ।
(ଚ) ଇନ୍ଦୋରରେ ଥିବା ଆଣବିକ ପ୍ରତିଷ୍ଠାନର ନାମ କ’ଣ ?
Answer:
ଇନ୍ଦୋରରେ ଥିବା ଆଣବିକ ପ୍ରତିଷ୍ଠାନର ନାମ ‘ଉନ୍ନତ ବୈଷୟିକ ଜ୍ଞାନ କେନ୍ଦ୍ର’ ।
(ଛ) ପ୍ରତିରକ୍ଷା ଗବେଷଣା ଓ ଉନ୍ନୟନ ସଙ୍ଗଠନ କେବେ ଗଠିତ ହୋଇଥିଲା ?
Answer:
ପ୍ରତିରକ୍ଷା ଗବେଷଣା ଓ ଉନ୍ନୟନ ସଙ୍ଗଠନ ୧୯୫୮ ମସିହାରେ ଗଠିତ ହୋଇଥିଲା ।
(ଜ) ଅଗ୍ନି କ୍ଷେପଣାସ୍ତ୍ର କେଉଁଠାରେ ପରୀକ୍ଷା କରାଯାଇଥିଲା ?
Answer:
ଅଗ୍ନି କ୍ଷେପଣାସ୍ତ୍ର ଓଡ଼ିଶାର ଚାନ୍ଦିପୁର ନିକଟସ୍ଥ ହୁଇଲର୍ ଦ୍ଵୀପରେ ପରୀକ୍ଷା କରାଯାଇଥିଲା ।
(ଝ) ଆନ୍ଧ୍ରପ୍ରଦେଶର କେଉଁ ସ୍ଥାନରେ ଏକ ରକେଟ୍ ଉକ୍ଷେପଣ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠିତ ହୋଇଛି ?
Answer:
ଆନ୍ଧ୍ରପ୍ରଦେଶର ଶ୍ରୀହରିକୋଟାଠାରେ ଏକ ରକେଟ୍ ଉତକ୍ଷେପଣ କେନ୍ଦ୍ର ପ୍ରତିଷ୍ଠିତ ହୋଇଅଛି ।
(ଞ) ‘‘ଭାସ୍କର-ପ୍ରଥମ’’ ଉପଗ୍ରହ ପ୍ରେରଣ ପାଇଁ କେଉଁ ଦେଶର ସହାୟତା ନିଆଯାଇଥିଲା ?
Answer:
‘ଭାସ୍କର-ପ୍ରଥମ’ ଉପଗ୍ରହ ପ୍ରେରଣ ପାଇଁ ରୁଷିଆର ସହାୟତା ନିଆଯାଇଥିଲା ।
![]()
୪. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନରେ ଦିଆଯାଇଥିବା ଚାରିଗୋଟି ବିକଳ୍ପ ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ତା’ର କ୍ରମିକ ନମ୍ବର ସହିତ ଲେଖ ।
(କ) କେଉଁଠାରେ ପ୍ରଥମ ଭାରତୀୟ ବୈଷୟିକ ଶିକ୍ଷାନୁଷ୍ଠାନ ପ୍ରତିଷ୍ଠା କରାଯାଇଥିଲା ?
(i) ମୁମ୍ବାଇ
(ii) ଦିଲ୍ଲୀ
(iii) ଖଡ଼ଗପୁର
(iv) ଚେନ୍ନାଇ
Answer:
(iii) ଖଡ଼ଗପୁର
(ଖ) ପରମାଣୁ ଶକ୍ତି ଆୟୋଗର ପ୍ରଥମ ଅଧ୍ୟକ୍ଷ କିଏ ଥିଲେ ?
(i) ଜବାହରଲାଲ ନେହେରୁ
(ii) ହୋମି ଜାହାଙ୍ଗୀର ଭାବା
(iii) ଅବଦୁଲ୍ କାଲାମ୍
(iv) ବିକ୍ରମ ସରାଭାଇ
Answer:
(ii) ହୋମି ଜାହାଙ୍ଗୀର ଭାବା
(ଗ) କେଉଁଟି ଆଣବିକ ରିଆକ୍ଟର ନୁହେଁ ?
(i) ଧ୍ରୁବ
(ii) ଆକାଶ
(iii) ଅପ୍ସରା
(iv) କାମିନା
Answer:
(ii) ଆକାଶ
(ଘ) ଏକୀଭୂତ ନିୟନ୍ତ୍ରିତ କ୍ଷେପଣାସ୍ତ୍ର ବିକାଶ କାର୍ଯ୍ୟକ୍ରମ କେବେଠାରୁ ଆରମ୍ଭ ହେଲା ?
(i) ୧୯୬୨
(ii) ୧୯୭୪
(iii) ୧୯୮୩
(iv) ୧୯୮୪
Answer:
(iii) ୧୯୮୩
(ଡ) ଉପଗ୍ରହ ଯୋଗଯୋଗ କେନ୍ଦ୍ର କେଉଁଠାରେ ଅବସ୍ଥିତ ?
(i) ଇଦୋର
(ii) ଟ୍ରମ୍ବେ
(iii) ଆର୍ଭି
(iv) ଲକ୍ଷ୍ନୌ
Answer:
(iii) ଆର୍ଭି
![]()
୫. ପାଠରେ ଦିଆଯାଇଥିବା ‘ତୁମ ପାଇଁ କାମ’’ଗୁଡ଼ିକ ଶିକ୍ଷକଙ୍କ ନିର୍ଦ୍ଦେଶନା ଓ ସହାୟତାରେ ସମ୍ପାଦନ କର ।
Answer:
(ପିଲାମାନେ ଶିକ୍ଷକଙ୍କ ସହାୟତା ଓ ନିର୍ଦ୍ଦେଶନାରେ ଉତ୍ତର ଲେଖିବେ ।)