Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 2 ଭଗ୍ନସଂଖ୍ୟା ଓ ଦଶମିକ ସଂଖ୍ୟା InText Questions Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 2 ଭଗ୍ନସଂଖ୍ୟା ଓ ଦଶମିକ ସଂଖ୍ୟା InText Questions
ନିଜେ କରି ଦେଖ :
(କ) \(\frac{12}{18}\) କୁ ଲଘିଷ୍ଠ ଆକାରରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:
\(\frac{12}{18}\) ରେ ଲବ 12, ହର 18
(ଖ) 2 × \(\frac{2}{5}\) = \(\frac{2 \times \ldots \ldots \ldots}{\ldots \ldots \ldots}=\frac{\ldots \ldots \ldots \ldots}{\ldots \ldots \ldots \ldots}\)
ସମାଧାନ:
= \(\frac{2 \times 2}{5}=\frac{4}{5}\)
(ଗ) 3 × \(\frac{5}{7}\) = \(\frac{\ldots \times \ldots}{\ldots \ldots}=\frac{\ldots \ldots}{\ldots \ldots}\)
ସମାଧାନ:
= \(\frac{3 \times 5}{7}=\frac{15}{7}=2 \frac{1}{7}\)
ନିଜେ କରି ଦେଖ :
କାଗଜକୁ ଦେଖୁ ନିମ୍ନରେ ଥିବା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :
(a) କାଗଜ ଖଣ୍ଡିକ ………. ଗୋଟି ସମାନ ଭାଗ ହେବାର ଦେଖାଯାଉଛି ।
ସମାଧାନ:
8
(b) କାଗଜର……………ସମାନ ଭାଗରୁ …..………. ସମାନ ଭାଗ ରଙ୍ଗିନ୍ ହୋଇଥିବାର ଦେଖାଯାଉଛି ।
ସମାଧାନ:
8, 1
(c) କାଗଜ ଖଣ୍ଡିକର ……………..ଅଂଶ ରଙ୍ଗିନ୍ ହୋଇଛି ।
ସମାଧାନ:
\(\frac{1}{8}\)
(d) କାଗଜଟିକୁ ପ୍ରଥମେ ………….ଗୋଟି ସମାନ ଭାଗରେ ଭାଙ୍ଗ କରାଯାଇଥିଲା ଓ ପରେ ଏହି ଭଙ୍ଗା ଯାଇଥିବା କାଗଜକୁ ପୁଣି ……….. ଗୋଟି ସମାନ ଭାଗରେ ଭାଙ୍ଗ କରାଗଲା । ତେଣୁ କାଗଜଟି ମୋଟ …… ଭାଗ ହେଲା
ସମାଧାନ:
4, 2
(e) ଆମେ ଜାଣିଲେ, କାଗଜ ଖଣ୍ଡିକର ……… ଅଂଶରେ ରଙ୍ଗ ଦିଆଯାଇଛି ।
ସମାଧାନ:
\(\frac{1}{8}\)

ଏଥୁରୁ ଆମେ କ’ଣ ଜାଣିଲେ?
……………. × ……………. = \(\frac{1}{8}\)
ସମାଧାନ:
ଏଥୁରୁ ଆମେ ଜାଣିଲେ \(\frac{1}{4} \times \frac{1}{2}=\frac{1}{8}\) ବତ୍ତମାନ ଦେଖ୍ ବା \(\frac{1}{8}=\frac{1}{4} \times \frac{1}{2}\)
ଏଣୁ \(\frac{1}{4} \times \frac{1}{2}=\frac{1 \times 1}{4 \times 2}=\frac{1}{8}\)
ଚିତ୍ର ଦେଖ୍ ଉତ୍ତର ଦିଅ ।
(କ)
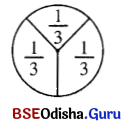
ଚିତ୍ର କ : 1 ରେ କେତୋଟି \(\frac{1}{3}\) ଅଛି? 1 ÷ \(\frac{1}{3}\) = କେତେ?
ସମାଧାନ:
3, 3
(ଖ)
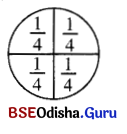
ଚିତ୍ର ଖ : 1 ରେ କେତୋଟି \(\frac{1}{4}\) ଅଛି? 1 ÷ \(\frac{1}{4}\) = କେତେ?
ସମାଧାନ:
4, 4
(ଗ)
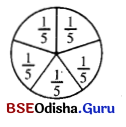
ଚିତ୍ର ଗ : 1 ରେ କେତୋଟି \(\frac{1}{5}\) ଅଛି? 1 ÷ \(\frac{1}{5}\) = କେତେ?
ସମାଧାନ:
5, 5
ନିମ୍ନରେ ଥିବା ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର।
(କ) \(\frac{2}{3}\) ର ବ୍ୟୁତ୍କ୍ରମ = …………
ସମାଧାନ:
\(\frac{3}{2}\)
(ଖ) \(\frac{3}{7}\) ର ବ୍ୟୁତ୍କ୍ରମ = ……….
ସମାଧାନ:
\(\frac{7}{3}\)
(ଗ) \(\frac{5}{2}\) ର ବ୍ୟୁତ୍କ୍ରମ = ………..
ସମାଧାନ:
\(\frac{2}{5}\)
(ଘ) 4 ର ବ୍ୟକ୍ରମ = ………..
ସମାଧାନ:
\(\frac{1}{4}\)
(ଙ) 1 ÷ \(\frac{2}{3}\) = …… × …….. = …….
ସମାଧାନ:
1 × \(\frac{5}{1}\) = 5
(ଚ) 2 ÷ \(\frac{3}{4}\) = …… × …….. = …….
ସମାଧାନ:
2 × \(\frac{4}{3}\) = \(\frac{8}{3}\)
(ଛ) \(\frac{4}{5}\) ÷ 3 = _____
ସମାଧାନ:
= \(\frac{4}{5} \times \frac{1}{3}=\frac{4}{15}\)
(ଜ) 3 \(\frac{1}{3}\) ÷ 4 = _____
ସମାଧାନ:
= \(\frac{10}{3} \times \frac{1}{4}=\frac{10}{12}=\frac{2 \times 5}{2 \times 6}=\frac{5}{6}\)
(ଝ) \(\frac{2}{7} \div \frac{3}{5}\)
ସମାଧାନ:
\(\frac{2}{7}\) × (\(\frac{3}{5}\) ର ବ୍ୟୁତ୍କ୍ରମ) = \(\frac{2}{7} \times \frac{5}{3}=\frac{10}{21}\)
(ଞ) 1 \(\frac{3}{4} \div \frac{5}{6}\)
ସମାଧାନ:
\(\frac{7}{4}\) × (\(\frac{5}{6}\) ର ବ୍ୟୁତ୍କ୍ରମ) = \(\frac{7}{4} \times \frac{6}{5}=\frac{42}{20}=\frac{21}{10}\)
(ଟ) 2 \(\frac{3}{5} \div 1 \frac{3}{5}\)
ସମାଧାନ:
\(\frac{13}{5} \div \frac{5}{3}=\frac{13}{5}\) × (\(\frac{5}{3}\) ର ବ୍ୟୁତ୍କ୍ରମ) = \(\frac{13}{5} \times \frac{3}{5}=\frac{39}{25}\) ବା \(\frac{14}{25}\)

ଗୁଣଫଳ ସ୍ଥିର କର :
(କ) 0.5 × 0.6
ସମାଧାନ:
ପ୍ରଥମ ସେପାନ : 5 × 6 = 30
ଦ୍ବିତୀୟ ସେପାନ : ସଂଖ୍ୟାଦ୍ଵୟର ଦଶମିକ ବିନ୍ଦୁ ପରବର୍ତ୍ତୀ ମୋଟ ଅଙ୍କ ସଂଖ୍ୟା = 1 + 1 = 2
ଦ୍ବିତୀୟ ସେପାନ : ଗୁଣଫଳର ଡାହାଣପଟୁ ଦୁଇଟି ଅଙ୍କଛାଡ଼ି ଦଶମିକ ବିନ୍ଦୁ ଦେଲେ ଗୁଣଫଳ ହେବ 0.30
∴ 0.5 × 0.6 = 0.30 ବା 0.3
(ଖ) 0.8 × 1.6
ସମାଧାନ:
ପ୍ରଥମ ସେପାନ : 8 × 16 = 128
ଦ୍ବିତୀୟ ସେପାନ : ସଂଖ୍ୟାଦ୍ଵୟର ଦଶମିକ ବିନ୍ଦୁ ପରବର୍ତ୍ତୀ ମୋଟ ଅଙ୍କ ସଂଖ୍ୟା = 1 + 1 = 2
ଦ୍ବିତୀୟ ସେପାନ : ଗୁଣଫଳର ଡାହାଣପଟୁ ଦୁଇଟି ଅଙ୍କଛାଡ଼ି ଦଶମିକ ବିନ୍ଦୁ ଦେଲେ ଗୁଣଫଳ ହେବ 1.28
∴ 0.8 × 1.6 = 1.28
(ଗ) 2.4 × 4.2
ସମାଧାନ:
ପ୍ରଥମ ସେପାନ : 24 × 42 = 1008
ଦ୍ବିତୀୟ ସେପାନ : ସଂଖ୍ୟାଦ୍ଵୟର ଦଶମିକ ବିନ୍ଦୁ ପରବର୍ତ୍ତୀ ମୋଟ ଅଙ୍କ ସଂଖ୍ୟା = 1 + 1 = 2
ଦ୍ବିତୀୟ ସେପାନ : ଗୁଣଫଳର ଡାହାଣପଟୁ ଦୁଇଟି ଅଙ୍କଛାଡ଼ି ଦଶମିକ ବିନ୍ଦୁ ଦେଲେ ଗୁଣଫଳ ହେବ 10.08
∴ 2.4 × 4.2 = 10.08
(ଘ) 1.5 × 1.25
ସମାଧାନ:
ପ୍ରଥମ ସେପାନ : 15 × 125 = 1875
ଦ୍ବିତୀୟ ସେପାନ : ସଂଖ୍ୟାଦ୍ଵୟର ଦଶମିକ ବିନ୍ଦୁ ପରବର୍ତ୍ତୀ ମୋଟ ଅଙ୍କ ସଂଖ୍ୟା = 1 + 1 = 2
ଦ୍ବିତୀୟ ସେପାନ : ଗୁଣଫଳର ଡାହାଣପଟୁ ଦୁଇଟି ଅଙ୍କଛାଡ଼ି ଦଶମିକ ବିନ୍ଦୁ ଦେଲେ ଗୁଣଫଳ ହେବ 1.875
∴ 1.5 × 1.25 = 1.875
(1) ଗୁଣଫଳ ଲେଖ–
(କ) 3.4 × 10 = _____
ସମାଧାନ:
34 (ଦଶମିକ ବିନ୍ଦୁ 1 ଟି ଅଙ୍କ ଡାହାଣକୁ ଘୁଞ୍ଚୁଲା)
(ଖ) 0.56 × 100 = _____
ସମାଧାନ:
56 (ଦଶମିକ ବିନ୍ଦୁ ଦୁଇଟି ଅଙ୍କ ଡାହାଣକୁ ଘୁଞ୍ଚିଲା )
(ଗ) 1.04 × 1000 = _____
ସମାଧାନ:
= 1.040 × 1000 = 1040
(ଘ) 0.3 × 100 = _____
ସମାଧାନ:
= 0.30 × 100 = 30

(2) ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର–
(କ) ଦଶମିକ ସଂଖ୍ୟାକୁ 100 ଦ୍ୱାରା ଗୁଣିବା ବେଳେ, ଦଶମିକ ବି…….ଗୋଟି ସ୍ଥାନ ଡାହାଣକୁ ଘୁଞ୍ଚିବ ।
ସମାଧାନ:
ଦୁଇ
(ଖ) ଦଶମିକ ସଂଖ୍ୟାକୁ 1000 ଦ୍ବାରା ଗୁଣନ କଲାବେଳେ ଦଶମିକ ବି………….ଗୋଟି ସ୍ଥାନ ଡାହାଣକୁ ଘୁଞ୍ଚୁବ ।
ସମାଧାନ:
ତିନି
ଉତ୍ତର ଲେଖ :
(କ) 125 ÷ 10 ର ଭାଗଫଳ କେତେ?
ସମାଧାନ:
12.5
(ଖ) 235.41 ÷ 100 ର ଭାଗଫଳ କେତେ?
ସମାଧାନ:
2.3541
(ଗ) 123.5 ÷ 1000 ର ଭାଗଫଳ କେତେ?
ସମାଧାନ:
.1235
ଉତ୍ତର କେତେ ହେବ ଲେଖ :
(କ) 2.4 ÷ 2
ସମାଧାନ:
= \(\frac{2.4 \times 5}{2 \times 5}=\frac{12.0}{10}\) = 1.20 ବା 1.2
(ଖ) 3.6 ÷ 4
ସମାଧାନ:
= \(\frac{3.6}{4}=\frac{3.6 \times 5 \times 5}{4 \times 5 \times 5}=\frac{18 \times 5}{20 \times 5}=\frac{90}{100}=\frac{9}{10}\) = 0.9
(ଗ) 3.3 ÷ 5
ସମାଧାନ:
= \(\frac{3.3 \times 2}{5 \times 2}=\frac{6.6}{10}\) = 0.66
(ଘ) 42.6 ÷ 25
ସମାଧାନ:
= \(\frac{42.6}{25}=\frac{42.6 \times 4}{25 \times 4}=\frac{170.4}{100}\) = 1.704
(ଙ) 73.8 ÷ 3
ସମାଧାନ:
= \(\frac{738}{10} \div 3=\frac{738}{10} \times \frac{1}{3} =\frac{ 738}{3} \times \frac{1}{10}=246 \times \frac{1}{10}\) = 24.6
(ଚ) 36.1 ÷ 14
ସମାଧାନ:
= \(\frac{361}{10} \div 19=\frac{ 361}{10} \times \frac{1}{19}=\frac{361}{19} \times \frac{1}{10}=19 \times \frac{1}{10}\) = 1.9
(ଛ) 32.72 ÷ 0.4
ସମାଧାନ:

(ଜ) 48.06 ÷ 0.9
ସମାଧାନ:

(ଝ) 90.48 ÷ 1.2
ସମାଧାନ:


ଉତ୍ତର ଲେଖ –
(କ) 2.6 ମିଟର କୁ ମିଟରରେ ପରିଣତ କର ।
ସମାଧାନ:
2.6 ମିଟର = (2.6 × 100) ସେ.ମି. = 260 ସେ.ମି. (1 ମି. = 100 ସେ.ମି.)
(ଖ) 3.24 ମିଟରକୁ ଡେସି ମିଟରରେ ପରିଣତ କର ।
ସମାଧାନ:
3.24 ମିଟର = (3.24 × 10) ଡେସିମିଟର = 32.4 ଡେସିମିଟର (1 ମି. = 10 ଡେସିମି)
(ଗ) 3.48 ସେ.ମି କୁ ମି. ଓ ସେ.ମି. ଏକକ ବ୍ୟବହାର କରି ଲେଖୁବା ପାଇଁ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର | _____ ମି _____ସେ.ମି ।
ସମାଧାନ:
3.48 ସେ.ମି. = 3 ମି. 48 ସେ.ମି.
(ଘ) 0.728 ଗ୍ରାମକୁ କି.ଗ୍ରା ରେ ପରିଣତ କର ।
ସମାଧାନ:
0.728 ଗ୍ରାମ୍ = \(\frac{0.728}{1000}\) କି.ଗ୍ରା = 0.000728 କି.ଗ୍ରା.
(ଙ) 3.2 କି.ଗ୍ରା.କୁ ଗ୍ରାମ୍ ଏକକରେ ପରିଣତ କର ।
ସମାଧାନ:
3.2 କିଗ୍ରା = (3.2 × 1000) ଗ୍ରାମ୍ = 3200 ଗ୍ରାମ୍ (1 କି.ଗ୍ରା. = 1000 ଗ୍ରାମ୍)
(ଚ) 4357 ଗ୍ରାମକୁ ନିମ୍ନମତେ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କରି ଲେଖ । 4357 ଗ୍ରାମ୍ = …… କି.ଗ୍ରା. …. ଗ୍ରାମ୍ ।
ସମାଧାନ:
4357 ଗ୍ରାମ୍ = 4 କି.ଗ୍ରା. 357 ଗ୍ରାମ୍ ।
![]()
![]()