Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 3 ମୌଳିକ ଜ୍ୟାମିତିକ ଚିତ୍ର InText Questions Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 3 ମୌଳିକ ଜ୍ୟାମିତିକ ଚିତ୍ର InText Questions
1. ନିମ୍ନରେ ଥିବା ଚିତ୍ରମାନଙ୍କ ମଧ୍ୟରେ ରେଖା, ରଶ୍ମି ଓ ରେଖାଖଣ୍ଡ ଚିହ୍ନଟ କର ।
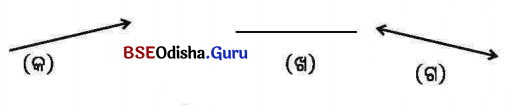
ସମାଧାନ:
ଚିତ୍ର (କ) – ରଶ୍ମି, ଚିତ୍ର (ଖ) – ରେଖାଖଣ୍ଡ ଓ ଚିତ୍ର (ଗ) – ରେଖା ।
2. ନିମ୍ନ ଚିତ୍ରରୁ ସୂକ୍ଷ୍ମକୋଣ, ସମକୋଣ ଓ ସ୍ଥୂଳକୋଣ ଚିହ୍ନଟ କର ।
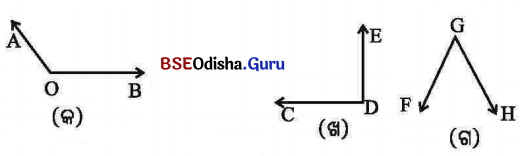
ସମାଧାନ:
ଚିତ୍ର (କ) ସ୍ଥୂଳକୋଣ, ଚିତ୍ର (ଖ) ସମକୋଣ, ଚିତ୍ର (ଗ) ସୂକ୍ଷ୍ମକୋଣ ।
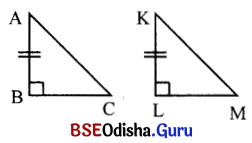
3. ନିମ୍ନ ଚିତ୍ରରୁ ସମକୋଣୀ ତ୍ରିଭୁଜ, ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜ ଓ ସୂକ୍ଷ୍ମକୋଣୀ ତ୍ରିଭୁଜ ଚିହ୍ନଟ କର ।
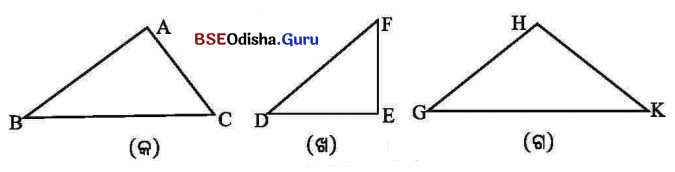
ସମାଧାନ:
ଚିତ୍ର (କ) – ସୂକ୍ଷ୍ମକୋଣୀ ତ୍ରିଭୁଜ, ଚିତ୍ର (ଖ) — ସମକୋଣୀ ତ୍ରିଭୁଜ, ଚିତ୍ର (ଗ) – ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜ ।
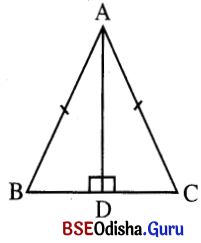
4. ନିମ୍ନ ଚିତ୍ରରୁ ସମବାହୁ, ସମଦ୍ବିବାହୁ ଓ ବିଷମବାହୁ ତ୍ରିଭୁଜ ଚିହ୍ନଟ କର ।
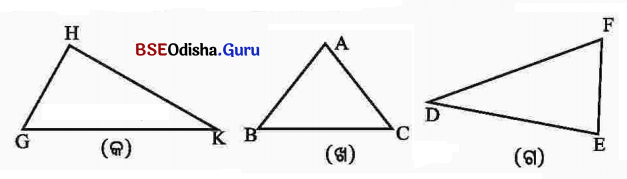
ସମାଧାନ:
ଚିତ୍ର (କ) – ବିଷମ ବାହୁ ତ୍ରିଭୁଜ, ଚିତ୍ର (ଖ) – ସମବାହୁ ତ୍ରିଭୁଜ, ଚିତ୍ର (ଗ) – ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
5. (କ) ନିମ୍ନ ଚିତ୍ରରୁ ଟ୍ରାପିଜିୟମ୍, ସାମାନ୍ତରିକ ଚିତ୍ର, ଆୟତଚିତ୍ର, ବର୍ଗଚିତ୍ର ଓ ରମ୍ବସ୍ ଚିହ୍ନଟ କର ।

ସମାଧାନ:
(କ) ଚିତ୍ରଟି ବର୍ଗଚିତ୍ର
(ଖ) ଚିତ୍ରଟି ସାମାନ୍ତରିକ ଚିତ୍ର
(ଗ) ଚିତ୍ରଟି ରମ୍ବସ୍
(ଘ) ଚିତ୍ରଟି ଟ୍ରାପିଜିୟମ୍
(ଙ) ଚିତ୍ରଟି ଆୟତଚିତ୍ର
(ଖ) ଉପରିସ୍ଥ ଚିତ୍ରମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁ କେଉଁ ଚିତ୍ରର ସମସ୍ତ କୋଣ ସମକୋଣ?
ସମାଧାନ:
ବର୍ଗଚିତ୍ର ଆୟତଚିତ୍ର

(ଗ) EFGH ଚିତ୍ରରେ କେଉଁ କୋଣମାନ ସମାନ ପରିମାଣ ବିଶିଷ୍ଟ? କେଉଁ ବାହୁଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟ ସମାନ?
ସମାଧାନ:
∠E = ∠G, ∠H = ∠F, EF = GH ଓ EH = FG
(ଘ) MJKL ଚିତ୍ରରେ କେଉଁ ବାହୁଗୁଡ଼ିକର ଦୈର୍ଘ୍ୟ ସମାନ?
ସମାଧାନ:
MJ = JK = KL = LM
ନିଜେ କରି ଦେଖ:
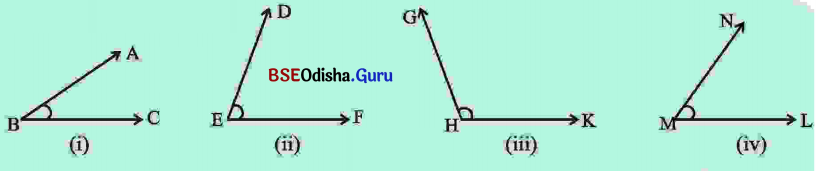
(କ) ଉପରିସ୍ଥ କୋଣଗୁଡ଼ିକର ପରିମାଣ ପ୍ରୋଟ୍ରାକ୍ଟର ସାହାଯ୍ୟରେ ମାପ ଓ ମାପଗୁଡ଼ିକୁ ସାରଣୀରେ ରଖ ।
| କୋଣ |
∠ABC |
∠DEF |
∠GHK |
∠LMN |
| ପରିମାଣ |
|
|
|
|
ସମାଧାନ:
| କୋଣ |
∠ABC |
∠DEF |
∠GHK |
∠LMN |
| ପରିମାଣ |
40° |
60° |
120° |
50° |
(ଖ) କେଉଁ କୋଣ ଦୁଇଟିର ପରିମାଣର ସମଷ୍ଟି 90° ସ୍ଥିର କର
ସମାଧାନ:
∠ABC ଓ ∠LMN କୋଣଦ୍ଵୟର ସମଷ୍ଟି 90° ।
(ଗ) କେଉଁ କୋଣ ଦୁଇଟିର ପରିମାଣର ସମଷ୍ଟି 180° ସ୍ଥିର କର ।
ସମାଧାନ:
∠GHK ଓ ∠DEF କୋଣଦ୍ୱୟର ସମଷ୍ଟି 180°
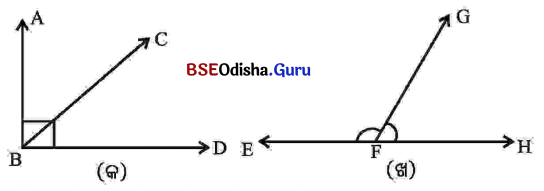
(ଘ) ଚିତ୍ର (କ)ରେ ∠ABC ଓ ∠CBD ଦୁଇଟି ପରସ୍ପର ସନ୍ନିହିତ କୋଣ ହେବେ କି? କାହିଁକି?
ଚିତ୍ର (ଖ)ରେ ∠EFG ଓ ∠GFH ଦୁଇଟି ପରସ୍ପର ସନ୍ନିହିତ କୋଣ ହେବେ କି? କାହିଁକି?
ସମାଧାନ:
ଚିତ୍ର (କ) ରେ ∠ABC ଓ ∠CBD କୋଣଦ୍ୱୟର ସାଧାରଣ ଶୀର୍ଷବିନ୍ଦୁ B, ସାଧାରଣ ବାହୁ \(\overrightarrow{\mathrm{BC}}\) କୋଣଦ୍ୱୟର ଅନ୍ତର୍ଦେଶରେ କୌଣସି ସାଧାରଣ ବିନ୍ଦୁ ନାହିଁ । ତେଣୁ କୋଣଦ୍ଵୟ ପରସ୍ପର ସନ୍ନିହିତ କୋଣ ଅଟନ୍ତି ।
ଚିତ୍ର (ଖ) ରେ ∠EFG ଓ ∠GFH କୋଣଦ୍ୱୟର ସାଧାରଣ ଶୀର୍ଷବିନ୍ଦୁ F, ସାଧାରଣ ବାହୁ \(\overrightarrow{\mathrm{FG}}\) ଓ କୋଣଦ୍ୱୟର ଅନ୍ତର୍ଦ୍ଦେଶରେ କୌଣସି ସାଧାରଣ ବିନ୍ଦୁ ନାହିଁ । ତେଣୁ କୋଣଦ୍ଵୟ ପରସ୍ପର ସନ୍ନିହିତ କୋଣ ଅଟନ୍ତି ।
⇒ ଚିତ୍ରରେ ଥିବା କୋଣଗୁଡ଼ିକ ମାପି ନିମ୍ନ ସାରଣୀ ପୂରଣ କର ।
| କୋଣର ନାମ |
∠ABC |
∠CBD |
∠EFG |
∠GFH |
| କୋଣର ପରିମାଣ |
|
|
|
|
ସମାଧାନ:
| କୋଣର ନାମ |
∠ABC |
∠CBD |
∠EFG |
∠GFH |
| କୋଣର ପରିମାଣ |
40° |
50° |
120° |
60° |
କ’ଣ ଦେଖିଲ?
(କ) କେଉଁ ଦୁଇଟି ସନ୍ନିହିତ କୋଣର ପରିମାଣର ସମଷ୍ଟି 90° ହେଲା?
ସମାଧାନ:
∠ABC ଓ ∠CBD
(ଖ) କେଉଁ ଦୁଇଟି ସନ୍ନିହିତ କୋଣର ପରିମାଣର ସମଷ୍ଟି 180° ହେଲା?
ସମାଧାନ:
∠EFG ଓ ∠GFH
(ଗ) କେଉଁ କୋଣ ଦୁଇଟି ପରସ୍ପର ଅନୁପୂରକ?
ସମାଧାନ:
∠ABC ଓ ∠CBD
(ଘ) କେଉଁ କୋଣ ଦୁଇଟି ପରସ୍ପର ପରିପୂରକ?
ସମାଧାନ:
∠EFG ଓ ∠GFH

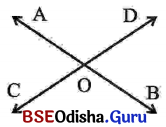
⇒ ଉପରିସ୍ଥ ଚିତ୍ରରେ କେତେ ଯୋଡ଼ା ପରସ୍ପର ପ୍ରତୀପ କୋଣ ଥିବାର ଦେଖୁଛ?
ସମାଧାନ:
ଚିତ୍ରରେ ଦୁଇଯୋଡ଼ା ପରସ୍ପର ପ୍ରତୀପ କୋଣ ଅଛି ।
ପରସ୍ପର ପ୍ରତୀପ କୋଣକୁ ପରସ୍ପର ବିପରୀତ କୋଣ କୁହାଯାଏ ।
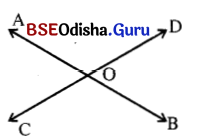
1. ବର୍ତ୍ତମାନ ତୁମ ପ୍ରୋଟ୍ରାକ୍ଟର ସାହାଯ୍ୟରେ ∠AOB, ∠BOC, ∠COD ଓ ∠DOA କୋଣ ସ୍ଫରୋଟିକୁ ମାପ ଓ ସେମାନଙ୍କର ପରିମାଣକୁ ନିମ୍ନରେ ଦିଆଯାଇଥିବା ଭଳି ଏକ ସାରଣୀ ତିଆରି କରି ଲେଖ।
| କୋଣର ନାମ |
∠AOC |
∠BOD |
∠BOC |
∠DOA |
| କୋଣର ପରିମାଣ |
|
|
|
|
ସମାଧାନ:
| କୋଣର ନାମ |
∠AOC |
∠BOD |
∠BOC |
∠DOA |
| କୋଣର ପରିମାଣ |
70° |
70° |
110° |
110° |
ତୁମେ ସାରଣୀ ଦେଖି ଓ ନିମ୍ନ ପ୍ରଶ୍ନ ଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
1. ∠AOC ର ପରିମାଣ ସହ କେଉଁ କୋଣର ପରିମାଣ ସମାନ?
ସମାଧାନ:
∠BOD
2. ∠BOC ର ପରିମାଣ ସହ କେଉଁ କୋଣର ପରିମାଣ ସମାନ?
ସମାଧାନ:
∠AOD
3. ∠AOC ଓ ∠BOD କୁ କି ପ୍ରକାର କୋଣ କୁହାଯାଏ?
ସମାଧାନ:
ପ୍ରତୀପ କୋଣ
4. ∠BOC ଓ ∠DOA କୁ କି ପ୍ରକାର କୋଣ କୁହାଯାଏ?
ସମାଧାନ:
ପ୍ରତୀପ କୋଣ
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରଦେଖୁ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଲେଖ ।
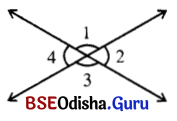
(କ) ∠1ସହ ଅନ୍ୟ କେଉଁ କୋଣ ସରଳ ଯୋଡ଼ି ଗଠନ କରେ?
ସମାଧାନ:
∠2 ଓ ∠1 କୋଣ
(ଖ) ∠3 ର ପ୍ରତୀପ କୋଣଟି କିଏ?
ସମାଧାନ:
∠1
(ଗ) ∠2 ର ପ୍ରତୀପ କୋଣଟି କିଏ?
ସମାଧାନ:
∠4
(ଘ) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ∠4 ର ପରିମାଣ 60° ହେଲେ, ଅନ୍ୟ କୋଣ ତିନୋଟିର ପରିମାଣ କେତେ?
ସମାଧାନ:
∠2 ର ପରିମାଣ = 60°, ∠1 ର ପରିମାଣ = 120° ଓ ∠3 ର ପରିମାଣ = 120°

⇒ ତୁମ ପରିବେଶରେ କେଉଁ କେଉଁଠାରେ ପରସ୍ପର ଛେଦୀ ରେଖା ଦେଖୁଛ ତାହାର ପାଞ୍ଚଟି ଉଦାହରଣ ଦିଅ ।
ସମାଧାନ:
ବାଟୁଳିଖଡ଼ା, ତାରଜାଲି, ଚଟ, ଚେସ୍ବୋର୍ଡ଼, ତାରବାଡ଼ ଆଦିରେ ପରସ୍ପରଛେଦୀ ରେଖା ଦେଖାଯାଏ ।
ନିଜେ କରି ଦେଖ:
(କ) ଚିତ୍ର ରେ ଦେଖୁଥିବା ପରସ୍ପର ଛେଦୀ ରେଖା ଯୋଡ଼ି ଓ ସେ ଦ୍ବୟର ଛେଦ ବିନ୍ଦୁର ନାମ ଲେଖ ।
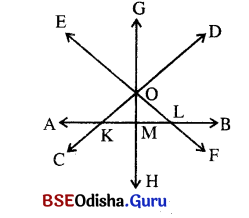
ସମାଧାନ:
\(\stackrel{\leftrightarrow}{\mathrm{EF}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) ପରସ୍ପରଛେଦୀ ରେଖା ଓ ଛେଦବିନ୍ଦୁ O,
\(\stackrel{\leftrightarrow}{\mathrm{EF}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{GH}}\) ପରସ୍ପରଛେଦୀ ରେଖା ଓ ଛେଦବିନ୍ଦୁ O,
\(\stackrel{\leftrightarrow}{\mathrm{EF}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{GH}}\) ପରସ୍ପରଛେଦୀ ରେଖା ଓ ଛେଦବିନ୍ଦୁ O,
\(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{EF}}\) ପରସ୍ପରଛେଦୀ ରେଖା ଓ ଛେଦବିନ୍ଦୁ L
\(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{GH}}\) ପରସ୍ପର ଛେଦୀରେଖା ଓ ଛେଦବିନ୍ଦୁ M
\(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{EF}}\) ପରସ୍ପରଛେଦୀ ରେଖା ଓ ଛେଦବିନ୍ଦୁ K ।
⇒ ଏହି ଚିତ୍ରରେ ସମାନ୍ତର ସରଳରେଖା ଥିବାର ଦେଖୁଛ କି?
ସମାଧାନ:
ନାହିଁ
(ଖ) ଦୁଇଟି ରେଖା ବା ରେଖାଖଣ୍ଡର ଗୋଟିଏରୁ ଅଧିକ ଛେଦବିନ୍ଦୁ ରହିବା ସମ୍ଭବ କି? ଯଦି ସମ୍ଭବ, ଏପରି ଦୁଇଟି ରେଖାର ଚିତ୍ର କର।
ସମାଧାନ:
ସମ୍ଭବ ନୁହେଁ ।
(ଗ) ତୁମ ପରିବେଶରେ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରୁଥିବା ରେଖା ବା ରେଖାଖଣ୍ଡର ଉଦାହରଣ କେଉଁଠି ଦେଖିବାକୁ ମିଳେ ତାହା ଲେଖ ।
ସମାଧାନ:
ଗୋଲ୍ପୋଷ୍ଟ, ଝରକାଜାଲି, ଇଟା, ଟେବୁଲ୍ର ଉପର ଧାର ଇତ୍ୟାଦି ।
(ଘ) ଗୋଟିଏ ଆୟତଚିତ୍ରର ପ୍ରତ୍ୟେକ ଯୋଡ଼ବାହୁର ଛେଦବିନ୍ଦୁରେ ଉତ୍ପନ୍ନ କୋଣର ପରିମାଣ କେତେ ମାପି ସ୍ଥିର କର। ଗୋଟିଏ ପୋଷ୍ଟକାର୍ଡ଼ ନେଇ ଏହି କାର୍ଯ୍ୟ କର ।
ସମାଧାନ:
90°
ଉତ୍ତର ଲେଖ :
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରକୁ ଦେଖ୍ ନିମ୍ନରେ ଦିଆଯାଇଥିବା କୋଣ
କୋଣ-ଯୋଡ଼ାଗୁଡ଼ିକ କି ପ୍ରକାର କୋଣ ଲେଖ ।
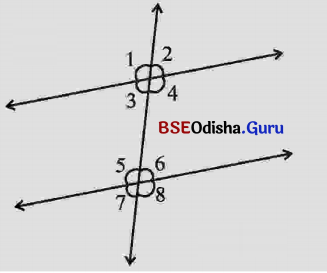
(କ) ∠1 ଓ ∠5
ସମାଧାନ:
∠1 ଓ ∠5 ଅନୁରୂପ କୋଣ
(ଖ) ∠3 ଓ ∠6
ସମାଧାନ:
∠3 ଓ ∠6 ଏକାନ୍ତର କୋଣ
(ଗ) ∠4 ଓ ∠6
ସମାଧାନ:
∠4 ଓ ∠6 ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୋଣ
(ଘ) ∠4 ଓ ∠5
ସମାଧାନ:
∠4 ଓ ∠5 ଏକାନ୍ତର କୋଣ
(ଘ) ∠3 ଓ ∠6
ସମାଧାନ:
∠3 ଓ ∠6 ଏକାନ୍ତର କୋଣ
(ଚ) ∠2 ଓ ∠6
ସମାଧାନ:
∠2 ଓ ∠6 ଅନୁରୂପ କୋଣ

1. ଏକ ଯୋଡ଼ା ସମାନ୍ତର ସରଳରେଖା ଅଙ୍କନ କର ଏବଂ ସେ ରେଖା ଦୁଇଟିର ଏକ ଛେଦକ ରେଖା ଅଙ୍କନ କର ।
ଛେଦକ ରେଖା ଦ୍ୱାରା ଉତ୍ପନ୍ନ କୋଣଗୁଡ଼ିକୁ ମାପି ନିମ୍ନ ଉକ୍ତିଗୁଡ଼ିକର ସତ୍ୟତା ପରୀକ୍ଷା କର ।
(କ) ଅନୁରୂପ କୋଣମାନ ସମପରିମାଣ ବିଶିଷ୍ଟ ।
(ଖ) ଏକାନ୍ତର କୋଣମାନ ସମ ପରିମାଣ ବିଶିଷ୍ଟ ।
(ଗ) ଛେଦକ ରେଖାର ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୌଣମାନ ପରସ୍ପର ପରିପୂରକ।
ସମାଧାନ:
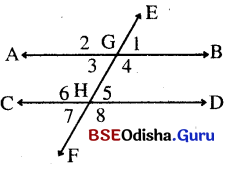
ଏଠାରେ \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ଓ \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖା ଗୋଟିଏ ସ୍କେଲର ଦୁଇଟି ଧାରରେ ଅଙ୍କନ କରାଯାଉ । \(\stackrel{\leftrightarrow}{\mathrm{EF}}\) ଏହାର ଛେଦକ ଅଙ୍କନ କରି AB ଓ CD ର ଛେଦବିନ୍ଦୁକୁ G ଓ H ରେ ନାମିତ କରାଯାଉ ।
କୋଣମାନଙ୍କୁ ଯଥାକ୍ରମେ 1, 2, 3, 4, 5, 6, 7, 8 ରେ ନାମିତ କରାଯାଉ । କୋଣମାନଙ୍କ ପରିମାଣକୁ ମାପି ନିମ୍ନ ସାରଣୀରେ ଦର୍ଶାଯାଇଛି ।
| କୋଣ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| କୋଣର ପରିମାଣ |
70° |
110° |
70° |
110° |
70° |
110° |
70° |
110° |
ଅନୁରୂପ କୋଣ ଯୋଡ଼ିମାନ ∠2 ଓ ∠6, ∠1 ଓ ∠5, ∠3 ଓ ∠7 ଏବଂ ∠4 ଓ ∠8 ।
ଏଠାରେ m∠1 = m∠5 = m∠3 = m∠7 = 70°
m∠2=m∠6=m∠4 = m∠8 = 110°
∴ ଅନୁରୂପ କୋଣମାନ ସମପରିମାଣ ବିଶିଷ୍ଟ ।
ଏକାନ୍ତର କୋଣଯୋଡ଼ି m∠3 ଓ m∠5 ଏବଂ m∠4 ଓ m∠6 ।
ଏଠାରେ m∠3 = m∠5 = 70°, m∠4 = m∠6 = 110°
∴ ଏକାନ୍ତର କୋଣମାନ ସମପରିମାଣ ବିଶିଷ୍ଟ ।
ଛେଦକରେଖାର ଏକ ପାର୍ଶ୍ବସ୍ଥ ଅନ୍ତଃସ୍ଥ କୋଣ ଯୋଡ଼ି ∠3, ∠6 ଏବଂ m∠4, ∠5
m∠3 + m∠6 = 70° + 110° = 180°, m∠4 + m∠5 = 110° + 70° = 180°
∴ ଛେଦକରେଖାର ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୋଣମାନ ପରସ୍ପର ପରିପୂରକ ।
![]()
![]()