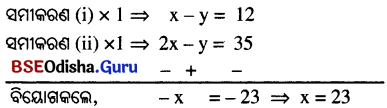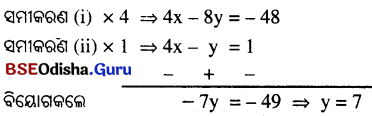Odisha State Board BSE Odisha 7th Class Geography Important Questions Chapter 4 ଜୈବମଣ୍ଡଳ Important Questions and Answers.
BE Odisha Class 7 Geography Important Questions Chapter 4 ଜୈବମଣ୍ଡଳ
Subjective Type Questions With Answers
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
Question 1.
ଶକ୍ତି ପ୍ରବାହ କ’ଶ ସଂକ୍ଷେପରେ ବୁଝାଅ ।
Answer:
- ଉଭିଦ ଜଗତ ଉତ୍ପାଦକ ଓ ପ୍ରାଣୀମାନେ ଭକ୍ଷକ ଅଟନ୍ତି ।
- ଉଭିଦ ଦ୍ୱାରା ମାଟିରୁ ସଂଗୃହୀତ ଖଣିଜ ଲବଣ ଓ ସୌରଶକ୍ତି ରାସାୟନିକ ଶକ୍ତିରେ ରୂପାନ୍ତରିତ ହୋଇ ରହେ ।
- ତୃଣଭୋଜୀ ପ୍ରାଣୀ ଉଭିଦର ବିଭିନ୍ନ ଅଂଶ ଖାଇବା ଦ୍ଵାରା ସେମାନେ ଉଭିଦଠାରୁ କିଛି ପରିମାଣର ରାସାୟନିକ ଶକ୍ତି (ପ୍ରାୟ ଉଭିଦଠାରେ ଥିବା ଶକ୍ତିର ଏକ-ଦଶମାଂଶ) ଗ୍ରହଣ କରନ୍ତି ।
- ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କଠାରୁ ଏହି ଶକ୍ତି (ପ୍ରାୟ ଏକ-ଦଶମାଂଶ) ମାଂସାଶୀ ପ୍ରାଣୀ ଓ ମନୁଷ୍ୟ ପାଖକୁ ଯାଏ ।
- ପରିସଂସ୍ଥାରେ ଏହିପରି ଶକ୍ତିର ସ୍ଥାନାନ୍ତରଣକୁ ଶକ୍ତି ପ୍ରବାହ କୁହାଯାଏ । ଶକ୍ତି ପ୍ରବାହ ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ହୁଏ ଓ ଶକ୍ତିର ପରିମାଣ ପ୍ରଥମ ସ୍ତରରୁ ଶୀର୍ଷ ସ୍ତର ଆଡ଼କୁ କ୍ରମଶଃ କମିଯାଏ ।
Question 2.
ଜଳ ଦୂଷିତ ହେବାର କାରଣଗୁଡ଼ିକ ଲେଖ ।
Answer:
ନିମ୍ନଲିଖୂତ କାରଣଗୁଡ଼ିକ ଦ୍ଵାରା ଜଳ ଦୂଷିତ ହୁଏ, ଯଥା-
- ବଡ଼ ବଡ଼ ସହରର ନର୍ଦ୍ଦମା ଜଳ, ଆବର୍ଜନା, କଳକାରଖାନାରୁ ବାହାରୁଥିବା ମଇଳା ଜଳରେ ମିଶିବା ।
- କୃଷି କ୍ଷେତ୍ରରେ ବ୍ୟବହୃତ ରାସାୟନିକ ସାର ଓ କୀଟନାଶକ ଔଷଧ ଜଳରେ ମିଶିବା ।
- ଭୂକ୍ଷୟ ଦ୍ବାରା ଜୀବଜନ୍ତୁଙ୍କର ପଚାସଢ଼ା ଶବ ଓ ଉଭିଦର ପତ୍ର ପାଣିରେ ପଢ଼ି ପଚିବା ଦ୍ଵାରା ।
- ଘରୋଇ କାର୍ଯ୍ୟ ଦ୍ବାରା ନିର୍ଗତ ମଇଳା ଓ ଆବର୍ଜନାଯୁକ୍ତ ଜଳ ମିଶିବା ।
Question 3.
ଜଳ, ବାୟୁ ଓ ମୃରିକା ପ୍ରଦୂଷଣ ରୋକିବା ପାଇଁ କି କି ପଦକ୍ଷେପମାନ ନିଆଯାଇ ପାରିବ ?
Answer:
ନିମ୍ନଲିଖତ ପଦକ୍ଷେପ ନିଆଗଲେ ଜଳ, ବାୟୁ ଓ ମୃରିକା ପ୍ରଦୂଷଣକୁ ରୋକି ହେବ, ଯଥା-
- ଜନସଂଖ୍ୟା ବୃଦ୍ଧିର ନିୟନ୍ତ୍ରଣ କରିବା ।
- ଜଳ, ଖଣିଜ ଲବଣ ଓ ଅନ୍ୟାନ୍ୟ ଖଣିଜ ଦ୍ରବ୍ୟର ନିୟନ୍ତ୍ରତ ବ୍ୟବହାର କରିବା ।
- ଜଙ୍ଗଲ କ୍ଷୟ ରୋକିବା ସହ ନୂତନ ଜଙ୍ଗଲ ସୃଷ୍ଟି ପାଇଁ ଉଦ୍ୟମ କରିବା ।
- କଳକାରଖାନାରୁ ନିର୍ଗତ ବିଷାକ୍ତ ଧୂଆଁକୁ ବିଭିନ୍ନ ପ୍ରକ୍ରିୟାରେ ବିଶୋଧ କରି ବାୟୁମଣ୍ଡଳକୁ ଛାଡ଼ିବା ଏବଂ ଶିଳ୍ପଜାତ ଆବର୍ଜନାର ପୁନଃଚକ୍ରଣ କରିବା ।
- ରାସାୟନିକ ସାର ଓ କୀଟନାଶକ ଔଷଧର ନିୟନ୍ତ୍ରିତ ବ୍ୟବହାର କରିବା ଏବଂ ଏହା ପରିବର୍ତ୍ତେ ଜୈବସାର ଓ ଜୈବ କୀଟନାଶକର ବ୍ୟବହାର ଉପରେ ଗୁରୁତ୍ଵ ଦେବା ।
- ଯାନବାହନରେ କୋଇଲା, ପେଟ୍ରୋଲ, ଡିଜେଲ ଇନ୍ଧନ ପରିବର୍ତ୍ତେ ବିଦ୍ୟୁତଶକ୍ତି, ସି.ଏଚ୍.ଜି. ଗ୍ୟାସ୍ ବ୍ୟବହାର କରିବା ।
- ଜୀବଜନ୍ତୁଙ୍କ ମଳ ଓ ଅନ୍ୟାନ୍ୟ ଜୈବିକ ଆବର୍ଜନାରୁ ବାୟୋଗ୍ୟାସ୍ ଓ ଜୈବିକ ସାର ପ୍ରସ୍ତୁତ କରିବା ।

Question 4.
ମୃରିକାରେ ଥିବା ବିଭିନ୍ନ ଉପାଦାନ ସମ୍ପର୍କରେ ଆଲୋଚନା କର ।
Answer:
- ମୃତ୍ତିକା କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ପଦାର୍ଥ ଉପାଦାନ ଦ୍ଵାରା ଗଠିତ । ଏହି ମୃତ୍ତିକାର କଠିନ ଅଂଶ ଉଭୟ ଅଜୈବିକ ଶିଳାରେଣୁ ଓ ଜୈବିକ ପଦାର୍ଥରେ ଗଠିତ ।
- ଏହି ଅଜୈବିକ ଶିଳାରେଣୁରେ ବୃକ୍ଷ ପାଇଁ ଆବଶ୍ୟକ ପଟାସିୟମ୍, ମାଗ୍ନେସିୟମ୍, ସଲ୍ଫର୍, ବୋରନ୍, ଫସ୍ଫରସ୍, କାଲ୍ସିୟମ୍, ଲୌହ ଓ ତମ୍ବା ଆଦି ପୋଷକ ପଦାର୍ଥ ରହିଥାଏ ।
- ମୁଭିକାର କଠିନ ଜୈବିକ ପଦାର୍ଥରେ ପ୍ରାଣୀ ଓ ଉଭିଦର ଅପଘଟିତ କ୍ଷୟାଂଶ ହିଁ ରହିଥାଏ ।
- ମୂରିକାରେ ଥିବା ଜଳ ଏହାର ତରଳ ଉପାଦାନ । କାରଣ ଜଳ ବିନା ମାଟିର ପ୍ରାଣ ପ୍ରଦାନକାରୀ ଶକ୍ତି ନ ଥାଏ ।
- ମୃତ୍ତିକାର ଛିଦ୍ରରେ ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ ଓ ଉଦ୍ଜାନ ଭଳି ଗ୍ୟାସ୍ ରହିଥାନ୍ତି ।
Question 5.
କ୍ରାନ୍ତୀୟ ପଶ୍ଚିମୋଚୀ ଅରଣ୍ୟ ସମ୍ପର୍କରେ ସଂକ୍ଷେପରେ ଲେଖ ।
Answer:
- ବାର୍ଷିକ ହାରାହାରି ୧୦୦ରୁ ୨୦୦ ସେ.ମି. ବୃଷ୍ଟିପାତ ପାଉଥିବା ଅଞ୍ଚଳରେ କ୍ରାନ୍ତୀୟ ପର୍ଶୁ ମୋଚୀ ଅରଣ୍ୟ ଦେଖାଯାଏ ।
- ବୃଷ୍ଟିପାତ ସାଧାରଣତଃ ଋତୁଭିଭିକ ହୋଇଥିବାରୁ ଏହାକୁ ମୌସୁମୀ ଅରଣ୍ୟ କୁହାଯାଏ ।
- ଭାରତର ଅଧିକାଂଶ ଅଞ୍ଚଳ, ଉତ୍ତର ଅଷ୍ଟ୍ରେଲିଆ ଓ ମଧ୍ୟ- ଆମେରିକାରେ ଏହିପ୍ରକାର ଅରଣ୍ୟ ଦେଖାଯାଏ ।
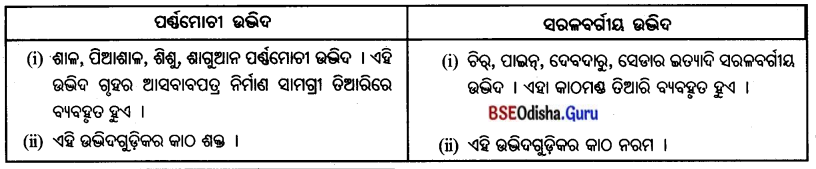
- ଶୁଷ୍କ ଋତୁରେ ଏହି ଅରଣ୍ୟର ବୃକ୍ଷଗୁଡ଼ିକ ପତ୍ରଝଡ଼ା ଦେଇଥାନ୍ତି ।
- ଏହି ଅରଣ୍ୟର ବୃକ୍ଷଗୁଡ଼ିକ ଗମ୍ବୁଜାକାର, ଶକ୍ତ ଓ ଉଚ୍ଚ । ଚନ୍ଦନ, ଶାଗୁଆନ, ଶାଳ, ପିଆଶାଳ, ଶିଶୁ, ଅସନ, କୁରୁମ ଆଦି ଏହି ଅରଣ୍ୟର ପ୍ରଧାନ ବୃକ୍ଷ ।
Question 6.
କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍ ଅରଣ୍ୟ ସମ୍ବନ୍ଧରେ ବର୍ଣ୍ଣନା କର ।
Answer:
- ବାର୍ଷିକ ହାରାହାରି ୨୦୦ ସେ.ମି.ରୁ ଅଧିକ ବୃଷ୍ଟିପାତ ହେଉଥିବା ଅଞ୍ଚଳରେ ଏ ପ୍ରକାର ଅରଣ୍ୟ ଦେଖାଯାଏ ।
- ଏହି ଅରଣ୍ୟ ଚିରସବୁଜ ରହିଥାଏ । ତେଣୁ ଏହାକୁ ଚିରହରିତ୍ ଅରଣ୍ୟ ମଧ୍ୟ କୁହାଯାଏ ।
- ଏହି ଅରଣ୍ୟ ଅତି ଘଞ୍ଚ ଓ ବୃକ୍ଷଗୁଡ଼ିକ ଅତି ଡେଙ୍ଗା, ଭୂମିରେ ସୂର୍ଯ୍ୟକିରଣ ପଡ଼ିପାରେ ନାହିଁ । ଫଳରେ ଭୂମି ସନ୍ତସନ୍ତିଆ ରହେ ।
- ଏହି ଅଞ୍ଚଳର ଅରଣ୍ୟରେ ବିଭିନ୍ନ ଜାତିର ପକ୍ଷୀ, ମାଙ୍କଡ଼, ସରୀସୃପ, କୁମ୍ଭୀର ଓ ଜଳହସ୍ତୀ ଆଦି ବାସ କରନ୍ତି ଏବଂ ଆବଲୁସ୍, ମେହୋଗାନୀ, ରୋଜ୍ଉଡ୍, ରେନିଲା, ରବର ଜାତୀୟ ବୃକ୍ଷ ଦେଖାଯାଏ ।
- ନିରକ୍ଷବୃତ୍ତର ଉଭୟ ପାର୍ଶ୍ଵରେ ୧୦° ଉତ୍ତର ଓ ଦକ୍ଷିଣ ସମାକ୍ଷରେଖା ଅନ୍ତର୍ଗତ ଅଞ୍ଚଳରେ ଏହି ଅରଣ୍ୟ ଦେଖାଯାଏ । କଙ୍ଗୋ ଓ ଆମାଜନ ନଦୀର ଅବବାହିକା, ପୂର୍ବ ଆଫ୍ରିକା ଓ ଇଣ୍ଡୋନେ ସିଆ, ଭାରତର ମେଘାଳୟ ଓ ପଶ୍ଚି ମଘାଟ ପର୍ବତମାଳାର ପଶ୍ଚିମ ପାର୍ଶ୍ବରେ ଏ ପ୍ରକାର ଅରଣ୍ୟ ଦେଖାଯାଏ ।

Question 7.
ବାୟୁ ପ୍ରଦୂଷଣର କାରଣଗୁଡ଼ିକ କ’ଣ ? ବାୟୁ ପ୍ରଦୂଷଣ କେଉଁ ରୋଗ ସୃଷ୍ଟି କରେ ?
Answer:
କାରଣ :
- ଅଗ୍ନି ଉଦ୍ଗିରଣ ସମୟରେ ଶହ ଶହ ଟନ୍ ପରିମାଣର ଆଗ୍ନେୟ ଭସ୍ମ ଓ ଗ୍ୟାସ୍ ବାୟୁମଣ୍ଡଳରେ ମିଶେ ।
- ବିଭିନ୍ନ କଳକାରଖାନା, ମଟରଗାଡ଼ି, ଉଡ଼ାଜାହାଜ, ଆଣବିକ ବିସ୍ଫୋରଣ, ତାପଜ ବିଦ୍ୟୁତ୍ କେନ୍ଦ୍ରରୁ ନିର୍ଗତ ବିଷାକ୍ତ ଧୂଳିଧୂଆଁ ବାୟୁରେ ମିଶେ ।
- ବିଭିନ୍ନ ପ୍ରକାର ଖଣିଜ ତଥା ଜୈବିକ ଜାଳେଣି (କୋଇଲା, ପେଟ୍ରୋଲ, ଡିଜେଲ ଆଦି)ର ବ୍ୟବହାର ଯୋଗୁ ବାୟୁ ପ୍ରଦୂଷଣ ହୁଏ ।
- ଗ୍ରାମାଞ୍ଚଳରେ ଶସ୍ୟ ଉତ୍ପାଦନ ସମୟରେ ତଥା କାଠ, ବାଉଁଶ ଓ ଗୋବର ଘସି ଆଦି ଜଳିବା ଦ୍ଵାରା ବାୟୁ ଦୂଷିତ ହୁଏ ।
- ଏହା ଶ୍ଵାସନଳୀ ଓ ଫୁସ୍ଫୁସ୍କୁ ସଂକ୍ରମିତ କରେ ଏବଂ ବିଭିନ୍ନ ପ୍ରକାର ଆଲର୍ଜି, ଚର୍ମକର୍କଟ, ଯକ୍ଷ୍ମା ତଥା ସ୍ନାୟବିକ ରୋଗ ସୃଷ୍ଟି କରେ ।
ସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
Question 1.
ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କ’ଣ ଉଦାହରଣ ସହ ବୁଝାଅ ।
Answer:
- ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କୁହାଯାଏ ।
- ଖାଦ୍ୟ ଶୃଙ୍ଖଳରେ ଥିବା ପ୍ରତ୍ୟେକ ଶ୍ରେଣୀଭୁକ୍ତ ଜୀବ ଏକ କଡ଼ି ପରି କାମ କରିଥାଏ । ଗୋଟିଏ କଡ଼ି ‘ଖାଦ୍ୟ’ ହେଲେ ଅନ୍ୟଟି ‘ଖାଦକ’ । ସେହିପରି ‘ଖାଦକ’ କଡ଼ି ଖାଦ୍ୟ ହେଲାବେଳେ ପରବର୍ତ୍ତୀ କଡ଼ି ଖାଦକ ହୁଏ ।
- ଉଦାହରଣ : ବିଭିନ୍ନ ପୋକଜୋକ ଆଦିକୁ ବେଙ୍ଗ ଖାଇଥାଏ ।
- ବେଙ୍ଗକୁ ଛୋଟ ସାପ, ଛୋଟ ସାପକୁ ବଡ଼ ସାପ, ବଡ଼ ସାପକୁ ନେଉଳ, ନେଉଳକୁ ଛଞ୍ଚାଣ ଖାଇ ବଞ୍ଚିଥାନ୍ତି । ପ୍ରାଣୀମାନେ ମରିଗଲା ପରେ ସେଗୁଡ଼ିକୁ ବ୍ୟାକ୍ଟେରିଆ ଅପଘଟନ କରି ମାଟିରେ ମିଶାଏ ।
Question 2.
ଜୈବ ଭାରସାମ୍ୟ କହିଲେ କ’ଣ ବୁଝାଯାଏ ?
Answer:
- ଖାଦ୍ୟ-ଖାଦକ ସମ୍ପର୍କ ଦୃଷ୍ଟିରୁ ଶକ୍ତି ପିରାମିଡ୍ର ପ୍ରଥମ ସ୍ତରରୁ ଚତୁର୍ଥ ସ୍ତର ଆଡ଼କୁ ଜୀବ ସଂଖ୍ୟା ହ୍ରାସ ପାଇବା ଜରୁରୀ ।
- ପ୍ରତ୍ୟେକ ସ୍ତରର ପ୍ରାଣୀମାନଙ୍କ ମଧ୍ଯରେ ସଂଖ୍ୟାଗତ ସୁସମ୍ପର୍କ ପ୍ରତିଷ୍ଠା ହୁଏ । ଏହି ପରି ସଂଖ୍ଯାଗତ ସୁସମ୍ପର୍କକୁ ଜୈବ ଭାରସାମ୍ୟ କୁହାଯାଏ ।
- ଅତ୍ୟଧିକ ଜଙ୍ଗଲ ଧ୍ଵଂସ ଫଳରେ ବିଭିନ୍ନ ଶକ୍ତି ସ୍ତର ମଧ୍ଯରେ ସଂଖ୍ୟାଗତ ସୁସମ୍ପର୍କ ନଷ୍ଟ ହେଉଛି । ଫଳରେ ଅନେକ ପ୍ରଜାତିର ବୃକ୍ଷଲତା ଓ ପ୍ରାଣୀ ନିଶ୍ଚିହ୍ନ ହେବାକୁ ବସିଲେଣି । ଫଳରେ ଜୈବ ଭାରସାମ୍ୟ ନଷ୍ଟ ହେବାରେ ଲାଗିଛି ।
- ନିମ୍ନ ସ୍ତରଗୁଡ଼ିକ କ୍ଷତିଗ୍ରସ୍ତ ହେଲେ ଚତୁର୍ଥ ସ୍ତରରେ ଥିବା ମଣିଷ | ନିଶ୍ଚିତଭାବେ ବିପଦଗ୍ରସ୍ତ ହେବ । ତେଣୁ ଜୈବ ଭାରସାମ୍ୟ ରକ୍ଷା ଦିଗରେ ଯନୂବାନ ହେବା ଆବଶ୍ୟକ ।
Question 3.
ମୃତ୍ତିକାର ରଙ୍ଗ କାହା କାହା ଉପରେ ନିର୍ଭର କରେ ଓ କିପରି ?
Answer:
- ମୃତ୍ତିକାର ରଙ୍ଗ ଶିଳାର ପ୍ରକାର, ଜୈବିକ ଅଂଶର ପରିମାଣ ଓ ଜଳବାୟୁ ଉପରେ ନିର୍ଭର କରେ ।
- ଜୀବାଂଶ କମ୍ ଥିଲେ ମୃତ୍ତିକାର ରଙ୍ଗ ହାଲୁକା ବା ଧଳା ଏବଂ ଜୀବାଂଶ ବେଶୀ ପରିମାଣରେ ଥିଲେ ମୃରିକା ଗାଢ଼ ରଙ୍ଗର ହୁଏ ।

Question 4.
ମୃରିକାରେ କେତୋଟି ଆକାରର ଶିଳାରେଣୁ ରହିଛି ଓ କ’ଣ କଣ ?
Answer:
- ମୃତ୍ତିକାରେ ଚାରୋଟି ଆକାରର ଶିଳାରେଣୁ ରହିଛି ।
- ସେଗୁଡ଼ିକ ହେଉଛି- ଗୋଡି଼, ବାଲି, ପଟୁ ଓ କର୍ଦ୍ଦମ ।
ଉଚ୍ଚ ପାର୍ବତ୍ୟ ଭୂମିରେ ଭିନ୍ନ ଭିନ୍ନ ପ୍ରକାର ଅରଣ୍ୟ
Question 1.
ଦେଖାଯାଏ କାହିଁକି ?
Answer:
- ଉଚ୍ଚତା ବଢ଼ିଲେ ତାପମାତ୍ରା ହ୍ରାସ ପାଏ । ଫଳରେ ଜଳବାୟୁରେ ପରିବର୍ତ୍ତନ ଘଟେ ଓ ଜଳବାୟୁ ଅନୁସାରେ ପ୍ରାକୃତିକ ଉଦ୍ଭଦ ଦେଖାଯାଏ ।
- ତେଣୁ ଉଚ୍ଚ ପାର୍ବତ୍ୟ ଭୂମିର ପାଦଦେଶରୁ ଶୀର୍ଷ ପର୍ଯ୍ୟନ୍ତ ଉଚ୍ଚତା ଭେଦରେ ଭିନ୍ନ ଭିନ୍ନ ଜଳବାୟୁ ଅନୁଭୂତ ହେଉଥିବାରୁ ଚିରହରିତ୍ ଅରଣ୍ୟ, ପର୍ଣ୍ଣମୋଚୀ ଅରଣ୍ୟ, ସରଳବର୍ଗୀୟ ଅରଣ୍ୟ ଓ ତୁନ୍ଦ୍ରା ଉଦ୍ଭିଦ ଦେଖିବାକୁ ମିଳେ ।
Question 2.
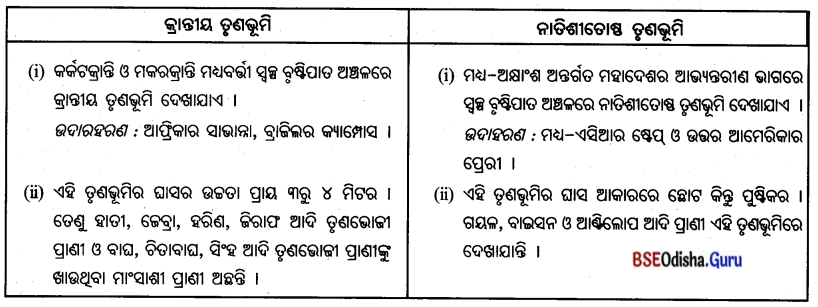
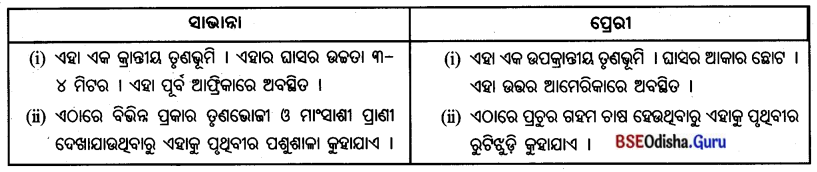
ସାଭାନାକୁ କାହିଁକି ପୃଥିବୀର ପଶୁଶାଳା କୁହାଯାଏ ?
Answer:
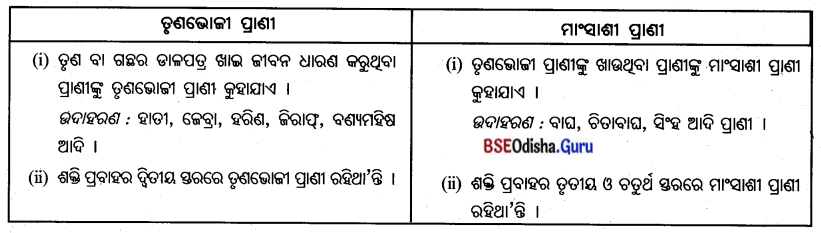
- ସାଭାନ୍ନା ତୃଣଭୂମିରେ ଖାଦ୍ୟ ସୁଲଭତା ଦୃଷ୍ଟିରୁ ହାତୀ, ଜେବ୍ରା, ହରିଣ, ଜିରାଫ୍, ବଣ୍ୟମହିଷ ଭଳି ତୃଣଭୋଜୀ ପ୍ରାଣୀ ଦେଖାଯାନ୍ତି ।
- ତୃଣଭୋଜୀ ପ୍ରାଣୀଙ୍କୁ ଖାଉଥିବା ମାଂସାଶୀ ପ୍ରାଣୀ, ଯଥା- ବାଘ, ଚିତାବାଘ, ସିଂହ ଆଦି ଏଠାରେ ରହିଥା’ନ୍ତି । ତେଣୁ ଏହାକୁ ପୃଥିବୀର ପ୍ରାକୃତିକ ପଶୁଶାଳା କୁହାଯାଏ ।
Question 3.
ବାୟୁ ପ୍ରଦୂଷଣର କୁଫଳଗୁଡ଼ିକ ଲେଖ ।
Answer:
- ଶ୍ଵାସନଳୀ ଓ ଫୁସ୍ଫୁସ୍ ସଂକ୍ରମଣ, ଆଲର୍ଜି, ଚର୍ମକର୍କଟ, ଯକ୍ଷ୍ମା ଓ ତଥା ସ୍ନାୟବିକ ରୋଗର ଶିକାର ହୋଇ ବହୁ ଲୋକ ମୃତ୍ୟୁବରଣ କରୁଛନ୍ତି ।
- ବାୟୁ ପ୍ରଦୂଷଣ ଯୋଗୁ ବାୟୁମଣ୍ଡଳ ଉତ୍ତପ୍ତ ହେଉଛି । ପୃଥିବୀର ବିଭିନ୍ନ ଅଞ୍ଚଳର ଜଳବାୟୁ ଓ ପାଣିପାଗରେ ଅନିୟମିତତା ଦେଖାଦେଉଛି ।
- କିଛି ସ୍ଥାନରେ ଅମ୍ଳବର୍ଷା ହେଉଛି । ଏହାର କୁପ୍ରଭାବ ମଣିଷ, ଜୀବଜଗତ ଓ ଉଭିଦ ଜଗତ ଉପରେ ପଡ଼ୁଛି ।

Question 4.
ଶବ୍ଦ ପ୍ରଦୂଷଣର କୁପ୍ରଭାବଗୁଡ଼ିକ ଲେଖ ।
Answer:
- ଆଜିକାଲି ଶବ୍ଦ ପ୍ରଦୂଷଣ ବୃଦ୍ଧି ପାଇବାରେ ଲାଗିଛି । ଗ୍ରାମାଞ୍ଚଳ ତୁଳନାରେ ସହରାଞ୍ଚଳରେ ଶବ୍ଦ ପ୍ରଦୂଷଣ ମାତ୍ରା ସର୍ବାଧିକ ଅନୁଭୂତ ହୁଏ ।
- ପ୍ରଚଣ୍ଡ ଘଡ଼ଘଡ଼ି ଶବ୍ଦରେ କିଛି ଲୋକ କାଲ ହୋଇଯାଇଥା’ନ୍ତି ।
- ସହରାଞ୍ଚଳରେ ଅତ୍ୟଧିକ ଯାନବାହନ ତଥା କଳକାରଖାନାରୁ ବାହାରୁଥିବା ଉଚ୍ଚ ଶବ୍ଦ ଯୋଗୁଁ ଲୋକଙ୍କର ଶ୍ରବଣ ଶକ୍ତି ଉପରେ କୁପ୍ରଭାବ ପଡ଼ୁଛି । ଲୋକମାନଙ୍କଠାରେ ମୁଖ୍ୟତଃ ମୁଣ୍ଡବ୍ୟଥା, ମସ୍ତିଷ୍କ ବିକୃତି ରୋଗ ବଢ଼ିବାରେ ଆଶଙ୍କା ସୃଷ୍ଟି ହୋଇଛି ।
Question 5.
କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍ ଅରଣ୍ୟରେ କେଉଁ ଜାତୀୟ ବୃକ୍ଷ ଦେଖାଯାଏ ?
Answer:
କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍ ଅରଣ୍ୟରେ ଆବରୁସ୍, ମେହୋଗାନୀ, ରୋଜ୍ଉଡ୍, ଆଇରନ ଉଡ୍, ଭେନିଲା ଓ ରବର ଜାତୀୟ ବୃକ୍ଷ ଦେଖାଯାଏ ।
Question 6.
କ୍ରାନ୍ତୀୟ ପର୍ଷ ମୋଚୀ ଅରଣ୍ୟରେ କେଉଁ ବୃକ୍ଷସବୁ ଦେଖାଯାଏ ?
Answer:
ଚନ୍ଦନ, ଶାଗୁଆନ, ଶାଳ, ପିଆଶାଳ, ଶିଶୁ, ଅସନ, କୁରୁମ ଆଦି ବୃକ୍ଷ କ୍ରାନ୍ତୀୟ ପର୍ଣ୍ଣ ମୋଚୀ ଅରଣ୍ୟରେ ଦେଖାଯାଏ ।
Question 7.
ଟାଇଗା ଅରଣ୍ୟରେ କେଉଁ ଜୀବଜନ୍ତୁ ଦେଖାଯା’ଛି ?
Answer:
ଟାଇଗା ଅରଣ୍ୟରେ ଧଳା କୋକିଶିଆଳି, ମିକ୍ସ୍, ଧଳାଭାଲୁ ଆଦି ଜୀବଜନ୍ତୁ ଦେଖାଯା’ନ୍ତି ।
Question 8.
ତୁନ୍ଦ୍ରାଞ୍ଚଳରେ ଦେଖାଯାଉଥିବା ପ୍ରାଣୀମାନଙ୍କର ନାମ ଲେଖ ।
Answer:
ସିଲ୍, ତିମି, ୱାଲ୍ରସ୍, ବଲ୍ଗା ହରିଣ, ମେରୁ ଭାଲୁ, ବରଫ କୋକିଶିଆଳୀ ଓ ମେରୁ ପେଚା ଆଦି ପ୍ରାଣୀମାନେ ତୁଦ୍ରାଞ୍ଚଳରେ ଦେଖାଯା’ନ୍ତି ।

Question 9.
ଜୁଆରିଆ ଅରଣ୍ୟ କ’ଣ ? ଏଠାରେ କି କି ବୃକ୍ଷ ଦେଖାଯାଇଥାଏ ?
Answer:
- କ୍ରାନ୍ତିମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ନଦୀମୁହାଣ ନିକଟବର୍ତ୍ତୀ ଜୁଆର ପାଣି ମାଡ଼ୁଥିବା ସନ୍ତସନ୍ତିଆ ଅଞ୍ଚଳରେ ଦେଖାଯାଉଥିବା ଅରଣ୍ୟକୁ ଜୁଆରିଆ ଅରଣ୍ୟ କୁହାଯାଏ ।
- ସୁନ୍ଦରୀ, ହେନ୍ତାଳ, ଝାଉଁ, ତାଳ, ନଡ଼ିଆ ଓ ଗୁଆ ଆଦି ଏ ଅରଣ୍ୟର ମୁଖ୍ୟ ବୃକ୍ଷ ଅଟେ ।
Question 10.
ତୁନ୍ଦ୍ରାଞ୍ଚଳରେ କେତେ ମାସ ଗ୍ରୀଷ୍ମଋତୁ ଓ ଏଠାରେ କି କି ପ୍ରକାର ଉଭିଦ ଦେଖାଯାଇଥାଏ ?
Answer:
- ତୁଦ୍ରାଞ୍ଚଳରେ ବର୍ଷରେ ମାତ୍ର ଦୁଇ ମାସ ଗ୍ରୀଷ୍ମଋତୁ ହୋଇଥାଏ ।
- ଗ୍ରୀଷ୍ମଋତୁରେ ବରଫ ତରଳିଲେ ଏହି ଅଞ୍ଚଳରେ ମସ୍, ଲାଇକେନ୍ ଭଳି ଛୋଟ ଗୁଳ୍ମ ଜନ୍ମିଥାଏ ।
ସଂକ୍ଷିପ୍ତ ଟିପ୍ପଣୀ ଲେଖ
1. ପରିସଂସ୍ଥା :
Answer:
- ଜୈବିକ ଓ ଅଜୈବିକ ଉପାଦାନ ମଧ୍ୟରେ ଥିବା ପାରସ୍ପରିକ ସଂବନ୍ଧି ଯୋଗୁ ସୃଷ୍ଟ ପରିବେଶକୁ ପରିସଂସ୍ଥା କୁହାଯାଏ । ଗଠନ ଓ କାର୍ଯ୍ୟ ଦୃଷ୍ଟିରୁ ପରିସଂସ୍ଥା ଏକ ପ୍ରାକୃତିକ ପରିସଂସ୍ଥା ।
- ପୃଥିବୀର ବିଭିନ୍ନ ଅଞ୍ଚଳରେ ଜୈବିକ ଓ ଅଜୈବିକ ଉପାଦାନ ମଧ୍ୟରେ ଅନ୍ତଃସମ୍ବନ୍ଧ ଯୋଗୁ ଅନେକ ଛୋଟବଡ଼ ପରିସଂସ୍ଥା ଗଢ଼ିଉଠିଛି ।
2. ଜୁଆରିଆ ଅରଣ୍ୟ :
Answer:
କ୍ରାନ୍ତମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ନଦୀମୁହାଣ ନିକଟବର୍ତ୍ତୀ ଜୁଆର ପାଣି ମାଡ଼ୁଥିବା ସନ୍ତ ସନ୍ତୋ ଆ ଅଞ୍ଚଳରେ ଜୁଆରିଆ ଅରଣ୍ୟ ଦେଖାଯାଏ । ସୁନ୍ଦରୀ, ହେନ୍ତାଳ, ଝାଉଁ, ତାଳ, ନଡ଼ିଆ, ଗୁଆ ଆଦି ଉଭୟ ମଧୁର ଓ ଲୁଣି ପାଣିରେ ବଢ଼ି ପାରୁଥିବା ବୃକ୍ଷ ଦେଖାଯାଏ ।
3. ତୁନ୍ଦ୍ରା ଉଭିଦ :
Answer:
- ମେରୁ ନିକଟବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ବର୍ଷର ୧୦ ମାସ ଅଧିକ ଥଣ୍ଡା ହୁଏ ଓ ଦୁଇ ମାସ ଗ୍ରୀଷ୍ମ ଋତୁ ।
- ଗ୍ରୀଷ୍ମଋତୁରେ ବରଫ ତରଳିଲେ ମସ୍, ଲାଇକେନ୍ ଭଳି ଛୋଟଛୋଟ ଗୁଳ୍ମ ଜନ୍ମେ । ଏଗୁଡ଼ିକୁ ତୁନ୍ଦ୍ରା ଉଭିଦ କହନ୍ତି ।
କାରଣ ଦର୍ଶାଅ
Question 1.
ମେରୁ ଅଞ୍ଚଳରେ ପ୍ରାଣୀମାନଙ୍କର ଚମଡ଼ା ଅଧିକ ଲୋମଯୁକ୍ତ ।
Answer:
- ମେରୁ ଅଞ୍ଚଳରେ ବର୍ଷର ୧୦ ମାସ ଅଧୁକ ଥଣ୍ଡା ଅନୁଭୂତ ହୁଏ ।
- ପ୍ରବଳ ଶୀତରୁ ରକ୍ଷା ପାଇବା ନିମନ୍ତେ ମେରୁ ଅଞ୍ଚଳର ପ୍ରାଣୀମାନଙ୍କର ଚମଡ଼ା ଅଧିକ ଲୋମଯୁକ୍ତ । ଲୋମ ତାପର କୁପରିବାହୀ ଥିବାରୁ ଶୀତର ପ୍ରଭାବରୁ ସେମାନେ ରକ୍ଷା ପାଆନ୍ତି ।

Question 2.
ସରଳବର୍ଗୀୟ ଅରଣ୍ୟରେ ଶଙ୍କୁ ଆକାରର ବୃକ୍ଷ ଦେଖାଯାଏ ।
Answer:
- ସରଳବର୍ଗୀୟ ଅରଣ୍ୟ ଥିବା ଅଞ୍ଚଳରେ ତୁନ୍ଦ୍ରାଞ୍ଚଳ ଅପେକ୍ଷା ଅଧିକ ତୁଷାରପାତ ହୋଇଥାଏ ।
- ଶଙ୍କୁ ଆକାର ବୃକ୍ଷରେ ତୁଷାରପାତ ହେଲେ ତାହା ଶୀଘ୍ର ଖସି ଭୂମିରେ ପଡ଼ିବା ସୁବିଧାଜନକ ହୋଇଥାଏ । ତେଣୁ ସରଳବର୍ଗୀୟ ଅରଣ୍ୟରେ ଶଙ୍କୁ ଆକାରର ବୃକ୍ଷ ଦେଖାଯାଏ ।
Question 3.
ଓଟକୁ ମରୁଭୂମିର ଜାହାଜ କୁହାଯାଏ ।
Answer:
- ଓଟ ଦୀର୍ଘଦିନ ଧରି ପାଣି ନ ପିଇ ବଞ୍ଚି ରହିପାରେ ଏବଂ ବାଲୁକାରାଶି ଉପରେ ସହଜରେ ଯିବାଆସିବା କରିପାରେ ।
- ତେଣୁ ଓଟକୁ ‘ମରୁଭୂମିର ଜାହାଜ’ କୁହାଯାଏ ।
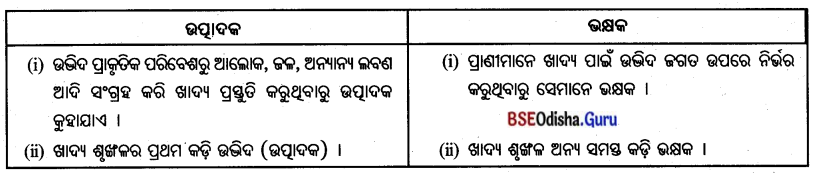
Question 4.
ଉଦ୍ଭଦକୁ ଉତ୍ପାଦକ କୁହାଯାଏ ।
Answer:
- ଉଦ୍ଭିଦ ପ୍ରାକୃତିକ ପରିବେଶରୁ ଆଲୋକ, ଜଳ ଓ ଅନ୍ୟାନ୍ୟ ଲବଣ ଆଦି ସଂଗ୍ରହ କରି ନିଜ ଖାଦ୍ୟ ପ୍ରସ୍ତୁତ କରିଥାଏ ।
- ତେଣୁ ଉଭିଦକୁ ଉତ୍ପାଦକ କୁହାଯାଏ ।
Question 5.
ଉତ୍ତର ଆମେରିକା ପ୍ରେରୀ ଅଞ୍ଚଳକୁ ‘ପୃଥିବୀର ରୁଟିଝୁଡ଼ି କୁହାଯାଏ ।
Answer:
- ଉତ୍ତର ଆମେରିକାର ପ୍ରେରୀ ଅଞ୍ଚଳ ଏକ ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି । ଏଠାରେ ପ୍ରଚୁର ଗହମ ଚାଷ ହୁଏ ।
- ପୃଥିବୀର ବିଭିନ୍ନ ଅଂଶକୁ ଗହମ ଯୋଗାଉଥିବାରୁ ଏହାକୁ ପୃଥିବୀର ରୁଟିଝୁଡ଼ି କୁହାଯାଏ ।

Question 6.
ମୃରିକା ଆମ ପାଇଁ ଏକ ଅମୂଲ୍ୟ ସମ୍ପଦ ।
Answer:
- ଉଭିଦଗୁଡ଼ିକ ବଞ୍ଚିବା ପାଇଁ ଭୂପୃଷ୍ଠର ମୃତ୍ତିକା ଉପରେ ନିର୍ଭର କରିଥାନ୍ତି । ପ୍ରତ୍ୟେକ ପ୍ରାଣୀ ବଞ୍ଚିବା ପାଇଁ ପ୍ରତ୍ୟକ୍ଷ ବା ପରୋକ୍ଷଭାବେ ଉଦ୍ଭାବ ଉପରେ ନିର୍ଭର କରିଥାଏ ।
- ମନୁଷ୍ୟ ତା’ର ମୌଳିକ ଆବଶ୍ୟକତା, ଯଥା- ଖାଦ୍ୟ, ବସ୍ତ୍ର ଓ ବାସଗୃହ ପାଇଁ ଭୂପୃଷ୍ଠସ୍ଥ ମୃତ୍ତିକା ଉପରେ ପ୍ରକାରାନ୍ତରେ ନିର୍ଭର କରିଥାଏ । ତେଣୁ ମୃରିକା ଆମ ପାଇଁ ଏକ ଅମୂଲ୍ୟ ସମ୍ପଦ ।
Question 7.
ମରୁ ଅଞ୍ଚଳରେ କଣ୍ଟାବୁଦାମାନ ଦେଖାଯାଏ ।
Answer:
ମରୁ ଅଞ୍ଚଳ ଅଧିକ ତାପମାତ୍ରା, ଅତି କମ୍ ବୃଷ୍ଟିପାତ ତଥା ଅନୁର୍ବର ବାଲିଆ ମାଟି ଯୋଗୁଁ ଏଠାରେ ଛୋଟ ଛୋଟ କଣ୍ଟାବୁଦାମାନ ଦେଖାଯାଏ ।
ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ
1. କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ଓ ନାତିଶୀତୋଷ୍ଣ ତୃଣଭୂମି
Answer:
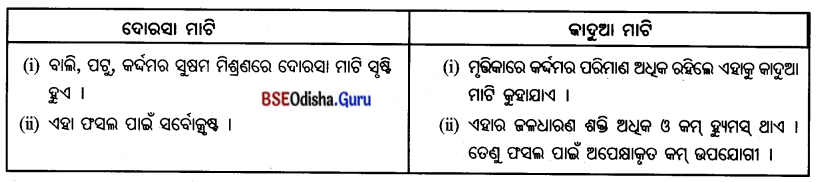
2. ଦୋରସା ମାଟି ଓ ଜାଦୁଆ ମାଟି
Answer:
3. ଅବଶିଷ୍ଟ ମୃତ୍ତିକା ଓ ଅପସୃତ ମୃରିକା
Answer:

4. ତୃଣଭୋଜୀ ପ୍ରାଣୀ ଓ ମାଂସାଶୀ ପ୍ରାଣୀ
Answer:
5. ଉତ୍ପାଦକ ଓ ଭକ୍ଷକ
Answer:
6. ସାଭାଜା ଓ ପ୍ରେରୀ
Answer:
7. ପଶ୍ଚିମୋଚୀ ଉଦ୍ଭବ ଓ ସରଳବର୍ଗୀୟ ଉଦ୍ଭଦ
Answer:
ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ।
Question i.
କାହାର ସମାହାରରେ ମଜ୍ଜିକା ଗଠିତ ?
Answer:
ମୃତ୍ତିକା କଠିନ, ତରଳ ଓ ଗ୍ୟାସୀୟ ପଦାର୍ଥର ସମାହାରରେ ଗଠିତ ।
Question ii.
ମୂଇଁକାର କଠିନ ଅଂଶ କେଉଁ ପଦାର୍ଥରେ ଗଠିତ ?
Answer:
ମୃତ୍ତିକାର କଠିନ ଅଂଶ ଉଭୟ ଶିଳାରେଣୁ ଓ ଜୈବିକ ପଦାର୍ଥରେ ଗଠିତ।
Question iii.
ମୃର୍ତ୍ତିକାର ରଙ୍ଗ କାହା ଉପରେ ନିର୍ଭର କରିଥାଏ ?
Answer:
ଶିଳାର ପ୍ରକାର, ଜୈବିକ ଅଂଶର ପରିମାଣ ଓ ଜଳବାୟୁ ଉପରେ ମୃତ୍ତିକାର ରଙ୍ଗ ନିର୍ଭର କରେ।

Question iv.
ମୂଇଁକାରେ ମୁଖ୍ୟତଃ କେତୋଟି ଆକାରର ଶିଳାରେଣୁ ରହିଥାଏ ଓ ସେଗୁଡ଼ିକ କ’ଣ କ’ଣ ?
Answer:
ମୃଭିକାରେ ମୁଖ୍ୟତଃ ଚାରୋଟି ଆକାରର ଶିଳାରେଣୁ ରହିଥାଏ; ଯଥା- ଗୋଡି଼, ବାଲି, ପଟୁ ଓ କର୍ଦ୍ଦମ।
Question v.
ଦୋରସା ମାଟି କିପରି ସୃଷ୍ଟି ହୁଏ ?
Answer:
ବାଲି, ପଟୁ, କର୍ଦ୍ଦମର ସୁଷମ ବିଶ୍ରଣରେ ଦୋରସା ମାଟି ସୃଷ୍ଟି ହୁଏ ।
Question vi.
ଅବଶିଷ୍ଟ ମୁଭିକା କାହାକୁ କୁହାଯାଏ ?
Answer:
ଶିଳା ଚୂର୍ଣ୍ଣବିଚୂର୍ଣ ହୋଇ ସେହି ସ୍ଥାନରେ ମୃତ୍ତିକାରେ ପରିଣତ ହେଲେ, ତାକୁ ଅବଶିଷ୍ଟ ମୃତ୍ତିକା କୁହାଯାଏ।
Question vii.
ଅପସୃତ ମୁଷ୍ଟିକା କାହାକୁ କୁହାଯାଏ ?
Answer:
ନଦୀ, ହିମବାହ ଓ ବାୟୁପ୍ରବାହଦ୍ଵାରା ଅପସୃତ ଶିଳାରେଣୁ ନିମ୍ନଭୂମିରେ ଜମା ମୃରିକାକୁ ଅପସୃତ ମୃଭିକା କୁହାଯାଏ।
Question viii.
ପରିସଂସ୍ଥା କାହାକୁ କୁହାଯାଏ ?
Answer:
ଜୈବିକ ଓ ଅଜୈବିକ (ଭୂମିରୂପ, ଜଳବାୟୁ, ମୃତ୍ତିକା) ଉପାଦାନ ମଧ୍ୟରେ ଥିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଯୋଗୁଁ ସୃଷ୍ଟ ପରିବେଶକୁ ପରିସଂସ୍ଥା କୁହାଯାଏ।
Question ix.
କାଦୁଆ ମାଟି କିପରି ଗଠିତ ହୁଏ ?
Answer:
ମୃତ୍ତିକାରେ କର୍ଦ୍ଦମ ପରିମାଣ ଅଧିକ ହେଲେ କାଦୁଆ ମାଟି ଗଠିତ ହୁଏ ।
Question x.
ଟାଇଗା କାହାକୁ କୁହାଯାଏ ?
Answer:
ଉତ୍ତର ଗୋଲାର୍ଦ୍ଧର ୫୦° ରୁ ୭୦° ସମାକ୍ଷରେଖା ମଧ୍ୟବର୍ତ୍ତୀ ଅଞ୍ଚଳରେ ସରଳବର୍ଗୀୟ ଅରଣ୍ୟ ଦେଖାଯାଏ ଓ ଏହି ଅଞ୍ଚଳକୁ ଟାଇଗା କୁହାଯାଏ ।

Question xi.
କାହାକୁ ପୃଥିବୀର ପଶୁଶାଳା କୁହାଯାଏ ?
Answer:
ସାଭାନ୍ନାକୁ ପୃଥିବୀର ପଶୁଶାଳା କୁହାଯାଏ ।
Question xii.
କେଉଁ ଅଞ୍ଚଳ ଶିକାରୀର ସ୍ବର୍ଗଭାବେ ପରିଚିତ ?.
Answer:
ସାଭାନ୍ନା ଅଞ୍ଚଳ ଶିକାରୀର ସ୍ଵର୍ଗଭାବେ ପରିଚିତ ।
Question xiii.
ମରୁଭୂମିର ମରୁଦ୍ୟାନମାନଙ୍କରେ କେଉଁ ବୃକ୍ଷ ଦେଖାଯାଏ ?
Answer:
ମରୁଭୂମିର ମରୁଦ୍ୟାନମାନଙ୍କରେ ନାଗଫେଣୀ, ଖଜୁରୀ, ସିଜୁ, ବାବୁଲ ଜାତୀୟ ବୃକ୍ଷ ଦେଖାଯାଏ ।
Question xiv.
ବ୍ରାଜିଲରେ ତୃଣଭୂମିକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ବ୍ରାଜିଲରେ ତୃଣଭୂମିକୁ କ୍ୟାମ୍ପାସ୍ କୁହାଯାଏ।
Question xv.
ଆର୍ଜେଣ୍ଟିନାରେ ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ କ’ଣ କୁହାଯାଏ ?
Answer:
ଆର୍ଜେଣ୍ଟିନାରେ ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ପମ୍ପାସ୍ କୁହାଯାଏ।
ପ୍ରତ୍ୟେକର ସଂଜ୍ଞା ଗୋଟିଏ ବାକ୍ୟରେ ପ୍ରକାଶ କର।
i. ପ୍ରାକୃତିକ ପରିବେଶ :
Answer:
ଜଳ, ସ୍ଥଳ, ଉଭିଦ ଓ ପ୍ରାଣୀମାନଙ୍କୁ ନେଇ ଗଠିତ ପରିବେଶକୁ ପ୍ରାକୃତିକ ପରିବେଶ କୁହାଯାଏ ।
ii. ଜୈବମଣ୍ଡଳ :
ଜୀବନ ଧାରଣ ପାଇଁ
Answer:
ଅଶ୍ମମଣ୍ଡଳ, ବାୟୁମଣ୍ଡଳ ଓ ବାରିମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଥିବା ତଥା ଆବଶ୍ୟକ ଉପାଦାନ ଥିବା ପତଳା କୁହାଯାଏ ।

iii. ପରିସଂସ୍ଥା :
Answer:
ସ୍ତରକୁ ଜୈବମଣ୍ଡଳ ଜୈବିକ ଓ ଅଜୈବିକ (ଭୂମିରୂପ, ଜଳବାୟୁ, ମୃତ୍ତିକା) ଉପାଦାନ ମଧ୍ୟରେ ଥିବା ପାରସ୍ପରିକ ସମ୍ବନ୍ଧ ଯୋଗୁଁ ସୃଷ୍ଟ ପରିବେଶକୁ ପରିସଂସ୍ଥା କୁହାଯାଏ ।
iv. ଜୀର୍ବାଳୀ :
Answer:
ଗୋଟିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଭୌଗୋଳିକ ସୀମାରେଖା ଭିତରେ ଥିବା ସମସ୍ତ ଛୋଟ ବଡ଼ ପରିସଂସ୍ଥାର ସମାହାରକୁ ଜୀବାଳୀ (Biome) କୁହାଯାଏ ।
v. ଖାଦ୍ୟ ଶୃଙ୍ଖଳ :
Answer:
କୌଣସି ପରିସଂସ୍ଥା ଅନ୍ତର୍ଗତ ପ୍ରତ୍ୟେକ ଜୀବ ଖାଦ୍ୟ ତଥା ଶକ୍ତି ପାଇଁ ଅନ୍ୟ ଜୀବ ଉପରେ ନିର୍ଭର କରିଥାଏ । ଏହାକୁ ଖାଦ୍ୟ ଶୃଙ୍ଖଳ କୁହାଯାଏ ।
vi. ଖାଦ୍ୟ କାଲକ :
Answer:
କୌଣସି ପରି ସଂସ୍ଥାରେ ଛନ୍ଦାଛନ୍ଦି ହୋଇ ରହିଥିବା ଖାଦ୍ୟଶୃଙ୍ଖଳଗୁଡ଼ିକୁ ଖାଦ୍ୟ ଜାଲକ (Food Web) କୁହାଯାଏ ।
vii. ମୁଭିକା :
Answer:
ମୃତ୍ତିକା ହେଉଛି କଠିନ (ଶିଳାରେଣୁ ଓ ଜୈବିକ ପଦାର୍ଥ), ତରଳ (ଜଳ) ଓ ଗ୍ୟାସୀୟ (ଅମ୍ଳଜାନ, ଅଙ୍ଗାରକାମ୍ଳ ଓ ଉଦ୍ଜାନ ଭଳି ଗ୍ୟାସ) ପଦାର୍ଥର ସମାହାର ।
viii. ଟାଇଗା
Answer:
ସରଳବର୍ଗୀୟ ଅରଣ୍ୟକୁ ରୁଷୀୟ ଭାଷାରେ ଟାଇଗା କୁହାଯାଏ । ଯାହାର ଅର୍ଥ ବିଶୁଦ୍ଧ, ଅସ୍ପୃଶ୍ୟ ।
ix. ସାଭାନ୍ନା :
Answer:
ଆଫ୍ରିକାର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
x. କ୍ୟାମ୍ବୋସ୍ :
Answer:
ବ୍ରାଜିଲ୍ରେ ଥିବା କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।

xi) ଲିଆନୋସ୍ :
Answer:
ଭେନେଜୁଏଲାରେ ଥିବା କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
xii. ପ୍ରେରୀ :
Answer:
ଉତ୍ତର ଆମେରିକାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
xiii. ଷ୍ଟେପ୍ :
Answer:
ମଧ୍ଯ-ଏସିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
xiv. ଡାଉନ୍ସ :
Answer:
ଅଷ୍ଟ୍ରେଲିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
xv. ପମ୍ପାସ :
Answer:
ଆର୍ଜେଣ୍ଟିନାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
xvi. ଭେଲ୍ :
Answer:
ଦକ୍ଷିଣ ଆଫ୍ରିକାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
xvii) ଶକ୍ତି ପିରାମିଡ୍ :
Answer:
ଖାଦ୍ୟ ଶୃଙ୍ଖଳର ପ୍ରତ୍ୟେକ ସ୍ତରରେ ଏକକ ସମୟ ଓ ଅଞ୍ଚଳରେ ଆହରଣ କରାଯାଉଥିବା ଶକ୍ତି ପରିମାଣ ଦର୍ଶାଉଥିବା ପିରାମିଡ୍ ସଦୃଶ ଗ୍ରାଫିକ୍ ଚିତ୍ର ।
ପ୍ରତ୍ୟେକ ବାକ୍ୟାଶକୁ ଗୋଟିଏ/ଦୁଇଟି ଭୌଗୋଳିକ ଶବ୍ଦରେ ପ୍ରକାଶ କର ।
i. କଙ୍ଗୋ ଓ ଆମାଜନ ଅବବାହିକାରେ ଦେଖାଯାଉଥିବା ଅରଣ୍ୟ ।
Answer
କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍ ଅରଣ୍ୟ
ii. ଶୁଷ୍କ ଋତୁରେ ପତ୍ରଝଡ଼ା ଦେଉଥିବା ଅରଣ୍ୟ ।
Answer
କ୍ରାନ୍ତୀୟ ପର୍ଣ୍ଣମୋଚୀ ଅରଣ୍ୟ

iii. ଭାରତର ଅଧିକାଂଶ ଅଞ୍ଚଳରେ ଦେଖାଯାଉଥିବା ଅରଣ୍ୟ ।
Answer
କ୍ରାନ୍ତୀୟ ପଶ୍ଚିମୋଚୀ ଅରଣ୍ୟ
iv. ଉଭୟ ମଧୁର ଓ ଲୁଣି ପାଣିରେ ବଢ଼ିପାରୁଥିବା ବୃକ୍ଷର ଅରଣ୍ୟ ।
Answer
ଜୁଆରିଆ ଅରଣ୍ୟ
v. ବ୍ରାଜିଲର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
Answer
କ୍ୟାସ
vi. ଶିକାରୀର ସ୍ଵର୍ଗ ଭାବେ ପରିଚିତ ଅଞ୍ଚଳ ।
Answer
ସାଇନ୍ନା
vii. ଦକ୍ଷିଣ ଆଫ୍ରିକାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ।
Answer
ଭେଲ୍ ଡ
viii. ଖାଦ୍ୟଶୃଙ୍ଖଳର ଶେଷ କଢ଼ି ।
Answer
ବ୍ୟାକ୍ଟେରିଆ
ix. କୌଣସି ବିସ୍ତୀର୍ଣ୍ଣ ସ୍ଥଳଭାଗ ଓ ଜଳରାଗ ଅନ୍ତର୍ଗତ ବୃହତ୍ ପରିସଂସ୍ଥା ।
Answer
ଜୀବାଳୀ
x. କ୍ରାନ୍ତିମଣ୍ଡଳ ଅନ୍ତର୍ଗତ ନଦୀମୁହାଣ ନିକଟବର୍ତ୍ତୀ ଜୁଆର ପାଣି ମାଡ଼ୁଥିବା ସନ୍ତସନ୍ତିଆ ଅରଣ୍ୟ ।
Answer
ଜୁଆରିଆ ଅରଣ୍ୟ

xi. ପୃଥିବୀର ରୁଟିଝୁଡ଼ି ।
Answer
ପ୍ରେରୀ
xii. ଦୀର୍ଘଦିନ ଧରି ପାଣି ନ ପିଇ ବଞ୍ଚୁରହି ବାଲୁକାରାଶି ଉପରେ ଯିବାଆସିବା କରିପାରୁଥିବା ପ୍ରାଣୀ ।
Answer
ଓଟ
xiii. ବାୟୁ ପ୍ରଦୂଷଣ ପାଇଁ ଦିଲ୍ଲୀ ଭଳି କେତେକ ସହରରେ ମଟରଗାଡ଼ିରେ ବ୍ୟବହୃତ ଗ୍ୟାସ୍ ।
Answer
କମ୍ରେସ୍ଡ଼ ନାଚୁରାଲ୍ ଗ୍ୟାସ୍
xiv. ଶବ୍ଦର ତୀବ୍ରତା ମାପିବାର ଏକକ ।
Answer
ଡେସିବେଲ୍
xv. ମେରୁ ଅଞ୍ଚଳରେ ଜନ୍ମ ଥିବା ଛୋଟ ଛୋଟ ମସ୍ ଓ ଲାଇକେନ୍ ଭଳି ଉଭିଦ ।
Answer
ଦ୍ରା ଉଭିଦ
xvi. ପୃଥିବୀର ପ୍ରାକୃତିକ ପଶୁଶାଳା ।
Answer
ସାଭାନା ।
ଠିକ୍ ଉତ୍ତର ବାଛି ଲେଖ ।
Question 1.
ମସ୍ ଓ ଲାଇକେନ୍ କେଉଁ ପ୍ରାକୃତିକ ଉଭିଦର ଅନ୍ତର୍ଗତ ?
(କ) ମରୁଭୂମି
(ଖ) କ୍ରାନ୍ତୀୟ ପଶ୍ଚିମୋଚୀ
(ଗ) କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍
(ଘ) ଶୀତଳ ମରୁ
Answer:
ଶୀତଳ ମରୁ

Question 2.
କେଉଁଠାରେ ବାବୁଲ ଜାତୀୟ ବୃକ୍ଷ ଦେଖାଯାଏ ?
(କ) କ୍ରାନ୍ତୀୟ ଅଞ୍ଚଳ
(ଖ) ନିରକ୍ଷୀୟ ଅଞ୍ଚଳ
(ଗ) ଉପକ୍ରାନ୍ତୀୟ ଅଞ୍ଚଳ
(ଘ) ମରୁ ଓ ଅଷ୍ଟମରୁ ଅଞ୍ଚଳ
Answer:
ମରୁ ଓ ଅଷ୍ଟମରୁ ଅଞ୍ଚଳ
Question 3.
କେଉଁ ଉଦ୍ଭିଦର କାଣ୍ଡ ମାଂସଳ ?
(କ) ଚିରହରିତ୍
(ଖ) ପର୍ଣ୍ଣମୋଚୀ
(ଗ) ତୁନ୍ଦ୍ରା.
(ଘ) ମରୁ
Answer:
ମରୁ
Question 4.
ଜିଆ, ଆଲକାତରା ଆଦି ଜୀବ ମୃର୍ତ୍ତିକାର କେଉଁ ଉପାଦାନକୁ ଧରି ରଖୁବାରେ ସାହାଯ୍ୟ କରେ ?
(କ) ଜଳ
(ଖ) ବାୟୁ
(ଗ) ଜଳବାୟୁ
(ଘ) ଜୈବାଂଶ
Answer:
ଜଳବାୟୁ
Question 5.
ବଡ଼ପାଟିରେ କଥାବାର୍ତ୍ତା ଶବ୍ଦ
(କ) ୪୦ ଡେସିବେଲ
(ଖ) ୫୦ ଡେସିବେଲ
(ଗ) ୬୦ ଡେସିବେଲ
(ଘ) ୭୦ ଡେସିବେଲ
Answer:
୬୦ ଡେସିବେଲ

Question 6.
ବିଶ୍ଵ ସ୍ଵାସ୍ଥ୍ୟ ସଂଗଠନ ଓ ବିଶ୍ଵବ୍ୟାଙ୍କର ସର୍ବେକ୍ଷଣ ଅନୁସାରେ ଭାରତରେ ସଂକ୍ରାମକ ରୋଗର କେତେ ଭାଗ ଦୂଷିତ ଜଳଯୋଗୁଁ ହୋଇଥାଏ ?
(କ) ଏକ-ତୃତୀୟାଂଶ
(ଖ) ଏକ-ଚତୁର୍ଥାଂଶ
(ଗ) ଏକ-ପଞ୍ଚମାଂଶ
(ଘ) ଏକ-ଷତାଂଶ
Answer:
ଏକ-ଚତୁର୍ଥାଂଶ
Question 7.
ବର୍ତମାନ ମଟରଗାଡ଼ିରେ କେଉଁ ଗ୍ୟାସ୍ର ବ୍ୟବହାର ହେଉଛି ?
(କ) ମିଥେନ୍
(ଖ) ଏଲ୍.ପି.ଜି.
(ଗ) ସି.ଏନ୍.ଜି.
(ଘ) ସି.ଏଫ୍.ଏସ୍
Answer:
ସି.ଏଚ୍.ଜି.
Question 8.
କେଉଁଟି ଚୁନ୍ଦ୍ରାଞ୍ଚଳ ପ୍ରାଣୀ ନୁହେଁ ?
(କ) ଓ୍ୱାଲରସ୍
(ଖ) ସିଲ୍
(ଗ) ଆଣ୍ଟିଲୋପ
(ଘ) ବଲ୍ ହରିଣ
Answer:
ଆଣ୍ଟିଲୋପ
Question 9.
କେଉଁଟି ଉପକ୍ରାନ୍ତୀୟ ପଶ୍ଚିମୋଚୀ ଅରଣ୍ୟର ବୃକ୍ଷ ନୁହେଁ ?
(କ) ବିବ୍
(ଖ) ଅସନ
(ଗ) ଆସ୍
(ଘ) ଓକ୍
Answer:
ଅସନ
Question 10.
‘ଫିଜାଣ୍ଟ’ କେଉଁ ପ୍ରାକୃତିକ ଅଞ୍ଚଳରେ ଦେଖାଯାନ୍ତି ?
(କ) କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍ ଅରଣ୍ୟ
(ଖ) ଉପକ୍ରାନ୍ତୀୟ ପର୍ଣ୍ଣମୋଚୀ ଅରଣ୍ୟ
(ଗ) ସରଳବର୍ଗୀୟ ଅରଣ୍ୟ
(ଘ) ଜୁଆରିଆ ଅରଣ୍ୟ
Answer:
ଉପକ୍ରାନ୍ତୀୟ ପର୍ଶୁ ମୋଚୀ ଅରଣ୍ୟ

Question 11.
କେଉଁଟି ଚିରହରିତ୍ ଅରଣ୍ୟର ଉଭିଦ ନୁହେଁ ?
(କ) ଆବଲୁସ୍
(ଖ) ମେହେଗାନୀ
(ଗ) ଶାଳ
(ଘ) ରୋଜ୍ଉଡ଼
Answer:
ଶାଳ
Question 12.
କେଉଁ ପ୍ରାଣୀ ସନ୍ତସନ୍ତିଆ ଅଞ୍ଚଳରେ ବାସ କରେ ?
(କ) ବାଘ
(ଖ) ମାଙ୍କଡ଼
(ଗ) ସରୀସୃପ
(ଘ) ଜଳହସ୍ତୀ
Answer:
ଜଳହସ୍ତୀ
Question 13.
ଧଳା ଭାଲୁ କେଉଁ ଅରଣ୍ୟର ଜୀବ ?
(କ) ଚିରହରିତ୍
(ଖ) ଜୁଆରିଆ
(ଗ) କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି
(ଘ) ସରଳବର୍ଗୀୟ
Answer:
ସର ଳ ବ ର୍ଗୀୟ
Question 14.
କେଉଁଟି ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି ଅଞ୍ଚଳର ପ୍ରାଣୀ ନୁହେଁ ?
(କ) ଗୟଳ
(ଖ) ସିଂହ
(ଗ) ବାଇସନ୍
(ଘ) ଆଣ୍ଟିଲୋପ
Answer:
ସିଂହ
Question 15.
କେଉଁ ପ୍ରଦୂଷଣ ହେତୁ ଅମ୍ଳବର୍ଷା ହୋଇଥାଏ ?
(କ) ଜଳ
(ଖ) ଶବ୍ଦ
(ଗ) ବାୟୁ
(ଘ) ମୃରିକା
Answer:
ବାୟୁ
ବନ୍ଧନୀ ମଧ୍ଯରୁ ଉପଯୁକ୍ତ ଶବ୍ଦ ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
1. ବାଲି, ପଟୁ, କର୍ଦ୍ଦମର ସୁଷମ ମିଶ୍ରଣରେ _____ ମାଟି ସୃଷ୍ଟି ହୁଏ । (ବାଲିଆ, ପଟୁ, କାଦୁଆ, ଦୋରସା)
Answer:
ଦୋରସା
2. ପଟୁମାଟି ଓ ଲୋଏସ୍. ______ ମୃତ୍ତିକାର ଅନ୍ତର୍ଗତ । (ଅବଶିଷ୍ଠ, ଅପସୃତ, ପଟୁ, କୃଷ୍ଣ)
Answer:
ଅପସୃତ

3. ୨୦୦ ସେ.ମି.ରୁ ଅଧିକ ବୃଷ୍ଟିପାତ ଅଞ୍ଚଳରେ _____ ଅରଣ୍ୟ ଦେଖାଯାଏ । (କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍, କ୍ରାନ୍ତୀୟ ପଶ୍ଚିମୋଚୀ, ଜୁଆରିଆ, ଟାଇଗା)
Answer:
କ୍ଳାନ୍ତୀୟ ଚିରହରିତ୍
4. କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍ ଅରଣ୍ୟରେ ______ ବୃକ୍ଷ ଦେଖାଯାଏ । (ସୁନ୍ଦରୀ, ଶିଶୁ, ଅସନ, ମେହୋଗାନୀ)
Answer:
ମେହୋଗାନୀ
5. କଙ୍ଗୋ ଓ ଆମାଜନ ଅବବାହିକାରେ ______ ଅରଣ୍ୟ ଦେଖାଯାଏ । (ଜୁଆରିଆ, ସରଳବର୍ଗୀୟ, ମୌସୁମୀ, ଚିରହରିତ)
Answer:
ଚିରହରିତ୍
6. ଭାରତର ଅଧିକାଂଶ ଅଞ୍ଚଳରେ _____ ଅରଣ୍ୟ ଦେଖାଯାଏ । (କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍, କ୍ରାନ୍ତୀୟ ମୌସୁମୀ, ଜୁଆରିଆ, ଟାଇଗା)
Answer:
କ୍ରାନ୍ତୀୟ ମୌସୁମୀ
7. ଜୁଆରିଆ ଅରଣ୍ୟରେ _______ ବୃକ୍ଷ ଦେଖାଯାଏ। (ସୁନ୍ଦରୀ ଓ ହେନ୍ତାଳ, ଆବଲୁସ ଓ ମେହୋଗାନୀ, ଶିଶୁ ଓ ଶାଳ, ଅସନ ଓ କୁରୁମ)
Answer:
ସୁନ୍ଦରୀ ଓ ହେନ୍ତାଳ
8. ଚିର ଓ ପାଇନ୍ ______ ଅରଣ୍ୟର ପ୍ରଧାନ ବୃକ୍ଷ । (ଜୁଆରିଆ, ସରଳବର୍ଗୀୟ, ଚିରହରିତ୍, ମୌସୁମୀ)
Answer:
ସରଳବର୍ଗୀୟ
9. ଧଳାଭାଲୁ ଓ ଧଳା କୋକିଶିଆଳି ______ ଅଟନ୍ତି। (ମୌସୁମୀ, ଚିରହରିତ୍, ଜୁଆରିଆ, ସରଳବର୍ଗୀୟ)
Answer:
ସରଳବର୍ଗୀୟ
10. ପୂର୍ବ ଆଫ୍ରିକାର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ _____ ଅରଣ୍ୟର ଜୀବଜନ୍ତୁ କୁହାଯାଏ । (ସାଭାନ୍ନା, କ୍ୟାମ୍ପାସ, ଲିଆନୋସ, ପମ୍ପାସ)
Answer:
ସାଭାନ୍ନା

11. ଦେଶର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ କ୍ୟାମ୍ପୋସ କୁହାଯାଏ । (ଭାରତ, ଜର୍ମାନ, ଜାପାନ, ବ୍ରାଜିଲ)
Answer:
ବ୍ରାଜିଲ
12. ଭେନଜୁଆଲାର କ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ _____ କୁହାଯାଏ। (ଲିଆନୋସ, କ୍ୟାମ୍ବୋସ, ପମ୍ପାସ, ସାଭାନ୍ନା)
Answer:
ଲିଆନୋସ
13. ଆର୍ଜେଣ୍ଟିନାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ _____ କୁହାଯାଏ । (କ୍ୟାମ୍ପୋସ, ପମ୍ପାସ, ସାରାନ୍ନା, ଲିଆନୋସ)
Answer:
ପମ୍ପାସ୍
14. ଉତ୍ତର ଆମେରିକାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ______ କୁହାଯାଏ । (ପମ୍ପାସ, କ୍ୟାମ୍ବୋସ, ପ୍ରେରୀ, ସାଭାନ୍ନା)
Answer:
ପ୍ରେରୀ
15. ଦକ୍ଷିଣ ଆଫ୍ରିକାର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ _____ କୁହାଯାଏ । (ପ୍ରେରୀ, ପମ୍ପାସ, ଷ୍ଟେପ୍, ଭେଲ୍)
Answer:
ଭେଲ୍
16. ମଧ୍ୟଏସିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ______ କୁହାଯାଏ । (ପମ୍ପାସ, ପ୍ରେରୀ, ଷ୍ଟେପ୍, ଭେଲ୍)
Answer:
ଷ୍ଟେପ୍
17. ଅଷ୍ଟ୍ରେଲିଆର ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମିକୁ ______ କୁହାଯାଏ । (ପ୍ରେରୀ, ଷ୍ଟେପ୍, ଭେଲ୍, ଡାଉନ୍ସ)
Answer:
ଡାଉନ୍ସ
18. _____ ଗୋଟିଏ ତୃଣଭୋଜୀ ପ୍ରାଣୀ ନୁହେଁ । (ଛେଳି, ବାଘ, ମେଣ୍ଢା, ହରିଣ)
Answer:
ବାଘ
19. ଆଲର୍ଜି ଓ ଚର୍ମ କର୍କଟ ______ ପ୍ରଦୂଷଣ ଯୋଗୁ ହୋଇଥାଏ । (ବାୟୁ, ଜଳ, ମୃତ୍ତିକା, ଶବ୍ଦ)
Answer:
ବାୟୁ
20. କାମଳ ରୋଗ _______ ପ୍ରଦୂଷଣ ଯୋଗୁ ହୋଇଥାଏ । (ବାୟୁ, ଜଳ, ମୃତ୍ତିକା, ଶବ୍ଦ)
Answer:
ଜଳ

21. ପ୍ଲାଷ୍ଟିକ ଦ୍ରବ୍ୟ ଓ ପଲିଥନ୍ର ବହୁଳ ବ୍ୟବହାର ଫଳରେ ______ ପ୍ରଦୂଷଣ ହୋଇଥାଏ। (ବାୟୁ, ଜଳ, ମୃତ୍ତିକା, ଶବ୍ଦ)
Answer:
ସୃଷ୍ଟିକା
22. ଶବ୍ଦ ପ୍ରଦୂଷଣ ବୃଦ୍ଧି ଯୋଗୁ _____ ରୋଗ ଦେଖାଯାଇଥାଏ । (ଆଲର୍ଜି, ଚର୍ମକର୍କଟ, କାମଳ, ମୁଣ୍ଡବ୍ୟଥା)
Answer:
ମୁଣ୍ଡବ୍ୟଥା
23. ସାଧାରଣ କଥାବାର୍ତ୍ତାର ଶବ୍ଦ ____ ଡେସିବେଲ୍ । (୨୦-୩୦, ୩୦-୩୫, ୩୫-୪୦, ୪୦-୪୫)
Answer:
୨୦-୩୦
24. ପୃଥିବୀର ରୁଟିଝୁଡ଼ି _____ ତୃଣଭୂମି ଅଞ୍ଚଳ ଅଟେ। (ସାରାନ୍ନା, ଲିଆନୋସ୍, ପମ୍ପାସ, କ୍ୟାମ୍ବୋସ)
Answer:
ପମ୍ପାସ୍
25. ପୃଥିବୀର ପଶୁଶାଳା _____ ତୃଣଭୂମି ଅଟେ । (କ୍ୟାମୋସ, ସାଭାନ୍ନା, ଷ୍ଟେପ୍, ପ୍ରେରୀ)
Answer:
ସାରାନ୍ନା
ସ୍ତମ୍ଭ ମିଳନ କର ।
Question 1.

Answer:

Question ii.
ସ୍ତମ୍ଭ ମିଳନ କର ।

Answer:

ପ୍ରଥମ ଯୋଡ଼ିକୁ ଦେଖୁ ଦ୍ଵିତୀୟ ଯୋଡ଼ି ପୂରଣ କର ।
1. କ୍ରାନ୍ତୀୟ ଚିରହରିତ୍ ଅରଣ୍ୟ : ରୋଜଉଡ୍ :: କ୍ରାନ୍ତୀୟ ପଶ୍ଚିମୋଚୀ ଅରଣ୍ୟ : _____।
Answer:
ଚନ୍ଦନ
2. ଜୁଆରିଆ ଅରଣ୍ୟ : ସୁନ୍ଦରୀ :: ସରଳବର୍ଗୀୟ ଅରଣ୍ୟ : _____।
Answer:
ପାଇନ
3. କ୍ରାନ୍ତୀୟ ତୃଣଭୂମି : ଜେବ୍ରା :: ଉପକ୍ରାନ୍ତୀୟ ତୃଣଭୂମି : _____।
Answer:
ଆଣ୍ଟିଲୋପ

4. ପୂର୍ବ ଆଫ୍ରିକା ; ସାମ୍ମାନା :: ବ୍ରାଜିଲ : _____।
Answer:
କାମ୍ବୋସ
5. ଭେନଜୁଏଲା : ଲିଆନୋସ :: ଆର୍ଜେଣ୍ଟିନା : _____।
Answer:
ପମ୍ପାସ
6. ଉତ୍ତର ଆମେରିକା : ପ୍ରେରୀ :: ଦକ୍ଷିଣ ଆଫ୍ରିକା : _____।
Answer:
ରେଲ୍
7. ମଧ୍ଯ-ଏସିଆ : ଷ୍ଟେପ୍ :: ଅଷ୍ଟ୍ରେଲିଆ : _____।
Answer:
ଡାଉନସ୍
8. ତୃଣଭୋଜୀ ପ୍ରାଣୀ : ଛେଳି :: ମାଂସାଶୀ ପ୍ରାଣୀ : _____।
Answer:
ବାଘ
9. ଖାଦ୍ୟ ଶୃଙ୍ଖଳର ପ୍ରଥମ କଡ଼ି : ଉଭିଦ :: ଖାଦ୍ୟଶୃଙ୍ଖଳର ଶେଷ କଡ଼ି : _____।
Answer:
ବ୍ୟାକ୍ଟେରିଆ

10. ଶକ୍ତି ପ୍ରବାହର ପ୍ରଥମ ସ୍ତର : ଉଭିଦ :: ଶକ୍ତି ପ୍ରବାହର ଦ୍ଵିତୀୟ ସ୍ତର : _____।
Answer:
ତୃଣଭୋଜୀ
11. ବାୟୁ ପ୍ରଦୂଷଣ : ଚର୍ମକର୍କଟ :: ଜଳ ପ୍ରଦୂଷଣ : _____।
Answer:
କାମଳ
12. ସାଧାରଣ କଥାବାର୍ତ୍ତା : ୨୦-୩୦ ଡେସିବେଲ :: ବଡ଼ପାଟିରେ କଥାବାର୍ତ୍ତା : _____।
Answer:
୬୦ ଡେସିବେଲ୍
![]()
![]()
![]()

![]()
![]()


![]()

![]()































 not built a nest. One day the crow was not in her nest. The cuckoo threw away the eggs and laid her own eggs there. The crow did not know this. She sat over the eggs for some days. Young ones came out. She took care of them. But when the young ones grew? up, they sang like cuckoos. So she drove them away. From that day the crow always drives away the cuckoo.
not built a nest. One day the crow was not in her nest. The cuckoo threw away the eggs and laid her own eggs there. The crow did not know this. She sat over the eggs for some days. Young ones came out. She took care of them. But when the young ones grew? up, they sang like cuckoos. So she drove them away. From that day the crow always drives away the cuckoo.