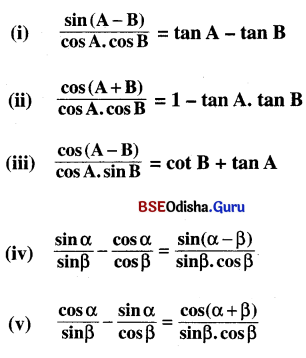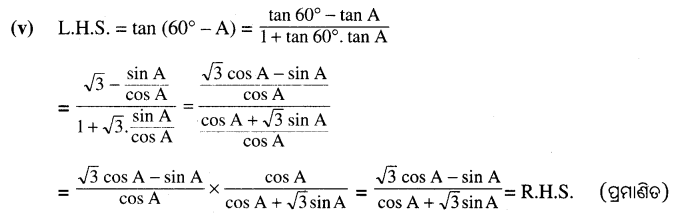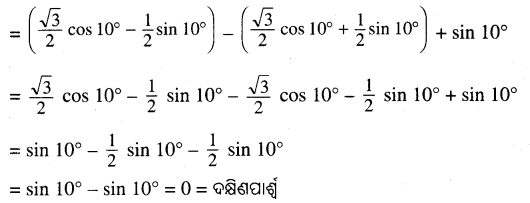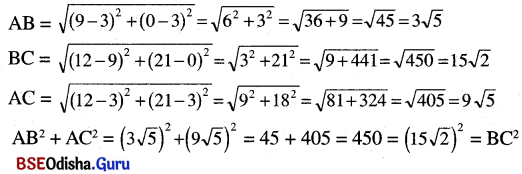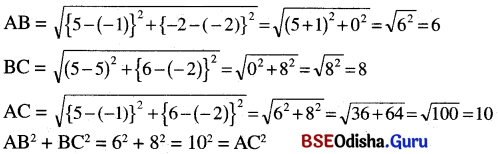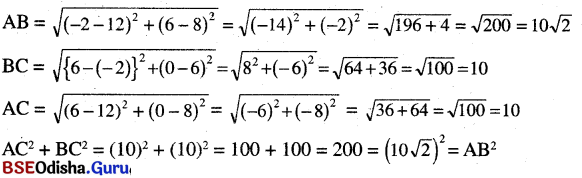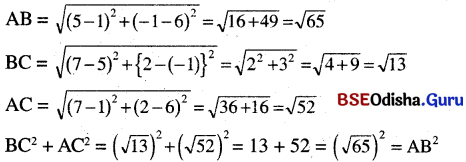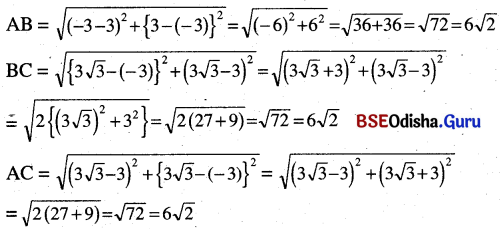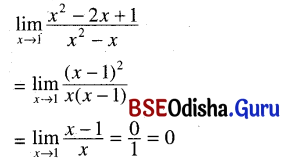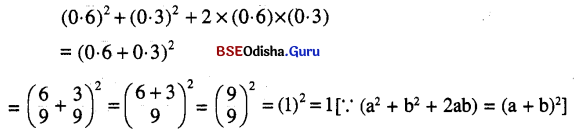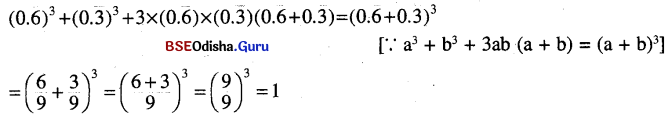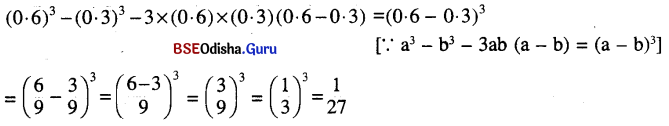Prasanna

Odisha State Board BSE Odisha 7th Class English Solutions Lesson 2 The Jackal and the Rooster Textbook Exercise Questions and Answers.

Class 7th English Chapter 2 The Jackal and the Rooster Question Answers BSE Odisha

The Jackal and the Rooster Class 7 Questions and Answers

Session – 1 (ପ୍ରଥମ ପର୍ଯ୍ୟାୟ)
I.Pre-Reading (ପୂର୍ବ-ପଠନ |)

→Socialization ( ସାମାଜିକୀକରଣ)
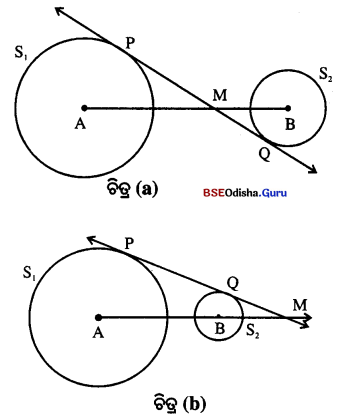
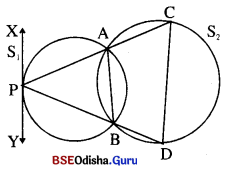
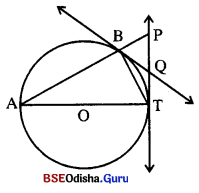
Look at the picture. (ଚିତ୍ରଟିକୁ ଧାନର ସହିତ ଲକ୍ଷ୍ୟକର)

→ What is the rooster doing? (ଗଞ୍ଜାଟି କ’ଣ କରୁଛି ?)
Answer:
The rooster is sitting in a high place and watching the jackal carefully.

Look at the second picture. (ଦ୍ଵିତୀୟ ଛବିକୁ ଦେଖ)
→ Who is the jackal carrying away? (କୋକିଶିଆଳ କ’ଣ ନେଇ ଚାଲିଯାଉଛି ? )
Answer:
The jackal is carrying away the rooster.

→ Why are people chasing after the jackal?
(ଲୋକମାନେ କୋକିଶିଆଳ ପଛରେ କାହିଁକି ଗୋଡ଼ାଉଛନ୍ତି ?)
Answer:
The people are chasing after the jackal to free the rooster.

→ How did the rooster escape from the jackal?
(ଗଞ୍ଜାଟି କୋକିଶିଆଳ କବଳରୁ କିପରି ମୁକୁଳିଗଲା ?)
Answer:
The rooster tricked the jackal and escaped from it.

Read the story to get answers to these questions.
(ଗପଟିକୁ ପାଠ କର ଏବଂ ଏସବୁ ପ୍ରଶ୍ନର ଉତ୍ତର ପାଅ ।)

II. While Reading (ପଠନ କାଳୀନ):
Text (ପାଠ୍ୟବସ୍ତୁ):

• SGP-1 (Sense Group Paragraph-1)
• Read para – 1 and 2 silently and answer the questions that follow.
(୧ମ ଓ ୨ୟ ଅନୁଚ୍ଛେଦକୁ ନୀରବରେ ପାଠ କର ଏବଂ ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡିକର ଉତ୍ତର ଦିଅ ।)
1. There was a very big and handsome rooster. He looked like a king with his beautiful red crown. He also felt like a king. He got up very early in the morning, sat in a high place, and sang non-stop-cock-koo-doodle doo, cock-koo-doodle doo. He knew that his song was much better than the songs of the other roosters in his locality. But he wanted to make his song still better, louder, and clearer. But how to do this was his problem. It was a problem till a jackal suggested a way out.
2. The jackal saw the rooster singing every day early in the morning. But it sang keeping his eyes open. If he would try to catch the rooster, the rooster would fly away to the tree. This was what happened the other day when he tried to catch a rooster. So he came to the rooster and said, “Oh great, handsome, king-like rooster! Your song will be really nice if you sing closing your eyes.”

ଓଡ଼ିଆ ଅନୁବାଦ
୧. ଗୋଟିଏ ବୃହଦାକାୟ ସୁନ୍ଦର ଗଞ୍ଜା ଥିଲା । ତା’ର ସୁନ୍ଦର ନାଲି ଚୂଳ ମୁକୁଟ ସଦୃଶ ଏବଂ ରାଜକୀୟ ଥିଲା । ସେ ମଧ୍ୟ ରାଜାପରି ଅନୁଭବ କରୁଥିଲା । ସେ ଖୁବ୍ ସକାଳରୁ ଉଠୁଥିଲା, ଗୋଟିଏ ଉଚ୍ଚ ଜାଗାରେ ବସୁଥିଲା ଏବଂ ନିରବଚ୍ଛିନ୍ନ ରାବ କରୁଥିଲା-କଲ୍‌ରେ-କୋ-ଡୁଡୁଲ୍ -ଡୋ-କକ୍‌କୋ -ଡୋଡୋଲ୍ -ଡୁ-….. ଜାଣିଥିଲା ଯେ ତା’ର ଗାନ ତା’ ଅଞ୍ଚଳର ଅନ୍ୟ ସମସ୍ତ ଗଞ୍ଜାମାନଙ୍କ ଗାନଠାରୁ ଅଧିକ ଭଲ ଥିଲା । ତଥାପି ତା’ଗାନକୁ ସେ ଆହୁରି ଅଧିକ ଭଲ କରିବାକୁ ଚାହୁଁଥିଲା ସ୍ବରର ଉଚ୍ଚତାରେ ଏବଂ ସ୍ପଷ୍ଟତାରେ । କିନ୍ତୁ କିଭଳି ଏପରି କରିବ, ତା’ପାଇଁ ସମସ୍ୟା ଥିଲା । ଏହା ତାକୁ ଏକ କୋକିଶିଆଳ ମାର୍ଗଦର୍ଶନ ଦେବା ପର୍ଯ୍ୟନ୍ତ ସମସ୍ୟା ଥିଲା ।

୨. କୋକିଶିଆଳଟି ଗଞ୍ଜାଟିକୁ ପ୍ରତ୍ୟହ ବଡ଼ିଭୋରରୁ ଗାନ କରୁଥିବାର ଲକ୍ଷ୍ୟ କଲା । କିନ୍ତୁ ସେ ଗାନ କଲାବେଳେ ଆଖୁକୁ ଖୋଲା ରଖୁଥିଲା । ଯଦି କେତେବେଳେ ସେ ଗଞ୍ଜାଟିକୁ ଧରି ନେବାକୁ ଚେଷ୍ଟା କରୁଥିଲା, ଗଞ୍ଜାଟି ତତ୍‌କ୍ଷଣାତ୍ ଗଛ ଉପରକୁ ଉଡ଼ି ଯାଉଥିଲା । ଆଉ ଗୋଟିଏ ଦିନ ମଧ୍ୟ ସେହିଭଳି ପୁନର୍ବାର ଘଟିଲା ଠିକ୍
ଯେତେବେଳେ ସେ ଗଞ୍ଜାଟିକୁ ଧରିବାକୁ ପୁନର୍ବାର ଚେଷ୍ଟା କରିଥିଲା । ତେଣୁ କୋକିଶିଆଳଟି ମନରେ ଉପାୟ ପାଞ୍ଚ୍ ଗଞ୍ଜା ପାଖକୁ ଆସିଲା ଏବଂ କହିଲା, ‘ହେ ମହାନ୍ ସୁନ୍ଦର ରାଜତୁଲ୍ୟ ଗଞ୍ଜା ।’ ତୁମର ଗାନ ବାସ୍ତବିକ ଅତୀବ ସୁନ୍ଦର ହେବ ଯଦି ତୁମେ ଆଖୁ ବନ୍ଦ କରି ଗାନ କରିବ ।

Notes And Glossary (ଶବ୍ଦାର୍ଥ):

handsome ( ପ୍ୟାଣ୍ଟ୍‌ସମ୍ ) – ସୁନ୍ଦର
rooster (ରୁଷ୍ଟର୍) – ଗଞ୍ଜା
beautiful (ବିଉଟିଫୁଲ୍) – ସୁନ୍ଦର
red crown (ରେଡ୍ କ୍ରାଉନ୍) – ନାଲି ମୁକୁଟ (ଚୂଳ)
felt (ଫେଲ୍‌ଟ) – ଅନୁଭବ କଲା
got up (ଗଟ୍ ଅପ୍) – ଉଠୁଥିଲା
early in the morning (ୟର୍ଲି ଇନ୍ ଦ ମଣ୍ଡିଙ୍ଗ୍)
sat (ସ୍ୟାଟ୍) – ବସୁଥିଲା
high place (ହାଇ ପ୍ଲେସ୍) – ଉଚ୍ଚ ଜାଗା
non-stop (ନନ୍-ଷ୍ଟପ୍ ) – ବନ୍ଦ ହେଉନଥୁବା
cock-koo-doodle doo (କକ୍-କୁ-ଡୁଡଲ୍ ଡୁ)– ଗଞ୍ଜାର ରାବ
much better (ମଚ୍ ବେଟର୍) – ବହୁତ ଭଲ
locality (ଲୋକାଲିଟି) – ଅଞ୍ଚଳ
wanted (ୱାଣ୍ଡେଡ୍) – ଇଚ୍ଛା କରୁଥିଲା | ଚାହୁଁଥିଲା
still better (ଷ୍ଟିଲ୍ ବେଟର୍) – ଅଧିକ ଭଲ
louder and clearer (ଲାଉଡ଼ର୍ ଆଣ୍ଡ୍ କ୍ଲିଅରର)
problem (ପ୍ରୋବ୍ଲେମ୍ ) – ସମସ୍ୟା
suggested (ସଜେଷ୍ଟେଡ୍) – ପ୍ରସ୍ତାବ ଦେଲେ
a way (ଏ ୱେ) – ଗୋଟିଏ ଉପାୟ
everyday (ଏଗ୍ରିଡ଼େ) – ପ୍ରତ୍ୟେକ ଦିନ
keeping (କିପିଙ୍ଗ୍) – ରଖୁ
open (ଓପନ୍) – ଖୋଲା
try (ଟ୍ରାଏ) – ଚେଷ୍ଟା କରିବା
to catch (ଟୁ କ୍ୟାଚ୍) – ଧରିବାକୁ
fly away (ଫ୍ଲାଏ ଆଷ୍ଟ୍ରେ) – ଦୂରକୁ ଉଡ଼ିଯିବା
happened (ହାପେନ୍‌ଡ୍) – ଘଟିଥିଲା
catch (କ୍ୟାଚ୍) – ଧରିବା
Oh great (ଓ ଗ୍ରେଟ୍ ) – ହେ ମହାନ୍
handsome (ହ୍ୟାଣ୍ଡସମ୍ ) – ସୁନ୍ଦର
closing (କ୍ଲୋଜିଙ୍ଗ୍) – ବନ୍ଦକରି

Comprehension Questions (ବୋଧପରିମାପକ ପ୍ରଶ୍ନବଳୀ):

Question 1.
Who are there in the story?
(ଗପଟିରେ କିଏ କିଏ ଅଛନ୍ତି ?
Answer:
The jackal and the rooster are there in the story.

Question 2.
What was the rooster like?
( ଗଞ୍ଜାଟି କିପରି ? )
Answer:
The rooster was handsome and king-like.

Question 3.
What did it do early in the morning?
(ବଡ଼ି ସକାଳୁ ଗଞ୍ଜାଟି କ’ଣ କରୁଥିଲା ?)
Answer:
The rooster sang non-stop cock-koo-doodle-doo every early morning sitting on a high place.

Question 4.
What did it know?
(ସେ (ଗଞ୍ଜାଟି) କ’ଣ ଜାଣିଥିଲା ?)
Answer:
It (the rooster) knew that his song was unique ( ଅସାଧାରଣ ) in sweetness and sound in his locality.

Question 5.
Is it true that the rooster’s song was better than the songs of other roosters?
(ଏହା କ’ଣ ସତ ଯେ, ଗଞ୍ଜାଟିର ଗାନ ତା’ ଅଞ୍ଚଳର ଅନ୍ୟ ଗଞ୍ଜାମାନଙ୍କ ଗାନଠାରୁ ଉତ୍କୃଷ୍ଟ ଥୁଲା )
Answer:
No, the song of the rooster was not so better than the song of the other roosters of his locality.

Question 6.
What did it want its song to be?
(ସେ ତା’ ଗାୟନ (ଗାଇବା)କୁ କିଭଳି କରିବାକୁ ଚାହୁଁଥିଲା ? )
Answer:
It wanted its song to be sweeter, louder and clearer.

Question 7.
Did it know how to do this ?
(ସେ କ’ଣ ତାହା କିପରି କରିବାକୁ ହେବ ଜାଣିଥିଲା ?)
Answer:
No, it not at all knew how to do this.

Question 8.
The jackal thought the rooster would fly away if it tried to catch it. Why?
(କୋକିଶିଆଳ ଜାଣିଥିଲା ଯେ, ଯଦି ସେ ଗଞ୍ଜାକୁ ଧରିବାକୁ ଚେଷ୍ଟା କରିବ, ସେ ତତ୍‌କ୍ଷଣାତ୍ ଉଡ଼ିକରି ଦୂରେଇ ଯିବ । କାହିଁକି ?)
Answer:
The Jackal is a hunter beast of small birds and animals. So he has natural experience (ସ୍ଵାଭାବିକ ଅନୁଭବ) of the latter getting escape in their way.

Question 9.
Did the jackal have similar experiences before?
(କୋକିଶିଆଳର କ’ଣ ଏକାଭଳି ପୂର୍ବାନୁଭୂତି ଥିଲା ?)
Answer:
Yes, the jackal had a similar experience before. This happened the other day when he tried to catch a rooster.

Question 10.
What did the jackal suggest the rooster make its song better?
(କୋକିଶିଆଳ ଗଞ୍ଜାଟିକୁ ତା’ର ଗାନକୁ ଅଧିକ ସୁମଧୁର କରିବାପାଇଁ କି ପ୍ରସ୍ତାବ ଦେଇଥିଲା ? )
Answer:
The jackal suggested the rooster close his eyes while singing in order to make its song better means sweeter, louder, and clearer.

Question 11.
Why did the jackal call the rooster ‘great, handsome. …?
(କୋକିଶିଆଳ କାହିଁକି ଗଞ୍ଜାଟିକୁ ମହାନ୍, ସୁନ୍ଦର ଇତ୍ୟାଦି ଶବ୍ଦଦ୍ୱାରା ସମ୍ବୋଧୃତ କରିଥିଲା ?)
Answer:
The Jackal is known for its wickedness, so that flattered (ଚାଟୁ କଲା) the rooster to make it his prey (ଶିକାର).

Question 12.
Will the rooster close its eyes and sing? Read the next part and see.
(ଗଞ୍ଜା କ’ଣ ସତରେ ଆଖୁ ବନ୍ଦକରି ଗାନ କଲା ? ପରବର୍ତୀ ଅନୁଚ୍ଛେଦ ପାଠ କର ଏବଂ ଲକ୍ଷ୍ୟ କର ।)

Session – 2 (ଦ୍ଵିତୀୟ ପର୍ଯ୍ୟାୟ):

• SGP-2 (Sense Group Paragraph-2)
• Read para – 3 silently and answer the questions that follow.
(୩ୟ ଅନୁଚ୍ଛେଦକୁ ପାଠ କର ଏବଂ ନିମ୍ନପ୍ରଦତ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)
3. The rooster closed his eyes and sang louder and clearer – cock koo-doodle- doo. Then SNAP !! The jackal caught the rooster by its neck and ran away. The owner of the rooster chased behind. His wife and sons joined him. Also joined his neighbors. But the jackal was much ahead of those running behind. The rooster, in the meantime, said, “Mr. Jackal, I’m so happy to be with you. Without walking I’m walking. Without flying, I’m flying. What a great feeling! And my owner is a miser. He never gives me anything to eat. Why don’t you tell this to them ?”
ଓଡ଼ିଆ ଅନୁବାଦ :
୩. ଗଞ୍ଜାଟି ଆଖ୍ ବନ୍ଦ କଲା ଏବଂ ଅଧିକ ଉଚ୍ଚ ସ୍ବରରେ ଏବଂ ସ୍ପଷ୍ଟ ଭାବରେ ଗାଇବାକୁ ଲାଗିଲା- କକ୍‌କ୍‌ରେ–କୁ-ଡୁଡୁଲେ-ଡୁ । ତା’ପରେ ଝାମ୍ପ । କୋକିଶିଆଳ ଗଞ୍ଜାଟିକୁ ବେକ ପାଖରୁ ଧରି ପକାଇଲା ଏବଂ ଦୌଡ଼ି ପଳାଇବାକୁ ଲାଗିଲା । ଗଞ୍ଜାର ମାଲିକ ପଛେ ପଛେ ଗୋଡ଼ାଇଲା । ତା’ର ସ୍ତ୍ରୀ ଓ ପୁଅମାନେ ସେହି ଦୌଡ଼ରେ ସାମିଲ ହେଲେ । ଆହୁରି ମଧ୍ୟ ତା’ର ସାଇପଡ଼ିଶାମାନେ ତାଙ୍କ ସହିତ ଯୋଗଦେଲେ । କିନ୍ତୁ କୋକିଶିଆଳଟି ପଛପଟୁ ଗୋଡ଼ାଉଥ‌ିବା ଦଳଠାରୁ ଖୁବ୍ ଆଗରେ ଥିଲା । ଇତି ଅବସରରେ ଗଞ୍ଜାଟି କହି ଉଠିଲା, ‘ହେ କୋକିଶିଆଳ, ମୁଁ ତୁମ ସହିତ ଥ‌ିବାରୁ ଭାରି ଖୁସି ।-ବିନା ଚାଲିବାରେ ମୁଁ ଚାଲି ପାରୁଛି । ବିନାଉଠିଲା, ‘ହେ କୋକିଶିଆଳ, ମୁଁ ତୁମ ସହିତ ଥବାରୁ ଭାରି ଖୁସି । ବିନା ଚାଲିବାରେ ମୁଁ ଚାଲି ପାରୁଛି । ବିନା ଉଡ଼ିବାରେ ମୁଁ ଉଡ଼ି ପାରୁଛି । କି’ ସୁନ୍ଦର ଅନୁଭୂତି ! କିନ୍ତୁ ମୋ ମାଲିକ ଗୋଟେ କୃପଣ । ସେ ମୋତେ କିଛି ଖାଇବାକୁ ଦିଏ ନାହିଁ । ତୁମେ କାହିଁକି ଏକଥା ସେମାନଙ୍କୁ କହିଦେଉ ନାହଁ ?”’

Notes And Glossary (ଶବ୍ଦାର୍ଥ):

closed (କ୍ଲୋଜଡ୍) – ବନ୍ଦ କଲା
Snap (ସ୍ନାପ୍) – ଝାମ୍ପ
jackal (ଜ୍ୟାକଲ୍) – କୋକିଶିଆଳ
caught (କଟ୍) – ଧରି ପକାଇଲା
neck (ନେକ୍) – ବେକ
owner (ଓନର୍) – ମାଲିକ
chased (ଚେଜ୍‌) – ପଶ୍ଚାତ୍‌ବନ କଲେ
joined (ଜଏନ୍‌ଡ୍) – ଯୋଗଦେଲେ
neighbours (ନେବର୍‌ସ) – ପଡ଼ୋଶୀମାନେ
ahead (ଆହେଡ଼) – ଆଗରେ
behind (ବିହାଇଣ୍ଡ୍) – ପଛରେ
feeling (ଫିଲିଙ୍ଗ୍) – ଅନୁଭୂତି
miser (ମାଇଜର) – କୃପଣ

Comprehension Questions (ବୋଧପରିମାପକ ପ୍ରଶ୍ନବଳୀ) :

Question 1.
Did the rooster sing closing its eyes ?
(ଗଞ୍ଜା କ’ଣ ଆଖୁ ବନ୍ଦ କରି ଗାନ କଲା ?)
Answer:
Yes, the rooster really sang closing its eyes.

Question 2.
What did the jackal do?
(କୋକିଶିଆଳ କ’ଣ କଲା ?)
Answer:
The jackal caught the rooster by its neck and ran away.

Question 3.
Who ran after the jackal?
(କିଏ କୋକିଶିଆଳ ପଛେ ପଛେ ଗୋଡ଼ାଇଲା ?)
Answer:
The owner of the rooster ran after the jackal. His wife and sons and his neighbors also joined him.

Question 4.
Why did they chase the jackal?
(କାହିଁକି ସେମାନେ କୋକିଶିଆଳକୁ ଗୋଡ଼ାଇଲେ ?)
Answer:
All they chased the jackal to free the rooster from its clutches (କବଳରୁ ).

Question 5.
Why couldn’t they catch the jackal?
(କାହିଁକି ସେମାନେ କୋକିଶିଆଳକୁ ଧରିପାରିଲେ ନାହିଁ ?)
Answer:
They could not be able to catch the jackal as it was far ahead of them.

Question 6.
Why did the rooster say that it was happy to be with the jackal?
(ଗଞ୍ଜା କାହିଁକି କୋକିଶିଆଳ ପାଖରେ ଥିବାରୁ ଖୁସି ବୋଲି କହିଲା ?)
Answer:
The rooster made a plan to escape from the jackal. So with this intention (ଇଚ୍ଛା ଥାଇ), it said so.

Question 7.
Was it really happy or telling a lie?
(ସେ କ’ଣ ସତରେ ଖୁସିଥିଲା ନା ମିଛ କହିଲା ?)
Answer:
He was not at all happy. He told a lie to work out (କାର୍ଯ୍ୟକାରୀ କରିବା) his plan.

Question 8.
What did it say about its owner?
(ସେ ତା’ର ମାଲିକ ବାବଦରେ କ’ଣ କହିଲା ?)
Answer:
It declared (ଘୋଷଣା କଲା) that its master was very miser. He did not give it anything to eat.

Question 9.
What did the rooster ask the jackal to do?
(ଗଞ୍ଜାଟି କୋକିଶିଆଳକୁ କ’ଣ କରିବାକୁ କହିଲା ?)
Answer:
The rooster requested the jackal to tell its master about its complaint (ଅଭିଯୋଗ ).
Will the jackal do what the rooster wanted him to do? Read the last part and see.

Session – 3 (ତୃତୀୟ ପର୍ଯ୍ୟାୟ)

SGP-3 (Sense Group Paragraph-3)
Read the rest part of the story and answer the questions that follow.
(ଗପଟିର ଅବଶିଷ୍ଟ ଅଂଶଟିକୁ ପଢ଼ ଏବଂ ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡିକର ଉତ୍ତର ଦିଅ ।)

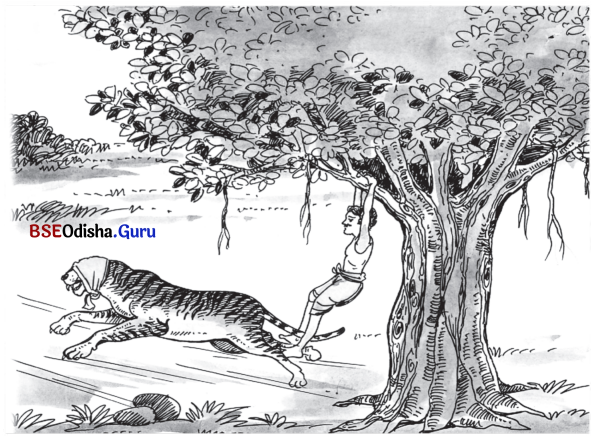
The jackal felt happy with these words of the rooster. As he opened his mouth to say something, the rooster flew up to a tree. Sitting on the branch of the tree, the rooster sang,

“I was a fool
To believe your lies
I closed instead of
Keeping open my eyes.”

The Jackal wept and said,
“I’m a great fool
To believe what you said,
For opening my mouth
I feel really repented.”

ଓଡ଼ିଆ ଅନୁବାଦ :
କୋକିଶିଆଳ ଗଞ୍ଜାଟିର ଏହି କଥାରେ ଖୁସି ହେଲା । ଯେତେବେଳେ ସେ କିଛି କହିବାକୁ ପାଟି ଖୋଲିଛି,
ତତ୍‌କ୍ଷଣାତ୍ ଗଞ୍ଜାଟି ଗଛ ଉପରକୁ ଉଡ଼ିଗଲା । ଗଛ ଡାଳରେ ବସି ଗଞ୍ଜାଟି ଗାଇବାକୁ ଲାଗିଲା ।
‘ମୁଁ ଥୁଲି ଗୋଟେ ବୋକା
ତୁମ ମିଛ କଥାକୁ ବିଶ୍ବାସ କରି
ଆଖ୍ ଖୋଲିବା ବଦଳେ ମୁଁ ବନ୍ଦ ରଖୁଥୁଲି ।’’
କାନ୍ଦି କାନ୍ଦି କୋକିଶିଆଳ କହିଲା,
‘ମୁଁ ତ ଗୋଟେ ମସ୍ତବଡ଼ ବୋକା
ଯେଣୁ ବିଶ୍ଵାସ କାଲି ତୁମ କଥା
ପାଟି ମେଲା କରି
ମୁଁ ବାସ୍ତବିକ ଅନୁତପ୍ତ ।

Notes And Glossary (ଶବ୍ଦାର୍ଥ):

felt (ଫେଲ୍‌ଟ) – ଅନୁଭବ କଲା
as (ଆଜ୍) – ଯେତେବେଳେ
flew up (ପ୍ଲିଜ ଅପ୍) – ଉପରକୁ ଉଡ଼ିଗଲା
fool (ଫୁଲ୍) – ନିବୋଧ | ବୋକା
lies (ଲାଇଜ୍) – ମିଛ କଥାସବୁ
instead of (ଇଡ୍‌ ଅଫ୍) – ପରିବର୍ତ୍ତେ
keeping open (କିପିଙ୍ଗ୍ ଓପନ୍) – ଖୋଲା ରଖୁ
wept (ୱେପ୍ଟ) – କାନ୍ଦିଲା
great (ଗ୍ରେଟ୍) – ବହୁତ ବଡ଼
believe (ବିଲିଭ୍) – ବିଶ୍ବାସ କରିବା
feel (ଫିଲ୍) – ଅନୁଭବ କରିବା
repented (ରିପେଣ୍ଡେଡ୍ ) – ଅନୁତାପ କଲା

Comprehension Questions (ବୋଧପରିମାପକ ପ୍ରଶ୍ନବଳୀ) :

Question 1.
Was the jackal happy with what the rooster said ?
(ଗଞ୍ଜା ଯାହା କହିଲା ସେଥୁରେ କୋକିଶିଆଳ ଖୁସି ଥିଲା କି ?)
Answer:
Yes, the jackal was happy with what the rooster said.

Question 2.
What did the rooster do when the jackal opened its mouth?
(କୋକିଶିଆଳ ପାଟି ଖୋଲିବାମାତ୍ରେ ଗଞ୍ଜାଟି କ’ଣ କଲା ?)
Answer:
The rooster immediately (ତତ୍‌କ୍ଷଣାତ୍) flew up to the tree when the jackal opened its mouth.

Question 3.
What did the rooster do sitting on the branch of a tree?
(ଗଞ୍ଜାଟି ଗଛଡାଳରେ ବସି କ’ଣ କଲା ?)
Answer:
The rooster sang a song sitting on the branch of the tree.

Question 4.
Did it realize the mistake it made?
(ସେ କ’ଣ ସେ କରିଥିବା ଭୁଲ ବୁଝିପାରିଲା ?)
Answer:
Yes, it (the rooster) realized the mistake it made.

Question 5.
What did the jackal do?
(କୋକିଶିଆଳ କ’ଣ କଲା ?)
Answer:
The jackal wept and repented (ରିପେଣ୍ଡେଡ୍ ) for its greater foolishness.

Question 6.
The jackal said something while weeping. What did it say?
(କୋକିଶିଆଳ କାନ୍ଦି କାନ୍ଦି କିଛି କହୁଥିଲା ? ସେ କ’ଣ କହୁଥିଲା ?)
Answer:
The jackal rebuked (ଗାଳି ଦେଲା) himself as he was a great fool.

Question 7.
What was the mistake of the rooster?
(ଗଞ୍ଜାଟିର ଭୁଲ କ’ଣ ଥିଲା ?)
Answer:
The mistake of the rooster was its plain belief (ସରଳ ବିଶ୍ଵାସ) to the jackal.

Question 8.
What was the mistake of the jackal?
(କୋକିଶିଆଳର ଭୁଲ୍ କ’ଣ ଥିଲା ?)
Answer:
The jackal believed the rooster and it let its prey (ଶିକାର) free. It was its greater mistake.

Question 9.
Both realized their mistakes. Who sang? Who wept? Why?
( ଉଭୟେ ନିଜ ନିଜ ଭୁଲ୍ ବୁଝିପାରିଲେ । କିଏ ଗାଇଲା ? କିଏ କାନ୍ଦିଲା ? କାହିଁକି ?)
Answer:
The rooster sang. It sang when it freed itself from the jackal. The jackal wept. It wept realizing (ଅନୁଭବ କରି) its foolishness losing its prey(ଶିକାର).

Question 10.
If two persons quarrel or fight, one that wins at the end is said to have the last laugh. Who had the last laugh in the story?
(ଯଦି ଦୁଇଜଣ ଝଗଡ଼ା ଲାଗନ୍ତି ବା ମରାମରି ହୁଅନ୍ତି; ଯିଏ ଶେଷରେ ଜିତିଯାଏ- କୁହାଯାଏ ଶେଷ ହସଟିଏ ହସେ । ଏ ଗପଟିରେ ସେହିପରି କିଏ ଶେଷ ହସଟିଏ ହସିଥିଲା ?)
Answer:
In this story, the rooster enjoyed its last laugh.

III. Post-Reading (ପଠନ ପରବର୍ତ୍ତୀ):
Session – 4 (ଚତୁର୍ଥ ପର୍ଯ୍ୟାୟ).
1.| Visual Memory Development Technique (VMDT) : (ଦୃଶ୍ୟ ସ୍ମୃତି ବିକାଶ କୌଶଳ):
Pictures : Place your index finger on the jackal, people and the rooster. (ସୂଚୀ ଅଙ୍ଗୁଳିଟିରେ ଛବିଟିରୁ ଦର୍ଶାଅ – କୋକିଶିଆଳ, ଲୋକମାନେ ଏବଂ ଗଞ୍ଜା)

→ Picture in SGP-3: on the jackal, on the rooster, and next on the tree. (କୋକିଶିଆଳ, ଗଞ୍ଜା ଏବଂ ପରେ ପରେ ଗଛ ଉପରେ)

→ Whole text : song of rooster, admitting mistake, jackal cuaght the – rooster, rooster singing cockoo-doodle-do. 123456789 ଗଞ୍ଜାର ସଙ୍ଗୀତ, ଭୁଲ୍ ବୁଝିବାରେ, କୋକିଶିଆଳ ଗଞ୍ଜାଟିକୁ ଧରିନେବା, ଗଞ୍ଜା ଗୀତ ଗାଇବା, କୋକୋ -ଡୋଡ଼ୋଲ୍ -ଡୁ )

2. Comprehension Activities (ବୋଧପରିମାପକ କାର୍ଯ୍ୟାବଳୀ):
(a) MCQ:
Choose the correct answer.
Question 1.
The rooster was ___________
(A) big
(B) handsome
(C) with a crown
(D) A, B and C
Answer:
(D) A, B and C

Question 2.
The rooster wanted to make his song ___________
(A) B, C and D
(B) louder
(C) clearer
(D) better
Answer:
(A) B, C and D

Question 3.
The jackal called the rooster_________________
(A) great
(B) handsome
(C) king-like
(D) all of A, B, and C
Answer:
(D) all of A, B, and C

Question 4.
Who chased after the jackal?
(A) the owner
(B) the neighbor of the owner
(C) his wife and sons
(D) all of them
Answer:
(D) all of them

Question 5.
The rooster said to the jackal ___________________
(A) his owner was a miser
(B) A and D
(C) his owner loved him
(D) his owner never gave him anything to eat
Answer:
(B) A and D

(b) Match, “Who said What”. Draw lines, one is done for you. (ମେଳ କର, ‘‘କିଏ କ’ଣ କହିଲା ?’’ ରେଖାଦ୍ଵାରା ଯୋଗକରି ଦର୍ଶାଅ ।) (ପ୍ରଶ୍ନ ସହ ଉତ୍ତର)

Answer:

Session – 5 (ପଞ୍ଚମ ପର୍ଯ୍ୟାୟ)
3. Listening (ଶ୍ରବଣ):
(a) Your teacher will read aloud some words from the list below. Tick those words which your teacher reads aloud. (ନିମ୍ନ ତାଲିକାରେ ଥ‌ିବା ଶବ୍ଦଗୁଡ଼ିକରୁ ତୁମ ଶିକ୍ଷକ କେତୋଟିକୁ ଉଚ୍ଚ ପାଟିରେ ପଢ଼ିବେ । ସେଗୁଡ଼ିକୁ ଟିକ୍ ଚିହ୍ନଦ୍ଵାରା ଦର୍ଶାଅ ।)
[handsome (‘d’ is silent), beautiful, problem, caught, neighbors, behind, instead, believe, repented]
(ହାଣ୍ଡସମ୍, ବିୟୁଟିଫୁଲ୍, ପ୍ରୋବ୍ଲେମ୍, କଅଟ୍, ନାଇବରସ୍, ବିହାଇଣ୍ଡ୍, ଇନ୍‌ଷ୍ଟେଡ୍, ବିଲିଭ୍, ରିପେଣ୍ଟେଡ୍)

(b) Your teacher will read aloud paragraph-3 (SGP-2). Listen to him / her and fill in the gaps. (ତୁମ ଶିକ୍ଷକ ତୃତୀୟ ଅନୁଚ୍ଛେଦଟିକୁ ପଠନ କରିବେ । ମନଯୋଗ ପୂର୍ବକ ଶୁଣି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।)

The _________ of the rooster chased _________. His _________ and sons joined _________. Also _________ his neighbors. But the _________was much _________of those _________ behind.
Answer:
The owner of the rooster chased behind. His wife and sons joined him. Also joined his neighbors. But the jackal was much ahead of those running behind.

4. Speaking (କହିବା):
(a) Chain-drill: ‘I was a fool to believe your lies.
(ଶୃଙ୍ଖଳ-ଅଭ୍ୟାସ : ମୁଁ ଗୋଟେ ବୋକା, ତୁମ ମିଛକୁ ବିଶ୍ଵାସ କଲି ।)
(b) Dialogue : Rehearsal[ Teacher vs. students , students vs. students, reading aloud the dialogues]
(ସଂଳାପ : ଶିକ୍ଷକ ଓ ଛାତ୍ରମାନେ, ଛାତ୍ରଛାତ୍ରୀ ଓ ଶିକ୍ଷକ ରୂପ କଥନ କରିବେ ।)

Jackal : I’m a fool.
(କୋକିଶିଆଳ: ମୁଁ ଗୋଟେ ବୋକା ।)
Rooster: I’m a fool too.
(ଗଞ୍ଜା: ମୁଁ ମଧ୍ୟ ଗୋଟେ ବୋକା ।)
Jackal : I opened my mouth.
(କୋକିଶିଆଳ: ମୁଁ ମୋ ପାଟି ମେଲା କଲି ।)
RoosterS I closed my eyes.
(ଗଞ୍ଜା: ମୁଁ ମୋ ଆଖୁ ବନ୍ଦ କଲି ।)
Jackal : You told lies.
( କୋକିଶିଆଳ : ତୁମେ ମିଛ କହିଲ ।)
Rooster: You too told lies.
(ଗଞ୍ଜା : ତୁମେ ମଧ୍ଯ ମିଛ କହିଲ ।)

(c) Words with ‘ie, ee, ei, ea, oo’ in spelling are generally spoken with a long sound taking more time. Given below are some such words from the lesson. Your teacher will read aloud each word, and you will repeat after him/her. (ଶିକ୍ଷକ କେତେକ ଶବ୍ଦ ଉଚ୍ଚାରଣ କରିବେ । ତୁମେ ତାଙ୍କ ସହିତ ସ୍ବର ମିଳାଇ ଉଚ୍ଚାରଣ କର ।)
[rooster, fool doodle , feel , free , believe, receive, repeat] (ରୁସ୍ତର, ଫୁଉଲ୍, ଡୋଡୋଲ୍, ଫିଇଲ୍, ଫ୍ରିଇ, ବିଲିଇଭ୍, ରିସିଲଭ୍, ରିଇପିଟ୍)

Session – 6 (ଷଷ୍ଠ ପର୍ଯ୍ୟାୟ)
5. Vocabulary (ଶବ୍ଦସମ୍ଭାର) :

(a) English spelling is difficult and tricky. One way of learning to spell is the four-step method: look>cover>write>verify. Learn the spelling of the following words from the lesson following the four-step method. (ଇଂରାଜୀ ଶବ୍ଦକୁ ଆୟତ୍ତ କରିବାରେ ଅନୁସରଣ କର-ଦେଖ > ଅତିକ୍ରମ କର > ଲେଖ > ପରଖ ।)
[beautiful, handsome, problem, neighbor, believe, instead, repent]

(b) Word Scramble (ଶବ୍ଦଗଠନ ଅସଜଡ଼ା ଅକ୍ଷରକୁ ନେଇ):
Find words from the scramble. In some cases, you may get two words.

Answer:
dre red (colour – ରଙ୍ଗ)
gib big (size – ଆକାର)
yrt try (begin with ‘t’ – t ରେ ଆରମ୍ଭ)
yee eye (body part – ଶରୀରର ଅଂଶ)
yad day (opposite of night – ରାତିର ବିପରୀତ)
yas say (begins with ‘s’ S ଲଗାଇ ଆରମ୍ଭ)
lyf fly (cock can but jackal cann’t – ଗଞ୍ଜା କରିପାରେ କୋକିଶିଆଳ କରିପାରେ ନାହିଁ)
aet eat (begins with ‘e’ e ଲଗାଇ ଆରମ୍ଭ)

6. Usage (ବ୍ୟବହାର) :
(a) Combine two sentences into one. One is done for you.
(ଦୁଇଟି ବାକ୍ୟକୁ ଯୋଡ଼ି ଗୋଟିଏ ବାକ୍ୟରେ ପ୍ରକାଶ କର ।)

(i) The rooster sang. It closed its eyes.
Answer:
The rooster sang closing its eyes.
(ii) The rooster sang. It sat on a tree.
Answer:
The rooster sang sitting on a tree.
(iii) Rakesh took tea. He sat on a chair.
Answer:
Rakesh took tea sitting on a chair.
(iv) Rabi went home. He rode on a bicycle.
Answer:
Rabi went home riding on a bicycle.
(v) The cat caught the rat. It climbed up the tree.
Answer:
The cat caught the rat climbing up the tree.
(vi) The jackal ran. It caught the rooster by its neck.
Answer:
The jackal ran catching the rooster by its neck.

(b) These sentences can also be written, beginning with the second part of the sentence. (ପୂର୍ବୋକ୍ତ ବାକ୍ୟଗୁଡ଼ିକୁ ବଦଳାଇ ଲେଖ । ଶେଷୋକ୍ତ ଅଂଶକୁ ପ୍ରଥମେ ଆରମ୍ଭ କରି ।)
Example :
Closing its eyes, the rooster sang.
Write all the sentences of 6(a) in this way.
___________________________________________
___________________________________________
___________________________________________
___________________________________________
Answer:
Answer:
(i) Closing its eyes, the rooster sang.
(ii) Sitting on a tree, the rooster sang.
(iii) Sitting on a chair, Rakesh took tea.
(iv) Riding on a bicycle, Rabi went home.
(v) Climbing up the tree, the cat caught the rat.
(vi) Catching the rooster by its neck, the jackal ran.’

Session – 7 (ସପ୍ତମ ପର୍ଯ୍ୟାୟ):
7. Writing (ଲିଖନାତ୍ମକ)
(a) Write answers to the following questions.

(i) What is the story about?
(ଗପଟି କେଉଁ ବିଷୟରେ ?)
Answer:
The story is about the rooster and the jackal.

(ii) What did the jackal ask the rooster to do ?
(କୋକିଶିଆଳ ଗଞ୍ଜାକୁ କ’ଣ କରିବାକୁ କହିଲା ?)
Answer:
The jackal asked the rooster to sing closing its eyes.

(iii) The rooster sang closing its eyes. What did the jackal do?
(ଗଞ୍ଜା ତା’ର ଆଖୁ ବନ୍ଦ କରି ଗୀତ ଗାଇଲା । କୋକିଶିଆଳ କ’ଣ କଲା ?)
Answer:
The jackal caught the rooster, his prey (ଶିକାର) by its neck whenever it started singing closing its eyes.

(iv) The jackal opened its mouth. What did the rooster do?
(କୋକିଶିଆଳ ତା’ର ପାଟି ଖୋଲିଲା । ଗଞ୍ଜାଟି କ’ଣ କଲା ?)
Answer:
The rooster freed itself from the jackal and flew up to a tree as soon as it (the jackal) opened its mouth.

(b) Given below is what the rooster told another rooster after the incident. Read what it said and fill in the gaps consulting the text. (ଘଟଣା ଘଟିଲା ପରେ ଗଞ୍ଜାଟି ଆଉ ଗୋଟିଏ ଗଞ୍ଜାକୁ କହିଲା । ପାଠ୍ୟ ଅନୁସରଣରେ ନିମ୍ନ ଶୂନ୍ୟସ୍ଥାନଗୁଡ଼ିକୁ ପୂରଣ କର ।)

Do you know what happened the other day? I was singing in the morning. A jackal came. He told me to sing ____________. I closed my _________ and _________. The jackal caught me by ___________ and ran away. My master, his ___________and ___________and his _________ chased the jackal. The jackal was much ahead. There was little chance of catching him. So I thought of a plan. I said to the jackal, “I’m happy with you. Why should they chase? Tell them this.” He _________ his _________to tell this. I quickly _________up on to the _________.
Answer:
Do you know what happened the other day? I was singing in the morning. A jackal came. He told me to sing closing my eyes. I closed my eyes and sang. The jackal caught me by my neck and ran away. My master, his wife and sons, and his neighbors chased the jackal. The jackal was much ahead. There was little chance of catching him. So I thought of a plan. I said to the jackal, “I’m happy with you. Why should they chase? Tell them this.” He opened his mouth to tell this. I quickly flew up onto the tree.

(c) You know what a rooster told another rooster about the incident. Consult the text and write what the jackal said to another jackal after the incident. (ତୁମେ ଜାଣିଲ ଗଞ୍ଜାଟି ଅନ୍ୟ ଗଞ୍ଜାଟିକୁ କ’ଣ କହିଲା । ପାଠ୍ୟ ଅନୁସରଣରେ ସେହିପରି କୋକିଶିଆଳଟି ଆଉ ଗୋଟିଏ କୋକିଶିଆଳକୁ କ’ଣ କହିଲା ?)
Do you know __________________________
_________________________________________
_________________________________________
_________________________________________
Answer:
Do you know I met a rooster singing in the early morning with open eyes? Cunningly (ଚାଲାକିରେ ) I told it to sing closing its eyes for it would be better, clear, and louder. As the rooster did so I caught it by its neck and ran away. Its owner, his wife, sons, and neighbors ran after me. The rooster told it had a nice feeling. It told its master was a miser and did not give it much to eat. It requested me to tell this to its master. As I opened my mouth to speak, it flew away up to a tree. I missed my prey (ଶିକାର).

8. Mental Talk (ମାନସ କଥନ) :
‘T was a fool to believe your lies.”
(ମନେ ମନେ – ମୁଁ ତୁମ ମିଛକୁ ବିଶ୍ଵାସ କରି ବୋକା ବନିଗଲି ।)

9. Let’s Think (ଚାଲ ଚିନ୍ତାମଗ୍ନ ହେବା):
We should know when to shut our mouths and to close or open our eyes.
(ଆମେ ଜାଣିବା ଉଚିତ ଯେ କେତେବେଳେ ପାଟି ବନ୍ଦ ରଖିବା ଏବଂ କେତେବେଳେ ଆଖୁ ଖୋଲା ରଖୁବା ବା ବନ୍ଦ ରଖିବା ।)

BSE Odisha 7th Class English Solutions Lesson 2 The Jackal and the Rooster Important Questions and Answers

(A) Choose the right answer from the options.

Question 1.
The rooster looked like a king with its ____________.
(i) power
(ii) large kingdom
(iii) large army
(iv) beautiful red crown
Answer:
(iv) beautiful red crown

Question 2.
Rooster always sang ___________.
(i) keeping its mouth open
(ii) keeping its eyes open
(iii) keeping its body open
(iv) None of the above
Answer:
(ii) keeping its eyes open

Question 3.
“Oh, great handsome king-like rooster !” Who said this?
(i) The jackal
(ii) Other animals
(iii) The hen
(iv) Both the jackal and other animals
Answer:
(i) The jackal

(B) Answer the following questions.

Question 1.
How did the rooster befool the jackal?
Answer:
The jackal was cunning enough to catch the rooster, but he was befooled when he opened his mouth listening to his praise from the rooster. The rooster flew up to a tree and freed itself.

Question 2.
What did the owner of the rooster do when he saw the jackal carrying away his rooster?
Answer:
The owner of the rooster saw the jackal carrying away his rooster. He, with his sons, wife, and neighbors chased behind, but they could not catch the jackal.

Question 3.
How did the rooster blame its owner?
Answer:
The rooster told its owner was a miser and he never gave it anything to eat. So it didn’t like its owner.

(C) Re-arrange the jumbled words to make meaningful sentences.
1. rooster / very / was / there / a / big/handsome / and
2. red / he / like / king/a / looked / with / beautiful / its / crown
3. king / like / he / felt / also / a
4. open / it / keeping / sang / his / but / eyes
5. ran / and / away / the / caught / jackal / the / its / rooster / by / neck
Answer:
1. There was a very big and handsome rooster.
2. He looked like a king with its beautiful red crown.
3. He also felt like a king.
4. But it sang keeping his eyes open.
5. The jackal caught the rooster by its neck and ran away.

(D) Find whether True or False.
1. He gives me everything to eat.
2. The jackal was not much ahead of those running behind.
3. He closed his eyes and sang louder and clearer.
4. The jackal felt unhappy with the words of the rooster.
5. The jackal saw the rooster singing every day early in the morning.
Answer:
(1) False (2) False (3) True (4) False (5) True

BSE Odisha 7th Class English Solutions Part – I

• Run! Run! Run! Question Answer
• The Jackal and the Rooster Question Answer
• The Camel Question Answer

Odisha State Board BSE Odisha 6th Class English Solutions Lesson 5 The Cat and the Dog Textbook Exercise Questions and Answers.

Class 6th English Chapter 5 The Cat and the Dog Question Answers BSE Odisha

The Cat and the Dog Class 6 Questions and Answers

Session – 1 (ସୋପାନ – ୧):
I. Pre-Reading (ପଢ଼ିବା ପୂର୍ବରୁ):

→  Socialisation (ସାମାଜିକୀକରଣ) :
→  There are some pairs of animals and birds who are always in the fight. They never can have a friendship. One is an enemy to the other. Can you guess the other such pair? Crow and cuckoo, for example. Look at the pictures and guess one pair of animals. Let’s read this very very interesting poem on dog and cat, and their relationship.
(କେତେକ ପଶୁ ଓ ପକ୍ଷୀଙ୍କର ଯୋଡ଼ା ଅଛି ଯେଉଁମାନେ ସର୍ବଦା ଯୁଦ୍ଧ କରନ୍ତି । ସେମାନଙ୍କର କେବେହେଲେ ବନ୍ଧୁତା ହୋଇନପାରେ । ଜଣେ ଅନ୍ୟ ଜଣଙ୍କର ଶତ୍ରୁ ଅଟେ । ତୁମେ ଏପରି ଅନ୍ୟ ଯୋଡ଼ାଙ୍କ ବିଷୟରେ ଅନୁମାନ କରିପାରିବ କି ? ଉଦାହରଣ ସ୍ଵରୂପ, କାଉ ଓ କୋଇଲି । ଛବିଗୁଡ଼ିକୁ ଦେଖ ଏବଂ ଅନ୍ୟ ଯୋଡ଼ା ପଶୁଙ୍କ ବିଷୟରେ ଅନୁମାନ କର । ଆସ ଆମେ କୁକୁର ଓ ବିଲେଇଙ୍କ ବିଷୟରେ ଏବଂ ସେମାନଙ୍କ ସମ୍ପର୍କ ବିଷୟରେ ଏହି ଅତି ଆନନ୍ଦଦାୟକ କବିତାଟିକୁ ପଢ଼ିବା ।)

II. While-Reading (ପଢ଼ିବା ସମୟରେ):
Text (ବିଷୟବସ୍ତୁ):
Follow three steps of teaching a poem-teacher reading aloud twice followed by a silent reading by the students.
(କବିତା ପଢ଼ିବାର ତିନିଗୋଟି ପର୍ଯ୍ୟାୟକୁ ଅନୁସରଣ କର – ଶିକ୍ଷକ ଦୁଇଥର ବଡ଼ପାଟିରେ ପଢ଼ିବେ ତାଙ୍କପଛରେ ଛାତ୍ରମାନଙ୍କଦ୍ୱାରା ନୀରବ ପଠନ ହେବ ।)

Read the poem silently and answer the questions that follow.
(କବିତାଟିକୁ ନୀରବରେ ପଢ଼ ଏବଂ ପରବର୍ତ୍ତୀ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

1. There was a dog and there was a cat.
One very thin and the other fat.
Neither of them was a pet.
But the cat always sat on a mat,
and claimed she was a loving pet.
As the fat cat saw one day,
the dog being chased away.

2. She said: “Chased here and chased there
No place to rest and retire
But look how I rest hither l
ike the owner’s grandmother.”

3. The dog saw the cat,
cursed his fate
and away he left.
Another day going that way
As the dog saw someone pack

4. the cat in the sack
and away her take,
He said; “Hey,
How is today ?”

5. The cat did say
from her gunny bag grey
“My wish was – ‘I may
go to a religious place one day’.
‘Carry me to Brindaban’ I say
and they obey.”

6. “But cat ‘nanny’
isn’t it funny
to go to Brindaban
in a bag gunny ?”

7. “I thought of going by bus but they are always rush.”
“What about trains Miss cat ?”

8. “Trains I hate,
They’re always late.”

କବିତାଟିର ଓଡ଼ିଆ ଉଚ୍ଚାରଣ :
(୧) ଦେୟାର୍ ୱାଜ୍ ଏ ଡ଼ଗ୍ ଆଣ୍ଡ୍ ଦେୟାର୍ ୱାଜ୍ ଏ କ୍ୟାଟ୍ ।
ୱାନ୍ ଭେରି ଥ୍ ଆଣ୍ଡ୍ ଦ’ ଅଦର୍ ପ୍ୟାଟ୍ ।
ନାଇଦର ଅଫ୍ ଦେମ୍ ୱାଜ୍ ଏ ପେଟ୍ ।
ବଟ୍ ଦ’ କ୍ୟାଟ୍ ଅଲୱେଜ୍ ସ୍ୟାଟ୍ ଅନ୍ ଏ ମ୍ୟାଚ୍,
ଆଣ୍ଡ୍ କ୍ଲେମ୍‌ଡ୍ ସି ୱାଜ୍ ଏ ଲଭିଙ୍ଗ୍ ପେଟ୍।
ଆଜ୍ ଦ’ ଫ୍ୟାଟ୍ କ୍ୟାଟ୍ ସିଅ ୱାନ୍ ଡେ,
ଦ’ ଡଗ୍ ବିଙ୍ଗ୍ ଚେକ୍‌ ଆମ୍ଭେ ।

(୨) ସି ସେଡ଼୍ : ‘‘ଚେକ୍‌ ହିଅର୍ ଆଣ୍ଡ ଚେକ୍‌ ଦେୟାର୍
ନୋ ପ୍ଲେସ୍ ଟୁ ରେଷ୍ଟ ଆଣ୍ଡ୍ ରିଟାୟାର୍
ବଟ୍ ଲୁକ୍ ହାସ୍‌ ଆଇ ରେଷ୍ଟ୍ ହିଦର୍
ଲାଇକ୍ ଦି ଓନର’ସ୍ ଗ୍ରାଣ୍ଡମଦର୍ ।’’

(୩) ଦି ଡଗ୍ ସ’ ଦ’ କ୍ୟାଟ୍,
କରସଡ୍ ହିଜ୍ ଫେଟ୍
ଆଣ୍ଡ୍ ଆମ୍ଭେ ହି ଲେଫ୍ଟ ।
ଆନାଦର୍ ଡେ ଗୋଇଙ୍ଗ୍ ଦ୍ୟାଟ୍ ୱେ
ଆଜ୍ ଦି’ ଡଗ୍ ସ’ ସମ୍ୱିନ୍‌ ପ୍ୟାକ୍

(୫) ଦ’ କ୍ୟାଟ୍ ଡିଡ୍ ସେ
ଫ୍ରମ୍ ହର୍ ଗନି ବ୍ୟାଗ୍ ଗ୍ରେ
‘‘ମାଇଁ ୱିଶ୍ ୱାଜ୍- ‘ ଆଇ ମେ
ଗୋ ଟୁ ଏ ରିଲିଜିଅସ୍ ପ୍ଲେସ୍ ୱାନ୍ ଡ଼େ’ ।
‘କ୍ୟାରି ମୁଁ ଟୁ ବ୍ରିନ୍ଦାବନ୍’ ଆଇ ସେ
ଆଣ୍ଡ ଦେ ଓବେ ।’’

(୬) ‘ବଟ୍ କ୍ୟାଟ୍ ‘ନାମ୍ନୀ’
ଇଜ୍ଣ୍ଟ ଇଟ୍ ଫନି
ଟୁ ଗୋ ଟୁ ବ୍ରିନ୍ଦାବନ୍
ଇନ୍ ଏ ବ୍ୟାଗ୍ ଗନି ?’’

(୭) ‘‘ଆଇ ଥଟ୍ ଅଫ୍ ଗୋଇଙ୍ଗ୍ ବାଇ ଏ ବସ୍
ବଟ୍ ଦେ ଆର୍ ଅଲୱେଜ୍ ରସ୍ ।’’
“ ହ୍ୱାଟ୍ ଏବାଉଟ୍ ଟ୍ରେନ୍‌ସ୍‌ ମିସ୍ କ୍ୟାଟ୍ ?””

(୮) ‘‘ଟ୍ରେନସ୍ ଆଈ ହେଟ୍,
ଦେ’ଆର୍ ଅଲୱେଜ୍ ଲେଟ୍ ।’’

ଓଡ଼ିଆ ଅନୁବାଦ :
(୧) କୁକୁରଟିଏ ଥିଲା ଓ ବିଲେଇଟିଏ ଥିଲା ।
ଜଣେ ବହୁତ ପତଳା ଓ ଅନ୍ୟ ଜଣଙ୍କ ମୋଟା ।
ସେମାନଙ୍କ ମଧ୍ୟରୁ କେହି ନଥିଲେ ପୋଷା ।
କିନ୍ତୁ ବିଲେଇ ସର୍ବଦା ଏକ ଆସନ (ମସିଣା) ଉପରେ ବସେ,
ଏବଂ ଦାବିକରୁଥିଲା ଯେ ସେ ଖୁବ୍ ପ୍ରିୟ ପୋଷା ।
ଯେତେବେଳେ ମୋଟା ବିଲେଇଟି ଦିନେ ଦେଖୁଲା,
କୁକୁରଟିକୁ ତଡ଼ିଦିଆଯାଉଥିଲା ।

(୨) ସେ (ସ୍ତ୍ରୀ) କହିଲା, ‘ଏଣେ ତଡ଼ିଦିଆ ଯାଉଛି ଓ ତେଣେ ତଡ଼ିଦିଆ ଯାଉଛି,
କୌଣସି ସ୍ଥାନ ନାହିଁ ବିଶ୍ରାମ ନେବାକୁ ଏବଂ ଶୟନ କରିବାକୁ
କିନ୍ତୁ ଦେଖ ମୁଁ କିପରି ଏଠାରେ ବିଶ୍ରାମ ନେଉଛି
ମାଲିକର ବୁଢ଼ୀମା’ (ଜେଜେମା’) ପରି ।’’

(୩) କୁକୁରଟି ବିଲେଇକୁ ଦେଖୁଲା,
ତାଙ୍କ ଭାଗ୍ୟକୁ ଅଭିଶାପ ଦେଲା |
ଏବଂ ସେ ଦୂରକୁ ଚାଲିଗଲା ।
ଆଉ ଏକ ଦିନେ ସେହି ବାଟଦେଇ ଯାଉଥିବାବେଳେ
ଯେତେବେଳେ କୁକୁରଟି ଦେଖିଲା କେହି ଜଣେ ବୁଜୁଳି ବାନ୍ଧୁଛି

(୪) ବିଲେଇଟିକୁ ଅଖା ବସ୍ତାରେ
ଏବଂ ତାକୁ ଦୂରକୁ ନେଇଯାଉଛି,
ସେ କହିଲା, ‘‘ହେ,
ଆଜି କିପରି ଅଛି ???

(୫) ବିଲେଇ ଜୋର୍ ଦେଇ କହିଲା
ତା’ର ଧୂସର ଅଖା ବସ୍ତାରୁ
‘ମୋ’ର ଇଚ୍ଛା ଥିଲା – ମୁଁ ଯାଆନ୍ତି
ଏକ ଧାର୍ମିକ ସ୍ଥାନକୁ ଦିନେ ।
‘ମୋତେ ନେଇଯାଅ ବୃନ୍ଦାବନକୁ’ ମୁଁ କହେ
ଏବଂ ସେମାନେ ପାଳନ କରନ୍ତି ।’’

(୬) ‘‘କିନ୍ତୁ ବିଲେଇ ‘ନାନୀ’
ଏହା କୌତୂହଳମୟ ନୁହେଁ କି
ବୃନ୍ଦାବନ ଯିବା
ଏକ ଅଖା ବସ୍ତା ଭିତରେ ?’’

(୭) ‘‘ମୁଁ ଭାବୁଥୁଲି ଯିବାକୁ ଏକ ବସ୍‌ରେ
କିନ୍ତୁ ସେଗୁଡ଼ାକ ସର୍ବଦା ଭିଡ଼ ରହୁଛି ।’’
‘ବିଲେଇ ମହାଶୟ ରେଳଗାଡ଼ିଗୁଡ଼ିକ ବିଷୟରେ କ’ଣ ?’’

(୮) ‘‘ମୁଁ ରେଳଗାଡ଼ିକୁ ଘୃଣା କରେ,
ସେଗୁଡ଼ାକ ସର୍ବଦା ବିଳମ୍ବରେ ଯାତ୍ରା କରନ୍ତି ।’’

Comprehension Questions (ବୋଧମୂଳକ ପ୍ରଶ୍ନବଳୀ):

Question 1.
What is the poem about?
(କବିତାଟି କାହା ଉପରେ ଆଧାରିତ ?)
Answer:
The poem is about a cat and a dog.

Question 2.
Who is thin?
(କିଏ ପତଳା ଅଟେ ?)
Answer:
The dog is thin.

Question 3.
Who is fat?
(କିଏ ମୋଟା ଅଟେ ?)
Answer:
The cat is fat.

Question 4.
Are they pets?
(ସେମାନେ ପୋଷା ଥିଲେ କି ?)
Answer:
No, they are not pets.

Question 5.
Who said, ‘She was a pet’.
(କିଏ କିହଲା, ‘‘ସେ ଗୋଟିଏ ପୋଷା ଥିଲା ।’’)
Answer:
The cat said, ‘She was a pet’.

Question 6.
What did the fat cat see one day?
(ଦିନେ ମୋଟା ବିଲେଇଟି କ’ଣ ଦେଖିଲା ?)
Answer:
One day the fat cat saw the dog being chased away.

Question 7.
What did she say about herself?
(ସେ ତା’ ନିଜ ବିଷୟରେ କ’ଣ କହିଲା ?)
Answer:
She said about herself that she rested there like the owner’s grandmother.

Question 8.
What do you mean by ‘curse’?
(ତୁମେ ‘ଅଭିଶାପ ଦେବା’’ର ଅର୍ଥ କ’ଣ ବୁଝୁଛ ?)
Answer:
By ‘curse’ we mean wishing or expressing misfortune for another (here) scold (ଗାଳିଦେବା).

Question 9.
Did the dog feel good or bad about himself?
(କୁକୁରଟା ତା’ ନିଜ ବିଷୟରେ ଭଲ ବା ଖରାପ ଭାବିଲା କି ?)
Answer:
The dog felt bad about himself.

Question 10.
What did the dog see one day?
(ଦିନେ କୁକୁର କ’ଣ ଦେଖୁଲା ?)
Answer:
One day, the dog saw someone pack the cat in a sack and took her away.

Question 11.
What did the dog tell the cat?
(କୁକୁର ବିଲେଇକୁ କ’ଣ କହିଲା ?)
Answer:
The dog told the cat how that day was.

Question 12.
What did the cat reply?
(କ’ଣ ବିଲେଇଟି ଉତ୍ତର ଦେଲା ?)
Answer:
The cat replied that her wish was to go to a religious place one day. She told them to carry her to Brindaban and they obeyed.

Question 13.
Is she telling the truth?
(ସେ (ସ୍ତ୍ରୀ) ସତ୍ୟ କହୁଅଛି କି ?)
Answer:
No, she is not telling the truth.

Question 14.
Where was the man carrying the cat?
(ଲୋକଟି ବିଲେଇକୁ କେଉଁଆଡ଼େ ବୋହିନେଇ ଯାଉଥିଲା ?)
Answer:
The man was carrying the cat to leave her in a distant place.

Question 15.
What did the dog ask the cat?
(କୁକୁରଟି ବିଲେଇକୁ କ’ଣ ପଚାରିଲା ?)
Answer:
The dog asked the cat, “Isn’t it funny to go to Brindaban in a gunny bag ?”

Question 16.
What did the cat reply?
(ବିଲେଇଟି କ’ଣ ଉତ୍ତର ଦେଲା ?)
Answer:
The cat replied that she had thought of going by bus but they were always rushed.

Question 17.
Was she telling the truth?
(ସେ (ସ୍ତ୍ରୀ) ସତ୍ୟ କହୁଥିଲା କି ?)
Answer:
No, she was not telling the truth.

Question 18.
What did the dog ask the cat next?
(ତା’ପରେ କୁକୁର ବିଲେଇକୁ କ’ଣ ପଚାରିଲା ?)
Answer:
Next, the dog asked the cat, “What about trains Miss Cat”.

Question 19.
What did the cat reply?
(ବିଲେଇଟି କ’ଣ ଉତ୍ତର ଦେଲା ?)
Answer:
The cat replied, “Trains I hate as they are always late.”
(Or) The cat replied that she hated trains as they were always late.

Question 20.
Is she telling the truth?
(ସେ (ସ୍ତ୍ରୀ) କ’ଣ ସତ୍ୟ କହୁ ଅଛି କି ?)
Answer:
No, she is not telling the truth.

Question 21.
Who do you like – the cat or the dog?
(ତୁମେ କାହାକୁ ଭଲପାଅ – ବିଲେଇକୁ ବା କୁକୁରକୁ ?)
Answer:
I like the dog very much.

Session – 2 (ସୋପାନ – ୨):
III. Post-Reading (ପଢ଼ିସାରିବା ପରେ):

1. Visual Memory Development Technique (VMDT) :
(ଦୃଶ୍ୟ ସ୍ମୃତି ଉନ୍ନୟନ କୌଶଳ (VMDT))
Pictures: a cat, a dog, a person carrying a cat, and a man chasing a dog.
(ଛବି)
Whole Text: Which stanza is on ‘Cat Brindaban T ‘dog chased away’, (ସମଗ୍ର ବିଷୟବସ୍ତୁ) ‘bus’, ‘train’.

2. Comprehension Activities (ବୋଧମୂଳକ କାର୍ଯ୍ୟାବଳୀ) :
(a)MCQs- Choose the correct alternative (ସଠିକ୍ ବିକଳ୍ପଟି ବାଛ) :

Question 1.
Who was a pet?
(a) the dog
(b) the cat
(c) both of them
(d) none of them
Answer:
(d) none of them

Question 2.
Who loves whom?
(a) The cat loves the dog.
(b) The dog loves the cat.
(c) Both of them love each other.
(d) None of them love each other.
Answer:
(d) None of them love each other.

Question 3.
The man was taking away the cat ______________.
(a) because the cat asked him to do so.
(b) to Brindaban
(c) to leave her in a distant place.
(d) to another house where she can live happily.
Answer:
(c) to leave her in a distant place.

Question 4.
The cat does not like to go by train because ______________.
(a) trains are late.
(b) trains are rush.
(c) train journey is expensive.
(d) she wants to tell a lie to the dog.
Answer:
(a) trains are late.

(b) Who said? (କିଏ କହିଲା ?)
(i) Tam a loving pet.’
(ii) ‘Chased here, chased there.’
(iii) ‘Hey, how is today ?’
(iv) ‘Why in a gunny bag ?”
(v) ‘Trains I hate.’
(vi) ‘Bus always rush.’

Answer:
The cat
The cat
The dog
The dog
The cat
The cat

Session – 3 (ସୋପାନ – ୩)
3. Listening (ମନଦେଇ ଶୁଣିବା) :
(a) Your teacher will read aloud some of the words listed below. Tick those which s/he reads aloud.
(ତଳେ ତାଲିକାଭୁକ୍ତ କେତେକ ଶବ୍ଦକୁ ତୁମ ଶିକ୍ଷକ ବଡ଼ପାଟିରେ ପଢ଼ିବେ । ସେ ଯେଉଁ ଶବ୍ଦଗୁଡ଼ିକ ବଡ଼ ପାଟିରେ ପଢ଼ିବେ ଠିକ୍ ( ✓) ଚିହ୍ନ ଦେଇ ଚିହ୍ନାଅ ।)
late, bus, train, bag, obey, pack, fate

(b) Your teacher reads aloud the first stanza, listen and fill in the blank. Do not look at the poem when doing the task. After doing the task see the poem and correct, if there is any mistake.
(ତୁମ ଶିକ୍ଷକ ବଡ଼ପାଟିରେ ପ୍ରଥମ ପଦଟି ପଢ଼ିବେ, ଶୁଣ ଏବଂ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର । କାର୍ଯ୍ୟଟି କଲାବେଳେ କବିତାଟି ଦେଖନାହିଁ । କାର୍ଯ୍ୟଟି କରିସାରିବା ପରେ କବିତାଟି ଦେଖ ଏବଂ ଯଦି କିଛି ଭୁଲ୍ ଥାଏ ସଂଶୋଧନ କର ।)
There was a _____________ and there was a ______________. One is very _____________ and the other is _____________. Neither of ___________ is a _____________. But the cat ___________ sat on a _____________ and claimed____________ was a _____________.
(Question with Answer)
Answer:
There was a dog and there was a cat. One is very thin and the other is fat. Neither of them is a pet. But the cat always sat on a mat and claimed she was a loving pet.

4. Speaking (କହିବା):
(a) Chain-drill: “There was a dog and there was a cat.”
(ଶୃଙ୍ଖଳ-ଅଭ୍ଯାସ)
(b) Reading aloud: Your teacher reads aloud one line, and you repeat after him/her. (First three stanzas)
(ବଡ଼ପାଟିରେ ପଢ଼ିବା)
(c) Dialogue: Teacher vs. students, students vs. students, two students in front of the class.
(ସଂଳାପ)
Dog: What about the train, Miss Cat?
Cat: Trains I hate.
They are always late.

5. Vocabulary (ଶବ୍ଦ ଜ୍ଞାନ) :
Write at least two holy places, (pilgrimage)
ଅନୂନ ଦୁଇଟି ସ୍ଥାନର ନାମ ଲେଖ । (ତୀର୍ଥସ୍ଥାନ) ।
(Question With Answers)

Answer:

6. Usage (ପ୍ରୟୋଗ):
See the example of how two sentences are joined together to make them one.
(ଉଦାହରଣ ଦେଖ କିପରି ବାକ୍ୟ ଦୁଇଟି ଯୋଗ ହୋଇ ଗୋଟିଏ ବାକ୍ୟ ହୋଇଛନ୍ତି ।)
Example (ଉଦାହରଣ) : I thought. I’ll go by bus.
Answer: I thought of going by bus.

Join the following pairs of sentences in this way.
(ଏହିପରି ଭାବରେ ନିମ୍ନଲିଖ୍ ବାକ୍ୟ ଯୋଡ଼ାଗୁଡ଼ିକୁ ଯୋଗକର ।)

Question (i).
I thought. I’ll buy a shirt.
Answer:
I thought of buying a shirt.

Question (ii).
I thought. I’ll help my friend.
Answer:
I thought of helping my friend.

Question (iii).
I thought. I’ll do the job myself.
Answer:
I thought of doing the job myself.

Question (iv).
I thought. I’ll not go to school today.
Answer:
I thought of not going to school today.

Session – 4 (ସୋପାନ — ୪):
7. Writing (ଲେଖିବା) :
(a) Answer the following questions.(ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

Question (i).
What is the poem about?
(କବିତାଟି କାହା ବିଷୟରେ ଲେଖାଯାଇଛି ?)
Answer:
The poem is about a dog and a cat.

Question (ii).
Who is thin?
(କିଏ ପତଳା ?)
Answer:
The dog is thin.

Question (iii).
Who is fat?
(କିଏ ମୋଟା ଅଟେ ?)
Answer:
The cat is fat.

Question (iv).
Who tells lies?
(କିଏ ମିଛ କହେ ?)
Answer:
The cat tells lie.

Question (v).
Who do you like?
(ତୁମେ କାହାକୁ ଭଲପାଅ ?)
Answer:
I like the dog.

Session – 5 (ସୋପାନ – ୫):
(b) Let’s write the story.
(ଆସ ଆମେ ଗପଟିକୁ ଲେଖିବା ।)
This poem is like a story. Fill in the blanks and write the story of the poem.
(କବିତାଟି ଗୋଟିଏ ଗପ ପରି । ଶୂନ୍ୟସ୍ଥାନଗୁଡ଼ିକୁ ପୂରଣ କର ଏବଂ କବିତାର ଗପଟିକୁ ଲେଖ ।) (Question with Answer)
There was _____________. The dog was _______________. But ___________ was thin. One day some people chased the ___________. The ___________saw this and said , “Chased ____________________. No place to ___________ to ____________ .“ Another day the _________saw the cat. The ___________ was being taken by a _________. The dog asked,” Hey, ___________? The ______________replied,” I ‘m going to ____________________ The dog asked , “Why not by ___________ ? The _____________replied ,“ Bus is ___________ .“ The ___________ then ___________ “Why not by _____________ ?“ The cat replied, ___________ ”.
Answer:
There was a dog and a cat. The dog was thin. But the cat was fat. One day some people chased the dog. The cat saw this and said, “Chased here and chased there. No place to rest and to retire.” Another day the dog saw the cat. The cat was being taken by a man. The dog asked, “Hey, How is today? The cat replied, “I’m going to Brindaban.” The dog asked, “Why not by bus? The cat replied, “Bus is always rush.” The dog then asked. “Why not by train?” The cat replied, “I hate trains because they are always late.”

8. Mental Talk (ମାନସିକ କଥୋପକଥନ) :
“Chased here, chased there.”

9. Let Us Think (ଆସ ଆମେ ଭାବିବା):
You came to know from the poem that cats and dogs are traditional enemies. But see this picture from a newspaper and think.
(ତୁମେ କବିତାରୁ ଜାଣିପାରିଲ ଯେ ବିଲେଇମାନେ ଏବଂ କୁକୁରମାନେ ପାରମ୍ପରିକ ଶତ୍ରୁ ଅଟନ୍ତି । କିନ୍ତୁ ଏକ ଖବର କାଗଜରୁ ଏହି ଚିତ୍ରଟିକୁ ଦେଖ ଏବଂ ଚିନ୍ତା କର ।)

BSE Odisha 6th Class English Part – II

•  Mice Question Answer
• The Foolish Son in Law Question Answer
• A Nail Question Answer
• The Deaf Friend Question Answer
• The Cat and the Dog Question Answer
• A Special School Question Answer
• When I Grow Up Question Answer
• Raghunath Murmu Question Answer

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a)

Question 1.
ନିମ୍ନଲିଖୂତ ମନୋମିଆଲଗୁଡ଼ିକୁ ସାନରୁ ବଡ଼ ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇ ଲେଖ ।
1.4y³, √2y², -51, 7y⁸, -8y⁴, \(\frac{11}{13}\)y⁹, √3y
ସମାଧାନ:
ମନୋମିଆଲଗୁଡ଼ିକୁ ସାନରୁ ବଡ଼ ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇ ଲେଖିଲେ ହେବ –
-51, √3y, √2y², 1.4y³, -8y⁴, 7y⁸, ଓ \(\frac{11}{13}\)y⁹ .

Question 2.
ନିମ୍ନରେ ପ୍ରଦତ୍ତ ମନୋମିଆଲ୍‌ଗୁଡ଼ିକ ମଧ୍ୟରୁ ସଦୃଶ ମନୋମିଆଲ୍‌ଗୁଡ଼ିକୁ ବାଛି ପୃଥକ୍ ଭାବେ ଲେଖ ।
12x², -3x, \(\frac{1}{\sqrt{2}}\) x³, -5x², \(\frac{x}{7}\), 15, √3x³, 10x⁴, \(\frac{8}{11}\)
ସମାଧାନ:
(12x², -5x²), (-3x, \(\frac{x}{7}\)), (\(\frac{1}{\sqrt{2}}\) x³, √3x³), (15, \(\frac{8}{11}\))
ସଦୃଶ ମନୋମିଆଲ୍‌ଗୁଡ଼ିକୁ ବନ୍ଧନୀ ମଧ୍ଯରେ ରଖାଯାଇଛି ।

Question 3.
ନିମ୍ନସ୍ଥ ପ୍ରତ୍ୟେକ ପ୍ରକାର ପଲିନୋମିଆଲ୍‌ରୁ ଦୁଇଟି ଲେଖାଏଁ ଉଦାହରଣ ଦିଅ ।

(i) ଣୂନଘାତା ପଲିନୋମିଆଲ୍
ସମାଧାନ:
2, –\(\frac{1}{4}\)

(ii) ଏକପଦ ବିଶିଷ୍ଟ ଦ୍ୱିଘାତୀ ପଲିନୋମିଆଲ୍
ସମାଧାନ:
5x², -3x²

(iii) ଦୁଇପଦ ବିଶିଷ୍ଟ ତ୍ରିଘାତୀ ପଲିନୋମିଆଲ୍
ସମାଧାନ:
2x³ – 3x², \(\frac{4}{5}\) x³ + 5x

(iv) ତିନିପଦ ବିଶିଷ୍ଟ ଦ୍ୱିଘାତୀ ପଲିନୋମିଆଲ୍
ସମାଧାନ:
x² – 3x + 2, 3x² – 4x – 5
(ଦତ୍ତ ଉଦାହରଣ ବ୍ୟତୀତ ଅନ୍ୟ ଉଦାହରଣ ଦିଆଯାଇପାରେ ।)

Question 4.
ଯାେଗ କର

(i) 2y³ – 3y – 4, 2 – y³ + 5y
ସମାଧାନ:
(2y³ – 3y –  4) + (2 – y³ + 5y)
= (2y² – 3y –  4) + (-y³ + 5y + 2) (ପ୍ରତ୍ୟେକ ପଲିନୋମିଆଲ୍‌କୁ ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇବା)
= (2y³ –  y³) + (-3y + 5y) + (- 4 + 2) (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି)
= y³ + 2y – 2
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = y³ + 2y – 2

(ii) 3x⁴ – 2x³ – 5 + x – 5x², 3x³ + 2x² – x⁴ – x + 1
ସମାଧାନ:
(3x⁴ – 2x³ – 5 + x – 5x²) + (3x³ + 2x² – x⁴ – x + 1)
= (3x⁴ – 2x³ – 5x² + x – 5) + (-x⁴ + 3x³ + 2x² – x + 1) (ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇ)
= (3x⁴ – x⁴) + (-2x³ + 3x³) + (-5x² + 2x²) + (x – x) + (-5 + 1) (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି)
= 2x⁴ + x³ – 3x² + 0 – 4 = 2x⁴ + x³ – 3x² – 4
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 2x⁴ + x³ – 3x² – 4

(iii) \(\frac{3}{4}\) x² – \(\frac{4}{5}\) x – 3, \(\frac{1}{4}\) x² + \(\frac{4}{5}\) x + 2
ସମାଧାନ:
\(\left(\frac{3}{4} x^2-\frac{4}{5} x-3\right)+\left(\frac{1}{4} x^2+\frac{4}{5} x+2\right)\)
= \(\left(\frac{3}{4} x^2+\frac{1}{4} x^2\right)+\left(-\frac{4}{5} x+\frac{4}{5} x\right)\) + (-3 + 2) (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି)
= \(\frac{4}{4}\) x² + 0.x – 1 = x² – 1
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x² – 1

(iv) 2.1x³ + 3.2x² + 5 – 3x, 1.9x³ – 1.2x² + 2x – 1
ସମାଧାନ:
(2.1x³ + 3.2x² + 5 – 3x) + (1.9x³ – 1.2x² + 2x – 1)
= (2.1x³ + 3.2x² – 3x + 5) + (1.9x³ – 1.2x² + 2x – 1)
= (2.1x³ + 1.9x³) + (3.2x² – 1.2x²) + (-3x + 2x) + (5 – 1)
= 4x³ + 2x² – x + 4
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 4x³ + 2x² – x + 4

(v) \(\frac{1}{2}\)z³ – \(\frac{3}{2}\) z² + 6z, \(\frac{1}{2}\) z² – \(\frac{1}{2}\) z³ – 3z – 1, z³ + 2z² + 3z – 4
ସମାଧାନ:

(vi) 8x – 3xy + 2xyz, 2xy – 5x + 3xyz, xy – 3x + 4xyz
ସମାଧାନ:
(8x – 3xy + 2xyz) + (2xy – 5x + 3xyz) + (xy – 3x + 4xyz)
= (2xyz – 3xy + 8x) + (3xyz + 2xy – 5x) + (4xyz + xy – 3x)
= (2xyz + 3xyz + 4xyz) + (- 3xy + 2xy + xy) + (8x- 5x – 3x)
= 9xyz + 0 + 0 = 9xyz
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 9xyz

(vii) 5x² – 2xy + y², 4xy – 2y² – 3x², 4y² – xy – x²
ସମାଧାନ:
(5x² – 2xy + y²) + (4xy – 2y² – 3x²) + (4y² – xy + x²)
= (5x² – 2xy + y²) + (-3x² + 4xy – 2y²) + (-x² – xy + 4y²)
= (5x² – 3x² – x²) + (-2xy + 4xy – xy) + (y² – 2y² + 4y²)
= x² + xy + 3y²
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x² + xy + 3y²

Question 5.
ବିୟୋଗ କର :

(i) 6x³ – 13x² + 14 ରୁ -x³ + 2x – 7x² + 11
ସମାଧାନ:
(6x³ – 13x² + 14) – (-x³ + 2x – 7x² + 11)
= (6x³ – 13x² + 14) – (-x³ – 7x² + 2x + 11) (ଘାତାଙ୍କ କ୍ରମରେ ଲେଖିଲେ)
= (6x³ – 13x² + 14) + {- (-x³ – 7x² + 2x + 11)} [∵ a – b = a + (- b)]
= (6x³ – 13x² + 14) + (x³ + 7x² – 2x – 11)
= 6x³ + x³ – 13x² + 7x² – 2x + 14 – 11 (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି ସଜାଇ ଲେଖିଲେ)
= 7x³ – 6x² – 2x + 3
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 7x³ – 6x² – 2x + 3

(ii) t⁴ – 11 + 2t² – t³ ରୁ 2t³ – 8t² – 10
ସମାଧାନ:
(t⁴ – 11 + 2t² – t³) – (2t³ – 8t² – 10)
= (t⁴ – t³ + 2t² – 11) – (2t³ – 8t² – 10)
= (t⁴ – t³ + 2t² – 11) + {-(2t³ – 8t² – 10)}
= (t⁴ – t³ + 2t² – 11) + (-2t³ + 8t² + 10)
= t⁴ – t³ – 2t³ + 2t² + 8t² – 11 + 10 = t⁴ – 3t³ + 10t² – 1
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = t⁴ – 3t³ + 10t² – 1

(iii) \(\frac{12}{13}\) y² – \(\frac{5}{13}\) y³ – 15 ରୁ – \(\frac{1}{13}\) y² + \(\frac{8}{13}\) y³ + 20
ସମାଧାନ:

(iv) 2.5x³ – 7 – 3.5x² ରୁ 2.5x² + 1.5x³ + 8 – 2x
ସମାଧାନ:
(2.5x³ – 7 – 3.5x²) – (2.5x² + 1.5x³ + 8 – 2x)
= (2.5x³ – 3.5x² – 7) – (1.5x³ + 2.5x² – 2x + 8)
= (2.5x³ – 3.5x² – 7) + {-(1.5x³ + 2.5x² – 2x + 8)}
= (2.5x³ – 3.5x² – 7) + (-1.5x³ – 2.5x² + 2x – 8)
= 2.5x³ – 1.5x³ – 3.5x² – 2.5x² + 2x – 7 – 8
= x³ – 6x² + 2x – 15
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x³ – 6x² + 2x – 15

(v) x² – 2xy + 3y² ରୁ 2x² – xy – 2y²
ସମାଧାନ:
(x² – 2xy + 3y²) – (2x² – xy – 2y²)
= (x² – 2xy + 3y²) + {-(2x² – xy – 2y²)}
= (x² – 2xy + 3y²) + (-2x² + xy + 2y²)
= x² – 2x² – 2xy + xy + 3y² + 2y² = -x² – xy + 5y²
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = -x² – xy + 5y²

(vi) 2x² – 3xy – 4xy² ରୁ x² – xy – 2xy²
ସମାଧାନ:
(2x² – 3xy- 4xy²) – (x² – xy – 2xy²)
= (2x² – 3xy – 4xy²) + {-(x² – xy – 2xy²)}
= (2x² – 3xy – 4xy²) + (-x² + xy + 2xy²)
= 2x² – x² – 3xy + xy – 4xy² + 2xy² = x² – 2xy – 2xy²
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x² – 2xy – 2xy²

(vii) a – 3b + 2c ରୁ 3b – 7c + 2a
ସମାଧାନ:
(a – 3b + 2c) – (3b – 7c + 2a) = (a – 3b + 2c) – (2a + 3b – 7c)
= (a – 3b + 2c) + {-(2a + 3b – 7c)} = (a – 3b + 2c) + (-2a – 3b + 7c)
= a – 2a – 3b – 3b + 2c + 7c = -a – 6b + 9c
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = -a – 6b + 9c

(viii) \(\frac{1}{2}\) a + \(\frac{2}{3}\) b – \(\frac{3}{2}\) c ରୁ a – \(\frac{1}{3}\) b + \(\frac{1}{2}\) c
ସମାଧାନ:

Question 6.
ନିମ୍ନରେ ଦତ୍ତ ପଲିନୋମିଆଲ୍‌ଗୁଡ଼ିକର ଗୁଣଫଳ ସ୍ଥିର କରି ଗୁଣଫଳର ଘାତ ନିରୂପଣ କର ।

(i) 2x² – 3x + 5 ଓ x² + 8x + 2
ସମାଧାନ:
(2x² – 3x + 5)(x² + 5x + 2)
= 2x²(x² + 5x + 2) -3x(x² + 5x + 2) + 5(x² + 5x + 2) ( ବଣ୍ଠନ ନିୟମ)
= 2x⁴ + 10x³ + 4x² – 3x³ – 15x² – 6x + 5x² + 25x + 10 (ପୁନଃବଣ୍ଟନ ନିୟମ)
= 2x⁴ + (10x³ – 3x³) + (4x² – 15x² + 5x²) + (-6x + 25x) + 10 (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି ରଖୁ)
= 2x⁴ + 7x³ – 6x² + 19x + 10
∴ ଗୁଣଫଳର ଘାତ = 4 ।
∴ ଯଦି p(x) ଓ q(x) ଦୁଇଟି ପଲିନୋମିଆଲ୍ ହୁଏ, ତେବେ {p(x) × g(x)} ର ଘାତ = p(x)ର ଘାତ + q(x)ର ଘାତ ।

(ii) y³ – 5y² + 11y ଓ y⁵ – 20y⁴ + 17
ସମାଧାନ:
(y³ – 5y² + 11y)(y⁵ – 20y⁴ + 17)
= y³(y⁵ – 20y⁴ + 17) – 5y²(y⁵ – 20y⁴ + 17) + 11y(y⁵ – 20y⁴ + 17)
=y⁸ – 20y⁷ + 17y³ – 5y⁷ + 100y⁶ – 85y² + 11y⁶ – 220y⁵ + 187y
=y⁸ + (-20y⁷ – 5y⁷) + (100y⁶ + 11y⁶) – 220y⁵ + 17y³ – 85y² + 187y
= y⁸ – 25y⁷ + 111y⁶ – 220y⁵ + 17y³ – 85y² + 187y
∴ ଗୁଣଫଳର ଘାତ = 8 ।

(iii) (2x + 3) ଓ 5x² – 7x + 8
ସମାଧାନ:
(2x + 3)(5x² – 7x + 8)
= 2x(5x² – 7x + 8) + 3(5x² – 7x + 8) = 10x³ – 14x² + 16x + 15x² – 21x + 24
= 10x³ + (-14x² + 15x²) + (16x – 21x) + 24 = 10x³ + x² – 5x + 24
∴ ଗୁଣଫଳର ଘାତ = 3 ।

(iv) (x – 1), (7x – 9) ଓ 3x³ – 14x² + 8
ସମାଧାନ:
(x – 1)(7x – 9)(3x³ – 14x² + 8)
= {(x – 1)(7x – 9)} (3x³ – 14x² + 8) = {x(7x – 9) – 1(7x – 9)} (3x³ – 14x² + 8)
= (7x² – 9x – 7x + 9)(3x³ – 14x² + 8) = (7x² – 16x + 9)(3x³ – 14x² + 8)
= 7x² (3x³ – 14x² + 8) – 16x(3x³ – 14x² + 8) + 9(3x³ – 14x² + 8)
= 21x⁵ – 98x⁴ + 56x² – 48x⁴ + 224x³ – 128x + 27x³ – 126x² + 72
= 21x⁵ + (- 98x⁴ – 48x⁴) + (224x³ + 27x³) + (56x² – 126x²) – 128x + 72
= 21x⁵ – 146x⁴ + 251x³ – 70x² – 128x + 72
∴ ଗୁଣଫଳର ଘାତ = 5 ।

(v) (x² + y²) ଓ (x⁴ – x²y² + y⁴)
ସମାଧାନ:
(x² + y²)(x⁴ – x²y² + y⁴)
= x² (x⁴ – x²y² + y⁴) + y² (x⁴ – x²y² + y⁴) = x⁶ – x⁴y² + x⁷y⁴ + x⁴y² – x²y⁴ + y⁶
= x⁶ + (-xy + x⁴y²) + (x²y⁴ – x²y⁴) + y⁶ = x⁶ + 0 + 0 + y⁶ = x⁶ + y⁶
∴ ଗୁଣଫଳର ଘାତ = 6 ।

(vi) (2x + 3y), (2x – 3y) ଓ (4x² + 9y²)
ସମାଧାନ:
(2x + 3y)(2x – 3y)(4x² + 9y²) = {(2x + 3y)(2x – 3y)} (4x² + 9y²)
= {2x(2x – 3y) + 3y(2x – 3y)} (4x² + 9y²)
= (4x² – 6xy + 6xy – 9y²)(4x² + 9y²) = (4x² – 9y²)(4x² + 9y²)
= 4x² (4x² + 9y²) – 9y² (4x² + 9y²) = 16x⁴ + 36x²y² – 36x²y² – 81y⁴
= 16x⁴ + 0 – 81y⁴ = 16x⁴ – 81y⁴
∴ ଗୁଣଫଳର ଘାତ = 4 ।

Question 7.
ଭାଗଫଳ ଓ ଭାଗଶେଷ ନିରୂପଣ କର ।

(i) (x³ – 1) + (x – 1)
ସମାଧାନ:

(ii) (-81y² + 64) + (8 – 9y)
ସମାଧାନ:

(iii) (2x³ – 7x² – x + 2) + (x² – 3x – 2)
ସମାଧାନ:

(iv) (x³ – 14x² + 37x – 26) + (x – 2)
ସମାଧାନ:

(v) (t³ – 6t² + 11t – 6) + (t² – 5t + 6)
ସମାଧାନ:

(vi) (8a² – 34ab + 21b²) + (4a + 3b)
ସମାଧାନ:

(vii) (16xy² – 21x²y + 9X³ – 4y3) + (x – y)
ସମାଧାନ:

(viii) (x⁴ + x²y² + y4) + (x² – xy + y²)
ସମାଧାନ:

ଭାଜ୍ୟ = ଭାଜକ x ଭାଗଫଳ + ଭାଗଶେଷ Euclidian Algorithmର ପ୍ରୟୋଗରେ ଭାରକ୍ରିୟାର ସତ୍ୟତା ନିରୂପଣ କରାଯାଇଥାଏ ।

Question 8.
ଯଦି p(x) = 3x³ – 6x² + 2 ଏବଂ q(x) = 2x² – 5x + 1 ତେବେ

(i) 2p(x) – 5q(x)
ସମାଧାନ:
ଯଦି p(x) = 3x³ – 6x² + 2 ଏବଂ q(x) = 2x² – 5x + 1
2p(x) – 5q(x) = 2(3x³ – 6x² + 2) – 5(2x² – 5x + 1)
= 6x³ – 12x² + 4 – 10x² + 25x – 5
= 6x³ – 12x² – 10x² + 25x + 4 – 5 = 6x³ – 22x² + 25x – 1

(ii) 4p(x) + 3q(x) ବମାନ ସ୍ଥିର କରା
ସମାଧାନ:
ଯଦି p(x) = 3x³ – 6x² + 2 ଏବଂ q(x) = 2x² – 5x + 1
4p(x) + 3q(x) = 4(3x³ – 6x² + 2) + 3(2x² – 5x + 1)
= 12x³ – 24x² + 8 + 6x² – 15x + 3
= 12x³ – 24x² + 6x² – 15x + 8 + 3 = 12x³ – 18x² – 15x + 11

Question 9.
ଯଦି p(x) = 2x³ + 3x + 5 ଏବଂ q(x) = x² + 4x + 1 ଓ r(x) = x – 1 ହୁଏ ତେବେ ଦର୍ଣ।ଅ ଯେ,

(i) p(x) × q(x) = q(x) × p(x)
ସମାଧାନ:
ଯଦି p(x) = 2x³ + 3x + 5 ଏବଂ q(x) = x² + 4x + 1 ଓ r(x) = x – 1
ବାମପାର୍ଶ୍ଵ = p(x) × q(x) = (2x³ + 3x + 5)(x² + 4x + 1)
= 2x³ (x² + 4x + 1) + 3x(x² + 4x + 1) + 5(x² + 4x + 1)
= 2x⁵ + 8x⁴ + 2x³ + 3x³ + 12x² + 3x + 5x² + 20x + 5
= 2x⁵ + 8x⁴ + 5x³ + 12x² + 5x² + 3x + 20x + 5
= 2x⁵ + 8x⁴ + 5x³ + 17x² + 23x + 5
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = q(x) × p(x) = (x² + 4x + 1)(2x³ + 3x + 5)
= x² (2x³ + 3x + 5) + 4x (2x³ + 3x + 5) + 1(2x³ + 3x + 5)
= 2x⁵ + 3x³ + 5x² + 8x⁴ + 12x² + 20x + 2x³ + 3x + 5
= 2x⁵ + 8x⁴ + 3x³ + 2x³ + 5x² + 12x² + 20x + 3x + 5
= 2x⁵ + 8x⁴ + 5x³ + 17x² + 23x + 5 (ପଲିନୋମିଆଲ୍ ଦ୍ଵୟର ଗୁଣନ କ୍ରମବିନିମୟୀ ।)
∴ ବାମପାର୍ଶ୍ଵ = ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ (ପ୍ରମାଣିତ)

(ii) p(x) × {(q(x) + r(x)} = p(x) . q(x) + p(x) . r(x)
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = P(x) × {q(x) + r(x)}
= (2x³ + 3x + 5) x {(x² + 4x + 1) + (x – 1)} = (2x³ + 3x + 5) + (x² + 4x + 1 + x – 1)
= (2x³ + 3x + 5)(x² + 5x) = 2x³ (x² + 5x) + 3x(x² + 5x) + 5(x² + 5x)
= 2x⁵ + 10x⁴ + 3x³ + 15x² + 5x² + 25x = 2x⁵ + 10x⁴ + 3x³ + 20x² + 25x
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = P(x) . q(x) + p(x) . r(x)
= (2x³ + 3x + 5)(x² + 4x + 1) + (2x³ + 3x + 5)(x – 1)
= 2x³ (x2 + 4x + 1) + 3x(x² + 4x + 1) + 5(x² + 4x + 1)+ 2x³ (x – 1) + 3x(x – 1) + 5(x – 1)
= 2x⁵ + 8x⁴ + 2x³ + 3x³ + 12x² + 3x + 5x² + 20x + 5 + 2x⁴ – 2x³ + 3x² – 3x + 5x – 5
= 2x⁵ + 8x⁴ + 2x⁴ + 2x³ + 3x³ – 2x³ + 12x² + 5x² + 3x² + 3x + 20x – 3x + 5x + 5 – 5
= 2x⁵ + 10x⁴ + 3x³ + 20x² + 25x
∴ ବାମପାର୍ଶ୍ଵ = ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ (ପ୍ରମାଣିତ)
(ପଲିନୋମିଆଲ୍ ଦ୍ଵୟର ଗୁଣନ କ୍ରମବିନିମୟୀ ।)

Question 10.
ସରଳ କର :

(i) (x² – 3x + 5) + (2x² – x – 2) – (3x² + 7x – 3)
ସମାଧାନ:
(x² – 3x + 5) + (2x² – x – 2) – (3x² + 7x – 3)
= x² – 3x + 5 + 2x² – x – 2 – 3x² – 7x + 3
= x² + 2x² – 3x² – 3x – x – 7x + 5 – 2 + 3
= 0 – 11x + 6 = -11x + 6

(ii) (x² – xy + 2y²) – (2x² + 4xy + 3y²) + (4x² – 2xy – y²)
ସମାଧାନ:
(x² – xy + 2y²) – (2x² + 4xy + 3y²) + (4x² – 2xy – y²)
= x² – xy + 2y² – 2x² – 4xy – 3y² + 4x² – 2xy – y²
= x² – 2x² + 4x² – xy – 4xy – 2xy + 2y² – 3y² – y²
= 3x² – 7xy – 2y²

(iii) (x + b + c) (a – b + c) – (a + b – c) (a – b – c)
ସମାଧାନ:
(a + b + c)(a – b + c) – (a + b – c)(a – b – c)
= [a(a – b + c) + b(a – b + c) + c(a – b + c)] – [a(a – b – c) + b(a – b – c) – c(a – b – c)]
= (a² – ab + ca + ab – b² + bc + ca –  bc + c²) – (a² – ab – ac + ab – b² – bc – ca + bc + c²)
= (a² – b² + c² – ab + ab + ca + ca + bc – bc) – (a² – b² + c² – ab + ab – ac – ac – bc + bc)
= (a² – b² + c² + 2ca) – (a² – b² + c² – 2ca) = a² – b² + c² + 2ca – a² + b² – c² + 2ca
= a² – a² – b² + b² + c² – c² + 2ca + 2ca = 4ca

Odisha State Board BSE Odisha 8th Class English Solutions Lesson 2 The Thief and the Tiger Textbook Exercise Questions and Answers.

Class 8th English Chapter 2 The Thief and the Tiger Question Answers BSE Odisha

The Thief and the Tiger Class 8 Questions and Answers

Session – 1
Pre-Reading (ପ୍ରାକ୍-ପଠନ):

→ Man rides a horse or an elephant or a donkey. Does he ever ride a lion or a tiger or a bear? Why? See the picture below. What do you see? A man is riding a tiger. Is it possible? When? Where? Let’s read the story and see how.

ଲୋକଟି ଗୋଟିଏ ଘୋଡ଼ା, କିମ୍ବା ହାତୀ କିମ୍ବା ଗଧ ଉପରେ ଚଢ଼ିଛି । ସେ କେବେ ସିଂହ, କିମ୍ବା ବାଘ କିମ୍ବା ଭାଲୁ ଉପରେ ଚଢ଼ିଥାଏ କି ? କାହିଁକି ? ତଳେ ଥ‌ିବା ଚିତ୍ରଟିକୁ ଦେଖ । କ’ଣ ଦେଖୁଛ ? ଗୋଟିଏ ଲୋକ ବାଘ ଉପରେ ଚଢ଼ିଛି କେତେବେଳେ ? କେଉଁଠି ? ଆସ ଗପଟି ପଢ଼ି ସବୁକଥା ଜାଣିବା ।

II. While Reading

Text

• SGP – I
• Read paragraphs 1-3 silently and answer the questions that follow.
  (୧ମରୁ ୩ୟ ଅନୁଚ୍ଛେଦ ପର୍ଯ୍ୟନ୍ତ ପାଠକରି ନୀରବରେ ପ୍ରଦତ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

1. Once …………………………………………… in the stable.
ଥରେ ଜଣେ ରାଜା ଥିଲେ । ସେ ତାଙ୍କର ବଳବାନ ଓ ଦ୍ରୁତଗାମୀ ଅଶୁମାନଙ୍କ ପାଇଁ ଖୁବ୍ ପ୍ରସିଦ୍ଧ ଥିଲେ । ସେ ସବୁଠାରୁ ଦକ୍ଷ ଶକ୍ତିଶାଳୀ ଘୋଡ଼ାମାନଙ୍କୁ ଆଣି ତାଙ୍କ ଘୋଡ଼ାଶାଳରେ ରଖୁଥିଲେ । ଦିନେ ଗୋଟିଏ ଚୋର ତାଙ୍କର ଗୋଟିଏ ଘୋଡ଼ାକୁ ଚୋରି କରିନେବାକୁ ଇଚ୍ଛା ପ୍ରକାଶ କଲା । ଗୋଟିଏ ବାଘ ଚୋରଟିର ଏ ଯୋଜନା ବିଷୟରେ ଜାଣିବାକୁ ପାଇଲା । ସେ ସେହି ଚୋରଟିର ମାଂସ ଖାଇବାକୁ ଚିନ୍ତାକଲା । ଏଣୁ ସେଇ ରାତିରେ ବାଘଟି ରାଜାଙ୍କ ଘୋଡ଼ାଶାଳରେ ଏକ ନିରାପଦ ସ୍ଥାନରେ ଛପିରହିଲା । ବାଘଟି ଘୋଡ଼ାମାନଙ୍କ ସହ ନୀରବରେ ଶାନ୍ତ ଅବସ୍ଥାରେ ଛିଡ଼ା ହୋଇ ରହିଲା । ସତେଯେମିତି ସେ ଘୋଡ଼ାଶାଳର ଅନ୍ୟ ଘୋଡ଼ାମାନଙ୍କ ପରି ଗୋଟିଏ ଘୋଡ଼ା ।

2. After sometime …………………………………………………… rode on it.
କିଛି ସମୟ ପରେ ଚୋରଟି ଘୋଡ଼ାଶାଳରେ ପ୍ରବେଶକଲା । ଘୋଡ଼ାଶାଳଟି ଅନ୍ଧାର ଥିଲା । ସେ ପ୍ରତ୍ୟେକ ଘୋଡ଼ାର ପିଠିରେ ହାତମାରି କେଉଁଟି ସବୁଠୁ ଶକ୍ତିଶାଳୀ ଘୋଡ଼ା ତାହା ପରୀକ୍ଷା କରିବାକୁ ଲାଗିଲା । ଶେଷରେ ସେ ବାଘର ପିଠିରେ ହାତ ପକାଇଲା । ଏଇଟି ସବୁଠୁ ଭଲ ଘୋଡ଼ା ବୋଲି ଚିନ୍ତାକଲା ଏବଂ ସେଇଟିକୁ ଘୋଡ଼ାଶାଳର ବାହାରକୁ ଆଣିଲା । ତା’ପରେ ସେ ବାଘର ପାଟିରେ ଲଗାମ ବାନ୍ଧିଲା ଏବଂ ତା’ଉପରେ ଚଢ଼ିଗଲା ।

3. The tiger ……………………………………… anything in the dark.
ବାଘର ଆଗରୁ ଏପରି କୌଣସି ଅଭିଜ୍ଞତା ନଥିଲା । ସେ ଚୋରକୁ ଅତି ଶକ୍ତିଶାଳୀ ବ୍ୟକ୍ତି ବୋଲି ଭାବିଲା । ସେ ଚୋରଟିକୁ ଭୟଙ୍କର ଭାବରେ ଡରିଯାଇଥିଲା । ଏଣୁ ଅତି ଦ୍ରୁତଗତିରେ ଦୌଡ଼ିବାକୁ ଲାଗିଲା । ଚୋରଟିର ମଧ୍ୟ ଏପରି ଏକ ପ୍ରାଣୀ ଉପରେ ଚଢ଼ିବାର ଅଭିଜ୍ଞତା ନଥିଲା । ସେ ଏହାକୁ ଅତି ଶକ୍ତିଶାଳୀ ଘୋଡ଼ା ବାଛି ଆଣିପାରିଛି ବୋଲି ଚିନ୍ତାକଲା । ସେ ଜାଣି ନଥିଲା ଯେ ସେ ଏକ ବାଘ ଉପରେ ଚଢ଼ିଛି କାରଣ ସ୍ଥାନଟି ସମ୍ପୂର୍ଣ୍ଣ ଅନ୍ଧକାର ଥିଲା ।

Word Meaning

famous : well-known to many people I renowned (ପ୍ରସିଦ୍ଧ, ବିଖ୍ୟାତ)
swift : fast moving (କ୍ଷିପ୍ର / ଶୀଘ୍ର ଗତି କରୁଥିବା)
stable : house for horses (ଘୋଡ଼ାଶାଳ)
steal : the act of taking something from someone unlawfully (ଚୋରିକରିବା)
plan : design / scheme (ଯୋଜନା)
flesh : meat (ମାଂସ)
hid : ଲୁଚାଇ

silently : without speaking / without making a sound (ନୀରବରେ )
touched: be in direct physical contact (ଛୁଇଁବା)
bridle: leather band put on the head of a horse to control its movement/reins
experience: the accumulation of knowledge or skills that results
from direct participation in events or activities (ଅନୁଭୂତି)
powerful : having great influence (କ୍ଷମତାଶାଳୀ / ବଳଶାଳୀ)
terribly : horribly / causing fear (ଭୟଙ୍କର ଭାବରେ)
imagine : fancy / think / suppose (କଳ୍ପନାକରିବା)

Comprehension Questions and Answers: (ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର)

Question 1.
What was the king famous for?
(ରାଜା କେଉଁଥୂପାଇଁ ପ୍ରସିଦ୍ଧ ଥିଲେ ?)
Answer:
The king was famous for his strong and swift horses.

Question 2.
What did the thief plan to do?
(ଚୋରଟି କ’ଣ କରିବାପାଇଁ ଯୋଜନା କଲା ?)
Answer:
The thief wanted to steal a horse.

Question 3.
Why did the tiger hide in the stable?
(ବାଘଟି ଘୋଡ଼ାଶାଳରେ ଛପିରହିଥିଲା କାହିଁକି ?)
Answer:
The tiger came to know about the thief’s plan and thought of eating the thief s flesh.

Question 4.
Why did the thief touch the back of each horse?
(ଚୋରଟି କାହିଁକି ପ୍ରତି ଘୋଡ଼ା ପିଠିରେ ହାତ ମାରୁଥିଲା ?)
Answer:
The thief touched the back of each horse to steal the best one.

Question 5.
Why did he think the tiger to be the best horse ?
(ସେ ବାଘକୁ କାହିଁକି ସର୍ବଶ୍ରେଷ୍ଠ ଘୋଡ଼ା ବୋଲି ଭାବୁଥିଲା ?)
Answer:
He thought the tiger was the best horse because he felt the tiger’s back was different from the other horses.

Question 6.
How did he ride on it?
(ସେ କିପରି ଏହା ଉପରେ ଚଢ଼ିଲା ?)
Answer:
He rode on the tiger putting a bridle on its mouth thinking it was a horse.

Question 7.
He did not know that he was riding a tiger. Why?
(ସେ ଜାଣି ନଥୁଲା ଯେ ସେ ଏକ ବାଘ ଉପରେ ଚଢ଼ିଥିଲା, ଏହାର କାରଣ କ’ଣ ?)
Answer:
He didn’t know that he was riding a tiger, because there was darkness inside the stable.

Question 8.
Where did the tiger run into?
(ବାଘ କେଉଁଠାକୁ ଦୌଡ଼ି ପଳାଇଲା ।)
Answer:
The tiger ran into the forest.

Session – 2

• SGP – 2
• Read paragraph 4 silently and answer the questions that follow.
  (ଚତୁର୍ଥ ଅନୁଚ୍ଛେଦଟି ପାଠକରି (ନୀରବରେ) ପ୍ରଦତ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

4. The day…………………………………… as it could.
ରାତି ପାହିଲା । ଅନ୍ଧକାର ଦୂରୀଭୂତ ହେଲା । ସେତେବେଳେ କେବଳ ସେ ଜାଣିପାରିଲା ଯେ ସେ ଭୁଲବଶତଃ ଗୋଟିଏ ବାଘ ଉପରେ ଚଢ଼ିଛି । ସେ ଭୟଭୀତ ହୋଇପଡ଼ିଲା । ବାଘଟି ମଧ୍ୟ ଭୟଭୀତ ହୋଇ ଅଧିକ ଦ୍ରୁତଗତିରେ ଦୌଡୁଥାଏ । ଚୋରଟି କ’ଣ କରିବ, ସ୍ଥିର କରିପାରିଲା ନାହିଁ । ସେ ପ୍ରାୟ ଅଚେତ ହେବାଭଳି ଅନୁଭବ କଲା । ଦୌଡୁଥିବାବେଳେ ବାଘ ଗୋଟିଏ ଗଛଦେଇ ଦୌଡ଼ୁଥିଲା । ଏହି ସମୟରେ ଚୋରଟି ଗଛର ଡାଳକୁ ଧରି ଗଛ ଉପରେ ଚଢ଼ିଗଲା । ବାଘ ଖୁସି ଅନୁଭବ କଲା । କାରଣ ସେ ଲୋକଟି ପାଇଁ ସେ ଅତ୍ୟଧ୍ୱ ଭୟଭୀତ ହୋଇପଡ଼ିଥିଲା । ପାରୁପର୍ଯ୍ୟନ୍ତ ଦ୍ରୁତ ବେଗରେ ବାଘଟି ବଣମଧ୍ୟକୁ ଦୌଡ଼ିଲା ।

Word Meaning

dawn : day break / beginning of the day (ପ୍ରଭାତ / ଉଷା)
disappear : vanish from sight (ଅନ୍ତର୍ଦ୍ଧାନ ହୋଇଯିବା / ଅଦୃଶ୍ୟ ହୋଇଯିବା)
frightened : scared / intense fear (ଭୟଭୀତ କରାଇବା)
fast : swift (ଦୃତ / ଦ୍ରୁତଗାମୀ)
faint : to feel weak and lose consciousness (ଅଚେତ ହୋଇଯିବା)
passed : to cross (ଅତିକ୍ରମ କରିବା)
branch : part of a tree (ଶାଖା)
climb : ascend (ଚଢ଼ିବା)

Comprehension Questions and Answers: (ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର)

Question 1.
When did the thief come to know that he was riding a tiger?
(ଚୋରଟି କେତେବେଳେ ଜାଣିପାରିଲା ଯେ ସେ ଏକ ବାଘ ଉପରେ ଚଢ଼ିଛି ?)
Answer:
When the day dawned and darkness disappeared the thief came to know that he was riding a tiger.

Question 2.
How did he save himself?
(ସେ କିପରି ନିଜକୁ ରକ୍ଷାକଲା ?)
Answer:
When the tiger ran by a tree beside the road the thief caught hold of one of the branches of the tree and climbed up.

Question 3.
Why was the tiger happy?
(ବାଘ କାହିଁକି ଖୁସି ହୋଇଗଲା ?)
Answer:
The tiger was terribly afraid of the rider. So when the rider climbed up the tree he was happy.

• SGP – 3 (Text book page No. 34)
• Read paragraphs 5 – 8 silently and answer the questions that follow.
  (୫ମ ଠାରୁ ଅଷ୍ଟମ ଅନୁଚ୍ଛେଦ ପର୍ଯ୍ୟନ୍ତ ନୀରବରେ ପାଠକରି ପ୍ରଦତ୍ତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

5. After…………………………………………. dead body.
କିଛି ସମୟ ପରେ ଚୋରଟି ଗଛ ଉପରୁ ଓହ୍ଲାଇ ଗଛତଳେ ବିଶ୍ରାମ ନେଲା । ଅତ୍ୟଧ‌ିକ ଭୟ ଓ କ୍ଳାନ୍ତ ଅନୁଭବ କରିଥିବାରୁ ସେ ସେଠାରେ ଶୋଇପଡିଲା । ଗଭୀର ନିଦ୍ରା ଯୋଗୁଁ ସେ ଗୋଟିଏ ମୃତ ଶବଭଳି ଜଣାପଡୁଥିଲା । ସେହି ବାଟଦେଇ ଗୋଟିଏ ଗଧ୍ଵ ଯାଉଥିଲା । ସେ ଲୋକଟିକୁ ଏକ ମୃତ ଶବ ଭାବି ତା’ର ମାଂସ ଖାଇବାକୁ ଇଚ୍ଛାକଲା । ସେ ମନକୁମନ କହିଲା, ମୁଁ କି ଭାଗ୍ୟବାନ, ଏଇ ଶବଟି ମୋର ସପ୍ତାହେରୁ ଅଧିକ କାଳ ଖାଦ୍ୟ ହୋଇପାରିବ । କିନ୍ତୁ କେହିଜଣେ ଏହାକୁ ବଣଭିତରକୁ ଟାଣିନେବାପାଇଁ ମୋତେ ସାହାଯ୍ୟ କରିବା ଦରକାର ।

6. Thinking so, ………………………………….. with a rope”.
ଏଇକଥା ଚିନ୍ତା କରି ଗଧ୍ଵ ଆଉ ଅନ୍ୟ ଗୋଟିଏ ପ୍ରାଣୀର ସାହାଯ୍ୟ ପାଇଁ ବଣ ଭିତରକୁ ଗଲା ଏବଂ ସେଇ ବାଘଟି ସହିତ ତା’ର ସାକ୍ଷାତ ହେଲା । ସେ ବାଘକୁ କହିଲା, ‘ବାଘ ମହାଶୟ’ ଗୋଟିଏ ମଣିଷର ଶବକୁ ଟାଣି ଆଣିବାରେ ମୋତେ ସାହାଯ୍ୟ କରିବ କି ? ମୁଁ ଏହାର ଅଧା ତୁମକୁ ଦେବି । ‘ଗତ ରାତିରେ ଘଟିଥିବା ଘଟଣାର ଅନୁଭୂତିରୁ ବାଘ କହିଲା, ‘ତୁମେ ମୋତେ ଠକିଦେବ ନାହିଁ ତ ? ମୋତେ ଏକା ଛାଡ଼ିଦେଇ ତୁମେ ଦୌଡ଼ି ପଳାଇଯିବନି ତ ? ‘ଗଧ୍ଵ କହିଲା, ‘ଆମେ ଦୁହେଁ ଦିହିଁଙ୍କୁ ଗୋଟିଏ ଦଉଡ଼ିରେ ବାନ୍ଧିଦେବା, ତା’ହେଲେ କେହି କାହାକୁ ଛାଡ଼ି ପଳାଇ ଯାଇପାରିବା ନାହିଁ ।’’

7. The wolf ……………………………………. wolf died.
ଗଧ୍ଵ ଓ ବାଘ ଦୁହେଁ ଦୁହିଁଙ୍କୁ ଗୋଟିଏ ଦଉଡ଼ିରେ ବାନ୍ଧି ସନ୍ତର୍ପଣରେ ଶବ ପାଖକୁ ଚାଲିଲେ । ଚୋରଟି ନିଦରୁ ଉଠିଯାଇଥିଲା । ସେ ଏମାନଙ୍କ ଆସିବା ଜାଣିପାରି ଭୟରେ ଚିତ୍କାର କରି କହିଲା, ‘ହଇରେ ବାଘ ତୁ ପୁଣି ଆସିଛୁ ?’’ ଏବେ ବାଘଟି ସେ ଚୋରକୁ ପୁଣି ଦେଖ୍ ଭୟଭୀତ ହୋଇପଡ଼ିଲା ଏବଂ ଗଧୂକୁ ଘୋଷାରିନେଇ ଯେତେ ପାରେ ସେତେ ଜୋର୍‌ରେ ଦଉଡ଼ିବାକୁ ଲାଗିଲା । ବିଚରା ଗଧୂଟି ବାଟରେ ମରିଗଲା ।

8. Since …………………………………………………… that day.
ସେବେଠୁ ବାଘ ଆଉ ମଣିଷ ମାଂସ ନ ଖାଇବା ପାଇଁ ପ୍ରତିଜ୍ଞାକଲା । ଚୋରଟି ମଧ୍ୟ ରକ୍ଷା ପାଇଯାଇଥିବାରୁ ଖୁସି ହେଲା ଏବଂ ସେ ମଧ୍ୟ ଆଉ ଚୋରି ନ କରିବାପାଇଁ ପ୍ରତିଜ୍ଞାକଲା ।

Word Meaning

tired: of strength or energy (କ୍ଳାନ୍ତ)
wolf: a wild carnivorous animal (ଗଧୂ)
luck : destiny/fate / fortune (ଭାଗ୍ୟ)
last : continue to stay (ଚାଲୁ ରଖୁବା | ତିଷ୍ଠିବା)
drag : to pull by force (ଘୋଷାରିଘୋଷାରି ଟାଣିନେବା)
suspicious: a doubtful condition, feeling that something is wrong (ସନ୍ଦେହପରାୟଣ )
cheat: betray/deceive (ଠକିବା)
leave: to give up/abandon (ଛାଡ଼ିବା)
alone : lonely (ଏକୁଟିଆ)
suggest : to give opinion (ମତାମତ ଦେବା)
tie : to tag/join (ବାନ୍ଧିବା / ସଂଯୁକ୍ତ କରିବା)
rope : twisted cord (ଦଉଡ଼ି / ରଜ୍ଜୁ)
awake: rise/get up (ଉଠିପଡ଼ିବା)
footsteps: found of feet/sound, of a person walking (ପାଦ ଶବ୍ଦ)
promised : to make a promise / assure (ପ୍ରତିଜ୍ଞାକରିବା)
desire: want/like to get (ଇଚ୍ଛା).
give up: to avoid/abandon (ଛାଡ଼ିଦେବା )
stealing: to take others without knowledge (ଚୋରି)

Comprehension Questions and Answers: (ସଂକ୍ଷିପ୍ତ ପ୍ରଶ୍ନୋତ୍ତର)

Question 1.
Why did the thief fall fast asleep?
(ଚୋରଟି ଗଭୀର ନିଦ୍ରାରେ ଶୋଇଁପଡ଼ିଲା କାହିଁକି ?)
Answer:
The thief fell fast asleep because he was afraid and tired.

Question 2.
Who saw him ? What was his plan ?
(କିଏ ତାକୁ ଦେଖୁଲା ? କ’ଣ ସେ ଚିନ୍ତାକଲା ?)
Answer:
A wolf saw him. He thought he as dead and planned to use him as his food for more than a week long.

Question 3.
What did he want the tiger to do?
(ସେ ବାଘକୁ କଣ କରିବାପାଇଁ ଚାହିଁଲା ?)
Answer:
He wanted the tiger to help him to drag the dead body into the forest.

Question 4.
What did the tiger say?
(ବାଘ କ’ଣ କହିଲା ?)
Answer:
The tiger asked him if he was going to cheat him or not.

Question 5.
“Won’t you run away leaving me alone ?” Who said this?
(ତୁ ମୋତେ ଏକୁଟିଆ ଛାଡ଼ି ପଳାଇଯିବୁନି ତ ? ଏକଥା କିଏ କହିଲା ?)
Answer:
“Won’t you run away leaving me alone ?” The tiger said this to the wolf.

Question 6.
What did the wolf say?
(ଗଧୂଟି କ’ଣ କହିଲା ?)
Answer:
The wolf suggested to the tiger that they would tie each other with a rope so that no one of them could run away leaving another.

Question 7.
What awoke the thief?
(ଚୋରଟି କାହିଁକି ଉଠିପଡ଼ିଲା ?)
Answer:
The footsteps of the tiger and the wolf awoke the thief.

Question 8.
Why did the tiger run away?
(ବାଘ କାହିଁକି ଦୌଡ଼ି ପଳାଇଲା ?)
Answer:
The tiger ran away frightened of the thief.

Question 9.
How did the wolf die?
(ଗଧୂ ମଲା କିପରି ?)
Answer:
The wolf died being dragged by the tiger as they tied each other with a rope.

Question 10.
What did the tiger promise?
(ବାଘ କ’ଣ ପ୍ରତିଜ୍ଞା କଲା ?)
Answer:
The tiger promised no to desire for human flesh any more.

Question 11.
What did the thief stop doing?
(ଚୋର ସେହିଦିନଠାରୁ କ’ଣ ନ କରିବାକୁ ସ୍ଥିରକଲା ?)
Answer:
The thief stopped stealing from that day.

Session – 3
III. Post-Reading (ପଢ଼ିବା ପରେ)

1. Visual Memory Development Technique (VMDT)
Whole Text : the tiger and the thief in the stable……
(ଘୋଡ଼ାଶାଳରେ ବାଘ ଏବଂ ଚୋର…
the tiger with the thief on its back ran for life
(ବାଘ ଚୋରକୁ ପିଠିରେ ବସାଇ ଜୀବନବିକଳରେ ପଳାଇଲା)
……….. the thief and the tiger save themselves
(ଚୋର ଏବଂ ବାଘ ଉଭୟେ ନିଜ ନିଜକୁ ରକ୍ଷାକଲେ ।
……………the wolf’s plan and he died.
(ଗଧୂର ଯୋଜନା ଏବଂ ତା’ର ମୃତ୍ୟୁ)

Part Text (Para-5): “What good luck !, This dead man will last me more than a week. But someone should help me drag the dead body”.
(କି ଭାଗ୍ୟ ! ଏହି ଶବଟି ମୋର ସପ୍ତାହେରୁ ଅଧିକକାଳ ଖାଦ୍ୟ ହୋଇ ପାରିବ । କିନ୍ତୁ ଏହାକୁ ଘୋଷାରିନେବାପାଇଁ ମୋତେ କେହିଜଣେ ସାହାଯ୍ୟ କରିବା ଦରକାର ।)

2. Comprehension Activity : (ବୋଧ ପରିମାପକ କାର୍ଯ୍ୟାବଳୀ)

(a) Choose the correct alternatives and complete each sentences.
(ଠିକ୍ ବିକଳ୍ପ ବାଛି ବାକ୍ୟଗୁଡ଼ିକ ପୂର୍ଣ କର ।)

Question 1.
The thief put a _______________ on the tiger’s mouth.
(A) saddle
(B) bridle
(C) chain
(D) rope
Answer:
(B) bridle

Question 2.
When the tiger and the thief saw each other, _______________.
(A) only the tiger was frightened
(B) only the thief was frightened
(C) both were frightened
(D) none was frightened
Answer:
(C) both were frightened

Question 3.
“What a good luck !“ said _______________.
(A) the king
(B) the tiger
(C) the thief
(D) the wolf
Answer:
(D) the wolf

Question 4.
The wolf’s final plan was to ________ the dead body.
(A) drag
(B) bury
(C) burn
(D) eat
Answer:
(D) eat

Question 5.
Seeing the thief, the tiger ran for life _______________ the wolf.
(A) dragging
(B) carrying
(C) leading
(D) following
Answer:
(A) dragging

(b) Given below are some sentences. They are about what happened in the story. But they are not in the right order. Fill in the boxes with correct serial numbers to rearrange the sentences. (ତଳେ କେତେକ ବାକ୍ୟ ଲେଖାହୋଇଛି । ସେଗୁଡ଼ିକ ଗଳ୍ପରେ ଘଟିଯାଇଥିବା ଘଟଣା ସମ୍ପର୍କିତ । କିନ୍ତୁ ସେଗୁଡ଼ିକ ଠିକ୍ କ୍ରମ ଅନୁସାରେ ନାହାନ୍ତି । ବାମପଟେ ଥ‌ିବା ଖାଲି ଘରଗୁଡ଼ିକରେ ଠିକ୍ କ୍ରମ ନମ୍ବର ଲେଖ୍ ବାକ୍ୟଗୁଡ଼ିକ ସଜାଅ ।)

[ ] The wolf requested the tiger to drag the man.
[ ] The thief got up.
[ ] The tiger among the horses stood silently.
[ ] Once, a thief came inside the stable to steal a horse.
[ ] It was dark everywhere.
[ ] The thief fell asleep like a dead man.
[ ] He climbed up a tree.
[ ] He thought the tiger to be the best horse.
[ ] The tiger ran for life dragging the wolf.
[ ] At night a tiger entered the stable.
[ ] The wolf and the tiger tied each other with a rope.

Answer:
[ 8 ] The wolf requested the tiger to drag the man.
[ 10] The thief got up.
[ 3 ] The tiger among the horses stood silently.
[ 1 ]Once, a thief came inside the stable to steal a horse.
[ 4 ] It was dark everywhere.
[ 7 ] The thief fell asleep like a dead man.
[ 6 ] He climbed up a tree.
[ 5 ] He thought the tiger to be the best horse.
[ 11] I The tiger ran for life dragging the wolf.
[ 2 ] At night a tiger entered the stable.
[ 9 ] The wolf and the tiger tied each other with a rope.

Session – 4

3. Listening : (ଶ୍ରବଣ)
On the chart below, the characters in the story are written in the boxes from left to right at the top. Some words related to the characters are given in the boxes from top to bottom at the left. Your teacher will read out the words one by one. Listen to him/her carefully and put a tick (✓) in the box on the word line below the character. One is done for you.
(ତଳ ଚାର୍ଟରେ ବିଷୟର ଚରିତ୍ରଗୁଡ଼ିକ ପୃଷ୍ଠାର ଅଗ୍ରଭାଗରେ ବାମରୁ ଡାହାଣକୁ ଲେଖାଯାଇଛି । ସେମାନଙ୍କ ଚରିତ୍ର ସହିତ ଖାପଖାଉଥ‌ିବା କେତେକ ଶବ୍ଦ ଉପରୁ ତଳକୁ ବାମପଟେ ଲେଖାଯାଇଛି । ତୁମ ଶିକ୍ଷକ ସେ ଶବ୍ଦଗୁଡ଼ିକୁ ଗୋଟିଏ ପରେ ଗୋଟିଏ ପାଠକରିବେ । ଯତ୍ନର ସହିତ ତାଙ୍କ ଶବ୍ଦଗୁଡ଼ିକ ଶୁଣ ଏବଂ ଶବ୍ଦ ଧାଡ଼ି ପାଖରେ ଥ‌ିବା ଖାଲି ଘରମାନଙ୍କରେ ସେମାନଙ୍କ ଚରିତ୍ରର ଗୁଣକୁ ଖାପଖାଉଥ‌ିବା ଶବ୍ଦ ପାଖରେ ଚିହ୍ନ ଦିଅ ।)

Answer:

Characters	thief	horse	tiger	wolf
Words
Strong			✓
flesh	✓
drag	✓
steal	✓
swift		✓	✓
speed			✓
Search	✓
ride	✓
stable	✓
run			✓
died				✓
branch
Forest			✓	✓
bridle		✓
slept	✓

4. Speaking : (କଥନ)
• Practise the following dialogues.
(ନିମ୍ନ ସଂଳାପଗୁଡ଼ିକ ଅଭ୍ୟାସ କର ।)
• Step : (କେଉଁ କେଉଁ ସ୍ତରଦେଇ ଏହି ସଂଳାପ ପାଠ କରାଯିବ ।)
• Rehearsal-teacher reads aloud, and students listen. The teacher reads aloud and students repeat after him/her dialogue by dialogue.
• Teacher vs Students.
• Students vs students (in two groups)
(ଶିକ୍ଷକ ପାଟି କରି ପଢ଼ିବେ – ଛାତ୍ରଛାତ୍ରୀମାନେ ଶୁଣିବେ)
ଶିକ୍ଷକ ପାଟି କରି ପାଠ କରିବାପରେ ଛାତ୍ରଛାତ୍ରୀ ସେଗୁଡ଼ିକୁ ଆଉଥରେ ଦୋହରାଇ କହିବେ ।
ଶିକ୍ଷକ –
କହିବେ –
ଛାତ୍ରଛାତ୍ରୀ କହିବେ – କହିବେ ।
ପରସ୍ପର ସହିତ – (ଦୁଇଟି ଦଳରେ ବିଭକ୍ତ ହୋଇ)
(They do this reading from the text.)

Wolf : Good Luck ! This dead man will last me more than a week.
But who will help me drag the dead body ?
Tiger: What are you looking for, Mr. Wolf?
Wolf: Mr. Tiger, will you help me drag this dead body?
Tiger: Why should I?
Wolf: I’ll give you half of it. ,
Tiger: Aren’t you going to cheat me?
Wolf: No, no, not at all. How can I?
Tiger: Won’t you run away leaving me alone?
Wolf: How can that be? We’ll tie each other with a rope.
Tiger: Good idea! That’ll do.

Session – 5

5. Vocabulary : (ଶବ୍ଦଜ୍ଞାନ)
Match who lives where. Write the serial numbers in brackets. One is done for you.

Answer:

Session  – 6

6.  Writing : (ଲିଖନ)

a. In comprehension Activity No. 2 b you have rearranged the sentences of the story. Use the sentences serially and write the story in the space given below. (ସଂପ୍ରତି କାର୍ଯ୍ୟ ପ୍ରକ୍ରିୟା No. 2(b)ରେ ଗଛର ବାକ୍ୟଗୁଡ଼ିକ ଠିକ୍ କ୍ରମରେ ସଜାଯାଇଛି ।ବାକ୍ୟଗୁଡ଼ିକ କ୍ରମ ଅନୁସାରେ ଲେଖୁ ଗଳ୍ପଟି ପ୍ରସ୍ତୁତ କର ।)

The Thief And The Tiger
______________________________________________
______________________________________________
______________________________________________
______________________________________________
Answer:

• Once a thief came inside the stable to steal a horse. At night a tiger entered the stable.
• The tiger among the horses stood silently.
• It was dark everywhere.
• He thought the tiger to be the best horse.
• He climbed up a tree.
• The thief fell asleep like a dead man.
• The wolf requested the tiger to drag the man.
• The wolf and the tiger tied each other with a rope.
• The thief got up.
• The tiger ran for life dragging the wolf.

(b). Write answers to the following questions.

Question (i).
Where did the thief and the tiger hide? Why?
(ଚୋର ଏବଂ ବାଘ କେଉଁଠି ଲୁଚିଥିଲେ ? କାହିଁକି ?)
Answer:
They hid in the king’s stable.
The thief wanted to steal a horse.
The tiger thought of eating man’s flesh.

Question (ii).
Why did the thief think the tiger to be the best horse?
(ଚୋର ବାଘକୁ କାହିଁକି ସର୍ବଶ୍ରେଷ୍ଠ ଘୋଡ଼ା ବୋଲି ଭାବିଲା ?)
Answer:
He thought so because the back of the tiger gave him a smooth silky touch.

Question (iii).
Why was the thief frightened when it was the day?
(ଦିନ ହୋଇଯିବା ପରେ ଚୋରଟି ଭୟଭୀତ ହୋଇପଡ଼ିଲା କାହିଁକି ?)
Answer:
The thief was frightened when it was the day because he could not see due to darkness inside the stable at night.

Question (iv).
How did he save himself?
(ସେ କିପରି ନିଜକୁ ରକ୍ଷାକଲା ?)
Answer:
When the tiger was running in fear with great speed passing under a tree the thief was caught hold of one branch of the tree and climbed up.

Question (v).
Where did the theif take rest? Why did he fall asleep?
(ଚୋର କେଉଁଠି ବିଶ୍ରାମ ନେଲା ? ସେ କାହିଁକି ଗଭୀର ନିଦ୍ରାରେ ଶୋଇପଡ଼ିଲା ?)
Answer:
The thief took rest under the tree.

Question (vi).
What was the wolf’s plan?
(ଗମ୍ଵାର ଯୋଜନା କ’ଣ ଥିଲା ?)
Answer:
The wolf planned to use the dead body as his food for more than a week long.

Question (vii).
What sort of help did the wolf want from the tiger? What was his offer to him?
(ଗଧୂଆ ବାଘ ନିକଟରୁ କିପରି ସାହାଯ୍ୟ ଆଶା କରିଥିଲା । ସେ ତାକୁ କେଉଁ ଉପହାର ଦେବାପାଇଁ ପ୍ରତିଶୃତି ଦେଲା ?)
Answer:
The wolf wanted the tiger to help him drag the body to the safest place in the forest.

Question (viii).
What was the tiger’s suspicion?
(ବାଘର ସନ୍ଦେହ କ’ଣ ଥିଲା ?)
Answer:
The tiger feared that the wolf would cheat him and run away leaving him alone.

Question (ix).
Why did the two animals tie each other with a rope?
(କାହିଁକି ଦୁଇଜଣ ପ୍ରାଣୀ ପରସ୍ପରକୁ ଏକ ଦଉଡ଼ିରେ ବାନ୍ଧିଲେ ?)
Answer:
The two animals tied each other with a rope so that neither of them could cheat or run away living another.

Question (x).
What did the tiger do when the thief shouted at him?
(ମଣିଷର ବଡ଼ପାଟି ଶୁଣି ବାଘ କ’ଣ କଲା ?)
Answer:
The tiger ran as fast as he could getting frightened and seeing the thief.

Question (xi).
What did the tiger promise?
(ବାଘ କ’ଣ ପ୍ରତିଜ୍ଞାକଲା ?)
Answer:
The tiger promised not to desire for human flesh anymore.

Question (xii).
What did the thief stop doing?
(ଚୋର କେଉଁ ଅଭ୍ୟାସ ବନ୍ଦ କରିଦେଲା ?)
Answer:
The thief stopped stealing anymore.

Session – 7

7. Mental Talk : (ମାନସିକ ଆଳାପ)

• The tiger was stronger than the thief, but not so clever. Fear made him weaker.
  (ବାଘ ମଣିଷଠାରୁ ବଳବାନ ଥିଲା; କିନ୍ତୁ ଚତୁର ନଥିଲା । ଭୟ ତାକୁ ଦୁର୍ବଳ କରିଦେଲା ।)
• Mind power is mightier than muscle power.
  (ମନର ବଳ ଶାରୀରିକ ବଳଠାରୁ ଅଧୁକ ଶକ୍ତିଶାଳୀ)

Tail-Piece

Did you like the story, “The Thief and The Tiger”?
(ଚୋର ଏବଂ ବାଘ ଗଳ୍ପଟି ଭଲ ଲାଗିଲା କି ?)
Read a story here, is more interesting than this.
(ଆଉ ଗୋଟିଏ ଏହିପରି ଗପ ପଢ଼ । ଏହାଠାରୁ ଅଧିକ ମନୋରଞ୍ଜନ କି)

The Liger On A Tiger (ବାଘ ଏବଂ ଫାଘ)

One day…………………………………………………. they could.

ଦିନେ ଗୋଟିଏ ଲୋକର ଘୋଡ଼ାଛୁଆଟି ହଜିଯାଇଥିଲା । ସେ ତାକୁ ଖୋଜି ଖୋଜି ବଣଭିତରକୁ ପଶିଯାଇଥିଲା । ସେ ବହୁତ କ୍ଳାନ୍ତ ହୋଇପଡ଼ିଥିଲା ଏବଂ ଆଗକୁ ଯିବାକୁ ଅକ୍ଷମ ହୋଇପଡ଼ିଥିଲା । ସେ ଘରକୁ ଫେରିଆସିବାକୁ ଇଚ୍ଛାକଲା । ମାତ୍ର ଘରକୁ ଫେରିବା ବାଟ ନପାଇ ବାଉଳା ହୋଇଗଲା । ସେତେବେଳକୁ ରାତି ହୋଇଯାଇଥିଲା । ଘରକୁ ଫେରିଯିବା ଆଉ ସମ୍ଭବ ନଥିଲା । ସେ ଗୋଟିଏ କୁଡ଼ିଆ ଦେଖିବାକୁ ପାଇଲା । ଏହା ଗୋଟିଏ ବୁଢ଼ୀଲୋକର କୁଡ଼ିଆ ଥିଲା । ଲୋକଟି ସେଠାରେ ଆଶ୍ରୟ ନେବାକୁ ବୁଢ଼ୀକୁ ଅନୁରୋଧ କଲା । ତା’ଘରେ ମାତ୍ର ଦୁଇଟି କୋଠରି ଥିଲା । ସେ ଗୋଟିଏ କୋଠରିରେ ତାରି ନାତୁଣୀ ସହିତ ରହୁଥିଲା ଏବଂ ଅନ୍ୟ କୋଠରିଟିରେ ଘରର ଜିନିଷପତ୍ର ସବୁ ରହିଥିଲା । ସେହି ଭଣ୍ଡାରଘରେ ତାକୁ ରହିବାକୁ ବୁଢ଼ୀ ଅନୁମତି ଦେଲା ।

ନାତୁଣୀଟି ଘୋଡ଼ାଛୁଆ ବିଷୟରେ କିଛିକିଛି ଶୁଣିଥିଲା । ଏଣୁ ସେ ଲୋକଟି ପାଖକୁ ଯାଇ ଘୋଡ଼ାଛୁଆ ବିଷୟରେ ସବୁକଥା ଜାଣିବାକୁ ଚାହିଁଲା । କିନ୍ତୁ ତା’ର ବୁଢ଼ୀ ମା’ ତାକୁ କହିଲା, ‘ଆଦୌ ନୁହେଁ । ତୁ ସେଠାକୁ ଆଦୌ ଯିବା ଉଚିତ ନୁହେଁ । ସେଠାରେ ବାଘ ଫାଘ ତୋତେ ଟେକିନେଇଯିବେ ।’’ ପ୍ରକୃତରେ ‘ଫାଘ’ ବୋଲି କୌଣସି ପ୍ରାଣୀ ନଥିଲା । କିନ୍ତୁ ବୁଢ଼ୀ ଘର ପଛପଟକୁ ପ୍ରତିଦିନ ଆସୁଥ‌ିବା ବାଘଟି ବୁଢ଼ୀ ମୁହଁରୁ ଫାଘ ସମ୍ପର୍କରେ ଶୁଣିବାକୁ ପାଇ ବିଚଳିତ ହୋଇପଡ଼ିଲା । ସେ ଭାବିଲା ବୋଧହୁଏ ଫାଘଟି ତା’ଅପେକ୍ଷା ଅଧିକ ଭୟଙ୍କର ଏକ ପ୍ରାଣୀ । ସେ ଗୋଟିଏ ରାକ୍ଷସ କିମ୍ବା ଭୂତ । ସେ ଖୁବ୍ ଭୟଭୀତ ହୋଇପଡ଼ିଲା । ସେ ସେଠାରୁ ପଳାଇଯିବାକୁ ଉପାୟ ଖୋଜିଲା । ଟିକିଏ ପରେ ଲୋକଟି ବାହାରକୁ ଆସି ଏହା ଦେଖିଲା ।

ସେତେବେଳକୁ ସକାଳ ହୋଇ ଆସୁଥାଏ । ସେଇ ଜାଲୁଜାଲୁଆ ଅନ୍ଧାର ଭିତରେ ଲୋକଟି ବାଘଟିକୁ ଦେଖି ତା’ର ଘୋଡ଼ାଛୁଆ ବୋଲି ଭାବିଲା । ସେ ସଙ୍ଗେ ସଙ୍ଗେ ସେଠାକୁ ଛୁଟିଯାଇ ବାଘର ମୁହଁକୁ ଗୋଟିଏ କନାରେ ବାନ୍ଧିପକାଇଲା । ଏହାଫଳରେ ବାଘର କାନ, ନାକ, ମୁଣ୍ଡ ଓ ବେକ ଜଣାପଡ଼ିଲା ନାହିଁ । ସେ ସଙ୍ଗେ ସଙ୍ଗେ ବାଘର ପିଠିରେ ବସିଗଲା । ବାଘର କି ଭୟ ! ସେ ଲୋକଟିକୁ ଫାଘ ବୋଲି ଭାବି ଜୀବନ ବିକଳରେ ଦୌଡ଼ିବାକୁ ଲାଗିଲା । ଯେତେବେଳେ ରାତି ପାହିଲା, ଲୋକଟି ଦେଖିଲା ଯେ ସେ ଗୋଟିଏ ବାଘ ପିଠିରେ ବସିଛି । କ’ଣ କରିବ ? କେମିତି ସେ ବାଘ ପିଠିରୁ ଖସି ଜୀବନ ବଞ୍ଚାଇବ ! ଯେତେବେଳେ ବାଘଟି ଗୋଟିଏ ବରଗଛ ତଳ ଦେଇ ଦୌଡୁଥିଲା, ଲୋକଟି ସେହି ସମୟରେ ବରଗଛର ଏକ ଡାଳକୁ ଧରି ଗଛ ଉପରେ ଚଢ଼ିଗଲା ଏବଂ କହିଲା, ‘ହେ ଭଗବାନ ! ତୁମକୁ ଧନ୍ୟବାଦ !

ଯାହାହେଉ ମୁଁ ବଞ୍ଚିଯାଇଛି ।’’ ବାଘଟି ମଧ୍ୟ ଫାଘ କବଳରୁ ମୁକ୍ତି ପାଇ ନିଜକୁ ଧନ୍ୟ ମନେକଲା । ବାଘଟି ଦୌଡ଼ି ନ ପଳାଇ ଗଛତଳେ ନିଶ୍ଵାସ ମାରିଲା ଏବଂ ଅନ୍ୟ ବାଘମାନଙ୍କୁ ଚିତ୍କାର କରି ଗଛ ଉପରେ ଥ‌ିବା ଭୟଙ୍କର ପ୍ରାଣୀ ଫାଘ ବିଷୟରେ ଜଣାଇଲା । ସବୁ ବାଘମାନେ ଆସି କହିଲେ, ‘ଖବର କ’ଣ ? କିଏ ତୁମର ମୁହଁ ବାନ୍ଧି ପକାଇଛି ?’’ ବାଘଟି ଦୀର୍ଘଶ୍ଵାସ ମାରି କହିଲା, ‘‘ଭାଇମାନେ ! ମୁଁ ମୃତ୍ୟୁମୁଖରୁ ବଞ୍ଚ୍ ଫେରିଆସିଛି । ମୋତେ ଗୋଟିଏ ‘ଫାଘ’ ଧରିନେଇଥିଲା । ମୁଁ ତାକୁ ପୂଜା ଅର୍ପଣ କରିବାକୁ ପ୍ରତିଜ୍ଞା କରିବାରୁ ସେ ମୋତେ ଛାଡ଼ିଦେଇଛି । ମୁଁ ଯଦି ତାକୁ ପୂଜା ଅର୍ପଣ ନଦିଏ; ତେବେ ସେ ମୋତେ ପୁଣି ଧରିନେଇଯିବ । ‘‘ଏକଥା ଶୁଣି ସବୁ ବାଘ ‘ଫାଘ’କୁ ପୂଜା କରି ଗଣ୍ଡା, ମଇଁଷି ପ୍ରଭୃତି ବିଭିନ୍ନ ଦ୍ରବ୍ୟ ଅର୍ପଣ କରିବାକୁ ଲାଗିଲେ । ଲୋକଟି ତା’ଜୀବନରେ କେବେ ହେଲେ ଏତେସଂଖ୍ୟକ ବାଘ ଏକାଠି ହେବାର ଦେଖି ନଥିଲା ।

ସେ ଖୁବ୍ ଭୟ ପାଇଗଲା । ସେ ଗଛ ଉପରେ ବସି ଥରିବାକୁ ଲାଗିଲା । ଉଭୟ ଲୋକ ଏବଂ ଗଛ ଦୋହଲୁଥିଲେ । ବାଘମାନେ ମଧ୍ୟ ଭୟ ପାଇ ଯାଇଥିଲେ । ସେମାନେ ଉପରକୁ ଚାହିଁଲେ; ମାତ୍ର ପତ୍ରଗହଳରେ ଲୋକଟିକୁ ଦେଖୁରିଲେ ନାହିଁ । ଲୋକର ପିନ୍ଧାଲୁଗାର ଶେଷ ଅଂଶଟି ଗୋଟିଏ ଡାଳରୁ ଓହଳିଥିଲା । ସେମାନେ ଏହା ପତ୍ରଗହଳ ମଧ୍ୟରେ ଜାଣିପାରିଲେ ନାହିଁ । ସେମାନେ ଏହାକୁ ଏକ ଲାଞ୍ଜ ବୋଲି ଭାବିଲେ । ଏହା ଦେଖ୍ ଗୋଟିଏ ବୁଢ଼ା ବାଘ କହିଲା, ‘ଏହା ଏକ ବିପଜ୍ଜନକ ଜୀବଭଳି ଲାଗୁଛି । ଏହା ନିଶ୍ଚୟ ଲାଇଗର ।’’ ଏହା ଶୁଣି ସମସ୍ତ ବାଘ ଚିତ୍କାର କରି ଉଠିଲେ, ‘‘ସେ ଆମକୁ ଧରିନେବ, ଜୀବନ ବଞ୍ଚାଇ ପଳାଇଯାଅ ।’’ ଏବଂ ସମସ୍ତେ ଯେତେ ଜୋର୍‌ରେ ପାରିଲେ ଦୌଡ଼ବାକୁ ଲାଗିଲେ ।

Word Meaning

dangle: to hang or swing loosely (ଉପରୁ ଓହଳିବା / ଝୁଲିରହିବା)
escape: to get free from something (ଖସି ପଳେଇବା)
flutter: to move by waving quickly and lightly
huge: very big (ବିରାଟ, ଖୁବ୍ ବଡ଼ ଆକାରର, ବିଶାଳ)
pant: to breathe quickly (ଅଣନିଶ୍ୱାସୀ ହୋଇପଡ଼ିବା)
rush out: to go or move suddenly with great speed (ହଠାତ୍ ଧାଇଁବା)
Search: to look for (ଖୋଜିବା)
shelter: a house or a place to stay (ଆଶ୍ରୟସ୍ଥଳୀ)

Class 8 Questions and Answers Part – I

• The Missing Ring Question Answer
• The Thief and the Tiger Question Answer
• A Wise Grandmother Question Answer
• The Stonecutter Question Answer

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 4 ତ୍ରିକୋଣମିତି Ex 4(b)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) sin (A – B) = sin A – cos A |
(ii) cos (θ + α) + cos (α – θ) = ……….. |
(iii) cos (60° – A) + ………. = cos A |
(iv) sin (30° + A) + sin (30° – A) = ……..|
(v) 2 sin A. sin B = ………… cos (A + B) |
(vi) tan (45° + θ). tan (45° – θ) = …………. |
Solution:

Question 2.

Solution:

Question 3.
ତ୍ପମାଣ କର:
(i) cos (A + 45°) = \(\frac{1}{\sqrt{2}}\) (cos A – sin A)
(ii) sin (45° – θ) = \(\frac{1}{\sqrt{2}}\) (sin θ – cos θ)
(iii) tan (45° + θ) = \(\frac{1+\tan \theta}{1-\tan \theta}\)
(iv) cot (45° + θ) = \(\frac{1+\tan \theta}{1-\tan \theta}\)
Solution:
(i) L.H.S. = cos (A + 45°) = cos A. cos 45° – sin A. sin 45°
= cos A . \(\frac{1}{\sqrt{2}}\) – sin A .\(\frac{1}{\sqrt{2}}\)

(ii) L.H.S. = sin (45° + θ) = sin 45° × cos θ – cos 45° 45° × sin θ
= \(\frac{1}{\sqrt{2}}\) cos θ – \(\frac{1}{\sqrt{2}}\) sin θ = – \(\frac{1}{\sqrt{2}}\) (sin θ – cos θ) = R.H.S.

(iii) L.H.S. = tan (45° + θ) = \(\frac{\tan 45^{\circ}+\tan \theta}{1-\tan 45^{\circ} \cdot \tan \theta}\) = \(\frac{1+\tan \theta}{1-1 \times \tan \theta}\)
= \(\frac{1+\tan \theta}{1-\tan \theta}\) = R.H.S.

(iv) L.H.S. = cot (45° – θ) = \(\frac{\cot 45^{\circ} \cdot \cot \theta+1}{\cot \theta-\cot 45^{\circ}}\) = \(\frac{1 \times \cot \theta+1}{\cot \theta-1}\) = \(\frac{\cot \theta+1}{\cot \theta-1}\)

Question 4.
ତ୍ପମାଣ କର:
(i) cos (45° – A). cos (45° – B) – sin (45° – A). sin (45° – B) = sin (A + B)
(ii) sin (45° + A). cos (20° – A) + cos (45° + A). sin (20° – A) = \(\frac{\sqrt{3}}{2}\)
(iii) cos (65° + θ). cos (35° + θ) + sin (65° + θ). sin (35° + θ) = \(\frac{\sqrt{3}}{2}\)
(iv) cos nθ . cos θ + sin nθ. sin θ = sin (n – 1) θ
(v) tan (60° – A) = \(\frac{\sqrt{3} \cos A-\sin A}{\cos A+\sqrt{3} \sin A}\)
Solution:
(i) L.H.S. = cos (45° – A). cos (45° – B) – sin (45° – A). sin (45° – B)
= cos (45° – A + 45° – B) = cos {90° – (A + B)}
= sin (A + B) = R.H.S.

(ii) L.H.S. = sin (40° + A). cos (20° – A) + cos (40° + A). sin (20° – A)
= sin (40° – A + 20° – A) = sin 60° = \(\frac{\sqrt{3}}{2}\) = R.H.S.

(iii) L.H.S. = cos (65° + θ). cos (35° + θ) + sin (65° + θ). sin (35° + θ)
= cos {(65° + θ) – (35° + θ)} = cos (65° + θ – 35° – θ)
= cos 30° = \(\frac{\sqrt{3}}{2}\) = R.H.S.

(iv) L.H.S. = cos nθ. cos θ + sin nθ. sin θ = cos (nθ – θ)
= sin (n – 1)θ = R.H.S.

Question 5.
ତ୍ପମାଣ କର:
(i) tan 62° = \(\frac{\cos 17^{\circ}+\sin 17^{\circ}}{\cos 17^{\circ}-\sin 17^{\circ}}\)
(ii) tan 70° = \(\frac{\cos 25^{\circ}+\sin 25^{\circ}}{\cos 25^{\circ}-\sin 25^{\circ}}\)
(iii) tan 7A. tan 4A. tan 3A = tan 7A – tan 4A – tan 3A
(iv) tan (x + y) – tan x – tan y = tan (x + y) . tan x . tan y
(v) (1 + tan 15°) (1 + tan 30°) = 2
(vi) (cot 10° – 1) (cot 35° – 1) = 2
(vii) \(\frac{1}{\cot A+\tan B}\) – \(\frac{1}{\tan A+\cot B}\) = tan (A – B)
(viii) √3 + cot 50° + tan 80° = √3 cot 50° . tan 80°
Solution:

Question 6.
cos 75° ଓ sin 15° ର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
cos 75° = cos (45° + 30°) = cos 45° . cos 30° – sin 45° . sin 30°
= \(\frac{1}{\sqrt{2}}\) . \(\frac{\sqrt{3}}{2}\) – \(\frac{1}{\sqrt{2}}\) × \(\frac { 1 }{ 2 }\) = \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
sin 15° = sin (60° – 45°) = sin 60° . cos 45° – cos 60° . sin 45°
= \(\frac{\sqrt{3}}{2}\) . \(\frac{1}{\sqrt{2}}\) – \(\frac { 1 }{ 2 }\) × \(\frac{1}{\sqrt{2}}\) = \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)

Question 7.
(i) cos α = \(\frac { 8 }{ 17 }\) ଓ sin β = \(\frac { 5 }{ 13 }\) ହେଲେ sin (α – β) ର ମାନ ନିଣ୍ଡଯ କର |
(ii) tan A = \(\frac { 1 }{ 2 }\), cot B = 3 ହେଲେ A + B ର ମାନ ନିଣ୍ଡଯ କର |
(iii) tan β = \(\frac{1-\tan \alpha}{1+\tan \alpha}\) ହେଲେ (α + β) ର ମାନ ନିଣ୍ଡଯ କର |
Solution:

Question 8.
A + B + C = 90° ହେଲେ ତ୍ପମାଣ କର ଯେ
(i) cot A + cot B + cot C = cot A . cot B . cot C
(ii) tan A . tan B + tan B . tan C + tan C . tan A = 1
Solution:
(i) A + B + C = 90° ⇒ A + B = 90° – C
⇒ cot (A + B) = cot (90° – C)
⇒ \(\frac{\cot A \cdot \cot B-1}{\cot B+\cot A}\) = tan C = \(\frac{1}{\cot \mathrm{C}}\)
⇒ cot C (cot A. cot B – 1) = 1 (cot B + cot A)
⇒ cot A. cot B. cot C – cot C = cot B + cot A
⇒ cot A. cot B. cot C = cot A + cot B + cot C

(ii) A + B + C = 90° ⇒ B + C = (90° – A)
⇒ tan (B + C) = tan (90° – A)
\(\frac{\tan B+\tan C}{1-\tan B \cdot \tan C}\) = cot A = \(\frac{1}{\tan \mathrm{A}}\)
⇒ tan A (tan B + tan C) = 1 – tan B. tan C
⇒ tan A. tan B + tan C. tan A = 1 – tan B. tan C
⇒ tan A. tan B + tan B. tan C + tan C. tan A = 1

Question 9.
(i) A + B + C = 180° ଏବଂ sin C = 1 ହେଲେ ପ୍ରମାଣ କର ଯେ tan A . tan B = 1
(ii) A + B + C = 180° ହେଲେ ପ୍ରମାଣ କର ଯେ cot A . cot B + cot B . cot C + cot C . cot A = 1
(iii) A + B + C = 180° ଏବଂ cos A = cot B . cos C ହେଲେ ପ୍ରମାଣ କର ଯେ
(a) tan A – tan B + tan C
(b) tan B . tan C = 2
Solution:
(i) sin C = 1 ⇒ sin C = sin 90° ⇒ C = 90°
A + B + C = 180° ⇒ A + B = 180° – C = 180° = 90° = 90°
⇒ A = 90° – B
∴ tan A . tan B = tan (90° – B) . tan B = cot B × tan B = 1

(ii) A + B + C = 180° ⇒ A + B = 180° – C
⇒ cot(A + B) = cot (180° – C)
⇒ \(\frac{\cot A \cdot \cot B-1}{\cot B+\cot A}\) = – cot C
⇒ cot A. cot B – 1=-cot C (cot B + cot A)
⇒cot A. cot B – 1=-cot B. cot C – cot C. cot A
⇒ cot A. cot B + cot B. cot C + cot C. cot A = 1

(iii) (a) A + B + C = 180° ⇒ (A + C) = 180° – A
⇒ sin (B + C) = sin (180° – A)
⇒ sin B . cos C + cos B . sin C = sin A
⇒ \(\frac { sin B. cos C }{ cos A }\) + \(\frac { cos B. sin C }{ cos A }\) = \(\frac { sin A }{ cos A }\) (ଭଉଯ ପାଣରେ cos A କାମାଗଣ)
⇒ \(\frac { sin B. cos C }{ cos B. cos C }\) + \(\frac { cos B. sin C }{ cos B. cos C }\) = tan A
⇒ tan B + tan C = tan A

(b) A + B + C = 180°
⇒ B + C = 180° – A
⇒ cos (B + C) = cos (180° – A) = – cos A
⇒ cos B. cos C – sin B. sin C = – cos B. cos C
⇒ 2cos B. cos C = sin B. sin C
⇒ 2 = \(\frac{\sin B \cdot \cos C}{\cos B \cdot \cos C}\) = tan B. tan C

Question 10.
ଜଣାଥ ଯେ : (i) sin (A + B) . sin (A – B) = sin² A – sin² B
(ii) cos (A + B) . cos (A – B) = cos² A – sin² B
Solution:
(i) L.H.S.= sin (A + B) . sin (A – B)
= (sin A. cos B + cos A· sin B) (sin A · cos B – cos A. sin B)
= (sin A. cos B)² – (cos A. sin B)²
= sin²A. cos²B – cos²A. sin²B
= sin²A (1 – sin²B) − (1 − sin²A) sin²B
= sin²A – sin²A. sin²B – sin²B + sin²A. sin²B
= sin²A – sin²B = R.H.S.

(ii) L.H.S.= cos (A + B) . cos (A – B)
= (cos A. cos B – sin A. sin B) (cos A. cos B + sin A. sin B)
= (cos A. cosB)² – (sin A. sin B)²
= cos²A cos²B – sin²A. sin²B
= cos²A (1 − sin²B) − (1 − cos²A) sin²B
= cos²A – cos²A. sin²B – sin²B + cos²A. sin²B
= cos²A – sin²B = R.H.S.

Question 11.
ପ୍ରମାଣ କର :
(i) sin 50° + sin 40° = √2 sin 85°
(ii) cos 50° + cos 40° = √2 cos 5°
(iii) sin 50° – sin 70° + sin 10° = 0
Solution:
(i) ଦାନପାଣ = sin 50° + sin 40°
= sin (45° +5°) + sin (45° – 5°)
= sin 45°. cos 5° + cos 45°. sin 5° + sin 45°. cos 5° – cos 45°. sin 5°
= 2 sin 45° × cos 5° = 2 × \(\frac{1}{\sqrt{2}}\) cos (90° – 85°)
= √2 sin 85° = ଦର୍ପଣପାଣ

(ii) ଦାନପାଣ = cos 50° + cos 40°
= cos (45° +5°) + cos (45° – 5°)
= cos 45°. cos 5° – sin 45°. sin 5° + cos 45°. cos 5° + sin 45°. sin 5°
= 2 cos 45°. cos 5°
= 2 × \(\frac{1}{\sqrt{2}}\) cos 5° = √2 cos 5° = ଦର୍ପଣପାଣ

(iii) ଦାନପାଣ = sin 50° – sin 70° + sin 10°
= sin (60° – 10°) – sin (60° – 10°) + sin 10°
= (sin 60° . cos 10° – cos 60° . sin 10°)
– (sin 60° . cos 10° + cos 60° . sin 10°) + sin 10°

Question 12.
ପ୍ରମାଣ କର :
(i) sin (A + B) = \(\frac{1}{\sqrt{2}}\) , cos (A – B) = \(\frac{1}{\sqrt{2}}\)
(ii) cos (A + B) = – \(\frac { 1 }{ 2 }\) , sin (A – B) = \(\frac { 1 }{ 2 }\)
(iii) tan (A – B) = \(\frac{1}{\sqrt{2}}\) = cot (A + B)
(iv) tan (A + B) = -1, cosec (A – B) = √2
Solution:
(i) sin (A + B) = \(\frac{1}{\sqrt{2}}\) = sin 45°ଦା, sin 135°
⇒ A + B = 45° ଦା, 135°
cos (A – B) = \(\frac{1}{\sqrt{2}}\) = cos 45° ⇒ A – B = 45°
A + B = 45° , A – B = 45°
ହେଲେ, (i) ଓ (ii) ରୁ A + B +A – B = 45° + 45° ⇒ 2A = 90° ⇒ A = 45°
B = 45° – 45° = 0°
ଯଦି A + B = 135°, A – B = 45°
∴ (i) ଓ (ii) ରୁ A + B + A – B = 135° + 45°
⇒ 2A = 180° ⇒ A = 90°
B = 135° – 90° = 45°
(∴ A = 45°, B = 0°) ଦା, (A = 90° , B = 45°)

(ii) cos (A + B) = – \(\frac { 1 }{ 2 }\) = cos 120°
⇒ A + B = 120°
sin (A – B) = \(\frac { 1 }{ 2 }\) = sin 30°
⇒ A – B = 30°
∴ (i) ଓ (ii) ରୁ A + B + A – B = 120° + 30°
⇒ 2A = 150° ⇒ A = 75°
B = 120° – 75° = 45° (∵ A = 75°, B = 45°)

(iii) tan (A – B) = \(\frac{1}{\sqrt{3}}\) = tan 30° ⇒ A – B = 30°
cot (A + B) = \(\frac{1}{\sqrt{3}}\) = cot 60° ⇒ A – B = 30°
∴ (i) ଓ (ii) ରୁ A + B + A – B = 60° + 30°
⇒ 2A = 90° ⇒ A = 45° , B = 60° – 45° = 15°
∴ A = 45° , B = 15°

(iv) tan (A + B) = -1 = tan 135° ⇒ A + B = 135°
cosec (A – B) = √2 = cosec 45° ⇒ A – B = 45°
(i) ଓ (ii) ରୁ 2A = 180° ⇒ A = 90°
∴ B = 135° – 90° = 45°
∴ A = 90° , B = 45°

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(a)

\(\left(\frac{{at}_1^2+{at} {t}_2^2}{2}, \frac{2 {at}_1+2 {at}_2}{2}\right)\)

Question 1.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ଯରେ ଦୂରତା ନିର୍ଣ୍ଣୟ କର ।
(i) (0, 0) ଓ (4, 3)
(ii) (0, 2) ଓ (-6, 2)
(iii) (-3, 0) ଓ (5, 6)
(iv) (2, 4) ଓ (1, 3)
(v) (-2, -2) ଓ (-3, -5)
(vi) (a, b) ଓ (- a, b)
ସମାଧାନ :
ମେନକର O(0, 0) ଓ P (4,3)
ମୂଳବିନ୍ଦୁଠାରୁ p(x, y)ର ଦୂରତା = \(\sqrt{x^2 + y^2}\)
OP = \(\sqrt{4^2 + 3^2}=\sqrt{16 + 9}=\sqrt{25}=5\)

(ii) ମେନକର A (0, 2), ଓ B (-6, 2)
ଏଠାରେ x₁ =0, y₁ = 2, x₂ = -6, y₂ = 2
AB = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) = √(-6-0)² +(2-2)² = √(36+0) = 6

(iii) P(-3, 0) ଓ Q (5, 6)
ଏଠାରେ x₁ = 3, y₁ = 0, x₂ = 5, y₂ = 6
PQ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)
= \(\sqrt{{5- (-3)}^2 +(6-0)^2}\) = \(\sqrt{8^2 + 6^2}\) = √64+36 = √100 = 10

(iv) P (2, 4) ଓ Q (1, 3)
PQ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) = \(\sqrt{(1-2)^2+(3-4)^2}\) = \(\sqrt{(-1)^2 +(-1)^2}\) =√2

(v) A (-2,-2) ଓ B (-3,-5).
AB = \(\sqrt{{-3-(-2)}^2 + {-5-(-2)}^2}\) = √1² +3² =√10

(vi) P (a, b) ଓ Q (a, b)
PQ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\) = \(\sqrt{(-a-a)^2+{b-(-b)}^2}\)
\(\sqrt{(-2a)^2+(2b)^2}\) = \(\sqrt{4a^2+4b^2}\) = 2√(a² + b²)

Question 2.
ନିମ୍ନଲିଖ କେଉଁ ବିନ୍ଦୁଦ୍ଵୟ ମୂଳବିନ୍ଦୁ ଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ସ୍ଥିର କର ।
(i) (0, 1) ଓ (- 1, 0)
(ii) (2,3) ଓ (4, \(\frac{3}{2}\))
(iii) (√7, √19) ଓ (-√7, – √19)
(iv) (4, – 2) ଓ (2, 4)
(v) (0, 4) ଓ (2, 2)
ସମାଧାନ :
(i) ଏଠାରେ ମୂଳବିନ୍ଦୁ O(0, 0) । A (0, 1) ଓ B(- 1, 0) ।
OA = \(\sqrt{1^2+0^2}\) = 1, OB = \(\sqrt{(-1)^2 +0^2}\) = 1 ∴ OA = OB
∴ (0, 1) ଓ ( 1, 0) ମୂଳବିନ୍ଦୁ ଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

(ii) ଏଠାରେ A(2,3) ଓ B(4, \(\frac{3}{2}\))
OA = √2^2+3^2 = √4+9 = √13
OB = \(\sqrt{4² + (\frac{3}{2})²}\) = \(\sqrt{16 + \frac{9}{4}}\) = \(\sqrt{\frac{64+9}{4}}\) = \(\sqrt{\frac{1}{2}}\)
OA ≠ OB ∴ A(2, 3) ଓ B(4, \(\frac{3}{2}\)) ବିଦୁ୍ୟଦ୍ଵୟ ମୂଳବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ନୁହେଁ ।

(iii) ଏଠାରେ A (√7, √19) ଓ B (-√7,-√19) ।
OA = \(\sqrt{(√7)^2+(√19)^2}\) = \(\sqrt{7+19}\) = √26
OB = \(\sqrt{(√7)^2+(-√19)^2}\) = \(\sqrt{7+19}\) = √26
∴ OA = OB ଅର୍ଥାତ୍‌ A(√7, √19) ଓ B(-√7, -√19) ବିନ୍ଦୁଦ୍ଵୟ ମୂଳ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

(iv) ଏଠାରେ A (4, – 2) ଓ B (2, 4) ।
OA = \(\sqrt{4^2 +(-2)^2}\) = \(\sqrt{16+4}\) = √20 = 2√5
OB = \(\sqrt{2^2 +4^2}\) = \(\sqrt{4+16}\) = √20 = 2√5
∴ OA = OB ଅର୍ଥାତ୍‌ A(4, – 2) ଓ B(2, 4) ବିନ୍ଦୁଦ୍ଵୟ ମୂଳ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

(v) ଏଠାରେ A(0, 4) ଓ B(2, 2)
OA = \(\sqrt{2^2+3^2}\) = √16 = 4
OB = \(\sqrt{2² + 2²}\) = \(\sqrt{4+4}\) = √8 = 2√2.
∴ OA ≠ OB ଅର୍ଥାତ୍ A(0, 4) ଓ B(2, 2) ବିଦୁ୍ୟଦ୍ଵୟ ମୂଳ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ନୁହେଁ ।

Question 3.
ପ୍ରମାଣ କର ଯେ, ନିମ୍ନୋକ୍ତ ଶୀର୍ଷବିନ୍ଦୁ ବିଶିଷ୍ଟ ABC ତ୍ରିଭୁଜମାନ ସମକୋଣୀ । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ କେଉଁ କୋଣଟି ସମକୋଣ ଦର୍ଶାଅ I
(i) A (3, 3), B (9, 0) ଓ C (12, 21)
(ii) A (1, 1), B (3, 4) ଓ C(0, 6)
(iii) A (-1, -2), B (5, -2) ଓ C (5, 6)
(iv) A (12, 8), B (- 2, 6) ଓ C (6, 0)
(v) A (1, 6), B (5, – 1) ଓ C (7, 2)
ସମାଧାନ :
P₁ = (x₁, y₁) ଓ P₂ (x₂, y₂) ହେଲେ, P₁P₂ = \(\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}\)

(i) A (3, 3), B (9, 0) ଓ C (12, 21)

∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(ii) A (1, 1), B (3, 4), C(0, 6)
AB = \(\sqrt{(3-1)^2+(4-1)^2}\) = \(\sqrt{2^2 +3^2}\) = √13
BC= \(\sqrt{(0-3)^2+(6-4)^2}\) = \(\sqrt{3^2 +2^2}\) = √13
AC = \(\sqrt{(0-1)^2+(6-1)^2}\) = \(\sqrt{1^2 +5^2}\) = √26
AB² + BC² = (√13)² +(√13)² = 13 + 13 = 26 = (√26)² =
∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(iii) A (-1,- 2), B (5, -2) ଓ C (5, 6)

∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(iv) A (12, 8), B (- 2, 6) ଓ C (6, 0)

∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

(v) A (1, 6), B (5, – 1) ଓ C (7, 2)

∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ। ⇒ m∠BAC = 90°

Question 4.
ଦର୍ଶାଅ ଯେ ନିମ୍ନୋକ୍ତ ଶୀର୍ଷବିନ୍ଦୁ ବିଶିଷ୍ଟ ABC ତ୍ରିଭୁଜମାନ ସମଦ୍ବିବାହୁ ।
(i) A (8, 2), B(5,- 3) ଓ C (0, 0)
(ii) A (0, 6), B (- 5, 3) ଓ C (3, 1)
(iii) A (8, 9), B(- 6, 1) ଓ C (0,-5)
(iv) A (7, 1), B (11, 4) ଓ C (4, – 3)
(v) A (0, 0), B (4, 0) ଓ C (0, -4)
(vi) A (2, 2) B (- 2, 4) ଓ C (2,6)

(i) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟର ସ୍ଥାନାଙ୍କ A (8, 2), B(5, – 3), C (0, 0) ।
AB = \(\sqrt{(5-8)^2+(-3-2)^2}\) = \(\sqrt{(-3)^2 +(-5)^2}\) = \(\sqrt{9+25}\)=√34
BC = \(\sqrt{(0-5)^2+{0-(-3)}^2}\) = \(\sqrt{25+9}\) = √34
CA = \(\sqrt{(8-0)^2+(2-0)^2}\) = \(\sqrt{64+4}\) = √68 = 2√17
∴ ∆ ABCର AB = BC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(ii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A(0, 6), B (- 5, 3) ଓ C (3, 1) ।
AB = \(\sqrt{(-5-0)^2+(3-6)^2}\) = \(\sqrt{(-5)^2 +(-3)^2}\) = \(\sqrt{25+9}\) = √34
BC= \(\sqrt{{3-(-5)}^2 +(1–3)^2}\) = \(\sqrt{8^2 +(-2)^2}\) = \(\sqrt{64+4}\)= √68
AC = \(\sqrt{(3-0)^2+(1-6)^2}\) = \(\sqrt{3^2 +(-5)^2}\) = \(\sqrt{9+25}\) = √34
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(iii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A(8, 9), B(- 6, 1) ଓ C (0, – 5) ।
AB = \(\sqrt{(-6-8)^2 +(1-9)^2}\) = \(\sqrt{(14)^2 +(8)^2}\) = \(\sqrt{196+64}\) = √260 = 2√65
BC = \(\sqrt{{0-(-6)}2 +(-5-1)^2}\) = \(\sqrt{62+(-6)^2}\) = \(\sqrt{36+36}\) = √72 = 6√2
AC = \(\sqrt{(0-8)^2 + (-5-9)^2}\) = \(\sqrt{(-8)^2 +(-14)^2}\) = \(\sqrt{64+196}\) = √260 = 2√65
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(iv) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A (7, 1), B (11, 4) ଓ C (4, – 3) ।
AB = \(\sqrt{(11-7)^2+(4-1)^2}\) = \(\sqrt{42+32}\) = \(\sqrt{16+9}\)= √25=5
BC = \(\sqrt{(4-11)^2+(-3-4)^2}\) = \(\sqrt{(-7)^2+(-7)^2}\) = \(\sqrt{49 +49}\) = √98 = 7√2
AC = \(\sqrt{(4-7)^2 +(-3-1)^2}\) = \(\sqrt{(-3)^2 + (-4)^2}\) = \(\sqrt{9 +16}\) = √25 = 5
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(v) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A (0, 0), B (4, 0), C (0, – 4) ।
AB = \(\sqrt{4^2 +0^2}\) = \(\sqrt{16}\) = 4,
AC = \(\sqrt{0^2 +(-4)^2}\) = √16 = 4
BC= \(\sqrt{(0-4)^2+(-4-0)^2}\) = \(\sqrt{(-4)^2 +(-4)^2}\) = \(\sqrt{16+16}\) = √32 = 4√2
∴ ∆ ABCର AB = AC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

(vi) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁତ୍ରୟ A (2, 2), B ( 2, 4) ଓ C (2, 6) ।
AB = \(\sqrt{(-2-2)^2 + (4 -2)^2}\) = \(\sqrt{4^2 +2^2}\) = \(\sqrt{16+4}\) = √20 = 2√5
BC = \(\sqrt{{2-(-2)}^2 +(6-4)^2}\) = \(\sqrt{4^2 +2^2}\) = \(\sqrt{16+4}\) = √20 = 2√5
∴ ∆ ABCର AB = BC ତେଣୁ ଏହା ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।

Question 5.
ଦର୍ଶାଅ ଯେ ନିମ୍ନଲିଖୂତ ବିନ୍ଦୁଗୁଡ଼ିକ ପାର୍ଶ୍ଵରେ ସୂଚିତ ଚିତ୍ରକୁ ଗଠନ କରିବ ।
(i) (1, 1), (- 1, – 1), (- √3, √3) (ସମବାହୁ ତ୍ରିଭୁଜ)
(ii) (3, – 3), (- 3, 3), (3√3, 3√3) (ସମବାହୁ ତ୍ରିଭୁଜ)
(iii) (1, 2), (3, 4) ଓ (5, 8) (ସମବାହୁ ତ୍ରିଭୁଜ)
(iv) (1, 2), (2, 4) ଓ (3, 5) (ବିଷମବାହୁ ତ୍ରିଭୁଜ)
(v) (-2, 3), (8, 3) ଓ (6, 7) (ସମକୋଣୀ ତ୍ରିଭୁଜ)
(vi) (-6, -8), (-16, 12) ଓ (- 26,- 18) (ସମକୋଣୀ ସମବାହୁ ତ୍ରିଭୁଜ)
ସମାଧାନ :
(i) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(1, 1), B(- 1, – 1), ଓ C (-√3, √3) ।

∴ ∆ ABCର AB = BC = AC । ତେଣୁ ଏହା ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।

(ii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(3, – 3), B(- 3, 3), C(3√3, 3√3) ।

∴ ∆ ABCର AB = BC = AC । ତେଣୁ ଏହା ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।

(iii) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(1, 2), B(3, 4) ଓ C(5, 8) ।

∴ ∆ ABCର AB ≠ BC ≠ AC । ତେଣୁ ଏହା ଏକ ବିଷମବାହୁ ତ୍ରିଭୁଜ ।

(iv) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(1, 2), B(2, 4) ଓ C(3, 5) ।

∴ ∆ ABCର AB ≠ BC ≠ AC । ତେଣୁ ABC ଏକ ବିଷମବାହୁ ତ୍ରିଭୁଜ ।

(v) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(-2, 3), B(8, 3) ଓ C(6, 7) ।

∴ ABC ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ।

(vi) ∆ ABCର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟ A(-2, 3), B(8, 3) ଓ C(6, 7) ।

∴ ABC ଏକ ସମକୋଣୀ ସମବାହୁ ତ୍ରିଭୁଜ ।

Question 6.
ଦର୍ଶାଅ ଯେ ନିମ୍ନଲିଖ୍ ବିନ୍ଦୁଗୁଡ଼ିକ ପାର୍ଶ୍ଵରେ ସୂଚିତ ଚିତ୍ରକୁ ଗଠନ କରିବ ।
(i) (-8, 3), (-2, -1), (6, -2) ଓ (0, 2) (ସାମାନ୍ତରିକ ଚିତ୍ର)
(ii) (-2, -1), (1, 0), (4, 3) ଓ (1, 2) (ସାମାନ୍ତରିକ ଚିତ୍ର)
(iii) (0, -1), (2, 1), (0, 3) ଓ (-2, 1) (ବର୍ଗ ଚିତ୍ର)
(iv) (0,5), (-1, 2), (-4, 3) ଓ (-3, 6) (ବର୍ଗ ଚିତ୍ର)
(v) (-2, 3), (-4, -1), (-6, 0) ଓ (-4, 4) (ଆୟତ ଚିତ୍ର)
ସମାଧାନ :
(i) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-8, 3), B (-2, -1), C (6,-2) ଓ D(0, 2)

∴ ABCD ଚତୁର୍ଭୁଜର AB = CD ଏବଂ AD = BC ।
⇒ ଚତୁର୍ଭୁଜଟି ସାମାନ୍ତରିକ ଚିତ୍ର ଅଟେ । (ପ୍ରମାଣିତ)
(ABCD ଚତୁର୍ଭୁଜର ବିପରୀତ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ)

(ii) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-2, -1), B(1, 0), C(4, 3) ଓ D(1, 2)

∴ ABCD ଚତୁର୍ଭୁଜର AB = CD ଏବଂ AD = BC ।
⇒ ଚତୁର୍ଭୁଜଟି ସାମାନ୍ତରିକ ଚିତ୍ର ଅଟେ । (ପ୍ରମାଣିତ)
(ABCD ଚତୁର୍ଭୁଜର ବିପରୀତ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ)

(iii) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-2, -1), B(1, 0), C(4, 3) ଓ D(1, 2)

(iv) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(0,5), B(-1, 2), C(-4, 3) ଓ D(-3, 6)

(v) ଦଉ ବିନ୍ଦୁ ଚତୁର୍ଭୁଜଟି A(-2, 3), B(-4, -1), C(-6, 0) ଓ D(-4, 4)

Question 7.
ଦର୍ଶାଅ ଯେ P (1, 1) ବିନ୍ଦୁ A (0, 2), B (2, 0) ଓ C (0, 0) ବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।
ସମାଧାନ :
AP = \(\sqrt{(0-1)^2 +(2-1)^2}\) = \(\sqrt{1^2 + 1^2}\) = √2
BP = \(\sqrt{(2-1)^2+(0-1)^2}\) = \(\sqrt{1^2+(-1)^2}\) = √2
CP = \(\sqrt{(0-1)^2+(0-1)^2}\) = \(\sqrt{(-1)^2 +(-1)^2}\) = √2
∴ AP = BP = CP ତେଣୁ ‘P’ ବିନ୍ଦୁ A, B ଓ C ବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

Question 8.
xର କେଉଁ ମାନ ପାଇଁ C (x, 3) ବିନ୍ଦୁ, A (2, 4) ଓ B (3, 5) ବିନ୍ଦୁଦ୍ଵୟ ଠାରୁ ସମାନ ଦୂରରେ ରହିବ ?
ସମାଧାନ :
C (x, 3), ବିନ୍ଦୁ A (2, 4), B (3, 5) ବିନ୍ଦୁଦ୍ଵୟଠାରୁ ସମଦୂରରେ ହେବେ।
AC² = (2 – x)² + (4 – 3)² = (2 – x)² + 1
BC² = (3 – x)² + (5 – 3)² = (3 – x)² + 4
କିନ୍ତୁ ଦଉ ଅନ୍ଥି AC = BC ⇒ AC2 = BC2
⇒ (2 – x)² + 1 = (3 – x)² + 4
⇒ 4 – 4x + x² + 1 = 9 – 6x + x² + 4
⇒ x² – x² + 6x – 4x = 9+ 4 – 5
⇒ 2x = 8 ⇒ x = \(\frac{8}{2}\) = 4
∴ xର ମାନ 4 ପାଇଁ C ବିନ୍ଦୁ A ଓ B ଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ହେବେ ।

Question 9.
P(2, y) ବିନ୍ଦୁ Q (-1, 2) ବିନ୍ଦୁଠାରୁ 5 ଏକକ ଦୂରରେ ରହିଲେ, ଦୁର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
P ଓ Q ବିନ୍ଦୁ ପରସ୍ପରଠାରୁ 5 ଏକକ ଦୂରରେ ଅବସ୍ଥିତ ।
P (2, y) Q) (-1, 2) ମଧ୍ୟରେ ଦୂରତା = \(\sqrt{(1-2)^2+(2-y)^2}\)
ପ୍ରଶ୍ମାନୁସାରେ \(\sqrt{(1-2)^2+(2-y)^2}\) = 5
ଉଭୟ ପାର୍ଶ୍ଵର ବର୍ଗ ନେଲେ, (- 1 – 2)² + (2 – y)² = 5²
⇒ (-3)² + 4 – 4y + y² = 25 ⇒ 9 + 4 + y² – 4y – 25 = 0
⇒ y² – 4y + 12 = 0 ⇒ y² – 6y + 2y + 12 = 0
⇒ y (y – 6) + 2 (y – 6) = 0 ⇒ (y – 6) (y + 2) = 0
⇒ y – 6 = 0 ବା y + 2 = 0 ⇒ y = 6 = 0 ବା y = -2
∴ yର ମାନ 6 କିମ୍ବା – 2 ହେଲେ, PQ = 5 ଏକକ ହେବ ।

Question 10.
ଦର୍ଶାଅ A (1, 1),B (2, 2) & C (3, 3) ଯେ ବିନ୍ଦୁତ୍ରୟ ଏକ ସରଳରେଖାରେ ରହିବେ ।
ସମାଧାନ :
AB = \(\sqrt{(2-1)^2 +(2-1)^2}\) = \(\sqrt{1^2 +1^2}\) = \(\sqrt{1+1}\) = √2
BC = \(\sqrt{(3-2)^2 +(3-2)^2}\) = \(\sqrt{1^2 +1^2}\) = \(\sqrt{1+1}\) = √2
AC = \(\sqrt{(3-1)^2+(3-1)^2}\) = \(\sqrt{2^2 +2^2}\) = \(\sqrt{4+4}\) = √8 = 2√2
AB + BC = √2 + √2 = 2√2 = AC
⇒ A, B, C ବିଦୁ୍ୟତ୍ରୟ ଏକ ସରଳରେଖାରେ ରହିବେ ।

Question 11.
ଦର୍ଶାଅ A (1, 4), B (-1, 6), C (2, 3) ଯେ ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ।
ସମାଧାନ :
AB = \(\sqrt{(-1-1)^2 +(6-4)^2}\) = \(\sqrt{(-2)^2 +(2)^2}\) = \(\sqrt{4+4}\) = √8 = 2√2
AC = \(\sqrt{(2-1)^2+(3-4)^2}\) = \(\sqrt{1^2 +1^2}\) = √2
BC = \(\sqrt{{2-(-1)}^2 +(3-6)^2}\) = \(\sqrt{(2+1)^2 +(-3)^2}\) = \(\sqrt{9+9}\) = √18 = 3√2
AB + AC = 2√2 + √2 = 3√2 = BC
⇒ B, A, C ଏକ ରେଖ୍ୟ ।

Question 12.
ପ୍ରମାଣ କର ଯେ, (1, 0), (2, -3) ଏବଂ (- 1, 6) ବିଦୁ୍ୟତ୍ରୟ ଏକରେଖ୍ୟ ଓ (1, 0) ବିନ୍ଦୁଟି ଅନ୍ୟ ଦୁଇ ବିନ୍ଦୁର ମଧ୍ୟବର୍ତ୍ତୀ ଅଟେ ।
ସମାଧାନ :
ମନେକର ବିଦୁ୍ୟତ୍ରୟ A (1, 0), B(2, -3) 3 C(-1, 6) ।
AB = \(\sqrt{(2-1)^2+(-3-0)^2}\) = \(\sqrt{1^2 +(-3)^2}\) = \(\sqrt{1+9}\) = √10
BC = \(\sqrt{(-1-2)^2+(6+3)^2}\) = \(\sqrt{(-3)^2+9^2}\) = \(\sqrt{9+81}\) = √90 = 3√10
AC = \(\sqrt{(-1-1)^2 + (6-0)^2}\) = \(\sqrt{(-2)^2 +6^2}\) = \(\sqrt{4+36}\) =√40 = 2√10
AB + AC = √10 + 2√10 = 3√10 = BC
∴ AB + AC = BC ⇒ B-A-C
⇒ A (1, 0), B (2, -3) 3 C (1, -6) ବିଦୁ୍ୟତ୍ରୟଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ହେବେ ।

Question 13.
x ଅକ୍ଷ ଉପରେ ଏକ ବିନ୍ଦୁର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ଯାହା (5, 4) ଓ (-2, 3) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିନ୍ଦୁଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ହେବ ।
ସମାଧାନ :
ମନେକର x ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ବିନ୍ଦୁଟି A (x,0) ।
ଦିଉ ବିଦୁ୍ଦ୍ଵୟ B (5, 4) ଓ C (- 2, 3) ।
AB² = (5 – x)² + (4 – 0)² = (5 – x)² + 16
AC² = (-2 – x)² + (3 – 0)² = (2 + x)² + 9
ପ୍ରଶ୍ମାବସାକ (2 + x)² + 9 = (5 – x)² + 16 ⇒ 4 + 4x + x² + 9 = 25 – 10x + x² + 16
= 4x + x² + 13 = 41 – 10x + x²
⇒ 14x = 28 ⇒ x =2
= 4x + 10x + x² – x = 41 – 13
∴ x ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ବିନ୍ଦୁଟିର ସ୍ଥାନାଙ୍କ (2, 0) ।

Question 14.
ଯଦି O (0, 0), A (1, 2), B (3, 8) ଏବଂ C (3, – 1) ହୁଏ, ତେବେ ଦର୍ଶାଅ ଯେ, AB = 2CO ।
ସମାଧାନ :
ଦର ବିନ୍ଦୁ ଚାରୋଟି O(0, 0), A(1, 2), B (3, 8) ଏବଂ C (3, – 1) ।
AB = \(\sqrt{(3-1)^2+(8-2)^2}\) = \(\sqrt{2^2+6^2}\) = \(\sqrt{4+36}\) = √40 = 2√10
CO = \(\sqrt{3^2 +(-1)^2}\) = \(\sqrt{9+1}\) = √10
∴ AB = 2√10 = 2CO ⇒ AB = 2CO ।

Question 15.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜର ଦୁଇ ଶୀର୍ଷବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 3) ବିନ୍ଦୁ (4, 3) ହେଲେ, ତୃତୀୟ ଶୀର୍ଷବିନ୍ଦୁର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ।
ସମାଧାନ :
ନିମ୍ନସ୍ଥ ଚିତ୍ରରେ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
ଏହାର ଶୀର୍ଷବିନ୍ଦୁ B (0, 3) ଏବଂ C (4, 3) । BC ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁ ।
BC = \(\sqrt{(4-0)^2 +(3-3)^2}\) = \(\sqrt{16+0}\) = √16 = 4 ଏକକ।
ଶୀର୍ଷବିନ୍ଦୁ Aରୁ BC ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ AD x ଅକ୍ଷକୁ P ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
∴ D ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{4+0}{2}\), \(\frac{3+3}{2}\)) = (2,3)

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 14 Limit and Differentiation Ex 14(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Exercise 14(b)

Question 1.

Using the ε – δ definition prove that
(i) \(\lim _{x \rightarrow 0}\) (2x + 3) = 3
Solution:
Let f(x) = 2x + 3
Here a = 0 and ℓ = 3
Let ε be any positive real number however small it may be.
Now |f(x) – ℓ| =| 2x + 3 – 3| =|2x|
Thus |f(x) – ℓ| < ε whenever
|2x| < ε i.e |x| < \(\frac{\varepsilon}{2}\)
Then |f(x) – ℓ| < ε
whenever |x – 0| < δ
under the condition δ = \(\frac{\varepsilon}{2}\)
∴ \(\lim _{x \rightarrow 0}\) (2x + 3) = 3

(ii) \(\lim _{x \rightarrow 1}\) (2x – 1) = 1
Solution:
Here f(x) = 2x – 1, ℓ = l and a = 1
Now |f(x)| = | 2x – 1 – 1|
= |2x – 2| = 2|x – 1|
Thus |f(x) –  ℓ| < ε
whenever 2|x – 1| < ε
i,e. |x – 1| < \(\frac{\varepsilon}{2}\) put δ = \(\frac{\varepsilon}{2}\)
Then |f(x) – ℓ| < ε
whenever|x – 1| < δ
Hence \(\lim _{x \rightarrow 1}\) (2x – 1) = 1

(iii) \(\lim _{x \rightarrow -2}\) (3x + 8) = 2
Solution:
|(3x + 8) – 2|
= |3x + 6| = 3|x + 2|
So |3x + 8 – 2| < ε
whenever 3|x + 2| < ε
i.e. |x + 2| < \(\frac{\varepsilon}{3}\)
Hence |(3x + 8) – 2| < ε
whenever | x + 2 | < δ
∴ \(\lim _{x \rightarrow -2}\) (3x + 8) = 2

(iv) \(\lim _{x \rightarrow 3}\) (x² + 2x – 8) = 7
Solution:
|(x² + 2x – 8) – 7|
= |(x² + 2x – 15|
= |(x + 5) (x – 3)|
=| x + 5| | x – 3|
If |x – 3| < 1 then| x + 5| =| x – 3 + 8| < |x – 3| + 8 < 9
Thus |(x² + 2x – 8) – 7| < 9 |x – 3|
So |(x² + 2x – 8) – 7| < ε
whenever 9|x – 3| < ε
i.e.| x – 3| < \(\frac{\varepsilon}{9}\)
Choose δ = minimum of 1 and \(\frac{\varepsilon}{9}\)
Then |(x² + 2x – 8) – 7| < ε
whenever |x – 3| < δ
∴ \(\lim _{x \rightarrow 3}\) (x² + 2x – 8) = 7   (proved)

(v) \(\lim _{x \rightarrow 9}\) √x = 3
Solution:
|√x – 3| = |\(\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{\sqrt{x}+3}\)|
= \(\frac{|x-9|}{|\sqrt{x}+3|}\)

(v) \(\lim _{x \rightarrow a}\) √x = √a, a > 0
Solution:

(vii) \(\lim _{x \rightarrow 1}\) |3x + 2| = 5
Solution:
When x → 1, 3x + 2 is always positive.
So |3x + 2| = 3x + 2
Thus ||3x + 2| -5| = |3x + 2 – 5|
= 3|x – 1|
∴ ||3x + 2| – 5 | < ε
whenever 3|x – 1| < ε
i.e. |x – 1| < \(\frac{\varepsilon}{3}\)
put δ = \(\frac{\varepsilon}{3}\)
Hence ||3x + 2| – 5| < ε
whenever |x – 1| < δ
∴ \(\lim _{x \rightarrow 1}\) |3x + 2| = 5

(viii) \(\lim _{x \rightarrow 2}\) |5x – 7| = 3
Solution:
Let any arbitrary ε > 0
then |5x – 7 – 3| < ε
If |5(x – 2)| < ε
i.e. if lx – 2| < \(\frac{\varepsilon}{5}\)
Choosing δ = \(\frac{\varepsilon}{5}\) we have
for any arbitrary ε > 0 there exists a δ > 0 depending on ε
Such that
|x – 2| < δ ⇒ |(5x – 7) – 3| < ε
∴ \(\lim _{x \rightarrow 2}\) |5x – 7| = 3

Question 2.
If \(\lim _{x \rightarrow a}\) f(x) = ℓ then prove that \(\lim _{x \rightarrow a}\) |f(x)| = | ℓ | Is the converse true ? Justify your answer with reasons.
Solution:
Let \(\lim _{x \rightarrow a}\) f(x) = ℓ
Then |f(x) – ℓ| < ε whenever |x – a| < δ
Now |f(x)| – ℓ| < |f(x) – ℓ| < ε
whenever |x – a| < δ
So \(\lim _{x \rightarrow a}\) |f(x)| = | ℓ |
The converse is not always true because | ℓ | = | -ℓ |
So \(\lim _{x \rightarrow a}\) f(x) = ℓ or -ℓ

Question 3.
(i) Prove that \(\lim _{x \rightarrow a}\) x = a
Solution:
Let ε is any positive number
Let f(x) = x
Now |f(x) – a| < ε
if |x – a| < ε
Choosing δ = ε we see that for each ε > 0 we find a δ > 0 depending on ε such that
|x – al < d ⇒ |f(x) – a| < ε
⇒ \(\lim _{x \rightarrow a}\) f(x) = a i,e. \(\lim _{x \rightarrow a}\) x = a

(ii) Using (i) and the laws of limits prove that \(\lim _{x \rightarrow a} x^n=a^n\), when n is an integer.
Solution:
Case-1: Let n > 0 and n ε z
Now \(\lim _{x \rightarrow a} x^n=\lim _{x \rightarrow a}\) (x. x. x…….. n factors)
= a. a …… n factors = aⁿ
Case-2: Let n = 0

(iii) Using (ii) and the laws of limits prove that \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}\) where n is an integer.
Solution:

Case-3: n = 0  Hence the case is obvious

(iv) Using (iii), the laws of limits and assuming that \(\lim _{x \rightarrow a} \frac{1}{x^m}=a^{\frac{1}{m}}\) where m is a non-zero integer prove that for any rational number n, \(\lim _{x \rightarrow a} \frac{x^n-a^n}{x-a}=n a^{n-1}\).
Solution:

Question 4.
Evaluate the following :
(i) \(\lim _{x \rightarrow 1}\) (1 + 2x – 3x² + 4x³ – 5x⁴)
Solution:
\(\lim _{x \rightarrow 1}\) (1 + 2x – 3x² + 4x³ – 5x⁴)
= 1 + 2 – 3 + 4 – 5 = 7 – 8 = -1

(ii) \(\lim _{x \rightarrow 0}\) (3x² + 4x – 1)(x⁴ + 2x³ – 3x² + 5x + 2)
Solution:
\(\lim _{x \rightarrow 0}\) (3x² + 4x – 1)(x⁴ + 2x³ – 3x² + 5x + 2)
=(-1). 2 = -2

(iii) \(\lim _{x \rightarrow 2}\) \(\frac{x^2+3 x-9}{x+1}\)
Solution:
\(\lim _{x \rightarrow 2}\) \(\frac{x^2+3 x-9}{x+1}\)
\(\frac{2^2+3 \cdot 2-9}{2+1}=\frac{1}{3}\)

(iv) \(\lim _{x \rightarrow 3}\) \(\frac{x^2-9}{x-3}\)
Solution:
\(\lim _{x \rightarrow 3}\) \(\frac{x^2-9}{x-3}\)
= \(\lim _{x \rightarrow 3} \frac{(x-3)(x+3)}{x-3}\)
= \(\lim _{x \rightarrow 3}\) (x + 3) = 3 + 3 = 6

(v) \(\lim _{x \rightarrow 1} \frac{x^3-1}{x-1}\)
Solution:
\(\lim _{x \rightarrow 1} \frac{x^3-1}{x-1}\)
= \(\lim _{x \rightarrow 1} \frac{(x-1)\left(x^2+x+1\right)}{x-1}\)
= \(\lim _{x \rightarrow 3}\) (x² + x + 1)
= 1 + 1 +1 = 3

(vi) \(\lim _{x \rightarrow 2} \frac{x-2}{x^4-16}\)
Solution:

(vii) \(\lim _{x \rightarrow 2} \frac{x^3-8}{x^5-32}\)
Solution:

(viii) \(\lim _{x \rightarrow 3} \frac{x^2+2 x-15}{x^2-x-6}\)
Solution:

(ix) \(\lim _{x \rightarrow 0} \frac{(3+x)^3-27}{x}\)
Solution:

(x) \(\lim _{x \rightarrow 2} \frac{\frac{1}{x^2}-\frac{1}{4}}{x-2}\)
Solution:

(xi) \(\lim _{x \rightarrow 1} \frac{1}{(x-1)}\left\{\frac{1}{x+3}-\frac{2}{3 x+5}\right\}\)
Solution:

(xii) \(\lim _{h \rightarrow 0} \frac{(x+h)^3-x^3}{h}\)
Solution:

(xiii) \(\lim _{h \rightarrow 0} \frac{(x+h)^4-x^4}{h}\)
Solution:

(xiv) \(\lim _{x \rightarrow 1} \frac{x^m-1}{x^n-1}\), where m, n are integers.
Solution:

(xv) \(\lim _{x \rightarrow 1} \frac{x^2-2 x+1}{x^2-x}\)
Solution:

(xvi) \(\lim _{x \rightarrow 1} \frac{x^2+x-2}{x^3-x^2-x+1}\)
Solution:

Question 5.
Evaluate the following :
(i) \(\lim _{x \rightarrow \infty} \frac{2 x+1}{3 x-2}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{2 x+1}{3 x-2}\)
= \(\lim _{x \rightarrow \infty} \frac{2+\frac{1}{x}}{3-\frac{2}{x}}=\frac{2}{3}\)
[ ∵ As x → ∞, \(\frac{1}{x}\) → 0]

(ii) \(\lim _{x \rightarrow \infty} \frac{3 x^2+x-1}{2 x^2-7 x+5}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{3 x^2+x-1}{2 x^2-7 x+5}\)
\(=\lim _{x \rightarrow \infty} \frac{3+\frac{1}{x}-\frac{1}{x^2}}{2-\frac{7}{x}+\frac{5}{x^2}}=\frac{3}{2}\)

(iii) \(\lim _{x \rightarrow \infty} \frac{x^3+2 x^2+3}{x^4-3 x^2+1}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{x^3+2 x^2+3}{x^4-3 x^2+1}\)
\(\lim _{x \rightarrow\infty}\frac{\frac{1}{x}+\frac{2}{x^2}+\frac{3}{x^4}}{1-\frac{3}{x^2}+\frac{1}{x^4}}=\frac{0}{1}\) =0
[ ∵ As x → ∞, \(\frac{1}{x}\) → 0]

(iv) \(\lim _{x \rightarrow \infty} \frac{x^4-5 x+2}{x^3-3 x+1}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{x^4-5 x+2}{x^3-3 x+1}\)
\(\lim _{x \rightarrow \infty} \frac{x-\frac{5}{x^2}+\frac{2}{x^3}}{1-\frac{3}{x^2}+\frac{1}{x^3}}\) = ∞

(v) \(\lim _{x \rightarrow \infty}\left(\frac{x^3}{2 x^2-1}-\frac{x^2}{2 x+1}\right)\)
Solution:

(vi) \(\lim _{n \rightarrow \infty} \frac{n}{n+1}\)
Solution:
\(\lim _{n \rightarrow \infty} \frac{n}{n+1}\)
= \(\lim _{n \rightarrow \infty} \frac{n}{1+\frac{1}{n}}\) = 1

(vii) \(\lim _{n \rightarrow \infty}\left(\frac{n^2+n+1}{5 n^2+2 n+1}\right)\)
Solution:

(viii) \(\lim _{n \rightarrow \infty}\left(\frac{\sqrt{n}-1}{\sqrt{n}+1}\right)\)
Solution:
\(\lim _{n \rightarrow \infty}\left(\frac{\sqrt{n}-1}{\sqrt{n}+1}\right)\)
= \(\lim _{n \rightarrow \infty} \frac{1-\frac{1}{\sqrt{n}}}{1+\frac{1}{\sqrt{n}}}\) = 1

(ix) \(\lim _{n \rightarrow \infty}\left(\frac{6 n^5+2 n+1}{n^5+n^4+3 n^3+2 n^2+n+1}\right)\)
Solution:

(x) \(\lim _{n \rightarrow \infty} \frac{1+2+3+\cdots+n}{n^2}\)
Solution:

(xi) \(\lim _{n \rightarrow \infty} \frac{1^2+2^2+3^2+\ldots+n^2}{n^3}\)
Solution:

(xii) \(\lim _{n \rightarrow \infty} \frac{1^3+2^3+3^3+\ldots+n^3}{n^4}\)
Solution:

(xiii)  \(\lim _{n \rightarrow \infty} \frac{1+\frac{1}{2}+\frac{1}{2^2}+\ldots+\frac{1}{2^n}}{1+\frac{1}{3}+\frac{1}{3^2}+\ldots \frac{1}{3^n}}\)
Solution:

(xiv) \(\lim _{n \rightarrow \infty} \frac{\lfloor n}{\mid n+1-\lfloor n}\)
Solution:

Question 6.
Examine the existence of the following limits :
(i) \(\lim _{x \rightarrow \sqrt{3}}\) [x]
Solution:
L.H.L. = \(\lim _{x \rightarrow \sqrt{3}-}\) [x] = \(\lim _{h \rightarrow 0}\) [√3 – h] = 1
R.H.L. = \(\lim _{x \rightarrow \sqrt{3}+}\) [x] = \(\lim _{h \rightarrow 0}\) [√3 + h] = 1
Thus L.H.L., R.H.L both
exist and L.H.L. = R.H.L.
So the limit exists and its value is 1.

(ii) \(\lim _{x \rightarrow 0}[x]\)
Solution:

(iii) \(\lim _{x \rightarrow-2}[x]\)
Solution:
L.H.L. = \(\lim _{x \rightarrow-2-} \frac{x-2}{|x-2|}\)
= \(\lim _{h \rightarrow 0}\)[-2 – h] = -3
R.H.L. \(\lim _{x \rightarrow-2+}\) [x] = \(\lim _{h \rightarrow 0}\)[-2 + h] = -2
Thus L.H.L. ≠ R.H.L.
So the limit does not exist.

(iv) \(\lim _{x \rightarrow 0} \frac{|x|}{x}\)
Solution:

(v) \(\lim _{x \rightarrow 2} \frac{x-2}{|x-2|}\)
Solution:

(vi) \(\lim _{x \rightarrow \frac{1}{2}} \frac{|2 x-1|}{2 x-1}\)
Solution:

(vii) \(\lim _{x \rightarrow 1}[2 x+3]\)
Solution:

(viii) \(\lim _{x \rightarrow \infty} \frac{x}{[x]}\)
Solution:

(ix) \(\lim _{x \rightarrow \infty} \frac{x^2-x}{\left[x^2-x\right]}\)
Solution:

(x) \(\lim _{x \rightarrow 1} \frac{\left|x^2-3 x+2\right|}{x^2-3 x+2}\)
Solution:

(xi) \(\lim _{x \rightarrow \infty}(-1)^{[x]}\)
Solution:
\(\lim _{x \rightarrow \infty}(-1)^{[x]}\)
[Put n ≤ n + 1,As n→ ∞, x → ∞
= \(\lim _{x \rightarrow \infty}(-1)^n\) [ ∵ [x] = n
= ± 1 [If n is odd, (-1)ⁿ = – 1 and if n is even (-1)ⁿ = 1 ]
We know that whenever the limit exists it must be unique.
So \(\lim _{x \rightarrow \infty}(-1)^{[x]}\) does not exist.

(xii) \(\lim _{x \rightarrow \infty} \sin x\)
Solution:

(xiii) \(\lim _{x \rightarrow \infty} \cos x\)
Solution:

(xiv) \(\lim _{x \rightarrow 0} \cos \frac{1}{x}\)
Solution:

(xv) \(\lim _{x \rightarrow \infty} \sin \frac{1}{x}\)
Solution:

(xvi) \(\lim _{x \rightarrow 1} f(x) \text { if } f(x)= \begin{cases}2 x-1, & x \leq 1 \\ 2 x+1, & x>1\end{cases}\)
Solution:

(xvii) \(\lim _{x \rightarrow 0} f(x) \text { and } \lim _{x \rightarrow 1} f(x)\)
if \(f(x)=\left\{\begin{array}{l}
0 . x \leq 0 \\
1-2 x, 0<x \leq 1 \\
3-4 x, x>1
\end{array}\right.\)
Solution:

Question 7.
Let f(x) = {1 if x is rational, 0 if x is irrational then show that \(\lim _{x \rightarrow a}\) f(x) does not exist for any a ∈ R.
Solution:
Let x → a through rational numbers.
Then \(\lim _{x \rightarrow a}\) f(x) = 1
If x → a through rational numbers.
Then \(\lim _{x \rightarrow a}\) f(x) = 0
Thus \(\lim _{x \rightarrow a}\) f(x) does not exist.

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 2 ବାସ୍ତବ ସଂଖ୍ୟା Ex 2(a)

Question 1.
ଭୁଲ୍ ଥିଲେ (F) ଓ ଠିକ୍ ଥିଲେ (T) ଲେଖ ।

(i) -1 ଦ୍ଵାରା -201 ବିଭାଜ୍ୟ ।
ସମାଧାନ:
T

(ii) 1 ଦ୍ଵାରା 0 ବିଭାଜ୍ୟ ।
ସମାଧାନ:
T

(iii) 0 ଦ୍ଵାରା 5 ବିଭାଜ୍ୟ ।
ସମାଧାନ:
F

(iv) ପୂର୍ଣ୍ଣସଂଖ୍ୟା ପରିମେୟ ନୁହେଁ ।
ସମାଧାନ:
F

(v) -5 < -3 ।
ସମାଧାନ:
T

(vi) 0.9 ଏକ ପରିମେୟ ସଂଖ୍ୟା ।
ସମାଧାନ:
T

(vii) 0 ଏକ ଗଣନ ସଂଖ୍ୟା ।
ସମାଧାନ:
F

(viii) -1/2 ଏକ ପରିମେୟ ସଂଖ୍ୟା ।
ସମାଧାନ:
T

(ix) a, b ∈ N ହେଲେ ab ∈ N ।
ସମାଧାନ:
T

(x) a, b ∈ N ହେଲେ a – b ∈ N ।
ସମାଧାନ:
F

(xi) a, b ∈ N ହେଲେ a – b ∈ Z ।
ସମାଧାନ:
T

(xii) a, b ∈ Z ହେଲେ a/b ∈ Z Q ।
ସମାଧାନ:
F

Question 2.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) \(\frac{1}{2}\) ର ଯୋଗାତ୍ମକ ବିଲୋମୀ । _____ ।
ସମାଧାନ:
\(-\frac{1}{2}\)

(ii) -7ରଗୁଣନାତ୍ମକ ବିଲୋମୀ ______ ।
ସମାଧାନ:
\(-\frac{1}{7}\)

(iii) _____ ତା’ ନିଜର ଯୋଗାତ୍ମକ ବିଲୋମୀ ।
ସମାଧାନ:
0

(iv) _____ ତା’ ନିଜର ଯୋଗାତ୍ମକ ବିଲୋମୀ ।
ସମାଧାନ:
1, -1

(v) ପୂର୍ବ ସଂଖ୍ୟା ସେଟ୍‌ରେ ଯୋଗାତ୍ମକ ଅଭେଦ ______
ସମାଧାନ:
0

(vi) ଯୁଗ୍ମ ଓ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଯୋଗଫଳ _____
ସମାଧାନ:
ଅଯୁଗ୍ମ

(vii) _____ ଏକମାତ୍ର ଯୁଗ୍ମ ମୌଳିକ ସଂଖ୍ୟା ଅଟେ ।
ସମାଧାନ:
2

(viii) ସର୍ବନିମ୍ନ ଅଯୁଗ୍ମ ମୌଳିକ ସଂଖ୍ୟାଟି _____ ଅଟେ ।
ସମାଧାନ:
3

(ix) ଗୁଣନ ପ୍ରକ୍ରିୟା _____ ପ୍ରକ୍ରିୟାକୁ ବଣ୍ଟନ କରେ ।
ସମାଧାନ:
ପୋଗ

(x) ପ୍ରକ୍ରିୟାକୁ ବଣ୍ଟନ କରେ । ଯୋଗାତ୍ମକ ବିଲୋମୀ ଉପାଦାନକୁ ମିଶାଇଲେ _____ ପକ ଅଟେ ।
ସମାଧାନ:
0

(xi) N ∩ N * = _____।
ସମାଧାନ:
N

(xii) ସେଟ୍‌ରେ – 1ର ଗୁଣନାତ୍ମକ ବିଲୋମୀ _____ ।
ସମାଧାନ:
-1

Question 3.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନପାଇଁ ପ୍ରଦତ୍ତ ସମ୍ଭାବ୍ୟ ଉତ୍ତରରୁ ଠିକ୍ ଉତ୍ତରଟିକୁ ବାଛ ।

(i) n, m ∈ Z ହେଲେ ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଅସତ୍ୟ ?
(a) m + n ∈ Z
(b) m – n ∈ Z
(c) m × n ∈ Z
(d) n ÷ m ∈ Z
ସମାଧାନ:
n + m ∈ Z

(ii) Z ସେଟ୍‌ରେ କେଉଁଟି ସତ୍ୟ ?
(a) ଯୋଗାତ୍ମକ ଅଭେଦ 0
(b) ଯୋଗାତ୍ମକ ଅଭେଦ 1
(c) ଗୁଣନାତ୍ମକ ଅଭେଦ 0
(d) ଯୋଗାତ୍ମକ ବିଲୋମୀ (−1)
ସମାଧାନ:
ଯୋଗାତ୍ମକ ଅଭେଦ 0

(iii) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ସତ୍ୟ ?
(a) ସବୁଠାରୁ କ୍ଷୁଦ୍ରତମ ମୌଳିକ ସଂଖ୍ୟାଟି 3 (b)
(b) ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଗୁଣଫଳ ଅଯୁଗ୍ମ
(c) ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଗୁଣଫଳ ଅଯୁଗ୍ମ (d)
(d) ଦୁଇଟି ମୌଳିକ ସଂଖ୍ୟାର ଗୁଣଫଳ ମୌଳିକ
ସମାଧାନ:
ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଗୁଣଫଳ ଅଯୁଗ୍ମ

(iv) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ସତ୍ୟ ?
(a) x < y ଓ y < z ହେଲେ x < z
(b) x< y 3 z ∈ Q ହେଲେ xz < yz
(c) x < y ଓ z ∈ Q ହେଲେ x + z < y + z ନ ହୋଇପାରେ ।
(d) ଦୁଇଟି ପରିମେୟ ସଂଖ୍ୟା ମଧ୍ୟରେ ସସୀମ ସଂଖ୍ୟକ ପରିମେୟ ବିଦ୍ୟାମନ ।
ସମାଧାନ:
x < y ଓ y < z ହେଲେ x < z ଓ x < z

(v) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁଟି ଠିକ୍ ?
(a) 0.9999 ……. < 1.0
(b) 1/5 ର ଦଶମିକ ପରିପ୍ରକାଶଟି 0.19999 …….
(c) 1/3 ର ଦଶମିକ ପରିପ୍ରକାଶ
(d) n ଏକ ମୌଳିକ ସଂଖ୍ୟା ହେଲେ 1/n ର ଦଶମିକ ପରିପ୍ରକାଶ ସର୍ବଦା ପୌନଃପୁନିକ ।
ସମାଧାନ:
1/5 ର ଦଶମିକ ପରିପ୍ରକାଶଟି 0.19999 …..

(vi) \(\frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{4}{7}\) ମଧ୍ୟରେ ବୃହତ୍ତମ ପରିମେୟ ସଂଖ୍ୟାଟି କେଉଁଟି ?
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{3}{5}\)
(d) \(\frac{4}{7}\)
ସମାଧାନ:
\(\frac{2}{3}\)

(vii) \(\frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{4}{7}\) ମଧ୍ୟରେ କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟା କେଉଁଟି ?
(a) \(\frac{1}{2}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{3}{5}\)
(d) \(\frac{4}{7}\)
ସମାଧାନ:
\(\frac{1}{2}\)

(viii) 1ର ଯୋଗାତ୍ମକ ବିଲୋମୀ କେଉଁଟି ? 
(a) 1
(b) 0
(c) -1
(d) ଏଥରୁ କୌଣସିଟି ନୁହେଁ
ସମାଧାନ:
-1

(ix) ନିମ୍ନଲିଖ ମଧ୍ୟରୁ କେଉଁ ଉଦ୍ଭଟି ଅସତ୍ୟ ?
(a) p ଓ q ମୌଳିକ ହେଲେ ସେମାନଙ୍କର ଗ.ସା.ଗୁ. = 1 ।
(b) p ଓ ୟୁ ଗଣନ ସଂଖ୍ୟା ହେଲେ p + g + pg ଏକ ଗଣନ ସଂଖ୍ୟା ।
(c) p ଓ ୟୁ ମୌଳିକ ସଂଖ୍ୟା ହେଲେ p + q ମଧ୍ୟ ଏକ ମୌଳିକ ସଂଖ୍ୟା ।
(d) p ଏକ ପୂର୍ବ ସଂଖ୍ୟା ଓ ଠୁ ଏକ ଗଣନ ସଂଖ୍ୟା ହେଲେ pg ଏକ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ।
ସମାଧାନ:
p ଓ ୟୁ ମୌଳିକ ସଂଖ୍ୟା ହେଲେ p + g ମଧ୍ଯ ଏକ ମୌଳିକ ସଂଖ୍ୟା ହେବ ।

Question 4.
ପ୍ରତି ଯୁଗ୍ମ ସଂଖ୍ୟା ଯୌଗିକ ଅଟେ କି ? କାରଣ ସହ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
2ର ଯୁଗ୍ମସଂଖ୍ୟା ଯାହା ଏକ ମୌଳିକ ସଂଖ୍ୟା ।
ପ୍ରତି ଯୁଗ୍ମସଂଖ୍ୟା ଯୌଗିକ ନୁହେଁ । କାରଣ 2 ବ୍ୟତୀତ ପ୍ରତି ଯୁଗ୍ମ ସଂଖ୍ୟା ଯୌଗିକ ।

Question 5.
କେଉଁ କେଉଁ ବୀଜଗାଣିତିକ ଧର୍ମଗୁଡ଼ିକ ପୂର୍ବ ସଂଖ୍ୟା ସେଟ୍ Zରେ ସତ୍ୟ, ମାତ୍ର ଗଣନ ସଂଖ୍ୟା ସେଟ୍‌ରେ ସତ୍ୟ ନୁହେଁ ସେଗୁଡ଼ିକ ଲେଖ ।
ସମାଧାନ:
ଯୋଗାତ୍ମକ ଅଭେଦ ଧର୍ମ ଏବଂ ଯୋଗାତ୍ମକ ବିଲୋମୀ ଧର୍ମ ଦ୍ଵୟ ପୂର୍ବସଂଖ୍ୟା ସେଟ୍ Zରେ ସତ୍ୟ ହେଲେ ହେଁ ତାହା ଗଣନ ସଂଖ୍ୟା ସେଟ୍ (N) ରେ ସତ୍ୟ ନୁହେଁ ।

Question 6.
କେଉଁ କେଉଁ ବୀଜଗାଣିତିକ ଧର୍ମଗୁଡ଼ିକ ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ ( ରେ ସତ୍ୟ, ମାତ୍ର ପୂର୍ବ ସଂଖ୍ୟା ସେଟ୍‌ରେ ଅସତ୍ୟ ସେଗୁଡ଼ିକ ଲେଖ ।
ସମାଧାନ:
ଗୁଣନାତ୍ମକ ବିଲୋମୀ ଧର୍ମ ପରିମେୟ ସଂଖ୍ୟା ସେଟ୍ (Q) ରେ ସତ୍ୟ ହେଲେ ହେଁ ପୂର୍ବସଂଖ୍ୟା ସେଟ୍ (Z) ରେ ଅସତ୍ୟ ।

Question 7.
x ଓ y ଅଯୁଗ୍ମ ହେଲେ ପ୍ରମାଣ କର ଯେ, xy ଅଯୁଗ୍ମ ମାତ୍ର x + y ଯୁଗ୍ମ ।
ସମାଧାନ:
ପ୍ରମାଣ : ମନେକର x ଓ y ଅଯୁଗ୍ମ ସଂଖ୍ୟା ଏବଂ x = 2n + 1 ଓ y = 2m + 1 (m, n ∈ Z) ।
xy = (2n + 1) (2m + 1 ) = 4mn + 2m + 2n + 1
= 2 (2 mn + m + n) + 1 (∴ m, n ∈ Z = 2mn + m + n ∈ Z)
x ଓ y ଅଯୁଗ୍ମ ⇒ xy ଅଯୁଗ୍ମ  … (i)  (ପ୍ରମାଣିତ)
x + y = (2n + 1) + (2m + 1 ) = 2n + 2m + 2
= 2(n + m + 1 ) (∴ m, n ∈ Z = m + n + 1 ∈ Z)
∴ x + y ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା  … (ii)
⇒ x ଓ y ଅଯୁଗ୍ମ = x + y ଯୁଗ୍ମ ।  (ପ୍ରମାଣିତ)
(i) ଓ (ii)ରୁ x ଓ y ଅଯୁଗ୍ମ ହେଲେ xy ଅଯୁଗ୍ମ ଏବଂ x + y ଯୁଗ୍ମ ହେବ ।

Question 8.
ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନେ ଯୋଗ ଜନିତ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରନ୍ତି କି ? କାରଣ ସହ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
ମନେକର ଦୁଇଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟା, x = 2n + 1 ଏବଂ
y = 2n+ 3 (n ∈ Z)
x + y ଏକ ଅଯୁଗ୍ମ ସଂଖ୍ୟା
ଦର୍ଶାଇବାକୁ ପଡ଼ିବ ।
2n + 1 + 2n + 3 = 4n + 4 = 2 (2n + 2)
ଅର୍ଥାତ୍ x + y ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା ।
ତେଣୁ ଅଯୁଗ୍ମ ସଂଖ୍ୟାମାନେ ଯୋଗ ଜନିତ ସଂବୃତ୍ତି ନିୟମ ପାଳନ କରନ୍ତି ନାହିଁ ।

Question 9.
15 ଅପେକ୍ଷା ବୃହତ୍ତର ଓ 100 ଠାରୁ କ୍ଷୁଦ୍ରତର ଯେଉଁ ପୂର୍ଣ ସଂଖ୍ୟାଗୁଡ଼ିକର ସାଧାରଣ ରୂପ 3x² +  2, n ∈ Z ସେଗୁଡ଼ିକ ଲେଖ ।
ସମାଧାନ:
ଦତ୍ତ ପୂର୍ଣ୍ଣସଂଖ୍ୟାର ସାଧାରଣ ରୂପ 3x? + 2 (n ∈ Z)
ଏଠାରେ ଲର ମାନ 1, 2, 3, ….. ହେଲେ, ଦତ୍ତ ପୂର୍ଣ୍ଣସଂଖ୍ୟାଗୁଡ଼ିକ ଯଥାକ୍ରମେ….
3(1)² + 2 = 5, 3(2)² + 2 = 12, 3(3)² + 2 = 29, 3(4)² + 2 = 50, 3(5)² + 2 = 77, 3(6)² + 2 = 110,
ଏଠାରେ nର ମାନ 3, 4 ଓ 5 ପାଇଁ ପୂର୍ବସଂଖ୍ୟାର ମାନ ଯଥାକ୍ରମେ 20, 50 ଓ 77 ହେବ ଯହା 15 ଓ 100 ମଧ୍ୟସ୍ଥ ପୂର୍ଣ୍ଣସଂଖ୍ୟା । ପ୍ରକାଶ ଥାଉକି nର ମାନ –3, –4 ଓ –5 ମଧ୍ଯ ପୂର୍ବସଂଖ୍ୟାର ମାନଗୁଡ଼ିକ ଯଥାକ୍ରମେ 29, 50, 77 ପ୍ରତ୍ୟେକ 15 ରୁ ବଡ଼ ଏବଂ 100 ରୁ ସାନ ।

Question 10.
0.123 123 123 …. ସଂଖ୍ୟାଟି ପରିମେୟ ସଂଖ୍ୟା ହେବ କି ? କାରଣ ସହ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
0.123 123 123 …..= 0.123
ପନେକବ x = 0. 123 ⇒ 1000 x = 123, \(\overline{123}\)
∴ 1000x -x= 123.0 – 0.0 = 123
⇒ 999x = 123 ⇒ x = \(\frac{123}{999}=\frac{41}{333}\)
ବି.ଦ୍ର. : ଏଥରୁ ସ୍ପଷ୍ଟ ଯେ, 0.123 123 123… ବ ପରିମେୟ ବୁପ \(\frac{41}{333}\) ହେତୁ ଦତ୍ତ ରାଶିଟି ଏକ ପରିମେୟ ସଂଖ୍ୟା ।

Question 11.
0.131 ସଂଖ୍ୟାକୁ, \(\frac{p}{q}\) ପରିମେୟ ରୂପରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:
0.131 = \(\frac{131}{1000}\)
0.131କୁ \(\frac{p}{q}\) ପରିମେୟ ରୂପରେ ପ୍ରକାଶ କଲେ ହେବ \(\frac{131}{1000}\)

Question 12.
\(\frac{1}{3}\) ପରିମେୟ ସଂଖ୍ୟାଟିକୁ ଅସରନ୍ତି ପୌନଃପୁନିକ ଦଶମିକ ରୂପେ ଲେଖ ।
ସମାଧାନ:
\(\frac{1}{3}\) = 1 ÷ 3 = 0. 333333…….= 0.3
∴ \(\frac{1}{3}\) ର ଅସରନ୍ତି ପୌନଃପୁନିକ ଦଶମିକ ରୂପ 0.333333….. ।

Question 13.
\(\frac{1}{3}\) ପରିମେୟ ସଂଖ୍ୟାଟିକୁ ଲଘିଷ୍ଠାକୃତି ନ ହୋଇଥବା \(\frac{100}{q_1}, \frac{p_1}{-102}, \frac{6 \times p_3}{q_3}\) ରୂପରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:

Question 14.
ସମାଧାନ:

ମେହିପରି \(\frac{-15}{15}=\frac{-15}{15}\) = 1 (n = 15 ପାଇଁ)
ପରିମେୟ ସଂଖ୍ୟାମାନ = -15, -7.5, – ….. -1
ଏଠାରେ –15 ଓ –1 ଯଥାକ୍ରମେ କ୍ଷୁଦ୍ରତମ ଏବଂ ବୃହତ୍ତମ ପରିମେୟ ସଂଖା ।

Question 15
ସମାଧାନ:

Question 16.
ସମାଧାନ:

Question 17.
ସମାଧାନ:

Question 18.
(i) \(0 . \overline{9}\) = 1
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{9}\) = 0.999…
⇒ 10 x = 9.999…
∴ 10x – x = 9.9999 …. – 0.999 … = 9
⇒ 9x = 9 ⇒ x = \(\frac{9}{9}\) = 1
∴ \(0 . \overline{9}\) = 1 (ପ୍ରମାଶିତ)

(ii) 1.29 = 1.3
ସମାଧାନ:
ମନେଳର x = 1.29
⇒ 10x = 12.9 = 12.999 ….
⇒ 100x = 129.9
⇒ 100x – 10x = 129.9 – 12.9
⇒ 90x = 117
⇒ x = \(\frac{117}{90}=\frac{13}{10}\) = 1.3
∴ 1.29 = 1.3 (ପ୍ରମାଶିତ)

(iii) 2.349 = 2.35
ସମାଧାନ:
ମନେଳର x = 2.349 ⇒ 100x = 234.9
⇒ 1000 x = 2349.9
∴ 1000 x – 100 x = 2349.9 – 234.9
⇒ 900 x = 2115 ⇒ x = \(\frac{2115}{900}=\frac{235}{100}\) = 2.35
∴ 234.9 = 2.35 (ପ୍ରମାଶିତ)

Question 19.
(i) \(0 . \overline{1}\)
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{1}\) = 0.11111 ….
⇒ 10x = 1.11…. = \(1 . \overline{1}\)
∴ 10x – x = \(1 . \overline{1}\) – \(0 . \overline{1}\)
⇒ 9x = 1 ⇒ x = \(\frac{1}{9}\)
∴ \(0 . \overline{1}\) = \(\frac{1}{9}\)

(ii) \(0 . \overline{11}\)
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{11}\) = 0.11111111….
⇒ 100x = 11.11
∴ 100x – x = 11.11 – 0.11
⇒ 99x = 11 ⇒ x = \(\frac{11}{99}=\frac{1}{9}\)
∴ \(0 . \overline{11}\) \(\frac{1}{9}\)

(iii) \(0 . \overline{89}\)
ସମାଧାନ:
ମନେଳର \(0 . \overline{89}\) = 0.898989 …..
⇒ 10x = \(8 . 9\overline{89}\) = 8.9898989….
⇒ 100 x = 89.898989 …..
∴ 100x – x = 89.898989 ….. – 0.898989 ….
⇒ 99 x = 89
⇒ x = \(\frac{89}{99}\)

(iv) \(0 . \overline{37}\)
ସମାଧାନ:
ମନେଳର x – \(0 . \overline{37}\) = 0.373737….
⇒ 100x = \(37 . \overline{37}\)
∴ 100x – x = 37.37 – 0.37
⇒ 99x = 37 ⇒ x = \(\frac{37}{99}\)
∴ 0.37 = \(\frac{37}{99}\)

(v) \(0 . \overline{123}\)
ସମାଧାନ:
ମନେଳର x = \(0 . \overline{123}\) = 0.123123123….
⇒ 10x = 1.23123 …..
⇒ 100x = 12.3123 …
⇒ 1000x = 123 .123
∴ 1000x – x = 123.123 – 0.123
⇒ 999x = 123 ⇒ x = \(\frac{123}{999}=\frac{41}{333}\)
∴ \(0 . \overline{123}\) = \(\frac{123}{999}=\frac{41}{333}\)

(vi) \(0 . 32\overline{1}\)
ସମାଧାନ:
ମନେଳର \(0 . 32\overline{1}\) = 0.3211111….
⇒ 100x = \(32\overline{1}\) ⇒ 1000x = \(321\overline{1}\)
∴ 1000x – 100x = \(321\overline{1}\) – \(32\overline{1}\)
⇒ 900x = 289 ⇒ x = \(\frac{289}{900}\)
∴ \(0 . 32\overline{1}\) = \(\frac{289}{900}\)

(vii) –\(0. 5\overline{4}\)
ସମାଧାନ:
ମନେଳର x = –\(0. 5\overline{4}\) = -0.5444….
⇒ 10x = –\(5\overline{4}\)
⇒ 100x = –\(54.\overline{4}\)
100x – 10x = –\(54.\overline{4}\) + \(5\overline{4}\)
⇒ 90x = -49 ⇒ x = \(\frac{-49}{90}\)
∴ –\(0. 5\overline{4}\) = \(\frac{-49}{90}\)

(viii) \(6. \overline{89}\)
ସମାଧାନ:
ମନେଳର x = \(6. \overline{89}\) = 6.8999 ….
⇒ 10x = \(68. \overline{9}\)
⇒ 100x = \(689. \overline{9}\)
∴ 100 x – 10 x = \(689. \overline{9}\) – \(68. \overline{9}\)
⇒ 90 x = 621
⇒ x = \(\frac{621}{90}=\frac{69}{10}\)

(ix) –\(0 . \overline{12}\)
ସମାଧାନ:
ମନେଳର –\(0 . \overline{12}\) = – 0.12121212….
⇒ 100x = –\(12 . \overline{12}\)
∴ 100x – x = –\(12 . \overline{12}\) + \(0 . \overline{12}\)
⇒ 99x = -12 ⇒ x = \(\frac{-12}{99}=\frac{-4}{33}\)
∴ –\(0 . \overline{12}\) = \(\frac{-4}{33}\)

(x) \(0 . 013\overline{05}\)
ସମାଧାନ:
ମନେଳର x = \(0 . 013\overline{05}\)
⇒ 1000x = \(13. \overline{05}\)
⇒ 100000 x = 1305.05
⇒ 100000 x – 1000 x = = 1305.05 – 13.05
⇒ 99000 x = 1292
⇒ x = \(\frac{1292}{99000}=\frac{323}{24750}\)

Question 20.
ମୂଲ୍ୟ ନିରୂପଣ କର (ପୂର୍ଣ ସଂଖ୍ୟା କିମ୍ବା ଭଗ୍ନ ସଂଖ୍ୟା ରୂପରେ)
(i) \(0 . \overline{6} + 0 . \overline{3} \)
ସମାଧାନ: 
\(0 . \overline{6} + 0 . \overline{3} \) = \(\frac{6}{9}=\frac{3}{9}\) = \(\frac{6+3}{9}\) = \(\frac{9}{9}\) = 1
(∵ \(0 . \overline{6}\) = \(\frac{6-0}{10-1}\) = \(\frac{6}{9}\))

(ii) \(0 . \overline{6} + (0 . \overline{3}) \) × 2
ସମାଧାନ: 
\(0 . \overline{6} + (0 . \overline{3}) \) × 2 = \(\frac{6}{9}-\frac{3}{9}\) × 2 = \(\frac{6}{9}-\frac{6}{9}\) = 0

(iii) \((0 \cdot \overline{6})^2+(0 \cdot \overline{3})^2+2 \times(0 \cdot \overline{6}) \times(0 \cdot \overline{3})\)
ସମାଧାନ: 

(iv) \((0 . \overline{6})^2+(0 \cdot \overline{3})^2-2 \times(0 . \overline{6}) \times(0 \cdot \overline{3})+0 . \overline{6}\)
ସମାଧାନ: 

(v) \((0 \cdot \overline{6})^2-(0 \cdot \overline{3})^2\)
ସମାଧାନ: 
\((0 \cdot 6)^2-(0 \cdot 3)^2=\left(\frac{6}{9}\right)^2-\left(\frac{3}{9}\right)^2=\frac{36}{81}-\frac{9}{81}=\frac{4}{9}-\frac{1}{9}=\frac{4-1}{9}=\frac{3}{9}=\frac{1}{3}\)

(vi) \((0 \cdot \overline{6})^3+(0 \cdot \overline{3})^3+3 \times(0 \cdot \overline{6}) \times(0 \cdot \overline{3})(0 \cdot \overline{6}+0 \cdot \overline{3})\)
ସମାଧାନ: 

(vii) \((0 . \overline{6})^3-(0 \cdot \overline{3})^3-3 \times(0 \cdot \overline{3}) \times(0 . \overline{6}) \times(0 \cdot \overline{6}-0 . \overline{3})\)
ସମାଧାନ: 

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ Ex 3 Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 3 ବୃତ୍ତର ସ୍ପର୍ଶକ Ex 3

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର O, ବୃତ୍ତ ବହିଃସ୍ଥ P କୌଣସି ଏକ ବିନ୍ଦୁ ଏବଂ \(\overline{\mathrm{PT}}\) ଉକ୍ତ ବୃତ୍ତର ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ହେଲେ, m∠OTP = _____ |
(ii) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ଠ । ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ \(\overline{\mathrm{PX}}\) ଓ \(\overline{\mathrm{PY}}\) ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ଦୁଇଟି ସ୍ପର୍ଶକଖଣ୍ଡ । ∠XPY ଏକ ସୂକ୍ଷ୍ମକୋଣ ହେଲେ, ∠XOY ଏକ
କୋଣ ।
(iii) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ଠ, ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ \(\overline{\mathrm{PT}}\) ଉକ୍ତ ବୃତ୍ତପ୍ରତି ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ହେଲେ, m∠TOP + m∠TPO = ____ |
(iv) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ଠ, ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ \(\overline{\mathrm{PX}}\) ଓ \(\overline{\mathrm{PY}}\) ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଦୁଇଟି ସ୍ପର୍ଶକ ଖଣ୍ଡ ହେଲେ,
(a) XOP କୋଣ ଓ ………………… କୋଣ ସମପରିମାଣ ବିଶିଷ୍ଟ;
(b) YPO କୋଣ ଓ ………………… କୋଣ ସମପରିମାଣ ବିଶିଷ୍ଟ ।
(v) ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର ୦ ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ । ବୃତ୍ତର ସମତଳରେ P ଏକ ବିନ୍ଦୁ ଏବଂ OP ଓ 1 ମଧ୍ଯରେ – ବୃହତ୍ତର ହେଲେ, P ବିନ୍ଦୁରୁ ବୃତ୍ତ ପ୍ରତି ଏକ ସ୍ପର୍ଶକ ଖଣ୍ଡ ଅଙ୍କନ ସମ୍ଭବ ।
(vi) 5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର କେନ୍ଦ୍ରଠାରୁ 13 ସେ.ମି. ଦୂରରେ ଓ ବୃତ୍ତର ସମତଳରେ ଅବସ୍ଥିତ ଏକ ବିନ୍ଦୁ P ହେଲେ, PT ସ୍ପର୍ଶକଖଣ୍ଡର ଦୈର୍ଘ୍ୟ ………………. ସେ.ମି.|
(vii) କେନ୍ଦ୍ର ୦ ଏବଂ 1 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ଏକ ସ୍ପର୍ଶକ ଖଣ୍ଡର ଦୈର୍ଘ୍ୟ t ସେ.ମି. ହେଲେ OP = ………………. ସେ.ମି.|
(viii) ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ବୃତ୍ତର (a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ………………… ଏକ
(b) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = …………………
(ix) ଦୁଇଟି ଅନ୍ତସ୍ପର୍ଶୀ ବୃତ୍ତର (a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ………………..
(b) ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ……………..
(x) ପରସ୍ପର ବହିଃସ୍ଥ ହୋଇଥ‌ିବା ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର
(a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ……………………
(b) ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ………………..
(xi) ପରସ୍ପର ବହିଃସ୍ଥ ହୋଇ ନ ଥ‌ିବା ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର
(a) ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = …………….
(b) ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ସଂଖ୍ୟା = ……………
(xii) △ABC ର AB =AC । △ABC ର ପରିବୃତ୍ତ ଉପରିସ୍ଥ A ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ ଉପରେ P ଏକ ବିନ୍ଦୁ, ଯେପରି P ଓ B ବିନ୍ଦୁଦ୍ଵୟ \(\overline{\mathrm{AC}}\) ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ।
m∠PAC = 70° ଦେଲେ, m∠ABC =
(xiii) ଗୋଟିଏ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ୫ ସେ.ମି. ହେଲେ ଏହାର ଦୁଇଟି ସମାନ୍ତର ସ୍ପର୍ଶକ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ………………. ସେ.ମି.|
(xiv) ଦୁଇଟି ବର୍ହିସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ହେଉଛି ବୃତ୍ତଦ୍ୱୟର ବ୍ୟାସାର୍ଦ୍ଧମାନଙ୍କର ………………. ସଦ୍ ପମାନ |
(xv) ଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ହେଉଛି ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧମାନଙ୍କର ……………… ସମାନ |
(xvi) ଏକ ସରଳରେଖା ଉପରିସ୍ଥ ଗୋଟିଏ ବିନ୍ଦୁ P ଠାରେ ସରଳରେଖାଟି ସର୍ବାଧିକ ……………… ହୋଇପାରିବ ।
Solution:
(i) 90°
(ii) ସ୍ଥୂଳକୋଣ
(iii) 90°
(iv) (a) YOP (b) XPO
(v) OP
(vi) 12
(vii) \(\sqrt{\mathrm{r}^2+\mathrm{t}^2}\)
(viii) (a) 2 (b) 1
(ix) (a)1 (b) 0
(x) (a) 2 (b) 0
(xi) (a) 0 (b) 0
(xii) 70°
(xiii) 16 ସେ.ମି.|
(xiv) ସମପୁ
(xv) ଥନ୍ତ୍ରର
(xvi) ଅସଂଖ୍ୟ

Question 2.
ଦତ୍ତ ଥ‌ିବା ଉକ୍ତି ଭୁଲ୍‌ଲେ (ଏହାକୁ ଦତ୍ତ ଉକ୍ତିର ନାସ୍ତିବାଚକ ଉକ୍ତି (Negative Statement) ବ୍ୟବହାର ନ କରି) ସଂଶୋଧନ କର ।
(i) r ଏକକ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତର L ରେଖା ଏକ ଛେଦକ ହେଲେ, ବୃତ୍ତର କେନ୍ଦ୍ରଠାରୁ L ର ଦୂରତା = r ଏକକ ।
(ii) ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତ ବହିଃସ୍ଥ କୌଣସି ଏକ ବିନ୍ଦୁ P | P ବିନ୍ଦୁରୁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ଏକ ସ୍ପର୍ଶକ ଖଣ୍ଡ \(\overline{\mathrm{PT}}\) ହେଲେ △OPT ରେ ∠POT ଏକ ସମକୋଣ ।
(iii) ଗୋଟିଏ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ । ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତ ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରୁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ \(\overline{\mathrm{PT}}\) ର ଦୈର୍ଘ୍ୟ t ଏକକ ଏବଂ ବୃତ୍ତର କେନ୍ଦ୍ର ୦ ଠାରୁ P ର ଦୂରତା d ଏକକ ହେଲେ, d² + r² = t²|
(iv) ଏକ ବୃତ୍ତର ସମତଳରେ ବୃତ୍ତ ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ Pରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ \(\overline{\mathrm{PT}}\); P ବିନ୍ଦୁଗାମୀ ଏକ ଛେଦକ, ବୃତ୍ତଟିକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରି P – A – B । ତେବେ PT² = PA × AB |
(v) ଏକ ବୃତ୍ତର ଅନ୍ତଃସ୍ଥ କୌଣସି ଏକ ବିନ୍ଦୁ Q ଠାରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଦୁଇଟି ସ୍ପର୍ଶକଖଣ୍ଡ ଅଙ୍କନ କରାଯାଇ ପାରିବ ।
(vi) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାସାର୍ଦ୍ଧ ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ କେବଳ ଗୋଟିଏ ବିନ୍ଦୁ P ଅଛି, ଯେଉଁଠାରୁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ହେବ ।
(vii) ଦୁଇଟି ସ୍ପର୍ଶକ ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ ଦ୍ଵୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା ସହ ଉକ୍ତ ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧର ସମଷ୍ଟି ସମାନ ହେଲେ, ବୃତ୍ତ ଦ୍ଵୟ ଅନ୍ତଃସ୍ପର୍ଶୀ ହେବେ ।
(viii) ଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶୀ ବୃତ୍ତର କେନ୍ଦ୍ରନ୍ବୟର ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା, ବୃତ୍ତଦ୍ଵୟର ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ବୟର ପାର୍ଥକ୍ୟ ସହ ସମାନ ।
(ix) ଦୁଇଟି ବୃତ୍ତ ମଧ୍ୟରୁ ଗୋଟିଏ ଅନ୍ୟଟିର ଅନ୍ତର୍ଦେଶରେ ଅବସ୍ଥିତ ହେଲେ, ସେ ଦୁଇଟି ବୃତ୍ତର ଗୋଟିଏ ମାତ୍ର ସାଧାରଣ ସ୍ପର୍ଶକ ରହିବ ।
(x) ଦୁଇଟି ବିନ୍ଦୁରେ ପରସ୍ପରକୁ ଛେଦ କରୁଥିବା ଦୁଇଟି ବୃତ୍ତର କେବଳ ଗୋଟିଏ ତୀର୍ଯ୍ୟକ ସାଧାରଣ ସ୍ପର୍ଶକ ଥାଏ ।
(xi) ଦୁଇଟି ଅନ୍ତଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତର ସ୍ପର୍ଶବିନ୍ଦୁ, ଅନ୍ତଃସ୍ଥ ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ ନୁହେଁ ।
(xii) ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ସ୍ପର୍ଶକ ବୃତ୍ତର ସ୍ପର୍ଶ ବିନ୍ଦୁ, ଉଭୟ ବୃତ୍ତ ମଧ୍ୟରୁ କୌଣସିଟିର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ନୁହେଁ ।
Solution:
(i) <r
(ii) ∠OTP ଟି ∠PTO
(iii) d² = t² + r²
(iv) PT² = PA × PB
(v) ଅନ୍ତର୍ ବଦଲରେ ଦହିମ
(vi) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଅସଂଖ୍ୟ ବିନ୍ଦୁ P ଅଛି ଯେଉଁଠାରୁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ହେବ ।
(vii) ସମଷ୍ଟି ବଦଳରେ ଅନ୍ତର ହେବ ।
(viii) ପାର୍ଥକ୍ୟ ବଦଳରେ ଅନ୍ତର ହେବ ।
(ix) ଗୋଟିଏ ମାତ୍ର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ହେବ ।
(x) ଗୋଟିଏ ତୀର୍ଯ୍ୟକ ବଦଳରେ ଦୁଇଟି ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ହେବ ।
(xi) ଉଭୟର ଏକ ସାଧାରଣ ବିନ୍ଦୁ ।
(xii) ଉଭୟ ବୃତ୍ତର ଏକ ସାଧାରଣ ବିନ୍ଦୁ ।

Question 3.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ O ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧ ୫ ସେ.ମି. । ଉକ୍ତ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ PO = 17 ସେ.ମି. ହେଲେ, P ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡର ଦୈର୍ଘ୍ୟ କେତେ ?
Solution:
ମନେକର S ବୃତ୍ତର କେନ୍ଦ୍ର 80 1
\(\overline{\mathrm{PT}}\) ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ।
ଓ ବ୍ୟାସାର୍ଦ୍ଧ (OT) = 8 ସେ.ମି., P ବହିଃସ୍ଥ ବିନ୍ଦୁ S ।
PO = 17 ସେ.ମି.|

\(\overline{\mathrm{PT}}\) ⊥ \(\overline{\mathrm{OT}}\)
POT ସମକୋଣା ତ୍ରିଭୁଜରେ PT = \(\sqrt{\mathrm{OP}^2-\mathrm{OT}^2}\)
= \(\sqrt{17^2-8^2}\) ସେ.ମି. = \(\sqrt{289-64}\) = \(\sqrt{225}\) = 15 ସେ.ମି.|
∴ P ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ pତୁର ଦୈର୍ଘ୍ୟ 15 ସେ.ମି. |

Question 4.
ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 4.5 ସେ.ମି. ଓ 12.5 ସେ.ମି. । ବୃତ୍ତ ଦ୍ଵୟର ଏକ ସାଧାରଣ ସ୍ପର୍ଶକ ବୃତ୍ତ ଦ୍ଵୟକୁ P ଓ Q ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କଲେ, \(\overline{\mathrm{PQ}}\)ର ଦୈର୍ଘ୍ୟ କେତେ ?
Solution:

Question 5.
ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର ଏକ ତୀର୍ଯ୍ୟକ ସାଧାରଣ ସ୍ପର୍ଶକ ବୃତ୍ତ ଦ୍ଵୟକୁ P ଓ ଠୁ ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । କେନ୍ଦ୍ରଦ୍ୱୟ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା 20 ସେ.ମି. ଏବଂ ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ୱୟ 7 ସେ.ମି. ଓ 5 ସେ.ମି. ହେଲେ, PQ କେତେ ସେ.ମି. ?
Solution:

Question 6.
ଚିତ୍ରରେ ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁ P | P ବିନ୍ଦୁଗାମୀ ଗୋଟିଏ ଛେଦକ ଦର ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରିକି P – A – B | P ବିଦୁଗାମୀ ଅନ୍ୟ ଏକ ଛେଦକ ଉକ୍ତ ବୃତ୍ତକୁ C ଓ D ବିନ୍ଦୁରେ ଛେଦ କରେ ଯେପରିକି P – C – D|
Solution:

(i) ସ୍ପର୍ଶକ-ସଂପୃକ୍ତ ଉପପାଦ୍ୟ ପ୍ରୟୋଗ କରି ପ୍ରମାଣ କର ।
PA × PB = PC × PD
(ii) PA = 10 ସେ.ମି., PB = 16 ସେ.ମି. ଓ PD = 20 ସେ.ମି. 6ହଲେ, CD କଣ୍ଡଯ କର |
(iii) PA = 8 ସେ.ମି. ଓ AB =10 ସେ.ମି. ହେଲେ, P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକଖଣ୍ଡର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ବଭ : ABCD ଦୂଇରେ P ଦହିମ ଏକ ଦିନ୍ଦୁ |
P – C – D ଓ P – A – B ଦୁଇଟି ଛେଦନ |
ତ୍ପ।ମାଣ୍ୟ : (i) PA × PB = PC × PD

ଅକନ : \(\overline{\text { PT }}\) ମ୍ଟଣକଖଣ୍ଡ ଅକନ କର |
ପ୍ତମାଣ: (i) PT² = PA × PB
PT² = PC × PD
∴ PA × PB = PC × PD

(ii) PC = \(\frac{PA \times PB}{PD}\) = \(\frac{10 \times 16}{20}\) ସେ.ମି = 8 ସେ.ମି
∴ CD = PD – PC = 20 ସେ.ମି – 8 ସେ.ମି = 12 ସେ.ମି |

(iii) PT² = PA × PB = PA (PA + AB)
= 8 × (8 + 10) = 8 × 18 ଦଗ ସେ.ମି |

Question 7.
ଚିତ୍ରରେ ଥ‌ିବା ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P | P ବିନ୍ଦୁଗାମୀ ଏକ ଛେଦକ ପୂର୍ବୋକ୍ତ ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ । ଯେପରି P – A – b | P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକରଶ୍ମିର ସ୍ପର୍ଶବିନ୍ଦୁ T |

(i) m\(\overparen{\text { AXT }}\) = 60° m\(\overparen{\text { BYT }}\) = 130° ଛେଦକ, m∠ATP, m∠APT, m∠ATB ଓ m∠BTQ ନିଣ୍ଡୟ କର |
(ii) m∠BTQ = 2m∠ATP ହେଲେ ,ପ୍ରମାଣ କର : (a) BT = TP (b) TA = AP
(iii) PA = 8 ସେ.ମି. ଓ PT = 12 ସେ.ମି. ହେଲେ , AB ନିଣ୍ଟୟ କର |
(iv) PT = 2AP ଏବଂ AB = 18 ସେ.ମି. ହେଲେ , PT ନିଣ୍ଟୟ କର |
(v) PT = 2AP ଏବଂ PB = 24 ସେ.ମି. ହେଲେ , PT ନିଣ୍ଟୟ କର |
Solution:
\(\overline{\mathrm{B} T}\) ଓ \(\overline{\mathrm{A} T}\) ଅଙ୍କନ କର ।

(i) m∠ABT = \(\frac { 1 }{ 2 }\)m\(\overparen{\text { AXT }}\) = \(\frac { 1 }{ 2 }\) × 60° = 30°
⇒ m∠ATP = m∠ABT = 30°
m∠BAT = \(\frac { 1 }{ 2 }\)m\(\overparen{\text { BYT }}\) = \(\frac { 1 }{ 2 }\) × 130° = 65°
△ATP ରେ ଦଦ୍ୱିମ m∠BAT = m∠ATP + m∠APT
⇒ m∠APT = m∠BAT – m∠ATP = 65° – 30° = 35°
m∠ATB = 180° – 30° – 65° = 85° (: ATB ଏକ ତ୍ରିଭୁବ)
m∠BTQ = m∠BAT = 65°

(ii) ମନେକର m∠ATP = θ ⇒ m∠ABT = θ
m∠BTQ = 2m∠ATP = 2θ
m∠BAT = m∠BTQ = 2θ
⇒ m∠APT = 2θ – θ = θ
△BTP ରେ m∠TBP = m∠TPB
⇒ BT = TP
△TAP ରେ m∠ATP = m∠APT ଦ୍ରେତୁ AT = AP

(iii) PT² = PA × PB
⇒ PB = \(\frac{\mathrm{PT}^2}{\mathrm{PA}}\) = \(\frac{12 \times 12}{8}\) = 18 ସେ.ମି
∴ AB = PB – PA = 18 ସେ.ମି – 8 ସେ.ମି = 10 ସେ.ମି |

(iv) PT² = PA × PB = PA × (PA + AB)
⇒ (2AP)² = PA (PA + 18)
⇒ \(\frac{4 \mathrm{AP}^2}{\mathrm{PA}}\) = PA + 18 ⇒ 4AP – AP = 18 ସେ.ମି.
⇒ 3AP = 18 ସେ.ମି. ⇒ PA = \(\frac { 18 }{ 3 }\) ସେ.ମି. = 6 ସେ.ମି.

(v) PT² = PA × PB
⇒ (2AP)² × (PA + AB)
⇒ PB = \(\frac{4 \mathrm{AP}^2}{\mathrm{PA}}\) = 4AP = 24 ସେ.ମି.
∴ PT = 2AP = \(\frac{4 \mathrm{AP}}{2}\) = \(\frac { 24 }{ 2 }\) ସେ.ମି. = 12 ସେ.ମି. |

Question 8.
(a) ଦୁଇଟି ବୃତ୍ତ ବହିଃସ୍ପର୍ଶୀ ହେଲେ, ପ୍ରମାଣ କର ଯେ, ଏହାର ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ବୟ ସର୍ବସମ ।
(b) ଦୁଇଟି ବୃତ୍ତ ଅନ୍ତସ୍ପର୍ଶୀ ହେଲେ, ପ୍ରମାଣ କର ଯେ, ସେମାନଙ୍କର ସାଧାରଣ ସ୍ପର୍ଶକ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁରୁ ଉକ୍ତ ବୃତ୍ତ ଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ଵୟ ସର୍ବସମ ।

Solution:
(a) ଦତ୍ତ : S ଓ S ବୃତ୍ତଦ୍ୱୟ ବହିଃସ୍ପର୍ଶୀ । ସେମାନଙ୍କର ସାଧାରଣ ସ୍ପର୍ଶକ L | L ଉପରିସ୍ଥ M ଏକ ବିନ୍ଦୁ | M ବିନ୍ଦୁରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡଦ୍ଵୟ \(\overline{\mathrm{MN}}\) ଓ \(\overline{\mathrm{MR}}\) |
ପ୍ରାମାଣ୍ୟ : MN = MR
ପ୍ରମାଣ : M ବିନ୍ଦୁରୁ S₁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MN = MP …(i)
ପୁନଶ୍ଚ M ବିନ୍ଦୁରୁ S₂ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MR = MP …(ii)
(i) ଓ (ii)ରୁ MN = MR (ପ୍ରମାଣିତ)

(b) ଦତ୍ତ : S₁ ଓ S₂ ବୃତ୍ତଦ୍ୱୟ ଅନ୍ତଃସ୍ପର୍ଶୀ । ସେମାନଙ୍କର ସାଧାରଣ ସ୍ପର୍ଶକ L । L ଉପରିସ୍ଥ M ଏକ ବିନ୍ଦୁ । M ବିନ୍ଦୁରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡଦ୍ଵୟ \(\overline{\mathrm{MN}}\) ଓ \(\overline{\mathrm{MR}}\) |

ପ୍ରାମାଣ୍ୟ : MN = MR
ପ୍ରମାଣ : M ବିନ୍ଦୁରୁ ଅନ୍ତବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MR = MP
ସେହିପରି M ବିନ୍ଦୁରୁ ବହିଃସ୍ଥ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ
ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
⇒ MN = MP
(i) ଓ (ii) ରୁ MN = MR (ପ୍ରମାଣିତ)

Question 9.
ପରସ୍ପରଛେଦୀ ଦୁଇଟି ବୃତ୍ତର ଛେଦବିନ୍ଦୁ A ଓ B । \(\overleftrightarrow{\mathbf{A B}}\) ଉପରିସ୍ଥ P ଏକ ବିନ୍ଦୁ ଯେପରି A – B – P। ପ୍ରମାଣ କର ଯେ, ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି P ବିନ୍ଦୁରୁ ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ଵୟ ସର୍ବସମ ।
ସମାଧାନ :
ଦତ୍ତ : ଦୁଇଟି ବୃତ୍ତ S₁ ଓ S₂, ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । \(\overleftrightarrow{\mathbf{A B}}\) ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରୁ ବୃତ୍ତଦ୍ଵୟ ପ୍ରତି \(\overrightarrow{\mathrm{PQ}}\) ଓ \(\overrightarrow{\mathrm{PR}}\) ସ୍ପର୍ଶକ ଅଙ୍କିତ ହୋଇଛି ।
ପ୍ରାମାଣ୍ୟ : PQ = PR
ପ୍ରମାଣ : S₁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overrightarrow{\mathrm{PQ}}\) |
S₁ ବୃତ୍ତର ଏକ ଛେଦକ \(\overleftrightarrow{\mathbf{P A B}}\) |
∴ PQ² = PA.PB …(i)

ସେହିପରି S₂ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overrightarrow{\mathrm{PR}}\) ।
S₂ ବୃତ୍ତର ଏକ ଛେଦକ \(\overleftrightarrow{\mathbf{P A B}}\) |
∴ PR² = PA·PB …(ii)
(i) ଓ (ii) ତି PQ² = PR² ⇒ PQ = PR (ପ୍ରମାଣିତ)

Question 10.
ଚିତ୍ରରେ r₁ ଓ x₂ ଏକକ ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ ବୃତ୍ତ S₁ ଓ S₂ ର କେନ୍ଦ୍ର ଯଥାକ୍ରମେ A ଓ B । ଚିତ୍ର (a)ରେ ବୃତ୍ତଦ୍ଵୟର ଗୋଟିଏ ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ \(\overline{\mathbf{A B}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ,
AM : MB = r₁ : r₂ |

ଚିତ୍ର (b)ରେ ବୃତ୍ତ ଦ୍ଵୟର ଗୋଟିଏ ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ \(\overrightarrow{\mathbf{A B}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରିକି A-B-M | ତ୍ପମାଣ କର ସେ AM : BM = r₁ : r₂ |
ସମାଧାନ :
ଦତ୍ତ : ଦୁଇଟି ଅଣଛେଦୀ ବୃତ୍ତର କେନ୍ଦ୍ର ଯଥାକ୍ରମେ O₁ ଓ O₂ |
\(\overline{\mathrm{PQ}}\) ଏକ ସାଧାରଣ ତୀର୍ଯ୍ୟକ ସ୍ପର୍ଶକ \(\overleftrightarrow{\mathrm{PQ}}\) ଓ O₁O₂ ର ଛେଦବିନ୍ଦୁ R |
ପ୍ରାମାଣ୍ୟ : \(\frac{\mathrm{O}_1 \mathrm{R}}{\mathrm{O}_2 \mathrm{R}}\) = \(\frac{r_1}{r_2}\)
ଅଙ୍କନ : \(\overline{\mathrm{O}_1 \mathrm{P}}\) ଓ \(\overline{\mathrm{O}_1 \mathrm{Q}}\) ଅକନ କର |
ପ୍ରମାଣ : O₁PR ଓ A O₂OR ମଧ୍ୟରେ
m∠O₁PR= m∠0₂QR (ପ୍ତତ୍ୟେକ ସମୟରେ)
m∠O₁RP = m∠O∠0₂RQ (ପ୍ତତ୍ୟେକ ସମୟରେ)
⇒ △O₁PR ~ △O₂QR (କୋ-କୋ ଗାଦଶ୍ୟ)
⇒ \(\frac{\mathrm{O}_1 \mathrm{R}}{\mathrm{O}_2 \mathrm{R}}\) = \(\frac{\mathrm{O}_1 \mathrm{P}}{\mathrm{O}_2 \mathrm{Q}}\) ⇒ \(\frac{r_1}{r_2}\) (ପ୍ରମାଣିତ)

(b) ଦତ୍ତ : S₁ ଓ S₂ ବୃତ୍ତଦ୍ୱୟ ଅଣଛେଦୀ । ସେମାନଙ୍କ କେନ୍ଦ୍ର ଯଥାକ୍ରମେ A ଓ B |
\(\overline{\mathrm{PQ}}\) ସେମାନଙ୍କର ଏକ ସାଧାରଣ ସ୍ପର୍ଶକ ।
\(\overrightarrow{\mathrm{PQ}}\) ଓ \(\overrightarrow{\mathrm{AB}}\) ର ଛେଦ ବିନ୍ଦୁ M, A – B – M |
ପ୍ରାମାଣ୍ୟ : \(\frac { AM }{ BM }\) = \(\frac{r_1}{r_2}\)
ଅଙ୍କନ : \(\overline{\mathrm{AP}}\) ଓ \(\overline{\mathrm{BQ}}\) ଅଙ୍କନ କର ।
ସ୍ତମାଣ: m∠APM = 90°

(\(\overline{\mathrm{PM}}\), S₁ ବୃତ୍ତର ସ୍ପର୍ଶକ ହେତୁ)
ସେହିପରି m∠BQM = 90°
⇒ m∠APM = = m∠BQM
m∠PMA = m∠QMB (ପାଧାରଣ କୋଣ)
⇒ △APM ~ △BQM (କୋ-କୋ ଗାଦଶ୍ୟ)
⇒ \(\frac { AM }{ BM }\) = \(\frac{r_1}{r_2}\)

Question 11.
ଗୋଟିଏ ବୃତ୍ତରେ \(\overline{\mathrm{PQ}}\) ଓ \(\overline{\mathrm{PR}}\) ଜ୍ୟା ଦ୍ଵୟ ସର୍ବସମ । ପ୍ରମାଣ କର ଯେ, ବୃତ୍ତ ପ୍ରତି P ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ, \(\overline{\mathrm{QR}}\) ସହ ସମାନ୍ତର ।

Solution:
ଦତ୍ତ : ବୃତ୍ତର \(\overline{\mathrm{PQ}}\) ଓ \(\overline{\mathrm{PR}}\) ଦୁଇଟି ସର୍ବସମ ଜ୍ୟା ।
P ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overleftrightarrow{M N}\) |
ପ୍ରାମାଣ୍ୟ : \(\overleftrightarrow{M N}\) || \(\overline{\mathrm{QR}}\)
ପ୍ରମାଣ : m∠MPQ = m∠PRQ (ଏକାନ୍ତର ଚାପାନ୍ତର୍ଲିଖ କୋଣ)
PQ = PR ⇒ m∠PQR = m∠PRQ
∴ m∠MPQ = m∠PQR
କିନ୍ତୁ ଏମାନେ ଏକାନ୍ତର ହେତୁ \(\overleftrightarrow{M N}\) || \(\overline{\mathrm{QR}}\) | (ପ୍ରମାଣିତ)

Question 12.
ଦୁଇଟି ଏକକେନ୍ଦ୍ରିକ ବୃତ୍ତ ମଧ୍ୟରୁ ଗୋଟିକର ଏକ ଜ୍ୟା \(\overline{\mathrm{AB}}\) ଅନ୍ୟ ବୃତ୍ତକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶକଲେ, ପ୍ରମାଣ କର ଯେ P ବିନ୍ଦୁରେ \(\overline{\mathrm{AB}}\) ସମଦ୍ଵିଖଣ୍ଡିତ ହୁଏ ।
Solution:

ଦତ୍ତ : S₁ ଓ S₂ ଦୁଇଟି ଏକକେନ୍ଦ୍ରିକ ବୃତ୍ତ । S₁ ବୃତ୍ତର ଜ୍ୟା \(\overline{\mathrm{AB}}\),
ଯାହା S₂ ବୃତ୍ତପ୍ରତି M ବିନ୍ଦୁରେ ସ୍ପର୍ଶକ ଅଟେ ।
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathrm{AB}}\) ଜ୍ୟା M ବିନ୍ଦୁରେ ସମଦ୍ବିଖଣ୍ଡିତ ହେବ । ଅର୍ଥାତ୍ AM = MB |
ଅଙ୍କନ : \(\overline{\mathrm{OM}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : S₂ ବୃତ୍ତର ‘M’ ସ୍ପର୍ଶବିନ୍ଦୁ । \(\overline{\mathrm{OM}}\) ସ୍ପର୍ଶବିନ୍ଦୁଗାମୀ ବ୍ୟାସାର୍ଦ୍ଧ । ⇒ \(\overline{\mathrm{OM}}\) ⊥ \(\overline{\mathrm{AB}}\)
ପୁନଶ୍ଚ S₂ ବୃତ୍ତର \(\overline{\mathrm{AB}}\) ଜ୍ୟା ପ୍ରତି \(\overline{\mathrm{OM}}\) ଲମ୍ବ ହେତୁ M, \(\overline{\mathrm{AB}}\) ର ମଧ୍ୟବିନ୍ଦୁ ।
ଅର୍ଥାତ୍ \(\overline{\mathrm{AB}}\) କ୍ୟାଟି M ବିନ୍ଦୁରେ ସମଦ୍ଵିଖଣ୍ଡିତ ହେବ । (ପ୍ରମାଣିତ)

Question 13.
ପ୍ରମାଣ କର ଯେ, ବୃତ୍ତର ଦୁଇ ସମାନ୍ତର ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ ଦ୍ଵୟର ସଂଯୋଜକ ରେଖାଖଣ୍ଡ ଉକ୍ତ ବୃତ୍ତର ଏକ ବ୍ୟାସ ।
Solution:
ଦତ୍ତ : S ବୃତ୍ତର ଠ କେନ୍ଦ୍ର ।
\(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{CD}}\) ଏବଂ \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ବୃତ୍ତ Sର ଦୁଇଟି ସ୍ପର୍ଶକ ।
ସେମାନଙ୍କ ସ୍ପର୍ଶବିନ୍ଦୁ ଯଥାକ୍ରମେ E ଓ F |
ପ୍ରାମାଣ୍ୟ : E-O-F ଏକ ରେଖ୍ୟ ଅର୍ଥାତ୍‌ \(\overline{\mathrm{EF}}\) ବୃତ୍ତର ବ୍ୟାସ ।
ଅଙ୍କନ : \(\overline{\mathrm{EO}}\) ଓ \(\overline{\mathrm{OF}}\) ଅଙ୍କନ କର । O ବିନ୍ଦୁରେ \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ସହ ସମାନ୍ତର କରି \(\overleftrightarrow{\mathrm{MON}}\) ଅଙ୍କନ କର ।

ତ୍ପମାଣ : m∠OEA = 90° ଓ \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) || \(\stackrel{\leftrightarrow}{\mathrm{MN}}\)
⇒ m∠EOM = 90°
ସେଦ୍ୱିପରି m∠FOM = 90°
∴ m∠EOM + m∠FOM = 90° + 90° = 180°
⇒ E-O-F ଏକରେଖ୍ୟ ଅର୍ଥାତ୍ \(\overline{\mathrm{EF}}\) ବୃତ୍ତର ବ୍ୟାସ ।

Question 14.
△ABC ସମ୍ପୃକ୍ତ \(\overline{\mathrm{BC}}\) ବାହୁ, \(\overrightarrow{\mathbf{A B}}\) ରଶ୍ମି ଓ \(\overrightarrow{\mathbf{A C}}\) ରଶ୍ମିକୁ POR ବୃତ୍ତ ଯଥାକ୍ରମେ P, Q ଓ R ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ | ତ୍ପମାଣ କର ଯେ, AQ = \(\frac { 1 }{ 2 }\) (AB + BC + AC)|
Solution:
ଦତ୍ତ : △ABC ର ବହିଃସ୍ଥ ଏକ ବୃତ୍ତ POR, \(\overline{\mathrm{BC}}\) ବାହୁକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ ଏବଂ \(\overrightarrow{\mathrm{AB}}\) ଓ \(\overrightarrow{\mathrm{AC}}\) ରଶ୍ମି ଦ୍ଵୟକୁ ଯଥାକ୍ରମେ Q ଓ R ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ ।
ପ୍ରାମାଣ୍ୟ : AQ = \(\frac { 1 }{ 2 }\) (AB + BC + CA)
ପ୍ରମାଣ : ବହିଃସ୍ଥ ବିନ୍ଦୁ A ରୁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ ।
∴ AQ = AR

ପୁନଶ୍ଚ BQ = BP ଏବଂ CP = CR
2AQ = AQ + AQ = AQ + AR = AB + BQ + AC + CR
= AB + BP + AC + CP = AB + (BP + CP) + AC = AB + BC + AC
∴ AQ = \(\frac { 1 }{ 2 }\) (AB + BC + AC) (ପ୍ରମାଣିତ)

Question 15.
ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର ସମସ୍ତ ବାହୁକୁ ଗୋଟିଏ ବୃତ୍ତ ସ୍ପର୍ଶ କଲେ, ପ୍ରମାଣ କର ଯେ ସାମାନ୍ତରିକ ଚିତ୍ରଟି ଏକ ରମ୍ବସ୍ ।
Solution:
ଦତ୍ତ :
ABCD ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ଏହାର \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CD}}\) ଓ \(\overline{\mathrm{DA}}\) ଯଥାକ୍ରମେ ଏକ ବୃତ୍ତକୁ P, Q, R, S ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ ।
ପ୍ରାମାଣ୍ୟ : ABCD ଏକ ରମ୍ବସ୍ ।
ପ୍ରମାଣ : ବହିଃସ୍ଥ ବିନ୍ଦୁ A ରୁ AP = AS
ସେହିପରି BP = BQ, DR = DS ଓ CR = CQ
∴ AP + BP + DR + CR = AS + BQ + DS + CQ = AS + DS + BQ + CQ

⇒ AB + CD = AD + BC
⇒ AB + AB = AD + AD (‘.’ AB = CD ଓ AD = BC)
⇒ 2AB = 2AD
⇒ AB = AD
ଅର୍ଥାତ୍ ABCD ଏକ ରମ୍ବସ୍ । (ପ୍ରମାଣିତ)

Question 16.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ ଏହି ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P | P ଠାରୁ ପୂର୍ବୋକ୍ତ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ ଦ୍ଵୟ ହେଉଛନ୍ତି \(\overline{\mathrm{PA}}\) ଓ \(\overline{\mathrm{PB}}\) | \(\overline{\mathrm{OP}}\) ର ଦୈର୍ଘ୍ୟ ବୃତ୍ତଟିର ବ୍ୟାସ ସହ ସମାନ ହେଲେ, ପ୍ରମାଣ କର ଯେ, △ABP ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
Solution:

ଦତ୍ତ : ABC ବୃତ୍ତର କେନ୍ଦ୍ର ଠ ଓ P ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ । \(\overline{\mathrm{PA}}\) ଓ \(\overline{\mathrm{PB}}\) ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ।
OP = ବୃତ୍ତର ବ୍ୟାସ ।
ପ୍ରାମାଣ୍ୟ : △ABP ଏକ ସମବାହୁ ଅର୍ଥାତ୍ AP = BP = AB |
ଅଙ୍କନ : \(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) ଓ \(\overline{\mathrm{AR}}\) ଅଙ୍କନ କର ।
∴ OP = 2r = 2OR ⇒ R, \(\overline{\mathrm{OP}}\) ର ମଧ୍ୟବିନ୍ଦୁ ।
∴ △OAP ସମକୋଣୀ (∵ m∠OAP = 90°)
ସମକୋଣରୁ କର୍ଣ୍ଣର ମଧ୍ୟବିନ୍ଦୁ Rକୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ \(\overline{\mathrm{AR}}\), \(\overline{\mathrm{OP}}\) ର ଅର୍ଦ୍ଧେକ ଦୈର୍ଘ୍ୟ ବିଶିଘୁ |
∴ AR = OA = OR
∴ AROA = OR
m∠AOR = 60°
ସେହିପରି m∠BOR = 60°
∴ m∠AOB 120° ⇒ m∠APB = 60°
ବର୍ତ୍ତମାନ △APBରେ PA = PB ଏବଂ m∠APB = 60°
∴ △APB ସମବାହୁ ।

Question 17.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ P ବୃତ୍ତର ବହିଃସ୍ଥ ଏକବିନ୍ଦୁ । \(\overrightarrow{\mathbf{P T}}\) ସ୍ପର୍ଶକରଶ୍ମିର ସ୍ପର୍ଶବିନ୍ଦୁ T, \(\overline{\mathrm{OP}}\)ର ମଧ୍ୟବିନ୍ଦୁ Q ହେଲେ ପ୍ରମାଣ କର ଯେ, QT = QP |
Solution:

ଦତ୍ତ : S ବୃତ୍ତର ‘O’ କେନ୍ଦ୍ର । P ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ ।
\(\overline{\mathrm{OP}}\) ର ମଧ୍ୟବିନ୍ଦୁ Q । \(\overrightarrow{\mathbf{P T}}\) ବୃତ୍ତପ୍ରତି P ବିନ୍ଦୁରୁ ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ।
ପ୍ରାମାଣ୍ୟ : QT = OP
ଅଙ୍କନ : \(\overline{\mathrm{OT}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : m∠OTP = 90° (ସ୍ପର୍ଶକ, ସ୍ପର୍ଶବିଦୁଗାମୀ ବ୍ୟାସାର୍ଦ୍ଧ ପ୍ରତି ଲମ୍ବ)
∴ △OTP ସମକୋଣୀ । ଉକ୍ତ ତ୍ରିଭୁଜର କର୍ଣ୍ଣର ମଧ୍ୟବିନ୍ଦୁ Q |
∴ ସମକୋଣା ତ୍ରିଭୁକର ସମକୋଣରୁ କଣ୍ଡର ମଧ୍ୟ ବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ସରକରେଖା କଣ୍ଡର ବୈଶ୍ୟର ଅର୍ଦ୍ଧେକ ।
∴ QT = \(\frac { 1 }{ 2 }\) OP = QP (ପ୍ରମାଣିତ)

Question 18.
ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ ସ୍ପର୍ଶକ ରଶ୍ମି \(\overrightarrow{\mathbf{P T}}\) ର ସ୍ପର୍ଶବିନ୍ଦୁ T | P ବିନ୍ଦୁଗାମୀ ଏକ ରେଖା ଉକ୍ତ ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରେ, ଯେପରିକି P-A-B | \(\overline{\mathrm{AB}}\) ଉପରେ A ଓ Bର ମଧ୍ୟବର୍ତ୍ତୀ C ଏକ ବିନ୍ଦୁ ।
ପ୍ରମାଣ କର :
(a) \(\overrightarrow{\mathbf{T C}}\), ∠ATB , ସମଦ୍ବିଖଣ୍ଡିତ ତ୍ରିଭୁଜର PC = PT
(b) PC = PT ହେଲେ \(\overrightarrow{\mathbf{T C}}\) ଦ୍ଵାରା ∠ATB ସମଦ୍ବିଖଣ୍ଡିତ ହୁଏ ।
Solution:
(a)
ଦତ୍ତ : ଏକ ବୃତ୍ତର ବହିଃସ୍ଥ ବିନ୍ଦୁ P । PT ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ଏବଂ P – A – B ଏକ ଛେଦକରେଖା ।
\(\overrightarrow{\mathbf{T C}}\), ∠ATBର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : PC = PT
ପ୍ରମାଣ : m∠PTA = m∠ABT (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ )

m∠ATC = m∠BTC (ଦଇ)
⇒ m∠PTA + m∠ATC = m∠ABT + m∠BTC
⇒ m∠ABT + m∠BTC = m∠CBT + m∠BTC = m∠TCA
(△BTCର ବହିଃସ୍ଥ କୋଣ)
ପୁନଶ୍ଚ m∠PTA + m∠ATC = m∠PTC
∴ m∠PTC = m∠TCA ⇒ m∠PTC = m∠TCP ⇒ PT = PC

(b) ଦତ୍ତ : ଏକ ବୃତ୍ତର P ବହିଃସ୍ଥ ବିନ୍ଦୁ । \(\overline{\mathrm{PT}}\) ଏକ ସ୍ପର୍ଶକଖଣ୍ଡ ଏବଂ P-A–B ଏକ ଛେଦକ ।
\(\overline{\mathrm{AB}}\) ର ମଧ୍ୟସ୍ଥ C ଏକ ବିନ୍ଦୁ ଓ PT = PC |
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathbf{T C}}\), ∠ATBର ସମଦ୍ଵିଖଣ୍ଡକ ।
ପ୍ରମାଣ : △PTCରେ PT = PC (ଦତ୍ତ)

⇒ m∠PTC= m∠PCT
⇒ m∠PTA + m∠ATC = m∠CBT + m∠BTC
(∵ △TBC ରେ ଦହିମ କୋଣ ∠PCT)
m∠PTA = m∠CBT (ଏକାନ୍ତ୍ରର ଦ୍ବରଖଣ୍ଡମ)
⇒ m∠ATC = m∠BTC ⇒ \(\overrightarrow{\mathbf{T C}}\), ∠ATBର ସମଦ୍ଵିଖଣ୍ଡକ (ପ୍ରମାଣିତ)

Question 19.
△ABCର ବାହୁ AB ଓ AC ଉପରେ ଯଥାକ୍ରମେ X ଓ Y ବିନ୍ଦୁ ଅବସ୍ଥିତ, ଯେପରିକି △ABCର ଅନ୍ତଃବୃତ୍ତକୁ \(\overline{\mathbf{XY}}\) ସ୍ପର୍ଶ କରିବ । ପ୍ରମାଣ କର ଯେ AX + XY+YA = AB + AC – BC |

Solution:
ଦତ୍ତ : △ABC ର ଅନ୍ତଃ ବୃ ତ୍ତ ବାହୁ ମାନ ଙ୍କୁ AB, BC, AC କୁ ଯଥାକ୍ରମେ P, Q, R ବିନ୍ଦୁ ରେ B ସ୍ପର୍ଶକରେ । △ABC ର AB ଓ AC ବାହୁ ଉପରେ X ଓ Y ଏପରି ଦୁଇରି ବିନ୍ଦୁ ଯେ XY, AABC Q ଅନ୍ତଃବୃତ୍ତକୁ M ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ ।
ହ୍ମାଣ୍ୟ: AX + XY + YA = AB + AC – BC
ପ୍ରମାଣ: AB+ AC – BC

= AP + BP + AR + RC − (BQ + QC)
= (AX + XP) + BP + (AY + YR) + RC – BQ – QC
[ଦତ୍ତ XM = XP, YM = YR, BP = BQ 19° RC = QC]
= AX + XM + BQ + AY + MY + QC − BQ – QC
= AX + AY + (XM + MY) = AX + AY + XY
∴ AX + AY + XY = AB + AC – BC

Question 20.
ବହିଃସ୍ପର୍ଶୀ ଦୁଇଟି ବୃତ୍ତ S₁ ଓ S₂ ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି ।
ବୃତ୍ତଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ S₁ ଓ S₂ ବୃତ୍ତ ଦ୍ଵୟକୁ ଯଥାକ୍ରମେ A ଓ B ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । P ବିନ୍ଦୁ ଦେଇ ଅଙ୍କିତ ସାଧାରଣ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{A B}}\) କୁ C ବିନ୍ଦୁରେ ଛେଦ କଲେ, ପ୍ରମାଣ କର :
(a) AC = BC ଏର୍ତ (b) m∠APB = 90° |

Solution:
ଦତ୍ତ : ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । ସାଧାରଣ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{A B}}\), ବୃତ୍ତଦ୍ଵୟକୁ A ଓ B ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରେ । P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{A B}}\) କୁ ‘C’ ବିନ୍ଦୁରେ ଛେଦ କରୁଛି ।
ପ୍ରାମଣ୍ୟ: (i) AC = CB (ii) m∠APB = 90°
ପ୍ରମାଣ : C ବହିଃସ୍ଥ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ ଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ । ଅର୍ଥାତ୍ CA = CP |
ସେହିପରି ଅନ୍ୟ ବୃତ୍ତରେ CP = CB ∴CA = CB .. (i) (ପ୍ରମାଣିତ)
∵ CA = CP → m∠CAP = m∠CPA
∵ CP = CB → m∠CBP = m∠CPB
∴ m∠CAP + m∠CBP = m∠CPA + m∠CPB
⇒ m∠CAP +m∠CBP = m∠APB
⇒ m∠CAP+m∠CBP + m∠APB = 2m∠APB
⇒ 180° = 2m∠APB ⇒ m∠APB = 90° …(ii) (ପ୍ରମାଣିତ)

Question 21.
S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟ ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । S₁ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ଦେଇ ଅଙ୍କିତ \(\overrightarrow{\mathbf{P A}}\) ଓ \(\overrightarrow{\mathbf{P B}}\) S, ବୃତ୍ତକୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ପ୍ରମାଣ କର ଯେ P ବିନ୍ଦୁରେ S₁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ, \(\overline{\mathbf{CD}}\) ସହ ସମାନ୍ତର ।
Solution:

ଦତ୍ତ : S₁ ଓ S₂ ବୃତ୍ତ ଦ୍ବୟ ପରସ୍ପରକୁ A ଓ B ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । P, S₁ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ । \(\overrightarrow{\mathbf{P A}}\) ଓ \(\overrightarrow{\mathbf{P B}}\), S₂ କୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : \(\overleftrightarrow{\mathrm{XY}}\) || \(\overline{\mathbf{CD}}\)
ଅଙ୍କନ : \(\overline{\mathbf{AB}}\) ଅଙ୍କନ କର ।

ପ୍ରମାଣ : m∠XPA = m∠ABP (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ)
ପୁନଶ୍ଚ ABDC ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖତ ଚତୁର୍ଭୁଜ ।
∠ABP ଚତୁର୍ଭୁଜଟିର ବହିଃସ୍ଥ କୋଣ ।
ଏଠାରେ m∠ABP = m∠ACD
∴ m∠XPA = m∠ACD କିନ୍ତୁ ଏମାନେ ଏକାନ୍ତର ।
∴ \(\overleftrightarrow{\mathrm{XY}}\) || \(\overline{\mathbf{CD}}\) (ପ୍ରମାଣିତ)

Question 22.
ଦୁଇଟି ପରସ୍ପର ଅଣଛେଦୀ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r₁ ଓ r₂ ଏକକ ଏବଂ r₁ > r₂ ବୃତ୍ତଦ୍ଵୟର କେନ୍ଦ୍ରଦ୍ଵୟ ମଧ୍ୟରେ ଦୂରତା d ଏକକ ହେଲେ ଏବଂ
(a) ଉଭୟ ବୃତ୍ତର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ A ଓ B ହେଲେ, ପ୍ରମାଣ କର ଯେ
AB² = d²(r₁ – r₂) ଏବଂ
(b) ଉଭୟ ବୃତ୍ତର ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ C ଓ D ହେଲେ, ପ୍ରମାଣ କର ଯେ CD² = d²(r₁ + r₂)²
Solution:
(a) ଦତ୍ତ : O ଓ P ଯଥାକ୍ରମେ S₁ ଓ S₂ ଦୁଇଟି ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ ଓ OP = d |
S₁ ଓ S₂ ବୃତ୍ତର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକର ସ୍ପର୍ଶବିନ୍ଦୁ
ଯଥାକ୍ରମେ A ଓ B|

OA = r, PB = r₂ , r₁ > r₂
ପ୍ରାମାଣ୍ୟ : AB² = d² – (r₁ – r₂)²
ଅଙ୍କନ : \(\overline{\mathbf{OA}}\) ଏବଂ \(\overline{\mathbf{PB}}\) ଅଙ୍କନ କର । \(\overline{\mathbf{PD}}\) ⊥ \(\overline{\mathbf{OA}}\) ଅଙ୍କନ କର ।
\(\overline{\mathbf{PD}}\) || \(\overleftrightarrow{\mathrm{AB}}\) ଅଙ୍କନ କର ।

ପ୍ରମାଣ : ADPB ଏକ ଆୟତକ୍ଷେତ୍ରର ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ
∴ AD = PB = r₂
⇒ OD = OA – AD = r₁ – r₂ ଓ AB = PD
△ODPରେ m∠ODP = 90°
⇒ OP² = OD² + PD² (ପିଥାଗୋରାସ୍ ଉପପାଦ୍ୟ)
⇒ PD² = OP² – OD² ⇒ AB = d² – (r₁ – r₂)²

(b) ଦତ୍ତ: O ଓ P ଯଥାକ୍ରମେ S₁ ଓ S₂ ବୃତ୍ତର କେନ୍ଦ୍ରବିନ୍ଦୁ ଏବଂ OP = d |
S₁ ଓ S₂ ବୃତ୍ତର ତୀର୍ଯ୍ୟକ୍ ସାଧାରଣ ସ୍ପର୍ଶକ ଯଥାକ୍ରମେ S₁ ଓ S₂ ବୃତ୍ତକୁ C ଓ D ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ ।
OC= r₁, PD = r₂ ଓ r₁ > r₂ |
ପ୍ରାମାଣ୍ୟ : CD² = d² – (r₁ + r₂)²
ଅଙ୍କନ : \(\overline{\mathbf{OC}}\), \(\overline{\mathbf{PD}}\) ଅଙ୍କନ କର ।
\(\overline{\mathbf{PE}}\) || \(\overline{\mathbf{CD}}\) ଅକନ କର ଯେବେକି \(\overline{\mathbf{PE}}\)
\(\overrightarrow{\mathrm{OF}}\) କୁ E ବିନ୍ଦୁରେ ଛେଦ କରିବ ।

ପ୍ରମାଣ : CEPD ଏକ ଆୟତଚିତ୍ର (ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ)
CE = PD = r₂
∴ OE = OC+CE = r₁ + r₂
OP = d (ଦତ୍ତ) ଓ PE = CD
m∠OCD = 90°, ∠CDP = 90°, m∠CEP = 90°
△OEPରେ OP² = OE² + PE² (ପିଥାଗୋରାସ୍ ଉପପାଦ୍ୟ)
∴PE² = OP² – OE²
⇒ CD² = OP² – OE² = d² – (r₁ + r₂)² (ପ୍ରମାଣିତ)

Question 23.
ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକ ରଶ୍ମିଦ୍ଵୟର ସ୍ପର୍ଶବିନ୍ଦୁ ଯଥାକ୍ରମେ Q ଏବଂ R | \(\overline{\mathbf{QR}}\) ଜ୍ୟାଦ୍ଵାରା ଛେଦିତ କ୍ଷୁଦ୍ରଚାପର ମଧ୍ୟବିନ୍ଦୁ S ହେଲେ, ପ୍ରମାଣ କର ଯେ, \(\overrightarrow{\mathrm{QS}}\) ଦ୍ଵାରା ∠PQR ସମଦ୍ବିଖଣ୍ଡିତ ହୁଏ |
Solution:
ଦତ୍ତ : ଗୋଟିଏ ବୃତ୍ତର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁ P ଏବଂ P ବିନ୍ଦୁଗାମୀ ସ୍ପର୍ଶକ ରଶ୍ମିଦ୍ବୟର ସ୍ପର୍ଶବିନ୍ଦୁ ଯଥାକ୍ରମେ Q ଏବଂ R । \(\overline{\mathbf{QR}}\) ଜ୍ୟାଦ୍ଵାରା ଛେଦିତ କ୍ଷୁଦ୍ରଚାପର ମଧ୍ୟବିନ୍ଦୁ S ।
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathbf{QS}}\), ∠PORର ସମଦ୍ବିଖଣ୍ଡକ ।
ଅଙ୍କନ : \(\overline{\mathbf{SR}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : \(\overparen{\mathrm{QSR}}\) ଚାପର ମଧ୍ୟବିନ୍ଦୁ S |

⇒ \(\overline{\mathbf{QS}}\) ≅ \(\overline{\mathbf{SR}}\) ⇒ m∠SRQ = m∠SQR
\(\overline{\mathbf{PQ}}\) ଏକ ସ୍ପର୍ଶକ ଏବଂ \(\overline{\mathbf{QS}}\) ସ୍ପର୍ଶକ ବିନ୍ଦୁଗାମୀ ଜ୍ୟା ।
⇒ m∠POS = m∠SRQ (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ )
∴ m∠PQS = m∠SQR
ଅର୍ଥାତ୍ \(\overrightarrow{\mathrm{SQ}}\), ∠PORର ସମଦ୍ବିଖଣ୍ଡକ ।

Question 24.
ଚିତ୍ରରେ ଥିବା ବୃତ୍ତର AT ଏକ ବ୍ୟାସ । ବୃତ୍ତ ଉପରିସ୍ଥ ଅନ୍ୟ ଏକ ବିନ୍ଦୁ B । \(\overrightarrow{\mathrm{AB}}\) ଏବଂ I ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ ପରସ୍ପରକୁ P ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । B ବିନ୍ଦୁରେ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overleftrightarrow{ T P}\) କୁ ( ବିନ୍ଦୁରେ ଛେଦ କଲେ, ପ୍ରମାଣ କର ଯେ Q ବିନ୍ଦୁ ହେଉଛି PT ର ମଧ୍ୟବିନ୍ଦୁ ।

Solution:
ଦତ୍ତ : \(\overline{\mathbf{AT}}\) ବୃତ୍ତର ଏକ ବ୍ୟାସ । ABT ବୃତ୍ତ ଉପରିସ୍ଥ B ଏକ ବିନ୍ଦୁ |
\(\overrightarrow{\mathrm{AB}}\) ଓ T ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶ \(\overleftrightarrow{ T P}\) ର ଛେଦବିନ୍ଦୁ Q |
ପ୍ରାମାଣ୍ୟ : Q, \(\overline{\mathbf{TP}}\)ର ମଧ୍ୟବିନ୍ଦୁ ।
ଅଙ୍କନ : \(\overline{\mathbf{BT}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ବହିଃସ୍ଥ ( ବିନ୍ଦୁରୁ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକଖଣ୍ଡ ଦ୍ଵୟ \(\overline{\mathbf{QB}}\) ଓ \(\overline{\mathbf{QT}}\) |
⇒ QB = QT
⇒ m∠QBT = m∠QTB
m∠ABT = 90° (∵ \(\overline{\mathbf{AT}}\) ବୃତ୍ତ ଏକ ବ୍ୟାସ)
m∠PBT = 90°
⇒ m∠PBQ + m∠QBT = 90°
ପୁନମ୍ନ m∠BTQ + m∠BPQ = 90°

⇒ m∠PBQ + m∠QBT = m∠BTQ + m∠BPQ
(: m∠QBT = m∠QTB)
⇒ m∠PBQ = m∠BPQ ⇒ BQ = QP
ପୁନମ୍ନ BQ = QT ⇒ QP = QT (ପ୍ରମାଣିତ)

Question 25.
ଗୋଟିଏ ବୃତ୍ତରେ \(\overline{\mathbf{AB}}\) ଏକ ବ୍ୟାସ । B ବିନ୍ଦୁରେ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଉପରେ C ଏପରି ଏକ ବିନ୍ଦୁ ଯେପରି \(\overline{\mathbf{CA}}\), ବୃତ୍ତକୁ D ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ AB² = AC × AD |

Solution:
ଦତ୍ତ : \(\overline{\mathbf{AB}}\), S ବୃତ୍ତର ଏକ ବ୍ୟାସ ।
\(\overrightarrow{\mathrm{BC}}\) ବୃତ୍ତପ୍ରତି B ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ C – D – A ଏକ ଛେଦକ ।
ପ୍ରାମାଣ୍ୟ : AB² = AC × AD
ଅଙ୍କନ : \(\overline{\mathbf{BD}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : BC ସ୍ପର୍ଶକ ⇒ ∠ABC = ସମକୋଣ
△ACBରେ AB² + BC² = AC² ⇒ AB² = AC² – BC²
ପୁନଶ୍ଚ CB² = CD · CA
⇒ AB² = AC² – BC² = AC² – CD · CA
= AC (AC – CD) = AC × AD (ପ୍ରମାଣିତ)

Question 26.
ଗୋଟିଏ ବୃତ୍ତରେ \(\overline{\mathbf{AB}}\) ଏକ ବ୍ୟାସ । B ବିନ୍ଦୁରେ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଉପରେ C ଓ D ଦୁଇଟି ବିନ୍ଦୁ ଯେପରି C-B-D | ଯଦି CA ଓ \(\overline{\mathbf{DA}}\) ଯଥାକ୍ରମେ ବୃତ୍ତକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି, ପ୍ରମାଣ କର ଯେ AC × AP = AD × AQ |
Solution:
ଦତ୍ତ : \(\overline{\mathbf{AB}}\) ଏକ ବୃତ୍ତର ବ୍ୟାସ । B ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{C D}\) । AC ଓ \(\overline{\mathbf{AD}}\) ବୃତ୍ତକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦକରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : AC × AP = AD × AQ
ଅଙ୍କନ : \(\overline{\mathbf{BP}}\) ଓ \(\overline{\mathbf{BQ}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △APB ଓ △ABC ମଧ୍ୟରେ
m∠APB m∠ABC (ପ୍ରତ୍ୟେକ ସମକୋଣ)
m∠PAB = m∠BAC (ସାଧାରଣ କୋଣ)

⇒ △APB ~ △ABC (କୋ.କୋ, ସାଦୃଶ୍ୟ)
⇒ \(\frac { AP }{ AB }\) = \(\frac { AB }{ AC }\) ⇒ AB² = AP × AC …(i)
ସେହିପରି △ABQ ~ △ABD
AB² = AD × AQ …(ii)
∴ (i) ଓ (ii)ରୁ AP × AC = AD × AQ (ପ୍ରମାଣିତ)

Question 27.
ଚିତ୍ରରେ S₁ ଓ S₂ ବୃତ୍ତ ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ଏବଂ G ସେମାନଙ୍କର ସ୍ପର୍ଶବିନ୍ଦୁ । ବୃତ୍ତଦ୍ଵୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ରଶ୍ମି \(\overrightarrow{\mathrm{PX}}\) ଓ \(\overrightarrow{\mathrm{PY}}\) ଦ୍ଵୟର ସାଧାରଣ ମୂଳ ବିନ୍ଦୁ P | S₁ ଓ S, ବୃତ୍ତକୁ \(\overrightarrow{\mathrm{PX}}\) ଯଥାକ୍ରମେ C ଓ ଯ ବିନ୍ଦୁରେ ଏବଂ \(\overrightarrow{\mathrm{PY}}\) ଯଥାକ୍ରମେ D ଓ F ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି ।
(a) ପ୍ରମାଣ କର :
(i) P, A, G, B ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ଓ
(ii) CE = DF

(b) ଉଭୟ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସାଧାରଣ ସ୍ପର୍ଶକ \(\overrightarrow{\mathrm{PX}}\) ଓ \(\overrightarrow{\mathrm{PY}}\) କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦକଲେ, ପ୍ରମାଣ କର :
(i) PM = PN, (ii) MG = NG ।
Solution:
ଦତ୍ତ : S₁ ଓ S₂ ଦୁଇଟି ବହିଃସ୍ପର୍ଶୀ ବୃତ୍ତ ପରସ୍ପରକୁ G ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । ବୃତ୍ତଦ୍ୱୟର ସରଳ ସାଧାରଣ ସ୍ପର୍ଶକ ରଶ୍ମି \(\overrightarrow{\mathrm{PX}}\) ଓ \(\overrightarrow{\mathrm{PY}}\), S₁ ଓ S₂ ବୃତ୍ତକୁ ଯଥାକ୍ରମେ C ଓ E ଏବଂ D ଓ F ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରନ୍ତି । ଓ ବିନ୍ଦୁରେ ଅଙ୍କିତ ସାଧାରଣ ସ୍ପର୍ଶକ PX ଓ PY କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ବୃତ୍ତଦ୍ୱୟର କେନ୍ଦ୍ର ଯଥାକ୍ରମେ A ଓ B |

ପ୍ରାମାଣ୍ୟ : (a) (i) P, A, G ଓ B ସରଳରେଖାରେ ଅବସ୍ଥିତ । (ii) CE = DF
(b) (i) PM = PN, (ii) MG = NG
ଅଙ୍କନ : \(\overline{\mathbf{AC}}\) ଓ \(\overline{\mathbf{AD}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : PE = PD (ବହିଃସ୍ଥ P ବିନ୍ଦୁରୁ S₂ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ)
ପୁନଶ୍ଚ PC = PD (ବହିଃସ୍ଥ P ବିନ୍ଦୁରୁ S₁ ବୃତ୍ତ ପ୍ରତି ଅଙ୍କିତ ସ୍ପର୍ଶକ ଖଣ୍ଡ)
∴ PE – PC = PF – PD ⇒ CE = DF (ପ୍ରମାଣିତ)
CM = MG ଏବଂ ME = MG ⇒ CM = ME
ସେହିପରି DN = NG ଏବଂ NG = NF
DN = NF, CE = DF (ପୂର୍ବରୁ ପ୍ରମାଣିତ)
⇒ 2 CM = 2 DN ⇒ CM = DN ….(i)
PC = PD = PC + CM = PD + DN → PM = PN
(i)ରୁ CM= DN →:MG = NG
(∵ MC = MG, DN = NG)
PM = PN (ପୂର୍ବରୁ ପ୍ରମାଣିତ)
⇒ m∠PMG = m∠PNG ⇒ m∠CMG = m∠DNG
ଦଇମାନ CAGM ଚତୁରିକରେ m∠ACM + m∠AGM = 180°
∴ m∠CMG + m∠CAG = 180° … (ii)
ସେହିପରି m∠DNG + m∠DAG = 180° …(iii)
m∠CMG + m∠CAG = m∠DNG + m∠DAG
m∠CAG = m∠DAG (∵ m∠CMG = m∠DNG)
m∠PAC = m∠PAD ….(iv)
(iv)ରୁ 2m∠CAG + 2m∠PAC = 360° ⇒ m∠CAG + m∠PAC = 180°
⇒ P, A, G ଏକରେଖ କିନ୍ତୁ A, G, B ଏକ ରେଞ୍ଜ
∴ P, A, G, B ଏକସରଳରେଖାରେ ଅବସ୍ଥିତ । (ପ୍ରମାଣିତ)

Question 28.
ପରସ୍ପର ଅନ୍ତଃସ୍ପର୍ଶୀ ଦୁଇଟି ବୃତ୍ତର ସ୍ପର୍ଶବିନ୍ଦୁ P । ଏକ ସରଳରେଖା ଗୋଟିଏ ବୃତ୍ତକୁ A ଓ B ବିନ୍ଦୁରେ ଓ ଅନ୍ୟ ବୃତ୍ତକୁ C ଓ Ð ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ ∠APC ଓ ∠BPD ସର୍ବସମ । [A-C-D ଓ A-D-C ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ପ୍ରମାଣ ଯୋଗ୍ୟ ।
Solution:

ଦତ୍ତ : ପରସ୍ପର ଅନ୍ତଃସ୍ପର୍ଶୀ ଦୁଇଟି ବୃତ୍ତର ସ୍ପର୍ଶବିନ୍ଦୁ P । ଏକ ସରଳରେଖା ବୃତ୍ତଦ୍ଵୟକୁ ଯଥାକ୍ରମେ A, B ଓ C, D ବିନ୍ଦୁରେ ଛେଦକରନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : ∠APC ≅ ∠BPD
ଅଙ୍କନ : P ବିନ୍ଦୁରେ ବୃତ୍ତପ୍ରତି ସାଧାରଣ ସ୍ପର୍ଶକ X – P – Y ଅଙ୍କନ କର ।
ମନେକର \(\overline{\mathrm{PC}}\)ର ଏକ ପାର୍ଶ୍ବରେ A ଓ X ଅବସ୍ଥାନ କରୁ ।
\(\overline{\mathrm{PA}}\), \(\overline{\mathrm{PD}}\), \(\overline{\mathrm{PC}}\) ଓ \(\overline{\mathrm{PB}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ମନେକର A – C – D – B|
m∠DPY = m∠DCP (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ)
ସେହିପରି m∠BPY = m∠DAP
∴ m∠DPY – m∠BPY = m∠DCP – m∠DAP
⇒ m∠DPB = m(∠CAP + m∠APC) – m∠DAP
(∵ ବହିଃସ୍ଥ m∠DCP = m∠CAP + m∠APC)
= m∠CAP + m∠APC – m∠CAP = m∠APC
ସେହିପରି A – D – C – B ହେଲେ ପ୍ରମାଣ ଅନୁରୂପ ।

Question 29.
△ABC ର ଅନ୍ତଃବୃତ୍ତ, \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) ଓ \(\overline{\mathrm{CA}}\) କୁ ଯଥାକ୍ରମେ P, Q ଓ R ବିନ୍ଦୁରେ ସ୍ପର୍ଶ କରେ । ଚିତ୍ରରେ BQ = 8 ସେ.ମି., CQ = 6 ସେ.ମି. ଏବଂ △ABCର ପରିସୀମା 36 ସେ.ମି. ହେଲେ, AB ଓ AC ନିର୍ଣ୍ଣୟ କର ।

Solution:
ଦତ୍ତ : △ABCର ଅନ୍ତଃବୃତ୍ତ \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\) ଓ \(\overline{\mathrm{CA}}\) କୁ ଯଥାକ୍ରମେ P, Q ଓ R ବିନ୍ଦୁରେ ଛେଦକରେ ।
BQ = 8 ସେ.ମି., CQ = 6 ସେ.ମି.
△ABCର ପରିସୀମା = 36 ସେ.ମି.
ନିର୍ଦେୟ : BQ = 8 ସେ.ମି. ⇒ BP = 8 ସେ.ମି.
CQ = 6 ସେ.ମି. ⇒ CR = 6 ସେ.ମି.
ମନେକର AP = AR = x ସେ.ମି.
△ABCର ପରିସୀମା = 36 ସେ.ମି.
⇒ AP + PB + BQ + QC +CR + RA = 36
⇒ (x + 8 + 8 + 6 + 6 + x) = 36 ⇒ 2x + 28 = 36
⇒ 2x = 36 – 28 = 8 ⇒ x = \(\frac { 8 }{ 2 }\) = 4
∴ AB = AP + BP = 4 ସେ.ମି. + 8 ସେ.ମି. = 12 ସେ.ମି.
AC = AR + CR = 4 ସେ.ମି. + 6 ସେ.ମି. = 10 ସେ.ମି. |

Question 30.
ଗୋଟିଏ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ ପରିଲିଖ୍ ଚତୁର୍ଭୁଜ ABCD ହେଲେ, ପ୍ରମାଣ କର ଯେ ∠AOB ଓ ∠COD ପରସ୍ପର ପରିପୂରକ । ∠B0C ଏବଂ ∠AOD ମଧ୍ୟରେ ଥ‌ିବା ସମ୍ପର୍କ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜ S ବୃତ୍ତର ପରିଲିଖ । ବୃତ୍ତର କେନ୍ଦ୍ର O |
gla: (i) m∠AOB + m∠COD = 180°
(ii) ∠BOC ଏବଂ ∠COD ମଧ୍ୟରେ ସଂପର୍କ ।
ପ୍ରମାଣ : m∠ABO = m∠CBO ⇒ m∠ABO = \(\frac { 1 }{ 2 }\) m∠B
m∠BAO = m∠DA0 ⇒ m∠BAO = \(\frac { 1 }{ 2 }\) m∠A
m∠OCD = m∠OCB ⇒ m∠OCD = \(\frac { 1 }{ 2 }\) m∠C
m∠ODC = m∠ODA ⇒ m∠ODC = \(\frac { 1 }{ 2 }\) m∠D

∴ m∠ABO + m∠BAO + m∠OCD + m∠ODC
= \(\frac { 1 }{ 2 }\) (m∠A + m∠B + m∠C + m∠D) = \(\frac { 1 }{ 2 }\) × 360° = 180°
ପୁନଶ୍ଚ m∠ABO + m∠BAO + m∠OCD + m∠ODC + m∠AOB + ∠COD = 180° + 180° = 360° …(ii)
∴ (i) ଓ (ii) ରୁ m∠AOB + m∠COD = 180° (ପ୍ରମାଣିତ)
ସେହିପରି m∠AOD + m∠BOC = 180° ଦେବ |

Question 31.
ଗୋଟିଏ ବୃତ୍ତର ଏକ ଜ୍ଯା \(\overline{\mathrm{AB}}\), ଏହି ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ P ଠାରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ ସହ ସମାନ୍ତର ହେଲେ, ପ୍ରମାଣ କର ଯେ P ବିନ୍ଦୁଠାରେ \(\overparen{\mathbf{A P B}}\) ସମଦ୍ବିଖଣ୍ଡିତ ହୁଏ ।
ସମାଧାନ :
ଦତ୍ତ : ABP ବୃତ୍ତର AB ଏକ ଜ୍ୟା । P ଠାରେ \(\overline{\mathrm{AB}}\) ସହ ସମାନ୍ତର ଭାବେ ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\overleftrightarrow{\mathrm{XY}}\), \(\overline{\mathrm{PB}}\)ର ଏକ ପାର୍ଶ୍ଵରେ X ଓ A ଅବସ୍ଥିତ ।
ପ୍ରାମାଣ୍ୟ : \(\widehat{\mathrm{AP}}\) ≅ \(\widehat{\mathrm{BP}}\)

ଅଙ୍କନ : \(\overline{\mathrm{PA}}\) ଓ \(\overline{\mathrm{PB}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : m∠XPA = m∠PBA (ଏକାନ୍ତର ବୃତ୍ତଖଣ୍ଡସ୍ଥ)
m∠XPA = m∠PAB (ଏକାନ୍ତର କରେ)
⇒ m∠PBA = m∠PAB
⇒ \(\widehat{\mathrm{PA}}\) ≅ \(\widehat{\mathrm{PB}}\)

Question 32.
ଚିତ୍ରରେ ଥ‌ିବା ବୃତ୍ତର କେନ୍ଦ୍ର 0, L₁ ଓ L₂ ଦୁଇଟି ସ୍ପର୍ଶକ ଏବଂ L₁ || L₂ | ବୃତ୍ତର K ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ \(\stackrel{\leftrightarrow}{\mathbf{P Q}}\), L₁ ଓ L₂ କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କରେ । ପ୍ରମାଣ କର ଯେ ∠MON ଏକ ସମକୋଣ ।

Solution:
ଦତ୍ତ : S ବୃତ୍ତର କେନ୍ଦ୍ର O,
L₁ ଓ L₂ ବୃତ୍ତପ୍ରତି ଦୁଇଟି ସ୍ପର୍ଶକ ଏବଂ L₁ || L₂| ବୃତ୍ତର K ବିନ୍ଦୁରେ ଅଙ୍କିତ ସ୍ପର୍ଶକ PO
L₁ ଓ L₂ କୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦକରେ ।
ପ୍ଵାମଣ୍ୟ: m∠MON = 90°
ଅଙ୍କନ : \(\overline{\mathrm{CO}}\), \(\overline{\mathrm{DO}}\), \(\overline{\mathrm{OK}}\), \(\overline{\mathrm{MO}}\) ଓ \(\overline{\mathrm{NO}}\) ଅଙ୍କନ କର ।
L₁ ଓ L₂, S ବୃତ୍ତକୁ ଯଥାକ୍ରମେ C ଓ D ବିନ୍ଦୁରେ ସ୍ପର୍ଶକରୁ ।
ପ୍ରମାଣ : △OCM ଓ △OKMରେ
MC = MK. \(\overline{\mathrm{MO}}\) ସାଧାରଣ ବାହୁ ।
ଓ m∠OCM= m∠OKM (ସାଧାରଣ)
∴ △OCM = △OKM = m∠CMO = m∠OMK

ସେହିପରି ପ୍ରମାଣ କରାଯାଇପାରେ ଯେ △OKN ≅ △ODN ⇒ m∠ONK = m∠OND L₁ || L₂, \(\stackrel{\leftrightarrow}{\mathrm{PQ}}\) ଛେଦକ ।
ତେଣୁ m∠CMK + m∠DNK= 180° ⇒ \(\frac { 1 }{ 2 }\) m∠CMK + \(\frac { 1 }{ 2 }\) m∠DNK = 90°
⇒ m∠KMO + m∠KNO = 90° …(i)
କିନ୍ତୁ m∠KMO + m∠KNO + m∠MON = 180°
90° + m∠MON = 180° [(i) ରୁ]
m∠MON = 180° – 90° = 90° (ପ୍ରମାଣିତ)

Odisha State Board BSE Odisha 10th Class Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Algebra Chapter 6 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି Ex 6(b)

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଯଦି (1, – 2) ବିନ୍ଦୁଟି (4, 2) ଓ (K, – 6) ବିନ୍ଦୁଦ୍ବୟର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ହୁଏ, ତେବେ k = ………. । [-2, 2, – 4, 4]
(ii) (- 2, 3) ଓ (3, – 2) ବିନ୍ଦୁଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ହେଉଛି ………. । [(1, 1), (\(\frac{1}{2}, \frac{1}{2}\)), (\(\frac{5}{2}, \frac{5}{2}\)) (\(-\frac{1}{2}, -\frac{1}{2}\))]
(iii) ଏକ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁ ହେଉଛି ମୂଳବିନ୍ଦୁ; ଯଦି ରେଖାଖଣ୍ଡଟିର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ (2, 3) ହୁଏ, ତେବେ ………. । [(-2, 3), (2,-3),(-2,-3) (\(\frac{1}{2}, \frac{3}{2}\))]
(iv) (0, 2) ଓ (2, 0) ବିନ୍ଦୁଦ୍ଵୟର ରେଖାଖଣ୍ଡକୁ 1 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥ‌ିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ………. । [(\(\frac{4}{3}, \frac{2}{3}\)), (\(\frac{4}{3}, \frac{2}{3}\)), (-2, 4),(4, -2)]
ଉତ୍ତର:
(i) -2
(ii) (\(\frac{1}{2}, \frac{1}{2}\))
(iii) (-2, -3)
(iv) (\(\frac{2}{3}, \frac{4}{3}\))

Question 2.
ନିମ୍ନଲିଖ ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଦତ୍ତ ବିନ୍ଦୁମାନଙ୍କୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
(i) (3, 4), (1,-2)
(ii) (-1,3), (4, 0)
(iii) (\(\frac{1}{2}, \frac{1}{3}\)), (\(\frac{1}{3}, \frac{1}{2}\))
(iv) (0,-3), (-4, 0)
(v) (-1,-2), (3, -1)
(vi) (a, b), (c, d)
(vii) (-2, 1), (-3, -4)
(viii) (at₁², 2at₁), (at₂², 2at₂)
ସମାଧାନ :
P (x,, y,) ଓ Q(x, y) ହେଲେ PQର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ = (\(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\))
(i) P (3, 4) ଓ Q (1, -2) PQର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{3+1}{2}, \frac{4+(-2)}{2}\)) = (2, 1)
(ii) (-1,3) ଓ (4, 0)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{-1+4}{2}, \frac{3+0)}{2}\)) = \(\frac{3}{2}, \frac{3}{2}\)
(iii) (\(\frac{1}{2}, \frac{1}{3}\)) ଓ (\(\frac{1}{3}, \frac{1}{2}\))ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ \(\left(\frac{\frac{1}{2}+\frac{1}{3}}{2}, \frac{\frac{1}{3}+\frac{1}{2}}{2}\right)=\left(\frac{5}{12}, \frac{5}{12}\right)\)
(iv) (0,-3) ଓ (-4,0)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{1-4}{2}, \frac{-3+0}{2}\)) = (-2, \(\frac{-3}{2}\))
(v) (-1, -2) ଓ (3, -1)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{-1+3}{2}, \frac{-2-1}{2}\)) = (1, \(\frac{-3}{2}\))
(vi) (a, b) ଓ (c, d)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+c}{2}, \frac{b+d}{2}\))
(vii) (-2, 1) ଓ (-3, -4)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{-1+3}{2}, \frac{-2-1}{2}\)) = (1, \(\frac{-3}{2}\))
(viii) (at₁², 2at₁) ଓ (at₂², 2at₂)ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ \(\left(\frac{{at}_1^2+{at}_2^2}{2}, \frac{2 {at}_1+2 {at}_2}{2}\right)\) = (\(\frac{a({t}_1^2+{t}_2^2)}{2}\), a(t₁+t₂))

Question 3.
ନିମ୍ନଲିଖତ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନରେ ଦତ୍ତ ଦୁଇବିନ୍ଦୁକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ହେଉଛି (-1, 2) । ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ । ଓ kର ମାନ ନିର୍ଣ୍ଣୟ କର ।
(i) (h, -1), (2, k)
(ii) (5, 3), (h, k)
(iii) (1+h, k), (k, -h – 1)
(iv) (h – k, k – h), (2h, 2k)
ସମାଧାନ :
(i) (h, 1 ) ଓ (2, k) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
∴ \(\frac{h+2}{2}\) = -1 ⇒ h + 2 = -2 ⇒ h = -4
ଏବଂ \(\frac{-1+k}{2}\) = 2 ⇒ -1 + k = 4 ⇒ k = 5
∴ h ଓ kର ମାନ ଯଥାକ୍ରମେ – 4 ଓ 5 ।

(ii) 5, 3) ଓ (h, k) ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
∴ \(\frac{5+h}{2}\) = -1 ⇒ 5 + h = -2 ⇒ h = -7
ଏବଂ \(\frac{3+k}{2}\) = 2 ⇒ 3 + k = 4 ⇒ k = 1
∴ h ଓ kର ମାନ ଯଥାକ୍ରମେ – 7 ଓ 1 ।

(iii) (1+h, k), (k, – h – 1) ବିଦୁ୍ୟଦ୍ୱୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
\(\frac{1+h+k}{2}\) = -1 ⇒ 1 + h + k = -2 ⇒ h + k = -3
ଏବଂ \(\frac{k-h-1}{2}\) = 2 ⇒ k – h – 1 = 4 ⇒ k – h = 5
ସମୀକରଣ (i) ଓ (ii) କୁ ଯୋଗକଲେ,

kର ମାନ ସମୀକରଣ (i)ରେ ପ୍ରୟୋଗ କଲେ, h + k = – 3
⇒ h + 1 = -3 ⇒ h – 1 – 3 = -4
∴ h = -4 ଓ k = 1

(iv) (h – k, k – h), (2h, 2k) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-1, 2) ।
\(\frac{h-k+2h}{2}\) = -1 ⇒ 3h – k = -2 ……(i)
ଏବଂ \(\frac{k-h-1}{2}\) = 2 ⇒ 3k – h = 4 …….(ii)

hର ମାନ ସମୀକରଣ (i)ରେ ପ୍ରୟୋଗ କଲେ, 3h – k = -2
⇒ \(\frac{-3}{4}\) – k = -2 = -k = -2 + \(\frac{-3}{4}\) = \(\frac{-8+3}{4}=\frac{-5}{4}\) ⇒ k = \(\frac{5}{4}\)
∴ h = \(\frac{-1}{4}\) ଓ k = \(\frac{5}{4}\)

Question 4.
(0, 0) ଏକ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ । ଯଦି ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (2, 3) ହୁଏ, ତେବେ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁଟିର ସ୍ଥାନଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏକ ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 0) ଏବଂ ଏକ ପ୍ରାନ୍ତ ବିଦୁର ସ୍ଥାନାଙ୍କ (2, 3) ।
ମନେକର ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶାନୁସାରେ, \(\frac{x+2}{2}\) = 0 ଏବଂ \(\frac{y+3}{2}\) = 0 ⇒ x = – 2 ଏବଂ y = -3
∴ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) = (-2, -3)

Question 5.
ଏକ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (-2, 4) ଏବଂ (1, 2), ତେବେ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁଟିର ସ୍ଥାନଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ଏକ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (-2, 4) ଓ (1, 2) ।
ମନେକର ଅନ୍ୟ ପ୍ରାନ୍ତ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶାନୁସାରେ, \(\frac{-2+x}{2}\) = 1 ⇒ x = 2 + 2 = 4 ଏବଂ \(\frac{4+ y}{2}\) = 2 ⇒ y = 4 – 4 = 0
∴ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (4, 0) ।

Question 6.
ଗୋଟିଏ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (3, 5) ଏବଂ (2, 1) ହେଲେ, ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁଟିର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ।
ସମାଧାନ :
ଗୋଟିଏ ରେଖାଖଣ୍ଡର ଏକ ପ୍ରାନ୍ତବିନ୍ଦୁ ଓ ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (3, 5) ଏବଂ (2, 1) |
ମନେକର ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶାନୁସାରେ, \(\frac{x+3}{2}\) = 2 ⇒ x = 4 – 3 = 1 ଏବଂ \(\frac{y+5}{2}\) = 1 ⇒ y = 2 – 5 = -3
∴ ଅନ୍ୟ ପ୍ରାନ୍ତବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, -3) ।

Question 7.
x ଓ yର କେଉଁ ମୂଲ୍ୟ ପାଇଁ (6, -2) ଓ (2, -4) ବିନ୍ଦୁଦ୍ଵୟକୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ଏବଂ (x, 1) ଓ (-2, y) ବିନ୍ଦୁଦ୍ଵୟକୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରିବେ ।
ସମାଧାନ :
ଗୋଟିଏ ରେଖାଖଣ୍ଡ PQର ପ୍ରାନ୍ତବିନ୍ଦୁଦ୍ଵୟର ସ୍ଥାନାଙ୍କ P(6, – 2) ଓ Q(2, – 4) ।
ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{6+2}{2}, \frac{-2-4}{2}\)) = (4, -3)
ଅନ୍ୟ ଏକ ରେଖାଖଣ୍ଡ \(\bar{RS}\)ର ପ୍ରାନ୍ତବିନ୍ଦୁ ଦ୍ବୟର ସ୍ଥାନାଙ୍କ R(x, 1) ଓ S(-2, y) ।
RS ରେଖାଖଣ୍ଡର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{x+(-2)}{2}, \frac{y+1}{2}\)) ।
PQ ଓ \(\bar{RS}\) ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରିବେ ।
ଅର୍ଥାତ୍ ରେଖାଖଣ୍ଡ ଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁ ଅଭିନ୍ନ ଅଟେ ।
ପ୍ରଶାନୁସାରେ, \(\frac{x+(-2)}{2}\) = 4 ⇒ x = 8 + 2 = 10 ଏବଂ \(\frac{1+y}{2}\) = -3 ⇒ y = – 6 – 1 = -7
∴ x = 10 ଓ y = -7।

Question 8.
(2, 3) ଓ (1, 4) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
A (x₁, y₁) ଓ B(x₂,y₂) ବିନ୍ଦୁଦ୍ଵୟର ସଂଯୋଗକାରୀ ରେଖାଖଣ୍ଡ \(\bar{AB}\) କୁ m : n ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା
ବିଦୁର ସ୍ଥାନାଙ୍କ (x, y) = \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)
(2, 3) ଓ (1, 4) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥ‌ିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ହେଉ ।
ଏଠାରେ x₁ = 2, y₁ = 3, x₂ = 1, y₂ = 4; m = 3 ଓ n = 2
x-ସ୍ଥାନାଙ୍କ = \(\frac{m x_2+n x_1}{m+n}=\frac{3×1+2×2}{3+2}=\frac{3+4}{5}=\frac{7}{5}\)
y-ସ୍ଥାନାଙ୍କ = \(\frac{m y_2+n y_1}{m+n}=\frac{3×4+2×3}{3+2}=\frac{12+6}{5}=\frac{18}{5}\)
∴ (2, 3) ଓ (1, 4) ରେଖାଖଣ୍ଡକୁ 3 : 2 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{7}{5}, \frac{18}{5}\))

Question 9.
(-2, 3) ଓ (5, -7) ବିନ୍ଦୁଦ୍ଵୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 4 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ମନେକର (-2, 3) ଓ (5, -7) ବିନ୍ଦୁଦ୍ୱୟକୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ 3 : 4 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ଏଠାରେ x₁ = -2, y₁ = 3, x₂ = 5, y₂ = -7; m = 3, n = 4 ।
∴ x-ସ୍ଥାନାଙ୍କ = \(\frac{m x_2+n x_1}{m+n}=\frac{3×5+4×(-2)}{3+4}=\frac{15-8}{7}=\frac{7}{7}=1\)
y-ସ୍ଥାନାଙ୍କ = \(\frac{m y_2+n y_1}{m+n}=\frac{3×(-7)+4(3)}{3+4}=\frac{-21+12}{7}=\frac{-9}{7}\)
∴ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (1, \(\frac{-9}{7}\)) ।

Question 10.
ଯଦି (5, 9) ବିନ୍ଦୁଟି, (7, -3) ଓ (4, k)କୁ ସଂଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ 2 : 1 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରେ, ତେବେ kର ମୂଲ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
(7, -3) ଓ (4, k) କୁ ଯୋଗକରୁଥିବା ରେଖାଖଣ୍ଡକୁ 2 : 1 ଅନୁପାତରେ ଅନ୍ତର୍ବିଭକ୍ତ କରୁଥିବା ବିନ୍ଦୁଟି (5, 9) ।
ଏଠାରେ x₁ = 7, y₁ = -3, x₂ = 4, y₂ = k; m = 2, n = 1
y-ସ୍ଥାନାଙ୍କ = \(\frac{m y_2+n y_1}{m+n}=\frac{2k+1(-3)}{2+1}\)
ପ୍ରଶାନୁସାରେ, \(\frac{2k+1(-3)}{2+1}\) = 9 = 2k – 3 = 9 × 3
⇒ 2k = 27 + 3 = 30 ⇒ k = \(\frac{30}{2}\) = 15
∴ kର ମୂଲ୍ୟ 15 ଅଟେ ।

Question 11.
ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ସାହାଯ୍ୟରେ ପ୍ରମାଣ କର ଯେ, କୌଣସି ତ୍ରିଭୁଜର ମଧ୍ଯମାତ୍ରୟ ଏକ ବିନ୍ଦୁଗାମୀ ।
ସମାଧାନ :
ମନେକର ABC ତ୍ରିଭୁଜର A, B ଓ C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ A (x₁,y₁), B (x₂, y₂) ଓ C (x₃, y₃) ।
ABC ତ୍ରିଭୁଜର ମଧ୍ଯମାତ୍ରୟ AD, BE, CF । BC ର ମଧ୍ୟବିନ୍ଦୁ D।
∴ D ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{x_2+x_3}{2}, \frac{y_2+y_3}{2}\)) ।
ସେହିପରି E ଓ F ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ
E(\(\frac{x_1+x_3}{2}, \frac{y_1+y_3}{2}\)), F(\(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\)) ।

ମଧ୍ୟମାତ୍ରୟର ଛେଦବିନ୍ଦୁ Gକୁ ତ୍ରିଭୁଜର ଭରକେନ୍ଦ୍ର କୁହାଯାଏ । ଭରକେନ୍ଦ୍ରଠାରେ ମଧ୍ୟମାତ୍ରୟ 2 : 1 ଅନୁପାତରେ ପରସ୍ପରକୁ ଅନ୍ତର୍ବିଭକ୍ତ କରନ୍ତି ।

∴ ତିନୋଟି ମଧ୍ଯମାଉପରିସ୍ଥ ଓ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଅଭିନ୍ନ ଅଟେ । ଏଥୁରୁ ସ୍ପଷ୍ଟ ଯେ କୌଣସି ତ୍ରିଭୁଜର ମଧ୍ଯମାତ୍ରୟ ଏକ ବିନ୍ଦୁଗାମୀ ।

Question 12.
(h, 5), (-4, k) ଓ (8, 9) ବିନ୍ଦୁମାନଙ୍କଦ୍ୱାରା ଗଠିତ ତ୍ରିଭୁଜର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (-2, 6) ହେଲେ h ଓ kର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ :
(h, 5), (-4, k) 8 (8, 9) ବିନ୍ଦୁମାନଙ୍କଦ୍ୱାରା ଗଠିତ ତ୍ରିଭୁଜର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (-2, 6) ।
ଏଠାରେ x₁ = h, x₂, = – 4, x₃ = 8, y₁ = 5, y₂ = k, y₃ = 9
ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (\(\frac{x_1+x_3+x_3}{3}, \frac{y_1+y_3+y_3}{3}\)
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{x_1+x_3+x_3}{3}=-2\) ଏବଂ \(\frac{y_1+y_3+y_3}{3}\) = 6
⇒ \(\frac{h-4+8}{3}=-2\) ⇒ \(\frac{5+k+9}{3}=6\)
⇒ h + 4 = -6 ⇒ k + 14 = 18
⇒ h = -6 – 4 =- 10 ⇒ k = 18 – 14 = 4
∴ h = 10 ଓ k = 4 ।

Question 13.
∆ ABCର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (1, 1) । A (3, -4), B (-4, 7) ହେଲେ, C ବିନ୍ଦୁର ସ୍ଥାନଙ୍କ ସ୍ଥିର କର ।
ସମାଧାନ :
∆ ABCର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (1, 1) । A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ A (3, -4) ଓ B(-4, 7) ।
ମନେକର ୯ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{3+(-4)+x}{3}=1\) ଏବଂ \(\frac{-4+7+y}{3}=1\)
⇒ -1 + x = 3 ⇒ y + 3 = 3
⇒ x = 3 + 1 = 4 ⇒ y = 3 – 3 = 0
∴ C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ C (4, 0) ।

Question 14.
ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ମାନ (-4, 1) ଓ (3,-4) ଏବଂ (1, 3) ହେଲେ, ଏହାର ଭରକେନ୍ଦ୍ର ସ୍ଥାନାଙ୍କ ହେବ ।
ସମାଧାନ :
ଗୋଟିଏ ∆ ର ଶୀର୍ଷବିଦୁ୍ୟତ୍ରୟର ସ୍ଥାନାଙ୍କ ( 4, 1), (3, -4) ଏବଂ (1, 3) ।
ଏହାର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ x = \(\frac{-4+3+1}{3}=\frac{0}{3}=0\) ଏବଂ y = \(\frac{1-4+3}{3}=\frac{4-4}{3}=0\)
∴ ∆ର ଭରକେନ୍ଦ୍ରର ସ୍ଥାନାଙ୍କ (0, 0) ଅର୍ଥାତ୍ ମୂଳବିନ୍ଦୁ ଅଟେ । (ପ୍ରମାଣିତ)

Question 15.
A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (1, 2) ଓ (5, -4) । AB ରେଖାଖଣ୍ଡ ଉପରେ ଏକ ବିନ୍ଦୁ ସ୍ଥିର କର, ଯେପରି ବିନ୍ଦୁଟିର A ବିନ୍ଦୁଠାରୁ ଦୂରତା, B ବିନ୍ଦୁଠାରୁ ଦୂରତାର 3 ଗୁଣ ହେବ ।
ସମାଧାନ :
AB ର A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (1, 2) ଓ (5,-4) ।
AB ଉପରେ ଏକ ବିନ୍ଦୁ P ଯେପରି AP = 3 BP ⇒ AP : BP=3 : 1
ଏଠାରେ x₁ = 1, y₁ = 2, x₂ = 5, y₂ = -4; m = 3, n = 1

Question 16.
(1, 5) ଓ (7, 2) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିଦୁ୍ୟଦ୍ୱୟକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ ସମତ୍ରିଖଣ୍ଡ କରୁଥିବା ବିନ୍ଦୁଦ୍ବୟର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
AB ର A ଓ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ (1, 5) ଓ (7, 2) ।
ମନେକର AB କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରୁଥିବା ବିଦୁ୍ୟଦ୍ଵୟ P ଏବଂ Q ।

∴ (1, 5) ଓ (7, 2) ସ୍ଥାନାଙ୍କ ବିଶିଷ୍ଟ ବିଦୁ୍ୟତ୍ବକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡକୁ ସମତ୍ରିଖଣ୍ଡ କରୁଥିବା ବିଦୁ୍ୟଦ୍ୱୟର ସ୍ଥାନାଙ୍କ (3, 4) ଏବଂ (5, 3) ।

Question 17.
O(0, 0), A (2a, 0) ଓ B (0, 2b) ହେଲେ ଦର୍ଶାଅ ଯେ OAB ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜ ଏବଂ ଏହାର କର୍ଣ୍ଣର ମଧ୍ୟବିନ୍ଦୁ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମାନ ଦୂରରେ ଅବସ୍ଥିତ ।
ସମାଧାନ :
∆ OABର ଶୀର୍ଷବିନ୍ଦୁ ତ୍ରୟର ସ୍ଥାନାଙ୍କ ଠ(0, 0), A(2a, 0) ଓ B (0, 2b) ।
A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (2a, 0) ଏହା x-ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ OA = 2a ଏକକ ।
B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 2b) ଏହା y-ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ OB = 2b ଏକକ !
⇒ କର୍ଣ୍ଣ AB = \(\sqrt{(0-2a)^2 +(2b-0)^2}\) = \(\sqrt{4a^2 +4b^2}\) = 2\(\sqrt{a^2 +b^2}\)

ମନେକର କର୍ପୂର ମଧ୍ୟବିନ୍ଦୁ P ।
AP = BP = \(\frac{\sqrt{a^2 +b^2}}{2}\) = \(\sqrt{a^2 +b^2}\)
∴ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{2a+0}{2}, \frac{0+2b}{2}\)) = (a,b)
∴ OP = \(\sqrt{a^2 +b^2}\)
∴ AP = BP = OP ଏଥରୁ ପ୍ରମାଣିତ ଯେ, କର୍ପୂର ମଧ୍ୟବିନ୍ଦୁ P ସମକୋଣୀ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁମାନଙ୍କଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ।

Question 18.
ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ସାହାଯ୍ୟରେ ପ୍ରମାଣ କର ଯେ, ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
ସମାଧାନ :
ପ୍ରଦତ୍ତ ଚିତ୍ରରେ OABC ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର । ମୂଳବିନ୍ଦୁ Oର ସ୍ଥାନାଙ୍କ (0, 0) ।
ମନେକର OA = a ∴ A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a, 0) ।
C ବିନ୍ଦୁରୁ OA ପ୍ରତି CD ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ ।
ମନେକର CD = b ଏବଂ OD = p ।
∴ C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (p, b) ଏବଂ B ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a + p, b) ।
ବର୍ତ୍ତମାନ OABC ସାମାନ୍ତରିକ ଚିତ୍ରର ଶୀର୍ଷବିନ୍ଦୁଗୁଡ଼ିକର ସ୍ଥାନାଙ୍କ O (0, 0), A (a, 0), B (a + p, b), C (p, b) ।

∴ କର୍ଣ୍ଣ AC ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+p}{2}, \frac{o+b}{2}\)) = (\(\frac{a+p}{2}, \frac{b}{2}\))
କର୍ଣ୍ଣ OBର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+p+0}{2}, \frac{b+0}{2}\)) = (\(\frac{a+p}{2}, \frac{b}{2}\))
∴ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟର ମଧ୍ୟବିନ୍ଦୁରୁ ସ୍ଥାନଙ୍କ ଅଭିନ୍ନ ।
ଅର୍ଥାତ୍ କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି । (ପ୍ରମାଣିତ)

Question 19.
ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ସାହାଯ୍ୟରେ ଦର୍ଶାଅ ଯେ, ଗୋଟିଏ ଆୟତଚିତ୍ରର କଣ୍ଠଦ୍ଵୟ ସର୍ବସମ ଏବଂ ପରସ୍ପରକୁ
ସମାଧାନ :
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ OABC ଏକ ଆୟତଚିତ୍ର ।
OABC ଆୟତଚିତ୍ରର ଶୀର୍ଷବିନ୍ଦୁ ଚାରୋଟିର ସ୍ଥାନାଙ୍କ ଯଥାକ୍ରମେ
O (0, 0), A (0, a), B (a, b), C (0, b) ।

କର୍ଣ୍ଣ AC = \(\sqrt{(0 – a)^2 + (b – 0)^2}\) = \(\sqrt{a^2 +b^2}\)
କର୍ଣ୍ଣ OB = \(\sqrt{(a-0)^2+(b-0)^2}\)= \(\sqrt{a^2 +b^2}\)
∴ AC = OB
କର୍ଣ୍ଣ ACର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{0+a}{2}, \frac{b+0}{2}\)) = (\(\frac{a}{2}, \frac{b}{2}\))
କର୍ଣ୍ଣ OB ର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (\(\frac{a+0}{2}, \frac{b+0}{2}\)) = (\(\frac{a}{2}, \frac{b}{2}\))
∴ OABC ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ଏବଂ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।

Question 20.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a, 0) ହେଲେ,
(i) ଅନ୍ୟ ଶୀର୍ଷବିନ୍ଦୁଦ୍ଵୟର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।
(ii) ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(iii) BE ମଧ୍ଯମାର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
(iv) G ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ ନିର୍ଣ୍ଣୟ କର ।

ସମାଧାନ :
ଦତ୍ତ ଚିତ୍ରରେ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । A ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (a, 0) ।
∴ CO ⊥ AB ⇒ ABର ମଧ୍ୟବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, 0) ।
ମନେକର \(\frac{a+x}{2}=0\) ⇒ x = -a
\(\frac{0+y}{2}=0\) ⇒ y = 0
∴ Bବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (-a, 0) ।

ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ (AB)
\(\sqrt{{a-(-a)}^2 +(0-0)^2}\) = √(2a)² = = √4a² = 2a
∴ ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା (OC)
= ବାହୁର ଦୈର୍ଘ୍ୟ × \(\frac{\sqrt{3}}{2}\) = 2a × \(\frac{\sqrt{3}}{2}\) = √3a
∴ C ବିନ୍ଦୁଟି y ଅକ୍ଷ ଉପରେ ଅବସ୍ଥିତ ହେତୁ ଏହାର y ସ୍ଥାନାଙ୍କ 0 ।
C ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (0, √3a) ।
(i) ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ୟ ଶୀର୍ଷବିନ୍ଦୁ ଦ୍ବୟର ସ୍ଥାନାଙ୍କ B (-a, 0) ଏବଂ C (0, √3a) ।
(ii) ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ = 2a
(iii)

(iv)

Odisha State Board BSE Odisha 10th Class English Solutions Chapter 7 The Flower-School Textbook Exercise Questions and Answers.

Class 10th English Chapter 7 The Flower-School Question Answers BSE Odisha

The Flower-School Class 10 Questions and Answers

H. Let’s Understand The Poem:
Read the poem silently and answer the following questions.
(କବିତାଟିକୁ ନୀରବରେ ପଢ଼ ଓ ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।)

Question 1.
What is the poem about?
(କବିତାଟି କେଉଁ ବିଷୟରେ ଲିଖ୍ ?)
Answer:
The poem is about the flower children.

Question 2.
What rumbles in the sky?
(ଆକାଶରେ କ’ଣ ଘଡ଼ଘଡ଼ିର ପ୍ରଚଣ୍ଡ ଧ୍ବନି ସୃଷ୍ଟି କରୁଛି ?)
Answer:
The storm-clouds rumble in the sky.

Question 3.
What comes marching over the heath?
(ବ୍ୟାପକ ତୃଣ ଅଞ୍ଚଳ ଉପରେ କ’ଣ ମାଡ଼ି ଆସୁଛି ?)
Answer:
The moist (slightly wet) east wind comes marching over the heath.

Question 4.
Which word tells that the east wind is not dry?
(କେଉଁ ଶବ୍ଦ ଦର୍ଶାଉଛି ଯେ ପୂବେଇ ପବନ ଶୁଖା ନୁହେଁ ?)
Answer:
The word ‘moist’ tells that the east wind is not dry.

Question 5.
How does the moist east wind come?
(ଆର୍ଦ୍ର ପୂବେଇ ପବନ କିଭଳି ଆସେ/ ଆସୁଛି ?)
Answer:
The moist east wind comes marching.

Question 6.
How do the crowds of flowers come out?
(ଫୁଲଗୁଡ଼ିକର ଦଳ କିପରି ବାହାରି ଆସୁଛି ?)
Answer:
The crowds of flowers come out suddenly from nowhere.

Question 7.
Where do the flowers dance and how?
(ଫୁଲସବୁ କେଉଁଠାରେ ନାଚୁଛି ଓ କିପରି ?)
Answer:
The flowers dance upon (ନୃତ୍ୟ କରୁଛି) the grass in wild excitement.

Question 8.
Which season is described in the poem ?
(ବର୍ଷସାରା ଫୁଲଗୁଡ଼ିକ କେଉଁଠାରେ ଥାଆନ୍ତି ?)
Answer:
In the poem, the rainy season is described.

Question 9.
Where are the flowers all year round?
( ବର୍ଷସାରା ଫୁଲଗୁଡ଼ିକ କେଉଁଠାରେ ଥାଆନ୍ତି ?)
Answer:
The flowers are at their school all year round.

Question 10.
Who are the flowers compared to?
(ଫୁଲଗୁଡ଼ିକୁ କାହା ସହିତ ତୁଳନା କରାଯାଇଛି ?)
Answer:
The flowers are compared to little children.

Question 11.
How do they do their lessons? Why?
(ସେମାନେ (ଫୁଲସବୁ) କିପରି ସେମାନଙ୍କର ପାଠପଢ଼ା କରନ୍ତି ? କାହିଁକି ?)
Answer:
The flowers do their lessons shutting their doors (ସେମାନଙ୍କର ଦ୍ଵାର ବନ୍ଦ କରି). Because this is their school hour and the time to come out hasn’t come yet.

Question 12.
Who does ‘their master’ refer to?
(‘ସେମାନଙ୍କର ମାଲିକ’ କାହାକୁ ସୂଚିତ କରୁଛି ?)
Answer:
‘Their master’ refers to their teacher.

Question 13.
Their master is strict or lenient? Which line in the poem tells us so?
( ସେମାନଙ୍କର ଗୁରୁ ବା ଶିକ୍ଷକ କଠୋର ବା ସରଳ ? କବିତାରେ କେଉଁ ଧାଡ଼ି ଏହା ଦର୍ଶାଉଛି ?)
Answer:
Their master is strict. The line in the poem telling us so is, “Their master makes them stand in a corner”.

Question 14.
When are they made to stand in a corner?
(ସେମାନଙ୍କୁ (ଫୁଲଗୁଡ଼ିକୁ) କେତେବେଳେ ଗୋଟିଏ କଣରେ ଠିଆ କରାଇ ଦିଆଯାଏ ?)
Answer:
They are made to stand in a comer when they play before school is over.

Question 15.
When do the flowers have their holidays?
(ଫୁଲସବୁ କେତେବେଳେ ସେମାନଙ୍କ ଛୁଟିଦିନ ପାଆନ୍ତି ?)
Answer:
When the rains come, the flowers have their holidays.

Question 16.
What changes take place in nature when the rain comes?
(ଯେତେବେଳେ ବର୍ଷା ଆସେ ପ୍ରକୃତିରେ କେଉଁସବୁ ପରିବର୍ତ୍ତନ ହୋଇଥାଏ ?)
Answer:
When the rain comes, branches clash together in the forest, the thunderclouds clap their giant hands, and the leaves rustle in the wild wind.

Question 17.
How do the flower children enjoy their holidays?
(ଫୁଲରୂପୀ ପିଲାମାନେ କିପରି ସେମାନଙ୍କର ଛୁଟି ଉପଭୋଗ କରନ୍ତି ?)
Answer:
The flower children enjoy their holidays by coming out in the rain dressed (ବର୍ଷା) in pink, yellow, and white.

Question 18.
Who is the speaker sharing his thoughts with?
(କବି କାହା ସହିତ ନିଜର ଭାବନା ବାଣ୍ଟିଛନ୍ତି ?)
Answer:
The speaker is sharing his thoughts with his mother.

Question 19.
Where is the home of the flower children?
(ଫୁଲରୂପୀ ପିଲାମାନଙ୍କର ଘର କେଉଁଠାରେ ?)
Answer:
The home of the flower children is in the sky.

Question 20.
Why are they eager to go to the sky ?
(ସେମାନେ (ଫୁଲସବୁ) କାହିଁକି ଆକାଶକୁ ଯିବା ପାଇଁ ଉତ୍ସୁକ/ବ୍ୟାକୁଳ ?)
Answer:
They are eager (ଉତ୍ସୁକ/ବ୍ୟାକୁଳ) to go to the sky as their mother in the sky calls them.

Question 21.
What does the speaker guess?
(ବକ୍ତା କ’ଣ ଅନୁମାନ କରିଛନ୍ତି ?)
Answer:
The speaker guesses to whom the flower children are raising their arms.

Question 22.
Why are the flower children raising their arms?
(ଫୁଲରୂପୀ ପିଲାମାନେ କାହିଁକି ସେମାନଙ୍କର ହାତ ଉଠାଉଛନ୍ତି ?)
Answer:
The flower children are raising (ଟେକୁଛନ୍ତି) their arms (ହାତ) to their mother living in the sky to embrace them (ସେମାନଙ୍କୁ କୋଳେଇ ନେବାପାଇଁ).

Question 23.
Why are they in a hurry?
(ସେମାନେ କାହିଁକି ଏତେ ଚଞ୍ଚଳ/ବ୍ୟଗ୍ର ହୋଇ ପଡ଼ିଛନ୍ତି ?)
Answer:
They are in a hurry as their mother in the sky calls them.

Question 24.
Which line tells that the speaker also longs for his mother?
(କବିତାରେ କେଉଁ ଧାଡ଼ି ଦର୍ଶାଉଛି ଯେ ବକ୍ତା ମଧ୍ୟ ତାଙ୍କ ମାଆଙ୍କ ପାଖକୁ ଯିବାକୁ ବ୍ୟାକୁଳ ହୋଇପଡ଼ିଛନ୍ତି ?)
Answer:
The line that tells that the speaker also longs for (wishes) his mother is “they have their mother as I have my own”.

I. Let’s Appreciate The Poem:
(A)
Question 1.
Why do you think the flowers dance upon the grass in wild glee?
(ତୁମେ କାହିଁକି ଭାବୁଛ ଫୁଲଗୁଡ଼ିକ ଘାସ ଉପରେ ପ୍ରବଳ ଉତ୍ତେଜନାରେ ନାଚୁଛନ୍ତି ?)
Answer:
I think the flowers dance upon the gears that come down with them. During storms, branches clash together in the forest and the leaves rustle in the wild wind. The moist east wind comes marching over the uncultivated land also.

Question 2.
Do you think the speaker feels that holidays are funnier than school days?
(ତୁମେ ଭାବୁଛ କି ସ୍କୁଲ ଦିନ ଅପେକ୍ଷା ଛୁଟିଦିନସବୁ ଅଧ୍ବକ କୌତୂହଳପ୍ରଦ ବୋଲି ବକ୍ତା ଅନୁଭବ କରୁଛନ୍ତି ?)
Answer:
Yes, I think so.

Question 3.
Why does the speaker think that the flowers go to school underground?
(ବକ୍ତା କାହିଁକି ଭାବୁଛନ୍ତି ଯେ ଫୁଲଗୁଡ଼ିକ ଭୂପୃଷ୍ଠ ତଳେ ଥ‌ିବା ବିଦ୍ୟାଳୟକୁ ଯାଆନ୍ତି ?)
Answer:
The speaker thinks that the flowers go to school underground as he notices them only when the monsoon rain comes and he does not notice the flowers anywhere in other seasons. So he thinks they must have been in school underground all year round.

Question 4.
How does the speaker describe the storm?
(ବକ୍ତା କିଭଳି ଝଡ଼କୁ ବର୍ଣ୍ଣନା କରିଛନ୍ତି ?)
Answer:
According to the speaker the storm-clouds rumble (make a long deep sound) as if they clap their giant hands and showers come down with them. During storms, branches clash together in the forest and the leaves rustle in the wild wind. The moist east wind comes marching over the uncultivated land also.

Question 5.
Do you think that the speaker’s description of the flowers and their school has any reality in real life?
ତୁମେ କ’ଣ ଭାବୁଛ ବକ୍ତାଙ୍କର ଫୁଲ ଓ ସେମାନଙ୍କର ବିଦ୍ୟାଳୟ ସମ୍ପର୍କିତ ବର୍ଣ୍ଣନାର ଜୀବନର ବାସ୍ତବତା ସହ କିଛି ସମ୍ପର୍କ ଅଛି ?)
Answer:
Yes, I think that the speaker’s description of the flowers and their school has a reality in real life.

Question 6.
Which elements of nature celebrate holidays with the flower children and how?
(ପ୍ରକୃତିର କେଉଁସବୁ ଉପାଦାନ ଫୁଲରୂପୀ ପିଲାମାନଙ୍କ ସହିତ ଛୁଟି ପାଳନ କରୁଛନ୍ତି ଓ କିପରି ?)
Answer:
Elements of nature like (ପରି) branches of trees in the forest, their leaves, and thunderclouds celebrate holidays with the flower children. With the blowing of wild wind, branches clash together in the forest and leaves make rustling sounds, and the thunderclouds rumble as if they clap with their big hands. In this way, they celebrate their holiday.

Question 7.
Identify the lines and phrases in the poem which indicate that the flower children have a strict system of schooling.
(କବିତାରେ ଫୁଲରୂପୀ ପିଲାମାନଙ୍କର କଠୋର ବିଦ୍ୟାଳୟ ବ୍ୟବସ୍ଥା ଥ‌ିବା କଥା ସୂଚିତ କରୁଥିବା ଧାଡ଼ି ଓ ବାକ୍ୟାଶଗୁଡ଼ିକୁ ଚିହ୍ନିତ କର ।)
Answer:
The lines and phrases in the poem which indicate that the flower children have a strict system of schooling are: “They do their lessons with doors shut, and if they want to come out to play before it is time, their master makes them stand in a comer. ”

(B)
Question 1.
The poet presents a lively description of nature during the monsoon
showers in June. The objects of nature seem to behave like human beings. Such a device in poetry is known as personification. (କବି ଜୁନ୍ ମାସର ମୌସୁମୀ ବର୍ଷା ସମୟର ପ୍ରକୃତିର ଏକ ଜୀବନ୍ତ ବିବରଣୀ ଉପସ୍ଥାପିତ କରିଛନ୍ତି । ପ୍ରକୃତିର ପଦାର୍ଥଗୁଡ଼ିକ ମନୁଷ୍ୟ ଭଳି ବ୍ୟବହାର କରୁଥ‌ିବାର ଜଣାଯାଉଛି । କବିତାରେ ଏଭଳି ଅଳଙ୍କାର କୁ personification ବା ‘ବ୍ୟକ୍ତିତ୍ବ ଆରୋପଣ’ କୁହାଯାଏ ।)
Personification is a device in which a thing or an idea or an animal is given human qualities and described as a living thing. (Personification ବା ବ୍ୟକ୍ତିତ୍ବ ଆରୋପଣ ହେଉଛି ଏକ ଅଳଙ୍କାର ଯେଉଁଥରେ ଏକ ପଦାର୍ଥ ବା ଏକ ଧାରଣା କିମ୍ବା ଏକ ପ୍ରାଣୀ ମାନବୀୟ ଗୁଣାବଳୀ ପ୍ରଦତ୍ତ ହୋଇଥାଏ ଏବଂ ଏକ ଜୀବନ୍ତ ପଦାର୍ଥ ଭଳି ବର୍ଣ୍ଣନା କରାଯାଇଥାଏ ।)
Pick out as many such examples as you can from the poem. One is done for you.
(ତୁମେ କବିତା ଯେତେ ପାରୁଛ ସେହିଭଳି ଉଦାହରଣ ବାହାର କର । ଗୋଟିଏ ତୁମ ପାଇଁ କରିଦିଆଯାଇଛି ।)
Answer:

• Storm clouds rumble in the sky.
• June showers come down.
• The moist east wind comes marching.
• Crowds of flowers come out and dance upon the grass in wild glee.
• Branches clash together in the forest.
• The leaves rustle in the wild wind.
• The thunderclouds clap their giant hands.
• The flower children rush out in dresses of pink and yellow and white.

Question 2.
Poets use words and pictures to bring out comparisons between persons, ideas or objects with similar quality or appearance. (ସମାନ ଗୁଣ ବା ଚେହେରା ଥ‌ିବା ବ୍ୟକ୍ତି, ଧାରଣା ବା ପଦାର୍ଥଗୁଡ଼ିକ ମଧ୍ୟରେ ତୁଳନା କରିବା ପାଇଁ କବିମାନେ ଶବ୍ଦ ଛବି ବ୍ୟବହାର କରିଥା’ନ୍ତି ।)
What are the things below compared to in the poem you just read?
(ତୁମେ ଏବେ ପଢ଼ିଥିବା କବିତାରେ ନିମ୍ନଲିଖୁ ଜିନିଷଗୁଡ଼ିକୁ କାହା ସହ ତୁଳନା କରାଯାଇଛି ?)
One is done for you.(ଗୋଟିଏ ତୁମପାଇଁ କରି ଦିଆଯାଇଛି ।)

• the bamboo — bagpipes
• the flowers —
• the underground —
• the rains —
• pink, yellow and white —
• the sky —
• the stars —

Answer.
the bamboo — bagpipes
the flowers — children
the underground — the flower-school
the rains — living animals
pink, yellow and white — colorful dresses
the sky — a living place like the earth
the stars — flower’s mothers

Question 3.
The theme of a poem is the main idea of the poem. The theme may not always be stated, but can be hinted at indirectly. Which of the following ideas supports the theme of ‘The Flower — School’? Tick your choice.
(କବିତାର ବିଷୟବସ୍ତୁ ହେଉଛି କବିତାର ମୁଖ୍ୟ ଧାରଣାସମୂହ । ବିଷୟବସ୍ତୁ ସର୍ବଦା ଉଲ୍ଲେଖ ହୋଇନଥାଏ, ମାତ୍ର ପରୋକ୍ଷରେ ସୂଚିତ କରାଯାଇଥାଏ । ‘The Flower – School’ ବା ‘ଫୁଲ-ବିଦ୍ୟାଳୟ’ର ବିଷୟବସ୍ତୁକୁ ନିମ୍ନଲିଖ୍ କେଉଁ ଧାରଣା ସମୂହ ସମର୍ଥନ କରୁଛି ।)

• love for wildlife
• appreciation of nature
• praise of God
• featuring imagination of a flower school
• dislike for the strict school system
• lauding the schoolmaster
• longing for the mother

Answer:

• appreciation of nature
• praise of God
• lauding the schoolmaster

Question 4.
The poet’s longing for his deceased mother creates _______ in the reader’s mind.
(କବିଙ୍କଦ୍ୱାରା ନିଜର ମୃତ ମାଆଙ୍କୁ ସ୍ମରଣ ପାଠକଙ୍କ ମନରେ ______________ସୃଷ୍ଟି କରିଛି ।)
(a) pity (b) panic
(c) pathos (d) pride
Answer:
(c) pathos (ପାଥୋସ୍)

J. Let’s Do The Activities:

Role-play
The students play the roles of ‘Small Boy’ and ‘Flower Child’ in pair and practise the dialogue naturally. They are to be invited to the front of the class to play the role. They change their role after the first round. (ଛାତ୍ରଛାତ୍ରୀମାନେ ଦୁଇଜଣିଆ ଦଳ ହୋଇ ‘ଛୋଟ ବାଳକ’ ଏବଂ ‘ଫୁଲରୂପୀ ପିଲା’ ଭୂମିକାରେ ଅଭିନୟ କରିବେ ଏବଂ ସଂଳାପଗୁଡ଼ିକ ସ୍ଵାଭାବିକ ଭାବେ ଅଭ୍ୟାସ କରିବେ । ସେମାନଙ୍କୁ ଅଭିନୟ କରିବା ପାଇଁ ବିଦ୍ୟାଳୟର ଆଗ ବେଞ୍ଚକୁ ଡକାଯିବ । ପ୍ରଥମ ରାଉଣ୍ଡ ପରେ ସେମାନେ ସେମାନଙ୍କ ଭୂମିକା ପରିବର୍ତ୍ତନ କରିବେ ।)

Small Boy        : Flower Child. Flower Child, where are you going?
Flower Child    : I’m going to school.
Small Boy        : School! You’re going to school! Which school do you go to?
Flower Child    :I go to school underground.
Small Boy        : Really? Who teaches you there?
Flower Child    : Our master.
Small Boy        : Nice. Does anybody disturb you there?
Flower Child    : No, not at all. We do our lessons with doors shut.
Small Boy        : How is your master?
Flower Child    : He’s very strict. He makes us stand in a corner when we play before school is over.
Small Boy        : Thank God. Do you always study? Don’t you have any holidays to enjoy?
Flower Child    : Of course. We have. We have holidays when the rains come.
Small Boy        : What do you do then?
Flower Child    : We wearcoIourfu1 dresses and come out to enjoy the beautiful nature.
Small Boy        : Where is your home?
Flower Child    : It is in the sky. My mother lives there. I am eager to go there.
Small Boy        : Oh really? My mother also lives there.

Question 2.
Listen and Correct:
The teacher reads aloud the following sentences with some intentional factual errors. The students listen and correct them saying: “Excuse me, Sir/Ma’m. I think it is ___________ not, but it is _____________.”
(ନିମ୍ନଲିଖ୍ ଉଦ୍ଦେଶ୍ୟମୂଳକ ଭାବେ ତଥ୍ୟଗତ ତୁଟି ସମ୍ବଳିତ ବାକ୍ୟଗୁଡ଼ିକୁ ଶିକ୍ଷକ ଉଚ୍ଚ ସ୍ୱରରେ ପଢ଼ିବେ । ପିଲାମାନେ ତାହାକୁ ଶୁଣିବେ ଏବଂ ସଂଶୋଧନ କରି କହିବେ ।)
Sentences (with errors):
(i) When the storm clouds rumble on the earth, June showers come down.
(ii) The moist west wind comes marching over the heath.
(iii) The wind blows the bagpipes among the pine trees.
(iv) The crowds of flowers dance upon the bamboos in a very excited way.
(v) The flowers go to school on the top of a hill.
(vi) The flower children do their lessons with their classroom doors open.
(vii) Their teacher makes them stand under a tree.
(viii) They have their holidays at the advent of summer.
(ix) Their home is in the sea.
(x) The flowers are eager to go to their school.
Answer:
(i) Excuse me, Sir/Ma’m. I think it is not ‘the storm clouds rumble on the earth’, but it is ‘the storm clouds rumble in the sky’.
(ii) Excuse me, Sir/Ma’m. I think it is not ‘the moist west wind comes marching’, but it is ‘the moist east wind comes marching’.
(iii) Excuse me, Sir/Ma’m. I think it is not ‘the pine trees’, but it is ‘the bamboos’.
(iv) Excuse me, Sir/Ma’m. I think it is not ‘the bamboos’, but it is ‘the grass’.
(v) Excuse me, Sir/Ma’m. I think it is not ‘on the top of a hill’, but it is ‘underground’.
(vi) Excuse me, Sir/Ma’m. I think it is not ‘classroom doors open’, but it is ‘classroom doors shut’.
(vii) Excuse me, Sir/Ma’m. I think it is not ‘stand under a tree’, but it is ‘stand in a comer’.
(viii) Excuse me, Sir/Ma’m. I think it is not ‘at the advent of summer’, but it is ‘at the advent of rain’.
(ix) Excuse me, Sir/Ma’m. I think it is not ‘in the sea’, but it is ‘in the sky’.
(x) Excuse me, Sir/Ma’m. I think it is not ‘go to their school’, but it is ‘go to their home’.

Question 3.
Writing
1. Given below is the summary of the poem “The Flower-School”. Fill in the blanks with suitable words to complete the summary. You may take the help of the “HELP BOX” given below. (ନିମ୍ନରେ “The Flower-School” ବା ‘ଫୁଲ-ବିଦ୍ୟାଳୟ’ର ସାରାଂଶ ଦିଆଯାଇଛି । ଶୂନ୍ୟସ୍ଥାନରେ ଉପଯୁକ୍ତ ଶବ୍ଦ ପୂରଣ କରି ସାରାଂଶକୁ ସମ୍ପୂର୍ଣ୍ଣ କର । ତୁମେ ନିମ୍ନରେ ପ୍ରଦତ୍ତ ‘HELP BOX’ ବା ‘ସହାୟକ ବାକ୍ସ’ର ସାହାଯ୍ୟ ନେଇପାର ।)

After the first shower of June, “hen the (a) _________ wind approaches blowing its (b) _________ to herald the advance of (c) ___________, the (d) _________ bloom and (e) ________ upon the grass in (f) ________ happiness. The poet thinks that before the arrival of spring, the flowers go to a school (g) ____________ and learn their lesson. They have their holidays only when it rains and they come out rushing in colorful dresses. The sky is their home towards which they raise their (h) _________ because their (i) _________ lives there and they are always in a (j) _______ to go home.

HELP BOX

mother     arms              hurry                 great        underground east          bagpipes       flowers            rain           dance

Answer:
After the first shower of June, when the (a) east wind approaches blowing its (b) bagpipes to herald (ଘୋଷଣା କରିବା ପାଇଁ) the advance of (c) rain, the (d) flowers bloom and (e) dance upon the grass in (f) great happiness. The poet thinks that before the arrival of spring, the flowers go to a school (g) underground and learn their lesson. They have their holidays only when it rains and they come out rushing in colorful dresses. The sky is their home towards which they raise their (h) arms because their (i) mother lives there and they are always in a (j) hurry (ତରବର) to go home.

Question 2.
Imagine that you are a child of the Flower-School. Write a letter to your mother describing your experience and feelings in your school. You may begin your letter as follows : (ମନେକର ତୁମେ Flower-Schoolର ଜଣେ ଶିଶୁ । ବିଦ୍ୟାଳୟରେ ତୁମର ଅଭିଜ୍ଞତା ଓ ଅନୁଭୂତିକୁ ବର୍ଣନା କରି ମା’ଙ୍କ ପାଖକୁ ଗୋଟିଏ ଚିଠି ଲେଖ । ତୁମେ ତୁମର ଚିଠି ନିମ୍ନ ପ୍ରକାରେ ଆରମ୍ଭ କରିପାର )

Flower School Date_______ Dear Mother, How are you? You’ll be glad to know that I go to school every day. Do you know how and where our school is? The school is situated under-ground. _____________________________________________ _____________________________________________We make a lot of fun. But our class teacher is _________________________________________________________________________________ _________________________________________________________________________________ _________________________________________________________________________________ I am looking forward to the holidays. I miss you a lot, Mom.                                                                                                                                                              Yours lovingly, (Name)

Answer:

Flower School
Date: 3rd June 2020

Dear Mother,

How are you? You’ll be glad to know that I go to school every day. Do you know how and where our school is? The school is situated underground (ଭୂତଳ). We do our lessons here. We make a lot of fun. But our class teacher is very strict ( ଅତି କଠୋର ). When we play before school is over, he makes us stand in a corner. When rains come. we enjoy our holidays a lot. We came out dressed in pink and yellow and white and joyfully dance up the grass. But, mother I long for you and am eager to go home.
lam looking forward to the holidays.
I miss you a lot, Mom.

Yours lovingly,
Pinky.

BSE Odisha 10th Class English The Flower-School Important Questions and Answers

Very Short & Objective Questions With Answers
Answer The Following Questions In A Word Or A Phrase.

Question 1.
Where do the storm-clouds rumble?
Answer:
in the sky

Question 2.
What showers come down with the storm clouds?
Answer:
June showers

Question 3.
Who blows bagpipes?
Answer:
the moist east wind

Question 4.
Where does it blow its bagpipes?
Answer:
among the bamboos

Question 5.
Where do the crowds of flowers dance?
Answer:
upon the grass

Question 6.
Whom does the wet east wind march over?
Answer:
the heath

Question 7.
Where is the school the flower go to?
Answer:
underground

Question 8.
How do flowers do their lessons?
Answer:
shutting their doors

Question 9.
Who makes the flowers stand in a corner?
Answer:
their master

Question 10.
When do the flowers have their holidays?
Answer:
with the coming of rains

Question 11.
What do branches do in the forest?
Answer:
clash (hit) together

Question 12.
What rustles in the wild wind?
Answer:
the leaves of the trees

Question 13.
Who claps their giant hands?
Answer:
the thunder-clouds

Question 14.
Where is the home of flower children?
Answer:
in the sky

Question 15.
How do flower children raise their hands?
Answer:
eagerly (ବ୍ୟାକୁଳ ଭାବରେ)

Fill In The Blanks With Right Words.

1. “The Flower School” is written by ____________.
Answer:
Rabindranath Tagore

2. ____________ bring rain in June.
Answer:
Storm-clouds

3. The moist east wind marches over ____________.
Answer:
the heath

4. ____________ blows its bagpipes.
Answer:
The moist east wind

5. The moist east wind blows its bagpipes among ____________.
Answer:
the bamboos

6. The moist east wind blows its bagpipes by ____________.
Answer:
blowing hard like the sound flowing from bagpipes

7. When the rains come, ____________ come out suddenly.
Answer:
crowds of flowers

8. In the phrase “crowds of flowers”, the word ‘crowds’ means ____________.
Answer:
a large number of

9. “Crowds of flowers come out.” Here ‘come out’ means ____________.
Answer:
bloom or appear

10. Crowds of flowers come out of ____________.
Answer:
from unknown places

11. Crowds of flowers dance upon ____________.
Answer:
the grass

12. Crowds of flowers dance upon the grass in ____________.
Answer:
wild glee

13. The flowers go to school ____________.
Answer:
underground

14. The flowers of their lessons ____________.
Answer:
with doors shut

15. The actual master of the flowers is ____________.
Answer:
God

Multiple Choice Questions(Mcqs) With Answers
Pick out the correct alternative.

Question 1.
‘’The wind comes marching”, What is the figure of speech used?
(A) Simile
(B) Metaphor
(C) Personification
(D) Alliteration
Answer:
(C) Personification

Question 2.
What do the flowers do in their holidays?
(A) They blossom
(B) They wither away
(C) They remain under the cover of the earth
(D) They become fragrant
Answer:
(A) They blossom

Question 3.
Who is the poet of the poem ‘The flower school’?
(A) Rudyard Kipling
(B) Humayun Kabir
(C) R.L. Stevenson
(D) Rabindranath Tagore
Answer:
(D) Rabindranath Tagore

Question 4.
Fill-in-the-Blank
The meaning of the word Rumble is ____________.
(A) a musical sound
(B) a loud resonating sound
(C) very high sound
(D) great excitement
Answer:
(B) a loud resonating sound

Question 5.
What is one word for ‘A large open area’
(A) Hall
(B) Heath
(C) Expanse
(D) Area
Answer:
(B) Heath

Question 6.
Which one below is an example of Alliteration in the poem The flower school?
(A) Bagpipes-Bamboos
(B) Storm-Sky
(C) Grass-Glee
(D) Thunder-Clouds
Answer:
(A) Bagpipes-Bamboos

Question 7.
What is the meaning of Glee?
(A) Surprised
(B) Excitement
(C) Restless
(D) Happiness
Answer:
(B) Excitement

Question 8.
‘They do their lessons with doors shut’ Who does ‘They’ refer to?
(A) Trees
(B) Clouds
(C) Leaves
(D) Flowers
Answer:
(D) Flowers

Question 9.
What is something the Crowd of Flowers does not do?
(A) clap their giant hands
(B) come out of a sudden
(C) do their lessons with doors shut
(D) dance upon the grass in wild glee
Answer:
(A) clap their giant hands

Question 10.
Who is the narrator of the poem “The flower school”
(A) Mother
(B) Father
(C) Brother
(D) Child
Answer:
(D) Child

Question 11.
From where do the children come out from
(A) Home
(B) Mud
(C) School underground
(D) ‘Vessel
(C) School underground

Question 12.
Which season is referred in the poem?
(A) Summer
(B) Winter
(C) Autumn
(D) Monsoon
Answer:
(D) Monsoon

Question 13.
What happens when the Monsoon arrives?
(A) The flower children die
(B) The flower children start eating food
(C) The flower children get their holidays
(D) The flower children take a bath
Answer:
(C) The flower children get their holidays

Question 14.
According to you who is the master of the Flower children?
(A) mother
(B) poet
(C) nature
(D) birds
Answer:
(C) nature

Question 15.
Synonym of the world ‘close’
(A) open
(B) together
(C) snow
(D) shut
Answer:
(B) together

Question 16.
What represents the mother in the poem?
(A) Mother nature
(B) Rabindranath Tagore
(C) School
(D) sky
Answer:
(D) sky

Question 17.
Which elements celebrate holidays with the flower children
(A) branches, leaves, and thunderclouds
(B) Thunder clouds, rigs, mud
(C) branches, twigs, leaves
(D) thunder clouds, twigs, mud
Answer:
(A) branches, leaves, and thunderclouds

The Flower-School Summary in English

Lead-In:
In this poem the speaker is excitedly (ପ୍ରବଳ ଆଗ୍ରହର ସହିତ) watching the monsoon rain (ମୌସୁମୀ ବର୍ଷା) and noticing (ଲକ୍ଷ୍ୟ କରୁଛନ୍ତି) small flowers that have bloomed (g© ©09) all over the place. He wonders (ଆଶ୍ଚର୍ଯ୍ୟ ପ୍ରକଟ କରିଛନ୍ତି) where they had been all the year round. He imagines (ଚିନ୍ତା|ଅନୁଭବ କରିଛନ୍ତି) they must have been in school just like him. The speaker wonders why the pretty flowers (ସୁନ୍ଦର ଫୁଲସବୁ) are so eager (ଉତ୍ସୁକ) to come out and play. He concludes (ଶେଷରେ ମତପ୍ରକାଶ କରିଛନ୍ତି) that they too need the warmth and love of their mother.

Stanzawise Explanation:
Stanza 1 (Lines 1 to 7)
When storm-clouds rumble in the sky and June showers
come down,
The moist east wind comes marching over the
heath to blow its bagpipes among the bamboo.
Then crowds of flowers come out of a sudden,
from nobody knows where, and dance upon
the grass in wild glee.

Gist: When storm clouds make a series of rumbling sounds in the sky and the heavy rain in June showers down, the soggy (wet) east wind blows over the large flat uncultivated areas with little shrubs as if blowing its bagpipes among the bamboo. All of a sudden plenty of flowers come out invisible and dance upon the grass in great delight or thrill.
ଅନୁବାଦ : ଯେତେବେଳେ ଆକାଶରେ ଝଡ଼ଜନିତ ବାଦଲ ଘଡ଼ଘଡ଼ି ଶବ୍ଦ କରେ ଓ ଜୁନ୍ ମାସର ବର୍ଷା ବର୍ଷ ଉଠେ, ଆର୍ଦ୍ରତାପୂର୍ଣ୍ଣ ପୂବେଇ ପବନ ଗୁଳ୍ମପୂର୍ଣ ବ୍ୟାପକ ପତିତ ଜମି ଉପରେ ବାଉଁଶ ବୃକ୍ଷ ମଧ୍ଯରେ ଭେରୀ ବଜାଇବାପାଇଁ ପ୍ରବାହିତ ହୋଇଆସେ । ହଠାତ୍ କେଉଁ ଅଜଣା ବା ଅଦୃଶ୍ୟ ସ୍ଥାନରୁ ଫୁଲସବୁ ଫୁଟି ବାହାରି ଆସନ୍ତି ଓ ଅତି ଆନନ୍ଦ ଓ ରୋମାଞ୍ଚରେ ସବୁଜ ଘାସ ଉପରେ ନୃତ୍ୟ କରନ୍ତି ।

Stanza 2 (Lines 8 to 13)
Mother, I really think the flowers go to school
underground.
They do their lessons with doors shut, and if
they want to come out to play before it is time,
their master makes them stand in a corner.
When the rains come they have their holidays.

Gist: The poet addresses or calls his mother and tells her that these flowers go to school underground. The flowers shutting (closing) the doors, do their lessons. Like little children at school, their master makes them stand in a corner if the flowers wish to come out to play in the gentle breeze before time. With the onset (beginning) of rain, these flowers enjoy their holidays.
ଅନୁବାଦ : କବି ଏହି ସମୟରେ ତାଙ୍କ ମାଆଙ୍କୁ ଡାକିଛନ୍ତି ଓ ସେ ତାଙ୍କୁ (ନିଜ ମା’ଙ୍କୁ) କହିଛନ୍ତି ଯେ ଏହି ଫୁଲସବୁ ଭୂପୃଷ୍ଠ ନିମ୍ନରେ ଥ‌ିବା ବିଦ୍ୟାଳୟକୁ ଯା’ନ୍ତି । ଫୁଲସବୁ ଦ୍ୱାର ବନ୍ଦ କରି ଭିତରେ ସେମାନଙ୍କ ପାଠ ପଢ଼ନ୍ତି । ଯଦି ସେମାନେ ସମୟ ପୂର୍ବରୁ ବାହାରକୁ ଆସି ମୁକ୍ତ ପବନରେ ଖେଳିବାକୁ ଚାହାନ୍ତି, ସେମାନଙ୍କର ଶିକ୍ଷକ (ମାଲିକ) ସେମାନଙ୍କୁ ଗୋଟିଏ କୋଣରେ ଠିଆ କରାଇ ଦିଅନ୍ତି । ବର୍ଷା ଆସିବାମାତ୍ରେ ଏହି ଫୁଲସବୁ ସେମାନଙ୍କର ଛୁଟି ସମୟକୁ ଖୁବ୍ ଉପଭୋଗ କରନ୍ତି ।

Stanza3. (Lines 14 to 17)
Branches clash together in the forest and the
leaves rustle in the wild wind, the thunder-clouds
clap their giant hands and the flower children
rush Out in dresses of pink and yellow and white.

Gist: Branches of trees strike hard with one another in the forest. The leaves rustle in the hard wind. With this, the thunder-clouds appear to clap their huge hands and the flower children come out quickly as if dressed in pink, yellow, and white colors.
ଅନୁବାଦ : ବୃକ୍ଷଗୁଡ଼ିକର ଡାଳ ବର୍ଷାରେ ଜଙ୍ଗଲରେ ପରସ୍ପର ମଧ୍ୟରେ ଘର୍ଷଣ ହୋଇ ବାଡ଼େଇ ହୁଏ । ପ୍ରଚଣ୍ଡ ପବନରେ ପତ୍ରସବୁ ଖସ୍ଖସ୍ ହୁଏ । ଏଥ୍ ସହିତ ଘଡ଼ଘଡ଼ି ନାଦ କରୁଥ‌ିବା ବାଦଲଖଣ୍ଡଗୁଡ଼ିକ ସେମାନଙ୍କର ବିଶାଳ ହାତରେ ତାଳି ମାରୁଥିବାର ପ୍ରତୀୟମାନ ହୁଏ । ଫୁଲରୂପୀ ପିଲାମାନେ ଗୋଲାପୀ, ହଳଦିଆ ଓ ଧବଳ ରଙ୍ଗର ପୋଷାକ ପରିଧାନ କରି ଶୀଘ୍ର ବାହାରି ଆସନ୍ତି ।

Stanza 4 (Lines 18 to 23)
Do you know, Mother, their home is in the sky,
where the stars are?
Haven’t you seen how eager they are to get there?
Don’t you know why they are in such a hurry?
Of course, I can guess to whom they raise their arms;
they have their mother as I have my own.

Gist: The narrator asks his mother if she knows that the home of these flower children is in the star-studded sky. He asks his mother if she can’t see how eagerly they wish to return to the sky. Certainly, he (the poet or the narrator) can guess that these flower children are raising their arms to their mother living in the sky, their mother as he (the poet) himself does.
ଅନୁବାଦ : କବି ତାଙ୍କ ମା’ଙ୍କୁ ପଚାରିଛନ୍ତି ଯେ ସେ କ’ଣ ଜାଣନ୍ତି ଯେ ଏହି ଫୁଲରୂପୀ ପିଲାମାନଙ୍କର ଘର ହେଉଛି ନକ୍ଷତ୍ର ବା ତାରାଖଚିତ ଆକାଶ । ସେ ପୁନଶ୍ଚ ତାଙ୍କ ମା’ଙ୍କୁ ପ୍ରଶ୍ନ କରିଛନ୍ତି ଯେ ସେ (ତାଙ୍କ ମା’) କ’ଣ ଜାଣିପାରୁ ନାହାନ୍ତି ଏହି ଫୁଲରୂପୀ ପିଲାମାନେ କିଭଳି ଆକାଶକୁ ଫେରିଯିବାକୁ ଏତେ ବ୍ୟଗ୍ର ବା ଉତ୍ସୁକ । ପ୍ରକୃତରେ କବି ଅନୁମାନ କରିପାରୁଛନ୍ତି ଯେ ସେ ଯେପରି ନିଜ ମା’ଙ୍କ ପାଖକୁ ଯିବା ପାଇଁ ନିଜ ହାତ ଦୁଇଟି ବଢ଼ାଇ ଦିଅନ୍ତି, ଠିକ୍ ସେଇଭଳି ଏହି ଫୁଲରୂପୀ ପିଲାମାନେ ଏବେ ଆକାଶରେ ଥ‌ିବା ସେମାନଙ୍କ ମା’ ଆଡ଼କୁ ସେମାନଙ୍କର ହାତ ଉଠାଇ ଦେଇଛନ୍ତି ।

About The Poet:
Rabindranath Tagore (1861-1941) was born in Kolkata on 7th May 1861. He was a great poet, painter, patriot (ଦେଶପ୍ରେମୀ), playwright (ନାଟ୍ୟକାର), novelist (ଔପନ୍ୟାସିକ), storyteller, philosopher and educationist (ଶିକ୍ଷାବିତ୍). The common theme (ସାଧାରଣ ଥିମ୍ |) in his writing is nature. Nature left a deep-seated impression (ଗଭୀର ଆସନ) on him. He was enchanted (ବିମୋହିତ ହୋଇ ପଡ଼ୁଥିଲେ) by nature. It inculcated (ଭର୍ତ୍ତି କରିଥିଲା) a sense of freedom in him. It is also the inner voice (ଅନ୍ତଃସ୍ୱର) of his poetry. He became the first Asian to win the Nobel Prize for Literature in 1913 for his collection of poems, “Gitanjali”. He is also well known for his contribution (ଅବଦାନ) to art and music.

Notes And Glossary:
rumble — make series of loud sounds (ଉଚ୍ଚ ସ୍ବରରେ ଗର୍ଜନ କରେ)
showers — rainfall lasting for a short time (କ୍ଷଣସ୍ଥାୟୀ ବର୍ଷା)
moist — slightly wet (ସାମାନ୍ୟ ଆର୍ଦ୍ର)
heath — large open uncultivated land
with shrub (ଗୁଳ୍ମପୂର୍ଣ୍ଣ ବିଶାଳ ଅଣକର୍ଷିତ ଭୂମି)
bagpipes — a musical tool (ବିଶାଳ ଭେରୀ)
in wild glee — in great excitement (ଅତି ଉତ୍ତେଜନା ବା ପ୍ରବଳ ଆନନ୍ଦରେ)
master — here, the teacher (ଶିକ୍ଷକ ବା ମାଲିକ)
clash — strike or hit against one another (ବାଡ଼େଇ ହୁଏ)
rustle — make sounds of blowing (ଖସ୍‌ଖସ୍ ହୁଏ (ପତ୍ରସବୁ))
giant — very large (ବିଶାଳ)
of course — certainly (ନିଶ୍ଚିତରୂପେ ବା ଅବଶ୍ୟ )
thunder-clouds clap — clapping of thunder clouds (ଘଡ଼ଘଡ଼ିର ଧ୍ଵନି)

BSE Odisha 10th Class English Detailed Text:

• All Things Bright and Beautiful Question Answer
• A letter to God Question Answer
• The Solitary Reaper Question Answer
• At the High School Question Answer
• Village Song Question Answer
• Festivals of North-East India Question Answer
• The Flower-School Question Answer
• Air Pollution: A Hidden Menace Question Answer
• From the Formalin Jar Question Answer
• School’s Goodbye Question Answer