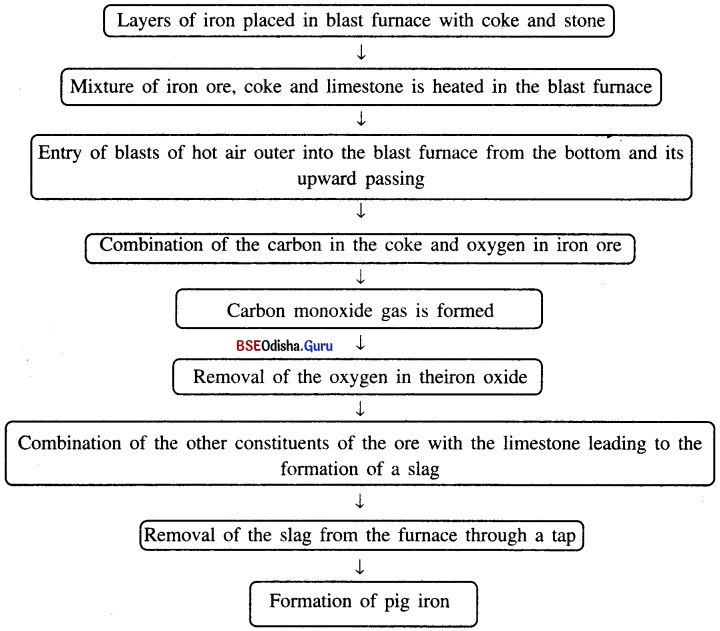
Odisha State Board CHSE Odisha Class 11 Political Science Solutions Unit 1 Understanding Political Theory Long Answer Questions.
CHSE Odisha 11th Class Political Science Unit 1 Understanding Political Theory Long Answer Questions
Long Questions With Answers
Question 1.
Define politics and discuss its nature. Or, Explain the meaning and nature of politics?
Answer :
‘Politics’ today has been more frequently used than that of political science. In most of the universities of the USA and UK, the department of political science is renamed as a department of politics.
The term ‘politics’ has been derived from the Greek word ‘polis’ which means the a days, politics is the central concept of the socio-political system. No one can avoid politics, as it encompasses different aspects of social, and political life. An individual today encounters politics in family, village, school, college, town, religious institution, business organization and human organizations.
Definition :
Scholars define politics in different ways. According to the Oxford English Dictionary politics is a science and art of government which deals with the organization of the state and the regulation of its relationship with other states.
Lasswell says politics is the study of influence and influential. David Easton defines politics as the authoritative allocation of values in society, and these values here mean material resources.
Butter says, politics is concerned with the people. It studies about their behaviour and support or reactions to decisions. Politics is a struggle for power to make authoritative decisions. It establishes a relationship between the government and every individual who seeks to maximize his interest best.
In the process, people fight with one another and make use of power and influence to realize their goals. In society, it is not possible for every individual to attain his goal and for the purpose he may have to enter into a conflict with others. To come out victorious in all such conflicts individuals use force and power. Thus, whenever people make use of power to achieve their goal in any conflicting situation it is called politics.
Nature :
- Politics is a social process, concerned with social conflicts and rivalry.
- It is a universal activity found everywhere and in every now and then.
- It is found in every organization and group activity, whether government or non-government, public or private. Political or non-political.
- Politics is based on morality. It seeks to establish an ideal society or state for the well-being of individuals.
- Politics is a struggle for power in a society where actors compete for power to maximize their gain.
- Politics seeks to resolve conflicts, bring peace and order and promote cooperation with the members of society.
Question 2.
Distinguish between politics and political science. Or, Make a comparison between politics and political science?
Answer :
Politics and political science the two terms have been derived from the same Greek word ‘polis’ that refers to the study of city-states in Greece. Both are social sciences dealing with individuals in society.
These two terms have been used interchangeably since the ancient era, but with the development of the concept of power, scholars started distinguishing between the two terms. In the modem age today, politics deals with power, conflict, political process and decision-making in controversial situations. But political science is the study of origin nature, structure and functions of state and government.
What is politics :
Politics is a socio-political concept associated with human organizations. Individual is the centre of politics. When every individual tries to protect and promote his interest he is likely to enter into a conflict with others. This conflict is a vital factor of politics. To resolve this conflict individuals accumulate and make use of power. Those who use it most proficiently they can safeguard their goal better.
Thus politics possesses three elements. Conflict, interest and power. It is a struggle for realise of interest in a conflicting situation
using power. Where there is conflict there is politics. Power is the epicentre of politics. So, people in society in to acquire and accumulate power and to use it to maximize one’s goals. Politics is always just and it promotes social welfare.
Politics is the study of power and influence. It believes in effective decision-making in any situation of conflict whereby social stability is maintained. Politics is a competition for power. Hence everybody tries to win. The political parties contest in elections to capture the power and this in politics.
Politics can be formal or informal when it is concerned with the formation of govt, a political party or policy-making it is formal politics. But informal politics is concerned with formation of alliances, use of power and the spread of ideology.
Political science :
Political science on the other hand is a science of state and government. It deals with the origin, nature, and basic principles of state and government. It also discusses about political theory, political philosophy, and government and individual state relationships.
The distinction between politics and political science may be analysed below.
Political science is the theoretical aspect of politics while politics is the reality. Political science is a science but politics is an art.
A student of political science undertakes a study of the origin, nature & development of state and government, the purpose and functions of the state. The goal of political science is to make men happy. But politics refers to the study of conflicts and controversy arising among groups of the political process.
The purpose of politics is to resolve social-political conflicts and to bring order and cooperation among people. The study of politics is universal and it touches everybody but study of political science is confined to educational institutions only.
Those concerned with political science are known as political thinkers or philosophers, but those dealing with politics are political leaders and statements. Political science undertakes a study of nature’s arid types of power but politics falls about the accumulation & use of power.
Politics is the realistic or behavioural dimension of political science. It is a factual and goal-oriented study. Political science is imaginary, ideological and based on value premises. The scope of politics and political science may not be completely separate but each of them has its own identity.
Question 3.
Examine the characteristics and features of politics, Politics has been a natural and essential aspect of social life. Discuss?
Answer :
Politics is a universal activity and there can be no society without politics. Therefore an individual encounters, politics in his village, family, town, schools, colleges, hospitals, temples, churches and in every social human organization.
Politics is associated with conflict, struggle, rivalry, cooperation and social integration. It seeks to promote the general good catlin says, politics is the study of organized human society and it deals primarily with the political aspects of the life of a community. When people express divergent views on any public issue it is called politics.
Morgenthau regards it as a struggle for power. It establishes a formal relationship between the people and the government. It influences policymaking both in positive and negative ways. The poor consider it as a struggle between power holders but the rich regard it ‘ as a source of social unity.
Characteristics :
The basic features of politics can be discussed below:
- Politics is concerned with socio-political disputes and conflicts. It cannot exist with conflict or controversy.
- It is a universal activity and people from all walks of life and involved in it
- Politics is concerned with government and the working of various organs of government.
- Power is the essence of politics. It seeks to maximize one’s power states to win over the opponents.
- Politics Organize conflicting claims and then by use of power resolve those conflicts.
- Politics is associated with the decision-making process.
- Politics believes in die study of the political process, which. means the study of public administration, election, political parties, pressure groups, laws making processes and administration of justice as well.
- Politics is an art whereby one group tries to achieve its goal against all others by using any means possible.
- Politics believes in bringing order out of disorder by resolving all issues, crises and conflicts arising between individuals and groups in social, and political life.
- Politics is also related to the distribution of material resources. Social economic privileges and opportunities.

Question 4.
Explain the meaning and scope of politics?
Answer :
The term ‘politics’ has been derived from the Greek word ‘polis’ which means the affairs of city-states. Aristotle was the first scholar to use the word politics, but scholars define it in their own way.
Traditional thinkers define politics as a socio-political process which promotes the public welfare. It gives more importance to the study of government and administration than that of individuals.
But, modem scholars consider politics as a study of conflicts. Rivalry and struggle in society. People living in society fight for their interests. The resources and opportunities are limited and they try to realize their interest by imposing power and influence. The study of this situation of conflict and cooperation in society and polity is known as politics.
Elements of politics :
- Interest or goal,
- Conflict over interest and
- use of power, are the true element of politics.
In every society, the goals of individuals are divergent. When two or more individuals go for the same interest it leads to conflict. To overcome this conflict individuals capture power and use it for the realization of their interests. Politics found everywhere, in society, in state and in the international sphere.
Scope of politics: The scope of politicsmay be explained below:
Study of society :
Politics is a social process and their can be no politics outside society. It deals with all situations of conflict and cooperation between individuals, groups and organizations and its mission is to resolve them.
Study of government :
The organs of government like the executive, legislature and judiciary are the main area of study in politics. Politics also studies policy making under crucial situations.
Study of power:
Power is the very basis of politics. Watkins says, not state but power is the centre of politics. It sheds light on the process of accumulation and exercise of power, sharing of power etc. those who can make the best use of power in any controversy or crisis they become victorious. Therefore, Morgenthau calls politics as a struggle for power.
Study on conflict and rivalry :
Politics seeks to study about social conflicts disputes and struggles over self-interests. Conflicts arise over self-interests. Conflicts arise over the distribution of power and socio-economic opportunities and resolving those peacefully is the prime concern of politics.
Study of the political process :
Political process refers to the formation of political parties, groups, elections, campaigns, government formation, decision-making, and performance of welfare. functions, a study of the law-making process, running of administration, adjudication etc. This is a never-ending process whereby all divergent views are resolved and social stability is maintained.
Study of the political system :
Politics is concerned with the study of the political system. The apolitical system comprises of the people. The government, the political parties. The groups, the executive, the religlatiure, the judiciary the people the political and non-political organizations and the disputes arising among them. Politics seeks to bring cooperation among rivals and discipline among warring groups.
Leadership :
Politics is concerned with leaders and their leadership qualities. The decisions taken by a lender in a crucial situation, his behaviour, temperament, attitude, reactions, likings and disliking, etc. are vital aspects of politics. The ability of a leader in realising his goals is an important aspect of politics.
Study of political reality :
Politics is always objective. It is concerned with the present social system, society-state relationships, group activity and with other sociopolitical organizations. It undertakes a realistic study as to resolve the crises and restore stability.
Besides, politics also undertakes a study of the international system. UNO, war and peace, inter-state rivalry, friendship, cooperation, terrorism, poverty, environmental concerns, human rights issues, etc.
It is also related to local government, group activity, communal tension, regional issues, the Caste system and the like. It is much broader in scope and all tissues facing mankind are the subject matter of politics.
Question 5.
Discuss the meaning of politics from traditional and modern points of view?
Answer :
‘Politics’ has become a natural and essential aspect of our social life. There can be no society without politics. An individual encounters politics in the village, in schools, colleges, towns, cities, hospitals, offices and in the government. As a universal activity it is closely linked with human existence. With the passage of time, everyone is becoming more and more political and all the aspects of human life is becoming free from state intervention.
Meaning:
“The Oxford dictionary defines politics as “a science and art of government which deals with the organization of state regulation of its relationship with other states.
Catlin links politics with the activities of an organized human society. He says, “Politics is the study of organized human society and it deals primarily with the political aspects of the life of the community.
Lasswell says, “Politics is the study of influence and influential.” David Easton defines politics as the ‘ study of the authoritative allocation of values as it is influenced by the distribution and use of power.
Thus everyone has tired to define politics in one’s own way, but there is no consensus. We can examine the traditional and modem view of politics below.
Traditional View, The traditional view of politics can be divided into:
- Philosophical,
- Institutional view
- Legalistic view.
Philosophical view:
The philosophical view is the oldest view of politics which includes all aspects of a person’s political activities. It regards ethics as the basis of politics. It aims to set up a good and just society and to end the evils of society. The Greek thinkers regard it as an all-embracing activity covering all aspects of human life.
Institutional view :
This view lays stress on formal aspects of formal political structures and processes. Van Dyke, an exponent of this approach has said that the study of politics is the study of govt. And its related institutions.
Legalistic view :
It stresses on the study of legal issues it emphasizes that the activities of the state must be in accordance with constitutional laws and based c proper interpretation and . execution of laws. Politics is a game of law-abiding political actors.
Criticism of traditional views :
The traditional view of politics neglects individual and international politics. It has failed to study the role of violence in politics.
Modern view of politics :
This view is given by the anglo American scholars and, Marxists. Basically, there are two views on politics. Politics and society are inseparable politics is a conflict for power and those who win it try to capture more and more power and to control the rest in society.
The second view regards politics as not as a conflict, but a cooperation which seeks to bring order and justice. It helps in maintaining collective interests and the common good against private interest.
The poor ones consider it as a conflict while the rich as a useful weapon for maintaining order.
Marxist view :
The Marxist scholar defines politics as a conflict between the haves and have-nots in society. This is a continuous process which will continue till the non-privileged section able to win and establish a class-less society.
Anglo-American view :
According to this view, political conflict is a part of human society. It is an activity which is linked with groups which have shared desires and who are ready to fight for their goal.
Quincy Wright says “Politics is the art of manipulation and group controlling and influencing others with a view to promoting some interests against others.
Politics revolves around the concept of power, Lasswell and Kaplan define it as “the study of shaping and sharing of power.” According to Morgenthau, “Politics is the struggle for power and the art of maintaining and retaining power.
” Power is the basis of all politics and study of politics is the study of power and power of the influence and influential. In the words of David Easton, “Politics is the authoritative allocation of values and it is influenced by the distribution and use of power.
Politics in the modem age is regarded as an interaction of all political activities and formal governmental institutions; It is a process by which policies are formulated and executed. It is a game of having maximum resources under disposal and for that each adopts several strategies tp get the decision in his favour.

Question 6.
Define Political theory and discuss its nature, Narrate the meaning and features of political theory. Narrate the meaning and features of political theory?
Answer :
Political theory is a part and parcel of political science. It deals not only with state or government but also with all other power-based organizations. Political theory undertakes the study of the origin, elements, future, problems and prospects of any-political event or issue. Political theory has two dimensions
It stands for the history of political ideas, such as Plata’s theory of justice, Hobbes’s sovereignty and Hegel’s theory of the state. From a modem point of view, the political theory deals with the political behaviour of both individual actors and political institutions like the executive, legislature and judiciary.
Political theory deals with the ideas and principles that shape constitutions governments and social life a systematic way. It makes us clear about our understanding of the concepts of freedom, equality, justice, democracy, secularism, etc. Besides’ examining arguments it reflects upon our current political experiences and indicates future trends.
Characteristics or features :
The fundamental characteristics or features of pol ideal theory can be stated below. Political theory deals with political concepts or ideas and it interprets them and indicates about their future. The political theory explains the factors behind every concept.
It unravels the truth and tries to realize the goal. Political theory is based on facts. It is universal and functions irrespective of time and place.
Political theory is based on mortality and this nature is found in classical theory. Theory develops out of issues, crises and situations. It is created out of social traditions, experiences of the people and general consciousness of society. It is not imaginary or speculative.
The political theory makes people conscious about politics. Political system political events.Concepts and sharpens our ideas and understanding about politics.
Question 7.
Explain the relevance of studying political theory Or, Describe the need for study of political theory Or, and Why should we study political theory?
Answer :
The term theory has been derived from the Greek word ’theoria’ which means deep thinking on any issue. Political theory is a part of social science that deals with state government and other political concepts. Political theory has three aspects.
- It is based on facts and evidence.
- There are factors or reasons behind every concept or argument.
- It is concerned with the well-being of the state and society.
Functions :
Political theory performs three functions
It seeks to describe the facts of political reality. It relies on a collection of data about reality through observation of arid experiences. It is logical and guided by reason It seeks to evaluate the behaviour of political actors on the basis of norms and values.
However, in order to be meaningful and relevant it must be normative and empirical. Political theory is both value-based and empirical. It believes in scientific analysis, observations inference, and study of ideas and values. The concepts of political theory explain about the political behaviour of individuals. Political theory emerges from socio-political crises.
Utility of political theory :
The study of political theory is useful to society, the state and citizens. Even students, teachers and administrators need to study political theory. Its relevance may be discussed below.
Understanding political concepts and ideals :
The study of political theory is essential for understanding various concepts and ideas. These concepts carry different meanings in different situations. So far the proper understanding of concepts study of theory is indispensable.
Social control and, reconstruction :
Every political system has some problems and prospects and for eradicating those problems, the study of theory is essential. The political theory provides remedies for various socio-political issues. Plato’s ideal State Marx’s class struggle, Hobbes’s absolute sovereignty etc. are examples of political theory helping social stability and reconstruction.
Mutual respect and tolerance:
The study of political theory helps in promoting mutual respect and tolerance. Political theory is a never-ending conversation among theorists and it helps in understanding reality.
Formulation of polity :
The study of political theory is useful for the formulation of public policy. The study of political history and political institutions is essential for policy-making.
Enriches the study of political science:
The study of politics enriches political science in two ways. It helps political scientists, and specify their research techniques and perceive their data. It suggests valuable hypotheses which are tested by political scientists. Again, study of political theory and its knowledge helps political analysis to understand facts, theories and events.
Thus, political theory broadens the knowledge of political science. The study of theory further informs about political organization, administration; functionaries and about experiences. It broadens our mind and introduces us with the future world.
Question 8.
Politics is a struggle for power Morgenthau?
Answer :
This statement of Hans J. Morgenthau is not about state, government or anything else, but power. It is the be all arid end all of politics. It covers all those activities that have their bearing on the struggle for power.
Politics and power are deeply attached. Without the accumulation of power or use of power no one can make his presence felt in politics. It is the fuel that runs the political machine. Therefore, Lasswell and Kaplan say, politics is the shaping and sharing of power in society. Besides Lasswell, David Easton, Robert A. Dahl, Morgenthau and Friechich Watkins also find power the core subject of politics.
Power is a coercive influence people remain loyal to it in fear of punishment. The laws of the state are obeyed by most people out of habit but some obey it out of fear. Therefore, Watkins says, politics deals not with the state but with power. Who gets what when and how is the subject matter of politics. In order to substantiate this statement of Morgenthau we have to analyse the following lines.
Power involves a conflict of purpose. It is a relationship. So it can’t be explained without an opponent or rival. Power may take any form, either knowledge, wealth, reputation or brute force.
Power manifests only in action. It is concerned with the wills and interests of various individuals and with their conflicting claims. In order to reconcile these claims power is used. Thus, it is the power that brings order out of disorder and unity out of disintegration.
Politics is also sustained by power politics is the study of the power holder and the way he exercises power over the opponent. It results in compromise and consensus, out of stiff rivalry and conflict. People having divergent interests come to compromise only because of the power factor.
Therefore, behavioural thinkers hold politics as the study of power. Authority and legitimacy. Power controls politics and through political power is enjoyed. Policy decisions are taken with the help of power and it is power that helps in executing those decisions.
If politics means the Resolution of social conflicts, without power it can’t be done thus power has varied dimensions and those who make use of it should legitimately use if for the achievement of their goal.
Question 9.
Distinguish between traditional and modern political theory?
Answer :
Political theory can be divided into classical and modem depending upon their subject matter and methods of study. The classical or traditional political theory stands for the history of political ideals and they are speculative in character. This type of theory is based on morality, values and ideals. Plato, Aristotle, Hobbes, Rousseau, Kant, Hegel, Marx and Laski, etc. belong to the classical theories.
Traditional political theory is mostly concerned with how the state should be what must be its goal. This is based on values & traditions.
But, modem political theory emerged after world war – II.
It was the product of behavioural revaluation which introduced scientific approach with too much stress on methods, techniques, data collection, analysis and systematization of facts David Easton. Truman, Herbert Siman, Robert Dali, Laswell, Kaplan, Karl Friedrich, etc. are the main exponents who popularized modem political theory.
Modem political theory is scientific in nature and based on reality. It is specifically believing in objective study based on facts and evidence. It is empirical in character and in most cases relies on data collection, observation, qualification, comparison and evaluation before arriving at any conclusion.
The modern political theory believes in an interdisciplinary approach and in most cases avoids value preferences. In place of studying political institutions and rules it believes in the study of political process, activity, structure, behaviour, culture and experiences for a better understanding of facts.
Question 10.
Define political theory and discuss how it differs from political philosophy, political thought and ideology?
Answer :
Political theory is a branch of political science which deals with the systematic study of State Government, political institutions, ideas and concepts.
It elaborates on the origin and nature of various organizations institutions, concepts and ideas and their values and importance in politics and society. It also sheds light on the behaviours reactions of individuals, groups and institutions.
Political theory is based on facts and evidence. The knowledge of political theory its ideas, concepts, and theories have relevance for society, study of political reality with the help of facts and evidence is a trade mark of political theory.
In order to have a clear understanding about political theory its relations to political philosophy, political thought and political ideologies must be studied.
Political theory and Political philosophy :
Political theory is different from political philosophy from different angles. Political theory is a part of political philosophy. So the scope of the latter is wider and vast than that of the former.
Political philosophy implies realists’ study of political events and situations with valid justifications. It may be factual or speculative. But, political theory is always based on facts and evidence.
Political theory studies the behaviour and functions of the political system, but political philosophy aims at studying about the goals of these institutions. A political philosopher may be a theorist but a theorist may not be a philosopher.
Political theory and political thought :
Political theory and political thought differ from each other on the following counts. Political though is the study of political speculation of a whole community, but political theory is the speculation of an individual thinker.
Political thought refers to the opinion & views of a political thinker on state government and other political organizations. It is a general statement of a political situation. But, political theory is the ideas of Plato, Aristotle, Rousseau, Hobbes and Marx on any political issue or event.
Political theory is universally applicable irrespective of time and place. But, political thought is the statement on state, government and political events of a definite period. The theory is factual & rational but political thought may be factual or may be based on imagination of the thinker.
Political theory & Politial Ideology :
Political ideology is a part of political theory’ but there are some distinctions between the two.
Ideology means emotional support for any concept or idea. Individuals express complete allegiance to ideas and get prepared to sacrifice anything for the same. But political theory is value-neutral.
Thinkers do not feel emotionally attached to their theory as they do to their ideology. It is realistic and permanent.
The scope of political theory is wider than that of political ideology. People may support or oppose an ideology but not any theory. Thus, political theory is an objective description of politics. It may be normative or empirical, but it seeks to explain political reality.

Question 11.
Define modern political theory and discuss its nature and significance Or, Examine the need for studying political theory?
Answer :
Modem political theory developed during the 2nd half of the 20th century. The behavioural revolution introduced new methods and technique’s for the study of political science and gave political theory the status of a scientific discipline.
Modem political theory is rational, neutral and based on facts. It is a statement about the political system. Political organizations and is based on facts and evidence, It seeks to make political science a pure science. Characteristics of modern political theory.
Modem political theory is based on the following features. It is based on facts & evidence and it can be studied empirically.
The modern political theory believes in the realistic study of political issues and (c) It’s the aries and propositions can be verified & tested through observation. It is scientific and value-free.
Modem political theory relies on data collection, observation and analysis of political data in order to arrive at any conclusion. It is objective in nature and believes in interdisciplinary study. Modem political theory seeks to solve political and social issues.
Significance of modern theory :
Modern political theory is relevant to formulating grounds.
It seeks to make political science a pure science. Through analysis and interpretation of political realities, it helps leaders, statesmen & administrators in taking appropriate decisions at the right time. It supplies facts about political behaviour and events, thus making it easy for the authority to solve any crisis.
Modem theory makes political science useful for the changing situation. Modem political theory supplies issues and problems for undertaking research. It broadens our knowledge by supplying facts, ideas and concepts.
For the understanding of complex political issues modem, political theory is regarded as useful. It works for the welfare of mankind. Thus, political theory, whether traditional or modem, always gives new ideas and concepts for the development and progress of the human race.
Question 12.
Examine the relevance of the scientific study of politics?
Answer :
The scientific study of politics began only after the second world war and thereafter political scientists started paying more attention to the various aspects of social life to know more about politics. This new approach turned its attention to the empirical study of relationships among people.
The process, first of all, began in USA and Britain and Scholars began to concentrate on the study of the behaviour of persons and groups instead of confining its study to the structure, institutions, ideologies and events. The scientific study of politics began with Aristotle.
Then Hobbes and Spencer in England used geometrical and biological methods of evolution and classification in the 16th – 17th centuries. In the modem age, students of political sociology.
Cybernetics and Operational Research have been insisting on the increasing use of scientific methods in the study of politics. Even in some spheres decision-making research, algebra and calculus and being used.
Now, there is a craze among scholars to make more use of scientific tools and techniques. As a result, efforts are being made in the field of voting behaviour studies, attitude measurements, opinions surveys etc. as an indication of the scientific study of politics.
Nowadays, political scientists have been trying to build models and test hypotheses of Political Science through the process of verification and empirical research.
They are trying to focus attention on the problems of facing mankind as a result of which they have been taking recourse to a multi-disciplinary approach to knowledge through the integral synthesis of available empirical information regarding the nature and behaviour of men.
Criticism :
The scientific approach can be criticized on the following grounds.
Duvenger criticizing the scientific approach says that politics cannot be scientific as a whole, it must be supplemented by moral Mid spiritual dimensions.
It cannot be successfully applied in the study of the policy formulation process, because the data available to political scientists are not adequate enough to know all the factors which influence the shaping of politics.
Political phenomena cannot be reproduced for scientific analysis. It is not possible to subject political data to quantitative measurement.
Political science tends to be influenced by the environment, emotions and value judgements and research cannot avoid them while making a study of politics. Therefore, a combination of empirical and philosophical methods is required.
Question 13.
Define the state and discuss its elements. Or, Explain the meaning and elements of the state?
Answer :
The state is regarded as the central theme of Political Science it is the most universal and most powerful of all social institutions. The term ‘state’ has been derived from its Teutonic root “Status’ which means ‘existence’.
It is a territorial unit where a group of people live under a political sovereign. State refers to a collection of human beings, occupying a definite area under an organized government and subject to no outside control.
Machiavelli was the first political thinker to use the word state and to popularize it. Bluntschli defines it as a politically organized people of a definite territory. Laski holds it as, “a territorial society divided into government and subjects claiming within its allotted physical area, supremacy over all other institutions.
According to Woodrow Wilson, “State is the people organized for law within a definite territory.
The state is thus a natural and universal institution and it exists for the good life of the citizens. It provides opportunities for the satisfaction of human desire and the development of human personality.
Elements :
The state has four elements, like
- population
- territory,
- sovereignty
- Government
which are: discussed below.
Population :
The population is the primary element of state Because a deserted or uninhabited surface might not be conceved in terms of state or association and the state being a human association must bear population as its constituent .element.
However, there is no consensus among political scientists regarding what should be the standard size of population for a state Aristotle, the father of Political Science, has advocated a minimum of ten thousand and a maximum a hundred thousand populations as the standard population for a state.
But in the context of modem state there are states like Maldives and Morrocco having a few thousand or population whereas there are large populations are like India and China.
Territory :
The next element of State is a fixed territory. Without a fixed territory there would be no state for which every state must have a territory of its own over which the state should have absolute control. Here the case of nomadic race and Jews could not have a state because of lack of a fixed territory.
The territory of State does not include only the surface territory but also the water and air surface. The concept of territory, is inseparable from that of the State in view of the fact the territory is an element which distinguishes the Site from other forms of associations.
If the population provides the physical basis, the territory provides the material basis of the State.
Government :
For the formation of State, there must be some sort of Political machinery which should exercise the supreme power of the state. So Government is the political machinery through which the will of the state is formulated, expressed and enforced Prof.
Gamer defines Government as “the agency through which common policies are determined and by which common affairs are regulated and common interest promoted.” Without Government, there must not be any concept of State.
Because the State has no life and it is the government through which the will and attention of the state are expressed and the government is the agent through which all the actions of the state are formulated and executed and without government, there will be anarchy or lawlessness.
Sovereignty:
The last important element of State is sovereignty. The word sovereignty has been derived from the Latin word ‘Supreanus’ which means supreme or absolute. Bodin, a French political philosopher defined sovereignty as “Supreme power over citizens and subjects unrestrained by law.
Sovereignty has also both internal and external meanings internally, it can be viewed that the state has complete legal authority over all the individuals who compose it and from an external point of view, it regards the State as legally independent of foreign dominations.
Other than the above four constituent elements of State in modem times, there is also another element, i.e, international recognition as the basis for the formation of the State. Nowadays international recognition is considered to be necessary not to constitute a state, but to enable it to participate in the community of nations.
Question 14.
Bring out the differences between State and Government?
Answer :
In common parlance, it is understood that there is no difference between State and Government. But in technical senses beyond the layman’s perception, there are basic differences between State and Government.
Some of the critical problems of Political Science are solved on the basis of distinction between the State and Government.
The following are the some of differences between State and the Government.
The state has four elements, namely, population; territory, sovereignty and government. So Government is one of the parts of the organic whole of the state. The Government is an agent of the state. It is the brain of the whole body of the state through which the will of the state is expressed.
Secondly, state is permanent whereas Government is temporary. A Government may come and go but the state is permanent. Ordinarily, there is no change of the state. The state continues forever but the Government is appointed for a fixed period of time.
The state is composed of all citizens whereas the Government by a few according to the provisions. The origins of the Government, the legislature, executives and judiciary through which along government runs. Thus, the state is broader than that of the Government.
The State possesses sovereign power, which is unlimited and absolute, but ordinarily, there is no such power of the Government. Whatever the Government enjoys is only derivative.
The state is an abstract concept whereas the Government is concrete. The state is invisible but Government is visible. The Government is a physical manifestation and it consists of people who can be seen and known.
All states are identical in character and there must be common aspects but all are not same but with regard to states whether long or small the characteristics of State do not change.
But the Government are of different types and they may vary from state to state. There are different classifications of government like monarchy, aristocracy, democracy, dictatorship etc.
So there is no uniform type of government but the state is a universal institution bearing four elements and if there is the absence of any single element three might not be any state.
Lastly, the citizens have a right against the government but not against the state. The government may commit mistakes and it is the genuine right of the individual to protest against any irrational actions of the Government.
But the citizens do not have any right to protest against state because state never commits any mistake. It is only Government which acts on behalf of the state.
A state is an indestructible unit but Government is destructible. The stability and permanence of state distinguish it from other organizations.
Question 15.
Distinguish between State and Association?
Answer :
The state is a sovereign political association and is superior to all other associations. Being a sovereign entity it is superior to all other associations, Associations are formed with a specific purpose but the state satisfies various needs of the people.
Association is a collection of individuals united for the achievement of certain specific goals. It is formed with a definite end, but state has a broader scope to serve the members. The differences between state and association can be stated below.
State is sovereign but associations are not:
The state is a sovereign political association and no other association enjoys this power. The state represents the collective will of its members and all the citizens are bound to obey its commands. It is a coercive agency it has armed forces, law courts and police.
But, associations are not sovereign, nor do they enjoy coercive authority. They cannot force their members to comply with their decisions. Association had no police army or court of law.
Membership :
Membership in a state is compulsory, but in the case of associations, it is voluntary.
State is national in character but associations can be local, national or international :
The state had a definite territory within which it enforces its commands. But, associations have no definite area or territory. Some are local or regional in character like clubs, some are national like, the national political parties, the R.S.S., the Muslim League, the VHP etc, and some others may be international like Red Cross-Society, the UNO etc.
One can be a member of one state, but of many associations :
An individual can join as many associations as he likes, but he can be a member of only one state at the same time. If he accepts the membership of another state he will have to lose her previous membership.
Territory :
The state has a definite territory and it can expand only by means of aggression or war, but the association has no fixed territory and it can be changed at will.
Scope :
The purpose and scope of the state is much wider than that of an association. The state aims at promoting the welfare of the common people. It makes plans for the all-around progress of its people but the scope of jurisdiction of an association is limited only to its member Associations are formed by those who need to be served by it.
State is superior to all other associations :
The state is an association of associations because it regulates the activities and existence of all other associations. All associations are subjected to the command of the state. Therefore, the state is considered to be superior to all other associations.

Question 16.
Critically examine the Individualistic theory of State regarding the sphere of State activity. Or “The State is best which governs the least.” Discuss this statement along with justification and criticism. Or, “State is a necessary evil.” Examine this statement along with its merits and demerits?
Answer :
Individualism or individualistic theory of state was a philosophy of the 18th century. But it has a long history and its roots can be traced from the writings of Greek Sophists and contractual thinkers like, Hobbes and Locke. It was further developed by Adamsmith, J.S. Mill and
Herbert Spencer, Hayek, Friedman and Oakesholt etc.
Theory: Individualism is based on the ultimate value of human personality. It * seeks to give the individual maximum freedom to develop his personality and restricts the functions of the state. It stands for maximum individual liberty and minimum functions for the state.
Features:
Individualism seeks to protect the liberty of the individual from the interference of the State.
It is based on the economic theory of Laissez-faire. It is based on a Capitalist economy, free trade and economic competition. The individual is demanded for the reduction of State activity in the economic sphere and it came to be known as the Laissez-faire theory.
It argues that the individual must be left alone to decide his future, and the State should not in any way restrain the scope of individual freedom and initiative.
The individualist theory regards the State as a necessary evil’. The state is necessary to stop the anti-social activities of individuals and, it is an evil because it encroaches upon the liberty of individuals.
This theory advocates for maximum liberty of the individual and minimum functions for the State. It pleads that the file State which governs the least is the best. The lesser the functions of State the better for individuals.
Individualist State is a police state which performs only negative or preventive functions. It prevents lawbreakers and checks the obstacles before individual liberty. The state is a negative institution and its functions are limited.
The state is compared to a night watchman which performs the following functions.
- Protection of the state and individuals from foreign aggression.
- Protection of property from robbery or damage.
- Protection of individuals against false contracts or breaches of contracts.
- Protection of the unfit; and
- Protection of individuals against diseases.
Merits
The individualistic theory is supported from four different angles.
From an ethical point of view, individualism is defended on the ground that, an individual personality can be best developed if he is left alone. If the individual is left free then the qualities like, self-reliance, initiative, enterprise and originality develop to the fullest extent.
Government interference kills initiative and cramps individual personality, The uniqueness of Individual personality characteristics are more likely to be destroyed by a uniform state which creates standardized values and reduces society to uniformity as a result of which both society and individuals are closers.
From the economic ground, it is also justified. Individualists hold that every man is self-seeking and he knows his interest best. If the individual is left to himself he would maximize his efforts and interests, Free competition increases production, ensures efficiency and maximizes economic well-being.
A free economy will provide incentives to people to work hard as a result trade, industry and commerce will flourish. So it advocated for non-interference of the state in the economic sphere.
Individualism is also justified on scientific grounds. Spencer favouring the theory holds that each individual should be allowed to stand or fall according to his worth without the support of the government.
Free competition among individuals would ensure the survival of the strong, the efficient, the intelligent and the virile and the elimination of the poor, the weak and the inefficient: He justifies it on the ground of survival of the fittest.
Practical experience shows how government interference leads to efficiency, corruption, red-tropism, delay and wastage., As the government is already over-burdened it can not deliver the goods.
In contrast, privately managed enterprises are more efficient and they make greater profits. Thus, the state should leave the individual to mobilize his own resources and attain his best interest.
Demerits :
The theory in spite of its value has been subjected to something criticism.
The individualistic assumption of state as a necessary evil is wrong. Because state is always considered to be a positive good it always protects, encourages and fosters common well-being it problems good life of the individuals rather than doing harm to them.
The role of state today has enormously increased for which, without state action, an individual’s all-around development can’t be attained. The state provides the basic needs like facilities for education, health and public services. So its powers should not be curtailed.
The basis of individualism is unsound. It regards human beings as self-seeking and thereby neglects the altruistic natures of man.
Individualism wrongly assumes that each individual knows his interest best. Because the ignorant ones can’t take effective precautions against dangers. It is the state which can judge an individual’s intellectual, moral and physical needs better than the individual.
The state does not encroach upon individual liberty. Actually, in a good state, the scope of individual action is enlarged and protected. All restraints of the state on individuals are not bad. Laws of the state are not anti-thetic to individual liberty,
Individualism seeks to create a division between individuals and society. Individual good and social welfare are not opposing but complementary,
The argument of survival of the fittest may not always prove survival of the best. This law is applicable for animals not for human beings. Man is the noblest of all animals and he posses reason, compassion and fellow feeling of love, and affection.
So it is human to say that the old, weak and invalid will have no right to live. The individualistic theory however good or bad it might be suffered, its decline in the 20th century with the emergence of modem welfare states.
Question 17.
Discuss, the origin and development of the concept of Welfare State and explain its merits, and demerits Or, Examine the meaning and nature of Welfare State along with its drawbacks.
Answer :
The concept of Welfare State is a by-product of communism and individualism. It is a social service agency which puts equal emphasis on individuals and society, It guarantees a minimum standard of subsistence to every individual.
According to Kent, a “Welfare State is a state that provides for its citizens a wide range of social services.” But G.D.H.Cole defines it is a society In which an assured minimum standard of living and opportunity becomes the possession of every individual. It seeks to maintain social justice.
Origin and Development :
The Concept of the Welfare State was first of all found in England. The following factors led to the evolution of the Welfare State.
- The evils of industrialization and urbanization.
- The New Deal Programme of U.S. President F.D. Roosevelt also contributed to its evolution.
Objectives:
A Welfare State seeks to fulfil the following objectives.
It checks the evil effects of the capitalist order and provides basic minimum needs to common man. It gives protection against natural and social contingencies. It seeks to ensure a fair standard of living to all.
Justification or Merits of Welfare State:
A Welfare State seeks or promotes people’s welfare by undertaking development activities relating to social welfare and security,
It guarantees a minimum standard of living and a reduction of economic inequality. It is a positive state which acts as a social service agency. The state looks after the individual from the cradle to the grave.
It puts equal emphasis on the individual and society on individual liberty and common goods. The State is considered a friend, philosopher and guide to the individual. Its function within the framework of democratic political institutions.
It regulates the national economy through planning. It postulates a mixed economy allows both the public and private sectors to play their part in the development of the national economy.
The State upholds the rights of all and gives equal treatment to all Individuals, groups and classes without discrimination.
Demerits:
- A Welfare State is an expensive model which puts pressure on public exchequer.
- It kills individual initiative and creates a pauper mentality in the minds of individuals.
- A Welfare State leads to bureaucratic despotism.
- It magnifies the state at the cost of individual
Question 18.
Discuss the function of the Welfare State in the modern age?
Answer :
The concept of the ‘Welfare State is a 20th-century phenomenon. The state in the modem age is wedded to the principle of welfare and every community seeks to provide for its members a large number of welfare measures or schemes. The state is considered as a positive instrument which guarantees to individuals a minimum standard of subsistence without removing incentives to private enterprises.
The state as a social service agency undertakes developmental activities relating to social welfare, security, and reduction of inequality and injustice. Welfare State is a community where every citizen has assured a minimum standard of living and opportunity.
The State protects the liberty and integrity of the individual and at the same time promotes common welfare. In a Welfare State, the individual has to get and the state does the rest.
Functions:
As a Positive State, the Welfare State performs a variety of functions concerning the life and happiness of the individual. The State provides conditions of social life, maintains law and order, guarantees fundamental rights, makes
provisions for social security and promotes common welfare. The State looks after the individual from cradle to grave. The State performs all those functions which the people expect from the state.
Gcttcll and Willoughby classified these functions into:
- Essential or obligatory functions and
- Optional functions
Obligatory functions:
These functions are essential and the State at all costs will have to perform these functions.
Defence or security of the State:
It is the most important function of a Welfare state. for which the statement maintains a strong army and defends the country from external aggression.
The State always seeks to enhance the strength of its armed forces, manufactures powerful weapons and increases its strength.lt maintains diplomatic relations with others to maintain a cordial atmosphere among the family of nations.
Maintenance of law and order :
A Welfare State maintains law and order and discipline all over the country. The State through its machinery creates conditions in which the life, liberty and property of the individuals can be protected. It ensures the supremacy of law and maintains peace.
Administration of justice:
The State makes adequate provisions for the administration of justice. It establishes courts of law and settles the disputes
arising between citizens and imposes punishment on the offenders.
Separate, courts are established to decide civil and criminal disputes. The State controls the life and activities the citizens and ensures supremacy to the law.
Protection of individual liberty and property :
The State protects the life, liberty and property of the individual from – possible threats. Thus, the State ensures a happy and peaceful life to the individual and grants fundamental freedoms.
Optional Functions.
These are the non-essential function of an individual. The State is never obliged to perform all these functions, however, most of the modem states do perform such functions. These are as follows.
The welfare of citizens :
A welfare State should perform all such functions as are necessary to promote welfare of the society has to make adequate provisions for medical facilities, sanitation a conservancy. The State should take care for public health, maintenance and construction of roads and must establish orphanages and child care centres.
Spread of education:
It is another important duty of a Welfare State. The State must introduce universal compulsory education for the children, encourages scientific and technological research and give patronage to art and literature. Care must be taken to maintain the spirit of unity among the people.
Regulation of tide and industry and development of agriculture:
The State as a welfare agency regulates, trade and commerce and controls the economy for the welfare Of the masses. It believes in a mixed economy, nationalization of big industries the other means of production regulating the prices of essentials, commodities and import-export.
The State introduces land- reforms irrigation measures, modernization of agriculture, cooperative farming and increases production. It checks, corruption and black-marketing in business.
Social Security :
This is one of the important functions of a welfare state. The state makes provisions, for the economic and social development of the weaker sections of society, prevents exploitation of the poor by the rich, and social security of widows, orphans, physically handicapped and distressed persons.
It prevents epidemics, provides insurance against accidents and unnatural deaths, undertakes family planning programmes and introduces measures like allowances to unemployed persons and pensions for old age persons.
Management of public utility services:
The State makes provisions for means of transport and communication, post and telegraph, supply of electricity and drinking water, road transport, railways and air transport etc.
Other functions:
A Welfare state undertakes economic planning for the rational utilisation of material and human resources. It safeguards the rights and liberties of the people, prevents adulteration of edible products, ensures free and fair elections and inspires public participation in political affairs.
The State takes all possible measures to develop the standard of living of the people and makes them lead happy and peaceful life.

Question 19.
Define Globalization and discuss its impact on the Indian economy?
Answer :
Globalization refers to a process of economic reforms introduced in 1990 with a view to integrating nation-states within the overall framework of WTO.
It is a modem version of the ‘Theory of, ‘Comparative Costs Advantage: propagated by classical economists to provide theoretical foundations for the unrestricted flow of goods from developed countries to developing and underdeveloped nations.
Globalization believes in the effective integration of economies through the exchange, of ideas, information, technologies, goods and, services. It is a product of the technological revolution in recent years and implies faster movement Of capital goods and services as a result of an increase in the speed of communication.
Globalization has four parameters :
Reduction of trade barriers so as to permit free flow of goods across national frontiers. Creation of an environment in which free flow of capital can take place among -nations States.
Creation of an environment permitting free flow of technology. Creation of an environment in which free movement of labour can take place in different countries of the world.
The developed nations consider globalization as a new mantra for world development. It started in India during 1991 with the hope of rapid economic growth. It has opened access to new markets and new technology.
Impact on the Indian Economy:
India has followed the policy of globalization for over a decade and it impact on our economy can be described below:
Increase in world export of goods and services:
As per the data supplied by the world bank during the last decade though we have hot been .able to compete with our neighbours like China and South Korea in the export of goods yet in the export of services India has done well. The Indian share in world export of goods and services has improved slightly.
The flow of foreign investment:
Globalisation has pledged a greater inflow of foreign investment to India and it has also picked up in India. But direct foreign investment in India has not been significant as yet.
Again, there is a wide gap between the approved investment and the actual flow of investment During 1996-2000 the inflow of foreign investment has decreased but still, there is a wide gap between promise and realization.
Import rate is higher than the rate of export:
The advocates of globalization argued in favour of export-oriented growth in place of import-oriented growth. But, actually, India is still relying on the import of foreign goods and our export has not picked up signs recently.
That means globalization has helped foreign countries to penetrate into Indian markets more than creating a favourable foreign market for Indian goods.
Indian Economy has become dependent:
It was hoped that globalization would help in increase of GDP growth, but in fact, our economy has become more and more dependent on the world economy after 12 years of experimentation.
Slowness in poverty, alleviation:
During the post-globalization period, India has failed to achieve any ‘progress in its programme of poverty alleviation. This is largely due to a reduction in agricultural productivity growth of non-farm sector development spending and inflation.
The policies of liberalization, privatization and globalization have affected the “performance of states in poverty eradication.
A decline in employment growth:
It is another major shortfall of globalization in the Indian economy. The rate of unemployment has gone up during the last five years. There has been a sharp decline in agriculture, community and personal services.
Effects of Indian industry:
Indian industry has been facing increasing competition from foreign industrial products. The indigenous industry has to pay excise. Sales tax, octroi and turnover tax while imported goods are given duty-free access to the market. As a result, most of industries are shut down and cheap imports have become a cause of recession in Indian industry.
A decline in agricultural export:
Prior to globalization and agreement on agriculture, Indian agricultural prices were lower than international prices. Due to heavy subsidies on agricultural export by developed countries, the international price of agricultural products has been lower, than Indian prices, thus Indian farmers have been put to a serious disadvantage.
Thus, after a. decade of globalization police being introduced in India, the hope of the nation has been sacked. It has affected badly our industry and agriculture. The process of development has not been encouraging. The. high hopes with which it was introduced in India had proved to be futile.
Question 20.
Analyse the socioeconomic functions of the Welfare State?
Answer :
The state in the modem age. has assumed the character of a welfare state. The idea of a welfare state emerged after World War II in Britain, USA, Germany and France. The Govt took the responsibility of providing all sorts of luxuries to ordinary citizens. The state provided a wide range of social services to the people.
Welfare State is a democratic state which seeks to secure socioeconomic welfare and development of its people with full respect to the rights and freedoms of the people. The socioeconomic functions of a welfare state can be discussed below.
Social functions :
A welfare state performs a good number of functions of securing socioeconomic reconstruction and development.
Securing social equality :
The state grants equal rights and freedoms to all its citizens. It ensures rule of law and abolishes all discrimination.
Secures social justice :
The state tries to establish a social order and gives special protection and Opportunities to the poor, and backward classes. The state enacts laws to reduce the gap between rich and poor and to secure social justice.
Provides social security :
A welfare state provides social security to the poor and needy. It gives financial- assistance to poor, disabled, diseased and unemployed people. It also makes provisions for insurance, provident fund, pension and health care facilities.
Fights social evils :
A welfare state seeks to eradicate social evils through legislation. The Govt, of India, has enacted laws to eradicate sati, child- marriage, dowry, prostitution and untouchability, etc.
Spread of education :
The state on a priority basis looks for the spread of education among the people. It establishes schools and colleges and provides free education up to secondary standards.
It sets up libraries, and reading rooms and provides financial assistance to private educational institutions. It also gives stipends and education loans to poor students.
Protection of public health :
A welfare state looks after public health and sanitation. It sets up hospitals, dispensaries and maternity homes and provides free medical aid to the people.
The state also initiates programmes for family planning and welfare.
Economic Functions :
The state undertakes a series of economic functions for rapid economic development.
Improvement of the economic condition of the people :
The state works for raising the living standard of the people by making provisions for food, clothing, shelter, education and health amenities. to all its citizens. The state tries to, eradicate poverty and unemployment
Economic planning :
Welfare stale undertakes economic planning for balanced utilization of its resources. Planning accelerates the pace of economic growth.
Development of agriculture :
A welfare state takes all possible steps for increasing agriculture production. It makes use of scientific known how, improved seeds, manures and machines. The state makes provisions for irrigation. conservation of crops and also fixes the prices of agricultural products.
Development of industry :
The state also facilities the development of the industry. It finalises national industrial policy and rules of export and import.
Regulates Trade and Commerce :
A welfare state regulates trade and commerce. It fixes customs duties, circulates currency establishes banks and insurance companies. It looks after the interests of the consumers and nationals.
The state also makes an equitable distribution of wealth, determines the fiscal policy of the nation and takes care so that wealth s not accumulated by few. It levies taxes to undertake socio-economic development.
The welfare state also takes care of the workers and labour class people. It determines their working hour, minimum wage, and proper working conditions. The state also makes special provisions for the upliftment of the poor working classes. In the age of privatization, the state today had to control unfair trading and ensure an efficient public distribution system for common goods.

Question 21.
Review the advantages and disadvantages of Globalisation?
Answer :
The 21st century is considered to be the age of globalisation. The concept involves a process of expanding business and trade relations among independent nations.
The aim of globalisation is to secure real socio-economic-political and cultural transformation of the world into a global community, It seeks the integration of the world economy into a common model.
Globalisation means a new world economic order based on free trade, free access to world markets and increased socio-economic and cultural linkage among nations. The aim of globalization is to secure the socio-economic integration and development of all the people of the world.
Features :
- Globalization believes in liberalization of trade industrial policy.
- It stands for the free flow of trade relations among nations.
- It seeks to integrate the domestic economy with world economy.
- It believes in liberalisation of imports and export.
- It believes in privatisation.
- Globalisation encourages cooperation among nations in order to; secure rapid development modernisation and technological advancement.
It introduces fiscal reforms strengthening free trade.
Globalisation stands for free trade, free access to world markets and. flow of investment across borders. Its motto is to bring about the unity of world culture, economy and infrastructure.
The developed nations of die world with a view to capturing the world market have designed the policy of globalisation, The World Trade Organisation has been set up replacing the GATT as per Dunkel’s Resolution and the big powers are now trying to capture the economies of poor countries.
India has adopted globalisation in 1991. During the last few years its impact has been mixed:
Advantages:
Globalisation constitutes a natural extension of the principles of inter¬dependence among nations. It leads to the socioeconomic and cultural integration of the people. It discourages war and aggression.
Liberal import-export policies encourage free flow of goods and services across the borders and accelerate the pace of economic industrial development.
It provides advanced technology to developing nations. A free-market economy encourages economic competition which brings development.
It has successfully fought against poverty, hunger and disease. Globalisation has brought about sustainable development all around the world.
Disadvantages:
The disadvantages of globalization outnumber its advantages.
Globalisation has enhanced the role of corporate business houses and capitalists and multi-national corporations have assumed an important role in international relations. The rich countries have taken undue control over the poor and developing countries.
Free market economy and free trade will make it difficult for developing countries to compete for protecting their interests. The rich nations have been protecting their trade interests through multi-national corporations.
It gives the state fewer financial resources to look after health, education and social security services. Globalisation has led to a widening of the gap between rich and poor.
Domestic markets of developing countries have been flooded with goods of rich countries. The small-scale and medium-range industries have suffered a loss.
The share of poor and developing countries in the world’s income and resources will be reduced because of the dominance of rich and developed countries. In the name of globalisation, the developed countries dictate terms to the poor countries.
It has adversely affected the interests . of labour and the govt, makes no effort to improve the conditions of the working class. The nations which have joined the globalisation process have been forced to abide by the suggestions of the World Bank, IMF and WTO.
It has given a setback to employment, and generation schemes followed by underdeveloped countries. As a whole, the globalisation concept is not wrong. It will yield positive results after a few years.
Question 22.
Review .the basic features of globalization and its impact on the state?
Answer :
Globalization is the process of the economic integration of the world. It started in the 2nd half of the 20th century under the initiative of rich and prosperous countries. Globalization seeks to ensure socioeconomic integration of the world through a free flow of goods. Services, information knowledge and people across the borders of the state.
Features :
Globalization believes in the integration of the domestic economy with the world economy. It aims at free trade with all other countries of the world.
As it believes in liberalization, each state has to open its domestic market for foreign companies. Globalization seeks to reduce state control over imports and export.
Globalisation seeks to keep the state away from ownership of means of production and distribution and allows free follows of industrial trade and economic activities among the people and their corporations.
It believes in the modernisation of transport and communication. It introduces economic reforms for giving maximum liberty to private organizations.
Impact on the state :
As a result of globalization, the scope of state activity and efficiency has been affected with the increase in investment privatization has encouraged the public sector to compete with the private sector.
The role of state has changed from a regulator to a facilitator. Though the state continues to be a welfare state its activity is confined to Ensuring a smooth and orderly functioning of the market. It tries to secure stability in the market through macroeconomic policies and
Providing social services, such as education, health care and social security measures. Regulating state economy in the interest of social justice and welfare.
The emergence of free trade, a market economy and multinational corporations have limited the scope of the role of state in the sphere of the international economy. Globalization has limited the sovereignty of the state. The WTO, World Bank and IMF have eroded into state autonomy.
The information technology revolution has led to the development of the means of transport and communication and the world is converted into a global village.
The movement for international peace and peaceful coexistence has reduced the importance of the military power of the state. The states are now concerned with the need to fight terrorism and safeguard human rights and the environment.
Try More:
LT Pivot Point Calculator