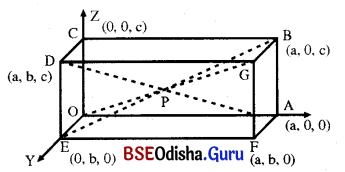
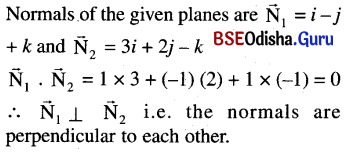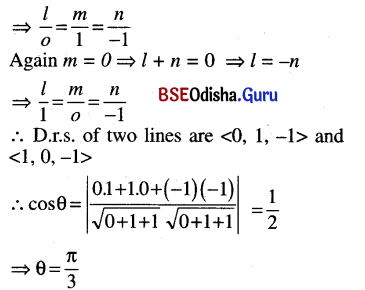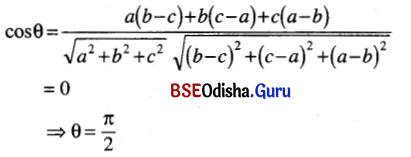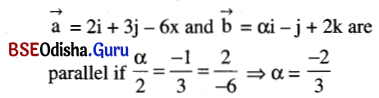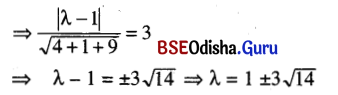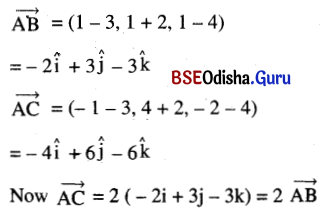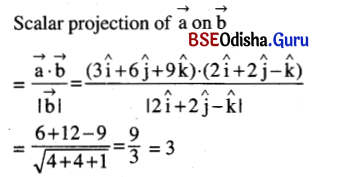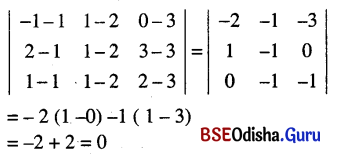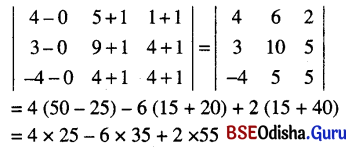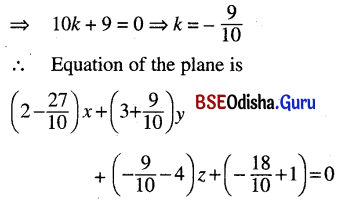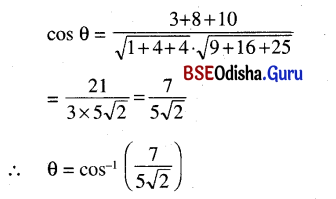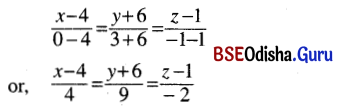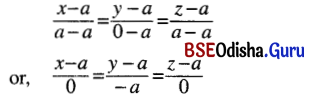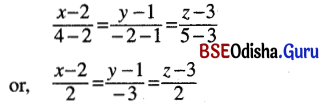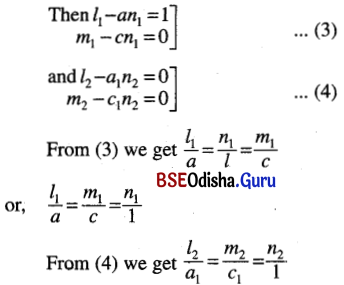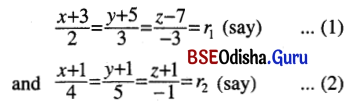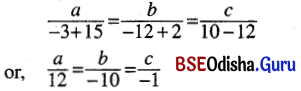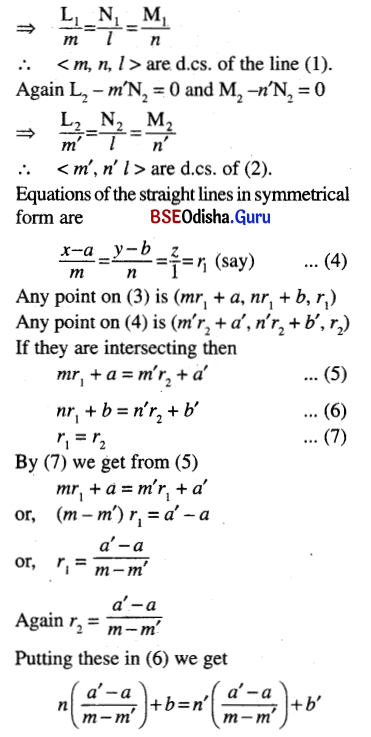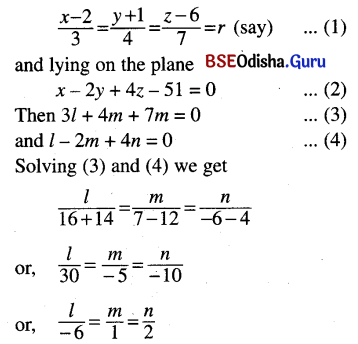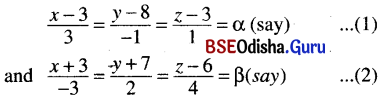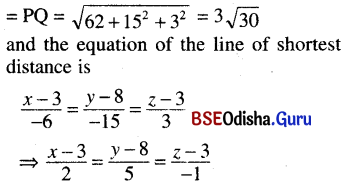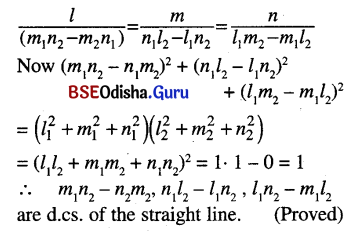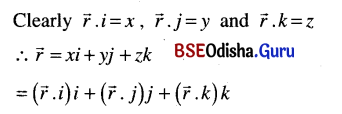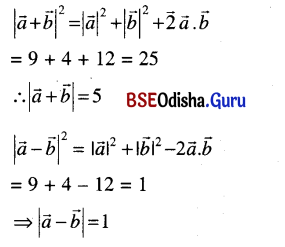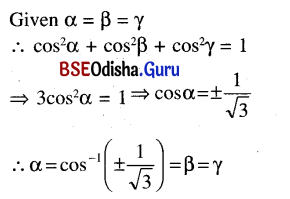Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 13 Three Dimensional Geometry Additional Exercise Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Additional Exercise
Question 1.
Find the equation in vector and Cartesian form of the plane passing through the point (3, -3, 1) and normal to the line joining the points (3, 4, -1) and (2, -1, 5)
Solution:

Changing the vector equation to cartesian form we have
(xi + yj + zk) . (-i – 5j + 6k) = 18
⇒ -x – 5y + 6z = 18
⇒ x + 5y – 6z + 18 = 0
Question 2.
Find the vector equation of the plane whose Cartesian form of equation is 3x – 4y + 2z = 5
Solution:
The cartesian equation is 3x – 4y + 2z = 5
The vector equation is \(\vec{r}\). (3i – 4j + 2k) = 5
Question 3.
Show that the normals to the planes \(\vec{r}\) . (î – ĵ + k̂) = 3 and \(\vec{r}\) . (3î + 2ĵ – k̂) = 0 are perpendicular to each other.
Solution:
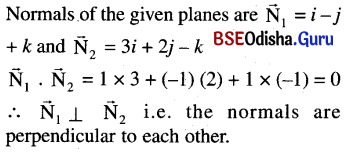

Question 4.
Find the angle between the planes \(\vec{r} \cdot(2 \hat{i}-\hat{j}+2 \hat{k})=6 \text { and } \vec{r} \cdot(3 \hat{i}+6 \hat{j}-2 \hat{k})=9\).
Solution:

Question 5.
Find the angle between the line \(\vec{r}=(\hat{i}+2 \hat{j}-\hat{k})+\lambda(\hat{i}-\hat{j}+\hat{k})\) and the \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})\) = 4.
Solution:

Question 6.
Prove that the acute angle between the lines whose direction cosines are given by the relations l + m + n = 0 and l2 + m2 – n2 = 0 is \(\frac{\pi}{3}\).
Solution:
l + m + n = 0 ⇒ n = -(l + m)
l2 + m2 – n2 = 0
⇒ l2 + m2 – (l + m)2 = 0
⇒ 2lm = 0
Now l = 0 ⇒ m + n = 0 ⇒ m = -n
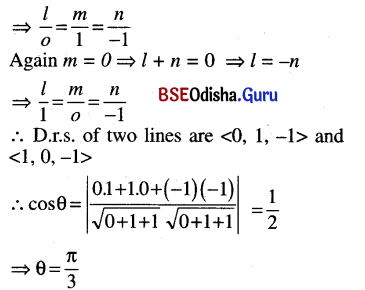
Question 7.
Prove that the three lines drawn from origin with direction cosines l1, m1, n1 ; l2, m2, n2 ; l3, m3, n3 are coplanar if \(\left|\begin{array}{lll}
l_1 & m_1 & n_1 \\
l_2 & m_2 & n_2 \\
l_3 & m_3 & n_3
\end{array}\right|\) = 0.
Solution:

Question 8.
Prove that three lines drawn from origin with direction cosines proportional to (1, -1, 1), (2, -3, 0), (1, 0, 3) lie on one plane.
Solution:

= 1 (-9) + 1 (6) + 1(3) = 0
∴ The lines are co-planar.
Question 9.
Determine k so that the lines joining the points P1 (k, 1, -1) and P2 (2k, 0, 2) shall be perpendicular to the line from P2 to P3 (2 + 2k, k, 1).
Solution:

Question 10.
Find the angle between the lines whose direction ratios are proportional to a, b, c and b-c, c-a, a-b.
Solution:
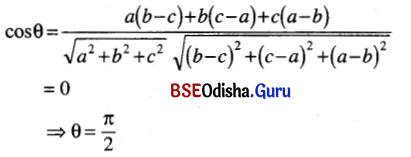

Question 11.
O is the origin and A is the point (a, b, c). Find the equation of the plane through A at right angles to \(\overrightarrow{OA}\).
Solution:

Question 12.
Find the equation of the plane through (6, 3, 1) and (8, -5, 3) parallel to x-axis.
Solution:
Given points are A (6, 3, 1) and B (8, -5, 3) D.C.S of x-axis are < 1, 0, 0 >
Let P (x, y, z) is any point on the plane.

⇒ 2 (y – 3) + 8 (z – 1) = 0
⇒ 2y – 6 + 8z – 8 = 0
⇒ y + 4z – 7 = 0
(A) Multiple Choice Questions (Mcqs) With Answers
Question 1.
Write the value of k such that the line \(\frac{x-4}{1}=\frac{y-2}{1}=\frac{z-k}{2}\) lies on the plane 2x – 4y + z = 7.
(a) k = 7
(b) k = 2
(c) k = 5
(d) k = 3
Solution:
(a) k = 7
Question 2.
If \((\vec{a} \times \vec{b})^2+(\vec{a} \cdot \vec{b})^2\) = 144, write the value of ab.
(a) 4
(b) 12
(c) 3
(d) 24
Solution:
(b) 12
Question 3.
If the vectors \(\vec{a}, \vec{b}\text { and }\vec{c}\) from the sides \(\overline{BC}, \overline{CA} \text { and } \overline{AB}\) respectively of a triangle ABC, then write the value of \(\vec{a} \times \vec{c}+\vec{b} \times \vec{c}\).
(a) 1
(b) -1
(c) 2
(d) 0
Solution:
(d) 0
Question 4.
If \(|\vec{a}|=3|\vec{b}|=2 \text { and } \vec{a} \cdot \vec{b}=0\), then write the value of \(|\vec{a} \times \vec{b}|\).
(a) 6
(b) 0
(c) 2
(d) 3
Solution:
(a) 6
Question 5.
If \(|\vec{a} \times \vec{b}|^2+|\vec{a} \cdot \vec{b}|^2\) = 144 and \(|\vec{a}|\) = 4 then \(|\vec{b}|\) is equal to:
(a) 3
(b) 8
(c) 12
(d) 16
Solution:
(a) 3
Question 6.
Write down the equation to the plane perpendicular to the y-axis at the point (0, -2, 0).
(a) y – 2 = 0
(b) y + 2 = 0
(c) y = 0
(d) 2y + 1 = 0
Solution:
(b) y + 2 = 0
Question 7.
How many straight lines in space through the origin are equally inclined to the coordinate axes?
(a) 2
(b) 1
(c) 0
(d) -1
Solution:
(a) 2
Question 8.
Write the value of a if the vectors \(\vec{a}=2 \hat{i}+3 \hat{j}-6 \hat{k} \text { and } \vec{b}=\alpha \hat{i}-\hat{j}+2 \hat{k}\) are parallel.
(a) \(\frac{2}{3}\)
(b) \(\frac{3}{2}\)
(c) \(\frac{-3}{2}\)
(d) \(\frac{-2}{3}\)
Solution:
(d) \(\frac{-2}{3}\)

Question 9.
Write the equation of the line passing through the point (4, -6, 1) and parallel to the line \(\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{-1}\).
(a) \(\frac{x+4}{1}=\frac{y+6}{3}=\frac{z+1}{-1}\)
(b) \(\frac{x-4}{1}=\frac{y+6}{3}=\frac{z-1}{-1}\)
(c) \(\frac{x-4}{1}=\frac{y-6}{3}=\frac{z-1}{-2}\)
(d) \(\frac{x+4}{-1}=\frac{y+6}{3}=\frac{z-1}{-1}\)
Solution:
(b) \(\frac{x-4}{1}=\frac{y+6}{3}=\frac{z-1}{-1}\)
Question 10.
What is the image of the point (-2, 3, -5) with respect to the zx-plane?
(a) (-2, -3, -5)
(b) (2, -3, -5)
(c) (2, 3, 5)
(d) (2, 3, -5)
Solution:
(a) (-2, -3, -5)
Question 11.
If \(|\vec{a} \times \vec{b}|^2=k|\vec{a} \cdot \vec{b}|^2+|\vec{a}|^2|\vec{b}|^2\), then what is the value of k?
(a) 1
(b) 2
(c) 0
(d) -1
Solution:
(d) -1
Question 12.
Write the value of m and n for which the vectors (m – 1) î + (n + 2) ĵ + 4k̂ and (m + 1) î + (n – 2) ĵ + 8k̂ will be parallel.
(a) m = 3 and n = 6
(b) m = -3 and n = 6
(c) m = -3 and n = -6
(d) m = 3 and n = -6
Solution:
(d) m = 3 and n = -6
Question 13.
For what value of λ the vectors λî + 3ĵ + λk̂ and λî – 2ĵ +k̂ are perpendicular to each other.
(a) (-2, -3)
(b) (2, 3)
(c) (2, -3)
(d) (-2, 3)
Solution:
(c) (2, -3)
Question 14.
If |x| = 1, |y| = 2 and |z| = 3, then how many points in R3 are there having coordinates (x, y, z)?
(a) 8
(b) 2
(c) 6
(d) 4
Solution:
(a) 8
Question 15.
Write the equation of the plane passing through the point (1, -2, 3) and perpendicular to the y-axis.
(a) y – 2 = 0
(b) y = -2
(c) y + 2 = 0
(d) 2y – 2 = 0
Solution:
(c) y + 2 = 0
Question 16.
What is the projection of î + ĵ – k̂ upon the vector î?
(a) 0
(b) 1
(c) 2
(d) None of the above
Solution:
(b) 1

Question 17.
If \(\vec{a}=2 \hat{i}+\hat{j}, \vec{b}=\hat{k}\) what is \(\vec{a} \cdot \vec{b}\)?
(a) 0
(b) 1
(c) 2
(d) None of the above
Solution:
(a) 0
Question 18.
What is the work done by a force \(\overrightarrow{\mathrm{F}}\) = 4i + 2j + 3k in displacing a particle from A (1, 2, 0) to B (2, -1, 3)?
(a) 5
(b) 6
(c) 7
(d) 8
Solution:
(c) 7
Question 19.
If \(\vec{a} \times \vec{b}=\hat{n}\) then what is the angle between \(\vec{a} \text { and } \vec{b}\)?
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{3}\)
(d) None of the above
Solution:
(b) \(\frac{\pi}{2}\)
Question 20.
The plane 2x + 3z = 5 is parallel to:
(a) x-axis
(b) y-axis
(c) z-axis
(d) line x = y = z
Solution:
(b) y-axis
Question 21.
The equation of the plane containing the points (1, 0, 0), (0, 2, 0) and (0, 0, 3) is given by:
(a) x + 2y + 3z = 1
(b) 3x + 2y + z = 2
(c) 6x + 3y + 2z = 6
(d) 6x + 3y + 2z = 8
Solution:
(c) 6x + 3y + 2z = 6
Question 22.
If on action of force f = 2i + j – k, a particle displaced from A (0, 1, 2) to B (-2, 3, 0) then what is the work done by the force?
(a) 1
(b) 2
(c) 0
(d) None of the above
Solution:
(c) 0
Question 23.
If \(\vec{a}, \vec{b}, \vec{c}\) are unit vectors and \(\vec{a}+\vec{b}+\vec{c}=0\) then evaluate \(\vec{a} \cdot \vec{b}+\vec{b} \cdot \vec{c}+\vec{c} \cdot \vec{a}\).
(a) \(\frac{3}{2}\)
(b) –\(\frac{3}{2}\)
(c) \(\frac{2}{3}\)
(d) –\(\frac{2}{3}\)
Solution:
(b) –\(\frac{3}{2}\)
Question 24.
What is the value of (î + ĵ) × (ĵ + k̂) × (k̂ + î)?
(a) 0
(b) 1
(c) 2
(d) 3
Solution:
(c) 2
Question 25.
Write the distance of the point of intersection of the plane, ax + by + cz + d = 0 and the z-axis from the origin.
(a) \(\left|\frac{d}{c}\right|\)
(b) \(\left|\frac{d}{a}\right|\)
(c) \(\left|\frac{a}{c}\right|\)
(d) \(\left|\frac{a}{d}\right|\)
Solution:
(a) \(\left|\frac{d}{c}\right|\)

Question 26.
Write down the equation of the plane through (0, 0, 0) perpendicular to the line joining (0, 0, 1) and (0, 0, -1).
(a) x = 0
(b) z = 0
(c) y = 0
(d) None of the above
Solution:
(b) z = 0
Question 27.
What is the distance of the point (1, 1, 1) from the plane y = x?
(a) 0
(b) 1
(c) -1
(d) None of the above
Solution:
(a) 0
Question 28.
What is the angle between the planes y + x = 0 and z = 0?
(a) 45°
(b) 60°
(c) 75°
(d) 90°
Solution:
(d) 90°
Question 29.
For what ‘k’ the line \(\frac{x-3}{2}=\frac{y+k}{-1}=\frac{z+1}{-5}\) lies on the plane 2x – y + z – 7 = 0.
(a) 0
(b) 1
(c) -1
(d) 2
Solution:
(d) 2
Question 30.
Projection of the line segment joining (1, 3, -1) and (3, 2, 4) on z-axis is
(a) 4
(b) 5
(c) 3
(d) 2
Solution:
(b) 5
Question 31.
The image of the point (6, 3, -4) with respect to yz-plane is ______.
(a) (-6, 3, 4)
(b) (6, 3, -4)
(c) (-6, 3, -4)
(d) (-6, -3, -4)
Solution:
(c) (-6, 3, -4)
Question 32.
Find the equation of a plane through (1, 1, 2) and parallel to x + y + z – 1 = 0
(a) x + y – z + 4 = 0
(b) x + y – z – 4 = 0
(c) x + y + z – 4 = 0
(d) x + y + z + 4 = 0
Solution:
(c) x + y + z – 4 = 0
Question 33.
The distance between the parallel planes 2x – 3y + 6z + 1 = 0 and 4x – 6y + 12z – 5 = 0 is ______.
(a) \(\frac{1}{4}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{1}{2}\)
(d) None
Solution:
(c) \(\frac{1}{2}\)
Question 34.
Find k if the normal to the plane parallel to the line joining (-1, 1, -4) and (5, 6, -2) has d.rs (3, -2, k).
(a) 1
(b) -1
(c) 2
(d) -2
Solution:
(b) -1

Question 35.
If a line makes angles 35° and 55° with x-axis and y-axis respectively, then the angle which this line subtends with z-axis is:-
(a) 35°
(b) 45°
(c) 55°
(d) 90°
Solution:
(d) 90°
Question 36.
Write the equation of the plane passing through (3, -6, -9) and parallel to xz-plane.
(a) z = -5
(b) z = -9
(c) z = 9
(d) z = -7
Solution:
(b) z = -9
Question 37.
In which condition x + y + z = α + β + γ will contain the line \(\frac{x-\alpha}{l}=\frac{y-\beta}{m}=\frac{z-\gamma}{n}\).
(a) l + m – n = 0
(b) l – m – n = 0
(c) l – m + n = 0
(d) l + m + n = 0
Solution:
(d) l + m + n = 0
Question 38.
The angle between the planes x + y + 1 = 0 and y + z + 1 = 0 is ______.
(a) 30°
(b) 45°
(c) 60°
(d) 75°
Solution:
(c) 60°
Question 39.
Find the number of points (x, y, z) in space other than the point (1, -2, 3) such that |x| = 1, |y|= 2, |z| = 3.
(a) 2
(b) 3
(c) 5
(d) 7
Solution:
(d) 7
Question 40.
Write the ratio in which the line segment joining the points (1, 2, -2) and (4, 3, 4) is divided by the xy-plane.
(a) 1:2
(b) 3:4
(c) 2:3
(d) 2:5
Solution:
(a) 1:2
(B) Very Short Type Questions With Answers
Question 1.
Write the value of k such that the line \(\frac{x-4}{1}=\frac{y-2}{1}=\frac{z-k}{2}\) lies on the plane 2x – 4y + z = 7.
Solution:
The line \(\frac{x-4}{1}=\frac{y-2}{1}=\frac{z-k}{2}\) lies on the plane 2x – 4y + z = 7.
Question 2.
Write the equations of the line 2x + z – 4 = 0 = 2y + z in the symmetrical form.
Solution:
Given line is 2x + z – 4 = 0 = 2y + z
⇒ z = -(2x – 4) = -2(x – 2) and z = -2y
∴ -2(x – 2) = -2y = z
∴ The equation of the line in symmetrical form is \(\frac{x-2}{1}=\frac{y}{1}=\frac{z}{-2}\).
Question 3.
Write the distance between parallel planes 2x – y + 3z = 4 and 2x – y + 3z = 18
Solution:
Distance between the given parallel planes
= \(\frac{|18-4|}{\sqrt{4+1+9}}=\frac{14}{\sqrt{14}}=\sqrt{14}\)
Question 4.
Write down the equation to the plane perpendicular to the y-axis at the point (0, -2, 0).
Solution:
The equation of the plane perpendicular to y-axis at (0, -2, 0) is
(x – 0) . 0 + (y + 2) . 1 + (z – 0) . 0 = 0
⇒ y + 2 = 0
Question 5.
Under which conditions the straight line \(\frac{\mathrm{x}-\mathrm{a}}{l}=\frac{\mathrm{y}-\mathrm{b}}{\mathrm{m}}=\frac{\mathrm{z}-\mathrm{c}}{\mathrm{n}}\) intersects the plane Ax + By + Cz = 0 at a point other than (a, b, c)?
Solution:
The line \(\frac{\mathrm{x}-\mathrm{a}}{l}=\frac{\mathrm{y}-\mathrm{b}}{\mathrm{m}}=\frac{\mathrm{z}-\mathrm{c}}{\mathrm{n}}\) will intersect the plane Ax + By + Cz + D = 0 at a point other than (a, b, c) if Al + Bm + Cn ≠ 0 and Aa + Bb + Cc + D ≠ 0.

Question 6.
How many straight lines in space through the origin are equally inclined to the coordinate axes?
Solution:
There are two lines in space through origin which are equally inclined to coordinate axes.
Question 7.
Write the value of a if the vectors \(\vec{a}=2 \hat{i}+3 \hat{j}-6 \hat{k} \text { and } \vec{b}=\alpha \hat{i}-\hat{j}+2 \hat{k}\) are parallel.
Solution:
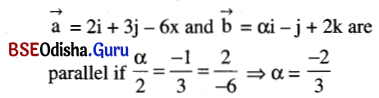
Question 8.
Write the equation of the line passing through the point (4, -6, 1) and parallel to the line \(\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{-1}\).
Solution:
Equation of the line passing through (4, -6, 1) and parallel to
\(\frac{x-1}{1}=\frac{y+2}{3}=\frac{z-1}{-1} \text { is } \frac{x-4}{1}=\frac{y+6}{3}=\frac{z-1}{-1}\).
Question 9.
What is the image of the point (-2, 3, -5) with respect to the zx-plane?
Solution:
Image of the point (-2, 3, -5) w.r.t. zx-plane is (-2, -3, -5)
Question 10.
What is the point of intersection of the line x = y = z with the plane x + 2y + 3z = 6?
Solution:
Given line is x = y = z = λ (say)
Any point on this line has coordinates (λ, λ, λ).
Putting x = y = z = λ in x + 2y + 3z = 6
We get 6λ = 6 ⇒ λ = 1
∴ The point of interesetion is (1, 1, 1).
Question 11.
How many directions a null vector has?
Solution:
A null vector has infinitely many directions (arbitrary direction).
Question 12.
For what value of λ the vectors λî + 3ĵ + λk̂ and λî – 2ĵ + k̂ are perpendicular to each other?
Solution:
Given vectors are perpendicular to each other iff λ2 – 6 + λ = 0.
⇒ λ2 + 3λ – 2λ- 6 = 0
⇒ λ (λ + 3) – 2 (λ + 3) = 0
⇒ (λ – 2) (λ + 3) = 0
⇒ λ = 2, λ = (-3)
Question 13.
If |x| = 1, |y| = 2 and |z| = 3, then how many points in R3 are there having coordinates (x, y, z)?
Solution:
Required number of points are ‘8’.
Question 14.
Write the equation of the plane passing through the point (1, -2, 3) and perpendicular to the y-axis.
Solution:
D.rs. of any line parallel to y-axis are < 0, 1, 0 >.
∴ The equation of required plane is
(x – 1) 0 + (y + 2) . 1 + (z – 3) . 0 = 0
⇒ y + 2 = 0
(C) Short Type Questions With Answers
Question 1.
Find the point where the line \(\frac{x-2}{1}=\frac{y}{-1}=\frac{z-1}{2}\) meets the plane 2x + y + z = 2.
Solution:
Equation of the line is \(\frac{x-2}{1}=\frac{y}{-1}=\frac{z-1}{2}\)
Co-ordinates of any point on the line are (k + 2, -k, 2k + 1)
This point lies on the plane
⇒ 2 (k + 2) + (-k) + (2k + 1) = 2
⇒ 3k + 5 = 2 ⇒ k = -1
⇒ The required point of intersection is (1, 2, -1)
Question 2.
If the sum of two unit vectors is a unit vector, show that the magnitude of their difference is √3.
Solution:


Question 3.
The position vectors of two points A and B are 3î + ĵ + 2k̂ and î – 2ĵ – 4k̂ respectively. Find the equation of the plane passing through B and perpendicular to \(\overrightarrow{AB}\).
Solution:

Question 4.
Find the equation of the plane through the point (2, 1, 0) and passing through the intersection of the planes 3x – 2y + z – 1 = 0 and x – 2y + 3z = 1.
Solution:
Equation of any plane passing through the intersection of given two planes is:
(3x – y + z – 1) + λ (x – 2y + 3z – 1) = 0
⇒ x (3 + 2λ) + y (-1 – 2λ) + z (1 + 3λ) – 1 – λ = 0
This plane passes through A (2, 1, 0)
⇒ 2 (3 + λ) – 1 – 2λ – 1 – λ = 0
⇒ 6 + 2λ – 2 – 3λ = 0
⇒ λ = 4
∴ Equation of the required plane is 7x – 9y + 13z – 5 = 0
Question 5.
Prove that the vectors 2î – ĵ + k̂, î – 3ĵ – 5k̂, 3î – 4ĵ – 4k̂ are the sides of a right angled triangle.
Solution:

Question 6.
Prove that \(|\overrightarrow{a}+\overrightarrow{b}| \leq|\overrightarrow{a}|+|\overrightarrow{b}|\). Write when equality will hold
Solution:

Question 7.
The projections of a line segment \(\overline{OP}\), through the origin O on the coordinate axes are 6, 2, 3. Find the length of the line segment \(\overline{OP}\) and its direction cosines.
Solution:

Question 8.
Prove that the lines \(\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}\) and 3x – 2y + z + 5 = 0 = 2x + 3y + 4z – 4 are coplanar.
Solution:
Given lines are
\(\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}\) = r (say) … (1)
and 3x – 2y + z + 5 = 0
2x + 3y + 4z – 4 = 0 … (2)
Two lines are coplanar if either they are parallel or intersecting coordinates of any point on the line (1) are P (3r – 4, -5r – 6, -2r + 1) putting in the equations (2) we get.
3 (3r – 4) – 2 (5r – 6) + (-2r + 1) + 5 = 0
and 2 (3r – 4) + 3 (5r – 6) + 4 (-2r + 1) -4 = 0
⇒ -3r + 6 = 0 and 13r – 26 = 0
⇒ r = 2 and r = 2
Thus two lines are intersecting.
⇒ The lines are co-planar.
Question 9.
If the sun of two unit vectors is a unit vector then find the magnitude of the difference.
Solution:


Question 10.
Find the equation of a plane parallel to the plane 2x – y + 3z + 1 = 0 and at a distance of 3 units away from it.
Solution:
Any plane parallel to 2x – y + 3z + 1 = 0 … (1)
has equation 2x – y + 3z + λ = 0.
Distance between two parallel planes (1) and (2) is 3 units.
Equation of required plane is.
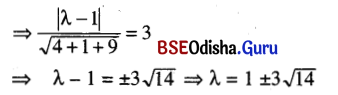
Question 11.
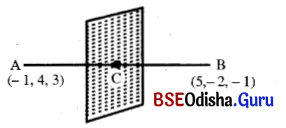
Show that the poiints (3, -2, 4), (1, 1, 1) and (-1, 4, -2) are collinear.
Solution:
Let the given points are A (3, -2, 4), B (1, 1, 1) and C (-1, 4, -2).
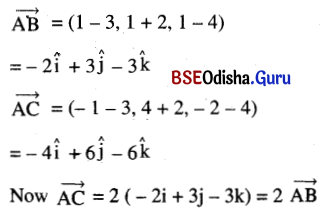
The points A, B and C are collinear.
Question 12.
Determine the value of m for which the following vectors are orthogonal:
(m + 1) j + m2ĵ – mk̂, (m2 – m + 1) î – mĵ + k̂
Solution:

Question 13.
Find the equation of the plane passing through the line x = y = z and the point (3, 2, 1).
Solution:
Equation of any plane through the line is (x – y) + λ (y – z) = 0 … (1)
Since the point (3, 2, 1) is on the plane, so it satisfies (1)
i.e., ( 3 – 2) + λ ( 2 – 1) = 0 ⇒ 1 + λ = 0
⇒ λ = -1
Using the value of λ in (1) we get
x – y + (-y) – z = 0 ⇒ x – 2y + z = 0 is the required equation of the plane.
Question 14.
Find the scalar projection of the vector \(\overrightarrow{a}=3 \hat{i}+6 \hat{j}+9 \hat{k} \text { on } \overrightarrow{b}=2 \hat{i}+2 \hat{j}-\hat{k}\).
Solution:
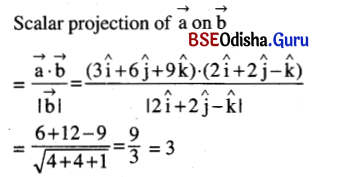
Question 15.
Prove that the straight line \(\frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-3}{1}\) lies on the plane 7x + 5y + z = 0.
Solution:
Given line is \(\frac{x-1}{2}=\frac{y+2}{-3}=\frac{z-3}{1}\) lies on the plane 7x + 5y + z = 0.
As 7 × 1 + 5 × (-2) + 3 = 0 the point (1,-2, 3) lies on the plane.
D.rs. of the given line = < 2, -3, 1 > and
d.rs. of the normal to the plane are < 7, 5, 1 >
As 2 × 7 + (-3) × 5 + 1 × 1 = 0
The given line is parallel to the given plane.
Hence the given line lies in the plane.
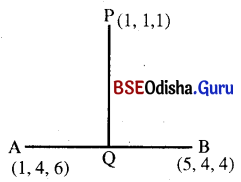
![]()

![]()